Important questions of thermal properties of matter
This assignment provides all important questions of this chapter , which will be important for examinations point of view.
1. Briefly describe the various scale of temperature and give the relation between them.
2.Define coefficient of linear ,area and volume expansion , also find the relation between them.
3.Show with the help of potential energy diagram that thermal expansion in solid is due to increase in interatomic distance.
4. What do you mean by the term thermal stress? Derive an expression for the same in case of a road fixed at both ends.
5. Define heat capacity, molar heat capacity and specific heat capacity also give their units and dimensions.
6. What do you mean by the term latent heat of fusion and latent heat of vaporization ?
7.Using P-T diagram of water , discuss the behavior of water when both pressure and temperature are (i) above the triple point (ii) at triple point (iii)below the triple point.
8. What is thermal conduction ? Discuss the variable and steady state of a rod being heated at one of its ends.
9. Define the coefficient of thermal conductivity and explain the formula used . Why do metals have higher conductivity then insulator?
10. Write the expression for the rate of flow of heat energy through a conductor maintained at different temperature at its two ends . Explain the symbols used . Given that heat is measured in joule , derive the units of thermal conductivity.
11.What is Newton’s law of cooling / how can it be experimentally verified? Plot the graph of log (T-T0) V/S time ‘t’.
12.Discuss energy distribution in the spectrum of perfectly black body. What conclusion do you derive from this distribution? Also explain the Wine’s displacement law of radiation.
13. State and explain Stefan’s law . How will you deduce Newton’s law of cooling from this law?
14. State and prove Kirchhoff’s law of heat radiation . Explain how Kirchhoff’s law leads to the conclusion that good absorber are good emitters.
Numericals-
1. A surveyor uses a steel measuring tape that is exactly 50m long at a temperature of 200C . What is the length on the hot summer day when the temperature is 350C? coefficient of linear expansion is 1.2 x 10-5K-1. . [ans-50.009m]
2. A glass flask with volume 200cm3 is filled to the brim with mercury at 200C . How much mercury overflows when temperature of the system is raised to 1000C ?[α for glass is 0.40x 10-5K-1.and cubical exp. For mercury is 1.2x 10-5K] . Ans-2.7cm3].
3. A pendulum clock consist of an iron rod connected to a small heavy bob. If it is designed to keep correct time at 200C, how fast or slow will it go in 24 hours at 400C. ( α for iron is 1.2×10-5K-1). Ans-10.4 sec
4.At what temperature is the Fahrenheit scale reading equal to(I) half that on the Celsius scale (II)Equal to the reading on Celsius scale?
5.A faulty thermometer reads 50C in melting ice and 990C in steam . Find the correct temperature in 0F when this faulty thermometer reads 520C.
6.
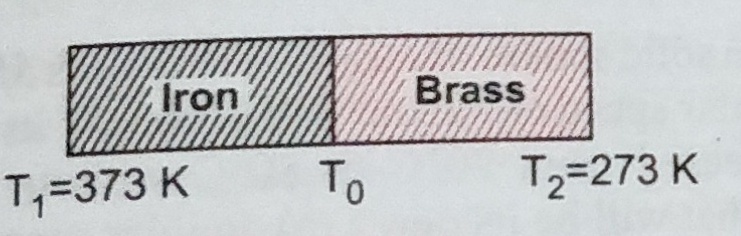
An iron bar of length l1=0.1m, A1=0.02m2, k1= 79w/mK and a brass bar of length l2=0.1m area 0.02m2 and K2=109 W/mK are soldered end to end as shown in fig. the free ends of the iron ball and brass bar maintained at 373K and 273K respectively . Obtain expression for and hence compute (a) the temperature of the junction(b) the equivalent thermal conductivity of the compound bar and (c)the heat current through the compound bar. Ans-315K ,91.6W/mK, 916W.
7. A body cools from 700c to 500C in 6 minutes and to 400C in 12 minutes . Find the temperature of the surroundings if cooling occur according to Newton’s law of cooling. Ans-300C.
8. A pan filled with hot food cools from 940C to 860C in 2 minutes when the room temperature is 200C . How long will it take to cool from 710C to 690c . Ans- 42sec.
9. The energy emitted per second by a black body at 12270C is E . If the temperature of the black body is increased to 27270C , calculate the energy emitted per second in terms of E in the second case. Ans-16E
10. Calculate the temperature in kelvin scale at which a perfectly black body radiates at the rate of 5.67 W/cm2. Given σ=5.67×10-8W/m2K4. Ans-1000K.