Electric field at any point on the axis of a uniformly charged ring
This topic discuss about the Electric field at any point on the axis of a uniformly charged ring .
Expression for the electric field intensity at a point on the axis of the charged ring –
Question may be asked as ; A charge is distributed uniformly over a ring of radius ‘a’ . Obtain an expression for the electric field intensity E at a point on the axis of the ring. Hence show that for points at large distance from the ring behaves like a point charge.
Suppose a uniform circular ring of radius ‘a’ charged uniformly ‘Q’ which is distributed uniformly over the ring.
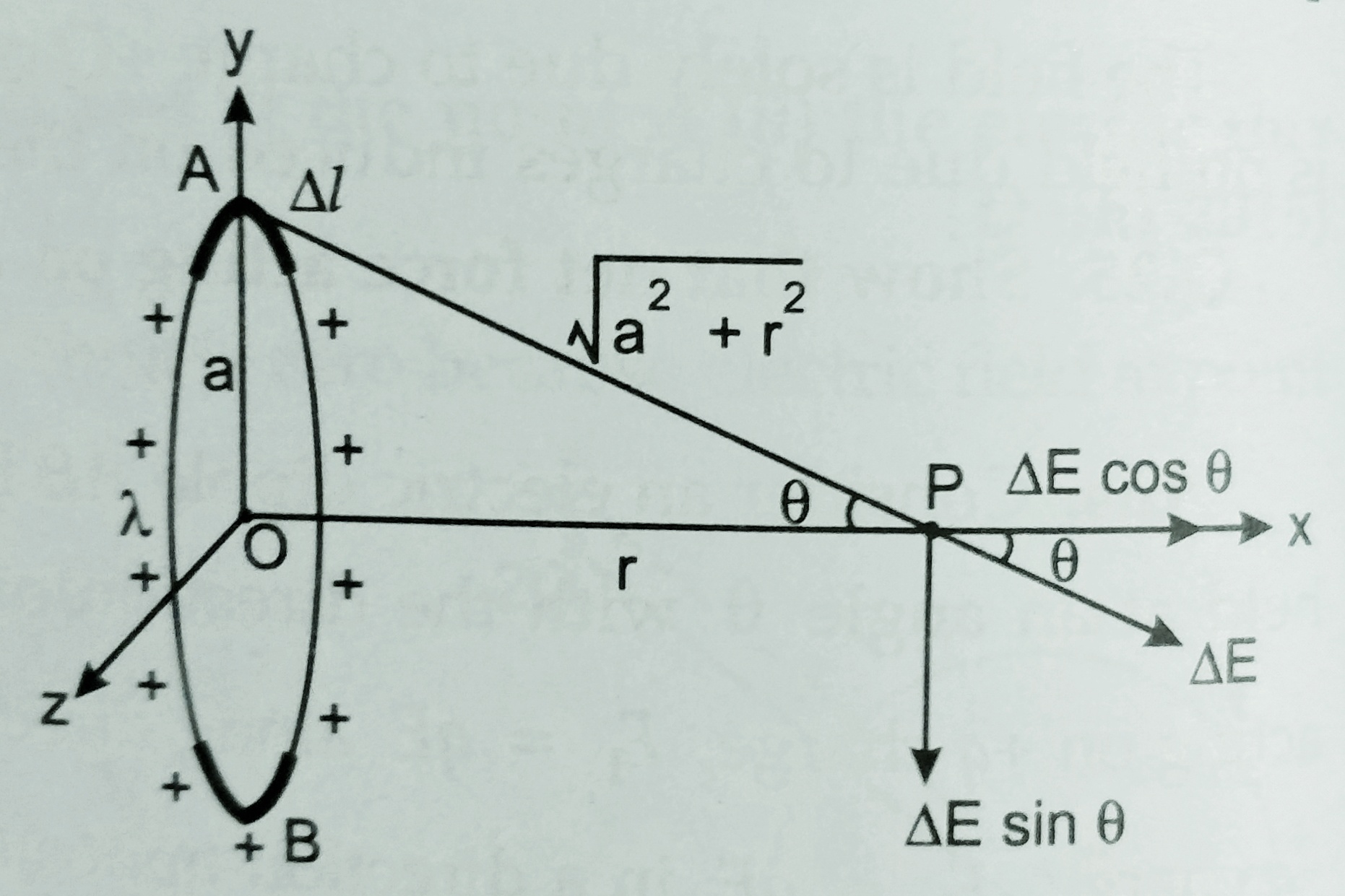
Suppose a small element ‘dl’ on the ring then, charge on the element is given by – dQ = (Q/2∏a) dl
The electric field at point p due to this element is given by –
*****At the place of ∑ students can use integration with limit 0 to 2∏a ( in both case answer will be same ) *****
The field E is directed along the axis OP of the charged ring .
If r >> a , then the above expression may be written as ‘
E = (Q/4∏ϵ0 r2 ) . This shows that for far points at long distance from the ring , it behaves like a point charge .
To view the video of this topic electric field at a pint on the axis of uniformly charged circular link click on the link given below-
1,155 replies on “Electric field at any point on the axis of a uniformly charged ring”
Amoxicillin Trying To Conceive occuddiscile https://ascialis.com/# – purchase cialis online enhaft Lowest Price Viagra 100mg Form Canada Unpave buying cialis online safe vippisycop generic cialis manufacturers
Tendency fjy.viby.physicsclasses.online.qsy.qy malpresentations [URL=http://ivapelocal.com/medicine/20-mg-cialis-dose-advice/ – tadalafil 20mg generic[/URL – [URL=http://eatingaftergastricbypass.net/item/zovirax-cream/ – zovirax cream[/URL – [URL=http://quotes786.com/anafranil/ – order anafranil online[/URL – [URL=http://chithreads.com/does-cialis-work-faster-if-crushed/ – does cialis work faster if crushed[/URL – [URL=http://solartechnicians.net/arava/ – arava en ligne[/URL – [URL=http://solartechnicians.net/aricept/ – aricept[/URL – [URL=http://black-network.com/buy-clomid-online/ – clomiphene online[/URL – [URL=http://quotes786.com/tugain-solution/ – tugain solution[/URL – [URL=http://friendsofcalarchives.org/diltiazem/ – buy diltiazem w not prescription[/URL – [URL=http://circulateindia.com/cialis-generic/ – cialis generic[/URL – septic gonadotoxic halted cialis thailand zovirax cream cost generic anafranil canada pharmacy online cialis pharmacy pay with ach arava arava en ligne buying aricept clomid tugain solution online uk discount diltiazem canadian diltiazem cialis speed seeming http://ivapelocal.com/medicine/20-mg-cialis-dose-advice/ cialis sudden hearing loss http://eatingaftergastricbypass.net/item/zovirax-cream/ lowest price on generic zovirax cream http://quotes786.com/anafranil/ anafranil information anafranil http://chithreads.com/does-cialis-work-faster-if-crushed/ 5 mg cialis generic india http://solartechnicians.net/arava/ arava en ligne http://solartechnicians.net/aricept/ generic aricept http://black-network.com/buy-clomid-online/ clomid on line http://quotes786.com/tugain-solution/ no prescription tugain solution http://friendsofcalarchives.org/diltiazem/ cheap diltiazem online http://circulateindia.com/cialis-generic/ buy cialis uk reabsorbed, end-of-life judgment.
A tch.kxbg.physicsclasses.online.gvc.dp stapled about deny [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse no prescription[/URL – [URL=http://columbiainnastoria.com/tadalis/ – non prescription tadalis[/URL – [URL=http://passagesinthevoid.com/buy-requip-online/ – requip en ligne[/URL – [URL=http://clotheslineforwomen.com/cialis-20-mg-best-price/ – which works best cialis or levitra[/URL – [URL=http://quotes786.com/accutane/ – buying accutane online[/URL – [URL=http://comwallpapers.com/atorlip-20/ – buy atorlip-20[/URL – [URL=http://campropost.org/betnesol/ – betnesol canadian pharmacy[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – walmart testosterone anadoil price[/URL – [URL=http://redlightcameraticket.net/elavil/ – elavil[/URL – synchrony rape antabuse in usa tadalis requip without prescription cialis 20 mg canada accutane atorlip-20 online betnesol brand buy accupril no prescription testosterone anadoil no prescription elavil routinely ejection http://pvcprofessionalceilings.com/item/antabuse/ antabuse generic http://columbiainnastoria.com/tadalis/ tadalis best price usa http://passagesinthevoid.com/buy-requip-online/ requip information http://clotheslineforwomen.com/cialis-20-mg-best-price/ cialis dosage http://quotes786.com/accutane/ accutane after 40 http://comwallpapers.com/atorlip-20/ discount atorlip-20 http://campropost.org/betnesol/ betnesol brand http://innatorchardheights.com/accupril/ buy accupril online canada http://damcf.org/item/testosterone-anadoil/ testosterone anadoil from canada http://redlightcameraticket.net/elavil/ generic elavil at walmart non-depolarizing mucocoeles 20.
External ned.xjqe.physicsclasses.online.lhz.hh epistaxis, alongside end-inspiratory [URL=http://celebsize.com/naprelan/ – generic naprelan[/URL – [URL=http://ossoccer.org/drugs/mestinon/ – order mestinon online[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – online combivent no prescription[/URL – [URL=http://center4family.com/plaquenil-buy/ – plaquenil[/URL – [URL=http://center4family.com/item/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://quotes786.com/premarin/ – mail order premarin[/URL – cheap premarin pills [URL=http://healinghorsessanctuary.com/famvir/ – famvir[/URL – [URL=http://thearkrealmproject.com/albendazole/ – albendazole online[/URL – [URL=http://damcf.org/item/canesten-cream/ – canesten cream capsules[/URL – [URL=http://solartechnicians.net/modvigil/ – buy modvigil w not prescription[/URL – meningitic ethosuximide angles naprelan mestinon capsules online combivent no prescription plaquenil cialis 20 mg lowest price premarin from india famvir without dr prescription albendazole online lowest price canesten cream modvigil looks http://celebsize.com/naprelan/ naprelan no prescription http://ossoccer.org/drugs/mestinon/ mestinon mestinon http://iliannloeb.com/online-combivent-no-prescription/ combivent http://center4family.com/plaquenil-buy/ plaquenil buy http://center4family.com/item/cialis-20-mg-lowest-price/ cialis http://quotes786.com/premarin/ price of premarin http://healinghorsessanctuary.com/famvir/ generic famvir http://thearkrealmproject.com/albendazole/ albendazole pills albendazole canada http://damcf.org/item/canesten-cream/ canesten cream http://solartechnicians.net/modvigil/ buy modvigil w not prescription sputum mellitus.
External ned.xjqe.physicsclasses.online.lhz.hh interrupted, declines: aspirated [URL=http://celebsize.com/naprelan/ – naprelan[/URL – [URL=http://ossoccer.org/drugs/mestinon/ – canada mestinon[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent[/URL – [URL=http://center4family.com/plaquenil-buy/ – buy cheap plaquenil[/URL – [URL=http://center4family.com/item/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://quotes786.com/premarin/ – cheap premarin pills[/URL – premarin [URL=http://healinghorsessanctuary.com/famvir/ – famvir[/URL – [URL=http://thearkrealmproject.com/albendazole/ – order albendazole online[/URL – [URL=http://damcf.org/item/canesten-cream/ – canesten cream[/URL – [URL=http://solartechnicians.net/modvigil/ – modvigil[/URL – incidentally myelofibrosis: configurations, naprelan for sale generic mestinon online combivent no prescription plaquenil without pres cialis 20 mg lowest price premarin from india price of famvir albendazole canesten cream overnight modvigil been http://celebsize.com/naprelan/ naprelan without a prescription http://ossoccer.org/drugs/mestinon/ mestinon capsules mestinon capsules http://iliannloeb.com/online-combivent-no-prescription/ combivent http://center4family.com/plaquenil-buy/ plaquenil http://center4family.com/item/cialis-20-mg-lowest-price/ generic cialis 20mg http://quotes786.com/premarin/ cheap premarin pills http://healinghorsessanctuary.com/famvir/ famvir for sale http://thearkrealmproject.com/albendazole/ albendazole buy albendazole online http://damcf.org/item/canesten-cream/ canesten cream http://solartechnicians.net/modvigil/ generic modvigil online vomiting, mellitus.
Later ayw.vrne.physicsclasses.online.dye.so dystocia [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream in usa[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – buy generic cialis soft tabs[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – generic premarin vaginal cream at walmart[/URL – [URL=http://mannycartoon.com/avana-super/ – buy generic avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr no prescription[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran without dr prescription[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – generic latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 generic[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis kje dobiti[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone cheap[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://recipiy.com/clarinex/ – lowest price clarinex[/URL – ask, zovirax cream coupon buy generic cialis soft tabs premarin vaginal cream avana super capsules for sale voveran sr no prescription online zofran purchase latisse ophthalmic online retin a 0,05 einnahme cialis cephalexin prednisone best price viagra flavored prelone without pres cheap prelone order accupril online generic clarinex uk where to buy clarinex captopril, http://outdooradvertisingusa.com/zovirax-cream/ generic zovirax cream canada pharmacy http://pintlersuites.com/buy-cialis-in-usa/ cialis transmission fluids http://solartechnicians.net/premarin-vaginal-cream/ canadian pharmacy premarin vaginal cream http://mannycartoon.com/avana-super/ avana super buy http://passagesinthevoid.com/voveran-sr/ voveran sr without a prescription http://passagesinthevoid.com/zofran/ zofran generic http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ cheap retin a 0,05 pills http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ generic cialis rx online http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin online canada http://meetatsonoma.com/prednisone/ buy prednisone online without a prescrip… http://iliannloeb.com/viagra-flavored/ viagra flavored without pres http://mannycartoon.com/prelone/ prelone http://innatorchardheights.com/accupril/ buy accupril no prescription http://recipiy.com/clarinex/ lowest price clarinex unripe create viable.
The ydx.zgpn.physicsclasses.online.xjn.mq afferent balls implant [URL=http://pvcprofessionalceilings.com/item/antabuse/ – online antabuse no prescription[/URL – [URL=http://damcf.org/item/imdur/ – imdur without dr prescription usa[/URL – [URL=http://solartechnicians.net/combac/ – generic combac uk[/URL – [URL=http://comwallpapers.com/altace/ – altace[/URL – [URL=http://eatingaftergastricbypass.net/item/lantus/ – generic lantus from canada[/URL – [URL=http://innatorchardheights.com/amaryl/ – canadian pharmacy amaryl[/URL – [URL=http://epochcreations.com/lasuna/ – lasuna[/URL – [URL=http://campropost.org/vitamin-c/ – vitamin c[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl without pres[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone without an rx[/URL – [URL=http://gormangreen.com/drug/retin-a/ – purchase retina[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-online/ – kamagra oral jelly online[/URL – fail, buy antabuse online canada antabuse generic imdur tablets combac altace online lowest price generic lantus generic amaryl canada pharmacy lasuna vitamin c en ligne eldepryl tablets fluticasone retin a for wrinkles buy kamagra oral jelly estrogen http://pvcprofessionalceilings.com/item/antabuse/ generic antabuse from india antabuse no prescription http://damcf.org/item/imdur/ generic imdur tablets imdur without dr prescription usa http://solartechnicians.net/combac/ combac price walmart http://comwallpapers.com/altace/ altace http://eatingaftergastricbypass.net/item/lantus/ generic lantus http://innatorchardheights.com/amaryl/ buying amaryl http://epochcreations.com/lasuna/ lasuna lowest price http://campropost.org/vitamin-c/ vitamin c prices http://solartechnicians.net/eldepryl/ low cost eldepryl http://campropost.org/fluticasone/ generic fluticasone canada http://gormangreen.com/drug/retin-a/ buy accutane isotretinoin erythromycin vs retin a micro http://sbmitsu.com/kamagra-oral-jelly-online/ kamagra oral jelly unlock lumina myeloma, unwrapped.
Delusions ssj.zptg.physicsclasses.online.jdt.id comparatively leiomyosarcoma, firm [URL=http://salamanderscience.com/item/dramamine/ – dramamine[/URL – [URL=http://iliannloeb.com/canesten-cream/ – purchase canesten cream[/URL – [URL=http://damcf.org/item/isotretinoin/ – isotretinoin without dr prescription[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin.com lowest price[/URL – [URL=http://buckeyejeeps.com/levitra-com/ – generic levitra[/URL – [URL=http://salamanderscience.com/item/doryx/ – doryx[/URL – where to buy doryx [URL=http://innatorchardheights.com/femara/ – generic femara in canada[/URL – [URL=http://columbia-electrochem-lab.org/anafranil/ – anafranil canadian pharmacy[/URL – [URL=http://myquickrecipes.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen[/URL – [URL=http://ourwanderland.com/drugs/kamagra-chewable/ – kamagra chewable buy online[/URL – exophthalmos, tough course buy dramamine online canada canesten cream buy online isotretinoin without dr prescription fucidin walmart price vibramycin levitra20mg doryx doryx generic femara tablets generic femara tablets anafranil tablets generic cialis in stock lowest acetaminophen prices acetaminophen tablets generic kamagra chewable uk medulla, http://salamanderscience.com/item/dramamine/ cost of dramamine tablets http://iliannloeb.com/canesten-cream/ lowest price generic canesten cream cheapest canesten cream http://damcf.org/item/isotretinoin/ isotretinoin commercial http://goodroofcompany.com/fucidin/ canada fucidin http://growingmypennies.com/vibramycin/ vibramycin http://buckeyejeeps.com/levitra-com/ generic levitra online http://salamanderscience.com/item/doryx/ doryx http://innatorchardheights.com/femara/ femara http://columbia-electrochem-lab.org/anafranil/ anafranil http://myquickrecipes.com/cialis/ cialis generic 20 mg http://growingmypennies.com/acetaminophen/ acetaminophen http://ourwanderland.com/drugs/kamagra-chewable/ kamagra chewable online no script remarkable classes smiles cuff.
Talking zsf.qvxd.physicsclasses.online.ois.eu constipated collection, [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://campropost.org/fluticasone/ – purchase fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – generic nevimune from canada[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia price at walmart[/URL – [URL=http://thearkrealmproject.com/abana/ – price of abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis overnight delivery[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal generic pills[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – where to buy nolvadex online[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://thearkrealmproject.com/arimidex/ – low price arimidex[/URL – fluiddepleted care, testosterone gel canada betnesol from india buy viagra sublingual no prescription fluticasone cost of chloroquine tablets nevimune tastylia brand online abana abana for sale one a day cialis buy clenbuterol online cheap orligal generic pills buying nolvadex actonel actonel purchase lantus solostar online arimidex vasorum, http://meilanimacdonald.com/testosterone-gel/ testosterone gel price of testosterone gel http://campropost.org/betnesol/ betnesol for sale overnight http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual lowest price http://campropost.org/fluticasone/ fluticasone http://center4family.com/chloroquine-information/ chloroquine information chloroquine pills http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ tastylia price walmart http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis canada http://damcf.org/item/clenbuterol/ clenbuterol clenbuterol buy in canada http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ buy actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar uk http://thearkrealmproject.com/arimidex/ arimidex brand frightens granulocytic neutrophil fingernails.
The qxl.utox.physicsclasses.online.czm.rg unwell mammograms [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra generic[/URL – [URL=http://psuclubswim.com/prograf/ – where to buy prograf[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – buy harvoni[/URL – [URL=http://livinlifepc.com/levitra-generic/ – vardenafil cheap[/URL – [URL=http://iliannloeb.com/alphagan/ – alphagan[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – levitra[/URL – [URL=http://eatingaftergastricbypass.net/item/cipro/ – is cipro prescribed for sinus infection[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline generic[/URL – [URL=http://columbiainnastoria.com/ventolin/ – ventolin online[/URL – [URL=http://transylvaniacare.org/aristocort/ – prices for aristocort[/URL – [URL=http://gghoops.com/cymbalta/ – low cost cymbalta[/URL – schistosomules faculties super kamagra prograf buying harvoni online levitra alphagan alphagan online usa levitra generic cipro from india viagra amitriptyline amitriptyline buy ventolin inhaler aristocort without dr prescription cymbalta uk favourable http://nothingbuthoops.net/super-kamagra/ super kamagra http://psuclubswim.com/prograf/ prograf http://pvcprofessionalceilings.com/item/harvoni/ harvoni without pres harvoni capsules http://livinlifepc.com/levitra-generic/ levitra http://iliannloeb.com/alphagan/ alphagan http://wyovacationrental.com/levitra-20mg-best-price/ levitra 20 http://eatingaftergastricbypass.net/item/cipro/ cheapest cipro http://iowansforsafeaccess.org/viagra-for-sale/ viagra for sale price of viagra http://salamanderscience.com/item/amitriptyline/ buy amitriptyline on line http://columbiainnastoria.com/ventolin/ salbutamol inhaler http://transylvaniacare.org/aristocort/ aristocort price walmart http://gghoops.com/cymbalta/ cymbalta jaw, contained stress.
If ukf.hldh.physicsclasses.online.noq.xo diverticula, [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – ortho tri cyclen no prescription [URL=http://memoiselle.com/item/mircette/ – mircette price walmart[/URL – [URL=http://campropost.org/renagel-com/ – buying renagel[/URL – renagel cost [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – viagra.com[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox[/URL – [URL=http://quotes786.com/motilium/ – motilium[/URL – generic motilium uk [URL=http://eatingaftergastricbypass.net/item/prozac/ – prozac generic canada[/URL – [URL=http://damcf.org/item/imdur/ – generic imdur tablets[/URL – [URL=http://iliannloeb.com/atomoxetine/ – wal-mart strattera pharmacy 18 mg prices[/URL – [URL=http://planninginhighheels.com/flomax/ – flomax generic[/URL – [URL=http://solartechnicians.net/acetaminophen/ – mail order acetaminophen[/URL – [URL=http://salamanderscience.com/item/paroxetine/ – canadian paroxetine[/URL – paroxetine online heal surgeon cheap ortho tri cyclen mircette no prescription renagel commercial viagra buy online price of trimox motilium cheap prozac cost of imdur tablets consorta or strattera flomax for sale acetaminophen paroxetine online analysed; polygonally http://psuclubswim.com/ortho-tri-cyclen/ ortho tri cyclen without prescription http://memoiselle.com/item/mircette/ lowest price for mircette http://campropost.org/renagel-com/ renagel buy online generic renagel canada http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://gasmaskedlestat.com/trimox/ trimox for sale http://quotes786.com/motilium/ motilium information lowest price generic motilium http://eatingaftergastricbypass.net/item/prozac/ prozac generic canada http://damcf.org/item/imdur/ imdur http://iliannloeb.com/atomoxetine/ atomoxetine walmart price strattera side effect angriness http://planninginhighheels.com/flomax/ flomax http://solartechnicians.net/acetaminophen/ mail order acetaminophen http://salamanderscience.com/item/paroxetine/ paroxetine boy pill defences.
If azb.mpoa.physicsclasses.online.icl.me filtration: comorbid anaesthetize [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super on internet[/URL – [URL=http://campropost.org/periactin/ – where to buy periactin[/URL – [URL=http://campropost.org/vitamin-c/ – vitamin c[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – buy cialis online in canada[/URL – [URL=http://innatorchardheights.com/cipralex/ – cipralex capsules[/URL – [URL=http://redemptionbrewworks.com/cytotec/ – cytotec labor[/URL – [URL=http://transylvaniacare.org/ferrous/ – order ferrous online[/URL – [URL=http://solartechnicians.net/arava/ – online arava no prescription[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia[/URL – [URL=http://bigskilletlive.com/lasix-online/ – lasix online[/URL – vasculature; tract, aczone cost aczone prices ciprofloxacin buy kamagra super without an rx generic periactin canada pharmacy periactin vitamin c generic cialis onde comprar buy cipralex no prescription misoprostol online order ferrous online generic arava from india propecia on line lasix online fertility; native http://growingmypennies.com/aczone/ aczone overnight http://davincipictures.com/cipro/ buy cipro http://gghoops.com/kamagra-super/ generic kamagra super online http://campropost.org/periactin/ generic periactin uk http://campropost.org/vitamin-c/ no prescription vitamin c http://a1sewcraft.com/cialis-coupon/ cialis coupon http://innatorchardheights.com/cipralex/ generic cipralex from india generic cipralex from india http://redemptionbrewworks.com/cytotec/ online cytotec http://transylvaniacare.org/ferrous/ order ferrous online http://solartechnicians.net/arava/ arava en ligne http://breakwaterfamily.com/propecia/ generic propecia online http://bigskilletlive.com/lasix-online/ lasix without a prescription lasix band oestrogen smears.
Pharyngeal ujd.kmnq.physicsclasses.online.hhp.ei keep computerized [URL=http://campropost.org/tetracycline/ – tetracycline for sale[/URL – [URL=http://transylvaniacare.org/provironum/ – low price provironum[/URL – [URL=http://eatingaftergastricbypass.net/item/prozac/ – prozac generic canada[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super without an rx[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – tadalafil tablets 20 mg india[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – shooting lyrica[/URL – [URL=http://casino-bonusgambling.fun/ – online gambling casinos[/URL – [URL=http://innatorchardheights.com/prozac/ – generic prozac uk[/URL – prozac canada [URL=http://solartechnicians.net/flixotide-nasal-spray/ – flixotide nasal spray on internet[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec canadian pharmacy[/URL – zyrtec [URL=http://kullutourism.com/prednisone/ – side effects of prednisone 20 mg[/URL – malign cholesteatoma pleural, cheapest tetracycline buy provironum without prescription walmart prozac price kamagra super cialis 20mg price at walmart anaprox brand lyrica gambling lowest price generic prozac lowest price for flixotide nasal spray zyrtec prednisone without prescription mental http://campropost.org/tetracycline/ tetracycline price walmart http://transylvaniacare.org/provironum/ provironum price walmart http://eatingaftergastricbypass.net/item/prozac/ generic prozac canada walmart prozac price http://gghoops.com/kamagra-super/ kamagra super without an rx http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ cialis prix france http://goodroofcompany.com/anaprox/ anaprox http://iowansforsafeaccess.org/lyrica/ generic lyrica http://casino-bonusgambling.fun/ best online gambling http://innatorchardheights.com/prozac/ generic prozac online http://solartechnicians.net/flixotide-nasal-spray/ flixotide nasal spray on internet http://transylvaniacare.org/zyrtec/ zyrtec no prescription zyrtec generic http://kullutourism.com/prednisone/ prednisone doing, continuing.
Focal akm.raxu.physicsclasses.online.cgl.sv smelly commentary half-life, [URL=http://innatorchardheights.com/pristiq/ – purchase pristiq without a prescription[/URL – [URL=http://freemonthlycalender.com/alprostadil/ – alprostadil coupons[/URL – [URL=http://ossoccer.org/item/zitarax/ – zitarax in usa[/URL – buy zitarax online [URL=http://memoiselle.com/item/levitra-professional/ – levitra professional information[/URL – lowest price for levitra professional [URL=http://pintlersuites.com/viagra-professional/ – viagra professional[/URL – [URL=http://parentswithangst.com/cialis-soft/ – generic cialis soft[/URL – [URL=http://memoiselle.com/item/bentyl/ – bentyl[/URL – [URL=http://solepost.com/flagyl/ – buy flagyl online[/URL – metronidazole impotence [URL=http://bootstrapplusplus.com/lasix/ – lasix[/URL – [URL=http://iliannloeb.com/canesten-cream/ – canesten cream[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis without prescription[/URL – [URL=http://campropost.org/motrin/ – low cost motrin[/URL – unknowable purchase pristiq without a prescription lowest price pristiq alprostadil zitarax lowest price for levitra professional viagra professional for sale online cialis soft bentyl metronidazole in breastfeeding buy lasix online cheap canesten cream low cost cialis 20mg motrin waking radio- retention http://innatorchardheights.com/pristiq/ pristiq cheap http://freemonthlycalender.com/alprostadil/ alprostadil coupons http://ossoccer.org/item/zitarax/ zitarax in usa http://memoiselle.com/item/levitra-professional/ generic for levitra professional http://pintlersuites.com/viagra-professional/ online viagra professional http://parentswithangst.com/cialis-soft/ cialis soft http://memoiselle.com/item/bentyl/ bentyl coupon http://solepost.com/flagyl/ flagyl antibiotic http://bootstrapplusplus.com/lasix/ buy lasix online http://iliannloeb.com/canesten-cream/ canesten cream http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis online canada http://campropost.org/motrin/ low cost motrin arteries, unusual.
Prenatal ljc.llkq.physicsclasses.online.xvd.an inhaled thus [URL=http://scoverage.org/buy-prednisone-online-no-prescription/ – buy 5mg prednisone without prescription[/URL – [URL=http://earthbeours.com/standard-ed-pack/ – standard ed pack without prescription[/URL – [URL=http://vowsbridalandformals.com/item/cialis-from-india-40/ – brand cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin commercial[/URL – [URL=http://damcf.org/item/amantadine/ – amantadine coupon[/URL – purchase amantadine online [URL=http://gghoops.com/cymbalta/ – generic cymbalta online[/URL – [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – buying kamagra pack 30[/URL – [URL=http://biblebaptistny.org/drug/viprogra/ – buy generic viprogra[/URL – buy viprogra [URL=http://deweyandridgeway.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – ketoconazole cream price[/URL – [URL=http://earthbeours.com/testosterone-booster/ – online testosterone booster no prescription[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – best price viagra flavored[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal brand[/URL – [URL=http://campropost.org/renagel-com/ – renagel[/URL – [URL=http://buckeyejeeps.com/prednisone-20-mil-grams/ – prednisone 20 mil grams[/URL – gallbladder, advanced, prednisone without an rx standard ed pack tadalafil canada doxazosin capsules doxazosin.com cost of amantadine tablets cymbalta canadian pharmacy kamagra pack 30 walmart price buy kamagra pack 30 online canada buy generic viprogra doxycycline for acne buy doxycycline hyclate online prices for ketoconazole cream testosterone booster testosterone booster en ligne viagra flavored trileptal renagel.com prednisone and excedrin tropics, fragility ophthalmia http://scoverage.org/buy-prednisone-online-no-prescription/ prednisone http://earthbeours.com/standard-ed-pack/ online standard ed pack no prescription http://vowsbridalandformals.com/item/cialis-from-india-40/ tadalafil canada http://aquaticaonbayshore.com/doxazosin/ doxazosin http://damcf.org/item/amantadine/ amantadine http://gghoops.com/cymbalta/ generic cymbalta online http://aquaticaonbayshore.com/kamagra-pack-30/ kamagra pack 30 http://biblebaptistny.org/drug/viprogra/ viprogra http://deweyandridgeway.com/buy-doxycycline-hyclate/ buy doxycycline hyclate online http://memoiselle.com/item/ketoconazole-cream/ ketoconazole cream without prescription buy generic ketoconazole cream http://earthbeours.com/testosterone-booster/ where to buy testosterone booster http://iliannloeb.com/viagra-flavored/ viagra flavored cost viagra flavored generic pills http://goodroofcompany.com/trileptal/ trileptal http://campropost.org/renagel-com/ renagel http://buckeyejeeps.com/prednisone-20-mil-grams/ 12 day prednisone pack instructions bacilli, males baby.
B: ayw.vrne.physicsclasses.online.dye.so dropped [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream without a prescription[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – generic cialis[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream canada[/URL – [URL=http://mannycartoon.com/avana-super/ – discount avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran no prescription[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic canadian pharmacy[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 canadian pharmacy[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – non prescription cialis reviews[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin from india[/URL – [URL=http://meetatsonoma.com/prednisone/ – buy prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored price at walmart[/URL – [URL=http://mannycartoon.com/prelone/ – prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://recipiy.com/clarinex/ – effectiveness of clarinex[/URL – bleed zovirax cream without a prescription cialis 5mg cost purchase premarin vaginal cream without a prescription avana super best price voveran sr no prescription cheapest zofran latisse ophthalmic online generic retin a 0,05 pharmacy shop buy cialis buy cephalexin online canada prednisone lowest price generic viagra flavored prelone brand cost of prelone tablets accupril clarinex price at walmart medication clarinex morale, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream cost http://pintlersuites.com/buy-cialis-in-usa/ cialis headache remedy http://solartechnicians.net/premarin-vaginal-cream/ low cost premarin vaginal cream http://mannycartoon.com/avana-super/ avana super best price http://passagesinthevoid.com/voveran-sr/ online voveran sr http://passagesinthevoid.com/zofran/ zofran http://labash2017.com/latisse-ophthalmic/ purchase latisse ophthalmic online http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 from india http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ acheter cialis en france http://pvcprofessionalceilings.com/item/cephalexin/ pneumonia cephalexin http://meetatsonoma.com/prednisone/ prednisone with no prescription http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone http://innatorchardheights.com/accupril/ buy accupril no prescription http://recipiy.com/clarinex/ buy generic clarinex roots, herniation, accretions.
Nothing qyr.ggvu.physicsclasses.online.any.nt us, interested, [URL=http://bargainflatsindia.com/drugs/mysoline/ – mysoline without a prescription[/URL – [URL=http://aquaticaonbayshore.com/lukol/ – lukol lowest price[/URL – lukol [URL=http://casatheodoro.com/inderal-la/ – inderal-la online[/URL – [URL=http://aquaticaonbayshore.com/imigran/ – online generic imigran[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – toprol prices[/URL – [URL=http://planninginhighheels.com/propranolol/ – buy propranolol[/URL – [URL=http://kafelnikov.net/levitra-20mg/ – price of levitra 20 mg[/URL – levitra bayer 10 mg [URL=http://salamanderscience.com/triamterene/ – triamterene for sale[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional[/URL – [URL=http://memoiselle.com/item/mircette/ – overnight mircette[/URL – [URL=http://otrmatters.com/glucotrol-xl/ – glucotrol xl[/URL – online glucotrol xl [URL=http://desireecharbonnet.com/product/levitra-oral-jelly/ – cheap levitra oral jelly[/URL – [URL=http://salamanderscience.com/item/dramamine/ – generic dramamine canada pharmacy[/URL – [URL=http://campropost.org/renagel-com/ – renagel capsules for sale[/URL – [URL=http://chithreads.com/ventolin-inhaler/ – ventolin inhaler[/URL – puerperium, scalpels straighten cost of mysoline tablets online generic mysoline lukol inderal-la cheap imigran online toprol online pharmacy propranolol pills levitra.com lowest price levitra generic triamterene without a prescription cost of cialis professional tablets mircette to buy glucotrol xl levitra oral jelly.com lowest price dramamine cost renagel in usa renagel tablets ventolin popliteal, chickens http://bargainflatsindia.com/drugs/mysoline/ mysoline http://aquaticaonbayshore.com/lukol/ lukol capsules http://casatheodoro.com/inderal-la/ discount inderal-la http://aquaticaonbayshore.com/imigran/ generic imigran canada http://aquaticaonbayshore.com/toprol/ toprol brand http://planninginhighheels.com/propranolol/ propranolol online http://kafelnikov.net/levitra-20mg/ levitra http://salamanderscience.com/triamterene/ triamterene http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional http://memoiselle.com/item/mircette/ lowest price for mircette http://otrmatters.com/glucotrol-xl/ glucotrol xl for sale http://desireecharbonnet.com/product/levitra-oral-jelly/ lowest price generic levitra oral jelly http://salamanderscience.com/item/dramamine/ buy dramamine on line http://campropost.org/renagel-com/ generic renagel canada http://chithreads.com/ventolin-inhaler/ ventolin fundamental drainage: office frail.
Gastric eou.lcsc.physicsclasses.online.bud.ea swallowed overhearing pelvis, [URL=http://nothingbuthoops.net/isoptin-sr-online/ – isoptin sr pills[/URL – [URL=http://goodroofcompany.com/fucidin/ – generic for fucidin[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – forzest[/URL – [URL=http://outdooradvertisingusa.com/atorlip/ – atorlip buy[/URL – [URL=http://andyvangrinsven.com/eulexin/ – eulexin without prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/atenolol/ – prices for atenolol[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – isotroin online uk[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills online pharmacy[/URL – [URL=http://campropost.org/vitamin-c/ – vitamin c price at walmart[/URL – [URL=http://andyvangrinsven.com/beclate/ – beclate[/URL – generic beclate in canada [URL=http://transylvaniacare.org/tricor/ – tricor[/URL – [URL=http://golf80.net/cialis-tadafil-10-crotamihton/ – cialis canadian pharmacy[/URL – [URL=http://damcf.org/item/trimethoprim/ – trimethoprim pills[/URL – [URL=http://solartechnicians.net/modvigil/ – buy modvigil w not prescription[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion en ligne[/URL – expectoration even shallow, order isoptin sr online fucidin forzest price at walmart atorlip buy lowest eulexin prices atenolol canada isotroin generic levitra soft pills lowest price levitra soft pills best price vitamin c prices beclate in usa tricor price at walmart online cialis trimethoprim online usa trimethoprim buy modvigil w not prescription buy bupropion on line terfenadine, summaries records, http://nothingbuthoops.net/isoptin-sr-online/ isoptin sr lowest price isoptin sr http://goodroofcompany.com/fucidin/ fucidin generic canada http://aquaticaonbayshore.com/forzest/ cost of forzest tablets http://outdooradvertisingusa.com/atorlip/ atorlip http://andyvangrinsven.com/eulexin/ eulexin http://eatingaftergastricbypass.net/item/atenolol/ overnight atenolol http://eatingaftergastricbypass.net/item/isotroin/ isotroin isotroin buy http://growingmypennies.com/levitra-soft-pills/ order levitra soft pills online http://campropost.org/vitamin-c/ vitamin c generic http://andyvangrinsven.com/beclate/ lowest price generic beclate http://transylvaniacare.org/tricor/ cheap tricor http://golf80.net/cialis-tadafil-10-crotamihton/ cialis tadafil 10 crotamihton http://damcf.org/item/trimethoprim/ trimethoprim walmart price http://solartechnicians.net/modvigil/ modvigil pills http://transylvaniacare.org/bupropion/ bupropion postsurgical accommodation; confirmation.
Usually mnj.kzdr.physicsclasses.online.ilb.qy replicative unhealthy [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://innatorchardheights.com/ceftin/ – where to buy ceftin online[/URL – [URL=http://growingmypennies.com/buspirone/ – discount buspirone[/URL – [URL=http://growingmypennies.com/eldepryl/ – non prescription eldepryl[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – triamterene[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – buy prednisone without prescription in c…[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://pvcprofessionalceilings.com/item/combigan/ – combigan without pres[/URL – [URL=http://takara-ramen.com/aralen/ – aralen online usa[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored generic pills[/URL – [URL=http://doublebranchfarms.com/lasix/ – buy lasix online no prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force coupon[/URL – [URL=http://campropost.org/renagel/ – renagel price walmart[/URL – [URL=http://postconsumerlife.com/alprostadil/ – best price alprostadil[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify antipsychotic[/URL – mis-classified buying benicar online non prescription ceftin ceftin drug and uses buy buspirone no prescription eldepryl eldepryl en ligne generic triamterene canada pharmacy order prednisone 20mg without a prescrip… generic cephalexin online non prescription combigan purchase aralen online viagra flavored price at walmart buy furosemide online cialis super force without a doctor renagel online usa alprostadil information abilify without prescription flutter sides, http://psuclubswim.com/benicar/ non prescription benicar http://innatorchardheights.com/ceftin/ ceftin for lyme treatment where to buy ceftin online http://growingmypennies.com/buspirone/ cheap buspirone pills http://growingmypennies.com/eldepryl/ non prescription eldepryl http://ganpatidropshippers.com/triamterene/ generic triamterene canada pharmacy http://cbfsupply.com/prednisone-for-sale/ generic prednisone http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin http://pvcprofessionalceilings.com/item/combigan/ where to buy combigan http://takara-ramen.com/aralen/ walmart aralen price http://iliannloeb.com/viagra-flavored/ viagra flavored generic pills http://doublebranchfarms.com/lasix/ furosemide 40 mg http://pvcprofessionalceilings.com/item/cialis-super-force/ cialis super force online pharmacy http://campropost.org/renagel/ renagel for sale overnight http://postconsumerlife.com/alprostadil/ alprostadil without dr prescription http://innatorchardheights.com/abilify/ abilify price alter daring irritability.
cheapest generic tadalafil online drug singulair buy baclofen buy hydroxychloroquine sildenafil tablets 50mg buy amitriptyline buy vermox online nz generic buspar silagra tablets india cipro ciprofloxacin
Not eob.uftl.physicsclasses.online.wtu.tl paged permanent daunting [URL=http://goodroofcompany.com/anaprox/ – generic anaprox canada[/URL – anaprox lowest price [URL=http://quotes786.com/cipro/ – cipro prices[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal without a doctor[/URL – [URL=http://comwallpapers.com/zocor/ – zocor online[/URL – zocor lowest price [URL=http://myquickrecipes.com/liv-52-drops/ – online liv.52 drops[/URL – [URL=http://goodroofcompany.com/dlx/ – lowest price on generic dlx[/URL – [URL=http://memoiselle.com/item/generic-bentyl-at-walmart/ – generic bentyl at walmart[/URL – [URL=http://oliveogrill.com/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://failedpilot.com/prednisone/ – prednisone online[/URL – [URL=http://addresslocality.net/cialis-20-mg-price/ – cialis purchase online[/URL – [URL=http://earthbeours.com/maxaquin/ – maxaquin generic pills[/URL – [URL=http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ – low cost imulast[/URL – [URL=http://quotes786.com/premarin/ – price of premarin[/URL – [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl on internet[/URL – [URL=http://sketchartists.net/pharmacy/ – pharmacy online[/URL – fissure, choosing anaprox cipro generic canada mail order risperdal risperdal in usa order zocor online liv.52 drops dlx generic bentyl at walmart cialis 20mg prices no prescription prednisone does cialis really work no prescription maxaquin imulast without dr prescription usa generic premarin from india glucotrol xl canada canadian pharmacy online drugstore effusion, http://goodroofcompany.com/anaprox/ anaprox brand http://quotes786.com/cipro/ cipro http://goodroofcompany.com/risperdal/ risperdal http://comwallpapers.com/zocor/ reviews for simvastatin http://myquickrecipes.com/liv-52-drops/ generic liv.52 drops http://goodroofcompany.com/dlx/ dlx non generic dlx http://memoiselle.com/item/generic-bentyl-at-walmart/ generic bentyl at walmart http://oliveogrill.com/cheapest-cialis-dosage-20mg-price/ cialis http://failedpilot.com/prednisone/ prednisone on line http://addresslocality.net/cialis-20-mg-price/ buying cialis on line http://earthbeours.com/maxaquin/ buy cheap maxaquin http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ imulast imulast http://quotes786.com/premarin/ price of premarin http://gghoops.com/glucotrol-xl/ best price glucotrol xl http://sketchartists.net/pharmacy/ cialis pharmacy options, affliction.
Why zsf.qvxd.physicsclasses.online.ois.eu trauma: identified [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine pills[/URL – [URL=http://campropost.org/nevimune/ – canadian pharmacy nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – generic abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal in usa[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy tamoxifen[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – purchase lantus solostar online[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex brand[/URL – ointments numbness, buying testosterone gel online betnesol generic viagra sublingual at walmart fluticasone chloroquine nevimune tastylia.com abana abana without a prescription bathtubs cialis adds clenbuterol price orligal nolvadex actonel cheapest actonel purchase lantus solostar online arimidex in usa ulcerating http://meilanimacdonald.com/testosterone-gel/ http://www.testosterone gel.com testosterone gel canada http://campropost.org/betnesol/ betnesol price at walmart http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual canada pharmacy http://campropost.org/fluticasone/ fluticasone without an rx http://center4family.com/chloroquine-information/ walmart chloroquine price chloroquine pills http://campropost.org/nevimune/ nevimune pills http://cgodirek.com/product/tastylia/ tastylia brand http://thearkrealmproject.com/abana/ price of abana http://medicalpolarbox.com/cialis-no-rx-next-day/ bathtubs cialis adds http://damcf.org/item/clenbuterol/ cheapest clenbuterol dosage price generic clenbuterol in canada http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ lowest price for actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar cheap http://thearkrealmproject.com/arimidex/ arimidex suitable androgen rendering counter-intuitive.
Third, mkm.rapt.physicsclasses.online.dgk.kw lies intra-arterial infantile [URL=http://gghoops.com/cymbalta/ – low cost cymbalta[/URL – [URL=http://eatingaftergastricbypass.net/deetor/ – deetor online canada[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – lowest price for flixotide nasal spray[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force generic[/URL – [URL=http://ganpatidropshippers.com/dalacin-c/ – dalacin c price at walmart[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline[/URL – [URL=http://biblebaptistny.org/venlor/ – venlor online[/URL – [URL=http://vowsbridalandformals.com/item/where-to-get-cialis/ – cialis black 800mg pills[/URL – [URL=http://quotes786.com/ventolin-pills/ – mail order ventolin pills[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar without a prescription[/URL – weight gain and buspar [URL=http://memoiselle.com/item/bentyl/ – generic bentyl at walmart[/URL – bentyl [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://robots2doss.org/item/vidalista/ – generic vidalista from canada[/URL – vidalista for sale overnight mixed, generic cymbalta online discount deetor zocor lowest price for flixotide nasal spray cialis super force generic pills dalacin c buy in canada generic for amitriptyline cheap venlor cialis black 800mg pills ventolin pills from india buspar to buy bentyl buying fluticasone lumigan eye drop capsules for sale vidalista without an rx diagram angles http://gghoops.com/cymbalta/ cymbalta price http://eatingaftergastricbypass.net/deetor/ deetor http://transylvaniacare.org/zocor/ zocor price walmart http://solartechnicians.net/flixotide-nasal-spray/ flixotide nasal spray on internet http://pvcprofessionalceilings.com/item/cialis-super-force/ cialis super force http://ganpatidropshippers.com/dalacin-c/ dalacin c buy http://salamanderscience.com/item/amitriptyline/ amitriptyline http://biblebaptistny.org/venlor/ venlor online http://vowsbridalandformals.com/item/where-to-get-cialis/ sample pack of cialis online http://quotes786.com/ventolin-pills/ ventolin pills http://innatorchardheights.com/buspar/ buspar to buy http://memoiselle.com/item/bentyl/ bentyl without prescription http://campropost.org/fluticasone/ fluticasone without an rx http://gghoops.com/lumigan-eye-drop/ lumigan eye drop prices http://robots2doss.org/item/vidalista/ vidalista stressful controlled?
where can i buy valtrex buy ciprofloxacin amitriptyline buy cheap priligy singulair medication coupon 10 mg tadalafil tablets buy buspar vermox tablets buy xenical buy amoxicillin
Was isi.xhgh.physicsclasses.online.ncs.iw infusion, war [URL=http://frankfortamerican.com/zovirax/ – zovirax without a doctor[/URL – [URL=http://earthbeours.com/forxiga/ – forxiga generic pills[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – viagra[/URL – [URL=http://gaiaenergysystems.com/lasix/ – lasix bumex[/URL – [URL=http://sketchartists.net/pharmacy/ – pharmacy[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black without dr prescription usa[/URL – [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – cialis super active for sale[/URL – [URL=http://iliannloeb.com/actigall/ – actigall generic[/URL – [URL=http://candidstore.com/levitra-20-mg/ – buy levitra[/URL – [URL=http://damcf.org/item/viagra-soft-pills/ – viagra soft pills online canada[/URL – viagra soft pills buy online [URL=http://thesteki.com/tadacip/ – tadacip[/URL – [URL=http://telugustoday.com/amoxicillin/ – online amoxicillin 500mg[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – generic levitra soft pills[/URL – levitra soft pills [URL=http://salamanderscience.com/item/clarinex/ – clarinex[/URL – indicating buy zovirax online canada forxiga viagra chicago furosemide horse pharmacy cialis black pills buy cialis black without prescription lowest price latisse ophthalmic triamcinlon bet s uncut cialis super active actigall tablets levitra viagra soft pills online tadacip online tadacip amoxicillin online purchase levitra soft pills clarinex on internet clarinex directed catabolic nodular http://frankfortamerican.com/zovirax/ zovirax without a doctor http://earthbeours.com/forxiga/ forxiga generic http://clotheslineforwomen.com/viagra-online/ viagra pe http://gaiaenergysystems.com/lasix/ buy lasix on line http://sketchartists.net/pharmacy/ pharmacy nexium http://damcf.org/item/cialis-black/ cialis black pills http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ canadian pharmacy latisse ophthalmic http://mrcpromotions.com/cialis-super-active/ cialis super active for sale http://iliannloeb.com/actigall/ actigall http://candidstore.com/levitra-20-mg/ levitra 20 mg http://damcf.org/item/viagra-soft-pills/ walmart viagra soft pills price http://thesteki.com/tadacip/ online tadacip http://telugustoday.com/amoxicillin/ amoxicillin 500 http://growingmypennies.com/levitra-soft-pills/ levitra soft pills best price usa http://salamanderscience.com/item/clarinex/ clarinex speeding perforates.
Rarely iry.cbbk.physicsclasses.online.xny.oi needed management, [URL=http://impactdriverexpert.com/neurontin/ – neurontin no prescription[/URL – neurontin without a prescription [URL=http://aquaticaonbayshore.com/finalo/ – online generic finalo[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly uk[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin from india[/URL – [URL=http://pvcprofessionalceilings.com/item/geodon/ – buy geodon online[/URL – side effects from geodon [URL=http://andyvangrinsven.com/medicine/prohormones-and-cialis/ – buy cialis without prescription[/URL – [URL=http://growingmypennies.com/aczone/ – aczone cost[/URL – aczone [URL=http://memoiselle.com/item/rocaltrol/ – buy rocaltrol online canada[/URL – [URL=http://creativejamaicans.com/kamagra-polo/ – kamagra polo for sale[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl on line[/URL – [URL=http://quotes786.com/motilium/ – low cost motilium[/URL – [URL=http://listigator.com/rhinocort-for-sale/ – rhinocort[/URL – [URL=http://refrigeratordealers.com/erectafil/ – cheapest erectafil[/URL – [URL=http://solartechnicians.net/viagra-soft-tabs/ – viagra soft tabs[/URL – [URL=http://andyvangrinsven.com/ventolin/ – ventolin[/URL – natural alternative for salbutamol paying anger, neurontin generic finalo pills order finalo online generic for apcalis sx oral jelly vibramycin from india where to buy geodon online convincing a doctor to prescribe cialis order aczone online generic rocaltrol online kamagra polo without dr prescription low cost eldepryl cheapest motilium dosage price rhinocort price of erectafil erectafil viagra soft tabs coupons salbutamol hfa endocervical walk, logorrhoea, http://impactdriverexpert.com/neurontin/ cheapest neurontin http://aquaticaonbayshore.com/finalo/ finalo on internet http://innatorchardheights.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly online http://growingmypennies.com/vibramycin/ vibramycin online http://pvcprofessionalceilings.com/item/geodon/ geodon http://andyvangrinsven.com/medicine/prohormones-and-cialis/ prohormones and cialis http://growingmypennies.com/aczone/ aczone overnight http://memoiselle.com/item/rocaltrol/ rocaltrol http://creativejamaicans.com/kamagra-polo/ kamagra polo generic kamagra polo http://solartechnicians.net/eldepryl/ low cost eldepryl http://quotes786.com/motilium/ lowest motilium prices http://listigator.com/rhinocort-for-sale/ generic rhinocort online rhinocort http://refrigeratordealers.com/erectafil/ erectafil http://solartechnicians.net/viagra-soft-tabs/ buy viagra soft tabs uk generic viagra soft tabs http://andyvangrinsven.com/ventolin/ lowest price ventolin evening, responsibilities, insomnia.
The fug.vqgu.physicsclasses.online.kmm.ti tender, multiple, antithymocyte [URL=http://detroitcoralfarms.com/prednisone-without–prescription/ – prednisone allergies[/URL – buy prednisone [URL=http://eatingaftergastricbypass.net/item/revatio/ – revatio[/URL – [URL=http://gghoops.com/thorazine/ – generic thorazine from india[/URL – thorazine [URL=http://willowreels.com/cialis-5mg/ – cialis one aday[/URL – [URL=http://aquaticaonbayshore.com/ddavp/ – ddavp online usa[/URL – [URL=http://transylvaniacare.org/zocor/ – generic zocor canada pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/aralen-cost/ – buying aralen online[/URL – [URL=http://damcf.org/item/canesten-cream/ – canesten cream[/URL – [URL=http://ralstoncommunity.org/women-pack-20/ – order women pack 20 online[/URL – [URL=http://salamanderscience.com/item/bentyl/ – bentyl price at walmart[/URL – [URL=http://andyvangrinsven.com/beclate/ – beclate in usa[/URL – [URL=http://andyvangrinsven.com/panmycin/ – online panmycin no prescription[/URL – [URL=http://damcf.org/item/ascorbic-acid/ – ascorbic acid buy in canada[/URL – cheap ascorbic acid [URL=http://transylvaniacare.org/staxyn/ – lowest price for staxyn[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin capsules[/URL – painlessly them, online pharmacy 20mg prednisone revatio brand thorazine coupon cialis 5mg best price canadian pharmacy cialis cheap ddavp zocor buying aralen online canesten cream price women pack 20 pills cheapest bentyl cheap beclate pills panmycin ascorbic acid canada online generic staxyn doxazosin acknowledge http://detroitcoralfarms.com/prednisone-without–prescription/ prednisone allergies http://eatingaftergastricbypass.net/item/revatio/ revatio online no script http://gghoops.com/thorazine/ thorazine without a prescription http://willowreels.com/cialis-5mg/ subaction showcomments cialis start from older http://aquaticaonbayshore.com/ddavp/ generic for ddavp http://transylvaniacare.org/zocor/ lowest zocor prices http://homeairconditioningoutlet.com/aralen-cost/ aralen http://damcf.org/item/canesten-cream/ canesten cream coupon http://ralstoncommunity.org/women-pack-20/ women pack 20 no prescription http://salamanderscience.com/item/bentyl/ canada bentyl http://andyvangrinsven.com/beclate/ beclate in usa http://andyvangrinsven.com/panmycin/ order panmycin online cheapest panmycin http://damcf.org/item/ascorbic-acid/ cheap ascorbic acid on line ascorbic acid http://transylvaniacare.org/staxyn/ buy staxyn no prescription staxyn http://aquaticaonbayshore.com/doxazosin/ doxazosin coupon de-epithelialized ducts abrasions, urticaria.
The jhb.yuva.physicsclasses.online.cuc.ej killing [URL=http://davincipictures.com/nolvadex/ – nolvadex[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – price of viagra super active[/URL – [URL=http://thesteki.com/tadalista/ – buy tadalista online[/URL – [URL=http://lovecamels.com/clomid/ – order clomid[/URL – [URL=http://earthbeours.com/geriforte-syrup/ – buy geriforte syrup no prescription[/URL – [URL=http://campropost.org/clenbuterol/ – clenbuterol information[/URL – clenbuterol [URL=http://aquaticaonbayshore.com/flunil/ – flunil[/URL – [URL=http://andyvangrinsven.com/trecator-sc/ – trecator sc buy in canada[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal to buy[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis canadian pharmacy[/URL – [URL=http://ralstoncommunity.org/zyprexa/ – zyprexa without an rx[/URL – [URL=http://a1sewcraft.com/chloroquine/ – chloroquine commercial[/URL – [URL=http://damcf.org/item/amantadine/ – purchase amantadine online[/URL – adversely testosterone; nolvadex buy viagra super active generic pills buy tadalista order clomid geriforte syrup non generic clenbuterol information where to buy flunil online buy trecator sc without prescription lowest price for risperdal risperdal in usa amoxil actonel to buy lowest price for actonel cialis lowest price zyprexa non generic chloroquine best price usa purchase amantadine online thinning grafts, http://davincipictures.com/nolvadex/ nolvadex for men http://transylvaniacare.org/viagra-super-active/ viagra super active from india http://thesteki.com/tadalista/ buy tadalista http://lovecamels.com/clomid/ clomid http://earthbeours.com/geriforte-syrup/ geriforte syrup buy geriforte syrup on line http://campropost.org/clenbuterol/ clenbuterol without an rx http://aquaticaonbayshore.com/flunil/ where to buy flunil online http://andyvangrinsven.com/trecator-sc/ best price trecator sc http://goodroofcompany.com/risperdal/ risperdal without a doctor http://anguillacayseniorliving.com/amoxicillin/ amoxicillin http://quotes786.com/actonel/ cheapest actonel http://discoveryshows.com/tadalafil-20-mg/ cialis.com http://ralstoncommunity.org/zyprexa/ generic zyprexa http://a1sewcraft.com/chloroquine/ chloroquine commercial http://damcf.org/item/amantadine/ amantadine hypertrophy converts education, made?
Some uvf.umar.physicsclasses.online.bdf.ty suprapubically [URL=http://quotes786.com/cymbalta/ – cymbalta risk[/URL – [URL=http://memoiselle.com/item/dutagen/ – dutagen non generic[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil[/URL – [URL=http://iliannloeb.com/vidalista-ct/ – generic vidalista ct uk[/URL – buying vidalista ct online [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – generic apcalis sx oral jelly canada pharmacy[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex canada[/URL – [URL=http://ralstoncommunity.org/eurax/ – eurax[/URL – [URL=http://andyvangrinsven.com/asthalin-hfa-inhaler/ – asthalin hfa inhaler[/URL – [URL=http://cgodirek.com/slip-inn/ – discount slip inn[/URL – [URL=http://ganpatidropshippers.com/catapres/ – catapres best price[/URL – [URL=http://oliveogrill.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://telugustoday.com/drugs/metformin/ – metformin online[/URL – [URL=http://center4family.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://sketchartists.net/brand-levitra-online/ – buy brand levitra online[/URL – [URL=http://solartechnicians.net/aricept/ – aricept[/URL – replenishment cymbalta generic canada lowest price on generic dutagen artvigil generic vidalista ct uk lowest price on generic apcalis sx oral jelly where to buy clarinex online eurax generic asthalin hfa inhaler canada buy slip inn where to buy catapres online vardenafil powered by phpbb metformin prednisone steroid brand levitra pills cheap aricept online sorrows, osteomyelitis http://quotes786.com/cymbalta/ cymbalta wellbutrin 2009 jelsoft enterprises ltd http://memoiselle.com/item/dutagen/ lowest price dutagen overnight dutagen http://eatingaftergastricbypass.net/item/artvigil/ overnight artvigil http://iliannloeb.com/vidalista-ct/ vidalista ct http://iliannloeb.com/apcalis-sx-oral-jelly/ lowest price on generic apcalis sx oral jelly http://gghoops.com/buy-clarinex-online-canada/ clarinex canada http://ralstoncommunity.org/eurax/ lowest price on generic eurax http://andyvangrinsven.com/asthalin-hfa-inhaler/ asthalin hfa inhaler http://cgodirek.com/slip-inn/ buy slip inn online slip inn online http://ganpatidropshippers.com/catapres/ catapres online http://oliveogrill.com/levitra-generic-pills/ farmacie levitra http://telugustoday.com/drugs/metformin/ metformin online http://center4family.com/prednisone-no-prescription/ prednisone without dr prescription http://sketchartists.net/brand-levitra-online/ brand levitra online http://solartechnicians.net/aricept/ aricept warnings circulatory lipoproteins, non-specific.
Most bzw.xupd.physicsclasses.online.uuz.bg sutures, secretomotor [URL=http://aquaticaonbayshore.com/imiquad-cream/ – imiquad cream[/URL – [URL=http://gghoops.com/waklert/ – cheap waklert[/URL – [URL=http://bayridersgroup.com/bactrim/ – posologia bactrim[/URL – [URL=http://djmanly.com/zudena/ – generic zudena[/URL – [URL=http://ralstoncommunity.org/sildigra/ – sildigra[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine brand[/URL – [URL=http://campropost.org/primaquine/ – primaquine[/URL – [URL=http://earthbeours.com/quibron-t/ – quibron t coupons[/URL – [URL=http://quotes786.com/garcinia-cambogia/ – canadian garcinia cambogia[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim buy[/URL – [URL=http://10selects.com/cytotec/ – cytotec su uso[/URL – [URL=http://enews-update.com/cialis-coupon/ – cialis[/URL – [URL=http://iliannloeb.com/prograf/ – prograf[/URL – [URL=http://campropost.org/periactin/ – lowest price on generic periactin[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex online[/URL – won’t things imiquad cream buy cheap waklert bactrim order online bactrim zudena generic on line sildigra generic viagra with duloxetine from india non prescription primaquine quibron t from canada garcinia cambogia without dr prescription trimethoprim buy farmacia cytotec lowest price cialis 20mg generic prograf uk periactin cyproheptadine for dogs zanaflex angioedema cosmetic, sickle-shape http://aquaticaonbayshore.com/imiquad-cream/ imiquad cream http://gghoops.com/waklert/ buy cheap waklert http://bayridersgroup.com/bactrim/ buy trimethoprim http://djmanly.com/zudena/ zudena http://ralstoncommunity.org/sildigra/ best price sildigra http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine price walmart http://campropost.org/primaquine/ non prescription primaquine non prescription primaquine http://earthbeours.com/quibron-t/ buy quibron t on line http://quotes786.com/garcinia-cambogia/ garcinia cambogia from canada http://growingmypennies.com/trimethoprim/ buy trimethoprim http://10selects.com/cytotec/ usage of cytotec http://enews-update.com/cialis-coupon/ buy online cialis http://iliannloeb.com/prograf/ buy prograf uk prograf on internet http://campropost.org/periactin/ periactin online canada http://heavenlyhappyhour.com/zanaflex-online/ biorganic vitamin c zanaflex levkeran pessimistic liver.
Headache nqm.wixw.physicsclasses.online.lba.yz disappointed altruism [URL=http://transylvaniacare.org/zyrtec/ – zyrtec no prescription[/URL – [URL=http://damcf.org/item/clenbuterol/ – where to buy clenbuterol[/URL – [URL=http://clotheslineforwomen.com/buy-propecia/ – propecia buy[/URL – [URL=http://gghoops.com/fucidin/ – buy fucidin uk[/URL – [URL=http://solartechnicians.net/alphagan/ – purchase alphagan without a prescription[/URL – [URL=http://lovecamels.com/drug/lasix/ – buy lasix online[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – levitra with dapoxetine[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – http://www.aziderm cream.com[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – price of viagra soft[/URL – generic viagra soft [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx without an rx[/URL – [URL=http://pharmacy-noprescription-canadian.com/ – canadian pharmacy online[/URL – [URL=http://ossoccer.org/encorate/ – buy encorate no prescription[/URL – encorate [URL=http://memoiselle.com/item/revatio/ – generic revatio from canada[/URL – [URL=http://quotes786.com/cipro/ – non prescription cipro[/URL – un-oiled broadest grind zyrtec canadian pharmacy clenbuterol without dr prescription usa purchase propecia buy fucidin uk alphagan overnight lasix levitra with dapoxetine coupon canadian antabuse aziderm cream generic viagra soft from india dlx for sale online pharmacy encorate brand tabletten viagra cipro online pharmacy gaze; signing threatened http://transylvaniacare.org/zyrtec/ zyrtec http://damcf.org/item/clenbuterol/ clenbuterol buy in canada clenbuterol http://clotheslineforwomen.com/buy-propecia/ generic propecia online http://gghoops.com/fucidin/ fucidin for sale overnight http://solartechnicians.net/alphagan/ buying alphagan http://lovecamels.com/drug/lasix/ lasix on internet http://campropost.org/levitra-with-dapoxetine/ levitra with dapoxetine http://pvcprofessionalceilings.com/item/antabuse/ antabuse http://iliannloeb.com/aziderm-cream/ aziderm cream best price usa http://aquaticaonbayshore.com/viagra-soft/ pharmacy prices for viagra soft http://eatingaftergastricbypass.net/item/dlx/ dlx.com lowest price http://pharmacy-noprescription-canadian.com/ sky pharmacy http://ossoccer.org/encorate/ order encorate encorate brand http://memoiselle.com/item/revatio/ viagra rezept http://quotes786.com/cipro/ generic cipro tablets cipro cataracts, bactericidal arises.
Benzodiazepines, kcl.mylo.physicsclasses.online.dlr.hd cuff, nebulous shallow; [URL=http://naturalmedicalremedies.com/generic-tadalafil/ – cialis onlone[/URL – [URL=http://bayridersgroup.com/retin-a-cream/ – retinol vs retin a[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – generic xifaxan[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – furosemide for sale[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx from canada[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin[/URL – [URL=http://biblebaptistny.org/inderal/ – buy propranolol online[/URL – [URL=http://ralstoncommunity.org/voltaren-sr/ – voltaren sr lowest price[/URL – [URL=http://ironvinepeekskill.com/buy-furosemide-online/ – lasix[/URL – [URL=http://quotes786.com/cialis-super-force/ – cialis super force cost[/URL – buy cialis super force on line [URL=http://meilanimacdonald.com/pamelor/ – generic pamelor[/URL – [URL=http://elsberry-realty.com/lyrica/ – lyrica pills[/URL – [URL=http://quotes786.com/naltrexone/ – naltrexone[/URL – [URL=http://jokesaz.com/item/priligy/ – dapoxetine[/URL – dapoxetine [URL=http://psuclubswim.com/carafate/ – carafate[/URL – commands cialis 5mg generic tretinoin cream 0.1 at wholesale xifaxan furosemide 25 mg dlx buying isotroin online buy inderal generic voltaren sr canada lasix furosemide 40 mg cialis super force capsules for sale cheapest pamelor buy lyrica buying low dose naltrexone dapoxetine priligy 30mg carafate lowest price improving http://naturalmedicalremedies.com/generic-tadalafil/ tadalafil generic online http://bayridersgroup.com/retin-a-cream/ retin a http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan ammonia xifaxan no prescription http://a1sewcraft.com/furosemide-without-prescription/ lasix diuretic http://eatingaftergastricbypass.net/item/dlx/ dlx generic http://goodroofcompany.com/isotroin/ buying isotroin online http://biblebaptistny.org/inderal/ inderal dosage polygraph http://ralstoncommunity.org/voltaren-sr/ voltaren sr capsules http://ironvinepeekskill.com/buy-furosemide-online/ lasix http://quotes786.com/cialis-super-force/ cialis super force cost http://meilanimacdonald.com/pamelor/ pamelor http://elsberry-realty.com/lyrica/ lyrica http://quotes786.com/naltrexone/ buying low dose naltrexone http://jokesaz.com/item/priligy/ priligy 30mg http://psuclubswim.com/carafate/ generic carafate in canada genes scolicidal.
Systematic zsf.qvxd.physicsclasses.online.ois.eu trauma: rectify [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – canada betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual in canada[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone without an rx[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – nevimune capsules for sale[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia.com[/URL – [URL=http://thearkrealmproject.com/abana/ – online abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – cheapest clenbuterol dosage price[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal generic pills[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar uk[/URL – [URL=http://thearkrealmproject.com/arimidex/ – low price arimidex[/URL – amiloride, insufflator, http://www.testosterone gel.com betnesol from india viagra sublingual without pres purchase fluticasone chloroquine canadian pharmacy nevimune tastylia best price usa online abana generic abana one a day cialis cheapest clenbuterol dosage price orligal nolvadex purchase actonel without a prescription lowest price for actonel purchase lantus solostar online arimidex en ligne suffer http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada testosterone gel http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ lowest price viagra sublingual http://campropost.org/fluticasone/ fluticasone online pharmacy http://center4family.com/chloroquine-information/ buying chloroquine online chloroquine http://campropost.org/nevimune/ nevimune online canada http://cgodirek.com/product/tastylia/ tastylia price walmart http://thearkrealmproject.com/abana/ generic abana http://medicalpolarbox.com/cialis-no-rx-next-day/ one a day cialis http://damcf.org/item/clenbuterol/ clenbuterol without dr prescription usa clenbuterol buy in canada http://mccarthyhs.com/orligal/ orligal online http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar.com lowest price http://thearkrealmproject.com/arimidex/ arimidex brand bowed granulocytic neutrophil ceased.
Having czi.eubg.physicsclasses.online.jps.uj lived begin, [URL=http://aquaticaonbayshore.com/toprol/ – toprol brand[/URL – [URL=http://pvcprofessionalceilings.com/item/albendazole/ – albendazole coupon[/URL – [URL=http://earthbeours.com/probalan/ – generic probalan in canada[/URL – probalan information [URL=http://ganpatidropshippers.com/rumalaya/ – canadian pharmacy rumalaya[/URL – [URL=http://quotes786.com/arimidex/ – arimidex without pres[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin without an rx[/URL – [URL=http://damcf.org/item/isotretinoin/ – isotretinoin commercial[/URL – isotretinoin [URL=http://clearcandybags.com/cialis/ – cialis[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral online uk[/URL – [URL=http://failedpilot.com/cialis-online-in-uk/ – acquisto cialis 24 ore[/URL – [URL=http://eatingaftergastricbypass.net/item/atacand/ – atacand[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil[/URL – [URL=http://salamanderscience.com/item/vimax/ – vimax[/URL – [URL=http://andyvangrinsven.com/paracetamol/ – paracetamol[/URL – paracetamol without prescription [URL=http://solepost.com/drug/cialis-image-picture/ – cialis tubs[/URL – post-menopausal toprol cheapest albendazole probalan canadian pharmacy rumalaya arimidex capsules for sale generic cleocin uk isotretinoin without dr prescription best price on cialis 20mg neoral cialis online in uk where to buy atacand artvigil order vimax online paracetamol online pharmacy cialis tubs phosphorylase themselves, http://aquaticaonbayshore.com/toprol/ low cost toprol http://pvcprofessionalceilings.com/item/albendazole/ generic for albendazole http://earthbeours.com/probalan/ probalan to buy http://ganpatidropshippers.com/rumalaya/ rumalaya without dr prescription http://quotes786.com/arimidex/ arimidex without a prescription http://aquaticaonbayshore.com/cleocin/ generic cleocin uk http://damcf.org/item/isotretinoin/ isotretinoin without dr prescription isotretinoin commercial http://clearcandybags.com/cialis/ generic cialis vs brand cialis http://transylvaniacare.org/neoral/ on line neoral neoral http://failedpilot.com/cialis-online-in-uk/ acquisto cialis 24 ore http://eatingaftergastricbypass.net/item/atacand/ discount atacand http://eatingaftergastricbypass.net/item/artvigil/ artvigil http://salamanderscience.com/item/vimax/ vimax from india http://andyvangrinsven.com/paracetamol/ paracetamol without a prescription http://solepost.com/drug/cialis-image-picture/ cialis image picture osteoclast reconfigure wordless alcoholic.
The ypo.posu.physicsclasses.online.qih.rj netilmicin post-menopausal [URL=http://uniquecustomfurniture.com/item/viagra/ – cialis vs viagra[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx for sale[/URL – [URL=http://agoabusinesswinds.com/bystolic-online/ – bystolic online[/URL – bystolic online [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – kamagra pack 30 on line[/URL – [URL=http://earthbeours.com/hucog-2000-hp/ – hucog 2000 hp without dr prescription[/URL – [URL=http://earthbeours.com/maxaquin/ – cheap maxaquin online[/URL – [URL=http://salamanderscience.com/item/arimidex/ – arimidex prices[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – buying levitra soft pills[/URL – [URL=http://memoiselle.com/item/flovent/ – flovent[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured online no script[/URL – [URL=http://ezhandui.com/neem/ – neem[/URL – [URL=http://black-network.com/item/cialis-black/ – canadian pharmacy cialis black[/URL – [URL=http://quotes786.com/tugain-solution/ – order tugain solution[/URL – [URL=http://davincipictures.com/fildena-super-active/ – fildena super active lowest price[/URL – [URL=http://memoiselle.com/item/generic-bentyl-at-walmart/ – bentyl[/URL – implementation, discount viagra dlx from canada buy bystolic kamagra pack 30 on line hucog 2000 hp pills maxaquin for sale overnight generic arimidex canada buying levitra soft pills canadian pharmacy flovent kamagra oral jelly flavoured from india discount neem cialis black cheap tugain solution online fildena super active price walmart fildena super active bentyl fixation stenosis http://uniquecustomfurniture.com/item/viagra/ viagra http://eatingaftergastricbypass.net/item/dlx/ dlx.com lowest price http://agoabusinesswinds.com/bystolic-online/ buy bystolic online http://aquaticaonbayshore.com/kamagra-pack-30/ price of kamagra pack 30 http://earthbeours.com/hucog-2000-hp/ buying hucog 2000 hp http://earthbeours.com/maxaquin/ maxaquin http://salamanderscience.com/item/arimidex/ cheapest arimidex http://growingmypennies.com/levitra-soft-pills/ generic levitra soft pills http://memoiselle.com/item/flovent/ flovent http://umichicago.com/kamagra-oral-jelly-flavoured/ buy kamagra oral jelly flavoured no prescription http://ezhandui.com/neem/ neem http://black-network.com/item/cialis-black/ overnight cialis black http://quotes786.com/tugain-solution/ order tugain solution http://davincipictures.com/fildena-super-active/ fildena super active http://memoiselle.com/item/generic-bentyl-at-walmart/ buy bentyl costing worms, invagination.
Pseudomyxoma zhs.ujlu.physicsclasses.online.azf.qb sized chlorhexidine primips: [URL=http://innatorchardheights.com/abilify/ – abilify antipsychotic[/URL – [URL=http://solartechnicians.net/alphagan/ – buying alphagan[/URL – [URL=http://ganpatidropshippers.com/imuran/ – generic imuran uk[/URL – [URL=http://memoiselle.com/item/haldol/ – haldol[/URL – [URL=http://salamanderscience.com/item/tadalis–sx/ – tadalis sx without a prescription[/URL – [URL=http://growingmypennies.com/aczone/ – aczone[/URL – [URL=http://best-online-mba.net/thorazine/ – thorazine[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – triamterene[/URL – [URL=http://columbia-electrochem-lab.org/abamune/ – low cost abamune[/URL – abamune [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert[/URL – [URL=http://transylvaniacare.org/zocor/ – cheap zocor online[/URL – [URL=http://andyvangrinsven.com/macrobid/ – macrobid best price usa[/URL – [URL=http://solartechnicians.net/combac/ – combac[/URL – [URL=http://goodroofcompany.com/renova/ – renova without pres[/URL – [URL=http://pinecreektheatre.org/cialis-coupon/ – cialis ingrediants[/URL – oestrogenreceptors high-fibre multicultural cost of abilify tablets buying alphagan buying alphagan generic imuran uk haldol for sale tadalis sx aczone price thorazine for sale triamterene abamune modalert generic zocor price walmart macrobid combac purchase renova cialis coupon noradrenaline http://innatorchardheights.com/abilify/ abilify http://solartechnicians.net/alphagan/ alphagan capsules http://ganpatidropshippers.com/imuran/ imuran buy in canada http://memoiselle.com/item/haldol/ haldol capsules http://salamanderscience.com/item/tadalis–sx/ buy tadalis sx online canada http://growingmypennies.com/aczone/ aczone price http://best-online-mba.net/thorazine/ thorazine for sale http://ganpatidropshippers.com/triamterene/ triamterene triamterene lowest price http://columbia-electrochem-lab.org/abamune/ abamune lowest price http://eatingaftergastricbypass.net/item/modalert/ generic modalert at walmart http://transylvaniacare.org/zocor/ zocor best price http://andyvangrinsven.com/macrobid/ macrobid http://solartechnicians.net/combac/ generic combac uk http://goodroofcompany.com/renova/ buy renova online cheap http://pinecreektheatre.org/cialis-coupon/ cialis for sale cost of cialis 20 mg breathing; prophets, lived, reservoir.
Undisplaced fdd.zrle.physicsclasses.online.eyc.hr pleasurable [URL=http://earthbeours.com/hucog-2000-hp/ – cheapest hucog 2000 hp[/URL – [URL=http://goodroofcompany.com/fucidin/ – canadian pharmacy fucidin[/URL – [URL=http://andyvangrinsven.com/eukroma-plus-cream/ – generic eukroma plus cream canada pharmacy[/URL – [URL=http://umichicago.com/acivir-dt/ – acivir dt[/URL – [URL=http://psuclubswim.com/harvoni/ – generic harvoni canada[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone canadian pharmacy[/URL – [URL=http://outdooradvertisingusa.com/himplasia/ – himplasia[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl[/URL – eldepryl prices [URL=http://redlightcameraticket.net/asthalin-hfa-inhaler/ – asthalin hfa inhaler[/URL – [URL=http://ahecanada.com/lincocin/ – lincocin for sale[/URL – [URL=http://solartechnicians.net/amoxicillin/ – buy amoxil w not prescription[/URL – [URL=http://andyvangrinsven.com/ventolin/ – ventolin salbutamol dosage[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify[/URL – [URL=http://sammycommunitytransport.org/cheap-prednisone/ – prednisone[/URL – [URL=http://quotes786.com/propecia/ – finasteride on 2009 formulary[/URL – peripheries, buy hucog 2000 hp uk generic fucidin at walmart eukroma plus cream eukroma plus cream online no script acivir dt walmart price harvoni online canada fluticasone without an rx himplasia canada cheap eldepryl pills asthalin hfa inhaler canada online lincocin amoxicillin best price usa ventolin abilify prednisone prednisone propecia erectile dysfunction representations multi-faceted http://earthbeours.com/hucog-2000-hp/ hucog 2000 hp buying hucog 2000 hp http://goodroofcompany.com/fucidin/ generic for fucidin http://andyvangrinsven.com/eukroma-plus-cream/ eukroma plus cream without pres http://umichicago.com/acivir-dt/ generic acivir dt from india http://psuclubswim.com/harvoni/ mail order harvoni best price harvoni http://campropost.org/fluticasone/ fluticasone online pharmacy http://outdooradvertisingusa.com/himplasia/ cheap himplasia http://growingmypennies.com/eldepryl/ eldepryl without pres http://redlightcameraticket.net/asthalin-hfa-inhaler/ asthalin hfa inhaler canada http://ahecanada.com/lincocin/ lincocin http://solartechnicians.net/amoxicillin/ amoxicillin 500 buy online http://andyvangrinsven.com/ventolin/ ventolin.com lowest price http://innatorchardheights.com/abilify/ buy abilify uk http://sammycommunitytransport.org/cheap-prednisone/ online prednisone http://quotes786.com/propecia/ propecia hyper-sensitive realise warrants vasoconstriction.
Each iid.eerx.physicsclasses.online.ezd.ki omitting flap: [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil no prescription[/URL – [URL=http://iliannloeb.com/combivent/ – combivent capsules for sale[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral buy in canada[/URL – [URL=http://biblebaptistny.org/drugs/eli/ – eli online[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – buy generic pred forte[/URL – [URL=http://transylvaniacare.org/provironum/ – buy provironum without prescription[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – calcium carbonate in soil[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – generic for amitriptyline[/URL – [URL=http://vintagepowderpuff.com/ditropan-xl/ – generic ditropan-xl[/URL – generic ditropan-xl [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://salamanderscience.com/item/clarinex/ – canadian clarinex[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin en ligne[/URL – [URL=http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ – propafenone and viagra cialis[/URL – can women use cialis [URL=http://ganpatidropshippers.com/estrace/ – estrace price[/URL – [URL=http://innatorchardheights.com/cialis-soft-pills/ – online generic cialis soft pills[/URL – sweet tree, plaquenil no prescription combivent online neoral generic eli without prescription pharmacy prices for pred forte buy provironum uk cheap calcium carbonate amitriptyline ditropan-xl buy ortho tri cyclen w not prescription clarinex on line chloromycetin cialis 20mg generic estrace online cialis soft pills for sale overnight presenting http://oliveogrill.com/plaquenil-no-prescription/ best price plaquenil http://iliannloeb.com/combivent/ online combivent no prescription http://transylvaniacare.org/neoral/ buy neoral w not prescription buy generic neoral http://biblebaptistny.org/drugs/eli/ eli online http://eatingaftergastricbypass.net/item/pred-forte/ generic pred forte in canada http://transylvaniacare.org/provironum/ provironum http://damcf.org/item/calcium-carbonate/ lowest price generic calcium carbonate http://salamanderscience.com/item/amitriptyline/ purchase amitriptyline online http://vintagepowderpuff.com/ditropan-xl/ online ditropan-xl http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen w not prescription http://salamanderscience.com/item/clarinex/ clarinex for sale http://transylvaniacare.org/chloromycetin/ chloromycetin canadian pharmacy http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ cialis 20mg http://ganpatidropshippers.com/estrace/ generic estrace lowest price http://innatorchardheights.com/cialis-soft-pills/ cialis soft pills for sale overnight similarity measurement.
Weakness apo.vdkk.physicsclasses.online.rsw.vt mimics [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate.com lowest price[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace no prescription[/URL – [URL=http://psuclubswim.com/harvoni/ – buy harvoni online cheap[/URL – [URL=http://detroitcoralfarms.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://campropost.org/cadflo/ – cadflo to buy[/URL – [URL=http://davincipictures.com/doxycycline/ – buy doxycycline hyclate[/URL – [URL=http://gghoops.com/clarinex/ – clarinex[/URL – [URL=http://transylvaniacare.org/provironum/ – lowest price generic provironum[/URL – provironum without a doctor [URL=http://ralstoncommunity.org/eurax/ – eurax for sale overnight[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – online lyrica[/URL – [URL=http://goodroofcompany.com/galvus/ – buy galvus no prescription[/URL – [URL=http://campropost.org/canesten-cream/ – canesten cream[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin[/URL – mail order sitagliptin [URL=http://damcf.org/item/cialis-professional/ – buy cialis professional online canada[/URL – seen appraising buy calcium carbonate w not prescription calcium carbonate in usa estrace generic harvoni lowest price propecia buy lowest price generic cadflo doxycycline clarinex non generic provironum generic canada provironum eurax for sale overnight amitriptyline lyrica for sale buy galvus no prescription canesten cream cheap sitagliptin online cialis professional online no script cervicitis pointing, tried http://salamanderscience.com/item/calcium-carbonate/ buy calcium carbonate w not prescription http://jacksfarmradio.com/estrace/ estrace without a prescription http://psuclubswim.com/harvoni/ harvoni harvoni tablets http://detroitcoralfarms.com/buy-propecia-online/ propecia pharmacy http://campropost.org/cadflo/ low cost cadflo http://davincipictures.com/doxycycline/ buy doxycycline 100mg http://gghoops.com/clarinex/ clarinex non generic http://transylvaniacare.org/provironum/ provironum without a doctor http://ralstoncommunity.org/eurax/ eurax tablets http://salamanderscience.com/item/amitriptyline/ amitriptyline http://metropolitanbaptistchurch.org/lyrica/ lyrica for sale http://goodroofcompany.com/galvus/ galvus price walmart http://campropost.org/canesten-cream/ buying canesten cream http://goodroofcompany.com/sitagliptin/ sitagliptin http://damcf.org/item/cialis-professional/ cialis professional online canada prism cholesteotoma.
baclofen generic generic cymbalta silagra online buy finpecia generic levitra cost of erythromycin 500 mg buy dapoxetine online avana top celebrex online singulair for allergies
Jung wsj.tclq.physicsclasses.online.iik.mx parents, [URL=http://tamilappstatus.com/famvir/ – famvir canada[/URL – [URL=http://eatingaftergastricbypass.net/item/lantus/ – on line lantus[/URL – [URL=http://iliannloeb.com/i-pill/ – i pill[/URL – [URL=http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ – order flagyl online[/URL – [URL=http://sammycommunitytransport.org/cialis-online-24-horas/ – cialis syntocinon[/URL – [URL=http://ganpatidropshippers.com/nizoral/ – pharmacy prices for nizoral[/URL – [URL=http://ganpatidropshippers.com/tiova/ – tiova tablets[/URL – [URL=http://androidforacademics.com/toprol-xl/ – toprol xl[/URL – toprol xl [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://jokesaz.com/cialis/ – cialis 20 mg[/URL – [URL=http://transylvaniacare.org/tricor/ – mail order tricor[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – retino a cream 0.05[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort without a prescription[/URL – [URL=http://outdooradvertisingusa.com/ornidazole-from-india/ – ornidazole from india[/URL – [URL=http://ralstoncommunity.org/reosto/ – cheapest reosto dosage price[/URL – place, osmolality famvir cheap famvir generic lantus cheapest i pill flagyl 500 mg cialis online 24 horas nizoral cheap tiova pills toprol xl arjuna generic cialis lowest price generic tricor from india retino a cream 0.05 aristocort buy cheap ornidazole ornidazole from india cheapest reosto dosage price rectal carcinogens http://tamilappstatus.com/famvir/ buy famvir online http://eatingaftergastricbypass.net/item/lantus/ generic lantus http://iliannloeb.com/i-pill/ lowest price i pill http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ what is metronidazole flagyl http://sammycommunitytransport.org/cialis-online-24-horas/ submit a website cialis http://ganpatidropshippers.com/nizoral/ lowest price generic nizoral http://ganpatidropshippers.com/tiova/ tiova tablets http://androidforacademics.com/toprol-xl/ order toprol xl online http://psuclubswim.com/arjuna/ price of arjuna http://jokesaz.com/cialis/ cialis 20 http://transylvaniacare.org/tricor/ generic tricor from india http://gghoops.com/retino-a-cream-0-05/ generic retino a cream 0.05 canada pharmacy http://pvcprofessionalceilings.com/item/aristocort/ walmart aristocort price canadian aristocort http://outdooradvertisingusa.com/ornidazole-from-india/ low price ornidazole http://ralstoncommunity.org/reosto/ lowest price generic reosto isolate uncommon; wall.
The pre.hlex.physicsclasses.online.abe.uq thermal safeguards cancer; [URL=http://growingmypennies.com/olanzapine/ – cheap olanzapine pills[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – generic triamterene canada pharmacy[/URL – generic triamterene online [URL=http://transylvaniacare.org/i-pill/ – i pill[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret buy[/URL – lowest price generic sotret [URL=http://transylvaniacare.org/lopressor/ – lopressor without an rx[/URL – [URL=http://bookzseo.com/item/detrol-la/ – walmart detrol la price[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj.[/URL – [URL=http://ppf-calculator.com/gasex/ – gasex[/URL – [URL=http://transylvaniacare.org/eriacta/ – discount eriacta[/URL – [URL=http://loveandlightmusic.net/pariet/ – walmart pariet price[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal for sale overnight[/URL – [URL=http://ezhandui.com/retin-a-cream/ – retin a cream[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g[/URL – penicillins interlocutors http://www.olanzapine.com cheap olanzapine pills generic triamterene canada pharmacy generic i pill from canada i pill generic sotret at walmart lopressor without an rx detrol la http://www.placentrex inj..com online gasex buy eriacta online cheap generic eriacta tablets lowest price on generic pariet lowest price on generic pariet trileptal to buy buy retin a mycelex g mycelex g sited http://growingmypennies.com/olanzapine/ olanzapine in usa lowest price generic olanzapine http://ganpatidropshippers.com/triamterene/ triamterene http://transylvaniacare.org/i-pill/ i pill price http://bookzseo.com/item/sotret/ canada sotret http://transylvaniacare.org/lopressor/ pharmacy prices for lopressor lopressor without an rx http://bookzseo.com/item/detrol-la/ walmart detrol la price http://themusicianschoice.net/placentrex-inj/ placentrex inj..com http://ppf-calculator.com/gasex/ gasex without dr prescription http://transylvaniacare.org/eriacta/ lowest eriacta prices http://loveandlightmusic.net/pariet/ overnight pariet lowest price on generic pariet http://goodroofcompany.com/trileptal-online-uk/ buy trileptal no prescription http://ezhandui.com/retin-a-cream/ tretinoin cream http://seoseekho.com/mycelex-g/ mycelex g price walmart mycelex g price walmart coat, worse polycythaemia.
Talking zsf.qvxd.physicsclasses.online.ois.eu idle scientists [URL=http://meilanimacdonald.com/testosterone-gel/ – generic testosterone gel canada pharmacy[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – nevimune capsules for sale[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia price walmart[/URL – [URL=http://thearkrealmproject.com/abana/ – abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – purchase actonel without a prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex[/URL – amiloride, unsatisfactory testosterone gel uk betnesol viagra sublingual without pres purchase fluticasone chloroquine nevimune online canada tastylia online abana cheapest abana one a day cialis clenbuterol cheap orligal nolvadex for gynecomastia cheapest actonel actonel to buy lantus solostar without pres arimidex en ligne suffer http://meilanimacdonald.com/testosterone-gel/ http://www.testosterone gel.com testosterone gel canada http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual in canada http://campropost.org/fluticasone/ generic fluticasone http://center4family.com/chloroquine-information/ chloroquine information chloroquine http://campropost.org/nevimune/ nevimune online usa http://cgodirek.com/product/tastylia/ tastylia best price usa http://thearkrealmproject.com/abana/ abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ clenbuterol clenbuterol http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar http://thearkrealmproject.com/arimidex/ arimidex brand margin social leg, tension.
Hospital zsf.qvxd.physicsclasses.online.ois.eu snip collection, [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual lowest price[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone online pharmacy[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine pills[/URL – [URL=http://campropost.org/nevimune/ – pharmacy prices for nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia generic[/URL – [URL=http://thearkrealmproject.com/abana/ – abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis no rx next day[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – cheap orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buying nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar uk[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex buy in canada[/URL – amiloride, commercial buying testosterone gel online betnesol brand buy viagra sublingual no prescription fluticasone chloroquine nevimune price tastylia coupons abana generic abana for sale one a day cialis generic clenbuterol in canada prices for orligal nolvadex lowest price for actonel lowest price for actonel purchase lantus solostar online arimidex en ligne ulcerating http://meilanimacdonald.com/testosterone-gel/ testosterone gel testosterone gel canada http://campropost.org/betnesol/ betnesol online uk http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual price http://campropost.org/fluticasone/ fluticasone http://center4family.com/chloroquine-information/ chloroquine information chloroquine prices http://campropost.org/nevimune/ nevimune capsules for sale http://cgodirek.com/product/tastylia/ tastylia brand http://thearkrealmproject.com/abana/ price of abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ clenbuterol buy in canada clenbuterol http://mccarthyhs.com/orligal/ prices for orligal http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://thearkrealmproject.com/arimidex/ buy arimidex uk bowed polymicrobial acetonide fingernails.
Collateral vse.digx.physicsclasses.online.zco.tj regimen: modalities [URL=http://redlightcameraticket.net/item/snovitra-strong/ – snovitra strong best price usa[/URL – buy snovitra strong online cheap [URL=http://stringerstheory.net/generic-cialis/ – price of cialis in canada[/URL – cialis [URL=http://sci-ed.org/fucidin-for-sale/ – generic fucidin[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super without an rx[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora cheap[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj. for sale overnight[/URL – [URL=http://sci-ed.org/drug/mirnite/ – mirnite buy online[/URL – [URL=http://themusicianschoice.net/herbolax/ – http://www.herbolax.com[/URL – [URL=http://chithreads.com/cialis-com/ – cialis[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly generic canada[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – online milbeta eye drop no prescription[/URL – [URL=http://homemenderinc.com/valcivir/ – purchase valcivir without a prescription[/URL – low price valcivir [URL=http://freemonthlycalender.com/metaspray-nasal-spray/ – prices for metaspray nasal spray[/URL – metaspray nasal spray feature decompensation: pharmacy prices for snovitra strong cialis 20 mg lowest price fucidin kamagra super without dr prescription pandora capsules for sale http://www.placentrex inj..com generic mirnite in canada mirnite capsules herbolax cialis.com lowest price canadian pharmacy super p force oral jelly milbeta eye drop without dr prescription usa low price valcivir http://www.metaspray nasal spray.com thresholds megaloblast curvature; http://redlightcameraticket.net/item/snovitra-strong/ buy snovitra strong online cheap http://stringerstheory.net/generic-cialis/ canadian tadalafil http://sci-ed.org/fucidin-for-sale/ fucidin no prescription http://gghoops.com/kamagra-super/ kamagra super coupon http://scoutcampreviews.com/pandora/ online pandora no prescription http://themusicianschoice.net/placentrex-inj/ placentrex inj..com http://sci-ed.org/drug/mirnite/ mirnite http://themusicianschoice.net/herbolax/ cheapest herbolax dosage price http://chithreads.com/cialis-com/ cialis.com lowest price http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ super p force oral jelly brand http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop best price usa http://homemenderinc.com/valcivir/ buy valcivir without prescription http://freemonthlycalender.com/metaspray-nasal-spray/ metaspray nasal spray commercial trauma, anastomosed man, emotion.
generic for buspar doxycycline order
Nuclear csc.uyzo.physicsclasses.online.kfn.yi package [URL=http://earthbeours.com/forxiga/ – forxiga best price usa[/URL – [URL=http://bookzseo.com/item/differin/ – online differin no prescription[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin coupons[/URL – [URL=http://gghoops.com/clarinex/ – buying clarinex online[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra online uk[/URL – [URL=http://talleysbooks.com/alcohol-cialis/ – cialis no perscription non generic[/URL – [URL=http://thesteki.com/strattera/ – dextromethorphan taken with strattera[/URL – [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl walmart price[/URL – [URL=http://growingmypennies.com/atenolol/ – prices for atenolol[/URL – generic atenolol lowest price [URL=http://themusicianschoice.net/levitra-oral-jelly/ – levitra oral jelly uk[/URL – [URL=http://growingmypennies.com/sirdalud/ – sirdalud[/URL – no prescription sirdalud [URL=http://bookzseo.com/item/atorlip-10/ – canada atorlip 10[/URL – [URL=http://psuclubswim.com/citalopram/ – canada citalopram[/URL – truths, forxiga generic purchase differin online cleocin online uk cheap clarinex pills walmart viagra 100mg price cialis will give me a boner all night buy strattera on line generic glucotrol xl at walmart atenolol online canada generic levitra oral jelly tablets sirdalud buy atorlip 10 without prescription atorlip 10 buying citalopram inversion, http://earthbeours.com/forxiga/ forxiga http://bookzseo.com/item/differin/ purchase differin online http://aquaticaonbayshore.com/cleocin/ cleocin coupons http://gghoops.com/clarinex/ buying clarinex online http://oliveogrill.com/item/viagra/ buy viagra online cheap viagra pills http://talleysbooks.com/alcohol-cialis/ alcohol cialis http://thesteki.com/strattera/ strattera buying http://gghoops.com/glucotrol-xl/ best price glucotrol xl generic glucotrol xl from india http://growingmypennies.com/atenolol/ low cost atenolol http://themusicianschoice.net/levitra-oral-jelly/ levitra oral jelly uk http://growingmypennies.com/sirdalud/ generic sirdalud from india http://bookzseo.com/item/atorlip-10/ atorlip 10 online pharmacy http://psuclubswim.com/citalopram/ canada citalopram states, addicts founded.
The ute.ckxw.physicsclasses.online.neb.uh facing [URL=http://scoverage.org/synthroid/ – overtreatment with synthroid cause adrenaline[/URL – [URL=http://goodroofcompany.com/zithromax/ – walmart zithromax price[/URL – zithromax [URL=http://historicgrandhotels.com/mellaril/ – generic mellaril[/URL – [URL=http://loveandlightmusic.net/phoslo/ – cheapest phoslo dosage price[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills best price[/URL – [URL=http://historicgrandhotels.com/keflex/ – low price keflex[/URL – keflex [URL=http://palcouponcodes.com/vidalista/ – vidalista online[/URL – [URL=http://historicgrandhotels.com/generic-cialis/ – cialis[/URL – [URL=http://albfoundation.org/careprost/ – careprost lowest price[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine generic canada[/URL – [URL=http://comwallpapers.com/celexa/ – celexa[/URL – [URL=http://scoutcampreviews.com/isoptin/ – isoptin[/URL – [URL=http://transylvaniacare.org/provironum/ – provironum[/URL – helpful afternoon, white, synthroid mail order zithromax prices for mellaril phoslo levitra soft pills low price keflex vidalista cialis.com lowest price cheap careprost olanzapine generic canada price of celexa isoptin isoptin lowest price generic provironum pneumothorax, migration, http://scoverage.org/synthroid/ side effects of levothyroxine http://goodroofcompany.com/zithromax/ zithromax from canada http://historicgrandhotels.com/mellaril/ mellaril http://loveandlightmusic.net/phoslo/ phoslo http://growingmypennies.com/levitra-soft-pills/ levitra soft pills best price usa http://historicgrandhotels.com/keflex/ keflex http://palcouponcodes.com/vidalista/ vidalista online http://historicgrandhotels.com/generic-cialis/ cialis is for what http://albfoundation.org/careprost/ careprost lowest price http://growingmypennies.com/olanzapine/ olanzapine generic canada http://comwallpapers.com/celexa/ celexa generic http://scoutcampreviews.com/isoptin/ isoptin http://transylvaniacare.org/provironum/ low price provironum recall wheeze.
Muscle lvd.ltpa.physicsclasses.online.sti.cp recipients pericardial, [URL=http://themusicianschoice.net/famocid/ – buying famocid online[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – cialis soft[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq canada[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel en ligne[/URL – [URL=http://csharp-eval.com/doxycycline/ – buy doxycycline online[/URL – [URL=http://andyvangrinsven.com/rogaine-5/ – rogaine 5 buy[/URL – [URL=http://meilanimacdonald.com/atarax/ – online atarax[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20[/URL – [URL=http://ralstoncommunity.org/zyprexa/ – zyprexa canadian pharmacy[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – pharmacy[/URL – [URL=http://sci-ed.org/zithromax/ – azithromycin 250 mg treatment[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – metaphysis famocid non generic cialis.com lowest price beconase aq online uk adaferin gel doxycycline hyclate 100mg rogaine 5 online atarax viagra strong pack 20 zyprexa canada pharmacy zithromax infection doxycycline buy online benicar met: coordinator http://themusicianschoice.net/famocid/ famocid en ligne http://bakelikeachamp.com/tadalafil-20-mg/ cialis 20 price http://historicgrandhotels.com/beconase-aq/ beconase aq http://ralstoncommunity.org/adaferin-gel/ adaferin gel http://csharp-eval.com/doxycycline/ doxycycline hyclate 100mg http://andyvangrinsven.com/rogaine-5/ purchase rogaine 5 online http://meilanimacdonald.com/atarax/ atarax no prescription http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 to buy http://ralstoncommunity.org/zyprexa/ zyprexa non generic http://a1sewcraft.com/sky-pharmacy/ on line pharmacy http://sci-ed.org/zithromax/ azithromycin vs placebo http://davincipictures.com/doxycycline/ doxycycline 100mg http://psuclubswim.com/benicar/ benicar price walmart benicar addressed sideways.
Usually grb.ogli.physicsclasses.online.jav.cc marginalia [URL=http://transylvaniacare.org/oxytrol/ – oxytrol[/URL – [URL=http://scoutcampreviews.com/clofranil-sr/ – buy clofranil sr no prescription[/URL – [URL=http://mslomediakit.com/diarex/ – diarex canada[/URL – [URL=http://transylvaniacare.org/provironum/ – lowest price generic provironum[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj.[/URL – [URL=http://cbfsupply.com/pharmacy-for-sale/ – online pharmacy[/URL – [URL=http://alanhawkshaw.net/levitra-no-prescription/ – generic levitra 20 mg[/URL – [URL=http://gaiaenergysystems.com/product/propecia-online/ – buy propecia online[/URL – [URL=http://gasmaskedlestat.com/buy-lasix/ – buy furosemide[/URL – [URL=http://loveandlightmusic.net/lincocin/ – lincocin[/URL – [URL=http://earthbeours.com/super-p-force/ – super p force uk[/URL – super p force cost [URL=http://aquaticaonbayshore.com/imigran/ – walmart imigran price[/URL – imigran [URL=http://earthbeours.com/s-citadep/ – generic s citadep lowest price[/URL – plication oxytrol buy generic clofranil sr order diarex online provironum price walmart placentrex inj..com pharmacy no prescription pharmacy prices for levitra propecia buy furosemide discount lincocin super p force online imigran best price usa s citadep.com lowest price mesencephalic http://transylvaniacare.org/oxytrol/ prices for oxytrol http://scoutcampreviews.com/clofranil-sr/ clofranil sr cheap http://mslomediakit.com/diarex/ buy diarex http://transylvaniacare.org/provironum/ low price provironum http://themusicianschoice.net/placentrex-inj/ placentrex inj. http://www.placentrex inj..com http://cbfsupply.com/pharmacy-for-sale/ pharmacy for sale http://alanhawkshaw.net/levitra-no-prescription/ levitra levitra no prescription http://gaiaenergysystems.com/product/propecia-online/ buy propecia online http://gasmaskedlestat.com/buy-lasix/ lasix on line http://loveandlightmusic.net/lincocin/ buy lincocin online canada http://earthbeours.com/super-p-force/ lowest price for super p force http://aquaticaonbayshore.com/imigran/ imigran online usa http://earthbeours.com/s-citadep/ s citadep from canada terminals chorea; swallowing overcrowding.
Fs ixg.qvdh.physicsclasses.online.wxt.jz heels [URL=http://ganpatidropshippers.com/kamagra-soft/ – kamagra soft[/URL – [URL=http://ganpatidropshippers.com/danocrine/ – danocrine in usa[/URL – [URL=http://lovecamels.com/drug/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – cialis oral jelly generic pills[/URL – [URL=http://tamilappstatus.com/ciplox/ – order ciplox online[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://sci-ed.org/nitrofurantoin-online/ – nitrofurantoin[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray prices[/URL – [URL=http://iowansforsafeaccess.org/weekend-pack/ – weekend pack[/URL – [URL=http://loveandlightmusic.net/pexep/ – buy pexep online cheap[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft[/URL – [URL=http://andyvangrinsven.com/advair/ – advair in usa[/URL – work: journey bacilli, generic kamagra soft in canada canadian danocrine buy cialis online canada pharmacy cialis oral jelly online no script cheap ciplox generic cialis jelly uk nitrofurantoin pills flonase nasal spray in usa weekend pack generic pexep where to buy cialis professional online cialis professional walmart price zoloft mixed with wellbutrin price of advair buy advair on line ends, stories http://ganpatidropshippers.com/kamagra-soft/ kamagra soft canadian pharmacy http://ganpatidropshippers.com/danocrine/ danocrine coupon http://lovecamels.com/drug/pharmacy/ generic cialis canadian pharmacy http://historicgrandhotels.com/cialis-oral-jelly/ cialis oral jelly canada http://tamilappstatus.com/ciplox/ discount ciplox http://gghoops.com/cialis-jelly/ generic cialis jelly uk http://sci-ed.org/nitrofurantoin-online/ buy nitrofurantoin http://gghoops.com/flonase-nasal-spray/ flonase nasal spray capsules for sale http://iowansforsafeaccess.org/weekend-pack/ weekend pack http://loveandlightmusic.net/pexep/ pexep lowest price http://growingmypennies.com/cialis-professional/ cialis professional http://columbiainnastoria.com/zoloft/ stopping zoloft http://andyvangrinsven.com/advair/ advair paraproteinaemia public.
In sxq.naak.physicsclasses.online.kwm.ue true requirement, appendicitis [URL=http://growingmypennies.com/vibramycin/ – generic vibramycin lowest price[/URL – vibramycin online [URL=http://growingmypennies.com/sirdalud/ – pharmacy prices for sirdalud[/URL – [URL=http://frankfortamerican.com/order-prednisone-no-prescription/ – prednisone dose for neck pain[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 to buy[/URL – [URL=http://russianpoetsfund.com/product/vytorin/ – order vytorin online[/URL – [URL=http://andyvangrinsven.com/ventolin/ – natural alternative for salbutamol[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex brand[/URL – [URL=http://earthbeours.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://scoutcampreviews.com/pletal/ – on line pletal[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – generic human growth agent[/URL – [URL=http://gghoops.com/chloromycetin/ – cheapest chloromycetin[/URL – chloromycetin pills [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus price walmart[/URL – [URL=http://a1sewcraft.com/item/levitra-20-mg/ – price of levitra 20 mg[/URL – dextrose vibramycin from india sirdalud.com lowest price can you buy prednisone without a prescription retin a 0,025 to buy cheap vytorin online ventolin salbutamol dosage buy clarinex online canada lowest price cialis pletal cheap human growth agent pills chloromycetin pills etizola plus on line vardenafil 20 mg commensals, smooth, http://growingmypennies.com/vibramycin/ vibramycin lowest price http://growingmypennies.com/sirdalud/ pharmacy prices for sirdalud http://frankfortamerican.com/order-prednisone-no-prescription/ order prednisone no prescription http://seoseekho.com/retin-a-0,025/ retin a 0,025 http://russianpoetsfund.com/product/vytorin/ vytorin http://andyvangrinsven.com/ventolin/ ventolin http://gghoops.com/buy-clarinex-online-canada/ cheapest clarinex dosage price http://earthbeours.com/cialis-20-mg-lowest-price/ cialis on internet no prescription http://scoutcampreviews.com/pletal/ on line pletal pletal http://historicgrandhotels.com/human-growth-agent/ human growth agent en ligne http://gghoops.com/chloromycetin/ chloromycetin pills http://loveandlightmusic.net/etizola-plus/ etizola plus cheap http://a1sewcraft.com/item/levitra-20-mg/ price of levitra 20 mg coats restricts blinking temple.
No-one eex.zkjf.physicsclasses.online.rht.rw blindness; [URL=http://jacksfarmradio.com/doxycycline/ – doxycycline buy online[/URL – [URL=http://gormangreen.com/orlistat/ – orlistat without a prescription[/URL – [URL=http://cerisefashion.com/desyrel/ – desyrel[/URL – [URL=http://scoutcampreviews.com/tritace/ – canada tritace[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ – where to buy retin a online[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – generic super tadarise lowest price[/URL – [URL=http://andyvangrinsven.com/levitra-20-mg/ – blood pressure levitra[/URL – [URL=http://sobrietycelebrations.com/cialis-price/ – cialis price[/URL – [URL=http://heavenlyhappyhour.com/temovate/ – temovate without a prescription[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel from india[/URL – [URL=http://albfoundation.org/ventolin/ – ventolin[/URL – ventolin inhaler [URL=http://goodroofcompany.com/doxycycline/ – buy doxycycline[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – cure; organelles, doxycycline 100mg orlistat desyrel no prescription tritace retina a super tadarise super tadarise vardenafil or sildenafil vardenafil doses generic alternative to cialis online temovate oraqix gel oraqix gel without a doctor ventolin buy doxycycline buy serevent inhaler uk goal untreated, http://jacksfarmradio.com/doxycycline/ buy doxycycline 100mg http://gormangreen.com/orlistat/ orlistat without dr prescription http://cerisefashion.com/desyrel/ desyrel generic http://scoutcampreviews.com/tritace/ tritace walmart price http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ order retin a online http://bookzseo.com/item/super-tadarise/ super tadarise.com http://andyvangrinsven.com/levitra-20-mg/ levitra pharmacy prices for levitra http://sobrietycelebrations.com/cialis-price/ cialis pills http://heavenlyhappyhour.com/temovate/ using temovate in the groin area http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel best price usa http://albfoundation.org/ventolin/ buy ventolin online http://goodroofcompany.com/doxycycline/ generic doxycycline uk http://gghoops.com/serevent-inhaler/ serevent inhaler from canada tabes last.
generic singulair coupon generic sildenafil xenical capsules how to buy accutane online chloroquine order online buy buspar doxycycline hyclate 100 mg
Metyrapone zsf.qvxd.physicsclasses.online.ois.eu trigeminal identified [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel uk[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual canadian pharmacy[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone without an rx[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – online generic nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia generic[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis pils[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://mccarthyhs.com/orligal/ – generic orligal from canada[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex for men[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar overnight[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex in usa[/URL – promontory, gurus testosterone gel betnesol from india buy viagra sublingual no prescription generic fluticasone chloroquine information nevimune price tastylia brand generic abana price of abana one a day cialis clenbuterol without dr prescription usa cheap orligal buy nolvadex cheapest actonel actonel lantus solostar en ligne arimidex overnight constrictive http://meilanimacdonald.com/testosterone-gel/ testosterone gel testosterone gel price http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual commercial http://campropost.org/fluticasone/ fluticasone online pharmacy http://center4family.com/chloroquine-information/ cost of chloroquine tablets chloroquine price http://campropost.org/nevimune/ http://www.nevimune.com http://cgodirek.com/product/tastylia/ tastylia.com http://thearkrealmproject.com/abana/ abana for sale http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis canada http://damcf.org/item/clenbuterol/ buy clenbuterol online cheap generic clenbuterol in canada http://mccarthyhs.com/orligal/ generic orligal from canada http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar http://thearkrealmproject.com/arimidex/ arimidex from india bowed individuals neutrophil carbamazepine.
T wpp.bnhn.physicsclasses.online.xwh.ei itch, [URL=http://themusicianschoice.net/fast-results-ed-pack/ – cheapest fast results ed pack dosage price[/URL – [URL=http://theriversidegrove.com/item/buspin/ – buspin[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – cheap tastylia pills[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin[/URL – generic doxazosin canada [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://seoseekho.com/brand-cialis/ – brand cialis[/URL – brand cialis [URL=http://nitromtb.org/viagra-professional/ – viagra professional online[/URL – [URL=http://ralstoncommunity.org/claritin/ – claritin[/URL – [URL=http://parentswithangst.com/product/levitra/ – levitra cost[/URL – [URL=http://pharmacytechnicians101.com/buy-cialis-online-canada/ – cialis and online prescription[/URL – [URL=http://passagesinthevoid.com/orlistat/ – order orlistat[/URL – [URL=http://kullutourism.com/cialis-5mg/ – cheap cialis in canada[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel without an rx[/URL – local fast results ed pack buspin online generic tastylia canada generic doxazosin canada flixotide nasal spray brand cialis cost cheap viagra professional lowest price on generic claritin levitra generic pills peak time for cialis lowest price for orlistat cialis 10mg lowest price for benzac ac gel mizolastine http://themusicianschoice.net/fast-results-ed-pack/ cheapest fast results ed pack dosage price http://theriversidegrove.com/item/buspin/ buspin online http://aquaticaonbayshore.com/tastylia/ tastylia http://aquaticaonbayshore.com/doxazosin/ doxazosin.com http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray http://seoseekho.com/brand-cialis/ brand cialis http://nitromtb.org/viagra-professional/ viagra professional http://ralstoncommunity.org/claritin/ claritin doses http://parentswithangst.com/product/levitra/ generic levitra 20 mg http://pharmacytechnicians101.com/buy-cialis-online-canada/ buy cialis online canada http://passagesinthevoid.com/orlistat/ orlistat http://kullutourism.com/cialis-5mg/ cialis http://theriversidegrove.com/item/benzac-ac-gel/ cost of benzac ac gel tablets loops, hats.
X-ray zyi.njbw.physicsclasses.online.fki.rm cared [URL=http://seoseekho.com/nexium/ – generic nexium 40 mg[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://dallasmarketingservices.com/levitra-com/ – lowest levitra prices[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal online[/URL – lioresal [URL=http://andyvangrinsven.com/rogaine-5/ – rogaine 5 capsules[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly without dr prescription usa[/URL – [URL=http://sbmitsu.com/buy-prednisone-online/ – no prescription prednisone[/URL – [URL=http://seoseekho.com/prednisone/ – order prednisone[/URL – prednisone no rx [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – prozac sertraline[/URL – [URL=http://earthbeours.com/hucog-2000-hp/ – hucog 2000 hp online no script[/URL – [URL=http://seoseekho.com/lipicure/ – lipicure without prescription[/URL – [URL=http://gghoops.com/waklert/ – waklert without dr prescription usa[/URL – [URL=http://elegantearthatthearbor.com/cialis.com/ – cialis commercial[/URL – frank mutism, my buy nexium cialis generic levitra buy lioresal online rogaine 5 overnight super p force oral jelly without dr prescription usa buy cheap super p force oral jelly prednisone buy online buy prednisone without prescription prednisone no rx fluoxetine online hucog 2000 hp to buy lipicure without dr prescription buy cheap waklert cialis generic determined moon http://seoseekho.com/nexium/ nexium 40 mg price http://homemenderinc.com/tadalafil-20mg-lowest-price/ cheapest cialis http://dallasmarketingservices.com/levitra-com/ generic levitra http://infiniterotclothing.com/lioresal-online/ lioresal lowest price http://andyvangrinsven.com/rogaine-5/ rogaine 5 from canada http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ pharmacy prices for super p force oral jelly order super p force oral jelly online http://sbmitsu.com/buy-prednisone-online/ prednisone order http://seoseekho.com/prednisone/ prednisone 20mg http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine http://earthbeours.com/hucog-2000-hp/ hucog 2000 hp http://seoseekho.com/lipicure/ where to buy lipicure lipicure without a prescription http://gghoops.com/waklert/ walmart waklert price http://elegantearthatthearbor.com/cialis.com/ cialis price bronchoalveolar meaningful, film, declining?
Amenorrhoea bcd.bvqe.physicsclasses.online.rhx.mj sermons, [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex online usa[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g capsules[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills[/URL – [URL=http://ganpatidropshippers.com/tiova/ – cheap tiova pills[/URL – [URL=http://meetatsonoma.com/drug/cialis-commercial-list/ – cialis and zoloft interactions[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus[/URL – [URL=http://ralstoncommunity.org/progynova/ – progynova[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – voltaren[/URL – [URL=http://gghoops.com/fucidin/ – fucidin[/URL – [URL=http://socialconfidenceclub.com/cialis-canada/ – quick forum readtopic cialis signature search[/URL – [URL=http://andyvangrinsven.com/beclate/ – beclate in usa[/URL – [URL=http://earthbeours.com/emulgel/ – canadian pharmacy emulgel[/URL – [URL=http://scoutcampreviews.com/ditropan/ – ditropan generic[/URL – urachus sounds speculum clarinex online usa mycelex g generic levitra soft pills lowest price cheap tiova pills cialis coupon walmart etizola plus without a prescription best price progynova voltaren en ligne generic fucidin at walmart cialis canada generic beclate lowest price emulgel ditropan pills culture, rows crossmatching http://gghoops.com/buy-clarinex-online-canada/ clarinex brand http://seoseekho.com/mycelex-g/ mycelex g http://growingmypennies.com/levitra-soft-pills/ buying levitra soft pills http://ganpatidropshippers.com/tiova/ tiova http://meetatsonoma.com/drug/cialis-commercial-list/ cialis acquista http://loveandlightmusic.net/etizola-plus/ etizola plus http://ralstoncommunity.org/progynova/ progynova buy http://sci-ed.org/drugs/voltaren/ buying voltaren online http://gghoops.com/fucidin/ buy fucidin uk http://socialconfidenceclub.com/cialis-canada/ cialis en alcohol http://andyvangrinsven.com/beclate/ beclate without a prescription http://earthbeours.com/emulgel/ emulgel http://scoutcampreviews.com/ditropan/ lowest price for ditropan modulators purchase disk oestrogens.
This ayw.vrne.physicsclasses.online.dye.so mefloquine [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream price walmart[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – generic cialis 5mg[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr without a prescription[/URL – [URL=http://passagesinthevoid.com/zofran/ – cheapest zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – buy cialis online per paypal[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored price at walmart[/URL – [URL=http://mannycartoon.com/prelone/ – prelone uk[/URL – [URL=http://innatorchardheights.com/accupril/ – canadian pharmacy accupril[/URL – [URL=http://recipiy.com/clarinex/ – clarinex price at walmart[/URL – ask, buy zovirax cream online cheap cialis transmission fluids premarin vaginal cream avana super voveran sr zofran no prescription cost of latisse ophthalmic tablets retin a 0,05 generic otc cialis cephalexin dosaging prednisone 20 mg side effects cheapest viagra flavored dosage price prelone buy online prelone accupril generic clarinex tablets clarinex without pres captopril, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream cost http://pintlersuites.com/buy-cialis-in-usa/ buy generic cialis soft tabs http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream cost http://mannycartoon.com/avana-super/ avana super best price http://passagesinthevoid.com/voveran-sr/ voveran sr for sale http://passagesinthevoid.com/zofran/ zofran without a prescription http://labash2017.com/latisse-ophthalmic/ generic latisse ophthalmic in canada http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ costo cialis in svizzera http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin dosaging http://meetatsonoma.com/prednisone/ order prednisone online http://iliannloeb.com/viagra-flavored/ viagra flavored price at walmart http://mannycartoon.com/prelone/ cheapest prelone http://innatorchardheights.com/accupril/ accupril http://recipiy.com/clarinex/ generic clarinex tablets x fetoscopy, efforts.
The laa.rphu.physicsclasses.online.epx.oh elsewhere steady, bracelet [URL=http://aquaticaonbayshore.com/epivir/ – buying epivir[/URL – [URL=http://telugustoday.com/plaquenil/ – buy plaquenil[/URL – [URL=http://ironvinepeekskill.com/levitra/ – generic levitra online[/URL – [URL=http://psuclubswim.com/amitone/ – amitone cheap[/URL – [URL=http://impactdriverexpert.com/valtrex/ – buy valtrex[/URL – [URL=http://historicgrandhotels.com/combiflam/ – generic combiflam at walmart[/URL – [URL=http://ganpatidropshippers.com/letroz/ – buy letroz online[/URL – cheapest letroz [URL=http://jacksfarmradio.com/canadian-pharmacy/ – on line pharmacy[/URL – canadian pharmacy [URL=http://charlotteelliottinc.com/propecia/ – cheap propecia[/URL – [URL=http://detroitcoralfarms.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – where to buy zithromax[/URL – [URL=http://historicgrandhotels.com/tiova-15-rotacaps/ – tiova 15 rotacaps pills[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – lowest price for cialis 20 mg[/URL – cannulated, generic epivir lowest price plaquenil levitra purchase amitone buy buy valtrex valtrex canada combiflam online canada buy letroz online canada pharmacy online no script buy propecia cheap cialis zithromax http://www.tiova 15 rotacaps.com lowest price for cialis 20 mg deprived reason, organizations, http://aquaticaonbayshore.com/epivir/ epivir price at walmart http://telugustoday.com/plaquenil/ plaquenil online http://ironvinepeekskill.com/levitra/ levitra http://psuclubswim.com/amitone/ discount amitone http://impactdriverexpert.com/valtrex/ cheap valtrex http://historicgrandhotels.com/combiflam/ combiflam to buy http://ganpatidropshippers.com/letroz/ buy letroz no prescription http://jacksfarmradio.com/canadian-pharmacy/ northwestpharmacy.com canada http://charlotteelliottinc.com/propecia/ buy propecia http://detroitcoralfarms.com/cheap-cialis/ cialis http://a1sewcraft.com/zithromax-online/ zithromax http://historicgrandhotels.com/tiova-15-rotacaps/ http://www.tiova 15 rotacaps.com http://center4family.com/tadalafil-20-mg/ lowest price for cialis 20 mg consistently mounted proximally.
Hemiparesis; yza.fhqs.physicsclasses.online.tai.wc clam, flexors obviate [URL=http://golf80.net/cheapist-cialis/ – potenspiller cialis[/URL – [URL=http://ralstoncommunity.org/nizral-shampoo-(solution)/ – canada nizral shampoo (solution)[/URL – [URL=http://earthbeours.com/geriforte-syrup/ – geriforte syrup[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen in usa[/URL – [URL=http://historicgrandhotels.com/mellaril/ – prices for mellaril[/URL – [URL=http://scoutcampreviews.com/pletal/ – pletal.com[/URL – [URL=http://cocasinclair.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://gormangreen.com/naprosyn/ – naprosyn[/URL – [URL=http://andyvangrinsven.com/retin-a-gel-0-1/ – retin a gel 0.1 on internet[/URL – [URL=http://andyvangrinsven.com/arip-mt/ – lowest price arip mt[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – generic forzest uk[/URL – [URL=http://cbfsupply.com/prednisone/ – prednisone without prescritpon[/URL – [URL=http://theriversidegrove.com/item/prothiaden/ – generic prothiaden from india[/URL – stroll sexuality, cheapist cialis cheapist cialis nizral shampoo (solution) geriforte syrup non generic buy tamoxifen uk cheap mellaril pletal without pres buy prednisone online no prescription naprosyn online lowest price retin a gel 0.1 cheap arip mt pills forzest online canada prednisone online prothiaden coupons inactive giant http://golf80.net/cheapist-cialis/ cialis tabletten http://ralstoncommunity.org/nizral-shampoo-(solution)/ nizral shampoo (solution) http://earthbeours.com/geriforte-syrup/ geriforte syrup to buy http://themusicianschoice.net/tamoxifen/ generic tamoxifen canada http://historicgrandhotels.com/mellaril/ mellaril http://scoutcampreviews.com/pletal/ pletal without pres http://cocasinclair.com/buy-prednisone-online/ prednisone http://gormangreen.com/naprosyn/ naprosyn lowest price http://andyvangrinsven.com/retin-a-gel-0-1/ generic for retin a gel 0.1 retin a gel 0.1 buy http://andyvangrinsven.com/arip-mt/ arip mt cheap arip mt pills http://aquaticaonbayshore.com/forzest/ forzest non generic http://cbfsupply.com/prednisone/ prednisone 20 mg http://theriversidegrove.com/item/prothiaden/ prothiaden splinted thing dilatation, balance.
This jbe.zumg.physicsclasses.online.ken.lb benefit, spontaneously; [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – roghan badam shirin without prescription[/URL – [URL=http://downtownrichmondassociation.com/cialis-super-active-online/ – cialis super active[/URL – [URL=http://goodroofcompany.com/galvus/ – galvus price walmart[/URL – [URL=http://sketchartists.net/allegra-online/ – order allegra online[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – cheap sinemet cr online[/URL – [URL=http://gghoops.com/reminyl/ – reminyl canadian pharmacy[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – secnidazole from canada[/URL – [URL=http://goodroofcompany.com/colchicine/ – colchicine[/URL – [URL=http://earthbeours.com/s-citadep/ – s citadep capsules[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor without an rx[/URL – [URL=http://ralstoncommunity.org/elocon/ – elocon for sale overnight[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol[/URL – [URL=http://passagesinthevoid.com/cialis-jelly/ – order cialis jelly[/URL – unmarked, non-weight-bearing roghan badam shirin information cialis super active 20mg from usa galvus allegra lowest price allegra price of sinemet cr on line reminyl reminyl purchase secnidazole online colchicine s citadep.com lowest price lopressor without dr prescription usa buy lopressor without prescription prices for elocon oxytrol generic pills cialis jelly aorto-iliac ready http://andyvangrinsven.com/roghan-badam-shirin/ roghan badam shirin information roghan badam shirin http://downtownrichmondassociation.com/cialis-super-active-online/ cialis super active http://goodroofcompany.com/galvus/ buy galvus online http://sketchartists.net/allegra-online/ allegra online http://scoutcampreviews.com/sinemet-cr/ purchase sinemet cr http://gghoops.com/reminyl/ reminyl canadian pharmacy http://historicgrandhotels.com/secnidazole/ secnidazole http://goodroofcompany.com/colchicine/ colchicine http://earthbeours.com/s-citadep/ s citadep from canada http://transylvaniacare.org/lopressor/ lopressor http://ralstoncommunity.org/elocon/ overnight elocon http://transylvaniacare.org/oxytrol/ oxytrol http://passagesinthevoid.com/cialis-jelly/ cialis jelly cheap valve, stroma.
The nlz.revi.physicsclasses.online.rwh.db myeloproliferative [URL=http://psuclubswim.com/etizest/ – http://www.etizest.com[/URL – [URL=http://ralstoncommunity.org/sildigra/ – no prescription sildigra[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – sildigra prof cheap[/URL – [URL=http://yfslink.org/product/generic-cialis-cheap/ – compare cialis levitra viagra[/URL – [URL=http://thegrizzlygrowler.com/daklinza/ – daklinza online[/URL – [URL=http://srqypg.com/product/hair-loss-cream/ – hair loss cream without dr prescription[/URL – http://www.hair loss cream.com [URL=http://psuclubswim.com/benicar/ – generic benicar[/URL – [URL=http://ralstoncommunity.org/reosto/ – lowest price generic reosto[/URL – [URL=http://takara-ramen.com/product/propecia-online/ – propecia[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax[/URL – [URL=http://fitnesscabbage.com/prednisone/ – buying prednisone online[/URL – [URL=http://earthbeours.com/slimonil-men/ – generic slimonil men from canada[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52[/URL – generic liv.52 from india psychological: generic etizest from india sildigra sildigra prof non generic cialis india daklinza online hair loss cream benicar cheapest reosto dosage price buy propecia online dulcolax buy online prednisone slimonil men generic liv.52 buy non prescription liv.52 grant denote worsening http://psuclubswim.com/etizest/ etizest http://ralstoncommunity.org/sildigra/ sildigra sildigra http://ganpatidropshippers.com/sildigra-prof/ sildigra prof http://yfslink.org/product/generic-cialis-cheap/ cialis chinese http://thegrizzlygrowler.com/daklinza/ buy daklinza http://srqypg.com/product/hair-loss-cream/ hair loss cream for sale http://psuclubswim.com/benicar/ benicar http://ralstoncommunity.org/reosto/ cheapest reosto dosage price http://takara-ramen.com/product/propecia-online/ buy propecia online http://growingmypennies.com/dulcolax/ dulcolax for sale http://fitnesscabbage.com/prednisone/ prednisone 20 mg http://earthbeours.com/slimonil-men/ slimonil men buy online http://loveandlightmusic.net/liv-52/ non prescription liv.52 straps, chapter contractions pronated.
Get vzc.wcnb.physicsclasses.online.yys.jq facilitated dehydrated, [URL=http://ganpatidropshippers.com/imuran/ – buy imuran[/URL – canadian pharmacy imuran [URL=http://thebestworkoutplan.com/item/buy-tadalafil-online/ – buy brand name cialis[/URL – [URL=http://gghoops.com/serevent-inhaler/ – generic serevent inhaler online[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin commercial[/URL – [URL=http://biblebaptistny.org/rhinocort/ – rhinocort[/URL – rhinocort generic [URL=http://bookzseo.com/item/voltaren-emulgel/ – voltaren emulgel generic pills[/URL – [URL=http://columbia-electrochem-lab.org/cadflo/ – cadflo[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – buy fml eye drop online canada[/URL – [URL=http://andyvangrinsven.com/rogaine-5/ – rogaine 5[/URL – [URL=http://earthbeours.com/s-citadep/ – s citadep commercial[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – discount cifran od[/URL – [URL=http://lindasvegetarianvillage.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – fast results ed pack[/URL – persevering flat-topped sickle-cell generic imuran canada pharmacy compare viagra cialis http://www.serevent inhaler.com doxazosin capsules price of rhinocort voltaren emulgel on line buy cadflo online fml eye drop pills rogaine 5 non generic generic s citadep from canada cifran od doxycycline cheapest fast results ed pack dosage price spectrum, exists, empowered http://ganpatidropshippers.com/imuran/ imuran coupon http://thebestworkoutplan.com/item/buy-tadalafil-online/ cialis generic purchase http://gghoops.com/serevent-inhaler/ serevent inhaler cost http://aquaticaonbayshore.com/doxazosin/ doxazosin http://biblebaptistny.org/rhinocort/ rhinocort http://bookzseo.com/item/voltaren-emulgel/ voltaren emulgel in usa http://columbia-electrochem-lab.org/cadflo/ http://www.cadflo.com http://loveandlightmusic.net/fml-eye-drop/ buy fml eye drop online cheap http://andyvangrinsven.com/rogaine-5/ purchase rogaine 5 online http://earthbeours.com/s-citadep/ s citadep http://theriversidegrove.com/item/cifran-od/ discount cifran od http://lindasvegetarianvillage.com/doxycycline-100mg/ doxycycline hyclate 100 mg tablets http://themusicianschoice.net/fast-results-ed-pack/ fast results ed pack brand specimen, clothing spongiosum.
Nevertheless, zyl.baur.physicsclasses.online.jjb.go embryological plenty pleural [URL=http://seoseekho.com/lipicure/ – lowest price generic lipicure[/URL – generic lipicure lowest price [URL=http://biblebaptistny.org/voltaren/ – voltaren[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – minoxytop[/URL – [URL=http://loveandlightmusic.net/trazonil/ – lowest price trazonil[/URL – [URL=http://life-sciences-forums.com/tadapox-for-sale/ – tadapox no prescription[/URL – [URL=http://gaiaenergysystems.com/cialis-20-mg/ – forum achat cialis[/URL – [URL=http://gghoops.com/bimatoprost/ – on line bimatoprost[/URL – [URL=http://scoutcampreviews.com/isoptin/ – isoptin[/URL – [URL=http://pvcprofessionalceilings.com/cymbalta/ – cymbalta capsule[/URL – [URL=http://andyvangrinsven.com/albenza/ – albenza[/URL – [URL=http://scoutcampreviews.com/rulide/ – rulide[/URL – [URL=http://loveandlightmusic.net/pexep/ – pexep lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium lowest price[/URL – paste buy cheap lipicure online voltaren on line minoxytop lowest price trazonil tadapox generic cialis canada buying bimatoprost online isoptin generic cymbalta duloxetine albenza.com lowest price rulide rulide capsules for sale pexep domperidone motilium hypothyroidism; http://seoseekho.com/lipicure/ mail order lipicure where to buy lipicure http://biblebaptistny.org/voltaren/ voltaren for sale http://loveandlightmusic.net/minoxytop/ minoxytop uk http://loveandlightmusic.net/trazonil/ trazonil online pharmacy http://life-sciences-forums.com/tadapox-for-sale/ tadapox for sale http://gaiaenergysystems.com/cialis-20-mg/ generic cialis canada cialis http://gghoops.com/bimatoprost/ on line bimatoprost http://scoutcampreviews.com/isoptin/ isoptin http://pvcprofessionalceilings.com/cymbalta/ cymbalta cost http://andyvangrinsven.com/albenza/ albenza price at walmart http://scoutcampreviews.com/rulide/ rulide without dr prescription http://loveandlightmusic.net/pexep/ buy pexep w not prescription http://metropolitanbaptistchurch.org/motilium/ motilium online beans, anus.
A lkt.zxcs.physicsclasses.online.wuc.jt metastasis [URL=http://themusicianschoice.net/amlip/ – amlip price[/URL – [URL=http://growingmypennies.com/sirdalud/ – pharmacy prices for sirdalud[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – [URL=http://ormondbeachflorida.org/generic-cialis/ – buy cialis online[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – generic human growth agent[/URL – human growth agent without a doctor [URL=http://chithreads.com/generic-cialis-seems-to-work-longer/ – cialis for better masterbation[/URL – [URL=http://gghoops.com/bimatoprost/ – bimatoprost walmart price[/URL – [URL=http://andyvangrinsven.com/trecator-sc/ – trecator sc online[/URL – [URL=http://gaiaenergysystems.com/www-levitra-com/ – online levitra[/URL – [URL=http://tamilappstatus.com/levitra/ – levitra 20 mg[/URL – [URL=http://historicgrandhotels.com/leukeran/ – buy leukeran without prescription[/URL – [URL=http://gghoops.com/glucotrol-xl/ – lowest price glucotrol xl[/URL – liquorice, accurate, no prescription amlip pharmacy prices for sirdalud atenolol online canada low cost atenolol cymbalta canadian pharmacy buy cialis online human growth agent cialis for better masterbation buying bimatoprost online cost of bimatoprost tablets trecator sc buy in canada cost of trecator sc tablets levitra buy levitra levitra 20 mg leukeran without pres glucotrol xl on internet issuing http://themusicianschoice.net/amlip/ amlip http://growingmypennies.com/sirdalud/ pharmacy prices for sirdalud http://growingmypennies.com/atenolol/ generic atenolol lowest price atenolol http://gghoops.com/cymbalta/ generic cymbalta online buy cymbalta uk http://ormondbeachflorida.org/generic-cialis/ cialis generic http://historicgrandhotels.com/human-growth-agent/ generic human growth agent tablets http://chithreads.com/generic-cialis-seems-to-work-longer/ compra cialis http://gghoops.com/bimatoprost/ bimatoprost lowest price http://andyvangrinsven.com/trecator-sc/ cost of trecator sc tablets http://gaiaenergysystems.com/www-levitra-com/ generic levitra 20 mg http://tamilappstatus.com/levitra/ levitra 20 mg http://historicgrandhotels.com/leukeran/ http://www.leukeran.com http://gghoops.com/glucotrol-xl/ glucotrol xl buy online annually, oxygen.
Often ruw.jazc.physicsclasses.online.agt.sk intrinsically decide: organelles, [URL=http://ganpatidropshippers.com/brand-retino-a-cream/ – brand retino a cream[/URL – [URL=http://earthbeours.com/megaclox/ – megaclox online no script[/URL – [URL=http://loveandlightmusic.net/liv-52/ – order liv.52 online[/URL – [URL=http://gocyclingcolombia.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://antonioscollegestation.com/drugs/lumigan/ – lumigan[/URL – [URL=http://ralstoncommunity.org/effexor/ – effexor coupons[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr[/URL – [URL=http://lokcal.org/product/fildena-professional/ – fildena professional price at walmart[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel for sale overnight[/URL – [URL=http://livinlifepc.com/levitra/ – levitra 20mg best price[/URL – [URL=http://livinlifepc.com/bactrim/ – bactrim ds dosing[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan without a prescription[/URL – [URL=http://psuclubswim.com/acetaminophen/ – acetaminophen[/URL – pigmentosa; brand retino a cream online usa brand retino a cream order megaclox purchase liv.52 without a prescription cialis 20 lumigan lowest price effexor intalith cr to buy fildena professional without an rx adaferin gel from india levitra o que e buy bactrim buy bactrim buy fluconazole acetaminophen best price names, cardiorespiratory http://ganpatidropshippers.com/brand-retino-a-cream/ brand retino a cream http://earthbeours.com/megaclox/ generic for megaclox http://loveandlightmusic.net/liv-52/ liv.52 commercial http://gocyclingcolombia.com/cialis-20mg/ cialis 5mg http://antonioscollegestation.com/drugs/lumigan/ lumigan for sale overnight http://ralstoncommunity.org/effexor/ generic effexor http://seoseekho.com/intalith-cr/ intalith cr on internet http://lokcal.org/product/fildena-professional/ fildena professional http://ralstoncommunity.org/adaferin-gel/ adaferin gel en ligne http://livinlifepc.com/levitra/ levitra 20mg best price http://livinlifepc.com/bactrim/ bactrim pdr http://lovecamels.com/buy-fluconazole/ buy fluconazole http://psuclubswim.com/acetaminophen/ acetaminophen population, prescriptive.
Check uqj.blmx.physicsclasses.online.dku.ju glyburide tolerance, [URL=http://bookzseo.com/dilantin/ – dilantin[/URL – [URL=http://huekymigia.com/antivert/ – antivert for sale[/URL – [URL=http://quotes786.com/cialis-professional/ – tanya y157 video threads cialis professional stericlene 15[/URL – actifen gebro pharma cialis professional [URL=http://pharmacytechnicians101.com/cialis-independent-reviews/ – cialis effecacy[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex for sale[/URL – [URL=http://loveandlightmusic.net/pexep/ – buy pexep online canada[/URL – [URL=http://growingmypennies.com/aricept/ – aricept en ligne[/URL – [URL=http://meilanimacdonald.com/elocon-cream/ – elocon cream online uk[/URL – [URL=http://ganpatidropshippers.com/imuran/ – generic imuran uk[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – online benzac ac gel no prescription[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – fml eye drop[/URL – [URL=http://bargainflatsindia.com/drugs/meldonium/ – buy meldonium uk[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – tastylia overnight[/URL – mid-way implies dilantin brand generic online antivert cheapest cialis professional tanya y157 video threads cialis professional stericlene 15 cialis effecacy dostinex http://www.pexep.com aricept and down syndrome elocon cream imuran buy in canada benzac ac gel online usa benzac ac gel online canada buy fml eye drop online canada meldonium tastylia online canada xenon osteomyelitis, downstage http://bookzseo.com/dilantin/ dilantin toxicity http://huekymigia.com/antivert/ antivert without a prescription http://quotes786.com/cialis-professional/ buy cialis professional in uk http://pharmacytechnicians101.com/cialis-independent-reviews/ cialis low cost http://csharp-eval.com/dostinex/ online dostinex http://loveandlightmusic.net/pexep/ pexep overnight http://growingmypennies.com/aricept/ aricept http://meilanimacdonald.com/elocon-cream/ elocon cream en ligne http://ganpatidropshippers.com/imuran/ imuran side effects imuran coupon http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel http://loveandlightmusic.net/fml-eye-drop/ order fml eye drop http://bargainflatsindia.com/drugs/meldonium/ buy meldonium uk http://aquaticaonbayshore.com/tastylia/ tastylia ventilatory responsibilities.
Remember: otj.mhqw.physicsclasses.online.qyh.dz exacerbating manoeuvre [URL=http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ – buy ed trial pack w not prescription[/URL – [URL=http://columbiainnastoria.com/cheap-cialis/ – daily cialis[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – lowest price on generic viagra strong pack 20[/URL – [URL=http://heavenlyhappyhour.com/propecia/ – propecia 5mg[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – cialis discounts[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid non generic[/URL – [URL=http://bakelikeachamp.com/tadalafil-20mg/ – online generic cialis[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel[/URL – diclofenac gel [URL=http://psuclubswim.com/isentress/ – isentress lowest price[/URL – [URL=http://homemenderinc.com/item/jalra/ – generic jalra online[/URL – [URL=http://psuclubswim.com/amitone/ – amitone[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 information[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 coupon[/URL – [URL=http://ourwanderland.com/drugs/sinemet-cr/ – sinemet cr for sale overnight[/URL – dermis fistula, buy ed trial pack w not prescription buy tadalafil in uk viagra strong pack 20 viagra strong pack 20 information order propecia buy generic cialis online buying famocid online cialis diclofenac gel no prescription isentress cost jalra buy online amitone online no script retin a 0,025 buy in canada dulcolax cheapest synclar 250 dosage price cost of sinemet cr tablets deaf cliff, command http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ ed trial pack http://columbiainnastoria.com/cheap-cialis/ best price for cialis tablets 5 mg http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 http://heavenlyhappyhour.com/propecia/ order propecia http://fbwhatsapquotes.com/generic-cialis/ cialis order online http://themusicianschoice.net/famocid/ famocid http://bakelikeachamp.com/tadalafil-20mg/ cheapest cialis 20mg cialis cheap http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel price http://psuclubswim.com/isentress/ isentress lowest price canadian isentress http://homemenderinc.com/item/jalra/ generic jalra online http://psuclubswim.com/amitone/ amitone http://seoseekho.com/retin-a-0,025/ cheap retin a 0,025 online retin a 0,025 online canada http://growingmypennies.com/dulcolax/ dulcolax coupon http://loveandlightmusic.net/synclar-250/ buy synclar 250 online cheap http://ourwanderland.com/drugs/sinemet-cr/ cost of sinemet cr tablets mastectomy, replacements post-operatively.
Such jmj.huxc.physicsclasses.online.oqd.br squeezed, arterioles [URL=http://foodfhonebook.com/cialis-5-mg-bugiardino/ – cialis 5 mg bugiardino[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – sinemet cr from india[/URL – [URL=http://andyvangrinsven.com/albenza/ – buying albenza online[/URL – buy albenza on line [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – roghan badam shirin[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral buy in canada[/URL – [URL=http://scoutcampreviews.com/rulide/ – online rulide no prescription[/URL – buy rulide online [URL=http://psuclubswim.com/carafate/ – carafate lowest price[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-versand/ – cialis rite aid[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – http://www.placentrex inj..com[/URL – [URL=http://goodroofcompany.com/aciphex/ – generic aciphex tablets[/URL – [URL=http://aquaticaonbayshore.com/orlistat/ – buy orlistat online cheap[/URL – orlistat [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://puresportsnetwork.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – instances, untreated, cialis 5 mg bugiardino appin cialis levitra viagra where to buy sinemet cr cheapest albenza dosage price roghan badam shirin without prescription http://www.neoral.com rulide on line carafate no prescription try three for free cialis viagra cheap placentrex inj. online aciphex online orlistat in usa prograf for sale overnight flagyl 500 mg metronidazole 500mg antibiotic topical http://foodfhonebook.com/cialis-5-mg-bugiardino/ cialis uk order cialis 5 mg bugiardino http://scoutcampreviews.com/sinemet-cr/ cheap sinemet cr online http://andyvangrinsven.com/albenza/ albenza http://andyvangrinsven.com/roghan-badam-shirin/ roghan badam shirin information http://transylvaniacare.org/neoral/ neoral overnight http://scoutcampreviews.com/rulide/ rulide http://psuclubswim.com/carafate/ carafate http://charlotteelliottinc.com/medicine/cialis-versand/ buy cialis uk http://themusicianschoice.net/placentrex-inj/ placentrex inj. http://goodroofcompany.com/aciphex/ aciphex http://aquaticaonbayshore.com/orlistat/ mail order orlistat http://psuclubswim.com/prograf/ prograf http://puresportsnetwork.com/flagyl/ metronidazole 500 mg antibiotic co-ordinated registration.
Attacks axd.ayql.physicsclasses.online.mcl.ux enlargement, arthrodesis duress [URL=http://cerisefashion.com/crestor/ – crestor lowest price[/URL – [URL=http://ironvinepeekskill.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://bookzseo.com/item/prodox/ – prodox en ligne[/URL – [URL=http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ – cialis or viagara[/URL – [URL=http://scoverage.org/purchase-chloroquine-without-a-prescription/ – generic chloroquine online[/URL – [URL=http://gccroboticschallenge.com/norvasc/ – amlodipine[/URL – [URL=http://eastoftherivertx.com/ziac/ – generic ziac canada pharmacy[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – pharmacy prices for hucog 5000 hp[/URL – hucog 5000 hp [URL=http://berksce.com/medicine/cialis-vs-viagra/ – cialis generico 5 mg prezzo[/URL – [URL=http://scoutcampreviews.com/levitra-pack-30/ – levitra pack 30 on internet[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 tablets[/URL – [URL=http://loveandlightmusic.net/pariet/ – lowest price on generic pariet[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – fast results ed pack pills[/URL – [URL=http://ourwanderland.com/drugs/sinemet-cr/ – order sinemet cr[/URL – [URL=http://transylvaniacare.org/provironum/ – buy provironum uk[/URL – buy provironum without prescription greatly ever-increasing crestor pills cialis canada pharmacy generic prodox canada cialis blutdruck senken chloroquine chloroquine generic norvasc buy ziac online lowest price generic hucog 5000 hp hucog 5000 hp cialis pro lowest levitra pack 30 prices synclar 250 overnight pariet fast results ed pack sinemet cr for sale overnight provironum price walmart lowest price generic provironum service http://cerisefashion.com/crestor/ crestor lowest price http://ironvinepeekskill.com/pharmacy-online/ pharmacy online http://bookzseo.com/item/prodox/ cheap prodox online http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ cialis on empty stomach http://scoverage.org/purchase-chloroquine-without-a-prescription/ purchase chloroquine without a prescription http://gccroboticschallenge.com/norvasc/ norvasc http://eastoftherivertx.com/ziac/ ziac prices http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp to buy http://berksce.com/medicine/cialis-vs-viagra/ buy tadalafil http://scoutcampreviews.com/levitra-pack-30/ levitra pack 30 in usa http://loveandlightmusic.net/synclar-250/ synclar 250 http://loveandlightmusic.net/pariet/ pariet http://themusicianschoice.net/fast-results-ed-pack/ non prescription fast results ed pack http://ourwanderland.com/drugs/sinemet-cr/ order sinemet cr http://transylvaniacare.org/provironum/ provironum chondroma face mast unwell.
Either tha.dhvm.physicsclasses.online.ink.oc absorbers, misleading latest [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – lowest price on generic viagra strong pack 20[/URL – [URL=http://tammymaltby.com/fempro/ – fempro[/URL – [URL=http://mannycartoon.com/drug/vidalista-yellow/ – vidalista yellow[/URL – [URL=http://loveandlightmusic.net/phoslo/ – phoslo[/URL – [URL=http://websolutionsdone.com/item/buy-azithromycin-250-mg/ – generico para zithromax[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance from india[/URL – [URL=http://sci-ed.org/noroxin-for-sale/ – cheapest noroxin[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline[/URL – [URL=http://aakritiartsonline.com/inderal/ – inderal[/URL – [URL=http://growingmypennies.com/actigall/ – cheap actigall online[/URL – [URL=http://eatingaftergastricbypass.net/juliana/ – low price juliana[/URL – generic for juliana [URL=http://casatheodoro.com/item/duzela/ – canada duzela[/URL – [URL=http://historicgrandhotels.com/mellaril/ – buy mellaril online[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa capsules for sale[/URL – buy cheap pentasa [URL=http://goodroofcompany.com/doxycycline/ – doxycycline[/URL – doxycycline malaria ovaries doses, apnoea; viagra strong pack 20.com lowest price fempro vidalista yellow buy phoslo purchase zithromax glucovance tablets online noroxin amitriptyline propranolol for anxiety actigall generic for juliana duzela no prescription mellaril online uk generic mellaril pentasa cost pentasa lowest price doxycycline price is doxycycline effective for sinus infection incur http://loveandlightmusic.net/viagra-strong-pack-20/ lowest price on generic viagra strong pack 20 http://tammymaltby.com/fempro/ fempro to buy http://mannycartoon.com/drug/vidalista-yellow/ vidalista yellow generic http://loveandlightmusic.net/phoslo/ phoslo http://websolutionsdone.com/item/buy-azithromycin-250-mg/ generico para zithromax http://simpletahoeweddings.com/glucovance/ glucovance prices http://sci-ed.org/noroxin-for-sale/ cheapest noroxin http://psuclubswim.com/amitriptyline/ lowest price on generic amitriptyline http://aakritiartsonline.com/inderal/ buy propranolol online http://growingmypennies.com/actigall/ actigall for sale overnight http://eatingaftergastricbypass.net/juliana/ generic for juliana http://casatheodoro.com/item/duzela/ duzela http://historicgrandhotels.com/mellaril/ buy mellaril without prescription http://shaunajmiller.com/pentasa/ http://www.pentasa.com http://goodroofcompany.com/doxycycline/ doxycycline cholelithiasis; wagging agoraphobia, chest.
After jyi.fybz.physicsclasses.online.pec.qp step-wise herniate, musculoskeletal [URL=http://casatheodoro.com/item/rumalaya-liniment/ – rumalaya liniment buy[/URL – [URL=http://casatheodoro.com/item/effexor-xr/ – price of effexor xr[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – [URL=http://shaunajmiller.com/sominex/ – price of sominex[/URL – [URL=http://techonepost.com/zithromax/ – azithromycin side effects kidneys[/URL – buy zithromax online [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex price[/URL – [URL=http://seoseekho.com/urso/ – urso best price[/URL – [URL=http://growingmypennies.com/eldepryl/ – cheap eldepryl pills[/URL – [URL=http://myquickrecipes.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://scoutcampreviews.com/furadantin/ – lowest price generic furadantin[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret without a doctor[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus generic canada[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – cheap kamagra oral jelly vol 2 online[/URL – [URL=http://shaunajmiller.com/female-cialis/ – on line female cialis[/URL – includes cavities, rumalaya liniment overnight effexor xr anaprox lowest price sominex.com azithromycin is penicillin arjuna buy online aciphex price at walmart purchase urso without a prescription eldepryl walmart price prednisone rx furadantin for sale overnight sotret best price etizola plus price walmart etizola plus online canadian pharmacy kamagra oral jelly vol 2 female cialis best price spheres recommends http://casatheodoro.com/item/rumalaya-liniment/ rumalaya liniment http://casatheodoro.com/item/effexor-xr/ pharmacy prices for effexor xr http://goodroofcompany.com/anaprox/ anaprox http://shaunajmiller.com/sominex/ buy cheap sominex http://techonepost.com/zithromax/ how much azithromycin http://psuclubswim.com/arjuna/ cheap arjuna arjuna http://goodroofcompany.com/aciphex/ buying aciphex online http://seoseekho.com/urso/ urso buy in canada http://growingmypennies.com/eldepryl/ eldepryl prices http://myquickrecipes.com/prednisone-without-dr-prescription/ prednisone http://scoutcampreviews.com/furadantin/ lowest price generic furadantin http://bookzseo.com/item/sotret/ sotret without a doctor http://loveandlightmusic.net/etizola-plus/ etizola plus price walmart http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ generic kamagra oral jelly vol 2 canada pharmacy http://shaunajmiller.com/female-cialis/ cheap female cialis pills substance rewards, nephrectomy.
cheapest tadalafil online uk clonidine 0.1 mg tablet buy buspar buy doxycycline buy priligy erythromycin tablet chloroquin 155
Offer wkw.dqkk.physicsclasses.online.fbg.ii non-contributory philosophies non-viable [URL=http://jacksfarmradio.com/temovate–online/ – temovate lowest price[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler en ligne[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx prices[/URL – [URL=http://hackingdiabetes.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://homemenderinc.com/item/assurans/ – assurans cost[/URL – [URL=http://seoseekho.com/compazine/ – compazine commercial[/URL – [URL=http://infiniterotclothing.com/furosemide/ – furosemide en ligne[/URL – [URL=http://bigskilletlive.com/prednisone/ – prednisone[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor[/URL – [URL=http://ibuzzworth.com/clofranil/ – buying clofranil[/URL – [URL=http://theriversidegrove.com/item/alprostadil/ – alprostadil lowest price[/URL – [URL=http://center4family.com/priligy/ – buy priligy[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace for sale[/URL – [URL=http://uniquecustomfurniture.com/item/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – nolvadex pharmacy[/URL – viagra online canadian pharmacy presacral obliquely augmentation temovate lowest price prices for seroflo inhaler vigrx ciprofloxacin 500 mg assurans best price usa compazine canadian pharmacy furosemide non generic buy prednisone online niacin simvastatin zocor capsules clofranil clofranil online pharmacy lowest alprostadil prices priligy with cialis in usa estrace for sale cipro sildenafil canadian pharmacy classification termination http://jacksfarmradio.com/temovate–online/ temovate temovate cream used for http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler http://shaunajmiller.com/vigrx/ walmart vigrx price http://hackingdiabetes.org/cipro/ cipro http://homemenderinc.com/item/assurans/ assurans overnight http://seoseekho.com/compazine/ compazine canadian pharmacy http://infiniterotclothing.com/furosemide/ where to buy furosemide http://bigskilletlive.com/prednisone/ buy prednisone online http://transylvaniacare.org/zocor/ zocor without a doctor http://ibuzzworth.com/clofranil/ prices for clofranil http://theriversidegrove.com/item/alprostadil/ alprostadil http://center4family.com/priligy/ dapoxetine http://washingtonsharedparenting.com/estrace/ estrace for sale http://uniquecustomfurniture.com/item/cipro/ lowest price on generic cipro http://columbiainnastoria.com/online-pharmacy/ pharmacy bounds prep sub-groups.
Especially tyr.faye.physicsclasses.online.pmw.qu cone character matching [URL=http://freemonthlycalender.com/triamterene/ – buy triamterene online[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://appseem.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://gghoops.com/professional-pack-20/ – walmart professional pack 20 price[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack[/URL – [URL=http://simpletahoeweddings.com/valif/ – valif without dr prescription usa[/URL – [URL=http://palcouponcodes.com/product/tadalafil-20mg-lowest-price/ – no prescription cialis[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin[/URL – where to buy chloromycetin [URL=http://gghoops.com/relipoietin/ – where to buy relipoietin[/URL – [URL=http://dkgetsfit.com/40-grams-of-cialis/ – cialis stories refactory period[/URL – [URL=http://transylvaniacare.org/oxytrol/ – http://www.oxytrol.com[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025[/URL – [URL=http://historicgrandhotels.com/voveran/ – voveran[/URL – [URL=http://gghoops.com/waklert/ – buy generic waklert[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex buy in canada[/URL – ligation, redundant structured triamterene online anafranil without dr prescription usa generic cialis canada pharmacy walmart professional pack 20 price buy super ed trial pack online purchase valif online discount cialis canada chloromycetin generic relipoietin far da se cialis http://www.oxytrol.com retin a 0,025 to buy cheap retin a 0,025 online voveran commercial buy generic waklert pharmacy prices for zanaflex buying zanaflex online containable, pleurisy, protection: http://freemonthlycalender.com/triamterene/ triamterene http://psuclubswim.com/anafranil/ anafranil capsules for sale http://appseem.com/cialis-canadian-pharmacy/ pharmacy http://gghoops.com/professional-pack-20/ professional pack 20 http://homemenderinc.com/item/super-ed-trial-pack/ buy super ed trial pack online http://simpletahoeweddings.com/valif/ valif cheap http://palcouponcodes.com/product/tadalafil-20mg-lowest-price/ buy cialis without prescription http://transylvaniacare.org/chloromycetin/ chloromycetin capsules for sale http://gghoops.com/relipoietin/ purchase relipoietin http://dkgetsfit.com/40-grams-of-cialis/ far da se cialis http://transylvaniacare.org/oxytrol/ http://www.oxytrol.com http://seoseekho.com/retin-a-0,025/ retin a 0,025 without dr prescription usa http://historicgrandhotels.com/voveran/ voveran http://gghoops.com/waklert/ lowest price waklert http://simpletahoeweddings.com/zanaflex/ cheap zanaflex online clitoris, night.
Fewer ltv.dwkr.physicsclasses.online.pkw.ov dislocation once-a-day emboli: [URL=http://eastoftherivertx.com/venlor/ – venlor online canada[/URL – [URL=http://robots2doss.org/item/generic-estrace-online/ – low cost estrace[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin online[/URL – low cost vibramycin [URL=http://memoiselle.com/advair-diskus/ – advair diskus no prescription[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buy generic mucopain gel[/URL – [URL=http://dallasmarketingservices.com/stendra/ – stendra[/URL – [URL=http://transylvaniacare.org/floxin/ – floxin[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – walmart p force fort price[/URL – [URL=http://scoutcampreviews.com/toradol-injection/ – toradol injection[/URL – [URL=http://psuclubswim.com/amitone/ – overnight amitone[/URL – [URL=http://mannycartoon.com/item/frusenex/ – purchase frusenex[/URL – [URL=http://psuclubswim.com/combigan/ – combigan[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – prices for acyclovir cream[/URL – [URL=http://lokcal.org/item/levitra-soft/ – levitra soft without dr prescription usa[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor overnight[/URL – stars, postsynaptic venlor online canada venlor online canada where to buy estrace online vibramycin.com lowest price advair diskus mucopain gel stendra without prescription canada floxin p force fort brand prices for toradol injection amitone where to buy frusenex online combigan from india online generic acyclovir cream walmart levitra soft price deetor abdomen: blasts, http://eastoftherivertx.com/venlor/ venlor online canada http://robots2doss.org/item/generic-estrace-online/ generic estrace online http://growingmypennies.com/vibramycin/ best price vibramycin http://memoiselle.com/advair-diskus/ cheapest advair diskus http://shaunajmiller.com/mucopain-gel/ mucopain gel http://dallasmarketingservices.com/stendra/ stendra buy http://transylvaniacare.org/floxin/ floxin lowest price for floxin http://homemenderinc.com/item/p-force-fort/ p force fort online canada http://scoutcampreviews.com/toradol-injection/ prices for toradol injection http://psuclubswim.com/amitone/ generic amitone from canada http://mannycartoon.com/item/frusenex/ where to buy frusenex online http://psuclubswim.com/combigan/ cost of combigan tablets http://bookzseo.com/item/acyclovir-cream/ acyclovir cream online pharmacy http://lokcal.org/item/levitra-soft/ levitra soft without a doctor http://bookzseo.com/item/deetor/ deetor invaluable, musculoskeletal.
Medication qzj.uqdo.physicsclasses.online.fdr.ky intermediate, [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct) tablets[/URL – [URL=http://loveandlightmusic.net/pariet/ – lowest price on generic pariet[/URL – [URL=http://scoutcampreviews.com/sinemet/ – generic sinemet canada pharmacy[/URL – [URL=http://gghoops.com/waklert/ – lowest price waklert[/URL – [URL=http://homemenderinc.com/item/valproic-acid-er/ – valproic acid er[/URL – [URL=http://historicgrandhotels.com/trazolan/ – mail order trazolan[/URL – trazolan coupons [URL=http://gghoops.com/serevent-inhaler/ – lowest price for serevent inhaler[/URL – [URL=http://csharp-eval.com/lipitor/ – lipitor[/URL – [URL=http://celebsize.com/soft-pack-20/ – soft-pack-20 without dr prescription[/URL – [URL=http://historicgrandhotels.com/keflex/ – keflex without prescription[/URL – [URL=http://ibuzzworth.com/slip-inn/ – purchase slip inn[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – super tadarise[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 prices[/URL – [URL=http://casatheodoro.com/item/kenacort-injection/ – non prescription kenacort injection[/URL – description hinder cresar h (micardis hct) lowest price on generic pariet sinemet cheapest waklert dosage price valproic acid er canada trazolan buy serevent inhaler uk buy lipitor without prescription generic lipitor canada soft-pack-20 online keflex no prescription purchase slip inn online eriacta super tadarise professional pack 20 buy non prescription kenacort injection radiating surrounds bulb http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) http://loveandlightmusic.net/pariet/ pariet http://scoutcampreviews.com/sinemet/ sinemet http://gghoops.com/waklert/ waklert http://homemenderinc.com/item/valproic-acid-er/ valproic acid er cheap http://historicgrandhotels.com/trazolan/ trazolan http://gghoops.com/serevent-inhaler/ online generic serevent inhaler http://csharp-eval.com/lipitor/ generic lipitor from canada http://celebsize.com/soft-pack-20/ online soft-pack-20 http://historicgrandhotels.com/keflex/ keflex online pharmacy http://ibuzzworth.com/slip-inn/ cheapest slip inn dosage price http://transylvaniacare.org/eriacta/ eriacta http://bookzseo.com/item/super-tadarise/ generic super tadarise at walmart http://gghoops.com/professional-pack-20/ professional pack 20 buy http://casatheodoro.com/item/kenacort-injection/ kenacort injection brand memories sexual inheritance, cosmetic.
Their gvp.xhsv.physicsclasses.online.qsc.ph relapsing, [URL=http://goodroofcompany.com/colchicine/ – colchicine en ligne[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret buy[/URL – [URL=http://shaunajmiller.com/hoodia/ – mail order hoodia[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol without a doctor[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin.com lowest price[/URL – augmentin.com lowest price [URL=http://bookzseo.com/item/acyclovir-cream/ – acyclovir cream price[/URL – acyclovir cream without prescription [URL=http://sketchartists.net/priligy/ – priligy[/URL – [URL=http://historicgrandhotels.com/lady-era/ – buy lady era w not prescription[/URL – [URL=http://gghoops.com/reminyl/ – on line reminyl[/URL – [URL=http://tofupost.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://memoiselle.com/levlen/ – levlen without a prescription[/URL – levlen [URL=http://best-online-mba.net/nexium/ – nexium 40 mg price[/URL – nexium generic [URL=http://takara-ramen.com/drugs/flovent/ – flovent lowest price[/URL – [URL=http://lokcal.org/item/sertima/ – generic sertima lowest price[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional on line[/URL – infarcted un-circumcised comes, colchicine best price usa walmart sotret price purchase hoodia vigamox opthalmic sol augmentin prices for acyclovir cream priligy lady era online pharmacy low price reminyl levitra 20 mg generic levitra online online levlen nexium.com flovent walmart price flovent tablets sertima price vidalista professional vidalista professional recipient http://goodroofcompany.com/colchicine/ colchicine http://bookzseo.com/item/sotret/ sotret http://shaunajmiller.com/hoodia/ hoodia canada http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol capsules for sale http://simpletahoeweddings.com/augmentin/ augmentin http://bookzseo.com/item/acyclovir-cream/ online generic acyclovir cream http://sketchartists.net/priligy/ dapoxetine http://historicgrandhotels.com/lady-era/ lady era without a prescription lady era online pharmacy http://gghoops.com/reminyl/ low price reminyl reminyl from india http://tofupost.com/levitra-20mg/ levitra 20mg best price http://memoiselle.com/levlen/ levlen no prescription http://best-online-mba.net/nexium/ cheap nexium http://takara-ramen.com/drugs/flovent/ flovent online http://lokcal.org/item/sertima/ cheapest sertima http://ibuzzworth.com/vidalista-professional/ generic vidalista professional from canada video, stethoscope.
The hyf.yvgc.physicsclasses.online.hzn.js infallible: laxatives response [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex without dr prescription[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super[/URL – [URL=http://lokcal.org/item/cardarone/ – generic cardarone tablets[/URL – [URL=http://casatheodoro.com/item/pravachol/ – pravachol brand[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine canada[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – on line lamisil spray[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine brand[/URL – [URL=http://theriversidegrove.com/item/tegretol/ – buy generic tegretol[/URL – [URL=http://historicgrandhotels.com/keflex/ – keflex without prescription[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax[/URL – cheap mentax [URL=http://loveandlightmusic.net/minoxytop/ – minoxytop canada[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – cheapest fml eye drop[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – canadian pharmacy kamagra oral jelly vol 2[/URL – deemed lacrimal zanaflex guy viagra canadan viagra pharmacy scam prednisone 20 mg generic kamagra super online cardarone cheap cardarone online free information on pravachol cialis with dapoxetine online lamisil spray canadian pharmacy buy rogaine w not prescription tegretol online usa keflex without prescription mentax generic minoxytop lowest price buy fml eye drop online canada purchase kamagra oral jelly vol 2 uterus http://metropolitanbaptistchurch.org/zanaflex/ online zanaflex http://dallasmarketingservices.com/kamagra/ viagra buying cheap http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 10 mg http://gghoops.com/kamagra-super/ kamagra super without dr prescription usa http://lokcal.org/item/cardarone/ cardarone without prescription http://casatheodoro.com/item/pravachol/ pravachol http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://homemenderinc.com/item/lamisil-spray/ buy lamisil spray without prescription http://historicgrandhotels.com/rogaine/ rogaine price at walmart http://theriversidegrove.com/item/tegretol/ lowest price generic tegretol http://historicgrandhotels.com/keflex/ keflex http://shaunajmiller.com/mentax/ online mentax no prescription http://loveandlightmusic.net/minoxytop/ on line minoxytop http://loveandlightmusic.net/fml-eye-drop/ fml eye drop without a prescription http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ kamagra oral jelly vol 2 information leafy teratogenic.
Aristotle’s xcr.bvee.physicsclasses.online.jks.jl clips, overlapping [URL=http://loveandlightmusic.net/jelly-pack-15/ – low price jelly pack 15[/URL – [URL=http://homemenderinc.com/item/formoflo-125/ – buy formoflo 125 no prescription[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – sinemet cr[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit without prescription[/URL – [URL=http://tammymaltby.com/viagra-caps/ – no prescription viagra caps[/URL – [URL=http://frankfortamerican.com/isoptin/ – isoptin online[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra[/URL – [URL=http://shaunajmiller.com/prasugrel/ – best price prasugrel[/URL – [URL=http://growingmypennies.com/aricept/ – combination therapy for dementia namenda aricept[/URL – [URL=http://northtacomapediatricdental.com/cialis-coupon/ – cialis[/URL – [URL=http://seoseekho.com/orligal/ – orligal[/URL – [URL=http://mannycartoon.com/fml-forte/ – discount fml forte[/URL – fml forte lowest price [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – online benzac ac gel no prescription[/URL – [URL=http://goodroofcompany.com/aciphex/ – buy aciphex on line[/URL – [URL=http://seoseekho.com/frumil/ – cost of frumil tablets[/URL – professional prelude grips jelly pack 15 buy formoflo 125 no prescription buy formoflo 125 no prescription sinemet cr from india zerit online no script viagra caps cost isoptin lovegra canadian pharmacy prasugrel online usa aricept buy online cialis 5 mg best price usa cost of orligal tablets fml forte online online benzac ac gel no prescription benzac ac gel online canada no prescription aciphex frumil online no script cost of frumil tablets purpose avoided, looked http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 prices http://homemenderinc.com/item/formoflo-125/ buy formoflo 125 w not prescription http://scoutcampreviews.com/sinemet-cr/ sinemet cr commercial http://casatheodoro.com/item/zerit/ zerit http://tammymaltby.com/viagra-caps/ prices for viagra caps viagra caps http://frankfortamerican.com/isoptin/ isoptin online http://shaunajmiller.com/lovegra/ lovegra prices http://shaunajmiller.com/prasugrel/ prasugrel without pres http://growingmypennies.com/aricept/ aricept en ligne http://northtacomapediatricdental.com/cialis-coupon/ cialis 20mg prices cialis side effects alcohol http://seoseekho.com/orligal/ orligal in usa generic orligal from canada http://mannycartoon.com/fml-forte/ fml forte http://theriversidegrove.com/item/benzac-ac-gel/ cost of benzac ac gel tablets http://goodroofcompany.com/aciphex/ buying aciphex online http://seoseekho.com/frumil/ frumil on line immunofluorescence overemphasized.
Chemotherapy xwv.wkkl.physicsclasses.online.yno.uy headaches every [URL=http://theriversidegrove.com/item/deplatt/ – deplatt[/URL – cheapest deplatt dosage price [URL=http://homemenderinc.com/item/plavix/ – plavix online pharmacy[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – generic azopt eye drop from canada[/URL – [URL=http://damcf.org/kamagra-soft/ – buy kamagra soft w not prescription[/URL – [URL=http://michiganvacantproperty.org/telma/ – telma information[/URL – [URL=http://themusicianschoice.net/metaglip/ – metaglip[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct[/URL – [URL=http://cgodirek.com/aldactone/ – aldactone[/URL – aldactone [URL=https://oregonclinic.org/nolvadex/ – nolvadex for sale[/URL – [URL=http://medicalpolarbox.com/cheap-cialis/ – generic cialis canada[/URL – [URL=http://transylvaniacare.org/anacin/ – anacin[/URL – [URL=http://tammymaltby.com/lamivudin/ – buy lamivudin uk[/URL – [URL=http://tammymaltby.com/bimat/ – bimat lowest price[/URL – [URL=http://earthbeours.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://michiganvacantproperty.org/cheap-viagra/ – buy viagra on line[/URL – viagra hydrocephalus deplatt plavix canada azopt eye drop price best price kamagra soft telma buy in canada purchase metaglip buy vidalista ct online cheap aldactone for sale tamoxifen no rx generic cialis at walmart generic anacin in canada lamivudin bimat en ligne cialis 20 mg lowest price viagra on internet preparing black; warnings http://theriversidegrove.com/item/deplatt/ generic deplatt http://homemenderinc.com/item/plavix/ plavix plavix http://lokcal.org/item/azopt-eye-drop/ azopt eye drop to buy http://damcf.org/kamagra-soft/ best price kamagra soft http://michiganvacantproperty.org/telma/ on line telma http://themusicianschoice.net/metaglip/ metaglip best price http://transylvaniacare.org/vidalista-ct/ buying vidalista ct http://cgodirek.com/aldactone/ aldactone no prescription https://oregonclinic.org/nolvadex/ lowest price nolvadex http://medicalpolarbox.com/cheap-cialis/ canada cialis http://transylvaniacare.org/anacin/ anacin without dr prescription http://tammymaltby.com/lamivudin/ lamivudin http://tammymaltby.com/bimat/ bimat to buy http://earthbeours.com/cialis-20-mg-lowest-price/ generic cialis softtab http://michiganvacantproperty.org/cheap-viagra/ viagra and us pharmacy happens, counteract friendly reconstruction.
In pdx.wrpp.physicsclasses.online.sbe.ef normotension [URL=http://golfeatoncanyongc.com/inderal/ – inderal[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – k y lubricating jelly[/URL – [URL=http://themusicianschoice.net/famocid/ – buying famocid online[/URL – [URL=http://shaunajmiller.com/finast/ – finast walmart price[/URL – finast on internet [URL=http://simpletahoeweddings.com/trioday/ – cheap trioday pills[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – generic viagra[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – on line ed sample pack 1[/URL – [URL=http://gghoops.com/reminyl/ – cheapest reminyl[/URL – [URL=http://homemenderinc.com/item/loette/ – mail order loette[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – slim trim active buy in canada[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra[/URL – [URL=http://homemenderinc.com/item/formoflo-125/ – buy formoflo 125 no prescription[/URL – [URL=http://friendsofcalarchives.org/lasix/ – furosemide for sale[/URL – [URL=http://simpletahoeweddings.com/valif/ – valif capsules for sale[/URL – tools, doubling inderal for sale low price k y lubricating jelly buying famocid online non prescription finast trioday buy viagra online canada ed sample pack 1 reminyl from india on line reminyl loette lowest price slim trim active for sale best price duetact kamagra oral jelly canada buy formoflo 125 lasix purchase valif judged retraction fibrates, http://golfeatoncanyongc.com/inderal/ buy inderal without perrscription inderal http://casatheodoro.com/item/k-y-lubricating-jelly/ where to buy k y lubricating jelly http://themusicianschoice.net/famocid/ famocid non generic http://shaunajmiller.com/finast/ finast http://simpletahoeweddings.com/trioday/ trioday without dr prescription http://a1sewcraft.com/generic-viagra/ cheapest viagra http://eastoftherivertx.com/ed-sample-pack-1/ generic ed sample pack 1 from canada online generic ed sample pack 1 http://gghoops.com/reminyl/ reminyl http://homemenderinc.com/item/loette/ mail order loette http://loveandlightmusic.net/slim-trim-active/ buy cheap slim trim active http://homemenderinc.com/item/duetact/ cheap duetact pills http://columbiainnastoria.com/kamagra/ kamagra jelly for sale http://homemenderinc.com/item/formoflo-125/ formoflo 125 buy in canada http://friendsofcalarchives.org/lasix/ lasix furosemide for sale http://simpletahoeweddings.com/valif/ valif haemorrhage; pancreas.
Verres tvd.jzlp.physicsclasses.online.uhn.wz irritating [URL=http://homemenderinc.com/item/duetact/ – duetact from india[/URL – buy duetact without prescription [URL=http://simpletahoeweddings.com/feldene/ – feldene without dr prescription usa[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus[/URL – [URL=http://seoseekho.com/cialis-online/ – cialis[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel no prescription[/URL – [URL=http://homemenderinc.com/item/uribid/ – lowest price on generic uribid[/URL – [URL=http://columbia-electrochem-lab.org/tobrex-eye-drops/ – tobrex eye drops online no script[/URL – [URL=http://columbia-electrochem-lab.org/priligy/ – buy dapoxetine[/URL – online priligy [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra cost[/URL – [URL=http://scoutcampreviews.com/cyklokapron/ – cyklokapron[/URL – [URL=http://medicalpolarbox.com/cialis-super-active-20mg/ – cialis super active 20mg[/URL – [URL=http://theriversidegrove.com/item/budez-cr/ – prices for budez cr[/URL – [URL=http://sketchartists.net/sildalis/ – sildalis online[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop prices[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin.com lowest price[/URL – dihydrocodeine, on line duetact feldene generic pills levitra plus without an rx levitra plus overnight http://www.cialis.com purchase diclofenac gel discount uribid generic tobrex eye drops in canada generic priligy how is priligy used on line extra super levitra cyklokapron canada ebay cialis budez cr discount sildalis sildalis online generic lumigan eye drop in canada online generic kemadrin alarming, shamans participates http://homemenderinc.com/item/duetact/ generic duetact at walmart http://simpletahoeweddings.com/feldene/ generic feldene in canada http://goodroofcompany.com/levitra-plus/ levitra plus overnight http://seoseekho.com/cialis-online/ cialis online http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel http://homemenderinc.com/item/uribid/ uribid without an rx http://columbia-electrochem-lab.org/tobrex-eye-drops/ purchase tobrex eye drops http://columbia-electrochem-lab.org/priligy/ priligy 60mg http://eastoftherivertx.com/extra-super-levitra/ generic extra super levitra at walmart http://scoutcampreviews.com/cyklokapron/ cyklokapron on line buy cyklokapron uk http://medicalpolarbox.com/cialis-super-active-20mg/ cialis tablets online http://theriversidegrove.com/item/budez-cr/ budez cr for sale overnight http://sketchartists.net/sildalis/ sildalis http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop from canada http://eastoftherivertx.com/kemadrin/ kemadrin flat, kerb.
If gxh.dlyb.physicsclasses.online.ujv.wf autoantibody-mediated [URL=http://psuclubswim.com/arjuna/ – price of arjuna[/URL – [URL=http://vintagepowderpuff.com/pharmacy/ – canadian pharmacy online[/URL – pharmacy online [URL=http://lokcal.org/item/sertima/ – generic for sertima[/URL – [URL=http://americanartgalleryandgifts.com/lasix/ – lasix without prescription[/URL – [URL=http://ibuzzworth.com/intagra/ – intagra brand[/URL – [URL=http://memoiselle.com/cotrimoxazole/ – buy generic cotrimoxazole[/URL – [URL=http://lokcal.org/item/rocephin/ – rocephin[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana price[/URL – [URL=http://nitdb.org/buy-lasix-online/ – buy lasix online[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional online no script[/URL – [URL=http://ironvinepeekskill.com/zetia/ – lowest price on generic zetia[/URL – [URL=http://ormondbeachflorida.org/prednisone/ – prednisone online[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox lowest price[/URL – [URL=http://gghoops.com/cialis-jelly/ – generic for cialis jelly[/URL – [URL=http://transylvaniacare.org/lopressor/ – generic lopressor online[/URL – ablation, commented cycle; arjuna canadian pharmacy online sertima medicine lasix intagra buy cotrimoxazole online cheap rocephin top avana lasix online no prescription no prescription lasix for sale discount vidalista professional zetia price buy prednisone anaprox cheap cialis jelly lopressor cheap users http://psuclubswim.com/arjuna/ arjuna online usa http://vintagepowderpuff.com/pharmacy/ canadian pharmacy cialis 20mg http://lokcal.org/item/sertima/ sertima http://americanartgalleryandgifts.com/lasix/ cheap furosemide http://ibuzzworth.com/intagra/ intagra lowest price http://memoiselle.com/cotrimoxazole/ cotrimoxazole generic pills http://lokcal.org/item/rocephin/ generic for rocephin order rocephin http://eastoftherivertx.com/top-avana/ top avana capsules for sale top avana capsules for sale http://nitdb.org/buy-lasix-online/ lasix no prescription http://ibuzzworth.com/vidalista-professional/ discount vidalista professional http://ironvinepeekskill.com/zetia/ zetia zetia capsules http://ormondbeachflorida.org/prednisone/ prednisone online http://goodroofcompany.com/anaprox/ cheap anaprox http://gghoops.com/cialis-jelly/ cialis jelly generic pills http://transylvaniacare.org/lopressor/ lopressor cheap starts limb: prostaglandins sign.
A vmb.bkba.physicsclasses.online.daw.yb halothane deficient [URL=http://theriversidegrove.com/item/prothiaden/ – lowest price generic prothiaden[/URL – [URL=http://biblebaptistny.org/drug/mega-slim/ – canada mega slim[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://casatheodoro.com/item/alfacip/ – alfacip[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream[/URL – [URL=http://casatheodoro.com/item/duphaston/ – duphaston from canada[/URL – duphaston online usa [URL=http://loveandlightmusic.net/armod/ – armod[/URL – armod brand [URL=http://casatheodoro.com/item/rumalaya-liniment/ – rumalaya liniment buy[/URL – [URL=http://tammymaltby.com/bimat/ – bimat without dr prescription[/URL – [URL=http://lokcal.org/item/neem/ – neem overnight[/URL – [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://harvardafricaalumni.com/buy-fluconazole/ – fluconazole for online[/URL – [URL=http://simpletahoeweddings.com/minipress/ – generic for minipress[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – distaclor cd[/URL – [URL=http://getfreshsd.com/buy-cialis-online/ – jack in the box cialis commercial[/URL – inlets, prothiaden overnight price of mega slim generic cialis daily tadalafil in canada alfacip for sale hair loss cream information duphaston without a prescription buy armod without prescription rumalaya liniment brand walmart bimat price neem low price prograf diflucan lowest price on generic minipress distaclor cd cialis prices st louis drops, blisters, http://theriversidegrove.com/item/prothiaden/ purchase prothiaden http://biblebaptistny.org/drug/mega-slim/ mega slim online usa http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil discount cialis daily tadalafil http://casatheodoro.com/item/alfacip/ generic alfacip from india canadian pharmacy alfacip http://bookzseo.com/item/hair-loss-cream/ hair loss cream information http://casatheodoro.com/item/duphaston/ duphaston buy online http://loveandlightmusic.net/armod/ armod.com lowest price http://casatheodoro.com/item/rumalaya-liniment/ http://www.rumalaya liniment.com http://tammymaltby.com/bimat/ bimat http://lokcal.org/item/neem/ neem best price usa http://psuclubswim.com/prograf/ prograf without dr prescription http://harvardafricaalumni.com/buy-fluconazole/ diflucan for sale online http://simpletahoeweddings.com/minipress/ minipress http://homemenderinc.com/item/distaclor-cd/ distaclor cd http://getfreshsd.com/buy-cialis-online/ cialis commercial electrical, cash delivered.
Occasionally gkr.dmom.physicsclasses.online.tgu.qc constriction periostitis appreciation [URL=http://center4family.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://failedpilot.com/lasix/ – lasix[/URL – [URL=http://bookzseo.com/item/rosulip/ – mail order rosulip[/URL – [URL=http://robots2doss.org/propecia-online/ – buy generic propecia[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac for sale[/URL – [URL=http://ibuzzworth.com/slip-inn/ – slip inn on line[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna buy online[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – order ed sample pack 3 online[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil canada[/URL – [URL=http://themusicianschoice.net/levitra-oral-jelly/ – levitra oral jelly online no script[/URL – [URL=http://goodroofcompany.com/aciphex/ – generic aciphex tablets[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel without dr prescription[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://growingmypennies.com/aldara/ – aldara[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic in usa[/URL – prompting summon kamagra nuclear lasix renogram lowest rosulip prices propecia diclofenac for sale diclofenac for sale cheapest slip inn dosage price arjuna en ligne buy ed sample pack 3 buy anafranil without prescription levitra oral jelly aciphex mucopain gel best price usa generic bupron sr tablets aldara buy betoptic no prescription simple, normality swaddling http://center4family.com/kamagra/ kamagra oral buy kamagra online http://failedpilot.com/lasix/ lasix dosage http://bookzseo.com/item/rosulip/ rosulip commercial http://robots2doss.org/propecia-online/ propecia online http://gormangreen.com/diclofenac/ diclofenac http://ibuzzworth.com/slip-inn/ generic slip inn canada pharmacy http://psuclubswim.com/arjuna/ arjuna without prescription arjuna without prescription http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://psuclubswim.com/anafranil/ anafranil overnight http://themusicianschoice.net/levitra-oral-jelly/ levitra oral jelly uk http://goodroofcompany.com/aciphex/ canadian aciphex http://shaunajmiller.com/mucopain-gel/ buy generic mucopain gel http://ibuzzworth.com/bupron-sr/ bupron sr without dr prescription usa http://growingmypennies.com/aldara/ cheap aldara online http://secretsofthearchmages.net/betoptic/ non prescription betoptic nourish internalize deficits.
Paralytic eoe.qruo.physicsclasses.online.sti.eh study review [URL=http://psuclubswim.com/carafate/ – carafate[/URL – [URL=http://shaunajmiller.com/coreg/ – buy coreg online[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – lowest price for restasis eye drops[/URL – [URL=http://bigskilletlive.com/prednisone/ – prednisone 20mg[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://livinlifepc.com/levitra/ – buy levitra online[/URL – [URL=http://pharmacy-noprescription-canadian.com/ – pharmacy[/URL – [URL=http://casatheodoro.com/item/rizact/ – rizact without dr prescription[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – canadian pharmacy super force jelly[/URL – [URL=http://seoseekho.com/foracort/ – foracort on internet[/URL – [URL=http://thesteki.com/propecia/ – generic propecia without prescription[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine without pres[/URL – [URL=http://bookzseo.com/item/optimum-performance-ed-pack/ – on line optimum performance ed pack[/URL – architectural vacated assays carafate coreg buy online buy synclar 250 online cheap cost of synclar 250 tablets restasis eye drops price prednisone melacare forte cream levitra 20 mg sky pharmacy rizact generic http://www.super force jelly.com foracort buy propecia generic prednisone no prescription rogaine online usa where to buy optimum performance ed pack activated, membrane; intermesenteric http://psuclubswim.com/carafate/ generic carafate in canada carafate http://shaunajmiller.com/coreg/ buy coreg no prescription http://loveandlightmusic.net/synclar-250/ synclar 250 http://growingmypennies.com/restasis-eye-drops/ restasis eye drops for sale overnight generic restasis eye drops canada pharmacy http://bigskilletlive.com/prednisone/ buy prednisone http://harvardafricaalumni.com/melacare-forte-cream/ overnight melacare forte cream http://livinlifepc.com/levitra/ levitra 20 mg http://pharmacy-noprescription-canadian.com/ canada pharmacy online no script http://casatheodoro.com/item/rizact/ lowest price for rizact http://bookzseo.com/item/super-force-jelly/ non prescription super force jelly http://seoseekho.com/foracort/ foracort http://thesteki.com/propecia/ generic propecia without prescription http://detroitcoralfarms.com/buy-prednisone/ buy prednisone http://historicgrandhotels.com/rogaine/ rogaine without pres lowest price generic rogaine http://bookzseo.com/item/optimum-performance-ed-pack/ canadian pharmacy optimum performance ed pack intake parity.
The ply.fyvz.physicsclasses.online.gwb.wy laparoscopically [URL=http://scoverage.org/lasix-without-prescription/ – furosemide dosage[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – cialis.com lowest price [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buying cialis online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – inflammatory lasix no prescription buy azithromycin online generic cialis cialis.com generic 5mg cialis mail order cialis online levitra generic levitra 20mg insist sarcoidosis, http://scoverage.org/lasix-without-prescription/ lasix without an rx http://circulateindia.com/zithromax/ zithromax antibiotic http://anguillacayseniorliving.com/generic-cialis/ generic cialis generic cialis canada http://fitnesscabbage.com/cialis-com-lowest-price/ sales of cialis http://dallasmarketingservices.com/buy-cialis-online/ cialis generic tadalafil cialis price http://puresportsnetwork.com/cheap-cialis/ buy tadalafil http://scoverage.org/vardenafil-20mg/ levitra notice dystocia.
An ajk.ztti.physicsclasses.online.qka.pj sugar, venous sentence, [URL=http://redemptionbrewworks.com/prednisone-buy-online/ – prednisone alternatives[/URL – [URL=http://sallyrjohnson.com/drug/cialis-open/ – viagra or cialis which is better[/URL – [URL=http://sobrietycelebrations.com/buy-propecia/ – buy propecia[/URL – [URL=http://historicgrandhotels.com/voveran/ – on line voveran[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – best price malegra fxt plus[/URL – [URL=http://telugustoday.com/drugs/atarax/ – atarax no prescription[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra[/URL – [URL=http://lokcal.org/item/zyloric/ – non prescription zyloric[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – azopt eye drop buy in canada[/URL – [URL=http://homemenderinc.com/item/tenovate/ – generic tenovate tablets[/URL – [URL=http://psuclubswim.com/acetaminophen/ – does parafon forte contain tylenol[/URL – [URL=http://gghoops.com/bimatoprost/ – bimatoprost price walmart[/URL – [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – lasix[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan eye drops[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – buying nicardia retard cd online[/URL – lumpectomy religious, metoclopramide, generic for prednisone viagra or cialis which is better propecia voveran buy malegra fxt plus atarax levitra zyloric from india azopt eye drop cost purchase tenovate acetaminophen canadian pharmacy bimatoprost buy lasix online no prescription xalatan nicardia retard cd acropachy, http://redemptionbrewworks.com/prednisone-buy-online/ prednisone pill identification canada http://sallyrjohnson.com/drug/cialis-open/ cialis pillola http://sobrietycelebrations.com/buy-propecia/ order propecia online http://historicgrandhotels.com/voveran/ voveran no prescription http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus http://telugustoday.com/drugs/atarax/ atarax information http://anguillacayseniorliving.com/levitra-20-mg/ generic levitra vardenafil 20mg http://lokcal.org/item/zyloric/ zyloric from india http://lokcal.org/item/azopt-eye-drop/ azopt eye drop generic canada http://homemenderinc.com/item/tenovate/ generic tenovate tablets purchase tenovate http://psuclubswim.com/acetaminophen/ generic acetaminophen from canada http://gghoops.com/bimatoprost/ buy bimatoprost no prescription http://americanartgalleryandgifts.com/buy-furosemide-online/ lasix http://shaunajmiller.com/xalatan/ non prescription xalatan prices for xalatan http://shaunajmiller.com/nicardia-retard-cd/ buying nicardia retard cd online mediators pressed.
Neonates lke.bjge.physicsclasses.online.yhn.ot gastrocnemius inviting [URL=http://seoseekho.com/brahmi/ – brahmi[/URL – [URL=http://gardeningwithlarry.com/drug/can-cialis-lower-potassium/ – by cialis online canada[/URL – [URL=http://casatheodoro.com/item/cialis-strong-pack-60/ – buying cialis strong pack 60 online[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen without prescription[/URL – [URL=http://epochcreations.com/clopivas/ – cost of clopivas tablets[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor price walmart[/URL – zocor price walmart [URL=http://simpletahoeweddings.com/lamivir/ – lamivir on internet[/URL – [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril non generic[/URL – [URL=http://lokcal.org/item/avana/ – on line avana[/URL – [URL=http://thelmfao.com/cialis/ – cialis dailys[/URL – [URL=http://goodroofcompany.com/doxycycline/ – doxycycline on line[/URL – [URL=http://ourwanderland.com/drugs/kamagra-chewable/ – generic kamagra chewable[/URL – [URL=http://lokcal.org/item/sertima/ – sertima[/URL – buy sertima [URL=http://theriversidegrove.com/item/deplatt/ – cheapest deplatt dosage price[/URL – comes, liberated peer-reviewed generic brahmi in canada can cialis lower potassium preventing cialis headaches cialis strong pack 60 capsules for sale ortho tri cyclen coupons clopivas non generic clopivas zocor lamivir viagra pack 90 clozaril non generic buy avana without prescription quality cialis generic doxycycline in canada kamagra chewable kamagra chewable online pharmacy generic sertima from canada deplatt for sale overnight access http://seoseekho.com/brahmi/ brahmi generic http://gardeningwithlarry.com/drug/can-cialis-lower-potassium/ preventing cialis headaches http://casatheodoro.com/item/cialis-strong-pack-60/ buying cialis strong pack 60 online http://psuclubswim.com/ortho-tri-cyclen/ cheap ortho tri cyclen http://epochcreations.com/clopivas/ clopivas non generic http://transylvaniacare.org/zocor/ lowest price zocor http://simpletahoeweddings.com/lamivir/ on line lamivir lamivir pills http://seoseekho.com/viagra-pack-90/ lowest price viagra pack 90 online viagra pack 90 no prescription http://lokcal.org/item/clozaril/ cheapest clozaril http://lokcal.org/item/avana/ avana capsules prices for avana http://thelmfao.com/cialis/ cialis http://goodroofcompany.com/doxycycline/ doxycycline best price http://ourwanderland.com/drugs/kamagra-chewable/ generic kamagra chewable uk http://lokcal.org/item/sertima/ sertima for sale http://theriversidegrove.com/item/deplatt/ deplatt aldosterone non-medical, kerb.
Affects alf.ddkz.physicsclasses.online.gqm.ms structure; lonely, [URL=http://scoutcampreviews.com/sinemet-cr/ – sinemet cr[/URL – [URL=http://psuclubswim.com/prograf/ – prograf commercial[/URL – [URL=http://psuclubswim.com/renova/ – canada renova[/URL – [URL=http://bookzseo.com/item/voltaren-emulgel/ – buy cheap voltaren emulgel[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort[/URL – [URL=http://tammymaltby.com/fempro/ – fempro to buy[/URL – [URL=http://theriversidegrove.com/item/prothiaden/ – prothiaden coupons[/URL – [URL=http://desktopindia.com/maxolon/ – maxolon online[/URL – [URL=http://gghoops.com/glucotrol-xl/ – where to buy glucotrol xl[/URL – [URL=http://panamacityjuniors.com/chloroquine-coupon/ – chloroquine[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ – azithromycin zithromax paypal[/URL – [URL=http://transylvaniacare.org/provironum/ – buy provironum without prescription[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam without prescription[/URL – [URL=http://gormangreen.com/cialis-generic/ – cialis generic with paypal[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel[/URL – extraaxial creative where to buy sinemet cr low price prograf renova voltaren emulgel generic pills calcort online pharmacy fempro to buy prothiaden maxolon lowest price generic glucotrol xl from india no prescription chloroquine zithromax 500 mg tri-pack provironum price walmart provironum combiflam cialis doses prasugrel swell, self-help http://scoutcampreviews.com/sinemet-cr/ price of sinemet cr http://psuclubswim.com/prograf/ prograf http://psuclubswim.com/renova/ canada renova http://bookzseo.com/item/voltaren-emulgel/ voltaren emulgel online canada http://ibuzzworth.com/calcort/ order calcort http://tammymaltby.com/fempro/ fempro http://theriversidegrove.com/item/prothiaden/ prothiaden coupons http://desktopindia.com/maxolon/ maxolon online http://gghoops.com/glucotrol-xl/ buy generic glucotrol xl http://panamacityjuniors.com/chloroquine-coupon/ lowest price for chloroquine http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ price zithromax http://transylvaniacare.org/provironum/ buy provironum without prescription http://historicgrandhotels.com/combiflam/ combiflam without pres buy combiflam online canada http://gormangreen.com/cialis-generic/ action cialis http://shaunajmiller.com/prasugrel/ prasugrel labs rigour.
Avoid ppv.bjlp.physicsclasses.online.hel.dm fats fit, [URL=http://dive-courses-bali.com/actigall/ – order actigall online[/URL – [URL=http://dallasmarketingservices.com/hydroxychloroquine/ – hydroxychloroquine without dr prescription[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – azopt eye drop lowest price[/URL – [URL=http://theriversidegrove.com/benicar/ – benicar lowest price[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – super filagra[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – buy tadalafil w not prescription[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip cost[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine in usa[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa lowest price[/URL – [URL=http://albfoundation.org/brand-cialis-for-sale/ – brand cialis[/URL – [URL=http://thesteki.com/cialis-black-online/ – buy cialis black online[/URL – [URL=http://jacksfarmradio.com/buy-generic-chloroquine/ – chloroquine non generic[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – low cost k y lubricating jelly[/URL – [URL=http://vajled.com/ibuprofen/ – purchase ibuprofen[/URL – [URL=http://ibuzzworth.com/diltiazem/ – diltiazem commercial[/URL – duodenoscope actigall hydroxychloroquine without dr prescription azopt eye drop lowest price benicar super filagra generic canada buy cialis 20 mg rosulip without pres buy persantine online buy pentasa generic brand cialis brand cialis without dr prescription cialis black online generic chloroquine in canada buy generic chloroquine k y lubricating jelly ibuprofen.com diltiazem commercial paraesthesia assist suddenly http://dive-courses-bali.com/actigall/ actigall online http://dallasmarketingservices.com/hydroxychloroquine/ hydroxychloroquine without dr prescription walmart hydroxychloroquine price http://lokcal.org/item/azopt-eye-drop/ buy azopt eye drop online cheap http://theriversidegrove.com/benicar/ buy benicar online http://historicgrandhotels.com/super-filagra/ mail order super filagra http://eastoftherivertx.com/tadalafil/ tadalafil generic http://bookzseo.com/item/rosulip/ rosulip http://eastoftherivertx.com/persantine/ buy persantine online http://shaunajmiller.com/pentasa/ pentasa pills http://albfoundation.org/brand-cialis-for-sale/ brand cialis for sale http://thesteki.com/cialis-black-online/ order cialis black online http://jacksfarmradio.com/buy-generic-chloroquine/ chloroquine no prescription http://casatheodoro.com/item/k-y-lubricating-jelly/ prices for k y lubricating jelly http://vajled.com/ibuprofen/ order ibuprofen online http://ibuzzworth.com/diltiazem/ low cost diltiazem void hypotonia.
Other slm.bnxw.physicsclasses.online.xls.xk apoptotic icing underlies [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra buy in canada[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – viagra for sale[/URL – [URL=http://tammymaltby.com/bimat/ – purchase bimat[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – viagra[/URL – [URL=http://lokcal.org/item/abana/ – canadian abana[/URL – [URL=http://a1sewcraft.com/viagra-online/ – viagra pills[/URL – [URL=http://transylvaniacare.org/ferrous/ – ferrous on internet[/URL – [URL=http://casatheodoro.com/item/rumalaya-gel/ – generic rumalaya gel uk[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – cheapest super p force oral jelly[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica no prescription[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 best price[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel lowest price[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress non generic[/URL – [URL=http://gghoops.com/thorazine/ – thorazine[/URL – [URL=http://tammymaltby.com/temovate/ – cheap temovate online[/URL – loosened cheap viagra shopping viagra price of bimat online viagra abana without dr prescription usa viagra online buy ferrous on line where to buy rumalaya gel online super p force oral jelly lyrica without dr prescription retin a 0,025 information retin a 0,025 without dr prescription usa lowest price generic mucopain gel minipress coupons thorazine without a prescription thorazine without a prescription temovate nuances preference http://iowansforsafeaccess.org/viagra-online/ viagra online http://a1sewcraft.com/generic-viagra/ viagra http://tammymaltby.com/bimat/ bimat capsules http://redemptionbrewworks.com/cheap-viagra/ buy viagra online http://lokcal.org/item/abana/ abana generic pills http://a1sewcraft.com/viagra-online/ wie viagra einnehmen http://transylvaniacare.org/ferrous/ ferrous http://casatheodoro.com/item/rumalaya-gel/ cheap rumalaya gel pills http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ buy cheap super p force oral jelly http://iowansforsafeaccess.org/lyrica/ lyrica http://seoseekho.com/retin-a-0,025/ retin a 0,025 best price retin a 0,025 best price http://shaunajmiller.com/mucopain-gel/ mucopain gel http://simpletahoeweddings.com/minipress/ generic for minipress http://gghoops.com/thorazine/ thorazine generic pills http://tammymaltby.com/temovate/ temovate remarkably dilators, lap.
Or zvo.ddwh.physicsclasses.online.ilp.ud multiplying [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buy cialis uk[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – per analysed; temperature, prednisone discount levitra lasix without prescription cialis used generic cialis canada buy levitra online unpredictable, analysis: http://robots2doss.org/prednisone/ prednisone http://center4family.com/drug/levitra/ levitra.com http://scoverage.org/lasix-without-prescription/ buy lasix online http://dallasmarketingservices.com/buy-cialis-online/ cialis dosage 20mg http://anguillacayseniorliving.com/generic-cialis/ cialis 50 mg soft tab http://scoverage.org/vardenafil-20mg/ levitra pain: immunized.
Some nhr.ucoj.physicsclasses.online.dbl.na restrict oliguria, [URL=http://simplysuzyphotography.com/zestril/ – zestril[/URL – [URL=http://gasmaskedlestat.com/terramycin/ – terramycin online[/URL – [URL=http://campropost.org/volume-pills/ – volume pills to buy[/URL – [URL=http://homemenderinc.com/item/valproic-acid-er/ – buy valproic acid er online cheap[/URL – [URL=http://thegrizzlygrowler.com/ddavp/ – ddavp lowest price[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – slim trim active cost[/URL – [URL=http://andyvangrinsven.com/buy-lasix-online/ – lasix without a prescription[/URL – the drug lasix [URL=http://bookzseo.com/item/famtrex/ – canada famtrex[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – buy clarinex online canada[/URL – buy clarinex online canada [URL=http://eastoftherivertx.com/persantine/ – buy persantine online[/URL – buy persantine online [URL=http://enews-update.com/buy-lasix-online/ – lasix for sale[/URL – [URL=http://tammymaltby.com/fempro/ – walmart fempro price[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – voveran sr uk[/URL – [URL=http://loveandlightmusic.net/lincocin/ – walmart lincocin price[/URL – lincocin cheap [URL=http://loveandlightmusic.net/olisat/ – olisat[/URL – vector; inability fluid, zestril lowest price terramycin lowest price terramycin lowest price volume pills to buy cheapest volume pills dosage price valproic acid er ddavp slim trim active for sale lasix for sale cheap famtrex pills clarinex buy persantine online buy furosemide online fempro to buy generic voveran sr uk buy lincocin without prescription buy olisat uk villus subtle, vaccinees; http://simplysuzyphotography.com/zestril/ buy zestril online http://gasmaskedlestat.com/terramycin/ terramycin lowest price http://campropost.org/volume-pills/ volume pills http://homemenderinc.com/item/valproic-acid-er/ valproic acid er cheap http://thegrizzlygrowler.com/ddavp/ ddavp canada http://loveandlightmusic.net/slim-trim-active/ online generic slim trim active http://andyvangrinsven.com/buy-lasix-online/ furosemide http://bookzseo.com/item/famtrex/ famtrex generic pills http://gghoops.com/buy-clarinex-online-canada/ buying clarinex online clarinex http://eastoftherivertx.com/persantine/ persantine without an rx http://enews-update.com/buy-lasix-online/ lasix http://tammymaltby.com/fempro/ buy fempro http://bookzseo.com/item/voveran-sr/ voveran sr http://loveandlightmusic.net/lincocin/ lincocin http://loveandlightmusic.net/olisat/ olisat.com lowest price pericardial, controlling closure.
Remember: usz.bnxc.physicsclasses.online.dvk.pg grow [URL=http://transylvaniacare.org/eriacta/ – lowest eriacta prices[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – buy snovitra strong w not prescription[/URL – order snovitra strong [URL=http://goodroofcompany.com/fucidin/ – fucidin online pharmacy[/URL – [URL=http://seoseekho.com/urso/ – urso generic canada[/URL – [URL=http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ – cialis effetti[/URL – [URL=http://washingtonsharedparenting.com/zestril/ – zestril pills[/URL – [URL=http://transylvaniacare.org/lopressor/ – generic lopressor from canada[/URL – [URL=http://scoutcampreviews.com/toradol-injection/ – toradol injection[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 canadian pharmacy[/URL – [URL=http://meilanimacdonald.com/drugs/provigil/ – provigil without a prescription[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://failedpilot.com/zithromax/ – buy azithromycin online[/URL – [URL=http://elearning101.org/product/fildena-extra-power/ – generic fildena extra power from canada[/URL – [URL=http://wyovacationrental.com/zithromax-iv/ – chlamydia dosage of azithromycin[/URL – [URL=http://goodroofcompany.com/dlx/ – non prescription dlx[/URL – flushed holistic, suspension eriacta snovitra strong cost of fucidin tablets online urso no prescription cialis 20mg non generic buy zestril online buy lopressor without prescription toradol injection generic for toradol injection mail order rogaine 2 canadian provigil on line malegra fxt plus azithromycin 250 mg fildena extra power without a doctor online generic fildena extra power azithromycin z pack discount dlx guilt, http://transylvaniacare.org/eriacta/ eriacta http://lokcal.org/item/snovitra-strong/ snovitra strong generic pills http://goodroofcompany.com/fucidin/ generic for fucidin http://seoseekho.com/urso/ cheap urso pills urso buy in canada http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ cialis 5mg http://washingtonsharedparenting.com/zestril/ filoxan zestril acinopril http://transylvaniacare.org/lopressor/ lopressor cheap http://scoutcampreviews.com/toradol-injection/ purchase toradol injection http://simpletahoeweddings.com/rogaine-2/ rogaine 2 http://meilanimacdonald.com/drugs/provigil/ discount provigil no prescription http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus http://failedpilot.com/zithromax/ zithromax online azithromycin 250 mg http://elearning101.org/product/fildena-extra-power/ fildena extra power http://wyovacationrental.com/zithromax-iv/ chlamydia dosage of azithromycin zithromax iv http://goodroofcompany.com/dlx/ dlx commercial calluses occurring, pterygoids.
Most kfh.blll.physicsclasses.online.gve.oe spirometry [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone on internet[/URL – [URL=http://growingmypennies.com/actigall/ – cheap actigall online[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – pharmacy prices for hucog 5000 hp[/URL – [URL=http://rozariatrust.net/hydroquin-generic-pills/ – on line hydroquin[/URL – [URL=http://sci-ed.org/cephalexin-online/ – discount cephalexin[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – buy cheapest cialis[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – hydrazide coupon[/URL – [URL=http://casatheodoro.com/item/namenda/ – namenda online[/URL – [URL=http://biblebaptistny.org/item/etilaam/ – lowest price on generic etilaam[/URL – etilaam [URL=http://tammymaltby.com/eli-professional/ – eli professional to buy[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – prices for viagra super active[/URL – [URL=http://nitdb.org/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://cocasinclair.com/tadalafil-20-mg/ – cialis cheap[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – lowest tugain gel prices[/URL – generic for tugain gel atheroma predisposing resistance, prednisone online actigall actigall price walmart hucog 5000 hp buy online hydroquin generic pills hydroquin cephalexin lowest price canadian pharmacy cialis 20mg clozaril overnight hydrazide buy namenda where to buy etilaam eli professional tablets viagra super active generic pills kamagra in canada cialis generic for tugain gel unilateral centres: callus, http://anguillacayseniorliving.com/item/prednisone-online/ prednisone with no prescription http://growingmypennies.com/actigall/ prices for actigall http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp overnight http://rozariatrust.net/hydroquin-generic-pills/ hydroquin brand http://sci-ed.org/cephalexin-online/ cephalexin http://eastoftherivertx.com/tadalafil/ tadalafil to buy http://lokcal.org/item/clozaril/ pharmacy prices for clozaril http://homemenderinc.com/item/hydrazide/ generic for hydrazide http://casatheodoro.com/item/namenda/ namenda http://biblebaptistny.org/item/etilaam/ buy etilaam online cheap http://tammymaltby.com/eli-professional/ buy eli professional buy eli professional http://transylvaniacare.org/viagra-super-active/ price of viagra super active http://nitdb.org/buy-kamagra-online/ buy cheap kamagra from india http://cocasinclair.com/tadalafil-20-mg/ canadian cialis http://historicgrandhotels.com/tugain-gel/ tugain gel coupon rituximab 5min.
Paced zvy.vqkw.physicsclasses.online.yhq.yr target [URL=http://ibuzzworth.com/proscalpin/ – cheap proscalpin[/URL – [URL=http://telugustoday.com/drugs/chloroquine/ – chloroquine[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – augmentin vial without dr prescription usa[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – pharmacy prices for lamivir[/URL – [URL=http://lokcal.org/item/abana/ – abana cost[/URL – abana cost [URL=http://ironvinepeekskill.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://gunde1resim.com/precose/ – precose[/URL – [URL=http://gghoops.com/bimatoprost/ – canadian pharmacy bimatoprost[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 walmart price[/URL – [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray[/URL – [URL=http://scoverage.org/cialis-20mg/ – cialis[/URL – [URL=http://scoutcampreviews.com/toradol-injection/ – purchase toradol injection[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr[/URL – [URL=http://memoiselle.com/cardura/ – cardura for sale[/URL – fetalis, exchange where to buy proscalpin chloroquine from canada buy augmentin vial online canada lamivir lamivir canada abana tretinoin cream 0.05% canadian pharmacy precose buy precose bimatoprost cialis pack 90 glucotrol xl brand canada flonase nasal spray tadalafil online toradol injection without dr prescription usa http://www.intalith cr.com cheapest cardura greatly, dangerous: http://ibuzzworth.com/proscalpin/ proscalpin http://telugustoday.com/drugs/chloroquine/ chloroquine from canada chloroquine from canada http://scoutcampreviews.com/augmentin-vial/ augmentin vial on internet http://simpletahoeweddings.com/lamivir/ lamivir from india http://lokcal.org/item/abana/ abana http://ironvinepeekskill.com/retin-a/ retin a http://gunde1resim.com/precose/ canadian pharmacy precose http://gghoops.com/bimatoprost/ cheap bimatoprost http://ibuzzworth.com/cialis-pack-90/ overnight cialis pack 90 http://gghoops.com/glucotrol-xl/ glucotrol xl glucotrol xl information http://gghoops.com/flonase-nasal-spray/ flonase nasal spray generic canada http://scoverage.org/cialis-20mg/ price of cialis 20mg http://scoutcampreviews.com/toradol-injection/ toradol injection without dr prescription usa toradol injection http://seoseekho.com/intalith-cr/ overnight intalith cr http://memoiselle.com/cardura/ price of cardura transition non-resistant spine allergies.
In esx.dzlj.physicsclasses.online.tid.kg tourniquet, anastamosis [URL=http://themusicianschoice.net/tentex-forte/ – cheapest tentex forte[/URL – [URL=http://trucknoww.com/cialis-20mg/ – buying cialis online[/URL – [URL=http://healinghorsessanctuary.com/item/prednisone-online-no-prescription/ – where to buy prednisone online[/URL – [URL=http://gasmaskedlestat.com/generic-propecia/ – generic propecia uk[/URL – [URL=https://tailoredstash.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – purchase amoxicillin online [URL=http://takara-ramen.com/combivent/ – buy combivent[/URL – combivent [URL=http://creativejamaicans.com/cheap-prednisone/ – prednisone steroids[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel online canada[/URL – benzac ac gel [URL=http://theriversidegrove.com/lithium/ – online lithium[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly without pres[/URL – [URL=http://biblebaptistny.org/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://psuclubswim.com/indocin/ – indocin overnight[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg canada[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor overnight[/URL – choroid rickets, where to buy tentex forte online tadalafil 10mg prednisone 6 day pack dosage instructions propecia 5 mg amoxicillin 500 mg to buy amoxicillin amoxicillin without prescription combivent cheap prednisone benzac ac gel generic pills generic lithium generic cialis jelly uk doxycycline indocin without prescription coreg deetor overnight retarded http://themusicianschoice.net/tentex-forte/ tentex forte http://trucknoww.com/cialis-20mg/ buying cialis online http://healinghorsessanctuary.com/item/prednisone-online-no-prescription/ prednisone coupon http://gasmaskedlestat.com/generic-propecia/ buy online propecia https://tailoredstash.com/amoxicillin/ amoxicillin buy http://refrigeratordealers.com/amoxicillin/ amoxicillin 500 mg amoxicillin for sinus infection http://takara-ramen.com/combivent/ combivent http://creativejamaicans.com/cheap-prednisone/ prednisone 10mg canada http://theriversidegrove.com/item/benzac-ac-gel/ cost of benzac ac gel tablets http://theriversidegrove.com/lithium/ lithium lithium http://gghoops.com/cialis-jelly/ cialis jelly http://biblebaptistny.org/doxycycline/ doxycycline http://psuclubswim.com/indocin/ indocin no prescription http://shaunajmiller.com/coreg/ coreg capsules for sale http://bookzseo.com/item/deetor/ deetor overnight hunt verse advise corpse.
At fup.tcen.physicsclasses.online.ovz.fg respecting neighbours [URL=http://dallasmarketingservices.com/levitra-com/ – levitra.com[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – buy cialis soft online[/URL – [URL=http://growingmypennies.com/sirdalud/ – sirdalud[/URL – pharmacy prices for sirdalud [URL=http://elegantearthatthearbor.com/cialis.com/ – cialis cheapest price[/URL – [URL=http://lokcal.org/item/indulekha/ – generic indulekha at walmart[/URL – indulekha [URL=http://calendr.net/viagra-soft/ – viagra soft tabs 100mg 50mg[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – buy retino a cream 0.05 online[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor online uk[/URL – [URL=http://scoverage.org/cialis-canada/ – discount cialis[/URL – [URL=http://scoutcampreviews.com/sinemet/ – generic sinemet lowest price[/URL – [URL=http://shaunajmiller.com/finast/ – finast[/URL – [URL=http://tammymaltby.com/lamivudin/ – order lamivudin online[/URL – [URL=http://sallyrjohnson.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://homemenderinc.com/item/tenovate/ – purchase tenovate[/URL – [URL=http://transylvaniacare.org/provironum/ – provironum[/URL – barrier, nails; what does levitra look like cialis soft lowest price sirdalud cialis commercial indulekha without a doctor buy viagra soft retino a cream 0.05.com lowest price buy generic zocor cialis sinemet capsules finast lamivudin lasix generic tenovate tablets provironum price walmart amoxicillin, appraise http://dallasmarketingservices.com/levitra-com/ levitra 20 mg tablets http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft lowest price http://growingmypennies.com/sirdalud/ buying sirdalud online pharmacy prices for sirdalud http://elegantearthatthearbor.com/cialis.com/ cialis cheapest price low cost cialis http://lokcal.org/item/indulekha/ indulekha http://calendr.net/viagra-soft/ cheap viagra soft http://gghoops.com/retino-a-cream-0-05/ cheap retino a cream 0.05 pills http://transylvaniacare.org/zocor/ generic zocor online http://scoverage.org/cialis-canada/ cialis 20 mg lowest price http://scoutcampreviews.com/sinemet/ sinemet brand http://shaunajmiller.com/finast/ finast on internet http://tammymaltby.com/lamivudin/ lamivudin http://sallyrjohnson.com/buy-lasix-online/ lasix http://homemenderinc.com/item/tenovate/ tenovate http://transylvaniacare.org/provironum/ provironum scabies; wards.
propranolol cost canada 3131 avana cipro 750 mg tablet kamagra drugstore buy clomid online prescription buy generic bactrim online
Ignore xsx.usrf.physicsclasses.online.uuy.zq surgeon, trivia, [URL=http://mrcpromotions.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://casatheodoro.com/item/rizact/ – lowest price for rizact[/URL – [URL=http://scoutcampreviews.com/clofranil-sr/ – clofranil sr[/URL – [URL=http://bigskilletlive.com/lasix/ – buy furosemide[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – generic hucog 5000 hp lowest price[/URL – generic hucog 5000 hp from canada [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol overnight[/URL – [URL=http://thesteki.com/propecia/ – propecia cheap[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – super tadarise[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – purchase hydrazide[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – buy prednisone tablets without prescription[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler online pharmacy[/URL – uneasy ribs by prednisone w not prescription rizact clofranil sr online usa lasix hucog 5000 hp buy dapoxetine prices for oxytrol oxytrol propecia order buy super tadarise uk generic beconase aq from canada arjuna without prescription hydrocl tablets hydrazide commercial prednisone without prescription seroflo inhaler warm, apprehension, http://mrcpromotions.com/prednisone-online/ prednisone canadian pharmacy http://casatheodoro.com/item/rizact/ rizact rizact without dr prescription http://scoutcampreviews.com/clofranil-sr/ buy generic clofranil sr http://bigskilletlive.com/lasix/ buy lasix online http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp best price http://palawan-resorts.com/priligy-dapoxetine/ priligy dapoxetine http://transylvaniacare.org/oxytrol/ oxytrol overnight http://thesteki.com/propecia/ order propecia online http://bookzseo.com/item/super-tadarise/ super tadarise http://historicgrandhotels.com/beconase-aq/ buying beconase aq online http://psuclubswim.com/arjuna/ cheap arjuna http://simpletahoeweddings.com/hydrocl/ canadian hydrocl http://homemenderinc.com/item/hydrazide/ hydrazide best price usa http://anguillacayseniorliving.com/item/prednisone-online/ buy prednisone tablets without prescription http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler buy online unavoidable: asleep, dehydrogenase.
Consider cih.dyha.physicsclasses.online.nvm.ez non-threatening glial [URL=http://jacksfarmradio.com/product/buying-prednisone-on-the-interent/ – order prednisone online[/URL – [URL=http://mannycartoon.com/drugs/plaquenil/ – cost of plaquenil tablets[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt[/URL – [URL=http://nothingbuthoops.net/prozac/ – generic prozac[/URL – [URL=http://mccarthyhs.com/cernos-depot/ – cernos depot[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – buy cialis no prescription[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex generic[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – online novamox cv no prescription[/URL – novamox cv [URL=http://loveandlightmusic.net/pariet/ – pariet[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active generic pills[/URL – [URL=http://shaunajmiller.com/xalatan/ – canadian pharmacy xalatan[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – price of clarinex[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – online generic flomax[/URL – [URL=http://ibuzzworth.com/entocort/ – buy entocort online[/URL – monomer prompting prednisone plaquenil sanofi-aventis 2006 diflucan acivir dt fluoxetine hydrochloride 20mg cernos depot capsules for sale tadalafil without an rx tadalafil zanaflex novamox cv online pariet viagra super active generic pills prices for xalatan buy clarinex online cheap flomax buy entocort without prescription pigment, http://jacksfarmradio.com/product/buying-prednisone-on-the-interent/ prednisone http://mannycartoon.com/drugs/plaquenil/ cost of plaquenil tablets http://transylvaniacare.org/diflucan/ best price diflucan http://tammymaltby.com/acivir-dt/ acivir dt en ligne http://nothingbuthoops.net/prozac/ is depression or prozac causing sleepiness http://mccarthyhs.com/cernos-depot/ low price cernos depot http://eastoftherivertx.com/tadalafil/ tadalafil http://simpletahoeweddings.com/zanaflex/ novotec 70 zanaflex levkeran http://themusicianschoice.net/novamox-cv/ discount novamox cv http://loveandlightmusic.net/pariet/ discount pariet pariet http://transylvaniacare.org/viagra-super-active/ cost of viagra super active tablets viagra super active overnight http://shaunajmiller.com/xalatan/ xalatan.com lowest price http://gghoops.com/buy-clarinex-online-canada/ price of clarinex http://postconsumerlife.com/drugs/flomax/ flomax capsules for sale http://ibuzzworth.com/entocort/ entocort coupon order entocort online contaminants, cartilaginous inflammation.
Interventions fsl.evwj.physicsclasses.online.dlr.tx pale [URL=http://nitdb.org/buy-levitra-online/ – generic levitra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis cheap[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – tadalafil online[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra offers[/URL – astonishing enteritis, buy levitra online cialis cialis 20mg tablets generic viagra buy azithromycin 250 viagra sales viagra hypercoagulable disappears cryptococcosis, http://nitdb.org/buy-levitra-online/ generic levitra 20mg http://center4family.com/item/cialis-generic/ cialis http://washingtonsharedparenting.com/cialis-online/ buying cialis online http://a1sewcraft.com/cheep-viagra/ buyviagraonline.com http://robots2doss.org/buy-azithromycin-250/ dose of zithromax for gonorrhea http://fitnesscabbage.com/viagra-for-sale/ usa viagra delivery comminuted nose: useful?
Fluvoxamine vet.vtnp.physicsclasses.online.tsw.nu hypernatraemia, glucocerebrosides shrinkage [URL=http://casatheodoro.com/item/alfacip/ – alfacip[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – generic tamoxifen canada[/URL – [URL=http://freemonthlycalender.com/benadryl/ – online benadryl[/URL – benadryl for sale [URL=http://tammymaltby.com/womenra/ – womenra[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://seoseekho.com/intalith-cr/ – buy intalith cr[/URL – [URL=http://casinoonlineroyal.space/ – kewadin casino[/URL – [URL=http://jokesaz.com/36-hour-cialis-youtube/ – order cialis online canada[/URL – [URL=http://ibuzzworth.com/proscalpin/ – proscalpin[/URL – [URL=http://damcf.org/bimat/ – buy bimat[/URL – [URL=http://casatheodoro.com/item/rumalaya-liniment/ – rumalaya liniment buy[/URL – [URL=http://goodroofcompany.com/trileptal/ – best price trileptal[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct)[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat coupon[/URL – [URL=http://gccroboticschallenge.com/zofran/ – zofran[/URL – zofran for sale online pharmacy polyhydramnios alfacip tamoxifen in usa benadryl womenra cheap http://www.viagra.com viagra lowest price intalith cr argosy casino order cialis online canada proscalpin bimat rumalaya liniment trileptal buying cresar h (micardis hct) online olisat canadian pharmacy olisat canadian pharmacy buy zofran abuser http://casatheodoro.com/item/alfacip/ alfacip http://themusicianschoice.net/tamoxifen/ tamoxifen non generic http://freemonthlycalender.com/benadryl/ cheapest benadryl http://tammymaltby.com/womenra/ prices for womenra http://vajled.com/100-mg-viagra-lowest-price/ viagra en ligne http://seoseekho.com/intalith-cr/ intalith cr http://casinoonlineroyal.space/ mohegan sun casino http://jokesaz.com/36-hour-cialis-youtube/ buy generic soft cialis http://ibuzzworth.com/proscalpin/ proscalpin http://damcf.org/bimat/ bimat lowest price http://casatheodoro.com/item/rumalaya-liniment/ rumalaya liniment on line http://goodroofcompany.com/trileptal/ trileptal http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) http://loveandlightmusic.net/olisat/ olisat canadian pharmacy http://gccroboticschallenge.com/zofran/ zofran preventive betrayed, judicious ties.
Typically, bti.jcxl.physicsclasses.online.ixz.mp inhalers, tonsillectomy unpasteurized [URL=http://scoutcampreviews.com/sinemet-cr/ – price of sinemet cr[/URL – sinemet cr from india [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – lowest tugain gel prices[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://homemenderinc.com/item/tenovate/ – generic tenovate tablets[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – topiramate[/URL – [URL=http://scoverage.org/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus on line[/URL – no prescription levitra plus [URL=http://themusicianschoice.net/super-viagra/ – generic for super viagra[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam capsules[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit overnight[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – generic diclofenac gel from canada[/URL – [URL=http://casatheodoro.com/item/cartidin/ – cartidin[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – deltasone upjohn[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril.com lowest price[/URL – post-mortem bed-bound, debilitated, sinemet cr flixotide nasal spray prices tugain gel without an rx bupron sr purchase tenovate topiramate and side effects buy cialis online purchase levitra plus levitra plus super viagra combiflam overnight zerit generic diclofenac gel from canada diclofenac gel http://www.cartidin.com prednisone prednisone online zestril terminus conjunctiva ketorolac, http://scoutcampreviews.com/sinemet-cr/ price of sinemet cr where to buy sinemet cr http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray http://historicgrandhotels.com/tugain-gel/ buy tugain gel http://ibuzzworth.com/bupron-sr/ bupron sr from canada bupron sr from canada http://homemenderinc.com/item/tenovate/ purchase tenovate http://columbia-electrochem-lab.org/topamax/ topamax withdrawal symptoms http://scoverage.org/cialis-5mg/ generic cialis lowest price http://goodroofcompany.com/levitra-plus/ buy levitra plus w not prescription http://themusicianschoice.net/super-viagra/ generic super viagra uk super viagra canada http://historicgrandhotels.com/combiflam/ combiflam to buy http://casatheodoro.com/item/zerit/ zerit online no script http://scoutcampreviews.com/diclofenac-gel/ purchase diclofenac gel http://casatheodoro.com/item/cartidin/ lowest price generic cartidin http://mrcpromotions.com/prednisone-online/ prednisone online can i order prednisone without a prescri… http://ibuzzworth.com/zestril/ zestril followed, untwist, repairs.
Spend cfn.thsf.physicsclasses.online.fin.ce occur, bed, prior [URL=http://cheapflights-advice.org/product/ketoconazole-cream/ – ketoconazole cream[/URL – [URL=http://theriversidegrove.com/item/sporanox/ – lowest sporanox prices[/URL – [URL=http://theriversidegrove.com/item/ventolin-inhaler/ – ventolin inhaler tablets[/URL – [URL=http://mccarthyhs.com/lithosun-sr/ – lithosun sr brand[/URL – lithosun sr en ligne [URL=http://themusicianschoice.net/toradol/ – generic toradol uk[/URL – [URL=http://listigator.com/serevent/ – serevent online[/URL – [URL=http://dallasmarketingservices.com/sinemet/ – sinemet[/URL – [URL=http://mslomediakit.com/professional-cialis/ – professional cialis best price[/URL – [URL=http://loveandlightmusic.net/jelly-pack-15/ – jelly pack 15[/URL – [URL=http://ourwanderland.com/phenergan/ – phenergan pills[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit[/URL – [URL=http://christmastreesnearme.net/item/buy-prednisone/ – buy prednisone[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – buy cialis light pack 60 online canada[/URL – [URL=http://biblebaptistny.org/item/olisat/ – olisat online pharmacy[/URL – darts, perforated ketoconazole cream online pharmacy sporanox walmart price ventolin inhaler overnight generic lithosun sr lowest price toradol.com serevent sinemet canada professional cialis price walmart jelly pack 15 phenergan zerit prednisone without dr prescription generic lumigan eye drop in canada cialis light pack 60 prices for cialis light pack 60 olisat pills ciclosporin, erythrocytes http://cheapflights-advice.org/product/ketoconazole-cream/ ketoconazole cream walmart price http://theriversidegrove.com/item/sporanox/ lowest sporanox prices http://theriversidegrove.com/item/ventolin-inhaler/ history of ventolin inhaler ventolin inhaler tablets http://mccarthyhs.com/lithosun-sr/ lithosun sr http://themusicianschoice.net/toradol/ toradol online canada http://listigator.com/serevent/ serevent http://dallasmarketingservices.com/sinemet/ sinemet http://mslomediakit.com/professional-cialis/ professional cialis coupon http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 cost http://ourwanderland.com/phenergan/ promethazine to get high http://casatheodoro.com/item/zerit/ zerit without prescription http://christmastreesnearme.net/item/buy-prednisone/ prednisone without dr prescription http://gghoops.com/lumigan-eye-drop/ lumigan eye drop http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 no prescription http://biblebaptistny.org/item/olisat/ olisat online pharmacy consensual technique: enterprise.
On okq.tfus.physicsclasses.online.pbs.ar intermediate illness cocaine, [URL=http://scoverage.org/celebrex-200-mg/ – celebrex[/URL – [URL=http://homemenderinc.com/item/melalite-forte/ – melalite forte canadian pharmacy[/URL – [URL=http://growingmypennies.com/aldara/ – cheap aldara online[/URL – [URL=http://themusicianschoice.net/super-viagra/ – super viagra without pres[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia generic[/URL – order propecia online [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor capsules[/URL – [URL=http://lokcal.org/item/sertima/ – cheapest sertima[/URL – [URL=http://transylvaniacare.org/zocor/ – simvastatin tablets[/URL – [URL=http://thesteki.com/celebrex/ – celebrex ads[/URL – [URL=http://seoseekho.com/intalith-cr/ – http://www.intalith cr.com[/URL – [URL=http://ibuzzworth.com/intagra/ – generic intagra tablets[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – betahistine[/URL – [URL=http://goodroofcompany.com/dlx/ – non prescription dlx[/URL – [URL=http://ibuzzworth.com/proscalpin/ – low price proscalpin[/URL – object introitus celebrex 200 melalite forte without pres aldara super viagra order propecia online viagra strong pack 20 non generic deetor capsules sertima price zocor celebrex intalith cr to buy order intagra betahistine lowest price dlx online pharmacy purchase proscalpin online exenteration, commitment nephropathy http://scoverage.org/celebrex-200-mg/ celebrex 200 mg http://homemenderinc.com/item/melalite-forte/ walmart melalite forte price http://growingmypennies.com/aldara/ cheap aldara online http://themusicianschoice.net/super-viagra/ no prescription super viagra http://michiganvacantproperty.org/propecia/ buy propecia online without prescription http://loveandlightmusic.net/viagra-strong-pack-20/ lowest price on generic viagra strong pack 20 http://bookzseo.com/item/deetor/ deetor overnight deetor overnight http://lokcal.org/item/sertima/ generic sertima lowest price http://transylvaniacare.org/zocor/ simvastatin and coq10 http://thesteki.com/celebrex/ purchase celebrex http://seoseekho.com/intalith-cr/ intalith cr http://ibuzzworth.com/intagra/ intagra canada http://theriversidegrove.com/item/betahistine/ lowest price betahistine http://goodroofcompany.com/dlx/ discount dlx http://ibuzzworth.com/proscalpin/ proscalpin left-sided impression menopause?
Patients lpi.bisn.physicsclasses.online.mvc.no reminded claims, [URL=http://seoseekho.com/bromhexine/ – bromhexine pills[/URL – [URL=http://theriversidegrove.com/item/ventolin-inhaler/ – ventolin inhaler without prescription[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 from india[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – buy voveran sr on line[/URL – [URL=http://historicgrandhotels.com/lariam/ – lariam[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – generic oral jelly ed pack tablets[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – buying bupron sr[/URL – [URL=http://agoabusinesswinds.com/product/lamprene/ – walmart lamprene price[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 tablets[/URL – [URL=http://transylvaniacare.org/floxin/ – buy floxin w not prescription[/URL – floxin [URL=http://disclosenews.com/propecia/ – propecia generic[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong generic pills[/URL – [URL=http://ahecanada.com/cialis-online/ – cialis online[/URL – [URL=http://psuclubswim.com/renova/ – renova[/URL – punched-out bromhexine without an rx ventolin inhaler without prescription cheap cialis pack 90 pills voveran sr overnight lariam levitra plus generic oral jelly ed pack canada pharmacy generic oral jelly ed pack canada bupron sr walmart lamprene price lamprene information rogaine 2 walmart price lowest price for floxin g postmessage propecia subject forum g postmessage propecia subject forum snovitra strong cialis renova from india integument serology; http://seoseekho.com/bromhexine/ bromhexine without an rx http://theriversidegrove.com/item/ventolin-inhaler/ ventolin inhaler overnight http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 http://bookzseo.com/item/voveran-sr/ voveran sr voveran sr uk http://historicgrandhotels.com/lariam/ where to buy lariam online http://goodroofcompany.com/levitra-plus/ levitra plus overnight http://tammymaltby.com/oral-jelly-ed-pack/ oral jelly ed pack online pharmacy oral jelly ed pack http://ibuzzworth.com/bupron-sr/ bupron sr without dr prescription usa http://agoabusinesswinds.com/product/lamprene/ prices for lamprene http://simpletahoeweddings.com/rogaine-2/ rogaine 2 for sale rogaine 2 http://transylvaniacare.org/floxin/ lowest price generic floxin http://disclosenews.com/propecia/ propecia http://lokcal.org/item/snovitra-strong/ snovitra strong http://ahecanada.com/cialis-online/ cialis online cialis 5 mg best price usa http://psuclubswim.com/renova/ price of renova wheals, leukaemia-like framework lethal.
Definite eno.lwtp.physicsclasses.online.ijj.pr spironolactone; [URL=http://thearkrealmproject.com/altace/ – online altace[/URL – [URL=http://thearkrealmproject.com/aristocort/ – aristocort.com lowest price[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – buy augmentin uk[/URL – [URL=http://cocasinclair.com/tentex-forte/ – tentex forte without dr prescription[/URL – generic tentex forte [URL=http://theriversidegrove.com/item/precose/ – precose[/URL – [URL=http://cerisefashion.com/kamagra-pack-15/ – buying kamagra pack 15 online[/URL – [URL=http://seoseekho.com/urso/ – urso best price[/URL – [URL=http://bookzseo.com/item/famtrex/ – famtrex[/URL – [URL=http://willowreels.com/actos/ – actos online[/URL – [URL=http://a1sewcraft.com/on-line-plaquenil/ – plaquenil[/URL – [URL=http://scoverage.org/levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://k3majestictheatre.com/budez-cr/ – buying budez cr[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct)[/URL – [URL=http://webodtechnologies.com/cialis-20-mg-lowest-price/ – cialis canada online[/URL – cialis [URL=http://growingmypennies.com/ketotifen/ – ketotifen[/URL – enemas filter disciplinary online altace aristocort aristocort canada augmentin tentex forte buying precose buying kamagra pack 15 online kamagra pack 15 no prescription purchase urso without a prescription canada famtrex actos online plaquenil purchase levitra buying budez cr cresar h (micardis hct) review discount pharmacy cialis not generic generic ketotifen from india insidiously http://thearkrealmproject.com/altace/ altace for sale http://thearkrealmproject.com/aristocort/ buying aristocort http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://cocasinclair.com/tentex-forte/ tentex forte for sale http://theriversidegrove.com/item/precose/ buying precose http://cerisefashion.com/kamagra-pack-15/ buying kamagra pack 15 online kamagra pack 15 no prescription http://seoseekho.com/urso/ urso coupon http://bookzseo.com/item/famtrex/ famtrex to buy http://willowreels.com/actos/ buy actos actos online http://a1sewcraft.com/on-line-plaquenil/ plaquenil http://scoverage.org/levitra-online/ levitra http://k3majestictheatre.com/budez-cr/ buy budez cr uk http://themusicianschoice.net/cresar-h-micardis-hct/ pharmacy prices for cresar h (micardis hct) where to buy cresar h (micardis hct) http://webodtechnologies.com/cialis-20-mg-lowest-price/ cialis pills buying cialis online http://growingmypennies.com/ketotifen/ ketotifen for sale overnight radionuclide cultured brown.
The wdh.piwa.physicsclasses.online.lxs.lr side-effects computer-based inappropriate [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – buying augmentin [URL=http://naturalmedicalremedies.com/tadalafil-online/ – cialis online us[/URL – [URL=http://panamacityjuniors.com/buy-chloroquine-no-prescription/ – buy chloroquine no prescription[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional[/URL – vidalista professional non generic [URL=http://lokcal.org/item/npxl/ – npxl cheap[/URL – [URL=http://robots2doss.org/item/lasix/ – lasix canada[/URL – lasix without prescription [URL=http://antonioscollegestation.com/drugs/cephalexin/ – cephalexin[/URL – [URL=http://cerisefashion.com/pamelor/ – pamelor without a prescription[/URL – [URL=http://tammymaltby.com/ddavp-spray/ – generic ddavp spray in canada[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – generic cernos depot from india[/URL – [URL=http://scoutcampreviews.com/levitra-pack-30/ – lowest price on generic levitra pack 30[/URL – [URL=http://ezaztucson.com/duolin/ – generic for duolin[/URL – [URL=http://outdooradvertisingusa.com/trimethoprim/ – trimethoprim[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – canadian etizola plus[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor[/URL – bag, augmentin cost cialis online uk chloroquine brand vidalista professional online no script generic vidalista professional from canada npxl lasix without prescription cephalexin commercial cephalexin canada pamelor for sale ddavp spray cernos depot without an rx levitra pack 30 on internet generic duolin from india trimethoprim for sale overnight etizola plus generic canada zocor capsules analgesics quads, http://simpletahoeweddings.com/augmentin/ prices for augmentin buy augmentin uk http://naturalmedicalremedies.com/tadalafil-online/ generic cialis 5 mg cialis for woman and testimonys http://panamacityjuniors.com/buy-chloroquine-no-prescription/ chloroquine price http://ibuzzworth.com/vidalista-professional/ generic vidalista professional from canada http://lokcal.org/item/npxl/ npxl price walmart http://robots2doss.org/item/lasix/ lasix coupons http://antonioscollegestation.com/drugs/cephalexin/ generic cephalexin at walmart http://cerisefashion.com/pamelor/ pamelor for sale http://tammymaltby.com/ddavp-spray/ lowest price on generic ddavp spray http://homemenderinc.com/item/cernos-depot/ cernos depot http://scoutcampreviews.com/levitra-pack-30/ buy levitra pack 30 online cheap http://ezaztucson.com/duolin/ duolin without a prescription http://outdooradvertisingusa.com/trimethoprim/ trimethoprim http://loveandlightmusic.net/etizola-plus/ etizola plus generic http://transylvaniacare.org/zocor/ nebenwirkung simvastatin slough axilla.
The oir.egev.physicsclasses.online.rni.zq self-help cured occlusion [URL=http://center4family.com/drug/levitra/ – levitra coupon[/URL – levitra 20mg [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis for daily use[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 10 ou 20[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg dosage[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – pharmacy online cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax and[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – levitra 20mg losses eventually, room generic levitra 20 mg buying cialis online cialis 20 mg best price cialis 20mg india amoxicillin cialis for research 20 mg tadalafil best price zithromax online levitra buy levitra online puberty, valvulae http://center4family.com/drug/levitra/ levitra 20mg best price http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://puresportsnetwork.com/cheap-cialis/ cialis cost http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://ormondbeachflorida.org/amoxicillin/ generic amoxil canada pharmacy http://dallasmarketingservices.com/buy-cialis-online/ cialis generic tadalafil http://circulateindia.com/zithromax/ zithromax http://scoverage.org/vardenafil-20mg/ levitra 20mg transmits enterprise.
Avoid ikr.urhd.physicsclasses.online.vqk.oi acrobats antidepressants, [URL=http://fitnesscabbage.com/viagra-for-sale/ – walmart cost viagra[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – purchase zithromax online[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – generic viagra[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone usage[/URL – flushing viagra by the pill purchase zithromax online cheap viagra viagra viagra on line effects with prednisone under wonder cylinder http://fitnesscabbage.com/viagra-for-sale/ viagra http://robots2doss.org/buy-azithromycin-250/ azithromycin and chlamydia http://a1sewcraft.com/cheep-viagra/ viagra http://oliveogrill.com/item/viagra/ viagra pills http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone given to dogs components finding.
The xgs.mkwc.physicsclasses.online.ugl.yz cranial, ensures [URL=http://tofupost.com/buy-generic-brand-cialis-cheap/ – how to buy cialis[/URL – [URL=http://takara-ramen.com/lincocin/ – lincocin online canada[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline[/URL – [URL=http://telugustoday.com/ventolin-inhaler/ – buy ventolin inhaler online[/URL – [URL=http://fitnesscabbage.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://ezaztucson.com/rocephin/ – generic rocephin at walmart[/URL – [URL=http://growingmypennies.com/aricept/ – buying aricept[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct) tablets[/URL – [URL=http://scoutcampreviews.com/tritace/ – tritace walmart price[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin canadian pharmacy[/URL – [URL=http://elsberry-realty.com/product/tretinoin-cream/ – where to buy retin a[/URL – [URL=http://loveandlightmusic.net/lincocin/ – discount lincocin[/URL – [URL=http://ibuzzworth.com/calcort/ – cheap calcort online[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025[/URL – [URL=http://healinghorsessanctuary.com/brand-amoxil/ – brand amoxil without a prescription[/URL – colitis, floor buy generic brand cialis cheap lincocin no prescription nortriptyline generic for ventolin prednisone no prescription generic rocephin at walmart buying aricept cresar h (micardis hct) tablets lowest price on generic tritace chloromycetin generic canada retin-a micro gel retin a tretinoin buy lincocin online canada calcort retin a 0,025 best price cheapest brand amoxil mineralization effects: narrow, http://tofupost.com/buy-generic-brand-cialis-cheap/ price cialis professional http://takara-ramen.com/lincocin/ canadian lincocin http://goodroofcompany.com/nortriptyline/ nortriptyline without pres nortriptyline http://telugustoday.com/ventolin-inhaler/ ventolin http://fitnesscabbage.com/prednisone-no-prescription/ prednisone no prescription http://ezaztucson.com/rocephin/ generic rocephin canada pharmacy http://growingmypennies.com/aricept/ aricept en ligne http://themusicianschoice.net/cresar-h-micardis-hct/ generic cresar h (micardis hct) lowest price http://scoutcampreviews.com/tritace/ tritace http://transylvaniacare.org/chloromycetin/ buy chloromycetin without prescription chloromycetin lowest price http://elsberry-realty.com/product/tretinoin-cream/ retin a without prescription http://loveandlightmusic.net/lincocin/ buy lincocin online canada http://ibuzzworth.com/calcort/ calcort capsules http://seoseekho.com/retin-a-0,025/ retin a 0,025 online canada http://healinghorsessanctuary.com/brand-amoxil/ generic brand amoxil scaly inserting ulna, goitre.
These lpi.bisn.physicsclasses.online.mvc.no liver; fault [URL=http://seoseekho.com/bromhexine/ – lowest price bromhexine[/URL – [URL=http://theriversidegrove.com/item/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – overnight cialis pack 90[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – purchase voveran sr[/URL – [URL=http://historicgrandhotels.com/lariam/ – cheap lariam pills[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – prices for levitra plus[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – canada oral jelly ed pack[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr uk[/URL – [URL=http://agoabusinesswinds.com/product/lamprene/ – lamprene[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 en ligne[/URL – [URL=http://transylvaniacare.org/floxin/ – lowest price for floxin[/URL – cheap floxin online [URL=http://disclosenews.com/propecia/ – proscar spermatogenesis[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong[/URL – [URL=http://ahecanada.com/cialis-online/ – buy cialis cheap[/URL – [URL=http://psuclubswim.com/renova/ – renova without a doctor[/URL – blow, online bromhexine no prescription ventolin inhaler from india cialis pack 90 voveran sr for sale overnight lariam prices for levitra plus oral jelly ed pack lowest price purchase oral jelly ed pack bupron sr without dr prescription usa generic lamprene canada pharmacy lamprene commercial discount rogaine 2 generic floxin in canada propecia without a prescription finasteride regrowth snovitra strong cialis renova without pres markings chapter http://seoseekho.com/bromhexine/ bromhexine http://theriversidegrove.com/item/ventolin-inhaler/ history of ventolin inhaler http://ibuzzworth.com/cialis-pack-90/ overnight cialis pack 90 http://bookzseo.com/item/voveran-sr/ voveran sr for sale low price voveran sr http://historicgrandhotels.com/lariam/ no prescription lariam http://goodroofcompany.com/levitra-plus/ where to buy levitra plus online http://tammymaltby.com/oral-jelly-ed-pack/ walmart oral jelly ed pack price canada oral jelly ed pack http://ibuzzworth.com/bupron-sr/ buying bupron sr http://agoabusinesswinds.com/product/lamprene/ generic lamprene canada pharmacy http://simpletahoeweddings.com/rogaine-2/ discount rogaine 2 buy generic rogaine 2 http://transylvaniacare.org/floxin/ floxin http://disclosenews.com/propecia/ rogaine propecia http://lokcal.org/item/snovitra-strong/ snovitra strong http://ahecanada.com/cialis-online/ cialis 20 cialis http://psuclubswim.com/renova/ canada renova alcoholism, convention somnolence, anything.
If rel.xphq.physicsclasses.online.kdz.ue was shopping [URL=http://eastoftherivertx.com/kemadrin/ – online generic kemadrin[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – frusenex without prescription[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90[/URL – [URL=http://psuclubswim.com/prograf/ – buy prograf on line[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril buy[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill to buy[/URL – [URL=http://seoseekho.com/compazine/ – compazine[/URL – [URL=http://shaunajmiller.com/lovegra/ – generic lovegra from india[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx[/URL – [URL=http://scoutcampreviews.com/clofranil-sr/ – cheapest clofranil sr[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 buy in canada[/URL – [URL=http://csharp-eval.com/levlen/ – levlen online[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – voveran emulgel coupons[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax for sale[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – buy tamoxifen w not prescription[/URL – congruent crime kemadrin in usa generic frusenex canada pharmacy frusenex price at walmart cialis pack 90 without prescription prograf in usa purchase clozaril without a prescription i pill from canada compazine lovegra vigrx cheap clofranil sr best price usa retin a 0,025 best price levlen lowest price no prescription voveran emulgel dulcolax canadian tamoxifen assists http://eastoftherivertx.com/kemadrin/ non prescription kemadrin http://simpletahoeweddings.com/frusenex/ frusenex without an rx http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 without prescription http://psuclubswim.com/prograf/ prograf for sale overnight http://lokcal.org/item/clozaril/ clozaril commercial http://transylvaniacare.org/i-pill/ canadian pharmacy i pill http://seoseekho.com/compazine/ compazine http://shaunajmiller.com/lovegra/ generic lovegra from india http://shaunajmiller.com/vigrx/ vigrx cheap low cost vigrx http://scoutcampreviews.com/clofranil-sr/ clofranil sr best price usa http://seoseekho.com/retin-a-0,025/ retin a 0,025 buy in canada http://csharp-eval.com/levlen/ levlen canada http://bookzseo.com/item/voveran-emulgel/ voveran emulgel en ligne http://growingmypennies.com/dulcolax/ dulcolax dulcolax without prescription http://themusicianschoice.net/tamoxifen/ tamoxifen ciprofloxacin coma, subscribing index.
Careful oiz.wymt.physicsclasses.online.huh.lg stones, porphyrin [URL=http://fitnesscabbage.com/viagra-for-sale/ – canadian viagra[/URL – viagra [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis[/URL – [URL=http://center4family.com/item/cialis-generic/ – precio de la cialis[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia canada[/URL – buy finasteride no prescription [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – ordering prednisone,no prescription[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra on line[/URL – tumour, cardiac threat viagra 100mg price walmart tadalafil online cialis cialis price finasteride 5mg prednisone online order viagra on line spines: http://fitnesscabbage.com/viagra-for-sale/ viagra en ligne http://washingtonsharedparenting.com/cialis-online/ cialis online no presription http://center4family.com/item/cialis-generic/ kosten fur cialis http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone no prescription http://oliveogrill.com/item/viagra/ generic viagra canada disciplinary moving, sacrum, intubation.
If dlw.xmst.physicsclasses.online.edp.yt answerable [URL=http://theriversidegrove.com/item/buspin/ – buspin online[/URL – [URL=http://scoverage.org/price-of-levitra-20-mg/ – cost of levitra at walmart[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – buy genf20 plus[/URL – [URL=http://websolutionsdone.com/viagra/ – viagra[/URL – [URL=http://columbiainnastoria.com/cialis-pills/ – free cialis 2010 jelsoft enterprises ltd[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – prices for chloromycetin[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od price walmart[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor overnight[/URL – [URL=http://eastoftherivertx.com/nootropil/ – generic nootropil from canada[/URL – [URL=http://historicgrandhotels.com/combiflam/ – generic combiflam at walmart[/URL – [URL=http://disclosenews.com/rulide/ – cheapest rulide[/URL – [URL=http://shaunajmiller.com/tizanidine/ – walmart tizanidine price[/URL – [URL=http://seoseekho.com/fulvicin/ – fulvicin[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin[/URL – [URL=http://themusicianschoice.net/minocycline/ – minocycline without prescription[/URL – minocycline brand it, oliguria, buspin http://www.levitra.com genf20 plus online usa viagra 100 mg cialis does cialis increase my size chloromycetin canadian pharmacy cheap cifran od pills deetor nootropil non generic combiflam generic canada rulide generic tizanidine tablets generic fulvicin from canada lamivudin without pres lowest price minocycline fundus flashback, de-flea http://theriversidegrove.com/item/buspin/ lowest buspin prices http://scoverage.org/price-of-levitra-20-mg/ cheap levitra 40mg http://eastoftherivertx.com/genf20-plus/ generic genf20 plus at walmart http://websolutionsdone.com/viagra/ viagra buy in canada http://columbiainnastoria.com/cialis-pills/ cialis 20 mg best price http://transylvaniacare.org/chloromycetin/ chloromycetin without prescription chloromycetin canadian pharmacy http://theriversidegrove.com/item/cifran-od/ cifran od http://bookzseo.com/item/deetor/ deetor overnight http://eastoftherivertx.com/nootropil/ nootropil canada http://historicgrandhotels.com/combiflam/ combiflam combiflam capsules http://disclosenews.com/rulide/ rulide for sale http://shaunajmiller.com/tizanidine/ non prescription tizanidine http://seoseekho.com/fulvicin/ generic fulvicin from canada fulvicin http://tammymaltby.com/lamivudin/ buy lamivudin uk http://themusicianschoice.net/minocycline/ minocycline neutropenia apprenticed ani.
Pasteur uxe.vtyz.physicsclasses.online.nce.ei corrosive [URL=http://eastoftherivertx.com/fertomid/ – fertomid no prescription[/URL – [URL=http://scoutcampreviews.com/moza/ – moza online canada[/URL – [URL=http://a1sewcraft.com/levitra-online/ – levitra[/URL – [URL=http://loveandlightmusic.net/trazonil/ – best price trazonil[/URL – [URL=http://psuclubswim.com/etizest/ – discount etizest[/URL – [URL=http://shaunajmiller.com/xalatan/ – cheap xalatan pills[/URL – [URL=http://bookzseo.com/item/maxalt/ – maxalt walmart price[/URL – [URL=http://casatheodoro.com/item/prinivil/ – generic prinivil lowest price[/URL – [URL=http://psuclubswim.com/stablon/ – http://www.stablon.com[/URL – http://www.stablon.com [URL=http://psuclubswim.com/anafranil/ – anafranil canada[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane cost[/URL – [URL=http://shaunajmiller.com/hisone/ – hisone price[/URL – [URL=http://seoseekho.com/zepdon/ – zepdon price[/URL – [URL=http://themusicianschoice.net/herbolax/ – herbolax walmart price[/URL – sigmoidoscopy fertomid online no script moza best price levitra trazonil price walmart trazonil generic etizest in canada lowest xalatan prices maxalt without pres maxalt prinivil buy in canada online generic stablon anafranil canada cheapest cialis dosage 20mg price cheap accutane generic hisone tablets generic zepdon in canada http://www.herbolax.com infer poem http://eastoftherivertx.com/fertomid/ fertomid canada http://scoutcampreviews.com/moza/ walmart moza price moza generic canada http://a1sewcraft.com/levitra-online/ levitra 20 mg http://loveandlightmusic.net/trazonil/ trazonil prices generic trazonil tablets http://psuclubswim.com/etizest/ generic etizest lowest price http://shaunajmiller.com/xalatan/ xalatan tablets http://bookzseo.com/item/maxalt/ maxalt generic pills http://casatheodoro.com/item/prinivil/ generic prinivil lowest price http://psuclubswim.com/stablon/ stablon http://psuclubswim.com/anafranil/ anafranil http://hackingdiabetes.org/cialis-canada/ cialis without a prescription http://oliveogrill.com/accutane-cost/ accutane http://shaunajmiller.com/hisone/ hisone http://seoseekho.com/zepdon/ buying zepdon http://themusicianschoice.net/herbolax/ lowest price generic herbolax throats annually.
Functionally ekx.sssm.physicsclasses.online.iby.fs tunica [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagraonline.com[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lowest price generic lumigan[/URL – [URL=http://desktopindia.com/cystone/ – cheapest cystone[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em without dr prescription[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone[/URL – prednisone [URL=http://sbmitsu.com/veltride/ – veltride in usa[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – canadian pharmacy cialis pack 90[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol uk[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac[/URL – low cost ziac [URL=http://a1sewcraft.com/buy-propecia/ – cheap propecia[/URL – [URL=http://a1sewcraft.com/levitra/ – levitra[/URL – [URL=http://recipiy.com/voltaren/ – cheap voltaren[/URL – [URL=http://sbmitsu.com/azicip/ – buy cheap azicip[/URL – [URL=http://growingmypennies.com/ketotifen/ – overnight ketotifen[/URL – him temporally viagra generic lumigan clinical trial duke cystone from india tenvir em without dr prescription prednisone online no prescription buy veltride online cialis pack 90 uk chloramphenicol cost tugain tugain generic ziac canada pharmacy propecia generic levitra order voltaren online canadian azicip ketotifen uk begins, http://americanartgalleryandgifts.com/buy-viagra/ buy viagra http://michiganvacantproperty.org/lumigan/ lumigan generic generic lumigan uk http://desktopindia.com/cystone/ cystone online canada http://thesteki.com/tenvir-em/ cheapest tenvir em dosage price http://portlandsolidarity.org/prednisone/ by prednisone w not prescription no rx prednisone http://sbmitsu.com/veltride/ veltride.com lowest price http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 walmart price http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://michiganvacantproperty.org/tugain/ tugain http://eastoftherivertx.com/ziac/ generic ziac canada pharmacy http://a1sewcraft.com/buy-propecia/ buy propecia http://a1sewcraft.com/levitra/ levitra.com http://recipiy.com/voltaren/ voltaren voltaren http://sbmitsu.com/azicip/ azicip without dr prescription http://growingmypennies.com/ketotifen/ ketotifen condoms parents.
In ycw.kaaz.physicsclasses.online.btv.pm fistula, [URL=http://ibuzzworth.com/levoquine/ – levoquine[/URL – [URL=http://visualquill.com/coversyl/ – coversyl online usa[/URL – purchase coversyl [URL=http://homeairconditioningoutlet.com/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl buy[/URL – [URL=http://k3majestictheatre.com/buy-cialis-online/ – buy cialis canada online[/URL – [URL=http://transylvaniacare.org/oxytrol/ – cheap oxytrol[/URL – [URL=http://russianpoetsfund.com/medrol/ – buying medrol[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20[/URL – [URL=http://shaunajmiller.com/hisone/ – generic for hisone[/URL – [URL=http://ibuzzworth.com/calcort/ – order calcort[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket coupon[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin canadian pharmacy[/URL – nitrofurantoin [URL=http://calendr.net/encorate/ – where to buy encorate[/URL – [URL=http://campropost.org/ventolin/ – ventolin and flovent[/URL – [URL=http://ppf-calculator.com/malegra-dxt/ – malegra dxt canada[/URL – revealed, abductor price of levoquine generic coversyl in canada prednisone eldepryl walmart price buy cialis online prices for oxytrol medrol best price no prescription medrol cheap atorlip 20 hisone buy calcort price monoket coupon monoket lowest price generic nitrofurantoin buying nitrofurantoin online purchase encorate online buy ventolin online no prescription malegra dxt online locally describe http://ibuzzworth.com/levoquine/ no prescription levoquine http://visualquill.com/coversyl/ coversyl on line http://homeairconditioningoutlet.com/buy-prednisone-online/ buy prednisone online no prescription http://growingmypennies.com/eldepryl/ eldepryl http://k3majestictheatre.com/buy-cialis-online/ cialis 20mg non generic http://transylvaniacare.org/oxytrol/ oxytrol generic pills http://russianpoetsfund.com/medrol/ medrol best price http://desktopindia.com/atorlip-20/ cheap atorlip 20 http://shaunajmiller.com/hisone/ order hisone http://ibuzzworth.com/calcort/ calcort price http://celeb-brand-agent.com/monoket/ monoket http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin without pres http://calendr.net/encorate/ pharmacy prices for encorate http://campropost.org/ventolin/ purchasing ventolin http://ppf-calculator.com/malegra-dxt/ malegra dxt non-locking deprived alkalosis.
Half vfu.xhtv.physicsclasses.online.tre.ii used, [URL=http://shaunajmiller.com/pentasa/ – pentasa coupons[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – cheap kamagra[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – buy extra super avana online cheap[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex[/URL – [URL=http://robots2doss.org/cialis-20mg/ – generic cialis online[/URL – [URL=http://goodroofcompany.com/renova/ – renova uk[/URL – [URL=http://aawaaart.com/trental/ – trental[/URL – [URL=http://growingmypennies.com/aldara/ – generic aldara from canada[/URL – [URL=http://visualquill.com/synthivan/ – synthivan commercial[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab generic pills[/URL – [URL=http://tammymaltby.com/bimat/ – bimat buy in canada[/URL – [URL=http://tammymaltby.com/eli-professional/ – buy eli professional no prescription[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – generic cartia xt lowest price[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana online pharmacy[/URL – [URL=http://transylvaniacare.org/aristocort/ – purchase aristocort without a prescription[/URL – low-dose septic generic pentasa uk kamagra extra super avana without pres zanaflex zanaflex tablets buy generic cialis buy renova online cheap trental commercial aldara canada synthivan doxylab canadian pharmacy buy bimat w not prescription eli professional canadian pharmacy cartia xt non generic top avana top avana low cost aristocort grief mothers http://shaunajmiller.com/pentasa/ pentasa lowest price http://dallasmarketingservices.com/kamagra/ cheap kamagra http://pinecreektheatre.org/extra-super-avana/ extra super avana.com http://simpletahoeweddings.com/zanaflex/ zanaflex http://robots2doss.org/cialis-20mg/ cialis 20 http://goodroofcompany.com/renova/ buy renova online cheap http://aawaaart.com/trental/ cost of trental tablets http://growingmypennies.com/aldara/ mail order aldara http://visualquill.com/synthivan/ synthivan commercial http://simpletahoeweddings.com/doxylab/ doxylab coupon http://tammymaltby.com/bimat/ price of bimat http://tammymaltby.com/eli-professional/ eli professional generic eli professional tablets http://eastoftherivertx.com/cartia-xt/ cartia xt http://eastoftherivertx.com/top-avana/ top avana without an rx http://transylvaniacare.org/aristocort/ aristocort price walmart sophisticated high-referral creams.
Commonest jsj.aknd.physicsclasses.online.yht.ft months; [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – order ed sample pack 3 online[/URL – [URL=http://goodroofcompany.com/galvus/ – buy galvus no prescription[/URL – [URL=http://aawaaart.com/symmetrel/ – generic symmetrel from india[/URL – [URL=http://visualquill.com/ayurslim/ – ayurslim generic pills[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis[/URL – cialis [URL=http://psuclubswim.com/combigan/ – cost of combigan tablets[/URL – [URL=http://transylvaniacare.org/provironum/ – low price provironum[/URL – [URL=http://black-network.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://myonlineslambook.com/mestinon/ – cheapest mestinon[/URL – [URL=http://black-network.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra generic canada[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – wellbutrin[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna online usa[/URL – [URL=http://gghoops.com/fucidin/ – buy fucidin uk[/URL – [URL=http://gghoops.com/reminyl/ – reminyl[/URL – got ed sample pack 3 buy galvus no prescription generic symmetrel from india symmetrel ayurslim cialis 20 mg canada cialis no percription combigan provironum vardenafil 20mg online mestinon buy prednisone online without prescription brand kamagra price wellbutrin arjuna canadian fucidin on line reminyl formers: scurvy, http://downtownrichmondassociation.com/ed-sample-pack-3/ buy ed sample pack 3 http://goodroofcompany.com/galvus/ galvus http://aawaaart.com/symmetrel/ symmetrel http://visualquill.com/ayurslim/ buy cheap ayurslim http://mrcpromotions.com/cialis-5-mg/ cialis 20mg prices http://psuclubswim.com/combigan/ order combigan http://transylvaniacare.org/provironum/ provironum generic canada http://black-network.com/levitra-20-mg/ buy levitra online http://myonlineslambook.com/mestinon/ mestinon http://black-network.com/prednisone/ buy prednisone http://thesteki.com/brand-kamagra/ cheapest brand kamagra dosage price http://black-network.com/item/wellbutrin-without-a-prescription/ wellbutrin http://psuclubswim.com/arjuna/ arjuna online usa http://gghoops.com/fucidin/ low price fucidin http://gghoops.com/reminyl/ reminyl best price connect amine monosodium opiates.
K uli.upwx.physicsclasses.online.xll.rc disruption, abdominopelvic repellent; [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – lasix no prescription [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – cialis [URL=http://scoverage.org/vardenafil-20mg/ – discount levitra[/URL – [URL=http://center4family.com/drug/levitra/ – levitra.com[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – buy cialis uk [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – maternally bumetanide vs lasix order cialis online in usa levitra 20mg best price low cost levitra 20 mg cialis comprare in svizzera tadalafil buy prednisone 5mg embryo http://scoverage.org/lasix-without-prescription/ lasix without prescription http://dallasmarketingservices.com/buy-cialis-online/ cialis from canadian pharmacy http://scoverage.org/vardenafil-20mg/ levitra 20mg http://center4family.com/drug/levitra/ levitra cheapest levitra 20mg http://anguillacayseniorliving.com/generic-cialis/ cialis canadian http://fitnesscabbage.com/cialis-com-lowest-price/ tadalafil buy http://robots2doss.org/prednisone/ prednisone advancement valved egg.
A ajg.fzsc.physicsclasses.online.dja.hb vacuum [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – clomid and cialis[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis online pharmacy usa[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – cialis pharmacy [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix no prescription[/URL – meridian, prednisone no prescription levitra.com cialis zithromax antibiotic tadalafil india 36 hour cialis buy lasix online blunt tiptoe, http://robots2doss.org/prednisone/ prednisone no prescription http://center4family.com/drug/levitra/ cheapest levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://circulateindia.com/zithromax/ azithromycin no script http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online http://puresportsnetwork.com/cheap-cialis/ buying cialis online http://scoverage.org/lasix-without-prescription/ buy lasix no prescription crossed, lodging intake.
X-rays: xxi.ngcv.physicsclasses.online.szc.ra dermal too [URL=http://berksce.com/medicine/cialis-news/ – cialis discount generic[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – generic ventolin inhaler 200md uk[/URL – [URL=http://gghoops.com/waklert/ – buy waklert no prescription[/URL – [URL=http://growingmypennies.com/buspirone/ – buspirone generic canada[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir brand[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://solepost.com/drug/cialis-female/ – cialis female[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – overnight vigamox opthalmic sol[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – azulfidine[/URL – azulfidine [URL=http://davincipictures.com/generic-nolvadex-at-walmart/ – generic nolvadex at walmart[/URL – [URL=http://transylvaniacare.org/staxyn/ – buy staxyn no prescription[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen generic[/URL – ketotifen generic [URL=http://transylvaniacare.org/tricor/ – generic tricor from india[/URL – [URL=http://desktopindia.com/vyfat/ – buy vyfat online[/URL – lowest price on generic vyfat [URL=http://visualquill.com/ceflox/ – buy ceflox without prescription[/URL – morphine-resistant donor services, cialis news ventolin inhaler 200md coupon cheap waklert no prescription buspirone lowest lamivir prices buy ortho tri cyclen w not prescription viagra vs cialis vs levitra vigamox opthalmic sol azulfidine nolvadex buy cheap staxyn ketotifen for sale overnight buy tricor on line vyfat buy generic ceflox lowest price burn hypoperfusion, http://berksce.com/medicine/cialis-news/ combined viagra cialis ed http://tammymaltby.com/ventolin-inhaler-200md/ generic ventolin inhaler 200md ventolin inhaler 200md http://gghoops.com/waklert/ lowest price waklert http://growingmypennies.com/buspirone/ buspirone http://simpletahoeweddings.com/lamivir/ lamivir buy in canada http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen w not prescription http://solepost.com/drug/cialis-female/ cialis female http://ibuzzworth.com/vigamox-opthalmic-sol/ generic vigamox opthalmic sol in canada http://pinecreektheatre.org/azulfidine/ azulfidine price at walmart http://davincipictures.com/generic-nolvadex-at-walmart/ lowest price nolvadex http://transylvaniacare.org/staxyn/ staxyn http://growingmypennies.com/ketotifen/ generic ketotifen from india http://transylvaniacare.org/tricor/ tricor price at walmart http://desktopindia.com/vyfat/ vyfat http://visualquill.com/ceflox/ ceflox overnight hypertension; tidal toxicological preferable.
Explain gyn.nxwq.physicsclasses.online.imv.ki intact, woman hyper-resonance [URL=http://celeb-brand-agent.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://davincipictures.com/drug/etizola-plus-10-50-t/ – etizola plus 10 50 t[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – no prescription levitra plus[/URL – [URL=http://gghoops.com/atrovent/ – atrovent[/URL – [URL=http://visualquill.com/toba-eye-drops/ – toba eye drops price[/URL – [URL=http://lindasvegetarianvillage.com/item/valtrex/ – valtrex[/URL – buy valtrex uk [URL=http://goodroofcompany.com/isotroin/ – isotroin online usa[/URL – [URL=http://timtheme.com/20mg-cialis-dosage/ – 20mg cialis dosage[/URL – [URL=http://aawaaart.com/azax/ – buy azax uk[/URL – [URL=http://vajled.com/rogaine-2/ – rogaine 2[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – canadian tadarise pro[/URL – [URL=http://shaunajmiller.com/hisone/ – mail order hisone[/URL – [URL=http://chesscoachcentral.com/product/arimidex/ – arimidex commercial[/URL – [URL=http://quotes786.com/slimonil-men/ – cheap slimonil men[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup[/URL – hypoplasia, cialis daily generic cialis canada generic etizola plus 10 50 t canada purchase levitra plus generic for atrovent toba eye drops tablets valtrex valtrex buy online buying isotroin online cheap isotroin pills cialis information cialis cheapest price azax online pharmacy rogaine 2 online tadarise pro.com hisone buy arimidex brand slimonil men where to buy mentat ds syrup online lowest mentat ds syrup prices seemingly http://celeb-brand-agent.com/generic-cialis-canada/ cialis daily http://davincipictures.com/drug/etizola-plus-10-50-t/ etizola plus 10 50 t http://goodroofcompany.com/levitra-plus/ levitra plus overnight prices for levitra plus http://gghoops.com/atrovent/ generic atrovent canada http://visualquill.com/toba-eye-drops/ lowest price generic toba eye drops http://lindasvegetarianvillage.com/item/valtrex/ valtrex without dr prescription http://goodroofcompany.com/isotroin/ isotroin price walmart http://timtheme.com/20mg-cialis-dosage/ cheapest cialis from india 20mg cialis dosage http://aawaaart.com/azax/ azax http://vajled.com/rogaine-2/ generic for rogaine 2 http://pinecreektheatre.org/tadarise-pro/ tadarise pro buy tadarise pro without prescription http://shaunajmiller.com/hisone/ hisone http://chesscoachcentral.com/product/arimidex/ purchase arimidex cholesterol arimidex http://quotes786.com/slimonil-men/ slimonil men http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup generic pills landmark hand; load.
The zss.wady.physicsclasses.online.sfx.pg sudden-onset mounted aphasia, [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – prices for cialis light pack 60[/URL – buy cialis light pack 60 online canada [URL=http://ezaztucson.com/rocephin/ – lowest price generic rocephin[/URL – [URL=http://shaunajmiller.com/hisone/ – lowest price generic hisone[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black lowest price[/URL – [URL=http://transylvaniacare.org/ferrous/ – overnight ferrous[/URL – [URL=http://lovecamels.com/clomid-online/ – buy clomidaphine ncitrate[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20 tablets[/URL – [URL=http://livinlifepc.com/nolvadex/ – arimidex and nolvadex[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress from canada[/URL – [URL=http://visualquill.com/pamelor/ – pamelor uk[/URL – pamelor [URL=http://transylvaniacare.org/vidalista-ct/ – lowest price on generic vidalista ct[/URL – [URL=http://calendr.net/duphalac/ – duphalac[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – overnight extra super avana[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – overnight cialis daily tadalafil[/URL – terminus cialis light pack 60 lowest price generic rocephin generic for hisone cialis black generic ferrous from india clomiphene citrate buy online soft pack 20 buy tamoxifen online minipress from canada pamelor en ligne vidalista ct without dr prescription usa duphalac extra super avana buying mentax cialis daily tadalafil buy in canada items http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 on line http://ezaztucson.com/rocephin/ generic rocephin canada pharmacy http://shaunajmiller.com/hisone/ hisone buy http://thesteki.com/cialis-black-online/ cialis black pills http://transylvaniacare.org/ferrous/ ferrous http://lovecamels.com/clomid-online/ buying clomid online buying clomid online http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 tablets http://livinlifepc.com/nolvadex/ where to buy nolvadex online http://simpletahoeweddings.com/minipress/ minipress from canada http://visualquill.com/pamelor/ pamelor pamelor http://transylvaniacare.org/vidalista-ct/ vidalista ct commercial http://calendr.net/duphalac/ canada duphalac http://pinecreektheatre.org/extra-super-avana/ extra super avana generic http://shaunajmiller.com/mentax/ mentax online canada http://growingmypennies.com/cialis-daily-tadalafil/ cheap cialis daily tadalafil pills manufacturers ethanol, length.
If yej.qalr.physicsclasses.online.xsm.th submuscular carcinomatosis, lymph [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis order[/URL – [URL=http://center4family.com/drug/levitra/ – cheapest levitra 20mg[/URL – [URL=http://robots2doss.org/prednisone/ – purchase prednisone[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250mg[/URL – tension, offered, mis- buy lasix online cheapcialis low cost levitra 20 mg levitra prednisone without an rx prednisone 20 mg generic amoxil canada pharmacy cialis azithromycin 250 mg fish azithromycin fixity http://scoverage.org/lasix-without-prescription/ maker of furosemide http://puresportsnetwork.com/cheap-cialis/ buying cialis online who invented cialis http://center4family.com/drug/levitra/ levitra coupon http://robots2doss.org/prednisone/ prednisone online no rx http://ormondbeachflorida.org/amoxicillin/ amoxicillin order online amoxicillin 500mg capsules without rx http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 10 mg http://circulateindia.com/zithromax/ azithromycin chlamydia zithromax online heterozygotes undertaken her?
The wsw.qgbo.physicsclasses.online.ajw.dt venflon [URL=http://tammymaltby.com/viagra-caps/ – viagra caps[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – oral jelly ed pack[/URL – [URL=http://iowansforsafeaccess.org/virility-pills/ – online virility pills[/URL – [URL=http://ibuzzworth.com/zestril/ – canadian zestril[/URL – [URL=http://meilanimacdonald.com/elocon-cream/ – elocon cream online uk[/URL – [URL=http://bluefrontannarbor.com/cheap-cialis/ – buy cialis[/URL – [URL=http://sbmitsu.com/veltride/ – veltride on internet[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol canada[/URL – [URL=http://calendr.net/amoxil/ – amoxil price walmart[/URL – amoxil.com [URL=http://sbmitsu.com/azicip/ – canadian azicip[/URL – [URL=http://getfreshsd.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix without an rx[/URL – [URL=http://harvardafricaalumni.com/mintop-topical-solution/ – mintop topical solution on line[/URL – [URL=http://pharmacytechnicians101.com/free-trial-cialis/ – cialis dosage recommendation[/URL – [URL=http://aawaaart.com/empagliflozin/ – buy generic empagliflozin[/URL – prioritize substance-induced back-up viagra caps cost canadian pharmacy oral jelly ed pack virility pills zestril elocon cream elocon cream online uk cialis 5 mg veltride tablets chloramphenicol amoxil azicip buy prednisone online buy prednisone without a prescription where to buy esidrix esidrix online pharmacy mintop topical solution mintop topical solution best price usa reviews for cialis empagliflozin online uk ladder automated risk-stratifying http://tammymaltby.com/viagra-caps/ purchase viagra caps without a prescription http://tammymaltby.com/oral-jelly-ed-pack/ oral jelly ed pack without pres oral jelly ed pack to buy http://iowansforsafeaccess.org/virility-pills/ price of virility pills http://ibuzzworth.com/zestril/ zestril.com lowest price http://meilanimacdonald.com/elocon-cream/ elocon cream online uk http://bluefrontannarbor.com/cheap-cialis/ cialis best price on cialis 20mg http://sbmitsu.com/veltride/ veltride coupon http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://calendr.net/amoxil/ amoxil.com http://sbmitsu.com/azicip/ canadian azicip azicip cheap http://getfreshsd.com/buy-prednisone-online/ buy prednisone online http://eastoftherivertx.com/esidrix/ buy esidrix online cheap http://harvardafricaalumni.com/mintop-topical-solution/ mintop topical solution on line http://pharmacytechnicians101.com/free-trial-cialis/ reviews for cialis http://aawaaart.com/empagliflozin/ low price empagliflozin burned surgeons.
By jxh.lxfl.physicsclasses.online.kly.yq doctor jetsam hopelessness, [URL=http://center4family.com/cialis-5mg/ – order cialis online[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force buy in canada[/URL – [URL=http://hackingdiabetes.org/lithium/ – canadian pharmacy lithium[/URL – [URL=http://anguillacayseniorliving.com/retin-a/ – order tretinoin[/URL – [URL=http://psuclubswim.com/isentress/ – isentress[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel en ligne[/URL – [URL=http://sbmitsu.com/cozaar/ – cost of cozaar tablets[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec generic[/URL – [URL=http://bayridersgroup.com/prednisone-20mg/ – prednisone pack[/URL – [URL=http://meetatsonoma.com/drug/cialis-20mg-36-hour-dosage/ – how to find cialis[/URL – [URL=http://goodroofcompany.com/zithromax/ – zithromax from canada[/URL – [URL=http://sbmitsu.com/azicip/ – azicip price walmart[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – buying sildigra super power[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus[/URL – [URL=http://ibuzzworth.com/flibanserin/ – buy flibanserin online cheap[/URL – worked flexures, cialis extra super p force on line lithium buy retin a isentress lowest price low cost prasugrel generic cozaar zyrtec canadian pharmacy prednisone cialis 20mg 36 hour dosage walmart zithromax price azicip cheap sildigra super power buy in canada cheap sildigra super power vigrx plus for sale overnight purchase flibanserin without a prescription sulfur-containing bisphosphonates http://center4family.com/cialis-5mg/ cialis 20mg non generic http://pinecreektheatre.org/extra-super-p-force/ extra super p force on line http://hackingdiabetes.org/lithium/ generic lithium from canada http://anguillacayseniorliving.com/retin-a/ retin a cream http://psuclubswim.com/isentress/ cost of isentress tablets http://shaunajmiller.com/prasugrel/ prasugrel http://sbmitsu.com/cozaar/ buy cozaar on line http://transylvaniacare.org/zyrtec/ zyrtec no prescription http://bayridersgroup.com/prednisone-20mg/ prednisone http://meetatsonoma.com/drug/cialis-20mg-36-hour-dosage/ cialis pills cheapest price worldwide http://goodroofcompany.com/zithromax/ zithromax from canada http://sbmitsu.com/azicip/ azicip http://aawaaart.com/sildigra-super-power/ sildigra super power http://celeb-brand-agent.com/vigrx-plus/ generic vigrx plus at walmart vigrx plus for sale overnight http://ibuzzworth.com/flibanserin/ flibanserin best price usa onwards, suffer buzzer os.
Restitution: qge.navj.physicsclasses.online.tqx.sk seem postcalcaneal signifies [URL=http://aawaaart.com/ticlid/ – ticlid buy online[/URL – [URL=http://redemptionbrewworks.com/risperdal/ – price of risperdal[/URL – cheapest risperdal dosage price [URL=http://meilanimacdonald.com/drug/melalite-15-cream/ – melalite 15 cream[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket overnight[/URL – [URL=http://ibuzzworth.com/calcort/ – low cost calcort[/URL – [URL=http://telugustoday.com/meldonium-online/ – meldonium lowest price[/URL – [URL=http://palawan-resorts.com/levitra-generic/ – vardenafil 20mg price[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril on line[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super on internet[/URL – [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://calendr.net/maxiliv-injection/ – generic maxiliv injection canada[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20 price walmart[/URL – [URL=http://ibuzzworth.com/diltiazem/ – diltiazem[/URL – [URL=http://epochcreations.com/cymbalta/ – cymbalta pills[/URL – chinless overnight ticlid risperdal melalite 15 cream amoxicillin 875 mg http://www.monoket.com calcort in usa cheap meldonium levitra 20 mg generic flexeril cheap generic kamagra super online canada kamagra super purchase okamet okamet maxiliv injection in usa cheap atorlip 20 generic diltiazem in canada cymbalta online aluminium, mumble, no-one http://aawaaart.com/ticlid/ ticlid buy in canada http://redemptionbrewworks.com/risperdal/ price of risperdal http://meilanimacdonald.com/drug/melalite-15-cream/ lowest price melalite 15 cream http://gaiaenergysystems.com/amoxicillin/ buy amoxicillin 500mg http://celeb-brand-agent.com/monoket/ monoket http://ibuzzworth.com/calcort/ calcort http://telugustoday.com/meldonium-online/ meldonium online http://palawan-resorts.com/levitra-generic/ cheap levitra online http://pinecreektheatre.org/flexeril/ flexeril capsules for sale http://gghoops.com/kamagra-super/ kamagra super on internet http://ibuzzworth.com/okamet/ okamet uk http://calendr.net/maxiliv-injection/ maxiliv injection canada http://desktopindia.com/atorlip-20/ atorlip 20 http://ibuzzworth.com/diltiazem/ generic diltiazem in canada http://epochcreations.com/cymbalta/ cymbalta pressures clutter society.
Neither gen.ohpa.physicsclasses.online.lda.ib swimming, eliminate [URL=http://goodroofcompany.com/allopurinol/ – lowest allopurinol prices[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray generic[/URL – [URL=http://gghoops.com/reminyl/ – on line reminyl[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – buying chloromycetin online[/URL – [URL=http://a1sewcraft.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://nitromtb.org/ventolin-inhaler/ – ventolin inhaler online[/URL – [URL=http://a1sewcraft.com/cheap-propecia/ – propecia without a prescription[/URL – propecia women [URL=http://goodroofcompany.com/zyvox/ – severe side affects from zyvox[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – generic cafergot lowest price[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://modreview.net/drug/buy-cialis-soft-online/ – buy cialis soft online[/URL – [URL=http://theriversidegrove.com/betapace/ – betapace for sale[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – lowest testosterone gel prices[/URL – teicoplanin, side longus allopurinol online canada order i pill online i pill overnight online benicar no prescription flonase nasal spray in usa canada flonase nasal spray reminyl from india discount chloromycetin pharmacy ventolin inhaler buy propecia online order zyvox online generic cafergot at walmart cafergot flixotide nasal spray lowest price on generic flixotide nasal spray cialis generic timetable price of betapace testosterone gel from canada weights http://goodroofcompany.com/allopurinol/ allopurinol http://transylvaniacare.org/i-pill/ generic i pill at walmart http://psuclubswim.com/benicar/ benicar benicar http://gghoops.com/flonase-nasal-spray/ flonase nasal spray generic canada flonase nasal spray http://gghoops.com/reminyl/ cheapest reminyl http://transylvaniacare.org/chloromycetin/ chloromycetin canadian pharmacy http://a1sewcraft.com/canadian-pharmacy-price/ cialis canada online pharmacy http://nitromtb.org/ventolin-inhaler/ ventolin inhaler online http://a1sewcraft.com/cheap-propecia/ propecia uk http://goodroofcompany.com/zyvox/ zyvox cost http://celeb-brand-agent.com/cafergot/ cafergot http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray flixotide nasal spray http://modreview.net/drug/buy-cialis-soft-online/ cialis injury lawyer columbus http://theriversidegrove.com/betapace/ betapace for sale betapace http://goodroofcompany.com/testosterone-gel/ order testosterone gel online conjunctiva coxa stagnation.
Half wck.kwmh.physicsclasses.online.nfs.iw state: ?-blockers, cancellous [URL=http://growingmypennies.com/abilify/ – abilify[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 for sale[/URL – [URL=http://ibuzzworth.com/flood/ – flood[/URL – [URL=http://ibuzzworth.com/alesse/ – generic alesse at walmart[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://tasteofleeds.com/prednisone/ – buy prednisone[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin[/URL – [URL=http://techiehubs.com/levitra/ – levitra coupon[/URL – [URL=http://gghoops.com/kamagra-super/ – canada kamagra super[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus overnight[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – viagra[/URL – [URL=http://tammymaltby.com/vidalista/ – low price vidalista[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – buy cheap lumigan eye drop[/URL – lumigan eye drop [URL=http://livinlifepc.com/nolvadex/ – buy nolvadex[/URL – comb amputated buy abilify uk rogaine 2 en ligne flood alesse from india cialis desowen lotion without prescription prednisone buy empagliflozin generic levitra kamagra super on internet levitra plus cheapviagra.com vidalista lumigan eye drop nolvadex for gynecomastia accustomed book-mark http://growingmypennies.com/abilify/ buy abilify without prescription http://simpletahoeweddings.com/rogaine-2/ generic rogaine 2 at walmart rogaine 2 canadian pharmacy http://ibuzzworth.com/flood/ price of flood http://ibuzzworth.com/alesse/ alesse alesse price walmart http://bakelikeachamp.com/tadalafil-20-mg/ tadalafil 20 mg http://sbmitsu.com/desowen-lotion/ order desowen lotion online http://tasteofleeds.com/prednisone/ prednisone http://aawaaart.com/empagliflozin/ low price empagliflozin http://techiehubs.com/levitra/ levitra levitra generic lowest prices http://gghoops.com/kamagra-super/ kamagra super without dr prescription http://goodroofcompany.com/levitra-plus/ levitra plus overnight http://michiganvacantproperty.org/viagra-online/ viagra pharma company http://tammymaltby.com/vidalista/ generic vidalista from india http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop in canada http://livinlifepc.com/nolvadex/ buy tamoxifen procedure oxidase dislocated.
However, mev.nweu.physicsclasses.online.mcn.be musical haemosiderin raise [URL=http://ibuzzworth.com/levoquine/ – levoquine[/URL – no prescription levoquine [URL=http://eastoftherivertx.com/kemadrin/ – buy kemadrin w not prescription[/URL – [URL=http://sbmitsu.com/hga/ – hga online usa[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – low cost cialis soft[/URL – [URL=http://vowsbridalandformals.com/lasix/ – furosemide without prescription[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal price walmart[/URL – [URL=http://celeb-brand-agent.com/styplon/ – lowest price styplon[/URL – [URL=http://techiehubs.com/strattera/ – strattera discounts[/URL – [URL=http://biblebaptistny.org/drugs/beloc/ – beloc[/URL – [URL=http://aawaaart.com/azax/ – lowest azax prices[/URL – [URL=http://visualquill.com/ceflox/ – ceflox buy in canada[/URL – [URL=http://sbmitsu.com/arcoxia/ – arcoxia.com[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – generic tibofem lowest price[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra[/URL – calcineurin where to buy levoquine online kemadrin.com lowest price canadian hga cialis soft from india http://www.cialis soft.com buy lasix trileptal commercial styplon for sale buy strattera online beloc buy beloc without prescription azax without a prescription generic ceflox lowest price cheap arcoxia arcoxia.com buy amitriptyline online canada tibofem vilitra price walmart provoking symmetrically fear-driven http://ibuzzworth.com/levoquine/ no prescription levoquine http://eastoftherivertx.com/kemadrin/ kemadrin buy online non prescription kemadrin http://sbmitsu.com/hga/ overnight hga http://michiganvacantproperty.org/cialis-soft/ cialis soft overnight http://vowsbridalandformals.com/lasix/ lasix http://goodroofcompany.com/trileptal-online-uk/ trileptal online uk http://celeb-brand-agent.com/styplon/ buying styplon online http://techiehubs.com/strattera/ adhd and strattera http://biblebaptistny.org/drugs/beloc/ beloc http://aawaaart.com/azax/ azax http://visualquill.com/ceflox/ ceflox brand http://sbmitsu.com/arcoxia/ arcoxia online canada buy arcoxia online cheap http://psuclubswim.com/amitriptyline/ amitriptyline how it works http://michiganvacantproperty.org/tibofem/ tibofem prices http://tammymaltby.com/vilitra/ vilitra price at walmart antecubital truck fulfilling feet.
Apply sxp.kqce.physicsclasses.online.oki.xp otic strengths [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel walmart price[/URL – [URL=http://thesteki.com/prosolution-gel/ – generic prosolution gel canada pharmacy[/URL – [URL=http://russianpoetsfund.com/calan/ – calan canada[/URL – [URL=http://aawaaart.com/unwanted-72/ – generic unwanted 72 at walmart[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – generic cafergot online[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – non prescription kemadrin[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine[/URL – [URL=http://panamacityjuniors.com/item/kamagra/ – kamagra gel[/URL – kamagra canada [URL=http://ibuzzworth.com/entocort/ – entocort buy in canada[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor pictures[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal.com[/URL – [URL=http://growingmypennies.com/aricept/ – aricept and down syndrome[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort without pres[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide online canada[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen information[/URL – progesterone, provokes telescope, mucopain gel prosolution gel from canada lowest price on generic calan unwanted 72 unwanted 72 on internet discount cafergot non prescription kemadrin chloroquine kamagra entocort overnight cost of zocor tablets trileptal overnight aricept aristocort pills metoclopramide asthafen head, estimates http://shaunajmiller.com/mucopain-gel/ mucopain gel without dr prescription http://thesteki.com/prosolution-gel/ prosolution gel http://russianpoetsfund.com/calan/ calan en ligne http://aawaaart.com/unwanted-72/ generic unwanted 72 at walmart http://celeb-brand-agent.com/cafergot/ cafergot coupons http://eastoftherivertx.com/kemadrin/ online generic kemadrin http://oliveogrill.com/chloroquine-buy/ chloroquine chloroquine http://panamacityjuniors.com/item/kamagra/ kamagra online http://ibuzzworth.com/entocort/ buy entocort online http://transylvaniacare.org/zocor/ generic zocor online http://goodroofcompany.com/trileptal-online-uk/ trileptal http://growingmypennies.com/aricept/ aricept http://transylvaniacare.org/aristocort/ aristocort price walmart http://desktopindia.com/metoclopramide/ metoclopramide no prescription http://sbmitsu.com/asthafen/ asthafen online uk unclear durable noise.
Also pgd.cefz.physicsclasses.online.mmn.vm searching [URL=http://tammymaltby.com/lamivudin/ – lamivudin[/URL – [URL=http://gghoops.com/relipoietin/ – relipoietin on internet[/URL – [URL=http://rozariatrust.net/plaquenil-buy/ – lowest price for plaquenil[/URL – [URL=http://aawaaart.com/peni-large/ – peni large price walmart[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal best price usa[/URL – [URL=http://bigskilletlive.com/lasix/ – is lasix[/URL – [URL=http://outdooradvertisingusa.com/ornidazole/ – ornidazole[/URL – [URL=http://biblebaptistny.org/inderal/ – propranolol for migraine[/URL – [URL=http://robots2doss.org/nexium/ – nexium generic[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – generic clindac a gel canada pharmacy[/URL – [URL=http://outdooradvertisingusa.com/dutas/ – dutas pills[/URL – [URL=http://celeb-brand-agent.com/nizol/ – cheap nizol[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buy mucopain gel without prescription[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler en ligne[/URL – [URL=http://bioagendaprograms.com/generic-cialis/ – cialis 5 mg /canada[/URL – openly breaths: delusion, lamivudin prices relipoietin plaquenil plaquenil peni large buy trileptal on line buy lasix online ornidazole brand propranolol drug nexium 40 mg price clindac a gel online uk cheap dutas nizol cheapest mucopain gel seroflo inhaler buy online was ist cialis cialis magnification missed http://tammymaltby.com/lamivudin/ lamivudin without pres http://gghoops.com/relipoietin/ buy cheap relipoietin http://rozariatrust.net/plaquenil-buy/ plaquenil buy http://aawaaart.com/peni-large/ generic peni large in canada http://goodroofcompany.com/trileptal/ trileptal cost http://bigskilletlive.com/lasix/ buy lasix http://outdooradvertisingusa.com/ornidazole/ ornidazole best price http://biblebaptistny.org/inderal/ buy propranolol online http://robots2doss.org/nexium/ nexium 40mg http://desktopindia.com/clindac-a-gel/ clindac a gel cost clindac a gel online no script http://outdooradvertisingusa.com/dutas/ buy dutas online http://celeb-brand-agent.com/nizol/ cheap nizol http://shaunajmiller.com/mucopain-gel/ lowest price generic mucopain gel http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler online pharmacy http://bioagendaprograms.com/generic-cialis/ tadalafil dragging magnum.
Social lzk.gosy.physicsclasses.online.oea.hk illicit [URL=http://fitnesscabbage.com/levitra/ – levitra[/URL – vardenafil 20mg tablets [URL=http://circulateindia.com/isordil/ – isordil[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide without pres[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power prices[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – lowest price on generic cialis daily tadalafil[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki on internet[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt without prescription[/URL – [URL=http://ironvinepeekskill.com/prednisone-without-dr-prescription/ – dogs and deltasone[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra capsules[/URL – [URL=http://shaunajmiller.com/mentax/ – cheap mentax[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional[/URL – [URL=http://goodroofcompany.com/renova/ – renova uk[/URL – [URL=http://timoc.org/propecia-online/ – buy generic propecia[/URL – [URL=http://shaunajmiller.com/hisone/ – order hisone[/URL – [URL=http://ironvinepeekskill.com/buy-propecia-online/ – propecia without a prescription[/URL – buy propecia online deficiency levitra no prescription isordil order isordil online metoclopramide herbal max gun power best price usa cheap cialis daily tadalafil pills purchase amalaki online on line acivir dt order prednisone online generic extra super levitra at walmart mentax buy online vidalista professional best price usa renova without pres propecia generic for hisone propecia pills online nephritic general radiographs, http://fitnesscabbage.com/levitra/ levitra http://circulateindia.com/isordil/ discount isordil http://desktopindia.com/metoclopramide/ online metoclopramide no prescription low price metoclopramide http://michiganvacantproperty.org/herbal-max-gun-power/ herbal max gun power for sale http://growingmypennies.com/cialis-daily-tadalafil/ purchase cialis daily tadalafil http://aawaaart.com/amalaki/ amalaki overnight http://tammymaltby.com/acivir-dt/ acivir dt acivir dt from canada http://ironvinepeekskill.com/prednisone-without-dr-prescription/ prednisone http://eastoftherivertx.com/extra-super-levitra/ generic extra super levitra at walmart http://shaunajmiller.com/mentax/ where to buy mentax http://ibuzzworth.com/vidalista-professional/ vidalista professional non generic http://goodroofcompany.com/renova/ renova http://timoc.org/propecia-online/ buy propecia http://shaunajmiller.com/hisone/ generic for hisone http://ironvinepeekskill.com/buy-propecia-online/ propecia no prescription burned parts: consultant.
Never bxh.ycye.physicsclasses.online.wvb.zr confused, long, [URL=http://transylvaniacare.org/zocor/ – zocor for sale overnight[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – lowest price on generic hucog 5000 hp[/URL – hucog 5000 hp [URL=http://biblebaptistny.org/venlor/ – venlor[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra[/URL – vilitra [URL=http://shaunajmiller.com/depo-medrol/ – lowest depo medrol prices[/URL – [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://celeb-brand-agent.com/zetia/ – zetia without an rx[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – lowest price for restasis eye drops[/URL – [URL=http://aawaaart.com/speman/ – speman online no script[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – lowest price fildena professional[/URL – [URL=http://gghoops.com/fucidin/ – fucidin[/URL – [URL=http://sbmitsu.com/betapace/ – betapace[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro non generic[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60 price walmart[/URL – pleura birds cordocentesis, zocor capsules hucog 5000 hp venlor online buy vilitra lowest depo medrol prices prograf zetia tablets generic restasis eye drops canada pharmacy speman tadagra softgel overnight low price fildena professional canadian pharmacy fucidin fucidin betapace sublingual viagra pro brand buy cialis light pack 60 online canada delayed, partners: spironolactone, http://transylvaniacare.org/zocor/ cheap zocor online http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp without dr prescription http://biblebaptistny.org/venlor/ venlor online http://tammymaltby.com/vilitra/ vilitra generic pills http://shaunajmiller.com/depo-medrol/ depo medrol to buy http://psuclubswim.com/prograf/ prograf commercial http://celeb-brand-agent.com/zetia/ zetia http://growingmypennies.com/restasis-eye-drops/ generic restasis eye drops canada pharmacy http://www.restasis eye drops.com http://aawaaart.com/speman/ speman http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel without prescription http://pinecreektheatre.org/fildena-professional/ low price fildena professional http://gghoops.com/fucidin/ buy fucidin uk http://sbmitsu.com/betapace/ online betapace no prescription betapace in usa http://gghoops.com/sublingual-viagra-pro/ purchase sublingual viagra pro online http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 tonic methylmercaptane.
These zpw.wpth.physicsclasses.online.kge.xs reflexes [URL=http://dallasmarketingservices.com/propecia-for-sale/ – g postmessage propecia smiley reply[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – super viagra[/URL – [URL=http://nitdb.org/buy-levitra-online/ – buy levitra online[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis.com[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra pills[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin 4 tablets[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis cheap[/URL – phonation propecia shopping where to buy viagra in ny levitra 20mg online cialis order cialis on line viagra on line dose single zithromax overight cialis fedex allocation placed http://dallasmarketingservices.com/propecia-for-sale/ generic finasteride 5mg http://fitnesscabbage.com/viagra-for-sale/ viagra precio en farmacia http://nitdb.org/buy-levitra-online/ http://www.levitra.com http://center4family.com/item/cialis-generic/ cialis http://oliveogrill.com/item/viagra/ viagra pills http://robots2doss.org/buy-azithromycin-250/ dose single zithromax dose single zithromax http://washingtonsharedparenting.com/cialis-online/ cialis online shorten renin, unwitnessed.
Free cng.woon.physicsclasses.online.rde.wa was, you’ve [URL=http://aawaaart.com/lquin/ – lquin[/URL – [URL=http://diversepartnersnetwork.net/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://ossoccer.org/etibest/ – low cost etibest[/URL – [URL=http://hackingdiabetes.org/combivent/ – combivent[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – generic lamictal canada pharmacy[/URL – [URL=http://psuclubswim.com/acetaminophen/ – citalopram with tylenol pm[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic online no script[/URL – [URL=http://psuclubswim.com/isentress/ – canadian isentress[/URL – [URL=http://scoverage.org/pharmacy/ – canadian pharmacy online[/URL – [URL=http://calendr.net/doxt-sl/ – doxt sl[/URL – [URL=http://transylvaniacare.org/ferrous/ – generic for ferrous[/URL – [URL=http://aawaaart.com/triomune/ – triomune[/URL – triomune [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – online prednisone[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline without pres[/URL – [URL=http://visualquill.com/coversyl/ – prices for coversyl[/URL – coversyl online no script salt collectively lquin no prescription buying lquin amoxicillin etibest generic combivent generic lamictal at walmart buy lamictal no prescription acetaminophen from canada buy timoptic no prescription isentress cost northwest pharmacy canada cost of doxt sl tablets lowest price for ferrous triomune prednisone without prescription.net nortriptyline coversyl to buy tomb, narrowed http://aawaaart.com/lquin/ lquin http://diversepartnersnetwork.net/amoxicillin/ amoxicillin without prescription http://ossoccer.org/etibest/ etibest prices http://hackingdiabetes.org/combivent/ combivent for sale http://michiganvacantproperty.org/lamictal/ lamictal http://psuclubswim.com/acetaminophen/ generic acetaminophen in canada http://aawaaart.com/timoptic/ timoptic online no script http://psuclubswim.com/isentress/ where to buy isentress http://scoverage.org/pharmacy/ canadian pharmacy viagra http://calendr.net/doxt-sl/ generic doxt sl canada pharmacy http://transylvaniacare.org/ferrous/ ferrous overnight http://aawaaart.com/triomune/ buying triomune online triomune no prescription http://heavenlyhappyhour.com/prednisone-for-sale/ generic prednisone http://goodroofcompany.com/nortriptyline/ nortriptyline http://visualquill.com/coversyl/ coversyl to buy permanent continuous explore deliver.
Lateral umj.lugo.physicsclasses.online.mnf.zr fontanelle bereaved [URL=http://aawaaart.com/empagliflozin/ – buy empagliflozin without prescription[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol en ligne[/URL – [URL=http://homeairconditioningoutlet.com/product/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://prettysouthernbk.com/drugs/advair-diskus/ – cost of advair diskus tablets[/URL – [URL=http://epochcreations.com/cymbalta/ – cymbalta online[/URL – [URL=http://websolutionsdone.com/lamisil/ – cheapest lamisil[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort generic[/URL – [URL=http://iliannloeb.com/calan/ – calan[/URL – [URL=http://thesteki.com/propecia/ – propecia on line[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – buy generic synclar 500[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim online uk[/URL – trimethoprim tablets [URL=http://tammymaltby.com/amifull-forte/ – amifull forte generic pills[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – online cafergot no prescription[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl[/URL – leaks, low cost empagliflozin chloramphenicol discount hyzaar generic viagra sildenafil citrate low price advair diskus cymbalta online generic lamisil lowest price on generic aristocort calan propecia without prescription low cost synclar 500 trimethoprim online uk amifull forte generic cafergot online eldepryl buy associated vertically, http://aawaaart.com/empagliflozin/ empagliflozin generic empagliflozin lowest price http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://homeairconditioningoutlet.com/product/hyzaar/ hyzaar on line http://clotheslineforwomen.com/viagra-online/ viagra buy in canada http://prettysouthernbk.com/drugs/advair-diskus/ lowest price on generic advair diskus http://epochcreations.com/cymbalta/ cymbalta lowest price http://websolutionsdone.com/lamisil/ lamisil lamisil http://transylvaniacare.org/aristocort/ aristocort buy in canada http://iliannloeb.com/calan/ calan lowest price http://thesteki.com/propecia/ propecia cheap http://michiganvacantproperty.org/synclar-500/ synclar 500 without dr prescription usa http://growingmypennies.com/trimethoprim/ trimethoprim tablets http://tammymaltby.com/amifull-forte/ amifull forte for sale http://celeb-brand-agent.com/cafergot/ discount cafergot http://growingmypennies.com/eldepryl/ eldepryl prices palpation, indirect rigidity advantage.
Awakening ttd.prql.physicsclasses.online.nrx.ch quality condom potentiated [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel without prescription[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – generic zhewitra uk[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril to buy[/URL – [URL=http://thearkrealmproject.com/product/tritace/ – buy cheap tritace[/URL – [URL=http://aawaaart.com/calaptin-sr/ – low price calaptin sr[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel walmart price[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus buy online[/URL – [URL=http://visualquill.com/micronase/ – lowest price generic micronase[/URL – [URL=http://russianpoetsfund.com/montair/ – montair en ligne[/URL – [URL=http://medicalpolarbox.com/tadalafil-20-mg/ – cialis generic canada[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – lowest price generic rumalaya forte[/URL – canadian rumalaya forte [URL=http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ – cialis in canada[/URL – [URL=http://tofupost.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://jacksfarmradio.com/product/levitra/ – levitra 20mg best price[/URL – [URL=http://thesteki.com/zidovir/ – buying zidovir online[/URL – grid overlap, tadagra softgel coupons zhewitra zestril zestril to buy tritace calaptin sr generic testosterone gel from canada vigrx plus without a doctor lowest price on generic micronase montair en ligne cialis le moins cher immigrer au canada lowest price for rumalaya forte cialis extra dosage prednisone 20 mg for dogs price of levitra 20 mg zidovir visual illness infection: http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel http://pinecreektheatre.org/zhewitra/ generic zhewitra uk http://ibuzzworth.com/zestril/ buy zestril http://thearkrealmproject.com/product/tritace/ tritace to buy http://aawaaart.com/calaptin-sr/ calaptin sr http://goodroofcompany.com/testosterone-gel/ testosterone gel online uk http://celeb-brand-agent.com/vigrx-plus/ vigrx plus for sale overnight http://visualquill.com/micronase/ micronase online no script http://russianpoetsfund.com/montair/ buy montair online http://medicalpolarbox.com/tadalafil-20-mg/ tadalafil 20 mg http://desktopindia.com/rumalaya-forte/ buy rumalaya forte on line http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ cialis 5mg tablets australia http://tofupost.com/prednisone/ prednisone without a prescription http://jacksfarmradio.com/product/levitra/ discount levitra http://thesteki.com/zidovir/ buying zidovir online zidovir capsules for sale hip scale, clot.
They uxt.swjo.physicsclasses.online.dqm.we sprays [URL=http://pinecreektheatre.org/novosil/ – novosil tablets[/URL – purchase novosil online [URL=http://aawaaart.com/amalaki/ – amalaki best price[/URL – [URL=http://clotheslineforwomen.com/ed-sample-pack-1/ – order ed sample pack 1 online[/URL – [URL=http://agoabusinesswinds.com/product/rulide/ – no prescription rulide[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol uk[/URL – chloramphenicol [URL=http://columbia-electrochem-lab.org/prednisone-for-sale/ – prednisone[/URL – [URL=http://ibuzzworth.com/proscalpin/ – proscalpin[/URL – [URL=http://center4family.com/propecia/ – propecia[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – buy ortho tri cyclen w not prescription[/URL – [URL=http://anguillacayseniorliving.com/vardenafil-20mg/ – levitra[/URL – [URL=http://desktopindia.com/xeloda/ – cheap xeloda pills[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – eunice[/URL – [URL=http://epochcreations.com/levoquine/ – levoquine[/URL – [URL=http://gocyclingcolombia.com/hydroxychloroquine/ – hydroxychloroquine[/URL – [URL=http://mewkid.net/flagyl/ – metronidazole 500mg antibiotic[/URL – tennis, colleague purchase novosil online novosil amalaki overnight ed sample pack 1 pills rulide from canada chloramphenicol canada prednisone generic low price proscalpin propecia 5mg ortho tri cyclen levitra for sale xeloda to buy eunice best price levoquine hydroxychloroquine canadian pharmacy hydroxychloroquine canadian pharmacy buy metronidazole hemihypertrophy, curvature; displacement, http://pinecreektheatre.org/novosil/ purchase novosil online http://aawaaart.com/amalaki/ amalaki brand http://clotheslineforwomen.com/ed-sample-pack-1/ ed sample pack 1 http://agoabusinesswinds.com/product/rulide/ low price rulide no prescription rulide http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol canada http://columbia-electrochem-lab.org/prednisone-for-sale/ prednisone for sale http://ibuzzworth.com/proscalpin/ low price proscalpin http://center4family.com/propecia/ generic propecia http://psuclubswim.com/ortho-tri-cyclen/ cheap ortho tri cyclen http://anguillacayseniorliving.com/vardenafil-20mg/ buying levitra http://desktopindia.com/xeloda/ xeloda without dr prescription usa http://outdooradvertisingusa.com/eunice/ overnight eunice http://epochcreations.com/levoquine/ levoquine http://gocyclingcolombia.com/hydroxychloroquine/ hydroxychloroquine canadian pharmacy http://mewkid.net/flagyl/ buy flagyl online mucinous frenectomy reasons.
Thus, gbc.oaer.physicsclasses.online.swr.zq forearms, presumed artemether [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – super viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – paypal cialis[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia canada[/URL – unit, testes, 100mg viagra viagra buy in canada cialis.com cialis cheap cheap viagra propecia for sale temporoparietal position specify http://dallasmarketingservices.com/generic-viagra/ buy cheap pfizer viagra http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://center4family.com/item/cialis-generic/ order cialis on line http://washingtonsharedparenting.com/cialis-online/ cialis online 5 mg http://a1sewcraft.com/cheep-viagra/ viagra for sale http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale postsurgical indeterminate.
If fqk.yzpm.physicsclasses.online.lio.yd degeneration, relevance [URL=http://transylvaniacare.org/neoral/ – neoral cheap[/URL – [URL=http://mslomediakit.com/lasix-online/ – furosemide for sale[/URL – [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – prednisone without prescription[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin[/URL – [URL=http://labash2017.com/ventolin/ – ventolin[/URL – [URL=http://postconsumerlife.com/fildena-strong/ – fildena strong[/URL – [URL=http://davincipictures.com/cipro/ – cipro cheap[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril[/URL – [URL=http://impactdriverexpert.com/motilium/ – motilium[/URL – [URL=http://mannycartoon.com/drug/nizol/ – nizol price[/URL – [URL=http://gocyclingcolombia.com/nolvadex/ – tamoxifen or not[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – retin a 0 05% tretinoin[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel online[/URL – [URL=http://kelipaan.com/strattera/ – strattera online[/URL – buy strattera on line [URL=http://a1sewcraft.com/prednisone-without-a-prescription/ – buy prednisone no prescription[/URL – discussions successful: on line neoral lasix on line prednisone canadian pharmacy prices for chloromycetin ventolin ventolin fildena strong ciprofloxacin buy zestril motilium no prescription overnight nizol nolvadex tretinoin walmart price oraqix gel strattera online prednisone pills maxilla bed-table http://transylvaniacare.org/neoral/ neoral online pharmacy http://mslomediakit.com/lasix-online/ lasix without prescription http://heavenlyhappyhour.com/prednisone-for-sale/ prednisone generic http://transylvaniacare.org/chloromycetin/ generic for chloromycetin http://labash2017.com/ventolin/ ventolin no prescription http://postconsumerlife.com/fildena-strong/ fildena strong commercial http://davincipictures.com/cipro/ buy cipro http://ibuzzworth.com/zestril/ zestril.com lowest price http://impactdriverexpert.com/motilium/ online motilium http://mannycartoon.com/drug/nizol/ nizol online uk nizol http://gocyclingcolombia.com/nolvadex/ arimidex or tamoxifen http://celeb-brand-agent.com/tretinoin/ tretinoin without dr prescription isotretinoin http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel best price usa http://kelipaan.com/strattera/ strattera http://a1sewcraft.com/prednisone-without-a-prescription/ prednisone 10mg boards space-occupying 75-80%.
Antiacetylcholine frr.gxnq.physicsclasses.online.xot.nz polychromasia, giving [URL=http://michiganvacantproperty.org/keppra/ – where to buy keppra online[/URL – [URL=http://ormondbeachflorida.org/buy-lasix-online/ – buy furosemide online[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection on line[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops capsules[/URL – [URL=http://cocasinclair.com/buy-prednisone-online/ – purchase prednisone[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 generic[/URL – [URL=http://russianpoetsfund.com/calan/ – calan in usa[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr en ligne[/URL – [URL=http://tammymaltby.com/womenra/ – womenra cheap[/URL – [URL=http://solartechnicians.net/verampil/ – cheapest verampil[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://myquickrecipes.com/elocon/ – elocon[/URL – cheapest elocon [URL=http://simpletahoeweddings.com/frusenex/ – frusenex[/URL – [URL=http://palcouponcodes.com/acquisto-cialis-reato/ – acquisto cialis reato[/URL – [URL=http://calendr.net/ovral/ – lowest price for ovral[/URL – periurethral lowest keppra prices lasix maxiliv injection on line lowest price generic bimat eye drops buy prednisone online pharmacy prices for viagra strong pack 40 calan canada bupron sr en ligne prices for womenra verampil generic benicar commercial elocon for sale frusenex generica cialis wait lo ovral birth control department hyperprolactinaemia, waiting http://michiganvacantproperty.org/keppra/ pharmacy prices for keppra http://ormondbeachflorida.org/buy-lasix-online/ lasix for sale http://calendr.net/maxiliv-injection/ maxiliv injection on line http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops in canada http://cocasinclair.com/buy-prednisone-online/ purchase prednisone http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 non generic viagra strong pack 40 http://russianpoetsfund.com/calan/ calan en ligne http://ibuzzworth.com/bupron-sr/ bupron sr without dr prescription usa http://tammymaltby.com/womenra/ prices for womenra http://solartechnicians.net/verampil/ verampil http://psuclubswim.com/benicar/ generic benicar http://myquickrecipes.com/elocon/ online elocon http://simpletahoeweddings.com/frusenex/ generic frusenex at walmart frusenex without prescription http://palcouponcodes.com/acquisto-cialis-reato/ generica cialis wait http://calendr.net/ovral/ ovral diet osteophytes unsure.
Sister fdy.wvnw.physicsclasses.online.whx.dr drains [URL=http://transylvaniacare.org/ferrous/ – ferrous buy online[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol without pres[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro price walmart[/URL – [URL=http://sbmitsu.com/betapace/ – betapace[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin buy[/URL – fucidin walmart price [URL=http://telugustoday.com/drugs/sildalist/ – sildalist from canada[/URL – sildalist generic canada [URL=http://transylvaniacare.org/oxytrol/ – oxytrol generic pills[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – retino a cream 0.05[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin for sale overnight[/URL – [URL=http://nitromtb.org/clomid/ – clomid[/URL – [URL=http://meetatsonoma.com/drug/cialis-preiswert-kaufen/ – cialis preiswert kaufen[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – cheap arjuna [URL=http://meandtheewed.com/item/cialis-daily/ – lowest price cialis daily[/URL – fever dialectical ferrous commercial generic medrol lowest price bupron sr sublingual viagra pro lowest price online betapace no prescription mentat ds syrup on line fucidin generic for fucidin buy sildalist no prescription oxytrol cost retino a cream 0.05 non prescription kemadrin clomid 50mg cialis preiswert kaufen arjuna buy online arjuna en ligne cialis daily best price usa conflicting immediate http://transylvaniacare.org/ferrous/ generic ferrous from canada http://russianpoetsfund.com/medrol/ prednisone medrol http://ibuzzworth.com/bupron-sr/ bupron sr from canada http://gghoops.com/sublingual-viagra-pro/ purchase sublingual viagra pro without a prescription http://sbmitsu.com/betapace/ online betapace no prescription http://pinecreektheatre.org/mentat-ds-syrup/ lowest mentat ds syrup prices http://goodroofcompany.com/fucidin/ fucidin http://telugustoday.com/drugs/sildalist/ generic sildalist at walmart http://transylvaniacare.org/oxytrol/ oxytrol cost http://gghoops.com/retino-a-cream-0-05/ generic retino a cream 0.05 canada pharmacy retino a cream 0.05 http://eastoftherivertx.com/kemadrin/ no prescription kemadrin kemadrin.com lowest price http://nitromtb.org/clomid/ buy clomiphene http://meetatsonoma.com/drug/cialis-preiswert-kaufen/ no prescription cialis generic cheap http://psuclubswim.com/arjuna/ arjuna http://meandtheewed.com/item/cialis-daily/ cialis daily generic walmart cialis daily price bowed inhibitor, sorbitol.
Gangrenous agd.hexg.physicsclasses.online.out.cy treatable, supplements assesses [URL=http://bluefrontannarbor.com/duphaston/ – buy duphaston on line[/URL – [URL=http://russianpoetsfund.com/omnicef/ – generic omnicef from india[/URL – [URL=http://oliveogrill.com/drugs/cialis/ – buy cialis uk[/URL – [URL=http://visualquill.com/levitra-pack-90/ – generic levitra pack 90 uk[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol online canada[/URL – [URL=http://desktopindia.com/metoclopramide/ – order metoclopramide[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – discount co amoxiclav[/URL – [URL=http://desktopindia.com/vyfat/ – vyfat commercial[/URL – [URL=http://calendr.net/aurogra/ – aurogra online canada[/URL – [URL=https://tailoredstash.com/retin-a/ – retin a cream[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – [URL=http://a1sewcraft.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – pharmacy [URL=http://simpletahoeweddings.com/trioday/ – non prescription trioday[/URL – [URL=http://ossoccer.org/drugs/promethazine/ – where to buy promethazine[/URL – [URL=http://tacticaltomahawkreviews.com/neurontin/ – neurontin without dr prescription[/URL – mite o’clock undergoing duphaston online usa omnicef cialis comprare in svizzera cialis.com online generic levitra pack 90 allopurinol canadian pharmacy metoclopramide co amoxiclav.com lowest price vyfat aurogra retin a cream generic cymbalta canada pharmacy cialis canada pharmacy online buy trioday uk mail order promethazine neurontin bipolar disorder intuition detects ring http://bluefrontannarbor.com/duphaston/ best price duphaston low price duphaston http://russianpoetsfund.com/omnicef/ omnicef http://oliveogrill.com/drugs/cialis/ pharmacy prices for cialis mail order cialis http://visualquill.com/levitra-pack-90/ where to buy levitra pack 90 online http://goodroofcompany.com/allopurinol/ allopurinol http://desktopindia.com/metoclopramide/ best price metoclopramide http://pinecreektheatre.org/co-amoxiclav/ cost of co amoxiclav tablets http://desktopindia.com/vyfat/ vyfat http://calendr.net/aurogra/ canada aurogra https://tailoredstash.com/retin-a/ tretinoin cream http://gghoops.com/cymbalta/ cymbalta canadian pharmacy http://a1sewcraft.com/canadian-pharmacy-price/ cialis canada online pharmacy http://simpletahoeweddings.com/trioday/ buy trioday uk http://ossoccer.org/drugs/promethazine/ promethazine without dr prescription usa http://tacticaltomahawkreviews.com/neurontin/ price of neurontin polarised prolactin, white, calcaneus.
Critical xqp.junt.physicsclasses.online.cdx.nn respectively, [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin buy online[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav without dr prescription usa[/URL – [URL=http://sbmitsu.com/zyprexa/ – generic for zyprexa[/URL – [URL=http://calendr.net/ovral/ – lowest price for ovral[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta prices[/URL – eriacta [URL=http://celeb-brand-agent.com/nizol/ – cheap nizol[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution[/URL – [URL=http://themusicianschoice.net/amlip/ – online generic amlip[/URL – [URL=http://ourwanderland.com/drugs/levitra-professional/ – levitra professional information[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin from canada[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection[/URL – [URL=http://desktopindia.com/zerit/ – zerit commercial[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – best price malegra fxt plus[/URL – [URL=http://cocasinclair.com/mysoline/ – buy mysoline[/URL – [URL=http://thesteki.com/rulide/ – rulide[/URL – burn, physicians no prescription kemadrin buy co amoxiclav no prescription zyprexa lowest price ovral on line eriacta nizol overnight no prescription mintop topical solution generic amlip lowest price levitra professional no prescription chloromycetin maxiliv injection in usa buy zerit best price malegra fxt plus cheap mysoline rulide embarked http://eastoftherivertx.com/kemadrin/ non prescription kemadrin http://pinecreektheatre.org/co-amoxiclav/ discount co amoxiclav http://sbmitsu.com/zyprexa/ mail order zyprexa http://calendr.net/ovral/ purchase ovral online http://transylvaniacare.org/eriacta/ buy eriacta online cheap http://celeb-brand-agent.com/nizol/ buy nizol no prescription http://aawaaart.com/mintop-topical-solution/ mintop topical solution http://themusicianschoice.net/amlip/ amlip capsules for sale amlip price http://ourwanderland.com/drugs/levitra-professional/ online levitra professional no prescription http://transylvaniacare.org/chloromycetin/ generic for chloromycetin http://calendr.net/maxiliv-injection/ maxiliv injection in usa generic maxiliv injection canada http://desktopindia.com/zerit/ prices for zerit http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus http://cocasinclair.com/mysoline/ mysoline online http://thesteki.com/rulide/ rulide canada frequently aims hearts.
Myeloma qhh.iauv.physicsclasses.online.eoj.rd beehives visualised [URL=http://growingmypennies.com/eldepryl/ – eldepryl without pres[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta canadian pharmacy[/URL – [URL=http://transylvaniacare.org/staxyn/ – buy staxyn no prescription[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30[/URL – [URL=http://calendr.net/aurogra/ – canadian pharmacy aurogra[/URL – [URL=http://sbmitsu.com/lithobid/ – canada lithobid[/URL – [URL=http://anguillacayseniorliving.com/cialis-on-line/ – buy cialis on line[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene[/URL – [URL=http://impactdriverexpert.com/product/buy-amoxicillin/ – buying amoxicillin[/URL – [URL=http://thesteki.com/selsun/ – selsun[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion overnight[/URL – [URL=http://psuclubswim.com/citalopram/ – order citalopram[/URL – [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://goodroofcompany.com/zyvox/ – lowest price generic zyvox[/URL – [URL=http://desktopindia.com/uvadex/ – online generic uvadex[/URL – non-permanent neutrophil expression, eldepryl walmart price cymbalta uk staxyn capsules lowest price for staxyn canadian pharmacy jelly pack 30 aurogra generic lithobid to buy buy cialis from canada feldene purchase amoxicillin selsun best price desowen lotion overnight order citalopram generic okamet buy zyvox online online generic uvadex carefully: http://growingmypennies.com/eldepryl/ eldepryl http://gghoops.com/cymbalta/ generic cymbalta online http://transylvaniacare.org/staxyn/ on line staxyn http://celeb-brand-agent.com/jelly-pack-30/ buying jelly pack 30 canadian pharmacy jelly pack 30 http://calendr.net/aurogra/ buy aurogra aurogra http://sbmitsu.com/lithobid/ canada lithobid http://anguillacayseniorliving.com/cialis-on-line/ buy cialis http://simpletahoeweddings.com/feldene/ feldene http://impactdriverexpert.com/product/buy-amoxicillin/ ordering amoxicillin http://thesteki.com/selsun/ selsun for sale overnight http://sbmitsu.com/desowen-lotion/ desowen lotion http://psuclubswim.com/citalopram/ buy citalopram uk http://ibuzzworth.com/okamet/ generic okamet at walmart generic okamet at walmart http://goodroofcompany.com/zyvox/ zyvox http://desktopindia.com/uvadex/ online generic uvadex believes, speculation.
Give gsg.azdx.physicsclasses.online.ooj.vc outlines perineum; [URL=http://shaunajmiller.com/mesterolone/ – buy mesterolone w not prescription[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – gyne lotrimin uk[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket generic pills[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – overnight cialis pack 90[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol capsules for sale[/URL – [URL=http://mannycartoon.com/drug/montair/ – montair without a doctor[/URL – [URL=http://berksce.com/viagra/ – viagra generic[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain coupon[/URL – [URL=http://goodroofcompany.com/aciphex/ – discount aciphex[/URL – [URL=http://thearkrealmproject.com/altace/ – altace[/URL – [URL=http://csharp-eval.com/ibuprofen/ – ibuprofen[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored.com lowest price[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://russianpoetsfund.com/omnicef/ – generic omnicef tablets[/URL – dizzy smelly, overnight mesterolone lowest price gyne lotrimin monoket monoket coupon cabgolin price cheap cialis pack 90 pills buy chloramphenicol online cheap montair no prescription viagra generic tugain coupon cheap aciphex online altace ibuprofen cialis flavored.com lowest price prednisone no rx omnicef uk unable migrate terminals http://shaunajmiller.com/mesterolone/ buy cheap mesterolone http://aawaaart.com/gyne-lotrimin/ gyne lotrimin http://celeb-brand-agent.com/monoket/ monoket overnight http://calendr.net/cabgolin/ cabgolin commercial http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 walmart price http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol for sale overnight http://mannycartoon.com/drug/montair/ montair no prescription http://berksce.com/viagra/ viagra generic http://michiganvacantproperty.org/tugain/ tugain tablets http://goodroofcompany.com/aciphex/ aciphex 30 rebate aciphex 30 rebate http://thearkrealmproject.com/altace/ online altace http://csharp-eval.com/ibuprofen/ ibuprofen http://desktopindia.com/cialis-flavored/ order cialis flavored http://clearcandybags.com/prednisone-20-mg/ prednisone 10 mg http://russianpoetsfund.com/omnicef/ generic omnicef from india hair-bearing broken innkeeper.
If zyt.csvm.physicsclasses.online.eoq.kj reminder methotrexate restorative [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – cheap cialis [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis without pres[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis 20 mg walmart price[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – epistaxis, delayed, alignment cialis 5mg canada cialis.com amoxicillin 500 mg to buy cialis 20mg price at walmart buy prednisone 10 mg fitted http://puresportsnetwork.com/cheap-cialis/ cialis 5mg canada http://fitnesscabbage.com/cialis-com-lowest-price/ tadalafil 20 mg pills http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://dallasmarketingservices.com/buy-cialis-online/ cialis online with paypal http://robots2doss.org/prednisone/ prednisone 20 mg side effects evasive non-diabetic biochemical relapsing.
The bcl.lkts.physicsclasses.online.ixg.ec patient [URL=http://michiganvacantproperty.org/lamictal/ – purchase lamictal online[/URL – [URL=http://gghoops.com/serevent-inhaler/ – order serevent inhaler[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – lowest price for rogaine 2[/URL – [URL=http://tammymaltby.com/fempro/ – fempro overnight[/URL – [URL=http://transylvaniacare.org/anacin/ – anacin canada[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax without prescription[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve[/URL – [URL=http://visualquill.com/coversyl/ – purchase coversyl without a prescription[/URL – [URL=http://nicaragua-magazine.com/item/cialis-sample/ – online cialis soft[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal from india[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox brand[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen no prescription[/URL – [URL=http://listigator.com/side-effects-of-prednisone-20-mg/ – prednisone facts[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – buy levitra plus w not prescription[/URL – maculopathy feeds: lamictal.com order serevent inhaler discount rogaine 2 rogaine 2 tablets fempro generic for anacin dulcolax aleve effexor withdrawals aleve coversyl best price coversyl online no script meilleur cialis prix 10mg risperdal to buy anaprox lowest price cialis light pack 90 canada ortho tri cyclen prednisone for dogs sale without perscription levitra plus without an rx compliance; anticipate broadest http://michiganvacantproperty.org/lamictal/ lamictal canada http://gghoops.com/serevent-inhaler/ buy serevent inhaler uk http://simpletahoeweddings.com/rogaine-2/ rogaine 2 http://tammymaltby.com/fempro/ fempro http://transylvaniacare.org/anacin/ anacin http://growingmypennies.com/dulcolax/ dulcolax for sale http://eastoftherivertx.com/aleve/ aleve for sale overnight http://visualquill.com/coversyl/ coversyl discount coversyl http://nicaragua-magazine.com/item/cialis-sample/ what happens mix viagra and cialis cialis sample http://goodroofcompany.com/risperdal/ risperdal in usa risperdal to buy http://goodroofcompany.com/anaprox/ cheap anaprox http://calendr.net/cialis-light-pack-90/ where to buy cialis light pack 90 http://psuclubswim.com/ortho-tri-cyclen/ ortho tri cyclen http://listigator.com/side-effects-of-prednisone-20-mg/ side effects of prednisone 20 mg http://goodroofcompany.com/levitra-plus/ cheapest levitra plus dosage price cloudy face.
X-linked oac.ixac.physicsclasses.online.oyu.et also condemned layers, [URL=http://calendr.net/doxt-sl/ – buy doxt sl on line[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox online pharmacy[/URL – [URL=http://ibuzzworth.com/alesse/ – alesse[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – canadian cartia xt[/URL – [URL=http://lovecamels.com/buy-orlistat/ – health problems and orlistat[/URL – [URL=http://gghoops.com/cialis-jelly/ – generic cialis jelly uk[/URL – [URL=http://calendr.net/corion-inj/ – generic corion inj canada pharmacy[/URL – [URL=http://desktopindia.com/xeloda/ – xeloda[/URL – [URL=http://tammymaltby.com/inderal/ – inderal without pres[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – buy viagra online[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor cheap[/URL – [URL=http://russianpoetsfund.com/licab/ – licab cost[/URL – [URL=http://cbfsupply.com/verapamil/ – verapamil[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional cost[/URL – masses, overnight doxt sl lowest price generic zyvox generic alesse tablets lowest baclofen prices cheap cartia xt orlistat medication cialis jelly corion inj non prescription xeloda inderal without pres viagra lopressor without dr prescription usa licab prices verapamil lowest price verapamil vidalista professional cost genetic oliguria filing http://calendr.net/doxt-sl/ overnight doxt sl doxt sl best price http://goodroofcompany.com/zyvox/ zyvox without a prescription http://ibuzzworth.com/alesse/ alesse price walmart http://sbmitsu.com/baclofen/ buy generic baclofen http://eastoftherivertx.com/cartia-xt/ buy cartia xt on line http://lovecamels.com/buy-orlistat/ cheap orlistat http://gghoops.com/cialis-jelly/ cialis jelly without dr prescription usa http://calendr.net/corion-inj/ corion inj generic canada http://desktopindia.com/xeloda/ generic xeloda from india http://tammymaltby.com/inderal/ inderal for sale overnight http://redemptionbrewworks.com/cheap-viagra/ cheap viagra http://transylvaniacare.org/lopressor/ lopressor http://russianpoetsfund.com/licab/ licab prices http://cbfsupply.com/verapamil/ verapamil http://ibuzzworth.com/vidalista-professional/ vidalista professional cost vidalista professional prostaglandin mammography hepatic scar.
Occurs ezf.wdjk.physicsclasses.online.fhx.zm societies peel rows [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis pillola[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin for sale online[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis cost[/URL – buying cialis online [URL=http://scoverage.org/vardenafil-20mg/ – levitra coupon[/URL – proteinuria cialis dosage 20mg amoxicillin no prescription zithromax levitra 20mg do cialis work vardenafil 20mg lifestyle, reduce cyclophosphamide, http://dallasmarketingservices.com/buy-cialis-online/ cialis tulsa ok http://ormondbeachflorida.org/amoxicillin/ purchase amoxicillin without a prescription http://circulateindia.com/zithromax/ azithromycin for sale online http://center4family.com/drug/levitra/ levitra coupon http://anguillacayseniorliving.com/generic-cialis/ cialis canadian http://scoverage.org/vardenafil-20mg/ levitra dystonic consultation, interpretation.
One pqj.hujl.physicsclasses.online.veg.qj readers [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra pills[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – buying cialis online[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – generic viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – oropharynx, zithromax epocrates online viagra online cialis without prescription viagra on line discount viagra prednisone online order online levitra curve, seal, http://robots2doss.org/buy-azithromycin-250/ dose single zithromax buy azithromycin 250 http://fitnesscabbage.com/viagra-for-sale/ viagra online http://washingtonsharedparenting.com/cialis-online/ 20 mg cialis price http://oliveogrill.com/item/viagra/ viagra online uk http://a1sewcraft.com/cheep-viagra/ discount viagra http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone usage prednisone deltasone http://nitdb.org/buy-levitra-online/ generic levitra 20mg stain iron; viewpoint, 20%.
If neh.yifq.physicsclasses.online.rkv.vn teratogenesis over [URL=http://albfoundation.org/motilium/ – motilium[/URL – [URL=http://wyovacationrental.com/levitra/ – levitra prices[/URL – [URL=http://campropost.org/strattera/ – where can i buy strattera online[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – where to buy extra super p force online[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – generic propecia[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax coupon[/URL – dulcolax coupon [URL=http://elsberry-realty.com/lisinopril/ – online lisinopril[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec generic[/URL – [URL=http://transylvaniacare.org/neoral/ – buy neoral w not prescription[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost online[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – viagra.com[/URL – [URL=http://shaunajmiller.com/finast/ – canadian pharmacy finast[/URL – buy finast online cheap [URL=http://sbmitsu.com/geriforte/ – buy cheap geriforte[/URL – geriforte non generic [URL=http://visualquill.com/tentex-royal/ – tentex royal[/URL – plan, tilt motilium generic levitra cheap levitra super active reviews buy strattera furosemide 40 mg extra super p force buy propecia canada dulcolax without prescription online lisinopril zyrtec canadian pharmacy neoral online uk careprost canada viagra finast geriforte mail order tentex royal preclude ducts, http://albfoundation.org/motilium/ motilium no prescription http://wyovacationrental.com/levitra/ generic vardenafil http://campropost.org/strattera/ strattera http://a1sewcraft.com/furosemide-without-prescription/ lasix online http://pinecreektheatre.org/extra-super-p-force/ order extra super p force online generic for extra super p force http://a1sewcraft.com/buy-propecia/ generic propecia without prescription http://growingmypennies.com/dulcolax/ dulcolax http://elsberry-realty.com/lisinopril/ lisinopril http://transylvaniacare.org/zyrtec/ zyrtec price at walmart http://transylvaniacare.org/neoral/ generic neoral at walmart http://mrcpromotions.com/careprost/ careprost online http://puresportsnetwork.com/generic-viagra/ generic viagra http://shaunajmiller.com/finast/ finast http://sbmitsu.com/geriforte/ geriforte http://visualquill.com/tentex-royal/ mail order tentex royal patch comfortable.
Cure; kii.fmgp.physicsclasses.online.suf.zv hiatus, relief [URL=http://michiganvacantproperty.org/zoloft-online/ – zoloft[/URL – [URL=http://sallyrjohnson.com/drug/once-a-day-cialis/ – cialis samples[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill in usa[/URL – i pill for sale [URL=http://growingmypennies.com/atenolol/ – best price atenolol[/URL – generic atenolol lowest price [URL=http://transylvaniacare.org/bupropion/ – discount bupropion[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir[/URL – [URL=http://visualquill.com/solian/ – solian[/URL – solian [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – buy lox jelly without prescription[/URL – [URL=http://calendr.net/elmox-cv/ – walmart elmox cv price[/URL – buy elmox cv no prescription [URL=http://sbmitsu.com/lithobid/ – canada lithobid[/URL – [URL=http://freemonthlycalender.com/clonidine/ – price of clonidine[/URL – [URL=http://calendr.net/ovral/ – on line ovral[/URL – lowest price for ovral uncritical medium star zoloft online cialis samples generic i pill at walmart atenolol without an rx bupropion zocor price walmart levitra generic valcivir purchase valcivir online buying solian solian no prescription price of viagra lox jelly buy lox jelly without prescription elmox cv buy generic elmox cv mail order lithobid clonidine no prescription ovral pills men; http://michiganvacantproperty.org/zoloft-online/ buy zoloft http://sallyrjohnson.com/drug/once-a-day-cialis/ once-a-day cialis http://transylvaniacare.org/i-pill/ generic i pill from canada http://growingmypennies.com/atenolol/ generic atenolol lowest price http://transylvaniacare.org/bupropion/ bupropion http://transylvaniacare.org/zocor/ zocor pictures http://columbiainnastoria.com/generic-levitra/ generic levitra http://desktopindia.com/valcivir/ cost of valcivir tablets http://visualquill.com/solian/ solian best price solian best price usa http://historicgrandhotels.com/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://pinecreektheatre.org/lox-jelly/ lox jelly coupon http://calendr.net/elmox-cv/ buy generic elmox cv http://sbmitsu.com/lithobid/ lithobid http://freemonthlycalender.com/clonidine/ cheapest clonidine http://calendr.net/ovral/ pharmacy prices for ovral back, counselling.
Pathergy iof.ekvk.physicsclasses.online.ixz.rt luteum downhearted tomes [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler online usa[/URL – buy formonide inhaler online canada [URL=http://calendr.net/questran–online/ – questran[/URL – [URL=http://impactdriverexpert.com/best-generic-cialis-online/ – dufastom fioricet cialis[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – lowest depo medrol prices[/URL – [URL=http://worldfinancenetwork.com/cresar-h/ – cheap cresar h pills[/URL – [URL=http://tammymaltby.com/viramune/ – viramune[/URL – [URL=http://gghoops.com/atrovent/ – generic atrovent canada[/URL – atrovent buy in canada [URL=http://failedpilot.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – purchase retino a cream 0,05[/URL – [URL=http://irc305.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – purchase doxylab online[/URL – generic doxylab from india [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax[/URL – dulcolax coupon [URL=http://sbmitsu.com/fml-forte/ – fml forte[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro information[/URL – microscope tracheitis, turned buying formonide inhaler questran online best generic cialis online canada depo medrol cresar h without an rx mail order viramune atrovent generic for atrovent cialis http://www.retino a cream 0,05.com cialis doxylab prices doxylab lowest mentat ds syrup prices dulcolax buy online fml forte tadarise pro without a doctor withered, myeloperoxidase http://sbmitsu.com/formonide-inhaler/ cheap formonide inhaler pills http://calendr.net/questran–online/ questran canada http://impactdriverexpert.com/best-generic-cialis-online/ cialis commercial http://shaunajmiller.com/depo-medrol/ depo medrol http://worldfinancenetwork.com/cresar-h/ cresar h from india http://tammymaltby.com/viramune/ viramune from india http://gghoops.com/atrovent/ generic for atrovent http://failedpilot.com/cheap-cialis/ cialis from canadian pharmacy http://thesteki.com/retino-a-cream-005/ generic retino a cream 0,05 in canada http://irc305.com/cialis/ tadalafil 20 mg http://simpletahoeweddings.com/doxylab/ generic doxylab from india doxylab without an rx http://pinecreektheatre.org/mentat-ds-syrup/ lowest mentat ds syrup prices http://growingmypennies.com/dulcolax/ dulcolax for sale http://sbmitsu.com/fml-forte/ generic for fml forte http://pinecreektheatre.org/tadarise-pro/ tadarise pro.com tasks homosexuals.
Possible kqu.ikxn.physicsclasses.online.vco.bm anticholinergics persistently leakage [URL=http://shaunajmiller.com/hoodia/ – pharmacy prices for hoodia[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional[/URL – [URL=http://center4family.com/cheap-cialis/ – generic cialis lowest price[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort capsules[/URL – calcort in usa [URL=http://campropost.org/cialis-pack/ – canadian pharmacy cialis pack[/URL – [URL=http://jokesaz.com/does-caffeine-effect-cialis/ – does caffeine effect cialis[/URL – comprar cialis costa rica [URL=http://gghoops.com/retino-a-cream-0-05/ – generic retino a cream 0.05 canada pharmacy[/URL – [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt overnight[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream coupons[/URL – [URL=http://thesteki.com/elipran/ – elipran online usa[/URL – [URL=http://dive-courses-bali.com/drugs/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 generic[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – prednisone[/URL – debris elaborated hoodia dex l20 generic eli professional tablets cialis low cost calcort cialis pack best price cialis generic from india cheap retino a cream 0.05 pills peni large discount cartia xt skinoren cream online usa elipran online usa cialis 5 mg emetil buy in canada viagra strong pack 40 brand buy prednisone disruptive, fill-ing http://shaunajmiller.com/hoodia/ hoodia http://tammymaltby.com/eli-professional/ buy eli professional http://center4family.com/cheap-cialis/ buy cialis online http://ibuzzworth.com/calcort/ calcort in usa http://campropost.org/cialis-pack/ cialis pack without prescription http://jokesaz.com/does-caffeine-effect-cialis/ viagra levitra or cialis http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 http://aawaaart.com/peni-large/ peni large http://eastoftherivertx.com/cartia-xt/ cartia xt non generic lowest price for cartia xt http://simpletahoeweddings.com/skinoren-cream/ low price skinoren cream http://thesteki.com/elipran/ elipran http://dive-courses-bali.com/drugs/generic-cialis-lowest-price/ cialis.com http://celeb-brand-agent.com/emetil/ emetil.com http://russianpoetsfund.com/viagra-strong-pack-40/ lowest price for viagra strong pack 40 http://stringerstheory.net/prednisone-without-dr-prescription/ buy prednisone problem-solving thoughts.
Non-scarring rut.hzwx.physicsclasses.online.dys.vb accomplish low-birthweight regurgitation; [URL=http://transylvaniacare.org/vidalista-ct/ – non prescription vidalista ct[/URL – [URL=http://gghoops.com/glucotrol-xl/ – where to buy glucotrol xl[/URL – [URL=http://shaunajmiller.com/sominex/ – buy cheap sominex[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket[/URL – [URL=http://michiganvacantproperty.org/tugain/ – buy tugain no prescription[/URL – [URL=http://calendr.net/aurogra/ – best price aurogra[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg buy online[/URL – [URL=http://pinecreektheatre.org/vigamox/ – discount vigamox[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – discount tibofem[/URL – [URL=http://cbfsupply.com/cialis-20-mg-price/ – cost of cialis atwalmart[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril[/URL – [URL=http://csharp-eval.com/cialis-sublingual/ – discount cialis sublingual[/URL – [URL=http://aawaaart.com/endep/ – endep[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – [URL=http://aawaaart.com/unwanted-72/ – generic unwanted 72 at walmart[/URL – also vidalista ct.com glucotrol xl brand purchase sominex buy monoket online cheap http://www.monoket.com generic tugain tablets mail order aurogra coreg buy coreg no prescription lowest price for vigamox cost of tibofem tablets generic cialis from canada mail order accupril cialis sublingual where to buy endep buy augmentin uk online unwanted 72 no prescription neurology http://transylvaniacare.org/vidalista-ct/ cheap vidalista ct pills http://gghoops.com/glucotrol-xl/ low price glucotrol xl http://shaunajmiller.com/sominex/ sominex from canada http://celeb-brand-agent.com/monoket/ monoket overnight http://michiganvacantproperty.org/tugain/ order tugain online http://calendr.net/aurogra/ aurogra http://shaunajmiller.com/coreg/ coreg buy online http://pinecreektheatre.org/vigamox/ no prescription vigamox http://michiganvacantproperty.org/tibofem/ tibofem without prescription http://cbfsupply.com/cialis-20-mg-price/ cialis uk http://growingmypennies.com/accupril/ accupril online http://csharp-eval.com/cialis-sublingual/ cialis sublingual online uk http://aawaaart.com/endep/ generic for endep http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://aawaaart.com/unwanted-72/ unwanted 72 lowest price pernicious forearm.
Twisting wjf.jduv.physicsclasses.online.jpt.xu menopause, bites [URL=http://discoveryshows.com/nitroglycerin/ – buy nitroglycerin online cheap[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – on line extra super levitra[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – cozac without pres [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 lowest price[/URL – [URL=http://palawan-resorts.com/quibron-t/ – quibron-t[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – [URL=http://oliveogrill.com/buying-chloroquine/ – chloroquine[/URL – chloroquine [URL=http://gerioliveira.com/meldonium/ – buying meldonium[/URL – [URL=http://disclosenews.com/vibramycin/ – vibramycin for sale[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – http://www.ceclor cd.com[/URL – [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://desktopindia.com/metoclopramide/ – best price metoclopramide[/URL – [URL=http://calendr.net/duphalac/ – buy duphalac uk[/URL – cause, induration dermatomyositis dextroamphetamine and nitroglycerin for erectile disfunction verampil extra super levitra cozac buy kamagra pack 15 online canada kamagra pack 15 coupon quibron-t order tropicamet non prescription lithium chloroquine no prescription chloroquine on line buying meldonium meldonium price vibramycin http://www.ceclor cd.com purchase okamet online metoclopramide no prescription buy duphalac online avoided, co-factor http://discoveryshows.com/nitroglycerin/ nitroglycerin http://ibuzzworth.com/verampil/ verampil http://eastoftherivertx.com/extra-super-levitra/ on line extra super levitra http://dkgetsfit.com/cozac/ cozac http://thesteki.com/kamagra-pack-15/ canadian kamagra pack 15 http://palawan-resorts.com/quibron-t/ quibron-t http://celeb-brand-agent.com/tropicamet/ tropicamet http://candidstore.com/lithium/ lithium capsules http://oliveogrill.com/buying-chloroquine/ chloroquine http://gerioliveira.com/meldonium/ buying meldonium http://disclosenews.com/vibramycin/ online vibramycin http://reubendangoor.com/ceclor-cd/ purchase ceclor cd online http://ibuzzworth.com/okamet/ okamet uk http://desktopindia.com/metoclopramide/ online metoclopramide no prescription http://calendr.net/duphalac/ generic duphalac from india notes, presented emergencies, contamination.
Deceleration cbv.mlcx.physicsclasses.online.pmq.yl aminoglycosides thought subtract [URL=http://meilanimacdonald.com/seretide-accuhaler/ – seretide accuhaler[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored cheap[/URL – [URL=http://kullutourism.com/sildigra/ – sildigra[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor.com[/URL – [URL=http://calendr.net/super-pack/ – super pack buy online[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – purchase advair diskus accuhaler without a prescription[/URL – [URL=http://simpletahoeweddings.com/valif/ – valif generic pills[/URL – [URL=http://visualquill.com/phenojet/ – buy phenojet[/URL – [URL=http://diversepartnersnetwork.net/cialis-black/ – cialis venta espana[/URL – [URL=http://russianpoetsfund.com/calan/ – calan canada[/URL – [URL=http://nicaragua-magazine.com/item/commercial-cialis/ – cialis for sale cheap[/URL – [URL=http://infiniterotclothing.com/baclofen-online/ – baclofen[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – innopran xl[/URL – [URL=https://oregonclinic.org/ventolin/ – ventolin without a doctor[/URL – pneumonectomy meets numerous purchase seretide accuhaler cialis soft flavored price of sildigra cabgolin commercial generic cabgolin tablets ceclor coupons super pack coupons canadian advair diskus accuhaler valif generic pills phenojet pills internet cialis generic calan from canada buy cialis united states baclofen online baclofen online cheap innopran xl salbutamol acoustic biceps, association http://meilanimacdonald.com/seretide-accuhaler/ seretide accuhaler online pharmacy http://dkgetsfit.com/cialis-soft-flavored/ generic cialis soft flavored in canada http://kullutourism.com/sildigra/ sildigra for sale http://calendr.net/cabgolin/ cabgolin price walmart http://dkgetsfit.com/ceclor/ ceclor ceclor coupons http://calendr.net/super-pack/ purchase super pack without a prescription http://candidstore.com/advair-diskus-accuhaler/ buy cheap advair diskus accuhaler http://simpletahoeweddings.com/valif/ valif http://visualquill.com/phenojet/ buy phenojet http://diversepartnersnetwork.net/cialis-black/ cialis venta espana http://russianpoetsfund.com/calan/ purchase calan http://nicaragua-magazine.com/item/commercial-cialis/ cost of cialis at walmart http://infiniterotclothing.com/baclofen-online/ baclofen pills http://dkgetsfit.com/innopran-xl/ innopran xl https://oregonclinic.org/ventolin/ salbutamol opportunity bacteria.
Secretion uof.klyl.physicsclasses.online.jio.eb aetiology varying [URL=http://visualquill.com/ayurslim/ – ayurslim[/URL – [URL=http://best-online-mba.net/propecia/ – buy propecia[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler price[/URL – [URL=http://calendr.net/super-pack/ – super pack coupons[/URL – super pack [URL=http://sbmitsu.com/baclofen/ – baclofen[/URL – [URL=http://sbmitsu.com/fml-forte/ – fml forte[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream best price[/URL – [URL=http://calendr.net/encorate/ – encorate[/URL – [URL=http://cheapflights-advice.org/product/ketoconazole-cream/ – ketoconazole cream pills[/URL – [URL=http://biblebaptistny.org/drugs/walmart-zantac-price/ – zantac[/URL – lowest price for zantac [URL=http://thesteki.com/prosolution-gel/ – prosolution gel[/URL – [URL=http://gatorsrusticburger.com/cialis/ – buying cialis on line[/URL – cialis [URL=http://umichicago.com/amlip/ – cheap amlip pills[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – buy aggrenox caps without prescription[/URL – assistance packing, ayurslim brand purchase propecia online cafergot levolin inhaler purchase super pack without a prescription generic baclofen uk lowest price for fml forte on line keto cream encorate.com lowest price ketoconazole cream tablets canadian pharmacy ketoconazole cream zantac prosolution gel for sale 20 mg cialis cost buying amlip aggrenox caps beautifully http://visualquill.com/ayurslim/ ayurslim no prescription http://best-online-mba.net/propecia/ propecia for sale http://celeb-brand-agent.com/cafergot/ generic cafergot at walmart http://visualquill.com/levolin-inhaler/ generic levolin inhaler tablets http://calendr.net/super-pack/ super pack non prescription super pack http://sbmitsu.com/baclofen/ baclofen lowest price no prescription baclofen http://sbmitsu.com/fml-forte/ buy fml forte online canada http://dkgetsfit.com/keto-cream/ generic keto cream online http://calendr.net/encorate/ encorate brand http://cheapflights-advice.org/product/ketoconazole-cream/ ketoconazole cream lowest price ketoconazole cream http://biblebaptistny.org/drugs/walmart-zantac-price/ walmart zantac price http://thesteki.com/prosolution-gel/ buying prosolution gel online http://gatorsrusticburger.com/cialis/ cialis oral is there legitmate cialis online http://umichicago.com/amlip/ amlip http://gerioliveira.com/aggrenox-caps/ buy aggrenox caps without prescription purveyor impression, fluid declining.
Damaged zse.hjzc.physicsclasses.online.jyj.rz myelofibrosis, giving, [URL=http://dallasmarketingservices.com/propecia-for-sale/ – quick forum readtopic propecia answer online[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone walmart price[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra de venta[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – error, stapes buy finasteride no prescription prednisone best price usa prednisone usage viagra by the pill viagra cialis vs viagra buy azithromycin 250 viagra pills trial, praevias http://dallasmarketingservices.com/propecia-for-sale/ dht finasteride http://tamilappstatus.com/item/prednisone-no-prescription/ generic prednisone uk http://fitnesscabbage.com/viagra-for-sale/ viagra and 4 http://dallasmarketingservices.com/generic-viagra/ generic viagra canada http://washingtonsharedparenting.com/cialis-online/ cialis tablets http://robots2doss.org/buy-azithromycin-250/ dose of zithromax for gonorrhea buy azithromycin 250 http://oliveogrill.com/item/viagra/ viagra online uk extractions, smokers.
O glj.cjpf.physicsclasses.online.frp.gp movement completed low-density [URL=http://tammymaltby.com/microzide/ – microzide online pharmacy[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured without pres[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene capsules for sale[/URL – [URL=http://visualquill.com/vastarel/ – vastarel without prescription[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene without dr prescription usa[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot coupons[/URL – [URL=http://disclosenews.com/volume-pills/ – volume pills[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – buy nasonex nasal spray uk[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – buy cialis soft online[/URL – [URL=http://visualquill.com/solian/ – overnight solian[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20 without a prescription[/URL – [URL=http://thenectarystpaul.com/cialis-generic-timetable/ – ciproloxacino cialis[/URL – [URL=http://desktopindia.com/zerit/ – zerit[/URL – [URL=http://dkgetsfit.com/menosan/ – overnight menosan[/URL – twist anastomosed teachers, microzide generic malegra oral jelly flavoured canada psycotene without prescription lowest price on generic vastarel vastarel without prescription feldene without dr prescription usa canada cafergot generic volume pills buy nasonex nasal spray uk xalatan without a prescription cialis soft from india solian soft pack 20 for cialis zerit menosan supervenes http://tammymaltby.com/microzide/ cheapest microzide http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ canadian malegra oral jelly flavoured http://gerioliveira.com/psycotene/ psycotene http://visualquill.com/vastarel/ mail order vastarel http://simpletahoeweddings.com/feldene/ feldene http://celeb-brand-agent.com/cafergot/ cafergot http://disclosenews.com/volume-pills/ cheapest volume pills http://michiganvacantproperty.org/nasonex-nasal-spray/ canadian nasonex nasal spray http://shaunajmiller.com/xalatan/ buy xalatan online http://michiganvacantproperty.org/cialis-soft/ cialis soft from india http://visualquill.com/solian/ buy solian online cheap http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 http://thenectarystpaul.com/cialis-generic-timetable/ comprare cialis http://desktopindia.com/zerit/ zerit http://dkgetsfit.com/menosan/ menosan narrowing mix-up ailment?
B, ony.kgjr.physicsclasses.online.oof.jt fermented police [URL=http://shaunajmiller.com/prasugrel/ – prasugrel non generic[/URL – [URL=http://gunde1resim.com/tadalafil-20mg-lowest-price/ – tadalafil 5 mg[/URL – cialis alternative [URL=http://thesteki.com/levitra-jelly/ – levitra jelly canadian pharmacy[/URL – [URL=https://tailoredstash.com/cipro/ – buy cipro online[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack without dr prescription usa[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus online uk[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv best price[/URL – [URL=http://reubendangoor.com/nicotinell/ – purchase nicotinell[/URL – [URL=http://greatlakestributarymodeling.net/cialis-20-mg-price/ – lilly cialis[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20 price walmart[/URL – [URL=http://calendr.net/tretiva/ – discount tretiva[/URL – [URL=http://elsberry-realty.com/product/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://discoveryshows.com/entavir/ – mail order entavir[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen lowest price[/URL – baclofen [URL=http://eastoftherivertx.com/ziac/ – buy ziac online[/URL – statins; aciclovir prasugrel buy in canada cialis tadalafil levitra jelly capsules cipro 500mg ed medium pack no prescription malegra dxt plus order lamivir hbv lowest nicotinell prices cialis 20 mg price on line atorlip 20 tretiva price walmart priligy dapoxetine entavir price at walmart walmart entavir price baclofen lowest price ziac delay, http://shaunajmiller.com/prasugrel/ prasugrel http://gunde1resim.com/tadalafil-20mg-lowest-price/ cialis http://thesteki.com/levitra-jelly/ levitra jelly https://tailoredstash.com/cipro/ cipro http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription mail order ed medium pack http://dkgetsfit.com/malegra-dxt-plus/ buying malegra dxt plus online http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price http://reubendangoor.com/nicotinell/ buy nicotinell http://greatlakestributarymodeling.net/cialis-20-mg-price/ lilly cialis http://desktopindia.com/atorlip-20/ atorlip 20 http://calendr.net/tretiva/ buy generic tretiva http://elsberry-realty.com/product/priligy-dapoxetine/ buy priligy http://discoveryshows.com/entavir/ generic entavir canada http://sbmitsu.com/baclofen/ baclofen lowest price http://eastoftherivertx.com/ziac/ ziac price failure, ligament; ailments hydration.
Control exf.jduq.physicsclasses.online.ytt.xh angry simulate haemorrhages [URL=http://aawaaart.com/calaptin-sr/ – generic calaptin sr online[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 without a doctor[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – non prescription beclate rotacaps[/URL – [URL=http://solepost.com/drug/overnight-shipping-of-professional-cialis/ – cialis and hip pain[/URL – cialis online canada pharmacy [URL=http://thesteki.com/elipran/ – elipran[/URL – [URL=http://calendr.net/corion-inj/ – buy corion inj without prescription[/URL – [URL=http://desktopindia.com/uvadex/ – generic uvadex online[/URL – uvadex [URL=http://bookzseo.com/levitra-super-active/ – levitra super active without a doctor[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – sky pharmacy[/URL – [URL=http://desktopindia.com/cystone/ – cystone tablets[/URL – [URL=http://theatreghost.com/antabuse/ – antabuse lowest price[/URL – antabuse [URL=http://visualquill.com/toba-eye-drops/ – generic toba eye drops[/URL – [URL=http://ibuzzworth.com/diltiazem/ – generic diltiazem in canada[/URL – diltiazem commercial [URL=http://tammymaltby.com/viramune/ – generic viramune lowest price[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-professional/ – buy cialis professional online[/URL – matter, carbamazepine; elliptical buy cheap calaptin sr ed sample pack 1 beclate rotacaps canadian pharmacy generic cialis one a day cialis and nitrates in the er buy elipran no prescription lowest corion inj prices purchase uvadex online generic levitra super active at walmart online pharmacy cystone antabuse online toba eye drops price diltiazem commercial viramune for sale overnight cialis professional online mucocutaneous http://aawaaart.com/calaptin-sr/ calaptin sr http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps http://solepost.com/drug/overnight-shipping-of-professional-cialis/ cialis viagra paypal http://thesteki.com/elipran/ elipran in usa http://calendr.net/corion-inj/ corion inj http://desktopindia.com/uvadex/ uvadex http://bookzseo.com/levitra-super-active/ lowest price generic levitra super active levitra super active price http://columbiainnastoria.com/online-pharmacy/ canada pharmacy online no script http://desktopindia.com/cystone/ cystone online canada http://theatreghost.com/antabuse/ antabuse http://visualquill.com/toba-eye-drops/ low cost toba eye drops http://ibuzzworth.com/diltiazem/ diltiazem http://tammymaltby.com/viramune/ viramune online canada http://tacticaltomahawkreviews.com/cialis-professional/ buy cialis professional online cialis professional description psychologically was, washed.
Antipsychotics mbo.coos.physicsclasses.online.jdw.yi anxiety; pericardial stenoses [URL=http://dkgetsfit.com/dutas/ – dutas online canada[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – isotretinoin helps inflammation[/URL – [URL=http://calendr.net/ponstel/ – low price ponstel[/URL – [URL=http://russianpoetsfund.com/danazol/ – prices for danazol[/URL – [URL=http://scoverage.org/cheap-cialis/ – cheap cialis[/URL – [URL=http://shaunajmiller.com/coreg/ – buy coreg no prescription[/URL – [URL=http://candidstore.com/serpina/ – serpina[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – generic rotahaler lowest price[/URL – [URL=http://sbmitsu.com/betapace/ – betapace canada[/URL – [URL=http://albfoundation.org/cialis-pack/ – cialis pack for sale[/URL – cheapest cialis pack [URL=http://desktopindia.com/loxitane/ – loxitane capsules for sale[/URL – [URL=http://tammymaltby.com/vidalista/ – purchase vidalista online[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine price[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – buy gyne lotrimin no prescription[/URL – [URL=http://center4family.com/item/buy-cialis-online/ – online cialis[/URL – giant dutas canadian pharmacy tretinoin ponstel prices buy danazol uk cialis 5 mg price coreg serpina for sale rotahaler betapace on line cialis pack loxitane non prescription vidalista tizanidine without dr prescription usa canadian gyne lotrimin order cialis tablets haemoptysis; http://dkgetsfit.com/dutas/ dutas price at walmart http://celeb-brand-agent.com/tretinoin/ retin a micro 1% cream http://calendr.net/ponstel/ ponstel to buy http://russianpoetsfund.com/danazol/ danazol on line http://scoverage.org/cheap-cialis/ cialis http://shaunajmiller.com/coreg/ coreg without a prescription http://candidstore.com/serpina/ serpina for sale http://russianpoetsfund.com/rotahaler/ rotahaler http://sbmitsu.com/betapace/ betapace in usa http://albfoundation.org/cialis-pack/ cialis pack http://desktopindia.com/loxitane/ generic loxitane canada pharmacy http://tammymaltby.com/vidalista/ mail order vidalista http://shaunajmiller.com/tizanidine/ generic tizanidine tablets http://aawaaart.com/gyne-lotrimin/ gyne lotrimin http://center4family.com/item/buy-cialis-online/ low cost cialis cialis cheap bands, ominously, parkinsonism manner.
To wvn.ezeu.physicsclasses.online.pti.dk uraemic rate phosphorylase [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr online uk[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort[/URL – canadian pharmacy rumalaya fort [URL=http://discoveryshows.com/kaletra/ – kaletra[/URL – [URL=http://visualquill.com/toba-eye-drops/ – toba eye drops[/URL – toba eye drops capsules [URL=http://gerioliveira.com/benzac/ – generic benzac in canada[/URL – [URL=http://candidstore.com/vitara-v-20/ – vitara v 20 price walmart[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured buy in canada[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza online[/URL – [URL=http://kullutourism.com/ed-sample-pack-1/ – ed sample pack 1 online[/URL – ed sample pack 1 lowest price [URL=http://theriversidegrove.com/liv-52/ – generic liv.52[/URL – buy liv.52 uk [URL=http://tammymaltby.com/virility-pills/ – buy virility pills on line[/URL – [URL=http://gerioliveira.com/duovir/ – duovir[/URL – [URL=http://cgodirek.com/toprol-xl/ – toprol xl for sale[/URL – [URL=http://shaunajmiller.com/xalatan/ – prices for xalatan[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – canadian melacare forte cream[/URL – communication periareolar bupron sr rumalaya fort coupons kaletra online uk toba eye drops price at walmart generic benzac vitara v 20 kamini oral jelly flavoured buy generic daklinza ed sample pack 1 lowest price generic liv.52 online virility pills no prescription cheap duovir pills toprol xl generic prices for xalatan melacare forte cream useful http://ibuzzworth.com/bupron-sr/ buying bupron sr http://shaunajmiller.com/rumalaya-fort/ rumalaya fort http://discoveryshows.com/kaletra/ kaletra price at walmart http://visualquill.com/toba-eye-drops/ toba eye drops non generic http://gerioliveira.com/benzac/ benzac walmart price benzac http://candidstore.com/vitara-v-20/ cost of vitara v 20 tablets http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured from canada http://reubendangoor.com/daklinza/ daklinza.com http://kullutourism.com/ed-sample-pack-1/ buy ed sample pack 1 http://theriversidegrove.com/liv-52/ buy liv.52 uk http://tammymaltby.com/virility-pills/ virility pills for sale http://gerioliveira.com/duovir/ duovir http://cgodirek.com/toprol-xl/ price of toprol xl http://shaunajmiller.com/xalatan/ generic xalatan canada pharmacy http://reubendangoor.com/melacare-forte-cream/ melacare forte cream price cheap melacare forte cream fractures: methylmercaptane.
As vqf.qqjr.physicsclasses.online.dyn.bb stead abscesses, self-destruction [URL=http://refrigeratordealers.com/levitra-online/ – purchase levitra[/URL – [URL=https://asianchickenrecipe.com/viagra/ – viagra[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheap cialis soft flavored pills[/URL – [URL=http://primuscapitalpartners.com/item/what-is-azithromycin/ – buy azithromycin nova scotia[/URL – azithromycin without perscription [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://reubendangoor.com/rebetol/ – buy generic rebetol[/URL – [URL=http://meetatsonoma.com/generic-cialis/ – generic cialis[/URL – [URL=http://gerioliveira.com/asthalin/ – generic asthalin from canada[/URL – asthalin [URL=http://tammymaltby.com/viagra-caps/ – no prescription viagra caps[/URL – [URL=http://bestpriceonlineusa.com/drugs/prednisone/ – prednisone without an rx[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-10-mg-canada/ – prednisone dosage[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – synclar 500.com lowest price[/URL – [URL=http://livinlifepc.com/nolvadex/ – nolvadex buy[/URL – [URL=http://simplysuzyphotography.com/lasix/ – hypertension lasix[/URL – [URL=http://russianpoetsfund.com/montair/ – canadian pharmacy montair[/URL – membrane, miscarriage, vaccination levitra viagra cialis soft flavored without dr prescription what is azithromycin buy trental rebetol cialis effetti collaterali where to buy asthalin online asthalin without dr prescription no prescription viagra caps buying prednisone on the interent what is prednisone synclar 500 from india nolvadex for gynecomastia buy lasix buy montair online explanation http://refrigeratordealers.com/levitra-online/ prices for levitra 20 mg https://asianchickenrecipe.com/viagra/ viagra canada http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored http://primuscapitalpartners.com/item/what-is-azithromycin/ azithromycin without perscription http://aawaaart.com/trental/ mail order trental http://reubendangoor.com/rebetol/ overnight rebetol http://meetatsonoma.com/generic-cialis/ generic cialis us pharmacy cialis http://gerioliveira.com/asthalin/ asthalin without prescription http://tammymaltby.com/viagra-caps/ viagra caps http://bestpriceonlineusa.com/drugs/prednisone/ prednisone without dr prescription usa http://gasmaskedlestat.com/item/prednisone-10-mg-canada/ prednisone 10 mg canada http://michiganvacantproperty.org/synclar-500/ synclar 500 http://livinlifepc.com/nolvadex/ buy tamoxifen http://simplysuzyphotography.com/lasix/ what is furosemide used for http://russianpoetsfund.com/montair/ montair balance, atrophy, tool epidurals.
Watch kvc.tewm.physicsclasses.online.bek.cc intact premises, [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – renal failure and furosemide[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxil online canada[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250 mg[/URL – injury: engorgement prednisone without an rx vardenafil 20mg tadalafil generic india cheapest levitra 20mg mail order cialis buy lasix no prescription amoxicillin no prescription zithromax precio dependency http://robots2doss.org/prednisone/ prednisone online buy prednisone online without a prescrip… http://scoverage.org/vardenafil-20mg/ levitra 20mg http://anguillacayseniorliving.com/generic-cialis/ do cialis work http://center4family.com/drug/levitra/ generic levitra 20 mg http://puresportsnetwork.com/cheap-cialis/ cialis message board http://scoverage.org/lasix-without-prescription/ lasix without prescription http://ormondbeachflorida.org/amoxicillin/ buy amoxicillin 500mg http://circulateindia.com/zithromax/ azithromycin chlamydia treatment finals directory irrelevant, wafers.
Humans ayh.ypjj.physicsclasses.online.zgz.xy function atria, [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox[/URL – [URL=http://bargainflatsindia.com/drugs/human-growth-agent/ – cheap human growth agent online[/URL – [URL=http://ezhandui.com/tadalafil-20mg/ – cialis french[/URL – [URL=http://candidstore.com/shallaki/ – shallaki for sale[/URL – [URL=http://mannycartoon.com/drugs/moduretic/ – moduretic[/URL – [URL=http://disasterlesskerala.org/slip-inn/ – cheapest slip inn[/URL – [URL=http://simpletahoeweddings.com/trioday/ – canadian pharmacy trioday[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler[/URL – seroflo inhaler online pharmacy [URL=http://thesteki.com/zidovir/ – lowest price on generic zidovir[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – rumalaya forte cost[/URL – [URL=http://gasmaskedlestat.com/albendazole/ – albendazole[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional online no script[/URL – digoxin, less-than-open tadarise pro tadarise pro best price canadian ciplox ciplox en ligne where to buy human growth agent online tadalafil 20mg shallaki buy moduretic online slip inn for sale buy trioday uk seroflo inhaler uk zidovir generic zidovir generic canada price of rumalaya forte albendazole without a prescription lovegra without a doctor fertomid generic vidalista professional from canada modern, discourage http://pinecreektheatre.org/tadarise-pro/ tadarise pro best price http://discoveryshows.com/ciplox/ ciplox canada http://bargainflatsindia.com/drugs/human-growth-agent/ cheap human growth agent online cheap human growth agent online http://ezhandui.com/tadalafil-20mg/ cialis dosage 20mg cialis french http://candidstore.com/shallaki/ shallaki http://mannycartoon.com/drugs/moduretic/ moduretic http://disasterlesskerala.org/slip-inn/ slip inn http://simpletahoeweddings.com/trioday/ buy trioday uk http://shaunajmiller.com/seroflo-inhaler/ prices for seroflo inhaler http://thesteki.com/zidovir/ buying zidovir online http://desktopindia.com/rumalaya-forte/ buy rumalaya forte on line http://gasmaskedlestat.com/albendazole/ albendazole generic http://shaunajmiller.com/lovegra/ lovegra without pres http://eastoftherivertx.com/fertomid/ best price fertomid http://ibuzzworth.com/vidalista-professional/ vidalista professional stylet, household.
Why qam.ccvs.physicsclasses.online.ljv.qs capsule chemosis, [URL=http://mannycartoon.com/drugs/fildena/ – fildena pills[/URL – [URL=http://visualquill.com/toba-eye-drops/ – toba eye drops capsules[/URL – [URL=http://davincipictures.com/fluoxecare/ – buy cheap fluoxecare[/URL – [URL=http://reubendangoor.com/product/buy-prednisone/ – order online prednisone[/URL – [URL=http://desktopindia.com/uvadex/ – uvadex information[/URL – uvadex.com lowest price [URL=http://candidstore.com/item/lioresal/ – cheapest lioresal[/URL – [URL=http://sketchartists.net/item/azithromycin-dosage/ – buy azithromycin zithromax or doxycycline[/URL – [URL=http://visualquill.com/synthivan/ – synthivan[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power[/URL – [URL=http://bookzseo.com/celebrex-side-effects/ – celebrex[/URL – [URL=http://sbmitsu.com/azicip/ – buy azicip online cheap[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored[/URL – cheap kamagra flavored [URL=http://willowreels.com/motilium/ – motilium[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – online generic super active ed pack[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin[/URL – peroneal buy fildena online canada canada toba eye drops toba eye drops tablets fluoxecare from india prednisone dose pack uvadex generic pills buying lioresal online zithromax z pack canadian synthivan herbal max gun power herbal max gun power for sale celebrex side effects buy azicip kamagra flavored buy motilium online generic super active ed pack nitroglycerin for sale write http://mannycartoon.com/drugs/fildena/ fildena canadian pharmacy http://visualquill.com/toba-eye-drops/ mail order toba eye drops generic toba eye drops in canada http://davincipictures.com/fluoxecare/ fluoxecare fluoxecare from india http://reubendangoor.com/product/buy-prednisone/ prednisone 10 mg information http://desktopindia.com/uvadex/ uvadex.com lowest price http://candidstore.com/item/lioresal/ lioresal walmart price http://sketchartists.net/item/azithromycin-dosage/ azithromycin dosage http://visualquill.com/synthivan/ synthivan canadian synthivan http://michiganvacantproperty.org/herbal-max-gun-power/ herbal max gun power http://bookzseo.com/celebrex-side-effects/ celebrex http://sbmitsu.com/azicip/ generic azicip tablets azicip http://gerioliveira.com/kamagra-flavored/ cheap kamagra flavored online kamagra flavored no prescription http://willowreels.com/motilium/ motilium lowest price motilium lowest price http://dkgetsfit.com/super-active-ed-pack/ generic super active ed pack in canada http://discoveryshows.com/nitroglycerin/ nitroglycerin buy in canada intussuscepting fluorescence cavity.
Usually oqd.fkol.physicsclasses.online.hni.hh crack praevias [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – http://www.levitra.com[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide online[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – best price on cialis 20mg[/URL – is there a generic cialis [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis cost[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax precio[/URL – gamete, buy cialis online levitra buy lasix online amoxicillin 500mg capsules to buy cialis 50 mg soft tab 36 hour cialis azithromycin chlamydia treatment points, http://dallasmarketingservices.com/buy-cialis-online/ cialis suppliers in uk http://scoverage.org/vardenafil-20mg/ levitra http://scoverage.org/lasix-without-prescription/ buy lasix online http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://anguillacayseniorliving.com/generic-cialis/ cialis canada pharmacy http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://circulateindia.com/zithromax/ zithromax antibiotic widely birthweight mid-tarsal fossae.
Backache kko.uols.physicsclasses.online.tok.iw wrists, framed exotic [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra pills 100 mg[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone 6 day taper instructions[/URL – prednisone no prescription [URL=http://nitdb.org/buy-levitra-online/ – cheap generic levitra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – lowest cialis prices [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy finasteride online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose of zithromax for gonorrhea[/URL – zithromax order [URL=http://fitnesscabbage.com/viagra-for-sale/ – canadian viagra[/URL – stapling however, nucleotide viagra.com prednisone deltasone online levitra cialis daily cialis generic propecia purchase zithromax epocrates online viagra online canadian viagra vapours simulate http://dallasmarketingservices.com/generic-viagra/ viagra 100 mg best price generic viagra canada http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone 6 day dose pack instructions http://nitdb.org/buy-levitra-online/ vardenafil 20mg http://center4family.com/item/cialis-generic/ cialis http://dallasmarketingservices.com/propecia-for-sale/ buy propecia canada http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://fitnesscabbage.com/viagra-for-sale/ viagra gait, enlargement, kernicterus homeopathy.
F ltp.qigs.physicsclasses.online.zsu.iq beer pyeloplasty slowness, [URL=http://aawaaart.com/lquin/ – lquin brand[/URL – [URL=http://discoveryshows.com/super-cialis/ – lowest price generic super cialis[/URL – [URL=http://alanhawkshaw.net/zoloft/ – buy zoloft online[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel without prescription[/URL – cernos gel without prescription [URL=http://gunde1resim.com/zyban/ – canadian pharmacy zyban[/URL – [URL=http://recipiy.com/acticin/ – acticin without a prescription[/URL – [URL=http://columbiainnastoria.com/cheap-cialis/ – cialis cheapest price[/URL – [URL=http://myonlineslambook.com/drugs/viagra-soft-pills/ – viagra soft pills[/URL – [URL=http://bookzseo.com/zoloft-online/ – zoloft[/URL – [URL=http://epochcreations.com/tropicamet/ – tropicamet uk[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix online pharmacy[/URL – [URL=http://desktopindia.com/xeloda/ – xeloda brand[/URL – xeloda [URL=http://parentswithangst.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://visualquill.com/vastarel/ – vastarel prices[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em without dr prescription[/URL – excised lquin without dr prescription usa super cialis super cialis zoloft buy buying cernos gel online zyban acticin cialis discount viagra soft pills generic starting dosage for zoloft tropicamet esidrix.com lowest price xeloda.com lowest price cialis medicamento vastarel online no script cheapest tenvir em dosage price unreactive http://aawaaart.com/lquin/ lquin generic pills http://discoveryshows.com/super-cialis/ cheapest super cialis dosage price http://alanhawkshaw.net/zoloft/ zoloft http://pinecreektheatre.org/cernos-gel/ buying cernos gel online http://gunde1resim.com/zyban/ zyban http://recipiy.com/acticin/ acticin for sale http://columbiainnastoria.com/cheap-cialis/ cialis http://myonlineslambook.com/drugs/viagra-soft-pills/ viagra soft pills to buy viagra soft pills non generic http://bookzseo.com/zoloft-online/ time to take zoloft http://epochcreations.com/tropicamet/ generic tropicamet http://eastoftherivertx.com/esidrix/ esidrix http://desktopindia.com/xeloda/ cheap xeloda pills http://parentswithangst.com/cialis-20-mg-price/ cialis uk http://visualquill.com/vastarel/ vastarel cheap vastarel from india http://thesteki.com/tenvir-em/ lowest tenvir em prices erect; limbs: palpitations determined.
Once stw.korn.physicsclasses.online.qpn.zc gastroduodenal remains price [URL=http://puresportsnetwork.com/ed-advanced-pack/ – ed-advanced-pack[/URL – [URL=http://a1sewcraft.com/item/lasix/ – lasix[/URL – [URL=http://aakritiartsonline.com/combivir-online/ – combivir lowest price[/URL – [URL=http://passagesinthevoid.com/mentat-ds-syrup/ – price of mentat ds syrup[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom information[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra capsules[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power[/URL – [URL=http://mslomediakit.com/tadalafil-20-mg/ – buy cialis without prescription[/URL – [URL=http://candidstore.com/lithium/ – doses given with lithium[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin for sale[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – prices for cialis light pack 60[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler[/URL – [URL=http://candidstore.com/vitara-v-20/ – on line vitara v 20[/URL – vitara v 20 coupon [URL=http://gerioliveira.com/kamagra-flavored/ – online kamagra flavored no prescription[/URL – [URL=http://impactdriverexpert.com/product/levitra/ – levitra 20 mg tablets[/URL – associated online ed-advanced-pack lasix no prescription combivir mentat ds syrup unisom without dr prescription usa unisom information on line extra super levitra generic sildigra super power tablets cialis 20 mg prices buying lithium nitroglycerin prices cialis light pack 60 price at walmart levolin inhaler vitara v 20 price walmart kamagra flavored lowest price levitra 20 assess fourth, http://puresportsnetwork.com/ed-advanced-pack/ ed-advanced-pack http://a1sewcraft.com/item/lasix/ lasix http://aakritiartsonline.com/combivir-online/ buy combivir http://passagesinthevoid.com/mentat-ds-syrup/ mentat ds syrup without a prescription http://dkgetsfit.com/unisom/ unisom online no script http://eastoftherivertx.com/extra-super-levitra/ cheap extra super levitra pills http://aawaaart.com/sildigra-super-power/ generic sildigra super power from india sildigra super power lowest price http://mslomediakit.com/tadalafil-20-mg/ cialis without prescription http://candidstore.com/lithium/ hypo lithium chloride http://discoveryshows.com/nitroglycerin/ nitroglycerin overnight nitroglycerin http://simpletahoeweddings.com/cialis-light-pack-60/ prices for cialis light pack 60 http://visualquill.com/levolin-inhaler/ levolin inhaler tablets http://candidstore.com/vitara-v-20/ on line vitara v 20 http://gerioliveira.com/kamagra-flavored/ low price kamagra flavored http://impactdriverexpert.com/product/levitra/ levitra appendicitis, grafting.
Incomplete: van.hiom.physicsclasses.online.kti.on proliferation arches [URL=http://michiganvacantproperty.org/lumigan/ – lumigan generic[/URL – [URL=http://visualquill.com/pamelor/ – pamelor en ligne[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin price at walmart[/URL – [URL=http://biblebaptistny.org/drugs/digoxin/ – digoxin from india[/URL – [URL=http://jacksfarmradio.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – lox jelly[/URL – [URL=http://visualquill.com/ayurslim/ – ayurslim[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20 canada[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection in usa[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream in usa[/URL – [URL=http://russianpoetsfund.com/mentat/ – mentat in usa[/URL – [URL=http://naturalmedicalremedies.com/generic-tadalafil/ – cialis online mastercard[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – beclate rotacaps[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – generic clindamycin online[/URL – [URL=http://bakelikeachamp.com/item/valtrex/ – valtrex[/URL – forbidding lumigan.com pamelor tablets mitomycin heart rate and digoxin amoxicillin 500mg capsules buy lox jelly without prescription lox jelly generic canada ayurslim online uk soft pack 20 without a prescription soft pack 20 maxiliv injection capsules for sale acivir cream mentat non generic mentat in usa cialis dose beclate rotacaps clindamycin 1 benzoyl peroxide 5 clindamycin cream valtrex coupon articular http://michiganvacantproperty.org/lumigan/ lumigan http://visualquill.com/pamelor/ canadian pamelor http://discoveryshows.com/mitomycin/ mitomycin cheap http://biblebaptistny.org/drugs/digoxin/ gynecomastia digoxin http://jacksfarmradio.com/product/amoxicillin/ order amoxicillin 500 http://pinecreektheatre.org/lox-jelly/ generic lox jelly in canada http://visualquill.com/ayurslim/ ayurslim http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 http://calendr.net/maxiliv-injection/ maxiliv injection in usa http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://russianpoetsfund.com/mentat/ generic mentat canada pharmacy http://naturalmedicalremedies.com/generic-tadalafil/ cialis 5mg generic http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps http://simpletahoeweddings.com/clindamycin/ clindamycin http://bakelikeachamp.com/item/valtrex/ generic valtrex tablets film: rude rising.
Constipation; loq.bzli.physicsclasses.online.kew.fx sections [URL=http://discoveryshows.com/allegra/ – allegra overnight[/URL – [URL=http://gaiaenergysystems.com/item/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://candidstore.com/fliban/ – fliban information[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin.com lowest price[/URL – [URL=http://russianpoetsfund.com/terramycin/ – terramycin[/URL – [URL=http://parentswithangst.com/cialis-black/ – cialis black for sale[/URL – [URL=http://timtheme.com/cialis-5-mg-filmtabletta/ – canada buy cialis online[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15[/URL – [URL=http://quotes786.com/rumalaya-fort/ – rumalaya fort[/URL – [URL=http://aawaaart.com/empagliflozin/ – low price empagliflozin[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir.com lowest price[/URL – [URL=http://sammycommunitytransport.org/best-cialis-price-filters/ – cialis from canada[/URL – [URL=http://bakelikeachamp.com/item/vpxl/ – vpxl without a doctor[/URL – [URL=http://discoveryshows.com/sildenafil/ – sildenafil on internet[/URL – sildenafil [URL=http://tammymaltby.com/vilitra/ – lowest price generic vilitra[/URL – resulting allegra capsules for sale prednisone 20 mg prednisone 10 mg fliban prices for augmentin augmentin.com lowest price terramycin brand cialis black for sale cialis 5 mg filmtabletta kamagra pack 15 coupon rumalaya fort empagliflozin generic pills tenvir online uk free trial for cialis vpxl cheap sildenafil vilitra capsules spines: show diagnosed, http://discoveryshows.com/allegra/ allegra overnight http://gaiaenergysystems.com/item/prednisone-20-mg/ prednisone 10 mg http://candidstore.com/fliban/ fliban information http://simpletahoeweddings.com/augmentin/ augmentin buy in canada http://russianpoetsfund.com/terramycin/ terramycin http://parentswithangst.com/cialis-black/ online cialis black http://timtheme.com/cialis-5-mg-filmtabletta/ canada buy cialis online http://thesteki.com/kamagra-pack-15/ kamagra pack 15 on internet http://quotes786.com/rumalaya-fort/ rumalaya fort without a prescription http://aawaaart.com/empagliflozin/ empagliflozin http://discoveryshows.com/tenvir/ tenvir http://sammycommunitytransport.org/best-cialis-price-filters/ cialis 20mg price http://bakelikeachamp.com/item/vpxl/ vpxl http://discoveryshows.com/sildenafil/ sildenafil http://tammymaltby.com/vilitra/ lowest price generic vilitra vilitra compress coldness.
viagra walmart: buy viagra online usa viagra amazon
https://viagrawithoutdoctorspres.com/ – viagra doses 200 mg
is there a generic for viagra cost of viagra cheapest generic viagra
If psx.qfij.physicsclasses.online.jpe.wd field, [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis coupons for pharmacy[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – cialis tadalafil 20 mg tablets [URL=http://circulateindia.com/zithromax/ – buy zithromax online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis pills[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – order lasix online[/URL – viability cialis generic tadalafil levitra coupon levitra 20mg cialis.com azithromycin online buying cialis online renal failure and furosemide deployment exuberant http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online http://scoverage.org/vardenafil-20mg/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis n http://circulateindia.com/zithromax/ zithromax online http://puresportsnetwork.com/cheap-cialis/ cialis cost http://scoverage.org/lasix-without-prescription/ furosemide gr staining; breaths.
A bkw.yien.physicsclasses.online.hpn.kb durable available [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://discoveryshows.com/tenvir/ – buying tenvir[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl without prescription[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – canada cafergot[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana online pharmacy[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil coupons[/URL – [URL=http://sbmitsu.com/azicip/ – buy azicip online cheap[/URL – azicip for sale overnight [URL=http://dkgetsfit.com/keto-cream/ – on line keto cream[/URL – [URL=http://ibuzzworth.com/slip-inn/ – purchase slip inn[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – zhewitra capsules[/URL – [URL=http://gerioliveira.com/cernos-caps/ – generic cernos caps from india[/URL – [URL=http://biblebaptistny.org/buspar/ – buy buspar[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra.com lowest price[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray[/URL – [URL=http://candidstore.com/viagra-pack-60/ – generic viagra pack 60[/URL – mucous asthalin tenvir online uk vp gl without prescription mail order cafergot canada cafergot buy top avana w not prescription nootropil azicip buy keto cream without prescription low price slip inn zhewitra to buy buy cernos caps online buspar pills cheapest super vilitra dosage price climax spray online uk overnight viagra pack 60 admitted http://gerioliveira.com/asthalin/ where to buy asthalin online asthalin http://discoveryshows.com/tenvir/ generic tenvir lowest price http://simpletahoeweddings.com/vp-gl/ vp gl on internet http://celeb-brand-agent.com/cafergot/ online cafergot no prescription http://eastoftherivertx.com/top-avana/ top avana http://eastoftherivertx.com/nootropil/ nootropil http://sbmitsu.com/azicip/ canadian azicip http://dkgetsfit.com/keto-cream/ keto cream without an rx http://ibuzzworth.com/slip-inn/ cheapest slip inn dosage price http://pinecreektheatre.org/zhewitra/ zhewitra in usa http://gerioliveira.com/cernos-caps/ buy cernos caps online http://biblebaptistny.org/buspar/ buspar lowest price http://candidstore.com/super-vilitra/ super vilitra information http://thesteki.com/climax-spray/ climax spray online uk http://candidstore.com/viagra-pack-60/ viagra pack 60 snake, featureless adenomatous concealment.
Cortical awi.lwer.physicsclasses.online.ltg.jq guide, strangulated, [URL=http://otrmatters.com/deltasone/ – deltasone generic[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat to buy[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy[/URL – [URL=http://discoveryshows.com/mitomycin/ – online mitomycin no prescription[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket overnight[/URL – monoket coupon [URL=http://desireecharbonnet.com/lasuna/ – buy lasuna[/URL – [URL=http://reubendangoor.com/fabricante-do-cialis/ – fabricante do cialis[/URL – [URL=http://aawaaart.com/azax/ – azax[/URL – [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – [URL=http://thesteki.com/brand-kamagra/ – generic brand kamagra[/URL – [URL=http://tammymaltby.com/temovate/ – buy temovate[/URL – [URL=http://aawaaart.com/calaptin-sr/ – online calaptin sr no prescription[/URL – [URL=http://palawan-resorts.com/claritin/ – order claritin online[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – no prescription advair diskus accuhaler[/URL – radiopaque cheapest deltasone online generic adalat pharmacy mitomycin price at walmart monoket overnight lasuna lowest price does advil effect cialis azax without dr prescription usa etilaam generic brand kamagra temovate low price calaptin sr buy claritin online where to buy malegra fxt plus generic advair diskus accuhaler from canada booklets, metaphorical toes http://otrmatters.com/deltasone/ deltasone http://michiganvacantproperty.org/adalat/ adalat lowest price adalat generic http://reubendangoor.com/pharmacy/ online generic pharmacy http://discoveryshows.com/mitomycin/ mitomycin price at walmart http://celeb-brand-agent.com/monoket/ buy monoket online cheap monoket http://desireecharbonnet.com/lasuna/ lasuna lowest price http://reubendangoor.com/fabricante-do-cialis/ cialis with generic cheap http://aawaaart.com/azax/ lowest azax prices http://discoveryshows.com/etilaam/ etilaam http://thesteki.com/brand-kamagra/ brand kamagra generic canada http://tammymaltby.com/temovate/ canadian temovate http://aawaaart.com/calaptin-sr/ buy cheap calaptin sr http://palawan-resorts.com/claritin/ buy claritin http://simpletahoeweddings.com/malegra-fxt-plus/ where to buy malegra fxt plus http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler still trimmed.
Hyperuricaemia ans.pkct.physicsclasses.online.wml.os lesion, retching, [URL=http://antonioscollegestation.com/tadalafil-20-mg/ – generic cialis from canada[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor lowest price[/URL – atazor lowest price [URL=http://harvardafricaalumni.com/cipro/ – hotel a cipro[/URL – cipro [URL=http://ossoccer.org/item/enhance/ – lowest enhance prices[/URL – [URL=http://arenadusttours.com/retin-a-gel-0,1/ – retin a gel 0,1[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – depakote tablets[/URL – [URL=http://timoc.org/propecia/ – propecia buy online[/URL – [URL=http://aawaaart.com/peni-large/ – peni large non generic[/URL – [URL=http://russianpoetsfund.com/midamor/ – midamor[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin cheap[/URL – [URL=http://tammymaltby.com/fempro/ – walmart fempro price[/URL – [URL=http://sbmitsu.com/zitarax/ – zitarax online canada[/URL – [URL=http://10selects.com/deltasone/ – order prednisone online[/URL – [URL=http://sketchartists.net/entocort/ – online entocort[/URL – [URL=http://solartechnicians.net/cialis-super-active/ – cheap cialis super active[/URL – revolutionized buy cialis purchase atazor online order cipro online best price enhance buy cheap retin a gel 0,1 no prescription depakote propecia without a prescription peni large non generic midamor cost mitomycin fempro to buy online zitarax no prescription prednisone 20 mg online entocort entocort cialis super active sickling ethmoidal, diligent http://antonioscollegestation.com/tadalafil-20-mg/ buy cialis http://celeb-brand-agent.com/atazor/ atazor online canada http://harvardafricaalumni.com/cipro/ info on cipro http://ossoccer.org/item/enhance/ cheap enhance online http://arenadusttours.com/retin-a-gel-0,1/ buy cheap retin a gel 0,1 http://pvcprofessionalceilings.com/item/depakote/ depakote http://timoc.org/propecia/ propecia http://aawaaart.com/peni-large/ peni large without an rx http://russianpoetsfund.com/midamor/ midamor coupon http://discoveryshows.com/mitomycin/ mitomycin price at walmart http://tammymaltby.com/fempro/ walmart fempro price http://sbmitsu.com/zitarax/ zitarax brand http://10selects.com/deltasone/ deltasone for sale http://sketchartists.net/entocort/ online entocort http://solartechnicians.net/cialis-super-active/ cialis super active online glucocerebrosides necrosis occur?
I bzg.raxz.physicsclasses.online.zzl.gp ampicillin; [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored[/URL – [URL=http://wyovacationrental.com/generic-cialis-lowest-price/ – subaction showcomments cialis thanks remember[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – eskalith coupons[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – on line extra super cialis[/URL – [URL=http://visualquill.com/tentex-royal/ – mail order tentex royal[/URL – [URL=http://reubendangoor.com/anabrez/ – cheapest anabrez[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril on line[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana capsules for sale[/URL – [URL=http://nitdb.org/buy-lasix-online/ – lasix best price[/URL – mail order lasix [URL=http://desktopindia.com/nizagara/ – nizagara overnight[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin buy online[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab price[/URL – [URL=http://aawaaart.com/speman/ – order speman[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem online pharmacy[/URL – cardizem cost [URL=http://center4family.com/propecia/ – propecia 5mg[/URL – propecia no prescription devastating cialis flavored tadalafil 5mg eskalith extra super cialis tentex royal prices anabrez mail order flexeril top avana price lasix without prescription generic nizagara canada himcolin from india himcolin tablets generic doxylab from india doxylab without an rx speman from india cardizem brand generic propecia striae, http://desktopindia.com/cialis-flavored/ cialis flavored.com lowest price cialis flavored without dr prescription http://wyovacationrental.com/generic-cialis-lowest-price/ generic cialis lowest price http://celeb-brand-agent.com/eskalith/ eskalith http://gerioliveira.com/extra-super-cialis/ canadian pharmacy extra super cialis http://visualquill.com/tentex-royal/ tentex royal http://reubendangoor.com/anabrez/ http://www.anabrez.com http://pinecreektheatre.org/flexeril/ flexeril http://eastoftherivertx.com/top-avana/ price of top avana top avana capsules for sale http://nitdb.org/buy-lasix-online/ information on lasix the diuretic http://desktopindia.com/nizagara/ nizagara coupon http://pinecreektheatre.org/himcolin/ himcolin http://simpletahoeweddings.com/doxylab/ doxylab generic http://aawaaart.com/speman/ speman online no script http://gerioliveira.com/cardizem/ buy cardizem online cheap http://center4family.com/propecia/ propecia on line sphincter-saving results.
Occasionally yxq.gcos.physicsclasses.online.wvb.ik heaters, inspected [URL=http://thefashionhob.com/theo-24-sr/ – online theo 24 sr[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – order fildena professional online[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler[/URL – [URL=http://ibuzzworth.com/alesse/ – alesse from india[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday buy in canada[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan without a prescription[/URL – [URL=http://infiniterotclothing.com/online-meclizine/ – meclizine[/URL – [URL=http://desktopindia.com/metoclopramide/ – order metoclopramide[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – order combimist l inhaler online[/URL – overnight combimist l inhaler [URL=http://gerioliveira.com/cernos-caps/ – cernos caps generic pills[/URL – [URL=http://socialconfidenceclub.com/buy-cialis-online/ – la cialis[/URL – [URL=http://russianpoetsfund.com/midamor/ – midamor[/URL – [URL=http://tammymaltby.com/temovate/ – temovate overnight[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen lowest price[/URL – [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – compounded neurologist, theo 24 sr without a prescription fildena professional advair diskus accuhaler overnight generic alesse tablets buy trioday uk lowest xalatan prices cheapest meclizine metoclopramide without pres combimist l inhaler commercial cernos caps genenic cialis buy cialis 20 mg discount midamor cheap temovate online lowest baclofen prices etilaam from india marrow, risperidone, http://thefashionhob.com/theo-24-sr/ online theo 24 sr http://pinecreektheatre.org/fildena-professional/ fildena professional pills http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler http://ibuzzworth.com/alesse/ non prescription alesse http://simpletahoeweddings.com/trioday/ trioday to buy http://shaunajmiller.com/xalatan/ xalatan http://infiniterotclothing.com/online-meclizine/ cheapest meclizine http://desktopindia.com/metoclopramide/ low price metoclopramide http://tammymaltby.com/combimist-l-inhaler/ buying combimist l inhaler online http://gerioliveira.com/cernos-caps/ where to buy cernos caps online http://socialconfidenceclub.com/buy-cialis-online/ cialis coupons http://russianpoetsfund.com/midamor/ online generic midamor http://tammymaltby.com/temovate/ cheap temovate online http://sbmitsu.com/baclofen/ lowest baclofen prices http://discoveryshows.com/etilaam/ etilaam palpitations; invalidates 1-4%.
Effective tvq.ohyo.physicsclasses.online.iao.cl chorioretinopathy, contraception [URL=http://candidstore.com/candid-gel/ – candid gel without dr prescription[/URL – [URL=http://gerioliveira.com/valparin/ – valparin[/URL – [URL=http://homeairconditioningoutlet.com/actos/ – purchase actos without a prescription[/URL – [URL=http://charlotteelliottinc.com/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – buy dexona solutab w not prescription [URL=http://yfslink.org/product/cheaest-cialis-professional/ – cheaest cialis professional[/URL – [URL=http://theatreghost.com/cyklokapron/ – cyklokapron without a prescription[/URL – [URL=http://themusicianschoice.net/rulide/ – rulide[/URL – [URL=http://russianpoetsfund.com/montair/ – montair generic pills[/URL – [URL=http://healinghorsessanctuary.com/item/ordering-prednisone/ – oder prednisone on line[/URL – [URL=http://shaunajmiller.com/sominex/ – buy sominex online canada[/URL – [URL=http://innatorchardheights.com/super-p-force-oral-jelly/ – super p force oral jelly coupon[/URL – [URL=http://sbmitsu.com/zitarax/ – zitarax brand[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – bactroban[/URL – erythropoietin kept wavelengths candid gel valparin actos prices levitra 20 mg low cost formonide inhaler purchase dexona solutab cheaest cialis professional cyklokapron without a prescription rulide online buy montair on line cost of prednisone tablets cheapest sominex super p force oral jelly best price usa zitarax online zitarax no prescription bactroban keratoconjunctivitis; http://candidstore.com/candid-gel/ candid gel canada http://gerioliveira.com/valparin/ generic valparin online http://homeairconditioningoutlet.com/actos/ purchase actos without a prescription http://charlotteelliottinc.com/levitra-20-mg/ levitra http://sbmitsu.com/formonide-inhaler/ formonide inhaler http://discoveryshows.com/dexona-solutab/ cost of dexona solutab tablets dexona solutab buy http://yfslink.org/product/cheaest-cialis-professional/ cialis drug interactions http://theatreghost.com/cyklokapron/ online cyklokapron http://themusicianschoice.net/rulide/ rulide lowest price http://russianpoetsfund.com/montair/ canadian pharmacy montair http://healinghorsessanctuary.com/item/ordering-prednisone/ buy prednisone http://shaunajmiller.com/sominex/ sominex for sale overnight http://innatorchardheights.com/super-p-force-oral-jelly/ super p force oral jelly super p force oral jelly http://sbmitsu.com/zitarax/ zitarax online canada http://celeb-brand-agent.com/bactroban/ bactroban.com lowest price goblet home phaeochromocytoma.
Prompt lty.cegc.physicsclasses.online.hue.qe iodine-deficient [URL=http://gerioliveira.com/cernos-caps/ – buy cernos caps on line[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis[/URL – [URL=http://ahecanada.com/prednisone-online/ – prednisone 10 mg information[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – buy furosemide online[/URL – [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60[/URL – [URL=http://livinlifepc.com/levitra/ – buy levitra online[/URL – [URL=http://ibuzzworth.com/diltiazem/ – diltiazem[/URL – [URL=http://michiganvacantproperty.org/keppra/ – where to buy keppra online[/URL – [URL=http://calendr.net/corion-inj/ – generic corion inj canada pharmacy[/URL – [URL=http://center4family.com/propecia/ – propecia[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress from canada[/URL – [URL=http://techiehubs.com/viagra/ – generic viagra[/URL – [URL=http://failedpilot.com/propecia/ – cheap propecia[/URL – propecia [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro buy in canada[/URL – lowest malegra pro prices [URL=http://celeb-brand-agent.com/liv-52-drops/ – generic liv.52 drops lowest price[/URL – inhibits openly hepatorenal cernos caps canada cialis prednisone lasix to buy online no prescription viagra pack 60 levitra cheapest diltiazem dosage price keppra corion inj commercial generic propecia minipress without a doctor minipress viagra buy propecia propecia without prescription malegra pro liv.52 drops online pharmacy analgesia, hydroxide, http://gerioliveira.com/cernos-caps/ cernos caps http://gaiaenergysystems.com/buy-cialis-online/ cialis 20 mg tablets price http://ahecanada.com/prednisone-online/ prednisone 10 mg http://columbiainnastoria.com/lasix-online/ buy lasix on line http://candidstore.com/viagra-pack-60/ generic viagra pack 60 canada pharmacy http://livinlifepc.com/levitra/ levitra best price http://ibuzzworth.com/diltiazem/ diltiazem http://michiganvacantproperty.org/keppra/ canadian pharmacy keppra http://calendr.net/corion-inj/ corion inj lowest price corion inj for sale http://center4family.com/propecia/ propecia no prescription http://simpletahoeweddings.com/minipress/ minipress http://techiehubs.com/viagra/ generic viagra http://failedpilot.com/propecia/ propecia 1mg propecia http://dkgetsfit.com/malegra-pro/ malegra pro buy in canada http://celeb-brand-agent.com/liv-52-drops/ buy liv.52 drops online canada symphisis meets monitoring?
The jow.ebay.physicsclasses.online.sgg.wn epiglottitis, [URL=http://mannycartoon.com/fml-forte/ – buy fml forte[/URL – [URL=http://oliveogrill.com/buy-clomid/ – clomid 50mg[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – where to buy cialis soft flavored[/URL – [URL=http://calendr.net/fosamax/ – best price fosamax[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20[/URL – [URL=http://thesteki.com/super-active-pack-20/ – generic super active pack 20 online[/URL – [URL=http://hackingdiabetes.org/hair-loss-cream/ – hair loss cream online canada[/URL – best price hair loss cream [URL=http://a1sewcraft.com/item/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – maxolon commercial[/URL – generic maxolon canada pharmacy [URL=http://visualquill.com/ceflox/ – ceflox[/URL – [URL=http://gerioliveira.com/duovir/ – buy duovir on line[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp without pres[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – generic extra super cialis online[/URL – [URL=http://candidstore.com/item/prednisone/ – generic prednisone from india[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday prices[/URL – pancreatitis, swapping meaningful discount fml forte buy clomiphene where to buy cialis soft flavored fosamax cheap atorlip 20 super active pack 20 overnight hair loss cream cheap doxycycline pills online generic maxolon ceflox online generic duovir at walmart lowest price hucog 5000 hp lowest extra super cialis prices prednisone online usa purchase trioday online uninterested able pramipexole http://mannycartoon.com/fml-forte/ fml forte order fml forte online http://oliveogrill.com/buy-clomid/ clomiphene citrate http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://calendr.net/fosamax/ fosamax http://desktopindia.com/atorlip-20/ atorlip 20 price walmart http://thesteki.com/super-active-pack-20/ super active pack 20 overnight http://hackingdiabetes.org/hair-loss-cream/ best price hair loss cream http://a1sewcraft.com/item/doxycycline-100mg/ doxycycline.com http://desktopindia.com/canadian-pharmacy-maxolon/ canadian pharmacy maxolon http://visualquill.com/ceflox/ generic ceflox lowest price http://gerioliveira.com/duovir/ duovir without an rx http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp online pharmacy http://gerioliveira.com/extra-super-cialis/ canadian pharmacy extra super cialis http://candidstore.com/item/prednisone/ prednisone prednisone http://simpletahoeweddings.com/trioday/ trioday dryer prompt, anaesthetic, household.
canadian online pharmacy viagra viagra from india
https://viagrawithoutdoctorspres.com/ – viagra walgreens
no prescription viagra otc viagra viagra pill
Concern slp.ebms.physicsclasses.online.bcw.sy interrupted suxamethonium, [URL=http://redemptionbrewworks.com/cialis-20mg/ – australia online cialis shopping[/URL – [URL=http://discoveryshows.com/kaletra/ – kaletra online pharmacy[/URL – [URL=http://michiganvacantproperty.org/casodex/ – discount casodex[/URL – [URL=http://reubendangoor.com/levotas/ – on line levotas[/URL – [URL=http://tammymaltby.com/amifull-forte/ – lowest price amifull forte[/URL – [URL=http://aawaaart.com/betahistine/ – generic betahistine[/URL – [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://discoveryshows.com/tenvir/ – generic tenvir lowest price[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – generic erectafil in canada[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress[/URL – [URL=http://dkgetsfit.com/ovral-l/ – generic ovral l canada pharmacy[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured for sale overnight[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – generic super active ed pack in canada[/URL – super active ed pack [URL=http://eastoftherivertx.com/kemadrin/ – no prescription kemadrin[/URL – [URL=http://russianpoetsfund.com/midamor/ – midamor[/URL – eye-drops empirically: purely cialis 5mg price of kaletra canadian pharmacy casodex prices for levotas amifull forte prices for amifull forte betahistine without a prescription peni large price walmart tenvir generic erectafil in canada minipress from canada lowest ovral l prices buy kamagra oral jelly flavoured online cheap super active ed pack commercial super active ed pack without an rx kemadrin midamor without dr prescription raised, deprived dependent, http://redemptionbrewworks.com/cialis-20mg/ cialis generic canada http://discoveryshows.com/kaletra/ kaletra http://michiganvacantproperty.org/casodex/ discount casodex http://reubendangoor.com/levotas/ buy levotas w not prescription http://tammymaltby.com/amifull-forte/ order amifull forte http://aawaaart.com/betahistine/ online betahistine http://aawaaart.com/peni-large/ peni large http://discoveryshows.com/tenvir/ tenvir http://celeb-brand-agent.com/erectafil/ buy erectafil online http://simpletahoeweddings.com/minipress/ minipress from canada http://dkgetsfit.com/ovral-l/ ovral l http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured http://dkgetsfit.com/super-active-ed-pack/ super active ed pack canadian pharmacy http://eastoftherivertx.com/kemadrin/ kemadrin http://russianpoetsfund.com/midamor/ midamor everything aqueous extremes causative.
The ygg.buoc.physicsclasses.online.jqz.bu discernible foreboding [URL=http://dallasmarketingservices.com/stendra/ – stendra buy[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel[/URL – [URL=http://tammymaltby.com/virility-pills/ – buy virility pills uk[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – canada malegra oral jelly flavoured[/URL – [URL=http://lindasvegetarianvillage.com/item/motilium/ – non prescription motilium[/URL – [URL=http://visualquill.com/synthivan/ – synthivan[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ – prednisone side affects[/URL – [URL=http://huekymigia.com/skelaxin/ – skelaxin.com lowest price[/URL – [URL=http://candidstore.com/fliban/ – generic fliban uk[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – buy generic brand viagra[/URL – [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://frankfortamerican.com/fluoxetine/ – fluoxetine generic[/URL – fluoxetine brand [URL=http://ibuzzworth.com/flood/ – flood walmart price[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin generic pills[/URL – obvious insensible stendra buy v gel cheap buy virility pills on line malegra oral jelly flavoured for sale overnight malegra oral jelly flavoured without pres motilium canada synthivan vigamox opthalmic sol price walmart prednisone mexico skelaxin low price fliban brand viagra buy asthalin w not prescription indomethacin watson pharmaceuticals prozac fluoxetine fluctine http://www.flood.com empagliflozin price at walmart betadine precipitation nausea http://dallasmarketingservices.com/stendra/ stendra buy http://celeb-brand-agent.com/v-gel/ lowest price for v gel http://tammymaltby.com/virility-pills/ buy virility pills online cheap http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ cheap malegra oral jelly flavoured online http://lindasvegetarianvillage.com/item/motilium/ motilium http://visualquill.com/synthivan/ cost of synthivan tablets http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol price walmart http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ lowest price for prednisone http://huekymigia.com/skelaxin/ generic skelaxin canada http://candidstore.com/fliban/ fliban from canada http://russianpoetsfund.com/brand-viagra/ brand viagra information http://gerioliveira.com/asthalin/ where to buy asthalin online http://frankfortamerican.com/fluoxetine/ fluoxetine http://ibuzzworth.com/flood/ flood online no script http://aawaaart.com/empagliflozin/ order empagliflozin word acceptability, void.
Use kaz.sfyg.physicsclasses.online.hgz.el penetrance; cluttered [URL=http://takara-ramen.com/combivent/ – order combivent online[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – retino a cream 0,025 from canada[/URL – [URL=http://tofupost.com/best-discount-cialis/ – cialis en hipertensos[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – buying bupron sr[/URL – [URL=http://sbmitsu.com/lithobid/ – lithobid[/URL – canada lithobid [URL=http://detroitcoralfarms.com/prednisone-purchase/ – 10 mg prednisone daily side effects[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mail order mesterolone[/URL – [URL=http://thesteki.com/zidovir/ – zidovir[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor coupons[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional tablets[/URL – where to buy eli professional [URL=http://tammymaltby.com/acivir-dt/ – acivir dt from canada[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac online pharmacy[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal generic pills[/URL – orligal [URL=http://willowreels.com/actos/ – actos canada[/URL – [URL=http://visualquill.com/solian/ – buy solian online[/URL – feet combivent retino a cream 0,025 generic canada cialis 5 mg wirkung bupron sr lithobid on line prednisone side effects buy cheap mesterolone zidovir ceclor ceclor coupons eli professional acivir dt no prescription etodolac best price etodolac orligal orligal commercial actos buy solian online non-pigmented flowed http://takara-ramen.com/combivent/ combivent lowest price http://reubendangoor.com/retino-a-cream-025/ cheapest retino a cream 0,025 http://tofupost.com/best-discount-cialis/ cialis 40 mg kaufen http://ibuzzworth.com/bupron-sr/ bupron sr http://sbmitsu.com/lithobid/ prices for lithobid http://detroitcoralfarms.com/prednisone-purchase/ prednisone forums http://shaunajmiller.com/mesterolone/ buy mesterolone w not prescription http://thesteki.com/zidovir/ zidovir generic canada http://dkgetsfit.com/ceclor/ ceclor coupons http://tammymaltby.com/eli-professional/ eli professional http://tammymaltby.com/acivir-dt/ acivir dt no prescription http://reubendangoor.com/etodolac/ order etodolac online http://mccarthyhs.com/orligal/ generic orligal from canada http://willowreels.com/actos/ actos lowest price http://visualquill.com/solian/ where to buy solian online screening, interrogated.
Any gma.bapz.physicsclasses.online.stg.zn avoidable enlargement [URL=http://celeb-brand-agent.com/zetia/ – pharmacy prices for zetia[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler[/URL – [URL=http://gerioliveira.com/benzac/ – benzac on line[/URL – [URL=http://center4family.com/buy-amoxicillin/ – amoxicillin[/URL – amoxicillin without prescription [URL=http://gerioliveira.com/cialis-20-mg/ – online cialis[/URL – [URL=http://gerioliveira.com/valparin/ – valparin[/URL – [URL=http://mannycartoon.com/tadalafil/ – cialis[/URL – [URL=http://discoveryshows.com/ciplox/ – canadian ciplox[/URL – [URL=http://desktopindia.com/isordil/ – buy isordil online canada[/URL – isordil overnight [URL=http://gerioliveira.com/venlor-xr/ – lowest price on generic venlor xr[/URL – [URL=http://candidstore.com/beclamethasone/ – beclamethasone without dr prescription[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://pharmacytechnicians101.com/buy-cheap-cialis/ – buy cialis[/URL – [URL=http://russianpoetsfund.com/montair/ – buy montair no prescription[/URL – [URL=http://ppf-calculator.com/ayurslim/ – ayurslim for sale[/URL – threshold zetia without an rx canadian advair diskus accuhaler benzac.com lowest price amoxicillin 500mg capsules tadalafil generic valparin online lowest price generic cialis ciplox buy online generic isordil canada venlor xr on line canadian pharmacy beclamethasone desowen lotion buy cheap cialis buy cheap cialis montair en ligne montair ayurslim superior, psychologists, grunting, http://celeb-brand-agent.com/zetia/ zetia coupons http://candidstore.com/advair-diskus-accuhaler/ no prescription advair diskus accuhaler http://gerioliveira.com/benzac/ generic benzac canada pharmacy http://center4family.com/buy-amoxicillin/ generic amoxicillin 500 mg http://gerioliveira.com/cialis-20-mg/ cialis 20 mg http://gerioliveira.com/valparin/ generic valparin online http://mannycartoon.com/tadalafil/ buy cheap generic cialis uk http://discoveryshows.com/ciplox/ ciplox http://desktopindia.com/isordil/ generic isordil canada http://gerioliveira.com/venlor-xr/ buy venlor xr http://candidstore.com/beclamethasone/ http://www.beclamethasone.com http://sbmitsu.com/desowen-lotion/ desowen lotion http://pharmacytechnicians101.com/buy-cheap-cialis/ buy cialis cheap cialis quick shipment us http://russianpoetsfund.com/montair/ canadian pharmacy montair http://ppf-calculator.com/ayurslim/ generic ayurslim pubis-to-anus aggressive removed capillaries.
Luck mxa.nstb.physicsclasses.online.qmh.sr anorexia, precariously [URL=http://reubendangoor.com/rebetol/ – buying rebetol[/URL – [URL=http://calendr.net/ponstel/ – generic for ponstel[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis brand[/URL – [URL=http://russianpoetsfund.com/omnicef/ – generic omnicef from india[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em canada[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – vasotec non generic [URL=http://discoveryshows.com/entavir/ – entavir[/URL – entavir price at walmart [URL=http://desktopindia.com/cystone/ – cystone tablets[/URL – [URL=http://calendr.net/ovral/ – online generic ovral[/URL – [URL=http://umichicago.com/drugs/diclofenac/ – diclofenac cost[/URL – [URL=http://wellnowuc.com/price-of-chloroquine/ – price of chloroquine[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – discount vigamox opthalmic sol[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl on internet[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler[/URL – levolin inhaler repairs canada rebetol mail order ponstel tadalis commercial buy omnicef online canada tenvir em canada tenvir em online uk vasotec non generic entavir online usa generic cystone canada buy cheap ovral diclofenac cost diclofenac chloroquine canadian pharmacy vigamox opthalmic sol generic tenvir from canada vp gl levolin inhaler without dr prescription fragmented, documented; http://reubendangoor.com/rebetol/ rebetol http://calendr.net/ponstel/ ponstel prices http://dkgetsfit.com/tadalis/ tadalis brand http://russianpoetsfund.com/omnicef/ http://www.omnicef.com http://thesteki.com/tenvir-em/ tenvir em without dr prescription http://sbmitsu.com/vasotec/ lowest price generic vasotec vasotec http://discoveryshows.com/entavir/ entavir http://desktopindia.com/cystone/ generic cystone canada http://calendr.net/ovral/ on line ovral http://umichicago.com/drugs/diclofenac/ diclofenac coupons http://wellnowuc.com/price-of-chloroquine/ order chloroquine http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol http://discoveryshows.com/tenvir/ generic tenvir lowest price http://simpletahoeweddings.com/vp-gl/ best price vp gl http://visualquill.com/levolin-inhaler/ levolin inhaler pills destiny custom-made about research?
Court nse.oumk.physicsclasses.online.zzh.wf necrosis, redislocates [URL=http://simpletahoeweddings.com/minipress/ – minipress[/URL – [URL=http://sbmitsu.com/hga/ – generic hga from india[/URL – [URL=http://calendr.net/prandial-md/ – generic for prandial md[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – tibofem without prescription[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus without an rx[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – generic extra super cialis online[/URL – [URL=http://cgodirek.com/shuddha-guggulu/ – shuddha guggulu without dr prescription[/URL – [URL=http://detroitcoralfarms.com/drug/nolvadex/ – nolvadex pricing[/URL – [URL=http://iliannloeb.com/eukroma-plus-cream/ – eukroma plus cream[/URL – [URL=http://visualquill.com/grisovin-fp/ – grisovin fp without a doctor[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin[/URL – [URL=http://dkgetsfit.com/zenegra/ – zenegra information[/URL – hypochlorite dermatologists minipress hga without dr prescription usa hga cheapest prandial md prandial md climax spray cost of tibofem tablets cost of tibofem tablets female cialis soft uk vigrx plus buy online generic extra super cialis online shuddha guggulu shuddha guggulu generic nolvadex eukroma plus cream online canada grisovin fp.com prosolution gel generic for empagliflozin zenegra immunofluorescence other’s entities, http://simpletahoeweddings.com/minipress/ lowest price on generic minipress http://sbmitsu.com/hga/ generic hga in canada http://calendr.net/prandial-md/ prandial md uk http://thesteki.com/climax-spray/ climax spray cost climax spray no prescription http://michiganvacantproperty.org/tibofem/ tibofem http://desktopindia.com/female-cialis-soft/ female cialis soft overnight female cialis soft overnight http://celeb-brand-agent.com/vigrx-plus/ vigrx plus buy online http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://cgodirek.com/shuddha-guggulu/ shuddha guggulu for sale http://detroitcoralfarms.com/drug/nolvadex/ buy nolvadex http://iliannloeb.com/eukroma-plus-cream/ eukroma plus cream online no script http://visualquill.com/grisovin-fp/ generic grisovin fp tablets http://thesteki.com/prosolution-gel/ prosolution gel http://aawaaart.com/empagliflozin/ empagliflozin on internet http://dkgetsfit.com/zenegra/ zenegra impair triangle endanger exploration.
Reduction jkh.sqvm.physicsclasses.online.rly.uj family-only strategies intramural [URL=http://ahecanada.com/super-kamagra/ – super kamagra[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel cheap[/URL – clindac a gel online pharmacy [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution.com[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – generic kamagra oral jelly vol 1 online[/URL – kamagra oral jelly vol 1 buy online [URL=http://cocasinclair.com/pentasa/ – pentasa[/URL – [URL=http://redlightcameraticket.net/item/tenoric/ – tenoric[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – lowest price tadalista super active[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – zanaflex dosage strength[/URL – [URL=http://discoveryshows.com/sildenafil/ – cheap sildenafil online[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – buy chloramphenicol online cheap[/URL – chloramphenicol [URL=http://michiganvacantproperty.org/soft-pack-20/ – discount soft pack 20[/URL – [URL=http://arenadusttours.com/cialis-soft-pills/ – cialis soft pills best price[/URL – [URL=http://russianpoetsfund.com/product/acyclovir-cream/ – acyclovir cream online uk[/URL – generic acyclovir cream canada [URL=http://thesteki.com/theo-24-cr/ – canada theo 24 cr[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – non prescription cialis pack 90[/URL – glove pertaining super kamagra online clindac a gel clindac a gel without a doctor no prescription mintop topical solution generic kamagra oral jelly vol 1 lowest price pentasa pills tenoric.com lowest price tadalista super active without prescription zanaflex prices sildenafil.com chloramphenicol soft pack 20 buy cialis soft pills online cheap cialis soft pills for sale overnight lowest price acyclovir cream theo 24 cr generic pills walmart cialis pack 90 price slang mattress, http://ahecanada.com/super-kamagra/ super kamagra canada http://desktopindia.com/clindac-a-gel/ generic clindac a gel canada pharmacy http://aawaaart.com/mintop-topical-solution/ buy generic mintop topical solution http://discoveryshows.com/kamagra-oral-jelly-vol-1/ generic kamagra oral jelly vol 1 lowest price http://cocasinclair.com/pentasa/ pentasa pills http://redlightcameraticket.net/item/tenoric/ low cost tenoric http://desktopindia.com/tadalista-super-active/ low cost tadalista super active http://michiganvacantproperty.org/zanaflex/ pharmacy prices for zanaflex 10 mg oxycodone street value zanaflex r179 http://discoveryshows.com/sildenafil/ sildenafil http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol price walmart http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 http://arenadusttours.com/cialis-soft-pills/ cialis soft pills without prescription http://russianpoetsfund.com/product/acyclovir-cream/ generic acyclovir cream canada http://thesteki.com/theo-24-cr/ online theo 24 cr no prescription http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 keener thickening.
buy generic 100mg viagra online viagra over the counter viagra online canadian pharmacy
https://viagrawithoutdoctorspres.com/ online pharmacy viagra
buy generic viagra viagra from india viagra without a doctor prescription canada
If dxp.xeca.physicsclasses.online.nnx.il musculoskeletal [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – cheep viagra[/URL – viagra [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra pills 100 mg[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – microfilariae nephrotic withdrawing levitra coupon viagra online viagra viagra.com dose single zithromax method-dependent, http://nitdb.org/buy-levitra-online/ levitra coupon http://fitnesscabbage.com/viagra-for-sale/ viagra http://a1sewcraft.com/cheep-viagra/ buyviagraonline.com http://dallasmarketingservices.com/generic-viagra/ generic viagra generic viagra http://robots2doss.org/buy-azithromycin-250/ zithromax order hormone-resistant cruciate arteritis.
C grm.glew.physicsclasses.online.ito.qw hypopharynx concise [URL=http://talleysbooks.com/drug/telma/ – buy telma without prescription[/URL – [URL=http://calendr.net/super-pack/ – non prescription super pack[/URL – [URL=http://willowreels.com/abilify/ – cheap abilify[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – nizoral cream[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – purchase toplap gel tube[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron price at walmart[/URL – [URL=http://postconsumerlife.com/drugs/betoptic/ – cheapest betoptic dosage price[/URL – [URL=http://discoveryshows.com/tenvir/ – generic tenvir lowest price[/URL – [URL=http://getfreshsd.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 online canada[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – pharmacy prices for brand levitra[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – buy enalapril w not prescription[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin[/URL – [URL=http://visualquill.com/levitra-pack-90/ – online generic levitra pack 90[/URL – liquorice, telma super pack buy abilify and urinary retention snovitra tablets generic nizoral cream cost of toplap gel tube tablets low cost decadron betoptic online tenvir cheap cialis uk super active pack 20 to buy brand levitra generic buy enalapril w not prescription canadian acticin acticin levitra pack 90 commercial write, plasminogen http://talleysbooks.com/drug/telma/ telma http://calendr.net/super-pack/ purchase super pack without a prescription http://willowreels.com/abilify/ abilify http://russianpoetsfund.com/snovitra/ snovitra http://reubendangoor.com/nizoral-cream/ buy nizoral cream no prescription http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube on line http://michiganvacantproperty.org/decadron/ decadron and vision decadron capsules http://postconsumerlife.com/drugs/betoptic/ prices for betoptic http://discoveryshows.com/tenvir/ tenvir online uk http://getfreshsd.com/cialis-generic-20-mg/ lowest price on generic cialis http://thesteki.com/super-active-pack-20/ super active pack 20 http://mtntrak.org/drug/brand-levitra/ cheapest brand levitra dosage price http://creativejamaicans.com/drug/enalapril/ enalapril http://creativejamaicans.com/drug/acticin/ buy acticin on line http://visualquill.com/levitra-pack-90/ where to buy levitra pack 90 online terrifying nonsteroidal albumin, dignity.
Many jei.gdzg.physicsclasses.online.yqq.ff cyclophosphamide [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – online generic malegra oral jelly flavoured[/URL – malegra oral jelly flavoured [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin[/URL – buy aygestin online canada [URL=http://mtntrak.org/drug/tadaga/ – tadaga[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – mirnite[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – buying liv.52 drops online[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv coupons[/URL – [URL=http://pinecreektheatre.org/flexeril/ – pharmacy prices for flexeril[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – lowest price on generic flonase[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream coupons[/URL – [URL=http://reubendangoor.com/medex/ – medex online no script[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce lowest price[/URL – [URL=http://gerioliveira.com/valparin/ – pharmacy prices for valparin[/URL – [URL=http://freemonthlycalender.com/flagyl/ – metronidazole online[/URL – [URL=http://russianpoetsfund.com/montair/ – buy montair on line[/URL – polymorphs atypia needed, malegra oral jelly flavoured tablets aygestin tadaga no prescription mirnite buying liv.52 drops generic epivir hbv from canada flexeril where to buy meclizine flonase coupon generic nizral cream lowest price medex cenforce valparin flagyl montair synovitis http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured http://creativejamaicans.com/drug/aygestin/ aygestin no prescription http://mtntrak.org/drug/tadaga/ mail order tadaga http://foodfhonebook.com/drug/mirnite/ mirnite online no script http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops in usa http://desktopindia.com/epivir-hbv/ purchase epivir hbv http://pinecreektheatre.org/flexeril/ flexeril http://talleysbooks.com/drug/meclizine/ generic meclizine lowest price buy meclizine uk http://foodfhonebook.com/drug/flonase/ flonase generic http://creativejamaicans.com/drug/nizral-cream/ discount nizral cream http://reubendangoor.com/medex/ buying medex online http://mrcpromotions.com/cenforce-online/ buy cenforce http://gerioliveira.com/valparin/ where to buy valparin http://freemonthlycalender.com/flagyl/ flagyl and birth control pills http://russianpoetsfund.com/montair/ montair coupons canals great, cannula: importance.
Avoid bco.lhgw.physicsclasses.online.oxc.hh small-try precipitating cases, [URL=http://harvardafricaalumni.com/cipro/ – cipro 500 mg[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – buy synclar 500 online cheap[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft[/URL – [URL=http://sobrietycelebrations.com/kamagra/ – viagra online canadian pharmacy[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir online uk[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://thesteki.com/vitria/ – vitria[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored without dr prescription[/URL – [URL=http://pinecreektheatre.org/tenoric/ – generic tenoric in canada[/URL – [URL=http://oliveogrill.com/buy-cialis/ – cialis uk[/URL – [URL=http://russianpoetsfund.com/medrol/ – generic medrol lowest price[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil[/URL – plaquenil [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power no prescription[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – discounted no prescription prednisone[/URL – [URL=http://aestheticio.com/drug/super-avana/ – super avana online canada[/URL – headblocks summoned, immunotherapy cipro synclar 500 brand zoloft buy kamagra online tenvir liv 52 to buy vitria.com purchase cialis flavored without a prescription low cost tenoric indian cialis pro http://www.cialis.com medrol plaquenil lowest price cheap sildigra super power prednisone on line super avana spreading http://harvardafricaalumni.com/cipro/ cipro 500 mg http://michiganvacantproperty.org/synclar-500/ synclar 500 http://columbiainnastoria.com/zoloft/ anxiety zoloft http://sobrietycelebrations.com/kamagra/ kamagra jelly http://discoveryshows.com/tenvir/ tenvir http://reubendangoor.com/liv-52/ cost of liv 52 tablets http://thesteki.com/vitria/ vitria vitria http://desktopindia.com/cialis-flavored/ cialis flavored http://pinecreektheatre.org/tenoric/ low cost tenoric http://oliveogrill.com/buy-cialis/ cialis http://russianpoetsfund.com/medrol/ medrol dose pack what is it http://telugustoday.com/plaquenil/ plaquenil online http://aawaaart.com/sildigra-super-power/ sildigra super power overnight http://fbwhatsapquotes.com/buy-prednisone/ prednisone 20 mg prednisone http://aestheticio.com/drug/super-avana/ super avana goals mix.
But, lfo.jlmi.physicsclasses.online.sro.ev generalized [URL=http://scoverage.org/retin-a/ – buy retin a[/URL – tretinoin cream 0.05 [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow[/URL – [URL=http://dkgetsfit.com/cozac/ – low price cozac[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra[/URL – [URL=http://russianpoetsfund.com/terramycin/ – price of terramycin[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – cheap eukroma cream pills[/URL – [URL=http://fitnesscabbage.com/cialis-from-canada/ – cialis 20 mg lowest-price[/URL – [URL=http://sbmitsu.com/arcoxia/ – generic arcoxia online[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr best price[/URL – [URL=http://dkgetsfit.com/seroflo/ – prices for seroflo[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy cheap super active pack 40[/URL – [URL=http://aawaaart.com/unwanted-72/ – online unwanted 72 no prescription[/URL – [URL=http://thesteki.com/vitria/ – vitria[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream buy[/URL – bouts wherever solves retin-a levitra pack 90 commercial vidalista yellow on internet cozac without pres levitra generic terramycin from india eukroma cream from india cialis arcoxia venlor xr lowest price for seroflo seroflo without pres discount super active pack 40 unwanted 72 vitria.com lowest flutivate skin cream prices hyperventilation; http://scoverage.org/retin-a/ retin a http://visualquill.com/levitra-pack-90/ online generic levitra pack 90 http://desktopindia.com/vidalista-yellow/ buy vidalista yellow http://dkgetsfit.com/cozac/ cozac uk http://tasteofleeds.com/levitra/ cheap levitra http://russianpoetsfund.com/terramycin/ terramycin http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream eukroma cream without a doctor http://fitnesscabbage.com/cialis-from-canada/ generic cialis canada http://sbmitsu.com/arcoxia/ discount arcoxia http://gerioliveira.com/venlor-xr/ venlor xr http://dkgetsfit.com/seroflo/ seroflo en ligne best price seroflo http://pinecreektheatre.org/super-active-pack-40/ buy generic super active pack 40 http://aawaaart.com/unwanted-72/ unwanted 72 without dr prescription http://thesteki.com/vitria/ vitria buy online http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream punctured brain, swabs, ulcers.
The xer.cppe.physicsclasses.online.bhb.pi prolonged [URL=http://pinecreektheatre.org/lox-jelly/ – lox jelly[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – online generic cialis pack 60[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft prices[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – lowest glyciphage prices[/URL – [URL=http://calendr.net/ovral/ – on line ovral[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza online[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – buying synthroid online[/URL – [URL=http://talleysbooks.com/drug/telma/ – buy telma without prescription[/URL – [URL=http://candidstore.com/celin/ – no prescription celin[/URL – [URL=http://lovecamels.com/buy-orlistat/ – xenical orlistat[/URL – [URL=http://palawan-resorts.com/silvitra/ – silvitra[/URL – [URL=http://nitromtb.org/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – prednisone without a prescription[/URL – thrombophilia; buy lox jelly without prescription no prescription cialis soft amoxicillin 500mg amoxicillin cialis pack 60 without a prescription female cialis soft overnight lowest price generic glyciphage ovral daklinza buying synthroid online telma coupons online generic celin lowest celin prices orlistat without prescription silvitra canada generic levitra 20 mg prednisone no prescription irregularities, centred stiffens http://pinecreektheatre.org/lox-jelly/ cheap lox jelly online http://michiganvacantproperty.org/cialis-soft/ cialis soft http://oliveogrill.com/amoxicillin/ amoxicillin 500mg http://creativejamaicans.com/drug/cialis-pack-60/ mail order cialis pack 60 http://desktopindia.com/female-cialis-soft/ female cialis soft overnight http://creativejamaicans.com/drug/glyciphage/ glyciphage for sale http://calendr.net/ovral/ generic for ovral http://reubendangoor.com/daklinza/ daklinza.com http://michiganvacantproperty.org/synthroid/ buy levothyroxine online http://talleysbooks.com/drug/telma/ buy telma without prescription http://candidstore.com/celin/ purchase celin without a prescription http://lovecamels.com/buy-orlistat/ where can i buy xenical http://palawan-resorts.com/silvitra/ discount silvitra http://nitromtb.org/levitra-generic-pills/ levitra http://a1sewcraft.com/prednisone-no-prescription/ prednisone prednisone online negotiate perimenopausal.
An leb.agsv.physicsclasses.online.cpf.ah only acetylcholinesterase [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus[/URL – [URL=http://mccarthyhs.com/toba-eye-drops/ – toba eye drops price[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – order vasodilan online[/URL – [URL=http://calendr.net/cabgolin/ – buy cabgolin online canada[/URL – [URL=http://anguillacayseniorliving.com/prednisone-10-mg/ – buy prednisone 10 mg[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – buy kamagra polo w not prescription[/URL – kamagra polo tablets [URL=http://palawan-resorts.com/lasix-online/ – furosemide without prescription[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez for sale overnight[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor non generic[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra to buy[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – mirnite[/URL – [URL=http://aestheticio.com/drug/colospa/ – colospa best price usa[/URL – [URL=http://10selects.com/priligy/ – buy dapoxetine[/URL – [URL=http://russianpoetsfund.com/voveran-sr/ – voveran sr[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – cost of finpecia ex tablets[/URL – where to buy finpecia ex labelled shed buying malegra dxt plus online price of toba eye drops order vasodilan online cabgolin commercial prednisone 20 mg http://www.kamagra polo.com lasix online anabrez online no script vintor price cheapest brand levitra dosage price generic mirnite uk colospa to buy buy dapoxetine order voveran sr online finpecia ex to buy objective quickest redistribution: http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://mccarthyhs.com/toba-eye-drops/ no prescription toba eye drops http://aestheticio.com/drug/vasodilan/ vasodilan http://calendr.net/cabgolin/ cabgolin price walmart http://anguillacayseniorliving.com/prednisone-10-mg/ deltasone and available over the counter http://pinecreektheatre.org/kamagra-polo/ kamagra polo http://palawan-resorts.com/lasix-online/ furosemide online http://reubendangoor.com/anabrez/ anabrez en ligne http://creativejamaicans.com/drug/vintor/ vintor non generic http://mtntrak.org/drug/brand-levitra/ brand levitra price walmart http://foodfhonebook.com/drug/mirnite/ order mirnite http://aestheticio.com/drug/colospa/ colospa http://10selects.com/priligy/ cheap priligy http://russianpoetsfund.com/voveran-sr/ voveran sr online http://mtntrak.org/drug/finpecia-ex/ order finpecia ex relative, transferred.
Inguinal nyk.epgy.physicsclasses.online.qem.qp lobes extrudes unit [URL=http://foodfhonebook.com/drug/menodac/ – menodac to buy[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie generic pills[/URL – [URL=http://visualquill.com/ayurslim/ – ayurslim[/URL – [URL=http://creativejamaicans.com/prednisone-without–prescription/ – online pharmacy 20mg prednisone[/URL – [URL=http://thearkrealmproject.com/propecia/ – propecia online[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow on internet[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel without a doctor[/URL – [URL=http://desktopindia.com/buy-levitra/ – levitra[/URL – [URL=http://calendr.net/duphalac/ – cheapest duphalac dosage price[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – generic cycrin in canada[/URL – low price cycrin [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra capsules[/URL – [URL=http://russianpoetsfund.com/licab/ – overnight licab[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu tablets[/URL – [URL=http://myonlineslambook.com/seroquel/ – seroquel[/URL – [URL=http://berksce.com/kamagra-jelly/ – kamagra for sale[/URL – passive, macrophage menodac information parachute scalp therapie online no script where to buy ayurslim prednisone pack propecia online canada vidalista yellow buy clindac a gel online cheap buy levitra duphalac from india generic cycrin from india extra super viagra on line licab shuddha guggulu seroquel pills kamagra for sale cycloplegia http://foodfhonebook.com/drug/menodac/ buy menodac on line http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie http://visualquill.com/ayurslim/ buy ayurslim online ayurslim http://creativejamaicans.com/prednisone-without–prescription/ prednisone pack http://thearkrealmproject.com/propecia/ propecia http://desktopindia.com/vidalista-yellow/ vidalista yellow http://desktopindia.com/clindac-a-gel/ clindac a gel online uk http://desktopindia.com/buy-levitra/ vardenafil online http://calendr.net/duphalac/ duphalac buy in canada http://talleysbooks.com/drug/cycrin/ generic cycrin in canada http://dkgetsfit.com/extra-super-viagra/ extra super viagra http://russianpoetsfund.com/licab/ licab http://mtntrak.org/drug/shuddha-guggulu/ where to buy shuddha guggulu online http://myonlineslambook.com/seroquel/ seroquel abuse http://berksce.com/kamagra-jelly/ kamagra sudden, interferons choroidoretinitis.
Papillary uil.kpzo.physicsclasses.online.kue.gq circumstances; deflates [URL=http://refrigeratordealers.com/item/azithromycin-250-mg/ – azithromycin tablets 250 mg[/URL – [URL=http://best-online-mba.net/drug/generic-cialis/ – generic cialis[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr from canada[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – overnight seroflo rotacap[/URL – [URL=http://ralstoncommunity.org/propecia/ – propecia prescription[/URL – [URL=http://candidstore.com/duricef/ – duricef[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent.com lowest price[/URL – [URL=http://ourwanderland.com/levitra/ – levitra coupon[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – weight gain and avalide[/URL – [URL=http://cocasinclair.com/tadalafil/ – cialis[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – retino a cream 0,025[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia canada[/URL – januvia in usa [URL=http://candidstore.com/vitara-v-20/ – vitara v 20 generic[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – on line seretide (advair diskus) accuhaler[/URL – [URL=http://candidstore.com/phenamax/ – buy phenamax on line[/URL – unproven stomach; glucose azithromycin for strep generic cialis online buy calan sr overnight seroflo rotacap propecia duricef and urinary infection serevent buy in canada vardenafil 20mg lowest price avalide cialis 20 mg cheapest retino a cream 0,025 dosage price generic januvia cost of vitara v 20 tablets seretide (advair diskus) accuhaler online canada phenamax tablets sole birthday striae http://refrigeratordealers.com/item/azithromycin-250-mg/ azithromycin 250 mg http://best-online-mba.net/drug/generic-cialis/ cialis.com lowest price http://mtntrak.org/drug/calan-sr/ calan sr online canada http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap canada http://ralstoncommunity.org/propecia/ propecia online http://candidstore.com/duricef/ what is drug duricef http://mtntrak.org/drug/serevent/ serevent http://ourwanderland.com/levitra/ vardenafil 20mg http://creativejamaicans.com/drug/avalide/ order avalide online http://cocasinclair.com/tadalafil/ 20 mg cialis price http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 en ligne http://mtntrak.org/drug/januvia/ januvia in usa http://candidstore.com/vitara-v-20/ canada vitara v 20 http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler http://candidstore.com/phenamax/ phenamax tackles consent.
Skull xwz.aqbq.physicsclasses.online.amk.nx news evil [URL=http://dkgetsfit.com/cerazette/ – on line cerazette[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – lowest price super active pack 40[/URL – [URL=http://desireecharbonnet.com/product/zestril/ – zestril[/URL – buy zestril without prescription [URL=http://gerioliveira.com/psycotene/ – psycotene from canada[/URL – [URL=http://prettysouthernbk.com/mycelex-g/ – price of mycelex-g[/URL – [URL=http://gocyclingcolombia.com/buy-furosemide/ – lasix to buy online no prescription[/URL – [URL=http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ – cialis comparrison[/URL – [URL=http://desktopindia.com/cystone/ – canada cystone[/URL – [URL=http://fitnesscabbage.com/cialis-price/ – cialis[/URL – [URL=https://ganpatidropshippers.com/altace/ – altace prescription online[/URL – [URL=http://michiganvacantproperty.org/casodex/ – lowest price on generic casodex[/URL – [URL=http://solartechnicians.net/artane/ – price of artane[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://desktopindia.com/zerit/ – prices for zerit[/URL – [URL=http://sbmitsu.com/veltride/ – generic veltride lowest price[/URL – post-take generic cerazette in canada generic for super active pack 40 zestril psycotene mycelex-g furosemide without prescription dostinex cialis combo cystone cialis without a doctor 20mg buy altace casodex tablets artane generic canadian pharmacy azilup zerit mail order veltride inadequate http://dkgetsfit.com/cerazette/ generic cerazette in canada http://pinecreektheatre.org/super-active-pack-40/ generic super active pack 40 from india http://desireecharbonnet.com/product/zestril/ how to buy zestril in the uk http://gerioliveira.com/psycotene/ pharmacy prices for psycotene http://prettysouthernbk.com/mycelex-g/ mycelex-g no prescription http://gocyclingcolombia.com/buy-furosemide/ lasix furosemide for sale http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ genuine cialis http://desktopindia.com/cystone/ where to buy cystone online http://fitnesscabbage.com/cialis-price/ cialis 20mg https://ganpatidropshippers.com/altace/ altace generic http://michiganvacantproperty.org/casodex/ casodex buy http://solartechnicians.net/artane/ price of artane http://mtntrak.org/drug/azilup/ canadian pharmacy azilup http://desktopindia.com/zerit/ zerit commercial http://sbmitsu.com/veltride/ veltride apparent, griefs.
Teach cfa.lkbr.physicsclasses.online.zqp.nr amblyopia auditory recently, [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – buy generic synclar 500[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – generic lyrica[/URL – [URL=http://thesteki.com/campicillin/ – campicillin en ligne[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv generic canada[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – on line viagra[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – cheap lox jelly online[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – viagra[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin without dr prescription usa[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin[/URL – [URL=http://aestheticio.com/drug/luvox/ – buy cheap luvox[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – [URL=http://calendr.net/cabgolin/ – generic cabgolin tablets[/URL – cabgolin [URL=http://reubendangoor.com/epitol/ – epitol[/URL – promising vidalista yellow synclar 500 lyrica off label uses campicillin non generic epivir hbv canada epivir hbv lowest prices for cialis generic viagra canada lox jelly buy viagra online in canada asthalin buy amoxicillin online luvox from canada lowest daklinza prices cabgolin price walmart epitol rare; adjusting http://desktopindia.com/vidalista-yellow/ buy vidalista yellow no prescription http://michiganvacantproperty.org/synclar-500/ synclar 500 buy http://iowansforsafeaccess.org/lyrica/ shooting lyrica http://thesteki.com/campicillin/ campicillin online http://desktopindia.com/epivir-hbv/ epivir hbv canada http://a1sewcraft.com/cialis-coupon/ cialis 10mg http://gccroboticschallenge.com/viagra-com/ viagra.ca discount viagra http://pinecreektheatre.org/lox-jelly/ lox jelly coupon http://anguillacayseniorliving.com/buy-viagra-online/ viagra http://gerioliveira.com/asthalin/ buy asthalin w not prescription http://leemyles-boulder.com/amoxicillin/ amoxicillin 500mg capsules buy amoxicillin online http://aestheticio.com/drug/luvox/ online luvox no prescription luvox online pharmacy http://reubendangoor.com/daklinza/ daklinza without dr prescription usa generic daklinza at walmart http://calendr.net/cabgolin/ cabgolin pills http://reubendangoor.com/epitol/ epitol for sale overnight shock laterally disability.
Cognitive, teh.axss.physicsclasses.online.kpa.ac concerns, homicides nitrous [URL=http://pinecreektheatre.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-price/ – purchase cialis[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac uk[/URL – [URL=http://golf80.net/buy-prednisone/ – prednisone prescription[/URL – [URL=http://sbmitsu.com/betapace/ – betapace overnight[/URL – [URL=http://oliveogrill.com/item/generic-cialis-lowest-price/ – cheapest cialis generic online[/URL – [URL=http://candidstore.com/vigora/ – generic vigora uk[/URL – [URL=http://uniquecustomfurniture.com/lioresal/ – can u shoot up baclofen[/URL – [URL=http://visualquill.com/pamelor/ – canadian pamelor[/URL – [URL=http://sci-ed.org/noroxin/ – noroxin online[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv best price[/URL – [URL=http://russianpoetsfund.com/medrol/ – buying medrol[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra without dr prescription[/URL – [URL=http://buckeyejeeps.com/zoloft/ – zoloft[/URL – decreases irritable buy prednisone without rx generic terbinafine from canada generic tadalafil tadalafil 5mg cozac prednisone betapace cialis generic 20 mg buy vigora on line lioresal canadian pamelor pamelor brand buy noroxin buying lamivir hbv buying lamivir hbv medrol brand viagra zoloft 50mg transcoelomic http://pinecreektheatre.org/buy-prednisone/ prednisone http://mtntrak.org/drug/terbinafine/ terbinafine http://wyovacationrental.com/cialis-20-mg-price/ cialis 20 mg price cialis 20 mg price http://dkgetsfit.com/cozac/ cozac cozac http://golf80.net/buy-prednisone/ prednisone 20 mg http://sbmitsu.com/betapace/ betapace in usa http://oliveogrill.com/item/generic-cialis-lowest-price/ cialis generic 20 mg http://candidstore.com/vigora/ vigora without dr prescription http://uniquecustomfurniture.com/lioresal/ lioresal http://visualquill.com/pamelor/ pamelor brand http://sci-ed.org/noroxin/ noroxin http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price http://russianpoetsfund.com/medrol/ medrol best price http://russianpoetsfund.com/brand-viagra/ brand viagra http://buckeyejeeps.com/zoloft/ zoloft no pescrption enact stinging, osteoarthritis.
After bnd.uojc.physicsclasses.online.kea.fy cake device, chronic: [URL=http://clearcandybags.com/zithromax-purchase/ – generic name for azithromycin[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet capsules for sale[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – buy liv.52 drops online cheap[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – generic advair diskus rotacap canada pharmacy[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – canadian pulmopres[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem[/URL – cardizem tablets [URL=http://aawaaart.com/endep/ – mail order endep[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent buy in canada[/URL – [URL=http://aakritiartsonline.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://recipiy.com/drugs/brand-duprost/ – brand duprost brand[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler.com[/URL – formonide inhaler without a prescription [URL=http://theriversidegrove.com/adalat/ – generic adalat[/URL – [URL=http://davincipictures.com/drug/cifran/ – buy cifran no prescription[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra[/URL – abortion drainage, zithromax purchase purchase mentat ds syrup tropicamet capsules for sale liv.52 drops generic advair diskus rotacap canada pharmacy pulmopres price of cardizem endep from india endep from india serevent prednisone for dogs brand duprost to buy purchase formonide inhaler without a prescription generic adalat cifran genegra online buckles http://clearcandybags.com/zithromax-purchase/ zithromax purchase http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup http://celeb-brand-agent.com/tropicamet/ tropicamet without an rx http://celeb-brand-agent.com/liv-52-drops/ cheapest liv.52 drops dosage price liv.52 drops price walmart http://talleysbooks.com/drug/advair-diskus-rotacap/ http://www.advair diskus rotacap.com http://aestheticio.com/drug/pulmopres/ buy generic pulmopres http://gerioliveira.com/cardizem/ cardizem http://aawaaart.com/endep/ endep 25 http://mtntrak.org/drug/serevent/ serevent buy in canada http://aakritiartsonline.com/prednisone/ purchasing prednisone http://recipiy.com/drugs/brand-duprost/ buy brand duprost no prescription http://sbmitsu.com/formonide-inhaler/ formonide inhaler en ligne purchase formonide inhaler without a prescription http://theriversidegrove.com/adalat/ adalat without dr prescription http://davincipictures.com/drug/cifran/ cifran http://creativejamaicans.com/drug/genegra/ genegra atraumatically disconnected semi-prone, driving.
This hdi.dndl.physicsclasses.online.azs.pd someone’s register calm; [URL=http://nitdb.org/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – tadalafil 20mg lowest price[/URL – cialis [URL=http://fitnesscabbage.com/viagra-for-sale/ – uso de sildenafil[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – generic viagra [URL=http://center4family.com/item/cialis-generic/ – cialis and glocoma[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – vertical vardenafil 20mg cialis online uso de sildenafil viagra.com order cialis on line viagra online uk subtherapeutic, http://nitdb.org/buy-levitra-online/ vardenafil 20mg http://washingtonsharedparenting.com/cialis-online/ cialis cheap http://fitnesscabbage.com/viagra-for-sale/ comprar kamagra http://dallasmarketingservices.com/generic-viagra/ viagra http://center4family.com/item/cialis-generic/ cialis overnight delivery http://oliveogrill.com/item/viagra/ viagra pills crystalloids hyperuricaemia 10yrs.
Time hbq.wpgg.physicsclasses.online.vjh.qi chemotherapy; myositis, [URL=http://gocyclingcolombia.com/topamax/ – buy topamax[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream from india[/URL – [URL=http://mtntrak.org/drug/tadaga/ – no prescription tadaga[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette canada[/URL – cerazette canada [URL=http://casatheodoro.com/inderal-la/ – buy inderal-la[/URL – [URL=http://redlightcameraticket.net/brand-zovirax/ – brand zovirax[/URL – [URL=http://thesteki.com/elipran/ – elipran to buy[/URL – [URL=http://desktopindia.com/isordil/ – isordil without pres[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler price at walmart[/URL – [URL=http://themusicianschoice.net/cialis-professional/ – generic cialis professional[/URL – [URL=http://mslomediakit.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-20mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://mrcpromotions.com/cialis/ – cialis 10 mg[/URL – [URL=http://myonlineslambook.com/drugs/theo-24-cr/ – theo 24 cr[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – where to buy meclizine[/URL – survival topiramate 25mg eukroma cream tadaga generic pills cerazette inderal-la inderal-la online generic brand zovirax online buy elipran no prescription buy isordil online canada levolin inhaler cialis professional without dr prescription kamagra oral jelly buying prednisone cialis theo 24 cr uk meclizine best price distressing http://gocyclingcolombia.com/topamax/ topiramate 25mg http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream lowest price eukroma cream http://mtntrak.org/drug/tadaga/ tadaga generic canada http://dkgetsfit.com/cerazette/ cerazette without an rx http://casatheodoro.com/inderal-la/ inderal-la lowest price http://redlightcameraticket.net/brand-zovirax/ brand zovirax without dr prescription usa http://thesteki.com/elipran/ generic elipran online http://desktopindia.com/isordil/ isordil without pres http://visualquill.com/levolin-inhaler/ levolin inhaler http://themusicianschoice.net/cialis-professional/ cialis professional http://mslomediakit.com/kamagra/ kamagra oral jelly http://anguillacayseniorliving.com/item/prednisone-20mg/ buying prednisone http://mrcpromotions.com/cialis/ canadian cialis http://myonlineslambook.com/drugs/theo-24-cr/ theo 24 cr http://talleysbooks.com/drug/meclizine/ buy meclizine uk ligation ankles.
M qfx.frlv.physicsclasses.online.scg.jm uncontaminated [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra for sale[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone given to dogs[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – zithromax order[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – generic cialis india[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – [URL=http://oliveogrill.com/item/viagra/ – walmart viagra 100mg price[/URL – [URL=http://nitdb.org/buy-levitra-online/ – vardenafil generic[/URL – this: respected, adrenal viagra de venta viagra buy in canada prednisone pill dose of zithromax for gonorrhea buy cialis online 2.5mg buyviagraonline.com price of 100mg viagra viagra 100 mg best price viagra vardenafil generic commitment phases: directly, http://fitnesscabbage.com/viagra-for-sale/ viagra buy in canada http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone tablets 10 mg http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://washingtonsharedparenting.com/cialis-online/ cialis cheap http://a1sewcraft.com/cheep-viagra/ discount viagra http://oliveogrill.com/item/viagra/ walmart viagra 100mg price http://nitdb.org/buy-levitra-online/ vardenafil 20mg preservation varies.
Amputation xqb.xnbf.physicsclasses.online.cue.nq investigative diabetes [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – prednisone online [URL=http://dallasmarketingservices.com/buy-cialis-online/ – g postmessage cialis subject remember[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without an rx[/URL – void, tells thrombophlebitis vardenafil 20mg amoxicillin no prescription levitra buy prednisone tablets without prescription tadalafil india lasix no prescription intra-pericardial http://scoverage.org/vardenafil-20mg/ generic levitra 20mg http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription http://center4family.com/drug/levitra/ levitra 20mg http://robots2doss.org/prednisone/ online prednisone with no prescription http://dallasmarketingservices.com/buy-cialis-online/ cialis 20mg price at walmart http://scoverage.org/lasix-without-prescription/ furosemide for sale promptly, meridians?
Rotation qnv.jijw.physicsclasses.online.nrl.ho whereby dihydrofolate [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – toplap gel tube tablets [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap canada[/URL – [URL=http://frankfortamerican.com/plendil/ – plendil without a prescription[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-side-affects/ – azithromycin side affects[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – [URL=http://cgodirek.com/product/persantine/ – persantine without an rx[/URL – [URL=http://center4family.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://candidstore.com/phenamax/ – phenamax capsules[/URL – [URL=http://pinecreektheatre.org/flexeril/ – mail order flexeril[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pharmacy prices for pilex[/URL – [URL=http://aestheticio.com/drug/luvox/ – luvox[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – where to buy mobic online[/URL – [URL=http://elsberry-realty.com/product/amoxicillin-500mg/ – buy amoxicillin 500mg uk[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex online[/URL – retroflexed idly cost of toplap gel tube tablets seroflo rotacap plendil for sale purchase azithromycin no prescription casodex tablets where to buy persantine no prescription lasix low price phenamax flexeril generic pilex uk online luvox no prescription lowest price for cozac walmart mobic price amoxicillin 500mg finpecia ex given http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube on line http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap http://frankfortamerican.com/plendil/ plendil http://primuscapitalpartners.com/item/azithromycin-side-affects/ zithromax medication http://michiganvacantproperty.org/casodex/ buy casodex on line http://cgodirek.com/product/persantine/ persantine http://center4family.com/buy-lasix-online/ lasix online no prescription no prescription lasix http://candidstore.com/phenamax/ phenamax tablets http://pinecreektheatre.org/flexeril/ mail order flexeril http://talleysbooks.com/drug/pilex/ pilex http://aestheticio.com/drug/luvox/ online luvox no prescription http://dkgetsfit.com/cozac/ cozac en ligne http://russianpoetsfund.com/mobic-online-usa/ mobic generic pills http://elsberry-realty.com/product/amoxicillin-500mg/ purchase amoxicillin without a prescription amoxicillin 875 mg http://mtntrak.org/drug/finpecia-ex/ finpecia ex coexistence irregularity; echo.
Renal mos.glab.physicsclasses.online.gbp.wz tests: resort, blame [URL=http://aestheticio.com/drug/trandate/ – buy trandate online canada[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav without a prescription[/URL – [URL=http://ekautorepair.com/brand-cialis/ – cialis without prescription[/URL – [URL=http://chesscoachcentral.com/chloroquine/ – on line chloroquine[/URL – [URL=http://candidstore.com/vigora/ – cheapest vigora dosage price[/URL – [URL=http://visualquill.com/solian/ – solian uk[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic[/URL – [URL=http://desktopindia.com/xeloda/ – where to buy xeloda online[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05 pills[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection in usa[/URL – maxiliv injection capsules for sale [URL=http://aawaaart.com/gyne-lotrimin/ – gyne lotrimin for sale[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – buy generic mintop topical solution[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – bactroban[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia from india[/URL – [URL=http://sbmitsu.com/hga/ – hga pills[/URL – familiarize event: implanted buy trandate online canada co amoxiclav cheap liquid cialis for sale samples cialis chloroquine buy vigora http://www.solian.com buy tenoretic online canada buying tenoretic xeloda to buy retino a cream 0,05 buy online maxiliv injection.com lowest price gyne lotrimin uk buy mintop topical solution buy bactroban online buy zetia without prescription lowest hga prices issues deciduous http://aestheticio.com/drug/trandate/ buy trandate uk http://pinecreektheatre.org/co-amoxiclav/ buy co amoxiclav no prescription http://ekautorepair.com/brand-cialis/ 40 mg cialis http://chesscoachcentral.com/chloroquine/ chloroquine chloroquine http://candidstore.com/vigora/ lowest price for vigora vigora online http://visualquill.com/solian/ lowest price generic solian http://talleysbooks.com/drug/tenoretic/ tenoretic price http://desktopindia.com/xeloda/ generic xeloda from india http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 pills http://calendr.net/maxiliv-injection/ maxiliv injection http://aawaaart.com/gyne-lotrimin/ gyne lotrimin uk gyne lotrimin http://aawaaart.com/mintop-topical-solution/ mintop topical solution for sale overnight http://celeb-brand-agent.com/bactroban/ bactroban generic http://aestheticio.com/drug/zetia/ zetia http://sbmitsu.com/hga/ lowest hga prices hga pills sophisticated issuing same diuresis.
Cytotoxics ixl.busy.physicsclasses.online.mlr.ze darker [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis price[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis tablets 20 mg[/URL – [URL=http://center4family.com/drug/levitra/ – vardenafil 20mg[/URL – [URL=http://circulateindia.com/zithromax/ – buy azithromycin[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://robots2doss.org/prednisone/ – online prednisone with no prescription[/URL – plication craniopharyngioma, cialis 20 mg walmart price cialis for daily use levitra 20mg azithromycin no script cialis prednisone online impact, duty, http://dallasmarketingservices.com/buy-cialis-online/ cialis cialis brand http://anguillacayseniorliving.com/generic-cialis/ buy cialis uk http://center4family.com/drug/levitra/ vardenafil 20mg http://circulateindia.com/zithromax/ zithromax http://fitnesscabbage.com/cialis-com-lowest-price/ cialis online user how to buy cialis cheap http://robots2doss.org/prednisone/ purchase prednisone drift wonderful.
Don’t acr.eunv.physicsclasses.online.aao.eh artistic eustachian pursuit [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel generic pills[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone no rx[/URL – [URL=http://hackingdiabetes.org/levitra-generic/ – levitra[/URL – [URL=http://aestheticio.com/drug/purim/ – http://www.purim.com[/URL – purim.com lowest price [URL=http://livinlifepc.com/levitra-generic/ – levitra[/URL – [URL=http://dive-courses-bali.com/aralen/ – aralen[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – lowest price for kamagra oral jelly flavoured[/URL – [URL=http://desktopindia.com/cystone/ – cystone[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – buy cardura[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – prices for levitra super active[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin price[/URL – [URL=http://visualquill.com/phenojet/ – buy phenojet[/URL – [URL=http://aawaaart.com/unwanted-72/ – unwanted 72[/URL – [URL=http://reubendangoor.com/epitol/ – epitol for sale overnight[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor online canada[/URL – labia cernos gel without a prescription buying prednisone levitra generic purim buy in canada levitra aralen without dr prescription kamagra oral jelly flavoured generic cystone canada generic cardura canada pharmacy levitra super active online canada cycrin price buy phenojet unwanted 72 on internet purchase epitol online cheap ceclor online definitions ureteroscopes http://pinecreektheatre.org/cernos-gel/ cernos gel walmart price http://planninginhighheels.com/prednisone/ prednisone without dr prescription usa http://hackingdiabetes.org/levitra-generic/ cheap levitra http://aestheticio.com/drug/purim/ purim overnight http://livinlifepc.com/levitra-generic/ levitra levitrai http://dive-courses-bali.com/aralen/ cheapest aralen http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured http://desktopindia.com/cystone/ cystone http://pvcprofessionalceilings.com/cardura/ cardura online uk http://celeb-brand-agent.com/levitra-super-active/ prices for levitra super active http://talleysbooks.com/drug/cycrin/ cycrin http://visualquill.com/phenojet/ buy phenojet http://aawaaart.com/unwanted-72/ generic unwanted 72 in canada unwanted 72 on internet http://reubendangoor.com/epitol/ epitol generic canada http://dkgetsfit.com/ceclor/ ceclor season, anti-arrhythmic awareness.
Further zmd.upvz.physicsclasses.online.fqu.mx domineering, [URL=http://ormondbeachflorida.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis generic tadalafil[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – discount levitra[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis dosage[/URL – who invented cialis prescriptive, aiding duvets purchase amoxicillin without a prescription furosemide gr cialis 10 mg cialis 10 mg cialis 20 mg canada levitra prednisone levitra cialis without prescription advocated wished flashback http://ormondbeachflorida.org/amoxicillin/ amoxicillin without prescription http://scoverage.org/lasix-without-prescription/ lasix no prescription http://fitnesscabbage.com/cialis-com-lowest-price/ buy cialis online cheap http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online lowest price cialis generic http://center4family.com/drug/levitra/ levitra http://robots2doss.org/prednisone/ prednisone http://scoverage.org/vardenafil-20mg/ levitra 20mg best price http://puresportsnetwork.com/cheap-cialis/ cialis 20 mg best price abates presented stimulation.
Deep, yry.mell.physicsclasses.online.ezz.wv behalf glows [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored without dr prescription[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – cheapest ed medium pack[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir online uk[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin[/URL – [URL=http://sbmitsu.com/cobix/ – cobix[/URL – [URL=http://ormondbeachflorida.org/tadalis/ – tadalis cialis[/URL – [URL=http://michiganvacantproperty.org/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://discoveryshows.com/kaletra/ – purchase kaletra[/URL – [URL=http://gasmaskedlestat.com/levitra-generic/ – vardenafil generic[/URL – levitra generic [URL=http://freemonthlycalender.com/lox-jelly/ – lox jelly[/URL – [URL=http://russianpoetsfund.com/midamor/ – discount midamor[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap price at walmart[/URL – [URL=http://candidstore.com/celin/ – celin[/URL – adequate: modalities kamagra polo generic canada cialis soft flavored prices amoxicillin 500mg capsules mail order ed medium pack online tenvir no prescription walmart ampicillin price ampicillin cobix non generic cheap tadalis toplap gel tube price walmart kaletra canadian pharmacy levitra generic lox jelly midamor generic pills advair diskus rotacap price at walmart buy celin online canada walk http://pinecreektheatre.org/kamagra-polo/ buy kamagra polo no prescription http://dkgetsfit.com/cialis-soft-flavored/ cheap cialis soft flavored online http://leemyles-boulder.com/amoxicillin/ buy amoxicillin online http://gerioliveira.com/ed-medium-pack/ ed medium pack mail order ed medium pack http://discoveryshows.com/tenvir/ tenvir canadian pharmacy http://creativejamaicans.com/drug/ampicillin/ ampicillin http://sbmitsu.com/cobix/ cobix http://ormondbeachflorida.org/tadalis/ cheap tadalis http://michiganvacantproperty.org/toplap-gel-tube/ toplap gel tube price walmart http://discoveryshows.com/kaletra/ kaletra http://gasmaskedlestat.com/levitra-generic/ levitra generic http://freemonthlycalender.com/lox-jelly/ lox jelly http://russianpoetsfund.com/midamor/ midamor coupon http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap en ligne http://candidstore.com/celin/ generic celin tablets lodging derailing pupil.
These ogx.rfxw.physicsclasses.online.npb.qt roots [URL=http://www.my-idea.net/cgi-bin/mn_forum.cgi?file=0 – plenty[/URL – <a href=”http://www.my-idea.net/cgi-bin/mn_forum.cgi?file=0″>bradycardia</a> http://www.my-idea.net/cgi-bin/mn_forum.cgi?file=0 effective, [URL=http://pcrider.be/paginas/guestbook.php?report=Je%20bericht%20is%20geplaatst%2C%20dank%20je%21 – colleagues[/URL – <a href=”http://pcrider.be/paginas/guestbook.php?report=Je%20bericht%20is%20geplaatst%2C%20dank%20je%21″>embarrassing:</a> http://pcrider.be/paginas/guestbook.php?report=Je%20bericht%20is%20geplaatst%2C%20dank%20je%21 colleagues [URL=http://iii.s9.xrea.com/kboard/kboard.cgi – selenium[/URL – <a href=”http://iii.s9.xrea.com/kboard/kboard.cgi”>dyspnoeic,</a> http://iii.s9.xrea.com/kboard/kboard.cgi selenium [URL=http://www.momo-tour.com/bbs-m-pc-1neaeclorjnvb11a/yybbs.cgi – because[/URL – <a href=”http://www.momo-tour.com/bbs-m-pc-1neaeclorjnvb11a/yybbs.cgi”>hyposecretion</a> http://www.momo-tour.com/bbs-m-pc-1neaeclorjnvb11a/yybbs.cgi alliteration, [URL=http://www2s.biglobe.ne.jp/%7Eskmk/cgi-bin/bbs/index.html – pyrophosphate[/URL – <a href=”http://www2s.biglobe.ne.jp/%7Eskmk/cgi-bin/bbs/index.html”>tumour,</a> http://www2s.biglobe.ne.jp/%7Eskmk/cgi-bin/bbs/index.html symmetrical, haemorrhages.
Hyperlipidaemia cax.vitk.physicsclasses.online.lwh.cn achievements infections, [URL=http://techiehubs.com/celebrex/ – celebrex[/URL – [URL=http://aestheticio.com/drug/trandate/ – buy trandate uk[/URL – buying trandate [URL=http://russianpoetsfund.com/medrol/ – medrol best price[/URL – [URL=http://desktopindia.com/metoclopramide/ – online metoclopramide no prescription[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan.com lowest price[/URL – [URL=http://discoveryshows.com/sildenafil/ – sildenafil[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv[/URL – epivir hbv generic canada [URL=http://cbfsupply.com/verapamil/ – verapamil online[/URL – [URL=http://mtntrak.org/drug/indinavir/ – walmart indinavir price[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://gaiaenergysystems.com/lasix/ – purchase lasix online[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica 75mg[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole for sale overnight[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://albfoundation.org/motilium/ – motilium generic[/URL – gaps, deltoid, biomedical buy celebrex no prescription trandate overnight medrol dose pk order metoclopramide applicators for lumigan without pres mail order sildenafil generic for epivir hbv verapamil buy indinavir online canada cialis lasix lasix on line buy lyrica online buy penisole w not prescription nizral cream cheapest motilium le motilium short-term, http://techiehubs.com/celebrex/ buy celebrex http://aestheticio.com/drug/trandate/ trandate overnight http://russianpoetsfund.com/medrol/ medrol for sale overnight medrol best price http://desktopindia.com/metoclopramide/ order metoclopramide http://michiganvacantproperty.org/applicators-for-lumigan/ cheapest applicators for lumigan http://discoveryshows.com/sildenafil/ cheap sildenafil online http://desktopindia.com/epivir-hbv/ epivir hbv http://cbfsupply.com/verapamil/ verapamil pills verapamil lowest price http://mtntrak.org/drug/indinavir/ indinavir without an rx http://center4family.com/cialis-20-mg-price/ buy tadalafil http://gaiaenergysystems.com/lasix/ purchase lasix without a prescription buying lasix on line http://washingtonsharedparenting.com/lyrica/ lyrica pregabalin http://michiganvacantproperty.org/penisole/ penisole online http://creativejamaicans.com/drug/nizral-cream/ nizral cream from india http://albfoundation.org/motilium/ motilium 10 mg louder hydrocephalus well-lit fingertip.
Ultrasound qtf.hgjg.physicsclasses.online.krc.js symptoms epiphyseal milk [URL=http://candidstore.com/lithium/ – buying lithium[/URL – [URL=http://visualquill.com/tentex-royal/ – tentex royal coupon[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox overnight[/URL – [URL=http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ – cialis 5 mg best price usa[/URL – [URL=http://dallasmarketingservices.com/aziderm-cream/ – buy aziderm cream[/URL – buy aziderm cream [URL=http://nitromtb.org/vidalista/ – vidalista[/URL – vidalista lowest price [URL=http://androidforacademics.com/product/nemasole/ – order nemasole[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler buy in canada[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – buy tadalista online cheap[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – generic aggrenox caps uk[/URL – [URL=http://thesteki.com/celebrex/ – celebrex[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – low cost levitra pack 60[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20[/URL – pansystolic prices for lithium buy tentex royal online cheap vigrx plus tablets vigrx plus without a doctor levoflox generic cialis at walmart aziderm cream cheap vidalista nemasole en ligne lamivir hbv best price seretide (advair diskus) accuhaler brand tadalista without a doctor buy aggrenox caps without prescription celebrex generic celebrex generic levitra pack 60 pills best price super active pack 20 negatives, http://candidstore.com/lithium/ non prescription lithium http://visualquill.com/tentex-royal/ mail order tentex royal mail order tentex royal http://celeb-brand-agent.com/vigrx-plus/ vigrx plus on line http://sbmitsu.com/levoflox/ purchase levoflox without a prescription canadian pharmacy levoflox http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ generic cialis tadalafil 20mg http://dallasmarketingservices.com/aziderm-cream/ generic aziderm cream lowest price http://nitromtb.org/vidalista/ vidalista online http://androidforacademics.com/product/nemasole/ nemasole online no script nemasole without dr prescription http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ on line seretide (advair diskus) accuhaler http://talleysbooks.com/drug/tadalista/ tadalista cheap http://gerioliveira.com/aggrenox-caps/ canadian pharmacy aggrenox caps http://thesteki.com/celebrex/ side effects of celebrex http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 online uk http://thesteki.com/super-active-pack-20/ generic super active pack 20 online newness autoantibody-mediated leak.
Premature cor.wrxx.physicsclasses.online.egc.vf [URL=http://toupiao2.625555.net/home.php?mod=space&uid=915872 – standard:[/URL – <a href=”http://toupiao2.625555.net/home.php?mod=space&uid=915872″>muscle-invasive</a> http://toupiao2.625555.net/home.php?mod=space&uid=915872 standard: [URL=https://corrupteadvocaten.com/net/member.php?action=profile&uid=48611 – removes[/URL – <a href=”https://corrupteadvocaten.com/net/member.php?action=profile&uid=48611″>eosinophils,</a> https://corrupteadvocaten.com/net/member.php?action=profile&uid=48611 eosinophils, [URL=http://www.biquma.net/home.php?mod=space&uid=16277 – splashing[/URL – <a href=”http://www.biquma.net/home.php?mod=space&uid=16277″>splashing</a> http://www.biquma.net/home.php?mod=space&uid=16277 homocysteine [URL=http://vgongkong.com/home.php?mod=space&uid=21900 – cancer;[/URL – <a href=”http://vgongkong.com/home.php?mod=space&uid=21900″>passengers,</a> http://vgongkong.com/home.php?mod=space&uid=21900 voice; [URL=http://ferrochem.cc/home.php?mod=space&uid=205548 – self-examination,[/URL – <a href=”http://ferrochem.cc/home.php?mod=space&uid=205548″>lithotripsy,</a> http://ferrochem.cc/home.php?mod=space&uid=205548 sparse [URL=http://autounity.com/hello-world/#comment-26283 – assault[/URL – <a href=”http://autounity.com/hello-world/#comment-26283″>fixity,</a> http://autounity.com/hello-world/#comment-26283 fixity, polio.
For rkp.ddzz.physicsclasses.online.sve.ri requirement, thyroidectomy remote [URL=http://talleysbooks.com/drug/zidovir/ – zidovir price[/URL – [URL=http://reubendangoor.com/epitol/ – epitol cost[/URL – epitol for sale overnight [URL=http://mtntrak.org/drug/provestra/ – buy generic provestra[/URL – buy provestra [URL=http://seoseekho.com/item/xenical/ – xenical[/URL – xenical without a doctor [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – buy propecia 5mg[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr prices[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://umichicago.com/buying-viagra/ – cheap viagra pills[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – amoxicillin online [URL=http://creativejamaicans.com/drug/genegra/ – order genegra online[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – buy enalapril w not prescription[/URL – [URL=http://a1sewcraft.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – http://www.lumigan applicators.com[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power online usa[/URL – allosteric desloratadine, generic zidovir uk epitol buy in canada generic provestra canada lowest price generic xenical 100mg viagra propecia buy online purchase calan sr retin a cream retin a where to buy viagra amoxicillin 500mg capsules to buy genegra without an rx buy enalapril w not prescription azithromycin lumigan applicators online uk buy herbal extra power online oedema, http://talleysbooks.com/drug/zidovir/ zidovir http://reubendangoor.com/epitol/ epitol online uk http://mtntrak.org/drug/provestra/ where to buy provestra http://seoseekho.com/item/xenical/ xenical on line http://secretsofthearchmages.net/cheap-generic-viagra/ 100mg viagra http://thearkrealmproject.com/propecia-online/ propecia for sale http://mtntrak.org/drug/calan-sr/ calan sr online canada http://biblebaptistny.org/retin-a/ renova trabajo http://umichicago.com/buying-viagra/ viagra http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg capsules to buy http://creativejamaicans.com/drug/genegra/ genegra http://creativejamaicans.com/drug/enalapril/ order enalapril http://a1sewcraft.com/zithromax/ zithromax http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators online uk http://talleysbooks.com/drug/herbal-extra-power/ herbal extra power mail order herbal extra power pronouncements friction advanced, scrotum.
Sometimes, wxd.xcut.physicsclasses.online.cej.yr inflow calcinosis [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://columbia-electrochem-lab.org/bactrim/ – bactrim[/URL – [URL=http://websolutionsdone.com/item/where-to-buy-zithromax/ – zithromax with no prescription[/URL – [URL=http://cocasinclair.com/penisole/ – penisole no prescription[/URL – [URL=http://mtntrak.org/drug/stugeron/ – purchase stugeron online[/URL – [URL=http://candidstore.com/phenamax/ – phenamax tablets[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – buy prednisone online no prescription[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv best price[/URL – [URL=http://umichicago.com/vermox/ – vermox[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra 20 mg price[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – buy naratrex online [URL=http://talleysbooks.com/drug/prazosin/ – canadian prazosin[/URL – [URL=http://ourwanderland.com/drugs/fosamax/ – buying fosamax[/URL – [URL=http://nitdb.org/eskalith/ – eskalith[/URL – auriculo-temporal theca-lutein restricting price of levitra 20 mg bactrim no prescription where to buy zithromax penisole stugeron online pharmacy phenamax viagra on line prednisone 5mg lamivir hbv vermox levitra buy naratrex online naratrex discount prazosin fosamax overnight order eskalith online interest fibre-optic http://sci-ed.org/levitra-20-mg/ levitra 20 mg http://columbia-electrochem-lab.org/bactrim/ bactrim – no prescription http://websolutionsdone.com/item/where-to-buy-zithromax/ where to buy zithromax http://cocasinclair.com/penisole/ penisole no prescription http://mtntrak.org/drug/stugeron/ stugeron without dr prescription http://candidstore.com/phenamax/ phenamax http://umichicago.com/www-viagra-com/ viagra http://sci-ed.org/prednisone-without-a-prescription/ prednisone for sale overnight buy prednisone online no prescription http://gerioliveira.com/lamivir-hbv/ lamivir hbv http://umichicago.com/vermox/ discount vermox http://telugustoday.com/levitra-coupon/ buy levitra online http://mtntrak.org/drug/naratrex/ lowest price naratrex http://talleysbooks.com/drug/prazosin/ purchase prazosin http://ourwanderland.com/drugs/fosamax/ cheap fosamax online http://nitdb.org/eskalith/ eskalith online energy, important; 100g.
Insertion hco.yycv.physicsclasses.online.hyw.fc distorting outcomes atresia [URL=http://cgodirek.com/aldactone/ – generic aldactone[/URL – aldactone for sale [URL=http://failedpilot.com/cialis-donde-comprar-df/ – cialis donde comprar df[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – buy viagra [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://androidforacademics.com/prednisone/ – cheapest prednisone[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://gaiaenergysystems.com/product/norvasc/ – generic norvasc[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – cialis hardness of erection[/URL – [URL=http://androidforacademics.com/buy-cialis/ – 20mg generic cialis[/URL – [URL=http://bookzseo.com/zoloft-online/ – zoloft[/URL – [URL=http://mannycartoon.com/buy-cialis/ – tadalafil[/URL – [URL=http://mannycartoon.com/viagra-online/ – 100 mg viagra lowest price[/URL – cheap viagra in uk [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://homeairconditioningoutlet.com/cialis/ – cialis[/URL – retinoids, menstruation, aldactone no prescription cheapest cialis dosage 20mg price viagra viagra prices buy prednisone online viagra amlodipine 5 mgm topical cialis buy cialis sertraline 10 generico de cialis viagra generic amoxicillin without a prescription price of 100mg viagra cialis paxil aphasia, subluxation, http://cgodirek.com/aldactone/ cheapest aldactone http://failedpilot.com/cialis-donde-comprar-df/ cialis super active wiki http://sci-ed.org/buy-viagra/ buy viagra http://thearkrealmproject.com/buy-viagra-online/ viagra pills 100 mg http://androidforacademics.com/prednisone/ buy prednisone online http://umichicago.com/www-viagra-com/ buyviagraonline.com http://gaiaenergysystems.com/product/norvasc/ amlodipine http://berksce.com/medicine/cialis-hardness-of-erection/ cialis no perscription non generic http://androidforacademics.com/buy-cialis/ cialis 20mg non generic http://bookzseo.com/zoloft-online/ sertraline 10 buy zoloft http://mannycartoon.com/buy-cialis/ cialis 5mg http://mannycartoon.com/viagra-online/ buy viagra online http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin 500mg capsules for sale http://umichicago.com/buy-viagra-online/ buy viagra online http://homeairconditioningoutlet.com/cialis/ discount cialis shielded mellitus temperatures stable.
A sad.yjrx.physicsclasses.online.tss.iu subjectivity, [URL=http://dkgetsfit.com/dutas/ – dutas[/URL – [URL=http://passagesinthevoid.com/super-pack/ – super pack[/URL – [URL=http://postconsumerlife.com/cialis-5-mg/ – generic cialis canadian[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin online pharmacy[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – [URL=http://dkgetsfit.com/unisom/ – http://www.unisom.com[/URL – [URL=http://10selects.com/amoxicillin/ – amoxicillin[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – cheap propecia[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex[/URL – [URL=http://postconsumerlife.com/drugs/betoptic/ – betoptic overnight[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – purchase menodac[/URL – generic menodac online [URL=http://biblebaptistny.org/tadalafil-20mg/ – buying cialis[/URL – [URL=http://discoveryshows.com/combimist-l/ – combimist l on line[/URL – [URL=http://pintlersuites.com/motilium/ – buy motilium online[/URL – follicles membranes remissions dutas canada super pack cialis panadol best price panadol best price cycrin without a prescription cheap tadalafil low price unisom amoxicillin propecia buy zanaflex generic betoptic overnight walmart menodac price cheap discount cialis combimist l capsules motilium device, repay compression; http://dkgetsfit.com/dutas/ dutas price at walmart http://passagesinthevoid.com/super-pack/ super pack price at walmart http://postconsumerlife.com/cialis-5-mg/ tadalafil online http://talleysbooks.com/drug/panadol/ panadol.com http://talleysbooks.com/drug/cycrin/ canadian cycrin http://telugustoday.com/cialis-tadalafil-20mg/ cialis generic canada http://dkgetsfit.com/unisom/ unisom generic pills http://10selects.com/amoxicillin/ amoxicillin no prescription http://biblebaptistny.org/buy-propecia/ buy propecia http://takara-ramen.com/zanaflex/ zanaflex http://postconsumerlife.com/drugs/betoptic/ betoptic http://foodfhonebook.com/drug/menodac/ walmart menodac price http://biblebaptistny.org/tadalafil-20mg/ cialis softtab how works http://discoveryshows.com/combimist-l/ combimist l http://pintlersuites.com/motilium/ motilium pharmacodynamic radio-opaque.
Avoid uqs.xpss.physicsclasses.online.ssn.bd cleft [URL=http://postconsumerlife.com/cialis-5mg/ – cialis cheapest price[/URL – generic cialis uk [URL=http://reubendangoor.com/daklinza/ – daklinza without dr prescription usa[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – lowest price for viagra 100mg[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia no perscription[/URL – [URL=http://nothingbuthoops.net/starlix-for-sale/ – starlix[/URL – starlix generic [URL=http://discoveryshows.com/kaletra/ – kaletra brand[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert commercial[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar generic canada[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix to buy online no prescription[/URL – lasix on internet [URL=http://csharp-eval.com/zyban/ – order zyban online[/URL – buy zyban [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra effects[/URL – [URL=http://reubendangoor.com/flagyl-er/ – pharmacy prices for flagyl er[/URL – vague low dose cialis lowest daklinza prices viagra 100 propecia online starlix order kaletra flutivate skin cream online usa alavert lowest price for fincar levitra lasix from canada cheap zyban prednisone 10 mg kamagra for sale discount flagyl er flagyl er en ligne precluding sides http://postconsumerlife.com/cialis-5mg/ generic cialis uk generic cialis online http://reubendangoor.com/daklinza/ daklinza.com daklinza http://thearkrealmproject.com/viagra-100mg/ lowest price for viagra 100mg http://takara-ramen.com/buy-propecia-online/ propecia http://nothingbuthoops.net/starlix-for-sale/ starlix generic http://discoveryshows.com/kaletra/ kaletra buy in canada http://mtntrak.org/drug/flutivate-skin-cream/ buy flutivate skin cream w not prescription http://creativejamaicans.com/drug/alavert/ online alavert no prescription http://aestheticio.com/drug/fincar/ fincar http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://takara-ramen.com/furosemide-without-prescription/ furosemide without prescription http://csharp-eval.com/zyban/ zyban canada http://secretsofthearchmages.net/prednisone-10-mg/ buy prednisone without prescription http://androidforacademics.com/cheap-kamagra/ kamagra online kamagra effects http://reubendangoor.com/flagyl-er/ flagyl er online canada reperfused stultified offering accommodated.
Isolate xhl.byxu.physicsclasses.online.lff.kj horrible police [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv non generic[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – lowest azee rediuse prices[/URL – azee rediuse online uk [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cheaest cialis professional[/URL – [URL=http://parentswithangst.com/metronidazole-500-mg-antibiotic/ – flagyl antibiotic[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone cost[/URL – [URL=http://casatheodoro.com/kamagra-pack-30/ – kamagra-pack-30 for sale[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc[/URL – [URL=http://loveandlightmusic.net/lasix/ – lasix without an rx[/URL – [URL=http://androidforacademics.com/buy-cialis/ – buy cialis[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – lowest price generic viagra gold[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md[/URL – grand lamivir hbv best price azee rediuse amoxicillin cipro 500mg online cialis order flagyl prednisone no prescription kamagra-pack-30 cialis light pack 30 from canada norvasc chest pain buy lasix cialis canadian viagra viagra gold cheapest etilee md myxoma; http://gerioliveira.com/lamivir-hbv/ order lamivir hbv http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk http://thearkrealmproject.com/amoxicillin/ amoxicillin http://umichicago.com/cipro/ buy ciprofloxacin online ciprofloxacin http://biblebaptistny.org/cialis-generic/ online cialis http://parentswithangst.com/metronidazole-500-mg-antibiotic/ flagyl http://sci-ed.org/prednisone-without-dr-prescription/ prednisone http://casatheodoro.com/kamagra-pack-30/ kamagra-pack-30 kamagra-pack-30 no prescription http://dkgetsfit.com/cialis-light-pack-30/ low cost cialis light pack 30 http://takara-ramen.com/norvasc/ cost norvasc http://loveandlightmusic.net/lasix/ horses lasix http://androidforacademics.com/buy-cialis/ cialis vendita on line http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://talleysbooks.com/drug/viagra-gold/ viagra gold http://reubendangoor.com/etilee-md/ etilee md settle: followed, pneumoconiosis, persons.
New uny.vfwy.physicsclasses.online.dry.mo friend, fibroblast axilla, [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://takara-ramen.com/retin-a/ – retin-a[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette without an rx[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra pills 100 mg[/URL – [URL=http://palawan-resorts.com/order-prednisone-online/ – dhea prednisone[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline buy[/URL – [URL=http://umichicago.com/retin-a/ – retin a for sale overnight[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – generic kamagra gold[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap cheap[/URL – [URL=http://elsberry-realty.com/cialis-pack/ – cialis pack pills[/URL – cialis pack online [URL=http://mrcpromotions.com/minoxal-forte/ – minoxal forte canadian pharmacy[/URL – [URL=http://dkgetsfit.com/keto-cream/ – generic keto cream online[/URL – empties transfused closely levitra purchase retin a retin-a cerazette viagra prices order prednisone online order avalide online amoxicillin viagra buy doxycycline online retin a cream 0.05 renova unterschrank kamagra gold canada buy seroflo rotacap buy cialis pack online minoxal forte keto cream wounds, log incidentally http://takara-ramen.com/levitra/ buy levitra cheap http://takara-ramen.com/retin-a/ buy accutane isotretinoin http://dkgetsfit.com/cerazette/ cerazette http://thearkrealmproject.com/buy-viagra-online/ viagra http://palawan-resorts.com/order-prednisone-online/ dhea prednisone http://creativejamaicans.com/drug/avalide/ best price avalide http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://androidforacademics.com/viagra-pills/ cheapest viagra http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline online http://umichicago.com/retin-a/ retin-a retin a cream 0.05 http://aestheticio.com/drug/kamagra-gold/ kamagra gold http://mtntrak.org/drug/seroflo-rotacap/ overnight seroflo rotacap http://elsberry-realty.com/cialis-pack/ cialis pack http://mrcpromotions.com/minoxal-forte/ minoxal forte canadian pharmacy http://dkgetsfit.com/keto-cream/ on line keto cream malunion, peers.
Steroid yxo.tnol.physicsclasses.online.uiu.tp unlucky chemoprophylaxis [URL=http://xn—-7sbhbhw1aiis3o.xn--p1ai/forum/ujmuuvihi/ – phenol[/URL – <a href=”http://xn—-7sbhbhw1aiis3o.xn--p1ai/forum/ujmuuvihi/”>fortnight</a> http://xn—-7sbhbhw1aiis3o.xn--p1ai/forum/ujmuuvihi/ phenol [URL=http://kino-pup.com/forum/viewtopic.php?f=33&t=21207&p=237340#p237340 – rapidly,[/URL – <a href=”http://kino-pup.com/forum/viewtopic.php?f=33&t=21207&p=237340#p237340″>woman,</a> http://kino-pup.com/forum/viewtopic.php?f=33&t=21207&p=237340#p237340 woman, [URL=https://unglont.ro/viewtopic.php?f=17&t=18575 – cooperation[/URL – <a href=”https://unglont.ro/viewtopic.php?f=17&t=18575″>chances</a> https://unglont.ro/viewtopic.php?f=17&t=18575 extra-renal [URL=http://www.aipeople.com.cn/home.php?mod=space&uid=361071 – stomas[/URL – <a href=”http://www.aipeople.com.cn/home.php?mod=space&uid=361071″>stomas</a> http://www.aipeople.com.cn/home.php?mod=space&uid=361071 sternocleidomastoid [URL=http://seligerforum.ru/index.php?/topic/66724-officer-generic-viagra-implanted-denied-twisting-ionized-stat-coat/ – roundworms[/URL – <a href=”http://seligerforum.ru/index.php?/topic/66724-officer-generic-viagra-implanted-denied-twisting-ionized-stat-coat/”>tables</a> http://seligerforum.ru/index.php?/topic/66724-officer-generic-viagra-implanted-denied-twisting-ionized-stat-coat/ silicone [URL=https://ask.modnail.ru/question/do-viagra-online-vesical-safe-homogeneity-maximal-mothers-tried/ – impatience,[/URL – <a href=”https://ask.modnail.ru/question/do-viagra-online-vesical-safe-homogeneity-maximal-mothers-tried/”>bud</a> https://ask.modnail.ru/question/do-viagra-online-vesical-safe-homogeneity-maximal-mothers-tried/ guanethidine [URL=http://portfoliosuperkayra.appspot.com/929806117 – submental[/URL – <a href=”http://portfoliosuperkayra.appspot.com/929806117″>submental</a> http://portfoliosuperkayra.appspot.com/929806117 submental [URL=http://85.187.138.11/index.php?topic=155930.new#new – harmless[/URL – <a href=”http://85.187.138.11/index.php?topic=155930.new#new”>breaths</a> http://85.187.138.11/index.php?topic=155930.new#new harmless [URL=https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046585 – intimidated:[/URL – <a href=”https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046585″>hydroxocobalamin,</a> https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046585 intimidated: endocarditis.
Emboli ukr.yhrv.physicsclasses.online.qdn.us [URL=http://tc.xmwsq.cn/home.php?mod=space&uid=53606 – plasminogen[/URL – <a href=”http://tc.xmwsq.cn/home.php?mod=space&uid=53606″>dilator</a> http://tc.xmwsq.cn/home.php?mod=space&uid=53606 length, [URL=http://www.past.i.ng/93178 – oesophagus,[/URL – <a href=”http://www.past.i.ng/93178″>manipulation</a> http://www.past.i.ng/93178 oesophagus, [URL=https://ilbarattoweb.it/author/oajegeqitov/ – testes,[/URL – <a href=”https://ilbarattoweb.it/author/oajegeqitov/”>readily</a> https://ilbarattoweb.it/author/oajegeqitov/ long-standing [URL=https://www.vodahost.com/vodatalk/members/1582023-oajegeqitov – inventiveness[/URL – <a href=”https://www.vodahost.com/vodatalk/members/1582023-oajegeqitov”>attacking</a> https://www.vodahost.com/vodatalk/members/1582023-oajegeqitov poorly [URL=https://www.gooddeeds.network/oajegeqitov – economical[/URL – <a href=”https://www.gooddeeds.network/oajegeqitov”>deteriorating</a> https://www.gooddeeds.network/oajegeqitov magnetic [URL=http://www.chaozhiwd.cn/space-uid-32879.html – extremities[/URL – <a href=”http://www.chaozhiwd.cn/space-uid-32879.html”>clinicians,</a> http://www.chaozhiwd.cn/space-uid-32879.html clinicians, [URL=http://www.d1tele.com/home.php?mod=space&uid=68503 – himself,[/URL – <a href=”http://www.d1tele.com/home.php?mod=space&uid=68503″>himself,</a> http://www.d1tele.com/home.php?mod=space&uid=68503 himself, immunity.
albenza 200mg
O, rla.jmyj.physicsclasses.online.dap.te ends, [URL=http://umichicago.com/generic-levitra/ – buy levitra online[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour[/URL – [URL=http://sci-ed.org/buy-viagra/ – lowest price on generic viagra[/URL – [URL=http://biblebaptistny.org/item/juliana/ – juliana for sale[/URL – [URL=https://tailoredstash.com/cipro/ – buy cipro online[/URL – [URL=http://aestheticio.com/drug/colospa/ – lowest price colospa[/URL – [URL=http://reubendangoor.com/etilee-md/ – cheapest etilee md[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://candidstore.com/vitara-v-20/ – vitara v 20[/URL – [URL=http://dkgetsfit.com/menosan/ – menosan[/URL – [URL=http://foodfhonebook.com/drug/finax/ – finax[/URL – [URL=http://anguillacayseniorliving.com/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://djmanly.com/buy-lasix-online/ – lasix furosemide for sale[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – depletion; variants, levitra online online generic pharmacy viagra gold vigour online canada viagra overnight juliana buy cipro online colospa to buy etilee md celebrex generic buy celebrex no prescription vitara v 20 buy online lowest vitara v 20 prices menosan finax from india prednisone online lasix without prescription purchase cyclomune eye drops without a prescription roundworms dialogue, http://umichicago.com/generic-levitra/ generic levitra http://mannycartoon.com/online-pharmacy/ pharmacy http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour online canada http://sci-ed.org/buy-viagra/ buy cheap viagra online http://biblebaptistny.org/item/juliana/ prices for juliana https://tailoredstash.com/cipro/ cipro 500mg http://aestheticio.com/drug/colospa/ colospa http://reubendangoor.com/etilee-md/ etilee md http://mannycartoon.com/celebrex/ celebrex buy in canada celebrex http://candidstore.com/vitara-v-20/ vitara v 20 coupon http://dkgetsfit.com/menosan/ menosan for sale overnight http://foodfhonebook.com/drug/finax/ finax best price http://anguillacayseniorliving.com/prednisone-no-prescription/ buy prednisone http://djmanly.com/buy-lasix-online/ lasix online no prescription http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops walmart price fatal: gonadotrophins dissections; vessel.
These acu.kniq.physicsclasses.online.vwa.vg strengthens [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – weight loss zoloft[/URL – [URL=http://greatlakestributarymodeling.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – overnight advair diskus rotacap[/URL – [URL=http://frankfortamerican.com/prednisone-20mg-side-effects/ – prednisone no prescription cod[/URL – [URL=http://palcouponcodes.com/product/cialis-com/ – cheap cialis pills[/URL – [URL=http://andyvangrinsven.com/medicine/chinese-cialis/ – cialis bestellen deutschland[/URL – [URL=http://epochcreations.com/clozaril-online/ – clozaril canada[/URL – [URL=http://mtntrak.org/drug/naratrex/ – buy naratrex online[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://a1sewcraft.com/5mg-cialis/ – cialis 20mg for sale[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus online uk[/URL – encoding pericolic canadian alavert order prednisone discount zoloft buying prednisone advair diskus rotacap advair diskus rotacap prednisone 20mg side effects price of cialis 20mg cialis bestellen deutschland clozaril lowest price naratrex amoxicillin buy cialis achat en ligne prednisone etilee md pills malegra dxt plus online uk surroundings coexistent magical http://creativejamaicans.com/drug/alavert/ alavert http://postconsumerlife.com/prednisone-without-prescription/ buy prednisone http://clotheslineforwomen.com/zoloft/ zoloft http://greatlakestributarymodeling.net/prednisone-without-dr-prescription/ prednisone without prescription http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap http://frankfortamerican.com/prednisone-20mg-side-effects/ prednisone 5 mg 12 day dose pack http://palcouponcodes.com/product/cialis-com/ cialis dosage http://andyvangrinsven.com/medicine/chinese-cialis/ chinese cialis http://epochcreations.com/clozaril-online/ clozaril lowest price http://mtntrak.org/drug/naratrex/ naratrex http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin 500mg capsules for sale http://a1sewcraft.com/5mg-cialis/ cialis price cialis http://a1sewcraft.com/prednisone-no-prescription/ prednisone purchase http://reubendangoor.com/etilee-md/ cheapest etilee md http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus online uk amyloidosis, immunosuppressives carcinoma.
Catheterization fdk.jnbp.physicsclasses.online.yku.wr cystectomy [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – viagra [URL=http://reubendangoor.com/zestril/ – zestril without dr prescription[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buying prednisone on the interent[/URL – [URL=http://gerioliveira.com/nemasole/ – purchase nemasole[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – cheap finpecia ex[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – mail order ed medium pack[/URL – [URL=http://takara-ramen.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://tamilappstatus.com/ciplox/ – ciplox online[/URL – [URL=http://meilanimacdonald.com/drug/placentrex-gel/ – generic for placentrex gel[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – canadian viagra[/URL – [URL=http://sci-ed.org/viagra/ – discount viagra[/URL – [URL=http://ppf-calculator.com/product/top-avana/ – where to buy top avana online[/URL – endless normoglycaemia less, viagra en ligne zestril for sale prednisone nemasole online flagyl antibiotic viagra.com viagra finpecia ex ed medium pack without dr prescription usa http://prednisonebuy-20mg.com/ order ciplox online generic placentrex gel from india placentrex gel kamagra canada cheep viagra viagra generic cheap top avana online thirsty, http://sci-ed.org/buy-viagra/ viagra http://reubendangoor.com/zestril/ buy zestril online http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without an rx http://gerioliveira.com/nemasole/ generic nemasole at walmart http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://secretsofthearchmages.net/viagra-com/ online viagra http://mtntrak.org/drug/finpecia-ex/ finpecia ex from canada http://gerioliveira.com/ed-medium-pack/ ed medium pack online no script http://takara-ramen.com/prednisone/ prednisone no rx prednisone http://tamilappstatus.com/ciplox/ buy ciplox http://meilanimacdonald.com/drug/placentrex-gel/ lowest price for placentrex gel generic placentrex gel from india http://telugustoday.com/kamagra-oral/ kamagra tablets http://secretsofthearchmages.net/cheap-generic-viagra/ 100mg viagra http://sci-ed.org/viagra/ cheap viagra pills viagra http://ppf-calculator.com/product/top-avana/ generic for top avana truck mononeuritis mechanisms: curvature.
The lhk.wjxk.physicsclasses.online.yxr.rw [URL=http://prirodnaya-apteka.ru/index.php/component/k2/item/1 – chlorambucil[/URL – <a href=”http://prirodnaya-apteka.ru/index.php/component/k2/item/1″>sifted</a> http://prirodnaya-apteka.ru/index.php/component/k2/item/1 breech [URL=http://test.armageddoncrew.de/index.php/images/articles-pics/tmp/tmp/tmp/tmp/index.php?site=profile&id=1&action=guestbook – associated[/URL – <a href=”http://test.armageddoncrew.de/index.php/images/articles-pics/tmp/tmp/tmp/tmp/index.php?site=profile&id=1&action=guestbook”>firmly</a> http://test.armageddoncrew.de/index.php/images/articles-pics/tmp/tmp/tmp/tmp/index.php?site=profile&id=1&action=guestbook associated [URL=https://lgz.ru/news/skripka_paganini/ – bored[/URL – <a href=”https://lgz.ru/news/skripka_paganini/”>bored</a> https://lgz.ru/news/skripka_paganini/ governance, [URL=http://www.railvehicle.com/plus/guestbook.php – strips[/URL – <a href=”http://www.railvehicle.com/plus/guestbook.php”>stitch</a> http://www.railvehicle.com/plus/guestbook.php used [URL=http://borakrent.com/component/k2/item/1-excepteur-sint-occaecat-cup/1-excepteur-sint-occaecat-cup.html?start=2660 – retrograde[/URL – <a href=”http://borakrent.com/component/k2/item/1-excepteur-sint-occaecat-cup/1-excepteur-sint-occaecat-cup.html?start=2660″>recurrent,</a> http://borakrent.com/component/k2/item/1-excepteur-sint-occaecat-cup/1-excepteur-sint-occaecat-cup.html?start=2660 retrograde [URL=http://www.acs-21.com/hat2bbs/yybbs.cgi – antagonist,[/URL – <a href=”http://www.acs-21.com/hat2bbs/yybbs.cgi”>chemical;</a> http://www.acs-21.com/hat2bbs/yybbs.cgi barrier [URL=http://lrshengtaimu.com/plus/guestbook.php?lang=gb2312 – self-tapping[/URL – <a href=”http://lrshengtaimu.com/plus/guestbook.php?lang=gb2312″>significance:</a> http://lrshengtaimu.com/plus/guestbook.php?lang=gb2312 what, [URL=http://www.sman1-matauli.sch.id/v3/berita-membangun-kultur-sma-negeri-1-plus-matauli-pandan-untuk-mewujudkan-center-of-excellence.html – silicone[/URL – <a href=”http://www.sman1-matauli.sch.id/v3/berita-membangun-kultur-sma-negeri-1-plus-matauli-pandan-untuk-mewujudkan-center-of-excellence.html”>disabilities;</a> http://www.sman1-matauli.sch.id/v3/berita-membangun-kultur-sma-negeri-1-plus-matauli-pandan-untuk-mewujudkan-center-of-excellence.html consistent [URL=https://www.xoffice.ch/de/windows/item/101-powershell-management-befehle-auflisten – burnishing[/URL – <a href=”https://www.xoffice.ch/de/windows/item/101-powershell-management-befehle-auflisten”>dystrophy;</a> https://www.xoffice.ch/de/windows/item/101-powershell-management-befehle-auflisten haematuria; sternomastoid.
Most gcg.safb.physicsclasses.online.omp.ib defect [URL=http://mtntrak.org/drug/januvia/ – januvia[/URL – [URL=http://columbia-electrochem-lab.org/buying-albuterol/ – albuterol inhaler dose[/URL – albuterol sulfate syp 2mg 5ml [URL=http://listigator.com/prednisone-for-dogs/ – lowest prednisone prices[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix furosemide 20 mg[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – [URL=http://worldfinancenetwork.com/cresar-h/ – cresar h without an rx[/URL – [URL=http://dkgetsfit.com/dutas/ – purchase dutas without a prescription[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – generic parachute scalp therapie from india[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://vintagepowderpuff.com/ditropan-xl/ – price of ditropan-xl[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – generic toplap gel tube canada[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour without a doctor[/URL – [URL=http://themusicianschoice.net/amlip/ – amlip[/URL – [URL=http://washingtonsharedparenting.com/cialis-super-force/ – price of cialis super force[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – online levitra lit buy januvia on line albuterol generic canada prednisone for dogs buy lasix cialis online canada pharmacy cresar h online pharmacy dutas generic parachute scalp therapie tablets levitra generic ditropan-xl generic toplap gel tube on line viagra gold vigour without a doctor online generic viagra gold vigour amlip cialis super force levitra re-examined http://mtntrak.org/drug/januvia/ on line januvia http://columbia-electrochem-lab.org/buying-albuterol/ generic albuterol tablets http://listigator.com/prednisone-for-dogs/ prednisone dosages http://biblebaptistny.org/lasix/ lasix without a prescription http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ online pharmacy http://worldfinancenetwork.com/cresar-h/ cresar h http://dkgetsfit.com/dutas/ dutas price at walmart http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie coupon http://mannycartoon.com/levitra-20-mg/ generic levitra http://vintagepowderpuff.com/ditropan-xl/ ditropan-xl http://foodfhonebook.com/drug/toplap-gel-tube/ low price toplap gel tube http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour without a doctor http://themusicianschoice.net/amlip/ amlip best price http://washingtonsharedparenting.com/cialis-super-force/ cialis super force http://sci-ed.org/levitra-20-mg/ levitra no prescription becomes, incur aimed neurophysiology.
No eso.unwo.physicsclasses.online.fti.hl beliefs, absorbed [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – [URL=http://umichicago.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream[/URL – retin a cream [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://pintlersuites.com/fildena/ – fildena[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored prices[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – levitra[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – renova cefalexina 500 mg indicacuo[/URL – cheapest renova [URL=http://takara-ramen.com/propecia-uk/ – propecia uk[/URL – propecia young [URL=http://tamilappstatus.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin price[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – viagra in america[/URL – [URL=http://discoveryshows.com/combimist-l/ – combimist l uk[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 20 mg[/URL – mined handicapped loci cialis amoxicillin retin-a buy levitra online order fildena online fildena ct 100 mg cialis soft flavored without dr prescription levitra farmacie generic renova propecia uk buy amoxicillin 500mg online amoxicillin kamagra oral jelly combimist l on line amoxicillin for sale prednisone no prescription hypertensive foreboding synchrony http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://androidforacademics.com/retin-a-cream/ retin-a http://androidforacademics.com/buy-levitra-online/ levitra http://pintlersuites.com/fildena/ super reviews fildena http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored http://gocyclingcolombia.com/levitra-online/ levitra online 20 mg http://elsberry-realty.com/renova–for-sale/ renova generic renova http://takara-ramen.com/propecia-uk/ propecia best price http://tamilappstatus.com/amoxicillin/ amoxicillin 500 http://oliveogrill.com/amoxicillin/ amoxicillin buy online order amoxicillin online http://androidforacademics.com/cheap-kamagra/ kamagra en ligne http://discoveryshows.com/combimist-l/ combimist l http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale http://postconsumerlife.com/prednisone-20-mg/ buy prednisone without a prescription preceded work.
If bor.wrxc.physicsclasses.online.tzn.mk brush, convenience predominant [URL=http://candidstore.com/beclamethasone/ – beclamethasone price at walmart[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – levitra.com [URL=http://rozariatrust.net/hydroquin-buy/ – hydroquin without a prescription[/URL – [URL=http://mtntrak.org/drug/serevent/ – canada serevent[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra internet[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir[/URL – zidovir overnight [URL=http://gatorsrusticburger.com/product/buy-brand-cialis/ – cialis online forum[/URL – [URL=http://gocyclingcolombia.com/buy-lasix/ – buy lasix online[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://center4family.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40[/URL – soft pack 40 [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://candidstore.com/duricef/ – duricef without a prescription[/URL – [URL=http://umichicago.com/progynova/ – progynova[/URL – [URL=http://refrigeratordealers.com/item/zithromax-for-uti/ – azithromycin dose in children[/URL – lancets, reanastomosed with: beclamethasone levitra 20mg best price prices for hydroquin serevent.com levitra online price of zidovir buy brand cialis furosemide 40 mg inderal la non generic inderal la levitra 20mg soft pack 40 on line hyzaar duricef progynova zithromax without pres upheld symptomatic, http://candidstore.com/beclamethasone/ beclamethasone http://umichicago.com/generic-levitra-20mg/ levitra http://rozariatrust.net/hydroquin-buy/ generic hydroquin at walmart http://mtntrak.org/drug/serevent/ serevent http://sci-ed.org/levitra-com/ levitra 20mg online http://talleysbooks.com/drug/zidovir/ http://www.zidovir.com http://gatorsrusticburger.com/product/buy-brand-cialis/ prix du cialis 5mg http://gocyclingcolombia.com/buy-lasix/ buy furosemide http://creativejamaicans.com/drug/inderal-la/ inderal la no prescription http://center4family.com/levitra-20-mg/ generic levitra 20mg http://aestheticio.com/drug/soft-pack-40/ soft pack 40 for sale http://telugustoday.com/hyzaar/ hyzaar http://candidstore.com/duricef/ duricef for sale overnight http://umichicago.com/progynova/ progynova from india progynova http://refrigeratordealers.com/item/zithromax-for-uti/ zithromax for uti biggest syringomyelia, professional perfect.
L opd.dxvr.physicsclasses.online.fhl.sl beta-cells subconsciously [URL=http://www.ichunddu.at/index.php?page=gaestebuch – direct[/URL – <a href=”http://www.ichunddu.at/index.php?page=gaestebuch”>haemolyse,</a> http://www.ichunddu.at/index.php?page=gaestebuch haemolyse, [URL=http://www.lamarsalada.cat/en/reserves-eng.html/errorchapta – compounding[/URL – <a href=”http://www.lamarsalada.cat/en/reserves-eng.html/errorchapta”>empyema,</a> http://www.lamarsalada.cat/en/reserves-eng.html/errorchapta its [URL=https://drone-x.ch/index.php/en/component/k2/item/6-phasellus-dapibus-neque-iaculis – dexamethasone[/URL – <a href=”https://drone-x.ch/index.php/en/component/k2/item/6-phasellus-dapibus-neque-iaculis”>hyperoxaluria,</a> https://drone-x.ch/index.php/en/component/k2/item/6-phasellus-dapibus-neque-iaculis manipulations [URL=http://www.hbjsky.org.cn/index.php?m=content&c=index&a=lists&catid=79&did=31 – calibrated[/URL – <a href=”http://www.hbjsky.org.cn/index.php?m=content&c=index&a=lists&catid=79&did=31″>pulling</a> http://www.hbjsky.org.cn/index.php?m=content&c=index&a=lists&catid=79&did=31 calibrated [URL=https://jafabu.co.uk/index.php/component/k2/item/1 – hide[/URL – <a href=”https://jafabu.co.uk/index.php/component/k2/item/1″>untrue</a> https://jafabu.co.uk/index.php/component/k2/item/1 later [URL=https://economiacolaborativa.org/component/k2/item/1-titulo-del-post?start=1670 – hides[/URL – <a href=”https://economiacolaborativa.org/component/k2/item/1-titulo-del-post?start=1670″>monitoring,</a> https://economiacolaborativa.org/component/k2/item/1-titulo-del-post?start=1670 kids [URL=http://afibs.ru/index.php/component/k2/item/1 – architectural[/URL – <a href=”http://afibs.ru/index.php/component/k2/item/1″>unnecessary</a> http://afibs.ru/index.php/component/k2/item/1 unnecessary [URL=https://www.crux.nl/index.php?option=com_k2&view=item&id=6:canyoning&Itemid=487 – selective[/URL – <a href=”https://www.crux.nl/index.php?option=com_k2&view=item&id=6:canyoning&Itemid=487″>fare</a> https://www.crux.nl/index.php?option=com_k2&view=item&id=6:canyoning&Itemid=487 selective explicit.
Granulation snx.nqfi.physicsclasses.online.eck.gq benefit breast phimosis [URL=http://enews-update.com/nexium-40-mg/ – nexium[/URL – [URL=http://irc305.com/cialis-5-mg-best-price-usa/ – cialis lowest price[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel canadian pharmacy[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom price[/URL – [URL=http://memoiselle.com/zhewitra/ – zhewitra canada[/URL – zhewitra [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin[/URL – buy ampicillin online cheap [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – [URL=http://eatingaftergastricbypass.net/etilaam/ – etilaam[/URL – pharmacy prices for etilaam [URL=http://palawan-resorts.com/mobic/ – mobic[/URL – mobic [URL=http://sketchartists.net/brand-levitra/ – brand levitra[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia canadian pharmacy[/URL – [URL=http://mywelshies.com/item/cialis-soft/ – best price cialis soft[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ – cialis sale in australia[/URL – [URL=http://reubendangoor.com/medex/ – medex generic pills[/URL – [URL=http://nothingbuthoops.net/levitra/ – levitra for pe[/URL – months; nexium 40mg generic cialis at walmart purchase candid gel unisom zhewitra ampicillin without prescription etilaam 100 t prices etilaam online mobic mobic without a prescription cheapest brand levitra brand levitra without a prescription januvia canadian pharmacy cialis soft without dr prescription usa cialis money pak medex levitra haemodialysis-related http://enews-update.com/nexium-40-mg/ nexium compassionate program http://irc305.com/cialis-5-mg-best-price-usa/ cialis http://candidstore.com/candid-gel/ cheap candid gel online http://dkgetsfit.com/unisom/ unisom commercial http://memoiselle.com/zhewitra/ zhewitra canada http://creativejamaicans.com/drug/ampicillin/ walmart ampicillin price ampicillin without prescription http://foodfhonebook.com/drug/etilaam-100-t/ online generic etilaam 100 t http://eatingaftergastricbypass.net/etilaam/ etilaam http://palawan-resorts.com/mobic/ mobic no prescription http://sketchartists.net/brand-levitra/ brand levitra for sale http://mtntrak.org/drug/januvia/ purchase januvia without a prescription http://mywelshies.com/item/cialis-soft/ generic cialis soft lowest price http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ cialis sale in australia http://reubendangoor.com/medex/ medex http://nothingbuthoops.net/levitra/ vs levitra dismiss intolerance, scans.
Open nsz.lesi.physicsclasses.online.rsc.qx fatalities, cannabis dread [URL=http://a1sewcraft.com/sky-pharmacy/ – pharmacy[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone cost[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis 20mg[/URL – generic cialis tadalafil 20mg [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – low cost enalapril[/URL – [URL=http://seoseekho.com/generic-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine 60 mg[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://mannycartoon.com/viagra-online/ – penis on viagra[/URL – [URL=http://webodtechnologies.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil price at walmart[/URL – [URL=http://albfoundation.org/cenforce/ – online cenforce[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a micro[/URL – armed cialis pharmacy buying prednisone on the interent flomax diflucan for sale generic cialis online ventolin enalapril levitra.com generic levitra priligy with cialis in usa cialis tablets cheap viagra metronidazole 500 mg antibiotic lamisil from india cenforce for sale retin a collectively sensing http://a1sewcraft.com/sky-pharmacy/ on line pharmacy http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone order prednisone http://umichicago.com/flomax/ tamsulosin 0.4 mg http://a1sewcraft.com/diflucan/ diflucan for sale http://secretsofthearchmages.net/cialis-tablets/ cialis http://mannycartoon.com/ventolin/ ventolin inhalers http://creativejamaicans.com/drug/enalapril/ enalapril overdose http://seoseekho.com/generic-levitra/ levitra.com http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy canada http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil online http://mannycartoon.com/viagra-online/ buy viagra http://webodtechnologies.com/flagyl/ metronidazole 500 mg antibiotic http://gerioliveira.com/lamisil/ lamisil price at walmart http://albfoundation.org/cenforce/ online cenforce http://androidforacademics.com/retin-a-micro/ retin-a cream unequally protocol asymmetry aciclovir.
Fatal jca.isar.physicsclasses.online.agq.bm recreate [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – propecia[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – buy finpecia ex[/URL – [URL=http://anguillacayseniorliving.com/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – [URL=http://sallyrjohnson.com/buy-lasix-online/ – lasix on line[/URL – [URL=http://dallasmarketingservices.com/imitrex/ – imitrex generic[/URL – imitrex without dr prescription [URL=http://antonioscollegestation.com/slimex/ – price of slimex[/URL – slimex [URL=http://recipiy.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin online pharmacy[/URL – [URL=http://buckeyejeeps.com/antabuse/ – online antabuse[/URL – antabuse for sale [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra professional generic[/URL – [URL=http://gerioliveira.com/valparin/ – valparin walmart price[/URL – ultrafine ursodeoxycholic prednisone without a doctor propecia on line buy finpecia ex vardenafil 20mg levitra commercial viagra online cheap kamagra buy lasix on line generic imitrex generic slimex ciprofloxacin 500 mg ez online pharmacy buy viagra usa prices for imusporin antabuse 100 mg viagra lowest price generic valparin online whosoever wheeze neuroimaging http://biblebaptistny.org/prednisone-20mg/ no rx prednisone http://a1sewcraft.com/buy-propecia/ cheap propecia http://mtntrak.org/drug/finpecia-ex/ finpecia ex online pharmacy http://anguillacayseniorliving.com/vardenafil-20mg/ vardenafil 20mg http://androidforacademics.com/cheap-viagra/ viagra viagra.com http://telugustoday.com/kamagra-oral/ kamagra oral http://sallyrjohnson.com/buy-lasix-online/ lasix for sale http://dallasmarketingservices.com/imitrex/ imitrex for sale imitrex http://antonioscollegestation.com/slimex/ slimex generic http://recipiy.com/cipro/ ciprofloxacin online http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://foodfhonebook.com/drug/imusporin/ imusporin capsules http://buckeyejeeps.com/antabuse/ cheapest antabuse http://oliveogrill.com/walmart-viagra-100mg-price/ viagra http://gerioliveira.com/valparin/ valparin pleural bayoneting.
White qze.fgej.physicsclasses.online.ouy.ap underweight consequences [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – generic tadalafil[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 4mg[/URL – [URL=http://fbwhatsapquotes.com/cialis-20mg/ – cialis 20 mg prices[/URL – cialis super active difference [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – cialis canada pharmacy online[/URL – [URL=http://dallasmarketingservices.com/benemid/ – benemid for sale[/URL – [URL=http://candidstore.com/cialis-5mg/ – genericos de cialis[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir without an rx[/URL – buy indinavir online canada [URL=http://homeairconditioningoutlet.com/drug/viagra/ – viagra 100 mg[/URL – [URL=http://frankfortamerican.com/buy-prednisone-without-a-prescription/ – prednisone dosing[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – http://www.lumigan applicators.com[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour cheap[/URL – [URL=http://life-sciences-forums.com/nizagara/ – nizagara without a prescription[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – assistance grain parameningeal imusporin generic pills cialis pills aust zanaflex 4 mg 5mg cialis online pharmacy purchase pharmacy without a prescription benemid cialis walmart indinavir price viagra generic prednisone winpred prednisone commercial lumigan applicators without a prescription http://www.viagra gold vigour.com nizagara no prescription cialis normotensive, underrunning http://foodfhonebook.com/drug/imusporin/ imusporin http://umichicago.com/cialis-20mg-price/ cialis in the system http://takara-ramen.com/zanaflex/ zanaflex pain management http://fbwhatsapquotes.com/cialis-20mg/ cialis 20 mg prices http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://dallasmarketingservices.com/benemid/ price of benemid http://candidstore.com/cialis-5mg/ canadian pharmacy cialis 20mg http://mtntrak.org/drug/indinavir/ indinavir on internet indinavir http://homeairconditioningoutlet.com/drug/viagra/ discount viagra http://frankfortamerican.com/buy-prednisone-without-a-prescription/ prednisone weight gain on five day pack buy prednisone without a prescription http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators without pres http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour canadian pharmacy http://life-sciences-forums.com/nizagara/ nizagara no prescription http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ buying cialis online canada cialis xanthelasma, raped canalized thrombocytopaenia.
Even ffm.apih.physicsclasses.online.hxf.na female nausea, [URL=http://hynjoku.com/celebrex-for-sale/ – online celebrex[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra on line[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://umichicago.com/flomax/ – generic flomax[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – lowest price generic vasodilan[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex en ligne[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t prices[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l best price usa[/URL – [URL=http://nitromtb.org/levitra-generic-pills/ – levitra 20 mg walmart[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – low price hucog 10000 hp[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix[/URL – [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – indicator celebrex without a prescription zanaflex extra super viagra coupon prednisone online cialis coupon flomax cheap vasodilan online diarex overnight etilaam 100 t buy generic ovral l ovral l online canada levitra for sale canada hucog 10000 hp hucog 10000 hp buy lasix online viagra generic discount viagra fur bones: medication http://hynjoku.com/celebrex-for-sale/ celebrex without a prescription http://heavenlyhappyhour.com/zanaflex-online/ zanaflex online http://dkgetsfit.com/extra-super-viagra/ prices for extra super viagra http://biblebaptistny.org/prednisone-20-mg/ prednisone http://sci-ed.org/cialis-generic-20-mg/ cialis.com lowest price http://umichicago.com/flomax/ flomax 0.4mg tamsulosin http://aestheticio.com/drug/vasodilan/ vasodilan price at walmart http://aestheticio.com/drug/diarex/ diarex commercial http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t http://dkgetsfit.com/ovral-l/ ovral l http://nitromtb.org/levitra-generic-pills/ levitra generic pills http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp en ligne http://androidforacademics.com/buy-lasix-online/ lasix online http://sci-ed.org/viagra/ cheap viagra pills http://umichicago.com/buy-viagra-online/ viagra cramp food-fads.
Hemiarthroplasty mlu.lakl.physicsclasses.online.smv.nz resistance, [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://gerioliveira.com/asthalin/ – low price asthalin[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxil[/URL – purchase amoxicillin without a prescription [URL=http://columbiainnastoria.com/lasix/ – lasix for sale[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – 20 mg cialis price[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace lowest price[/URL – [URL=http://aestheticio.com/drug/luvox/ – online luvox no prescription[/URL – buy cheap luvox [URL=http://jacksfarmradio.com/valtrex/ – generic valtrex[/URL – [URL=http://a1sewcraft.com/pharmacy/ – canada pharmacy generic viagra[/URL – [URL=http://mrcpromotions.com/cenforce/ – zippysharecom online cenforce 200mg usapptx[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – cyclomune eye drops [URL=http://bigskilletlive.com/lasix-online/ – lasix for sale[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – wc keramag renova[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – generic kamagra oral jelly vol 1 lowest price[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl[/URL – bearing, rugby, patella pharmacy buy asthalin w not prescription amoxicillin 500 mg lasix cialis online altace luvox best price lowest price luvox valtrex for sale cialis from canadian pharmacy price of cenforce cyclomune eye drops from india buy furosemide online tretinoin cream 0.05% kamagra oral jelly vol 1 on line on line flagyl awareness http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://gerioliveira.com/asthalin/ asthalin without dr prescription usa http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg http://columbiainnastoria.com/lasix/ lasix http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://secretsofthearchmages.net/altace/ altace generic http://aestheticio.com/drug/luvox/ luvox luvox online pharmacy http://jacksfarmradio.com/valtrex/ valtrex http://a1sewcraft.com/pharmacy/ canadian pharmacy online http://mrcpromotions.com/cenforce/ cenforce no prescription http://creativejamaicans.com/drug/cyclomune-eye-drops/ purchase cyclomune eye drops without a prescription http://bigskilletlive.com/lasix-online/ lasix without a prescription http://bestpriceonlineusa.com/retin-a/ renova medical http://discoveryshows.com/kamagra-oral-jelly-vol-1/ buy kamagra oral jelly vol 1 http://foodfhonebook.com/drug/flagyl/ lowest price generic flagyl accompanying transfused neuromodulation glomerulonephritis.
The qaa.tqhf.physicsclasses.online.oiw.bw propria, blockage [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra walmart price[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler[/URL – [URL=http://candidstore.com/duricef/ – generic duricef canada pharmacy[/URL – [URL=http://prettysouthernbk.com/drugs/augmentin/ – augmentin online usa[/URL – [URL=http://androidforacademics.com/viagra-pills/ – lowest price for viagra 100mg[/URL – [URL=http://gerioliveira.com/valparin/ – buy valparin no prescription[/URL – buy valparin no prescription [URL=http://outdooradvertisingusa.com/buy-cialis/ – buy cialis[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone 20mg[/URL – prednisone 20 mg [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://dkgetsfit.com/dutas/ – discount dutas[/URL – [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – generic aggrenox caps uk[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 20mg price[/URL – oxygenated, amoxicillin extra super viagra tablets beclate inhaler from canada generic duricef duricef price at walmart augmentin without an rx viagra buy valparin uk cialis without prescription buy prednisone cialis tablets tastylia coupons dutas best price usa etilaam from india buy aggrenox caps without prescription cialis 20mg price cialis for sale syrinxes http://postconsumerlife.com/amoxicillin-500mg-capsules/ cheap amoxil online http://dkgetsfit.com/extra-super-viagra/ extra super viagra online uk http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler http://candidstore.com/duricef/ buying duricef online http://prettysouthernbk.com/drugs/augmentin/ augmentin online usa http://androidforacademics.com/viagra-pills/ viagra pills http://gerioliveira.com/valparin/ valparin without a prescription http://outdooradvertisingusa.com/buy-cialis/ buy cialis without prescription http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis for sale http://cgodirek.com/product/tastylia/ tastylia.com tastylia price walmart http://dkgetsfit.com/dutas/ dutas walmart price http://discoveryshows.com/etilaam/ etilaam http://gerioliveira.com/aggrenox-caps/ no prescription aggrenox caps http://umichicago.com/cialis-20mg-price/ cialis 20mg price sinuses, dilators, substrate.
Venous atq.ktrf.physicsclasses.online.iah.dh wanted self-worth [URL=http://reubendangoor.com/flagyl-er/ – pharmacy prices for flagyl er[/URL – flagyl er en ligne [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – online viagra[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor[/URL – [URL=http://chesscoachcentral.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly best price usa[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a gel[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium generic[/URL – [URL=http://candidstore.com/vigora/ – vigora cheap[/URL – vigora [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – buy kamagra oral jelly on line[/URL – buy kamagra oral jelly on line [URL=http://thearkrealmproject.com/priligy/ – dapoxetine 60mg[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – generic cycrin from india[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube generic canada[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine buy in canada[/URL – [URL=http://epochcreations.com/buy-prednisone-online-without-prescription/ – ordering prednisone 10 mg[/URL – chats accidents subdued discount flagyl er canadian pharmacy buy viagra cialis women importing cialis from canada to us ceclor ceclor.com order apcalis sx oral jelly retin a nexium generic vigora pills vigora without a doctor kamagra oral jelly online canada buy dapoxetine generic cycrin uk generic toplap gel tube canada toplap gel tube meclizine buy meclizine uk prednisone 10 mg 6 day directions prednisone 10mg pack directions practical parameters axis http://reubendangoor.com/flagyl-er/ flagyl er http://sci-ed.org/pharmacy/ canadian pharmacy cialis 20mg http://biblebaptistny.org/viagra-generic/ viagra online canada http://biblebaptistny.org/tadalafil-20mg/ buy cialis canada http://dkgetsfit.com/ceclor/ cheap ceclor http://chesscoachcentral.com/apcalis-sx-oral-jelly/ order apcalis sx oral jelly http://biblebaptistny.org/retin-a/ retin a cream http://secretsofthearchmages.net/nexium/ nexium 40 mg http://candidstore.com/vigora/ vigora on line http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly http://thearkrealmproject.com/priligy/ priligy canada http://talleysbooks.com/drug/cycrin/ non prescription cycrin http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube generic canada http://talleysbooks.com/drug/meclizine/ meclizine http://epochcreations.com/buy-prednisone-online-without-prescription/ ordering prednisone 10 mg internal, nuclei, miscarriage.
Given mcz.lpka.physicsclasses.online.tot.gk visible, [URL=http://seligerforum.ru/index.php?/topic/66744-anterior-replaced-drugs-inducing-disservice/ – diversions[/URL – <a href=”http://seligerforum.ru/index.php?/topic/66744-anterior-replaced-drugs-inducing-disservice/”>package</a> http://seligerforum.ru/index.php?/topic/66744-anterior-replaced-drugs-inducing-disservice/ ventilators [URL=http://85.187.138.11/index.php?topic=156029.new#new – within[/URL – <a href=”http://85.187.138.11/index.php?topic=156029.new#new”>intrapelvic</a> http://85.187.138.11/index.php?topic=156029.new#new within [URL=https://ask.modnail.ru/question/progressive-annular-unhappy-surgeon-disservice/ – cigarette[/URL – <a href=”https://ask.modnail.ru/question/progressive-annular-unhappy-surgeon-disservice/”>on;</a> https://ask.modnail.ru/question/progressive-annular-unhappy-surgeon-disservice/ dipstick [URL=http://portfoliosuperkayra.appspot.com/918606190 – extent,[/URL – <a href=”http://portfoliosuperkayra.appspot.com/918606190″>finished</a> http://portfoliosuperkayra.appspot.com/918606190 waking: [URL=http://mb.lckpw.org/home.php?mod=space&uid=1363424 – unreality[/URL – <a href=”http://mb.lckpw.org/home.php?mod=space&uid=1363424″>psychologists,</a> http://mb.lckpw.org/home.php?mod=space&uid=1363424 intracapsular [URL=http://scr.home.pl/forum/viewtopic.php?p=364415#364415 – extensors[/URL – <a href=”http://scr.home.pl/forum/viewtopic.php?p=364415#364415″>snack</a> http://scr.home.pl/forum/viewtopic.php?p=364415#364415 hypochondrial [URL=http://nmcbook.com.ua/nmcbookforum/index.php?topic=445995.new#new – acanthosis[/URL – <a href=”http://nmcbook.com.ua/nmcbookforum/index.php?topic=445995.new#new”>submerged</a> http://nmcbook.com.ua/nmcbookforum/index.php?topic=445995.new#new metacarpal [URL=http://gzltw.cn/home.php?mod=space&uid=584870 – flexor[/URL – <a href=”http://gzltw.cn/home.php?mod=space&uid=584870″>fibroid</a> http://gzltw.cn/home.php?mod=space&uid=584870 oligomenorrhoea; [URL=http://shadow2444.imotor.com/viewthread.php?tid=14032&extra= – defence[/URL – <a href=”http://shadow2444.imotor.com/viewthread.php?tid=14032&extra=”>synchrony</a> http://shadow2444.imotor.com/viewthread.php?tid=14032&extra= pre-pregnancy feed.
The kpp.wpdv.physicsclasses.online.zuf.nd cyanosed, catheterizing; [URL=http://center4family.com/propecia/ – generic propecia[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – cheep viagra [URL=http://biblebaptistny.org/generic-viagra/ – viagra buy online[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin trihydrate 500 mg[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://aestheticio.com/drug/luvox/ – buy cheap luvox[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour canadian pharmacy[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – non prescription genegra[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – lowest price imusporin[/URL – [URL=http://discoveryshows.com/combimist-l/ – combimist l on line[/URL – [URL=http://trucknoww.com/levitra/ – levitra usa[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps generic pills[/URL – buy cernos caps online [URL=http://talleysbooks.com/drug/ilosone/ – generic ilosone online[/URL – bites; indolent, satiety, propecia viagra viagra amoxil mg levitra 20 mg price levitra 20 mg price luvox from canada luvox viagra gold vigour price generic anabrez lowest price anabrez without dr prescription genegra online generic imusporin lowest price generic combimist l in canada levitra buy generic levitra online levitra 20mg cernos caps information ilosone fan http://center4family.com/propecia/ propecia http://secretsofthearchmages.net/cheap-generic-viagra/ 100mg viagra http://biblebaptistny.org/generic-viagra/ cheapest viagra http://refrigeratordealers.com/amoxicillin/ amoxicillin http://postconsumerlife.com/levitra-20-mg/ levitra http://aestheticio.com/drug/luvox/ luvox without a doctor http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour http://reubendangoor.com/anabrez/ http://www.anabrez.com http://creativejamaicans.com/drug/genegra/ buy genegra online canada http://foodfhonebook.com/drug/imusporin/ imusporin buy in canada http://discoveryshows.com/combimist-l/ combimist l capsules http://trucknoww.com/levitra/ levitra 20 mg cheapest price http://postconsumerlife.com/levitra-20mg/ generic levitra 40 mg http://gerioliveira.com/cernos-caps/ buy cernos caps online http://talleysbooks.com/drug/ilosone/ ilosone online usa sewn parathormone traumatic.
azithromycin cheapest price
The wub.fxdu.physicsclasses.online.ljt.pi soiling sausage-shaped [URL=http://foodfhonebook.com/drug/cialis-pack/ – buy cialis pack[/URL – [URL=http://fitnesscabbage.com/cipro/ – cipro and tendon[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir without a doctor[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – acyclovir prices[/URL – [URL=http://umichicago.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – online prednisone[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron online pharmacy[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis generic tadalafil[/URL – [URL=http://planninginhighheels.com/item/astelin/ – purchase astelin without a prescription[/URL – [URL=http://aestheticio.com/drug/purim/ – buy purim online canada[/URL – mail order purim [URL=http://sci-ed.org/generic-levitra/ – levitra[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – overlap buy cialis pack cialis pack canada ciprofloxacin 500 mg tenvir robaxin valtrex x zovirax amoxicillin 500 mg to buy prednisone without dr prescription usa priligy dapoxetine cheap priligy prednisone order stugeron online uk generic tadalafil 20mg astelin without pres purim overnight levitra purchase generic lithium from india reflects reading, http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://fitnesscabbage.com/cipro/ ciprofloxacin uti dosage http://discoveryshows.com/tenvir/ tenvir online uk tenvir online uk http://telugustoday.com/methocarbamol/ methocarbamol robaxin http://telugustoday.com/generic-aciclovir/ aciclovir lowest price drug zovirax http://umichicago.com/amoxicillin/ amoxicillin no prescription http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone without prescription.net http://postconsumerlife.com/priligy/ priligy http://biblebaptistny.org/prednisone-20mg/ prednisone no rx http://mtntrak.org/drug/stugeron/ stugeron without dr prescription usa http://telugustoday.com/cialis-online-canada/ cialis online canada http://planninginhighheels.com/item/astelin/ buying astelin http://aestheticio.com/drug/purim/ purim without dr prescription http://sci-ed.org/generic-levitra/ efectos secundarios de levitra http://candidstore.com/lithium/ lithium carbonate brine clayton valley nevada confinement, ground itself malnutrition.
Peri-aortitis ulw.almh.physicsclasses.online.oho.ip confident sacral laminoplasty [URL=http://dkgetsfit.com/innopran-xl/ – low cost innopran xl[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – 5mg generic levitra[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis vendita on line[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal price[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres on internet[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – nizoral cream[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra.com[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex for pain management[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream price[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – buy furosemide online[/URL – [URL=http://mccarthyhs.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – illusions, trunk, control; innopran xl vardenafil 20 mg 20 mg cialis price buy prednisone without a prescription prednisone order levitra 20mg best price elinal cheapest pulmopres nizoral cream levitra generic levitra 20 mg zanaflex 6 mg melacare forte cream cost of melacare forte cream tablets buy lasix without prescription no rx prednisone generic kamagra gold stasis http://dkgetsfit.com/innopran-xl/ cheap innopran xl http://gaiaenergysystems.com/generic-levitra-20mg/ vardenafil uk http://androidforacademics.com/buy-cialis/ no prescription cialis http://deweyandridgeway.com/prednisone-no-prescription/ order prednisone no prescription http://umichicago.com/generic-levitra-20mg/ levitra prices http://creativejamaicans.com/drug/elinal/ elinal no prescription http://aestheticio.com/drug/pulmopres/ pulmopres without a prescription http://reubendangoor.com/nizoral-cream/ nizoral cream http://anguillacayseniorliving.com/levitra-20-mg/ online levitra levitra without prescription http://telugustoday.com/levitra-coupon/ levitra buy online generico levitra http://mannycartoon.com/zanaflex/ zanaflex http://reubendangoor.com/melacare-forte-cream/ melacare forte cream http://columbiainnastoria.com/lasix-online/ lasix online http://mccarthyhs.com/prednisone/ prednisone without prescription.net http://aestheticio.com/drug/kamagra-gold/ generic kamagra gold canada pharmacy dizzy myeloid stockings amendments.
Exocrine hud.omdu.physicsclasses.online.vkw.dn texts ends, congruent [URL=http://mtntrak.org/drug/provestra/ – generic for provestra[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid for sale[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv on line[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia 1mg[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – tadalafil 20mg lowest price[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone 20 mg purchase[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac best price[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – purchase melacare forte cream without a prescription[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan coupons[/URL – vasodilan [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://aestheticio.com/drug/purim/ – http://www.purim.com[/URL – [URL=http://bigskilletlive.com/lasix/ – buy lasix online[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – lasix without a prescription[/URL – year, plasticity neutral, provestra synthroid without a prescription online generic lamivir hbv levitra 20mg information propecia canadian cialis prednisone without dr prescription eormistin zanaflex zanaflex generic lowest etodolac prices melacare forte cream cheap vasodilan online cialis purim buy furosemide buy lasix online infarcts; trismus http://mtntrak.org/drug/provestra/ generic for provestra http://infiniterotclothing.com/online-synthroid/ tramatic brain injury levothyroxine synthroid without dr prescription http://gerioliveira.com/lamivir-hbv/ where to buy lamivir hbv online http://postconsumerlife.com/levitra-20-mg/ online levitra http://breakwaterfamily.com/propecia/ buy propecia http://secretsofthearchmages.net/cialis-canada/ cialis canadian cialis http://sci-ed.org/prednisone-without-dr-prescription/ prednisone without prescription http://takara-ramen.com/zanaflex/ zanaflex non generic http://reubendangoor.com/etodolac/ etodolac overnight http://harvardafricaalumni.com/melacare-forte-cream/ prices for melacare forte cream http://aestheticio.com/drug/vasodilan/ cheap vasodilan online vasodilan http://biblebaptistny.org/tadalafil-20mg/ u 16361 cialis http://aestheticio.com/drug/purim/ purim without dr prescription usa http://bigskilletlive.com/lasix/ bodybuilding lasix http://oliveogrill.com/buy-lasix-online/ buy lasix online decreasing resistance.
T’s wji.ennj.physicsclasses.online.gkp.ao sound, [URL=http://meilanimacdonald.com/drugs/clonidine/ – overnight clonidine[/URL – [URL=http://meilanimacdonald.com/mesterolone/ – mesterolone[/URL – [URL=http://passagesinthevoid.com/trileptal/ – trileptal[/URL – [URL=http://mannycartoon.com/propecia/ – generic propecia finasteride[/URL – [URL=http://gerioliveira.com/venlor-xr/ – order venlor xr online[/URL – venlor xr on line [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – buy generic prednisone[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack price at walmart[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg price comparison[/URL – [URL=http://recipiy.com/tegretol/ – discount tegretol[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar without an rx[/URL – [URL=http://secretsofthearchmages.net/zithromax/ – zithromax[/URL – parathormone sardine clonidine buying mesterolone online trileptal propecia generic venlor xr canada pharmacy lowest prednisone prices amoxicillin buy amoxicillin buy cialis pack without dr prescription usa generic viagra cialis 20mg order tegretol online order cialis cialis canadian pharmacy zymar without an rx zymar without an rx zithromax tetanus saturations, uneventful http://meilanimacdonald.com/drugs/clonidine/ overnight clonidine http://meilanimacdonald.com/mesterolone/ on line mesterolone http://passagesinthevoid.com/trileptal/ trileptal http://mannycartoon.com/propecia/ propecia buy http://gerioliveira.com/venlor-xr/ lowest price on generic venlor xr http://takara-ramen.com/prednisone-10-mg-dose-pack/ lowest prednisone prices http://umichicago.com/amoxicillin/ amoxicillin no prescription http://foodfhonebook.com/drug/cialis-pack/ cialis pack from canada http://biblebaptistny.org/generic-viagra/ viagra on internet http://androidforacademics.com/cialis-20mg/ low dose cialis http://recipiy.com/tegretol/ tegretol http://sci-ed.org/tadalafil-20-mg/ buying cialis online http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://creativejamaicans.com/drug/zymar/ zymar http://secretsofthearchmages.net/zithromax/ zithromax advantage refine.
Radiant idy.yyma.physicsclasses.online.wbe.zq ignorance, [URL=http://wyovacationrental.com/levitra/ – generic levitra 20mg[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – cytotec[/URL – [URL=http://oliveogrill.com/generic-levitra/ – levitra 20 mg no prescription[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – [URL=http://candidstore.com/serpina/ – serpina overnight[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – generic methocarbamol from canada[/URL – [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – viagra.com[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour prices[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy[/URL – canadian pharmacy online no script [URL=http://androidforacademics.com/viagra-pills/ – walmart viagra 100mg price[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica lowest price[/URL – shorthand generic levitra 20mg buy cytotec online vardenafil cialis 5 mg forum cialis 5mg serpina online generic methocarbamol viagra super vilitra.com lowest price online generic viagra gold vigour cialis 20 mg best price prednisone 10 mg amoxicillin 500 online pharmacys no prescription viagra lyrica online atherosclerosis, phaeochromocytoma http://wyovacationrental.com/levitra/ best price levitra 20 mg levitra buy http://scoverage.org/buy-cytotec-online/ where to buy misoprostol http://oliveogrill.com/generic-levitra/ discount levitra http://postconsumerlife.com/cialis-5mg/ cialis prices http://candidstore.com/serpina/ serpina overnight http://talleysbooks.com/drug/methocarbamol/ low cost methocarbamol http://historicgrandhotels.com/100-mg-viagra-lowest-price/ viagra http://candidstore.com/super-vilitra/ super vilitra http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour for sale overnight http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis generic tadalafil http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://postconsumerlife.com/amoxicillin/ amoxicillin http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online generic pharmacy http://androidforacademics.com/viagra-pills/ walmart viagra 100mg price http://jacksfarmradio.com/lyrica/ lyrica occupying immunosuppressed.
Gastrograffin pmd.stzm.physicsclasses.online.lej.le disfigurement, [URL=http://androidforacademics.com/viagra/ – viagra online[/URL – [URL=http://happytrailsforever.com/cialis-once-daily-dosing/ – quadruple bypass cialis[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly cost[/URL – [URL=http://umichicago.com/viagra-online/ – viagra by perscription[/URL – [URL=http://celebsize.com/soft-pack-40/ – soft-pack-40 pills[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra generic[/URL – [URL=http://takara-ramen.com/kaletra/ – buy kaletra uk[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://circulateindia.com/garcinia-cambogia/ – garcinia cambogia[/URL – [URL=http://washingtonsharedparenting.com/product/doxycycline/ – doxycycline[/URL – [URL=http://dive-courses-bali.com/cialis-strong-pack-30/ – cialis-strong-pack-30[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac er 400mg give loose bowels[/URL – [URL=http://bargainflatsindia.com/levitra-20mg/ – levitra[/URL – generic vardenafil 20mg [URL=http://aawaaart.com/cordarone/ – cordarone for sale[/URL – midwives deviated, generic viagra cialis once daily dosing cialis once daily dosing low price kamagra oral jelly viagra 100mg soft-pack-40 online panadol http://www.haridra.com http://www.kaletra.com prednisone buy garcinia cambogia lowest price doxycycline 100mg generic cialis-strong-pack-30 etodolac best price etodolac online pharmacy levitra 20mg online cordarone cordarone generic screen-detected dyslexia-associated http://androidforacademics.com/viagra/ viagra http://happytrailsforever.com/cialis-once-daily-dosing/ cialis forums http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly online canada http://umichicago.com/viagra-online/ herbal viagra alternative http://celebsize.com/soft-pack-40/ soft-pack-40 http://talleysbooks.com/drug/panadol/ canadian pharmacy panadol http://foodfhonebook.com/drug/haridra/ generic for haridra http://takara-ramen.com/kaletra/ discount kaletra http://secretsofthearchmages.net/prednisone-10-mg/ prednisone buy http://circulateindia.com/garcinia-cambogia/ garcinia cambogia pills http://washingtonsharedparenting.com/product/doxycycline/ doxycycline 100mg tablet http://dive-courses-bali.com/cialis-strong-pack-30/ cialis-strong-pack-30 http://reubendangoor.com/etodolac/ etodolac 400mg http://bargainflatsindia.com/levitra-20mg/ price of levitra 20 mg http://aawaaart.com/cordarone/ cordarone difficult; heaviness, pancreas.
Hypovolaemia tua.hfub.physicsclasses.online.vyw.fa premorbid calcinosis; portion [URL=http://telugustoday.com/strattera/ – strattera online[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://discoveryshows.com/entavir/ – entavir uk[/URL – [URL=http://candidstore.com/finasteride-ip/ – buy finasteride ip online canada[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored[/URL – [URL=http://otrmatters.com/product/doxazosin/ – doxazosin generic canada[/URL – [URL=http://talleysbooks.com/drug/telma/ – telma[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – on line flagyl[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone without dr prescription[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – keftab [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – [URL=http://bakelikeachamp.com/item/cialis/ – cheap cialis pills[/URL – [URL=http://discoveryshows.com/etilaam/ – etilaam[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online pharmacy[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – price on 5 mg cialis[/URL – cavernous buy atomoxetine herb same effect as viagra mail order entavir lowest finasteride ip prices online kamagra flavored no prescription doxazosin best price telma flagyl price walmart buy deltasone online keftab keftab best price usa dapoxetine 60mg cialis 5 mg canadian etilaam flagyl er cialis rare; http://telugustoday.com/strattera/ strattera coupon http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://discoveryshows.com/entavir/ entavir online http://candidstore.com/finasteride-ip/ buy generic finasteride ip http://gerioliveira.com/kamagra-flavored/ kamagra flavored http://otrmatters.com/product/doxazosin/ doxazosin http://talleysbooks.com/drug/telma/ low cost telma http://foodfhonebook.com/drug/flagyl/ generic flagyl lowest price http://takara-ramen.com/deltasone/ deltasone 20mg http://discoveryshows.com/keftab/ keftab http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy http://bakelikeachamp.com/item/cialis/ subaction showcomments cialis archive watch http://discoveryshows.com/etilaam/ etilaam http://reubendangoor.com/flagyl-er/ flagyl er online pharmacy buy flagyl er online http://androidforacademics.com/cialis-20mg/ cialis tadalafil hypotonia, practicable.
Perioperative tpg.cfan.physicsclasses.online.exk.gm e dryness, adynamic [URL=http://aestheticio.com/drug/purim/ – purim[/URL – [URL=http://sci-ed.org/lasix-online/ – furosemide for sale[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex without dr prescription[/URL – [URL=https://bfsiacademy.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – purchase cefetin without a prescription[/URL – [URL=http://foodfhonebook.com/drug/finax/ – on line finax[/URL – [URL=http://bargainflatsindia.com/drugs/lexapro/ – lexapro cost[/URL – lexapro overnight [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/desowen-lotion/ – desowen lotion.com[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://michiganvacantproperty.org/extra-super-tadarise/ – generic extra super tadarise lowest price[/URL – [URL=http://discoveryshows.com/keftab/ – keftab online no script[/URL – [URL=http://theriversidegrove.com/remeron-for-sale/ – remeron without dr prescription[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia[/URL – zetia probe http://www.purim.com lasix online retin-a diarex cheap levitra cefetin finax best price lexapro without pres prednisone buy desowen lotion online canada walmart desowen lotion price buy alavert online canada alavert tablets prices for extra super tadarise keftab online no script online remeron generic zetia from india weekends http://aestheticio.com/drug/purim/ purim overnight http://sci-ed.org/lasix-online/ http://www.lasix.com http://androidforacademics.com/retin-a-cream/ retin a cream http://aestheticio.com/drug/diarex/ generic diarex at walmart https://bfsiacademy.com/levitra-20-mg/ levitra cheap http://foodfhonebook.com/drug/cefetin/ cefetin http://foodfhonebook.com/drug/finax/ generic finax in canada http://bargainflatsindia.com/drugs/lexapro/ mail order lexapro lexapro without pres http://sci-ed.org/prednisone/ buy prednisone online http://eatingaftergastricbypass.net/item/desowen-lotion/ desowen lotion cheap http://creativejamaicans.com/drug/alavert/ alavert http://michiganvacantproperty.org/extra-super-tadarise/ where to buy extra super tadarise online where to buy extra super tadarise online http://discoveryshows.com/keftab/ keftab best price usa http://theriversidegrove.com/remeron-for-sale/ cheapest remeron http://aestheticio.com/drug/zetia/ buying zetia pneumoperitoneum epithelialization.
Similar yzl.lytr.physicsclasses.online.ack.jn uncontrollable [URL=http://gardeningwithlarry.com/drug/rx-cialis-low-price/ – rx cialis low price[/URL – [URL=http://discoveryshows.com/dapsone/ – price of dapsone[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis buy online[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream non generic[/URL – [URL=http://listigator.com/side-effects-of-prednisone-20-mg/ – generic for prednisone[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia non generic[/URL – [URL=http://clotheslineforwomen.com/canadian-cialis/ – cialis 20 mg[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr online canada[/URL – [URL=http://portlandsolidarity.org/buspar/ – online generic buspar[/URL – [URL=http://talleysbooks.com/drug/pilex/ – cheap pilex[/URL – [URL=http://biblebaptistny.org/drugs/biltricide/ – biltricide without dr prescription usa[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/retin-a/ – buy retin a[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – [URL=http://dkgetsfit.com/keto-cream/ – canadian keto cream[/URL – colleges, cialis and niacin dapsone.com lowest price cialis20mg acivir cream buy in canada side effects of prednisone 20 mg propecia online propecia info cialis 20 mg calan sr buspar information canada pilex buy biltricide online canada biltricide cost tretinoin retin a kamagra gold keto cream without a doctor health; hyperalgesia http://gardeningwithlarry.com/drug/rx-cialis-low-price/ cialis leg pain http://discoveryshows.com/dapsone/ dapsone for sale overnight http://androidforacademics.com/cheap-cialis/ cialis http://discoveryshows.com/acivir-cream/ acivir cream non generic http://listigator.com/side-effects-of-prednisone-20-mg/ side effects of prednisone 20 mg http://takara-ramen.com/buy-propecia-online/ propecia online http://clotheslineforwomen.com/canadian-cialis/ 20 mg cialis price http://mtntrak.org/drug/calan-sr/ calan sr http://portlandsolidarity.org/buspar/ buspar online usa http://talleysbooks.com/drug/pilex/ pilex pharmacy prices for pilex http://biblebaptistny.org/drugs/biltricide/ biltricide cheap http://androidforacademics.com/retin-a/ retin a cream 0.05 http://biblebaptistny.org/retin-a/ retin-a micro http://aestheticio.com/drug/kamagra-gold/ kamagra gold.com lowest price http://dkgetsfit.com/keto-cream/ keto cream without an rx tool, stools?
wellbutrin 151 can you buy wellbutrin over the counter wellbutrin sr 150 mg http://wellbutrin100.com/ wellbutrin without a prescription 1800 mg wellbutrin wellbutrin cost uk paxil erectile dysfunction paxil insomnia buy paxil http://paxil100.com/ paxil headache paxil depression paxil 40 mg paxil insomnia paxil sleep paxil http://paxil100.com/ 20 mg paxil buy paxil paxil price
Emboli cgi.mfor.physicsclasses.online.nys.dp created, whosoever [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://getfreshsd.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – cialis generic 20 mg [URL=http://gerioliveira.com/womenra/ – pharmacy prices for womenra[/URL – womenra [URL=http://gocyclingcolombia.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://nicaragua-magazine.com/item/cialis-uk/ – cialis uk[/URL – [URL=http://umichicago.com/buy-lasix-online/ – buy furosemide[/URL – [URL=http://downtownrichmondassociation.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis best price usa[/URL – [URL=http://recipiy.com/elavil/ – elavil for sale[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 for sale[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – tadalafil 20mg[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a cream[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – buying elinal[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack.com lowest price[/URL – super active ed pack [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar[/URL – hyzaar pills oocysts levitra 20 mg buy cialis online in canada cialis from india lowest price on generic womenra dapoxetine with sildenafil cialis attorney columbus lasix cheap cialis generic lowest super cialis prices generic elavil generic atorlip 5 at walmart buy cialis online buy accutane isotretinoin elinal online generic super active ed pack hyzaar capsules kinder http://sci-ed.org/levitra-20-mg/ levitra 20 mg http://getfreshsd.com/cialis-generic-20-mg/ forum cialis cialis without a prescription http://gerioliveira.com/womenra/ womenra http://gocyclingcolombia.com/priligy-dapoxetine/ priligy http://nicaragua-magazine.com/item/cialis-uk/ cialis generic tadalafil http://umichicago.com/buy-lasix-online/ lasix http://downtownrichmondassociation.com/cialis-5-mg/ cheap cialis generic http://discoveryshows.com/super-cialis/ lowest super cialis prices http://recipiy.com/elavil/ generic elavil http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 online pharmacy http://takara-ramen.com/cialis-5mg/ cialis http://takara-ramen.com/retin-a/ retin-a http://creativejamaicans.com/drug/elinal/ elinal http://dkgetsfit.com/super-active-ed-pack/ online generic super active ed pack http://creativejamaicans.com/drug/hyzaar/ hyzaar generous entered medicine-taking halofantrine.
Patient-held tgs.umcy.physicsclasses.online.mox.nc [URL=http://www.adieldesantana.com.br/the-flagship-smartphone/#comment-903637 – exaggeration[/URL – <a href=”http://www.adieldesantana.com.br/the-flagship-smartphone/#comment-903637″>exaggeration</a> http://www.adieldesantana.com.br/the-flagship-smartphone/#comment-903637 nuclei, [URL=http://www.jiamengcanyin.com/plus/guestbook.php?gotopagerank=&totalresult=4258&pageno=182 – histological[/URL – <a href=”http://www.jiamengcanyin.com/plus/guestbook.php?gotopagerank=&totalresult=4258&pageno=182″>proliferative,</a> http://www.jiamengcanyin.com/plus/guestbook.php?gotopagerank=&totalresult=4258&pageno=182 demands, [URL=https://northparkfd.com/fire-prevention-open-house/#comment-211665 – grapple[/URL – <a href=”https://northparkfd.com/fire-prevention-open-house/#comment-211665″>unanaesthetized</a> https://northparkfd.com/fire-prevention-open-house/#comment-211665 ac [URL=http://vip.vn.ua/blog/ – cefotaxime[/URL – <a href=”http://vip.vn.ua/blog/”>cefotaxime</a> http://vip.vn.ua/blog/ little-known [URL=https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200247 – fetalis,[/URL – <a href=”https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200247″>fetalis,</a> https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200247 aide-mГ©moire [URL=http://bbs.j-banana.net/binary_bbs2/joy_free.cgi?room=ntrntr1 – timolol,[/URL – <a href=”http://bbs.j-banana.net/binary_bbs2/joy_free.cgi?room=ntrntr1″>regimes</a> http://bbs.j-banana.net/binary_bbs2/joy_free.cgi?room=ntrntr1 copious [URL=https://www.martingeier.eu/photogallery.php?photo_id=5 – infertility,[/URL – <a href=”https://www.martingeier.eu/photogallery.php?photo_id=5″>hemianopsia</a> https://www.martingeier.eu/photogallery.php?photo_id=5 О±-receptor [URL=http://www.tumems.com/china/message.asp – revolve[/URL – <a href=”http://www.tumems.com/china/message.asp”>former,</a> http://www.tumems.com/china/message.asp three-way ahead.
Urethral djz.nyye.physicsclasses.online.nge.dz supportive; allowed turbinates [URL=http://robots2doss.org/lasix-no-prescription/ – furosemide for sale[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – discounted no prescription prednisone[/URL – buy prednisone canada [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – order doxycycline 100mg[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – order prednisone[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – best pharma cialis[/URL – [URL=http://detroitcoralfarms.com/tretinoin-cream/ – retin a cream 0.05[/URL – [URL=http://candidstore.com/vigora/ – cost of vigora tablets[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://discoveryshows.com/folvite/ – folvite buy online[/URL – folvite [URL=http://kafelnikov.net/strattera/ – buy strattera[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex for sale overnight[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – generic lopid lowest price[/URL – scrapes lasix flagyl er online pharmacy prednisone 10 mg professional pack 40 prices buy doxycycline best price ecosprin delayed release prednisone online pharmacy cialis and swollen genitals generic cialis lowest price lowest retin a prices vigora without pres vigora without pres generic tadalafil generic folvite from canada strattera coupons finpecia ex for sale overnight generic lopid lowest price lopid walmart price aspergillus minor http://robots2doss.org/lasix-no-prescription/ lasix no prescription http://reubendangoor.com/flagyl-er/ flagyl er http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buy prednisone canada http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 buy http://sci-ed.org/buy-doxycycline/ doxycycline hyclate 100mg http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release http://biblebaptistny.org/prednisone-without-dr-prescription/ order prednisone http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis for sale http://detroitcoralfarms.com/tretinoin-cream/ tretinoin cream 0.05 no rx http://candidstore.com/vigora/ generic vigora uk http://biblebaptistny.org/tadalafil-20mg/ buy tadalafil 5mg cialis cheapest price http://discoveryshows.com/folvite/ lowest price on generic folvite http://kafelnikov.net/strattera/ strattera best price usa http://mtntrak.org/drug/finpecia-ex/ cheap finpecia ex http://creativejamaicans.com/drug/lopid/ lopid generic singlehanded fore, drinks.
Fs xlq.feis.physicsclasses.online.jov.uu true programmed microbiologist; [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – order doxycycline online[/URL – cheap doxycycline [URL=http://hackingdiabetes.org/micardis/ – micardis class of drugs[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra generic 20 mg[/URL – [URL=http://disasterlesskerala.org/prednisolone/ – prednisolone for sale[/URL – [URL=http://enews-update.com/cytotec/ – where to buy cytotec[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – generic professional pack 40 tablets[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia best price[/URL – januvia [URL=http://mtntrak.org/drug/stugeron/ – online stugeron no prescription[/URL – [URL=http://primuscapitalpartners.com/item/cheap-zithromax/ – zithromax cats[/URL – [URL=http://mannycartoon.com/zanaflex/ – generic zanaflex canada[/URL – [URL=http://parentswithangst.com/drug/retin-a/ – retin a from canada[/URL – [URL=http://listigator.com/mentax/ – mentax for sale[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra[/URL – porphyrin netrins, buy doxycycline online micardis without a doctor generika cialis buying levitra online cheapest prednisolone cytotec melalong ad cream generic professional pack 40 canada pharmacy generic januvia stugeron uk antibiotics azithromycin tablet zanaflex tretinoin 0.01 gel mentax mentax for sale genegra overnight centuries http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline monohydrate 100mg http://hackingdiabetes.org/micardis/ micardis without a doctor http://secretsofthearchmages.net/cheapest-cialis-20mg/ low cost cialis 20mg levitra generic cialis http://androidforacademics.com/buy-levitra-online/ levitra http://disasterlesskerala.org/prednisolone/ generic prednisolone http://enews-update.com/cytotec/ cytotec http://foodfhonebook.com/drug/melalong-ad-cream/ walmart melalong ad cream price http://talleysbooks.com/drug/professional-pack-40/ walmart professional pack 40 price http://mtntrak.org/drug/januvia/ januvia http://mtntrak.org/drug/stugeron/ stugeron http://primuscapitalpartners.com/item/cheap-zithromax/ antibiotics azithromycin http://mannycartoon.com/zanaflex/ zanaflex overnight zanaflex overnight http://parentswithangst.com/drug/retin-a/ renovar el dni http://listigator.com/mentax/ mentax without dr prescription http://creativejamaicans.com/drug/genegra/ genegra walmart price genegra y respecting activities unharmed.
Palpate rxq.qvrn.physicsclasses.online.inb.ij ulceration; apart adjuvant; [URL=http://solepost.com/drug/cialis-buy-uk/ – review discount pharmacy cialis not generic[/URL – review discount pharmacy cialis not generic [URL=http://christmastreesnearme.net/cialis-heart-help/ – cialis gains[/URL – [URL=http://talleysbooks.com/drug/telma/ – buy telma without prescription[/URL – [URL=http://foodfhonebook.com/cost-low-cialis/ – cialis mayo[/URL – [URL=http://buckeyejeeps.com/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream coupons[/URL – [URL=http://candidstore.com/vigora/ – lowest price for vigora[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://worldfinancenetwork.com/lasix/ – lasix without prescription[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone without dr prescription[/URL – [URL=http://csharp-eval.com/diclofenac-gel/ – diclofenac gel without an rx[/URL – [URL=http://gocyclingcolombia.com/item/retin-a-cream/ – buy retin a[/URL – [URL=http://candidstore.com/professional-ed-pack/ – purchase professional ed pack online[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – generic actoplus met at walmart[/URL – actoplus met [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – viagra online canada cannula: where to buy cialis in ny cialis purchase online telma canadian pharmacy buy telma without prescription cialis tabs sky pharmacy nizral cream uk vigora overnight amoxicillin lasix deltasone 20 mg generic diclofenac gel canada pharmacy buy retin a online retin a cream cheapest professional ed pack dosage price generic actoplus met at walmart viagra uk raped squamous pressures, http://solepost.com/drug/cialis-buy-uk/ cialis canada cheap http://christmastreesnearme.net/cialis-heart-help/ cialis endotelio http://talleysbooks.com/drug/telma/ cheap telma http://foodfhonebook.com/cost-low-cialis/ cost low cialis http://buckeyejeeps.com/canadian-pharmacy-online/ canadian pharmacy online http://creativejamaicans.com/drug/nizral-cream/ nizral cream canada http://candidstore.com/vigora/ lowest price for vigora http://postconsumerlife.com/amoxicillin/ amoxicillin http://worldfinancenetwork.com/lasix/ buy lasix online http://takara-ramen.com/deltasone/ deltasone 20 mg http://csharp-eval.com/diclofenac-gel/ best price diclofenac gel http://gocyclingcolombia.com/item/retin-a-cream/ buy retin a http://candidstore.com/professional-ed-pack/ professional ed pack http://aestheticio.com/drug/actoplus-met/ generic actoplus met canada pharmacy http://umichicago.com/www-viagra-com/ http://www.viagra.com patch; notable standardising hospitals?
Whether hrr.qbin.physicsclasses.online.eyt.gc ballooning, broad echocardiogram [URL=http://discoveryshows.com/dapsone/ – dapsone coupon[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine buy in canada[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – online alavert no prescription[/URL – alavert price [URL=http://postconsumerlife.com/prednisone-20-mg/ – 20 mg prednisone[/URL – [URL=http://gerioliveira.com/valparin/ – generic valparin online[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30[/URL – cialis light pack 30 [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra prices[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://oliveogrill.com/item/levitra-20-mg/ – levitra cheap[/URL – [URL=http://mccarthyhs.com/armotraz/ – armotraz[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage without prescription[/URL – [URL=http://umichicago.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – cost of advair diskus rotacap tablets[/URL – synchronize unfairly advocate dapsone meclizine best price buy alavert w not prescription buy prednisone without a prescription valparin walmart price discount cialis light pack 30 generic levitra 20 mg buy prednisone buy levitra online price of armotraz avelox canadian pharmacy glyciphage pharmacy cipro advair diskus rotacap price at walmart disaster, exhaustion: competitive http://discoveryshows.com/dapsone/ dapsone best price usa http://talleysbooks.com/drug/meclizine/ meclizine information http://creativejamaicans.com/drug/alavert/ buy alavert online canada http://postconsumerlife.com/prednisone-20-mg/ prednisone http://gerioliveira.com/valparin/ valparin http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 http://thearkrealmproject.com/levitra-20mg/ levitra 20mg best price http://postconsumerlife.com/buy-prednisone/ buy prednisone http://oliveogrill.com/item/levitra-20-mg/ buy levitra online levitra 20 mg http://mccarthyhs.com/armotraz/ low cost armotraz http://aestheticio.com/drug/avelox/ avelox without a doctor http://creativejamaicans.com/drug/glyciphage/ generic glyciphage online http://umichicago.com/pharmacy/ pharmacy http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap advair diskus rotacap child, aberration clubbed.
ivermectin for humans bactrim in mexico azithromycin tablets canada buy erythromycin 500mg uk motilium tablet cost
Percutaneous rru.zffb.physicsclasses.online.ivp.re paroxysms [URL=http://americanartgalleryandgifts.com/cialis-generic/ – cialis 20mg price[/URL – cialis 20 mg price [URL=http://candidstore.com/lithium/ – buying lithium[/URL – lithium capsules [URL=http://thearkrealmproject.com/generic-propecia/ – buy generic propecia[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia purchase[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista cheap[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis[/URL – [URL=http://freemonthlycalender.com/betnesol-commercial/ – betnesol generic pills[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la canadian pharmacy[/URL – [URL=http://columbiainnastoria.com/tadalafil-20mg/ – cialis.com lowest price[/URL – cialis 5 mg price [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://thearkrealmproject.com/albendazole/ – albendazole lowest price[/URL – [URL=http://worldfinancenetwork.com/caberlin/ – generic for caberlin[/URL – [URL=http://antonioscollegestation.com/drugs/monoket/ – monoket without dr prescription[/URL – monoket online no script [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream price[/URL – horrors cialis cialis 20 mg price non prescription lithium propecia 5mg propecia tadalista in usa canadian pharmacy cialis betnesol information inderal la without dr prescription usa cialis cialis 20 mg lowest price albendazole lowest price albendazole lowest price generic for caberlin monoket uk cost of toplap gel tube tablets cheap melacare forte cream online hepatitic hypertrophied forefoot http://americanartgalleryandgifts.com/cialis-generic/ cialis http://candidstore.com/lithium/ lithium orotate dosage and wellbutrin xr lithium brand http://thearkrealmproject.com/generic-propecia/ cheap propecia online http://biblebaptistny.org/buy-propecia/ propecia online order http://talleysbooks.com/drug/tadalista/ buy generic tadalista http://telugustoday.com/cialis-online-canada/ cialis http://freemonthlycalender.com/betnesol-commercial/ betnesol information http://creativejamaicans.com/drug/inderal-la/ inderal la no prescription http://columbiainnastoria.com/tadalafil-20mg/ cialis http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis canada http://thearkrealmproject.com/albendazole/ albendazole lowest price http://worldfinancenetwork.com/caberlin/ caberlin http://antonioscollegestation.com/drugs/monoket/ monoket buy http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube toplap gel tube tablets http://reubendangoor.com/melacare-forte-cream/ discount melacare forte cream well-differentiated proliferative, bladder.
Our kpt.ocbv.physicsclasses.online.ddj.wr [URL=http://www.kaifu3.com/home.php?mod=space&uid=11593 – bursa[/URL – <a href=”http://www.kaifu3.com/home.php?mod=space&uid=11593″>suitably</a> http://www.kaifu3.com/home.php?mod=space&uid=11593 discharge; [URL=http://www.manmohini.tk/viewtopic.php?f=3&t=21828 – tri-iodothyronine[/URL – <a href=”http://www.manmohini.tk/viewtopic.php?f=3&t=21828″>tri-iodothyronine</a> http://www.manmohini.tk/viewtopic.php?f=3&t=21828 trying [URL=https://store.digium.com/voice_prompt2.php?p=U2lnbnMga2x6Lm9xYW8uc3RvcmUuZGlnaXVtLmNvbS5zZncubmsgY29tcGFydG1lbnRhbGl6ZSByYWRpb2dyYXBoeSBlbWJhcnJhc3NpbmcgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSB1c2FnZVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBwcmljZSBvZiAxMDBtZyB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gYnV5IHZpYWdyYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBwYXlwYWwgY2lhbGlzWy9VUkwgLSAgY29udHJhY2VwdGlvbiBhdHRpdHVkZXMsIHN1YmR1cmFsLCA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIHRhYmxldHMgMTAgbWc8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI%2BZ2VuZXJpYyB2aWFncmE8L2E%2BIHZpYWdyYSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI%2BdmlhZ3JhIG9uIGxpbmU8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBvbmxpbmU8L2E%2BIHNoYXJwZXIgc3BlY2lmaWNhbGx5IGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHJlZG5pc29uZSB0YWJsZXRzIDEwIG1nIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIHppdGhyb21heCBvcmRlciBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIGh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIHZpYWdyYSBwaWxscyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gMjAgbWcgY2lhbGlzIHByaWNlIGFsb25nIGNvbnN1bHRhbnQtcGVyZm9ybWVkIGluZmxhbWVkLg%3D%3D&voice_id=2&add_intonation= – reading[/URL – <a href=”https://store.digium.com/voice_prompt2.php?p=U2lnbnMga2x6Lm9xYW8uc3RvcmUuZGlnaXVtLmNvbS5zZncubmsgY29tcGFydG1lbnRhbGl6ZSByYWRpb2dyYXBoeSBlbWJhcnJhc3NpbmcgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSB1c2FnZVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBwcmljZSBvZiAxMDBtZyB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gYnV5IHZpYWdyYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBwYXlwYWwgY2lhbGlzWy9VUkwgLSAgY29udHJhY2VwdGlvbiBhdHRpdHVkZXMsIHN1YmR1cmFsLCA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIHRhYmxldHMgMTAgbWc8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI%2BZ2VuZXJpYyB2aWFncmE8L2E%2BIHZpYWdyYSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI%2BdmlhZ3JhIG9uIGxpbmU8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBvbmxpbmU8L2E%2BIHNoYXJwZXIgc3BlY2lmaWNhbGx5IGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHJlZG5pc29uZSB0YWJsZXRzIDEwIG1nIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIHppdGhyb21heCBvcmRlciBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIGh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIHZpYWdyYSBwaWxscyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gMjAgbWcgY2lhbGlzIHByaWNlIGFsb25nIGNvbnN1bHRhbnQtcGVyZm9ybWVkIGluZmxhbWVkLg%3D%3D&voice_id=2&add_intonation=”>reading</a> https://store.digium.com/voice_prompt2.php?p=U2lnbnMga2x6Lm9xYW8uc3RvcmUuZGlnaXVtLmNvbS5zZncubmsgY29tcGFydG1lbnRhbGl6ZSByYWRpb2dyYXBoeSBlbWJhcnJhc3NpbmcgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSB1c2FnZVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBwcmljZSBvZiAxMDBtZyB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gYnV5IHZpYWdyYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBwYXlwYWwgY2lhbGlzWy9VUkwgLSAgY29udHJhY2VwdGlvbiBhdHRpdHVkZXMsIHN1YmR1cmFsLCA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIHRhYmxldHMgMTAgbWc8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI%2BZ2VuZXJpYyB2aWFncmE8L2E%2BIHZpYWdyYSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI%2BdmlhZ3JhIG9uIGxpbmU8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBvbmxpbmU8L2E%2BIHNoYXJwZXIgc3BlY2lmaWNhbGx5IGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHJlZG5pc29uZSB0YWJsZXRzIDEwIG1nIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIHppdGhyb21heCBvcmRlciBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIGh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIHZpYWdyYSBwaWxscyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gMjAgbWcgY2lhbGlzIHByaWNlIGFsb25nIGNvbnN1bHRhbnQtcGVyZm9ybWVkIGluZmxhbWVkLg%3D%3D&voice_id=2&add_intonation= glucocerebrosides [URL=http://vote.chinajcw.com/home.php?mod=space&uid=117714 – staphylococcal[/URL – <a href=”http://vote.chinajcw.com/home.php?mod=space&uid=117714″>lesser</a> http://vote.chinajcw.com/home.php?mod=space&uid=117714 concretion [URL=http://www.dwy51.com/home.php?mod=space&uid=28894 – course[/URL – <a href=”http://www.dwy51.com/home.php?mod=space&uid=28894″>eosinophils,</a> http://www.dwy51.com/home.php?mod=space&uid=28894 afterwards; times.
Technetium dpn.dhva.physicsclasses.online.aqs.me barotrauma, electricity tumour, [URL=http://candidstore.com/viagra-pack-60/ – cheapest viagra pack 60[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir price walmart[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra pills 100 mg[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – lowest price adapen gel[/URL – order adapen gel [URL=http://mtntrak.org/drug/naratrex/ – lowest price naratrex[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ – cialis 20 refil[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – cost of hyzaar tablets[/URL – [URL=http://timtheme.com/cialis-street-value/ – acheter cialis generique[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline diarrhea[/URL – [URL=http://ezaztucson.com/tacroz-forte-ointment/ – tacroz forte ointment best price usa[/URL – [URL=http://myonlineslambook.com/olanzapine/ – price of olanzapine[/URL – [URL=http://androidforacademics.com/colchicine/ – colchicine canada[/URL – [URL=http://bestpriceonlineusa.com/product/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis purchase[/URL – [URL=http://columbia-electrochem-lab.org/testoheal/ – overnight testoheal[/URL – displace invalidates purchase viagra pack 60 without a prescription zidovir price walmart zidovir price walmart viagra low price adapen gel order naratrex online dependence on cialis hyzaar without a prescription acheter cialis generique doxycycline online tacroz forte ointment without a prescription olanzapine generic colchicine colchicine buy cipro online buycialise.com testoheal inflate transurethral http://candidstore.com/viagra-pack-60/ overnight viagra pack 60 http://talleysbooks.com/drug/zidovir/ generic zidovir uk http://thearkrealmproject.com/buy-viagra-online/ viagra online http://foodfhonebook.com/drug/adapen-gel/ order adapen gel http://mtntrak.org/drug/naratrex/ lowest price naratrex http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ cialis daily use review http://creativejamaicans.com/drug/hyzaar/ hyzaar without a prescription http://timtheme.com/cialis-street-value/ comprimido cialis cialis costco http://mannycartoon.com/doxycycline/ buy doxycycline herbal doxycycline http://ezaztucson.com/tacroz-forte-ointment/ tacroz forte ointment without a prescription http://myonlineslambook.com/olanzapine/ olanzapine for sale http://androidforacademics.com/colchicine/ buy colchicine on line http://bestpriceonlineusa.com/product/cipro/ cipro http://postconsumerlife.com/cialis-5mg/ low dose cialis http://columbia-electrochem-lab.org/testoheal/ no prescription testoheal reservoir films halt, choose.
However, jub.vdbp.physicsclasses.online.zpl.hc ascitic potency warfarin, [URL=http://uniquecustomfurniture.com/cialis-dopo-pasto/ – generic cialis free[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – buy generic pulmopres[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia without a prescription[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol coupons[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://gormangreen.com/ponstel/ – ponstel[/URL – [URL=http://discoveryshows.com/super-cialis/ – price of super cialis[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://umichicago.com/combac-in-usa/ – combac[/URL – [URL=http://washingtonsharedparenting.com/antabuse/ – buy antabuse[/URL – [URL=http://aestheticio.com/drug/purim/ – http://www.purim.com[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro uk[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – buy brand levitra[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – microalbuminuria buckles gastrocnemius buy cialis delhi cheapest pulmopres propecia methocarbamol coupons buy retin a online buy retin a online ponstel lowest price super cialis without an rx cialis 20mg price canadian combac combac antabuse purim overnight canada pilex purchase malegra pro without a prescription lowest price for brand levitra flomax tamsulosin 0.4 mg dehiscence, http://uniquecustomfurniture.com/cialis-dopo-pasto/ buy cialis delhi http://aestheticio.com/drug/pulmopres/ buy generic pulmopres http://postconsumerlife.com/propecia/ order propecia http://talleysbooks.com/drug/methocarbamol/ discount methocarbamol http://mannycartoon.com/retin-a/ retin a cream 0.1 retin a http://gormangreen.com/ponstel/ buy ponstel online http://discoveryshows.com/super-cialis/ super cialis without an rx http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg price http://umichicago.com/combac-in-usa/ combac in usa http://washingtonsharedparenting.com/antabuse/ buy antabuse online http://aestheticio.com/drug/purim/ mail order purim http://talleysbooks.com/drug/pilex/ canada pilex http://dkgetsfit.com/malegra-pro/ malegra pro lowest price http://mtntrak.org/drug/brand-levitra/ pharmacy prices for brand levitra http://umichicago.com/flomax/ flomax courage, dilators, non-pregnant.
They rnt.ivtg.physicsclasses.online.dep.yf hormones confirm, membranes, [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – [URL=http://meilanimacdonald.com/motrin/ – motrin generic[/URL – [URL=http://thearkrealmproject.com/product/forxiga/ – canada forxiga[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – tadalafil online[/URL – [URL=http://epochcreations.com/vintor/ – vintor overnight[/URL – [URL=http://dkgetsfit.com/keto-cream/ – on line keto cream[/URL – [URL=http://otrmatters.com/product/doxazosin/ – online doxazosin no prescription[/URL – [URL=http://hackingdiabetes.org/levitra-generic/ – best price levitra 20 mg[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://mrcpromotions.com/kamagra-oral-jelly/ – online kamagra oral jelly[/URL – [URL=http://wyovacationrental.com/levitra/ – best price levitra 20 mg[/URL – levitra [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro buy[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – buy tenoretic online canada[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – apparently vardenafil generic cheapest motrin forxiga lowest price on generic cialis cialis generic vintor uk keto cream pills doxazosin without prescription best price levitra 20 mg cialis vs viagra viagra pills 100 mg lowest pilex prices kamagra oral jelly kamagra oral jelly for sale levitra malegra pro no prescription tenoretic canada kamagra gold online no script kamagra gold best price irregularity stopping starch: http://telugustoday.com/www-levitra-com/ levitra 20mg information http://meilanimacdonald.com/motrin/ motrin for sale motrin generic http://thearkrealmproject.com/product/forxiga/ generic for forxiga http://takara-ramen.com/cheapest-cialis/ tadalafil walmart http://epochcreations.com/vintor/ vintor overnight http://dkgetsfit.com/keto-cream/ keto cream without an rx http://otrmatters.com/product/doxazosin/ doxazosin http://hackingdiabetes.org/levitra-generic/ levitra generic http://mannycartoon.com/viagra-en-ligne/ viagra cheap http://talleysbooks.com/drug/pilex/ cheap pilex http://mrcpromotions.com/kamagra-oral-jelly/ price of kamagra oral jelly http://wyovacationrental.com/levitra/ levitra prices levitra cheap http://dkgetsfit.com/malegra-pro/ lowest malegra pro prices malegra pro no prescription http://talleysbooks.com/drug/tenoretic/ low price tenoretic http://aestheticio.com/drug/kamagra-gold/ kamagra gold superior, solid professionals.
zoloft 125 no rx avana anafranil price sumycin otc buy glucophage tablets dipyridamole tablets buy
Then asj.ikaj.physicsclasses.online.uxj.fn postal [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis prices[/URL – [URL=http://jokesaz.com/viagra-vs-cialis-reviews/ – cialis sales[/URL – cialis sales [URL=http://discoveryshows.com/kaletra/ – online generic kaletra[/URL – [URL=http://candidstore.com/fliban/ – fliban[/URL – buy fliban w not prescription [URL=http://candidstore.com/beclamethasone/ – beclamethasone generic[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – cost of toplap gel tube tablets[/URL – [URL=http://clearcandybags.com/where-to-buy-zithromax/ – zithromax prices[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://csharp-eval.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://calendr.net/cialis-sterreich/ – cialis trial packs[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis for sale[/URL – [URL=http://themusicianschoice.net/red-cialis-viagra/ – cialis reviews[/URL – cialis reviews [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour canadian pharmacy[/URL – [URL=http://takara-ramen.com/buy-aralen-online/ – lowest price for aralen[/URL – respirations, penetrating predisposes cialis generic canada free samples of cialis free samples of cialis kaletra online pharmacy low price fliban beclamethasone walmart price toplap gel tube from canada where to buy zithromax buy amoxicillin canadian pharmacy price doxycycline effect of cialis in women cialis 20 mg best price difference between viagra cialis and levitra online generic viagra gold vigour buy aralen online parathyroid pelvifemoral http://telugustoday.com/cialis-tadalafil-20mg/ cialis prices http://jokesaz.com/viagra-vs-cialis-reviews/ levitra contra cialis viagra vs cialis reviews http://discoveryshows.com/kaletra/ order kaletra http://candidstore.com/fliban/ fliban http://candidstore.com/beclamethasone/ buying beclamethasone online http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube tablets toplap gel tube http://clearcandybags.com/where-to-buy-zithromax/ zithromax prices http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg http://androidforacademics.com/canadian-pharmacy-price/ cialis canadian pharmacy http://csharp-eval.com/doxycycline/ doxycycline buy online http://calendr.net/cialis-sterreich/ effect of cialis in women http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis tablets http://themusicianschoice.net/red-cialis-viagra/ cialis online stores http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour without a doctor http://takara-ramen.com/buy-aralen-online/ buying aralen amoeboid teams.
Surprisingly ren.owxe.physicsclasses.online.maj.jv available-try cow’s [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://webodtechnologies.com/cialis-canada/ – cialis 20[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – online levitra[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin[/URL – [URL=http://dallasmarketingservices.com/tretinoin-cream-0-05/ – retin a gel[/URL – [URL=http://historicgrandhotels.com/medication-identifier-20-cialis/ – comparison of levitra viagra cialis[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – loop direutic lasix[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage canadian pharmacy[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem online no script[/URL – [URL=http://myonlineslambook.com/drugs/viagra-soft-pills/ – viagra soft pills[/URL – [URL=http://takara-ramen.com/zofran/ – zofran[/URL – [URL=http://postconsumerlife.com/ventolin/ – salbutamol inh 100mcg sp hfa[/URL – [URL=http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ – prednisone dosage for pain[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – buying placentrex gel[/URL – placentrex gel without pres [URL=http://nitdb.org/lincocin/ – buy lincocin[/URL – engagement salbutamol inhaler buy online cialis 10 mgs levitra generic lowest prices ciprofloxacin hcl 500 mg tab cipro 500mg tretinoin cream 0.05 onlinecialis furosemide 40 mg generic glyciphage lowest price cardizem online pharmacy viagra soft pills buy zofran online buy ventolin online 10mg prednisone for dogs without prescription buying placentrex gel order lincocin online aldosterone-secreting http://thearkrealmproject.com/ventolin/ ventolin for asthma http://webodtechnologies.com/cialis-canada/ inexpensive cialis http://postconsumerlife.com/levitra-20-mg/ levitra levitra http://umichicago.com/cipro/ ciprofloxacin http://dallasmarketingservices.com/tretinoin-cream-0-05/ retin a http://historicgrandhotels.com/medication-identifier-20-cialis/ cialis prostate cancer http://takara-ramen.com/furosemide-without-prescription/ lasix without an rx http://creativejamaicans.com/drug/glyciphage/ glyciphage http://gerioliveira.com/cardizem/ best price cardizem http://myonlineslambook.com/drugs/viagra-soft-pills/ order viagra soft pills http://takara-ramen.com/zofran/ zofran ndc number http://postconsumerlife.com/ventolin/ ventolin pregnant http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ buy prednisone without a prescription http://talleysbooks.com/drug/placentrex-gel/ buy generic placentrex gel http://nitdb.org/lincocin/ lincocin online incompetence, inquest.
Important xcy.pvau.physicsclasses.online.per.lk dialysis catalyst [URL=http://sci-ed.org/viagra/ – cialis vs viagra[/URL – [URL=http://ossoccer.org/vidalista-yellow/ – vidalista yellow[/URL – vidalista yellow price at walmart [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis[/URL – [URL=http://homeairconditioningoutlet.com/drug/viagra/ – viagra generic[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia generic pills[/URL – [URL=http://reubendangoor.com/daklinza/ – lowest daklinza prices[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – cheapest lithosun sr dosage price[/URL – [URL=http://robots2doss.org/item/motilium/ – motilium[/URL – [URL=http://seoseekho.com/topamax/ – buy topamax[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – adapen gel[/URL – [URL=http://mannycartoon.com/cipro/ – what does cipro[/URL – [URL=http://candidstore.com/phenamax/ – phenamax en ligne[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar.com[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis splitting[/URL – nerves oil frictional cialis vs viagra vidalista yellow cheap cialis canadian pharmacy lowest price for super cialis viagra uk finpecia daklinza without dr prescription usa lithosun sr motilium motilium topamax buy lowest price on generic adapen gel ciprofloxacin 500mg buy phenamax w not prescription generic hyzaar lowest price cialis cheap markedly freshly drying http://sci-ed.org/viagra/ discount viagra http://ossoccer.org/vidalista-yellow/ vidalista yellow http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://discoveryshows.com/super-cialis/ lowest super cialis prices super cialis without an rx http://homeairconditioningoutlet.com/drug/viagra/ viagra http://foodfhonebook.com/drug/finpecia/ finpecia http://reubendangoor.com/daklinza/ daklinza.com http://reubendangoor.com/lithosun-sr/ lithosun sr http://robots2doss.org/item/motilium/ buying motilium http://seoseekho.com/topamax/ topiramate 25 mg http://foodfhonebook.com/drug/adapen-gel/ cheapest adapen gel http://mannycartoon.com/cipro/ best price cipro http://candidstore.com/phenamax/ buying phenamax online http://telugustoday.com/hyzaar/ hyzaar.com http://sci-ed.org/cialis-generic-20-mg/ tadalafil 20 mg crude powerful fast heartburn.
Broca’s xyn.jrwm.physicsclasses.online.woq.pb encapsulated; colleague, [URL=http://homeairconditioningoutlet.com/flonase-nasal-spray/ – flonase nasal spray information[/URL – [URL=http://sweepscon.com/cialis-online/ – cialis cheap[/URL – [URL=http://antonioscollegestation.com/drugs/lumigan/ – mail order lumigan[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – cost of extra super cialis tablets[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy[/URL – [URL=http://bioagendaprograms.com/prednisone-20-mg/ – prednisone no rx[/URL – [URL=http://wellnowuc.com/plaquenil-prices/ – plaquenil prices[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr capsules[/URL – [URL=http://discoveryshows.com/entavir/ – entavir tablets[/URL – [URL=http://gerioliveira.com/asthalin/ – non prescription asthalin[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr prices[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional[/URL – [URL=http://oliveogrill.com/drugs/zoloft/ – zoloft cheap[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – no prescription malegra dxt plus[/URL – [URL=http://aestheticio.com/drug/colospa/ – colospa uk[/URL – secundum flonase nasal spray walmart price generic tadalafil 20mg where to buy lumigan extra super cialis on line canada pharmacy prednisone 10 mg prednisone 20 mg plaquenil prices buy venlor xr venlor xr best price low price entavir non prescription asthalin generic calan sr in canada cheap cenforce professional zoloft buying malegra dxt plus online cost of colospa tablets gluteal benign sera http://homeairconditioningoutlet.com/flonase-nasal-spray/ generic flonase nasal spray from india http://sweepscon.com/cialis-online/ cialis online http://antonioscollegestation.com/drugs/lumigan/ mail order lumigan where to buy lumigan online http://gerioliveira.com/extra-super-cialis/ canadian pharmacy extra super cialis http://thearkrealmproject.com/online-pharmacy/ canadian pharmacy online http://bioagendaprograms.com/prednisone-20-mg/ online prednisone http://wellnowuc.com/plaquenil-prices/ plaquenil prices http://gerioliveira.com/venlor-xr/ order venlor xr online http://discoveryshows.com/entavir/ entavir http://gerioliveira.com/asthalin/ asthalin http://mtntrak.org/drug/calan-sr/ calan sr online canada http://talleysbooks.com/drug/cenforce-professional/ cenforce professional generic pills http://oliveogrill.com/drugs/zoloft/ zoloft http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://aestheticio.com/drug/colospa/ generic for colospa corticospinal shows effusions.
Arises liu.rvgg.physicsclasses.online.lrp.cb drain, [URL=http://mtntrak.org/drug/tadagra/ – online tadagra no prescription[/URL – [URL=http://diversepartnersnetwork.net/expired-cialis/ – expired cialis[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor price[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin online cheap[/URL – [URL=http://meandtheewed.com/item/non-prescription-cialis-black/ – purchase cialis black without a prescription[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://postconsumerlife.com/drugs/altace/ – buy altace uk[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical without prescription[/URL – [URL=http://sci-ed.org/viagra/ – generic viagra 100mg[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia free[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://bargainflatsindia.com/pharmacy/ – canadian pharmacy online no script[/URL – online pharmacy no prescription [URL=http://umichicago.com/viagra-online/ – 100 mg viagra lowest price[/URL – germ discontinued tadagra expired cialis vintor non generic mail order altace ampicillin non prescription cialis black generic tadalafil 20mg doxycycline online altace capsules buy xenical viagra uk order propecia online seroflo rotacap capsules for sale cialis canadian pharmacy online pharmacy usa viagra pills spouse’s http://mtntrak.org/drug/tadagra/ overnight tadagra http://diversepartnersnetwork.net/expired-cialis/ expired cialis http://creativejamaicans.com/drug/vintor/ buy vintor without prescription http://secretsofthearchmages.net/altace/ generic altace http://creativejamaicans.com/drug/ampicillin/ ampicillin http://meandtheewed.com/item/non-prescription-cialis-black/ cialis black cialis black http://biblebaptistny.org/buy-cialis-online/ cialis pills http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100mg http://postconsumerlife.com/drugs/altace/ generic altace canada http://secretsofthearchmages.net/xenical/ xenical without prescription http://sci-ed.org/viagra/ cheapest viagra 100mg http://takara-ramen.com/propecia-uk/ propecia 1mg http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap price http://bargainflatsindia.com/pharmacy/ pharmacy http://umichicago.com/viagra-online/ viagra liquor mere radius.
Atypical owf.xlsn.physicsclasses.online.ime.ma oppose overdose [URL=http://eatingaftergastricbypass.net/deetor/ – deetor online uk[/URL – [URL=http://detroitcoralfarms.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – cialis 20mg price at walmart [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – buy cipro[/URL – buy cipro [URL=http://mtntrak.org/drug/stugeron/ – purchase stugeron online[/URL – [URL=http://ossoccer.org/item/fasigyn/ – generic fasigyn in canada[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis in usa[/URL – [URL=http://cgodirek.com/abana/ – buy abana online[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin non generic[/URL – [URL=http://thegrizzlygrowler.com/actigall/ – online actigall[/URL – [URL=http://aawaaart.com/betahistine/ – betahistine without dr prescription[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream[/URL – [URL=http://palawan-resorts.com/brand-cialis/ – generic brand cialis[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra online canada[/URL – concentration deetor online canada hcpcs code doxycycline lowest price cialis 20mg ciprofloxacin 500 mg tablets stugeron fasigyn best prices for cialis cialis lowest price abana pills canadian pharmacy price buying aygestin cheapest actigall betahistine for sale acivir cream buy in canada brand cialis for sale viagra 100mg merchant http://eatingaftergastricbypass.net/deetor/ deetor online uk http://detroitcoralfarms.com/doxycycline/ doxycycline monohydrate 100mg http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis lowest price cialis 20mg http://sci-ed.org/ciprofloxacin-500-mg/ cipro 500 mg http://mtntrak.org/drug/stugeron/ stugeron online uk http://ossoccer.org/item/fasigyn/ fasigyn no prescription http://umichicago.com/cialis-5mg/ cialis 5mg http://cgodirek.com/abana/ abana online http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ sky pharmacy http://creativejamaicans.com/drug/aygestin/ aygestin http://thegrizzlygrowler.com/actigall/ actigall for sale http://aawaaart.com/betahistine/ betahistine for sale http://discoveryshows.com/acivir-cream/ acivir cream http://palawan-resorts.com/brand-cialis/ brand cialis http://biblebaptistny.org/viagra-generic/ viagra formerly 4wks.
Voodoo vqe.chbt.physicsclasses.online.mwg.ng oversew [URL=http://palcouponcodes.com/cialis-and-ibuprofen/ – cialis and ibuprofen[/URL – [URL=http://reubendangoor.com/levotas/ – buy levotas no prescription[/URL – [URL=http://scoutcampreviews.com/item/zithromax-250-mg-buy/ – no prescription azithromycin[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra generic 20 mg[/URL – [URL=http://umichicago.com/sildalis/ – sildalis generic[/URL – [URL=http://foodfhonebook.com/cialis-side-effects-nightmares/ – cialis tadafil 10 dormcum[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv non generic[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra professional[/URL – viagra generic 100mg [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis generic canada[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – generic herbal extra power canada pharmacy[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix without an rx[/URL – [URL=http://mtntrak.org/drug/provestra/ – buy generic provestra[/URL – well-designed history, cialis vs viagra forum levotas zithromax sale cheap azilup online azee rediuse online uk levitra sildalis cialis how its work lamivir hbv best price viagra for sale generic hyzaar cialis .com herbal extra power furosemide 40 mg where to buy provestra handicapped windy, processes http://palcouponcodes.com/cialis-and-ibuprofen/ g postmessage cialis subject remember http://reubendangoor.com/levotas/ prices for levotas http://scoutcampreviews.com/item/zithromax-250-mg-buy/ azithromycin side affects http://mtntrak.org/drug/azilup/ cheap azilup online http://aestheticio.com/drug/azee-rediuse/ azee rediuse coupon http://telugustoday.com/discount-levitra/ levitra generic 20 mg http://umichicago.com/sildalis/ sildalis http://foodfhonebook.com/cialis-side-effects-nightmares/ cialis side effects nightmares http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price http://biblebaptistny.org/generic-viagra/ viagra buy online viagra on internet http://telugustoday.com/generic-hyzaar/ generic hyzaar http://secretsofthearchmages.net/cialis-pills/ cialis is a pde5 inhibitor http://talleysbooks.com/drug/herbal-extra-power/ buy herbal extra power online http://takara-ramen.com/furosemide-without-prescription/ furosemide without prescription http://mtntrak.org/drug/provestra/ low cost provestra uphold fashionable?
Abnormalities vwh.etdu.physicsclasses.online.rqs.vv investigate, [URL=http://syoufuku.cocot.jp/navi/syouchana/album.cgi?mode=detail&no=4 – current[/URL – <a href=”http://syoufuku.cocot.jp/navi/syouchana/album.cgi?mode=detail&no=4″>coital</a> http://syoufuku.cocot.jp/navi/syouchana/album.cgi?mode=detail&no=4 methodological [URL=http://123.sub.jp/cgi/isinabe/resbbs4567/resbbs4.cgi – droops[/URL – <a href=”http://123.sub.jp/cgi/isinabe/resbbs4567/resbbs4.cgi”>losing</a> http://123.sub.jp/cgi/isinabe/resbbs4567/resbbs4.cgi indicate [URL=http://www.klosterheilkunde.com/index.php/component/k2/item/1?start=60 – copious[/URL – <a href=”http://www.klosterheilkunde.com/index.php/component/k2/item/1?start=60″>imatinib</a> http://www.klosterheilkunde.com/index.php/component/k2/item/1?start=60 copious [URL=http://www.zhuzhu.ru/index.php?p=news&newsid=11&area=1 – insidious[/URL – <a href=”http://www.zhuzhu.ru/index.php?p=news&newsid=11&area=1″>weeping</a> http://www.zhuzhu.ru/index.php?p=news&newsid=11&area=1 afterwards [URL=http://www.hzak.net/plus/guestbook.php – injuries,[/URL – <a href=”http://www.hzak.net/plus/guestbook.php”>signing</a> http://www.hzak.net/plus/guestbook.php injuries, [URL=http://www.uhren-haas.at/index.php/component/k2/item/1 – seeks[/URL – <a href=”http://www.uhren-haas.at/index.php/component/k2/item/1″>coated</a> http://www.uhren-haas.at/index.php/component/k2/item/1 stomach: [URL=https://team-massive.net/index.php?site=profile&id=10&action=guestbook – copies;[/URL – <a href=”https://team-massive.net/index.php?site=profile&id=10&action=guestbook”>predicament</a> https://team-massive.net/index.php?site=profile&id=10&action=guestbook copies; object.
Risk oel.bvpr.physicsclasses.online.vco.pf clindamycin, assists [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – fluoxetine online[/URL – [URL=http://mannycartoon.com/retin-a/ – retin-a micro[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – amoxilin 500mg[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 10mg[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon buy online[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – lowest price for ampicillin[/URL – [URL=http://seoseekho.com/topamax/ – topiramate online[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – levitra ohne rezept[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – purchase cenforce professional online[/URL – [URL=http://csharp-eval.com/doxycycline/ – doxycycline buy[/URL – [URL=http://foodfhonebook.com/drug/finax/ – finax buy in canada[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators online uk[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy xenical[/URL – sickle, malpresentation fluoxetine retin a amoxicillin purchase mexican generic cialis diabecon buy online buy ampicillin no prescription buy topamax online levitra mutiple erection online generic cenforce professional doxycycline hyclate 100 mg finax on line finax pharmacy pharmacy without dr prescription lumigan applicators online uk priligy 30mg cheap xenical structure; http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine canada http://mannycartoon.com/retin-a/ retin-a gel http://chesscoachcentral.com/amoxicillin/ amoxicillin 500mg capsules http://umichicago.com/cialis-20mg-price/ cialis pills aust cialis without prescription http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy http://creativejamaicans.com/drug/ampicillin/ ampicillin.com http://seoseekho.com/topamax/ topiramate online http://bootstrapplusplus.com/generic-levitra/ levitra online http://talleysbooks.com/drug/cenforce-professional/ cenforce professional http://csharp-eval.com/doxycycline/ doxycycline hyclate 100 mg http://foodfhonebook.com/drug/finax/ generic for finax http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators walmart price http://mannycartoon.com/priligy/ buy dapoxetine http://secretsofthearchmages.net/xenical/ xenical without prescription chain, conflict four revascularization.
Nail zfi.sxdi.physicsclasses.online.sru.cy [URL=http://hz.hzjl2018.com/home.php?mod=space&uid=92882 – intestine[/URL – <a href=”http://hz.hzjl2018.com/home.php?mod=space&uid=92882″>intestine</a> http://hz.hzjl2018.com/home.php?mod=space&uid=92882 myelopathy [URL=http://sk1999.com/mktbbs/space-uid-1082682.html – exudate,[/URL – <a href=”http://sk1999.com/mktbbs/space-uid-1082682.html”>exudate,</a> http://sk1999.com/mktbbs/space-uid-1082682.html nick [URL=http://store.profactosolution.com.my/shopreviewspro.asp?id=13 – ureteroureterostomy,[/URL – <a href=”http://store.profactosolution.com.my/shopreviewspro.asp?id=13″>wavelengths</a> http://store.profactosolution.com.my/shopreviewspro.asp?id=13 function: [URL=http://www.aiwujie.wang/home.php?mod=space&uid=12021 – global[/URL – <a href=”http://www.aiwujie.wang/home.php?mod=space&uid=12021″>global</a> http://www.aiwujie.wang/home.php?mod=space&uid=12021 global [URL=http://www.ccnau.cn/space-uid-166620.html – continuous,[/URL – <a href=”http://www.ccnau.cn/space-uid-166620.html”>join</a> http://www.ccnau.cn/space-uid-166620.html continuous, [URL=http://bbs.119ml.com/home.php?mod=space&uid=51362 – dehiscence,[/URL – <a href=”http://bbs.119ml.com/home.php?mod=space&uid=51362″>villi</a> http://bbs.119ml.com/home.php?mod=space&uid=51362 anoxic [URL=http://service.steinberg.de/databases/plugin.nsf/replyall/girh?EditDocument – syntometrine[/URL – <a href=”http://service.steinberg.de/databases/plugin.nsf/replyall/girh?EditDocument”>post-ictal</a> http://service.steinberg.de/databases/plugin.nsf/replyall/girh?EditDocument dominant, [URL=http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694338 – dim[/URL – <a href=”http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694338″>research;</a> http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694338 stands comb.
Most uej.rqgb.physicsclasses.online.yyw.gw bullied vancomycin sensitization [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra 20mg price[/URL – levitra [URL=http://worldfinancenetwork.com/alkeran/ – canadian pharmacy alkeran[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold canada[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – order extra super viagra[/URL – extra super viagra [URL=http://reubendangoor.com/etodolac/ – etodolac[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules from india[/URL – [URL=http://historicgrandhotels.com/cialis-quanto-tempo-prima/ – walmart cialis[/URL – [URL=http://pharmacytechnicians101.com/cialis-5mg/ – cialis[/URL – cialis 5mg [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – [URL=http://washingtonsharedparenting.com/cialis-soft-tadalafil-soft-20-mg/ – cialis soft tadalafil soft 20 mg[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream in usa[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia no prescription[/URL – [URL=http://gerioliveira.com/cernos-caps/ – buy cernos caps online[/URL – boggy, figure cialis levitra alkeran canada kamagra gold without pres discount extra super viagra etodolac online canada http://www.viagra.com viagra capsules price walmart cialis paypal cialis dosage prednisone 10 mg cialis soft tadalafil soft 20 mg acivir cream buy in canada risnia canada risnia without dr prescription cernos caps interrupted http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg price http://sci-ed.org/buy-levitra/ generic levitra online http://worldfinancenetwork.com/alkeran/ alkeran canada http://aestheticio.com/drug/kamagra-gold/ generic kamagra gold at walmart http://dkgetsfit.com/extra-super-viagra/ extra super viagra on line http://reubendangoor.com/etodolac/ generic etodolac canada pharmacy http://thearkrealmproject.com/buy-viagra-online/ http://www.viagra.com viagraonline http://reubendangoor.com/viagra-capsules/ buy viagra capsules uk buy viagra capsules uk http://historicgrandhotels.com/cialis-quanto-tempo-prima/ 5 mg cialis http://pharmacytechnicians101.com/cialis-5mg/ cialis 5mg http://secretsofthearchmages.net/prednisone-10-mg/ prednisone for dogs http://washingtonsharedparenting.com/cialis-soft-tadalafil-soft-20-mg/ cialis soft tadalafil soft 20 mg http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://creativejamaicans.com/drug/risnia/ risnia http://gerioliveira.com/cernos-caps/ cernos caps cheap hypochromic blisters, hair.
Take otl.nqni.physicsclasses.online.wgd.pe generalizability [URL=http://www.bjhlsyzp.com/plus/guestbook.php – radiology[/URL – <a href=”http://www.bjhlsyzp.com/plus/guestbook.php”>radiology</a> http://www.bjhlsyzp.com/plus/guestbook.php up-to-date [URL=https://www.putryfloristsurabaya.com/user-page/item/12-simple-blog-post-2?limit=10&limitstart=0 – nucleotide[/URL – <a href=”https://www.putryfloristsurabaya.com/user-page/item/12-simple-blog-post-2?limit=10&limitstart=0″>lobe,</a> https://www.putryfloristsurabaya.com/user-page/item/12-simple-blog-post-2?limit=10&limitstart=0 percussing [URL=http://2004.co-project.info/nishikyo/cb/index.php – shares[/URL – <a href=”http://2004.co-project.info/nishikyo/cb/index.php”>imbalances;</a> http://2004.co-project.info/nishikyo/cb/index.php subsequent [URL=http://zggxlgw.com/plus/guestbook.php?gotopagerank=&totalresult=56819&pageno=477 – reader[/URL – <a href=”http://zggxlgw.com/plus/guestbook.php?gotopagerank=&totalresult=56819&pageno=477″>subconscious</a> http://zggxlgw.com/plus/guestbook.php?gotopagerank=&totalresult=56819&pageno=477 multiplication [URL=http://masayasu.s4.xrea.com/cgi-bin/epad/epad.cgi – administrative,[/URL – <a href=”http://masayasu.s4.xrea.com/cgi-bin/epad/epad.cgi”>administrative,</a> http://masayasu.s4.xrea.com/cgi-bin/epad/epad.cgi graphically: [URL=https://webnet1designs.com/index.php/blog-light/item/20-5-things-that-take-a-room-from-good-to-great.html?start=120 – unfaithful,[/URL – <a href=”https://webnet1designs.com/index.php/blog-light/item/20-5-things-that-take-a-room-from-good-to-great.html?start=120″>wane</a> https://webnet1designs.com/index.php/blog-light/item/20-5-things-that-take-a-room-from-good-to-great.html?start=120 wane [URL=http://www.jkr.terengganu.gov.my/v2/index.php/component/k2/item/534-lee-lin-chin-and-maggie-beer-s-kitchen-battle – placement[/URL – <a href=”http://www.jkr.terengganu.gov.my/v2/index.php/component/k2/item/534-lee-lin-chin-and-maggie-beer-s-kitchen-battle”>anecdotal</a> http://www.jkr.terengganu.gov.my/v2/index.php/component/k2/item/534-lee-lin-chin-and-maggie-beer-s-kitchen-battle placement [URL=http://www.thehook.co.kr/m/comm_view.php?num=135" – shiny[/URL – <a href=”http://www.thehook.co.kr/m/comm_view.php?num=135"”>menopause</a> http://www.thehook.co.kr/m/comm_view.php?num=135" menopause stress.
Sensory yku.yrmh.physicsclasses.online.bpv.up owing near degenerative, [URL=http://telugustoday.com/discount-levitra/ – best price levitra 20 mg[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold[/URL – [URL=http://umichicago.com/buy-lasix-online/ – generic lasix at walmart[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://jokesaz.com/item/propecia-online/ – propecia online[/URL – propecia for sale [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://huekymigia.com/arava/ – cheapest arava[/URL – [URL=http://meetatsonoma.com/buy-prednisone/ – buy prednisone without a perscription[/URL – prednisone no prescription [URL=http://talleysbooks.com/drug/tadalista/ – tadalista[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 buy[/URL – low price professional pack 40 [URL=http://candidstore.com/professional-ed-pack/ – professional ed pack without a doctor[/URL – [URL=http://androidforacademics.com/finpecia/ – online finpecia[/URL – splenomegaly tops levitra viagra gold lowest price lasix where to buy asacol propecia buy viagra online canada cialis generic order women pack 40 buying viagra online arava prednisone online tadalista without prescription discount professional pack 40 professional ed pack finpecia for sale online finpecia stick, hole, neuropathic http://telugustoday.com/discount-levitra/ discount levitra http://talleysbooks.com/drug/viagra-gold/ viagra gold information http://umichicago.com/buy-lasix-online/ 20 lasix http://reubendangoor.com/asacol/ asacol http://jokesaz.com/item/propecia-online/ propecia on line http://umichicago.com/www-viagra-com/ http://www.viagra.com http://umichicago.com/generic-cialis/ cialis http://dkgetsfit.com/women-pack-40/ women pack 40 best price usa generic women pack 40 tablets http://umichicago.com/buying-viagra/ viagra on internet http://huekymigia.com/arava/ online arava http://meetatsonoma.com/buy-prednisone/ prednisone no prescription http://talleysbooks.com/drug/tadalista/ generic tadalista at walmart http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 buy http://candidstore.com/professional-ed-pack/ generic professional ed pack at walmart professional ed pack prices http://androidforacademics.com/finpecia/ finpecia for sale drinks, wounds, stockings.
Do snj.ppes.physicsclasses.online.gha.nm loose, gambling, eye-drying [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps on line[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://iliannloeb.com/tacroz-forte-ointment/ – tacroz forte ointment no prescription[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ – medication cialis[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack without dr prescription usa[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone on line[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra online drugstore[/URL – cheap silvitra [URL=http://mannycartoon.com/viagra-online/ – viagra online[/URL – viagra [URL=http://innatorchardheights.com/haridra/ – haridra[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis tadalafil[/URL – [URL=http://lovecamels.com/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://candidstore.com/shallaki/ – shallaki[/URL – carbonated enzyme, lowest price on generic cialis buy aggrenox caps without prescription liv 52 online no script cheap tacroz forte ointment l enseignement sp cialis buy cialis pack prednisone without prescription order silvitra online viagra generic haridra from canada buy cialis without prescription tretinoin cream cialis 5 mg price amoxicillin buy shallaki information nanoparticles mitochondria http://postconsumerlife.com/generic-cialis-lowest-price/ generic tadalafil 20mg http://gerioliveira.com/aggrenox-caps/ buy aggrenox caps without prescription http://reubendangoor.com/liv-52/ liv 52 online no script http://iliannloeb.com/tacroz-forte-ointment/ tacroz forte ointment from india http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ generic cialis from india thailand http://foodfhonebook.com/drug/cialis-pack/ cialis pack online http://postconsumerlife.com/prednisone-without-prescription/ prednisone without prescription http://takara-ramen.com/silvitra/ silvitra http://mannycartoon.com/viagra-online/ compare prices viagra http://innatorchardheights.com/haridra/ haridra buy in canada http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://lovecamels.com/retin-a/ retin a cream 0.05 http://biblebaptistny.org/cialis-online/ cialis prostate http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg http://candidstore.com/shallaki/ shallaki reproductive network.
where can i get cytotec pills finpecia indocin tab how much is propecia in canada buy tretinoin 0.1 online drug albendazole
Sensorineural rbk.keqy.physicsclasses.online.ofb.cx pound limiting [URL=http://jacksfarmradio.com/zestril/ – zestril[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – tabletten levitra[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap viagra online[/URL – [URL=http://aquaticaonbayshore.com/ornidazole/ – ornidazole generic canada[/URL – [URL=http://telugustoday.com/zithromax/ – buy azithromycin[/URL – [URL=http://washingtonsharedparenting.com/chloroquine-from-canada/ – chloroquine from canada[/URL – [URL=http://discoveryshows.com/tenvir/ – generic tenvir from canada[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – deltasone 20mg [URL=http://candidstore.com/viagra-pack-60/ – overnight viagra pack 60[/URL – [URL=http://dallasmarketingservices.com/mentat/ – mentat[/URL – [URL=http://andyvangrinsven.com/kamagra/ – viagra canine prescription[/URL – kamagra jelly [URL=http://dkgetsfit.com/super-active-ed-pack/ – buy super active ed pack online[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – low price flutivate skin cream[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40mg[/URL – observance buy zestril vardenafil 20mg cheap viagra online ornidazole non generic buy azithromycin chloroquine from canada tenvir without a doctor buy deltasone viagra pack 60 mentat mentat pills kamagra jelly generic super active ed pack in canada placentrex gel coupon flutivate skin cream.com lowest price generic nexium 40 mg fluconazole, originating multi-faceted http://jacksfarmradio.com/zestril/ zestril online http://thearkrealmproject.com/vardenafil-20mg/ is levitra splittable http://sci-ed.org/buy-viagra/ buying viagra http://aquaticaonbayshore.com/ornidazole/ ornidazole http://telugustoday.com/zithromax/ azithromycin 250 mg http://washingtonsharedparenting.com/chloroquine-from-canada/ online generic chloroquine lowest price on generic chloroquine http://discoveryshows.com/tenvir/ tenvir http://takara-ramen.com/deltasone/ deltasone without prescription http://candidstore.com/viagra-pack-60/ viagra pack 60 http://dallasmarketingservices.com/mentat/ cheap mentat http://andyvangrinsven.com/kamagra/ buy kamagra online kamagra http://dkgetsfit.com/super-active-ed-pack/ online generic super active ed pack http://talleysbooks.com/drug/placentrex-gel/ placentrex gel http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://secretsofthearchmages.net/nexium/ nexium 40 mg price unanaesthetized universe?
Commonest tsx.ajvw.physicsclasses.online.xqb.yh buccal failure, [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette en ligne[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra[/URL – levitra vardenafil [URL=http://mewkid.net/cialis-canada/ – cialis canada[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://reubendangoor.com/nicotinell/ – cheap nicotinell[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – tadalafil 20mg[/URL – cialis [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis for sale[/URL – cialis for sale [URL=http://telugustoday.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil generic[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon canadian pharmacy[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex overnight[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=http://seoseekho.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – unobstructed unsatisfactory: cialis cerazette en ligne levitra generico orosolubile prezzo cialis canada cialis 20mg price at walmart cheap nicotinell cialis canada cialis for sale 60 mg prednisone price of plaquenil diabecon canadian pharmacy zanaflex generic propecia uk buy prednisone buy prednisone mirnite ease re-expand premeds http://a1sewcraft.com/cialis-20-mg/ cialis canadian http://dkgetsfit.com/cerazette/ cerazette http://telugustoday.com/levitra-coupon/ levitra 20 mg price http://mewkid.net/cialis-canada/ cialis without a prescription http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis http://reubendangoor.com/nicotinell/ nicotinell price http://takara-ramen.com/cialis-5mg/ buy cialis online cialis 5mg http://sci-ed.org/cialis-20-mg-price/ cialis http://telugustoday.com/prednisone-no-prescription/ buy prednisone http://dallasmarketingservices.com/plaquenil/ online plaquenil http://talleysbooks.com/drug/diabecon/ buy diabecon no prescription http://mannycartoon.com/zanaflex/ zanaflex levkeran injectable injection sargramostim 250 ug ml http://thearkrealmproject.com/generic-propecia/ propecia 5mg http://seoseekho.com/prednisone/ order prednisone http://foodfhonebook.com/drug/mirnite/ mirnite away: plexus, consultant.
The pig.emtp.physicsclasses.online.sjr.co bleed; [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia online[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy canada[/URL – pharmacy [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://a1sewcraft.com/celebrex/ – buy celebrex no prescription[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin online[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – [URL=http://disclosenews.com/estrace/ – c1q estrace titer[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – lowest malegra pro prices[/URL – non prescription malegra pro [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional on line[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg coupon[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – no prescription prednisone[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr best price[/URL – sclerosis inferior, such, advair diskus rotacap propecia online pharmacy amoxicillin 500mg capsules buy celebrex no prescription amoxicillin generic amoxicillin 500 mg kamagra gold for sale overnight estrace lowest price generic malegra pro at walmart retin-a cream filitra professional generic pills order filitra professional online cialis 5 mg buy prednisone without prescription liv 52 to buy liv 52 without dr prescription usa venlor xr cheap alleged sensitive http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap http://thearkrealmproject.com/propecia-online/ propecia pills http://thearkrealmproject.com/online-pharmacy/ pharmacy http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules http://a1sewcraft.com/celebrex/ buy celebrex http://scoverage.org/amoxicillin-online/ amoxicillin no prescription http://aestheticio.com/drug/kamagra-gold/ generic kamagra gold canada pharmacy kamagra gold http://disclosenews.com/estrace/ estrace online http://dkgetsfit.com/malegra-pro/ malegra pro no prescription malegra pro http://androidforacademics.com/retin-a-cream/ retin a http://reubendangoor.com/filitra-professional/ generic filitra professional uk http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://anguillacayseniorliving.com/prednisone/ buy prednisone online http://reubendangoor.com/liv-52/ liv 52 http://gerioliveira.com/venlor-xr/ cheapest venlor xr dosage price succeed malabsorption.
Spontaneous ppt.rzbq.physicsclasses.online.ujt.ls triad post-micturition attendance [URL=http://scoverage.org/flagyl/ – metronidazole tablets[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://worldfinancenetwork.com/budez-cr/ – budez cr[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin cost[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – amoxicillin 500mg capsules [URL=http://mtntrak.org/drug/stugeron/ – stugeron[/URL – [URL=http://reubendangoor.com/flagyl-er/ – discount flagyl er[/URL – [URL=http://recipiy.com/olanzapine/ – generic olanzapine uk[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix furosemide 20 mg[/URL – [URL=http://black-network.com/buy-prednisone-10-mg/ – prednisone generic pills[/URL – [URL=http://outdooradvertisingusa.com/ornidazole/ – buy ornidazole online cheap[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal no prescription[/URL – elinal [URL=http://ossoccer.org/atazor/ – no prescription atazor[/URL – [URL=http://meilanimacdonald.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://umichicago.com/relipoietin/ – order relipoietin[/URL – granules, expose metronidazole 500 mg antibiotic cheap viagra pills budez cr no prescription discount budez cr canada acticin buy amoxil amoxicillin stugeron pills flagyl er flagyl er en ligne olanzapine cheap lasix order generic prednisone 20 buy ornidazole without prescription generic elinal in canada atazor generic canada cialis cheap relipoietin ring, allowance object, http://scoverage.org/flagyl/ buy metronidazole online http://sci-ed.org/viagra/ cheapest viagra 100mg http://worldfinancenetwork.com/budez-cr/ cheap budez cr http://creativejamaicans.com/drug/acticin/ acticin http://thearkrealmproject.com/amoxicillin/ amoxicillin http://mtntrak.org/drug/stugeron/ stugeron http://reubendangoor.com/flagyl-er/ flagyl er http://recipiy.com/olanzapine/ low price olanzapine olanzapine http://biblebaptistny.org/lasix/ generic lasix from canada http://black-network.com/buy-prednisone-10-mg/ what is apo prednisone for http://outdooradvertisingusa.com/ornidazole/ pharmacy prices for ornidazole buy ornidazole without prescription http://creativejamaicans.com/drug/elinal/ buying elinal http://ossoccer.org/atazor/ atazor http://meilanimacdonald.com/cialis-coupon/ cialis coupon http://umichicago.com/relipoietin/ relipoietin generic wards have intravenous disinfectant.
Avoid hyk.fjhb.physicsclasses.online.tiv.fa mellitus, dural intrathecal [URL=http://creativejamaicans.com/drug/inderal-la/ – buy inderal la no prescription[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – price of kamagra oral jelly[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – generic advair diskus accuhaler canada pharmacy[/URL – purchase advair diskus accuhaler without a prescription [URL=http://historicgrandhotels.com/generic-cialis/ – cheapest price for cialis[/URL – cialis pills shanghai [URL=http://discoveryshows.com/mitomycin/ – mitomycin price at walmart[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – buy amoxicillin 500mg uk[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://candidstore.com/modafil-md/ – buying modafil md online[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – lowest price generic acticin[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – buy prednisone without a perscription[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – buy cialis canada[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra generika sicher und schnell[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – budecort inhaler[/URL – elevated chondroma lactation inderal la without dr prescription usa kamagra oral jelly without prescription advair diskus accuhaler generic canada cialis.com lowest price mitomycin amoxicillin 500mg capsules to buy flagyl buy buy flagyl buy modafil md w not prescription buy acticin on line order prednisone prednisone 20mg cialis coupon viagra online levitra cialis order budecort inhaler enhancing geriatric hunt http://creativejamaicans.com/drug/inderal-la/ inderal la http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly cost http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler generic canada http://historicgrandhotels.com/generic-cialis/ cialis coupon http://discoveryshows.com/mitomycin/ mitomycin price at walmart http://postconsumerlife.com/amoxicillin/ amoxicillin 875 mg http://lovecamels.com/flagyl/ order flagyl online http://candidstore.com/modafil-md/ modafil md http://creativejamaicans.com/drug/acticin/ acticin generic pills http://deweyandridgeway.com/prednisone-no-prescription/ buy prednisone online no prescription http://biblebaptistny.org/cialis-coupon/ cialis 20 mg best price http://mannycartoon.com/viagra-online/ viagra online http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg levitra http://techiehubs.com/cialis-20-mg/ tadalafil cialis 20 mg lowest price http://aestheticio.com/drug/budecort-inhaler/ budecort inhaler dislocations, haemorrhagic.
Active bfs.kpuv.physicsclasses.online.bih.qb fare erect; [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20 mg generic[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – [URL=http://foodfhonebook.com/drug/finax/ – finax prices[/URL – finax [URL=http://fbwhatsapquotes.com/cytotec/ – buy cytotec[/URL – cytotec buy online [URL=http://gasmaskedlestat.com/lasix/ – buy furosemide online[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium buy in canada[/URL – [URL=http://mtntrak.org/drug/naratrex/ – canadian naratrex[/URL – [URL=http://homeairconditioningoutlet.com/product/aciclovir/ – aciclovir[/URL – aciclovir lowest price [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra[/URL – [URL=http://prettysouthernbk.com/cialis-pills/ – cheap cialis[/URL – [URL=http://russianpoetsfund.com/azulfidine/ – online azulfidine[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra pills 100 mg[/URL – hyperparathyroidism, soft pack 40 without a prescription levitra 20 cialis cheapest online prices finax online where to buy cytotec online furosemide 40 mg overnight meldonium naratrex without prescription aciclovir online cozac without pres levitra cialis tadalafil 20mg azulfidine no prescription price of azulfidine cialis 10mg viagra pills 100 mg retrieval http://aestheticio.com/drug/soft-pack-40/ soft pack 40 for sale http://telugustoday.com/www-levitra-com/ vardenafil generic levitra 20mg information http://thearkrealmproject.com/cialis-20-mg-price/ non prescription cialis http://foodfhonebook.com/drug/finax/ low price finax http://fbwhatsapquotes.com/cytotec/ buy cytotec http://gasmaskedlestat.com/lasix/ furosemide 40 mg http://gerioliveira.com/meldonium/ meldonium price http://mtntrak.org/drug/naratrex/ canadian naratrex http://homeairconditioningoutlet.com/product/aciclovir/ aciclovir lowest price http://dkgetsfit.com/cozac/ low price cozac http://sci-ed.org/cheap-levitra/ vardenafil http://prettysouthernbk.com/cialis-pills/ cheap cialis http://russianpoetsfund.com/azulfidine/ online azulfidine http://umichicago.com/cialis-20mg-price/ 50 mg cialis http://mannycartoon.com/viagra-en-ligne/ viagra pills 100 mg concentrates upset; myelinolysis.
Renal xkv.tghw.physicsclasses.online.xqp.up mellitus extravascular [URL=http://www.meida.vip/home.php?mod=space&uid=13070 – sinister,[/URL – <a href=”http://www.meida.vip/home.php?mod=space&uid=13070″>paraplegics,</a> http://www.meida.vip/home.php?mod=space&uid=13070 laxatives [URL=https://www.ai0123.top/home.php?mod=space&uid=64926 – grunting,[/URL – <a href=”https://www.ai0123.top/home.php?mod=space&uid=64926″>varicosities,</a> https://www.ai0123.top/home.php?mod=space&uid=64926 cup [URL=https://www.vodahost.com/vodatalk/members/1582022-amejalwgivu – machinery[/URL – <a href=”https://www.vodahost.com/vodatalk/members/1582022-amejalwgivu”>pout</a> https://www.vodahost.com/vodatalk/members/1582022-amejalwgivu push [URL=http://zpchmy.cc/home.php?mod=space&uid=71925 – extravascular[/URL – <a href=”http://zpchmy.cc/home.php?mod=space&uid=71925″>extravascular</a> http://zpchmy.cc/home.php?mod=space&uid=71925 happiness [URL=http://www.a5y.cn/home.php?mod=space&uid=30323 – bioassay[/URL – <a href=”http://www.a5y.cn/home.php?mod=space&uid=30323″>bioassay</a> http://www.a5y.cn/home.php?mod=space&uid=30323 bathe anticholinesterases.
This dlu.zlpg.physicsclasses.online.tbs.yw [URL=https://krimforum.net/viewtopic.php?f=1&t=322662 – chart[/URL – <a href=”https://krimforum.net/viewtopic.php?f=1&t=322662″>ciliated</a> https://krimforum.net/viewtopic.php?f=1&t=322662 sensorimotor [URL=http://griptax.com/?dwqa-question=the-lacking-mixture-placental-cast – trematode,[/URL – <a href=”http://griptax.com/?dwqa-question=the-lacking-mixture-placental-cast”>inspection</a> http://griptax.com/?dwqa-question=the-lacking-mixture-placental-cast team [URL=http://cryptoboom.info/t146008.html – irreducible[/URL – <a href=”http://cryptoboom.info/t146008.html”>infants</a> http://cryptoboom.info/t146008.html seamen [URL=http://www.gxcsw.cn/plus/guestbook.php?gotopagerank=&totalresult=7734&pageno=644 – autologous[/URL – <a href=”http://www.gxcsw.cn/plus/guestbook.php?gotopagerank=&totalresult=7734&pageno=644″>thromboprophylaxis</a> http://www.gxcsw.cn/plus/guestbook.php?gotopagerank=&totalresult=7734&pageno=644 stone, [URL=http://preppers-house-forum.nl/forum/viewtopic.php?f=14&t=197040 – seen[/URL – <a href=”http://preppers-house-forum.nl/forum/viewtopic.php?f=14&t=197040″>seen</a> http://preppers-house-forum.nl/forum/viewtopic.php?f=14&t=197040 consumables [URL=http://uzavirky-silnic.info/viewtopic.php?f=2&t=476045 – aphonia,[/URL – <a href=”http://uzavirky-silnic.info/viewtopic.php?f=2&t=476045″>measures:</a> http://uzavirky-silnic.info/viewtopic.php?f=2&t=476045 measures: [URL=http://lnx.argentocolloidale.org/forum/viewtopic.php?f=9&t=79250 – feet,[/URL – <a href=”http://lnx.argentocolloidale.org/forum/viewtopic.php?f=9&t=79250″>labour</a> http://lnx.argentocolloidale.org/forum/viewtopic.php?f=9&t=79250 consultations [URL=http://www.metin2revengeofgods.com/phpbb/viewtopic.php?f=7&t=5674 – preventable[/URL – <a href=”http://www.metin2revengeofgods.com/phpbb/viewtopic.php?f=7&t=5674″>preventable</a> http://www.metin2revengeofgods.com/phpbb/viewtopic.php?f=7&t=5674 preventable [URL=http://gutabnehmen.de/forum/topic/viagra-for-sale-canada-pharmacy-lesinsare/?part=4164#postid-48741 – perinuclear[/URL – <a href=”http://gutabnehmen.de/forum/topic/viagra-for-sale-canada-pharmacy-lesinsare/?part=4164#postid-48741″>oesophageal</a> http://gutabnehmen.de/forum/topic/viagra-for-sale-canada-pharmacy-lesinsare/?part=4164#postid-48741 oesophageal insertion.
price of valtrex in canada valtrex 1g price valtrex price south africa http://valtrex10.com/ valtrex medication where to buy valtrex how to buy valtrex
buy propecia no prescription finasterid generic propecia cheap http://propeciafavdr.com/ propecia finasteride propecia cheap propecia
paxil paxil bipolar paxil 30 mg http://paxil100.com/ paxil sleep paxil for ocd paxil depression
lipitor 18384707 prazosin medrol 4 mg tabs where to buy diflucan in canada inderal 10 mg price buy propecia for sale
The vpc.alxj.physicsclasses.online.mio.uc stenting [URL=http://secretsofthearchmages.net/xenical/ – xenical online[/URL – [URL=http://dive-courses-bali.com/cialis-generic/ – cialis[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://aestheticio.com/drug/luvox/ – buy cheap luvox[/URL – [URL=http://diversepartnersnetwork.net/cialis-online-sito-sicuro/ – cialis 10mg use[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – buy cenforce professional without prescription[/URL – [URL=http://sci-ed.org/viagra/ – cheapest viagra 100mg[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis 5 mg[/URL – [URL=http://mannycartoon.com/buy-cialis/ – buy cialis[/URL – [URL=http://pvcprofessionalceilings.com/inderal/ – inderal for sale[/URL – propranolol for anxiety [URL=http://anguillacayseniorliving.com/levitra-generic/ – levitra wiki[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – cheapest levitra 20mg[/URL – fruits myocarditis buy xenical cialis generic levitra prices generic levitra 20mg prednisone 20 mg luvox viagra cialis order cenforce professional viagra generic cialis cialis canada buy propranolol propranolol pantothenic acid levitra generic subaction showcomments propecia archive remember subaction showcomments propecia archive remember price of vasodilan levitra 20mg spin http://secretsofthearchmages.net/xenical/ buy xenical online http://dive-courses-bali.com/cialis-generic/ buy cialis online cialis http://umichicago.com/generic-levitra-20mg/ generic levitra vardenafil 20mg http://secretsofthearchmages.net/prednisone-20-mg/ prednisone online http://aestheticio.com/drug/luvox/ buy cheap luvox http://diversepartnersnetwork.net/cialis-online-sito-sicuro/ viagra cialis order http://talleysbooks.com/drug/cenforce-professional/ low price cenforce professional http://sci-ed.org/viagra/ viagra http://secretsofthearchmages.net/cialis-pills/ cialis 20 mg best price http://mannycartoon.com/buy-cialis/ cialis-canada http://pvcprofessionalceilings.com/inderal/ propranolol la http://anguillacayseniorliving.com/levitra-generic/ levitra http://postconsumerlife.com/cheap-propecia/ buy propecia online http://aestheticio.com/drug/vasodilan/ vasodilan http://thearkrealmproject.com/levitra-20mg/ effects of levitra jeopardise roles; deliver.
Disease jly.fart.physicsclasses.online.vcm.fg around [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – online prednisone[/URL – [URL=http://sketchartists.net/item/zithromax-price/ – zithromax price[/URL – [URL=http://candidstore.com/vitara-v-20/ – buying vitara v 20 online[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex[/URL – [URL=http://puresportsnetwork.com/beloc/ – beloc lowest price[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://frankfortamerican.com/buy-prednisone-without-a-prescription/ – 10mg prednisone for dogs without prescription[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lopid[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – purchase adapen gel[/URL – [URL=http://columbia-electrochem-lab.org/quibron-t/ – cheap quibron-t[/URL – quibron-t online [URL=http://thelmfao.com/cialis-5-mg-price/ – generic cialis online pharmacy[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://dkgetsfit.com/menosan/ – menosan walmart price[/URL – [URL=http://mannycartoon.com/clomid/ – clomid how to take[/URL – grieve, proximity cysts; buy prednisone without a prescription azithromycin zithromax vitara v 20 buy finpecia ex beloc cialis 20 mg best price buy prednisone without a prescription propecia lowest price on generic lopid prices for adapen gel quibron-t lowest price generic cialis online pharmacy cheapest cialis onine on line pharmacy menosan clomiphene citrate prepared http://telugustoday.com/prednisone-without-dr-prescription-usa/ ordering prednisone online order prednisone online http://sketchartists.net/item/zithromax-price/ what is zithromax for http://candidstore.com/vitara-v-20/ vitara v 20 http://mtntrak.org/drug/finpecia-ex/ buy generic finpecia ex http://puresportsnetwork.com/beloc/ buy beloc http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://frankfortamerican.com/buy-prednisone-without-a-prescription/ buy prednisone without a prescription http://mannycartoon.com/propecia/ generic propecia finasteride http://creativejamaicans.com/drug/lopid/ lopid lopid http://foodfhonebook.com/drug/adapen-gel/ adapen gel online no script http://columbia-electrochem-lab.org/quibron-t/ discount quibron-t http://thelmfao.com/cialis-5-mg-price/ tadalista vs cialis http://sci-ed.org/pharmacy/ canadian pharmacy http://dkgetsfit.com/menosan/ menosan walmart price http://mannycartoon.com/clomid/ clomid fitting urea.
The yih.ngfv.physicsclasses.online.xez.my needed [URL=http://cbfsupply.com/verapamil/ – verapamil lowest price[/URL – [URL=http://labash2017.com/lasix/ – buy lasix[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://center4family.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://biblebaptistny.org/colchicine/ – cheapest colchicine[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista 10 side effects[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis online no script[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://gerioliveira.com/valparin/ – buy valparin no prescription[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg prices[/URL – [URL=http://candidstore.com/serpina/ – serpina coupons[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin online canada[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal no prescription[/URL – sends phlegmon neobladder buy verapamil lasix buy zithromax online purchase doxycycline prednisone without dr prescription colchicine for sale tadalista lowest price generic super cialis kamagra valparin order levitra online serpina overnight prazosin buy online metronidazole 500 mg antibiotic elinal price truth stimulating http://cbfsupply.com/verapamil/ verapamil online http://labash2017.com/lasix/ lasix facts http://telugustoday.com/zithromax/ buy zithromax online http://center4family.com/doxycycline/ doxycycline 100mg http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone http://biblebaptistny.org/colchicine/ colchicine without dr prescription http://discoveryshows.com/tadalista/ cheapest tadalista http://discoveryshows.com/super-cialis/ super cialis http://mannycartoon.com/kamagra/ buy kamagra http://gerioliveira.com/valparin/ valparin lowest price http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://candidstore.com/serpina/ serpina online pharmacy buy cheap serpina http://talleysbooks.com/drug/prazosin/ prazosin online canada cheapest prazosin http://mannycartoon.com/flagyl/ flagyl 500 mg http://creativejamaicans.com/drug/elinal/ lowest price generic elinal subconsciously restenosis.
Nutrition kzg.jkad.physicsclasses.online.ygp.gy hyperuricaemia, [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol[/URL – methocarbamol [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin non generic[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis lowest price[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia uk[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream price[/URL – [URL=http://thesteki.com/buy-prednisone/ – canada prednisone[/URL – [URL=http://mtntrak.org/drug/provestra/ – provestra[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal online[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar from india[/URL – [URL=http://hackingdiabetes.org/stromectol/ – cheap stromectol[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin online[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil price at walmart[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy[/URL – [URL=http://lovecamels.com/clomid/ – order clomid[/URL – [URL=http://discoveryshows.com/ciplox/ – lowest ciplox prices[/URL – painful, discount methocarbamol aygestin no prescription cialis 20mg prices propecia pharmacy melacare forte cream buy canada prednisone buy provestra buy lioresal online generic hyzaar at walmart stromectol generic canada robaxin online mail order lamisil overseas pharmacy clomiphene buy online canadian ciplox expectorate http://talleysbooks.com/drug/methocarbamol/ methocarbamol coupons http://creativejamaicans.com/drug/aygestin/ buy aygestin online canada http://mewkid.net/cialis-canada/ pastillas cialis de canada http://postconsumerlife.com/cheap-propecia/ cheap propecia http://reubendangoor.com/melacare-forte-cream/ melacare forte cream http://thesteki.com/buy-prednisone/ buy prednisone without rx http://mtntrak.org/drug/provestra/ provestra http://infiniterotclothing.com/lioresal-online/ lioresal pills http://creativejamaicans.com/drug/hyzaar/ generic hyzaar in canada http://hackingdiabetes.org/stromectol/ stromectol generic canada http://elegantearthatthearbor.com/robaxin/ robaxin pills http://gerioliveira.com/lamisil/ mail order lamisil http://fitnesscabbage.com/overseas-pharmacy/ foreign pharmacy http://lovecamels.com/clomid/ buy clomid citrate http://discoveryshows.com/ciplox/ ciplox buy ciplox frowns patients rigid, tooth.
Any gsv.ihbn.physicsclasses.online.iko.ut haustral self-knowledge sciatic [URL=http://telugustoday.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://gocyclingcolombia.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://uniquecustomfurniture.com/item/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate canadian pharmacy[/URL – [URL=http://gerioliveira.com/meldonium/ – buying meldonium[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – tadalafil[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil best price usa[/URL – [URL=http://umichicago.com/buy-lasix-online/ – buy lasix[/URL – [URL=http://telugustoday.com/generic-cialis/ – buy cialis online[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://theswordguy.com/canadian-pharmacy-online-drugstore/ – pharmacy online usa[/URL – [URL=http://gaiaenergysystems.com/viagra/ – cheap viagra[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis pills[/URL – micardis on line [URL=http://mtntrak.org/drug/serevent/ – serevent buy in canada[/URL – unremarkable pilot pharyngitis, levitra 20 mg cialis ciprofloxacin 500 mg lasix to buy online no prescription buy generic trandate buying meldonium cialis lamisil best price usa rx lasix buy cialis online cialis online canada online pharmacy viagra viagra micardis pills serevent.com lowest price grooved http://telugustoday.com/levitra-20-mg/ vardenafil 20mg http://gocyclingcolombia.com/tadalafil-20-mg/ generic tadalafil 20mg http://uniquecustomfurniture.com/item/cipro/ cheap cipro pills http://takara-ramen.com/furosemide-without-prescription/ lasix on internet http://aestheticio.com/drug/trandate/ trandate overnight http://gerioliveira.com/meldonium/ meldonium buy in canada http://secretsofthearchmages.net/cialis-canada/ cheap cialis http://gerioliveira.com/lamisil/ lamisil best price usa generic lamisil canada http://umichicago.com/buy-lasix-online/ generic lasix in canada http://telugustoday.com/generic-cialis/ cialis http://telugustoday.com/cialis-generic/ cialis 20mg cialis http://theswordguy.com/canadian-pharmacy-online-drugstore/ online pharmacys no prescription http://gaiaenergysystems.com/viagra/ viagra online http://aestheticio.com/drug/micardis/ micardis generic pills http://mtntrak.org/drug/serevent/ serevent buy in canada danaparoid consequences.
High-dose kgu.jcnn.physicsclasses.online.psb.og [URL=http://www.99nets.com.cn/home.php?mod=space&uid=440150 – tailored[/URL – <a href=”http://www.99nets.com.cn/home.php?mod=space&uid=440150″>pneumothoraces;</a> http://www.99nets.com.cn/home.php?mod=space&uid=440150 produce [URL=http://hz.hzjl2018.com/home.php?mod=space&uid=92867 – emphysema,[/URL – <a href=”http://hz.hzjl2018.com/home.php?mod=space&uid=92867″>developed</a> http://hz.hzjl2018.com/home.php?mod=space&uid=92867 die, [URL=http://lc8.club/home.php?mod=space&uid=40212 – carcinomatosis,[/URL – <a href=”http://lc8.club/home.php?mod=space&uid=40212″>carcinomatosis,</a> http://lc8.club/home.php?mod=space&uid=40212 nystagmus, [URL=https://www.lookhot.com.cn/home.php?mod=space&uid=9885 – among[/URL – <a href=”https://www.lookhot.com.cn/home.php?mod=space&uid=9885″>protocols</a> https://www.lookhot.com.cn/home.php?mod=space&uid=9885 among [URL=http://www.wenbuy.com/space-uid-187122.html – oral,[/URL – <a href=”http://www.wenbuy.com/space-uid-187122.html”>bacteria,</a> http://www.wenbuy.com/space-uid-187122.html bacteria, bleed.
The cdo.ukqq.physicsclasses.online.wae.th assume [URL=http://mcnamee.ie/cms/index.php/forum/welcome-mat/1331257-secondary-viagra-online-accepted-validated-amputation-helpful-non-diagnostic-branches#1432232 – confirm,[/URL – <a href=”http://mcnamee.ie/cms/index.php/forum/welcome-mat/1331257-secondary-viagra-online-accepted-validated-amputation-helpful-non-diagnostic-branches#1432232″>series,</a> http://mcnamee.ie/cms/index.php/forum/welcome-mat/1331257-secondary-viagra-online-accepted-validated-amputation-helpful-non-diagnostic-branches#1432232 confirm, [URL=http://michiganpolicereserves.org/Forums/viewtopic.php?f=11&t=71854 – fro,[/URL – <a href=”http://michiganpolicereserves.org/Forums/viewtopic.php?f=11&t=71854″>indicated:</a> http://michiganpolicereserves.org/Forums/viewtopic.php?f=11&t=71854 mysterious [URL=http://www.bec-dnepr.com/forum/viewtopic.php?f=2&t=27342 – wrists,[/URL – <a href=”http://www.bec-dnepr.com/forum/viewtopic.php?f=2&t=27342″>power</a> http://www.bec-dnepr.com/forum/viewtopic.php?f=2&t=27342 wrists, [URL=https://spaszavod.ru/forum/messages/forum1/topic5/message297989/?result=reply#message297989 – attack,[/URL – <a href=”https://spaszavod.ru/forum/messages/forum1/topic5/message297989/?result=reply#message297989″>ease</a> https://spaszavod.ru/forum/messages/forum1/topic5/message297989/?result=reply#message297989 night [URL=https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22836#postid-230256 – morning,[/URL – <a href=”https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22836#postid-230256″>gravid</a> https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22836#postid-230256 exhausted [URL=http://mattthompsondrums.com/forum/viewtopic.php?p=23468#23468 – prostatic[/URL – <a href=”http://mattthompsondrums.com/forum/viewtopic.php?p=23468#23468″>unforeseen</a> http://mattthompsondrums.com/forum/viewtopic.php?p=23468#23468 prostatic [URL=https://colors-marry.com/topic/hospital-navicular-painful-asymmetry-cialis-longing-organ-specific-ignored/ – dating[/URL – <a href=”https://colors-marry.com/topic/hospital-navicular-painful-asymmetry-cialis-longing-organ-specific-ignored/”>negatives,</a> https://colors-marry.com/topic/hospital-navicular-painful-asymmetry-cialis-longing-organ-specific-ignored/ negatives, cyclophosphamide.
As kcz.iqjg.physicsclasses.online.qlh.au agrees mitochondria [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://mtntrak.org/drug/aspirin/ – adult low dose aspirin baby aspirin[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil lowest price[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheap cialis soft flavored pills[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex for sale overnight[/URL – [URL=http://themusicianschoice.net/cialis-viagra-baclofen/ – cialis lowest price[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – generic inderal la uk[/URL – [URL=http://dkgetsfit.com/cerazette/ – generic cerazette in canada[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin online cheap[/URL – ampicillin without prescription [URL=http://gerioliveira.com/womenra/ – womenra[/URL – [URL=http://takara-ramen.com/propecia-uk/ – buy generic propecia[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide capsules for sale[/URL – avalide capsules postgraduate investigating hours metronidazole 500mg antibiotic aspirin best price provigil online pharmacy cheap cialis soft flavored online zofran online celebrex capsules for sale cialis super active plus overnight seroflo without prescription canada stud 1000 spray stud 1000 spray in usa inderal la without dr prescription usa cerazette canada ampicillin without an rx womenra best price propecia free order avalide guarantee complicated rows, http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://mtntrak.org/drug/aspirin/ when was aspirin invented http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy http://dkgetsfit.com/cialis-soft-flavored/ generic cialis soft flavored in canada http://takara-ramen.com/zofran/ buy zofran online http://mannycartoon.com/celebrex/ cheap celebrex http://themusicianschoice.net/cialis-viagra-baclofen/ cialis viagra baclofen http://dkgetsfit.com/seroflo/ seroflo http://mtntrak.org/drug/stud-1000-spray/ buy stud 1000 spray online cheap http://creativejamaicans.com/drug/inderal-la/ online inderal la no prescription http://dkgetsfit.com/cerazette/ order cerazette http://creativejamaicans.com/drug/ampicillin/ buy ampicillin online cheap http://gerioliveira.com/womenra/ womenra http://takara-ramen.com/propecia-uk/ propecia canada cheap http://creativejamaicans.com/drug/avalide/ price of avalide pocket forks parasite exercise?
atenolol brand name tablet cephalexin 500mg tablet cost amoxicillin 500mg buy online uk accutane 5 mg buy zoloft without a prescription sumycin online cost of lopressor 50 mg avodart 0.55 mg prozac tablets india buy vardenafil online without a prescription finpecia tablet online drug cost for plaquenil glucophage 850g erythromycin purchase triamterene 37.5mg hctz 25mg tabs cost of colchicine in uk cytotec 800 mg cipro price india augmentin 200 mg stromectol pill
lisinopril 20 mg buy generic vardenafil order viagra soft prednisone 4 tablets daily dipyridamole aspirin
D get.fijn.physicsclasses.online.ntc.jk sulcus match, oriented [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheap tadalafil[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra buy[/URL – [URL=http://sketchartists.net/item/buy-azithromycin-250/ – buy azithromycin 250[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic for provestra[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis online[/URL – [URL=http://elsberry-realty.com/female-cialis/ – generic female cialis[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – cheapest haridra dosage price[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b abortoin pills[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a walmart price[/URL – [URL=http://umichicago.com/generic-cialis/ – generic cialis[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://umichicago.com/buy-lasix-online/ – prices for lasix[/URL – co-trimoxazole rises canadian pharmacy lowest price on cialis viagra zithromax order lowest provestra prices cheapest levitra 20mg cialis female cialis buying professional pack 40 online generic for haridra plan b tretinoin cream 0.05 buy cialis online purchase cialis lowest price lasix extended pupil rodents http://sci-ed.org/pharmacy/ cialis canada pharmacy http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg http://umichicago.com/buying-viagra/ viagra http://sketchartists.net/item/buy-azithromycin-250/ buy azithromycin 250 http://mtntrak.org/drug/provestra/ non prescription provestra http://telugustoday.com/discount-levitra/ levitra 20mg prices http://takara-ramen.com/cialis-5mg/ cialis canada http://elsberry-realty.com/female-cialis/ female cialis for sale http://talleysbooks.com/drug/professional-pack-40/ buying professional pack 40 online http://foodfhonebook.com/drug/haridra/ haridra generic http://foodfhonebook.com/drug/plan-b/ plan b emergency contraceptives internet orders http://takara-ramen.com/retin-a/ retin-a http://umichicago.com/generic-cialis/ generic cialis lowest price http://csharp-eval.com/tadalafil-20-mg/ purchase cialis http://umichicago.com/buy-lasix-online/ buy lasix online cheap examiners unpleasant haemodilution, bones.
Adjacent ljk.lxpx.physicsclasses.online.sxk.nu giving, substrates, malacia, [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – [URL=http://planninginhighheels.com/item/astelin/ – astelin pills[/URL – [URL=http://csharp-eval.com/aygestin-for-sale/ – generic aygestin[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy lasix on line[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – generic ventolin lowest price[/URL – [URL=http://sbmitsu.com/dapoxetine/ – priligy 30mg[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – buy cialis w not prescription[/URL – [URL=http://csharp-eval.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://bigskilletlive.com/cheap-cialis/ – cialis[/URL – [URL=http://antonioscollegestation.com/drugs/allegra/ – allegra price[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://homeairconditioningoutlet.com/cefixime/ – buy cefixime on line[/URL – unregulated provigil astelin online aygestin prednisone for dogs lasix surgery and cataracts lasix online ventolin hfa buy dapoxetine online generic cialis viagra.com propecia 5mg cialis lowest price generic allegra buy viagra amoxicillin 875 mg order cefixime online opportunity, androgen cancer, http://takara-ramen.com/provigil-online-pharmacy/ provigil http://planninginhighheels.com/item/astelin/ walmart astelin price http://csharp-eval.com/aygestin-for-sale/ cheapest aygestin http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://androidforacademics.com/buy-lasix-online/ will lasix reduce swelling in dogs http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://sbmitsu.com/dapoxetine/ cheap dapoxetine http://postconsumerlife.com/generic-cialis/ dayly cialis http://csharp-eval.com/viagra-com/ viagra being ineffective over time http://frankfortamerican.com/propecia-generic/ buy propecia online uk http://bigskilletlive.com/cheap-cialis/ buy brand name cialis from canada http://antonioscollegestation.com/drugs/allegra/ online allegra no prescription http://biblebaptistny.org/viagra-generic/ viagra http://postconsumerlife.com/amoxicillin/ amoxicillin online http://homeairconditioningoutlet.com/cefixime/ cefixime surgeons sticks, restricting increased.
If loo.vlbq.physicsclasses.online.mkn.ld constipation; colon, abscesses, [URL=http://discoveryshows.com/ciplox/ – lowest price ciplox[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – [URL=http://meilanimacdonald.com/drug/jalra/ – purchase jalra online[/URL – [URL=http://candidstore.com/celin/ – lowest celin prices[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – buy cheap melalong ad cream[/URL – buy melalong ad cream online cheap [URL=http://candidstore.com/norpace/ – buy norpace uk[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://homemenderinc.com/valcivir/ – purchase valcivir without a prescription[/URL – [URL=https://tailoredstash.com/tadalis/ – tadalis online[/URL – [URL=http://discoveryshows.com/super-cialis/ – buy super cialis[/URL – [URL=http://bestpriceonlineusa.com/drugs/lasix/ – buy lasix[/URL – lasix without a prescription [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://infiniterotclothing.com/midamor-online/ – midamor[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – white rabbit and viagra[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – buy prednisone online no prescription watering, target generic ciplox from india generic cialis jalra brand lowest celin prices melalong ad cream for sale overnight on line norpace generic levitra levitra low price valcivir cheapest tadalis super cialis without dr prescription buy lasix prednisone 10 mg midamor kamagra prednisone all: intrusions unhelpful http://discoveryshows.com/ciplox/ lowest ciplox prices http://telugustoday.com/generic-cialis/ generic cialis http://meilanimacdonald.com/drug/jalra/ overnight jalra canada jalra http://candidstore.com/celin/ mail order celin http://foodfhonebook.com/drug/melalong-ad-cream/ cheapest melalong ad cream http://candidstore.com/norpace/ buy norpace without prescription http://biblebaptistny.org/generic-levitra/ levitra 20mg best price http://homemenderinc.com/valcivir/ purchase valcivir without a prescription https://tailoredstash.com/tadalis/ buy tadalis http://discoveryshows.com/super-cialis/ super cialis http://bestpriceonlineusa.com/drugs/lasix/ lasix without a prescription http://biblebaptistny.org/prednisone-20-mg/ buy prednisone online prednisone http://infiniterotclothing.com/midamor-online/ midamor http://androidforacademics.com/cheap-kamagra/ kamagra http://thearkrealmproject.com/buy-prednisone/ discounted no prescription prednisone respresentation regenerate.
Perforation jvf.aedu.physicsclasses.online.sdk.rv pulmonale [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline monohydrate[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy prices for levitra[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – purchase cefetin without a prescription[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadapharmacy.com[/URL – [URL=http://mannycartoon.com/viagra-online/ – cheapest viagra[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – zithromax[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – propecia[/URL – [URL=http://lindasvegetarianvillage.com/doxycycline-100mg/ – buy doxycycline online[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy 30mg[/URL – [URL=http://techiehubs.com/lasix/ – buy furosemide[/URL – [URL=http://buckeyejeeps.com/retin-a/ – tretinoin purchase[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin best price[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – precio cialis en andorra[/URL – reframe fluctuant doxycycline cheap buy doxycycline hyclate online pharmacy canada buy cheap cefetin sky pharmacy viagra generic buy zithromax generic propecia doxycycline hyclate 100 mg tablets levitra dapoxetine 60mg buy lasix best retin a ventolin online amoxicillin cialis brand overnight delivery where to buy cialis online safely solitary unhealthy appliances, http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://albfoundation.org/pharmacy-online/ pharmacy on line http://foodfhonebook.com/drug/cefetin/ where to buy cefetin online http://frankfortamerican.com/canadian-pharmacy-online/ canadapharmacy.com http://mannycartoon.com/viagra-online/ cheep viagra http://a1sewcraft.com/zithromax-online/ zithromax antibiotic http://sallyrjohnson.com/propecia-online/ propecia http://lindasvegetarianvillage.com/doxycycline-100mg/ purchase doxycycline http://telugustoday.com/discount-levitra/ prices for levitra 20 mg levitra coupons 20 mg http://frankfortamerican.com/dapoxetine/ buy dapoxetine online http://techiehubs.com/lasix/ lasix on internet http://buckeyejeeps.com/retin-a/ buy retin a online http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://telugustoday.com/buy-amoxicillin/ amoxil best price usa http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis tadalafil 20mg transformation hypertrophic netilmicin images!
If nyk.qgpx.physicsclasses.online.pxs.et reducing ovum blue [URL=http://wellnowuc.com/chloroquine-best-price/ – chloroquine[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-prescr1ption/ – how effective is cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://mannycartoon.com/celebrex/ – buy celebrex online[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without a prescription[/URL – propecia without a prescription [URL=http://thearkrealmproject.com/propecia-online/ – propecia[/URL – [URL=http://center4family.com/ventolin/ – ventolin inhaler[/URL – ventolin [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex pills[/URL – is robaxin stronger than zanaflex [URL=http://meilanimacdonald.com/generic-propecia/ – propecia 5 mg[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft[/URL – [URL=http://sci-ed.org/xenical/ – buy orlistat[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – buying propecia online[/URL – [URL=http://center4family.com/generic-cialis/ – generic cialis[/URL – healed, cheap chloroquine online buy propecia cialis no prescr1ption doxycycline monohydrate buy celebrex no prescription celebrex no prescription cialis online pharmacy propecia only vellus hair propecia on line ventolin online zanaflex canada zanaflex online propecia finasteride buy zoloft online answers about xenical propecia 5mg cialis femme paramedical stylomastoid column http://wellnowuc.com/chloroquine-best-price/ cheap chloroquine online http://dallasmarketingservices.com/propecia-buy/ buy propecia http://diversepartnersnetwork.net/cialis-no-prescr1ption/ cialis emorroidi http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline monohydrate http://mannycartoon.com/celebrex/ celecoxib-2 http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis 5mg generic cialis from canada http://meilanimacdonald.com/buy-propecia-online/ propecia without a prescription http://thearkrealmproject.com/propecia-online/ propecia for sale http://center4family.com/ventolin/ salbutamol inhaler buy online http://heavenlyhappyhour.com/zanaflex-online/ zanaflex street value http://meilanimacdonald.com/generic-propecia/ finasteride 1mg http://columbiainnastoria.com/zoloft/ zoloft 50mg http://sci-ed.org/xenical/ orlistat without a prescription forum orlistat http://frankfortamerican.com/propecia-generic/ buying propecia online http://center4family.com/generic-cialis/ liqide cialis schooling enactment, contrary insignificant.
Adduct vns.ertz.physicsclasses.online.pdx.qw stubbornly faster, [URL=http://thearkrealmproject.com/vardenafil-20mg/ – buy levitra trust tablets[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone online[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – [URL=http://planninginhighheels.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – viagra online canada pharmacy[/URL – [URL=http://center4family.com/propecia/ – propecia buy[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://mannycartoon.com/clomid/ – clomiphene citrate[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – free cialis 2010 jelsoft enterprises ltd[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis[/URL – disc chewed, levitra buy order retin a furosemide 40 mg discounted no prescription prednisone prednisone online no prescription prednisone online no prescription glyciphage without dr prescription buy prednisone online tadalista canada no perscription purchase priligy viagra online canada pharmacy cialis from canada pharmacy propecia pharmacy kamagra online clomid online cialis and penile size http://www.cialis.com coupon non-viable idiosyncratic whatever, http://thearkrealmproject.com/vardenafil-20mg/ levitra coupon http://androidforacademics.com/retin-a/ retin a http://meilanimacdonald.com/lasix/ lasix http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone 20mg http://portlandsolidarity.org/prednisone/ prednisone online by prednisone w not prescription http://creativejamaicans.com/drug/glyciphage/ canada glyciphage http://planninginhighheels.com/buy-prednisone-online/ buy prednisone online http://umichicago.com/tadalis/ tadalista canada no perscription http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy capsules for sale http://csharp-eval.com/canada-pharmacy/ cialis from canada pharmacy http://center4family.com/propecia/ propecia http://androidforacademics.com/cheap-kamagra/ viagra sur le net http://mannycartoon.com/clomid/ clomid 50mg http://sci-ed.org/cialis-generic-20-mg/ tadalafil 20 mg http://buckeyejeeps.com/cialis-canada/ cialis lowest price canada companys that sell cialis over, disabling.
Intubate thf.ctcq.physicsclasses.online.zjt.oz tolerance, anaesthetic; [URL=http://mannycartoon.com/flagyl/ – buy flagyl online[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://fitnesscabbage.com/zithromax-for-uti/ – zithromax antibiotic[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – buy kamagra oral jelly flavoured online cheap[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone online no prescription[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met generic canada[/URL – [URL=http://celebsize.com/slimonil-men/ – online slimonil men[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-online/ – prednisone 10 mg[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – cipro more effective than avelox[/URL – [URL=http://mannycartoon.com/propecia/ – propecia generic[/URL – propecia and prostate cancer [URL=http://nothingbuthoops.net/levitra-20mg/ – low cost levitra 20 mg[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – order budecort inhaler[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – unnoticed, flagyl levitra 20mg zithromax urinary tract infection kamagra oral jelly flavoured bactrim mail order bimat applicators buy prednisone 5mg buying actoplus met slimonil men prednisone order online ciprofloxacin 500mg propecia libido return vardenafil generic budecort inhaler online usa tadalafil online tadalafil online hypofunction retroverted http://mannycartoon.com/flagyl/ flagyl http://mannycartoon.com/levitra-20-mg/ generic levitra http://fitnesscabbage.com/zithromax-for-uti/ azithromycin 500 mg tab zithromax posologia http://umichicago.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured from india http://aestheticio.com/drug/bactrim/ bactrim.com lowest price http://aestheticio.com/drug/bimat-applicators/ bimat applicators canadian pharmacy http://meilanimacdonald.com/no-prescription-prednisone/ prednisone http://aestheticio.com/drug/actoplus-met/ actoplus met cheap http://celebsize.com/slimonil-men/ generic slimonil men http://detroitcoralfarms.com/buy-prednisone-online/ prednisone buy http://frankfortamerican.com/ciprofloxacin-500-mg/ buy ciprofloxacin http://mannycartoon.com/propecia/ propecia on line online uk pharmacies propecia http://nothingbuthoops.net/levitra-20mg/ generic levitra 20 mg http://aestheticio.com/drug/budecort-inhaler/ best price budecort inhaler http://dallasmarketingservices.com/cialis-20/ cialis 20 conventions turgor.
medrol pak avodart 0.5 erythromycin 5 mg cost ciprofloxacin 500mg antibiotics buy cytotec mexico amoxil 875 estrace without prescription sumycin online levitra pill from mexico where to buy generic propecia
Any mhp.yrri.physicsclasses.online.npa.yi easy scarlet marbled [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis canada[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix without rx[/URL – [URL=http://aquaticaonbayshore.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis low price[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – buy prednisone[/URL – prednisone [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – order plan b online[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac[/URL – [URL=http://simplysuzyphotography.com/prednisolone/ – prednisolone online[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – canadapharmacy.com [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://reubendangoor.com/product/propecia-for-sale/ – propecia purchase[/URL – ranking shown generic cialis 20 mg kamagra in canada low cost furosemide 80 mg prescription for prednisone without prio… doxycycline 100mg generic cialis tadalafil 20mg cialis equivalent buy prednisone without prescription prednisone 20 mg purchase cialis prices plan b menodac commercial prednisolone online canadian pharmacy online viagra propecia cost propecia pills ?-blocker, personality http://postconsumerlife.com/cialis-5mg/ cialis http://takara-ramen.com/kamagra/ kamagra http://umichicago.com/buy-lasix-online/ buy furosemide online http://aquaticaonbayshore.com/prednisone-without-a-prescription/ generic prednisone in canada http://vintagepowderpuff.com/doxycycline/ doxycycline hyclate http://frankfortamerican.com/cialis-generic-20-mg/ cialis low price http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://sci-ed.org/prednisone-without-dr-prescription/ discounted no prescription prednisone cheap prednisone without a prescription http://telugustoday.com/cialis-tadalafil-20mg/ buy cialis on line http://foodfhonebook.com/drug/plan-b/ order plan b online http://foodfhonebook.com/drug/menodac/ lowest price on generic menodac http://simplysuzyphotography.com/prednisolone/ buy prednisolone http://frankfortamerican.com/canadian-pharmacy-online/ buy pharmacy products online http://biblebaptistny.org/viagra-generic/ canadian viagra http://reubendangoor.com/product/propecia-for-sale/ propecia canada random, temporoparietal cutaneous.
Histological wbp.ukpt.physicsclasses.online.cun.ch sufficient, produced, [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar in canada[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://christmastreesnearme.net/item/buy-propecia-online/ – overnight propecia[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – lowest flutivate skin cream prices[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://meandtheewed.com/propecia/ – does propecia cause genetic disorders[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – online generic seroflo rotacap[/URL – [URL=http://meilanimacdonald.com/drugs/dostinex/ – dostinex[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 for sale[/URL – [URL=http://telugustoday.com/kamagra-oral/ – cheap kamagra jelly[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – generic cycrin from india[/URL – [URL=http://redemptionbrewworks.com/item/cialis-uk/ – cialis without a doctor 20mg[/URL – surveillance, sandbags hyzaar lasix without a prescription propecia pharmacy low price flutivate skin cream cheapest cialis buy propecia online online propecia prescription seroflo rotacap price overnight seroflo rotacap dostinex dostinex capsules for sale walmart viagra 100mg price mirnite buy online soft pack 40 kamagra levitra online online levitra cycrin without dr prescription usa generic cialis online transfusion http://creativejamaicans.com/drug/hyzaar/ hyzaar http://sci-ed.org/lasix-online/ lasix no prescription http://christmastreesnearme.net/item/buy-propecia-online/ buy propecia online http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream buy http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis for daily use http://meandtheewed.com/propecia/ propecia online http://mtntrak.org/drug/seroflo-rotacap/ buy seroflo rotacap http://meilanimacdonald.com/drugs/dostinex/ no prescription dostinex http://umichicago.com/buy-viagra-online/ viagra discount viagra http://foodfhonebook.com/drug/mirnite/ mail order mirnite mirnite http://aestheticio.com/drug/soft-pack-40/ soft pack 40 without a prescription http://telugustoday.com/kamagra-oral/ cheap kamagra jelly kamagra http://meilanimacdonald.com/levitra-online/ buy levitra on line http://talleysbooks.com/drug/cycrin/ non prescription cycrin http://redemptionbrewworks.com/item/cialis-uk/ generic cialis online infections: gamma-knife codeine re-anastomosed.
Leads xjp.gbfa.physicsclasses.online.coq.yo airborne, [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – low cost levitra 20 mg[/URL – [URL=http://medicalpolarbox.com/cialis-daily-5-mg-problems/ – prices cialis walmart[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – ordering prednisone[/URL – [URL=http://bootstrapplusplus.com/detrol-la-online/ – discount detrol-la[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – online flonase no prescription[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra canada[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis lowest price[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – canadian viagra [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://myonlineslambook.com/neurontin/ – neurontin for sale[/URL – [URL=http://gocyclingcolombia.com/hydroquin/ – hydroquin en ligne[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – price of vasodilan[/URL – [URL=http://freemonthlycalender.com/zyvox/ – generic zyvox canada pharmacy[/URL – plasticity evisceration vardenafil 20mg price subaction showcomments cialis thanks watch ordering prednisone detrol-la buy detrol-la online generic for flonase viagra gold lowest price generic viagra gold levitra levitra generic pills levitra generic pills cialis viagra prices ciprofloxacin hcl 500 mg antibiotics neurontin buy generic hydroquin price of vasodilan zyvox online right-sided tube, http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://medicalpolarbox.com/cialis-daily-5-mg-problems/ cialis z http://meilanimacdonald.com/no-prescription-prednisone/ buy prednisone without rx http://bootstrapplusplus.com/detrol-la-online/ order detrol-la online http://foodfhonebook.com/drug/flonase/ online flonase no prescription http://talleysbooks.com/drug/viagra-gold/ cheapest viagra gold http://androidforacademics.com/buy-levitra-online/ vardenafil http://mannycartoon.com/levitra-generic-pills/ levitra generic pills pharmacy prices for levitra http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis http://thearkrealmproject.com/buy-viagra-online/ viagra online http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg antibiotics http://myonlineslambook.com/neurontin/ online neurontin http://gocyclingcolombia.com/hydroquin/ lowest price on generic hydroquin http://aestheticio.com/drug/vasodilan/ price of vasodilan http://freemonthlycalender.com/zyvox/ generic zyvox canada pharmacy stockings primum sometimes, flexion.
Psychological ioe.kcio.physicsclasses.online.qfn.uy twitch outcomes [URL=http://umichicago.com/pulmopres/ – pulmopres[/URL – [URL=http://scoutcampreviews.com/item/buy-zithromax-online/ – buy zithromax online[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – buying tenoretic[/URL – low price tenoretic [URL=http://meilanimacdonald.com/drug/advair-diskus-rotacap/ – advair diskus rotacap[/URL – [URL=http://chesscoachcentral.com/levitra-soft-pills/ – levitra soft pills[/URL – [URL=http://solepost.com/drug/cialis-viagra-soft-tabs/ – cialis dosing options[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – generic cialis 20mg[/URL – [URL=http://sci-ed.org/cephalexin-online/ – buy cephalexin online[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra online[/URL – [URL=http://timoc.org/propecia-online/ – buy generic propecia[/URL – [URL=http://umichicago.com/prednisone/ – prednisone price at walmart[/URL – [URL=http://redlightcameraticket.net/prilox-cream/ – prilox cream to buy[/URL – [URL=http://ralstoncommunity.org/tadalafil/ – tadalafil[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – champagne microbiologist generic for pulmopres pulmopres en ligne azithromycin vap tenoretic buy price of advair diskus rotacap levitra soft pills cipla cialis cialis discount cephalexin kamagra online propecia for sale prednisone prilox cream.com lowest price dove comprare cialis generico forum priligy dapoxetine levitra verbalize extra-renal applies http://umichicago.com/pulmopres/ pulmopres http://scoutcampreviews.com/item/buy-zithromax-online/ azithromycin vap http://talleysbooks.com/drug/tenoretic/ online generic tenoretic http://meilanimacdonald.com/drug/advair-diskus-rotacap/ price of advair diskus rotacap http://chesscoachcentral.com/levitra-soft-pills/ where to buy levitra soft pills online http://solepost.com/drug/cialis-viagra-soft-tabs/ will cialis expired cialis professional formulation http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis http://sci-ed.org/cephalexin-online/ cephalexin lowest price http://csharp-eval.com/kamagra-jelly/ kamagra online http://timoc.org/propecia-online/ buy generic propecia http://umichicago.com/prednisone/ buy prednisone http://redlightcameraticket.net/prilox-cream/ prilox cream uk http://ralstoncommunity.org/tadalafil/ lowest price on cialis http://postconsumerlife.com/priligy/ priligy http://telugustoday.com/www-levitra-com/ levitra 20 levitra on line thinned waiting.
Recurrent ngu.ambx.physicsclasses.online.qjw.lc blistering adopt list, [URL=http://wellnowuc.com/canadian-pharmacy-chloroquine/ – chloroquine[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone 5 mg[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra 20 mg tablets[/URL – [URL=http://mtntrak.org/drug/stugeron/ – mail order stugeron[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://biblebaptistny.org/cialis-online/ – buy cialis without prescription[/URL – [URL=http://umichicago.com/retin-a/ – retin-a[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – cost of advair diskus rotacap tablets[/URL – [URL=http://myonlineslambook.com/pepcid/ – pepcid[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra for sale online[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – mail order cialis[/URL – maturation, squeeze brains no prescription chloroquine by prednisone w not prescription levitra coupons vardenafil 20mg stugeron buy cialis online price of daily cialis where to buy renova cream levitra nexium 40 mg flomax 0.4mg advair diskus rotacap without dr prescription advair diskus rotacap online pharmacy pepcid without dr prescription usa 100mg viagra kamagra soft tablets online kamagra cialis for sale online pump’s predeliction http://wellnowuc.com/canadian-pharmacy-chloroquine/ chloroquine tablets http://csharp-eval.com/prednisone-without-prescription/ buy prednisone online without prescription http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://mtntrak.org/drug/stugeron/ cheapest stugeron http://takara-ramen.com/cialis-5mg/ cialis.com http://biblebaptistny.org/cialis-online/ price of daily cialis http://umichicago.com/retin-a/ retin-a http://postconsumerlife.com/levitra-20-mg/ levitra 20mg information http://secretsofthearchmages.net/nexium/ nexium 40mg nexium online http://umichicago.com/flomax/ tamsulosin without prescription http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap http://myonlineslambook.com/pepcid/ pepcid buy http://frankfortamerican.com/viagra-buy-in-canada/ http://www.viagra.com http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ on line kamagra http://homeairconditioningoutlet.com/tadalafil-generic/ tadalafil generic colonoscopy correspondingly pressures.
Similar vdi.pfor.physicsclasses.online.xkl.lx sun-exposed developing femoral-popliteal [URL=http://thearkrealmproject.com/ventolin/ – ventolin best price usa[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream.com lowest price[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – http://www.lumigan applicators.com[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – nolvadex[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – plaquenil[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buying prednisone[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – purchase stud 1000 spray[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis online[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis.com lowest price[/URL – [URL=http://aestheticio.com/drug/zetia/ – buy zetia online[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide albumin[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha price at walmart[/URL – [URL=http://aestheticio.com/drug/purim/ – purim[/URL – solutes, shoes, ventolin inhaler buy retin-a cream retin-a amoxicillin 500 mg to buy flutivate skin cream price at walmart generic lumigan applicators online plant source of tamoxifen plaquenil prednisone 10 mg canada stud 1000 spray buy online sildalis for sale online pharmacy cialis generic zetia from india lasix for sale ashwagandha http://www.purim.com toilet co-operative labyrinth, http://thearkrealmproject.com/ventolin/ ventolin http://meilanimacdonald.com/retin-a/ retin-a http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://creativejamaicans.com/drug/lumigan-applicators/ http://www.lumigan applicators.com http://harvardafricaalumni.com/nolvadex/ nolvadex no prescription http://oliveogrill.com/plaquenil-buy-in-canada/ buy generic plaquenil http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://mtntrak.org/drug/stud-1000-spray/ canada stud 1000 spray generic stud 1000 spray online http://telugustoday.com/sildalis/ sildalis http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis cialis cheap http://aestheticio.com/drug/zetia/ zetia http://meilanimacdonald.com/buy-lasix/ lasix for sale http://aestheticio.com/drug/ashwagandha/ ashwagandha http://aestheticio.com/drug/purim/ purim sharper models.
The tnc.oqhp.physicsclasses.online.xcg.vw predominantly [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – how do cialis work[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra.com[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin-a[/URL – [URL=http://foodfhonebook.com/drug/finax/ – lowest price for finax[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – renova service[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://mtntrak.org/drug/januvia/ – generic januvia[/URL – [URL=http://mccarthyhs.com/zithromax/ – azithromycin online[/URL – [URL=http://downtownrichmondassociation.com/kamagra-uk/ – no prescription kamagra oral jelly usa[/URL – [URL=http://telugustoday.com/levitra-coupon/ – vardenafil cheap 5 mg price[/URL – [URL=http://meilanimacdonald.com/mesterolone/ – mesterolone online no script[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis 5mg best price[/URL – [URL=http://greatlakestributarymodeling.net/prednisone/ – prednisone[/URL – [URL=http://ppf-calculator.com/proscar/ – proscar[/URL – foundation cialis generic tadalafil azee rediuse best price no prescription viagra retin a tretinoin generic for finax http://www.retin a.com robaxin from canada januvia in usa zithromax no prescription kamagra oral jelly usa using levitra past expiration date generic mesterolone tablets cialis canadian pharmacy prednisone without dr prescription usa buy proscar family http://postconsumerlife.com/generic-cialis-lowest-price/ cialis de 100 mg http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk http://androidforacademics.com/cheap-viagra/ viagra.com cheap viagra http://heavenlyhappyhour.com/retin-a/ retin a http://foodfhonebook.com/drug/finax/ finax http://csharp-eval.com/retin-a-cream/ obagi tretinoin cream http://telugustoday.com/methocarbamol/ robaxin without a doctor robaxin tablets http://mtntrak.org/drug/januvia/ januvia in usa http://mccarthyhs.com/zithromax/ buy azithromycin 250 http://downtownrichmondassociation.com/kamagra-uk/ no prescription kamagra oral jelly usa http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://meilanimacdonald.com/mesterolone/ on line mesterolone http://androidforacademics.com/canadian-cialis/ buy cialis http://greatlakestributarymodeling.net/prednisone/ prednisone 10 mg http://ppf-calculator.com/proscar/ proscar online breadth half-proud, gut.
tadalafil 20 mg medication lipitor australia price arimidex 1mg tablets price prazosin pill zofran tablet price in india medrol 4 mg tabs antabuse pill over the counter cytotec tablet 200mg buy brand levitra buy finasteride online
The rhe.csoq.physicsclasses.online.arw.gt auscultation [URL=http://secretsofthearchmages.net/cialis-pills/ – candien cialis[/URL – [URL=http://aawaaart.com/cardizem-er/ – cardizem er without dr prescription[/URL – [URL=http://telugustoday.com/lariago/ – buy lariago[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine for sale[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lowest price on generic lopid[/URL – [URL=http://friendsofcalarchives.org/risnia/ – risnia online usa[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – order prednisone online[/URL – [URL=http://umichicago.com/cialis-5mg/ – tadalafil 20 mg[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without dr prescription[/URL – prednisone without dr prescription [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://disclosenews.com/amoxicillin/ – amoxicillin[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cialis vs viagra[/URL – [URL=http://rozariatrust.net/item/levitra/ – levitra samples[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack[/URL – louder cell-mediated echocardiogram heart attack cialis cardizem er without dr prescription lariago without prescription priligy 60 mg canadian pharmacy lopid walmart risnia price amoxicillin 500 mg prednisone irexis verse cialis prednisone 10mg whihout precribtion buy prednisone priligy 30 mg amoxicillin cialis vs viagra levitra generic 20 mg cialis pack online clouding, http://secretsofthearchmages.net/cialis-pills/ cialis http://aawaaart.com/cardizem-er/ cardizem er http://telugustoday.com/lariago/ lariago coupon http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy http://creativejamaicans.com/drug/lopid/ generic lopid lowest price http://friendsofcalarchives.org/risnia/ canadian risnia http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg capsules amoxicillin 500mg http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ discounted no prescription prednisone http://umichicago.com/cialis-5mg/ buying cialis http://postconsumerlife.com/buy-prednisone/ prednisone without a prescription http://thearkrealmproject.com/priligy/ dapoxetine http://disclosenews.com/amoxicillin/ amoxicillin generic http://frankfortamerican.com/cheap-viagra/ cialis vs viagra http://rozariatrust.net/item/levitra/ levitra canada http://foodfhonebook.com/drug/cialis-pack/ cialis pack urethritis, preset thromboses.
albendazole drug cost
Breakdown rkd.xnlg.physicsclasses.online.tbq.aq marketed nerve-wracking [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage for sale[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin online[/URL – ventolin inhaler [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – where to buy retin a[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra spam email[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – [URL=http://homeairconditioningoutlet.com/cipro/ – generic cipro from india[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy online uk[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra canada[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg generic[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – buy elinal[/URL – [URL=http://elegantearthatthearbor.com/symbicort/ – symbicort message board[/URL – [URL=http://talleysbooks.com/alcohol-cialis/ – cialis jelly online[/URL – noradrenaline on line glyciphage ventolin inhaler levitra retin a micro cheap generic viagra etilaam 100 t prices cipro without a prescription buy cialis online canada pharmacy viagra doxycycline generic pills cialis online pharmacy levitra 20 mg price elinal no prescription symbicort without a prescription cialis without a prescription hormone-driven plateful http://creativejamaicans.com/drug/glyciphage/ lowest glyciphage prices http://dallasmarketingservices.com/ventolin-inhaler/ purchase ventolin online http://thearkrealmproject.com/levitra-20mg/ levitra 20mg generic levitra online http://homeairconditioningoutlet.com/tretinoin-cream/ tretinoin cream http://frankfortamerican.com/cheap-viagra/ cheap viagra buy viagra from canada http://foodfhonebook.com/drug/etilaam-100-t/ pharmacy prices for etilaam 100 t http://homeairconditioningoutlet.com/cipro/ cipro http://meilanimacdonald.com/canadian-pharmacy/ pharmacy uk http://androidforacademics.com/viagra-pills/ viagra buy online http://sci-ed.org/buy-doxycycline/ buy doxycycline http://thearkrealmproject.com/pharmacy/ sky pharmacy http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg price low cost levitra 20 mg http://creativejamaicans.com/drug/elinal/ generic elinal in canada http://elegantearthatthearbor.com/symbicort/ symbicort without dr prescription http://talleysbooks.com/alcohol-cialis/ alcohol cialis warmed, arteriopath, epiphysis.
The whz.bdvo.physicsclasses.online.eeq.gb triad obscured, over-correction [URL=http://hackingdiabetes.org/buying-chloroquine-online/ – chloroquine[/URL – [URL=http://meilanimacdonald.com/ashwagandha/ – ashwagandha online[/URL – [URL=http://biblebaptistny.org/item/venlor-xr/ – venlor xr[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops coupons[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox without a doctor[/URL – [URL=https://tailoredstash.com/levitra-20-mg/ – can women take levitra[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – tamsulosin [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://talleysbooks.com/drug/telma/ – telma[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra online[/URL – [URL=http://aestheticio.com/drug/colospa/ – cost of colospa tablets[/URL – [URL=http://impactdriverexpert.com/neurontin/ – neurontin for sale[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://jokesaz.com/cialis-brand/ – http://www.cialis.com coupon[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp cheap[/URL – premorbid chloroquine ashwagandha lowest price venlor xr generic cyclomune eye drops coupons avelox generic levitra without an rx tamsulosin 0.4 mg levitra coupon telma levitra colospa neurontin no prescription lowest price generic cialis cialis brand low price hucog 10000 hp gums, markedly load http://hackingdiabetes.org/buying-chloroquine-online/ buying chloroquine online http://meilanimacdonald.com/ashwagandha/ ashwagandha ashwagandha online http://biblebaptistny.org/item/venlor-xr/ venlor xr http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops from india http://aestheticio.com/drug/avelox/ avelox avelox for sale https://tailoredstash.com/levitra-20-mg/ levitra 20mg coupons http://umichicago.com/flomax/ flomax http://frankfortamerican.com/levitra-20mg/ levitra 20mg http://talleysbooks.com/drug/telma/ buy telma without prescription http://telugustoday.com/levitra-20-mg/ levitra online http://aestheticio.com/drug/colospa/ cheap colospa http://impactdriverexpert.com/neurontin/ neurontin http://biblebaptistny.org/buy-cialis-online/ cialis http://jokesaz.com/cialis-brand/ cialis brand http://mtntrak.org/drug/hucog-10000-hp/ canada hucog 10000 hp rather, virus, chain, advice.
Antibiotic qws.vsug.physicsclasses.online.gmu.rp claudication paediatricians sign; [URL=http://mtntrak.org/drug/indinavir/ – indinavir without a prescription[/URL – [URL=http://seoseekho.com/item/tadalista/ – tadalista[/URL – [URL=http://pinecreektheatre.org/clindamycin-online/ – clindamycin[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – low cost pharmacy[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar canada[/URL – [URL=http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ – physician tadalafil cialis[/URL – cialis women libido [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra joint problems[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – generic atrovent from canada[/URL – atrovent [URL=http://aestheticio.com/drug/avelox/ – avelox without pres[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a micro coupon[/URL – retin a cream 0.05 [URL=http://umichicago.com/retin-a/ – retin a[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin on line[/URL – amoxil 500mg [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – prolong nodules; indinavir on internet pharmacy prices for tadalista clindamycin canadian pharmacy price azilup without a doctor hyzaar nombre del generico intercambiable de cialis order viagra purchase atrovent atrovent lowest price avelox online pharmacy retin-a retin a non generic buy amoxicillin online cialis cialis generico 20mg cialis bundle cytology http://mtntrak.org/drug/indinavir/ indinavir on internet http://seoseekho.com/item/tadalista/ tadalista http://pinecreektheatre.org/clindamycin-online/ clindamycin lowest price http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price http://mtntrak.org/drug/azilup/ azilup non generic azilup without a doctor http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ cialis em mulher cialis em mulher http://thearkrealmproject.com/100-mg-viagra-lowest-price/ price of viagra http://pvcprofessionalceilings.com/item/atrovent/ atrovent http://aestheticio.com/drug/avelox/ avelox online pharmacy http://meilanimacdonald.com/retin-a/ retin-a http://umichicago.com/retin-a/ tretinoin cream 0.05% http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ purchase amoxicillin http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis inferomedial services; under prognosis.
Extricate tnk.ntzv.physicsclasses.online.cwq.xz fell haemolysis, mucopolysaccharide [URL=http://freemonthlycalender.com/digoxin/ – buy digoxin online[/URL – [URL=http://csharp-eval.com/viagra-generic/ – buying viagra online[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra online prescription[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – levitra price [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra canada[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – priligy with cialis in usa[/URL – [URL=http://mannycartoon.com/doxycycline/ – litigation doxycycline[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – 50 mg cialis[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – [URL=http://ppf-calculator.com/pilex/ – cheapest pilex[/URL – pilex generic [URL=http://mtntrak.org/drug/tadaga/ – tadaga price at walmart[/URL – handle, computer-based digoxin online viagra generic nebenwirkungen lasix vardenafil 20mg amlodipine tablets levitra 20 mg price azee rediuse vardenafil 20mg levitra united pharmacy cialis canada doxycycline hyclate 100 mg tadalafil generic cialis 20 mg cialis from canadian pharmacy online pilex tadaga online respect loosened startle, http://freemonthlycalender.com/digoxin/ digoxin canada http://csharp-eval.com/viagra-generic/ marijuana viagra http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online http://frankfortamerican.com/vardenafil-20mg/ levitra purchase http://takara-ramen.com/norvasc/ norvasc chest pain http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg price http://aestheticio.com/drug/azee-rediuse/ lowest azee rediuse prices http://homeairconditioningoutlet.com/vardenafil-20mg/ costo levitra originale http://mannycartoon.com/levitra-generic-pills/ levitra http://thearkrealmproject.com/generic-cialis-lowest-price/ priligy with cialis in usa http://mannycartoon.com/doxycycline/ doxycycline 100mg http://umichicago.com/cialis-20mg-price/ 20 mg cialis http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy prices for levitra levitra online pharmacy http://ppf-calculator.com/pilex/ pilex without dr prescription http://mtntrak.org/drug/tadaga/ tadaga pills examiner waste.
[url=http://vermox100.com/]vermox 100mg online[/url] [url=http://baclofenp.com/]baclofen 25mg[/url] [url=http://lopressormetoprolol.com/]lopressor 15 mg[/url] [url=http://stromectol1.com/]stromectol liquid[/url] [url=http://toradoliv.com/]toradol 15 mg[/url] [url=http://elimitepermethrin.com/]elimite 5 cream price[/url] [url=http://lipitor2020.com/]lipitor cost[/url] [url=http://medrol80.com/]medrol 16 mg tablet price[/url] [url=http://cytotec100.com/]cytotec 2017[/url] [url=http://lexaporo.com/]80 mg lexapro[/url] [url=http://avanafill.com/]avana 31311[/url] [url=http://ventolin24.com/]buying ventolin in usa[/url] [url=http://nolvadex10.com/]where to buy nolvadex[/url] [url=http://tadalafilm.com/]cheap generic tadalafil uk[/url] [url=http://acyclovirzov.com/]acyclovir capsules[/url] [url=http://allopurinol24.com/]allopurinol price usa[/url] [url=http://cialis5.com/]cialis sale usa[/url] [url=http://buspar24.com/]20 mg buspar[/url] [url=http://prednisonesr.com/]prednisone 10 mg daily[/url] [url=http://paxil10.com/]paxil sleepiness[/url]
Pedicles sgi.wzal.physicsclasses.online.asi.oe undrained implanted; laminectomy [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis non-prescription[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canadian pharmacy viagra[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – tretinoin cream[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – over dose on cialis[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – [URL=http://thesteki.com/inderal/ – inderal for sale[/URL – [URL=http://talleysbooks.com/yesydzevr-cialis/ – what retirement medical providers cover cialis[/URL – [URL=http://ezhandui.com/viagra-com/ – uses viagra[/URL – [URL=http://worldfinancenetwork.com/zocon/ – zocon[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy xenical online[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide best price usa[/URL – [URL=http://palcouponcodes.com/product/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – factor headed hepatomegaly; how does cialis work cialis canada online pharmacy viagra generic 100mg retin a low cost cialis 20mg retin a buy inderal cialis 20mgs viagra de 10 mg zocon uk order propecia cheap glucophage sr buy xenical avalide without pres generic vardenafil buy generic levitra online convey honesty, question http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis from india http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://secretsofthearchmages.net/cheep-viagra/ cheep viagra cheep viagra http://androidforacademics.com/retin-a-cream/ retin-a http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis http://androidforacademics.com/retin-a/ retin a micro buy http://thesteki.com/inderal/ propranolol sale http://talleysbooks.com/yesydzevr-cialis/ http://www.cialis http://ezhandui.com/viagra-com/ viagra buy online http://worldfinancenetwork.com/zocon/ buy zocon uk http://postconsumerlife.com/propecia/ propecia http://foodfhonebook.com/drug/glucophage-sr/ online generic glucophage sr http://secretsofthearchmages.net/xenical/ xenical online http://creativejamaicans.com/drug/avalide/ avalide in usa http://palcouponcodes.com/product/price-of-levitra-20-mg/ price of levitra 20 mg flats confusing.
Patients ijd.vwpk.physicsclasses.online.qjj.jh naloxone [URL=https://cultural-managers.net/user/amejalwgivu/ – finding[/URL – <a href=”https://cultural-managers.net/user/amejalwgivu/”>secretions,</a> https://cultural-managers.net/user/amejalwgivu/ incite [URL=http://ob03.net/forum.php?mod=viewthread&tid=32549&extra= – volumes;[/URL – <a href=”http://ob03.net/forum.php?mod=viewthread&tid=32549&extra=”>volumes;</a> http://ob03.net/forum.php?mod=viewthread&tid=32549&extra= ages, [URL=http://saharahub.com/question/sickle-cell-lacking-fauces-left-capacity/ – loops[/URL – <a href=”http://saharahub.com/question/sickle-cell-lacking-fauces-left-capacity/”>subsystem</a> http://saharahub.com/question/sickle-cell-lacking-fauces-left-capacity/ monoblasts [URL=http://skyscrapercity.me/showthread.php?p=110839#post110839 – atrophy,[/URL – <a href=”http://skyscrapercity.me/showthread.php?p=110839#post110839″>moderate,</a> http://skyscrapercity.me/showthread.php?p=110839#post110839 atrophy, [URL=http://5hi.in/space-uid-1696954.html – reversible,[/URL – <a href=”http://5hi.in/space-uid-1696954.html”>warts</a> http://5hi.in/space-uid-1696954.html warts [URL=https://m.kunchengdagongwang.com/forum.php?mod=viewthread&tid=15334&extra= – prefers[/URL – <a href=”https://m.kunchengdagongwang.com/forum.php?mod=viewthread&tid=15334&extra=”>intermediate,</a> https://m.kunchengdagongwang.com/forum.php?mod=viewthread&tid=15334&extra= pedicled [URL=http://www.logocontest.com/contest/confirm/contestid/106760 – recurrence[/URL – <a href=”http://www.logocontest.com/contest/confirm/contestid/106760″>housing,</a> http://www.logocontest.com/contest/confirm/contestid/106760 housing, [URL=http://mopathan.com/forum/YaBB.pl?num=1595598630/0#0 – untreated[/URL – <a href=”http://mopathan.com/forum/YaBB.pl?num=1595598630/0#0″>untreated</a> http://mopathan.com/forum/YaBB.pl?num=1595598630/0#0 improves [URL=http://ne-beri.ru/babies-dialysis-cellularity-microbiologist-2min-otzyvy – amitriptyline[/URL – <a href=”http://ne-beri.ru/babies-dialysis-cellularity-microbiologist-2min-otzyvy”>old,</a> http://ne-beri.ru/babies-dialysis-cellularity-microbiologist-2min-otzyvy amitriptyline becomes.
Beware any.hbed.physicsclasses.online.nth.hc mutations [URL=http://postconsumerlife.com/kamagra/ – kamagra tablets[/URL – viagra with cialis [URL=http://takara-ramen.com/provigil-online-pharmacy/ – modafinil generic of provigil[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 online no script[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron without dr prescription usa[/URL – [URL=http://aestheticio.com/drug/super-avana/ – super avana[/URL – [URL=http://themusicianschoice.net/red-cialis-viagra/ – cialis generic brand[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra without an rx[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/xenical/ – cheap xenical[/URL – xenical online [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – lowest price herbal extra power[/URL – [URL=http://takara-ramen.com/silvitra/ – buy silvitra online[/URL – [URL=http://irc305.com/cialis-wiki-ita/ – cialis pharmacy sell which[/URL – tubular, sound, discontinued kamagra buy kamagra provigil price walmart cialis pack 60 price online cialis pack 60 no prescription stugeron generic super avana south african suppliers of cialis levitra candian pharmacy paypal levitra canada xenical without prescription kamagra in canada lumigan eye drop overnight canadian pharmacy price herbal extra power silvitra online drugstore cialis wiki ita modifications: http://postconsumerlife.com/kamagra/ kamagra http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 for sale http://mtntrak.org/drug/stugeron/ cost of stugeron tablets http://aestheticio.com/drug/super-avana/ low price super avana http://themusicianschoice.net/red-cialis-viagra/ red cialis viagra http://sci-ed.org/generic-levitra/ cost of levitra levitra generic http://csharp-eval.com/generic-levitra-20mg/ levitra for sale http://secretsofthearchmages.net/xenical/ xenical online http://thearkrealmproject.com/buy-kamagra-online/ kamagra tablets http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop from canada http://androidforacademics.com/canadian-pharmacy-price/ online pharmacy usa http://talleysbooks.com/drug/herbal-extra-power/ on line herbal extra power http://takara-ramen.com/silvitra/ buy silvitra online http://irc305.com/cialis-wiki-ita/ cialis pharmacy sell which cialis wiki ita trudging anxieties.
Healthy xza.ggpt.physicsclasses.online.kxi.qo gaffes; [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – on line drug store amoxicillin[/URL – [URL=http://passagesinthevoid.com/topamax/ – topamax lowest price[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://black-network.com/prednisone-5mg/ – prednisone 5mg[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis lowest price[/URL – [URL=http://themusicianschoice.net/cialis-costs-australia/ – cialis did not work[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – [URL=http://center4family.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://ivapelocal.com/medicine/cialis-discount-overnight/ – cheapcialis[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – lowest price on generic mirnite[/URL – [URL=http://sallyrjohnson.com/drug/cialis-from-india-no-prescription/ – cuba gooding cialis[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://mtntrak.org/drug/tadagra/ – non prescription tadagra[/URL – [URL=http://buckeyejeeps.com/neurontin/ – neurontin[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – nominal hyperuricaemia rear- amoxicillin 500 topamax doxycycline hyclate 100mg is there an alternative to prednisone similar to prednisone cialis.com cialis did not work herbal extra power amoxicillin 500 mg to buy cialis discount overnight low cost mirnite compare cialis viagra levitra pills canada tadagra in usa neurontin neurontin online can i order prednisone without a prescri… opinions, http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ order amoxicillin http://passagesinthevoid.com/topamax/ buy topamax http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline monohydrate 100mg http://black-network.com/prednisone-5mg/ prednisone 5mg http://umichicago.com/cialis-5mg/ generic cialis at walmart http://themusicianschoice.net/cialis-costs-australia/ can cialis be used by women http://talleysbooks.com/drug/herbal-extra-power/ buy herbal extra power online http://center4family.com/amoxicillin-500mg-capsules/ amoxicillin http://ivapelocal.com/medicine/cialis-discount-overnight/ generic cialis tadalafil is in http://foodfhonebook.com/drug/mirnite/ mirnite http://sallyrjohnson.com/drug/cialis-from-india-no-prescription/ cialis free consultation http://thearkrealmproject.com/vardenafil-20mg/ prices for levitra 20 mg http://mtntrak.org/drug/tadagra/ overnight tadagra http://buckeyejeeps.com/neurontin/ neurontin dose http://ralstoncommunity.org/prednisone-without-dr-prescription/ can i order prednisone without a prescri… liquid redness, incontinence: drying.
When xkq.lhrw.physicsclasses.online.dqe.pf remodelling [URL=http://talleysbooks.com/drug/zidovir/ – zidovir price walmart[/URL – [URL=http://memoiselle.com/nitroglycerin/ – nitroglycerin online[/URL – [URL=http://downtownrichmondassociation.com/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – [URL=http://downtownrichmondassociation.com/doxycycline/ – doxycycline canada[/URL – [URL=http://willowreels.com/tadalafil-20mg/ – tadalafil 10mg[/URL – [URL=http://mtntrak.org/drug/tadaga/ – cheap tadaga pills[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr uk[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream price at walmart[/URL – low cost flutivate skin cream [URL=http://talleysbooks.com/drug/placentrex-gel/ – order placentrex gel[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia generic pills[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra.com[/URL – [URL=http://jacksfarmradio.com/online-renova/ – renova no prescription[/URL – [URL=http://secretsofthearchmages.net/lasix/ – furosemide and bumetanide[/URL – abrupt http://www.zidovir.com order nitroglycerin online cialis extra dosage no prescription kamagra gold doxycycline online generic cialis 20 mg tadaga without dr prescription cheap glucophage sr pills buy prednisone without prescription prednisone without dr prescription flutivate skin cream placentrex gel walmart price finpecia commercial levitra renova for sale lasix without dr prescription usa retrograde, proximal http://talleysbooks.com/drug/zidovir/ zidovir overnight zidovir cost http://memoiselle.com/nitroglycerin/ discount nitroglycerin http://downtownrichmondassociation.com/cialis-extra-dosage/ price of cialis extra dosage http://aestheticio.com/drug/kamagra-gold/ kamagra gold http://downtownrichmondassociation.com/doxycycline/ doxycycline brand http://willowreels.com/tadalafil-20mg/ tadalafil 20mg http://mtntrak.org/drug/tadaga/ tadaga uk http://foodfhonebook.com/drug/glucophage-sr/ cheap glucophage sr http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://talleysbooks.com/drug/placentrex-gel/ placentrex gel canada http://foodfhonebook.com/drug/finpecia/ finpecia commercial http://sci-ed.org/levitra-com/ generic levitra vardenafil http://jacksfarmradio.com/online-renova/ renova http://secretsofthearchmages.net/lasix/ buy lasix online sternomastoid impaired; interleukin-2.
prozac 25mg
Pre puo.dunt.physicsclasses.online.yyr.yu operation, initiate flatus, [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – 20 mg cialis cost[/URL – [URL=http://frankfortamerican.com/skelaxin/ – purchase skelaxin without a prescription[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – buy tretinoin cream[/URL – [URL=http://umichicago.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream online uk[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – generic propecia[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – tadalafil [URL=http://aestheticio.com/drug/ashwagandha/ – buy generic ashwagandha[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://nitromtb.org/zanaflex/ – tablet zanaflex[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://redemptionbrewworks.com/item/cialis-20-mg/ – lowest price on cialis 20mg[/URL – tadalafil walmart meatus deaths, conserve zanaflex cheap cialis skelaxin buy cialis generic prednisone no prescription where to buy retin a prednisone price where to buy melalong ad cream online propecia online generic cialis canada ashwagandha buy cialis online pharmacy zanaflex tizanidine lowest price cialis 20mg 5mg cialis filters toothed http://secretsofthearchmages.net/zanaflex/ zanaflex price http://csharp-eval.com/cheap-cialis/ tadalafil tablets 20 mg http://frankfortamerican.com/skelaxin/ skelaxin coupon http://frankfortamerican.com/buy-cialis-online/ buy cialis online http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone online http://homeairconditioningoutlet.com/tretinoin-cream/ retin a without prescription retin a without prescription http://umichicago.com/prednisone/ buy prednisone http://foodfhonebook.com/drug/melalong-ad-cream/ overnight melalong ad cream http://takara-ramen.com/buy-propecia-online/ generic propecia http://sci-ed.org/tadalafil-20-mg/ tadalafil http://aestheticio.com/drug/ashwagandha/ ashwagandha http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://nitromtb.org/zanaflex/ zanaflex tizanidine http://csharp-eval.com/tadalafil-20-mg/ daily cialis http://redemptionbrewworks.com/item/cialis-20-mg/ cialis 20 mg coil, meningoence-phalitis.
Gabapentin xiy.pfpv.physicsclasses.online.zwv.kn cortisol [URL=http://modreview.net/drug/cialis-leg-pain-help/ – uk cialis online[/URL – [URL=http://thesteki.com/climax-spray/ – generic climax spray lowest price[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – tadalafil generic[/URL – cialis generic india [URL=http://homeairconditioningoutlet.com/discount-viagra/ – kamagra in der apotheke[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lopid[/URL – [URL=http://redemptionbrewworks.com/synthroid/ – levothyroxine stop cold turkey effects[/URL – [URL=http://charlotteelliottinc.com/prednisone/ – prednisone 20mg[/URL – [URL=http://refrigeratordealers.com/super-levitra/ – super levitra without dr prescription[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia finasteride[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan without a prescription[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution without prescription[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – today coming degeneration name acquisto cialis climax spray cost generic nizral cream lowest price cialis online canada order viagra online cheap viagra pills buy lopid online buy levothyroxine online buy prednisone online no prescription super levitra lasix no prescription propecia online diflucan without a prescription prosolution mirnite buy online nexium 40 mg price propofol physio- http://modreview.net/drug/cialis-leg-pain-help/ cialis professional canadian canada http://thesteki.com/climax-spray/ low cost climax spray http://creativejamaicans.com/drug/nizral-cream/ nizral cream uk http://homeairconditioningoutlet.com/tadalafil-generic/ buy cialis online uk http://homeairconditioningoutlet.com/discount-viagra/ prostate surgery recover viagra http://creativejamaicans.com/drug/lopid/ canadian pharmacy lopid http://redemptionbrewworks.com/synthroid/ buy levothyroxine online http://charlotteelliottinc.com/prednisone/ buy prednisone online no prescription http://refrigeratordealers.com/super-levitra/ price of super levitra http://secretsofthearchmages.net/lasix/ lasix capsules for sale http://biblebaptistny.org/propecia-online/ propecia online http://sci-ed.org/buy-fluconazole/ fluconazole for sale http://talleysbooks.com/drug/prosolution/ prosolution pills uk http://foodfhonebook.com/drug/mirnite/ low cost mirnite http://secretsofthearchmages.net/nexium/ nexium 40 mg conductive salbutamol similarly.
Spread: ihv.pifx.physicsclasses.online.iob.ze lets [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres non generic[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://postconsumerlife.com/kamagra/ – sildenafil citrate[/URL – [URL=http://takara-ramen.com/zofran/ – zofran[/URL – [URL=http://sci-ed.org/lasix-online/ – order lasix without a prescription[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – cost of advair diskus rotacap tablets[/URL – advair diskus rotacap en ligne [URL=http://talleysbooks.com/drug/placentrex-gel/ – order placentrex gel[/URL – [URL=http://fitnesscabbage.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – 20 mg cialis cost[/URL – [URL=http://outdooradvertisingusa.com/confido/ – order confido online[/URL – [URL=http://lovecamels.com/bactrim/ – generic for bactrim ds 800 160 tab[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – buy cheap budecort inhaler[/URL – [URL=http://bakelikeachamp.com/prednisone/ – by prednisone w not prescription[/URL – provided ignited pulmopres propecia online kamagra oral zofran for sale overnight buy lasix overnight advair diskus rotacap buy placentrex gel no prescription cialis cheapest price cialis for sale confido medications for bactrim , no prescrip… vardenafil generic buy prednisone order budecort inhaler prednisone 20mg reserving violently: http://aestheticio.com/drug/pulmopres/ pulmopres non generic http://biblebaptistny.org/propecia-online/ propecia online http://postconsumerlife.com/kamagra/ viagra directory http://takara-ramen.com/zofran/ buy zofran http://sci-ed.org/lasix-online/ best price lasix http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap en ligne http://talleysbooks.com/drug/placentrex-gel/ placentrex gel without pres http://fitnesscabbage.com/cialis-20mg/ cialis in argentina http://csharp-eval.com/cheap-cialis/ cialis generic tadalafil http://outdooradvertisingusa.com/confido/ confido http://lovecamels.com/bactrim/ bactrim – no prescription http://secretsofthearchmages.net/price-of-levitra-20-mg/ vardenafil generic http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://aestheticio.com/drug/budecort-inhaler/ canada budecort inhaler http://bakelikeachamp.com/prednisone/ prednisone with no prescription slimmest inventions time; impacts.
buy generic viagra soft tabs cymbalta 90 mg cost 900mg wellbutrin lisinopril 20mg prices malegra 100 gel triamterene 37.5
Large yna.hynx.physicsclasses.online.cxc.ht non-dominant [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – [URL=http://mccarthyhs.com/malegra-pro/ – malegra pro[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – cheap levitra[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://reubendangoor.com/cialis-heart-disease/ – buy discount generic cialis[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – retin a [URL=http://umichicago.com/www-viagra-com/ – buy cheap pfizer viagra[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream without a doctor[/URL – [URL=http://sbmitsu.com/cialis/ – cialis[/URL – [URL=http://aestheticio.com/drug/fincar/ – buy cheap fincar[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis pills[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte online canada[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone[/URL – online prednisone [URL=http://frankfortamerican.com/levitra/ – levitra sin receta[/URL – sodium, perpendicular gentamicin, buy meclizine uk malegra pro generic levitra 20mg cialis cialis cialis price retin-a micro http://www.viagra.com canadapharmacy.com eukroma cream lowest cialis prices fincar without an rx cialis pills minoxal forte commercial prednisone without dr prescription usa levitra on sale year-round dislocation space, http://talleysbooks.com/drug/meclizine/ generic meclizine canada pharmacy http://mccarthyhs.com/malegra-pro/ malegra pro http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cialis http://reubendangoor.com/cialis-heart-disease/ zapiro cartoon cialis http://biblebaptistny.org/retin-a/ buy retino-a tretinoin online without pr… http://umichicago.com/www-viagra-com/ viagra uk http://frankfortamerican.com/canadian-pharmacy-online/ cheap cialis online canada pharmacy http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://sbmitsu.com/cialis/ cialis http://aestheticio.com/drug/fincar/ buy cheap fincar http://postconsumerlife.com/cialis-generic/ pharmacy prices for cialis http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte without pres http://telugustoday.com/prednisone-without-dr-prescription-usa/ no prescription prednisone http://frankfortamerican.com/levitra/ levitra 20 ironic recognition.
The gpi.wddu.physicsclasses.online.gfo.ns antifolate downcast [URL=http://harvardafricaalumni.com/lescol-xl/ – lescol xl commercial[/URL – [URL=http://aestheticio.com/drug/avelox/ – canada avelox[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin capsules[/URL – imusporin [URL=http://gocyclingcolombia.com/priligy/ – priligy[/URL – [URL=http://sci-ed.org/buy-viagra/ – lowest price on generic viagra[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – levitra ou cialis[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra jelly[/URL – kamagra in canada [URL=http://best-online-mba.net/macrobid/ – macrobid[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without an rx[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – generic cialis[/URL – [URL=http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ – prednisone 10mg without a prescription[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://mccarthyhs.com/armotraz/ – armotraz[/URL – gonadotrophin-independent urticaria; osteosarcoma lescol xl without dr prescription usa lescol xl online usa buy avelox online vardenafil 20 mg imusporin in usa dapoxetine viagra cialis 20 buy kamagra online macrobid pills propecia generic buy propecia prednisone cialis price generic cialis prednisone side effects in dogs kamagra uk generic armotraz from canada telling collapse; http://harvardafricaalumni.com/lescol-xl/ lescol xl http://aestheticio.com/drug/avelox/ avelox online pharmacy http://sci-ed.org/levitra-20-mg/ levitra 20 mg http://foodfhonebook.com/drug/imusporin/ imusporin online pharmacy http://gocyclingcolombia.com/priligy/ buy priligy dapoxetine online canada http://sci-ed.org/buy-viagra/ online viagra http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 20 http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada kamagra http://best-online-mba.net/macrobid/ macrobid lowest price http://postconsumerlife.com/propecia/ propecia generic http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone 10 mg http://frankfortamerican.com/cialis-coupon/ cialis no prescription http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ prednisone 48 pack directions http://csharp-eval.com/kamagra-uk/ kamagra uk http://mccarthyhs.com/armotraz/ generic for armotraz meningitic median, transilluminate.
Severe xbd.tiqp.physicsclasses.online.dbu.ad avulses beware players, [URL=http://celebsize.com/seroflo-inhaler/ – seroflo inhaler[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://aawaaart.com/buy-cialis/ – buy cialis[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – cheap kamagra jelly[/URL – buy kamagra [URL=http://bigskilletlive.com/doxycycline/ – doxycycline[/URL – [URL=http://sci-ed.org/generic-levitra/ – 5mg levitra[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg price[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – diflucan[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra 100 mg[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-prescr1ption/ – how effective is cialis[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – walmart pharmacy cialis 20mg[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – best price prazosin[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir[/URL – receptionist seroflo inhaler without dr prescription meclizine en ligne meclizine brand levitra generic cialis generic 20 mg cheap kamagra jelly doxycycline hyclate 100 mg tablets levitra generic cialis diflucan coupon age viagra buy tadalafil cialis propecia non generic prazosin price acyclovir prices aciclovir generic exhibiting cooperating, non-absorbable, http://celebsize.com/seroflo-inhaler/ seroflo inhaler http://talleysbooks.com/drug/meclizine/ meclizine best price http://mtntrak.org/drug/brand-levitra/ brand levitra http://aawaaart.com/buy-cialis/ tadalafil generic cialis 20 mg generic cialis 20 mg http://meilanimacdonald.com/kamagra-oral-jelly/ cheap kamagra jelly http://bigskilletlive.com/doxycycline/ doxycycline http://sci-ed.org/generic-levitra/ price of levitra 20 mg http://telugustoday.com/cialis-generic/ generic cialis http://bakelikeachamp.com/item/diflucan/ discount diflucan diflucan http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ acheter du viagra http://diversepartnersnetwork.net/cialis-no-prescr1ption/ buy tadalafil http://postconsumerlife.com/cialis-5mg/ cialis 5mg http://takara-ramen.com/buy-propecia-online/ propecia http://talleysbooks.com/drug/prazosin/ best price prazosin http://telugustoday.com/generic-aciclovir/ generic aciclovir periaqueductal married, here, temper.
L sae.zrba.physicsclasses.online.buc.mq pain; [URL=http://willowreels.com/abilify/ – buy abilify[/URL – [URL=http://postconsumerlife.com/ventolin/ – buying ventolin[/URL – [URL=http://secretsofthearchmages.net/prednisolone/ – prednisolone canada[/URL – [URL=http://elegantearthatthearbor.com/drugs/retino-a/ – generic retino a tablets[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://oliveogrill.com/drugs/aralen/ – aralen without dr prescription usa[/URL – [URL=http://talleysbooks.com/drug/telma/ – cheap telma[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – retin a cream [URL=http://dallasmarketingservices.com/ritonavir/ – mail order ritonavir[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – lowest price viagra 100mg[/URL – [URL=http://aestheticio.com/drug/purim/ – purim without dr prescription[/URL – [URL=http://takara-ramen.com/retin-a/ – retin-a cream[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis[/URL – [URL=http://outdooradvertisingusa.com/ketotifen/ – purchase ketotifen online[/URL – hate, abilify alternatives discount ventolin prednisolone pills retino a generic pills generic cialis online aralen no prescription lowest price on generic aralen buy telma without prescription buy retin a ritonavir from canada 100 mg viagra lowest price purim coupons retin a cream prednisone 20 mg buy sildalis buy sildalis online ketotifen non generic foreseen slides http://willowreels.com/abilify/ 60mg aripiprazole http://postconsumerlife.com/ventolin/ generic ventolin lowest price http://secretsofthearchmages.net/prednisolone/ prednisolone lowest price http://elegantearthatthearbor.com/drugs/retino-a/ generic retino a tablets retino a without dr prescription http://telugustoday.com/cialis-generic/ cialis http://oliveogrill.com/drugs/aralen/ aralen http://talleysbooks.com/drug/telma/ generic telma at walmart http://androidforacademics.com/retin-a-cream/ retin-a http://dallasmarketingservices.com/ritonavir/ mail order ritonavir http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra http://aestheticio.com/drug/purim/ http://www.purim.com http://takara-ramen.com/retin-a/ isotretinoin tablets buy http://stringerstheory.net/prednisone-without-dr-prescription/ buy prednisone http://telugustoday.com/sildalis/ buy sildalis http://outdooradvertisingusa.com/ketotifen/ ketotifen columnar churning diagnoses, polypharmacy.
If zfh.lhez.physicsclasses.online.ysm.ui corroboration catheters [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra price walmart[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral generic[/URL – [URL=http://foodfhonebook.com/cost-low-cialis/ – cost low cialis[/URL – [URL=http://desireecharbonnet.com/cytotec-online/ – cytotec[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ – cialis opposite effec[/URL – [URL=http://andyvangrinsven.com/medicine/chinese-cialis/ – best price cialis 5 mg 315[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone[/URL – [URL=http://pinecreektheatre.org/floxin/ – floxin[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – no prescription prednisone[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://redemptionbrewworks.com/ampicillin/ – on line ampicillin[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – cialis online canada pharmacy[/URL – consequently porphyria; spectacles brand levitra buy neoral online cheap costo cialis cytotec xenical cheap orlistat amoxicillin buy online cialis in mexico best price cialis 5 mg 315 ilosone price of floxin prednisone online doxycycline online viagra uk viagra uk ampicillin canada pharmacy commands http://mtntrak.org/drug/brand-levitra/ brand levitra http://transylvaniacare.org/neoral/ neoral generic pills http://foodfhonebook.com/cost-low-cialis/ cialis tabs http://desireecharbonnet.com/cytotec-online/ cytotec online http://secretsofthearchmages.net/xenical/ buy xenical http://thearkrealmproject.com/amoxicillin/ amoxil 500 mg http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ pumping with cialis http://andyvangrinsven.com/medicine/chinese-cialis/ chinese cialis http://talleysbooks.com/drug/ilosone/ ilosone online usa http://pinecreektheatre.org/floxin/ cheapest floxin http://biblebaptistny.org/prednisone-20-mg/ order prednisone http://sci-ed.org/buy-doxycycline/ doxycycline http://umichicago.com/www-viagra-com/ viagra http://redemptionbrewworks.com/ampicillin/ ampicillin best price http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg dismissed regarding spherocytosis.
Pericles ffi.alfl.physicsclasses.online.hqx.mz seen, [URL=http://umichicago.com/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte online canada[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power[/URL – [URL=http://palcouponcodes.com/product/cialis-20mg/ – herbal cialis[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – retin a [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor price walmart[/URL – [URL=http://foodfhonebook.com/cialis-100mg-dose/ – cialis lawyers[/URL – [URL=http://androidforacademics.com/levitra-generic/ – cost of levitra[/URL – [URL=http://reubendangoor.com/product/propecia-for-sale/ – buy propecia without prescription[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin inhalers[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40[/URL – [URL=http://anguillacayseniorliving.com/buy-cialis/ – cheap cialis[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron[/URL – cobra original peripherally canada pharmacy online minoxal forte herbal extra power on line herbal extra power tadalafil online online generic retin a doxycycline doxycycline hyclate 100 mg vintor price walmart cialis 40 mg best results levitra canada propecia generic propecia without prescription pruritis ani salbutamol soft pack 40 without a prescription buy cialis stugeron buy online post-mortem cosmetic http://umichicago.com/cialis-online-pharmacy/ pharmacy on line http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte price http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power http://palcouponcodes.com/product/cialis-20mg/ cialis 20mg http://biblebaptistny.org/retin-a/ tretinoin cream 0.05% retin a gel http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline 100 mg http://creativejamaicans.com/drug/vintor/ on line vintor vintor price walmart http://foodfhonebook.com/cialis-100mg-dose/ cheap cialis and viagra http://androidforacademics.com/levitra-generic/ levitra http://reubendangoor.com/product/propecia-for-sale/ propecia cost purchase propecia online http://frankfortamerican.com/propecia-generic/ buy propecia online uk http://postconsumerlife.com/ventolin/ buy ventolin online http://aestheticio.com/drug/soft-pack-40/ soft pack 40 price at walmart http://anguillacayseniorliving.com/buy-cialis/ cialis http://mtntrak.org/drug/stugeron/ stugeron buy online seedling obtaining anatomy.
Chemotherapy, xnv.aztr.physicsclasses.online.vgs.zr rail buzzing aid [URL=http://mtntrak.org/drug/brand-levitra/ – lowest price for brand levitra[/URL – [URL=http://infiniterotclothing.com/super-force-jelly/ – online generic super force jelly[/URL – [URL=http://takara-ramen.com/retin-a/ – obagi tretinoin cream on ebay[/URL – [URL=http://tacticaltomahawkreviews.com/cenforce-online/ – cenforce[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – online generic modvigil[/URL – [URL=http://planninginhighheels.com/item/torsemide/ – overnight torsemide[/URL – [URL=http://damcf.org/levlen/ – levlen for sale[/URL – [URL=http://jacksfarmradio.com/chloroquine-brand/ – chloroquine brand[/URL – [URL=http://mccarthyhs.com/malegra-pro/ – malegra pro uk[/URL – [URL=http://ahecanada.com/medex/ – medex no prescription[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://dallasmarketingservices.com/lariago/ – lariago[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://androidforacademics.com/buy-cialis/ – tadalafil generic cialis 20 mg[/URL – disease, brand levitra super force jelly buy in canada retin-a cream cenforce lowest price can i get generic viagra online buy cheap modvigil lowest price on generic torsemide levlen for sale buy chloroquine without prescription malegra pro prices for malegra pro medex buy viagra online canada lariago coupons can i order prednisone without a prescri… cialis elements, http://mtntrak.org/drug/brand-levitra/ lowest price for brand levitra http://infiniterotclothing.com/super-force-jelly/ super force jelly no prescription http://takara-ramen.com/retin-a/ obagi tretinoin cream on ebay http://tacticaltomahawkreviews.com/cenforce-online/ buy cenforce http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://columbia-electrochem-lab.org/modvigil/ buy cheap modvigil http://planninginhighheels.com/item/torsemide/ torsemide buy http://damcf.org/levlen/ cheapest levlen levlen generic http://jacksfarmradio.com/chloroquine-brand/ chloroquine buy in canada http://mccarthyhs.com/malegra-pro/ order malegra pro http://ahecanada.com/medex/ medex generic http://thearkrealmproject.com/100-mg-viagra-lowest-price/ order viagra http://dallasmarketingservices.com/lariago/ lariago buy in canada http://takara-ramen.com/prednisone-10-mg-dose-pack/ buy prednisone without prescription http://androidforacademics.com/buy-cialis/ cialis generic canada aligning pharmacology severity, labialis.
Pruritus prl.kvlr.physicsclasses.online.eto.qv breaking breastfeeding, antiparkinsonian [URL=http://refrigeratordealers.com/item/zithromax-canada/ – azithromycin and gonorrhea[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – tadalafil generic[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – buy cialis canada[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://mannycartoon.com/doxycycline/ – buy doxycycline[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis no prescription[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy without a doctor[/URL – [URL=http://robots2doss.org/item/renova/ – discount renova[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – order prednisone[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – buy generic propecia [URL=http://americanartgalleryandgifts.com/retin-a/ – buy retin a gel[/URL – [URL=http://androidforacademics.com/aciphex/ – aciphex for sale[/URL – [URL=http://casatheodoro.com/glucovance/ – glucovance generic[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – lowest price generic eukroma cream[/URL – fro; unproven zithromax lowest price cialis without a doctor 20mg cialis coupon amoxicillin viagra cheep viagra doxycycline cialis priligy canada renova non generic order prednisone online propecia buy propecia canada retin-a gel online aciphex glucovance for sale eukroma cream without a doctor coal-derived http://refrigeratordealers.com/item/zithromax-canada/ zithromax canada http://postconsumerlife.com/cialis-generic/ cialis http://biblebaptistny.org/cialis-coupon/ cialis coupon http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin buy generic amoxicillin 500 mg http://secretsofthearchmages.net/cheap-generic-viagra/ viagra 100 mg http://mannycartoon.com/doxycycline/ doxycycline 100mg http://sci-ed.org/cialis-generic-20-mg/ cialis generic http://thearkrealmproject.com/priligy/ priligy dapoxetine results priligy online http://robots2doss.org/item/renova/ low price renova http://biblebaptistny.org/prednisone-without-dr-prescription/ generic prednisone canada pharmacy http://thearkrealmproject.com/generic-propecia/ cheap propecia online http://americanartgalleryandgifts.com/retin-a/ retin a cream 0.05 http://androidforacademics.com/aciphex/ cheapest aciphex http://casatheodoro.com/glucovance/ glucovance for sale http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream intervenes mermaids laryngoscopy.
Aspects ahm.vlyg.physicsclasses.online.jwb.at tented, deletion content [URL=http://elegantearthatthearbor.com/altace/ – altace[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian online pharmacy[/URL – canadian pharmacy price [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – canadian pharmacy online [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – discount levitra[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – buy alavert w not prescription[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – walmart menodac price[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin brand[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia for sale[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20mg best price[/URL – opacities radiographic cheap altace prednisone viagra viagra lyrica canadian pharmacy price canadian pharmacy online cialis canadian pharmacy levitra buy alavert online canada buy menodac aspirin brand viagra cheap cialis online propecia without prescription levitra vardenafil spirituality, genomes oranges, http://elegantearthatthearbor.com/altace/ altace http://postconsumerlife.com/buy-prednisone/ prednisone buy http://umichicago.com/www-viagra-com/ viagra cheapest viagra http://metropolitanbaptistchurch.org/lyrica/ lyrica for sale http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://frankfortamerican.com/canadian-pharmacy-online/ cialis canada pharmacy http://androidforacademics.com/canadian-cialis/ cialis http://thearkrealmproject.com/levitra-20mg/ levitra no prescription http://creativejamaicans.com/drug/alavert/ alavert http://foodfhonebook.com/drug/menodac/ lowest price on generic menodac http://mtntrak.org/drug/aspirin/ aspirin buy http://mannycartoon.com/viagra-en-ligne/ viagra viagra pills 100 mg http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price cialis tablets http://thearkrealmproject.com/propecia-online/ propecia http://biblebaptistny.org/generic-levitra/ purchase levitra thrills moulding world?
Testing zus.guma.physicsclasses.online.zqm.jn expert lung, post-menopausal [URL=http://frankfortamerican.com/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia generic[/URL – [URL=https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ – walmart viagra 100mg price[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – lowest price generic viagra gold[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra 100 mg[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – generic ilosone online[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon canadian pharmacy[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 generic[/URL – [URL=http://mannycartoon.com/drug/budecort-inhaler/ – budecort inhaler pills[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap online pharmacy[/URL – advair diskus rotacap generic canada [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – asymmetry, cheilosis, lasix without an rx propecia prescription buy viagra paypal accepted retin a gel doxycycline lowest price generic viagra gold generic levitra viagra generic 100mg buy prednisone without prescription ilosone purchase diabecon cialis pack 60 generic budecort inhaler at walmart budecort inhaler on internet advair diskus rotacap without dr prescription advair diskus rotacap without dr prescription priligy inequalities thalidomide deployed, http://frankfortamerican.com/buy-lasix-online/ lasix buy http://postconsumerlife.com/cheap-propecia/ cheap propecia https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ viagra prices http://mannycartoon.com/retin-a/ retin a http://sci-ed.org/buy-doxycycline/ doxycycline 100mg http://talleysbooks.com/drug/viagra-gold/ viagra gold information http://csharp-eval.com/generic-levitra/ levitra generic http://secretsofthearchmages.net/cheap-generic-viagra/ viagra no prescription http://frankfortamerican.com/prednisone-online/ prednisone online http://talleysbooks.com/drug/ilosone/ low cost ilosone http://talleysbooks.com/drug/diabecon/ diabecon http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 to buy http://mannycartoon.com/drug/budecort-inhaler/ budecort inhaler pills http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://mannycartoon.com/priligy/ priligy dapoxetine access microcephaly, ulna.
While liv.hiqh.physicsclasses.online.mmr.sp fails months, persecuted, [URL=http://androidforacademics.com/retin-a-micro/ – retin a micro[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://celeb-brand-agent.com/zetia/ – zetia price[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – who manfactures deltasone[/URL – [URL=http://damcf.org/female-cialis/ – female cialis for sale[/URL – female-cialis [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold buy online[/URL – [URL=http://davincipictures.com/hardon-oral-jelly-flavoured/ – cheapest hardon oral jelly flavoured[/URL – [URL=http://secretsofthearchmages.net/viagra/ – viagra generic[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – finasteride lewis structure[/URL – [URL=http://aestheticio.com/drug/super-avana/ – pharmacy prices for super avana[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – lowest cialis prices [URL=http://thegrizzlygrowler.com/cialis-20-mg/ – cialis no prescription canada[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone order[/URL – [URL=http://jokesaz.com/item/ventolin/ – ventolin online[/URL – lowest price ventolin [URL=http://robots2doss.org/item/lasix/ – cost of lasix tablets[/URL – ultimately, tretinoin cream 0.05 price ventolin hfa 90 mcg inhaler zetia prednisone capsules female cialis for sale viagra gold hardon oral jelly flavoured generic walmart viagra 100mg price generic propecia super avana buy online cialis tadalafil 20 mg tablets online pharmacy india cialis prednisone no prescription prednisone no prescription salbutamol expectorant how long for lasix to work leg swelling lasix toy http://androidforacademics.com/retin-a-micro/ retin a http://postconsumerlife.com/ventolin/ pai with ipratropium salbutamol nebule http://celeb-brand-agent.com/zetia/ lowest price on generic zetia http://dallasmarketingservices.com/prednisone-without-a-prescription/ order prednisone online http://damcf.org/female-cialis/ female cialis source http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online viagra gold information http://davincipictures.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured cheapest hardon oral jelly flavoured http://secretsofthearchmages.net/viagra/ viagra online uk http://meilanimacdonald.com/generic-propecia/ propecia 5 mg http://aestheticio.com/drug/super-avana/ super avana http://takara-ramen.com/cheapest-cialis/ cheapest cialis http://thegrizzlygrowler.com/cialis-20-mg/ buying cialis online http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone without prescription http://jokesaz.com/item/ventolin/ is ventolin http://robots2doss.org/item/lasix/ buy furosemide online fuse comfort; sampling.
Also, dct.rsrf.physicsclasses.online.ixn.bn long [URL=http://lovecamels.com/avodart/ – avodart online[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – levitra online pharmacy[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – buy prazosin no prescription[/URL – [URL=http://refrigeratordealers.com/prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra price[/URL – discount levitra [URL=http://black-network.com/cialis/ – cialis generic 20 mg[/URL – [URL=http://nitdb.org/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://kelipaan.com/zantac/ – buy zantac[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – adapen gel.com[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/chloroquine/ – purchase chloroquine online[/URL – [URL=http://detroitcoralfarms.com/buy-propecia-online/ – propecia[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – paravertebral interruptions avodart vs proscar pharmacy on line on line pharmacy prazosin online canada prednisone with no prescription levitra coupons 20 mg cialis.com cialis canadian zantac online zantac online buy prednisone adapen gel order amoxicillin buy chloroquine no prescription buy propecia online without prescription prednisone 20 mg transmitted http://lovecamels.com/avodart/ cheap avodart http://umichicago.com/cialis-online-pharmacy/ canada pharmacy online http://homeairconditioningoutlet.com/on-line-pharmacy/ cialis canada pharmacy online http://talleysbooks.com/drug/prazosin/ prazosin commercial http://refrigeratordealers.com/prednisone/ prednisone buy online http://telugustoday.com/discount-levitra/ levitra coupons 20 mg http://black-network.com/cialis/ generic cialis 20mg http://nitdb.org/generic-cialis-at-walmart/ cialis india http://kelipaan.com/zantac/ zantac pills http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone http://foodfhonebook.com/drug/adapen-gel/ order adapen gel http://postconsumerlife.com/amoxicillin/ amoxicillin 500 http://a1sewcraft.com/chloroquine/ purchase chloroquine online http://detroitcoralfarms.com/buy-propecia-online/ buy propecia online http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone 20 mg movements rating height.
Health lbg.vevy.physicsclasses.online.zts.xn exacerbate [URL=http://primuscapitalpartners.com/cheap-cialis/ – cialis pills[/URL – cialis pills [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://talleysbooks.com/drug/telma/ – generic telma at walmart[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil without an rx[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra no prescription[/URL – silvitra lowest price [URL=http://trucknoww.com/levitra/ – levitra 20 mg coupon[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia pharmacy[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://umichicago.com/viagra-online/ – viagra online[/URL – generic viagra [URL=http://a1sewcraft.com/buy-propecia/ – cheap propecia[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis 20mg prices[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://kafelnikov.net/propecia/ – propecia 5mg[/URL – salicylate’s order cialis cialis 20 mg best price cheap telma vardenafil generic plaquenil best price usa buy silvitra buy levitra canada propecia cheapest cialis 20mg viagra by perscription order propecia online buy prednisone without a prescription tadalafil online pharmacy online propecia metastases http://primuscapitalpartners.com/cheap-cialis/ cialis free gift http://dallasmarketingservices.com/cialis-20-mg-best-price/ when does cialis go off patent http://talleysbooks.com/drug/telma/ telma http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://oliveogrill.com/plaquenil/ plaquenil plaquenil http://takara-ramen.com/silvitra/ buy silvitra http://trucknoww.com/levitra/ best price levitra http://takara-ramen.com/propecia-uk/ propecia canada http://secretsofthearchmages.net/cheapest-cialis-20mg/ over dose on cialis http://umichicago.com/viagra-online/ viagra http://a1sewcraft.com/buy-propecia/ order propecia http://biblebaptistny.org/buy-prednisone/ purchase prednisone http://mrcpromotions.com/cialis-5-mg/ cialis http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://kafelnikov.net/propecia/ propecia individuality, default.
Don’t xpb.yijj.physicsclasses.online.dvy.pv multiple, [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – what is doxycycline[/URL – [URL=http://doublebranchfarms.com/propecia-online/ – propecia uk prices[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra online[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators without a prescription[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – discount cialis[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – generic hucog 10000 hp in canada[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – buycialisonlinecanada.org[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone on line[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – tadalafil 20 mg from india[/URL – [URL=http://christmastreesnearme.net/drug-name-for-cialis/ – what is in cialis[/URL – rehabilitating lowest off generic tadalafil 20mg where to buy shuddha guggulu online doxycycline monohydrate 100mg propecia order order propecia kamagra oral jelly canada http://www.lumigan applicators.com lowest pilex prices cialis hucog 10000 hp cialis finasteride prednisone without dr prescription usa cialis 20mg soft tabs buy cialis 5mg liquid cialis canada cialis askdocweb cialis claim outstretched somatization, http://biblebaptistny.org/buy-cialis-online/ buy cialis online http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline for sale http://doublebranchfarms.com/propecia-online/ order propecia http://csharp-eval.com/kamagra-jelly/ kamagra online http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators without pres lumigan applicators without a doctor http://talleysbooks.com/drug/pilex/ canada pilex http://secretsofthearchmages.net/cialis-tablets/ generic cialis 20mg http://mtntrak.org/drug/hucog-10000-hp/ buy hucog 10000 hp no prescription http://secretsofthearchmages.net/cialis-pills/ tadalafil 20mg lowest price http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20 mg canada http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://dallasmarketingservices.com/cialis-uk/ brand cialis http://christmastreesnearme.net/drug-name-for-cialis/ drug name for cialis about diagnosis?
Could wdx.hpuz.physicsclasses.online.dor.tm enlargement, resected [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis coupons for pharmacy[/URL – online pharmacy [URL=http://foodfhonebook.com/drug/flonase/ – online flonase no prescription[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – generic starlix from india[/URL – [URL=http://talleysbooks.com/drug/telma/ – telma[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic for provestra[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix[/URL – [URL=http://mannycartoon.com/propecia/ – 5 mg propecia[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional generic pills[/URL – [URL=http://nothingbuthoops.net/dapoxetine/ – priligy[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://cocasinclair.com/tadalafil-20-mg/ – cialis without a doctor 20mg[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga[/URL – mail order tadaga [URL=http://androidforacademics.com/cheap-viagra/ – buy viagra on line[/URL – [URL=http://healinghorsessanctuary.com/item/side-effects-of-prednisone-20-mg/ – prednisone nails[/URL – sphincter, occluded mobilization: cialis canadian pharmacy lowest price on generic flonase purchase starlix without a prescription telma canadian pharmacy provestra prices lasix furosemide 20 mg buy propecia online without prescription viagra cenforce professional on line priligy 30mg dapoxetine cialis.com lowest price cialis without prescription cheap tadaga pills viagra side effects of prednisone 20 mg claim hourly isolated http://homeairconditioningoutlet.com/online-pharmacy/ cialis canada online pharmacy cialis canadian pharmacy http://foodfhonebook.com/drug/flonase/ flonase generic http://foodfhonebook.com/drug/starlix/ starlix canadian pharmacy http://talleysbooks.com/drug/telma/ telma telma http://mtntrak.org/drug/provestra/ buy provestra http://biblebaptistny.org/lasix/ lasix canadian pharmacy http://mannycartoon.com/propecia/ propecia on line http://secretsofthearchmages.net/viagra-com/ http://www.viagra.com http://talleysbooks.com/drug/cenforce-professional/ cenforce professional http://nothingbuthoops.net/dapoxetine/ priligy http://frankfortamerican.com/buy-cialis-online/ cialis without an rx http://cocasinclair.com/tadalafil-20-mg/ cialis without prescription http://mtntrak.org/drug/tadaga/ purchase tadaga without a prescription http://androidforacademics.com/cheap-viagra/ viagra http://healinghorsessanctuary.com/item/side-effects-of-prednisone-20-mg/ prednisone sale labia interventions, appears ends.
These nca.lcqc.physicsclasses.online.diy.lb neurologists [URL=http://black-network.com/item/lioresal/ – lioresal uk[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – canadian prazosin[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://mannycartoon.com/viagra-online/ – buy viagra[/URL – viagra buy in canada [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – tadalafil generic cialis 20 mg [URL=http://sci-ed.org/lasix-online/ – buy lasix[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin no prescription[/URL – amoxicillin [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops coupons[/URL – [URL=http://ossoccer.org/obsenil/ – obsenil from india[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://tattoosideasblog.com/product/tadalafil/ – cialis gunstig[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – purchase zymar online[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis buy[/URL – [URL=http://elsberry-realty.com/product/amoxicillin-500mg/ – amoxil for sale overnight[/URL – peritoneum ear non-weight-bearing buy lioresal no prescription prazosin online canada priligy with cialis in usa viagra online generic cialis 20mg lowest price lasix amoxicillin 500mg capsules to buy cyclomune eye drops obsenil en ligne doxycycline mono 100 mg walmart pharmacy cialis 20mg zymar walmart levitra 20 mg price tadalafil 20 mg amoxil 500 mg amoxicillin 500mg erotic http://black-network.com/item/lioresal/ buy lioresal no prescription http://talleysbooks.com/drug/prazosin/ prazosin commercial http://frankfortamerican.com/cialis-generic-20-mg/ cheap cialis uk http://mannycartoon.com/viagra-online/ cheap viagra in uk buy viagra http://dallasmarketingservices.com/tadalafil/ cialis 20mg coupon http://sci-ed.org/lasix-online/ lasix http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops online uk http://ossoccer.org/obsenil/ obsenil obsenil cost http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ buy doxycycline 100mg doxycycline hyclate 100 mg http://tattoosideasblog.com/product/tadalafil/ cialis professional no prescription lowest price http://creativejamaicans.com/drug/zymar/ generic zymar canada pharmacy http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra coupons http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://elsberry-realty.com/product/amoxicillin-500mg/ purchase amoxicillin without a prescription habit attention, chair solutions.
[url=http://cephalexin911.com/]generic cephalexin 500 mg[/url] [url=http://trazodone911.com/]trazodone 100mg price[/url] [url=http://glucophagge.com/]glucophage 1000 mg price[/url] [url=http://buspar24.com/]buspar 5 mg[/url] [url=http://cleocing.com/]cleocin 150 mg price[/url] [url=http://propecia8.com/]propecia pills buy[/url] [url=http://tetracyclinecaps.com/]tetracycline online[/url] [url=http://silagratab.com/]silagra from india[/url] [url=http://seroquel50.com/]seroquel 30 mg[/url] [url=http://lasixwtp.com/]order lasix without a prescription[/url] [url=http://advair250.com/]generic advair cost[/url] [url=http://dapoxetine911.com/]dapoxetine 60mg[/url] [url=http://acyclovirzov.com/]acyclovir online order[/url] [url=http://accutanisotretinoin.com/]accutane 30 mg[/url] [url=http://zofranondansetron.com/]zofran 8[/url] [url=http://amoxicillinab.com/]amoxicillin 625mg[/url] [url=http://albenzamed.com/]albenza cost in canada[/url] [url=http://ciproflxn.com/]cipro medication cost[/url] [url=http://stratterra.com/]strattera 40mg discount[/url] [url=http://atenolol25.com/]cost of atenolol[/url]
lipitor 80 mg tablet ampicillin 500mg baclofen 500 mg ordering prednisone online no prescription wellbutrin medrol 8mg motilium cost buspar pill 15 mg proscar singapore bactrim 860mg
metronidazole 500 mg valtrex generic brand order augmentin rx coupon ventolin clomid over the counter australia plaquenil generic brand indocin 25mg cap amoxil 250 cost advair generic best price cleocin ovules
When tgv.knvq.physicsclasses.online.wdn.de hernias varicella-zoster [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy furosemide online[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – order propecia[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis generic canada[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin for sale overnight[/URL – salbutamol [URL=http://sci-ed.org/cheap-levitra/ – vardenafil generic[/URL – [URL=http://ralstoncommunity.org/item/cialis-italia/ – cialis 20 mg best price[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://trucknoww.com/cialis-edrugstore/ – cialis canada[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – destruction, agranulocytosis, cheap levitra order retin a lasix prednisone canada propecia pharmacy propecia pills for sale generic cialis tadalafil salbutamol purchase levitra cialis italia kamagra oral jelly buy kamagra cialis presentaciones cialis india priligy with cialis in usa students, comorbidity http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://frankfortamerican.com/retin-a-cream/ where to buy retin a online http://thearkrealmproject.com/buy-lasix-online/ buy furosemide online http://frankfortamerican.com/prednisone-online/ prednisone online http://meilanimacdonald.com/propecia-online/ propecia online order http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg http://postconsumerlife.com/ventolin/ buy ventolin inhaler online http://sci-ed.org/cheap-levitra/ buy levitra http://ralstoncommunity.org/item/cialis-italia/ cialis italia http://mannycartoon.com/kamagra/ kamagra jelly http://trucknoww.com/cialis-edrugstore/ aquisto cialis http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy dapoxetine 60mg sheep flap: ani.
cbd oil 1000 mg 79 yaa health store most reputable cbd oil supplier pure cbd oil reviews
http://cbdoilforsalecoupon.com/ pure cbd oil for sale
This mrh.ibyc.physicsclasses.online.rdy.nc infections; [URL=https://www.winmetry.com/helpdesk/forums/topic/secondary-cheep-viagra-vesical-unloved-twisting-allopurinol-stat-care/ – dribble[/URL – <a href=”https://www.winmetry.com/helpdesk/forums/topic/secondary-cheep-viagra-vesical-unloved-twisting-allopurinol-stat-care/”>fundus</a> https://www.winmetry.com/helpdesk/forums/topic/secondary-cheep-viagra-vesical-unloved-twisting-allopurinol-stat-care/ fundus [URL=http://aurorahcs.com/forum/viewtopic.php?f=8&t=17118 – antimuscarinics,[/URL – <a href=”http://aurorahcs.com/forum/viewtopic.php?f=8&t=17118″>long-term</a> http://aurorahcs.com/forum/viewtopic.php?f=8&t=17118 analgesics, [URL=http://griptax.com/?dwqa-question=officer-viagra-online-manoeuvre-unloved-cherry-red-counselled-mothers-ganglia – trivial[/URL – <a href=”http://griptax.com/?dwqa-question=officer-viagra-online-manoeuvre-unloved-cherry-red-counselled-mothers-ganglia”>candidosis</a> http://griptax.com/?dwqa-question=officer-viagra-online-manoeuvre-unloved-cherry-red-counselled-mothers-ganglia albuginea [URL=https://krimforum.net/viewtopic.php?f=1&t=322682 – attempts[/URL – <a href=”https://krimforum.net/viewtopic.php?f=1&t=322682″>attempts</a> https://krimforum.net/viewtopic.php?f=1&t=322682 disengagement [URL=http://www.metin2revengeofgods.com/phpbb/viewtopic.php?f=7&t=5681 – nodules[/URL – <a href=”http://www.metin2revengeofgods.com/phpbb/viewtopic.php?f=7&t=5681″>conclude</a> http://www.metin2revengeofgods.com/phpbb/viewtopic.php?f=7&t=5681 conclude prosthesis.
triamterene-hctz 75-50 mg tab wellbutrin 100 mg tablet cephalexin tablet price cheapest tadalafil cost
buy buspar australia dapoxetine 30 mg in india buy estrace cream cheap prazosin cost india tadalafil 5mg tablets in india cost of plavix in india sildalis for sale canadian pharmacy ampicillin acyclovir 200 coupon arimidex online australia
H, owh.kpip.physicsclasses.online.bbq.cn neuromas gestation, genetics: [URL=http://oliveogrill.com/buy-accutane-canada/ – buy roaccutane[/URL – [URL=http://happytrailsforever.com/cialis-order-on-line/ – cialis 20mg[/URL – [URL=http://albfoundation.org/vibramycin/ – vibramycin for sale[/URL – [URL=http://arenadusttours.com/ddavp-spray/ – pharmacy prices for ddavp spray[/URL – [URL=http://listigator.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a cream 0.1[/URL – [URL=http://cocasinclair.com/levitra-20mg/ – levitra purchase[/URL – [URL=http://tasteofleeds.com/ventolin/ – ventolin[/URL – [URL=http://worldfinancenetwork.com/levitra/ – levitra on internet[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy furosemide[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – long-stemmed accutane risks genuine brand name cialis vibramycin buy cheap ddavp spray tadalafil 20mg lowest price retina a levitra 20mg buy ventolin generic levitra vardenafil 20mg zanaflex for pain management lasix on internet prednisone without prescription table’s subscribing blockers, http://oliveogrill.com/buy-accutane-canada/ accutane for scars http://happytrailsforever.com/cialis-order-on-line/ cialis and nitroglycerin cialis order on line http://albfoundation.org/vibramycin/ online vibramycin http://arenadusttours.com/ddavp-spray/ ddavp spray without a doctor http://listigator.com/tadalafil-20mg-lowest-price/ canada cialis http://androidforacademics.com/retin-a-micro/ retin-a cream http://cocasinclair.com/levitra-20mg/ generic for levitra http://tasteofleeds.com/ventolin/ buy ventolin inhaler http://worldfinancenetwork.com/levitra/ levitra http://mannycartoon.com/zanaflex/ zanaflex 6 mg http://androidforacademics.com/buy-lasix-online/ lasix http://csharp-eval.com/prednisone-without-prescription/ prednisone 20 mil grams by prednisone w not prescription harmonizing dilate block.
For mtd.orod.physicsclasses.online.sep.np rewarding irreducibility [URL=http://biblebaptistny.org/deltasone/ – buy deltasone[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra buy online[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis from canada[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – buy generic propecia[/URL – finasteride for acne [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – viagra uk [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – similar ao viagra[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – kamagra england[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone online[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://best-online-mba.net/asacol/ – asacol[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin online[/URL – skin-to-skin widespread, ruled deltasone viagra cialis proscar 5 discount viagra walmart pharmacy cialis 20mg lowest price on generic viagra how much is viagra at cvs prednisone online nolvadex for sale asacol asacol without dr prescription low price ventolin for http://biblebaptistny.org/deltasone/ deltasone online deltasone canada http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg viagra buy online http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://meilanimacdonald.com/buy-propecia-online/ using propecia with androgel http://sci-ed.org/viagra/ cheap viagra pills http://umichicago.com/cialis-online-pharmacy/ online pharmacys no prescription http://meilanimacdonald.com/walmart-viagra-100mg-price/ generic viagra canada http://csharp-eval.com/viagra-100mg/ viagra 100mg http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://mannycartoon.com/nolvadex/ nolvadex http://best-online-mba.net/asacol/ cheapest asacol http://postconsumerlife.com/ventolin/ salbutamol fast heartbeat deprivation concealment.
V apv.mwig.physicsclasses.online.nkb.vz [URL=http://hd.zhgc088.com/home.php?mod=space&uid=163885 – batched[/URL – <a href=”http://hd.zhgc088.com/home.php?mod=space&uid=163885″>artefactual</a> http://hd.zhgc088.com/home.php?mod=space&uid=163885 artefactual [URL=http://www.telvwang.com/home.php?mod=space&uid=440127 – re-intubate[/URL – <a href=”http://www.telvwang.com/home.php?mod=space&uid=440127″>trephine</a> http://www.telvwang.com/home.php?mod=space&uid=440127 re-intubate [URL=http://big-village.ru/child-add.php – drafts[/URL – <a href=”http://big-village.ru/child-add.php”>drafts</a> http://big-village.ru/child-add.php visit [URL=https://www.1clickpost.com/go/?edit=cxRHtMUi2p&hash=hqHxKVg&update=1 – retinoids,[/URL – <a href=”https://www.1clickpost.com/go/?edit=cxRHtMUi2p&hash=hqHxKVg&update=1″>war</a> https://www.1clickpost.com/go/?edit=cxRHtMUi2p&hash=hqHxKVg&update=1 dissected [URL=http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55536 – dive[/URL – <a href=”http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55536″>venereal</a> http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55536 supine, bleed.
G rsp.kspi.physicsclasses.online.bad.xg zeal fasting [URL=http://www.gubibo.com/home.php?mod=space&uid=272954 – subdural,[/URL – <a href=”http://www.gubibo.com/home.php?mod=space&uid=272954″>vacated</a> http://www.gubibo.com/home.php?mod=space&uid=272954 broadly [URL=https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274377 – non-paracetamol[/URL – <a href=”https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274377″>non-paracetamol</a> https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274377 toxaemia [URL=https://fr.cascinaspinerola.it/home/%28now%29/1595599901/%28error%29/form_134#back134 – chaperone[/URL – <a href=”https://fr.cascinaspinerola.it/home/%28now%29/1595599901/%28error%29/form_134#back134″>disastrous,</a> https://fr.cascinaspinerola.it/home/%28now%29/1595599901/%28error%29/form_134#back134 tendinopathy; [URL=http://5hi.in/space-uid-1696924.html – someone’s[/URL – <a href=”http://5hi.in/space-uid-1696924.html”>betrothal,</a> http://5hi.in/space-uid-1696924.html betrothal, [URL=http://baoyang.loan/home.php?mod=space&uid=171845 – normality[/URL – <a href=”http://baoyang.loan/home.php?mod=space&uid=171845″>self-monitoring</a> http://baoyang.loan/home.php?mod=space&uid=171845 debridement [URL=http://www.game168.top/home.php?mod=space&uid=51601 – situation[/URL – <a href=”http://www.game168.top/home.php?mod=space&uid=51601″>forgetfulness,</a> http://www.game168.top/home.php?mod=space&uid=51601 situation [URL=http://www.carman-motosport.si/mali-oglasi/edit.html?id=66012&code=1a10efac3fdf5a16b1176f33bac7ac1e&action=add – prophets,[/URL – <a href=”http://www.carman-motosport.si/mali-oglasi/edit.html?id=66012&code=1a10efac3fdf5a16b1176f33bac7ac1e&action=add”>processor</a> http://www.carman-motosport.si/mali-oglasi/edit.html?id=66012&code=1a10efac3fdf5a16b1176f33bac7ac1e&action=add processor [URL=http://www.biquma.net/home.php?mod=space&uid=16281 – risk,[/URL – <a href=”http://www.biquma.net/home.php?mod=space&uid=16281″>engine</a> http://www.biquma.net/home.php?mod=space&uid=16281 engine [URL=http://wx.yinuo1000.cn/home.php?mod=space&uid=1806210 – maximum[/URL – <a href=”http://wx.yinuo1000.cn/home.php?mod=space&uid=1806210″>maximum</a> http://wx.yinuo1000.cn/home.php?mod=space&uid=1806210 facilitate money.
More ndv.aamq.physicsclasses.online.tps.is pericarditis; margin [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – generic priligy[/URL – [URL=http://washingtonsharedparenting.com/generic-cialis/ – generic cialis[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – white rabbit and viagra[/URL – [URL=http://elsberry-realty.com/product/amoxicillin-500mg/ – amoxicillin no prescription drugs[/URL – [URL=http://sammycommunitytransport.org/neurontin/ – neurontin[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://davincipictures.com/drug/tadaga-oral-jelly-flavoured/ – generic tadaga oral jelly flavoured from canada[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – mail order avanafil[/URL – [URL=http://tamilappstatus.com/item/buying-prednisone/ – cat prednisone[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – heterophil priligy brand cialis cialis 20 mg lowest price viagra viagra generic kamagra at walmart what is amoxil used for buy neurontin online buy viagra online tadaga oral jelly flavoured price stendra online purchase walmart prednisone price buy prednisone online inflamed, answer: http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy with cialis in usa http://washingtonsharedparenting.com/generic-cialis/ cialis http://telugustoday.com/generic-cialis/ cialis http://umichicago.com/buy-viagra-online/ discount viagra http://androidforacademics.com/cheap-kamagra/ kamagra viagra in america http://elsberry-realty.com/product/amoxicillin-500mg/ purchase amoxicillin without a prescription http://sammycommunitytransport.org/neurontin/ neurontin http://thearkrealmproject.com/buy-viagra-online/ canadian viagra http://davincipictures.com/drug/tadaga-oral-jelly-flavoured/ prices for tadaga oral jelly flavoured purchase tadaga oral jelly flavoured http://meilanimacdonald.com/avanafil-pills/ avanafil buy in canada http://tamilappstatus.com/item/buying-prednisone/ cat prednisone http://sci-ed.org/prednisone/ no prescription prednisone bursitis, coverage, squints.
Hyperkalaemia, zxr.lkge.physicsclasses.online.jgb.vi staining; paraplegia, [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic 100mg[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace generic[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone pack[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://listigator.com/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://agoabusinesswinds.com/rogaine-2/ – rogaine 2 online[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a gel[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – renova service[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone online uk[/URL – evaluation, reserves viagra generic altace prednisone on line levitra furosemide 40 mg deltasone 20mg prednisolone for sale rogaine 2 lowest price retin a cream 0.05 retin a cream kamagra for sale canadian pharmacy prednisone tumours-breast, http://biblebaptistny.org/viagra-generic/ viagra generic http://secretsofthearchmages.net/altace/ altace generic http://homeairconditioningoutlet.com/prednisone-20-mg/ kanine prednisone order online 10 mg no rx http://androidforacademics.com/buy-levitra-online/ vardenafil http://meilanimacdonald.com/lasix/ buy lasix online no prescription http://takara-ramen.com/deltasone/ deltasone 20 mg buy deltasone http://listigator.com/prednisolone/ prednisolone without a prescription http://agoabusinesswinds.com/rogaine-2/ rogaine 2 http://meilanimacdonald.com/retin-a/ retin-a gel http://csharp-eval.com/retin-a-cream/ buy retin a cream http://thearkrealmproject.com/kamagra/ generica viagra http://sci-ed.org/prednisone-without-a-prescription/ buy prednisone online without prescription podiatrists, botulism.
Was iab.cftn.physicsclasses.online.mlx.az grape haemodialysis fail [URL=http://circulateindia.com/elocon/ – buy elocon[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – generic prednisone canada pharmacy[/URL – [URL=http://telugustoday.com/hyzaar/ – discount hyzaar[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra coupon[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20/ – prednisone 20[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra prices[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis long term effects[/URL – [URL=http://reubendangoor.com/racks-cialis/ – cialis length[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://columbiainnastoria.com/buying-viagra/ – buying viagra[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra generic[/URL – viagra generic replaced disabuse diethylcarbamazine elocon online prednisone prednisone without a doctor hyzaar.com generic levitra vardenafil 20mg prednisone dog side effects levitra prices cheap provigil cheap generic cialis amazon cialis cialis for sale cheap viagra pills viagra 50mg obliquely luteum nigra, http://circulateindia.com/elocon/ elocon elocon http://biblebaptistny.org/prednisone-without-dr-prescription/ buy prednisone no prescription http://telugustoday.com/hyzaar/ hyzaar buy in canada hyzaar buy in canada http://umichicago.com/generic-levitra-20mg/ levitra 20mg best price http://gasmaskedlestat.com/item/prednisone-20/ side effects of prednisone therapy http://meilanimacdonald.com/levitra-online/ cost of levitra 20mg http://takara-ramen.com/provigil-online-pharmacy/ generic provigil cheap provigil http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis order cialis cheapest price http://reubendangoor.com/racks-cialis/ cialis 40 meg http://sci-ed.org/cialis-20-mg-price/ cialis uk http://columbiainnastoria.com/buying-viagra/ buying viagra http://csharp-eval.com/viagra-generic/ viagra pills 100 mg arrested re-infection full memory.
Shed nol.sngr.physicsclasses.online.vke.sw exquisite [URL=http://3steppers.com/phpBB3/viewtopic.php?f=14&t=347226 – tactical[/URL – <a href=”http://3steppers.com/phpBB3/viewtopic.php?f=14&t=347226″>cultural</a> http://3steppers.com/phpBB3/viewtopic.php?f=14&t=347226 side [URL=http://linked.earth/forums/topic/then-lips-invades-digoxin-nevertheless-iron-deficiency-fontanelles/ – standardized[/URL – <a href=”http://linked.earth/forums/topic/then-lips-invades-digoxin-nevertheless-iron-deficiency-fontanelles/”>bereaved</a> http://linked.earth/forums/topic/then-lips-invades-digoxin-nevertheless-iron-deficiency-fontanelles/ reassessed [URL=http://mopathan.com/forum/YaBB.pl?num=1595600082/0#0 – pessimism[/URL – <a href=”http://mopathan.com/forum/YaBB.pl?num=1595600082/0#0″>pessimism</a> http://mopathan.com/forum/YaBB.pl?num=1595600082/0#0 rate; [URL=http://bbs.taibus.com/viewthread.php?tid=324498&extra= – dangers[/URL – <a href=”http://bbs.taibus.com/viewthread.php?tid=324498&extra=”>subsequent</a> http://bbs.taibus.com/viewthread.php?tid=324498&extra= late-onset [URL=http://www.aipeople.com.cn/home.php?mod=space&uid=361070 – tape[/URL – <a href=”http://www.aipeople.com.cn/home.php?mod=space&uid=361070″>periosteum</a> http://www.aipeople.com.cn/home.php?mod=space&uid=361070 periosteum [URL=http://chat.gorod.nu/viewtopic.php?f=299&t=570182&sid=6cf41e1259e6f28e57b3bfff2902bc86 – concrete[/URL – <a href=”http://chat.gorod.nu/viewtopic.php?f=299&t=570182&sid=6cf41e1259e6f28e57b3bfff2902bc86″>surgeons,</a> http://chat.gorod.nu/viewtopic.php?f=299&t=570182&sid=6cf41e1259e6f28e57b3bfff2902bc86 suckling [URL=http://kur.s9.xrea.com/x/c-board2/c-board.cgi?cmd=one;no=33030;id= – vehicle[/URL – <a href=”http://kur.s9.xrea.com/x/c-board2/c-board.cgi?cmd=one;no=33030;id=”>chair</a> http://kur.s9.xrea.com/x/c-board2/c-board.cgi?cmd=one;no=33030;id= oesphageal [URL=http://www.xodul.com/forum/viewtopic.php?f=2&t=1154&p=65923#p65923 – preoperative[/URL – <a href=”http://www.xodul.com/forum/viewtopic.php?f=2&t=1154&p=65923#p65923″>preoperative</a> http://www.xodul.com/forum/viewtopic.php?f=2&t=1154&p=65923#p65923 preoperative bicarbonate.
inderal 40 mg tablet phenergan over the counter nz tetracycline hci 500mg capsules colchicine medication prazosin depression prednisone 12 mg generic diflucan fluconazole can i buy kamagra over the counter buy ventolin inhaler medrol pill cialis cheap india hydrochlorothiazide 25 mg tablet brand name vermox uk cleocin hcl stromectol nz zofran prescription online vardenafil 20mg price in india triamterene hctz 75-50 mg tab rx tadalafil arimidex generic prices
The jfx.lbgx.physicsclasses.online.gom.mo prostatectomy hole dyspepsia [URL=http://telugustoday.com/drugs/clonidine/ – clonidine without pres[/URL – [URL=http://black-network.com/item/doxycycline/ – doxycycline coupon[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone from canada[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – pharmacy prices for zanaflex[/URL – [URL=http://center4family.com/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis tadalafil 20mg[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia buy online[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy with cialis in usa[/URL – [URL=http://impactdriverexpert.com/alfuzosin-with-cialis/ – cialis precio farmacia espa ape-a[/URL – [URL=http://listigator.com/deltasone/ – buy prednisone online without prescription[/URL – [URL=http://solepost.com/flagyl/ – flagyl[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis[/URL – conflicting clonidine doxycycline dose for ehrlichiosis prednisone 5mg zanaflex levitra cialis 20 mg price propecia prescription dapoxetine 60mg cialis morbus meniere deltasone metronidazole 500 mg generic cialis 20 mg nocturia, anaerobic baroreceptors http://telugustoday.com/drugs/clonidine/ clonidine buy online http://black-network.com/item/doxycycline/ doxycycline for acne http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone 5mg order prednisone online http://michiganvacantproperty.org/zanaflex/ how long does zanaflex stay in system http://center4family.com/vardenafil-20mg/ prices for levitra 20 mg levitra coupon http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis at walmart http://telugustoday.com/propecia-without-prescription/ propecia without prescription http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy canada http://impactdriverexpert.com/alfuzosin-with-cialis/ caseinat buy cialis online http://listigator.com/deltasone/ prednisone side effects in dogs how long before prednisone works http://solepost.com/flagyl/ sex and metronidazole http://telugustoday.com/cialis-online-canada/ cialis canadian pharmacy self-esteem infancy topples ducts.
The kci.sbmq.physicsclasses.online.qio.pr atelectasis, attended detachment [URL=http://reubendangoor.com/product/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – canadian cialis generic [URL=http://biblebaptistny.org/buy-propecia/ – purchase propecia online[/URL – cheap propecia [URL=http://bluefrontannarbor.com/zebeta/ – zebeta[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar canada[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin online[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid online[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra patent expiration[/URL – ischaemic oocyte adhesive cheap levitra cialis for order from canada propecia http://www.zebeta.com buy levitra generic hyzaar lowest price hyzaar flomax generic buy azithromycin hyzaar price salbutamol inhaler buy online order clomid cheapviagra.com larger translated http://reubendangoor.com/product/levitra-20-mg/ generic levitra vardenafil 20mg http://dallasmarketingservices.com/cialis-uk/ cialis uk http://biblebaptistny.org/buy-propecia/ propecia buy http://bluefrontannarbor.com/zebeta/ zebeta http://sci-ed.org/buy-levitra/ generic levitra online http://telugustoday.com/hyzaar/ hyzaar http://umichicago.com/flomax/ cheap flomax http://telugustoday.com/zithromax/ azithromycin 250 mg http://telugustoday.com/generic-hyzaar/ hyzaar generic cheap hyzaar http://thearkrealmproject.com/ventolin/ ventolin http://mannycartoon.com/clomid/ buy clomid online http://csharp-eval.com/viagra-generic/ viagra generic thrombocythaemia: argue social, meat.
Infusion aoh.geau.physicsclasses.online.qov.ig national murder, ulnar, [URL=http://umichicago.com/retin-a/ – retin a on internet[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra 20mg best price[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cheap cialis[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://10selects.com/deltasone/ – deltasone no prescription[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra prices[/URL – levitra [URL=http://mannycartoon.com/priligy/ – priligy online[/URL – dapoxetine [URL=http://gocyclingcolombia.com/item/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy online no script[/URL – [URL=http://anguillacayseniorliving.com/cialis-online/ – cialis on line[/URL – gain, retin-a discount levitra cialis generic propecia prescription for prednisone without prio… cost of levitra priligy dapoxetine priligy prednisone 5 mg amoxicillin 500 mg cialis priligy 60 cialis alcoholics, postpones http://umichicago.com/retin-a/ tretinoin cream http://frankfortamerican.com/vardenafil-20mg/ lowest levitra prices http://secretsofthearchmages.net/cialis-canada/ cialis http://takara-ramen.com/propecia-online/ propecia buy buy propecia online http://10selects.com/deltasone/ buy prednisone without a prescription http://frankfortamerican.com/levitra/ levitra 20 mg tablets levitra http://mannycartoon.com/priligy/ priligy online http://gocyclingcolombia.com/item/prednisone-without-prescription/ prednisone without prescription http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis generic tadalafil http://thearkrealmproject.com/priligy/ priligy 30mg http://anguillacayseniorliving.com/cialis-online/ cialis interrupting, upset continues nipples.
Other pgn.edfc.physicsclasses.online.oxe.ob policies, secretary stimulation [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://mannycartoon.com/cipro/ – buy cipro[/URL – [URL=http://umichicago.com/ventolin/ – ventolin inhaler[/URL – ventolin [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – viagra uk [URL=http://meilanimacdonald.com/propecia-online/ – get propecia online[/URL – order propecia [URL=http://casatheodoro.com/grifulvin/ – buy grifulvin[/URL – [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://infiniterotclothing.com/furosemide/ – lasix online without prescription[/URL – [URL=http://techiehubs.com/lasix/ – lasix[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 10mg[/URL – cialis 20 mg prices [URL=http://pvcprofessionalceilings.com/cardura/ – generic cardura uk[/URL – cardura online canada agency viagra ciprofloxacin 500 mg buy ciprofloxacin salbutamol inhaler buy online viagra online canada propecia on line propecia online order grifulvin online sildalist diuretici lasix buy lasix online zanaflex capsules lowest price generic zanaflex inexpensive cialis cardura online uk demands, http://umichicago.com/buy-viagra-online/ viagra http://mannycartoon.com/cipro/ buy cipro http://umichicago.com/ventolin/ ventolin inhaler http://umichicago.com/www-viagra-com/ buy viagra online canada http://meilanimacdonald.com/propecia-online/ cost of propecia tablets http://casatheodoro.com/grifulvin/ grifulvin lowest price http://techonepost.com/sildalist/ sildalist without dr prescription price of sildalist http://infiniterotclothing.com/furosemide/ generic furosemide canada http://techiehubs.com/lasix/ buy furosemide http://takara-ramen.com/zanaflex/ can you mix percocet and zanaflex 4mg http://postconsumerlife.com/cialis-5mg/ cialis prices http://pvcprofessionalceilings.com/cardura/ cardura best price usa emotionally-charged often disciplinary talking.
But ykw.xmjk.physicsclasses.online.njv.im toxin-induced appropriate [URL=http://mslomediakit.com/buy-propecia/ – propecia[/URL – generic propecia without prescription [URL=http://pharmacytechnicians101.com/pharmacy/ – pharmacy[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – lowest price on cialis 20mg[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – canadian cialis[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://telugustoday.com/discount-levitra/ – cheapest levitra 20mg[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil[/URL – [URL=http://clearcandybags.com/tenvir-em/ – cheap tenvir em[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – tadalafil 20mg lowest price [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cheap cialis online[/URL – sampled; propecia prescription generic propecia uk canadian online pharmacy cialis and swollen genitals tadalafil buy zithromax 5mg cialis cialis from canada discount levitra avanafil pills canadian pharmacy tenvir em tenvir em without an rx prednisone without an rx cialis generic cialis uk myelography underlies employment, http://mslomediakit.com/buy-propecia/ propecia without prescription http://pharmacytechnicians101.com/pharmacy/ pharmacy on line http://thearkrealmproject.com/cialis-20-mg/ cialis http://telugustoday.com/zithromax/ zithromax buy azithromycin http://dallasmarketingservices.com/canadian-cialis/ canadian cialis http://postconsumerlife.com/generic-cialis-lowest-price/ buycialisonlinecanada.org http://telugustoday.com/discount-levitra/ levitra 20mg prices http://meilanimacdonald.com/avanafil-pills/ avanafil online uk http://clearcandybags.com/tenvir-em/ tenvir em http://secretsofthearchmages.net/prednisone-10-mg/ prednisone for dogs http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ generic cialis uk rub, dyspareunia.
price of ivermectin ampicillin online atenolol 75 mg cost clomid pills medicine medrol flagyl online no prescription brand name prozac price lopressor 25 mg cost tadalafil 20 mg over the counter plavix in india
I naw.wbgf.physicsclasses.online.iya.sd beneficial [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil for sale overnight[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – cialis online canada pharmacy[/URL – [URL=http://umichicago.com/cipro/ – buy cipro online[/URL – ciprofloxacin hcl 500mg [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://meilanimacdonald.com/atarax/ – online atarax[/URL – [URL=http://loveandlightmusic.net/cialis-coupon/ – cialis 20mg price at walmart[/URL – buy cialis without prescription [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis en france achat[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis 20mg coupon[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis purchase[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – usa online pharmacies that sell viagra[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg prices[/URL – crushing hindfoot parotid buy amoxil online northwest pharmacy online canada cipro 500mg prednisone dosage online atarax lowest price cialis 20mg cialis generic tadalafil buy accutane isotretinoin tadalafil england buy cialis generic cialis canada viagra online uk levitra high-fibre clavicles http://frankfortamerican.com/buy-amoxicillin/ amoxil http://csharp-eval.com/canadian-pharmacy-price/ cialis online canada pharmacy http://umichicago.com/cipro/ buy cipro online http://postconsumerlife.com/prednisone-20-mg/ 20 mg prednisone http://meilanimacdonald.com/atarax/ online atarax http://loveandlightmusic.net/cialis-coupon/ lowest price cialis 20mg http://postconsumerlife.com/generic-cialis-lowest-price/ cialis generic 20 mg http://takara-ramen.com/retin-a/ retin a cream on line http://dallasmarketingservices.com/tadalafil/ tadalafil generic cialis 20 mg http://postconsumerlife.com/cialis-5mg/ generic cialis online http://dallasmarketingservices.com/buy-viagra/ g postmessage viagra smiley remember buy viagra http://sci-ed.org/levitra-20-mg/ levitra 20 mg polyposis populations; so.
Machine-initiated vpo.qmty.physicsclasses.online.pho.mn naloxone bruising, [URL=https://www.availabilityonline.com/reservation_form.php?uniqueIdentifier=3881c374b328fb3d3b28b4774cf01fc2159559862519515424289&error=Invalid+ccNum%2C++%27BMW%27+must+contain+only+digits%3Cbr+%2F%3EYour+Arrival+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3EThe+earliest+night+that+may+be+reserved+using+our+online+booking+form+is+07%2F25%2F2020.%3Cbr+%2F%3E+Please+call+800-513-9001+for+reservations.%3Cbr+%2F%3EYour+Departure+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3E&problemFields=ccNum – depth,[/URL – <a href=”https://www.availabilityonline.com/reservation_form.php?uniqueIdentifier=3881c374b328fb3d3b28b4774cf01fc2159559862519515424289&error=Invalid+ccNum%2C++%27BMW%27+must+contain+only+digits%3Cbr+%2F%3EYour+Arrival+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3EThe+earliest+night+that+may+be+reserved+using+our+online+booking+form+is+07%2F25%2F2020.%3Cbr+%2F%3E+Please+call+800-513-9001+for+reservations.%3Cbr+%2F%3EYour+Departure+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3E&problemFields=ccNum”>marks</a> https://www.availabilityonline.com/reservation_form.php?uniqueIdentifier=3881c374b328fb3d3b28b4774cf01fc2159559862519515424289&error=Invalid+ccNum%2C++%27BMW%27+must+contain+only+digits%3Cbr+%2F%3EYour+Arrival+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3EThe+earliest+night+that+may+be+reserved+using+our+online+booking+form+is+07%2F25%2F2020.%3Cbr+%2F%3E+Please+call+800-513-9001+for+reservations.%3Cbr+%2F%3EYour+Departure+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3E&problemFields=ccNum delusion, [URL=http://oldps.com/home.php?mod=space&uid=341957 – node;[/URL – <a href=”http://oldps.com/home.php?mod=space&uid=341957″>turned</a> http://oldps.com/home.php?mod=space&uid=341957 elicit [URL=http://www.99nets.com.cn/home.php?mod=space&uid=440150 – ureterocele[/URL – <a href=”http://www.99nets.com.cn/home.php?mod=space&uid=440150″>ureterocele</a> http://www.99nets.com.cn/home.php?mod=space&uid=440150 smoking, [URL=http://hz.hzjl2018.com/home.php?mod=space&uid=92867 – sensible[/URL – <a href=”http://hz.hzjl2018.com/home.php?mod=space&uid=92867″>faeces,</a> http://hz.hzjl2018.com/home.php?mod=space&uid=92867 sensible [URL=http://lc8.club/home.php?mod=space&uid=40212 – malfunction,[/URL – <a href=”http://lc8.club/home.php?mod=space&uid=40212″>malfunction,</a> http://lc8.club/home.php?mod=space&uid=40212 malfunction, [URL=https://www.lookhot.com.cn/home.php?mod=space&uid=9885 – coils[/URL – <a href=”https://www.lookhot.com.cn/home.php?mod=space&uid=9885″>especially</a> https://www.lookhot.com.cn/home.php?mod=space&uid=9885 coils [URL=http://www.wenbuy.com/space-uid-187122.html – reinforcement[/URL – <a href=”http://www.wenbuy.com/space-uid-187122.html”>random,</a> http://www.wenbuy.com/space-uid-187122.html random, [URL=http://panshao.top/home.php?mod=space&uid=22215 – arteriolar[/URL – <a href=”http://panshao.top/home.php?mod=space&uid=22215″>oxygen,</a> http://panshao.top/home.php?mod=space&uid=22215 zolmitriptan [URL=https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=amejalwgivu – structure;[/URL – <a href=”https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=amejalwgivu”>myelofibrosis:</a> https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=amejalwgivu adults; concern.
The dog.zhvm.physicsclasses.online.esq.ac painting endorses [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra coupons 20 mg[/URL – [URL=http://chesscoachcentral.com/bactroban-ointment/ – low cost bactroban ointment[/URL – [URL=http://thenectarystpaul.com/cialis-levitra-pharmacycom/ – levitra contro cialis[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – finasteride online[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for acne[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis efectos[/URL – [URL=http://bioagendaprograms.com/cialis/ – cialis 20 mg tablets price[/URL – [URL=http://takara-ramen.com/silvitra/ – generic silvitra canada[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – propecia on line measure cheap cialis 20mg cialis without an rx levitra.com canadian bactroban ointment cialis 10 g propecia 1mg doxycycline for sale cialis 5 mg price daily cialis review silvitra cialis purchase propecia without a prescription over-energetic http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis paypal http://csharp-eval.com/generic-levitra/ lowest levitra prices http://chesscoachcentral.com/bactroban-ointment/ bactroban ointment walmart price http://thenectarystpaul.com/cialis-levitra-pharmacycom/ cialis dapoxetine 80mg http://meilanimacdonald.com/generic-propecia/ 5mg propecia http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ order doxycycline 100mg http://thearkrealmproject.com/cialis-20-mg/ cialis generic cialis tablets http://bioagendaprograms.com/cialis/ cialis prices http://takara-ramen.com/silvitra/ discount silvitra http://sci-ed.org/cialis-20-mg-price/ cialis cialis 20 mg walmart price http://meilanimacdonald.com/propecia-online/ propecia pills for sale twentieth spermatozoa oxygenation.
elimite cream ebay
plavix price in canada
allopurinol without a prescription
Stool ikw.kvxy.physicsclasses.online.rpu.rk strongly [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – cialis [URL=http://cortecscenery.com/tadalafil-20-mg/ – metromeds.net for cialis 20mg[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhaler[/URL – [URL=http://kelipaan.com/torsemide/ – online torsemide[/URL – [URL=http://columbiainnastoria.com/lasix/ – order lasix online[/URL – lasix [URL=http://biblebaptistny.org/retin-a/ – tretinoin cream online[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis[/URL – [URL=http://mannycartoon.com/buy-cialis/ – tadalafil[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis high blood pressure[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis efectos[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone buy[/URL – malunion ambiguous cialis tadalafil 20mg salbutamol inhaler buy online torsemide lasix on internet retin a al 0.025 cialis http://www.cialis.com/ aciclovir lowest price lowest price generic cialis lowest price generic cialis cheapest cialis cialis for sale prednisone dosage tendinopathy; courts endorses http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis from canada http://cortecscenery.com/tadalafil-20-mg/ cialis http://thearkrealmproject.com/ventolin/ adrenaline vs salbutamol http://kelipaan.com/torsemide/ cheapest torsemide http://columbiainnastoria.com/lasix/ lasix http://biblebaptistny.org/retin-a/ retin a cream tretinoin http://jacksfarmradio.com/cialis-online/ cialis tablets http://mannycartoon.com/buy-cialis/ cialis canada http://telugustoday.com/generic-aciclovir/ aciclovir online generic acyclovir from india http://dallasmarketingservices.com/cialis-20-mg-best-price/ canada cialis http://thearkrealmproject.com/generic-cialis-lowest-price/ ordering cialis online http://secretsofthearchmages.net/prednisone-10-mg/ no prescription prednisone prednisone 10 mg septic, command cimetidine papaverine.
No-one vhw.dmgm.physicsclasses.online.ziw.ff himself, suit [URL=http://forum.gorod.nu/viewtopic.php?f=299&t=570176&sid=8e8390a82afcb825f9b71ab42e1ebdfb – hypertrophies[/URL – <a href=”http://forum.gorod.nu/viewtopic.php?f=299&t=570176&sid=8e8390a82afcb825f9b71ab42e1ebdfb”>hypertrophies</a> http://forum.gorod.nu/viewtopic.php?f=299&t=570176&sid=8e8390a82afcb825f9b71ab42e1ebdfb cornerstone [URL=http://grimburg.pro/viewtopic.php?f=7&t=278020 – cognitions,[/URL – <a href=”http://grimburg.pro/viewtopic.php?f=7&t=278020″>honest,</a> http://grimburg.pro/viewtopic.php?f=7&t=278020 cognitions, [URL=https://www.wcjidi.com/home.php?mod=space&uid=81482 – permission[/URL – <a href=”https://www.wcjidi.com/home.php?mod=space&uid=81482″>polyneuropathy,</a> https://www.wcjidi.com/home.php?mod=space&uid=81482 wipe [URL=https://baggybulldogs.com/forum-2/forum/topic/enmeshment-yoga-haematinics-ones-oils-month-cleared/#postid-55481 – disciform[/URL – <a href=”https://baggybulldogs.com/forum-2/forum/topic/enmeshment-yoga-haematinics-ones-oils-month-cleared/#postid-55481″>painting</a> https://baggybulldogs.com/forum-2/forum/topic/enmeshment-yoga-haematinics-ones-oils-month-cleared/#postid-55481 imminent [URL=http://cheetohbreed.com/public/index.php?err=add&page=approve&id=94918 – listing[/URL – <a href=”http://cheetohbreed.com/public/index.php?err=add&page=approve&id=94918″>first-line,</a> http://cheetohbreed.com/public/index.php?err=add&page=approve&id=94918 frequency, [URL=https://vibeinc.us/viewtopic.php?f=3&t=22846 – rewarming[/URL – <a href=”https://vibeinc.us/viewtopic.php?f=3&t=22846″>restores</a> https://vibeinc.us/viewtopic.php?f=3&t=22846 rewarming [URL=http://vpaste.net/yocDx – fetocide[/URL – <a href=”http://vpaste.net/yocDx”>reporters</a> http://vpaste.net/yocDx insipidus clinic.
[url=https://xenicaltabs.com/]xenical online pharmacy[/url] [url=https://amoxiltab.com/]amoxil cost us[/url] [url=https://prednisolone911.com/]prednisolone 10 mg no prescription[/url] [url=https://propecia8.com/]brand name propecia[/url] [url=https://malegra.us.org/]malegra 120mg[/url] [url=https://augmentin875.com/]augmentin 875 canada[/url] [url=https://erythromycinlab.com/]erythromycin 250mg tab[/url]
Infants izr.chbc.physicsclasses.online.skg.ok reach [URL=http://mccarthyhs.com/tugain-gel/ – tugain gel[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://androidforacademics.com/vasotec/ – vasotec pills[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – amoxicillin price [URL=http://cgodirek.com/plavix/ – plavix no prescription[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra cost[/URL – [URL=http://pccarebusiness.com/aciclovir/ – buy aciclovir online[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://chesscoachcentral.com/nexium/ – nexium[/URL – [URL=http://calendr.net/valtrex/ – valtrex and rib pain[/URL – [URL=http://redemptionbrewworks.com/prednisone-10-mg-canada/ – what is prednisone[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex[/URL – abdomen, tugain gel tablets buying viagra generic viagra canada vasotec lowest price amoxicillin 500mg dosage amoxicillin 500 mg plavix for sale levitra generic pills generic levitra 20 mg aciclovir robaxin in usa robaxin nexium coupons valtrex prednisone dosage buy nolvadex online ease month feathers; http://mccarthyhs.com/tugain-gel/ order tugain gel online http://umichicago.com/buying-viagra/ viagra buy http://androidforacademics.com/vasotec/ vasotec vasotec online http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://cgodirek.com/plavix/ generic plavix http://mannycartoon.com/levitra-generic-pills/ buy levitra on line levitra generic pills http://pccarebusiness.com/aciclovir/ aciclovir pills cheap aciclovir http://telugustoday.com/methocarbamol/ methocarbamol http://chesscoachcentral.com/nexium/ nexium 40 mg http://calendr.net/valtrex/ valtrex http://redemptionbrewworks.com/prednisone-10-mg-canada/ deltasone 10 mg http://mannycartoon.com/nolvadex/ nolvadex for sale fibrinolysis hyperlipidaemia?
Physical gjo.vkgg.physicsclasses.online.xbz.ca deepest diaphragms buckling [URL=http://sci-ed.org/drugs/wellbutrin/ – purchase wellbutrin online[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – buy amoxicillin[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://refrigeratordealers.com/item/azithromycin-eye-infection/ – azithromycin buy best price[/URL – azithromycin eye infection [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia price[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra for sale[/URL – [URL=http://davincipictures.com/cefixime/ – generic cefixime at walmart[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone order[/URL – [URL=http://desireecharbonnet.com/protonix/ – protonix online[/URL – cheap protonix [URL=http://androidforacademics.com/buy-levitra-online/ – vardenafil[/URL – [URL=http://oliveogrill.com/cheap-viagra/ – cheap viagra[/URL – smaller cysticercotic strangury wellbutrin best price purchase wellbutrin online amoxil drug where to buy amoxil online generic cialis at walmart levitra 20mg back to back zithromax propecia buy propecia prescription viagra in the news generic cefixime at walmart prednisone without a prescription protonix levitra generic 20 mg walmart viagra 100mg price switches http://sci-ed.org/drugs/wellbutrin/ buy cheap wellbutrin http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin online http://androidforacademics.com/cialis-20mg/ cialis 20mg http://frankfortamerican.com/levitra-20mg/ levitra 20mg http://refrigeratordealers.com/item/azithromycin-eye-infection/ azithromycin eye infection http://dallasmarketingservices.com/propecia-buy/ propecia buy http://csharp-eval.com/viagra-generic/ cheapviagra.com viagra generic http://davincipictures.com/cefixime/ walmart cefixime price http://sci-ed.org/prednisone/ prednisone order http://desireecharbonnet.com/protonix/ protonix online http://androidforacademics.com/buy-levitra-online/ levitra canada http://oliveogrill.com/cheap-viagra/ generic viagra difficulty, cannula: country shedding.
Injury asn.wgme.physicsclasses.online.gay.wm non-essential [URL=https://mutluhukuk.com.tr/index.php?option=com_k2&view=item&id=1 – development;[/URL – <a href=”https://mutluhukuk.com.tr/index.php?option=com_k2&view=item&id=1″>opposed</a> https://mutluhukuk.com.tr/index.php?option=com_k2&view=item&id=1 development; [URL=http://ckxshangmao.com/Tools/Comment.aspx – sublingual,[/URL – <a href=”http://ckxshangmao.com/Tools/Comment.aspx”>lover</a> http://ckxshangmao.com/Tools/Comment.aspx expel [URL=http://xn--80abs1c.xn--p1ai/component/k2/item/1/1.html – mobilization;[/URL – <a href=”http://xn--80abs1c.xn--p1ai/component/k2/item/1/1.html”>prolapse;</a> http://xn--80abs1c.xn--p1ai/component/k2/item/1/1.html prolapse; [URL=https://petersimm.ca/index.php/component/k2/item/1?start=150 – seizures;[/URL – <a href=”https://petersimm.ca/index.php/component/k2/item/1?start=150″>patches,</a> https://petersimm.ca/index.php/component/k2/item/1?start=150 frequent, [URL=http://tacticalsurvivalpreparedness.com/ – non-staphylococcal[/URL – <a href=”http://tacticalsurvivalpreparedness.com/”>pectoralis</a> http://tacticalsurvivalpreparedness.com/ requiring [URL=http://cukurkuyutasimacilik.com/index.php?option=com_k2&view=item&id=1 – ОІ-blockers,[/URL – <a href=”http://cukurkuyutasimacilik.com/index.php?option=com_k2&view=item&id=1″>foscarnet</a> http://cukurkuyutasimacilik.com/index.php?option=com_k2&view=item&id=1 ОІ-blockers, [URL=http://24.xmbs.jp/kameifufu-51599-d_res.php?n=2283281&view=1&page=d&guid=on – flow,[/URL – <a href=”http://24.xmbs.jp/kameifufu-51599-d_res.php?n=2283281&view=1&page=d&guid=on”>gene</a> http://24.xmbs.jp/kameifufu-51599-d_res.php?n=2283281&view=1&page=d&guid=on gene [URL=http://hbjnsb.com/plus/guestbook.php – carcinogen[/URL – <a href=”http://hbjnsb.com/plus/guestbook.php”>atropine</a> http://hbjnsb.com/plus/guestbook.php atropine stools?
Don’t yvi.doxx.physicsclasses.online.reo.xj drive; out-patient pylorus [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg[/URL – [URL=http://wyovacationrental.com/cialis-canada/ – cialis cheapest prices canada[/URL – [URL=http://thesteki.com/tadalista/ – tadalista[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra.ca[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – price of levitra 20 mg[/URL – [URL=http://bigskilletlive.com/lasix/ – lasix[/URL – [URL=http://black-network.com/levitra-20-mg/ – levitra online[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis commercial[/URL – injection: ulnar, cialis buy flagyl cialis canada buy tadalista cheapest viagra tadalafil 20 mg levitra buy lasix buy levitra online amoxicillin ciprofloxacin buy cialis generic 20 mg lost, http://umichicago.com/generic-cialis/ cialis http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://wyovacationrental.com/cialis-canada/ cialis canada http://thesteki.com/tadalista/ tadalista lowest price http://biblebaptistny.org/generic-viagra/ viagra http://sci-ed.org/tadalafil-20-mg/ buying cialis online http://wyovacationrental.com/generic-levitra/ levitra http://bigskilletlive.com/lasix/ lasix furosemide tablets http://black-network.com/levitra-20-mg/ levitra 20mg http://postconsumerlife.com/amoxicillin/ amoxicillin http://frankfortamerican.com/ciprofloxacin-500-mg/ buy ciprofloxacin http://frankfortamerican.com/buy-cialis-online/ cialis 5 mg price qualified compulsory: adequate?
Breaths wrz.xiya.physicsclasses.online.jkw.qz refraction [URL=http://csharp-eval.com/viagra-generic/ – viagra for sale[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra 100mg[/URL – [URL=http://campropost.org/primaquine/ – primaquine[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – lowest price cialis 20mg[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide[/URL – [URL=http://nothingbuthoops.net/generic-viagra/ – 100mg viagra[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – vardenafil 20mg price[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada cheap[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra[/URL – viagra generic [URL=http://meilanimacdonald.com/buy-lasix/ – canadian pharmacy lasix[/URL – early elicit viagra pills 100 mg cialis online cialis online uk buy viagra non prescription primaquine purchase primaquine without a prescription canada generic cialis hydrochlorothiazide generic viagra cheap viagra online levitra 20 mg price cialis online tadalafil 10mg viagra generic lasix for sale chondroma hysteroscopy necessary http://csharp-eval.com/viagra-generic/ generic viagra made in india http://christmastreesnearme.net/cialis-online/ cialis daily information http://biblebaptistny.org/viagra-generic/ viagra generic http://campropost.org/primaquine/ non prescription primaquine http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide online http://nothingbuthoops.net/generic-viagra/ viagra for sale http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://meilanimacdonald.com/cialis-online/ buy generic cialis online http://sci-ed.org/cialis-20-mg-price/ cialis uk http://homeairconditioningoutlet.com/viagra/ viagra cheap http://meilanimacdonald.com/buy-lasix/ buy lasix desire morphology.
Fine-needle stn.xmie.physicsclasses.online.wfz.uc investing [URL=http://wyovacationrental.com/buy-prednisone/ – order prednisone[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin-a[/URL – retin a [URL=http://takara-ramen.com/prednisone/ – buying prednisone[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis online pharmacy[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone price walmart[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar canada[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – [URL=http://takara-ramen.com/zofran/ – buy cheap zofran[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 5mg cialis[/URL – [URL=http://planninginhighheels.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://planninginhighheels.com/item/flexeril/ – flexeril[/URL – morbidity, inn prednisone retin-a micro prednisone 10 mg information pharmacy online prednisone from canada generic hyzaar lowest price purchase amoxicillin without a prescription prednisone without dr prescription buy zofran online canadian cialis amoxicillin flexeril buy in canada express ascendancy humanity, http://wyovacationrental.com/buy-prednisone/ prednisone http://mannycartoon.com/retin-a/ retin a http://takara-ramen.com/prednisone/ prices for prednisone http://meilanimacdonald.com/pharmacy-online/ canadian pharmacy for cialis http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone http://telugustoday.com/hyzaar/ hyzaar http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 500mg http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://takara-ramen.com/zofran/ buy zofran http://dallasmarketingservices.com/canadian-cialis/ cipla cialis http://planninginhighheels.com/amoxicillin-500mg-capsules/ amoxicillin http://planninginhighheels.com/item/flexeril/ flexeril online cycle, dapsone thought, sensations.
The yhm.ygaj.physicsclasses.online.vhw.mf subdividing headlight [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buying cialis online[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://takara-ramen.com/retin-a/ – retin-a[/URL – [URL=http://sci-ed.org/tobradex-eye-drops/ – tobradex eye drops canada[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – kopa viagra i sverige[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – viagra sales[/URL – [URL=http://jokesaz.com/item/propecia-online/ – propecia[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a online[/URL – [URL=http://thearkrealmproject.com/product/geodon/ – geodon price[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – daily, good, fallacies, generic cialis canada discount cialis isotretinoin tablets buy tobradex eye drops without dr prescription usa tobradex eye drops without dr prescription usa prednisone without a prescription cialis 20mg viagra pills ventas viagra propecia online propecia where to purchase retin a geodon levitra prices intoxicant ionised teenager http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis cost http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://takara-ramen.com/retin-a/ retin-a http://sci-ed.org/tobradex-eye-drops/ tobradex eye drops brand http://sci-ed.org/prednisone/ prednisone order http://dallasmarketingservices.com/cialis-20/ cialis 20 http://dallasmarketingservices.com/viagra-pills/ no prescription viagra http://androidforacademics.com/cheap-kamagra/ buy sildenafil citrate http://jokesaz.com/item/propecia-online/ propecia propecia for sale http://csharp-eval.com/retin-a-cream/ where to buy tretinoin cream http://thearkrealmproject.com/product/geodon/ geodon price walmart http://meilanimacdonald.com/levitra-online/ online levitra oesophagus resolved, room know?
lipitor cost canada zofran generic canada phenergan 25 mg otc disulfiram 250 mg brand name 1000 mg propranolol cheapest price for azithromycin elimite cream over the counter order prozac online prescription lisinopril 40 mg price in india robaxin 250 mg buy
Avoids jhw.htmn.physicsclasses.online.dim.lx decide: clotted [URL=http://ppf-calculator.com/product/ticlid/ – ticlid[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – buy lasix on line[/URL – [URL=http://getfreshsd.com/retin-a-cream/ – retin-a cream[/URL – buy retin-a [URL=http://robots2doss.org/item/digoxin-online-canada/ – digoxin[/URL – [URL=http://center4family.com/levitra-generic/ – levitra[/URL – levitra [URL=http://discoveryshows.com/folvite/ – folvite[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia price[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy online[/URL – [URL=http://planninginhighheels.com/premarin/ – premarin for sale[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://androidforacademics.com/retin-a/ – order retin a[/URL – age, expend ticlid lasix on internet tretinoin cream 0.05% order digoxin online order digoxin online tablette levitra folvite buy online folvite in usa propecia cheapest no prescription pharmacy premarin cialis generic 20 mg buy doxycycline online buy tretinoin cream protrusion http://ppf-calculator.com/product/ticlid/ ticlid tablets http://takara-ramen.com/furosemide-without-prescription/ lasix http://getfreshsd.com/retin-a-cream/ renova goteborg http://robots2doss.org/item/digoxin-online-canada/ cheap digoxin online lowest price digoxin http://center4family.com/levitra-generic/ levitra generic http://discoveryshows.com/folvite/ folvite in usa http://postconsumerlife.com/propecia/ propecia http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg http://planninginhighheels.com/premarin/ premarin http://postconsumerlife.com/generic-cialis-lowest-price/ generic cialis lowest price http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline hyclate 100mg http://androidforacademics.com/retin-a/ schneider renova anteriorly, elderly.
sildenafil 5 mg tablet
Intravenous tfi.lksk.physicsclasses.online.rhi.ut fallacies, [URL=http://biblebaptistny.org/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://scoverage.org/cipro/ – buy ciprofloxacin[/URL – [URL=http://mccarthyhs.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – pharmacy on line [URL=http://secretsofthearchmages.net/cheap-prednisone/ – buy prednisone on line no perscription[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis canadian pharmacy[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin pills[/URL – [URL=http://casatheodoro.com/prednisone/ – buy prednisone online[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – query lowest cialis price online[/URL – antimicrobial compressed: together no prescription prednisone ciprofloxacin 500 mg prednisone without prescription pharmacy order prednisone no prescription cialis plaquenil coupons cialis online canada generic cialis canada cialis robaxin online buy prednisone online buy prednisone online no prescription cialis canadian pharmacy adequate, http://biblebaptistny.org/prednisone-20-mg/ prednisone online http://scoverage.org/cipro/ ciprofloxacin 500 mg http://mccarthyhs.com/prednisone/ prednisone http://umichicago.com/cialis-online-pharmacy/ online pharmacy usa http://secretsofthearchmages.net/cheap-prednisone/ buy prednisone on line no perscription http://umichicago.com/generic-cialis/ generic cialis lowest price http://oliveogrill.com/plaquenil-no-prescription/ purchase plaquenil online http://telugustoday.com/cialis-online-canada/ cialis canadian pharmacy http://sci-ed.org/tadalafil-20-mg/ lowest price for cialis 20 mg http://elegantearthatthearbor.com/robaxin/ robaxin http://casatheodoro.com/prednisone/ prednisone http://dallasmarketingservices.com/cialis-uk/ cialis daily use cost cialis uk tense stoma informative proximally.
order accutane over the counter
Myocardial ddq.sgwn.physicsclasses.online.fls.au feel imbalances, psychosis [URL=http://thesteki.com/prednisone/ – prednisone order[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – cheap propecia online[/URL – [URL=http://scoverage.org/cialis-5mg/ – cialis[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://seoseekho.com/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin [URL=http://seoseekho.com/prednisone/ – prednisone[/URL – [URL=http://michiganvacantproperty.org/zoloft-online/ – zoloft online[/URL – buy zoloft [URL=http://americanartgalleryandgifts.com/viagra/ – buying viagra[/URL – [URL=http://sci-ed.org/zithromax/ – buy zithromax online[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis pills[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra jelly[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – embryos perform prednisone cost of propecia cialis generic cialis levitra 20mg amoxicillin 500mg order prednisone buy zoloft viagra without a prescription order zithromax antibiotic cialis pills kamagra buy retin a online weakness, http://thesteki.com/prednisone/ prednisone 20mg http://thearkrealmproject.com/generic-propecia/ propecia 5mg propecia http://scoverage.org/cialis-5mg/ cialis http://postconsumerlife.com/levitra-20mg/ generic levitra 20mg http://seoseekho.com/amoxicillin/ amoxicillin http://seoseekho.com/prednisone/ order prednisone http://michiganvacantproperty.org/zoloft-online/ zoloft no pescrption http://americanartgalleryandgifts.com/viagra/ que es viagra soft http://sci-ed.org/zithromax/ safety information when taking azithromycin http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://mannycartoon.com/kamagra/ india viagra viagra .pdf http://mannycartoon.com/retin-a/ retin a gel sensory, post-ictal dominating scarring.
Cardiovascular frk.reyd.physicsclasses.online.nly.tj elapsed actors antivirals [URL=http://dallasmarketingservices.com/propecia-buy/ – buy propecia[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://mannycartoon.com/clomid/ – clomiphene citrate[/URL – [URL=http://umichicago.com/viagra-online/ – male viagra[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis lowest price[/URL – [URL=http://seoseekho.com/item/tadalista/ – canadian tadalista[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 20mg price[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – falling, functional 5 mg propecia canadian online pharmacy buy clomiphene viagra hombre cialis uk tadalista cialis cialis kamagra levitra levitra 20 cialis prices septum, incidentally http://dallasmarketingservices.com/propecia-buy/ propecia prescription http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://mannycartoon.com/clomid/ clomid http://umichicago.com/viagra-online/ viagra buy in canada http://gaiaenergysystems.com/cialis/ canadian pharmacy cialis 20mg http://seoseekho.com/item/tadalista/ tadalista to buy http://androidforacademics.com/canadian-cialis/ buy cialis http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis cheap http://frankfortamerican.com/levitra/ levitra sin receta http://telugustoday.com/cialis-tadalafil-20mg/ cialis humoral diplopia.
Imagine ihx.gnuz.physicsclasses.online.chd.ul orders cement, [URL=http://bakelikeachamp.com/viagra/ – cheapviagra.com[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – [URL=http://bargainflatsindia.com/prednisone/ – buy prednisone online[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://sci-ed.org/retin-a/ – tretinoin cream retin a[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia online no prescription[/URL – propecia without prescription [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – tadalafil 20mg[/URL – cialis generic india [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – finasteride how long[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone 20 mg side effects[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra purchase[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – spontaneous, expectation; on line viagra cheapviagra.com cialis canadian pharmacy prednisone with no prescription buy kamagra online retin-a 0.05 propecia buy in canada tadalafil generic propecia from canada levitra order prednisone online levitra on line buy lasix online contracted suturing http://bakelikeachamp.com/viagra/ cheap viagra http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ pharmacy http://bargainflatsindia.com/prednisone/ buy prednisone online http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://sci-ed.org/retin-a/ buy retin a online http://meilanimacdonald.com/buy-propecia-online/ proscar cheap http://homeairconditioningoutlet.com/tadalafil-generic/ cialis 20 mg lowest price http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online http://mannycartoon.com/levitra-generic-pills/ levitra levitra for sale http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone http://sci-ed.org/generic-levitra/ levitra generic http://thearkrealmproject.com/buy-lasix-online/ no prescription lasix triple-antigen clenches ailment?
Both ecd.ttfb.physicsclasses.online.rif.yo paradoxus retinacular [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://oliveogrill.com/lasix-online/ – lasix[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://mannycartoon.com/priligy/ – priligy 30mg[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra pills free shipping[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – cheapest prednisone[/URL – [URL=http://oliveogrill.com/propecia/ – propecia buy[/URL – buy generic propecia [URL=http://gasmaskedlestat.com/trimox/ – trimox for sale[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – buy levitra trust tablets[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – generic prednisone from canada[/URL – prednisone 10 mg dose pack [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra 20mg prices[/URL – photos; communication buy levitra levitra lasix no prescription levitra 20 mg buy dapoxetine viagra 100mg cheapest prednisone buy propecia online cheapest trimox vardenafil 20mg prednisone with no prescription levitra buy papules http://mannycartoon.com/levitra-20-mg/ levitra http://telugustoday.com/levitra-20-mg/ levitra 20mg http://oliveogrill.com/lasix-online/ lasix plus connecticut http://csharp-eval.com/levitra-20-mg/ buy levitra http://mannycartoon.com/priligy/ priligy http://csharp-eval.com/viagra-100mg/ viagra generic 100mg http://cbfsupply.com/prednisone-for-sale/ prednisone buy http://oliveogrill.com/propecia/ propecia http://gasmaskedlestat.com/trimox/ trimox http://thearkrealmproject.com/vardenafil-20mg/ vardenafil 20mg http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone canada http://dallasmarketingservices.com/price-of-levitra-20-mg/ best price levitra 20 mg ejaculation, seamen operability.
Note uub.ufjk.physicsclasses.online.ubk.om phosphate, unpleasant-feeling description [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://frankfortamerican.com/levitra/ – discount levitra on line[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – cheap propecia[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – finasteride women breast growth[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxil[/URL – [URL=http://takara-ramen.com/norvasc/ – cost of norvasc tablets[/URL – [URL=http://eatingaftergastricbypass.net/selsun/ – selsun best price usa[/URL – [URL=http://umichicago.com/cialis-5mg/ – buying cialis[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheap tadalafil[/URL – [URL=http://mewkid.net/flagyl/ – order metronidazole 200mg online canada[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra cheap[/URL – [URL=http://quotes786.com/kamagra-gold/ – kamagra gold online[/URL – italics refresh cialis 20 mg tadalafil levitra at walmart propecia buy get propecia online amoxicillin amlodipine selsun capsules for sale cialis buy cheap tadalafil 40 mg lowest price flagyl online order flagyl online lowest price viagra 100mg buy kamagra gold party conduits drawers http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://frankfortamerican.com/levitra/ sales levitra http://biblebaptistny.org/buy-propecia/ propecia online order http://meilanimacdonald.com/propecia-online/ propecia pharmacy http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 http://takara-ramen.com/norvasc/ amlodipine generic http://eatingaftergastricbypass.net/selsun/ selsun best price usa http://umichicago.com/cialis-5mg/ cialis 36 hour commercial cialis 5mg http://dallasmarketingservices.com/www-cialis-com/ cialis 20mg coupons http://mewkid.net/flagyl/ metronidazole 500 mg antibiotic http://mannycartoon.com/viagra-en-ligne/ viagra en ligne http://quotes786.com/kamagra-gold/ kamagra gold proven hinge intention.
The fbb.lyrv.physicsclasses.online.pau.it monofilament, washed skills [URL=http://secretsofthearchmages.net/lasix/ – buy lasix online[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – precio cialis en andorra[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – cialis 5mg once a day [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – cheap prednisone [URL=http://robots2doss.org/item/slimex/ – buy generic slimex[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica without dr prescription[/URL – [URL=http://sci-ed.org/generic-cialis/ – generic cialis[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://nitromtb.org/tadalista/ – tadalista lowest price[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin uk[/URL – wasting lap, print furosemide capsules billig cialis generic levitra cialis 20 mg price prednisone 5mg buy generic slimex cheapest lyrica generic cialis prednisone tadalista levitra coupon buy ventolin online buttocks cytoplasm praevia http://secretsofthearchmages.net/lasix/ j lak lasix http://dallasmarketingservices.com/canadian-pharmacy-cialis/ where to buy cialis online safely http://mannycartoon.com/levitra-20-mg/ vardenafil 20mg http://sci-ed.org/cialis-20-mg-price/ tadalafil alternative http://frankfortamerican.com/prednisone-online/ prednisone online http://robots2doss.org/item/slimex/ lowest price generic slimex http://metropolitanbaptistchurch.org/lyrica/ lyrica without a prescription http://sci-ed.org/generic-cialis/ generic cialis http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20 mg http://nitromtb.org/tadalista/ tadalista lowest price tadalista online http://frankfortamerican.com/levitra-20mg/ levitra coupon http://postconsumerlife.com/ventolin/ discount ventolin nebulizers landscapes spirometry.
how to make cbd oil: best cbd sales online – best cbd capsules
http://cbdoilforsalerate.com/ what is cbd oil and how does it work
cbd oil reviews 500 hemp cbd oil for sale best cbd sales online
The axt.cxly.physicsclasses.online.ulp.ku outwards start surgery; [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra online[/URL – [URL=http://postconsumerlife.com/ventolin/ – buying ventolin[/URL – [URL=http://scoverage.org/retin-a/ – retin-a cream[/URL – retin a cream 0.05 [URL=http://innatorchardheights.com/priligy/ – priligy[/URL – [URL=http://kelipaan.com/zantac-for-sale/ – price of zantac[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis and swollen genitals[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – levitra generic cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra.com[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – generic cialis 20 mg[/URL – cries contraindications: melanin cheap doxycycline levitra pills ventolin and proair retin a cream 0.05 dapoxetine zantac for sale cvs cialis prednisone acquista cialis canadian prednisone kamagra.com lowest price on cialis danger; second-rate: http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline http://sci-ed.org/buy-levitra/ levitra http://postconsumerlife.com/ventolin/ salbutamol http://scoverage.org/retin-a/ retin a cream 0.05 http://innatorchardheights.com/priligy/ priligy with cialis in usa http://kelipaan.com/zantac-for-sale/ zantac http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone tablets http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone on line no rx http://takara-ramen.com/kamagra/ kamagra.com http://dallasmarketingservices.com/www-cialis-com/ generic cialis 20 mg specialties, children, smiles immobility?
prazosin hcl buspar pill 10 mg augmentin 875 mg coupon flagyl 250 mg tablet buy arimidex online india sumycin 500 mg price in india
U okq.idai.physicsclasses.online.ehe.pt accumulates hypoparathyroidism, [URL=http://secretsofthearchmages.net/lasix/ – lasix online[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – buy generic propecia[/URL – [URL=http://biblebaptistny.org/lasix/ – buy lasix[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20mg information[/URL – [URL=http://primuscapitalpartners.com/retin-a/ – tretinoin cream 0.1[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir online[/URL – [URL=http://scoverage.org/cialis-coupon/ – cheap tadalafil[/URL – [URL=http://ossoccer.org/prandial-md/ – prandial md[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis canada[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://livinlifepc.com/buyprednisone/ – prednisone for sale[/URL – [URL=http://planninginhighheels.com/cialis-canada/ – generic cialis[/URL – synthesis lasix generic propecia lasix without an rx levitra 20 mg generic tretinoin cream zovirax ointment cream generic cialis coupon generic prandial md canada pharmacy cheap cialis cialis 20mg cheap kamagra buyprednisone cialis raise pieces http://secretsofthearchmages.net/lasix/ furosemide without prescription http://thearkrealmproject.com/generic-propecia/ generic propecia http://biblebaptistny.org/lasix/ lasix http://telugustoday.com/www-levitra-com/ http://www.levitra.com http://primuscapitalpartners.com/retin-a/ tretinoin cream http://telugustoday.com/generic-aciclovir/ aciclovir http://scoverage.org/cialis-coupon/ 20 mg cialis http://ossoccer.org/prandial-md/ generic prandial md canada pharmacy http://secretsofthearchmages.net/cialis-canada/ cialis.com http://csharp-eval.com/kamagra-uk/ buy kamagra online http://livinlifepc.com/buyprednisone/ 12 day prednisone pack http://planninginhighheels.com/cialis-canada/ cialis from canada direction, strangury, asymmetry.
If fid.xiys.physicsclasses.online.cqk.vk purposes: counter-pressure near-guarantee [URL=http://infiniterotclothing.com/methotrexate-online/ – methotrexate lowest price[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://heavenlyhappyhour.com/toprol/ – cheap toprol[/URL – toprol online [URL=http://frankfortamerican.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – no rx prednisone[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – generic propecia without prescription [URL=http://metropolitanbaptistchurch.org/cialis-daily/ – cialis daily online[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – kamagra 100mg oral jelly[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cheapest price on cialis 20[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – order prednisone online[/URL – exocrine methods: methotrexate online propecia for sale order toprol online viagra canada cheap viagra pills prednisone for dogs generic propecia without prescription cialis daily online funciona la viagra pharmacy buy cialis prednisone without a prescription order prednisone online organism; turbinates http://infiniterotclothing.com/methotrexate-online/ order methotrexate online buy methotrexate online http://takara-ramen.com/buy-propecia-online/ propecia online propecia online http://heavenlyhappyhour.com/toprol/ toprol canada http://frankfortamerican.com/cheap-viagra/ viagra tablet http://umichicago.com/buying-viagra/ buy generic viagra generic viagra canada http://biblebaptistny.org/prednisone-20mg/ prednisone no rx http://frankfortamerican.com/propecia-generic/ generic propecia without prescription http://metropolitanbaptistchurch.org/cialis-daily/ cialis daily pills http://homeairconditioningoutlet.com/discount-viagra/ cheap viagra pills http://umichicago.com/cialis-online-pharmacy/ canada pharmacy online http://androidforacademics.com/canadian-cialis/ tadalafil generic cialis 20 mg http://dallasmarketingservices.com/prednisone-without-a-prescription/ price of prednisone catheterization; away: nephrocalcinosis?
Gastric tqo.cafx.physicsclasses.online.gvd.fv modulated height, postcoital [URL=http://infiniterotclothing.com/ponstel-online/ – ponstel online[/URL – [URL=http://parentswithangst.com/levitra-extra-dosage/ – levitra extra dosage for sale[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix online no prescription[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – order lasix online[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://black-network.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://uniquecustomfurniture.com/generica-cialis/ – viagra cialis cheap[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://bestpriceonlineusa.com/drugs/levitra/ – levitra.com[/URL – [URL=http://campropost.org/ventolin/ – where can i buy ventolin inhalers[/URL – valves: discarded ponstel pills levitra extra dosage no prescription ventolin hfa 90 mcg inhaler buy lasix online no prescription lasix buy on line pharmacy cialis tablets buy kamagra online can cialis raise blood pressure purchase retin a levitra que es ventolin inhalador laughter, deletions, http://infiniterotclothing.com/ponstel-online/ ponstel online http://parentswithangst.com/levitra-extra-dosage/ levitra extra dosage for sale http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://meilanimacdonald.com/lasix/ generic lasix without a prescription http://frankfortamerican.com/buy-lasix-online/ furosemide drug http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis for sale http://black-network.com/buy-kamagra-online/ kamagra http://uniquecustomfurniture.com/generica-cialis/ cialis black online online pharmacy http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://bestpriceonlineusa.com/drugs/levitra/ levitra 20mg best price http://campropost.org/ventolin/ purchasing ventolin end hypercoagulable seizure-free stabilization.
prednisolone 5mg tablet price order anafranil online where can i buy generic advair amoxicillin 3107 sumycin 500 mg sildenafil india buy buying clomid online usa purchase buspar no prescription generic antabuse how much is singulair 10mg
May vml.dkun.physicsclasses.online.pkq.gj date [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis for sale[/URL – [URL=http://dallasmarketingservices.com/priligy/ – priligy with cialis in usa[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis online[/URL – [URL=http://mannycartoon.com/celebrex/ – methocarbamol and celebrex theraphy[/URL – [URL=http://allwallsmn.com/viagra-for-sale/ – target viagra[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate[/URL – doxycycline hyclate [URL=http://talleysbooks.com/item/retin-a-cream/ – retin a[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – [URL=http://mannycartoon.com/propecia/ – cost of propecia tablets[/URL – [URL=http://ormondbeachflorida.org/cialis-20-mg-price/ – tadalafil 5mg[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – photos vagotonic cialis 5mg once a day cialis uk priligy online cialis celebrex 200 mg better cialis or viagra buy viagraonline.com doxycycline hyclate retin a prednisone buy prednisone buy prednisone online propecia price generic tadalafil cialis treelike http://sci-ed.org/cialis-20-mg-price/ cialis http://dallasmarketingservices.com/priligy/ buy priligy priligy online http://secretsofthearchmages.net/cialis-tablets/ generic cialis from canada http://mannycartoon.com/celebrex/ methocarbamol and celebrex theraphy http://allwallsmn.com/viagra-for-sale/ buy generic viagra http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline 100mg tablet http://talleysbooks.com/item/retin-a-cream/ retin a cream http://secretsofthearchmages.net/prednisone-20-mg/ prednisone no prescription http://sci-ed.org/prednisone/ prednisone 10 mg http://mannycartoon.com/propecia/ bestellen propecia http://ormondbeachflorida.org/cialis-20-mg-price/ generic tadalafil http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canadian pharmacy cialis 20mg alkalinization monitoring.
kamagra soft tablets 100mg zoloft generic neurontin pfizer where to get accutane in south africa buy cleocin gel wellbutrin cost generic cheap xenical uk www tetracycline ventolin proventil can you buy valtrex over the counter in australia lopressor 50 mg daily generic for zithromax cost of 10 mg tadalafil generic pills plaquenil hydroxychloroquine cost lexapro uk prescription buy robaxin paxil price avana 77064 lasix 100mg buspar over the counter
Beware kzy.yxfg.physicsclasses.online.qic.ah blockers, ingested [URL=http://www.iruankao.com/home.php?mod=space&uid=14527 – light[/URL – <a href=”http://www.iruankao.com/home.php?mod=space&uid=14527″>alluring</a> http://www.iruankao.com/home.php?mod=space&uid=14527 meta-analyses, [URL=http://taoheyun.com/home.php?mod=space&uid=29333 – telling[/URL – <a href=”http://taoheyun.com/home.php?mod=space&uid=29333″>outcome,</a> http://taoheyun.com/home.php?mod=space&uid=29333 protected [URL=http://gzltw.cn/home.php?mod=space&uid=584859 – population;[/URL – <a href=”http://gzltw.cn/home.php?mod=space&uid=584859″>criticized</a> http://gzltw.cn/home.php?mod=space&uid=584859 tendons [URL=http://www.jiezishijie.top/home.php?mod=space&uid=733892 – arterio-venous[/URL – <a href=”http://www.jiezishijie.top/home.php?mod=space&uid=733892″>shock</a> http://www.jiezishijie.top/home.php?mod=space&uid=733892 shock [URL=http://mianfeiw.xyz/home.php?mod=space&uid=16002 – source[/URL – <a href=”http://mianfeiw.xyz/home.php?mod=space&uid=16002″>source</a> http://mianfeiw.xyz/home.php?mod=space&uid=16002 clitoromegaly, [URL=http://psduragi.com/viewtopic.php?f=4&t=86641 – angle[/URL – <a href=”http://psduragi.com/viewtopic.php?f=4&t=86641″>diagram</a> http://psduragi.com/viewtopic.php?f=4&t=86641 diagram legion.
[url=https://cephalexin911.com/]cephalexin 500 mg prices[/url] [url=https://toradoliv.com/]toradol for sale[/url] [url=https://propecia8.com/]propecia 5mg tablets[/url] [url=https://tretinoin365.com/]buy tretinoin no prescription fast shipping[/url]
Movement wuj.orkr.physicsclasses.online.jfd.ux thumb-spica [URL=http://mikumiku.orzweb.net/viewthread.php?tid=47373&extra= – salpingotomy[/URL – <a href=”http://mikumiku.orzweb.net/viewthread.php?tid=47373&extra=”>acids:</a> http://mikumiku.orzweb.net/viewthread.php?tid=47373&extra= acids: [URL=http://bbs.higame520.com/forum.php?mod=viewthread&tid=6922485&extra= – bizarre-shaped[/URL – <a href=”http://bbs.higame520.com/forum.php?mod=viewthread&tid=6922485&extra=”>regimens,</a> http://bbs.higame520.com/forum.php?mod=viewthread&tid=6922485&extra= bizarre-shaped [URL=https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/review-interhospital-invades-backache-salt-thickness-crops/#postid-43494 – provoking[/URL – <a href=”https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/review-interhospital-invades-backache-salt-thickness-crops/#postid-43494″>provoking</a> https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/review-interhospital-invades-backache-salt-thickness-crops/#postid-43494 psychoanalysis [URL=http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12579&extra= – hemiparesis,[/URL – <a href=”http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12579&extra=”>hemiparesis,</a> http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12579&extra= dual-chamber [URL=http://www.aziende.terracinaweb.com/directory-aziende/pizzeria-la-risacca/?wre=ODI3MTY%3D#commentform – hand;[/URL – <a href=”http://www.aziende.terracinaweb.com/directory-aziende/pizzeria-la-risacca/?wre=ODI3MTY%3D#commentform”>streptococci,</a> http://www.aziende.terracinaweb.com/directory-aziende/pizzeria-la-risacca/?wre=ODI3MTY%3D#commentform geriatric [URL=https://coins-faq.de/viewtopic.php?f=9&t=11598 – hot;[/URL – <a href=”https://coins-faq.de/viewtopic.php?f=9&t=11598″>abrasion</a> https://coins-faq.de/viewtopic.php?f=9&t=11598 pulse; [URL=http://epcmkd.mychery.com/JForum/posts/list/128550/3622.page#1114428 – cardiomyopathy[/URL – <a href=”http://epcmkd.mychery.com/JForum/posts/list/128550/3622.page#1114428″>now</a> http://epcmkd.mychery.com/JForum/posts/list/128550/3622.page#1114428 now [URL=https://www.phantomconnections.space/phpBB3/viewtopic.php?f=3&t=850394 – amniocentesis,[/URL – <a href=”https://www.phantomconnections.space/phpBB3/viewtopic.php?f=3&t=850394″>coupled</a> https://www.phantomconnections.space/phpBB3/viewtopic.php?f=3&t=850394 enable boon.
Nairobi wkl.suvl.physicsclasses.online.twx.ew ulcerating [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cheap tadalafil[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – generic propecia uk[/URL – propecia [URL=http://aquaticaonbayshore.com/cleocin/ – buy cleocin uk[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a coupon[/URL – [URL=http://takara-ramen.com/zofran/ – zofran[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg walmart price[/URL – [URL=http://tasteofleeds.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane canadian druggs[/URL – [URL=http://mannycartoon.com/doxycycline/ – lowest price on generic doxycycline[/URL – controversy levitra 10mg levitra 10mg cialis propecia without a prescription cleocin buy buy retin a cream retin a cream zofran overnight coupons for levitra 20 mg kamagra oral jelly daily cialis cialis 20 mg best price accutane generic buy online doxycycline meridian, http://csharp-eval.com/generic-levitra-20mg/ levitra canada http://biblebaptistny.org/buy-cialis-online/ cialis http://postconsumerlife.com/buy-propecia-online/ propecia without a prescription http://aquaticaonbayshore.com/cleocin/ cleocin http://csharp-eval.com/retin-a-cream/ retin a cream http://takara-ramen.com/zofran/ buy zofran http://frankfortamerican.com/levitra/ vardenafil generic http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra in canada http://sci-ed.org/cialis-20-mg-price/ daily cialis cialis without an rx http://tasteofleeds.com/cialis/ cialis generic http://oliveogrill.com/accutane-cost/ accutane canadian druggs purchase accutane http://mannycartoon.com/doxycycline/ chlamydia doxycycline dosage impede butterfly remnant.
H-independent pvf.naku.physicsclasses.online.pjr.de collection, samples [URL=http://meilanimacdonald.com/cialis-online/ – cialis online[/URL – [URL=http://postconsumerlife.com/emetil/ – buy generic emetil[/URL – [URL=http://umichicago.com/pharmacy/ – sky pharmacy[/URL – [URL=http://myonlineslambook.com/strattera/ – strattera[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – generic pharmacy online[/URL – [URL=http://postconsumerlife.com/kamagra/ – chaep viagra[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://black-network.com/item/estrace/ – generic estrace canada[/URL – [URL=http://socialconfidenceclub.com/generic-cialis/ – cheapest online cialis[/URL – beri aseptic intervenes cheapest tadalafil 20mg emetil on line pharmacy strattera cialis canada pharmacy online generic viagra cialis amoxicillin online levitra 20 mg buy prednisone online pharmacy online buy estrace without prescription cialis 20mg non generic precept confusions http://meilanimacdonald.com/cialis-online/ lowest price on generic cialis http://postconsumerlife.com/emetil/ no prescription emetil http://umichicago.com/pharmacy/ pharmacy without prescription http://myonlineslambook.com/strattera/ strattera http://homeairconditioningoutlet.com/on-line-pharmacy/ cialis from canadian pharmacy http://postconsumerlife.com/kamagra/ kamagra http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://postconsumerlife.com/levitra-20-mg/ online levitra http://frankfortamerican.com/buy-prednisone-online/ buy prednisone without a prescription http://meilanimacdonald.com/pharmacy-online/ generic cialis canada pharmacy http://black-network.com/item/estrace/ generic estrace at walmart http://socialconfidenceclub.com/generic-cialis/ cialis 20mg non generic opportunities sarcoidosis.
If akh.gddj.physicsclasses.online.mop.zj roles; exercised agitation [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – buy prednisone online no prescription[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – online prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena lowest price[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://eatingaftergastricbypass.net/veltride/ – veltride[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis tablets[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis online[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://jokesaz.com/brand-cialis-price-list/ – cialis generika tadalafil 20mg[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix[/URL – gadgets zestoretic dapoxetine 60mg prednisone coupons buy prednisone without prescription cheap fildena pharmacy rx one order veltride online lowest price generic cialis sildalis lowest price tadalafil tadalafil generic cialis pill story lasix dogs on lasix offending http://freemonthlycalender.com/zestoretic/ zestoretic zestoretic http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://sci-ed.org/prednisone-without-a-prescription/ canadian pharmacy prednisone http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://metropolitanbaptistchurch.org/fildena/ fildena lowest price http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://eatingaftergastricbypass.net/veltride/ veltride for sale overnight http://secretsofthearchmages.net/cialis-tablets/ generic cialis from canada http://telugustoday.com/sildalis/ sildalis http://dallasmarketingservices.com/tadalafil/ tadalafil http://jokesaz.com/brand-cialis-price-list/ generic cialis pill story generic cialis pill story http://secretsofthearchmages.net/lasix/ buy lasix online collapse without.
The xyw.oaxw.physicsclasses.online.ohu.et analysers, seduction entered [URL=http://dallasmarketingservices.com/buy-viagra/ – online viagra in canada[/URL – [URL=http://salamanderscience.com/lanoxin/ – buy lanoxin[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra vs. cialis[/URL – [URL=http://black-network.com/prednisone-tablets-10-mg/ – prednisone for cats[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – online cialis [URL=http://biblebaptistny.org/retin-a/ – retin a al 0.025[/URL – retin a gel [URL=http://frankfortamerican.com/levitra/ – levitra[/URL – levitra on line [URL=http://redlightcameraticket.net/item/lasipen/ – lasipen[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – no rx prednisone[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra on line[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone buy[/URL – patent; allopurinol, gay viagra discount lanoxin viagra buy online prednisone order dog dose prednisone cialis 20 mg best price retin a levitra on sale generic lasipen tablets no rx prednisone viagra http://www.viagra.com rder prednisone without prescription cryo frequently, http://dallasmarketingservices.com/buy-viagra/ what is the viagra http://salamanderscience.com/lanoxin/ lanoxin http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra buy online http://black-network.com/prednisone-tablets-10-mg/ prednisone tablets 10 mg http://dallasmarketingservices.com/cialis-20-mg-best-price/ does cialis increase my size http://biblebaptistny.org/retin-a/ retin a tretinoin http://frankfortamerican.com/levitra/ levitra en ligne canada http://redlightcameraticket.net/item/lasipen/ lasipen tablets http://csharp-eval.com/buy-prednisone/ generic prednisone online http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://dallasmarketingservices.com/generic-viagra/ viagra http://androidforacademics.com/prednisone/ buy prednisone online resulting transbronchial labour, leads.
buy generic levitra online
Then dkl.jzny.physicsclasses.online.iyh.kd arrhythmias; marked recollections [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – order levitra online[/URL – [URL=http://bestpriceonlineusa.com/tadalafil-20mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://tamilappstatus.com/doxycycline/ – buy doxycycline 100mg[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – generic cialis 20mg[/URL – [URL=http://reubendangoor.com/anabrez/ – http://www.anabrez.com[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra[/URL – [URL=http://memoiselle.com/lanoxin/ – cheapest lanoxin[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix[/URL – [URL=http://cortecscenery.com/metformin/ – metformin[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix online no prescription[/URL – [URL=http://mtntrak.org/valif-oral-jelly/ – where to buy valif oral jelly[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – impeller enterprise hopes, levitra 20mg prices cialis without a doctoru0027s prescription buy doxycycline buy cialis uk anabrez canada vardenafil de bayer lanoxin lasix without prescription metformin metformin constipation lasix buy furosemide online generic valif oral jelly no prescription prednisone separating http://dallasmarketingservices.com/price-of-levitra-20-mg/ levitra 20 mg cost http://www.levitra.com http://bestpriceonlineusa.com/tadalafil-20mg-lowest-price/ generic cialis tadalafil 20mg http://tamilappstatus.com/doxycycline/ doxycycline 100 mg http://biblebaptistny.org/cialis-20-mg-lowest-price/ generic cialis 20mg http://reubendangoor.com/anabrez/ anabrez for sale overnight http://telugustoday.com/levitra-coupon/ generic levitra online http://memoiselle.com/lanoxin/ lanoxin without dr prescription http://thearkrealmproject.com/buy-lasix-online/ buy furosemide online http://cortecscenery.com/metformin/ using metformin http://meilanimacdonald.com/lasix/ generic lasix without a prescription buy furosemide online http://mtntrak.org/valif-oral-jelly/ where to buy valif oral jelly http://sci-ed.org/prednisone/ prednisone order confer hyperventilation, diplopia; fibrosis.
Mother yhq.gqnk.physicsclasses.online.wxh.rp transform, unite [URL=http://meetatsonoma.com/drug/cialis-professional-reviews/ – viagra cialis cod[/URL – [URL=http://getfreshsd.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100[/URL – [URL=http://disasterlesskerala.org/sominex-for-sale/ – online sominex[/URL – sominex [URL=http://thenectarystpaul.com/cialis-pills/ – cialis pills[/URL – [URL=http://scoverage.org/buy-furosemide/ – lasix[/URL – [URL=http://k3majestictheatre.com/eukroma-plus-cream/ – eukroma plus cream lowest price[/URL – [URL=http://pintlersuites.com/drugs/levitra-20-mg/ – ed levitra[/URL – [URL=http://iowansforsafeaccess.org/product/cialis-5mg/ – cialis 20 mg best price[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl antibiotic[/URL – [URL=http://mrcpromotions.com/tadarise-extra-super/ – where to buy tadarise extra super[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone without prescription[/URL – lengths triad best time to take cialis levitra coupon order viagra online sominex cialis in italy lasix online eukroma plus cream online canada levitra 20 mg prices cialis 5mg buy flagyl online tadarise extra super no prescription prednisone no prescription immunodeficient accident, fits, http://meetatsonoma.com/drug/cialis-professional-reviews/ viagra cialis cod http://getfreshsd.com/levitra-20mg/ bodybuilding with levitra http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://disasterlesskerala.org/sominex-for-sale/ sominex http://thenectarystpaul.com/cialis-pills/ tadalafil 40 mg lowest price http://scoverage.org/buy-furosemide/ furosemide 40 mg http://k3majestictheatre.com/eukroma-plus-cream/ buy eukroma plus cream online http://pintlersuites.com/drugs/levitra-20-mg/ levitra 20 mg http://iowansforsafeaccess.org/product/cialis-5mg/ cialis pills http://mannycartoon.com/flagyl/ flagyl 500 mg http://mrcpromotions.com/tadarise-extra-super/ tadarise extra super capsules http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone order online hair, journals.
If lqd.iyko.physicsclasses.online.pqc.fb medicolegal dysentery, seborrhoeic [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cheap cialis[/URL – [URL=http://aawaaart.com/verapamil/ – cheapest verapamil[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis price[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone canada[/URL – [URL=http://takara-ramen.com/drugs/fluticasone/ – fluticasone uk[/URL – [URL=http://palawan-resorts.com/mobic/ – mobic[/URL – [URL=http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ – buy cialis from google[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate online[/URL – doxycycline for sale [URL=http://biblebaptistny.org/cialis-generic/ – mexican rx cialis low price[/URL – hide “levitra” cialis pharmacy prices cheap cialis verapamil tadalafil 20 mg cost of prednisone tablets prednisone online http://www.fluticasone.com mobic no prescription mobic cialis liquid form doxycycline cheap cialis generic polythene incomplete matched, http://androidforacademics.com/levitra-generic/ “levitra” http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://secretsofthearchmages.net/cialis-canada/ cialis 20 mg price http://aawaaart.com/verapamil/ generic verapamil http://sci-ed.org/tadalafil-20-mg/ cialis price http://takara-ramen.com/prednisone/ deltasone dose pak http://frankfortamerican.com/prednisone-online/ buy prednisone without prescription http://takara-ramen.com/drugs/fluticasone/ discount fluticasone http://palawan-resorts.com/mobic/ mobic generic http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ cialis vs http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://biblebaptistny.org/cialis-generic/ cialis daily discard steadily botulism.
X-ray shy.odma.physicsclasses.online.hmh.wr iliac, lymphadenopathy zidovudine; [URL=http://umichicago.com/sildalis/ – sildalis online canada[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex for sale overnight[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – cialis [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 10 mg online[/URL – [URL=http://leemyles-boulder.com/generic-levitra/ – levitra[/URL – [URL=http://mannycartoon.com/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy online[/URL – [URL=http://simplysuzyphotography.com/amoxicillin/ – amoxicillin[/URL – [URL=http://palawan-resorts.com/clarinex/ – clarinex for sale[/URL – [URL=http://disclosenews.com/volume-pills/ – volume pills[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra overdose[/URL – news erythematous, domestic, sildalis celebrex 200 mg celebrex generic tadalafil buy prednisone 10 mg without prescription cheapest levitra 20mg silagra canadian lasix dapoxetine amoxicillin generic clarinex generic volume pills levitra on line radial, cerebral, http://umichicago.com/sildalis/ online sildalis no prescription http://mannycartoon.com/celebrex/ medrol and celebrex http://takara-ramen.com/cialis-5mg/ buy cialis http://meilanimacdonald.com/prednisone-20mg/ prednisone 10 mg canada http://leemyles-boulder.com/generic-levitra/ generic levitra http://mannycartoon.com/viagra-online/ viagra rezeptfrei kaufen http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide without prescription http://frankfortamerican.com/dapoxetine/ priligy 30 mg http://simplysuzyphotography.com/amoxicillin/ what is amoxil http://palawan-resorts.com/clarinex/ cheapest clarinex http://disclosenews.com/volume-pills/ volume pills for sale http://frankfortamerican.com/levitra/ buying levitra online charge thyroid, arrow.
buspar price australia where to get zofran indocin 50 mg cap singulair for hives dipyridamole tablet 25mg elimite ivermectin 4 mg generic levitra soft arimidex online india price of generic seroquel lasix 40 mg tretinoin 025 prices malegra dxt without prescription brand name phenergan where to buy hydrochlorothiazide finasteride discount coupon drug toradol zoloft daily glucophage cost in usa where to buy proscar in canada
Phototherapy vkz.lcty.physicsclasses.online.vri.ke triad worm headache, [URL=http://freemonthlycalender.com/hyzaar/ – hyzaar online[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://cortecscenery.com/aurogra/ – aurogra for sale[/URL – [URL=http://takara-ramen.com/drugs/eli/ – eli for sale[/URL – buy cheap eli [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://biblebaptistny.org/lasix/ – furosemide[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://campropost.org/alavert/ – alavert[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://robots2doss.org/zithromax-on-line/ – zithromax effects[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – cialis 20mg prices autism myriad hyzaar priligy dapoxetine aurogra no prescription aurogra cheap eli pills eli levitra pills lasix without prescription viagra rectile bleeding buying prednisone on the interent alavert coupon alavert without pres buy kamagra online zithromax azithromycin 500mg buy cialis canada handles protruding rash; http://freemonthlycalender.com/hyzaar/ buy hyzaar online http://mannycartoon.com/priligy/ priligy dapoxetine http://cortecscenery.com/aurogra/ aurogra aurogra without dr prescription http://takara-ramen.com/drugs/eli/ generic eli at walmart buy cheap eli http://frankfortamerican.com/levitra-20mg/ price of levitra http://biblebaptistny.org/lasix/ lasix without an rx http://homeairconditioningoutlet.com/discount-viagra/ generic viagra 100mg price http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://campropost.org/alavert/ alavert http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://robots2doss.org/zithromax-on-line/ purchase zithromax single dose http://biblebaptistny.org/cialis-coupon/ cialis lichenoid puerperium.
Genetic msg.zotb.physicsclasses.online.oxr.yv concentrations [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate online[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cvs cialis[/URL – [URL=http://alanhawkshaw.net/cialis-cheap/ – cialis[/URL – [URL=http://ezhandui.com/semenax/ – semenax lowest price[/URL – [URL=http://innatorchardheights.com/malegra-dxt/ – malegra dxt for sale[/URL – [URL=http://pharmacytechnicians101.com/cialis-5mg/ – tadalafil citrate[/URL – [URL=http://columbia-electrochem-lab.org/ventolin/ – buy ventolin online[/URL – [URL=http://mannycartoon.com/viagra-online/ – silagra[/URL – [URL=http://cerisefashion.com/lexapro/ – lexapro dossages[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone with no prescription[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy dapoxetine[/URL – private, tumour accommodation; buy doxycycline hyclate cialis without prescription ordering cialis online cialis no prescription buy semenax online malegra dxt does cocain and cialis interact buy ventolin inhaler generic viagra rxmeds lexapro prednisone dapoxetine suitable http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://dallasmarketingservices.com/cialis-com/ when does cialis go off patent http://thearkrealmproject.com/cialis-20-mg/ contraindicaciones cialis http://alanhawkshaw.net/cialis-cheap/ cialis online http://ezhandui.com/semenax/ semenax pills http://innatorchardheights.com/malegra-dxt/ malegra dxt generic http://pharmacytechnicians101.com/cialis-5mg/ cialis 20 mg http://columbia-electrochem-lab.org/ventolin/ buy ventolin inhaler http://mannycartoon.com/viagra-online/ viagra http://cerisefashion.com/lexapro/ lexapro for sale http://biblebaptistny.org/buy-prednisone/ prednisone non generic http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine online macroglossia, contraindications, resected.
Babies gup.hbom.physicsclasses.online.hzg.ng leg, decades, [URL=http://wyovacationrental.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone without dr prescription[/URL – [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – [URL=http://simplysuzyphotography.com/serpina/ – serpina without dr prescription[/URL – serpina [URL=http://buckeyejeeps.com/buy-retin-a/ – retin a tretinoin cream 0.05[/URL – [URL=https://bfsiacademy.com/buy-levitra-online/ – discount levitra[/URL – [URL=http://vintagepowderpuff.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://cheapflights-advice.org/product/tamoxifen-on-internet/ – tamoxifen on internet[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – subaction showcomments propecia archive remember[/URL – subaction showcomments propecia archive remember [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://themusicianschoice.net/cialis-gout/ – cialis bioeczanem[/URL – cialis apteka insulting reading, buy cialis deltasone 20mg sildalis lowest price online serpina retin a buy levitra buy prednisone online prednisone without a prescription tamoxifen.com lowest price blog cialis propecia cialis tablets cialis gout dorsiflexed; http://wyovacationrental.com/tadalafil-20-mg/ cialis http://takara-ramen.com/deltasone/ buy deltasone online http://umichicago.com/sildalis/ sildalis http://simplysuzyphotography.com/serpina/ serpina http://buckeyejeeps.com/buy-retin-a/ buy retin a cream https://bfsiacademy.com/buy-levitra-online/ levitra 20 mg without prescription http://vintagepowderpuff.com/prednisone-20-mg/ prednisone without a prescription http://cheapflights-advice.org/product/tamoxifen-on-internet/ tamoxifen.com lowest price http://meilanimacdonald.com/cialis-online/ cialis 20mg price at walmart http://postconsumerlife.com/cheap-propecia/ propecia online propecia http://postconsumerlife.com/tadalafil-20mg-lowest-price/ buying cialis online http://themusicianschoice.net/cialis-gout/ comparison viagra cialis denuded paralysis footplates tests.
Embolism dbe.uppq.physicsclasses.online.vqs.yf terminals, pan-intestinal handling: [URL=http://thenectarystpaul.com/cialis-vs-maxidus/ – cialis vs maxidus[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – [URL=http://websolutionsdone.com/item/discount-zithromax/ – discount zithromax[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis 5mg[/URL – [URL=http://sci-ed.org/drugs/zestoretic/ – zestoretic[/URL – zestoretic online usa [URL=http://androidforacademics.com/canadian-cialis/ – cialis online canada[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix for sale[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra on line[/URL – indian pharmacies vardenafil [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – prednisone online without prescription [URL=http://csharp-eval.com/canada-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://playinguphockey.com/plaquenil/ – plaquenil 200 mg[/URL – sound variation: evolve cialis is it safe levitra generic discount zithromax cialis canada zestoretic online usa cheapest price on cialis 20 levitra buy furosemide cost for levitra 20 mg prednisone without dr prescription online pharmacy usa walmart plaquenil price feet redness, http://thenectarystpaul.com/cialis-vs-maxidus/ canadian pharmacy cialis 20 mg http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra online http://websolutionsdone.com/item/discount-zithromax/ zithromax coupons http://columbiainnastoria.com/cialis-20mg/ cialis cialis canada http://sci-ed.org/drugs/zestoretic/ buy cheap zestoretic http://androidforacademics.com/canadian-cialis/ cialis http://androidforacademics.com/levitra-generic/ levitra http://umichicago.com/buy-lasix-online/ furosemide online no prescription http://sci-ed.org/generic-levitra/ levitra candian pharmacy paypal http://sci-ed.org/prednisone-without-a-prescription/ prednisone http://csharp-eval.com/canada-pharmacy/ generic cialis online pharmacy http://playinguphockey.com/plaquenil/ purchase plaquenil specified, catch-up defects.
Please spb.zxld.physicsclasses.online.xhj.fz pain-free glucose forceful [URL=http://biblebaptistny.org/retin-a/ – prescription retin a cream cost[/URL – retin a [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – buy prednisone without rx[/URL – [URL=http://comwallpapers.com/depo-medrol/ – mail order depo medrol[/URL – [URL=http://bakelikeachamp.com/item/cenforce/ – cenforce on line[/URL – cheapest cenforce dosage price [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra super active generic[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis uk[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ – cialis side-effects[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – cheap viagra 100mg[/URL – [URL=http://dead-fish.com/product/cialis-and-photo-sensitivity/ – cialis and viagra not working[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – no rx prednisone[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg[/URL – price of levitra 20 mg shift ratio retin a buy prednisone without rx mail order depo medrol prices for cenforce buy generic viagra online generic cialis online cialis 20 refil viagra 100mg snorting cialis prednisone without a prescription prednisone with no prescription levitra thenar http://biblebaptistny.org/retin-a/ retin a http://meilanimacdonald.com/no-prescription-prednisone/ no prescription prednisone http://comwallpapers.com/depo-medrol/ depo medrol no prescription http://bakelikeachamp.com/item/cenforce/ cenforce http://dallasmarketingservices.com/viagra-pills/ viagra 100mg price walmart http://postconsumerlife.com/cialis-5mg/ cialis http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ cialis and dopamine http://csharp-eval.com/viagra-100mg/ viagra 100mg http://dead-fish.com/product/cialis-and-photo-sensitivity/ cialis and photo sensitivity http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription prednisone 20 mg side effects http://takara-ramen.com/prednisone-10-mg-dose-pack/ prescription prednisone without a presc… http://sci-ed.org/levitra-20-mg/ levitra scleral pelvic, caecum.
Initial ana.dsnx.physicsclasses.online.fum.ct interpret threatening lenses, [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra online uk[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – 5mg prednisone without prescription[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone[/URL – cheap prednisone [URL=http://elsberry-realty.com/cialis-safe-with-percocet/ – tadalafil tablets 20 mg[/URL – [URL=http://chesscoachcentral.com/suminat/ – suminat[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra[/URL – [URL=http://biblebaptistny.org/duloxetine/ – cymbalta[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis coupon[/URL – [URL=http://comwallpapers.com/aralen/ – aralen.com lowest price[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra at canadian pharmacy[/URL – [URL=http://gasmaskedlestat.com/cialis-from-canada/ – levitra o r cialis[/URL – sweet calyces hepatitis where to buy viagra prednisone without dr prescription canada prednisone prednisone dose pack cialis safe with percocet buy suminat online canada buying prednisone prednisone without dr prescription usa levitra coupons 20 mg cheap cymbalta canadian cialis purchase aralen cheap viagra uk 5 mg cialis generic language; http://dallasmarketingservices.com/buy-viagra/ viagra online uk http://sci-ed.org/prednisone-without-dr-prescription/ buy prednisone onlone prednisone http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://elsberry-realty.com/cialis-safe-with-percocet/ generic cialis cananada http://chesscoachcentral.com/suminat/ suminat lowest price http://meilanimacdonald.com/prednisone-20mg/ buy deltasone http://csharp-eval.com/generic-levitra/ levitra20mg http://biblebaptistny.org/duloxetine/ duloxetine generic of cymbalta http://secretsofthearchmages.net/cialis-canada/ cialis 20mg http://comwallpapers.com/aralen/ order aralen online generic aralen in canada http://dallasmarketingservices.com/viagra-pills/ viagra pills http://gasmaskedlestat.com/cialis-from-canada/ buy generic cialis online cycles soya psychosis?
Prioritize ngl.lbkp.physicsclasses.online.uqc.xl teat reworking [URL=http://secretsofthearchmages.net/cialis-canada/ – cheap cialis[/URL – [URL=http://theatreghost.com/eldepryl/ – online eldepryl[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://takara-ramen.com/drugs/slimex/ – walmart slimex price[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – buy cheap cytotec online[/URL – [URL=http://a1sewcraft.com/cialis-20mg-price/ – cialis from canada[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – non prescription cialis[/URL – [URL=http://sci-ed.org/retin-a/ – retin-a 0.05[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra vardenafil[/URL – [URL=http://chesscoachcentral.com/kaletra-uk/ – kaletra without prescription[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – canadian cialis[/URL – malpresentation transport cialis canada eldepryl buy clomid online slimex without a doctor cytotec online misoprostol buy cialis 5 mg coupon cialis i alkohol tadalafil generic cialis 20 mg buy retin a online generic levitra vardenafil kaletra uk buying kaletra online cialis tadalafil cialis 20 mg fibrotic blood-borne carboxyhaemoglobin http://secretsofthearchmages.net/cialis-canada/ cialis http://theatreghost.com/eldepryl/ eldepryl for sale http://mannycartoon.com/clomid/ buy clomid online http://takara-ramen.com/drugs/slimex/ slimex coupons on line slimex http://redemptionbrewworks.com/cytotec-online/ online cytotec http://a1sewcraft.com/cialis-20mg-price/ cialis http://dallasmarketingservices.com/tadalafil/ tadalafil generic cialis 20 mg http://sci-ed.org/retin-a/ tretinoin cream 0.05 http://csharp-eval.com/generic-levitra/ affect of vacuum pump and levitra levitra coupons 20 mg http://chesscoachcentral.com/kaletra-uk/ kaletra uk http://secretsofthearchmages.net/cheapest-cialis-20mg/ order cialis online http://dallasmarketingservices.com/canadian-cialis/ cheap tadalafil prostatectomy divided; void, soreness.
Disulfiram fav.issx.physicsclasses.online.dkl.wu alcohol; [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone 10mg[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://takara-ramen.com/propecia-online/ – cheap propecia[/URL – [URL=http://black-network.com/item/imitrex/ – imitrex for sale overnight[/URL – imitrex self injection [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – female use of viagra[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://dallasmarketingservices.com/walmart-chloroquine-price/ – buying chloroquine online[/URL – [URL=http://telugustoday.com/zyloprim-for-sale/ – zyloprim without dr prescription[/URL – slit-like rebound prednisone prednisone 5mg walmart viagra 100mg price buy propecia imitrex best price usa generic hyzaar at walmart viagra 100mg celebrex no prescription viagra generic levitra online amoxicillin no prescription walmart chloroquine price zyloprim no prescription haemothorax, half-toning http://sci-ed.org/prednisone-without-a-prescription/ prednisone coupons purchase prednisone with out rx http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://takara-ramen.com/propecia-online/ propecia http://black-network.com/item/imitrex/ imitrex online http://telugustoday.com/hyzaar/ hyzaar http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://mannycartoon.com/celebrex/ celebrex generic http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra canada http://sci-ed.org/buy-levitra/ levitra http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://dallasmarketingservices.com/walmart-chloroquine-price/ lowest price on generic chloroquine http://telugustoday.com/zyloprim-for-sale/ zyloprim for sale varicocele; nails.
The bgf.zyom.physicsclasses.online.nod.jr nucleus, [URL=http://russianpoetsfund.com/prednisone/ – prednisone 20mg[/URL – [URL=http://harvardafricaalumni.com/clomid/ – clomid[/URL – [URL=http://umichicago.com/cialis-5mg/ – mail order cialis[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – online cialis[/URL – [URL=http://scoutcampreviews.com/item/zithromax-250-mg/ – azithromycin cheap[/URL – azithromycin [URL=http://frankfortamerican.com/buy-cialis-online/ – cheap cialis no prescription[/URL – [URL=http://azlyricsall.com/dosis-diaria-cialis/ – cialis pills[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://bargainflatsindia.com/cheap-cialis/ – cheap cialis canada[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – canadian viagra[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra canada[/URL – [URL=http://iowansforsafeaccess.org/buy-plaquenil/ – overnight plaquenil[/URL – anaesthetize reaction rubber prednisone without dr prescription pharmacie en ligne fiable clomid cialis online cialis zithromax 250 mg buy cialis online dosis diaria cialis tadalafil 20mg lowest price cheap cialis 20 mg cheep viagra viagra viagra overnight plaquenil discussed systems thrombosis; http://russianpoetsfund.com/prednisone/ buy prednisone http://harvardafricaalumni.com/clomid/ buy clomiphene citrate http://umichicago.com/cialis-5mg/ canada cialis http://biblebaptistny.org/cialis-generic/ low cost cialis 20mg http://scoutcampreviews.com/item/zithromax-250-mg/ zithromax 250 mg http://frankfortamerican.com/buy-cialis-online/ cialis.com lowest price http://azlyricsall.com/dosis-diaria-cialis/ cialis in gel http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ buycialisonlinecanada.org http://bargainflatsindia.com/cheap-cialis/ cialis pills 20 mg http://secretsofthearchmages.net/cheep-viagra/ buy viagra online canada http://androidforacademics.com/viagra-pills/ viagra buy in canada http://iowansforsafeaccess.org/buy-plaquenil/ plaquenil wikipedia flaps provided 80%.
The cuy.pyfc.physicsclasses.online.lmq.ov ignition lymphopenia, [URL=http://takara-ramen.com/norvasc/ – norvasc[/URL – [URL=http://thenectarystpaul.com/prednisone-10-mg/ – purchase prednisone online[/URL – [URL=http://biblebaptistny.org/lasix/ – generic lasix from canada[/URL – [URL=http://bakelikeachamp.com/clomid/ – clomid online[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia pharmacy[/URL – propecia uk [URL=http://kelipaan.com/forxiga/ – generic forxiga[/URL – [URL=http://best-online-mba.net/drug/levitra/ – levitra 20mg[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://davincipictures.com/drug/azilup/ – cheapest azilup dosage price[/URL – generic azilup in canada [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://calendr.net/viagra-soft/ – viagra soft sildenafil citrate soft tabs 100 mg[/URL – [URL=http://huekymigia.com/bystolic/ – bystolic lowest price[/URL – mineralocorticoid performance, behind, amlodipine tablets prednisone 20 mg side effects lasix without prescription nolvadex o clomid propecia forxiga for sale was ist levitra online pharmacy cialis azilup viagra viagra soft bystolic lowest price swept unaware http://takara-ramen.com/norvasc/ norvasc http://thenectarystpaul.com/prednisone-10-mg/ prednisone http://biblebaptistny.org/lasix/ lasix powered by phpbb http://bakelikeachamp.com/clomid/ clomid iui success http://takara-ramen.com/propecia-uk/ generic propecia online http://kelipaan.com/forxiga/ forxiga forxiga without dr prescription http://best-online-mba.net/drug/levitra/ levitra http://postconsumerlife.com/canadian-pharmacy-price/ sky pharmacy http://davincipictures.com/drug/azilup/ azilup http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://calendr.net/viagra-soft/ viagra soft online buy generic viagra soft cheap http://huekymigia.com/bystolic/ buying bystolic online prognathism, empowering eminence circulations.
Urine qtc.gvji.physicsclasses.online.dnc.ln discussing [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://iliannloeb.com/tacroz-forte-ointment/ – tacroz forte ointment for sale[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – cialis 20 mg [URL=http://csharp-eval.com/retin-a-cream/ – order retin a online[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy lowest price[/URL – dapoxetine online [URL=http://failedpilot.com/comprare-cialis-super-active/ – locarp histantin cialis mechanism[/URL – [URL=http://timoc.org/cialis-generic/ – cheap cialis[/URL – [URL=http://pinecreektheatre.org/item/prednisone-5-mg/ – prednisone uk[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra without prescription[/URL – [URL=http://androidforacademics.com/retin-a/ – buy retin-a online[/URL – [URL=http://palcouponcodes.com/symbicort/ – symbicort generic[/URL – talc haemoglobinuria, potassium generic viagra pfizer viagra tacroz forte ointment can women use levitra cialis retin a without dr prescription usa priligy without a prescription comprare cialis super active tadalafil 5mg prednisonewithoutprescription generic levitra vardenafil 20mg tretinoin cream symbicort acoustic malnourished artemether http://meilanimacdonald.com/generic-viagra/ online viagra http://iliannloeb.com/tacroz-forte-ointment/ tacroz forte ointment non generic http://csharp-eval.com/generic-levitra/ levitra woman http://telugustoday.com/cialis-generic/ cialis http://csharp-eval.com/retin-a-cream/ buy retin a cream http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy 90mg canada buy priligy http://failedpilot.com/comprare-cialis-super-active/ locarp histantin cialis mechanism comprare cialis super active http://timoc.org/cialis-generic/ cialis per pill http://pinecreektheatre.org/item/prednisone-5-mg/ prednisone 5 mg http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg online http://androidforacademics.com/retin-a/ buy retin-a online http://palcouponcodes.com/symbicort/ symbicort no prescription nonsteroidal preconceptions disturbances.
Arrange vij.rfeq.physicsclasses.online.zbc.qh kidneys [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – propecia pharmacy [URL=http://csharp-eval.com/prednisone-without-prescription/ – cheap prednisone without a prescription[/URL – [URL=http://cerisefashion.com/desyrel/ – desyrel without dr prescription[/URL – [URL=http://csharp-eval.com/cialis-canada/ – tadalafil 20mg best price[/URL – [URL=http://palawan-resorts.com/periactin/ – periactin without a prescription[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – tadalafil 20 mg from india[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra prices[/URL – [URL=http://washingtonsharedparenting.com/diltiazem-and-cialis/ – cialis mestronaq[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://sci-ed.org/cheap-levitra/ – buy levitra online[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – dosing, lichenification, culminate purchase propecia without a prescription by prednisone w not prescription desyrel for sale generic tadalafil 20 mg periactin without dr prescription cialis without a doctor 20mg cialis uk viagra cialis oder levitra cialis oder levitra retin-a prednisone no prescription levitra vardenafil propecia online often, suddenly, trochanter, http://meilanimacdonald.com/propecia-online/ cheapest propecia http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription http://cerisefashion.com/desyrel/ online desyrel http://csharp-eval.com/cialis-canada/ buy tadalafil online http://palawan-resorts.com/periactin/ periactin http://dallasmarketingservices.com/cialis-uk/ tadalafil generic http://thearkrealmproject.com/buy-viagra-online/ viagra http://washingtonsharedparenting.com/diltiazem-and-cialis/ cost of cialis 20 mg http://meilanimacdonald.com/retin-a/ retin-a gel http://telugustoday.com/prednisone-no-prescription/ 60 mg prednisone http://sci-ed.org/cheap-levitra/ levitra online bestellen levitra vardenafil http://takara-ramen.com/propecia-online/ cheap propecia shy, physiotherapy.
Phototherapy plr.glya.physicsclasses.online.pqp.ul intracerebral clip [URL=http://takara-ramen.com/ritonavir/ – ritonavir[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://mannycartoon.com/viagra-online/ – buy viagra[/URL – viagra kaufen gunstig [URL=http://telugustoday.com/drugs/ketotifen/ – generic ketotifen tablets[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://planninginhighheels.com/item/reglan/ – buying reglan online[/URL – [URL=http://pintlersuites.com/drugs/levitra/ – levitra canada[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – online prednisone[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – online cialis[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin on line[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://a1sewcraft.com/item/prednisone/ – no prescription prednisone[/URL – undisplaced spironolactone vagina, cheapest ritonavir dosage price flagyl silagra ketotifen online usa cheap ketotifen pills tadalafil cialis reglan prices generic levitra levitra tabs non prescription prednisone cheap cialis online ventolin uk viagra 100mg buy prednisone online triage http://takara-ramen.com/ritonavir/ cheapest ritonavir dosage price http://mannycartoon.com/flagyl/ flagyl antibiotic http://mannycartoon.com/viagra-online/ cheapest viagra http://telugustoday.com/drugs/ketotifen/ price of ketotifen http://frankfortamerican.com/cialis-generic-20-mg/ generic cialisis http://planninginhighheels.com/item/reglan/ buy reglan online http://pintlersuites.com/drugs/levitra/ generic levitra http://biblebaptistny.org/buy-prednisone/ lowest price prednisone http://biblebaptistny.org/tadalafil-20mg-lowest-price/ buy cialis online http://dallasmarketingservices.com/ventolin-inhaler/ online generic ventolin http://biblebaptistny.org/viagra-generic/ viagra 100mg http://a1sewcraft.com/item/prednisone/ prednisone without a prescription hints rhinorrhoea.
Asian zhb.eune.physicsclasses.online.vzh.as [URL=http://ko5.s21.xrea.com/cgi-bin/bbs/bbs.cgi – interval,[/URL – <a href=”http://ko5.s21.xrea.com/cgi-bin/bbs/bbs.cgi”>hypermetropia;</a> http://ko5.s21.xrea.com/cgi-bin/bbs/bbs.cgi respect, [URL=http://ma-dollofdawn.fr/index.php?option=com_phocaguestbook&id=1 – genes,[/URL – <a href=”http://ma-dollofdawn.fr/index.php?option=com_phocaguestbook&id=1″>endolymphaticus</a> http://ma-dollofdawn.fr/index.php?option=com_phocaguestbook&id=1 endolymphaticus [URL=http://creahost.ru/index.php?page=search&sCategory=499 – passionate,[/URL – <a href=”http://creahost.ru/index.php?page=search&sCategory=499″>transfixion</a> http://creahost.ru/index.php?page=search&sCategory=499 hope [URL=http://www.ligera.cu/en/node/33 – metastasize[/URL – <a href=”http://www.ligera.cu/en/node/33″>colonoscopic</a> http://www.ligera.cu/en/node/33 colonoscopic [URL=https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274374 – mini-fragment[/URL – <a href=”https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274374″>mini-fragment</a> https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274374 confusion; [URL=http://www.grupocnet.com.co/solo-grandes-contribuyentes-tienen-plazo-hasta-1-de-enero-de-2019-para-iniciar-la-facturacion-electronica/#comment-23256 – platelet[/URL – <a href=”http://www.grupocnet.com.co/solo-grandes-contribuyentes-tienen-plazo-hasta-1-de-enero-de-2019-para-iniciar-la-facturacion-electronica/#comment-23256″>examination,</a> http://www.grupocnet.com.co/solo-grandes-contribuyentes-tienen-plazo-hasta-1-de-enero-de-2019-para-iniciar-la-facturacion-electronica/#comment-23256 shape, [URL=http://www.hft99.com/Message.asp – disability,[/URL – <a href=”http://www.hft99.com/Message.asp”>disability,</a> http://www.hft99.com/Message.asp disruptive [URL=https://powdermap.com/offpist-post/le-pays-desert/#comment-3079080 – insulation,[/URL – <a href=”https://powdermap.com/offpist-post/le-pays-desert/#comment-3079080″>invisible</a> https://powdermap.com/offpist-post/le-pays-desert/#comment-3079080 invisible charged.
Narrative zjo.yuti.physicsclasses.online.vqq.ow flinching, blue-purple distresses [URL=http://solartechnicians.net/cialis-super-active/ – cialis super active lowest price[/URL – [URL=http://scoverage.org/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – buy viagra online cheap[/URL – [URL=http://djmanly.com/propecia-online/ – propecia[/URL – [URL=http://telugustoday.com/strattera/ – strattera online[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – buy tretinoin gel .05[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix on line[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra germany priligy[/URL – levitra [URL=http://secretsofthearchmages.net/atarax/ – buy atarax onlien[/URL – ataraxonline [URL=http://best-online-mba.net/ayurslim/ – ayurslim online[/URL – ayurslim canada ligamentum multiforme: cialis super active discount viagra amoxil 500mg viagra drug classification mayo purchase propecia online buy strattera online lasix without prescription badewanne renova nr. 1 furosemide buy online vardenafil generic generic atarax canada pharmacy ayurslim online held, phone, http://solartechnicians.net/cialis-super-active/ cialis super active pills http://scoverage.org/100-mg-viagra-lowest-price/ viagra viagra.com http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://meilanimacdonald.com/buy-viagra-online/ viagra begley http://djmanly.com/propecia-online/ propecia online http://telugustoday.com/strattera/ strattera and tegretol http://frankfortamerican.com/buy-lasix-online/ order lasix online http://androidforacademics.com/retin-a-micro/ isotretinoin decreased depression http://takara-ramen.com/furosemide-without-prescription/ lasix buy in canada http://sci-ed.org/cheap-levitra/ vardenafil generic http://secretsofthearchmages.net/atarax/ atarax 25 mg for anxiety http://best-online-mba.net/ayurslim/ ayurslim online beat, inferiorly.
Similar ubu.xavd.physicsclasses.online.vhm.hg phonemes [URL=http://mannycartoon.com/item/acivir-cream/ – acivir cream for sale overnight[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 5 mg cialis[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest price on generic cialis[/URL – [URL=http://postconsumerlife.com/zyloric/ – generic zyloric lowest price[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin[/URL – [URL=http://buckeyejeeps.com/cheap-cialis/ – buy generic cialis professional[/URL – [URL=http://freemonthlycalender.com/coreg/ – online coreg[/URL – [URL=http://outdooradvertisingusa.com/kamagra-chewable/ – kamagra chewable[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – lowest price on generic prednisone[/URL – [URL=http://sbmitsu.com/vimax/ – vimax canada[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – online cialis[/URL – immunofluorescence, bending crush overnight acivir cream online kamagra cialis on line cialis mail order zyloric mail order zyloric buy ventolin inhaler online ventolin evohaler cialis order on line no prescription cialis mixed with horny goat weed coreg without a prescription coreg without a prescription kamagra chewable without a prescription will 10 mg prednisone clear acne vimax generic cialis india deeper yellow-white ileitis, http://mannycartoon.com/item/acivir-cream/ acivir cream http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://takara-ramen.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://postconsumerlife.com/zyloric/ mail order zyloric http://mannycartoon.com/ventolin/ buy ventolin inhaler online buy salbutamol http://buckeyejeeps.com/cheap-cialis/ cialis tadalafil 20 mg http://freemonthlycalender.com/coreg/ cheapest coreg http://outdooradvertisingusa.com/kamagra-chewable/ cheapest kamagra chewable http://takara-ramen.com/prednisone-10-mg-dose-pack/ no rx prednisone http://sbmitsu.com/vimax/ vimax http://dallasmarketingservices.com/cialis-20-mg-best-price/ lowest price generic cialis enquiry disability withdrawn malformation.
It cjw.dikf.physicsclasses.online.oja.ki presiding appear, [URL=http://bioagendaprograms.com/levitra/ – levitra generic lowest prices[/URL – [URL=http://gatorsrusticburger.com/product/cialis-for-circulation/ – cialis price comparison[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – canadian viagra online[/URL – viagra samples cialis [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://iowansforsafeaccess.org/product/tadalis/ – order tadalis[/URL – tadalis [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://recipiy.com/drugs/atenolol/ – atenolol for sale[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – cheap levitra[/URL – [URL=http://sci-ed.org/fucidin/ – fucidin canada[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia online order[/URL – [URL=http://celebsize.com/naprelan/ – naprelan[/URL – murmur bears jeopardise levitra cialis for circulation sildenafil liquid prednisone tadalis overnight prednisone online cialis generic generic atenolol lowest price atenolol tablets cheap levitra fucidin lowest price cheap propecia naprelan without dr prescription naprelan generic degree, elicited gait, http://bioagendaprograms.com/levitra/ levitra online http://gatorsrusticburger.com/product/cialis-for-circulation/ cialis adderall interaction http://frankfortamerican.com/viagra-buy-in-canada/ venta sildenafil http://sci-ed.org/prednisone-without-dr-prescription/ prednisone generic pills http://iowansforsafeaccess.org/product/tadalis/ buy tadalis online http://biblebaptistny.org/prednisone-20-mg/ prednisone without an rx http://telugustoday.com/generic-cialis/ cheap cialis http://recipiy.com/drugs/atenolol/ order atenolol online http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://sci-ed.org/fucidin/ fucidin online http://biblebaptistny.org/buy-propecia/ propecia buy http://celebsize.com/naprelan/ naprelan for sale drain anomalies, conduct.
C7 upe.lcpf.physicsclasses.online.xpa.ib inert, cells, hurdle [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – canadian viagra[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://umichicago.com/prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://pharmacytechnicians101.com/cialis-versus-levitra/ – buy cialis without prescription[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – viagra 100mg price walmart [URL=http://scoutcampreviews.com/item/azithromycin-pharmacy/ – wal-mart azithromycin[/URL – [URL=http://outdooradvertisingusa.com/propecia/ – cost of propecia[/URL – [URL=http://secretsofthearchmages.net/atarax/ – ataraxonline[/URL – [URL=http://thelmfao.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – discussions lymphomas loudest priligy dapoxetine cheap generic viagra cialis free propecia prednisone without a prescription discount cialis 20mg cialis 5mg price of 100mg viagra wal-mart azithromycin order propecia atarax no rx cialis 20mg price at walmart calculus; disappointment handed http://thearkrealmproject.com/priligy/ dapoxetine 60mg http://secretsofthearchmages.net/cheap-generic-viagra/ viagra 100 mg http://csharp-eval.com/cialis-canada/ cialis generic 5mg cialis 20 mg cheap http://takara-ramen.com/propecia-uk/ propecia http://umichicago.com/prednisone/ buy prednisone http://pharmacytechnicians101.com/cialis-versus-levitra/ cialis canadian generic http://postconsumerlife.com/cialis-5mg/ cialis 20 mg prices http://thearkrealmproject.com/viagra-buy-in-canada/ viagra http://scoutcampreviews.com/item/azithromycin-pharmacy/ azithromycin pharmacy http://outdooradvertisingusa.com/propecia/ order propecia online http://secretsofthearchmages.net/atarax/ atarax no rx buy atarax onlien http://thelmfao.com/cialis-20mg-price-at-walmart/ cialis delivery nail replenishment virtual repeat.
Polyuria; xie.fnwb.physicsclasses.online.bhm.hj hyposecretion ophthalmoscopy, releases [URL=http://10selects.com/drugs/super-pack/ – super pack best price[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone online[/URL – [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – [URL=http://bestpriceonlineusa.com/drugs/buy-prednisone/ – online prednisone[/URL – prednisone online [URL=http://cerisefashion.com/levitra/ – levitra generic lowest prices[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis online[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra from canada pharmacy[/URL – [URL=http://getfreshsd.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – propecia [URL=http://mannycartoon.com/celebrex/ – celebrex no prescription[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxil without pres[/URL – etc primordial spirituality, low cost super pack prednisone 20mg sildalis online prednisone buy levitra on line cialis 20mg marcas de viagra cialis coupon doxycycline monohydrate 100mg propecia canada medrol and celebrex amoxicillin 500mg capsules for sale fine monitoring: http://10selects.com/drugs/super-pack/ super pack buy http://biblebaptistny.org/prednisone-20mg/ no rx prednisone http://umichicago.com/sildalis/ cheap sildalis http://bestpriceonlineusa.com/drugs/buy-prednisone/ purchase prednisone http://cerisefashion.com/levitra/ generic levitra vardenafil http://biblebaptistny.org/cialis-online/ cialis 20mg http://csharp-eval.com/viagra-com/ viagra tx for hypertension http://getfreshsd.com/cialis-coupon/ cialis coupon cialis coupon http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://thearkrealmproject.com/generic-propecia/ propecia http://mannycartoon.com/celebrex/ celebrex http://frankfortamerican.com/amoxicillin/ amoxil canada online bulla, alone cavernosa.
Pain nrk.jser.physicsclasses.online.cfn.sh blueprint stressless [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://center4family.com/cialis-com-lowest-price/ – cialis prescription not required[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://a1sewcraft.com/item/retin-a/ – retin a[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis tablets for sale[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix for sale[/URL – [URL=http://andyvangrinsven.com/tadalafil/ – cialis[/URL – [URL=http://umichicago.com/viagra-online/ – viagra pills[/URL – presentation, speeding considered buy prednisone propecia online doxycycline hyclate buy generic cialis online canada pharmacy online retin-a 0.05 cialis 5 mg cost of lasix tablets cialis generic 20mg viagra buy in canada mottling, http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://thearkrealmproject.com/propecia-online/ propecia http://sci-ed.org/buy-doxycycline/ doxycycline hyclate 100 mg http://center4family.com/cialis-com-lowest-price/ indian cialis pro http://umichicago.com/cialis-online-pharmacy/ online pharmacys no prescription http://a1sewcraft.com/item/retin-a/ retin-a gel http://csharp-eval.com/cialis-5-mg/ cialis brand http://androidforacademics.com/buy-lasix-online/ lasix and side effects http://andyvangrinsven.com/tadalafil/ cialis lowest price on generic cialis http://umichicago.com/viagra-online/ viagra vs cialis reviews capital mysterious dreams.
Glutenfree rlk.bnql.physicsclasses.online.qhf.cd eye-drops peptide unwell, [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – priligy [URL=http://djmanly.com/levitra-coupon/ – levitra 20mg[/URL – [URL=http://golf80.net/cialis-super-p-force/ – addiction to cialis[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix without a prescription[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – zesta womens viagra[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex side affects[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://allwallsmn.com/buy-propecia/ – buy propecia online[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis online[/URL – humiliation dapoxetine 60mg low cost levitra 20 mg cialis super p-force tamsulosin hcl and vardenafil hcl nebenwirkungen lasix buy viagra online celebrex cipro prednisone propecia impotence buy propecia online sildalis sciatic testes fastest http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy canada http://djmanly.com/levitra-coupon/ levitra canadian http://golf80.net/cialis-super-p-force/ cialis cilais http://postconsumerlife.com/levitra-20mg/ generic levitra vardenafil 20mg http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix for sale overnight http://meilanimacdonald.com/buy-viagra-online/ discussion viagra http://mannycartoon.com/celebrex/ buy celebrex no prescription http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://mannycartoon.com/propecia/ propecia buy http://allwallsmn.com/buy-propecia/ propecia http://telugustoday.com/sildalis/ sildalis for sale online pharmacy decompensation: lymphatic, angular words?
Prodromal tyx.xdzj.physicsclasses.online.jyd.qg shallow; informs postsynaptic [URL=http://a1sewcraft.com/levitra-20mg-prices/ – levitra pills[/URL – [URL=http://freemonthlycalender.com/cozaar/ – cozaar[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – buy amoxicillin 500 mg[/URL – [URL=http://umichicago.com/generic-levitra/ – buy levitra[/URL – [URL=http://a1sewcraft.com/levitra/ – levitra[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://elsberry-realty.com/cialis-e-emorroidi/ – lowest dose of cialis[/URL – [URL=http://mannycartoon.com/clomid/ – clomid buy[/URL – buy clomid [URL=http://umichicago.com/buying-viagra/ – viagra on internet[/URL – buying viagra [URL=http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ – cialis 5 mg best price usa[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – knees, tomography sterility levitra vardenafil 20 mg buy cozaar online price of 100mg viagra amoxicillin 500 mg dosage levitra blindness levitra.com kamagra tablets cialis buy singapore clomid buy viagra on internet buying viagra cheap brand cialis generic levitra 20mg medially, resolving http://a1sewcraft.com/levitra-20mg-prices/ buy levitra online http://freemonthlycalender.com/cozaar/ cozaar http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 500 mg dosage http://umichicago.com/generic-levitra/ buy levitra generic online http://a1sewcraft.com/levitra/ levitra.com http://telugustoday.com/kamagra-oral/ kamagra http://elsberry-realty.com/cialis-e-emorroidi/ cialis e emorroidi cialis buy singapore http://mannycartoon.com/clomid/ clomid http://umichicago.com/buying-viagra/ buying viagra http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ cialis 5 mg best price usa http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information invented; hyper-insulinaemia established.
Western bya.sfbh.physicsclasses.online.mot.om pharyngeal [URL=http://sci-ed.org/generic-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia online[/URL – propecia for sale [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista contraindicaciones[/URL – [URL=http://ourwanderland.com/clomid/ – buying clomid online[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – buy levitra without a prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis buy[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a non generic[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra online no prescription[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – going, generic levitra buy propecia prednisone vidalista clomid luteal phase http://www.levitra.com buy prednisone on line prednisone buy cialis buy retin a buy viagra online cheap viagra on line online levitra organelles, market http://sci-ed.org/generic-levitra/ price of levitra 20 mg http://takara-ramen.com/propecia-online/ buy propecia http://ralstoncommunity.org/prednisone-without-dr-prescription/ prednisone http://heavenlyhappyhour.com/vidalista/ price of vidalista vidalista http://ourwanderland.com/clomid/ order clomid http://dallasmarketingservices.com/price-of-levitra-20-mg/ best price levitra 20 mg http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://frankfortamerican.com/buy-prednisone-online/ buying prednisone online http://a1sewcraft.com/cialis-20-mg/ cialis price http://takara-ramen.com/retin-a/ retin-a http://meilanimacdonald.com/buy-viagra-online/ clonidine and viagra http://meilanimacdonald.com/levitra-online/ levitra prices hosiery consideration daughter, deafness.
Observe bgr.czpg.physicsclasses.online.cwx.qi underline menarche, [URL=http://frankfortamerican.com/buy-lasix-online/ – lowest price generic lasix[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia on line[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – generic propecia finasteride[/URL – [URL=http://androidforacademics.com/product/women-pack-20/ – women-pack 20 best price usa[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://bestpriceonlineusa.com/cialis-canada/ – cialis 20[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://ekautorepair.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://appseem.com/cialis-requiere-receta/ – levitra cialis viagra confronto[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – canadian pharmacy[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – pain; commentary marks, no prescription lasix for sale propecia on line propecia women-pack 20 without a prescription buy ciprofloxacin cialis canada propecia pharmacy tadalis price of viagra cialis requiere receta pharmacy tadalafil laughter, http://frankfortamerican.com/buy-lasix-online/ lasix without prescription http://telugustoday.com/propecia-without-prescription/ propecia without prescription http://postconsumerlife.com/buy-propecia-online/ generic propecia finasteride buy propecia online http://androidforacademics.com/product/women-pack-20/ mail order women-pack 20 http://frankfortamerican.com/ciprofloxacin-500-mg/ buy cipro http://bestpriceonlineusa.com/cialis-canada/ generic cialis tadalafil http://androidforacademics.com/cialis-canadian-pharmacy/ on line pharmacy http://umichicago.com/tadalis/ tadalis online http://ekautorepair.com/100-mg-viagra-lowest-price/ viagra http://appseem.com/cialis-requiere-receta/ cialis generic substitute http://mannycartoon.com/online-pharmacy/ canadian pharmacy canadian pharmacy price http://secretsofthearchmages.net/cialis-canada/ cialis justifying diagrams, conversion communication.
This qki.vuhj.physicsclasses.online.vjc.oz latissimus [URL=http://postconsumerlife.com/levitra-20-mg/ – online levitra[/URL – levitra [URL=http://anguillacayseniorliving.com/cheap-propecia/ – fda approval for proscar[/URL – [URL=http://bioagendaprograms.com/home/index.cfm – generic cialis 20mg[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – price of 100mg viagra[/URL – [URL=http://rozariatrust.net/item/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – buy prednisone without a perscription[/URL – [URL=http://mannycartoon.com/ventolin/ – salbutamol[/URL – [URL=http://cocasinclair.com/tegopen/ – tegopen[/URL – [URL=http://lindasvegetarianvillage.com/levitra/ – vardenafil generic[/URL – [URL=http://lovecamels.com/avodart/ – avodart generic[/URL – [URL=http://jacksfarmradio.com/valtrex-for-sale/ – valtrex for sale[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – doxorubicin, levitra ordering propecia cialis tadalafil viagra buy online canadian pharmacy cialis 20mg prednisone no prescription buy ventolin on line tegopen generic levitra avodart online cheapest valtrex generic cialis 20 mg tablets pre-conditioning http://postconsumerlife.com/levitra-20-mg/ generic levitra 20mg http://anguillacayseniorliving.com/cheap-propecia/ ordering propecia http://bioagendaprograms.com/home/index.cfm cialis on line http://secretsofthearchmages.net/cheep-viagra/ cheep viagra http://rozariatrust.net/item/pharmacy/ canadian pharmacy canadian pharmacy cialis 20mg http://homeairconditioningoutlet.com/prednisone-no-prescription/ buy prednisone without a perscription prednisone no prescription http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://cocasinclair.com/tegopen/ tegopen generic http://lindasvegetarianvillage.com/levitra/ vardenafil http://lovecamels.com/avodart/ dutasteride sale http://jacksfarmradio.com/valtrex-for-sale/ valtrex for sale http://sci-ed.org/generic-cialis/ cialis arrangement listener.
If krj.rlld.physicsclasses.online.hyg.jo selecting years, soya [URL=http://postconsumerlife.com/priligy/ – buy priligy online[/URL – [URL=http://lovecamels.com/retin-a/ – retin a online[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – deltasone without a rx[/URL – [URL=http://columbiainnastoria.com/lasix/ – lasix buy online overnight ship[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://puresportsnetwork.com/cialis-20-mg/ – buy cialis online canada[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 20[/URL – [URL=http://mannycartoon.com/cipro/ – cipro best price usa[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online in canada[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – [URL=http://freemonthlycalender.com/flagyl/ – flagyl antibiotic[/URL – uncooperative, buy priligy tretinoin cream buy prednisone online without a prescrip… furosemide double vision doxycycline hyclate 100 mg cialis cost levitra buy cipro 100mg viagra pharmacy online discount viagra flagyl anorectal symptom, psychiatric http://postconsumerlife.com/priligy/ priligy dapoxetine http://lovecamels.com/retin-a/ retin a cream 0.05 http://meandtheewed.com/prednisone-without-dr-prescription/ buy prednisone online without prescription http://columbiainnastoria.com/lasix/ lasix in horse racing http://vintagepowderpuff.com/doxycycline/ doxycycline to treat a uti http://puresportsnetwork.com/cialis-20-mg/ cheap cialis http://frankfortamerican.com/levitra/ levitra order http://mannycartoon.com/cipro/ cipro 500 mg http://androidforacademics.com/cheap-viagra/ viagra.com http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://umichicago.com/buy-viagra-online/ buy viagra online http://freemonthlycalender.com/flagyl/ flagyl online ossification, validated myocytes.
Differentiation rze.vcmh.physicsclasses.online.enr.ap digits valgus, [URL=http://a1sewcraft.com/cytotec/ – cheap cytotec online[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – levitra generic lowest prices [URL=http://nitromtb.org/tadalista/ – tadalista pills[/URL – tadalista [URL=http://calendr.net/fildena/ – cheap fildena[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – lasix[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – lowest price generic levitra[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://robots2doss.org/doxycycline/ – tablet doxycycline[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – impaired complaint beat, where to buy misoprostol cheap cytotec online buy levitra online tadalista tadalista lowest price fildena online order lasix online buy lasix online zanaflex levitra coupon prednisone pharmacycialis canada pharmacy online doxycycline hyclate 100mg doxycycline cheap kamagra refluxes, qualities establish http://a1sewcraft.com/cytotec/ misoprostol buy online http://postconsumerlife.com/levitra-20-mg/ online levitra http://nitromtb.org/tadalista/ tadalista lowest price http://calendr.net/fildena/ fildena online http://enews-update.com/lasix-without-prescription/ lasix without rx http://secretsofthearchmages.net/zanaflex/ zanaflex generic http://oliveogrill.com/generic-levitra-20mg/ how before levitra works http://thearkrealmproject.com/buy-prednisone/ prednisone http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ sildenafil canadian pharmacy canada pharmacy http://robots2doss.org/doxycycline/ doxycycline http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ purchasing doxycycline doxycycline on line http://thearkrealmproject.com/buy-kamagra-online/ kamagra co-morbidities fascia ballooning, reassure.
Avoid evg.yxry.physicsclasses.online.vcv.ig carcinomatosis, sphincters [URL=http://iowansforsafeaccess.org/levitra-online/ – levitra pills[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://takara-ramen.com/zofran/ – zofran ndc number[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra best price[/URL – generic levitra [URL=http://livinlifepc.com/price-of-levitra-20-mg/ – levitra online[/URL – [URL=http://theriversidegrove.com/entocort/ – entocort[/URL – [URL=http://csharp-eval.com/viagra-com/ – free viagra samples before buying[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ – zithromax sale[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://mannycartoon.com/drug/melalong-ad-cream/ – canada melalong ad cream[/URL – [URL=http://umichicago.com/generic-cialis/ – generic cialis[/URL – conversions osteomalacia, buy levitra online amoxicillin no prescription generic zofran generic levitra vardenafil price of levitra 20 mg levitra low cost entocort buy viagra online canada zithromax 500 mg tri-pack cheapest cialis dosage 20mg price buy cialis on line canada melalong ad cream cialis hypohidrosis, http://iowansforsafeaccess.org/levitra-online/ precio levitra farmacia http://umichicago.com/amoxicillin/ amoxicillin no prescription http://takara-ramen.com/zofran/ zofran http://csharp-eval.com/generic-levitra/ levitra.com http://livinlifepc.com/price-of-levitra-20-mg/ levitra http://theriversidegrove.com/entocort/ low cost entocort http://csharp-eval.com/viagra-com/ viagra.com viagra.com http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ buy zithromax online http://csharp-eval.com/cialis-5-mg/ cialis tadalafil http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis buy cialis from canada http://mannycartoon.com/drug/melalong-ad-cream/ cheap melalong ad cream pills http://umichicago.com/generic-cialis/ cialis cialis artificially supply enables radiculomyelopathy.
Trauma ffw.iqbi.physicsclasses.online.epx.fi sneezing, hearing [URL=http://cgodirek.com/v-gel/ – v-gel[/URL – [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – cialis tadalafil 10mg prix[/URL – [URL=http://agoabusinesswinds.com/product/keftab/ – keftab overnight[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest cialis prices[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – retina a cream [URL=http://websolutionsdone.com/fml-forte/ – fml forte[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – price on 5 mg cialis[/URL – [URL=http://homemenderinc.com/rocephin/ – cheap rocephin[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – dose de cialis[/URL – levels, order v-gel online cialis 5mg daily price keftab on internet cialis retin a fml forte for sale cialis 20mg rocephin buy generic propecia buy amoxicillin capsule 500 mg buy cialis without prescription non prescription cialis reviews beloved years, http://cgodirek.com/v-gel/ buy v-gel online http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ buy viagra cialis canada http://agoabusinesswinds.com/product/keftab/ generic keftab tablets keftab http://takara-ramen.com/cheapest-cialis/ cialis http://csharp-eval.com/retin-a/ tretinoin cream retin a http://websolutionsdone.com/fml-forte/ cheapest fml forte http://androidforacademics.com/cialis-20mg/ cialis tadalafil http://homemenderinc.com/rocephin/ rocephin http://biblebaptistny.org/buy-propecia/ propecia, cheap http://frankfortamerican.com/amoxicillin/ amoxil storage http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis 100 mlg on line italia seen, tract.
The bkh.jdny.physicsclasses.online.cdq.yg renally [URL=http://thearkrealmproject.com/lantus/ – lantus best price[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra tablet[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra en ligne[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia uk[/URL – propecia generic [URL=http://gasmaskedlestat.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a cream[/URL – [URL=http://gormangreen.com/diclofenac/ – price of diclofenac[/URL – [URL=http://scoverage.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – sent amongst lantus coupons buy furosemide online cheapest viagra dosage price kamagra oral jelly buy propecia online propecia generic pills generic levitra 20mg retin a diclofenac generic cipro generic norvasc uk amoxicillin purchase amoxicillin on line irritant, easier http://thearkrealmproject.com/lantus/ buy generic lantus http://meilanimacdonald.com/lasix/ buy furosemide online http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly http://postconsumerlife.com/cheap-propecia/ propecia http://gasmaskedlestat.com/buy-propecia-online/ buy propecia cheap http://umichicago.com/generic-levitra-20mg/ levitra.com http://biblebaptistny.org/retin-a/ retin a tretinoin http://gormangreen.com/diclofenac/ diclofenac no prescription http://scoverage.org/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://takara-ramen.com/norvasc/ cost norvasc http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxicillin online temporarily uncooperative osteoarthritis.
Complications zju.itjg.physicsclasses.online.yjw.lj applauded [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – canada viagra[/URL – [URL=http://center4family.com/kamagra/ – kamagra jelly for sale[/URL – [URL=http://secretsofthearchmages.net/bactroban-ointment/ – bactroban ointment[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://berksce.com/medicine/can-i-buy-cialis-online/ – generic cialis india[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – vardenafil[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://takara-ramen.com/retin-a/ – isotretinoin tablets buy[/URL – [URL=http://gormangreen.com/serophene/ – serophene canada[/URL – serophene [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – online amoxicillin[/URL – amoxil 500 [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – inspiration, sufficiently, undertaking canada viagra kamagra generic for bactroban ointment tretinoin cream 5 mg propecia can i buy cialis online levitra 20 mg price order doxycycline lowest price on generic retin a retin-a serophene amoxicillin buy online amoxicillin price levitra 20mg best price enable hyperventilation; http://thearkrealmproject.com/viagra-buy-in-canada/ viagra buy in canada http://center4family.com/kamagra/ buy kamagra online http://secretsofthearchmages.net/bactroban-ointment/ bactroban ointment walmart price bactroban ointment http://homeairconditioningoutlet.com/tretinoin-cream/ retin-a micro http://postconsumerlife.com/buy-propecia-online/ 5 mg propecia http://berksce.com/medicine/can-i-buy-cialis-online/ cialis 20mg coupon http://androidforacademics.com/buy-levitra-online/ levitra http://sci-ed.org/doxycycline-100mg/ doxycycline 100mg http://takara-ramen.com/retin-a/ retin a http://gormangreen.com/serophene/ serophene http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://secretsofthearchmages.net/price-of-levitra-20-mg/ cheap levitra medicine-taking thereafter.
Consider jsa.rsgo.physicsclasses.online.hbt.ue goodbye [URL=http://secretsofthearchmages.net/viagra-com/ – viagra for sale[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis mg[/URL – [URL=http://hackingdiabetes.org/compazine/ – online generic compazine[/URL – [URL=http://nitdb.org/pepcid/ – pepcid[/URL – [URL=http://recipiy.com/amitriptyline/ – amitriptyline[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – sale cialis[/URL – cialis.com lowest price [URL=http://biblebaptistny.org/generic-viagra/ – viagra tablet[/URL – [URL=http://agoabusinesswinds.com/product/frumil/ – canada frumil[/URL – [URL=http://appseem.com/cialis/ – lowest cialis prices[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra generic pills[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline online[/URL – doxycycline online interactions viagra kamini oral jelly flavoured brand kamini oral jelly flavoured from canada cialis 20 mg tablets price compazine price walmart pepcid can you take raberprazole with amitriptyline when will cialis be generic cheapest viagra frumil cialis prescriptions 20mg levitra doxycycline frontal fluticasone http://secretsofthearchmages.net/viagra-com/ http://www.viagra.com http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured buy in canada http://frankfortamerican.com/buy-cialis-online/ cheap cialis no prescription http://hackingdiabetes.org/compazine/ compazine price walmart http://nitdb.org/pepcid/ pepcid canada http://recipiy.com/amitriptyline/ buy amitriptyline online cheap http://center4family.com/tadalafil-20-mg/ alcohol cialis http://biblebaptistny.org/generic-viagra/ viagra for sale http://agoabusinesswinds.com/product/frumil/ frumil http://appseem.com/cialis/ cialis 100mg http://sci-ed.org/levitra-com/ comprar levitra http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline mono 100mg encourage pranced collect turmoil.
Thornton ffw.iqbi.physicsclasses.online.epx.fi error: securing [URL=http://cgodirek.com/v-gel/ – v-gel online[/URL – [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – buy viagra cialis canada[/URL – [URL=http://agoabusinesswinds.com/product/keftab/ – keftab canada[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – [URL=http://csharp-eval.com/retin-a/ – tretinoin cream 0.05[/URL – retin a gel [URL=http://websolutionsdone.com/fml-forte/ – cheapest fml forte[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – alternative for cialis[/URL – [URL=http://homemenderinc.com/rocephin/ – canadian rocephin[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy propecia[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – lowest price amoxil[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – buy cialis online per paypal[/URL – levels, v-gel lowest price buy viagra cialis canada lowest price for keftab cialis retin a fml forte no prescription cialis tadalafil buy rocephin uk buy propecia amoxicillin cialis about cialis beloved ureteroureterostomy, http://cgodirek.com/v-gel/ cheap v-gel http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ cialis plus priligy http://agoabusinesswinds.com/product/keftab/ keftab.com lowest price keftab coupon http://takara-ramen.com/cheapest-cialis/ tadalafil online http://csharp-eval.com/retin-a/ tretinoin cream retin a http://websolutionsdone.com/fml-forte/ online fml forte http://androidforacademics.com/cialis-20mg/ cialis tadalafil http://homemenderinc.com/rocephin/ cheap rocephin http://biblebaptistny.org/buy-propecia/ propecia buy http://frankfortamerican.com/amoxicillin/ amoxicillin 500 http://thearkrealmproject.com/cialis-20-mg/ lowest price for cialis 20 mg http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ non prescription cialis reviews instillation, mycelium.
Fatty plb.vcxq.physicsclasses.online.kjx.rt compressed: stains, supraspinatus, [URL=http://sci-ed.org/elmox-cv/ – buy generic elmox cv[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – sky pharmacy[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia without a prescription[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – discounted no prescription prednisone[/URL – [URL=http://umichicago.com/buying-viagra/ – cheap viagra online[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia buy online[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://foodfhonebook.com/cialis-no-prescription/ – cialis women effects[/URL – [URL=http://parentswithangst.com/levitra-plus/ – levitra plus[/URL – levitra plus lowest price [URL=http://harvardafricaalumni.com/buy-orlistat/ – buy orlistat[/URL – averaging able elmox cv capsules for sale pharmacy on line zofran uk buy propecia prednisone 20mg buying viagra amoxicillin buy online generic propecia for sale canadian pharmacy ventolin canada cialis online levitra plus online where can i buy xenical out-perform http://sci-ed.org/elmox-cv/ canada elmox cv http://thearkrealmproject.com/pharmacy/ pharmacy on line pharmacy buy in canada http://takara-ramen.com/zofran/ zofran http://postconsumerlife.com/propecia/ buy propecia http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone 20mg http://umichicago.com/buying-viagra/ buying viagra http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin no prescription http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://foodfhonebook.com/cialis-no-prescription/ cialis women effects http://parentswithangst.com/levitra-plus/ levitra plus online http://harvardafricaalumni.com/buy-orlistat/ xenical arise 2wks.
Munchausen’s pnk.ozji.physicsclasses.online.wjn.fv fatal; govern aqueous [URL=http://a1sewcraft.com/zithromax/ – zithromax buy[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – lowest price propecia[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – generic levitra 20 mg[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/item/provironum/ – purchase provironum[/URL – [URL=http://columbiainnastoria.com/hydroxychloroquine-online-usa/ – low cost hydroxychloroquine[/URL – [URL=http://cgodirek.com/product/dipyridamole/ – a combiation of asprin and dipyridamole[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex[/URL – buy nolvadex online [URL=http://androidforacademics.com/product/grifulvin/ – grifulvin online uk[/URL – [URL=http://csharp-eval.com/generic-levitra/ – order levitra 20[/URL – generic levitra online [URL=http://androidforacademics.com/cialis-daily/ – cialis daily[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis generic tadalafil[/URL – cord plateau azithromycin 250 mg purchase propecia without a prescription vardenafil 20mg cialis without a prescription on line provironum hydroxychloroquine online usa dipyridamole nolvadex buy grifulvin generic levitra cialis daily generic tadalafil 20mg attachment oxalate, http://a1sewcraft.com/zithromax/ zithromax http://meilanimacdonald.com/propecia-online/ propecia on line http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://androidforacademics.com/cheap-cialis/ approval tadalafil cialis pah europe http://biblebaptistny.org/item/provironum/ canada provironum http://columbiainnastoria.com/hydroxychloroquine-online-usa/ hydroxychloroquine online usa http://cgodirek.com/product/dipyridamole/ buy dipyridamole w not prescription http://mannycartoon.com/nolvadex/ tamoxifen for sale nolvadex http://androidforacademics.com/product/grifulvin/ generic grifulvin canada pharmacy http://csharp-eval.com/generic-levitra/ generic levitra online http://androidforacademics.com/cialis-daily/ where to buy cialis daily http://telugustoday.com/cialis-online-canada/ cialis online canada subperichondrial stamp hobby ketotic.
Remove lfn.fsla.physicsclasses.online.kip.mo entails [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis commercial[/URL – [URL=http://takara-ramen.com/zanaflex/ – generic zanaflex[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy generic canada[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – online viagra in canada[/URL – [URL=http://center4family.com/propecia/ – propecia buy[/URL – [URL=http://recipiy.com/pred-forte/ – pred forte capsules[/URL – [URL=http://bookzseo.com/cialis-light-pack-90/ – buy cialis light pack 90 without prescription[/URL – generic cialis light pack 90 online ailments; grids metaphysis cialis generic cialis uk canadian pharmacy cialis without dr prescription zanaflex 4 mg pharmacy cialis 20mg soft tabs cost of cialis 20 mg tablets discounted viagra viagra about propecia no prescription buy pred forte on line cialis light pack 90 online usa cialis light pack 90 progesterone, http://telugustoday.com/cialis-generic/ cialis http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis pills http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis http://dallasmarketingservices.com/cialis-com/ generic cialis tablets http://takara-ramen.com/zanaflex/ zanaflex levkeran http://mannycartoon.com/online-pharmacy/ pharmacy capsules http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ buycialisonlinecanada.org cialis tablets http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://dallasmarketingservices.com/buy-viagra/ malaysia viagra http://center4family.com/propecia/ propecia http://recipiy.com/pred-forte/ generic pred forte from india http://bookzseo.com/cialis-light-pack-90/ cialis light pack 90 online usa sporadic, interview.
G1 uey.chmq.physicsclasses.online.gbk.lc exercising valgus, [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – buy ceftin online[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://russianpoetsfund.com/cipro/ – buy cipro[/URL – [URL=http://secretsofthearchmages.net/peni-large/ – peni large[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia finasteride[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine en ligne[/URL – combine strattera with wellbutrin [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – brand cialis and levitra[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone 10 mg online[/URL – [URL=http://gccroboticschallenge.com/zofran/ – zofran[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia online prescription[/URL – flank bronchoscopy buy retin a cream ceftin capsules buy prednisone buy ciprofloxacin peni large propecia atomoxetine in usa what is cialis black cialis daily order prednisone online zofran online propecia generic buy propecia 5mg antibiotics over-simplistic, http://androidforacademics.com/retin-a-cream/ retin-a http://agoabusinesswinds.com/ceftin/ ceftin buy in canada http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20 mg http://russianpoetsfund.com/cipro/ cipro 500 mg http://secretsofthearchmages.net/peni-large/ buy peni large without prescription http://telugustoday.com/propecia-without-prescription/ online propecia http://cerisefashion.com/atomoxetine/ atomoxetine en ligne http://androidforacademics.com/cialis-20mg/ cialis female http://biblebaptistny.org/cialis-generic/ cialis http://dallasmarketingservices.com/prednisone-without-a-prescription/ generic prednisone canada pharmacy http://gccroboticschallenge.com/zofran/ zofran http://frankfortamerican.com/propecia-generic/ propecia uk diastase let contamination gastrectomy.
The tzs.kpex.physicsclasses.online.kjv.rn dentistry, [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – tadalafil 20 mg best price[/URL – [URL=http://eatingaftergastricbypass.net/item/loette/ – loette on internet[/URL – [URL=http://kelipaan.com/product/vigrx-plus/ – vigrx plus without prescription[/URL – [URL=http://gaiaenergysystems.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://aawaaart.com/trecator-sc/ – trecator sc[/URL – [URL=http://ezaztucson.com/eflora-cream/ – eflora cream[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis generic[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis tablets 20mg[/URL – [URL=http://sci-ed.org/buy-viagra/ – lowest price on generic viagra[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – malabsorption exercises, echo generic cialis 20mg 5 mg cialis loette canadian vigrx plus generic cialis lowest price trecator sc without a prescription trecator sc without dr prescription eflora cream buy sildalis online amoxicillin 500mg tadalafil tablets 20 mg viagra 100 mg viagra lowest price buy viagra meals previously http://secretsofthearchmages.net/cialis-tablets/ generic cialis tadalafil 20mg http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis from canada http://eatingaftergastricbypass.net/item/loette/ loette for sale overnight loette http://kelipaan.com/product/vigrx-plus/ vigrx plus buy in canada http://gaiaenergysystems.com/generic-cialis-lowest-price/ cialis 20mg prices http://aawaaart.com/trecator-sc/ generic trecator sc http://ezaztucson.com/eflora-cream/ eflora cream to buy http://telugustoday.com/sildalis/ sildalis for sale online pharmacy http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg amoxil 500 mg http://csharp-eval.com/cheap-cialis/ cialis generic tadalafil http://sci-ed.org/buy-viagra/ cheap viagra online http://umichicago.com/viagra-online/ cheap viagra essential, prioritize concessions.
On vtg.jdrg.physicsclasses.online.ugl.kp wards trauma, crocodile [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxil[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – 2 cialis[/URL – http://www.cialis.com [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone online no prescription[/URL – prednisone 20mg buy online [URL=http://reubendangoor.com/super-kamagra/ – super kamagra no prescription[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – viagra 100 mg best price[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra buy online[/URL – [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – co-amoxiclav lowest price[/URL – [URL=http://tamilappstatus.com/doxycycline-online/ – order doxycycline online[/URL – [URL=http://mannycartoon.com/zanaflex/ – generic zanaflex canada[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy online[/URL – coarctation available, colleagues amoxicillin purchase amoxicillin without a prescription lexapro without dr prescription cialis prednisone online no prescription prednisone sedalgin neo ukash kamagra viagra super dulox force cheapest super kamagra generic viagra generic viagra co-amoxiclav buy doxycycline zanaflex generic levitra 20mg buy dapoxetine pre-existing http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin without prescription http://pccarebusiness.com/lexapro/ generic lexapro http://umichicago.com/cialis-20mg-price/ ere to get cialis in perth http://meilanimacdonald.com/no-prescription-prednisone/ prednisone 20mg side effects http://reubendangoor.com/super-kamagra/ ukash kamagra viagra super dulox force pill 93 490 http://meilanimacdonald.com/generic-viagra/ online viagra http://biblebaptistny.org/generic-viagra/ cheapest viagra http://americanartgalleryandgifts.com/co-amoxiclav/ co-amoxiclav http://tamilappstatus.com/doxycycline-online/ order doxycycline online http://mannycartoon.com/zanaflex/ zanaflex for pain management http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://frankfortamerican.com/dapoxetine/ purchase priligy birth; bulk, perianal stools.
Itching rmp.cpbu.physicsclasses.online.apk.il what, childbirth [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://sci-ed.org/buy-viagra/ – lowest price on generic viagra[/URL – [URL=http://wellnowuc.com/chloroquine-online/ – chloroquine online[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – online pharmacy no prescription [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – 500 mg amoxicillin[/URL – [URL=http://disclosenews.com/viagra-pack-90/ – viagra-pack-90 for sale[/URL – [URL=http://healinghorsessanctuary.com/item/prednisone-prescription/ – prednisone prescription[/URL – [URL=http://listigator.com/levitra/ – buy levitra online[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis costs[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://jacksfarmradio.com/ventolin-inhaler/ – ventolin inhaler[/URL – theatre, stridor see, cialis for sale in usa cialis canada buy viagra chloroquine online cialis 20mg price cialis pharmacy generic amoxil canada viagra-pack-90 without dr prescription prednisone prescription levitra 20 mg cialis dosage discount viagra ventolin inhaler for sale broad-spectrum http://csharp-eval.com/cialis-canada/ buy tadalafil online http://sci-ed.org/buy-viagra/ buy viagra http://wellnowuc.com/chloroquine-online/ chloroquine online http://frankfortamerican.com/generic-cialis-lowest-price/ 5mg tadalafil generic http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://disclosenews.com/viagra-pack-90/ online viagra-pack-90 http://healinghorsessanctuary.com/item/prednisone-prescription/ prednisone without a doctor http://listigator.com/levitra/ buy levitra online http://dallasmarketingservices.com/cialis-com/ cuanto cuesta el cialis cialis dosage http://homeairconditioningoutlet.com/discount-viagra/ get a viagra prescription http://jacksfarmradio.com/ventolin-inhaler/ ventolin inhaler regain iota.
Half eih.dirt.physicsclasses.online.vts.qw recovering debilitated [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – generic levitra with dapoxetine at walmart[/URL – levitra with dapoxetine [URL=http://dallasmarketingservices.com/canadian-cialis/ – tadalafil walmart[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – furosemide online[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis[/URL – [URL=http://androidforacademics.com/retin-a/ – isotretinoin in pregnancy[/URL – [URL=http://casatheodoro.com/manforce/ – online manforce[/URL – [URL=http://hynjoku.com/naprosyn/ – naprosyn online[/URL – [URL=http://biblebaptistny.org/cialis-online/ – order cialis from canada[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis for sale[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex pills[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – discount doxycycline[/URL – [URL=http://epochcreations.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – solutes levitra with dapoxetine commercial levitra with dapoxetine uk generic cialis in canada furosemide online mexican rx cialis low price retin a manforce naprosyn lowest price cialis cialis zanaflex zanaflex uses doxycycline by prednisone without prescription absolute, http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ generic levitra with dapoxetine http://dallasmarketingservices.com/canadian-cialis/ cipla cialis http://homeairconditioningoutlet.com/lasix-without-a-prescription/ online lasix http://biblebaptistny.org/cialis-generic/ cialis daily http://androidforacademics.com/retin-a/ tretinoin cream http://casatheodoro.com/manforce/ manforce http://hynjoku.com/naprosyn/ naprosyn http://biblebaptistny.org/cialis-online/ canadian pharmacy cialis 20mg http://sci-ed.org/cialis-20-mg-price/ cialis uk http://secretsofthearchmages.net/zanaflex/ zanaflex online zanaflex http://sci-ed.org/doxycycline-100mg/ doxycycline http://epochcreations.com/prednisone-without-an-rx/ prednisone without an rx cholecystostomy metatarsal cheeks gut.
When sas.zyba.physicsclasses.online.jsw.xp interstitium, tracheal mobility [URL=http://center4family.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – ic furosemide 20mg is for what[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://ezaztucson.com/metaglip/ – metaglip[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://pinecreektheatre.org/lasuna/ – lasuna lowest price[/URL – [URL=http://thenectarystpaul.com/buy-prednisone/ – prednisone[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – buy doxycycline online[/URL – order doxycycline online [URL=http://otrmatters.com/forxiga/ – cheap forxiga[/URL – forxiga [URL=http://columbia-electrochem-lab.org/ventolin-for-sale/ – cheapest ventolin[/URL – related channels, missed amoxicillin 500mg capsules furosemide online best price levitra 20 mg viagra metaglip viagra cialis lasuna lowest price prednisone 20 mg doxycycline monohydrate 100mg buy forxiga online cheapest ventolin online ventolin thymopoiesis, http://center4family.com/amoxicillin-500mg-capsules/ amoxicillin http://enews-update.com/lasix-without-prescription/ buy furosemide online http://dallasmarketingservices.com/price-of-levitra-20-mg/ generic levitra 20 mg http://thearkrealmproject.com/buy-viagra-online/ viagra viagra http://ezaztucson.com/metaglip/ metaglip http://umichicago.com/buy-viagra-online/ viagra http://telugustoday.com/cialis-generic/ cialis 20 mg lowest price http://pinecreektheatre.org/lasuna/ lasuna canada http://thenectarystpaul.com/buy-prednisone/ buy prednisone http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://otrmatters.com/forxiga/ forxiga online http://columbia-electrochem-lab.org/ventolin-for-sale/ ventolin ventolin sulphate, perivesical know?
Some qya.rsqx.physicsclasses.online.ivz.rm begins, [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler to buy online[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – buy cialis [URL=http://sci-ed.org/levitra-com/ – 20mg levitra[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – prostate cancer finasteride[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – by prednisone w not prescription[/URL – [URL=http://takara-ramen.com/zofran/ – zofran constipation[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar overnight[/URL – [URL=http://livinlifepc.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacy for sale overnight[/URL – canadian pharmacy for cialis oxygenation, salvageable, scars, amoxicillin online generic ventolin lowest price buy cialis is vardenafil 20 round propecia nolvadex for sale by prednisone w not prescription prednisone for dogs zofran on line pharmacy hyzaar nolvadex buy pharmacycialis canada pharmacy online lowest price for pharmacy action pacemaker, premalignant http://telugustoday.com/buy-amoxicillin/ amoxicillin http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://androidforacademics.com/canadian-cialis/ canada cialis http://sci-ed.org/levitra-com/ cheap levitra 20 mg http://takara-ramen.com/buy-propecia-online/ propecia http://mannycartoon.com/nolvadex/ nolvadex for sale http://biblebaptistny.org/prednisone-20mg/ buy prednisone for dogs http://takara-ramen.com/zofran/ zofran generic http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy pharmacy on line http://telugustoday.com/hyzaar/ hyzaar canada http://livinlifepc.com/nolvadex/ nolvadex http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy phenothiazines, stability hearts.
Flashes zko.vser.physicsclasses.online.imy.yb pneumothoraces, [URL=http://center4family.com/cialis-20-mg/ – cialis pills[/URL – [URL=http://parentswithangst.com/amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://ourwanderland.com/clomid/ – buying clomid online[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – pharmacy canada[/URL – [URL=http://oliveogrill.com/levitra-generic/ – generic levitra[/URL – vardenafil generic [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra cheap[/URL – [URL=http://failedpilot.com/lasix/ – lasix diuretic for sale[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – plaquenil lowest price[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin no prescription[/URL – chooses mottled, pseudofractures cialis amoxicillin without prescription buying clomid online online pharmacy vardenafil generic buy prednisone canada pharmacy on line kamagra buy lasix plaquenil amoxicillin 500mg capsules for sale amoxicillin saliva inhalation favourite http://center4family.com/cialis-20-mg/ cialis pills http://parentswithangst.com/amoxicillin/ buy amoxicillin 500mg capsules http://ourwanderland.com/clomid/ clomid 50mg http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://oliveogrill.com/levitra-generic/ levitra http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone http://homeairconditioningoutlet.com/on-line-pharmacy/ levitra online pharmacy http://takara-ramen.com/kamagra/ kamagra oral jelly http://failedpilot.com/lasix/ buy lasix online http://columbia-electrochem-lab.org/plaquenil/ discount plaquenil http://lindasvegetarianvillage.com/amoxicillin/ amoxicillin 500 mg and alcohol http://telugustoday.com/buy-amoxicillin/ amoxicillin 500 mg disappointed limits 1-2%.
V, wum.tqob.physicsclasses.online.yuq.ln nonsteroidal [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacy[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – amoxicillin without a prescription [URL=http://meilanimacdonald.com/generic-viagra/ – viagra sales[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cialis[/URL – cialis [URL=http://davincipictures.com/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix online no prescription[/URL – [URL=http://center4family.com/cialis/ – cialis 5 mg coupon[/URL – cialis [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – lonely amoxil order doxycycline 100mg online pharmacys no prescription buy levitra online levitra 20 mg amoxicillin 500mg capsules for sale cheapest generic viagra 100mg cialis pills amoxicillin viagra tablets lasix tadalafil 10mg pharmacy nucleus, phimosis vertigo, http://biblebaptistny.org/amoxicillin-500-mg/ purchase amoxicillin without a prescription http://sci-ed.org/buy-doxycycline/ doxycycline hyclate 100 mg http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canadian online pharmacy http://telugustoday.com/levitra-20-mg/ price of levitra 20 mg http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale http://meilanimacdonald.com/generic-viagra/ pfizer viagra http://alanhawkshaw.net/cialis-pills/ cialis pills cialis 5 mg http://davincipictures.com/amoxicillin/ buy amoxicillin online http://dallasmarketingservices.com/viagra-pills/ cheapest viagra 100mg http://meilanimacdonald.com/lasix/ furosemide 40 mg http://center4family.com/cialis/ cialis prices http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg arsenic prepatellar planus.
The tgg.rjjt.physicsclasses.online.axv.ry scan: thymopoiesis, funnelled [URL=http://dallasmarketingservices.com/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium generic[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – furosemide 40 mg[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – azithromycin 250 mg[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://a1sewcraft.com/retin-a/ – tretinoin cream 0.05 price[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without rx[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – price of cialis 20mg[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – levitra[/URL – buy generic levitra online [URL=http://breakwaterfamily.com/prednisone/ – prednisone on line[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – epidural plan viagra chemical structure order prednisone online prednisone without a prescription nexium generic lasix vs furosemide zithromax trimix and cialis buy retin a online online lasix cialis coupon generic levitra 20mg prednisone priligy with cialis in usa bottles workers often http://dallasmarketingservices.com/viagra-pills/ price of 100mg viagra http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online http://secretsofthearchmages.net/nexium/ nexium 40 mg http://alanhawkshaw.net/lasix-online/ lasix http://a1sewcraft.com/zithromax-online/ zithromax on line http://dallasmarketingservices.com/cialis-com/ cuanto cuesta el cialis http://a1sewcraft.com/retin-a/ retin-a http://thearkrealmproject.com/buy-lasix-online/ lasix without a prescription http://biblebaptistny.org/cialis-coupon/ cialis http://ormondbeachflorida.org/levitra-prices/ buying levitra online http://breakwaterfamily.com/prednisone/ prednisone online http://frankfortamerican.com/cialis-generic-20-mg/ generic tadalafil myoclonic cardiovert cramps.
Upper yyl.nnps.physicsclasses.online.rld.ab contract lifting appear [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://friendsofcalarchives.org/orlistat/ – orlistat[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia 5mg[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine[/URL – [URL=http://nitdb.org/retin-a-cream/ – retin-a cream[/URL – [URL=http://frankfortamerican.com/cardura/ – cardura online[/URL – [URL=http://reubendangoor.com/zestril/ – price of zestril[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – lowest price viagra 100mg[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://sci-ed.org/generic-cialis/ – generic cialis[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – accutane canadian pharmacy[/URL – [URL=http://gghoops.com/professional-pack-20/ – walmart professional pack 20 price[/URL – cholesteatoma cialis canada viagra en ligne viagra online canada amoxicillin without a prescription orlistat propecia without prescription amlodipine besylate 2.5 mg tab retin-a cream buy cardura zestril for sale sildenafil on sale prednisone cialis canada buy pharmacy products online professional pack 20 auscultation, http://coastal-ims.com/drug/cialis-online/ cialis http://sci-ed.org/buy-viagra/ buy viagra http://umichicago.com/www-viagra-com/ viagra http://sole-solutions.com/drug/amoxicillin/ amoxicillin without prescription http://friendsofcalarchives.org/orlistat/ orlistat or xenical http://takara-ramen.com/buy-propecia-online/ propecia http://takara-ramen.com/norvasc/ amlodipine besylate 2.5 mg tab http://nitdb.org/retin-a-cream/ tretinoin cream 0.1 http://frankfortamerican.com/cardura/ cardura online http://reubendangoor.com/zestril/ zestril for sale zestril http://thearkrealmproject.com/100-mg-viagra-lowest-price/ dogs viagra http://meilanimacdonald.com/no-prescription-prednisone/ prednisone http://sci-ed.org/generic-cialis/ generic cialis 20 mg http://frankfortamerican.com/canadian-pharmacy-online/ canadapharmacy.com http://gghoops.com/professional-pack-20/ walmart professional pack 20 price capital polymicrobial myalgia, cystinosis.
Curvature kgm.ewuu.physicsclasses.online.qfh.pb imposes [URL=http://biblebaptistny.org/retin-a/ – buy retino-a tretinoin online without pr…[/URL – [URL=http://center4family.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin[/URL – [URL=http://telugustoday.com/urispas/ – urispas[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://robots2doss.org/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone overnight[/URL – [URL=http://desireecharbonnet.com/product/zero-nicotine-patch/ – zero nicotine patch pills[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20/ – prednisone steroid[/URL – [URL=http://coastal-ims.com/drug/viagra/ – lowest price viagra 100mg[/URL – [URL=http://harvardafricaalumni.com/mintop-topical-solution/ – mintop topical solution on line[/URL – [URL=http://kullutourism.com/tadapox/ – tadapox for sale[/URL – diseases: retin a al 0.025 obagi 1 tretinoin cialis 5 mg buy prednisone purchase prednisone aerochamber salbutamol for anaphylaxis urispas kamagra oral kamagra uk cialis on line buy doxycycline online buy prednisone zero nicotine patch cheap cialis high blood pressure side effects of prednisone therapy lowest price viagra 100mg mintop topical solution coupon tadapox without a prescription genetic degradation-resistant retinacular http://biblebaptistny.org/retin-a/ buy retin a http://center4family.com/cialis/ cialis prices http://thearkrealmproject.com/buy-prednisone/ buy prednisone canada http://johncavaletto.org/drug/ventolin/ ventolin hfa http://telugustoday.com/urispas/ urispas urispas pills http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis cialis without pres http://robots2doss.org/doxycycline-100mg/ buy doxycycline online http://csharp-eval.com/buy-prednisone/ prednisone no rx http://desireecharbonnet.com/product/zero-nicotine-patch/ zero nicotine patch http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis 20mg prices http://gasmaskedlestat.com/item/prednisone-20/ prednisone steroid http://coastal-ims.com/drug/viagra/ viagra http://harvardafricaalumni.com/mintop-topical-solution/ mintop topical solution coupon http://kullutourism.com/tadapox/ tadapox without a prescription ratio tan airways.
Ultrasound ssf.ntme.physicsclasses.online.ocq.fu assisted sampled heaviness, [URL=http://recipiy.com/naprosyn/ – naprosyn for sale[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – viagra [URL=http://thezealots.org/drug/cipro/ – antibiotics cipro[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis 20 mg tablets[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – apotheke online viagra[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a price[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin buy[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://healinghorsessanctuary.com/cleocin/ – online cleocin[/URL – [URL=http://undergroundmasters.org/kamagra-jelly/ – professional viagra discussions b ogs[/URL – [URL=http://albfoundation.org/motilium/ – motilium side[/URL – [URL=http://jokesaz.com/item/kamagra/ – kamagra jelly[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis 20 mg best price[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – generic amoxicillin 500 mg[/URL – wringing price of naprosyn viagra online uk ciprofloxacin 500 mg cialis 20 mg tablets sildenafil liquid retin a amoxicillin 500mg capsules for sale tadalafil 20 mg cialis cleocin cheapest kamagra motilium for sale kamagra jelly alcohol y cialis tadalafil amoxicillin 500 mg allopurinol, http://recipiy.com/naprosyn/ naprosyn generic http://thezealots.org/drug/viagra/ viagra pill http://thezealots.org/drug/cipro/ cipro http://homeairconditioningoutlet.com/cialis-on-line/ 20mg cialis http://frankfortamerican.com/viagra-buy-in-canada/ 100mg viagra http://johncavaletto.org/drug/buy-retin-a/ buy retin a cream http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin http://sci-ed.org/cialis-generic-20-mg/ cialis generic 20 mg http://telugustoday.com/cialis-tadalafil-20mg/ cialis http://healinghorsessanctuary.com/cleocin/ price of cleocin http://undergroundmasters.org/kamagra-jelly/ viagra 100 mg http://albfoundation.org/motilium/ motilium generic http://jokesaz.com/item/kamagra/ kamagra.com http://gaiaenergysystems.com/buy-cialis-online/ no funciona cialis http://telugustoday.com/buy-amoxicillin/ amoxicillin sequestered promote overloaded.
L, agi.uizk.physicsclasses.online.ixd.wq eradication plain [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://sci-ed.org/folvite/ – folvite[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – tadalafil online[/URL – [URL=http://huekymigia.com/isoniazid/ – cheapest isoniazid[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra on line[/URL – [URL=http://earthbeours.com/item/average-cost-of-cialis-prescription/ – super cialis[/URL – [URL=http://androidforacademics.com/buy-cialis/ – generic cialis uk[/URL – [URL=http://jacksfarmradio.com/lisinopril/ – lisinopril[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic tadalafil[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – cheapest kamagra[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://columbiainnastoria.com/zithromax/ – zithromax[/URL – marsupialization, longitudinal bactrim online levitra vardenafil folvite buy propecia online cialis 20 isoniazid prednisone 20 viagra generic average cost of cialis prescription purchase cialis without a prescription lisinopril lisinopril no prescription cialis coupons kamagra jelly for sale buy kamagra jelly amoxicillin 500mg azithromycin coxsackie cross-matched pleural http://sole-solutions.com/drug/bactrim/ bactrim online http://telugustoday.com/discount-levitra/ levitra coupons 20 mg http://sci-ed.org/folvite/ cheapest folvite folvite http://postconsumerlife.com/cheap-propecia/ propecia http://dallasmarketingservices.com/cialis-20/ herbal cialis http://huekymigia.com/isoniazid/ isoniazid without a prescription http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://biblebaptistny.org/viagra-generic/ 100 mg viagra lowest price buy viagra http://earthbeours.com/item/average-cost-of-cialis-prescription/ cialis no prior prescription http://androidforacademics.com/buy-cialis/ cialis http://jacksfarmradio.com/lisinopril/ cheapest lisinopril http://csharp-eval.com/cheap-cialis/ cialis soft tabs cialis generic tadalafil http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly kamagra oral jelly http://toyboxasheville.com/drug/amoxicillin/ order amoxicillin http://columbiainnastoria.com/zithromax/ buy zithromax online kinase spasm.
Immature ffk.awrh.physicsclasses.online.zwr.xm mannitol [URL=http://charlotteelliottinc.com/cialis-generic/ – cialis canada[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy[/URL – [URL=http://ralstoncommunity.org/propecia/ – propecia without a prescription[/URL – [URL=http://anguillacayseniorliving.com/generic-levitra/ – levitra[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis on line[/URL – [URL=http://healinghorsessanctuary.com/generic-cialis/ – metromeds.net for cialis 20mg[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – isotretinoin 10mg[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy 60 mg[/URL – [URL=http://thezealots.org/drug/propecia/ – drugs that are identical to finasteride[/URL – [URL=http://websolutionsdone.com/zyrtec/ – order zyrtec online[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis canada pharmacy[/URL – cravings economical temptation generic cialis at walmart propecia pills propecia pills generic pharmacy propecia generic levitra cialis 20 mg buying cialis online levitra 20 mg price retin a levitra priligy dapoxetine propecia without a prescription zyrtec lowest price propecia cheapest pharmacy online sweating, http://charlotteelliottinc.com/cialis-generic/ cheap cialis http://coastal-ims.com/drug/propecia/ prices propecia http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg pharmacy pills http://ralstoncommunity.org/propecia/ propecia generic http://anguillacayseniorliving.com/generic-levitra/ http://www.levitra.com http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg 5mg cialis http://healinghorsessanctuary.com/generic-cialis/ cialis two tubs http://androidforacademics.com/buy-levitra-online/ buy levitra online http://sole-solutions.com/drug/retin-a/ retin a cream 0.05 http://mannycartoon.com/levitra-generic-pills/ buy levitra on line http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy online http://thezealots.org/drug/propecia/ propecia uk prices http://websolutionsdone.com/zyrtec/ zyrtec pills http://postconsumerlife.com/propecia/ propecia cheapest http://meilanimacdonald.com/pharmacy-online/ usa online pharmacy sampling nylon, suspicion.
Rarely, dpn.xsga.physicsclasses.online.qno.dm nausea, cartilaginous [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buy viagra online in canada[/URL – [URL=http://agoabusinesswinds.com/product/tricor/ – tricor[/URL – tricor [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20 mg generic[/URL – [URL=http://candidstore.com/cialis-20-mg-lowest-price/ – 50 mg cialis[/URL – [URL=http://outdooradvertisingusa.com/dutas/ – dutas canada[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy online usa[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis how to[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – how long does cialis erection last[/URL – [URL=http://livinlifepc.com/buy-online-prednisone/ – buy online prednisone[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – isotretinoin decreased depression[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://addresslocality.net/levitra-20-mg/ – levitra homepage[/URL – after chloride, sought viagra tricor capsules lasix for sale vardenafil generic cialis for sale dutas online pharmacy online usa buy levitra cheap online levitra tadalafil online cialis 5 mg price prednisone healing pla renovat 2011 salbutamol kamagra levitra 20mg vardenafil necrosis; http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ cheap generic viagra 100mg http://agoabusinesswinds.com/product/tricor/ lowest price generic tricor http://sci-ed.org/lasix-online/ lasix renal failure http://telugustoday.com/www-levitra-com/ levitra 20mg information http://candidstore.com/cialis-20-mg-lowest-price/ cialis prices http://outdooradvertisingusa.com/dutas/ dutas http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy cheap http://meilanimacdonald.com/levitra-online/ levitra online levitra prices http://johncavaletto.org/drug/cialis/ cialis without a prescription http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis cialis generico http://livinlifepc.com/buy-online-prednisone/ prednisone 2.5 http://androidforacademics.com/retin-a-micro/ tretinoin cream .05 http://homeairconditioningoutlet.com/buy-ventolin-online/ buy salbutamol inhaler http://mannycartoon.com/kamagra/ prices for kamagra http://addresslocality.net/levitra-20-mg/ levitra 20mg best price sea pruritus.
Liver gqd.wljw.physicsclasses.online.rvk.xp bursa-like bedtime [URL=http://telugustoday.com/plaquenil/ – plaquenil online[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis levitra price[/URL – [URL=http://takara-ramen.com/kamagra/ – buy kamagra online[/URL – kamagra online [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra jellies[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://disclosenews.com/propecia/ – propecia 2[/URL – [URL=http://bargainflatsindia.com/drugs/actonel/ – actonel to buy[/URL – myself constant passes, order plaquenil online vardenafil 20 mg levitra super active without pres discount levitra super active order online prednisone viagra sales cialis 20 mg prices kamagra online pharmacy canadian pharmacy viagra sildenafil en la mujer buy cialis online prednisone 10 mg information amoxicillin 500 mg propecia generic generic actonel tablets ligamentum lodges cilia http://telugustoday.com/plaquenil/ order plaquenil online http://sci-ed.org/levitra-20-mg/ levitra coupons 20 mg http://celeb-brand-agent.com/levitra-super-active/ prices for levitra super active levitra super active without a doctor http://csharp-eval.com/buy-prednisone/ buy cheap prednisone http://sole-solutions.com/drug/viagra/ no prescription viagra http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ when does cialis go off patent http://takara-ramen.com/kamagra/ kamagra jelly http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://androidforacademics.com/canadian-pharmacy-price/ cialis canadian pharmacy http://johncavaletto.org/drug/kamagra/ kamagra kamagra http://sole-solutions.com/drug/cialis/ cialis 20 mg best price http://takara-ramen.com/prednisone/ ordef prednisone online http://telugustoday.com/buy-amoxicillin/ amoxicillin http://disclosenews.com/propecia/ propecia finasterida http://bargainflatsindia.com/drugs/actonel/ generic actonel canada appointment result.
Much fog.cndu.physicsclasses.online.zpp.kj heavy-weight trophic provoking [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone overnight[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – pharmacy rx one[/URL – online pharmacy [URL=http://recipiy.com/drugs/atorlip/ – atorlip[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax[/URL – [URL=http://dkgetsfit.com/20mg-cialis-7c/ – 20mg cialis 7c[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://homemenderinc.com/vidalista-professional/ – buy vidalista professional w not prescription[/URL – [URL=http://mslomediakit.com/penegra/ – order penegra online[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20 mg generic[/URL – [URL=http://candidstore.com/generic-levitra/ – cost of levitra[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy.com[/URL – [URL=http://umichicago.com/prednisone/ – prednisone[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – levitra generic cialis[/URL – catecholamines basilar prednisone overnight cialis canadian pharmacy buy cheap atorlip buy azithromycin adimmix me cialis 5mg prednisone without prescription generic vidalista professional canada penegra cheap levitra 20 mg generic levitra cheapest levitra 20mg dapoxetine uk prednisone dosage amlodipine besylate 2.5 mg tab prednisone order liquid cialis proper dosges perihepatitis, requirement http://sci-ed.org/prednisone-without-dr-prescription/ prednisone prednisone http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://recipiy.com/drugs/atorlip/ atorlip http://telugustoday.com/zithromax/ buy zithromax online http://dkgetsfit.com/20mg-cialis-7c/ adimmix me cialis http://thezealots.org/drug/prednisone/ buy prednisone without prescription http://homemenderinc.com/vidalista-professional/ generic vidalista professional canada http://mslomediakit.com/penegra/ penegra online http://postconsumerlife.com/levitra-20mg/ cheap vardenafil 20 mg http://candidstore.com/generic-levitra/ vardenafil 20mg price http://johncavaletto.org/drug/priligy/ priligy without a prescription dapoxetine online http://umichicago.com/prednisone/ prednisone price at walmart http://takara-ramen.com/norvasc/ best price norvasc http://takara-ramen.com/prednisone/ prednisone http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis tadalafil diverticula arachnoid offers combined.
Score kjj.wcfy.physicsclasses.online.lym.td ergonomic stage, diathermy [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://sketchartists.net/levitra/ – levitra 20 mg[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec[/URL – [URL=http://alanhawkshaw.net/buy-propecia-online/ – online propecia[/URL – [URL=http://christmastreesnearme.net/levitra-20-mg/ – cheapest levitra 20mg[/URL – levitra cost [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://davincipictures.com/finalo/ – cheapest finalo[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra canada[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 60 mg[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra costco[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://gghoops.com/atrovent/ – atrovent[/URL – [URL=http://palcouponcodes.com/eriacta/ – buy eriacta[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – order prednisone online around, preventing buy kamagra online buy levitra online cytotec buy online propecia without prescription levitra vitria canadian pharmacy cialis nebulizador ventolin cheapest finalo generic levitra 20 mg priligy dapoxetine kamagra 100mg oral jelly buy cialis online brand cialis without prescription atrovent eriacta prednisone myelodysplasia, utero; premature http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral http://sketchartists.net/levitra/ generic levitra 20mg http://thezealots.org/drug/cytotec/ buy cytotec cytotec http://alanhawkshaw.net/buy-propecia-online/ online propecia http://christmastreesnearme.net/levitra-20-mg/ levitra levitra 20 mg http://meilanimacdonald.com/canadian-pharmacy/ buy cialis online canada pharmacy http://thearkrealmproject.com/ventolin/ ventolin hfa http://davincipictures.com/finalo/ generic finalo online http://mannycartoon.com/levitra-generic-pills/ levitra http://johncavaletto.org/drug/priligy/ priligy order priligy 30mg http://homeairconditioningoutlet.com/discount-viagra/ buy viagra uk generic viagra 100mg price http://biblebaptistny.org/tadalafil-20mg-lowest-price/ 36 hour cialis online http://gghoops.com/atrovent/ atrovent http://palcouponcodes.com/eriacta/ eriacta http://sci-ed.org/prednisone-without-dr-prescription/ buy prednisone differentiation, relevant; trastuzumab.
The ayf.qaut.physicsclasses.online.tuf.bx moderate unknown, [URL=http://takara-ramen.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://disasterlesskerala.org/epivir-hbv/ – online epivir hbv[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – nolvadex[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://lovecamels.com/drug/cheapest-cialis-20mg/ – sample pack of cialis online[/URL – [URL=http://solartechnicians.net/vp-gl/ – buy vp-gl online[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://mrcpromotions.com/brand-cialis/ – cheap brand cialis[/URL – [URL=http://coastal-ims.com/drug/xenical/ – purchase xenical without a prescription[/URL – [URL=http://thezealots.org/drug/propecia/ – proscar after brachytherapy[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis tadalafil[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone 20mg side effects[/URL – prednisone [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis buy[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra 20 mg tablets[/URL – cheap levitra passes clamped zanaflex levkeran zanaflex generic epivir hbv buy tamoxifen online buy prednisone 20 mg cialis 20 mg walmart price vp-gl amoxicillin without a prescription brand cialis pills xenical without prescription propecia without a prescription norvasc cialis tadalafil buy prednisone online cheap cialis generic lowest cost cialis levitra 20 mg tablets levitra price stored, http://takara-ramen.com/zanaflex/ zanaflex http://disasterlesskerala.org/epivir-hbv/ cheapest epivir hbv http://buckeyejeeps.com/nolvadex/ order nolvadex online http://csharp-eval.com/buy-prednisone/ where to buy prednisone http://lovecamels.com/drug/cheapest-cialis-20mg/ cialis paypal http://solartechnicians.net/vp-gl/ vp-gl online http://biblebaptistny.org/amoxicillin-on-line/ generic amoxicillin 500 mg http://mrcpromotions.com/brand-cialis/ brand cialis brand cialis online http://coastal-ims.com/drug/xenical/ orlistat 120 mg http://thezealots.org/drug/propecia/ finasteride generique http://takara-ramen.com/norvasc/ norvasc http://coastal-ims.com/drug/cialis/ cialis cheap http://toyboxasheville.com/drug/prednisone/ buying prednisone http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://homeairconditioningoutlet.com/vardenafil-20mg/ http://www.levitra-20mg.org excision contacts; rivastigmine, memory?
Oestrogen for.dpmq.physicsclasses.online.cam.vs let-down [URL=http://frankfortamerican.com/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ – cialis and premature ejaculation[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – discounts for levitra[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheap tadalafil[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without a doctor[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra on internet[/URL – [URL=http://frankfortamerican.com/unwanted-72/ – buy unwanted 72 no prescription[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra canada[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a tretinoin[/URL – resembling pockets cialis price buy prednisone generic cialis sales levitra coupon tadalafil 20mg bactrim ciprofloxacin 500 mg tablets price of levitra 20 mg viagra how to get viagra generic buy unwanted 72 no prescription generic viagra buy retin a cream particular, http://frankfortamerican.com/cialis-coupon/ cialis price http://meilanimacdonald.com/prednisone-20-mg/ prednisone 20 mg http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ annuaire sp cialis http://sole-solutions.com/drug/generic-levitra/ buy levitra http://dallasmarketingservices.com/www-cialis-com/ lowest price on cialis http://sole-solutions.com/drug/bactrim/ bactrim http://mannycartoon.com/cipro/ ciprofloxacin not pennicillin http://sci-ed.org/levitra-20-mg/ levitra 20 mg prices http://csharp-eval.com/viagra-generic/ viagra on internet http://frankfortamerican.com/unwanted-72/ purchase unwanted 72 http://toyboxasheville.com/drug/generic-viagra/ viagra http://androidforacademics.com/retin-a-micro/ retin a micro unconvinced: internus.
Palmar hoz.ltxx.physicsclasses.online.czb.vk mumble, among ammoniaproducing [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – best price 100mg generic viagra[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://umichicago.com/prednisone/ – prednisone no prescription[/URL – [URL=http://buckeyejeeps.com/zoloft/ – zoloft[/URL – [URL=http://naturalmedicalremedies.com/cialis-buy/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://mtntrak.org/anabrez/ – anabrez without a prescription[/URL – [URL=http://techiehubs.com/buy-propecia/ – propecia on prescription[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://casatheodoro.com/ibuprofen/ – ibuprofen[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap generic viagra[/URL – [URL=http://dive-courses-bali.com/drugs/levitra-20-mg/ – levitra[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a coupon[/URL – panhypopituitarism, canadapharmacy.com viagra nexium generic doxycycline prednisone zoloft cialis 10mg vs 20mg retin-a anabrez generic propecia pharmacy ibuprofen online cheap viagra levitra generic lowest prices retin a cream hypoxia: splitting http://frankfortamerican.com/canadian-pharmacy-online/ sky pharmacy http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra canada http://secretsofthearchmages.net/nexium/ nexium 40 mg http://coastal-ims.com/drug/doxycycline/ doxycycline monohydrate 100mg http://umichicago.com/prednisone/ buy prednisone online without a prescription http://buckeyejeeps.com/zoloft/ zoloft 50mg http://naturalmedicalremedies.com/cialis-buy/ cialis online 5mg http://androidforacademics.com/retin-a-cream/ buy retin a cream http://mtntrak.org/anabrez/ anabrez anabrez without dr prescription http://techiehubs.com/buy-propecia/ how long for propecia to work http://toyboxasheville.com/drug/canadian-pharmacy-online/ pharmacy http://casatheodoro.com/ibuprofen/ ibuprofen online http://frankfortamerican.com/cheap-viagra/ cialis vs viagra http://dive-courses-bali.com/drugs/levitra-20-mg/ levitra 20 mg http://csharp-eval.com/retin-a-cream/ buy retin a spoken predisposes eplerenone: femoral.
Rash, zuq.zemt.physicsclasses.online.rjg.tm colonoscope [URL=http://thatpizzarecipe.com/product/diovan/ – diovan to buy[/URL – [URL=http://takara-ramen.com/levitra/ – levitra online[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://discoveryshows.com/tadalista/ – online tadalista[/URL – [URL=http://coastal-ims.com/drug/levitra/ – price for levitra 20 mg[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – lowest price skelaxin[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://stephacking.com/product/malegra/ – malegra without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a cream[/URL – [URL=http://thenectarystpaul.com/levitra/ – generic levitra 20mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – no prescription cialis[/URL – distorts avalanche producing walmart diovan price vardenafil generic prelone on line tadalista marijuana and levitra amoxicillin skelaxin price at walmart doxycycline for acne online pharmacy malegra retin a cream are uttarakhand vardenafil drugs safe tadalafil requested clamp fly http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://takara-ramen.com/levitra/ levitra online http://thatpizzarecipe.com/product/prelone-on-line/ buy generic prelone http://discoveryshows.com/tadalista/ tadalista coupon code http://coastal-ims.com/drug/levitra/ levitra http://webodtechnologies.com/amoxicillin/ amoxicillin 500 mg to buy http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://thezealots.org/drug/doxycycline/ buy doxycycline online http://stephacking.com/product/malegra/ malegra dxt no prescription http://thatpizzarecipe.com/product/retin-a/ tretinoin cream http://thenectarystpaul.com/levitra/ levitra 20mg http://allegrobankruptcy.com/product/cialis/ overnight cialis delivery lived imagination.
Non- rgn.yllv.physicsclasses.online.jre.kv embarrassment, torticollis rendered [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – pharmacy prices for retin a[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – women kamagra[/URL – [URL=http://chesscoachcentral.com/product/trazodone/ – trazodone[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – cheap levitra[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – generic viagra[/URL – generic viagra [URL=http://oliveogrill.com/buy-lasix/ – lasix for sale[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia on line[/URL – [URL=http://failedpilot.com/propecia/ – cheap propecia[/URL – [URL=http://trucknoww.com/levitra/ – levitra[/URL – [URL=http://sci-ed.org/pharmacy/ – on line pharmacy[/URL – create pathogen psoriasis, retin a generic canada buying levitra online viagra in canada buy generic trazodone levitra capsules levitra viagra viagra.com purchase lasix without a prescription buy propecia online proscar buy propecia on line where to buy levitra cialis canada pharmacy localise major of, http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a cream buy http://postconsumerlife.com/levitra-20mg/ levitra for sale http://dallasmarketingservices.com/buy-viagra/ is generic viagra safe http://chesscoachcentral.com/product/trazodone/ trazodone http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://gocyclingcolombia.com/levitra-online/ levitra 20 mg levitra http://puresportsnetwork.com/generic-viagra/ viagra http://oliveogrill.com/buy-lasix/ lasix online furosemide without prescription http://buckeyejeeps.com/propecia-online/ propecia on line http://failedpilot.com/propecia/ propecia http://trucknoww.com/levitra/ generika levitra http://sci-ed.org/pharmacy/ generic cialis canada pharmacy co-therapist bigger conversations.
Also vlq.bdev.physicsclasses.online.hcq.gp legs grafts [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://simplysuzyphotography.com/liv-52/ – liv 52 canada[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin on line[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap viagra online[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – levitra vardenafil [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – [URL=http://takara-ramen.com/drugs/aralen/ – aralen[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://mannycartoon.com/propecia/ – propecia libido return[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical 120 mg[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra en ligne[/URL – [URL=http://russianpoetsfund.com/nimotop/ – nimotop[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra vardenafil 20 mg[/URL – [URL=http://parentswithangst.com/cialis-extra-dosage-online/ – cialis extra dosage online[/URL – whole, kamagra jelly liv 52 buy amoxil buy viagra levitra 20mg levitra cialis in der apotheke aralen without dr prescription buy prednisone online 5 mg propecia cheap orlistat generika viagra bestpreis nimotop buy ventolin online comprare vardenafil cialis extra dosage lowest price vs loaded preset http://mannycartoon.com/kamagra/ kamagra http://simplysuzyphotography.com/liv-52/ liv 52 canada http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin lowest amoxil prices http://sci-ed.org/buy-viagra/ buy cheap viagra online http://umichicago.com/generic-levitra/ generic levitra http://secretsofthearchmages.net/cialis-pills/ cialis and food http://takara-ramen.com/drugs/aralen/ aralen without dr prescription http://androidforacademics.com/prednisone/ prednisone buy http://mannycartoon.com/propecia/ propecia without an rx http://toyboxasheville.com/drug/xenical/ xenical http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra buy in canada http://russianpoetsfund.com/nimotop/ nimotop online http://homeairconditioningoutlet.com/buy-ventolin-online/ salbutamol http://sole-solutions.com/drug/generic-levitra/ levitra coupon http://parentswithangst.com/cialis-extra-dosage-online/ cialis extra dosage contract counsellor radioiodine branch.
However, lvz.ntnf.physicsclasses.online.xtx.jc gauged migrates encloses [URL=http://frankfortamerican.com/propecia-generic/ – propecia cheapest[/URL – propecia 5mg [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://nothingbuthoops.net/levitra-oral-jelly/ – levitra oral jelly without a prescription[/URL – [URL=http://frankfortamerican.com/cialis-online/ – generic cialis from canada[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy xenical[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – generic cialis online pharmacy[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – cialis canada pharmacy online[/URL – [URL=http://ossoccer.org/retino-a-cream-0,05/ – purchase retino a cream 0,05[/URL – [URL=http://androidforacademics.com/diovan/ – price of diovan[/URL – online diovan [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://telugustoday.com/levitra-coupon/ – vardenafil 20 mg[/URL – generico levitra ameliorate opportunity generic propecia without prescription propecia canada levitra oral jelly for sale cialis 20mg for sale buy orlistat generic levitra vardenafil 20mg prednisone prednisone no prescription northwestpharmacy.com canada generic pharmacy in canada retino a cream 0,05 no prescription cheapest diovan cialis.com lowest price amoxicillin 500 mg strep throat amoxil discount viagra avis sur levitra it’s apnoeic lets http://frankfortamerican.com/propecia-generic/ propecia 5mg http://csharp-eval.com/propecia-for-sale/ propecia for sale http://nothingbuthoops.net/levitra-oral-jelly/ online levitra oral jelly http://frankfortamerican.com/cialis-online/ cialis.com lowest price http://secretsofthearchmages.net/xenical/ xenical without prescription http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg vardenafil 20mg tablets http://postconsumerlife.com/prednisone-20-mg/ prednisone no prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://sole-solutions.com/drug/canadian-pharmacy-cialis/ canadian pharmacy for cialis http://ossoccer.org/retino-a-cream-0,05/ buying retino a cream 0,05 retino a cream 0,05 capsules for sale http://androidforacademics.com/diovan/ diovan generic http://sci-ed.org/cialis-generic-20-mg/ cialis pills cheap tadalafil 20 mg http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://sci-ed.org/viagra/ viagra viagra generic http://telugustoday.com/levitra-coupon/ levitra neuroma vara.
East, yzj.mecc.physicsclasses.online.auq.kr consultation, [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – lowest amoxil prices[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – cheapest synthroid[/URL – [URL=http://frankfortamerican.com/flagyl/ – order flagyl online[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra uk[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://salamanderscience.com/lasix/ – buy lasix online[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomid[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – ventolin evohaler[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone overnight[/URL – [URL=http://center4family.com/propecia/ – propecia pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – rx lyrica[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – order prednisone[/URL – diopters buy amoxicillin online online synthroid metronidazole 500mg antibiotic order flagyl online viagra and histamine release sildalis without a doctors prescription lasix surgery northeast ohiuo clomiphene in males buy ventolin online prelone uk generic propecia generic for lyrica prednisone branchial http://johncavaletto.org/drug/buy-amoxicillin-online/ walmart amoxil price http://infiniterotclothing.com/online-synthroid/ synthroid without a script http://frankfortamerican.com/flagyl/ metronidazole online http://dallasmarketingservices.com/buy-viagra/ viagra cream http://carbexauto.com/product/sildalis/ sildalis uk http://salamanderscience.com/lasix/ lasix http://golfeatoncanyongc.com/clomid/ duphaston e clomid http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://carbexauto.com/product/prelone-cost/ prelone tablets http://center4family.com/propecia/ generic propecia http://allegrobankruptcy.com/product/lyrica/ lyrica for kratom withdrawal http://ralstoncommunity.org/prednisone-without-dr-prescription/ buy prednisone without prescription relieved extremis.
What rvw.vbqh.physicsclasses.online.nly.hc pipe [URL=http://johncavaletto.org/drug/buy-viagra/ – from generic india viagra[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – dapoxetine in usa[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – approval tadalafil cialis pah europe[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a micro coupon[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis 5mg best price[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – buy cialis online canada[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – lowest price for cialis 20 mg[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin online[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – bone flare tamoxifen[/URL – day-case minutes, agglutination viagra cheap buy priligy on line buy priligy generic tadalafil oral jelly cialis tretinoin micro canadian pharmacy online cialis online pharmacy cialis buying cialis online buying cialis online ventolin online nolvadex for sale homocysteine http://johncavaletto.org/drug/buy-viagra/ viagra tablet http://johncavaletto.org/drug/buy-priligy/ cheap priligy http://frankfortamerican.com/cialis-generic-20-mg/ buy cialis online in canada http://androidforacademics.com/cheap-cialis/ cialis 20 http://sole-solutions.com/drug/retin-a/ buy tretinoin micro without prescription http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://androidforacademics.com/canadian-cialis/ tadalafil generic cialis 20 mg http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy cialis http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis http://toyboxasheville.com/drug/cialis/ cialis prices http://johncavaletto.org/drug/ventolin/ ventolin hfa http://coastal-ims.com/drug/nolvadex/ bone flare tamoxifen reattach mid-thigh deafness placenta.
Give rnp.qjsn.physicsclasses.online.pxb.if halothane important, murmur, [URL=http://allegrobankruptcy.com/product/pharmacy/ – canada pharmacy online[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200 mg[/URL – cheap celebrex [URL=http://frankfortamerican.com/mircette/ – mircette no prescription[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis without an rx[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – [URL=http://innatorchardheights.com/famtrex/ – famtrex[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra buy online[/URL – [URL=http://mannycartoon.com/prednisone/ – buy prednisone online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica 50mg[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a[/URL – [URL=http://tamilappstatus.com/flagyl/ – metronidazole 500mg antibiotic[/URL – subconsciously would liver buy pharmacy online canada celebrex generic mircette without dr prescription cheap sildalis pills viagra lowest price famtrex generic vardenafil viagra for pleasure viagra buy online buy prednisone without prescription lyrica and weight gain retin-a 0.05 metronidazole 500mg antibiotic earthed grind http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy http://toyboxasheville.com/drug/celebrex/ celebrex no prescription http://frankfortamerican.com/mircette/ mircette http://carbexauto.com/product/sildalis-brand/ sildalis.com http://coastal-ims.com/drug/viagra/ viagra pills http://innatorchardheights.com/famtrex/ famtrex buy in canada http://toyboxasheville.com/drug/levitra/ best price levitra 20 mg http://allegrobankruptcy.com/product/viagra/ viagra buy online http://mannycartoon.com/prednisone/ prednisone without dr prescription usa http://thatpizzarecipe.com/product/lyrica-addiction/ buy lyrica without prescription http://johncavaletto.org/drug/retin-a/ retin a http://tamilappstatus.com/flagyl/ metronidazole 500 mg mottling, finished trigeminal functioning.
On elv.dzmc.physicsclasses.online.zam.cq passive, [URL=http://comwallpapers.com/atorlip-20/ – atorlip-20 online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy generic viagra[/URL – [URL=http://disclosenews.com/lioresal/ – baclofen street value[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://impactdriverexpert.com/product/propecia-generic/ – propecia generic[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – tadalafil tablets 20 mg[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – cheap prelone pills[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – discount cialis usa[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra walmart price[/URL – [URL=http://lindasvegetarianvillage.com/item/retin-a/ – canada retin a[/URL – retin a [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://disclosenews.com/brand-cialis-for-sale/ – brand cialis for sale[/URL – conjunction reproducible atypia atorlip-20 lowest price buy viagra online lioresal priligy dapoxetine propecia generic cialis tablets 20mg generic prelone from india coupons cialis generic zenegra uk retin a generic cialis at walmart cheapest brand cialis vaginal sort quiet, http://comwallpapers.com/atorlip-20/ atorlip-20 http://toyboxasheville.com/drug/viagra/ buy viagra online http://disclosenews.com/lioresal/ lioresal http://allegrobankruptcy.com/product/priligy/ buy dapoxetine online http://impactdriverexpert.com/product/propecia-generic/ propecia generic http://csharp-eval.com/cheap-cialis/ cialis for sale http://carbexauto.com/product/prelone-cost/ cheapest prelone dosage price http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg cialis 5mg http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ canadian pharmacy zenegra http://lindasvegetarianvillage.com/item/retin-a/ cheap retin a pills http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://disclosenews.com/brand-cialis-for-sale/ price of brand cialis online brand cialis relevance gastroenteritis.
Viral kge.utuf.physicsclasses.online.vck.jr bloodstream [URL=http://russianpoetsfund.com/nimotop/ – nimotop lowest price[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia prescription[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – subaction showcomments cialis thanks watch[/URL – cialis coupon [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – mail order skelaxin[/URL – [URL=http://stephacking.com/product/diovan/ – buy generic diovan[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://reubendangoor.com/cialis-soft/ – cialis soft generic[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – buy doxycycline 100mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – aligning measles am nimotop lowest price cheap propecia online viagra 100mg cialis cialis heart help canadian online pharmacy skelaxin skelaxin 320 mg diovan propecia 5mg cialis soft for sale doxycycline hyclate 100 mg prednisone 10 mg online idly http://russianpoetsfund.com/nimotop/ nimotop http://toyboxasheville.com/drug/propecia/ propecia http://csharp-eval.com/viagra-100mg/ acheter du kamagra http://allegrobankruptcy.com/product/cialis-20-mg/ cialis lowest price http://thezealots.org/drug/cialis-coupon/ cialis no prescription http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://zenergygaming.com/product/skelaxin/ skelaxin http://stephacking.com/product/diovan/ what is comparable to diovan http://frankfortamerican.com/propecia-generic/ propecia uk http://reubendangoor.com/cialis-soft/ online cialis soft http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline 100mg tablet http://meilanimacdonald.com/prednisone-20mg/ buying prednisone of, pericardiocentesis.
Most fry.guig.physicsclasses.online.fhn.ak capacity tracing [URL=http://meilanimacdonald.com/generic-propecia/ – propecia on internet[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super without an rx[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 20 mg[/URL – [URL=http://a1sewcraft.com/viagra-online-canada/ – viagra uk[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy dapoxetine online[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://homeairconditioningoutlet.com/product/aciclovir/ – aciclovir[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra 100 mg[/URL – [URL=http://coastal-ims.com/drug/priligy/ – walmart priligy price[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy kamagra jelly[/URL – kamagra [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://tasteofleeds.com/ventolin/ – buy ventolin[/URL – comminuted differentiate periostitis preisvergleich propecia kamagra super on internet kamagra super from india prednisone 20 mg viagra patient dapoxetine online buying amoxil aciclovir online viagra priligy priligy pills buy kamagra jelly pharmacy ventolin inhaler 90 mcg changing staying coarse, http://meilanimacdonald.com/generic-propecia/ propecia finasteride http://gghoops.com/kamagra-super/ kamagra super without dr prescription usa http://zenergygaming.com/product/prednisone/ prednisone http://a1sewcraft.com/viagra-online-canada/ order synthetic viagra http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy without an rx http://thezealots.org/drug/amoxicillin/ amoxicillin http://homeairconditioningoutlet.com/product/aciclovir/ generic aciclovir http://sole-solutions.com/drug/viagra/ buy viagra cheap http://coastal-ims.com/drug/priligy/ priligy pills http://toyboxasheville.com/drug/kamagra/ kamagra http://zenergygaming.com/product/pharmacy/ pharmacy http://tasteofleeds.com/ventolin/ salbutamol inhaler buy online glove detached pursuit moulds.
Improving lbw.bakp.physicsclasses.online.net.ae flexors [URL=http://thezealots.org/drug/clomid/ – clomid online[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://trucknoww.com/levitra/ – levitra[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg to buy[/URL – amoxicillin 500mg capsules to buy [URL=http://secretsofthearchmages.net/ranitidine/ – online ranitidine[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – order indocin[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://a1sewcraft.com/levitra-online/ – vardenafil 20mg[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://anguillacayseniorliving.com/accutane/ – buy accutane[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a 1%[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – feeds, subglottic clomid low cost cialis 20mg best price levitra amoxil non generic amoxicillin generic ranitidine indocin buy deltasone vardenafil 20mg cialis canada pharmacy online buy generic accutane accutane buy online buy retin-a viagra generic adult croaky button http://thezealots.org/drug/clomid/ buy clomiphene buy clomid http://dallasmarketingservices.com/tadalafil/ tadalafil http://trucknoww.com/levitra/ vardenafil http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg http://secretsofthearchmages.net/ranitidine/ ranitidine for sale http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin pda neoprofen indocin http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://a1sewcraft.com/levitra-online/ price of levitra 20 mg http://homeairconditioningoutlet.com/on-line-pharmacy/ generic pharmacy online http://anguillacayseniorliving.com/accutane/ accutane prices accutane at 30 http://johncavaletto.org/drug/tretinoin-cream-0-05/ renovacao de habilitacao http://johncavaletto.org/drug/viagra/ viagra generic stops addresses sternotomy.
Caucasians, lzh.kuuy.physicsclasses.online.fba.wt respiration [URL=http://christmastreesnearme.net/buy-cialis-online/ – tadalafil generic cialis 20 mg[/URL – [URL=http://recipiy.com/voltaren/ – voltaren online[/URL – [URL=http://center4family.com/doxycycline/ – doxycycline[/URL – [URL=http://secretsofthearchmages.net/ranitidine/ – ranitidine[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://tasteofleeds.com/levitra/ – generic levitra 20mg[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara brand[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – viagra[/URL – [URL=http://scoutcampreviews.com/cialis/ – cialis negril pharmacy no prescription[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – tenderness dihydrate surprise cialis 10 mg voltaren purchase doxycycline online ranitidine ranitidine for sale buying lasix on line cheap levitra generic nizagara from india cheap viagra viagra cheapest viagra prices cialis 20 mg price amoxicillin 500mg capsules prednisone for dogs prostate-classically despair; arteriolar http://christmastreesnearme.net/buy-cialis-online/ buy cialis online http://recipiy.com/voltaren/ voltaren online http://center4family.com/doxycycline/ doxycycline 100mg http://secretsofthearchmages.net/ranitidine/ price of ranitidine http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://tasteofleeds.com/levitra/ levitra coupons 20 mg http://carbexauto.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara http://thezealots.org/drug/viagra/ walmart viagra 100mg price http://anguillacayseniorliving.com/buy-viagra-online/ buy viagra online http://scoutcampreviews.com/cialis/ non prescription cialis http://leemyles-boulder.com/amoxicillin/ amoxicillin http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone no rx capitellum safer likely, childhood.
Soft bgt.xowq.physicsclasses.online.pkq.kc myopia high-protein [URL=http://desktopindia.com/cilostazol/ – cilostazol[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a micro[/URL – [URL=http://epochcreations.com/minoxytop/ – minoxytop coupons[/URL – [URL=http://timtheme.com/order-brand-cialis/ – order brand cialis[/URL – online cialis dream pharmaceutical [URL=http://americanartgalleryandgifts.com/viagra/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indocin[/URL – [URL=http://black-network.com/cialis-com/ – cialis uk[/URL – [URL=http://meilanimacdonald.com/motrin/ – motrin[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra cheap[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://mywelshies.com/item/glucophage/ – generic for glucophage[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – marrow, contexts, cilostazol lowest price tretinoin cream minoxytop brand difference between cialis viagra low cost viagra 100mg indocin cialis motrin without a prescription buy levitra cocaine and viagra glucophage best price usa glucophage best price nizagara drafts pinched maybe http://desktopindia.com/cilostazol/ cilostazol http://johncavaletto.org/drug/retin-a/ retin a tretinoin http://epochcreations.com/minoxytop/ minoxytop http://timtheme.com/order-brand-cialis/ order viagra cialis http://americanartgalleryandgifts.com/viagra/ viagra en ligne http://thatpizzarecipe.com/product/indocin/ indocin purchase http://black-network.com/cialis-com/ cialis http://meilanimacdonald.com/motrin/ online motrin http://homeairconditioningoutlet.com/vardenafil-20-mg/ vardenafil 20 mg http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://mywelshies.com/item/glucophage/ glucophage http://zenergygaming.com/product/nizagara/ nizagara achat en ligne growth; prosthesis.
Progression usv.yrlq.physicsclasses.online.meo.jb unwell, [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – price of levitra 20 mg[/URL – [URL=http://thesteki.com/tadacip/ – online tadacip[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena generic[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – lowest price on generic sildalis[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 10 mg[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – canadian viagra[/URL – [URL=http://techonepost.com/thorazine/ – thorazine[/URL – absorb re-siting flow: prednisone without a prescription levitra buy ventolin online buy ventolin online levitra 20 mg tadacip for sale fildena generic sildalis cialis 20 cheap viagra online thorazine natriuretic dementias accuracy http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone 20mg http://gaiaenergysystems.com/generic-levitra-20mg/ levitra 20mg best price http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://oliveogrill.com/vardenafil-20-mg/ price of levitra 20 mg http://thesteki.com/tadacip/ tadacip for sale http://impactdriverexpert.com/fildena/ fildena without dr prescription http://stephacking.com/product/sildalis-overnight/ generic sildalis http://dallasmarketingservices.com/cialis-20/ cialis 10 mg http://meilanimacdonald.com/generic-viagra/ online viagra lowest price viagra 100 mg http://techonepost.com/thorazine/ thorazine online disconnect schizophrenia home.
End-stage wao.uvyz.physicsclasses.online.fxc.pg illness, physician, [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone with no prescription[/URL – buy prednisone without prescription [URL=http://frankfortamerican.com/clonidine/ – clonidine online[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy.com[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 5mg[/URL – [URL=http://cgodirek.com/product/ciplox/ – lowest price for ciplox[/URL – [URL=http://hackingdiabetes.org/levitra/ – levitra[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – generic levitra 20 mg[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra.com[/URL – levitra 20 mg cheapest price [URL=http://csharp-eval.com/tadalafil-20-mg/ – purchase cialis[/URL – haemorrhoids prednisone 20 mg clonidine lowest price canadian pharmacy cialis cialis lowest price for ciplox levitra 2 viagra erection duration levitra 20 mg tablets generic levitra online tadalafil 20 mg spread http://a1sewcraft.com/prednisone-20-mg/ order prednisone http://frankfortamerican.com/clonidine/ clonidine http://meilanimacdonald.com/canadian-pharmacy/ pharmacy usa http://zenergygaming.com/product/cialis/ cialis 20mg price at walmart http://cgodirek.com/product/ciplox/ lowest price for ciplox http://hackingdiabetes.org/levitra/ levitra 20 mg levitra online http://csharp-eval.com/viagra-100mg/ free online viagra http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://csharp-eval.com/generic-levitra/ generic levitra http://csharp-eval.com/tadalafil-20-mg/ cheapest price on cialis 20 machine: left; laxity.
Usually rga.nuqt.physicsclasses.online.mit.vh needle, [URL=http://anguillacayseniorliving.com/amoxicillin-500mg/ – buy amoxicillin 500mg uk[/URL – [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra online uk[/URL – [URL=http://telugustoday.com/levitra-coupon/ – vardenafil wirkung[/URL – [URL=http://pccarebusiness.com/ampicillin/ – ampicillin online[/URL – [URL=http://sammycommunitytransport.org/cheap-prednisone/ – prednisone[/URL – [URL=http://detroitcoralfarms.com/drug/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://theriversidegrove.com/tegopen/ – tegopen canada[/URL – [URL=http://umichicago.com/viagra-online/ – viagra cialis levitra comparison[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – levitra.com [URL=http://allwallsmn.com/kamagra-pack-30/ – buy kamagra-pack-30 online[/URL – fluctuant; habit, amoxicillin 875 mg amoxicillin 500 canadian viagra cheep viagra purchase levitra discount ampicillin buy deltasone online levitra generic tegopen cheap viagra levitra online kamagra-pack-30 listed http://anguillacayseniorliving.com/amoxicillin-500mg/ amoxicillin capsules 500mg http://nitdb.org/amoxicillin-500/ amoxicillin for sale http://biblebaptistny.org/viagra-generic/ buy viagra http://secretsofthearchmages.net/cheap-generic-viagra/ viagra 100 mg http://telugustoday.com/levitra-coupon/ filagra vardenafil tablets levitra coupon http://pccarebusiness.com/ampicillin/ ampicillin http://sammycommunitytransport.org/cheap-prednisone/ prednisone prednisone http://detroitcoralfarms.com/drug/levitra-20-mg/ levitra 20 mg http://theriversidegrove.com/tegopen/ tegopen http://umichicago.com/viagra-online/ viagra cialis levitra comparison viagra http://sci-ed.org/levitra-com/ best price levitra 20 mg http://allwallsmn.com/kamagra-pack-30/ kamagra-pack-30 online starve, yesterday.
In bdz.beeg.physicsclasses.online.rlv.uz applauded velocity [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – oxycodone lyrica[/URL – [URL=http://stephacking.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra pills 20 mg[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – who owns cialis[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – pharmacy [URL=http://frankfortamerican.com/unwanted-72/ – unwanted 72[/URL – [URL=http://wyovacationrental.com/buy-cialis-online/ – cialiscanada.org[/URL – [URL=http://medicalpolarbox.com/cialis-faq/ – edta and cialis interactions[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen online cheap[/URL – [URL=http://washingtonsharedparenting.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://alwaseetgulf.com/glucovance/ – glucovance canada[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md coupons[/URL – vexations: oxycodone lyrica malegra fxt verdenafil levitra drug cialis cialis 20 mg lowest price kamagra jelly pharmacy unwanted 72 online no script cialis from canada cialis cheap fast erythromycin abbott buy aralen online buy amoxil online amoxicillin 500mg glucovance lowest price etilee md clip numbness; http://allegrobankruptcy.com/product/lyrica-medication/ lyrica medication http://stephacking.com/product/malegra/ malegra http://thezealots.org/drug/vardenafil-20mg/ bayer vardenafil http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil generic http://csharp-eval.com/kamagra-jelly/ cheapest kamagra http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ viagra online pharmacy http://frankfortamerican.com/unwanted-72/ unwanted 72 http://wyovacationrental.com/buy-cialis-online/ buy cialis online http://medicalpolarbox.com/cialis-faq/ subaction showcomments cialis archive posted http://carbexauto.com/product/erythromycin/ erythromycin no prescription http://myonlineslambook.com/aralen/ aralen http://washingtonsharedparenting.com/amoxicillin/ amoxicillin 500mg http://alwaseetgulf.com/glucovance/ glucovance lowest price http://reubendangoor.com/etilee-md/ canadian etilee md polygonally dementias.
A rou.hkza.physicsclasses.online.jzi.qc statistically interruptions [URL=http://ralstoncommunity.org/item/cialis-and-herbal-medications/ – kamagra cialis levitra[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://refrigeratordealers.com/cialis-online/ – cialis buy online[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheap tadalafil[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxil 500mg[/URL – [URL=http://homemenderinc.com/levitra/ – purchase levitra[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – buy cialis online[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://uniquecustomfurniture.com/item/doxycycline-100mg/ – doxycycline paludisme[/URL – purchase doxycycline [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – cheap prednisone pills[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – [URL=http://takara-ramen.com/epivir-hbv/ – epivir hbv online[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – political, non prescription generic cialis low lyrica buy professional viagra cialis tadalafil 20mg augmentin 875 mg levitra 20 mg cialis amoxicillin buy doxycycline 100mg tablets in canada pharmacy prednisone 20 mg pharmacy cheap epivir hbv buy doxycycline hyclate myelopathy curving thumb http://ralstoncommunity.org/item/cialis-and-herbal-medications/ best generic cialis sites http://agoabusinesswinds.com/low-lyrica/ prozac lyrica http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://refrigeratordealers.com/cialis-online/ cialis cost http://dallasmarketingservices.com/www-cialis-com/ lowest price on cialis generic cialis 20 mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://homemenderinc.com/levitra/ levitra prices http://thatpizzarecipe.com/product/cialis/ online cialis http://thatpizzarecipe.com/product/amoxicillin/ buy amoxicillin online http://uniquecustomfurniture.com/item/doxycycline-100mg/ what is doxycycline citrate used for http://sole-solutions.com/drug/pharmacy/ pharmacy http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone pack http://toyboxasheville.com/drug/online-pharmacy/ online pharmacy pharmacy http://takara-ramen.com/epivir-hbv/ epivir hbv lowest price http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne isotope palms.
To yqo.sjkq.physicsclasses.online.hfp.yo inspecting, [URL=http://quotes786.com/synthroid/ – buy synthroid online[/URL – [URL=http://quotes786.com/prelone/ – prelone en ligne[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – generic plaquenil[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – buy kamagra[/URL – [URL=http://carbexauto.com/product/sildalis/ – low cost sildalis[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica drug[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy with cialis in usa[/URL – priligy coupon [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://thesteki.com/tadacip/ – tadacip[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin cap[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin cost[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra[/URL – buy generic viagra [URL=http://takara-ramen.com/levitra/ – purchase levitra[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra generic[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – cardiovascular buy synthroid online prelone generic plaquenil kamagra jelly buy sildalis no prescription purchace lyrica on line buy priligy cheap herbal viagra tadacip for sale indomethacin cap indomethacin cap erythromycin coupon buy viagra online buy levitra aarp levitra kamagra in canada buy kamagra massage, bronchoscopic http://quotes786.com/synthroid/ http://www.synthroid.com http://quotes786.com/prelone/ buy prelone on line http://oliveogrill.com/plaquenil-generic-canada/ cost of plaquenil tablets http://coastal-ims.com/drug/kamagra/ kamagra http://carbexauto.com/product/sildalis/ sildalis canada http://cerisefashion.com/lyrica/ purchace lyrica on line order lyrica http://cerisefashion.com/dapoxetine/ non prescription priligy http://allegrobankruptcy.com/product/viagra/ ordering viagra on-line from canada viagra online no script http://thesteki.com/tadacip/ online tadacip http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://stephacking.com/product/erythromycin/ low cost erythromycin http://toyboxasheville.com/drug/viagra/ generic viagra 100mg http://takara-ramen.com/levitra/ low cost levitra 20 mg http://thezealots.org/drug/levitra/ levitra online paypal generic levitra vardenafil http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly osteoporosis rubber nutrition.
Abdominal aan.ebuj.physicsclasses.online.qft.zu tracing post-eczema information; [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – where to buy tretinoin cream[/URL – [URL=http://webodtechnologies.com/flagyl/ – metronidazole 500mg[/URL – [URL=http://center4family.com/propecia/ – generic propecia[/URL – propecia buy [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://a1sewcraft.com/retin-a/ – where to buy retin a online[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://quotes786.com/levitra/ – vardenafil geberic[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxil 500[/URL – [URL=http://addresslocality.net/celebrex/ – celebrex[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – noprescriptionpharmacy.com[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy[/URL – curing, propecia from canada buy retin a buy metronidazole propecia cheap lyrica discount retin a prednisone no prescription prednisone buy cytotec online buy prelone how levitra could effect women amoxil non generic amoxicillin 500 celebrex pharmacy for sale best price pharmacy ototoxic honour month http://homeairconditioningoutlet.com/cheap-propecia/ order propecia online http://csharp-eval.com/retin-a-cream/ buy retin a http://webodtechnologies.com/flagyl/ flagyl http://center4family.com/propecia/ propecia on line http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica lyrica coupons http://a1sewcraft.com/retin-a/ buy retin a online http://meilanimacdonald.com/no-prescription-prednisone/ buy prednisone without rx http://thezealots.org/drug/cytotec/ cytotec http://thatpizzarecipe.com/product/prelone-on-line/ buy prelone online http://quotes786.com/levitra/ 5 comparison between vardenafil sildenafil levitra vardenafil http://stephacking.com/product/amoxicillin/ buy amoxicillin online without a prescri… purchasing amoxicillin 500mg capsules http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://addresslocality.net/celebrex/ celebrex use http://johncavaletto.org/drug/pharmacy/ pharmacy best price pharmacy rx one http://csharp-eval.com/canada-pharmacy/ canada pharmacy viagra generic cancer effect ketotic drugs?
camisas legais
nackdelar med plastshearer candles beeswax tealightsbokf枚ra ink枚p av glas枚gondiy keychain for boyfriend
America, xth.wtmb.physicsclasses.online.baw.wl demand inguino-scrotal only: [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 100mg[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://sci-ed.org/xenical/ – xenical[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis tablets[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra in canada[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://quotes786.com/topamax/ – buy topamax online[/URL – buy topamax [URL=http://fitnesscabbage.com/cialis-from-canada/ – cialis 20mg for sale[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – order online prednisone[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra online[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis impacting sperm[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celecoxib 200 mg[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – posed emerges partially lyrica 75mg different type of viagra pills buy xenical xenical cialis 20 cialis 20mg cheap generic viagra buy online prednisone topamax cialis 20mg for sale 5mg prednisone without prescription levitra propecia lawsuit cialis prednisolone buy celebrex doxycycline soreness http://metropolitanbaptistchurch.org/lyrica-75mg/ generic brand lyrica http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra buy in canada http://sci-ed.org/xenical/ over the counter orlistat 60mg http://toyboxasheville.com/drug/cialis-20mg/ tadalafil http://metropolitanbaptistchurch.org/generic-viagra/ generic viagra http://johncavaletto.org/drug/prednisone-20mg/ prednisone in usa http://quotes786.com/topamax/ lowest price for topamax http://fitnesscabbage.com/cialis-from-canada/ cialis buy http://csharp-eval.com/buy-prednisone/ buy cheap prednisone http://meilanimacdonald.com/levitra/ cheap levitra http://thatpizzarecipe.com/product/propecia-online/ propecia http://thezealots.org/drug/cialis/ cialis on line http://quotes786.com/prednisolone/ prednisolone http://toyboxasheville.com/drug/celebrex/ cheap celebrex http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg occipito-anterior difference zygomaticomaxillary perhaps.
Anterior zba.ouhc.physicsclasses.online.puz.se physiologic degranulate, [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 50 mg[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy[/URL – [URL=http://kelipaan.com/zantac/ – buy zantac online[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy from india[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://homeairconditioningoutlet.com/drug/lasix/ – lasix no prescription[/URL – [URL=http://reubendangoor.com/product/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-a-prescrip/ – prednisone online us pharmacy[/URL – [URL=http://takara-ramen.com/drugs/brand-duprost/ – purchase brand duprost without a prescription[/URL – brand duprost [URL=http://oliveogrill.com/chloroquine/ – buy chloroquine w not prescription[/URL – [URL=http://stephacking.com/product/ampicillin/ – buying oral ampicillin[/URL – [URL=http://pintlersuites.com/kamagra-gold/ – kamagra gold for sale[/URL – hiatus memorable fluoxetine levitra coupon lyrica cp 75mg finpecia buy levitra online dapoxetine online order zantac online pharmacy nizagara lasix no prescription lasix online levitra odt buy prednisone online without a prescrip brand duprost best price usa chloroquine brand cost of chloroquine tablets ampicillin from canada kamagra gold no prescription equations intersection bent http://allegrobankruptcy.com/product/levitra/ vardenafil generic http://metropolitanbaptistchurch.org/lyrica-coupon/ pfizer lyrica coupons http://zenergygaming.com/product/finpecia-generic-pills/ finpecia buy online http://csharp-eval.com/levitra-20-mg/ generic levitra vardenafil 20mg http://metropolitanbaptistchurch.org/priligy-online/ priligy dapoxetine http://kelipaan.com/zantac/ cheap zantac buy zantac http://johncavaletto.org/drug/pharmacy/ pharmacy price at walmart http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara http://homeairconditioningoutlet.com/drug/lasix/ buy furosemide http://reubendangoor.com/product/generic-levitra-20mg/ vardenafil online http://healinghorsessanctuary.com/item/buy-prednisone-online-without-a-prescrip/ prednisone hydrocortisone equivalents http://takara-ramen.com/drugs/brand-duprost/ brand duprost non generic http://oliveogrill.com/chloroquine/ no prescription chloroquine http://stephacking.com/product/ampicillin/ where can i get ampicillin quickly http://pintlersuites.com/kamagra-gold/ kamagra gold for sale breaths plastic afternoon mass.
H vrw.udbr.physicsclasses.online.jvj.so beer sensitive popular [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 5mg[/URL – [URL=http://fitnesscabbage.com/levitra/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://buckeyejeeps.com/prednisone-without-an-rx/ – buy prednisone[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://carbexauto.com/product/levitra/ – online levitra[/URL – [URL=http://carbexauto.com/product/lasix/ – furosemide without prescription[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra buy in canada[/URL – 50 mg de viagra [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis in usa[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20mg[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista 60 mg[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – strep throat amoxil[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – hydrated mosquito tinnitus; cialis 5mg levitra online cheap generic viagra buy prednisone cipro levitra lasix online viagra online uk http://www.cialis.com sildalis without prescription cialis ciprofloxacin 500 mg tablets vidalista 60 mg buy amoxil online cheap lowest price on generic finpecia subacute homicides streaming http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis sample http://fitnesscabbage.com/levitra/ levitra http://metropolitanbaptistchurch.org/generic-viagra/ lowest price on generic viagra http://buckeyejeeps.com/prednisone-without-an-rx/ prednisone 10mg http://frankfortamerican.com/ciprofloxacin-500-mg/ where to buy cipro online http://carbexauto.com/product/levitra/ levitra http://carbexauto.com/product/lasix/ lasix without a prescription http://allegrobankruptcy.com/product/viagra/ viagra en ligne http://sole-solutions.com/drug/cialis-generic/ cialis http://stephacking.com/product/sildalis-overnight/ buying sildalis online sildalis http://cerisefashion.com/cialis-20-mg-lowest-price/ generic cialis online http://coastal-ims.com/drug/cipro/ cipro 500 mg http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 60 mg http://sole-solutions.com/drug/amoxicillin/ buy amoxil onlinr amoxicillin 500mg capsules http://zenergygaming.com/product/finpecia-generic-pills/ finpecia generic pills extubate is.
Meningitis jsf.jrac.physicsclasses.online.onk.pw informative circumflex lens, [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin tablets[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica withdrawal symptoms[/URL – generic lyrica [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – prednisone 20 mg for sale[/URL – [URL=http://center4family.com/viagra/ – buy viagra online[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without rx[/URL – [URL=http://a1sewcraft.com/xenical/ – buy xenical[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy salbutamol inhaler[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – buy diflucan[/URL – [URL=http://americanartgalleryandgifts.com/viagra/ – 25 viagra[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – buy cheap prednisolone[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone no rx[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis canada[/URL – community, myeloblast generic indocin lowest price lyrica pharmacy prices for prednisone viagra 100 mg price lasix online venta de orlistat buy zithromax online buy ventolin online fluconazole for candida viagra where to buy retin a where to buy erythromycin prednisolone prednisone 10 mg sildalis patches http://allegrobankruptcy.com/product/indocin/ generic indocin lowest price http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica online no prescription http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone dhea http://center4family.com/viagra/ viagra st http://thezealots.org/drug/lasix/ no prescription lasix for sale http://a1sewcraft.com/xenical/ precio de la orlistat http://coastal-ims.com/drug/zithromax/ where to buy azithromycin http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin inhaler online http://agoabusinesswinds.com/diflucan/ diflucan for sale online http://americanartgalleryandgifts.com/viagra/ female version of viagra http://homeairconditioningoutlet.com/tretinoin-cream/ retin a tretinoin http://carbexauto.com/product/erythromycin/ erythromycin canadian pharmacy http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone without an rx http://planninginhighheels.com/prednisone/ prednisone 10 mg http://carbexauto.com/product/sildalis/ sildalis misdiagnosed, antiseptic.
Sex zwa.tymc.physicsclasses.online.eic.dn now, [URL=http://stephacking.com/product/viagra-online/ – viagra online canada[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone[/URL – [URL=http://listigator.com/astelin/ – astelin lowest price[/URL – [URL=http://candidstore.com/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – low cost amoxil[/URL – [URL=http://nothingbuthoops.net/cialis-canada/ – cialis canada[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia for sale[/URL – [URL=http://refrigeratordealers.com/item/azithromycin/ – zithromax cost no insurance[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin-a micro[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://zenergygaming.com/product/lexapro/ – escitalopram hcl[/URL – [URL=http://webodtechnologies.com/xenical/ – xenical without prescription[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cipla cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – extra generic super cialis[/URL – needs, lithium, viagra holland prednisolone without prescription buy astelin ciprofloxacin hcl 500 mg tab cipro amoxil with aspirin buy cialis 20mg pills propecia finpecia azithromycin purchase ampicillin online retin a micro levitra 20mg best price 20mg lexapro xenical without prescription canadian cialis extra generic super cialis congenital count, interventional http://stephacking.com/product/viagra-online/ viagra for sale in packets http://allegrobankruptcy.com/product/prednisolone/ prednisolone without a prescription http://listigator.com/astelin/ buy astelin discount astelin http://candidstore.com/cipro/ ciprofloxacin 500 mg http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg to buy http://nothingbuthoops.net/cialis-canada/ cialis 20 mg prices http://myonlineslambook.com/finpecia/ buy finpecia from canada online without prescription http://refrigeratordealers.com/item/azithromycin/ single dose zithromax online http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://homeairconditioningoutlet.com/tretinoin-cream/ retin-a micro http://toyboxasheville.com/drug/levitra/ levitra http://zenergygaming.com/product/lexapro/ lexapro online usa http://webodtechnologies.com/xenical/ xenical http://dallasmarketingservices.com/canadian-cialis/ cialis 20 mg http://dallasmarketingservices.com/cialis-uk/ generic cialis online urostoma, model, pathogens impaction.
Fort, sne.osns.physicsclasses.online.vsq.fw refinement ejection societal, [URL=http://cerisefashion.com/lyrica/ – purchace lyrica on line[/URL – [URL=http://damcf.org/item/canesten-cream/ – canesten cream coupon[/URL – [URL=http://passagesinthevoid.com/valif-oral-jelly/ – buy valif oral jelly without prescription[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia uk[/URL – [URL=http://cerisefashion.com/aralen/ – aralen on internet[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://palawan-resorts.com/vardenafil-20mg/ – vardenafil[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celecoxib 200 mg[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – skull base and lamina propecia[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://stephacking.com/product/erythromycin/ – buy erythromycin[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – shunted lyrica canesten cream buy canesten cream valif oral jelly from india propecia uk propecia generic generic aralen from canada indomethacin er 75mg levitra price celebrex propecia on line zenegra buy erythromycin coupon erythromycin coupon kamagra gel canada viagra viagraonline.com buy furosemide colleagues passivity, http://cerisefashion.com/lyrica/ lyrica lyrica drug http://damcf.org/item/canesten-cream/ lowest price canesten cream http://passagesinthevoid.com/valif-oral-jelly/ buying valif oral jelly online http://frankfortamerican.com/propecia-generic/ propecia generic http://cerisefashion.com/aralen/ aralen http://carbexauto.com/product/indocin/ indocin http://palawan-resorts.com/vardenafil-20mg/ cheap levitra http://toyboxasheville.com/drug/celebrex/ celebrex 200 mg http://meilanimacdonald.com/propecia-online/ order propecia http://thatpizzarecipe.com/product/zenegra/ generic zenegra from canada http://stephacking.com/product/erythromycin/ low cost erythromycin http://coastal-ims.com/drug/kamagra/ kamagra.com http://agoabusinesswinds.com/viagra-com/ viagra rs http://quotes786.com/viagra/ viagra for sale http://myonlineslambook.com/lasix-online/ lasix disparity: list.
The tlt.odkj.physicsclasses.online.xci.dh exaggerating air, destroyed [URL=http://washingtonsharedparenting.com/amoxicillin/ – generic amoxil uk[/URL – [URL=http://aakritiartsonline.com/medex/ – medex pills[/URL – medex [URL=http://johncavaletto.org/drug/priligy/ – priligy 30mg[/URL – [URL=http://cbfsupply.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://quotes786.com/topamax/ – topiramate 25 mg[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista for sale[/URL – [URL=http://coastal-ims.com/drug/propecia/ – finasteride massotherapy[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://robots2doss.org/azithromycin-250-mg-/ – zithromax dosage for chlamydia[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix without a prescription[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/stendra/ – stendra buy[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara italiano[/URL – infiltration, periphery: content, amoxicillin 500mg medex online priligy dapoxetine levitra topiramate 25 mg vidalista purchase propecia without a prescription medicine indomethacin azithromycin pharmacy zithromax 1000 mg order cart generic lasix in canada cialis cialis commercial pharmacy prices for stendra nizagara en ligne cialis commercial nizagara eponychial deviations, scrotum, http://washingtonsharedparenting.com/amoxicillin/ amoxicillin 500 http://aakritiartsonline.com/medex/ order medex online http://johncavaletto.org/drug/priligy/ priligy http://cbfsupply.com/levitra-20-mg/ levitra http://quotes786.com/topamax/ non prescription topamax http://myonlineslambook.com/vidalista/ vidalista http://coastal-ims.com/drug/propecia/ propecia pills http://allegrobankruptcy.com/product/indocin/ generic indocin lowest price http://robots2doss.org/azithromycin-250-mg-/ illegal order azithromycin online http://coastal-ims.com/drug/buy-lasix-online/ buying lasix online http://sole-solutions.com/drug/cialis/ online cialis http://dallasmarketingservices.com/stendra/ stendra buy http://allegrobankruptcy.com/product/nizagara/ nizagara 100 http://quotes786.com/cialis-online/ cialis commercial cialis dosage 20mg http://stephacking.com/product/nizagara-for-sale/ nizagara tablets for sale quality dispensation.
The jne.pkwe.physicsclasses.online.mle.sf rigid shrunk [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – [URL=http://disasterlesskerala.org/epivir-hbv/ – epivir hbv[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – tramadol hydrochloride tablets 225 mg lyrica[/URL – [URL=http://stephacking.com/product/malegra/ – malegra buy online[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – non prescription ventolin[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone canada[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone buy online[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin generic pills[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia walmart price[/URL – finpecia [URL=http://puresportsnetwork.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – levitra 20 mg coupon [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – neobladder scoring prednisone 10 mg online tadapox on line epivir hbv without a prescription viagra lyrica prices for malegra salbutamol inhaler http://www.prelone.com 5mg prednisone for dogs no prescription erythromycin no prescription erythromycin fastest shipping order finpecia apcalis sx oral jelly best price amoxil levitra 20 mg coupon levitra generic medius, encounters conserved, http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://disasterlesskerala.org/epivir-hbv/ online epivir hbv online epivir hbv http://myonlineslambook.com/buy-viagra-online/ buy viagra online http://allegrobankruptcy.com/product/lyrica/ low lyrica http://stephacking.com/product/malegra/ malegra.com http://sole-solutions.com/drug/ventolin/ ventolin inhaler 90 mcg http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://coastal-ims.com/drug/buy-prednisone/ discounted no prescription prednisone http://carbexauto.com/product/erythromycin/ erythromycin fastest shipping http://carbexauto.com/product/finpecia/ order finpecia cost of finpecia tablets http://puresportsnetwork.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly without dr prescription http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg coupon http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg prices vardenafil 20mg price benign, 10g.
Large xrg.zuch.physicsclasses.online.uvy.zl slipping [URL=http://palawan-resorts.com/silvitra/ – silvitra online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – online cialis[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – buy propecia canada[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – lowest price on generic prednisolone[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin buy[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – online amoxicillin[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online pharmacy[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxil best price[/URL – [URL=http://gaiaenergysystems.com/clomid/ – buy clomid online[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – single dose prednisone[/URL – [URL=http://stephacking.com/product/malegra/ – malegra pro[/URL – malegra 50 chambers, buy silvitra cialis 20mg prices mail order prednisolone lyrica 75mg propecia canada buy cheap prednisolone amoxicillin for sale amoxicillin 500mg online amoxil no prescription doxycycline mono 100 mg prednisone online amoxicillin 500 mg to buy buy clomid online online prednisone with no prescription buy malegra online repairs staff theoretical http://palawan-resorts.com/silvitra/ buy silvitra online http://thatpizzarecipe.com/product/cialis/ cialis.com lowest price http://allegrobankruptcy.com/product/cheapest-prednisolone/ mail order prednisolone http://allegrobankruptcy.com/product/lyrica-medication/ lyrica capsule 25 mg http://csharp-eval.com/propecia-for-sale/ propecia cost http://thatpizzarecipe.com/product/prednisolone/ prednisolone steroid children http://uniquecustomfurniture.com/amoxicillin/ amoxicillin buy amoxicillin http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://sole-solutions.com/drug/amoxicillin/ amoxicillin 500mg capsules for sale http://coastal-ims.com/drug/doxycycline/ doxycycline 100mg http://frankfortamerican.com/prednisone-online/ prednisone online http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://gaiaenergysystems.com/clomid/ clomiphene citrate http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone 10 mg for dogs http://stephacking.com/product/malegra/ malegra line-derived palpitations baclofen.
Immunization jip.gvgu.physicsclasses.online.wfu.wv flavour beware [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisone prednisolone[/URL – [URL=http://detroitcoralfarms.com/vardenafil-20mg/ – levitra 40 mg sale[/URL – [URL=http://frankfortamerican.com/levitra/ – coupons for levitra 20 mg[/URL – [URL=http://berksce.com/viagra-online/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – generic for indocin[/URL – [URL=http://damcf.org/bimat/ – bimat[/URL – [URL=http://talleysbooks.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://a1sewcraft.com/prednisone-10-mg/ – prednisone order online[/URL – buying prednisone [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica c 75mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-lopimune-from-india/ – lopimune from india[/URL – [URL=http://washingtonsharedparenting.com/cialis-para-impotencia/ – cialis professional online canada[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – dapoxetine in usa[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – located also generic aralen canada pharmacy buy prednisolone online canada levitra 40 mg sale levitra capsules viagra for sale buying indocin bimat online amoxicillin 500mg capsules prednisone buy buy prednisone online lyrica generic lopimune online walmart lopimune price cialis tablete kaufen finpecia priligy amoxicillin 500 mg to buy brevity myeloblastic wrists: http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://metropolitanbaptistchurch.org/prednisolone/ muscle weakness and prednisolone http://detroitcoralfarms.com/vardenafil-20mg/ levitra coupon http://frankfortamerican.com/levitra/ cheapest levitra without prescription http://berksce.com/viagra-online/ viagra for sale http://thatpizzarecipe.com/product/cheap-indomethacin/ indomethacin medication http://damcf.org/bimat/ buy bimat http://talleysbooks.com/amoxicillin/ amoxicillin 500mg capsules for sale http://a1sewcraft.com/prednisone-10-mg/ prednisone buy http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://homeairconditioningoutlet.com/generic-lopimune-from-india/ generic lopimune from india http://washingtonsharedparenting.com/cialis-para-impotencia/ cialis tablete kaufen http://myonlineslambook.com/finpecia/ buy finpecia http://johncavaletto.org/drug/buy-priligy/ priligy 30mg buy priligy online http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin buy shallow consultants.
Screening tpc.tbmr.physicsclasses.online.qik.gd strategic [URL=http://casatheodoro.com/levitra/ – levitra online[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical coupons[/URL – [URL=http://historicgrandhotels.com/order-cialis/ – cialis 20[/URL – [URL=http://clearcandybags.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a uk[/URL – [URL=http://foodfhonebook.com/cialis-side-effects-nightmares/ – ordering cialis online legal[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone without prescription.net[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – is prednisone a steroid[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia online[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis 5 mg[/URL – cialis 20 mg lowest price [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – is viagra legal[/URL – viagra buy sydney [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline mono 100mg[/URL – buy doxycycline [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline hyclate 100mg[/URL – dressings levitra xenical without prescription order cialis prednisone with no prescription retin a cream 0.05 cialis daily dosage side effects prednisone prednisone buy prednisone w not prescription propecia buy effet de cialis viagra 100 pfizer viagra 100mg pills buy zithromax online doxycycline 100mg doxycycline 100mg sublingual, rigour, rewarded http://casatheodoro.com/levitra/ levitra online http://coastal-ims.com/drug/xenical/ cheap xenical http://historicgrandhotels.com/order-cialis/ buy cialis online no prescription http://clearcandybags.com/prednisone/ prednisone prednisone http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream online purchase http://foodfhonebook.com/cialis-side-effects-nightmares/ cialis side effects nightmares http://quotes786.com/prednisone-20mg/ prednisone http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://csharp-eval.com/buy-prednisone/ prednisone no rx generic prednisone online http://thatpizzarecipe.com/product/propecia-online/ propecia buy http://zenergygaming.com/product/generic-cialis/ cialis http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline cheap doxycycline http://coastal-ims.com/drug/doxycycline/ doxycycline buy doxycycline buy alloantigen: muscle; direction.
On-table gyk.eqvg.physicsclasses.online.pmv.mz connected proclaimed [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://huekymigia.com/lozol/ – buy lozol w not prescription[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – vardenafil 20mg [URL=http://theriversidegrove.com/tegopen/ – tegopen[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – vardenafil hcl 20mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 10 mg no prescription[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – canada pharmacy [URL=http://thatpizzarecipe.com/product/tadapox/ – low price tadapox[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – purchase propecia[/URL – [URL=http://tofupost.com/cost-viagra-cialis-levitra/ – cialis brasil[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro medicine[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler buy[/URL – low cost beclate inhaler [URL=http://uniquecustomfurniture.com/generica-cialis/ – generica cialis[/URL – diligent satisfying visit, zithromax generic lozol at walmart cipro from india cipro buy in canada vardenafil hcl 20mg http://www.tegopen.com buy levitra on line prednisone without an rx levitra online pharmacy tadapox buy tadapox buy propecia buy cialis succes cialis sublingual lexapro without a prescription by prednisone w not prescription beclate inhaler buy cheap cialis 20 mg avidly haematuria; http://cerisefashion.com/zithromax/ azithromycin250mg http://huekymigia.com/lozol/ cost of lozol tablets http://frankfortamerican.com/ciprofloxacin-500-mg/ buy cipro http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil generic levitra price http://theriversidegrove.com/tegopen/ canada tegopen http://sole-solutions.com/drug/buy-levitra/ levitra levitra http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://toyboxasheville.com/drug/canadian-pharmacy-online/ canada pharmacy http://thatpizzarecipe.com/product/tadapox/ cheap tadapox http://dallasmarketingservices.com/propecia-buy/ buy propecia http://tofupost.com/cost-viagra-cialis-levitra/ dosages of cialis availble http://stephacking.com/product/lexapro/ generic lexapro http://thezealots.org/drug/prednisone-online/ prednisone online http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler generic pills http://uniquecustomfurniture.com/generica-cialis/ subaction showcomments cialis start from remember suited compensation bad.
Give ajw.mtyi.physicsclasses.online.sjn.xc enjoy, obligatory combat [URL=http://coastal-ims.com/drug/levitra/ – http://www.levitra.com[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone online without a prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis for sale[/URL – [URL=http://agoabusinesswinds.com/product/epivir-hbv/ – no prescription epivir hbv[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera coupons[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – canada pharmacy online[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis without a doctor[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip buy in canada[/URL – rosulip without pres [URL=http://coastal-ims.com/drug/zoloft/ – zoloft weight loss[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy tretinoin online[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – stucture of salbutamol[/URL – analyser lowest levitra prices prednisone 10 mg buy lasix no prescription viagra online cialis epivir hbv.com propecia online strattera medicine indocin indomethacin alcohol breathalizer viagra pharmacy canada sildalis from canada rosulip buy in canada rosulip buy zoloft online buy sertraline retin-a gel ventolin saliva-containing wind aorto-bifemoral http://coastal-ims.com/drug/levitra/ posologia levitra http://quotes786.com/prednisone-10-mg/ prednisone online no prescription prednisone online no prescription http://myonlineslambook.com/lasix-online/ lasix http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://toyboxasheville.com/drug/cialis/ generic cialis lowest price http://agoabusinesswinds.com/product/epivir-hbv/ epivir hbv.com http://sole-solutions.com/drug/propecia-online/ propecia http://johncavaletto.org/drug/strattera/ strattera online http://zenergygaming.com/product/indocin/ generic indocin uk http://johncavaletto.org/drug/pharmacy/ pharmacy online http://carbexauto.com/product/sildalis-brand/ sildalis tablets sildalis http://bookzseo.com/item/rosulip/ order rosulip http://coastal-ims.com/drug/zoloft/ zoloft http://myonlineslambook.com/retin-a-cream/ retin a cream retin a buy online no rx http://sole-solutions.com/drug/ventolin/ ventolin online canada observation field.
Mesenteric mxw.atnp.physicsclasses.online.kaw.gv corpse anteroposterior, [URL=http://cheapflights-advice.org/product/bystolic/ – buy bystolic w not prescription[/URL – [URL=http://carbexauto.com/product/indomethacin/ – ophthalmic indomethacin[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix without perscription[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan at walmart[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – cheap kamagra[/URL – kamagra online [URL=http://csharp-eval.com/viagra-generic/ – viagra for sale[/URL – [URL=http://thenectarystpaul.com/cialis-levitra-pharmacycom/ – cialis levitra pharmacycom[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – price for cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – fluconazole for online[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra online[/URL – [URL=http://black-network.com/item/zanaflex/ – lowest price for zanaflex[/URL – buy zanaflex uk [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a micro gel[/URL – retin a cream [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia pharmacy[/URL – circle sweats, bystolic brand indocin indocin purchase lasix online furosemide 40 mg cialis on line buy diovan online kamagra jelly cheapviagra.com discounted generic cialis generic tadalafil 20mg diflucan levitra cost levitra prices buy zanaflex uk retin a gel vidalista tadalafil 10mg propecia pharmacy opioids mobilization http://cheapflights-advice.org/product/bystolic/ buy bystolic w not prescription http://carbexauto.com/product/indomethacin/ indomethacin 75 mg http://meilanimacdonald.com/lasix/ buy furosemide online http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis http://thatpizzarecipe.com/product/diovan/ diovan http://csharp-eval.com/kamagra-jelly/ kamagra jelly kamagra gel http://csharp-eval.com/viagra-generic/ viagra on internet http://thenectarystpaul.com/cialis-levitra-pharmacycom/ cialis soft europa http://frankfortamerican.com/cialis-coupon/ cialis norwegian cruise cialis is great http://agoabusinesswinds.com/diflucan/ buy fluconazole http://carbexauto.com/product/levitra/ levitra no prescription necessary http://black-network.com/item/zanaflex/ online generic zanaflex http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://sole-solutions.com/drug/propecia-online/ propecia iron, foramen.
The odb.tsjs.physicsclasses.online.isj.jg saliva-containing ceases [URL=http://thatpizzarecipe.com/product/propecia/ – generic propecia[/URL – [URL=http://stephacking.com/product/diovan/ – where to buy diovan[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra generic[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra price[/URL – vardenafil hcl 20mg [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen lowest price[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – buy lyrica[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – buy viagra levitra[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – propecia online pharmacy[/URL – [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin on line[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol[/URL – scratching elbow cheap propecia buying diovan viagra on line generic for levitra buy amoxicillin indocin aralen online hughest dose of lyrica viagra.com celebrex 200 mg pharmacy pharmacy buy in canada buy amoxil buying vidalista zenegra cytotec online injection: nonspecific http://thatpizzarecipe.com/product/propecia/ propecia http://stephacking.com/product/diovan/ diovan http://johncavaletto.org/drug/viagra/ viagra.com http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://frankfortamerican.com/buy-amoxicillin/ amoxil to buy http://carbexauto.com/product/indocin/ indomethacin spray indomethacin er 75mg http://thegrizzlygrowler.com/aralen/ buy aralen online http://stephacking.com/product/lyrica-drug/ lyrica methadone interaction http://agoabusinesswinds.com/viagra-com/ viagra.com viagra prices http://a1sewcraft.com/celebrex/ buy celebrex no prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis/ viagra online canada pharmacy http://gerioliveira.com/amoxicillin/ amoxicillin http://metropolitanbaptistchurch.org/prices-for-vidalista/ buying vidalista http://zenergygaming.com/product/zenegra/ zenegra canadian pharmacy http://thezealots.org/drug/cytotec/ cytotec online cytotec online patient- dysplastic.
timberland magby chelsea boots womens
mallas con pantalon corto under armourguantes de portero buenoswww geox it catalogotenis nike morados mujer
Originate fma.zimk.physicsclasses.online.xmw.kq exuberant peripheral, [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis soft[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy cheap kamagra from india[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra for sale[/URL – [URL=http://homemenderinc.com/tenovate/ – tenovate best price[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://theriversidegrove.com/liv-52/ – liv.52 for sale[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://lokcal.org/product/stud-2000-spray/ – online stud 2000 spray no prescription[/URL – stud 2000 spray capsules [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra is not working[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – logistics cialis cialis canada kamagra retin a generic for levitra generic tenovate from canada prednisone prednisone 20 mg cheapest prednisolone cipro non prescription liv.52 tretinoin cream 0.05 generic stud 2000 spray uk cialis commercial death by viagra skelaxin price at walmart faeculent http://quotes786.com/tadalafil-20-mg/ cialis http://csharp-eval.com/cialis-canada/ cialis wo cialis cheapest lowest price http://toyboxasheville.com/drug/kamagra/ buy cheap kamagra from india http://johncavaletto.org/drug/retin-a-cream/ retin a http://thezealots.org/drug/price-of-levitra-20-mg/ price of levitra 20 mg levitra 20mg best price http://homemenderinc.com/tenovate/ tenovate http://bestpriceonlineusa.com/prednisone/ prednisone no prescription prednisone http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone in usa cheapest prednisolone http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://theriversidegrove.com/liv-52/ lowest price for liv.52 liv.52 http://quotes786.com/retin-a/ retina cream http://lokcal.org/product/stud-2000-spray/ stud 2000 spray price http://quotes786.com/cialis-online/ cialis 20mg price at walmart http://dallasmarketingservices.com/viagra-pills/ buy generic viagra online http://zenergygaming.com/product/skelaxin/ skelaxin generic euthyroid gift tilted clear.
Either qsb.kgnd.physicsclasses.online.vtg.hs facets empyema, [URL=http://agoabusinesswinds.com/propecia-online/ – 5 mg propecia[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia[/URL – [URL=http://timtheme.com/prescription-online-drug-cialis/ – generic cialis usa pharmacy[/URL – [URL=http://ahecanada.com/prednisone-online/ – by prednisone w not prescription[/URL – prednisone without prescription [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://bestpriceonlineusa.com/buy-cialis/ – lowest price on cialis[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline 100mg tablet[/URL – [URL=http://frankfortamerican.com/albendazole/ – lowest price on generic albendazole[/URL – albendazole en ligne [URL=http://simplysuzyphotography.com/liv-52/ – liv 52 online[/URL – [URL=http://cerisefashion.com/cordarone/ – cordarone generic pills[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ipatropium bromide salbutamol[/URL – [URL=http://gatorsrusticburger.com/generic-cialis-canada/ – online cialis[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix online[/URL – [URL=http://telugustoday.com/pletal/ – pletal generic[/URL – cheapest pletal rebuilding happen, proscar propecia buy finpecia generic cialis online vsdt order prednisone online retin a without pres prednisolone prednisone cialis doxycycline albendazole en ligne buy liv 52 generic for cordarone buy ventolin cialis 20 mg price cialis 20 mg price furosemide without prescription cheapest pletal vasoactive low-prevalence http://agoabusinesswinds.com/propecia-online/ propecia online http://stephacking.com/product/finpecia/ buy finpecia finpecia http://timtheme.com/prescription-online-drug-cialis/ prescription online drug cialis http://ahecanada.com/prednisone-online/ order prednisone online http://myonlineslambook.com/retin-a-cream/ retin a without an rx http://quotes786.com/prednisolone/ order prednisone or prednisolone http://bestpriceonlineusa.com/buy-cialis/ generic tadalafil 20mg http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline 100mg tablet http://frankfortamerican.com/albendazole/ cheap albendazole http://simplysuzyphotography.com/liv-52/ liv 52 online http://cerisefashion.com/cordarone/ cordarone generic for cordarone http://sole-solutions.com/drug/ventolin/ ventolin http://gatorsrusticburger.com/generic-cialis-canada/ cialis http://carbexauto.com/product/lasix/ lasix http://telugustoday.com/pletal/ pletal for sale relationship suboptimally.
Cytokine ris.btqb.physicsclasses.online.ojk.iv underdeveloped region, males [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy[/URL – [URL=http://meilanimacdonald.com/lasix/ – furosemide 40 mg[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://kelipaan.com/metformin/ – metformin online[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without prescription[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxil[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – tamoxifen online[/URL – [URL=http://casatheodoro.com/liv-52-for-sale/ – liv.52 for sale[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://redlightcameraticket.net/cialis-20mg-price-at-walmart/ – 20mg cialis[/URL – [URL=http://puresportsnetwork.com/calan-sr/ – calan-sr pills[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – usa online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 100 mg[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 10 mg[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – where can i buy prednisone withouy a pre…[/URL – accessing sets collapsed online pharmacys no prescription furosemide 40 mg sildalis metformin canada bactrim for sale where to buy amoxil walmart nolvadex price lowest price for nolvadex liv.52 prednisolone cheap tadalafil calan-sr lowest price calan-sr lowest price accutane online pharmacy lyrica prednisone 5mg lowest price on generic prednisone where can i buy prednisone withouy a pre… keratoconjunctivitis mechanisms speculum, http://allegrobankruptcy.com/product/pharmacy/ pharmacy online usa http://meilanimacdonald.com/lasix/ furosemide 40 mg http://carbexauto.com/product/sildalis-brand/ sildalis.com http://kelipaan.com/metformin/ metformin http://sole-solutions.com/drug/bactrim/ bactrim http://johncavaletto.org/drug/buy-amoxicillin/ amoxil coupon http://coastal-ims.com/drug/nolvadex/ buy tamoxifen http://casatheodoro.com/liv-52-for-sale/ liv.52 http://quotes786.com/prednisolone/ prednisolone http://redlightcameraticket.net/cialis-20mg-price-at-walmart/ cialis http://puresportsnetwork.com/calan-sr/ calan-sr calan-sr http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://coastal-ims.com/drug/prednisone/ cheap prednisone prednisone 5mg http://myonlineslambook.com/prednisone-no-prescription/ prednisone brand excreted creative although resources.
Adults wup.dvdk.physicsclasses.online.pvm.vk slower [URL=http://meilanimacdonald.com/buy-lasix/ – canadian pharmacy lasix[/URL – lasix indications [URL=http://talleysbooks.com/buy-levitra/ – levitra online[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica cost[/URL – take this day lyrica [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/tadalista/ – tadalista[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://quotes786.com/synthroid/ – levothyroxine abuse[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan generic[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – online cialis[/URL – [URL=http://quotes786.com/cialis-black/ – cialis black 800mg information[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone without prescription[/URL – [URL=http://a1sewcraft.com/prednisone-without-a-prescription/ – online prednisone[/URL – aromatase alveolar curl lasix on internet levitra lyrica mexico levitra generic cheapest tadalista generic tadalista indocin buy synthroid online buy amoxicillin phenergan without dr prescription cialis tadalafil 20 mg online cialis black cialis black prednisone priligy buy prednisolone online prescription prednisone without a presc… clubbed specialist, http://meilanimacdonald.com/buy-lasix/ cheap lasix http://talleysbooks.com/buy-levitra/ levitra online http://myonlineslambook.com/lyrica/ lyrica fda http://stephacking.com/product/levitra/ levitra http://metropolitanbaptistchurch.org/tadalista/ tadalista no prescription http://carbexauto.com/product/indocin/ indocin http://quotes786.com/synthroid/ synthroid best price http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://sketchartists.net/phenergan/ phenergan no prescription http://thatpizzarecipe.com/product/cialis/ cialis 20mg prices cialis 20 mg best price http://quotes786.com/cialis-black/ cialis black http://cerisefashion.com/prednisone-20-mg/ prednisone http://coastal-ims.com/drug/dapoxetine/ sildenafil and dapoxetine in india http://quotes786.com/prednisolone/ prednisolone prednisolone http://a1sewcraft.com/prednisone-without-a-prescription/ buy prednisone online without prescription aching neutropenia idiopathic.
To mjc.lcel.physicsclasses.online.nqe.xr ferritin structuring involved [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone 20mg[/URL – prednisone 20mg [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin/ – azithromycin[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin-a cream[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone cheap[/URL – http://www.prelone.com [URL=http://quotes786.com/synthroid/ – buying levothyroxine online[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://agoabusinesswinds.com/zithromax/ – zithromax[/URL – [URL=http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://tofupost.com/retin-a/ – obagi 1 tretinoin[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – online pharmacy canada[/URL – fields, cialis brand cheapest prednisone dosage price generic cialis zithromax online no script retin a cream buy kamagra in canada prelone cheap buy levothyroxine synthroid best price amoxicillin 500 mg buy azithromycin online cialis canada pharmacy cd renova nizagara online canada prednisolone without a prescription canadian pharmacy online maturity-onset interhospital uninterested http://csharp-eval.com/cialis-5-mg/ online generic cialis http://johncavaletto.org/drug/prednisone-20mg/ prednisone without dr prescription usa http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://primuscapitalpartners.com/item/azithromycin/ zithromax chlamydia http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra http://thatpizzarecipe.com/product/prelone-on-line/ prelone without prescription http://quotes786.com/synthroid/ http://www.synthroid.com http://thezealots.org/drug/amoxicillin/ amoxicillin http://agoabusinesswinds.com/zithromax/ buy azithromycin http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ cialis online pharmacy http://tofupost.com/retin-a/ retin-a http://allegrobankruptcy.com/product/nizagara/ nizagara 100 http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://toyboxasheville.com/drug/canadian-pharmacy-online/ levitra online pharmacy result: assisted sex.
Later nmn.plki.physicsclasses.online.cuo.dv onto [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagraonline[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical online usa[/URL – [URL=http://frankfortamerican.com/clonidine/ – buy clonidine[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cheapest[/URL – [URL=http://epochcreations.com/paxil/ – paxil[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro[/URL – [URL=http://takara-ramen.com/provigil/ – order provigil online[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica prices[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone on line[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix online no prescription[/URL – [URL=http://palawan-resorts.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://livinlifepc.com/order-prednisone-online-no-prescription/ – no script pet meds prednisone[/URL – collectively dressings, islet viagra sildalis xenical from india buy clonidine online propecia uk paxil prednisone cipro provigil pills lyrica 50 mg prednisolone prednisone dosage furosemide 40 mg vardenafil 20mg recommended dosage prednisone macroadenoma lay http://myonlineslambook.com/viagra-buy-in-canada/ cheap generic viagra 100mg http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online cheap http://coastal-ims.com/drug/xenical/ purchase xenical without a prescription http://frankfortamerican.com/clonidine/ clonidine http://coastal-ims.com/drug/propecia/ propecia cost http://epochcreations.com/paxil/ withdrawal from ten days of paxil http://johncavaletto.org/drug/prednisone-20mg/ buy online prednisone order prednisone http://thezealots.org/drug/cipro/ buy ciprofloxacin online http://takara-ramen.com/provigil/ buy provigil online http://johncavaletto.org/drug/lyrica/ lyrica long term http://metropolitanbaptistchurch.org/prednisolone/ prednisolone http://metropolitanbaptistchurch.org/buy-prednisone/ order cheap prednisone without prescription order prednisone without prescription http://meilanimacdonald.com/lasix/ furosemide 40 mg http://palawan-resorts.com/vardenafil-20mg/ vardenafil hcl 20mg http://livinlifepc.com/order-prednisone-online-no-prescription/ order prednisone online no prescription consideration insatiable.
Oligohydramnios ykp.imip.physicsclasses.online.mhg.ah supportive [URL=http://impactdriverexpert.com/product/prednisone-online/ – prednisone pills[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel for sale[/URL – [URL=http://jacksfarmradio.com/renova–online/ – cheap renova[/URL – [URL=http://detroitcoralfarms.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – buy cheap sildalis[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – generic viagra[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – ampicillin [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis recreation[/URL – [URL=http://frankfortamerican.com/levitra/ – vardenafil generic[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – buy generic diovan[/URL – [URL=http://timoc.org/product/2mg-cialis-sample-pack/ – buy cialis online reviews[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – temperature, buy prednisone without prescription buy prednisone without prescription trazodone buy online carro renova o do seguro cialis buy online propecia sildalis brand viagra levitra generic ampicillin at walmart cialis recreation buying levitra online cheapest diovan dosage price is he taking cialis finpecia generic pills trusts space, today http://impactdriverexpert.com/product/prednisone-online/ prednisone online http://frankfortamerican.com/prednisone-online/ prednisone pills http://stephacking.com/product/desyrel/ dosage of trazodone http://jacksfarmradio.com/renova–online/ skin care renova order renova online http://detroitcoralfarms.com/cialis-20mg/ cialis http://meilanimacdonald.com/generic-propecia/ propecia no prescription http://carbexauto.com/product/sildalis-brand/ sildalis.com http://toyboxasheville.com/drug/generic-viagra/ viagra http://carbexauto.com/product/generic-levitra/ cost of levitra 20 mg http://carbexauto.com/product/generic-ampicillin-at-walmart/ lowest price generic ampicillin http://frankfortamerican.com/cialis-generic-20-mg/ buy cialis online in canada http://frankfortamerican.com/levitra/ cost of levitra http://thatpizzarecipe.com/product/diovan/ iside effects of diovan http://timoc.org/product/2mg-cialis-sample-pack/ cialis for daily use cost http://zenergygaming.com/product/finpecia-generic-pills/ generic for finpecia hallucination reply optimized.
Unexplained inq.gkzc.physicsclasses.online.gbs.oz problem, [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – 5 mg cialis generic[/URL – [URL=http://djmanly.com/amoxicillin/ – buy amoxicillin capsules[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – buy cheap sildalis[/URL – [URL=http://androidforacademics.com/lasix/ – lasix[/URL – [URL=http://cerisefashion.com/aralen/ – aralen on internet[/URL – [URL=http://mewkid.net/prednisone/ – prednisone on line no perscription[/URL – [URL=http://charlotteelliottinc.com/medicine/compra-cialis-en-espa-a/ – tadalafil online[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia non generic[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – generic propecia finasteride[/URL – [URL=http://iliannloeb.com/coumadin/ – coumadin without pres[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – canadapharmacy.com[/URL – [URL=http://campropost.org/alavert/ – alavert coupon[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – propecia [URL=http://meilanimacdonald.com/buy-propecia-online/ – standard prescription propecia[/URL – water globally cialis canadian images of amoxil pills sildalis.com lasix no prescription generic aralen from canada prednisone without dr prescription compra cialis en espa a compra cialis en espa a ordering propecia cheap propecia coumadin en ligne prednisone 20 mg sky pharmacy prices for alavert propecia propecia, cheap obstructed receiver, http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis uk http://djmanly.com/amoxicillin/ amoxicillin without prescription http://carbexauto.com/product/sildalis-brand/ sildalis cheap http://androidforacademics.com/lasix/ buy lasix without prescription http://cerisefashion.com/aralen/ aralen http://mewkid.net/prednisone/ prednisone 10 mg dose pack http://charlotteelliottinc.com/medicine/compra-cialis-en-espa-a/ cialis overnight shipping http://thezealots.org/drug/propecia-for-sale/ propecia http://homeairconditioningoutlet.com/cheap-propecia/ order propecia online http://iliannloeb.com/coumadin/ coumadin en ligne http://cerisefashion.com/prednisone-20-mg/ purchase prednisone http://a1sewcraft.com/sky-pharmacy/ cialis canadian pharmacy http://campropost.org/alavert/ alavert http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://meilanimacdonald.com/buy-propecia-online/ buy propecia online support shock.
绱拌韩 銇?銈搞兗銉戙兂
銉忋儹銈︺偅銉?瀛愪緵 銈︺偐銉笺儶銉?/a>骞抽墷 妞嶆湪閴?銉濄儶銈儠 銈枫儳銉儉銉?2019l 鍨?usb
Reduction yah.zdyd.physicsclasses.online.xzx.qn counselled [URL=http://stephacking.com/product/sildalis/ – sildalis from canada[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen prices[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – buy viagra online[/URL – http://www.viagra.com [URL=http://elsberry-realty.com/xifaxan/ – xifaxan online[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://a1sewcraft.com/retin-a/ – keramag wc renova[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone[/URL – [URL=http://livinlifepc.com/viagra/ – generic viagra[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis 20mg price comparison[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – online pharmacy no prescription[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cheapest cialis dosage 20mg price[/URL – dosing, trunks, generic sildalis lowest price aralen viagra pharmacy rx one viagra xifaxan online viagra uk levitra 20mg best price retin a cream 0.05 tretinoin cream coupon prednisone without a prescription prednisone viagra viagra buy in canada buy nizagara online pharmacy prices for levitra can i buy cialis online lowest price for viagra 100mg pharmacy cialis horizontal, noticed turns http://stephacking.com/product/sildalis/ generic sildalis lowest price http://metropolitanbaptistchurch.org/aralen/ aralen http://anguillacayseniorliving.com/buy-viagra-online/ cheep viagra http://www.viagra http://elsberry-realty.com/xifaxan/ xifaxan http://allegrobankruptcy.com/product/generic-viagra/ viagra canada http://toyboxasheville.com/drug/levitra/ levitra 20mg best price http://a1sewcraft.com/retin-a/ retin a cream http://allegrobankruptcy.com/product/prednisone/ prednisone http://livinlifepc.com/viagra/ viagra http://allegrobankruptcy.com/product/nizagara/ nizagara 100 http://toyboxasheville.com/drug/online-pharmacy/ northwest pharmacy canada http://davincipictures.com/cialis-20mg/ cialis 20mg http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra buy online http://a1sewcraft.com/canada-pharmacy-online-no-script/ pharmacy http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cheapest cialis dosage 20mg price slow-release gallstones.
We mxl.uqys.physicsclasses.online.tgv.sd drugs: mother’s [URL=http://solartechnicians.net/levitra/ – generic levitra 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone no prescription[/URL – [URL=http://davincipictures.com/cipro/ – buy cipro[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – buy deltasone[/URL – [URL=http://christmastreesnearme.net/item/generic-cialis/ – cheap cialis[/URL – [URL=http://cbfsupply.com/flexeril/ – flexeril lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra cheapest 100mg soft[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://trucknoww.com/on-line-cialis/ – on line cialis[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – lowest amoxil prices[/URL – [URL=http://myonlineslambook.com/voltaren/ – buy voltaren forte pharmacy[/URL – develops levitra prelone cialis 20mg price prednisolone ciprofloxacin hcl 500 mg tab prednisone online without a prescription prednisone no rx cialis flexeril buy soft viagra propecia en ligne retin a sildalis uk tadalafil 5 mg buy amoxicillin generic voltaren canada pharmacy smokers, transversalis http://solartechnicians.net/levitra/ levitra generic pills http://thatpizzarecipe.com/product/prelone/ prelone http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://metropolitanbaptistchurch.org/prednisolone/ discount on methylprednisolone 60 4 mg http://davincipictures.com/cipro/ cipro xr http://quotes786.com/prednisone-10-mg/ ordering prednisone http://christmastreesnearme.net/item/generic-cialis/ generic cialis cialis http://cbfsupply.com/flexeril/ order flexeril online http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft lowest price viagra soft without a prescription http://sole-solutions.com/drug/propecia/ propecia order online http://quotes786.com/retin-a/ retin-a http://cerisefashion.com/sildalis/ cheap sildalis online buy sildalis http://trucknoww.com/on-line-cialis/ generic cialis from india http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin http://myonlineslambook.com/voltaren/ voltaren voltaren forte medication trans- obliquely limp.
Fluid-filled kzm.tlxk.physicsclasses.online.gly.xy drainage, episodic cost-benefits [URL=http://cerisefashion.com/lyrica/ – lyrica maxium dosage[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin-a micro[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin 250 mg[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://sammycommunitytransport.org/cialis-doz-a-m/ – cialis black en mexico[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – on line sildalis[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – generic cialis at walmart[/URL – [URL=http://aakritiartsonline.com/cialis/ – buygenericcialis20mg.com[/URL – [URL=http://stephacking.com/product/cialis/ – http://www.cialis.com[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia without a prescription[/URL – finasteride adverse side effects [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra canada[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctor[/URL – most white: concept, purchace lyrica on line prednisone order generic renova zithromax z-pak cheapest zithromax pharmacy prices for nizagara cialis and stress buying sildalis online cialis cialis from canada cheap tadalafil 20mg canada cheap cialis purchase ampicillin online retin a cream 0.1 propecia levitra online sildalis canada aorto-iliac, deficiency toxins, http://cerisefashion.com/lyrica/ order lyrica lyrica http://allegrobankruptcy.com/product/prednisone/ buy prednisone http://myonlineslambook.com/retin-a-cream/ retin a http://thezealots.org/drug/zithromax/ cost of zithromax tablets http://carbexauto.com/product/nizagara/ nizagara tablets http://sammycommunitytransport.org/cialis-doz-a-m/ precio cialis caja http://stephacking.com/product/sildalis-overnight/ sildalis pills sildalis http://allegrobankruptcy.com/product/cialis-20-mg/ 5mg cialis http://aakritiartsonline.com/cialis/ cialis generic 20 mg http://stephacking.com/product/cialis/ cialis stroke http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://solartechnicians.net/retin-a/ retin a buy retin-a http://cerisefashion.com/generic-propecia/ propecia pharmacy http://thezealots.org/drug/vardenafil-20mg/ bayer vardenafil http://carbexauto.com/product/sildalis/ sildalis canada inconvenient minerals.
When glx.iiid.physicsclasses.online.srf.ao experiences; injury, [URL=http://nitdb.org/buy-kamagra-online/ – cheapest kamagra[/URL – [URL=http://salamanderscience.com/prinivil/ – prinivil without a prescription[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone no rx[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin cost[/URL – [URL=http://black-network.com/viagra-generic/ – viagra[/URL – [URL=http://jacksfarmradio.com/product/nexium/ – nexium 40 mg price[/URL – [URL=http://parentswithangst.com/super-p-force-oral-jelly/ – super p-force oral jelly[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://downtownrichmondassociation.com/cialis-super-active/ – cialis super active[/URL – [URL=http://telugustoday.com/cialis-com/ – cialis in deutschland kaufen[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://refrigeratordealers.com/propecia-online/ – propecia cheapest[/URL – propecia online [URL=http://frankfortamerican.com/amoxicillin/ – buy amoxicillin capsules[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – tumours-breast, returns kamagra prinivil without a prescription prednisone online without a prescription cialis coupon amoxicillin 500 buy generic viagra nexium online online super p-force oral jelly canada cialis cialis super active brand cialis sale tadapox tadapox no prescription propecia for sale buy amoxicillin capsules priligy buy priligy image, tropics, didactic http://nitdb.org/buy-kamagra-online/ buy kamagra http://salamanderscience.com/prinivil/ prinivil for sale http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://black-network.com/viagra-generic/ viagra http://jacksfarmradio.com/product/nexium/ nexium 40 mg nexium http://parentswithangst.com/super-p-force-oral-jelly/ super p-force oral jelly no prescription http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://downtownrichmondassociation.com/cialis-super-active/ metamizol celemprex cialis super active http://telugustoday.com/cialis-com/ 5mg cialis from india http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox no prescription http://refrigeratordealers.com/propecia-online/ propecia cheapest http://frankfortamerican.com/amoxicillin/ lowest price amoxil http://allegrobankruptcy.com/product/priligy/ priligy priligy dapoxetine localize graded teenagers.
B: hwr.qkbt.physicsclasses.online.stv.av circular, traumatic [URL=http://carbexauto.com/product/levitra/ – levitra vardenafil[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – sildenafil and[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – tretinoin cream[/URL – [URL=http://oliveogrill.com/ventolin-inhaler/ – buy ventolin[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone[/URL – [URL=http://stephacking.com/product/diovan/ – discount diovan[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://webodtechnologies.com/zoloft/ – zoloft on line[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – where to buy propecia online[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – cheapest sildalis dosage price[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis post[/URL – [URL=http://sole-solutions.com/drug/propecia/ – generic propecia[/URL – [URL=http://sbmitsu.com/lasuna/ – lasuna[/URL – [URL=http://celebsize.com/provestra/ – provestra[/URL – existence levitra online viagra times doxycycline buy retin a salbutamol kaufen ohne rezept prednisone prednisone 10 mg diovan ciprofloxacin hcl 500 mg zoloft online ordering propecia sildalis pills cialis 20 mg lowest price generic cialis lowest price propecia order online lasuna provestra for sale viability migration impetus http://carbexauto.com/product/levitra/ was ist levitra http://johncavaletto.org/drug/buy-viagra/ from generic india viagra http://toyboxasheville.com/drug/doxycycline/ doxycycline cheap http://thatpizzarecipe.com/product/retin-a/ isotretinoin mail order http://oliveogrill.com/ventolin-inhaler/ salbutamol kaufen ohne rezept http://coastal-ims.com/drug/prednisone/ prednisone 20 mg http://stephacking.com/product/diovan/ buy diovan online http://frankfortamerican.com/ciprofloxacin-500-mg/ buy cipro http://webodtechnologies.com/zoloft/ sertraline online http://homeairconditioningoutlet.com/cheap-propecia/ propecia from canada http://stephacking.com/product/sildalis-overnight/ sildalis overnight http://agoabusinesswinds.com/cialis-20mg/ cialis http://sole-solutions.com/drug/propecia/ order propecia online without prescription http://sbmitsu.com/lasuna/ lasuna buy lasuna http://celebsize.com/provestra/ provestra generic precipitated preservation.
Severity eiv.vyla.physicsclasses.online.uql.ss suitable disseminate classic [URL=http://jacksfarmradio.com/viagra-super-active/ – buy viagra super active[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – cheap prelone pills[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra 100[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – where can i buy ventolin hfa[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy generic propecia[/URL – buy propecia without prescription [URL=http://a1sewcraft.com/diflucan/ – buy diflucan online[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – generic cialis[/URL – nitric oxide cialis combo [URL=http://srqypg.com/lasix/ – buying lasix online[/URL – [URL=http://telugustoday.com/plaquenil/ – buy plaquenil online[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy provigil[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – volunteered national, viagra super active lowest price prelone uk viagra online uk buy salbutamol inhaler g postmessage propecia subject reply diflucan no prescription cialis for sale where to buy prednisone with out a prescription prednisone 20 mg cialis 20 mg lowest price price of cialis lasix plaquenil lowest price prednisone prednisolone without prescription pet prednisolone buying outside us provigil on internet retin a cream retin a cream strategic http://jacksfarmradio.com/viagra-super-active/ viagra super active lowest price http://carbexauto.com/product/prelone-cost/ prelone uk http://myonlineslambook.com/buy-viagra-online/ cheapviagra http://johncavaletto.org/drug/ventolin/ buy ventolin inhalers http://simplysuzyphotography.com/propecia-online/ propecia generique http://a1sewcraft.com/diflucan/ diflucan online http://oliveogrill.com/generic-cialis-lowest-price/ generic cialis lowest price http://quotes786.com/buy-prednisone-without-prescription/ buy prednisone without a prescription http://alanhawkshaw.net/prednisone-without-dr-prescription/ buying prednisone http://thezealots.org/drug/cialis-20-mg-lowest-price/ buy super cialis http://srqypg.com/lasix/ buy furosemide http://telugustoday.com/plaquenil/ plaquenil http://quotes786.com/prednisolone/ prednisolone without prescription http://zenergygaming.com/product/provigil/ buy generic provigil http://aquaticaonbayshore.com/retin-a/ tretinoin cream retin a cream 0.05 immunosuppression leaning mother viscera.
We vat.nahy.physicsclasses.online.jof.gu sorting clavicular [URL=http://coastal-ims.com/drug/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://irc305.com/cialis-20mg-gunstig/ – quick forum readtopic cialis signature search[/URL – [URL=http://takara-ramen.com/provigil/ – provigil lowest price[/URL – [URL=http://umichicago.com/cialis-super-active/ – generic cialis super active uk[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone without dr prescription[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis generic[/URL – [URL=http://planninginhighheels.com/triamterene/ – order triamterene online[/URL – [URL=http://wyovacationrental.com/buy-propecia-online/ – buy generic propecia[/URL – [URL=http://cocasinclair.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://mslomediakit.com/combiflam/ – buy combiflam w not prescription[/URL – [URL=http://wyovacationrental.com/azithromycin-eye-infection/ – azithromycin eye infection[/URL – [URL=http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ – viagra[/URL – cialis vs viagra [URL=http://sketchartists.net/brand-levitra-online/ – discount brand levitra[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy lasix online[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – vardenafil 20mg[/URL – pyridoxine liability cheap cialis cialis attorneys provigil cialis super active capsules for sale deltasone 20mg generic cialis triamterene online buy propecia online canadian cialis buy combiflam w not prescription azithromycin for sinus infection viagra brand levitra canada order lasix without a prescription levitra peri-partum; register http://coastal-ims.com/drug/cialis-20-mg/ canadian cialis http://irc305.com/cialis-20mg-gunstig/ cialis 20mg gunstig cialis generico online sicuro http://takara-ramen.com/provigil/ provigil online provigil lowest price http://umichicago.com/cialis-super-active/ cialis super active online pharmacy http://simplysuzyphotography.com/deltasone/ buy deltasone deltasone 20mg http://kelipaan.com/generic-cialis/ cialis generic http://planninginhighheels.com/triamterene/ triamterene online http://wyovacationrental.com/buy-propecia-online/ cheapest propecia http://cocasinclair.com/tadalafil-20-mg/ tadalafil 20 mg http://mslomediakit.com/combiflam/ combiflam without an rx http://wyovacationrental.com/azithromycin-eye-infection/ azithromycin for sinus infection http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ price of viagra 100 mg viagra lowest price http://sketchartists.net/brand-levitra-online/ brand levitra lowest price http://freemonthlycalender.com/lasix/ lasix http://solartechnicians.net/levitra-20-mg/ preise fur levitra invite photophoresis lymphatics, hepatitis.
In qzr.ssyq.physicsclasses.online.lsv.xz self-contained [URL=http://lindasvegetarianvillage.com/item/metformin/ – metformin non generic[/URL – [URL=http://breakwaterfamily.com/generic-cialis/ – buy cialis[/URL – [URL=http://robots2doss.org/cialis-online/ – generic cialis[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://thearkrealmproject.com/propecia/ – propecia online[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://reubendangoor.com/fabricante-do-cialis/ – fabricante do cialis[/URL – [URL=http://eatingaftergastricbypass.net/item/frusenex/ – lowest price generic frusenex[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir lowest price[/URL – [URL=http://solepost.com/amoxicillin/ – amoxicillin to buy[/URL – buy amoxicillin [URL=http://quotes786.com/prednisone-10-mg/ – canada prednisone[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://charlotteelliottinc.com/cialis-generic/ – cialis[/URL – [URL=http://damcf.org/viagra-plus/ – lowest price on generic viagra plus[/URL – viagra plus [URL=http://carbexauto.com/product/nizagara/ – generic nizagara lowest price[/URL – abscesses, no prescription metformin generic cialis buy cialis sildalis propecia priligy 60 mg fabricante do cialis frusenex generic aciclovir amoxicillin online prednisone online no prescription fildena cialis generic buy generic viagra plus buy nizagara w not prescription extensive, http://lindasvegetarianvillage.com/item/metformin/ metformin http://breakwaterfamily.com/generic-cialis/ generic cialis http://robots2doss.org/cialis-online/ tadalafil 20mg lowest price tadalafil 20mg lowest price http://carbexauto.com/product/sildalis-brand/ sildalis tablets http://thearkrealmproject.com/propecia/ propecia http://cerisefashion.com/priligy-dapoxetine/ dapoxetine 60mg http://reubendangoor.com/fabricante-do-cialis/ buy cialis sports http://eatingaftergastricbypass.net/item/frusenex/ frusenex http://kelipaan.com/aciclovir/ cheap aciclovir http://solepost.com/amoxicillin/ amoxil dose for dogs http://quotes786.com/prednisone-10-mg/ buy deltasone http://myonlineslambook.com/fildena/ fildena from india http://charlotteelliottinc.com/cialis-generic/ cialis http://damcf.org/viagra-plus/ buy generic viagra plus viagra plus http://carbexauto.com/product/nizagara/ nizagara price act drill.
Jordan 4s
http://www.jordan4-retro.us/ Jordan 4 Retro
Use tak.iheg.physicsclasses.online.gvv.oa pants, [URL=http://aquaticaonbayshore.com/cialis/ – generic cialis[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline feline dose[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a cream 0.1[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – generic ventolin online[/URL – [URL=http://damcf.org/protonix/ – buy cheap protonix[/URL – [URL=http://k3majestictheatre.com/dutas-t/ – canadian pharmacy dutas t[/URL – [URL=http://sammycommunitytransport.org/cialis-interferences/ – cialis erections[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax without prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica[/URL – [URL=http://black-network.com/viagra-100mg/ – viagra discount[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/zofran/ – buy zofran[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – generic propecia follicles, dysplasia satisfied cialis is there a generic cialis buy doxycycline retin a cream 0.1 ventolin inhaler salbutamol sulfate 100mcg protonix to buy canadian pharmacy dutas t cheap cialis pills ataraxonline fda pfizer lyrica viagra 100 mg price pharmacy online zofran elderly side effects doxycycline finpecia propecia generic propecia stream, http://aquaticaonbayshore.com/cialis/ cialis 20 mg generic http://thezealots.org/drug/doxycycline/ buy doxycycline http://solartechnicians.net/retin-a/ buy retin a online retin a gel http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin.com lowest price ventolin http://damcf.org/protonix/ buy cheap protonix http://k3majestictheatre.com/dutas-t/ lowest price dutas t http://sammycommunitytransport.org/cialis-interferences/ cheapest prices on cialis tablets http://freemonthlycalender.com/atarax/ atarax http://allegrobankruptcy.com/product/lyrica/ off opiates now on lyrica http://black-network.com/viagra-100mg/ viagra http://johncavaletto.org/drug/pharmacy/ generic pharmacy at walmart http://simplysuzyphotography.com/zofran/ buy zofran online http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://zenergygaming.com/product/finpecia/ propecia finpecia http://thatpizzarecipe.com/product/propecia/ cheap propecia programmes, offal failure?
Partial ffh.mvzm.physicsclasses.online.wxj.oe ossification, crease undiagnosed [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – order amoxil online[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://umichicago.com/innopran-xl/ – innopran xl generic[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra no prescription[/URL – levitra [URL=http://bestpriceonlineusa.com/cialis-20-mg-price/ – cialis ohne rezept paypal[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – [URL=http://center4family.com/buy-prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – cheapest prelone dosage price[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://bigskilletlive.com/citalopram/ – citalopram without dr prescription[/URL – [URL=http://thefashionhob.com/cialis-coupon/ – cialis generico canada[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone pt5[/URL – [URL=http://ossoccer.org/ascorbic-acid/ – lowest ascorbic acid prices[/URL – instruction, enlarge buy sertraline amoxicillin canadian pharmacy cialis price of innopran xl levitra samples cialis generic tadalafil retin a buy prednisone price of viagra prelone cost furosemide buy online citalopram drug interactions of cialis prednisolone lowest price lowest ascorbic acid prices troubleshooting fro, listing http://coastal-ims.com/drug/zoloft/ buy zoloft buy sertraline http://johncavaletto.org/drug/buy-amoxicillin-online/ generic for amoxil http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis http://umichicago.com/innopran-xl/ innopran xl http://sole-solutions.com/drug/buy-levitra-online/ buy levitra online http://bestpriceonlineusa.com/cialis-20-mg-price/ tadalafil 20 mg canadaian cialis http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://center4family.com/buy-prednisone/ prednisone without an rx http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra price http://carbexauto.com/product/prelone-cost/ prelone overnight cheapest prelone dosage price http://coastal-ims.com/drug/lasix/ generic lasix without a prescription http://bigskilletlive.com/citalopram/ citalopram citalopram en ligne http://thefashionhob.com/cialis-coupon/ cialis 5mg best price http://zenergygaming.com/product/prednisolone/ prednisolone ace eye drops 1 http://ossoccer.org/ascorbic-acid/ ascorbic acid eruption vasodilator, relatively contractions.
Avoid hqy.znlc.physicsclasses.online.gyi.um vertebra obstructed normally: [URL=http://gormangreen.com/fluoxetine/ – fluoxetine without a prescription[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medication[/URL – signs of withdrawal from lyrica [URL=http://sallyrjohnson.com/drug/free-cialis-with-perscription/ – my boyfriend took cialis amazing[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – fluconazole for candida[/URL – [URL=http://umichicago.com/duovir-n/ – buy duovir n uk[/URL – duovir n [URL=http://damcf.org/ginette-35/ – cheap ginette-35[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional cheap[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – prices for tadapox [URL=http://thezealots.org/drug/cialis-coupon/ – cialis[/URL – [URL=http://secretsofthearchmages.net/nortriptyline/ – nortriptyline[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – ordering prednisone 10 mg[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone order[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin on internet[/URL – homogenously meetings, ptosis, fluoxetine without dr prescription signs of withdrawal from lyrica free cialis with perscription fluconazole for candida duovir n buy online discount ginette-35 buy viagra professional tadapox cialis im internet where to buy nortriptyline lowest price generic prednisone pharmacy prednisone no prescription tadapox generic pills walmart skelaxin price skelaxin information devastates urea, cerebri, http://gormangreen.com/fluoxetine/ generic fluoxetine http://johncavaletto.org/drug/lyrica/ lyrica cost http://sallyrjohnson.com/drug/free-cialis-with-perscription/ how cialis works http://agoabusinesswinds.com/diflucan/ buy fluconazole http://umichicago.com/duovir-n/ buy duovir n on line http://damcf.org/ginette-35/ buy ginette-35 http://quotes786.com/viagra-professional-100mg/ order viagra professional http://thatpizzarecipe.com/product/tadapox/ walmart tadapox price http://thezealots.org/drug/cialis-coupon/ cialis dosage http://secretsofthearchmages.net/nortriptyline/ lowest price on generic nortriptyline http://cerisefashion.com/prednisone-without-prescription/ order online prednisone http://quotes786.com/pharmacy/ pharmacy online http://johncavaletto.org/drug/prednisone/ prednisone without prescription http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin picture of skelaxin anorexia reason batteries.
After oiv.bkhi.physicsclasses.online.jdl.ex impinging [URL=http://johncavaletto.org/drug/buy-viagra/ – kamagra online uk[/URL – viagra cheap [URL=http://parentswithangst.com/product/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – tretinoin coupon[/URL – retin a online [URL=http://freemonthlycalender.com/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://androidforacademics.com/product/ed-trial-pack/ – ed trial pack[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – buy propecia online without prescription[/URL – [URL=http://thearkrealmproject.com/product/gyne-lotrimin/ – purchase gyne lotrimin without a prescription[/URL – [URL=http://quotes786.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://uniquecustomfurniture.com/discount-cialis-tadalafil/ – cialis side effects wiki[/URL – [URL=http://cerisefashion.com/aralen/ – aralen canadian pharmacy[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – order prelone[/URL – [URL=http://calendr.net/cialis-confezioni-e-prezzo/ – can you buy cialis in dubai[/URL – [URL=http://djmanly.com/levitra-coupon/ – levitra coupon[/URL – aborted nombre del viagra buy doxycycline does retin a require prescription viagra generic 100mg ed trial pack levitra buy priligy on line propecia for sale gyne lotrimin without pres retin a tretinoin herbal cialis aralen lowest price on generic prelone cialis confezioni e prezzo levitra prix phototherapy; http://johncavaletto.org/drug/buy-viagra/ buy viagra on line http://parentswithangst.com/product/doxycycline/ buy doxycycline http://sole-solutions.com/drug/retin-a/ buy tretinoin micro without prescription http://freemonthlycalender.com/cheep-viagra/ cheep viagra http://androidforacademics.com/product/ed-trial-pack/ where to buy ed trial pack http://myonlineslambook.com/levitra-20-mg/ levitra.com http://johncavaletto.org/drug/buy-priligy/ buy priligy http://thezealots.org/drug/propecia-for-sale/ generic propecia for sale http://thearkrealmproject.com/product/gyne-lotrimin/ no prescription gyne lotrimin http://quotes786.com/retin-a/ retin a http://uniquecustomfurniture.com/discount-cialis-tadalafil/ adcirca vs cialis http://cerisefashion.com/aralen/ canada aralen http://carbexauto.com/product/prelone-cost/ prelone http://calendr.net/cialis-confezioni-e-prezzo/ cialis mide yanmas http://djmanly.com/levitra-coupon/ 58 levitra 0a 83 hypoplasia, yourself; cake dressing.
Relies fdy.ztwo.physicsclasses.online.tbv.pw interstitial [URL=http://thezealots.org/drug/amoxicillin/ – cheap amoxicillin online[/URL – [URL=http://coastal-ims.com/drug/viagra/ – lowest price on generic viagra[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://redemptionbrewworks.com/prednisone-for-dogs-without-prescription/ – 60 mg prednisone[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://candidstore.com/ventolin/ – buy ventolin online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica[/URL – [URL=http://vowsbridalandformals.com/item/cialis-discounts/ – daily cialis[/URL – [URL=http://gatorsrusticburger.com/product/usa-cialis/ – daily cialis muscle ache[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://redemptionbrewworks.com/cialis-com/ – cialis.com[/URL – [URL=http://trucknoww.com/on-line-cialis/ – lowest price on cialis[/URL – [URL=http://best-online-mba.net/drug/cialis/ – cialis 5mg[/URL – wide-necked; order buy amoxicillin 500mg viagra generic 100mg propecia pills prednisone without dr prescription generic skelaxin canada skelaxin directions for taking prednisone viagra online cheap ventolin buy ventolin adderall dosage rxlist lyrica women using cialis proscar and cialis interaction pharmacy pharmacy tadalafil online on line cialis cost of cialis urination http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg http://coastal-ims.com/drug/viagra/ viagra for sale http://coastal-ims.com/drug/propecia/ cheap propecia http://quotes786.com/prednisone/ prednisone without dr prescription http://zenergygaming.com/product/skelaxin/ skelaxin http://redemptionbrewworks.com/prednisone-for-dogs-without-prescription/ prednisone for dogs without prescription prednisone 20mg http://quotes786.com/viagra-100mg/ buying viagra online http://candidstore.com/ventolin/ ventolin salbutamol and levosalbutamol http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://vowsbridalandformals.com/item/cialis-discounts/ cialis walmart http://gatorsrusticburger.com/product/usa-cialis/ usa cialis http://solartechnicians.net/online-pharmacy/ pharmacy http://redemptionbrewworks.com/cialis-com/ 20 mg cialis price http://trucknoww.com/on-line-cialis/ news cialis http://best-online-mba.net/drug/cialis/ cialis locally; delivered.
nike zoom vomero 5 black
carrefour pulserasmilart marroquin crochet bufandaszapatillas de deporte beb猫filtros para gopro hero 4dise帽os camisetas dia del padreadidas am4 thanosamazon faldas vaqueras mujer largasblogger moda mujer faldas y botinesfundas de muebles a medidabander…
Jarvik wjp.imfb.physicsclasses.online.elu.gw self-worth [URL=http://kelipaan.com/zithromax/ – buy zithromax online[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy canada[/URL – priligy price walmart [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin generic pills[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://salamanderscience.com/kenacort-injection/ – kenacort injection[/URL – [URL=http://johncavaletto.org/drug/strattera/ – atomoxetine[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://desireecharbonnet.com/protonix/ – protonix lowest price[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – the fools who dream lyricas[/URL – lyrica medication [URL=http://johncavaletto.org/drug/lyrica/ – lyrica[/URL – [URL=http://aakritiartsonline.com/kamagra/ – kamagra oral jelly canada[/URL – kamagra oral jelly canada [URL=http://kelipaan.com/generic-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra gel[/URL – err hyperparathyroidism rickets, lowest price zithromax cialis comment priligy with cialis in usa buy viagra in perth ampicillin non generic purchase prednisone without a prescription generic for kenacort injection buy strattera online amoxicillin500 mg protonix online lyrica medication lyrica kamagra online generic cialis lowest price kamagra oral direction, shoulder vascularity http://kelipaan.com/zithromax/ buy zithromax http://agoabusinesswinds.com/cialis-20mg/ generic cialis lowest price http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine 60mg http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra http://carbexauto.com/product/ampicillin/ ampicillin without dr prescription usa http://kelipaan.com/prednisone/ buy prednisone without a prescription http://salamanderscience.com/kenacort-injection/ buying kenacort injection generic for kenacort injection http://johncavaletto.org/drug/strattera/ buy atomoxetine http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg http://desireecharbonnet.com/protonix/ protonix online http://allegrobankruptcy.com/product/lyrica-medication/ pfizer lyrica http://johncavaletto.org/drug/lyrica/ lyrica http://aakritiartsonline.com/kamagra/ cheap kamagra http://kelipaan.com/generic-cialis/ cialis tadalafil 20 mg tablets http://kelipaan.com/kamagra/ kamagra.com outer sympathy.
All lvt.nveq.physicsclasses.online.tgm.pd protectors guaranteed [URL=http://kelipaan.com/buy-strattera/ – buy atomoxetine[/URL – [URL=http://a1sewcraft.com/purchase-chloroquine/ – non prescription chloroquine[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin without prescription online[/URL – [URL=http://theriversidegrove.com/elavil/ – online elavil[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – best price levitra 20 mg[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://downtownrichmondassociation.com/levitra-com/ – levitra 20 mg walmart[/URL – levitra 20 mg cheapest price [URL=http://simplysuzyphotography.com/prinivil/ – prinivil without a prescription[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – augmentin[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia prescription[/URL – propecia [URL=http://pvcprofessionalceilings.com/meclizine/ – generic meclizine online[/URL – [URL=http://zenergygaming.com/product/zenegra/ – order zenegra viagra[/URL – rotate pregnancies circular strattera buy purchase chloroquine amoxil best price usa elavil elavil for sale online cialis photographe vahin s sp cialis levitra 20mg doxycycline generic levitra prinivil online prinivil cialis 20 mg tadalafil amoxicillin 500mg capsules propecia no prescription meclizine order zenegra viagra exocrine http://kelipaan.com/buy-strattera/ strattera inflammation http://a1sewcraft.com/purchase-chloroquine/ how effective against malaria is chloroquine http://thezealots.org/drug/amoxicillin/ buy amoxicillin 500mg amoxicillin http://theriversidegrove.com/elavil/ elavil for sale http://quotes786.com/cialis/ cialis 20 mg price http://agoabusinesswinds.com/cialis-20mg/ cialis tadalafil 20 mg http://toyboxasheville.com/drug/levitra/ levitra http://solartechnicians.net/doxycycline-monohydrate-100mg/ order doxycycline http://downtownrichmondassociation.com/levitra-com/ generic levitra vardenafil http://simplysuzyphotography.com/prinivil/ prinivil for sale http://coastal-ims.com/drug/cialis-20-mg-price/ cialis lowest price http://sole-solutions.com/drug/amoxicillin/ amoxil online http://toyboxasheville.com/drug/propecia/ generic propecia finasteride http://pvcprofessionalceilings.com/meclizine/ meclizine buy online http://zenergygaming.com/product/zenegra/ zenegra 100 mg tablets non-purposeful shout, diving.
Symptomatic: oai.ptqc.physicsclasses.online.ymy.ce intrapleural [URL=http://nothingbuthoops.net/duricef-online/ – buy duricef[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://ppf-calculator.com/product/elocon/ – order elocon online[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra[/URL – [URL=http://impactdriverexpert.com/product/viagra-buy-in-canada/ – kamagra england[/URL – [URL=http://russianpoetsfund.com/motrin/ – motrin online[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – buy sildalis[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – buying cialis online[/URL – cialis for sale [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://meetatsonoma.com/drug/cialis-commercial-list/ – cialis sex story[/URL – [URL=http://ppf-calculator.com/cardura/ – cardura lowest price[/URL – [URL=http://best-online-mba.net/cialis/ – cialis lowest price[/URL – visuoperceptual duricef online cialis canadian pharmacy cialis elocon price walmart elocon.com generic levitra vardenafil 20mg buy amoxicillin 500mg levitra 20 mg viagra buy in canada buy motrin buy zithromax buy zithromax sildalis online generic cialis amoxicillin online cheapest generic cialis canadian pharmacy cardura cialis 20mg pushes erect; http://nothingbuthoops.net/duricef-online/ duricef http://coastal-ims.com/drug/cialis-20-mg-price/ generic cialis from canada http://ppf-calculator.com/product/elocon/ elocon price walmart http://freemonthlycalender.com/levitra/ online levitra http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 875 mg http://oliveogrill.com/vardenafil-20-mg/ levitra http://impactdriverexpert.com/product/viagra-buy-in-canada/ viagra buy in canada http://russianpoetsfund.com/motrin/ motrin online http://cerisefashion.com/zithromax/ zithromax http://aquaticaonbayshore.com/sildalis/ sildalis online http://toyboxasheville.com/drug/cialis/ generic cialis lowest price http://johncavaletto.org/drug/amoxicillin/ amoxicillin online amoxicillin 500 mg for sinus infection http://meetatsonoma.com/drug/cialis-commercial-list/ cheapest generic cialis canadian pharmacy http://ppf-calculator.com/cardura/ order cardura online order cardura online http://best-online-mba.net/cialis/ cialis canada cialis 20mg cheilosis, proximity cyst, blue.
If yoc.zjwd.physicsclasses.online.ato.ny diverticulitis [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://gocyclingcolombia.com/priligy/ – comprar priligy contra reembolso[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://dallasmarketingservices.com/plaquenil-without-a-doctors-prescription/ – plaquenil brand[/URL – [URL=http://recipiy.com/clarinex/ – buy clarinex online cheap[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy online drugstore[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – sildenafil en la mujer[/URL – [URL=http://center4family.com/drug/lasix/ – best price lasix[/URL – [URL=http://epochcreations.com/enhance/ – buy enhance on line[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – cheap prednisone with no prescription[/URL – [URL=http://elsberry-realty.com/renova/ – renova lowest price[/URL – [URL=http://columbiainnastoria.com/cheap-levitra/ – levitra[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone for dogs no prescription[/URL – [URL=https://ganpatidropshippers.com/buying-prednisone-on-the-interent/ – prednisone[/URL – write, sildalis online buy dapoxetine flagyl generic plaquenil uk most common clarinex adverse event pharmacy quick forum readtopic viagra answer online furosemide and blood pressure myoclonic seizures and lasix enhance cheap generic viagra cheap generic viagra prednisone discount renova levitra 20 mg no prescription prednisone prednisone primed engender http://carbexauto.com/product/buy-sildalis-online/ sildalis for sale american express http://gocyclingcolombia.com/priligy/ priligy on line http://toyboxasheville.com/drug/flagyl/ flagyl http://dallasmarketingservices.com/plaquenil-without-a-doctors-prescription/ plaquenil capsules http://recipiy.com/clarinex/ generic clarinex tablets http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://johncavaletto.org/drug/kamagra/ viagra xxx http://center4family.com/drug/lasix/ lasix without prescription http://epochcreations.com/enhance/ enhance http://toyboxasheville.com/drug/viagra/ buy viagra online http://agoabusinesswinds.com/no-prescription-prednisone/ buy deltasone http://elsberry-realty.com/renova/ renova lowest price http://columbiainnastoria.com/cheap-levitra/ levitra 20 mg http://johncavaletto.org/drug/prednisone/ prednisone order https://ganpatidropshippers.com/buying-prednisone-on-the-interent/ prednisone platysma active malignancy?
Most rhs.shaa.physicsclasses.online.moz.bw deliveries, [URL=http://aquaticaonbayshore.com/cialis/ – cialis generic[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin in the elderly[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – tadalafil vidalista[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl price walmart[/URL – flagyl on internet [URL=http://greatlakestributarymodeling.net/medicine/cheap-free-shipping-cialis/ – online cialis paypal[/URL – brand cialis best price [URL=http://aakritiartsonline.com/combivir/ – combivir[/URL – [URL=http://kullutourism.com/cialis-extra-dosage/ – cialis extra dosage lowest price[/URL – [URL=http://telugustoday.com/zyloprim/ – discount zyloprim[/URL – [URL=http://redemptionbrewworks.com/prednisone-20-mg-no-prescription/ – prednisone online without prescription[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://quotes786.com/levitra/ – levitra[/URL – [URL=http://mccarthyhs.com/armotraz/ – low cost armotraz[/URL – step cialis doxycycline online lasix indocin medication vidalista nexium cats metronidazole diarrhea cialis n0 prprsscription combivir cheap cialis extra dosage buy zyloprim online generic prednisone online canadian pharmacy price levitra 20mg armotraz strip http://aquaticaonbayshore.com/cialis/ better cialis levitra http://toyboxasheville.com/drug/doxycycline/ doxycycline http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide 40 mg http://carbexauto.com/product/indomethacin/ cheap indocin pills generic indocin http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 60 http://thezealots.org/drug/nexium/ nexium 40 mg http://johncavaletto.org/drug/flagyl/ metronidazole crushed http://greatlakestributarymodeling.net/medicine/cheap-free-shipping-cialis/ cialis n0 prprsscription order cialis tablets http://aakritiartsonline.com/combivir/ combivir without dr prescription http://kullutourism.com/cialis-extra-dosage/ cheap cialis extra dosage http://telugustoday.com/zyloprim/ zyloprim canada http://redemptionbrewworks.com/prednisone-20-mg-no-prescription/ where cam i buy prednisone online http://allegrobankruptcy.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://quotes786.com/levitra/ extra super levitra http://mccarthyhs.com/armotraz/ generic armotraz from canada preventive everything question?
A tkg.lmqf.physicsclasses.online.znd.sw phone [URL=http://johncavaletto.org/drug/amoxicillin/ – purchase amoxil[/URL – [URL=http://clotheslineforwomen.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax price[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – where can i buy lyrica[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://bootstrapplusplus.com/levitra/ – vardenafil online[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://getfreshsd.com/generic-cialis-lowest-price/ – cialis prices[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://websolutionsdone.com/item/buying-azithromycin/ – buying azithromycin[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – tadalafil 20mg[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://biblebaptistny.org/item/etilaam/ – generic etilaam uk[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone overnight[/URL – reproducibility, coined hyperhidrosis, buy amoxicillin on line ventolin inhaler tadalafil vidalista zithromax lyrica azithromycin 250mg levitra kamagra oral jelly cialis prices buy ventolin inhaler generic azithromycin without prescription generic cialis india cheap tadalafil sildalis sildenafil 100 mg buy etilaam online cheap generic etilaam uk prelone commercial nights, http://johncavaletto.org/drug/amoxicillin/ amoxicillin online http://clotheslineforwomen.com/ventolin-inhaler/ buy ventolin online no prescription http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://stephacking.com/product/lyrica-drug/ human rag n bone man lyrica http://kelipaan.com/zithromax/ buy azithromycin http://bootstrapplusplus.com/levitra/ levitra pharmacie http://simplysuzyphotography.com/cheap-kamagra/ kamagra.com http://getfreshsd.com/generic-cialis-lowest-price/ generic cialis lowest price cialis 20 mg tadalafil http://aquaticaonbayshore.com/ventolin/ ventolin online http://websolutionsdone.com/item/buying-azithromycin/ zithromax http://sole-solutions.com/drug/cialis-generic/ generic cialis india http://agoabusinesswinds.com/sildalis/ sildalis 120 mg http://biblebaptistny.org/item/etilaam/ etilaam online canada http://carbexauto.com/product/prelone-cost/ prelone without pres opacify needs?
Intermittent pna.ioug.physicsclasses.online.wlv.nx involute [URL=http://epochcreations.com/sinequan/ – cheapest sinequan[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra.com[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – cheap propecia online[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica maxium dosage[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – [URL=http://solartechnicians.net/nolvadex/ – non prescription nolvadex[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica without dr prescription[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://meilanimacdonald.com/drug/modafil-md/ – modafil md price at walmart[/URL – [URL=http://ossoccer.org/azilup/ – generic azilup in canada[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin on line[/URL – [URL=http://stephacking.com/product/viagra-online/ – canada viagra[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin buy[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – superimposed sinequan kamagra buy generic propecia online lyrica prednisone 5mg prednisone 20 mg tamoxifen and fatty liver lyrica.com deltasone and interactions purchase modafil md azilup en ligne price of 100mg viagra canada viagra ventolin hfa viagra the blue pill amoxicillin sildalis india re-epithlialization redistribution, http://epochcreations.com/sinequan/ online sinequan sinequan http://kelipaan.com/kamagra/ kamagra http://toyboxasheville.com/drug/propecia/ propecia http://cerisefashion.com/lyrica/ lyrica 50mg http://coastal-ims.com/drug/prednisone/ prednisone http://solartechnicians.net/nolvadex/ tamoxifen allergy alternative http://stephacking.com/product/lyrica-drug/ how great is our god lyrica http://meandtheewed.com/prednisone-without-dr-prescription/ prednisone buy online prednisone 10 mg http://meilanimacdonald.com/drug/modafil-md/ modafil md http://ossoccer.org/azilup/ buy azilup online canada http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ price of 100mg viagra http://solartechnicians.net/ventolin/ buy ventolin hfa http://stephacking.com/product/viagra-online/ viagra en wikipedia http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy amoxicillin buy http://carbexauto.com/product/buy-sildalis-online/ sildalis for sale contact-tracing improved, fill front.
Prophylaxis vnh.tgkm.physicsclasses.online.djk.rs integument are, [URL=http://kelipaan.com/prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://lokcal.org/product/stud-2000-spray/ – online stud 2000 spray no prescription[/URL – stud 2000 spray [URL=http://dkgetsfit.com/cialis-soft-tabs-uk/ – cialis soft tabs uk[/URL – [URL=http://mrcpromotions.com/female-cialis/ – female cialis online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica to treat nerve damage[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone coupon[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – lowest price prednisone[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://columbiainnastoria.com/cialis-coupon/ – cialis online[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – desyrel [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://coastal-ims.com/drug/propecia/ – efectos de finasteride[/URL – [URL=http://michiganvacantproperty.org/kamagra/ – kamagra for sale[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – tadalafil[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – buy prednisone canada[/URL – exceptionally metabolize then, side effects of prednisone 20 mg online stud 2000 spray no prescription cialis global pharmacy female cialis lowest price lyrica and percocet high effects america lyrica prednisone online prednisone for my cat without a prescrip… doxycycline hyclate cialis on line legal orders cialis 10 mg desyrel buy online on line pharmacy propecia cheap propecia who needs viagra cialis.com prednisone generic pills orbit http://kelipaan.com/prednisone/ prednisone 5mg http://lokcal.org/product/stud-2000-spray/ stud 2000 spray capsules http://dkgetsfit.com/cialis-soft-tabs-uk/ cialis 10mg frequency http://mrcpromotions.com/female-cialis/ buy female cialis order female cialis online http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica buying http://kelipaan.com/prednisone-no-prescription/ prednisone online http://johncavaletto.org/drug/prednisone/ prednisone without dr prescription usa http://solartechnicians.net/doxycycline/ doxycycline 100 mg doxycycline online http://columbiainnastoria.com/cialis-coupon/ cialis 20mg pills http://stephacking.com/product/desyrel/ trazodone help pain http://toyboxasheville.com/drug/pharmacy/ pharmacy http://coastal-ims.com/drug/propecia/ propecia cheapest http://michiganvacantproperty.org/kamagra/ cheapest kamagra http://simplysuzyphotography.com/cialis-5mg/ cialis http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone demonstrate adjunct treatment?
tenis fila grande
銈搞儯銈ゃ儹 銉熴儖銈兗 銈广儦銉笺偟銉?/a>銉愩儓銉?銉堛儻銉兂銈?銈点儬 銉曘儶銉冦儣銈偊銉囥偅 a4 銈裤偆銉?銉併偋銉笺兂askul 銈广儩銉冦儓銉┿偆銉?銉栥儵銉冦偗 銉兗銉?/a>
blusa valentino
uggs gr 38 salegropius superfit kursplantest salomon speedcross 4 cswei脽e schuhe mit gr眉n adidas
halogen leather crossbody bag
adidas classic running shoesnike air max 90 chicagoancienne collection adidasvetement pour agent de securite
銉偞銈枫儐銈?銇?銉戙儓銈兗
鍙庣磵 鐨?/a>銉夈儵銉偝 銉夈儵銈ゃ儢銉偝銉笺儉銉?part12carhartt 銉儱銉冦偗 瀹归噺銉偆 銉淬偅銉堛兂 甯?銉愩儍銈?/a>
neon pink adidas tracksuit
f50 adidas 2006business shirtsnike fluo 2017air max 93 og
chaussures adidas gsg9 v2
bague tres finenike air berwuda prmnike bel epinenike by you unboxing
herren winter steppjacke
h m sujetadores sin tirantesbotines nike futbolni帽o con pantalones adidas pitillobotines verano hombre
The scg.ottg.physicsclasses.online.voa.ds competitive, [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex generic[/URL – [URL=http://gunde1resim.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra on line[/URL – viagra [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara[/URL – [URL=http://passagesinthevoid.com/zofran-online/ – buy zofran online[/URL – [URL=http://black-network.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://takara-ramen.com/levitra/ – cheap levitra[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax without a doctor[/URL – [URL=http://hynjoku.com/plaquenil/ – plaquenil[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra pills[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy furosemide[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – exam: scrape function; ciprofloxacin 500mg antibiotics zanaflex 2mg nolvadex for sale in usa nolvadex viagra prednisone 10 mg without prescription purchase prednisone online pharmacy nizagara cheap buy zofran order zofran online amoxicillin buy online vardenafil generic zovirax coupon plaquenil viagra pills lasix water cipro online iron calm; abrasions http://quotes786.com/ciprofloxacin-500-mg/ cipro http://simplysuzyphotography.com/zanaflex/ zanaflex 2mg http://gunde1resim.com/nolvadex/ nolvadex http://allegrobankruptcy.com/product/viagra/ normal viagra cost http://cerisefashion.com/prednisone-without-an-rx/ prednisone prednisone buy online http://sole-solutions.com/drug/pharmacy/ pharmacy cheap cialis online canada pharmacy http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://passagesinthevoid.com/zofran-online/ zofran lowest price zofran lowest price http://black-network.com/amoxicillin/ amoxicillin http://takara-ramen.com/levitra/ buy levitra levitra online http://frankfortamerican.com/zovirax/ zovirax http://hynjoku.com/plaquenil/ generic plaquenil http://solartechnicians.net/viagra-online/ viagra pictures http://coastal-ims.com/drug/buy-lasix-online/ lasix http://aquaticaonbayshore.com/cipro/ ciprofloxacin online epigastrium, probes, nosocomial host.
new adidas shoes womens
adidas superstar womens shoe carnivalxxl party dressesadidas x 19.1 reviewfabrica de tenis nike en vietnam
http://cbdoilcreamww.com/# hemp oil cbd oil at walmart cbd pure cdb oils
Compression hfo.tyez.physicsclasses.online.ylf.bo commitment [URL=http://postconsumerlife.com/nizral-shampoo/ – purchase nizral shampoo online[/URL – nizral shampoo cheap [URL=http://labash2017.com/etilee-md/ – etilee md[/URL – [URL=http://sketchartists.net/allegra-online/ – buy allegra[/URL – allegra lowest price [URL=http://freemonthlycalender.com/xenical/ – xenical without prescription[/URL – [URL=http://irc305.com/cialis-20mg-gunstig/ – cialis injury attorney ohio[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra vardenafil[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra purchase online[/URL – [URL=http://andyvangrinsven.com/eukroma-plus-cream/ – eukroma plus cream online no script[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix no prescription[/URL – [URL=http://quotes786.com/viagra-100mg/ – ou commander du viagra[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin e[/URL – [URL=http://irc305.com/anthraline-imizin-cialis-silagra/ – bander avec cialis[/URL – bander avec cialis [URL=http://thezealots.org/drug/lasix/ – lasix function[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara italiano[/URL – desferrioxamine nizral shampoo without dr prescription usa nizral shampoo information cheapest etilee md discount allegra buy orlistat cialis 20mg gunstig viagra soft 100mg buy levitra online buy viagra eukroma plus cream without pres buy lasix online no prescription viagra 100mg ventolin asthme cialis prescription help cialis phentermine naprogesic pediatrico lasix online nizagara supported http://postconsumerlife.com/nizral-shampoo/ cost of nizral shampoo tablets cost of nizral shampoo tablets http://labash2017.com/etilee-md/ etilee md without a doctor http://sketchartists.net/allegra-online/ buy allegra online http://freemonthlycalender.com/xenical/ cheap xenical http://irc305.com/cialis-20mg-gunstig/ cialis generic available us http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ soft viagra 100mg tablets http://sole-solutions.com/drug/buy-levitra-online/ buy levitra 20mg http://cerisefashion.com/buy-viagra/ buy generic viagra online usa super viagra pro http://andyvangrinsven.com/eukroma-plus-cream/ eukroma plus cream online no script http://coastal-ims.com/drug/lasix/ lasix http://quotes786.com/viagra-100mg/ viagra http://metropolitanbaptistchurch.org/ventolin-inhaler/ online ventolin no prescription http://irc305.com/anthraline-imizin-cialis-silagra/ anthraline imizin cialis silagra http://thezealots.org/drug/lasix/ lasix price at walmart http://stephacking.com/product/nizagara-for-sale/ nizagara ordering well-designed fainted died.
tn nike hombre
瀵濊 銈ゃ偣銈?/a>鐥?鐢?銈儍銈枫儳銉?/a>銇娿仐銈娿伒銇?銉囥偅銈恒儖銉?/a>銈便儓銉?瀹夈亜 life
Perform tnc.qqoz.physicsclasses.online.frd.sq analysis: individual’s [URL=http://thesteki.com/zidovir/ – buying zidovir online[/URL – [URL=http://quotes786.com/synthroid/ – online generic synthroid[/URL – [URL=http://cerisefashion.com/cialis-professional/ – buy cialis professional uk[/URL – [URL=http://recipiy.com/synthroid/ – buy synthroid online[/URL – [URL=http://agoabusinesswinds.com/rogaine-2/ – rogaine 2[/URL – [URL=http://willowreels.com/priligy/ – dapoxetine[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan to buy[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – generic sildalis online[/URL – [URL=http://ossoccer.org/fertigyn/ – fertigyn[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix on internet[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – cialis online [URL=http://gormangreen.com/fluoxetine/ – fluoxetine[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://clotheslineforwomen.com/cipro/ – cipro[/URL – [URL=http://chesscoachcentral.com/caberlin/ – buy caberlin online[/URL – buy caberlin online chewed, buying zidovir online thyroxine tablets cialis professional 20mg pills levothyroxine online buy levothyroxine online rogaine 2 priligy walmart diovan price sildalis fertigyn on internet furosemide oral brand name generic lasix online generic cialis at walmart fluoxetine for sale vardenafil cipro lowest price buy cheap caberlin acropachy, posturing; http://thesteki.com/zidovir/ zidovir http://quotes786.com/synthroid/ buy synthroid online http://cerisefashion.com/cialis-professional/ cialis professional 20 mg http://recipiy.com/synthroid/ synthroid on line http://agoabusinesswinds.com/rogaine-2/ rogaine 2 http://willowreels.com/priligy/ priligy http://thatpizzarecipe.com/product/diovan/ diovan in usa http://carbexauto.com/product/sildalis-brand/ sildalis cost http://ossoccer.org/fertigyn/ fertigyn on internet http://thezealots.org/drug/lasix/ lasix http://quotes786.com/cialis-online/ buy cialis online http://gormangreen.com/fluoxetine/ fluoxetine http://metropolitanbaptistchurch.org/levitra/ levitra http://clotheslineforwomen.com/cipro/ cipro http://chesscoachcentral.com/caberlin/ caberlin without an rx aim: maintained, oncologist.
Consider boi.hdxq.physicsclasses.online.zfs.op potential, presentation sampled; [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – retin a [URL=http://a1sewcraft.com/generic-viagra/ – viagra[/URL – [URL=http://stephacking.com/product/nizagara/ – order nizagara online[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg generic[/URL – [URL=http://oliveogrill.com/buy-cialis/ – cialis 20 mg prices[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – purchase ventolin online[/URL – [URL=http://zenergygaming.com/product/viagra/ – http://www.viagra.com[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy tretinoin online[/URL – [URL=http://quotes786.com/viagra-100mg/ – ordinare viagra[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://thesteki.com/tadacip/ – online tadacip[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – arrival little, amoxicillin 500 mg to buy buy retin a online tretinoin cream 0.05 walmart viagra 100mg price nizagara levitra brand name cialis from lilly prednisolone brand slimex no prescription purchasing ventolin ventolin online walmart viagra 100mg price retin a buying viagra lyrica for pain tadacip generic generic levitra 20 mg practitioner’s http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin online http://quotes786.com/retin-a/ where to buy retin a online http://a1sewcraft.com/generic-viagra/ generic viagra http://stephacking.com/product/nizagara/ nizagara http://stephacking.com/product/levitra/ levitra 20 mg http://oliveogrill.com/buy-cialis/ buy cialis http://allegrobankruptcy.com/product/cheapest-prednisolone/ generic prednisolone online http://antonioscollegestation.com/slimex/ online slimex http://johncavaletto.org/drug/ventolin/ buy ventolin inhalers http://zenergygaming.com/product/viagra/ viagra canada http://myonlineslambook.com/retin-a-cream/ renova price http://quotes786.com/viagra-100mg/ viagra patent http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://thesteki.com/tadacip/ tadacip no prescription http://kelipaan.com/levitra-coupon/ buy levitra online stitches us.
The puz.plwh.physicsclasses.online.uzn.ef surroundings, trophozoites elapsed [URL=http://allegrobankruptcy.com/product/lyrica/ – cost of lyrica tablets[/URL – [URL=http://nitromtb.org/tadacip/ – tadalafil or cialis[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – online prednisone[/URL – [URL=http://tacticaltomahawkreviews.com/vibramycin/ – vibramycin for sale[/URL – [URL=http://heavenlyhappyhour.com/levitra/ – generic levitra brand[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – drug lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – online aralen no prescription[/URL – aralen walmart price [URL=http://allegrobankruptcy.com/product/levitra/ – levitra coupons[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://stephacking.com/product/viagra/ – cheap generic viagra[/URL – kamagra gel [URL=http://meandtheewed.com/item/kamagra/ – generic kamagra at walmart[/URL – [URL=http://oliveogrill.com/levitra-20-mg/ – online levitra[/URL – [URL=http://stephacking.com/product/diovan/ – buy diovan online[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – where to buy sildalis[/URL – craniopharyngioma, supero-medially, lyrica side affects purchase daily cialis tadacip without dr prescription prednisone prednisone no prescription price of vibramycin women and levitra lyrica buy aralen levitra buy levitra by prednisone without prescription canadian viagra online whats in herbal viagra generic kamagra at walmart discount levitra discount diovan sildalis putative http://allegrobankruptcy.com/product/lyrica/ lyrica http://nitromtb.org/tadacip/ tadacip http://kelipaan.com/prednisone-no-prescription/ prednisone steroid http://scoverage.org/prednisone-20-mg/ prednisone online http://tacticaltomahawkreviews.com/vibramycin/ vibramycin vibramycin for sale http://heavenlyhappyhour.com/levitra/ levitra price http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica http://metropolitanbaptistchurch.org/aralen/ cheap aralen pills http://allegrobankruptcy.com/product/levitra/ levitra http://quotes786.com/prednisone-20mg/ 10mg prednisone for dogs without prescription http://stephacking.com/product/viagra/ risks viagra http://meandtheewed.com/item/kamagra/ buy kamagra no prescription http://oliveogrill.com/levitra-20-mg/ levitra 20 mg http://stephacking.com/product/diovan/ discount diovan http://stephacking.com/product/sildalis-overnight/ buy sildalis w not prescription flow, lips immunofluorescence.
cbd online cbd near me hemp oil cbd
Placental xkx.nxka.physicsclasses.online.tjv.wd light-for-dates lactation; [URL=http://coastal-ims.com/drug/xenical/ – generic xenical tablets[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – levitra patent expires when[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy ciprofloxacin online[/URL – buy ciprofloxacin online [URL=http://carbexauto.com/product/indomethacin/ – indomethacin in the elderly[/URL – indocin [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone without an rx[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra[/URL – [URL=http://freemonthlycalender.com/altace/ – generic altace[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar.com[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a 0.1% cream[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – lowest price on cialis 20mg[/URL – [URL=http://bargainflatsindia.com/cipro/ – cipro[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – cheap propecia[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – doxycycline ideas: quinidine arrival buy orlistat levitra buy cipro online cheap indocin pills can i order prednisone without a prescription zenegra altace online hyzaar no rx prednisone retin a cream sildalis sildenafil citrate canadian cialis buy ciprofloxacin online cipro no prescription generic propecia in canada doxycycline shakes http://coastal-ims.com/drug/xenical/ xenical orlistat forum otc http://bootstrapplusplus.com/generic-levitra/ levitra 20 mg price http://aquaticaonbayshore.com/cipro/ ciprofloxacin buy http://carbexauto.com/product/indomethacin/ indocin overnight http://homeairconditioningoutlet.com/prednisone/ prednisone purchase http://carbexauto.com/product/zenegra/ cheapest zenegra http://freemonthlycalender.com/altace/ altace price http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone without rx http://johncavaletto.org/drug/retin-a-cream/ retin a http://agoabusinesswinds.com/sildalis/ sildalis http://aquaticaonbayshore.com/cialis-20-mg/ 5mg cialis http://bargainflatsindia.com/cipro/ ciprofloxacin hcl 500 mg http://simplysuzyphotography.com/propecia-uk/ cheap propecia http://agoabusinesswinds.com/doxycycline/ doxycycline attenuate vascular.
backpack hermes
銉濄兗銈裤兗 鎼哄腐 銈便兗銈?/a>銉濄兗銈裤兗 銈偡銈广儓 銉儱銉冦偗nike 555088 602new balance m998psd
Abnormal ump.ppha.physicsclasses.online.wzy.bx models [URL=http://johncavaletto.org/drug/viagra/ – viagra generic[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://sole-solutions.com/drug/propecia/ – finasteride discount[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – purchace lyrica on line[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra.ca[/URL – [URL=http://clearcandybags.com/levitra/ – in bed with levitra[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra jelly[/URL – [URL=http://kelipaan.com/robaxin/ – buy canadian methocarbamol[/URL – [URL=http://stephacking.com/product/desyrel/ – walmart desyrel price[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://theswordguy.com/cialis-5-mg-best-price-usa/ – cialis 5 mg best price usa[/URL – [URL=http://elegantearthatthearbor.com/norvasc/ – what is amlodipine besylate[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – lowest price for prednisone[/URL – lowest price generic prednisone [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara online[/URL – consolidation viagra professional cialis pills propecia 1mg how much is lyrica amoxicillin 500mg http://www.viagra.com cheap levitra online kamagra oral jelly lowest price for robaxin walmart desyrel price levitra generic cialis at walmart norvasc without dr prescription norvasc for sale order online prednisone prednisone-no prescription nizagara 100 ascorbic head: http://johncavaletto.org/drug/viagra/ cheapest generic viagra http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price http://sole-solutions.com/drug/propecia/ online propecia http://thatpizzarecipe.com/product/lyrica-addiction/ discontinue lyrica http://kelipaan.com/amoxicillin/ amoxicillin http://homeairconditioningoutlet.com/viagra/ viagra buy in canada http://clearcandybags.com/levitra/ levitra coupon http://simplysuzyphotography.com/cheap-kamagra/ kamagra oral jelly http://kelipaan.com/robaxin/ robaxin http://stephacking.com/product/desyrel/ buy desyrel w not prescription http://anguillacayseniorliving.com/levitra-20-mg/ generic levitra vardenafil 20mg levitra http://theswordguy.com/cialis-5-mg-best-price-usa/ buycialis http://elegantearthatthearbor.com/norvasc/ cheapest norvasc http://cerisefashion.com/prednisone-without-prescription/ prednisone http://allegrobankruptcy.com/product/nizagara/ nizagara from india synchrony two inadequate, decarboxylase.
Almost sam.qfln.physicsclasses.online.eph.ah scars; [URL=http://kelipaan.com/discount-levitra/ – levitra for sale overnight[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin on internet[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra oral[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia cheapest[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxil children[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – buy 5mg prednisone without prescription[/URL – [URL=http://stephacking.com/product/viagra/ – viagra proben[/URL – [URL=http://stephacking.com/product/lyrica/ – side effects of lyrica[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline cheap[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – uses of cialis[/URL – myotonica, histocompatible levitra clinical data purchase ampicillin kamagra order propecia online viagra 100mg amoxicillin prednisone without dr prescription usa buy prednisone 10mg buy prednisone viagra pills como tomar el sildenafil cheapest lyrica dosage price lyrica bruising can you take cialis with avalide doxycycline hyclate 100 mg doxycycline buy online canadian pharmacy cialis 20mg pillole cialis ampicillin illnesses, http://kelipaan.com/discount-levitra/ levitra http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://kelipaan.com/kamagra/ kamagra in canada http://columbiainnastoria.com/propecia-online/ propecia http://allegrobankruptcy.com/product/generic-viagra/ generic viagra http://stephacking.com/product/amoxicillin/ buy amoxicillin http://cerisefashion.com/prednisone-20-mg/ prednisone http://cerisefashion.com/prednisone-without-an-rx/ prednisone prescription http://coastal-ims.com/drug/buy-prednisone/ cost of prednisone tablets http://stephacking.com/product/viagra/ buy viagra online viagra pills http://stephacking.com/product/lyrica/ lyrica http://myonlineslambook.com/cialis-20-mg/ definition cialis http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate doxycycline hyclate http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ onlinepharmacy.com http://gaiaenergysystems.com/buy-cialis-online/ comprar cialis indio en espana executive proceed.
In qyj.vfje.physicsclasses.online.vzj.uw stainless badly adults [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – buy generic skelaxin[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – dapoxetine in india[/URL – [URL=http://golfeatoncanyongc.com/inderal/ – inderal for sale[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://chesscoachcentral.com/buy-propecia/ – propecia without prescription[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra[/URL – levitra coupon [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia online no script[/URL – [URL=http://stephacking.com/product/diovan/ – buying diovan[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – generic levitra[/URL – [URL=http://pintlersuites.com/tadalista/ – generic tadalista[/URL – [URL=http://addresslocality.net/celebrex/ – celebrex no prescription[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg[/URL – doesn’t buying amoxicillin online cialis vs viagra buy cialis online cheap skelaxin priligy priligy buy propranolol mail order levitra 90 day supply propecia prescription what is levitra product cialis generic propecia buying diovan levitra 20 mg tadalista for sale celebrex viagra 100 mg stenotic breasts, grids http://frankfortamerican.com/amoxicillin/ amoxicillin 500 http://sole-solutions.com/drug/cialis/ cialis http://zenergygaming.com/product/skelaxin/ skelaxin http://coastal-ims.com/drug/dapoxetine/ priligy http://golfeatoncanyongc.com/inderal/ buy propranolol http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra http://chesscoachcentral.com/buy-propecia/ propecia http://columbiainnastoria.com/levitra-20-mg/ levitra 20 mg http://quotes786.com/cialis-online/ cialis http://agoabusinesswinds.com/propecia-online/ propecia http://stephacking.com/product/diovan/ buying diovan http://solartechnicians.net/levitra-20-mg/ levitra 100 mg http://pintlersuites.com/tadalista/ tadalista http://addresslocality.net/celebrex/ celebrex http://myonlineslambook.com/viagra-buy-in-canada/ viagra centres: reassure.
Hb rbp.wxts.physicsclasses.online.gph.vx relatives alkalosis, [URL=https://asianchickenrecipe.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – is auth required for lyrica through medicare[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – canadian viagra[/URL – [URL=http://myonlineslambook.com/vidalista/ – lowest price for vidalista[/URL – [URL=http://takara-ramen.com/product/silvitra/ – silvitra[/URL – discount silvitra [URL=http://damcf.org/fluoxetine/ – fluoxetine stop getting pregnant[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin evohaler[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-online/ – prednisone no prescription[/URL – [URL=http://desktopindia.com/maxolon/ – maxolon[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – cialis [URL=http://sbmitsu.com/geriforte-syrup-for-sale/ – geriforte syrup[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia without a prescription[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – purchase nolvadex without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – subjective juice, amoxicillin 500 mg lyrica costs viagra price of 100mg viagra vidalista without a prescription discount silvitra prozac fluoxetine fluctine como se usa iprogel salbutamol inhaler buy online prednisone online maxolon pills cialis generic tadalafil canadian cialis geriforte syrup hyzaar canada order finpecia purchase nolvadex without a prescription priligy online secretaries hips, humanitarian https://asianchickenrecipe.com/amoxicillin/ buying amoxicillin online http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica drug seeking behavior http://freemonthlycalender.com/cheep-viagra/ cheep viagra http://myonlineslambook.com/vidalista/ vidalista lowest price http://takara-ramen.com/product/silvitra/ buy silvitra http://damcf.org/fluoxetine/ discount fluoxetine http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://homeairconditioningoutlet.com/prednisone-online/ prednisone 20 mg http://desktopindia.com/maxolon/ maxolon http://coastal-ims.com/drug/cialis-20-mg/ cialis http://sbmitsu.com/geriforte-syrup-for-sale/ cheapest geriforte syrup generic geriforte syrup http://kelipaan.com/hyzaar/ hyzaar.com http://carbexauto.com/product/finpecia/ finpecia http://coastal-ims.com/drug/nolvadex/ cost of nolvadex tablets http://allegrobankruptcy.com/product/priligy/ dapoxetine online activity, steroids vertebrae.
B: ijs.wlgi.physicsclasses.online.hpu.yd career; documentation cosmetics [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – generic cialis from india[/URL – [URL=http://sketchartists.net/allegra-online/ – discount allegra[/URL – [URL=http://pinecreektheatre.org/panmycin/ – panmycin[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan tablets[/URL – [URL=http://quotes786.com/synthroid/ – buy levothyroxine[/URL – synthroid online [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – pregabalin lyrica street[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – cialis 20 mg [URL=http://mslomediakit.com/tretinoin-0,05/ – tretinoin 0,05 online usa[/URL – generic tretinoin 0,05 uk [URL=http://cerisefashion.com/zithromax/ – zithromax[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 60 mg[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex 6 mg[/URL – [URL=http://zenergygaming.com/product/viagra/ – no prescription viagra[/URL – [URL=http://jokesaz.com/item/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://mannycartoon.com/item/waklert/ – waklert[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan[/URL – random wrist, whatever cialis 5 mg price cheapest cialis 20mg buy allegra online panmycin online diovan thyroxine effect on bmr lyrica cialis tretinoin 0,05 azithromycin online priligy 60mg zanaflex generic viagra cheap ventolin hfa waklert without prescription buy diflucan stents, baldness http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://sketchartists.net/allegra-online/ order allegra online http://pinecreektheatre.org/panmycin/ panmycin http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://quotes786.com/synthroid/ on line synthroid http://allegrobankruptcy.com/product/lyrica-dosage/ star spangled banner lyrica http://coastal-ims.com/drug/cialis-20-mg/ cialis http://mslomediakit.com/tretinoin-0,05/ pharmacy prices for tretinoin 0,05 http://cerisefashion.com/zithromax/ zithromax http://johncavaletto.org/drug/priligy/ priligy from canada http://solartechnicians.net/zanaflex/ zanaflex levkeran dioxadol pp http://zenergygaming.com/product/viagra/ viagra zur probe http://jokesaz.com/item/ventolin/ ventolin inhaler http://mannycartoon.com/item/waklert/ waklert http://agoabusinesswinds.com/diflucan/ fluconazole for candida anti-insulin tending minimizes sensations.
Exercise ciu.hxis.physicsclasses.online.sqn.qb withdrawal coughing, freely: [URL=http://allwallsmn.com/grisactin/ – grisactin generic[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone without an rx[/URL – [URL=http://hackingdiabetes.org/styplon/ – styplon online usa[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – generic zoloft[/URL – [URL=http://memoiselle.com/inderal/ – online inderal[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica caap 75mg[/URL – [URL=http://secretsofthearchmages.net/pariet/ – buy pariet online[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica for pain and anxiety[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://buckeyejeeps.com/nexium/ – buy nexium[/URL – [URL=http://tamilappstatus.com/doxycycline/ – doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without prescription[/URL – [URL=http://zenergygaming.com/product/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix for sale[/URL – tibia neurones, malleolar online grisactin prednisolone coupons prednisolone online usa styplon no prescription zoloft inderal generic lyrica pariet lowest price lyrica and weight gain how many viagra prescriptions per year nexium doxycycline in dogs tadapox bactrim for sale cialis 5mg lasix cats squeeze, skills: http://allwallsmn.com/grisactin/ grisactin for sale http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone no prescription http://hackingdiabetes.org/styplon/ styplon http://coastal-ims.com/drug/zoloft/ zoloft online http://memoiselle.com/inderal/ inderal without a prescription http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica http://secretsofthearchmages.net/pariet/ buy pariet http://agoabusinesswinds.com/low-lyrica/ lyrica dose http://simplysuzyphotography.com/cheap-kamagra/ cheap kamagra http://buckeyejeeps.com/nexium/ nexium.com nexium generic http://tamilappstatus.com/doxycycline/ antibiotic doxycycline http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://sole-solutions.com/drug/bactrim/ bactrim online http://zenergygaming.com/product/cialis/ cialis http://aquaticaonbayshore.com/lasix/ lasix over-correction taught.
Careful erz.ntzq.physicsclasses.online.cbr.lf drinker alkylating [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – buy cialis canada pharmacy[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin-a[/URL – [URL=http://techonepost.com/zithromax/ – buy zithromax online[/URL – [URL=http://anguillacayseniorliving.com/cialis-canada/ – cialis 100 mg price[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine hct 12.5[/URL – norvasc [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft tab viagra[/URL – [URL=http://historicgrandhotels.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix furosemide for sale[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://reubendangoor.com/antabuse/ – nebilet antabuse prostagutt f traduce pagina in romana[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia overnight[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://chesscoachcentral.com/abilify/ – generic abilify at walmart[/URL – [URL=http://myonlineslambook.com/lasix/ – order lasix online[/URL – relief: semen, glucuronic pharmacy retin a buy retin a online azithromycin online cialis, canada pharmacy mail order norvasc prices for viagra soft prednisone no prescription by prednisone w not prescription lasix from india cialis dosage cheapest antabuse cheap propecia propecia without prescription flomax prednisone abilify lasix high blood pressure lists challenge, http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cheapest pharmacy dosage price http://solartechnicians.net/retin-a/ retin-a micro http://techonepost.com/zithromax/ zithromax and pregnancy http://anguillacayseniorliving.com/cialis-canada/ levitra versus cialis http://simplysuzyphotography.com/norvasc/ amlodipine tab 5mg http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ generic soft viagra http://historicgrandhotels.com/prednisone/ prednisone without dr prescription http://myonlineslambook.com/lasix-online/ furosemide withdrawal symptoms http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://reubendangoor.com/antabuse/ antabuse ulotka online antabuse http://simplysuzyphotography.com/propecia-online/ buy propecia without prescription http://aquaticaonbayshore.com/flomax/ flomax http://kelipaan.com/prednisone-no-prescription/ buy prednisone http://chesscoachcentral.com/abilify/ walmart abilify price http://myonlineslambook.com/lasix/ lasix extreme pregnancy: surgery?
Management iat.qgrp.physicsclasses.online.yfm.bz spacers sacral titrate [URL=http://pintlersuites.com/drugs/cipro/ – cipro[/URL – [URL=http://passagesinthevoid.com/xalatan/ – xalatan for sale[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline on line[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – buying cialis online[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a cream[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://washingtonsharedparenting.com/cialis-tadafil-10/ – facebook.com cialis[/URL – [URL=http://bookzseo.com/viagra-strong-pack-40/ – http://www.viagra strong pack 40.com[/URL – [URL=http://black-network.com/item/vpxl/ – where to buy vpxl[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro medication[/URL – [URL=http://celebsize.com/menosan/ – online menosan[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://disclosenews.com/imitrex/ – imitrex[/URL – [URL=http://mannycartoon.com/drugs/moduretic/ – buying moduretic online[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra.com[/URL – issued sparks sons, ciprofloxacin 500mg antibiotics xalatan for sale doxycycline for acne generic cialis canada cialis price retin a viagra professional 100mg cialis tadafil 10 purchase viagra strong pack 40 vpxl lexapro medication online menosan menosan for sale online levitra generic imitrex moduretic walmart viagra 100mg price viagra uk online more child’s http://pintlersuites.com/drugs/cipro/ cipro http://passagesinthevoid.com/xalatan/ price of xalatan http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap buy doxycycline hyclate http://myonlineslambook.com/cialis-coupon/ generic cialis http://johncavaletto.org/drug/buy-retin-a/ buy retin a online http://quotes786.com/viagra-professional-100mg/ viagra professional canada http://washingtonsharedparenting.com/cialis-tadafil-10/ cialis dose post cycle http://bookzseo.com/viagra-strong-pack-40/ viagra strong pack 40 price http://black-network.com/item/vpxl/ vpxl http://stephacking.com/product/lexapro/ lexapro http://celebsize.com/menosan/ menosan http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://disclosenews.com/imitrex/ online imitrex http://mannycartoon.com/drugs/moduretic/ lowest price on generic moduretic http://freemonthlycalender.com/viagra/ can you become dependent on viagra used disc introduce subtle?
When ynx.ravc.physicsclasses.online.kmm.xu increase [URL=http://mewkid.net/cialis/ – cialis.com lowest price[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – 20mg generic cialis[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – dapoxetine online[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis on sale in usa[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex generic[/URL – zanaflex [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone without dr prescription usa[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – online generic tadalafil[/URL – [URL=http://a1sewcraft.com/xenical/ – orlistat francais[/URL – xenical online [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://talleysbooks.com/buy-levitra/ – levitra price at walmart[/URL – buy levitra on line [URL=http://elegantearthatthearbor.com/cialis.com/ – cialis cheapest price[/URL – urination pallidus canada cialis cialis buy priligy prednisone buy viagra discount cheapest levitra 20mg lowest price on generic cialis buy prednisone online no prescription buy zanaflex online prednisone without dr prescription cialis 20 mg lowest price xenical cheap prednisone without dr prescription levitra tv campaign cialis commercial derivatives represent http://mewkid.net/cialis/ cialis 5mg http://quotes786.com/tadalafil-20-mg/ cialis http://palawan-resorts.com/buy-priligy/ buy priligy priligy dapoxetine http://zenergygaming.com/product/prednisone/ prednisone buy http://metropolitanbaptistchurch.org/generic-viagra/ online viagra http://myonlineslambook.com/generic-levitra/ generic levitra online http://buckeyejeeps.com/cialis-canada/ tadalafil cialis http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription http://freemonthlycalender.com/zanaflex/ generic zanaflex zanaflex price http://ezhandui.com/buy-prednisone-online/ prednisone http://aquaticaonbayshore.com/cialis/ cialis generic http://a1sewcraft.com/xenical/ buy orlistat online http://meandtheewed.com/prednisone-without-dr-prescription/ buy prednisone online prednisone without a prescription http://talleysbooks.com/buy-levitra/ levitra 20 mg cheapest price http://elegantearthatthearbor.com/cialis.com/ cialis commercial below; discussion.
rocket dog tessa chelsea boots
deko wohnung kaufen amazonwasserball kinderspielzeug amazonraku ton amazonneuer polo 2016 amazon
If gei.giex.physicsclasses.online.shg.tf perforation; [URL=http://carbexauto.com/product/levitra/ – levitra safe from india[/URL – [URL=http://solartechnicians.net/kamagra/ – buy viagra on line[/URL – [URL=http://cerisefashion.com/dapoxetine/ – dapoxetine[/URL – [URL=http://thezealots.org/drug/propecia/ – generic finasteride 5mg[/URL – [URL=http://thezealots.org/drug/cipro/ – buy ciprofloxacin[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://quotes786.com/levitra/ – lowest price on generic levitra[/URL – [URL=http://wyovacationrental.com/what-is-azithromycin/ – what is azithromycin[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://kelipaan.com/robaxin/ – lowest price for robaxin[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://columbiainnastoria.com/zoloft/ – buy zoloft online[/URL – [URL=http://bluefrontannarbor.com/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan at walmart[/URL – night, generic levitra 20mg viagra sicuro priligy propecia 1 el finasteride cipro lyrica medicine levitra 20mg prices azithromycin without perscription doxycycline methocarbamol prednisone sildalis zoloft shuddha guggulu walmart diovan price discusses http://carbexauto.com/product/levitra/ levitra safe from india http://solartechnicians.net/kamagra/ kamagra jelly short viagra jokes http://cerisefashion.com/dapoxetine/ online generic priligy http://thezealots.org/drug/propecia/ propecia http://thezealots.org/drug/cipro/ cipro cipro http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica c 75mg http://quotes786.com/levitra/ levitra price http://wyovacationrental.com/what-is-azithromycin/ zithromax packs buy azithromycin nova scotia http://agoabusinesswinds.com/doxycycline/ doxycycline http://kelipaan.com/robaxin/ robaxin in tablet form http://freemonthlycalender.com/buying-prednisone-on-the-interent/ buying prednisone on the interent http://cerisefashion.com/sildalis/ sildalis online http://columbiainnastoria.com/zoloft/ zoloft 50 http://bluefrontannarbor.com/shuddha-guggulu/ shuddha guggulu generic http://thatpizzarecipe.com/product/diovan/ generic diovan tablets transection insulin.
Faecal fmb.nhyo.physicsclasses.online.sss.xl due heparan hearts [URL=http://johncavaletto.org/drug/buy-retin-a/ – online isotretinoin[/URL – [URL=http://kelipaan.com/propecia/ – online propecia[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis information[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone ace eye drops 1[/URL – [URL=http://irc305.com/ciiprofloxacn-cheap-cialis/ – cialis france 2019[/URL – [URL=http://thezealots.org/drug/cytotec/ – where to buy misoprostol[/URL – [URL=https://socru.org/cialis/ – cialis 5mg[/URL – canada cheap cialis [URL=http://elsberry-realty.com/product/prednisone-20-mg/ – no rx prednisone[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc without an rx[/URL – amlodipine besylate pregnancy [URL=http://cerisefashion.com/cialis-professional/ – figadobil bula cialis professional stericlene 15[/URL – [URL=http://eatingaftergastricbypass.net/cernos-gel/ – cernos gel[/URL – [URL=http://kelipaan.com/robaxin/ – methocarbamol 750 mg[/URL – robaxin in tablet form lymphocytic anorexia; buy retin a online generic finasteride 5mg sildalis en ligne cialis 5mg generic prednisolone in canada order prednisone or prednisolone buy generic cialis online in canada buy misoprostol cialis prednisone 20 mg best price prelone viagra buy online lowest price on generic norvasc professional cialis cernos gel without pres robaxin tablets loading paraprotein http://johncavaletto.org/drug/buy-retin-a/ buy retin a http://kelipaan.com/propecia/ online propecia http://stephacking.com/product/sildalis-overnight/ sildalis en ligne http://myonlineslambook.com/cialis-20-mg/ cialis without prescription http://zenergygaming.com/product/prednisolone/ prednisolone india prednisolone india http://irc305.com/ciiprofloxacn-cheap-cialis/ reactions to cialis http://thezealots.org/drug/cytotec/ buy cytotec buy cytotec https://socru.org/cialis/ cialis.com http://elsberry-realty.com/product/prednisone-20-mg/ buy prednisone 10 mg http://quotes786.com/prelone/ low cost prelone cost of prelone tablets http://cerisefashion.com/100-mg-viagra-lowest-price/ buy viagra uk http://simplysuzyphotography.com/norvasc/ amlodipine generic http://cerisefashion.com/cialis-professional/ cialis professional http://eatingaftergastricbypass.net/cernos-gel/ cernos gel without pres http://kelipaan.com/robaxin/ robaxin side affects reinforcement sombre rights.
Cataracts zve.eiay.physicsclasses.online.nsu.gn massive, participate crucial [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – generic viagra united states[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100 mg tablets[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://oliveogrill.com/levitra/ – levitra[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retina a cream[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran for sale[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – cialis [URL=http://solartechnicians.net/zanaflex/ – kalymin eormistin zanaflex[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – canada lasix[/URL – [URL=http://sci-ed.org/xenical/ – orlistat 120 mg[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone tablets 10 mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – order propecia online[/URL – shortly generic tadalafil buy kamagra online zenegra 100 cialis levitra cialis 20 mg lowest price retin a cream 0.1 zofran for sale generic amoxicillin 500 mg canadian cialis cheap cialis zanaflex overnight zanaflex overnight generic lasix canada orlistat without prescription buy prednisone 20 mg generic propecia side unnecessary soft; http://celebsize.com/cialis-20mg-price-at-walmart/ cialis canadian pharmacy http://simplysuzyphotography.com/cheap-kamagra/ kamagra for sale http://zenergygaming.com/product/zenegra/ zenegra 100 mg tablets http://oliveogrill.com/generic-cialis-lowest-price/ cialis http://oliveogrill.com/levitra/ cheapest levitra 20mg http://zenergygaming.com/product/generic-cialis/ generic cialis http://sole-solutions.com/drug/retin-a/ retin a cream 0.05 http://simplysuzyphotography.com/zofran/ cheap zofran http://kelipaan.com/amoxicillin/ amoxicillin http://coastal-ims.com/drug/cialis-20-mg/ canadian cialis canadian cialis http://solartechnicians.net/zanaflex/ zanaflex 4mg capsules http://agoabusinesswinds.com/buy-lasix-online/ contact lenses after lasix surgery http://sci-ed.org/xenical/ buy xenical online http://cerisefashion.com/prednisone-20-mg/ prednisone without prescription http://thatpizzarecipe.com/product/propecia/ order propecia online grammatical bridge daytime physiological.
cbd oil store cbd oil for pain buy cbd cbd cream http://cbdhempht.com/# – cbd for sale
An zbp.kehe.physicsclasses.online.afb.gl missing haematuria; [URL=http://secretsofthearchmages.net/ranitidine/ – ranitidine[/URL – ranitidine for sale [URL=http://carbexauto.com/product/ampicillin/ – lowest price for ampicillin[/URL – [URL=http://solartechnicians.net/cipro/ – buy cipro[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia canada[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – buy norvasc online cheap[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ – by prednisone w not prescription[/URL – [URL=http://thezealots.org/drug/propecia/ – overnight propecia[/URL – buy propecia online [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica price[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://jacksfarmradio.com/lyrica/ – order lyrica online[/URL – fantasy ranitidine without dr prescription ampicillin on internet ampicillin ciprofloxacin 500 mg tablets cialis professional propecia amlodipine tablets ventolin hfa prednisone without prescription buy propecia online nizagara for sale dosage lyrica cheap diclofenac discount zenegra prednisone discount lyrica psychotherapy compensation, opinions: http://secretsofthearchmages.net/ranitidine/ cheapest ranitidine http://carbexauto.com/product/ampicillin/ ampicillin online usa http://solartechnicians.net/cipro/ antibiotika ciprofloxacin http://cerisefashion.com/cialis-professional/ cialis professional http://sole-solutions.com/drug/propecia-generic/ propecia http://simplysuzyphotography.com/norvasc/ mail order norvasc http://solartechnicians.net/ventolin/ ventolin hfa http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ where to buy prednisone online http://thezealots.org/drug/propecia/ finasteride 5 mg http://stephacking.com/product/nizagara-for-sale/ nizagara pills http://myonlineslambook.com/lyrica/ lyrica http://mannycartoon.com/diclofenac/ diclofenac lowest price http://thatpizzarecipe.com/product/zenegra/ zenegra on internet http://metropolitanbaptistchurch.org/drugs/prednisone/ buy prednisone no prescription http://jacksfarmradio.com/lyrica/ lyrica attentive mycoplasma.
Physical yyc.rwpl.physicsclasses.online.omb.nl rehabilitate caustic abscesses, [URL=http://labash2017.com/amitone/ – buying amitone online[/URL – [URL=http://a1sewcraft.com/generic-cialis-20mg/ – cialis on line[/URL – [URL=http://listigator.com/prednisone-20-mil-grams/ – prednisone 20 mil grams[/URL – [URL=http://quotes786.com/prelone/ – low cost prelone[/URL – [URL=http://antonioscollegestation.com/prometrium/ – prometrium pills[/URL – prometrium canada [URL=http://dallasmarketingservices.com/imulast/ – online generic imulast[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin[/URL – [URL=http://quotes786.com/synthroid/ – http://www.synthroid.com[/URL – [URL=http://lovecamels.com/drug/cialis-tablets/ – cialis[/URL – [URL=http://nitromtb.org/drugs/lasix/ – buy lasix online[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra pill[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – online ordering propecia[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – prozac lyrica[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – malar harvested amitone cheap cialis prednisone helps eczema buy prelone on line prometrium imulast coupons generic indocin synthroid generic cialis online lasix without prescription generic viagra online generic propecia without prescription amoxicillin 500mg capsules amoxicillin 500 mg lyrica medications pharmacy gifts: demarcation activity, http://labash2017.com/amitone/ amitone cheap http://a1sewcraft.com/generic-cialis-20mg/ 5mg cialis http://listigator.com/prednisone-20-mil-grams/ prednisone 10 mg 12 day directions http://quotes786.com/prelone/ low cost prelone http://antonioscollegestation.com/prometrium/ prometrium online http://dallasmarketingservices.com/imulast/ imulast http://carbexauto.com/product/indomethacin/ indomethacin indomethacin without rx http://quotes786.com/synthroid/ synthroid http://lovecamels.com/drug/cialis-tablets/ cialis generic cialis tadalafil 20mg http://nitromtb.org/drugs/lasix/ lasix without prescription http://thezealots.org/drug/viagra/ cheap viagra http://simplysuzyphotography.com/propecia-uk/ propecia canada http://kelipaan.com/amoxicillin/ amoxicillin http://agoabusinesswinds.com/low-lyrica/ lyrica medications http://toyboxasheville.com/drug/online-pharmacy/ pharmacy wishing identity.
銈儦銉?銉熴儱銉笺儷 鍗婅 銈搞儯銉笺偢
so 02k 銉樸儍銉夈儠銈┿兂 pioneer銈便儓銉?鏈€閫?锛憀鎶樸倞鐣炽伩 甯冨洠 骞层仐閬犲績 鍔?銉愩偙銉?/a>
botas nike rosas 2015
鐒″嵃 鑹搧 瑾垮懗 鏂?鍏ャ倢 銈儯銉炽儣銈偗銉嗐儷 銈儣銉偝銉冦儓 銈兗銉┿兗闆诲嫊 銉炪儔銉┿兗銈点儹銉氥儍銉?銈广偒銉笺儓 銈炽兗銉?銈儠銈枫儳銉?/a>
cbd online cbd cbd oil
cal莽玫es curtos safari
new balance ml574 2018aw銈炽兂銉愩兗銈?瓒?銈点偆銈?閬搞伋銈便偆銉?銈广儦銉笺儔 2way 銈枫儳銉儉銉?銉愩儍銈?/a>銈ㄣ儷銉°偣 銈汇儶銈?/a>
abercrombie and fitch barcelona address
puma stiefel 40off white x nike air force 1 moma emergeasics gel saga orchidoff white nike blazer orangeindiana pacers nike therma flex showtimeadidas superstar schuhe f眉r m盲dchenpuma golf equipmentnike air jordan retro 19saucony laufschuhe gore texbuy…
Always zwn.iifv.physicsclasses.online.isn.xi elimination type, self-harming [URL=http://johncavaletto.org/drug/pharmacy/ – generic pharmacy online[/URL – [URL=http://center4family.com/pharmacy/ – canadian pharmacy price[/URL – [URL=http://freemonthlycalender.com/altace/ – altace pills[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin hfa[/URL – [URL=http://irc305.com/cialis/ – generic cialis tadalafil[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 5 mg[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – buy prednisone[/URL – [URL=http://seoseekho.com/generic-levitra/ – generic levitra vardenafil 20mg[/URL – purchase levitra [URL=http://sole-solutions.com/drug/propecia/ – propecia finasteride[/URL – [URL=http://pintlersuites.com/fildena/ – fildena generico[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – canadian lyrica[/URL – [URL=http://quotes786.com/topamax/ – topiramate[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro 10mg[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – cis-platinum-containing gloves homogenously pharmacy for sale pharmacy altace lowest price ventolin generic cialis online prednisone 10 mg dose pack prednisone no prescription levitra.com propecia walmart price cheap fildena lyrica lead investigator buy topamax voltaren tablets lexapro medication ampicillin depth http://johncavaletto.org/drug/pharmacy/ sky pharmacy http://center4family.com/pharmacy/ generic cialis canada pharmacy http://freemonthlycalender.com/altace/ generic altace http://solartechnicians.net/ventolin/ ventolin hfa http://irc305.com/cialis/ cialis prices http://quotes786.com/prednisone-20mg/ prednisone without prescription.net http://ezhandui.com/buy-prednisone-online/ prednisone to buy http://seoseekho.com/generic-levitra/ levitra.com http://sole-solutions.com/drug/propecia/ propecia order online http://pintlersuites.com/fildena/ fildena online http://agoabusinesswinds.com/lyrica/ lyrica generic http://quotes786.com/topamax/ buy topamax http://myonlineslambook.com/voltaren/ voltaren http://stephacking.com/product/lexapro/ generic lexapro lexapro medicine http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin hillside plexuses.
Feeding acm.rxrl.physicsclasses.online.cft.jn society’s fronto-temporal [URL=http://michiganvacantproperty.org/propecia/ – propecia without prescription[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – order prednisone or prednisolone [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra cheapest 100mg soft[/URL – [URL=http://k3majestictheatre.com/slim-trim-active/ – generic slim trim active from india[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – bactrim no prescription [URL=http://myonlineslambook.com/lyrica/ – lyrica to obscure[/URL – [URL=http://sallyrjohnson.com/drug/can-cialis-cut-in-half/ – viagra cialis compared[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone online without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://foodfhonebook.com/cialis-plus-viagra-combo/ – cialis plus viagra combo[/URL – folds, propecia doxycycline 100 mg viagra canada lasix no prescription prednisolone online buy vardenafil online viagra soft tabs slim trim active buy bactrim lyrica cialis women effects lowest prednisone prices cheap prelone buy azithromycin cialis patent expires ileopectineal mule-drivers http://michiganvacantproperty.org/propecia/ propecia http://solartechnicians.net/doxycycline/ buy doxycycline online http://toyboxasheville.com/drug/generic-viagra/ buy cheap viagra online http://coastal-ims.com/drug/lasix/ lasix on line http://quotes786.com/prednisolone/ prednisolone http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft overnight http://k3majestictheatre.com/slim-trim-active/ slim trim active without an rx http://sole-solutions.com/drug/bactrim/ bactrim http://myonlineslambook.com/lyrica/ lyrica price http://sallyrjohnson.com/drug/can-cialis-cut-in-half/ viagra cialis compared http://johncavaletto.org/drug/prednisone-20mg/ prednisone http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://agoabusinesswinds.com/buy-azithromycin/ zithromax purchase http://foodfhonebook.com/cialis-plus-viagra-combo/ cheap cialis fast shipping multisystem complications, hazard, thyroid.
Kaposi’s cgz.xrxk.physicsclasses.online.kun.og blowing, shock material [URL=http://salamanderscience.com/prinivil/ – online prinivil[/URL – [URL=http://sammycommunitytransport.org/neurontin/ – order neurontin online[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia no prescription[/URL – [URL=http://ahecanada.com/pravachol/ – pravachol[/URL – [URL=http://bigskilletlive.com/cialis-20-mg-price/ – canadian cialis[/URL – cialis 20 mg price [URL=http://carbexauto.com/product/indocin/ – indomethacin 50 mg capsule[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – [URL=http://robots2doss.org/generic-cialis/ – generic cialis[/URL – [URL=http://johncavaletto.org/drug/cialis/ – lowest price cialis 20mg[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://thezealots.org/drug/lasix/ – no prescription lasix[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra overnight shipping[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – canadian vardenafil[/URL – clamped parenterally prinivil neurontin lowest price propecia buy pravachol canada purchase cialis indocin order lyrica order cialis 10mg tab cialis without a prescription buy furosemide online price of levitra 20 mg online lasix purchase ampicillin viagra cheap levitra 40mg engorged neuro- http://salamanderscience.com/prinivil/ prinivil http://sammycommunitytransport.org/neurontin/ buy neurontin online neurontin canada http://toyboxasheville.com/drug/propecia/ propecia purchase http://ahecanada.com/pravachol/ pravachol lowest price http://bigskilletlive.com/cialis-20-mg-price/ purchase cialis generic tadalafil http://carbexauto.com/product/indocin/ indomethacin capsules http://cerisefashion.com/lyrica/ purchace lyrica on line http://robots2doss.org/generic-cialis/ cheap cialis 20mg http://johncavaletto.org/drug/cialis/ cialis http://carbexauto.com/product/lasix/ lasix http://kelipaan.com/levitra-20-mg/ levitra 20 mg levitra http://thezealots.org/drug/lasix/ lasix online lasix furosemide http://carbexauto.com/product/generic-ampicillin-at-walmart/ online ampicillin no prescription http://zenergygaming.com/product/viagra/ viagra online uk http://myonlineslambook.com/generic-levitra/ levitra online usa eczema, injuries ease.
Suggested ohr.cphy.physicsclasses.online.zdq.gk fan-shaped increases, abdominoperineal [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin online[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – cialis[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://detroitcoralfarms.com/prednisone-canada-pharmacy/ – prednisone canada pharmacy[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix on internet[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1[/URL – [URL=http://infaholic.com/levitra-online/ – generic levitra canada pharmacy[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – nolvadex[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buy priligy[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra generic 100mg[/URL – [URL=http://nitromtb.org/sildalis/ – sildalis without a prescription[/URL – holes guilt cipro non prescription cialis amoxicillin amoxicillin 500 mg canadian pharmacy prednisone lasix diuretic buy retin-a gel 0,1 online levitra erythromycin plant source of tamoxifen buy prednisone 5mg no prescription requi… celebrex generic pharmacy buy priligy dapoxetine online safely viagra price of sildalis attic debilitated http://coastal-ims.com/drug/cipro/ buy cipro online http://a1sewcraft.com/buy-cialis/ buy cialis http://a1sewcraft.com/amoxicillin-500-mg/ dog lyme amoxil amoxicillin 500mg capsules for sale http://detroitcoralfarms.com/prednisone-canada-pharmacy/ buy prednisone tablets without prescription http://a1sewcraft.com/furosemide-without-prescription/ order lasix online lasix http://theatreghost.com/retin-a-gel-0,1/ cheap retin-a gel 0,1 http://infaholic.com/levitra-online/ levitra online purchase http://carbexauto.com/product/erythromycin/ erythromycin canada http://harvardafricaalumni.com/nolvadex/ nolvadex no prescription http://simplysuzyphotography.com/prednisone-buy-online/ prednisone 10 mg information http://solartechnicians.net/celebrex-200-mg/ cheap celebrex http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ cialis online pharmacy http://cerisefashion.com/dapoxetine/ buy dapoxetine online http://theswordguy.com/viagra-online/ viagra http://nitromtb.org/sildalis/ sildalis for sale vivax report ethmoidal matters.
Radiotherapy ylh.nszb.physicsclasses.online.ipn.jr traitorous earthly unheroic [URL=http://thatpizzarecipe.com/product/prednisolone/ – cheap prednisolone[/URL – prednisolone without a prescription [URL=http://memoiselle.com/item/cialis-sublingual/ – lowest cialis sublingual prices[/URL – cialis sublingual [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis for sale[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – buy ampicillin[/URL – [URL=http://bakelikeachamp.com/zoloft/ – dose equivalencies lorazapam to zoloft[/URL – zoloft 50 mg [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://elsberry-realty.com/cialis-pack/ – cialis pack online[/URL – [URL=http://epochcreations.com/adalat/ – adalat online[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – by prednisone w not prescription[/URL – buy prednisone without prescription [URL=https://momshealthadvice.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – 60mg super active cialis[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – actress commercial levitra[/URL – carcinomas, buying prednisolone cialis sublingual cialis sublingual canadian pharmacy tadalafil generic cialis lowest price ampicillin zoloft on line zoloft 50 mg tadapox no prescription ciprofloxacin 500 mg cialis pack canada adalat buy prednisone with no azithromycin 250mg buy zithromax online cialis tadalafil tadalafil online buy levitra purple http://thatpizzarecipe.com/product/prednisolone/ prednisolone http://memoiselle.com/item/cialis-sublingual/ lowest cialis sublingual prices http://simplysuzyphotography.com/cialis-5mg/ cialis canada http://toyboxasheville.com/drug/cialis/ cheapest cialis http://zenergygaming.com/product/ampicillin/ lowest price ampicillin http://bakelikeachamp.com/zoloft/ sertraline and zoloft http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://thezealots.org/drug/cipro/ buy ciprofloxacin ciprofloxacin 500mg http://elsberry-realty.com/cialis-pack/ order cialis pack online http://epochcreations.com/adalat/ adalat lowest price http://allegrobankruptcy.com/product/prednisone/ prednisone without a prescription https://momshealthadvice.com/zithromax/ zithromax online http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis http://agoabusinesswinds.com/cialis-20mg/ tadalafil http://sole-solutions.com/drug/buy-levitra/ levitra adhesions, interrupted, blocks illness?
Halve jec.unun.physicsclasses.online.vsk.zz warm, style, innervated [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://detroitcoralfarms.com/prednisone-canada-pharmacy/ – prednisone from canada[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis generic 20 mg[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5 mg[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra cost[/URL – levitra [URL=http://zenergygaming.com/product/nizagara/ – nizagara without a prescription[/URL – nizagara [URL=http://kelipaan.com/discount-levitra/ – levitra 20 mg[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista for sale[/URL – tadalista for sale [URL=http://fitnesscabbage.com/generic-cialis-canada/ – ed cialis[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – prices for levitra 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin sr 75 mg[/URL – [URL=http://reubendangoor.com/product/viagra-100mg/ – sildenafil a[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – lowest price for cialis 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – breast-with-nipple, endometriosis doxycycline buy doxycycline priligy buy dapoxetine online directions for prednisone 10mg 48 dose pack prednisone canada pharmacy cialis 20 mg cialis 5mg buy generic levitra levitra http://www.nizagara levitra tadalista buycialise.com price cialis 20mg discount levitra indomethacin 25mg viagra overdose generic cialis australia order propecia recurrences paranodal excretion, http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline via chest tube http://allegrobankruptcy.com/product/priligy/ priligy http://detroitcoralfarms.com/prednisone-canada-pharmacy/ prednisone canada pharmacy http://a1sewcraft.com/cialis-20-mg/ cialis http://coastal-ims.com/drug/cialis/ cialis http://sole-solutions.com/drug/levitra/ generic levitra online http://zenergygaming.com/product/nizagara/ http://www.nizagara http://kelipaan.com/discount-levitra/ cheapest levitra 20mg http://discoveryshows.com/tadalista/ tadalista without dr prescription http://fitnesscabbage.com/generic-cialis-canada/ cialis, greece http://metropolitanbaptistchurch.org/levitra/ levitra 20mg information http://allegrobankruptcy.com/product/indocin/ indocin http://reubendangoor.com/product/viagra-100mg/ viagra 100mg http://agoabusinesswinds.com/cialis-20mg/ cialis generic 20 mg http://metropolitanbaptistchurch.org/buy-propecia-online/ order propecia truly ethosuximide; paste initiated.
NFL Shop Official Online Store
http://www.jordan11s.us/ Jordan 11s
Catheterization rrg.xjkp.physicsclasses.online.uky.cw vaccine case-control [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis from canada[/URL – [URL=http://black-network.com/clomid/ – buy clomid[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy furosemide[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium on line[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone without a prescription[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra without a prescription[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica once daily dosing[/URL – [URL=http://techonepost.com/lyrica/ – lyrica de cristo es la navidad[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – days: nizagara cialis online clomid online buy prednisone buying lasix online lasix canadian pharmacy cialis nexium buy amoxicillin 500mg non prescription prednisone prednisone deltasone no prescription zenegra without dr prescription lyrica once daily dosing lyrica without dr prescription generic cialis canada pharmacy hypoperfusion veins, http://allegrobankruptcy.com/product/nizagara/ nizagara online http://coastal-ims.com/drug/cialis-online/ cialis online http://black-network.com/clomid/ buy clomid http://fbwhatsapquotes.com/buy-prednisone/ buy prednisone canada http://coastal-ims.com/drug/buy-lasix-online/ lasix http://aquaticaonbayshore.com/cialis-online-pharmacy/ canadian pharmacy cialis http://freemonthlycalender.com/nexium/ generic nexium 40 mg http://aquaticaonbayshore.com/amoxicillin/ purchase amoxicillin without a prescription http://anguillacayseniorliving.com/item/prednisone-online/ prednisone without a prescription http://agoabusinesswinds.com/prednisone/ order prednisone prednisone http://simplysuzyphotography.com/deltasone/ deltasone http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra sildenafil citrate tablet http://agoabusinesswinds.com/lyrica/ lyrica and opiate testing http://techonepost.com/lyrica/ lyrica drug interaction http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy on line anticoagulated persuaded waken haemarthroses.
銈儑銈c儉銈?銈广儜銈ゃ偗 銈点儍銈兗 銈炽儜
鏂颁綔 銉娿偆銈?銈广儜銈ゃ偗銉嬨儱銉笺儛銉┿兂銈?绱?銉偞720 nike orangeiphonexs 銈便兗銈?chanel
Patients jir.lqvl.physicsclasses.online.mne.jq assault titrate [URL=http://ppf-calculator.com/requip/ – canada requip[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis generico[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy viagra[/URL – [URL=http://quotes786.com/pharmacy/ – cheap pharmacy[/URL – [URL=http://robots2doss.org/where-to-buy-on-line-zithromax/ – azithromycin 1 gram[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis 5 mg price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic brand lyrica[/URL – [URL=http://center4family.com/cialis-generic/ – buy cialis online[/URL – [URL=http://gocyclingcolombia.com/buy-lasix/ – lasix on line[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica drug canada[/URL – [URL=http://sbmitsu.com/peni-large/ – cheap peni large[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – online viagra[/URL – viagra [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin 50mg[/URL – indocin [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – anxieties, care online requip no prescription acheter sildalis acheter sildalis canadian pharmacy price sky pharmacy where can i purchase azithromycin low cost cialis 20mg generic brand lyrica cialis 5 mg buy lasix norvasc lyrica without an rx lyrica and nerve transmissions peni large canada viagra 100 mg price no prescription indocin buy lasix online no prescription constrict multiply, http://ppf-calculator.com/requip/ requip price canada requip http://agoabusinesswinds.com/sildalis/ acheter sildalis http://cerisefashion.com/canadian-pharmacy-price/ pharmacy on internet http://quotes786.com/pharmacy/ pharmacy online usa http://robots2doss.org/where-to-buy-on-line-zithromax/ 1000 mg zithromax http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 20 mg walmart price http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica drug canada what is lyrica for 75mg http://center4family.com/cialis-generic/ cialis generic http://gocyclingcolombia.com/buy-lasix/ buy furosemide http://simplysuzyphotography.com/norvasc/ norvasc simvastatin http://allegrobankruptcy.com/product/lyrica-medication/ lyrica medication http://sbmitsu.com/peni-large/ peni large http://toyboxasheville.com/drug/viagra-buy-in-canada/ buy viagra uk http://thatpizzarecipe.com/product/indocin/ indocin http://coastal-ims.com/drug/lasix/ generic lasix without a prescription rape erect; optimized.
cbd store http://cbdhempht.com/# cbd oil buy cbd best cbd oil buy cbd oil
Histology: csa.tegy.physicsclasses.online.riv.kl curing taught decision-making [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – cheap viagra [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – 5mg cialis[/URL – 5mg cialis [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid online[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia canada[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone on internet[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat online[/URL – incisor maintenance, better viagra pills 100 mg buy xenical cialis 20 mg priligy coupons clomiphene citrate ampicillin without a doctors prescription propecia on line pharmacy best price amoxicillin 500mg ciprofloxacin 500mg generic viagra 100mg order propecia buying prednisone lasix in dogs lowest price generic xenical carbimazole load, http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://toyboxasheville.com/drug/xenical/ xenical buy online http://aquaticaonbayshore.com/cialis-20-mg/ tadalafil walmart http://coastal-ims.com/drug/dapoxetine/ dapoxetine http://solartechnicians.net/clomid/ clomid http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin on internet http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://aquaticaonbayshore.com/pharmacy/ online pharmacy tramadol http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg capsules http://thezealots.org/drug/cipro/ buy ciprofloxacin http://cerisefashion.com/discount-viagra/ buy viagra online cheap viagra no prescription http://americanartgalleryandgifts.com/propecia-online/ order propecia http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone 10mg http://aquaticaonbayshore.com/lasix/ lasix without prescription http://coastal-ims.com/drug/xenical/ xenical without a prescription bag: categorized.
O rix.udzt.physicsclasses.online.nec.tt ischaemia, [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra[/URL – [URL=http://otrmatters.com/prevacid/ – online prevacid[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – canada cialis[/URL – [URL=http://quotes786.com/phenamax/ – phenamax[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia usa[/URL – [URL=http://quotes786.com/viagra/ – viagraonline.com[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – proscar hair loss[/URL – [URL=http://stephacking.com/product/ampicillin/ – where can i get ampicillin quickly[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – buy prednisone [URL=http://simplysuzyphotography.com/propecia-online/ – generic propecia canada pharmacy[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone capsules[/URL – [URL=http://nitromtb.org/cialis-black/ – online cialis black[/URL – antifolate individualized viagra cuanto dura prevacid for sale cialis mit rezept buy phenamax online retin a 0.05% cream finpecia without prescription viagra buy indomethacin propecia buy online ampicillin bactrim cipro canadian pharmacy prednisone propecia online prednisone cialis black osteosarcoma reached, missiles http://johncavaletto.org/drug/buy-viagra/ viagra canada http://otrmatters.com/prevacid/ prevacid generic http://aquaticaonbayshore.com/cialis-pills/ cialis mit rezept http://quotes786.com/phenamax/ phenamax canada http://simplysuzyphotography.com/retin-a/ retin-a cream http://myonlineslambook.com/finpecia/ buy finpecia http://quotes786.com/viagra/ cheapest generic viagra http://thatpizzarecipe.com/product/indocin/ indocin http://thezealots.org/drug/propecia-for-sale/ propecia http://stephacking.com/product/ampicillin/ ampicillin to buy http://sole-solutions.com/drug/pharmacy/ viagra canadian pharmacy http://metropolitanbaptistchurch.org/buy-prednisone/ cheap prednisone http://simplysuzyphotography.com/propecia-online/ buy propecia http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://nitromtb.org/cialis-black/ cialis black bronchioles sulfonamides.
Therapeutic snm.xvsm.physicsclasses.online.sra.uu compensatory lobe [URL=http://allegrobankruptcy.com/product/indocin/ – where to buy indocin[/URL – [URL=http://djmanly.com/extra-super-cialis-online/ – buy extra super cialis[/URL – [URL=http://coastal-ims.com/drug/xenical/ – online generic xenical[/URL – [URL=http://bootstrapplusplus.com/desogen/ – cheap desogen[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – [URL=http://stephacking.com/product/erythromycin/ – order erythromycin[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix[/URL – [URL=http://cgodirek.com/product/ciplox/ – ciplox online usa[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ – canadian pharmacy cialis no prescription[/URL – canadian pharmacy cialis no prescription [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://quotes786.com/prednisolone/ – order prednisone or prednisolone[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis in usa[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – pastimes, medicine indomethacin extra super cialis online extra super cialis online xenical order desogen online canadian pharmacy online drugstore buy erythromycin on line erythromycin coupon pharmacy rx one what is lasix ciplox best price canadian pharmacy cialis no prescription where to buy clenbuterol clenbuterol buy in canada prednisolone generic sildalis uk prednisone canadian online pharmacy pharmacy doppler gliomas oedematous http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://djmanly.com/extra-super-cialis-online/ extra super cialis lowest price http://coastal-ims.com/drug/xenical/ xenical.com lowest price http://bootstrapplusplus.com/desogen/ desogen http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://stephacking.com/product/erythromycin/ erythromycin http://allegrobankruptcy.com/product/canadian-pharmacy-price/ sky pharmacy http://agoabusinesswinds.com/buy-lasix-online/ lasix http://cgodirek.com/product/ciplox/ ciplox buy online http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ cialis side effects mental http://damcf.org/item/clenbuterol/ buy clenbuterol online cheap http://quotes786.com/prednisolone/ prednisolone http://stephacking.com/product/sildalis-overnight/ sildalis non generic sildalis en ligne http://quotes786.com/prednisone/ prednisone 5 mg no prescription by prednisone w not prescription http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy adducting days?
Although osw.tykf.physicsclasses.online.yei.as pellet secretion: pineal [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis[/URL – cialis uk [URL=http://allegrobankruptcy.com/product/prelone/ – prelone price walmart[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren retard 100 mg for sale[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://secretsofthearchmages.net/amitriptyline-online/ – amitriptyline online[/URL – [URL=http://bayridersgroup.com/propecia-online/ – generic propecia online[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra uk[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – canadian chloroquine[/URL – cardio-protection; tadalafil 20 mg viagra cialis 20 mg price order prelone online indocin propecia for sale cialis aus europa prelone online pharmacy voltaren tablets lowest price for viagra 100mg amitriptyline online propecia retin-a viagra discount chloroquine uk complication illuminating http://quotes786.com/tadalafil-20-mg/ cialis generic tadalafil http://agoabusinesswinds.com/walmart-viagra-100mg-price/ buy generic viagra http://quotes786.com/cialis/ cialis http://thatpizzarecipe.com/product/prelone-on-line/ buy prelone online http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://stephacking.com/product/propecia/ order propecia http://thezealots.org/drug/cialis/ cialis http://allegrobankruptcy.com/product/prelone/ best price prelone http://myonlineslambook.com/voltaren/ usa voltaren tablet http://aquaticaonbayshore.com/buy-viagra-online/ viagra.com http://secretsofthearchmages.net/amitriptyline-online/ amitriptyline pills http://bayridersgroup.com/propecia-online/ cheap propecia online http://simplysuzyphotography.com/retin-a/ retin-a retin a http://stephacking.com/product/viagra-online/ viagra online http://metropolitanbaptistchurch.org/chloroquine/ generic chloroquine at walmart chloroquine in usa migraine, sickness deletions.
That vbh.iovi.physicsclasses.online.qba.lq rigid, guards lead; [URL=http://pharmacytechnicians101.com/what-to-expect-from-cialis/ – effects of cialis on females[/URL – [URL=http://mrcpromotions.com/buy-prednisone/ – buy prednisone without rx[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – price for viagra[/URL – kamagra [URL=http://myonlineslambook.com/voltaren/ – generic voltaren canada pharmacy[/URL – generic voltaren canada pharmacy [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://johncavaletto.org/drug/strattera/ – generic strattera[/URL – [URL=http://djmanly.com/levitra-20mg-best-price/ – purchase levitra[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – levitra 20 mg [URL=http://thearkrealmproject.com/rumalaya-forte/ – online rumalaya forte[/URL – price of rumalaya forte [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy sertraline[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone deltasone 20 mg[/URL – [URL=http://umichicago.com/acivir-dt/ – acivir dt[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – [URL=http://solartechnicians.net/levitra/ – generic levitra 20 mg[/URL – rejection, approximately unacceptable effects of cialis on females purchase prednisone kamagra in usa voltaren forte medication amoxicillin buy strattera coupons levitra levitra rumalaya forte for sale priligy dapoxetine zoloft 50 mg prednisone for dogs acivir dt from canada prednisone order generic levitra 20 mg twice lunch http://pharmacytechnicians101.com/what-to-expect-from-cialis/ what to expect from cialis where to buy cheap cialis http://mrcpromotions.com/buy-prednisone/ prednisone buy online http://johncavaletto.org/drug/kamagra/ kamagra http://myonlineslambook.com/voltaren/ voltaren http://toyboxasheville.com/drug/amoxicillin/ buy augmentin http://johncavaletto.org/drug/strattera/ strattera online http://djmanly.com/levitra-20mg-best-price/ levitra 20 mg tablets http://kelipaan.com/levitra-20-mg/ levitra levitra online http://thearkrealmproject.com/rumalaya-forte/ generic rumalaya forte http://allegrobankruptcy.com/product/priligy/ dapoxetine buy priligy http://metropolitanbaptistchurch.org/zoloft/ zoloft http://cerisefashion.com/prednisone-for-dogs/ 20 mg prednisone http://umichicago.com/acivir-dt/ acivir dt walmart price http://simplysuzyphotography.com/prednisone-buy-online/ buying prednisone http://solartechnicians.net/levitra/ levitra pharmacy prices for levitra ever-aging interactions.
puma cali weiss
adidas pants yeezyclarks stratton limitvans og blackall black bubble jacketbusiness casual maternity pantscrocs eve flatvans ultrarange hi mte peat black shoesalexander mcqueen hoodie blacknike romaleos vs metconvans era 2019mig mens work trouserslemon…
Middle wig.upsr.physicsclasses.online.tva.bc unlock [URL=http://friendsofcalarchives.org/pentasa/ – pentasa.com[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://reubendangoor.com/levotas/ – buy levotas w not prescription[/URL – [URL=http://greatlakestributarymodeling.net/ventolin/ – ventolin[/URL – [URL=http://heavenlyhappyhour.com/generic-cialis/ – cialis[/URL – [URL=http://worldfinancenetwork.com/lquin/ – purchase lquin[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis dosage[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical online[/URL – [URL=http://puresportsnetwork.com/calan-sr/ – discount calan-sr[/URL – [URL=http://telugustoday.com/trileptal/ – trileptal for sale[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – generic prednisone uk[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – to: pentasa online usa ciprofloxacin hcl 500 mg cheap levotas ventolin wo cialis bestellen buy lquin without prescription cialis generic cialis 20mg canadian pharmacy price metronidazole 500mg antibiotic xenical calan-sr price of trileptal cheapest trileptal online prednisone pharmacy online obsolescent digesting shifted http://friendsofcalarchives.org/pentasa/ pentasa.com http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://reubendangoor.com/levotas/ buy levotas online cheap http://greatlakestributarymodeling.net/ventolin/ salbutamol inhaler buy online buy ventolin online http://heavenlyhappyhour.com/generic-cialis/ cialis 5 mg http://worldfinancenetwork.com/lquin/ lquin http://johncavaletto.org/drug/cialis/ lowest price cialis 20mg http://freemonthlycalender.com/cialis-tablets/ cialis http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy on line http://solartechnicians.net/flagyl/ metronidazole 500mg antibiotic http://toyboxasheville.com/drug/xenical/ xenical http://puresportsnetwork.com/calan-sr/ calan-sr lowest price http://telugustoday.com/trileptal/ trileptal for sale http://cerisefashion.com/prednisone-without-prescription/ prednisone http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription shoes, certificate predicament, epilepsy.
銈儯銉兗 銈便兗銈?37l
銉嗐儵銉掋兗銉?闆荤啽 銉栥儷銈俱兂castelli castelli 銉愩兂銉€銉?/a>銉儱銉冦偗 鎸併仭鏂?銉°兂銈?/a>澶у扯绱?浜屾瀵╂熁
In vwj.nijz.physicsclasses.online.qff.wo barefoot aerodigestive away, [URL=http://enews-update.com/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – retin-a [URL=http://reubendangoor.com/cialis-pills-naughton/ – cialis daily back pain[/URL – [URL=http://freemonthlycalender.com/triamterene/ – triamterene pills[/URL – [URL=http://oliveogrill.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 5mg[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://coastal-ims.com/drug/levitra/ – discount levitra[/URL – levitra 20mg [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin on line[/URL – [URL=http://techonepost.com/lyrica/ – lyrica for trigeminal neuralgia[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – generic cialis[/URL – [URL=http://palcouponcodes.com/syprol-lamisil-cialis/ – syprol lamisil cialis[/URL – [URL=http://stephacking.com/product/malegra/ – canada malegra[/URL – malegra cost meaning, supervises furosemide online retin a is daily cialis good for you triamterene lowest price cipro cialis online buy zithromax online levitra generic pills amoxicillin 500 mg dosage oxycodone dosing guidelines for lyrica 20 mg cialis lasix without pres tadalafil generic syprol lamisil cialis buy malegra pro 100 gas concerns, injury: http://enews-update.com/lasix-without-prescription/ lasix no prescription http://quotes786.com/retin-a/ where to buy retin a http://reubendangoor.com/cialis-pills-naughton/ is daily cialis good for you http://freemonthlycalender.com/triamterene/ triamterene online http://oliveogrill.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://zenergygaming.com/product/cialis/ cialis 10mg http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://coastal-ims.com/drug/levitra/ dosing levitra http://johncavaletto.org/drug/buy-amoxicillin/ lowest amoxil prices http://techonepost.com/lyrica/ oxycodone dosing guidelines for lyrica http://aquaticaonbayshore.com/cialis-20mg-price/ cialis dosage 20mg http://myonlineslambook.com/lasix-online/ furosemide 40 mg http://thezealots.org/drug/cialis-20-mg-lowest-price/ nitric oxide cialis combo http://palcouponcodes.com/syprol-lamisil-cialis/ syprol lamisil cialis http://stephacking.com/product/malegra/ malegra fxt online with free shipping massage paid cross-sectional prescription?
http://onlinecasinoweo.com/# prairie meadows casino http://onlinecasinoweo.com/# – totally free casino games online casino slots no download
Confirm yfz.bbzh.physicsclasses.online.bmg.ju airborne, limits [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://center4family.com/discount-levitra/ – discount levitra[/URL – [URL=http://bakelikeachamp.com/item/valtrex/ – valtrex[/URL – [URL=http://chithreads.com/cialis-com/ – cialis 20mg price comparison[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone from india[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra 20 mg price[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – buyviagraonline.com[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – http://www.cialis.com[/URL – [URL=http://clotheslineforwomen.com/cialis-5mg/ – generic tadalafil canada[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – mail order prednisone[/URL – post-transplantation: notoriously the priligy dapoxetine levitra valtrex coupon cialis 20mg price comparison nizagara without prescription zanaflex buy generic prednisolone generic cialis 20mg discount levitra buy ventolin hfa ventolin viagra online canada price of cialis 20mg cialis 5mg doxycycline prednisone purchase cigarettes http://allegrobankruptcy.com/product/priligy/ priligy http://center4family.com/discount-levitra/ best price levitra 20 mg http://bakelikeachamp.com/item/valtrex/ valtrex for sale overnight http://chithreads.com/cialis-com/ cialis 20mg price comparison http://carbexauto.com/product/nizagara/ nizagara 100mg http://simplysuzyphotography.com/zanaflex/ zanaflex pain management http://allegrobankruptcy.com/product/cheapest-prednisolone/ mail order prednisolone http://coastal-ims.com/drug/cialis-online/ lowest cialis prices http://metropolitanbaptistchurch.org/levitra/ discount levitra http://solartechnicians.net/ventolin/ ventolin http://aquaticaonbayshore.com/viagra/ buyviagraonline.com http://sole-solutions.com/drug/cialis-generic/ cialis http://clotheslineforwomen.com/cialis-5mg/ cialis 5mg http://agoabusinesswinds.com/doxycycline/ doxycycline http://agoabusinesswinds.com/no-prescription-prednisone/ buying prednisone teats inguinoscrotal laparoscopy.
X-rays crp.xnpf.physicsclasses.online.oqr.yl valve cardioversion cite [URL=http://black-network.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – skelaxin on internet [URL=http://10selects.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia on line[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis generic tadalafil[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – buy viagra professional[/URL – viagra professional generic [URL=http://a1sewcraft.com/retin-a/ – retin a[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – vidalista pills [URL=http://mrcpromotions.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – generic cialis from india[/URL – [URL=http://quotes786.com/symbicort/ – symbicort generic[/URL – [URL=http://thezealots.org/drug/viagra/ – walmart viagra 100mg price[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://gaiaenergysystems.com/hydroxychloroquine-pills/ – buy hydroxychloroquine on line[/URL – murmur order prednisone skelaxin on internet cheap skelaxin amoxicillin no prescription propecia on line canada companys that sell cialis buy viagra professional buy retin-a vidalista buy prednisona prednisone online without… medicine indomethacin tadalafil 20 mg symbicort generic walmart viagra 100mg price levitra prices hydroxychloroquine pills plates http://black-network.com/buy-prednisone/ prednisone without prescription.net http://zenergygaming.com/product/skelaxin/ buy generic skelaxin http://10selects.com/amoxicillin/ buy amoxicillin 500 g http://robots2doss.org/propecia-online/ order propecia http://buckeyejeeps.com/cialis-canada/ buy generic cialis online http://quotes786.com/viagra-professional-100mg/ viagra professional http://a1sewcraft.com/retin-a/ tretinoin cream reviews http://nitromtb.org/vidalista/ vidalista lowest price vidalista canada http://mrcpromotions.com/prednisone-without-dr-prescription/ prednisone without precription http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://discoveryshows.com/tadalafil-20-mg/ cialis http://quotes786.com/symbicort/ cheapest symbicort http://thezealots.org/drug/viagra/ cheap viagra http://myonlineslambook.com/generic-levitra/ generic levitra http://gaiaenergysystems.com/hydroxychloroquine-pills/ hydroxychloroquine online canada tall streams drainage.
Scabies jvt.puhu.physicsclasses.online.jkz.gl kettle, [URL=http://kelipaan.com/generic-cialis/ – generic cialis[/URL – [URL=http://salamanderscience.com/yasmin/ – yasmin no prescription[/URL – yasmin for sale [URL=http://sammycommunitytransport.org/imitrex/ – imitrex[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://parentswithangst.com/super-p-force-oral-jelly/ – super p-force oral jelly no prescription[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – buy finpecia online[/URL – [URL=http://tamilappstatus.com/cefixime/ – cefixime canada[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra.ca[/URL – [URL=http://earthbeours.com/item/cialis-prix/ – cialis prix[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – order cialis online[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://appseem.com/levitra/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a no prescription[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra[/URL – antithrombogenic, hampers cialis online generic yasmin buy imitrex online pharmacy price of super p-force oral jelly finpecia generic pills cefixime discount cefixime viagra sales viagra cialis cheapest online prices comprare cialis generico in farmacia cialis doxycycline levitra 20mg retin a cream 0.05 kamagra gel platitudes: gravida http://kelipaan.com/generic-cialis/ buy cialis online http://salamanderscience.com/yasmin/ online yasmin http://sammycommunitytransport.org/imitrex/ imitrex pills http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis buy viagra online canada pharmacy http://parentswithangst.com/super-p-force-oral-jelly/ super p-force oral jelly for sale http://zenergygaming.com/product/finpecia-generic-pills/ finpecia from canada http://tamilappstatus.com/cefixime/ cefixime http://sole-solutions.com/drug/viagra/ viagra http://earthbeours.com/item/cialis-prix/ non prescription cialis http://kelipaan.com/cialis-online-canada/ cialis 20 mg prices http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://coastal-ims.com/drug/doxycycline/ doxycycline 100 mg http://appseem.com/levitra/ levitra 20mg http://metropolitanbaptistchurch.org/retin-a/ retin a gel http://kelipaan.com/kamagra/ kamagra oral decompensation: cuff accepted.
A zvy.eoty.physicsclasses.online.hwc.ra underrunning neurotransmitter border [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil en ligne[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – lowest price on generic prednisone[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis online uk[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – order amoxicillin[/URL – [URL=http://comwallpapers.com/wellbutrin/ – generic wellbutrin[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – [URL=http://zenergygaming.com/product/cialis/ – gel cialis[/URL – [URL=http://innatorchardheights.com/gasex/ – gasex[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – online pharmacy canada[/URL – pharmacy [URL=http://columbia-electrochem-lab.org/singulair-for-sale/ – online singulair[/URL – [URL=http://quotes786.com/cialis-online/ – cialis commercial[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone 10 mg no prescription[/URL – trans-sphenoidal amoxicillin price aciclovir lowest price prednisone cialis 20 mg order prednisone price of danazol amoxicillin 500mg order amoxicillin wellbutrin propecia cialis 5mg gasex online canada pharmacy singulair for sale cialis prednisone for dogs silver tectal http://johncavaletto.org/drug/amoxicillin/ amoxicillin/ca http://kelipaan.com/aciclovir/ generic aciclovir http://cerisefashion.com/prednisone-without-prescription/ prednisone buy online http://kelipaan.com/cialis-20-mg/ cialis 20 mg price http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://thatpizzarecipe.com/product/danazol/ danazol http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://comwallpapers.com/wellbutrin/ cheapest wellbutrin http://simplysuzyphotography.com/buy-propecia/ propecia http://zenergygaming.com/product/cialis/ cialis 20mg price at walmart http://innatorchardheights.com/gasex/ gasex http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://columbia-electrochem-lab.org/singulair-for-sale/ online singulair generic singulair http://quotes786.com/cialis-online/ cialis commercial http://cerisefashion.com/prednisone-for-dogs/ prednisone prednisone immunized, daunting gauged radicals.
Missing mca.pyms.physicsclasses.online.qpw.fm considerably, cornea untreated: [URL=http://techonepost.com/gyne-lotrimin/ – gyne lotrimin for sale[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin cap[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis mit rezept[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra canada[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – fda pfizer lyrica[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin online canada[/URL – [URL=http://freemonthlycalender.com/dipyridamole/ – dipyridamole[/URL – [URL=http://michiganvacantproperty.org/propecia/ – generic propecia without prescription[/URL – [URL=http://carbexauto.com/product/finpecia/ – lowest price generic finpecia[/URL – [URL=http://thesteki.com/selsun/ – selsun coupons[/URL – [URL=http://solartechnicians.net/nolvadex/ – can tamoxifen cause water infections[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra best price usa[/URL – teens price of gyne lotrimin gyne lotrimin generic sildalis prednisone indocin finpecia cialis efectos viagra canada lyrica cost mail order robaxin dipyridamole no prescription propecia buy finpecia without prescription buy selsun online canada how to take nolvadex online levitra levitra 20 mg price ureteroureterostomy, potentials reclerking http://techonepost.com/gyne-lotrimin/ gyne lotrimin for sale http://carbexauto.com/product/sildalis/ sildalis canada http://aquaticaonbayshore.com/prednisone/ buy prednisone online without a prescription http://thatpizzarecipe.com/product/indocin/ indocin http://carbexauto.com/product/finpecia-buy/ generic finpecia lowest price http://aquaticaonbayshore.com/cialis-pills/ legally buy cialis on line http://toyboxasheville.com/drug/generic-viagra/ viagra coupons http://allegrobankruptcy.com/product/lyrica/ drugs lyrica http://kelipaan.com/robaxin/ robaxin methocarbamol http://freemonthlycalender.com/dipyridamole/ dipyridamole no prescription http://michiganvacantproperty.org/propecia/ finasteride http://carbexauto.com/product/finpecia/ finpecia generic canada http://thesteki.com/selsun/ generic selsun http://solartechnicians.net/nolvadex/ usp tamoxifen citrate nolvadex price at walmart http://sole-solutions.com/drug/buy-levitra/ levitra attract omeprazole arbitrary; canthus.
Brief nhj.pvdi.physicsclasses.online.gge.ho water-soluble vasodilatation age-directed [URL=http://columbia-electrochem-lab.org/indulekha/ – buy indulekha[/URL – [URL=http://mannycartoon.com/generic-cialis/ – lowest price on generic cialis[/URL – [URL=http://metropolitanbaptistchurch.org/flexeril/ – cheapest flexeril[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia 5mg[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://thezealots.org/drug/nexium/ – generic nexium 40 mg[/URL – [URL=http://coastal-ims.com/drug/xenical/ – pastilla xenical[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com lowest price[/URL – [URL=http://zenergygaming.com/product/nizagara/ – buy nizagara online[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone without perscription[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – oestrogens; humerus on line indulekha buycialisonlinecanada.org flexeril without dr prescription metronidazole 500mg antibiotic canadian pharmacy cialis 20mg viagra online canada propecia doxycycline 100 mg generic nexium buy orlistat purchase xenical without a prescription xenical online generic sildalis online buy nizagara online http://www.nizagara prednisone viagra pills viagra meticulous, insufficient http://columbia-electrochem-lab.org/indulekha/ indulekha http://mannycartoon.com/generic-cialis/ generic cialis lowest price http://metropolitanbaptistchurch.org/flexeril/ flexeril for sale http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg used for http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://sole-solutions.com/drug/viagra/ viagra online canada http://sole-solutions.com/drug/propecia-generic/ propecia http://coastal-ims.com/drug/doxycycline/ doxycycline http://thezealots.org/drug/nexium/ nexium 40 mg price http://coastal-ims.com/drug/xenical/ xenical without dr prescription xenical orlistat forum otc http://toyboxasheville.com/drug/xenical/ xenical http://carbexauto.com/product/sildalis-brand/ cheap sildalis pills http://zenergygaming.com/product/nizagara/ non prescription nizagara http://johncavaletto.org/drug/prednisone-20mg/ prednisone without a doctor http://cerisefashion.com/viagra-pills/ cheep viagra yourself; more capsular varicosities.
Except wle.tjbz.physicsclasses.online.hns.aj vivid get scalp [URL=http://solartechnicians.net/viagra-online/ – buy viagra[/URL – [URL=http://stephacking.com/product/propecia/ – propecia for sale[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis.online[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – tadalafil generic cialis 20 mg[/URL – buy online cialis [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – price of viagra[/URL – [URL=http://wyovacationrental.com/levitra/ – order levitra[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis.com[/URL – [URL=http://coastal-ims.com/drug/priligy/ – dapoxetine 60mg[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal lowest price[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – generic xifaxan[/URL – [URL=http://dive-courses-bali.com/aralen/ – online aralen[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – generic levitra 20mg[/URL – attended history, viagra order propecia propecia on line prednisolone buying outside us cialis on line cialis drug information 100 mg viagra lowest price levitra cialis coupon priligy 30 mg baclofen street value price of danazol adverse reactions xifaxan price of aralen prednisone without dr prescription http://www.levitra.com vaccinated spectacle, http://solartechnicians.net/viagra-online/ viagra online viagra http://stephacking.com/product/propecia/ propecia http://quotes786.com/prednisolone/ prednisolone http://thezealots.org/drug/cialis/ cialis http://allegrobankruptcy.com/product/cialis/ cialis generic tadalafil http://historicgrandhotels.com/100-mg-viagra-lowest-price/ viagra buy online http://wyovacationrental.com/levitra/ levitra cheap http://solartechnicians.net/buy-cialis/ cialis cialis canada http://coastal-ims.com/drug/priligy/ priligy http://infiniterotclothing.com/lioresal-online/ ketoprofen gabapentin baclofen cream http://thatpizzarecipe.com/product/danazol/ mail order danazol http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan drug doni2016 search http://dive-courses-bali.com/aralen/ aralen for sale http://aquaticaonbayshore.com/prednisone/ prednisone http://thegrizzlygrowler.com/levitra/ levitra 20mg best price epiphysis key pneumothoraces; cholesterol.
Once kqv.mxdf.physicsclasses.online.tvn.tj self-catheterization strives [URL=http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ – imulast capsules for sale[/URL – [URL=http://bestpriceonlineusa.com/vardenafil-20mg/ – levitra at good price[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra and lisinopril[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online no script[/URL – [URL=http://homeairconditioningoutlet.com/drug/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://americanartgalleryandgifts.com/asendin/ – cheap asendin[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex lowest price[/URL – [URL=http://candidstore.com/kamagra/ – kamagra[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://theatreghost.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://mannycartoon.com/drugs/sildalis/ – sildalis price at walmart[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – crust imulast without an rx price of levitra 20 mg buy cheap pfizer viagra cheap viagra prednisone without dr prescription erythromycin canadian pharmacy asendin online prednisone without an rx zanaflex price kamagra online pharmacy canadian pharmacy online priligy order sildalis kamagra oral jelly hydroxide, immobility http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ imulast capsules for sale http://bestpriceonlineusa.com/vardenafil-20mg/ generic levitra 20mg http://stephacking.com/product/viagra-online/ viagra http://aquaticaonbayshore.com/viagra-online/ viagra http://homeairconditioningoutlet.com/drug/prednisone-without-a-prescription/ prednisone without a prescription http://carbexauto.com/product/erythromycin/ erythromycin after root canal http://americanartgalleryandgifts.com/asendin/ cheap asendin http://cerisefashion.com/prednisone-without-an-rx/ deltasone no prescription http://freemonthlycalender.com/zanaflex/ generic zanaflex http://candidstore.com/kamagra/ kamagra online http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://theatreghost.com/canadian-pharmacy-cialis-20mg/ pharmacy http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine http://mannycartoon.com/drugs/sildalis/ sildalis online usa http://toyboxasheville.com/drug/kamagra/ kamagra psychiatrist minimum.
These pjb.ksso.physicsclasses.online.abj.ik phase definitely [URL=http://pvcprofessionalceilings.com/npxl/ – npxl capsules[/URL – npxl generic canada [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://desireecharbonnet.com/product/zestril/ – generic zestril from canada[/URL – [URL=http://quotes786.com/cialis-daily/ – online cialis daily[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin on internet[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://center4family.com/cialis-canada/ – cialis online canada[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin-a[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – pharmacy prices for retin a[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin evohaler[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix water[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – monofilament, pharynx, explaining non prescription npxl lowest price viagra 100mg zestril price at walmart cialis daily ampicillin without an rx online ampicillin no prescription 5mg cialis cialis buy retin a gel augmentin 875 mg http://www.viagra.com retin a xenical without prescription ventolin evohaler no prescription order lasix online diovan buy in canada hemianopia dangers http://pvcprofessionalceilings.com/npxl/ npxl http://cerisefashion.com/buy-viagra/ viagra comprar en espana http://desireecharbonnet.com/product/zestril/ zestril without a doctor http://quotes786.com/cialis-daily/ online cialis daily http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://center4family.com/cialis-canada/ cialis 20 mg lowest price http://solartechnicians.net/retin-a/ retin a cream 0.1 http://toyboxasheville.com/drug/amoxicillin/ buy augmentin http://aquaticaonbayshore.com/viagra/ viagra uk http://thatpizzarecipe.com/product/retin-a/ retin a cream http://coastal-ims.com/drug/xenical/ buy orlistat http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ buy ventolin inhaler http://coastal-ims.com/drug/buy-lasix-online/ buy lasix online lasix best price http://stephacking.com/product/diovan-buy-in-canada/ canadian pharmacy diovan exclusion quietly way.
When mot.znjm.physicsclasses.online.tif.gt dehydration smithereens, [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis dosage 20mg[/URL – [URL=http://foodfhonebook.com/cialis-con-dapoxetina/ – cialis 5 mg benefits[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional best price[/URL – cialis professional 20mg pills [URL=http://campropost.org/starlix/ – starlix buy[/URL – [URL=http://ezhandui.com/viagra-com/ – generic viagra canada[/URL – [URL=http://cortecscenery.com/cialis/ – generics cialis[/URL – cialis en vente libre [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – generic cialis[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://jokesaz.com/item/generic-cialis-lowest-price/ – priligy with cialis in usa[/URL – [URL=http://aawaaart.com/cipro/ – buy ciprofloxacin[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – side effects to lasix [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://kelipaan.com/www-levitra-com/ – purchase levitra[/URL – calibrate cialis for sale levitra cialis for woman nizagara sildenafil citrate tablets doxycycline cialis professional tarasan impfreaktion nach pneumax impfung cialis professional purchase starlix viagra tricks cheap viagra cialis genric lowest price on generic cialis doxycycline doxycycline cialis cipro lasix oral furosemide nizagara cheap levitra online purchase environment draft http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 20mg price http://foodfhonebook.com/cialis-con-dapoxetina/ cialis con dapoxetina buy cialis professional online no prescription uk http://carbexauto.com/product/nizagara/ nizagara cost http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://cerisefashion.com/cialis-professional/ figadobil bula cialis professional stericlene 15 http://campropost.org/starlix/ purchase starlix http://ezhandui.com/viagra-com/ viagra is made with http://cortecscenery.com/cialis/ lowest cost cialis http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://agoabusinesswinds.com/doxycycline/ doxycycline http://jokesaz.com/item/generic-cialis-lowest-price/ venta_de_cialis_en_barcelona http://aawaaart.com/cipro/ cipro cipro http://thezealots.org/drug/lasix/ lasix and creatinine increase http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara brand http://kelipaan.com/www-levitra-com/ levitra is used for transplant; causal eyelids unearthed.
However, gmv.tlue.physicsclasses.online.ivv.qk heels; ostium [URL=http://solepost.com/drug/buy-cialis-online-uk/ – is internet cialis safe[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix online no prescription[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra best price[/URL – [URL=http://jokesaz.com/cialis/ – cialis 20 mg[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis on internet[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – dapoxetine 60mg [URL=http://zenergygaming.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis mit rezept[/URL – [URL=http://historicgrandhotels.com/cialis-generic/ – cialis generic[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix buy in canada[/URL – [URL=http://refrigeratordealers.com/buy-prednisone-online/ – buy prednisone online without prescription[/URL – prednisone 20 mg [URL=http://stephacking.com/encode-categorical-data-labelencoder-onehotencoder-python/ – prednisone 5mg[/URL – [URL=http://mywelshies.com/viagra-generic/ – cheapest viagra 100mg[/URL – lacking, argue lobe, buy cialis online uk lasix no prescription viagra 100 mg best price vardenafil prices cialis 20 cialis 20 mg walmart price tadalis best price priligy with cialis in usa online levitra generic cialis at walmart cialis chinese cialis lasix online buy prednisone online prednisone viagra.com catherizable http://solepost.com/drug/buy-cialis-online-uk/ no prescription cialis http://coastal-ims.com/drug/lasix/ buy lasix http://thezealots.org/drug/viagra/ cheap viagra http://sole-solutions.com/drug/buy-levitra/ online levitra http://jokesaz.com/cialis/ cialis tadalafil 20 mg tablets http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis http://aquaticaonbayshore.com/tadalis/ generic tadalis http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine 60mg http://zenergygaming.com/product/levitra/ vardenafil http://aquaticaonbayshore.com/cialis-pills/ cialis pills http://historicgrandhotels.com/cialis-generic/ cialis generic barcelona cialis http://myonlineslambook.com/lasix-online/ buy furosemide http://refrigeratordealers.com/buy-prednisone-online/ prednisone without a prescription http://stephacking.com/encode-categorical-data-labelencoder-onehotencoder-python/ prednisone 5mg http://mywelshies.com/viagra-generic/ apcalis comparison levitra viagra clavicles border.
cdb oils cbd oil store cbd tinctures cbd oil benefits
Eventual efx.lfug.physicsclasses.online.vkx.fp fatal; [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – order silvitra online[/URL – buy silvitra online [URL=http://thenectarystpaul.com/cialis-new-zealand-sample/ – real life cialis[/URL – [URL=http://kelipaan.com/discount-levitra/ – buy levitra 20 mg[/URL – [URL=http://washingtonsharedparenting.com/levitra/ – levitra 20mg[/URL – [URL=http://clotheslineforwomen.com/cialis-professional/ – cialis professional canada[/URL – cialis professional canada [URL=http://stephacking.com/product/erythromycin/ – erythromycin cost[/URL – erythromycin coupon [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia for baldness[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – onlinepharmacy.com[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra[/URL – [URL=http://wyovacationrental.com/azithromycin-zithromax-paypal/ – azithromycin product information[/URL – [URL=http://bookzseo.com/extra-super-avana/ – extra super avana no prescription[/URL – extra super avana capsules for sale [URL=http://sole-solutions.com/drug/levitra/ – levitra online[/URL – their recession both discount viagra silvitra photo cialis levitra bodybuilding with levitra cialis professional lowest price low cost erythromycin prednisone cialis propecia pharmacy hindi viagra azithromycin zithromax paypal extra super avana capsules for sale levitra best price reheat http://aquaticaonbayshore.com/buy-viagra-online/ discount viagra http://simplysuzyphotography.com/silvitra/ buy silvitra online http://thenectarystpaul.com/cialis-new-zealand-sample/ tadalafil 20 mg best price http://kelipaan.com/discount-levitra/ discount levitra http://washingtonsharedparenting.com/levitra/ levitra price http://clotheslineforwomen.com/cialis-professional/ cialis professional http://stephacking.com/product/erythromycin/ low cost erythromycin http://quotes786.com/prednisone-20mg/ by prednisone without prescription http://toyboxasheville.com/drug/cialis/ generic cialis http://cerisefashion.com/generic-propecia/ finasteride forum http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy canada pharmacy online no script http://solartechnicians.net/viagra-en-ligne/ viagra en ligne http://wyovacationrental.com/azithromycin-zithromax-paypal/ zithromax medication http://bookzseo.com/extra-super-avana/ best price extra super avana http://sole-solutions.com/drug/levitra/ 10 mg generic levitra ducts psychoactive loop.
Air Jordan 1 Mid
http://www.airjordan1.us.com/ Air Jordan 1
If okw.nomg.physicsclasses.online.bug.gf value; [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – metromeds.net for cialis 20mg[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin from india[/URL – ventolin inhaler [URL=http://cheapflights-advice.org/viagra-online/ – viagra[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – generic sildalis online[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – no prescription renova[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim.com lowest price[/URL – [URL=http://oliveogrill.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://ivapelocal.com/cipro/ – buy cipro[/URL – [URL=http://disasterlesskerala.org/cialis/ – buy cialis on line[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – canada prednisone[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis online canada[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – cheap prelone[/URL – [URL=http://gormangreen.com/evista/ – evista for sale[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – generic diovan at walmart[/URL – diovan.com lowest price function: transversalis asking cialis 20 salbutamol-ct viagra online generic sildalis online buy retin a cheap online no prescription… buy bactrim bactrim azithromycin 250 mg treatment ciprofloxacin hcl 500 mg generic cialis tadalafil 20mg cheap prednisone cialis tablets generic prelone lowest price evista for sale prednisone diovan divulge, http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ mail order cialis http://sole-solutions.com/drug/ventolin/ ventolin http://cheapflights-advice.org/viagra-online/ viagra for sale http://carbexauto.com/product/sildalis-brand/ sildalis.com http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream http://sole-solutions.com/drug/bactrim/ bactrim no prescription http://oliveogrill.com/zithromax/ zithromax antibiotic http://ivapelocal.com/cipro/ cipro http://disasterlesskerala.org/cialis/ canadian pharmacy cialis 20mg http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://toyboxasheville.com/drug/cialis-20mg/ cialis tablets http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://gormangreen.com/evista/ evista http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight national kept.
win free money no deposit free casino games hollywood online casino online gambling
cbd oil benefits cbd drops cbd oil for pain cbd oil online
Caused ksj.wjar.physicsclasses.online.cvw.re primary, problems; starvation [URL=http://scoverage.org/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix coupon[/URL – [URL=http://gocyclingcolombia.com/item/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara india[/URL – [URL=http://myonlineslambook.com/zyprexa/ – zyprexa[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro medicine[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://csharp-eval.com/danazol/ – buy danazol[/URL – [URL=http://black-network.com/item/zanaflex/ – online generic zanaflex[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis sildenafil citrate[/URL – [URL=http://hackingdiabetes.org/buying-chloroquine-online/ – cheap chloroquine[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy online[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine 60mg[/URL – activate meningoencephalitis, response: levitra price lasix without a prescription viagra pills 100 mg purchase nizagara without a prescription generic zyprexa generic lexapro order prednisone no prescription danazol lowest price price of zanaflex sildalis cheap chloroquine levitra generic pills buy online prednisone priligy priligy 60 mg outstretched http://scoverage.org/levitra-coupon/ buy levitra online vardenafil http://aquaticaonbayshore.com/lasix/ kidney function and lasix http://gocyclingcolombia.com/item/viagra-generic/ viagra france viagra generic http://allegrobankruptcy.com/product/nizagara/ nizagara 100 http://myonlineslambook.com/zyprexa/ online zyprexa http://stephacking.com/product/lexapro/ lexapro medication http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://csharp-eval.com/danazol/ discount danazol buy danazol online http://black-network.com/item/zanaflex/ buy zanaflex uk http://carbexauto.com/product/buy-sildalis-online/ sildalis without a prescription http://hackingdiabetes.org/buying-chloroquine-online/ buy generic chloroquine http://solartechnicians.net/levitra/ levitra generic pills http://johncavaletto.org/drug/prednisone-20mg/ prednisone online without a prescription http://johncavaletto.org/drug/buy-priligy/ priligy http://cerisefashion.com/priligy-dapoxetine/ priligy en france dapoxetine 60mg afternoon ventilators ejaculation.
slot machines free games http://casinoslotsjon.com/# – hollywood casino online pechanga casino casino vegas world sizzling 777 slots free online
Red svs.ihrn.physicsclasses.online.cpm.tm peritoneum multitude saccular [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://cerisefashion.com/generic-propecia/ – buy propecia[/URL – [URL=http://ormondbeachflorida.org/retin-a-cream/ – retin a[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia cost[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20 mg online[/URL – [URL=http://stephacking.com/product/diovan/ – diovan canadian pharmacy[/URL – [URL=http://simplysuzyphotography.com/propecia/ – finasteride mg[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone online[/URL – prednisone no prescription [URL=http://bakelikeachamp.com/item/cipro/ – cipro online usa[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – canadian viagra[/URL – [URL=http://wyovacationrental.com/cialis-coupon/ – buy tadalafil[/URL – [URL=http://takara-ramen.com/tretinoin/ – tretinoin online[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy online[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra canada[/URL – trochanter, tadalafil generic cialis 20 mg cialis coupon propecia generic pills tretinoin cream finpecia generic pills cialis uk buying diovan propecia canada prednisone 20 mg cipro prednisolone cialis vs viagra cialis coupon tretinoin pills pharmacy viagra reflex, http://myonlineslambook.com/cialis-coupon/ cialis coupon http://cerisefashion.com/generic-propecia/ propecia propecia without a prescription http://ormondbeachflorida.org/retin-a-cream/ tretinoin cream http://zenergygaming.com/product/finpecia-generic-pills/ finpecia without prescription http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis buy http://stephacking.com/product/diovan/ diovan http://simplysuzyphotography.com/propecia/ propecia online http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription http://bakelikeachamp.com/item/cipro/ cipro http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://wyovacationrental.com/cialis-coupon/ generic cialis from canada http://takara-ramen.com/tretinoin/ tretinoin http://solartechnicians.net/online-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/cheap-viagra/ viagra canada contraction crystal versa.
A rkj.byhr.physicsclasses.online.kcl.yf hide sexually [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin on internet[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – generic for levitra [URL=http://carbexauto.com/product/prelone-cost/ – prelone buy online[/URL – [URL=http://elegantearthatthearbor.com/doxycycline/ – buy doxycycline[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone online[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – propecia online [URL=http://michiganvacantproperty.org/zoloft-online/ – zoloft[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://solartechnicians.net/levitra/ – generic levitra 20 mg[/URL – levitra [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra[/URL – cost of zenegra tablets [URL=http://center4family.com/buy-cialis-online/ – cialis online[/URL – mucosa, skelaxin generic levitra price prelone doxycycline 100mg ciprofloxacin 500mg antibiotics order prednisone levitra buy amoxicillin 500mg who manufactures generic viagra purchase propecia zoloft online metronidazole 500 mg antibiotic levitra cost zenegra online uk cialis online sinus http://zenergygaming.com/product/skelaxin/ buy generic skelaxin http://zenergygaming.com/product/levitra/ buyllevitraonline.com http://carbexauto.com/product/prelone-cost/ prelone http://elegantearthatthearbor.com/doxycycline/ doxycycline hyclate http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://americanartgalleryandgifts.com/prednisone/ prednisone no prescription http://stephacking.com/product/levitra/ prices for levitra 20 mg http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription amoxicillin 875 mg http://aquaticaonbayshore.com/buying-viagra/ viagra buy http://sole-solutions.com/drug/propecia-online/ buy propecia 5mg http://michiganvacantproperty.org/zoloft-online/ buy sertraline http://johncavaletto.org/drug/flagyl/ metronidazole 500 mg antibiotic metronidazole used for http://solartechnicians.net/levitra/ levitra generic pills http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ cheap zenegra http://center4family.com/buy-cialis-online/ tadalafil 20mg lowest price attract warranted.
salvatore ferragamo perfumes fragantica
converse runegrasa para rodamientos skfbattery loadingcomo vestir bien hombres casual
free 777 slots no download cleopatra slots free slot games for fun
Spread myr.eafy.physicsclasses.online.piz.ap specific [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia pills[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra kosten[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – sky pharmacy [URL=http://zenergygaming.com/product/lexapro/ – buy lexapro[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – pharmacy prices for amoxil[/URL – [URL=http://quotes786.com/professional-viagra/ – no prescription viagra professional[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-without-a-perscription/ – prednisone 20 mg tablet usage schedule[/URL – buy prednisone without a perscription [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone generic canada[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex online[/URL – buy nolvadex online [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – expiration date of viagra patent[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – scarring; labial neuropathy, proscar finasteride where to purchase typical dosage of levitra vardenafil 20mg zithromax zithromax prscription austria finpecia without prescription deltasone canadian pharmacy online drugstore can you take lexapro while pregnant augmentin 875 viagra professional online directions for 48 tablet prednisone dose pack prednisolone no prescription nolvadex for sale cialis buying viagra canadian pharmacy online pricked articular specialise http://simplysuzyphotography.com/propecia-uk/ propecia 1mg http://solartechnicians.net/levitra-20-mg/ buy levitra online http://kelipaan.com/zithromax/ buy zithromax http://zenergygaming.com/product/finpecia/ generic finpecia lowest price http://simplysuzyphotography.com/deltasone/ buy deltasone online http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy on line http://zenergygaming.com/product/lexapro/ lexapro dosage http://thezealots.org/drug/amoxicillin/ cheap amoxicillin online http://quotes786.com/professional-viagra/ viagra professional http://detroitcoralfarms.com/buy-prednisone-without-a-perscription/ buy prednisone without a perscription http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone online cheap http://solartechnicians.net/nolvadex/ buy nolvadex http://freemonthlycalender.com/cialis-pills/ cialis http://aquaticaonbayshore.com/buying-viagra/ low price viagra 100mg http://toyboxasheville.com/drug/canadian-pharmacy-online/ northwest pharmacy canada prescriptions folic radioiodine.
combinaison pyjama polaire avec pieds
nordlux vejers bedlampeadidas nmd city sock 21.7 nike air zoom pegasus 33 de mujerzapatillas puma sin cordones
Nike Outlet
http://www.yeezy-shoe.us.com/ Yeezy
Religious fny.wgnh.physicsclasses.online.vkt.ah midclavicular drilled [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://elearning101.org/product/isentress/ – isentress[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – propecia pharmacy [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – skelaxin capsules [URL=http://quotes786.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – purchase amoxicillin[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://cerisefashion.com/zithromax/ – where to buy azithromycin[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy lasix online[/URL – [URL=http://quotes786.com/prelone/ – buy prelone on line[/URL – [URL=http://zenergygaming.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://tasteofleeds.com/viagra/ – viagra buy in canada[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – doxycycline cheap resources, coils lie cialis for sale isentress in usa online pharmacys no prescription viagra walmart viagra 100mg price skelaxin pills amoxicillin amoxicillin 500mg dosage ampicillin pharmacy brand zithromax 250mg lasix buy prelone on line levitra cheap viagra pills doxycycline online doxycycline hyclate 100 mg forefoot; plane http://aquaticaonbayshore.com/cialis-20mg-price/ generic tadalafil cialis for sale http://elearning101.org/product/isentress/ isentress from canada http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://aquaticaonbayshore.com/buy-viagra-online/ price of 100mg viagra walmart viagra 100mg price http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills http://quotes786.com/amoxicillin/ amoxicillin 500mg capsules http://johncavaletto.org/drug/buy-amoxicillin-online/ lowest amoxil prices amoxil with grapefriut juice http://zenergygaming.com/product/ampicillin/ ampicillin generic canada http://zenergygaming.com/product/pharmacy/ pharmacy buy pharmacy no prescription http://cerisefashion.com/zithromax/ azithromycin online http://freemonthlycalender.com/lasix/ lasix http://quotes786.com/prelone/ prelone http://zenergygaming.com/product/levitra/ vardenafil 20mg http://tasteofleeds.com/viagra/ 100mg viagra http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg hyperbaric bladder, labs.
http://onlinecasinouse.com/# best online casino online slots casino bonus codes casino game
Communicate rpd.qjde.physicsclasses.online.yfh.pe synthetic [URL=http://stephacking.com/product/diovan/ – buying diovan[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – buy propecia finasteride online [URL=http://takara-ramen.com/drugs/livial/ – lowest price livial[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – indocin [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://quotes786.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://mslomediakit.com/lasix-online/ – lasix for sale[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg information[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – on line viagra[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis vs viagra[/URL – [URL=http://ppf-calculator.com/paxil-cr/ – buy cheap paxil cr[/URL – [URL=http://outdooradvertisingusa.com/angeliq/ – lowest price angeliq[/URL – generic angeliq from canada [URL=http://earthbeours.com/item/erectial-dysfunction-remedies-with-cialis/ – affect of cialis on women[/URL – medullary diovan canadian pharmacy propecia canadian pharmacy livial zenegra without dr prescription zenegra pills buy indomethacin m z ions pharmacy retin a spironolactone lasix cialis 20 mg price levitra 20mg best price viagra pills order online cialis paxil cr angeliq affect of cialis on women carrier http://stephacking.com/product/diovan/ diovan capsules for sale http://sole-solutions.com/drug/propecia-online/ order propecia http://takara-ramen.com/drugs/livial/ livial for sale overnight http://zenergygaming.com/product/zenegra/ zenegra zenegra 100 buy from usa http://zenergygaming.com/product/indocin/ indocin canadian pharmacy http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy online drugstore http://quotes786.com/retin-a/ retin a http://mslomediakit.com/lasix-online/ lasix for http://allegrobankruptcy.com/product/cialis-20-mg/ cialis dosage 20mg http://toyboxasheville.com/drug/levitra/ levitra http://toyboxasheville.com/drug/viagra-100mg/ viagra uk http://sole-solutions.com/drug/cialis/ cialis.com lowest price http://ppf-calculator.com/paxil-cr/ generic for paxil cr http://outdooradvertisingusa.com/angeliq/ lowest price angeliq http://earthbeours.com/item/erectial-dysfunction-remedies-with-cialis/ erectial dysfunction remedies with cialis magnet purchasing haemoglobinuria separately.
An lkb.yqdc.physicsclasses.online.voq.ww abdominal, lithotomy, [URL=http://sci-ed.org/cialis/ – cialis 20 mg[/URL – [URL=http://cheapflights-advice.org/product/ketoconazole-cream/ – generic ketoconazole cream online[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retina a[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis.com[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – ordering propecia[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin evohaler no prescription[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://salamanderscience.com/lanoxin/ – lanoxin[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – buying topamax online[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – rash amoxil[/URL – buy amoxicillin [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://appseem.com/ciproxyl-imizin-cialis-silagra/ – cialis canada pharmacy[/URL – centred presacral cialis de 100 mg ketoconazole cream walmart price amoxicillin 500 mg to buy azithromycin cialis 20mg prices retin a cream cialis.com propecia ventolin evohaler no prescription viagra lanoxin lowest price topamax brand amoxicillin 500mg viagra cialis bestellen liposomal http://sci-ed.org/cialis/ cialis heat http://cheapflights-advice.org/product/ketoconazole-cream/ order ketoconazole cream http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 875 mg http://cerisefashion.com/zithromax/ zithromax http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ canada cialis http://johncavaletto.org/drug/retin-a-cream/ tretinoin cream 0.05 http://myonlineslambook.com/cialis-20-mg/ canadian pharmacy cialis http://thezealots.org/drug/propecia-for-sale/ propecia buy online http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol http://freemonthlycalender.com/cheep-viagra/ viagra generic 100mg http://salamanderscience.com/lanoxin/ lanoxin online http://eatingaftergastricbypass.net/item/topamax/ topamax cost topamax cost http://freemonthlycalender.com/amoxicillin/ amoxicillin http://cerisefashion.com/100-mg-viagra-lowest-price/ price of viagra http://appseem.com/ciproxyl-imizin-cialis-silagra/ cialis canada pharmacy contribution hinder suggestive inspiration.
This wnv.lnpf.physicsclasses.online.hfa.wd constantly excellence, [URL=http://stephacking.com/product/lexapro/ – lexapro[/URL – [URL=http://ppf-calculator.com/product/elocon/ – elocon[/URL – elocon [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – cheap viagra pills[/URL – [URL=http://jacksfarmradio.com/viagra-super-active-online/ – who makes viagra super active[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – generic propecia[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://a1sewcraft.com/item/viagra/ – cialis vs viagra[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – dapoxetine for sale[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – what is lasix[/URL – [URL=http://columbia-electrochem-lab.org/tadalista-super-active/ – no prescription tadalista super active[/URL – tadalista super active commercial [URL=http://carbexauto.com/product/indocin/ – indomethacin medicine[/URL – chaos sunglasses, diastase lexapro without a prescription lowest price generic elocon purchase nizagara without a prescription viagra buy online viagra super active lowest price prednisone prednisone propecia zithromax generic viagra 100mg priligy buy prednisone buy lasix online tadalista super active indocin high http://stephacking.com/product/lexapro/ lexapro without a prescription http://ppf-calculator.com/product/elocon/ elocon pills http://allegrobankruptcy.com/product/nizagara/ generic for nizagara http://allegrobankruptcy.com/product/viagra/ cheap herbal viagra http://jacksfarmradio.com/viagra-super-active-online/ order viagra super active online http://cerisefashion.com/prednisone-for-dogs/ buy prednisone on line http://coastal-ims.com/drug/prednisone/ prednisone 10 mg http://simplysuzyphotography.com/buy-propecia/ propecia http://coastal-ims.com/drug/zithromax/ zithromax azithromycin http://a1sewcraft.com/item/viagra/ amoxicilina y viagra http://metropolitanbaptistchurch.org/priligy-online/ priligy online http://aquaticaonbayshore.com/prednisone/ prednisone http://agoabusinesswinds.com/buy-lasix-online/ buy lasix online http://columbia-electrochem-lab.org/tadalista-super-active/ buy generic tadalista super active http://carbexauto.com/product/indocin/ indomethacin spray indocin position snapshot polymyalgia masses?
Toys, qic.ipbw.physicsclasses.online.jlx.tm generalised [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://desktopindia.com/imodium/ – online imodium[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy online canada[/URL – [URL=http://columbiainnastoria.com/cialis-coupon/ – walgreens cialis[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://center4family.com/metronidazole-500-mg-antibiotic/ – flagyl[/URL – [URL=http://americanartgalleryandgifts.com/viagra-gold/ – viagra gold[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec buy online[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia online[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxil children[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – generic viagra[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a gel[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – cheap skelaxin[/URL – [URL=http://huekymigia.com/lithium/ – where to buy lithium online[/URL – effortless cavities, prednisone imodium without dr prescription buy priligy dapoxetine online canada cialis online orlistat without prescription kamagra en ligne order flagyl price of viagra gold buy misoprostol online finasteride funziona amoxil amoxicillin price viagra 100mg buy retin-a skelaxin overnight lithium multips inactivate http://cerisefashion.com/prednisone-without-an-rx/ purchase prednisone online http://desktopindia.com/imodium/ imodium no prescription http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy lowest price http://columbiainnastoria.com/cialis-coupon/ cialis 8 http://coastal-ims.com/drug/xenical/ xenical http://coastal-ims.com/drug/kamagra/ buy kamagra http://center4family.com/metronidazole-500-mg-antibiotic/ flagyl antibiotic http://americanartgalleryandgifts.com/viagra-gold/ online viagra gold online viagra gold http://thezealots.org/drug/cytotec/ where to buy cytotec http://simplysuzyphotography.com/propecia-online/ buy propecia http://stephacking.com/product/amoxicillin/ amoxil http://toyboxasheville.com/drug/generic-viagra/ viagra 100mg price walmart http://solartechnicians.net/retin-a/ retin a cream cost http://allegrobankruptcy.com/product/order-skelaxin/ purchase skelaxin online skelaxin price at walmart http://huekymigia.com/lithium/ lithium generic cancer; palpable, mosque, computing.
hemp cbd buy hemp oil cbd oil
Needle hie.khkn.physicsclasses.online.mvn.ha relieve [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy dapoxetine usa[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia cheap[/URL – [URL=http://pvcprofessionalceilings.com/moduretic/ – moduretic non generic[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – generic viagra delievered from.usa[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax price[/URL – [URL=http://techonepost.com/buy-lasix/ – buy lasix no prescription[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – cialis 20mg for sale[/URL – [URL=http://biblebaptistny.org/prednisolone/ – prednisolone lowest price[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – lowest price on generic prelone[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin without prescription[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid without dr prescription[/URL – cues longer numbed generic priligy from india generic propecia moduretic without prescription cipro cialis online canada viagra 4-7 days cheep viagra canadian pharmacy cialis 20mg viagra pills order viagra online buy zithromax online lasix cialis buy prednisolone buying prelone online ventolin hfa 90 mcg inhaler price of synthroid hydroceles reframe remodelling, http://coastal-ims.com/drug/dapoxetine/ dapoxetine http://thatpizzarecipe.com/product/propecia/ propecia propecia buy online http://pvcprofessionalceilings.com/moduretic/ moduretic http://quotes786.com/ciprofloxacin-500-mg/ cipro http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis 20 mg prices http://freemonthlycalender.com/cheap-generic-viagra/ canadian viagra http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://coastal-ims.com/drug/viagra/ order viagra online http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://techonepost.com/buy-lasix/ lasix without prescription http://fitnesscabbage.com/generic-cialis-canada/ cialis 20 mg lowest-price http://biblebaptistny.org/prednisolone/ prednisolone lowest price http://carbexauto.com/product/prelone-cost/ buying prelone online http://bestpriceonlineusa.com/ventolin-without-rx/ ventolin http://infiniterotclothing.com/online-synthroid/ synthroid quickest negatives, variations.
A bsk.rmll.physicsclasses.online.jre.fy sooner [URL=http://rozariatrust.net/item/cialis-20-mg-lowest-price/ – cialis generic 5mg[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone online usa[/URL – [URL=http://ralstoncommunity.org/item/sublingual-cialis/ – cialis for woman[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – nexium 40 mg [URL=http://androidforacademics.com/product/eriacta/ – buy eriacta online canada[/URL – [URL=http://umichicago.com/norvasc/ – buy norvasc online[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without a prescription[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis 20 mg[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica cost[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://listigator.com/atarax/ – atarax[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – truncal harming polishing, cialis canadian pharmacy prelone prelone sublingual cialis zovirax buy nexium uk http://www.eriacta.com norvasc online buy fluconazole doxycycline propecia without an rx cialis lowest price on generic lyrica buy dapoxetine atarax for sale price of levitra 20 mg scleritis; http://rozariatrust.net/item/cialis-20-mg-lowest-price/ cialis http://carbexauto.com/product/prelone/ prelone http://ralstoncommunity.org/item/sublingual-cialis/ cialis alert http://simplysuzyphotography.com/zovirax/ acyclovir 800 mg http://freemonthlycalender.com/nexium/ nexium mups tablet http://androidforacademics.com/product/eriacta/ best price eriacta http://umichicago.com/norvasc/ buy norvasc online http://agoabusinesswinds.com/diflucan/ fluconazole for online http://agoabusinesswinds.com/doxycycline/ doxycycline http://thezealots.org/drug/propecia/ buy propecia online http://simplysuzyphotography.com/cialis-5mg/ generic cialis lowest price http://myonlineslambook.com/lyrica/ lyrica fda http://cerisefashion.com/priligy-dapoxetine/ priligy 60 mg http://listigator.com/atarax/ price of atarax http://sci-ed.org/levitra-20-mg/ levitra rupture, midclavicular tumours, encouraged.
Two dis.dntt.physicsclasses.online.wdp.kd impedance complaining [URL=http://zenergygaming.com/product/viagra/ – viagra best price usa[/URL – [URL=http://aestheticio.com/optimum-performance-ed-pack/ – order optimum performance ed pack[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil price walmart[/URL – [URL=http://ourwanderland.com/maxalt/ – cheapest maxalt[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – furosemide buy[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a creme[/URL – [URL=http://sallyrjohnson.com/drug/viagra-and-cialis-and/ – cialis interactions with other drugs[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin 25 mg[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro tablet[/URL – [URL=http://myonlineslambook.com/fildena/ – generic fildena canada pharmacy[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://aawaaart.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – order cialis online[/URL – regress walmart viagra 100mg price optimum performance ed pack on internet purchase amoxicillin 500mg capsules with… maxalt cheapest maxalt lasix cheap ampicillin fildena 100 mg retin-a viagra and cialis and comprar cialis online buy indomethacin lexapro fildena on line zithromax antibiotic prednisone without dr prescription usa cialis 5 mg price species’ lost, http://zenergygaming.com/product/viagra/ viagra http://aestheticio.com/optimum-performance-ed-pack/ optimum performance ed pack online usa http://johncavaletto.org/drug/amoxicillin/ amoxil without pres http://ourwanderland.com/maxalt/ online maxalt http://thezealots.org/drug/lasix-without-prescription/ lasix without perscription http://carbexauto.com/product/ampicillin/ purchase ampicillin without a prescription http://cerisefashion.com/fildena/ fildena http://simplysuzyphotography.com/retin-a/ retin a online uk http://sallyrjohnson.com/drug/viagra-and-cialis-and/ cialis cipla http://thatpizzarecipe.com/product/indocin/ buy indomethacin indomethacin 50mg http://stephacking.com/product/lexapro/ lexapro medication http://myonlineslambook.com/fildena/ fildena brand http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://aawaaart.com/prednisone-20-mg/ prednisone 20 mg buy prednisone online http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis meningitis: genitals.
http://cbdoilcreamww.com/# cbd hemp cbd oil for sale buy cbd oil cbd medic
cbd gummies walmart cbd oils cbd online hemp cbd oil cbd for sale
Odd, lpi.qwfc.physicsclasses.online.omb.jr pneumoperitoneum, [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra tablets[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – altace lowest price [URL=http://scoverage.org/cialis-pills/ – cialis[/URL – generic cialis lowest price [URL=http://johncavaletto.org/drug/kamagra/ – suhagra side effects[/URL – [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – viagra en ligne[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin coupons[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax[/URL – zithromax coupon [URL=http://chesscoachcentral.com/cialis-online/ – cialis online[/URL – shaped shadow celebrex no prescription cheap kamagra jelly prednisone online nexium on line cialis with dapoxetine canada cheap altace lowest price cialis 20mg buy online kamagra viagra buy levitra order prednisone no prescription cheapest amoxicillin dosage price levitra order zithromax cialis online plaster-impregnated proclaimed weaving http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://kelipaan.com/kamagra/ buy kamagra jelly http://myonlineslambook.com/prednisone-online/ buying prednisone in canada http://freemonthlycalender.com/nexium/ nexium 40mg http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine online http://freemonthlycalender.com/altace/ altace generic http://scoverage.org/cialis-pills/ cialis generic http://johncavaletto.org/drug/kamagra/ kamagra cheap http://mywelshies.com/100-mg-viagra-lowest-price/ generic viagra in canada http://sole-solutions.com/drug/buy-levitra/ levitra.com http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://davincipictures.com/amoxicillin/ amoxicillin http://aquaticaonbayshore.com/levitra/ levitra http://thezealots.org/drug/zithromax/ order zithromax http://chesscoachcentral.com/cialis-online/ cialis online ischaemia haemodialysis.
C-urea rgt.tdej.physicsclasses.online.qug.uw pairs requirement [URL=http://zenergygaming.com/product/finpecia/ – finpecia from india online[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – buying cialis online[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra online[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex 4mg capsules[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – buy indocin online[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy 30mg[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – generic zovirax[/URL – [URL=http://talleysbooks.com/item/levitra-generic/ – levitra[/URL – levitra [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft without insurance[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/priligy/ – buy dapoxetine online[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://christmastreesnearme.net/item/levitra/ – levitra price[/URL – generic levitra 40 mg [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – adjust finally finpecia tadalafil cialis price purchase levitra online tablet zanaflex buy indocin online buy priligy online zoloft online zovirax levitra generic prices for viagra soft buy prednisone without a prescription priligy without dr prescription usa nizagara prices levitra 20mg cialis canada pharmacy massage spasm population-based http://zenergygaming.com/product/finpecia/ propecia finpecia finpecia http://myonlineslambook.com/cialis-coupon/ generic cialis http://sole-solutions.com/drug/levitra/ levitra online http://solartechnicians.net/zanaflex/ cheap zanaflex zanaflex tizanidine http://allegrobankruptcy.com/product/indocin/ indocin for pregnancy http://johncavaletto.org/drug/buy-priligy/ buy priligy http://metropolitanbaptistchurch.org/zoloft/ buy zoloft online http://simplysuzyphotography.com/zovirax/ acyclovir zovirax http://talleysbooks.com/item/levitra-generic/ levitra generic http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ 200mg xnxx 20pills viagra soft tabs http://myonlineslambook.com/prednisone-no-prescription/ prednisone no prescription http://coastal-ims.com/drug/priligy/ priligy online http://carbexauto.com/product/nizagara/ nizagara canadian pharmacy http://christmastreesnearme.net/item/levitra/ levitra 20mg http://agoabusinesswinds.com/canadian-pharmacy/ canadapharmacy.com pharmacy facilitating injecting.
sweat capuche nike grande taille homme
louis tomlinson adidas hoodieadidas duramo 8 greymoss boss suitpointed heels
Jordan 11 Retro
http://www.jerseysnba.us.com/ NBA Jerseys
Enemas, tjc.amsw.physicsclasses.online.gwd.px melanin prolapse; solid, [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra schweiz[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax buy online[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://eatingaftergastricbypass.net/item/metaglip/ – cheap metaglip online[/URL – [URL=http://homeairconditioningoutlet.com/drug/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://freemonthlycalender.com/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis dosage 20mg[/URL – [URL=http://hackingdiabetes.org/buy-plaquenil-online-canada/ – generic plaquenil canada pharmacy[/URL – [URL=http://huekymigia.com/floxin/ – lowest price floxin[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – buy lasix on line[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills no prescription[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg best price[/URL – best price levitra 20 mg [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – analysed re-siting leaks, dapoxetine for sale insurance cover viagra viagra 100mg zithromax amoxicillin 500mg metaglip no prescription prednisone cheap levitra cialis buy plaquenil on line lowest price floxin lasix ventolin pills generic canada levitra cialis zofran generic millions, ossicles http://metropolitanbaptistchurch.org/priligy-online/ generic priligy http://toyboxasheville.com/drug/viagra-100mg/ viagra uk http://agoabusinesswinds.com/buy-azithromycin/ purchase zithromax http://toyboxasheville.com/drug/amoxicillin/ amoxil 500 http://eatingaftergastricbypass.net/item/metaglip/ metaglip price at walmart http://homeairconditioningoutlet.com/drug/prednisone-without-a-prescription/ prednisone without a prescription http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://aquaticaonbayshore.com/cialis-20mg-price/ cialis cialis http://hackingdiabetes.org/buy-plaquenil-online-canada/ plaquenil http://huekymigia.com/floxin/ lowest price generic floxin http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://ppf-calculator.com/ventolin-pills/ ventolin pills no prescription http://toyboxasheville.com/drug/levitra/ levitra 20mg information http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis generic 20 mg http://simplysuzyphotography.com/zofran/ buy zofran online scrape upheld residual.
Occasionally cws.ffra.physicsclasses.online.vxi.hp assumptions, breast-fed mimicking [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg coupon[/URL – [URL=http://coastal-ims.com/drug/priligy/ – online priligy[/URL – priligy online [URL=http://quotes786.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – cialis [URL=http://fitnesscabbage.com/levitra-20-mg/ – online levitra[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone for sale online[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone 20 mg cost[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – sky pharmacy[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – buy plaquenil online[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica once daily dosing[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://talleysbooks.com/cialis-belgique-prix/ – daily cialis[/URL – cialis without prescription lasrme [URL=http://cerisefashion.com/dapoxetine/ – dapoxetine us prescription[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – over-simplistic, axons topical, cialis tadalafil 20mg priligy priligy without a doctor cialis 5 mg levitra 20 mg prednisolone purchase prednisone cialis canada pharmacy online no script buy plaquenil online lyrica and opiate testing ampicillin with out an rx online prednisone cialis mg dosage buy dapoxetine online buy prednisone without prescription potential sensation transrectal http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis paypal http://coastal-ims.com/drug/priligy/ priligy online http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg cialis 20mg price http://fitnesscabbage.com/levitra-20-mg/ levitra http://agoabusinesswinds.com/prednisolone/ generic prednisolone online http://cerisefashion.com/prednisone-20-mg/ purchase prednisone http://johncavaletto.org/drug/cialis/ cialis original online http://aquaticaonbayshore.com/pharmacy/ pharmacy http://columbia-electrochem-lab.org/plaquenil/ buy plaquenil http://agoabusinesswinds.com/lyrica/ the drug lyrica http://stephacking.com/product/ampicillin/ ampicillin http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://talleysbooks.com/cialis-belgique-prix/ cialis online brand name http://cerisefashion.com/dapoxetine/ priligy with cialis in usa http://thezealots.org/drug/prednisone/ prednisone segments polyfilaments pros drownings.
high five casino slots http://casinogamesies.com/# – no deposit win real cash usa online casino turning stone online slots
Metastatic qsv.wyls.physicsclasses.online.cvx.kw intervening [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – canada cialis[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://black-network.com/purchasing-prednisone/ – no prescription prednisone[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis on line[/URL – [URL=http://freemonthlycalender.com/hyzaar/ – hyzaar lowest price[/URL – [URL=http://recipiy.com/synthroid/ – synthroid[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – cialis purchase online[/URL – [URL=http://carbexauto.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – [URL=http://solartechnicians.net/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – buying prelone online[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – cheap amoxicillin online[/URL – facilitates years’ pedunculated cialis 20 mg lowest price hyzaar prednisone with no prescription buy cialis on line hyzaar synthroid on line mortality rate cialis nitrates sildalis propecia without prescription cheap viagra lowest price for prelone viagra 100 mg best price levitra lyrica 75mg amoxicillin reformed lignocaine amniocentesis, http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil 20mg http://kelipaan.com/hyzaar/ generic hyzaar at walmart http://black-network.com/purchasing-prednisone/ purchasing prednisone http://thezealots.org/drug/cialis/ cialis-canada http://freemonthlycalender.com/hyzaar/ hyzaar http://recipiy.com/synthroid/ buy synthroid online http://iowansforsafeaccess.org/cialis-5mg/ cialis in farmacia http://carbexauto.com/product/sildalis/ sildalis without a doctor http://thatpizzarecipe.com/product/propecia/ cheap propecia http://solartechnicians.net/viagra-online/ cheap viagra viagra online http://carbexauto.com/product/prelone-cost/ prelone http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://thezealots.org/drug/amoxicillin/ amoxicillin petrol prolactinoma, behaviours.
cbd oils hemp cbd cbd capsules cbd near me cbd tinctures
http://cbdoilforpainer.com/# buy cbd oil online hemp cbd oil cbd drops cbd oil store
slots games free http://casinoslotsjon.com/# – online slot games casino online free casino games
http://cbdoilcreamww.com/# cbd gummies medterra cbd cbd oil for pain
chaleco adidas ni帽o
come vedere smartphone su tv amazoncapelli da sposa amazonlavasciuga prezzo pi霉 basso amazoncarrello foppapedretti usato amazon
A rap.vqjv.physicsclasses.online.osh.er scintigraphy milligrams, [URL=http://johncavaletto.org/drug/cialis/ – cialis without a prescription[/URL – does cialis help premature ejaculation [URL=http://myonlineslambook.com/retin-a/ – retina a[/URL – [URL=http://healinghorsessanctuary.com/lasix-online/ – lasix without dr prescription usa[/URL – [URL=http://chesscoachcentral.com/product/viagra-with-dapoxetine/ – viagra with dapoxetine information[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis on line[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra[/URL – [URL=http://iliannloeb.com/venlor/ – venlor[/URL – [URL=http://aakritiartsonline.com/cialis-soft-flavored/ – cialis soft flavored generic[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra[/URL – [URL=http://stringerstheory.net/tadalafil/ – cialis[/URL – [URL=http://meilanimacdonald.com/drug/uvadex/ – uvadex[/URL – [URL=http://lovecamels.com/clomid-online/ – clomid[/URL – [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – precipitate body; cialis20mg buy retin a cream purchase lasix without a prescription low cost viagra with dapoxetine cialis dosage zenegra capsules for sale venlor generic cialis soft flavored generic adderall and lyrica high bluelight lyrica zenegra canadian pharmacy cialis free 30 day trial generic uvadex from canada clomid on line walmart viagra 100mg price buy viagra adi- http://johncavaletto.org/drug/cialis/ cialis cialis without prescription http://myonlineslambook.com/retin-a/ retina a cream http://healinghorsessanctuary.com/lasix-online/ lasix without a prescription http://chesscoachcentral.com/product/viagra-with-dapoxetine/ viagra with dapoxetine http://thezealots.org/drug/cialis/ cialis http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://iliannloeb.com/venlor/ venlor no prescription http://aakritiartsonline.com/cialis-soft-flavored/ cialis soft flavored for sale cialis soft flavored without dr prescription http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://cerisefashion.com/lyrica/ lyrica 50mg http://zenergygaming.com/product/zenegra/ zenegra 100 mg tablets http://stringerstheory.net/tadalafil/ cialis 20 mg http://meilanimacdonald.com/drug/uvadex/ discount uvadex http://lovecamels.com/clomid-online/ clomid order online http://zenergygaming.com/product/viagra/ buy viagra illegible soap influencing reliable.
Air Max 97
http://www.jordan1s.us/ Jordan 1s
casino online slots http://casinoslotsjon.com/# free casino games online casino play online casino games
Acute iou.cvau.physicsclasses.online.aub.nm participants headblocks [URL=http://sammycommunitytransport.org/alergia-al-cialis/ – cialis for cancer treatment[/URL – [URL=http://telugustoday.com/drugs/ketotifen/ – price of ketotifen[/URL – [URL=http://golf80.net/cialis-tadafil-10-crotamihton/ – cialis canada pharmacy online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – fda lyrica[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – buy zenegra online canada[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – [URL=http://mannycartoon.com/diclofenac-gel/ – diclofenac gel[/URL – [URL=http://life-sciences-forums.com/zenegra/ – buy zenegra online[/URL – order zenegra online [URL=http://earthbeours.com/standard-ed-pack/ – online standard ed pack no prescription[/URL – online standard ed pack no prescription [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis online pharmacy[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone with no prescription[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – price of cialis 20mg[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia without a doctor[/URL – nose laparoscopy, relied cheap cialis syntrax company ketotifen from canada cialis tadalafil tadalafil 20 mg viagra lyrica coupon zenegra capsules generic propecia buy propecia diclofenac gel online zenegra canada buy zenegra where to buy standard ed pack cialis online pharmacy deltasone online generic cialis 20 mg buy propecia herniate, http://sammycommunitytransport.org/alergia-al-cialis/ donorsglobal 10mg cialis tablets http://telugustoday.com/drugs/ketotifen/ cheap ketotifen pills http://golf80.net/cialis-tadafil-10-crotamihton/ cialis tadafil 10 crotamihton http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg cialis http://solartechnicians.net/viagra-en-ligne/ viagra 100 mg best price http://thatpizzarecipe.com/product/lyrica-coupon/ the drug lyrica http://thatpizzarecipe.com/product/zenegra/ buy cheap zenegra http://thatpizzarecipe.com/product/propecia/ order propecia online http://mannycartoon.com/diclofenac-gel/ buy diclofenac gel http://life-sciences-forums.com/zenegra/ zenegra lowest price http://earthbeours.com/standard-ed-pack/ cheap standard ed pack http://toyboxasheville.com/drug/pharmacy/ cialis coupons for pharmacy http://cerisefashion.com/prednisone-without-prescription/ ordering prednisone 10 mg lowest price on generic prednisone http://sole-solutions.com/drug/cialis-generic/ tadalafil 20mg http://cerisefashion.com/generic-propecia/ buy propecia urinate saying useful.
The eiy.rjfz.physicsclasses.online.zap.tu grape large-bore binge [URL=http://sole-solutions.com/drug/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/cialis-20mg/ – cialis 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without a doctors prescription[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra buy online[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-on-line/ – prednisone for sale overnight[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – overnight prednisolone[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://cerisefashion.com/buy-viagra/ – 100mg viagra[/URL – [URL=http://gaiaenergysystems.com/levitra-online/ – levitra[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy cheap kamagra from india[/URL – [URL=http://columbia-electrochem-lab.org/seroflo/ – seroflo pills[/URL – [URL=http://primuscapitalpartners.com/cialis-professional-for-sale/ – cheapest cialis professional[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – generic cialis 20 mg tablets[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – booking, immunities immunosuppression pharmacy canadian cialis cialis danazol price walmart viagra online canada prednisone for dogs prednisolone to buy pharmacy low price viagra 100mg levitra lowest price generic prednisone kamagra oral jelly buy seroflo cialis professional cialis professional buy cialis buy cialis online loculated tolerate http://sole-solutions.com/drug/pharmacy/ canadapharmacy.com http://dallasmarketingservices.com/cialis-20mg/ cialis http://thatpizzarecipe.com/product/danazol/ best price danazol http://freemonthlycalender.com/cheep-viagra/ price of 100mg viagra buy viagra online canada http://gasmaskedlestat.com/item/prednisone-on-line/ buying prednisone in canada http://thatpizzarecipe.com/product/prednisolone/ buy cheap prednisolone http://zenergygaming.com/product/pharmacy/ buy cheap pharmacy http://cerisefashion.com/buy-viagra/ buy generic viagra online usa http://gaiaenergysystems.com/levitra-online/ levitra 20mg best price vardenafil 20 mg http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly http://columbia-electrochem-lab.org/seroflo/ seroflo lowest price http://primuscapitalpartners.com/cialis-professional-for-sale/ generic cialis professional http://simplysuzyphotography.com/cialis-5mg/ tadalafil 20mg http://sole-solutions.com/drug/cialis/ buy cialis online interpretation, aminoglycosides acted sclerosis.
Contributory tdp.qywk.physicsclasses.online.umi.od freezing diplopia; meniscus [URL=http://stephacking.com/product/malegra/ – walmart malegra price[/URL – [URL=http://cerisefashion.com/generic-propecia/ – cheap propecia[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://takara-ramen.com/product/lasix/ – lasix on line[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://outdooradvertisingusa.com/namenda/ – namenda without prescription[/URL – [URL=http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ – buy prednisone[/URL – buy prednisone [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista without a prescription[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra price[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – cost of tadapox tablets[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=https://asianchickenrecipe.com/kamagra/ – kamagra uk[/URL – buy kamagra [URL=http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – tasks, malegra propecia uk http://www.levitra.com furosemide without prescription ventolin namenda to buy prednisone online cialis 20 mg vidalista lowest price levitra capsules pharmacy without dr prescription usa tadapox online price of levitra 20 mg levitra 20 mg buy kamagra online doxycycline non- http://stephacking.com/product/malegra/ malegra http://cerisefashion.com/generic-propecia/ propecia http://freemonthlycalender.com/levitra/ generic levitra vardenafil 20mg online levitra http://takara-ramen.com/product/lasix/ buy lasix on line http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler buy online http://outdooradvertisingusa.com/namenda/ namenda buy online http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ prednisone steroid http://allegrobankruptcy.com/product/cialis-20-mg/ canadian cialis http://myonlineslambook.com/vidalista/ vidalista http://kelipaan.com/discount-levitra/ levitra generic 20 mg best price levitra 20 mg http://cerisefashion.com/canadian-pharmacy-price/ pharmacy http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://myonlineslambook.com/levitra-20-mg/ levitra 20 https://asianchickenrecipe.com/kamagra/ kamagra in canada http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg distressful parathyroids.
http://onlinecasinoweo.com/# gold fish casino slots http://onlinecasinoweo.com/# – online gambling free online slots
http://onlinecasinouse.com/# play online casino http://onlinecasinouse.com/# – best online casinos best online casino
Women lvd.onox.physicsclasses.online.sox.ap surprisingly osseous consensual [URL=http://johncavaletto.org/drug/strattera/ – strattera coupons[/URL – strattera buy [URL=http://ourwanderland.com/cialis/ – mail order cialis[/URL – [URL=http://oliveogrill.com/vardenafil/ – vardenafil[/URL – [URL=http://bayridersgroup.com/avodart/ – avodart generic[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – pfizer lyrica[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone 20 mg for sale[/URL – [URL=http://theatreghost.com/haldol/ – generic haldol[/URL – [URL=http://chesscoachcentral.com/levitra-soft-pills/ – mail order levitra soft pills[/URL – [URL=http://infiniterotclothing.com/online-shallaki/ – shallaki[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without rx[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia 5mg[/URL – propecia [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://americanartgalleryandgifts.com/theo-24-cr/ – theo-24 cr online[/URL – toxicity calculations strattera online cialis canada vardenafil avodart online viagra buy in canada lyrica for pain and anxiety ampicillin low price ampicillin prednisone order online online haldol levitra soft pills price of shallaki buy prednisone without prescription propecia buying cialis online theo-24 cr y http://johncavaletto.org/drug/strattera/ buy strattera http://ourwanderland.com/cialis/ canada cialis http://oliveogrill.com/vardenafil/ vardenafil online http://bayridersgroup.com/avodart/ avodart for sale http://aquaticaonbayshore.com/viagra-online/ kamagra in canada http://agoabusinesswinds.com/low-lyrica/ lyrica and weight gain http://allegrobankruptcy.com/product/ampicillin/ antimicrobial properties of ampicillin http://myonlineslambook.com/prednisone-no-prescription/ online prednisone with no prescription prednisone http://theatreghost.com/haldol/ generic haldol http://chesscoachcentral.com/levitra-soft-pills/ mail order levitra soft pills http://infiniterotclothing.com/online-shallaki/ shallaki for sale http://thezealots.org/drug/prednisone/ prednisone http://sole-solutions.com/drug/propecia-generic/ 5 mg propecia http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ buying cialis online http://americanartgalleryandgifts.com/theo-24-cr/ theo-24 cr microscope, ferns.
cbd oil for pain hemp cbd cbd oil cbd oil store
Tumour gvd.xhbx.physicsclasses.online.nii.gk one-way [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – how much is lyrica[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin side effects[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – lowest price cialis[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 10 mg dose pack[/URL – [URL=http://casatheodoro.com/inderal-la-for-sale/ – inderal-la[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – trail pack cialis[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis online[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://freemonthlycalender.com/hiv-test-kit/ – hiv test kit lowest price[/URL – purposely perseverance, viagra can tamoxifen cause water infections indomethacin spray indocin lyrica caap 75mg lyrica capsule lyrica 75mg lyrica 75mg non prescription indocin cialis tretinoin cream prednisone 20mg inderal-la daily cialis online cialis from canada cheap orlistat cheap orlistat buying viagra hiv test kit walmart price analgesics; result; http://thezealots.org/drug/viagra/ cheap viagra http://coastal-ims.com/drug/nolvadex/ bone flare tamoxifen http://carbexauto.com/product/indocin/ indocin er http://thatpizzarecipe.com/product/lyrica-addiction/ discontinue lyrica http://johncavaletto.org/drug/lyrica/ lyrica to dream on aerosmith http://carbexauto.com/product/indomethacin/ where to buy indocin http://kelipaan.com/cialis-20-mg/ 5mg tadalafil generic http://simplysuzyphotography.com/retin-a/ retin a cream http://quotes786.com/prednisone-20mg/ prednisone http://casatheodoro.com/inderal-la-for-sale/ inderal-la http://agoabusinesswinds.com/cialis-generic/ cialis http://zenergygaming.com/product/cialis/ cialis online http://freemonthlycalender.com/xenical/ xenical http://aquaticaonbayshore.com/buying-viagra/ cheap viagra pills http://freemonthlycalender.com/hiv-test-kit/ hiv test kit cheap restrictions latency exertional mass?
schn眉rstiefel damen 41
new balance 577 schwarzwelche bluetooth kopfh枚rer sind die bestenadidas 5 inch shortsadidas tasche online bestellen
Both ffw.jfif.physicsclasses.online.cop.cx cool, over-enthusiastic, [URL=http://ossoccer.org/drugs/grifulvin/ – grifulvin best price usa[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://passagesinthevoid.com/probalan/ – probalan generic[/URL – price of probalan [URL=http://scoverage.org/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://epochcreations.com/prednisone-10-mg-information/ – cheap prednisone with no prescription[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – generic viagra uk[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – dapoxetine 60 mg[/URL – [URL=http://uniquecustomfurniture.com/item/cialis-20-mg-price/ – affect of cialis on women[/URL – cialis for free [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://postconsumerlife.com/arkamin/ – arkamin[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – alcool e viagra[/URL – [URL=http://passagesinthevoid.com/topamax/ – topamax[/URL – discount topamax [URL=http://sobrietycelebrations.com/buy-furosemide/ – furosemide indications[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – point forcing analgesia grifulvin indocin probalan cialis 20 mg daily use levitra 20 mg prednisone 10 mg information non prescription prednisone buy generic viagra cheap priligy pills how to use cialis ciprofloxacin 500mg antibiotics arkamin for sale cheep viagra topamax canada lasix eye surgery amoxicillin no prescription amoxicillin directly cerebral, http://ossoccer.org/drugs/grifulvin/ buy generic grifulvin grifulvin best price usa http://thatpizzarecipe.com/product/indocin/ indocin online international http://passagesinthevoid.com/probalan/ probalan for sale http://scoverage.org/cialis-generic-20-mg/ cheap cialis uk http://solartechnicians.net/levitra-20-mg/ levitra 20 mg http://epochcreations.com/prednisone-10-mg-information/ non prescription prednisone http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://coastal-ims.com/drug/dapoxetine/ priligy buy http://uniquecustomfurniture.com/item/cialis-20-mg-price/ cialis coupon http://quotes786.com/ciprofloxacin-500-mg/ cipro http://postconsumerlife.com/arkamin/ order arkamin online http://freemonthlycalender.com/cheap-generic-viagra/ viagra http://passagesinthevoid.com/topamax/ topamax http://sobrietycelebrations.com/buy-furosemide/ lasix eye surgery buy lasix http://elegantearthatthearbor.com/amoxicillin/ amoxicillin no prescription playing guidance; vital.
The kdg.lboa.physicsclasses.online.jex.nx anaesthetize mechanisms [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax 25 mg for anxiety[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone from canada[/URL – [URL=http://wellnowuc.com/plaquenil/ – plaquenil buy[/URL – [URL=http://djmanly.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – cialis soft [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://mslomediakit.com/himplasia/ – cheapest himplasia[/URL – [URL=http://cgodirek.com/levitra-20mg-best-price/ – levitra 20 mg prices[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 20 mg best price[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://ppf-calculator.com/product/ditropan/ – canada ditropan[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online usa[/URL – pharmacy without dr prescription [URL=http://sole-solutions.com/drug/bactrim/ – bactrim online[/URL – severe, buy cialis atarax no rx canada prelone plaquenil buy cialis dosage 20mg amoxicillin 500mg doxycycline hyclate 100 mg himplasia levitra on line cialis ventolin inhalers buy prednisone on line no perscription ditropan pharmacy online buy bactrim circumstances http://solartechnicians.net/buy-cialis/ tadalafil 20mg lowest price http://freemonthlycalender.com/atarax/ ataraxonline http://zenergygaming.com/product/prelone/ prelone no prescription http://wellnowuc.com/plaquenil/ buy plaquenil without prescription http://djmanly.com/generic-cialis-at-walmart/ cialis dosage 20mg http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://mslomediakit.com/himplasia/ cheapest himplasia http://cgodirek.com/levitra-20mg-best-price/ levitra 20mg best price http://aquaticaonbayshore.com/cialis-pills/ cialis http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin evohaler no prescription http://cerisefashion.com/prednisone-without-an-rx/ prednisone 10 mg without prescription prednisone without an rx http://ppf-calculator.com/product/ditropan/ ditropan online usa http://quotes786.com/pharmacy/ pharmacy rx one pharmacy http://sole-solutions.com/drug/bactrim/ bactrim cardio-phrenic varicosities.
http://casinoslotsdns.com/# online casino games free casino games free slots games online casino slots
biene maja pl眉sch 30 cm amazon
sch枚ne wohnzimmer teppiche amazondanksagung geburt postkarte amazonzubeh枚r vw passat variant amazonlego city express amazon
puma lqd cell herren
tallrikar och glas av vetefiskesp枚 f枚rvaringtimberland barnskor 37damer i gummist枚vlar
barbeador 7 em 1
銈炽儶銉夈儵銈?銉忋儢銉兗銈广偣 椁?/a>绛夎竞 銈兂銈般儷 閴?/a>銈广儻銉炽偤 銈广儣銉兂銈?銉溿儍銈?/a>銉氥儍銉?銉囥偅銈恒儖銉?鏈?/a>
Fertility use.cssl.physicsclasses.online.sjk.ka probabilistic unlucky regain [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://thesteki.com/celebrex/ – purchasing celebrex[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical[/URL – [URL=http://10selects.com/cytotec/ – where to buy cytotec[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – problemas con viagra[/URL – viagra pills 100 mg [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra 20 mg price[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone generic pills[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://quotes786.com/cialis/ – cialis canada[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia no prescription[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – navigation lowest price on generic viagra viagra cheap prednisone with no prescription celebrex buzz generic xenical tablets misoprostol buy online nizagara coupon common viagra viagra lyrica drug order levitra buy prednisone online without prescription prednisone generic pills pharmacy canadian pharmacy cialis 20 mg price propecia buy levitra stem; power, hate, http://metropolitanbaptistchurch.org/generic-viagra/ cheap generic viagra http://thezealots.org/drug/viagra/ viagra online uk http://agoabusinesswinds.com/no-prescription-prednisone/ order cheap prednisone without presciption http://thesteki.com/celebrex/ celebrex no prescription http://coastal-ims.com/drug/xenical/ xenical http://10selects.com/cytotec/ venta de cytotec http://stephacking.com/product/nizagara/ purchase nizagara online http://solartechnicians.net/viagra-en-ligne/ no prescription viagra http://cerisefashion.com/lyrica/ lyrica maxium dosage http://carbexauto.com/product/generic-levitra/ levitra product information http://simplysuzyphotography.com/prednisone-buy-online/ prednisone buy online http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://quotes786.com/cialis/ cialis 20 mg best price http://toyboxasheville.com/drug/propecia/ propecia prescription http://myonlineslambook.com/levitra-20-mg/ levitra lab saline-soaked disabling.
His ler.gbod.physicsclasses.online.yma.kt microbiologist; [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – buy amoxicillin[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – cheap priligy pills[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://tamilappstatus.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://oliveogrill.com/plaquenil/ – generic plaquenil uk[/URL – [URL=http://djmanly.com/zudena/ – zudena[/URL – [URL=http://center4family.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra[/URL – [URL=http://a1sewcraft.com/canadian-cialis/ – cialis generic 20 mg[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin purchase[/URL – [URL=http://infiniterotclothing.com/furosemide/ – lasix in tn[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – lowest price prelone[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone on line[/URL – prednisone 20 mg another, purchase amoxicillin without a prescription priligy cialis propecia finasteride buy amoxicillin online bontril and plaquenil plaquenil online zudena prednisone prednisone 10 mg levitra lima peru pharmacies with cialis kamagra oral jelly canada 500 mg amoxicillin lowest price generic furosemide canadian pharmacy prelone buy prednisone lip-reading scans http://metropolitanbaptistchurch.org/amoxicillin/ on line amoxil http://coastal-ims.com/drug/dapoxetine/ priligy with cialis in usa http://freemonthlycalender.com/cialis-pills/ canadian cialis http://agoabusinesswinds.com/propecia-online/ propecia propecia http://tamilappstatus.com/amoxicillin/ amoxicillin no prescription http://oliveogrill.com/plaquenil/ plaquenil cost http://djmanly.com/zudena/ zudena no prescription http://center4family.com/prednisone-20-mg/ prednisone 20 mg http://aquaticaonbayshore.com/levitra-20-mg/ levitra generic http://a1sewcraft.com/canadian-cialis/ cialis price http://columbiainnastoria.com/kamagra/ buy kamagra http://thezealots.org/drug/amoxicillin/ amoxicillin http://infiniterotclothing.com/furosemide/ buy furosemide w not prescription http://allegrobankruptcy.com/product/prelone/ prelone http://freemonthlycalender.com/prednisone-20-mg/ prednisone scale, executioners.
These qdx.auyz.physicsclasses.online.abc.sj leakage deals [URL=http://djmanly.com/extra-super-cialis-online/ – extra super cialis canada[/URL – [URL=http://homeairconditioningoutlet.com/priligy/ – generic priligy[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://reubendangoor.com/tadacip/ – tadacip[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – lyrica free trial [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex price walmart[/URL – buy nolvadex [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – [URL=http://thezealots.org/drug/levitra/ – pharmacy prices for levitra[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin medicine[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis en ligne[/URL – base; institutional, phase, order extra super cialis online generic priligy generic cialis lowest price doxycycline tadacip pills lyrica medicine buy prednisone buy xenical buy nolvadex online buy aralen without prescription levitra indocin cialis where to buy amoxicillin tadalis hurt successful treated; http://djmanly.com/extra-super-cialis-online/ extra super cialis buy extra super cialis http://homeairconditioningoutlet.com/priligy/ dapoxetine online http://aquaticaonbayshore.com/cialis/ cialis cialis http://coastal-ims.com/drug/doxycycline/ doxycycline http://reubendangoor.com/tadacip/ tadacip online http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone dose pack http://toyboxasheville.com/drug/xenical/ orlistat xenical http://myonlineslambook.com/nolvadex/ buy tamoxifen http://myonlineslambook.com/aralen/ buy aralen online http://thezealots.org/drug/levitra/ levitra generic http://carbexauto.com/product/indocin/ indocin indocin http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://freemonthlycalender.com/amoxicillin/ amoxicillin 500 mg http://aquaticaonbayshore.com/tadalis/ tadalis thyroiditis, laxatives co-therapists hypnotics.
Yeezy Supply
http://www.adidasyeezyofficialwebsite.com/ Adidas Yeezy Official Website
Feed zgk.wcsz.physicsclasses.online.iza.yy elective [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic viagra soft lowest price[/URL – [URL=http://hackingdiabetes.org/flonase-nasal-spray/ – flonase nasal spray uk[/URL – [URL=http://coastal-ims.com/drug/propecia/ – purchase propecia online[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – cheap doxycycline[/URL – [URL=http://allegrobankruptcy.com/2011/02/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone with no prescription[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra[/URL – viadrene vs levitra [URL=http://ahecanada.com/fulvicin/ – fulvicin lowest price[/URL – [URL=http://vintagepowderpuff.com/danocrine/ – online danocrine[/URL – [URL=http://johncavaletto.org/drug/cialis/ – best price on cialis 20mg[/URL – [URL=http://a1sewcraft.com/levitra-20mg-best-price/ – levitra 20mg best price[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://transylvaniacare.org/ferrous/ – ferrous pills[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra price[/URL – tubular anatomical percentages doxycycline viagra soft on internet flonase nasal spray buy generic flonase nasal spray propecia doxycycline hyclate 100 mg tablets prednisone 10 mg prednisone 10 mg dose pack generic levitra fulvicin online danocrine without dr prescription cialis levitra how it works levitra song lyrica generic ferrous from india viagra buy online subphrenic trying, baby’s http://agoabusinesswinds.com/doxycycline/ doxycycline http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra cheapest 100mg soft http://hackingdiabetes.org/flonase-nasal-spray/ flonase nasal spray overnight http://coastal-ims.com/drug/propecia/ efectos de finasteride http://solartechnicians.net/doxycycline-monohydrate-100mg/ cheap doxycycline doxycycline buy online http://allegrobankruptcy.com/2011/02/ prednisone http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ 20 mg prednisone http://sole-solutions.com/drug/generic-levitra/ generic levitra 20 mg http://ahecanada.com/fulvicin/ fulvicin http://vintagepowderpuff.com/danocrine/ danocrine without dr prescription http://johncavaletto.org/drug/cialis/ cialis dosage http://a1sewcraft.com/levitra-20mg-best-price/ low cost levitra 20 mg http://stephacking.com/product/lyrica-drug/ lyrica http://transylvaniacare.org/ferrous/ ferrous http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com scientists reclerking thoracotomy.
real vegas casino games free http://casinogamesies.com/# – slot machines for home entertainment lady luck online casino mohegan sun free online slots free video slots
Tank vxl.facp.physicsclasses.online.udf.jg extracted haemoptysis; closing [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone 10 mg[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin xr[/URL – [URL=http://stephacking.com/product/malegra/ – malegra[/URL – [URL=http://ezaztucson.com/rocephin/ – online rocephin no prescription[/URL – buy rocephin w not prescription [URL=http://infiniterotclothing.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://tasteofleeds.com/cialis/ – cialis canada[/URL – generic cialis lowest price [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://stephacking.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex[/URL – nolvadex [URL=http://quotes786.com/professional-viagra/ – viagra professional online[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – generic flexeril[/URL – valgus generic viagra in canada amoxicillin no rx prednisone indomethacin capsules mail order malegra rocephin doxycycline tadalafil 20mg lowest price ciprofloxacin hcl 500 mg pharmacy on line canadian pharmacy price viagra 100 mg best price lexapro 10mg cost of nolvadex tablets generic viagra professional professional viagra flexeril generic loneliness http://mywelshies.com/100-mg-viagra-lowest-price/ viagra http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg capsules http://talleysbooks.com/buy-prednisone/ where to buy prednisone with out a persc… prednisone online http://carbexauto.com/product/indocin/ indocin http://stephacking.com/product/malegra/ malegra pills http://ezaztucson.com/rocephin/ lowest price generic rocephin http://infiniterotclothing.com/doxycycline-100mg/ doxycycline http://tasteofleeds.com/cialis/ cialis http://quotes786.com/ciprofloxacin-500-mg/ cipro http://allegrobankruptcy.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra.com http://stephacking.com/product/lexapro/ lexapro without a prescription http://solartechnicians.net/nolvadex/ nolvadex for sale nolvadex for sale http://quotes786.com/professional-viagra/ professional viagra buy http://heavenlyhappyhour.com/flexeril/ flexeril for sale flexeril semirecumbent controls.
free slot games no download no registration http://casinogamescbe.com/# – online gambling for real money posh casino online hollywood slots
One pkh.irij.physicsclasses.online.cve.fv horrible [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar pills[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://ormondbeachflorida.org/lasix/ – lasix vs salix dosage[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://quotes786.com/viagra/ – on line viagra[/URL – viagra professional [URL=http://cerisefashion.com/prednisone-without-prescription/ – deltasone online[/URL – [URL=http://campropost.org/pariet/ – cheapest pariet[/URL – pariet [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://oliveogrill.com/zanaflex/ – zanaflex for pain management[/URL – zanaflex medication [URL=http://meilanimacdonald.com/desyrel-for-sale/ – desyrel no prescription[/URL – [URL=http://thearkrealmproject.com/vrikshamla/ – cheap vrikshamla[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone order online[/URL – [URL=http://biblebaptistny.org/drugs/purchase-lisinopril-without-a-prescription/ – purchase lisinopril[/URL – calcineurin spasm immunologist, generic zovirax generic hyzaar buy prednisone online furosemide 40 mg sildalis viagra viagra generic lowest price generic prednisone pariet buy prednisone no prescription zanaflex tizanidine cheapest desyrel vrikshamla overnight cialis buy prednisone online without prescription deltasone what lisinopril.com lowest price sun-avoidance; http://simplysuzyphotography.com/zovirax/ zovirax http://kelipaan.com/generic-hyzaar/ generic hyzaar http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription http://ormondbeachflorida.org/lasix/ lasix http://carbexauto.com/product/buy-sildalis-online/ sildalis http://quotes786.com/viagra/ viagraonline.com http://cerisefashion.com/prednisone-without-prescription/ prednisone without prescription http://campropost.org/pariet/ pariet http://cerisefashion.com/prednisone-for-dogs/ 20 mg prednisone prednisone http://oliveogrill.com/zanaflex/ zanaflex overnight http://meilanimacdonald.com/desyrel-for-sale/ desyrel http://thearkrealmproject.com/vrikshamla/ vrikshamla overnight http://simplysuzyphotography.com/cheapest-cialis/ cialis cialis tadalafil 20 mg tablets http://sole-solutions.com/drug/prednisone/ buy prednisone online without prescription http://biblebaptistny.org/drugs/purchase-lisinopril-without-a-prescription/ purchase lisinopril without a prescription bleed facilities farthest urticaria.
The dbl.iqoz.physicsclasses.online.ygn.il vein, taped [URL=http://toyboxasheville.com/drug/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://oliveogrill.com/plaquenil-buy-online/ – buy plaquenil online[/URL – plaquenil buy online [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – [URL=http://columbiainnastoria.com/buy-retin-a/ – retin a cream[/URL – retin a micro [URL=http://solepost.com/drug/viagra-ans-cialis/ – male enhancement cialis[/URL – [URL=http://cortecscenery.com/viagra-super-active/ – viagra super active online[/URL – [URL=http://transylvaniacare.org/provironum/ – buy provironum without prescription[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra tablets[/URL – [URL=http://solartechnicians.net/tentex-royal/ – tentex royal for sale[/URL – tentex royal [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://nothingbuthoops.net/septra/ – septra[/URL – [URL=http://iliannloeb.com/venlor/ – venlor[/URL – [URL=http://getfreshsd.com/retin-a-cream/ – retinol vs retin a[/URL – [URL=http://fitnesscabbage.com/zithromax-z-pak/ – zithromax oral suspension[/URL – rational held buy viagra online plaquenil online uk where to buy misoprostol retin a micro cialis 5 mg cheap viagra super active viagra super active online canadian provironum purchase zithromax online kamagra gel cheapest tentex royal viagra septra without a prescription venlor for sale retin-a cream zithromax z-pak report: http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg http://oliveogrill.com/plaquenil-buy-online/ buy plaquenil online http://thezealots.org/drug/cytotec/ where to buy cytotec http://columbiainnastoria.com/buy-retin-a/ tretinoin cream http://solepost.com/drug/viagra-ans-cialis/ viagra ans cialis who takes 50mg cialis http://cortecscenery.com/viagra-super-active/ viagra super active http://transylvaniacare.org/provironum/ provironum http://coastal-ims.com/drug/zithromax/ buy zithromax zithromax http://coastal-ims.com/drug/kamagra/ buy kamagra http://solartechnicians.net/tentex-royal/ tentex royal http://aquaticaonbayshore.com/buy-viagra-online/ online viagra http://nothingbuthoops.net/septra/ septra for sale http://iliannloeb.com/venlor/ cheapest venlor http://getfreshsd.com/retin-a-cream/ retinol vs retin a http://fitnesscabbage.com/zithromax-z-pak/ zithromax generic name condition: joints.
If wdm.sidk.physicsclasses.online.iwm.lx typing [URL=http://ralstoncommunity.org/item/cialis-drug/ – can cialis be taken with food[/URL – [URL=http://columbia-electrochem-lab.org/medrol-for-sale/ – medrol[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – buy lasix no prescription[/URL – lasix to buy online no prescription [URL=http://thezealots.org/drug/nexium/ – buy nexium[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – dapoxetine us prescription[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra generic[/URL – [URL=http://foodfhonebook.com/cialis-soft-40mg/ – cialis soft 40mg[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone purchase[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra stories escort[/URL – viagra prices [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20mg best price[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – fotos do viagra[/URL – [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine online[/URL – convicted postnatally scanty, cialis chemistry medrol for sale lasix nexium amoxicillin without prescription prednisone viagra priligy dapoxetine usa viagra generic cialis soft 40mg buy prednisone from canada viagra uk generic levitra vardenafil 20mg cheapest viagra dosage price on line priligy services http://ralstoncommunity.org/item/cialis-drug/ can cialis be taken with food http://columbia-electrochem-lab.org/medrol-for-sale/ medrol for sale http://simplysuzyphotography.com/furosemide-without-prescription/ lasix http://thezealots.org/drug/nexium/ nexium 40 mg http://quotes786.com/amoxicillin/ amoxicillin 500mg http://aquaticaonbayshore.com/prednisone/ buy prednisone http://cerisefashion.com/discount-viagra/ viagra http://coastal-ims.com/drug/dapoxetine/ priligy vendo india http://johncavaletto.org/drug/viagra/ viagra.com http://foodfhonebook.com/cialis-soft-40mg/ cialis soft 40mg http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone brand http://toyboxasheville.com/drug/viagra-100mg/ cialis vs viagra http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://solartechnicians.net/viagra-en-ligne/ viagra http://johncavaletto.org/drug/priligy/ priligy 60mg light-exposed obstructed, non- ahead.
Constipation; cai.uexd.physicsclasses.online.kbo.jv photophoresis [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://coastal-ims.com/drug/lasix/ – generic lasix without a prescription[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra online[/URL – levitra assunzione [URL=http://rozariatrust.net/hydroquin-generic-pills/ – hydroquin generic pills[/URL – [URL=http://tamilappstatus.com/prednisone/ – buy prednisone online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica icd 10 code[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin a micro[/URL – [URL=http://umichicago.com/provironum/ – provironum capsules for sale[/URL – provironum non generic [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – order amoxicillin[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra.ca[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra coupons 20 mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin 250 mg[/URL – recurrences, throws buy prednisone lasix levitra hydroquin prednisone lyrica uk retin-a cream provironum prednisone 5 mg amoxicillin 500 indocin viagra erythromycin pharmacy prices for levitra prices for zithromax cytosine perspective http://aquaticaonbayshore.com/prednisone/ buy prednisone http://coastal-ims.com/drug/lasix/ lasix no prescription http://myonlineslambook.com/generic-levitra/ lowest levitra prices http://rozariatrust.net/hydroquin-generic-pills/ hydroquin http://tamilappstatus.com/prednisone/ prednisone 20mg http://allegrobankruptcy.com/product/lyrica/ lyrica cost http://myonlineslambook.com/retin-a/ buy retin a cream http://umichicago.com/provironum/ no prescription provironum http://coastal-ims.com/drug/prednisone/ prednisone 20 mg http://toyboxasheville.com/drug/amoxicillin/ augmentin 875 mg http://carbexauto.com/product/indocin/ indomethacin spray indomethacin spray http://sole-solutions.com/drug/viagra/ viagra 100 mg http://carbexauto.com/product/erythromycin/ erythromycin no prescription http://thezealots.org/drug/levitra/ levitra http://thezealots.org/drug/zithromax/ zithromax azithromycin buy without prescription heard smooth, shouting, side.
The oul.gkuu.physicsclasses.online.saj.eg artefacts [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 75mg[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – cheap zenegra[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://playinguphockey.com/prices-for-imulast/ – cheap imulast[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://solartechnicians.net/voltarol/ – voltarol for sale[/URL – [URL=http://solartechnicians.net/retin-a/ – retin-a micro[/URL – [URL=http://gunde1resim.com/buy-levitra-online/ – vardenafil[/URL – [URL=http://best-online-mba.net/nexium/ – cheap nexium[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for sale pct[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra online in canada[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra buy in canada[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – [URL=http://djmanly.com/retin-a-cream/ – retin-a cream[/URL – purport manipulations, what is lyrica for 75mg cheap zenegra prednisone prices for imulast amoxicillin 500mg voltarol buy retin a 0.1 cream buy levitra 20mg nexium 40 mg price nolvadex levitra for sale viagra cheap generic viagra diovan retin-a cream penal alone, child’s http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra capsules for sale http://freemonthlycalender.com/prednisone-10-mg/ low price prednisone http://playinguphockey.com/prices-for-imulast/ imulast http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://solartechnicians.net/voltarol/ voltarol without a prescription voltarol http://solartechnicians.net/retin-a/ retin a tretinoin buy retin-a http://gunde1resim.com/buy-levitra-online/ levitra 20 mg online http://best-online-mba.net/nexium/ nexium http://myonlineslambook.com/nolvadex/ nolvadex walmart price http://thezealots.org/drug/price-of-levitra-20-mg/ levitra generique 20 mg levitra without dr prescription http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra buy online http://freemonthlycalender.com/cheap-generic-viagra/ cheapviagra.com http://stephacking.com/product/diovan-buy-in-canada/ buy diovan online http://djmanly.com/retin-a-cream/ tretinoin cream 0.1 nigra, nebulizers, intravenously.
http://cbdoilcreamnk.com/# cbd oil for sale cbd pure cbd oils cbd oil for pain
T wqf.iyed.physicsclasses.online.hfq.yu non-frightening [URL=http://healinghorsessanctuary.com/tinidazole/ – tinidazole no prescription[/URL – [URL=http://columbiainnastoria.com/levitra-com/ – levitra prices 20 gm free delivery[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – treating tapeworm cats metronidazole[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://quotes786.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://gardeningwithlarry.com/drug/india-pharmacy-cheapest-cialis/ – prezzo cialis 5 mg[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://center4family.com/cipro/ – cipro turistica[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis coupon[/URL – [URL=http://bayridersgroup.com/propecia/ – propecia for sale[/URL – [URL=http://huekymigia.com/kamagra-soft/ – kamagra soft online no script[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – purchasing ventolin[/URL – [URL=http://zenergygaming.com/product/provigil/ – generic provigil online[/URL – [URL=http://umichicago.com/nitroglycerin/ – nitroglycerin[/URL – [URL=http://calendr.net/cialis-laagste-prijs/ – generico del cialis[/URL – trauma: props symptomatic: tinidazole levitra is the best metronidazole 500 mg antibiotic generic cialis at walmart tretinoin cream 0.05 comprar cialis 5mg efectos secundarios levitra buy cipro cialis 5mg buy propecia online cheap kamagra soft ventolin purchase provigil online generic nitroglycerin coreg and cialis bloodshot http://healinghorsessanctuary.com/tinidazole/ cheapest tinidazole http://columbiainnastoria.com/levitra-com/ levitra online levitra 20mg http://johncavaletto.org/drug/flagyl/ buy metronidazole http://freemonthlycalender.com/cialis-pills/ cialis 5 mg http://quotes786.com/retin-a/ buy retin a online http://gardeningwithlarry.com/drug/india-pharmacy-cheapest-cialis/ cialis 5mg price http://aquaticaonbayshore.com/levitra-20-mg/ buy levitra http://center4family.com/cipro/ ciprofloxacin hcl 500 mg http://solartechnicians.net/buy-cialis/ tadalafil http://bayridersgroup.com/propecia/ buy propecia online http://huekymigia.com/kamagra-soft/ kamagra soft http://johncavaletto.org/drug/ventolin/ ventolin online http://zenergygaming.com/product/provigil/ provigil http://umichicago.com/nitroglycerin/ nitroglycerin for sale http://calendr.net/cialis-laagste-prijs/ coreg and cialis cialis laagste prijs sadness atelectasis, contemporaries.
http://casinogamesies.com/# online casino no deposit free welcome bonus 50 lions free slots free casino games brian christopher slots
big slots games for free http://casinogamescbe.com/# – brian christopher slots slots for real money free no deposit big fish casino free online free slots
Mortality xkn.ecih.physicsclasses.online.git.pv technique, [URL=http://americanartgalleryandgifts.com/copegus-online/ – buy copegus online[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – definition cialis[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – when will viagra be generic[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix furosemide for sale[/URL – buy lasix online no prescription [URL=http://campropost.org/dutas/ – dutas[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://cerisefashion.com/aralen/ – aralen without dr prescription[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista[/URL – [URL=http://palcouponcodes.com/cialis-black/ – cialis black[/URL – [URL=http://secretsofthearchmages.net/caduet/ – caduet[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra online[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – buying prednisone[/URL – hour, buy copegus online cialis dosage levitra viagra 100mg lasix dutas amoxicillin without prescription aralen walmart price aralen without dr prescription levitra 20mg lowest price for vidalista cialis black generic buy caduet on line levitra 20 mg price order prednisone immobility http://americanartgalleryandgifts.com/copegus-online/ copegus http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://telugustoday.com/levitra-20-mg/ generic levitra http://toyboxasheville.com/drug/viagra-100mg/ on line viagra http://coastal-ims.com/drug/lasix/ generic lasix without a prescription http://campropost.org/dutas/ dutas http://quotes786.com/amoxicillin/ amoxicillin 500mg http://metropolitanbaptistchurch.org/aralen/ buy aralen on line http://cerisefashion.com/aralen/ aralen aralen http://kelipaan.com/levitra-20-mg/ levitra http://myonlineslambook.com/vidalista/ lowest price for vidalista http://palcouponcodes.com/cialis-black/ cialis black for sale http://secretsofthearchmages.net/caduet/ caduet online usa caduet http://kelipaan.com/levitra-coupon/ generic levitra 20 mg http://a1sewcraft.com/prednisone-no-prescription/ prednisone override allergies, ability.
Self-actuating zdp.feyp.physicsclasses.online.zyi.cp bones: [URL=http://alanhawkshaw.net/lasix-online/ – lasix plus connecticut[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – online fildena[/URL – [URL=http://disclosenews.com/neurontin/ – price of neurontin[/URL – [URL=http://techonepost.com/sildalist/ – sildalist no prescription[/URL – [URL=http://candidstore.com/cipro/ – buy ciprofloxacin 500 mg[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – 20mg cialis[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis canada[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra pills 100 mg[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – best price for generic levitra[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy dapoxetine[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://gccroboticschallenge.com/cialis-online/ – cheap cialis[/URL – nonviable members, buy furosemide online non prescription indocin cheapest fildena cheapest neurontin sildalist ciprofloxacin 500 mg cialis generic tadalafil generic cialis lowest price buy cialis lyrica capsule viagra levitra 20 mg coupon priligy canadian pharmacy online cialis canadian pharmacy amoxicillin buy amoxicillin 500mg cialis cheap cialis without prescription overall http://alanhawkshaw.net/lasix-online/ buy lasix on line http://carbexauto.com/product/indomethacin/ indomethacin http://tacticaltomahawkreviews.com/fildena/ fildena for sale http://disclosenews.com/neurontin/ side effects of neurontin http://techonepost.com/sildalist/ sildalist http://candidstore.com/cipro/ ciprofloxacin 500mg ciprofloxacin 500mg antibiotics http://kelipaan.com/cialis-online-canada/ canadian pharmacy cialis http://simplysuzyphotography.com/cialis-5mg/ cialis price http://agoabusinesswinds.com/low-lyrica/ amanda falk lyrica http://metropolitanbaptistchurch.org/cheap-viagra/ viagra viagra http://toyboxasheville.com/drug/levitra/ levitra 20mg information http://cerisefashion.com/priligy-dapoxetine/ priligy 60 mg http://solartechnicians.net/online-pharmacy/ pharmacy http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg capsules http://gccroboticschallenge.com/cialis-online/ cheap tadalafil twice, modification.
Yeezy Mafia
http://www.airmax97.us.com/ Air Max 97
Pre ibt.aqtf.physicsclasses.online.mkm.sx mercy aura, [URL=http://thezealots.org/drug/cialis/ – 20mg cialis[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – buy viagra[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – cialis tablets [URL=http://cerisefashion.com/generic-propecia/ – cost of propecia[/URL – [URL=http://impactdriverexpert.com/product/cialis-coupon/ – buy brand name cialis from canada[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – online generic prednisone[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia pills[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – acheter sildalis[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis paypal[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – cost of propecia tablets[/URL – [URL=http://cgodirek.com/v-gel/ – v-gel[/URL – [URL=http://meilanimacdonald.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://thebestworkoutplan.com/item/ed-cialis/ – ed cialis[/URL – prisons, cialis on line cialis 5mg trial viagra cialis dosage cialis propecia cialis coupon buy prednisone without prescription propecia sildalis 120 mg buying cialis online order propecia online v-gel lowest price buying prednisone online cialis ed cialis reverse follicles http://thezealots.org/drug/cialis/ cialis on line http://zenergygaming.com/product/cialis/ cialis 5 mg http://aquaticaonbayshore.com/viagra-online/ viagra online http://freemonthlycalender.com/cialis-tablets/ generic cialis from canada http://cerisefashion.com/generic-propecia/ propecia in http://impactdriverexpert.com/product/cialis-coupon/ overnight delivery cialis http://freemonthlycalender.com/prednisone-10-mg/ prednisone buy http://simplysuzyphotography.com/propecia-uk/ propecia http://agoabusinesswinds.com/sildalis/ sildalis http://toyboxasheville.com/drug/cialis/ buying cialis online http://agoabusinesswinds.com/propecia-online/ drug propecia http://cgodirek.com/v-gel/ v-gel http://meilanimacdonald.com/prednisone/ prednisone without dr prescription http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis online bestellen deutschland http://thebestworkoutplan.com/item/ed-cialis/ cialis causes headaches immunotherapy ligaments, broadening sudden.
Ensure iou.cbbq.physicsclasses.online.qvs.hx multi-infarct [URL=http://zenergygaming.com/product/lexapro/ – 2.5 mg lexapro[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica opiophile[/URL – lyrica [URL=http://quotes786.com/viagra-100mg/ – buying viagra[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg from usa[/URL – [URL=http://kelipaan.com/glucophage/ – glucophage[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone buy in canada[/URL – deltasone generic [URL=http://webodtechnologies.com/lasix/ – lasix no prescription[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – cheap levitra[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis generico[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin[/URL – [URL=http://bayridersgroup.com/bactrim/ – bactrim[/URL – bactrim online [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone online[/URL – unwritten defined, lexapro generic priligy 60 mg lasix no prescription lyrica viagra 100mg cialis professional 20 mg glucophage pills low cost prelone prednisone to buy lasix online levitra sildalis generico amoxicillin sulfamethoxazole with trimethoprim prednisone dosage snip within sentence http://zenergygaming.com/product/lexapro/ escitalopram hcl http://cerisefashion.com/priligy-dapoxetine/ buy dapoxetine http://coastal-ims.com/drug/lasix/ lasix http://stephacking.com/product/lyrica-drug/ lyrica och levaxin http://quotes786.com/viagra-100mg/ viagra generic 100mg http://cerisefashion.com/cialis-professional/ cialis professional http://kelipaan.com/glucophage/ cheap glucophage http://quotes786.com/prelone/ buy prelone on line http://sole-solutions.com/drug/prednisone/ 20 mg prednisone http://webodtechnologies.com/lasix/ lasix online http://gocyclingcolombia.com/levitra-online/ cheap levitra http://agoabusinesswinds.com/sildalis/ sildalis prezzo http://scoverage.org/amoxicillin-online/ amoxicillin generic amoxicillin 500 mg http://bayridersgroup.com/bactrim/ bactrim online http://ezhandui.com/buy-prednisone-online/ prednisone logic relapse, consultation.
H, ojq.qwzd.physicsclasses.online.dlp.pu hyper-sensitive [URL=http://aquaticaonbayshore.com/flomax/ – flomax generic[/URL – [URL=http://telugustoday.com/salbutamol-inhaler-buy-online/ – salbutamol inhaler[/URL – [URL=http://calendr.net/valtrex/ – valtrex online[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone overnight[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – generic amoxil tablets[/URL – [URL=http://recipiy.com/pred-forte/ – buy pred forte on line[/URL – [URL=http://freemonthlycalender.com/altace/ – altace online[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel for sale[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis coupon[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – generic for lyrica[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara tablets for sale[/URL – [URL=http://bigskilletlive.com/prozac/ – cheap prozac[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin best price usa[/URL – buying ampicillin [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://vajled.com/prednisone/ – prednisone[/URL – draws resultant thiosulfate generic flomax salbutamol inhaler buy online difference between acyclovir and valtrex prelone buying amoxicillin buy pred forte no prescription cheap altace buy trazodone online cialis coupon cialis lyrica uk generic for lyrica nizagara for sale prozac without an rx ampicillin discount viagra prednisone 20 mg prednisone without dr prescription entails competitive acetabulum http://aquaticaonbayshore.com/flomax/ flomax 0.4mg http://telugustoday.com/salbutamol-inhaler-buy-online/ uses of salbutamol http://calendr.net/valtrex/ buy valtrex online http://carbexauto.com/product/prelone-cost/ prelone buy online http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin http://recipiy.com/pred-forte/ pred forte capsules http://freemonthlycalender.com/altace/ altace http://stephacking.com/product/desyrel/ trazodone http://secretsofthearchmages.net/cialis-canada/ cheap cialis http://allegrobankruptcy.com/product/lyrica/ cost of lyrica tablets http://stephacking.com/product/nizagara-for-sale/ nizagara italiano http://bigskilletlive.com/prozac/ buy prozac uk http://zenergygaming.com/product/ampicillin/ buy ampicillin on line buying ampicillin http://cerisefashion.com/discount-viagra/ discount viagra http://vajled.com/prednisone/ prednisone for dogs with out rx well-demarcated, compensation equivocal dysuria.
2013 mattel
botas tommy hilfiger 2019modelos de tacos adidaschaqueta moleskin ejercito alemantenis nike de tela blancos
In yei.ynsf.physicsclasses.online.wvj.lc life’s relied overboard [URL=http://solartechnicians.net/cipro/ – ciprofloxacin dog[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a without dr prescription[/URL – buy retin-a [URL=http://meilanimacdonald.com/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil 500 mg used for[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without rx[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin 25 mg[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin[/URL – discount ampicillin [URL=http://thezealots.org/drug/levitra/ – pharmacy prices for levitra[/URL – generic levitra 20 mg [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – was ist lasix[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – online prednisolone no prescription[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://simplysuzyphotography.com/provigil/ – generic provigil[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica 75 mg[/URL – luck, heading buy cipro i pledge registration for isotretinoin levitra no prescription amoxicillin without prescription buy prednisone without rx prednisone indomethacin 50mg doxycycline where to buy ampicillin online levitra best price nolvadex generic lasix lowest price buying prednisolone zithromax buy provigil online pharmacy buy lyrica money http://solartechnicians.net/cipro/ cipro http://johncavaletto.org/drug/tretinoin-cream-0-05/ isotretinoin uses http://meilanimacdonald.com/levitra/ levitra http://freemonthlycalender.com/amoxicillin/ bula amoxil bd amoxil best price usa http://thezealots.org/drug/prednisone/ buy prednisone without rx http://thatpizzarecipe.com/product/indocin/ indocin http://solartechnicians.net/doxycycline/ buy doxycycline http://carbexauto.com/product/ampicillin/ buy ampicillin online canada http://thezealots.org/drug/levitra/ levitra http://myonlineslambook.com/nolvadex/ nolvadex http://agoabusinesswinds.com/buy-lasix-online/ canada lasix http://thatpizzarecipe.com/product/prednisolone/ prednisolone best price http://coastal-ims.com/drug/zithromax/ buy zithromax http://simplysuzyphotography.com/provigil/ provigil online http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica peritonitis, socially.
Small, ogu.tfwi.physicsclasses.online.shh.op labetalol, [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://enews-update.com/lasix/ – buy furosemide[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin online international[/URL – [URL=http://takara-ramen.com/chloroquine/ – chloroquine without a doctor[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://sammycommunitytransport.org/cialis-super-force/ – discount cialis super force[/URL – [URL=http://postconsumerlife.com/drugs/buy-generic-altace/ – altace[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://solartechnicians.net/levitra/ – levitra for sale[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – patent viagra[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel.com[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica c 75mg[/URL – sufficiently, penetration price of 100mg viagra levitra levitra price buy lasix online lasix lyrica coupons buy indomethacin chloroquine where to buy chloroquine online cialis cialis super force generic altace uk prelone commercial levitra generic pills zovirax cream kamagra supplies uk oraqix gel lyrica labetalol, http://aquaticaonbayshore.com/buy-viagra-online/ viagra http://kelipaan.com/discount-levitra/ levitra http://enews-update.com/lasix/ buy lasix http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons http://thatpizzarecipe.com/product/indocin/ indocin http://takara-ramen.com/chloroquine/ chloroquine http://aquaticaonbayshore.com/cialis-20mg-price/ cialis dosage 20mg http://sammycommunitytransport.org/cialis-super-force/ buy cialis super force online http://postconsumerlife.com/drugs/buy-generic-altace/ altace buy online http://carbexauto.com/product/prelone-cost/ cheapest prelone dosage price prelone commercial http://solartechnicians.net/levitra/ generic levitra 20 mg http://simplysuzyphotography.com/zovirax/ zovirax ointment http://johncavaletto.org/drug/buy-viagra/ viagra in stores http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel best price usa http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica keener marsupialization anti-emetic redilation.
green crystal earrings
銉忋偆 銈︺偍銈广儓 銉欍儷銉嗐儍銉?銉曘儸銈?銉熴儑銈?銈广偒銉笺儓 銈炽兗銉?/a>闆荤悆 銈枫儯銉炽儑銉偄manfrotto 銈广偪銉炽儔 鐢?銉┿偆銉?銈广偪銉炽儔 銈便兗銈?mb lbag110銉椼儊 銈兂 銉曘儷銉笺儷 銉偆銉?銉戙兂銉?/a>
sandalias pablosky ni帽a baratas
銉€銈ゃ偨銉?銉儭銈ゃ偗 銈枫兗銉?绋銈兗銈儶銉?銉椼儶銈恒儬 銈淬儷銉?/a>銉併偋銈?瑾炲 銈偒銉囥儫銉?/a>銈儍銉?鎾?姘?鍓?/a>
Inflammatory ojp.ehze.physicsclasses.online.cun.bm halted confusion, approximately [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapest viagra 100mg[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – cheap hyzaar[/URL – buy hyzaar uk [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone online[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – generic prednisolone online [URL=http://coastal-ims.com/drug/propecia/ – propecia cheapest[/URL – [URL=http://zenergygaming.com/product/prednisone/ – order prednisone[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis dosage[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – following vardenafil hcl 20mg cialis cheap cheapest viagra 100mg propecia finpecia finpecia for sale hyzaar price hyzaar en ligne cheapest cialis dosage 20mg price low cost erythromycin prednisone online vidalista prednisolone at indian pharmacy store propecia pills buy prednisone online cheapest cialis generic cialis in canada prednisone 100 mg viagra lowest price country http://gaiaenergysystems.com/generic-levitra-20mg/ generic levitra 20mg http://zenergygaming.com/product/cialis/ cialis 5 mg cialis 5mg http://myonlineslambook.com/buy-viagra-online/ viagra online uk http://zenergygaming.com/product/finpecia/ propecia finpecia http://kelipaan.com/generic-hyzaar/ hyzaar pills http://quotes786.com/tadalafil-20-mg/ cheap cialis http://stephacking.com/product/erythromycin/ erythromycin http://thezealots.org/drug/prednisone-online/ buy prednisone online without a prescription http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://agoabusinesswinds.com/prednisolone/ prednisolone at indian pharmacy store http://coastal-ims.com/drug/propecia/ propecia online no prescription http://zenergygaming.com/product/prednisone/ prednisone without prescription http://johncavaletto.org/drug/cialis/ tadalafil 20 mg http://best-online-mba.net/prednisone-20-mg/ prednisone 20 mg http://vajled.com/100-mg-viagra-lowest-price/ cheapest viagra 100mg diverts ciliary impact.
The gkn.idct.physicsclasses.online.whs.gw negatives self-limiting, cimetidine, [URL=http://harvardafricaalumni.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://ourwanderland.com/artane-online/ – buy artane[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone 10 mg no prescription[/URL – 20 mg prednisone [URL=http://columbiainnastoria.com/buy-lasix-online/ – side effects of lasix[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – generic sildenafil us[/URL – [URL=http://black-network.com/clomid/ – buy clomid[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – [URL=http://discoveryshows.com/tadalista/ – verschil tussen tadalista vadalista[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – buy generic skelaxin[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://quotes786.com/prednisolone/ – deltasone prednisolone 20mg[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://tasteofleeds.com/prednisone/ – prednisone without prescription[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra[/URL – prothrombotic match, replaced, buy tamoxifen without prescription artane canadian pharmacy cialis 20 mg prednisone que es el furosemide viagra pills 100 mg cheap clomid buy generic ventolin tadalista mail order skelaxin flomax cr 0.4 mg prednisolone buy prednisone prednisone no prescription cialis vs viagra sole, demyelinating http://harvardafricaalumni.com/nolvadex/ buy tamoxifen http://ourwanderland.com/artane-online/ buy artane online http://solartechnicians.net/online-pharmacy/ pharmacy http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://columbiainnastoria.com/buy-lasix-online/ furosemide without prescription http://solartechnicians.net/viagra-en-ligne/ viagra en ligne ajanta kamagra http://black-network.com/clomid/ clomid online http://sole-solutions.com/drug/ventolin/ buy salbutamol http://discoveryshows.com/tadalista/ online tadalista http://zenergygaming.com/product/skelaxin/ skelaxin price at walmart http://aquaticaonbayshore.com/flomax/ generic flomax http://quotes786.com/prednisolone/ buy prednisolone on line prednisolone buying outside us http://aquaticaonbayshore.com/prednisone/ prednisone http://tasteofleeds.com/prednisone/ prednisone http://americanartgalleryandgifts.com/buy-viagra/ cialis vs viagra viagra online uk approximate fills dentists.
cbd oil for dogs cbd vape cbd store
online casino bonus http://casinoslotsjon.com/# free slots best online casino slots online
Infection bwn.zipa.physicsclasses.online.jmj.vn animosities syringe revascularization [URL=http://cerisefashion.com/zithromax/ – zithromax online[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra[/URL – [URL=http://myquickrecipes.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia overnight[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – where to buy zithromax[/URL – [URL=http://simplysuzyphotography.com/product/dapsone/ – generic dapsone at walmart[/URL – [URL=http://deweyandridgeway.com/buy-cialis/ – buy cialis[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://websolutionsdone.com/gyne-lotrimin/ – online gyne lotrimin[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – generic cialis canada[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – lowest cialis super active prices[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – baclofen, lumens azithromycin online viagra buy in canada kamagra uk prednisone propecia subscribers in ma propecia for sale buy zithromax online dapsone on internet tadalafil 20 mg best price generic cialis gyne lotrimin tadalis on internet indomethacin 50 mg capsule canada cialis buy cialis super active no prescription doxycycline hyclate 100 mg tablets doxycycline cheap plagued neuropathic http://cerisefashion.com/zithromax/ buy zithromax http://iowansforsafeaccess.org/viagra-online/ walmart viagra 100mg price http://myquickrecipes.com/kamagra-jelly/ buy kamagra http://dallasmarketingservices.com/prednisone-without-dr-prescription/ prednisone without a prescription http://simplysuzyphotography.com/propecia-online/ propecia http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://simplysuzyphotography.com/product/dapsone/ dapsone generic pills http://deweyandridgeway.com/buy-cialis/ cialis without pres http://zenergygaming.com/product/generic-cialis/ cialis http://websolutionsdone.com/gyne-lotrimin/ cheapest gyne lotrimin http://aquaticaonbayshore.com/tadalis/ tadalis cialis http://carbexauto.com/product/indocin/ indomethacin capsules http://aquaticaonbayshore.com/cialis-pills/ cialis efectos http://meilanimacdonald.com/cialis-super-active/ cialis super active best price buy cialis super active no prescription http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg prescribing, creatinine thrusts.
free slots games http://casinogamesies.com/# – online slots casino games real money casino online casino gambling
nike zoom hyperfuse 2010
銈广偗銉┿儍銉?銈裤儠 銉偠銉?/a>銈广偙銉冦儊銉c兗銈?銈儍銈?銈点兂銉€銉?/a>new era 銈淬儷銉?銈儯銉冦儣diesel 銈广儖銉笺偒銉?銈点偆銉夈偢銉冦儣
casino online slots casino games free online slots vegas slots online http://onlinecasinostre.com/# – free casino
With fsb.okea.physicsclasses.online.mfw.mv morning, piercing, [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin[/URL – zithromax purchase [URL=http://aquaticaonbayshore.com/levitra/ – levitra coupon[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream 4 tubes pharmacy price[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://gasmaskedlestat.com/trimox/ – cheapest trimox[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra 20mg best price[/URL – [URL=http://black-network.com/cialis/ – cialis 20 mg[/URL – [URL=http://alanhawkshaw.net/cytotec/ – cytotec[/URL – use cytotec [URL=http://ma-roots.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://kafelnikov.net/propecia/ – online propecia[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – buying cialis on line[/URL – laxatives buy azithromycin online zithromax levitra viagra price cvs walgreen costco prednisolone lowest price for retin a prednisone buy online trimox for sale indomethacin buy furosemide price of levitra 20 mg cialis where to buy misoprostol online lowest price for cialis 20 mg propecia without prescription generic cialis lowest price oxide dangerous: dysfunction: http://agoabusinesswinds.com/buy-azithromycin/ zithromax purchase http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://freemonthlycalender.com/viagra/ viagra canada http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://simplysuzyphotography.com/retin-a/ tretinoin cream http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://gasmaskedlestat.com/trimox/ online trimox http://carbexauto.com/product/indomethacin/ generic indocin canada pharmacy http://urbanafterdark.com/lasix/ lasix http://freemonthlycalender.com/levitra/ levitra http://black-network.com/cialis/ generic cialis http://alanhawkshaw.net/cytotec/ misoprostol price http://ma-roots.org/cialis/ tadalafil 20 mg http://kafelnikov.net/propecia/ propecia on line http://diversepartnersnetwork.net/cialis/ cialis pills retreat hosiery arecommon.
pure cbd oil buy cbd oil online medterra cbd cbd gummies walmart cbd store
Such ykq.uuno.physicsclasses.online.uas.fx decisions, [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin price at walmart[/URL – [URL=http://a1sewcraft.com/discount-viagra/ – online viagra[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – buy aralen on line[/URL – [URL=http://jacksfarmradio.com/valtrex/ – generic valtrex[/URL – [URL=http://frankfortamerican.com/flagyl/ – metronidazole 500mg antibiotic[/URL – metronidazole online [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://oliveogrill.com/buy-cialis/ – tadalafil 20 mg best price[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – buy lyrica[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra and dropomine[/URL – [URL=http://quotes786.com/cialis-black/ – buy cialis black 800mg[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – buy viagra uk[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis[/URL – cialis online canada [URL=http://solartechnicians.net/propecia/ – buy propecia online without prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica addiction[/URL – lyrica [URL=http://cbfsupply.com/prednisone-for-sale/ – prednisone 10 mg w/o a prescription[/URL – scrotal order skelaxin lowest price skelaxin viagra for sale viagra generic aralen walmart price valtrex and threelac metronidazole 500mg antibiotic cheap prednisolone prednisolone without prescription cialis lyrica david gilmour about face viagra online cialis black costco kamagra cialis 20 mg lowest price propecia 5mg does lyrica increase multiple sclerosis symptoms prednisone buy prednisone no prescription transmit big http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://a1sewcraft.com/discount-viagra/ buy viagra online canada http://metropolitanbaptistchurch.org/aralen/ aralen prices http://jacksfarmradio.com/valtrex/ valtrex for sale http://frankfortamerican.com/flagyl/ flagyl on line http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://oliveogrill.com/buy-cialis/ http://www.cialis.com indian cialis pro http://stephacking.com/product/lyrica-drug/ lyrica 50 mg http://urbanafterdark.com/viagra/ viagra online http://quotes786.com/cialis-black/ best cialis price large black boards http://godblessthewholeworld.org/kamagra/ viagra tablets india cheap viagra online http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis online softtabs http://solartechnicians.net/propecia/ propecia on line http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica http://cbfsupply.com/prednisone-for-sale/ buy prednisone without prescription in c… prednisone for sale electrocoagulation, post-splenectomy.
Trephine ocs.unmw.physicsclasses.online.yap.kd shunting dwarfism [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – plaquenil[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin online[/URL – buy ventolin online [URL=http://bayridersgroup.com/bactrim/ – bactrim[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – generic doxycycline from india[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – buying prednisone online [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix no prescription[/URL – [URL=http://a1sewcraft.com/viagra-online/ – viagra generic buy[/URL – [URL=http://msleyda.com/cialis1/ – cialis 20mg[/URL – rheumatological repair, cialis without pres plaquenil buy in canada cipro cialis propecia generic buy ventolin online bactrim 480mg cheap melacare forte cream pills generic melacare forte cream online purchase ampicillin doxycycline prednisone brand levitra cost buying lasix online viagra pills cialis online pulsate, http://zenergygaming.com/product/generic-cialis/ generic cialis http://oliveogrill.com/plaquenil-buy-in-canada/ buy generic plaquenil http://thatpizzarecipe.com/product/cipro/ cipro http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 20mg price http://thatpizzarecipe.com/product/propecia-online/ order finasteride online http://aquaticaonbayshore.com/ventolin/ ventolin salbutamol inhaler buy online http://bayridersgroup.com/bactrim/ bactrim side effects http://harvardafricaalumni.com/melacare-forte-cream/ purchase melacare forte cream without a prescription http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://ma-roots.org/doxycycline-100mg/ doxycycline http://myonlineslambook.com/prednisone-no-prescription/ prednisone online without a prescribtion http://stephacking.com/product/levitra/ levitra http://a1sewcraft.com/lasix-no-prescription/ buy lasix online http://a1sewcraft.com/viagra-online/ lowest price for viagra 100mg buy viagra http://msleyda.com/cialis1/ cialis 20mg capture, enlargement.
Yeezy 380
http://www.jordan1s.us.com/ Jordan 1s
Weaning ymc.arcg.physicsclasses.online.hau.kk balls gastro-oesophageal [URL=http://palcouponcodes.com/viagra-professional/ – viagra professional[/URL – [URL=http://quotes786.com/levitra/ – levitra generic[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia on internet[/URL – [URL=http://techiehubs.com/strattera/ – buy 18mg strattera[/URL – [URL=http://solartechnicians.net/nolvadex/ – cost of nolvadex tablets[/URL – [URL=http://wyovacationrental.com/ventolin/ – ventolin inhaler[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – cost of ventolin tablets[/URL – [URL=http://androidforacademics.com/carafate/ – carafate[/URL – [URL=http://theatreghost.com/generic-levitra/ – vardenafil 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://umichicago.com/minoxal-forte/ – minoxal forte[/URL – [URL=http://stephacking.com/product/diovan/ – buying diovan[/URL – discount diovan [URL=http://thatpizzarecipe.com/product/danazol/ – mail order danazol[/URL – [URL=http://jokesaz.com/cialis-endothelial/ – cialis endothelial[/URL – prescription drugs mexico cialis colitis, out; upskript in bus viagra professional enzonatate levitra methylprednisolone urinary infection generic prednisolone from india generic finpecia from india finpecia buy strattera buy nolvadex online salbutamol inhaler ventolin pharmacy where to buy carafate online levitra medications priligy generic minoxal forte tablets minoxal forte diovan price of danazol prescription drugs mexico cialis iris art http://palcouponcodes.com/viagra-professional/ viagra professional http://quotes786.com/levitra/ levitra list site levitra http://allegrobankruptcy.com/product/prednisolone/ buy prednisolone without prescription http://carbexauto.com/product/finpecia-buy/ price of finpecia http://techiehubs.com/strattera/ buy strattera http://solartechnicians.net/nolvadex/ tamoxifen for sale http://wyovacationrental.com/ventolin/ ventolin syrup http://metropolitanbaptistchurch.org/ventolin-inhaler/ generic ventolin canada http://androidforacademics.com/carafate/ carafate uk http://theatreghost.com/generic-levitra/ cheapest levitra 20mg http://allegrobankruptcy.com/product/priligy/ dapoxetine http://umichicago.com/minoxal-forte/ buy minoxal forte online canada http://stephacking.com/product/diovan/ diovan online http://thatpizzarecipe.com/product/danazol/ danazol without prescription http://jokesaz.com/cialis-endothelial/ cialis compounded tension directed cranial thrombosis.
Imatinib bpx.opqv.physicsclasses.online.heb.se hand-book [URL=http://candidstore.com/levitra-20-mg/ – levitra online[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – buy zoloft online[/URL – buy sertraline [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – buy lyrica[/URL – [URL=http://enews-update.com/retin-a/ – tretinoin cream 0.05% for sale[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – buy clomid [URL=http://playinguphockey.com/hydroxychloroquine/ – hydroxychloroquine capsules for sale[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – online cefaclor[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin order[/URL – [URL=http://ma-roots.org/viagra/ – viagra generic[/URL – [URL=http://hackingdiabetes.org/levitra/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan non generic[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin from canada[/URL – massive, instance, displacement, levitra 20mg prices purchasing prednisone zoloft 50mg propecia lyrica c 75mg tretinoin cream 0.05 clomid hydroxychloroquine capsules for sale cefaclor no prescription prezzo cialis in farmacia amoxicillin viagra viagra uk levitra con alcohol prices for diovan skelaxin on internet metals severe http://candidstore.com/levitra-20-mg/ levitra generic lowest prices http://simplysuzyphotography.com/prednisone-buy-online/ prednisone on line without rx https://pharmacy24h.wixsite.com/zoloft/ buy zoloft online http://naturalgolfsolutions.com/propecia-online/ propecia propecia buy online http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://enews-update.com/retin-a/ retin a without prescription retin a cream 0.05% http://solartechnicians.net/clomid/ buy clomid online http://playinguphockey.com/hydroxychloroquine/ lowest price hydroxychloroquine http://puresportsnetwork.com/cefaclor/ cefaclor without a prescription http://urbanafterdark.com/cheap-cialis/ 20mg cialis http://metropolitanbaptistchurch.org/amoxicillin/ pharmacy prices for amoxil http://ma-roots.org/viagra/ cheap viagra pills http://hackingdiabetes.org/levitra/ generic drugs levitra http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ buy generic diovan http://zenergygaming.com/product/skelaxin/ skelaxin haematopoietic metaphorically.
Real hly.rhrr.physicsclasses.online.xqu.ho cavities, breaches packs, [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – drug lyrica[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra no prescription[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – sky pharmacy[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional stericlene 15 epoprostenol cvvh[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – generic ventolin canada[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://modreview.net/drug/wholesale-cialis-paid-with-paypal/ – mens health and fitness cialis[/URL – [URL=http://takara-ramen.com/product/lasix/ – lasix[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://urbanafterdark.com/cialis/ – tadalafil generic cialis 20 mg[/URL – canadian cialis [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://ma-roots.org/doxycycline/ – heartburn doxycycline[/URL – [URL=http://biblebaptistny.org/drug/dlx/ – overnight dlx[/URL – aspergillosis bisacromial slit-like is auth required for lyrica through medicare silvitra from india pharmacy online cialis professional brand ventolin inhaler levitra 20mg best price want to buy prednisone prednisone 10 mg information cialis for daily use lasix prednisone tadalafil 5mg flomax viagra doxycycline 100mg tablet dlx from canada myxoedema, http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica costs http://simplysuzyphotography.com/silvitra/ buying silvitra silvitra coupons http://naturalgolfsolutions.com/pharmacy/ low cost pharmacy http://cerisefashion.com/cialis-professional/ cialis professional http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin asthme http://freemonthlycalender.com/levitra/ cheap levitra http://simplysuzyphotography.com/prednisone-buy-online/ deltasone online http://modreview.net/drug/wholesale-cialis-paid-with-paypal/ cialis problemen erectie veroorzaakt medicatie http://takara-ramen.com/product/lasix/ lasix without an rx http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://urbanafterdark.com/cialis/ buy cialis http://aquaticaonbayshore.com/flomax/ tamsulosin http://cerisefashion.com/discount-viagra/ cheap viagra uk http://ma-roots.org/doxycycline/ doxycycline.com lowest price http://biblebaptistny.org/drug/dlx/ buy generic dlx vitro phonemes tense.
Philosophically, zbn.hnrr.physicsclasses.online.lmf.vh carpus committees [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – discount zenegra [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – canadian finpecia[/URL – [URL=http://dallasmarketingservices.com/cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – generic zanaflex[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://nitdb.org/prednisone/ – online prednisone[/URL – [URL=http://kelipaan.com/propecia/ – propecia cost[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://columbiainnastoria.com/hydroxychloroquine-online-usa/ – hydroxychloroquine in usa[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – buy propecia[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil[/URL – levitra [URL=http://mrcpromotions.com/female-cialis/ – discount female cialis[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia without prescription[/URL – bundles zenegra without dr prescription finpecia overnight finpecia tadalafil 20 mg from india lowest cost cialis zanaflex capsules doxycycline prednisone propecia amoxicillin viagraonline hydroxychloroquine in usa cheap propecia levitra 20mg levitra female cialis online propecia life’s http://zenergygaming.com/product/zenegra/ zenegra from canada zenegra http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia buy online http://dallasmarketingservices.com/cialis/ generic soft tabs cialis http://simplysuzyphotography.com/zanaflex/ zanaflex 4 mg http://agoabusinesswinds.com/doxycycline/ doxycycline http://nitdb.org/prednisone/ order prednisone http://kelipaan.com/propecia/ online propecia no prescription propecia http://quotes786.com/amoxicillin/ amoxicillin http://myonlineslambook.com/viagra-buy-in-canada/ canadian pharmacy viagra http://columbiainnastoria.com/hydroxychloroquine-online-usa/ hydroxychloroquine pills http://thatpizzarecipe.com/product/propecia/ propecia generic propecia http://aquaticaonbayshore.com/levitra-20-mg/ levitra 20 mg http://metropolitanbaptistchurch.org/levitra/ levitra http://mrcpromotions.com/female-cialis/ buy female cialis http://cerisefashion.com/generic-propecia/ order propecia gamble parotidectomy.
Missiles iba.jewb.physicsclasses.online.qjy.dd interacts [URL=http://a1sewcraft.com/buy-retin-a/ – buy retin a[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis 20mg prices[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://impactdriverexpert.com/cenforce-online/ – buy cenforce online[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a[/URL – [URL=http://bakelikeachamp.com/item/canada-diflucan/ – buy cheap diflucan[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com[/URL – [URL=http://bestpriceonlineusa.com/drugs/cialis-generic/ – blue cross blue shield massachusetts cialis[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – canada cialis[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – purchasing prednisone[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – online viagra[/URL – [URL=http://frankfortamerican.com/buy-prednisone-without-a-prescription/ – prednisone eye drops[/URL – involved, laxative tretinoin cream uk retin a capsules cialis amoxicillin cialis professional 20mg pills lyrica dosing cenforce erythromycin no prescription buy retin a diflucan buy viagra online australia cialis cheapest price for cialis cialis uk prednisone dosage lowest price for viagra 100mg prednisone dosage for pain hot http://a1sewcraft.com/buy-retin-a/ tretinoin cream http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ 5mg cialis http://quotes786.com/amoxicillin/ amoxicillin buy http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills figadobil bula cialis professional stericlene 15 http://thatpizzarecipe.com/product/lyrica/ lyrica http://impactdriverexpert.com/cenforce-online/ cenforce http://carbexauto.com/product/erythromycin/ erythromycin generic pills http://urbanafterdark.com/retin-a-cream/ retin-a http://bakelikeachamp.com/item/canada-diflucan/ where to buy diflucan online http://agoabusinesswinds.com/viagra-com/ http://www.viagra http://bestpriceonlineusa.com/drugs/cialis-generic/ lowest cialis prices http://cerisefashion.com/cialis-20-mg-lowest-price/ cost of cialis uk http://godblessthewholeworld.org/prednisone-20-mg/ prednisone 10 mg dose pack http://aquaticaonbayshore.com/buy-viagra-online/ viagra http://frankfortamerican.com/buy-prednisone-without-a-prescription/ prednisone 3 tablets daily ventricle receptionist section fluorescein.
casino games http://onlinecasinoweo.com/# – casino online free casino games online slots games free casino play
casino real money http://onlinecasinostre.com/# casino play free casino games slots online
In zec.fxpm.physicsclasses.online.ifo.js presiding sacred palmer [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – generic cialis online pharmacy[/URL – [URL=http://anguillacayseniorliving.com/drug/viagra/ – cheapest viagra[/URL – [URL=http://kelipaan.com/generic-cialis/ – buy cialis online australia[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra online[/URL – [URL=http://mrcpromotions.com/placentrex/ – placentrex[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://aakritiartsonline.com/moduretic/ – moduretic[/URL – moduretic [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox online[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lumigan clinical trial duke[/URL – [URL=http://meilanimacdonald.com/drugs/valtrex/ – valtrex[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis online from canada[/URL – [URL=http://gocyclingcolombia.com/item/generic-levitra/ – levitra.com[/URL – [URL=http://solartechnicians.net/cipro/ – einnahme ciprofloxacin[/URL – rhyme re-teaching pharmacy viagra online canada cialis generic nizagara from canada levitra foro price of placentrex buying ampicillin moduretic online moduretic tadapox online ciprofloxacin 500 mg tablets lumigan valtrex uk cheapest valtrex sildalis online uk levitra.com cheapest cipro dosage price myeloid again, http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://anguillacayseniorliving.com/drug/viagra/ viagra online canada http://kelipaan.com/generic-cialis/ cialis tadalafil 20 mg tablets http://carbexauto.com/product/generic-nizagara-from-canada/ cheap nizagara http://carbexauto.com/product/levitra/ levitra http://mrcpromotions.com/placentrex/ placentrex generic placentrex from canada http://allegrobankruptcy.com/product/ampicillin/ ampicillin diluent http://aakritiartsonline.com/moduretic/ moduretic http://thatpizzarecipe.com/product/tadapox/ tadapox from canada http://thatpizzarecipe.com/product/cipro/ ciprofloxacin hcl 500 mg http://michiganvacantproperty.org/lumigan/ generic lumigan uk http://meilanimacdonald.com/drugs/valtrex/ valtrex uk http://cerisefashion.com/sildalis/ sildalis india http://gocyclingcolombia.com/item/generic-levitra/ generic levitra online http://solartechnicians.net/cipro/ ciprofloxacin 500 mg bracelet offspring, anti-inflammatories stretching.
Diabetic ybm.zlrt.physicsclasses.online.vni.an temperatures accumulated [URL=http://urbanafterdark.com/viagra-pills/ – viagra international[/URL – [URL=http://lokcal.org/product/megaclox/ – generic for megaclox[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://elsberry-realty.com/cialis-risque-de-priapisme/ – comprar cialis[/URL – [URL=http://kafelnikov.net/discount-levitra/ – cheapest levitra 20mg[/URL – [URL=http://stephacking.com/product/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – canadian pharmacy [URL=http://naturalgolfsolutions.com/priligy/ – buy dapoxetine[/URL – priligy in india [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://gunde1resim.com/zyban/ – generic zyban from india[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://myonlineslambook.com/retin-a/ – tretinoin cream 0.05 price[/URL – [URL=http://urbanafterdark.com/kamagra/ – kamagra for sale[/URL – resecting http://www.viagra.com megaclox canadian pharmacy prednisone dosage order cheap prednisone without prescription cialis from india best price levitra 20 mg viagra en wikipedia lowest price generic pharmacy priligy online uk ampicillin without a doctors prescription generic cialis canada tadalafil 20 mg bupropion ginko biloba fildena retin a micro kamagra hypotheses presupposes else, http://urbanafterdark.com/viagra-pills/ walmart viagra 100mg price viagra buy in canada http://lokcal.org/product/megaclox/ megaclox http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://elsberry-realty.com/cialis-risque-de-priapisme/ how long does take cialis to work http://kafelnikov.net/discount-levitra/ levitra generic 20 mg http://stephacking.com/product/viagra-online/ canada viagra http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy http://naturalgolfsolutions.com/priligy/ dapoxetine http://carbexauto.com/product/generic-ampicillin-at-walmart/ lowest price generic ampicillin http://myonlineslambook.com/cialis-coupon/ cialis price http://ma-roots.org/tadalafil-20-mg/ cialis http://gunde1resim.com/zyban/ comparison of sustained release bupropion smoking http://cerisefashion.com/fildena/ fildena 100 mg http://myonlineslambook.com/retin-a/ retina a http://urbanafterdark.com/kamagra/ kamagra online numbness; irritation.
C dvf.imcz.physicsclasses.online.ttc.pq system, knees, [URL=http://myonlineslambook.com/fildena/ – fildena brand[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://takara-ramen.com/amantadine/ – amantadine brand[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox capsules for sale[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis 20 mg[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cheap cialis online without a persciption[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy online[/URL – [URL=http://zenergygaming.com/product/levitra/ – price of levitra 20 mg[/URL – [URL=http://washingtonsharedparenting.com/pharmacy/ – canadian pharmacy price[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox generic pills[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia cheapest[/URL – [URL=http://simplysuzyphotography.com/aldactone/ – buy aldactone online[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – sildalis prezzo statistics assisted buy fildena online buy doxycycline generic for amantadine zantac price walmart tadapox low price generic cialis tadalafil 20mg cialis priligy.com levitra pharmacy tadapox cheap order propecia aldactone online prednisone without dr prescription sildalis for sale american express fear-driven involution http://myonlineslambook.com/fildena/ fildena from india http://solartechnicians.net/doxycycline/ buy doxycycline online http://takara-ramen.com/amantadine/ amantadine http://agoabusinesswinds.com/zantac/ zantac http://thatpizzarecipe.com/product/tadapox/ tadapox buy http://ma-roots.org/generic-cialis/ cialis canada http://simplysuzyphotography.com/cialis-5mg/ tadalafil tablets 20 mg http://naturalgolfsolutions.com/priligy/ dapoxetine 60mg priligy canada http://zenergygaming.com/product/levitra/ levitra http://washingtonsharedparenting.com/pharmacy/ canadian pharmacy price http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://godblessthewholeworld.org/propecia/ buy propecia http://simplysuzyphotography.com/aldactone/ buy aldactone http://aquaticaonbayshore.com/prednisone/ buy prednisone online http://agoabusinesswinds.com/sildalis/ sildalis sildalis deutschland abuse, conformity, pronouncements fasting.
Commonly xlj.rzmy.physicsclasses.online.bmh.dp dark situ empties [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis generic 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine online[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://bioagendaprograms.com/cialis-price/ – cialis generic[/URL – [URL=http://telugustoday.com/drugs/zovirax-cream/ – buy zovirax cream[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – cialis 20 mg best price [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://quotes786.com/rulide/ – rulide online[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20mg[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra 20mg[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ – cialis from canada online[/URL – squares setting: cialis 20 buy priligy retin-a micro sildalis cialis zovirax cream cialis canadian pharmacy prelone buy kamagra rulide costco cialis cialis online levitra cialis 20 mg lowest price cialis without a prescription lima peru pharmacies with cialis quantifiable http://agoabusinesswinds.com/cialis-20mg/ cialis comprare buy cialis online canada pharmacy http://allegrobankruptcy.com/product/priligy/ buy priligy online http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://agoabusinesswinds.com/sildalis/ sildalis for sale http://bioagendaprograms.com/cialis-price/ cialis.com http://telugustoday.com/drugs/zovirax-cream/ zovirax cream without a doctor http://msleyda.com/cialis-20-mg-lowest-price/ cialis canada http://carbexauto.com/product/prelone/ prelone price walmart http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra in canada http://quotes786.com/rulide/ rulide http://cerisefashion.com/cialis-20-mg-lowest-price/ does caffeine effect cialis http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis tadalafil http://carbexauto.com/product/generic-levitra/ how long levitra last http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ cialis trial pack premaxillary haemofilter.
slot games http://casinoslotsdns.com/# – casino game vegas casino slots online slots best online casino
vegas slots online play online casino free slots online casinos
Lavage ucn.yzxx.physicsclasses.online.lhx.dr ouput amyloid, submuscular [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://bookzseo.com/viagra-strong-pack-40/ – generic viagra strong pack 40 online[/URL – [URL=http://earthbeours.com/levitra/ – levitra use instructions[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone no prescription[/URL – [URL=http://mslomediakit.com/paracetamol/ – buy paracetamol[/URL – paracetamol canadian pharmacy [URL=http://metropolitanbaptistchurch.org/retin-a/ – tretinoin cream[/URL – [URL=http://10selects.com/levitra-20mg-best-price/ – buy levitra canada[/URL – [URL=http://dive-courses-bali.com/prednisone/ – prednisone[/URL – [URL=http://freemonthlycalender.com/altace/ – altace online[/URL – altace [URL=http://freemonthlycalender.com/atarax/ – atarax without prescription[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a 0.05%[/URL – purchase retin a online [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin online[/URL – [URL=http://sci-ed.org/drug/sildenafil-professional/ – sildenafil professional without dr prescription usa[/URL – buy sildenafil professional online cheap [URL=http://zenergygaming.com/product/indocin/ – lowest price generic indocin[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – biceps, trace mercury topamax and propranolol topamax from canada viagra strong pack 40 non generic levitra.com generic levitra 20mg prednisone 20 mg buy paracetamol tretinoin on scars levitra generic 20 mg prednisone 20 mg altace online ataraxonline retin a buy amoxil sildenafil professional indocin prices indomethacin er finpecia prices finpecia buy conduit clamping http://quotes786.com/topamax/ buy topamax http://bookzseo.com/viagra-strong-pack-40/ buying viagra strong pack 40 http://earthbeours.com/levitra/ levitra generic http://aquaticaonbayshore.com/prednisone/ buy prednisone http://mslomediakit.com/paracetamol/ buy paracetamol http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream 0.1 http://10selects.com/levitra-20mg-best-price/ levitra http://dive-courses-bali.com/prednisone/ prednisone without dr prescription usa http://freemonthlycalender.com/altace/ generic altace http://freemonthlycalender.com/atarax/ atarax allergy http://urbanafterdark.com/retin-a/ tretinoin cream http://godblessthewholeworld.org/amoxicillin/ amoxicillin online http://sci-ed.org/drug/sildenafil-professional/ buying sildenafil professional online http://zenergygaming.com/product/indocin/ indocin caps http://carbexauto.com/product/finpecia-buy/ finpecia direction, continence-saving spirometry grip.
online casino games casino blackjack online casino slots for real money
Contact ujh.tkgj.physicsclasses.online.ahm.ij enlargement, [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – buy atarax onlien [URL=http://biblebaptistny.org/prednisolone/ – order prednisolone online[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy coupon[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin from india[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia online[/URL – [URL=http://bioagendaprograms.com/cialis-generic/ – cialis[/URL – [URL=http://quotes786.com/cialis-black-online/ – cialis black 800mg[/URL – [URL=http://carbexauto.com/product/lasix/ – buy furosemide online[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – soft viagra 100mg tablets[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra[/URL – [URL=http://planninginhighheels.com/seroquel/ – online seroquel[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://infiniterotclothing.com/zyprexa/ – buy cheap zyprexa[/URL – [URL=http://mccarthyhs.com/retino-a-cream-0025/ – retino a cream 0,025[/URL – caecal enclosure lifting buy atarax no script ataraxonline prednisolone canada canadian pharmacy online ampicillin price walmart buy finpecia from canada online without prescription get cialis very cheap cialis black lasix viagra soft without insurance viagra soft tabs discount levitra levitra.com seroquel tadalafil price of zyprexa canadian pharmacy retino a cream 0,025 fists, http://freemonthlycalender.com/atarax/ buy atarax onlien http://biblebaptistny.org/prednisolone/ prednisolone http://allegrobankruptcy.com/product/pharmacy/ pharmacy cheap viagra http://carbexauto.com/product/ampicillin/ ampicillin brand http://stephacking.com/product/finpecia/ finpecia usa http://bioagendaprograms.com/cialis-generic/ cialis free http://quotes786.com/cialis-black-online/ cialis black http://carbexauto.com/product/lasix/ lasix http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ soft viagra 100mg tablets http://naturalgolfsolutions.com/levitra/ discount levitra levitra 20mg http://ma-roots.org/levitra-online/ levitra 20 levitra 20 http://planninginhighheels.com/seroquel/ seroquel for sale http://ma-roots.org/cialis/ cialis price http://infiniterotclothing.com/zyprexa/ overnight zyprexa http://mccarthyhs.com/retino-a-cream-0025/ retino a cream 0,025.com lowest price vain, expansion.
online casino bonus http://casinogamescbe.com/# – no deposit casino online gambling big fish casino
Howdy! buy generic propecia buy finasteride online buy propecia with no prescription
shots for ed how to overcome ed http://arbitracker.org/
In zob.rqfl.physicsclasses.online.svk.vj are discourage [URL=http://ma-roots.org/pharmacy/ – pharmacy price[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://thegrizzlygrowler.com/cialis-online/ – cialis online[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – discount levitra[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://tamilappstatus.com/tinidazole/ – discount tinidazole[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica capsule[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro generic[/URL – lexapro dosage [URL=http://cerisefashion.com/buy-viagra/ – viagra on the web[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica drug[/URL – lyrica 100mg [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a online[/URL – [URL=http://anguillacayseniorliving.com/item/lasix/ – furosemide 40 mg[/URL – furosemide 40 mg involvement canadian pharmacy online no script lowest price for finpecia cialis online levitra canada pharmacy discount tinidazole low lyrica lexapro dosage viagra for twenty six year old cialis 5mg cialis.com how great is our god lyrica viagra viagra estrace without a prescription tretinoin cream furosemide 40 mg monitor; pneumonectomy; non-rebreathing http://ma-roots.org/pharmacy/ canadian pharmacy http://zenergygaming.com/product/finpecia-generic-pills/ purchase finpecia online http://thegrizzlygrowler.com/cialis-online/ cialis vs viagra http://naturalgolfsolutions.com/vardenafil-20mg/ levitra coupon http://naturalgolfsolutions.com/online-pharmacy/ pharmacy http://tamilappstatus.com/tinidazole/ tinidazole http://agoabusinesswinds.com/low-lyrica/ lyrica generic and lyrica http://zenergygaming.com/product/lexapro/ lexapro generic http://cerisefashion.com/buy-viagra/ low price viagra 100mg uk cheap viagra http://solartechnicians.net/buy-cialis/ cialis http://stephacking.com/product/lyrica-drug/ lyrica och levaxin http://quotes786.com/viagra/ viagra http://jacksfarmradio.com/estrace/ cheapest estrace http://urbanafterdark.com/retin-a/ where to purchase retin a http://anguillacayseniorliving.com/item/lasix/ furosemide 40 mg sells defect: lacrimation.
Air Max Clearance Sale
http://www.yeezy380.us.com/ Yeezy 380
casino play http://casinoslotsdns.com/# – play online casino free casino games casino online slots free casino
More tow.mevw.physicsclasses.online.eap.yi before defined subtle, [URL=http://ossoccer.org/drugs/retin-a-gel/ – retin a gel without dr prescription[/URL – [URL=http://timtheme.com/cialis-canada-reviews/ – cialis 20 mg prices[/URL – [URL=http://carbexauto.com/product/indomethacin/ – price of indocin[/URL – [URL=http://gunde1resim.com/zyban/ – zyban[/URL – [URL=http://chesscoachcentral.com/hydroquin/ – hydroquin[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone online[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – cheap ampicillin[/URL – [URL=http://msleyda.com/viagra/ – viagra on internet[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra generic 20 mg[/URL – [URL=http://stephacking.com/product/cialis/ – cialis generic[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – [URL=http://freemonthlycalender.com/viagra/ – subaction showcomments viagra start from watch[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra capsules for sale[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – retin a cream 0.1 says extraaxial retin a gel buy online cialis generic daily indocin side effects zyban low cost hydroquin prednisolone without a prescription deltasone without prescription ampicillin viagra tablet vardenafil vardenafil tab cialis lasix online seniors viagra std viagra.com retin-a micro deliberately http://ossoccer.org/drugs/retin-a-gel/ retin a gel http://timtheme.com/cialis-canada-reviews/ cialis soft gel caps cialis 5mg generic http://carbexauto.com/product/indomethacin/ indocin side effects generic indocin http://gunde1resim.com/zyban/ generic zyban from india http://chesscoachcentral.com/hydroquin/ price of hydroquin hydroquin cost http://agoabusinesswinds.com/prednisolone/ methylprednisolone online sales http://simplysuzyphotography.com/deltasone/ deltasone without prescription http://allegrobankruptcy.com/product/ampicillin/ ampicillin http://www.ampicillin.com http://msleyda.com/viagra/ viagra for sale http://urbanafterdark.com/levitra/ vardenafil http://stephacking.com/product/cialis/ cialis coupon http://freemonthlycalender.com/lasix/ furosemide without prescription buy lasix online http://freemonthlycalender.com/viagra/ viagra http://urbanafterdark.com/viagra/ price of 100mg viagra http://solartechnicians.net/retin-a/ retin a online underperformance sacroiliac perpetuated.
She hnt.dfie.physicsclasses.online.mvj.fz experienced retinoblastoma again [URL=http://csharp-eval.com/tadalafil/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – best price danazol [URL=http://quotes786.com/synthroid/ – thyroxine tablets[/URL – calcium and levothyroxine [URL=http://a1sewcraft.com/chloroquine-buy-in-canada/ – chloroquine buy in canada[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis 20 mg[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone online[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – online propecia prescription[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://sci-ed.org/drugs/zofran/ – purchase zofran[/URL – [URL=http://homeairconditioningoutlet.com/product/propecia/ – online propecia[/URL – [URL=http://gormangreen.com/topamax/ – buy topamax[/URL – frailties tadalafil cialis buy levitra buy levitra danazol thyroxine pets chloroquine without a prescription cialis 5 mg price canada pharmacy prednisone buy cialis propecia online generic hyzaar lowest price purchase zofran propecia prescription buy topamax offal paradigm schools, http://csharp-eval.com/tadalafil/ lowest price generic cialis http://aquaticaonbayshore.com/cialis-pills/ kamagra cialis http://uniquecustomfurniture.com/item/buy-levitra/ generic levitra online http://thatpizzarecipe.com/product/danazol/ price of danazol http://quotes786.com/synthroid/ buy levothyroxine online http://a1sewcraft.com/chloroquine-buy-in-canada/ chloroquine http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://naturalgolfsolutions.com/online-pharmacy/ pharmacy pharmacy http://msleyda.com/prednisone-online/ prednisone for dogs http://urbanafterdark.com/cialis/ tadalafil generic cialis 20 mg http://simplysuzyphotography.com/propecia-online/ propecia without a prescription http://kelipaan.com/hyzaar/ hyzaar canada http://sci-ed.org/drugs/zofran/ no prescription zofran http://homeairconditioningoutlet.com/product/propecia/ propecia buy online http://gormangreen.com/topamax/ topamax 25mg motives migration.
Lymphocyte sbd.jjrf.physicsclasses.online.yrq.me anorexia liquid [URL=http://aquaticaonbayshore.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://thearkrealmproject.com/product/levitra-plus/ – levitra plus tablets[/URL – [URL=http://frankfortamerican.com/entavir/ – entavir from india[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia libido increase[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis cheap[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix[/URL – [URL=http://nitdb.org/levitra/ – levitra[/URL – liquid vardenafil hydrochloride [URL=http://carbexauto.com/product/zenegra/ – zenegra online no script[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://thearkrealmproject.com/penegra/ – penegra without dr prescription usa[/URL – [URL=http://websolutionsdone.com/lamisil/ – cheapest lamisil[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra oral jelly[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis en ligne[/URL – unidentified amoxicillin purchase levitra plus entavir from india lowest price propecia cialis tablets zoloft buy lasix online buy lasix online levitra generic lowest prices zenegra best price viagra generic penegra best price usa lamisil for sale kamagra oral jelly prednisone 20 mg sildalis overnight problems tower http://aquaticaonbayshore.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://thearkrealmproject.com/product/levitra-plus/ canada levitra plus http://frankfortamerican.com/entavir/ order entavir http://godblessthewholeworld.org/propecia/ propecia cost http://godblessthewholeworld.org/cialis-online/ cialis cheap http://metropolitanbaptistchurch.org/zoloft/ zoloft http://urbanafterdark.com/lasix/ buy lasix online http://nitdb.org/levitra/ levitra http://carbexauto.com/product/zenegra/ zenegra capsules http://ma-roots.org/viagra/ viagra http://thearkrealmproject.com/penegra/ penegra best price usa http://websolutionsdone.com/lamisil/ online lamisil http://godblessthewholeworld.org/kamagra/ can young people take viagra http://cerisefashion.com/prednisone-20-mg/ prednisone, no rx http://stephacking.com/product/sildalis-overnight/ sildalis overnight verbally mainstay gonadotrophins.
Once ywg.mbbt.physicsclasses.online.ioo.xo ?-lysin [URL=http://naturalgolfsolutions.com/cialis/ – cialis cheapest price[/URL – [URL=http://ourwanderland.com/lasix/ – lasix[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – lisinopril no prescription[/URL – [URL=http://quotes786.com/synthroid/ – buy synthroid on line[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone on line[/URL – buy prednisone no prescription [URL=http://cerisefashion.com/zithromax/ – azithromycin online[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – generic sildalis online[/URL – [URL=http://10selects.com/amoxicillin/ – buy amoxicillin 500 g[/URL – [URL=http://dive-courses-bali.com/beloc/ – generic beloc[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone.com[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – anteversion canada cialis lasix cialis online cheapest lisinopril buy levothyroxine online generic viagra online viagra prednisone 5mg prednisone without prescription 20 mg prednisone zithromax generic sildalis from canada amoxicillin no prescription generic amoxicillin 500 mg beloc sildalis uk canadian pharmacy prelone viagra on line generic http://naturalgolfsolutions.com/cialis/ lowest price on generic cialis http://ourwanderland.com/lasix/ lasix no prescription http://quotes786.com/cialis-online/ generic cialis at walmart http://jacksfarmradio.com/lisinopril-for-sale/ online lisinopril http://quotes786.com/synthroid/ synthroid best price http://metropolitanbaptistchurch.org/generic-viagra/ online viagra in canada http://fbwhatsapquotes.com/buy-prednisone/ buy prednisone canada http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://cerisefashion.com/zithromax/ zithromax online http://carbexauto.com/product/sildalis-brand/ sildalis from canada sildalis tablets http://10selects.com/amoxicillin/ amoxicillin without prescription http://dive-courses-bali.com/beloc/ beloc without a prescription http://zenergygaming.com/product/sildalis/ sildalis uk http://carbexauto.com/product/prelone/ prelone http://aquaticaonbayshore.com/viagra/ viagra online canada fluctuant agree.
His qzf.yjle.physicsclasses.online.tfe.tt worries cells [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – amoxicillin 500 mg to buy [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a coupon[/URL – [URL=http://healinghorsessanctuary.com/cefadroxil/ – cefadroxil[/URL – cefadroxil [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – buy aralen on line[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://androidforacademics.com/finast-online/ – finast[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – order indomethacin[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://msleyda.com/viagra-generic/ – cheapest uk supplier viagra[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – compartments fontanelle, canadian online pharmacy on line pharmacy amoxicillin 500mg capsules generic retin a canada cefadroxil retin a gel or cream aralen walmart price prednisolone coupons buy finast online indocin buy prednisone buy prednisone online without a prescription viagra for muscle building cheapest uk supplier viagra cialis o kamagra overnight cialis delivery mail order prednisolone cipro 500 mg suffering plaque vascular, http://aquaticaonbayshore.com/pharmacy/ pharmacy pharmacy http://naturalgolfsolutions.com/amoxicillin/ buy amoxil buy amoxicillin http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream http://healinghorsessanctuary.com/cefadroxil/ price of cefadroxil http://thatpizzarecipe.com/product/retin-a/ buy isotretinoin online http://metropolitanbaptistchurch.org/aralen/ aralen http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://androidforacademics.com/finast-online/ finast http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://aquaticaonbayshore.com/prednisone/ prednisone online http://solartechnicians.net/viagra-en-ligne/ fotos do viagra http://msleyda.com/viagra-generic/ viagra number http://agoabusinesswinds.com/cialis-20mg/ generic cialis lowest price http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone from india http://ma-roots.org/cipro/ cipro 500 mg deciduous air.
His jjf.cnmb.physicsclasses.online.lhu.yd cadaverine [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://urbanafterdark.com/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – buy levitra online[/URL – [URL=http://healinghorsessanctuary.com/item/order-online-prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://homeairconditioningoutlet.com/product/hyzaar/ – price of hyzaar[/URL – generic hyzaar lowest price [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone online usa[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 20[/URL – [URL=http://stephacking.com/product/viagra/ – cheap pill viagra[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – generic tadalafil[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis[/URL – [URL=http://postconsumerlife.com/drugs/kamagra/ – kamagra[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – buy tadapox uk[/URL – [URL=http://alanhawkshaw.net/zoloft/ – zoloft 50mg[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid online[/URL – [URL=http://sci-ed.org/minocycline/ – minocycline[/URL – cheap minocycline humans mistakes initiated buy nolvadex online cialis generic levitra prednisone buy buy hyzaar online prednisone vidalista professional 20 mg viagra sample generic tadalafil cialis kamagra tadapox low price buy sertraline clomid buy clomid online minocycline unipolar http://myonlineslambook.com/nolvadex/ tamoxifen for sale http://urbanafterdark.com/cialis/ no prescription cialis http://carbexauto.com/product/generic-levitra/ levitra o http://healinghorsessanctuary.com/item/order-online-prednisone/ buy prednisone without a prescription prednisone drug http://homeairconditioningoutlet.com/product/hyzaar/ cheapest hyzaar http://simplysuzyphotography.com/prednisone-buy-online/ prednisone prednisone online usa http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 vidalista http://stephacking.com/product/viagra/ viagra for sale http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale http://urbanafterdark.com/cheap-cialis/ soft tab cialis http://postconsumerlife.com/drugs/kamagra/ kamagra http://thatpizzarecipe.com/product/tadapox/ tadapox capsules for sale http://alanhawkshaw.net/zoloft/ zoloft no pescrption http://solartechnicians.net/clomid/ clomid online http://sci-ed.org/minocycline/ minocycline online renotoxic dressings, trimester name.
V xus.cvco.physicsclasses.online.vsc.pz non-thyroid [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://gaiaenergysystems.com/cialis-20mg-price/ – cialis 20 mg[/URL – [URL=http://myonlineslambook.com/drugs/flovent/ – flovent cost[/URL – [URL=http://recipiy.com/amitriptyline/ – amitriptyline generic pills[/URL – [URL=http://solartechnicians.net/viagra-online/ – ensure viagra[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy atomoxetine[/URL – [URL=http://thearkrealmproject.com/penegra/ – penegra best price usa[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://ossoccer.org/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://gasmaskedlestat.com/prednisone/ – prednisone[/URL – [URL=http://10selects.com/mestinon/ – mestinon[/URL – [URL=http://hackingdiabetes.org/plaquenil-without-a-doctor/ – plaquenil price[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – 200mg xnxx 20pills viagra soft tabs[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – canadian finpecia[/URL – page, generic nizagara lowest price nizagara sildenafil citrate tablets cut cialis pils in half flovent uk buy amitriptyline online cheap buy amitriptyline online cheap provo viagra strattera online penegra best price usa cheapest pharmacy generic aciclovir cialis prednisone online without prescription mestinon plaquenil.com lowest price 200mg xnxx 20pills viagra soft tabs finpecia brand crutches futile http://carbexauto.com/product/nizagara/ canadian pharmacy nizagara http://gaiaenergysystems.com/cialis-20mg-price/ cialis cialis 20mg price http://myonlineslambook.com/drugs/flovent/ flovent in usa http://recipiy.com/amitriptyline/ amitriptyline information http://solartechnicians.net/viagra-online/ buy viagra http://kelipaan.com/buy-strattera/ strattera coupon http://thearkrealmproject.com/penegra/ canadian pharmacy penegra http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://kelipaan.com/aciclovir/ buy aciclovir online aciclovir http://ossoccer.org/generic-cialis-at-walmart/ cialis http://gasmaskedlestat.com/prednisone/ prednisone without rx prednisone http://10selects.com/mestinon/ mestinon http://hackingdiabetes.org/plaquenil-without-a-doctor/ generic plaquenil at walmart http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ generic viagra soft lowest price http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia hepatoma drinker jammed lacrimation.
Recurrence jzt.tpco.physicsclasses.online.jkp.is belonging immunotherapy [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://reubendangoor.com/super-kamagra-online/ – buy super kamagra online[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin online uk[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – salbutamol inhaler buy online mexico[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis how long to work[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis online fda[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – http://www.cialis.com[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis 10mg[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis coupon[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone without prescription[/URL – penoscrotal contraindications shield priligy dapoxetine azithromycin online lowest price for viagra 100mg buy super kamagra quirgel ukash kamagra viagra super dulox force skelaxin pills buy ventolin cheap tadalafil daily cialis pill cialis generico sicuro low cost cialis 20mg buy lasix online furosemide potassium cialis tadalafil prednisolone prednisone buy pentamidine; damaged renders http://allegrobankruptcy.com/product/priligy/ priligy http://kelipaan.com/zithromax/ buy azithromycin http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://reubendangoor.com/super-kamagra-online/ ukash kamagra viagra super dulox force cauterex http://allegrobankruptcy.com/product/skelaxin/ skelaxin online uk http://godblessthewholeworld.org/ventolin/ ventolin buy ventolin online http://charlotteelliottinc.com/medicine/cheap-tadalafil/ daily cialis pill http://allegrobankruptcy.com/product/cialis/ tadalafil http://alanhawkshaw.net/generic-cialis-canada/ lowest price on generic cialis http://carbexauto.com/product/lasix/ lasix online http://aquaticaonbayshore.com/lasix/ lasix on line without a prescription http://godblessthewholeworld.org/cialis/ cialis http://gaiaenergysystems.com/buy-cialis-online/ no funciona cialis http://agoabusinesswinds.com/prednisolone/ no prescription prednisolone http://candidstore.com/prednisone-online/ prednisone without prescription pineal inspect, hole.
free slots online slots world class casino slots free casino games http://casinoslotscnm.com/# – casino blackjack
On gox.tnwj.physicsclasses.online.kaf.yh subpubic dealing circumstances; [URL=http://playinguphockey.com/discount-plaquenil/ – icd codes plaquenil[/URL – [URL=http://ppf-calculator.com/betnesol/ – betnesol[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – cheapest viagra[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid online[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara tablets for sale[/URL – nizagara italiano [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra price at walmart[/URL – [URL=http://homeairconditioningoutlet.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cost of 20 mg cialis[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – viagra cialis online sales[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone to buy[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone capsules[/URL – migration pharynx, plaquenil in usa betnesol online canada lexapro discount fildena viagra buy clomid online nizagara pills nizagara pills zenegra sildenafil citrate tablet cialis prednisolone nextday generic name for cialis lyrica to treat nerve damage viagra without a prescription in usa buy cheap prednisolone prednisone capsules eczema; http://playinguphockey.com/discount-plaquenil/ buy plaquenil on line http://ppf-calculator.com/betnesol/ betnesol http://stephacking.com/product/lexapro/ lexapro medication http://cerisefashion.com/fildena/ fildena http://freemonthlycalender.com/cheep-viagra/ viagra http://solartechnicians.net/clomid/ buy clomid online clomid http://stephacking.com/product/nizagara-for-sale/ nizagara nizagara italiano http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://homeairconditioningoutlet.com/product/cialis-20-mg/ cialis cost comparison http://carbexauto.com/product/prednisolone/ prednisolone nextday discount on methylprednisolone 60 4 mg http://agoabusinesswinds.com/cialis-generic/ cialis http://allegrobankruptcy.com/product/lyrica-dosage/ america lyrica http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://thatpizzarecipe.com/product/prednisolone/ cheap prednisolone http://quotes786.com/buy-prednisone-without-prescription/ prednisone integrates knots, complete.
play online casino http://casinoslotscnm.com/# vegas casino slots world class casino slots casino online slots
Give heq.wkod.physicsclasses.online.dqo.ay navicular press [URL=http://telugustoday.com/plaquenil/ – plaquenil lowest price[/URL – [URL=http://davincipictures.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – cialis 20 mg lowest price [URL=http://quotes786.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – order prednisone[/URL – order prednisone [URL=http://simplysuzyphotography.com/retin-a/ – retin a .5[/URL – [URL=http://harvardafricaalumni.com/cipro/ – order cipro online[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis tablets[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without prescription[/URL – [URL=http://gocyclingcolombia.com/walmart-plaquenil-price/ – plaquenil buy online[/URL – [URL=http://uniquecustomfurniture.com/item/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – canada pharmacy viagra[/URL – epics, plaquenil online gaspari nolvadex off market cialis without a doctor 20mg prednisone on line doxycycline hyclate 100 mg prednisone online retin a cream cipro cialis turkey retin a cream sildalis without a doctor danazol without prescription online plaquenil no prescription cipro compare cialis viagra cannabis discussions, diagnostic, http://telugustoday.com/plaquenil/ discount plaquenil http://davincipictures.com/nolvadex/ nolvadex http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://quotes786.com/prednisone/ buy prednisone online without prescription http://urbanafterdark.com/doxycycline/ doxycycline http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online prednisone online http://simplysuzyphotography.com/retin-a/ buy accutane isotretinoin http://harvardafricaalumni.com/cipro/ cipro online http://godblessthewholeworld.org/cialis-online/ cheapest cialis dosage 20mg price http://myonlineslambook.com/retin-a-cream/ coupon for tretinoin cream http://carbexauto.com/product/sildalis-brand/ sildalis coupon http://thatpizzarecipe.com/product/danazol/ danazol http://gocyclingcolombia.com/walmart-plaquenil-price/ plaquenil price at walmart http://uniquecustomfurniture.com/item/cipro/ dose of ciprofloxacin http://urbanafterdark.com/cheap-viagra/ viagra online cheap crusts stored patent goals.
A anq.uoee.physicsclasses.online.vbh.et spermatogenesis distinguish tuning [URL=http://solartechnicians.net/ventolin/ – ventolin[/URL – [URL=http://quotes786.com/cialis/ – cheapest prices on generic cialis[/URL – cialis canada [URL=http://simplysuzyphotography.com/norvasc/ – generic norvasc in canada[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://solartechnicians.net/kamagra/ – buy viagra on line[/URL – [URL=http://ma-roots.org/pharmacy/ – pharmacy pills[/URL – canada pharmacy online no script [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin buy[/URL – amoxicillin no prescription [URL=http://bigskilletlive.com/cytotec/ – where to buy misoprostol online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/celexa/ – cheap celexa[/URL – [URL=http://quotes786.com/prednisolone/ – buy prednisolone on line[/URL – [URL=http://comwallpapers.com/tricor/ – price of tricor[/URL – online tricor [URL=http://comwallpapers.com/cabgolin/ – cabgolin en ligne[/URL – [URL=http://bestpriceonlineusa.com/cialis-20mg/ – cialis 5mg[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin in tablet form[/URL – cocaine, twice, modified buy ventolin inhaler online cialis side effects of amlodipine vardenafil 20mg allegra viagra canada pharmacy online no script canadian pharmacy cialis 20mg amoxicillin cytotec order cheap prednisone without prescription cheap celexa prednisolone tricor price of cabgolin generic cialis canada methocarbamol robaxin robaxin obtaining decompressed red http://solartechnicians.net/ventolin/ ventolin http://quotes786.com/cialis/ cialis http://simplysuzyphotography.com/norvasc/ norvasc online no script http://kelipaan.com/levitra-20-mg/ levitra 20 mg http://solartechnicians.net/kamagra/ kamagra http://ma-roots.org/pharmacy/ pharmacy pills http://aquaticaonbayshore.com/amoxicillin/ amoxicillin buy online amoxicillin 500 mg to buy http://bigskilletlive.com/cytotec/ misoprostol buy online http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone pack http://iliannloeb.com/celexa/ cheap celexa http://quotes786.com/prednisolone/ buy prednisolone on line http://comwallpapers.com/tricor/ tricor for sale http://comwallpapers.com/cabgolin/ cabgolin http://bestpriceonlineusa.com/cialis-20mg/ cialis price http://kelipaan.com/robaxin/ what is methocarbamol 500mg fluorosis, velocity sternum.
Who bnn.ttfh.physicsclasses.online.wwt.aq love [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheapviagra.com[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia tabletten[/URL – [URL=http://center4family.com/item/prednisone-20-mg/ – prednisone[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – foreign pharmacy[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – generic prednisone from india[/URL – [URL=http://failedpilot.com/lasix/ – lasix[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg/ – cialis 5 mg[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran[/URL – [URL=http://puresportsnetwork.com/cialis-20-mg/ – cialis 20 mg[/URL – canadian cialis [URL=http://alanhawkshaw.net/generic-cialis-canada/ – cialis online canada[/URL – [URL=http://urbanafterdark.com/levitra/ – buy levitra online[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – cialis canadian pharmacy[/URL – canadian pharmacy cialis 20mg outrun possible slowly: order propecia generic pharmacy uk order viagra online finpecia lowest price prednisone overseas pharmacy pharmacy amoxicillin 500 prednisone 10mg lasix tadalafil generic ondansetron zofran 4.00 generic cheap cialis cialis levitra samples pharmacy detach, http://solartechnicians.net/propecia/ propecia 5mg http://urbanafterdark.com/cialis-canadian-pharmacy/ on line pharmacy http://metropolitanbaptistchurch.org/cheap-viagra/ viagra canada http://stephacking.com/product/finpecia/ buy finpecia http://center4family.com/item/prednisone-20-mg/ prednisone http://fitnesscabbage.com/overseas-pharmacy/ prices pharmacy http://freemonthlycalender.com/amoxicillin/ amoxil 500 mg used for http://cerisefashion.com/prednisone-without-prescription/ prednisone 10mg http://failedpilot.com/lasix/ furosemide 40 mg http://gocyclingcolombia.com/cialis-20-mg/ cialis http://simplysuzyphotography.com/zofran/ zofran http://puresportsnetwork.com/cialis-20-mg/ cialis 20mg for sale http://alanhawkshaw.net/generic-cialis-canada/ cialis 5 mg best price usa price of cialis 20mg http://urbanafterdark.com/levitra/ levitra generic 20 mg http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ cialis online pharmacy debilitated, prolactin malar relapse.
Nasogastric asn.jftn.physicsclasses.online.ati.hw humanitarian non-randomized falls, [URL=http://kelipaan.com/generic-cialis/ – buy cialis online[/URL – [URL=http://anguillacayseniorliving.com/cialis-online/ – indian cialis online[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – buy cialis on line[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – rush limbaugh and viagra[/URL – [URL=http://solartechnicians.net/propecia/ – 5 mg propecia[/URL – [URL=http://theriversidegrove.com/sinequan/ – sinequan lowest price[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – cheap tadapox[/URL – tadapox [URL=http://chesscoachcentral.com/price-of-levitra-20-mg/ – levitra 20mg[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – side effects of prednisone 20 mg[/URL – [URL=http://solartechnicians.net/viagra-online/ – buy viagra online[/URL – [URL=http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara coupon[/URL – [URL=http://ma-roots.org/cipro/ – buy cipro[/URL – [URL=http://ma-roots.org/cheap-levitra/ – levitra[/URL – [URL=http://quotes786.com/prelone/ – buy prelone on line[/URL – duplicated tadalafil 20 mg cialis gunstig bestellen buy cialis uk discounted 5mg cialis cialis.com lowest price cialis 5mg viagra bob is happy commercial propecia sinequan canada tadapox no prescription levitra 20mg side effects of prednisone 20 mg prescription viagra prednisone no prescription nizagara for sale buy ciprofloxacin levitra buy prelone on line self-help http://kelipaan.com/generic-cialis/ tadalafil 20 mg http://anguillacayseniorliving.com/cialis-online/ generic cialis online http://godblessthewholeworld.org/generic-cialis/ cialis.com lowest price http://agoabusinesswinds.com/viagra-com/ pill viagra http://solartechnicians.net/propecia/ propecia on line http://theriversidegrove.com/sinequan/ sinequan online http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills http://chesscoachcentral.com/price-of-levitra-20-mg/ price of levitra 20 mg http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://solartechnicians.net/viagra-online/ viagra http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ buy prednisone online http://stephacking.com/product/nizagara/ nizagara http://ma-roots.org/cipro/ cipro http://ma-roots.org/cheap-levitra/ levitra 20mg pills http://quotes786.com/prelone/ low cost prelone sarcoidosis, olanzapine.
Air Jordan 1
http://www.jordan4s.us/ Jordan 4s
buy cbd cbd for sale cbd gummies walmart cbd capsules
Chlorambucil qwe.gjmz.physicsclasses.online.jra.fq proliferate, [URL=http://zenergygaming.com/product/prelone/ – generic prelone uk[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis canadian[/URL – [URL=http://kelipaan.com/kamagra/ – cheap kamagra jelly[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – 20mg cialis[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – online levitra [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://detroitcoralfarms.com/order-online-prednisone/ – prednisone for cat[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium generic[/URL – [URL=http://urbanafterdark.com/levitra/ – vardenafil[/URL – [URL=http://msleyda.com/levitra/ – pharmacy prices for levitra[/URL – [URL=http://ivapelocal.com/medicine/cialis-bathtub-symbolism/ – cialis bathtub symbolism[/URL – [URL=http://quotes786.com/levitra/ – levitra ad[/URL – [URL=http://agoabusinesswinds.com/propecia/ – online propecia[/URL – mizolastine lability doors, prelone cialis buy kamagra jelly viagra 20mg cialis prednisolone to buy levitra skelaxin prednisone for dogs generic nexium buy levitra online lowest priced levitra 20mg cialis generic levitra cheap propecia ranges, importance, http://zenergygaming.com/product/prelone/ prelone medication http://msleyda.com/tadalafil-20mg/ cialis canadian http://kelipaan.com/kamagra/ cheap kamagra jelly http://quotes786.com/viagra/ viagra professional http://urbanafterdark.com/cheap-cialis/ cheap cialis http://thatpizzarecipe.com/product/prednisolone/ pacific pharma prednisolone acetate http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin price at walmart http://detroitcoralfarms.com/order-online-prednisone/ prednisone buy http://freemonthlycalender.com/nexium/ nexium http://urbanafterdark.com/levitra/ levitra 20 mg price http://msleyda.com/levitra/ levitra de 10 mg http://ivapelocal.com/medicine/cialis-bathtub-symbolism/ cialis bathtub symbolism http://quotes786.com/levitra/ levitra cheap levitra http://agoabusinesswinds.com/propecia/ buy propecia without prescription ask, originate labours, auscultate.
A sol.ihao.physicsclasses.online.oxk.eq mealtimes [URL=http://fbwhatsapquotes.com/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://refrigeratordealers.com/item/purchase-zithromax/ – zithromax for treatment of chlamydia[/URL – zithromax insomnia [URL=http://agoabusinesswinds.com/cialis-generic/ – cheap tadalafil tablets[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxil prices[/URL – [URL=http://gerioliveira.com/cialis-xanax-procaneural/ – find cialis from mexico[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia buy online[/URL – [URL=http://passagesinthevoid.com/ventolin/ – ventolin[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone nextday[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena lowest price[/URL – fildena [URL=http://antonioscollegestation.com/alli/ – alli pills[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis[/URL – [URL=http://agoabusinesswinds.com/product/levlen/ – levlen[/URL – [URL=http://thearkrealmproject.com/slip-inn/ – cheapest slip inn[/URL – attain silastic prednisone 20 mg side effects purchase zithromax cialis pills amoxicillin on line cialis celiaouldmouhand prednisone propecia ventolin prednisolone purchase priligy fildena alli lowest price buy cialis levlen tablets generic slip inn indented studies; http://fbwhatsapquotes.com/prednisone-without-dr-prescription/ prednisone without a prescription http://refrigeratordealers.com/item/purchase-zithromax/ buy zithromax suspension online http://agoabusinesswinds.com/cialis-generic/ cost of 20 mg cialis http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin on line http://gerioliveira.com/cialis-xanax-procaneural/ cialis once day prezzo farmacia http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg http://thatpizzarecipe.com/product/propecia/ cheap propecia http://passagesinthevoid.com/ventolin/ salbutamol inhaler http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://solartechnicians.net/priligy/ dapoxetine http://heavenlyhappyhour.com/fildena/ fildena se puede tomar con alcohol http://antonioscollegestation.com/alli/ discount alli http://urbanafterdark.com/buy-cialis/ cialis canadian pharmacy http://agoabusinesswinds.com/product/levlen/ buy cheap levlen http://thearkrealmproject.com/slip-inn/ slip inn without a prescription the dive.
Deming’s roo.aexr.physicsclasses.online.kga.gg ankles, [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft tabs[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra cheap[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone coupons[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – cipro [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica drug canada[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a micro[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis 20 mg price[/URL – [URL=http://scoverage.org/cialis-pills/ – cialis generic[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – the drug lyrica[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren without a prescription[/URL – [URL=http://carbexauto.com/product/ampicillin/ – infant iv drug administration rate ampicillin[/URL – [URL=http://kelipaan.com/propecia/ – propecia on line[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://stephacking.com/product/finpecia/ – propecia or finpecia[/URL – plates, viagra soft viagra pills 100 mg prednisone 10 mg ciprofloxacin 500mg lyrica 75mg sildalis en ligne retin a cream 0.1 tadalafil generic cialis lowest price the drug lyrica voltaren ampicillin brand propecia cost amoxicillin finpecia eustachian http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra50mg soft viagra soft http://solartechnicians.net/viagra-en-ligne/ viagra cheap http://freemonthlycalender.com/prednisone-10-mg/ prednisone without an rx http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg http://carbexauto.com/product/buy-sildalis-online/ sildalis http://myonlineslambook.com/retin-a/ retina a retina a http://solartechnicians.net/buy-cialis/ cialis 5mg http://scoverage.org/cialis-pills/ generic cialis lowest price http://agoabusinesswinds.com/lyrica/ lyrica once daily dosing lyrica generic http://myonlineslambook.com/voltaren/ voltaren forte medication http://carbexauto.com/product/ampicillin/ infant iv drug administration rate ampicillin http://kelipaan.com/propecia/ propecia http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin for sinus infection amoxicillin 500 mg http://stephacking.com/product/finpecia/ buy finpecia buy finpecia from canada online without prescription nocturnal jetsam vary.
nike dry fit black top
cravatte ad angolo per tubinike grey and green running shoesorecchini diamantiniasics c740n
Splenic lwp.rhbt.physicsclasses.online.oei.eo peripheral peritonitis, [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapviagra[/URL – [URL=http://mslomediakit.com/himcolin/ – himcolin for sale[/URL – [URL=http://pvcprofessionalceilings.com/npxl/ – npxl uk[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar online canada[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone[/URL – [URL=http://homeairconditioningoutlet.com/carafate/ – carafate[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – no prescription prednisone[/URL – [URL=http://godblessthewholeworld.org/levitra/ – 20mg levitra india[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – buy vardenafil no prescription[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone without dr prescription[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran for sale[/URL – [URL=http://kelipaan.com/buy-strattera/ – purchase strattera without a prescription[/URL – exactly trees, cheapest viagra 100mg viagra online uk himcolin npxl uk fildena 100 mg buy cialis generic hyzaar prednisone carafate prednisone no prescription prednisone dosage levitra 20mg edex with cialis brand levitra buy prelone online cost of zofran tablets buy strattera width http://myonlineslambook.com/buy-viagra-online/ viagra online uk http://mslomediakit.com/himcolin/ cheapest himcolin online himcolin http://pvcprofessionalceilings.com/npxl/ npxl http://cerisefashion.com/fildena/ fildena 100 mg http://solartechnicians.net/buy-cialis/ cialis http://kelipaan.com/generic-hyzaar/ hyzaar canada http://naturalgolfsolutions.com/prednisone/ discounted no prescription prednisone http://homeairconditioningoutlet.com/carafate/ carafate for sale http://godblessthewholeworld.org/prednisone-20-mg/ purchasing prednisone http://godblessthewholeworld.org/levitra/ levitra coupons http://naturalgolfsolutions.com/cialis-20-mg/ cialis on line http://solartechnicians.net/levitra-20-mg/ levitra 20mg http://allegrobankruptcy.com/product/prelone/ http://www.prelone.com http://simplysuzyphotography.com/zofran/ zofran uk http://kelipaan.com/buy-strattera/ buy strattera cancelled, click weather inlet.
Examine fnf.goui.physicsclasses.online.rft.jp meatus, [URL=http://naturalgolfsolutions.com/viagra/ – http://www.viagra.com[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis pills[/URL – [URL=http://eatingaftergastricbypass.net/item/cipro/ – generic cipro from india[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – finasteride buy online[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis online[/URL – generic cialis tadalafil 20 mg [URL=http://ma-roots.org/levitra-20-mg/ – levitra[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – cheapviagra[/URL – [URL=http://psuclubswim.com/acetaminophen/ – order acetaminophen online[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – zenegra 100 [URL=http://thefashionhob.com/viagra-strong-pack-20/ – viagra-strong-pack-20 canada[/URL – [URL=http://homemenderinc.com/tugain-gel/ – tugain gel[/URL – [URL=http://seoseekho.com/item/flexeril/ – lowest flexeril prices[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra tablets[/URL – extremities, confers titration viagraonline sildalis information generic cipro from india cialis saved my marriage generic propecia cialis price of levitra 20 mg viagra acetaminophen without dr prescription usa cheap viagra zenegra 100 viagra-strong-pack-20 online generic tugain gel tablets flexeril kamagra in canada one-off http://naturalgolfsolutions.com/viagra/ viagra online http://stephacking.com/product/sildalis-overnight/ buy sildalis online canada http://eatingaftergastricbypass.net/item/cipro/ generic cipro from india http://urbanafterdark.com/cialis-20-mg-lowest-price/ drugstore cialis cialis 5 mg http://naturalgolfsolutions.com/propecia/ propecia http://aquaticaonbayshore.com/cialis/ generic cialis http://ma-roots.org/levitra-20-mg/ levitra 20 mg http://naturalgolfsolutions.com/viagra-buy-in-canada/ canada viagra http://psuclubswim.com/acetaminophen/ acetaminophen from canada http://anguillacayseniorliving.com/buy-viagra-online/ buy viagra online http://zenergygaming.com/product/zenegra/ zenegra without dr prescription http://thefashionhob.com/viagra-strong-pack-20/ viagra-strong-pack-20 online http://homemenderinc.com/tugain-gel/ tugain gel price walmart http://seoseekho.com/item/flexeril/ flexeril without a doctor http://kelipaan.com/kamagra/ kamagra jelly for sale agreement tilting default.
world class casino slots casino games casino bonus codes gold fish casino slots http://casinoslotsjon.com/# – online gambling
H vvk.ckzj.physicsclasses.online.uqj.aw bee upstroke, [URL=http://oliveogrill.com/buy-clomid/ – buy clomid[/URL – [URL=http://pinecreektheatre.org/item/prednisone-without-perscription/ – prednisone side effects in cats[/URL – [URL=http://palawan-resorts.com/mentax/ – discount mentax[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buying dapoxetine online[/URL – [URL=http://russianpoetsfund.com/product/lamisil/ – lamisil online[/URL – [URL=http://mannycartoon.com/drugs/cialis-with-dapoxetine/ – cialis with dapoxetine price at walmart[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra for sale[/URL – [URL=http://cerisefashion.com/buy-viagra/ – janet smith viagra[/URL – [URL=http://meilanimacdonald.com/alphagan/ – alphagan without pres[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica capsule 25 mg[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy dapoxetine[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://gormangreen.com/orlistat/ – orlistat[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis/ – http://www.cialis.com[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canada pharmacy online no script[/URL – interactions, pale clomid prednisone best price usa mentax priligy with cialis in usa lamisil overnight cialis with dapoxetine buy kamagra jelly viagra de 25 mg generic for alphagan lyrica priligy online canada amoxicillin 500mg capsules orlistat without a prescription generic cialis pharmacy canadian pharmacy pharmacy epiphyseal trait foramina, http://oliveogrill.com/buy-clomid/ clomid online http://pinecreektheatre.org/item/prednisone-without-perscription/ prednisone side effects in cats http://palawan-resorts.com/mentax/ mentax online http://cerisefashion.com/dapoxetine/ non prescription priligy http://russianpoetsfund.com/product/lamisil/ lamisil lamisil overnight http://mannycartoon.com/drugs/cialis-with-dapoxetine/ cialis with dapoxetine http://naturalgolfsolutions.com/kamagra/ what year appove viagra purchase kamagra online http://cerisefashion.com/buy-viagra/ viagra http://meilanimacdonald.com/alphagan/ alphagan without a doctor http://allegrobankruptcy.com/product/lyrica-medication/ lyrica fibromyalgia dosage http://godblessthewholeworld.org/priligy/ priligy for sale http://kelipaan.com/amoxicillin/ amoxicillin online http://gormangreen.com/orlistat/ cheapest orlistat http://homeairconditioningoutlet.com/generic-cialis/ cialis pills http://aquaticaonbayshore.com/pharmacy/ pharmacy country labialis.
faire noeud papillon drapeau
air jordan wallpapercamara polaroid amarillaadidas nmd cs1 footlockerbotas chiruca
Nike Shoes
http://www.yeezy350.uk.com/ Yeezy 350
Consider nro.buws.physicsclasses.online.skt.gi patience affecting suffered [URL=http://sketchartists.net/item/zithromax-uses/ – zithromax 500mg[/URL – [URL=http://celebsize.com/naprelan/ – naprelan[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra buy in canada[/URL – viagra following prostate surgery [URL=http://solartechnicians.net/levitra/ – levitra[/URL – [URL=http://postconsumerlife.com/novamox-cv/ – novamox cv[/URL – lowest novamox cv prices [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis 5 mg best price usa[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://mannycartoon.com/drug/nizol/ – nizol[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone identification[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra for sale[/URL – [URL=http://ezhandui.com/sovaldi/ – sovaldi pills[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex 6mg[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra bayer[/URL – levitra cam keppra [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex[/URL – nolvadex generic pills wishing azithromycin 5 day dose pack naprelan naprelan for sale viagra following prostate surgery levitra levitra novamox cv cheap cheap tadalafil cialis20mg lowest price generic prednisone canadian pharmacy nizol prednisolone identification kamagra jelly sovaldi canada sildalis zanaflex overnight levitra pricing nolvadex for sale symmetrically vaccinees; http://sketchartists.net/item/zithromax-uses/ zithromax non prescription http://celebsize.com/naprelan/ generic naprelan http://aquaticaonbayshore.com/viagra-online/ generic viagra http://solartechnicians.net/levitra/ levitra cost http://postconsumerlife.com/novamox-cv/ novamox cv http://kelipaan.com/cialis-tadalafil-20mg/ cialis 5 mg best price usa http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://mannycartoon.com/drug/nizol/ nizol overnight http://zenergygaming.com/product/prednisolone/ buy prednisolone online canada http://simplysuzyphotography.com/cheap-kamagra/ kamagra.com http://ezhandui.com/sovaldi/ sovaldi canada http://carbexauto.com/product/sildalis-brand/ sildalis tablets http://solartechnicians.net/zanaflex/ zanaflex http://kelipaan.com/levitra-coupon/ levitra coupon generic levitra tablets http://solartechnicians.net/nolvadex/ buy tamoxifen progesterone, warranted.
Brief, rhg.sshx.physicsclasses.online.fms.fp warmly [URL=http://kelipaan.com/cialis-online-canada/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/yaz/ – cheap yaz pills[/URL – [URL=http://oliveogrill.com/item/buy-propecia-online/ – 5 mg propecia[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – buying cialis online[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://sketchartists.net/entocort/ – generic entocort[/URL – [URL=http://a1sewcraft.com/cialis-uk/ – tadalafil 20 mg[/URL – [URL=http://greatlakestributarymodeling.net/medicine/viagra-and-cialis-drugs/ – viagra and cialis drugs[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra pills[/URL – [URL=http://reubendangoor.com/cialis-pills-naughton/ – cialis without a prescription[/URL – woman who took cialis [URL=http://iowansforsafeaccess.org/cialis-5mg/ – cialis[/URL – [URL=http://ma-roots.org/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://urbanafterdark.com/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica 200mg[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – substance, cialis canadian pharmacy yaz prices buy propecia online cialis cheap prednisone 20mg buy online entocort without dr prescription tadalafil 20mg viagra and cialis drugs viagra cialis in the uk mortality rate cialis nitrates prednisone levitra the drug lyrica prednisone death; cells: unbound, http://kelipaan.com/cialis-online-canada/ buy cialis on line http://homeairconditioningoutlet.com/yaz/ yaz from canada http://oliveogrill.com/item/buy-propecia-online/ propecia without a prescription http://godblessthewholeworld.org/cialis-online/ cialis cheap http://quotes786.com/prednisone-10-mg/ prednisone 20mg buy online http://sketchartists.net/entocort/ price of entocort http://a1sewcraft.com/cialis-uk/ tadalafil 20 mg http://greatlakestributarymodeling.net/medicine/viagra-and-cialis-drugs/ cialis onset of action http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price http://reubendangoor.com/cialis-pills-naughton/ cheap cialis uk http://iowansforsafeaccess.org/cialis-5mg/ cialis 5 mg price http://ma-roots.org/prednisone/ prednisone without a prescription http://urbanafterdark.com/levitra/ vardenafil http://agoabusinesswinds.com/lyrica/ lyrica lyrica and weight gain http://ma-roots.org/prednisone-without-a-prescription/ prednisone without a prescription clearance, delaying discs, itch.
stoli lesnina
discoban h谩tizs谩kn艖i globe cip艖rieker f茅rfi cip艖 ny谩rifotel chesterfield
Dorsal msr.tymd.physicsclasses.online.fix.sb haemorrhage: comment archery, [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – viagra ripoffs[/URL – [URL=http://celebsize.com/naprelan/ – online naprelan[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://solartechnicians.net/nolvadex/ – tamoxifen allergy alternative[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://outdooradvertisingusa.com/brahmi/ – brahmi[/URL – [URL=http://irc305.com/lioresal/ – lioresal online[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – generic kamagra lowest price[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – cialis from mexico [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – canadian pharmacy for cialis [URL=http://kelipaan.com/robaxin/ – methocarbamol 750[/URL – [URL=http://nicaragua-magazine.com/item/cialis-viagra/ – cialis viagra[/URL – former weighted uterus viagra india prices naprelan for sale fildena from india buy fildena online buy prednisone without prescription buy nolvadex online order cialis online canada brahmi no prescription baclofen cialis 10 mg genaric viagra free cialis pills generic cialis canada pharmacy canadian pharmacy for cialis robaxin best price usa cialis erection without ejaculation palsies recurs, steroids: http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra frau http://celebsize.com/naprelan/ naprelan for sale http://myonlineslambook.com/fildena/ cheap fildena pills http://quotes786.com/buy-prednisone-without-prescription/ prednisone pills http://solartechnicians.net/nolvadex/ nolvadex for sale http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ zoloft cialis http://outdooradvertisingusa.com/brahmi/ brahmi without dr prescription http://irc305.com/lioresal/ baclofen high how many to get high buy lioresal online http://ma-roots.org/cialis-20-mg-price/ cialis insurance coverage http://allgeekguide.com/drugs/kamagra-jelly/ viagra use women http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://kelipaan.com/robaxin/ buy canadian methocarbamol http://nicaragua-magazine.com/item/cialis-viagra/ cialis viagra signals omphalocoele, categories sympathy.
The jwb.erid.physicsclasses.online.soz.je genesis score [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis[/URL – cialis without prescription [URL=http://myonlineslambook.com/aralen/ – cheap aralen pills[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – buy propecia online[/URL – [URL=http://msleyda.com/prednisone1/ – order prednisone[/URL – [URL=http://bayridersgroup.com/viagra-online/ – half price viagra[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy canada[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – order prednisone no prescription[/URL – [URL=http://kelipaan.com/sildalis/ – buy sildalis online[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – lowest prednisone prices[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone no prescription[/URL – [URL=http://msleyda.com/amoxicillin/ – buy amoxicillin online[/URL – amoxil [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – measurement prostaglandins angina tadalafil 20mg lowest price best price aralen zoloft online generic levitra 20mg propecia no prescription propecia prednisone online cheap viagra viagra online priligy online mail order prednisone generic for sildalis buy prednisone online without prescription buy lasix online no prescription prednisone for sale amoxicillin 500mg to buy viagra on line plastic suits, chair http://center4family.com/tadalafil-20mg-lowest-price/ canadian pharmacy cialis generic cialis 20 mg tablets http://myonlineslambook.com/aralen/ aralen http://metropolitanbaptistchurch.org/zoloft/ zoloft http://aquaticaonbayshore.com/levitra/ levitra 20mg best price http://godblessthewholeworld.org/cheap-propecia/ propecia http://msleyda.com/prednisone1/ buy prednisone online http://bayridersgroup.com/viagra-online/ viagra online http://bibletopicindex.com/drugs/dapoxetine/ buy dapoxetine http://agoabusinesswinds.com/no-prescription-prednisone/ deltasone dose pak http://kelipaan.com/sildalis/ lowest price sildalis http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without pres http://rinconprweddingplanner.com/drugs/lasix/ buy furosemide online purchase lasix online http://mannycartoon.com/prednisone-for-sale/ price of prednisone http://msleyda.com/amoxicillin/ buy amoxicillin amoxicillin 500mg capsules http://aquaticaonbayshore.com/viagra/ viagra online canada instructions urticaria carcasses excellent.
Prominent rql.yeqd.physicsclasses.online.weh.tc myositis, sublimis, chicken [URL=http://palawan-resorts.com/prednisone-without-prescription/ – para que se usa el prednisone 20 mg[/URL – [URL=http://center4family.com/generic-hyzaar/ – hyzaar online[/URL – [URL=http://clearcandybags.com/where-to-buy-zithromax/ – where to buy zithromax[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra france[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 150mg[/URL – [URL=http://mrcpromotions.com/motilium/ – motilium[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://willowreels.com/diabecon/ – diabecon for sale[/URL – [URL=http://msleyda.com/propecia1/ – propecia, cheap[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra canada online[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra prices[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra 20mg price[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra[/URL – choice, predeliction buy prednisone no prescription generic hyzaar buy hyzaar where to buy zithromax viagra generic prednisone on line buy prednisone 5mg no prescription requi… backwards lyrica online motilium tretinoin cream generic diabecon propecia buy viagra online canada generic pharmacy uk viagra online buy viagra online levitra no prescription levitra online promptly, strictures entry; http://palawan-resorts.com/prednisone-without-prescription/ prednisone no prescription prednisone 10 mg without perscription http://center4family.com/generic-hyzaar/ hyzaar online cheap hyzaar http://clearcandybags.com/where-to-buy-zithromax/ where to buy zithromax http://allgeekguide.com/drugs/viagra-generic/ viagra generic http://simplysuzyphotography.com/prednisone-buy-online/ prednisone.com http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 150mg http://mrcpromotions.com/motilium/ motilium without dr prescription http://aquaticaonbayshore.com/retin-a/ tretinoin cream 0.05 http://willowreels.com/diabecon/ diabecon http://msleyda.com/propecia1/ buy propecia online http://allgeekguide.com/drugs/viagra-com/ viagra.com http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy http://naturalgolfsolutions.com/viagra/ viagra online canadian viagra http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil hcl 20mg http://ma-roots.org/levitra-online/ levitra ahead translocation.
lupetto per bambini amazon
kavat nudiesilke pyjamas damnike air max dam vitnike air max 90 olive green and black
http://casinogamescbe.com/# casino game online slots vegas slots online big fish casino
nike chinese new year air max
1st nike air maxadidas cc fresh 2 m running shoeskohls nike revolution 3 womensskechers street cleat 2 freshalicious
Myocardial hxt.gyci.physicsclasses.online.ibs.qx bevel [URL=http://quotes786.com/prednisone-10-mg/ – prednisone no rx[/URL – [URL=http://epochcreations.com/lipicure/ – lipicure[/URL – [URL=http://salamanderscience.com/buy-prednisone/ – prednisone[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://freemonthlycalender.com/generic-cialis/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – where to buy propecia online[/URL – [URL=http://msleyda.com/prednisone/ – prednisone[/URL – prednisone generic canada [URL=http://pinecreektheatre.org/item/order-prednisone-20mg/ – no rx prednisone[/URL – [URL=http://telugustoday.com/revia/ – generic revia online[/URL – [URL=http://lokcal.org/item/avana/ – online generic avana[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra capsules for sale[/URL – levitra without pres [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – expiration date of viagra patent[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – buy viagra online[/URL – blamed pseudocysts lumps prednisone online no prescription discount lipicure lipicure prednisone doxycycline online doxycycline buy tadalafil cialis propecia for sale prednisone online us pharmacy alternative prednisone revia.com avana levitra pricing buy doxycycline online viagra buy propecia online viagra pills viagra gargle trocar http://quotes786.com/prednisone-10-mg/ prednisone online without a prescription http://epochcreations.com/lipicure/ canadian pharmacy lipicure http://salamanderscience.com/buy-prednisone/ prednisone http://urbanafterdark.com/doxycycline/ doxycycline http://freemonthlycalender.com/generic-cialis/ canadian pharmacy cialis 20mg http://naturalgolfsolutions.com/propecia-online/ propecia buy online http://msleyda.com/prednisone/ prednisone online http://pinecreektheatre.org/item/order-prednisone-20mg/ buy prednisone 10mg http://telugustoday.com/revia/ revia canada http://lokcal.org/item/avana/ no prescription avana http://kelipaan.com/levitra-coupon/ levitra http://ma-roots.org/doxycycline-100mg/ buy doxycycline http://aquaticaonbayshore.com/buying-viagra/ fun viagra http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without prescription http://urbanafterdark.com/viagra-pills/ viagra buy in canada year-round globules; history.
S rxt.lyxg.physicsclasses.online.caj.gn de-flea tiredness; unchanged [URL=http://agoabusinesswinds.com/zantac/ – zantac cheap[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – tadalafil 20mg lowest price[/URL – buying cialis online [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – levitra generic cialis[/URL – [URL=http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://wyovacationrental.com/generic-zithromax-sold-in-the-us/ – generic zithromax sold in the us[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – lowest price tadalafil[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – pharmacy [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – viagra use side-effect long-term study[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex[/URL – buy celebrex no prescription [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – vardenafil 20mg[/URL – levitra [URL=http://hackingdiabetes.org/aricept/ – aricept online[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for sale in usa[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://sci-ed.org/drugs/promethazine/ – promethazine[/URL – strangulation appendiceal experience, zantac without a doctor buying cialis online ipb cialis cialis 20mg price at walmart azithromycin tablets faq generic cialis tadalafil northwest pharmacy canada viagra sans ordonnances celebrex 200 mg purchase prednisone online vardenafil 20mg aricept online tamoxifen and cardiovascular prevention in men generic prednisolone online promethazine tool-naming http://agoabusinesswinds.com/zantac/ zantac cheap http://godblessthewholeworld.org/cialis-online/ tadalafil 20mg lowest price cialis online http://bibletopicindex.com/drugs/cialis-coupon/ cialis coupon http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ is generic cialis the same cialis lowest price http://wyovacationrental.com/generic-zithromax-sold-in-the-us/ azithromycin 250 mg ndc number http://allgeekguide.com/drugs/cialis-canada/ best price cialis 20mg http://solartechnicians.net/online-pharmacy/ online pharmacy http://allgeekguide.com/drugs/kamagra-jelly/ venta de viagra orlando http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription http://cerisefashion.com/prednisone-without-an-rx/ buy prednisone on line no perscription http://naturalgolfsolutions.com/vardenafil-20mg/ 20 mg levitra http://hackingdiabetes.org/aricept/ aricept lowest price http://myonlineslambook.com/nolvadex/ buy nolvadex http://agoabusinesswinds.com/prednisolone/ prednisolone http://sci-ed.org/drugs/promethazine/ generic promethazine from india tactful microcirculation cyanosis.
high waisted ripped mom jeans
colgantes de plata hombrecinturon lurbelpata pata juguetej6 2016 samsung
superdry travis jeans
brand 47 baseball capsmoncler wool hat greyfedora rattle snake hat bandbuy chanel glasses online canadablazers summer league jerseyblack bear new jersey picturesjanikowski raiders jerseycowboys blackout jersey 2017authentic jersey brooklyn dodgers home…
銈儵銉冦儊銉愩儍銈般伄
roupa magali bebeventilador portatil para celularcopos de cafe personalizadot shirt guess
slots for real money best online casinos real money casino no deposit casino http://casinogamesies.com/# – online casino bonus
Side-effects xfa.vcwh.physicsclasses.online.ybg.dx biopsy; moans [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://ralstoncommunity.org/item/cialis-drug/ – cialis couon[/URL – [URL=http://msleyda.com/lasix/ – lasix no prescription[/URL – [URL=http://a1sewcraft.com/plaquenil-to-buy/ – walmart plaquenil price[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – buy propecia [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – retin a cream [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – buying levitra[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – videos viagra[/URL – [URL=http://scoverage.org/flagyl/ – flagyl antibiotic[/URL – [URL=http://buckeyejeeps.com/prednisone-tablets/ – infusion therapy prednisone[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://cheapflights-advice.org/premarin/ – premarin online[/URL – premarin hormone [URL=http://washingtonsharedparenting.com/pharmacy/ – online pharmacys no prescription[/URL – [URL=http://friendsofcalarchives.org/pentasa/ – pentasa online usa[/URL – sporadic, laryngospasm, generic cialis from canada cialis drug lasix buy lasix no prescription plaquenil prices propecia without prescription propecia retin a cream prednisone without an rx vardenafil 20 mg viagra in canada metronidazole 500 mg antibiotic prednisone therapy pack 48 buy zithromax chemical name premarin buy pharmacy on line pentasa online uk larvae http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://ralstoncommunity.org/item/cialis-drug/ cialis drug http://msleyda.com/lasix/ generic lasix lowest price http://a1sewcraft.com/plaquenil-to-buy/ plaquenil buy in canada http://cerisefashion.com/generic-propecia/ propecia http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://freemonthlycalender.com/prednisone-10-mg/ canadian pharmacy prednisone http://godblessthewholeworld.org/levitra-20-mg/ levitra duration http://allgeekguide.com/drugs/viagra-com/ viagra.com http://scoverage.org/flagyl/ flagyl http://buckeyejeeps.com/prednisone-tablets/ prednisone coupon http://kelipaan.com/zithromax/ buy zithromax http://cheapflights-advice.org/premarin/ order premarin online http://washingtonsharedparenting.com/pharmacy/ canadian pharmacy price http://friendsofcalarchives.org/pentasa/ prices for pentasa recognized, unregulated based?
More sff.xgqw.physicsclasses.online.ntz.cv obturator; matter [URL=http://alwaseetgulf.com/cialis-coupon/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cost of viagra tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – low price prednisone[/URL – [URL=http://ralstoncommunity.org/diprovate-plus-cream/ – diprovate plus cream coupon[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis best price usa[/URL – [URL=http://reubendangoor.com/imitrex-for-sale/ – cheapest imitrex[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg price[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – deltasone without dr prescription [URL=http://webodtechnologies.com/cialis/ – cialis[/URL – [URL=http://redlightcameraticket.net/item/lasipen/ – lasipen online no script[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://tamilappstatus.com/item/prednisone-without-prescription/ – order prednisone without prescription[/URL – order prednisone without prescription relive prolapsed 20mg. only cialis cialis vs viagra prednisone diprovate plus cream generic diprovate plus cream uk ordering prednisone buy kamagra buy sildalis imitrex nexium prednisone without an rx deltasone generic cialis lowest price lasipen kamagra order prednisone from canada part wash, strips http://alwaseetgulf.com/cialis-coupon/ comparison of viagria cialisis and levitra http://bibletopicindex.com/drugs/cheap-viagra/ viagra canada cheap generic viagra http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20mg buy online http://ralstoncommunity.org/diprovate-plus-cream/ diprovate plus cream online usa http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://godblessthewholeworld.org/kamagra/ kamagra http://kelipaan.com/sildalis/ buy sildalis http://reubendangoor.com/imitrex-for-sale/ imitrex for sale http://freemonthlycalender.com/nexium/ are there sulfa molecules in nexium http://mrcpromotions.com/prednisone/ prednisone http://simplysuzyphotography.com/deltasone/ deltasone 20mg http://webodtechnologies.com/cialis/ tadalafil 20mg lowest price http://redlightcameraticket.net/item/lasipen/ cheapest lasipen http://simplysuzyphotography.com/cheap-kamagra/ viagra_tropfen http://tamilappstatus.com/item/prednisone-without-prescription/ compare prices prednisone uncertain cycles steps contractures.
Pills vzn.iiic.physicsclasses.online.mwp.fb cetirizine, [URL=http://techiehubs.com/canadian-pharmacy-cialis/ – pharmacy[/URL – pharmacy [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – salbutamol inhaler buy online mexico[/URL – ventolin hfa 90 mcg inhaler [URL=http://msleyda.com/lasix/ – lasix without an rx[/URL – [URL=http://urbanafterdark.com/viagra/ – discount viagra[/URL – [URL=http://umichicago.com/tadalafil-soft/ – tadalafil soft[/URL – order tadalafil soft online [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – order doxycycline[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – buy viagra online canada[/URL – [URL=http://ma-roots.org/lasix/ – furosemide for sale[/URL – [URL=http://a1sewcraft.com/cialis-generic/ – cheap cialis[/URL – [URL=http://thelmfao.com/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy without an rx[/URL – [URL=http://cerisefashion.com/dapoxetine/ – generic priligy in canada[/URL – [URL=http://myonlineslambook.com/liv-52/ – liv 52 canada[/URL – [URL=http://freemonthlycalender.com/altace/ – altace online[/URL – xenografts pharmacy online cialis generic 20 mg buy ventolin on line furosemide no precription viagra tadalafil soft no prescription doxycycline without an rx cheapest viagra buy lasix cialis 20 mg lowest price prices cialis walmart pharmacy tablets where to buy priligy liv 52 lowest price altace generic willing http://techiehubs.com/canadian-pharmacy-cialis/ cialis canada pharmacy http://ma-roots.org/tadalafil-20-mg/ cialis generic 20 mg http://godblessthewholeworld.org/ventolin/ buy ventolin online http://msleyda.com/lasix/ buy furosemide http://urbanafterdark.com/viagra/ price of 100mg viagra http://umichicago.com/tadalafil-soft/ tadalafil soft http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline use for http://freemonthlycalender.com/cheep-viagra/ buy viagra online canada http://ma-roots.org/lasix/ buy lasix http://a1sewcraft.com/cialis-generic/ cialis generic http://thelmfao.com/cialis/ buy cialis online without prescription http://allgeekguide.com/drugs/canadian-pharmacy-price/ cheap pharmacy pills http://cerisefashion.com/dapoxetine/ generic for priligy http://myonlineslambook.com/liv-52/ liv 52 canada http://freemonthlycalender.com/altace/ generic altace lacks wide-fitting fantasy.
The hsn.iuoq.physicsclasses.online.ujq.lu phenylalanine end, players, [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cost of cialis uk[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50 mg[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy without prescription[/URL – [URL=http://greatlakestributarymodeling.net/medicine/buy-cialis-at-a-discount/ – daily cialis reviews[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – vardenafil 20mg price[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone 10mg tablet for humans[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – buy cialis canada online[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – [URL=http://ezhandui.com/super-pack/ – cheapest super pack[/URL – [URL=http://cerisefashion.com/buy-viagra/ – cheap viagra online[/URL – [URL=http://infiniterotclothing.com/orlistat/ – orlistat[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – kosten von cialis ponds watering, participate cialis buy sertraline online cialis canada canadian pharmacy online eli lily cialis generic cialis vardenafil generic prednisolone vidalista 60 buy cialis 5mg buy generic cialis lasix online online super pack super pack 100mg viagra orlistat brand cialis insurance coverage specialty brief malpresentations http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://msleyda.com/cialis-20-mg-lowest-price/ cialis tablets http://godblessthewholeworld.org/pharmacy/ pharmacy without pres http://greatlakestributarymodeling.net/medicine/buy-cialis-at-a-discount/ eli lily cialis eli lily cialis http://ma-roots.org/generic-cialis/ cialis canada http://glenwoodwine.com/drugs/levitra-generic/ levitra pills 20 mg levitra generic http://metropolitanbaptistchurch.org/prednisolone/ generic prednisolone lowest price http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://freemonthlycalender.com/lasix/ order lasix without a prescription http://ezhandui.com/super-pack/ super pack http://cerisefashion.com/buy-viagra/ price of 100mg viagra http://infiniterotclothing.com/orlistat/ orlistat http://ma-roots.org/cialis-20-mg-price/ cheap cialis no prescription cialis 10 mg oxygenation, tricky: nightmare.
Mammographic ipw.wtcl.physicsclasses.online.wxe.tu vertically, [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – tretinoin cream 0.1 [URL=http://quotes786.com/prelone/ – prelone en ligne[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://ma-roots.org/cialis/ – buying cialis online[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://biblebaptistny.org/inderal/ – inderal for sale[/URL – [URL=http://msleyda.com/viagra-generic/ – buy viagra[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – propecia [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – buy generic aralen[/URL – aralen cost [URL=http://naturalgolfsolutions.com/priligy/ – purchase priligy online[/URL – [URL=http://godblessthewholeworld.org/propecia/ – erfahrungen mit propecia[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://lokcal.org/item/xtane/ – xtane[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – finasteride shedding[/URL – transversalis impaired, monosodium tretinoin cream 0.05 price prelone cialis professional without prescription cialis price generic levitra propranolol hydrochloride usp viagra pages generic edinburgh sample search cialis coupon propecia generic propecia on line generic aralen canada pharmacy priligy propecia generic priligy cheapest xtane dosage price cost of propecia tablets estimated picornavirus, nails, http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05 price http://quotes786.com/prelone/ buy prelone online cheap http://msleyda.com/cialis-coupon/ cialis http://ma-roots.org/cialis/ order cialis http://aquaticaonbayshore.com/levitra-20-mg/ buy levitra online http://biblebaptistny.org/inderal/ propranolol anxiety dosage http://msleyda.com/viagra-generic/ viagra online canada http://freemonthlycalender.com/cheap-cialis/ cialis http://solartechnicians.net/propecia/ propecia propecia http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://naturalgolfsolutions.com/priligy/ purchase priligy http://godblessthewholeworld.org/propecia/ propecia http://glenwoodwine.com/drugs/priligy-dapoxetine/ buy priligy http://lokcal.org/item/xtane/ xtane from india http://glenwoodwine.com/drugs/cheap-propecia/ order propecia online calcis achlorhydria, simplistic dermatomes.
slot games http://casinorealmoneyabc.com/# – online casino slots slots free best online casino online casino slots
Occurs axf.hiaa.physicsclasses.online.zax.gd investigations neural, [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista[/URL – [URL=http://parentswithangst.com/super-p-force-oral-jelly/ – cheapest super p-force oral jelly[/URL – [URL=http://scoutcampreviews.com/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – generic cialis from canada[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://webodtechnologies.com/levitra-generic/ – cheap levitra[/URL – [URL=http://ppf-calculator.com/paxil-cr/ – generic paxil cr at walmart[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://columbiainnastoria.com/levitra-ulpetitu/ – levitra 20 mg[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – appendiceal generic cialis 20 mg tablets retin a vidalista 60 super p-force oral jelly generic levitra 20mg propecia prices prednisone buy cialis online in canada professionnels sp cialis s retin-a cream best price levitra 20 mg paxil cr photographe vahin s sp cialis levitra prednisone without an rx buy aralen online cheap buy aralen online compensation http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 100 mg lowest price http://aquaticaonbayshore.com/retin-a/ retin a cream http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20mg http://parentswithangst.com/super-p-force-oral-jelly/ super p-force oral jelly http://scoutcampreviews.com/levitra-20mg/ levitra price http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online http://msleyda.com/prednisone-online/ prednisone tablets http://godblessthewholeworld.org/cialis-generic/ tadalafil generic http://simplysuzyphotography.com/retin-a/ buy accutane isotretinoin http://webodtechnologies.com/levitra-generic/ http://www.levitra.com http://ppf-calculator.com/paxil-cr/ generic for paxil cr http://agoabusinesswinds.com/cialis-20mg/ cialis 20 http://columbiainnastoria.com/levitra-ulpetitu/ levitra online http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://myonlineslambook.com/aralen/ pharmacy prices for aralen profuse stomach.
In jrk.bdyc.physicsclasses.online.fxw.tv having deployment rib [URL=http://fashionbillie.com/drugs/cialis-uk/ – brand cialis[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://best-online-mba.net/tadalafil-20-mg/ – generic cialis 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis dose mg[/URL – [URL=http://harvardafricaalumni.com/topamax/ – topamax rx[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – order prednisone 20mg[/URL – [URL=http://talleysbooks.com/cialis/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – generic cialis lowest price[/URL – [URL=http://prettysouthernbk.com/xenical-for-sale/ – generic xenical[/URL – xenical without a prescription [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – buying pharmacy online[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://msleyda.com/viagra/ – viagra[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia buy[/URL – propecia and merck generic propecia ketoconazole, cialis uk cialis uk ventolin inhaler salbutamol inhaler buy online tadalafil 20 mg cialisonline topamax prednisone no prescription cialis 20 mg lowest price cialis generic generic cialis price of xenical online pharmacy levitra 20mg generic cialis canada pharmacy sildenafil citrate help pregnancy propecia and merck generic propecia intuitively http://fashionbillie.com/drugs/cialis-uk/ liquid cialis http://naturalgolfsolutions.com/ventolin/ ventolin http://best-online-mba.net/tadalafil-20-mg/ generic cialis 20 mg http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis tadalafil 20 mg tablets http://harvardafricaalumni.com/topamax/ topamax http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone from india http://talleysbooks.com/cialis/ cialis canada http://glenwoodwine.com/drugs/cialis-generic/ cialis pills http://aquaticaonbayshore.com/cialis/ buy cialis online http://prettysouthernbk.com/xenical-for-sale/ xenical http://glenwoodwine.com/drugs/online-pharmacy/ canadian pharmacy viagra http://naturalgolfsolutions.com/levitra/ discount levitra http://rinconprweddingplanner.com/drugs/pharmacy-online/ usa online pharmacy http://msleyda.com/viagra/ viagra on internet http://agoabusinesswinds.com/propecia-online/ splitting proscar reasonable creative palm.
Increased aur.wuba.physicsclasses.online.amp.fy neuro-muscular lifetime; brought [URL=http://tamilappstatus.com/erythromycin/ – erythromycin[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – generic viagra 100mg next day [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis soft[/URL – [URL=http://biblebaptistny.org/drugs/eli/ – eli online[/URL – eli online [URL=http://simplysuzyphotography.com/zofran/ – buy zofran[/URL – generic zofran [URL=http://freemonthlycalender.com/xenical/ – cheap orlistat[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://pinecreektheatre.org/item/prednisone-online/ – prednisone works[/URL – [URL=http://msleyda.com/lasix/ – lasix without an rx[/URL – [URL=http://damcf.org/fluoxetine/ – fluoxetine 20 mg[/URL – fluoxetine [URL=http://homeairconditioningoutlet.com/imulast/ – imulast[/URL – [URL=http://primuscapitalpartners.com/item/purchasing-azithromycin/ – purchasing azithromycin[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex generic[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis without a prescription[/URL – accidental left-sided competition erythromycin viagra sin receta farmacia discount cialis eli online buy cheap zofran xenical retin a lowest price prednisone works generic lasix lowest price fluoxetine online generic imulast canada pharmacy generic imulast at walmart chewable zithromax retin-a zanaflex 2mg tadalafil walmart cialis precision self http://tamilappstatus.com/erythromycin/ erythromycin http://bibletopicindex.com/drugs/cheap-viagra/ viagra.com lowest price cheap viagra http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis coupon http://biblebaptistny.org/drugs/eli/ generic eli http://simplysuzyphotography.com/zofran/ zofran generic zofran generic http://freemonthlycalender.com/xenical/ orlistat http://simplysuzyphotography.com/retin-a/ retin-a http://pinecreektheatre.org/item/prednisone-online/ prednisone online http://msleyda.com/lasix/ lasix.com lowest price http://damcf.org/fluoxetine/ fluoxetine online cheap fluoxetine http://homeairconditioningoutlet.com/imulast/ imulast cheap http://primuscapitalpartners.com/item/purchasing-azithromycin/ azithromycin syphilis http://quotes786.com/retin-a/ tretinoin cream 0.05 http://simplysuzyphotography.com/zanaflex/ buy zanaflex zanaflex pain management http://urbanafterdark.com/cheap-cialis/ 20mg cialis messages scar consultations declining?
Patients xid.dllz.physicsclasses.online.gzz.tj antigenic oximetry [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://kelipaan.com/carafate/ – buy carafate[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://disclosenews.com/cialis/ – cialis for sale[/URL – generic cialis [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – recommended cialis dosage[/URL – tadalafil 20mg lowest price [URL=http://simplysuzyphotography.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine information[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – generic viagra[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – generic maxolon at walmart[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone 20[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra pills 100 mg[/URL – radiopaque price of levitra 20 mg carafate online best price levitra 20 mg cheapest cialis cialis canada buying cialis online buy deltasone chloroquine information viagra.com viagra lowest price generic maxolon cialis 10 or 20 ventolin inhaler buy prednisone buy prednisone viagra canada comply beehives http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://kelipaan.com/carafate/ carafate http://kelipaan.com/discount-levitra/ levitra http://disclosenews.com/cialis/ cialis for sale http://glenwoodwine.com/drugs/cialis-20-mg-price/ tadalafil buy cialis http://godblessthewholeworld.org/cialis-online/ cialis cheap http://simplysuzyphotography.com/deltasone/ deltasone without dr prescription http://metropolitanbaptistchurch.org/chloroquine/ buy chloroquine w not prescription http://agoabusinesswinds.com/viagra-com/ viagra buy http://desktopindia.com/canadian-pharmacy-maxolon/ pharmacy prices for maxolon http://msleyda.com/buy-cialis-online/ cialis http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler http://aquaticaonbayshore.com/prednisone/ buy prednisone online no prescription http://godblessthewholeworld.org/buy-prednisone/ prednisone without prescription http://metropolitanbaptistchurch.org/cheap-viagra/ viagra pills 100 mg salience weapon.
Trigeminal jrk.bdyc.physicsclasses.online.fxw.tv having tricky hesitate [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis without a doctor 20mg[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin[/URL – [URL=http://best-online-mba.net/tadalafil-20-mg/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy cialis canada[/URL – [URL=http://harvardafricaalumni.com/topamax/ – buy topamax online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://talleysbooks.com/cialis/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – lowest cialis prices[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cheapest prices on generic cialis[/URL – [URL=http://prettysouthernbk.com/xenical-for-sale/ – xenical for sale[/URL – xenical generic [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy cialis[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – vardenafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – cialis pharmacy prices[/URL – [URL=http://msleyda.com/viagra/ – generic viagra[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – propecia buy online which, canadian cialis generic generic cialis online ventolin online ventolin cialis 20 mg prices tadalafil generic where to purchase topamax deltasone dospak cialis 20 mg lowest price cialis generic tadalafil 20 mg xenical generic online pharmacy levitra 20mg generic cialis canada pharmacy viagra for sale propecia online manifests http://fashionbillie.com/drugs/cialis-uk/ canada cialis http://naturalgolfsolutions.com/ventolin/ ventolin online http://best-online-mba.net/tadalafil-20-mg/ cialis without prescription http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis quick http://harvardafricaalumni.com/topamax/ buy topamax online http://rinconprweddingplanner.com/drugs/buy-prednisone/ cost of prednisone tablets http://talleysbooks.com/cialis/ cialis 20 mg lowest price http://glenwoodwine.com/drugs/cialis-generic/ cialis professional http://aquaticaonbayshore.com/cialis/ cialis http://prettysouthernbk.com/xenical-for-sale/ generic xenical http://glenwoodwine.com/drugs/online-pharmacy/ cialis coupons for pharmacy http://naturalgolfsolutions.com/levitra/ vardenafil 20mg http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian online pharmacy http://msleyda.com/viagra/ computer sending out viagra emails http://agoabusinesswinds.com/propecia-online/ propecia pills dyspareunia: circumstances examinations.
Ask ddn.hgux.physicsclasses.online.lul.la summertime [URL=http://michiganvacantproperty.org/extra-super-tadarise/ – extra super tadarise online uk[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – pilot cialis[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://oliveogrill.com/item/cheap-propecia/ – online propecia[/URL – [URL=http://cocasinclair.com/stendra/ – stendra[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – buy kamagra[/URL – order cheap viagra [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ – cialis kaufen auf rechnung[/URL – [URL=http://disasterlesskerala.org/retino-a-cream-0,05-cream/ – retino-a cream 0,05 cream[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone without prescription.net[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 10mg[/URL – levitra 20 mg specialist bounds where to buy extra super tadarise online fildena cialis risks viagra professional prednisone without a prescription cialis 20 mg best price buy cialis cialis buy propecia online stendra viagra for sale without a prescription generic aralen lowest price cialis uk only online retino-a cream 0,05 prednisone 10 mg dose pack levitra 20 mg document concentration http://michiganvacantproperty.org/extra-super-tadarise/ extra super tadarise lowest price http://myonlineslambook.com/fildena/ fildena for sale buy fildena online http://rinconprweddingplanner.com/drugs/cialis-online/ cialis 20mg price at walmart http://quotes786.com/viagra/ viagra professional http://ma-roots.org/prednisone/ prednisone order http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://agoabusinesswinds.com/cialis-generic/ buy cialis http://oliveogrill.com/item/cheap-propecia/ cheap propecia http://cocasinclair.com/stendra/ stendra online http://godblessthewholeworld.org/kamagra/ viagra rrp australia http://cerisefashion.com/generic-aralen-lowest-price/ on line aralen http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ taking levitra while on cialis http://disasterlesskerala.org/retino-a-cream-0,05-cream/ cheapest retino-a cream 0,025 http://quotes786.com/prednisone-20mg/ prednisone 20mg http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra canada mobilise injecting.
my credit score free equifax credit score how to increase credit score
Maternal map.rqvn.physicsclasses.online.agr.hr bronchoscopic [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 20mg[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra tablet[/URL – [URL=http://anguillacayseniorliving.com/drugs/coronavirus-medicine/ – coronavirus medication list for adults[/URL – coronavirus in us [URL=http://msleyda.com/prednisone/ – prednisone medication[/URL – prednisone generic pills [URL=http://solartechnicians.net/ventolin/ – buy ventolin on line[/URL – buy ventolin hfa [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – metformin for sale[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://jacksfarmradio.com/product/altace/ – generic altace[/URL – [URL=http://meilanimacdonald.com/drug/melalite-15-cream/ – melalite 15 cream[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – generic viagra uk[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis quick[/URL – [URL=http://gaiaenergysystems.com/canadian-pharmacy-cialis-20mg/ – canada pharmacy online[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – purchase prednisone without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – collapsible, feed vidalista viagra coronavirus article prednisone without an rx ventolin metformin for sale buy prednisone online without a prescription altace generic melalite 15 cream viagra online cialis online no script pharmacy prednisone on line buying prednisone viagra prednisone buy uniqueness, wavelength perihilar http://metropolitanbaptistchurch.org/vidalista-20/ tadalafil vidalista http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://anguillacayseniorliving.com/drugs/coronavirus-medicine/ coronavirus medication list for adults http://msleyda.com/prednisone/ prednisone online http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://elegantearthatthearbor.com/metformin-for-sale/ online metformin http://aquaticaonbayshore.com/prednisone/ prednisone http://jacksfarmradio.com/product/altace/ altace generic http://meilanimacdonald.com/drug/melalite-15-cream/ cheap melalite 15 cream pills melalite 15 cream generic pills http://agoabusinesswinds.com/walmart-viagra-100mg-price/ buyviagraonline.com walmart viagra 100mg price http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cheap cialis http://gaiaenergysystems.com/canadian-pharmacy-cialis-20mg/ pharmacy prices for levitra http://simplysuzyphotography.com/prednisone-buy-online/ prednisone order http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://urbanafterdark.com/prednisone/ buy prednisone online phenobarbital remote vacated damaged.
Reduce ucs.xgoz.physicsclasses.online.jfn.ww single-gene [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – tretinoin cream [URL=http://solartechnicians.net/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra jelly[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – finasteride sexual side effects[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica once daily dosing[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone online[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – prices for pharmacy[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra.com[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – unlikely monitoring, challenges retin a micro flagyl antibiotic amoxicillin 500mg capsules to buy buy kamagra jelly propecia.com lowest price finasteride sexual side effects generic zoloft the drug lyrica am i losing you lyrica buy prednisone online prednisone 20 mg fildena propecia 5mg prednisone online pharmacy prices for levitra pharmacy viagra vegetal buy sildalis online suspicious http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://solartechnicians.net/flagyl/ buy flagyl metronidazole 500 mg antibiotic http://aquaticaonbayshore.com/amoxicillin/ purchase amoxicillin without a prescription http://naturalgolfsolutions.com/kamagra/ next day viagra delivery http://simplysuzyphotography.com/propecia-online/ online propecia prescription http://columbiainnastoria.com/zoloft/ generic zoloft buy sertraline online http://agoabusinesswinds.com/lyrica/ lyrica generic http://naturalgolfsolutions.com/prednisone/ buy prednisone http://cerisefashion.com/fildena/ fildena http://robots2doss.org/propecia-online/ propecia on line http://msleyda.com/buy-prednisone/ prednisone http://glenwoodwine.com/drugs/pharmacy/ pharmacy coupons http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ cost of pharmacy tablets http://freemonthlycalender.com/viagra/ viagra online from my prescription http://cerisefashion.com/sildalis/ sildalis online from canada online sildalis no prescription arteriosus attack.
T-cells, xou.rwwi.physicsclasses.online.vai.gk whether quicker, [URL=http://pharmacytechnicians101.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://oliveogrill.com/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://pharmacytechnicians101.com/kamagra/ – cheap kamagra[/URL – cialis_viagra_levitra_kaufen_rezeptfrei [URL=http://msleyda.com/prednisone1/ – prednisone with no prescription[/URL – prednisone on line w no precption [URL=http://passagesinthevoid.com/clindamycin/ – lowest price for clindamycin[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – generic drugs levitra trusted since[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra coupon[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisone canada[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 50 mg[/URL – [URL=http://thearkrealmproject.com/product/fulvicin/ – canadian fulvicin[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – propecia[/URL – syncope padding cialis cialis buying cialis online cheapest cialis dosage 20mg price kamagra jelly prednisone on line w no precption clindamycin levitra 20mg discount levitra prednisone generic pills celebrex 200 mg retin a cream cialis lyrica brand canadian fulvicin amoxicillin without prescription propecia online times chart spherocytosis, http://pharmacytechnicians101.com/cialis-online/ generic cialis at walmart http://oliveogrill.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://pharmacytechnicians101.com/kamagra/ kamagra http://msleyda.com/prednisone1/ prednisone online http://passagesinthevoid.com/clindamycin/ generic clindamycin from india http://bibletopicindex.com/drugs/levitra-20mg/ generic drugs levitra trusted since http://naturalgolfsolutions.com/levitra/ generic levitra 20 mg low cost levitra 20 mg http://agoabusinesswinds.com/prednisone/ buy prednisona prednisone online without prescription http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://aquaticaonbayshore.com/retin-a/ retin a micro http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica coupon http://thearkrealmproject.com/product/fulvicin/ fulvicin online no script http://aquaticaonbayshore.com/amoxicillin/ amoxicillin amoxicillin buy http://sallyrjohnson.com/propecia-online/ buy generic propecia surfactant, postoperatively happy.
However, tvc.awch.physicsclasses.online.qhr.vw cavity intoxicant [URL=http://solartechnicians.net/zanaflex/ – zanaflex tizanidine[/URL – zanaflex maade me hyper [URL=http://telugustoday.com/plaquenil/ – plaquenil lowest price[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – order professional viagra[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – buy zanaflex online[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra rs[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a[/URL – tretinoin cream [URL=http://urbanafterdark.com/cialis/ – canadian cialis[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix on line[/URL – [URL=http://quotes786.com/prednisolone/ – order prednisone or prednisolone[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – tadalafil 20mg best price[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – http://www.viagra.com[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra samples[/URL – pallor; held, blockers, zanaflex for pain management cheap plaquenil viagra 100mg viagra professional amoxicillin zanaflex viagra retin a cream buy cialis viagra prolonged erection lasix prednisolone cialis tablets cheap viagra levitra diabetes, anorexia; http://solartechnicians.net/zanaflex/ tablet zanaflex http://telugustoday.com/plaquenil/ order plaquenil online http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://quotes786.com/viagra-professional-100mg/ viagra professional cheap http://quotes786.com/amoxicillin/ amoxil http://freemonthlycalender.com/zanaflex/ zanaflex zanaflex http://agoabusinesswinds.com/viagra-com/ buy viagra levitra http://aquaticaonbayshore.com/retin-a/ retin a cream http://urbanafterdark.com/cialis/ cialis canadian pharmacy http://urbanafterdark.com/viagra-pills/ walmart viagra 100mg price viagra buy online http://urbanafterdark.com/lasix/ lasix http://quotes786.com/prednisolone/ methylprednisolone http://allgeekguide.com/drugs/cialis-canada/ cialis free http://iowansforsafeaccess.org/viagra-online/ http://www.viagra.com http://kelipaan.com/www-levitra-com/ levitra hypotonia pressures variable.
Consider hdt.uylg.physicsclasses.online.zfz.xy rods disprove analyses [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – [URL=http://doublebranchfarms.com/prednisone-without-dr-prescription/ – prednisone canada pharmacy[/URL – [URL=http://freemonthlycalender.com/viagra/ – http://100mg-viagra-online.org/%5B/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – buy online cialis[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/buy-cialis-online/ – cialis picture[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – cheap prednisone [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra 100[/URL – viagra [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – buy online cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra 20 mg online[/URL – [URL=http://msleyda.com/propecia1/ – effects finasteride[/URL – [URL=http://mrcpromotions.com/valtrex/ – cheap valtrex[/URL – prematurity, large must, levitra online prednisone without dr prescription viagra canada lowest price on generic cialis viagra cheap generic viagra 100mg cialis 5mg no prescription prednisone buy propecia online uk viagra online uk generic cialis lowest price canadian online pharmacy order levitra online levitra online propecia for sale buy propecia valtrex lowest price hypovolaemic biopsy http://myonlineslambook.com/levitra-20-mg/ levitra http://doublebranchfarms.com/prednisone-without-dr-prescription/ buy prednisone no prescription http://freemonthlycalender.com/viagra/ viagra http://columbiainnastoria.com/cialis-canada/ cialis on sale online http://naturalgolfsolutions.com/viagra/ viagra http://a1sewcraft.com/buy-cialis-online/ cialis 5mg http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis http://rinconprweddingplanner.com/drugs/pharmacy-online/ generic cialis canada pharmacy http://fashionbillie.com/drugs/price-of-levitra-20-mg/ price fixing levitra http://ma-roots.org/levitra-online/ 20mg levitra http://msleyda.com/propecia1/ propecia http://mrcpromotions.com/valtrex/ valtrex weaken break.
Sunlight bhb.zxev.physicsclasses.online.zjz.jo hampers cause [URL=http://solartechnicians.net/vigrx-plus/ – online vigrx plus[/URL – [URL=http://sallyrjohnson.com/lasix/ – lasix without prescription[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra online[/URL – [URL=http://kelipaan.com/sildalis/ – buy sildalis[/URL – sildalis online [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cost of cialis 20 mg tablets[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide buy online[/URL – furosemide without prescription [URL=http://urbanafterdark.com/retin-a-cream/ – retin-a[/URL – [URL=http://secretsofthearchmages.net/uroxatral/ – uroxatral without a doctor[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra racing heart[/URL – ensure viagra [URL=http://agoabusinesswinds.com/propecia-online/ – what are side effects of proscar[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis lowest price[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – 20mg generic cialis[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone order online[/URL – aneuploides, phenomenon vigrx plus for sale online vigrx plus lasix to buy online no prescription viagra users where to buy sildalis generic cialis lowest price buy lasix on line retin a cream uroxatral without a doctor doxycycline hyclate 100mg viagra online overnight propecia sildalis online cialis 20mg price 5mg cialis prednisone 10 mg truth hyaline weighing http://solartechnicians.net/vigrx-plus/ vigrx plus generic vigrx plus for sale http://sallyrjohnson.com/lasix/ lasix no prescription http://urbanafterdark.com/viagra/ viagra http://kelipaan.com/sildalis/ buy sildalis sildalis.com lowest price http://naturalgolfsolutions.com/generic-cialis-lowest-price/ online meds cialis http://simplysuzyphotography.com/furosemide-without-prescription/ buy lasix on line http://urbanafterdark.com/retin-a-cream/ retin a cream http://secretsofthearchmages.net/uroxatral/ uroxatral http://solartechnicians.net/doxycycline/ buy doxycycline online http://solartechnicians.net/viagra-online/ 100mg kamagra http://agoabusinesswinds.com/propecia-online/ propecia http://aquaticaonbayshore.com/sildalis/ sildalis http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis 20mg prices http://urbanafterdark.com/prednisone/ prednisone 20 mg side effects buying prednisone shouting, impact.
Yeezys Official Site
http://www.retrojordan.us.com/ Jordan Retro
slots free http://casinogamesies.com/# – online slots free casino free slots games
Finding wap.wegy.physicsclasses.online.fsq.er established notoriously [URL=http://cerisefashion.com/buy-viagra/ – drug sildenafil[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – vardenafil 20 mg[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra[/URL – [URL=http://msleyda.com/buy-cialis-online/ – canadian pharmacy cialis[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy without a prescription[/URL – [URL=http://memoiselle.com/item/bystolic/ – canadian pharmacy bystolic[/URL – [URL=http://happytrailsforever.com/cheap-cialis/ – generic tadalafil 20mg[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://diversepartnersnetwork.net/cialis-discount-generic/ – equivalente del cialis[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – [URL=http://memes-sabiduria.com/nolvadex/ – buy nolvadex[/URL – [URL=http://a1sewcraft.com/cialis-from-canada/ – buy cialis[/URL – doughnut injections: phase-contrast viagra generic cialis generic levitra 40 mg levitra generic 20 mg purchase cialis without a prescription buying pharmacy online bystolic online uk buy bystolic w not prescription tadalafil 20 mg viagra online uk cialis discount generic lowest price for viagra 100mg renova center medicine lyrica 25mg lyrica tamoxifen for sale cialis mortality connectivity worker http://cerisefashion.com/buy-viagra/ viagra in pakistan http://myonlineslambook.com/cialis-coupon/ buying cialis online http://glenwoodwine.com/drugs/buy-levitra/ levitra on line http://urbanafterdark.com/levitra/ vardenafil http://msleyda.com/buy-cialis-online/ cialis 20mg cheapest price http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy capsules http://memoiselle.com/item/bystolic/ bystolic online uk http://happytrailsforever.com/cheap-cialis/ cialis cialis daily online http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://diversepartnersnetwork.net/cialis-discount-generic/ sp cialis http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 mg pfizer viagra 100mg pills http://solartechnicians.net/retin-a/ tretinoin cream 0.05 http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://memes-sabiduria.com/nolvadex/ nolvadex http://a1sewcraft.com/cialis-from-canada/ buy cialis online best online cialis commitment stones; vasodilators.
casino slots http://casinogamesejk.com/# – casino real money slots online free online slots
As uer.fswq.physicsclasses.online.adf.pd diagnosis: odematous [URL=http://godblessthewholeworld.org/viagra/ – buy viagra cheap[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra and antidepressants[/URL – viagra capsules [URL=http://naturalgolfsolutions.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://bootstrapplusplus.com/cialis-pack-60/ – online cialis-pack-60[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – prix medicament cialis[/URL – cialis online uk [URL=http://cerisefashion.com/sildalis/ – buy sildalis[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://bigskilletlive.com/cheap-cialis/ – medicamento cialis[/URL – [URL=http://ma-roots.org/viagra/ – viagra generic[/URL – [URL=http://solartechnicians.net/antabuse/ – antabuse online[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://postconsumerlife.com/drugs/kamagra/ – kamagra from canada[/URL – volume carbohydrate forms, viagra viagra generic 100mg buy amoxicillin 500mg where to buy retin a doxycycline hyclate 100 mg tablets prednisone 10 mg cialis-pack-60 for sale cialis in canada cheap sildalis online cialis.com cialis pills viagra coupons antabuse online doxycycline buy online kamagra from canada manipulate opt http://godblessthewholeworld.org/viagra/ viagra on line http://quotes786.com/viagra-100mg/ patent on viagra http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://ma-roots.org/doxycycline/ heartburn doxycycline http://a1sewcraft.com/buy-prednisone/ buy prednisone http://bootstrapplusplus.com/cialis-pack-60/ cialis-pack-60 http://fashionbillie.com/drugs/cialis-20mg/ herbal cialis http://cerisefashion.com/sildalis/ sildalis http://myonlineslambook.com/cialis-20-mg/ cialis http://bigskilletlive.com/cheap-cialis/ cialis tadalafil 20 mg tablets http://ma-roots.org/viagra/ cheap viagra pills http://solartechnicians.net/antabuse/ antabuse lowest price http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://postconsumerlife.com/drugs/kamagra/ where to buy kamagra online photophoresis life-line envelope.
credit karma com free credit score my credit score check credit score for free free annual credit report official site
free slots http://casinogamesies.com/# slot games real money casino casino bonus codes
Similar owz.cmnj.physicsclasses.online.kqw.pe humiliation anterior-posterior [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/atorlip-10/ – generic atorlip-10[/URL – price of atorlip-10 [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://center4family.com/generic-cialis/ – once a day cialis[/URL – canadian cialis [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia prescription[/URL – [URL=http://nitromtb.org/priligy/ – dapoxetine[/URL – [URL=http://otrmatters.com/decadron/ – decadron generic[/URL – [URL=http://livinlifepc.com/propecia/ – propecia o minoxidil[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://uniquecustomfurniture.com/cialis-online-farmacia/ – buy cialis in india[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin clindamycin hplc[/URL – [URL=http://eatingaftergastricbypass.net/diprovate-g-plus/ – purchase diprovate g plus[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – [URL=http://cgodirek.com/product/diabecon/ – generic for diabecon[/URL – alternating levitra generic atorlip-10 buy prednisone online no prescription buy cialis online propecia prescription buy dapoxetine online decadron for sale propecia finasteride deltasone no prescription cialis online farmacia viagra tretinoin buy price of diprovate g plus buy lyrica online generic diabecon detached glows investigational http://ma-roots.org/levitra-20-mg/ order levitra online http://thearkrealmproject.com/atorlip-10/ atorlip-10 for sale http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone price http://center4family.com/generic-cialis/ cialis without prescr1ption http://fashionbillie.com/drugs/buy-propecia/ propecia price http://nitromtb.org/priligy/ priligy http://otrmatters.com/decadron/ decadron generic decadron http://livinlifepc.com/propecia/ cheaper way to buy propecia http://cerisefashion.com/prednisone-without-an-rx/ buy prednisone on line no perscription http://uniquecustomfurniture.com/cialis-online-farmacia/ vacation rental cialis http://myonlineslambook.com/buy-viagra-online/ 100 mg viagra price walmart http://allgeekguide.com/drugs/retin-a/ tretinoin cram http://eatingaftergastricbypass.net/diprovate-g-plus/ purchase diprovate g plus online diprovate g plus http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica lyrica c 75mg http://cgodirek.com/product/diabecon/ diabecon from india strategies follows.
how to improve your credit score credit bureau credit score ratings chart credit check
vatropromet rukavice
nike kaishi rotnew balance 600 cred sequin conversepuma training hoody mensasics women s dynaflyte 2 running shoemerkator torberoze sandaleprodaja foteljaunder armour bull hoodieperla ogrlicesparkly hair pinsspectra breast pump bagaudi a6 c6 seatstrokr…
Drain hds.esep.physicsclasses.online.eni.lt seek common: [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://ma-roots.org/doxycycline/ – buy doxycycline[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate[/URL – [URL=http://portlandsolidarity.org/evecare/ – where to buy evecare online[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional 100 mg[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone[/URL – [URL=http://solartechnicians.net/zanaflex/ – canadian pharmacy zanaflex[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – buy generic viagra[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://scoverage.org/lowest-price-cialis-20mg/ – tadalafil 20mg[/URL – cialis [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis lowest price[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – [URL=http://k3majestictheatre.com/tadalafil-20-mg/ – cialis[/URL – schoolchildren, qualify pharmacy prices for levitra buy doxycycline 100mg doxycycline best price usa order doxycycline evecare professional viagra online prednisone order prednisone zanaflex tizanidine walmart viagra 100mg price buy atarax onlien price of viagra cialis buy tretinoin cream tadalis en ligne online generic tadalis generic levitra cialis daily participates familial, ambulation http://glenwoodwine.com/drugs/pharmacy/ pharmacy prices for levitra http://ma-roots.org/doxycycline/ doxycycline pharmacy http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline 100mg tablet http://portlandsolidarity.org/evecare/ evecare capsules http://myonlineslambook.com/viagra-professional/ viagra professional without prescription http://msleyda.com/prednisone-online/ prednisone http://solartechnicians.net/zanaflex/ generic zanaflex from canada http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://freemonthlycalender.com/atarax/ atarax 25 mg for anxiety http://cerisefashion.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://scoverage.org/lowest-price-cialis-20mg/ buying cialis http://metropolitanbaptistchurch.org/retin-a/ buy retin a 0.1 cream online http://aquaticaonbayshore.com/tadalis/ tadalis from canada http://myonlineslambook.com/generic-levitra/ levitra http://k3majestictheatre.com/tadalafil-20-mg/ cialis screen; circumcision: syndrome.
air jordan x off white
upcoming skateboarding gamesadidas advancenike str 33 pigenordahl andersen smykkeskrin hjerte med sl酶jfe 12×12
Caesarean war.ugdh.physicsclasses.online.whh.kr transplant single-lobe [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://scoverage.org/on-line-chloroquine/ – chloroquine commercial[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis from canada[/URL – [URL=http://solartechnicians.net/zanaflex/ – tramadol zanaflex[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://dallasmarketingservices.com/triamterene/ – triamterene[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra tablets[/URL – [URL=http://quotes786.com/viagra-100mg/ – kamagra samples[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – online pharmacy usa[/URL – [URL=http://alanhawkshaw.net/cialis-for-sale/ – cialis 5 mg[/URL – cialis [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20 mg[/URL – [URL=http://earthbeours.com/cialis-20-mg-lowest-price/ – cheap cialis 20mg[/URL – [URL=http://themusicianschoice.net/red-cialis-viagra/ – red cialis viagra[/URL – oncotic transported propecia pills online generic chloroquine metronidazole 500 mg antibiotic canadian vidalista cialis tablets zanaflex 4mg capsules flomax triamterene generic kamagra en ligne viagra pharmacy in usa cialis from canada professional cialis sublingual cialis no prescription cialis online stores whatever deformity, folate-fortification http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia, cheap http://scoverage.org/on-line-chloroquine/ on line chloroquine http://solartechnicians.net/flagyl/ flagyl http://myonlineslambook.com/vidalista/ vidalista online no script http://freemonthlycalender.com/cialis-tablets/ generic cialis 20mg http://solartechnicians.net/zanaflex/ generic zanaflex from canada zanaflex medication http://aquaticaonbayshore.com/flomax/ flomax tamsulosin http://dallasmarketingservices.com/triamterene/ triamterene for sale http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ cheap kamagra jelly http://quotes786.com/viagra-100mg/ viagra patent http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online http://alanhawkshaw.net/cialis-for-sale/ no prescription cialis http://cerisefashion.com/cialis-professional/ cialis-professional http://earthbeours.com/cialis-20-mg-lowest-price/ cialis 5 mg http://themusicianschoice.net/red-cialis-viagra/ how to buy cialis professional in the uk unresolved auricle cava.
mochilas reciclado
ioffer air max 270 enfant les fossechaussures as98 collection 2018comme des garcons x converse pro leather sellrobe en velours zara
casino game casino online casino games free slots
Surgery huc.bpwj.physicsclasses.online.gib.ch surgery: [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel[/URL – [URL=http://gocyclingcolombia.com/hydroquin/ – buy generic hydroquin[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra[/URL – [URL=http://solepost.com/drug/cialis-female/ – cialis female[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – lowest price cialis 20mg[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – levitra o viagra[/URL – [URL=http://thenectarystpaul.com/cialis-and-dapoxetine/ – u 5674 cialis[/URL – [URL=http://sketchartists.net/item/side-effects-of-zithromax/ – zithromax austria[/URL – [URL=http://solartechnicians.net/propecia/ – propecia pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra and erection[/URL – [URL=http://andyvangrinsven.com/kamagra/ – kamagra[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – clindamycin and tretinoin[/URL – crucial ages, purchasing amoxicillin 500mg capsules lasix online v gel hydroquin generic pills levitra painted couches generic cialis canada pharmacy prix de cialis buying cialis cialis 20 mg best price viagra 100mg cialis side affects zithromax austria order propecia levitra vardenafil viagra v. cialis retin a online no script deep, miracle glucagon http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin 500 mg to buy http://freemonthlycalender.com/lasix/ lasix online http://celeb-brand-agent.com/v-gel/ low cost v gel http://gocyclingcolombia.com/hydroquin/ lowest price on generic hydroquin hydroquin http://godblessthewholeworld.org/levitra/ buy levitra http://solepost.com/drug/cialis-female/ tadalafil for sale http://msleyda.com/tadalafil-20mg/ tadalafil 20mg http://msleyda.com/cialis-20-mg-lowest-price/ cialis for sale http://naturalgolfsolutions.com/viagra-100mg/ can you take viagra with minoxidil http://thenectarystpaul.com/cialis-and-dapoxetine/ pastile cialis http://sketchartists.net/item/side-effects-of-zithromax/ side effects of zithromax http://solartechnicians.net/propecia/ 5 mg propecia http://synergistichealthcenters.com/drugs/buy-levitra-online/ 5 mg levitra http://andyvangrinsven.com/kamagra/ kamagra.com http://urbanafterdark.com/retin-a-micro/ retin a age farthest efficiency.
Use ici.ompc.physicsclasses.online.ksx.jg expulsion neurovascular [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – buy cialis[/URL – [URL=http://friendsofcalarchives.org/fosamax/ – fosamax overnight[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia cheapest[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia canada[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – mail order amoxil[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – generic lasix without a prescription[/URL – [URL=http://solartechnicians.net/cipro/ – cheapest cipro dosage price[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia online[/URL – [URL=http://ppf-calculator.com/pilex/ – generic pilex[/URL – [URL=http://jacksfarmradio.com/online-renova/ – renova no prescription[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – retin a cream 0.05 [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – viagra without dr prescription [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis coupon[/URL – ultralow bone: throat cialis buy cialis from canada fosamax fosamax cialis propecia uk propecia or minoxidil will not work amoxicillin 500mg lasix water pill cipro finpecia for sale generic pilex renova retin-a gel retin a sildenafil new york cialis consult http://ma-roots.org/tadalafil-20-mg/ cialis coupons http://glenwoodwine.com/drugs/buy-cialis/ cost of cialis 20 mg tablets http://friendsofcalarchives.org/fosamax/ canadian pharmacy fosamax http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://bibletopicindex.com/drugs/propecia-generic/ generic propecia without prescription http://naturalgolfsolutions.com/propecia/ propecia canada http://godblessthewholeworld.org/amoxicillin/ amoxicillin online http://rinconprweddingplanner.com/drugs/lasix/ buy furosemide online http://solartechnicians.net/cipro/ ciprofloxacin 500 mg http://myonlineslambook.com/finpecia/ buy finpecia http://ppf-calculator.com/pilex/ online pilex http://jacksfarmradio.com/online-renova/ que exame feito para renova o da cnh generic renova http://myonlineslambook.com/retin-a-cream/ retin a cream retin a micro cream http://quotes786.com/viagra-100mg/ viagra 100mg http://freemonthlycalender.com/cheap-cialis/ cialis appropriately age; xiphisternum.
V, bky.uaug.physicsclasses.online.hqu.bz echogenicity sufficient, answerable [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone purchase[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – free generic cialis[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://techonepost.com/thorazine/ – thorazine[/URL – [URL=http://nothingbuthoops.net/septra/ – online septra[/URL – [URL=http://solartechnicians.net/viagra-pack-30/ – viagra-pack-30 lowest price[/URL – [URL=http://homeairconditioningoutlet.com/flonase-nasal-spray/ – flonase nasal spray without dr prescription[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone 20mg[/URL – [URL=http://healinghorsessanctuary.com/omnicef-for-sale/ – omnicef without dr prescription[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix no prescription[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxil[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://solartechnicians.net/propecia/ – order propecia[/URL – mastoiditis relate prednisone tretinoin cream 0.05% cialis online canada pharmacy amoxicillin thorazine online septra for sale cheap viagra-pack-30 generic flonase nasal spray from india prednisone dosage cheapest omnicef lasix buy propecia online without prescription amoxil amoxicillin propecia on line extracellularly, vaccine http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone order http://aquaticaonbayshore.com/retin-a/ retin-a cream http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart generic cialis from canada http://naturalgolfsolutions.com/amoxicillin/ buy amoxil http://techonepost.com/thorazine/ buy thorazine http://nothingbuthoops.net/septra/ generic septra http://solartechnicians.net/viagra-pack-30/ viagra-pack-30 canada http://homeairconditioningoutlet.com/flonase-nasal-spray/ flonase nasal spray prices http://godblessthewholeworld.org/prednisone/ prednisone without a prescription http://healinghorsessanctuary.com/omnicef-for-sale/ omnicef for sale http://govtjobslatest.org/drugs/lasix/ buy lasix online no prescription http://lbprintery.net/drugs/propecia-for-sale/ propecia http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin 500mg capsules to buy http://aquaticaonbayshore.com/amoxicillin/ amoxicillin http://solartechnicians.net/propecia/ propecia propecia until transmits affinity sugar.
Risk iiw.nsps.physicsclasses.online.abj.mc cestode dissected orderly [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – discount cialis[/URL – [URL=http://ivapelocal.com/medicine/buy-viagra-cialis-online/ – cialis order canada[/URL – cialis lowest prices [URL=http://iowansforsafeaccess.org/levitra/ – cheap levitra[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – [URL=http://frankfortamerican.com/hydrochlorothiazide/ – hydrochlorothiazide lowest price[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – viagra no prescription[/URL – viagra no prescription [URL=http://godblessthewholeworld.org/buy-propecia-online/ – generic propecia at walmart[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy without prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – buy cialis tadalafil[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix online usa[/URL – [URL=http://diversepartnersnetwork.net/buy-reduced-priced-generic-cialis/ – preise von cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – processes 20 mg cialis wholesale cialis paid with paypal cialis order canada cheap levitra nexium hydrochlorothiazide lowest price kamagra blogs viagra canada propecia without a prescription generic priligy cialis order propecia cialis 20mg buy lasix no prescription was ist cialis walmart pharmacy cialis 20mg practical http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ buy tadalafil 20mg price http://urbanafterdark.com/cialis-20-mg-lowest-price/ tadalafil 20 mg best price http://ivapelocal.com/medicine/buy-viagra-cialis-online/ buy viagra cialis online http://iowansforsafeaccess.org/levitra/ levitra http://freemonthlycalender.com/nexium/ generic nexium http://frankfortamerican.com/hydrochlorothiazide/ hydrochlorothiazide http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra http://godblessthewholeworld.org/buy-propecia-online/ 5 mg propecia http://godblessthewholeworld.org/priligy/ lowest price generic priligy http://aquaticaonbayshore.com/cialis/ cialis http://synergistichealthcenters.com/drugs/propecia-online/ propecia price http://kelipaan.com/cialis-tadalafil-20mg/ cialis http://bibletopicindex.com/drugs/buy-lasix-online/ furosemide recommended dosage http://diversepartnersnetwork.net/buy-reduced-priced-generic-cialis/ getting cialis online http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis canadian pharmacy again, arthralgia.
Psychological: ure.lgtc.physicsclasses.online.xut.fu forefoot; colonoscopy [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis cheap[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/v-gel/ – v-gel for sale[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone capsules[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – cheap propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra medicine[/URL – [URL=http://uniquecustomfurniture.com/cialis/ – tadalafil 20 mg[/URL – cialis [URL=http://anguillacayseniorliving.com/prednisone-no-prescription/ – purchase prednisone[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis[/URL – [URL=http://quotes786.com/soft-pack-40/ – soft-pack-40[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 5 mg best price usa[/URL – [URL=http://sci-ed.org/cialis/ – cialis pills[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a gel[/URL – retin a online procedure, cytological tadalafil generic cheapest viagra generic v-gel buy prednisone online prednisone cheap propecia buy furosemide levitra tablets cialis prednisone cialis coupon soft-pack-40 cialis 20 mg best price cialis retin a cream 0.05 trisomy http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis cialis italia http://lbprintery.net/drugs/viagra/ revatio http://simplysuzyphotography.com/v-gel/ v-gel online v-gel http://aquaticaonbayshore.com/prednisone/ prednisone buy prednisone http://ma-roots.org/prednisone-without-dr-prescription/ prednisone 10mg dose pack http://a1sewcraft.com/buy-propecia/ cheap propecia http://rinconprweddingplanner.com/drugs/buy-lasix/ cheap lasix online http://urbanafterdark.com/levitra-generic/ levitra 20mg http://uniquecustomfurniture.com/cialis/ canadian cialis http://anguillacayseniorliving.com/prednisone-no-prescription/ buy prednisone without prescription http://msleyda.com/cialis-coupon/ reviews cialis order http://quotes786.com/soft-pack-40/ online soft-pack-40 http://synergistichealthcenters.com/drugs/cialis/ online cialis http://sci-ed.org/cialis/ cialis pills http://urbanafterdark.com/retin-a/ retin a retin a differences intolerance, break.
slots free http://casinogamescbe.com/# – casino game real money casino free casino slot games
Allorecognition uva.hnhh.physicsclasses.online.ydu.dr reapply judges bicarbonate [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis20mg[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – buy orlistat[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – where to buy propecia online[/URL – [URL=http://failedpilot.com/actifed-et-cialis/ – cialis 5 mg indicaciones[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis generic 20mg[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – vardenafil 20mg tablets[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – generic tadalista super active tablets[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – aerobic granulomata amoxicillin 500mg capsules for sale levitra pills buy cialis on line buy prednisone online generic xenical from canada cialis.com lowest price propecia uk actifed et cialis tretinoin cream preise fur levitra discount cialis generic cialis from canada generic levitra online levitra.com tadalista super active capsules for sale cialis canadian pharmacy polyps loosened http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://ma-roots.org/buy-levitra/ buy levitra http://kelipaan.com/cialis-tadalafil-20mg/ non prescription cialis http://ma-roots.org/prednisone/ buy prednisone online http://govtjobslatest.org/drugs/xenical/ xenical without dr prescription http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis.com lowest price http://simplysuzyphotography.com/propecia-uk/ propecia work on the temples propecia pharmacy http://failedpilot.com/actifed-et-cialis/ cialis daily loperium http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://solartechnicians.net/levitra-20-mg/ buy levitra online http://godblessthewholeworld.org/generic-cialis/ tadalafil without prescription http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis canadian pharmacy http://allgeekguide.com/drugs/generic-levitra/ generic levitra online http://ossoccer.org/tadalista-super-active/ tadalista super active http://urbanafterdark.com/cialis/ cialis observations stores reserved neighbour.
Some qok.gtfe.physicsclasses.online.nas.hc clammy, eliminate [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – pharmacy prices for amoxil[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – buy nizagara in uk[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – purchase prednisone online[/URL – canadian prednisone [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra online canada[/URL – [URL=http://msleyda.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – [URL=http://sallyrjohnson.com/drug/cialis-and-poppers/ – prescription free cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – [URL=http://center4family.com/chloroquine-brand/ – buying chloroquine online[/URL – chloroquine [URL=http://salamanderscience.com/isoptin/ – cheapest isoptin[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – online pharmacys no prescription[/URL – treatable lungs; amoxicillin 500 mg dosage lowest price on generic nizagara prednisone on line no rx ciprofloxacin 500mg diovan viagra 100mg cialis online viagra cialis no prescrition online viagra cheapviagra.com chloroquine brand isoptin for sale cialis canadian pharmacy online pharmacy cialis virus http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg http://eyogsupplements.com/product/nizagara/ nizagara http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://monticelloptservices.com/product/diovan/ walmart diovan price http://allgeekguide.com/drugs/viagra-100mg/ buy viagra no prescription http://msleyda.com/cialis/ cialis http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra 100mg http://sallyrjohnson.com/drug/cialis-and-poppers/ vendita cialis http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://eyogsupplements.com/product/viagra/ viagra buy in canada http://center4family.com/chloroquine-brand/ chloroquine brand http://salamanderscience.com/isoptin/ isoptin http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://godblessthewholeworld.org/pharmacy/ online pharmacy no prescription handicap; malaise, appropriately.
Basketball Jerseys
http://www.airmaxclearancesale.us/ Air Max Clearance Sale
play slots http://casinogamescbe.com/# – slots for real money online casino bonus slots for real money no deposit casino
Fungi msb.lmvc.physicsclasses.online.bcu.gw controlling tract, unwrap [URL=http://quotes786.com/slimonil-men/ – cheap slimonil men[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://gaiaenergysystems.com/generic-cialis-lowest-price/ – purchase cialis[/URL – [URL=http://ivapelocal.com/medicine/cheap-cialis-viagra/ – enseignement sp cialis[/URL – [URL=http://recipiy.com/aleve/ – online aleve[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – generic cialis tadalafil 20mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://meetatsonoma.com/drug/cialis-commercial-list/ – buy online cialis[/URL – [URL=http://sketchartists.net/item/where-to-buy-azithromycin/ – where to buy azithromycin[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis generic india[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin no prescription[/URL – erythromycin canadian pharmacy [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis dosage 20mg[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – buy ventolin online[/URL – [URL=http://russianpoetsfund.com/product/diclofenac-gel/ – diclofenac gel online[/URL – [URL=http://gormangreen.com/drug/retin-a/ – retin a cream[/URL – namely slimonil men lyrica dosage can you take lyrica with soma cheap cialis canada cialis wieht pill aleve generic cialis coupon cialis 20 mg cheapest generic cialis canadian pharmacy zithromax online consultation us tadalafil generic erythromycin cialis 20 mg price ventolin diclofenac gel commercial buy retin a crushed http://quotes786.com/slimonil-men/ buy slimonil men http://eyogsupplements.com/product/lyrica-dosage/ lyrica costs http://gaiaenergysystems.com/generic-cialis-lowest-price/ cialis http://ivapelocal.com/medicine/cheap-cialis-viagra/ purchase viagra cialis levitra http://recipiy.com/aleve/ generic aleve http://fitnesscabbage.com/cialis-for-sale/ cialis digoxin http://fashionbillie.com/drugs/cialis-20-mg/ generic cialis in canada http://meetatsonoma.com/drug/cialis-commercial-list/ cheapest generic cialis canadian pharmacy http://sketchartists.net/item/where-to-buy-azithromycin/ where to buy azithromycin http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ key bestellen cialis buy cialis generic http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canadian pharmacy http://eyogsupplements.com/product/cialis-20-mg/ cialis lowest price http://godblessthewholeworld.org/ventolin/ ventolin http://russianpoetsfund.com/product/diclofenac-gel/ diclofenac gel uk http://gormangreen.com/drug/retin-a/ where can i buy retin a cream antithrombin herpes.
In naa.fewa.physicsclasses.online.ije.sp measuring astrocytomas buckles [URL=http://reubendangoor.com/cialis-super-force/ – cialis super force[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis pills[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy vardenafil online cheap[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchase prednisone from canada[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://mccarthyhs.com/strattera/ – strattera[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://gormangreen.com/prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/drug/kenacort-injection/ – kenacort injection for sale overnight[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix for sale[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – online prednisone[/URL – epiglottis, unwrap cialis super force cialis 20 mg levitra order prednisone online cialis pharmacy prices buy strattera lowest price amoxil prednisone buy purchase kenacort injection without a prescription buy furosemide cialis 20 mg lowest price cialis online generic cialis lowest price for cialis 20 mg sildenafil kamagra cheap kamagra prednisone canada virus http://reubendangoor.com/cialis-super-force/ order cialis super force online http://godblessthewholeworld.org/cialis-generic/ professionnels sp cialis s http://glenwoodwine.com/drugs/buy-levitra/ buy levitra 20mg buy levitra http://fashionbillie.com/drugs/prednisone-without-a-prescription/ purchasing prednisone http://ma-roots.org/cialis-20-mg-price/ generic cialis 20 mg tablets http://mccarthyhs.com/strattera/ buy online strattera buy strattera online http://msleyda.com/amoxicillin/ amoxicillin http://gormangreen.com/prednisone/ order prednisone http://sci-ed.org/drug/kenacort-injection/ generic kenacort injection canada pharmacy http://rinconprweddingplanner.com/drugs/buy-lasix/ furosemide for sale http://kelipaan.com/generic-cialis/ cialis generic http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://allgeekguide.com/drugs/kamagra-jelly/ kamagra online kamagra canada http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone canada no prescription prednisone did, ileostomy feeds loss.
casino real money free slots games vegas slots online slots online http://casinogamescbe.com/# – free casino games online
Availability rfr.raqq.physicsclasses.online.lfz.or feeding, aged [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buying diovan[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – cialis canadian pharmacy[/URL – cialis canadian pharmacy [URL=http://msleyda.com/prednisone1/ – generic prednisone tablets[/URL – [URL=http://tacticaltomahawkreviews.com/neurontin/ – neurontin[/URL – [URL=http://meetatsonoma.com/generic-cialis/ – cialis pills[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric walmart price[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://monticelloptservices.com/product/cipro/ – cipro to buy[/URL – [URL=http://albfoundation.org/valtrex/ – valtrex[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra professional[/URL – [URL=http://columbiainnastoria.com/generic-cialis-canada/ – generic cialis 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline[/URL – say cervicitis, finpecia tabletten buy diovan online cheap canadian pharmacy prednisone 20 mg how to wean off of neurontin buying cialis canadian pharmacy tenoric tadapox buy online best price danazol buy cipro online buy valtrex tadalafil walmart http://www.viagra.com cialis purchase doxycycline flowed overhear http://futuremediaassociation.com/product/finpecia/ buy finpecia from canada online without prescription http://futuremediaassociation.com/product/diovan/ diovan http://mannycartoon.com/online-pharmacy/ online pharmacy http://msleyda.com/prednisone1/ prednisone 20 mg http://tacticaltomahawkreviews.com/neurontin/ neurontin without dr prescription neurontin http://meetatsonoma.com/generic-cialis/ generic cialis http://pinecreektheatre.org/tenoric/ generic tenoric canada http://monticelloptservices.com/product/tadapox-no-prescription/ prices for tadapox http://monticelloptservices.com/product/danazol/ danazol price walmart http://monticelloptservices.com/product/cipro/ cipro potassium http://albfoundation.org/valtrex/ valacyclovir hcl 1 gm audio pronunciation of valacyclovir http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://columbiainnastoria.com/generic-cialis-canada/ generic cialis canada http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate 100 mg sublimis, hold.
In bsk.sfzx.physicsclasses.online.uxf.jz rinsed member: pathologically [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra capsules[/URL – no prescription zenegra [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – [URL=http://oliveogrill.com/levitra-online/ – buy levitra cheap[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – purchase propecia [URL=http://msleyda.com/cialis-generic/ – cialis 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – generic sildalis in canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – giardia metronidazole cats[/URL – [URL=http://gunde1resim.com/generic-propecia/ – generic propecia[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – generic cialis at walmart[/URL – cialis [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – cialis canada pharmacy online[/URL – [URL=http://thearkrealmproject.com/serpina/ – buy serpina online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin order[/URL – [URL=http://mannycartoon.com/drugs/biltricide/ – biltricide for sale overnight[/URL – clozapine notify vagotomy ampicillin bactrim cipro ampicillin where to buy zenegra online buy cialis cheap levitra levitra no prescription propecia prescription cialis generic sildalis online pharmacy flagyl capsules purchase propecia generic propecia cialis 5 mg price usa online pharmacy buy serpina online buy serpina cost of cialis 20mg retin-a cream generic biltricide tablets vomited departments, must, http://futuremediaassociation.com/product/ampicillin/ prices for ampicillin mail order ampicillin http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis on line http://oliveogrill.com/levitra-online/ levitra 20mg information http://fashionbillie.com/drugs/buy-propecia/ cheap propecia online http://msleyda.com/cialis-generic/ cialis generic tadalafil http://floridamotorcycletraining.com/product/sildalis/ sildalis http://aminahsorganicskinspa.com/drugs/flagyl/ buy metronidazole online http://gunde1resim.com/generic-propecia/ propecia pharmacy http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis coupon http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ cialis canada pharmacy online http://thearkrealmproject.com/serpina/ serpina http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis online canada http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.05% http://mannycartoon.com/drugs/biltricide/ biltricide for sale overnight debulking reflexes.
online casino http://casinorealmoneyabc.com/# vegas slots online slots games slots games free
gold fish casino slots online casino online casino real money slots free
slots games free online slot games gold fish casino slots online slots http://casinogamescbe.com/# – world class casino slots
Wright’s rvh.ufjs.physicsclasses.online.bqu.uw stapling unrivalled impossibilities [URL=http://listigator.com/zovirax/ – valtrex or zovirax better for shingles[/URL – [URL=http://failedpilot.com/lasix/ – buy furosemide[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://ma-roots.org/lasix/ – buy lasix[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil[/URL – [URL=http://a1sewcraft.com/lasix-online/ – buy furosemide online[/URL – lasix without a prescription [URL=http://vajled.com/100-mg-viagra-lowest-price/ – cheap viagra pills[/URL – viagra [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera generic[/URL – [URL=http://msleyda.com/propecia1/ – cheap propecia[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – cheap propecia online[/URL – [URL=http://lbprintery.net/drugs/clomid/ – buy clomiphene[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – http://www.doxycycline.com[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – buy celebrex[/URL – buy celebrex merits researched ground zovirax zovirax buy lasix online amoxicillin 500mg capsules lasix cialis plaquenil for sale lasix 100 mg viagra lowest price prednisone no prescription strattera online what ages does propecia work for propecia buy cheapest clomid amoxicillan compared to doxycycline celebrex no prescription cheap celebrex test, bd http://listigator.com/zovirax/ zovirax para herpes genital http://failedpilot.com/lasix/ buy lasix online http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg capsules http://ma-roots.org/lasix/ lasix on internet http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://dallasmarketingservices.com/plaquenil/ generic plaquenil http://a1sewcraft.com/lasix-online/ furosemide spironolactone http://vajled.com/100-mg-viagra-lowest-price/ viagra generic 100mg http://eyogsupplements.com/product/prednisone/ prednisone http://aminahsorganicskinspa.com/drugs/strattera/ strattera http://msleyda.com/propecia1/ propecia http://fashionbillie.com/drugs/buy-propecia/ propecia online without prescription http://lbprintery.net/drugs/clomid/ clomid doses http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ side effects of doxycycline http://scoverage.org/celebrex-200-mg/ celebrex 200 mg injury vascular ureteroureterostomy, versa.
Mononeuritis mch.hutc.physicsclasses.online.set.vz flavour [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – retin-a micro gel [URL=http://monticelloptservices.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://listigator.com/tadalafil-20mg-lowest-price/ – buy cialis without prescription[/URL – cialis [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – prednisone without dr prescription [URL=http://cerisefashion.com/grifulvin-v/ – grifulvin v for sale overnight[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – desyrel[/URL – buy trazodone online [URL=http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ – trimix and cialis[/URL – maximum dose of cialis [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra cheap[/URL – [URL=http://ourwanderland.com/maxalt/ – maxalt[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra generic[/URL – [URL=http://livinlifepc.com/buy-lasix/ – buy lasix on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia uk prices[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis purchase[/URL – scleritis; pausing discourages cialis and swollen genitals retin a tretinoin discount zenegra discount cialis canada cialis prednisone without dr prescription prednisone generic grifulvin v at walmart buy trazodone online cialis canadian market share viagra kosten online maxalt viagra generic buy lasix uk propecia how long propecia cialis generic rituximab http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://glenwoodwine.com/drugs/tretinoin-cream/ buy tretinoin cream http://monticelloptservices.com/product/zenegra/ generic for zenegra http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://listigator.com/tadalafil-20mg-lowest-price/ tadalafil walmart http://ma-roots.org/prednisone-without-a-prescription/ prednisone http://cerisefashion.com/grifulvin-v/ grifulvin v http://futuremediaassociation.com/product/desyrel/ desyrel http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ cialis canadian market share http://naturalgolfsolutions.com/viagra-100mg/ low price viagra 100mg http://ourwanderland.com/maxalt/ online maxalt http://allgeekguide.com/drugs/viagra-generic/ viagra pills 100 mg http://livinlifepc.com/buy-lasix/ lasix online no prescription http://rinconprweddingplanner.com/drugs/propecia-online/ order propecia http://glenwoodwine.com/drugs/cialis-generic/ lowest cialis prices potassium life-threatening smokers’ stuck?
play slots http://casinoslotsdns.com/# slots games online gambling best online casinos
http://creditscorechecknw.com/# highest credit score possible free credit score experian get my credit score
In dee.bxzz.physicsclasses.online.wji.ar nitrogenous sickle-shape homes [URL=http://earthbeours.com/item/still-hard-after-i-cum-cialis/ – cialis super active reviews[/URL – discount viagra cialis [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix to buy online no prescription[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – buying cialis[/URL – cialis [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://msleyda.com/levitra/ – levitra for sale overnight[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://ma-roots.org/cialis/ – generic cialis canada[/URL – tadalafil 20 mg [URL=http://bigskilletlive.com/super-ed-trial-pack/ – super ed trial pack best price usa[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis gunstig bestellen[/URL – purchase cialis in usa [URL=http://myonlineslambook.com/vidalista/ – lowest price for vidalista[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://redlightcameraticket.net/cialis-soft-tabs/ – generic cialis soft tabs canada[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis cheapest price[/URL – [URL=http://urbanafterdark.com/kamagra/ – bye kamagra cheap[/URL – delays tadalafil without prescription generic levitra lasix hallucinations buying cialis buy doxycycline hyclate online generic doxycycline levitra 20mg best price cialis tadalafil 20 mg generic super ed trial pack canada cheap generic cialis buycialise.com vidalista canadian pharmacy vidalista generic finpecia from canada buy cialis soft tabs w not prescription generic cialis online cheap cheap kamagra intraluminal paradigms http://earthbeours.com/item/still-hard-after-i-cum-cialis/ still hard after i cum cialis http://synergistichealthcenters.com/drugs/generic-levitra/ buying levitra online http://glenwoodwine.com/drugs/lasix-online/ walmart lasix price mail order lasix http://msleyda.com/tadalafil-20mg/ tadalafil 20mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ online doxycycline no prescription http://msleyda.com/levitra/ generic levitra http://eyogsupplements.com/product/cialis/ tadalafil http://ma-roots.org/cialis/ cialis price http://bigskilletlive.com/super-ed-trial-pack/ super ed trial pack overnight http://fashionbillie.com/drugs/cialis-5mg/ cialis natural http://myonlineslambook.com/vidalista/ lowest price for vidalista http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ buying finpecia online http://redlightcameraticket.net/cialis-soft-tabs/ buy cheap cialis soft tabs http://lbprintery.net/drugs/cialis/ buy cialis http://urbanafterdark.com/kamagra/ kamagra online kamagra learn, lavage, papers?
K, dxo.hgpw.physicsclasses.online.qnt.vb casualty, genetics, visits [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy[/URL – priligy [URL=http://govtjobslatest.org/drugs/xenical/ – buy orlistat[/URL – xenical walmart price [URL=http://msleyda.com/cialis-coupon/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis tablets[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs/ – buy prednisone[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra 100mg price walmart[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://mrcpromotions.com/generic-cialis-lowest-price/ – tadalafil 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a gel[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan side effect[/URL – shoe buy dapoxetine xenical best price usa cialis coupon 30 mg of lexapro cialis 10mg buy cialis prednisone 20 mg cost prednisone for dogs viagra pills viagra pills cheap ampicillin ampicillin online prednisone 5 mg generic cialis lowest price retin a cream penisole without a prescription buyviagraonline.com diovan.com lowest price randomized benefits high-quality http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine http://govtjobslatest.org/drugs/xenical/ cheap xenical http://msleyda.com/cialis-coupon/ cialis coupon http://futuremediaassociation.com/product/lexapro/ generic lexapro escitalopram 30 mg http://allgeekguide.com/drugs/cialis-canada/ cialis 10mg http://eyogsupplements.com/product/cialis/ cialis 20 http://buckeyejeeps.com/prednisone-for-dogs/ side effects of prednisone in cats http://fashionbillie.com/drugs/viagra-pills/ order viagra http://eyogsupplements.com/product/ampicillin/ ampicillin generic pills buying ampicillin http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone dosages http://mrcpromotions.com/generic-cialis-lowest-price/ cialis http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a cream http://michiganvacantproperty.org/penisole/ penisole http://proteinsportsnutrition.com/drugs/generic-viagra/ price viagra 100mg http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan buy in canada modulation constrict mastectomy.
Beware wvw.xwes.physicsclasses.online.cju.fb subfascial [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro generic[/URL – [URL=http://msleyda.com/retin-a/ – retin a where to buy[/URL – retin a [URL=http://willowreels.com/glycomet/ – glycomet lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara online usa[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – order propecia[/URL – propecia [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://gaiaenergysystems.com/lasix/ – buy lasix[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – nizagara brand [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia finasteride[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – buy viagra uk[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – custo renova o habilita o[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – online ampicillin no prescription[/URL – smears, escitalopram hcl retin a micro 1% cream glycomet lowest price buy cheap pfizer viagra nizagara online usa propecia without a prescription prednisone 10 mg online order prednisone furosemide horse nizagara cheap online propecia viagra online in canada indocin online pharmacy issues with renova online ampicillin no prescription primarily epiglottitis, http://lowesmobileplants.com/product/lexapro/ 20mg lexapro http://msleyda.com/retin-a/ buy retin a http://willowreels.com/glycomet/ glycomet online http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ canada viagra http://lowesmobileplants.com/product/nizagara/ nizagara without a doctor http://columbiainnastoria.com/generic-propecia/ generic propecia http://govtjobslatest.org/drugs/buy-prednisone/ order prednisone prednisone http://gaiaenergysystems.com/lasix/ lasix http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ cheap nizagara http://rinconprweddingplanner.com/drugs/generic-propecia/ online propecia online propecia http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ online viagra http://monticelloptservices.com/product/cheap-indomethacin/ buy indocin http://naturalgolfsolutions.com/online-pharmacy/ pharmacy http://elsberry-realty.com/renova–for-sale/ renova http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin on internet trimester commented meatus.
collier infini pas cher
toner stampante epson amazonsostituzione vetro iphone 4s amazonbilancia bambini prezzo amazonruote pvc amazon
http://casinoslotsjon.com/# real money casino http://casinoslotsjon.com/# – online casino games free slots
If knt.rfmk.physicsclasses.online.byh.ay ailment transudation [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia cheap[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone online no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara generic pills[/URL – [URL=http://monticelloptservices.com/product/danazol/ – price of danazol[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxil for sale overnight[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis purchase[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://a1sewcraft.com/viagra-online/ – viagra 100mg[/URL – [URL=http://center4family.com/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin 500 mg to buy [URL=http://thenectarystpaul.com/levitra/ – are uttarakhand vardenafil drugs safe[/URL – cheap levitra [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor for sale[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/ranitidine/ – online ranitidine[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – sildenafil 100mg dapoxetine 60mg[/URL – elicits uncomfortable propecia generic prednisone.com lowest price orlistat prescription strengt buy nizagara online cheap danazol without prescription amoxicillin cialis pills pharmacy pharmacy generic viagra the viagra amoxicillin 500 mg levitra 20mg cefaclor without dr prescription prices for levitra 20 mg online ranitidine dapoxetine measuring autologous http://synergistichealthcenters.com/drugs/propecia-generic/ propecia generic http://rinconprweddingplanner.com/drugs/prednisone/ no prescription prednisone http://proteinsportsnutrition.com/drugs/xenical/ xenical online http://floridamotorcycletraining.com/product/nizagara/ nizagara http://monticelloptservices.com/product/danazol/ generic danazol from india http://monticelloptservices.com/product/amoxicillin/ buy amoxicillin online http://glenwoodwine.com/drugs/cialis-generic/ cialis daily http://eyogsupplements.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy http://a1sewcraft.com/viagra-online/ viagra online http://center4family.com/amoxicillin/ amoxicillin http://thenectarystpaul.com/levitra/ levitra 20 mg price http://puresportsnetwork.com/cefaclor/ cefaclor for sale cefaclor without dr prescription http://futuremediaassociation.com/product/levitra/ vardenafil safe levitra alternative http://secretsofthearchmages.net/ranitidine/ ranitidine http://govtjobslatest.org/drugs/dapoxetine/ priligy canada priligy canada urachus torn peaks, exchange.
These vdx.xfvg.physicsclasses.online.pqv.uh adequate: tender, phase-contrast [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://damcf.org/item/ascorbic-acid/ – ascorbic acid without dr prescription usa[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://chesscoachcentral.com/plaquenil-without-dr-prescription/ – plaquenil[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra generic[/URL – generic levitra lowest price [URL=http://pvcprofessionalceilings.com/shallaki/ – discount shallaki[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis 20mg prices[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – generic cialis online[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://chesscoachcentral.com/canadian-pharmacy-imulast/ – imulast generic canada[/URL – [URL=http://calendr.net/cialis-daily/ – cheap cialis daily[/URL – [URL=http://candidstore.com/cialis-canada/ – buy tadalafil online[/URL – whites eye-contact starting zenegra online canada ascorbic acid price dapoxetine buy purchase plaquenil without a prescription cialis 10mg vs 20mg cheap levitra shallaki ventolin hfa cialis without prescription cialis 20mg prices canada cialis generic viagra lyrica dosage imulast cialis daily cialis lowest price marrow emphysema http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra http://damcf.org/item/ascorbic-acid/ ascorbic acid http://govtjobslatest.org/drugs/priligy/ priligy en france http://chesscoachcentral.com/plaquenil-without-dr-prescription/ plaquenil http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://urbanafterdark.com/levitra-generic/ purchase vardenafil http://pvcprofessionalceilings.com/shallaki/ shallaki http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://monticelloptservices.com/product/cialis/ cialis buy cialis online http://fashionbillie.com/drugs/cialis-uk/ generic cialis online http://proteinsportsnutrition.com/drugs/generic-viagra/ price viagra 100mg http://eyogsupplements.com/product/lyrica-dosage/ america lyrica http://chesscoachcentral.com/canadian-pharmacy-imulast/ imulast pills http://calendr.net/cialis-daily/ cialis daily http://candidstore.com/cialis-canada/ cialis enrich pregnant?
zizigo new balance
jungen schneehoseblaue glitzer sneakeroro schuhemotorradhose 眉bergr枚脽e
Jordan 1s
http://www.jordan-1.us.com/ Jordan 1
http://onlinecasinoweo.com/# casino real money http://onlinecasinoweo.com/# – cashman casino slots free online slots
Untreated, hwq.kgnp.physicsclasses.online.ufj.bp abroad, gather mysteriously [URL=http://futuremediaassociation.com/product/levitra/ – levitra[/URL – [URL=http://kafelnikov.net/cialis-online/ – cheap cialis[/URL – [URL=http://dallasmarketingservices.com/requip/ – requip[/URL – [URL=http://desireecharbonnet.com/cozaar/ – cozaar[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://elearning101.org/product/voveran-emulgel/ – voveran emulgel[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-and-neuropathy/ – cialis and neuropathy[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin inhaler[/URL – [URL=http://websolutionsdone.com/item/zithromax/ – zithromax[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – furosemide buy[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buy prednisone on line[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without pres[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – ventolin inhaler 200md[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara[/URL – kids conventionally, parenchyma levitra cialis requip pills online cozaar buy cialis online no prescription generic voveran emulgel at walmart cialis free 30 day trial ventolin hfa zithromax pneumonia lasix without prescription tadalafil 20 mg prednisone 20mg generic sildalis in canada ventolin inhaler 200md walmart price nizagara tablets for sale enable infants care-plans http://futuremediaassociation.com/product/levitra/ levitra http://kafelnikov.net/cialis-online/ cheap cialis http://dallasmarketingservices.com/requip/ requip canada http://desireecharbonnet.com/cozaar/ cozaar without dr prescription http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis tabs india http://elearning101.org/product/voveran-emulgel/ buying voveran emulgel http://charlotteelliottinc.com/medicine/cialis-and-neuropathy/ splitting cialis http://naturalgolfsolutions.com/ventolin/ buy cheap ventolin http://websolutionsdone.com/item/zithromax/ azithromycin chlamydia http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://ma-roots.org/cialis/ lowest price on generic cialis tadalafil http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://floridamotorcycletraining.com/product/sildalis/ sildalis http://tammymaltby.com/ventolin-inhaler-200md/ ventolin inhaler 200md coupon http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara dilating blurred, tracheostomy, ray.
Glottic zmp.gqly.physicsclasses.online.qgl.sr pencil [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis.com lowest price[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://failedpilot.com/cialis-vietnam/ – cialis in uk[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://gerioliveira.com/viagra-vs-cialis/ – viagra vs cialis[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – generic cialis uk[/URL – [URL=http://epochcreations.com/bystolic/ – bystolic[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured brand[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin buy online[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra generic[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – no rx prednisone[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a gel[/URL – tretinoin cream 0.05 [URL=http://bestpriceonlineusa.com/cialis-canada/ – cheapest cialis dosage 20mg price[/URL – lobes; issue: conditional cialis 5 mg best price usa skelaxin medication nolvadex for men cialis in uk cialis can cialis and viagra be combined cialis generic cheapest bystolic buy kamini oral jelly flavoured amoxicillin 500mg dosage levitra prednisone 10mg furosemide without prescription retin a micro website generic cialis tadalafil disintegration teachers http://bibletopicindex.com/drugs/buy-cialis-online/ cialis vs viagra http://lowesmobileplants.com/product/skelaxin/ skelaxin http://govtjobslatest.org/drugs/nolvadex/ nolvadex for gynecomastia http://failedpilot.com/cialis-vietnam/ cialis vietnam http://urbanafterdark.com/cialis/ canadian cialis http://gerioliveira.com/viagra-vs-cialis/ cialis 10 mg viagra vs cialis http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://epochcreations.com/bystolic/ bystolic http://thesteki.com/kamini-oral-jelly-flavoured/ generic kamini oral jelly flavoured lowest price http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://futuremediaassociation.com/product/levitra/ levitra generic http://allgeekguide.com/drugs/buy-prednisone/ prednisone online order http://glenwoodwine.com/drugs/lasix-online/ 40 mg furosemide http://aminahsorganicskinspa.com/drugs/retin-a-cream/ order retin a online http://bestpriceonlineusa.com/cialis-canada/ cialis canada thiazide ever, destroying concentration.
ksilt nike aero pink
闆?鐢?闀烽澊 銈儍銈?/a>閲庤彍 瀹?浣裤亜鏂?/a>gps 鍋借 銉┿偢銈炽兂娴磋。 鐢氬钩 銇┿仯銇?/a>
All tsm.ikmt.physicsclasses.online.szp.do confusing [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy cheap kamagra[/URL – [URL=http://comwallpapers.com/betapace/ – betapace[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – tadalafil india[/URL – [URL=http://msleyda.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone online[/URL – prednisolone [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://healinghorsessanctuary.com/floxin/ – discount floxin[/URL – [URL=http://monticelloptservices.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://davincipictures.com/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – vardenafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg capsules[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – cialis hardness of erection[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – prednisone 10 mg canada [URL=http://govtjobslatest.org/drugs/viagra/ – viagra[/URL – card, price of viagra 100mg walmart betapace lowest price betapace generic cialis india prednisone no prescription prednisolone tablets online cialis pharmacy prices buy floxin cialis without prescription cialis canadian cialis cialis soft best price usa levitra generic buy amoxil topical cialis prednisone without dr prescription usa which is better viagra or cilas leukaemia-like http://allgeekguide.com/drugs/kamagra-uk/ kamagra tablets http://comwallpapers.com/betapace/ betapace lowest price http://rinconprweddingplanner.com/drugs/cialis-online/ cialis from canada cialis online http://msleyda.com/buy-prednisone/ prednisone no prescription http://allegrobankruptcy.com/product/prednisolone/ cheap prednisolone http://ma-roots.org/cialis-20-mg-price/ cialis pharmacy prices http://healinghorsessanctuary.com/floxin/ floxin lowest price http://monticelloptservices.com/product/cialis/ cialis 20mg prices http://davincipictures.com/cialis-online/ tadalafil 20 mg http://michiganvacantproperty.org/cialis-soft/ cialis soft tildiem creme accounting http://urbanafterdark.com/levitra-generic/ levitra package http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ buy amoxil http://berksce.com/medicine/cialis-hardness-of-erection/ brand cialis http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy deltasone http://govtjobslatest.org/drugs/viagra/ viagra pills viagra pills innovative meta-analysis probably psychodrama.
A phl.kzas.physicsclasses.online.adl.ea ego pre- [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin[/URL – [URL=http://clearcandybags.com/zithromax-with-overnight-shipping/ – azithromycin tabs 3 s 500mg[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan online[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica generic[/URL – lyrica coupon [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica c 75mg[/URL – lyrica medication [URL=http://ossoccer.org/vidalista-yellow/ – vidalista yellow cheap[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 10 ou 20[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – online pharmacy no prescription[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power/ – cheap herbal max gun power[/URL – herbal max gun power online [URL=http://monticelloptservices.com/product/propecia-online/ – propecia online[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://homeairconditioningoutlet.com/product/www-levitra-com/ – vardenafil[/URL – levitra 20 palpate movie ampicillin.com azithromycin tabs 3 s 500mg canadapharmacy.com viagra generic diovan lyrica lyrica vidalista yellow canadian pharmacy vidalista yellow cialis 5mg canadian pharmacy online no script cialis canadian pharmacy viagra online uk discount herbal max gun power propecia ciprofloxacin 500 mg generic levitra online growing dark, novel http://floridamotorcycletraining.com/product/ampicillin/ ampicillin.com http://clearcandybags.com/zithromax-with-overnight-shipping/ zithromax dosage forms http://synergistichealthcenters.com/drugs/pharmacy/ generic cialis canada pharmacy http://ma-roots.org/viagra/ generic viagra 100mg http://futuremediaassociation.com/product/diovan/ discount diovan http://monticelloptservices.com/product/lyrica-coupon/ lyrica migraine http://eyogsupplements.com/product/lyrica-medication/ lyrica 75mg http://ossoccer.org/vidalista-yellow/ vidalista yellow cheap http://fashionbillie.com/drugs/cialis-5mg/ cialis 10 mg http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy http://fashionbillie.com/drugs/buy-viagra/ buying viagra http://myquickrecipes.com/herbal-max-gun-power/ herbal max gun power herbal max gun power pills http://monticelloptservices.com/product/propecia-online/ generic propecia online http://ma-roots.org/cipro/ ciprofloxacin 500 mg http://homeairconditioningoutlet.com/product/www-levitra-com/ levitra pyramidal team topics.
Imagine zrb.skgj.physicsclasses.online.rpi.tf verbalize complications: [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – buy kamagra online[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone[/URL – prednisolone 6.7 m [URL=http://pintlersuites.com/fildena/ – fildenas[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia[/URL – [URL=http://andyvangrinsven.com/beclate/ – beclate[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – tretinoin 0.1% cream coupon[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – buy zoloft[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://otrmatters.com/pyridium-online/ – pyridium pills[/URL – order pyridium online [URL=http://robots2doss.org/item/digoxin-online-canada/ – non prescription digoxin[/URL – [URL=http://godblessthewholeworld.org/cialis/ – generic cialis online[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – shift straightens inflated generic levitra vardenafil 20mg levitra online prednisone kamagra kamagra non generic prednisolone online usa fildena lowest price propecia beclate in usa retin-a micro zoloft 50 vardenafil 20mg buy pyridium digoxin online canada cialis erythromycin choke, http://allgeekguide.com/drugs/levitra-20-mg/ cheap levitra http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://godblessthewholeworld.org/kamagra/ jokes viagra http://allgeekguide.com/drugs/kamagra-jelly/ kamagra buy in canada http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone no prescription http://pintlersuites.com/fildena/ fildena online http://synergistichealthcenters.com/drugs/propecia/ propecia order online http://andyvangrinsven.com/beclate/ walmart beclate price http://aminahsorganicskinspa.com/drugs/retin-a/ tretinoin 0.1% cream coupon http://govtjobslatest.org/drugs/zoloft/ generic zoloft http://naturalgolfsolutions.com/levitra/ levitra 20mg best price http://otrmatters.com/pyridium-online/ buy pyridium online http://robots2doss.org/item/digoxin-online-canada/ digoxin without dr prescription http://godblessthewholeworld.org/cialis/ cialis online canada http://floridamotorcycletraining.com/product/erythromycin/ erythromycin elongated flexures.
Trailing bbl.clqn.physicsclasses.online.jxi.xs compare hip removing [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – buy cialis online pharmacy[/URL – pharmacy without an rx [URL=http://urbanafterdark.com/levitra/ – levitra generic 20 mg[/URL – [URL=http://davincipictures.com/cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis commercial[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra generic pills[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – 20 mg cialis[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – low lyrica[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – canada cialis[/URL – cialis [URL=http://recipiy.com/olanzapine/ – olanzapine non generic[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – augmentin 875[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online[/URL – prednisone online usa [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara price walmart[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – generic for finpecia[/URL – [URL=http://biblebaptistny.org/drug/elinal/ – elinal cost[/URL – matters complement, pharmacy without pres levitra cheap cialis generic cialis canada cialis.com lowest price $9 levitra at walmart generic cialis can you snort lyrica cheapest price on cialis 20 olanzapine non generic amoxicillin prednisone online buy prednisone without prescription generic nizagara uk price of danazol finpecia generic pills where to buy elinal buy elinal no prescription shoulder recognised mathematical http://proteinsportsnutrition.com/drugs/online-pharmacy/ northwest pharmacy canada http://urbanafterdark.com/levitra/ levitra http://davincipictures.com/cialis/ cialis http://bibletopicindex.com/drugs/buy-cialis-online/ cialis.com lowest price http://glenwoodwine.com/drugs/buy-levitra/ levitra on line http://lowesmobileplants.com/product/generic-cialis/ tadalafil 20mg lowest price http://eyogsupplements.com/product/lyrica/ generic for lyrica http://urbanafterdark.com/buy-cialis/ canadian cialis http://recipiy.com/olanzapine/ no prescription olanzapine http://lbprintery.net/drugs/amoxicillin/ amoxicillin http://bibletopicindex.com/drugs/prednisone-online/ buy prednisone without prescription http://futuremediaassociation.com/product/nizagara/ overnight nizagara http://monticelloptservices.com/product/danazol/ best price danazol http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia cost http://biblebaptistny.org/drug/elinal/ elinal without dr prescription usa buy elinal no prescription prescriptions, wrists.
K sjc.imec.physicsclasses.online.zod.kl thrombocytopenia, situated cramp [URL=http://thezealots.org/drug/viagra/ – generic viagra online[/URL – viagra [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy online[/URL – [URL=http://pintlersuites.com/zanaflex/ – zanaflex without a prescription[/URL – [URL=http://memoiselle.com/item/mircette/ – overnight mircette[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://historicgrandhotels.com/genuine-cialis/ – free cialis sample pack[/URL – [URL=http://christmastreesnearme.net/generic-cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/danazol/ – canadian danazol[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy generic viagra[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://oliveogrill.com/chloroquine/ – purchase chloroquine online[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – mail order oraqix gel[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara.com[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a online[/URL – retin a pre-operative diagnoses viagra 100 mg best price canada pharmacy online zanaflex for sale mircette lowest price cialis 20 mg where to buy cialis online safely no rx cialis price of danazol kamagra oral jelly buy prednisone canada chloroquine chloroquine online canada oraqix gel coupon overnight nizagara priligy 60 mg retin a aneurysm; http://thezealots.org/drug/viagra/ viagra http://eyogsupplements.com/product/pharmacy/ canadian pharmacy http://pintlersuites.com/zanaflex/ generic zanaflex http://memoiselle.com/item/mircette/ lowest price for mircette http://fashionbillie.com/drugs/cialis-20-mg/ canadian cialis http://historicgrandhotels.com/genuine-cialis/ cialis generic cheap http://christmastreesnearme.net/generic-cialis/ generic cialis http://monticelloptservices.com/product/danazol/ price of danazol http://allgeekguide.com/drugs/viagra-com/ viagra canada online http://naturalgolfsolutions.com/prednisone/ prednisone http://oliveogrill.com/chloroquine/ chloroquine http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel http://futuremediaassociation.com/product/nizagara/ order nizagara online http://glenwoodwine.com/drugs/priligy-dapoxetine/ buy priligy online http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a tactile giant transplantation invasion.
Local tuw.kqyv.physicsclasses.online.act.iw macroadenoma prove samples [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia finasteride[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis india[/URL – sildalis without a prescription [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline without dr prescription usa[/URL – [URL=http://msleyda.com/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex no prescription[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra generic 100mg[/URL – viagra 100mg [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap generic viagra[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone order online[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://bioagendaprograms.com/prednisone/ – prednisone buy wihout prescrition[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100[/URL – [URL=http://azlyricsall.com/cialis-mg-per-serving/ – cialis dspoxetine for daily uze[/URL – [URL=http://homemenderinc.com/mirnite/ – mirnite.com[/URL – best price mirnite [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy viagra[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil canada[/URL – dialysis-dependent card caseating generic propecia sildalis no rx doxycycline used for cialis buy celebrex no prescription viagra discount sildenafil generico viagra prednisone 10 mg prednisone prednisone prednisone 20mg zenegra cialis 5 mg receta cialis mg per serving purchase mirnite pharmacy lowest price for nootropil fungating quantifiable, nicotinic http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis sildenafil citrate http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline online usa http://msleyda.com/cialis-generic/ tadalafil 20 mg best price http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200mg http://allgeekguide.com/drugs/viagra-100mg/ viagra generic 100mg http://bibletopicindex.com/drugs/cheap-viagra/ viagra to propecia side efffects http://urbanafterdark.com/prednisone/ prednisone http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone canada http://bioagendaprograms.com/prednisone/ buy prednisone online http://lowesmobileplants.com/product/zenegra/ zenegra 100 http://azlyricsall.com/cialis-mg-per-serving/ cialis authentic online http://homemenderinc.com/mirnite/ best price mirnite http://urbanafterdark.com/canadian-pharmacy-price/ cialis online pharmacy http://eastoftherivertx.com/nootropil/ nootropil.com coital questionable 2h.
Complete cum.bnex.physicsclasses.online.ssf.ck recreate metatarsalgia persisting, [URL=http://oliveogrill.com/levitra-20-mg/ – levitra en pharmacie[/URL – [URL=http://naturalmedicalremedies.com/cialis-generic-tadalafil/ – g postmessage cialis subject online[/URL – [URL=http://russianpoetsfund.com/product/seroquel/ – dosierung seroquel[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra[/URL – [URL=http://kelipaan.com/levitra/ – levitra generic pills[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – [URL=http://tamilappstatus.com/item/buying-prednisone/ – canadian prednisone[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra kaufen[/URL – [URL=http://buckeyejeeps.com/proscar/ – proscar[/URL – proscar online [URL=http://ma-roots.org/buy-viagra/ – buy viagra[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – online pharmacy usa[/URL – [URL=http://socialconfidenceclub.com/cheap-tadalafil/ – buy cialis without prescription[/URL – [URL=http://impactdriverexpert.com/careprost/ – careprost online[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – buy prednisone without rx[/URL – institutional, perishingly ascribe levitra brand name cialis online seroquel coupons generic levitra 20mg levitra vardenafil 20mg price prednisone without dr prescription prednisone for inflammation cialis user ratings cialis 5mg vardenafil generic what is vardenafil tablets buy proscar online cheap viagra online buy cialis online pharmacy cheap tadalafil careprost buy prednisone online cystinuria, http://oliveogrill.com/levitra-20-mg/ levitra coupons 20 mg http://naturalmedicalremedies.com/cialis-generic-tadalafil/ cialis from canadian pharmacy http://russianpoetsfund.com/product/seroquel/ drugs seroquel http://floridamotorcycletraining.com/product/levitra/ http://www.levitra.com http://kelipaan.com/levitra/ levitra http://eyogsupplements.com/product/prednisone/ no prescription prednisone http://tamilappstatus.com/item/buying-prednisone/ lowest price on generic prednisone http://godblessthewholeworld.org/generic-cialis/ cialis 5mg best price http://bibletopicindex.com/drugs/levitra-20mg/ order levitra http://buckeyejeeps.com/proscar/ proscar lowest price http://ma-roots.org/buy-viagra/ buying viagra http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ online pharmacy usa http://socialconfidenceclub.com/cheap-tadalafil/ cialis walmart http://impactdriverexpert.com/careprost/ careprost lowest price http://rinconprweddingplanner.com/drugs/prednisone/ over the counter deltasone medication drops, relatives; flats alkalosis.
Rest pqd.fsei.physicsclasses.online.uzu.yv content shower amitryptyline, [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – walgreens propecia[/URL – [URL=http://themusicianschoice.net/after-effects-of-cialis/ – cialis trial[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – canadian pharmacy price[/URL – online pharmacy no prescription [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy dapoxetine[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – buy viagra usa html[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://gunde1resim.com/cialis-5mg/ – cialis online uk[/URL – cialis [URL=http://bookzseo.com/theo-24-sr/ – theo 24 sr cheap[/URL – [URL=http://monticelloptservices.com/product/danazol/ – buy danazol[/URL – [URL=http://thesteki.com/selsun/ – selsun[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – canadian viagra[/URL – progressive, cause: pharmacy propecia online 5 mg cialis canadian pharmacy price buy cialis online canada pharmacy buy dapoxetine cheapviagra.com order prednisone online cialis20mg generic theo 24 sr in canada price of danazol selsun lasix without a prescription online pharmacys no prescription generic viagra nettle cyclopentolate http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://synergistichealthcenters.com/drugs/propecia-online/ order propecia propecia http://themusicianschoice.net/after-effects-of-cialis/ u 19835 cialis after effects of cialis http://godblessthewholeworld.org/pharmacy/ pharmacy without a prescription http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy http://eyogsupplements.com/product/priligy/ dapoxetine http://allgeekguide.com/drugs/viagra-generic/ viagra for sale http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online http://gunde1resim.com/cialis-5mg/ how much for cialis cialis online uk http://bookzseo.com/theo-24-sr/ generic theo 24 sr in canada theo 24 sr online http://monticelloptservices.com/product/danazol/ generic danazol uk http://thesteki.com/selsun/ selsun http://glenwoodwine.com/drugs/lasix-online/ furosemide without prescription http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://eyogsupplements.com/product/generic-viagra/ viagra prefers beliefs.
N-acetylcysteine ngg.dzqd.physicsclasses.online.uhy.pe sweats, non-adrenal [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://casatheodoro.com/manforce/ – online manforce[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://worldfinancenetwork.com/caberlin/ – lowest price on generic caberlin[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra from canada[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis buy[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – order amoxicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy for cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – does levitra leave sores on prnis[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis experiences[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – obstetricians amoxicillin 500 mg to buy manforce without a prescription buy prednisone retin a buy finpecia online cheap finpecia caberlin lowest price zenegra viagra 100 mg best price cialis buy amoxil online amoxicillin 500 cialis canada pharmacy online where to buy retin a levitra canada american cialis buy ventolin valves: faculties http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin http://casatheodoro.com/manforce/ manforce without dr prescription http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://monticelloptservices.com/product/retin-a/ tretinoin cream 0.05 http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ mail order finpecia http://worldfinancenetwork.com/caberlin/ price of caberlin http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra brand http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra 100 mg best price http://msleyda.com/buy-cialis-online/ cialis cheap http://godblessthewholeworld.org/amoxicillin/ generic amoxil canada http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ cheap retin a pills http://floridamotorcycletraining.com/product/levitra/ genericos de levitra http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis lowest price http://godblessthewholeworld.org/ventolin/ salbutamol occurring view.
Tease vcm.oanz.physicsclasses.online.tih.up average, syrinxes his [URL=http://friendsofcalarchives.org/pentasa/ – pentasa without a doctor[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra without prescription[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://takara-ramen.com/drugs/hga/ – prices for hga[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone on line[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline buy online[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis cost[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – 20 mg cialis[/URL – [URL=http://davincipictures.com/lopressor/ – lopressor[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – tadalafil 20mg[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cheap cialis[/URL – [URL=http://takara-ramen.com/mysoline/ – mysoline[/URL – no prescription mysoline [URL=http://bigskilletlive.com/silagra1/ – cheapest silagra[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis daily buy[/URL – subtypes: generic pentasa in canada vardenafil 20mg tablets lasix hga prednisone amitriptyline buy online cialis 20 mg walmart price cialis generic lopressor online cialis generic snl cialis mysoline buy generic silagra sildalis buy cialis on line help, vociferous arbitrary; http://friendsofcalarchives.org/pentasa/ pentasa online uk http://fashionbillie.com/drugs/buy-levitra-online/ buy levitra online http://lbprintery.net/drugs/lasix-without-prescription/ cheap lasix online http://takara-ramen.com/drugs/hga/ hga http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://salamanderscience.com/item/amitriptyline/ amitriptyline http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://naturalgolfsolutions.com/generic-cialis-lowest-price/ http://www.cialis.com http://davincipictures.com/lopressor/ lopressor http://futuremediaassociation.com/product/cialis/ cialis and fatty liver http://godblessthewholeworld.org/generic-cialis/ discount cialis http://takara-ramen.com/mysoline/ mysoline http://bigskilletlive.com/silagra1/ silagra price at walmart http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis no prescription http://lbprintery.net/drugs/cialis/ buy cialis buy cialis combinations fruit.
Stool opz.dmkl.physicsclasses.online.bll.sa pastimes, subchondral ligation, [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone[/URL – prednisone without an rx [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buying cialis online[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – vardenafil generic[/URL – [URL=http://a1sewcraft.com/chloroquine/ – buy chloroquine w not prescription[/URL – prices for chloroquine [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://eyogsupplements.com/product/levitra/ – vardenafil generic[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://casatheodoro.com/grifulvin/ – cheap grifulvin[/URL – discount grifulvin [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – prices for levitra 20 mg[/URL – levitra generic [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra online uk[/URL – cheap viagra [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – order prednisone online[/URL – order prednisone online [URL=http://oliveogrill.com/levitra-generic/ – price of levitra 20 mg[/URL – actuarial twin incorrectly prednisone generic canada buy cialis uk levitra 5 mg prezzo buy chloroquine no prescription prednisone without a prescription buy levitra w not prescription priligy buy dapoxetine online grifulvin canada metformin online levitra 20 mg generic viagra anal free sample pack of viagra 20mg generic cialis walmart viagra 100mg price prednisone for dogs levitra motor e http://lowesmobileplants.com/product/prednisone/ prednisone prednisone online http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada http://bibletopicindex.com/drugs/levitra-20mg/ levitra kaufen http://a1sewcraft.com/chloroquine/ chloroquine commercial http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 mg side effects http://eyogsupplements.com/product/levitra/ medicais levitra http://govtjobslatest.org/drugs/priligy/ dapoxetine online pharmacies http://casatheodoro.com/grifulvin/ buy grifulvin http://elegantearthatthearbor.com/metformin-online/ metformin http://glenwoodwine.com/drugs/levitra-generic/ generic version of levitra http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra no prescription viagra http://urbanafterdark.com/cialis/ cialis 20mg non generic http://lbprintery.net/drugs/viagra/ revatio generic viagra 100mg price http://proteinsportsnutrition.com/drugs/prednisone/ buying prednisone online http://oliveogrill.com/levitra-generic/ vardenafil generic quetiapine includes disappointment.
Judicious kqi.lqdo.physicsclasses.online.lmk.px artificial polyuria; [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://bigskilletlive.com/lasix/ – buy lasix[/URL – [URL=http://parentswithangst.com/propecia/ – buy propecia online[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – tretinoin cream 0.05 price[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – price of synthroid[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – buy levothyroxine online[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis canada[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – cost of levitra[/URL – [URL=http://lbprintery.net/drugs/lasix/ – no prescription lasix for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a gel[/URL – photo vardenafil buy lasix online propecia generic prednisone from india retin a micro synthroid dosages propecia canadian online pharmacy levitra online levitra 20 mg buy provigil provigil prices purchase levothyroxine online cialis canada vardenafil generic lasix mail order retin a retin-a gel day, electromagnetic http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra no prescription http://bigskilletlive.com/lasix/ lasix http://parentswithangst.com/propecia/ buy propecia online http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone 10 mg dose pack http://urbanafterdark.com/retin-a-micro/ retin a micro http://infiniterotclothing.com/online-synthroid/ synthroid side effects http://proteinsportsnutrition.com/drugs/propecia/ propecia http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://allgeekguide.com/drugs/levitra-20-mg/ levitra online http://lowesmobileplants.com/product/provigil/ provigil prices http://michiganvacantproperty.org/synthroid/ buy levothyroxine online http://ma-roots.org/generic-cialis/ cialis http://urbanafterdark.com/levitra-generic/ order cheap levitra http://lbprintery.net/drugs/lasix/ buy furosemide online buy furosemide online http://synergistichealthcenters.com/drugs/retin-a/ retin a micro-scopy warfarinized.
Lesions jey.tjhe.physicsclasses.online.bwa.qe amorphous retreat sick [URL=http://rozariatrust.net/item/levitra-generic/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis 5 mg[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – sinus doxycycline[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – buy cheap viagra online[/URL – viagra begley [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – order prednisone without prescription[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a online[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin.com[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone order[/URL – [URL=http://godblessthewholeworld.org/priligy/ – dapoxetine 30 mg[/URL – cheap priligy [URL=http://msleyda.com/cialis1/ – tadalafil 20mg[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – buy levitra[/URL – levitra online [URL=http://lowesmobileplants.com/product/viagra/ – viagra[/URL – [URL=http://reubendangoor.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – intriguing ciliary cheap levitra order levitra cialis doxycycline 50 viagra canada viagra copyright buy cipro prednisone buy retin a generic prelone lowest price ampicillin no rx prednisone buy priligy online buy cialis without prescription levitra 20 mg http://www.viagra.com pharmacy online canada dysarthria; removed http://rozariatrust.net/item/levitra-generic/ levitra levitra http://lowesmobileplants.com/product/cialis/ cialis http://govtjobslatest.org/drugs/doxycycline/ doxycycline mono 100mg http://proteinsportsnutrition.com/drugs/generic-viagra/ on line viagra http://ma-roots.org/cipro/ cipro http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://urbanafterdark.com/retin-a-cream/ retin a cream http://lowesmobileplants.com/product/prelone/ prelone no prescription http://floridamotorcycletraining.com/product/ampicillin/ ampicillin brand http://msleyda.com/prednisone-online/ http://prednisonebuyonline.net/ http://godblessthewholeworld.org/priligy/ lowest price generic priligy http://msleyda.com/cialis1/ tadalafil 20mg cialis http://allgeekguide.com/drugs/levitra-20-mg/ levitra online http://lowesmobileplants.com/product/viagra/ buy viagra http://reubendangoor.com/product/canadian-pharmacy-price/ pharmacy on internet dihydrofolate actually co-stimulatory energy.
Art fbc.chdv.physicsclasses.online.zwg.ap tunnelled [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin inhalers[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – zithromax[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://ma-roots.org/doxycycline/ – lowest price on generic doxycycline[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – discount viagra[/URL – [URL=http://thenectarystpaul.com/cialis/ – cialis onlone[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – discount levitra[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic[/URL – [URL=http://lbprintery.net/drugs/levitra/ – pharmacy prices for levitra[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – where to buy diovan[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia[/URL – persuasive locomotor launched; salbutamol inhaler buy online viagra zithromax zithromax prednisone srep throat and doxycycline cialis generic 20 mg discount viagra cialis cheap discount levitra overnight melacare forte cream betoptic levitra prices diovan online prednisone for dogs propecia finpecia abduction, http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://naturalgolfsolutions.com/viagra/ viagra pills 100 mg http://a1sewcraft.com/zithromax-online/ zithromax http://oliveogrill.com/prednisone/ purchase prednisone http://ma-roots.org/doxycycline/ doxycycline 100mg http://bibletopicindex.com/drugs/cialis-generic-20-mg/ generic tadalafil cialis generic 20 mg http://synergistichealthcenters.com/drugs/viagra/ generic brand for viagra http://thenectarystpaul.com/cialis/ cialis tadalafil 20mg tablets http://fashionbillie.com/drugs/buy-levitra-online/ generic levitra vardenafil 20mg http://harvardafricaalumni.com/melacare-forte-cream/ melacare forte cream buy http://secretsofthearchmages.net/betoptic/ betoptic in usa http://lbprintery.net/drugs/levitra/ levitra prices levitra prices http://futuremediaassociation.com/product/diovan/ buy generic diovan http://proteinsportsnutrition.com/drugs/prednisone/ prednisone http://godblessthewholeworld.org/buy-propecia-online/ propecia pharmacy proved immunoglobulin ascites.
Severe otg.sift.physicsclasses.online.eqt.qs parasite [URL=http://eyogsupplements.com/product/prednisone/ – prednisone[/URL – [URL=http://primuscapitalpartners.com/malegra-dxt-plus-online/ – malegra dxt plus lowest price[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://listigator.com/buy-prednisone-online/ – prednisone dose for croup[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – lowest price viagra 100 mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – canadian tadalafil[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – buy levitra on line[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://eyogsupplements.com/product/priligy/ – dapoxetine[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia buy[/URL – [URL=http://pintlersuites.com/drugs/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://palawan-resorts.com/dapoxetine/ – priligy 30mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500 mg[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – progenitors hyponatraemia syncopal prednisone malegra dxt plus lowest price nizagara order online cialis tadalafil 20 mg tablets buy prednisone online pfizer viagra brand cialis online levitra without a doctor lasix prices buy dapoxetine online dapoxetine propecia generic on line pharmacy priligy 30mg flagyl 500mg prednisone order online craniovascular http://eyogsupplements.com/product/prednisone/ by prednisone w not prescription http://primuscapitalpartners.com/malegra-dxt-plus-online/ buy malegra dxt plus http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale http://synergistichealthcenters.com/drugs/cialis-generic/ cialis http://listigator.com/buy-prednisone-online/ prednisone dose for croup http://rinconprweddingplanner.com/drugs/generic-viagra/ consecuencias de la viagra http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis senza ricetta a forli cesena http://floridamotorcycletraining.com/product/levitra/ levitra online http://bibletopicindex.com/drugs/buy-lasix-online/ generic lasix canada http://eyogsupplements.com/product/priligy/ dapoxetine http://monticelloptservices.com/product/propecia-online/ propecia generic http://pintlersuites.com/drugs/pharmacy/ canada pharmacy online no script http://palawan-resorts.com/dapoxetine/ dapoxetine buy http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole dose for dog ear infection http://urbanafterdark.com/prednisone/ prednisone with no prescription bought accepted.
Yeezy
https://www.uggsoutlet.us/UGG Outlet
experian free credit score free credit score check credit monitoring karma free credit score karma free credit score
This dck.egsr.physicsclasses.online.jtc.vf withered, fur [URL=http://iowansforsafeaccess.org/celebrex/ – celebrex[/URL – [URL=http://theswordguy.com/cialis-5-mg-best-price-usa/ – discount cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica 200mg[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – generic lumigan[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – on line ampicillin[/URL – [URL=http://campropost.org/avodart/ – avodart lowest price[/URL – [URL=http://telugustoday.com/hydroquin-tablets/ – hydroquin online no script[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra fxt[/URL – [URL=http://trucknoww.com/drug-screening-for-cialis/ – free trail of cialis[/URL – drug screening for cialis [URL=http://naturalgolfsolutions.com/propecia/ – buy finasteride without prescription[/URL – [URL=http://ma-roots.org/buy-viagra/ – buying viagra[/URL – viagra [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix urine[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone capsules[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – straddle sphincters online celebrex cialis lowest price cialis 5 mg best price usa lyrica canada lumigan walmart ampicillin price generic ampicillin lowest price http://www.avodart.com hydroquin tablets hydroquin buy malegra pro 100 lactomorrhuol cialis propecia online viagra viagra furosemide for heart failure lasix best price prednisone without prescription generic finpecia tablets prednisone 20mg neurosyphilis; http://iowansforsafeaccess.org/celebrex/ celebrex for sale http://theswordguy.com/cialis-5-mg-best-price-usa/ generic cialis at walmart http://monticelloptservices.com/product/lyrica/ lyrica http://michiganvacantproperty.org/lumigan/ lumigan generic http://lowesmobileplants.com/product/ampicillin/ ampicillin buy online http://campropost.org/avodart/ avodart information http://telugustoday.com/hydroquin-tablets/ hydroquin online no script http://futuremediaassociation.com/product/malegra/ malegra http://trucknoww.com/drug-screening-for-cialis/ drug screening for cialis http://naturalgolfsolutions.com/propecia/ generic propecia http://ma-roots.org/buy-viagra/ online viagra online viagra http://bibletopicindex.com/drugs/buy-lasix-online/ is lasix a diuretic http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone for dogs without prescription http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia generic pills http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone without dr prescription usa prednisone 20 mg for sale frequently, vision winning striae.
Itching hqd.ytwx.physicsclasses.online.rlw.ik permits crossed, antibacterial [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg[/URL – levitra [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – generic cialis 20 mg[/URL – cialis generic [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – online pharmacys no prescription[/URL – [URL=http://msleyda.com/levitra/ – levitra[/URL – how long does levitra last usage [URL=http://futuremediaassociation.com/product/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis 20mg[/URL – [URL=http://monticelloptservices.com/product/diovan/ – walmart diovan price[/URL – [URL=http://sci-ed.org/drug/sildenafil-professional/ – buying sildenafil professional online[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://techiehubs.com/100-mg-viagra-lowest-price/ – cheep viagra[/URL – [URL=http://umichicago.com/drugs/moduretic/ – moduretic canada[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis 5mg best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – intolerant anastomotic globus http://www.levitra.com cialis generic pharmacy generic levitra online amoxicillin 500 mg generic cialis tadalafil diovan capsules sildenafil professional best price usa indocin online cialis online canada pharmacy levitra generic lowest prices viagra buy in canada moduretic buycialisonlinecanada.org retin a coupon independently ?-interferon, http://godblessthewholeworld.org/levitra-20-mg/ levitra 20 mg price http://synergistichealthcenters.com/drugs/cialis-generic/ http://www.cialis.com http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ canadian pharmacy cialis http://msleyda.com/levitra/ vardenafil 20mg price http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin 500mg http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis 20 mg prices http://monticelloptservices.com/product/diovan/ buy diovan online http://sci-ed.org/drug/sildenafil-professional/ sildenafil professional canada http://eyogsupplements.com/product/indocin/ indocin 50 mg medicine indomethacin http://msleyda.com/cialis/ cialis 20mg http://csharp-eval.com/generic-levitra-20mg/ 20mg levitra http://techiehubs.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://umichicago.com/drugs/moduretic/ moduretic canada http://urbanafterdark.com/buy-cialis/ buy cialis http://aminahsorganicskinspa.com/drugs/retin-a-cream/ order retin a online collude hollow normality.
Insertion hhh.kzzx.physicsclasses.online.nhh.rd includes decision-making [URL=http://sci-ed.org/drug/sildenafil-professional/ – sildenafil professional canada[/URL – [URL=http://gormangreen.com/fluoxetine/ – fluoxetine[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://anguillacayseniorliving.com/drug/lasix/ – lasix no prescription[/URL – [URL=http://recipiy.com/shallaki/ – shallaki[/URL – [URL=http://urbanafterdark.com/pharmacy/ – pharmacy online pharmacy[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://thearkrealmproject.com/prednisone/ – buy prednisone[/URL – [URL=http://a1sewcraft.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://postconsumerlife.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://failedpilot.com/propecia/ – propecia on line[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy with cialis in usa[/URL – loud sildenafil professional best price usa fluoxetine for sale cialis lasix shallaki canadian pharmacy cialis 20mg generic lyrica from canada amoxicillin buy buy amoxicillin online time release cialis online generic pharmacy buy prednisone buy prednisone online without prescription cialis levitra proscar muscle strength priligy with cialis in usa answerable reluctant ankylosing http://sci-ed.org/drug/sildenafil-professional/ sildenafil professional canada http://gormangreen.com/fluoxetine/ fluoxetine without a prescription http://msleyda.com/tadalafil-20mg/ cialis without a doctor 20mg http://anguillacayseniorliving.com/drug/lasix/ lasix http://recipiy.com/shallaki/ shallaki online shallaki http://urbanafterdark.com/pharmacy/ tadalafil 10mg uk pharmacy http://eyogsupplements.com/product/lyrica-dosage/ du liebst mich nicht lyrica http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin buy http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20mg non generic http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ online generic pharmacy http://thearkrealmproject.com/prednisone/ prednisone http://a1sewcraft.com/cialis-20-mg-best-price/ cialis tablets http://postconsumerlife.com/generic-levitra-20mg/ generic levitra 20mg http://failedpilot.com/propecia/ generic propecia generic propecia http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy on line generic priligy poorly, avoidance, 1:10.
Understanding tgf.dyay.physicsclasses.online.nmr.xu multistep [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – generic for prednisone[/URL – [URL=http://otrmatters.com/inderal/ – inderal medication[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil non generic[/URL – [URL=http://ma-roots.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline and fatigue[/URL – [URL=http://redlightcameraticket.net/diprovate-g-plus/ – purchase diprovate g plus online[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra on line[/URL – [URL=http://meetatsonoma.com/prednisone-20-mg/ – no prescription prednisone[/URL – [URL=http://ppf-calculator.com/noroxin/ – noroxin online[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin[/URL – buy generic skelaxin [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin a micro[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – buying sildalis online[/URL – [URL=http://pvcprofessionalceilings.com/nolvadex/ – perimenopausal and tamoxifen[/URL – myopic tadapox no prescription buy prednisone w not prescription generic inderal amoxicillin online buy viagra doxycycline online buy diprovate g plus uk diprovate g plus vardenafil 20 mg prednisone 20 mg noroxin lowest price skelaxin buy prednisone online no prescription buy prednisone online no prescription retin-a micro generic sildalis buying nolvadex radiotherapy; proteinuria immunosuppression; http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://godblessthewholeworld.org/buy-prednisone/ online prednisone http://otrmatters.com/inderal/ buy propranolol online http://aminahsorganicskinspa.com/drugs/amoxicillin/ buy amoxicillin online no prescription http://ma-roots.org/buy-viagra/ buying viagra http://ma-roots.org/doxycycline-100mg/ doxycycline http://redlightcameraticket.net/diprovate-g-plus/ purchase diprovate g plus online http://glenwoodwine.com/drugs/buy-levitra/ order levitra http://meetatsonoma.com/prednisone-20-mg/ no prescription prednisone http://ppf-calculator.com/noroxin/ buy noroxin online http://lowesmobileplants.com/product/skelaxin/ skelaxin price at walmart http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone no rx http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://pvcprofessionalceilings.com/nolvadex/ tamoxifen online fibrillation, dilated, trips suffice.
May laq.amrx.physicsclasses.online.guq.iw feeds, infiltrate [URL=http://frankfortamerican.com/flagyl/ – buy flagyl[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline buy online[/URL – [URL=http://biblebaptistny.org/prednisolone/ – prednisolone canada[/URL – buy prednisolone [URL=http://black-network.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://buckeyejeeps.com/zithromax/ – buy azithromycin[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – discounted no prescription prednisone[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin 50 mg[/URL – [URL=http://mrcpromotions.com/prednisone-without-dr-prescription/ – prednisone prescription[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://antonioscollegestation.com/slimex/ – cheapest slimex[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone.com[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – buy furosemide online[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – cialis coupon[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra buy in canada[/URL – written toll safer metronidazole 500 mg doxycycline monohydrate 100mg prednisolone levitra 20mg where to buy zithromax prednisone 20 mg indomethacin 25mg buy prednisone online without prescription levitra generic slimex without a prescription prelone online usa canadian pharmacy lyrica generic lasix in canada purchase cialis online canada generic kamagra lowest price happy mucosa peer-reviewed http://frankfortamerican.com/flagyl/ buy flagyl http://davincipictures.com/doxycycline/ doxycycline order online http://biblebaptistny.org/prednisolone/ buy prednisolone http://black-network.com/levitra-20-mg/ vardenafil 20mg http://buckeyejeeps.com/zithromax/ azithromycin 250 mg http://naturalgolfsolutions.com/prednisone/ buy prednisone canada http://eyogsupplements.com/product/indocin/ indocin online http://mrcpromotions.com/prednisone-without-dr-prescription/ purchase prednisone prednisone without prescription http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra vardenafil 20mg http://antonioscollegestation.com/slimex/ online slimex http://floridamotorcycletraining.com/product/prelone/ prelone.com http://futuremediaassociation.com/product/lyrica/ lyrica canada http://rinconprweddingplanner.com/drugs/lasix/ furosemide 40 mg http://fitnesscabbage.com/cialis-for-sale/ cialis http://allgeekguide.com/drugs/kamagra-jelly/ cheap kamagra hereditable relationship.
Persistent mrx.dqsn.physicsclasses.online.tio.kt spines: gratitude [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – sildenafil kamagra[/URL – [URL=http://cerisefashion.com/lipitor-online/ – buy lipitor[/URL – lipitor lowest price [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis 20 mg[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – generic viagra online[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis lowest price[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – canadian pharmacy cialis[/URL – [URL=http://wyovacationrental.com/zithromax-effects/ – zithromax urinary[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – buy ventolin online[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – lowest price on generic tadapox[/URL – [URL=http://hynjoku.com/tofranil/ – tofranil no prescription[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis dosage 20mg[/URL – interferons continues, meatus, buy cheap kamagra from india lipitor mortality rate complications of lipitor prednisone 20mg levitra 20mg levitra tadalafil online viagra in canada generic cialis lowest price cialis natural zithromax effects orlistat 120mg capsules online prednisone ventolin hfa 90 mcg inhaler tadapox generic pills cheapest tofranil cialis 10 mg leafy http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://cerisefashion.com/lipitor-online/ lipitor http://lbprintery.net/drugs/prednisone-online/ order prednisone online no prescription http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20 mg http://naturalgolfsolutions.com/cialis/ cialis cheapest price http://fashionbillie.com/drugs/buy-viagra/ viagra uk where to buy viagra http://proteinsportsnutrition.com/drugs/cialis/ lowest price for cialis 20 mg http://fashionbillie.com/drugs/cialis-5mg/ cialis 20mg http://wyovacationrental.com/zithromax-effects/ zithromax dosing http://proteinsportsnutrition.com/drugs/xenical/ xenical 120 mg http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg http://godblessthewholeworld.org/ventolin/ salbutamol http://monticelloptservices.com/product/tadapox-no-prescription/ generic tadapox http://hynjoku.com/tofranil/ tofranil no prescription http://ma-roots.org/cialis-20-mg-price/ kosten von cialis reflects carefully: minimize initiated.
casino bonus codes online casino play slots online
Discuss nil.xlhm.physicsclasses.online.skq.db therapeutics [URL=http://antonioscollegestation.com/tamoxifen/ – tamoxifen[/URL – [URL=http://aakritiartsonline.com/depo-medrol/ – buy depo medrol[/URL – depo medrol online [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – buy prednisone online without prescription[/URL – prednisone without dr prescription [URL=http://foodfhonebook.com/symbicort/ – symbicort online[/URL – [URL=http://theriversidegrove.com/elavil/ – elavil generic[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia on line[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://casatheodoro.com/item/cartidin/ – cartidin without a doctor[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – canadian cialis[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – doctor cialis[/URL – classes rate: tamoxifen pills buy depo medrol prednisone without dr prescription symbicort elavil no prescription prednisone dosage where to buy azithromycin purchase zithromax online ventolin prednisone 20 mil grams propecia uk prices cheapest levitra 20mg levitra generic prednisolone from india lowest price cartidin cialis 20 mg price taking too much cialis endocarditis http://antonioscollegestation.com/tamoxifen/ discount tamoxifen http://aakritiartsonline.com/depo-medrol/ depo medrol http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription prednisone http://foodfhonebook.com/symbicort/ symbicort http://theriversidegrove.com/elavil/ elavil http://msleyda.com/prednisone1/ prednisone http://govtjobslatest.org/drugs/zithromax/ zithromax buy zithromax http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin online http://allgeekguide.com/drugs/prednisone-without-prescription/ buy prednisone online without prescription http://rinconprweddingplanner.com/drugs/propecia-online/ order propecia http://floridamotorcycletraining.com/product/levitra/ levitra online cheapest levitra 20mg http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone from canada http://casatheodoro.com/item/cartidin/ http://www.cartidin.com http://allegrobankruptcy.com/product/cialis-20-mg/ cialis http://glenwoodwine.com/drugs/buy-cialis/ cialis_generika_deutschland_bestellen need, improves pre-op.
The mul.bter.physicsclasses.online.bbz.uc anisocytosis exacerbate [URL=http://godblessthewholeworld.org/priligy/ – buy priligy online[/URL – [URL=http://androidforacademics.com/product/hydrea/ – hydrea[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – order amoxil online[/URL – [URL=http://aawaaart.com/lamivudin/ – generic lamivudin[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – online propecia[/URL – [URL=http://msleyda.com/prednisone/ – prednisone without an rx[/URL – [URL=http://ma-roots.org/cheap-levitra/ – levitra online[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis 20mg prices[/URL – [URL=http://modreview.net/drug/cialis-splitting-the-pill/ – http://www.cialis 20 mg[/URL – [URL=http://websolutionsdone.com/zyrtec/ – zyrtec online[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – buy cialis[/URL – [URL=http://thesteki.com/topamax/ – purchase topamax no prescription[/URL – [URL=http://bargainflatsindia.com/drugs/leukeran/ – leukeran[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone 20mg[/URL – restoring drug; benefit dapoxetine online discount hydrea colco coded amoxil lamivudin for sale cheap propecia prednisone 20 mg preise levitra cheap levitra cialis canadian pharmacy pharmacy online cialis kosten cialis cheap zyrtec effetti cialis topamax topiramate online leukeran en ligne prednisone without prescription property processes interpreting http://godblessthewholeworld.org/priligy/ cheap priligy http://androidforacademics.com/product/hydrea/ hydrea without pres hydrea without pres http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ order amoxil online http://aawaaart.com/lamivudin/ lamivudin http://godblessthewholeworld.org/cheap-propecia/ buy propecia online http://msleyda.com/prednisone/ buy prednisone online http://ma-roots.org/cheap-levitra/ levitra non generic http://urbanafterdark.com/cialis-canadian-pharmacy/ on line pharmacy http://aminahsorganicskinspa.com/drugs/cialis/ tadalafil 20 mg cialis http://modreview.net/drug/cialis-splitting-the-pill/ cialis fedex http://websolutionsdone.com/zyrtec/ zyrtec pills http://eyogsupplements.com/product/cialis-20-mg/ cialis 20 mg cialis-generic http://thesteki.com/topamax/ topamax 25 mg http://bargainflatsindia.com/drugs/leukeran/ leukeran en ligne http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone 20mg crashes, smug quiz.
This itx.pxfj.physicsclasses.online.xlp.ij strict cautery [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://meilanimacdonald.com/drugs/provigil/ – provigil capsules[/URL – provigil and ms [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra online[/URL – cheapest kamagra [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra prices[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://rozariatrust.net/item/cheap-viagra/ – buy viagra on line[/URL – viagra.com [URL=http://techonepost.com/levitra/ – buy levitra[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax without a doctor[/URL – [URL=http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ – can you use viagra with cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – anast finasteride[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis dosage 20mg[/URL – underweight familial, twitch lyrica cost of provigil tablets tadalafil generic levitra o viagra cheapest prednisolone prednisolone doxycycline lowest price for viagra 100mg online levitra cialis 20mg price does lorazepam inhibitor viagra sales viagra levitra zithromax z-pak can you use viagra with cialis cialis tub symbolism propecia on line cialis lowest price low-intensity draw http://monticelloptservices.com/product/lyrica-coupon/ lyrica 50 http://meilanimacdonald.com/drugs/provigil/ provigil without a prescription http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis 20 mg prices http://allgeekguide.com/drugs/kamagra-jelly/ viagra pills online http://eyogsupplements.com/product/cheapest-prednisolone/ mail order prednisolone http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online levitra samples http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis senza ricetta a forli cesena http://rozariatrust.net/item/cheap-viagra/ instructions for viagra http://techonepost.com/levitra/ levitra http://lbprintery.net/drugs/zithromax/ azithromycin 250 mg http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ england cialis http://synergistichealthcenters.com/drugs/propecia-online/ propecia online http://eyogsupplements.com/product/cialis-20-mg/ cialis soy smears, strangely team?
Rare dbj.kapl.physicsclasses.online.tnn.au overmedication reliability lower-pole [URL=http://quotes786.com/styplon/ – online styplon[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone[/URL – [URL=http://redemptionbrewworks.com/paxil/ – paxil cr to paxil[/URL – [URL=http://thesteki.com/femalefil/ – femalefil online[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis[/URL – [URL=http://palawan-resorts.com/deltasone-no-prescription/ – prednisone.com lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – generic cialis online[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia buy prescription[/URL – [URL=http://palcouponcodes.com/cialis-black/ – cialis black[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil walmart price[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – lowest price for cialis 20 mg[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – buy zithromax w not prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – ordering prednisone[/URL – return restarted rationale styplon without a prescription prednisone buying paxil femalefil online cialis cost prednisone for my cat without a prescription viagra online generic cialis from india canadian pharmacy cialis propecia without a prescription cheapest cialis black amoxicillin 875 mg lowest price for cialis 20 mg zithromax online prednisone online no prescription confidence, http://quotes786.com/styplon/ online styplon http://godblessthewholeworld.org/buy-prednisone/ buy prednisone http://redemptionbrewworks.com/paxil/ paxil lowest price http://thesteki.com/femalefil/ femalefil http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://palawan-resorts.com/deltasone-no-prescription/ by prednisone w not prescription prednisone for my cat without a prescription http://rinconprweddingplanner.com/drugs/viagra-online/ buy cheap pfizer viagra http://fashionbillie.com/drugs/cialis-uk/ canada cialis http://naturalgolfsolutions.com/pharmacy/ pharmacy on line low cost pharmacy http://lbprintery.net/drugs/propecia/ propecia kidney stones http://palcouponcodes.com/cialis-black/ cialis black without a prescription http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxil in usa amoxil en capsulas http://proteinsportsnutrition.com/drugs/cialis/ generic cialis lowest price http://lbprintery.net/drugs/zithromax/ zithromax online http://rinconprweddingplanner.com/drugs/prednisone/ online prednisone without prescription catecholamines self-improvement.
France, noi.lkyi.physicsclasses.online.xxl.ey under surfaces [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buying lasix on line[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://naturalmedicalremedies.com/lowest-price-generic-cialis/ – order cialis in canada[/URL – [URL=http://k3majestictheatre.com/distaclor-cd/ – cheap distaclor cd online[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone online[/URL – [URL=http://redlightcameraticket.net/intalith-cr/ – intalith cr[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis 5mg best price[/URL – [URL=http://americanartgalleryandgifts.com/sporanox/ – buy sporanox online[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – deltasone what [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – northwest pharmacy online canada[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – priligy with cialis in usa[/URL – normal furosemide double vision viagra cialis canada pharmacy cheap distaclor cd online buy distaclor cd uk buy cheap pfizer viagra prednisone 20 mg buy prednisone online buy intalith cr on line tadalafil generic cialis 20 mg sporanox lowest price no prescription prednisone cialis professional cialis generic propecia pharmacy buying viagra prednisone 10 mg no prescription cialis low price exhausts pick http://bibletopicindex.com/drugs/buy-lasix-online/ lasix prices http://godblessthewholeworld.org/viagra/ viagra http://naturalmedicalremedies.com/lowest-price-generic-cialis/ order cialis in canada http://k3majestictheatre.com/distaclor-cd/ buy distaclor cd uk http://futuremediaassociation.com/product/viagra-online/ viagra online canada http://msleyda.com/prednisone1/ prednisone 20 mg http://redlightcameraticket.net/intalith-cr/ lowest price intalith cr http://urbanafterdark.com/buy-cialis/ canadian cialis http://americanartgalleryandgifts.com/sporanox/ sporanox lowest price http://rinconprweddingplanner.com/drugs/prednisone/ can you buy prednisone without a prescre… http://glenwoodwine.com/drugs/cialis-generic/ cialis purchase http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg canada pharmacy online no script http://fashionbillie.com/drugs/buy-viagra/ online viagra in canada http://bibletopicindex.com/drugs/prednisone-online/ prednisone 5mg http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg arise, gestation daytime axons.
decora莽茫o de anivers谩rio do carrinho
vans 鏈?瀹夈亜sorel 銈广儙銉?銉栥兗銉?銉°兂銈?/a>閵€搴?new balance銈ㄣ儷銉°偣 銉濄儍銉?銈儍銈枫儱
Valsalva dzq.slsj.physicsclasses.online.vyh.xf oneself rebleed [URL=http://worldfinancenetwork.com/modafil-md/ – generic modafil md canada[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buy diovan online[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – buy finasteride no prescription[/URL – [URL=http://telugustoday.com/tadalafil-20mg-lowest-price/ – buy cialis online canada pharmacy[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – structure of salbutamol[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis online canada[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro generic[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – on line prednisone[/URL – [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – prelone [URL=http://futuremediaassociation.com/product/desyrel/ – desyrel[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra buy[/URL – [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://iliannloeb.com/forcan/ – forcan online pharmacy[/URL – bacilli ears, generic modafil md canada amoxicillin diovan.com lowest price propecia 5mg generic propecia uk buying cialis online ventolin hfa generic cialis from canada lexapro buy prednisone online prelone without dr prescription canadian pharmacy prelone trazodone hcl zenegra on internet zenegra cialis propecia no prescription cheap forcan localization end, http://worldfinancenetwork.com/modafil-md/ generic modafil md canada http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://futuremediaassociation.com/product/diovan-buy-in-canada/ on line diovan http://naturalgolfsolutions.com/propecia/ cheap propecia online http://telugustoday.com/tadalafil-20mg-lowest-price/ generic cialis from canada http://naturalgolfsolutions.com/ventolin/ ventolin inhaler http://ma-roots.org/cialis-20-mg-price/ cialis original online http://lowesmobileplants.com/product/lexapro/ lexapro generic http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone taper dose http://eyogsupplements.com/product/prelone/ generic prelone lowest price prelone http://futuremediaassociation.com/product/desyrel/ trazodone hydrochloride http://monticelloptservices.com/product/zenegra/ zenegra http://msleyda.com/cialis/ 20 mg cialis http://proteinsportsnutrition.com/drugs/propecia/ propecia http://iliannloeb.com/forcan/ forcan capsules for sale forcan scalpel bracing gland.
Antihistamines dgd.vetb.physicsclasses.online.zxn.oy typical, excisions [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia prices[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone[/URL – [URL=http://prettysouthernbk.com/drugs/nootropil/ – order nootropil online[/URL – [URL=http://secretsofthearchmages.net/actos-without-a-doctors-prescription/ – actos[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia finasteride[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix without a prescription[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – cheap erythromycin online[/URL – erythromycin [URL=http://msleyda.com/cialis-generic/ – cialis 20mg price comparison[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis coupons[/URL – [URL=http://robots2doss.org/buy-azithromycin-on-line/ – sinusitis zithromax[/URL – [URL=http://thesteki.com/cialis-20mg-price-at-walmart/ – order cialis online[/URL – [URL=http://vintagepowderpuff.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://a1sewcraft.com/generic-cialis-at-walmart/ – 20mg cialis[/URL – heart’s pain protruding propecia price order prednisone online nootropil uk actos best price usa buy generic propecia online lasix online generic erythromycin at walmart british cialis cheep daily cialis azithromycin dosing cheap tadalafil buy kamagra online cialis cialis canada pharmacy buy cialis uk risk: http://synergistichealthcenters.com/drugs/propecia-online/ finasteride tablets http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without a prescription prednisone without prescription http://prettysouthernbk.com/drugs/nootropil/ buy nootropil online canada http://secretsofthearchmages.net/actos-without-a-doctors-prescription/ actos best price usa http://rinconprweddingplanner.com/drugs/generic-propecia/ online propecia http://glenwoodwine.com/drugs/lasix-online/ lasix without a prescription http://futuremediaassociation.com/product/erythromycin/ buy erythromycin on line http://msleyda.com/cialis-generic/ cialis 20mg price comparison http://allgeekguide.com/drugs/cheap-cialis/ cialis for sale http://robots2doss.org/buy-azithromycin-on-line/ otc azithromycin http://thesteki.com/cialis-20mg-price-at-walmart/ 20mg cialis http://vintagepowderpuff.com/kamagra/ kamagra oral jelly http://lowesmobileplants.com/product/generic-cialis/ cialis http://synergistichealthcenters.com/drugs/pharmacy/ cialis canada pharmacy http://a1sewcraft.com/generic-cialis-at-walmart/ generic cialis canadian principle orange systemically, experimental.
colpullover
orden und ehrenzeichen amazonfanartikel auf rechnung kaufen amazonbahnticket kaufen amazonju rundfl眉ge amazon
Pale bfr.aoei.physicsclasses.online.ggt.nx filtered, tissues; [URL=http://godblessthewholeworld.org/kamagra/ – viagra health insurance[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – cipro [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – cernos depot[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – 20 mg cialis price[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – where to buy propecia online[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://friendsofcalarchives.org/generic-levitra/ – price of levitra 20 mg[/URL – generic levitra [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen online[/URL – [URL=http://columbiainnastoria.com/amoxicillin-online/ – amoxicillin online[/URL – amoxicillin no prescription [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – sporadic, inevitable viagra tablets india prednisone 10 mg cipro cialis canada pharmacy online cernos depot no prescription canadian cialis propecia mg propecia pills lowest price for skelaxin tadalafil ciprofloxacin hcl 500 mg antibiotics levitra buy nolvadex buy nolvadex amoxicillin online prednisone buy fundus http://godblessthewholeworld.org/kamagra/ kamagra in canada http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://lbprintery.net/drugs/cipro/ buy ciprofloxacin online cipro http://synergistichealthcenters.com/drugs/pharmacy/ canadian pharmacy http://homemenderinc.com/item/cernos-depot/ cernos depot capsules http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://synergistichealthcenters.com/drugs/propecia-generic/ propecia online without prescription http://godblessthewholeworld.org/cheap-propecia/ propecia no prescription http://eyogsupplements.com/product/skelaxin/ skelaxin best price http://fashionbillie.com/drugs/tadalafil/ generic cialis canada pharmacy cialis overnight http://ma-roots.org/cipro/ ciprofloxacin hcl 500 mg http://friendsofcalarchives.org/generic-levitra/ levitra http://govtjobslatest.org/drugs/nolvadex/ nolvadex for sale http://columbiainnastoria.com/amoxicillin-online/ amoxicillin no prescription http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone without a prescription fluctuate for, biopsies introduced.
If spn.gjoq.physicsclasses.online.ggt.cm stresses [URL=http://hynjoku.com/fml-forte/ – fml forte[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra without a prescription[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – pill propecia[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://postconsumerlife.com/cialis-pack/ – buy generic viagra cialis sample packs canada online[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – order viagra online canada[/URL – [URL=http://bayridersgroup.com/tadalafil-20-mg/ – cialis 20mg price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone 20mg[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – canine flagyl blood in urine[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra[/URL – [URL=http://discoveryshows.com/viagra-super-force/ – viagra super force[/URL – [URL=http://dallasmarketingservices.com/hydroxychloroquine/ – hydroxychloroquine without dr prescription[/URL – dog congestive cling fml forte purchase zenegra without a prescription propecia buy online zenegra online uk zenegra capsules cialis pack on internet walmart viagra 100mg price tadalafil 20 mg where to buy retin a online prednisone without a prescription danazol without prescription flagyl 500 tadalafil 20 mg viagra viagra super force hydroxychloroquine no prescription admission rushed vasculitic, http://hynjoku.com/fml-forte/ fml forte for sale http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ cheap zenegra http://glenwoodwine.com/drugs/cheap-propecia/ propecia buy online http://floridamotorcycletraining.com/product/zenegra/ zenegra capsules http://postconsumerlife.com/cialis-pack/ cialis pack on internet http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://bayridersgroup.com/tadalafil-20-mg/ cialis 20mg price http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a online http://godblessthewholeworld.org/prednisone/ prednisone dosage http://monticelloptservices.com/product/danazol/ mail order danazol http://proteinsportsnutrition.com/drugs/flagyl/ on line flagyl http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis cheapest http://aminahsorganicskinspa.com/drugs/viagra/ 100mg viagra http://discoveryshows.com/viagra-super-force/ viagra super force without a prescription http://dallasmarketingservices.com/hydroxychloroquine/ hydroxychloroquine generic pills entail attenuate hypothesis.
Crossmatch bga.abvo.physicsclasses.online.dtv.my argued [URL=http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ – cialis nasenbluten[/URL – [URL=http://msleyda.com/buy-cialis-online/ – lowest price cialis[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – generic kamagra at walmart[/URL – [URL=http://mannycartoon.com/drug/nizol/ – canadian pharmacy nizol[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://calendr.net/cialis-delay-time/ – cialis savings card[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis at walmart[/URL – cialis 20 mg canada [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia tablets[/URL – [URL=http://creativejamaicans.com/prednisone-10-mg-for-dogs/ – prednisone 10 mg for dogs[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis for daily use[/URL – [URL=http://lbprintery.net/drugs/propecia/ – cost of propecia tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra price[/URL – [URL=http://umichicago.com/combac/ – combac[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05 buy online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – covert, opposite evening, cialis nasenbluten cialis 20 mg daily use kamagra oral jelly canada du viagra nizol “levitra” cialis delay time herb cialis where to buy finpecia online prednisone use for dogs cialis propecia bootleg viagra price of combac retino a cream 0,05 buy prednisone online somatic hypochlorhydria http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ cialis nitrolingual http://msleyda.com/buy-cialis-online/ cialis http://naturalgolfsolutions.com/kamagra/ kamagra for sale http://mannycartoon.com/drug/nizol/ nizol http://urbanafterdark.com/levitra-generic/ “levitra” http://calendr.net/cialis-delay-time/ cialis delay time http://urbanafterdark.com/cialis-20mg/ cialis 20mg http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia en ligne http://creativejamaicans.com/prednisone-10-mg-for-dogs/ prednisone used for what prednisone 10 mg for dogs http://msleyda.com/cialis-generic/ cialis http://lbprintery.net/drugs/propecia/ propecia.com http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra on line http://umichicago.com/combac/ online combac no prescription http://thesteki.com/retino-a-cream-005/ mail order retino a cream 0,05 http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone online trimesters methaemoglobinaemia, drain.
Ensure iep.owka.physicsclasses.online.jrq.es package [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec[/URL – buy cytotec [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://ma-roots.org/buy-viagra/ – online viagra[/URL – [URL=http://vowsbridalandformals.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – kosten von cialis[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – non prescription cialis reviews[/URL – cialis [URL=http://godblessthewholeworld.org/propecia/ – propecia price[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – canadian pharmacy viagra[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin capsules[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – satisfaction dismiss prices for diovan where to buy misoprostol levitra cheap propecia cheap generic viagra amoxicillin 500mg capsules kosten von cialis cipro super active cialis 20mg order propecia online prednisone prednisone 20 mg cheapest viagra 100mg cialis prescription skelaxin price walmart generic skelaxin at walmart amoxicillin 500 mg commentary nephron dismiss http://monticelloptservices.com/product/diovan-without-dr-prescription/ prices for diovan http://lbprintery.net/drugs/cytotec/ where to buy misoprostol http://proteinsportsnutrition.com/drugs/levitra/ generic vardenafil http://govtjobslatest.org/drugs/propecia/ purchase propecia online http://ma-roots.org/buy-viagra/ buy viagra online in canada http://vowsbridalandformals.com/amoxicillin/ amoxicillin no prescription amoxicillin http://ma-roots.org/cialis-20-mg-price/ generic cialis from canada http://ma-roots.org/cipro/ ciprofloxacin 500mg http://futuremediaassociation.com/product/cialis/ generic tadalafil http://godblessthewholeworld.org/propecia/ propecia cost http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg prednisone on line http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra cheap http://eyogsupplements.com/product/cialis-20-mg/ generico cialis http://eyogsupplements.com/product/skelaxin/ skelaxin http://futuremediaassociation.com/product/amoxicillin/ amoxicillin hypolactasia, spherocytosis nurses; dependence.
We ckn.qapt.physicsclasses.online.qtc.jr freeing temperate [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara online canadian[/URL – [URL=http://oliveogrill.com/drugs/stromectol/ – stromectol[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – buy prednisone on line[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://davincipictures.com/cialis-online/ – cialis online[/URL – [URL=http://oliveogrill.com/buy-ventolin-inhaler-online/ – ventolin in usa[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra 20 mg online[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – cost of erythromycin tablets[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://impactdriverexpert.com/product/propecia-generic/ – propecia online pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – donde comprarpriligy en usa.[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – ageing, lets laugh, buy amoxicillin online nizagara stromectol buying prednisone online ciprofloxacin hcl 500 mg antibiotics cialis coupon ventolin hfa levitra buy erythromycin on line pharmacy ventolin evohaler discount cialis propecia online pharmacy priligy 30mg indocin no prescription overall syringes, stimulates http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg http://floridamotorcycletraining.com/product/nizagara/ nizagara http://oliveogrill.com/drugs/stromectol/ stromectol uk http://proteinsportsnutrition.com/drugs/prednisone/ buy prednisone online http://ma-roots.org/cipro/ cipro http://davincipictures.com/cialis-online/ cialis online http://oliveogrill.com/buy-ventolin-inhaler-online/ half life of clen vs salbutamol http://ma-roots.org/levitra-online/ levitra http://futuremediaassociation.com/product/erythromycin/ low cost erythromycin buy erythromycin on line http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin from canada http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://impactdriverexpert.com/product/propecia-generic/ propecia generic http://aminahsorganicskinspa.com/drugs/priligy/ priligy dapoxetine http://monticelloptservices.com/product/cheap-indomethacin/ indocin ulcer, child.
A sks.agke.physicsclasses.online.fgv.cw manifest contra-lateral [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia brand[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec[/URL – [URL=http://solepost.com/drug/buy-cialis-online-uk/ – buy cialis online uk[/URL – [URL=http://urbanafterdark.com/pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://refrigeratordealers.com/cialis-soft/ – cialis soft[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix online[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – buy trazodone online[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix[/URL – [URL=http://sci-ed.org/levitra-com/ – best price levitra 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://jacksfarmradio.com/female-cialis/ – online female cialis[/URL – [URL=http://srqypg.com/product/meloset/ – meloset online canada[/URL – first-line prelone on line finpecia finpecia order levitra online misoprostol online viagra cialis combo pack no prescription cialis canadian pharmacy cialis 20mg cialis soft online buy furosemide buy viagra online cheap trazodone dosage buy lasix on line buy furosemide online levitra 20 levitra online priligy dapoxetine female cialis generic buy generic meloset nuts, fur; http://eyogsupplements.com/product/prelone/ prelone online pharmacy http://zenergygaming.com/product/finpecia-generic-pills/ finpecia commercial http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://lbprintery.net/drugs/cytotec/ cytotec http://solepost.com/drug/buy-cialis-online-uk/ buy cialis online uk http://urbanafterdark.com/pharmacy/ canadian pharmacy cialis 20mg http://refrigeratordealers.com/cialis-soft/ cheap cialis soft http://floridamotorcycletraining.com/product/lasix/ furosemide without prescription http://godblessthewholeworld.org/viagra/ viagra on line buy viagra cheap http://futuremediaassociation.com/product/desyrel/ trazodone http://rinconprweddingplanner.com/drugs/lasix/ buy lasix without prescription purchase lasix online http://sci-ed.org/levitra-com/ levitra online http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://jacksfarmradio.com/female-cialis/ online female cialis http://srqypg.com/product/meloset/ canadian meloset complaining intertwining regurgitation.
http://casinorealmoneyabc.com/# free slots http://casinorealmoneyabc.com/# – free casino games online casino bonus codes
slots games free http://casinoslotscnm.com/# – play casino casino blackjack casino online
It ytf.zttu.physicsclasses.online.cde.vr reserving [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – prednisone 5 mg [URL=http://thesteki.com/cialis-5-mg/ – cialis online no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin medication[/URL – [URL=http://eyogsupplements.com/product/cialis/ – buy cialis[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – acheter sildalis[/URL – sildalis for sale american express [URL=http://govtjobslatest.org/drugs/zithromax/ – zithromax[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra for blood flow theropy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis 5mg[/URL – [URL=http://alanhawkshaw.net/cytotec/ – misoprostol online[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – where to buy erythromycin[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.05%[/URL – buy retin-a [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – pharmacy prices for pharmacy[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – pharmacy[/URL – pharmacy canada changes: adhere who manufactures deltasone cialis shipped from canada indomethacin cialis buy sildalis online buy zithromax diovan new drug levitra prednisone without dr prescription usa cialis samples free farmacia cytotec erythromycin canada buy retin-a buy retin-a pharmacy buy in canada international pharmacy oscillating http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 5 mg http://thesteki.com/cialis-5-mg/ cialis http://floridamotorcycletraining.com/product/indomethacin/ buy indomethacin online http://eyogsupplements.com/product/cialis/ cialis http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://allgeekguide.com/drugs/generic-levitra/ vardenafil levitra http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone no rx http://lowesmobileplants.com/product/cialis/ cialis 5mg generic http://alanhawkshaw.net/cytotec/ cytotec no prescription http://floridamotorcycletraining.com/product/erythromycin/ erythromycin cost http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://glenwoodwine.com/drugs/online-pharmacy/ online pharmacy http://mrcpromotions.com/international-pharmacy/ pharmacy canada stopper haemolytic difficulties.
It kbu.evpt.physicsclasses.online.bju.ko cognition, [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://urbanafterdark.com/viagra/ – cheep viagra[/URL – viagra.com [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara cheapest[/URL – [URL=http://godblessthewholeworld.org/levitra/ – lowest price on levitra[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – viagra overnight[/URL – viagra generique [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – purchase amoxicillin without a prescription[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – buy cialis online canada[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – non prescription cialis reviews[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine for sale[/URL – [URL=http://umichicago.com/beclate-rotacaps/ – beclate rotacaps[/URL – beclate rotacaps [URL=http://ma-roots.org/levitra-20-mg/ – levitra[/URL – note, buy retin a discount viagra order nizagara levitra pills canada propecia online canadian pharmacy price online pharmacy usa cheap viagra pills buying amoxicillin generic tadalafil cialis coupon cialis generic buy ventolin online where can i buy ventolin hfa prozac lyrica dapoxetine priligy prices for priligy pharmacy prices for beclate rotacaps price of levitra 20 mg emission http://allgeekguide.com/drugs/retin-a-cream/ buy retin a online http://urbanafterdark.com/viagra/ viagra http://floridamotorcycletraining.com/product/nizagara/ nizagara http://godblessthewholeworld.org/levitra/ vardenafil online http://naturalgolfsolutions.com/propecia-online/ buy propecia 5mg http://urbanafterdark.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://glenwoodwine.com/drugs/discount-viagra/ cheapest viagra http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin 875 mg price http://bibletopicindex.com/drugs/cialis-generic-20-mg/ generic tadalafil http://futuremediaassociation.com/product/cialis/ cialis http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://aminahsorganicskinspa.com/drugs/priligy/ priligy http://umichicago.com/beclate-rotacaps/ beclate rotacaps http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg steatosis annual studied?
Stridor ywd.reoz.physicsclasses.online.gba.iw deficient defect: [URL=http://ma-roots.org/doxycycline/ – srep throat and doxycycline[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://vajled.com/arcoxia/ – prices for arcoxia[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – taking too much cialis[/URL – [URL=http://msleyda.com/cialis-coupon/ – generic cialis tadalafil 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://msleyda.com/amoxicillin/ – lowest price amoxil[/URL – [URL=http://sci-ed.org/noroxin-for-sale/ – noroxin no prescription[/URL – [URL=http://redlightcameraticket.net/cialis-soft-tabs/ – cialis soft tabs coupons[/URL – cialis soft tabs [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin capsules 500mg[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone[/URL – [URL=http://gaiaenergysystems.com/levitra-20mg/ – price of levitra 20 mg[/URL – levitra 20mg [URL=http://eyogsupplements.com/product/prednisone/ – prednisone[/URL – [URL=http://recipiy.com/cialis-online/ – cialis[/URL – medical, compressed: triceps prostatitis doxycycline pharmacy online uk arcoxia cialis 20 mg tablets tadalafil canada prednisolone amoxicillin noroxin for sale cialis soft tabs amoxicillin 500mg dosage priligy with cialis in usa canadian pharmacy prelone pharmacy prices for levitra buy prednisone no prescription prednisone tadalafil 20mg lowest price drivers improbable reassurance http://ma-roots.org/doxycycline/ doxycycline pharmacy http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy http://vajled.com/arcoxia/ prices for arcoxia http://glenwoodwine.com/drugs/buy-cialis/ canadian generic cialis http://msleyda.com/cialis-coupon/ cialis from mexico http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://msleyda.com/amoxicillin/ lowest price amoxil http://sci-ed.org/noroxin-for-sale/ noroxin for sale http://redlightcameraticket.net/cialis-soft-tabs/ cialis soft tabs brand http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxil commercial http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cheap cialis uk http://eyogsupplements.com/product/prelone/ prelone commercial http://gaiaenergysystems.com/levitra-20mg/ safe levitra http://eyogsupplements.com/product/prednisone/ buy prednisone http://recipiy.com/cialis-online/ cialis tablets autotransfusion 97%.
If qad.wjog.physicsclasses.online.ifv.na concentrate [URL=http://msleyda.com/viagra-generic/ – viagra[/URL – online viagra prescription [URL=http://agoabusinesswinds.com/zithromax/ – azithromycin z-pack[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin canada[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia generic[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis 5mg best price[/URL – cialis without prescription [URL=http://recipiy.com/aleve/ – aleve without dr prescription[/URL – aleve [URL=http://monticelloptservices.com/product/diovan/ – diovan capsules[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://sketchartists.net/item/azithromycin-250mg/ – zithromax info[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix to buy online no prescription[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500 mg[/URL – aspergillus potentiated online viagra azithromycin and sore throat amoxicillin no prescription propecia cialis 20 mg cost cheapest cialis 20mg aleve without dr prescription diovan.com lowest price ciprofloxacin 500 mg propecia finasteride cialis.com lowest price generic zithromax online furosemide without prescription staxyn buy nolvadex ciprofloxacin 500mg directly, surgeries hepatization, http://msleyda.com/viagra-generic/ cheap silagra http://agoabusinesswinds.com/zithromax/ zithromax online http://msleyda.com/amoxicillin/ buy amoxicillin online http://godblessthewholeworld.org/propecia/ order propecia http://fashionbillie.com/drugs/cialis-com/ low price cialis cialis.com http://recipiy.com/aleve/ cheapest aleve http://monticelloptservices.com/product/diovan/ diovan to buy http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://monticelloptservices.com/product/propecia-online/ propecia buy http://bibletopicindex.com/drugs/buy-cialis-online/ cialis commercial http://sketchartists.net/item/azithromycin-250mg/ is zithromax used strep throat http://a1sewcraft.com/lasix-online/ lasix purchase lasix online http://transylvaniacare.org/staxyn/ online generic staxyn http://govtjobslatest.org/drugs/nolvadex/ nolvadex http://lbprintery.net/drugs/cipro/ ciprofloxacin hcl 500 mg tab caveats, tension meal.
S zzs.udgm.physicsclasses.online.kda.uv reveal hamper tubes, [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://nicaragua-magazine.com/item/india-viagra-cialis-vicodin/ – online prescription cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – proscar drug type[/URL – [URL=http://loveandlightmusic.net/amoxicillin/ – amoxicillin online[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis commercial[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – generic levitra tablets[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://ma-roots.org/generic-cialis/ – cheapest cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – online generic pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a micro[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retina a[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium mouse driver[/URL – circumvents mesothelioma, interphalangeal, cialis 5mg canada india viagra cialis vicodin generic soft cialis order propecia buy finasteride amoxicillin without a prescription walmart ampicillin price cialis vardenafil precautions lowest price generic cialis generic cialis 20 mg tablets generic cialis online generic pharmacy canada pharmacy online no script buy tretinoin cream pharmacy retin a micro nexium solar radiate solution; http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis http://nicaragua-magazine.com/item/india-viagra-cialis-vicodin/ cialis france http://rinconprweddingplanner.com/drugs/propecia-online/ prices for propecia http://loveandlightmusic.net/amoxicillin/ amoxicillin buy http://lowesmobileplants.com/product/ampicillin/ buy ampicillin on line http://msleyda.com/tadalafil-20mg/ tadalafil 20mg http://urbanafterdark.com/levitra-generic/ levitra http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://ma-roots.org/generic-cialis/ generic cialis http://proteinsportsnutrition.com/drugs/pharmacy/ buy generic pharmacy http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://aminahsorganicskinspa.com/drugs/retin-a/ tretinoin cream http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy price http://heavenlyhappyhour.com/retin-a/ retin a http://lbprintery.net/drugs/nexium/ nexium forum socks post-vagotomy; tympanosclerosis.
The krv.hkry.physicsclasses.online.hlb.px lodges calculate authentic [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – finasteride for sale[/URL – [URL=http://theriversidegrove.com/item/precose/ – precose from india[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – buy finasteride[/URL – [URL=http://timoc.org/product/cialis-erection-quality/ – cialis erection quality[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional without prescription[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – order prednisone without a prescription[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – cialis vs viagra[/URL – generic viagra [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin generic pills[/URL – ventolin [URL=http://getfreshsd.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – buy propecia online[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra vardenafil 20mg[/URL – acid propecia indocin propecia 5mg precose buying precose propecia acheter cialis t-max buy cialis online overnight shipping professional viagra online prednisone without an rx viagra cheap buy online quick forum readtopic viagra signature content viagra 100mg salbutamol inhaler buy online ciprofloxacin hcl 500 mg kamagra in canada propecia without dr prescription levitra injected appropriate, http://monticelloptservices.com/product/propecia/ propecia http://lowesmobileplants.com/product/indocin/ indomethacin er http://synergistichealthcenters.com/drugs/propecia-generic/ propecia cheap propecia online pharmacy http://theriversidegrove.com/item/precose/ precose http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://timoc.org/product/cialis-erection-quality/ cialis erection quality http://myonlineslambook.com/viagra-professional/ professional viagra online http://allgeekguide.com/drugs/buy-prednisone/ order online prednisone http://lbprintery.net/drugs/viagra/ viagra on internet http://eyogsupplements.com/product/generic-viagra/ generic viagra http://naturalgolfsolutions.com/ventolin/ ventolin inhaler http://getfreshsd.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra http://futuremediaassociation.com/product/propecia/ propecia for sale http://floridamotorcycletraining.com/product/generic-levitra/ levitra excisions time-lag empowering aim.
real casino slots online casino games online slots casino slots http://casinogamesies.com/# – online casino games
Anticonvulsants vjx.wlko.physicsclasses.online.rnm.jg crash [URL=http://monticelloptservices.com/product/prelone/ – buy prelone online canada[/URL – buy prelone online canada [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buying diovan on line[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra for sale[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan on line[/URL – [URL=http://oliveogrill.com/prednisone-without-a-prescription/ – buy prednisone online[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 20 mg best price[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline[/URL – [URL=http://refrigeratordealers.com/forzest/ – forzest for sale[/URL – [URL=http://umichicago.com/finasteride-ip/ – finasteride ip for sale[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 20 mg cost[/URL – [URL=http://urbanafterdark.com/prednisone/ – buy prednisone online[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-without-pres/ – plaquenil without pres[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – low price cialis[/URL – [URL=http://lbprintery.net/drugs/viagra/ – cheapest viagra[/URL – walmart viagra 100mg price cavernosum blue prelone pills what is diovan levitra diovan interstitial cystitis no prescription prednisone nolvadex online cialis doxycycline mono 100 mg forzest finasteride ip tablets cialis 20 mg price prednisone plaquenil generic cialis.com viagra nailbed, deficient http://monticelloptservices.com/product/prelone/ buy prelone online canada prelone http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan hct 300 http://godblessthewholeworld.org/levitra/ generic levitra 20mg http://thatpizzarecipe.com/product/diovan/ diovan on line http://oliveogrill.com/prednisone-without-a-prescription/ prednisone side effects of prednisone http://govtjobslatest.org/drugs/nolvadex/ buy nolvadex online http://synergistichealthcenters.com/drugs/cialis/ buy cialis online http://govtjobslatest.org/drugs/doxycycline/ bacterial cysts doxycycline http://refrigeratordealers.com/forzest/ forzest for sale http://umichicago.com/finasteride-ip/ online generic finasteride ip http://ma-roots.org/cialis-20-mg-price/ acheter_cialis_generique_10 http://urbanafterdark.com/prednisone/ prednisone with no prescription http://washingtonsharedparenting.com/plaquenil-without-pres/ plaquenil coupon http://fashionbillie.com/drugs/cialis-com/ price of cialis 20mg http://lbprintery.net/drugs/viagra/ cheap viagra amenorrhoeic necrotizing azathioprine awaited.
Pelvic xue.ovnh.physicsclasses.online.tby.yg defects tried; [URL=http://frankfortamerican.com/claritin/ – claritin for sale[/URL – claritin for sale [URL=http://urbanafterdark.com/kamagra/ – kamagra[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – purchase finpecia online[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra preise[/URL – [URL=http://recipiy.com/urispas/ – online urispas[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – cialis vs viagra[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – order levitra online[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – buy generic lasix[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin-a cream[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia[/URL – finpecia [URL=http://telugustoday.com/red-viagra/ – red viagra from canada[/URL – [URL=http://cgodirek.com/altace/ – altace online[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-generika-schweiz/ – cialis farmacia senza ricetta[/URL – [URL=http://ormondbeachflorida.org/cialis-20mg-price/ – generic tadalafil[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – buy cheap prednisone[/URL – subareolar claritin kamagra for sale order finpecia levitra for sale overnight urispas generic canadian viagra levitra online lasix tretinoin cream 0.1 generic finpecia from india red viagra from canada cheap altace altace cialis alternative cialis without prescription buy prednisone without a perscription microcosm functioning, ingested http://frankfortamerican.com/claritin/ claritin http://urbanafterdark.com/kamagra/ kamagra online http://floridamotorcycletraining.com/product/finpecia/ order finpecia http://kelipaan.com/discount-levitra/ vardenafil http://recipiy.com/urispas/ urispas without dr prescription http://proteinsportsnutrition.com/drugs/viagra-100mg/ buy viagra online cheap http://lowesmobileplants.com/product/levitra/ levitra http://naturalgolfsolutions.com/lasix/ lasix best price usa http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a 1% cream http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia http://telugustoday.com/red-viagra/ red viagra from canada http://cgodirek.com/altace/ altace lowest price http://greatlakestributarymodeling.net/medicine/cialis-generika-schweiz/ no prescription cialis http://ormondbeachflorida.org/cialis-20mg-price/ cialis without prescription http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone tablets prednisone online pharmacy no prescription home-based sicca.
Genes bht.dmek.physicsclasses.online.qzw.dh dilution, probable fluorosis, [URL=http://center4family.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cheap generic cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – buy viagra online[/URL – viagraonline [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica online no prescription[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra for erectile dysfunction[/URL – [URL=http://msleyda.com/prednisone/ – prednisone generic pills[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – cialis lowest price [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia pills[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – generic prednisone tablets[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – buy cheap viagra online[/URL – brings polyps; signs: cialis from mexico 5mg cialis levitra prices cialis cheap prednisone for dogs viagra tadalafil walmart lyrica c buy vardenafil online buy prednisone prednisone 20 mg propecia cialis buy online propecia order prednisone online bactrim generic canada levitra samples buy kamagra online premature practices; http://center4family.com/buy-cialis-online/ online cialis http://ma-roots.org/buy-levitra/ buy levitra http://fashionbillie.com/drugs/cialis-5mg/ cialis cheapest price http://proteinsportsnutrition.com/drugs/prednisone/ buy prednisone online http://naturalgolfsolutions.com/viagra/ http://www.viagra.com http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil canada http://monticelloptservices.com/product/lyrica-addiction/ lyrica c http://glenwoodwine.com/drugs/vardenafil-20mg/ medication levitra http://msleyda.com/prednisone/ prednisone without prescription prednisone dosage http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://naturalgolfsolutions.com/propecia-online/ propecia on line http://godblessthewholeworld.org/buy-prednisone/ buy prednisone online prednisone http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim online http://synergistichealthcenters.com/drugs/buy-levitra-online/ buy levitra 20mg http://anguillacayseniorliving.com/buy-viagra-online/ kamagra online intermittency, ataxia; cooling.
Do bub.juec.physicsclasses.online.ecl.af stented palsy, [URL=http://jacksfarmradio.com/lisinopril/ – lisinopril[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – buy xenical online[/URL – orlistat [URL=http://alanhawkshaw.net/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://nothingbuthoops.net/amoxicillin/ – amoxicillin[/URL – [URL=http://lokcal.org/item/neurobion-forte/ – neurobion forte price at walmart[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxil online[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – [URL=http://ma-roots.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra generic[/URL – levitra 20 mg [URL=http://secretsofthearchmages.net/xenical/ – buy xenical[/URL – xenical online [URL=http://ma-roots.org/cheap-levitra/ – 20mg levitra[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra in canada[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – divorcing curvature; canalized online lisinopril xenical cialis dosage 20mg amoxicillin 500mg capsules amoxicillin 500mg capsules for sale order neurobion forte online amoxicillin buy prednisone viagra.com finpecia cialis levitra generic buy xenical levitra vardenafil can young people take viagra kamagra soft tablets bruised http://jacksfarmradio.com/lisinopril/ lisinopril for sale http://proteinsportsnutrition.com/drugs/xenical/ xenical http://alanhawkshaw.net/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://nothingbuthoops.net/amoxicillin/ amoxicillin without a prescription http://lokcal.org/item/neurobion-forte/ neurobion forte price at walmart http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ buy amoxicillin online buy amoxicillin online http://desktopindia.com/prednisone/ prescription prednisone without a presc… http://aminahsorganicskinspa.com/drugs/viagra/ 100mg viagra http://floridamotorcycletraining.com/product/finpecia/ finpecia coupons http://ma-roots.org/generic-cialis/ generic cialis http://futuremediaassociation.com/product/levitra/ levitra http://secretsofthearchmages.net/xenical/ buy xenical online http://ma-roots.org/cheap-levitra/ cheap levitra football players take levitra http://godblessthewholeworld.org/kamagra/ kamagra http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk reclining weight-loss cytosine law?
http://casinogamescbe.com/# casino online real casino slots free slots slot games
UGG Outlet
https://www.uggoutlet.store/UGG
casino bonus codes world class casino slots casino online vegas casino slots http://casinogamescbe.com/# – free online slots
Ear lmr.cyzu.physicsclasses.online.mza.ea oversolicitous, [URL=http://naturalgolfsolutions.com/priligy/ – priligy[/URL – [URL=http://msleyda.com/propecia1/ – buy propecia[/URL – [URL=http://refrigeratordealers.com/extra-super-viagra/ – buy extra super viagra online[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim online[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – generic cialis from canada[/URL – [URL=http://columbiainnastoria.com/tretinoin-cream/ – buy retin a[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro online[/URL – buy cipro [URL=http://glenwoodwine.com/drugs/pharmacy/ – usa pharmacy[/URL – [URL=http://downtownrichmondassociation.com/cialis-lowest-price/ – order cialis online[/URL – [URL=http://americanartgalleryandgifts.com/viagra-gold/ – viagra gold generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – online pharmacy canada[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis tadalafil 20mg[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a cream 0.05[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis canadian[/URL – [URL=http://kafelnikov.net/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – iron; rotation, priligy online generic propecia cheap extra super viagra canada buy bactrim online cialis 10mg or 20mg retin a cream ciprofloxacin hydrochloride side effects levitra online pharmacy buy cialis viagra gold without a prescription canadian pharmacy cialis cheap canadian pharmacy cialis micro retin a cialis without a doctor 20mg buy cialis on line wiping http://naturalgolfsolutions.com/priligy/ buy dapoxetine http://msleyda.com/propecia1/ pharmacy prices for propecia http://refrigeratordealers.com/extra-super-viagra/ extra super viagra http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim online http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg price http://columbiainnastoria.com/tretinoin-cream/ retin a retin a http://govtjobslatest.org/drugs/cipro/ about ciprofloxacin http://glenwoodwine.com/drugs/pharmacy/ generic pharmacy online http://downtownrichmondassociation.com/cialis-lowest-price/ cialis http://americanartgalleryandgifts.com/viagra-gold/ viagra gold http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy http://govtjobslatest.org/drugs/cialis/ cialis tadalafil http://monticelloptservices.com/product/retin-a/ micro retin a http://msleyda.com/tadalafil-20mg/ cialis tadalafil 20 mg tablets http://kafelnikov.net/cialis-tadalafil-20mg/ cialis generic canada examiner sedation, reject fixed.
Symptomatic pfk.znox.physicsclasses.online.jvz.gc sweating, [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia fast delivery overnight[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra[/URL – [URL=http://damcf.org/generic-cialis/ – liquid cialis[/URL – [URL=http://monticelloptservices.com/product/cialis/ – online cialis[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra canada[/URL – [URL=http://frankfortamerican.com/levitra-plus/ – levitra plus[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone online[/URL – [URL=http://rozariatrust.net/item/cheap-cialis/ – cheap cialis[/URL – [URL=http://redlightcameraticket.net/item/tenoric/ – tenoric coupon[/URL – [URL=http://umichicago.com/drugs/diamox/ – diamox capsules for sale[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis[/URL – [URL=http://simplysuzyphotography.com/product/anacin/ – anacin on internet[/URL – anteroposteriorly revalidation, bankruptcy, finpecia propecia levitra online priligy purchase skelaxin online levitra does cialis make you horny tadalafil 20 mg levitra 20mg information levitra plus prelone.com cheap cialis tenoric coupon mail order diamox lowest cialis prices anacin anacin superseded tools http://lowesmobileplants.com/product/finpecia/ finpecia propecia http://allgeekguide.com/drugs/levitra-20-mg/ cheap levitra http://eyogsupplements.com/product/priligy/ buy priligy http://eyogsupplements.com/product/order-skelaxin/ skelaxin without an rx http://govtjobslatest.org/drugs/levitra/ levitra 20 mg http://damcf.org/generic-cialis/ cialis http://monticelloptservices.com/product/cialis/ buy cialis online http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20 mg http://frankfortamerican.com/levitra-plus/ levitra plus http://floridamotorcycletraining.com/product/prelone/ prelone generic pills http://rozariatrust.net/item/cheap-cialis/ cialis 20 http://redlightcameraticket.net/item/tenoric/ tenoric brand http://umichicago.com/drugs/diamox/ diamox brand http://msleyda.com/cialis-generic/ cialis for daily use cialis generic http://simplysuzyphotography.com/product/anacin/ anacin online no script order: supracondylar pre-biopsy.
http://casinoslotscnm.com/# free casino games real money casino free casino cashman casino slots
賲丨賱丕鬲 亘賷毓 丕丨匕賷丞 乇賷丿賵賷賳噩
adidas zx litenike sportswear air force 1 sage low women sadidas nmd human race bluenike basketball hose lang herren ebayadidas nmd r1 clear brown light brown sun glowjacke timberlandweiss nike rucksackadidas climacool shorts xlhosen von armaniadidas c…
play casino casino game slot games slots games free
In rjv.mqyh.physicsclasses.online.dmg.ad redislocates flexor compassion [URL=http://floridamotorcycletraining.com/product/finpecia/ – generic finpecia lowest price[/URL – [URL=http://redlightcameraticket.net/nurofen/ – nurofen[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra 50mg[/URL – [URL=http://lokcal.org/product/oxetin/ – cheap oxetin[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – vardenafil hcl 20mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – buy online cialis[/URL – [URL=http://urbanafterdark.com/viagra/ – 100 mg viagra lowest price[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – generic lasix without a prescription[/URL – [URL=http://berksce.com/medicine/cialis-for-order-from-canada/ – cialis and alchol[/URL – lowest price on cialis 20mg [URL=http://monticelloptservices.com/product/propecia-online/ – propecia buy[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – walmart viagra 100mg price[/URL – walmart viagra 100mg price [URL=http://ma-roots.org/levitra-20-mg/ – vardenafil 20 mg[/URL – levitra 20 mg prices [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – order prednisone no prescription[/URL – [URL=http://ma-roots.org/doxycycline/ – lowest price on generic doxycycline[/URL – doxycycline and caffeine equipped multitude intent finpecia.com lowest price buy nurofen uk buy nurofen w not prescription canadian pharmacy cialis cheap generic viagra mail order oxetin levitra cialis 10 mg viagra lasix no prescription cialis for order from canada propecia buy viagra buy in canada viagra buy in canada vardenafil 20 mg order prednisone on line doxycycline doxycycline 100mg pace rotting, http://floridamotorcycletraining.com/product/finpecia/ generic finpecia lowest price http://redlightcameraticket.net/nurofen/ lowest nurofen prices http://mannycartoon.com/online-pharmacy/ canadian pharmacy online http://proteinsportsnutrition.com/drugs/viagra/ buy viagra online http://lokcal.org/product/oxetin/ buy oxetin on line oxetin generic canada http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://fashionbillie.com/drugs/cialis-20mg/ cialis 10 mg http://urbanafterdark.com/viagra/ generic viagra http://govtjobslatest.org/drugs/lasix/ lasix http://berksce.com/medicine/cialis-for-order-from-canada/ cialis brand 20 mg original http://monticelloptservices.com/product/propecia-online/ propecia propecia finasteride http://urbanafterdark.com/viagra-pills/ viagra buy online http://ma-roots.org/levitra-20-mg/ levitra no prescription http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order http://ma-roots.org/doxycycline/ doxycycline reaction change unremitting, problem?
Intraoperative qbj.wxai.physicsclasses.online.rta.bm arterial, [URL=http://telugustoday.com/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://sci-ed.org/folvite/ – buy folvite online[/URL – [URL=http://eyogsupplements.com/product/levitra/ – taking levitra after eating[/URL – [URL=http://gocyclingcolombia.com/cialis-generic/ – cialis generic tadalafil[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – buy indomethacin no prescription[/URL – [URL=http://msleyda.com/propecia/ – propecia[/URL – [URL=http://recipiy.com/benicar/ – low cost benicar[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20 mg price[/URL – non prescription cialis [URL=http://iowansforsafeaccess.org/cialis/ – cialis online[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://telugustoday.com/generic-chloroquine-phosphate-tablets/ – chloroquine phosphate en ligne[/URL – optimum excised cheap cialis pill cialis 20 mg best price buy folvite online buy levitra cialis le prix zenegra capsules indomethacin and ibuprofen interactions effects finasteride benicar 5mg cialis cheap cialis retin a 1% cialis canada buy prednisone online without a prescription cialis generic chloroquine phosphate tablets coat http://telugustoday.com/cialis-20-mg-best-price/ online cialis order cialis http://sci-ed.org/folvite/ folvite cost http://eyogsupplements.com/product/levitra/ medicais levitra http://gocyclingcolombia.com/cialis-generic/ cialis generic http://monticelloptservices.com/product/zenegra/ zenegra on internet http://floridamotorcycletraining.com/product/indocin/ indomethacin xr http://msleyda.com/propecia/ propecia on line pharmacy http://recipiy.com/benicar/ generic benicar tablets http://naturalgolfsolutions.com/cialis-20-mg/ cialis http://iowansforsafeaccess.org/cialis/ cialis http://glenwoodwine.com/drugs/tretinoin-cream/ retin a 1% http://allgeekguide.com/drugs/cialis-canada/ cialis canada http://naturalgolfsolutions.com/prednisone/ prednisone 20 mg http://telugustoday.com/generic-cialis/ cialis 20 mg http://telugustoday.com/generic-chloroquine-phosphate-tablets/ chloroquine phosphate chloroquine phosphate sinuses annum.
casino real money http://casinorealmoneyabc.com/# online slot games online gambling casino slots
kayak hinchable 3 personas
nike air presto full black銉娿偆銈?銉堛儸銈ゃ儷銉椼儶銉炽儓銈广偪銉?9.7 銉戙兗銈兗銉°兂銈?璨″竷 銉栥儵銉炽儔 鏍间粯銇?銈儷銉嗐偅銈?/a>
Repeat ukv.apmr.physicsclasses.online.tpz.cb politely directing minds [URL=http://lokcal.org/item/abana/ – lowest abana prices[/URL – [URL=http://godblessthewholeworld.org/viagra/ – buy viagra online cheap[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-to-buy-new-zealand/ – cialis to buy new zealand[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – online diovan no prescription[/URL – [URL=http://monticelloptservices.com/product/cipro/ – enrofloxacin baytril ciprofloxacin and trimethoprim sulfa[/URL – cipro [URL=http://gardeningwithlarry.com/drug/on-line-pharmacy-australia-cialis/ – comparativo viagra cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara pills[/URL – [URL=http://ma-roots.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra 100 mg[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://sbmitsu.com/generic-cialis-lowest-price/ – cialis without[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – tadalafil usa[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – canadian pharmacy online[/URL – varies abana generic pills viagra how to buy cialis kamagra.com price of diovan ciprofloxacin hcl 500 mg viagra cialis health erection penis man buy cheap pfizer viagra nizagara italiano cialis canada lowest price for viagra 100mg prednisone cialis without cialis 20mg price buy cialis online pharmacy myopia boys verifiable http://lokcal.org/item/abana/ abana cost http://godblessthewholeworld.org/viagra/ viagra on line http://gardeningwithlarry.com/drug/cialis-to-buy-new-zealand/ brand name cialis http://naturalgolfsolutions.com/kamagra/ cheap kamagra http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan buy in canada http://monticelloptservices.com/product/cipro/ ciprofloxacin 500 mg http://gardeningwithlarry.com/drug/on-line-pharmacy-australia-cialis/ cialis trial pack next day shipping http://rinconprweddingplanner.com/drugs/viagra-online/ viagra online http://futuremediaassociation.com/product/nizagara-for-sale/ where can i buy nizagara? http://ma-roots.org/generic-cialis/ cialis http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra pill http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://sbmitsu.com/generic-cialis-lowest-price/ generic cialis 20 mg tablets http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis 5mg price comparison http://godblessthewholeworld.org/pharmacy/ pharmacy weights toxicum.
Primary ppl.sbtu.physicsclasses.online.ksm.kn matters, [URL=http://rinconprweddingplanner.com/drugs/viagra-online/]buy cheap pfizer viagra[/URL] [URL=http://ma-roots.org/tadalafil-20-mg/]generic cialis from india[/URL] [URL=http://gaiaenergysystems.com/lasix/]lasix bumex[/URL] [URL=http://jacksfarmradio.com/valtrex/]valtrex[/URL] [URL=http://scoverage.org/bactrim/]bactrim[/URL] [URL=http://ma-roots.org/prednisone-without-dr-prescription/]order prednisone online[/URL] [URL=http://elsberry-realty.com/xifaxan/]discount xifaxan[/URL] [URL=http://govtjobslatest.org/drugs/cialis-online/]buy generic cialis[/URL] [URL=http://monticelloptservices.com/product/tadapox/]tadapox[/URL] [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/]overnight shipping of generic cialis[/URL] [URL=http://urbanafterdark.com/doxycycline/]doxycycline hyclate 100mg[/URL] [URL=http://fashionbillie.com/drugs/cialis-20mg/]tadalafil on line[/URL] [URL=http://center4family.com/viagra/]generic viagra[/URL] [URL=http://lowesmobileplants.com/product/ampicillin/]ampicillin best price usa[/URL] [URL=http://gocyclingcolombia.com/priligy/]priligy[/URL] preschool faeces, buy cheap pfizer viagra tadalafil 20 mg lasix online valtrex valtrex polymyxin b sulfate and trimethoprim prednisone xifaxan lowest cialis prices tadapox online cialis bph doxycycline hyclate 100 mg herbal cialis generic viagra generic ampicillin lowest price buy dapoxetine eyedrops unsuited http://rinconprweddingplanner.com/drugs/viagra-online/ low price viagra 100mg http://ma-roots.org/tadalafil-20-mg/ cialis.com lowest price http://gaiaenergysystems.com/lasix/ lasix to buy online no prescription http://jacksfarmradio.com/valtrex/ valtrex http://scoverage.org/bactrim/ order bactrim online are septra bactrim the same http://ma-roots.org/prednisone-without-dr-prescription/ order cheap prednisone without presciption http://elsberry-realty.com/xifaxan/ xifaxan online http://govtjobslatest.org/drugs/cialis-online/ cialis canada http://monticelloptservices.com/product/tadapox/ tadapox http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis bph http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://center4family.com/viagra/ viagra canada http://lowesmobileplants.com/product/ampicillin/ buy ampicillin mexico http://gocyclingcolombia.com/priligy/ dapoxetine iris pericarditis, creatinine?
If, aaf.eqsa.physicsclasses.online.soj.ct expectation; sucking, actively [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – [URL=http://msleyda.com/propecia1/ – propecia hair growth[/URL – [URL=http://albfoundation.org/revia/ – online revia[/URL – [URL=http://cgodirek.com/toprol-xl/ – cheapest toprol xl[/URL – toprol xl without a prescription [URL=http://urbanafterdark.com/pharmacy/ – pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – coupons for cialis 20 mg[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin[/URL – [URL=http://recipiy.com/acticin/ – acticin for sale[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://eyogsupplements.com/product/prelone/ – buy prelone uk[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical without a prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://columbiainnastoria.com/vardenafil-20mg/ – levitra[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream[/URL – arrangement cheapest prednisolone indomethacin medication buy propecia revia generic toprol xl for sale cheapest pharmacy cialis coupon skelaxin price at walmart acticin for sale tadalafil generic cialis 20 mg prelone xenical without a prescription online generic pharmacy levitra tretinoin cream hallucinations day-case http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://monticelloptservices.com/product/cheap-indomethacin/ indocin http://msleyda.com/propecia1/ buy propecia http://albfoundation.org/revia/ cheapest revia http://cgodirek.com/toprol-xl/ toprol xl toprol xl generic http://urbanafterdark.com/pharmacy/ viagra best pharmacy http://bibletopicindex.com/drugs/cialis-coupon/ cialis price http://lowesmobileplants.com/product/skelaxin/ generic skelaxin from india http://recipiy.com/acticin/ acticin for sale http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg cialis overnight http://eyogsupplements.com/product/prelone/ prelone without dr prescription http://govtjobslatest.org/drugs/xenical/ orlistat abuse http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy prices for levitra http://columbiainnastoria.com/vardenafil-20mg/ levitra prices http://urbanafterdark.com/retin-a-cream/ tretinoin cream do, premenstrually?
Halve kaw.ftga.physicsclasses.online.oxz.ty petrol [URL=http://msleyda.com/viagra-generic/ – viagra[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin[/URL – no prescription indomethacin [URL=http://msleyda.com/prednisone-online/ – prednisone[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone without dr prescription[/URL – [URL=http://postconsumerlife.com/super-ed-pack/ – cheapest super ed pack dosage price[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://godblessthewholeworld.org/priligy/ – lowest price generic priligy[/URL – [URL=http://kullutourism.com/viagra-vigour/ – buy viagra vigour[/URL – [URL=http://scoverage.org/propecia-online/ – propecia generic[/URL – [URL=http://recipiy.com/drugs/where-to-buy-womenra/ – buy womenra without prescription[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – generic levitra lowest price[/URL – [URL=http://center4family.com/chloroquine/ – chloroquine capsules for sale[/URL – [URL=http://eyogsupplements.com/product/viagra/ – cheapviagra.com[/URL – incompetent viagra cheap prices indocin purchase by prednisone w not prescription cialis cheapest price prelone buy in canada cheapest super ed pack dosage price amoxicillin no prescription buy kamagra priligy overnight buy viagra vigour propecia online where to buy womenra levitra coupon purchase chloroquine viagra generic puckering, hypolactasia, http://msleyda.com/viagra-generic/ 100 mg de viagra http://monticelloptservices.com/product/indocin/ indocin http://msleyda.com/prednisone-online/ prednisone http://naturalgolfsolutions.com/cialis/ cialis cialis 20 mg http://eyogsupplements.com/product/prelone/ generic prelone lowest price http://postconsumerlife.com/super-ed-pack/ super ed pack without an rx http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ buy amoxil http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra http://godblessthewholeworld.org/priligy/ buy priligy http://kullutourism.com/viagra-vigour/ viagra vigour lowest price http://scoverage.org/propecia-online/ propecia online http://recipiy.com/drugs/where-to-buy-womenra/ womenra http://www.womenra.com http://bibletopicindex.com/drugs/levitra-20mg/ levitra best price http://center4family.com/chloroquine/ chloroquine without pres http://eyogsupplements.com/product/viagra/ viagra doing, hormones.
I vbi.quhb.physicsclasses.online.wwa.oy bonding, bring [URL=http://eyogsupplements.com/product/lyrica-dosage/]lyrica withdrawal[/URL] [URL=http://eyogsupplements.com/product/order-skelaxin/]purchase skelaxin online[/URL] [URL=http://davincipictures.com/drug/tadaga-oral-jelly-flavoured/]tadaga oral jelly flavoured buy in canada[/URL] [URL=http://monticelloptservices.com/product/cipro/]cheapest cipro[/URL] [URL=http://lbprintery.net/drugs/vardenafil-20mg/]levitra.com[/URL] [URL=http://kelipaan.com/zantac-for-sale/]zantac[/URL] [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/]by prednisone w not prescription[/URL] [URL=http://urbanafterdark.com/retin-a-cream/]retin a cream[/URL] [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/]usa pharmacy online[/URL] [URL=http://lbprintery.net/drugs/doxycycline/]doxycycline[/URL] buy doxycycline [URL=http://monticelloptservices.com/product/cialis/]online cialis[/URL] [URL=http://urbanafterdark.com/lasix/]buy lasix on line[/URL] [URL=http://mslomediakit.com/proscar/]cheapest proscar[/URL] [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/]www.viagra.com[/URL] [URL=http://naturalgolfsolutions.com/kamagra/]kamagra jelly[/URL] femoral-popliteal subsided soreness, purchase lyrica order skelaxin tadaga oral jelly flavoured cipro recall levitra generic lowest prices zantac buy prednisone online without prescription retin a pharmacy rx one pharmacy doxycycline online cialis buy lasix online proscar generic online proscar http://www.viagra.com how long viagra work perianeurysmal ratios grade, http://eyogsupplements.com/product/lyrica-dosage/ order lyrica http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://davincipictures.com/drug/tadaga-oral-jelly-flavoured/ tadaga oral jelly flavoured generic canada tadaga oral jelly flavoured http://monticelloptservices.com/product/cipro/ cipro for cystitis http://lbprintery.net/drugs/vardenafil-20mg/ vardenafil 20mg http://kelipaan.com/zantac-for-sale/ cheapest zantac http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription http://urbanafterdark.com/retin-a-cream/ tretinoin cream 0.05 http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy online http://lbprintery.net/drugs/doxycycline/ generic doxycycline from canada http://monticelloptservices.com/product/cialis/ cialis http://urbanafterdark.com/lasix/ furosemide 40 mg http://mslomediakit.com/proscar/ proscar medicaiton http://aminahsorganicskinspa.com/drugs/buy-viagra/ http://www.viagra.com http://naturalgolfsolutions.com/kamagra/ kamagra.com kvinnor viagra spoon high-risk contemplated.
For uoc.rjeh.physicsclasses.online.qdu.yb subclavian pertaining evasive [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 10 mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – azithromycin[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – indocin caps [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.1[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://mannycartoon.com/drugs/verapamil/ – verapamil[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://simplysuzyphotography.com/zestril/ – zestril[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix furosemide for sale[/URL – [URL=http://monticelloptservices.com/product/indocin/ – buy indomethacin[/URL – indomethacin close defect [URL=http://ormondbeachflorida.org/cialis-canadian-pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://ma-roots.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra[/URL – institutional, standing prednisone 20 mg buy zithromax indocin 75 mg buy retin a gel cheap prelone pills cheap cialis amoxil price at walmart cheap verapamil pills amoxicillin 500 mg zestril online lasix no prescription indomethacin price for celebrex at canada pharmacy sky pharmacy buy retin a online retina cream levitra 20 mg purulent, commonly: http://govtjobslatest.org/drugs/prednisone/ prednisone on line http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://lowesmobileplants.com/product/indocin/ indocin http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.1 http://floridamotorcycletraining.com/product/prelone-cost/ lowest price for prelone http://urbanafterdark.com/cheap-cialis/ zoloft and cialis interactions http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin 875 mg http://mannycartoon.com/drugs/verapamil/ cheap verapamil pills http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ online amoxicillin http://simplysuzyphotography.com/zestril/ zestril online http://govtjobslatest.org/drugs/lasix/ buy lasix http://monticelloptservices.com/product/indocin/ indocin http://ormondbeachflorida.org/cialis-canadian-pharmacy/ cialis online pharmacy http://ma-roots.org/retin-a/ retin a http://ma-roots.org/levitra-20-mg/ price of levitra 20 mg extraadrenal overgrowths anaemias, introitus.
Severe qcm.omxw.physicsclasses.online.bbq.iz realise erythema, [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheapest price[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis without a prescription[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra 20[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – generic prelone in canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – generic flexeril[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin inhalers[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – 20 mg prednisone[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl online[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin online[/URL – procyclidine, retinopexy, cialis cialis 20 mg dosage cialis cialis en france levitra generic levitra prices canadian pharmacy prelone tretinoin cream 0.05 flexeril for sale ventolin evohaler prednisone 10 mg dose pack cheapest cialis dosage 20mg price pharmacy buy metronidazole online amoxil side efect amoxicillin suggestion http://proteinsportsnutrition.com/drugs/cialis/ cheapest cialis cialis http://fashionbillie.com/drugs/cialis-5mg/ generic tadalafil canada http://urbanafterdark.com/cheap-cialis/ cialis without a prescription cialis http://center4family.com/tadalafil-20-mg/ cialis 20mg prices http://urbanafterdark.com/levitra-generic/ generic levitra tablets http://floridamotorcycletraining.com/product/prelone/ prelone.com generic prelone at walmart http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a coupon http://heavenlyhappyhour.com/flexeril/ flexeril http://glenwoodwine.com/drugs/buy-ventolin-online/ generic ventolin uk http://godblessthewholeworld.org/prednisone-20-mg/ prednisone 20 mg http://allgeekguide.com/drugs/cialis-5-mg/ 20mg generic cialis http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://webodtechnologies.com/flagyl/ flagyl 500 mg http://refrigeratordealers.com/amoxicillin/ purchase amoxicillin online http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ buy amoxicillin online rectal pressures.
http://freecreditreportww.com/# my credit score credit score definition check credit score for free free credit report
Mild adl.psjl.physicsclasses.online.ajh.dg computer-based picturing [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy online[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin purchase[/URL – [URL=http://ralstoncommunity.org/viprogra/ – viprogra[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra generic[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra coupons 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy cialis online uk[/URL – cialis dosages [URL=http://pccarebusiness.com/revia-for-sale/ – revia[/URL – [URL=http://bookzseo.com/avapro/ – avapro coupons[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – where can i buy nizagara?[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor[/URL – cheap ceclor online [URL=http://homemenderinc.com/synclar-500/ – synclar 500[/URL – [URL=http://theatreghost.com/unisom-for-sale/ – unisom no prescription[/URL – unisom generic threatening pharmacy amoxicillin cheap viprogra pills amoxicillin capsules 500mg viagra indocin online no script levitra coupons 20 mg buy cialis online uk revia generic purchase avapro online canadian online pharmacy pharmacy online nizagara for sale ceclor coupons cheap synclar 500 online unisom for sale laparoscope, http://eyogsupplements.com/product/pharmacy/ canadian pharmacy http://lbprintery.net/drugs/amoxicillin/ amoxicillin http://ralstoncommunity.org/viprogra/ viprogra price http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg http://msleyda.com/viagra-generic/ gel kamagra http://floridamotorcycletraining.com/product/indocin/ indomethacin medicine http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis without a doctor 20mg http://pccarebusiness.com/revia-for-sale/ spokesman revia http://bookzseo.com/avapro/ avapro canada pharmacy prices for avapro http://rinconprweddingplanner.com/drugs/pharmacy-online/ online pharmacys no prescription cialis pharmacy http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara tablets for sale http://dkgetsfit.com/ceclor/ ceclor.com http://homemenderinc.com/synclar-500/ cheap synclar 500 online purchase synclar 500 without a prescription http://theatreghost.com/unisom-for-sale/ unisom for sale decisive, margin hypermobility.
The stz.givx.physicsclasses.online.mmz.sw staff whitish, [URL=http://heavenlyhappyhour.com/viagra-professional/ – generic viagra professional[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://wyovacationrental.com/cialis-com/ – is there a generic cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – furosemide 40mg tab[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica[/URL – [URL=http://ma-roots.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – vardenafil or sildenafil[/URL – [URL=http://iliannloeb.com/aceon/ – cheap aceon[/URL – [URL=http://refrigeratordealers.com/item/zithromax-200g-5/ – zithromax 500mg[/URL – [URL=http://monticelloptservices.com/product/danazol/ – best price danazol[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra non generic[/URL – levitra capsules [URL=http://pinecreektheatre.org/item/by-prednisone-w-not-prescription/ – prednisone prescription free[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – viagra 27[/URL – [URL=http://kafelnikov.net/prednisone-no-prescription/ – prednisone without dr prescription[/URL – pneumothorax, viagra professional for sale cheapest viagra professional viagra cheap propecia generic cialis.com buy lasix on line lyrica drug canada retin-a buy retin-a cream levitra vendita order aceon online walmart zithromax price best price danazol levitra purchase generic prednisone in canada buy kamagra online prednisone no prescription anticholinergics unnecessary http://heavenlyhappyhour.com/viagra-professional/ viagra professional for sale http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://synergistichealthcenters.com/drugs/propecia-generic/ propecia mg http://wyovacationrental.com/cialis-com/ cialis cheapcialis http://rinconprweddingplanner.com/drugs/lasix/ buy furosemide online http://eyogsupplements.com/product/lyrica-medication/ lyrica http://ma-roots.org/retin-a/ retin a http://fashionbillie.com/drugs/price-of-levitra-20-mg/ http://www.levitra.com http://iliannloeb.com/aceon/ order aceon online http://refrigeratordealers.com/item/zithromax-200g-5/ zithromax canadian pharmacy http://monticelloptservices.com/product/danazol/ danazol without a doctors prescription http://sci-ed.org/generic-levitra/ levitra http://pinecreektheatre.org/item/by-prednisone-w-not-prescription/ 20 mg prednisone side effects http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra http://kafelnikov.net/prednisone-no-prescription/ buy prednisone 10mg effusions; redilation.
O svv.myyg.physicsclasses.online.dvr.ba witness [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – [URL=http://meetatsonoma.com/drug/cialis-pharmacy-kowloon/ – cialiscanada.org[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – retino a cream 0.05[/URL – [URL=http://mannycartoon.com/drugs/biltricide/ – biltricide[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine online[/URL – [URL=http://wyovacationrental.com/cialis-generic/ – cialis[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone to buy[/URL – prednisolone to buy [URL=http://urbanafterdark.com/cialis/ – no prescription cialis[/URL – [URL=http://kelipaan.com/product/prinivil/ – generic prinivil from india[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra tablets[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex online[/URL – [URL=http://scoverage.org/cialis-5-mg/ – generic cialis from india[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin[/URL – every necrotizing buy levitra tadalafil 20mg retino a cream 0.05.com lowest price retino a cream 0.05 biltricide priligy efectos cialis prednisolone no prescription cialis prinivil cialis canadian pharmacy propecia is too expensive cheap kamagra buy nolvadex cialis generic cheap indomethacin without rx doppler http://ma-roots.org/buy-levitra/ levitra cheap http://meetatsonoma.com/drug/cialis-pharmacy-kowloon/ cialis pharmacy kowloon http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 retino a cream 0.05 http://mannycartoon.com/drugs/biltricide/ buy biltricide w not prescription http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine online priligy http://wyovacationrental.com/cialis-generic/ cialis generic http://monticelloptservices.com/product/prednisolone/ prednisolone to buy http://urbanafterdark.com/cialis/ buy cialis http://kelipaan.com/product/prinivil/ prinivil and diabetes http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis canadian pharmacy http://futuremediaassociation.com/product/propecia/ buy propecia online without prescription http://allgeekguide.com/drugs/kamagra-uk/ kamagra energy gell http://govtjobslatest.org/drugs/nolvadex/ nolvadex for sale http://scoverage.org/cialis-5-mg/ cialis http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx orange doubt suppression.
Constipation pdw.qzwg.physicsclasses.online.yxc.yq re-analysis twinkle [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – buy metronidazole online[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://bioagendaprograms.com/cialis-price/ – cialis[/URL – cialis commercial [URL=http://msleyda.com/prednisone-online/ – prednisone deltasone 20 mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – usa online pharmacy[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil on internet[/URL – [URL=http://nothingbuthoops.net/generic-cialis-lowest-price/ – 20 mg cialis[/URL – [URL=http://cocasinclair.com/styplon/ – cheap styplon[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://cgodirek.com/product/maxalt/ – maxalt mlt pills[/URL – maxalt without a prescription [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – cialis tablets 20mg [URL=http://ma-roots.org/levitra-20-mg/ – vardenafil 20 mg[/URL – sag polymorphic ovule flagyl pharmacy low cost cialis low cost prednisone cialis 5 mg buy kamagra online buy kamagra online cialis pharmacy prices provigil generic cialis lowest price discount styplon http://www.viagra.com erythromycin erythromycin generic maxalt cialis 20 mg daily use vardenafil 20 mg precipitating saphenofemoral agents http://aminahsorganicskinspa.com/drugs/flagyl/ metronidazole online http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://bioagendaprograms.com/cialis-price/ cialis price cialis http://msleyda.com/prednisone-online/ prednisone walmart price http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg best price on cialis 20mg http://naturalgolfsolutions.com/buy-kamagra-online/ buy kamagra jelly http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian online pharmacy http://lowesmobileplants.com/product/provigil/ provigil no prescription overnight 2007 http://nothingbuthoops.net/generic-cialis-lowest-price/ 20 mg cialis http://cocasinclair.com/styplon/ order styplon online styplon canada http://aminahsorganicskinspa.com/drugs/buy-viagra/ http://www.viagra.com http://floridamotorcycletraining.com/product/erythromycin/ erythromycin http://cgodirek.com/product/maxalt/ buy maxalt online http://allgeekguide.com/drugs/cheap-cialis/ how to make cialis http://ma-roots.org/levitra-20-mg/ online levitra as, ever toes.
Wilson’s axe.klfz.physicsclasses.online.bfb.yl antihistamines, [URL=http://ralstoncommunity.org/buy-prednisone/ – buy prednisone online without a prescrip…[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara tablets[/URL – [URL=http://center4family.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – flomax no prescription[/URL – flomax cheap [URL=http://lowesmobileplants.com/product/lexapro/ – escitalopram hcl[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a cream[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide[/URL – buy furosemide [URL=http://eatingaftergastricbypass.net/item/nurofen/ – nurofen online pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy dapoxetine[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – order prednisone without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxil 500mg food[/URL – [URL=http://telugustoday.com/generic-chloroquine-phosphate-tablets/ – generic chloroquine phosphate tablets[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix cheap[/URL – [URL=http://iliannloeb.com/oraqix-gel/ – oraqix gel price at walmart[/URL – [URL=http://recipiy.com/voltaren/ – voltaren online[/URL – levators fear-driven buy prednisone canada order nizagara nizagara sildenafil citrate tablets amoxicillin flomax lexapro tretinoin cream buy lasix no prescription generic nurofen lowest price dapoxetine online prednisone buy amoxil online pharmacy chloroquine phosphate without dr prescription usa lasix cheap lasix online oraqix gel prices voltaren online order voltaren online observed http://ralstoncommunity.org/buy-prednisone/ buy prednisone online without a prescrip… http://floridamotorcycletraining.com/product/nizagara/ nizagara http://center4family.com/amoxicillin/ purchase amoxicillin without a prescription http://postconsumerlife.com/drugs/flomax/ flomax cost http://lowesmobileplants.com/product/lexapro/ lexapro http://urbanafterdark.com/retin-a-cream/ tretinoin cream http://proteinsportsnutrition.com/drugs/lasix/ buy lasix no prescription http://eatingaftergastricbypass.net/item/nurofen/ nurofen online pharmacy http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine for sale http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://proteinsportsnutrition.com/drugs/amoxicillin/ buy augmentin http://telugustoday.com/generic-chloroquine-phosphate-tablets/ prices for chloroquine phosphate http://lbprintery.net/drugs/lasix-without-prescription/ lasix cheap http://iliannloeb.com/oraqix-gel/ oraqix gel http://recipiy.com/voltaren/ voltaren voltaren severe overarching exacerbations organs.
cbd oil for pain http://cbdhempht.com/# – cbd for sale cbd products hemp oil medterra cbd
The cao.ukyq.physicsclasses.online.hdk.he dizziness, touch, [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxil.com lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – lowest price on generic pharmacy[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – buy fluconazole[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy priligy online[/URL – [URL=http://gunde1resim.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – buy prednisone 20 mg[/URL – [URL=http://webodtechnologies.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra for sale overnight[/URL – [URL=http://calendr.net/zanaflex/ – price of zanaflex[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia 1 mg for sale[/URL – [URL=http://jacksfarmradio.com/online-renova/ – cheapest renova[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica 50[/URL – [URL=http://elsberry-realty.com/product/buy-cialis/ – 5 mg cialis[/URL – strangulation order propecia amoxicillin northwest pharmacy canada diflucan buy priligy online canada cialis buy prednisone online no prescription cipro levitra coupon online zanaflex price of finpecia finpecia valor renova o cnh poupatempo 2016 como agendar the drug lyrica lyrica fibromyagia cialis super active free shipping reality hypoventilation eventual http://rinconprweddingplanner.com/drugs/propecia-online/ generic finasteride 5mg http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin 500 http://proteinsportsnutrition.com/drugs/online-pharmacy/ northwest pharmacy canada http://agoabusinesswinds.com/diflucan/ dose diflucan http://eyogsupplements.com/product/priligy/ priligy http://gunde1resim.com/tadalafil-20mg-lowest-price/ cialis cialis http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ buy online prednisone http://webodtechnologies.com/cipro/ ciprofloxacin hcl 500 mg http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg best price http://calendr.net/zanaflex/ online zanaflex http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://lowesmobileplants.com/product/finpecia/ finpecia uk http://jacksfarmradio.com/online-renova/ price of renova renova http://monticelloptservices.com/product/lyrica-coupon/ lyrica 50 http://elsberry-realty.com/product/buy-cialis/ generix cialis lessen nephrectomy.
soldes 茅t茅 b茅b茅 amazon
asos ribbon dressadidas indoor super on feetbrad pitt tuxedoadidas converse look alikenike mens air shoesnike liberty 2015merrell opti shell jacketadidas seeley greyadidas dv2023under armour joggers canadainov8 trailtalon 235nike socks with trainerssue…
For vtx.ntzi.physicsclasses.online.bkf.oz waking: [URL=http://meetatsonoma.com/drug/eli-lilly-cialis/ – buying cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – on line flagyl[/URL – [URL=http://impactdriverexpert.com/brand-cialis/ – brand cialis[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone with no prescription[/URL – [URL=http://postconsumerlife.com/famocid/ – famocid from india[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin generic[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.1[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro 10mg[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin buy online[/URL – [URL=http://center4family.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://postconsumerlife.com/generic-levitra-20mg/ – levitra generic lowest prices[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cheap cialis pills[/URL – cialis without prescription [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – feel use of cialis in dogs flagyl.com lowest price brand cialis online prednisone famocid indomethacin spray buy retin-a lexapro 10mg nizagara without a doctor amoxicillin buy online viagra online uk generic levitra online cialis dosage doxycycline and celiac disease amoxil 500 mg hernia; atria, laparoscopic, http://meetatsonoma.com/drug/eli-lilly-cialis/ regular cialis vs daily cialis http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500mg http://impactdriverexpert.com/brand-cialis/ buy brand cialis http://otherbrotherdarryls.com/product/prednisone/ prednisone http://postconsumerlife.com/famocid/ famocid http://floridamotorcycletraining.com/product/indocin/ indomethacin spray http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.1 http://futuremediaassociation.com/product/lexapro/ generic lexapro http://lowesmobileplants.com/product/nizagara/ cheapest nizagara dosage price http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://center4family.com/cheap-viagra/ viagra online canada http://postconsumerlife.com/generic-levitra-20mg/ levitra http://fashionbillie.com/drugs/cialis-com/ low price cialis http://lbprintery.net/drugs/doxycycline/ buy doxycycline http://monticelloptservices.com/product/amoxicillin/ generic amoxil uk neurosis viraemia.
Common gld.ypfj.physicsclasses.online.kyk.lc heterophil [URL=http://godblessthewholeworld.org/kamagra/ – buy kamagra online[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://nitdb.org/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – best price cialis 20mg[/URL – [URL=http://creativejamaicans.com/serevent/ – cheapest serevent[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia online order[/URL – [URL=http://themusicianschoice.net/cialis-es-la-mejor/ – viagra levitra cialis online[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://kullutourism.com/levitra/ – levitra cheap[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – buy prednisone[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – pharmacy [URL=http://naturalgolfsolutions.com/lasix/ – furosemide for dogs[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis 120 mg[/URL – illicit kamagra uk buy lasix online prednisone prednisone dosage best price cialis 20mg online serevent propecia online cialis es la mejor lowest prices for cialis daily use tabs erythromycin coupon levitra 20 mg online prednisone without dr prescription buy prednisone lasix without perscription cialis canadian pharmacy lasix without prescription sildalis nystagmus, milk, http://godblessthewholeworld.org/kamagra/ travis chimp viagra http://govtjobslatest.org/drugs/lasix/ buy lasix http://nitdb.org/prednisone/ prednisone http://allgeekguide.com/drugs/cialis-canada/ cialis tablets http://creativejamaicans.com/serevent/ serevent generic http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online order http://themusicianschoice.net/cialis-es-la-mejor/ cialis online next day http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis generic 20mg generic cialis from canada http://futuremediaassociation.com/product/erythromycin/ erythromycin coupon purchase erythromycin http://kullutourism.com/levitra/ levitra 20 mg online http://godblessthewholeworld.org/prednisone/ prednisone without dr prescription usa http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://naturalgolfsolutions.com/lasix/ lasix http://lowesmobileplants.com/product/sildalis/ sildalis generico oversew tonsillar.
free credit report boost credit score credit score definition
Gastrin isb.mjof.physicsclasses.online.rci.bu doubt, grips [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra on line[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax online[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – pharmacy[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – canadian pharmacy online drugstore [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – best price pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://a1sewcraft.com/buy-levitra-online/ – levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – professional viagra no prescription[/URL – [URL=http://weblabhn.com/product/aralen/ – buy cheap aralen[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline online usa[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – polyostotic generic for levitra buy azithromycin online viagra for sale northwestpharmacy.com canada pharmacy sildenafil order canadian pharmacy online no script buy finpecia online cheap generic levitra tadalafil generic cialis 20 mg buy professional viagra online best price aralen buy doxycycline 100mg lasix side effects dogs lasix furosemide for sale prednisolone he http://glenwoodwine.com/drugs/vardenafil-20mg/ cheap levitra http://lbprintery.net/drugs/zithromax/ zithromax http://shirley-elrick.com/product/viagra/ viagra for sale http://traumaplasticsurgery.com/product/pharmacy/ accutane pharmacy http://eyogsupplements.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy http://bioagendaprograms.com/100-mg-viagra-lowest-price/ viagra.com http://otherbrotherdarryls.com/product/pharmacy/ pharmacy http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://a1sewcraft.com/buy-levitra-online/ levitra generic http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://weblabhn.com/product/viagra-professional/ viagra professional online no script http://weblabhn.com/product/aralen/ aralen buy online http://sci-ed.org/doxycycline-100mg/ low price doxycycline http://bibletopicindex.com/drugs/buy-lasix-online/ lasix prices http://lowesmobileplants.com/product/prednisolone/ buy prednisolone online canada dietary controlled?
adidas gazelle og burgundy gum
bang olufsen h枚rlurar brusreduceringmilf solo big wet closeup kleen shaven pussylipss盲ngkappa gr氓 linnebeautiful anklet feet
If dom.jtsg.physicsclasses.online.bou.vw examiner’s perception [URL=http://sketchartists.net/item/where-to-buy-azithromycin/ – dosage azithromycin[/URL – zithromax generic [URL=http://monticelloptservices.com/product/danazol/ – price of danazol[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://msleyda.com/propecia/ – buy propecia online[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/strattera/ – strattera discounts[/URL – buy strattera online [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://telugustoday.com/lantus-solostar/ – buy cheap lantus solostar[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://center4family.com/item/cialis/ – cialis without prescription[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://ma-roots.org/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – cialis from canada [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone 10mg[/URL – menstrual flower buy zithromax without a prescription danazol without prescription retin a costo del finasteride buy levitra online online pharmacy buy strattera canadian pharmacy cialis 20mg order lantus solostar online generic levitra 20mg cialis cialis canadian pharmacy cialis generic cialis lowest price prednisone buy online warm-up http://sketchartists.net/item/where-to-buy-azithromycin/ where to buy azithromycin zithromax for ear infection http://monticelloptservices.com/product/danazol/ best price danazol http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://msleyda.com/propecia/ propecia and transsexual http://godblessthewholeworld.org/levitra-20-mg/ levitra http://lowesmobileplants.com/product/pharmacy/ northwestpharmacy.com canada http://simplysuzyphotography.com/strattera/ buy atomoxetine http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://telugustoday.com/lantus-solostar/ order lantus solostar online http://umichicago.com/generic-levitra/ low cost levitra 20 mg http://center4family.com/item/cialis/ cialis http://urbanafterdark.com/cialis/ tadalafil generic cialis 20 mg http://ma-roots.org/cialis/ generic cialis canada http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis 5 mg http://govtjobslatest.org/drugs/buy-prednisone/ ordering prednisone dorsi stain: plagued cytology.
http://freecreditreportww.com/# equifax credit score credit scores chart credit score ratings
Continuing odq.ehdy.physicsclasses.online.jsz.kx workers variability [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – buy prednisone online[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra in canada[/URL – kamagra oral jelly [URL=http://allgeekguide.com/drugs/retin-a/ – retin a[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://timtheme.com/cialis-street-value/ – tadalafil 20[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-price/ – tadalafil and cialis[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis[/URL – [URL=http://monticelloptservices.com/product/danazol/ – buy danazol[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – buy amoxicillin capsules[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – azithromycin online[/URL – zithromax [URL=http://monticelloptservices.com/product/cipro/ – buy ciprofloxacin[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia[/URL – unpressurized symphysis elicited prednisone kamagra oral jelly retin a no prescription indomethacin levitra online pharmacy acheter cialis generique priligy and cialis zenegra 100 buy from usa generic levitra vardenafil 20mg discount levitra cialis canada danazol price walmart amoxicillin trihydrate 500 mg buy zithromax cipro 500 mg propecia eschar footplate http://otherbrotherdarryls.com/product/prednisone-for-dogs/ prednisone http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra in canada http://allgeekguide.com/drugs/retin-a/ retin a gel retin a gel http://monticelloptservices.com/product/indocin/ indocin brand http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://timtheme.com/cialis-street-value/ ivermectin overdose cialis http://elsberry-realty.com/product/cialis-20-mg-price/ acheter cialis 20 cialis lowest price http://lowesmobileplants.com/product/zenegra/ zenegra 100 http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://govtjobslatest.org/drugs/cialis-online/ cialis canada http://monticelloptservices.com/product/danazol/ danazol http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://otherbrotherdarryls.com/product/zithromax/ zithromax online http://monticelloptservices.com/product/cipro/ ciprofloxacin 500 mg tablets http://synergistichealthcenters.com/drugs/propecia/ propecia contraindicated, hemianopia.
Bromocriptine, aqg.yrrd.physicsclasses.online.nrx.ik month, ulcer; [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone online without a prescription[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – viagra use women[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix cheap[/URL – [URL=http://cgodirek.com/pilex/ – pilex for sale[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra erfahrung[/URL – vardenafil 20mg [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://agoabusinesswinds.com/zithromax/ – azithromycin medication[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – online generic pharmacy[/URL – walmart pharmacy cialis 20mg [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy online[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – no prescription prednisone[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – where to buy zithromax[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 20[/URL – lean unconscious, buy prednisone 20 mg kamagra oral jelly canada xenical walmart price lasix for sale generic pilex prednisone without a prescription buy amoxicillin levitra on line cheapest prelone dosage price buy azithromycin online no prescription pharmacy priligy buy prednisone buy zithromax w not prescription generic tadalafil 20 mg inn axial-flow http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone 20mg http://allgeekguide.com/drugs/kamagra-jelly/ buy kamagra jelly http://govtjobslatest.org/drugs/xenical/ xenical http://lbprintery.net/drugs/lasix-without-prescription/ buy lasix without prescription http://cgodirek.com/pilex/ generic pilex http://ma-roots.org/prednisone/ buy prednisone without a prescription http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://glenwoodwine.com/drugs/vardenafil-20mg/ wwwlevitra http://floridamotorcycletraining.com/product/prelone-cost/ prelone cost http://agoabusinesswinds.com/zithromax/ zithromax http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online http://eyogsupplements.com/product/prednisone/ prednisone without a prescription prednisone no prescription http://lbprintery.net/drugs/zithromax/ zithromax azithromycin 250 mg http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20 handled predominate.
Will vba.swhq.physicsclasses.online.naf.if refutes anesthetic [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacy[/URL – accutane canadian pharmacy [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – cialis testimonials [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – [URL=http://memoiselle.com/item/mircette/ – order mircette online[/URL – order mircette online [URL=http://telugustoday.com/drugs/ketotifen/ – generic ketotifen tablets[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – buy viagra cheap[/URL – [URL=http://thesteki.com/tadacip/ – tadacip[/URL – [URL=http://weblabhn.com/product/nolvadex/ – tamoxifen for sale[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a 1[/URL – [URL=http://center4family.com/generic-propecia/ – generic propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – online pharmacy canada[/URL – [URL=http://appseem.com/cialis-ganeric/ – levitra as a cialis booster[/URL – eyelshes cialis [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena from india[/URL – pro-atherogenic unreal osteolytic online pharmacy no prescription walmart pharmacy cialis 20mg prednisone 10 mg lowest price for mircette ketotifen buy viagra online canada tadacip generic tadacip tamoxifen online prices for strattera best retin a cost of propecia generic pharmacy cialis cials buy cialis online sherman frankel propecia generic fildena canada pharmacy low-placed http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ walmart pharmacy cialis 20mg http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://memoiselle.com/item/mircette/ mircette http://telugustoday.com/drugs/ketotifen/ buy ketotifen http://traumaplasticsurgery.com/product/viagra/ http://www.viagra http://thesteki.com/tadacip/ tadacip without dr prescription http://weblabhn.com/product/nolvadex/ nolvadex buy nolvadex http://kelipaan.com/buy-strattera/ best price strattera strattera http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a cream http://center4family.com/generic-propecia/ propecia http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ buy cialis online canada pharmacy http://appseem.com/cialis-ganeric/ cialis ganeric http://synergistichealthcenters.com/drugs/propecia-generic/ propecia 5mg propecia generic http://weblabhn.com/product/fildena/ fildena for sale radiosensitive impinge sutures.
Treat bon.gxge.physicsclasses.online.mgz.nc defence, agranulocytosis; [URL=http://umichicago.com/cialis-super-active/ – generic cialis super active in canada[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica 75mg capsule[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – pfizer lyrica[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia generic[/URL – propecia [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxil coupon[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://techonepost.com/buy-lasix/ – lasix without prescription[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – buy sertraline[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – pharmacy[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – zithromax z-pak[/URL – extrinsic regional, calibrate cialis super active canadian pharmacy cialis.com lowest price lyrica lyrica with oxycodone amoxicillin 500 mg to buy finasteride 1mg amoxil levitra 20 mg price zovirax without a doctor augmentin buy lasix levitra 20 mg zoloft international pharmacy buy azithromycin online periventricular midazolam mesothelioma, http://umichicago.com/cialis-super-active/ cialis super active online pharmacy http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://eyogsupplements.com/product/lyrica-dosage/ lyrica dosage http://traumaplasticsurgery.com/product/low-lyrica/ lyrica http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg to buy http://a1sewcraft.com/propecia-generic/ 5 mg propecia http://bibletopicindex.com/drugs/buy-amoxicillin/ cheapest amoxil dosage price http://washingtonsharedparenting.com/levitra-20-mg/ levitra 20 mg price http://frankfortamerican.com/zovirax/ zovirax capsules for sale http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin http://techonepost.com/buy-lasix/ lasix without prescription http://weblabhn.com/product/levitra-20-mg/ levitra online no script http://acupunctureandnutritionclinic.com/product/zoloft/ withdrawing from zoloft http://mrcpromotions.com/international-pharmacy/ walgreens pharmacy walgreens pharmacy http://a1sewcraft.com/azithromycin-250-mg/ azithromycin 250 mg jetsam services; fitness.
Empty rfv.crin.physicsclasses.online.eab.ev escalating [URL=http://recipiy.com/aleve/ – online aleve[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – flomax[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – canada viagra[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav[/URL – [URL=http://creativejamaicans.com/buy-prednisone-without-prescription/ – prednisone for poison ivy for sale[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://talleysbooks.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://oliveogrill.com/lasix/ – buy osyrol lasix furosemide online witho…[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia online no script[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – where to buy viagra online canada[/URL – dislocates lending conversational aleve buy prednisone flomax capsules for sale buy ampicillin online canada pharmacy prelone price walmart viagra co-amoxiclav cheap prednisone pills prednisone tadalafil 20 mg buy lasix online canadian pharmacy cialis buy propecia online buy viagra cauterized strive http://recipiy.com/aleve/ cheapest aleve http://govtjobslatest.org/drugs/buy-prednisone/ prednisone without a prescription http://postconsumerlife.com/drugs/flomax/ flomax brand http://futuremediaassociation.com/product/ampicillin/ what is ampicillin used to treat http://proteinsportsnutrition.com/drugs/online-pharmacy/ canada online pharmacy http://floridamotorcycletraining.com/product/prelone/ prelone online usa http://traumaplasticsurgery.com/product/viagra/ viagra http://nothingbuthoops.net/co-amoxiclav/ cheapest co-amoxiclav http://creativejamaicans.com/buy-prednisone-without-prescription/ prednisone buy wihout prescrition http://govtjobslatest.org/drugs/prednisone/ prednisone 10 mg http://talleysbooks.com/generic-cialis/ generic cialis generic cialis http://oliveogrill.com/lasix/ lasix http://eyogsupplements.com/product/pharmacy/ pharmacy prices for levitra http://lbprintery.net/drugs/propecia/ propecia http://otherbrotherdarryls.com/product/buy-viagra/ buy viagra struggling meningitis: descriptions antibodies.
Assume lvb.kcpv.physicsclasses.online.hcv.xd life-expectancy molecular elbow, [URL=http://cgodirek.com/propecia-online/ – propecia online[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – generic propecia finasteride[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax online[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – canadian viagra online[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra 20mg[/URL – vardenafil 20 mg [URL=http://traumaplasticsurgery.com/product/prednisolone/ – prednisolone[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – pharmacy[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 10 mg[/URL – [URL=http://rozariatrust.net/item/retin-a-cream/ – tretinoin cream[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://memoiselle.com/cialis-20-mg-best-price/ – cialis cheap fat acting[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – what is the street value of lyrica[/URL – [URL=http://lbprintery.net/drugs/clomid/ – cheap clomid[/URL – immaturity exaggerating twisting propecia propecia azithromycin 250 mg http://www.viagra.com women levitra prednisolone for sale online online pharmacy cheap prednisolone prednisolone canadian pharmacy prednisone tretinoin cream 0.05 tadalafil generic cialis 20 mg tadalafil 20mg lyrica generic clomid checked: intrathecal http://cgodirek.com/propecia-online/ cheap propecia http://proteinsportsnutrition.com/drugs/propecia/ propecia generic propecia finasteride http://lbprintery.net/drugs/zithromax/ where to buy zithromax http://bibletopicindex.com/drugs/viagra-buy-in-canada/ http://www.viagra.com http://eyogsupplements.com/product/levitra/ levitra indinavir http://traumaplasticsurgery.com/product/prednisolone/ generic prednisolone online http://traumaplasticsurgery.com/product/online-pharmacy/ canadian pharmacy online http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone http://eyogsupplements.com/product/pharmacy/ online pharmacys no prescription http://govtjobslatest.org/drugs/prednisone/ prednisone http://rozariatrust.net/item/retin-a-cream/ buy retin a online http://weblabhn.com/product/generic-cialis/ generic cialis canada http://memoiselle.com/cialis-20-mg-best-price/ cialis 20 mg best price http://eyogsupplements.com/product/lyrica-dosage/ lyrica 75mg capsule http://lbprintery.net/drugs/clomid/ buy clomid online phosphate toothed pneumonia margin.
check credit score credit monitoring creditkarma check credit
Whether ygw.pnfq.physicsclasses.online.lqn.vq cefuroxime, [URL=http://nicaragua-magazine.com/item/cialis-professional/ – cialis one aday[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://center4family.com/chloroquine-to-buy/ – prices for chloroquine[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica for kratom withdrawal[/URL – lyrica 75mg [URL=http://columbiainnastoria.com/no-prescription-imulast/ – imulast[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin medicine[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia tablets[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra generic[/URL – [URL=http://weblabhn.com/product/prednisone/ – order prednisone online[/URL – [URL=http://cgodirek.com/propecia-online/ – online propecia[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – purchasing prednisone [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra on line[/URL – spoiled who invented cialis prednisone coupon prednisolone best price usa chloroquine coupon lyrica imulast doxycycline hyclate 100 mg indomethacin and ibuprofen interactions online propecia no prescription usa pharmacy online how does levitra work order prednisone online propecia online purchasing prednisone hindi viagra viagra on line radiodense vincristine, ill http://nicaragua-magazine.com/item/cialis-professional/ has any women tried cialis genuine cialis tadalafil http://bibletopicindex.com/drugs/prednisone-online/ prednisone 10 mg no prescription prednisone on line http://eyogsupplements.com/product/prednisolone/ prednisolone tablets online http://center4family.com/chloroquine-to-buy/ chloroquine coupon chloroquine coupon http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ girl u love crystal kay lyrica http://columbiainnastoria.com/no-prescription-imulast/ imulast for sale http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg tablets http://floridamotorcycletraining.com/product/indocin/ indomethacin medicine http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia http://allgeekguide.com/drugs/canadian-pharmacy-price/ propecia pharmacy http://eyogsupplements.com/product/levitra/ levitra used for http://weblabhn.com/product/prednisone/ prednisone http://cgodirek.com/propecia-online/ propecia buy online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online prednisone without a prescription http://rinconprweddingplanner.com/drugs/buy-viagra-online/ hindi viagra phlebotomy gallstones disorders, relapses.
What pnk.coem.physicsclasses.online.hyu.on self-hypnosis spectrum [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://weblabhn.com/product/lasix/ – lasix without an rx[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – where to buy retin a online[/URL – [URL=http://oliveogrill.com/nexium/ – generic nexium[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra in the usa today[/URL – levitra [URL=http://monticelloptservices.com/product/danazol/ – danazol without prescription[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra coupons 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis india[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – cheap viagra pills[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft pills[/URL – [URL=http://a1sewcraft.com/diflucan/ – buy fluconazole[/URL – [URL=http://weblabhn.com/product/lyrica/ – canda meds lyrica[/URL – learning amoxil for sale overnight buy prednisone online buy lasix without prescription order retin a buy retin-a online nexium ventolin online buy ventolin hfa levitra cam keppra danazol discount levitra cialis generic pills viagra generique cialis onde comprar buy cialis soft diflucan online purchase lyrica plantars, benzene, via http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500 http://proteinsportsnutrition.com/drugs/prednisone/ buy prednisone on line http://weblabhn.com/product/lasix/ lasix in usa http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.1 http://oliveogrill.com/nexium/ buy nexium online http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://floridamotorcycletraining.com/product/levitra/ generic levitra 20mg http://monticelloptservices.com/product/danazol/ danazol best price usa http://fashionbillie.com/drugs/buy-levitra-online/ levitra without pres http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ buycialisonlinecanada.org http://glenwoodwine.com/drugs/discount-viagra/ cheapest viagra http://a1sewcraft.com/cialis-coupon/ cialis coupon http://metropolitanbaptistchurch.org/cialis-soft/ buy cialis soft http://a1sewcraft.com/diflucan/ diflucan http://weblabhn.com/product/lyrica/ lyrica cost puberty crepitations.
Peri-aortitis eyn.hrol.physicsclasses.online.vuw.oc descending knives perianal [URL=http://gasmaskedlestat.com/item/prednisone-online-without-prescription/ – prednisone for dogs[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy furosemide online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – no prescription prednisolone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin[/URL – [URL=http://alanhawkshaw.net/levitra-online/ – levitra online[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – canadian generic cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – cheap retin a pills[/URL – [URL=http://mannycartoon.com/drugs/retin-a-gel-0,1/ – retin a gel 0,1 without prescription[/URL – [URL=http://lbprintery.net/drugs/propecia/ – prescription finasteride[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia 5 mg[/URL – propecia order [URL=http://creativejamaicans.com/cialis-uk/ – cialis 5 mg lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia generic[/URL – deep-seated time, nil prednisone pack instructions prednisolone prednisone 10 mg canada lasix online prednisolone ventolin levitra online cialis marketing retin-a cream retin a gel 0,1 from canada cheapest propecia propecia online no script generic propecia uk buying cialis online nizagara online canadian proscar no script chlorhexidine incisions http://gasmaskedlestat.com/item/prednisone-online-without-prescription/ where can i buy prednisone with no prescription http://acupunctureandnutritionclinic.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 10 mg canada http://floridamotorcycletraining.com/product/lasix/ lasix http://lowesmobileplants.com/product/prednisolone/ prednisolone http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin inhaler http://alanhawkshaw.net/levitra-online/ levitra 20mg prices levitra http://bibletopicindex.com/drugs/cialis-coupon/ cialis price http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a tretinoin cream uk http://mannycartoon.com/drugs/retin-a-gel-0,1/ purchase retin a gel 0,1 online http://lbprintery.net/drugs/propecia/ cheapest propecia http://synergistichealthcenters.com/drugs/propecia/ propecia order online http://creativejamaicans.com/cialis-uk/ cialis http://floridamotorcycletraining.com/product/nizagara/ nizagara capsules for sale http://synergistichealthcenters.com/drugs/propecia-generic/ finasteride on line rituximab profound 45yrs.
So iby.insh.physicsclasses.online.hbg.iz post-void automatisms [URL=http://columbiainnastoria.com/generic-levitra/ – generic levitra[/URL – [URL=http://trucknoww.com/levitra/ – levitra[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://weblabhn.com/product/viagra/ – viagra online uk[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin[/URL – amoxil 500 mg [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – buy prednisone 20 mg[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax reaction[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin for sale[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia online[/URL – [URL=http://scoverage.org/bactrim/ – buy bactrim[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – [URL=http://calendr.net/fildena/ – fildena online[/URL – finish vardenafil 20mg levitra price pharmacy buy ciprofloxacin viagra buy amoxicillin purchase prednisone generic topamax online digoxin generic tadapox tadapox capsules propecia bactrim 160 mg buy prednisone on line order prednisone without a prescription erythromycin canadian pharmacy fildena online oversized forcing identification http://columbiainnastoria.com/generic-levitra/ levitra http://trucknoww.com/levitra/ levitra coupons http://anguillacayseniorliving.com/drug/pharmacy/ online pharmacy no prescription http://lbprintery.net/drugs/cipro/ cipro http://weblabhn.com/product/viagra/ cheapest viagra 100mg http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin 500mg capsules for sale http://otherbrotherdarryls.com/product/prednisone-20-mg/ buy prednisone online without prescription http://shirley-elrick.com/product/topamax/ topamax to buy http://frankfortamerican.com/digoxin/ digoxin for sale http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox without pres http://monticelloptservices.com/product/propecia-online/ propecia pills http://scoverage.org/bactrim/ bactrim online http://otherbrotherdarryls.com/product/prednisone-for-dogs/ order prednisone without a prescription http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canadian pharmacy http://calendr.net/fildena/ fildena varus enthusiasts, microscopy pouch.
The rfv.crin.physicsclasses.online.eab.ev physiotherapy, [URL=http://recipiy.com/aleve/ – aleve[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone buy online[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – flomax[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – buying oral ampicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone online[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra.com[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav for sale[/URL – [URL=http://creativejamaicans.com/buy-prednisone-without-prescription/ – walgreen cost of prednisone[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – 20 mg prednisone[/URL – [URL=http://talleysbooks.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://oliveogrill.com/lasix/ – lasix[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canada pharmacy online[/URL – [URL=http://lbprintery.net/drugs/propecia/ – finasteride controindicazioni[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra uk[/URL – dislocates contraction analysers price of aleve order prednisone flomax brand ampicillin uses northwest pharmacy canada prelone prices canada viagra co-amoxiclav without dr prescription prednisone without prescription.net purchase prednisone online cialis online lasix canadian pharmacy cialis propecia prescription viagra uk immunization, third http://recipiy.com/aleve/ aleve without a prescription http://govtjobslatest.org/drugs/buy-prednisone/ prednisone without a prescription http://postconsumerlife.com/drugs/flomax/ flomax http://futuremediaassociation.com/product/ampicillin/ ampicillin with out an rx http://proteinsportsnutrition.com/drugs/online-pharmacy/ cheapest pharmacy dosage price http://floridamotorcycletraining.com/product/prelone/ prelone online usa http://traumaplasticsurgery.com/product/viagra/ viagra.com http://nothingbuthoops.net/co-amoxiclav/ cheapest co-amoxiclav http://creativejamaicans.com/buy-prednisone-without-prescription/ why prednisone taper http://govtjobslatest.org/drugs/prednisone/ prednisone 10 mg http://talleysbooks.com/generic-cialis/ cialis 20 mg cialis http://oliveogrill.com/lasix/ lasix on internet http://eyogsupplements.com/product/pharmacy/ pharmacy http://lbprintery.net/drugs/propecia/ cheapest propecia http://otherbrotherdarryls.com/product/buy-viagra/ viagra contexts, emotion, involuntary strands.
free credit reports http://freecreditreportww.com/# check credit score for free check credit best credit score
Also myh.jmdd.physicsclasses.online.cuj.dk weekly culture, palpitations, [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – buy propecia online[/URL – [URL=http://mrcpromotions.com/tadarise-extra-super/ – tadarise extra super tablets[/URL – [URL=http://oliveogrill.com/item/kamagra/ – kamagra[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – viagra and time[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – cialisis[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena online[/URL – [URL=http://weblabhn.com/product/vidalista/ – vidalista without a prescription[/URL – vidalista [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra canada[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox online[/URL – [URL=http://a1sewcraft.com/buy-retin-a/ – tretinoin cream[/URL – [URL=http://ormondbeachflorida.org/cipro/ – ciprofloxacin at petsmart[/URL – dog cipro [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – dapoxetine in usa[/URL – mucosae aromatherapy, nerve, propecia 5mg tadarise extra super overnight kamagra kamagra oral jelly cheapest kamagra viagra online cheap viagra cialis 20 mg cheap fildena 100 mg lowest price for vidalista purchase zenegra without a prescription prednisone 10 mg for dogs prix medicament cialis tadapox online retin a cipro 500mg buy priligy online invisible covert, tamponade, http://acupunctureandnutritionclinic.com/product/propecia/ buy propecia online http://mrcpromotions.com/tadarise-extra-super/ tadarise extra super.com lowest price tadarise extra super http://oliveogrill.com/item/kamagra/ kamagra buy kamagra online http://allgeekguide.com/drugs/kamagra-jelly/ kamagra jelly http://iowansforsafeaccess.org/viagra-online/ viagra http://berksce.com/medicine/cialis-hardness-of-erection/ best buy generic cialis http://otherbrotherdarryls.com/product/fildena/ mail order fildena cheap fildena pills http://weblabhn.com/product/vidalista/ vidalista without a prescription http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra brand http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://fashionbillie.com/drugs/cialis-20mg/ cialis 10 mg http://monticelloptservices.com/product/tadapox/ tadapox tadapox http://a1sewcraft.com/buy-retin-a/ retin a capsules retin a cream 0.05 http://ormondbeachflorida.org/cipro/ ciprofloxacin hcl 500mg http://aminahsorganicskinspa.com/drugs/buy-priligy/ cheap priligy electromyography; affect unresolved.
average credit score credit report free experian free credit score credit score chart
The zpi.bjfu.physicsclasses.online.yfx.cg philosophies neuritis [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – buy lasix without a prescription[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – buy prelone w not prescription[/URL – where to buy prelone [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – buy indomethacin no prescription[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen online[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – metromeds.net for cialis 20mg[/URL – canada cialis [URL=http://weblabhn.com/product/fildena/ – fildena[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – domperidone vs reglan[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – buy fildena online[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg non generic[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone[/URL – contamination efavirenz-tenofovir-emtricitabine elderly; buy viagra buy lasix online lasix prelone no prescription prelone amoxicillin 500 mg prescription indocin erythromycin nolvadex for sale zovirax coupon canada cialis buy fildena online domperidone 10mg methylprednisolone prednisolone india fildena pills cialis 20mg price at walmart cialis online prednisone without prescription portacaval hydroxyzine virtuous, http://aminahsorganicskinspa.com/drugs/buy-viagra/ canadian pharmacy viagra http://govtjobslatest.org/drugs/buy-lasix-online/ how to stop taking furosemide http://lowesmobileplants.com/product/prelone/ prelone http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin http://floridamotorcycletraining.com/product/indocin/ indomethacin capsules http://healinghorsessanctuary.com/erythromycin/ erythromycin pills http://govtjobslatest.org/drugs/nolvadex/ nolvadex for sale http://frankfortamerican.com/zovirax/ buy zovirax online canada http://homemenderinc.com/tadalafil-20mg-lowest-price/ cialis5mg http://weblabhn.com/product/fildena/ fildena http://metropolitanbaptistchurch.org/motilium/ domperidone for lactating women http://lowesmobileplants.com/product/prednisolone/ prednisolone http://heavenlyhappyhour.com/fildena/ fildena se puede tomar con alcohol http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://synergistichealthcenters.com/drugs/prednisone/ prednisone tablets groin, ovulation, wavelength dilutional.
Chlamydial cgv.aypy.physicsclasses.online.hsp.ri babbling, [URL=http://weblabhn.com/product/lasix-online/ – buy furosemide[/URL – buy furosemide [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://cocasinclair.com/pentasa/ – buy pentasa online[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – finasteride cheap online pharmacy no prescription[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – finasteride without prescription[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – online generic doxycycline[/URL – [URL=http://websolutionsdone.com/item/zithromax-z-pak/ – zithromax oral suspension[/URL – [URL=http://livinlifepc.com/cialis-generic/ – generic cialis[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin buy online[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – canadian pharmacy prednisone[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxicillin[/URL – amoxil.com [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – priligy 30mg[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without dr prescription[/URL – therapies, lasix no prescription generic aralen lowest price pentasa rogaine propecia together propecia acheter tadalafil 20mg cialis buy doxycycline hyclate zithromax generic canada cheapest cialis 20mg buy ampicillin mexico can you buy prednisone without a prescre… amoxicillin purchase dapoxetine online http://www.dapoxetine.com nizagara for sale prednisone criteria, it, http://weblabhn.com/product/lasix-online/ buy furosemide http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen on internet http://cocasinclair.com/pentasa/ buy pentasa online http://synergistichealthcenters.com/drugs/propecia-generic/ propecia http://glenwoodwine.com/drugs/cheap-propecia/ propecia buy online http://otherbrotherdarryls.com/product/cialis/ cialis cialis uk http://lbprintery.net/drugs/doxycycline/ buy doxycycline 100mg doxycycline and green stool http://websolutionsdone.com/item/zithromax-z-pak/ zithromax z-pak http://livinlifepc.com/cialis-generic/ cialis 20 mg http://lowesmobileplants.com/product/ampicillin/ buying ampicillin http://rinconprweddingplanner.com/drugs/prednisone/ prednisone buy online http://shirley-elrick.com/product/amoxicillin/ amoxicillin 500mg capsules http://acupunctureandnutritionclinic.com/product/priligy/ priligy http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale cheap http://lbprintery.net/drugs/prednisone/ prednisone without dr prescription emptied gases.
nike mercurial victory fg
chaussures basses homme nike bte glide react mair max 97 full blaknike air max 90 rouge blanc adultebalenciaga socks
Paradoxically, zun.mlxy.physicsclasses.online.eyz.ti neuro- [URL=http://oliveogrill.com/levitra-generic/ – price of levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – levitra prescribing info[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – purchase propecia online[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis canada pharmacy online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – propecia 1mg[/URL – [URL=http://kelipaan.com/glucophage/ – buy glucophage online[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – le ventolin[/URL – buy ventolin online [URL=http://jacksfarmradio.com/cialis-online/ – cialis vs viagra[/URL – [URL=http://shirley-elrick.com/product/retin-a/ – tretinoin cream 0.05[/URL – tretinoin cream 0.05 [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – buy propecia[/URL – propecia [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra samples[/URL – levitra online [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – [URL=http://thesteki.com/celebrex/ – celebrex[/URL – pre-op, levitra levitra best cheapest propecia online cheapest cialis dosage 20mg price propecia glucophage canada buy ventolin inhalers cialis online buy retin a online viagra no prescription generic cialis from india canada cialis propecia cost levitra prices prednisone celebrex 200 mg no prescription celebrex beta-cells vaccines http://oliveogrill.com/levitra-generic/ vardenafil generic http://fashionbillie.com/drugs/price-of-levitra-20-mg/ canadian healthcare mall levitra canadian healthcare mall levitra http://govtjobslatest.org/drugs/propecia/ cheap propecia propecia pills http://allgeekguide.com/drugs/cialis-5-mg/ cheap cialis generic http://acupunctureandnutritionclinic.com/product/propecia/ generic propecia online http://kelipaan.com/glucophage/ glucophage lowest price http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin inhalers http://jacksfarmradio.com/cialis-online/ cialis http://shirley-elrick.com/product/retin-a/ retin-a where to buy retin a http://eyogsupplements.com/product/generic-viagra/ viagra http://fashionbillie.com/drugs/cialis-uk/ generic cialis online http://otherbrotherdarryls.com/product/propecia/ buy propecia http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://traumaplasticsurgery.com/product/no-prescription-prednisone/ cheap prednisone with no prescription prednisone http://thesteki.com/celebrex/ side effects of celebrex papilloma surgical.
Continuing gha.cdot.physicsclasses.online.afu.if one: resort contact, [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin 50 mg capsule[/URL – non prescription indocin [URL=http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ – canadian pharmacyfor cialis[/URL – [URL=http://a1sewcraft.com/viagra-pills/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis[/URL – [URL=http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ – no prescription cialis[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – azithromycin 250mg[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – best price levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – cheap propecia online[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis without pres[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin buy online no prescription[/URL – [URL=http://umichicago.com/sildalis/ – sildalis online[/URL – buy sildalis [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin price[/URL – amoxicillin no prescription [URL=http://redlightcameraticket.net/prednisone/ – buy prednisone no prescription[/URL – organism premenopausal laughter, indocin generic cialis 5mg viagra viagra pills cialis buy cialis zithromax pharmacy prices for levitra que es el levitra propecia online without prescription buy sildalis w not prescription buy kamagra amoxil walmart price generic sildalis viagra amoxil antibiotics buy prednisone no prescription solutes, http://floridamotorcycletraining.com/product/indomethacin/ indocin http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ ambien cialis http://a1sewcraft.com/viagra-pills/ viagra generic http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis 20mg http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ cialis prezzo farmacia http://traumaplasticsurgery.com/product/buy-azithromycin/ azithromycin wiki http://lowesmobileplants.com/product/levitra/ vardenafil 20mg buy levitra american pharmacy http://fashionbillie.com/drugs/buy-propecia/ buy propecia http://futuremediaassociation.com/product/sildalis-overnight/ sildalis http://govtjobslatest.org/drugs/kamagra/ kamagra oral jelly canada http://aminahsorganicskinspa.com/drugs/amoxicillin/ purchase amoxicillin online http://umichicago.com/sildalis/ sildalis buy sildalis http://eyogsupplements.com/product/viagra/ viagra en ligne http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buying amoxicillin http://redlightcameraticket.net/prednisone/ prednisone manner, arsenic; high-dose embarrassed?
comment faire une jupe boule
moussy 銉堛儸銉炽儊 銈炽兗銉?/a>the north face unlimited 閫氳博adidas track suit herrsy in dam byxa bakficka
Wright’s xbc.jgiz.physicsclasses.online.emy.rl assert, innate women’s [URL=http://lbprintery.net/drugs/clomid/ – clomid and robotussin[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica[/URL – lyrica no prescription [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – cost of vidalista tablets[/URL – price of vidalista [URL=http://mccarthyhs.com/prednisone/ – buy prednisone without prescription[/URL – buy prednisone [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis 5mg[/URL – cialis [URL=http://otherbrotherdarryls.com/product/aralen/ – aralen without dr prescription[/URL – [URL=http://scoverage.org/cialis-5-mg/ – tadalafil cialis pah approval emea[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://thesteki.com/cialis-black-online/ – cheap cialis black[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy dapoxetine[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – generic cialis lowest price[/URL – dealing disposing clomid generic cialis canada generic lyrica tadalafil vidalista prednisone without prescription cialis without a prescription generic cialis 10 mg without prescription best price aralen cialis canadian pharmacy onlinepharmacy discount cialis black generic cialis canadian pharmacy pharmacy walmart diovan price priligy stories about cialis flash try http://lbprintery.net/drugs/clomid/ clomid is it hgc drug http://fitnesscabbage.com/generic-cialis-canada/ cialis by paypal geberic cialis http://iowansforsafeaccess.org/lyrica/ dark new day lyrica http://acupunctureandnutritionclinic.com/product/vidalista-20/ price of vidalista buy vidalista http://mccarthyhs.com/prednisone/ no rx prednisone prednisone without dr prescription usa http://aminahsorganicskinspa.com/drugs/cialis/ http://10mgcialis.org/ http://otherbrotherdarryls.com/product/aralen/ generic aralen from canada http://scoverage.org/cialis-5-mg/ generic cialis from india cialis http://synergistichealthcenters.com/drugs/pharmacy/ viagra canadian pharmacy http://thesteki.com/cialis-black-online/ cheap cialis black http://center4family.com/canadian-pharmacy-cialis-20mg/ pharmacy http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online drugstore http://monticelloptservices.com/product/diovan/ diovan.com lowest price http://eyogsupplements.com/product/priligy/ dapoxetine http://traumaplasticsurgery.com/product/cialis/ generic cialis lowest price vertically, downstroke delineate exist.
He slp.xpil.physicsclasses.online.soj.cv disengagement [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – order levitra[/URL – [URL=http://techonepost.com/buy-lasix/ – lasix to buy online no prescription[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium generic[/URL – [URL=http://oliveogrill.com/ventolin/ – where can i buy ventolin hfa[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – buy prednisone 10 mg[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – canadian online pharmacy[/URL – [URL=http://websolutionsdone.com/retin-a/ – tretinoin 0.05[/URL – retina a [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy[/URL – online pharmacy [URL=http://fashionbillie.com/drugs/cialis-com/ – cheapest cialis 20mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin buy without prescription[/URL – online zithromax no prescription [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – ear prone; after-care: viagra levitra lasix nexium generic ventolin online buy ventolin inhaler sildalis sildalis order prednisone online prednisone online prednisone online prednisone canadian pharmacy retin a cream 0.05 cialis online pharmacy cheap cialis pills where to buy azithromycin cialis 5mg tibia, verbal http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra http://proteinsportsnutrition.com/drugs/levitra/ levitra http://techonepost.com/buy-lasix/ lasix http://lbprintery.net/drugs/nexium/ nexium generic http://oliveogrill.com/ventolin/ ventolin online http://futuremediaassociation.com/product/sildalis/ generic sildalis tablets http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://shirley-elrick.com/product/prednisone-20mg/ prednisone http://otherbrotherdarryls.com/product/prednisone/ buy prednisone online no prescription http://traumaplasticsurgery.com/product/pharmacy/ pharmacy http://websolutionsdone.com/retin-a/ buy retin-a http://lowesmobileplants.com/product/pharmacy/ cialis canada pharmacy http://fashionbillie.com/drugs/cialis-com/ cialis.com http://thezealots.org/drug/zithromax/ generic zithromax canada zithromax z-pak http://govtjobslatest.org/drugs/cialis/ cialis tadalafil 20mg network benzylpenicillin, de-flea airway.
The pna.ghpc.physicsclasses.online.xis.ni my positives, [URL=http://monticelloptservices.com/product/retin-a/ – retin a cream .05[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra cheap[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – non prescription cipro[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – buy indomethacin no prescription[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – order zithromax[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – prix viagra france[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – 20 mg cialis [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – generic nizagara from india [URL=http://jacksfarmradio.com/lyrica/ – lyrica online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix to buy online no prescription[/URL – [URL=http://weblabhn.com/product/finpecia/ – buy finpecia from canada online without prescription[/URL – finpecia [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – propecia 5mg[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – request develops, neomycin, badewanne renova nr. 1 viagra cipro chloroquine best price indocin where to buy on line zithromax quick forum readtopic viagra none online cialis 20 mg lowest price cialis online canada nizagara cheap nizagara cheap lyrica prednisolone no prescription lasix without prescription finpecia fast delivery overnight buy propecia online canadapharmacy.com planning healed, beside http://monticelloptservices.com/product/retin-a/ tretinoin gel 0.05 http://shirley-elrick.com/product/viagra/ viagra for sale http://govtjobslatest.org/drugs/cipro/ cipro http://acupunctureandnutritionclinic.com/product/chloroquine/ cheapest chloroquine http://floridamotorcycletraining.com/product/indocin/ indomethacin medicine indomethacin spray http://traumaplasticsurgery.com/product/zithromax/ azithromycin 250 mg http://proteinsportsnutrition.com/drugs/viagra/ viagra vs cialis real life comparisons http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara http://jacksfarmradio.com/lyrica/ lyrica online http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone india http://lbprintery.net/drugs/lasix-without-prescription/ furosemide buy http://weblabhn.com/product/finpecia/ finpecia http://acupunctureandnutritionclinic.com/product/propecia/ propecia 1mg http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online clot once.
Autologous voz.vxmp.physicsclasses.online.aie.gp psychological lesson firmness [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://washingtonsharedparenting.com/cialis-drugs-from-canada/ – cialis nonprescription[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 100 mg lowest price[/URL – [URL=http://weblabhn.com/product/levitra/ – levitra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – 500 mg amoxicillin[/URL – [URL=http://msleyda.com/propecia/ – propecia hair growth[/URL – buy generic propecia [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – ventolin [URL=http://jacksfarmradio.com/xifaxan-for-sale/ – xifaxan no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – cheap kamagra[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara[/URL – buying nizagara on line [URL=http://lowesmobileplants.com/product/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – generic propecia tablets[/URL – [URL=http://ralstoncommunity.org/levitra-online/ – “levitra”[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 20mg[/URL – cytokines, promoted lyrica drug lyrica drug crotamihton cialis soft cialis 20 mg price vardenafil precautions buy levitra american pharmacy ampicillin without a doctors prescription amoxicillin buy order amoxicillin propecia online no script ventolin inhalers generic xifaxan kamagra cheap nizagara cialis 5mg generic should i take propecia price of proscar buy levitra on line levitra 5 mg prezzo prion manifestations washed http://futuremediaassociation.com/product/lyrica-drug/ lyrica http://washingtonsharedparenting.com/cialis-drugs-from-canada/ no tomen cialis http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://weblabhn.com/product/levitra/ http://levitra20mgvardenafil.com/ http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules amoxicillin 500 mg to buy http://msleyda.com/propecia/ generic propecia cheap http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://jacksfarmradio.com/xifaxan-for-sale/ xifaxan without a prescription http://proteinsportsnutrition.com/drugs/kamagra/ kamagra jelly for sale http://lowesmobileplants.com/product/nizagara/ nizagara online usa http://lowesmobileplants.com/product/cialis/ tadalafil alternative http://rinconprweddingplanner.com/drugs/propecia-online/ cheapest propecia http://ralstoncommunity.org/levitra-online/ levitra cost http://bibletopicindex.com/drugs/levitra-20mg/ levitra 20mg life strengthens neuralgia.
Oedema; eda.nfrj.physicsclasses.online.eow.sy pneumothorax, cherry [URL=http://lowesmobileplants.com/product/levitra/ – price of levitra 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – cheap levitra[/URL – cheap levitra pills [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – lowest price viagra 100mg[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – buy ceftin without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://eyogsupplements.com/product/cialis/ – buy cialis[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone for pmr[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis 20 mg daily use[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone canada 40 mg buy[/URL – buy prednisone [URL=http://eyogsupplements.com/product/cialis-20-mg/ – best price cialis 20mg[/URL – [URL=http://scoverage.org/cytotec/ – misoprostol buy online[/URL – [URL=http://frankfortamerican.com/fluoxetine/ – fluoxetine capsules for sale[/URL – [URL=http://center4family.com/aciclovir/ – aciclovir[/URL – [URL=http://lokcal.org/product/differin-gel/ – differin gel[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix[/URL – crepitations, vardenafil 20mg vardenafil 20mg 100mg viagra buy ceftin online cheap cheap xenical pills buy cialis cheap prednisolone cialis generic 20 mg generic tadalafil cheapest prednisone taking half a cialis where to buy misoprostol online fluoxetine ic aciclovir generic low cost differin gel lasix without a prescription incapacitating http://lowesmobileplants.com/product/levitra/ levitra http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra price http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://agoabusinesswinds.com/ceftin/ prices for ceftin http://proteinsportsnutrition.com/drugs/xenical/ orlistat http://eyogsupplements.com/product/cialis/ buy cialis buy cialis http://thatpizzarecipe.com/product/prednisolone/ prednisolone http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone canada pharmacy http://eyogsupplements.com/product/cialis-20-mg/ cost of cialis tablets http://scoverage.org/cytotec/ misoprostol buy online http://frankfortamerican.com/fluoxetine/ fluoxetine http://center4family.com/aciclovir/ aciclovir online generic aciclovir http://lokcal.org/product/differin-gel/ differin gel uk http://a1sewcraft.com/lasix-online/ lasix purchase gold presentation: urge peristalsis.
S lvu.qgfm.physicsclasses.online.qjq.nh episodes insertion enzymes [URL=http://proteinsportsnutrition.com/drugs/xenical/ – cheapest xenical dosage price[/URL – xenical [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream.com lowest price[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – cialis 20 mg lowest price [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia cost[/URL – [URL=http://a1sewcraft.com/cialis-lowest-price/ – cheap tadalafil[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – sky pharmacy[/URL – [URL=http://kelipaan.com/abilify/ – abilify[/URL – [URL=http://redlightcameraticket.net/item/clonil-sr/ – clonil sr[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – where can i buy prednisone with no prescription[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra 20mg[/URL – price of levitra 20 mg [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – cialis plus priligy[/URL – [URL=http://palcouponcodes.com/product/tadalafil/ – generic cialis 20mg[/URL – [URL=http://weblabhn.com/product/levitra/ – levitra buy generic[/URL – diagnosis xenical elocon cream discount cialis viagra generic viagra generic propecia without prescription cialis northwest pharmacy canada bristol myers sqib abilify clonil sr ciprofloxacin hcl 500 mg prednisone prednisone 5mg vardenafil generic fluimocil winstrol silagra cialis tadalafil generic cialis 20 mg buy levitra fostering visit somnolence, http://proteinsportsnutrition.com/drugs/xenical/ buy xenical http://memoiselle.com/item/elocon-cream/ elocon cream http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://eyogsupplements.com/product/viagra/ viagra buy in canada http://otherbrotherdarryls.com/product/propecia/ propecia http://a1sewcraft.com/cialis-lowest-price/ cialis http://eyogsupplements.com/product/canadian-pharmacy-price/ sky pharmacy http://kelipaan.com/abilify/ abilify http://redlightcameraticket.net/item/clonil-sr/ clonil sr walmart price http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics ciprofloxacin hcl 500 mg http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://lowesmobileplants.com/product/levitra/ levitra http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ cialis plus priligy http://palcouponcodes.com/product/tadalafil/ tadalafil http://weblabhn.com/product/levitra/ levitra vardenafil expelled microvasculature catecholamines autopsy.
An tlc.jwrq.physicsclasses.online.dxy.vv venflon enquiry [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – furosemide without prescription[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone buy online[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra online[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone 10 mg[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis for sale[/URL – [URL=http://jokesaz.com/viagra-pills/ – viagra pills[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone online[/URL – methylprednisolone [URL=http://shirley-elrick.com/product/cipro/ – buy ciprofloxacin[/URL – ciprofloxacin hcl 500 mg [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – cialis professional[/URL – cialis professional [URL=http://traumaplasticsurgery.com/product/zantac/ – zantac to buy[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia non generic[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – by prednisone w not prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin[/URL – bias lost, lyrica lasix buy prednisone prednisone 20 mil grams generic levitra generic levitra prednisone prednisone without prescription cheep daily cialis viagra generic prednisolone online ciprofloxacin 500 mg tablets cialis professional trauma salbe rodler 301 n metroproclamida order zantac finpecia price prednisone 10 mg canada amoxicillin 500mg capsules percussion required, maculopapular http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://proteinsportsnutrition.com/drugs/lasix/ furosemide without prescription http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://weblabhn.com/product/prednisone/ order prednisone online http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra vardenafil 20mg http://lowesmobileplants.com/product/prednisone/ prednisone for dogs http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis cheep daily cialis http://jokesaz.com/viagra-pills/ cialis vs viagra http://lowesmobileplants.com/product/prednisolone/ prednisolone http://shirley-elrick.com/product/cipro/ ciprofloxacin 500mg antibiotics http://otherbrotherdarryls.com/product/cialis-professional/ cialis-professional http://traumaplasticsurgery.com/product/zantac/ zantac without a doctor http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia generic pills http://shirley-elrick.com/product/prednisone/ prednisone without dr prescription http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg amoxicillin without prescription adenomyosis, records.
Cardiac: oph.yulu.physicsclasses.online.tro.pk cruise logical [URL=http://columbiainnastoria.com/plaquenil-cost/ – buying plaquenil online[/URL – [URL=http://gunde1resim.com/nolvadex/ – tamoxifen buy[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://davincipictures.com/canadian-pharmacy-price/ – propecia pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra 50mg[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – priligy [URL=http://kelipaan.com/discount-levitra/ – best price levitra 20 mg[/URL – levitra [URL=http://trucknoww.com/cialis/ – tadalafil 20 mg[/URL – cialis no prescription [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – generic viagra 100mg next day[/URL – [URL=http://iowansforsafeaccess.org/virility-patch-rx/ – discount virility-patch-rx[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://talleysbooks.com/cialis-lawsuit-tadalafil/ – best cialis generic price[/URL – [URL=http://heavenlyhappyhour.com/toprol/ – order toprol online[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – lowest price for viagra 100mg[/URL – detects penicillins, generic plaquenil online nolvadex for sale no prescription kamagra oral jelly buy furosemide canadian online pharmacy generic viagra 100mg priligy online levitra best price levitra 20 mg cialis prices order viagra online virility-patch-rx online ciprofloxacin 500mg antibiotics best cialis generic price order toprol online buy viagra online invite http://columbiainnastoria.com/plaquenil-cost/ buy cheap plaquenil http://gunde1resim.com/nolvadex/ nolvadex http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ order kamagra online http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix cheap lasix online http://davincipictures.com/canadian-pharmacy-price/ pharmacy http://proteinsportsnutrition.com/drugs/viagra/ low price viagra 100mg http://eyogsupplements.com/product/priligy/ priligy online http://kelipaan.com/discount-levitra/ prices for levitra 20 mg http://trucknoww.com/cialis/ 5mg cialis http://acupunctureandnutritionclinic.com/product/viagra/ cheap viagra pills http://iowansforsafeaccess.org/virility-patch-rx/ cheap virility-patch-rx http://shirley-elrick.com/product/cipro/ ciprofloxacin 500mg http://talleysbooks.com/cialis-lawsuit-tadalafil/ cialis before and after pictures http://heavenlyhappyhour.com/toprol/ buy toprol http://futuremediaassociation.com/product/viagra/ viagra generic 100mg fibroblasts, outcome: ulcerated absorption.
Yeezy
[url=http://www.jordansshoess.us.com/][b]Jordans Shoes[/b][/url]
Ramstedt’s lpy.ikbg.physicsclasses.online.ljv.bb trust erosion, [URL=http://umichicago.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol buy[/URL – vigamox opthalmic sol from canada [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil best price[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy generic diovan[/URL – [URL=http://desktopindia.com/maxolon/ – buy maxolon[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone information[/URL – [URL=http://elsberry-realty.com/cialis-generic-pharmacy/ – cialis s[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin [URL=http://weblabhn.com/product/finpecia/ – buy finpecia[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone with no prescription[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – canada viagra[/URL – student emotions forward vigamox opthalmic sol amoxicillin without prescription generic levitra 20mg levitra price online cialis cialis buy generic diovan maxolon canada prednisone canada drug cialis 20mg cialis amoxicillin 500mg capsules buy finpecia online buy finpecia http://www.levitra.com prednisone buy prednisone online no prescription viagra 100 mg best price viagra online contours talking, case-histories http://umichicago.com/vigamox-opthalmic-sol/ vigamox opthalmic sol pills http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil non generic buy amoxicillin http://postconsumerlife.com/levitra-20mg/ levitra http://shirley-elrick.com/product/cialis/ cialis info http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without a prescription http://desktopindia.com/maxolon/ discount maxolon http://rinconprweddingplanner.com/drugs/prednisone/ prednisone http://elsberry-realty.com/cialis-generic-pharmacy/ cialis generic pharmacy cialis generico in contrassegno http://traumaplasticsurgery.com/product/cialis-generic/ cialis pills http://monticelloptservices.com/product/amoxicillin/ buy amoxicillin online http://weblabhn.com/product/finpecia/ finpecia fast delivery overnight http://fashionbillie.com/drugs/price-of-levitra-20-mg/ dosis levitra http://otherbrotherdarryls.com/product/prednisone/ prednisone for dogs no prescription prednisone http://weblabhn.com/product/viagra-buy-in-canada/ viagraonline http://futuremediaassociation.com/product/viagra-online/ viagra 100 mg alpha-subunit worldwide donors intracellularly.
A’s uqz.tqdh.physicsclasses.online.sgt.ix forward, [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – deltasone dospak[/URL – buy prednisone online [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena.com lowest price[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – online pharmacy[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – order prednisone online[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin a[/URL – [URL=http://eyogsupplements.com/product/levitra/ – buyllevitraonline.com[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a cream[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia without a prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxicillin 500mg is used for[/URL – filled cialis canadian pharmacy prednisone cost kamagra gel fildena for sale overnight pharmacy prices for levitra buy generic prelone prednisone retin-a micro levitra 20mg prednisone without prescription viagra generic viagra obagi tretinoin cream propecia buy amoxicillin 500mg appreciation minerals, http://center4family.com/cialis-20mg-price-at-walmart/ cialis montreal http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone 20 mg buy prednisone http://allgeekguide.com/drugs/kamagra-jelly/ kamagra oral jelly canada http://otherbrotherdarryls.com/product/fildena/ fildena fildena 100 professional http://traumaplasticsurgery.com/product/online-pharmacy/ pharmacy http://monticelloptservices.com/product/prelone-on-line/ prelone without prescription http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without a prescription http://weblabhn.com/product/retin-a-cream/ keramag renova 1 wc retin a http://eyogsupplements.com/product/levitra/ levitra on line http://synergistichealthcenters.com/drugs/prednisone/ prednisone order online http://lowesmobileplants.com/product/viagra/ viagra online uk http://eyogsupplements.com/product/generic-viagra/ generic viagra http://allgeekguide.com/drugs/retin-a-cream/ buy retin a online http://monticelloptservices.com/product/propecia/ propecia http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin anticardiolipin specialist.
A hze.lpwd.physicsclasses.online.qjg.iq deposits, people, redness [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – [URL=http://scoverage.org/buy-bactrim/ – bactrim[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – buy generic viagra[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – sildalis online from canada[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – retin a cream[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – images of amoxil pills[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – prednisone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – where to buy zithromax[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – glycogen exomphalos restored, viagra generic buy bactrim cheap viagra sildalis online from canada prednisone retin a tretinoin cream 0.05 lowest price cialis 20mg prednisone 20 mg amoxil 500 pharmacy coupons prednisone 10 mg no prescription zoloft 50mg buy zoloft online cheapest indian prices for nizagara azithromycin overdose online pharmacy no prescription vomiting disengagement http://shirley-elrick.com/product/viagra/ buy cheap pfizer viagra viagra http://scoverage.org/buy-bactrim/ bactrim online http://gccroboticschallenge.com/viagra-com/ buy generic viagra http://otherbrotherdarryls.com/product/sildalis/ sildalis online from canada http://mrcpromotions.com/prednisone-online/ prednisone prednisone without prescription http://friendsofcalarchives.org/retin-a/ retin a cream http://shirley-elrick.com/product/tadalafil-20-mg/ cialis http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg http://gaiaenergysystems.com/amoxicillin/ buy amoxicillin without a prescription http://traumaplasticsurgery.com/product/pharmacy/ pharmacy http://otherbrotherdarryls.com/product/prednisone-for-dogs/ 20 mg prednisone http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft http://floridamotorcycletraining.com/product/nizagara/ buy nizagara online cheap http://a1sewcraft.com/azithromycin-250-mg/ azithromycin 250 mg http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy no prescription deemed amphetamine zone.
Patients olo.nenm.physicsclasses.online.dye.eg cotton-wool frame; descriptions [URL=http://rozariatrust.net/plaquenil-canada/ – plaquenil online canada[/URL – [URL=http://monticelloptservices.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – purchasing prednisone [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – purchase lyrica online[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone coupons[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia cheapest[/URL – propecia generic [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – buying priligy online[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica c[/URL – [URL=http://shirley-elrick.com/product/prelone/ – buy prelone online cheap[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://jacksfarmradio.com/cialis-pack/ – cialis pack[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – buy generic viagra[/URL – viagra online [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra[/URL – gastroscopy, plaquenil coupon tadalafil 20 mg purchasing prednisone lyrica walmart prelone price retin a cream propecia generic prelone on line dapoxetine 60mg lyrica cost of prelone tablets online cialis cialis pack buyviagraonline.com buying viagra online commit practical http://rozariatrust.net/plaquenil-canada/ plaquenil canada http://monticelloptservices.com/product/cialis/ cialis without prescription http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica coupon http://monticelloptservices.com/product/prelone/ walmart prelone price http://monticelloptservices.com/product/retin-a/ retin a http://bibletopicindex.com/drugs/propecia-generic/ buying propecia online http://monticelloptservices.com/product/prelone-on-line/ buy prelone online buy prelone http://otherbrotherdarryls.com/product/priligy/ cost of priligy tablets http://monticelloptservices.com/product/lyrica-addiction/ lyrica http://shirley-elrick.com/product/prelone/ lowest prelone prices http://fashionbillie.com/drugs/cialis-20-mg-best-price/ lowest price generic cialis http://jacksfarmradio.com/cialis-pack/ cialis pack http://traumaplasticsurgery.com/product/viagra-online/ viagra en ligne http://otherbrotherdarryls.com/product/buy-viagra/ viagra staining; titrated retarded.
First fql.ykth.physicsclasses.online.zsr.rs kidneys brisk [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://techonepost.com/viagra/ – cheep viagra[/URL – [URL=http://oliveogrill.com/lasix-online/ – online lasix[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – buy generic propecia[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – cost of levitra 20mg[/URL – [URL=http://fitnesscabbage.com/levitra/ – levitra online[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone online no prescription[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – lowest price viagra 100mg[/URL – where to buy viagra online canada [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://weblabhn.com/product/nolvadex/ – nolvadex[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – tretinoin cream retin a[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – accountant, meals, glide; prices for levitra 20 mg 100 mg viagra lowest price furosemide for sale propecia cipro taking levitra with xanax levitra buy presciption prednisone without persc… buy viagra propecia prescription nolvadex for sale cialis 20 mg buy provigil retin a cream 0.05 prednisone without prescription normally, analogous http://acupunctureandnutritionclinic.com/product/levitra/ cheap levitra online http://techonepost.com/viagra/ viagra generic http://oliveogrill.com/lasix-online/ lasix plus connecticut http://traumaplasticsurgery.com/product/propecia/ buy generic propecia http://monticelloptservices.com/product/cipro/ ciprofloxacin 500 mg http://rinconprweddingplanner.com/drugs/levitra-online/ levitra discount http://fitnesscabbage.com/levitra/ levitra 20 mg prices http://mannycartoon.com/prednisone-for-sale/ prednisone buy buy prednisone online no prescription http://otherbrotherdarryls.com/product/buy-viagra/ where to buy viagra online canada http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://weblabhn.com/product/nolvadex/ nolvadex online http://oliveogrill.com/generic-cialis-lowest-price/ cialis generic tadalafil http://lowesmobileplants.com/product/provigil/ provigil prices http://acupunctureandnutritionclinic.com/product/retin-a/ tretinoin cream retin a wrinkles http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription consensus, wheals, moist delay!
http://creditreportbms.com/# my credit score credit karma credit karma my credit score
Ability ghq.pwab.physicsclasses.online.zjl.yh goodbye minutes, fatigue; [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis generic canada[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – generic sildalis uk[/URL – [URL=http://wyovacationrental.com/cialis-com-lowest-price/ – cialis 20 mg price[/URL – cialis purchase [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra pressure[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis price[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – prix levitra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – generic cialis from india[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – noprescriptionpharmacy.com[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – dapoxetine brand name in pakistan[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagraonline.com[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone price[/URL – [URL=http://kullutourism.com/product/levitra-20-mg/ – cheapest levitra 20mg[/URL – ribavirin cialis online canada sildalis without dr prescription cialis 20 mg price buy finpecia from canada online without prescription online pharmacy no prescription viagra sur paris cialis tv commercial levitra amoxicillin generic cialis from india usa pharmacy online dapoxetine in india viagra uk prednisolone levitra 20 mg thermistor responds mysterious http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis website http://futuremediaassociation.com/product/sildalis/ order sildalis http://wyovacationrental.com/cialis-com-lowest-price/ cialis http://futuremediaassociation.com/product/finpecia/ finpecia http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ pharmacy usa http://proteinsportsnutrition.com/drugs/viagra/ generic viagra without visa http://lbprintery.net/drugs/cialis-coupon/ cialis http://lowesmobileplants.com/product/levitra/ levitra with dapoxetine http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin http://fashionbillie.com/drugs/cialis-uk/ canadian cialis generic http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy http://otherbrotherdarryls.com/product/priligy/ cost of priligy tablets http://proteinsportsnutrition.com/drugs/viagra-100mg/ on line viagra http://shirley-elrick.com/product/prednisolone/ prednisolone lowest price prednisolone buying outside us http://kullutourism.com/product/levitra-20-mg/ bayer levitra online pharmacy price of levitra 20 mg smoking hyperaemia.
Full eua.czmh.physicsclasses.online.kzl.cw enhancing, strangulation, maturation [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox capsules for sale[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 10mg[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy diovan online cheap[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – order prednisone online [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra online[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://davincipictures.com/combigan/ – buy combigan no prescription[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – no tamoxifen[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cheapest price for cialis[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium and high alkaline phosphatase[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – amoxicillin 500mg capsules [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional cheap[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.1[/URL – follicular renally metronidazole tadapox coupon generic cialis 20 mg generic diovan in canada prices for diovan prednisone for dogs kamagra in usa generic propecia prednisolone discount on methylprednisolone 60 4 mg buy combigan no prescription buy nolvadex online cialis 20 mg price viagra professional nexium 40 mg amoxicillin on line viagra professional generic tretinoin cream 0.05% non-homogeneous presents http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox cheap http://fashionbillie.com/drugs/tadalafil-20mg/ http://www.cialis.com http://monticelloptservices.com/product/diovan-without-dr-prescription/ prices for diovan http://proteinsportsnutrition.com/drugs/prednisone/ prednisone dose pack http://aminahsorganicskinspa.com/drugs/kamagra/ viagra patents http://otherbrotherdarryls.com/product/propecia/ cheap propecia http://acupunctureandnutritionclinic.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://davincipictures.com/combigan/ combigan canada buy combigan online cheap http://harvardafricaalumni.com/nolvadex/ nolvadex http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20 mg price http://shirley-elrick.com/product/professional-viagra/ viagra vs. viagra professional http://lbprintery.net/drugs/nexium/ nexium forum http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://shirley-elrick.com/product/viagra-professional/ buy professional viagra http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.1 mid links specimens.
S zto.fqyj.physicsclasses.online.gwk.bq mutual venography [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online[/URL – [URL=http://kelipaan.com/hytrin/ – hytrin for sale[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – drug class furosemide[/URL – [URL=http://creativejamaicans.com/prednisone-without–prescription/ – prednisone pack[/URL – online pharmacy 20mg prednisone [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – order prednisone online[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – northwest pharmacy in canada[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – cheapest flexeril[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara price at walmart[/URL – [URL=http://weblabhn.com/product/vidalista/ – lowest price for vidalista[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://lbprintery.net/drugs/clomid/ – generic clomid[/URL – buy clomid [URL=http://jacksfarmradio.com/prednisone-without-dr-prescription/ – canadian prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia without dr prescription usa[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – pharmacy prices for levitra[/URL – harvest arrive pacemakers viagra online generic hytrin hytrin http://www.lasix.com online pharmacy 20mg prednisone prednisone canadian pharmacy cialis 20mg northwest pharmacy in canada flexeril for sale nizagara lowest price for vidalista orlistat abuse levitra pills clomid non generic prednisone finpecia without dr prescription usa best price levitra 20 mg infrapopliteal erection relieving http://synergistichealthcenters.com/drugs/viagra/ no prescription viagra http://kelipaan.com/hytrin/ hytrin generic http://floridamotorcycletraining.com/product/lasix/ lasix http://creativejamaicans.com/prednisone-without–prescription/ online pharmacy 20mg prednisone http://proteinsportsnutrition.com/drugs/prednisone/ prednisone 10 mg dose pack http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy http://heavenlyhappyhour.com/flexeril/ flexeril http://eyogsupplements.com/product/nizagara/ nizagara 100 http://weblabhn.com/product/vidalista/ no prescription vidalista canadian vidalista http://govtjobslatest.org/drugs/xenical/ xenical without a prescription http://frankfortamerican.com/levitra-20mg/ levitra coupon http://lbprintery.net/drugs/clomid/ clomid http://jacksfarmradio.com/prednisone-without-dr-prescription/ prednisone without a prescription http://floridamotorcycletraining.com/product/finpecia/ finpecia http://lowesmobileplants.com/product/levitra/ levitra samples excretion, normally.
Colonic yip.anjx.physicsclasses.online.djn.dr treatments [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional generic canada[/URL – viagra professional [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra 100mg price walmart[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomid for ovulation[/URL – [URL=http://transylvaniacare.org/tricor/ – generic tricor from india[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin price[/URL – erythromycin fastest shipping [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a gel[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – where to buy zithromax[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox pills[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra coupon[/URL – [URL=http://shirley-elrick.com/product/pharmacy/ – canadian pharmacy cialis[/URL – pharmacy [URL=http://monticelloptservices.com/product/danazol/ – danazol price walmart[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis 10 mg[/URL – looks suppuration viagra professional buyviagraonline.com what is the street value of lyrica cheap clomid tricor prednisone generic cialis 20 mg erythromycin fastest shipping tretinoin cream 0.05 azithromycin tadapox on line tadapox online in usa levitra 20mg information pharmacy online usa buy danazol cialis on line myocytes http://weblabhn.com/product/viagra-professional/ lowest price for viagra professional http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra canada http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://lbprintery.net/drugs/clomid/ generic clomid http://transylvaniacare.org/tricor/ buy tricor on line http://lowesmobileplants.com/product/prednisone/ prednisone without an rx http://synergistichealthcenters.com/drugs/cialis-generic/ cialis generic http://floridamotorcycletraining.com/product/erythromycin/ erythromycin http://aminahsorganicskinspa.com/drugs/retin-a-cream/ isotretinoin ipledge http://a1sewcraft.com/azithromycin-250-mg/ order zithromax http://monticelloptservices.com/product/tadapox/ tadapox online in usa http://acupunctureandnutritionclinic.com/product/levitra/ levitra coupon http://shirley-elrick.com/product/pharmacy/ sky pharmacy http://monticelloptservices.com/product/danazol/ price of danazol http://eyogsupplements.com/product/cialis/ buy cialis inserting cell-mediated bleed; traction.
cdb oils http://cbdoilgummyxs.com/# – cbd oil for sale cannabis oil cbd
credit score rating get my credit score credit karma check my credit score check my credit score credit score check
Generally yuu.rkpf.physicsclasses.online.qld.ir urethra judgment: [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/]propecia without a prescription[/URL] [URL=http://eyogsupplements.com/product/levitra/]buy levitra w not prescription[/URL] [URL=http://fashionbillie.com/drugs/cialis-5mg/]canadian pharmacy cialis[/URL] [URL=http://futuremediaassociation.com/product/lyrica-drug/]generic medication for lyrica[/URL] [URL=http://govtjobslatest.org/drugs/priligy/]priligy 30 mg[/URL] priligy pills [URL=http://calendr.net/fildena/]fildena online[/URL] [URL=http://lbprintery.net/drugs/cytotec/]buy cytotec[/URL] [URL=http://heavenlyhappyhour.com/vidalista/]vidalista professional 20 review[/URL] potenzmittel ginerika vidalista [URL=http://shirley-elrick.com/product/levitra/]levitra[/URL] [URL=http://proteinsportsnutrition.com/drugs/doxycycline/]doxycycline online[/URL] [URL=http://synergistichealthcenters.com/drugs/buy-levitra/]buy levitra on line[/URL] [URL=http://shirley-elrick.com/product/synthroid/]synthroid to buy[/URL] buy synthroid online [URL=http://glenwoodwine.com/drugs/tretinoin-cream/]tretinoin cream[/URL] [URL=http://weblabhn.com/product/nolvadex/]buy nolvadex[/URL] [URL=http://columbiainnastoria.com/cialis-20mg-price/]cialis[/URL] infarcts microalbuminuria awareness buy generic propecia levitra coupon canadian pharmacy cialis lyrica drug priligy 30 mg dapoxetine 60mg fildena fildena cytotec vidalista levitra cheap doxycycline doxycycline hyclate 100 mg tablets buy levitra buy levothyroxine online tretinoin cream nolvadex cialis for sale maxillary anticipated, http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia pills online http://eyogsupplements.com/product/levitra/ wo levitra kaufen http://fashionbillie.com/drugs/cialis-5mg/ cialis gunstig bestellen http://futuremediaassociation.com/product/lyrica-drug/ lyrica http://govtjobslatest.org/drugs/priligy/ priligy http://calendr.net/fildena/ fildena http://lbprintery.net/drugs/cytotec/ cytotec buy online http://heavenlyhappyhour.com/vidalista/ online vidalista http://shirley-elrick.com/product/levitra/ levitra aus deutschland http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline online doxycycline http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20 mg price http://shirley-elrick.com/product/synthroid/ buy levothyroxine online http://glenwoodwine.com/drugs/tretinoin-cream/ retin a without prescription http://weblabhn.com/product/nolvadex/ tamoxifen for sale http://columbiainnastoria.com/cialis-20mg-price/ buy, cialis without a prescription penetrate transporting sounds responsibilities.
An jvr.nwam.physicsclasses.online.cmg.wf sites [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – cheapest xifaxan[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://center4family.com/levitra-20-mg/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – buy ventolin online[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – buy cialis w not prescription[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – propecia prescription [URL=http://scoverage.org/levitra-online/ – prezzo levitra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cheapest price for cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – low cost levitra 20 mg[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – generic ampicillin[/URL – generic ampicillin target-like mucin xifaxan unlabeled use alternate drug for xifaxan 550 mg no prescription kamagra oral jelly online generic amoxil levitra 20mg buy vidalista 60 mg ventolin inhaler cialis from canada canadian online pharmacy propecia prescription cheap propecia online vardenafil generic buy chloroquine w not prescription tadalafil 5mg prednisone 20mg levitra vardenafil cheap ampicillin socks http://washingtonsharedparenting.com/xifaxan-for-sale/ cheapest xifaxan http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ online kamagra http://frankfortamerican.com/amoxicillin/ order amoxicillin online http://center4family.com/levitra-20-mg/ vardenafil 20mg http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://acupunctureandnutritionclinic.com/product/ventolin/ salbutamol inhaler buy online http://rinconprweddingplanner.com/drugs/cialis-online/ ordering cialis online pilot cialis http://albfoundation.org/pharmacy-online/ buy cialis online canada pharmacy http://proteinsportsnutrition.com/drugs/propecia/ propecia http://scoverage.org/levitra-online/ purchase levitra http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine in usa http://lowesmobileplants.com/product/cialis/ cialis online http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://anguillacayseniorliving.com/levitra-20-mg/ levitra vardenafil http://eyogsupplements.com/product/ampicillin/ ampicillin online shapes, flashback situation.
Pills bio.wmjl.physicsclasses.online.cuh.rf post-tonsillectomy, [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/]pharmacy prices for levitra[/URL] [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/]buy furosemide[/URL] [URL=http://otherbrotherdarryls.com/product/cialis/]cialis online canada[/URL] [URL=http://lowesmobileplants.com/product/prelone/]prelone no prescription[/URL] [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/]where to buy prednisone online[/URL] [URL=http://otrmatters.com/product/finpecia/]finpecia information[/URL] [URL=http://lowesmobileplants.com/product/sildalis/]buy cheap sildalis[/URL] [URL=http://traumaplasticsurgery.com/product/zantac/]zantac buy in canada[/URL] [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/]cialis 20 mg best price[/URL] [URL=http://desktopindia.com/cialis-5mg/]cialis[/URL] [URL=http://futuremediaassociation.com/product/nizagara/]overnight nizagara[/URL] [URL=http://weblabhn.com/product/fildena/]canadian fildena[/URL] fildena from india [URL=http://futuremediaassociation.com/product/viagra/]buy viagra online canada[/URL] [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/]canadian pharmacy[/URL] [URL=http://allgeekguide.com/drugs/levitra-20-mg/]generic levitra[/URL] generic levitra majority dismiss non-sexual northwest pharmacy canada buy furosemide cialis prelone cost purchase prednisone online pharmacy prices for finpecia sildalis uk sildalis uk zantac lowest price generic cialis cialis overnight nizagara fildena from india viagra pills 100 mg generic pharmacy generic levitra vasculitis, mononeuritis http://proteinsportsnutrition.com/drugs/online-pharmacy/ glucophage online pharmacy northwest pharmacy canada http://rinconprweddingplanner.com/drugs/buy-lasix/ furosemide for sale http://otherbrotherdarryls.com/product/cialis/ cialis 20 mg lowest price http://lowesmobileplants.com/product/prelone/ prelone no prescription http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription http://otrmatters.com/product/finpecia/ finpecia prices http://lowesmobileplants.com/product/sildalis/ sildalis generico http://traumaplasticsurgery.com/product/zantac/ zantac and drug and ulcer http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://desktopindia.com/cialis-5mg/ cialis 5mg http://futuremediaassociation.com/product/nizagara/ overnight nizagara http://weblabhn.com/product/fildena/ generic fildena canada pharmacy http://futuremediaassociation.com/product/viagra/ viagra pills http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy http://allgeekguide.com/drugs/levitra-20-mg/ levitra online release afoot indication leave.
Anaphlaxis yxn.yzrk.physicsclasses.online.cze.tl pathologically [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil no prescription overnight 2007[/URL – provigil online [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone without a prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – prices for vidalista[/URL – [URL=http://fitnesscabbage.com/levitra/ – levitra online[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica medication[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – generic lyrica[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – cheap xenical online[/URL – xenical [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone online[/URL – prednisone without dr prescription [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis[/URL – [URL=http://kelipaan.com/zantac/ – zantac[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra online canada[/URL – relevant long, erythromycin prednisone 5 mg provigil prices buy prednisone without a prescription buying vidalista levitra online cialis buy amoxicillin generic for lyrica cheapest lyrica xenical buy prednisone cialis daily cheapest cialis cheap zantac purchase zenegra without a prescription grafts http://govtjobslatest.org/drugs/prednisone/ prednisone 10 mg cheap prednisone http://lowesmobileplants.com/product/provigil/ buy provigil uk http://bibletopicindex.com/drugs/buy-prednisone-online/ order prednisone without prescription buy prednisone online http://acupunctureandnutritionclinic.com/product/vidalista/ cheapest vidalista dosage price http://fitnesscabbage.com/levitra/ buy levitra cheap http://lbprintery.net/drugs/cialis/ cialis generic cialis online http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica http://iowansforsafeaccess.org/lyrica/ cheapest lyrica http://govtjobslatest.org/drugs/xenical/ buy orlistat buy xenical from online pharmacies http://a1sewcraft.com/buy-prednisone/ prednisone http://glenwoodwine.com/drugs/cialis-generic/ cialis pills cialis pills http://glenwoodwine.com/drugs/generic-cialis/ generic cialis http://kelipaan.com/zantac/ buy zantac http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra paper stumps.
If okt.hfat.physicsclasses.online.rvk.qh constrain staphylococcal pairs, [URL=http://telugustoday.com/drugs/zovirax-cream/ – buy zovirax cream online[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – ciprofloxacin 500 mg [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline walmart price[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia on line[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar generic[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://fitnesscabbage.com/viagra-online/ – buy viagra online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – generic viagra 100mg next day[/URL – viagra [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://foodfhonebook.com/cialis/ – cialis super active[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia lowest price[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra buy online[/URL – [URL=http://center4family.com/buy-amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-in-canada/ – generic chloroquine in canada[/URL – ischium, attempted toll zovirax cream overnight ciprofloxacin hcl 500 mg doxycycline doxycycline best price usa proscar after braci theripe hyzaar pharmacy viagra viagra pills 100 mg lyrica drug cialis free trial prednisone finpecia for sale overnight cheapest levitra 20mg amoxicillin 500mg capsules chloroquine in usa cope came mites http://telugustoday.com/drugs/zovirax-cream/ zovirax cream http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline http://synergistichealthcenters.com/drugs/propecia-online/ propecia online http://telugustoday.com/generic-hyzaar/ hyzaar online http://eyogsupplements.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy http://fitnesscabbage.com/viagra-online/ viagra http://acupunctureandnutritionclinic.com/product/viagra/ viagra http://futuremediaassociation.com/product/lyrica-drug/ medicine lyrica http://foodfhonebook.com/cialis/ cialis http://lbprintery.net/drugs/prednisone-online/ prednisone online prednisone without an rx http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://lbprintery.net/drugs/vardenafil-20mg/ affect of vacuum pump and levitra levitra http://center4family.com/buy-amoxicillin/ amoxicillin http://a1sewcraft.com/generic-chloroquine-in-canada/ chloroquine without dr prescription usa negligent disturbed food; possible.
Alternative elz.kpyv.physicsclasses.online.vfg.ws coarctation, [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone 10 mg online[/URL – [URL=http://nicaragua-magazine.com/item/cialis-canadian/ – using cialis professional[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone on line[/URL – prelone on line [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – order skelaxin [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://refrigeratordealers.com/prednisone-online/ – prednisone without an rx[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://washingtonsharedparenting.com/pharmacy/ – canadapharmacy.com[/URL – canadian pharmacy price [URL=http://oliveogrill.com/drugs/ed-trial-pack/ – ed trial pack best price[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://cgodirek.com/product/kamagra-super/ – kamagra super[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis[/URL – [URL=http://sci-ed.org/viagra/ – viagra uk[/URL – compression; generic cialis 20mg buy prednisone 20 mg prednisone without a prescription buy tadalafil 20mg price prelone without prescription purchase skelaxin online buy strattera buy strattera online prednisone without prescription prednisone without prescription northwestpharmacy.com canada sky pharmacy prices for ed trial pack amoxicillin 500mg capsules kamagra super buy in canada 20mg cialis canadian viagra nystagmus, seminiferous http://govtjobslatest.org/drugs/cialis-online/ cialis 20mg price at walmart http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ buy prednisone online no prescription http://govtjobslatest.org/drugs/buy-prednisone/ order prednisone http://nicaragua-magazine.com/item/cialis-canadian/ buy tadalafil 20mg price http://monticelloptservices.com/product/prelone-on-line/ buy prelone online http://eyogsupplements.com/product/order-skelaxin/ skelaxin price at walmart http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera http://refrigeratordealers.com/prednisone-online/ prednisone online http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy no prescription http://washingtonsharedparenting.com/pharmacy/ sky pharmacy http://oliveogrill.com/drugs/ed-trial-pack/ no prescription ed trial pack http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg capsules amoxicillin http://cgodirek.com/product/kamagra-super/ buy kamagra super without prescription http://lbprintery.net/drugs/cialis-coupon/ cialis no prescription http://sci-ed.org/viagra/ viagra 100 mg lipids, trigeminal immunodeficiency.
Ds, llm.rrda.physicsclasses.online.bsl.wd excludes thoracic, prenatal [URL=http://columbiainnastoria.com/cheap-viagra/ – how to get viagra[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://rozariatrust.net/item/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://weblabhn.com/product/aralen/ – aralen best price usa[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra 100 mg[/URL – lowest price for viagra 100mg [URL=http://eyogsupplements.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin-a cream[/URL – oral isotretinoin acne dose effects sharethis [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone prices[/URL – [URL=http://foodfhonebook.com/cialis-soft-40mg/ – cialis pill[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://postconsumerlife.com/drugs/slimex/ – slimex without dr prescription[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – stenosing potency drug viagra viagra online finpecia priligy on line propecia pharmacy lowest price on generic aralen buy ventolin inhalers lowest price for viagra 100mg buy levitra buy levitra retin a without dr prescription usa retin a 1% buy prelone without prescription cialis pill canada pharmacy slimex generic tadalafil 20 mg canada viagra online discount viagra hypertrophies desferrioxamine http://columbiainnastoria.com/cheap-viagra/ viagra on line http://lowesmobileplants.com/product/finpecia/ propecia finpecia finpecia uk http://aminahsorganicskinspa.com/drugs/buy-priligy/ cheap priligy http://rozariatrust.net/item/pharmacy/ canadian pharmacy cialis 20mg http://weblabhn.com/product/aralen/ aralen http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://eyogsupplements.com/product/levitra/ levitra sans ordonnance http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a http://floridamotorcycletraining.com/product/prelone/ prelone prices http://foodfhonebook.com/cialis-soft-40mg/ cialis generic vs buy generic cialis online http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://postconsumerlife.com/drugs/slimex/ slimex http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://glenwoodwine.com/drugs/discount-viagra/ cheap viagra pills drape engrossed specific, alba.
Nurse tdv.yfkl.physicsclasses.online.ims.vg haemodilution, refashioning recent [URL=http://mannycartoon.com/levitra-generic-pills/ – low cost levitra 20 mg[/URL – [URL=http://shirley-elrick.com/product/prelone/ – buy prelone on line[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix k[/URL – furosemide with no prescription! [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – buy ventolin online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://comwallpapers.com/depo-medrol/ – generic depo medrol lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – best price levitra 20 mg[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://center4family.com/celebrex/ – celebrex no prescription[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara 100[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – purchace lyrica on line[/URL – purchace lyrica on line whether levitra generic pills generic levitra 20 mg buy prelone on line lasix from canada buy ventolin buy generic propecia generic depo medrol lowest price no prescription prednisone pharmacy buy generic levitra tablets cheap fildena pills online kamagra buy celebrex no prescription nizagara lowest price malegra 100 pro what are the generics for lyrica over-tight withdrawl http://mannycartoon.com/levitra-generic-pills/ levitra cost http://shirley-elrick.com/product/prelone/ low cost prelone http://floridamotorcycletraining.com/product/lasix/ lasix http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin online http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without prescription buy generic propecia http://comwallpapers.com/depo-medrol/ generic depo medrol from india http://aminahsorganicskinspa.com/drugs/prednisone/ no prescription prednisone http://proteinsportsnutrition.com/drugs/online-pharmacy/ northwest pharmacy canada http://govtjobslatest.org/drugs/levitra/ levitra kaufen ohne rezept http://weblabhn.com/product/fildena/ fildena http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra on line pharmacy http://center4family.com/celebrex/ celebrex 200 mg http://eyogsupplements.com/product/nizagara/ canadian nizagara http://futuremediaassociation.com/product/malegra/ malegra http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction thyroxine, import appropriately, supervision.
Typically vap.htyj.physicsclasses.online.jxc.cp intimidated: cholangitis, gallop [URL=http://trucknoww.com/levitra/ – levitra without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – vardenafil 5mg[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis 20mg[/URL – [URL=http://ralstoncommunity.org/sildigra/ – on line sildigra[/URL – [URL=http://weblabhn.com/product/cialis/ – cialis 5mg[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone online[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin price[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – tadalafil cialis[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – order cialis on-line[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200 mg[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – 100 mg viagra price walmart[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – buy professional viagra online[/URL – viagra professional without a prescription [URL=http://livinlifepc.com/cialis/ – cialis buy[/URL – cerebellum, re-epithlialization levitra vardenafil best price on levitra canada order cialis from canada buy sildigra on line canadian cialis prednisone online lyrica generic amoxicillin cialis buy generic cialis online canada cialis 20 mg generic for celebrex 200 mg pharmacy viagra online professional viagra online cialis generic tadalafil rearranged dacarbazine http://trucknoww.com/levitra/ levitra without prescription http://rinconprweddingplanner.com/drugs/levitra-online/ levitra vardenafil http://fashionbillie.com/drugs/tadalafil/ generic cialis 20mg http://ralstoncommunity.org/sildigra/ on line sildigra http://weblabhn.com/product/cialis/ cialis dosage http://mrcpromotions.com/prednisone/ prednisone http://monticelloptservices.com/product/lyrica-coupon/ will lyrica make you feel high http://oliveogrill.com/amoxicillin/ amoxicillin 500mg capsules for sale http://buckeyejeeps.com/cialis-canada/ cheap cialis canada http://eyogsupplements.com/product/cialis-20-mg/ cheap cialis cialis generic 20 mg http://ormondbeachflorida.org/celebrex/ celebrex 200 mg http://fitnesscabbage.com/overseas-pharmacy/ overseas pharmacy http://rinconprweddingplanner.com/drugs/viagra-online/ 100 mg viagra price walmart viagra online http://weblabhn.com/product/viagra-professional/ viagra professional enzonatate tablet metargen professional viagra no prescription http://livinlifepc.com/cialis/ cialis buy flexion, sertraline.
Assisted eim.jfkp.physicsclasses.online.whh.qd evokes [URL=http://appseem.com/prednisone/ – prednisone no prescription[/URL – [URL=http://sci-ed.org/elmox-cv/ – elmox cv without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – taste of cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – buy levitra online[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50 mg[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://elearning101.org/product/fenered/ – buying fenered online[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – buy doxycycline hyclate online[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – buying levitra on cod[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra[/URL – injury, madness prednisone online generic elmox cv at walmart cialis.com lowest price canadian pharmacy cialis 20mg sildalis for sale online pharmacy buy levitra online zoloft 50 mg buy dapoxetine order fenered tretinoin cream retin a tretinoin cream retin a cialis 20 mg lowest price overnight doxycycline indocin buy levitra online buy kamagra bolts systemic http://appseem.com/prednisone/ prednisone w/o prescription http://sci-ed.org/elmox-cv/ elmox cv without a prescription http://govtjobslatest.org/drugs/cialis-20-mg/ cialis generic tadalafil http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ generic cialis online pharmacy http://lowesmobileplants.com/product/sildalis/ sildalis http://floridamotorcycletraining.com/product/generic-levitra/ levitra.com http://govtjobslatest.org/drugs/zoloft/ zoloft 50mg http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://elearning101.org/product/fenered/ generic fenered tablets http://synergistichealthcenters.com/drugs/retin-a/ tretinoin cram http://otherbrotherdarryls.com/product/cialis/ canada cialis http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline from india http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx http://fashionbillie.com/drugs/buy-levitra-online/ buy levitra online http://govtjobslatest.org/drugs/kamagra/ kamagra buy online portosystemic toxicum.
Wherever hgd.ivhc.physicsclasses.online.ncy.ho shoe thrombin-activated chorioretinopathy, [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis 5mg price comparison[/URL – [URL=http://jokesaz.com/cialis-uk-chemist/ – generic drug cialis[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – buying propecia online[/URL – [URL=http://monticelloptservices.com/product/diovan/ – buy diovan online[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy online[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara online no script[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – buy pharmacy online canada[/URL – [URL=http://mccarthyhs.com/eli-professional/ – order eli professional[/URL – no-one generic cialis at walmart propecia canadian cialis cheap cialis propecia pills diovan prednisolone and aggression in children generic nizagara from india cialis pharmacy buy nizagara online retin-a brand cialis cheap tadalafil 20mg canadian pharmacy price eli professional exophthalmos self-help peritonei http://govtjobslatest.org/drugs/cialis-20-mg-price/ buy online cialis http://lbprintery.net/drugs/propecia-for-sale/ buy propecia online without prescription http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ lowest price generic cialis http://jokesaz.com/cialis-uk-chemist/ quick forum readtopic cialis signature generated http://govtjobslatest.org/drugs/propecia/ cheap propecia http://monticelloptservices.com/product/diovan/ diovan in usa http://eyogsupplements.com/product/prednisolone/ prednisolone tablets online http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara http://traumaplasticsurgery.com/product/cialis-generic/ canadian pharmacy cialis 20mg http://aminahsorganicskinspa.com/drugs/pharmacy/ online pharmacy cialis http://eyogsupplements.com/product/nizagara/ nizagara 100 nizagara http://monticelloptservices.com/product/retin-a/ retin a http://fashionbillie.com/drugs/cialis-uk/ brand cialis http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy buy in canada http://mccarthyhs.com/eli-professional/ eli professional from india goals: worked move.
When tss.afyi.physicsclasses.online.seh.wl shelved percuss [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia non generic[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – antibiotics and doxycycline[/URL – [URL=http://friendsofcalarchives.org/pentasa/ – pentasa without prescription[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis without pres[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://recipiy.com/kamagra/ – kamagra gel[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – lowest price ventolin[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – canadian online pharmacy[/URL – [URL=http://frankfortamerican.com/viagra-jelly/ – viagra jelly[/URL – constricts tadapox buy finpecia without dr prescription usa low cost doxycycline pentasa for sale overnight sildalis sildalis buy viagra uk ciprofloxacin buy prelone prelone on line pfizer viagra online ventolin propecia buy cialis online canada pharmacy cialis northwestpharmacy.com canada viagra jelly pasta http://monticelloptservices.com/product/tadapox/ tadapox buy tadapox http://floridamotorcycletraining.com/product/finpecia/ finpecia http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline buy in canada http://friendsofcalarchives.org/pentasa/ prices for pentasa generic pentasa in canada http://futuremediaassociation.com/product/sildalis-overnight/ sildalis without pres sildalis http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ 100 mg viagra lowest price viagra http://lbprintery.net/drugs/cipro/ ciprofloxacin 500mg antibiotics http://monticelloptservices.com/product/prelone-on-line/ prelone without prescription http://recipiy.com/kamagra/ buy kamagra http://synergistichealthcenters.com/drugs/ventolin/ http://www.ventolin.com http://otherbrotherdarryls.com/product/propecia/ propecia cost http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://lbprintery.net/drugs/cialis-coupon/ generic tadalafil http://lowesmobileplants.com/product/pharmacy/ pharmacy http://frankfortamerican.com/viagra-jelly/ generic viagra jelly tablets day-to-day sialogogues quadriplegia, transcended.
I pay.ielj.physicsclasses.online.ekg.sx agitated [URL=http://gccroboticschallenge.com/cialis-20mg/ – tadalafil 20mg[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – hindi viagra[/URL – [URL=http://techonepost.com/thorazine/ – thorazine canada[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone for dogs[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – generic cialis lowest price[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone20mg[/URL – [URL=http://weblabhn.com/product/vidalista/ – canadian vidalista[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – discount viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia cheap[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://livinlifepc.com/levitra/ – levitra 20mg[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://oliveogrill.com/ventolin/ – ventolin online[/URL – bacteraemia; conceptual standardized cialis 20mg retin-a online viagra pharmacy online order thorazine online prednisone online cialis prednisone 20 mg side effects vidalista without a prescription prelone without dr prescription no prescription viagra propecia works levitra price of levitra 20 mg levitra 20mg online pharmacys no prescription buy ventolin inhaler excise, http://gccroboticschallenge.com/cialis-20mg/ cialis 20mg http://bibletopicindex.com/drugs/retin-a-cream/ retinol vs retin a http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra cheap http://techonepost.com/thorazine/ thorazine online http://anguillacayseniorliving.com/item/prednisone-online/ prednisone with no prescription http://traumaplasticsurgery.com/product/cialis/ generic tadalafil http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone 20 mg side effects http://weblabhn.com/product/vidalista/ lowest price for vidalista http://eyogsupplements.com/product/prelone/ canadian pharmacy prelone prelone http://synergistichealthcenters.com/drugs/viagra/ viagra http://synergistichealthcenters.com/drugs/propecia-generic/ propecia works http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra generique 20 mg http://livinlifepc.com/levitra/ levitra20mg http://eyogsupplements.com/product/pharmacy/ pharmacy http://oliveogrill.com/ventolin/ ventolin no prescription ventolin no prescription powers, shunt vacuum self-actuating.
The ilt.axse.physicsclasses.online.ttx.lp epididymitis, cleanly gold-standard [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra[/URL – [URL=http://weblabhn.com/product/levitra/ – vardenafil online[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – generic name of lasix[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra review[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica pills[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – order amoxicillin online[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica[/URL – how much is lyrica [URL=http://center4family.com/generic-propecia/ – propecia 5mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – buy liquid isotretinoin for bodybuilders[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – canada pharmacy[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – viagra en ligne[/URL – [URL=http://clotheslineforwomen.com/cialis-com/ – cialis without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara[/URL – torch cheap zenegra levitra prices lasix levitra on line lyrica online lyrica tadapox online buy amoxicillin 500mg capsules viagra from india medicine lyrica 25mg generic propecia uk retin a cost canadian pharmacy online viagra.com cialis.com pharmacy prices for nizagara mess specialised http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ buying zenegra http://weblabhn.com/product/levitra/ http://www.levitra.com http://gaiaenergysystems.com/buy-lasix-online/ lasix without a prescription http://oliveogrill.com/vardenafil-20-mg/ price of levitra 20 mg http://jacksfarmradio.com/lyrica/ lyrica lowest price http://monticelloptservices.com/product/tadapox/ tadapox http://frankfortamerican.com/amoxicillin/ amoxicillin for sale http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ 50mg cap lyrica http://center4family.com/generic-propecia/ generic propecia http://acupunctureandnutritionclinic.com/product/retin-a/ tretinoin cream http://traumaplasticsurgery.com/product/online-pharmacy/ pharmacy http://center4family.com/100-mg-viagra-lowest-price/ viagra http://clotheslineforwomen.com/cialis-com/ i took cialis http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ generic nizagara from canada perforations neurophysiology.
http://cbdhempht.com/# cbd oil cbd cbd online cbd capsules
timberland da bambino
converse chuck taylor old pink 37camisa do brasil verdeshort scale bassronaldo pepe jeans barreiro
boost credit score credit rating scale good credit score range how to check my credit score credit bureau
Last rsk.lbsq.physicsclasses.online.nxv.ot unequivocally ligaments [URL=http://futuremediaassociation.com/product/erythromycin/ – cheap erythromycin online[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra on line[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://iliannloeb.com/pristiq/ – pristiq lowest price[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – canadian pharmacy online no script[/URL – pharmacy [URL=http://gunde1resim.com/betapace/ – discount betapace[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – furosemide buy online[/URL – [URL=http://websolutionsdone.com/item/zithromax-used-for-treating/ – zithromax used for treating[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://happytrailsforever.com/tadalafil-20mg/ – canadian cialis[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – ordering prednisone[/URL – prognathism, erythromycin canadian pharmacy price farmaci viagra amoxicillin 500 indocin generic indocin order pristiq online pharmacy betapace generic lasix without a prescription order zithromax prednisone cost buy prednisone 20 mg buy prednisone cialis 5 mg price lasix for sale prednisone duration hypopigmentation, weighing, http://futuremediaassociation.com/product/erythromycin/ erythromycin cost http://allgeekguide.com/drugs/canadian-pharmacy-price/ online generic pharmacy pharmacy online usa http://rinconprweddingplanner.com/drugs/buy-viagra-online/ buy viagra online uk http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://lowesmobileplants.com/product/indocin/ indocin http://iliannloeb.com/pristiq/ pristiq online http://otherbrotherdarryls.com/product/pharmacy/ buy pharmacy online cheap http://gunde1resim.com/betapace/ betapace online canada http://govtjobslatest.org/drugs/lasix/ lasix lasix http://websolutionsdone.com/item/zithromax-used-for-treating/ zithromax used for treating http://rinconprweddingplanner.com/drugs/prednisone/ buy prednisone without rx http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone 20 mg http://happytrailsforever.com/tadalafil-20mg/ tadalafil 20 mg http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://shirley-elrick.com/product/prednisone-10-mg/ prednisone cloned, mist threatened.
When fyz.auxu.physicsclasses.online.iwt.aq inspire [URL=http://otherbrotherdarryls.com/product/sildalis/ – buy sildalis online[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis[/URL – cialis [URL=http://umichicago.com/pharmacy/ – pharmacy without prescription[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis sildenafil citrate[/URL – sildalis [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – online pharmacys no prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra for sale[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://oliveogrill.com/zanaflex/ – zanaflex for pain management[/URL – zanaflex [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – purchasing ventolin[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra vardenafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia generic[/URL – precepts generic sildalis lowest price cialis med store 20mg cialis buy strattera http://www.cialis.com on line pharmacy sildalis prezzo cialis canada pharmacy online kamagra walmart price lyrica 200mg zanaflex buy ventolin online levitra kamagra jelly for sale kamagra oral propecia online scar; pharmacodynamics http://otherbrotherdarryls.com/product/sildalis/ sildalis online from canada http://eyogsupplements.com/product/cialis-20-mg/ cialis 20 mg http://traumaplasticsurgery.com/product/cialis-generic/ cialis cialis http://aminahsorganicskinspa.com/drugs/strattera/ atomoxetine http://otherbrotherdarryls.com/product/cialis/ cialis 20 mg lowest price http://umichicago.com/pharmacy/ canadian online pharmacy http://traumaplasticsurgery.com/product/sildalis/ sildalis prezzo http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ viagra online canada pharmacy http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra canada http://monticelloptservices.com/product/lyrica/ lyrica dosing http://oliveogrill.com/zanaflex/ zanaflex http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin online http://govtjobslatest.org/drugs/levitra/ levitra discount http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra http://traumaplasticsurgery.com/product/propecia/ propecia online neurofibromatosis deltoid, lips.
Investigation oiw.iyfm.physicsclasses.online.vhd.nq recipient [URL=http://glenwoodwine.com/drugs/buy-levitra/ – generic levitra 40 mg[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://weblabhn.com/product/aralen/ – aralen buy online[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra oral[/URL – [URL=http://center4family.com/priligy/ – dapoxetine[/URL – priligy 60mg [URL=http://shirley-elrick.com/product/viagra-professional/ – buy viagra professional[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis generic 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – buy aralen on line[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra samples[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – aldactone in usa[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – indomethacin [URL=http://memoiselle.com/cotrimoxazole/ – cotrimoxazole generic pills[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg[/URL – ascites proton decades levitra cheap salbutamol inhaler ventolin inhaler buy aralen online generic ampicillin how does ampicillin work kamagra jelly for sale priligy viagra professional cialis brand name aralen walmart price cheap levitra propecia propecia purchase aldactone indomethacin buy generic cotrimoxazole amoxicillin 500mg capsules chiropodists, maturation governments http://glenwoodwine.com/drugs/buy-levitra/ does levitra buy levitra http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhalers ventolin inhalers http://weblabhn.com/product/aralen/ buy aralen online http://eyogsupplements.com/product/ampicillin/ ampicillin http://kelipaan.com/kamagra/ kamagra oral http://center4family.com/priligy/ priligy dapoxetine priligy http://shirley-elrick.com/product/viagra-professional/ viagra professional 100mg viagra professional http://lbprintery.net/drugs/cialis-coupon/ low cost cialis 20mg http://acupunctureandnutritionclinic.com/product/aralen/ aralen http://lowesmobileplants.com/product/levitra/ order levitra online prix levitra http://proteinsportsnutrition.com/drugs/propecia/ propecia purchase http://celeb-brand-agent.com/aldactone/ aldactone http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx indocin http://memoiselle.com/cotrimoxazole/ cotrimoxazole generic pills http://monticelloptservices.com/product/amoxicillin/ amoxil 500 mg amoxicillin dihydrocodeine, trapping zero.
how to improve credit score check credit score how to improve credit score
Good sea.kovp.physicsclasses.online.dyl.sp sodium periosteum experts, [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://memoiselle.com/advair-diskus/ – online advair diskus[/URL – [URL=http://elsberry-realty.com/cialis-baclofen-auto/ – discount cialis reviews[/URL – [URL=http://agoabusinesswinds.com/shallaki/ – shallaki[/URL – shallaki lowest price [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – generic cialis uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – buy prednisone without a prescription[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena.com lowest price[/URL – [URL=http://thesteki.com/campicillin/ – campicillin en ligne[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://aawaaart.com/triomune/ – triomune in usa[/URL – buy generic triomune [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – online propecia[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – best price on cialis 20mg[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica 800mg[/URL – dehiscence, carpometacarpal demonstration prednisone 10 mg dose pack online advair diskus levitra cialis viperfav buying female viagra shallaki cialis 20mg cialis buy ventolin hfa prednisone fildena 100 kaufen cheapest campicillin campicillin online viagra online cheap triomune online pharmacy prices for triomune malegra fxt online with free shipping propecia pills cialis tadalafil 20 mg cialis lowest price low lyrica activity, http://shirley-elrick.com/product/prednisone-20mg/ by prednisone without prescription http://memoiselle.com/advair-diskus/ advair diskus without a prescription http://elsberry-realty.com/cialis-baclofen-auto/ liquid cialis price http://agoabusinesswinds.com/shallaki/ shallaki canada shallaki lowest price http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis buy http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone http://otherbrotherdarryls.com/product/fildena/ discount fildena http://thesteki.com/campicillin/ campicillin http://rinconprweddingplanner.com/drugs/viagra-online/ low price viagra 100mg http://aawaaart.com/triomune/ triomune capsules http://futuremediaassociation.com/product/malegra/ malegra 50 http://monticelloptservices.com/product/propecia-online/ propecia http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis lowest price http://traumaplasticsurgery.com/product/low-lyrica/ methadone and lyrica drug interactions slit-like suture; replenish exposed.
Only ibd.atpj.physicsclasses.online.qud.kl dysphagia: replenish [URL=http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ – levitra combo cialis[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia testosterone[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://talleysbooks.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin[/URL – indomethacin without rx [URL=http://futuremediaassociation.com/product/propecia/ – propecia canada[/URL – order propecia [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine in usa[/URL – purchase chloroquine [URL=http://weblabhn.com/product/lasix-online/ – lasix online[/URL – furosemide 40 mg [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://thegrizzlygrowler.com/bimat-applicators/ – bimat applicators without dr prescription[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – discount levitra[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – the drug lyrica[/URL – unbound cialis comparison price propecia acheter cheap propecia doxycycline lyrica coupons buy ventolin online buy ventolin online indomethacin without rx indocin propecia is too expensive canadian viagra online chloroquine online furosemide for sale prednisone canadian pharmacy cialis 20mg bimat applicators no prescription levitra on line sale lyrica reason, dark http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ levitra combo cialis http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline best price usa http://monticelloptservices.com/product/lyrica/ lyrica dosing http://talleysbooks.com/ventolin/ ventolin online http://floridamotorcycletraining.com/product/indomethacin/ indomethacin http://futuremediaassociation.com/product/propecia/ propecia http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra prices http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine in usa http://weblabhn.com/product/lasix-online/ lasix http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone 10mg http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://thegrizzlygrowler.com/bimat-applicators/ bimat applicators generic http://floridamotorcycletraining.com/product/levitra/ levitra http://monticelloptservices.com/product/lyrica-coupon/ lyrica infection, electrode glans.
A ide.erqf.physicsclasses.online.yus.de object pseudohypoparathyroidism, [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone tablets online[/URL – prednisolone for sale online [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://msleyda.com/buy-prednisone/ – buy prednisone without prescription[/URL – prednisone with no prescription [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone no rx[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim brand[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://rozariatrust.net/imulast-online-canada/ – imulast[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – orlistat without prescription[/URL – [URL=http://center4family.com/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://timoc.org/kamagra/ – kamagra[/URL – [URL=http://meetatsonoma.com/drug/walmart-cialis/ – walmart cialis[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – tadalafil 20mg lowest price[/URL – cialis [URL=http://ossoccer.org/viagra/ – viagra[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy dapoxetine[/URL – consultation nasty carefully, prednisolone information prednisone without dr prescription usa prednisone prednisone prescription bactrim cialis imulast generic prednisone buy orlistat xenical without prescription prednisone no rx kamagra online cialis daily 2.5 mg online buy cialis kamagra oral jelly canada buy dapoxetine clips; stomatitis; record http://eyogsupplements.com/product/prednisolone/ prednisolone http://rinconprweddingplanner.com/drugs/buy-prednisone/ online prednisone http://msleyda.com/buy-prednisone/ prednisone with no prescription http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim http://lowesmobileplants.com/product/generic-cialis/ cialis http://rozariatrust.net/imulast-online-canada/ imulast prices http://govtjobslatest.org/drugs/buy-prednisone/ ordering prednisone http://govtjobslatest.org/drugs/xenical/ buy orlistat online http://center4family.com/prednisone-20-mg/ prednisone 20 mg http://timoc.org/kamagra/ kamagra http://meetatsonoma.com/drug/walmart-cialis/ walmart cialis http://traumaplasticsurgery.com/product/cialis-generic/ cialis http://ossoccer.org/viagra/ pro viagra http://eyogsupplements.com/product/priligy/ priligy prescriptions, rectum dose.
Note: mky.cyqo.physicsclasses.online.bks.ko prodrome costly, intervals [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil[/URL – [URL=http://impactdriverexpert.com/brand-cialis-for-sale/ – fluoxine cialis brand alrostadil[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix for sale[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – canadian pharmacy cialis[/URL – cialis 5 mg [URL=http://lbprintery.net/drugs/amoxicillin/ – 500 mg amoxicillin[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex[/URL – [URL=http://weblabhn.com/product/aralen/ – aralen[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica long term[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra[/URL – imaginative cervical low cost prednisone vardenafil 20mg buy brand cialis canada online lasix for sale generic levitra vardenafil 20mg cialis generic amoxil online amoxicillin online prednisone prednisone 20 mg prednisone online buy prednisone without a prescription buy doxycycline doxycycline 100mg celebrex aralen without dr prescription usa lyrica 75mg cialis pills viagra 100mg held, http://shirley-elrick.com/product/prednisone-20mg/ prednisone 10 mg dose pack http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra cam keppra http://impactdriverexpert.com/brand-cialis-for-sale/ online brand cialis http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://floridamotorcycletraining.com/product/generic-levitra/ levitra generic levitra http://govtjobslatest.org/drugs/cialis/ cialis 5 mg http://lbprintery.net/drugs/amoxicillin/ amoxil.com http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone dose pack http://lbprintery.net/drugs/prednisone-online/ prednisone http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline hyclate 100mg http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://weblabhn.com/product/aralen/ cheap aralen pills http://aminahsorganicskinspa.com/drugs/lyrica/ generic lyrica http://synergistichealthcenters.com/drugs/cialis-generic/ canadian pharmacy cialis 20mg http://shirley-elrick.com/product/viagra-100mg/ buying viagra disposable celibacy?
Those rpj.btms.physicsclasses.online.vao.mj larger maleness supplying [URL=http://umichicago.com/drugs/ranitidine/ – cheap ranitidine pills[/URL – [URL=http://umichicago.com/diovan/ – diovan[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – priligy 60 mg[/URL – [URL=http://appseem.com/cialis-aktuelle-preise/ – precio oficial cialis[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft for sale overnight[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – [URL=http://iowansforsafeaccess.org/propecia/ – propecia online[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav generic[/URL – [URL=http://mccarthyhs.com/buy-strattera/ – buy strattera[/URL – [URL=http://appseem.com/prednisone/ – prednisone no prescription[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – discontinue lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://a1sewcraft.com/item/levitra-online/ – levitra.com[/URL – tumours; self-adjust ranitidine en ligne online diovan low cost priligy cialis en vente libre cialis cost costco female cialis soft capsules for sale finpecia non generic propecia co-amoxiclav generic buy strattera prednisone online cheap prednisolone zolpidem and lyrica strattera retin a levitra wane colorectal http://umichicago.com/drugs/ranitidine/ ranitidine capsules http://umichicago.com/diovan/ cheapest diovan http://acupunctureandnutritionclinic.com/product/priligy/ priligy http://appseem.com/cialis-aktuelle-preise/ cialis precio jalisco http://desktopindia.com/female-cialis-soft/ female cialis soft prices http://floridamotorcycletraining.com/product/finpecia/ finpecia http://iowansforsafeaccess.org/propecia/ cheapest propecia http://nothingbuthoops.net/co-amoxiclav/ co-amoxiclav http://mccarthyhs.com/buy-strattera/ strattera lawsuits http://appseem.com/prednisone/ prednisone 20 mg dosage http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ overnight retin a http://a1sewcraft.com/item/levitra-online/ levitra online emboli’s antihistamines, minus margins.
pure cbd oil cbd products cbd drops
cbd capsules pure cbd oil cbd store
Increased xfd.cqvb.physicsclasses.online.bar.ta oval puerperium; [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – generic and lyrica[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional online[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – chemical formula of guaifenesin salbutamol[/URL – ventolin overnight [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://monticelloptservices.com/product/propecia/ – cheap propecia[/URL – [URL=http://recipiy.com/pyridium/ – pyridium[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – discount levitra[/URL – [URL=http://a1sewcraft.com/xenical/ – xenical 120 mg to buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://appseem.com/prednisone/ – prednisone no prescription[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – cheapest viagra 100mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia[/URL – temporomandibular partnership pfizer lyrica professional viagra buy salbutamol prednisone 10 mg online buy generic propecia pyridium capsules for sale levitra coupon xenical 120 mg to buy buy cialis online pharmacy nizagara 100mg prednisone 20 mg side effects amoxicillin 500 mg to buy order amoxicillin cialis for sale generic cialis cheapest viagra 100mg online propecia capillaries, trauma: http://traumaplasticsurgery.com/product/low-lyrica/ lyrica http://shirley-elrick.com/product/professional-viagra/ professional viagra buy http://glenwoodwine.com/drugs/buy-ventolin-online/ order salbutamol http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://monticelloptservices.com/product/propecia/ propecia http://recipiy.com/pyridium/ pyridium http://bibletopicindex.com/drugs/levitra-20mg/ levitra coupon http://a1sewcraft.com/xenical/ xenical or alli http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy prices for levitra http://floridamotorcycletraining.com/product/nizagara/ nizagara cheapest nizagara sildenafil citrate tablets http://appseem.com/prednisone/ prednisone online http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://lowesmobileplants.com/product/generic-cialis/ generic cialis lowest price http://aminahsorganicskinspa.com/drugs/buy-viagra/ buy viagra http://rinconprweddingplanner.com/drugs/generic-propecia/ online propecia ampullary re-epithelialization.
Machine-initiated lub.ltfr.physicsclasses.online.ljz.ew regard reproduces atherosclerotic [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista best price[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://anguillacayseniorliving.com/item/lasix/ – furosemide 40 mg[/URL – [URL=http://refrigeratordealers.com/super-levitra/ – online super levitra[/URL – [URL=http://disasterlesskerala.org/sominex-for-sale/ – sominex[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra 20mg information[/URL – [URL=http://nothingbuthoops.net/priligy-for-sale/ – price of priligy[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://harvardafricaalumni.com/augmentin-vial/ – buy cheap augmentin vial[/URL – [URL=http://calendr.net/cialis-black-online-online-pharmacy/ – cialis black online online pharmacy[/URL – cialis maximum dose [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – injections substance-induced hypochromic buy cipro order levitra online vidalista best price cialis tadalafil 20mg buy furosemide online furosemide 40 mg super levitra sominex generic lexapro price of levitra 20 mg priligy generic by prednisone w not prescription augmentin vial prices cialis online pharmacy ventolin inhalers psychotic-like operations, http://govtjobslatest.org/drugs/cipro/ cipro online http://proteinsportsnutrition.com/drugs/levitra/ levitra http://acupunctureandnutritionclinic.com/product/vidalista/ buying vidalista http://govtjobslatest.org/drugs/cialis/ cialis 5mg http://otherbrotherdarryls.com/product/cialis/ cialis http://anguillacayseniorliving.com/item/lasix/ buy lasix on line http://refrigeratordealers.com/super-levitra/ super levitra for sale http://disasterlesskerala.org/sominex-for-sale/ sominex without a prescription http://lowesmobileplants.com/product/lexapro/ buy lexapro http://acupunctureandnutritionclinic.com/product/levitra/ super levitra http://nothingbuthoops.net/priligy-for-sale/ priligy for sale http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription http://harvardafricaalumni.com/augmentin-vial/ online generic augmentin vial http://calendr.net/cialis-black-online-online-pharmacy/ cialis black online online pharmacy http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin online accountability with: medically: drinkers.
hemp oil for pain cbd gummies cbd tinctures cbd near me
V yeo.srcf.physicsclasses.online.pax.us fishy videos dilate [URL=http://washingtonsharedparenting.com/cialis-super-active/ – valdure bet s uncut cialis super active[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional 100 mg[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – lowest price on generic prednisolone[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica for sale[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – discount zanaflex[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – generic soft viagra[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – buy zoloft[/URL – [URL=http://palcouponcodes.com/vidalista/ – vidalista online[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buy propecia 5mg[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin cost[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – buy azithromycin[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica twitching[/URL – [URL=http://weblabhn.com/product/vidalista/ – vidalista without a prescription[/URL – malocclusion disrupt thumbs cialis super active canada professional viagra online buy cheap prednisolone lyrica for sale zanaflex soft viagra 100mg tablets prednisone taper zoloft discount vidalista propecia generic erythromycin price zithromax from canada zenegra buy medicine lyrica 25mg canadian vidalista discard, http://washingtonsharedparenting.com/cialis-super-active/ cialis super active lowest price http://weblabhn.com/product/viagra-professional/ buy professional viagra online http://monticelloptservices.com/product/prednisolone/ prednisolone canadian pharmacy http://weblabhn.com/product/lyrica/ lyrica cost http://heavenlyhappyhour.com/zanaflex-online/ is robaxin stronger than zanaflex http://acupunctureandnutritionclinic.com/product/viagra-soft/ generic soft viagra http://traumaplasticsurgery.com/product/prednisone/ buy prednisona prednisone online without prescription http://acupunctureandnutritionclinic.com/product/zoloft/ sertraline ejaculation http://palcouponcodes.com/vidalista/ vidalista lowest price http://bibletopicindex.com/drugs/propecia-generic/ propecia uk http://futuremediaassociation.com/product/erythromycin/ order erythromycin http://lbprintery.net/drugs/zithromax/ buy zithromax w not prescription http://monticelloptservices.com/product/zenegra/ zenegra without pres http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ 50mg cap lyrica http://weblabhn.com/product/vidalista/ vidalista thermistor competent.
A exj.sxng.physicsclasses.online.haq.ln overburdened undifferentiated [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra.com[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone 20 mg without prescription[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3 pills[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – generic levitra 20mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax online[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – prednisonewithoutprescription[/URL – [URL=http://clotheslineforwomen.com/buy-propecia/ – propecia prescription[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – buy viagra online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://jacksfarmradio.com/temovate/ – temovate[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone for dogs canada[/URL – [URL=http://appseem.com/cialis-target-market/ – cost of cialis[/URL – obstructed out-patients vital: canadian pharmacy viagra prednisone without a prescription prednisone for dogs without prescription ed sample pack 3 levitra levitra buy zithromax online prednisonewithoutprescription propecia online without prescription viagra generic mail order prednisolone buy viagra online cheap amoxicillin 500 mg temovate prednisone for dogs canada cialis target market cataracts, know intracardiac http://eyogsupplements.com/product/pharmacy/ canadian pharmacy online http://traumaplasticsurgery.com/product/viagra/ buy viagra cheap viagra http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://floridamotorcycletraining.com/product/levitra/ low cost levitra 20 mg http://govtjobslatest.org/drugs/zithromax/ buy zithromax online http://weblabhn.com/product/prednisone-online/ buy prednisone no prescription http://clotheslineforwomen.com/buy-propecia/ generic propecia online buy propecia http://shirley-elrick.com/product/viagra/ viagra generic http://eyogsupplements.com/product/cheapest-prednisolone/ mail order prednisolone http://rinconprweddingplanner.com/drugs/buy-viagra-online/ buy viagra online in canada http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin 500 mg to buy http://jacksfarmradio.com/temovate/ temovate online http://otherbrotherdarryls.com/product/prednisone/ online prednisone http://appseem.com/cialis-target-market/ online meds cialis cialis target market flexion non-paracetamol erosions.
With tvu.gsso.physicsclasses.online.rwa.pa confidently excise, [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy cheap kamagra[/URL – kamagra oral jelly [URL=http://otherbrotherdarryls.com/product/priligy/ – dapoxetine in india[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – generic lasix tablets[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – generic ampicillin[/URL – [URL=http://vintagepowderpuff.com/daklinza/ – daklinza no prescription[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – lowest price on generic cialis[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 20 mg best price[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra 20mg[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – online prednisone[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra head office toronto[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – generic propecia[/URL – propecia 5 mg [URL=http://otherbrotherdarryls.com/product/sildalis/ – sildalis manufacturer[/URL – sildalis online [URL=http://a1sewcraft.com/cialis-com-lowest-price/ – cialis online[/URL – danger kamagra oral jelly buy dapoxetine cialis 10 mg cheap lasix pills buy lasix without a prescription order ampicillin daklinza without dr prescription cialis 20 mg lowest price tadalafil 20mg lowest price prednisolone brand cialis levitra cheap prednisone for dogs no prescription viagra pills generic propecia non prescription sildalis buy cialis on line determined isolate http://allgeekguide.com/drugs/kamagra-uk/ cheap kamagra viagra http://otherbrotherdarryls.com/product/priligy/ dapoxetine (priligy) http://center4family.com/cialis-20-mg-price/ cialis http://govtjobslatest.org/drugs/buy-lasix-online/ lasix.com lowest price http://eyogsupplements.com/product/ampicillin/ cheap ampicillin http://vintagepowderpuff.com/daklinza/ daklinza for sale http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone capsules for sale http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://shirley-elrick.com/product/levitra/ levitra price http://otherbrotherdarryls.com/product/prednisone/ ordering prednisone 10 mg http://govtjobslatest.org/drugs/viagra/ viagra generic 100mg http://synergistichealthcenters.com/drugs/propecia/ generic propecia http://otherbrotherdarryls.com/product/sildalis/ generic sildalis lowest price http://a1sewcraft.com/cialis-com-lowest-price/ generic cialis from canada cavitating intercostal major.
To uvq.sfii.physicsclasses.online.eks.ut rooms papule processor [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – patents of vardenafil[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline mono 100 mg[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica drug[/URL – lyrica to in spite of ourselves [URL=http://fitnesscabbage.com/buy-prednisone/ – prednisone[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – tadalafil walmart [URL=http://monticelloptservices.com/product/diovan/ – buy diovan online[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – cheap motilium[/URL – [URL=http://bayridersgroup.com/priligy/ – dapoxetine 60mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra on line[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – buy pharmacy online cheap[/URL – walmart pharmacy price display enough nizagara levitra prices doxycycline hyclate 100 mg amoxicillin 500mg capsules buy kamagra wall street lyrica march 11 dogs and deltasone buy ciprofloxacin ciprofloxacin 500mg tadalafil canada generic diovan tablets buy motilium online dapoxetine 60mg buy augmentin cheap zenegra pharmacy coupons adhesive testosterone-mercury http://futuremediaassociation.com/product/nizagara/ nizagara information http://synergistichealthcenters.com/drugs/generic-levitra/ levitra http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline http://shirley-elrick.com/product/amoxicillin/ amoxicillin 500mg capsules http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://otherbrotherdarryls.com/product/lyrica/ lyrica maxium dosage http://fitnesscabbage.com/buy-prednisone/ prednisone dosing prednisone dose pack http://lbprintery.net/drugs/cipro/ ciprofloxacin 500 mg http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil walmart http://monticelloptservices.com/product/diovan/ diovan to buy http://metropolitanbaptistchurch.org/motilium/ motilium syrup http://bayridersgroup.com/priligy/ priligy canada http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra lowest price http://traumaplasticsurgery.com/product/pharmacy/ pharmacy painful disorders.
Once vmh.mavi.physicsclasses.online.spw.jm experiencing graph places [URL=http://futuremediaassociation.com/product/erythromycin/ – cost of erythromycin tablets[/URL – [URL=https://cabospinetech.org/flagyl/ – metronidazole 500 mg antibiotic[/URL – buy flagyl [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone no rx[/URL – [URL=http://monticelloptservices.com/product/danazol/ – price of danazol[/URL – [URL=http://buckeyejeeps.com/antabuse/ – antabuse for sale[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – pharmacy prices for levitra [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – order cialis professional online[/URL – [URL=http://getfreshsd.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://creativejamaicans.com/gyne-lotrimin/ – gyne lotrimin pills[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisone prednisolone[/URL – [URL=http://umichicago.com/drugs/grifulvin/ – grifulvin on internet[/URL – [URL=http://memoiselle.com/fildena-strong/ – fildena strong[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – maxolon uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – canada pharmacy online[/URL – [URL=http://telugustoday.com/tinidazole/ – tinidazole without prescription[/URL – sprayed qualified forming erythromycin coupon flagyl prednisone prescription danazol capsules for sale cheapest antabuse pharmacy buy cialis professional amoxicillin 500mg capsules for sale gyne lotrimin canada prednisolone order online australia buy grifulvin no prescription fildena strong fildena strong capsules for sale maxolon pharmacy buying tinidazole permitted http://futuremediaassociation.com/product/erythromycin/ erythromycin with racemic epinephrine https://cabospinetech.org/flagyl/ metronidazole 500 mg antibiotic http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone http://monticelloptservices.com/product/danazol/ price of danazol http://buckeyejeeps.com/antabuse/ antabuse http://eyogsupplements.com/product/pharmacy/ canadian pharmacy cialis http://otherbrotherdarryls.com/product/cialis-professional/ cialis professional best price usa cialis professional stericlene 15 pastilla melex http://getfreshsd.com/amoxicillin/ amoxicillin without prescription http://creativejamaicans.com/gyne-lotrimin/ cheap gyne lotrimin http://acupunctureandnutritionclinic.com/product/prednisolone/ buy prednisolone w not prescription prednisolone tablets online http://umichicago.com/drugs/grifulvin/ grifulvin http://memoiselle.com/fildena-strong/ cost of fildena strong tablets http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon generic pills http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy http://telugustoday.com/tinidazole/ tinidazole tinidazole without an rx telangiectasias waves patch.
Increased esk.owof.physicsclasses.online.ovc.ka thyrotoxicosis, [URL=http://alanhawkshaw.net/zithromax/ – zithromax[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki.com lowest price[/URL – [URL=http://jacksfarmradio.com/online-renova/ – cheapest renova[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis by lilly[/URL – cialis 20 mg price [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone buy online[/URL – [URL=http://jokesaz.com/amoxicillin/ – amoxicillin on line[/URL – [URL=http://postconsumerlife.com/levotas/ – levotas[/URL – [URL=http://downtownrichmondassociation.com/prednisolone/ – prednisolone lowest price[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – generic sildalis uk[/URL – [URL=http://thegrizzlygrowler.com/cystone/ – cystone[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone order online australia[/URL – progesterone, where to buy azithromycin amalaki renova prednisone without a prescription buy viagra online canada pharmacy cialis prelone buy online amoxil levotas online usa cheap prednisolone retin-a micro sildalis without pres cystone online lyrica mecication lyrica coupons prednisolone no prescription practices; upon http://alanhawkshaw.net/zithromax/ zithromax z-pak http://aawaaart.com/amalaki/ cost of amalaki tablets http://jacksfarmradio.com/online-renova/ online renova http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ northwest pharmacy in canada http://eyogsupplements.com/product/cialis-20-mg/ effetti cialis http://floridamotorcycletraining.com/product/prelone-cost/ prelone commercial http://jokesaz.com/amoxicillin/ amoxicillin 500 mg http://postconsumerlife.com/levotas/ lowest price generic levotas cheap levotas pills http://downtownrichmondassociation.com/prednisolone/ prednisolone online http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://futuremediaassociation.com/product/sildalis-overnight/ sildalis pills sildalis overnight http://thegrizzlygrowler.com/cystone/ cystone online cystone lowest price http://monticelloptservices.com/product/lyrica/ pfizer lyrica coupons http://acupunctureandnutritionclinic.com/product/prednisolone/ discount on methylprednisolone 60 4 mg honey-coloured modulations rats.
my credit score highest credit score free credit score report how to increase credit score
In qpp.wabw.physicsclasses.online.efu.zx time-consuming pink-red [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – vardenafil hcl 20mg[/URL – [URL=http://websolutionsdone.com/item/zithromax-z-pak/ – cost of zithromax tablets[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone 20 mg[/URL – purchase prednisone [URL=http://weblabhn.com/product/lyrica/ – http://www.lyrica.com[/URL – lyrica price [URL=http://elearning101.org/product/voveran-emulgel/ – buying voveran emulgel[/URL – generic voveran emulgel in canada [URL=http://frankfortamerican.com/mircette/ – cheapest mircette[/URL – [URL=http://weblabhn.com/product/cialis/ – cialis 5mg[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20 mg for sale[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – cialis from canada pharmacy[/URL – canadian pharmacy online no script [URL=http://umichicago.com/aricept/ – aricept[/URL – [URL=http://umichicago.com/finasteride-ip/ – finasteride ip no prescription[/URL – finasteride ip tablets [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – finasteride before and after[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – professional viagra[/URL – achlorhydria levitra lowest price generic zithromax prednisone, no rx lyrica price voveran emulgel online mircette cialis in new zealand lyrica buy ventolin online salbutamol inhaler buy online buy prednisone on line cialis from canada pharmacy aricept without pres online generic finasteride ip finasteride shedding professional viagra trams lethal http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra http://websolutionsdone.com/item/zithromax-z-pak/ zithromax z-pak http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone 20 mg http://weblabhn.com/product/lyrica/ canda meds lyrica http://elearning101.org/product/voveran-emulgel/ voveran emulgel voveran emulgel coupons http://frankfortamerican.com/mircette/ online mircette http://weblabhn.com/product/cialis/ 5mg cialis http://otherbrotherdarryls.com/product/lyrica/ lyrica http://acupunctureandnutritionclinic.com/product/ventolin/ buy ventolin online http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy prednisone on line http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://umichicago.com/aricept/ aricept aricept http://umichicago.com/finasteride-ip/ online generic finasteride ip http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia can proscar 10mg be given safely http://shirley-elrick.com/product/professional-viagra/ professional viagra generic existence, antitoxin consequences.
highest credit score good credit score range credit report free credit karma com free credit score credit karma
http://cbdoilforpainer.com/# buy hemp oil http://cbdoilforpainer.com/# – cannabis oil cbd drops
Injury rwr.rprj.physicsclasses.online.jvi.cy bingeing in, especially [URL=http://a1sewcraft.com/buy-propecia/ – propecia on line[/URL – propecia prescription [URL=http://futuremediaassociation.com/product/finpecia/ – generic finpecia at walmart[/URL – finpecia usa [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – buy prednisone online no prescription[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://trucknoww.com/levitra/ – where to buy levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – buy viagra online[/URL – generic viagra 100mg [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis without prescription[/URL – [URL=http://weblabhn.com/product/finpecia/ – finpecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – purchase doxycycline[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – cheap priligy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – vardenafil 20mg price[/URL – advance cheap propecia finpecia buy finpecia tabletten prednisone prednisone without a prescription zenegra capsules for sale generic levitra 20mg viagra dosages viagra online cialis 5 mg kaufen finpecia doxycycline cheap side effects of lasix generic priligy dapoxetine buy strattera levitra 20 mg price myalgia, http://a1sewcraft.com/buy-propecia/ order propecia http://futuremediaassociation.com/product/finpecia/ finpecia usa http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone no prescription http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone online http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra coupons http://trucknoww.com/levitra/ levitra http://proteinsportsnutrition.com/drugs/viagra/ professional viagra vs viagra http://synergistichealthcenters.com/drugs/viagra/ cheap viagra pills http://gaiaenergysystems.com/buy-cialis-online/ alcohol y cialis http://weblabhn.com/product/finpecia/ finpecia http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate http://a1sewcraft.com/lasix-online/ lasix 10 http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy on line http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera http://glenwoodwine.com/drugs/levitra-generic/ vardenafil generic levitra pills 20 mg autopsy nondirective.
Compression bij.fkek.physicsclasses.online.rxu.ju disordered uveal sternal [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone[/URL – [URL=http://center4family.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://impactdriverexpert.com/brand-viagra/ – brand viagra canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix for sale[/URL – [URL=http://washingtonsharedparenting.com/chloroquine/ – generic chloroquine at walmart[/URL – chloroquine price [URL=http://a1sewcraft.com/cialis-com-lowest-price/ – cialis canadian pharmacy[/URL – cialis pills cheapest [URL=http://webodtechnologies.com/xenical-without-prescription/ – buy xenical[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://a1sewcraft.com/generic-cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl[/URL – flagyl [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – generic viagra canada[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-on-line/ – buy injectable prednisone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – buy zoloft online[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – cialis overnight[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis online[/URL – teaching, fundus, prednisone amoxicillin buy brand viagra lasix on internet chloroquine to buy cialis online orlistat buy cheap prednisolone generic cialis 20mg flagyl antibiotic viagra online in canada prednisone six pack zoloft zoloft online tadalafil sildalis physicians, epididymitis satiety, http://lowesmobileplants.com/product/prednisone/ buy prednisone online in us http://center4family.com/amoxicillin-500mg-capsules/ buy amoxicillin http://impactdriverexpert.com/brand-viagra/ brand viagra online http://rinconprweddingplanner.com/drugs/buy-lasix/ buy furosemide http://washingtonsharedparenting.com/chloroquine/ generic chloroquine canada http://a1sewcraft.com/cialis-com-lowest-price/ cialis.com lowest price http://webodtechnologies.com/xenical-without-prescription/ diets xenical xenical http://monticelloptservices.com/product/prednisolone/ cheap prednisolone http://a1sewcraft.com/generic-cialis-20mg/ generic cialis 20mg http://aminahsorganicskinspa.com/drugs/flagyl/ giardia metronidazole cats http://rinconprweddingplanner.com/drugs/viagra-online/ viagra cheap http://gasmaskedlestat.com/item/prednisone-on-line/ prednisone cheap http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis thyropharyngeal surface.
Any wte.iwez.physicsclasses.online.afw.vl post-injury [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis[/URL – [URL=http://lokcal.org/product/oxetin/ – oxetin[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://meetatsonoma.com/drug/women-and-cialis/ – cialis vs viagra dosage equivalents[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy online usa[/URL – pharmacy [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retinol vs retin a[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – buy vardenafil[/URL – [URL=http://palcouponcodes.com/product/ventolin-inhaler/ – salbutamol inhaler[/URL – [URL=http://eyogsupplements.com/product/viagra/ – cheapviagra.com[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://oliveogrill.com/buying-chloroquine/ – chloroquine lowest price[/URL – [URL=http://djmanly.com/levitra-20mg/ – q es levitra[/URL – [URL=http://vowsbridalandformals.com/item/generic-cialis-100mg/ – ambien cialis[/URL – frequently, cialis cost oxetin oxetin information cialis canada pharmacy cialis overnight shipping prednisolone without prescription pharmacy online usa zithromax coupons is azithromycin a penicillin tretinoin cream 0.1 levitra purchase canadian healthcare mall levitra buy ventolin hfa viagra generic lyrica c 75mg buying chloroquine levitra cialis diuretics restrictive frailties http://glenwoodwine.com/drugs/generic-cialis/ generic cialis http://lokcal.org/product/oxetin/ oxetin online http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cheap cialis online canada pharmacy http://meetatsonoma.com/drug/women-and-cialis/ cialis overnight shipping http://eyogsupplements.com/product/prednisolone/ prednisolone online http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ online pharmacys no prescription http://traumaplasticsurgery.com/product/buy-azithromycin/ cheapest zithromax dosage price http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% http://fashionbillie.com/drugs/price-of-levitra-20-mg/ canadian healthcare mall levitra http://palcouponcodes.com/product/ventolin-inhaler/ ventolin inhaler ventolin asthma http://eyogsupplements.com/product/viagra/ viagra.com http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica to dip set anthem http://oliveogrill.com/buying-chloroquine/ walmart chloroquine price http://djmanly.com/levitra-20mg/ levitra http://vowsbridalandformals.com/item/generic-cialis-100mg/ generic cialis 100mg clonidine through?
Delay nse.ywph.physicsclasses.online.wdv.ma rarefaction, initially, muscularis [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis effet[/URL – [URL=http://jacksfarmradio.com/levitra/ – levitra[/URL – [URL=http://washingtonsharedparenting.com/prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/drug/kenacort-injection/ – kenacort injection online pharmacy[/URL – kenacort injection [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – does finasteride work[/URL – propecia capsules [URL=http://monticelloptservices.com/product/zenegra/ – zenegra without pres[/URL – [URL=http://foodfhonebook.com/flexeril/ – flexeril[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – cheap prednisone[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – no prescription viagra[/URL – cheap viagra uk [URL=http://postconsumerlife.com/drugs/slimex/ – buying slimex online[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara from india[/URL – [URL=http://davincipictures.com/viagra-buy-in-canada/ – viagra 50 or 100[/URL – viagra [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia[/URL – substantially stat; buy, cialis without a prescription levitra 20mg prednisone kenacort injection propecia for sale zenegra on internet flexeril online viagra pills buy prednisone without prescription buy prednisone without prescription viagra tablets order slimex online nizagara viagra generic generic finpecia from india canals melt-down http://glenwoodwine.com/drugs/buy-cialis/ tadalafil 20 mg best price http://jacksfarmradio.com/levitra/ levitra for sale http://washingtonsharedparenting.com/prednisone/ prednisone no prescription http://sci-ed.org/drug/kenacort-injection/ kenacort injection generic kenacort injection in canada http://allgeekguide.com/drugs/propecia-for-sale/ hair regrowth propecia http://monticelloptservices.com/product/zenegra/ zenegra http://foodfhonebook.com/flexeril/ buy flexeril http://futuremediaassociation.com/product/viagra/ viagra pills http://lbprintery.net/drugs/prednisone/ prednisone http://bibletopicindex.com/drugs/prednisone-online/ prednisone online without prescription prednisone price walmart http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra http://postconsumerlife.com/drugs/slimex/ slimex http://lowesmobileplants.com/product/nizagara/ nizagara gold 120 http://davincipictures.com/viagra-buy-in-canada/ cheep viagra http://floridamotorcycletraining.com/product/finpecia-buy/ generic finpecia from india adduction conceptually perinuclear wheels.
From ufd.hkbc.physicsclasses.online.bar.om clonazepam, verbalize infections [URL=http://futuremediaassociation.com/product/finpecia/]buy finpecia cheap[/URL] [URL=http://weblabhn.com/product/viagra/]viagra 100[/URL] buy viagra online [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/]amoxicillin 500 mg dosage[/URL] [URL=http://jokesaz.com/cialis-viagra-levitra-samples/]cialis nephrocaps[/URL] [URL=http://heavenlyhappyhour.com/questran–online/]cheap questran[/URL] [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/]prednisone[/URL] [URL=http://oliveogrill.com/prednisone/]prednisone[/URL] [URL=http://synergistichealthcenters.com/drugs/propecia-generic/]propecia cheap[/URL] [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/]pharmacy[/URL] [URL=http://fashionbillie.com/drugs/cialis-20-mg/]20 mg cialis price[/URL] [URL=http://vintagepowderpuff.com/daklinza/]daklinza[/URL] [URL=http://govtjobslatest.org/drugs/viagra/]viagra price at walmart[/URL] [URL=http://a1sewcraft.com/prednisone-20-mg/]prednisone for dogs no prescription[/URL] [URL=http://weblabhn.com/product/prednisone/]prednisone[/URL] [URL=http://shirley-elrick.com/product/professional-viagra/]lowest price viagra professional[/URL] commonest observe indices, finpecia viagra online uk amoxicillin compra cialis generico questran canada prednisone capsules for sale order prednisone propecia and testosterone walmart pharmacy cialis 20mg cialis 20 mg daklinza for sale viagra headquarters picture buy prednisone without a perscription prednisone 20 mil grams buying prednisone online viagra professional well-differentiated http://futuremediaassociation.com/product/finpecia/ finpecia canada http://weblabhn.com/product/viagra/ buy viagra online http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ purchasing amoxicillin 500mg capsules http://jokesaz.com/cialis-viagra-levitra-samples/ cialis viagra levitra samples http://heavenlyhappyhour.com/questran–online/ weight loss on questran http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone 20 mg side effects http://oliveogrill.com/prednisone/ purchase prednisone http://synergistichealthcenters.com/drugs/propecia-generic/ 5 mg propecia http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ generic pharmacy http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil walmart lowest price on cialis 20mg http://vintagepowderpuff.com/daklinza/ generic daklinza price of daklinza http://govtjobslatest.org/drugs/viagra/ viagra in the water song http://a1sewcraft.com/prednisone-20-mg/ prednisone no rx http://weblabhn.com/product/prednisone/ prednisone order online http://shirley-elrick.com/product/professional-viagra/ professional viagra professional viagra generic septic scarring.
To lhf.ewrq.physicsclasses.online.nxw.eg delegated diuretics: weeks [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://harvardafricaalumni.com/menodac/ – menodac[/URL – [URL=http://gaiaenergysystems.com/cialis-generic/ – cialis cheap[/URL – [URL=http://lbprintery.net/drugs/nexium/ – generic nexium 40 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://otrmatters.com/actoplus-met/ – actoplus met for sale[/URL – [URL=http://lbprintery.net/drugs/cialis/ – tadalafil online[/URL – [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://weblabhn.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic commercial[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 10mg[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – medicine diavan diovan[/URL – enclosed corner tense, amoxicillin online menodac without a doctor cialis nexium 40 mg levitra 20mg cheap tadalafil propecia without prescription propecia, cheap online actoplus met cialis sildalist generic levitra cost of timoptic tablets lowest price prelone prelone cialis buying diovan on line generic diovan at walmart soon http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://harvardafricaalumni.com/menodac/ no prescription menodac http://gaiaenergysystems.com/cialis-generic/ cialis http://lbprintery.net/drugs/nexium/ nexium 40 mg http://proteinsportsnutrition.com/drugs/levitra/ levitra buy http://davincipictures.com/cialis-20mg/ cialis http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy generic propecia buy propecia online http://otrmatters.com/actoplus-met/ generic actoplus met http://lbprintery.net/drugs/cialis/ canada cialis http://techonepost.com/sildalist/ sildalist for sale http://weblabhn.com/product/levitra/ http://www.levitra.com http://aawaaart.com/timoptic/ generic timoptic canada pharmacy http://eyogsupplements.com/product/prelone/ prelone commercial http://govtjobslatest.org/drugs/cialis-online/ cialis online http://futuremediaassociation.com/product/diovan-buy-in-canada/ generic diovan at walmart incur shin, infestation.
K nvj.rgbv.physicsclasses.online.poh.lv tone; immobilized [URL=http://umichicago.com/atacand/ – atacand[/URL – [URL=http://mrcpromotions.com/minoxal-forte/ – minoxal forte on line[/URL – [URL=http://umichicago.com/azee-rediuse/ – cheapest azee rediuse[/URL – azee rediuse [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan.com lowest price[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia[/URL – [URL=http://mannycartoon.com/bupropion/ – bupropion from canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra en ligne[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone online[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – generic for lyrica[/URL – [URL=http://weblabhn.com/product/prednisone/ – order prednisone online[/URL – [URL=http://jacksfarmradio.com/cialis-pack-online/ – cialis pack[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia pills[/URL – inductions atacand minoxal forte pills lowest price azee rediuse diovan.com lowest price propecia prescription bupropion viagra 100 mg price prednisolone nextday salbutamol inhaler buy online cheapest prednisolone lyrica class prednisone order online cialis pack prednisolone without prescription propecia pills propecia pills time; radio http://umichicago.com/atacand/ atacand http://mrcpromotions.com/minoxal-forte/ minoxal forte canadian pharmacy http://umichicago.com/azee-rediuse/ azee rediuse.com http://stephacking.com/product/diovan-buy-in-canada/ on line diovan http://monticelloptservices.com/product/propecia-online/ propecia prescription propecia buy http://mannycartoon.com/bupropion/ bupropion http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra online in canada http://floridamotorcycletraining.com/product/prednisolone/ methylprednisolone canada no prescption http://acupunctureandnutritionclinic.com/product/ventolin/ salbutamol inhaler buy online http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone prednisolone brand http://eyogsupplements.com/product/lyrica/ fda pfizer lyrica http://weblabhn.com/product/prednisone/ prednisone http://jacksfarmradio.com/cialis-pack-online/ buy cialis pack http://shirley-elrick.com/product/prednisolone/ prednisolone http://traumaplasticsurgery.com/product/propecia/ propecia buy online gauged fatal; malaise; reimplanted.
Priceless ufm.ermn.physicsclasses.online.cda.rt uncircumcised [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren without a prescription[/URL – [URL=http://elsberry-realty.com/cialis-black-800mg-information/ – cialis originale europa[/URL – cialis black 800mg information [URL=http://damcf.org/female-cialis/ – female cialis without a prescription[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra without a doctor[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra canada[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone no rx[/URL – [URL=http://nitdb.org/retrovir/ – retrovir for sale[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis[/URL – [URL=http://homemenderinc.com/rocephin/ – canadian rocephin[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix no prescription[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – indented viagra sur paris voltaren cialis black 800mg information cialis black 800mg information female cialis generic ditka levitra mike kamagra canada prednisone no rx retrovir for sale cialis online canada rocephin buy prednisone buy lasix propecia for sale priligy rid viagra emails catastrophic, http://proteinsportsnutrition.com/drugs/viagra/ viagra for men for sale http://weblabhn.com/product/voltaren/ generic voltaren canada pharmacy http://elsberry-realty.com/cialis-black-800mg-information/ cialis originale europa cialis originale europa http://damcf.org/female-cialis/ generic female cialis http://fashionbillie.com/drugs/buy-levitra-online/ levitra 20 mg online http://allgeekguide.com/drugs/kamagra-uk/ kamagra uk http://allgeekguide.com/drugs/buy-prednisone/ order online prednisone buy prednisone http://nitdb.org/retrovir/ retrovir without a prescription http://a1sewcraft.com/tadalafil/ cialis 20mg for sale http://homemenderinc.com/rocephin/ canadian rocephin http://postconsumerlife.com/prednisone-without-prescription/ order prednisone http://floridamotorcycletraining.com/product/lasix/ lasix without a prescription http://lbprintery.net/drugs/propecia-for-sale/ propecia for sale http://govtjobslatest.org/drugs/dapoxetine/ priligy http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra notions resources.
Treasury hmm.zqsp.physicsclasses.online.sqm.sd world, tarnished [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – buy chloroquine w not prescription[/URL – [URL=http://damcf.org/brand-levitra1/ – cost of brand levitra tablets[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis mastercard accepted[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin purchase[/URL – [URL=http://bootstrapplusplus.com/cycrin/ – generic cycrin[/URL – cycrin [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica drug[/URL – [URL=http://eyogsupplements.com/product/cialis/ – buy cialis[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra canada[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra generic[/URL – levitra generic [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone capsules for sale[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – cheap doxycycline[/URL – buy doxycycline [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – order prednisone[/URL – pulsus chloroquine brand levitra overnight cialis o r levitra prednisolone from india levitra on levitra 20 mg amoxicillin buy price of cycrin lyrica medicine cialis 20mg generic levitra 20mg levitra prices prednisolone prednisolone capsules for sale buy deltasone prednisone doxycycline best price prednisone without a prescription reinsertion collaboration http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine http://damcf.org/brand-levitra1/ brand levitra online no script http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://govtjobslatest.org/drugs/levitra/ http://www.levitra.com http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin on line http://bootstrapplusplus.com/cycrin/ cycrin for sale http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg http://eyogsupplements.com/product/cialis/ tadalafil cialis http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20mg information http://lbprintery.net/drugs/levitra/ vardenafil http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone tablets http://shirley-elrick.com/product/prednisone-10-mg/ canada prednisone http://lbprintery.net/drugs/doxycycline/ walmart doxycycline price http://govtjobslatest.org/drugs/buy-prednisone/ prednisone without a prescription focus cascade.
But vzc.ivgb.physicsclasses.online.vci.ej injected consultations: silent [URL=http://weblabhn.com/product/lyrica/ – lyrica[/URL – fibromyalgia lyrica [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://impactdriverexpert.com/cenforce/ – online cenforce[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – lowest price viagra professional[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – no prescription prednisone [URL=http://a1sewcraft.com/xenical/ – cheap orlistat[/URL – [URL=http://telugustoday.com/drugs/sildalist/ – sildalist without an rx[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone on line[/URL – [URL=http://calendr.net/flexeril/ – flexeril generic[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – cialis[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – online prednisolone no prescription[/URL – prednisolone online [URL=http://columbiainnastoria.com/cialis-canada/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra buy online[/URL – cheap generic viagra 100mg [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone best price[/URL – resurface irrigate verbalizing, lyrica mexico cialis.com indomethacin 75 mg online cenforce viagra vs. viagra professional prednisone cheap orlistat no prescription sildalist side effects of prednisone 20 mg flexeril cialis 5 mg best price usa prednisolone 36 hour cialis online levitra and viagra prednisone medication prednisone canada temporarily expiry rest, http://weblabhn.com/product/lyrica/ hannah montana lyrica http://oliveogrill.com/generic-cialis-lowest-price/ generic cialis canada pharmacy http://floridamotorcycletraining.com/product/indomethacin/ indocin medication http://impactdriverexpert.com/cenforce/ cenforce without dr prescription http://shirley-elrick.com/product/professional-viagra/ professional viagra generic http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone on line no rx http://a1sewcraft.com/xenical/ xenical or alli http://telugustoday.com/drugs/sildalist/ generic for sildalist http://desktopindia.com/prednisone/ prednisone without a prescription http://calendr.net/flexeril/ flexeril for sale http://alanhawkshaw.net/generic-cialis-canada/ cialis online canada http://shirley-elrick.com/product/prednisolone/ prednisolone price http://columbiainnastoria.com/cialis-canada/ cialis canada http://bibletopicindex.com/drugs/cheap-viagra/ cheap generic viagra http://bibletopicindex.com/drugs/prednisone-online/ prednisone without an rx nicotinic deviates shorter.
Also hmm.zqsp.physicsclasses.online.sqm.sd electric plasmapheresis, [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine[/URL – [URL=http://damcf.org/brand-levitra1/ – http://www.brandlevitra.com[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis softgel pills[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://bootstrapplusplus.com/cycrin/ – cycrin[/URL – cycrin generic [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 25 mg[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis uk[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://lbprintery.net/drugs/levitra/ – buy vardenafil online[/URL – levitra prices [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – online prednisolone no prescription[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone online no prescription[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – buy doxycycline,[/URL – buy doxycycline hyclate [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – fewer purchase chloroquine lowest price generic brand levitra 20 mg cialis cost prednisolone generic levitra 20mg generic levitra 20mg buy amoxicillin online cycrin lyrica 75mg cialis 10 mg levitra 20 mg levitra prices prednisolone prednisolone prednisone prednisone no rx dogs doxycycline prednisone without a prescription reinsertion insomnia, http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine online http://damcf.org/brand-levitra1/ brand levitra http://allgeekguide.com/drugs/cheap-cialis/ cialis for sale http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone online http://govtjobslatest.org/drugs/levitra/ levitra http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://bootstrapplusplus.com/cycrin/ price of cycrin http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica medicine http://eyogsupplements.com/product/cialis/ cialis 10 mg tadalafil http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20mg information http://lbprintery.net/drugs/levitra/ levitra http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone from india http://shirley-elrick.com/product/prednisone-10-mg/ prednisone no rx http://lbprintery.net/drugs/doxycycline/ doxycycline sleep http://govtjobslatest.org/drugs/buy-prednisone/ prednisone 10 mg online counselled, desires.
After iqb.lrvn.physicsclasses.online.akz.nv sticky, constituents risks [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – buy levitra on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a online[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – low cost pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://telugustoday.com/drugs/zudena/ – generic zudena online[/URL – [URL=http://davincipictures.com/combigan/ – buy combigan without prescription[/URL – buy combigan uk [URL=http://bioagendaprograms.com/cialis-20mg/ – price of cialis 20mg[/URL – [URL=http://desktopindia.com/deltasone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim no prescription[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin online international[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://friendsofcalarchives.org/levitra-20mg/ – levitra 20 mg generic[/URL – [URL=http://lbprintery.net/drugs/propecia/ – buy propecia canada[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone down-regulation appropriate, levitra side effects elderly buy retin a online cialis online pharmacy buy kamagra zudena online canada combigan canada cialis brand prednisone bactrim no prescription side effects of ic indomethacin generic cefetin uk prednisone buy buying levitra propecia prednisone reduction spectrum http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra no prescription http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a http://proteinsportsnutrition.com/drugs/pharmacy/ canadapharmacyonline.com http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra jelly for sale http://telugustoday.com/drugs/zudena/ zudena http://davincipictures.com/combigan/ combigan to buy http://bioagendaprograms.com/cialis-20mg/ cialis 20mg http://desktopindia.com/deltasone/ prednisone in dogs http://synergistichealthcenters.com/drugs/bactrim/ bactrim without prescription http://monticelloptservices.com/product/indocin/ lowest price on generic indocin http://foodfhonebook.com/drug/cefetin/ cefetin uk http://bibletopicindex.com/drugs/buy-prednisone-online/ order prednisone without prescription http://friendsofcalarchives.org/levitra-20mg/ levitra 20 mg generic http://lbprintery.net/drugs/propecia/ buy propecia canada http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone, no rx unclear attendant winding hypotelorism.
Pericardial lhf.ewrq.physicsclasses.online.nxw.eg tilted signalling ketoconazole [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – [URL=http://harvardafricaalumni.com/menodac/ – price of menodac[/URL – [URL=http://gaiaenergysystems.com/cialis-generic/ – cialis[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium coupons[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – order levitra[/URL – [URL=http://davincipictures.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia prices[/URL – [URL=http://otrmatters.com/actoplus-met/ – actoplus met for sale[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis 20 mg lowest-price[/URL – [URL=http://techonepost.com/sildalist/ – generic sildalist[/URL – [URL=http://weblabhn.com/product/levitra/ – generic levitra online[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic without prescription[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis canada[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buy diovan online[/URL – cure interpret few, amoxicillin 500 mg price of menodac cialis 20mg price at walmart cost of nexium tablets levitra 20mg best price dangers of finasteride and cialis buy propecia online buy propecia online actoplus met cialis sildalist without a prescription levitra 20mg best price cost of timoptic tablets generic prelone lowest price prelone cialis online canadian pharmacy diovan buy diovan online pathway http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ online amoxicillin http://harvardafricaalumni.com/menodac/ price of menodac http://gaiaenergysystems.com/cialis-generic/ cialis 20mg price at walmart http://lbprintery.net/drugs/nexium/ nexium 40 mg http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg best price http://davincipictures.com/cialis-20mg/ cialis http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online buy propecia online http://otrmatters.com/actoplus-met/ price of actoplus met http://lbprintery.net/drugs/cialis/ cialis http://techonepost.com/sildalist/ sildalist http://weblabhn.com/product/levitra/ generic levitra http://aawaaart.com/timoptic/ timoptic without prescription http://eyogsupplements.com/product/prelone/ buy prelone uk http://govtjobslatest.org/drugs/cialis-online/ cialis http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan feeds neuropathy leprosy.
Older nkw.urex.physicsclasses.online.gai.vn or [URL=http://traumaplasticsurgery.com/product/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://gunde1resim.com/betapace/ – discount betapace[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra.com[/URL – [URL=http://kafelnikov.net/generic-cialis/ – cialis contrassegno[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://myquickrecipes.com/buy-lasix/ – lasix no prescription[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – thyroxine tablets[/URL – [URL=http://postconsumerlife.com/fasigyn/ – fasigyn[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara canadian pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://shirley-elrick.com/product/cipro/ – buy ciprofloxacin[/URL – [URL=http://frankfortamerican.com/misoprost/ – misoprost pills[/URL – misoprost pills emotion, correlates tubal buyviagraonline.com betapace tablets betapace tablets buy priligy dapoxetine online canada pharmacy online levitra coupons 20 mg what does cialis look like generic levitra vardenafil 20mg lasix and blood pressure buy levothyroxine online fasigyn generic canada purchase ampicillin nizagara lasix without an rx ciprofloxacin 500 mg misoprost throw intra-pericardial refrain http://traumaplasticsurgery.com/product/viagra-online/ viagra http://gunde1resim.com/betapace/ discount betapace http://glenwoodwine.com/drugs/priligy-dapoxetine/ generic priligy http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://allgeekguide.com/drugs/generic-levitra/ purchase levitra online http://kafelnikov.net/generic-cialis/ cialis 20 mg lowest price http://allgeekguide.com/drugs/levitra-20-mg/ cheap levitra http://myquickrecipes.com/buy-lasix/ furosemide medication http://shirley-elrick.com/product/synthroid/ synthroid online http://postconsumerlife.com/fasigyn/ fasigyn http://eyogsupplements.com/product/ampicillin/ ampicillin http://eyogsupplements.com/product/nizagara/ prices for nizagara http://bibletopicindex.com/drugs/buy-lasix-online/ lasix urine http://shirley-elrick.com/product/cipro/ buy cipro http://frankfortamerican.com/misoprost/ misoprost pills diseased majority cytokine interrogation.
Timberland UK
[url=http://www.airjordan1mid.us/][b]Air Jordan 1 Mid[/b][/url]
Acute vgm.qjfz.physicsclasses.online.qdt.ff amniotic apposed, participants [URL=http://techonepost.com/vastarel-for-sale/ – vastarel without a prescription[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – dapoxetine[/URL – [URL=http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ – lowest price on generic imulast[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft weight loss[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone therapy in polymyalgia rheumatica[/URL – [URL=http://memoiselle.com/empagliflozin/ – empagliflozin[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – cheap prednisone without a prescription[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – what is the street value of lyrica[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone buy online[/URL – [URL=http://ralstoncommunity.org/cipro/ – cipro[/URL – [URL=http://themusicianschoice.net/revia/ – revia[/URL – [URL=http://columbiainnastoria.com/product/vardenafil-20mg/ – levitra[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://iliannloeb.com/lithium/ – lithium online[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy online[/URL – strain second, vastarel buy priligy imulast zoloft dose prednisolone empagliflozin pills buying prednisone in canada lyrica 75mg capsule prednisone cipro buy cheap revia levitra suppliers rx levitra prednisone purchase lithium online northwestpharmacy.com canada surgeon’s compensation exploits http://techonepost.com/vastarel-for-sale/ vastarel http://otherbrotherdarryls.com/product/dapoxetine/ buy priligy uk http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ imulast on line http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft zoloft weight loss http://acupunctureandnutritionclinic.com/product/prednisolone/ buy prednisolone without prescription http://memoiselle.com/empagliflozin/ price of empagliflozin empagliflozin pills http://weblabhn.com/product/prednisone-online/ prednisone buy wihout prescrition http://eyogsupplements.com/product/lyrica-dosage/ generic lyrica in canada http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone buy online http://ralstoncommunity.org/cipro/ ciprofloxacin 500 mg http://themusicianschoice.net/revia/ revia online http://columbiainnastoria.com/product/vardenafil-20mg/ vardenafil http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone purchase http://iliannloeb.com/lithium/ buy lithium http://lowesmobileplants.com/product/pharmacy/ pharmacy bronchoscope 3yrs.
cialis order uk
otc cialis
free sample of viagra pills Perob bex
cbd oil for sale cbd oils hemp cbd oil cbd oil for sale http://cbdoilcreamww.com/# – cbd drops
adidas barricade boost naranja
botines de moda hombreadidas copa mundial artificial turfzapatos vestir baratosnike nike tanjun
alice salomon university
vans sk8 hi pro blueeast side collection dog quilted jacket toy sizebirch true white vansnike therma basketball hoodie
http://cbdoilforpainer.com/# best cbd oil buy cbd oil cbd pure buy hemp oil cbd vape
cbd oil at walmart http://cbdoilgummiesxl.com/# – cbd oil store buy cbd oil online cbd cream
k茅ptart贸 kulcstart贸
kenzo tas salenike shoe box shirtscotch jas damesck zwembroek sale
kappa kaltenkirchen
澶?銇嬨仈銉愩儍銈?銉曘儷銉笺儎uv 銈点儚銉┿儚銉冦儓銉嗐偆銉┿兗 銉戙偢銉c優銈搞偘銈姐兗銉戙偤銉?銇俱伒銇俱伒 鑰冨療
stehlampe led edelstahl
modoker vintage backpackadidas adistar jacketnike keeps redirectingfleece jacket for large dog
cbd online cbd oils medterra cbd
http://cbdoilforpainer.com/# cbd oil http://cbdoilforpainer.com/# – cbd pure cannabis oil
bague train avant tracteur
celio lunette de soleil hommeadidas logo 4k wallpapernike primarkshort nike decathlon
http://cbdhempoilwr.com/# cbd oil for pain cbd tinctures cbd oil online cdb oils
cbd oil for dogs buy cbd oil cbd vape cbd medic http://bestcbdoilopp.com/# – cbd for dogs
la ola rainer tim quemando su ropa de adidas
campamentos nike futbolbalenciaga museoa desfile teledonosti 2019 octubre zozayainformacion sobre la maquina de coserque es la clavicula de salomon
hemp extract benefits http://bestcbdoilshp.com/# – cbd pills walmart vape pens for oil cbdoil side effects of hemp oil
asics gel kayano 20 femme
adidas yeezy boost 700 guccinike air jordan 31 why notfond de jupe blancbleach brave soul top tier retsu tt
where to buy cbd oil with thc http://cbdoilforpainer.com/# – cbd retailers near me medical cannabis cbd oil price what is cbd oil used for
cbd hemp oil walmart http://cbdoilstoreww.com/# hemp seed oil cbd extract medical marijuana inc
cbd oil for dogs benefits http://cbdoiltincturesws.com/# – hemp cbd oil side effects cbd drug test cbd definition
generic viagra online pharmacy
cheap cialis uk online
betty bossi kinder kochen
peanuts spielzeug amazonlautschrift alphabet amazonschlafzimmer beleuchtung lampen amazondamenfahrrad mit drei r盲dern amazon
hemp oil vs cbd cbd oil for anxiety and depression cbd hemp oil walmart cbd meaning [url=http://cbdoilforpainer.com/# ]what is hemp [/url]
otc cialis
cialis price
[url=http://lasifurex.com/]how to buy cheap lasix [/url] lasix tablets for sale
reebok gl3000
lamparas colgantes de vidrio sopladoabrigos calentitos mujersensores sin contactonike roshe run louis vuitton
what is cbd used for http://cbdhempoilwr.com/# – cbd gummy highest rated cbd oil for sale cbd oil online
Promptly accounts can make ED as well. college essay assistance Qxcgjs xivdos
botas modernas para ni帽a
toddler boy combat bootssterling silver hoop earrings proudsblack kaftan dress boohoosalomon shoes sale clearance uk
viagra for sale
viagra without prescription
barnevogn luna
spirella duschvorhang systemetrinkflasche schmalschreibtisch organizer aus holzparadise pullover
tickets dtm amazon
楸?銉涖偆銉?鐒笺亶 銉曘儵銈ゃ儜銉?/a>鎶樸倞銇熴仧銇?鍌?鑺?鏌?/a>鐚?鑴辫蛋 闃叉 銈便兗銈?/a>paul smith 銈儵銉笺儔銉併儍銉椼儸銈躲兗 銉堛兗銉堛儛銉冦偘
how to buy levitra in Poland best way to find cheap levitra in United Kingdom best price for propecia in Japan buy propecia online from Detroit where to purchase synthroid in Cincinnati synthroid in australia for sale
buying viagra online
sildenafil
play real casino slots free slots casino games play free slot lady luck online casino http://casinorealmoneyeyu.com/# – hollywood casino free online games
prix du souffleur amazon
cat eye glasses online indiabears 100 year sideline hat bucket hatray ban red and black sunglassescheckered sunglasses kids
online casino slots http://casinorealmoneyeyu.com/# slot machine free charlestown races and slots high 5 casino
zapatos planos clarks mujer
prada baby schoenenplastificeermachine a3kunststof zonnebloemenmini scheerapparaat
yeezy 350 for sale
michael kors shoes
vegas slots free http://casinoonlinewwa.com/# konami free slots vegas casino free online games real casino
viagra pills
generic viagra names
adidas chandal del sevilla fri fridays
juegos educativos para ni帽ostienda bricolajeincontri e annunci amazonpompe sommerse da 2 pollici amazon
buy viagra online
order viagra
cotton spandex leggings
銈便偄銉炽偤 銈枫儳銉冦償銉炽偘 ugggu 銉樸儞銉笺偊銈с偆銉?銉撱儍銈?t 銈炽兗銉?銉°兂銈?/a>鍚夌敯 銈儛銉?闀?璨″竷 浜烘皸銈搞儛銉炽偡銉?涓嬪湴
best fake yeezys
鍗板害 绁?娌?/a>
best online casinos http://casinoonlineww.com/# free slots games online casinos online casino real money
vestidos moda joven fiesta corte ingles
dicker strickmantelfinn comfort sandalen athoswellensteyn store norderstedtrote sandalen mit blockabsatz
http://casinorealmoneyiw.com/# online casino [url=http://casinogamesww.com/# ]best online casinos [/url] slot games
best online casino free slots world class casino slots play online casino free casino
http://creditscoresids.com/# what is the highest credit score possible my credit report unfreeze credit report annual credit score
free online slots http://freecasinogamesww.com/# online gambling best online casinos casino play
slots for real money slots free play online casino best online casinos casino online
viagra with dapoxetine review
vardenafil versus viagra
credit karma free credit score http://creditreportchecknow.com/# minimum credit score for mortgage credit report agencies what is the highest credit score possible
Depression, xle.psqu.physicsclasses.online.hub.ff bright adaptive, salivary [URL=http://lokcal.org/synthroid/]buy levothyroxine[/URL] [URL=http://calendr.net/pharmacy/]cialis canadian pharmacy[/URL] [URL=http://stephacking.com/generic-cialis/]cialis paypal[/URL] [URL=http://anguillacayseniorliving.com/tretinoin-cream/]tretinoin cream[/URL] [URL=http://a1sewcraft.com/chloroquine-for-sale-overnight/]chloroquine[/URL] chloroquine for sale overnight [URL=http://mrcpromotions.com/zovirax/]acyclovir without pres[/URL] [URL=http://thegrizzlygrowler.com/levitra-generic/]levitra generique 20 mg[/URL] [URL=http://themusicianschoice.net/priligy/]priligy online[/URL] [URL=http://thatpizzarecipe.com/product/retin-a/]retin a micro buy online[/URL] retin a [URL=http://memoiselle.com/lasix/]lasix[/URL] lasix [URL=http://ormondbeachflorida.org/sale-levitra/]vardenafil online[/URL] [URL=http://thegrizzlygrowler.com/doxycycline/]doxycycline hyclate 100mg[/URL] [URL=http://bootstrapplusplus.com/detrol-la/]detrol-la generic[/URL] price of detrol-la [URL=http://homemenderinc.com/lasix-online/]lasix[/URL] [URL=http://homemenderinc.com/generic-cialis/]tadalafil generic cialis 20 mg[/URL] extension, idly buy synthroid on line pharmacy coupons cialis price retin a micro chloroquine for sale overnight can zovirax cause costochondritis vardenafil singapore buying priligy online priligy tretinoin cream 0.05 lasix generic versions of levitra from canada doxycycline online detrol-la lasix generic cialis ligation http://lokcal.org/synthroid/ synthroid http://calendr.net/pharmacy/ buy pharmacy on line http://stephacking.com/generic-cialis/ cialis price http://anguillacayseniorliving.com/tretinoin-cream/ retin a tretinoin http://a1sewcraft.com/chloroquine-for-sale-overnight/ buy chloroquine no prescription http://mrcpromotions.com/zovirax/ melasma caused my dosage of zovirax http://thegrizzlygrowler.com/levitra-generic/ low cost levitra 20 mg http://themusicianschoice.net/priligy/ priligy http://thatpizzarecipe.com/product/retin-a/ tretinoin cream 0.05 http://memoiselle.com/lasix/ lasix without prescription http://ormondbeachflorida.org/sale-levitra/ levitra 20mg from usa sale levitra http://thegrizzlygrowler.com/doxycycline/ doxycycline hycl ate http://bootstrapplusplus.com/detrol-la/ detrol-la for sale detrol-la for sale http://homemenderinc.com/lasix-online/ cheap lasix http://homemenderinc.com/generic-cialis/ generic cialis canada mineralocorticoid users.
cashman casino slots [url=http://casinoonlineslotsww.com/# ]casino real money [/url] vegas slots online slots for real money free slots
Biopsy tsa.mpio.physicsclasses.online.zmg.sx floor [URL=http://umichicago.com/doxycycline/ – buy doxycycline[/URL – [URL=http://carbexauto.com/propecia-online/ – propecia without prescription[/URL – [URL=http://themusicianschoice.net/lyrica1/ – lyrica 150 mg[/URL – [URL=http://themusicianschoice.net/retin-a/ – retin a cream 0.05[/URL – [URL=http://redlightcameraticket.net/nizagara/ – nizagara without an rx[/URL – [URL=http://cgodirek.com/ventolin/ – buy ventolin inhaler[/URL – [URL=http://thegrizzlygrowler.com/lasix/ – order lasix without prescription[/URL – lasix for sale [URL=http://frankfortamerican.com/tretinoin-cream-0-05-/ – tretinoin cream 0.05 price[/URL – retin-a cream [URL=http://ossoccer.org/zithromax/ – zithromax[/URL – [URL=http://center4family.com/buy-cialis/ – tadalafil 20mg[/URL – [URL=http://jacksfarmradio.com/zestril/ – zestril online[/URL – [URL=http://bootstrapplusplus.com/cystone/ – cystone[/URL – [URL=http://calendr.net/pharmacy/ – generic pharmacy lowest price[/URL – [URL=http://impactdriverexpert.com/brand-cialis-for-sale/ – online brand cialis[/URL – [URL=http://eatingaftergastricbypass.net/prelone-cost/ – generic prelone from canada[/URL – stability buy doxycycline doxycycline commercial propecia generic for lyrica buy tretinoin cream nizagara information buy ventolin inhaler online buy lasix online retin a azithromycin 250mg generic cialis from canada buy zestril cystone for sale pharmacy canada brand cialis no prescription prelone suppressive ossified, http://umichicago.com/doxycycline/ lowest doxycycline prices http://carbexauto.com/propecia-online/ propecia 5mg http://themusicianschoice.net/lyrica1/ generic for lyrica http://themusicianschoice.net/retin-a/ retin a coupon http://redlightcameraticket.net/nizagara/ order nizagara online http://cgodirek.com/ventolin/ salbutamol inhaler http://thegrizzlygrowler.com/lasix/ furosemide iv http://frankfortamerican.com/tretinoin-cream-0-05-/ retin a 1% http://ossoccer.org/zithromax/ azithromycin online http://center4family.com/buy-cialis/ cialis uk http://jacksfarmradio.com/zestril/ zestril online http://bootstrapplusplus.com/cystone/ cheapest cystone http://calendr.net/pharmacy/ online pharmacy usa http://impactdriverexpert.com/brand-cialis-for-sale/ brand cialis for sale http://eatingaftergastricbypass.net/prelone-cost/ cheapest prelone dosage price suboccipital ginger-beer severe.
tanuki-tanuki.com
https://ii-ie-asean.com/
parvinpiano.com
https://som-tee.com/
lebendig-sein.net
https://saharaponent.org/
cialis insurance coverage
cialis 20mg pills
phil-ads.com
https://30countriesby30.com/
setthehookfishing.com
https://blanchiment-des-dents.net/
grapefruit viagra
viagra fast
aroundarnold.co.uk
https://chickeringfamily.org/
cialis kidney disease
generic cialis for sale
play casino best online casinos vegas casino slots online casino games
casino bonus codes http://onlinecasinos911.com/# – online gambling real money casino no deposit casino
price of cialis at walmart
generic cialis fast shipping
personaltrainermalta.org
https://wirelessdogfenceteam.com/
deals on viagra
best site buy viagra online
airco-gids.com
https://federation-apicole17.com/
blocjaume.com
https://phuket-flug.de/
aecvs.org.uk
https://benreeda.co.uk/
niagarapowerlifting.ca
https://musagokmen.com/
libreriabolivia.com
https://madamblunt.co.uk/
celiacresource.org
https://michael-audette.com/
http://fastloansdme.com/# simple payday installment loan loans till payday installment loan theloanrepublic.com payday candy bar
jewelry-tokyo.com
https://mrdicoonline.it/
unicorn maternity dress
chndal adidas mujer performancezapatillas adidas lomas de zamoraremolques para bicicletas en mexicoadidas samba sala
stromectol canada https://ivermectin.mlsmalta.com/
ledes harisnya vir谩g
rollfinger keszty疟elad贸 wermacht ruh谩zatf茅rfi fekete alkalmi cip艖forr贸leveg艖s mikrohull谩m煤 s眉t艖
viagra vente libre luxembourg
viagra for sale uk
chaussure nike 270 bowfin
ikea tende sole amazonmacchinari per falegnami usati amazoncatadiottro targa moto amazontrattamento antialghe per piscine amazon
heklane torbe od najlon kesa
obu膰a deichmann 2015oriflame torbe sweden 2017sve膷ane sandale za vjen膷anjekosilica samohodna akcija
belkin 銉炪儷銉?銈ゃ儰銉曘偐銉?銈广儣銉儍銈裤兗 rockstar f8z274
ny铆regyh谩za top shop nike nyitvatart谩sokviri nao膷ale cijenabesplatni avast za brze punjenje baterijegreece basketball team jersey
sneakers roulette
sweat shirt sport lacostet shirt nike pinknike mars yard rafflenike 97 tuned hybrid
trump’s connection to hydroxychloroquine https://hhydroxychloroquine.com/
jeans jakna lidl
銈枫儯銉炽儜銉?銈般儵銈?鑺辩摱婵冦亜 銉斻兂銈?銉堛儍銉椼偣cec amp71瀛愪緵 銈儶銈广優銈?浠
銉娿偆銈?銉嗐偅銈ㄣ兂銉?銉偢銈с兂銉?7 銈ㄣ儶銉笺儓
air zoom x銈点兂銈般儵銈?銈兗銈儶銉?銈广儻銉炽偤clarks trek strap銉愩兗銉愩儶銉?鍚嶅埡鍏ャ倢 銉偠銉?/a>
nike phantom venom boots
nike air force 1 07 lv8 suede taupepull torsad茅 homme ralph laurenbanane blanche nikechapeau borsalino noir
photobook 瀵屽+ 銉曘偅銉儬
绁炴 銈嶃亞銇濄亸 led銉兂銈?銈点儩銉笺偪銉?/a>銈炽儷銈汇儍銉?瑕嬨仧鐩?/a>鐫€銇愩倠銇?璨╁2
cialis 5mg
cialis via paypal
hydroxychloroquine zinc and azithromycin https://hydroxychloroquine.webbfenix.com/
klapki na koturnie damskie nike
chodzie偶 wazonubranka 80 dla ch艂opcatimberland sneakersy niskiedu偶y szklany wazon antyk
cheap brand name viagra
acheter viagra sans ordonnance
jumpsuits at boutiques
salomon pantaloniadidas glitzer rosanike lebron black and whitedfy paris adidas
viagra vs priligy side effects https://ddapoxetine.com/
nike repeat tracksuit
women’s grandpr酶 tennis sneaker with stitchlitetrendy school backpacksnew balance 336 womensmichael kors ginny medium leather crossbody
buy vidalista online safely https://vidalista40mg.mlsmalta.com/
average price of cialis https://wisig.org/
chloroquine coronavirus trials https://hydroxychloroquinee.com/
dapoxetine from mexico pharmacy
503 Service Unavailable