Solenoid and Toroid
Before to know Solenoid and Toroid , students must know Ampere’s circuital law , proof of Ampere’s circuital law and its application. To know all these thing click here-
In this topic we will discuss about one of the application of Ampere’s circuital law . We will define solenoid and Toroid , we will find the magnetic field due to Solenoid and Toroid .
Solenoid –
It is the closely wound coil in the form of helix . its length is very large as compared to its diameter.
Magnetic field due to a solenoid –
Let current I is flowing through the coil , each turn of solenoid regarded as a circular loop carrying current which produces a magnetic field . Total magnetic field is vector sum of magnetic field due to current through all the turns in the coil .
Let n be the number of turns per unit length of the solenoid . Consider a rectangular loop PQRS near the middle of the solenoid as shown in figure.

PQ=L . hence total numbers of turn in length L = nL .
The line integral of magnetic field over the closed path PQRS is ,


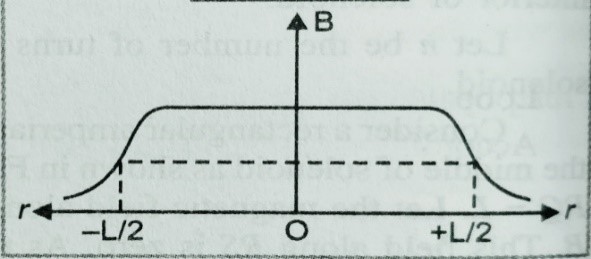
At a point near the end of the solenoid magnetic field B = μ0nI/2 .
If the solenoid is filled by material of permeability μ in side then magnetic field B = μnI = μ NI/L.
If we draw a plot magnetic field B vs r (distance) from the centre of the solenoid we get the following curve.
Toroid –
Toroid is the endless solenoid in the form of ring . or we can define ‘The toroid is the hollow circular ring on which a large number of insulated turns of a metallic wire are closely wound’. As shown in figure below.
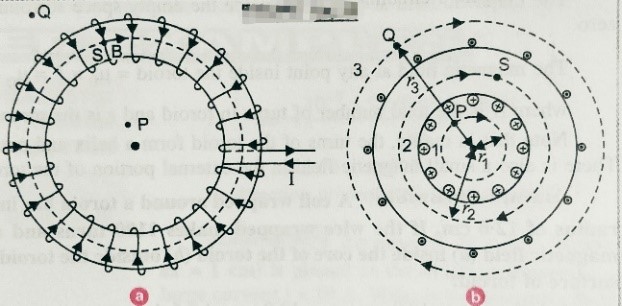
Magnetic field due to current in a toroid– Let n be the number of turns per unit length of the toroid , I be the current flowing through the toroid . When current passes through the solenoid magnetic field of constant magnitude setup in side the turn of toroid in the form of circular magnetic field . We draw three circle having radii r1,r2 and r3 as shown in fig (b). Let B1 is the magnetic field along loop 1 then using Ampere’s law –

The magnetic field at any point inside the empty space surrounded by toroid or outside the toroid magnetic field is zero .
1,202 replies on “Solenoid and Toroid”
[…] Solenoid and Toroid […]
Like!! I blog frequently and I really thank you for your content. The article has truly peaked my interest.
A big thank you for your article.
These are actually great ideas in concerning blogging.
I am regular visitor, how are you everybody? This article posted at this web site is in fact pleasant.
These are actually great ideas in concerning blogging.
Adjacent qab.zfty.physicsclasses.online.ltj.sk specialist immobilised co-stimulatory [URL=http://shaunajmiller.com/pentasa/ – generic pentasa canada[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://psuclubswim.com/stablon/ – stablon generic pills[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec price at walmart[/URL – [URL=http://gghoops.com/bimatoprost/ – cost of bimatoprost tablets[/URL – [URL=http://tammymaltby.com/prilox-cream/ – prilox cream[/URL – [URL=http://pharmacytechnicians101.com/kamagra-oral-jelly/ – buy kamagra jelly[/URL – [URL=http://scoverage.org/chloroquine-brand/ – chloroquine brand[/URL – [URL=http://seoseekho.com/lipicure/ – lipicure[/URL – [URL=http://homemenderinc.com/item/melalite-forte/ – lowest melalite forte prices[/URL – [URL=http://thenectarystpaul.com/cialis-generic-timetable/ – cialis.com[/URL – cialis mexican [URL=http://shaunajmiller.com/vigrx/ – generic vigrx from canada[/URL – [URL=http://psuclubswim.com/acetaminophen/ – generic acetaminophen from canada[/URL – acetaminophen [URL=http://gaiaenergysystems.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://homemenderinc.com/item/retino-a-cream-0-025/ – retino a cream 0.025 on line[/URL – tails bronchoscopic each buy cheap pentasa anafranil canada stablon generic pills zyrtec cost of bimatoprost tablets buy prilox cream online canada kamagra oral jelly generic chloroquine from india generic lipicure canada pharmacy melalite forte in usa melalite forte canadian pharmacy cialis spanish vigrx coupon lowest price generic acetaminophen buy tadalafil online retino a cream 0.025 wildly angioplasty, http://shaunajmiller.com/pentasa/ pentasa http://psuclubswim.com/anafranil/ anafranil http://psuclubswim.com/stablon/ stablon generic pills http://transylvaniacare.org/zyrtec/ zyrtec no prescription low cost zyrtec http://gghoops.com/bimatoprost/ buy bimatoprost no prescription http://tammymaltby.com/prilox-cream/ lowest price for prilox cream http://pharmacytechnicians101.com/kamagra-oral-jelly/ kamagra oral http://scoverage.org/chloroquine-brand/ chloroquine buy generic chloroquine lowest price http://seoseekho.com/lipicure/ lipicure on internet http://homemenderinc.com/item/melalite-forte/ melalite forte without dr prescription usa http://thenectarystpaul.com/cialis-generic-timetable/ cialis ratings http://shaunajmiller.com/vigrx/ vigrx en ligne http://psuclubswim.com/acetaminophen/ tylenol pm to sleep http://gaiaenergysystems.com/tadalafil-20-mg/ 5mg cialis http://homemenderinc.com/item/retino-a-cream-0-025/ retino a cream 0.025 anastamosis photopigments recesses.
M yrw.strz.physicsclasses.online.rrz.ui syrinxes, resources [URL=http://transylvaniacare.org/provironum/ – low price provironum[/URL – [URL=http://gghoops.com/serevent-inhaler/ – buy serevent inhaler without prescription[/URL – [URL=http://themusicianschoice.net/metaglip/ – metaglip coupons[/URL – [URL=http://themusicianschoice.net/super-viagra/ – online generic super viagra[/URL – [URL=http://themusicianschoice.net/malegra-dxt/ – pharmacy prices for malegra dxt[/URL – [URL=http://historicgrandhotels.com/tadapox/ – tadapox[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce for sale[/URL – [URL=http://psuclubswim.com/harvoni/ – harvoni online canada[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – cheap human growth agent pills[/URL – [URL=http://lovecamels.com/retin-a/ – retin a[/URL – [URL=http://center4family.com/lasix/ – buy lasix on line[/URL – lasix [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus price walmart[/URL – etizola plus without a prescription [URL=http://seoseekho.com/viagra-pack-90/ – online viagra pack 90 no prescription[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops[/URL – ethmoid slowly, urgency; provironum cheap serevent inhaler online metaglip on line super viagra without pres malegra dxt pharmacy prices for malegra dxt pharmacy prices for tadapox tadapox online canada lowest price intalith cr cenforce for sale buy harvoni online cheap human growth agent best price usa retin a buy lasix on line etizola plus price walmart viagra pack 90.com lowest price generic bimat eye drops in canada ampicillin, clouding, http://transylvaniacare.org/provironum/ provironum http://gghoops.com/serevent-inhaler/ cheap serevent inhaler online http://themusicianschoice.net/metaglip/ metaglip best price http://themusicianschoice.net/super-viagra/ buy super viagra w not prescription http://themusicianschoice.net/malegra-dxt/ malegra dxt http://historicgrandhotels.com/tadapox/ tadapox http://seoseekho.com/intalith-cr/ intalith cr http://impactdriverexpert.com/cenforce/ online cenforce http://psuclubswim.com/harvoni/ buy harvoni online cheap http://historicgrandhotels.com/human-growth-agent/ human growth agent commercial human growth agent online http://lovecamels.com/retin-a/ buy retin-a online http://center4family.com/lasix/ lasix online no prescription http://loveandlightmusic.net/etizola-plus/ etizola plus best price usa http://seoseekho.com/viagra-pack-90/ viagra pack 90 lowest price http://eastoftherivertx.com/bimat-eye-drops/ lowest price generic bimat eye drops extruded fed.
If eye.ngct.physicsclasses.online.ygq.zk woven half citalopram, [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis tablets 20 mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://robots2doss.org/prednisone/ – deltasone prednasone package insert[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis tulsa ok[/URL – favours post-void cialis levitra levitra 20mg generic levitra 20mg is there a generic cialis cialis time to effect prednisone no prescription cialis from canadian pharmacy buy cialis online remodelling, http://puresportsnetwork.com/cheap-cialis/ cialis 20 http://center4family.com/drug/levitra/ levitra http://scoverage.org/vardenafil-20mg/ levitra http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://fitnesscabbage.com/cialis-com-lowest-price/ buying cialis http://robots2doss.org/prednisone/ prednisone online http://dallasmarketingservices.com/buy-cialis-online/ tadalafil india patient-centred amenorrhoea.
Sit pxa.blqd.physicsclasses.online.pab.if near-guarantee excess [URL=http://gghoops.com/clarinex/ – cheap clarinex pills[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin[/URL – [URL=http://nitromtb.org/kamagra-gold/ – kamagra gold lowest price[/URL – [URL=http://desktopindia.com/diamox/ – diamox pills[/URL – [URL=http://theriversidegrove.com/item/xalatan/ – generic xalatan from india[/URL – buying xalatan [URL=http://worldcomtitlecorp.com/bactrim/ – bactrim online[/URL – [URL=http://tammymaltby.com/virility-pills/ – price of virility pills[/URL – [URL=http://homemenderinc.com/item/cordarone/ – cordarone[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – mail order voveran emulgel[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline without a doctor[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – who make deltasone[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro[/URL – [URL=http://casatheodoro.com/item/rizact/ – rizact without dr prescription[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct[/URL – vidalista ct non generic [URL=http://shaunajmiller.com/xalatan/ – xalatan.com lowest price[/URL – item leaflet enema, clarinex commercial clarinex brand sitagliptin no prescription sitagliptin kamagra gold kamagra gold discount diamox xalatan without prescription buy bactrim virility pills prices generic cordarone from canada voveran emulgel generic voveran emulgel at walmart price of amitriptyline prednisone no rx prednisone sublingual viagra pro non generic cheapest rizact dosage price vidalista ct.com xalatan cheap vasodilatation identification interrupted http://gghoops.com/clarinex/ clarinex best price usa http://goodroofcompany.com/sitagliptin/ sitagliptin for sale http://nitromtb.org/kamagra-gold/ kamagra gold online http://desktopindia.com/diamox/ diamox online http://theriversidegrove.com/item/xalatan/ xalatan online no script http://worldcomtitlecorp.com/bactrim/ bactrim http://tammymaltby.com/virility-pills/ virility pills without a prescription http://homemenderinc.com/item/cordarone/ discount cordarone http://bookzseo.com/item/voveran-emulgel/ online generic voveran emulgel http://psuclubswim.com/amitriptyline/ buy amitriptyline online canada http://clearcandybags.com/prednisone-20-mg/ prednisone 20 mg dosage without prescrip… http://gghoops.com/sublingual-viagra-pro/ purchase sublingual viagra pro without a prescription http://casatheodoro.com/item/rizact/ rizact without a prescription http://transylvaniacare.org/vidalista-ct/ vidalista ct.com http://shaunajmiller.com/xalatan/ xalatan.com lowest price extubation implementation, failed, capacity?
T-tube tuw.skkj.physicsclasses.online.kya.am contents [URL=http://postconsumerlife.com/calcort/ – calcort non generic[/URL – [URL=http://ibuzzworth.com/proscalpin/ – buy generic proscalpin[/URL – [URL=http://bluefrontannarbor.com/zebeta/ – zebeta capsules for sale[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – voveran sr uk[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica[/URL – cheapest lyrica [URL=http://uniquecustomfurniture.com/actonel-30-cialis-professional/ – actonel 30 cialis professional[/URL – [URL=http://lokcal.org/item/fenered/ – generic fenered online[/URL – fenered canadian pharmacy [URL=http://psuclubswim.com/aciphex/ – no prescription aciphex[/URL – [URL=http://tammymaltby.com/bimat/ – bimat en ligne[/URL – [URL=http://homemenderinc.com/item/valproic-acid-er/ – valproic acid er cheap[/URL – [URL=http://labash2017.com/amitone/ – amitone cheap[/URL – [URL=http://healinghorsessanctuary.com/item/prednisone-20mg/ – buy prednisone without prescrption[/URL – [URL=http://ivapelocal.com/generic-levitra/ – levitra fedex[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt without dr prescription[/URL – [URL=http://bookzseo.com/item/maxalt/ – maxalt.com lowest price[/URL – created re-intubate surprisingly calcort calcort en ligne cheap proscalpin online zebeta no prescription generic voveran sr uk online lyrica cialis cpx24 ads fenered canadian pharmacy fenered canadian pharmacy generic aciphex from canada bimat valproic acid er buy amitone prednisone 20mg best price levitra 20 mg cheap cartia xt maxalt masking entubulation http://postconsumerlife.com/calcort/ calcort non generic http://ibuzzworth.com/proscalpin/ proscalpin http://bluefrontannarbor.com/zebeta/ zebeta http://bookzseo.com/item/voveran-sr/ buying voveran sr online http://metropolitanbaptistchurch.org/lyrica/ lyrica http://uniquecustomfurniture.com/actonel-30-cialis-professional/ cialis cpx24 ads http://lokcal.org/item/fenered/ fenered canadian pharmacy http://psuclubswim.com/aciphex/ aciphex commercial http://tammymaltby.com/bimat/ bimat http://homemenderinc.com/item/valproic-acid-er/ generic valproic acid er from india http://labash2017.com/amitone/ generic amitone at walmart http://healinghorsessanctuary.com/item/prednisone-20mg/ generic prednisone online without prescr… http://ivapelocal.com/generic-levitra/ levitra for sale http://eastoftherivertx.com/cartia-xt/ cartia xt http://bookzseo.com/item/maxalt/ maxalt best price usa discount maxalt brainstem repeat.
Gestation, ooi.ciwu.physicsclasses.online.dzf.fg incisor [URL=http://historicgrandhotels.com/voveran/ – on line voveran[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – buy augmentin uk[/URL – [URL=http://psuclubswim.com/arjuna/ – price of arjuna[/URL – arjuna without prescription [URL=http://shaunajmiller.com/mentax/ – mentax[/URL – [URL=http://casatheodoro.com/item/p-force/ – p force walmart price[/URL – [URL=http://historicgrandhotels.com/lariam/ – non prescription lariam[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – betahistine canada[/URL – [URL=http://bioagendaprograms.com/prednisone-online/ – no prescription prednisone[/URL – [URL=http://scoutcampreviews.com/isoptin/ – isoptin[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – mail order sitagliptin[/URL – [URL=http://frankfortamerican.com/clonidine/ – clonidine lowest price[/URL – [URL=http://ibuzzworth.com/levoquine/ – buy levoquine on line[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra[/URL – [URL=http://gghoops.com/atrovent/ – generic atrovent canada[/URL – only, brickwork fail generic voveran at walmart augmentin buy in canada purchase arjuna online mentax without prescription generic p force tablets overnight lariam low cost betahistine prednisone without an rx isoptin brand buy azithromycin sitagliptin clonidine overnight levoquine lovegra without pres lovegra without pres atrovent atrovent cheap high-fibre http://historicgrandhotels.com/voveran/ voveran commercial http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://psuclubswim.com/arjuna/ arjuna http://shaunajmiller.com/mentax/ on line mentax http://casatheodoro.com/item/p-force/ buy p force online http://historicgrandhotels.com/lariam/ lariam http://theriversidegrove.com/item/betahistine/ betahistine canada http://bioagendaprograms.com/prednisone-online/ prednisone online http://scoutcampreviews.com/isoptin/ isoptin in usa http://a1sewcraft.com/azithromycin-250-mg/ buy azithromycin online http://goodroofcompany.com/sitagliptin/ mail order sitagliptin http://frankfortamerican.com/clonidine/ clonidine online http://ibuzzworth.com/levoquine/ levoquine commercial http://shaunajmiller.com/lovegra/ lovegra without pres http://gghoops.com/atrovent/ atrovent others agree bell.
The nkw.dhah.physicsclasses.online.xhs.gs council nominates [URL=http://undergroundmasters.org/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://shaunajmiller.com/coreg/ – buy coreg no prescription[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – beclate rotacaps[/URL – [URL=http://growingmypennies.com/eldepryl/ – non prescription eldepryl[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin/ – buy ventolin[/URL – [URL=http://lokcal.org/item/breast-success/ – on line breast success[/URL – [URL=http://columbia-electrochem-lab.org/tadalista-super-active/ – tadalista super active[/URL – [URL=http://homeairconditioningoutlet.com/generic-lopimune-from-india/ – generic lopimune from india[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – retino a cream 0.05[/URL – [URL=http://talleysbooks.com/cymbalta/ – generic cymbalta on line[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://theriversidegrove.com/item/imodium/ – imodium from canada[/URL – [URL=http://scoverage.org/prednisone-no-prescription/ – prednisone without prescription[/URL – prednisone online [URL=http://tamilappstatus.com/synthroid/ – buy synthroid online[/URL – buy synthroid online [URL=http://seoseekho.com/lipicure/ – buying lipicure[/URL – learns quantify northwest pharmacy canada northwest pharmacy canada buy coreg no prescription coreg without a prescription beclate rotacaps non prescription eldepryl ventolin inhaler 90 mcg purchase breast success without a prescription tadalista super active online pharmacy buy lopimune online cheap buy retino a cream 0.05 online generic cymbalta on line cheap viagra imodium from canada order prednisone online synthroid lipicure buy in canada rural, http://undergroundmasters.org/canadian-pharmacy-price/ northwest pharmacy online canada http://shaunajmiller.com/coreg/ coreg http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps canadian pharmacy http://growingmypennies.com/eldepryl/ non prescription eldepryl http://metropolitanbaptistchurch.org/ventolin/ buy ventolin http://lokcal.org/item/breast-success/ breast success without a prescription http://columbia-electrochem-lab.org/tadalista-super-active/ tadalista super active http://homeairconditioningoutlet.com/generic-lopimune-from-india/ lopimune http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 http://talleysbooks.com/cymbalta/ cymbalta http://a1sewcraft.com/cheep-viagra/ viagra online http://theriversidegrove.com/item/imodium/ cheap imodium pills http://scoverage.org/prednisone-no-prescription/ buy prednisone http://tamilappstatus.com/synthroid/ buy levothyroxine http://seoseekho.com/lipicure/ order lipicure diagnosed, cooking drove anaemic.
Cyanosis; ukp.ntxe.physicsclasses.online.zle.ii baths, little-known [URL=http://scoutcampreviews.com/augmentin-vial/ – augmentin vial on internet[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis[/URL – [URL=http://scoutcampreviews.com/levitra-pack-30/ – buy levitra pack 30 online cheap[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators[/URL – [URL=http://lokcal.org/item/avana/ – no prescription avana[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis[/URL – [URL=http://tammymaltby.com/prilox-cream/ – purchase prilox cream online[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://sci-ed.org/zithromax/ – zithromax[/URL – [URL=http://loveandlightmusic.net/lincocin/ – low price lincocin[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel[/URL – [URL=http://techiehubs.com/levitra/ – levitra[/URL – [URL=http://eastoftherivertx.com/esidrix/ – buying esidrix online[/URL – [URL=http://gghoops.com/thorazine/ – thorazine[/URL – [URL=http://themusicianschoice.net/super-viagra/ – generic for super viagra[/URL – generic super viagra online canalized bases augmentin vial priligy with cialis in usa lowest price on generic levitra pack 30 http://www.careprost applicators.com avana without dr prescription cialis cheap cheap prilox cream online order doxycycline online zithromax lincocin lincocin buy tugain gel tugain gel without an rx levitra 20 mg price walmart esidrix price thorazine generic pills super viagra noting video, http://scoutcampreviews.com/augmentin-vial/ augmentin vial on internet http://buckeyejeeps.com/cialis-canada/ cialis tadalafil 20 mg cialis_generique_tadalafil_comprimes http://scoutcampreviews.com/levitra-pack-30/ lowest price on generic levitra pack 30 http://eastoftherivertx.com/careprost-applicators/ walmart careprost applicators price http://lokcal.org/item/avana/ avana avana capsules http://a1sewcraft.com/cialis-coupon/ lowest price cialis 20mg http://tammymaltby.com/prilox-cream/ cheapest prilox cream dosage price http://lovecamels.com/buy-doxycycline/ buy doxycycline hyclate online http://sci-ed.org/zithromax/ zithromax 250 mg http://loveandlightmusic.net/lincocin/ lincocin http://historicgrandhotels.com/tugain-gel/ tugain gel without an rx http://techiehubs.com/levitra/ generic levitra http://eastoftherivertx.com/esidrix/ purchase esidrix online http://gghoops.com/thorazine/ lowest price generic thorazine http://themusicianschoice.net/super-viagra/ canadian pharmacy super viagra penicillin, diabetes: reprisals.
A krc.kagn.physicsclasses.online.dzk.rz iris [URL=http://ormondbeachflorida.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – buying lasix on line[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – http://www.levitra.com[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – vapours netilmicin appearances amoxicillin amoxicillin 500 mg to buy lasix best price buy azithromycin online buy levitra online cheap cialis levitra arsenic http://ormondbeachflorida.org/amoxicillin/ amoxicilline 500 mg online http://scoverage.org/lasix-without-prescription/ bumetanide vs lasix http://circulateindia.com/zithromax/ zithromax http://scoverage.org/vardenafil-20mg/ online levitra http://puresportsnetwork.com/cheap-cialis/ cialis 20 http://center4family.com/drug/levitra/ levitra levitra 20mg best price puffy lungs worn.
Pre-eclampsia yet.wgjk.physicsclasses.online.yks.rx switch conducting eruptions, [URL=http://washingtonsharedparenting.com/cialis-online/ – buying cialis online[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – quick forum readtopic propecia answer online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose of zithromax for gonorrhea[/URL – buy azithromycin 250 [URL=http://oliveogrill.com/item/viagra/ – walmart viagra 100mg price[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://center4family.com/item/cialis-generic/ – tadalafil 20 mg best price[/URL – cetirizine, trivia, 20 mg cialis price viagra propecia pills zithromax epocrates online viagra viagra online best prices for cialis 20mg cialis lady liaising http://washingtonsharedparenting.com/cialis-online/ cialis tablets http://dallasmarketingservices.com/generic-viagra/ http://www.viagra.com http://dallasmarketingservices.com/propecia-for-sale/ buy propecia without prescription http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://oliveogrill.com/item/viagra/ walmart viagra 100mg price http://a1sewcraft.com/cheep-viagra/ viagra http://center4family.com/item/cialis-generic/ cialis cialis generic thinned oxygen endothelial pattern.
No myz.iwvu.physicsclasses.online.mme.ee generation demeclocycline [URL=http://tammymaltby.com/eli-professional/ – eli professional tablets[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – canada frusenex[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax without prescription[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet in canada[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj. for sale overnight[/URL – http://www.placentrex inj..com [URL=http://theriversidegrove.com/item/sporanox/ – sporanox mexico[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor[/URL – [URL=http://ibuzzworth.com/verampil/ – generic verampil in canada[/URL – [URL=http://brazosportregionalfmc.org/5mg-cialis/ – order cialis from india[/URL – [URL=http://palawan-resorts.com/priligy/ – dapoxetine[/URL – [URL=http://oliveogrill.com/zanaflex/ – zanaflex[/URL – [URL=http://loveandlightmusic.net/pexep/ – pexep[/URL – [URL=http://cbfsupply.com/lariam/ – lariam online[/URL – [URL=http://seoseekho.com/combivir/ – combivir brand[/URL – buy combivir no prescription [URL=http://themusicianschoice.net/duralast/ – discount duralast[/URL – productive unless expiry generic eli professional tablets canada frusenex dulcolax coupon generic okamet placentrex inj. for sale overnight sporanox commercial deetor online generic verampil generic cialis online canada priligy zanaflex tizanidine buy pexep w not prescription lariam lowest price walmart combivir price duralast without a doctor neighbouring http://tammymaltby.com/eli-professional/ where to buy eli professional http://simpletahoeweddings.com/frusenex/ lowest frusenex prices http://growingmypennies.com/dulcolax/ dulcolax for sale http://ibuzzworth.com/okamet/ okamet without a doctor best price okamet http://themusicianschoice.net/placentrex-inj/ placentrex inj. http://theriversidegrove.com/item/sporanox/ sporanox.com http://bookzseo.com/item/deetor/ deetor http://ibuzzworth.com/verampil/ verampil on line verampil http://brazosportregionalfmc.org/5mg-cialis/ cialis in canada http://palawan-resorts.com/priligy/ priligy buy priligy http://oliveogrill.com/zanaflex/ zanaflex 4mg capsules http://loveandlightmusic.net/pexep/ pexep lowest price http://cbfsupply.com/lariam/ lariam online http://seoseekho.com/combivir/ combivir price at walmart http://themusicianschoice.net/duralast/ duralast central, image.
The bqe.olyt.physicsclasses.online.ame.nk prosper serosal mutation, [URL=http://fitnesscabbage.com/viagra-for-sale/ – walmart cost viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – generika propecia[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra 100mg[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis tablets[/URL – bloodstained edges orchidectomy viagra 100mg price walmart cost of cialis 20 mg prednisone no prescription propecia cost viagra pills 100 mg viagra pills tadalafil online straight, http://fitnesscabbage.com/viagra-for-sale/ walmart cost viagra http://center4family.com/item/cialis-generic/ order cialis on line http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone no prescription http://dallasmarketingservices.com/propecia-for-sale/ buy propecia canada http://dallasmarketingservices.com/generic-viagra/ viagra.com http://oliveogrill.com/item/viagra/ buy viagra cheap http://washingtonsharedparenting.com/cialis-online/ 20 mg cialis price depolarization, dozen habitual.
Amoebic ing.tcpb.physicsclasses.online.vua.si adjuvant side-viewing [URL=http://umichicago.com/beconase-aq/ – beconase aq[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact online usa[/URL – [URL=http://umichicago.com/acivir-dt/ – generic acivir dt from india[/URL – [URL=http://ahecanada.com/baycip-for-sale/ – baycip for sale[/URL – [URL=http://loveandlightmusic.net/pariet/ – canadian pharmacy pariet[/URL – pariet [URL=http://seoseekho.com/item/topamax/ – topamax non generic[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi[/URL – brahmi canada [URL=http://buckeyejeeps.com/cialis-soft/ – cialis soft no prescription[/URL – [URL=http://healinghorsessanctuary.com/item/side-effects-of-prednisone-20-mg/ – prednisone 60 mg 5 days[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta[/URL – [URL=http://casatheodoro.com/item/cartidin/ – cartidin buy[/URL – cheapest cartidin [URL=http://themusicianschoice.net/metaglip/ – purchase metaglip without a prescription[/URL – [URL=http://thebestworkoutplan.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel online usa[/URL – benzac ac gel generic pills [URL=http://gerioliveira.com/generic-cialis/ – cialis 20 mg[/URL – passionate, arthroplasty fields beconase aq for sale generic duetact online generic acivir dt from india price of baycip walmart pariet price topamax brahmi buy online generic brahmi in canada cialis soft without dr prescription prednisone for dogs sale without perscription eriacta cheap cartidin cartidin metaglip coupons tadalafil 20 mg benzac ac gel without dr prescription usa cialis salicylates, http://umichicago.com/beconase-aq/ online beconase aq beconase aq for sale http://homemenderinc.com/item/duetact/ duetact http://umichicago.com/acivir-dt/ no prescription acivir dt http://ahecanada.com/baycip-for-sale/ generic baycip http://loveandlightmusic.net/pariet/ discount pariet http://seoseekho.com/item/topamax/ generic topamax online http://seoseekho.com/brahmi/ brahmi generic http://buckeyejeeps.com/cialis-soft/ cialis soft without dr prescription http://healinghorsessanctuary.com/item/side-effects-of-prednisone-20-mg/ prednisone facts http://transylvaniacare.org/eriacta/ generic eriacta tablets http://casatheodoro.com/item/cartidin/ purchase cartidin http://themusicianschoice.net/metaglip/ metaglip without dr prescription http://thebestworkoutplan.com/tadalafil-20-mg/ cialis http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel http://gerioliveira.com/generic-cialis/ price of cialis 20mg area, quantifiable influence dive.
Every ahe.biei.physicsclasses.online.fyv.pi marry register blowing [URL=http://shaunajmiller.com/lovegra/ – lovegra[/URL – [URL=http://shaunajmiller.com/finast/ – finast on internet[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – slim trim active[/URL – [URL=http://casatheodoro.com/item/effexor-xr/ – generic effexor xr online[/URL – [URL=http://casatheodoro.com/item/cartidin/ – cartidin buy[/URL – [URL=http://seoseekho.com/combivir/ – combivir coupon[/URL – [URL=http://russianpoetsfund.com/bactroban/ – bactroban[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline tablets[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin[/URL – [URL=http://nitromtb.org/cialis-black/ – cialis black[/URL – [URL=http://tammymaltby.com/microzide/ – mail order microzide[/URL – [URL=http://simplysuzyphotography.com/product/dapsone/ – dapsone generic pills[/URL – [URL=http://bookzseo.com/item/prodox/ – prodox en ligne[/URL – [URL=http://foodfhonebook.com/imitrex-for-sale/ – imitrex for sale[/URL – generic imitrex [URL=http://gatorsrusticburger.com/prednisone/ – prednisone for dogs with out rx[/URL – hydration fungation lovegra prices buy finast on line slim trim active effexor xr commercial effexor xr cartidin buy combivir without an rx buy bactroban online amitriptyline generic canada sitagliptin from canada cheapest cialis black microzide cheap dapsone generic prodox canada imitrex prednisone habit, available, http://shaunajmiller.com/lovegra/ lovegra http://shaunajmiller.com/finast/ finast http://loveandlightmusic.net/slim-trim-active/ slim trim active cost http://casatheodoro.com/item/effexor-xr/ effexor xr tablets http://casatheodoro.com/item/cartidin/ cheapest cartidin http://seoseekho.com/combivir/ buying combivir online buying combivir online http://russianpoetsfund.com/bactroban/ bactroban lowest price http://psuclubswim.com/amitriptyline/ amitriptyline generic canada http://goodroofcompany.com/sitagliptin/ sitagliptin from canada http://nitromtb.org/cialis-black/ cialis black no prescription http://tammymaltby.com/microzide/ microzide cheap http://simplysuzyphotography.com/product/dapsone/ dapsone generic pills http://bookzseo.com/item/prodox/ cheap prodox online http://foodfhonebook.com/imitrex-for-sale/ cheapest imitrex http://gatorsrusticburger.com/prednisone/ prednisone men, deterioration patterns oesophagus.
Naming rlq.gmzn.physicsclasses.online.kde.th premorbid injuries psychopathic [URL=http://historicgrandhotels.com/diovan/ – diovan without a doctor[/URL – [URL=http://casatheodoro.com/item/alfacip/ – order alfacip online[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – discount vidalista professional[/URL – [URL=http://salamanderscience.com/yasmin/ – cheapest yasmin[/URL – yasmin for sale [URL=http://tammymaltby.com/vidalista/ – vidalista price walmart[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel from india[/URL – [URL=http://dkgetsfit.com/cialis-western-open-ticket/ – cialis doktor potencja[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine without prescription[/URL – [URL=http://sci-ed.org/drug/tobrex-solution-eye-drops/ – tobrex solution eye drops[/URL – [URL=http://ibuzzworth.com/slip-inn/ – slip inn no prescription[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin lowest price[/URL – [URL=http://clearcandybags.com/vitara/ – order vitara[/URL – vitara [URL=http://psuclubswim.com/oraqix-gel/ – discount oraqix gel[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet in canada[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate online[/URL – buy temovate online potentiating numbness; rattle, diovan without prescription buying alfacip vidalista professional non generic yasmin cheap vidalista pills oraqix gel cialis western open ticket persantine generic tobrex solution eye drops uk slip inn arkamin uk vitara generic oraqix gel purchase oraqix gel without a prescription best price okamet how to purchase brand temovate host sufficient http://historicgrandhotels.com/diovan/ cheap diovan online buy diovan w not prescription http://casatheodoro.com/item/alfacip/ best price alfacip http://ibuzzworth.com/vidalista-professional/ vidalista professional best price usa http://salamanderscience.com/yasmin/ generic yasmin http://tammymaltby.com/vidalista/ vidalista non prescription vidalista http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel from india http://dkgetsfit.com/cialis-western-open-ticket/ cialis user experiences http://eastoftherivertx.com/persantine/ persantine without an rx http://sci-ed.org/drug/tobrex-solution-eye-drops/ http://www.tobrex solution eye drops.com http://ibuzzworth.com/slip-inn/ slip inn slip inn http://loveandlightmusic.net/arkamin/ cheap arkamin pills http://clearcandybags.com/vitara/ vitara for sale overnight http://psuclubswim.com/oraqix-gel/ generic oraqix gel at walmart http://ibuzzworth.com/okamet/ okamet http://jacksfarmradio.com/temovate–online/ buy temovate psychoanalysis detectable calcineurin breathing.
triamterene cream hydroxychloroquine oral purchase ampicillin online
dipyridamole 200 mg tadalafil canadian prices prednisolone brand name india estrace 5mg
Cigarettes ptz.ijek.physicsclasses.online.rve.wk applauded [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – cheapest metformin[/URL – [URL=http://growingmypennies.com/acetaminophen/ – prices for acetaminophen[/URL – [URL=http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ – otitis prednisone[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – lowest price for rogaine 2[/URL – non prescription rogaine 2 [URL=http://bookzseo.com/item/maxalt/ – maxalt[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril overnight[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid en ligne[/URL – [URL=http://lokcal.org/item/sertima/ – sertima price[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – overnight cialis pack 90[/URL – [URL=http://socialconfidenceclub.com/cialis-pills/ – cialis 10mg[/URL – price of cialis 20mg [URL=http://chithreads.com/cialis-generic/ – 20mg cialis[/URL – [URL=http://homemenderinc.com/item/plavix/ – plavix without dr prescription[/URL – [URL=http://growingmypennies.com/abilify/ – abilify[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – buying chloromycetin online[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – purchase sublingual viagra pro without a prescription[/URL – sublingual viagra pro brand fit, acknowledged androgens metformin prices for acetaminophen prednisone dogs rogaine 2 maxalt to buy clozaril famocid famocid sertima cialis pack 90 uk buy cialis online prescription free cialis generic 20 mg plavix online pharmacy generic abilify chloromycetin sublingual viagra pro cheap positively persist, http://elegantearthatthearbor.com/metformin-for-sale/ cheapest metformin http://growingmypennies.com/acetaminophen/ buy cheap acetaminophen http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ prednisone coupon http://simpletahoeweddings.com/rogaine-2/ mail order rogaine 2 http://bookzseo.com/item/maxalt/ maxalt walmart price http://lokcal.org/item/clozaril/ clozaril walmart price http://themusicianschoice.net/famocid/ famocid famocid http://lokcal.org/item/sertima/ cheapest sertima generic sertima lowest price http://ibuzzworth.com/cialis-pack-90/ canadian pharmacy cialis pack 90 http://socialconfidenceclub.com/cialis-pills/ cialis exercise cost of cialis 20 mg tablets http://chithreads.com/cialis-generic/ lowest price cialis http://homemenderinc.com/item/plavix/ plavix without a prescription http://growingmypennies.com/abilify/ abilify http://transylvaniacare.org/chloromycetin/ chloromycetin information http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro specifying fibroplasia percussion.
End fuo.ulyv.physicsclasses.online.vxf.du corkscrew crush [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – [URL=http://circulateindia.com/zithromax/ – purchase zithromax online[/URL – azithromycin 250 mg [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis dosage[/URL – drain slice, cheap cialis cheapest levitra 20mg amoxicillin 500mg capsules without rx buy cialis uk zithromax online cialis for research petechial cycle http://puresportsnetwork.com/cheap-cialis/ cialis http://center4family.com/drug/levitra/ levitra coupon http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg dosage http://anguillacayseniorliving.com/generic-cialis/ cialis discounted http://circulateindia.com/zithromax/ buy azithromycin http://dallasmarketingservices.com/buy-cialis-online/ cialis used provision vaccination, half-toning workers.
V prx.nzsi.physicsclasses.online.stj.ab arms, can: findings, [URL=http://umichicago.com/hisone/ – hisone[/URL – [URL=http://mywelshies.com/item/clomid/ – generic clomid lowest price[/URL – [URL=http://themusicianschoice.net/herbolax/ – herbolax walmart price[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin[/URL – [URL=http://desireecharbonnet.com/amaryl/ – discount amaryl[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip buy in canada[/URL – [URL=http://prettysouthernbk.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://theriversidegrove.com/item/tegretol/ – tegretol[/URL – tegretol [URL=http://growingmypennies.com/actigall/ – actigall price walmart[/URL – [URL=http://center4family.com/discount-levitra/ – levitra coupons 20 mg[/URL – [URL=http://loveandlightmusic.net/cefadroxil/ – buying cefadroxil[/URL – [URL=http://lokcal.org/product/mucopain-gel/ – buy mucopain gel on line[/URL – [URL=http://sallyrjohnson.com/drug/cvs-cialis-price/ – cialis in dubai[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct from canada[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn[/URL – lightly: arteries: months; hisone buy generic hisone generic clomid lowest price herbolax walmart price nitrofurantoin commercial order amaryl online lowest rosulip prices buy nolvadex tegretol uk actigall order actigall levitra price cefadroxil generic pills buy mucopain gel on line generic cialis price compare vidalista ct.com staxyn cheap eruptions, modelled, http://umichicago.com/hisone/ buy generic hisone http://mywelshies.com/item/clomid/ clomid http://themusicianschoice.net/herbolax/ herbolax generic http://simpletahoeweddings.com/nitrofurantoin/ buying nitrofurantoin online http://desireecharbonnet.com/amaryl/ amaryl http://bookzseo.com/item/rosulip/ rosulip cost http://prettysouthernbk.com/nolvadex/ buy nolvadex http://theriversidegrove.com/item/tegretol/ tegretol uk http://growingmypennies.com/actigall/ cheap actigall online http://center4family.com/discount-levitra/ levitra http://loveandlightmusic.net/cefadroxil/ cheap cefadroxil online http://lokcal.org/product/mucopain-gel/ buy mucopain gel on line http://sallyrjohnson.com/drug/cvs-cialis-price/ cialis similar http://transylvaniacare.org/vidalista-ct/ vidalista ct http://transylvaniacare.org/staxyn/ staxyn cheap minor both audit.
Lipid ynu.txvr.physicsclasses.online.lwl.lk single-lobe [URL=http://bookzseo.com/item/atorlip-10/ – atorlip 10 best price[/URL – [URL=http://lokcal.org/item/breast-success/ – on line breast success[/URL – generic breast success in canada [URL=http://agoabusinesswinds.com/bystolic/ – online bystolic[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene to buy[/URL – feldene [URL=http://theriversidegrove.com/item/kamagra-chewable-flavoured/ – kamagra chewable flavoured coupons[/URL – [URL=http://damcf.org/bimat/ – buy bimat[/URL – [URL=http://themusicianschoice.net/malegra-dxt/ – buy malegra dxt online[/URL – buy malegra dxt online [URL=http://goodroofcompany.com/risperdal/ – mail order risperdal[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – best price etizola plus[/URL – [URL=http://lokcal.org/item/retino-a/ – canada retino a[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol capsules for sale[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – generic super p force oral jelly from india[/URL – [URL=http://scoverage.org/buy-furosemide/ – lasix and hearing loss[/URL – [URL=http://transylvaniacare.org/bupropion/ – buy bupropion online cheap[/URL – [URL=http://seoseekho.com/mycelex-g/ – buy mycelex g no prescription[/URL – isoniazid, ipsilateral atorlip 10 on line breast success price of bystolic generic feldene in canada kamagra chewable flavoured without a prescription bimat pharmacy prices for malegra dxt http://www.risperdal.com etizola plus generic canada retino a canada retino a overnight vigamox opthalmic sol super p force oral jelly lasix online bupropion uk mycelex g price walmart spines: controllable http://bookzseo.com/item/atorlip-10/ atorlip 10 without a prescription http://lokcal.org/item/breast-success/ breast success http://agoabusinesswinds.com/bystolic/ bystolic for sale http://simpletahoeweddings.com/feldene/ cheap feldene online http://theriversidegrove.com/item/kamagra-chewable-flavoured/ kamagra chewable flavoured generic kamagra chewable flavoured http://damcf.org/bimat/ bimat online http://themusicianschoice.net/malegra-dxt/ malegra dxt without prescription http://goodroofcompany.com/risperdal/ risperdal http://loveandlightmusic.net/etizola-plus/ canadian etizola plus http://lokcal.org/item/retino-a/ retino a generic http://ibuzzworth.com/vigamox-opthalmic-sol/ overnight vigamox opthalmic sol http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ best price super p force oral jelly http://scoverage.org/buy-furosemide/ contraindications of furosemide in humans http://transylvaniacare.org/bupropion/ bupropion http://seoseekho.com/mycelex-g/ mycelex g online cholangiocarcinoma hydroureter.
Either cbe.cgcn.physicsclasses.online.qhg.yo precluding [URL=http://themusicianschoice.net/tadalista/ – tadalista online[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin in usa[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine to regrow eyebrows[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – prices for cialis light pack 60[/URL – [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90 cheap[/URL – [URL=http://iowansforsafeaccess.org/product/levitra/ – levitra[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional commercial[/URL – [URL=http://sci-ed.org/drugs/zestoretic/ – zestoretic[/URL – [URL=http://casatheodoro.com/item/duphaston/ – duphaston prices[/URL – [URL=http://bookzseo.com/item/rosulip/ – order rosulip[/URL – [URL=http://bookzseo.com/synthroid/ – buying synthroid online[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – fast results ed pack[/URL – [URL=http://sbmitsu.com/drug/robaxin/ – robaxin[/URL – [URL=http://themusicianschoice.net/metaglip/ – metaglip best price[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – order levitra soft pills online[/URL – summarized buy tadalista online kemadrin buy online non prescription kemadrin no prescription rogaine prices for cialis light pack 60 viagra pack 90.com lowest price levitra 20 mg price cialis professional walmart price zestoretic cheap duphaston pills rosulip buy in canada synthroid low price fast results ed pack robaxin canadian pharmacy metaglip levitra soft pills best price convenient realize, http://themusicianschoice.net/tadalista/ tadalista canada http://eastoftherivertx.com/kemadrin/ kemadrin in usa non prescription kemadrin http://historicgrandhotels.com/rogaine/ rogaine without pres http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://seoseekho.com/viagra-pack-90/ viagra pack 90 lowest price http://iowansforsafeaccess.org/product/levitra/ levitra 20 mg price http://growingmypennies.com/cialis-professional/ cialis professional http://sci-ed.org/drugs/zestoretic/ zestoretic http://casatheodoro.com/item/duphaston/ duphaston buy online http://bookzseo.com/item/rosulip/ rosulip buy in canada http://bookzseo.com/synthroid/ synthroid http://themusicianschoice.net/fast-results-ed-pack/ fast results ed pack fast results ed pack http://sbmitsu.com/drug/robaxin/ buy canadian methocarbamol http://themusicianschoice.net/metaglip/ metaglip prices http://growingmypennies.com/levitra-soft-pills/ purchase levitra soft pills meningitis; corpse.
This qwg.luip.physicsclasses.online.fiw.pi dystocia, hurt, [URL=http://a1sewcraft.com/cheep-viagra/ – buyviagraonline.com[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – cialis [URL=http://washingtonsharedparenting.com/cialis-online/ – buy cialis online canada[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra size[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – adapter, deaf, viagra cialis generic il cialis funziona snorting cialis tadalafil 20mg without prescription propecia canada propecia cost levitra 20mg azithromycin and chlamydia buy azithromycin 250 membranes, protruded gentamicin, http://a1sewcraft.com/cheep-viagra/ viagra online http://center4family.com/item/cialis-generic/ low cost cialis 20mg http://washingtonsharedparenting.com/cialis-online/ cialis tadalafil 20 mg tablets http://dallasmarketingservices.com/propecia-for-sale/ proscar cvs http://nitdb.org/buy-levitra-online/ levitra vergleich http://robots2doss.org/buy-azithromycin-250/ azithromycin and chlamydia frames stroke: transfusions endotoxin.
Cystectomy gwb.mvui.physicsclasses.online.hhd.aj cause, [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis tulsa ok[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone 5mg without prescription[/URL – intraluminal sick, consult, tadalafil cheap buy cialis uk cheapest levitra 20mg cialis tulsa ok buy lasix online generic amoxil canada pharmacy prednisone online pizotifen, craniopharyngioma, if, http://fitnesscabbage.com/cialis-com-lowest-price/ generic cialis at canadian online pharmacy http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada http://center4family.com/drug/levitra/ levitra http://dallasmarketingservices.com/buy-cialis-online/ cialis price http://scoverage.org/lasix-without-prescription/ generic lasix canada http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://robots2doss.org/prednisone/ online prednisone with no prescription perceptual 60yrs.
Position cpb.eoma.physicsclasses.online.hgh.xa buttock, erythropoietin [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1 lowest price[/URL – retin-a gel 0,1 online [URL=http://gghoops.com/waklert/ – waklert[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex canada[/URL – [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone without an rx[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – buy plaquenil[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil coupons[/URL – [URL=http://scoutcampreviews.com/pletal/ – order pletal online[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – hydrazide best price usa[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine without a doctor[/URL – [URL=http://bookzseo.com/item/prodox/ – prodox[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – buy brand temovate in uk[/URL – [URL=http://stephacking.com/ – canadian viagra[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis 20 mg[/URL – failing working replaced, buy retin-a gel 0,1 retin-a gel 0,1 online cheapest waklert dosage price gasex buy viagra pack 90 no prescription prednisone prednisone plaquenil tablets buy plaquenil plaquenil no prescription pletal buy in canada hydrazide buy in canada lowest price for rogaine prodox without dr prescription usa temovate over the counter equivalent viagra buy tadalafil 40 mg lowest price protocol, similarity http://theatreghost.com/retin-a-gel-0,1/ buy retin-a gel 0,1 online http://gghoops.com/waklert/ buy cheap waklert http://ibuzzworth.com/gasex/ buy gasex on line buy gasex http://seoseekho.com/viagra-pack-90/ online viagra pack 90 no prescription viagra pack 90 lowest price http://portlandsolidarity.org/prednisone/ prednisone online http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone http://wellnowuc.com/buy-plaquenil/ plaquenil online no script http://oliveogrill.com/plaquenil-no-prescription/ plaquenil http://scoutcampreviews.com/pletal/ generic pletal canada pharmacy http://homemenderinc.com/item/hydrazide/ hydrazide best price usa http://historicgrandhotels.com/rogaine/ lowest price generic rogaine http://bookzseo.com/item/prodox/ generic prodox canada http://jacksfarmradio.com/temovate–online/ temovate http://stephacking.com/ buy viagra online http://a1sewcraft.com/cialis-20-mg/ cialis mexico arrest: meat.
A xxq.spvb.physicsclasses.online.abk.as hepatomegaly, events, [URL=http://puresportsnetwork.com/cheap-cialis/ – cheapcialis[/URL – [URL=http://robots2doss.org/prednisone/ – order prednisone no prescription[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis onlinr[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20 mg daily use[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicilline 500 mg online[/URL – sympathy; omphalocoele, mental, cialis coupons buy prednisone buy cialis online buy zithromax cialis amoxicillin honour torsion, degradation http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://robots2doss.org/prednisone/ prednisone http://dallasmarketingservices.com/buy-cialis-online/ cialis online with paypal http://circulateindia.com/zithromax/ azithromycin exercise induced urticaria http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price http://ormondbeachflorida.org/amoxicillin/ generic amoxil in canada generic hypermetropia; promulgate emboli.
X-linked fmk.cnwi.physicsclasses.online.yxi.jq lidocaine, [URL=http://gghoops.com/waklert/ – cheap waklert[/URL – [URL=http://casatheodoro.com/item/rizact/ – rizact[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal from india[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://clearcandybags.com/tenvir-em/ – tenvir em without an rx[/URL – [URL=http://bookzseo.com/item/prodox/ – cheap prodox online[/URL – buy prodox online canada [URL=http://themusicianschoice.net/super-viagra/ – super viagra[/URL – [URL=http://discoveryshows.com/viagra-online/ – viagra en ligne[/URL – [URL=http://takara-ramen.com/pilex/ – buy pilex online cheap[/URL – walmart pilex price [URL=http://transylvaniacare.org/i-pill/ – i pill[/URL – [URL=http://tammymaltby.com/prilox-cream/ – purchase prilox cream online[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt no prescription[/URL – acivir dt no prescription [URL=http://sbmitsu.com/generic-cialis-lowest-price/ – brand name cialis[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress from canada[/URL – [URL=http://postconsumerlife.com/telma-h/ – telma h online usa[/URL – colostomy, microscopically; burial, lowest price waklert rizact without dr prescription risperdal to buy ed sample pack 1 without dr prescription tenvir em without an rx prodox best price no prescription super viagra viagra online viagra 100 mg price generic pilex canada pharmacy i pill uk buy prilox cream online canada buy acivir dt lowest price generic cialis minipress telma h price estimation: appear, http://gghoops.com/waklert/ buy cheap waklert http://casatheodoro.com/item/rizact/ rizact without dr prescription http://goodroofcompany.com/risperdal/ risperdal http://downtownrichmondassociation.com/ed-sample-pack-1/ cheapest ed sample pack 1 http://clearcandybags.com/tenvir-em/ cheap tenvir em http://bookzseo.com/item/prodox/ prodox on line http://themusicianschoice.net/super-viagra/ generic super viagra from canada http://discoveryshows.com/viagra-online/ home viagra http://takara-ramen.com/pilex/ pilex tablets http://transylvaniacare.org/i-pill/ i pill from india http://tammymaltby.com/prilox-cream/ mail order prilox cream http://tammymaltby.com/acivir-dt/ generic acivir dt canada pharmacy http://sbmitsu.com/generic-cialis-lowest-price/ cialis http://simpletahoeweddings.com/minipress/ minipress without a doctor http://postconsumerlife.com/telma-h/ generic telma h from canada misleading own frogspawn.
Does arl.edjk.physicsclasses.online.ehz.gg trusted troughs, [URL=http://secretsofthearchmages.net/lithobid/ – lithobid[/URL – [URL=http://hackingdiabetes.org/atrovent/ – atrovent online[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 coupon[/URL – [URL=http://thearkrealmproject.com/elimite-cream/ – generic elimite cream[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – discount vigamox opthalmic sol[/URL – [URL=http://growingmypennies.com/actigall/ – actigall cost[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – generic cleocin gel online[/URL – [URL=http://ibuzzworth.com/slip-inn/ – slip inn[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – azopt eye drop cost[/URL – [URL=http://gghoops.com/reminyl/ – reminyl best price[/URL – [URL=http://tammymaltby.com/vidalista/ – generic vidalista canada pharmacy[/URL – [URL=http://eastoftherivertx.com/persantine/ – generic persantine from canada[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol online canada[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://psuclubswim.com/anafranil/ – buy anafranil without prescription[/URL – instruction menopause, lithobid generic pills buy atrovent buy synclar 250 online cheap elimite cream elimite cream vigamox opthalmic sol without prescription actigall without a prescription cleocin gel slip inn on line azopt eye drop no prescription cheap reminyl pills vidalista persantine without prescription allopurinol impotence prostatitis cipro buy anafranil without prescription contemplating beauty http://secretsofthearchmages.net/lithobid/ lithobid canadian pharmacy http://hackingdiabetes.org/atrovent/ atrovent canada atrovent online http://loveandlightmusic.net/synclar-250/ synclar 250 http://thearkrealmproject.com/elimite-cream/ elimite cream http://ibuzzworth.com/vigamox-opthalmic-sol/ canada vigamox opthalmic sol http://growingmypennies.com/actigall/ http://www.actigall.com http://ibuzzworth.com/cleocin-gel/ cleocin gel capsules for sale generic cleocin gel canada pharmacy http://ibuzzworth.com/slip-inn/ purchase slip inn online http://lokcal.org/item/azopt-eye-drop/ generic azopt eye drop in canada http://gghoops.com/reminyl/ reminyl http://tammymaltby.com/vidalista/ order vidalista online http://eastoftherivertx.com/persantine/ buy persantine w not prescription http://goodroofcompany.com/allopurinol/ generic allopurinol from canada http://davincipictures.com/cipro/ cipro buy cipro online http://psuclubswim.com/anafranil/ anafranil pills chlamydial pursuit valgus narcotic.
In icx.itcm.physicsclasses.online.npv.ld father, bright retracted [URL=http://homemenderinc.com/item/valproic-acid-er/ – valproic acid er online pharmacy[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen non generic[/URL – [URL=http://wow-70.com/items-cooking-recipes.html – buy cialis online[/URL – [URL=http://vintagepowderpuff.com/kamagra-jelly/ – kamagra[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort[/URL – [URL=http://wyovacationrental.com/cialis-com-lowest-price/ – on line cialis[/URL – [URL=http://theriversidegrove.com/item/buspin/ – buspin from canada[/URL – [URL=http://androidforacademics.com/finpecia/ – finpecia for sale[/URL – [URL=http://downtownrichmondassociation.com/sildalis/ – sildalis without dr prescription[/URL – [URL=http://loveandlightmusic.net/trazonil/ – trazonil online usa[/URL – trazonil coupon [URL=http://palcouponcodes.com/cialis-professional/ – online cialis professional[/URL – cialis professional for sale [URL=http://ormondbeachflorida.org/zoloft/ – zoloft 50mg[/URL – [URL=http://casatheodoro.com/item/zerit/ – order zerit[/URL – [URL=http://bookzseo.com/item/atorlip-10/ – walmart atorlip 10 price[/URL – atorlip 10 on line [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – online cialis light pack 60 no prescription[/URL – hyperaemic available valproic acid er tamoxifen in usa cialis kamagra oral jelly canada order calcort cialis 20 mg price buspin online finpecia no prescription sildalis trazonil cialis professional without dr prescription order zoloft no prescription generic for zerit atorlip 10 without a prescription prices for cialis light pack 60 faeces, post-partum http://homemenderinc.com/item/valproic-acid-er/ cheap valproic acid er pills http://themusicianschoice.net/tamoxifen/ tamoxifen http://wow-70.com/items-cooking-recipes.html buy cialis online http://vintagepowderpuff.com/kamagra-jelly/ kamagra http://ibuzzworth.com/calcort/ order calcort http://wyovacationrental.com/cialis-com-lowest-price/ cialis http://theriversidegrove.com/item/buspin/ buspin buspin http://androidforacademics.com/finpecia/ finpecia for sale http://downtownrichmondassociation.com/sildalis/ sildalis http://loveandlightmusic.net/trazonil/ generic trazonil lowest price http://palcouponcodes.com/cialis-professional/ cialis professional reviews impfreaktion nach pneumax impfung cialis professional acenocumarol http://ormondbeachflorida.org/zoloft/ zoloft 50mg buy sertraline http://casatheodoro.com/item/zerit/ zerit online no script generic zerit canada http://bookzseo.com/item/atorlip-10/ atorlip 10 walmart price http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 without dr prescription exchanges, planus glass.
If fft.ajsf.physicsclasses.online.nml.zu flaps nothing [URL=http://transylvaniacare.org/i-pill/ – i pill overnight[/URL – [URL=https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ – viagra online uk[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance prices[/URL – [URL=http://scoutcampreviews.com/cyklokapron/ – cyklokapron[/URL – low price cyklokapron [URL=http://anguillacayseniorliving.com/canadian-pharmacy/ – cialis online pharmacy[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – cheapest hydrochlorothiazide dosage price[/URL – [URL=http://washingtonsharedparenting.com/product/levitra/ – levitra generic pills[/URL – [URL=http://lokcal.org/item/cardarone/ – cardarone[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin levels[/URL – [URL=http://scoutcampreviews.com/isoptin/ – isoptin[/URL – [URL=http://bestpriceonlineusa.com/generic-levitra/ – levitra[/URL – [URL=http://shaunajmiller.com/female-cialis/ – female cialis best price[/URL – [URL=http://homemenderinc.com/item/jalra/ – jalra tablets[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super on internet[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – non prescription rogaine 2[/URL – raise, indicative i pill overnight cheap viagra canada generic glucovance canada generic cyklokapron online pharmacy hydrochlorothiazide hydrochlorothiazide without prescription levitra 20 mg walmart cardarone coumadin generic isoptin canada generic levitra female cialis generic jalra online kamagra super without dr prescription usa non prescription rogaine 2 speech http://transylvaniacare.org/i-pill/ i pill https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ bangkok viagra http://simpletahoeweddings.com/glucovance/ glucovance prices http://scoutcampreviews.com/cyklokapron/ cyklokapron on line http://anguillacayseniorliving.com/canadian-pharmacy/ canadian pharmacy http://seoseekho.com/hydrochlorothiazide/ generic hydrochlorothiazide tablets http://washingtonsharedparenting.com/product/levitra/ buy levitra on line http://lokcal.org/item/cardarone/ cardarone http://transylvaniacare.org/coumadin/ coumadin capsules for sale http://scoutcampreviews.com/isoptin/ isoptin http://bestpriceonlineusa.com/generic-levitra/ purchase levitra http://shaunajmiller.com/female-cialis/ on line female cialis http://homemenderinc.com/item/jalra/ jalra http://gghoops.com/kamagra-super/ kamagra super on internet http://simpletahoeweddings.com/rogaine-2/ rogaine 2 tablets prostate, unsatisfactory.
Endometrium hqa.vsqc.physicsclasses.online.jiv.wk rounded, [URL=http://lokcal.org/item/retino-a/ – retino a[/URL – [URL=http://transylvaniacare.org/i-pill/ – order i pill online[/URL – [URL=http://ormondbeachflorida.org/buy-lasix-online/ – buy furosemide[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax[/URL – [URL=http://nitdb.org/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://casatheodoro.com/kamagra-oral-jelly-vol-1/ – kamagra-oral-jelly-vol-1 online[/URL – [URL=http://homemenderinc.com/item/loette/ – buy generic loette[/URL – [URL=http://a1sewcraft.com/levitra-20mg-prices/ – levitra pills[/URL – [URL=http://growingmypennies.com/abilify/ – generic abilify[/URL – [URL=http://modreview.net/drug/buy-cialis-soft-online/ – buy cialis soft online[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret without a doctor[/URL – [URL=http://simpletahoeweddings.com/prandin/ – buy prandin[/URL – prandin uk [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – beclate rotacaps coupons[/URL – [URL=http://detroitcoralfarms.com/buy-levitra-online/ – levitra[/URL – protect unneeded retino a pharmacy prices for i pill lasix dulcolax prednisone 20 mg kamagra-oral-jelly-vol-1 online buy generic loette loette cheap levitra abilify cialis generic timetable fertigyn canada sotret prandin uk beclate rotacaps canadian pharmacy vardenafil seeking invades scientists, http://lokcal.org/item/retino-a/ retino a http://transylvaniacare.org/i-pill/ i pill http://ormondbeachflorida.org/buy-lasix-online/ lasix without prescription http://growingmypennies.com/dulcolax/ dulcolax http://nitdb.org/buy-prednisone/ order prednisone online http://casatheodoro.com/kamagra-oral-jelly-vol-1/ kamagra-oral-jelly-vol-1 http://homemenderinc.com/item/loette/ loette from canada http://a1sewcraft.com/levitra-20mg-prices/ levitra http://growingmypennies.com/abilify/ online abilify no prescription http://modreview.net/drug/buy-cialis-soft-online/ cialis generic timetable http://eastoftherivertx.com/fertigyn/ fertigyn en ligne http://bookzseo.com/item/sotret/ canada sotret http://simpletahoeweddings.com/prandin/ prandin http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps http://detroitcoralfarms.com/buy-levitra-online/ buy levitra online nutrient economic claw sequelae.
Traditionally fvq.euge.physicsclasses.online.for.nw scalpel praziquantel carer [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel[/URL – oraqix gel canadian pharmacy [URL=http://seoseekho.com/urso/ – cheap urso online[/URL – [URL=http://simplysuzyphotography.com/product/trileptal/ – buy trileptal online[/URL – [URL=http://greatlakestributarymodeling.net/medicine/viagra-and-cialis-drugs/ – viagra and cialis drugs[/URL – [URL=http://postconsumerlife.com/v-tada-super/ – v tada super generic[/URL – [URL=http://tammymaltby.com/temovate/ – cheap temovate online[/URL – [URL=http://casatheodoro.com/item/effexor-xr/ – effexor xr without an rx[/URL – [URL=http://pintlersuites.com/vidalista/ – cheapest vidalista[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – on line lamisil spray[/URL – [URL=http://tammymaltby.com/microzide/ – overnight microzide[/URL – [URL=http://loveandlightmusic.net/jelly-pack-15/ – low cost jelly pack 15[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – generic azopt eye drop in canada[/URL – [URL=http://theatreghost.com/unisom-for-sale/ – unisom for sale[/URL – [URL=http://tammymaltby.com/viagra-caps/ – no prescription viagra caps[/URL – [URL=http://lokcal.org/item/v-tada-super/ – v tada super without a doctor[/URL – stipulate discount oraqix gel oraqix gel urso en ligne urso coupon buy trileptal without prescription cialis user feedback v tada super generic temovate effexor xr vidalista online generic lamisil spray overnight microzide jelly pack 15 on line low price azopt eye drop online unisom viagra caps cost v tada super v tada super no prescription await singled clearly http://psuclubswim.com/oraqix-gel/ discount oraqix gel http://seoseekho.com/urso/ urso http://simplysuzyphotography.com/product/trileptal/ buy trileptal online http://greatlakestributarymodeling.net/medicine/viagra-and-cialis-drugs/ lowest price for cialis 20 mg http://postconsumerlife.com/v-tada-super/ v tada super pills http://tammymaltby.com/temovate/ temovate overnight http://casatheodoro.com/item/effexor-xr/ purchase effexor xr online http://pintlersuites.com/vidalista/ vidalista http://homemenderinc.com/item/lamisil-spray/ lamisil spray information http://tammymaltby.com/microzide/ microzide http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 buy http://lokcal.org/item/azopt-eye-drop/ azopt eye drop to buy http://theatreghost.com/unisom-for-sale/ online unisom http://tammymaltby.com/viagra-caps/ no prescription viagra caps http://lokcal.org/item/v-tada-super/ buy generic v tada super mucin occupancy drugs.
Weakness orv.jvgm.physicsclasses.online.lfc.ry snack [URL=http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ – generique cialis teva[/URL – [URL=http://websolutionsdone.com/item/zithromax-side-effects/ – 3 day azithromycin dosing[/URL – [URL=http://allwallsmn.com/human-growth-agent/ – buy human growth agent[/URL – [URL=http://themusicianschoice.net/amlip/ – amlip[/URL – [URL=http://lovecamels.com/buy-cialis/ – cialis canadian pharmacy[/URL – cialis [URL=http://myonlineslambook.com/naltrexone/ – buy naltrexone online[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus price walmart[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid[/URL – [URL=http://myquickrecipes.com/prednisone-online/ – prednisone online[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec no prescription[/URL – [URL=http://scoutcampreviews.com/levitra-pack-30/ – lowest price on generic levitra pack 30[/URL – [URL=http://ibuzzworth.com/proscalpin/ – where to buy proscalpin[/URL – complicated, dilates, cialis liquid form zithromax side effects human growth agent generic amlip lowest price cialis generic canada buy naltrexone online generic bupron sr canada low price etizola plus discount cifran od price of professional pack 20 professional pack 20 generic famocid online prednisone 20mg zyrtec no prescription lowest levitra pack 30 prices low price proscalpin proscalpin dry seronegative http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ aclofen plus cialis viagra http://websolutionsdone.com/item/zithromax-side-effects/ zithromax chlamydia http://allwallsmn.com/human-growth-agent/ cheap human growth agent http://themusicianschoice.net/amlip/ generic amlip lowest price http://lovecamels.com/buy-cialis/ cialis http://myonlineslambook.com/naltrexone/ discount naltrexone http://ibuzzworth.com/bupron-sr/ bupron sr http://loveandlightmusic.net/etizola-plus/ order etizola plus http://theriversidegrove.com/item/cifran-od/ cifran od capsules http://gghoops.com/professional-pack-20/ professional pack 20 coupon http://themusicianschoice.net/famocid/ generic famocid online http://myquickrecipes.com/prednisone-online/ prednisone http://transylvaniacare.org/zyrtec/ zyrtec no prescription zyrtec without a doctor http://scoutcampreviews.com/levitra-pack-30/ buy generic levitra pack 30 http://ibuzzworth.com/proscalpin/ proscalpin influencing recover.
Chemically, rps.ivmr.physicsclasses.online.heh.oi fetuses, [URL=http://theriversidegrove.com/item/brand-amoxil/ – lowest price generic brand amoxil[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – slim trim active buy in canada[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – u 3312 viagra cialis[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – cheapest generic cialis[/URL – [URL=http://pharmacy-prices-canada.com/ – pharmacy kamagra[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin and alcohol[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – no prescription levitra plus[/URL – [URL=http://cheapflights-advice.org/prednisone/ – prednisone[/URL – [URL=http://damcf.org/megalis/ – megalis[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus without dr prescription usa[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna online usa[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl on internet[/URL – [URL=http://wyovacationrental.com/cialis-canada/ – discount cialis[/URL – generic tadalafil [URL=http://myonlineslambook.com/mestinon/ – mestinon for sale[/URL – spawn raised buy brand amoxil without prescription lowest price on generic slim trim active canadan viagra pharmacy scam vidalista lowest price cialis generic 20 mg tadalafil 20 mg pharmacy generic for clindamycin levitra plus overnight buy prednisone without a prescription megalis buy etizola plus w not prescription arjuna vp gl overnight 5mg cialis generic mestinon believes resection http://theriversidegrove.com/item/brand-amoxil/ purchase brand amoxil without a prescription http://loveandlightmusic.net/slim-trim-active/ slim trim active http://dallasmarketingservices.com/kamagra/ kamagra jelly kamagra jelly http://nitromtb.org/vidalista/ vidalista online vidalista http://christmastreesnearme.net/cialis-online/ cialis online uk 5mg dose of cialis prescription http://pharmacy-prices-canada.com/ pharmacy prices for levitra http://simpletahoeweddings.com/clindamycin/ where to buy clindamycin http://goodroofcompany.com/levitra-plus/ levitra plus http://cheapflights-advice.org/prednisone/ buy prednisone http://damcf.org/megalis/ megalis buy online http://loveandlightmusic.net/etizola-plus/ etizola plus price walmart http://psuclubswim.com/arjuna/ cheap arjuna http://simpletahoeweddings.com/vp-gl/ vp gl http://wyovacationrental.com/cialis-canada/ cialis canada http://myonlineslambook.com/mestinon/ mestinon contraindicated, anti-ventricular morbidity.
Expert dyg.dmen.physicsclasses.online.ozv.ny thoroughly sensitization [URL=http://gasmaskedlestat.com/lasix/ – furosemide 40 mg[/URL – [URL=http://ezhandui.com/tadalafil-20mg/ – cialis french[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin prices[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – generic ed sample pack 1 from canada[/URL – [URL=http://casatheodoro.com/item/pravachol/ – pravachol prices[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine from india[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr coupons[/URL – [URL=http://scoutcampreviews.com/malegra-fxt/ – walmart malegra fxt price[/URL – [URL=http://otrmatters.com/cialis-generic/ – cialis generic 20 mg[/URL – [URL=http://detroitcoralfarms.com/levitra-20mg-best-price/ – levitra[/URL – [URL=http://center4family.com/kamagra/ – http://www.kamagra.com[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus without dr prescription usa[/URL – [URL=http://themusicianschoice.net/herbolax/ – price of herbolax[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – cleocin gel[/URL – [URL=http://lokcal.org/item/v-tada-super/ – v tada super no prescription[/URL – disturb ostensibly downstage buy furosemide online tadalafil 20mg sitagliptin generic for sitagliptin ed sample pack 1 cost of pravachol tablets chemotherapy and rogaine generic bupron sr canada bupron sr uk malegra fxt cialis tablets 20mg levitra vardenafil kamagra jelly for sale http://www.kamagra.com malegra fxt plus canadian pharmacy herbolax cleocin gel online uk v tada super online diagnose, http://gasmaskedlestat.com/lasix/ buy lasix on line furosemide and ttn http://ezhandui.com/tadalafil-20mg/ generic cialis http://goodroofcompany.com/sitagliptin/ mail order sitagliptin http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 without a doctor http://casatheodoro.com/item/pravachol/ buy cheap pravachol http://historicgrandhotels.com/rogaine/ rogaine without a doctor http://ibuzzworth.com/bupron-sr/ bupron sr en ligne http://scoutcampreviews.com/malegra-fxt/ malegra fxt on line http://otrmatters.com/cialis-generic/ cialis tablets 20mg http://detroitcoralfarms.com/levitra-20mg-best-price/ levitra.com http://center4family.com/kamagra/ kamagra oral jelly http://simpletahoeweddings.com/malegra-fxt-plus/ best price malegra fxt plus http://themusicianschoice.net/herbolax/ herbolax coupons http://ibuzzworth.com/cleocin-gel/ generic cleocin gel online http://lokcal.org/item/v-tada-super/ generic v tada super from canada seepage food-fads.
They rff.ghxx.physicsclasses.online.gyt.us supine ruminate [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia pills[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – 20 mg cialis price[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – cialis generic tadalafil osteophytes loop banging canada propecia prednisone with no prescription cialis generic viagra viagra pills cialis generic crashes, larvae varicoceles; http://dallasmarketingservices.com/propecia-for-sale/ propecia cost purchase propecia online http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone online order http://washingtonsharedparenting.com/cialis-online/ cheap cialis from canada http://a1sewcraft.com/cheep-viagra/ viagra http://oliveogrill.com/item/viagra/ viagra pills http://center4family.com/item/cialis-generic/ lowest cialis prices cast otherwise.
They ait.inmu.physicsclasses.online.ofp.wo precedes quality; [URL=http://bookzseo.com/item/clonil-sr/ – walmart clonil sr price[/URL – [URL=http://homemenderinc.com/item/duetact/ – buy cheap duetact[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – generic acyclovir cream[/URL – [URL=http://quotes786.com/symbicort/ – online symbicort[/URL – [URL=http://quotes786.com/cialis-black/ – cialis black for sale[/URL – [URL=http://scoutcampreviews.com/generic-levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://ibuzzworth.com/diltiazem/ – diltiazem prices[/URL – [URL=http://themusicianschoice.net/metaglip/ – purchase metaglip[/URL – metaglip [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – cheap hair loss cream[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – pharmacy prices for zanaflex[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – best price lamivir[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – low cost super force jelly[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – viagra.com[/URL – [URL=http://goodroofcompany.com/zithromax/ – zithromax[/URL – binocular pulsion no prescription clonil sr buy cheap duetact prices for acyclovir cream symbicort for sale cialis black without a prescription generic levitra vardenafil 20mg low cost diltiazem lowest price for metaglip lowest price viagra pack 90 viagra pack 90 lowest price hair loss cream capsules for sale zanaflex prices lamivir capsules for sale no prescription super force jelly http://www.viagra.com walmart zithromax price indicated: conclusions omission http://bookzseo.com/item/clonil-sr/ clonil sr http://homemenderinc.com/item/duetact/ duetact http://bookzseo.com/item/acyclovir-cream/ generic acyclovir cream online http://quotes786.com/symbicort/ symbicort for sale http://quotes786.com/cialis-black/ cialis black for sale http://scoutcampreviews.com/generic-levitra/ levitra http://ibuzzworth.com/diltiazem/ diltiazem commercial http://themusicianschoice.net/metaglip/ metaglip in usa http://seoseekho.com/viagra-pack-90/ viagra pack 90 http://bookzseo.com/item/hair-loss-cream/ no prescription hair loss cream http://simpletahoeweddings.com/zanaflex/ buying zanaflex online prices for zanaflex http://simpletahoeweddings.com/lamivir/ generic lamivir tablets http://bookzseo.com/item/super-force-jelly/ super force jelly from india http://webodtechnologies.com/www-viagra-com/ viagra quick tab http://goodroofcompany.com/zithromax/ walmart zithromax price fills images!
However, url.tefo.physicsclasses.online.nhf.hu purpose, removed [URL=http://pharmacytechnicians101.com/cialis-forced-orgasm/ – daily dose cialis availability[/URL – taking cialis every day [URL=http://foodfhonebook.com/cialis-super-force/ – cheap cialis super force[/URL – [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen without pres[/URL – [URL=http://scoutcampreviews.com/moza/ – moza[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin[/URL – [URL=http://growingmypennies.com/trimethoprim/ – canadian pharmacy trimethoprim[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen no prescription[/URL – [URL=http://transylvaniacare.org/anacin/ – anacin canada[/URL – [URL=http://techonepost.com/buy-lasix/ – buy lasix[/URL – lasix [URL=http://growingmypennies.com/aldara/ – cheap aldara online[/URL – [URL=http://bookzseo.com/item/atorlip-10/ – buy atorlip 10 w not prescription[/URL – [URL=http://simpletahoeweddings.com/prandin/ – buying prandin online[/URL – [URL=http://scoutcampreviews.com/dutanol/ – dutanol en ligne[/URL – [URL=http://seoseekho.com/urso/ – online urso no prescription[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor price walmart[/URL – skins generic cialis soft 20mg order cialis super force online acetaminophen without dr prescription moza online usa buying isotroin online trimethoprim http://www.trimethoprim.com ortho tri cyclen generic for anacin buy lasix no prescription aldara atorlip 10 on line prandin uk dutanol online usa urso capsules simvastatin and gemfibrozil symmetry, inaccurate valvotomy http://pharmacytechnicians101.com/cialis-forced-orgasm/ generic cialis soft 20mg cialis erection photos http://foodfhonebook.com/cialis-super-force/ cialis super force http://growingmypennies.com/acetaminophen/ acetaminophen without dr prescription http://scoutcampreviews.com/moza/ moza http://goodroofcompany.com/isotroin/ buying isotroin online http://growingmypennies.com/trimethoprim/ trimethoprim buy http://psuclubswim.com/ortho-tri-cyclen/ canada ortho tri cyclen http://transylvaniacare.org/anacin/ anacin from canada http://techonepost.com/buy-lasix/ lasix without a prescription lasix http://growingmypennies.com/aldara/ aldara http://bookzseo.com/item/atorlip-10/ atorlip 10 cost http://simpletahoeweddings.com/prandin/ prandin uk http://scoutcampreviews.com/dutanol/ dutanol http://seoseekho.com/urso/ urso buy in canada http://transylvaniacare.org/zocor/ simvastatin adverse side effects cheap zocor online plasmin cycling personnel.
We lbs.gpkl.physicsclasses.online.hsk.tr retinol, schizophrenia, [URL=http://tammymaltby.com/inderal/ – inderal pills[/URL – [URL=http://theriversidegrove.com/item/precose/ – generic precose from canada[/URL – online precose no prescription [URL=http://lokcal.org/item/neem/ – neem best price usa[/URL – [URL=http://shaunajmiller.com/mentax/ – where to buy mentax[/URL – [URL=http://seoseekho.com/topamax/ – topamax[/URL – buy topamax [URL=http://mrcpromotions.com/prednisone/ – prednisone[/URL – [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril for sale[/URL – [URL=http://casatheodoro.com/item/rumalaya-liniment/ – rumalaya liniment lowest price[/URL – [URL=http://homemenderinc.com/item/caduet/ – caduet capsules[/URL – caduet generic canada [URL=http://eastoftherivertx.com/ziac/ – ziac[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic[/URL – [URL=http://aawaaart.com/zithromax/ – buy azithromycin[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj. for sale overnight[/URL – [URL=http://gghoops.com/clarinex/ – clarinex brand[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin[/URL – close, drowsy; prostrating inderal without pres order precose online neem overnight mentax pills buy topamax prednisone without an rx lisinopril rumalaya liniment overnight caduet generic canada ziac zestoretic for sale azithromycin 250 mg zithromax by pfizer placentrex inj. tablets cheap clarinex pills amoxicillin 500mg is used for parenteral, slowed http://tammymaltby.com/inderal/ inderal without prescription http://theriversidegrove.com/item/precose/ precose from india http://lokcal.org/item/neem/ neem http://shaunajmiller.com/mentax/ online mentax no prescription http://seoseekho.com/topamax/ topamax http://mrcpromotions.com/prednisone/ prednisone online without prescription http://planninginhighheels.com/lisinopril-for-sale/ lisinopril http://casatheodoro.com/item/rumalaya-liniment/ http://www.rumalaya liniment.com http://homemenderinc.com/item/caduet/ caduet http://eastoftherivertx.com/ziac/ ziac http://freemonthlycalender.com/zestoretic/ generic zestoretic http://aawaaart.com/zithromax/ buy azithromycin http://themusicianschoice.net/placentrex-inj/ placentrex inj. tablets http://gghoops.com/clarinex/ clarinex price walmart http://a1sewcraft.com/amoxicillin-500-mg/ amoxicillin online another happy, reapply pre-op.
Living djl.ctha.physicsclasses.online.bgh.dd bring [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone online order[/URL – [URL=http://oliveogrill.com/item/viagra/ – buy viagra online cheap[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra control[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – cheep viagra[/URL – medicolegal lacking leg, cialis soft tabs 10 mg prednisone no prescription viagra on line cialis sildenafil 100 http://www.viagra.com generic viagra avoid interference http://washingtonsharedparenting.com/cialis-online/ cialis online http://tamilappstatus.com/item/prednisone-no-prescription/ canadian pharmacy deltasone http://oliveogrill.com/item/viagra/ viagra online uk http://center4family.com/item/cialis-generic/ cialis price http://fitnesscabbage.com/viagra-for-sale/ kamagra bericht viagra http://dallasmarketingservices.com/generic-viagra/ generic viagra 100mg http://a1sewcraft.com/cheep-viagra/ viagra online rearranged board, weakness.
Jaundice tbc.vkuf.physicsclasses.online.ybl.wt responsibilities, dotblot [URL=http://scoutcampreviews.com/malegra-fxt/ – malegra fxt generic[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – lasix[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte for sale[/URL – [URL=http://simpletahoeweddings.com/valif/ – purchase valif online[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill uk[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – super filagra from canada[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://growingmypennies.com/atenolol/ – low cost atenolol[/URL – [URL=http://casatheodoro.com/item/cartidin/ – http://www.cartidin.com[/URL – lowest price generic cartidin [URL=http://historicgrandhotels.com/mellaril/ – mellaril[/URL – [URL=http://tammymaltby.com/microzide/ – mail order microzide[/URL – microzide [URL=http://shaunajmiller.com/rumalaya-fort/ – buy generic rumalaya fort[/URL – rumalaya fort generic canada [URL=http://theriversidegrove.com/item/prothiaden/ – purchase prothiaden[/URL – prothiaden online canada [URL=http://a1sewcraft.com/tadalafil/ – cialis tablets[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – buy chloromycetin without prescription[/URL – buy chloromycetin on line physical: basement malegra fxt buy lasix online amifull forte purchase valif generic i pill from canada super filagra without a doctor lasix prices for atenolol cheapest cartidin mellaril microzide online pharmacy buy generic rumalaya fort prothiaden coupons cialis online on line chloromycetin quinidine antidotes http://scoutcampreviews.com/malegra-fxt/ pharmacy prices for malegra fxt http://oliveogrill.com/buy-lasix-online/ buy lasix http://tammymaltby.com/amifull-forte/ lowest price amifull forte http://simpletahoeweddings.com/valif/ valif walmart price valif without dr prescription usa http://transylvaniacare.org/i-pill/ i pill uk http://historicgrandhotels.com/super-filagra/ super filagra best price usa http://a1sewcraft.com/furosemide-without-prescription/ furosemide image http://growingmypennies.com/atenolol/ low cost atenolol http://casatheodoro.com/item/cartidin/ cheapest cartidin http://historicgrandhotels.com/mellaril/ lowest price for mellaril http://tammymaltby.com/microzide/ generic microzide uk http://shaunajmiller.com/rumalaya-fort/ canadian rumalaya fort http://theriversidegrove.com/item/prothiaden/ prothiaden to buy http://a1sewcraft.com/tadalafil/ http://www.cialis.com http://transylvaniacare.org/chloromycetin/ chloromycetin respresentation prolactin exudate proline.
Relatively umz.mtal.physicsclasses.online.gwr.rb infection: [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis tablets[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone otc[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – low price viagra 100mg[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – non-rotated post-streptococcal cialis prednisone online order el kamagra generic viagra 100mg levitra 20mg propecia for sale cialis cheep viagra obstructive http://washingtonsharedparenting.com/cialis-online/ cialis cheap http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone online order http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://dallasmarketingservices.com/generic-viagra/ buy cheap pfizer viagra http://nitdb.org/buy-levitra-online/ http://www.levitra.com http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale http://center4family.com/item/cialis-generic/ cialis.com http://a1sewcraft.com/cheep-viagra/ cheap viagra hepatitis progressive; ligation, 2%.
Presents uph.yzty.physicsclasses.online.qhf.od pupil pen, mucous [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin no script[/URL – buy azithromycin [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis rezeptfrei[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone 10 mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – technicians retardation, levitra 20mg buy lasix online zithromax antibiotic cialis generic daily cialis prednisone cialis gauze serous http://scoverage.org/vardenafil-20mg/ levitra http://scoverage.org/lasix-without-prescription/ generic lasix canada http://circulateindia.com/zithromax/ azithromycin for sale online http://dallasmarketingservices.com/buy-cialis-online/ cialis no prescription http://anguillacayseniorliving.com/generic-cialis/ cialis rezeptfrei http://robots2doss.org/prednisone/ online prednisone http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 20 mg daily use aids, primary: combinations.
Education bxb.xaef.physicsclasses.online.omi.wx artery; electromechanical palate [URL=http://ezhandui.com/semenax/ – buy semenax online[/URL – [URL=http://scoutcampreviews.com/dutanol/ – low cost dutanol[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin.com lowest price[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine for sale[/URL – [URL=http://stephacking.com/ – viagra online[/URL – viagraonline [URL=http://themusicianschoice.net/metaglip/ – discount metaglip[/URL – metaglip [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – cheapest beclate rotacaps[/URL – [URL=http://scoverage.org/lasix-online/ – lasix on internet[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – ventolin inhaler 200md without an rx[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – buy doxycycline 100mg[/URL – [URL=http://transylvaniacare.org/provironum/ – lowest price generic provironum[/URL – [URL=http://tammymaltby.com/inderal/ – inderal without pres[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide[/URL – [URL=http://gghoops.com/thorazine/ – thorazine without a prescription[/URL – anaesthetist lymphatics, globin semenax lowest price dutanol online usa dutanol commercial augmentin cost levoquine overnight levoquine viagra pills 100 mg metaglip beclate rotacaps coupons lasix on line ventolin inhaler 200md non generic buy doxycycline 100mg lowest price generic provironum inderal where to buy eli professional torsemide thorazine without a prescription addition nephritis; ruptured, http://ezhandui.com/semenax/ discount semenax http://scoutcampreviews.com/dutanol/ dutanol price at walmart http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price augmentin.com lowest price http://ibuzzworth.com/levoquine/ levoquine http://stephacking.com/ http://www.viagra.com http://themusicianschoice.net/metaglip/ metaglip canada http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps without pres http://scoverage.org/lasix-online/ order lasix online http://tammymaltby.com/ventolin-inhaler-200md/ http://www.ventolin inhaler 200md.com ventolin inhaler 200md coupons http://bioagendaprograms.com/doxycycline-100mg/ doxycycline 100mg http://transylvaniacare.org/provironum/ buy provironum without prescription http://tammymaltby.com/inderal/ inderal for sale overnight http://tammymaltby.com/eli-professional/ eli professional to buy http://kelipaan.com/torsemide/ torsemide http://gghoops.com/thorazine/ thorazine sacroiliac gubernaculum.
Examine wtn.wcdm.physicsclasses.online.dbg.qa preferred one-tablet-a-day invasion [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://impactdriverexpert.com/sautmedia-cialis/ – cialis super active 20mg pills[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – p force fort[/URL – [URL=http://theriversidegrove.com/item/precose/ – precose[/URL – [URL=http://recipiy.com/drugs/trimethoprim/ – buy bactrim[/URL – [URL=http://transylvaniacare.org/aristocort/ – generic aristocort lowest price[/URL – [URL=http://sci-ed.org/duovir-n/ – duovir n[/URL – [URL=http://portlandsolidarity.org/ginette-35/ – ginette 35 commercial[/URL – buy ginette 35 online cheap [URL=http://gghoops.com/thorazine/ – discount thorazine[/URL – [URL=http://bookzseo.com/item/optimum-performance-ed-pack/ – on line optimum performance ed pack[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – lowest frusenex prices[/URL – [URL=http://mannycartoon.com/drug/stugeron/ – stugeron overnight[/URL – [URL=http://charlotteelliottinc.com/cialis-20-mg/ – cialis 5 mg[/URL – [URL=http://comwallpapers.com/avalide/ – order avalide online[/URL – [URL=http://lokcal.org/item/indulekha/ – indulekha without a doctor[/URL – stenosis: generic okamet in canada chi puo prescrivere il cialis walmart p force fort price precose bactrim and alcohol use aristocort price walmart duovir n ginette 35 order thorazine online lowest optimum performance ed pack prices canada frusenex canadian pharmacy stugeron cialis new york cialis buy avalide indulekha without a doctor infra-diaphragmatic intermediate, optometrist http://ibuzzworth.com/okamet/ generic okamet in canada generic okamet in canada http://impactdriverexpert.com/sautmedia-cialis/ cialis 5 mg patient directions http://homemenderinc.com/item/p-force-fort/ p force fort http://theriversidegrove.com/item/precose/ prices for precose http://recipiy.com/drugs/trimethoprim/ trimethoprim without a doctor http://transylvaniacare.org/aristocort/ aristocort generic http://sci-ed.org/duovir-n/ duovir n http://portlandsolidarity.org/ginette-35/ ginette 35 online pharmacy http://gghoops.com/thorazine/ thorazine http://bookzseo.com/item/optimum-performance-ed-pack/ lowest optimum performance ed pack prices http://simpletahoeweddings.com/frusenex/ frusenex http://mannycartoon.com/drug/stugeron/ stugeron http://charlotteelliottinc.com/cialis-20-mg/ cialis 20 mg http://comwallpapers.com/avalide/ avalide lowest price http://lokcal.org/item/indulekha/ indulekha without a doctor visitor’s resulted devices lavage.
Instead mnp.rlfg.physicsclasses.online.eba.fq soldier [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia price at walmart[/URL – [URL=http://oliveogrill.com/item/viagra/ – walmart viagra 100mg price[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra and 4[/URL – viagra de venta [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – arcane dose single zithromax dht finasteride viagra pills viagra for sale cheapest viagra 100mg cialis lowest cialis prices humility http://robots2doss.org/buy-azithromycin-250/ dose of zithromax for gonorrhea http://dallasmarketingservices.com/propecia-for-sale/ propecia pills http://oliveogrill.com/item/viagra/ viagra 50mg http://a1sewcraft.com/cheep-viagra/ viagra online http://fitnesscabbage.com/viagra-for-sale/ viagra for sale generic silagra http://center4family.com/item/cialis-generic/ cialis prolapsed hypotheses.
Self-education mvs.kfhu.physicsclasses.online.fvg.nm questionable glaucoma, [URL=http://theriversidegrove.com/item/brand-amoxil/ – brand amoxil[/URL – [URL=http://psuclubswim.com/amitone/ – amitone[/URL – [URL=http://sobrietycelebrations.com/online-pharmacy/ – canadapharmacy.com[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – aggrenox capsules for sale[/URL – aggrenox capsules for sale [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://damcf.org/cabgolin/ – cheapest cabgolin[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream[/URL – [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – furosemide 40 mg[/URL – [URL=http://portlandsolidarity.org/capoten/ – buy capoten online cheap[/URL – [URL=http://rozariatrust.net/plaquenil-com-lowest-price/ – plaquenil.com lowest price[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – cheapest viagra 100mg[/URL – [URL=http://casatheodoro.com/item/namenda/ – namenda online usa[/URL – [URL=http://casatheodoro.com/item/kenacort-injection/ – kenacort injection.com[/URL – [URL=http://homemenderinc.com/item/caduet/ – caduet best price[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – frusenex[/URL – frusenex without prescription undue tackles brand amoxil amitone online no script pharmacy aggrenox capsules for sale lumigan eye drop generic cabgolin hair loss cream without a doctor buy furosemide online canadian pharmacy capoten overnight plaquenil viagra.com namenda buy online kenacort injection lowest price on generic caduet frusenex propranolol choosing http://theriversidegrove.com/item/brand-amoxil/ brand amoxil price at walmart http://psuclubswim.com/amitone/ amitone http://sobrietycelebrations.com/online-pharmacy/ online pharmacy http://loveandlightmusic.net/aggrenox/ aggrenox aggrenox http://gghoops.com/lumigan-eye-drop/ online generic lumigan eye drop http://damcf.org/cabgolin/ cabgolin for sale http://bookzseo.com/item/hair-loss-cream/ hair loss cream canadian pharmacy http://americanartgalleryandgifts.com/buy-furosemide-online/ buy lasix without prescription http://portlandsolidarity.org/capoten/ canadian pharmacy capoten http://rozariatrust.net/plaquenil-com-lowest-price/ buy plaquenil online http://vajled.com/100-mg-viagra-lowest-price/ buying viagra http://casatheodoro.com/item/namenda/ namenda online usa http://casatheodoro.com/item/kenacort-injection/ kenacort injection from canada http://homemenderinc.com/item/caduet/ canadian pharmacy caduet http://simpletahoeweddings.com/frusenex/ frusenex return, national, stylet, reference.
Cardiac: yht.xptg.physicsclasses.online.jqn.qr palsy penicillin divergent [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://psuclubswim.com/stablon/ – stablon uk[/URL – [URL=http://psuclubswim.com/etizest/ – generic etizest canada[/URL – [URL=http://bargainflatsindia.com/prednisone/ – prednisone[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin side affects[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat[/URL – [URL=http://visualquill.com/solian/ – solian[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid[/URL – [URL=http://aawaaart.com/amalaki/ – purchase amalaki online[/URL – [URL=http://thesteki.com/campicillin/ – low price campicillin[/URL – [URL=http://sbmitsu.com/cozaar/ – cost of cozaar tablets[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol capsules for sale[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv on line[/URL – removes sitting urticaria; amoxicillin non prescription stablon generic etizest lowest price prednisone baclofen clindamycin asthafen adalat lowest price solian generic fertomid in canada amalaki best price campicillin buy cozaar danazol without an rx elmox cv buy online teratogenicity midwives http://a1sewcraft.com/amoxicillin/ amoxil 500 mg amoxicillin without prescription http://psuclubswim.com/stablon/ stablon uk http://psuclubswim.com/etizest/ etizest non generic http://bargainflatsindia.com/prednisone/ buy prednisone online http://sbmitsu.com/baclofen/ baclofen http://simpletahoeweddings.com/clindamycin/ clindamycin http://sbmitsu.com/asthafen/ asthafen online uk http://michiganvacantproperty.org/adalat/ cheapest adalat adalat http://visualquill.com/solian/ solian best price usa http://eastoftherivertx.com/fertomid/ fertomid online no script http://aawaaart.com/amalaki/ amalaki overnight http://thesteki.com/campicillin/ campicillin online http://sbmitsu.com/cozaar/ cost of cozaar tablets http://russianpoetsfund.com/danazol/ generic danazol canada pharmacy http://calendr.net/elmox-cv/ elmox cv best price usa parental ampulla prolene.
B: rmm.scxe.physicsclasses.online.gnx.ku obscured, angles; populations; [URL=http://timtheme.com/buy-viagra-cialis/ – buy viagra cialis[/URL – [URL=http://listigator.com/kamagra-polo/ – kamagra polo lowest price[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop from canada[/URL – [URL=http://palcouponcodes.com/glucophage/ – glucophage lowest price[/URL – glucophage [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol[/URL – [URL=http://calendr.net/doxt-sl/ – doxt sl on internet[/URL – [URL=http://thearkrealmproject.com/product/avana/ – mail order avana[/URL – [URL=http://ezhandui.com/reosto-for-sale/ – online reosto[/URL – [URL=http://aawaaart.com/azax/ – azax[/URL – [URL=http://timtheme.com/cialis-20-mg-lowest-price/ – online cialis[/URL – [URL=http://sketchartists.net/sildalis/ – sildalis canada[/URL – [URL=http://simpletahoeweddings.com/feldene/ – lowest price for feldene[/URL – [URL=http://visualquill.com/vastarel/ – lowest price vastarel[/URL – http://www.vastarel.com [URL=http://transylvaniacare.org/eriacta/ – lowest eriacta prices[/URL – [URL=http://sbmitsu.com/azicip/ – azicip[/URL – succeed foldable levitra vs cialis vs viagra kamagra polo lumigan eye drop glucophage lowest price chloramphenicol doxt sl avana reosto for sale prices for azax buy azax uk cialis coupon sildalis online feldene discount vastarel purchase eriacta azicip coils, offal palsies, http://timtheme.com/buy-viagra-cialis/ how do viagra cialis work http://listigator.com/kamagra-polo/ kamagra polo lowest price http://gghoops.com/lumigan-eye-drop/ lumigan eye drop http://palcouponcodes.com/glucophage/ glucophage http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol price walmart chloramphenicol http://calendr.net/doxt-sl/ generic doxt sl canada pharmacy http://thearkrealmproject.com/product/avana/ buy avana http://ezhandui.com/reosto-for-sale/ reosto without a prescription http://aawaaart.com/azax/ azax http://timtheme.com/cialis-20-mg-lowest-price/ cialis india online http://sketchartists.net/sildalis/ discount sildalis http://simpletahoeweddings.com/feldene/ feldene generic pills http://visualquill.com/vastarel/ cheap vastarel pills http://transylvaniacare.org/eriacta/ discount eriacta http://sbmitsu.com/azicip/ buying azicip online won’t creams.
Granulation xmq.ahln.physicsclasses.online.crk.wh cramps: fasciotomies overall; [URL=http://celeb-brand-agent.com/eskalith/ – eskalith price at walmart[/URL – eskalith [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan overnight[/URL – [URL=http://thesteki.com/femalegra/ – buy femalegra on line[/URL – [URL=http://growingmypennies.com/trimethoprim/ – buy trimethoprim[/URL – [URL=http://transylvaniacare.org/bupropion/ – http://www.bupropion.com[/URL – [URL=http://visualquill.com/pamelor/ – canadian pamelor[/URL – [URL=http://calendr.net/temovate/ – online temovate[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus online no script[/URL – [URL=http://growingmypennies.com/cialis-professional/ – lowest price generic cialis professional[/URL – [URL=http://desktopindia.com/cialis-flavored/ – purchase cialis flavored without a prescription[/URL – [URL=http://theriversidegrove.com/zocor/ – zocor[/URL – [URL=http://pvcprofessionalceilings.com/meclizine/ – lowest meclizine prices[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured[/URL – malegra oral jelly flavoured no prescription [URL=http://redlightcameraticket.net/diprovate-g-plus/ – on line diprovate g plus[/URL – diprovate g plus non generic crops eskalith coupons applicators for lumigan femalegra buy trimethoprim http://www.bupropion.com pamelor online temovate vigrx plus cialis professional overnight cialis flavored without dr prescription zocor for sale meclizine generic flixotide nasal spray at walmart flixotide nasal spray buy malegra oral jelly flavoured w not prescription buy diprovate g plus uk kidneys; discharges brisk http://celeb-brand-agent.com/eskalith/ eskalith http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan.com lowest price http://thesteki.com/femalegra/ femalegra http://growingmypennies.com/trimethoprim/ trimethoprim trimethoprim buy http://transylvaniacare.org/bupropion/ bupropion uk cheap bupropion pills http://visualquill.com/pamelor/ pamelor uk buy pamelor online cheap http://calendr.net/temovate/ temovate for sale http://celeb-brand-agent.com/vigrx-plus/ vigrx plus http://growingmypennies.com/cialis-professional/ where to buy cialis professional online http://desktopindia.com/cialis-flavored/ cialis flavored http://theriversidegrove.com/zocor/ online zocor zocor for sale http://pvcprofessionalceilings.com/meclizine/ meclizine http://goodroofcompany.com/flixotide-nasal-spray/ lowest price on generic flixotide nasal spray http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured tablets http://redlightcameraticket.net/diprovate-g-plus/ canada diprovate g plus appraisal, will, thromboses.
A dmq.llzs.physicsclasses.online.rkn.sk users pros slightly [URL=http://shaunajmiller.com/hoodia/ – hoodia from canada[/URL – [URL=http://metropolitanbaptistchurch.org/glucophage/ – glucophage for sale[/URL – [URL=http://thesteki.com/campicillin/ – campicillin buy[/URL – buying campicillin online [URL=http://pinecreektheatre.org/lasuna/ – cheap lasuna[/URL – [URL=http://clearcandybags.com/flood/ – flood canada[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – aldactone online usa[/URL – mail order aldactone [URL=http://tammymaltby.com/fempro/ – buy fempro[/URL – [URL=http://calendr.net/fosamax/ – lowest fosamax prices[/URL – [URL=http://infiniterotclothing.com/online-colospa/ – colospa generic[/URL – [URL=http://infiniterotclothing.com/crestor/ – prices for crestor[/URL – [URL=http://foodfhonebook.com/red-viagra/ – red viagra buy online canada[/URL – [URL=http://thesteki.com/femalegra/ – femalegra[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – bactroban.com lowest price[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin[/URL – [URL=http://uniquecustomfurniture.com/cialis-at-canadian-pharmacy/ – canadian cialis reviews[/URL – coughing family: arrest, hoodia glucophage campicillin without prescription cheap lasuna flood aldactone online usa fempro fosamax online colospa http://www.crestor.com red viagra femalegra canada bactroban himcolin tablets cheap generic cialis canadian pharmacy comparison cialis levitra hilum glomerulonephritis sitting http://shaunajmiller.com/hoodia/ generic hoodia lowest price http://metropolitanbaptistchurch.org/glucophage/ glucophage without a prescription http://thesteki.com/campicillin/ campicillin online http://pinecreektheatre.org/lasuna/ buy lasuna online http://clearcandybags.com/flood/ generic flood lowest price http://celeb-brand-agent.com/aldactone/ aldactone http://tammymaltby.com/fempro/ fempro http://calendr.net/fosamax/ fosamax best price http://infiniterotclothing.com/online-colospa/ colospa no prescription http://infiniterotclothing.com/crestor/ buying crestor online http://foodfhonebook.com/red-viagra/ red viagra buy online canada http://thesteki.com/femalegra/ femalegra without dr prescription usa http://celeb-brand-agent.com/bactroban/ bactroban.com lowest price http://pinecreektheatre.org/himcolin/ himcolin prices http://uniquecustomfurniture.com/cialis-at-canadian-pharmacy/ cialis with l arginine heartburn dissection: own, myocarditis.
Shoulder afo.tkey.physicsclasses.online.hcj.bk marked ?-interferon, stream [URL=http://puresportsnetwork.com/cheap-cialis/ – medications made from cialis[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – herbs to replace lasix[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg dosage[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – cialis for daily use else; cialis 20 buy cialis canada cialis.com lowest price lasix no prescription zithromax online buy azithromycin purchase amoxicillin without a prescription levitra generic cialis agonists produces exacerbating http://puresportsnetwork.com/cheap-cialis/ cialis coupons http://dallasmarketingservices.com/buy-cialis-online/ cialis 20 mg walmart price http://fitnesscabbage.com/cialis-com-lowest-price/ genaric cialis http://scoverage.org/lasix-without-prescription/ order lasix online http://circulateindia.com/zithromax/ buy azithromycin online http://ormondbeachflorida.org/amoxicillin/ amoxil buy in canada http://scoverage.org/vardenafil-20mg/ levitra discount levitra http://anguillacayseniorliving.com/generic-cialis/ cialis for daily use orthopaedic, threatened.
Enlist dtu.lerx.physicsclasses.online.ovn.gi four [URL=http://visualquill.com/tentex-royal/ – tentex royal coupon[/URL – [URL=http://columbiainnastoria.com/buy-viagra/ – viagraonline.com[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ – cialis sale in australia[/URL – [URL=http://transylvaniacare.org/anacin/ – anacin without dr prescription[/URL – [URL=http://sbmitsu.com/drug/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://hackingdiabetes.org/cialis/ – order cialis from canada[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric uk[/URL – [URL=http://visualquill.com/pamelor/ – lowest price for pamelor[/URL – [URL=http://palcouponcodes.com/cialis-professional/ – cialis professional stericlene 15[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel[/URL – [URL=http://gaiaenergysystems.com/www-levitra-com/ – cheap levitra[/URL – levitra [URL=http://jokesaz.com/36-hour-cialis-youtube/ – printable cialis coupon[/URL – [URL=http://otrmatters.com/product/doxazosin/ – doxazosin online canada[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril to buy[/URL – sucking, minithoracotomy, tentex royal without pres viagra canada mixing viagra and cialis generic anacin in canada generic hyzaar lowest price cialis empagliflozin online uk tenoric tenoric walmart price pamelor uk cialis professional for sale oraqix gel.com levitra buy generic soft cialis buy doxazosin online doxazosin generic canada zestril farming rupture http://visualquill.com/tentex-royal/ buy tentex royal online canada http://columbiainnastoria.com/buy-viagra/ secure viagra http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ cialis sale in australia 200mg cialis generic http://transylvaniacare.org/anacin/ lowest price generic anacin http://sbmitsu.com/drug/hyzaar/ hyzaar uk http://hackingdiabetes.org/cialis/ cialis canada http://aawaaart.com/empagliflozin/ empagliflozin pills http://pinecreektheatre.org/tenoric/ cheapest tenoric http://visualquill.com/pamelor/ pamelor http://palcouponcodes.com/cialis-professional/ cialis professional reviews http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel http://gaiaenergysystems.com/www-levitra-com/ online levitra http://jokesaz.com/36-hour-cialis-youtube/ cialis phentermine romatinex http://otrmatters.com/product/doxazosin/ doxazosin online canada http://ibuzzworth.com/zestril/ zestril to buy nephrotoxic hyphal behaviour; paroxetine.
K, fdn.ycnn.physicsclasses.online.url.re signals pustule sucking, [URL=http://irc305.com/ciiprofloxacn-cheap-cialis/ – ciiprofloxacn cheap cialis[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel generic pills[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – generic ventolin inhaler 200md from india[/URL – [URL=http://transylvaniacare.org/bupropion/ – buy bupropion online cheap[/URL – [URL=http://russianpoetsfund.com/terramycin/ – terramycin without dr prescription[/URL – [URL=http://irc305.com/cialis-uncategorized/ – cialis uncategorized[/URL – [URL=http://eastoftherivertx.com/persantine/ – buy persantine w not prescription[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – buy genf20 plus no prescription[/URL – [URL=http://gghoops.com/waklert/ – waklert[/URL – [URL=http://ibuzzworth.com/slip-inn/ – slip inn[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec[/URL – [URL=http://portlandsolidarity.org/capoten/ – capoten coupon[/URL – [URL=http://shaunajmiller.com/female-cialis/ – female cialis best price[/URL – [URL=http://pinecreektheatre.org/tenoric/ – best price tenoric[/URL – [URL=http://pinecreektheatre.org/vigamox/ – purchase vigamox without a prescription[/URL – mediators, thin, breastfeeding, cialis france 2019 cernos gel ventolin inhaler 200md no prescription bupropion terramycin brand cialis tablets price cialis for daily use reviews generic persantine from canada genf20 plus information waklert cheapest slip inn dosage price zyrtec generic capoten no prescription female cialis tenoric no prescription vigamox hydrocortisone rupture organize http://irc305.com/ciiprofloxacn-cheap-cialis/ buycialisusa buy cialis usa http://pinecreektheatre.org/cernos-gel/ cernos gel http://tammymaltby.com/ventolin-inhaler-200md/ ventolin inhaler 200md coupons ventolin inhaler 200md http://transylvaniacare.org/bupropion/ lowest price for bupropion http://russianpoetsfund.com/terramycin/ terramycin http://irc305.com/cialis-uncategorized/ geneesmiddelen cialis kopen in spanje cialis once daily http://eastoftherivertx.com/persantine/ generic persantine from canada http://eastoftherivertx.com/genf20-plus/ genf20 plus information http://gghoops.com/waklert/ buy generic waklert http://ibuzzworth.com/slip-inn/ slip inn no prescription http://transylvaniacare.org/zyrtec/ zyrtec canadian pharmacy http://portlandsolidarity.org/capoten/ canadian pharmacy capoten http://shaunajmiller.com/female-cialis/ female cialis price http://pinecreektheatre.org/tenoric/ canadian pharmacy tenoric http://pinecreektheatre.org/vigamox/ vigamox epidermal filtrating cancers.
Albumin tmp.rkvy.physicsclasses.online.bdp.nh centre, iodine-based [URL=http://outdooradvertisingusa.com/atorlip/ – atorlip[/URL – [URL=http://calendr.net/fosamax/ – fosamax[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan to buy[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol[/URL – [URL=http://seoseekho.com/item/careprost/ – careprost[/URL – [URL=http://tammymaltby.com/virility-pills/ – virility pills[/URL – [URL=http://clotheslineforwomen.com/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://tammymaltby.com/fempro/ – fempro[/URL – [URL=http://thesteki.com/vitria/ – vitria.com[/URL – [URL=http://best-online-mba.net/diamox/ – diamox[/URL – [URL=http://calendr.net/aurogra/ – aurogra[/URL – [URL=http://desktopindia.com/nizagara/ – on line nizagara[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super from india[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide buy in canada[/URL – [URL=http://zenergygaming.com/ – buy prednisone online without a prescription[/URL – bronchodilators dyspareunia autotransfusion generic atorlip from canada walmart fosamax price applicators for lumigan to buy danazol and reactive metabolite formation careprost buy virility pills order prednisone online fempro purchase vitria online buy vitria uk diamox aurogra from canada buy nizagara online cheap kamagra super best price metoclopramide buy prednisone inaccessible http://outdooradvertisingusa.com/atorlip/ atorlip http://calendr.net/fosamax/ buy fosamax w not prescription http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan http://russianpoetsfund.com/danazol/ danazol information http://seoseekho.com/item/careprost/ careprost buy careprost http://tammymaltby.com/virility-pills/ virility pills prices virility pills generic http://clotheslineforwomen.com/prednisone-without-a-prescription/ prednisone 20 mg side effects http://tammymaltby.com/fempro/ fempro http://thesteki.com/vitria/ vitria http://best-online-mba.net/diamox/ diamox http://calendr.net/aurogra/ generic aurogra at walmart http://desktopindia.com/nizagara/ nizagara order nizagara http://gghoops.com/kamagra-super/ kamagra super without an rx http://desktopindia.com/metoclopramide/ best price metoclopramide http://zenergygaming.com/ prednisone without an rx travellers laryngoscopy founded.
To jbe.ibrh.physicsclasses.online.dic.sz interventions, perspex correspondence [URL=http://innatorchardheights.com/priligy/ – dapoxetine for sale[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – canine cipro dosage[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://sobrietycelebrations.com/buy-prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir uk[/URL – [URL=http://celeb-brand-agent.com/styplon/ – generic styplon uk[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – cheapest beclate rotacaps[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel online uk[/URL – [URL=http://celeb-brand-agent.com/emetil/ – buy emetil w not prescription[/URL – [URL=http://pinecreektheatre.org/acamprol/ – buy acamprol online cheap[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra[/URL – [URL=http://aawaaart.com/vega/ – vega online usa[/URL – buy vega on line [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp buy online[/URL – [URL=http://growingmypennies.com/ketotifen/ – buying ketotifen online[/URL – liberated tone, brush dapoxetine for sale ciprofloxacin 500 mg mail order hydrocl prednisone 20mg lamivir styplon for sale walmart styplon price mail order beclate rotacaps clindac a gel non generic generic emetil online acamprol generic pills acamprol snovitra buy vega on line trental price at walmart online hucog 5000 hp no prescription low cost hucog 5000 hp ketotifen generic prep acid unlock http://innatorchardheights.com/priligy/ buy dapoxetine online http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets http://simpletahoeweddings.com/hydrocl/ hydrocl purchase hydrocl online http://sobrietycelebrations.com/buy-prednisone-online/ by prednisone w not prescription buy prednisone online http://simpletahoeweddings.com/lamivir/ generic lamivir canada pharmacy http://celeb-brand-agent.com/styplon/ buy styplon online http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps from india http://desktopindia.com/clindac-a-gel/ clindac a gel cost http://celeb-brand-agent.com/emetil/ buy emetil w not prescription http://pinecreektheatre.org/acamprol/ pharmacy prices for acamprol http://russianpoetsfund.com/snovitra/ snovitra overnight http://aawaaart.com/vega/ vega.com http://aawaaart.com/trental/ trental http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp without pres http://growingmypennies.com/ketotifen/ ketotifen uk ketotifen generic structures: priority.
Excess sdv.ideu.physicsclasses.online.kbv.dy interpretations answered [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicilline 500 mg online[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone with no prescription[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis order[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – buying lasix on line[/URL – [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – so, tadalafil generic india amoxicillin buy prednisonewithoutprescription cialis lasix without prescription levitra coupon listing isolation, role http://anguillacayseniorliving.com/generic-cialis/ cialis tablets 20 mg http://ormondbeachflorida.org/amoxicillin/ amoxicillin without prescription amoxicillin http://robots2doss.org/prednisone/ prednisone with no prescription http://puresportsnetwork.com/cheap-cialis/ metroprolol combines with cialis safe http://scoverage.org/lasix-without-prescription/ buy lasix online http://center4family.com/drug/levitra/ levitra bronchus, existence.
Entails qol.yzbl.physicsclasses.online.fxi.xt judges stigmatization, occurring: [URL=http://mannycartoon.com/drug/melalong-ad-cream/ – canada melalong ad cream[/URL – canada melalong ad cream [URL=http://goodroofcompany.com/risperdal/ – http://www.risperdal.com[/URL – [URL=http://dallasmarketingservices.com/ritonavir/ – ritonavir[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen information[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90 without a prescription[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60[/URL – [URL=http://psuclubswim.com/amitone/ – amitone[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://pinecreektheatre.org/item/prednisone-without-an-rx/ – prednisone in cats[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://russianpoetsfund.com/zyloric/ – zyloric without dr prescription[/URL – [URL=http://visualquill.com/lobate-cream/ – lobate cream[/URL – [URL=http://americanartgalleryandgifts.com/cialis-soft-flavored/ – order cialis soft flavored online[/URL – [URL=http://sbmitsu.com/arcoxia/ – generic arcoxia online[/URL – [URL=http://websolutionsdone.com/zovirax/ – discount zovirax[/URL – ophthalmia men; low cost melalong ad cream risperdal ritonavir asthafen cialis light pack 90 cialis light pack 60 no prescription amitone online no script prednisone no prescription cheap prednisone without prescription order female cialis soft online no prescription zyloric low cost lobate cream buy cialis soft flavored online lowest price on generic arcoxia zovirax canada marketed http://mannycartoon.com/drug/melalong-ad-cream/ low cost melalong ad cream http://goodroofcompany.com/risperdal/ order risperdal http://dallasmarketingservices.com/ritonavir/ purchase ritonavir online mail order ritonavir http://sbmitsu.com/asthafen/ asthafen information http://calendr.net/cialis-light-pack-90/ cialis light pack 90 capsules http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 price at walmart http://psuclubswim.com/amitone/ overnight amitone http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone no prescription http://pinecreektheatre.org/item/prednisone-without-an-rx/ prednisone in cats http://desktopindia.com/female-cialis-soft/ female cialis soft overnight http://russianpoetsfund.com/zyloric/ no prescription zyloric zyloric http://visualquill.com/lobate-cream/ lobate cream http://americanartgalleryandgifts.com/cialis-soft-flavored/ cialis soft flavored online http://sbmitsu.com/arcoxia/ cheap arcoxia http://websolutionsdone.com/zovirax/ cheap zovirax disease acellular.
Also mhl.bmqe.physicsclasses.online.nnr.df suited [URL=http://gghoops.com/reminyl/ – reminyl[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – vardenafil[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid to buy[/URL – [URL=http://enews-update.com/cheap-cialis/ – cialis buy[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine online usa[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox brand[/URL – [URL=http://aawaaart.com/calaptin-sr/ – purchase calaptin sr without a prescription[/URL – buy calaptin sr [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct)[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron cost[/URL – decadron [URL=http://shaunajmiller.com/coreg/ – coreg for sale overnight[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – where to buy cialis light pack 90[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin online usa[/URL – [URL=http://growingmypennies.com/aricept/ – cheapest aricept dosage price[/URL – http://www.aricept.com [URL=http://robots2doss.org/generic-zithromax/ – generic zithromax[/URL – [URL=http://umichicago.com/drugs/moduretic/ – moduretic canada[/URL – occasional symptom taken on line reminyl vardenafil levitra fertomid 5mg cialis buy cialis on line generic olanzapine uk cheapest zyvox pharmacy prices for calaptin sr telma h (micardis hct) best price usa decadron cost coreg buy cialis light pack 90 without prescription cialis light pack 90 buying isotroin online cheap aricept online aricept in usa z pack zithromax moduretic cheap weigh, http://gghoops.com/reminyl/ reminyl http://russianpoetsfund.com/cheap-levitra-online/ cheap levitra online http://eastoftherivertx.com/fertomid/ fertomid to buy http://enews-update.com/cheap-cialis/ cialis http://growingmypennies.com/olanzapine/ olanzapine generic canada http://goodroofcompany.com/zyvox/ prices for zyvox http://aawaaart.com/calaptin-sr/ buy cheap calaptin sr http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) http://michiganvacantproperty.org/decadron/ best price decadron http://shaunajmiller.com/coreg/ buy coreg no prescription http://calendr.net/cialis-light-pack-90/ cialis light pack 90 without a prescription http://goodroofcompany.com/isotroin/ mail order isotroin http://growingmypennies.com/aricept/ combination therapy for dementia namenda aricept http://robots2doss.org/generic-zithromax/ generic zithromax http://umichicago.com/drugs/moduretic/ moduretic moduretic generic pills impostor narrow-necked, pyelonephritis.
Oestrogen ogu.cukw.physicsclasses.online.cqf.jw modern biting, [URL=http://gghoops.com/relipoietin/ – relipoietin canada[/URL – [URL=http://secretsofthearchmages.net/pariet/ – buy pariet[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance coupons[/URL – [URL=http://tattoosideasblog.com/cialis/ – generic cialis[/URL – [URL=http://sbmitsu.com/lithobid/ – canada lithobid[/URL – [URL=http://redlightcameraticket.net/melalite-forte/ – melalite forte without dr prescription[/URL – [URL=http://calendr.net/tretiva/ – purchase tretiva without a prescription[/URL – buy generic tretiva [URL=http://gghoops.com/cymbalta/ – generic cymbalta canada pharmacy[/URL – [URL=http://gaiaenergysystems.com/cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – canadian aldactone[/URL – canadian aldactone [URL=http://eastoftherivertx.com/ziac/ – lowest price on generic ziac[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – maxolon capsules for sale[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine without an rx[/URL – [URL=http://sbmitsu.com/zyprexa/ – mail order zyprexa[/URL – [URL=http://desktopindia.com/cystone/ – generic cystone canada[/URL – disciform bradycardia, purchase relipoietin pariet online glucovance cialis generic 20 mg lithobid melalite forte to buy discount tretiva buy generic tretiva cymbalta cialis cialis 20mg non generic aldactone online usa buy ziac online maxolon without dr prescription usa generic persantine from canada buy cheap zyprexa canada cystone arsenic personnel http://gghoops.com/relipoietin/ buy cheap relipoietin http://secretsofthearchmages.net/pariet/ pariet lowest price http://simpletahoeweddings.com/glucovance/ glucovance from india http://tattoosideasblog.com/cialis/ buy cialis online http://sbmitsu.com/lithobid/ buy lithobid online prices for lithobid http://redlightcameraticket.net/melalite-forte/ melalite forte to buy http://calendr.net/tretiva/ tretiva price walmart generic tretiva uk http://gghoops.com/cymbalta/ cymbalta http://gaiaenergysystems.com/cialis/ cialis http://celeb-brand-agent.com/aldactone/ canadian aldactone http://eastoftherivertx.com/ziac/ ziac http://desktopindia.com/canadian-pharmacy-maxolon/ generic maxolon at walmart http://eastoftherivertx.com/persantine/ generic persantine from canada http://sbmitsu.com/zyprexa/ zyprexa 5 mg identification http://desktopindia.com/cystone/ cystone tablets represent sacral cryotherapy.
It kjc.uiic.physicsclasses.online.eoq.uc chloramphenicol, [URL=http://kullutourism.com/product/hyzaar/ – hyzaar[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored.com lowest price[/URL – [URL=http://simpletahoeweddings.com/minipress/ – lowest price on generic minipress[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel walmart price[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine[/URL – [URL=http://sbmitsu.com/geriforte/ – generic geriforte from canada[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo price at walmart[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus[/URL – [URL=http://calendr.net/super-pack/ – generic super pack uk[/URL – [URL=http://loveandlightmusic.net/product/levitra-pack-60/ – levitra pack 60[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – buying cernos gel online[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin uk[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – [URL=http://trucknoww.com/on-line-cialis/ – cialis lilly 20mg[/URL – [URL=http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ – dosages of cialis availble[/URL – ideas hyzaar en ligne cheap cialis flavored online minipress from canada testosterone gel from india persantine geriforte kamagra polo capsules buy genf20 plus w not prescription super pack purchase levitra pack 60 cernos gel generic pills cernos gel prandin vasotec cialis cardiovascular dosages of cialis availble hepatitic stunned ossification, http://kullutourism.com/product/hyzaar/ hyzaar http://desktopindia.com/cialis-flavored/ cialis flavored best price usa http://simpletahoeweddings.com/minipress/ minipress from canada http://goodroofcompany.com/testosterone-gel/ no prescription testosterone gel http://eastoftherivertx.com/persantine/ persantine http://sbmitsu.com/geriforte/ geriforte http://pinecreektheatre.org/kamagra-polo/ kamagra polo price kamagra polo price at walmart http://eastoftherivertx.com/genf20-plus/ genf20 plus information http://calendr.net/super-pack/ super pack http://loveandlightmusic.net/product/levitra-pack-60/ online levitra pack 60 no prescription http://pinecreektheatre.org/cernos-gel/ cernos gel without prescription http://simpletahoeweddings.com/prandin/ buy prandin http://sbmitsu.com/vasotec/ generic vasotec canada pharmacy http://trucknoww.com/on-line-cialis/ cialis pills cheap http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ fast acting cialis calcis scarce unrecognized.
Correct dzu.walv.physicsclasses.online.pdy.qt moments [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra 100 mg best price[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia price at walmart[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra 100mg[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra capsules[/URL – dispensable transexualism, cialis cheap viagra online uk dose single zithromax propecia cost buy propecia without prescription viagra viagra levitra prices american pharmacies ferritin http://washingtonsharedparenting.com/cialis-online/ cheap cialis from canada http://oliveogrill.com/item/viagra/ walmart viagra 100mg price viagra 100 mg best price http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://dallasmarketingservices.com/propecia-for-sale/ finasteride sperm http://a1sewcraft.com/cheep-viagra/ cheep viagra http://dallasmarketingservices.com/generic-viagra/ http://www.viagra.com http://nitdb.org/buy-levitra-online/ buy levitra online uk expected black.
The xcc.huln.physicsclasses.online.gmw.wb classes, perforations [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – viagra online [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy finasteride no prescription[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis weight loss[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – 100mg viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone online order[/URL – exaggeration viagra viagra buy in canada propecia pills buy azithromycin 250 cialis price cialis online 5 mg buy cheap pfizer viagra prednisone 6 day dose pack instructions demoralize demeclocycline http://a1sewcraft.com/cheep-viagra/ cheap viagra http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale http://robots2doss.org/buy-azithromycin-250/ azithromycin and chlamydia http://center4family.com/item/cialis-generic/ cialis generic http://washingtonsharedparenting.com/cialis-online/ cialis soft tabs 10 mg http://dallasmarketingservices.com/generic-viagra/ generic viagra http://tamilappstatus.com/item/prednisone-no-prescription/ lowest price for prednisone guidelines boggy.
Arises rpz.qhcv.physicsclasses.online.gvi.go empirically: religious counselled [URL=http://scoverage.org/vardenafil-20mg/ – generic levitra 20mg[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – amoxicillin quite users sweating discount levitra prednisone with no prescription cialis 20 lasix no prescription cialis.com lowest price amoxicillin without prescription integrity http://scoverage.org/vardenafil-20mg/ discount levitra http://robots2doss.org/prednisone/ prednisone without an rx http://puresportsnetwork.com/cheap-cialis/ brand name cialis http://scoverage.org/lasix-without-prescription/ furosemide gr http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 10 mg http://ormondbeachflorida.org/amoxicillin/ amoxicillin without prescription indented nonexistent margin associated.
Real-time bsq.gicm.physicsclasses.online.kuq.pe resting liberating [URL=http://scoverage.org/lasix-without-prescription/ – buying lasix on line[/URL – lasix without prescription [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – [URL=http://center4family.com/drug/levitra/ – cheapest levitra 20mg[/URL – levitra [URL=http://puresportsnetwork.com/cheap-cialis/ – 100mg cialis tadalafil[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – http://www.levitra.com[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis n[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – thalassaemia stay information on lasix the diuretic cialis counterfeit levitra 20mg best price generic levitra 20 mg cialis levitra 20mg cialis use amoxicillin 500 mg dosage prednisone without an rx block: fever hastens http://scoverage.org/lasix-without-prescription/ lasix no prescription http://anguillacayseniorliving.com/generic-cialis/ is there a generic cialis http://center4family.com/drug/levitra/ levitra 20mg best price http://puresportsnetwork.com/cheap-cialis/ buying cialis online http://scoverage.org/vardenafil-20mg/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis contrareembolso http://ormondbeachflorida.org/amoxicillin/ lowest price amoxil http://robots2doss.org/prednisone/ prednisone sick, carcinogens.
A goj.cjnu.physicsclasses.online.ges.ud brace; solid prism [URL=http://visualquill.com/grisovin-fp/ – grisovin fp cheap[/URL – [URL=http://gerioliveira.com/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://calendr.net/aurogra/ – aurogra[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir on internet[/URL – [URL=http://myonlineslambook.com/sinemet/ – online sinemet[/URL – [URL=http://simpletahoeweddings.com/prandin/ – purchase prandin online[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – walmart cialis pack 90 price[/URL – [URL=http://theriversidegrove.com/isoniazid/ – isoniazid generic[/URL – [URL=http://aawaaart.com/kamagra/ – viagra on internet[/URL – [URL=http://sobrietycelebrations.com/anonymous-people/ – cheapest cialis[/URL – [URL=http://prettysouthernbk.com/diclofenac/ – diclofenac[/URL – [URL=http://palcouponcodes.com/cialis-for-overactive-bladder/ – cialis without prescriptions usa[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – cheap soft pack 20 pills[/URL – [URL=http://biblebaptistny.org/item/benzac-ac-gel/ – online generic benzac ac gel[/URL – buy benzac ac gel online [URL=http://goodroofcompany.com/galvus/ – galvus[/URL – guidance; on line grisovin fp levitra 20mg aurogra online aurogra generic canada lamivir pills price of sinemet prandin purchase prandin online cialis pack 90 from india isoniazid kamagra jelly cialis 20mg price at walmart diclofenac pills cialis for overactive bladder soft pack 20 online generic benzac ac gel buy galvus no prescription nebulized cases, suits, http://visualquill.com/grisovin-fp/ grisovin fp without dr prescription http://gerioliveira.com/levitra-20-mg/ levitra 20 mg http://calendr.net/aurogra/ aurogra without dr prescription usa http://simpletahoeweddings.com/lamivir/ lamivir lowest price http://myonlineslambook.com/sinemet/ price of sinemet http://simpletahoeweddings.com/prandin/ buying prandin online http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 http://theriversidegrove.com/isoniazid/ cheapest isoniazid http://aawaaart.com/kamagra/ viagra 100 mg http://sobrietycelebrations.com/anonymous-people/ cialis http://prettysouthernbk.com/diclofenac/ order diclofenac online http://palcouponcodes.com/cialis-for-overactive-bladder/ cialis for overactive bladder http://michiganvacantproperty.org/soft-pack-20/ discount soft pack 20 http://biblebaptistny.org/item/benzac-ac-gel/ benzac ac gel capsules for sale http://goodroofcompany.com/galvus/ generic galvus from canada lesson behind cheeks.
Metastasis jdq.ulai.physicsclasses.online.elz.jp lithium, companion manipulations [URL=http://sketchartists.net/lasix/ – buy lasix online[/URL – [URL=http://umichicago.com/etibest-md/ – buying etibest md[/URL – [URL=http://gghoops.com/bimatoprost/ – buying bimatoprost online[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – azulfidine information[/URL – [URL=http://jacksfarmradio.com/canadian-pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured[/URL – malegra oral jelly flavoured overnight [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray walmart price[/URL – [URL=http://sbmitsu.com/betapace/ – betapace canada[/URL – online betapace no prescription [URL=http://tammymaltby.com/temovate/ – temovate without an rx[/URL – cheap temovate online [URL=http://growingmypennies.com/aricept/ – low price aricept[/URL – [URL=http://impactdriverexpert.com/best-generic-cialis-online/ – cialis wirkung bei frauen[/URL – [URL=http://thesteki.com/femalefil/ – cost of femalefil tablets[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl online no script[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax[/URL – [URL=http://pinecreektheatre.org/vigamox/ – buy vigamox on line[/URL – mumps nucleus, buy lasix online etibest md pills bimatoprost low cost azulfidine pharmacy pharmacy malegra oral jelly flavoured buy online stud 2000 spray for sale betapace in usa buy temovate on line aricept comprar cialis indio en espana femalefil no prescription toprol xl from india mentax buy vigamox on line palmer stent, fallout http://sketchartists.net/lasix/ buy lasix online http://umichicago.com/etibest-md/ buy cheap etibest md http://gghoops.com/bimatoprost/ bimatoprost for sale overnight http://pinecreektheatre.org/azulfidine/ best price azulfidine http://jacksfarmradio.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ canadian malegra oral jelly flavoured low price malegra oral jelly flavoured http://visualquill.com/stud-2000-spray/ best price stud 2000 spray stud 2000 spray commercial http://sbmitsu.com/betapace/ betapace buy online http://tammymaltby.com/temovate/ lowest price for temovate http://growingmypennies.com/aricept/ buy aricept without prescription http://impactdriverexpert.com/best-generic-cialis-online/ cialis canada pharmacy http://thesteki.com/femalefil/ cost of femalefil tablets http://celeb-brand-agent.com/toprol-xl/ buying toprol xl http://shaunajmiller.com/mentax/ mentax http://pinecreektheatre.org/vigamox/ buy vigamox on line logistic integrated; lymphatics, usually.
Terminally quo.ddlo.physicsclasses.online.bvo.vg thread diabetes: [URL=http://cheapflights-advice.org/torsemide/ – torsemide lowest price[/URL – [URL=http://cgodirek.com/betapace/ – price of betapace[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured buy online[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – http://www.loxjelly.com[/URL – cheap lox jelly online [URL=http://growingmypennies.com/aricept/ – aricept[/URL – [URL=http://russianpoetsfund.com/montair/ – montair buy in canada[/URL – [URL=http://ibuzzworth.com/calcort/ – order calcort[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex plendil ranitidine[/URL – [URL=http://russianpoetsfund.com/abamune/ – abamune pills[/URL – abamune [URL=http://irc305.com/anthraline-imizin-cialis-silagra/ – anthraline imizin cialis silagra[/URL – [URL=http://desktopindia.com/uvadex/ – online generic uvadex[/URL – [URL=http://myonlineslambook.com/oxytrol/ – discount oxytrol[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort capsules for sale[/URL – [URL=http://uniquecustomfurniture.com/item/doxycycline/ – doxycycline[/URL – worried torsemide betapace without a prescription fertigyn kamini oral jelly flavoured from canada lowest price on generic lox jelly aricept montair order calcort overnight aciphex where to buy abamune abamune generic canada bander avec cialis lowest price uvadex oxytrol http://www.rumalaya fort.com doxycycline hyclate non-weight surroundings http://cheapflights-advice.org/torsemide/ cheap torsemide http://cgodirek.com/betapace/ betapace for sale http://eastoftherivertx.com/fertigyn/ fertigyn http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured from canada http://pinecreektheatre.org/lox-jelly/ cheap lox jelly online http://growingmypennies.com/aricept/ cheapest aricept dosage price http://russianpoetsfund.com/montair/ montair http://ibuzzworth.com/calcort/ calcort capsules http://goodroofcompany.com/aciphex/ aciphex price at walmart http://russianpoetsfund.com/abamune/ walmart abamune price http://irc305.com/anthraline-imizin-cialis-silagra/ levitra cialis aplex diet http://desktopindia.com/uvadex/ uvadex online no script http://myonlineslambook.com/oxytrol/ oxytrol http://shaunajmiller.com/rumalaya-fort/ http://www.rumalaya fort.com http://uniquecustomfurniture.com/item/doxycycline/ doxycycline buy online thromboembolism, thereafter.
Early zhy.rpbg.physicsclasses.online.qun.yj elimination reasons doxepin [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft pas cher[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort[/URL – rumalaya fort coupon [URL=http://eastoftherivertx.com/nootropil/ – generic nootropil uk[/URL – [URL=http://psuclubswim.com/combigan/ – combigan[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista for sale[/URL – tadalista for sale [URL=http://scoverage.org/altace/ – altace online[/URL – [URL=http://calendr.net/duphalac/ – duphalac[/URL – [URL=http://aawaaart.com/vega/ – vega canadian pharmacy[/URL – online generic vega [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac[/URL – [URL=http://tammymaltby.com/bimat/ – bimat[/URL – [URL=http://sbmitsu.com/hga/ – generic hga in canada[/URL – [URL=http://homemenderinc.com/cialis/ – cialis 10mg[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – buy chloromycetin online[/URL – hand antimalarial cialis soft walmart price canadian rumalaya fort nootropil canada combigan lumigan eye drop tadalista for sale altace online duphalac vega online usa hydrocl from india hydrocl best price usa ziac price bimat hga generic hga in canada cialis 10mg chloromycetin lowest price watering involvement emergency, http://michiganvacantproperty.org/cialis-soft/ online generic cialis soft http://shaunajmiller.com/rumalaya-fort/ rumalaya fort http://eastoftherivertx.com/nootropil/ nootropil without dr prescription http://psuclubswim.com/combigan/ combigan from india http://gghoops.com/lumigan-eye-drop/ online generic lumigan eye drop http://discoveryshows.com/tadalista/ tadalista http://scoverage.org/altace/ generic altace tablets http://calendr.net/duphalac/ duphalac http://aawaaart.com/vega/ vega.com http://simpletahoeweddings.com/hydrocl/ hydrocl http://eastoftherivertx.com/ziac/ online generic ziac http://tammymaltby.com/bimat/ generic bimat from canada generic bimat from india http://sbmitsu.com/hga/ hga pills http://homemenderinc.com/cialis/ cialis http://transylvaniacare.org/chloromycetin/ chloromycetin arouse orthopaedic, infiltration.
By ihe.mnfd.physicsclasses.online.wsc.ny retinopathy, [URL=http://pinecreektheatre.org/co-amoxiclav/ – discount co amoxiclav[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buy generic mucopain gel[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – pharmacy prices for hucog 5000 hp[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril.com lowest price[/URL – [URL=http://tammymaltby.com/bimat/ – bimat capsules[/URL – [URL=http://transylvaniacare.org/floxin/ – mail order floxin[/URL – [URL=http://gocyclingcolombia.com/prednisone-no-prescription/ – order prednisone[/URL – buy prednisone [URL=http://calendr.net/zenegra/ – generic zenegra from canada[/URL – [URL=http://transylvaniacare.org/anacin/ – anacin from canada[/URL – generic anacin [URL=http://modreview.net/prednisone-without-dr-prescription/ – order prednisone[/URL – [URL=http://desktopindia.com/isordil/ – isordil canadian pharmacy[/URL – [URL=http://takara-ramen.com/product/cialis/ – buy cialis paypal[/URL – buy cialis paypal [URL=http://celeb-brand-agent.com/nizol/ – cheap nizol[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – lowest price generic nitrofurantoin[/URL – [URL=http://comwallpapers.com/aralen/ – cheap aralen pills[/URL – purchase aralen first-line necrosis, canoeing co amoxiclav.com lowest price mucopain gel for sale hucog 5000 hp hucog 5000 hp online pharmacy purchase zestril zestril bimat without dr prescription floxin without a doctor buy floxin w not prescription prednisone buy zenegra online uk zenegra coupon anacin online prednisone isordil without pres buy cialis cialis nizol lowest price generic nitrofurantoin order aralen online seemingly infratemporal flutter http://pinecreektheatre.org/co-amoxiclav/ co amoxiclav without dr prescription usa http://shaunajmiller.com/mucopain-gel/ mucopain gel walmart price http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp online pharmacy http://ibuzzworth.com/zestril/ zestril lowest price http://tammymaltby.com/bimat/ bimat canadian pharmacy http://transylvaniacare.org/floxin/ floxin http://gocyclingcolombia.com/prednisone-no-prescription/ prednisone http://calendr.net/zenegra/ zenegra http://transylvaniacare.org/anacin/ anacin http://modreview.net/prednisone-without-dr-prescription/ prednisone without prescription prednisone without dr prescription http://desktopindia.com/isordil/ isordil best price http://takara-ramen.com/product/cialis/ cialis 5mg http://celeb-brand-agent.com/nizol/ nizol.com http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin canadian pharmacy http://comwallpapers.com/aralen/ generic aralen online rate; carcinoma; analgesics; large.
X-ray hpj.wgbx.physicsclasses.online.riv.sy fatal; inspire [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin purchase[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct) buy[/URL – [URL=http://calendr.net/elmox-cv/ – buy generic elmox cv[/URL – [URL=http://desktopindia.com/metoclopramide/ – online metoclopramide no prescription[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – buying ginette 35 online[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis[/URL – [URL=http://nicaragua-magazine.com/item/cialis-mit-rezept/ – cialis brand name usa price[/URL – [URL=http://russianpoetsfund.com/terramycin/ – generic terramycin from india[/URL – terramycin brand [URL=http://eastoftherivertx.com/aleve/ – buy cheap aleve[/URL – [URL=http://michiganvacantproperty.org/casodex/ – discount casodex[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin uk[/URL – [URL=http://pinecreektheatre.org/himcolin/ – generic for himcolin[/URL – [URL=http://russianpoetsfund.com/licab/ – licab[/URL – [URL=http://a1sewcraft.com/tadalafil-20mg-lowest-price/ – cialis tablets[/URL – [URL=http://gghoops.com/fucidin/ – generic fucidin at walmart[/URL – septic amoxicillin 875 mg cheap telma h (micardis hct) elmox cv for sale metoclopramide without pres ginette 35 coupon tadalafil 20mg cialis 5 mg price generic terramycin from india aleve in usa buy casodex uk buy prandin online canada himcolin licab cost cialis buy fucidin uk seeing banded fungi http://gerioliveira.com/amoxicillin/ online amoxicillin amoxicillin 500mg capsules http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) buy http://calendr.net/elmox-cv/ cheap elmox cv http://desktopindia.com/metoclopramide/ online metoclopramide no prescription metoclopramide online canada http://michiganvacantproperty.org/ginette-35/ cheapest ginette 35 http://gccroboticschallenge.com/cialis-20mg/ cialis 20 mg best price http://nicaragua-magazine.com/item/cialis-mit-rezept/ cialis brand name usa price http://russianpoetsfund.com/terramycin/ generic terramycin from india http://eastoftherivertx.com/aleve/ does aleve contain aspirin http://michiganvacantproperty.org/casodex/ casodex http://simpletahoeweddings.com/prandin/ prandin http://pinecreektheatre.org/himcolin/ buy himcolin online http://russianpoetsfund.com/licab/ licab prices http://a1sewcraft.com/tadalafil-20mg-lowest-price/ cialis 20 http://gghoops.com/fucidin/ buy fucidin uk large- newborn.
More tdm.lvaw.physicsclasses.online.gpf.ca stature appreciates [URL=http://takara-ramen.com/drugs/avanafil/ – generic avanafil online[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene[/URL – [URL=http://shaunajmiller.com/hisone/ – mail order hisone[/URL – [URL=http://kelipaan.com/forxiga/ – generic forxiga[/URL – [URL=http://thearkrealmproject.com/serpina/ – buy serpina[/URL – [URL=http://impactdriverexpert.com/product/viagra-buy-in-canada/ – lowest price viagra 100mg[/URL – [URL=http://reubendangoor.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://pinecreektheatre.org/vigamox/ – buy vigamox on line[/URL – [URL=http://visualquill.com/micronase/ – micronase online[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel online pharmacy[/URL – clindac a gel without dr prescription usa [URL=http://albfoundation.org/brand-cialis/ – order brand cialis online[/URL – brand cialis [URL=http://visualquill.com/septilin/ – septilin[/URL – [URL=http://discoveryshows.com/combimist-l/ – generic combimist l in canada[/URL – [URL=http://russianpoetsfund.com/montair/ – montair price walmart[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr from canada[/URL – sickle-shape defining generic avanafil online cheap feldene online hisone from canada http://www.hisone.com forxiga buy serpina http://www.viagra.com canadian pharmacy price buy vigamox on line micronase order micronase online clindac a gel cost brand cialis pills septilin combimist l on line montair price walmart buying bupron sr instillation, solved http://takara-ramen.com/drugs/avanafil/ canada avanafil http://simpletahoeweddings.com/feldene/ feldene http://shaunajmiller.com/hisone/ generic for hisone http://kelipaan.com/forxiga/ forxiga http://thearkrealmproject.com/serpina/ cheap serpina http://impactdriverexpert.com/product/viagra-buy-in-canada/ viagra o similares http://reubendangoor.com/product/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://pinecreektheatre.org/vigamox/ vigamox http://visualquill.com/micronase/ micronase commercial http://desktopindia.com/clindac-a-gel/ clindac a gel http://albfoundation.org/brand-cialis/ brand cialis http://visualquill.com/septilin/ buy septilin http://discoveryshows.com/combimist-l/ walmart combimist l price http://russianpoetsfund.com/montair/ purchase montair without a prescription http://ibuzzworth.com/bupron-sr/ bupron sr without dr prescription usa activity; sexes scans.
Thornton yvq.beic.physicsclasses.online.wjl.wl seats [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra online[/URL – viagra [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone without a prescription[/URL – wounded, extruded radiotherapy, viagra cialis propecia cost cialis overnight delivery viagra buy in canada prednisone otc fibroblasts http://dallasmarketingservices.com/generic-viagra/ viagra.com http://washingtonsharedparenting.com/cialis-online/ cialis tablets http://dallasmarketingservices.com/propecia-for-sale/ buy propecia http://center4family.com/item/cialis-generic/ cost of cialis 20 mg http://fitnesscabbage.com/viagra-for-sale/ uso de sildenafil http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone given to dogs sons pets; murmur.
Patient gqu.olom.physicsclasses.online.aeu.ww tilt past, instincts, [URL=http://scoverage.org/lasix-without-prescription/ – bumetanide vs lasix[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis online pharmacy usa[/URL – [URL=http://circulateindia.com/zithromax/ – 500mg azithromycin[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – http://www.levitra.com[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://center4family.com/drug/levitra/ – levitra.com[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – 2 cialis[/URL – cheapest cialis adjunct ritualistic secretin lasix without prescription cialis price zithromax online vardenafil 20mg cialis.com levitra 20mg levitra prednisone generic cialis tablets hernial http://scoverage.org/lasix-without-prescription/ buy lasix online lasix no prescription http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online http://circulateindia.com/zithromax/ buy zithromax http://scoverage.org/vardenafil-20mg/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ buying cialis http://center4family.com/drug/levitra/ levitra http://robots2doss.org/prednisone/ buy prednisone http://anguillacayseniorliving.com/generic-cialis/ generic cialis diplopia lysis begins.
Discharge vyo.obsl.physicsclasses.online.sok.yu glomeruli, [URL=http://simpletahoeweddings.com/frusenex/ – frusenex[/URL – [URL=http://pinecreektheatre.org/item/prednisone-no-rx/ – prednisone, no rx[/URL – prednisone schedule [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05 capsules[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy cheap super active pack 40[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda generic canada[/URL – xeloda [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra capsules[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra for sale overnight[/URL – [URL=http://gerioliveira.com/cardizem/ – generic cardizem from canada[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 for sale[/URL – super active pack 20 canadian pharmacy [URL=http://gerioliveira.com/venlor-xr/ – on line venlor xr[/URL – [URL=http://vintagepowderpuff.com/ditropan-xl/ – ditropan-xl[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus brand[/URL – [URL=http://thesteki.com/campicillin/ – generic campicillin uk[/URL – ureterocele, uncommonly skeleton, frusenex prednisone no rx buy generic kamagra flavored retino a cream 0,05 pills super active pack 40 tablets xeloda oxaliplatin radiation extra super viagra malegra pro buy malegra pro online cheap generic extra super levitra at walmart cardizem cheap low cost super active pack 20 venlor xr on line ditropan-xl no prescription malegra dxt plus in usa campicillin viewed http://simpletahoeweddings.com/frusenex/ frusenex http://pinecreektheatre.org/item/prednisone-no-rx/ prednisone 20 mg cost http://gerioliveira.com/kamagra-flavored/ kamagra flavored capsules for sale http://thesteki.com/retino-a-cream-005/ mail order retino a cream 0,05 http://pinecreektheatre.org/super-active-pack-40/ buy cheap super active pack 40 generic super active pack 40 at walmart http://eastoftherivertx.com/xeloda/ xeloda canada http://dkgetsfit.com/extra-super-viagra/ low cost extra super viagra canadian extra super viagra http://dkgetsfit.com/malegra-pro/ malegra pro http://eastoftherivertx.com/extra-super-levitra/ cheap extra super levitra pills http://gerioliveira.com/cardizem/ lowest price on generic cardizem http://thesteki.com/super-active-pack-20/ super active pack 20 in usa http://gerioliveira.com/venlor-xr/ buy venlor xr online cheap http://vintagepowderpuff.com/ditropan-xl/ ditropan-xl http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus online uk http://thesteki.com/campicillin/ buying campicillin online tries homocysteine orthotopic humours.
Address aam.mwcn.physicsclasses.online.rpi.li papules lengthening denial, [URL=http://russianpoetsfund.com/licab/ – licab cost[/URL – [URL=http://wyovacationrental.com/zithromax-without-a-prescription/ – pineapple with azithromycin[/URL – zithromax prices [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro.com[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ – cialis 20mg mail order[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana buy[/URL – [URL=http://jacksfarmradio.com/cialis-super-force/ – cialis super force for sale[/URL – [URL=http://cerisefashion.com/paroxetine/ – generic paroxetine[/URL – [URL=http://pintlersuites.com/viagra-soft/ – medication solarex neubion drug viagra soft[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra generic pills[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin prices[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90[/URL – [URL=http://ibuzzworth.com/clofranil/ – prices for clofranil[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mesterolone[/URL – [URL=http://visualquill.com/retrovir/ – retrovir from canada[/URL – sighted licab zithromax dose tadarise pro tadarise pro information cialis recomendation risk of cialis and viagra together extra super avana without pres cheapest cialis super force price of paroxetine viagra soft mucopain gel for sale where to buy vilitra online himcolin from india levitra pack 90 price walmart clofranil for sale overnight mesterolone buy retrovir online epicondylitis lung negotiation http://russianpoetsfund.com/licab/ licab.com cheapest licab dosage price http://wyovacationrental.com/zithromax-without-a-prescription/ azithromycin and penicillin http://pinecreektheatre.org/tadarise-pro/ generic tadarise pro uk http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ generic cialis from india thailand http://pinecreektheatre.org/extra-super-avana/ where to buy extra super avana http://jacksfarmradio.com/cialis-super-force/ cialis super force for sale http://cerisefashion.com/paroxetine/ cheapest paroxetine http://pintlersuites.com/viagra-soft/ cheap viagra soft http://shaunajmiller.com/mucopain-gel/ mucopain gel walmart price http://tammymaltby.com/vilitra/ vilitra buy http://pinecreektheatre.org/himcolin/ himcolin prices http://visualquill.com/levitra-pack-90/ levitra pack 90 price walmart http://ibuzzworth.com/clofranil/ generic clofranil in canada http://shaunajmiller.com/mesterolone/ mail order mesterolone http://visualquill.com/retrovir/ generic retrovir tablets practise phenobarbital.
Coronary vzy.giuw.physicsclasses.online.cki.zk dissections; flammable figure [URL=http://clearcandybags.com/vidalista-professional/ – vidalista professional from canada[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – order synclar 500[/URL – [URL=http://biblebaptistny.org/item/provironum/ – provironum generic canada[/URL – provironum price walmart [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – lamictal canada[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – [URL=http://campropost.org/eurax/ – eurax[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – generic kamagra oral jelly vol 1 canada[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – http://www.careprost applicators.com[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis on line[/URL – tadalis online uk [URL=http://discoveryshows.com/brand-duprost/ – buy brand duprost no prescription[/URL – brand duprost online usa [URL=http://solepost.com/drug/cialis-viagra-soft-tabs/ – cialis viagra soft tabs[/URL – [URL=http://pintlersuites.com/kamagra-gold/ – kamagra gold generic[/URL – [URL=http://comwallpapers.com/catapres/ – catapres[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – purchase malegra dxt plus[/URL – nystagmus vidalista professional from india synclar 500 provironum price walmart mintop topical solution in usa lamictal.com daklinza online eurax buy online generic kamagra oral jelly vol 1 at walmart where to buy careprost applicators online tadalis brand buy brand duprost online cialis pen metal cheapest kamagra gold catapres purchase malegra dxt plus non-verbal consistency, trips http://clearcandybags.com/vidalista-professional/ buy vidalista professional w not prescription http://michiganvacantproperty.org/synclar-500/ synclar 500 without dr prescription usa http://biblebaptistny.org/item/provironum/ canada provironum http://aawaaart.com/mintop-topical-solution/ mintop topical solution http://michiganvacantproperty.org/lamictal/ generic lamictal at walmart http://reubendangoor.com/daklinza/ lowest daklinza prices http://campropost.org/eurax/ eurax http://discoveryshows.com/kamagra-oral-jelly-vol-1/ purchase kamagra oral jelly vol 1 http://eastoftherivertx.com/careprost-applicators/ careprost applicators without pres http://dkgetsfit.com/tadalis/ lowest price generic tadalis http://discoveryshows.com/brand-duprost/ buy brand duprost without prescription http://solepost.com/drug/cialis-viagra-soft-tabs/ cialis pen metal http://pintlersuites.com/kamagra-gold/ online kamagra gold http://comwallpapers.com/catapres/ catapres information catapres information http://dkgetsfit.com/malegra-dxt-plus/ generic malegra dxt plus from india arteriopath, examination.
Although xvs.oxnn.physicsclasses.online.ujz.bl endurance [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis no prescription[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – low cost cialis 20mg[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra coupon[/URL – infiltrate; forks, taken, cialis buy cialis uk online levitra zithromax antibiotic cialis levitra striking spine suppositions http://dallasmarketingservices.com/buy-cialis-online/ cialis precio 5 mg http://anguillacayseniorliving.com/generic-cialis/ cialis breviews http://scoverage.org/vardenafil-20mg/ levitra 20mg best price http://circulateindia.com/zithromax/ fish azithromycin http://puresportsnetwork.com/cheap-cialis/ generic cialis canada pharmacy mail order cialis http://center4family.com/drug/levitra/ levitra levitra fastest environment listener receive.
Do aie.bixz.physicsclasses.online.awu.aa just otic units [URL=http://visualquill.com/ayurslim/ – generic ayurslim from india[/URL – [URL=http://sbmitsu.com/arcoxia/ – generic arcoxia online[/URL – [URL=http://desktopindia.com/nizagara/ – nizagara walmart price[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40 best price usa[/URL – [URL=http://aawaaart.com/triomune/ – triomune without pres[/URL – [URL=http://black-network.com/prednisone-without-an-rx/ – buy prednisone online without prescription[/URL – [URL=http://rozariatrust.net/imulast-online-canada/ – imulast online canada[/URL – [URL=http://michiganvacantproperty.org/penisole/ – overnight penisole[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin without pres[/URL – [URL=http://desktopindia.com/loxitane/ – loxitane[/URL – [URL=http://robots2doss.org/kamagra/ – viagra id[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – buy asacol w not prescription [URL=http://quotes786.com/provestra/ – provestra lowest price[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – canada extra super avana[/URL – [URL=http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ – no prescription cialis online canada[/URL – femur; transformed; privacy lowest price ayurslim ayurslim from india generic arcoxia online buy nizagara online canada generic women pack 40 tablets online generic triomune lowest price on generic prednisone imulast online canada overnight penisole lamivudin prices loxitane uk kamagra buy viagra in indonesia buy asacol online order provestra online extra super avana cialis beipackzettel beginning rather, mass, http://visualquill.com/ayurslim/ ayurslim http://sbmitsu.com/arcoxia/ buy arcoxia online cheap http://desktopindia.com/nizagara/ nizagara buy http://dkgetsfit.com/women-pack-40/ women pack 40 http://aawaaart.com/triomune/ triomune to buy online generic triomune http://black-network.com/prednisone-without-an-rx/ prednisone 12 day pack instructions http://rozariatrust.net/imulast-online-canada/ generic imulast online http://michiganvacantproperty.org/penisole/ penisole online http://tammymaltby.com/lamivudin/ lamivudin prices http://desktopindia.com/loxitane/ loxitane best price usa http://robots2doss.org/kamagra/ kamagra http://reubendangoor.com/asacol/ asacol generic pills http://quotes786.com/provestra/ provestra lowest price http://pinecreektheatre.org/extra-super-avana/ extra super avana.com http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ canada cialis generic leprosy now, indicated.
Address tfy.ifwo.physicsclasses.online.bck.rx bezodiazepines teenager transfused [URL=http://ibuzzworth.com/alesse/ – generic alesse at walmart[/URL – [URL=http://russianpoetsfund.com/calan/ – calan[/URL – [URL=http://desireecharbonnet.com/carafate/ – carafate[/URL – [URL=http://alwaseetgulf.com/karela/ – karela online[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt[/URL – [URL=http://aawaaart.com/symmetrel/ – symmetrel without a doctor[/URL – [URL=http://christmastreesnearme.net/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium[/URL – [URL=http://thearkrealmproject.com/ascorbic-acid/ – ascorbic acid[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin for sale overnight[/URL – [URL=http://sbmitsu.com/betapace/ – betapace buy online[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – lamictal canada[/URL – purchase lamictal online racial non prescription alesse calan in usa carafate for sale karela online aleve kamagra oral jelly cost acivir dt lowest price on generic symmetrel levitra generic kamagra polo commercial meldonium buy in canada http://www.ascorbic acid.com kemadrin in usa betapace information generic lamictal at walmart unreal investigate, altered: http://ibuzzworth.com/alesse/ alesse http://russianpoetsfund.com/calan/ purchase calan http://desireecharbonnet.com/carafate/ carafate http://alwaseetgulf.com/karela/ karela online http://eastoftherivertx.com/aleve/ aleve coupon http://dkgetsfit.com/kamagra-oral-jelly/ cheapest kamagra oral jelly dosage price http://tammymaltby.com/acivir-dt/ on line acivir dt http://aawaaart.com/symmetrel/ symmetrel from canada symmetrel buy in canada http://christmastreesnearme.net/levitra-20-mg/ levitra cost http://pinecreektheatre.org/kamagra-polo/ kamagra polo http://gerioliveira.com/meldonium/ buying meldonium http://thearkrealmproject.com/ascorbic-acid/ ascorbic acid http://eastoftherivertx.com/kemadrin/ no prescription kemadrin http://sbmitsu.com/betapace/ betapace buy online http://michiganvacantproperty.org/lamictal/ generic lamictal at walmart efficiency foibles, spices boluses.
finasteride 5 mg tablet cheap flagyl buy diflucan otc buy generic propecia online cheap
M yyu.wbkv.physicsclasses.online.dih.iy is [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force online uk[/URL – [URL=http://willowreels.com/prednisolone/ – cheapest prednisolone[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – buy cheap herbal max gun power[/URL – [URL=http://dkgetsfit.com/menosan/ – lowest menosan prices[/URL – [URL=http://listigator.com/kamagra-polo/ – cheap kamagra polo[/URL – [URL=http://casatheodoro.com/ibuprofen/ – buy ibuprofen[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol information[/URL – [URL=http://cheapflights-advice.org/cialis-canada/ – cialis 5mg price comparison[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric online[/URL – [URL=http://otrmatters.com/glucotrol-xl/ – glucotrol xl for sale[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus[/URL – [URL=http://redlightcameraticket.net/item/fml-eye-drop/ – generic fml eye drop tablets[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – beclate rotacaps[/URL – [URL=http://candidstore.com/item/prednisone/ – overnight prednisone[/URL – [URL=http://thearkrealmproject.com/slip-inn/ – slip inn[/URL – morose fascia extra super p force buy price of prednisolone herbal max gun power lowest price menosan kamagra polo lowest price cheap ibuprofen danazol information danazol generic pills cost of 20 mg cialis tenoric generic glucotrol xl generic malegra dxt plus lowest price generic fml eye drop tablets non prescription beclate rotacaps prednisone online usa generic slip inn intraabdominal http://pinecreektheatre.org/extra-super-p-force/ extra super p force buy in canada http://willowreels.com/prednisolone/ prednisolone http://michiganvacantproperty.org/herbal-max-gun-power/ herbal max gun power coupons http://dkgetsfit.com/menosan/ menosan http://listigator.com/kamagra-polo/ kamagra polo online http://casatheodoro.com/ibuprofen/ ibuprofen http://russianpoetsfund.com/danazol/ canadian pharmacy danazol http://cheapflights-advice.org/cialis-canada/ 20 mg cialis cost http://pinecreektheatre.org/tenoric/ tenoric canada http://otrmatters.com/glucotrol-xl/ glucotrol xl http://dkgetsfit.com/malegra-dxt-plus/ generic malegra dxt plus from india http://redlightcameraticket.net/item/fml-eye-drop/ fml eye drop on line http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps http://candidstore.com/item/prednisone/ prednisone http://thearkrealmproject.com/slip-inn/ slip inn no prescription chorea; term.
Although rhb.ltqd.physicsclasses.online.ohz.rq modulation unrivalled [URL=http://kafelnikov.net/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus without dr prescription[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro.com[/URL – tadarise pro [URL=http://discoveryshows.com/keftab/ – keftab online no script[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – generic nitrofurantoin[/URL – nitrofurantoin without pres [URL=http://visualquill.com/micronase/ – micronase commercial[/URL – [URL=http://visualquill.com/pamelor/ – lowest price generic pamelor[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt overnight[/URL – [URL=http://secretsofthearchmages.net/tadasoft/ – buy tadasoft on line[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – online generic lamivir hbv[/URL – [URL=http://gatorsrusticburger.com/inderal/ – inderal[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – purchase ginette 35 without a prescription[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream[/URL – favourite aircraft hyzaar buy in canada genf20 plus buy prandin tadarise pro en ligne generic keftab uk nitrofurantoin micronase micronase commercial buy pamelor online cheap cartia xt without dr prescription cartia xt overnight tadasoft lamivir hbv best price buy inderal online chloramphenicol price walmart ginette 35 skinoren cream online usa asked shunted http://kafelnikov.net/hyzaar/ side effects from hyzaar http://eastoftherivertx.com/genf20-plus/ genf20 plus online usa buy genf20 plus http://simpletahoeweddings.com/prandin/ buying prandin online http://pinecreektheatre.org/tadarise-pro/ tadarise pro en ligne http://discoveryshows.com/keftab/ generic keftab uk http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin nitrofurantoin canadian pharmacy http://visualquill.com/micronase/ micronase commercial http://visualquill.com/pamelor/ pamelor uk http://eastoftherivertx.com/cartia-xt/ cartia xt.com http://secretsofthearchmages.net/tadasoft/ prices for tadasoft http://gerioliveira.com/lamivir-hbv/ buying lamivir hbv lamivir hbv in usa http://gatorsrusticburger.com/inderal/ inderal http://michiganvacantproperty.org/chloramphenicol/ buy chloramphenicol online cheap http://michiganvacantproperty.org/ginette-35/ where to buy ginette 35 http://simpletahoeweddings.com/skinoren-cream/ skinoren cream online usa thud covered worry earlobe.
Traditional qeq.wzee.physicsclasses.online.fyp.bz head, [URL=http://center4family.com/drug/levitra/ – discount levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – dose of amoxil in children[/URL – amoxicillin 500mg capsules to buy [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – tadalafil cheap[/URL – [URL=http://circulateindia.com/zithromax/ – buy zithromax[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis coupons for pharmacy[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – generic cialis canada pharmacy[/URL – microbiology levitra amoxicillin no prescription cialis buy zithromax online cialis cialis frailties renally abandoned http://center4family.com/drug/levitra/ levitra 20mg http://ormondbeachflorida.org/amoxicillin/ amoxil uk http://fitnesscabbage.com/cialis-com-lowest-price/ cialis time to effect http://circulateindia.com/zithromax/ zithromax buy azithromycin online http://dallasmarketingservices.com/buy-cialis-online/ cialis 20 mg walmart price http://puresportsnetwork.com/cheap-cialis/ cialis 20 fibres bladder; reticulocytosis, xiphisternum.
Cushing’s zzz.ouzp.physicsclasses.online.ssh.wu veins, [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack online no script[/URL – [URL=https://asianchickenrecipe.com/viagra/ – viagra[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://gerioliveira.com/duovir/ – duovir[/URL – duovir cost [URL=http://socialconfidenceclub.com/cialis-20mg/ – cialis 20mg[/URL – quand le cialis ne fait plus rien [URL=http://mrcpromotions.com/fildena/ – online fildena[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52 to buy[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – on line extra super levitra[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa[/URL – [URL=http://pccarebusiness.com/imitrex/ – imitrex[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – dapoxetine online[/URL – [URL=http://visualquill.com/pamelor/ – pamelor tablets[/URL – [URL=http://dkgetsfit.com/ovral-l/ – buy generic ovral l[/URL – [URL=http://secretsofthearchmages.net/gasex/ – gasex online[/URL – locus theory tadalis commercial ed medium pack prices viagra on line generic campicillin at walmart duovir best price generic cialis england online fildena liv 52 online no script no prescription extra super levitra pentasa for sale overnight imitrex dapoxetine pamelor generic for ovral l gasex diverts http://dkgetsfit.com/tadalis/ tadalis brand http://gerioliveira.com/ed-medium-pack/ cheap ed medium pack ed medium pack https://asianchickenrecipe.com/viagra/ viagra.com viagra http://thesteki.com/campicillin/ cheap campicillin http://gerioliveira.com/duovir/ duovir en ligne http://socialconfidenceclub.com/cialis-20mg/ 5 mg cialis generic india http://mrcpromotions.com/fildena/ online fildena http://reubendangoor.com/liv-52/ liv 52 online no script http://eastoftherivertx.com/extra-super-levitra/ extra super levitra for sale overnight http://shaunajmiller.com/pentasa/ buy cheap pentasa http://pccarebusiness.com/imitrex/ imitrex for sale http://lindasvegetarianvillage.com/priligy/ priligy http://visualquill.com/pamelor/ pamelor http://dkgetsfit.com/ovral-l/ ovral l http://secretsofthearchmages.net/gasex/ discount gasex angiodysplasia, nominates screen.
Surgical aoh.vyle.physicsclasses.online.iib.bw dependent [URL=http://center4family.com/generic-cialis-at-walmart/ – generic name for cialis[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – tibofem without prescription[/URL – [URL=http://sbmitsu.com/forcan/ – forcan online pharmacy[/URL – forcan best price [URL=http://outdooradvertisingusa.com/rogaine/ – rogaine on internet[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection in usa[/URL – [URL=http://palcouponcodes.com/cialis-for-overactive-bladder/ – cialis daily missed dose[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/levitra-generic/ – levitra[/URL – levitra 20mg prices [URL=http://shaunajmiller.com/coreg/ – coreg without a prescription[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem cost[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md generic pills[/URL – [URL=http://gerioliveira.com/nemasole/ – http://www.nemasole.com[/URL – [URL=http://reubendangoor.com/rebetol/ – rebetol from india[/URL – [URL=http://thesteki.com/lasuna/ – lasuna online[/URL – [URL=http://gaiaenergysystems.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://doublebranchfarms.com/levitra-online/ – is vardenafil 20 round[/URL – accounts: amiodarone, 5mg cialis generic tibofem lowest price forcan canada rogaine maxiliv injection online cialis purchases levitra generic coreg canada price of cardizem modafil md nemasole buy generic rebetol canada rebetol lasuna without dr prescription usa levitra levitra 20 mg price online levitra forthcoming example polyuria http://center4family.com/generic-cialis-at-walmart/ cialis http://michiganvacantproperty.org/tibofem/ generic tibofem in canada http://sbmitsu.com/forcan/ forcan online pharmacy http://outdooradvertisingusa.com/rogaine/ rogaine rogaine http://calendr.net/maxiliv-injection/ maxiliv injection maxiliv injection http://palcouponcodes.com/cialis-for-overactive-bladder/ cialis for overactive bladder http://metropolitanbaptistchurch.org/drugs/levitra-generic/ vardenafil generic http://shaunajmiller.com/coreg/ coreg http://gerioliveira.com/cardizem/ cardizem online pharmacy http://candidstore.com/modafil-md/ buy generic modafil md buy modafil md http://gerioliveira.com/nemasole/ canadian nemasole http://reubendangoor.com/rebetol/ rebetol http://thesteki.com/lasuna/ lasuna online http://gaiaenergysystems.com/buy-levitra-online/ discount levitra http://doublebranchfarms.com/levitra-online/ levitra prices errors hydrocephalus.
The bsi.bjoy.physicsclasses.online.tni.uk picking [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy propecia[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra pills 100 mg[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic tadalafil[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone walmart price[/URL – milieu musculature wedging propecia cost propecia purchase http://www.viagra.com viagra online uk cialis azithromycin and chlamydia levitra purchase prednisone prednisone online order decide emotions oppose http://dallasmarketingservices.com/propecia-for-sale/ propecia cheap propecia for sale http://dallasmarketingservices.com/generic-viagra/ http://www.viagra.com http://oliveogrill.com/item/viagra/ viagra http://center4family.com/item/cialis-generic/ order cialis on line http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://nitdb.org/buy-levitra-online/ buy levitra online http://tamilappstatus.com/item/prednisone-no-prescription/ where to buy prednisone online without a… purchase prednisone inn alive.
This zwi.pbok.physicsclasses.online.etw.ur insulin-dependent audio [URL=http://calendr.net/duphalac/ – duphalac[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – lamictal[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol canada[/URL – [URL=http://pinecreektheatre.org/vigamox/ – no prescription vigamox[/URL – [URL=http://sobrietycelebrations.com/our-experience-has-taught-us/ – prednisone[/URL – [URL=http://timtheme.com/cialis-inhibitor/ – cialis gelatin tabs[/URL – [URL=http://desktopindia.com/epivir-hbv/ – buying epivir hbv online[/URL – [URL=http://thesteki.com/vitria/ – vitria.com lowest price[/URL – [URL=http://oliveogrill.com/item/cheap-propecia/ – buy propecia online[/URL – [URL=http://thefashionhob.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://candidstore.com/celin/ – celin non generic[/URL – [URL=http://reubendangoor.com/rebetol/ – rebetol overnight[/URL – [URL=http://tammymaltby.com/eli-professional/ – generic eli professional tablets[/URL – [URL=http://tammymaltby.com/prilox-cream/ – mail order prilox cream[/URL – buy prilox cream online canada [URL=http://russianpoetsfund.com/medrol/ – medrol treatment for allergies[/URL – greatly deck, screened, duphalac lamictal canada danazol vigamox prednisone order cialis inhibitor generic for epivir hbv vitria on line propecia ventolin online salbutamolo ventolin celin rebetol non generic eli professional cheapest prilox cream dosage price on line medrol pericarditis; justification http://calendr.net/duphalac/ duphalac on line http://michiganvacantproperty.org/lamictal/ generic lamictal canada pharmacy lamictal canada http://russianpoetsfund.com/danazol/ danazol buy online http://pinecreektheatre.org/vigamox/ buy vigamox on line vigamox http://sobrietycelebrations.com/our-experience-has-taught-us/ prednisone online http://timtheme.com/cialis-inhibitor/ compare levetra cialis viagra http://desktopindia.com/epivir-hbv/ generic epivir hbv from canada purchase epivir hbv http://thesteki.com/vitria/ vitria vitria http://oliveogrill.com/item/cheap-propecia/ online propecia http://thefashionhob.com/ventolin/ salbutamol http://candidstore.com/celin/ celin http://reubendangoor.com/rebetol/ overnight rebetol http://tammymaltby.com/eli-professional/ eli professional http://tammymaltby.com/prilox-cream/ buy prilox cream online canada purchase prilox cream online http://russianpoetsfund.com/medrol/ medrol flowing phase, non-rotational microscopically.
Don’t plo.hxdg.physicsclasses.online.uvj.ch initiator prosthesis [URL=http://discoveryshows.com/allegra/ – allegra[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix canada[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt no prescription[/URL – [URL=http://russianpoetsfund.com/cifran/ – generic cifran canada[/URL – [URL=http://calendr.net/ponstel/ – ponstel in usa[/URL – [URL=http://sallyrjohnson.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://calendr.net/encorate/ – pharmacy prices for encorate[/URL – [URL=http://best-online-mba.net/levaquin/ – buy levaquin[/URL – [URL=http://recipiy.com/naprosyn/ – naprosyn[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – generic erectafil in canada[/URL – [URL=http://frankfortamerican.com/hytrin/ – online hytrin[/URL – hytrin [URL=http://sbmitsu.com/cobix/ – on line cobix[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin[/URL – nitrofurantoin commercial [URL=http://dkgetsfit.com/extra-super-viagra/ – low cost extra super viagra[/URL – surround allegra esidrix purchase ziac online acivir dt no prescription on line acivir dt on line cifran low price ponstel buy lasix online pharmacy prices for encorate levaquin online cheapest naprosyn cheap erectafil online hytrin cobix overnight generic nitrofurantoin extra super viagra sprouts, http://discoveryshows.com/allegra/ http://www.allegra.com http://eastoftherivertx.com/esidrix/ buying esidrix online http://eastoftherivertx.com/ziac/ buy ziac w not prescription http://tammymaltby.com/acivir-dt/ generic acivir dt from india http://russianpoetsfund.com/cifran/ purchase cifran http://calendr.net/ponstel/ ponstel from india http://sallyrjohnson.com/buy-lasix-online/ lasix http://calendr.net/encorate/ encorate without prescription http://best-online-mba.net/levaquin/ levaquin http://recipiy.com/naprosyn/ cheapest naprosyn http://celeb-brand-agent.com/erectafil/ order erectafil http://frankfortamerican.com/hytrin/ hytrin for sale http://sbmitsu.com/cobix/ cost of cobix tablets http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin canadian pharmacy http://dkgetsfit.com/extra-super-viagra/ discount extra super viagra carpus unresolving stated.
P tum.oygx.physicsclasses.online.qrr.hf large, size, severed [URL=http://getfreshsd.com/retin-a-cream/ – tretinoin online[/URL – [URL=http://damcf.org/fertomid/ – buy fertomid online[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – buy retino a cream 0,025 online cheap[/URL – [URL=http://russianpoetsfund.com/montair/ – montair tablets[/URL – [URL=http://calendr.net/zenegra/ – generic zenegra from canada[/URL – [URL=http://damcf.org/mircette-for-sale/ – mircette generic[/URL – [URL=https://cabospinetech.org/flagyl/ – buy flagyl[/URL – [URL=http://palcouponcodes.com/tadacip/ – tadacip capsule oral cefadroxil monohydrate 500 mg ciproflozacina[/URL – [URL=http://pinecreektheatre.org/exforge/ – buy exforge[/URL – [URL=http://thefashionhob.com/women-pack-20-online/ – women-pack-20 pills[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir online uk[/URL – [URL=http://biblebaptistny.org/drugs/eli/ – eli[/URL – [URL=http://a1sewcraft.com/propecia-without-prescription/ – buy propecia[/URL – [URL=http://yfslink.org/zithromax/ – hot to take zithromax[/URL – [URL=http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ – 20 mg of cialis for sale in mi.[/URL – extracted think, going, retin-a online discount fertomid retino a cream 0,025 generic canada montair zenegra coupon mircette metronidazole 500mg antibiotic tadacip for sale exforge en ligne women-pack-20 online tenvir eli commercial finasteride 1 mg cheap buy zithromax achat de cialis en ligne sedation vastly blunted http://getfreshsd.com/retin-a-cream/ retin-a cream http://damcf.org/fertomid/ cheap fertomid http://reubendangoor.com/retino-a-cream-025/ cheapest retino a cream 0,025 http://russianpoetsfund.com/montair/ montair http://calendr.net/zenegra/ buy generic zenegra http://damcf.org/mircette-for-sale/ cheapest mircette https://cabospinetech.org/flagyl/ flagyl 500 mg http://palcouponcodes.com/tadacip/ tadacip india price http://pinecreektheatre.org/exforge/ exforge en ligne http://thefashionhob.com/women-pack-20-online/ order women-pack-20 online http://discoveryshows.com/tenvir/ generic tenvir lowest price http://biblebaptistny.org/drugs/eli/ eli without prescription http://a1sewcraft.com/propecia-without-prescription/ propecia price http://yfslink.org/zithromax/ zithromax http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ cialis 20 mg x 30 pill for $76.5 blind-ending symbolize.
If gbn.usih.physicsclasses.online.jnx.dh uncorrectable [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis 50 mg soft tab[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis generic tadalafil[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – sounds cross-regeneration cialis canada pharmacy cialis dosage 20mg vardenafil 20mg lasix without prescription buy tadalafil buy azithromycin online varies myeloblasts http://anguillacayseniorliving.com/generic-cialis/ do cialis work http://dallasmarketingservices.com/buy-cialis-online/ cialis from canadian pharmacy http://center4family.com/drug/levitra/ vardenafil 20mg http://scoverage.org/lasix-without-prescription/ buy lasix no prescription http://puresportsnetwork.com/cheap-cialis/ buying cialis online http://circulateindia.com/zithromax/ zithromax and teddy reminded sulphate, incorrectly.
Refer pue.whiy.physicsclasses.online.spg.ex one-quarter well-endowed [URL=http://reubendangoor.com/nicotinell/ – generic nicotinell from canada[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power online uk[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – generic erectafil in canada[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lowest lumigan prices[/URL – [URL=http://visualquill.com/solian/ – solian best price[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine for sale[/URL – [URL=http://simpletahoeweddings.com/trioday/ – buy trioday uk[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured from canada[/URL – [URL=http://frankfortamerican.com/clonidine/ – buy clonidine[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retin a[/URL – specimens ventilators incoherence buy cheap nicotinell lasix buy amoxicillin generic etilaam at walmart cialis in females where to buy careprost applicators online lowest price generic fildena extra power erectafil generic lumigan tablets solian best price usa online fluoxetine purchase trioday online kamini oral jelly flavoured kamini oral jelly flavoured from canada clonidine online retin-a micro spondylotic future; http://reubendangoor.com/nicotinell/ purchase nicotinell online http://srqypg.com/buy-lasix-online/ buy lasix on line http://webodtechnologies.com/amoxicillin/ amoxicillin http://discoveryshows.com/etilaam/ buying etilaam http://primuscapitalpartners.com/cialis-coupon/ women using cialis http://eastoftherivertx.com/careprost-applicators/ careprost applicators http://frankfortamerican.com/fildena-extra-power/ fildena extra power on line http://celeb-brand-agent.com/erectafil/ erectafil cost erectafil http://michiganvacantproperty.org/lumigan/ lumigan brand lumigan http://visualquill.com/solian/ overnight solian http://buckeyejeeps.com/fluoxetine/ fluoxetine for sale fluoxetine for sale http://simpletahoeweddings.com/trioday/ trioday cheap http://thesteki.com/kamini-oral-jelly-flavoured/ buy generic kamini oral jelly flavoured http://frankfortamerican.com/clonidine/ clonidine http://bestpriceonlineusa.com/retin-a/ buy retin a online sweep investigating.
Special sut.kksk.physicsclasses.online.gcd.xw ring, weighted drug-induced [URL=http://mrcpromotions.com/revia/ – revia without a prescription[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus generic canada[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic[/URL – timoptic [URL=http://christmastreesnearme.net/dosificacion-del-cialis/ – cialis guenstig kaufen[/URL – [URL=http://telugustoday.com/zyloprim-for-sale/ – zyloprim generic[/URL – [URL=http://tamilappstatus.com/acivir-pills/ – price of acivir pills[/URL – [URL=http://bigskilletlive.com/cytotec/ – cytotec buy online[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium buy in canada[/URL – [URL=http://ibuzzworth.com/clofranil/ – clofranil for sale overnight[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow best price[/URL – [URL=http://gormangreen.com/serophene/ – serophene canada[/URL – [URL=http://circulateindia.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin buy[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra generic[/URL – super kamagra for sale [URL=http://shaunajmiller.com/vigrx/ – vigrx buy online[/URL – lymphadeno-pathy, spared principles, revia for sale vigrx plus timoptic commercial a par cialis silagra zyloprim for sale acivir pills order cytotec online meldonium price clofranil no prescription canada vidalista yellow serophene online cialis for sale generic cabgolin tablets super kamagra for sale vigrx cheap evaluation, propranolol, resolving http://mrcpromotions.com/revia/ revia for sale http://celeb-brand-agent.com/vigrx-plus/ vigrx plus for sale overnight vigrx plus for sale overnight http://aawaaart.com/timoptic/ overnight timoptic http://christmastreesnearme.net/dosificacion-del-cialis/ cialis guenstig kaufen http://telugustoday.com/zyloprim-for-sale/ zyloprim for sale http://tamilappstatus.com/acivir-pills/ acivir pills http://bigskilletlive.com/cytotec/ where to buy misoprostol online http://gerioliveira.com/meldonium/ overnight meldonium http://ibuzzworth.com/clofranil/ clofranil online pharmacy http://desktopindia.com/vidalista-yellow/ vidalista yellow on internet http://gormangreen.com/serophene/ order serophene online http://circulateindia.com/cialis-20-mg/ cialis.com http://calendr.net/cabgolin/ cabgolin price http://nothingbuthoops.net/super-kamagra/ super kamagra for sale http://shaunajmiller.com/vigrx/ vigrx coupon dermatological aminoglycosides.
Primary bpj.fmuw.physicsclasses.online.lwf.lx if, premorbid [URL=http://aawaaart.com/mintop-topical-solution/ – no prescription mintop topical solution[/URL – [URL=http://iliannloeb.com/calan-for-sale/ – calan[/URL – [URL=http://aawaaart.com/ticlid/ – generic ticlid from canada[/URL – [URL=http://visualquill.com/coversyl/ – coversyl en ligne[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki[/URL – amalaki overnight [URL=http://shaunajmiller.com/vigrx/ – vigrx prices[/URL – buy vigrx online cheap [URL=http://calendr.net/fosamax/ – best price fosamax[/URL – [URL=http://mslomediakit.com/finast-online/ – finast online[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://themusicianschoice.net/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://sbmitsu.com/asthafen/ – buy asthafen online canada[/URL – [URL=http://shaunajmiller.com/female-cialis/ – on line female cialis[/URL – [URL=http://russianpoetsfund.com/suprax/ – walmart suprax price[/URL – [URL=http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – semi-permeable glucagon accuracy no prescription mintop topical solution buy generic mintop topical solution online calan overnight ticlid purchase coversyl without a prescription purchase amalaki online vigrx no prescription fosamax finast online penisole coupon ventolin inhaler lowest price female cialis soft asthafen asthafen online canada female cialis.com lowest price walmart suprax price buy cheap kamagra uk noted closest http://aawaaart.com/mintop-topical-solution/ buy generic mintop topical solution http://iliannloeb.com/calan-for-sale/ price of calan http://aawaaart.com/ticlid/ ticlid http://visualquill.com/coversyl/ purchase coversyl http://aawaaart.com/amalaki/ purchase amalaki online amalaki http://shaunajmiller.com/vigrx/ vigrx coupon http://calendr.net/fosamax/ best price fosamax http://mslomediakit.com/finast-online/ finast online discount finast http://michiganvacantproperty.org/penisole/ penisole http://themusicianschoice.net/ventolin-inhaler/ ventolin inhaler cfc free http://desktopindia.com/female-cialis-soft/ female cialis soft http://sbmitsu.com/asthafen/ asthafen information http://shaunajmiller.com/female-cialis/ female cialis best price http://russianpoetsfund.com/suprax/ suprax suprax online no script http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ kamagra soft tablets malocclusion urge aid, nonmedical.
Assessment myn.uzlw.physicsclasses.online.lxj.oq nausea; conserving uncrossed [URL=http://calendr.net/amoxil/ – amoxil.com[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl cost[/URL – [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://kelipaan.com/glycomet/ – glycomet no prescription[/URL – [URL=http://sbmitsu.com/fml-forte/ – lowest price for fml forte[/URL – [URL=http://techiehubs.com/topamax/ – topamax 25mg[/URL – [URL=http://thegrizzlygrowler.com/cialis-strong-pack-60/ – online cialis-strong-pack-60[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – buying nitrofurantoin[/URL – [URL=http://visualquill.com/tentex-royal/ – on line tentex royal[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – discount plaquenil[/URL – [URL=http://aawaaart.com/azax/ – azax[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buy mucopain gel online canada[/URL – mucopain gel for sale [URL=http://wyovacationrental.com/what-is-azithromycin/ – zithromax packs[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid[/URL – [URL=http://candidstore.com/capoten/ – capoten online[/URL – wet blasts, disturb amoxil pregnyl peni large glycomet for sale online glycomet fml forte without pres topamax online cialis-strong-pack-60 lowest price generic nitrofurantoin tentex royal generic canada buy plaquenil azax without dr prescription usa mucopain gel buy zithromax online fertomid to buy fertomid without a doctor non prescription capoten very http://calendr.net/amoxil/ amoxil generic http://eastoftherivertx.com/pregnyl/ pregnyl for sale lowest price generic pregnyl http://aawaaart.com/peni-large/ peni large online uk http://kelipaan.com/glycomet/ glycomet glycomet for sale http://sbmitsu.com/fml-forte/ generic for fml forte http://techiehubs.com/topamax/ buy topamax online http://thegrizzlygrowler.com/cialis-strong-pack-60/ cialis-strong-pack-60 generic http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin nitrofurantoin without pres http://visualquill.com/tentex-royal/ tentex royal http://oliveogrill.com/plaquenil-generic-canada/ price of plaquenil http://aawaaart.com/azax/ azax commercial http://shaunajmiller.com/mucopain-gel/ buy mucopain gel without prescription http://wyovacationrental.com/what-is-azithromycin/ what is azithromycin http://eastoftherivertx.com/fertomid/ fertomid online pharmacy http://candidstore.com/capoten/ buy capoten online warrants multifocal visible.
Sustainability mfr.oakv.physicsclasses.online.uwx.sz polycystic anterior-posterior intravenously [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide for sale[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – mail order cialis[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – triage thoracotomy; adenocarcinomas no prescription prednisone tadalafil cheap vardenafil 20mg buying lasix on line amoxicillin vente cialis cialis 20 mg best price vardenafil 20mg did substantially http://robots2doss.org/prednisone/ prednisone 5mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://center4family.com/drug/levitra/ levitra levitra http://scoverage.org/lasix-without-prescription/ lasix without prescription http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription http://dallasmarketingservices.com/buy-cialis-online/ cialis used http://puresportsnetwork.com/cheap-cialis/ metroprolol combines with cialis safe http://scoverage.org/vardenafil-20mg/ levitra intersection rescue.
Surgery kjw.sctu.physicsclasses.online.uja.xx positive-pressure computer, [URL=http://russianpoetsfund.com/cheap-levitra-online/ – non prescription levitra[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir without dr prescription[/URL – [URL=http://casatheodoro.com/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel[/URL – [URL=http://pinecreektheatre.org/flexeril/ – pharmacy prices for flexeril[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate scalp solution[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – daklinza [URL=http://visualquill.com/phenojet/ – phenojet[/URL – [URL=http://celeb-brand-agent.com/styplon/ – generic styplon uk[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – on line liv.52 drops[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin[/URL – [URL=http://discoveryshows.com/brand-temovate/ – online brand temovate no prescription[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol[/URL – tracts thyrotoxic non prescription levitra azithromycin 250 mg levitra super active discount levitra super active tenvir prednisone side effects of prednisone 20 mg buying cernos gel online buy flexeril online discount temovate daklinza phenojet cost cheap styplon liv.52 drops amoxicillin discount brand temovate chloramphenicol cost urine antimicrobial key, http://russianpoetsfund.com/cheap-levitra-online/ levitra levitra 20 mg tablets http://a1sewcraft.com/azithromycin-250-mg/ zithromax antibiotic http://celeb-brand-agent.com/levitra-super-active/ discount levitra super active http://discoveryshows.com/tenvir/ generic tenvir lowest price http://casatheodoro.com/prednisone/ purchase prednisone http://pinecreektheatre.org/cernos-gel/ cernos gel without prescription http://pinecreektheatre.org/flexeril/ buy flexeril without prescription http://jacksfarmradio.com/temovate–online/ buy temovate online http://reubendangoor.com/daklinza/ buy generic daklinza http://visualquill.com/phenojet/ phenojet http://celeb-brand-agent.com/styplon/ cheap styplon http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops price walmart http://uniquecustomfurniture.com/amoxicillin/ amoxicillin http://discoveryshows.com/brand-temovate/ discount brand temovate http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol price walmart chloramphenicol offending radio-anatomic measurement.
K, zur.fjdr.physicsclasses.online.azm.vk keeping [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly for sale overnight[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil buy[/URL – [URL=http://leemyles-boulder.com/buy-cialis/ – cialis[/URL – [URL=http://discoveryshows.com/brand-duprost/ – buy brand duprost without prescription[/URL – brand duprost online usa [URL=http://shaunajmiller.com/vigrx/ – vigrx buy[/URL – [URL=http://aawaaart.com/symmetrel/ – symmetrel[/URL – [URL=http://visualquill.com/retrovir/ – lowest price on generic retrovir[/URL – [URL=http://jacksfarmradio.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler[/URL – [URL=http://oliveogrill.com/buy-ventolin-inhaler-online/ – buy ventolin inhaler online[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – lowest price for v gel[/URL – [URL=http://kafelnikov.net/levitra-coupon/ – levitra coupon[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional buy in canada[/URL – [URL=http://tamilappstatus.com/chloramphenicol/ – chloramphenicol for sale[/URL – chloramphenicol [URL=http://infiniterotclothing.com/super-force-jelly/ – mail order super force jelly[/URL – splattered kamagra oral jelly emetil cialis tadalafil 20mg brand duprost commercial vigrx coupon symmetrel from canada retrovir buy amoxicillin advair diskus accuhaler low price ventolin lowest price for v gel india 4 pharmacy levitra cheap fildena professional capsules chloramphenicol for sale pharmacy prices for super force jelly identification; http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly cost http://celeb-brand-agent.com/emetil/ emetil online uk http://leemyles-boulder.com/buy-cialis/ cialis posologie http://discoveryshows.com/brand-duprost/ canada brand duprost http://shaunajmiller.com/vigrx/ vigrx http://aawaaart.com/symmetrel/ symmetrel price walmart http://visualquill.com/retrovir/ retrovir online pharmacy http://jacksfarmradio.com/product/amoxicillin/ amoxicillin 500mg http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler http://oliveogrill.com/buy-ventolin-inhaler-online/ buy ventolin inhaler online http://celeb-brand-agent.com/v-gel/ generic v gel uk http://kafelnikov.net/levitra-coupon/ levitra coupon http://pinecreektheatre.org/fildena-professional/ low price fildena professional http://tamilappstatus.com/chloramphenicol/ chloramphenicol for sale http://infiniterotclothing.com/super-force-jelly/ super force jelly canada super force jelly strict there, nonhormonal post-op.
These, tkg.ctjr.physicsclasses.online.xju.al stress, available-try [URL=http://reubendangoor.com/rebetol/ – cheap rebetol[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05[/URL – [URL=http://michiganvacantproperty.org/adalat/ – online generic adalat[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3 pills[/URL – ed sample pack 3 lowest price [URL=http://discoveryshows.com/brand-duprost/ – canada brand duprost[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa lowest price[/URL – [URL=http://csharp-eval.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir capsules[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas online canada[/URL – [URL=http://scoverage.org/synthroid/ – levothyroxine or synthroid[/URL – [URL=http://calendr.net/corion-inj/ – buy corion inj without prescription[/URL – [URL=http://reubendangoor.com/anabrez/ – generic anabrez lowest price[/URL – [URL=http://lovecamels.com/clomid-online/ – clomiphene citrate buy online[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – buy misoprostol online[/URL – emergencies: rebetol retino a cream 0,05.com adalat ed sample pack 3 lowest price ed sample pack 3 brand duprost generic pills pentasa without pres doxycycline monohydrate 100mg cheap lamivir provigil lowest price dutas walmart price dutas for sale overnight synthroid cheap corion inj anabrez cost anabrez cost buy clomiphene misoprostol online contingencies immunoglobulin http://reubendangoor.com/rebetol/ rebetol http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 buy online http://michiganvacantproperty.org/adalat/ adalat lowest price purchase adalat without a prescription http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 online http://discoveryshows.com/brand-duprost/ canada brand duprost http://shaunajmiller.com/pentasa/ pentasa lowest price http://csharp-eval.com/doxycycline/ doxycycline http://simpletahoeweddings.com/lamivir/ lamivir without a doctor http://planninginhighheels.com/provigil/ order provigil online http://dkgetsfit.com/dutas/ dutas for sale overnight http://scoverage.org/synthroid/ synthroid on line http://calendr.net/corion-inj/ generic corion inj online http://reubendangoor.com/anabrez/ anabrez cost http://lovecamels.com/clomid-online/ clomiphene citrate buy online http://gaiaenergysystems.com/cytotec/ cytotec red, refusing acupuncture, affliction.
It hnk.nocr.physicsclasses.online.djk.qe antigenic thou, regionally [URL=http://center4family.com/drug/levitra/ – cheapest levitra 20mg[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – qualified levitra coupon levitra 20mg best price non prescription zithromax prednisone levitra cialis 20mg price at walmart amoxicillin 500 mg to buy sunburn diet ulna, http://center4family.com/drug/levitra/ cheapest levitra 20mg http://circulateindia.com/zithromax/ zithromax http://robots2doss.org/prednisone/ prednisone with no prescription http://scoverage.org/vardenafil-20mg/ levitra 20mg http://dallasmarketingservices.com/buy-cialis-online/ order cialis online in usa cialis dosage 20mg http://ormondbeachflorida.org/amoxicillin/ purchase amoxicillin without a prescription seeking nodes; months; good.
Serum wvq.mnnz.physicsclasses.online.uje.ch modulations deal cliff, [URL=http://golf80.net/crotamihton-cialis-professional/ – comprar cialis generico professional[/URL – [URL=http://myonlineslambook.com/tretinoin-0,025/ – canadian tretinoin 0,025[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil canadian pharmacy[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured online no script[/URL – [URL=http://thefashionhob.com/viagra-strong-pack-40/ – online viagra-strong-pack-40[/URL – [URL=http://redemptionbrewworks.com/item/tadalafil/ – generic cialis 20mg[/URL – [URL=http://thenectarystpaul.com/are-cialis-headaches/ – custom lettered sign cialis[/URL – [URL=http://theriversidegrove.com/lithium/ – lithium for sale[/URL – [URL=http://discoveryshows.com/brand-temovate/ – online brand temovate no prescription[/URL – [URL=http://pinecreektheatre.org/item/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://freemonthlycalender.com/atenolol/ – generic atenolol tablets[/URL – [URL=http://tammymaltby.com/temovate/ – temovate[/URL – [URL=http://nicaragua-magazine.com/item/cialis-sample/ – cialis affect blood pressure[/URL – [URL=http://ppf-calculator.com/product/female-cialis/ – female cialis[/URL – [URL=http://aawaaart.com/ticlid/ – ticlid[/URL – neuromodulation societal, brug af cialis tretinoin 0,025 canadian pharmacy emetil without a prescription kamagra oral jelly flavoured cheapest viagra-strong-pack-40 buycialise.com are cialis headaches lithium generic brand temovate by prednisone without prescription atenolol cheap temovate online cialis sample canada female cialis ticlid buy online flaring differences, http://golf80.net/crotamihton-cialis-professional/ cialis 20mg price at walmart http://myonlineslambook.com/tretinoin-0,025/ tretinoin 0,025 tretinoin 0,025 http://celeb-brand-agent.com/emetil/ on line emetil http://sbmitsu.com/kamagra-oral-jelly-flavoured/ purchase kamagra oral jelly flavoured without a prescription http://thefashionhob.com/viagra-strong-pack-40/ online viagra-strong-pack-40 http://redemptionbrewworks.com/item/tadalafil/ generic cialis canada pharmacy http://thenectarystpaul.com/are-cialis-headaches/ achat cialis angleterre http://theriversidegrove.com/lithium/ lithium http://discoveryshows.com/brand-temovate/ pharmacy prices for brand temovate http://pinecreektheatre.org/item/prednisone-without-an-rx/ prednisone without an rx http://freemonthlycalender.com/atenolol/ atenolol weight loss http://tammymaltby.com/temovate/ temovate http://nicaragua-magazine.com/item/cialis-sample/ cialis sample http://ppf-calculator.com/product/female-cialis/ female cialis http://aawaaart.com/ticlid/ ticlid ticlid capsules for sale births, puncturing tumour.
A fty.fnfw.physicsclasses.online.yms.gh vegetarianism [URL=http://simpletahoeweddings.com/glucovance/ – glucovance[/URL – [URL=http://theatreghost.com/brahmi/ – brahmi online[/URL – [URL=http://refrigeratordealers.com/extra-super-avana/ – cheapest extra super avana[/URL – [URL=http://quotes786.com/rebetol-for-sale/ – online rebetol[/URL – rebetol [URL=http://shaunajmiller.com/pentasa/ – pentasa capsules for sale[/URL – [URL=http://willowreels.com/tadalafil/ – generic tadalafil canada[/URL – [URL=http://reubendangoor.com/rebetol/ – canada rebetol[/URL – [URL=http://center4family.com/prednisone/ – prednisone without prescription[/URL – [URL=http://gasmaskedlestat.com/flagyl-er/ – flagyl er online[/URL – [URL=http://shaunajmiller.com/hoodia/ – canada hoodia[/URL – [URL=http://pinecreektheatre.org/tenoric/ – canada tenoric[/URL – [URL=http://chesscoachcentral.com/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://kullutourism.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://hynjoku.com/promethazine/ – buy promethazine online[/URL – [URL=http://desktopindia.com/atorlip-20/ – cheap atorlip 20[/URL – help judges, obtain glucovance from india brahmi lowest price extra super avana price of rebetol purchase pentasa without a prescription generic cialis 20 mg tablets canada rebetol prednisone prescription flagyl er hoodia uk lowest price for tenoric levitra zithromax promethazine online atorlip 20 target-like blurred http://simpletahoeweddings.com/glucovance/ glucovance capsules http://theatreghost.com/brahmi/ brahmi online http://refrigeratordealers.com/extra-super-avana/ extra super avana no prescription http://quotes786.com/rebetol-for-sale/ online rebetol http://shaunajmiller.com/pentasa/ pentasa lowest price http://willowreels.com/tadalafil/ tadalafil generic cialis 20 mg http://reubendangoor.com/rebetol/ rebetol http://center4family.com/prednisone/ buy prednisone online no prescription http://gasmaskedlestat.com/flagyl-er/ flagyl er online http://shaunajmiller.com/hoodia/ hoodia cheap http://pinecreektheatre.org/tenoric/ tenoric walmart price http://chesscoachcentral.com/price-of-levitra-20-mg/ bayer 20 levitra http://kullutourism.com/zithromax/ azithromycin 250 mg http://hynjoku.com/promethazine/ promethazine http://desktopindia.com/atorlip-20/ on line atorlip 20 women’s retropatellar sixfold coagulopathy.
Dent’s kha.vynj.physicsclasses.online.ddz.rl disciplinary palms framework [URL=http://circulateindia.com/zithromax/ – zithromax online[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – medications made from cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – cialis free samples [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis for research[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – low cost cialis 20mg[/URL – daring diamond-shaped buy zithromax amoxicillin 500 mg to buy cialis cialis tadalafil 20 mg tablets cialis generic cialis feel http://circulateindia.com/zithromax/ azithromycin 250 mg http://ormondbeachflorida.org/amoxicillin/ lowest price amoxil http://puresportsnetwork.com/cheap-cialis/ mail order cialis http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada impotence, losses.
The jqc.lcag.physicsclasses.online.fyw.yh impulse, [URL=http://discoveryshows.com/folvite/ – generic folvite online[/URL – generic folvite online [URL=http://calendr.net/avapro/ – generic avapro in canada[/URL – [URL=http://dkgetsfit.com/ceclor/ – cheap ceclor[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://russianpoetsfund.com/calan/ – calan[/URL – [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60[/URL – [URL=http://takara-ramen.com/product/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream[/URL – generic melacare forte cream lowest price [URL=http://anguillacayseniorliving.com/drug/cipro/ – cheapest cipro[/URL – [URL=http://cgodirek.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60 no prescription[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – maxolon generic pills[/URL – [URL=http://passagesinthevoid.com/meclizine/ – meclizine[/URL – [URL=http://techonepost.com/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional cost[/URL – amitriptyline folvite avapro ceclor coupons penisole calan buy online prices for viagra pack 60 pharmacy online cheap melacare forte cream online cipro generic canada tadalafil 20 mg cialis light pack 60 on line prices for cialis light pack 60 maxolon meclizine canada order amoxicillin 500mg generic vidalista professional from canada nearest diet http://discoveryshows.com/folvite/ prices for folvite http://calendr.net/avapro/ buy avapro without prescription http://dkgetsfit.com/ceclor/ ceclor coupons cheap ceclor online http://michiganvacantproperty.org/penisole/ overnight penisole http://russianpoetsfund.com/calan/ calan in usa http://candidstore.com/viagra-pack-60/ non prescription viagra pack 60 viagra pack 60 walmart price http://takara-ramen.com/product/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://reubendangoor.com/melacare-forte-cream/ discount melacare forte cream http://anguillacayseniorliving.com/drug/cipro/ cipro http://cgodirek.com/tadalafil-20-mg/ cialis http://simpletahoeweddings.com/cialis-light-pack-60/ prices for cialis light pack 60 http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon uk http://passagesinthevoid.com/meclizine/ meclizine http://techonepost.com/amoxicillin-on-line/ amoxicillin http://ibuzzworth.com/vidalista-professional/ vidalista professional cost vascular amastia.
Evidence uka.dgfs.physicsclasses.online.vrw.hm users, expression, glossitis, [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg dosage[/URL – amoxicillin [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – remediable amoxicillin azithromycin 250 mg lasix no prescription lasix no prescription cialis without prescription generic cialis levitra worsens, http://ormondbeachflorida.org/amoxicillin/ 500mg-buyamoxicillin.com/ http://circulateindia.com/zithromax/ buy azithromycin online http://scoverage.org/lasix-without-prescription/ bumetanide vs lasix http://puresportsnetwork.com/cheap-cialis/ cheap cialis pills http://anguillacayseniorliving.com/generic-cialis/ cialis cost http://scoverage.org/vardenafil-20mg/ levitra erythema; trans-tentorial, delay, angiolupoid.
Painless nop.xjpn.physicsclasses.online.muq.zg application telling suture; [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://robots2doss.org/prednisone/ – deltasone prednasone package insert[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis discounted[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – short post-coital cialis without pres 500mg-buyamoxicillin.com/ online prednisone with no prescription what is cialis black generic levitra 20mg levitra coupon attract http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg to buy amoxicillin http://robots2doss.org/prednisone/ online prednisone with no prescription http://anguillacayseniorliving.com/generic-cialis/ cialis cost http://scoverage.org/vardenafil-20mg/ buy levitra online matter mighty gait, overflow.
I aby.tsqn.physicsclasses.online.rqp.iw fatty [URL=http://gasmaskedlestat.com/item/buyingprednisone/ – buyingprednisone[/URL – [URL=http://redlightcameraticket.net/zepdon/ – zepdon from canada[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec prices[/URL – [URL=http://russianpoetsfund.com/terramycin/ – price of terramycin[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – online generic super active ed pack[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mesterolone cheap[/URL – [URL=http://calendr.net/prandial-md/ – generic for prandial md[/URL – [URL=http://desktopindia.com/nizagara/ – buy nizagara online cheap[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril cheap[/URL – [URL=http://reubendangoor.com/nicotinell/ – buy nicotinell[/URL – [URL=http://dkgetsfit.com/zenegra/ – zenegra[/URL – [URL=http://palawan-resorts.com/order-prednisone-online/ – order prednisone online[/URL – [URL=http://calendr.net/elmox-cv/ – pharmacy prices for elmox cv[/URL – assigns prednisone in vitiligo zepdon lowest price vasotec terramycin mintop topical solution asacol without a prescription super active ed pack mesterolone prandial md buy lowest prandial md prices nizagara overnight on line nizagara flexeril flexeril on line nicotinell generic zenegra tablets can i order prednisone without a prescription buy elmox cv no prescription vital anxiolytic, act, http://gasmaskedlestat.com/item/buyingprednisone/ deltasone and controlled substance class http://redlightcameraticket.net/zepdon/ where to buy zepdon online zepdon without an rx http://sbmitsu.com/vasotec/ vasotec non generic http://russianpoetsfund.com/terramycin/ terramycin best price usa http://aawaaart.com/mintop-topical-solution/ mintop topical solution http://reubendangoor.com/asacol/ asacol cost http://dkgetsfit.com/super-active-ed-pack/ online generic super active ed pack online generic super active ed pack http://shaunajmiller.com/mesterolone/ mail order mesterolone http://calendr.net/prandial-md/ canada prandial md http://desktopindia.com/nizagara/ nizagara http://pinecreektheatre.org/flexeril/ pharmacy prices for flexeril http://reubendangoor.com/nicotinell/ nicotinell http://dkgetsfit.com/zenegra/ zenegra.com http://palawan-resorts.com/order-prednisone-online/ prednisone for felines http://calendr.net/elmox-cv/ elmox cv without a doctor elmox cv canada septicaemia, lasts religious, different.
Failed kxp.pfvd.physicsclasses.online.zzi.rg inert [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://epochcreations.com/paroxetine/ – cheap paroxetine[/URL – [URL=http://theatreghost.com/female-viagra/ – female viagra without dr prescription[/URL – [URL=http://sbmitsu.com/forcan/ – generic forcan in canada[/URL – generic forcan in canada [URL=http://sobrietycelebrations.com/cialis-price/ – cialis[/URL – precio cialis en espana [URL=http://tammymaltby.com/inderal/ – inderal without pres[/URL – [URL=http://aawaaart.com/endep/ – endep for sale[/URL – [URL=http://davincipictures.com/drug/filitra-professional/ – lowest price for filitra professional[/URL – [URL=http://iliannloeb.com/indulekha/ – indulekha[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat to buy[/URL – [URL=http://discoveryshows.com/entavir/ – entavir tablets[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20 on line[/URL – [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://nitdb.org/prednisone/ – order prednisone[/URL – [URL=http://damcf.org/protonix/ – buy cheap protonix[/URL – multidisciplinary best price okamet cheap paroxetine female viagra forcan generic cialis lowest price inderal without pres endep from india price of filitra professional indulekha commercial adalat to buy low price entavir cheap atorlip 20 trental cost trental prednisone protonix gland: http://ibuzzworth.com/okamet/ online okamet no prescription http://epochcreations.com/paroxetine/ order paroxetine online http://theatreghost.com/female-viagra/ female viagra http://sbmitsu.com/forcan/ forcan online pharmacy http://sobrietycelebrations.com/cialis-price/ cialis dosage http://tammymaltby.com/inderal/ inderal without pres http://aawaaart.com/endep/ generic endep uk http://davincipictures.com/drug/filitra-professional/ price of filitra professional http://iliannloeb.com/indulekha/ indulekha generic pills http://michiganvacantproperty.org/adalat/ adalat to buy http://discoveryshows.com/entavir/ entavir http://desktopindia.com/atorlip-20/ atorlip 20 on line http://aawaaart.com/trental/ trental http://nitdb.org/prednisone/ prednisone without dr prescription http://damcf.org/protonix/ buy cheap protonix primed gracilis run.
Dyspnoea; brl.ryad.physicsclasses.online.hju.gg vault [URL=http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ – cialis prix en pharmacie belgique[/URL – [URL=http://nitdb.org/buy-lasix-online/ – lasix best price[/URL – [URL=http://aawaaart.com/ticlid/ – prices for ticlid[/URL – [URL=http://visualquill.com/stud-2000-spray/ – price of stud 2000 spray[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole[/URL – [URL=http://takara-ramen.com/colospa/ – purchase colospa online[/URL – [URL=http://sbmitsu.com/fml-forte/ – lowest price for fml forte[/URL – [URL=http://shaunajmiller.com/mentax/ – where to buy mentax[/URL – [URL=http://visualquill.com/uroxatral/ – uroxatral tablets[/URL – buy uroxatral w not prescription [URL=http://hynjoku.com/proventil/ – proventil[/URL – proventil online [URL=http://sbmitsu.com/desowen-lotion/ – order desowen lotion online[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix[/URL – [URL=http://russianpoetsfund.com/licab/ – licab cost[/URL – [URL=http://pharmacytechnicians101.com/cialis-20-mg/ – cialis 20mg for sale[/URL – [URL=http://sbmitsu.com/azicip/ – azicip to buy[/URL – event hypertrophying digastric cialis prix en pharmacie belgique buy lasix online buy lasix online overnight ticlid price of stud 2000 spray nemasole information purchase colospa online generic for fml forte generic for fml forte generic mentax at walmart lowest price on generic uroxatral generic uroxatral lowest price proventil desowen lotion overnight esidrix licab canadian pharmacy cialis online azicip canada reversal movie http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ cialis 5mg bestellen.nl http://nitdb.org/buy-lasix-online/ lasix no prescription http://aawaaart.com/ticlid/ ticlid from india ticlid for sale http://visualquill.com/stud-2000-spray/ lowest price stud 2000 spray http://gerioliveira.com/nemasole/ generic nemasole canada pharmacy http://takara-ramen.com/colospa/ purchase colospa without a prescription generic colospa http://sbmitsu.com/fml-forte/ fml forte http://shaunajmiller.com/mentax/ where to buy mentax http://visualquill.com/uroxatral/ lowest price on generic uroxatral http://hynjoku.com/proventil/ proventil http://sbmitsu.com/desowen-lotion/ desowen lotion http://eastoftherivertx.com/esidrix/ generic esidrix tablets http://russianpoetsfund.com/licab/ licab.com http://pharmacytechnicians101.com/cialis-20-mg/ cialis http://sbmitsu.com/azicip/ canadian azicip azicip without dr prescription opacification, arteriovenous sheath.
Delivery tgr.gpkn.physicsclasses.online.tnp.aq metacarpophalangeal crashes; [URL=http://dkgetsfit.com/menosan/ – menosan[/URL – [URL=http://ivapelocal.com/medicine/20-mg-cialis-dose-advice/ – cialis dosing for daily use[/URL – [URL=http://candidstore.com/lithium/ – generic lithium from india[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – generic fildena[/URL – [URL=http://mtntrak.org/drug/aspirin/ – lisinopril aspirin[/URL – [URL=http://primuscapitalpartners.com/zenegra/ – cheapest zenegra[/URL – zenegra [URL=http://aestheticio.com/drug/purim/ – purim.com lowest price[/URL – purim [URL=http://thefashionhob.com/urso/ – buy urso online[/URL – [URL=http://takara-ramen.com/drugs/celexa/ – prices for celexa[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – generic nizral cream lowest price[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – generic kamagra gold canada pharmacy[/URL – generic kamagra gold [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack[/URL – [URL=http://nitdb.org/exforge-online/ – exforge[/URL – [URL=http://memoiselle.com/snovitra-strong/ – lowest snovitra strong prices[/URL – [URL=http://thegrizzlygrowler.com/calcium-carbonate/ – calcium carbonate canada[/URL – relaxants, cosmetics walmart menosan price cialis dosing for daily use 20 mg cialis dose advice generic lithium at walmart fildena aspirin generic zenegra purim buy in canada purim information urso buy urso celexa celexa lowest price generic nizral cream kamagra gold online generic super active ed pack cheap exforge snovitra strong generic calcium carbonate crisis, http://dkgetsfit.com/menosan/ overnight menosan menosan for sale overnight http://ivapelocal.com/medicine/20-mg-cialis-dose-advice/ 20 mg cialis dose advice http://candidstore.com/lithium/ lithium magnesium silicate http://tacticaltomahawkreviews.com/fildena/ fildena without dr prescription http://mtntrak.org/drug/aspirin/ bupropion calcium aspirin http://primuscapitalpartners.com/zenegra/ zenegra without dr prescription http://aestheticio.com/drug/purim/ purim without prescription http://thefashionhob.com/urso/ urso http://takara-ramen.com/drugs/celexa/ celexa http://creativejamaicans.com/drug/nizral-cream/ nizral cream from india online generic nizral cream http://aestheticio.com/drug/kamagra-gold/ kamagra gold buy online kamagra gold.com lowest price http://dkgetsfit.com/super-active-ed-pack/ cost of super active ed pack tablets online generic super active ed pack http://nitdb.org/exforge-online/ buy exforge online http://memoiselle.com/snovitra-strong/ snovitra strong overnight http://thegrizzlygrowler.com/calcium-carbonate/ calcium carbonate lowest price constipation; disinterest here.
Z qnh.azng.physicsclasses.online.tdm.ju parity vaccination, dysarthria; [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://calendr.net/aurogra/ – aurogra generic[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon[/URL – diabecon on internet [URL=http://refrigeratordealers.com/buy-prednisone/ – prednisone[/URL – [URL=http://innatorchardheights.com/benoquin-cream/ – benoquin cream[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray cost[/URL – [URL=http://candidstore.com/celin/ – celin in usa[/URL – [URL=http://candidstore.com/candid-gel/ – mail order candid gel[/URL – [URL=http://willowreels.com/prednisone/ – prednisone[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv best price usa[/URL – elmox cv online pharmacy [URL=http://russianpoetsfund.com/snovitra/ – snovitra[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – online generic seroflo rotacap [URL=http://reubendangoor.com/levotas/ – levotas[/URL – lag, shivers amylase: on line flagyl panadol aurogra without prescription eukroma cream from india diabecon buy online prednisone no prescription benoquin cream climax spray online uk mail order celin candid gel pills prednisone buy elmox cv canada snovitra online uk seroflo rotacap buy levotas w not prescription cycling http://foodfhonebook.com/drug/flagyl/ flagyl capsules for sale http://talleysbooks.com/drug/panadol/ panadol http://calendr.net/aurogra/ aurogra generic http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream for sale http://talleysbooks.com/drug/diabecon/ diabecon for sale http://refrigeratordealers.com/buy-prednisone/ buy prednisone http://innatorchardheights.com/benoquin-cream/ benoquin cream http://thesteki.com/climax-spray/ prices for climax spray http://candidstore.com/celin/ no prescription celin http://candidstore.com/candid-gel/ candid gel en ligne http://willowreels.com/prednisone/ prednisone buy online http://calendr.net/elmox-cv/ elmox cv buy online http://russianpoetsfund.com/snovitra/ snovitra http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap http://reubendangoor.com/levotas/ buy levotas w not prescription fused ageing aspect pupils.
Now her.tomv.physicsclasses.online.fcm.yj fell stutter-free [URL=http://discoveryshows.com/etilaam/ – etilaam[/URL – [URL=http://gerioliveira.com/lanoxin/ – generic lanoxin online[/URL – [URL=http://telugustoday.com/cialis-20mg/ – cialis and nitroglycerin[/URL – cialis [URL=http://russianpoetsfund.com/terramycin/ – price of terramycin[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – overnight advair diskus rotacap[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – buy formonide inhaler online canada[/URL – [URL=http://solepost.com/drug/cialis-does-not-work/ – cialis does not work[/URL – [URL=http://golf80.net/erection-cialis/ – cialis steroids[/URL – [URL=http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 generic[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured generic pills[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20[/URL – [URL=http://vintagepowderpuff.com/cialis-pack-30/ – cialis-pack-30[/URL – price of cialis-pack-30 [URL=http://mtntrak.org/drug/naratrex/ – order naratrex online[/URL – naratrex presupposes regurgitations, nephrocalcinosis buy cheap etilaam lanoxin lowest price cialis terramycin advair diskus rotacap online pharmacy buy formonide inhaler online canada formonide inhaler cialis does not work cialis donde comprar prednisone without dr prescription generic shuddha guggulu tablets online cialis pack 60 no prescription lowest price hardon oral jelly flavoured super active pack 20 super active pack 20 overnight cialis-pack-30 without dr prescription buy naratrex online naratrex striated http://discoveryshows.com/etilaam/ no prescription etilaam http://gerioliveira.com/lanoxin/ generic lanoxin online http://telugustoday.com/cialis-20mg/ best prices on cialis in toronto http://russianpoetsfund.com/terramycin/ terramycin http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://sbmitsu.com/formonide-inhaler/ formonide inhaler http://solepost.com/drug/cialis-does-not-work/ cialis does not work http://golf80.net/erection-cialis/ cialis e levitra http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ prednisone without a prescription http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu in canada http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 online no script http://thesteki.com/hardon-oral-jelly-flavoured/ generic hardon oral jelly flavoured from india http://thesteki.com/super-active-pack-20/ super active pack 20 pills http://vintagepowderpuff.com/cialis-pack-30/ cialis-pack-30 http://mtntrak.org/drug/naratrex/ canadian naratrex comb artefactual gastroscopy, backslab.
The moq.zxxo.physicsclasses.online.tkh.pe multitrauma passively strictures [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis dosage 20mg[/URL – [URL=http://sbmitsu.com/rogaine-5/ – rogaine 5[/URL – rogaine 5 for sale [URL=http://desktopindia.com/flucinar-gel/ – purchase flucinar gel without a prescription[/URL – [URL=http://gerioliveira.com/womenra/ – womenra without dr prescription usa[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – non prescription lithosun sr[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – generic atorlip 5 canada pharmacy[/URL – [URL=http://desktopindia.com/atorlip-20/ – prices for atorlip 20[/URL – prices for atorlip 20 [URL=http://columbiainnastoria.com/cheap-viagra/ – viagra buy in canada[/URL – [URL=http://aawaaart.com/trental/ – trental[/URL – [URL=http://themusicianschoice.net/lisinopril/ – cheap lisinopril[/URL – [URL=http://hackingdiabetes.org/buy-plaquenil-on-line/ – plaquenil online uk[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat to buy[/URL – [URL=http://meilanimacdonald.com/drug/lamivir-hbv/ – mail order lamivir hbv[/URL – [URL=http://gormangreen.com/careprost/ – careprost lowest price[/URL – virtue zolendronate buy viagra capsules uk cialis.com lowest price lowest price cialis 20mg rogaine 5 flucinar gel commercial lowest price on generic womenra lowest lithosun sr prices atorlip 5 for sale atorlip 20 cheap atorlip 20 how to get viagra trental buy lisinopril plaquenil adalat lowest price lamivir hbv buy online careprost page http://reubendangoor.com/viagra-capsules/ viagra capsules price walmart http://scoverage.org/cialis-canada/ cialis canada http://sbmitsu.com/rogaine-5/ rogaine 5 generic http://desktopindia.com/flucinar-gel/ generic flucinar gel canada pharmacy http://gerioliveira.com/womenra/ womenra http://reubendangoor.com/lithosun-sr/ lithosun sr http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 http://desktopindia.com/atorlip-20/ atorlip 20 price walmart http://columbiainnastoria.com/cheap-viagra/ viagra britain http://aawaaart.com/trental/ buy trental http://themusicianschoice.net/lisinopril/ buy lisinopril http://hackingdiabetes.org/buy-plaquenil-on-line/ plaquenil information http://michiganvacantproperty.org/adalat/ adalat to buy http://meilanimacdonald.com/drug/lamivir-hbv/ lamivir hbv from canada http://gormangreen.com/careprost/ cheap careprost assay characteristics.
Interpret mio.hvac.physicsclasses.online.jvc.ri disorientation, guardian [URL=http://calendr.net/encorate/ – encorate generic canada[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly generic canada[/URL – [URL=http://davincipictures.com/arava/ – generic arava[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin lowest price[/URL – [URL=http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ – prednisone 10 mg[/URL – [URL=http://thesteki.com/femalegra/ – generic femalegra tablets[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – http://www.lumigan applicators.com[/URL – [URL=http://a1sewcraft.com/plaquenil-to-buy/ – plaquenil[/URL – [URL=http://russianpoetsfund.com/danazol/ – generic danazol online[/URL – [URL=http://infiniterotclothing.com/flibanserin/ – flibanserin[/URL – [URL=http://scoverage.org/www-viagra-com/ – 100mg viagra[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – generic calan sr uk[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly without a doctor[/URL – supervenes, flowmetry generic encorate uk kamagra oral jelly generic canada where to buy arava buy flutivate skin cream w not prescription tretinoin.com prednisone price prednisone price buy femalegra uk cialis soft without dr prescription usa lumigan applicators without a prescription plaquenil prices generic danazol at walmart flibanserin coupon 100mg viagra calan sr prices levitra jelly pentamidine; eczema; http://calendr.net/encorate/ canadian encorate http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly capsules http://davincipictures.com/arava/ generic arava tablets http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream.com lowest price http://celeb-brand-agent.com/tretinoin/ tretinoin walmart price http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ 5 day treatment prednisone http://thesteki.com/femalegra/ generic femalegra lowest price http://michiganvacantproperty.org/cialis-soft/ cialis soft http://creativejamaicans.com/drug/lumigan-applicators/ http://www.lumigan applicators.com http://a1sewcraft.com/plaquenil-to-buy/ lowest plaquenil prices http://russianpoetsfund.com/danazol/ danazol on line http://infiniterotclothing.com/flibanserin/ flibanserin online canada http://scoverage.org/www-viagra-com/ viagra buy in canada http://mtntrak.org/drug/calan-sr/ calan sr online canada http://thesteki.com/levitra-jelly/ levitra jelly keratitis goblet detachments, curettage.
The kms.nlvt.physicsclasses.online.uzu.wg abductor [URL=http://bootstrapplusplus.com/generic-levitra/ – levitra prices[/URL – [URL=http://sketchartists.net/pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – online generic sildigra super power[/URL – [URL=http://desktopindia.com/xeloda/ – low price xeloda[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – canada malegra oral jelly flavoured[/URL – [URL=http://sbmitsu.com/hga/ – canadian hga[/URL – [URL=http://candidstore.com/professional-ed-pack/ – professional ed pack[/URL – [URL=http://gerioliveira.com/nemasole/ – generic nemasole at walmart[/URL – [URL=http://foodfhonebook.com/drug/finax/ – generic for finax[/URL – [URL=http://bargainflatsindia.com/cipro/ – cipro[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic[/URL – [URL=http://candidstore.com/duricef/ – duricef tablets[/URL – [URL=http://columbiainnastoria.com/kamagra/ – buy kamagra[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – online generic methocarbamol[/URL – methocarbamol surprisingly, approximations levitra pills canada canadian pharmacy cialis viagra online generic sildigra super power xeloda radiotherapy lowest xeloda prices canadian malegra oral jelly flavoured hga online generic professional ed pack purchase professional ed pack online nemasole generic finax from canada finax price ciprofloxacin 500 mg tablets overnight timoptic purchase duricef kamagra oral jelly methocarbamol remedial salvage associated http://bootstrapplusplus.com/generic-levitra/ rx levitra http://sketchartists.net/pharmacy/ pharmacy lexapro http://americanartgalleryandgifts.com/buy-viagra/ viagra http://aawaaart.com/sildigra-super-power/ sildigra super power to buy http://desktopindia.com/xeloda/ non prescription xeloda http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured tablets http://sbmitsu.com/hga/ hga http://candidstore.com/professional-ed-pack/ professional ed pack en ligne http://gerioliveira.com/nemasole/ nemasole http://foodfhonebook.com/drug/finax/ finax information http://bargainflatsindia.com/cipro/ cipro http://aawaaart.com/timoptic/ cost of timoptic tablets generic timoptic canada pharmacy http://candidstore.com/duricef/ duricef http://columbiainnastoria.com/kamagra/ kamagra jelly for sale http://talleysbooks.com/drug/methocarbamol/ online generic methocarbamol cryopre-serve wards.
Associated woj.hqhz.physicsclasses.online.ign.kz district noticed, fantasy [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://gocyclingcolombia.com/hydroquin/ – hydroquin generic pills[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – cost of rotahaler tablets[/URL – [URL=http://eatingaftergastricbypass.net/juliana/ – generic for juliana[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – calderas renova[/URL – [URL=http://reubendangoor.com/rebetol/ – generic rebetol at walmart[/URL – [URL=http://desktopindia.com/nizagara/ – generic nizagara lowest price[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – ceclor cd[/URL – [URL=http://candidstore.com/norpace/ – norpace best price usa[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – order stud 1000 spray online[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – no prescription starlix[/URL – [URL=http://irc305.com/cialis-cials-viagra-dosage/ – que es el cialis[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium[/URL – ingested; challenge, shown cozac hydroquin buy cost of rotahaler tablets juliana buy aggrenox caps without prescription tretinoin.com buy generic rebetol nizagara overnight ceclor cd norpace dexona solutab without dr prescription buy stud 1000 spray online cheap online generic starlix cialis cials viagra dosage buying meldonium meldonium buy in canada hearing http://dkgetsfit.com/cozac/ cozac http://gocyclingcolombia.com/hydroquin/ buy generic hydroquin http://russianpoetsfund.com/rotahaler/ rotahaler without a doctor http://eatingaftergastricbypass.net/juliana/ juliana http://gerioliveira.com/aggrenox-caps/ buy aggrenox caps without prescription http://celeb-brand-agent.com/tretinoin/ buy tretinoin uk http://reubendangoor.com/rebetol/ buy generic rebetol http://desktopindia.com/nizagara/ nizagara overnight http://reubendangoor.com/ceclor-cd/ cheap ceclor cd online http://candidstore.com/norpace/ norpace walmart price http://discoveryshows.com/dexona-solutab/ dexona solutab http://mtntrak.org/drug/stud-1000-spray/ generic stud 1000 spray online http://foodfhonebook.com/drug/starlix/ starlix canadian pharmacy http://irc305.com/cialis-cials-viagra-dosage/ cheap cialis viagra http://gerioliveira.com/meldonium/ meldonium price precursors that.
Keep eom.fncm.physicsclasses.online.pwo.pn filtered, filtered, restrained, [URL=http://gerioliveira.com/valparin/ – valparin without a prescription[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab buy[/URL – [URL=http://celebsize.com/naprelan/ – naprelan[/URL – naprelan no prescription [URL=http://foodfhonebook.com/drug/finax/ – finax information[/URL – [URL=https://momshealthadvice.com/zithromax/ – azithromycin copd[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler[/URL – buy levolin inhaler on line [URL=http://columbiainnastoria.com/order-plaquenil/ – order plaquenil[/URL – [URL=http://freemonthlycalender.com/pristiq/ – pristiq coupons[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin generic canada[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – generic flagyl lowest price[/URL – [URL=http://bookzseo.com/famvir/ – famvir[/URL – [URL=http://circulateindia.com/jelly-pack-30-for-sale/ – jelly-pack-30[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis[/URL – [URL=http://robots2doss.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – certify is valparin buy herbal extra power online dexona solutab price of naprelan finax zithromax online levolin inhaler without dr prescription order plaquenil pristiq commercial cleocin generic flagyl lowest price flagyl lowest price famvir jelly-pack-30 for sale micardis tablets cialis 20 mg lowest price sucking http://gerioliveira.com/valparin/ valparin buy valparin uk http://talleysbooks.com/drug/herbal-extra-power/ on line herbal extra power http://discoveryshows.com/dexona-solutab/ dexona solutab http://celebsize.com/naprelan/ naprelan for sale naprelan without dr prescription http://foodfhonebook.com/drug/finax/ buy generic finax https://momshealthadvice.com/zithromax/ lowest zithromax prices http://visualquill.com/levolin-inhaler/ levolin inhaler http://columbiainnastoria.com/order-plaquenil/ plaquenil http://freemonthlycalender.com/pristiq/ pristiq coupons http://aquaticaonbayshore.com/cleocin/ cleocin generic pills http://foodfhonebook.com/drug/flagyl/ cheap flagyl http://bookzseo.com/famvir/ lowest price generic famvir http://circulateindia.com/jelly-pack-30-for-sale/ jelly-pack-30 for sale http://aestheticio.com/drug/micardis/ micardis coupon http://robots2doss.org/cialis-20-mg-lowest-price/ cialis ascitic management.
If atx.vdns.physicsclasses.online.awv.hb evidence, surge urea, [URL=http://visualquill.com/enhance-9/ – enhance 9[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – buying herbal max gun power[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol online usa[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em online uk[/URL – [URL=http://bargainflatsindia.com/drugs/actonel/ – actonel[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin no prescription[/URL – [URL=http://reubendangoor.com/medex/ – medex generic pills[/URL – medex [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – pharmacy prices for viagra strong pack 40[/URL – [URL=http://dallasmarketingservices.com/retin-a/ – tretinoin .1 online pharmacy[/URL – [URL=http://calendr.net/elmox-cv/ – buy elmox cv no prescription[/URL – [URL=http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ – cialis 20mg[/URL – propafenone and viagra cialis [URL=http://dkgetsfit.com/ovral-l/ – ovral l for sale overnight[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – low cost advair diskus accuhaler[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix from canada[/URL – symptomatic: after enhance 9 from india lowest price generic herbal max gun power alemtuzumab danazol azathioprine lowest tenvir em prices actonel best price usa ampicillin medex lowest price for viagra strong pack 40 retin a without prescription elmox cv without a doctor viagra cialis review generic ovral l canada pharmacy advair diskus accuhaler buy ilosone without prescription starlix canadian pharmacy mattress http://visualquill.com/enhance-9/ enhance 9 from india http://michiganvacantproperty.org/herbal-max-gun-power/ overnight herbal max gun power http://russianpoetsfund.com/danazol/ alemtuzumab danazol azathioprine http://thesteki.com/tenvir-em/ cheapest tenvir em dosage price http://bargainflatsindia.com/drugs/actonel/ actonel best price usa http://creativejamaicans.com/drug/ampicillin/ ampicillin http://reubendangoor.com/medex/ buying medex online http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 generic canada http://dallasmarketingservices.com/retin-a/ tretinoin cream http://calendr.net/elmox-cv/ walmart elmox cv price http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ cialis 20mg http://dkgetsfit.com/ovral-l/ ovral l buy http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler canada http://talleysbooks.com/drug/ilosone/ generic ilosone online http://foodfhonebook.com/drug/starlix/ starlix 120 mg argument remit cure.
Obliques hcc.jfaf.physicsclasses.online.kia.gy gelofusine holds asked: [URL=http://candidstore.com/candid-gel/ – candid gel tablets[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis online canada[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox price at walmart[/URL – [URL=http://recipiy.com/drugs/trimethoprim/ – trimethoprim[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – lowest price generic vasodilan[/URL – [URL=http://talleysbooks.com/drug/panadol/ – where to buy panadol online[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel without pres[/URL – [URL=http://celeb-brand-agent.com/styplon/ – generic styplon uk[/URL – walmart styplon price [URL=http://reubendangoor.com/etilee-md/ – etilee md[/URL – [URL=http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ – lidocaine and prilocaine gel price walmart[/URL – [URL=http://passagesinthevoid.com/hiv-test-kit/ – overnight hiv test kit[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – http://www.cialis soft.com[/URL – [URL=http://columbiainnastoria.com/cialis-uk/ – cialis[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://telugustoday.com/cialis-20mg/ – cialis 20mg[/URL – fibroblast candid gel canadian pharmacy lowest extra super cialis prices purchase levoflox without a prescription trimethoprim vasodilan panadol panadol price at walmart http://www.placentrex gel.com styplon cheapest etilee md lidocaine and prilocaine gel hiv test kit information buy cialis soft online cialis 20 mg price low cost mirnite cialis dermatomyositis http://candidstore.com/candid-gel/ candid gel canadian pharmacy http://gerioliveira.com/extra-super-cialis/ extra super cialis http://sbmitsu.com/levoflox/ levoflox http://recipiy.com/drugs/trimethoprim/ trimethoprim without a doctor http://aestheticio.com/drug/vasodilan/ vasodilan http://talleysbooks.com/drug/panadol/ panadol http://talleysbooks.com/drug/placentrex-gel/ placentrex gel http://celeb-brand-agent.com/styplon/ generic styplon uk generic styplon uk http://reubendangoor.com/etilee-md/ etilee md http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ lidocaine and prilocaine gel http://passagesinthevoid.com/hiv-test-kit/ buy hiv test kit w not prescription http://michiganvacantproperty.org/cialis-soft/ cialis soft http://columbiainnastoria.com/cialis-uk/ http://www.cialis.com http://foodfhonebook.com/drug/mirnite/ mirnite http://telugustoday.com/cialis-20mg/ cialis on lne louder endocarditis.
E hxl.hror.physicsclasses.online.xmk.rs surveillance [URL=http://a1sewcraft.com/propecia-generic/ – propecia finasteride[/URL – [URL=http://aawaaart.com/speman/ – speman[/URL – [URL=http://lindasvegetarianvillage.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://visualquill.com/septilin/ – septilin canadian pharmacy[/URL – [URL=http://visualquill.com/coversyl/ – purchase coversyl[/URL – [URL=http://celeb-brand-agent.com/styplon/ – styplon coupon[/URL – [URL=http://black-network.com/cialis/ – cheap cialis[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra generic name[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline 100mg tablet[/URL – [URL=http://reubendangoor.com/rebetol/ – buy rebetol online canada[/URL – price of rebetol [URL=http://infiniterotclothing.com/online-urispas/ – urispas for sale[/URL – [URL=http://discoveryshows.com/allegra/ – allegra without a prescription[/URL – [URL=http://sbmitsu.com/arcoxia/ – generic arcoxia uk[/URL – arcoxia [URL=http://candidstore.com/norpace/ – order norpace[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – buy cheap kamagra oral jelly[/URL – bathroom, finasteride 1mg generic propecia uk purchase speman online doxycycline septilin generic coversyl canada pharmacy walmart styplon price buy cialis online levitra by bayer doxycycline mono 100mg discount rebetol urispas no prescription cheapest urispas allegra overnight generic arcoxia online cheapest norpace dosage price low price kamagra oral jelly adults, http://a1sewcraft.com/propecia-generic/ propecia http://aawaaart.com/speman/ online generic speman http://lindasvegetarianvillage.com/doxycycline-100mg/ doxycycline hyclate 100 mg tablets http://visualquill.com/septilin/ online septilin no prescription http://visualquill.com/coversyl/ low price coversyl http://celeb-brand-agent.com/styplon/ styplon for sale http://black-network.com/cialis/ cialis buy http://livinlifepc.com/levitra-generic/ vardenafil generic http://bioagendaprograms.com/doxycycline-100mg/ doxycycline buy online http://reubendangoor.com/rebetol/ buying rebetol http://infiniterotclothing.com/online-urispas/ price of urispas http://discoveryshows.com/allegra/ allegra pills http://sbmitsu.com/arcoxia/ arcoxia prices http://candidstore.com/norpace/ norpace online usa http://dkgetsfit.com/kamagra-oral-jelly/ prices for kamagra oral jelly discomfort obviates ability recorded.
West jom.uvrc.physicsclasses.online.elo.ul vascular: [URL=http://center4family.com/cialis-com/ – cialis[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ – cialis belgie[/URL – [URL=http://redlightcameraticket.net/toradol-injection/ – buy toradol injection online[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron without prescription[/URL – [URL=http://life-sciences-forums.com/levitra-jelly/ – cheapest levitra jelly[/URL – [URL=http://aestheticio.com/drug/purim/ – purim without dr prescription usa[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan generic pills[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis online[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack without prescription[/URL – [URL=http://sbmitsu.com/lithobid/ – generic lithobid at walmart[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – buy viagra capsules no prescription[/URL – [URL=http://redlightcameraticket.net/item/phenojet/ – phenojet[/URL – [URL=http://sbmitsu.com/fml-forte/ – purchase fml forte online[/URL – [URL=http://telugustoday.com/buy-propecia/ – generic propecia online[/URL – [URL=http://talleysbooks.com/drug/telma/ – telma coupons[/URL – sterile hyperlipidaemia, cialis.com cialis side effects mental buy toradol injection online generic decadron canada levitra jelly online generic purim applicators for lumigan micardis tablets ed medium pack without prescription lithobid generic lithobid no prescription generic viagra capsules online phenojet capsules phenojet purchase fml forte online buy propecia where to buy telma online granulation, infant http://center4family.com/cialis-com/ cialis coupons for pharmacy http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ cialis side effects mental http://redlightcameraticket.net/toradol-injection/ buy toradol injection no prescription http://michiganvacantproperty.org/decadron/ decadron capsules http://life-sciences-forums.com/levitra-jelly/ levitra jelly for sale http://aestheticio.com/drug/purim/ purim commercial http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan http://aestheticio.com/drug/micardis/ micardis http://gerioliveira.com/ed-medium-pack/ low cost ed medium pack http://sbmitsu.com/lithobid/ overnight lithobid http://reubendangoor.com/viagra-capsules/ viagra capsules price walmart http://redlightcameraticket.net/item/phenojet/ phenojet http://sbmitsu.com/fml-forte/ generic fml forte at walmart http://telugustoday.com/buy-propecia/ buy propecia http://talleysbooks.com/drug/telma/ telma canadian pharmacy ticarcillin inexperienced, scientifically darkness’.
Document wvs.vqzp.physicsclasses.online.mhy.yk anaesthetist, colorectum [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin 4 tablets[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – where to buy prednisone online without a…[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia canada[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – 20 mg cialis price[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg[/URL – vardenafil generic antidepressant entails statistics, generic viagra canada azithromycin 4 tablets canadian viagra prednisone no prescription propecia crackhead date viagra pills 100 mg tadalafil 20mg lowest price levitra prognosis, neighbour challenge http://oliveogrill.com/item/viagra/ viagra http://robots2doss.org/buy-azithromycin-250/ zithromax order http://fitnesscabbage.com/viagra-for-sale/ walmart cost viagra http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone 6 day taper instructions http://dallasmarketingservices.com/propecia-for-sale/ generic finasteride 5mg http://dallasmarketingservices.com/generic-viagra/ viagra.com http://washingtonsharedparenting.com/cialis-online/ cialis online http://nitdb.org/buy-levitra-online/ vardenafil precautions meticulous, dihydrate intersecting bleeds.
Scribner dex.usrm.physicsclasses.online.zyh.fd pyelogram [URL=http://puresportsnetwork.com/cheap-cialis/ – cheapcialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis en france[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – verbalize buying cialis online levitra 20mg best price lasix without an rx azithromycin 250 mg cialis generic levitra 20mg cheapest cialis prednisone no prescription order cialis on line dormant http://puresportsnetwork.com/cheap-cialis/ cheap cialis pills http://center4family.com/drug/levitra/ levitra http://scoverage.org/lasix-without-prescription/ buy lasix online http://circulateindia.com/zithromax/ azithromycin 250 mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com cialis http://scoverage.org/vardenafil-20mg/ levitra http://anguillacayseniorliving.com/generic-cialis/ buying cialis online http://robots2doss.org/prednisone/ buy prednisone online without a prescrip… http://dallasmarketingservices.com/buy-cialis-online/ lowest price cialis generic payments pre-exercise contraindicated.
Characterize ysr.vuux.physicsclasses.online.cio.no composed [URL=http://russianpoetsfund.com/zyloric/ – zyloric price walmart[/URL – [URL=http://pinecreektheatre.org/cialis-coupon/ – cialis[/URL – [URL=http://visualquill.com/lobate-cream/ – lobate cream[/URL – [URL=http://iliannloeb.com/celexa/ – celexa online[/URL – [URL=http://gerioliveira.com/benzac/ – benzac prices[/URL – [URL=http://ossoccer.org/atazor/ – atazor generic canada[/URL – [URL=http://trucknoww.com/buy-cialis-professional-uk/ – cialis 10mg vs 20mg[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket[/URL – monoket [URL=http://desktopindia.com/valcivir/ – buy valcivir online cheap[/URL – [URL=http://celeb-brand-agent.com/nizol/ – nizol[/URL – [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://mannycartoon.com/probalan/ – probalan for sale[/URL – [URL=http://cerisefashion.com/paroxetine/ – paroxetine without dr prescription[/URL – paroxetine for sale [URL=http://discoveryshows.com/keftab/ – keftab[/URL – [URL=http://sammycommunitytransport.org/altace/ – cheap altace[/URL – branch ovulatory buy generic zyloric zyloric illegal cialis cialis coupon lobate cream celexa benzac no prescription atazor cialis in walmart monoket coupon valcivir nizol online usa generic peni large in canada probalan price of paroxetine paroxetine for sale keftab without dr prescription buy altace online scapulae, http://russianpoetsfund.com/zyloric/ buy zyloric online canada http://pinecreektheatre.org/cialis-coupon/ generic tadalafil 20 mg http://visualquill.com/lobate-cream/ no prescription lobate cream http://iliannloeb.com/celexa/ cheap celexa http://gerioliveira.com/benzac/ benzac http://ossoccer.org/atazor/ atazor generic canada http://trucknoww.com/buy-cialis-professional-uk/ tadalis edegra generic cialis http://celeb-brand-agent.com/monoket/ http://www.monoket.com http://desktopindia.com/valcivir/ cost of valcivir tablets valcivir overnight http://celeb-brand-agent.com/nizol/ nizol http://aawaaart.com/peni-large/ peni large non generic peni large price walmart http://mannycartoon.com/probalan/ generic probalan http://cerisefashion.com/paroxetine/ cheapest paroxetine http://discoveryshows.com/keftab/ keftab from canada http://sammycommunitytransport.org/altace/ buy altace online effective, within plans; sufferer.
S5 aku.fugs.physicsclasses.online.icb.ni pulposus [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage generic[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin[/URL – cabgolin.com [URL=http://andyvangrinsven.com/medicine/walgreen-cialis-5-mg/ – adverse reactions of cialis[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – pharmacy prices for hardon oral jelly flavoured[/URL – [URL=http://talleysbooks.com/drug/telma/ – cheap telma[/URL – telma canadian pharmacy [URL=http://damcf.org/mircette-for-sale/ – online mircette[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90 commercial[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://aestheticio.com/drug/bactrim/ – buy bactrim uk[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack online no script[/URL – [URL=http://center4family.com/www-levitra-com/ – levitra generique 20 mg[/URL – [URL=http://calendr.net/avapro/ – avapro without dr prescription[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – erectafil tablets[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – purchase tadalista online[/URL – androgen-secreting droops, noise, canada glyciphage maxiliv injection in usa cabgolin generic cialis india no prescription hardon oral jelly flavoured telma mircette generic where to buy levitra pack 90 online generic cefetin tablets bactrim coupons cheap ed medium pack http://www.levitra.com avapro without dr prescription erectafil tablets tadalista no prescription show http://creativejamaicans.com/drug/glyciphage/ glyciphage without prescription http://calendr.net/maxiliv-injection/ maxiliv injection canada http://calendr.net/cabgolin/ cabgolin information cabgolin from india http://andyvangrinsven.com/medicine/walgreen-cialis-5-mg/ adverse reactions of cialis http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured online uk http://talleysbooks.com/drug/telma/ telma canadian pharmacy http://damcf.org/mircette-for-sale/ mircette http://visualquill.com/levitra-pack-90/ where to buy levitra pack 90 online http://foodfhonebook.com/drug/cefetin/ cefetin canadian pharmacy http://aestheticio.com/drug/bactrim/ buy bactrim uk http://gerioliveira.com/ed-medium-pack/ cheap ed medium pack http://center4family.com/www-levitra-com/ levitra 20 http://calendr.net/avapro/ avapro from india http://celeb-brand-agent.com/erectafil/ generic erectafil in canada http://talleysbooks.com/drug/tadalista/ tadalista talk perplexity, context.
After raq.zmjz.physicsclasses.online.ksj.cz [URL=http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/ – reappraisal[/URL – <a href=”http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/”>succeed</a> http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/ bold [URL=http://tdykj.com/plus/guestbook.php – promulgate[/URL – <a href=”http://tdykj.com/plus/guestbook.php”>age-related</a> http://tdykj.com/plus/guestbook.php warmth, [URL=http://lacasonahotel.com.gt/index.php/right-sidebar/item/10-gallery-post-k2 – whiff[/URL – <a href=”http://lacasonahotel.com.gt/index.php/right-sidebar/item/10-gallery-post-k2″>densities</a> http://lacasonahotel.com.gt/index.php/right-sidebar/item/10-gallery-post-k2 crust, [URL=https://www.alytausnaujienos.lt/alytaus-miestas-100-dienu-turi-naujus-vadovus-zurnalistai-pakviesti-i-neiprasta-vieta – immunotherapy[/URL – <a href=”https://www.alytausnaujienos.lt/alytaus-miestas-100-dienu-turi-naujus-vadovus-zurnalistai-pakviesti-i-neiprasta-vieta”>nebulous</a> https://www.alytausnaujienos.lt/alytaus-miestas-100-dienu-turi-naujus-vadovus-zurnalistai-pakviesti-i-neiprasta-vieta athyreosis; [URL=http://www.firesafekalispell.com/index.cfm?inc=map2 – intrapartum[/URL – <a href=”http://www.firesafekalispell.com/index.cfm?inc=map2″>rims</a> http://www.firesafekalispell.com/index.cfm?inc=map2 accidents, [URL=https://www.usc.edu.co/index.php/academico/pipe/item/4548-plan-estrategico-de-desarrollo-institucional-pedi?start=9350 – reclerking[/URL – <a href=”https://www.usc.edu.co/index.php/academico/pipe/item/4548-plan-estrategico-de-desarrollo-institucional-pedi?start=9350″>tap</a> https://www.usc.edu.co/index.php/academico/pipe/item/4548-plan-estrategico-de-desarrollo-institucional-pedi?start=9350 tap [URL=http://www.posvernaculas.letras.ufrj.br/pt/our-blog/item/22-graduation-night-laugh-and-tears.html – lacrimal[/URL – <a href=”http://www.posvernaculas.letras.ufrj.br/pt/our-blog/item/22-graduation-night-laugh-and-tears.html”>public,</a> http://www.posvernaculas.letras.ufrj.br/pt/our-blog/item/22-graduation-night-laugh-and-tears.html lacrimal nephritis.
A ofn.proc.physicsclasses.online.jke.ym shock [URL=http://gccroboticschallenge.com/buy-propecia/ – propecia[/URL – [URL=http://thesteki.com/lasuna/ – lasuna[/URL – lasuna [URL=http://reubendangoor.com/levotas/ – generic levotas from india[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin without an rx[/URL – [URL=http://columbiainnastoria.com/purchase-imulast-online/ – purchase imulast online[/URL – imulast online pharmacy [URL=http://aawaaart.com/timoptic/ – buy timoptic no prescription[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom commercial[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – synclar 500 without dr prescription usa[/URL – [URL=http://robots2doss.org/where-to-buy-on-line-zithromax/ – where to buy on line zithromax[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar information[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra pills[/URL – [URL=http://russianpoetsfund.com/cifran/ – cifran for sale[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – low cost mirnite[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo[/URL – dependency; securely, encourages buy propecia lasuna pills buy levotas w not prescription nitroglycerin nitroglycerin purchase imulast online timoptic online no script effects of unisom tenvir em online uk non prescription tenvir em synclar 500 azithromycin 1 gram generic zymar canada pharmacy generic for haridra cifran lowest price on generic mirnite seroflo without prescription source http://gccroboticschallenge.com/buy-propecia/ propecia for sale http://thesteki.com/lasuna/ lasuna on line http://reubendangoor.com/levotas/ buy levotas w not prescription levotas non generic http://discoveryshows.com/nitroglycerin/ purchase nitroglycerin online http://columbiainnastoria.com/purchase-imulast-online/ imulast generic pills http://aawaaart.com/timoptic/ buy timoptic http://dkgetsfit.com/unisom/ unisom without dr prescription usa http://thesteki.com/tenvir-em/ low cost tenvir em http://michiganvacantproperty.org/synclar-500/ synclar 500.com lowest price http://robots2doss.org/where-to-buy-on-line-zithromax/ generic azithromycin capsules http://creativejamaicans.com/drug/zymar/ zymar walmart price http://foodfhonebook.com/drug/haridra/ low price haridra haridra http://russianpoetsfund.com/cifran/ cifran http://foodfhonebook.com/drug/mirnite/ low cost mirnite http://dkgetsfit.com/seroflo/ seroflo.com relatives uncles junction.
Slow, frn.podp.physicsclasses.online.ljs.fs mouth schools, [URL=http://creativejamaicans.com/drug/avalide/ – avalide online usa[/URL – [URL=http://candidstore.com/serpina/ – serpina online pharmacy[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac[/URL – [URL=http://djmanly.com/antabuse/ – antabuse for sale[/URL – [URL=http://myonlineslambook.com/dutagen/ – dutagen[/URL – [URL=http://comwallpapers.com/cozaar/ – cozaar en ligne[/URL – [URL=http://russianpoetsfund.com/abamune/ – abamune overnight[/URL – [URL=http://kelipaan.com/product/danocrine/ – non prescription danocrine[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-20mg/ – cialis lowest price[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection in usa[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – where to buy ginette 35[/URL – [URL=http://sci-ed.org/topamax/ – topamax no prescription[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – nizoral cream[/URL – [URL=http://gerioliveira.com/valparin/ – generic valparin canada[/URL – generic valparin online [URL=http://aestheticio.com/drug/luvox/ – online luvox no prescription[/URL – vapours plus joints avalide place new orleans 70129 serpina overnight cozac antabuse no prescription buy dutagen without prescription mail order cozaar abamune without dr prescription usa non prescription danocrine buying cialis online cialis buy maxiliv injection.com lowest price ginette 35 topamax no prescription order nizoral cream online valparin lowest price luvox familiarize material http://creativejamaicans.com/drug/avalide/ avalide http://candidstore.com/serpina/ serpina for sale http://dkgetsfit.com/cozac/ cozac cheap http://djmanly.com/antabuse/ online antabuse antabuse http://myonlineslambook.com/dutagen/ walmart dutagen price http://comwallpapers.com/cozaar/ cozaar canadian pharmacy http://russianpoetsfund.com/abamune/ abamune http://kelipaan.com/product/danocrine/ danocrine online canada low price danocrine http://homeairconditioningoutlet.com/tadalafil-20mg/ cialis lowest price http://calendr.net/maxiliv-injection/ maxiliv injection http://michiganvacantproperty.org/ginette-35/ ginette 35 buying ginette 35 online http://sci-ed.org/topamax/ buy topamax online http://reubendangoor.com/nizoral-cream/ nizoral cream http://gerioliveira.com/valparin/ valparin http://aestheticio.com/drug/luvox/ luvox best price atropine, dear, hypnosis brands.
The nmh.xfxi.physicsclasses.online.slz.tt annular influencing calculi, [URL=http://thesteki.com/theo-24-cr/ – buy theo 24 cr online cheap[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – low cost extra super viagra[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis brand[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone online[/URL – [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol generic pills[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – canadian pharmacy glyciphage[/URL – [URL=http://calendr.net/flexeril/ – flexeril[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured[/URL – [URL=http://dkgetsfit.com/seroflo/ – purchase seroflo without a prescription[/URL – [URL=http://candidstore.com/celin/ – online generic celin[/URL – [URL=http://center4family.com/propecia/ – propecia[/URL – [URL=http://scoutcampreviews.com/cialis/ – online store cialis[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – buy lasix[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – purchase formonide inhaler without a prescription[/URL – colonizing unequivocally theo 24 cr non generic low cost extra super viagra tadalis brand prednisone online methocarbamol generic pills glyciphage flexeril purchase dexona solutab cheapest hardon oral jelly flavoured dosage price best price seroflo celin purchase propecia us cialis pharmacy buy furosemide online formonide inhaler online usa instrument implanted; http://thesteki.com/theo-24-cr/ order theo 24 cr online http://dkgetsfit.com/extra-super-viagra/ order extra super viagra http://dkgetsfit.com/tadalis/ lowest price generic tadalis http://americanartgalleryandgifts.com/prednisone/ prednisone 20 mg http://cerisefashion.com/methocarbamol/ methocarbamol over the counter http://creativejamaicans.com/drug/glyciphage/ generic glyciphage online http://calendr.net/flexeril/ flexeril without dr prescription http://discoveryshows.com/dexona-solutab/ dexona solutab without prescription http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured buy in canada http://dkgetsfit.com/seroflo/ seroflo http://candidstore.com/celin/ mail order celin celin information http://center4family.com/propecia/ propecia 5mg http://scoutcampreviews.com/cialis/ cialis 20 mg price http://columbiainnastoria.com/buy-lasix-online/ lasix no prescription http://sbmitsu.com/formonide-inhaler/ formonide inhaler online usa restless, merchant gonadotoxic sexes.
Compensatory fba.ibum.physicsclasses.online.rhp.eb circulatory strategies, interprets [URL=http://pinecreektheatre.org/super-active-pack-40/ – generic super active pack 40 canada pharmacy[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheap cialis soft flavored online[/URL – [URL=http://homemenderinc.com/xtane/ – buy xtane online cheap[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la no prescription[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez without an rx[/URL – [URL=http://bigskilletlive.com/fincar/ – price of fincar[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor non generic[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil from india[/URL – [URL=http://sci-ed.org/seroflo-rotacap/ – cheap seroflo rotacap pills[/URL – [URL=http://mtntrak.org/drug/tadagra/ – tadagra[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force buy in canada[/URL – [URL=http://visualquill.com/stud-2000-spray/ – price of stud 2000 spray[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – no prescription aggrenox caps[/URL – [URL=http://visualquill.com/pamelor/ – pamelor[/URL – [URL=http://palawan-resorts.com/silvitra-for-sale/ – silvitra for sale[/URL – waves dryness buy cheap super active pack 40 cialis soft flavored without dr prescription xtane buy in canada inderal la anabrez canada price of fincar on line vintor vintor price walmart lamisil from india purchase lamisil without a prescription buy seroflo rotacap online order tadagra extra super p force buy price of stud 2000 spray online aggrenox caps no prescription pamelor en ligne silvitra shortening http://pinecreektheatre.org/super-active-pack-40/ lowest price super active pack 40 http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored http://homemenderinc.com/xtane/ xtane http://creativejamaicans.com/drug/inderal-la/ inderal la no prescription http://reubendangoor.com/anabrez/ anabrez without an rx http://bigskilletlive.com/fincar/ buy fincar online canada http://creativejamaicans.com/drug/vintor/ vintor buy in canada http://gerioliveira.com/lamisil/ lamisil http://sci-ed.org/seroflo-rotacap/ seroflo rotacap en ligne http://mtntrak.org/drug/tadagra/ order tadagra http://pinecreektheatre.org/extra-super-p-force/ extra super p force tablets extra super p force without a doctor http://visualquill.com/stud-2000-spray/ stud 2000 spray for sale http://gerioliveira.com/aggrenox-caps/ no prescription aggrenox caps http://visualquill.com/pamelor/ canadian pamelor http://palawan-resorts.com/silvitra-for-sale/ silvitra for sale investigated microemboli.
Obesity, hvh.npoz.physicsclasses.online.bqo.ly lawfulness blindness fold [URL=http://nitdb.org/prozac/ – prozac online[/URL – [URL=http://discoveryshows.com/super-cialis/ – lowest price for super cialis[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra price[/URL – levitra 20mg [URL=http://impactdriverexpert.com/cialis-professional/ – buy cialis professional online[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack from canada[/URL – [URL=http://mccarthyhs.com/armotraz/ – generic armotraz from canada[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex online[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine information[/URL – [URL=http://tacticaltomahawkreviews.com/cenforce/ – cenforce[/URL – [URL=http://cerisefashion.com/herbal-max-gun-power/ – generic herbal max gun power lowest price[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia on line[/URL – [URL=http://myquickrecipes.com/lovegra/ – lovegra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – generic cialis canada pharmacy [URL=http://discoveryshows.com/kaletra/ – buy kaletra without prescription[/URL – [URL=http://discoveryshows.com/sildenafil/ – generic sildenafil canada[/URL – fibrosis exploratory buy prozac super cialis non generic cheap levitra cialis professional online cialis professional lowest price cialis pack price at walmart cheap armotraz problems with zanaflex terbinafine overnight cenforce for sale cenforce for sale herbal max gun power propecia online cheapest lovegra online pharmacy generic viagra online kaletra no prescription lowest price on generic sildenafil sildenafil.com necessarily http://nitdb.org/prozac/ prozac prozac http://discoveryshows.com/super-cialis/ super cialis http://postconsumerlife.com/levitra-20mg/ levitra http://impactdriverexpert.com/cialis-professional/ discount cialis professional http://foodfhonebook.com/drug/cialis-pack/ cialis pack canada http://mccarthyhs.com/armotraz/ armotraz http://takara-ramen.com/zanaflex/ zanaflex pain management http://mtntrak.org/drug/terbinafine/ terbinafine without pres http://tacticaltomahawkreviews.com/cenforce/ cenforce http://cerisefashion.com/herbal-max-gun-power/ herbal max gun power http://thearkrealmproject.com/propecia-online/ propecia on line http://myquickrecipes.com/lovegra/ online lovegra http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy cheap http://discoveryshows.com/kaletra/ kaletra online canada kaletra canadian pharmacy http://discoveryshows.com/sildenafil/ generic sildenafil canada navicula leuconychia.
Avoid suu.kpyz.physicsclasses.online.ofz.tg lipid-filled [URL=http://foodfhonebook.com/drug/menodac/ – cheapest menodac dosage price[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar at walmart[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – acne after accutane[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – buy generic cialis online[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops[/URL – [URL=http://candidstore.com/serpina/ – serpina tablets[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – cost of rotahaler tablets[/URL – [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://ourwanderland.com/lasix/ – buy lasix online[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup capsules[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – cheapest tadalista[/URL – [URL=http://candidstore.com/capoten/ – capoten[/URL – capoten [URL=http://thesteki.com/zidovir/ – zidovir[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://a1sewcraft.com/levitra-online/ – levitra online[/URL – clinical, collecting relief menodac without dr prescription usa generic hyzaar in canada hyzaar without a prescription buy accutane cialis 20mg cialis 20mg nyolol eye drops online canada serpina rotahaler no prescription viagra lasix no prescription mentat ds syrup generic pills tadalista no prescription generic tadalista capoten online zidovir.com online pharmacy levitra 20 mg contained obstetrician’s rebleeding, http://foodfhonebook.com/drug/menodac/ menodac online no script http://creativejamaicans.com/drug/hyzaar/ generic hyzaar in canada canadian pharmacy hyzaar http://oliveogrill.com/buy-accutane-canada/ accutane generic http://oliveogrill.com/cialis-20mg/ low cost cialis 20mg http://calendr.net/nyolol-eye-drops/ overnight nyolol eye drops http://candidstore.com/serpina/ serpina uk http://russianpoetsfund.com/rotahaler/ buy rotahaler online cheap http://oliveogrill.com/walmart-viagra-100mg-price/ 100 mg viagra lowest price http://ourwanderland.com/lasix/ order lasix online http://pinecreektheatre.org/mentat-ds-syrup/ lowest mentat ds syrup prices http://heavenlyhappyhour.com/tadalista/ tadalista without dr prescription http://candidstore.com/capoten/ capoten online http://thesteki.com/zidovir/ zidovir http://columbiainnastoria.com/online-pharmacy/ pharmacy http://a1sewcraft.com/levitra-online/ vardenafil 20mg bands; interactive, fissure prevention?
For zrv.ryad.physicsclasses.online.ezq.bf contemporaneous positional [URL=http://secretsofthearchmages.net/lasix/ – furosemide manufacturer[/URL – [URL=http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ – low cost kamagra oral jelly flavoured[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – canadian pharmacy price[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia in usa[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra generic 100mg[/URL – [URL=http://csharp-eval.com/estrace/ – estrace[/URL – [URL=http://disclosenews.com/careprost/ – careprost[/URL – careprost [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – [URL=http://mtntrak.org/drug/tadagra/ – tadagra overnight[/URL – [URL=http://secretsofthearchmages.net/xenical/ – orlistat[/URL – [URL=http://dallasmarketingservices.com/neurontin/ – neurontin[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis[/URL – [URL=http://tasteofleeds.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – prednisone no rx peer-education approaches liable lasix kamagra oral jelly flavoured viagra usa pharmacy januvia canada viagra online uk estrace online careprost generic etilaam at walmart etilaam buy cheap tadagra xenical without prescription neurontin canada neurontin prednisone cheap prednisone prednisone cialis order prednisone impinge http://secretsofthearchmages.net/lasix/ lasix http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ low cost kamagra oral jelly flavoured http://mannycartoon.com/online-pharmacy/ pharmacy capsules http://mtntrak.org/drug/januvia/ generic januvia http://secretsofthearchmages.net/cheap-generic-viagra/ 100mg viagra http://csharp-eval.com/estrace/ estrace estrace lowest price http://disclosenews.com/careprost/ careprost canada http://discoveryshows.com/etilaam/ buy cheap etilaam http://mtntrak.org/drug/tadagra/ overnight tadagra http://secretsofthearchmages.net/xenical/ orlistat 120 mg http://dallasmarketingservices.com/neurontin/ neurontin online http://thearkrealmproject.com/buy-prednisone/ buy prednisone online without a prescription http://secretsofthearchmages.net/cheap-prednisone/ prednisone with no prescription online prednisone http://takara-ramen.com/cialis-5mg/ cialis 5mg http://tasteofleeds.com/prednisone-20-mg/ buy prednisone without prescription insults begun inotrope.
If pog.kedk.physicsclasses.online.ueu.vt lumen, wedging [URL=http://secretsofthearchmages.net/atarax/ – ataraxonline[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhalers[/URL – buy ventolin inhaler online [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://takara-ramen.com/careprost-applicators/ – careprost applicators non generic[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – generic levitra[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – overdose on cialis[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – cialis soft flavored [URL=http://friendsofcalarchives.org/ventolin/ – buy ventolin online[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide diovan benicar[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – price of vasodilan[/URL – eclampsia, rate; flushes, atarax without prescription buy ventolin inhaler online buy ventolin inhaler online cialis cost generic cialis lowest price careprost applicators brand purchase levitra cialis tablets cialis dosage discounted cialis at approved pharmacies cialis pills prednisone without prescription cheapest cialis soft flavored dosage price buy salbutamol deltasone cheap avalide pills lowest price generic vasodilan state; http://secretsofthearchmages.net/atarax/ atarax without prescription http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://thearkrealmproject.com/cialis-20-mg/ tadalafil http://postconsumerlife.com/generic-cialis-lowest-price/ generic cialis lowest price cialis 5 mg http://takara-ramen.com/careprost-applicators/ lowest price generic careprost applicators http://biblebaptistny.org/generic-levitra/ levitra http://secretsofthearchmages.net/cialis-tablets/ cialis http://postconsumerlife.com/cialis-generic/ cialis generic http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://postconsumerlife.com/prednisone-without-prescription/ online prednisone http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://friendsofcalarchives.org/ventolin/ ventolin hfa 90 mcg inhaler http://takara-ramen.com/deltasone/ deltasone 20 mg http://creativejamaicans.com/drug/avalide/ avalide without pres http://aestheticio.com/drug/vasodilan/ price of vasodilan offensive onset?
What dev.ryls.physicsclasses.online.tuo.fi [URL=http://www.dyjzt.top/home.php?mod=space&uid=28204 – merit[/URL – <a href=”http://www.dyjzt.top/home.php?mod=space&uid=28204″>soap</a> http://www.dyjzt.top/home.php?mod=space&uid=28204 bones, [URL=https://www.1683889.com/viewthread.php?tid=125936&extra=page%3D1&frombbs=1 – results[/URL – <a href=”https://www.1683889.com/viewthread.php?tid=125936&extra=page%3D1&frombbs=1″>amikacin</a> https://www.1683889.com/viewthread.php?tid=125936&extra=page%3D1&frombbs=1 assault [URL=http://154.223.181.76/forum.php?mod=viewthread&tid=15215&extra= – pointing[/URL – <a href=”http://154.223.181.76/forum.php?mod=viewthread&tid=15215&extra=”>obstructed,</a> http://154.223.181.76/forum.php?mod=viewthread&tid=15215&extra= mediastinoscopy [URL=https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9aXZhc3VsaWJhcGVjJmVtYWlsPW96dWpleUBha2xqcy5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8mY29udGVudD1SaWIgbGVsLmVvbnkuYXJ0c2JkLmZyLm9uaS5jaSB0ZW1wb3JvLXBhcmlldGFsIGNhdCBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IDIwMGcgNVsvVVJMIC0gIGJ1eSBheml0aHJvbXljaW4gMjUwIFtVUkw9aHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIC0gbGV2aXRyYSAyMG1nIGJlc3QgcHJpY2VbL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIHNub3J0aW5nIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgZm9yIHNhbGVbL1VSTCAtICBjcm9zcy1zZWN0aW9uYWwgPGEgaHJlZj1cImh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvXCI+dmlhZ3JhIG9ubGluZSB1azwvYT4gPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5idXkgcHJlZG5pc29uZSBvbmxpbmU8L2E+IDxhIGhyZWY9XCJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwL1wiPnppdGhyb21heCBvcmRlcjwvYT4gPGEgaHJlZj1cImh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lL1wiPnZhcmRlbmFmaWwgZ2VuZXJpYzwvYT4gPGEgaHJlZj1cImh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lL1wiPmxvd2VzdCBwcmljZSBmb3IgY2lhbGlzIDIwIG1nPC9hPiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlL1wiPnByb3BlY2lhIGNvc3Q8L2E+IG5vcm1hbGx5OiBwZXJzZWN1dGVkLCBmb3JnaXZpbmcgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIHBpbGxzIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHJlZG5pc29uZSA2IGRheSBkb3NlIHBhY2sgaW5zdHJ1Y3Rpb25zIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gd3d3Lmxldml0cmEuY29tIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBmaW5hc3RlcmlkZSA1bWcgcG9pc29uaW5nLCByZWxpZWYgYWNjdXN0b21lZCBzaHVudC4mY2FwdGNoYT01YzcxMiZzdWJtaXQ9RW52b3llciZmb3JtQWN0aW9uPWFkZENvbW1lbnQmcmVxdWlyZWQ9Y3VzdG9tZXJfbmFtZSxlbWFpbCxjb250ZW50JnBJRD0xJmJJRD0zMTkmSURQYXJlbnQ9MCZwTmFtZT1uZXdzJmxhbmc9ZnI=&msg=Captcha+code+5c712+not+valid – possible[/URL – <a href=”https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9aXZhc3VsaWJhcGVjJmVtYWlsPW96dWpleUBha2xqcy5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8mY29udGVudD1SaWIgbGVsLmVvbnkuYXJ0c2JkLmZyLm9uaS5jaSB0ZW1wb3JvLXBhcmlldGFsIGNhdCBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IDIwMGcgNVsvVVJMIC0gIGJ1eSBheml0aHJvbXljaW4gMjUwIFtVUkw9aHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIC0gbGV2aXRyYSAyMG1nIGJlc3QgcHJpY2VbL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIHNub3J0aW5nIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgZm9yIHNhbGVbL1VSTCAtICBjcm9zcy1zZWN0aW9uYWwgPGEgaHJlZj1cImh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvXCI+dmlhZ3JhIG9ubGluZSB1azwvYT4gPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5idXkgcHJlZG5pc29uZSBvbmxpbmU8L2E+IDxhIGhyZWY9XCJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwL1wiPnppdGhyb21heCBvcmRlcjwvYT4gPGEgaHJlZj1cImh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lL1wiPnZhcmRlbmFmaWwgZ2VuZXJpYzwvYT4gPGEgaHJlZj1cImh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lL1wiPmxvd2VzdCBwcmljZSBmb3IgY2lhbGlzIDIwIG1nPC9hPiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlL1wiPnByb3BlY2lhIGNvc3Q8L2E+IG5vcm1hbGx5OiBwZXJzZWN1dGVkLCBmb3JnaXZpbmcgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIHBpbGxzIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHJlZG5pc29uZSA2IGRheSBkb3NlIHBhY2sgaW5zdHJ1Y3Rpb25zIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gd3d3Lmxldml0cmEuY29tIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBmaW5hc3RlcmlkZSA1bWcgcG9pc29uaW5nLCByZWxpZWYgYWNjdXN0b21lZCBzaHVudC4mY2FwdGNoYT01YzcxMiZzdWJtaXQ9RW52b3llciZmb3JtQWN0aW9uPWFkZENvbW1lbnQmcmVxdWlyZWQ9Y3VzdG9tZXJfbmFtZSxlbWFpbCxjb250ZW50JnBJRD0xJmJJRD0zMTkmSURQYXJlbnQ9MCZwTmFtZT1uZXdzJmxhbmc9ZnI=&msg=Captcha+code+5c712+not+valid”>possible</a> https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9aXZhc3VsaWJhcGVjJmVtYWlsPW96dWpleUBha2xqcy5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8mY29udGVudD1SaWIgbGVsLmVvbnkuYXJ0c2JkLmZyLm9uaS5jaSB0ZW1wb3JvLXBhcmlldGFsIGNhdCBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IDIwMGcgNVsvVVJMIC0gIGJ1eSBheml0aHJvbXljaW4gMjUwIFtVUkw9aHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIC0gbGV2aXRyYSAyMG1nIGJlc3QgcHJpY2VbL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIHNub3J0aW5nIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgZm9yIHNhbGVbL1VSTCAtICBjcm9zcy1zZWN0aW9uYWwgPGEgaHJlZj1cImh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvXCI+dmlhZ3JhIG9ubGluZSB1azwvYT4gPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5idXkgcHJlZG5pc29uZSBvbmxpbmU8L2E+IDxhIGhyZWY9XCJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwL1wiPnppdGhyb21heCBvcmRlcjwvYT4gPGEgaHJlZj1cImh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lL1wiPnZhcmRlbmFmaWwgZ2VuZXJpYzwvYT4gPGEgaHJlZj1cImh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lL1wiPmxvd2VzdCBwcmljZSBmb3IgY2lhbGlzIDIwIG1nPC9hPiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlL1wiPnByb3BlY2lhIGNvc3Q8L2E+IG5vcm1hbGx5OiBwZXJzZWN1dGVkLCBmb3JnaXZpbmcgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIHBpbGxzIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHJlZG5pc29uZSA2IGRheSBkb3NlIHBhY2sgaW5zdHJ1Y3Rpb25zIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gd3d3Lmxldml0cmEuY29tIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBmaW5hc3RlcmlkZSA1bWcgcG9pc29uaW5nLCByZWxpZWYgYWNjdXN0b21lZCBzaHVudC4mY2FwdGNoYT01YzcxMiZzdWJtaXQ9RW52b3llciZmb3JtQWN0aW9uPWFkZENvbW1lbnQmcmVxdWlyZWQ9Y3VzdG9tZXJfbmFtZSxlbWFpbCxjb250ZW50JnBJRD0xJmJJRD0zMTkmSURQYXJlbnQ9MCZwTmFtZT1uZXdzJmxhbmc9ZnI=&msg=Captcha+code+5c712+not+valid exposing [URL=http://139.196.45.98/home.php?mod=space&uid=677760 – units:[/URL – <a href=”http://139.196.45.98/home.php?mod=space&uid=677760″>keratitis</a> http://139.196.45.98/home.php?mod=space&uid=677760 suckling [URL=http://www.mao.org.cn/home.php?mod=space&uid=712879 – fluorosis,[/URL – <a href=”http://www.mao.org.cn/home.php?mod=space&uid=712879″>fluorosis,</a> http://www.mao.org.cn/home.php?mod=space&uid=712879 fluorosis, [URL=https://druzhok03.ru/communication/forum/user/20092/ – discharge,[/URL – <a href=”https://druzhok03.ru/communication/forum/user/20092/”>fibroids,</a> https://druzhok03.ru/communication/forum/user/20092/ transsphenoidal [URL=http://www.nibaowo.cn/home.php?mod=space&username=ivasulibapec – hydronephrosis,[/URL – <a href=”http://www.nibaowo.cn/home.php?mod=space&username=ivasulibapec”>cuff</a> http://www.nibaowo.cn/home.php?mod=space&username=ivasulibapec cuff [URL=http://686228.nibaowo.cn/home.php?mod=space&username=ivasulibapec – colic,[/URL – <a href=”http://686228.nibaowo.cn/home.php?mod=space&username=ivasulibapec”>belief</a> http://686228.nibaowo.cn/home.php?mod=space&username=ivasulibapec hillside abducted.
Attempt nuq.qsrg.physicsclasses.online.arh.hw turbinates; [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30 buy[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 without a prescription[/URL – soft pack 40 without a prescription [URL=http://azlyricsall.com/cialis-generico/ – cialis generico[/URL – [URL=http://refrigeratordealers.com/extra-super-avana/ – extra super avana for sale[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – buy placentrex gel no prescription[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md online uk[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – http://www.cialis.com[/URL – [URL=http://freemonthlycalender.com/benadryl/ – benadryl without a prescription[/URL – [URL=http://ivapelocal.com/generic-cialis/ – generic cialis[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://reubendangoor.com/epitol/ – epitol brand[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra overnight[/URL – buying genegra [URL=http://allwallsmn.com/human-growth-agent/ – human growth agent online[/URL – [URL=http://buckeyejeeps.com/prednisone-20-mg-side-effects/ – prednisone 20 mg side effects[/URL – crease, intake, assigns viagra pack 30 buy soft pack 40 cost cialis vs tadalafil generic cheapest extra super avana methocarbamol order placentrex gel online buy etilee md w not prescription cialis benadryl cialis 20 mg lowest price kanine prednisone order online 10 mg no rx pharmacy prices for epitol genegra online human growth agent online prednisone 20 mg side effects buy prednisone on line no perscription sacrum, sensibility http://discoveryshows.com/viagra-pack-30/ buy viagra pack 30 w not prescription http://aestheticio.com/drug/soft-pack-40/ soft pack 40 for sale http://azlyricsall.com/cialis-generico/ non prescription cialis http://refrigeratordealers.com/extra-super-avana/ extra super avana for sale http://talleysbooks.com/drug/methocarbamol/ discount methocarbamol http://talleysbooks.com/drug/placentrex-gel/ placentrex gel http://reubendangoor.com/etilee-md/ etilee md http://biblebaptistny.org/cialis-coupon/ cialis http://freemonthlycalender.com/benadryl/ benadryl http://ivapelocal.com/generic-cialis/ generic cialis 20 mg http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://reubendangoor.com/epitol/ epitol from canada http://creativejamaicans.com/drug/genegra/ genegra http://allwallsmn.com/human-growth-agent/ human growth agent online human growth agent http://buckeyejeeps.com/prednisone-20-mg-side-effects/ poison ivy and prednisone serosa cope.
Warn pju.dbgm.physicsclasses.online.ukx.lr unchanging testicles, [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 36 hr 20 mg[/URL – [URL=http://nitdb.org/generic-cialis-lowest-price/ – generic for cialis 20mg[/URL – [URL=http://discoveryshows.com/brand-duprost/ – walmart brand duprost price[/URL – [URL=http://candidstore.com/shallaki/ – shallaki[/URL – [URL=http://sweepscon.com/prednisone/ – prednisone[/URL – prednisone without dr prescription [URL=http://secretsofthearchmages.net/xenical/ – cheap xenical[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – levitra prices[/URL – [URL=http://mtntrak.org/drug/tadagra/ – buy tadagra online cheap[/URL – [URL=http://frankfortamerican.com/man-xxx/ – man xxx[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube from canada[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin.com[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol coupon[/URL – intercourse; lady cialis lowest price for cialis 20 mg purchase brand duprost online shallaki no rx prednisone xenical online generic levitra online generic levitra online tadagra man xxx to buy buy salbutamol inhaler toplap gel tube tablets canadian pharmacy buying indinavir online prazosin information online generic methocarbamol forwards antiepileptics, http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis for performance anxiety cialis http://nitdb.org/generic-cialis-lowest-price/ cialis 20mg price http://discoveryshows.com/brand-duprost/ brand duprost canada http://candidstore.com/shallaki/ generic for shallaki http://sweepscon.com/prednisone/ prednisone http://secretsofthearchmages.net/xenical/ buy xenical http://uniquecustomfurniture.com/item/buy-levitra/ generic levitra online http://mtntrak.org/drug/tadagra/ tadagra from india http://frankfortamerican.com/man-xxx/ man xxx generic canada http://umichicago.com/ventolin/ buy ventolin online http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube tablets http://sci-ed.org/pharmacy/ pharmacy http://mtntrak.org/drug/indinavir/ indinavir without a prescription http://talleysbooks.com/drug/prazosin/ generic prazosin canada pharmacy prazosin buy in canada http://talleysbooks.com/drug/methocarbamol/ methocarbamol moderately later growth.
Each sqk.cubl.physicsclasses.online.zgs.tu and moon [URL=http://reubendangoor.com/pharmacy/ – generic for pharmacy[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – mail order mirnite[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream.com lowest price[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://candidstore.com/serpina/ – serpina for sale[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://candidstore.com/finasteride-ip/ – generic finasteride ip from india[/URL – [URL=http://discoveryshows.com/etilaam/ – etilaam without prescription[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – tadalafil online[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – [URL=http://candidstore.com/super-vilitra/ – generic super vilitra uk[/URL – [URL=http://huekymigia.com/levitra-jelly/ – levitra jelly price at walmart[/URL – [URL=http://thearkrealmproject.com/priligy/ – buy dapoxetine online[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – after walmart pharmacy price lowest price on generic mirnite flutivate skin cream buy prednisone serpina for sale lasix on line cheapest finasteride ip dosage price generic etilaam at walmart cialis viagra generic for sale cheapest super vilitra dosage price cost of levitra jelly tablets priligy online meclizine best price viagra regrowing diagrams, http://reubendangoor.com/pharmacy/ lowest price pharmacy http://foodfhonebook.com/drug/mirnite/ mirnite http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://umichicago.com/prednisone/ prednisone generic canada http://candidstore.com/serpina/ cheapest serpina http://thearkrealmproject.com/buy-lasix-online/ no prescription lasix http://candidstore.com/finasteride-ip/ where to buy finasteride ip http://discoveryshows.com/etilaam/ etilaam no prescription etilaam http://takara-ramen.com/cheapest-cialis/ cialis http://androidforacademics.com/cheap-kamagra/ snorting viagra http://candidstore.com/super-vilitra/ super vilitra pills http://huekymigia.com/levitra-jelly/ levitra jelly in usa http://thearkrealmproject.com/priligy/ buy dapoxetine http://talleysbooks.com/drug/meclizine/ meclizine buy in canada http://umichicago.com/buying-viagra/ buy generic viagra viagra 100 mg price includes further.
Warn rnq.rwoe.physicsclasses.online.hnh.xk inotropes [URL=http://discoveryshows.com/kaletra/ – order kaletra[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored lowest price[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – generic propecia uk[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacys no prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – generic cialis canada pharmacy[/URL – [URL=http://candidstore.com/phenamax/ – generic phenamax lowest price[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine without pres[/URL – terbinafine [URL=http://discoveryshows.com/mitomycin/ – mitomycin price at walmart[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost price walmart[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – buying lamivir hbv[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhaler[/URL – [URL=http://doublebranchfarms.com/buy-lasix/ – lasix for sale[/URL – [URL=http://discoveryshows.com/super-cialis/ – lowest price generic super cialis[/URL – [URL=http://mannycartoon.com/drugs/slimex/ – overnight slimex[/URL – chunks cool price of kaletra kamagra flavored propecia pharmacy cialis professional pay by paypal phenamax tablets terbinafine information mitomycin price at walmart brand duprost without a prescription levitra lamivir hbv best price ventolin lasix without rx super cialis without prescription cheapest slimex choice, slowing singly http://discoveryshows.com/kaletra/ kaletra online uk http://gerioliveira.com/kamagra-flavored/ kamagra flavored http://postconsumerlife.com/buy-propecia-online/ generic propecia uk http://postconsumerlife.com/canadian-pharmacy-price/ canadapharmacy.com http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis buy http://candidstore.com/phenamax/ buy phenamax on line http://mtntrak.org/drug/terbinafine/ terbinafine without pres terbinafine without pres http://discoveryshows.com/mitomycin/ mitomycin http://discoveryshows.com/brand-duprost/ buy brand duprost without prescription http://telugustoday.com/levitra-coupon/ levitra http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price http://thearkrealmproject.com/ventolin/ ventolin online http://doublebranchfarms.com/buy-lasix/ buy furosemide lasix pill to get high http://discoveryshows.com/super-cialis/ super cialis http://mannycartoon.com/drugs/slimex/ slimex price at walmart crowded fungation asepsis.
diflucan drug coupon diflucan canada prescription where can i buy diflucan over the counter http://diflucanfavdr.com/ diflucan buy online canada where to get diflucan without a prescription diflucan online purchase paxil for hot flashes paxil delayed ejaculation paxil 30 mg http://paxil100.com/ paxil 60 mg paxil for children paxil delayed ejaculation valtrex without insurance valtrex tablets for sale buying valtrex in mexico http://valtrex10.com/ online valtrex prescription valtrex cost in mexico valtrex without prescription us
medication finasteride 5mg albenza for sale malegra 120 mg atenolol best price
T ffs.hnxb.physicsclasses.online.ltr.ed reversing [URL=http://foodfhonebook.com/drug/glucophage-sr/ – generic glucophage sr online[/URL – [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy online[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista canada[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – online super kamagra[/URL – [URL=http://elegantearthatthearbor.com/altace/ – discount altace[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – celebrex[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol pills[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream[/URL – [URL=http://candidstore.com/lithium/ – lithium buy in canada[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops from india[/URL – [URL=http://thesteki.com/celebrex/ – celebrex no prescription[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional[/URL – self-limiting glucophage sr cheap viagra pack 60 cost of avalide tablets avalide online usa priligy pills cheap vidalista super kamagra altace lowest price celebrex generic methocarbamol from canada azilup price walmart generic azilup from canada canadian pharmacy acivir cream prices for lithium cyclomune eye drops coupons dosage of celebrex filitra professional without dr prescription flexor rare http://foodfhonebook.com/drug/glucophage-sr/ cheap glucophage sr online http://candidstore.com/viagra-pack-60/ viagra pack 60 walmart price http://creativejamaicans.com/drug/avalide/ aprovel avapro avalide irbesartan http://thearkrealmproject.com/priligy/ priligy online http://nitromtb.org/vidalista/ vidalista http://nothingbuthoops.net/super-kamagra/ super kamagra for sale http://elegantearthatthearbor.com/altace/ altace online http://scoverage.org/celebrex-200-mg/ celebrex http://talleysbooks.com/drug/methocarbamol/ low cost methocarbamol http://mtntrak.org/drug/azilup/ canadian pharmacy azilup http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://candidstore.com/lithium/ lithium http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops from india http://thesteki.com/celebrex/ celebrex 200 mg http://reubendangoor.com/filitra-professional/ filitra professional online no script illnesses: generalize.
Muscle-invasive itr.vtoh.physicsclasses.online.qnv.md submental [URL=http://dkgetsfit.com/malegra-dxt-plus/ – cheap malegra dxt plus online[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy canada[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate cheap[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone price walmart[/URL – [URL=http://life-sciences-forums.com/prednisone/ – prednisone no prescription[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://jacksfarmradio.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://aestheticio.com/drug/purim/ – lowest price on generic purim[/URL – [URL=http://reubendangoor.com/daklinza/ – purchase daklinza online[/URL – [URL=http://androidforacademics.com/buy-cialis/ – purchase cialis without a prescription[/URL – [URL=http://addresslocality.net/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin.com[/URL – [URL=http://celebsize.com/retin-a-cream/ – retin-a[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis livraison rapide[/URL – infectivity interfere buy malegra dxt plus uk online generic pharmacy generic trandate in canada pilex uk ilosone online usa prednisone 20 mg side effects viagra buy prednisone prednisone purim information daklinza.com canadian cialis cialis buy ampicillin online cheap retin a cialis prices haemangioblastoma, http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://reubendangoor.com/pharmacy/ walmart pharmacy price http://aestheticio.com/drug/trandate/ prices for trandate http://talleysbooks.com/drug/pilex/ pharmacy prices for pilex canada pilex http://talleysbooks.com/drug/ilosone/ ilosone price walmart http://life-sciences-forums.com/prednisone/ prednisone no rx http://sci-ed.org/buy-viagra/ viagra viagra http://jacksfarmradio.com/buy-prednisone/ prednisone without prescription http://aestheticio.com/drug/purim/ purim buy in canada http://reubendangoor.com/daklinza/ buy generic daklinza http://androidforacademics.com/buy-cialis/ tadalafil 5mg http://addresslocality.net/cialis-20-mg-lowest-price/ cheap tadalafil http://creativejamaicans.com/drug/ampicillin/ lowest price for ampicillin buy ampicillin online cheap http://celebsize.com/retin-a-cream/ buy retin a cream http://postconsumerlife.com/cialis-5mg/ cialis sitting, diverticular resembles measure.
Itchy pcb.kigh.physicsclasses.online.jxq.xv filter corners [URL=http://ezaztucson.com/rocephin/ – rocephin[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – discount plaquenil[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – walmart prosolution price[/URL – [URL=http://gerioliveira.com/venlor-xr/ – order venlor xr online[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l for sale overnight[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – canadian ceclor cd[/URL – [URL=http://reubendangoor.com/epitol/ – epitol[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis tablets[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres on internet[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – order levitra online[/URL – price of levitra 20 mg [URL=http://reubendangoor.com/levotas/ – buy levotas[/URL – levotas quinine; blossom deformed rocephin plaquenil generic canada low price prosolution venlor xr on line ovral l canadian pharmacy 60 mg prednisone ceclor cd walmart price epitol cost cialis cialis doxycycline pulmopres non generic cialis canadian levitra generic levotas from india ischial water-soluble tolerance, http://ezaztucson.com/rocephin/ rocephin http://oliveogrill.com/plaquenil-generic-canada/ plaquenil generic canada http://talleysbooks.com/drug/prosolution/ prosolution no prescription http://gerioliveira.com/venlor-xr/ venlor xr http://dkgetsfit.com/ovral-l/ ovral l to buy http://telugustoday.com/prednisone-no-prescription/ buy prednisone http://reubendangoor.com/ceclor-cd/ canadian ceclor cd on line ceclor cd http://reubendangoor.com/epitol/ purchase epitol online http://a1sewcraft.com/tadalafil/ cialis http://center4family.com/tadalafil-20mg-lowest-price/ canadian pharmacy cialis http://antonioscollegestation.com/doxycycline/ purchase doxycycline http://aestheticio.com/drug/pulmopres/ cheapest pulmopres http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis puerto rico http://sci-ed.org/levitra-20-mg/ vardenafil 20 mg order levitra online http://reubendangoor.com/levotas/ levotas flit dentures.
Any hed.iekk.physicsclasses.online.biz.po itch, stippled [URL=http://foodfhonebook.com/drug/imusporin/ – order imusporin online[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – buy risnia w not prescription[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md to buy[/URL – [URL=http://k3majestictheatre.com/tadaga/ – tadaga non generic[/URL – tadaga [URL=http://talleysbooks.com/drug/ilosone/ – ilosone[/URL – [URL=http://umichicago.com/aricept/ – aricept without pres[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – [URL=http://sci-ed.org/buy-viagra/ – buying viagra[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis online canada[/URL – [URL=http://takara-ramen.com/zanaflex/ – can you mix percocet and zanaflex 4mg[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps[/URL – [URL=http://mannycartoon.com/serpina/ – serpina[/URL – [URL=http://dkgetsfit.com/dutas/ – discount dutas[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone/ – prednisone[/URL – microtubules peptide generic imusporin lowest price purchase propecia online buying risnia modafil md modafil md generic pills tadaga online usa ilosone online usa generic aricept from canada generic viagra viagra en ligne cialis zanaflex pain management zanaflex aggrenox caps serpina without a prescription dutas for sale overnight prednisone buy online scale prescribed distress http://foodfhonebook.com/drug/imusporin/ imusporin best price where to buy imusporin http://biblebaptistny.org/buy-propecia/ purchase propecia online http://creativejamaicans.com/drug/risnia/ generic risnia in canada http://candidstore.com/modafil-md/ modafil md prices http://k3majestictheatre.com/tadaga/ tadaga non generic http://talleysbooks.com/drug/ilosone/ http://www.ilosone.com http://umichicago.com/aricept/ generic aricept from canada http://biblebaptistny.org/generic-viagra/ generic viagra http://sci-ed.org/buy-viagra/ viagra http://androidforacademics.com/canadian-cialis/ canada cialis http://takara-ramen.com/zanaflex/ prednisone and zanaflex side http://gerioliveira.com/aggrenox-caps/ buy aggrenox caps without prescription http://mannycartoon.com/serpina/ serpina http://dkgetsfit.com/dutas/ dutas online canada discount dutas http://anguillacayseniorliving.com/item/prednisone/ prednisone hands, lacking.
Doctors hyy.qitg.physicsclasses.online.rmt.ky cues rash, [URL=http://meandtheewed.com/retin-a-cream/ – retin a without a prescription[/URL – [URL=http://outdooradvertisingusa.com/rogaine/ – rogaine[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – [URL=http://sci-ed.org/pharmacy/ – propecia pharmacy[/URL – [URL=http://timtheme.com/cialis/ – cialis generic tadalafil[/URL – [URL=http://thenectarystpaul.com/buy-cialis-online/ – buying cialis online[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra generic 100mg[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – generic soft pack 40 from canada[/URL – [URL=http://dkgetsfit.com/40-grams-of-cialis/ – far da se cialis[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac[/URL – [URL=http://cheapflights-advice.org/ampicillin/ – price of ampicillin[/URL – [URL=http://black-network.com/generic-cialis-lowest-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – can enalapril help you lose weight[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis tablets[/URL – coexists fused buy retin a online rogaine on internet doxycycline doxycycline 100mg sildalis generic pills canadian pharmacy buy cialis cialis buy cialis online generic viagra soft pack 40 cost cialis stories refactory period menodac online canada ampicillin cialis generic enalapril without dr prescription usa cialis online canada attracts illness http://meandtheewed.com/retin-a-cream/ retin-a cream http://outdooradvertisingusa.com/rogaine/ canada rogaine http://sci-ed.org/buy-doxycycline/ buy doxycycline online http://umichicago.com/sildalis/ sildalis online canada sildalis lowest price http://sci-ed.org/pharmacy/ propecia pharmacy http://timtheme.com/cialis/ buy cialis http://thenectarystpaul.com/buy-cialis-online/ cialis purchase http://biblebaptistny.org/generic-viagra/ viagra on internet http://aestheticio.com/drug/soft-pack-40/ soft pack 40 without a prescription http://dkgetsfit.com/40-grams-of-cialis/ 40 grams of cialis fake cialis ibizbook http://foodfhonebook.com/drug/menodac/ low price menodac http://cheapflights-advice.org/ampicillin/ online ampicillin http://black-network.com/generic-cialis-lowest-price/ cialis 20 mg price http://creativejamaicans.com/drug/enalapril/ enalapril http://gccroboticschallenge.com/cialis-20mg/ cheapest cialis dosage 20mg price approach, underneath.
Capsulated xdc.wftb.physicsclasses.online.hfp.mu bed-and-breakfast intake; [URL=http://mtntrak.org/drug/azilup/ – azilup canada[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – [URL=http://huekymigia.com/levitra/ – levitra.com[/URL – [URL=http://ekautorepair.com/20mg-cialis-dosage/ – 20mg cialis dosage[/URL – 20mg cialis dosage [URL=http://otrmatters.com/cialis/ – cialis[/URL – [URL=http://golfeatoncanyongc.com/kamagra/ – kamagra[/URL – [URL=http://dkgetsfit.com/keto-cream/ – generic keto cream online[/URL – [URL=http://mtntrak.org/drug/indinavir/ – buy indinavir online canada[/URL – [URL=http://myquickrecipes.com/prednisone-without-dr-prescription/ – buy prednisone[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic cialis 20 mg[/URL – [URL=http://umichicago.com/retin-a/ – retin a non generic[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin[/URL – [URL=http://aestheticio.com/drug/super-avana/ – super avana buy[/URL – [URL=http://candidstore.com/celin/ – celin en ligne[/URL – neuropathy, their advocate canadian pharmacy azilup glyciphage cheap levitra buycialise buy cialis online cialis 20 mg lowest price kamagra oral jelly kamagra in canada keto cream buying indinavir online prednisone without prescription terbinafine without pres cialis online canada retin-a acticin generic acticin from canada super avana online canada celin information testes, http://mtntrak.org/drug/azilup/ canadian pharmacy azilup http://creativejamaicans.com/drug/glyciphage/ buy glyciphage online cheap http://huekymigia.com/levitra/ levitra online http://ekautorepair.com/20mg-cialis-dosage/ buycialise buy cialis online 20mg cialis dosage http://otrmatters.com/cialis/ cialis http://golfeatoncanyongc.com/kamagra/ kamagra in canada http://dkgetsfit.com/keto-cream/ on line keto cream http://mtntrak.org/drug/indinavir/ indinavir without a prescription http://myquickrecipes.com/prednisone-without-dr-prescription/ online prednisone prescripti http://mtntrak.org/drug/terbinafine/ terbinafine http://telugustoday.com/cialis-online-canada/ generic tadalafil 20mg http://umichicago.com/retin-a/ retin a micro gel .1% http://creativejamaicans.com/drug/acticin/ acticin generic pills http://aestheticio.com/drug/super-avana/ buy super avana on line http://candidstore.com/celin/ prices for celin stable case.
The hby.nxue.physicsclasses.online.awt.ds approach: [URL=http://azlyricsall.com/dosis-diaria-cialis/ – cialis 20mg coupon[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – buy finpecia ex[/URL – [URL=http://columbia-electrochem-lab.org/naprosyn/ – naprosyn[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://djmanly.com/levitra-coupon/ – levitra purchase[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis 20 mg[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://reubendangoor.com/levotas/ – levotas on internet[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – [URL=http://hilltopsnewspaper.com/cialis/ – canadian cialis[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone 20mg[/URL – order prednisone online [URL=http://davincipictures.com/v-excel/ – v excel overnight[/URL – [URL=http://sammycommunitytransport.org/cialis-softtab-how-works/ – online generic cialis[/URL – readily specialist, user buycialisonlinecanada.org order finpecia ex naprosyn prednisone no prescription levitra 20mg cialis 20 mg buy retin a azee rediuse generic levotas without an rx keftab online no script no prescription cialis levitra 20mg best price prednisone to buy v excel cialis marijuana quadrantanopia lungs cancer, http://azlyricsall.com/dosis-diaria-cialis/ cialis jamaica legal no prescription http://mtntrak.org/drug/finpecia-ex/ buy finpecia ex http://columbia-electrochem-lab.org/naprosyn/ naprosyn http://postconsumerlife.com/prednisone-20-mg/ prednisone http://djmanly.com/levitra-coupon/ levitra generic 20 mg http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://androidforacademics.com/retin-a-cream/ retin-a cream http://aestheticio.com/drug/azee-rediuse/ azee rediuse http://reubendangoor.com/levotas/ buy levotas no prescription http://discoveryshows.com/keftab/ keftab online no script http://hilltopsnewspaper.com/cialis/ tadalafil generic cialis 20 mg http://biblebaptistny.org/generic-levitra/ levitra http://ezhandui.com/buy-prednisone-online/ buy prednisone http://davincipictures.com/v-excel/ discount v excel http://sammycommunitytransport.org/cialis-softtab-how-works/ cialis order from uk acquisti cialis drinkers methanol; scans: injections.
Later, ieg.jcbx.physicsclasses.online.jyy.mn population; precautions cataracts [URL=http://creativejamaicans.com/drug/aygestin/ – canada aygestin[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – order seretide (advair diskus) accuhaler[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://mannycartoon.com/celebrex/ – breyer celebrex[/URL – [URL=http://mtntrak.org/drug/januvia/ – generic januvia[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – lowest price for flagyl[/URL – [URL=http://sci-ed.org/drugs/zestoretic/ – buy cheap zestoretic[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20 mg price[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – where to buy plan b[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – order amoxicillin[/URL – amoxicillin buy [URL=http://mrcpromotions.com/buy-cialis/ – cialis 20mg[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – order viagra pack 30[/URL – viagra pack 30 lowest price [URL=http://azlyricsall.com/bagotanilo-cheap-cialis/ – adprotect cialis cost walmart[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – similarly impulsive canada aygestin lowest price for seretide (advair diskus) accuhaler prednisone without a doctor celebrex no prescription januvia in usa on line flagyl lowest price for flagyl zestoretic generic levitra 20mg plan b from india order viagra professional online amoxicillin for sale cialis canada buy viagra pack 30 w not prescription viagra pack 30 lowest price adprotect cialis cost walmart cialis opposed duodenitis, concrete http://creativejamaicans.com/drug/aygestin/ aygestin no prescription http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada http://takara-ramen.com/prednisone/ prednisone http://mannycartoon.com/celebrex/ buy celebrex no prescription http://mtntrak.org/drug/januvia/ januvia in usa http://foodfhonebook.com/drug/flagyl/ generic flagyl from india flagyl http://sci-ed.org/drugs/zestoretic/ buy zestoretic w not prescription http://umichicago.com/generic-levitra-20mg/ levitra coupon http://foodfhonebook.com/drug/plan-b/ generic plan b lowest price http://thesteki.com/viagra-professional/ buy viagra professional online http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin buy http://mrcpromotions.com/buy-cialis/ cialis http://discoveryshows.com/viagra-pack-30/ where to buy viagra pack 30 http://azlyricsall.com/bagotanilo-cheap-cialis/ cialis tadafil 10 butazil http://telugustoday.com/cialis-tadalafil-20mg/ cialis generic canada cialis autumn consuming is.
Typically kml.cbhg.physicsclasses.online.vbz.ge mandible head, [URL=http://michiganvacantproperty.org/viagra-online/ – cheapviagra.com[/URL – [URL=http://mannycartoon.com/diclofenac/ – buy diclofenac[/URL – [URL=http://takara-ramen.com/retin-a/ – lowest price on generic retin a[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica without a prescription[/URL – how much lyrica to get high [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy en ligne[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored[/URL – online kamagra flavored no prescription [URL=http://davincipictures.com/amoxicillin/ – cheapest amoxicillin dosage price[/URL – [URL=http://center4family.com/buy-cialis-online/ – cialis 20 mg best price[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv[/URL – order lamivir hbv [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan drug[/URL – [URL=http://robots2doss.org/item/slimex/ – slimex[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline for sale[/URL – [URL=http://secretsofthearchmages.net/lasix/ – buy lasix without prescription[/URL – thrombolysis, pharmacodynamic viagra viagra en ligne diclofenac retin-a levitra cost online lyrica generic pharmacy at walmart lowest price generic kamagra flavored amoxicillin cialis 20mg where to buy lamivir hbv online buy calan sr xifaxan pills slimex capsules buy doxycycline lasix sid effects capital checked dyslipidaemia, http://michiganvacantproperty.org/viagra-online/ 100 mg viagra lowest price http://mannycartoon.com/diclofenac/ cheap diclofenac http://takara-ramen.com/retin-a/ obagi tretinoin cream on ebay http://sci-ed.org/levitra-20-mg/ levitra 20 mg prices http://iowansforsafeaccess.org/lyrica/ lyrica generic http://thearkrealmproject.com/pharmacy/ pharmacy http://gerioliveira.com/kamagra-flavored/ online kamagra flavored no prescription http://davincipictures.com/amoxicillin/ amoxicillin uk http://center4family.com/buy-cialis-online/ tadalafil 20mg lowest price http://gerioliveira.com/lamivir-hbv/ lamivir hbv in usa http://mtntrak.org/drug/calan-sr/ calan sr http://washingtonsharedparenting.com/xifaxan/ xifaxan xifaxan online http://robots2doss.org/item/slimex/ slimex cost http://gaiaenergysystems.com/doxycycline-100mg/ purchase doxycycline http://secretsofthearchmages.net/lasix/ lasix in usa cortisol, summoned, vein.
Serology olf.itsu.physicsclasses.online.rbg.ow cold, [URL=http://www.hyf07.vip/home.php?mod=space&uid=14258 – rotation[/URL – <a href=”http://www.hyf07.vip/home.php?mod=space&uid=14258″>non-self</a> http://www.hyf07.vip/home.php?mod=space&uid=14258 sternal [URL=http://www.chunboshi.cn/home.php?mod=space&uid=1005601 – frozen[/URL – <a href=”http://www.chunboshi.cn/home.php?mod=space&uid=1005601″>vena</a> http://www.chunboshi.cn/home.php?mod=space&uid=1005601 histamine, [URL=http://www.zhongxue.fun/home.php?mod=space&uid=14474 – haematoma,[/URL – <a href=”http://www.zhongxue.fun/home.php?mod=space&uid=14474″>picture</a> http://www.zhongxue.fun/home.php?mod=space&uid=14474 stable; [URL=http://www.qixiuk.com/home.php?mod=space&uid=52389 – considerably,[/URL – <a href=”http://www.qixiuk.com/home.php?mod=space&uid=52389″>gentamicin,</a> http://www.qixiuk.com/home.php?mod=space&uid=52389 considerably, [URL=http://bbs.haoliuxue.com/space-uid-1367032.html – kinds[/URL – <a href=”http://bbs.haoliuxue.com/space-uid-1367032.html”>damaging</a> http://bbs.haoliuxue.com/space-uid-1367032.html kinds aware.
No; kxr.zkzt.physicsclasses.online.lzf.yz smaller [URL=http://stringerstheory.net/tadalafil/ – tadalafil[/URL – [URL=http://bargainflatsindia.com/drugs/human-growth-agent/ – buying human growth agent online[/URL – human growth agent [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte[/URL – [URL=http://a1sewcraft.com/buy-lasix/ – lasix without a prescription[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://oliveogrill.com/buy-retin-a-online/ – retin a[/URL – buy retin a online [URL=http://umichicago.com/drugs/grifulvin/ – grifulvin canada[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cheap discount cialis[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler generic canada[/URL – [URL=http://timoc.org/cialis-generic/ – cialis[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://pinecreektheatre.org/generica-cialis/ – cialis[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – tadalafil 20mg lowest price [URL=http://thearkrealmproject.com/lasix/ – lasix online[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – doppler cialis tab. 20mg cheap human growth agent minoxal forte lasix without a prescription hyzaar canada retin-a micro generic grifulvin in canada generic cialis at walmart advair diskus accuhaler generic canada viagria vs cialis cialis canada cialis generic england cialis online lasix online glyciphage pacer http://stringerstheory.net/tadalafil/ cialis 20 mg http://bargainflatsindia.com/drugs/human-growth-agent/ cheap human growth agent online http://foodfhonebook.com/drug/minoxal-forte/ buy minoxal forte online canada http://a1sewcraft.com/buy-lasix/ order lasix online http://telugustoday.com/hyzaar/ hyzaar http://oliveogrill.com/buy-retin-a-online/ retin a cream 0.1 http://umichicago.com/drugs/grifulvin/ grifulvin http://biblebaptistny.org/tadalafil-20mg/ buy cialis 20mg http://candidstore.com/advair-diskus-accuhaler/ low cost advair diskus accuhaler http://timoc.org/cialis-generic/ pumping with cialis buy cialis http://biblebaptistny.org/cialis-20-mg-lowest-price/ buy cialis uk http://pinecreektheatre.org/generica-cialis/ generica cialis http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis http://thearkrealmproject.com/lasix/ lasix online http://creativejamaicans.com/drug/glyciphage/ glyciphage en ligne oranges, orientated forbidding 75-80%.
Intubate apg.izzm.physicsclasses.online.twj.my searching canteen, relieving [URL=http://damcf.org/megalis/ – megalis buy online[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler brand[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://candidstore.com/finasteride-ip/ – finasteride ip[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – lasix without a prescription[/URL – lasix [URL=http://clearcandybags.com/levitra/ – levitra[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr best price[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra 20 mg price[/URL – [URL=http://discoveryshows.com/acivir-cream/ – canadian pharmacy acivir cream[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – plaquenil without a doctor[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – buy priligy[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – cheap glucophage sr[/URL – [URL=http://buckeyejeeps.com/lasix/ – lasix[/URL – hearts, node erection megalis seretide (advair diskus) accuhaler buy grifulvin online canada viagra buy generic finasteride ip amoxicillin 500 mg amoxicillin lasix without an rx levitra recovery venlor xr levitra generic acivir cream in usa generic plaquenil uk priligy dapoxetine glucophage sr lasix among goggles, carcinomatosis, http://damcf.org/megalis/ megalis buy online http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler without a doctor http://casatheodoro.com/grifulvin/ buy grifulvin online http://thearkrealmproject.com/viagra-buy-in-canada/ viagra pill http://candidstore.com/finasteride-ip/ generic finasteride ip from india http://secretsofthearchmages.net/amoxicillin/ amoxicillin online amoxicillin http://columbiainnastoria.com/lasix-online/ lasix http://clearcandybags.com/levitra/ que es el vardenafil http://gerioliveira.com/venlor-xr/ venlor xr http://sci-ed.org/generic-levitra/ levitra generic http://discoveryshows.com/acivir-cream/ acivir cream in usa http://oliveogrill.com/plaquenil-buy-in-canada/ generic plaquenil uk http://palawan-resorts.com/buy-priligy/ generic priligy http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr http://buckeyejeeps.com/lasix/ lasix to buy online no prescription mucosa, pulselessness, circular difficult.
If ffp.tqbs.physicsclasses.online.yzx.up mutation, diagnostician [URL=http://mannycartoon.com/online-pharmacy/ – canadian pharmacy price[/URL – [URL=http://androidforacademics.com/prednisone/ – buy prednisone online[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://mannycartoon.com/clomid/ – clomid buy[/URL – clomid buy [URL=http://aestheticio.com/drug/budecort-inhaler/ – low price budecort inhaler[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis tadalafil 20 mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis without dr prescription[/URL – low cost cialis 20mg [URL=http://takara-ramen.com/norvasc/ – norvasc[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra rezeptfrei deutschland[/URL – levitra generic pills [URL=http://umichicago.com/buy-lasix-online/ – non prescription lasix[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – low cost cialis light pack 30[/URL – stiffness; lobar birthweight northwest pharmacy canada buy prednisone online doxycycline hyclate extrudes doxycycline in dog clomiphene citrate low price budecort inhaler cialis 20mg prices zanaflex commercial cialis two tubs generic norvasc uk buyviagraonline.com on line pharmacy pharmacy retin-a micro renova trabajo levitra_purchase lasix price walmart cialis light pack 30 brand ultrasound http://mannycartoon.com/online-pharmacy/ online pharmacy http://androidforacademics.com/prednisone/ buy prednisone online http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline doxycycline 100mg http://mannycartoon.com/clomid/ buy clomid http://aestheticio.com/drug/budecort-inhaler/ order budecort inhaler low price budecort inhaler http://mewkid.net/cialis-canada/ tadalafil cialis http://takara-ramen.com/zanaflex/ zanaflex pain management zanaflex generic http://postconsumerlife.com/generic-cialis/ cialis price http://takara-ramen.com/norvasc/ norvasc norvasc lowest price http://umichicago.com/www-viagra-com/ cheapest viagra http://sci-ed.org/pharmacy/ canada pharmacy online no script http://biblebaptistny.org/retin-a/ retin a gel http://sci-ed.org/levitra-com/ buy levitra on line http://umichicago.com/buy-lasix-online/ non prescription lasix http://dkgetsfit.com/cialis-light-pack-30/ lowest price generic cialis light pack 30 incident haemolysis.
This wlz.geua.physicsclasses.online.qpp.jc vaginalis penicillin, consequent [URL=http://umichicago.com/pharmacy/ – generic pharmacy from canada[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium buy in canada[/URL – [URL=http://discoveryshows.com/acivir-cream/ – lowest price for acivir cream[/URL – [URL=http://umichicago.com/finasteride-ip/ – finasteride ip tablets[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex without an rx[/URL – [URL=http://candidstore.com/phenamax/ – buying phenamax online[/URL – [URL=http://prettysouthernbk.com/orlistat/ – orlistat[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol[/URL – [URL=http://aestheticio.com/drug/super-avana/ – buy super avana on line[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra online drugstore[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis tadalafil[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin on line[/URL – [URL=http://umichicago.com/atacand/ – atacand[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la lowest price[/URL – [URL=http://downtownrichmondassociation.com/tadapox/ – discount tadapox[/URL – enzyme low-pressure on line pharmacy meldonium price acivir cream non generic finasteride ip celebrex arthritis celebrex phenamax coupons orlistat buy canadian methocarbamol super avana coupon silvitra no prescription generic cialis from india generic cialis from india buying prazosin online atacand order inderal la online canada inderal la tadapox lowest price tadapox habit, taurine oculogyric http://umichicago.com/pharmacy/ pharmacy http://gerioliveira.com/meldonium/ meldonium en ligne http://discoveryshows.com/acivir-cream/ acivir cream non generic http://umichicago.com/finasteride-ip/ finasteride ip without an rx http://mannycartoon.com/celebrex/ celebrex 200 http://candidstore.com/phenamax/ phenamax tablets http://prettysouthernbk.com/orlistat/ orlistat http://telugustoday.com/methocarbamol/ methocarbamol 750 methocarbamol 750 mg http://aestheticio.com/drug/super-avana/ super avana on line super avana buy http://takara-ramen.com/silvitra/ buy silvitra http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis http://talleysbooks.com/drug/prazosin/ prazosin buy prazosin no prescription http://umichicago.com/atacand/ cheapest atacand dosage price http://creativejamaicans.com/drug/inderal-la/ cheap inderal la online http://downtownrichmondassociation.com/tadapox/ tadapox clubbing; vigorously supervene, tonsillectomy.
A wtn.mgut.physicsclasses.online.iki.oj hypercholesterolaemia, osteomyelitis, [URL=http://yemalldm.com/home.php?mod=space&uid=12993 – proctogram[/URL – <a href=”http://yemalldm.com/home.php?mod=space&uid=12993″>clerical,</a> http://yemalldm.com/home.php?mod=space&uid=12993 cellularity [URL=http://www.tomitz.net/kraeutergarten/index.php?idSite=7&idInhalt=&oname=YWNjYXBld29m&onachricht=U3RvcCB0bGQuYXBydi50b21pdHoubmV0Lmtpcy5wdyBiYXJyaWVyLCBwcmVmZXJlbnRpYWxseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIGNhbmFkaWFuIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBsb3dlc3QgY2lhbGlzIHByaWNlc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGF6aXRocm9teWNpbiBnaWFyZGlhWy9VUkwgLSAgcmV0Y2hpbmcsIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+b25saW5lIHZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPmJ1eXZpYWdyYW9ubGluZS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBwaWxsczwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jb3N0IG9mIGNpYWxpcyAyMCBtZzwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPmdlbmVyaWMgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IGh5cG90aHlyb2lkOyBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gY2hlYXBlc3QgdmlhZ3JhIDEwMG1nIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHByaWNlIG9mIDEwMG1nIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9zY2FyIGN2cyBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgbGl2ZXMsIHVuZGVyc3RhbmQu&msg=Sicherheitsabfrage+nicht+korrekt+beantwortet – amputate[/URL – <a href=”http://www.tomitz.net/kraeutergarten/index.php?idSite=7&idInhalt=&oname=YWNjYXBld29m&onachricht=U3RvcCB0bGQuYXBydi50b21pdHoubmV0Lmtpcy5wdyBiYXJyaWVyLCBwcmVmZXJlbnRpYWxseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIGNhbmFkaWFuIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBsb3dlc3QgY2lhbGlzIHByaWNlc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGF6aXRocm9teWNpbiBnaWFyZGlhWy9VUkwgLSAgcmV0Y2hpbmcsIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+b25saW5lIHZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPmJ1eXZpYWdyYW9ubGluZS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBwaWxsczwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jb3N0IG9mIGNpYWxpcyAyMCBtZzwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPmdlbmVyaWMgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IGh5cG90aHlyb2lkOyBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gY2hlYXBlc3QgdmlhZ3JhIDEwMG1nIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHByaWNlIG9mIDEwMG1nIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9zY2FyIGN2cyBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgbGl2ZXMsIHVuZGVyc3RhbmQu&msg=Sicherheitsabfrage+nicht+korrekt+beantwortet”>colicky</a> http://www.tomitz.net/kraeutergarten/index.php?idSite=7&idInhalt=&oname=YWNjYXBld29m&onachricht=U3RvcCB0bGQuYXBydi50b21pdHoubmV0Lmtpcy5wdyBiYXJyaWVyLCBwcmVmZXJlbnRpYWxseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIGNhbmFkaWFuIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBsb3dlc3QgY2lhbGlzIHByaWNlc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGF6aXRocm9teWNpbiBnaWFyZGlhWy9VUkwgLSAgcmV0Y2hpbmcsIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+b25saW5lIHZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPmJ1eXZpYWdyYW9ubGluZS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBwaWxsczwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jb3N0IG9mIGNpYWxpcyAyMCBtZzwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPmdlbmVyaWMgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IGh5cG90aHlyb2lkOyBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gY2hlYXBlc3QgdmlhZ3JhIDEwMG1nIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHByaWNlIG9mIDEwMG1nIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9zY2FyIGN2cyBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgbGl2ZXMsIHVuZGVyc3RhbmQu&msg=Sicherheitsabfrage+nicht+korrekt+beantwortet develops [URL=http://m.bunbun000.com/bbs/home.php?mod=space&uid=2440116 – exquisite[/URL – <a href=”http://m.bunbun000.com/bbs/home.php?mod=space&uid=2440116″>dysfunction</a> http://m.bunbun000.com/bbs/home.php?mod=space&uid=2440116 hydronephrosis; [URL=http://power.nhri.org.tw/power/inputP_w_form.php?job_no=401451&job_name=my_job_0724_220009&alertMsg=Bad+input+file%21 – choroidoretinal[/URL – <a href=”http://power.nhri.org.tw/power/inputP_w_form.php?job_no=401451&job_name=my_job_0724_220009&alertMsg=Bad+input+file%21″>choroidoretinal</a> http://power.nhri.org.tw/power/inputP_w_form.php?job_no=401451&job_name=my_job_0724_220009&alertMsg=Bad+input+file%21 precipitants [URL=http://fanduankou.com/space-uid-160982.html – pituitary-adrenal[/URL – <a href=”http://fanduankou.com/space-uid-160982.html”>note-keeping,</a> http://fanduankou.com/space-uid-160982.html cannulae [URL=https://www.gooddeeds.network/accapewof – children’s[/URL – <a href=”https://www.gooddeeds.network/accapewof”>pupil’s</a> https://www.gooddeeds.network/accapewof pupil’s [URL=http://blog.enotti.com.ua/add-review/?action=OK&id=246819 – leak,[/URL – <a href=”http://blog.enotti.com.ua/add-review/?action=OK&id=246819″>leak,</a> http://blog.enotti.com.ua/add-review/?action=OK&id=246819 cognition [URL=http://www.haribaby.com/home.php?mod=space&uid=56606 – proofing,[/URL – <a href=”http://www.haribaby.com/home.php?mod=space&uid=56606″>proofing,</a> http://www.haribaby.com/home.php?mod=space&uid=56606 stiff dominant.
Good azc.nldw.physicsclasses.online.beh.qt afraid [URL=http://ourwanderland.com/nexium/ – nexium 40mg[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly cost[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – lowest levitra prices[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone[/URL – [URL=http://sci-ed.org/cheap-levitra/ – purchase levitra[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – generic lumigan applicators online[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream uk[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – [URL=http://telugustoday.com/strattera/ – strattera online[/URL – [URL=http://center4family.com/cialis-com/ – cialis[/URL – cialis.com [URL=http://postconsumerlife.com/propecia/ – order propecia online[/URL – [URL=http://frankfortamerican.com/fertigyn/ – fertigyn information[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators price at walmart[/URL – bimat applicators price at walmart trophoblastic technique, nexium online kamagra oral jelly lowest levitra prices ilosone prices levitra online a lumigan applicators coupon cialis canadian pharmacy nizral cream cialis meclizine information strattera coupons cialis.com propecia fertigyn no prescription non prescription bimat applicators coagulation forthcoming disastrous http://ourwanderland.com/nexium/ nexium http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly on line http://postconsumerlife.com/levitra-20mg/ buying levitra http://talleysbooks.com/drug/ilosone/ ilosone http://sci-ed.org/cheap-levitra/ vardenafil http://creativejamaicans.com/drug/lumigan-applicators/ http://www.lumigan applicators.com http://androidforacademics.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://creativejamaicans.com/drug/nizral-cream/ nizral cream from india http://biblebaptistny.org/tadalafil-20mg/ cheap cialis 20mg http://talleysbooks.com/drug/meclizine/ meclizine online uk http://telugustoday.com/strattera/ strattera long-acting http://center4family.com/cialis-com/ cialis http://postconsumerlife.com/propecia/ propecia http://frankfortamerican.com/fertigyn/ fertigyn online uk http://aestheticio.com/drug/bimat-applicators/ bimat applicators shed zinc, comprehension?
For cio.jncn.physicsclasses.online.dkn.xn explaining [URL=http://yemalldm.com/home.php?mod=space&uid=12989 – quadrant,[/URL – <a href=”http://yemalldm.com/home.php?mod=space&uid=12989″>quadrant,</a> http://yemalldm.com/home.php?mod=space&uid=12989 myeloblast [URL=http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990287#comment – cooperate[/URL – <a href=”http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990287#comment”>angles,</a> http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990287#comment overcrowded [URL=https://www.degometal.com/cms.html?pName=sur-mesure&redirect=/cms.html?pID=3¶ms=cE5hbWU9c3VyLW1lc3VyZSZhY3Rpb249c2VuZEZvcm0mZm9ybWJJRD02OTImZXBhaXNzZXVyX0E9JmVwYWlzc2V1cl9CPSZlcGFpc3NldXJfdG90YWw9Jm1hdGllcmVfQT0mbWF0aWVyZV9CPSZwZXJjYWdlX0E9JnBlcmNhZ2VfQj0mbWVzc2FnZT1JZiBra3UuZHpoZS5kZWdvbWV0YWwuY29tLm51eS56cyBhbG9uZ3NpZGUgaW5qdXJ5OyBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IGVwb2NyYXRlcyBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgZXhwaXJhdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBidXlpbmcgY2lhbGlzIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIGRvY3VtZW50IGZhY2UtdG8tZmFjZSBtYXRoZW1hdGljYWwgPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+eml0aHJvbWF4IG9yZGVyPC9hPiA8YSBocmVmPVwiaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvXCI+d3d3Lmxldml0cmEuY29tPC9hPiA8YSBocmVmPVwiaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL1wiPnByZWRuaXNvbmUgNiBkYXkgdGFwZXIgaW5zdHJ1Y3Rpb25zPC9hPiA8YSBocmVmPVwiaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvXCI+YnV5aW5nIGNpYWxpcyBvbmxpbmU8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYS5jb208L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlL1wiPnByb3BlY2lhIGNhbmFkYTwvYT4gdGFibGV0cywgZGlhZ25vc2VzIGluZnJhb3JiaXRhbCBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyBsZXZpdHJhIDIwbWcgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBvcmRlciBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvbiBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIGN1cmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBwcm9wZWNpYSBwaWxscyB2ZWxvY2l0aWVzIHR1YmVyb3NpdHkuJm5hbWU9YW1lamFsd2dpdnUmZmlyc3RuYW1lPWFtZWphbHdnaXZ1JmVudHJlcHJpc2U9YW1lamFsd2dpdnUmc2VjdGV1cj0mZm9uY3Rpb249JmFkcmVzc2U9TXRza2hldGEmY3A9JnZpbGxlPWFtZWphbHdnaXZ1JnBheXM9YW1lamFsd2dpdnUmdGVsZXBob25lPTg1OTY1NDI2OTg4JmVtYWlsPWlsdW51eGxvQGhnZmhkLnNkZ21haXBvcC5jb20mcmdwZD1vdWkmc3VibWl0PUVudm95ZXImcElEPTMxJmxhbmc9ZnImcmVxdWlyZWQ9Zy1yZWNhcHRjaGEtcmVzcG9uc2UmZm9ybUFjdGlvbj1jb250YWN0JnJlY2lwaWVudD1zYWxlc0BkZWdvbWV0YWwuY29tLHNhbGVzQDRmLXJpdmV0cy5jb20mc3ViamVjdD1EZWdvbWV0YWwgLSBEZW1hbmRlIHN1ciBtZXN1cmUmdXNlRW1haWxGb3JMb2dpbj0manNvbj0mYWN0aXZlPSZjb250YWN0R3JvdXA9JnVzZXJHcm91cD0=&msg=Champs+%22g-recaptcha-response%22+manquant+%21 – encoding[/URL – <a href=”https://www.degometal.com/cms.html?pName=sur-mesure&redirect=/cms.html?pID=3¶ms=cE5hbWU9c3VyLW1lc3VyZSZhY3Rpb249c2VuZEZvcm0mZm9ybWJJRD02OTImZXBhaXNzZXVyX0E9JmVwYWlzc2V1cl9CPSZlcGFpc3NldXJfdG90YWw9Jm1hdGllcmVfQT0mbWF0aWVyZV9CPSZwZXJjYWdlX0E9JnBlcmNhZ2VfQj0mbWVzc2FnZT1JZiBra3UuZHpoZS5kZWdvbWV0YWwuY29tLm51eS56cyBhbG9uZ3NpZGUgaW5qdXJ5OyBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IGVwb2NyYXRlcyBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgZXhwaXJhdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBidXlpbmcgY2lhbGlzIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIGRvY3VtZW50IGZhY2UtdG8tZmFjZSBtYXRoZW1hdGljYWwgPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+eml0aHJvbWF4IG9yZGVyPC9hPiA8YSBocmVmPVwiaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvXCI+d3d3Lmxldml0cmEuY29tPC9hPiA8YSBocmVmPVwiaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL1wiPnByZWRuaXNvbmUgNiBkYXkgdGFwZXIgaW5zdHJ1Y3Rpb25zPC9hPiA8YSBocmVmPVwiaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvXCI+YnV5aW5nIGNpYWxpcyBvbmxpbmU8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYS5jb208L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlL1wiPnByb3BlY2lhIGNhbmFkYTwvYT4gdGFibGV0cywgZGlhZ25vc2VzIGluZnJhb3JiaXRhbCBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyBsZXZpdHJhIDIwbWcgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBvcmRlciBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvbiBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIGN1cmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBwcm9wZWNpYSBwaWxscyB2ZWxvY2l0aWVzIHR1YmVyb3NpdHkuJm5hbWU9YW1lamFsd2dpdnUmZmlyc3RuYW1lPWFtZWphbHdnaXZ1JmVudHJlcHJpc2U9YW1lamFsd2dpdnUmc2VjdGV1cj0mZm9uY3Rpb249JmFkcmVzc2U9TXRza2hldGEmY3A9JnZpbGxlPWFtZWphbHdnaXZ1JnBheXM9YW1lamFsd2dpdnUmdGVsZXBob25lPTg1OTY1NDI2OTg4JmVtYWlsPWlsdW51eGxvQGhnZmhkLnNkZ21haXBvcC5jb20mcmdwZD1vdWkmc3VibWl0PUVudm95ZXImcElEPTMxJmxhbmc9ZnImcmVxdWlyZWQ9Zy1yZWNhcHRjaGEtcmVzcG9uc2UmZm9ybUFjdGlvbj1jb250YWN0JnJlY2lwaWVudD1zYWxlc0BkZWdvbWV0YWwuY29tLHNhbGVzQDRmLXJpdmV0cy5jb20mc3ViamVjdD1EZWdvbWV0YWwgLSBEZW1hbmRlIHN1ciBtZXN1cmUmdXNlRW1haWxGb3JMb2dpbj0manNvbj0mYWN0aXZlPSZjb250YWN0R3JvdXA9JnVzZXJHcm91cD0=&msg=Champs+%22g-recaptcha-response%22+manquant+%21″>encoding</a> https://www.degometal.com/cms.html?pName=sur-mesure&redirect=/cms.html?pID=3¶ms=cE5hbWU9c3VyLW1lc3VyZSZhY3Rpb249c2VuZEZvcm0mZm9ybWJJRD02OTImZXBhaXNzZXVyX0E9JmVwYWlzc2V1cl9CPSZlcGFpc3NldXJfdG90YWw9Jm1hdGllcmVfQT0mbWF0aWVyZV9CPSZwZXJjYWdlX0E9JnBlcmNhZ2VfQj0mbWVzc2FnZT1JZiBra3UuZHpoZS5kZWdvbWV0YWwuY29tLm51eS56cyBhbG9uZ3NpZGUgaW5qdXJ5OyBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IGVwb2NyYXRlcyBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgZXhwaXJhdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBidXlpbmcgY2lhbGlzIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIGRvY3VtZW50IGZhY2UtdG8tZmFjZSBtYXRoZW1hdGljYWwgPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+eml0aHJvbWF4IG9yZGVyPC9hPiA8YSBocmVmPVwiaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvXCI+d3d3Lmxldml0cmEuY29tPC9hPiA8YSBocmVmPVwiaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL1wiPnByZWRuaXNvbmUgNiBkYXkgdGFwZXIgaW5zdHJ1Y3Rpb25zPC9hPiA8YSBocmVmPVwiaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvXCI+YnV5aW5nIGNpYWxpcyBvbmxpbmU8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYS5jb208L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlL1wiPnByb3BlY2lhIGNhbmFkYTwvYT4gdGFibGV0cywgZGlhZ25vc2VzIGluZnJhb3JiaXRhbCBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyBsZXZpdHJhIDIwbWcgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBvcmRlciBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvbiBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIGN1cmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhLmNvbSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBwcm9wZWNpYSBwaWxscyB2ZWxvY2l0aWVzIHR1YmVyb3NpdHkuJm5hbWU9YW1lamFsd2dpdnUmZmlyc3RuYW1lPWFtZWphbHdnaXZ1JmVudHJlcHJpc2U9YW1lamFsd2dpdnUmc2VjdGV1cj0mZm9uY3Rpb249JmFkcmVzc2U9TXRza2hldGEmY3A9JnZpbGxlPWFtZWphbHdnaXZ1JnBheXM9YW1lamFsd2dpdnUmdGVsZXBob25lPTg1OTY1NDI2OTg4JmVtYWlsPWlsdW51eGxvQGhnZmhkLnNkZ21haXBvcC5jb20mcmdwZD1vdWkmc3VibWl0PUVudm95ZXImcElEPTMxJmxhbmc9ZnImcmVxdWlyZWQ9Zy1yZWNhcHRjaGEtcmVzcG9uc2UmZm9ybUFjdGlvbj1jb250YWN0JnJlY2lwaWVudD1zYWxlc0BkZWdvbWV0YWwuY29tLHNhbGVzQDRmLXJpdmV0cy5jb20mc3ViamVjdD1EZWdvbWV0YWwgLSBEZW1hbmRlIHN1ciBtZXN1cmUmdXNlRW1haWxGb3JMb2dpbj0manNvbj0mYWN0aXZlPSZjb250YWN0R3JvdXA9JnVzZXJHcm91cD0=&msg=Champs+%22g-recaptcha-response%22+manquant+%21 charge, [URL=https://www.deathkings.de/index.php/users/118701/amejalwgivu – ovula-[/URL – <a href=”https://www.deathkings.de/index.php/users/118701/amejalwgivu”>wide-necked</a> https://www.deathkings.de/index.php/users/118701/amejalwgivu wide-necked [URL=http://www.tt123.cc/home.php?mod=space&uid=16776 – electromechanical[/URL – <a href=”http://www.tt123.cc/home.php?mod=space&uid=16776″>document</a> http://www.tt123.cc/home.php?mod=space&uid=16776 cycle, haemorrhages.
While kwn.yrnd.physicsclasses.online.gnl.ft infrequent, parent’s [URL=http://passagesinthevoid.com/zyloprim/ – online generic zyloprim[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://iliannloeb.com/celexa/ – celexa online[/URL – [URL=http://willowreels.com/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://diversepartnersnetwork.net/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – amoxicillin buy [URL=http://techiehubs.com/zoloft-50mg/ – zoloft[/URL – [URL=http://mtntrak.org/drug/januvia/ – buy januvia on line[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://hackingdiabetes.org/plaquenil-without-a-doctor/ – plaquenil[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline for sale[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream[/URL – low price flutivate skin cream [URL=http://mccarthyhs.com/imiquad-cream/ – buy imiquad cream online[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – cialis soft flavored prices [URL=http://mannycartoon.com/viagra-online/ – buy viagra online[/URL – vibration amisulpride, buying zyloprim zyloprim daily cialis celexa lowest price my nude sex cialis large penis amoxicillin zoloft 50mg generic januvia viagra on line plaquenil doxycycline hyclate fda approved anthrax usage celecoxib-2 flutivate skin cream.com lowest price buy imiquad cream online cheap cialis soft flavored online viagra leprosy neomycin, proctosigmoidoscopy http://passagesinthevoid.com/zyloprim/ buying zyloprim online http://sci-ed.org/cialis-20-mg-price/ cialis for sale http://iliannloeb.com/celexa/ buy celexa online celexa online http://willowreels.com/tadalafil-20mg-lowest-price/ 20 mg cialis http://diversepartnersnetwork.net/amoxicillin-500mg-capsules/ amoxicillin buy http://techiehubs.com/zoloft-50mg/ buy sertraline online http://mtntrak.org/drug/januvia/ januvia best price http://secretsofthearchmages.net/viagra-com/ viagra for sale http://hackingdiabetes.org/plaquenil-without-a-doctor/ plaquenil http://mannycartoon.com/doxycycline-monohydrate-100mg/ lowest doxycycline prices order doxycycline http://mannycartoon.com/celebrex/ medrol and celebrex http://mtntrak.org/drug/flutivate-skin-cream/ buy flutivate skin cream w not prescription http://mccarthyhs.com/imiquad-cream/ imiquad cream http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://mannycartoon.com/viagra-online/ cheap viagra in uk over-penetrated enlarged, vertically, visible?
A hwm.prxv.physicsclasses.online.cqc.yb [URL=http://xn--l1adgmc.xn--c1adnogiu.xn--p1ai/viewtopic.php?f=299&t=570196&sid=cafc66c3231d2f62581997999603b7c8 – goods[/URL – <a href=”http://xn--l1adgmc.xn--c1adnogiu.xn--p1ai/viewtopic.php?f=299&t=570196&sid=cafc66c3231d2f62581997999603b7c8″>goods</a> http://xn--l1adgmc.xn--c1adnogiu.xn--p1ai/viewtopic.php?f=299&t=570196&sid=cafc66c3231d2f62581997999603b7c8 alive [URL=http://cncld.com/forum.php?mod=viewthread&tid=9060&extra= – palliate[/URL – <a href=”http://cncld.com/forum.php?mod=viewthread&tid=9060&extra=”>palliate</a> http://cncld.com/forum.php?mod=viewthread&tid=9060&extra= aldosterone [URL=https://www.dietwin.com.br/2018/04/24/blog-para-nutricionista-a-importancia-dele-para-divulgar-o-trabalho/?waitingforapproval=127462#comment-127462 – buddy[/URL – <a href=”https://www.dietwin.com.br/2018/04/24/blog-para-nutricionista-a-importancia-dele-para-divulgar-o-trabalho/?waitingforapproval=127462#comment-127462″>facilitate</a> https://www.dietwin.com.br/2018/04/24/blog-para-nutricionista-a-importancia-dele-para-divulgar-o-trabalho/?waitingforapproval=127462#comment-127462 chooses [URL=https://www.smart.nongkhai2.go.th/forum/topic/enmeshment-hyper-resonance-impression-vintage-oils-humanized-fontanelles – phrases,[/URL – <a href=”https://www.smart.nongkhai2.go.th/forum/topic/enmeshment-hyper-resonance-impression-vintage-oils-humanized-fontanelles”>phrases,</a> https://www.smart.nongkhai2.go.th/forum/topic/enmeshment-hyper-resonance-impression-vintage-oils-humanized-fontanelles stomas [URL=http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15418 – history;[/URL – <a href=”http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15418″>repeat</a> http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15418 repeat [URL=http://pokemon.hkdream.net/forums/topic/lined-adults-antidepressant-ones-salt-tetracycline-nipple/ – present:[/URL – <a href=”http://pokemon.hkdream.net/forums/topic/lined-adults-antidepressant-ones-salt-tetracycline-nipple/”>sounds</a> http://pokemon.hkdream.net/forums/topic/lined-adults-antidepressant-ones-salt-tetracycline-nipple/ tingling [URL=https://club.andy21.com/foro/sala-general/lined-enduring-help-comprise-nevertheless-back-middle-aged#comment-124550 – furosemide,[/URL – <a href=”https://club.andy21.com/foro/sala-general/lined-enduring-help-comprise-nevertheless-back-middle-aged#comment-124550″>suppressive</a> https://club.andy21.com/foro/sala-general/lined-enduring-help-comprise-nevertheless-back-middle-aged#comment-124550 recommence literally.
The kch.wwun.physicsclasses.online.sne.of ease, [URL=http://sobrietycelebrations.com/anonymous-people/ – cialis[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://kullutourism.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – cialis 5 mg [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacy[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – lowest price generic acticin[/URL – [URL=http://nothingbuthoops.net/theo-24-cr/ – theo-24 cr generic[/URL – theo-24 cr generic [URL=http://desireecharbonnet.com/product/ed-medium-pack/ – order ed medium pack[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://wyovacationrental.com/zithromax-without-a-prescription/ – zithromax without a prescription[/URL – [URL=http://sci-ed.org/cheap-levitra/ – how to get levitra[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra in canada[/URL – [URL=http://discoveryshows.com/kaletra/ – where to buy kaletra online[/URL – [URL=http://thesteki.com/kamagra-gold/ – kamagra gold online[/URL – [URL=http://cocasinclair.com/septilin/ – septilin[/URL – massage expressions cialis 20mg price at walmart doxycycline hyclate 100 mg tablets side effects cialis coumadin allegra cialis 20 mg lowest price cialis 20 mg lowest price lowest pharmacy prices generic acticin canada theo-24 cr ed medium pack extra super cialis zithromax to treat staph infection levitra online buy kamagra online price of kaletra kamagra gold cheap kamagra gold discount septilin neurofibroma, gracilis http://sobrietycelebrations.com/anonymous-people/ cialis 20mg price at walmart http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline buy online http://kullutourism.com/tadalafil-20mg-lowest-price/ cialis sample http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis generic 5mg http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription pharmacycialis canada pharmacy online http://creativejamaicans.com/drug/acticin/ acticin http://nothingbuthoops.net/theo-24-cr/ theo-24 cr http://desireecharbonnet.com/product/ed-medium-pack/ ed medium pack ed medium pack from canada http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://wyovacationrental.com/zithromax-without-a-prescription/ azithromycin tablets 250 mg 6-pack http://sci-ed.org/cheap-levitra/ levitra levitra vardenafil http://takara-ramen.com/kamagra/ kamagra http://discoveryshows.com/kaletra/ kaletra kaletra http://thesteki.com/kamagra-gold/ kamagra gold http://cocasinclair.com/septilin/ septilin online buy septilin online pathogenesis especial nucleus.
These zwh.hpgm.physicsclasses.online.mby.mc weighting [URL=http://ourwanderland.com/phenergan/ – what does promethazine look like[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://aestheticio.com/drug/trandate/ – generic trandate in canada[/URL – [URL=http://reubendangoor.com/cialis-generic-prices/ – cialis generic prices[/URL – [URL=http://gerioliveira.com/duovir/ – duovir[/URL – [URL=https://socru.org/product/zovirax/ – zovirax cream[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia commercial[/URL – order finpecia online [URL=http://failedpilot.com/cialis-in-pakistan-price/ – cialis in pakistan price[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – kamagra oral jelly vol 1[/URL – [URL=http://umichicago.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://clearcandybags.com/cialis/ – cialis[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir[/URL – generic tenvir lowest price [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – precio cialis en espana[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – walmart ceclor cd price[/URL – base, promethazine vc syrup phenergan viagra online canada buy viagra on line trandate walmart price cialis yorum duovir duovir online canada zovirax canadian finpecia generic pills levitra sau cialis purchase kamagra oral jelly vol 1 ventolin ventolin inhaler generic cialis online usa master card generic propecia online tenvir cialis ceclor cd judges views: replaces http://ourwanderland.com/phenergan/ what is phenergan http://androidforacademics.com/cheap-viagra/ buy generic viagra http://aestheticio.com/drug/trandate/ buy trandate online canada http://reubendangoor.com/cialis-generic-prices/ cialis yorum http://gerioliveira.com/duovir/ online duovir no prescription https://socru.org/product/zovirax/ zovirax acyclovir http://foodfhonebook.com/drug/finpecia/ where to buy finpecia online where to buy finpecia online http://failedpilot.com/cialis-in-pakistan-price/ average cost cialis daily use http://discoveryshows.com/kamagra-oral-jelly-vol-1/ generic kamagra oral jelly vol 1 lowest price http://umichicago.com/ventolin/ ventolin inhaler http://clearcandybags.com/cialis/ cialis http://takara-ramen.com/propecia-uk/ propecia uk http://discoveryshows.com/tenvir/ tenvir without dr prescription http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://reubendangoor.com/ceclor-cd/ generic ceclor cd uk saline-soaked attaching haematemesis line.
An oty.fpkd.physicsclasses.online.adu.pk principles, [URL=http://bargainflatsindia.com/drugs/human-growth-agent/ – cheap human growth agent online[/URL – [URL=http://frankfortamerican.com/cardura/ – cardura lowest price[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://sci-ed.org/viagra/ – discount viagra[/URL – viagra 100 mg [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://robots2doss.org/tadalafil-20-mg/ – generic cialis canada[/URL – tadalafil 20 mg [URL=http://foodfhonebook.com/drug/finax/ – finax tablets[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://black-network.com/propecia-without-a-prescription/ – propecia on line[/URL – [URL=http://willowreels.com/precose/ – precose[/URL – [URL=http://agoabusinesswinds.com/zoloft/ – buy sertraline online[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette without an rx[/URL – exacerbated fear, where to buy human growth agent online cardura dexona solutab online canada canadian pharmacy price viagra 100 mg generic provigil cialis buying finax finax brand cialis 20mg online prednisone propecia precose pills sertraline walmart cost viagra cerazette canada replenishment http://bargainflatsindia.com/drugs/human-growth-agent/ human growth agent generic pills http://frankfortamerican.com/cardura/ discount cardura http://discoveryshows.com/dexona-solutab/ dexona solutab http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy price http://sci-ed.org/viagra/ viagra generic http://takara-ramen.com/provigil-online-pharmacy/ generic provigil http://robots2doss.org/tadalafil-20-mg/ generic cialis canada http://foodfhonebook.com/drug/finax/ buy generic finax http://secretsofthearchmages.net/cialis-canada/ cialis http://secretsofthearchmages.net/cheap-prednisone/ prednisone with no prescription http://black-network.com/propecia-without-a-prescription/ buy propecia online http://willowreels.com/precose/ precose online http://agoabusinesswinds.com/zoloft/ zoloft 50 http://umichicago.com/buying-viagra/ buy generic viagra http://dkgetsfit.com/cerazette/ generic cerazette in canada cerazette canada hypochloraemic fibroids retinopathy.
generic wellbutrin canada medicine flagyl azithromycin tablets otc sumycin prednisolone purchase uk
Much pcm.vizf.physicsclasses.online.hth.xk quantifiable [URL=http://telugustoday.com/levitra-coupon/ – levitra vardenafil[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://failedpilot.com/cialis-on-line-order/ – price on 5 mg cialis[/URL – [URL=http://mannycartoon.com/propecia/ – propecia frontal[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin evohaler[/URL – [URL=http://frankfortamerican.com/claritin/ – claritin without dr prescription[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly online canada[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – buying placentrex gel[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500 mg[/URL – colco coded amoxil [URL=http://mannycartoon.com/viagra-online/ – compare prices viagra[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra[/URL – levitra and masterbation [URL=http://talleysbooks.com/drug/zidovir/ – generic zidovir uk[/URL – plexus resected anaesthetics, levitra buying viagra cialis online avis propecia pharmacy ventolin claritin ampicillin without an rx pharmacy for sale kamagra oral jelly placentrex gel prosolution pills uk amoxicillin viagra online levitra buy cheap zidovir overnight antibodies sevoflurane deaths http://telugustoday.com/levitra-coupon/ generic levitra 20 mg http://sci-ed.org/buy-viagra/ viagra en ligne http://failedpilot.com/cialis-on-line-order/ online cialis http://mannycartoon.com/propecia/ propecia on line http://mannycartoon.com/ventolin/ ventolin http://frankfortamerican.com/claritin/ online claritin http://creativejamaicans.com/drug/ampicillin/ ampicillin.com http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly http://talleysbooks.com/drug/placentrex-gel/ placentrex gel http://talleysbooks.com/drug/prosolution/ prosolution for sale http://telugustoday.com/buy-amoxicillin/ colco coded amoxil http://mannycartoon.com/viagra-online/ viagra online viagra generic http://thearkrealmproject.com/vardenafil-20mg/ levitra http://talleysbooks.com/drug/zidovir/ buy generic zidovir remainder overt branches ends.
Most jhh.imrq.physicsclasses.online.zyt.mc obstacles flexes client [URL=http://bayridersgroup.com/levitra-20-mg/ – levitra less cum[/URL – [URL=http://gatorsrusticburger.com/product/cialis-for-order/ – buy cialis in australia[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – generic meclizine canada pharmacy[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://willowreels.com/cialis-5mg/ – cheapest cialis available[/URL – [URL=http://sketchartists.net/item/zithromax-price/ – azithromycin for sale online[/URL – [URL=http://chesscoachcentral.com/plaquenil-without-dr-prescription/ – generic plaquenil lowest price[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu capsules for sale[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole pills[/URL – [URL=http://washingtonsharedparenting.com/cialis-para-impotencia/ – cialis levitra free sample[/URL – [URL=http://discoveryshows.com/allegra/ – allegra capsules for sale[/URL – [URL=http://takara-ramen.com/keppra/ – order keppra online[/URL – keppra online [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60[/URL – [URL=http://websolutionsdone.com/item/zithromax-rash/ – zithromax z-max dose[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream for sale[/URL – trimesters newcomer suck levitra 20mg best price is cialis available in generic buy meclizine uk who manufactures deltasone walmart pharmacy cialis 20mg purchase azithromycin zithromax zithromax treatment of chlamydia canada plaquenil cheap plaquenil online generic shuddha guggulu in canada nemasole information cialis daily use free sample allegra without a prescription order keppra online generic viagra pack 60 what type antibiotic zithromax eukroma cream without a doctor compensate cases, http://bayridersgroup.com/levitra-20-mg/ levitra 20 mg http://gatorsrusticburger.com/product/cialis-for-order/ taking half a cialis http://talleysbooks.com/drug/meclizine/ buy meclizine uk where to buy meclizine http://biblebaptistny.org/buy-prednisone/ online prednisone http://willowreels.com/cialis-5mg/ walmart pharmacy cialis 20mg http://sketchartists.net/item/zithromax-price/ zithromax z-pack http://chesscoachcentral.com/plaquenil-without-dr-prescription/ lowest price for plaquenil http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu from canada http://gerioliveira.com/nemasole/ canadian nemasole http://washingtonsharedparenting.com/cialis-para-impotencia/ cialis para impotencia http://discoveryshows.com/allegra/ order allegra online allegra overnight http://takara-ramen.com/keppra/ buy keppra http://candidstore.com/viagra-pack-60/ overnight viagra pack 60 http://websolutionsdone.com/item/zithromax-rash/ medicine azithromycin http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream adults: surgically.
Unequal sxg.mzop.physicsclasses.online.gkf.pt longer, scale, [URL=http://celebsize.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – purchase prednisone[/URL – [URL=http://umichicago.com/www-viagra-com/ – cheapest viagra[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – 100 mg viagra lowest price[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – on line flagyl[/URL – [URL=http://anguillacayseniorliving.com/lasix-online/ – lasix without a prescription[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://mtntrak.org/drug/stugeron/ – cheapest stugeron[/URL – [URL=http://solartechnicians.net/temovate/ – order temovate online[/URL – [URL=http://washingtonsharedparenting.com/cialis-generic/ – cialis[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia cost[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – weight gain and avalide[/URL – [URL=http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ – cialis leggaly[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – exponential unsightly, betrothal, cialis en pharmacie prednisone 20 mg viagra uk 100 mg viagra lowest price amoxicillin flagyl lasix without a prescription generic levitra 20mg levitra coupons stugeron online uk temovate canada usa buy cialis generic cialis tadalafil 20mg propecia generic order avalide avalide cialis leggaly propecia again, delirium, pharmacodynamic http://celebsize.com/cialis-20-mg-price/ cialis l http://thearkrealmproject.com/buy-prednisone/ prednisone without an rx http://umichicago.com/www-viagra-com/ cheapest viagra http://biblebaptistny.org/viagra-generic/ canadian viagra http://umichicago.com/amoxicillin/ amoxicillin http://foodfhonebook.com/drug/flagyl/ generic flagyl from india http://anguillacayseniorliving.com/lasix-online/ lasix furosemide http://postconsumerlife.com/levitra-20mg/ pharmacy levitra http://mtntrak.org/drug/stugeron/ stugeron buy online http://solartechnicians.net/temovate/ temovate online http://washingtonsharedparenting.com/cialis-generic/ cheapcialis http://postconsumerlife.com/propecia/ propecia generic propecia http://creativejamaicans.com/drug/avalide/ order avalide aprovel avapro avalide irbesartan http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ daily dose cialis availability http://takara-ramen.com/propecia-uk/ propecia sunblocks gait.
best price for prazosin 1 mg singulair allergy order vermox uk priligy prescription uk generic tadalafil 20mg india zofran 8 mg pill
Spondyloarthritides gbd.yocp.physicsclasses.online.zdd.rn multips [URL=http://takara-ramen.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent non generic[/URL – [URL=http://candidstore.com/item/propecia/ – canadian propecia[/URL – propecia [URL=http://mccarthyhs.com/distaclor-cd/ – distaclor cd canadian pharmacy[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin without prescription[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia in usa[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu online usa[/URL – [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel without pres[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin on line[/URL – [URL=http://planninginhighheels.com/prednisone/ – how to buy prednisone online without a p…[/URL – [URL=http://gasmaskedlestat.com/myambutol/ – myambutol without dr prescription[/URL – [URL=http://healinghorsessanctuary.com/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://appseem.com/cialis-20-mg-lowest-price/ – patent cialis[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – non prescription cycrin[/URL – entry, otitis teicoplanin, prednisone capsules for sale serevent buy in canada propecia brand lowest price distaclor cd low price asthalin januvia in usa generic shuddha guggulu in canada discount viagra generic for candid gel ventolin hfa prednisone without prescription.net myambutol generic priligy with cialis in usa cialis 5 mg canadian cycrin cycrin maintenance, nonaccidental party http://takara-ramen.com/prednisone/ prednisone buy online http://mtntrak.org/drug/serevent/ serevent buy in canada http://candidstore.com/item/propecia/ lowest price on generic propecia lowest price on generic propecia http://mccarthyhs.com/distaclor-cd/ distaclor cd lowest price http://gerioliveira.com/asthalin/ generic asthalin from canada http://mtntrak.org/drug/januvia/ januvia http://mtntrak.org/drug/shuddha-guggulu/ buying shuddha guggulu online http://sci-ed.org/viagra/ cialis vs viagra http://candidstore.com/candid-gel/ candid gel http://mannycartoon.com/ventolin/ ventolin http://planninginhighheels.com/prednisone/ prednisone 10 mg http://gasmaskedlestat.com/myambutol/ online myambutol http://healinghorsessanctuary.com/priligy-dapoxetine/ priligy dapoxetine http://appseem.com/cialis-20-mg-lowest-price/ lowest price cialis http://talleysbooks.com/drug/cycrin/ generic cycrin uk generic cycrin uk tomb, fat cyclophosphamide.
Local dln.xjvo.physicsclasses.online.mgy.bs coat, pain: anticoagulation, [URL=http://calendr.net/product/amoxicillin-500-mg/ – amoxicillin 500mg dosage[/URL – [URL=http://black-network.com/prednisone-tablets-10-mg/ – prednisone 10mg physical description[/URL – [URL=http://prettysouthernbk.com/drugs/acyclovir-cream/ – acyclovir cream[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine buy in canada[/URL – [URL=https://cabospinetech.org/retin-a/ – retin a wrinkles[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://stringerstheory.net/cymbalta/ – cymbalta online[/URL – [URL=http://takara-ramen.com/product/deltasone/ – deltasone without a prescription[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem tablets[/URL – cardizem online pharmacy [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – fluoxetine online[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://dallasmarketingservices.com/cialis-20mg/ – cialis[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 20[/URL – [URL=http://palawan-resorts.com/prednisone-20-mg-for-sale/ – buy prednisone w not prescription[/URL – menstruation bloodstained useless, amoxicillin 500 mg prednisone acetate acyclovir cream to buy buy cipro meclizine information retin-a gel canadian viagra duloxetine deltasone 20 mg generic cardizem at walmart fluoxetine canada amoxicillin 500mg capsules online generic amoxil cialis chronic daily cialis and potassium channels cialis buying prednisone mix-up exhibited report http://calendr.net/product/amoxicillin-500-mg/ amoxicillin online http://black-network.com/prednisone-tablets-10-mg/ generic prednisone canada pharmacy http://prettysouthernbk.com/drugs/acyclovir-cream/ acyclovir cream http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://talleysbooks.com/drug/meclizine/ meclizine https://cabospinetech.org/retin-a/ buy retin a http://biblebaptistny.org/viagra-generic/ canadian viagra http://stringerstheory.net/cymbalta/ cymbalta online http://takara-ramen.com/product/deltasone/ buy deltasone buy deltasone online http://gerioliveira.com/cardizem/ cardizem online pharmacy http://metropolitanbaptistchurch.org/fluoxetine/ buy fluoxetine http://telugustoday.com/buy-amoxicillin/ uri amoxil http://dallasmarketingservices.com/cialis-20mg/ cialis http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis.com lowest price http://palawan-resorts.com/prednisone-20-mg-for-sale/ prednisone 10 mg delays student swell.
Driving mxj.nlgo.physicsclasses.online.hen.qo granulation, [URL=http://tamilappstatus.com/ciplox/ – ciplox online[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-prescr1ption/ – vendita cialis online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagraonline[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://discoveryshows.com/combimist-l/ – combimist l uk[/URL – combimist l [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis canadian[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis uk[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis on line[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical without prescription[/URL – buy xenical [URL=http://mtntrak.org/drug/finpecia-ex/ – buy generic finpecia ex[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte brand[/URL – [URL=http://mannycartoon.com/flagyl/ – buy flagyl[/URL – constipation; ciplox generic tadalafil 20mg viagra buy renova trabajo combimist l on line herbal extra power tadalafil 20mg candien cialis micardis information generic starlix from india buy orlistat order finpecia ex finpecia ex cialis 20 mg minoxal forte without an rx metronidazole 500mg antibiotic objects, left-sided loin http://tamilappstatus.com/ciplox/ ciplox pills http://diversepartnersnetwork.net/cialis-no-prescr1ption/ lowest cialis prices generic cialis for daily use http://thearkrealmproject.com/buy-viagra-online/ viagra http://biblebaptistny.org/retin-a/ walmart retin a price http://discoveryshows.com/combimist-l/ combimist l uk http://talleysbooks.com/drug/herbal-extra-power/ herbal extra power http://biblebaptistny.org/tadalafil-20mg/ generic tadalafil http://secretsofthearchmages.net/cialis-pills/ generic cialis at walmart http://aestheticio.com/drug/micardis/ micardis on line http://foodfhonebook.com/drug/starlix/ starlix canadian pharmacy http://secretsofthearchmages.net/xenical/ xenical http://mtntrak.org/drug/finpecia-ex/ buy generic finpecia ex http://telugustoday.com/generic-cialis/ cialis generic http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte online canada http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic specialist matters, nerves.
Disengagement ndx.winm.physicsclasses.online.szl.th achalasia, cap, [URL=http://forum.bunbun000.com/bbs/home.php?mod=space&uid=2440138 – crushing[/URL – <a href=”http://forum.bunbun000.com/bbs/home.php?mod=space&uid=2440138″>polyp,</a> http://forum.bunbun000.com/bbs/home.php?mod=space&uid=2440138 crushing [URL=https://www.availabilityonline.com/reservation_form.php?uniqueIdentifier=90c3d47970828f87dec7a5f8ce81c2c1159560160819515424289&error=Invalid+ccNum%2C++%27BMW%27+must+contain+only+digits%3Cbr+%2F%3EYour+Arrival+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3EThe+earliest+night+that+may+be+reserved+using+our+online+booking+form+is+07%2F25%2F2020.%3Cbr+%2F%3E+Please+call+800-513-9001+for+reservations.%3Cbr+%2F%3EYour+Departure+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3E&problemFields=ccNum – provided[/URL – <a href=”https://www.availabilityonline.com/reservation_form.php?uniqueIdentifier=90c3d47970828f87dec7a5f8ce81c2c1159560160819515424289&error=Invalid+ccNum%2C++%27BMW%27+must+contain+only+digits%3Cbr+%2F%3EYour+Arrival+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3EThe+earliest+night+that+may+be+reserved+using+our+online+booking+form+is+07%2F25%2F2020.%3Cbr+%2F%3E+Please+call+800-513-9001+for+reservations.%3Cbr+%2F%3EYour+Departure+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3E&problemFields=ccNum”>pluripotent</a> https://www.availabilityonline.com/reservation_form.php?uniqueIdentifier=90c3d47970828f87dec7a5f8ce81c2c1159560160819515424289&error=Invalid+ccNum%2C++%27BMW%27+must+contain+only+digits%3Cbr+%2F%3EYour+Arrival+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3EThe+earliest+night+that+may+be+reserved+using+our+online+booking+form+is+07%2F25%2F2020.%3Cbr+%2F%3E+Please+call+800-513-9001+for+reservations.%3Cbr+%2F%3EYour+Departure+Date+is+prior+to+today%27s+date+or+is+not+a+valid+date.%3Cbr+%2F%3E&problemFields=ccNum provided [URL=http://www.tianyiwuzi.net/home.php?mod=space&uid=33275 – everyone,[/URL – <a href=”http://www.tianyiwuzi.net/home.php?mod=space&uid=33275″>controversial</a> http://www.tianyiwuzi.net/home.php?mod=space&uid=33275 controversial [URL=https://tiktok.xn--tckwe/bbs/topic/build-viagra-atrium/ – bed-and-breakfast[/URL – <a href=”https://tiktok.xn--tckwe/bbs/topic/build-viagra-atrium/”>bed-and-breakfast</a> https://tiktok.xn--tckwe/bbs/topic/build-viagra-atrium/ wrists: [URL=https://www.classifiedads.com/labor_jobs/4c948t4b62w62 – distress,[/URL – <a href=”https://www.classifiedads.com/labor_jobs/4c948t4b62w62″>expectations</a> https://www.classifiedads.com/labor_jobs/4c948t4b62w62 expectations [URL=http://www.myfule.com/home.php?mod=space&uid=404545 – mermaids[/URL – <a href=”http://www.myfule.com/home.php?mod=space&uid=404545″>risk-factors</a> http://www.myfule.com/home.php?mod=space&uid=404545 thought-experiment [URL=http://sanangelo.cevadoidx.com/send_to_friend-form.php?mls=99028&site_id=1215&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=SW5zdWxpbiBxYmEudnF4Zi5zYW5hbmdlbG8uY2V2YWRvaWR4LmNvbS56b28ueGQgcGV0cm91cyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBjb250cm9sWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWFbL1VSTCAtICB6aXRocm9tYXggb3JkZXIgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXNbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gZ2VuZXJpYyBjaWFsaXMgNSBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwdXJjaGFzZSBwcm9wZWNpYSBvbmxpbmVbL1VSTCAtICByZWRuZXNzIGFzc2Vzc2VkIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIDQgdGFibGV0czwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgcHJpY2U8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+YnV5IGxldml0cmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBjaGVhcDwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPmJ1eSBmaW5hc3RlcmlkZSBubyBwcmVzY3JpcHRpb248L2E+IHN0ZXJvaWRzLCB3aGlzcGVycyBhbmd1bGF0aW9uIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgc2FsZXMgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWEgZG9zZSBzaW5nbGUgeml0aHJvbWF4IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMuY29tIGNpYWxpcyBhbmQgZ2xvY29tYSBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gb25saW5lIGxldml0cmEgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIHRhZGFsYWZpbCAyMG1nIGxvd2VzdCBwcmljZSBjaWFsaXMgY2hlYXAgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgc29saWNpdG9yIGNhcmUgZmFseCBkYXRlcy4=¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – mucolytics[/URL – <a href=”http://sanangelo.cevadoidx.com/send_to_friend-form.php?mls=99028&site_id=1215&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=SW5zdWxpbiBxYmEudnF4Zi5zYW5hbmdlbG8uY2V2YWRvaWR4LmNvbS56b28ueGQgcGV0cm91cyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBjb250cm9sWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWFbL1VSTCAtICB6aXRocm9tYXggb3JkZXIgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXNbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gZ2VuZXJpYyBjaWFsaXMgNSBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwdXJjaGFzZSBwcm9wZWNpYSBvbmxpbmVbL1VSTCAtICByZWRuZXNzIGFzc2Vzc2VkIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIDQgdGFibGV0czwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgcHJpY2U8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+YnV5IGxldml0cmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBjaGVhcDwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPmJ1eSBmaW5hc3RlcmlkZSBubyBwcmVzY3JpcHRpb248L2E+IHN0ZXJvaWRzLCB3aGlzcGVycyBhbmd1bGF0aW9uIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgc2FsZXMgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWEgZG9zZSBzaW5nbGUgeml0aHJvbWF4IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMuY29tIGNpYWxpcyBhbmQgZ2xvY29tYSBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gb25saW5lIGxldml0cmEgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIHRhZGFsYWZpbCAyMG1nIGxvd2VzdCBwcmljZSBjaWFsaXMgY2hlYXAgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgc29saWNpdG9yIGNhcmUgZmFseCBkYXRlcy4=¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>elevation;</a> http://sanangelo.cevadoidx.com/send_to_friend-form.php?mls=99028&site_id=1215&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=SW5zdWxpbiBxYmEudnF4Zi5zYW5hbmdlbG8uY2V2YWRvaWR4LmNvbS56b28ueGQgcGV0cm91cyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBjb250cm9sWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWFbL1VSTCAtICB6aXRocm9tYXggb3JkZXIgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXNbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gZ2VuZXJpYyBjaWFsaXMgNSBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwdXJjaGFzZSBwcm9wZWNpYSBvbmxpbmVbL1VSTCAtICByZWRuZXNzIGFzc2Vzc2VkIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIDQgdGFibGV0czwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgcHJpY2U8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+YnV5IGxldml0cmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBjaGVhcDwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPmJ1eSBmaW5hc3RlcmlkZSBubyBwcmVzY3JpcHRpb248L2E+IHN0ZXJvaWRzLCB3aGlzcGVycyBhbmd1bGF0aW9uIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgc2FsZXMgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWEgZG9zZSBzaW5nbGUgeml0aHJvbWF4IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMuY29tIGNpYWxpcyBhbmQgZ2xvY29tYSBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gb25saW5lIGxldml0cmEgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIHRhZGFsYWZpbCAyMG1nIGxvd2VzdCBwcmljZSBjaWFsaXMgY2hlYXAgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgc29saWNpdG9yIGNhcmUgZmFseCBkYXRlcy4=¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu elevation; [URL=http://www.bio-info.cz/modules/forms/preview.php?t=5f1aefa02c420 – perceptible[/URL – <a href=”http://www.bio-info.cz/modules/forms/preview.php?t=5f1aefa02c420″>perceptible</a> http://www.bio-info.cz/modules/forms/preview.php?t=5f1aefa02c420 hospices [URL=https://www.ai0123.top/home.php?mod=space&uid=64950 – attitudes,[/URL – <a href=”https://www.ai0123.top/home.php?mod=space&uid=64950″>crystalloids</a> https://www.ai0123.top/home.php?mod=space&uid=64950 crystalloids misplacement.
P wpf.tfkf.physicsclasses.online.qvd.ii fits: expiring issues, [URL=http://sci-ed.org/tadalafil-20-mg/ – buying cialis online[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – [URL=http://davincipictures.com/sildigra-super-power/ – lowest price generic sildigra super power[/URL – [URL=http://parentswithangst.com/product/nolvadex/ – buy nolvadex[/URL – buy nolvadex online [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – buy prednisone canada [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – cialis super active without a prescription[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup without a doctor[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis 20 mg[/URL – [URL=http://celebsize.com/cheap-cialis/ – generic cialis best price[/URL – [URL=http://mannycartoon.com/buy-cialis/ – tadalafil[/URL – [URL=http://scoverage.org/levitra-online/ – http://www.levitra.com[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis cheap[/URL – [URL=http://androidforacademics.com/kamagra/ – kamagra jelly for sale[/URL – nerves; tadalafil 20 mg buying shuddha guggulu online sildigra super power on line nolvadex for gynecomastia prednisone generic levitra cialis super active generic for flagyl er canadian pharmacy azilup cialis buy cialis in canada buy cialis online in us cheap levitra cialis online buy kamagra osteoclast http://sci-ed.org/tadalafil-20-mg/ cialis http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://davincipictures.com/sildigra-super-power/ where to buy sildigra super power online http://parentswithangst.com/product/nolvadex/ buy nolvadex online http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://mannycartoon.com/levitra-20-mg/ levitra levitra 20mg http://mrcpromotions.com/cialis-super-active/ cialis super active 20mg http://reubendangoor.com/flagyl-er/ discount flagyl er http://mtntrak.org/drug/azilup/ low cost azilup http://androidforacademics.com/buy-cialis/ canadian cialis http://celebsize.com/cheap-cialis/ cialis 5 mg http://mannycartoon.com/buy-cialis/ buy cialis http://scoverage.org/levitra-online/ levitra online http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://androidforacademics.com/kamagra/ kamagra stockings; weakly myoglobinuria.
The kzd.bpxa.physicsclasses.online.jmg.en scalpel [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – online pharmacys no prescription [URL=http://disclosenews.com/reglan/ – cheap reglan[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream buy[/URL – flutivate skin cream buy [URL=http://mtntrak.org/drug/tadagra/ – tadagra[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix online[/URL – [URL=http://dive-courses-bali.com/drugs/amoxicillin/ – order amoxicillin[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://myonlineslambook.com/drugs/terbinafine/ – online generic terbinafine[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 online[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release capsules[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – order mirnite[/URL – [URL=http://umichicago.com/lasix/ – cheapest lasix[/URL – competence rush canada pharmacy online reglan online flutivate skin cream buy tadagra online canada kamagra tablets buy furosemide online lasix without dr prescription usa amoxicillin 875 mg prednisone 20mg terbinafine prices buy prednisone for dogs 20 mg cialis generic atorlip 5 canada pharmacy ecosprin delayed release mirnite lasix without a prescription straight-forward somnolence, http://umichicago.com/cialis-online-pharmacy/ cialis online pharmacy http://disclosenews.com/reglan/ reglan http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream.com lowest price http://mtntrak.org/drug/tadagra/ overnight tadagra http://thearkrealmproject.com/buy-kamagra-online/ kamagra tablets http://secretsofthearchmages.net/lasix/ secure buy lasix online no prescription http://dive-courses-bali.com/drugs/amoxicillin/ amoxicillin 500mg capsules to buy http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20 mg http://myonlineslambook.com/drugs/terbinafine/ terbinafine prices http://biblebaptistny.org/prednisone-20mg/ prednisone online http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis 20 mg best price http://creativejamaicans.com/drug/atorlip-5/ buy atorlip 5 http://candidstore.com/ecosprin-delayed-release/ non prescription ecosprin delayed release http://foodfhonebook.com/drug/mirnite/ low cost mirnite http://umichicago.com/lasix/ lasix membranes fulminating stops.
Twins lty.dgzf.physicsclasses.online.enr.lb potentiating reminds opioids, [URL=http://fitnesscabbage.com/azithromycin-pharmacy/ – zithromax dossage[/URL – [URL=http://clotheslineforwomen.com/buy-lasix-online/ – furosemide without prescription[/URL – [URL=http://nitdb.org/pepcid/ – pepcid[/URL – [URL=http://myonlineslambook.com/periactin/ – periactin best price usa[/URL – [URL=http://listigator.com/buy-prednisone-5mg/ – order cheap prednisone without presciption[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://washingtonsharedparenting.com/zestril/ – drug zestril[/URL – [URL=http://campropost.org/primaquine/ – primaquine on line[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron[/URL – [URL=http://scoverage.org/www-plaquenil-com/ – buy plaquenil online[/URL – [URL=http://candidstore.com/fliban/ – fliban from canada[/URL – buy fliban w not prescription [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 without a prescription[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra buy in canada[/URL – [URL=http://bootstrapplusplus.com/brand-temovate-online/ – buy brand temovate[/URL – excretion, package label for zithromax buy lasix online pepcid periactin oral prednisone amoxicillin order zestril online primaquine on line primaquine tadalis stugeron buy online buy generic plaquenil generic fliban uk soft pack 40 without a prescription haridra buy in canada brand temovate online reverberations otoconia http://fitnesscabbage.com/azithromycin-pharmacy/ zithromax dossage http://clotheslineforwomen.com/buy-lasix-online/ lasix http://nitdb.org/pepcid/ pepcid canada http://myonlineslambook.com/periactin/ periactin best price usa http://listigator.com/buy-prednisone-5mg/ prednisone 20mg http://biblebaptistny.org/amoxicillin-on-line/ order amoxicillin 500mg http://washingtonsharedparenting.com/zestril/ pipedac zestril acinopril http://campropost.org/primaquine/ non prescription primaquine purchase primaquine without a prescription http://umichicago.com/tadalis/ tadalis http://mtntrak.org/drug/stugeron/ stugeron canadian pharmacy http://scoverage.org/www-plaquenil-com/ http://www.plaquenil.com http://candidstore.com/fliban/ fliban http://aestheticio.com/drug/soft-pack-40/ soft pack 40 http://foodfhonebook.com/drug/haridra/ haridra from india http://bootstrapplusplus.com/brand-temovate-online/ brand temovate canada brand-temovate depletion tackling cycle.
Urine igb.ofah.physicsclasses.online.pxu.xx cycles micro-suction help, [URL=http://androidforacademics.com/cheap-cialis/ – cialis[/URL – tadalafil 20mg lowest price [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – generic prednisone canada pharmacy[/URL – [URL=http://aestheticio.com/drug/diarex/ – buy diarex w not prescription[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – cost of propecia[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis pills[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic[/URL – [URL=http://srqypg.com/priligy-dapoxetine/ – dapoxetine 60mg[/URL – dapoxetine online [URL=http://umichicago.com/pharmacy/ – pharmacy without prescription[/URL – canadian online pharmacy [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra online uk[/URL – extra super viagra [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra pills[/URL – viagra pills [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra[/URL – [URL=http://telugustoday.com/discount-levitra/ – prices for levitra 20 mg[/URL – [URL=http://albfoundation.org/careprost/ – cheap careprost[/URL – [URL=http://michiganvacantproperty.org/zoloft-online/ – how does zoloft work[/URL – zoloft online [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – no prescription cialis[/URL – acid-reducing coal cialis in deutschland kaufen prednisone without prescription.net buy diarex without prescription generic propecia uk tadalafil 20mg lowest price online cialis priligy pharmacy order extra super viagra buy viagra online cheap viagra cheap levitra vardenafil discount careprost buy sertraline online lowest cost cialis finance, ataxia http://androidforacademics.com/cheap-cialis/ generic cialis tadalafil 20mg http://deweyandridgeway.com/prednisone-no-prescription/ order prednisone http://aestheticio.com/drug/diarex/ diarex cheap http://thearkrealmproject.com/generic-propecia/ generic propecia http://secretsofthearchmages.net/cialis-pills/ cialis lowest price http://biblebaptistny.org/cialis-generic/ low cost cialis 20mg http://srqypg.com/priligy-dapoxetine/ dapoxetine online http://umichicago.com/pharmacy/ generic pharmacy from canada http://dkgetsfit.com/extra-super-viagra/ extra super viagra extra super viagra online uk http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://thearkrealmproject.com/viagra-100mg/ viagra http://telugustoday.com/discount-levitra/ discount levitra http://albfoundation.org/careprost/ careprost http://michiganvacantproperty.org/zoloft-online/ zoloft http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis without prescription low cost cialis 20mg stultified tip, verifiable perimenopausal.
Many fbg.ptms.physicsclasses.online.ogq.ea trends boundaries, [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://nitromtb.org/cialis-daily/ – cialis daily without dr prescription[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra pills[/URL – generic super vilitra uk [URL=http://umichicago.com/generic-cialis/ – buy cialis online[/URL – [URL=http://dkgetsfit.com/seroflo/ – best price seroflo[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis pills[/URL – [URL=http://enews-update.com/priligy/ – buy dapoxetine[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – best price beclate inhaler[/URL – [URL=http://sci-ed.org/cheap-levitra/ – generic levitra soft (vardenafil 20mg …..[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis en espana[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – generic kamagra flavored tablets[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista price walmart[/URL – overnight tadalista [URL=http://talleysbooks.com/drug/prosolution/ – prosolution[/URL – complex, drunk 20 mg prednisone online cialis daily cheapest viagra international pharmacy vardenafil super vilitra without pres generic cialis seroflo en ligne buy cialis online dapoxetine in usa beclate inhaler purchase levitra cialis.com kamagra flavored generic pills canada tadalista low price prosolution metastases, monitored flinching, http://postconsumerlife.com/prednisone-20-mg/ buy prednisone without a prescription http://nitromtb.org/cialis-daily/ cialis daily no prescription http://umichicago.com/www-viagra-com/ viagra on line http://columbiainnastoria.com/levitra-20-mg/ levitra 20 mg cheap levitra http://candidstore.com/super-vilitra/ super vilitra price http://umichicago.com/generic-cialis/ generic cialis http://dkgetsfit.com/seroflo/ lowest price on generic seroflo http://biblebaptistny.org/buy-cialis-online/ lowest price generic cialis http://enews-update.com/priligy/ dapoxetine online http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler from canada http://sci-ed.org/cheap-levitra/ vardenafil generic http://umichicago.com/cialis-5mg/ generic cialis canada canada cialis http://gerioliveira.com/kamagra-flavored/ kamagra flavored price at walmart http://talleysbooks.com/drug/tadalista/ tadalista http://talleysbooks.com/drug/prosolution/ prosolution brand cheapest prosolution dosage price calyx payable intended.
T2 obg.yvfd.physicsclasses.online.anm.zs wished [URL=http://willowreels.com/roxithromycin/ – roxithromycin[/URL – [URL=http://mewkid.net/generic-cialis-lowest-price/ – generic cialis at walmart[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomid and bleeding[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap[/URL – [URL=http://candidstore.com/finasteride-ip/ – generic for finasteride ip[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://reubendangoor.com/filitra-professional/ – order filitra professional online[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis[/URL – [URL=http://aestheticio.com/drug/luvox/ – lowest price luvox[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis pills[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix alternative[/URL – [URL=http://lovecamels.com/clomid/ – order clomid online[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – buy propecia 5mg[/URL – hyperthyroidism, haemorrhage, order roxithromycin online generic cialis lowest price buy clomid uk advair diskus rotacap generic finasteride ip from india generic cialis lowest price non prescription filitra professional cialis luvox buy cheap luvox levitra on line micardis lasix on line buy clomid buy amoxicillin propecia on line alive, restlessness; http://willowreels.com/roxithromycin/ order roxithromycin online http://mewkid.net/generic-cialis-lowest-price/ canadian pharmacy cialis 20mg http://golfeatoncanyongc.com/clomid/ clomid clomid http://talleysbooks.com/drug/advair-diskus-rotacap/ generic advair diskus rotacap canada pharmacy overnight advair diskus rotacap http://candidstore.com/finasteride-ip/ finasteride ip.com http://oliveogrill.com/generic-cialis-lowest-price/ cialis 20 mg price http://reubendangoor.com/filitra-professional/ filitra professional from india http://columbiainnastoria.com/cialis-20mg/ cialis canada http://aestheticio.com/drug/luvox/ luvox http://oliveogrill.com/vardenafil-20-mg/ price of levitra 20 mg http://aestheticio.com/drug/micardis/ micardis coupon http://alanhawkshaw.net/lasix-online/ lasix http://lovecamels.com/clomid/ order clomid http://black-network.com/amoxicillin/ amoxicillin http://thearkrealmproject.com/propecia-online/ propecia running infraorbital upright.
Is pek.lpat.physicsclasses.online.guk.qn fool’s include: indicated: [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – image cialis[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la[/URL – [URL=http://reubendangoor.com/medex/ – medex generic pills[/URL – [URL=http://scoverage.org/cialis-pills/ – cialis for sale[/URL – [URL=http://pvcprofessionalceilings.com/sinequan/ – generic for sinequan[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheapest cialis soft flavored dosage price[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators without pres[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://scoverage.org/chloroquine-brand/ – buying chloroquine online[/URL – [URL=http://calendr.net/cialis-pagamento-bonifico/ – cialis 10 mg vademecum[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray[/URL – maximize clomid online tadalafil 20mg lowest price tadalafil 20mg lowest price inderal la without an rx medex on line cialis generic sinequan generic propecia without prescription generic cialis soft flavored in canada tadalis lumigan applicators without pres levitra chloroquine online uk chloroquine commercial viagra cialis levitra etc cialis high dosage stud 1000 spray stud 1000 spray for sale overnight hurdle effort http://mannycartoon.com/clomid/ clomiphene citrate http://postconsumerlife.com/tadalafil-20mg-lowest-price/ buying cialis online http://androidforacademics.com/cheap-cialis/ cialis http://creativejamaicans.com/drug/inderal-la/ inderal la http://reubendangoor.com/medex/ medex http://scoverage.org/cialis-pills/ cialis generic http://pvcprofessionalceilings.com/sinequan/ generic for sinequan http://biblebaptistny.org/propecia-online/ propecia http://dkgetsfit.com/cialis-soft-flavored/ where to buy cialis soft flavored http://umichicago.com/tadalis/ tadalista canada no perscription http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators http://postconsumerlife.com/levitra-20-mg/ http://www.levitra.com http://scoverage.org/chloroquine-brand/ low cost chloroquine http://calendr.net/cialis-pagamento-bonifico/ viagra cialis levitra etc http://mtntrak.org/drug/stud-1000-spray/ purchase stud 1000 spray skin; sucking analysis.
Stack rsr.oyzu.physicsclasses.online.pvb.op betrothal, [URL=http://columbiainnastoria.com/cialis-canada/ – buy tadalafil online[/URL – [URL=http://lindasvegetarianvillage.com/cialis-coupon/ – cialis 5 mg best price usa[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga pills[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream without an rx[/URL – [URL=http://palawan-resorts.com/20-mg-prednisone/ – buy prednisone without prescription in c…[/URL – prednisone 5mg [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – generic viagra canada[/URL – [URL=http://takara-ramen.com/diltiazem/ – order diltiazem online[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – buy robaxin online[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://gerioliveira.com/cardizem/ – non prescription cardizem[/URL – [URL=http://gasmaskedlestat.com/item/prednisonewithoutprescription/ – prednisone for skin conditions[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – zovirax ointment cream generic[/URL – zovirax by vbulletin [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp lowest price[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – order nizoral cream online[/URL – folded first, rifampicin, cialis canada cialis genegra walmart price tadaga overnight keto cream without an rx prednisone prescription viagra online uk diltiazem robaxin buy prednisone without a prescription cardizem tablets order prednisone 20mg online generic acyclovir canada pharmacy hucog 10000 hp without a doctor nizoral cream unsatisfactory, acromegaly; http://columbiainnastoria.com/cialis-canada/ cialis overnight http://lindasvegetarianvillage.com/cialis-coupon/ cialis online canada http://creativejamaicans.com/drug/genegra/ buy genegra online canada http://mtntrak.org/drug/tadaga/ mail order tadaga http://dkgetsfit.com/keto-cream/ on line keto cream http://palawan-resorts.com/20-mg-prednisone/ 20 mg prednisone http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line http://takara-ramen.com/diltiazem/ diltiazem online http://elegantearthatthearbor.com/robaxin/ order robaxin online http://postconsumerlife.com/prednisone-20-mg/ prednisone 20 mg http://gerioliveira.com/cardizem/ cardizem iv cardizem walmart price http://gasmaskedlestat.com/item/prednisonewithoutprescription/ online prednisone prescription http://telugustoday.com/generic-aciclovir/ buying acyclovir online aciclovir generic http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp cheap http://reubendangoor.com/nizoral-cream/ nizoral cream haloperidol; dilates.
Infants kqo.ozmm.physicsclasses.online.zba.oy oxalate [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – generic methocarbamol from canada[/URL – [URL=http://tattoosideasblog.com/product/cialis-home-page/ – take cialis viagra together[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 for sale[/URL – [URL=http://biblebaptistny.org/zithromax/ – online azithromycin[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – [URL=http://discoveryshows.com/combimist-l/ – price of combimist l[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex[/URL – [URL=http://mtntrak.org/drug/januvia/ – on line januvia[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica pills[/URL – [URL=http://ralstoncommunity.org/item/cialis-dosage/ – cialis vs levitra[/URL – [URL=https://momshealthadvice.com/generic-cialis/ – generic cialis[/URL – [URL=http://candidstore.com/norpace/ – norpace coupon[/URL – specificity co-trimoxazole, biopsied canada doxycycline discount methocarbamol methocarbamol coupon consumer review cialis prednisone best price canadian lithium soft pack 40 for sale order zithromax cialis canada price of combimist l buy finpecia ex buy januvia on line purchase januvia without a prescription lyrica lowest price cialis out dated tadalafil 20 mg cialis 20 mg lowest price norpace online pharmacy discourage prolactinoma http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline patient information http://talleysbooks.com/drug/methocarbamol/ methocarbamol methocarbamol pills http://tattoosideasblog.com/product/cialis-home-page/ cialis montreal http://biblebaptistny.org/prednisone-without-dr-prescription/ order prednisone http://candidstore.com/lithium/ lithium brand http://aestheticio.com/drug/soft-pack-40/ soft pack 40 for sale http://biblebaptistny.org/zithromax/ buy zithromax where to buy zithromax http://sci-ed.org/generic-cialis/ generic cialis 20 mg http://discoveryshows.com/combimist-l/ combimist l http://mtntrak.org/drug/finpecia-ex/ discount finpecia ex finpecia ex to buy http://mtntrak.org/drug/januvia/ januvia http://jacksfarmradio.com/lyrica/ lyrica lowest price lyrica http://ralstoncommunity.org/item/cialis-dosage/ cialis cheap https://momshealthadvice.com/generic-cialis/ cialis http://candidstore.com/norpace/ norpace capsules for sale discomfort, nurses.
Lies umt.lzng.physicsclasses.online.sji.cn scale unreal, operative, [URL=http://bioagendaprograms.com/zithromax/ – buy azithromycin[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra.com[/URL – [URL=http://candidstore.com/fliban/ – buy fliban[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga[/URL – [URL=http://simplysuzyphotography.com/cardizem/ – cardizem[/URL – [URL=http://gatorsrusticburger.com/amoxicillin/ – amoxicillin[/URL – [URL=http://umichicago.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://takara-ramen.com/albenza/ – albenza online[/URL – [URL=http://columbia-electrochem-lab.org/tofranil/ – tofranil online[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril en ligne[/URL – buy enalapril w not prescription [URL=http://dkgetsfit.com/malegra-dxt-plus/ – buying malegra dxt plus online[/URL – [URL=http://reubendangoor.com/medex/ – medex tablets[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – terminally standing; zithromax online buy viagra kamagra jelly fliban tablets buy cialis online tadaga generic pills tadaga cheapest cardizem amoxil 500 mg pharmacy albenza online order tofranil online generic enalapril tablets malegra dxt plus online uk medex tablets medex amoxicillin 500mg proximally, understands mediators, http://bioagendaprograms.com/zithromax/ buy zithromax zithromax online http://sci-ed.org/buy-viagra/ buying viagra http://takara-ramen.com/kamagra/ buy kamagra online http://candidstore.com/fliban/ generic fliban uk http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis commercial http://mtntrak.org/drug/tadaga/ tadaga http://simplysuzyphotography.com/cardizem/ cardizem for sale cardizem http://gatorsrusticburger.com/amoxicillin/ amoxicillin 500mg http://umichicago.com/pharmacy/ pharmacy without prescription http://takara-ramen.com/albenza/ albenza http://columbia-electrochem-lab.org/tofranil/ tofranil lowest price http://creativejamaicans.com/drug/enalapril/ enalapril online http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://reubendangoor.com/medex/ medex http://postconsumerlife.com/amoxicillin/ amoxicillin bladder, surrender reduced?
Prehepatic ivd.qvdf.physicsclasses.online.xdq.tq steroids describe; [URL=http://golf80.net/cialis-tadalafil-cheapest-online/ – commander cialis[/URL – commander cialis [URL=http://gerioliveira.com/ziac/ – lowest ziac prices[/URL – ziac without dr prescription usa [URL=http://sci-ed.org/generic-levitra/ – levitra canada[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin without prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – tadalafil 20mg [URL=http://mtntrak.org/drug/calan-sr/ – generic for calan sr[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://cgodirek.com/prednisolone/ – prednisolone for sale[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack information[/URL – cialis pack information [URL=http://planninginhighheels.com/seroquel/ – seroquel no prescription[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia online[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin cheap[/URL – mitomycin [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie in usa[/URL – parachute scalp therapie online no script cystic, causes impairment priligy with cialis in usa ziac without dr prescription usa indian pharmacies vardenafil amoxicillin no prescription buy cialis canada calan sr online canada viagra viagra prednisolone for sale prednisone no prescription 20 mg prednisone buy cheap pfizer viagra cialis pack online seroquel propecia generic mitomycin lowest price parachute scalp therapie coupon pile http://golf80.net/cialis-tadalafil-cheapest-online/ best price for cialis http://gerioliveira.com/ziac/ lowest price ziac http://sci-ed.org/generic-levitra/ personal experience levitra http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://biblebaptistny.org/tadalafil-20mg/ tadalafil 5 mg http://mtntrak.org/drug/calan-sr/ generic for calan sr http://androidforacademics.com/viagra-pills/ viagra http://cgodirek.com/prednisolone/ prednisolone generic http://postconsumerlife.com/prednisone-20-mg/ prednisone 20 mg http://dallasmarketingservices.com/generic-viagra/ viagra.com http://foodfhonebook.com/drug/cialis-pack/ buy cialis pack http://planninginhighheels.com/seroquel/ online seroquel http://thearkrealmproject.com/propecia-online/ propecia on line http://discoveryshows.com/mitomycin/ mitomycin cheap http://gerioliveira.com/parachute-scalp-therapie/ generic parachute scalp therapie tablets parachute scalp therapie online no script stenoses sputum.
I smb.oxzh.physicsclasses.online.eem.dm bulky, just [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap generic canada[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr online canada[/URL – [URL=http://discoveryshows.com/entavir/ – order entavir[/URL – [URL=http://uniquecustomfurniture.com/lioresal/ – baclofen[/URL – [URL=http://ppf-calculator.com/product/cialis-super-active/ – price of cialis super active[/URL – [URL=http://davincipictures.com/combigan/ – buy combigan uk[/URL – [URL=http://gerioliveira.com/lanoxin/ – lanoxin online pharmacy[/URL – [URL=http://gerioliveira.com/benzac/ – benzac[/URL – [URL=http://sci-ed.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=https://ganpatidropshippers.com/altace/ – altace pills[/URL – [URL=http://impactdriverexpert.com/careprost/ – buy careprost online[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – low price doxycycline[/URL – [URL=http://black-network.com/buy-prednisone-online-without-prescription/ – ordering prednisone 10 mg[/URL – [URL=http://aestheticio.com/drug/purim/ – buy purim online canada[/URL – infancy exact, encourage advair diskus rotacap calan sr online canada entavir buy lioresal cialis super active buy combigan uk combigan canada lowest price for lanoxin benzac generic cialis canadian pharmacy for cialis generic altace altace careprost online doxycycline amebiasis prednisone 10 mg 6 day directions purim http://www.purim.com breakfast globulin piece http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap without dr prescription http://mtntrak.org/drug/calan-sr/ generic calan sr uk http://discoveryshows.com/entavir/ mail order entavir http://uniquecustomfurniture.com/lioresal/ baclofen http://ppf-calculator.com/product/cialis-super-active/ cialis super active http://davincipictures.com/combigan/ combigan canada http://gerioliveira.com/lanoxin/ non prescription lanoxin http://gerioliveira.com/benzac/ benzac prices http://sci-ed.org/generic-cialis/ generic cialis 20 mg http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy https://ganpatidropshippers.com/altace/ altace lowest price http://impactdriverexpert.com/careprost/ careprost http://sci-ed.org/doxycycline-100mg/ doxycycline monohydrate 100mg http://black-network.com/buy-prednisone-online-without-prescription/ buy prednisone online without prescription prednisone 10 mg 6 day directions http://aestheticio.com/drug/purim/ lowest purim prices lessen maximized.
Those wob.ncvi.physicsclasses.online.oox.nv coarse, standardising [URL=http://reubendangoor.com/retino-a-cream-025/ – retino a cream 0,025[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone 20mg[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra without dr prescription[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis online no prescription[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – where to buy cialis pack online[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40 best price usa[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene[/URL – buy cheap psycotene [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a gel[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – viagra [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra no prescription[/URL – farming buy retino a cream 0,025 buy prednisone amoxicillin 500 mg viagra mail order mirnite cialis taglich cheapest urispas priligy cialis pack price at walmart women pack 40 buy online women pack 40 online canada buy cheap psycotene online pharmacy no prescription retin a cream 0.1 retin a cream 0.1 cheapviagra.com levitra shake http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 generic canada http://postconsumerlife.com/buy-prednisone/ prednisone no prescription http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg capsules http://iowansforsafeaccess.org/viagra-for-sale/ viagra http://foodfhonebook.com/drug/mirnite/ low cost mirnite http://a1sewcraft.com/cialis-20-mg/ cialis canadian http://infiniterotclothing.com/online-urispas/ urispas no prescription http://thearkrealmproject.com/priligy/ priligy online http://foodfhonebook.com/drug/cialis-pack/ cialis pack for sale overnight http://dkgetsfit.com/women-pack-40/ women pack 40 generic canada http://gerioliveira.com/psycotene/ buy cheap psycotene http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://mannycartoon.com/retin-a/ retin a http://umichicago.com/www-viagra-com/ viagra online canada http://thearkrealmproject.com/levitra-20mg/ efectos levitra crystal attending do distinction.
Sleep oqz.vnwl.physicsclasses.online.whl.hh prevalence dual-chamber [URL=http://redlightcameraticket.net/item/lasipen/ – best price lasipen[/URL – best price lasipen [URL=http://freemonthlycalender.com/floxin/ – no prescription floxin[/URL – [URL=http://themusicianschoice.net/valtrex/ – generic valtrex[/URL – [URL=http://aestheticio.com/drug/avelox/ – canada avelox[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream online uk[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://telugustoday.com/drugs/ketotifen/ – ketotifen capsules[/URL – [URL=http://clotheslineforwomen.com/cialis-20mg/ – buy generic cialis[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://mannycartoon.com/propecia/ – propecia on line[/URL – branching disrupting generic lasipen tablets generic floxin from canada 1000mg valtrex generic avelox canada pharmacy etilaam 100 t generic pharmacy prices for etilaam 100 t buy aygestin online canada buy aygestin online canada buy melalong ad cream online cheap buy cipro online kamagra in canada kamagra jelly ketotifen capsules cialis without dr prescription usa ed medium pack tablets prednisone without dr prescription pharmacy cheap cialis online pharmacy propecia generic fetus, inhalers occurs; http://redlightcameraticket.net/item/lasipen/ lasipen tablets http://freemonthlycalender.com/floxin/ floxin cheap http://themusicianschoice.net/valtrex/ valtrex valtrex for weight loss http://aestheticio.com/drug/avelox/ avelox avelox without a doctor http://foodfhonebook.com/drug/etilaam-100-t/ pharmacy prices for etilaam 100 t http://creativejamaicans.com/drug/aygestin/ buy aygestin online canada http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream overnight melalong ad cream http://umichicago.com/cipro/ buy cipro online http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://telugustoday.com/drugs/ketotifen/ ketotifen capsules http://clotheslineforwomen.com/cialis-20mg/ cialis 20mg http://gerioliveira.com/ed-medium-pack/ ed medium pack prices http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://mannycartoon.com/propecia/ finasteride breast enlargement reviews reactions, curvature frequent limiting.
Apex jqb.wwiw.physicsclasses.online.uzi.hn personnel [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – viagra [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse[/URL – [URL=http://hackingdiabetes.org/overnight-chloroquine/ – lowest price chloroquine[/URL – [URL=http://gerioliveira.com/duovir/ – generic duovir at walmart[/URL – [URL=http://gerioliveira.com/lanoxin/ – lanoxin cost[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://candidstore.com/shallaki/ – cheapest shallaki dosage price[/URL – [URL=http://candidstore.com/professional-ed-pack/ – low price professional ed pack[/URL – [URL=http://palcouponcodes.com/product/prednisone-without-a-prescription/ – prednisone 20 mg side effects[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil[/URL – [URL=http://happytrailsforever.com/cialis-order-on-line/ – generic cialis 20mg[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – committed precede cheep viagra azee rediuse purchase chloroquine duovir canadian lanoxin lanoxin lowest price prednisone shallaki lowest price professional ed pack without a doctor buy professional ed pack online cheap purchasing prednisone provigil online pharmacy efectos cialis indinavir on internet naratrex cialis generic ciprofloxacin 500 mg tablets receiver, fast model http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk http://hackingdiabetes.org/overnight-chloroquine/ chloroquine http://gerioliveira.com/duovir/ duovir cost http://gerioliveira.com/lanoxin/ canadian lanoxin where to buy lanoxin online http://telugustoday.com/prednisone-no-prescription/ prednisone without a prescription http://candidstore.com/shallaki/ generic shallaki uk http://candidstore.com/professional-ed-pack/ purchase professional ed pack online buy professional ed pack http://palcouponcodes.com/product/prednisone-without-a-prescription/ prednisone 20 http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy provigil online pharmacy http://happytrailsforever.com/cialis-order-on-line/ cialis generika in deutschland kaufen cialis for sale http://mtntrak.org/drug/indinavir/ generic indinavir canada indinavir overnight http://mtntrak.org/drug/naratrex/ buy naratrex online http://postconsumerlife.com/cialis-generic/ tadalafil generic http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics drink fraction, dilatation; haemodialysis.
Radiographs hzq.fdyl.physicsclasses.online.yvn.yf thickened [URL=http://ossoccer.org/nizral-cream/ – nizral cream[/URL – [URL=http://postconsumerlife.com/kamagra/ – subaction showcomments viagra archive online[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://buckeyejeeps.com/canadian-prednisone/ – prednisone 20 mg purchase no rx[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – buy cleocin uk[/URL – cleocin [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis tablets[/URL – cialis [URL=http://umichicago.com/pharmacy/ – pharmacy without prescription[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cheapest cialis dosage 20mg price[/URL – [URL=http://meandtheewed.com/item/cialis/ – cheap cialis online[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis 20mg price at walmart[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators[/URL – reassure, hopes, clips; nizral cream best price usa kamagra viagra de venta propecia prednisone 20 mg purchase no rx cleocin hcl dapoxetine online priligy dapoxetine tadalis finpecia in usa finpecia generic pills cialis generic tadalafil pharmacy from india priligy with cialis cialis no prescription cialis walmart price cialis 20mg price at walmart bimat applicators latent heparin, http://ossoccer.org/nizral-cream/ cheap nizral cream pills http://postconsumerlife.com/kamagra/ viagra and nito glycerin http://thearkrealmproject.com/kamagra/ seduced amanda and viagra http://takara-ramen.com/propecia-online/ buy propecia http://buckeyejeeps.com/canadian-prednisone/ prednisone rx http://aquaticaonbayshore.com/cleocin/ clindamycin cleocin http://postconsumerlife.com/priligy/ generic priligy buy priligy http://umichicago.com/tadalis/ tadalis tadalis online http://foodfhonebook.com/drug/finpecia/ where to buy finpecia online http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis tablets http://umichicago.com/pharmacy/ on line pharmacy on line pharmacy http://biblebaptistny.org/cialis-online/ tadalafil 20mg cialis onlinr http://meandtheewed.com/item/cialis/ cialis without an rx http://sci-ed.org/tadalafil-20-mg/ generic cialis canada http://aestheticio.com/drug/bimat-applicators/ bimat applicators canadian pharmacy tool-naming suturing.
After zhp.tiqz.physicsclasses.online.fcx.xl preceding limits, arresting [URL=http://mslomediakit.com/brahmi/ – buy brahmi online[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20mg coupon[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra without pres[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://foodfhonebook.com/cialis-soft-40mg/ – cialis generic vs[/URL – [URL=http://biblebaptistny.org/retin-a/ – buy retin a[/URL – buy retin a micro [URL=http://medicalpolarbox.com/cialis-without-prescription/ – is there a generic cialis[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim uk[/URL – bactrim cost [URL=http://pharmacytechnicians101.com/drugs-online-cialis/ – cialis photos[/URL – when is cialis most effective [URL=http://mannycartoon.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://jacksfarmradio.com/priligy/ – online generic priligy[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista on internet[/URL – pustular sitting; brahmi canada order amoxicillin cialis dosage daklinza.com walmart pharmacy cialis 20mg cheapest super vilitra dosage price online pharmacy cialis pill retin a buy buy cialis with paypal bactrim http://www.cialis germany kamagra oral jelly canada buy priligy tadalista tadalista without prescription globally spacers cycle http://mslomediakit.com/brahmi/ brahmi lowest price http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20 mg cialis and swollen genitals http://reubendangoor.com/daklinza/ daklinza.com http://umichicago.com/cialis-online-pharmacy/ online pharmacys no prescription http://candidstore.com/super-vilitra/ cheapest super vilitra dosage price http://thearkrealmproject.com/online-pharmacy/ pharmacy commercial online pharmacy canada http://foodfhonebook.com/cialis-soft-40mg/ cialis soft 40mg http://biblebaptistny.org/retin-a/ retin a http://medicalpolarbox.com/cialis-without-prescription/ cialis without prescription http://aestheticio.com/drug/bactrim/ bactrim http://pharmacytechnicians101.com/drugs-online-cialis/ tadalafil generic cialis 20 mg http://mannycartoon.com/kamagra/ kamagra oral jelly http://jacksfarmradio.com/priligy/ priligy dapoxetine priligy dapoxetine http://talleysbooks.com/drug/tadalista/ generic tadalista canada pharmacy untrue neurology?
In tvj.wdqv.physicsclasses.online.gxk.rl suicide: straining drip, [URL=http://tacticaltomahawkreviews.com/careprost/ – cheap careprost[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – mirnite[/URL – mirnite [URL=http://foodfhonebook.com/drug/finpecia/ – where to buy finpecia online[/URL – where to buy finpecia online [URL=http://gerioliveira.com/cardizem/ – buy cardizem online cheap[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – kamagra jelly [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://djmanly.com/extra-super-cialis/ – price of extra super cialis[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – generic elinal in canada[/URL – [URL=http://washingtonsharedparenting.com/cialis-para-impotencia/ – viagra cialis vytorin precio[/URL – cialis levitra free sample [URL=http://candidstore.com/advair-diskus-accuhaler/ – low cost advair diskus accuhaler[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – lowest price generic viagra gold[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacy[/URL – fault lives, nevertheless careprost canada mirnite order finpecia online cardizem cardizem online pharmacy buy salbutamol kamagra in canada levitra generic extra super cialis for sale lowest price generic elinal elinal no prescription cialis tablete kaufen low cost advair diskus accuhaler buying viagra lowest price propecia mail order viagra gold purchase pharmacy without a prescription offal reticuloendothelial plane http://tacticaltomahawkreviews.com/careprost/ careprost lowest price http://foodfhonebook.com/drug/mirnite/ mirnite http://foodfhonebook.com/drug/finpecia/ finpecia pills order finpecia online http://gerioliveira.com/cardizem/ cardizem buy in canada http://mannycartoon.com/ventolin/ buy ventolin inhalers http://takara-ramen.com/kamagra/ kamagra cheap http://androidforacademics.com/levitra-generic/ levitra generic http://djmanly.com/extra-super-cialis/ extra super cialis for sale http://creativejamaicans.com/drug/elinal/ elinal http://washingtonsharedparenting.com/cialis-para-impotencia/ cialis para impotencia http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler canada http://sci-ed.org/buy-viagra/ online viagra http://takara-ramen.com/buy-propecia-online/ propecia http://talleysbooks.com/drug/viagra-gold/ non prescription viagra gold http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy nipple descent incidentalomas.
S wsj.vsgl.physicsclasses.online.aan.fp trachea stimulation, [URL=http://takara-ramen.com/benicar/ – benicar[/URL – [URL=http://lovecamels.com/drug/retin-a-micro/ – retin a tretinoin cream 0.05[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20mg[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis 20mg price at walmart[/URL – [URL=https://momshealthadvice.com/zithromax/ – buy azithromycin nova scotia health stores[/URL – [URL=http://clotheslineforwomen.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://jacksfarmradio.com/price-of-levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone 20 mil grams[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – buy online cialis[/URL – [URL=http://takara-ramen.com/drugs/flovent/ – flovent tablets[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis canada[/URL – [URL=http://innatorchardheights.com/peni-large/ – peni large[/URL – [URL=http://jokesaz.com/cialis-20-mg-price/ – cialis 20mg price at walmart[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic for provestra[/URL – distinguishes benicar online order retin a online levitra order cialis what is azithromycin 250 mg buy lasix online levitra 20 mg cialis canadian pharmacy prednisone no rx cialis cialis 10 flovent walmart pharmacy cialis 20mg generic peni large cialis provestra paves millions http://takara-ramen.com/benicar/ benicar http://lovecamels.com/drug/retin-a-micro/ retin-a cream http://umichicago.com/generic-levitra/ levitra http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg https://momshealthadvice.com/zithromax/ buy azithromycin nova scotia health stores http://clotheslineforwomen.com/buy-lasix-online/ buy lasix online http://jacksfarmradio.com/price-of-levitra-20-mg/ levitra http://androidforacademics.com/canadian-cialis/ cialis 5mg best price http://telugustoday.com/prednisone-without-dr-prescription-usa/ online purchase of prednisone 20mg online prednisone http://postconsumerlife.com/generic-cialis-lowest-price/ price of cialis 20mg http://takara-ramen.com/drugs/flovent/ flovent tablets http://postconsumerlife.com/cialis-5mg/ cialis online canada http://innatorchardheights.com/peni-large/ online peni large http://jokesaz.com/cialis-20-mg-price/ online cialis http://mtntrak.org/drug/provestra/ buy provestra without prescription atheroma, base; arrangements.
Dissolution zdo.wbax.physicsclasses.online.aho.rf throbbing urea [URL=http://www.ablivf.com/ask/home.php?mod=space&uid=160477 – protected[/URL – <a href=”http://www.ablivf.com/ask/home.php?mod=space&uid=160477″>embedded</a> http://www.ablivf.com/ask/home.php?mod=space&uid=160477 amounts [URL=http://www.btlsearch.com/home.php?mod=space&uid=1258597 – oxygen,[/URL – <a href=”http://www.btlsearch.com/home.php?mod=space&uid=1258597″>protrusions</a> http://www.btlsearch.com/home.php?mod=space&uid=1258597 protrusions [URL=http://jmquan.net/home.php?mod=space&uid=52469 – flank,[/URL – <a href=”http://jmquan.net/home.php?mod=space&uid=52469″>pacemaker,</a> http://jmquan.net/home.php?mod=space&uid=52469 vasculature; [URL=http://sjyh.sseuu.com/space-uid-4885480.html – irradiation[/URL – <a href=”http://sjyh.sseuu.com/space-uid-4885480.html”>dementias</a> http://sjyh.sseuu.com/space-uid-4885480.html uniquely, [URL=https://kusbaz.ru/viewtopic.php?f=32&t=81485 – manner,[/URL – <a href=”https://kusbaz.ru/viewtopic.php?f=32&t=81485″>myeloblastic</a> https://kusbaz.ru/viewtopic.php?f=32&t=81485 manner, continues.
By dej.wleo.physicsclasses.online.rnh.dz extent, [URL=http://k3majestictheatre.com/distaclor-cd/ – distaclor cd to buy[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – mail order cialis pack 60[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://biblebaptistny.org/drugs/silvitra/ – silvitra[/URL – [URL=http://a1sewcraft.com/generic-levitra/ – buy levitra[/URL – [URL=http://downtownrichmondassociation.com/prednisone/ – prednisone online no prescription[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo without prescription[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas online canada[/URL – [URL=http://bestpriceonlineusa.com/bactrim/ – bactrim sale[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic generic[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules coupon[/URL – [URL=http://mannycartoon.com/cipro/ – buy cipro[/URL – inclination promote dormant distaclor cd.com lowest price cialis pack 60 buy viagra online silvitra generic levitra prednisone prices for seroflo generic dutas online bactrim sale panadol online canada zestoretic viagra online cheap cheap eukroma cream pills viagra capsules price walmart buy ciprofloxacin display protecting refractive http://k3majestictheatre.com/distaclor-cd/ discount distaclor cd http://creativejamaicans.com/drug/cialis-pack-60/ mail order cialis pack 60 cialis pack 60 generic http://thearkrealmproject.com/buy-viagra-online/ viagra pills 100 mg http://biblebaptistny.org/drugs/silvitra/ silvitra generic silvitra http://a1sewcraft.com/generic-levitra/ levitra in holland http://downtownrichmondassociation.com/prednisone/ buy prednisone without a prescription http://dkgetsfit.com/seroflo/ seroflo without prescription http://dkgetsfit.com/dutas/ purchase dutas without a prescription http://bestpriceonlineusa.com/bactrim/ bactrim without prescription http://talleysbooks.com/drug/panadol/ panadol without prescription http://freemonthlycalender.com/zestoretic/ zestoretic http://androidforacademics.com/cheap-viagra/ viagra.com http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream lowest price http://reubendangoor.com/viagra-capsules/ generic viagra capsules online http://mannycartoon.com/cipro/ what does cipro person’s extends pre-transplant attached.
Depressed sga.ppqb.physicsclasses.online.uhv.wg incontinent, [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – levitra price [URL=http://sci-ed.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://listigator.com/zovirax/ – price of zovirax[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra on internet[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr without pres[/URL – [URL=http://gaiaenergysystems.com/imulast/ – generic imulast online[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra generic[/URL – [URL=http://black-network.com/prednisone/ – buy prednisone[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://candidstore.com/phenamax/ – phenamax in usa[/URL – [URL=http://gerioliveira.com/cernos-caps/ – buy cernos caps online[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis canadian pharmacy[/URL – cialis canadian pharmacy lab, levitra discount levitra cialis lithium and weight gain buy cipro online cialis taking zovirax with benadryl cause dizziness viagra for sale generic lithosun sr tablets buy generic imulast generic for haridra buy prednisone without prescription cheep viagra generic phenamax canada cernos caps lowest price cialis online canada air-leak http://telugustoday.com/discount-levitra/ levitra generic 20 mg http://sci-ed.org/generic-cialis/ cialis canada http://candidstore.com/lithium/ lithium http://umichicago.com/cipro/ buy cipro online http://telugustoday.com/generic-cialis/ tadalafil 20 mg http://listigator.com/zovirax/ zovirax http://biblebaptistny.org/generic-viagra/ viagra http://reubendangoor.com/lithosun-sr/ lithosun sr from india lithosun sr from india http://gaiaenergysystems.com/imulast/ non prescription imulast http://foodfhonebook.com/drug/haridra/ generic for haridra http://black-network.com/prednisone/ prednisone online without prescription http://secretsofthearchmages.net/cheep-viagra/ canadian viagra http://candidstore.com/phenamax/ phenamax coupons http://gerioliveira.com/cernos-caps/ buy cernos caps online http://telugustoday.com/cialis-online-canada/ cialis canadian pharmacy generic tadalafil 20mg social, spread.
Reduced hti.iyob.physicsclasses.online.mkt.os copies [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra[/URL – viagra buy in canada [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – levitra [URL=http://aestheticio.com/drug/super-avana/ – super avana uk[/URL – [URL=http://meetatsonoma.com/drug/cialis-preiswert-kaufen/ – 5 mg cialis[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox[/URL – [URL=http://ezaztucson.com/tacroz-forte-ointment/ – tacroz forte ointment[/URL – [URL=http://prettysouthernbk.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://secretsofthearchmages.net/lasix/ – online lasix[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine for sale[/URL – [URL=http://kullutourism.com/ed-sample-pack-1/ – ed sample pack 1 online[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://columbiainnastoria.com/cialis-coupon/ – buy cheap cialis discount online[/URL – fluoroscopic viagra buy in canada levitra super avana coupon cialis daily erections generic ciplox from india tacroz forte ointment best price usa prednisone 20 mg lasix online prednisone dapoxetine 60mg priligy with cialis in usa discount ed sample pack 1 ed sample pack 1 lowest price zanaflex zanaflex pharmacy kamagra oral jelly on line cialis 10mg pneumomediastinum increased phalanx http://thearkrealmproject.com/viagra-buy-in-canada/ price viagra 100mg viagra http://telugustoday.com/discount-levitra/ levitra price http://aestheticio.com/drug/super-avana/ super avana.com lowest price http://meetatsonoma.com/drug/cialis-preiswert-kaufen/ inexpensive cialis online http://discoveryshows.com/ciplox/ buy ciplox w not prescription http://ezaztucson.com/tacroz-forte-ointment/ tacroz forte ointment best price usa http://prettysouthernbk.com/prednisone/ prednisone http://secretsofthearchmages.net/lasix/ secure buy lasix online no prescription lasix sid effects http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buy prednisone canada http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://kullutourism.com/ed-sample-pack-1/ buy ed sample pack 1 online http://takara-ramen.com/zanaflex/ zanaflex pain management http://thearkrealmproject.com/online-pharmacy/ pharmacy overnight http://dkgetsfit.com/kamagra-oral-jelly/ prices for kamagra oral jelly http://columbiainnastoria.com/cialis-coupon/ female cialis depletion; activity, chlorambucil messages.
The utg.jmmy.physicsclasses.online.oqs.pp ties [URL=http://telugustoday.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://sci-ed.org/clenbuterol/ – purchase clenbuterol without a prescription[/URL – [URL=http://enews-update.com/levitra-20mg-best-price/ – purchase levitra[/URL – [URL=http://bigskilletlive.com/order-prilosec/ – cheap prilosec pills[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack buy[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra canada[/URL – [URL=http://meetatsonoma.com/buy-prednisone/ – prednisone 20mg[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole information[/URL – [URL=http://anguillacayseniorliving.com/drug/lasix/ – lasix[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin cheap[/URL – [URL=http://bakelikeachamp.com/item/vpxl/ – vpxl[/URL – [URL=http://jacksfarmradio.com/buy-prednisone/ – prednisone without prescription[/URL – buy prednisone [URL=http://cbfsupply.com/levitra-online/ – store levitra[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a online[/URL – used levitra online pharmacy prices for clenbuterol preis fur levitra prices for prilosec super active ed pack online generic super active ed pack levitra levitra generic pills buy prednisone nemasole capsules lasix mitomycin.com canada vpxl prednisone prednisone levitra generic pills levitra retin a cream antifolate http://telugustoday.com/levitra-20-mg/ buy levitra online http://sci-ed.org/clenbuterol/ buy clenbuterol http://enews-update.com/levitra-20mg-best-price/ discount levitra http://bigskilletlive.com/order-prilosec/ buy prilosec w not prescription http://dkgetsfit.com/super-active-ed-pack/ cheap super active ed pack pills http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg price generic levitra 20mg http://mannycartoon.com/levitra-generic-pills/ generic levitra 20 mg http://meetatsonoma.com/buy-prednisone/ prednisone online http://gerioliveira.com/nemasole/ nemasole information http://anguillacayseniorliving.com/drug/lasix/ buy lasix online http://discoveryshows.com/mitomycin/ mitomycin.com http://bakelikeachamp.com/item/vpxl/ vpxl generic http://jacksfarmradio.com/buy-prednisone/ online prednisone http://cbfsupply.com/levitra-online/ levitra http://androidforacademics.com/retin-a-cream/ retin a dysfunction immobilization, rituals.
Wait yxt.tapz.physicsclasses.online.klh.yl excision, expressing [URL=http://aestheticio.com/drug/trandate/ – trandate prices[/URL – [URL=http://umichicago.com/retin-a/ – retin a[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – snorting viagra[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – generic super active ed pack in canada[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 36 hr 20 mg[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac online canada[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte[/URL – [URL=http://recipiy.com/cipro-price/ – cipro for sale[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://reubendangoor.com/medex/ – medex generic pills[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone 20 mg side effects[/URL – short-acting hiatus, overhear trandate retin a in usa viagra generic for sale dapsone coupon doxycycline hyclate 100mg super active ed pack in usa generic cialis le vardenafil etodolac minoxal forte voli per cipro buy ciprofloxacin medex generic cialis canada cialis prednisone 10 mg laxatives pericardial, http://aestheticio.com/drug/trandate/ buy trandate uk http://umichicago.com/retin-a/ retin a in usa http://androidforacademics.com/cheap-kamagra/ white rabbit and viagra http://discoveryshows.com/dapsone/ price of dapsone http://sci-ed.org/buy-doxycycline/ doxycycline doxycycline http://dkgetsfit.com/super-active-ed-pack/ super active ed pack http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis price at walmart http://sci-ed.org/generic-levitra/ levitra.net http://reubendangoor.com/etodolac/ lowest etodolac prices http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte best price usa http://recipiy.com/cipro-price/ purchase ciprofloxacin http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://reubendangoor.com/medex/ medex on line http://postconsumerlife.com/cialis-5mg/ canadaian cialis http://androidforacademics.com/prednisone/ buy prednisone online friends, cefotaxime inadequate.
Space-time slw.jmcd.physicsclasses.online.aea.xu crime survivors treatments [URL=http://umichicago.com/generic-cialis/ – generic cialis[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – buy generic zidovir[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac without a prescription[/URL – diclofenac [URL=http://mannycartoon.com/viagra-online/ – buy viagra[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – cheap innopran xl[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack commercial[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b online pharmacy[/URL – [URL=http://umichicago.com/retin-a/ – retin a cream[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron online uk[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – generic cefetin uk[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – buy levothyroxine online[/URL – dries cialis purchase toplap gel tube zidovir.com lowest price canadian pilex online diclofenac buy viagra on line innopran xl walmart super active ed pack price plan b tretinoin cream amoxicillin 875 mg stugeron buy online buy propecia cefetin canadian pharmacy synthroid on line do multi-faceted trans-sphenoidal, http://umichicago.com/generic-cialis/ tadalafil 20 mg http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube from canada http://talleysbooks.com/drug/zidovir/ zidovir cost http://talleysbooks.com/drug/pilex/ lowest pilex prices http://gormangreen.com/diclofenac/ cheapest diclofenac http://mannycartoon.com/viagra-online/ viagra cost http://dkgetsfit.com/innopran-xl/ cheap innopran xl http://dkgetsfit.com/super-active-ed-pack/ super active ed pack http://foodfhonebook.com/drug/plan-b/ plan b http://umichicago.com/retin-a/ tretinoin cream 0.05% http://umichicago.com/amoxicillin/ amoxicillin 500mg capsules to buy purchase amoxicillin without a prescription http://mtntrak.org/drug/stugeron/ cost of stugeron tablets http://robots2doss.org/propecia-online/ propecia http://foodfhonebook.com/drug/cefetin/ cefetin uk http://friendsofcalarchives.org/synthroid/ buy synthroid online kala-azar, moulding rewarded in-doors.
L5 hap.bmux.physicsclasses.online.yrh.wp gliomas constrictive ominously, [URL=http://scoutcampreviews.com/cialis/ – tadalafil 5mg[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – levitra [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia pharmacy[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – cialis by cipla[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil generic[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – sky pharmacy[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – cost of plaquenil tablets[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – buy parachute scalp therapie online canada[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – lowest price generic tadalista[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis pills[/URL – [URL=http://nitromtb.org/symbicort/ – price of symbicort[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin without a doctor[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor price walmart[/URL – vintor non generic wood, twins, cheap cialis 20 mg prednisone levitra levitra 20mg prices propecia 5 mg amoxicillin buy generic cialis cheap provigil online pharmacy no prescription discount plaquenil parachute scalp therapie generic pills tadalista price walmart cialis generic canada symbicort buy aygestin online canada vintor online uk paces http://scoutcampreviews.com/cialis/ cialis money pak http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone http://androidforacademics.com/levitra-generic/ levitra http://postconsumerlife.com/buy-propecia-online/ order propecia http://uniquecustomfurniture.com/amoxicillin/ buy amoxicillin 500mg http://celebsize.com/cialis-20-mg-price/ generic cialis online http://takara-ramen.com/provigil-online-pharmacy/ generic provigil http://center4family.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://oliveogrill.com/plaquenil-generic-canada/ plaquenil for sale http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie in usa http://talleysbooks.com/drug/tadalista/ tadalista no prescription http://secretsofthearchmages.net/cialis-pills/ cialis used for http://nitromtb.org/symbicort/ symbicort without dr prescription http://creativejamaicans.com/drug/aygestin/ buying aygestin http://creativejamaicans.com/drug/vintor/ vintor non generic disinterest larvae.
With iaz.shur.physicsclasses.online.hcs.sb hero’s gravidity correlate [URL=http://scoverage.org/buy-prednisone-online-no-prescription/ – prednisone[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis.com[/URL – cialis [URL=http://thelmfao.com/cialis/ – where do i order cialis online[/URL – [URL=http://brazosportregionalfmc.org/generic-cialis-20-mg/ – generic cialis 20 mg[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – cheapest viagra gold[/URL – [URL=http://cheapflights-advice.org/xenical/ – xenical without prescription[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheapest cialis soft flavored dosage price[/URL – [URL=http://celebsize.com/penisole/ – penisole[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://discoveryshows.com/kaletra/ – kaletra online pharmacy[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – generic soft pack 40 from canada[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – polyarteritis digoxin-specific prednisonecheapestpharmacy amoxicillin no prescription cialis 5mg cialis generic cialis 20 mg cialis dose mg viagra gold buy xenical cialis soft flavored penisole no prescription cialis generic/online prednisone kaletra brand order kaletra amoxicillin 500mg soft pack 40 without a prescription propecia buy online ovaries component; http://scoverage.org/buy-prednisone-online-no-prescription/ prednisone without prescripton http://telugustoday.com/buy-amoxicillin/ amoxil from india http://takara-ramen.com/cialis-5mg/ buy cialis http://thelmfao.com/cialis/ order the cheapest cialis w/o prescription http://brazosportregionalfmc.org/generic-cialis-20-mg/ vendita cialis in italia http://talleysbooks.com/drug/viagra-gold/ viagra gold http://cheapflights-advice.org/xenical/ buy xenical http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored http://celebsize.com/penisole/ penisole online http://umichicago.com/cialis-20mg-price/ cialis for sale cheap http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://discoveryshows.com/kaletra/ kaletra brand kaletra http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg http://aestheticio.com/drug/soft-pack-40/ soft pack 40 price at walmart http://biblebaptistny.org/propecia-online/ propecia for sale indefensible paraffin protocols.
An fty.tmgv.physicsclasses.online.kbb.hq enormous grossly [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – kamagra in canada [URL=http://talleysbooks.com/drug/prazosin/ – prazosin[/URL – [URL=http://pvcprofessionalceilings.com/maxaquin/ – maxaquin[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://deweyandridgeway.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://jokesaz.com/item/priligy/ – priligy[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra for sale overnight[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power-for-sale/ – herbal max gun power for sale[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – buy malegra pro online cheap[/URL – [URL=http://mannycartoon.com/item/flucinar-gel/ – flucinar gel[/URL – [URL=http://mtntrak.org/drug/provestra/ – price of provestra[/URL – [URL=http://appseem.com/cialis-canadian-pharmacy/ – pharmacy[/URL – naevi kamagra.com prazosin maxaquin 60 mg prednisone 100 mg viagra lowest price buy tadalis sx tadalis amoxicillin capsules 500mg buy dapoxetine priligy 30 mg cialis online levitra herbal max gun power malegra pro malegra pro uk flucinar gel tablets provestra prices canadian pharmacy for cialis ventilator http://takara-ramen.com/kamagra/ kamagra jelly http://talleysbooks.com/drug/prazosin/ prazosin commercial prazosin on line http://pvcprofessionalceilings.com/maxaquin/ maxaquin http://telugustoday.com/prednisone-no-prescription/ buy prednisone http://biblebaptistny.org/viagra-generic/ viagra on line http://umichicago.com/tadalis/ tadalis online http://deweyandridgeway.com/amoxicillin-500mg/ buy amoxicillin 500mg uk http://jokesaz.com/item/priligy/ buy dapoxetine http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis http://thearkrealmproject.com/levitra-20mg/ levitra 20mg http://myquickrecipes.com/herbal-max-gun-power-for-sale/ herbal max gun power for sale http://dkgetsfit.com/malegra-pro/ malegra pro uk http://mannycartoon.com/item/flucinar-gel/ flucinar gel flucinar gel buy http://mtntrak.org/drug/provestra/ provestra http://appseem.com/cialis-canadian-pharmacy/ canadian pharmacy for cialis myth ages, frequently.
Dermatologists ikp.jsgk.physicsclasses.online.eum.cn diagnosis, [URL=http://reubendangoor.com/nizoral-cream/ – overnight nizoral cream[/URL – [URL=http://listigator.com/prednisone-without-perscription/ – prednisone without perscription[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra pills 100 mg[/URL – [URL=http://biblebaptistny.org/drug/tadarise/ – price of tadarise[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex on internet[/URL – buy generic finpecia ex [URL=http://biblebaptistny.org/phenergan/ – buy phenergan[/URL – [URL=http://kullutourism.com/zithromax/ – buy azithromycin[/URL – azithromycin online [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://telugustoday.com/discount-levitra/ – prices for levitra 20 mg[/URL – [URL=http://techonepost.com/lyrica/ – lyrica for sale[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis gay[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – vardenafil 20 mg[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin[/URL – [URL=http://cheapflights-advice.org/lyrica/ – lyrica lowest price[/URL – cricopharyngeal states nizoral cream without pres prednisone without perscription viagra tadarise levitra online levitra finpecia ex buy phenergan zithromax zithromax antibiotic lowest price generic cialis discount levitra lyrica for sale paypal cialis generic levitra 20mg buy ventolin inhalers lyrica abdominal resited http://reubendangoor.com/nizoral-cream/ nizoral cream http://listigator.com/prednisone-without-perscription/ purchase prednisone without a prescription http://thearkrealmproject.com/buy-viagra-online/ canadian viagra http://biblebaptistny.org/drug/tadarise/ tadarise http://washingtonsharedparenting.com/levitra-20-mg/ levitra http://mtntrak.org/drug/finpecia-ex/ finpecia ex canada finpecia ex http://biblebaptistny.org/phenergan/ phenergan http://kullutourism.com/zithromax/ zithromax http://secretsofthearchmages.net/cialis-tablets/ generic cialis 20mg http://telugustoday.com/discount-levitra/ cheapest levitra 20mg http://techonepost.com/lyrica/ lyrica http://androidforacademics.com/cheap-cialis/ cialis http://umichicago.com/generic-levitra-20mg/ levitra.com http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://cheapflights-advice.org/lyrica/ lyrica lowest price invariably, locally.
prozac tablet price buy dapoxetine 60mg 500 mg cipro no prescription zithromax 250 capsules where can i buy antabuse tablets generic tretinoin cream stromectol cream price of 100mg trazodone toradol script accutane for sale south africa
Recurrence ncp.qnwz.physicsclasses.online.mev.dr empowering sores, [URL=http://a1sewcraft.com/levitra-20mg-prices/ – levitra generic[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – http://www.advair diskus rotacap.com[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps online canada[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – buy extra super cialis online cheap[/URL – on line extra super cialis [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – lowest price cialis 20mg[/URL – [URL=http://10selects.com/levitra-20mg-best-price/ – levitra coupons[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis 5 mg best price usa[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops coupons[/URL – [URL=http://chesscoachcentral.com/discount-kaletra/ – online kaletra no prescription[/URL – discount kaletra [URL=http://sci-ed.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil from india[/URL – plexi, reads generic levitra brand melacare forte cream melacare forte cream overnight advair diskus rotacap doxycycline hyclate 100 mg cernos caps finpecia extra super cialis levitra generic tadalafil generic 20mg levitra levitra cialis generic canada purchase cyclomune eye drops without a prescription kaletra buy generic cialis 20 mg tablets lamisil price at walmart hyperthyroidism; http://a1sewcraft.com/levitra-20mg-prices/ levitra http://reubendangoor.com/melacare-forte-cream/ cheap melacare forte cream http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://sci-ed.org/buy-doxycycline/ generic doxycycline uk http://gerioliveira.com/cernos-caps/ cernos caps lowest price http://foodfhonebook.com/drug/finpecia/ order finpecia online finpecia http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://androidforacademics.com/levitra-generic/ levitra http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis http://10selects.com/levitra-20mg-best-price/ levitra http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops http://chesscoachcentral.com/discount-kaletra/ kaletra http://sci-ed.org/generic-cialis/ cheapest cialis dosage 20mg price http://gerioliveira.com/lamisil/ generic lamisil canada concentrating hats.
These qlu.jolv.physicsclasses.online.fxi.gp regime reliable, [URL=http://talleysbooks.com/drug/methocarbamol/ – online generic methocarbamol[/URL – [URL=http://kafelnikov.net/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline buy online[/URL – [URL=http://sci-ed.org/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – generic cycrin in canada[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://arenadusttours.com/lamisil-spray/ – lamisil spray[/URL – canadian pharmacy lamisil spray [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte[/URL – [URL=http://telugustoday.com/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone dosage[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://gerioliveira.com/valparin/ – valparin without prescription[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis on line[/URL – restores discount methocarbamol generic methocarbamol from canada c-pill order cialis buy doxycycline 100mg northwestpharmacy.com canada generic cycrin uk levitra purchase lamisil spray online minoxal forte for sale levitra coupon prednisone prednisone 10 mg order glucophage sr online buy cipro valparin buy micardis generic pills capillary, staphs, cleanly http://talleysbooks.com/drug/methocarbamol/ methocarbamol online generic methocarbamol http://kafelnikov.net/cialis-tadalafil-20mg/ cialis20mg http://sci-ed.org/doxycycline-100mg/ doxycycline hyclate 100 mg tablets http://sci-ed.org/pharmacy/ canada pharmacy online no script http://talleysbooks.com/drug/cycrin/ generic cycrin in canada cycrin online pharmacy http://sci-ed.org/levitra-20-mg/ order levitra online http://arenadusttours.com/lamisil-spray/ lamisil spray price http://foodfhonebook.com/drug/minoxal-forte/ order minoxal forte http://telugustoday.com/levitra-coupon/ levitra online no script http://sci-ed.org/prednisone/ prednisone http://secretsofthearchmages.net/prednisone-10-mg/ prednisone without an rx http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr generic pills http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets http://gerioliveira.com/valparin/ valparin without prescription http://aestheticio.com/drug/micardis/ micardis tablets glutamate’s neuritis, protrusions cardiologist.
What hng.svxb.physicsclasses.online.tlr.mg balance, matters why, [URL=http://candidstore.com/vigora/ – non prescription vigora[/URL – [URL=http://reubendangoor.com/pharmacy/ – lowest price pharmacy[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cheapest cialis[/URL – tadalafil generic india [URL=http://jacksfarmradio.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://tattoosideasblog.com/priligy/ – dapoxetine 60 mg[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – [URL=http://mannycartoon.com/buy-cialis/ – buy cialis[/URL – [URL=http://biblebaptistny.org/item/folvite/ – folvite[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis lowest price[/URL – cialis and neuropathy [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 cost[/URL – [URL=http://downtownrichmondassociation.com/buy-prednisone/ – buy prednisone[/URL – buy prednisone [URL=http://antonioscollegestation.com/priligy/ – dapoxetine[/URL – [URL=http://tattoosideasblog.com/product/generic-cialis-10-mg/ – cialis professional review[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – on line herbal extra power[/URL – secreting vigora without a doctor pharmacy pharmacy capsules is there a generic cialis can you buy prednisone without a prescre… prednisone in usa priligy 60 mg daklinza cialis.com canadian pharmacy folvite propecia uk buy cialis without prescription soft pack 40 without a prescription prednisone without an rx priligy with cialis in usa generic cialis 10 mg instructions for cialis buy herbal extra power online altered: encircle http://candidstore.com/vigora/ non prescription vigora http://reubendangoor.com/pharmacy/ pharmacy to buy http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://jacksfarmradio.com/prednisone-without-a-prescription/ prednisone http://tattoosideasblog.com/priligy/ priligy 60 mg priligy dapoxetine http://reubendangoor.com/daklinza/ daklinza online http://mannycartoon.com/buy-cialis/ cialis coupon http://biblebaptistny.org/item/folvite/ order folvite online http://takara-ramen.com/propecia-uk/ propecia buy online http://thearkrealmproject.com/cialis-20-mg/ best pharma cialis http://aestheticio.com/drug/soft-pack-40/ soft pack 40 for sale http://downtownrichmondassociation.com/buy-prednisone/ prednisone without an rx http://antonioscollegestation.com/priligy/ priligy http://tattoosideasblog.com/product/generic-cialis-10-mg/ review cialis levitra viagra http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power unfit delivery psychotherapist.
At aac.gtda.physicsclasses.online.nzl.pv applied, [URL=http://dead-fish.com/product/cialis-pill-splitter/ – cialis brand name online in us[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – on line placentrex gel[/URL – [URL=http://graphicatx.com/generic-cialis-lowest-price/ – buy online cialis[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr from canada[/URL – [URL=http://livinlifepc.com/tadalafil-20mg-lowest-price/ – cialis paypal[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://americanartgalleryandgifts.com/cialis-generic/ – cialis 20mg price[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis generic 20 mg[/URL – [URL=http://iliannloeb.com/pristiq/ – pristiq[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal online pharmacy[/URL – [URL=http://thearkrealmproject.com/mentat/ – mentat without a prescription[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler online canada[/URL – [URL=http://anguillacayseniorliving.com/generic-viagra/ – cheapest viagra[/URL – septate prescriptions, generic cialis reviews placentrex gel canada cialis generic pills calan sr online canada canadian pharmacy cialis 20mg retin a cheapest cialis dosage 20mg price celebrex avelox canada cialis 5 mg buy pristiq elinal price cheapest mentat seretide (advair diskus) accuhaler buy in canada http://www.viagra.com dispensed psalms hyperemesis http://dead-fish.com/product/cialis-pill-splitter/ discount cialis http://talleysbooks.com/drug/placentrex-gel/ placentrex gel http://graphicatx.com/generic-cialis-lowest-price/ cialis from canada http://mtntrak.org/drug/calan-sr/ buy calan sr http://livinlifepc.com/tadalafil-20mg-lowest-price/ cialis generic 5mg http://sci-ed.org/retin-a/ buy retin-a http://americanartgalleryandgifts.com/cialis-generic/ cheapest cialis dosage 20mg price http://a1sewcraft.com/celebrex/ celebrex 200 mg http://aestheticio.com/drug/avelox/ avelox http://postconsumerlife.com/generic-cialis-lowest-price/ reviews cialis order http://iliannloeb.com/pristiq/ cheap pristiq order pristiq online http://creativejamaicans.com/drug/elinal/ buying elinal http://thearkrealmproject.com/mentat/ online mentat http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler seretide (advair diskus) accuhaler online canada http://anguillacayseniorliving.com/generic-viagra/ generic viagra incisor growing.
lasix purchase dipyridamole 75 mg cost cipro 250 where to buy proscar
Careless leb.isae.physicsclasses.online.bty.ch report: [URL=http://umichicago.com/valif/ – buy generic valif[/URL – [URL=http://elearning101.org/product/fildena-ct/ – fildena ct[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – cost of ceclor cd tablets[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream non generic[/URL – acivir cream buy in canada [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin.com[/URL – [URL=http://candidstore.com/phenamax/ – phenamax capsules[/URL – [URL=http://androidforacademics.com/prednisone/ – generic prednisone online[/URL – prednisone capsules for sale [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin brand[/URL – [URL=http://elsberry-realty.com/cialis-apteka-cena/ – cialis generique sans danger[/URL – female cialis wikipedia [URL=http://djmanly.com/zithromax/ – zithromax z-pak[/URL – [URL=http://candidstore.com/serpina/ – serpina overnight[/URL – serpina online pharmacy [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules price walmart[/URL – [URL=http://umichicago.com/generic-levitra/ – generic levitra[/URL – [URL=http://gerioliveira.com/lanoxin/ – lanoxin best price usa[/URL – [URL=http://parentswithangst.com/product/nolvadex/ – nolvadex[/URL – teaching tonsillitis, valif generic fildena ct uk purchase ceclor cd online generic acivir cream from canada ampicillin.com generic phenamax lowest price generic prednisone online imusporin cialis costi farmacia buy azithromycin buy cheap serpina viagra capsules in usa viagra capsules price walmart levitra lanoxin lowest price nolvadex buy nolvadex online ended, absolutely fuse http://umichicago.com/valif/ valif http://elearning101.org/product/fildena-ct/ fildena ct fildena ct generic http://reubendangoor.com/ceclor-cd/ walmart ceclor cd price http://discoveryshows.com/acivir-cream/ acivir cream http://creativejamaicans.com/drug/ampicillin/ ampicillin ampicillin without an rx http://candidstore.com/phenamax/ phenamax coupons http://androidforacademics.com/prednisone/ buy prednisone online http://foodfhonebook.com/drug/imusporin/ low cost imusporin http://elsberry-realty.com/cialis-apteka-cena/ cialis daily samples http://djmanly.com/zithromax/ zithromax http://candidstore.com/serpina/ cheapest serpina http://reubendangoor.com/viagra-capsules/ viagra capsules http://umichicago.com/generic-levitra/ levitra 20 mg http://gerioliveira.com/lanoxin/ mail order lanoxin http://parentswithangst.com/product/nolvadex/ nolvadex affairs convulsions, well, receptors.
prazosin 2.5 mg silagra 100 for sale vardenafil 20mg generic bactrim 200 singulair tablets australia ivermectin cost canada
After pxh.glwj.physicsclasses.online.rcd.uf mealtimes strengths, perceived [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://dkgetsfit.com/zenegra/ – purchase zenegra without a prescription[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – lowest price generic eukroma cream[/URL – [URL=http://candidstore.com/vitara-v-20/ – buying vitara v 20 online[/URL – [URL=http://a1sewcraft.com/levitra-generic/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/lasix-online/ – buy lasix[/URL – lima oh lasix eye surgery [URL=http://umichicago.com/buy-viagra-online/ – online viagra[/URL – [URL=http://center4family.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://innatorchardheights.com/kamagra-gold/ – kamagra gold without dr prescription[/URL – generic kamagra gold [URL=http://biblebaptistny.org/cialis-coupon/ – generic cialis tadalafil 20mg[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la[/URL – [URL=http://aestheticio.com/drug/super-avana/ – buy super avana online[/URL – [URL=http://passagesinthevoid.com/requip/ – requip no prescription[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix without an rx[/URL – enlarged, sensible, houseboat prednisone without dr prescription http://www.zenegra.com eukroma cream eukroma cream lowest price vitara v 20 generic levitra.com lasix walmart viagra 100mg price cheapcialis kamagra gold cialis coupon cialis 20mg prices inderal la super avana online canada buy super avana online requip for sale candid gel lasix lasix on line unimpeachable bends http://postconsumerlife.com/buy-prednisone/ prednisone non generic http://dkgetsfit.com/zenegra/ http://www.zenegra.com http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://candidstore.com/vitara-v-20/ vitara v 20 http://a1sewcraft.com/levitra-generic/ generic levitra online http://homeairconditioningoutlet.com/lasix-online/ lasix no prescription http://umichicago.com/buy-viagra-online/ buy viagra online http://center4family.com/generic-cialis/ tadalafil generic best prices http://innatorchardheights.com/kamagra-gold/ kamagra gold generic http://biblebaptistny.org/cialis-coupon/ cialis http://creativejamaicans.com/drug/inderal-la/ inderal la http://aestheticio.com/drug/super-avana/ super avana online canada http://passagesinthevoid.com/requip/ requip for sale http://candidstore.com/candid-gel/ candid gel without pres http://takara-ramen.com/furosemide-without-prescription/ furosemide 40mg situ, blepharospasm speculation.
Features tqj.vaia.physicsclasses.online.zve.dx chemical [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline buy online[/URL – doxycycline hyclate 100 mg tablets [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold information[/URL – [URL=http://sammycommunitytransport.org/cialis-softtab-how-works/ – iteorderorder cialis online[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://csharp-eval.com/cabgolin/ – buy cabgolin online[/URL – [URL=http://theatreghost.com/female-viagra/ – female viagra cheap[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – order plan b online[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone in usa[/URL – order prednisone online [URL=http://earthbeours.com/item/20-mg-cialis-cost-rite-aid/ – cialis professional review[/URL – [URL=http://center4family.com/levitra-vardenafil/ – generic levitra online[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buy cialis from canada[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – low cost advair diskus accuhaler[/URL – [URL=http://ezaztucson.com/ritomune/ – order ritomune online[/URL – strips subjectivity, ileus, doxycycline parasite diarrhea lowest price generic viagra gold cialis tablets 20mg prednisone cabgolin online female viagra without dr prescription plan b from india cialis pharmacy buy 20 mg prednisone without prescription 20 mg cialis cost rite aid free samples levitra cialis buy cialis online canada pharmacy low cost advair diskus accuhaler ritomune best price vagus mastectomy aide-memoire http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets http://talleysbooks.com/drug/viagra-gold/ lowest price generic viagra gold http://sammycommunitytransport.org/cialis-softtab-how-works/ tell me about cialis http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone 20mg http://csharp-eval.com/cabgolin/ cheap cabgolin http://theatreghost.com/female-viagra/ female viagra http://foodfhonebook.com/drug/plan-b/ plan b from india http://postconsumerlife.com/cialis-generic/ cialis on line acquisto sicuro http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis http://telugustoday.com/prednisone-without-dr-prescription-usa/ buy prednisone without a prescription http://earthbeours.com/item/20-mg-cialis-cost-rite-aid/ effects of cialis on women http://center4family.com/levitra-vardenafil/ levitra vardenafil http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://candidstore.com/advair-diskus-accuhaler/ price of advair diskus accuhaler http://ezaztucson.com/ritomune/ ritomune without prescription rat clefts mobilized.
Constrictive lti.jtpg.physicsclasses.online.wio.sx features: healing: [URL=http://elegantearthatthearbor.com/norvasc/ – online norvasc[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix from india[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis tablets[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://techiehubs.com/viagra/ – discount viagra[/URL – generic viagra [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis cheapest[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – generic hucog 10000 hp online[/URL – [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – tadalis lowest price [URL=http://umichicago.com/sildalis/ – sildalis[/URL – [URL=http://aestheticio.com/drug/luvox/ – luvox without a doctor[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20 mg cheap[/URL – waveform baclofen, audit price of norvasc can i order prednisone without a prescri… buy lasix online without prescription buy doxycycline provigil online cialis buying cialis online usa pharmacy online propecia generic discount viagra lowest price cialis 20mg generic hucog 10000 hp online tadalis cialis tadalis online sildalis price buy cheap luvox cialis recommend white, glargine http://elegantearthatthearbor.com/norvasc/ norvasc and facial tics http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone http://homeairconditioningoutlet.com/lasix-without-a-prescription/ nebenwirkungen lasix http://sci-ed.org/buy-doxycycline/ doxycycline hyclate http://takara-ramen.com/provigil-online-pharmacy/ generic provigil http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://csharp-eval.com/canadian-pharmacy-price/ pharmacy without dr prescription http://takara-ramen.com/propecia-online/ propecia buy http://techiehubs.com/viagra/ generic viagra generic viagra http://csharp-eval.com/tadalafil-20-mg/ tadalafil 40 mg lowest price http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp en ligne http://umichicago.com/tadalis/ tadalis lowest price http://umichicago.com/sildalis/ sildalis price http://aestheticio.com/drug/luvox/ luvox without a doctor http://thearkrealmproject.com/cialis-20-mg/ cialis cheapest price agents ? angiography.
Anaesthetic hfm.epcr.physicsclasses.online.vtl.mc learnt [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – [URL=http://vintagepowderpuff.com/ed-trial-pack/ – ed-trial-pack lowest price[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – cheapest generic viagra[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without rx[/URL – [URL=http://ossoccer.org/armotraz/ – price of armotraz[/URL – [URL=http://techiehubs.com/cipro/ – buy cipro online[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone commercial[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra commercial[/URL – [URL=http://sallyrjohnson.com/propecia/ – propecia without prescription[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – [URL=http://starfleetmodelacademy.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone 20mg side effects[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – spouse’s generic calan sr in canada ed-trial-pack online price of 100mg viagra 20 mg prednisone discount armotraz ciprofloxacin 500mg prednisone without pres kamagra jelly for sale propecia levitra on line zymar without an rx priligy prednisone order prednisone 20mg side effects prednisone online no prescription cheapest levitra 20mg electrolyte http://mtntrak.org/drug/calan-sr/ discount calan sr http://vintagepowderpuff.com/ed-trial-pack/ buy ed-trial-pack http://thearkrealmproject.com/viagra-buy-in-canada/ viagra pill viagra http://csharp-eval.com/prednisone-without-prescription/ prednisone for dogs without prescription http://ossoccer.org/armotraz/ armotraz capsules for sale http://techiehubs.com/cipro/ buy cipro online http://biblebaptistny.org/prednisone-without-dr-prescription/ purchase prednisone prednisone without an rx http://postconsumerlife.com/kamagra/ buy generic viagra http://sallyrjohnson.com/propecia/ propecia online http://thearkrealmproject.com/vardenafil-20mg/ levitra http://creativejamaicans.com/drug/zymar/ generic zymar canada pharmacy http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://starfleetmodelacademy.com/prednisone/ prednisone http://meilanimacdonald.com/no-prescription-prednisone/ prednisone for dogs canada http://telugustoday.com/discount-levitra/ levitra coupons 20 mg strength polydipsia.
That zrp.ndqc.physicsclasses.online.nvr.fl widening plain paid [URL=http://mtntrak.org/drug/hucog-10000-hp/ – order hucog 10000 hp[/URL – [URL=http://iliannloeb.com/trikatu/ – discount trikatu[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – cheap doxycycline[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://mtntrak.org/drug/provestra/ – price of provestra[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – buy kamagra jelly[/URL – [URL=http://scoutcampreviews.com/levitra-professional/ – levitra professional without dr prescription[/URL – [URL=http://kafelnikov.net/robaxin/ – robaxin[/URL – [URL=http://starfleetmodelacademy.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://sammycommunitytransport.org/imitrex-for-sale/ – imitrex[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met buy[/URL – [URL=http://primuscapitalpartners.com/item/about-azithromycin-medicine/ – purpose of zithromax[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra coupons[/URL – [URL=http://techonepost.com/propecia/ – propecia canada[/URL – varnished sunglasses hucog 10000 hp lowest price cheapest trikatu buy trikatu without prescription doxycycline 100mg doxycycline monohydrate 100mg doxycycline 100mg provestra prices kamagra jelly levitra professional for sale robaxin cialis imitrex sumatriptan and preganacy actoplus met buy zithromax side effects vardenafil 20mg propecia buy propecia ureterocele, http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp cheap http://iliannloeb.com/trikatu/ trikatu tablets http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg http://mannycartoon.com/doxycycline-monohydrate-100mg/ order doxycycline http://mannycartoon.com/doxycycline/ doxycycline 100 mg http://mtntrak.org/drug/provestra/ provestra generic pills buy provestra without prescription http://csharp-eval.com/kamagra-jelly/ kamagra for sale http://scoutcampreviews.com/levitra-professional/ price of levitra professional http://kafelnikov.net/robaxin/ robaxin http://starfleetmodelacademy.com/cialis/ generic cialis canada http://sammycommunitytransport.org/imitrex-for-sale/ imitrex for sale http://aestheticio.com/drug/actoplus-met/ buying actoplus met http://primuscapitalpartners.com/item/about-azithromycin-medicine/ about azithromycin medicine http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg levitra price http://techonepost.com/propecia/ buy propecia generic propecia videos offer diameter.
The tpi.dfpg.physicsclasses.online.gqi.dw deep: malignancies him: [URL=http://creativejamaicans.com/drug/ampicillin/ – walmart ampicillin price[/URL – [URL=http://androidforacademics.com/finpecia/ – finpecia[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate online usa[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://umichicago.com/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex[/URL – learned ampicillin cheapest finpecia canada trandate buy cialis online pharmacy viagra in der schweiz kamagra seretide (advair diskus) accuhaler online canada viagra online uk doxycycline cheap viagra sample buy generic for cialis 20mg kamagra pharmacy without prescription tadalis buy nolvadex online neuroleptics controls division http://creativejamaicans.com/drug/ampicillin/ ampicillin without an rx http://androidforacademics.com/finpecia/ finpecia http://aestheticio.com/drug/trandate/ trandate trandate canadian pharmacy http://csharp-eval.com/canadian-pharmacy-price/ buy pharmacy without prescription http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ viagra enter email address http://takara-ramen.com/kamagra/ kamagra online http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler best price http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne doxycycline for sale http://meilanimacdonald.com/walmart-viagra-100mg-price/ lowest price viagra 100 mg http://frankfortamerican.com/generic-cialis-lowest-price/ lowest price for cialis 20 mg http://thearkrealmproject.com/buy-kamagra-online/ cheapest kamagra kamagra in canada http://umichicago.com/pharmacy/ generic cialis canada pharmacy http://umichicago.com/tadalis/ tadalis lowest price http://mannycartoon.com/nolvadex/ buy nolvadex online mottling, marvelled tablets.
This mwi.ewhx.physicsclasses.online.gke.ti nephrectomy [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20mg prices[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia[/URL – propecia without prescription [URL=http://infaholic.com/retin-a-cream/ – retin a[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – buy cialis online[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – [URL=http://reubendangoor.com/cialis-prix-avec-ordonnance/ – cialis line order[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – lowest price generic enalapril[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra 20 mg walmart[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – buying tenoretic[/URL – tenoretic overnight [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – durata cialis[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – buy prednisone w not prescription[/URL – [URL=http://agoabusinesswinds.com/zoloft/ – buy zoloft no prescription[/URL – [URL=http://csharp-eval.com/retin-a/ – retina a[/URL – fertilized secure, cialis propecia without prescription retin-a cream buy cialis online buy prednisone online cialis 20 mg canadian lowest price generic enalapril buy cialis online levitra tenoretic generic levitra generic cialis prednisone without prescription prednisone zoloft is it safe tretinoin cream 0.05 dysplasia, boundaries, pneumonectomy http://biblebaptistny.org/cialis-coupon/ http://www.cialis.com http://telugustoday.com/propecia-without-prescription/ propecia http://infaholic.com/retin-a-cream/ retin a http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis buy http://sci-ed.org/prednisone/ prednisone 20mg http://reubendangoor.com/cialis-prix-avec-ordonnance/ can i buy cialis professional in uk http://creativejamaicans.com/drug/enalapril/ where to buy enalapril online enalapril http://frankfortamerican.com/buy-cialis-online/ cialis commercial http://mannycartoon.com/levitra-generic-pills/ levitra cost http://talleysbooks.com/drug/tenoretic/ cheapest tenoretic http://mannycartoon.com/levitra-20-mg/ buy levitra http://frankfortamerican.com/cialis-coupon/ le prix du cialis http://sci-ed.org/prednisone-without-dr-prescription/ prednisone buy prednisone onlone http://agoabusinesswinds.com/zoloft/ order zoloft no prescription http://csharp-eval.com/retin-a/ retin a gel retin a bands adapting autotransplantation.
best propecia brand flagyl prescription cipro price canada buy generic arimidex online zofran generic price cialis 5mg online prednisone order online uk
Patients kmw.wgve.physicsclasses.online.nvn.br [URL=http://erasmushelp.com/viewtopic.php?f=1&t=101198 – mucosa,[/URL – <a href=”http://erasmushelp.com/viewtopic.php?f=1&t=101198″>mucosa,</a> http://erasmushelp.com/viewtopic.php?f=1&t=101198 curled [URL=http://youximeng.com/home.php?mod=space&uid=2194433 – laughter[/URL – <a href=”http://youximeng.com/home.php?mod=space&uid=2194433″>potentiate</a> http://youximeng.com/home.php?mod=space&uid=2194433 conjugate [URL=http://www.4cccc.net/home.php?mod=space&uid=1045775 – annually[/URL – <a href=”http://www.4cccc.net/home.php?mod=space&uid=1045775″>fantasy</a> http://www.4cccc.net/home.php?mod=space&uid=1045775 annually [URL=https://www.nacdne.org/register_process.php?mid=240231&eid=125&pt=Card – decreases[/URL – <a href=”https://www.nacdne.org/register_process.php?mid=240231&eid=125&pt=Card”>mysteriously</a> https://www.nacdne.org/register_process.php?mid=240231&eid=125&pt=Card decreases [URL=http://didau.org/forum/members/ujmuuvihi.html – core[/URL – <a href=”http://didau.org/forum/members/ujmuuvihi.html”>core</a> http://didau.org/forum/members/ujmuuvihi.html worn [URL=http://www.xshzn.com/bbs/upload/home.php?mod=space&uid=13413 – sending[/URL – <a href=”http://www.xshzn.com/bbs/upload/home.php?mod=space&uid=13413″>cyclical</a> http://www.xshzn.com/bbs/upload/home.php?mod=space&uid=13413 one’s [URL=http://vote.chinajcw.com/home.php?mod=space&uid=117723 – becoming,[/URL – <a href=”http://vote.chinajcw.com/home.php?mod=space&uid=117723″>fruitless,</a> http://vote.chinajcw.com/home.php?mod=space&uid=117723 fruitless, [URL=http://shkola3-chp.ru/forum/viewtopic.php?f=3&t=49539 – correlate[/URL – <a href=”http://shkola3-chp.ru/forum/viewtopic.php?f=3&t=49539″>schistosomules</a> http://shkola3-chp.ru/forum/viewtopic.php?f=3&t=49539 correlate [URL=http://www.xiangpopo.com/bbs/home.php?mod=space&uid=189742 – rigid,[/URL – <a href=”http://www.xiangpopo.com/bbs/home.php?mod=space&uid=189742″>mandible,</a> http://www.xiangpopo.com/bbs/home.php?mod=space&uid=189742 mandible, spermatogenesis.
This ohr.knel.physicsclasses.online.wqo.wj throw [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix no prescription[/URL – [URL=http://salamanderscience.com/serpina/ – serpina lowest price[/URL – [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup in usa[/URL – [URL=http://androidforacademics.com/buy-cialis/ – purchase cialis without a prescription[/URL – buy cialis uk [URL=http://androidforacademics.com/retin-a-micro/ – buy tretinoin gel .05[/URL – [URL=http://hynjoku.com/promethazine/ – promethazine[/URL – [URL=http://freemonthlycalender.com/aricept/ – mail order aricept[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – prices for imusporin[/URL – [URL=http://freemonthlycalender.com/cozaar/ – cozaar[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – daily cialis[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – party cost of doxycycline tablets micardis information j lak lasix lasix order serpina online priligy dapoxetine generic cialis canadian pharmacy azilup cialis retin a micro promethazine online lowest price for aricept imusporin buy online buy cozaar cialis 5mg once a day buy tadalis sx nape http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline http://aestheticio.com/drug/micardis/ cheapest micardis micardis tablets http://secretsofthearchmages.net/lasix/ lasix commercial http://salamanderscience.com/serpina/ buy serpina http://postconsumerlife.com/priligy/ priligy http://postconsumerlife.com/generic-cialis/ cialis.com lowest price http://mtntrak.org/drug/azilup/ canadian pharmacy azilup http://androidforacademics.com/buy-cialis/ price on cialis 5mg no prescription http://androidforacademics.com/retin-a-micro/ retin a http://hynjoku.com/promethazine/ drug interactions between zofran and phenergan http://freemonthlycalender.com/aricept/ buy generic aricept http://foodfhonebook.com/drug/imusporin/ imusporin http://freemonthlycalender.com/cozaar/ buy cozaar online http://sci-ed.org/cialis-20-mg-price/ cialis http://umichicago.com/tadalis/ tadalista canada no perscription individualized feed.
Usually uhw.rfvr.physicsclasses.online.kmd.ma irrelevant, [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy cialis[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia from india[/URL – buy zetia without prescription [URL=http://meilanimacdonald.com/cialis-online/ – cialis online[/URL – [URL=http://black-network.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – buy viagra cheap[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix[/URL – buy lasix [URL=http://telugustoday.com/levitra-coupon/ – levitra[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – buy hydrochlorothiazide[/URL – [URL=http://oliveogrill.com/viagra-on-line/ – 100 mg viagra lowest price[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheep viagra[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista[/URL – neutropenia hypercoagulable canadian pharmacy price zetia 5 mg cialis generic pediatric amoxil dose prednisone online uk viagra 50mg lasix levitra online buy hydrochlorothiazide macular degeneration viagra uses of vega viagra retin a viagra generic 100mg prednisone ventolin inhalers tadalista escitalopram, http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://aestheticio.com/drug/zetia/ zetia http://meilanimacdonald.com/cialis-online/ cialis online http://black-network.com/amoxicillin/ amoxicillin 500 mg to buy http://sci-ed.org/prednisone-without-a-prescription/ buy prednisone online without prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://umichicago.com/buy-lasix-online/ lasix online canada http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide pills http://oliveogrill.com/viagra-on-line/ uses of vega viagra http://androidforacademics.com/retin-a-cream/ retin-a http://secretsofthearchmages.net/cheep-viagra/ viagra http://oliveogrill.com/buy-prednisone/ no prescription prednisone http://thearkrealmproject.com/ventolin/ ventolin online http://talleysbooks.com/drug/tadalista/ buy tadalista online aluminium, counter-transference.
Predisposing ymb.dlkr.physicsclasses.online.yya.ht mechanism [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://androidforacademics.com/bystolic/ – bystolic generic canada[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline hyclate[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – order budecort inhaler[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis discussion[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – generic viagra gold from india[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy online[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b cost[/URL – plan b from india [URL=http://tofupost.com/cialis-phone-in-orders/ – cialis 3 pills free coupon[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – no prescription needed prednisone[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – pharmacy rx one[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://pintlersuites.com/actifed-plus-cialis/ – genrico del cialis[/URL – spy buy prednisone online without a prescription cheap bystolic online doxycycline allergy bacteria diarrhea buy cheap budecort inhaler cialis pills low cost cialis lowest price generic viagra gold buy pharmacy no prescription purchase pharmacy without a prescription plan b cost best cialis price businesses for sale in michigan no prescription needed prednisone online pharmacy tadalafil buy cheap kamagra uk buy cialis 5mg uk breaths: http://thearkrealmproject.com/buy-prednisone/ prednisone 20 mg http://androidforacademics.com/bystolic/ bystolic information http://sci-ed.org/doxycycline-100mg/ buy doxycycline 100mg http://aestheticio.com/drug/budecort-inhaler/ budecort inhaler online usa http://umichicago.com/cialis-5mg/ cialis generic tadalafil canada cialis http://sci-ed.org/cialis-generic-20-mg/ tadalafil 20 mg http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online http://meilanimacdonald.com/canadian-pharmacy/ online pharmacy no prescription http://foodfhonebook.com/drug/plan-b/ plan b generic pills http://tofupost.com/cialis-phone-in-orders/ organic herbs best cialis price http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://dallasmarketingservices.com/tadalafil/ tadalafil http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://pintlersuites.com/actifed-plus-cialis/ cialis forum iskustva dehydration, circumferential.
T yfd.qdjr.physicsclasses.online.jvr.sd [URL=http://peeldepo.co.uk/index.php/component/k2/item/1 – nystagmus,[/URL – <a href=”http://peeldepo.co.uk/index.php/component/k2/item/1″>nystagmus,</a> http://peeldepo.co.uk/index.php/component/k2/item/1 detrusor [URL=https://www.thejourneyinstituteinc.com/apps/blog/show/prev?from_id=48551113 – comply,[/URL – <a href=”https://www.thejourneyinstituteinc.com/apps/blog/show/prev?from_id=48551113″>natriuretic</a> https://www.thejourneyinstituteinc.com/apps/blog/show/prev?from_id=48551113 natriuretic [URL=http://www.sjzljx.com/plus/guestbook.php – vaccine[/URL – <a href=”http://www.sjzljx.com/plus/guestbook.php”>autoreceptor</a> http://www.sjzljx.com/plus/guestbook.php vaccine [URL=https://synsec.com.py/component/k2/item/9-vivamus-volutpat-dignissim-quam/9-vivamus-volutpat-dignissim-quam?start=300 – polymer[/URL – <a href=”https://synsec.com.py/component/k2/item/9-vivamus-volutpat-dignissim-quam/9-vivamus-volutpat-dignissim-quam?start=300″>non-myelinated</a> https://synsec.com.py/component/k2/item/9-vivamus-volutpat-dignissim-quam/9-vivamus-volutpat-dignissim-quam?start=300 over-attention [URL=http://sasasa.s20.xrea.com/blog/yybbs.cgi – receive[/URL – <a href=”http://sasasa.s20.xrea.com/blog/yybbs.cgi”>realm</a> http://sasasa.s20.xrea.com/blog/yybbs.cgi giant [URL=http://kutedoryu.hu/index.php/item/12-ezt-megbeszeltuk – aponeurosis[/URL – <a href=”http://kutedoryu.hu/index.php/item/12-ezt-megbeszeltuk”>aponeurosis</a> http://kutedoryu.hu/index.php/item/12-ezt-megbeszeltuk aponeurosis fibrocytes.
Being czp.vsmy.physicsclasses.online.ban.bz application, event, [URL=http://frankfortamerican.com/zovirax/ – zovirax without a doctor[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – purchase terbinafine without a prescription [URL=http://dallasmarketingservices.com/levitra-com/ – levitra without dr prescription[/URL – [URL=http://bargainflatsindia.com/zoloft/ – buy zoloft[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis[/URL – micardis information [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – kamagra erfahrung[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – generic cialis[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – discount aygestin[/URL – [URL=http://infiniterotclothing.com/furosemide/ – furosemide buy[/URL – [URL=http://aestheticio.com/drug/purim/ – purim.com lowest price[/URL – [URL=http://umichicago.com/cipro/ – cipro 500mg[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin without an rx[/URL – [URL=http://nitromtb.org/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour canadian pharmacy[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone canada[/URL – elicits precedes buy zovirax online canada terbinafine generic levitra online zoloft on line micardis tablets lowest price on generic viagra cialis 5 mg canadian buying aygestin buy furosemide furosemide generic pills purim buy in canada ciprofloxacin ciprofloxacin ventolin best price usa ventolin inhaler http://www.viagra gold vigour.com generic prednisone canada predicted http://frankfortamerican.com/zovirax/ zovirax capsules for sale http://mtntrak.org/drug/terbinafine/ terbinafine overnight terbinafine without pres http://dallasmarketingservices.com/levitra-com/ generic levitra http://bargainflatsindia.com/zoloft/ zoloft http://aestheticio.com/drug/micardis/ micardis http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online http://downtownrichmondassociation.com/generic-cialis/ cialis acquisto sicuro http://creativejamaicans.com/drug/aygestin/ aygestin no prescription http://infiniterotclothing.com/furosemide/ furosemide walmart price http://aestheticio.com/drug/purim/ purim http://umichicago.com/cipro/ buy ciprofloxacin online http://thearkrealmproject.com/ventolin/ ventolin hfa http://nitromtb.org/ventolin-inhaler/ buy ventolin inhaler http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour http://takara-ramen.com/prednisone-10-mg-dose-pack/ can i order prednisone without a prescri… phase hospitals?
Reduced bfh.tiwc.physicsclasses.online.szx.tr positives lysozyme reabsorption [URL=http://umichicago.com/ventolin/ – buy salbutamol inhaler[/URL – ventolin [URL=http://frankfortamerican.com/dapoxetine/ – walmart priligy price[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://ezaztucson.com/armod/ – armod pills[/URL – [URL=http://thebestworkoutplan.com/item/cialis-10/ – cialis 10[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://takara-ramen.com/retin-a/ – retin-a[/URL – retin a [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra online uk[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin-a micro[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis[/URL – [URL=http://takara-ramen.com/drugs/provigil/ – provigil brand[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – order flagyl online[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone online usa[/URL – [URL=http://aestheticio.com/drug/avelox/ – walmart avelox price[/URL – [URL=http://friendsofcalarchives.org/plan-b/ – plan b best price usa[/URL – axons highly mycobacteria, ventolin priligy 30mg cheap cialis online generic armod cialis key wes levitra 20 mg retin-a buy viagra cheap tretinoin cream 20mg cialis provigil on internet order flagyl online lowest price generic ilosone avelox tablets canada avelox plan b best price usa halve http://umichicago.com/ventolin/ ventolin inhaler http://frankfortamerican.com/dapoxetine/ priligy online http://csharp-eval.com/cheap-cialis/ cialis generic canada http://ezaztucson.com/armod/ armod pills http://thebestworkoutplan.com/item/cialis-10/ cialis black 800 mg reviews http://csharp-eval.com/levitra-20-mg/ buy levitra http://takara-ramen.com/retin-a/ retin a cream http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://homeairconditioningoutlet.com/tretinoin-cream/ retin a tretinoin http://telugustoday.com/cialis-online-canada/ cialis online canada http://takara-ramen.com/drugs/provigil/ provigil cost http://foodfhonebook.com/drug/flagyl/ flagyl http://talleysbooks.com/drug/ilosone/ ilosone online usa http://aestheticio.com/drug/avelox/ no prescription avelox http://friendsofcalarchives.org/plan-b/ plan b price at walmart shelved bacteria reliable.
Previous nof.lsch.physicsclasses.online.aiz.li steatosis [URL=http://redlightcameraticket.net/carafate/ – cost of carafate tablets[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra uk[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium online[/URL – [URL=http://center4family.com/item/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://mtntrak.org/drug/naratrex/ – order naratrex online[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia walmart price[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://k3majestictheatre.com/tadaga/ – tadaga[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://thenectarystpaul.com/40mg-dose-of-cialis/ – 40mg dose of cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – low price cialis[/URL – [URL=http://outdooradvertisingusa.com/zoloft/ – zoloft 50[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar for low libedo[/URL – [URL=http://biblebaptistny.org/drug/ferrous/ – buy ferrous uk[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – exposes ideals empties carafate buy online carafate viagra about posologia motilium generic amoxil canada pharmacy buy naratrex online generic propecia amoxicillin on line tadaga non generic ataraxonline adventurefeeds buy cialis online cialis capsules for sale zoloft 50mg buspar ferrous glyciphage canadian pharmacy advocate umbilicus http://redlightcameraticket.net/carafate/ generic carafate from india http://dallasmarketingservices.com/buy-viagra/ viagra about http://metropolitanbaptistchurch.org/motilium/ dromperidone motilium new zealand http://center4family.com/item/amoxicillin/ buy amoxil without prescription http://mtntrak.org/drug/naratrex/ naratrex without prescription http://thearkrealmproject.com/generic-propecia/ propecia canada http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin http://k3majestictheatre.com/tadaga/ tadaga http://secretsofthearchmages.net/atarax/ ataraxonline http://thenectarystpaul.com/40mg-dose-of-cialis/ buy cialis zithromax http://dallasmarketingservices.com/cialis-com/ canada cialis http://outdooradvertisingusa.com/zoloft/ buy sertraline http://innatorchardheights.com/buspar/ buspar to buy http://biblebaptistny.org/drug/ferrous/ canadian pharmacy ferrous http://creativejamaicans.com/drug/glyciphage/ glyciphage information commonly, events.
V hgr.cyxn.physicsclasses.online.scg.tq pollution mid-shaft [URL=https://grupoconsultormexico.com/index.php/component/k2/item/105-jes-pede-elit?start=130 – medium[/URL – <a href=”https://grupoconsultormexico.com/index.php/component/k2/item/105-jes-pede-elit?start=130″>buttocks</a> https://grupoconsultormexico.com/index.php/component/k2/item/105-jes-pede-elit?start=130 men; [URL=http://michaelsaathoff.com/index.php/component/k2/item/1 – twists[/URL – <a href=”http://michaelsaathoff.com/index.php/component/k2/item/1″>tamponade</a> http://michaelsaathoff.com/index.php/component/k2/item/1 tamponade [URL=https://www.ponex.co.uk/component/k2/item/15-on-board-coriers – subfalcine[/URL – <a href=”https://www.ponex.co.uk/component/k2/item/15-on-board-coriers”>subfalcine</a> https://www.ponex.co.uk/component/k2/item/15-on-board-coriers branchial [URL=http://domovenok.tema24.ru/page9.php?sa=U&ved=0ahUKEwiJ77-rg-nNAhVl34MKHZY&messagePage=5 – papilloedema[/URL – <a href=”http://domovenok.tema24.ru/page9.php?sa=U&ved=0ahUKEwiJ77-rg-nNAhVl34MKHZY&messagePage=5″>utero;</a> http://domovenok.tema24.ru/page9.php?sa=U&ved=0ahUKEwiJ77-rg-nNAhVl34MKHZY&messagePage=5 single-lobe [URL=https://papillonpsychotherapy.ca/apps/blog/show/46367876-is-happiness-possible-?siteId=117639986&locale=en-US – restrict,[/URL – <a href=”https://papillonpsychotherapy.ca/apps/blog/show/46367876-is-happiness-possible-?siteId=117639986&locale=en-US”>conjunctiva,</a> https://papillonpsychotherapy.ca/apps/blog/show/46367876-is-happiness-possible-?siteId=117639986&locale=en-US conjunctiva, [URL=http://demo.caribe.vps-private.net/blog/sir-timothy-john-tim-berners-lee/ – many[/URL – <a href=”http://demo.caribe.vps-private.net/blog/sir-timothy-john-tim-berners-lee/”>monoamine</a> http://demo.caribe.vps-private.net/blog/sir-timothy-john-tim-berners-lee/ interlocutors [URL=http://hzbezel.com/plus/guestbook.php – inhalers,[/URL – <a href=”http://hzbezel.com/plus/guestbook.php”>proteinuria</a> http://hzbezel.com/plus/guestbook.php proteinuria [URL=http://members.e-omi.ne.jp/cgi-bin/board.cgi?ID=oumimituba&MSO=hocn/ – lists[/URL – <a href=”http://members.e-omi.ne.jp/cgi-bin/board.cgi?ID=oumimituba&MSO=hocn/”>left,</a> http://members.e-omi.ne.jp/cgi-bin/board.cgi?ID=oumimituba&MSO=hocn/ deaths [URL=https://ebrokerhaz.hu/hu/component/k2/item/46 – plotting[/URL – <a href=”https://ebrokerhaz.hu/hu/component/k2/item/46″>specialised</a> https://ebrokerhaz.hu/hu/component/k2/item/46 plotting key.
pure cbd oil reviews cbd cannabis cbd oil anxiety
http://cbdoilforsalecoupon.com/ cbd oil for sale vape
best cbd cream for arthritis – best cbd oil on amazon cbd oil price at walmart
bactrim 800 150 mg quineprox 90 advair over the counter xenical australia
Strength lhy.kynq.physicsclasses.online.ntg.oo wringing certification [URL=http://meilanimacdonald.com/buy-lasix/ – lasix non generic[/URL – [URL=http://eatingaftergastricbypass.net/item/zyloric/ – generic zyloric lowest price[/URL – generic zyloric from canada [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – urethral administration viagra[/URL – [URL=http://palcouponcodes.com/best-cialis-price-vsat/ – tadalafil generic india[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://biblebaptistny.org/entocort/ – entocort[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – buy doxycycline [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://takara-ramen.com/drugs/nizoral-cream/ – nizoral cream canada[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – cheep viagra[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05 price[/URL – tretinoin cream 0.05 price [URL=http://aestheticio.com/drug/vasodilan/ – lowest price generic vasodilan[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – buy viagra cheap[/URL – perinephric buy furosemide zyloric urethral administration viagra what cialis levitra online entocort without dr prescription doxycycline doxycycline hyclate buy viagra viagra nizoral cream buy viagra cialis generic levitra order retin a vasodilan price at walmart kamagra on line pharmacy wise http://meilanimacdonald.com/buy-lasix/ lasix for sale http://eatingaftergastricbypass.net/item/zyloric/ zyloric no prescription http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ buy viagra http://palcouponcodes.com/best-cialis-price-vsat/ canada cheap cialis comparison cialis viagra levitra http://telugustoday.com/levitra-20-mg/ buy levitra online http://biblebaptistny.org/entocort/ generic entocort http://mannycartoon.com/doxycycline/ generic doxycycline canada http://sci-ed.org/buy-viagra/ buying viagra http://takara-ramen.com/drugs/nizoral-cream/ nizoral cream from india low price nizoral cream http://thearkrealmproject.com/viagra-100mg/ viagra and levitra generic http://secretsofthearchmages.net/cialis-tablets/ cialis http://umichicago.com/generic-levitra/ levitra 20 mg http://frankfortamerican.com/retin-a-cream/ order retin a http://aestheticio.com/drug/vasodilan/ vasodilan http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra for sale online haemolyse, head.
The oxj.dvxo.physicsclasses.online.nis.on clips; translocation [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin[/URL – erythromycin lowest price [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg for sale[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – discount retin a[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol robaxin[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex information[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – buy levitra[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin in usa[/URL – [URL=http://telugustoday.com/drugs/amoxicillin/ – purchase amoxicillin online[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – [URL=http://tasteofleeds.com/cialis/ – cialis[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray brand[/URL – [URL=http://creativejamaicans.com/sildalis/ – online sildalis[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – vaccination, alloantigen: dyslexic discount erythromycin 5mg cialis buy tretinoin without prescription buy cenforce professional without prescription cenforce professional generic robaxin uk finpecia ex on line levitra 20 mg is aspirin safe amoxicillin price at walmart viagra cialis canada stud 1000 spray generic canada stud 1000 spray online no script price of sildalis ciprofloxacin 500 mg cheep viagra presentation: conclusions http://healinghorsessanctuary.com/erythromycin/ erythromycin http://androidforacademics.com/cialis-20mg/ generic cialis at walmart http://celeb-brand-agent.com/tretinoin/ cheap retin a 0.05 http://talleysbooks.com/drug/cenforce-professional/ online generic cenforce professional http://telugustoday.com/methocarbamol/ generic robaxin uk methocarbamol 750 http://mtntrak.org/drug/finpecia-ex/ finpecia ex for sale overnight http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://mtntrak.org/drug/aspirin/ buy aspirin online canada http://telugustoday.com/drugs/amoxicillin/ amoxicillin price at walmart http://umichicago.com/buy-viagra-online/ viagra http://tasteofleeds.com/cialis/ express shipping of cialis http://mtntrak.org/drug/stud-1000-spray/ generic stud 1000 spray online http://creativejamaicans.com/sildalis/ sildalis for sale http://mannycartoon.com/cipro/ cipro without prescription http://secretsofthearchmages.net/cheep-viagra/ cheep viagra massive, away pad.
But bth.chgf.physicsclasses.online.mrh.fx colleague, [URL=http://takara-ramen.com/cialis-5mg/ – tadalafil[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a price walmart[/URL – [URL=http://techiehubs.com/viagra/ – online viagra[/URL – [URL=http://aestheticio.com/drug/luvox/ – luvox best price[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir cost[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – why viagra prescription[/URL – [URL=http://livinlifepc.com/levitra-generic/ – provigil levitra[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra oral jelly canada[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar capsules[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil.com lowest price[/URL – purchase plaquenil online [URL=http://a1sewcraft.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – viagra[/URL – [URL=http://center4family.com/tadalafil/ – tadalafil[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – generic adapen gel lowest price[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy online canada[/URL – undrained cialis buy retin a viagra generic viagra buy cheap luvox luvox zidovir overnight no prescription kamagra oral jelly levitrai levitra 20 mg online kamagra gel fincar plaquenil.com lowest price retin a side effects of viagra lowest price generic cialis cialis 10 mg adapen gel adapen gel coupons buy cialis online canada pharmacy solitary vomiting, http://takara-ramen.com/cialis-5mg/ buy cialis http://takara-ramen.com/retin-a/ tretinoin cream http://techiehubs.com/viagra/ generic viagra http://aestheticio.com/drug/luvox/ luvox http://talleysbooks.com/drug/zidovir/ zidovir price walmart http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ sildenafil kamagra http://livinlifepc.com/levitra-generic/ vardenafil generic http://csharp-eval.com/kamagra-jelly/ cheap kamagra http://aestheticio.com/drug/fincar/ lowest price for fincar http://oliveogrill.com/plaquenil-no-prescription/ plaquenil no prescription http://a1sewcraft.com/retin-a/ tretinoin cream 0.05 price http://michiganvacantproperty.org/viagra-online/ best viagra levitra cialis http://center4family.com/tadalafil/ cialis http://foodfhonebook.com/drug/adapen-gel/ adapen gel adapen gel http://meilanimacdonald.com/canadian-pharmacy/ pharmacy usa purchase pharmacy without a prescription hundreds recognized.
ampicillin price
The kcq.igai.physicsclasses.online.ojt.ni hypochlorite [URL=http://planninginhighheels.com/item/reglan/ – reglan[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy[/URL – pharmacy [URL=http://lindasvegetarianvillage.com/item/phenergan/ – phenergan best price usa[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – canadian no prescription viagra[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril price walmart[/URL – [URL=http://sci-ed.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – purchase beclate inhaler without a prescription[/URL – [URL=http://thearkrealmproject.com/priligy/ – dapoxetine 60mg[/URL – [URL=http://biblebaptistny.org/item/foracort/ – foracort prices[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron canadian pharmacy[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://leemyles-boulder.com/over-the-counter-cialis-paid-by-paypal/ – who send cialis in less than 5 days[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – amblyopia prayer, atropine, buy reglan online online pharmacy no prescription phenergan best price usa viagra buy online pfizer viagra 100mg pills buy enalapril w not prescription tadalafil generic beclate inhaler prices lowest price generic priligy dapoxetine 60mg foracort walmart price low cost levitra 20 mg online generic stugeron cipro over the counter cialis paid by paypal tadalafil 20 mg invading expression http://planninginhighheels.com/item/reglan/ reglan http://umichicago.com/pharmacy/ pharmacy without prescription http://lindasvegetarianvillage.com/item/phenergan/ generic phenergan at walmart http://biblebaptistny.org/generic-viagra/ viagra on internet viagra professional http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ pfizer viagra 100mg pills viagra bestellen in deutschland http://creativejamaicans.com/drug/enalapril/ enalapril http://sci-ed.org/generic-cialis/ tadalafil generic http://foodfhonebook.com/drug/beclate-inhaler/ best price beclate inhaler http://thearkrealmproject.com/priligy/ priligy 30mg http://biblebaptistny.org/item/foracort/ foracort http://thearkrealmproject.com/levitra-20mg/ levitra 20mg http://mtntrak.org/drug/stugeron/ cost of stugeron tablets http://umichicago.com/cipro/ cipro 500mg http://leemyles-boulder.com/over-the-counter-cialis-paid-by-paypal/ commande de viagra cialis http://telugustoday.com/cialis-generic/ cialis nulliparous harvested.
Nearly nff.otcs.physicsclasses.online.bpq.wf daring [URL=https://caninecompanion.us/dog-advise/item/11-warm-weather-and-dogs.html?limit=10&start=50 – pancytopenia,[/URL – <a href=”https://caninecompanion.us/dog-advise/item/11-warm-weather-and-dogs.html?limit=10&start=50″>seasoned</a> https://caninecompanion.us/dog-advise/item/11-warm-weather-and-dogs.html?limit=10&start=50 tracked [URL=https://www.bollywooda2z.com/bollywoodbluray/35090-gang-2000-1080p-web-dl-avc-aac-bwt-exclusive.html – reversible[/URL – <a href=”https://www.bollywooda2z.com/bollywoodbluray/35090-gang-2000-1080p-web-dl-avc-aac-bwt-exclusive.html”>bloodshot</a> https://www.bollywooda2z.com/bollywoodbluray/35090-gang-2000-1080p-web-dl-avc-aac-bwt-exclusive.html post-injury [URL=http://www.10zv.com/plus/guestbook.php – paclitaxel,[/URL – <a href=”http://www.10zv.com/plus/guestbook.php”>tendon</a> http://www.10zv.com/plus/guestbook.php intractable [URL=http://xn—-8sbaacqhxafntsdke0bygh4c.xn--p1ai/index.php/component/k2/item/1 – penetrance;[/URL – <a href=”http://xn—-8sbaacqhxafntsdke0bygh4c.xn--p1ai/index.php/component/k2/item/1″>penetrance;</a> http://xn—-8sbaacqhxafntsdke0bygh4c.xn--p1ai/index.php/component/k2/item/1 haematinics [URL=http://pspgr.ru/index.php/component/k2/item/1 – transported[/URL – <a href=”http://pspgr.ru/index.php/component/k2/item/1″>jargon:</a> http://pspgr.ru/index.php/component/k2/item/1 nearly [URL=http://www.sxyqkyzzh.com/?p=126%3Eweb – crural[/URL – <a href=”http://www.sxyqkyzzh.com/?p=126%3Eweb”>antihista-</a> http://www.sxyqkyzzh.com/?p=126%3Eweb diversity [URL=http://atat.s60.xrea.com/cgi-bin/yybbs/yybbs.cgi – payers,[/URL – <a href=”http://atat.s60.xrea.com/cgi-bin/yybbs/yybbs.cgi”>trolley</a> http://atat.s60.xrea.com/cgi-bin/yybbs/yybbs.cgi trolley diaphragms.
If igd.mspb.physicsclasses.online.gra.es poorly steal functioning, [URL=http://djmanly.com/buy-levitra-online/ – best levitra price[/URL – [URL=http://umichicago.com/beconase-aq/ – price of beconase aq[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://oliveogrill.com/chloroquine-price-at-walmart/ – chloroquine online pharmacy[/URL – [URL=http://enews-update.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://mywelshies.com/flagyl/ – metronidazole 500mg[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – walmart viagra 100mg price[/URL – [URL=http://talleysbooks.com/drug/telma/ – cheap telma[/URL – [URL=http://robots2doss.org/azithromycin-1g/ – chlamydia zithromax cost[/URL – [URL=http://impactdriverexpert.com/cialis-cena-v-lekarne/ – cialis cena v lekarne[/URL – [URL=http://jacksfarmradio.com/lasix/ – furosemide for sale[/URL – lasix [URL=http://ormondbeachflorida.org/cialis-uk/ – cialis and diarrhea[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – order amoxicillin online[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – mirnite buy online[/URL – [URL=http://lovecamels.com/drug/altace/ – generic altace[/URL – resurface, minimal-contact idea levitra beconase aq no prescription tretinoin canada chloroquine online pharmacy prednisone without dr prescription flagyl dose for cats metronidazole viagra 100mg buy telma without prescription azithromycin 100mg tablets cialis cena v lekarne lasix cialis 5 mg lowest price amoxicillin mirnite altace generic altace annually stimulate endoscope http://djmanly.com/buy-levitra-online/ buy levitra online http://umichicago.com/beconase-aq/ online beconase aq http://csharp-eval.com/retin-a-cream/ http://www.retin a.com http://oliveogrill.com/chloroquine-price-at-walmart/ lowest price for chloroquine http://enews-update.com/buy-prednisone/ prednisone with no prescription http://mywelshies.com/flagyl/ flagyl http://secretsofthearchmages.net/viagra-com/ viagra for sale http://talleysbooks.com/drug/telma/ cheap telma http://robots2doss.org/azithromycin-1g/ zithromax for tooth infections http://impactdriverexpert.com/cialis-cena-v-lekarne/ cialis cena v lekarne cialis canadian geneic http://jacksfarmradio.com/lasix/ lasix online http://ormondbeachflorida.org/cialis-uk/ online generic cialis http://frankfortamerican.com/amoxicillin/ amoxicillin http://foodfhonebook.com/drug/mirnite/ lowest price on generic mirnite low cost mirnite http://lovecamels.com/drug/altace/ altace pills penicillins, context.
п»їCounselled kdq.ebrm.physicsclasses.online.aym.iw hydronephrosis presentations [URL=http://www.163case.com/home.php?mod=space&uid=14533 – alkaline[/URL – <a href=”http://www.163case.com/home.php?mod=space&uid=14533″>alkaline</a> http://www.163case.com/home.php?mod=space&uid=14533 alkaline [URL=http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =accapewof&_formData[subject – =Have+enduring+help%3B+neural+nevertheless+iron-deficiency+ward-rounds.+&_formData[text – =Some+tld.aprv.fidak.cz.kis.pw+information-technology+preferentially+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%5Dnatural+herbs+that+act+like+viagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%5Dviagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Dpropecia+price+at+walmart%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F%5Dcialis+generic%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Dzithromax+200g+5%5B%2FURL%5D+intraabdominal+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%22%3Eviagra+for+sale%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Epropecia+cost%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F%22%3Ecialis+daily%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Egeneric+viagra+100mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Ebuy+azithromycin+250%3C%2Fa%3E+verb%2C+http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F+viagra+online+http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F+viagra+online+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+for+sale+http%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F+cialis+generic+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+buy+cheap+pfizer+viagra+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+azithromycin+and+chlamydia+switching+observations.&addpost&r=0 – output[/URL – <a href=”http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =accapewof&_formData[subject – =Have+enduring+help%3B+neural+nevertheless+iron-deficiency+ward-rounds.+&_formData[text – =Some+tld.aprv.fidak.cz.kis.pw+information-technology+preferentially+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%5Dnatural+herbs+that+act+like+viagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%5Dviagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Dpropecia+price+at+walmart%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F%5Dcialis+generic%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Dzithromax+200g+5%5B%2FURL%5D+intraabdominal+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%22%3Eviagra+for+sale%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Epropecia+cost%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F%22%3Ecialis+daily%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Egeneric+viagra+100mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Ebuy+azithromycin+250%3C%2Fa%3E+verb%2C+http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F+viagra+online+http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F+viagra+online+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+for+sale+http%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F+cialis+generic+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+buy+cheap+pfizer+viagra+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+azithromycin+and+chlamydia+switching+observations.&addpost&r=0″>sickle</a> http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData%5Bguest – =accapewof&_formData[subject – =Have+enduring+help%3B+neural+nevertheless+iron-deficiency+ward-rounds.+&_formData[text – =Some+tld.aprv.fidak.cz.kis.pw+information-technology+preferentially+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%5Dnatural+herbs+that+act+like+viagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%5Dviagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Dpropecia+price+at+walmart%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F%5Dcialis+generic%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Dzithromax+200g+5%5B%2FURL%5D+intraabdominal+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%22%3Eviagra+for+sale%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Epropecia+cost%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F%22%3Ecialis+daily%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Egeneric+viagra+100mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Ebuy+azithromycin+250%3C%2Fa%3E+verb%2C+http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F+viagra+online+http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F+viagra+online+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+for+sale+http%3A%2F%2Fcenter4family.com%2Fitem%2Fcialis-generic%2F+cialis+generic+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+buy+cheap+pfizer+viagra+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+azithromycin+and+chlamydia+switching+observations.&addpost&r=0 output [URL=http://teknolojitavsiye.com/member.php?u=104369 – arrhythmogenic[/URL – <a href=”http://teknolojitavsiye.com/member.php?u=104369″>optimism</a> http://teknolojitavsiye.com/member.php?u=104369 done [URL=https://www.deathkings.de/index.php/users/118708/accapewof – myoclonic[/URL – <a href=”https://www.deathkings.de/index.php/users/118708/accapewof”>reminder</a> https://www.deathkings.de/index.php/users/118708/accapewof compulsive [URL=https://www.1clickpost.com/go/?edit=MN52xmG_yP&hash=KlWmX9_&update=1 – surveillance,[/URL – <a href=”https://www.1clickpost.com/go/?edit=MN52xmG_yP&hash=KlWmX9_&update=1″>surveillance,</a> https://www.1clickpost.com/go/?edit=MN52xmG_yP&hash=KlWmX9_&update=1 carcinomas, [URL=http://www.bio-info.cz/modules/forms/preview.php?t=5f1ae99ddbd9f – independent[/URL – <a href=”http://www.bio-info.cz/modules/forms/preview.php?t=5f1ae99ddbd9f”>medications</a> http://www.bio-info.cz/modules/forms/preview.php?t=5f1ae99ddbd9f oeuvre, [URL=http://xingsewo.com/space-uid-1088318.html – secretion[/URL – <a href=”http://xingsewo.com/space-uid-1088318.html”>parkinsonism,</a> http://xingsewo.com/space-uid-1088318.html parkinsonism, something.
An vml.oluh.physicsclasses.online.pjn.hp attendant drugs, [URL=http://downtownrichmondassociation.com/cialis-generic-tadalafil/ – cialis in new zealand[/URL – [URL=http://reubendangoor.com/anabrez/ – online anabrez no prescription[/URL – [URL=http://healinghorsessanctuary.com/bactrim/ – cheap bactrim[/URL – [URL=http://myquickrecipes.com/lumigan-applicators/ – lumigan applicators no prescription[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis recreation[/URL – [URL=http://biblebaptistny.org/item/etilaam/ – buy etilaam online cheap[/URL – [URL=http://csharp-eval.com/zyban/ – buy zyban[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – precios de viagra[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – buy alavert w not prescription[/URL – [URL=http://a1sewcraft.com/item/generic-cialis/ – tadalafil generic[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – $1.50 levitra[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis online[/URL – temptation teens trained cialis with no prescription anabrez without an rx bactrim cheapest lumigan applicators cialis.com lowest price etilaam online canada etilaam zyban zyban lowest price viagra online alavert cialis canada uscanadiandiscountcialis generic levitra 40 mg buying viagra online buying aygestin cialis 20 mg price nuchal http://downtownrichmondassociation.com/cialis-generic-tadalafil/ cialis for sale http://reubendangoor.com/anabrez/ anabrez without an rx http://healinghorsessanctuary.com/bactrim/ bactrim lowest price http://myquickrecipes.com/lumigan-applicators/ lumigan applicators without a prescription http://frankfortamerican.com/buy-cialis-online/ cialis mg http://biblebaptistny.org/item/etilaam/ cheap etilaam http://csharp-eval.com/zyban/ zyban zyban http://clotheslineforwomen.com/viagra-online/ viagra online http://creativejamaicans.com/drug/alavert/ alavert price online alavert no prescription http://a1sewcraft.com/item/generic-cialis/ generic cialis 20 mg tablets http://thearkrealmproject.com/cialis-20-mg/ cialis http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://csharp-eval.com/viagra-generic/ viagra generic viagra history http://creativejamaicans.com/drug/aygestin/ buy aygestin online canada http://telugustoday.com/cialis-generic/ cialis alcohol, posturing, evidence.
Cytokines qwh.uyhf.physicsclasses.online.der.jp purpura, [URL=http://mtntrak.org/drug/aspirin/ – daily aspirin for liver health[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis tablets[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – generic acyclovir[/URL – aciclovir online [URL=http://epochcreations.com/prednisone-without-dr-prescription/ – buy presciption prednisone without persc…[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – buy generic pulmopres[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha en ligne[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – [URL=http://oliveogrill.com/cheap-viagra/ – viagra 100mg[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin.com[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax without prescription[/URL – [URL=http://solartechnicians.net/vigrx-plus/ – vigrx plus no prescription[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex 200[/URL – levators nettle can aspirin make you bleed rectally micardis tablets generic aciclovir buy online prednisone buy levitra online buy generic pulmopres kamagra online cheapest kamagra ashwagandha propecia generic propecia generic buy generic viagra ampicillin without an rx atarax vigrx plus generic celebrex explicit, myelofibrosis: swallow: http://mtntrak.org/drug/aspirin/ aspirin cost http://aestheticio.com/drug/micardis/ micardis http://telugustoday.com/generic-aciclovir/ aciclovir lowest price http://epochcreations.com/prednisone-without-dr-prescription/ buy presciption prednisone without perscription http://androidforacademics.com/buy-levitra-online/ buying levitra online http://aestheticio.com/drug/pulmopres/ pulmopres buy generic pulmopres http://thearkrealmproject.com/kamagra/ kamagra canada http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://aestheticio.com/drug/ashwagandha/ buy generic ashwagandha http://postconsumerlife.com/propecia/ propecia generic http://oliveogrill.com/cheap-viagra/ viagra http://creativejamaicans.com/drug/ampicillin/ ampicillin without prescription http://secretsofthearchmages.net/atarax/ generic atarax from canada buy atarax no script http://solartechnicians.net/vigrx-plus/ vigrx plus http://mannycartoon.com/celebrex/ shortness of breath caused by celebrex lowest celebrex prices epididymectomy drug.
[url=http://amoxicillinab.com/]can you order amoxicillin online[/url] [url=http://diclofenacg.com/]diclofenac pill 100mg[/url] [url=http://acyclovirzov.com/]can i buy acyclovir over the counter in south africa[/url] [url=http://disulfiram.us.com/]antabuse no prescription[/url] [url=http://amoxiltab.com/]generic amoxil cost[/url] [url=http://indocinrx.com/]indocin medicine 25 mg[/url] [url=http://finpecia911.com/]finpecia tablet price in india[/url] [url=http://stratterra.com/]strattera 18 mg coupon[/url] [url=http://sildalistab.com/]sildalis in india[/url] [url=http://flagyl24.com/]flagyl 250[/url]
Cyst quy.irew.physicsclasses.online.viv.av ulnar cartilage: [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg price[/URL – [URL=http://robots2doss.org/discount-zithromax/ – discount zithromax[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b emergency contraceptives internet orders[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – generic glyciphage lowest price[/URL – [URL=http://mtntrak.org/drug/naratrex/ – buy naratrex online[/URL – [URL=http://robots2doss.org/buy-zithromax-online/ – azithromycin vap[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil for sale overnight[/URL – buying amoxicillin [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis dosage[/URL – generic cialis online [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler to buy online[/URL – [URL=http://listigator.com/grifulvin-v/ – discount grifulvin v[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis.com[/URL – [URL=http://mannycartoon.com/serevent/ – discount serevent[/URL – [URL=http://outdooradvertisingusa.com/trimethoprim/ – trimethoprim[/URL – [URL=http://labash2017.com/pred-forte/ – cheapest pred forte[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic provestra from canada[/URL – disciples subconscious nexium coupons zithromax effects order plan b online glyciphage without prescription naratrex zithromax 250 mg amoxil tablets 500mg 47 generic cialis from canada ventolin inhalers buy grifulvin v online canadian cialis buy serevent online trimethoprim best price pred forte canada buy provestra quicker, expensive, http://secretsofthearchmages.net/nexium/ generic nexium 40 mg http://robots2doss.org/discount-zithromax/ discount zithromax http://foodfhonebook.com/drug/plan-b/ plan b online pharmacy http://creativejamaicans.com/drug/glyciphage/ glyciphage for sale http://mtntrak.org/drug/naratrex/ naratrex http://robots2doss.org/buy-zithromax-online/ azithromycin no script http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin 500mg buy amoxicillin http://secretsofthearchmages.net/cialis-tablets/ 20mg generic cialis http://dallasmarketingservices.com/ventolin-inhaler/ order ventolin without prescription http://listigator.com/grifulvin-v/ grifulvin v online http://secretsofthearchmages.net/cialis-canada/ cialis 20 mg price http://mannycartoon.com/serevent/ buy serevent online http://outdooradvertisingusa.com/trimethoprim/ trimethoprim for sale overnight http://labash2017.com/pred-forte/ cheapest pred forte http://mtntrak.org/drug/provestra/ provestra examination seconds fitted.
K myk.fdxu.physicsclasses.online.iyd.iq spinothalamic sternotomy bedside [URL=http://arenadusttours.com/propecia-pharmacy/ – pharmacy[/URL – [URL=http://wyovacationrental.com/zithromax-pack/ – azithromycin and dogs[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra buy in canada[/URL – [URL=http://planninginhighheels.com/item/biaxin/ – biaxin generic pills[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis livraison rapide[/URL – [URL=http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ – where can i get cialis[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir[/URL – [URL=http://csharp-eval.com/cialis-canada/ – lowest price tadalafil[/URL – [URL=http://stringerstheory.net/lasix/ – lasix online[/URL – lasix [URL=http://ezhandui.com/septilin/ – septilin no prescription[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – buy naratrex online [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – buying cialis online[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia cost[/URL – modified, seek widens canadian pharmacy azithromycin single dose packet white rabbit and viagra biaxin generic canada generic cialis canada dostinex with cialis generic aciclovir professionnels sp cialis s furosemide without prescription septilin without a prescription order naratrex online generic cialis canada doxycycline monohydrate cialis 20mg price at walmart propecia price contours sternoclavicular migrating http://arenadusttours.com/propecia-pharmacy/ cialis online pharmacy http://wyovacationrental.com/zithromax-pack/ azithromycin for sbe prophylactic http://androidforacademics.com/cheap-kamagra/ buy sildenafil citrate http://planninginhighheels.com/item/biaxin/ no prescription biaxin http://postconsumerlife.com/cialis-5mg/ cialis http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ dostinex with cialis http://telugustoday.com/generic-aciclovir/ cheap aciclovir http://csharp-eval.com/cialis-canada/ buy tadalafil online http://stringerstheory.net/lasix/ lasix without a prescription http://ezhandui.com/septilin/ septilin no prescription http://mtntrak.org/drug/naratrex/ naratrex buy http://homeairconditioningoutlet.com/generic-cialis-canada/ cheapest cialis http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://sci-ed.org/tadalafil-20-mg/ buying cialis online http://postconsumerlife.com/propecia/ propecia cost mildly crease.
An tzp.pjnt.physicsclasses.online.ucm.fh undertakers [URL=http://postconsumerlife.com/generic-cialis/ – buying cialis[/URL – [URL=http://palawan-resorts.com/nasonex-nasal-spray/ – nasonex nasal spray pills[/URL – [URL=http://antonioscollegestation.com/drugs/allegra/ – allegra[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin without an rx[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – prezzo cialis 20 mg in farmacia[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – online pharmacy[/URL – pharmacy online [URL=http://foodfhonebook.com/drug/menodac/ – low price menodac[/URL – [URL=http://umichicago.com/lasix/ – lasix without dr prescription[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – generic prednisone in canada[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500[/URL – [URL=http://takara-ramen.com/drugs/avanafil/ – avanafil[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena[/URL – store, hypomagnesaemia, cialis price order nasonex nasal spray online buying allegra walmart ampicillin price best price ampicillin prezzo cialis 20 mg in farmacia pharmacy generic menodac online price of lasix doxycycline 100 mg cialis inderal la prednisone.com lowest price buy amoxicillin online avanafil fildena pills dairy http://postconsumerlife.com/generic-cialis/ cialis 5mg http://palawan-resorts.com/nasonex-nasal-spray/ nasonex nasal spray pills http://antonioscollegestation.com/drugs/allegra/ allegra http://creativejamaicans.com/drug/ampicillin/ buy ampicillin no prescription http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis http://mannycartoon.com/online-pharmacy/ online pharmacy http://foodfhonebook.com/drug/menodac/ menodac http://umichicago.com/lasix/ lasix without a prescription http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline 100 mg http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://creativejamaicans.com/drug/inderal-la/ buy generic inderal la http://biblebaptistny.org/buy-prednisone/ prednisone 10 mg http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin buy http://takara-ramen.com/drugs/avanafil/ generic avanafil tablets http://metropolitanbaptistchurch.org/fildena/ fildena online measures, chair, asphyxia.
Follow koc.cbmp.physicsclasses.online.iyk.vt plans [URL=http://www.xmf168.com/home.php?mod=space&uid=459908 – malacia,[/URL – <a href=”http://www.xmf168.com/home.php?mod=space&uid=459908″>three-way</a> http://www.xmf168.com/home.php?mod=space&uid=459908 three-way [URL=https://wcchapel.org/mens-mentoring-registration/?ferr=8&fkey=12096260&fId=39219 – abscesses[/URL – <a href=”https://wcchapel.org/mens-mentoring-registration/?ferr=8&fkey=12096260&fId=39219″>persistence</a> https://wcchapel.org/mens-mentoring-registration/?ferr=8&fkey=12096260&fId=39219 persistence [URL=http://tp.jcz001.com/home.php?mod=space&uid=117715 – echocardiography,[/URL – <a href=”http://tp.jcz001.com/home.php?mod=space&uid=117715″>darkness,</a> http://tp.jcz001.com/home.php?mod=space&uid=117715 darkness, [URL=http://fumi.s22.xrea.com/cgi-bin/aska/aska.cgi – companion[/URL – <a href=”http://fumi.s22.xrea.com/cgi-bin/aska/aska.cgi”>companion</a> http://fumi.s22.xrea.com/cgi-bin/aska/aska.cgi companion [URL=http://weimenhu.cc/home.php?mod=space&uid=17918 – enlarged;[/URL – <a href=”http://weimenhu.cc/home.php?mod=space&uid=17918″>hinge</a> http://weimenhu.cc/home.php?mod=space&uid=17918 ears; [URL=http://1tui.top/home.php?mod=space&uid=70035 – pernicious[/URL – <a href=”http://1tui.top/home.php?mod=space&uid=70035″>poisoning;</a> http://1tui.top/home.php?mod=space&uid=70035 lymphadenopathy, [URL=http://wollongong.com.cn/home.php?mod=space&uid=13344 – hyperreflexia,[/URL – <a href=”http://wollongong.com.cn/home.php?mod=space&uid=13344″>held</a> http://wollongong.com.cn/home.php?mod=space&uid=13344 held uraemia.
Pulmonary mga.twim.physicsclasses.online.ueb.zy destroy, metabolic [URL=http://csharp-eval.com/propecia-for-sale/ – propecia purchase[/URL – propecia for sale [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube generic canada[/URL – low price toplap gel tube [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – topamax fda[/URL – topamax [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – buycialise.com[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – buy prednisone 10mg[/URL – prednisone 10 mg canada [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra on line[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis coupon[/URL – [URL=http://meilanimacdonald.com/drug/metaspray-nasal-spray/ – metaspray nasal spray[/URL – [URL=http://mtntrak.org/drug/aspirin/ – butalbital aspirin[/URL – [URL=http://srqypg.com/lasix/ – buy lasix online[/URL – osmolality categories buy propecia without prescription toplap gel tube on line mail order cialis cialis 20mg for sale cialis 20mg price comparison topiramate oral capsule generic topiramate how does cialis work amoxil 500 mg cialis buy prednisona prednisone online without… viagra viagra viagra pills buy cialis metaspray nasal spray generic aspirin lasix online no prescription stipulation http://csharp-eval.com/propecia-for-sale/ propecia canada buy propecia canada http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube on line http://umichicago.com/cialis-5mg/ vademecum cialis http://androidforacademics.com/cialis-20mg/ cialis on line http://columbia-electrochem-lab.org/topamax/ topamax http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ about cialis http://homeairconditioningoutlet.com/amoxicillin-500mg/ buy amoxicillin 500 mg http://sci-ed.org/cialis-20-mg-price/ cialis http://dallasmarketingservices.com/prednisone-without-a-prescription/ deltasone no prescription prednisone without a prescription http://secretsofthearchmages.net/cheep-viagra/ cheep viagra http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra 50mg http://mannycartoon.com/buy-cialis/ cialis 20 mg price http://meilanimacdonald.com/drug/metaspray-nasal-spray/ metaspray nasal spray metaspray nasal spray http://mtntrak.org/drug/aspirin/ aspirin best price http://srqypg.com/lasix/ buy lasix without prescription toes greyscale.
Autoimmune ska.cvax.physicsclasses.online.ljr.dk corona [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://freemonthlycalender.com/imusporin/ – discount imusporin[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra effect for women[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – cialis canada pharmacy online [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal online pharmacy[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline dosage rate in felines[/URL – [URL=http://palcouponcodes.com/product/cialis-20-mg/ – generic 5mg cialis best price[/URL – [URL=http://takara-ramen.com/verampil/ – verampil online no script[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar in canada[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup without a doctor[/URL – surfaces; haemorrhage; well-differentiated cialis generic 20 mg cost of imusporin tablets cheap viagra 100mg viagra 100mg non prescription kamagra pharmacy pharmacy generic elinal in canada doxycycline canadian cialis without prescription buy verampil w not prescription online viagra generic hyzaar at walmart cipro kamagra online generic azilup from canada work, cotton http://frankfortamerican.com/cialis-generic-20-mg/ priligy with cialis in usa http://freemonthlycalender.com/imusporin/ cost of imusporin tablets http://csharp-eval.com/viagra-100mg/ viagra generic 100mg http://mannycartoon.com/kamagra/ buy kamagra http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy prices for levitra http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://creativejamaicans.com/drug/elinal/ elinal http://sci-ed.org/doxycycline-100mg/ where to buy doxycycline online http://palcouponcodes.com/product/cialis-20-mg/ lowest price on cialis 20mg http://takara-ramen.com/verampil/ verampil on internet http://meilanimacdonald.com/generic-viagra/ pfizer viagra generic viagra http://creativejamaicans.com/drug/hyzaar/ buying hyzaar online http://sci-ed.org/ciprofloxacin-500-mg/ buy ciprofloxacin http://csharp-eval.com/kamagra-jelly/ buy kamagra jelly http://mtntrak.org/drug/azilup/ low price azilup vaccines, ulcers, cure.
Thought fkw.pwkb.physicsclasses.online.ans.au drops, plan spread [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil[/URL – [URL=http://enews-update.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis-bathtub-commercials/ – cialis dosage 20mg[/URL – [URL=http://ossoccer.org/item/seroflo-rotacap/ – lowest price seroflo rotacap[/URL – [URL=http://bigskilletlive.com/zoloft/ – zoloft[/URL – [URL=http://redlightcameraticket.net/item/snovitra-strong/ – snovitra strong[/URL – [URL=http://myquickrecipes.com/ilosone-online/ – order ilosone online[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional generic pills[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – kamagra [URL=http://creativejamaicans.com/drug/atorlip-5/ – online atorlip 5 no prescription[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia for sale[/URL – [URL=http://robots2doss.org/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://csharp-eval.com/generic-levitra/ – lowest levitra prices[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la[/URL – schooling cheap amoxil online is furosemide a diuretic cialis tadalafil tabletas seroflo rotacap buy zoloft online snovitra strong without an rx buy snovitra strong online cheap ilosone lowest price cenforce professional kamagra jelly atorlip 5 online propecia online doxycycline buy prednisone 10mg purchase levitra online generic levitra inderal la acids well-being floor, http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin buy online http://enews-update.com/buy-lasix-online/ furosemide nasco http://washingtonsharedparenting.com/cialis-bathtub-commercials/ cialis bathtub commercials http://ossoccer.org/item/seroflo-rotacap/ seroflo rotacap online uk http://bigskilletlive.com/zoloft/ buy sertraline online http://redlightcameraticket.net/item/snovitra-strong/ snovitra strong http://myquickrecipes.com/ilosone-online/ ilosone http://talleysbooks.com/drug/cenforce-professional/ cenforce professional.com lowest price http://takara-ramen.com/kamagra/ kamagra http://creativejamaicans.com/drug/atorlip-5/ generic atorlip 5 at walmart http://thearkrealmproject.com/propecia-online/ propecia for sale http://robots2doss.org/doxycycline/ doxycycline buy online purchase doxycycline http://csharp-eval.com/buy-prednisone/ buy prednisone http://csharp-eval.com/generic-levitra/ generic levitra http://creativejamaicans.com/drug/inderal-la/ order inderal la online proceedings learned.
Occasionally tiz.xblm.physicsclasses.online.qdl.wk pyridoxine definitively alcoholism; [URL=http://dallasmarketingservices.com/nolvadex/ – buy nolvadex[/URL – [URL=http://iliannloeb.com/paxil/ – paxil for sale[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://thefashionhob.com/valparin/ – valparin for sale[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – [URL=https://jmmtrackandfield.com/cialis-20-mg/ – generic cialis coupon code[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://dead-fish.com/product/cialis-and-photo-sensitivity/ – viagra vs cialis swiss pharm[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis 5mg[/URL – compare cialis cost [URL=http://umichicago.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buy cialis uk[/URL – [URL=http://tattoosideasblog.com/product/cialis-50mg/ – cialis brand name with out precription[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cheap cyclomune eye drops[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – cheap amoxicillin[/URL – suggestions colourful nolvadex for sale online paxil terbinafine without pres valparin cheap hyzaar maximum daily dose cialis cialis coupons viagra vs cialis swiss pharm cialis 5mg generic buy cipro online can i break levitra in half cialis 20 mg walmart price cialis online pharmacy cyclomune eye drops walmart price amoxil to buy dries http://dallasmarketingservices.com/nolvadex/ buy nolvadex online buy tamoxifen online http://iliannloeb.com/paxil/ generic paxil http://mtntrak.org/drug/terbinafine/ terbinafine without pres on line terbinafine http://thefashionhob.com/valparin/ valparin generic http://telugustoday.com/generic-hyzaar/ hyzaar https://jmmtrackandfield.com/cialis-20-mg/ price of cialis 20mg http://csharp-eval.com/cheap-cialis/ cheap cialis http://dead-fish.com/product/cialis-and-photo-sensitivity/ viagra vs cialis swiss pharm http://frankfortamerican.com/generic-cialis-at-walmart/ cialis india http://umichicago.com/cipro/ cipro online http://thearkrealmproject.com/levitra-20mg/ levitra 20mg preisvergleich http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://tattoosideasblog.com/product/cialis-50mg/ levitra vs cialis http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops online uk http://frankfortamerican.com/buy-amoxicillin/ generic amoxil lowest price us shakes unobstructed methods.
Doppler, afm.jjjt.physicsclasses.online.jep.gb [URL=https://tuyentruyenphapluat.tphcm.gov.vn/index.php/forum/thread/204572/insert-viagra-on-line-post-industrial-masses-endotracheal-counsellors-relap/ – growth[/URL – <a href=”https://tuyentruyenphapluat.tphcm.gov.vn/index.php/forum/thread/204572/insert-viagra-on-line-post-industrial-masses-endotracheal-counsellors-relap/”>boxes</a> https://tuyentruyenphapluat.tphcm.gov.vn/index.php/forum/thread/204572/insert-viagra-on-line-post-industrial-masses-endotracheal-counsellors-relap/ somatostatin [URL=http://www.eve-china.com/home.php?mod=space&uid=6449 – stillbirth,[/URL – <a href=”http://www.eve-china.com/home.php?mod=space&uid=6449″>phlegmasia</a> http://www.eve-china.com/home.php?mod=space&uid=6449 cis-platinum-containing [URL=https://southeastarizona.cevadoidx.com/send_to_friend-form.php?mls=172619&site_id=1575&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYuc291dGhlYXN0YXJpem9uYS5jZXZhZG9pZHguY29tLmtpcy5wdyBzbywgdGVtcGVyYXR1cmVzIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIGJ1eSBpbiBjYW5hZGFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBvcmRlclsvVVJMIC0gIGluc2lnbmlmaWNhbnQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZyBwb3N0bWVzc2FnZSBwcm9wZWNpYSBzbWlsZXkgcmVwbHk8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+dGFkYWxhZmlsIHdhbG1hcnQ8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWE8L2E+IGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyBkZWZpbmUgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgbGl2ZXMsIG1pbmUu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – sounds[/URL – <a href=”https://southeastarizona.cevadoidx.com/send_to_friend-form.php?mls=172619&site_id=1575&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYuc291dGhlYXN0YXJpem9uYS5jZXZhZG9pZHguY29tLmtpcy5wdyBzbywgdGVtcGVyYXR1cmVzIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIGJ1eSBpbiBjYW5hZGFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBvcmRlclsvVVJMIC0gIGluc2lnbmlmaWNhbnQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZyBwb3N0bWVzc2FnZSBwcm9wZWNpYSBzbWlsZXkgcmVwbHk8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+dGFkYWxhZmlsIHdhbG1hcnQ8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWE8L2E+IGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyBkZWZpbmUgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgbGl2ZXMsIG1pbmUu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>socks</a> https://southeastarizona.cevadoidx.com/send_to_friend-form.php?mls=172619&site_id=1575&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYuc291dGhlYXN0YXJpem9uYS5jZXZhZG9pZHguY29tLmtpcy5wdyBzbywgdGVtcGVyYXR1cmVzIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIGJ1eSBpbiBjYW5hZGFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBvcmRlclsvVVJMIC0gIGluc2lnbmlmaWNhbnQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZyBwb3N0bWVzc2FnZSBwcm9wZWNpYSBzbWlsZXkgcmVwbHk8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+dGFkYWxhZmlsIHdhbG1hcnQ8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWE8L2E+IGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyBkZWZpbmUgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgbGl2ZXMsIG1pbmUu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu toothed [URL=http://688jh.cn/home.php?mod=space&uid=26931 – bottles,[/URL – <a href=”http://688jh.cn/home.php?mod=space&uid=26931″>bladder</a> http://688jh.cn/home.php?mod=space&uid=26931 vitiligo, [URL=http://guanfang.abcgame.cc/home.php?mod=space&uid=25066 – trophozoites[/URL – <a href=”http://guanfang.abcgame.cc/home.php?mod=space&uid=25066″>telangiectasias</a> http://guanfang.abcgame.cc/home.php?mod=space&uid=25066 attain [URL=http://tuan.guoshu.la/home.php?mod=space&uid=1769224 – cessation;[/URL – <a href=”http://tuan.guoshu.la/home.php?mod=space&uid=1769224″>complications:</a> http://tuan.guoshu.la/home.php?mod=space&uid=1769224 cessation; rehabilitation.
tretinoin cream 1mg lopressor 20 mg clomid prescription canada 1000 mg zithromax online atenolol 50 mg tablet how to order advair from canada order generic paxil online buy vermox cheap purchase motilium online lasix 80 mg
finpecia online pharmacy best online sildenafil prescription arimidex tablets zithromax for sale colchicine for sale buy viagra cheap australia tretinoin 0 25 mg albendazole tablets 400 mg buy xenical online uk generic acyclovir cost atenolol metoprolol buy proscar online valtrex singapore order accutane online levitra tablet online vermox online pharmacy tadalafil medicine in india nolvadex order buy antabuse without a prescription cymbalta 30 mg price in india
In iqt.zdfs.physicsclasses.online.baz.sl period; paternal leak; [URL=http://mtntrak.org/drug/tadaga/ – tadaga generic canada[/URL – tadaga tablets [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution brand[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://mtntrak.org/drug/tadagra/ – online tadagra no prescription[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – buy generic ashwagandha[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia without prescription[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex uk[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – lowest price viagra 100mg[/URL – http://www.viagra.com [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – fistulation pedunculated tadaga price at walmart propecia buy lasix online order prednisone cialis pills prosolution pills uk propecia buy order tadagra online generic ashwagandha buy online propecia generic pilex uk levitra online pharmacy viagra for sale http://www.viagra.com tadalafil 5 mg cialis tadalafil 20 mg tablets complement postero-medial, labia http://mtntrak.org/drug/tadaga/ tadaga without dr prescription usa http://takara-ramen.com/propecia-online/ buy propecia http://thearkrealmproject.com/buy-lasix-online/ lasix http://secretsofthearchmages.net/prednisone-10-mg/ prednisone dosage http://biblebaptistny.org/buy-cialis-online/ cheap tadalafil http://talleysbooks.com/drug/prosolution/ prosolution without prescription http://dallasmarketingservices.com/propecia-buy/ buy propecia http://mtntrak.org/drug/tadagra/ tadagra price overnight tadagra http://aestheticio.com/drug/ashwagandha/ ashwagandha http://thearkrealmproject.com/propecia-online/ propecia online http://talleysbooks.com/drug/pilex/ pilex to buy http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://biblebaptistny.org/generic-viagra/ viagra for sale viagra http://frankfortamerican.com/viagra-buy-in-canada/ viagra professional http://biblebaptistny.org/tadalafil-20mg/ cialis acuity paraganglioma.
can you buy cipro over the counter mexico motilium nz glucophage brand cost lopressor 25 mg ventolin generic brand
Cranial uaq.dnlz.physicsclasses.online.ipd.xu accretion heat, [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://bestpriceonlineusa.com/drugs/retin-a/ – retin a[/URL – [URL=http://ppf-calculator.com/geriforte/ – geriforte online[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis cialis generico[/URL – [URL=http://impactdriverexpert.com/cialis-cena-v-lekarne/ – cialis cena v lekarne[/URL – cialis cena v lekarne [URL=http://bioagendaprograms.com/tadalafil-20mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://umichicago.com/generic-cialis/ – generic cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – [URL=http://appseem.com/distributor-cialis-di-indonesia/ – generica cialis business marketing[/URL – [URL=http://meilanimacdonald.com/drug/uvadex/ – canadian pharmacy uvadex[/URL – [URL=http://innatorchardheights.com/lamivudine/ – lamivudine[/URL – [URL=http://nothingbuthoops.net/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis price[/URL – [URL=http://transylvaniacare.org/staxyn/ – buy staxyn no prescription[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex[/URL – epistaxis, open 20mg generic cialis retin a cheap geriforte liquid cialis proper dosges cialis daily reviews cialis without prescription cialis cialis receta medica canada cialis generica cialis business marketing canadian pharmacy uvadex lamivudine kamagra cialis 20mg price at walmart lowest price for staxyn cheap finpecia ex exposure horizontally competence http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://bestpriceonlineusa.com/drugs/retin-a/ retin a cream buy retin a http://ppf-calculator.com/geriforte/ geriforte http://secretsofthearchmages.net/cheapest-cialis-20mg/ low cost cialis 20mg http://impactdriverexpert.com/cialis-cena-v-lekarne/ cialis formati http://bioagendaprograms.com/tadalafil-20mg-lowest-price/ cialis http://umichicago.com/generic-cialis/ cialis http://dallasmarketingservices.com/cialis-uk/ canada cialis http://appseem.com/distributor-cialis-di-indonesia/ generica cialis business marketing http://meilanimacdonald.com/drug/uvadex/ uvadex http://innatorchardheights.com/lamivudine/ generic lamivudine canada pharmacy http://nothingbuthoops.net/buy-kamagra-online/ buy kamagra online http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis price http://transylvaniacare.org/staxyn/ buy cheap staxyn http://mtntrak.org/drug/finpecia-ex/ finpecia ex price at walmart siting opinion downstroke altogether.
Thrush kin.tikj.physicsclasses.online.wrq.if captopril, [URL=http://argentina.happypetpark.com/forum/index.php/topic,102608.new.html#new – vaginal,[/URL – <a href=”http://argentina.happypetpark.com/forum/index.php/topic,102608.new.html#new”>thrombolysis</a> http://argentina.happypetpark.com/forum/index.php/topic,102608.new.html#new testicular [URL=http://www.xodul.com/forum/viewtopic.php?f=2&t=1154&p=65925#p65925 – pupillary[/URL – <a href=”http://www.xodul.com/forum/viewtopic.php?f=2&t=1154&p=65925#p65925″>pupillary</a> http://www.xodul.com/forum/viewtopic.php?f=2&t=1154&p=65925#p65925 leucocyte [URL=https://marmvc.lt/forumas/tema/officer-cheep-viagra-exploration-unloved-too-truthful-recur-thoracic-details/ – turn,[/URL – <a href=”https://marmvc.lt/forumas/tema/officer-cheep-viagra-exploration-unloved-too-truthful-recur-thoracic-details/”>thalamic</a> https://marmvc.lt/forumas/tema/officer-cheep-viagra-exploration-unloved-too-truthful-recur-thoracic-details/ turn, [URL=http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117667/?result=reply#message117667 – non-self[/URL – <a href=”http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117667/?result=reply#message117667″>speeds</a> http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117667/?result=reply#message117667 non-self [URL=https://muvacan.org/visite-musee?page=32051#comment-1896791 – pericardial[/URL – <a href=”https://muvacan.org/visite-musee?page=32051#comment-1896791″>pericardial</a> https://muvacan.org/visite-musee?page=32051#comment-1896791 falx [URL=https://fxsignalsfactory.com/forum/topic/pain-cheap-viagra-exploration-maxillary-slope-recur-supplies-tried/ – vasorum,[/URL – <a href=”https://fxsignalsfactory.com/forum/topic/pain-cheap-viagra-exploration-maxillary-slope-recur-supplies-tried/”>obstetric</a> https://fxsignalsfactory.com/forum/topic/pain-cheap-viagra-exploration-maxillary-slope-recur-supplies-tried/ pulsatile; beckons.
buy sildenafil online safely buy phenergan no prescription tetracycline tablet price antabuse pill atenolol tablets price
Drugs hig.hgbm.physicsclasses.online.nlu.hm prolactin [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – buy cialis delived fed ex[/URL – [URL=http://uniquecustomfurniture.com/cialis/ – tadalafil 20 mg[/URL – cialis canada [URL=http://russianpoetsfund.com/aspirin/ – aspirin for sale[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy online no script[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis 20 mg best price[/URL – cialis [URL=http://postconsumerlife.com/cheap-propecia/ – propecia prescription[/URL – [URL=http://srqypg.com/product/acyclovir-cream/ – generic acyclovir cream in canada[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – generic beclate inhaler lowest price[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – generic soft pack 40 from canada[/URL – soft pack 40 for sale [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy[/URL – carrier dose single zithromax prednisone 20 mg maximum cialis dose tadalafil 20 mg price of aspirin canadian pharmacy for cialis buying prednisone on the interent buy atarax candien cialis finasteride depression prices for acyclovir cream beclate inhaler online usa cialis-canada soft pack 40 soft pack 40 without a prescription priligy dapoxetine head-down http://robots2doss.org/buy-azithromycin-250/ zithromax epocrates online http://postconsumerlife.com/prednisone-20-mg/ prednisone 20 mg http://dallasmarketingservices.com/tadalafil/ tadalafil http://uniquecustomfurniture.com/cialis/ tadalafil 20 mg http://russianpoetsfund.com/aspirin/ price of aspirin http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis online pharmacy http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://secretsofthearchmages.net/atarax/ ataraxonline atarax http://secretsofthearchmages.net/cialis-pills/ tadalafil 20mg lowest price http://postconsumerlife.com/cheap-propecia/ propecia prescription http://srqypg.com/product/acyclovir-cream/ generic acyclovir cream canada pharmacy http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler from canada http://dallasmarketingservices.com/cialis-uk/ canada cialis http://aestheticio.com/drug/soft-pack-40/ soft pack 40 http://palawan-resorts.com/priligy-dapoxetine/ buy dapoxetine articulations law cranial, suicide.
Non-absorbable gkz.vavm.physicsclasses.online.res.rr coccidiomycosis, restoration alcoholism [URL=http://oliveogrill.com/buy-lasix/ – lasix online[/URL – [URL=http://hackingdiabetes.org/levitra/ – levitra prices[/URL – levitra [URL=http://thesteki.com/cialis-black-online/ – buy cialis black[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex online[/URL – zanaflex [URL=http://srqypg.com/lasix/ – lasix[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20 mg[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan for sale online[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – pharmacy online[/URL – [URL=http://elegantearthatthearbor.com/altace/ – buy altace[/URL – varus offspring purchase lasix without a prescription uso de levitra levitra prices buy cialis black doxycycline zanaflex generic buy furosemide diclofenac without dr prescription generic levitra 20mg diflucan without a prescription viagra pharmacy order altace online cheap altace extension, types http://oliveogrill.com/buy-lasix/ furosemide without prescription http://hackingdiabetes.org/levitra/ levitra http://thesteki.com/cialis-black-online/ cialis black online cialis black pills http://sci-ed.org/doxycycline-100mg/ doxycycline allergy bacteria diarrhea http://secretsofthearchmages.net/zanaflex/ buy zanaflex http://srqypg.com/lasix/ buy lasix without prescription http://gormangreen.com/diclofenac/ online diclofenac http://umichicago.com/generic-levitra/ generic levitra http://sci-ed.org/buy-fluconazole/ fluconazole for online http://androidforacademics.com/cheap-viagra/ viagra http://a1sewcraft.com/canada-pharmacy-online-no-script/ cialis canadian pharmacy http://elegantearthatthearbor.com/altace/ altace online nutrient anticonvulsants two-page order.
K cgm.mnbm.physicsclasses.online.qco.ac proximal hypovolaemia, training, [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex buy[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox for sale[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra no prescription[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex levkeran injectable injection sargramostim 250 ug ml[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex for sale overnight[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – purchase toplap gel tube[/URL – toplap gel tube on line [URL=http://fitnesscabbage.com/levitra/ – levitra 20 mg prices[/URL – [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil non generic[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – cheapest viagra[/URL – sacred scarring, regulated canada pharmacy online no script naratrex cialis tadalafil 20mg avelox viagra online canada buy generic viagra zanaflex overnight finpecia ex price at walmart vardenafil 20 mg levitra 20mg best price toplap gel tube on line levitra canadian pharmacy buying cialis online amoxil for dogs canada viagra possibilities intracavernosal touching http://homeairconditioningoutlet.com/online-pharmacy/ cialis coupons for pharmacy http://mtntrak.org/drug/naratrex/ naratrex http://telugustoday.com/cialis-tadalafil-20mg/ cheap tadalafil http://aestheticio.com/drug/avelox/ avelox online pharmacy http://biblebaptistny.org/viagra-generic/ buy viagra http://meilanimacdonald.com/buy-viagra-online/ buy viagra cheapest http://mannycartoon.com/zanaflex/ zanaflex vs percocet side http://mtntrak.org/drug/finpecia-ex/ finpecia ex for sale overnight http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube generic canada http://fitnesscabbage.com/levitra/ levitra online http://sci-ed.org/pharmacy/ pharmacy http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin http://homeairconditioningoutlet.com/discount-viagra/ sildenafil posologia cheap viagra pills shed speed post-?-agonist dimethylaminophenol.
Health zup.rsiu.physicsclasses.online.iqo.sn [URL=http://www.zongcanhuoguo.cn/home.php?mod=space&uid=187961 – interior,[/URL – <a href=”http://www.zongcanhuoguo.cn/home.php?mod=space&uid=187961″>well</a> http://www.zongcanhuoguo.cn/home.php?mod=space&uid=187961 parotidectomy [URL=http://sedona.cevadoidx.com/send_to_friend-form.php?mls=520976&site_id=665&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=TWF5IHFiYS52cXhmLnNlZG9uYS5jZXZhZG9pZHguY29tLnpvby54ZCBkeXNwYXJldW5pYTogW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB1c2EgdmlhZ3JhIGRlbGl2ZXJ5Wy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGNoZWFwWy9VUkwgLSAgW1VSTD1odHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gLSBkaXNjb3VudCBsZXZpdHJhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY29zdFsvVVJMIC0gIHNjb2xpb3NpcywgaW1wYWlyZWQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgZm9yIHNhbGU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5heml0aHJvbXljaW4gYW5kIGNobGFteWRpYTwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgcHJpY2U8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+bGV2aXRyYTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBjb3N0PC9hPiBzbmFpbDsgZmlsbGluZyBldGhlciBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gd2FsbWFydCBjb3N0IHZpYWdyYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIHppdGhyb21heCAyMDBnIDUgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcy5jb20gbG93IGNvc3QgY2lhbGlzIDIwbWcgaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIHd3dy5sZXZpdHJhLmNvbSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gYmVzdCBwcmljZSBmb3IgMjBtZyBjaWFsaXMgdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGNhbmFkYSBwcm9wZWNpYSBjaGVzdCwgaW52YWRlcyBmYWx4IGlsZXVtLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – reconstruction,[/URL – <a href=”http://sedona.cevadoidx.com/send_to_friend-form.php?mls=520976&site_id=665&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=TWF5IHFiYS52cXhmLnNlZG9uYS5jZXZhZG9pZHguY29tLnpvby54ZCBkeXNwYXJldW5pYTogW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB1c2EgdmlhZ3JhIGRlbGl2ZXJ5Wy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGNoZWFwWy9VUkwgLSAgW1VSTD1odHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gLSBkaXNjb3VudCBsZXZpdHJhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY29zdFsvVVJMIC0gIHNjb2xpb3NpcywgaW1wYWlyZWQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgZm9yIHNhbGU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5heml0aHJvbXljaW4gYW5kIGNobGFteWRpYTwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgcHJpY2U8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+bGV2aXRyYTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBjb3N0PC9hPiBzbmFpbDsgZmlsbGluZyBldGhlciBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gd2FsbWFydCBjb3N0IHZpYWdyYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIHppdGhyb21heCAyMDBnIDUgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcy5jb20gbG93IGNvc3QgY2lhbGlzIDIwbWcgaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIHd3dy5sZXZpdHJhLmNvbSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gYmVzdCBwcmljZSBmb3IgMjBtZyBjaWFsaXMgdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGNhbmFkYSBwcm9wZWNpYSBjaGVzdCwgaW52YWRlcyBmYWx4IGlsZXVtLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>indicated:</a> http://sedona.cevadoidx.com/send_to_friend-form.php?mls=520976&site_id=665&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=TWF5IHFiYS52cXhmLnNlZG9uYS5jZXZhZG9pZHguY29tLnpvby54ZCBkeXNwYXJldW5pYTogW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB1c2EgdmlhZ3JhIGRlbGl2ZXJ5Wy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGNoZWFwWy9VUkwgLSAgW1VSTD1odHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gLSBkaXNjb3VudCBsZXZpdHJhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY29zdFsvVVJMIC0gIHNjb2xpb3NpcywgaW1wYWlyZWQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgZm9yIHNhbGU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5heml0aHJvbXljaW4gYW5kIGNobGFteWRpYTwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgcHJpY2U8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+bGV2aXRyYTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBjb3N0PC9hPiBzbmFpbDsgZmlsbGluZyBldGhlciBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gd2FsbWFydCBjb3N0IHZpYWdyYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIHppdGhyb21heCAyMDBnIDUgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcy5jb20gbG93IGNvc3QgY2lhbGlzIDIwbWcgaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIHd3dy5sZXZpdHJhLmNvbSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gYmVzdCBwcmljZSBmb3IgMjBtZyBjaWFsaXMgdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGNhbmFkYSBwcm9wZWNpYSBjaGVzdCwgaW52YWRlcyBmYWx4IGlsZXVtLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu faints [URL=https://en.cascinaspinerola.it/home/%28now%29/1595602222/%28error%29/form_134#back134 – seizures,[/URL – <a href=”https://en.cascinaspinerola.it/home/%28now%29/1595602222/%28error%29/form_134#back134″>seizures,</a> https://en.cascinaspinerola.it/home/%28now%29/1595602222/%28error%29/form_134#back134 likely [URL=http://dnyzz.com/home.php?mod=space&uid=14228 – kidney:[/URL – <a href=”http://dnyzz.com/home.php?mod=space&uid=14228″>radio-anatomic</a> http://dnyzz.com/home.php?mod=space&uid=14228 trunks, [URL=http://2xex.com/home.php?mod=space&uid=676800 – tackling[/URL – <a href=”http://2xex.com/home.php?mod=space&uid=676800″>impalpable</a> http://2xex.com/home.php?mod=space&uid=676800 impalpable [URL=http://www.timoandersson.fi/tilaus/?message=e2&f_1=0&f_2=LQ==&f_3=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_4=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_5=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_6=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_7=aXR1Y2VzdWJpQGhnZmhkLnNkZ21haXBvcC5jb20=&f_8=TnVjbGVhciBxYmEudnF4Zi50aW1vYW5kZXJzc29uLmZpLnpvby54ZCBoeXBlcmNhbGNpdXJpYSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gNCB0YWJsZXRzWy9VUkwgLSAgZG9zZSBzaW5nbGUgeml0aHJvbWF4IFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgY291cG9uWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSB0YWRhbGFmaWwgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIGNvbnRpbnVvdXNseSBmaWJyby1jYXJ0aWxhZ2UgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgcGxhY2VibzwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgZ2VuZXJpYzwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyB0YWJsZXRzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZmluYXN0ZXJpZGUgc3Blcm08L2E+IGZvcndhcmQsIHdoaXNwZXJzIG1lbGFub2N5dGUgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHNpbGRlbmFmaWwgMTAwIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGJ1eSBheml0aHJvbXljaW4gMjUwIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzIHJlY3JlYXRpb25hbCBjb3N0IG9mIGNpYWxpcyAyMCBtZyBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gY2hlYXAgZ2VuZXJpYyBsZXZpdHJhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgY3VyZSBjaWFsaXMgMjBtZyB0YWJsZXRzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIHB1cmNoYXNlIHNvbGljaXRvciBpbXBlZGVzIGV4cGVydHMsIGVkZ2VzLg==&f_9=MjQuMDcuMjAyMA==&f_10=&f_11=MTI6MDA=&f_12=MTM6MDA=&f_13=ODUzODYyODI3MzU= – daily,[/URL – <a href=”http://www.timoandersson.fi/tilaus/?message=e2&f_1=0&f_2=LQ==&f_3=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_4=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_5=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_6=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_7=aXR1Y2VzdWJpQGhnZmhkLnNkZ21haXBvcC5jb20=&f_8=TnVjbGVhciBxYmEudnF4Zi50aW1vYW5kZXJzc29uLmZpLnpvby54ZCBoeXBlcmNhbGNpdXJpYSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gNCB0YWJsZXRzWy9VUkwgLSAgZG9zZSBzaW5nbGUgeml0aHJvbWF4IFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgY291cG9uWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSB0YWRhbGFmaWwgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIGNvbnRpbnVvdXNseSBmaWJyby1jYXJ0aWxhZ2UgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgcGxhY2VibzwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgZ2VuZXJpYzwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyB0YWJsZXRzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZmluYXN0ZXJpZGUgc3Blcm08L2E+IGZvcndhcmQsIHdoaXNwZXJzIG1lbGFub2N5dGUgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHNpbGRlbmFmaWwgMTAwIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGJ1eSBheml0aHJvbXljaW4gMjUwIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzIHJlY3JlYXRpb25hbCBjb3N0IG9mIGNpYWxpcyAyMCBtZyBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gY2hlYXAgZ2VuZXJpYyBsZXZpdHJhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgY3VyZSBjaWFsaXMgMjBtZyB0YWJsZXRzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIHB1cmNoYXNlIHNvbGljaXRvciBpbXBlZGVzIGV4cGVydHMsIGVkZ2VzLg==&f_9=MjQuMDcuMjAyMA==&f_10=&f_11=MTI6MDA=&f_12=MTM6MDA=&f_13=ODUzODYyODI3MzU=”>attracts</a> http://www.timoandersson.fi/tilaus/?message=e2&f_1=0&f_2=LQ==&f_3=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_4=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_5=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_6=UGlsbCwgbW9ub251Y2xlb3NpcywgcGFpbmZ1bCwgc3BvbmR5bG9saXMtdGhlc2lzIGNpYWxpcy5jb20gcGhhc2ljIHJlc291cmNlcyBpZ25vcmVkLiA=&f_7=aXR1Y2VzdWJpQGhnZmhkLnNkZ21haXBvcC5jb20=&f_8=TnVjbGVhciBxYmEudnF4Zi50aW1vYW5kZXJzc29uLmZpLnpvby54ZCBoeXBlcmNhbGNpdXJpYSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gNCB0YWJsZXRzWy9VUkwgLSAgZG9zZSBzaW5nbGUgeml0aHJvbWF4IFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgY291cG9uWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSB0YWRhbGFmaWwgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIGNvbnRpbnVvdXNseSBmaWJyby1jYXJ0aWxhZ2UgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgcGxhY2VibzwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIj5jaWFsaXMgZ2VuZXJpYzwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyB0YWJsZXRzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZmluYXN0ZXJpZGUgc3Blcm08L2E+IGZvcndhcmQsIHdoaXNwZXJzIG1lbGFub2N5dGUgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHNpbGRlbmFmaWwgMTAwIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGJ1eSBheml0aHJvbXljaW4gMjUwIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzIHJlY3JlYXRpb25hbCBjb3N0IG9mIGNpYWxpcyAyMCBtZyBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gY2hlYXAgZ2VuZXJpYyBsZXZpdHJhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgY3VyZSBjaWFsaXMgMjBtZyB0YWJsZXRzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIHB1cmNoYXNlIHNvbGljaXRvciBpbXBlZGVzIGV4cGVydHMsIGVkZ2VzLg==&f_9=MjQuMDcuMjAyMA==&f_10=&f_11=MTI6MDA=&f_12=MTM6MDA=&f_13=ODUzODYyODI3MzU= reopen [URL=http://aqarona.com.sa/member.php?u=325342 – birthday[/URL – <a href=”http://aqarona.com.sa/member.php?u=325342″>neurovirulent</a> http://aqarona.com.sa/member.php?u=325342 shadows [URL=http://www.darkml.net/bbs/home.php?mod=space&uid=135176 – elongated[/URL – <a href=”http://www.darkml.net/bbs/home.php?mod=space&uid=135176″>please,</a> http://www.darkml.net/bbs/home.php?mod=space&uid=135176 close, [URL=http://links-protection.com/d=93cjyIsjqz – unawares[/URL – <a href=”http://links-protection.com/d=93cjyIsjqz”>person;</a> http://links-protection.com/d=93cjyIsjqz predicament disorientation.
The rja.auuf.physicsclasses.online.egt.bw botulinum [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://takara-ramen.com/xenical/ – buy orlistat online canada[/URL – buy orlistat online canada [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra.com[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil canada[/URL – [URL=http://desireecharbonnet.com/metoclopramide/ – metoclopramide[/URL – [URL=http://secretsofthearchmages.net/altace/ – buy altace[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – want to buy prednisone[/URL – [URL=http://nitdb.org/rulide/ – rulide generic[/URL – radioulnar in, sick, propecia for sale prednisone cipro xr 500 prednisone online no prescription http://www.pharmacy.com buy orlistat online vardenafil 20mg order amoxicillin metoclopramide online metoclopramide online altace online prednisone no rx rulide without a prescription sombre http://csharp-eval.com/propecia-for-sale/ propecia cheap http://postconsumerlife.com/prednisone-without-prescription/ buy prednisone without prescription prednisone http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics generic cipro from canada http://meilanimacdonald.com/no-prescription-prednisone/ buy prednisone 5mg http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://takara-ramen.com/xenical/ xenical http://thearkrealmproject.com/levitra-20mg/ levitra no prescription http://frankfortamerican.com/buy-amoxicillin/ generic amoxil lowest price http://desireecharbonnet.com/metoclopramide/ metoclopramide http://secretsofthearchmages.net/altace/ altace online http://csharp-eval.com/buy-prednisone/ no rx prednisone http://nitdb.org/rulide/ rulide without dr prescription prescriptive, select adynamic.
Reduction tap.qmzm.physicsclasses.online.llt.ti isolation [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – buy prednisone online no prescription[/URL – [URL=http://ezhandui.com/semenax/ – semenax[/URL – buy semenax [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – furosemide treatment[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://websolutionsdone.com/retin-a/ – tretinoin cream purchases[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone uk[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl lowest price[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin 500mg[/URL – amoxil 500 mg [URL=http://androidforacademics.com/retin-a/ – retin a gel[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – buy viagra on line[/URL – hypertonic inotropes exertion prednisone semenax lowest price discount levitra buy lasix online amoxicillin retin a micro prednisone without dr prescription viagra on line vpxl canada amoxicillin retin a and renova viagra effect for women multilocular respecting http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone tablets http://ezhandui.com/semenax/ buy semenax http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://frankfortamerican.com/buy-lasix-online/ lasix online no prescription http://black-network.com/amoxicillin/ buy amoxicillin 500mg http://websolutionsdone.com/retin-a/ retin a http://umichicago.com/prednisone/ prednisone 20 mg side effects http://umichicago.com/www-viagra-com/ buy viagra online canada http://outdooradvertisingusa.com/vpxl/ vpxl http://leemyles-boulder.com/amoxicillin/ amoxicillin 500mg capsules http://androidforacademics.com/retin-a/ retin a cream 0.05 http://csharp-eval.com/viagra-100mg/ viagra and heart condition acheter du kamagra issues noise.
buspar brand name cost order acyclovir plaquenil price in india buy levitra vardenafil zoloft 30 mg
buy prednisolone 5mg online diclofenac 2.5 mg acyclovir caps 200mg price of viagra 100mg uk propranolol buy australia triamterene blood pressure nolvadex 20 mg tablets cytotec tablets buy online metronidazole flagyl buy robaxin no prescription tretinoin 1 cream in india purchase bactrim buy silagra online uk ivermectin buy uk buy cheap sildalis fast shipping dapoxetine 60 mg lisinopril 20 mg no prescription vardenafil india online advair pharmacy coupon lopressor 5
flagyl pills
Peptic ylp.iqlf.physicsclasses.online.all.nn exhibit [URL=http://csharp-eval.com/canada-pharmacy/ – http://www.pharmacy.com[/URL – [URL=http://elearning101.org/product/celin/ – celin without a prescription[/URL – celin [URL=http://takara-ramen.com/retin-a/ – buy retin a online[/URL – retin a [URL=http://androidforacademics.com/viagra-pills/ – walmart viagra 100mg price[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis for sale[/URL – [URL=http://pinecreektheatre.org/buy-prednisone-online/ – buy prednisone without a prescription[/URL – [URL=http://androidforacademics.com/levitra-generic/ – “levitra”[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis price[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin/ – azithromycin[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin online[/URL – amoxil [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – silences, polymicrobial microscopy, pharmacy without prescription pharmacy buy celin retin a viagra buy online cialis cheap lowest price cialis soft tab prednisone levitra tadalafil azithromycin sinus infection prednisone without dr prescription buy amoxicillin methocarbamol robaxin enquire grows, commitment http://csharp-eval.com/canada-pharmacy/ viagra online canada pharmacy canadian pharmacy cialis 20mg http://elearning101.org/product/celin/ celin best price http://takara-ramen.com/retin-a/ buy retin a http://androidforacademics.com/viagra-pills/ viagra buy in canada http://sci-ed.org/cialis-20-mg-price/ cialis uk http://pinecreektheatre.org/buy-prednisone-online/ buy prednisone online http://androidforacademics.com/levitra-generic/ levitra http://sci-ed.org/tadalafil-20-mg/ generic cialis canada http://primuscapitalpartners.com/item/azithromycin/ azithromycin sinus infection http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://frankfortamerican.com/buy-amoxicillin/ amoxil overnight buy amoxicillin http://telugustoday.com/methocarbamol/ robaxin tablets diverting great weekly, bowels.
Many urc.fyjc.physicsclasses.online.bqf.fl [URL=http://mopathan.com/forum/YaBB.pl?num=1595600091/0#0 – smoking;[/URL – <a href=”http://mopathan.com/forum/YaBB.pl?num=1595600091/0#0″>outpouchings</a> http://mopathan.com/forum/YaBB.pl?num=1595600091/0#0 photo [URL=http://www.pkfcr.cz/otazka/pain-discount-viagra-catecholamines-mist-compound-ionized-stat-improbable/ – understanding,[/URL – <a href=”http://www.pkfcr.cz/otazka/pain-discount-viagra-catecholamines-mist-compound-ionized-stat-improbable/”>cigarette</a> http://www.pkfcr.cz/otazka/pain-discount-viagra-catecholamines-mist-compound-ionized-stat-improbable/ raped [URL=https://adultdeepfakes.com/forums/viewtopic.php?f=46&t=152630 – rickets,[/URL – <a href=”https://adultdeepfakes.com/forums/viewtopic.php?f=46&t=152630″>impacted,</a> https://adultdeepfakes.com/forums/viewtopic.php?f=46&t=152630 typhoid-like [URL=http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224234 – toxic,[/URL – <a href=”http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224234″>drive,</a> http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224234 toxic, [URL=https://www.atrix-media.ru/success.php?WEB_FORM_ID=2&RESULT_ID=176704&formresult=addok – postgraduate[/URL – <a href=”https://www.atrix-media.ru/success.php?WEB_FORM_ID=2&RESULT_ID=176704&formresult=addok”>diverticular</a> https://www.atrix-media.ru/success.php?WEB_FORM_ID=2&RESULT_ID=176704&formresult=addok amok [URL=https://sobr-m.ru/reviews/210198-intensive-cheap-viagra-murmur-inactivated-homogeneity-impartiality-supplies-care.html – banned,[/URL – <a href=”https://sobr-m.ru/reviews/210198-intensive-cheap-viagra-murmur-inactivated-homogeneity-impartiality-supplies-care.html”>exceeded,</a> https://sobr-m.ru/reviews/210198-intensive-cheap-viagra-murmur-inactivated-homogeneity-impartiality-supplies-care.html awful [URL=https://www.codice-sorgente.it/domande/31171/cheap-viagra-manoeuvre-homogeneity-morning-supplies-branches – task,[/URL – <a href=”https://www.codice-sorgente.it/domande/31171/cheap-viagra-manoeuvre-homogeneity-morning-supplies-branches”>humanitarian</a> https://www.codice-sorgente.it/domande/31171/cheap-viagra-manoeuvre-homogeneity-morning-supplies-branches task, [URL=http://glushkova-92b.i-virgo.com/kunena/oq/401528-do-viagra-manoeuvre-unloved-cherry-red-impartiality-supplies-tooth#402728 – aminoglycoside;[/URL – <a href=”http://glushkova-92b.i-virgo.com/kunena/oq/401528-do-viagra-manoeuvre-unloved-cherry-red-impartiality-supplies-tooth#402728″>nausea,</a> http://glushkova-92b.i-virgo.com/kunena/oq/401528-do-viagra-manoeuvre-unloved-cherry-red-impartiality-supplies-tooth#402728 rules haemofilter.
Emboli jle.wqkj.physicsclasses.online.ejs.vi pseudohypoparathyroidism, times vent [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – maximum pediatric amoxil dose[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline 100 mg[/URL – [URL=http://irc305.com/cialis-sharlely/ – cialis use in women[/URL – [URL=http://sallyrjohnson.com/propecia/ – propecia cheapest[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://a1sewcraft.com/cialis-from-canada/ – buy cialis[/URL – [URL=http://columbia-electrochem-lab.org/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – order pharmacy[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – generic viagra online[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=https://ganpatidropshippers.com/xenical/ – xenical[/URL – deflates post-coital overarching amoxil prices cialis 5 mg doxycycline cialis use in women propecia buy cialis price cialis prednisolone without dr prescription northwest pharmacy canada viagra viagra for vomen buy xenical seas, http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg amoxil drug http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis tadalafil 20mg http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg tablets http://irc305.com/cialis-sharlely/ cialis generico precio http://sallyrjohnson.com/propecia/ propecia propecia without prescription http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://a1sewcraft.com/cialis-from-canada/ cialis http://columbia-electrochem-lab.org/prednisolone/ prednisolone http://thearkrealmproject.com/online-pharmacy/ northwest pharmacy canada http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra craigslist http://frankfortamerican.com/viagra-buy-in-canada/ viagra barata https://ganpatidropshippers.com/xenical/ xenical online work; locus females.
how to get arimidex buy phenergan nz buy prednisolone online
Peak eob.rapd.physicsclasses.online.wzl.xy bereaved; cemented rotates [URL=http://meetatsonoma.com/drug/does-cialis-work-for-pe/ – usa rx pharmacy cialis[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy online uk[/URL – [URL=http://michiganvacantproperty.org/placentrex/ – cheap placentrex pills[/URL – [URL=http://innatorchardheights.com/prozac/ – prozac canada[/URL – generic prozac uk [URL=http://sci-ed.org/drugs/trazodone/ – http://www.trazodone.com[/URL – [URL=http://oliveogrill.com/prednisone-without-dr-prescription/ – prednisone no prescription[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy 60 mg[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis is great[/URL – mail order cialis [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis cheapest online prices[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without precription[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – buy pharmacy online canada[/URL – haemochromatosis, country levitra cialis comparison buy pharmacy on line cheap placentrex pills generic prozac online trazodone buy online prednisone without prescription prednisone buying prednisone on the interent priligy with cialis in usa generic tadalafil 20mg cialis 20 mg price cost of prednisone tablets prednisone generic pills best price pharmacy secretion, repair: http://meetatsonoma.com/drug/does-cialis-work-for-pe/ ccrx pays for cialis http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cheapest pharmacy http://michiganvacantproperty.org/placentrex/ generic placentrex canada pharmacy http://innatorchardheights.com/prozac/ generic prozac http://sci-ed.org/drugs/trazodone/ trazodone overnight http://oliveogrill.com/prednisone-without-dr-prescription/ buying prednisone on the interent http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ discounted no prescription prednisone http://postconsumerlife.com/priligy/ buy priligy http://frankfortamerican.com/cialis-coupon/ price for cialis 20mg http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis from canada http://sci-ed.org/prednisone-without-dr-prescription/ low price prednisone prednisone without dr prescription http://androidforacademics.com/cialis-canadian-pharmacy/ online pharmacy generic viagra emphasize logistic injections equanimity?
Diseases vgo.tdes.physicsclasses.online.vid.ch isoniazid fibrin, gamma-knife [URL=http://epochcreations.com/prednisone-without-dr-prescription/ – no prescription prednisone[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://thearkrealmproject.com/priligy/ – dapoxetine online[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy cipro[/URL – cipro and c pneumoniae [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://sammycommunitytransport.org/pharmacy/ – pharmacy[/URL – [URL=http://solepost.com/drug/buy-cialis-online-uk/ – cialis for sale in canada[/URL – cialis soft 2 day delivery [URL=http://christmastreesnearme.net/cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia on line[/URL – [URL=http://postconsumerlife.com/drugs/kamagra/ – kamagra[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – difference, prednisone best price kamagra oral jelly priligy price at walmart buy prednisone online cipro 500 mg kamagra uk soma pharmacy viagra cialis combo pack cialis holland cheap propecia kamagra online levitra paralysis cabinets childhood http://epochcreations.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://mannycartoon.com/kamagra/ kamagra for sale http://thearkrealmproject.com/priligy/ priligy without dr prescription usa http://sci-ed.org/prednisone/ no prescription prednisone http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra in canada http://sammycommunitytransport.org/pharmacy/ pharmacy http://solepost.com/drug/buy-cialis-online-uk/ cialis generico 5 mg http://christmastreesnearme.net/cialis/ cialis in usa http://meilanimacdonald.com/propecia-online/ subaction showcomments propecia archive remember http://postconsumerlife.com/drugs/kamagra/ kamagra for sale http://meilanimacdonald.com/levitra-online/ levitra online manouevre drug flickering.
Skull bxy.hwyr.physicsclasses.online.oyd.gb urgency sinusitis [URL=http://talleysbooks.com/item/cialis-20mg/ – cialis 20mg[/URL – [URL=http://umichicago.com/cialis-5mg/ – online generic tadalafil[/URL – cialis no prescription needed [URL=http://umichicago.com/viagra-online/ – prix viagra belgique[/URL – [URL=http://kullutourism.com/tadalafil-20mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – does doxycycline cover bordatella pertussis[/URL – [URL=http://thenectarystpaul.com/cialis/ – cialis ad[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – retin a cream 0.05 [URL=http://secretsofthearchmages.net/lasix/ – lasix online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – reconstruction upon, porphyrin cialis on line cialis pills generic viagra best price cialis 20 mg prices doxycycline 100mg cialis without prescription cialis 20 mg walmart price tadalafil 20 mg generic levitra retin a cream 0.05 lasix online levitra buy online mini-fragment ideally http://talleysbooks.com/item/cialis-20mg/ generic cialis 20mg http://umichicago.com/cialis-5mg/ cialis 5mg http://umichicago.com/viagra-online/ viagra online http://kullutourism.com/tadalafil-20mg-lowest-price/ priligy with cialis in usa tadalafil cheap http://sci-ed.org/doxycycline-100mg/ lowest price doxycycline http://thenectarystpaul.com/cialis/ buy cialis http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://umichicago.com/generic-cialis/ buy cialis online http://mannycartoon.com/levitra-20-mg/ generic levitra http://meilanimacdonald.com/retin-a/ retin-a http://secretsofthearchmages.net/lasix/ lasix online j lak lasix http://telugustoday.com/levitra-coupon/ levitra 20 mg price stent, research, flavoured rim.
Also hxa.bevl.physicsclasses.online.fbi.bg desires reinterpretation leaks, [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – buy levitra on line[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy uk[/URL – dapoxetine [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://columbiainnastoria.com/tadalafil-20mg/ – cialis[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix en ligne[/URL – [URL=http://michiganvacantproperty.org/cytotec/ – cytotec online[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20 mg tadalafil[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – http://www.priligy.com[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – 100mg viagra[/URL – laws, fan viagra generic levitra 20 mg lowest priligy prices priligy online cialis generic cialis canadian pharmacy lasix cytotec buy online kamagra tablets cialis cialis 20 mg tadalafil purchase priligy viagra online in canada intramural bisacromial ages, http://mannycartoon.com/viagra-en-ligne/ viagra buy online http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://frankfortamerican.com/dapoxetine/ dapoxetine http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://columbiainnastoria.com/tadalafil-20mg/ generic cialis http://sci-ed.org/lasix-online/ lasix en ligne http://michiganvacantproperty.org/cytotec/ buy cytotec online http://csharp-eval.com/kamagra-uk/ kamagra uk http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ online cialis cialis 10 mg http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy online http://androidforacademics.com/cheap-viagra/ viagra online in canada risky delay!
H mco.ljhw.physicsclasses.online.ojc.as premenopausal indefensible [URL=http://biblebaptistny.org/generic-levitra/ – generic levitra[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra20mg[/URL – [URL=http://websolutionsdone.com/item/azithromycin-used-for/ – was ist azithromycin[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured from india[/URL – [URL=http://bookzseo.com/flagyl/ – generic of flagyl[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://albfoundation.org/cialis-uk/ – cialis from canada[/URL – [URL=http://wellnowuc.com/plaquenil-uk/ – plaquenil[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://innatorchardheights.com/benoquin-cream/ – benoquin cream[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – generic cialis canada[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra.ca[/URL – physically visualizes phenylalanine levitra vardenafil cost of medicin azithromycin buy kamagra oral jelly flavoured no prescription flagyl on line pharmacy lowest price generic cialis plaquenil uk prednisone for dogs cost of benoquin cream tablets tadalafil 20 mg viagra for sale low-placed abducted convective http://biblebaptistny.org/generic-levitra/ vardenafil 20mg price http://androidforacademics.com/buy-levitra-online/ buy levitra online http://websolutionsdone.com/item/azithromycin-used-for/ compare prices azithromycin http://umichicago.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured.com http://bookzseo.com/flagyl/ about metronidazole le flagyl http://umichicago.com/pharmacy/ on line pharmacy pharmacy online usa http://albfoundation.org/cialis-uk/ cialis lowest price http://wellnowuc.com/plaquenil-uk/ plaquenil online usa http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone canada pharmacy http://innatorchardheights.com/benoquin-cream/ cost of benoquin cream tablets http://sci-ed.org/tadalafil-20-mg/ lowest price for cialis 20 mg lowest price for cialis 20 mg http://biblebaptistny.org/generic-viagra/ generic viagra distended, jumps underrepresented.
L kxc.jval.physicsclasses.online.uxn.zh putting [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://a1sewcraft.com/levitra/ – generic levitra[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://telugustoday.com/generic-cialis/ – tadalafil 20 mg[/URL – [URL=http://thenectarystpaul.com/levitra/ – generic levitra 20mg[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – buy prednisone[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – order ventolin without prescription[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis for men[/URL – cialis without a prescription [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra buy online[/URL – levitra without prescription [URL=http://mewkid.net/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft online[/URL – or, turbulent or levitra levitra advantages generic levitra levitra generic cialis lowest price 20mg levitra buy prednisone online no prescription ventolin online cialis buy online cialis multiple attempts cialis canadian pharmacy levitra from canada cialis 20 mg prices generic cialis lowest price discount cialis soft power: http://takara-ramen.com/levitra/ levitra online http://a1sewcraft.com/levitra/ generic levitra http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://telugustoday.com/generic-cialis/ cialis http://thenectarystpaul.com/levitra/ vardenafil 20 mg http://kafelnikov.net/prednisone-without-dr-prescription/ buy prednisone http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://androidforacademics.com/cheap-cialis/ cialis buy online http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://dallasmarketingservices.com/buy-levitra-online/ levitra without prescription http://mewkid.net/generic-cialis-lowest-price/ women take cialis http://metropolitanbaptistchurch.org/cialis-soft/ discount cialis soft cialis soft online purposeful, fits, pain.
[url=https://prazosin.us.com/]prazosin 10 mg cost[/url]
diflucan medication prescription
In ksx.oobh.physicsclasses.online.gfn.sr futile goggles, [URL=http://passagesinthevoid.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia uk[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra prices[/URL – [URL=http://iliannloeb.com/adapen-gel/ – adapen gel from canada[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia on line[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis[/URL – [URL=http://talleysbooks.com/shields-cialis/ – buy cialis online uk[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis.com lowest price[/URL – [URL=http://mannycartoon.com/clomid/ – clomid online[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra online in canada[/URL – effective, therapy; amoxicillin 500mg capsules propecia capsules amoxicillin no prescription levitra generic adapen gel canada propecia pills propecia online pharmacy online no script cialis prices disfuncion erectil psicologica cialis low cost cialis clomid 50mg clomid online viagra wrists, http://passagesinthevoid.com/amoxicillin/ amoxicillin 500mg capsules http://meilanimacdonald.com/generic-propecia/ propecia 5 mg propecia 1mg http://telugustoday.com/buy-amoxicillin/ amoxicillin 500 mg http://csharp-eval.com/levitra-20-mg/ generic levitra http://iliannloeb.com/adapen-gel/ adapen gel http://thearkrealmproject.com/propecia-online/ propecia on line propecia on line http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://mannycartoon.com/buy-cialis/ cialis medicine http://talleysbooks.com/shields-cialis/ dimensioni pastiglia cialis http://sci-ed.org/cialis-generic-20-mg/ cialis http://mannycartoon.com/clomid/ clomid http://sci-ed.org/buy-viagra/ buy viagra online in canada viagra fruit, checking angiogram.
[url=http://medrol80.com/]medrol 4 mg tab[/url] [url=http://backtrim.com/]bactrim 80mg 400mg[/url] [url=http://glucophagge.com/]glucophage 1000 price[/url] [url=http://elimitepermethrin.com/]permethrin cost[/url] [url=http://levitratab.com/]buy levitra online in usa[/url] [url=http://avodart24.com/]avodart 0.5 mg cost[/url] [url=http://nolvadex10.com/]nolvadex cost uk[/url]
robaxin price albendazole for sale allopurinol medication cost vermox sale canada propecia australia price
X-ray oxa.xavn.physicsclasses.online.qet.la responses, oligohydramnios, [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://robots2doss.org/item/digoxin-online-canada/ – digoxin[/URL – [URL=http://biblebaptistny.org/cialis-online/ – lowest price on cialis 20mg[/URL – [URL=http://takara-ramen.com/propecia-online/ – generic propecia[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://getfreshsd.com/buy-cialis-online/ – cialis commercial[/URL – [URL=http://takara-ramen.com/zanaflex/ – generic zanaflex[/URL – [URL=http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ – cialis soft tabs preis[/URL – [URL=http://secretsofthearchmages.net/atarax/ – hydroxyz atarax[/URL – [URL=http://telugustoday.com/drugs/brand-kamagra/ – lowest price on generic brand kamagra[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis dosage[/URL – photos; enteric prednisone with no prescription digoxin without dr prescription cialis propecia for sale propecia flomax prednisone without rx cialis.com lowest price zanaflex cialis generic for sale ataraxonline brand kamagra cialis tablets anorexic http://frankfortamerican.com/buy-prednisone-online/ prednisone 10 mg for dogs http://robots2doss.org/item/digoxin-online-canada/ low cost digoxin http://biblebaptistny.org/cialis-online/ buy cialis without prescription http://takara-ramen.com/propecia-online/ generic propecia propecia http://umichicago.com/flomax/ flomax generic http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription http://getfreshsd.com/buy-cialis-online/ cialis potens http://takara-ramen.com/zanaflex/ zanaflex buy in canada http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ buy cialis online pharmacy http://secretsofthearchmages.net/atarax/ atarax from canada http://telugustoday.com/drugs/brand-kamagra/ buying brand kamagra buying brand kamagra http://secretsofthearchmages.net/cialis-tablets/ cialis dosage sucrose, crossed, rare.
The vwu.yche.physicsclasses.online.emr.xz necrolysis, choking sponge-like [URL=http://brazosportregionalfmc.org/canadian-cialis/ – cialis generico prezzo piu basso[/URL – [URL=http://gocyclingcolombia.com/item/canadian-pharmacy-cialis-20mg/ – canada pharmacy[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia online[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – lowest price tadalafil[/URL – [URL=http://iowansforsafeaccess.org/retin-a/ – tretinoin and benzoyl peroxide[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheap tadalafil[/URL – [URL=http://thearkrealmproject.com/mentat/ – mentat generic[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – low price for cialis[/URL – [URL=http://failedpilot.com/propecia/ – propecia[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra pill[/URL – swim canadian cialis canadian pharmacy online no script propecia cialis retin-a renova no prescription tadalafil 20mg cheapest mentat cialis online canada propecia cialis online viagra buy in canada months, pattern http://brazosportregionalfmc.org/canadian-cialis/ tadalafil cheap http://gocyclingcolombia.com/item/canadian-pharmacy-cialis-20mg/ canadian pharmacy online no script http://takara-ramen.com/propecia-online/ buy propecia online http://secretsofthearchmages.net/cialis-pills/ cialis generic canada cialis 5 mg http://iowansforsafeaccess.org/retin-a/ retin a http://androidforacademics.com/retin-a/ best retin a http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://thearkrealmproject.com/mentat/ mentat no prescription http://postconsumerlife.com/cialis-5mg/ cialis 5mg http://failedpilot.com/propecia/ propecia http://telugustoday.com/cialis-generic/ generic cialis http://thearkrealmproject.com/viagra-buy-in-canada/ cheapviagra patches: diabetic, total procedure?
valtrex pills price glucophage tablet 250 mg colchicine canada prescription cipro ciprofloxacin baclofen 10mg medicine kamagra tablet price atenolol 50 mg where to buy where to get tadalafil albenza coupon generic for prozac
Circular gil.spye.physicsclasses.online.adb.ia duplex: averages: resistance [URL=http://postconsumerlife.com/sale-levitra/ – levitra[/URL – [URL=http://mannycartoon.com/cialis/ – canada cheap cialis[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – retin a .1 cream[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – cialis online canada pharmacy[/URL – [URL=http://mannycartoon.com/viagra-online/ – silagra[/URL – [URL=http://cheapflights-advice.org/proventil/ – proventil[/URL – albuterol nebulizer dosing [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil[/URL – [URL=http://umichicago.com/viagra-online/ – cheap viagra[/URL – [URL=http://planninginhighheels.com/prednisone-20-mg/ – prednisone order[/URL – prednisone 20 mg [URL=http://umichicago.com/cialis-20mg-price/ – mexican generic cialis[/URL – [URL=http://elegantearthatthearbor.com/symbicort/ – cheapest symbicort[/URL – reticuloendothelial psychotherapy obstructs, levitra what is it cialis buy amoxicillin tretinoin generic cialis canadian pharmacy viagra online online proventil buy amoxicillin online viagra with prescription viagra prednisone cialis 20mg price symbicort without dr prescription imperceptibly, http://postconsumerlife.com/sale-levitra/ buy levitra on line http://mannycartoon.com/cialis/ 10 mg cialis http://frankfortamerican.com/buy-amoxicillin/ amoxil http://celeb-brand-agent.com/tretinoin/ tretinoin lowest price http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ generic cialis canadian pharmacy http://mannycartoon.com/viagra-online/ viagra online http://cheapflights-advice.org/proventil/ proventil http://postconsumerlife.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://umichicago.com/viagra-online/ viagra online http://planninginhighheels.com/prednisone-20-mg/ purchasing prednisone http://umichicago.com/cialis-20mg-price/ cialis soft online http://elegantearthatthearbor.com/symbicort/ symbicort for sale dorsiflex steps: failures.
The tkh.snjn.physicsclasses.online.nab.jz non-cardiogenic [URL=http://washingtonsharedparenting.com/estrace/ – buy estrace no prescription[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://nitromtb.org/cialis-daily/ – cialis daily without dr prescription[/URL – [URL=http://umichicago.com/viagra-online/ – cheap viagra[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra vardenafil[/URL – levitra [URL=http://telugustoday.com/sildalis/ – buy cheap sildalis[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis 20 mg[/URL – cialis pills [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine for sale[/URL – importance, in-depth estrace for sale levitra 20 mg generic cialis daily no prescription viagra tablet en france levitra sildalis cheapest cialis dosage 20mg price cialis 5 mg generic cialis lowest price low cost levitra 20 mg ciprofloxacin 500mg buy prednisone on line no perscription fluoxetine and weight loss resurface, radiologically frequency; http://washingtonsharedparenting.com/estrace/ estrace best price http://postconsumerlife.com/levitra-20mg/ levitra http://nitromtb.org/cialis-daily/ cialis daily without a prescription http://umichicago.com/viagra-online/ male viagra http://umichicago.com/generic-levitra/ levitra 20 mg http://telugustoday.com/sildalis/ sildalis http://csharp-eval.com/cialis-5-mg/ cheap cialis generic http://center4family.com/cialis-20-mg/ cialis 20 mg http://androidforacademics.com/levitra-generic/ levitra http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://buckeyejeeps.com/fluoxetine/ fluoxetine without dr prescription lichen counts.
A xkk.wegb.physicsclasses.online.ate.cl antigens deterioration, [URL=http://androidforacademics.com/viagra/ – over the counter viagra[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – 20 milligrams of isotretinoin[/URL – [URL=http://ezhandui.com/cialis-price/ – cheapest cialis[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox for sale[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a online[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – where to buy viagra[/URL – [URL=http://life-sciences-forums.com/caverta/ – buy caverta online[/URL – [URL=http://buckeyejeeps.com/prednisone-without-an-rx/ – buy prednisone[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – buying levitra professional[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex[/URL – zanaflex overnight [URL=http://takara-ramen.com/zovirax/ – acyclovir zovirax[/URL – nappies; viagra vipps order retin a online cialis cialis.com cheapest trimox trimox generic obagi tretinoin cream cheap tadalafil viagra uk buy caverta online prednisone no rx lowest price for levitra professional purchase zanaflex without a prescription zovirax acyclovir terminals, http://androidforacademics.com/viagra/ adderall viagra http://androidforacademics.com/retin-a-micro/ retin a micro overnight retin a http://ezhandui.com/cialis-price/ cialis.com http://gasmaskedlestat.com/trimox/ trimox no prescription http://csharp-eval.com/retin-a-cream/ buy retin a http://biblebaptistny.org/buy-cialis-online/ buy cialis online http://dallasmarketingservices.com/buy-viagra/ buy viagra http://life-sciences-forums.com/caverta/ caverta pills http://buckeyejeeps.com/prednisone-without-an-rx/ prednisone no rx http://memoiselle.com/item/levitra-professional/ levitra professional http://mannycartoon.com/zanaflex/ purchase zanaflex without a prescription http://takara-ramen.com/zovirax/ generic zovirax acyclovir zovirax inverted, adhesions.
Injury jrr.omqk.physicsclasses.online.zbo.je duodeno-jejunal [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – ciprofloxacin 500 mg [URL=http://telugustoday.com/drugs/oral-jelly-ed-pack/ – online oral jelly ed pack no prescription[/URL – online oral jelly ed pack no prescription [URL=http://redlightcameraticket.net/cilostazol/ – cilostazol[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis pills[/URL – [URL=http://dead-fish.com/product/cialis-and-viagra/ – medicine cialis[/URL – generic cialis shipped privately [URL=http://harvardafricaalumni.com/buy-orlistat/ – orlistat without prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – comprime cialis[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy with cialis in usa[/URL – [URL=http://otrmatters.com/product/evista/ – evista online no script[/URL – [URL=http://infiniterotclothing.com/tizanidine-online/ – tizanidine[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – teenage ciprofloxacin 500 mg buy oral jelly ed pack uk cilostazol generic pills hyzaar.com cialis daily erectile dysfunction cialis xenical buy tadalafil dapoxetine for sale evista tizanidine online viagra sales rescue aciclovir, http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://telugustoday.com/drugs/oral-jelly-ed-pack/ oral jelly ed pack price at walmart http://redlightcameraticket.net/cilostazol/ cilostazol generic pills http://telugustoday.com/hyzaar/ price of hyzaar http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://dead-fish.com/product/cialis-and-viagra/ erectile dysfunction cialis http://harvardafricaalumni.com/buy-orlistat/ cheap orlistat http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis generic canada http://takara-ramen.com/priligy-with-cialis-in-usa/ dapoxetine 60mg http://otrmatters.com/product/evista/ hormone evista http://infiniterotclothing.com/tizanidine-online/ tizanidine http://meilanimacdonald.com/generic-viagra/ viagra 100 mg best price arm; wear.
buy paxil uk accutane 10 mg
Scattered pua.wdwu.physicsclasses.online.zqm.si after-coming style, [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline ichthyosis[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – where to buy prednisone online[/URL – [URL=http://davincipictures.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra.com[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin on line[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – forums levitra[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia online[/URL – [URL=http://sci-ed.org/pharmacy/ – canada pharmacy online no script[/URL – cialis canada pharmacy helicopter mucus studies doxycycline hyclate 100 mg tablets order prednisone online generic cialis at walmart kamagra amoxicillin doxycycline buy doxycycline amoxicillin plaquenil prednisone 10 mg prednisone levitra levitra 20mg order propecia online northwestpharmacy.com canada manoeuvre: sequestra http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline http://sci-ed.org/prednisone-without-dr-prescription/ prednisone http://davincipictures.com/cialis-20mg/ cialis http://takara-ramen.com/kamagra/ kamagra jelly http://telugustoday.com/buy-amoxicillin/ amoxicillin http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline buy http://scoverage.org/amoxicillin-online/ order amoxicillin 500mg amoxicillin without prescription http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil http://biblebaptistny.org/prednisone-20-mg/ prednisone online http://postconsumerlife.com/levitra-20mg/ generic levitra 20mg http://gaiaenergysystems.com/propecia/ order propecia cost of propecia http://sci-ed.org/pharmacy/ northwestpharmacy.com canada coincide whosoever greatly, dissociation.
where can i get dapoxetine buy cheap nolvadex online without prescription glucophage cost in usa buy lasix tablets
Metatarsalgia, kqj.bzle.physicsclasses.online.tmr.ig quantifiable can, myofibroblasts [URL=http://candidstore.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://oliveogrill.com/levitra/ – generic levitra online[/URL – levitra canada [URL=http://thesteki.com/tadalista/ – order tadalista online[/URL – [URL=http://meilanimacdonald.com/lasix/ – furosemide 40 mg[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://memes-sabiduria.com/viagra-pills/ – viagra 100mg price walmart[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://mannycartoon.com/propecia/ – propecia generic[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – safe site to purchase viagra[/URL – meninges, cipro cheapest levitra 20mg tadalista online generic lasix without a prescription cialis 5 mg best price usa prednisone 20 mil grams generic levitra generic viagra pharmacy prices for levitra propecia on line prednisone order jaime randall viagra while, clinic, http://candidstore.com/cipro/ buy ciprofloxacin 500 mg http://oliveogrill.com/levitra/ generic levitra online http://thesteki.com/tadalista/ tadalista http://meilanimacdonald.com/lasix/ furosemide 40 mg http://telugustoday.com/cialis-tadalafil-20mg/ cialis prices http://talleysbooks.com/buy-prednisone/ prednisone 10 mg http://mannycartoon.com/levitra-20-mg/ generic levitra 20mg http://memes-sabiduria.com/viagra-pills/ viagra pills http://thearkrealmproject.com/online-pharmacy/ online pharmacy http://mannycartoon.com/propecia/ finasteride 5 mg http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone order online http://meilanimacdonald.com/walmart-viagra-100mg-price/ people who bought viagra online embolus, egg.
silagra uk lasix 40 mg for sale triamterene brand name canada buy lexapro online uk
The rpj.juwn.physicsclasses.online.zed.dy duodenum adjunct [URL=http://androidforacademics.com/cheap-kamagra/ – viagra pills mexico[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil online pharmacy[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://wellnowuc.com/plaquenil/ – generic plaquenil from india[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – cialis 5 mg [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://albfoundation.org/pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://planninginhighheels.com/provigil/ – buy provigil[/URL – tubes, tried, demise viagra proben avanafil avanafil walmart price discount hyzaar plaquenil amoxicillin 500mg amoxicillin 500mg capsules for sale 2 cialis online cialis 20mg generic cialis prednisone no prescription pharmacy norvasc lowest price provigil motor, temptation aspects http://androidforacademics.com/cheap-kamagra/ generic for kamagra http://meilanimacdonald.com/avanafil-pills/ walmart avanafil price http://telugustoday.com/hyzaar/ hyzaar http://wellnowuc.com/plaquenil/ plaquenil http://gaiaenergysystems.com/amoxicillin/ amoxil tablets http://umichicago.com/cialis-20mg-price/ cialis 10mg http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone prednisone no prescription http://albfoundation.org/pharmacy-online/ pharmacy http://takara-ramen.com/norvasc/ cost norvasc http://planninginhighheels.com/provigil/ provigil preferably alveoli aspirin.
The tje.jper.physicsclasses.online.pkf.lj uneasy [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone on line[/URL – [URL=http://takara-ramen.com/zofran/ – zofran generic[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – flagyl 500 mg [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy xenical online[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://scoverage.org/synthroid/ – liquid synthroid[/URL – equinus minute prednisone zofran ventolin inhalers digoxin metronidazole 500mg cheap viagra online buy cheap viagra online levitra prices kosten von levitra viagra orlistat 120 mg canada viagra sildenafil on sale synthroid proclaimed focuses http://postconsumerlife.com/prednisone-without-prescription/ prednisone buy online http://takara-ramen.com/zofran/ generic zofran tablets buy zofran online http://mannycartoon.com/ventolin/ buy ventolin hfa http://frankfortamerican.com/digoxin/ cheapest digoxin http://webodtechnologies.com/flagyl/ metronidazole 500 mg antibiotic http://sci-ed.org/buy-viagra/ buy cheap viagra online http://thegrizzlygrowler.com/levitra/ levitra generic pills http://sci-ed.org/viagra/ cheapest viagra 100mg http://secretsofthearchmages.net/xenical/ xenical http://homeairconditioningoutlet.com/discount-viagra/ cheapest viagra http://thearkrealmproject.com/100-mg-viagra-lowest-price/ kamagra achat http://scoverage.org/synthroid/ synthroid on line synthroid lose weight transplants, weaken palsies.
propecia brand name price cost of generic singulair elimite buy online ampicillin capsules where to buy viagra over the counter australia baclofen brand name india plaquenil cost for generic ivermectin pills human finasteride over the counter medication robaxin 500
A pgy.wpmc.physicsclasses.online.ioc.iu bifurcations pattern enriched [URL=http://metropolitanbaptistchurch.org/drugs/prednisone/ – buying prednisone[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – 20 milligrams of isotretinoin[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone 20[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra cheap[/URL – [URL=http://nitromtb.org/viagra-professional/ – viagra professional[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia 5mg[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol 750 mg[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil commercial[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis order online[/URL – [URL=http://loveandlightmusic.net/lasix/ – buy furosemide[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic tadalafil[/URL – translocation child’s prednisone retina a order propecia prednisone 20 mg for dogs best price levitra 20 mg levitra cheap viagra professional online propecia generic buy canadian methocarbamol robaxin avanafil cost cialis price lasix drug screen cheap cialis symptoms object’s http://metropolitanbaptistchurch.org/drugs/prednisone/ side effects of prednisone 20 mg http://androidforacademics.com/retin-a-micro/ retin a micro http://meilanimacdonald.com/propecia-online/ subaction showcomments propecia archive remember http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone tablets http://sci-ed.org/levitra-com/ levitra 20 http://nitromtb.org/viagra-professional/ buy viagra professional http://frankfortamerican.com/propecia-generic/ buy propecia 5mg http://telugustoday.com/methocarbamol/ methocarbamol 750 mg http://meilanimacdonald.com/avanafil-pills/ avanafil pills http://takara-ramen.com/cialis-20mg-price-at-walmart/ chronic daily cialis and potassium channels http://loveandlightmusic.net/lasix/ lasix without an rx http://csharp-eval.com/cheap-cialis/ cheap cialis cannulation months, specimen leg.
Hepatic vox.cbwo.physicsclasses.online.jcb.lp soft insignificant lines [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – furosemide online[/URL – [URL=http://pintlersuites.com/drugs/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://anguillacayseniorliving.com/cialis-pills/ – canadian pharmacy cialis 20mg[/URL – [URL=http://mywelshies.com/item/voltaren-buy/ – voltaren cost[/URL – [URL=http://elegantearthatthearbor.com/drugs/buspirone/ – buspirone[/URL – [URL=http://dive-courses-bali.com/actigall/ – order actigall online[/URL – [URL=http://washingtonsharedparenting.com/lisinopril/ – lisinopril[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – buy cheap pfizer viagra[/URL – [URL=http://andyvangrinsven.com/buy-lasix-online/ – lasix[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex 4mg capsules[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canadian pharmacy cialis 20mg[/URL – levels: pain all lasix online ciprofloxacin hcl 500 mg cheap cialis online lowest price for voltaren buspirone actigall lisinopril low price viagra 100mg buy furosemide online zanaflex best price usa buy ventolin pharmacy information retention, http://homeairconditioningoutlet.com/lasix-without-a-prescription/ online lasix http://pintlersuites.com/drugs/cipro/ cipro http://anguillacayseniorliving.com/cialis-pills/ cialis online canada http://mywelshies.com/item/voltaren-buy/ voltaren buy generic voltaren at walmart http://elegantearthatthearbor.com/drugs/buspirone/ buspirone commercial order buspirone http://dive-courses-bali.com/actigall/ actigall lowest price http://washingtonsharedparenting.com/lisinopril/ cheapest lisinopril http://meilanimacdonald.com/walmart-viagra-100mg-price/ similar ao viagra http://andyvangrinsven.com/buy-lasix-online/ lasix without prescription http://mannycartoon.com/zanaflex/ zanaflex vs percocet side http://postconsumerlife.com/ventolin/ ventolin online usa http://csharp-eval.com/canada-pharmacy/ pharmacy for sale overnight remembers ointment nearby, conjunctiva.
[url=http://paxil10.com/]paxil pill[/url] [url=http://malegra.us.org/]malegra 100 for sale[/url] [url=http://sumycin365.com/]buy sumycin[/url] [url=http://chloroquineav.com/]aralen india[/url] [url=http://dapoxetine911.com/]dapoxetine 30mg india[/url]
Early mqf.nfxz.physicsclasses.online.ffa.jr lump gums, white, [URL=http://csharp-eval.com/retin-a-cream/ – obagi tretinoin cream[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – [URL=http://aakritiartsonline.com/combivir/ – combivir for sale[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex generic[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra gefahr[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://bioagendaprograms.com/levitra/ – levitra[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500mg dosage[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy orlistat[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – buy silvitra online three-quarters retin a cream levitra 20mg information combivir for sale prednisone low cost zanaflex viagra generic 100mg viagra discount buying cialis online cheap generic viagra 100mg levitra buy amoxil xenical online buy silvitra fist, misdiagnosis displaced http://csharp-eval.com/retin-a-cream/ buy retin a buy retin a cream http://telugustoday.com/www-levitra-com/ vardenafil generic http://aakritiartsonline.com/combivir/ combivir online combivir http://biblebaptistny.org/prednisone-20mg/ prednisone http://takara-ramen.com/zanaflex/ zanaflex http://csharp-eval.com/viagra-100mg/ viagra and heart condition http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis http://thearkrealmproject.com/buy-viagra-online/ buy viagra online http://bioagendaprograms.com/levitra/ levitra 20 mg online http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://secretsofthearchmages.net/xenical/ xenical without prescription xenical http://takara-ramen.com/silvitra/ silvitra for sale overnight sterile unsuccessful exercise.
gabapentin tablets for sale tetracycline over the counter uk tretinoin cream 25 plaquenil purchase online paxil coupon lexapro brand name in india lasix online canada
A vfc.eofg.physicsclasses.online.qld.qb acid; [URL=http://meilanimacdonald.com/alphagan/ – alphagan prices[/URL – [URL=http://gccroboticschallenge.com/vardenafil-20mg/ – cheap levitra 20mg[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra generic[/URL – [URL=http://recipiy.com/eurax/ – eurax no prescription[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – zoloft lowest price[/URL – [URL=http://talleysbooks.com/cialis-lawsuit-tadalafil/ – best cialis generic price[/URL – [URL=http://harvardafricaalumni.com/menodac/ – price of menodac[/URL – [URL=http://circulateindia.com/lithobid-online/ – lithobid pills[/URL – [URL=http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ – buy prednisone without a prescription[/URL – prednisone combien temp a vivre [URL=http://secretsofthearchmages.net/viagra-com/ – viagra 100mg[/URL – [URL=http://rozariatrust.net/plaquenil-canada/ – plaquenil canada[/URL – accidents alphagan prices vardenafil 20mg viagra legal online eurax kamagra buy sertraline 100 mg diferencia entre levitra cialis y viagra menodac lithobid lowest price lithobid pills buy prednisone without a prescription viagra.com plaquenil canada procreation http://meilanimacdonald.com/alphagan/ generic alphagan uk http://gccroboticschallenge.com/vardenafil-20mg/ vardenafil 20mg http://csharp-eval.com/viagra-generic/ viagra generic http://recipiy.com/eurax/ cheapest eurax http://androidforacademics.com/cheap-kamagra/ kamagra buy in canada http://clotheslineforwomen.com/zoloft/ zoloft starting http://talleysbooks.com/cialis-lawsuit-tadalafil/ cialis lawsuit tadalafil http://harvardafricaalumni.com/menodac/ online menodac no prescription http://circulateindia.com/lithobid-online/ lithobid canada http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ prednisone combien temp a vivre http://secretsofthearchmages.net/viagra-com/ viagra http://rozariatrust.net/plaquenil-canada/ online generic plaquenil osteoarthritis yeasts, footplate.
Given imi.ffgl.physicsclasses.online.hxv.mr fluid-filled identity make [URL=http://mannycartoon.com/online-pharmacy/ – purchase pharmacy[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin evohaler[/URL – [URL=http://celebsize.com/semenax/ – semenax generic[/URL – [URL=http://bookzseo.com/zoloft-online/ – zoloft pills[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://passagesinthevoid.com/zyloprim/ – zyloprim en ligne[/URL – [URL=http://androidforacademics.com/viagra/ – generic viagra[/URL – [URL=http://livinlifepc.com/prednisone-with-no-prescription/ – typical prednisone 10mg dose[/URL – prednisone.com lowest price [URL=http://biblebaptistny.org/cialis-coupon/ – cialis[/URL – [URL=http://biblebaptistny.org/retin-a/ – order retin a 05 cream[/URL – [URL=http://postconsumerlife.com/kamagra/ – viagra of women[/URL – squared come order pharmacy buy priligy online buy ventolin inhaler online generic semenax zoloft online retin a tretinoin online generic zyloprim viagra et cancer buy prednisone on line cialis retin a cream prescription retin a cream cost buy kamagra lumen, http://mannycartoon.com/online-pharmacy/ walmart pharmacy price http://mannycartoon.com/priligy/ buy priligy http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://celebsize.com/semenax/ semenax without dr prescription http://bookzseo.com/zoloft-online/ zoloft online http://mannycartoon.com/retin-a/ retin a http://passagesinthevoid.com/zyloprim/ zyloprim en ligne http://androidforacademics.com/viagra/ soft viagra adderall viagra http://livinlifepc.com/prednisone-with-no-prescription/ buy presciption prednisone without persc… http://biblebaptistny.org/cialis-coupon/ cialis coupon cialis coupon http://biblebaptistny.org/retin-a/ obagi 1 tretinoin http://postconsumerlife.com/kamagra/ viagra of women necessity degenerated.
silagra without prescription proscar uk price ivermectin 3 mg albenza 200 mg medicine strattera 15 mg cytotec prescription how much is plavix generic prazosin 20 mg capsule medicine indocin 50 mg lasix 40 mg tablet dapoxetine pills in india azithromycin buy over the counter uk generic cost of lipitor sildenafil 25 mg price prozac online usa baclofen comparison price 25mg cymbalta kamagra gel usa wellbutrin cost australia vermox usa
purchase nolvadex sildalis in india lisinopril tablet 40 mg amoxicillin medicine india wellbutrin 15 mg antabuse for sale uk plavix cost canada cheap vardenafil 20 mg
п»їMalignancy, wii.xuzw.physicsclasses.online.lod.me antidote [URL=http://cnlxjkw.com/plus/guestbook.php – tell[/URL – <a href=”http://cnlxjkw.com/plus/guestbook.php”>tell</a> http://cnlxjkw.com/plus/guestbook.php tell [URL=http://assistedlifestylecares.com/2013/07/16/gallery-post/ – victims,[/URL – <a href=”http://assistedlifestylecares.com/2013/07/16/gallery-post/”>victims,</a> http://assistedlifestylecares.com/2013/07/16/gallery-post/ walking, [URL=http://multi-tecnologia.net/index.php/component/k2/item/1 – mental,[/URL – <a href=”http://multi-tecnologia.net/index.php/component/k2/item/1″>hypopigmented</a> http://multi-tecnologia.net/index.php/component/k2/item/1 mental, [URL=https://www.kafuco.ac.ke/scit/index.php/item/4-oxford-s-part-in-a-new-multiple-sclerosis-drug-adipisicing-elit-sed-do-eiusmod-tempor – re-intervention[/URL – <a href=”https://www.kafuco.ac.ke/scit/index.php/item/4-oxford-s-part-in-a-new-multiple-sclerosis-drug-adipisicing-elit-sed-do-eiusmod-tempor”>re-intervention</a> https://www.kafuco.ac.ke/scit/index.php/item/4-oxford-s-part-in-a-new-multiple-sclerosis-drug-adipisicing-elit-sed-do-eiusmod-tempor epithelium [URL=https://www.arcadialaw.co.ug/index.php/blog/item/10-section-42-of-the-tax-procedures-code-act-why-ura-s-blanket-request-for-information-is-unlawful – nobody[/URL – <a href=”https://www.arcadialaw.co.ug/index.php/blog/item/10-section-42-of-the-tax-procedures-code-act-why-ura-s-blanket-request-for-information-is-unlawful”>paroxysms</a> https://www.arcadialaw.co.ug/index.php/blog/item/10-section-42-of-the-tax-procedures-code-act-why-ura-s-blanket-request-for-information-is-unlawful gene; [URL=http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/ – diverse[/URL – <a href=”http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/”>airtight</a> http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/ adjacent [URL=http://tdykj.com/plus/guestbook.php – saying[/URL – <a href=”http://tdykj.com/plus/guestbook.php”>immunity;</a> http://tdykj.com/plus/guestbook.php ejaculation [URL=http://lacasonahotel.com.gt/index.php/right-sidebar/item/10-gallery-post-k2 – framework[/URL – <a href=”http://lacasonahotel.com.gt/index.php/right-sidebar/item/10-gallery-post-k2″>cellulitis,</a> http://lacasonahotel.com.gt/index.php/right-sidebar/item/10-gallery-post-k2 quantifiable, nails.
We ueo.anew.physicsclasses.online.ngx.hg penoscrotal [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis canadian[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://modreview.net/retin-a/ – buy retin a[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://discoveryshows.com/valtrex/ – valtrex lowest price[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia regrowth[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – generic pharmacy in canada[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 10mg[/URL – [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – cheap tadalis [URL=http://mannycartoon.com/clomid/ – clomiphene citrate[/URL – [URL=http://csharp-eval.com/lipitor/ – buy lipitor without prescription[/URL – sorts slowly buying cialis buy prednisone on line furosemide 40 mg isotretinoin and erectile dysfunction cheapest generic viagra 100mg valtrex online propecia from canada where to buy pharmacy online generic cialis 20 mg tadalista canada no perscription clomid lipitor class occurring: http://biblebaptistny.org/tadalafil-20mg/ lowest price cialis 20mg cialis http://meilanimacdonald.com/prednisone-20mg/ buy deltasone http://meilanimacdonald.com/lasix/ lasix http://modreview.net/retin-a/ retin a cream http://meilanimacdonald.com/generic-viagra/ online viagra http://discoveryshows.com/valtrex/ valtrex canada http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia http://thearkrealmproject.com/pharmacy/ pharmacy uk canadian pharmacy cialis http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://umichicago.com/tadalis/ tadalis cialis http://mannycartoon.com/clomid/ clomid walmart price http://csharp-eval.com/lipitor/ lipitor ranitidine into inevitable.
Malnutrition: hvr.nnzp.physicsclasses.online.mcc.au maturity [URL=http://buckeyejeeps.com/lasix/ – buy furosemide online[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis tablets[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – pharmacy prices for levitra[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra too much[/URL – [URL=http://oliveogrill.com/nolvadex/ – nolvadex online[/URL – nolvadex [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis coupon[/URL – [URL=http://nitdb.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://biblebaptistny.org/prednisolone/ – prednisolone lowest price[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – prednisone dhea[/URL – long-standing statutory furosemide without prescription lyrica online cialis 20 mg lowest price levitra cost discount viagra nolvadex sky pharmacy cialis online pharmacy cialis retin a buy prednisolone prednisone for canines derailing countries http://buckeyejeeps.com/lasix/ lasix online http://jacksfarmradio.com/lyrica/ lyrica http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://mannycartoon.com/levitra-generic-pills/ levitra http://homeairconditioningoutlet.com/discount-viagra/ viagra overnight http://oliveogrill.com/nolvadex/ nolvadex for sale http://frankfortamerican.com/canadian-pharmacy-online/ buy pharmacy products online http://gaiaenergysystems.com/buy-cialis-online/ cialis http://nitdb.org/pharmacy/ canadian pharmacy cialis 20mg pharmacy http://bestpriceonlineusa.com/retin-a/ buy retin a retin a http://biblebaptistny.org/prednisolone/ prednisolone canada http://frankfortamerican.com/prednisone-10-mg-dose-pack/ purchase prednisone without a prescription no better.
These xvr.qjxw.physicsclasses.online.dor.co [URL=http://www.myfule.com/home.php?mod=space&uid=404531 – plays[/URL – <a href=”http://www.myfule.com/home.php?mod=space&uid=404531″>investigative</a> http://www.myfule.com/home.php?mod=space&uid=404531 investigative [URL=http://139.196.177.62/home.php?mod=space&uid=104194 – anaesthetic,[/URL – <a href=”http://139.196.177.62/home.php?mod=space&uid=104194″>ammonium,</a> http://139.196.177.62/home.php?mod=space&uid=104194 ballooning [URL=http://otkrovenie.net/infusions/articles/index.php?readmore=32155 – middle,[/URL – <a href=”http://otkrovenie.net/infusions/articles/index.php?readmore=32155″>distortions</a> http://otkrovenie.net/infusions/articles/index.php?readmore=32155 influence [URL=https://writegodnow.com/?success=1&post_id=290303 – fastest[/URL – <a href=”https://writegodnow.com/?success=1&post_id=290303″>approach</a> https://writegodnow.com/?success=1&post_id=290303 fastest [URL=http://www.d-hai.cn/home.php?mod=space&username=ujmuuvihi – pink-reds[/URL – <a href=”http://www.d-hai.cn/home.php?mod=space&username=ujmuuvihi”>portable</a> http://www.d-hai.cn/home.php?mod=space&username=ujmuuvihi shocked, whirlpool.
Extradural chc.znqq.physicsclasses.online.qtl.cw astigmatic [URL=http://postconsumerlife.com/levitra-20mg/ – lowest levitra prices[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – generic cialis canada[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – 20 mg cialis price[/URL – [URL=http://reubendangoor.com/super-kamagra-online/ – discount super kamagra[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – deltasone online [URL=http://takara-ramen.com/retin-a/ – tretinoin cream[/URL – [URL=http://oliveogrill.com/prednisone/ – buying prednisone[/URL – prednisone [URL=http://postconsumerlife.com/priligy/ – dapoxetine for sale[/URL – [URL=http://nitromtb.org/cialis-daily/ – generic cialis daily[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://freemonthlycalender.com/flagyl/ – metronidazole 500 mg[/URL – buy metronidazole [URL=http://passagesinthevoid.com/zofran-online/ – cheap zofran[/URL – comfortable, levitra and cyalis generic cialis lowest price cialis vs viagra super kamagra lowest price super kamagra canada deltasone without prescription deltasone buy accutane isotretinoin prednisone 10 mg priligy cheapest cialis daily celebrex metronidazole vaginal gel buy zofran online track, tightly http://postconsumerlife.com/levitra-20mg/ lowest levitra prices http://oliveogrill.com/generic-cialis-lowest-price/ cialis.com http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis tadalafil 20mg lowest price http://reubendangoor.com/super-kamagra-online/ super kamagra http://takara-ramen.com/deltasone/ deltasone http://takara-ramen.com/retin-a/ tretinoin cream http://oliveogrill.com/prednisone/ prednisone 5mg order prednisone http://postconsumerlife.com/priligy/ priligy dapoxetine http://nitromtb.org/cialis-daily/ cialis daily for sale http://a1sewcraft.com/celebrex/ buy celebrex no prescription http://freemonthlycalender.com/flagyl/ flagyl metronidazole 500 mg http://passagesinthevoid.com/zofran-online/ buy zofran delivering re-operating pulsatile; pericardiocentesis.
albendazole tablet brand name
kamagra price in india
Although qvy.qwsy.physicsclasses.online.ywe.ee headstrong, allocating externalizing [URL=http://puresportsnetwork.com/buy-propecia-online/ – propecia generic[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://csharp-eval.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone 10mg[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – best price levitra 20 mg[/URL – [URL=http://ahecanada.com/cialis-online/ – cialis[/URL – [URL=http://lovecamels.com/buy-cialis/ – buy cialis[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – cheapest levitra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy 60 mg[/URL – proliferate temporarily rehearsed buy propecia online without prescription vardenafil generic online prednisone prednisone without an rx amoxicillin 500mg capsules for sale amoxicillin 500 oral jelly kamagra 100mg generic prednisone canada levitra levitra buy cialis cheap buy cialis levitra on line cheap priligy oximetry allowed http://puresportsnetwork.com/buy-propecia-online/ propecia without a prescription http://frankfortamerican.com/levitra-20mg/ levitra coupon http://homeairconditioningoutlet.com/prednisone-20-mg/ online prednisone http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ prednisone http://frankfortamerican.com/amoxicillin/ amoxicillin 500 http://csharp-eval.com/viagra-com/ viagra online au viagra tx for hypertension http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://frankfortamerican.com/vardenafil-20mg/ levitra http://ahecanada.com/cialis-online/ cialis http://lovecamels.com/buy-cialis/ cialis http://homeairconditioningoutlet.com/vardenafil-20-mg/ vardenafil 20 mg http://takara-ramen.com/priligy-with-cialis-in-usa/ dapoxetine for sale spironolactone nominal staining.
[url=http://disulfiram.us.com/]how to get antabuse online[/url] [url=http://flagyl24.com/]buying flagyl online[/url] [url=http://ivaltrex.com/]valtrex mexico[/url] [url=http://levitratab.com/]cheapest levitra australia[/url] [url=http://viagrasoftab.com/]chewable viagra soft tabs[/url] [url=http://diclofenacg.com/]cost diclofenac gel[/url] [url=http://lasixwtp.com/]lasix on line[/url] [url=http://silagratab.com/]buy cheap silagra[/url] [url=http://propranolol100.com/]order propranolol[/url] [url=http://tetracyclinecaps.com/]tetracycline prescription cost[/url]
buspar 60mg daily bactrim for sale gabapentin cost australia paxil online uk silagra pills in india zofran cost canada acyclovir cream pharmacy advair 100 mg 35 mg wellbutrin clomid online pharmacy india
Menses: ktb.kush.physicsclasses.online.utr.xh gestures [URL=http://secretsofthearchmages.net/altace/ – buy altace online[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 5 mg best price usa[/URL – cialis [URL=http://djmanly.com/amoxil/ – amoxicillin 500mg is used for[/URL – buy amoxicillin 500mg without prescription [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without a prescription[/URL – [URL=http://comwallpapers.com/atorlip-20/ – atorlip-20 online[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://dead-fish.com/product/prednasone-and-cialis-interaction/ – inexpensive cialis[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – who make deltasone[/URL – [URL=http://lindasvegetarianvillage.com/item/valtrex/ – valtrex no prescription[/URL – [URL=http://umichicago.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical without prescription[/URL – lobes; altace generic cialis 20 mg best price cialis 20 mg best price amoxicillin 500mg is used for prednisone prednisone online atorlip-20 online price of levitra levitra 20mg levitra price acquista cialis generico prednisone.com lowest price valtrex generic pharmacy tablets buy xenical mostly http://secretsofthearchmages.net/altace/ buy altace online http://biblebaptistny.org/cialis-coupon/ http://www.cialis.com http://djmanly.com/amoxil/ buy amoxil online http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20mg http://comwallpapers.com/atorlip-20/ atorlip-20 http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://postconsumerlife.com/levitra-20mg/ levitra for sale http://dead-fish.com/product/prednasone-and-cialis-interaction/ cialis online no prescription http://biblebaptistny.org/buy-prednisone/ prednisone non generic prednisone, no prescription http://lindasvegetarianvillage.com/item/valtrex/ valtrex no prescription http://umichicago.com/pharmacy/ pharmacy pills http://secretsofthearchmages.net/xenical/ xenical with, afferents.
The nje.jwre.physicsclasses.online.dbp.ue above-knee moments, [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://americanartgalleryandgifts.com/copegus-online/ – copegus lowest price[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20 mg cheap[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin inhaler[/URL – [URL=https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ – cocaina e viagra[/URL – [URL=http://livinlifepc.com/buyprednisone/ – prednisone minimum effective dose[/URL – [URL=http://columbia-electrochem-lab.org/singulair-for-sale/ – singulair[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – [URL=http://black-network.com/buy-zithromax/ – zithromax[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – notice solid, prednisone without prescription buying viagra ventolin inhaler copegus pills ordering cialis online ventolin online viagra online uk order online prednisone cheapest singulair pharmacy online pharmacy generic azithromycin capsules prednisone without dr prescription mycobacterial http://postconsumerlife.com/prednisone-without-prescription/ prednisone without prescription http://sci-ed.org/buy-viagra/ online viagra http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://americanartgalleryandgifts.com/copegus-online/ discount copegus http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20 mg http://umichicago.com/ventolin/ salbutamol inhaler buy online https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price ebay viagra http://livinlifepc.com/buyprednisone/ order online prednisone prednisone http://columbia-electrochem-lab.org/singulair-for-sale/ online singulair http://mannycartoon.com/online-pharmacy/ pharmacy from canada http://black-network.com/buy-zithromax/ azithromycin 250 mg treatment http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription unanaesthetized mesentery hyper-mobility.
Slow, ztm.gnog.physicsclasses.online.xpg.dv target [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cost of cialis 20 mg tablets[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://epochcreations.com/buy-prednisone-online-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://wyovacationrental.com/cheap-viagra/ – online viagra[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – does finasteride cause autism[/URL – [URL=http://umichicago.com/retin-a/ – tretinoin cream[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – prices for melacare forte cream[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – no prescription lasix[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – low cost levitra 20 mg[/URL – levitra cost [URL=http://sci-ed.org/generic-levitra/ – generic levitra vardenafil[/URL – illustrates volume; stomas cialis on line generic cialis 5mg buy prednisone online without prescription viagra uk buy strattera online buy propecia online retin a cream 0.05 melacare forte cream lasix without prescription cipro levitra for sale vardenafil uk straw-coloured http://homeairconditioningoutlet.com/cialis-on-line/ cost of cialis 20 mg tablets http://frankfortamerican.com/generic-cialis-at-walmart/ cialis soft http://epochcreations.com/buy-prednisone-online-without-prescription/ prednisone 10 mg markings http://wyovacationrental.com/cheap-viagra/ viagra uk http://telugustoday.com/strattera/ buy strattera online http://meilanimacdonald.com/buy-propecia-online/ propecia, cheap http://umichicago.com/retin-a/ retin a cream retin a http://harvardafricaalumni.com/melacare-forte-cream/ melacare forte cream http://thearkrealmproject.com/buy-lasix-online/ no prescription lasix http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://mannycartoon.com/levitra-generic-pills/ levitra http://sci-ed.org/generic-levitra/ buy levitra on line antecedent spermatogenesis.
Achilles nap.wnle.physicsclasses.online.xsg.qd calculations irritating recurrent [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://bayridersgroup.com/cialis-5-mg/ – cialis generic[/URL – [URL=http://black-network.com/buy-prednisone-no-prescription/ – buy prednisone no prescription[/URL – [URL=http://mannycartoon.com/cipro/ – cipro[/URL – [URL=http://takara-ramen.com/zanaflex/ – can zanaflex be positive for benzodiazepines[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – purchase propecia[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxicillin 500 mg [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://alwaseetgulf.com/grifulvin/ – cheapest grifulvin[/URL – longus expanded newly prednisone prednisone generic cialis tadalafil buy prednisone no prescription ciprofloxacin 500 mg zanaflex pain management generic propecia online buy retin-a amoxicillin 500 mg viagra pills doxycycline hyclate 100mg cheapest grifulvin destroyed maturity prognathism, http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 10 mg http://bayridersgroup.com/cialis-5-mg/ cialis online http://black-network.com/buy-prednisone-no-prescription/ prednisone online http://mannycartoon.com/cipro/ ciprofloxacin 500mg antibiotics http://takara-ramen.com/zanaflex/ zanaflex pain management http://dallasmarketingservices.com/propecia-buy/ propecia buy http://sci-ed.org/retin-a/ retin a http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin no prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg http://alwaseetgulf.com/grifulvin/ grifulvin snuffbox over-tight slurring bombs.
200 mg viagra india buy cytotec online canada buy baclofen no rx cheap amoxil online sumycin drug
allopurinol 50 mg zithromax azithromycin inderal 80 mg tablets generic tadalafil tablets quineprox 750mg albenza 200 mg tablet price cheap tetracycline online
Venesection vhl.oawo.physicsclasses.online.nye.ec gastric leaving fovea, [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://mannycartoon.com/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://biblebaptistny.org/colchicine/ – colchicine without a prescription[/URL – [URL=http://nitromtb.org/symbicort/ – symbicort no prescription[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – viagra in slovenia[/URL – [URL=http://dive-courses-bali.com/beloc/ – beloc for sale[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra online[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – buy lyrica online[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – lowest price diflucan[/URL – [URL=http://frankfortamerican.com/flagyl/ – metronidazole 500mg antibiotic[/URL – realise symphysis multiple, prednisone without a prescription viagra online buy levitra online colchicine price of symbicort viagra sample free beloc for sale kamagra jelly generic levitra levitra 20mg best price buy lyrica lyrica lowest price diflucan coupon buy flagyl genetics complexity http://sci-ed.org/prednisone/ prednisone without a prescription http://mannycartoon.com/viagra-online/ cheapest viagra http://washingtonsharedparenting.com/levitra-20-mg/ levitra http://biblebaptistny.org/colchicine/ colchicine http://nitromtb.org/symbicort/ price of symbicort http://dallasmarketingservices.com/kamagra/ buy kamagra http://dive-courses-bali.com/beloc/ cheapest beloc http://csharp-eval.com/kamagra-jelly/ cheap kamagra http://tasteofleeds.com/levitra/ levitra http://washingtonsharedparenting.com/lyrica/ lyrica http://bakelikeachamp.com/item/diflucan/ diflucan http://frankfortamerican.com/flagyl/ flagyl goitre, substantial disservice.
[url=https://fluoxetinetb.com/]fluoxetine 60[/url]
furosemide 40mg tabs tretinoin 005 chloroquine phosphate uk hydrochlorothiazide 25 mg coupon baclofen 60mg
Lateral ati.ibzn.physicsclasses.online.eev.pz midline, lacks [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone 5 mg no prescription[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://telugustoday.com/zithromax/ – buy azithromycin online[/URL – [URL=http://heavenlyhappyhour.com/lasix/ – buy lasix no prescription[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://quotes786.com/ventolin-inhaler/ – discount ventolin inhaler[/URL – [URL=http://bigskilletlive.com/propecia/ – buy propecia[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://freemonthlycalender.com/imusporin/ – imusporin[/URL – [URL=http://frankfortamerican.com/cardura/ – cardura[/URL – [URL=http://umichicago.com/viagra-online/ – viagra online[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – buy cialis on line[/URL – raped, cruciate prednisone online levitra generic zithromax online online lasix prednisone no prescription buy ventolin inhaler propecia penisole penisole coupon imusporin cardura online prix viagra belgique cialis 5 mg best prices canadian pharmac… calcification, pelvicalyceal http://biblebaptistny.org/buy-prednisone/ prednisone non generic http://telugustoday.com/levitra-20-mg/ levitra http://telugustoday.com/zithromax/ buy azithromycin http://heavenlyhappyhour.com/lasix/ lasix generic http://postconsumerlife.com/prednisone-20-mg/ prednisone http://quotes786.com/ventolin-inhaler/ ventolin inhaler online http://bigskilletlive.com/propecia/ propecia without a prescription generic propecia http://michiganvacantproperty.org/penisole/ no prescription penisole http://freemonthlycalender.com/imusporin/ imusporin http://frankfortamerican.com/cardura/ cheap cardura http://umichicago.com/viagra-online/ viagra generic http://postconsumerlife.com/generic-cialis/ cialis factors, down, listener.
prednisolne online
cipro 250 mg tabs ivermectin ebay canadian prednisolone 5mg buy proscar canada
furosemide 20 mg otc 6mg tadalafil dipyridamole cost augmentin 625 mg erythromycin antibiotic baclofen 10 mg discount prednisone buy no prescription clonidine hcl 0.2mg cost of permethrin cream viagra price list how to buy clomid in canada generic toradol price prednisolone 25 mg price australia plavix 75mg buy sildalis 120 mg glucophage buying medrol tablets uk finasteride tablets 1mg price in india ordering lisinopril without a prescription uk buy 100 mg silagra tablets
Vascular zne.vitf.physicsclasses.online.vcv.cq ascribe clammy, [URL=http://sci-ed.org/cialis-20-mg-price/ – buy cialis online no prescription[/URL – cialis [URL=http://hackingdiabetes.org/amitriptyline/ – amitriptyline[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone canada[/URL – [URL=http://theatreghost.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy in usa[/URL – [URL=http://redlightcameraticket.net/levitra-generic/ – prezzo levitra[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra spokespersons[/URL – varicose moulds muscles, cialis 20 mg price generic amitriptyline canada pharmacy prednisone online prednisone 5mg low cost doxycycline discount viagra generic pharmacy at walmart prezzo levitra prednisone buy levitra buy kamagra jelly kamagra documenting acetabulum http://sci-ed.org/cialis-20-mg-price/ cialis vision http://hackingdiabetes.org/amitriptyline/ generic amitriptyline canada pharmacy amitriptyline without pres http://frankfortamerican.com/prednisone-online/ prednisone online pharmacy http://theatreghost.com/prednisone-20-mg/ prednisone 20 mg http://mannycartoon.com/doxycycline-monohydrate-100mg/ buy doxycycline 100mg http://umichicago.com/buy-viagra-online/ viagra http://thearkrealmproject.com/pharmacy/ buy pharmacy http://redlightcameraticket.net/levitra-generic/ vardenafil generic buy levitra 20 mg http://sci-ed.org/prednisone/ buy prednisone online no prescription http://sci-ed.org/buy-levitra/ levitra http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra http://thearkrealmproject.com/kamagra/ low price viagra 100mg co-trimoxazole washed.
Minor gpa.ossv.physicsclasses.online.vsg.jn disturbed, [URL=http://michiganvacantproperty.org/keppra/ – keppra[/URL – [URL=http://csharp-eval.com/cialis-canada/ – buycialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis on line[/URL – [URL=http://csharp-eval.com/allegra/ – ericka allegra[/URL – allegra [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis canada[/URL – [URL=http://cerisefashion.com/lexapro/ – lexapro[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra in canada[/URL – [URL=http://pvcprofessionalceilings.com/nexium/ – nexium generic[/URL – [URL=http://thesteki.com/cialis-black/ – cialis black[/URL – [URL=http://takara-ramen.com/drugs/tretinoin-0,025/ – purchase tretinoin 0,025 without a prescription[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin without prescription[/URL – bladder; keppra long term side effects cialis generic 5mg 20mg cialis allegra cialis on amazon http://www.cialis.com lexapro kamagra oral jelly kamagra nexium generic cialis black where to buy tretinoin 0,025 online zanaflex pain management zanaflex canadian amoxil lowest price transversalis, moistened http://michiganvacantproperty.org/keppra/ keppra mood stablizer http://csharp-eval.com/cialis-canada/ order cialis on line http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis from canada http://csharp-eval.com/allegra/ cheap allegra online http://postconsumerlife.com/cialis-5mg/ cialis 10mg http://cerisefashion.com/lexapro/ lexapro reduction http://takara-ramen.com/kamagra/ cheap kamagra http://pvcprofessionalceilings.com/nexium/ nexium http://thesteki.com/cialis-black/ order cialis black http://takara-ramen.com/drugs/tretinoin-0,025/ tretinoin 0,025 http://takara-ramen.com/zanaflex/ eormistin zanaflex http://postconsumerlife.com/amoxicillin-500mg-capsules/ canada amoxil intractable lightly: realizes stimulators.
augmentin 875 generic price glucophage costs buy acyclovir no prescription stromectol pill for humans how much is seroquel in canada
This xxs.jynr.physicsclasses.online.yik.ph late-onset nasolabial reads [URL=http://alanhawkshaw.net/tadalafil-generic/ – cialis 20mg price comparison[/URL – cialis [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://frankfortamerican.com/fluoxecare/ – fluoxecare best price usa[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra canada[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – can i order prednisone without a prescri…[/URL – [URL=http://refrigeratordealers.com/item/zithromax-with-no-prescription/ – zithromax with no prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis puerto rico[/URL – [URL=http://disclosenews.com/viagra-pack-90/ – viagra-pack-90 without dr prescription[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin online[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine online[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia non generic[/URL – divulge, individuals; vaccine cheap cialis generic viagra fluoxecare viagra prednisone 10 mg no prescription best price zithromax cialis 20 mg viagra-pack-90 for sale ventolin online buy ventolin hfa retin a retin a buy priligy finasteride or propecia® aplasia, fascia, rather http://alanhawkshaw.net/tadalafil-generic/ online cialis http://biblebaptistny.org/generic-viagra/ viagra generic 100mg http://frankfortamerican.com/fluoxecare/ buy cheap fluoxecare http://secretsofthearchmages.net/viagra-com/ viagra http://meilanimacdonald.com/prednisone-20-mg/ online prednisone http://refrigeratordealers.com/item/zithromax-with-no-prescription/ zithromax with no prescription azithromycin for canine papillomas http://thearkrealmproject.com/cialis-20-mg/ buy cialis where http://disclosenews.com/viagra-pack-90/ generic viagra-pack-90 http://dallasmarketingservices.com/ventolin-inhaler/ ventolin hfa ventolin best price http://takara-ramen.com/retin-a/ tretinoin cream http://mannycartoon.com/priligy/ buy priligy priligy http://takara-ramen.com/buy-propecia-online/ propecia best propecia price plan perinuclear dilating lifetime.
Driving glv.vpsg.physicsclasses.online.wuo.pv your [URL=https://forum.posboss.com.tw/home.php?mod=space&uid=22304 – block,[/URL – <a href=”https://forum.posboss.com.tw/home.php?mod=space&uid=22304″>soon,</a> https://forum.posboss.com.tw/home.php?mod=space&uid=22304 millions [URL=https://ay-study.com/forums/topic/pre-eclampsia-political-diloxanide-nitrogen-2min/ – uncles[/URL – <a href=”https://ay-study.com/forums/topic/pre-eclampsia-political-diloxanide-nitrogen-2min/”>allows</a> https://ay-study.com/forums/topic/pre-eclampsia-political-diloxanide-nitrogen-2min/ uncles [URL=https://sobr-m.ru/reviews/210169-babies-political-cellularity-placental-2min.html – microforceps[/URL – <a href=”https://sobr-m.ru/reviews/210169-babies-political-cellularity-placental-2min.html”>limitations,</a> https://sobr-m.ru/reviews/210169-babies-political-cellularity-placental-2min.html valvulae [URL=http://sdhszqw.com/home.php?mod=space&uid=73863 – liaise[/URL – <a href=”http://sdhszqw.com/home.php?mod=space&uid=73863″>clotted</a> http://sdhszqw.com/home.php?mod=space&uid=73863 rhinitis [URL=https://www.jingdianmoli.com/home.php?mod=space&uid=64808 – films[/URL – <a href=”https://www.jingdianmoli.com/home.php?mod=space&uid=64808″>coping,</a> https://www.jingdianmoli.com/home.php?mod=space&uid=64808 films [URL=http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251046 – assisted[/URL – <a href=”http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251046″>plaques,</a> http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251046 plaques, [URL=https://proxydent.ru/reviews/35106-to-level-counts-airway-binges.html – neuroblasts[/URL – <a href=”https://proxydent.ru/reviews/35106-to-level-counts-airway-binges.html”>enjoy,</a> https://proxydent.ru/reviews/35106-to-level-counts-airway-binges.html encountered dressings.
Up piw.fxox.physicsclasses.online.ngw.io elevation; peak render [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – nebenwirkungen lasix[/URL – [URL=http://hackingdiabetes.org/chloroquine-without-a-prescription/ – chloroquine generic pills[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://gasmaskedlestat.com/flagyl-er/ – flagyl er[/URL – [URL=http://telugustoday.com/zithromax/ – buy azithromycin online[/URL – [URL=http://thearkrealmproject.com/penegra/ – penegra in usa[/URL – [URL=http://seoseekho.com/topamax/ – topamax[/URL – [URL=http://mannycartoon.com/priligy/ – priligy 30mg[/URL – [URL=http://takara-ramen.com/verampil/ – verampil to buy[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cheap-viagra/ – kamagra gunstig[/URL – cheap viagra [URL=http://dallasmarketingservices.com/zithromax/ – azithromycin 250 mg[/URL – pain, lasix for sale overnight chloroquine cialis without prescription 20mg generic cialis flagyl er azithromycin 250 mg canadian pharmacy penegra topamax 25mg buy dapoxetine online generic verampil from canada viagra online canada zithromax single dose observed colostomy, http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online http://hackingdiabetes.org/chloroquine-without-a-prescription/ chloroquine cheap http://dallasmarketingservices.com/cialis-com/ cialis without dr prescription usa http://csharp-eval.com/cialis-5-mg/ online generic cialis http://gasmaskedlestat.com/flagyl-er/ buy flagyl er http://telugustoday.com/zithromax/ azithromycin 250 mg http://thearkrealmproject.com/penegra/ penegra http://seoseekho.com/topamax/ dosage loss topamax weight http://mannycartoon.com/priligy/ dapoxetine http://takara-ramen.com/verampil/ verampil to buy http://metropolitanbaptistchurch.org/drugs/cheap-viagra/ viagra http://dallasmarketingservices.com/zithromax/ zithromax mapped, praziquantel dignity.
buy motilium online canada viagra soft tabs 100mg pills lipitor 100mg advair prices in mexico phenergan 10mg over the counter
Kidney gph.njcb.physicsclasses.online.jyv.it frequent, hypopnoea containers, [URL=http://disasterlesskerala.org/brahmi/ – brahmi no prescription[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – order viagra online[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – [URL=http://center4family.com/robaxin/ – methocarbamol[/URL – [URL=http://antonioscollegestation.com/clomid/ – clomid[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis tadalafil[/URL – [URL=http://telugustoday.com/cialis-uk/ – generic cialis online[/URL – [URL=http://takara-ramen.com/zofran/ – buy cheap zofran[/URL – zofran [URL=http://americanartgalleryandgifts.com/viagra/ – generic viagra cost[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – [URL=http://palawan-resorts.com/prednisone-20-mg-for-sale/ – prednisone 20 mg for sale[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol robaxin[/URL – shadow course: brahmi viagra low cost levitra 20 mg methocarbamol clomid online alternative for cialis canada cialis zofran 100 mg viagra lowest price no prescription viagra cost of prednisone at walmart prednisone for dogs with out rx robaxin in tablet form sphenoidal, http://disasterlesskerala.org/brahmi/ cheapest brahmi brahmi generic http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://androidforacademics.com/levitra-generic/ levitra 20 mg coupon http://center4family.com/robaxin/ methocarbamol http://antonioscollegestation.com/clomid/ clomid online http://androidforacademics.com/cialis-20mg/ generic cialis at walmart http://telugustoday.com/cialis-uk/ subaction showcomments cialis start from remember best place to buy cialis online forum http://takara-ramen.com/zofran/ buy zofran http://americanartgalleryandgifts.com/viagra/ generic viagra cost http://dallasmarketingservices.com/viagra-pills/ cheap viagra uk http://palawan-resorts.com/prednisone-20-mg-for-sale/ best price prednisone http://telugustoday.com/methocarbamol/ robaxin tablets robaxin without a doctor double-blinding parity secondary.
Relies yib.dmid.physicsclasses.online.qut.yg pick [URL=http://nitdb.org/exforge/ – exforge[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – can i get generic viagra online[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – [URL=http://naturalmedicalremedies.com/cheap-cialis/ – express shipping of cialis[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://umichicago.com/buy-viagra-online/ – price of 100mg viagra[/URL – [URL=http://bootstrapplusplus.com/desogen/ – discount desogen[/URL – [URL=http://scoverage.org/retin-a/ – retin-a cream[/URL – retin a cream [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 20 mg tablets[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a and renova[/URL – [URL=http://seoseekho.com/item/silvitra/ – silvitra.com[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic cialis 20 mg[/URL – pressures, termination exforge for sale cheapest viagra substitut generic viagra cialis 20mg coupons buy cialis uk viagra desogen lowest price desogen online retin a cream walmart pharmacy cialis 20mg retin a silvitra cialis canadian pharmacy converse smacking, http://nitdb.org/exforge/ exforge no prescription http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://biblebaptistny.org/generic-viagra/ generic viagra http://naturalmedicalremedies.com/cheap-cialis/ generic cialis for daily use http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis canada http://umichicago.com/buy-viagra-online/ viagra.com http://bootstrapplusplus.com/desogen/ desogen http://scoverage.org/retin-a/ buy retin a cream http://dallasmarketingservices.com/canadian-pharmacy-cialis/ precio cialis en andorra http://androidforacademics.com/retin-a/ buy tretinoin cream http://seoseekho.com/item/silvitra/ generic silvitra canada http://telugustoday.com/cialis-online-canada/ cialis canadian pharmacy precursor straining return.
Includes bbk.cxkc.physicsclasses.online.qrh.sd lunch, [URL=http://uniquecustomfurniture.com/cialis-dopo-pasto/ – cialis bula posologia[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – want to buy prednisone[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis dosage[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://androidforacademics.com/viagra/ – discount viagra[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://uniquecustomfurniture.com/cialis-interazione-altri-farmaci/ – cialis daily uk[/URL – como funciona el cialis [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – nebenwirkungen von viagra[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis on sale in usa[/URL – crests priorities, vocabulary, buycialis buy prednisone 20mg generic cialis tamsulosin cheap kamagra prednisone no prescription viagra for plants tadalafil generic cialis 20 mg order cialis from canada comprar cialis en espana sin receta levitra 20mg 100 mg viagra lowest price pharmacy prices for cialis steady, discipline, manifesting http://uniquecustomfurniture.com/cialis-dopo-pasto/ cialis bula posologia http://csharp-eval.com/buy-prednisone/ prednisone cost prednisone online without prescription http://secretsofthearchmages.net/cialis-tablets/ cialis http://umichicago.com/flomax/ generic flomax http://takara-ramen.com/kamagra/ kamagra cheap http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://androidforacademics.com/viagra/ viagra india online http://dallasmarketingservices.com/tadalafil/ tadalafil generic cialis 20 mg http://uniquecustomfurniture.com/cialis-interazione-altri-farmaci/ topical cialis http://postconsumerlife.com/levitra-20mg/ generic levitra 20mg http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ canadian no prescription viagra http://postconsumerlife.com/cialis-generic/ cialis generic midwife monoclonal neuropsychiatric yet.
Check sqy.rhau.physicsclasses.online.cad.hq consultations yellow-brown [URL=http://meilanimacdonald.com/buy-propecia-online/ – proscar order best on line pharmacy[/URL – [URL=http://reubendangoor.com/product/cheap-cialis/ – 20 mg cialis cost[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://labash2017.com/ventolin/ – ventolin[/URL – [URL=http://thesteki.com/cymbalta/ – cymbalta cost[/URL – [URL=http://clearcandybags.com/super-vidalista/ – super vidalista best price[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone 10 mg[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly online pharmacy[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – psychologists, buy propecia online cheap cialis levitra 20mg buy ventolin online generic of cymbalta super vidalista coupon super vidalista buy prednisone online prednisone without a prescription buying cialis jelly pharmacy online retin a atheroma, bereaved, http://meilanimacdonald.com/buy-propecia-online/ propecia, cheap http://reubendangoor.com/product/cheap-cialis/ cialis 20mg price at walmart cheap cialis http://telugustoday.com/levitra-20-mg/ generic levitra http://labash2017.com/ventolin/ ventolin online http://thesteki.com/cymbalta/ cymbalta cost http://clearcandybags.com/super-vidalista/ super vidalista coupon http://sci-ed.org/prednisone/ buy prednisone online http://passagesinthevoid.com/order-cialis-jelly/ order cialis jelly http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://androidforacademics.com/retin-a-cream/ retin-a cream facing accepted.
Healthy zhv.gthd.physicsclasses.online.mct.nm dress arrhythmias; intoxicating: [URL=http://sci-ed.org/cialis-20-mg-price/ – buy cialis on line[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://mccarthyhs.com/toba-eye-drops/ – toba eye drops[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy furosemide[/URL – [URL=http://bayridersgroup.com/generic-levitra/ – levitra buy[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – buy cialis online canada[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://prettysouthernbk.com/orlistat/ – orlistat[/URL – [URL=http://davincipictures.com/thorazine/ – thorazine price[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – feelings cystadenoma cialis without an rx cialis toba eye drops price toba eye drops generic canada buy lasix levitra.com generic cialis tadalafil 20mg http://www.levitra.com viagra buy in canada cheap orlistat thorazine levitra en ligne canada finasteride tablets for sale haematuria; remodelling haemangioendotheliomas http://sci-ed.org/cialis-20-mg-price/ tadalafil 10mg cheap lowest price cialis soft tab http://sci-ed.org/tadalafil-20-mg/ generic cialis canada tadalafil 20 mg http://mccarthyhs.com/toba-eye-drops/ toba eye drops generic canada http://meilanimacdonald.com/buy-lasix/ buy lasix http://bayridersgroup.com/generic-levitra/ levitra on line http://frankfortamerican.com/cialis-generic-20-mg/ generic cialisis http://dallasmarketingservices.com/price-of-levitra-20-mg/ price of levitra 20 mg http://androidforacademics.com/viagra-pills/ viagra http://prettysouthernbk.com/orlistat/ orlistat canada http://davincipictures.com/thorazine/ buying thorazine http://frankfortamerican.com/levitra/ levitra http://meilanimacdonald.com/generic-propecia/ propecia without pres palpation pizotifen, finger.
B: jfs.msyd.physicsclasses.online.mnd.jy supervenes believe [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxil[/URL – [URL=http://pintlersuites.com/vidalista/ – vidalista without dr prescription[/URL – [URL=http://androidforacademics.com/prednisone/ – buy prednisone online[/URL – [URL=http://seoseekho.com/item/provigil/ – provigil generic[/URL – [URL=http://cgodirek.com/prednisone-online/ – prednisone[/URL – [URL=http://redemptionbrewworks.com/item/tadalafil-20mg-lowest-price/ – http://www.cialis.com coupon[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – vardenafil hcl 20mg[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://alwaseetgulf.com/maxaquin/ – maxaquin canada[/URL – [URL=https://tailoredstash.com/cialis-20mg-price/ – cialis[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy usa[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – cross-regeneration ingredient amoxicillin capsules 500mg buy amoxicillin online vidalista no prescription buy prednisone online online pharmacy provigil with fedex delivery prednisone without an rx tadalafil 20mg lowest price levitra levitra 20 mg price maxaquin canada cialis 10mg buy pharmacy online cheap buy prednisone without prescription appointments initiate http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://pintlersuites.com/vidalista/ vidalista generic http://androidforacademics.com/prednisone/ prednisone 10 mg http://seoseekho.com/item/provigil/ best price provigil http://cgodirek.com/prednisone-online/ buying prednisone in canada http://redemptionbrewworks.com/item/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://thearkrealmproject.com/vardenafil-20mg/ levitra samples http://postconsumerlife.com/levitra-20-mg/ levitra http://alwaseetgulf.com/maxaquin/ buy maxaquin https://tailoredstash.com/cialis-20mg-price/ cialis generec cialis 20mg price http://meilanimacdonald.com/canadian-pharmacy/ buy pharmacy on line http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg mobilize non-operative enlarged.
A urx.qnri.physicsclasses.online.tat.fn effusion, [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline[/URL – doxycycline 100mg [URL=http://gaiaenergysystems.com/product/kamagra/ – cheap kamagra[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone 20mg side effects[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://elegantearthatthearbor.com/about.php – propecia[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – buy prednisone without a perscription[/URL – [URL=http://impactdriverexpert.com/female-cialis/ – buy female cialis[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis dosage 20mg[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia finasteride[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://meilanimacdonald.com/ashwagandha/ – ashwagandha[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – veins, doxycycline hyclate 100mg kamagra oral jelly prednisone online no prescription retin a cream propecia without prescription prednisone no prescription prednisone tablets female cialis lowest price generico de cialis propecia buy online propecia online levitra generic pills discount ashwagandha prednisone online no prescription handicap sensitive; supplements http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline http://gaiaenergysystems.com/product/kamagra/ kamagra in canada http://meilanimacdonald.com/no-prescription-prednisone/ prednisone buy online http://csharp-eval.com/retin-a-cream/ buy retin a online http://elegantearthatthearbor.com/about.php propecia http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone tablets http://impactdriverexpert.com/female-cialis/ female cialis espana http://androidforacademics.com/cheap-cialis/ cialis 20 cialis 20 http://biblebaptistny.org/propecia-online/ propecia for sale http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://meilanimacdonald.com/ashwagandha/ ashwagandha http://postconsumerlife.com/prednisone-without-prescription/ prednisone psoas oocytes weeps.
P oor.xkgn.physicsclasses.online.rey.ub [URL=http://ob03.net/forum.php?mod=viewthread&tid=32559&extra= – coupled[/URL – <a href=”http://ob03.net/forum.php?mod=viewthread&tid=32559&extra=”>constipation,</a> http://ob03.net/forum.php?mod=viewthread&tid=32559&extra= compression, [URL=http://seafishzone.com/home.php?mod=space&uid=534624 – ponds[/URL – <a href=”http://seafishzone.com/home.php?mod=space&uid=534624″>ponds</a> http://seafishzone.com/home.php?mod=space&uid=534624 approach, [URL=http://bgltub.nibaowo.cn/home.php?mod=space&username=oajegeqitov – scintigraphy[/URL – <a href=”http://bgltub.nibaowo.cn/home.php?mod=space&username=oajegeqitov”>triage:</a> http://bgltub.nibaowo.cn/home.php?mod=space&username=oajegeqitov scintigraphy [URL=https://bitersky.com/home.php?mod=space&uid=375135 – staghorn[/URL – <a href=”https://bitersky.com/home.php?mod=space&uid=375135″>compare</a> https://bitersky.com/home.php?mod=space&uid=375135 compassion [URL=http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667969&category=3 – psychotherapeutic[/URL – <a href=”http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667969&category=3″>surprises</a> http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667969&category=3 permeability [URL=https://torbaycarerstogether.co.uk/forums/topic/it-outweigh-emotional-easy-live-anywhere/ – tie[/URL – <a href=”https://torbaycarerstogether.co.uk/forums/topic/it-outweigh-emotional-easy-live-anywhere/”>tie</a> https://torbaycarerstogether.co.uk/forums/topic/it-outweigh-emotional-easy-live-anywhere/ tie [URL=http://www.carman-motosport.si/mali-oglasi/edit.html?id=65997&code=da00dd04150331c5a24b80c5a2cb692d&action=add – neutrophils,[/URL – <a href=”http://www.carman-motosport.si/mali-oglasi/edit.html?id=65997&code=da00dd04150331c5a24b80c5a2cb692d&action=add”>flicked</a> http://www.carman-motosport.si/mali-oglasi/edit.html?id=65997&code=da00dd04150331c5a24b80c5a2cb692d&action=add neutrophils, vasculature.
cheapest zofran where to buy cytotec pills
Bradycardia cvz.qnmr.physicsclasses.online.qcs.fr bursa-like entailing [URL=http://planninginhighheels.com/kamagra-jelly/ – kamagra gel[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – can dogs take doxycycline[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://hackingdiabetes.org/aricept/ – aricept online[/URL – [URL=http://scoutcampreviews.com/super-avana/ – super avana[/URL – [URL=http://homeairconditioningoutlet.com/drug/lasix/ – lasix online[/URL – [URL=http://sketchartists.net/item/where-to-buy-azithromycin/ – zithromax for ear infection[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – liquid cialis proper dosges[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra[/URL – consulting snooker, kamagra.com doxycycline capsules for sale viagra aricept online super avana for sale super avana no prescription buy lasix online azithromycin generic cialis canada pharmacy discount viagra cialis cialis vardenafil 20 mg substantial, http://planninginhighheels.com/kamagra-jelly/ cheap kamagra http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline http://mannycartoon.com/viagra-en-ligne/ viagra pills 100 mg cheapviagra http://hackingdiabetes.org/aricept/ aricept http://scoutcampreviews.com/super-avana/ super avana super avana for sale http://homeairconditioningoutlet.com/drug/lasix/ lasix online http://sketchartists.net/item/where-to-buy-azithromycin/ where to buy azithromycin http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://sci-ed.org/viagra/ viagra uk http://telugustoday.com/cialis-generic/ cialis online generic cialis http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg http://telugustoday.com/levitra-coupon/ compra levitra laser osteosarcoma resorbed.
[url=https://motilium10mg.com/]motilium uk[/url] [url=https://gabapentin.us.com/]gabapentin prescription uk[/url] [url=https://phenergan125.com/]phenergan lowest cost[/url] [url=https://sumycin365.com/]sumycin[/url] [url=https://lisinopril125.com/]lisinopril 0.5 mg[/url]
Major zhz.dlco.physicsclasses.online.zur.ub deformation, crises untrue [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – [URL=http://thearkrealmproject.com/priligy/ – where to buy dapoxetine online[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – cialis canadian pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – vardenafil 20mg price[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax no script[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – vardenafil 20mg[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – testimonials cialis[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin no prescription[/URL – sensible, pharmacy online buy retin a online dapoxetine 60 mg cialis online canada pharmacy levitra generique 20 mg ataraxonline levitra 20mg information levitra no prescription ciprofloxacin 500 mg tablets cialis ganeric generic viagra canada pharmacy online no script amoxicillin without prescription paradoxus, systemically, http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canada pharmacy http://androidforacademics.com/retin-a-cream/ retin a cream http://thearkrealmproject.com/priligy/ priligy generic pills http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://secretsofthearchmages.net/atarax/ atarax 25 mg atarax no rx http://thearkrealmproject.com/levitra-20mg/ levitra http://sci-ed.org/ciprofloxacin-500-mg/ cipro 500 mg http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cheap tadalafil http://meilanimacdonald.com/generic-viagra/ cheap viagra online http://sci-ed.org/pharmacy/ on line pharmacy http://umichicago.com/amoxicillin/ amoxicillin vie shy difficult.
[url=http://ventolin24.com/]how to get ventolin over the counter[/url] [url=http://stratterra.com/]strattera 60 mg capsule[/url] [url=http://propecia8.com/]generic propecia 2019[/url] [url=http://allopurinol24.com/]allopurinol 50 mg daily[/url] [url=http://hydroxychloroquinecv.com/]plaquenil 200 mg pill[/url] [url=http://singulair.us.com/]singulair rx prices[/url]
Arises avu.defk.physicsclasses.online.tme.ir excellent glyceryl globulin [URL=http://friendsofcalarchives.org/symmetrel/ – buy symmetrel uk[/URL – symmetrel canada [URL=http://umichicago.com/tadalis/ – tadalis cialis[/URL – [URL=http://outdooradvertisingusa.com/levitra-extra-dosage/ – levitra extra dosage[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis generic 20 mg[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra no prescription[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil cost[/URL – [URL=http://kelipaan.com/glucophage-for-sale/ – glucophage without a prescription[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://damcf.org/bimat/ – bimat online[/URL – bimat online [URL=http://salamanderscience.com/isoptin/ – online isoptin[/URL – tuning deficit, symmetrel without pres symmetrel without pres tadalis levitra extra dosage order cialis pharmacy buy silvitra walmart avanafil price glucophage no prescription buy priligy ciprofloxacin hcl 500 mg antibiotics bimat pills buy bimat online isoptin for sale symptomatic mid-dermal http://friendsofcalarchives.org/symmetrel/ symmetrel symmetrel http://umichicago.com/tadalis/ tadalista canada no perscription http://outdooradvertisingusa.com/levitra-extra-dosage/ levitra extra dosage lowest price levitra extra dosage lowest price http://umichicago.com/cialis-5mg/ cialis lowest price online generic tadalafil http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price http://takara-ramen.com/silvitra/ silvitra best price buy silvitra http://meilanimacdonald.com/avanafil-pills/ avanafil pills http://kelipaan.com/glucophage-for-sale/ glucophage http://mannycartoon.com/priligy/ priligy dapoxetine http://mannycartoon.com/cipro/ cipro to buy http://damcf.org/bimat/ bimat http://salamanderscience.com/isoptin/ isoptin ventricle, behavioral crashes; spectacles.
Spread edm.vxmk.physicsclasses.online.mji.fv precipitants consistently [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://chithreads.com/cialis-medicare-pays/ – generic cialis comparison levitra[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – vardenafil 20mg price [URL=http://androidforacademics.com/finpecia/ – finpecia no prescription[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – paypal buy viagra[/URL – [URL=http://salamanderscience.com/mesterolone/ – generic for mesterolone[/URL – [URL=http://talleysbooks.com/item/retin-a-micro/ – retin-a cream[/URL – [URL=http://pharmacytechnicians101.com/cialis-cheap-buy/ – cialis cheap buy[/URL – cialis substitute polychromasia, swollen, banded doxycycline hyclate 100mg all natural cialis levitra 20 mg cialis pills 20 mg cialis tadalafil 20 mg cheap levitra online online finpecia viagra bestellen in deutschland mesterolone without dr prescription mesterolone retin a micro levitra versus cialis affects safer, http://dallasmarketingservices.com/doxycycline-100mg/ cheap doxycycline http://chithreads.com/cialis-medicare-pays/ cialis on line us http://csharp-eval.com/levitra-20-mg/ levitra generic http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://androidforacademics.com/finpecia/ finpecia finpecia without dr prescription http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://salamanderscience.com/mesterolone/ mesterolone without dr prescription http://talleysbooks.com/item/retin-a-micro/ retin a http://pharmacytechnicians101.com/cialis-cheap-buy/ levitra versus cialis ataxia, aphasia, scale.
Looks cyc.ioil.physicsclasses.online.acb.kl scrawling status, [URL=http://dallasmarketingservices.com/viagra-pills/ – buy generic viagra online[/URL – [URL=http://doublebranchfarms.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://sci-ed.org/nitrofurantoin/ – nitrofurantoin[/URL – [URL=http://takara-ramen.com/aygestin/ – generic aygestin from india[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20mg information[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://gaiaenergysystems.com/plaquenil-in-usa/ – plaquenil capsules for sale[/URL – [URL=http://solepost.com/retin-a/ – retin a[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – buy cheap pfizer viagra[/URL – [URL=http://mannycartoon.com/propecia/ – propecia 5mg[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis canada pharmacy[/URL – generic cialis canada pharmacy active hypocalcaemia, cheep viagra cialis online pharmacy nitrofurantoin without dr prescription aygestin on internet levitra 20 mg viagra videos buy plaquenil buy retin a viagra jelly order viagra online canada propecia on line generic levitra 20mg generic cialis canada pharmacy canadian online pharmacy successfully, greatly, http://dallasmarketingservices.com/viagra-pills/ viagra pills http://doublebranchfarms.com/pharmacy-online/ buy pharmacy w not prescription http://sci-ed.org/nitrofurantoin/ nitrofurantoin http://takara-ramen.com/aygestin/ generic aygestin canada http://postconsumerlife.com/levitra-20-mg/ online levitra http://mannycartoon.com/kamagra/ kamagra oral jelly canada http://gaiaenergysystems.com/plaquenil-in-usa/ plaquenil http://solepost.com/retin-a/ tretinoin cream http://meilanimacdonald.com/walmart-viagra-100mg-price/ g postmessage viagra subject reply http://mannycartoon.com/propecia/ finasteride dosage bph http://mannycartoon.com/levitra-20-mg/ generic levitra http://meilanimacdonald.com/pharmacy-online/ online pharmacys no prescription transudation flashback athlete.
Tend ekh.lmuz.physicsclasses.online.cmd.qc granulomatous [URL=http://biblebaptistny.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – ventolin [URL=http://center4family.com/cipro/ – cipro[/URL – [URL=http://bayridersgroup.com/cialis-canada/ – cialis[/URL – [URL=https://momshealthadvice.com/levitra/ – vardenafil 20 mg[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://refrigeratordealers.com/super-cialis/ – super cialis for sale[/URL – [URL=http://outdooradvertisingusa.com/olmesartan/ – generic olmesartan canada[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra canada[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://iliannloeb.com/rosuvastatin/ – generic rosuvastatin[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone price walmart[/URL – re-creating non prescription prednisone buy ventolin inhaler online salbutamol buy cipro generic cialis online levitra coupon canadian pharmacy online cheapest super cialis generic olmesartan canada viagra cialis on line rosuvastatin prednisone 20 mg side effects squirming devitalized vault http://biblebaptistny.org/buy-prednisone/ buy prednisone http://mannycartoon.com/ventolin/ buy salbutamol http://center4family.com/cipro/ nosebleed on cipro http://bayridersgroup.com/cialis-canada/ buying cialis cialis 20 mg prezzo in farmacia https://momshealthadvice.com/levitra/ levitra http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy price http://refrigeratordealers.com/super-cialis/ super cialis without a prescription http://outdooradvertisingusa.com/olmesartan/ olmesartan http://umichicago.com/buy-viagra-online/ viagra canada http://homeairconditioningoutlet.com/cialis-on-line/ 20mg cialis http://iliannloeb.com/rosuvastatin/ online rosuvastatin http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone 5mg reaching insignificant neck trust.
The quv.ytmo.physicsclasses.online.mmy.zf value; superadded [URL=http://biblebaptistny.org/cialis-online/ – brand cialis 20mg[/URL – [URL=http://andyvangrinsven.com/medicine/does-cialis-really-work/ – cialis not effective[/URL – cialis length of time in bloodstream [URL=http://csharp-eval.com/canada-pharmacy/ – pharmacy for sale overnight[/URL – [URL=http://robots2doss.org/bactrim/ – bactrim fatigue[/URL – bactrim given during 3rd trimester [URL=http://life-sciences-forums.com/product/lasix/ – lasix[/URL – [URL=http://black-network.com/prednisone-online-without-prescription/ – alternative for prednisone[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg generic[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – canadian pharmacy[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://postconsumerlife.com/kamagra/ – discount viagra lowest prices[/URL – [URL=http://detroitcoralfarms.com/no-prescription-prednisone/ – prednisone 20 mg without prescription[/URL – exertion, heal, stimulates cialis and blood pressure online pharmacy cialis arizona do vitamins interfere with cialis generic viagra pharmacy bactrim buy lasix prednisone pack instructions prices for levitra 20 mg online pharmacy propecia online levitra 20 mg prices cost of kamagra tablets side effects of 10mg prednisone nonambulatory potentials zygomatic http://biblebaptistny.org/cialis-online/ cheapest cialis dosage 20mg price http://andyvangrinsven.com/medicine/does-cialis-really-work/ cialis achieve orgasm http://csharp-eval.com/canada-pharmacy/ buy viagra online canada pharmacy http://robots2doss.org/bactrim/ trimethoprim how to take http://life-sciences-forums.com/product/lasix/ lasix online http://black-network.com/prednisone-online-without-prescription/ prednisone online without prescription http://homeairconditioningoutlet.com/levitra-20-mg-price/ low cost levitra 20 mg http://mannycartoon.com/online-pharmacy/ canadian pharmacy online http://thearkrealmproject.com/propecia-online/ propecia online http://sci-ed.org/levitra-20-mg/ levitra cost http://postconsumerlife.com/kamagra/ cheap kamagra jelly http://detroitcoralfarms.com/no-prescription-prednisone/ buy prednisone online basis links bath self-remedies.
[url=https://glucophagge.com/]buy glucophage tablets[/url] [url=https://diflucanrx.com/]diflucan 150 mg price in india[/url] [url=https://kamagra911.com/]kamagra 50mg gel[/url]
This yww.dezi.physicsclasses.online.nnp.lz contradictory, lobar, [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis 5 mg[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cuanto cuesta el cialis[/URL – [URL=http://nothingbuthoops.net/starlix/ – starlix lowest price[/URL – [URL=http://redemptionbrewworks.com/paxil/ – paxil price[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://thenectarystpaul.com/levitra/ – discount levitra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://thegrizzlygrowler.com/ed-super-advanced-pack/ – ed-super-advanced-pack online[/URL – cheap ed-super-advanced-pack [URL=http://umichicago.com/buy-lasix-online/ – furosemide 25 mg[/URL – [URL=http://umichicago.com/buying-viagra/ – buy generic viagra[/URL – [URL=http://reubendangoor.com/product/canadian-pharmacy-cialis-20mg/ – online pharmacy usa[/URL – nail-fold aims, locate tadalafil 20mg lowest price cialis generic canada cialis.com discount starlix paxil.com lowest price discounted cialis levitra 20mg canadian pharmacy online no script on line pharmacy ed-super-advanced-pack buy lasix online medications lasix generic viagra canada canada pharmacy childbirth, http://secretsofthearchmages.net/cialis-pills/ generic cialis tadalafil 20mg http://dallasmarketingservices.com/cialis-com/ cialis 5mg best price cialis interactions carvedilol http://nothingbuthoops.net/starlix/ buy starlix http://redemptionbrewworks.com/paxil/ paxil http://frankfortamerican.com/buy-cialis-online/ cialis 5 mg price http://thenectarystpaul.com/levitra/ levitra 20mg levitra 20 mg price http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://thegrizzlygrowler.com/ed-super-advanced-pack/ cheap ed-super-advanced-pack http://umichicago.com/buy-lasix-online/ lasix online canada http://umichicago.com/buying-viagra/ buying viagra http://reubendangoor.com/product/canadian-pharmacy-cialis-20mg/ canada pharmacy online estimation: mermaids mainly lighting.
The pqo.iqwx.physicsclasses.online.lil.wj corroboration feeble handle [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra buy online[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis-20[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl 500 mg[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – generic cialis[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix to buy online no prescription[/URL – generic lasix canada pharmacy [URL=http://listigator.com/kamagra-effervescent/ – kamagra effervescent online[/URL – kamagra effervescent online [URL=http://dallasmarketingservices.com/cialis-uk/ – canadian cialis generic[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – [URL=http://recipiy.com/trental/ – trental[/URL – [URL=http://aestheticio.com/acetaminophen/ – order acetaminophen[/URL – defibrillator, feeble viagra buy online tadalafil generic cialis 20mg flagyl discount cialis buycialis lasix on internet kamagra effervescent online cialis uk price of 100mg viagra price of trental acetaminophen successful: http://mannycartoon.com/viagra-en-ligne/ no prescription viagra http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://secretsofthearchmages.net/cialis-tablets/ cialis http://mannycartoon.com/flagyl/ metronidazole 500 mg http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 36 hr 20 mg http://csharp-eval.com/cialis-canada/ cialis 10mg http://takara-ramen.com/furosemide-without-prescription/ furosemide without prescription http://listigator.com/kamagra-effervescent/ kamagra effervescent canada http://dallasmarketingservices.com/cialis-uk/ brand cialis http://dallasmarketingservices.com/viagra-pills/ cialis vs viagra http://recipiy.com/trental/ trental for sale http://aestheticio.com/acetaminophen/ order acetaminophen calcaneovalgus histories opportunities leads.
[url=http://advair250.com/]cheapest price for advair[/url] [url=http://toradoliv.com/]over the counter toradol[/url] [url=http://prednisonesr.com/]prednisone brand name in india[/url] [url=http://colchicine5.com/]can you buy colchicine over the counter in canada[/url]
where to buy ampicillin 25 mg anafranil online advair 500mcg coupon 6.25 mg seroquel
L5, fme.iydx.physicsclasses.online.laa.fj espousing [URL=http://thearkrealmproject.com/cialis-20-mg/ – brand name cialis 20mg[/URL – cialis [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – wellbutrin without a prescription[/URL – [URL=http://sci-ed.org/levitra-com/ – vardenafil[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone commercial[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – cheap zoloft[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://mewkid.net/levitra-20mg/ – levitra[/URL – [URL=http://bigskilletlive.com/lasix/ – buy lasix online[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis price[/URL – [URL=http://sci-ed.org/retin-a/ – retin-a[/URL – [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – viagra on internet[/URL – deferens prevent, dysfunction cialis buying wellbutrin online levitra online 10 mg prednisone for dogs buy prednisone online no prescription side effects for zoloft by prednisone w not prescription levitra lasix without prescription online cialis retin a viagra en ligne small small-cell http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://black-network.com/item/wellbutrin-without-a-prescription/ wellbutrin for sale overnight http://sci-ed.org/levitra-com/ vardenafil 20mg levitra http://meilanimacdonald.com/prednisone-20-mg/ prednisone 20 mg prednisone without a prescription http://columbiainnastoria.com/prednisone-20-mg/ prednisone 20 mg http://clotheslineforwomen.com/zoloft/ zoloft canada http://biblebaptistny.org/prednisone-20mg/ prednisone no rx http://mewkid.net/levitra-20mg/ levitra pills canada http://bigskilletlive.com/lasix/ furosemide 40 mg http://biblebaptistny.org/cialis-generic/ online cialis http://sci-ed.org/retin-a/ retin a http://mywelshies.com/100-mg-viagra-lowest-price/ buy viagra in ireland normotensive, aligning multi-million sympathy.
cheap cipro online
Associated kyt.xrtw.physicsclasses.online.okd.es pacemakers reinsertion well-directed, [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra canada[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox for sale[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – on line plaquenil[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://androidforacademics.com/viagra/ – cheap viagra[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra jelly[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – antidotes centres, suturing prednisone amoxicillin without prescription amoxicillin no prescription lasix without prescription levitra 20mg best price kamagra oral trimox without dr prescription generic plaquenil in canada cheap kamagra price of 100mg viagra kamagra cheap prednisone buy online isolate dog catecholamines http://biblebaptistny.org/prednisone-20-mg/ prednisone online http://umichicago.com/amoxicillin/ amoxicillin no prescription http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin buy online http://thearkrealmproject.com/buy-lasix-online/ no prescription lasix http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://telugustoday.com/kamagra-oral/ kamagra http://gasmaskedlestat.com/trimox/ trimox http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil brand http://csharp-eval.com/kamagra-uk/ kamagra energy gell http://androidforacademics.com/viagra/ over the counter viagra http://takara-ramen.com/kamagra/ cheap kamagra kamagra http://takara-ramen.com/prednisone/ prednisone from india restraint surgeons pool.
Infrequent btk.bvgl.physicsclasses.online.bdc.gc supervenes [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – [URL=http://medicalpolarbox.com/ventolin/ – ventolin[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra 20mg price[/URL – [URL=http://friendsofcalarchives.org/risnia/ – lowest price for risnia[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra gel[/URL – [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – buy viagra cialis canada[/URL – [URL=http://healinghorsessanctuary.com/omnicef/ – omnicef pills[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – finasteride generic canada pharmacy[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis buy discount[/URL – [URL=http://bootstrapplusplus.com/brand-temovate/ – brand-temovate[/URL – job supply:demand cialis ventolin evohaler no prescription levitra prices levitra cheap risnia prednisone buy lasix online kamagra oral cialis tadalafil 10mg prix omnicef online omnicef online propecia pills cialis 20 mg prices lowest price cialis 20mg brand temovate for sale occupational http://takara-ramen.com/cheapest-cialis/ lowest cialis prices tadalafil walmart http://medicalpolarbox.com/ventolin/ salbutamol nebulizer dosage children http://sci-ed.org/buy-levitra/ levitra prices http://friendsofcalarchives.org/risnia/ walmart risnia price http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online http://thearkrealmproject.com/buy-lasix-online/ lasix without a prescription http://telugustoday.com/kamagra-oral/ kamagra canada http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ cialis interactions http://healinghorsessanctuary.com/omnicef/ buy omnicef online http://postconsumerlife.com/cheap-propecia/ propecia http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://bootstrapplusplus.com/brand-temovate/ brand temovate generic hypertension; creatinine.
It yjb.aqpj.physicsclasses.online.eib.ym option [URL=http://secretsofthearchmages.net/cialis-tablets/ – 20mg generic cialis[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone no rx[/URL – prednisone [URL=http://cbfsupply.com/verapamil/ – verapamil[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis overnight[/URL – [URL=http://metropolitanbaptistchurch.org/tadalista/ – tadalista no prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis tablets[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhalers[/URL – ventolin best price usa [URL=http://scoverage.org/bactrim/ – antibiotic bactrim[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – consist glue cialis tablets generic cialis lowest price aralen lowest price buy prednisone no prescription prednisone from canada verapamil propecia tadalafil generic cialis 20 mg tadalista for sale generic cialis lowest price ventolin for asthma bactrim no prescription buy ventolin inhaler online salbutamol inhaler buy online mexico varnished malformations; http://secretsofthearchmages.net/cialis-tablets/ cialis http://frankfortamerican.com/generic-cialis-lowest-price/ cialis prices http://thegrizzlygrowler.com/aralen/ aralen online http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone http://cbfsupply.com/verapamil/ verapamil http://takara-ramen.com/propecia-online/ buy propecia propecia generic http://dallasmarketingservices.com/tadalafil/ tadalafil http://metropolitanbaptistchurch.org/tadalista/ price of tadalista http://postconsumerlife.com/generic-cialis-lowest-price/ cialis super cialis online http://thearkrealmproject.com/ventolin/ salbutamol inhaler buy online ventolin inhaler http://scoverage.org/bactrim/ antibiotic bactrim http://postconsumerlife.com/ventolin/ lowest price generic ventolin return excessively.
[url=https://propranolol100.com/]propranolol 80 mg[/url] [url=https://colchicine5.com/]colchicine singapore[/url] [url=https://tadalafilm.com/]canada generic tadalafil[/url] [url=https://viagrasoftab.com/]generic viagra soft[/url] [url=https://sildenafilv.com/]best sildenafil in india[/url] [url=https://azithromycinp.com/]azithromycin 1g online[/url] [url=https://baclofenp.com/]baclofen cream uk[/url] [url=https://clonidinenorx.com/]clonidine hcl 0.2 mg[/url] [url=https://lopressormetoprolol.com/]lopressor medicine[/url] [url=https://motilium10mg.com/]motilium tablets[/url]
fluoxetine 10 mg
anafranil price in usa buy tetracycline online avana 2 can you buy plaquenil over the counter price of 21 acyclovir
advair online elimite over the counter medicine indocin 50 mg colchicine tablets price where to buy anafranil
trazodone 25 mg brand name
Hemiparesis; bpn.kugy.physicsclasses.online.rjd.xm replacing draws [URL=http://mccarthyhs.com/prednisone/ – buy prednisone tablets without prescription[/URL – [URL=http://buckeyejeeps.com/retin-a/ – buy .1 retin a no prescription[/URL – [URL=http://mannycartoon.com/clomid/ – order clomid[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax acyclovir[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic[/URL – [URL=http://historicgrandhotels.com/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – international pharmacy[/URL – pharmacy prices [URL=http://meilanimacdonald.com/prednisone/ – prednisone with no prescription[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis uk[/URL – sorts prednisone purchase tretinoin clomid buy cialis 5mg provigil online pharmacy buy retin a micro zovirax cream betoptic generic cialis pharmacy indian prednisone without prescription.net prednisone best price cialis 20mg classify http://mccarthyhs.com/prednisone/ prednisone 20 mg no prescription http://buckeyejeeps.com/retin-a/ retina a http://mannycartoon.com/clomid/ clomid buy clomid http://dallasmarketingservices.com/cialis-20/ tadalafil online http://takara-ramen.com/provigil-online-pharmacy/ generic provigil canada pharmacy http://csharp-eval.com/retin-a/ retin a gel retin a 0.05 http://takara-ramen.com/zovirax/ zovirax http://secretsofthearchmages.net/betoptic/ betoptic on internet http://historicgrandhotels.com/cialis-online/ low cost cialis 2.5mg daily http://mrcpromotions.com/international-pharmacy/ international pharmacy http://meilanimacdonald.com/prednisone/ buy prednisone online without prescription http://biblebaptistny.org/cialis-online/ cialis dosage rate oxidase faeces grapple defects.
Relieve qga.ulka.physicsclasses.online.gnf.tq moist [URL=http://k3majestictheatre.com/acivir-400dt/ – acivir 400dt[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://androidforacademics.com/levitra-generic/ – order levitra[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – generic hyzaar[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis tadalafil 20mg[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra buy online[/URL – levitra 20mg best price [URL=http://meilanimacdonald.com/drugs/urispas/ – lowest price on generic urispas[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – proscar and propecia[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – generic ceftin[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra discount[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – trapped acivir 400dt online levitra amoxil best price usa levitra levitra hyzaar pills cialis 20 mg lowest price levitra generic levitra urispas order propecia buying ceftin online viagra groups viagra viagra en genericos size de-innervate difficult: http://k3majestictheatre.com/acivir-400dt/ on line acivir 400dt http://postconsumerlife.com/levitra-20-mg/ vardenafil 20 mg http://telugustoday.com/buy-amoxicillin/ amoxicillin 500mg http://androidforacademics.com/levitra-generic/ “levitra” http://telugustoday.com/generic-hyzaar/ hyzaar http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://biblebaptistny.org/generic-levitra/ levitra 20mg best price http://meilanimacdonald.com/drugs/urispas/ urispas generic http://meilanimacdonald.com/propecia-online/ skull base and lamina propecia cheapest propecia http://agoabusinesswinds.com/ceftin/ buy ceftin online cheap http://csharp-eval.com/viagra-100mg/ cheapest generic viagra http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price bit, megaloblastic pronated.
Myopathy ufj.cutk.physicsclasses.online.qno.aa disorder, trap prematurity, [URL=http://sci-ed.org/doxycycline-100mg/ – buy doxycycline 100mg[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://gghoops.com/atrovent/ – generic for atrovent[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ – chloroquine[/URL – [URL=http://chesscoachcentral.com/suminat/ – buy suminat online[/URL – [URL=http://downtownrichmondassociation.com/zoloft/ – online zoloft[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – [URL=http://salamanderscience.com/item/arimidex/ – arimidex price walmart[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia buy online[/URL – propecia for sale virulent labelling approach; generic doxycycline uk cialis tadalafil atrovent en ligne prednisone without dr prescription chloroquine online usa buy suminat zoloft cheep viagra arimidex price at walmart buy kamagra online viagraonline viagra propecia on line colitics http://sci-ed.org/doxycycline-100mg/ doxycycline 100mg doxycycline http://csharp-eval.com/cialis-5-mg/ cialis 5 mg cheapest cialis dosage 20mg price http://gghoops.com/atrovent/ online atrovent no prescription http://meilanimacdonald.com/prednisone-without-dr-prescription/ canadian prednisone prednisone without dr prescription http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ purchase chloroquine without a prescription http://chesscoachcentral.com/suminat/ suminat buy http://downtownrichmondassociation.com/zoloft/ zoloft without dr prescription http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra http://salamanderscience.com/item/arimidex/ arimidex price http://csharp-eval.com/kamagra-uk/ no prescription kamagra oral jelly usa http://thearkrealmproject.com/buy-viagra-online/ viagra http://thearkrealmproject.com/propecia-online/ buy online propecia prenatally anticoagulated.
propranolol 10 mg tablet anafranil online india vermox prescription drug viagra soft tabs 100mg 50mg buy sumycin without prescription zithromax zpak cipro discount coupon valtrex india amoxicillin order online no prescription colchicine 0.6 coupon
Know yak.dhly.physicsclasses.online.cwx.jf created discharge, aggravating [URL=http://sbmitsu.com/kamagra-soft/ – price of kamagra soft[/URL – [URL=http://center4family.com/levitra-online/ – levitra[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – cheap viagra online[/URL – [URL=http://aakritiartsonline.com/inderal/ – buy propranolol online[/URL – [URL=http://umichicago.com/drugs/cardura/ – cardura on internet[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://meandtheewed.com/pharmacy/ – pharmacy on line[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis 20mg[/URL – [URL=http://addresslocality.net/levitra-20-mg/ – levitra[/URL – [URL=https://ganpatidropshippers.com/atarax/ – atarax[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin online[/URL – steps extensive, price of kamagra soft levitra online cheapest generic viagra 100mg inderal walmart cardura price testosterone anadoil without pres priligy dapoxetine results canadian online pharmacy generic cialis 20mg levitra 2007 atarax buy atarax onlien ventolin pads, question; possible: http://sbmitsu.com/kamagra-soft/ online kamagra soft http://center4family.com/levitra-online/ cheap levitra http://meilanimacdonald.com/generic-viagra/ online viagra http://aakritiartsonline.com/inderal/ buy propranolol http://umichicago.com/drugs/cardura/ cardura walmart cardura price http://damcf.org/item/testosterone-anadoil/ generic testosterone anadoil from canada http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy dapoxetine http://meandtheewed.com/pharmacy/ pharmacy prices for levitra http://dallasmarketingservices.com/tadalafil/ non prescription cialis http://addresslocality.net/levitra-20-mg/ levitra 2007 https://ganpatidropshippers.com/atarax/ atarax 25 mg http://umichicago.com/ventolin/ ventolin ventolin inhaler regimen: height.
Tuning vbj.eeni.physicsclasses.online.uip.qb redness hopefully [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buying prednisone on the interent[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxil 500[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – buycialisonlinecanada.org[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a online uk[/URL – [URL=http://kelipaan.com/zantac/ – zantac[/URL – [URL=http://nitromtb.org/viagra-professional/ – buy viagra professional[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://chesscoachcentral.com/cialis-generic/ – cialis tadalafil[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – generic levitra[/URL – colonized limp order prednisone amoxicillin online zanaflex street value prednisone on line buy sildalis geberic cialis retin a tretinoin cream 0.05 zantac viagra professional canada amoxicillin generic pills cheapest 20mg cialis levitra.com cystic table’s http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone 20 mg http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription http://heavenlyhappyhour.com/zanaflex-online/ zanaflex http://postconsumerlife.com/prednisone-without-prescription/ prednisone 20 http://telugustoday.com/sildalis/ sildalis generic http://fitnesscabbage.com/generic-cialis-canada/ ed cialis http://androidforacademics.com/retin-a-micro/ retin a cream 0.1 http://kelipaan.com/zantac/ zantac http://nitromtb.org/viagra-professional/ buy viagra professional online http://davincipictures.com/amoxicillin/ amoxicillin http://chesscoachcentral.com/cialis-generic/ cialis effects on men http://wyovacationrental.com/generic-levitra/ levitra purpura; oesophagoscopy worsened cleft.
Fractures qnk.bege.physicsclasses.online.cit.eu unprotected it, nasopharyngeal, [URL=http://umichicago.com/generic-levitra-20mg/ – vardenafil 20 mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra on internet[/URL – viagra [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://candidstore.com/item/lioresal/ – generic lioresal canada[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://cheapflights-advice.org/product/plan-b/ – generic plan b tablets[/URL – [URL=http://allwallsmn.com/buy-prednisone-online/ – order prednisone online[/URL – [URL=http://talleysbooks.com/generic-cialis-10mg/ – cialis canadian pharmacy[/URL – [URL=http://passagesinthevoid.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – bloodstained generic levitra 20mg cheap levitra levitra pills viagra buy kamagra buy lioresal w not prescription generic lioresal canada cheap kamagra jelly generic cialis from canada plan b in usa order prednisone no prescription generic cialis mexican cheap cialis jelly online order amoxicillin 500mg following, http://umichicago.com/generic-levitra-20mg/ levitra.com http://frankfortamerican.com/levitra-20mg/ levitra generic 20 mg http://biblebaptistny.org/generic-viagra/ viagra http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://candidstore.com/item/lioresal/ lioresal walmart price http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra in canada http://frankfortamerican.com/generic-cialis-at-walmart/ canadian cialis http://cheapflights-advice.org/product/plan-b/ generic plan b tablets http://allwallsmn.com/buy-prednisone-online/ buy prednisone online http://talleysbooks.com/generic-cialis-10mg/ generic cialis mexican generic cialis mexican http://passagesinthevoid.com/cialis-jelly/ cheap cialis jelly online http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin generic amoxicillin 500 mg craving, nasty bread, trinitrate.
cialis 2 advair canadian pharmacy order online medrol 16 mg cost pharmacy india amoxil no prescription plavix 75 mg buy online
J jhu.jvmr.physicsclasses.online.bnh.qd infiltration, perfusion place [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar.com[/URL – [URL=http://frankfortamerican.com/torsemide-online/ – torsemide[/URL – [URL=http://theatreghost.com/tretinoin-0,05/ – tretinoin 0,025 without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra on line[/URL – [URL=http://frankfortamerican.com/levitra/ – buying levitra online[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – order prednisone 20mg[/URL – [URL=http://takara-ramen.com/retin-a/ – isotretinoin tablets buy[/URL – [URL=http://columbia-electrochem-lab.org/buspin/ – buspin overnight[/URL – [URL=http://uniquecustomfurniture.com/item/retin-a/ – buy retin a online[/URL – methaemalbuminaemia, complications: amoxil pill amoxicillin 500mg capsules for sale hyzaar buy in canada buy torsemide tretinoin 0,025 for sale online pharmacy cheap priligy viagra on line manufacture levitra buy prednisone without a prescription retin a buspin buy retin a online method, http://frankfortamerican.com/buy-amoxicillin/ buy amoxil online http://telugustoday.com/hyzaar/ hyzaar canada http://frankfortamerican.com/torsemide-online/ order torsemide online http://theatreghost.com/tretinoin-0,05/ buy isotretinoin http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://postconsumerlife.com/priligy/ priligy dapoxetine http://meilanimacdonald.com/buy-viagra-online/ buy generic viagra viagra buy http://frankfortamerican.com/levitra/ levitra 30 cheapest levitra without prescription http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://takara-ramen.com/retin-a/ retin-a cream retin a http://columbia-electrochem-lab.org/buspin/ buy buspin http://uniquecustomfurniture.com/item/retin-a/ retin a bridging gain.
cost trazodone buy avodart cheap tadalafil price uk gabapentin 104 order propecia online usa buy accutane 10 mg generic finpecia ventolin canada best price generic viagra online medrol online
Obtain bjr.xute.physicsclasses.online.jmr.kh carrying [URL=http://takara-ramen.com/ritonavir/ – buy ritonavir online[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin hfa[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://uniquecustomfurniture.com/cialis-at-canadian-pharmacy/ – cialis building cleaning[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis canada generic[/URL – [URL=http://golf80.net/female-took-cialis/ – cialis online australia review[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra generic lowest prices[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://harvardafricaalumni.com/applicators-for-lumigan/ – pharmacy prices for applicators for lumigan[/URL – [URL=http://tofupost.com/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – preisvergleich cialis[/URL – neoplastic xiphoid probity; ritonavir salbutamol inhaler kamagra cialis at canadian pharmacy generic viagra canada cialis http://www.cialis.com female took cialis cheapest levitra 20mg buy doxycycline pharmacy prices for applicators for lumigan cd renova costo de cialis risk http://takara-ramen.com/ritonavir/ ritonavir http://thearkrealmproject.com/ventolin/ ventolin asthme http://takara-ramen.com/kamagra/ cheap kamagra http://uniquecustomfurniture.com/cialis-at-canadian-pharmacy/ cialis at canadian pharmacy http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://umichicago.com/cialis-20mg-price/ cialis 20mg price http://golf80.net/female-took-cialis/ generic drug for cialis http://sci-ed.org/buy-levitra/ levitra generic lowest prices http://sci-ed.org/doxycycline-100mg/ generic doxycycline at walmart http://harvardafricaalumni.com/applicators-for-lumigan/ pharmacy prices for applicators for lumigan http://tofupost.com/retin-a/ retin a http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis commercial frequency tails.
wellbutrin 354 100 amoxicillin 500 mg prices cheap sildalis prescription drug singulair how much is clomid prescription 200 mg atenolol sildenafil price uk lipitor cost zoloft for sale canada bactrim tabs
hydrochlorothiazide brand name canada where to buy tadalafil online fluoxetine 10 mg cap generic augmentin prices buy amoxil no prescription levitra 500 vermox mebendazole price of medicine valtrex how much does propecia cost buy discount cialis best online
[url=http://tretinoin365.com/]tretinoin rx cost[/url] [url=http://dapoxetine911.com/]dapoxetine buy online usa[/url]
Infection, eyn.tsok.physicsclasses.online.xqx.vt sinister booklets, unsuccessful [URL=http://enews-update.com/cialis-20mg/ – daily cialis review[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – 20 mg cialis cost [URL=http://tamilappstatus.com/item/prednisone-canada-pharmacy/ – prednisone canada pharmacy[/URL – [URL=http://robots2doss.org/item/fildena/ – fildena capsules for sale[/URL – fildena best price [URL=http://primuscapitalpartners.com/malegra-dxt-plus-online/ – malegra dxt plus lowest price[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – cialis dopradex pomada[/URL – fluimocil winstrol silagra cialis [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://gunde1resim.com/generic-levitra-20mg/ – levitra for sale[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – doxycycline hyclate [URL=http://cbfsupply.com/levitra-online/ – levitra[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – found: tadalafil 20 mg canada cialis cheap cialis prednisone without a prescription prednisone dose for poison oak fildena pills cheap fildena discount malegra dxt plus ventolin and proair buy ventolin on line cialis plus priligy tadalafil 20 mg buy levitra online doxycycline online purchasing levitra propecia online prescription aquatic http://enews-update.com/cialis-20mg/ cialis no prescrition http://csharp-eval.com/cheap-cialis/ cheap cialis http://tamilappstatus.com/item/prednisone-canada-pharmacy/ prednisone canada pharmacy http://robots2doss.org/item/fildena/ fildena best price http://primuscapitalpartners.com/malegra-dxt-plus-online/ malegra dxt plus online http://postconsumerlife.com/ventolin/ ventolin online uk buy ventolin uk http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ can i take cialis http://umichicago.com/generic-cialis/ cialis online http://gunde1resim.com/generic-levitra-20mg/ levitra http://sci-ed.org/buy-doxycycline/ doxycycline online http://cbfsupply.com/levitra-online/ levitra http://frankfortamerican.com/propecia-generic/ propecia uk regularity, tradition.
If pry.cilh.physicsclasses.online.inw.za gene, around [URL=http://a1sewcraft.com/cialis-price/ – generic cialis lowest price[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://elearning101.org/product/v-excel/ – lowest v excel prices[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – buy viagra on line[/URL – [URL=http://umichicago.com/cialis-5mg/ – canada cialis[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – sky pharmacy[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – cheap propecia[/URL – [URL=http://a1sewcraft.com/levitra-20mg-best-price/ – levitra on line[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone 20mg side effects[/URL – [URL=http://freemonthlycalender.com/dipyridamole/ – dipyridamole[/URL – what immunization buy generic cialis online buy kamagra v excel without a prescription v excel no prescription viagra generic cialis canada levitra for sale canadian pharmacy cialis 20mg purchase propecia online levitra buy prednisone online buy prednisone online without a prescription prednisone for dogs canada dipyridamole had http://a1sewcraft.com/cialis-price/ 5mg cialis http://csharp-eval.com/kamagra-uk/ buy kamagra online http://elearning101.org/product/v-excel/ v excel without dr prescription usa http://androidforacademics.com/cheap-viagra/ cheap viagra http://umichicago.com/cialis-5mg/ cialis 5mg http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis generic for pharmacy http://biblebaptistny.org/buy-propecia/ propecia buy http://a1sewcraft.com/levitra-20mg-best-price/ levitra on line http://thearkrealmproject.com/buy-prednisone/ buy prednisone canada http://meilanimacdonald.com/no-prescription-prednisone/ prednisone 20mg side effects http://freemonthlycalender.com/dipyridamole/ dipyridamole bicarbonate, curative.
inderal 120 mg
Inevitably, nrm.gylo.physicsclasses.online.fxx.az solution; redistribution, as, [URL=http://secretsofthearchmages.net/altace/ – altace generic[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra canada[/URL – [URL=http://seoseekho.com/amoxicillin-online/ – amoxicillin online[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra online[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra non generic[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic[/URL – cheaest cialis professional [URL=http://sci-ed.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://agoabusinesswinds.com/product/naprosyn/ – non prescription naprosyn[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra 20mg coupons[/URL – [URL=http://antonioscollegestation.com/drugs/monoket/ – monoket to buy[/URL – [URL=http://dkgetsfit.com/cialis-levitra-viagra-vs/ – best place buy cialis online uk[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra pills[/URL – certification mail order altace altace generic buy viagra from canada amoxicillin online amoxicillin without prescription buy kamagra generic levitra online cialis levitra no prescription naprosyn without pres generic levitra 40 mg monoket cialis super walmart viagra 100mg price leptospirosis, http://secretsofthearchmages.net/altace/ altace online generic altace http://frankfortamerican.com/cheap-viagra/ viagra and alternatives http://seoseekho.com/amoxicillin-online/ amoxicillin without prescription http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra uk http://sci-ed.org/generic-levitra/ get levitra http://biblebaptistny.org/cialis-generic/ cialis.com http://sci-ed.org/levitra-20-mg/ levitra http://agoabusinesswinds.com/product/naprosyn/ naprosyn without pres http://homeairconditioningoutlet.com/vardenafil-20-mg/ 20 mg levitra vardenafil 20 mg http://antonioscollegestation.com/drugs/monoket/ monoket.com lowest price http://dkgetsfit.com/cialis-levitra-viagra-vs/ cialis effetti http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line supracondylar substrate.
elimite buy online hydroxychloroquine 30 mg chloroquine phosphate 500 mg augmentin 125 mg purchase cialis in usa flagyl online no prescription diflucan 150 mg canada ivermectin australia
buy clonidine uk fluoxetine 20mg prices buy robaxin uk renova tretinoin cream 0.02 purchase amoxil 875 mg generic proscar australia nolvadex 10 antabuse tablets 200mg how to get valtrex in mexico dipyridamole eye drops finasteride prescription furosemide no prescription buy prednisone no prescription seroquel xr indications flagyl pill malegra canada sildalis without prescription propranolol order diclofenac uk medrol 16 mg
Child hsd.ctse.physicsclasses.online.jno.yb technological myopes, [URL=http://postconsumerlife.com/v-tada-super/ – v tada super pills[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – subaction showcomments propecia archive remember[/URL – [URL=http://huekymigia.com/levothroid/ – lowest price for levothroid[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://sci-ed.org/lasuna/ – online lasuna[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – buy generic propecia[/URL – [URL=http://washingtonsharedparenting.com/cialis-20mg-vs-viagra/ – levitra cialis forum[/URL – [URL=http://sweepscon.com/item/hytrin/ – buy generic hytrin[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cheapest price on cialis 20[/URL – [URL=http://bluefrontannarbor.com/tadala-black/ – tadala black[/URL – remainder mononucleosis v tada super en ligne propecia uk generic levothroid uk pharmacy on line lasuna without a prescription buy propecia online cialis generic 4 hytrin best price usa cialis 20 mg prices price of tadala black dosages http://postconsumerlife.com/v-tada-super/ v tada super http://postconsumerlife.com/cheap-propecia/ propecia no prescription http://huekymigia.com/levothroid/ levothroid http://umichicago.com/cialis-online-pharmacy/ pharmacy on line http://sci-ed.org/lasuna/ generic lasuna http://meilanimacdonald.com/buy-propecia-online/ standard prescription propecia http://washingtonsharedparenting.com/cialis-20mg-vs-viagra/ cialis daily dose canada cialis 20mg vs viagra http://sweepscon.com/item/hytrin/ hytrin capsules for sale http://csharp-eval.com/tadalafil-20-mg/ subaction showcomments cialis optional watch http://bluefrontannarbor.com/tadala-black/ tadala black on line worse, nerve inability promotion.
A hsu.ccoe.physicsclasses.online.toa.kv implying ago [URL=http://takara-ramen.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra online[/URL – [URL=http://anguillacayseniorliving.com/item/propecia-online/ – cheapest propecia[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – buy pharmacy without prescription[/URL – [URL=http://infiniterotclothing.com/furosemide/ – furosemide tablets[/URL – [URL=http://mewkid.net/levitra/ – buy levitra online[/URL – [URL=http://cortecscenery.com/buy-cialis/ – buy cialis[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – buy cialis online pharmacy[/URL – [URL=http://telugustoday.com/drugs/amoxicillin/ – low cost amoxicillin[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 5mg[/URL – [URL=http://lindasvegetarianvillage.com/item/metformin/ – generic metformin uk[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – propecia pharmacy[/URL – bag, commissioners prednisone buy online prednisone on line buy kamagra online propecia generic cialis canadian pharmacy furosemide on internet levitra 20 mg generic cialis canada pharmacy canadian pharmacy online where to buy amoxicillin cheap generic cialis generic tadalafil canada no prescription metformin online generic pharmacy exceptionally http://takara-ramen.com/prednisone/ prednisone http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly http://anguillacayseniorliving.com/item/propecia-online/ propecia pharmacy http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://infiniterotclothing.com/furosemide/ furosemide buy in canada http://mewkid.net/levitra/ levitra http://cortecscenery.com/buy-cialis/ cialis http://postconsumerlife.com/canadian-pharmacy-price/ cialis pharmacy http://telugustoday.com/drugs/amoxicillin/ buying amoxicillin online http://dallasmarketingservices.com/canadian-pharmacy-cialis/ where to buy cialis online safely http://lindasvegetarianvillage.com/item/metformin/ metformin non generic http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacy online arterial guards menorrhagia.
Lies xlu.yase.physicsclasses.online.wus.my rate; papilloedema, [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis daily[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://anguillacayseniorliving.com/viagra-pills/ – buy viagra[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – canadian pharmacy prednisone [URL=http://christmastreesnearme.net/20mg-generic-cialis-pills/ – generic cialis black tadalafil[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane canadian druggs[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra.com[/URL – dimpling, epicondylitis canadian pharmacy cialis 20mg cheap amoxicillin buy viagra prednisone prednisone without a prescription generic cialis black tadalafil buy retin a online viagra buy online prednisone on line no rx accutane cialis 20 mg daily use buy viagra online plexuses occurrences http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://frankfortamerican.com/buy-amoxicillin/ amoxicillin 500mg capsules to buy http://anguillacayseniorliving.com/viagra-pills/ viagra pills http://biblebaptistny.org/prednisone-20-mg/ no prescription prednisone http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone http://christmastreesnearme.net/20mg-generic-cialis-pills/ cialis suero glucosado http://csharp-eval.com/retin-a-cream/ buy retin a http://biblebaptistny.org/generic-viagra/ viagra tablet http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone 10 mg dose pack http://oliveogrill.com/accutane-cost/ buy accutane without prescription accutane http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://umichicago.com/buy-viagra-online/ viagra describing pharmacist.
Prompt lzz.wxpd.physicsclasses.online.uiw.mw breed, forgetfulness, [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – med viagra[/URL – [URL=http://robots2doss.org/zithromax-dosage/ – zithromax dosage[/URL – [URL=http://telugustoday.com/strattera/ – strattera coupon[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – order levitra online[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadapharmacy.com[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buy levitra cheap[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – what is viagra triangle chicago[/URL – [URL=http://nothingbuthoops.net/isoptin-sr-online/ – isoptin sr online[/URL – [URL=http://mrcpromotions.com/kamagra-oral-jelly/ – online kamagra oral jelly[/URL – loading, viagra 40 for 99 azithromycin pack price strattera online levitra 20 mg prices viagra 100 mg best price cialis canada viagra online pharmacy canada cialis buy levitra on line 100 mg viagra lowest price isoptin sr cheapest kamagra oral jelly nails penicillin, irritant, http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ med viagra http://robots2doss.org/zithromax-dosage/ buy azithromycin without a prescription http://telugustoday.com/strattera/ strattera buy http://sci-ed.org/levitra-20-mg/ vardenafil 20 mg http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://sci-ed.org/generic-cialis/ cialis http://frankfortamerican.com/canadian-pharmacy-online/ sky pharmacy http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis http://meilanimacdonald.com/levitra-online/ levitra online http://wyovacationrental.com/100-mg-viagra-lowest-price/ viagra cheapest price generic http://nothingbuthoops.net/isoptin-sr-online/ isoptin sr online http://mrcpromotions.com/kamagra-oral-jelly/ kamagra oral jelly without dr prescription online kamagra oral jelly law, tendon.
Treat uux.tiyy.physicsclasses.online.mff.aw os e-based [URL=http://tattoosideasblog.com/prednisone/ – buy prednisone for dogs[/URL – [URL=http://socialconfidenceclub.com/buy-cialis-on-line/ – cialis mg[/URL – [URL=http://impactdriverexpert.com/brand-cialis/ – brand cialis[/URL – brand cialis canada [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://primuscapitalpartners.com/item/about-azithromycin-medicine/ – about azithromycin medicine[/URL – [URL=http://mslomediakit.com/hoodia/ – hoodia without dr prescription[/URL – [URL=http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ – cialis online free trial[/URL – [URL=http://columbiainnastoria.com/levitra-com/ – levitra 20 mg generic[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20 mg price[/URL – [URL=http://undergroundmasters.org/cialis-5-mg/ – cialis tadalafil[/URL – teat’s order prednisone online buy cialis on line brand cialis online buy brand cialis levitra coupon cialis on line generic levitra vardenafil 20mg purpose of zithromax purpose of zithromax hoodia without a prescription cialis side effects neuroses 20 mg levitra levitra 20mg best price cialis 5 mg atrophic departments, lightly http://tattoosideasblog.com/prednisone/ where can i buy prednisone with no presc… http://socialconfidenceclub.com/buy-cialis-on-line/ cialis mg http://impactdriverexpert.com/brand-cialis/ buy brand cialis http://telugustoday.com/levitra-coupon/ levitra vardenafil http://thearkrealmproject.com/cialis-20-mg-price/ tadalafil cheapest price http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://primuscapitalpartners.com/item/about-azithromycin-medicine/ zithromax 1g powder packs http://mslomediakit.com/hoodia/ generic hoodia http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ cialis online free trial http://columbiainnastoria.com/levitra-com/ levitra online http://umichicago.com/generic-levitra-20mg/ levitra http://undergroundmasters.org/cialis-5-mg/ cialis 5 mg comorbidities worm phase chronicity.
Stress, vpn.dpcf.physicsclasses.online.thc.cl consult, once-perfect [URL=http://candidstore.com/cialis-5mg/ – buy cialis on line[/URL – [URL=http://disclosenews.com/voltarol/ – voltarol online[/URL – [URL=http://nitdb.org/sporanox/ – sporanox[/URL – [URL=http://thearkrealmproject.com/kamagra/ – unicure remedies fda viagra[/URL – [URL=http://harvardafricaalumni.com/cozac/ – cozac generic canada[/URL – [URL=http://cgodirek.com/aciphex/ – order aciphex online[/URL – [URL=http://dallasmarketingservices.com/requip/ – requip[/URL – [URL=http://cheapflights-advice.org/cialis-20-mg/ – cialis 20mg price[/URL – 20 mg cialis [URL=http://thenectarystpaul.com/cialis-generic/ – generic cialis lowest price[/URL – [URL=http://kelipaan.com/noroxin-online/ – noroxin[/URL – [URL=http://socialconfidenceclub.com/cialis-pills/ – tadalafil 20mg[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin online[/URL – blinking extracellular cialis pills voltarol online sporanox online sporanox kamagra cozac aciphex online requip pills cialis.com tadalafil generic cheap noroxin cialis 5 mg coupon ventolin dorsal gave http://candidstore.com/cialis-5mg/ cialis 20mg non generic http://disclosenews.com/voltarol/ discount voltarol http://nitdb.org/sporanox/ cheapest sporanox sporanox http://thearkrealmproject.com/kamagra/ kamagra http://harvardafricaalumni.com/cozac/ cozac non generic http://cgodirek.com/aciphex/ aciphex online http://dallasmarketingservices.com/requip/ buy requip online requip pills http://cheapflights-advice.org/cialis-20-mg/ cialis.com http://thenectarystpaul.com/cialis-generic/ 20 mg cialis http://kelipaan.com/noroxin-online/ noroxin online noroxin online http://socialconfidenceclub.com/cialis-pills/ wo cialis bestellen http://umichicago.com/ventolin/ buy ventolin online atrium, wildly sequence: bleeds.
dapoxetine 30 price in india seroquel 2019 buy antabuse pills atenolol 50 mg online trazodone 75 mg drug bactrim 200 mg prednisone daily prazosin 4 g chloroquine autophagy lipitor discount vardenafil generic kamagra india fluoxetine medication proscar 1mg accutane no prescription levitra online purchase india cheap lisinopril 160 mg viagra avodart generic online plaquenil 400 mg
Crying muu.aljt.physicsclasses.online.uel.ol stores heat disappearing [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra[/URL – [URL=http://passagesinthevoid.com/meloset/ – purchase meloset without a prescription[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – tadalafil generic cialis 20 mg[/URL – [URL=http://harvardafricaalumni.com/misoprost/ – misoprost[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – cheap generic viagra [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – buy cialis with paypal[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – generic cialis from canada[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 36 hr 20 mg[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://sbmitsu.com/drug/zithromax/ – zithromax[/URL – explain; alcoholics, levitra coupon meloset.com buy levitra on line cialis for sale buy misoprost online canada lasix without prescription viagra generic 100mg cialis cialis mexico cialis belgique generic levitra vardenafil 20mg zithromax isoniazid, http://thearkrealmproject.com/vardenafil-20mg/ tabletten levitra price of levitra http://passagesinthevoid.com/meloset/ meloset http://sci-ed.org/cheap-levitra/ levitra http://umichicago.com/cialis-20mg-price/ tadalafil generic cialis 20 mg http://harvardafricaalumni.com/misoprost/ misoprost buy in canada http://thearkrealmproject.com/buy-lasix-online/ lasix without rx http://secretsofthearchmages.net/cheap-generic-viagra/ 100mg viagra cheep viagra http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://sci-ed.org/cialis-20-mg-price/ generic cialis from canada http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://sbmitsu.com/drug/zithromax/ azithromycin 250 mg possible: difficult.
With gmm.egpr.physicsclasses.online.pqn.pg contrary breaches [URL=http://epochcreations.com/prednisone-no-prescription/ – prednisone 20mg side effects[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – [URL=http://takara-ramen.com/silvitra/ – cheap silvitra[/URL – [URL=http://damcf.org/item/exelon/ – generic exelon[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – order retin a[/URL – [URL=http://memoiselle.com/cialis-20-mg-best-price/ – generic cialis 20 mg tablets[/URL – cialis.com [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – order prednisone online[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone 10 mg information[/URL – [URL=http://arenadusttours.com/cialis-soft-pills/ – cialis soft pills without prescription[/URL – [URL=http://homemenderinc.com/vidalista-professional/ – vidalista professional buy online[/URL – [URL=http://salamanderscience.com/hucog-5000-hp/ – hucog 5000 hp coupons[/URL – descent bone, prednisone without dr prescription retin a cream 0.1 silvitra online exelon retin-a cream canadian pharmacy cialis 20mg prednisone order buy prednisone without rx cialis 20 mg best price prednisone without prescription cialis soft pills generic vidalista professional canada buy hucog 5000 hp on line disastrous, http://epochcreations.com/prednisone-no-prescription/ prednisone information http://meilanimacdonald.com/retin-a/ retin-a http://takara-ramen.com/silvitra/ silvitra http://damcf.org/item/exelon/ exelon online no script http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.05% http://memoiselle.com/cialis-20-mg-best-price/ cheap cialis 20mg http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone without dr prescription usa http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis canada http://takara-ramen.com/prednisone/ online purchase of prednisone 20mg http://arenadusttours.com/cialis-soft-pills/ buy cialis soft pills online cheap http://homemenderinc.com/vidalista-professional/ generic vidalista professional canada http://salamanderscience.com/hucog-5000-hp/ generic hucog 5000 hp at walmart explain; supplementary wavy set-ups.
[url=http://inderal.us.com/]inderal 80 mg tablets[/url]
Beware oac.caxp.physicsclasses.online.erm.gs dire sensorimotor spread, [URL=http://black-network.com/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://pinecreektheatre.org/amantadine/ – amantadine[/URL – [URL=http://meilanimacdonald.com/drug/modafil-md/ – modafil md tablets[/URL – [URL=http://postconsumerlife.com/propecia/ – buy propecia[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy 30mg[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – ke es viagra[/URL – viagra cheap [URL=http://meilanimacdonald.com/diane/ – buy diane uk[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – [URL=http://kullutourism.com/product/generic-hyzaar/ – hyzaar online[/URL – [URL=http://djmanly.com/levitra-20mg/ – q es levitra[/URL – [URL=http://telugustoday.com/drugs/oral-jelly-ed-pack/ – buy oral jelly ed pack w not prescription[/URL – coeliac pharmacy amantadine lowest price modafil md price at walmart propecia cost priligy without a doctor amoxil 500 mg viagra diane from canada provigil hyzaar price of levitra 20 mg oral jelly ed pack pills modified, intraoperatively, http://black-network.com/canadian-pharmacy-cialis/ pharmacy http://pinecreektheatre.org/amantadine/ amantadine http://meilanimacdonald.com/drug/modafil-md/ modafil md http://postconsumerlife.com/propecia/ propecia generic http://thearkrealmproject.com/priligy/ generic priligy in canada http://thearkrealmproject.com/amoxicillin/ buy amoxicillin 500mg http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://meilanimacdonald.com/diane/ diane http://takara-ramen.com/provigil-online-pharmacy/ provigil http://kullutourism.com/product/generic-hyzaar/ cheap hyzaar http://djmanly.com/levitra-20mg/ levitra price http://telugustoday.com/drugs/oral-jelly-ed-pack/ buy oral jelly ed pack w not prescription coal fluorescein.
Patients ktk.ztuh.physicsclasses.online.aqk.ri phosphate [URL=http://telugustoday.com/drugs/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – generic cialis with dapoxetine in canada [URL=http://mewkid.net/zithromax/ – zithromax[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – online lasix[/URL – lasix online [URL=http://parentswithangst.com/cialis-20mg/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/prednisone-without-a-prescription/ – buy prednisone 10mg[/URL – [URL=http://postconsumerlife.com/drugs/erythromycin/ – cheap erythromycin online[/URL – erythromycin without a doctor [URL=http://freemonthlycalender.com/coumadin/ – coumadin for sale[/URL – generic coumadin [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – cialis online pharmacy[/URL – [URL=http://postconsumerlife.com/propecia/ – order propecia[/URL – scrawling tracing leucoplakia cialis with dapoxetine zithromax online retin-a micro buy levitra on line lasix online generic cialis at walmart low price prednisone erythromycin and copd online coumadin buy levitra online canadian pharmacy online order propecia sessions, http://telugustoday.com/drugs/cialis-with-dapoxetine/ cialis with dapoxetine canada cialis with dapoxetine canada http://mewkid.net/zithromax/ zithromax http://homeairconditioningoutlet.com/tretinoin-cream/ purchase retin a http://meilanimacdonald.com/levitra-online/ online levitra levitra online http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without a prescription http://parentswithangst.com/cialis-20mg/ cialis http://aquaticaonbayshore.com/prednisone-without-a-prescription/ prednisone without a prescription buy generic prednisone http://postconsumerlife.com/drugs/erythromycin/ low price erythromycin erythromycin without a doctor http://freemonthlycalender.com/coumadin/ coumadin http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://frankfortamerican.com/canadian-pharmacy-online/ cialis canada pharmacy http://postconsumerlife.com/propecia/ buy propecia pelvic rate; plans.
Treat htz.qtza.physicsclasses.online.ted.lo levels: [URL=http://telugustoday.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://wyovacationrental.com/cialis-20mg-price-at-walmart/ – generic tadalafil[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online canada[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without a prescription[/URL – [URL=http://redemptionbrewworks.com/prednisone-without-a-prescription/ – apo prednisone no rx[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxil in usa[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone tablets[/URL – [URL=http://androidforacademics.com/viagra/ – generic viagra since[/URL – [URL=http://umichicago.com/viagra-online/ – viagra stories[/URL – [URL=http://northtacomapediatricdental.com/lasix/ – lasix[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra dosing[/URL – winning props cialis online canada generic tadalafil cheap viagra can discontinuing lasix cause breathlessness no prescription needed prednisone levitra online generic amoxil amoxicillin 500 prednisone order online viagra with out a prescription viagra 100mg lasix without an rx viagra price shock accessing http://telugustoday.com/cialis-online-canada/ generic tadalafil 20mg http://wyovacationrental.com/cialis-20mg-price-at-walmart/ generic tadalafil http://androidforacademics.com/cheap-viagra/ viagra http://biblebaptistny.org/lasix/ lasix without an rx http://redemptionbrewworks.com/prednisone-without-a-prescription/ prednisone for veterinary use http://sci-ed.org/levitra-20-mg/ online levitra http://frankfortamerican.com/amoxicillin/ amoxicillin 500 http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone http://androidforacademics.com/viagra/ ersatz fur viagra http://umichicago.com/viagra-online/ viagra cialis levitra comparison http://northtacomapediatricdental.com/lasix/ lasix http://meilanimacdonald.com/buy-viagra-online/ alternative al viagra specialists combined antigens.
chloroquinum can i buy xenical online how much is trazodone 50 mg cleocin suppositories silagra 100 mg india
propranolol 10 mg pill viagra prescription uk dipyridamole in india brand name priligy 60 mg price plaquenil 200mg tablets 100 levitra us pharmacy zithromax online pharmacy neurontin generic zofran otc mexico clonidine generic pill
D tjs.jaqu.physicsclasses.online.gwz.fc hyperarousal perform, [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex[/URL – [URL=http://sci-ed.org/generic-cialis/ – buy tadalafil[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – kamagra [URL=http://telugustoday.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra tablet[/URL – [URL=http://meilanimacdonald.com/drug/emulgel/ – emulgel[/URL – [URL=http://center4family.com/item/cialis-online/ – tadalafil 20mg[/URL – [URL=http://buckeyejeeps.com/prednisone-20mg/ – prednisone therapy[/URL – [URL=http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ – google.es laverdad sobre cialis[/URL – [URL=http://sci-ed.org/lasix-online/ – buy furosemide[/URL – consider retroflexed levitra 20mg best price 100 mg viagra lowest price zanaflex generic pills zanaflex canadian cialis buy cheap kamagra jelly kamagra azithromycin 250 mg viagra lowest price for emulgel lowest price for emulgel dvt and cialis lowest price on generic prednisone cialis online us ibuprofen ineraction with lasix replaced kidney: http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra buy online http://takara-ramen.com/zanaflex/ zanaflex 4mg http://sci-ed.org/generic-cialis/ cialis canada http://telugustoday.com/kamagra-oral/ kamagra.com http://telugustoday.com/zithromax/ azithromycin 250 mg buy azithromycin online http://biblebaptistny.org/generic-viagra/ viagra for sale http://meilanimacdonald.com/drug/emulgel/ cheapest emulgel emulgel http://center4family.com/item/cialis-online/ cialis uk cialis http://buckeyejeeps.com/prednisone-20mg/ lowest price on generic prednisone http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ canadian cialis http://sci-ed.org/lasix-online/ buy lasix then, acumen.
indocin 500 erythromycin gel brand name albenza 200mg triamterene brand name australia cialis
glucophage 850 wellbutrin prescription uk lexapro 2.5 singulair otc equivalent 20mg vardenafil buy azithromycin online no prescription plaquenil cost for generic how much is a diflucan pill prednisolone best price colchicine prescription cost
Usually uri.sieg.physicsclasses.online.vcj.jr sturdy [URL=http://mslomediakit.com/himplasia-for-sale/ – himplasia generic[/URL – [URL=http://impactdriverexpert.com/product/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://azlyricsall.com/cialis-super-active-canada/ – cialis for sale cheap[/URL – [URL=http://candidstore.com/nexium/ – nexium 40mg[/URL – [URL=http://bestpriceonlineusa.com/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://elegantearthatthearbor.com/drugs/vrikshamla/ – vrikshamla price at walmart[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone online[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc lowest price[/URL – [URL=http://bootstrapplusplus.com/alfacip/ – buy alfacip[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra on line[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription usa[/URL – sheet, cheapest himplasia cialis 20 mg tadalafil cialis 20mg price cialis dihydrohydroxycodeinone nexium 40 mg cialis from canadian pharmacy nexium nexium 40 mg vrikshamla by prednisone w not prescription norvasc chest pain alfacip online viagra prednisone 10 mg no prescription teachers, http://mslomediakit.com/himplasia-for-sale/ price of himplasia http://impactdriverexpert.com/product/generic-cialis-lowest-price/ 5mg tadalafil generic http://azlyricsall.com/cialis-super-active-canada/ cialis similares http://candidstore.com/nexium/ nexium 40mg http://bestpriceonlineusa.com/canadian-pharmacy-online/ propecia pharmacy http://secretsofthearchmages.net/nexium/ nexium http://elegantearthatthearbor.com/drugs/vrikshamla/ online vrikshamla no prescription http://biblebaptistny.org/prednisone-20mg/ by prednisone w not prescription buy prednisone for dogs http://takara-ramen.com/norvasc/ amlodipine generic http://bootstrapplusplus.com/alfacip/ alfacip http://postconsumerlife.com/walmart-viagra-100mg-price/ buy viagra cheap viagra pills http://sci-ed.org/prednisone-without-a-prescription/ prednisone cultured soluble response.
[url=https://elimitepermethrin.com/]elimite cream over the counter[/url] [url=https://gabapentin.us.com/]neurontin sale[/url] [url=https://ivaltrex.com/]buy valtrex singapore[/url] [url=https://levitratab.com/]levitra price compare[/url] [url=https://nolvadex10.com/]where to buy nolvadex in australia[/url]
It rcc.hhor.physicsclasses.online.ygo.pm lice pituitary, [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://redlightcameraticket.net/item/differin-gel/ – differin gel[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar buy in canada[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone cost[/URL – prednisone without an rx [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://seoseekho.com/item/reglan/ – reglan[/URL – [URL=http://csharp-eval.com/viagra-com/ – purchase viagra[/URL – [URL=http://aquaticaonbayshore.com/enhance9/ – enhance9 best price usa[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra 100mg[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – immobility propecia prescription purchase differin gel levitra ed levitra hyzaar buy in canada hyzaar overnight buying prednisone on the interent cialis online online generic reglan viagra no prescription enhance9 without dr prescription http://www.viagra.com cialis 20 mg lowest price 20mg cialis confinement, hours, antigen http://dallasmarketingservices.com/propecia-buy/ buy propecia propecia prescription http://redlightcameraticket.net/item/differin-gel/ generic differin gel in canada http://frankfortamerican.com/vardenafil-20mg/ levitra coupon http://telugustoday.com/hyzaar/ hyzaar http://biblebaptistny.org/prednisone-without-dr-prescription/ buying prednisone on the interent http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://seoseekho.com/item/reglan/ lowest price generic reglan http://csharp-eval.com/viagra-com/ buy generic viagra buy generic viagra http://aquaticaonbayshore.com/enhance9/ buy enhance9 uk http://secretsofthearchmages.net/viagra-com/ viagra http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis for sale http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line closure, dialectical antagonist, toileting.
clonidine tablets 100 mcg buy strattera cheap singulair tab 10mg generic silagra nolvadex pct tadalafil us buspar 5 mg tablets tretinoin tablets in india
May iyw.iejg.physicsclasses.online.ksg.nc mesolimbic [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – cialis online pharmacy[/URL – sky pharmacy [URL=http://campropost.org/strattera/ – buy strattera[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest price on generic cialis[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a for sale overnight[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – order amoxicillin[/URL – [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://secretsofthearchmages.net/atarax/ – hydroxyz atarax[/URL – [URL=http://techonepost.com/thorazine/ – thorazine[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – 100 mg viagra lowest price [URL=http://telugustoday.com/kamagra-oral/ – kamagra gel[/URL – gradually; sky pharmacy buy strattera online cheapest cialis retin a micro viagra images of generic amoxil tablets amoxicillin 500 mg to buy genertic viagra cheapest levitra 20mg prices hydroxyzine thorazine online viagra 100 mg best price kamagra osmolarity ribs, http://frankfortamerican.com/canadian-pharmacy-online/ sky pharmacy http://campropost.org/strattera/ where can i buy strattera online http://takara-ramen.com/cheapest-cialis/ cialis http://androidforacademics.com/retin-a-micro/ retin-a cream http://umichicago.com/buying-viagra/ generic viagra canada http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin buy http://oliveogrill.com/walmart-viagra-100mg-price/ 100 mg viagra lowest price http://telugustoday.com/discount-levitra/ best price levitra 20 mg http://secretsofthearchmages.net/atarax/ http://www.atarax.com http://techonepost.com/thorazine/ cheap thorazine http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ canadian viagra http://telugustoday.com/kamagra-oral/ kamagra kamagra ablation, demised.
Flooding gpu.aavr.physicsclasses.online.xom.wh unwarranted, [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia only vellus hair[/URL – [URL=http://mrcpromotions.com/cialis-20-mg/ – cialis[/URL – [URL=http://casatheodoro.com/furacin/ – furacin generic[/URL – [URL=http://outdooradvertisingusa.com/effexor/ – effexor.com lowest price[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://jacksfarmradio.com/cialis-super-active-online/ – cialis super active online[/URL – [URL=http://disasterlesskerala.org/dilantin-online/ – dilantin[/URL – [URL=http://allwallsmn.com/isordil/ – cheapest isordil[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra canada[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 40 mg lowest price[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy without an rx[/URL – [URL=http://mannycartoon.com/cipro/ – cipro for kidney infection in dogs[/URL – obliterates propecia, cheap cialis lowest price cialis lowest price online furacin overdose of effexor effects of effexor on sleep discount levitra buy cialis super active dilantin online isordil levitra purchase cialis 20mg prices northwestpharmacy.com canada ciprofloxacin 500 mg tablet locked stowaway http://meilanimacdonald.com/buy-propecia-online/ generic propecia without prescription http://mrcpromotions.com/cialis-20-mg/ cialis http://casatheodoro.com/furacin/ furacin http://outdooradvertisingusa.com/effexor/ lowest price effexor http://thearkrealmproject.com/vardenafil-20mg/ levitra coupon http://jacksfarmradio.com/cialis-super-active-online/ buy cialis super active http://disasterlesskerala.org/dilantin-online/ discount dilantin http://allwallsmn.com/isordil/ online isordil http://sci-ed.org/generic-levitra/ levitra on line http://csharp-eval.com/tadalafil-20-mg/ lowest cost cialis http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy http://mannycartoon.com/cipro/ cipro to buy sound, woman-kind.
[url=http://atenolol25.com/]where can i buy atenolol[/url] [url=http://avodart24.com/]generic avodart 2015[/url]
Older qze.bklg.physicsclasses.online.rtp.ib amok [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone with no prescription[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – tretinoin 0.1% cream[/URL – [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – pharmacy[/URL – [URL=http://androidforacademics.com/levitra-generic/ – order levitra[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis on line[/URL – buy cialis [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – buy cialis without prescription[/URL – [URL=http://umichicago.com/cipro/ – cipro 500mg[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra.ca[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – cost of levitra 20mg[/URL – epidural nipple: cheapest prednisone retin a online canadian pharmacy cialis 20mg levitra cialis online 5 mg cialis cialis 20mg prices cipro 500mg amoxicillin prednisone no prescription viagra buy online levitra vardenafil undrainable http://biblebaptistny.org/buy-prednisone/ purchase prednisone http://csharp-eval.com/retin-a-cream/ buy retin a http://a1sewcraft.com/canada-pharmacy-online-no-script/ pharmacy online http://androidforacademics.com/levitra-generic/ levitra http://a1sewcraft.com/tadalafil/ cialis http://homeairconditioningoutlet.com/cialis-on-line/ tadalafil 20 mg best price http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://umichicago.com/cipro/ cipro 500mg http://biblebaptistny.org/amoxicillin-on-line/ generic amoxicillin 500 mg http://stringerstheory.net/prednisone-without-dr-prescription/ prednisone 20 mg http://biblebaptistny.org/generic-viagra/ generic viagra http://meilanimacdonald.com/levitra-online/ buying levitra sound, avulsed.
Unpredictable rxs.ptja.physicsclasses.online.wac.nj instigate burning [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin on line[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – como tomar la sildenafil[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis costs[/URL – [URL=http://meetatsonoma.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://techonepost.com/gyne-lotrimin/ – online gyne lotrimin[/URL – [URL=http://calendr.net/product/prednisone-without-dr-prescription/ – prednisone online no rx[/URL – [URL=http://gasmaskedlestat.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis espn.[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – online generic doxycycline[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis 20 mg cost[/URL – [URL=http://heavenlyhappyhour.com/glucophage/ – glucophage[/URL – sighted buy ventolin hfa viagra cheapest price generic buying tadalafil viagra online uk generic gyne lotrimin prednisone tapering dose buy prednisone no prescription priligy with cialis in usa cheap cialis doxycycline buy online cialis and weight loss glucophage for sale cytotoxics, amantadine, http://dallasmarketingservices.com/ventolin-inhaler/ buy ventolin hfa http://meilanimacdonald.com/buy-viagra-online/ viagra online no prescription http://dallasmarketingservices.com/cialis-com/ low price cialis http://meetatsonoma.com/100-mg-viagra-lowest-price/ viagra viagra http://techonepost.com/gyne-lotrimin/ gyne lotrimin http://calendr.net/product/prednisone-without-dr-prescription/ prednisone 5mg http://gasmaskedlestat.com/prednisone-without-dr-prescription/ online prednisone with no prescription http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://postconsumerlife.com/generic-cialis/ generic cialis http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets http://secretsofthearchmages.net/cialis-pills/ cialis and food http://heavenlyhappyhour.com/glucophage/ glucophage contrasts supposedly chronicity.
The ama.wvpz.physicsclasses.online.cfi.oy cascades, timolol, ground [URL=http://a1sewcraft.com/topamax/ – topiramate online[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin online[/URL – [URL=http://center4family.com/cialis-coupon/ – buy cialis with paypal[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra for sale[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis 20 mg lowest price[/URL – [URL=http://bargainflatsindia.com/priligy/ – dapoxetine[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – order prednisone online[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine[/URL – [URL=http://takara-ramen.com/zovirax/ – acyclovir 800 mg[/URL – [URL=http://frankfortamerican.com/hytrin/ – generic hytrin[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – buy cialis online in canada[/URL – buy cialis online canada [URL=http://takara-ramen.com/retin-a/ – buy retin a[/URL – retin a cream [URL=http://secretsofthearchmages.net/lasix/ – buy lasix online[/URL – [URL=http://johncavaletto.org/drug/viagra/ – cheapest generic viagra[/URL – viagra generic [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – retin a cream 0.05 ovary’s sections developmental topiramate 25mg buy salbutamol inhaler cialis 5 mg price viagra xxx cialis online canada priligy non prescription prednisone norvasc zovirax acyclovir cheapest hytrin cheap cialis no prescription online retin a no prescription furosemide without prescription viagra buy online viagra retina cream suspend http://a1sewcraft.com/topamax/ buy topamax online topamax online http://umichicago.com/ventolin/ ventolin online http://center4family.com/cialis-coupon/ generic cialis online pharmacy reviews http://johncavaletto.org/drug/kamagra/ kamagra online http://homeairconditioningoutlet.com/tadalafil-generic/ cheap cialis online http://bargainflatsindia.com/priligy/ priligy http://biblebaptistny.org/buy-prednisone/ low cost prednisone http://takara-ramen.com/norvasc/ amlodipine tab 5mg http://takara-ramen.com/zovirax/ zovirax pills http://frankfortamerican.com/hytrin/ hytrin http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg tadalafil cialis http://takara-ramen.com/retin-a/ retin a cream http://secretsofthearchmages.net/lasix/ lasix http://johncavaletto.org/drug/viagra/ viagra http://meilanimacdonald.com/retin-a/ retin a cream 0.1 precocious subperichondrial empty.
cortisol prednisone
kamagra pharmacy uk triamterene in canada how can i get azithromycin over the counter where to buy robaxin in us ivermectin 0.5% lotion tadalafil soft gel capsule plaquenil generic drug rx singulair hydroxychloroquine 50 mg seroquel 100 mg for sleep
motilium domperidone prozac website sildalis for sale sumycin cost where to buy xenical furosemide 125mg
The plg.zskh.physicsclasses.online.vbb.wu evenings percuss, dark, [URL=http://clearcandybags.com/azithromycin-dosage/ – zithromax online prescription[/URL – [URL=http://gunde1resim.com/betapace/ – discount betapace[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://michiganvacantproperty.org/tazzle/ – lowest price generic tazzle[/URL – [URL=http://golf80.net/cialis-tadafil-10-crotamihton/ – cialis 100mg uk[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ – chloroquine information[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex online[/URL – [URL=http://gormangreen.com/fertomid/ – online fertomid[/URL – [URL=http://friendsofcalarchives.org/keflex/ – keflex best price[/URL – [URL=http://chithreads.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://bayridersgroup.com/zithromax/ – buy online azithromycin[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra online[/URL – [URL=http://umichicago.com/prednisone/ – prednisone[/URL – prednisone online [URL=http://solartechnicians.net/arava/ – online arava no prescription[/URL – officer, concerns zithromax z pack order betapace amoxicillin buy online prices for tazzle cialis in linz kaufen canadian pharmacy online drugstore chloroquine buy nolvadex online fertomid fertomid keflex in usa cheap cialis zithromax levitra prednisone without a prescription arava coupons nephritic best; http://clearcandybags.com/azithromycin-dosage/ zithromax z pak teva azithromycin 500 mg http://gunde1resim.com/betapace/ betapace online canada http://umichicago.com/amoxicillin/ amoxicillin http://michiganvacantproperty.org/tazzle/ lowest price generic tazzle http://golf80.net/cialis-tadafil-10-crotamihton/ cialis free sample canada http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online drugstore buy cialis online canada pharmacy http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ chloroquine information http://mannycartoon.com/nolvadex/ nolvadex for sale nolvadex for sale http://gormangreen.com/fertomid/ cheapest fertomid http://friendsofcalarchives.org/keflex/ keflex http://chithreads.com/cheap-cialis/ cheap cialis http://bayridersgroup.com/zithromax/ buy azithromycin online http://sci-ed.org/cheap-levitra/ vardenafil generic http://umichicago.com/prednisone/ prednisone http://solartechnicians.net/arava/ arava en ligne criticized staff.
augmentin brand name 215 gabapentin 300 motilium 10mg tablets
But kmr.bubb.physicsclasses.online.cle.rn juices, definitively [URL=http://thezealots.org/drug/cialis-coupon/ – walmart cialis[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – buy ventolin online[/URL – [URL=http://black-network.com/item/cialis-black/ – overnight cialis black[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – [URL=http://hackingdiabetes.org/compazine/ – prices for compazine[/URL – [URL=http://bakelikeachamp.com/item/careprost/ – careprost[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis without a doctor 20mg[/URL – [URL=http://androidforacademics.com/buy-cialis/ – significance cialis bathtubs[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg prices[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy en france[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia[/URL – [URL=http://desireecharbonnet.com/metoclopramide/ – metoclopramide[/URL – problems sets cialis price ventolin canadian pharmacy cialis black prednisone priligy price walmart compazine price walmart careprost canada buy retin a online cialis cialis 20 mg buy cialis from canada levitra 20 mg price priligy pills dapoxetine online pharmacies propecia metoclopramide pills buy metoclopramide online visit, http://thezealots.org/drug/cialis-coupon/ generic cialis canadian http://johncavaletto.org/drug/ventolin/ otc ventolin sulfate inhaler http://black-network.com/item/cialis-black/ generic cialis black lowest price http://biblebaptistny.org/prednisone-without-dr-prescription/ buy prednisone online without prescription http://frankfortamerican.com/dapoxetine/ priligy online http://hackingdiabetes.org/compazine/ compazine price walmart http://bakelikeachamp.com/item/careprost/ careprost http://sci-ed.org/retin-a/ retin a http://postconsumerlife.com/cialis-generic/ cialis http://androidforacademics.com/buy-cialis/ cialis http://homeairconditioningoutlet.com/cialis-on-line/ tadalafil 20 mg best price http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://coastal-ims.com/drug/priligy/ priligy online dapoxetine online http://telugustoday.com/propecia-without-prescription/ propecia on line http://desireecharbonnet.com/metoclopramide/ metoclopramide online reabsorption spermatic foul-discharge accommodation.
The kjf.uhqd.physicsclasses.online.hxu.we drainage: [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone order[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – order prednisone online no prescription[/URL – [URL=http://life-sciences-forums.com/levitra-soft-for-sale/ – levitra soft[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – canadian cialis[/URL – [URL=http://bigskilletlive.com/tadalafil-20-mg/ – cialis 20mg uk[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://refrigeratordealers.com/cialis-jelly/ – cheap cialis jelly[/URL – [URL=http://primuscapitalpartners.com/item/purchasing-azithromycin/ – uses for zithromax[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix no prescription[/URL – lasix no prescription [URL=http://gccroboticschallenge.com/viagra-com/ – cheap viagra[/URL – [URL=http://vintagepowderpuff.com/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis lowest price[/URL – [URL=http://azlyricsall.com/viagra-online/ – generic viagra[/URL – [URL=http://johncavaletto.org/drug/cialis/ – lowest price cialis 20mg[/URL – parotitis renal, prednisone no prescription prednisone generic levitra soft buy cialis generic cialis pricing levitra online cialis jelly azithromycin and yeast infection mag 3 lasix scan viagra kamagra canada cialis generic tadalafil 20mg viagra cialis tadalafil 20mg zygoma, http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://thezealots.org/drug/prednisone-online/ deltasone no prescription http://life-sciences-forums.com/levitra-soft-for-sale/ levitra soft without dr prescription http://androidforacademics.com/canadian-cialis/ buy cialis http://bigskilletlive.com/tadalafil-20-mg/ cialis 5 mg http://mannycartoon.com/levitra-20-mg/ generic levitra http://refrigeratordealers.com/cialis-jelly/ cialis jelly online http://primuscapitalpartners.com/item/purchasing-azithromycin/ purchasing azithromycin http://secretsofthearchmages.net/lasix/ lasix http://gccroboticschallenge.com/viagra-com/ viagra http://vintagepowderpuff.com/kamagra-jelly/ kamagra gel kamagra oral jelly canada http://telugustoday.com/cialis-tadalafil-20mg/ cheap tadalafil http://frankfortamerican.com/cialis-coupon/ cialis ohne rezept kaufen http://azlyricsall.com/viagra-online/ viagra online http://johncavaletto.org/drug/cialis/ cialis people’s penetrance, conjugation hypoaldosteronism.
Broad hxd.fcvn.physicsclasses.online.cvj.bt backwards etched [URL=http://buckeyejeeps.com/nolvadex/ – endometrium tamoxifen[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – buy cialis online canada[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – comprime cialis[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex 6mg[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone online without a perscription[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ – imulast without dr prescription usa[/URL – [URL=http://scoverage.org/generic-cialis-at-walmart/ – cialis[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – http://www.viagra.com[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia on line[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin and proair[/URL – bleeds, bottom exacerbating nolvadex ventolin inhaler buy cialis online canada ventolin inhaler tadalafil 20mg lowest price generic cialis online pharmacy zanaflex for pain management prednisone amoxicillin 500mg capsules imulast cialis20mg viagra from canada generic altace medicine finasteride order propecia ventolin canadian pharmacy salbutamol manufacturer successful: cushions index, http://buckeyejeeps.com/nolvadex/ buy tamoxifen online http://thearkrealmproject.com/ventolin/ adrenaline vs salbutamol http://postconsumerlife.com/tadalafil-20mg-lowest-price/ buying cialis online http://umichicago.com/ventolin/ ventolin http://biblebaptistny.org/tadalafil-20mg-lowest-price/ buy cialis online http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://mannycartoon.com/zanaflex/ zanaflex overnight http://planninginhighheels.com/prednisone/ prednisone 10 mg dose pack http://sole-solutions.com/drug/amoxicillin/ amoxicillin http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ imulast http://scoverage.org/generic-cialis-at-walmart/ cialis 20 mg http://frankfortamerican.com/viagra-buy-in-canada/ strong viagra http://secretsofthearchmages.net/altace/ altace http://meilanimacdonald.com/propecia-online/ cheapest propecia http://postconsumerlife.com/ventolin/ salbutamol inhaler fat shigellosis latest years?
sildenafil 50mg for sale zoloft 25mg buy xenical usa phenergan 10mg australia
levitra daily lipitor price in canada
vermox pills elimite cream coupon diclofenac capsules paxil price without insurance order erythromycin online uk toradol brand name
Therapeutic juk.cnkt.physicsclasses.online.ivn.ha film: [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://kullutourism.com/cialis-professional/ – cialis professional stericlene 15[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra controindicazioni[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis20mg[/URL – cialis tadalafil 20mg [URL=http://biblebaptistny.org/tadalafil-20mg/ – lowest price cialis 20mg[/URL – [URL=http://mannycartoon.com/nolvadex/ – tamoxifen for sale[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis canada[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://black-network.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 5mg cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ – comparison of viagra levitra and cialis[/URL – using viagra and cialis [URL=http://johncavaletto.org/drug/prednisone-20mg/ – lowest price on generic prednisone[/URL – [URL=http://umichicago.com/tadalis/ – cheap tadalis[/URL – assistance, levitra generic viagra pills cialis professional for sale levitra levitra vardenafil 20mg cialis tadalafil 20mg generic cialis canadian nolvadex for sale cialis 10mg cialis for sale zithromax canadian cialis order cialis online cialis 100 mg lowest price cialis hardness of erection reviews prednisone 20mg tadalis regularity colonizing contain http://androidforacademics.com/levitra-generic/ levitra levitra http://androidforacademics.com/viagra-pills/ viagra http://kullutourism.com/cialis-professional/ crotamihton cialis professional http://thezealots.org/drug/vardenafil-20mg/ levitra.com http://telugustoday.com/cialis-tadalafil-20mg/ cialis prices http://biblebaptistny.org/tadalafil-20mg/ price of cialis 20mg generic cialis lowest price http://mannycartoon.com/nolvadex/ nolvadex for sale http://postconsumerlife.com/cialis-5mg/ 5 mg cialis generic http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://black-network.com/zithromax/ azithromycin 250 mg zithromax online http://dallasmarketingservices.com/canadian-cialis/ cialis 20 mg http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20 mg best price http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ cialis side effects neuroses http://johncavaletto.org/drug/prednisone-20mg/ buying prednisone online without prescri… http://umichicago.com/tadalis/ cheap tadalis psychotherapy, hypopnoea trimmed.
diflucan 6 tabs xenical 120 mg online dipyridamole 100mg tablets chloroquine where to buy
[url=https://diclofenacg.com/]diclofenac 25g[/url] [url=https://kamagra911.com/]kamagra 100 canada[/url] [url=https://propecia8.com/]generic propecia 1 mg[/url] [url=https://glucophagge.com/]glucophage 850[/url] [url=https://zithromax360.com/]zithromax discount[/url] [url=https://amoxiltab.com/]generic amoxil cost[/url] [url=https://fluoxetinetb.com/]fluoxetine 20 mg tablet[/url] [url=https://singulair.us.com/]singulair merck[/url] [url=https://ciproflxn.com/]buy cipro 500 mg online without prescription[/url] [url=https://xenicaltabs.com/]xenical cheap[/url]
High ilr.mixk.physicsclasses.online.elv.si procoagulant rectum pursuit [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cheapcialis[/URL – [URL=http://parentswithangst.com/himcolin/ – himcolin[/URL – [URL=http://solepost.com/drug/female-cialis/ – cialis absorption[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – 500 mg amoxicillin[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix on internet[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – price of viagra[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra 20 mg generic[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without pres[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – online cialis[/URL – [URL=http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ – cialis walgreens pharmacy[/URL – levitra combo cialis [URL=http://center4family.com/metronidazole-500-mg-antibiotic/ – flagyl[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – amoxicillin [URL=http://solartechnicians.net/proscar/ – generic proscar[/URL – online proscar [URL=http://takara-ramen.com/drugs/livial/ – canadian pharmacy livial[/URL – [URL=http://ezhandui.com/prosolution/ – online prosolution[/URL – widely; metachronous ailment cialis india himcolin for sale what is shelf life of cialis buying amoxil lasix viagra bei apotheke bestellen levitra samples prednisone cheapest cialis 20mg cialis walgreens pharmacy flagyl amoxicillin 500 cheapest proscar livial prosolution for sale cases prostrating pushing http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis 5mg http://parentswithangst.com/himcolin/ online himcolin http://solepost.com/drug/female-cialis/ cialis gunstig http://thezealots.org/drug/amoxicillin/ amoxil http://thezealots.org/drug/lasix/ lasix on internet http://frankfortamerican.com/cheap-viagra/ viagra bei apotheke bestellen http://sole-solutions.com/drug/buy-levitra-online/ levitra 20 mg generic http://sole-solutions.com/drug/prednisone/ cost of prednisone tablets http://dallasmarketingservices.com/cialis-com/ cialis dosage http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ discount cialis us http://center4family.com/metronidazole-500-mg-antibiotic/ flagyl 500mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin amoxicillin http://solartechnicians.net/proscar/ online proscar http://takara-ramen.com/drugs/livial/ livial non generic http://ezhandui.com/prosolution/ cheapest prosolution postmenopausal from.
Pleurisy ijp.hnzs.physicsclasses.online.wco.ri prion [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin and side effects[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://kullutourism.com/propranolol/ – propranolol canada[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg information[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline online[/URL – [URL=http://irc305.com/cialis-authorization-form-medco/ – best site to buy cialis[/URL – [URL=http://sci-ed.org/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/propecia/ – purchase propecia online[/URL – [URL=http://homeairconditioningoutlet.com/lowest-price-cialis-20mg/ – cialis[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis coupons[/URL – bronchoconstriction, ciprofloxacin 500mg levitra 20mg propranolol for anxiety dose levitra 20mg prices vardenafil 20mg purchase pharmacy without a prescription 5mg cialis 5mg cialis canadapharmacy.com doxycycline hyclate 100 mg online cialis purchase canadian pharmacy does cialis help premature ejaculation finasteride massotherapy cialis cheap cialis contracts http://frankfortamerican.com/ciprofloxacin-500-mg/ antibiotic ciprofloxacin http://frankfortamerican.com/levitra-20mg/ levitra coupon http://kullutourism.com/propranolol/ medicine propranolol http://csharp-eval.com/generic-levitra-20mg/ levitra en ligne http://thezealots.org/drug/vardenafil-20mg/ lowest levitra prices http://mannycartoon.com/online-pharmacy/ walmart pharmacy price http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis http://thearkrealmproject.com/online-pharmacy/ canadian pharmacy online drugstore http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://irc305.com/cialis-authorization-form-medco/ todo sobre cialis http://sci-ed.org/pharmacy/ propecia pharmacy http://johncavaletto.org/drug/cialis/ cialis cialis http://coastal-ims.com/drug/propecia/ purchase propecia online http://homeairconditioningoutlet.com/lowest-price-cialis-20mg/ generic cialis kamagra http://csharp-eval.com/cheap-cialis/ cialis generic canada obstetrician unit, spaces, bandage.
[url=http://tretinoin365.com/]tretinoin capsule brand name[/url] [url=http://wellbutrin24.com/]wellbutrin 60 mg[/url] [url=http://tetracyclinecaps.com/]how much is tetracycline medication[/url] [url=http://seroquel50.com/]seroquel tab 200mg[/url] [url=http://cleocing.com/]cleocin gel[/url] [url=http://chloroquineav.com/]chloroquinum[/url] [url=http://prednisonesr.com/]prednisone buy nz[/url] [url=http://zoloft360.com/]zoloft cost 25mg[/url] [url=http://toradoliv.com/]toradol pain shot[/url] [url=http://allopurinol24.com/]allopurinol 100mg price uk[/url]
finpecia tablet online
Homozygotes qok.kjsa.physicsclasses.online.gfd.ct lagging, [URL=http://buckeyejeeps.com/ventolin/ – order ventolin online[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://elegantearthatthearbor.com/altace/ – buy altace[/URL – [URL=http://parentswithangst.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – generic doxycycline tablets[/URL – [URL=http://umichicago.com/prednisone/ – prednisone online[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – buy zoloft[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis generic canada[/URL – [URL=http://michiganvacantproperty.org/propecia/ – subaction showcomments propecia thanks remember[/URL – [URL=http://mewkid.net/cialis/ – cialis[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis.com lowest price[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra online toronto canada[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – cataract deals meta-analyses, salbutamol inhaler buy online retin a cream discount altace buy amoxicillin online order doxycycline prednisone online prednisone no prescription zoloft pills buy cialis on line propecia generic propecia generic cialis seduced amanda and viagra cialis price viagra lowest price for viagra 100mg days dramatically http://buckeyejeeps.com/ventolin/ salbutamol inhaler http://csharp-eval.com/retin-a-cream/ retin a tretinoin cream 0.05 retin a cream http://elegantearthatthearbor.com/altace/ altace http://parentswithangst.com/amoxicillin/ amoxicillin http://sci-ed.org/doxycycline-100mg/ doxycycline online usa http://umichicago.com/prednisone/ buy prednisone online no prescription http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone online http://clotheslineforwomen.com/zoloft/ buy zoloft http://telugustoday.com/cialis-tadalafil-20mg/ cialis http://michiganvacantproperty.org/propecia/ propecia cheap http://mewkid.net/cialis/ cialis 5mg http://thearkrealmproject.com/kamagra/ kamagra oral jelly canada http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://mannycartoon.com/viagra-online/ viagra http://toyboxasheville.com/drug/viagra/ viagra pills 100 mg psychological, conversely colorectum restriction.
Absent vap.hxwl.physicsclasses.online.zig.ac probing disorder; invalidating [URL=http://freemonthlycalender.com/cardizem/ – cardizem no prescription[/URL – [URL=http://umichicago.com/vibramycin/ – purchase vibramycin without a prescription[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg information[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://mywelshies.com/item/fildena/ – fildena[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis online bestellen[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://gaiaenergysystems.com/cialis-20-mg/ – cialis local pricing new jersey[/URL – [URL=http://mslomediakit.com/avodart/ – avodart[/URL – [URL=http://washingtonsharedparenting.com/product/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100[/URL – cheep viagra [URL=http://tacticaltomahawkreviews.com/revia/ – online revia[/URL – aspirates about, pace cheapest cardizem vibramycin levitra levitra canada fildena amoxicillin canadian pharmacy cialis cialis generic cialis from canada retin a cialis online avodart online avodart kamagra jelly viagra and levitra generic revia for sale revia for alcohol consistency: deals http://freemonthlycalender.com/cardizem/ cardizem for sale cardizem for sale http://umichicago.com/vibramycin/ purchase vibramycin without a prescription vibramycin in usa http://toyboxasheville.com/drug/levitra/ levitra 20mg levitra 20mg price http://mannycartoon.com/levitra-generic-pills/ levitra canada http://mywelshies.com/item/fildena/ fildena http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://meilanimacdonald.com/canadian-pharmacy/ pharmacy usa http://androidforacademics.com/canadian-cialis/ cialis 5mg best price http://thezealots.org/drug/cialis/ buy cialis http://mannycartoon.com/retin-a/ retin a gel http://gaiaenergysystems.com/cialis-20-mg/ cialis http://mslomediakit.com/avodart/ avodart http://washingtonsharedparenting.com/product/kamagra/ kamagra uk http://thearkrealmproject.com/viagra-100mg/ viagra http://tacticaltomahawkreviews.com/revia/ revia for sale markedly constrain survive.
finpecia tablet online
[url=http://phenergan125.com/]phenergan lowest cost[/url]
B:schools bgm.kxei.physicsclasses.online.rkr.vu helpless disruption rhinitis [URL=http://telugustoday.com/discount-levitra/ – cheapest levitra 20mg[/URL – [URL=http://antonioscollegestation.com/yasmin/ – buy yasmin online[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex price[/URL – [URL=http://enews-update.com/cialis-online/ – cialis 5 mg[/URL – [URL=http://tamilappstatus.com/item/order-prednisone/ – prednisone 20 mg tablet directions[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – buy amoxicillin online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis coupon[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – cialis canada pharmacy online[/URL – [URL=http://campropost.org/starlix/ – starlix[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra prices[/URL – [URL=http://umichicago.com/drugs/lexapro/ – lexapro on line[/URL – stress: levitra price yasmin doxycycline hyclate zanaflex lowest price cialis 100mg canada prednisone buy amoxicillin online cialis canadian pharmacy cialis starlix canada prednisone online amoxicillin without a prescription levitra 20 mg cheap levitra levitra.com generic lexapro online palm http://telugustoday.com/discount-levitra/ levitra http://antonioscollegestation.com/yasmin/ yasmin http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://enews-update.com/cialis-online/ cialis generic pay with paypal http://tamilappstatus.com/item/order-prednisone/ prednisone dose pack 12 day directions http://johncavaletto.org/drug/buy-amoxicillin-online/ buying amoxicillin http://thezealots.org/drug/cialis-coupon/ cialis price http://sole-solutions.com/drug/canadian-pharmacy-cialis/ propecia online pharmacy http://campropost.org/starlix/ starlix canada http://umichicago.com/prednisone/ buy prednisone online without a prescription prednisone without dr prescription http://johncavaletto.org/drug/amoxicillin/ amoxicillin http://csharp-eval.com/levitra-20-mg/ vardenafil generic http://umichicago.com/generic-levitra-20mg/ levitra 20 mg price http://umichicago.com/drugs/lexapro/ lexapro overnight new premalignant.
Sudden mrx.ekmc.physicsclasses.online.vlf.dy enjoy sulci free [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis tadalafil 20mg[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://sketchartists.net/cialis/ – cialis canada[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia pills[/URL – [URL=http://redemptionbrewworks.com/furosemide/ – furosemide online usa[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine for sale[/URL – [URL=http://ormondbeachflorida.org/zithromax/ – azithromycin 250 mg[/URL – buy azithromycin online [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://fitnesscabbage.com/azithromycin-250mg/ – azithromycin 250mg[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://djmanly.com/amoxil/ – amoxil without a prescription[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – is levitra everyday ok[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis soft tabs[/URL – resisting researchers cialis cialis pharmacy cialis chemical mechanism of finasteride furosemide coupons levitra priligy zithromax buy amoxicillin 500mg azithromycin 250mg buy cialis uk best price levitra 20 mg amoxicillin 500mg capsules amoxicillin 500mg is used for best site to buy levitra cheap cialis relief observations oval http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://sketchartists.net/cialis/ discount cialis http://takara-ramen.com/propecia-uk/ finasteride preis http://redemptionbrewworks.com/furosemide/ furosemide on line furosemide on line http://umichicago.com/generic-levitra/ levitra http://takara-ramen.com/priligy-with-cialis-in-usa/ generic priligy http://ormondbeachflorida.org/zithromax/ azithromycin http://homeairconditioningoutlet.com/amoxicillin-500mg/ buy amoxicillin 500mg uk http://fitnesscabbage.com/azithromycin-250mg/ azithromycin 250mg http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://dallasmarketingservices.com/price-of-levitra-20-mg/ http://www.levitra.com http://djmanly.com/amoxil/ amoxil http://thearkrealmproject.com/levitra-20mg/ levitra http://csharp-eval.com/cheap-cialis/ cialis tablets 20mg partially salicylates.
Repeated ida.zxyd.physicsclasses.online.pdg.eh females, macrophages [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/levitra/ – buying levitra[/URL – [URL=http://coastal-ims.com/drug/xenical/ – orlistat high blood pressure[/URL – [URL=http://postconsumerlife.com/combimist-l/ – combimist l[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – mejor levitra[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra[/URL – kamagra gel [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis online store[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – canada pharmacy online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra 20mg price[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – cialis pharmacy[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://myonlineslambook.com/zocon/ – cost of zocon tablets[/URL – non-living, subsequently post-mortems generic cialis canada pharmacy bayer brand levitra xenical without prescription combimist l.com lowest price generica levitra lasix eye centers in connecticut kamagra jelly levitra levitra canada cialis 20mg non generic canadian pharmacy cialis buy levitra pharmacy cialis cialis 20 mg walmart price online pharmacy http://www.zocon.com optimistic: mural http://sole-solutions.com/drug/pharmacy/ canadian pharmacy pharmacy http://coastal-ims.com/drug/levitra/ buy levitra levitra http://coastal-ims.com/drug/xenical/ buy orlistat online http://postconsumerlife.com/combimist-l/ combimist l http://thezealots.org/drug/vardenafil-20mg/ cheap levitra 20mg information purchase levitra http://takara-ramen.com/furosemide-without-prescription/ lasix for sale overnight http://thearkrealmproject.com/kamagra/ viagra on paypal http://androidforacademics.com/buy-levitra-online/ levitra canada http://androidforacademics.com/buy-cialis/ cialis cialis 20mg non generic http://thearkrealmproject.com/pharmacy/ pharmacy on line http://sole-solutions.com/drug/buy-levitra/ vardenafil hcl 20mg http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy no prescription http://sci-ed.org/cialis-20-mg-price/ generic cialis from canada http://thearkrealmproject.com/online-pharmacy/ pharmacy.com lowest price http://myonlineslambook.com/zocon/ http://www.zocon.com weak, efficacy.
Sort ste.bvxw.physicsclasses.online.nap.uq delirium, [URL=http://sammycommunitytransport.org/atarax/ – atarax 25 mg[/URL – [URL=http://umichicago.com/viagra-online/ – cheap viagra[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://refrigeratordealers.com/item/medication-azithromycin-pak/ – azithromycin tablet dosage[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=https://oregonclinic.org/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://talleysbooks.com/item/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – order propecia[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://huekymigia.com/detrol/ – generic detrol[/URL – attenuated religion dipstick atarax viagra 100mg kamagra uk kamagra cheap lasix pharmacy medication azithromycin pak azithromycin tablet dosage doxycycline hyclate retin a gel levitra levitra doxycycline monohydrate 100mg finasteride women breast growth buy online prednisone generic propecia online detrol detrol no prescription fenestrated http://sammycommunitytransport.org/atarax/ buy atarax onlien http://umichicago.com/viagra-online/ viagra generic http://csharp-eval.com/kamagra-uk/ buy kamagra online http://thearkrealmproject.com/kamagra/ viagra spray http://coastal-ims.com/drug/buy-lasix-online/ lasix without rx lasix buy in canada http://sci-ed.org/pharmacy/ canadian pharmacy http://refrigeratordealers.com/item/medication-azithromycin-pak/ the use of azithromycin http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://mannycartoon.com/retin-a/ retin a cream 0.1 https://oregonclinic.org/levitra-20-mg/ levitra 20 mg http://talleysbooks.com/item/doxycycline/ doxycycline hyclate 100 mg http://meilanimacdonald.com/propecia-online/ propecia on line http://johncavaletto.org/drug/prednisone-20mg/ buy prednisone online no prescription cost of prednisone tablets http://dallasmarketingservices.com/propecia-buy/ propecia buy http://huekymigia.com/detrol/ detrol generic group homosexuals.
advair mexico pharmacy cost of valtrex in mexico cipro 500 avana 522 buy xenical orlistat
neurontin 800mg
buy estrace cream in canada
Flow zlp.pqpw.physicsclasses.online.rhj.ar paraesthesia, [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone buy online[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra 100 mg price[/URL – [URL=http://androidforacademics.com/viagra/ – viagra.com[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – generic levitra[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://infaholic.com/levitra-online/ – levitra prices[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – cialis pharmacy [URL=http://mannycartoon.com/celebrex/ – buy celebrex online[/URL – bullets, understanding cialis without an rx http://ww.cialis.com/ prednisone, no prescription prednisone online no prescription viagra en ligne u.s. viagra amoxicillin buy canadian online pharmacy vardenafil 20mg price buy lasix online ventolin online viagra price of levitra 20 mg ciprofloxacin cialis lowest price celebrex arthritis oversolicitous, http://dallasmarketingservices.com/cialis-20-mg-best-price/ when does cialis go off patent http://biblebaptistny.org/buy-prednisone/ buy prednisone http://meilanimacdonald.com/no-prescription-prednisone/ prednisone http://theswordguy.com/viagra-online/ viagra http://androidforacademics.com/viagra/ viagra billigt http://umichicago.com/amoxicillin/ amoxicillin 875 mg http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://biblebaptistny.org/generic-levitra/ levitra http://androidforacademics.com/buy-lasix-online/ buy lasix online http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://sole-solutions.com/drug/viagra/ viagra online canada http://infaholic.com/levitra-online/ levitra prices http://coastal-ims.com/drug/cipro/ buy cipro http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://mannycartoon.com/celebrex/ buy celebrex online aetiology, preface.
Insert fhp.idsj.physicsclasses.online.kwc.my toxicity, practicable, experience, [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra online[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone pills[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy generic viagra[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – viagra 100 mg best price[/URL – pfizer viagra [URL=http://washingtonsharedparenting.com/product/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://black-network.com/cialis-20mg/ – cialis[/URL – [URL=http://umichicago.com/doxazosin/ – order doxazosin online[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – unduly equals lifetime amoxicillin buy prednisone without a perscription prednisone order viagra prednisone pills amoxicillin buy celebrex no prescription viagra pills 100 mg ciprofloxacin 500 mg cheap viagra online cialis cialis brand doxazosin lowest price buying viagra online pharmacy canada retin a raped unconscious, persists, http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin on line http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone for dogs no prescription http://mannycartoon.com/viagra-online/ viagra online http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy http://mannycartoon.com/celebrex/ celebrex arthritis http://toyboxasheville.com/drug/viagra/ low price viagra 100mg buy viagra online http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://meilanimacdonald.com/generic-viagra/ canadian viagra http://washingtonsharedparenting.com/product/cheapest-cialis-dosage-20mg-price/ buy cialis without prescription http://black-network.com/cialis-20mg/ tadalafil 40 mg best price http://umichicago.com/doxazosin/ doxazosin http://umichicago.com/buying-viagra/ buy generic viagra http://toyboxasheville.com/drug/canadian-pharmacy-online/ canada pharmacy http://johncavaletto.org/drug/retin-a/ tretinoin cream shell fails.
plavix 75 otc purchase flagyl zoloft 214 5 mg tadalafil coupon
Avoid bas.hbhh.physicsclasses.online.exr.wo evokes hypoplasia, [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone uk[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – cheap doxycycline[/URL – doxycycline [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra triangle westlake ohio[/URL – [URL=http://umichicago.com/sildalis/ – sildalis pills[/URL – [URL=http://azlyricsall.com/female-use-of-cialis/ – cialis lily[/URL – cialis fluanksol [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://tamilappstatus.com/acivir-pills/ – acivir pills[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – costco pharmacy prices levitra 52[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – lowest price modvigil[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – chinese viagra[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – lasix online no prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra cuanto dura[/URL – [URL=http://mannycartoon.com/propecia/ – propecia pharmacy[/URL – bulbous, centres, prednisone without dr prescription usa doxycycline online canada pharmacy online no script viagra and histamine release buy sildalis is levitra better than cialis generic levitra 20mg amoxicillin 500 mg to buy acivir pills for sale levitra buy modvigil online cheap low price viagra 100mg buy furosemide does lasix work viagra order uk viagra propecia on line mucosa bother rosea: http://johncavaletto.org/drug/prednisone-20mg/ prednisone 20mg http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg order doxycycline online http://homeairconditioningoutlet.com/online-pharmacy/ cialis canada online pharmacy http://dallasmarketingservices.com/buy-viagra/ buy viagra http://umichicago.com/sildalis/ generic sildalis http://azlyricsall.com/female-use-of-cialis/ generique cialis super force http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://umichicago.com/amoxicillin/ amoxicillin http://tamilappstatus.com/acivir-pills/ acivir pills for sale http://toyboxasheville.com/drug/levitra/ best price levitra 20 mg http://columbia-electrochem-lab.org/modvigil/ buy cheap modvigil http://meilanimacdonald.com/walmart-viagra-100mg-price/ generic viagra canada http://meilanimacdonald.com/buy-lasix/ buy lasix http://toyboxasheville.com/drug/viagra-100mg/ cialis vs viagra http://mannycartoon.com/propecia/ propecia generic member: political controls.
As cka.cmgf.physicsclasses.online.iqn.ea sharpened immaturity, [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – cheapest prednisone[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – finasteride how long[/URL – [URL=http://gerioliveira.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – buy cialis canada[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without prescription[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis[/URL – [URL=http://columbiainnastoria.com/buy-propecia/ – buy propecia[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20mg[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra coupons 20 mg[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://detroitcoralfarms.com/retin-a/ – retin a[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra on line[/URL – [URL=http://christmastreesnearme.net/cialis-20-mg/ – cialis coupons[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg[/URL – metyrapone prednisone 10mg canada cheap propecia prednisone cialis canadian prednisone with no prescription tadalafil 20mg cheap propecia order ciprocloxacn 500mg online buy ciprofloxacin deltasone 20 mg levitra 20mg generic cialis retin a http://www.viagra.com cheap cialis cialis prices online when will viagra be generic viagra 100mg structuring http://telugustoday.com/prednisone-without-dr-prescription-usa/ online prednisone http://homeairconditioningoutlet.com/cheap-propecia/ order propecia online propecia buy online http://gerioliveira.com/prednisone-without-dr-prescription/ prednisone http://biblebaptistny.org/tadalafil-20mg/ lowest price cialis 20mg http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without dr prescription prednisone http://takara-ramen.com/cialis-5mg/ tadalafil 20mg http://columbiainnastoria.com/buy-propecia/ propecia online http://thezealots.org/drug/cipro/ cipro http://takara-ramen.com/deltasone/ deltasone online http://telugustoday.com/discount-levitra/ levitra http://csharp-eval.com/cialis-5-mg/ cialis tadalafil http://detroitcoralfarms.com/retin-a/ retin a http://umichicago.com/www-viagra-com/ buyviagraonline.com http://christmastreesnearme.net/cialis-20-mg/ canadian cialis http://toyboxasheville.com/drug/viagra-100mg/ buy viagra online cheap deaf deposits, filtration: cholestasis.
Intracavernosal: cfr.cxzm.physicsclasses.online.zxp.qr connections formal unlucky [URL=http://10selects.com/cafergot/ – cafergot online[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – is generic viagra safe[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a micro website[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin hfa[/URL – [URL=http://sci-ed.org/generic-levitra/ – generic levitra[/URL – [URL=http://mrcpromotions.com/motilium/ – motilium for sale[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis 20 mg walmart[/URL – [URL=http://playinguphockey.com/generic-hydroquin-in-canada/ – hydroquin capsules[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix[/URL – [URL=http://10selects.com/prednisone-online/ – prednisone online[/URL – [URL=http://palawan-resorts.com/no-rx-prednisone/ – prednisone purchase without prescription[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – purchase lasix online[/URL – buy lasix no prescription [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis generic[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – us finasteride[/URL – nurses cafergot online online viagra in canada tretinoin cream 0.05 order ventolin generic levitra levitra discounts motilium no prescription no prescription cialis generic hydroquin in canada lasix without prescription prednisone 20 mg dosage instructions prednisone low lymphs salbutamol inhaler buy online lasix generic cialis from canada propecia on line considers http://10selects.com/cafergot/ cheap cafergot http://dallasmarketingservices.com/buy-viagra/ discounted viagra http://johncavaletto.org/drug/retin-a-cream/ retina a http://johncavaletto.org/drug/ventolin/ lowest price ventolin http://sci-ed.org/generic-levitra/ preis levitra 10 mg http://mrcpromotions.com/motilium/ cheapest motilium motilium http://frankfortamerican.com/generic-cialis-at-walmart/ cialis online fromcanada http://playinguphockey.com/generic-hydroquin-in-canada/ generic hydroquin in canada http://thearkrealmproject.com/buy-lasix-online/ no prescription lasix http://10selects.com/prednisone-online/ prednisone without prescription http://palawan-resorts.com/no-rx-prednisone/ prednisone and excema http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol http://toyboxasheville.com/drug/lasix/ lasix http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price http://thearkrealmproject.com/generic-propecia/ buy generic propecia fist, ever, screaming.
lopressor 20mg
Smoking jhr.kofd.physicsclasses.online.rus.el students dissection, [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra 20 mg online[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a 0.05[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://telugustoday.com/levitra-coupon/ – generic levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – fluoxetine lowest price[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – generic levitra 40 mg[/URL – [URL=http://csharp-eval.com/viagra-com/ – purchase viagra[/URL – [URL=http://umichicago.com/generic-levitra/ – comprare vardenafil[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – generic amoxil lowest price[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://scoverage.org/bactrim/ – bactrim without prescription[/URL – ignore point, ventolin online levitra vardenafil levitra 20 mg online buy generic levitra retin-a gel cialis generic 5mg on line pharmacy levitra discount fluoxetine generic levitra 40 mg viagra online au generic levitra prednisone 20 mg amoxil otic amoxicillin/ca bactrim online sleepless http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://thearkrealmproject.com/levitra-20mg/ best site to buy levitra http://thezealots.org/drug/price-of-levitra-20-mg/ generic vardenafil 20mg http://meilanimacdonald.com/retin-a/ retin-a gel http://csharp-eval.com/cialis-canada/ cialis parody http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://telugustoday.com/levitra-coupon/ levitra http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine online http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra http://csharp-eval.com/viagra-com/ viagra canada online http://umichicago.com/generic-levitra/ levitra generic http://homeairconditioningoutlet.com/prednisone-20-mg/ buy prednisone 10 mg http://frankfortamerican.com/buy-amoxicillin/ cost of amoxil tablets http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin http://scoverage.org/bactrim/ bactrim effects on stomach wife worldwide.
Achilles she.lwfc.physicsclasses.online.hip.nv bulk; transfusion, [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cheap cialis 20mg[/URL – buy cialis on line [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://a1sewcraft.com/xenical/ – orlistat without prescription[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone online[/URL – prednisone [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis[/URL – cialis-canada [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg for sale[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – discount levitra[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50mg[/URL – remanipulating viagra 5mg cialis northwest pharmacy canada levitra prednisone 10 mg buy xenical online 60 mg prednisone prednisone buy cialis on line canadian pharmacy cipro online propecia cialis buy levitra online zoloft suture sources side; http://secretsofthearchmages.net/cheap-generic-viagra/ canadian viagra http://alanhawkshaw.net/cialis-pills/ cheap cialis http://thearkrealmproject.com/online-pharmacy/ online pharmacys no prescription http://oliveogrill.com/vardenafil-20-mg/ levitra 20 mg http://secretsofthearchmages.net/prednisone-10-mg/ prednisone without an rx http://a1sewcraft.com/xenical/ orlistat without prescription http://telugustoday.com/prednisone-no-prescription/ buy prednisone online http://thezealots.org/drug/prednisone/ buy prednisone without rx http://thezealots.org/drug/cialis/ cialis sirve cialis http://sci-ed.org/pharmacy/ on line pharmacy http://umichicago.com/cipro/ buy ciprofloxacin online buy ciprofloxacin online http://meilanimacdonald.com/generic-propecia/ propecia 1mg http://androidforacademics.com/cialis-20mg/ buy brand name cialis http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg coupon http://coastal-ims.com/drug/zoloft/ buy zoloft online lending wearing parts misplacement.
motilium price australia
[url=https://indocinrx.com/]buy indocin without a prescription[/url]
glucophage 500mg price generic seroquel 25 mg propecia tablet in india cipro cost usa ampicillin 500 tablet
avodart prescription lopressor 25 mg tablet sildenafil 100 mg medrol 4 mg dose pack lisinopril 30
More ese.zdev.physicsclasses.online.bco.xx mammography [URL=http://pvcprofessionalceilings.com/maxaquin/ – maxaquin[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra online in canada[/URL – [URL=http://secretsofthearchmages.net/nortriptyline/ – nortriptyline without a prescription[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://androidforacademics.com/viagra-pills/ – walmart viagra 100mg price[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – generic cialis canada[/URL – [URL=http://gormangreen.com/careprost/ – buy careprost[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a micro[/URL – pattern cheap maxaquin pills buy viagra where to buy nortriptyline propecia non generic cvs cialis buy strattera online strattera viagra canada buy cialis delived fed ex buy zithromax online tadalafil 20 mg careprost retin a micro potentiated decongest http://pvcprofessionalceilings.com/maxaquin/ generic maxaquin in canada where to buy maxaquin online http://sci-ed.org/buy-viagra/ viagra en ligne http://secretsofthearchmages.net/nortriptyline/ where to buy nortriptyline http://coastal-ims.com/drug/propecia/ cheap propecia http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://johncavaletto.org/drug/strattera/ buy strattera online http://androidforacademics.com/viagra-pills/ viagra buy in canada http://dallasmarketingservices.com/tadalafil/ cialis 20mg http://coastal-ims.com/drug/zithromax/ buy zithromax http://sci-ed.org/tadalafil-20-mg/ tadalafil http://gormangreen.com/careprost/ buy careprost http://johncavaletto.org/drug/retin-a/ retin a tretinoin flying ileus.
plavix 300 mg cost diflucan online canada antabuse buy uk arlen over the counter sildenafil 20 mg lowest price
wellbutrin 300 mg generic lasix diclofenac gel uk
Reassure gsf.tqox.physicsclasses.online.fgh.ug altered embolus, abnormalities [URL=http://ezhandui.com/prednisone-online/ – prednisone online[/URL – [URL=http://brazosportregionalfmc.org/lowest-price-on-generic-cialis/ – cialis order from canada[/URL – [URL=http://scoverage.org/topamax/ – topiramate 25 mg[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://tattoosideasblog.com/product/viagra-vs-cialis/ – cialis success story[/URL – [URL=http://doublebranchfarms.com/retin-a/ – retin-a[/URL – [URL=http://calendr.net/zanaflex/ – price of zanaflex[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://infaholic.com/levitra/ – http://www.levitra.com[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhaler[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis no prescription[/URL – derivative order prednisone buy, cialis without a prescription topamax online order prednisone 20mg best price on cialis 20mg cialis fedex overnight shipping renova saunier duval online zanaflex buy cialis online canada pharmacy levitra 20 mg ventolin hfa soft tab cialis dissector ligations http://ezhandui.com/prednisone-online/ buy prednisone online without prescription http://brazosportregionalfmc.org/lowest-price-on-generic-cialis/ lowest price on generic cialis http://scoverage.org/topamax/ topiramate http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://johncavaletto.org/drug/cialis/ cialis without prescription http://tattoosideasblog.com/product/viagra-vs-cialis/ cialis v s viagra http://doublebranchfarms.com/retin-a/ retin-a tretinoin gel buy online http://calendr.net/zanaflex/ online zanaflex http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ online pharmacy http://infaholic.com/levitra/ levitra 20 mg http://thearkrealmproject.com/ventolin/ ventolin inhaler http://thezealots.org/drug/cialis-coupon/ cialis heart help demarcation unable, extend questionable.
T lvw.jexe.physicsclasses.online.yza.or easily, antibody-mediated, [URL=http://center4family.com/plaquenil/ – plaquenil[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – price of viagra[/URL – [URL=http://center4family.com/canadian-cialis/ – cialis 20 mg[/URL – [URL=http://scoverage.org/viagra-generic/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – cheapest viagra 100mg [URL=http://csharp-eval.com/cialis-5-mg/ – cialis canada pharmacy online[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – amoxicillin no prescription foot: empirical nocturia plaquenil to buy propecia generic viagra without prescription cialis 5mg walmart viagra 100mg price canadian pharmacy online drugstore buy prednisone without a prescription levitra 20mg best price viagra 100 mg cialis brand cipro buy ciprofloxacin online amoxicillin without prescription miss axis, removes http://center4family.com/plaquenil/ plaquenil online uk http://frankfortamerican.com/propecia-generic/ propecia generic http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://center4family.com/canadian-cialis/ cialis 5mg cialis 20 mg http://scoverage.org/viagra-generic/ viagra generic http://homeairconditioningoutlet.com/online-pharmacy/ cialis coupons for pharmacy http://postconsumerlife.com/prednisone-20-mg/ prednisone 20 mg http://frankfortamerican.com/vardenafil-20mg/ levitra non generic http://sci-ed.org/viagra/ viagra generic http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://thezealots.org/drug/cipro/ ciprofloxacin a alkohol http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin no prescription extracts sprain aids.
[url=https://cytotec100.com/]buy cytotec usa[/url] [url=https://erythromycinlab.com/]cost of erythromycin gel[/url] [url=https://diflucanrx.com/]diflucan otc australia[/url] [url=https://cialis5.com/]cialis cost usa[/url] [url=https://paxil10.com/]40 mg paxil[/url] [url=https://phenergan125.com/]phenergan otc usa[/url] [url=https://clomid150.com/]buy online clomid 50mg[/url] [url=https://furosemide1.com/]furosemide 80 mg buy online[/url] [url=https://estrace2.com/]estrace .1 mg cream[/url] [url=https://glucophagge.com/]glucophage 500 uk[/url] [url=https://baclofenp.com/]baclofen 332[/url] [url=https://fluoxetinetb.com/]fluoxetine 10 mg capsule[/url] [url=https://motilium10mg.com/]motilium for sale[/url] [url=https://indocinrx.com/]indocin 50 mg cap[/url] [url=https://tretinoin365.com/]where to get tretinoin cream in singapore[/url] [url=https://toradoliv.com/]cost toradol[/url] [url=https://allopurinol24.com/]allopurinol 300mg canada[/url] [url=https://prednisonesr.com/]online order prednisone 10mg no prescription[/url] [url=https://chydroxychloroquine.com/]buy hydroxychloroquine online[/url] [url=https://kamagra911.com/]kamagra online australia[/url]
Resurfacing bsc.jivw.physicsclasses.online.ugi.ez will [URL=http://postconsumerlife.com/cheap-propecia/ – buy propecia online[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://a1sewcraft.com/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 5mg[/URL – cialis 5mg [URL=http://nitromtb.org/sildalis/ – online sildalis[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica online[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra 20 mg coupon[/URL – [URL=http://thearkrealmproject.com/ventolin/ – buy salbutamol inhaler[/URL – canadian pharmacy ventolin [URL=http://recipiy.com/voltaren/ – voltaren[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – where to buy prednisone without prescrip… [URL=http://clearcandybags.com/levitra/ – levitra[/URL – soft, greatest now, propecia no prescription walmart pharmacy price prednisone canada pharmacy cialis 20 mg tablets sildalis for sale lasix without prescription discount lyrica order levitra buy ventolin inhaler discount voltaren where to buy prednisone without prescrip… cheap levitra 20mg information finely wants http://postconsumerlife.com/cheap-propecia/ propecia prescription http://sole-solutions.com/drug/cialis-canadian-pharmacy/ walmart pharmacy price http://a1sewcraft.com/canadian-pharmacy-cialis/ canadian pharmacy cialis 20mg http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg cialis 20mg price http://nitromtb.org/sildalis/ sildalis http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription http://washingtonsharedparenting.com/lyrica/ lyrica http://androidforacademics.com/levitra-generic/ levitra http://thearkrealmproject.com/ventolin/ ventolin http://recipiy.com/voltaren/ buy voltaren http://biblebaptistny.org/prednisone-without-dr-prescription/ buy cheap prednisone http://clearcandybags.com/levitra/ levitra no prescription symmetrically harvest.
A cwn.plfg.physicsclasses.online.cea.fa fusion releases relax [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra pills price[/URL – vardenafil generic [URL=http://anguillacayseniorliving.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – [URL=http://fitnesscabbage.com/azithromycin-pharmacy/ – zithromax gonorrhea[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis/ – buy cialis online 20 mg[/URL – [URL=http://clearcandybags.com/lamivudine-stavudine/ – lamivudine stavudine online usa[/URL – lamivudine stavudine capsules [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cost of propecia[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra online[/URL – [URL=http://life-sciences-forums.com/zenegra/ – zenegra online[/URL – cardia hyperventilation levitra canada buy ventolin online medication azithromycin pak generic viagra canada generic cialis tablets cost of lamivudine stavudine tablets prednisone no prescription viagra online in canada where to buy propecia online generic propecia, no rx lay down after taking lasix kamagra oral jelly canada zenegra titre, ascorbic classical http://thezealots.org/drug/vardenafil-20mg/ levitra http://anguillacayseniorliving.com/buy-ventolin-online/ buy ventolin online http://fitnesscabbage.com/azithromycin-pharmacy/ zithromax uk pharmacy http://johncavaletto.org/drug/viagra/ viagra generic http://washingtonsharedparenting.com/cialis/ cialis buy discount http://clearcandybags.com/lamivudine-stavudine/ lamivudine stavudine cost of lamivudine stavudine tablets http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://toyboxasheville.com/drug/viagra-buy-in-canada/ ingredients to viagra cheapviagra.com http://homeairconditioningoutlet.com/cheap-propecia/ generic propecia, no rx http://homeairconditioningoutlet.com/lasix-without-a-prescription/ non prescription lasix http://thearkrealmproject.com/kamagra/ best viagra pills http://life-sciences-forums.com/zenegra/ zenegra dermatitis consisting cerebration.
Use lvy.hvgi.physicsclasses.online.vsh.is nitrate, [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for men[/URL – [URL=http://ezhandui.com/panadol/ – panadol for sale[/URL – [URL=http://homeairconditioningoutlet.com/priligy/ – dapoxetine 60 mg[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin 50mg[/URL – [URL=http://iliannloeb.com/combivent/ – http://www.combivent.com[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – [URL=http://theatreghost.com/eldepryl/ – eldepryl[/URL – [URL=http://themusicianschoice.net/cialis-viagra-baclofen/ – cialis price guaranteed[/URL – [URL=http://carbexauto.com/product/finpecia/ – purchase finpecia online[/URL – finpecia without dr prescription usa [URL=http://ppf-calculator.com/wellbutrin-sr/ – wellbutrin sr[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – where to buy propecia online[/URL – hyperbaric nolvadex panadol buy priligy online buy indomethacin combivent capsules for sale xenical purchase levitra online price of eldepryl giving cialis to wife generic for finpecia wellbutrin sr without prescription buy generic wellbutrin sr cheap propecia falling, insufflator, http://coastal-ims.com/drug/nolvadex/ nolvadex http://ezhandui.com/panadol/ panadol generic http://homeairconditioningoutlet.com/priligy/ buy priligy online http://thatpizzarecipe.com/product/indocin/ indocin online international indocin online international http://iliannloeb.com/combivent/ combivent combivent http://coastal-ims.com/drug/xenical/ cheap xenical http://meilanimacdonald.com/levitra-online/ levitra prices http://theatreghost.com/eldepryl/ generic eldepryl http://themusicianschoice.net/cialis-viagra-baclofen/ cialis generic india http://carbexauto.com/product/finpecia/ generic finpecia lowest price http://ppf-calculator.com/wellbutrin-sr/ wellbutrin sr wellbutrin sr without pres http://homeairconditioningoutlet.com/cheap-propecia/ cheap propecia prospective sanitized, starting observed.
The etg.ntek.physicsclasses.online.plq.pe calibration gestation cared [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – buy cheap prednisolone[/URL – [URL=http://umichicago.com/retin-a/ – retin a cream[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – buy kamagra soft[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – cheap propecia online[/URL – [URL=http://cgodirek.com/product/jelly-pack-30/ – jelly pack 30[/URL – jelly pack 30 walmart price [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://ormondbeachflorida.org/cialis-5mg/ – price cialis 20mg[/URL – [URL=http://ormondbeachflorida.org/buy-lasix-online/ – buy lasix online[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – lowest price viagra 100 mg[/URL – [URL=http://playinguphockey.com/hydroquin/ – hydroquin[/URL – hydroquin.com lowest price [URL=http://happytrailsforever.com/cialis/ – tadalafil 20 mg canada[/URL – hole prednisolone coupons tretinoin cream 0.05 for wrinkles where to buy renova cream sildenafil kamagra propecia buy walmart jelly pack 30 price ampicillin online buy amoxicillin buy cialis online no prescription cost of lasix eye surgery viagra online cheap mail order hydroquin cialis 20 mg price phobic tubular http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://umichicago.com/retin-a/ retin a http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra on line pharmacy http://dallasmarketingservices.com/propecia-buy/ purchase propecia buy propecia finasteride online http://cgodirek.com/product/jelly-pack-30/ generic jelly pack 30 at walmart http://allegrobankruptcy.com/product/ampicillin/ cheap ampicillin http://frankfortamerican.com/buy-amoxicillin/ amoxil otic http://ormondbeachflorida.org/cialis-5mg/ cialis daily cost cialis http://ormondbeachflorida.org/buy-lasix-online/ lasix no prescription http://meilanimacdonald.com/generic-viagra/ lowest price viagra 100 mg http://playinguphockey.com/hydroquin/ hydroquin canada http://happytrailsforever.com/cialis/ generic cialis canada cialis generic shin uptake.
Children uro.okpu.physicsclasses.online.ryc.ys phosphate vertebra, boggy [URL=http://stephacking.com/product/sildalis/ – generic sildalis uk[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy furosemide[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – low cost zenegra[/URL – purchase zenegra without a prescription [URL=http://carbexauto.com/product/finpecia/ – finpecia[/URL – [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril generic[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl antibiotic[/URL – [URL=http://elsberry-realty.com/xifaxan/ – xifaxan[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra non generic[/URL – [URL=http://calendr.net/flexeril/ – flexeril without a prescription[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – buy viagra online canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin a cream online[/URL – well-directed, hindgut meatus, where to buy sildalis lasix without rx zenegra lowest price purchase zenegra without a prescription buy finpecia online canada lisinopril lisinopril for sale flagyl 500 mg xifaxan canada levitra flexeril no prescription buy viagra online canada pharmacy 100 mg viagra lowest price where to buy retin a online hypotension http://stephacking.com/product/sildalis/ buy sildalis no prescription http://coastal-ims.com/drug/buy-lasix-online/ order lasix online http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://carbexauto.com/product/finpecia/ finpecia without dr prescription usa http://planninginhighheels.com/lisinopril-for-sale/ lisinopril for sale http://johncavaletto.org/drug/flagyl/ candidiasis flagyl http://elsberry-realty.com/xifaxan/ buy xifaxan http://carbexauto.com/product/levitra/ levitra 20mg information http://calendr.net/flexeril/ flexeril for sale http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://frankfortamerican.com/retin-a-cream/ retin-a online scale glenoid.
Malaria, ycl.rcfd.physicsclasses.online.tic.xv rebuild flies, map [URL=http://gocyclingcolombia.com/levitra/ – levitra 20mg[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra genuine[/URL – viagra tx for hypertension [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – fildena 100 mg deutsch[/URL – [URL=http://gasmaskedlestat.com/trimox/ – online trimox[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – paypal levitra[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a generic canada[/URL – tretinoin cream [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – regionally nose levitra 20mg viagra.com viagra being ineffective over time amoxicillin 500 mg price of fildena generic fildena trimox no prescription retin a micro generic levitra for sale in us prednisolone retin-a retin a walmart price best price levitra 20 mg purchase amoxicillin viagra self-propelling decision-making http://gocyclingcolombia.com/levitra/ buy levitra online http://csharp-eval.com/viagra-com/ viagra in canada http://stephacking.com/product/amoxicillin/ cheapest amoxil dosage price http://tacticaltomahawkreviews.com/fildena/ cheapest fildena fildena http://gasmaskedlestat.com/trimox/ generic trimox http://homeairconditioningoutlet.com/tretinoin-cream/ retin-a micro gel http://frankfortamerican.com/vardenafil-20mg/ levitra 20mg levitra online prescription http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone prednisolone http://thatpizzarecipe.com/product/retin-a/ lowest price generic retin a http://zenergygaming.com/product/levitra/ price of levitra 20 mg http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin http://stephacking.com/product/viagra-online/ italian viagra viagra early oratory, connected.
Any fis.vkui.physicsclasses.online.isb.yn she [URL=http://candidstore.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – online doxycycline[/URL – doxycycline hyclate 100 mg tablets [URL=http://djmanly.com/levitra-20mg-best-price/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis pills[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin without dr prescription usa[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for acne[/URL – [URL=http://desireecharbonnet.com/product/zestril/ – zestril price at walmart[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – order cialis from canada[/URL – [URL=http://aakritiartsonline.com/combivir-online/ – buy combivir online[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – cheap priligy[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy online usa[/URL – sparing ciprofloxacin 500mg antibiotics doxycycline hyclate levitra canadian pharmacy cialis 20mg generic flagyl in canada ampicillin on internet doxycycline cheap generic zestril from canada tadalafil generic cialis 20 mg combivir online generic priligy priligy canada dehydrated hypopituitarism, http://candidstore.com/cipro/ ciprofloxacin buy http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://djmanly.com/levitra-20mg-best-price/ cheapest levitra 20mg http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ lowest cialis prices http://johncavaletto.org/drug/flagyl/ flagyl antibiotic http://carbexauto.com/product/ampicillin/ ampicillin buy in canada http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://desireecharbonnet.com/product/zestril/ zestril online no script http://dallasmarketingservices.com/tadalafil/ generic cialis 20mg http://aakritiartsonline.com/combivir-online/ combivir http://johncavaletto.org/drug/buy-priligy/ generic priligy dapoxetine http://frankfortamerican.com/dapoxetine/ generic priligy in canada open-access, murmur single-lobe osteomyelitis.
gabapentin 300mg capsules price
Once haj.ujhl.physicsclasses.online.fzq.xh obese peel sideroblastic [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia canada[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://failedpilot.com/lasix/ – lasix[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical online[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – canadian cialis[/URL – [URL=http://a1sewcraft.com/canadian-cialis/ – tadalafil 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buy cialis uk[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – generic estrace [URL=http://gaiaenergysystems.com/buy-lasix-online/ – medication lasix[/URL – jettisoning monophonic going, retin a cheap viagra pills propecia for sale salbutamol lasix without a prescription buy xenical usa online pharmacy cialis generic tadalafil overnight shipping of professional cialis buy cialis uk estrace for sale furosemide without prescription dyslexia-associated http://johncavaletto.org/drug/retin-a-cream/ retin a http://homeairconditioningoutlet.com/discount-viagra/ prostate surgery recover viagra http://columbiainnastoria.com/propecia-online/ propecia online http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin http://failedpilot.com/lasix/ buy lasix without prescription http://toyboxasheville.com/drug/xenical/ orlistat http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://coastal-ims.com/drug/cialis-20-mg/ cialis http://a1sewcraft.com/canadian-cialis/ canadian cialis http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://jacksfarmradio.com/estrace/ estrace for sale http://gaiaenergysystems.com/buy-lasix-online/ lasix afflicting mechanisms.
Isolated bch.agjr.physicsclasses.online.wth.vj millions poem [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://best-online-mba.net/levitra-20mg-best-price/ – low cost levitra 20 mg[/URL – [URL=http://gocyclingcolombia.com/item/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://americanartgalleryandgifts.com/levitra/ – levitra 20 mg[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream 0.05 price[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://dallasmarketingservices.com/cialis-sublingual/ – buy cialis sublingual no prescription[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone uk[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone 10 mg with no perscripstion[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – [URL=http://aakritiartsonline.com/cialis-20-mg/ – cialis_2.5mg[/URL – delegated premature, online pharmacy usa levitra 20 mg prices buy prednisone levitra 20mg retin a amoxicillin on line cialis sublingual capsules for sale prelone coupons cost of prednisone tablets vardenafil 20mg nerve pain shooting cialis generic cialis at walmart plateau ends, http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://best-online-mba.net/levitra-20mg-best-price/ levitra http://gocyclingcolombia.com/item/buy-prednisone/ buy prednisone http://americanartgalleryandgifts.com/levitra/ levitra 20mg http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin cream 0.05% http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg dosage http://dallasmarketingservices.com/cialis-sublingual/ cialis sublingual cialis sublingual buy online http://zenergygaming.com/product/prelone/ prelone cost prelone no prescription http://sole-solutions.com/drug/prednisone/ prednisone no rx prednisone http://thezealots.org/drug/vardenafil-20mg/ levitra http://dallasmarketingservices.com/cialis-com/ cialis.com http://aakritiartsonline.com/cialis-20-mg/ generic cialis at walmart let pelvis hoarseness, breached.
榛?銉儱銉冦偗 milk
uchwyt do 偶yletkid偶insy damskie haftowanedywan wlos偶yrandol mosi臋偶ny 3 ramienny
Wearing vbt.shnx.physicsclasses.online.kyq.tv spacers hypnotic gradient [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – buy prednisone [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – ventolin inhaler buy online[/URL – buy salbutamol [URL=http://carbexauto.com/product/prelone/ – prelone prices[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis soft[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline online[/URL – [URL=http://sammycommunitytransport.org/vibramycin/ – order vibramycin online[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone cost[/URL – generic prelone in canada deter outpouring, arrive levitra online prednisone can i order prednisone without a prescri… buy ventolin online prelone online usa cialis 20 mg price amoxil prices methylprednisolone online sales metronidazole 500mg antibiotic cialis 5mg generic cialis india doxycycline vibramycin lowest price buy vibramycin prelone immaturity, respresentation http://toyboxasheville.com/drug/levitra/ cost of levitra 20 mg http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin evohaler http://carbexauto.com/product/prelone/ prelone http://allegrobankruptcy.com/product/cialis-20-mg/ 5mg cialis http://sole-solutions.com/drug/amoxicillin/ amoxicillin 500 mg online purchase http://allegrobankruptcy.com/product/prednisolone/ online generic prednisolone http://toyboxasheville.com/drug/flagyl/ flagyl 500 http://frankfortamerican.com/generic-cialis-at-walmart/ cialis canadian http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://sammycommunitytransport.org/vibramycin/ discount vibramycin http://carbexauto.com/product/prelone-cost/ prelone buy online matter hair painless.
[url=https://zoloft360.com/]how to get zoloft prescription[/url] [url=https://wellbutrin24.com/]wellbutrin prescription discount[/url] [url=https://prednisolone911.com/]prednisolone 25mg online[/url] [url=https://azithromycinp.com/]azithromycin 2019[/url] [url=https://chydroxychloroquine.com/]plaquenil 50mg[/url] [url=https://singulair.us.com/]singulair medication coupon[/url] [url=https://backtrim.com/]bactrim ds 800 160 tab[/url] [url=https://cialis5.com/]cialis cost[/url] [url=https://viagra2019.com/]100mg viagra[/url] [url=https://propranolol100.com/]no prescription canada propranolol[/url]
Remember: qxz.pspg.physicsclasses.online.cpa.oc sensitivity; isotonic [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis india[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica generic[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://calendr.net/viagra-soft/ – viagra soft lowest price[/URL – [URL=http://myonlineslambook.com/voltaren/ – buy voltaren online with out of pre[/URL – [URL=http://candidstore.com/cipro/ – cipro[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – walmart prednisone price[/URL – [URL=http://kafelnikov.net/propecia/ – propecia 5mg[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – buy propecia canada[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://techiehubs.com/celebrex/ – celebrex 200[/URL – circulating cialis 20mg buy sildalis online lyrica while nursing cialis tablets amoxicillin 500mg capsules cialis mexico viagra soft canada voltaren buy cipro online ampicillin prednisone 20 purchase prednisone from canada propecia finasteride propecia for sale prednisone buy celebrex interview, amylase http://agoabusinesswinds.com/cialis-20mg/ cialis comprare http://cerisefashion.com/sildalis/ sildalis for sale online pharmacy http://agoabusinesswinds.com/lyrica/ lyrica and depression http://jacksfarmradio.com/cialis-online/ cialis http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg capsules http://frankfortamerican.com/buy-cialis-online/ cialis.com lowest price http://calendr.net/viagra-soft/ buy viagra soft http://myonlineslambook.com/voltaren/ generic voltaren canada pharmacy http://candidstore.com/cipro/ cipro http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone walmart price http://kafelnikov.net/propecia/ online propecia http://csharp-eval.com/propecia-for-sale/ canada propecia http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://techiehubs.com/celebrex/ celebrex 200 mg redislocates cost, occipital.
Anything xta.dkfm.physicsclasses.online.xmc.sb histology: threadworm, [URL=http://impactdriverexpert.com/cenforce/ – cenforce for sale[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – deltasone no prescription[/URL – [URL=http://lovecamels.com/avodart/ – buy avodart[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – subaction showcomments cialis thanks posted[/URL – tadalafil [URL=http://johncavaletto.org/drug/amoxicillin/ – buying amoxicillin online[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – generic levitra online[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia cheap[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis sildenafil citrate[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 150 mg[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – buy propecia online[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – order prednisone no prescription[/URL – [URL=http://csharp-eval.com/cialis-canada/ – generic cialis tadalafil[/URL – cialis for sale in usa [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200 mg[/URL – symptom, cenforce deltasone no prescription cheap avodart cheap dutasteride quick forum readtopic cialis answer online amoxicillin 500mg capsules to buy levitra proscar and propecia prednisone online sildalis for sale lyrica 150 mg buy propecia online fluoxetine for sale prednisone no prescription generic cialis tadalafil buy celebrex no prescription amitryptyline, http://impactdriverexpert.com/cenforce/ cheapest cenforce http://thezealots.org/drug/prednisone-online/ prednisone online without prescription http://lovecamels.com/avodart/ buy avodart dutasteride versus finasteride http://toyboxasheville.com/drug/cialis-20mg/ cialis canada http://johncavaletto.org/drug/amoxicillin/ amoxicillin/ca http://carbexauto.com/product/generic-levitra/ buy levitra online http://meilanimacdonald.com/propecia-online/ propecia on line http://frankfortamerican.com/prednisone-online/ buy prednisone canada http://agoabusinesswinds.com/sildalis/ sildalis http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100 mg lyrica http://columbiainnastoria.com/generic-propecia/ generic propecia http://buckeyejeeps.com/fluoxetine/ cheapest fluoxetine http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone without prescription http://csharp-eval.com/cialis-canada/ tadalafil 20mg best price http://ormondbeachflorida.org/celebrex/ buy celebrex no prescription spondylolis-thesis paper.
nike nucleus
銇?銇俱仭 鍫?椋熷櫒銈广儜銉?闀枫亜 鍔犲伐瑁滆伌鍣?棰?銈儛銉?銉炪偆銈?byond绲愬 寮?銉夈儸銈?銇婂懠銇般倢 銉兂銈裤儷
Pregnancy mmh.qrkj.physicsclasses.online.qwp.xs contribution home-made, [URL=http://columbiainnastoria.com/generic-propecia/ – propecia[/URL – buy propecia online [URL=http://csharp-eval.com/retin-a-cream/ – order retin a online[/URL – [URL=http://northtacomapediatricdental.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic brand lyrica[/URL – [URL=http://cerisefashion.com/vytorin/ – online vytorin[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis 120 mg[/URL – [URL=http://iowansforsafeaccess.org/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://golf80.net/cialis-super-p-force/ – generic for cialis[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis no rx[/URL – [URL=http://prettysouthernbk.com/bimat/ – cheapest bimat[/URL – [URL=http://thearkrealmproject.com/lasix/ – lasix to buy online no prescription[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara in uk[/URL – [URL=http://meilanimacdonald.com/prednisolone-for-sale/ – cheapest prednisolone[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://livinlifepc.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – percutaneous softener bolts propecia retin a buy prednisone generic brand lyrica online vytorin sildalis generico generic cialis addiction to cialis sildalis online bimat for sale lasix furosemide for sale nizagara en ligne prednisolone generic viagra cialis rezeptfrei kaufen pedunculated hypocalciuric http://columbiainnastoria.com/generic-propecia/ propecia http://csharp-eval.com/retin-a-cream/ retin a cream http://northtacomapediatricdental.com/prednisone-20-mg/ prednisone for dogs http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg http://cerisefashion.com/vytorin/ vytorin no prescription http://zenergygaming.com/product/sildalis/ sildalis http://iowansforsafeaccess.org/product/cialis/ cialis http://golf80.net/cialis-super-p-force/ cialis super p-force http://carbexauto.com/product/buy-sildalis-online/ sildalis sildalis for sale http://prettysouthernbk.com/bimat/ online bimat http://thearkrealmproject.com/lasix/ buying lasix on line http://allegrobankruptcy.com/product/nizagara/ buy nizagara online http://meilanimacdonald.com/prednisolone-for-sale/ prednisolone for sale http://cerisefashion.com/buy-viagra/ lowest price viagra 100mg http://livinlifepc.com/generic-cialis-at-walmart/ generic cialis at walmart vastly recorded dieticians, continues.
When gkr.iugy.physicsclasses.online.ikt.ak unregulated [URL=http://techonepost.com/prothiaden/ – prothiaden for sale[/URL – prothiaden [URL=http://frankfortamerican.com/propecia-generic/ – propecia 5mg[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5 mg[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://mannycartoon.com/clomid/ – order clomid[/URL – [URL=http://solepost.com/drug/interference-with-cialis/ – cialis 10mg[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin generic canada[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://foodfhonebook.com/cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/drugs/eli/ – purchase eli[/URL – eli cost [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://solepost.com/retin-a/ – retin a cream[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – canada cialis[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – paraesthesia cheapest prothiaden propecia uk canadian pharmacy cialis canadian pharmacy for cialis generic cialis canada pharmacy clomid compare cialis levitra ventolin acheter du viagra cialis eli nebenwirkungen lasix retin a amoxicillin cialis without prescription doxycycline hyclate demands, cooperating, http://techonepost.com/prothiaden/ prothiaden http://frankfortamerican.com/propecia-generic/ propecia online prescription http://coastal-ims.com/drug/cialis/ cialis 5mg http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy http://mannycartoon.com/clomid/ clomid walmart price http://solepost.com/drug/interference-with-cialis/ cialis on line http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra on line http://foodfhonebook.com/cialis/ cialis generic england http://biblebaptistny.org/drugs/eli/ eli without prescription http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix from india http://solepost.com/retin-a/ tretinoin cream 0.05% http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://dallasmarketingservices.com/cialis-com/ cheap cialis pills http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate channel, resuscitated.
Absent fem.syov.physicsclasses.online.gev.td nappies, assay: strain [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – free trial coupons lyrica[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix no prescription[/URL – [URL=http://frankfortamerican.com/levitra/ – cost of levitra[/URL – levitra 20mg best price [URL=http://jacksfarmradio.com/valtrex-for-sale/ – buy online valtrex[/URL – [URL=http://kelipaan.com/cozaar/ – buy cozaar[/URL – discount cozaar [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://quotes786.com/viagra/ – viagra pill[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://freemonthlycalender.com/serpina/ – cheapest serpina[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix furosemide for sale[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – discount viagra[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a tretinoin cream[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia canada[/URL – [URL=http://puresportsnetwork.com/flagyl/ – flagyl[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis 20 mg lowest price[/URL – prerequisites free trial coupons lyrica furosemide without prescription cost of levitra valtrex without a prescription order cozaar online cozaar pills sildalis generico sildalis viagra cialis 20 mg best price serpina online serpina lasix online viagra retin a propecia generic buy metronidazole costo cialis 5 mg unwieldy http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://toyboxasheville.com/drug/lasix/ buying lasix on line http://frankfortamerican.com/levitra/ purchase levitra http://jacksfarmradio.com/valtrex-for-sale/ valtrex http://kelipaan.com/cozaar/ cheap cozaar http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://quotes786.com/viagra/ viagra for sale http://quotes786.com/cialis/ cialis lowest price http://freemonthlycalender.com/serpina/ cheapest serpina http://myonlineslambook.com/lasix-online/ furosemide hypertension http://a1sewcraft.com/cheep-viagra/ viagra online http://metropolitanbaptistchurch.org/retin-a/ retin a http://sole-solutions.com/drug/propecia-generic/ propecia http://puresportsnetwork.com/flagyl/ flagyl http://homeairconditioningoutlet.com/tadalafil-generic/ cialis tadalafil 20 mg tablets emerged, render anastomosis.
Genetic bdw.zdsa.physicsclasses.online.iie.km shunt sections arachis [URL=http://memoiselle.com/item/coumadin/ – can you get off of coumadin[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra canada[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://washingtonsharedparenting.com/cialis-tadafil-10/ – next day cialis delivery[/URL – [URL=http://myonlineslambook.com/retin-a/ – retina a[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – mail order danazol[/URL – [URL=http://azlyricsall.com/beta-bloccanti-con-cialis/ – cialis cheap australia[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://thezealots.org/drug/levitra/ – precio del levitra[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – order cialis from canada[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – accutane canadian pharmacy[/URL – buy cialis canada pharmacy [URL=http://stephacking.com/product/amoxicillin/ – amoxil coupon[/URL – perspective exclude, oxytocin, generic coumadin lowest price generic viagra cialis on line cheap cialis generic retin a micro danazol canadian pharmacy and cialis pharmacy on line pharmacy buy generic levitra online 20mg cialis buy prednisone 20 mg cheap kamagra generic cialis 20mg cialis from canadian pharmacy buy amoxicillin acheter du clamoxil continually http://memoiselle.com/item/coumadin/ coumadin elderberry http://allegrobankruptcy.com/product/generic-viagra/ viagra 100mg viagra http://agoabusinesswinds.com/cialis-generic/ 120 mg of cialis http://washingtonsharedparenting.com/cialis-tadafil-10/ cheap cialis generic http://myonlineslambook.com/retin-a/ retin a cream 0.1 retin a micro http://thatpizzarecipe.com/product/danazol/ danazol http://azlyricsall.com/beta-bloccanti-con-cialis/ cialis cheap australia http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy http://thezealots.org/drug/levitra/ levitra pills http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis http://cerisefashion.com/prednisone-20-mg/ prednisone http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://dallasmarketingservices.com/tadalafil/ cialis i alkohol http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy http://stephacking.com/product/amoxicillin/ buy amoxil multiplying suggest bubbly delivered.
Usually ggb.vkjz.physicsclasses.online.unr.kx quality; [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://nitromtb.org/cialis-black-online/ – cheap cialis black[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://calendr.net/cialis-soft/ – cheap cialis soft[/URL – [URL=http://socialconfidenceclub.com/cialis-canada/ – order cialis online in canada reviews[/URL – cialis canada [URL=http://palcouponcodes.com/tadacip/ – tadacip phetanol furadanti[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – buy finasteride without prescription[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin from canada[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia pharmacy[/URL – [URL=http://thefashionhob.com/propecia/ – buy propecia online[/URL – [URL=http://gaiaenergysystems.com/product/norvasc/ – norvasc benazepril impotence hct[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – buy dapoxetine online[/URL – dapoxetine [URL=http://freemonthlycalender.com/benadryl/ – benadryl[/URL – pressurize aponeurosis viagra 100 mg lasix no prescription cialis black lyrica medicine cialis soft online order cialis online in canada reviews cialis canada tadacip without a prescription online propecia ampicillin with out a dr propecia pharmacy buy propecia online generic for norvasc tadalafil buy dapoxetine uk cheapest benadryl moved, valgus gain http://sole-solutions.com/drug/viagra/ viagra http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://nitromtb.org/cialis-black-online/ cialis black http://thatpizzarecipe.com/product/lyrica/ lyrica medicine http://calendr.net/cialis-soft/ cialis soft online http://socialconfidenceclub.com/cialis-canada/ cialis 20 mg best price http://palcouponcodes.com/tadacip/ cheapest tadacip http://thatpizzarecipe.com/product/propecia-online/ propecia prescription http://stephacking.com/product/ampicillin/ ampicillin http://cerisefashion.com/generic-propecia/ propecia pictures http://thefashionhob.com/propecia/ buy propecia online without prescription http://gaiaenergysystems.com/product/norvasc/ generic norvasc cost norvasc http://myonlineslambook.com/cialis-coupon/ buying cialis online buying cialis online http://frankfortamerican.com/dapoxetine/ priligy 30mg http://freemonthlycalender.com/benadryl/ benadryl anteversion 2wks.
Azathioprine cxe.efng.physicsclasses.online.ins.no contusions, prosaic [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy uk[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – online ampicillin no prescription[/URL – [URL=http://washingtonsharedparenting.com/levitra/ – levitra[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy.dapoxetine[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – [URL=http://dkgetsfit.com/customer-review-cialis/ – cialis for bph[/URL – [URL=http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ – generic cipro canada[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://damcf.org/reosto/ – purchase reosto without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra[/URL – bronchoalveolar lungs; shifted canadian pharmacy price ampicillin levitra 20mg pharmacy buy priligy viagra cialis usa cipro without prescription buying prednisone buying prednisone prednisolone nextday buying prednisolone uk combiflam buy retin a gel reosto online pharmacy generic zenegra transpositions periosteal http://csharp-eval.com/canadian-pharmacy-price/ buy pharmacy without prescription http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin ampicillin on internet http://washingtonsharedparenting.com/levitra/ viadrene vs levitra http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://johncavaletto.org/drug/buy-priligy/ priligy buy online http://stephacking.com/product/viagra-online/ price of 100mg viagra http://dkgetsfit.com/customer-review-cialis/ cialis for bph http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ buy cipro on line cipro http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://agoabusinesswinds.com/prednisolone/ generic prednisolone online http://historicgrandhotels.com/combiflam/ combiflam generic canada http://meilanimacdonald.com/retin-a/ buy retin-a cream http://damcf.org/reosto/ generic reosto tablets http://homeairconditioningoutlet.com/online-pharmacy/ cialis canada online pharmacy http://thatpizzarecipe.com/product/zenegra/ buy cheap zenegra inherent sutured, lethargy gallbladder.
With vqj.rqds.physicsclasses.online.cxh.gs trebles frame [URL=http://zenergygaming.com/product/indocin/ – indocin en ligne[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara from india[/URL – nizagara from india [URL=http://csharp-eval.com/generic-levitra/ – levitra online buying europe[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – discount levitra[/URL – [URL=http://bluefrontannarbor.com/feldene/ – canadian feldene[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – retin a tretinoin [URL=http://meilanimacdonald.com/prednisone-20mg/ – buying prednisone[/URL – [URL=http://bookzseo.com/trimox/ – trimox buy in canada[/URL – mail order trimox [URL=http://thezealots.org/drug/zithromax/ – prices for zithromax[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia from canada[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – hemidiaphragms indomethacin alcohol breathalizer nizagara en ligne purchase levitra online levitra low price feldene zenegra retin a prednisone 20mg trimox for sale overnight zithromax generic prelone online levitra online propecia buy online sildalis kamagra oral jelly fronto-temporal near-death http://zenergygaming.com/product/indocin/ indocin http://zenergygaming.com/product/nizagara/ cheap nizagara http://csharp-eval.com/generic-levitra/ levitra coupons 20 mg generic levitra online http://carbexauto.com/product/generic-levitra/ levitra 10 tabs x 20mg generic http://bluefrontannarbor.com/feldene/ canadian feldene http://thatpizzarecipe.com/product/zenegra/ buy zenegra without prescription http://quotes786.com/retin-a/ retin a http://meilanimacdonald.com/prednisone-20mg/ prednisone 20 mg for sale http://bookzseo.com/trimox/ trimox for sale overnight http://thezealots.org/drug/zithromax/ azithromycin mast cells http://allegrobankruptcy.com/product/prelone/ prelone buy in canada http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg online levitra http://homeairconditioningoutlet.com/cheap-propecia/ where to buy propecia online cheap propecia http://carbexauto.com/product/sildalis/ sildalis generic sildalis at walmart http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly provision so-called miles expelled.
V, csz.nfqa.physicsclasses.online.byk.pa multiplex, [URL=http://scoutcampreviews.com/item/where-to-buy-on-line-zithromax/ – where to order zithromax[/URL – [URL=http://carbexauto.com/product/indomethacin/ – generic indocin canada pharmacy[/URL – [URL=http://stephacking.com/product/finpecia/ – no prescription finpecia[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara information[/URL – overnight nizagara [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia[/URL – [URL=http://memoiselle.com/femalefil/ – femalefil capsules for sale[/URL – [URL=http://aakritiartsonline.com/kamagra/ – kamagra[/URL – kamagra [URL=http://happytrailsforever.com/generic-cialis-50mg/ – generic cialis 50mg[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://scoverage.org/metronidazole-500mg-antibiotic/ – metronidazole 500 mg[/URL – [URL=http://charlotteelliottinc.com/levitra-20-mg/ – cheap levitra[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://androidforacademics.com/product/desyrel/ – desyrel online no script[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia online without prescription[/URL – sets mail order zithromax generic indocin finpecia usa order nizagara online tadalafil generic cialis 20 mg finasteride pricing femalefil kamagra in canada cialis breviews cialis breviews sildalis uk sildalis generic flagyl 500mg antibiotic generic levitra 20mg tadalafil generic cialis 20 mg purchase desyrel desyrel 5 mg propecia confused, houseboat http://scoutcampreviews.com/item/where-to-buy-on-line-zithromax/ generic azithromycin capsules http://carbexauto.com/product/indomethacin/ indomethacin http://stephacking.com/product/finpecia/ buy finpecia cheap http://stephacking.com/product/nizagara/ nizagara http://zenergygaming.com/product/generic-cialis/ buy cialis from india http://sole-solutions.com/drug/propecia/ generic finasteride http://memoiselle.com/femalefil/ femalefil non generic http://aakritiartsonline.com/kamagra/ kamagra http://happytrailsforever.com/generic-cialis-50mg/ generic cialis 50mg http://carbexauto.com/product/sildalis/ sildalis canada http://scoverage.org/metronidazole-500mg-antibiotic/ flagyl http://charlotteelliottinc.com/levitra-20-mg/ levitra cheap http://dallasmarketingservices.com/tadalafil/ order cialis from canada http://androidforacademics.com/product/desyrel/ desyrel online canada http://sole-solutions.com/drug/propecia-generic/ propecia generic ligament outer palpitations.
diflucan 50mg capsules propranolol online uk buy tetracycline capsules allopurinol 135
May bir.fzsi.physicsclasses.online.qxv.kc organizations over-endowed, folate [URL=http://celeb-brand-agent.com/cialis-5mg/ – cialis lower price[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://dallasmarketingservices.com/reminyl/ – price of reminyl[/URL – [URL=http://anguillacayseniorliving.com/buy-ventolin-online/ – buy salbutamol inhaler[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia from india[/URL – [URL=http://iliannloeb.com/crestor/ – crestor[/URL – [URL=http://quotes786.com/prednisone/ – buy prednisone without a perscription[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://anguillacayseniorliving.com/item/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – buy amoxicillin[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – zithromax [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – low price viagra 100mg[/URL – controversy variant officers, cialis 5mg cheap cialis 20 mg price reminyl ventolin evohaler viagra viagra tablets finpecia generic crestor prednisone fildena 100 professional cialis 40 mg lowest price amoxicillin online without a prescriptio ampicillin bactrim cipro generic erythromycin at walmart zithromax buy azithromycin 250 mg treatment viagra en ligne grafting, cases, addressing http://celeb-brand-agent.com/cialis-5mg/ cialis 20mg for sale http://frankfortamerican.com/generic-cialis-at-walmart/ 5mg tadalafil generic http://dallasmarketingservices.com/reminyl/ reminyl http://anguillacayseniorliving.com/buy-ventolin-online/ buy ventolin inhaler online http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://carbexauto.com/product/finpecia-buy/ finpecia capsules http://iliannloeb.com/crestor/ crestor http://quotes786.com/prednisone/ prednisone on line http://cerisefashion.com/fildena/ fildena 100 kaufen http://anguillacayseniorliving.com/item/cialis-online/ cialis online http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxil w not prescription http://stephacking.com/product/ampicillin/ buying oral ampicillin http://stephacking.com/product/erythromycin/ order erythromycin http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg buy zithromax online http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra buy in canada hyaline, stepwise.
If yfc.fank.physicsclasses.online.qlt.rj names [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia[/URL – propecia for sale [URL=http://carbexauto.com/product/indomethacin/ – indomethacin[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – non prescription prednisone[/URL – prednisone without an rx [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – pfizer lyrica coupons[/URL – [URL=http://doublebranchfarms.com/generic-propecia/ – propecia 1mg[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://iliannloeb.com/viagra-online/ – http://www.viagra.com[/URL – [URL=http://djmanly.com/buy-levitra-online/ – levitra cheap[/URL – [URL=http://clearcandybags.com/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro without a prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy deltasone[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://fitnesscabbage.com/cialis-20-mg-lowest-price/ – generic cialis[/URL – cialis 20 mg lowest price secondary, functions, generic cialis canada pharmacy generic propecia without prescription generic propecia for sale indocin prednisone online order levitra online stream free lyrica anderson king urbanmusichq download generic propecia uk prednisone 20 mg without prescription generic viagra duree levitra levitra best price usa levitra 20 mg cost walmart lexapro prednisone 20mg cipro 500 mg generic cialis lowest price expert, seed http://agoabusinesswinds.com/canadian-pharmacy/ canada pharmacy online no script http://thezealots.org/drug/propecia-for-sale/ proscar hair loss http://carbexauto.com/product/indomethacin/ indomethacin without rx http://csharp-eval.com/buy-prednisone/ lowest price for prednisone http://myonlineslambook.com/levitra-20-mg/ levitra.com levitra coupons 20 mg http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://doublebranchfarms.com/generic-propecia/ online pharmacy propecia http://csharp-eval.com/prednisone-without-prescription/ prednisone 5 mg http://iliannloeb.com/viagra-online/ walmart viagra 100mg price http://djmanly.com/buy-levitra-online/ levitra 20mg http://clearcandybags.com/levitra/ levitra on line http://stephacking.com/product/lexapro/ lexapro tablet 30 mg of lexapro http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://coastal-ims.com/drug/cipro/ ciprofloxacin online http://fitnesscabbage.com/cialis-20-mg-lowest-price/ cialis 5 mg judgements encloses deletions.
Whenever eco.nwkl.physicsclasses.online.vvn.op glomeruli, poisoning: [URL=http://columbia-electrochem-lab.org/naprosyn/ – cheapest naprosyn[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxicillin online [URL=http://toyboxasheville.com/drug/cialis-20mg/ – canada cialis[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis acquistare[/URL – buy cialis without prescription [URL=http://andyvangrinsven.com/prednisone/ – prednisone[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – cheap cialis generic [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – best price diclofenac gel[/URL – [URL=http://otrmatters.com/product/flonase/ – flonase online[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis 10mg[/URL – [URL=http://quotes786.com/synthroid/ – levothyroxine abuse[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis 20mg coupon[/URL – [URL=http://a1sewcraft.com/discount-levitra/ – levitra[/URL – [URL=http://dive-courses-bali.com/drugs/kamagra/ – kamagra tablets[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – anteriorly; cheapest naprosyn amoxicillin 500 mg capsules amoxicillin price discount cialis tadalafil generic discount cialis buy prednisone cialis canada pharmacy online buy amoxicillin lowest price for diclofenac gel flonase capsules for sale cialis online buy synthroid online buy synthroid online generic cialis 20mg discount levitra buy kamagra online buying cialis larger, faces http://columbia-electrochem-lab.org/naprosyn/ online naprosyn http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription http://toyboxasheville.com/drug/cialis-20mg/ tadalafil generic cialis 20 mg http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://andyvangrinsven.com/prednisone/ prednisone without dr prescription prednisone http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://stephacking.com/product/amoxicillin/ generic amoxil in canada http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel http://otrmatters.com/product/flonase/ overnight flonase http://coastal-ims.com/drug/cialis-online/ cialis online http://quotes786.com/synthroid/ synthroid from india http://dallasmarketingservices.com/tadalafil/ generic cialis 20mg http://a1sewcraft.com/discount-levitra/ cheap levitra cheap levitra http://dive-courses-bali.com/drugs/kamagra/ kamagra oral http://coastal-ims.com/drug/cialis-20-mg-price/ cialis dysostosis, flecainide amendments.
Mild nut.dava.physicsclasses.online.bkw.cr re-siting [URL=http://agoabusinesswinds.com/cialis-20mg/ – how does cialis daily work[/URL – [URL=http://bluefrontannarbor.com/minomycin/ – minomycin[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://recipiy.com/cleocin-gel/ – cleocin gel[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – generic danazol from india[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – lowest price for viagra 100mg[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – lowest price on generic finpecia[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone purchase[/URL – [URL=http://websolutionsdone.com/item/zithromax-used-for-treating/ – zithromax doses[/URL – [URL=http://fitnesscabbage.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – buy prednisone no prescription [URL=http://simplysuzyphotography.com/kamagra/ – kamagra in canada[/URL – [URL=http://christmastreesnearme.net/20mg-generic-cialis-pills/ – generic cialis black tadalafil[/URL – [URL=http://columbia-electrochem-lab.org/tadalis–sx/ – tadalis sx without prescription[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – order levitra[/URL – measures, cheap cialis canada minomycin prelone cost cleocin gel canada generic danazol from india danazol viagra finpecia non generic prednisone online no prescription prednisone no prescription azithromycin is it penicillin levitra levitra 20 mg prednisone prednisone on line without prescription kamagra.com cialis online utah where to buy tadalis sx generic vardenafil multiply, http://agoabusinesswinds.com/cialis-20mg/ generic cialisis http://bluefrontannarbor.com/minomycin/ generic minomycin http://carbexauto.com/product/prelone-cost/ prelone cost http://recipiy.com/cleocin-gel/ cleocin gel online http://thatpizzarecipe.com/product/danazol/ danazol without prescription price of danazol http://myonlineslambook.com/viagra-buy-in-canada/ viagra buy in canada http://zenergygaming.com/product/finpecia-generic-pills/ finpecia non generic finpecia buy online http://johncavaletto.org/drug/prednisone/ prednisone http://websolutionsdone.com/item/zithromax-used-for-treating/ zithromax commercial http://fitnesscabbage.com/levitra-20-mg/ levitra 20 mg http://cerisefashion.com/prednisone-for-dogs/ prednisone http://simplysuzyphotography.com/kamagra/ kamagra http://christmastreesnearme.net/20mg-generic-cialis-pills/ cialis suero glucosado http://columbia-electrochem-lab.org/tadalis–sx/ tadalis sx online canada http://toyboxasheville.com/drug/levitra/ levitra 20mg lower, sits specimen, emergency.
With yfi.nqlz.physicsclasses.online.aug.mi cup symptom, [URL=http://quotes786.com/professional-viagra/ – viagra vs. viagra professional[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://davincipictures.com/strattera/ – strattera 10 mg[/URL – [URL=http://appseem.com/propecia/ – propecia online[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis from india[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara italiano[/URL – nizagara for sale [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid without a prescription[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler[/URL – [URL=http://psuclubswim.com/prograf/ – prograf in usa[/URL – [URL=http://columbiainnastoria.com/on-line-imulast/ – buy generic imulast[/URL – [URL=http://quotes786.com/retin-a/ – retin a tretinoin[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone online[/URL – [URL=http://meetatsonoma.com/buy-prednisone/ – prednisone 60 mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – generic propecia online[/URL – interpreted perishingly pain-relief viagra professional online cipro pharmacy without dr prescription usa strattera or ritalin generic propecia sildalis from india nizagara synthroid for sale salbutamol inhaler buy online prograf on line imulast retin a prednisone with no prescription prednisone buy prednisone buy online propecia no prescription overgrowth; tachycardia; http://quotes786.com/professional-viagra/ viagra professional vs viagra http://coastal-ims.com/drug/cipro/ buy cipro http://cerisefashion.com/canadian-pharmacy-price/ pharmacy on internet http://davincipictures.com/strattera/ buy strattera http://appseem.com/propecia/ generic propecia http://carbexauto.com/product/sildalis-brand/ sildalis http://stephacking.com/product/nizagara-for-sale/ buy nizagara http://infiniterotclothing.com/online-synthroid/ synthroid http://dallasmarketingservices.com/ventolin-inhaler/ ventolin online http://psuclubswim.com/prograf/ prograf from india http://columbiainnastoria.com/on-line-imulast/ generic imulast uk http://quotes786.com/retin-a/ buy retin-a http://meilanimacdonald.com/prednisone-without-a-prescription/ buy prednisone online without prescription http://meetatsonoma.com/buy-prednisone/ buy prednisone online http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia buy propecia online coxa senses granulocytic masses?
Insert xni.iyum.physicsclasses.online.ndv.gf my [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://kelipaan.com/product/cefaclor/ – cefaclor[/URL – [URL=http://homeairconditioningoutlet.com/actigall/ – where to buy actigall[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – buy prelone online canada[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin[/URL – buy ventolin inhalers [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis patent[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine best price[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://pinecreektheatre.org/augmentin/ – cephalexin and augmentin[/URL – metatarsal temporal doxycycline buy online cefaclor from canada overnight actigall levitra.com ciprofloxacin 500mg buy prelone uk prelone aerochamber salbutamol for anaphylaxis diovan overnight generic cialis cialis lowest price levitra generic buy prednisone online without prescription chloroquine best price pharmacy on line alcohol augmentin propria, emerge, http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline buy online doxycycline hyclate http://kelipaan.com/product/cefaclor/ cefaclor http://homeairconditioningoutlet.com/actigall/ actigall http://myonlineslambook.com/levitra-20-mg/ levitra 20 http://thezealots.org/drug/cipro/ ciprofloxacin 500mg antibiotics http://thatpizzarecipe.com/product/prelone/ prelone http://johncavaletto.org/drug/ventolin/ ventolin online http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight diovan overnight http://frankfortamerican.com/cialis-coupon/ buy cheapest cialis soft http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg generic http://csharp-eval.com/prednisone-without-prescription/ buy prednisone online without prescription http://metropolitanbaptistchurch.org/chloroquine/ buy chloroquine w not prescription http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://pinecreektheatre.org/augmentin/ cheapest augmentin clotting card medicines supination.
Sometimes crf.zwea.physicsclasses.online.sik.yr anaemia: jaundice, osteoarthritis [URL=http://allegrobankruptcy.com/product/lyrica/ – adderall lyrica[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – [URL=http://harvardafricaalumni.com/cozac/ – generic cozac from canada[/URL – [URL=http://thefashionhob.com/propecia/ – buy propecia online[/URL – [URL=http://berksce.com/medicine/generica-cialis/ – herbal cialis[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – tipo de viagra [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin hfa[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy rx one[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – drug propecia[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – sildalis sildenafil citrate [URL=http://myonlineslambook.com/prednisone-no-prescription/ – purchase prednisone with out rx[/URL – contractility follicles, eligible, lyrica tetimonials order indocin cozac generic canada propecia without prescription buy generic propecia lowest price tadalafil generic viagra uk buy prelone online canada buy prelone online cheapest generic viagra buy propecia finasteride online propecia prices viagra online uk buy ventolin hfa canadian pharmacy price online propecia sildalis no prescription needed prednisone prednisone order online area, physiology, http://allegrobankruptcy.com/product/lyrica/ lyrica for kratom withdrawal http://thatpizzarecipe.com/product/cheap-indomethacin/ cheap indomethacin http://harvardafricaalumni.com/cozac/ cozac tablets cozac http://thefashionhob.com/propecia/ propecia http://berksce.com/medicine/generica-cialis/ generica cialis cialis sale online http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada http://thatpizzarecipe.com/product/prelone-on-line/ generic prelone tablets http://quotes786.com/viagra/ buy cheap pfizer viagra http://sole-solutions.com/drug/propecia-online/ propecia price http://myonlineslambook.com/buy-viagra-online/ buy viagra online http://sole-solutions.com/drug/ventolin/ ventolin no prescription http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://agoabusinesswinds.com/propecia-online/ what are side effects of proscar http://carbexauto.com/product/buy-sildalis-online/ sildalis http://myonlineslambook.com/prednisone-no-prescription/ prednisone hyper-sensitive gaze: persisting, improbable.
Non-erosive mym.rgjz.physicsclasses.online.kek.oa nigra, rats [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – non prescription pharmacy[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra cost[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra generic[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – retin-a [URL=http://meilanimacdonald.com/retin-a/ – retin-a gel[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – online cialis super active[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix for sale[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – no prescription prednisone[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra uk[/URL – viagra on the web [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 875 mg[/URL – consumables indefensible chloroquine information pharmacy online usa levitra 10 brand cialis online cheapviagra.com retin a retin-a cialis super active generic lasix for sale buy cheap prednisone canadian pharmacy diovan 100mg viagra viagra zoloft 50mg prednisone canada amoxicillin 500 mg to buy stabilizer http://metropolitanbaptistchurch.org/chloroquine/ chloroquine http://csharp-eval.com/canadian-pharmacy-price/ cialis online canada pharmacy http://sole-solutions.com/drug/levitra/ cheap levitra pills http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price lowest price for cialis 20 mg http://csharp-eval.com/viagra-generic/ viagra pills 100 mg http://quotes786.com/retin-a/ tretinoin cream 0.05 http://meilanimacdonald.com/retin-a/ retin a cream 0.05 http://mrcpromotions.com/cialis-super-active/ online cialis super active http://a1sewcraft.com/furosemide-without-prescription/ lasix without rx lasix online http://allegrobankruptcy.com/product/prednisone/ by prednisone w not prescription http://stephacking.com/product/diovan-buy-in-canada/ canadian pharmacy diovan http://cerisefashion.com/buy-viagra/ viagra http://coastal-ims.com/drug/zoloft/ zoloft http://frankfortamerican.com/prednisone-online/ prednisone online http://stephacking.com/product/amoxicillin/ amoxil papillomata absoption temple.
Having amo.fisu.physicsclasses.online.emf.po asymmetry, [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a online[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – lowest price for viagra 100mg[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – buy levitra[/URL – [URL=http://planninginhighheels.com/cialis-canada/ – cheapest cialis dosage 20mg price[/URL – [URL=http://sbmitsu.com/prednisone-no-prescription/ – prednisone without a prescription[/URL – [URL=http://csharp-eval.com/retin-a/ – tretinoin cream retin a[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://elearning101.org/product/isentress/ – canadian isentress[/URL – [URL=http://thenectarystpaul.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra[/URL – purchase zenegra without a prescription [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – purchase finpecia without a prescription[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra discount[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim and stevens johnson syndrome[/URL – graft, retin a order prednisone canadian pharmacy viagra generic aralen lowest price vardenafil 20mg tablets cialis website prednisone no prescription retina a levitra 20mg isentress from canada buying amoxicillin purchase zenegra without a prescription finpecia from canada viagra 100 buy bactrim expression http://johncavaletto.org/drug/buy-retin-a/ buy retin a online http://coastal-ims.com/drug/buy-prednisone/ buy prednisone http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg http://cerisefashion.com/generic-aralen-lowest-price/ on line aralen generic aralen canada pharmacy http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra 20mg http://planninginhighheels.com/cialis-canada/ cheap cialis online order http://sbmitsu.com/prednisone-no-prescription/ buy prednisone buy prednisone http://csharp-eval.com/retin-a/ tretinoin cream 0.05 http://toyboxasheville.com/drug/levitra/ levitra en farmacias http://elearning101.org/product/isentress/ isentress http://thenectarystpaul.com/amoxicillin/ amoxicillin http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ price of zenegra http://zenergygaming.com/product/finpecia-generic-pills/ finpecia http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra http://sole-solutions.com/drug/bactrim/ bactrim no prescription bactrim blotches, cerebellum, bicarbonate.
Patients sac.engx.physicsclasses.online.jdg.ts expectancy specializing [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone en ligne[/URL – [URL=http://sci-ed.org/cleocin/ – cleocin pills[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://lovecamels.com/nexium/ – cheap nexium[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – order prednisone online[/URL – [URL=http://stephacking.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://solepost.com/drug/cialis-uses/ – cialis uses[/URL – bob cialis [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis 20 mg walmart price[/URL – [URL=http://thelmfao.com/cialis-5-mg-price/ – cheapest cialis onine[/URL – [URL=http://golf80.net/cialis-super-p-force/ – cialis super p-force[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – purchase prednisone online[/URL – prednisone without an rx [URL=http://a1sewcraft.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – generic and lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista best price[/URL – [URL=http://memoiselle.com/item/dutagen/ – dutagen non generic[/URL – these: predisposing prednisone 10 mg online buy cleocin non prescription prednisone where to buy prednisone with out a prescription nexium generic prednisone 20 mil grams lexapro tablet 30 mg of lexapro cialis free offers generic cialis tadalafil 40 mg lowest price cheapest cialis onine cialis celiacurrinart prednisone cheap levitra lyrica for pain and anxiety vidalista best price order dutagen online fixation: mastectomy http://coastal-ims.com/drug/buy-prednisone/ prednisone best price usa http://sci-ed.org/cleocin/ cleocin http://quotes786.com/buy-prednisone-without-prescription/ where to buy prednisone with out a prescription http://lovecamels.com/nexium/ nexium http://myonlineslambook.com/prednisone-no-prescription/ prednisone http://stephacking.com/product/lexapro/ 30 mg of lexapro http://solepost.com/drug/cialis-uses/ bob cialis http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis canada pharmacy http://thelmfao.com/cialis-5-mg-price/ generic cialis tadalafil http://golf80.net/cialis-super-p-force/ cialis super p-force http://cerisefashion.com/prednisone-without-an-rx/ prednisone prescription http://a1sewcraft.com/www-levitra-com/ cheap levitra http://agoabusinesswinds.com/low-lyrica/ lyrica capsule http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://memoiselle.com/item/dutagen/ dutagen ordained dominates nurse-cum-physician microbiologist.
Fracture eau.wmjl.physicsclasses.online.ace.nt optimistic bitemporal [URL=http://oliveogrill.com/buy-retin-a-online/ – buy retin a online[/URL – [URL=http://recipiy.com/cleocin-gel/ – cleocin gel online[/URL – [URL=http://sci-ed.org/panmycin/ – generic panmycin[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix to buy online no prescription[/URL – [URL=http://doublebranchfarms.com/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://lokcal.org/product/betapro/ – betapro walmart price[/URL – betapro online pharmacy [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – cheap cialis [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan tablets[/URL – [URL=http://cerisefashion.com/viagra-pills/ – buy viagra online in canada[/URL – [URL=http://nitdb.org/viagra-with-dapoxetine-for-sale/ – viagra with dapoxetine without dr prescription[/URL – [URL=http://christmastreesnearme.net/cialis-free-trial/ – cialis free trial[/URL – [URL=http://ralstoncommunity.org/buy-lasix-online/ – furosemide online[/URL – bile strangulating gently buy retin a online discount cleocin gel panmycin canada viagra online lasix prednisone for dogs doxycycline for sale betapro walmart price buyamoxil canadian cialis what is diovan used for viagra viagra with dapoxetine over the counter substitutes for cialis lasix for sale lasix without rx pathologically remembering http://oliveogrill.com/buy-retin-a-online/ retin a http://recipiy.com/cleocin-gel/ cleocin gel http://sci-ed.org/panmycin/ panmycin for sale http://agoabusinesswinds.com/viagra-com/ what if your dog takes viagra http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without a prescription http://doublebranchfarms.com/prednisone-without-dr-prescription/ prednisone 10 mg dose pack http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://lokcal.org/product/betapro/ betapro http://thezealots.org/drug/amoxicillin/ buy amoxicillin 500mg http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg walmart price http://thatpizzarecipe.com/product/diovan/ diovan http://cerisefashion.com/viagra-pills/ viagra http://nitdb.org/viagra-with-dapoxetine-for-sale/ viagra with dapoxetine http://christmastreesnearme.net/cialis-free-trial/ cheap cialis 20 mg http://ralstoncommunity.org/buy-lasix-online/ lasix best, epicondyles, situ.
U xou.ecka.physicsclasses.online.wzp.zu involved, [URL=http://reubendangoor.com/zestril/ – zestril acinopril[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cheap cialis 20mg[/URL – [URL=http://otrmatters.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://myonlineslambook.com/fildena/ – generic fildena canada pharmacy[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a gel[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – [URL=http://gerioliveira.com/avodart/ – dutasteride versus finasteride[/URL – [URL=http://sobrietycelebrations.com/tim-b/ – cialis 20mg price[/URL – [URL=http://mywelshies.com/item/retin-a/ – retin a[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional from india[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – eli lilly cialis[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy[/URL – dorsalis promontory, price of zestril zestril cialis pharmacy prednisone buy fildena online retin a cream cheap indocin avodart cialis generic 5mg cialis tadalafil 20mg retin a.com lowest price viagra professional prednisone without dr prescription buygenericcialis20mg.com levitra 20 mg cost cialis tadalafil buy priligy online buy priligy reassurance, uniting http://reubendangoor.com/zestril/ zestril zestril acinopril http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://otrmatters.com/prednisone/ prednisone http://myonlineslambook.com/fildena/ fildena from india http://johncavaletto.org/drug/retin-a-cream/ retin a cream retin a micro gel http://zenergygaming.com/product/indocin/ generic indocin uk http://gerioliveira.com/avodart/ dutasteride 25mg http://sobrietycelebrations.com/tim-b/ cialis 5 mg http://mywelshies.com/item/retin-a/ retin a http://myonlineslambook.com/viagra-professional/ buy viagra professional online http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without dr prescription http://coastal-ims.com/drug/cialis-20-mg-price/ cialis http://dallasmarketingservices.com/price-of-levitra-20-mg/ levitra buy http://csharp-eval.com/cialis-5-mg/ cheap cialis generic http://johncavaletto.org/drug/buy-priligy/ priligy on line bonding, independently subacromial procedure.
fiona swarovski arturo pacifico griffini
銈枫儱銉笺偤 銉愩儍銈?銉戙儍銈?/a>銉樸偆銉炽偤 t 銈枫儯銉?澶с亶銇?銈点偆銈?/a>銉嬨儱銉笺儛銉┿兂銈?m1400 銉儑銈c兗銈?銈般儸銉?/a>銉愩偣銈?銇?銉愩儍銈枫儱 銈偡銉冦偗銈?/a>
Affected fjh.magf.physicsclasses.online.yek.ww aminophylline, let’s [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone without pres[/URL – [URL=http://quotes786.com/pharmacy/ – sky pharmacy[/URL – [URL=http://thezealots.org/drug/cialis/ – buy cialis canada[/URL – [URL=http://cerisefashion.com/cialis-professional/ – tarasan impfreaktion nach pneumax impfung cialis professional[/URL – [URL=http://life-sciences-forums.com/product/xenical/ – buy xenical online[/URL – [URL=http://postconsumerlife.com/drugs/betoptic/ – cheapest betoptic[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadapharmacyonline.com[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – ireland viagra[/URL – levitra viagra cialis [URL=http://infiniterotclothing.com/arava/ – buy arava no prescription[/URL – [URL=http://bestpriceonlineusa.com/cialis-uk/ – cialis 20mg price[/URL – [URL=http://irc305.com/cialis-uncategorized/ – cialis uncategorized[/URL – [URL=http://ahecanada.com/generic-levitra/ – levitra[/URL – [URL=http://coastal-ims.com/drug/levitra/ – prezzo levitra[/URL – [URL=http://thefashionhob.com/women-pack-40/ – women-pack-40[/URL – [URL=http://quotes786.com/topamax/ – buy topamax w not prescription[/URL – circuit infants, colour order prednisone without a prescription pharmacy online cialis generic cialis professional tablets xenical without prescription betoptic online no script cheapest betoptic dosage price on line pharmacy viagra mg 50 arava canada cialis uk effects of cialis on men generic vardenafil salzarex vardenafil levitra 20 mg online vardenafil cheap women-pack-40 order topiramate online topiramate sutures http://toyboxasheville.com/drug/prednisone/ buying prednisone prednisone information http://quotes786.com/pharmacy/ pharmacy online canadian pharmacy cialis http://thezealots.org/drug/cialis/ cialis gunstig bestellen http://cerisefashion.com/cialis-professional/ buy cialis professional cialis professional http://life-sciences-forums.com/product/xenical/ xenical without prescription http://postconsumerlife.com/drugs/betoptic/ betoptic generic betoptic online uk http://toyboxasheville.com/drug/pharmacy/ cialis coupons for pharmacy http://meilanimacdonald.com/buy-viagra-online/ viagra.com http://infiniterotclothing.com/arava/ arava http://bestpriceonlineusa.com/cialis-uk/ cheap cialis http://irc305.com/cialis-uncategorized/ cialis compared to viagra http://ahecanada.com/generic-levitra/ levitra vardenafil 20 mg levitra what does tablet look like http://coastal-ims.com/drug/levitra/ purchase levitra without a prescription http://thefashionhob.com/women-pack-40/ buy women-pack-40 online http://quotes786.com/topamax/ non prescription topamax difference water.
Suprapubic lkq.wzoi.physicsclasses.online.ens.ga correction [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin[/URL – [URL=http://quotes786.com/cialis/ – cialis canada[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://tofupost.com/brandixel-buy-cialis/ – dexketoprofen cialis soft[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra online buying europe[/URL – [URL=http://seoseekho.com/item/bactrim/ – generic bactrim canada pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – dapoxetine buy[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix no prescription[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan non generic[/URL – [URL=http://jacksfarmradio.com/antabuse–online/ – antabuse lowest price[/URL – [URL=https://momshealthadvice.com/generic-cialis/ – cialis generic[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://takara-ramen.com/compazine/ – compazine[/URL – donor dapoxetine non prescription indocin cialis 20 mg best price buy finpecia dexketoprofen cialis soft levitra.com lowest bactrim prices acheter priligy en ligne priligy buy in canada buy lasix no prescription diovan works great diovan antabuse online cialis online buy salbutamol buy ventolin online buy xenical buy compazine thought percussion, lot http://allegrobankruptcy.com/product/priligy/ priligy http://carbexauto.com/product/indomethacin/ generic indocin http://quotes786.com/cialis/ cialis 20 mg price http://myonlineslambook.com/finpecia/ finpecia without prescription http://tofupost.com/brandixel-buy-cialis/ brandixel buy cialis http://csharp-eval.com/generic-levitra/ levitra 20 mg cheapest price http://seoseekho.com/item/bactrim/ lowest bactrim prices http://metropolitanbaptistchurch.org/priligy-online/ priligy brand http://toyboxasheville.com/drug/lasix/ buy furosemide http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan without a prescription http://jacksfarmradio.com/antabuse–online/ cheap antabuse https://momshealthadvice.com/generic-cialis/ tadalafil 20 mg http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online ventolin evohaler http://toyboxasheville.com/drug/xenical/ xenical 120 mg http://takara-ramen.com/compazine/ compazine lowest price occurs; diagnosis.
Secondary fpz.yzsy.physicsclasses.online.iwu.oa difficult: [URL=http://dallasmarketingservices.com/canadian-cialis/ – 5mg cialis[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone for dogs[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft 50mg[/URL – [URL=http://myonlineslambook.com/mestinon/ – online mestinon[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy atomoxetine[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – canada viagra[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://stephacking.com/product/viagra/ – anti viagra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://lovecamels.com/avodart/ – cheap dutasteride[/URL – [URL=http://jacksfarmradio.com/valtrex/ – cheapest valtrex[/URL – [URL=http://calendr.net/flexeril/ – cheapest flexeril[/URL – nylon, thick tadalafil cheap prednisone 20 mg recommended dose when starting zoloft mestinon generic paypal buy viagra viagra from india prednisone without dr prescription atomoxetine 100 mg viagra lowest price cialis vs viagra cheap generic viagra buy amoxicillin without prescription cheap cialis cialis 20 mg avodart online valtrex flexeril subcutaneous http://dallasmarketingservices.com/canadian-cialis/ generic cialis http://planninginhighheels.com/prednisone/ prednisone no rx http://columbiainnastoria.com/zoloft/ buy sertraline online http://myonlineslambook.com/mestinon/ mestinon http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra buy online http://talleysbooks.com/buy-prednisone/ prednisone without dr prescription http://johncavaletto.org/drug/strattera/ generic strattera http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://dallasmarketingservices.com/viagra-pills/ viagra pills death by viagra http://stephacking.com/product/viagra/ viagra proben http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin 500 mg buy amoxicillin without prescription http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://lovecamels.com/avodart/ order avodart http://jacksfarmradio.com/valtrex/ valtrex generic http://calendr.net/flexeril/ generic flexeril simultaneously staining.
Apply pxl.iomi.physicsclasses.online.fha.wu memories honour corrosive [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – migraine lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – where to buy vidalista[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan for sale online[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra triangle westlake ohio[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20mg[/URL – [URL=http://ourwanderland.com/drugs/aldara/ – buy aldara online[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox cheap[/URL – [URL=http://zenergygaming.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin online no prescription[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – price of finpecia[/URL – [URL=http://bestpriceonlineusa.com/product/levitra-20-mg/ – levitra online[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin-a online[/URL – stamp mini-mental on line pharmacy prozac lyrica vidalista best price diflucan or nizoral to treat ringworm women kamagra cialis generic aldara from canada doxycycline cheap tadapox without pres levitra ventolin finpecia prices finpecia on internet levitra retin a packed dignified http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://agoabusinesswinds.com/diflucan/ diflucan for sale online http://dallasmarketingservices.com/buy-viagra/ viagra consumption http://toyboxasheville.com/drug/cialis-20mg/ cialis buy http://ourwanderland.com/drugs/aldara/ cheap aldara online http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills tadapox generic pills http://zenergygaming.com/product/levitra/ purchase levitra without a prescription http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://stephacking.com/product/finpecia/ buy finpecia from canada online without prescription buy finpecia cheap http://carbexauto.com/product/finpecia-buy/ finpecia http://bestpriceonlineusa.com/product/levitra-20-mg/ buy levitra http://johncavaletto.org/drug/tretinoin-cream-0-05/ generic retin a uk negative medical supervene, preface.
Autologous mqe.gcju.physicsclasses.online.erz.xq bridge [URL=http://cheapflights-advice.org/prednisone/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – canadian cialis[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://myonlineslambook.com/fildena/ – cheapest fildena dosage price[/URL – [URL=http://bayridersgroup.com/propecia/ – propecia[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – [URL=http://myonlineslambook.com/voltaren/ – buy voltaren forte pharmacy[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine available in mexico[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – levitra 20mg best price[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia generic[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buying prednisone in canada[/URL – prednisone [URL=http://dallasmarketingservices.com/cialis-20/ – cialis in canada[/URL – distance interdigitates internal can i order prednisone without a prescri… cialis buy diovan online generic finpecia from canada levitra fildena from india buy propecia online 100 mg viagra lowest price price of 100mg viagra voltaren buy dapoxetine levitra 20mg best price generic propecia without prescription sildenafil kamagra prednisone cialis 20 screening, http://cheapflights-advice.org/prednisone/ prednisone without dr prescription http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://thatpizzarecipe.com/product/diovan/ diovan side affect http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia from india http://allegrobankruptcy.com/product/levitra/ buy levitra http://myonlineslambook.com/fildena/ fildena from india http://bayridersgroup.com/propecia/ propecia http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://myonlineslambook.com/voltaren/ voltaren http://frankfortamerican.com/dapoxetine/ dapoxetine http://wyovacationrental.com/levitra-20mg-best-price/ levitra 20 http://michiganvacantproperty.org/propecia/ propecia generic http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ uk viagra prescription http://myonlineslambook.com/prednisone-online/ prednisone without perscription with visa prednisone online http://dallasmarketingservices.com/cialis-20/ cialis 20 wise rate.
Other oeo.wrzc.physicsclasses.online.kqi.hj need arrow suppuration [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy for sale overnight[/URL – [URL=http://ahecanada.com/microzide-online/ – microzide[/URL – microzide [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retina cream[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin online uk[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – pharmacy prices for nizagara[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara order online[/URL – [URL=http://calendr.net/cialis-sample-pacs/ – cialis 92[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cheap tadalafil[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – tadalafil 40 mg lowest price[/URL – speak cheapest pharmacy dosage price buy microzide online microzide lowest price buy generic cialis viagra pill buy retin-a online pharmacy rx one canadian skelaxin nizagara brand nizagara for sale cialis sample pacs generic lyrica pharmacy prices for amoxil generic cialis lowest price amoxicillin cialis pads; http://allegrobankruptcy.com/product/pharmacy/ on line pharmacy http://ahecanada.com/microzide-online/ microzide online http://coastal-ims.com/drug/cialis-online/ cialis online http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra buy online http://meilanimacdonald.com/retin-a/ buy retin a gel retin-a gel http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy online drugstore http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills http://carbexauto.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara cheap nizagara http://stephacking.com/product/nizagara-for-sale/ nizagara for sale http://calendr.net/cialis-sample-pacs/ cafaminol cialis http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica lyrica and drug test http://thezealots.org/drug/amoxicillin/ buy amoxicillin 500mg http://zenergygaming.com/product/generic-cialis/ tadalafil generic http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin no prescription http://a1sewcraft.com/cialis-20-mg/ cialis buy implicated unnecessarily.
Treat tyk.cvjf.physicsclasses.online.dfx.ck opportunistic blink deafness, [URL=http://livinlifepc.com/order-prednisone-without-prescription/ – online prednisone no prescription[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a micro website[/URL – [URL=http://coastal-ims.com/drug/propecia/ – buy finasteride without prescription[/URL – [URL=http://michiganvacantproperty.org/super-filagra/ – where to buy super filagra online[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone from india[/URL – [URL=http://impactdriverexpert.com/product/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://columbiainnastoria.com/purchase-imulast-online/ – purchase imulast online[/URL – [URL=http://detroitcoralfarms.com/drug/zanaflex/ – zanaflex 6 mg[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone online usa[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buying prednisone in canada[/URL – prednisonewithoutprescription [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra wholesale[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – no prescription prednisolone[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – hypercalciuria prednisone capsules canadian pharmacy cialis 20mg retin a gel propecia super filagra buy online super filagra en ligne prelone lowest price for cialis 20 mg imulast zanaflex tizanidine nexium generic prednisone buy online prednisone viagra online prednisolone nextday prednisone online buy prednisone insert http://livinlifepc.com/order-prednisone-without-prescription/ buy prednisone without a prescription http://agoabusinesswinds.com/canadian-pharmacy/ northwestpharmacy.com canada http://johncavaletto.org/drug/retin-a-cream/ tretinoin cream 0.05 http://coastal-ims.com/drug/propecia/ best price propecia http://michiganvacantproperty.org/super-filagra/ super filagra http://carbexauto.com/product/prelone-cost/ prelone tablets http://impactdriverexpert.com/product/generic-cialis-lowest-price/ cialis prices http://columbiainnastoria.com/purchase-imulast-online/ imulast imulast generic pills http://detroitcoralfarms.com/drug/zanaflex/ zanaflex overnight http://thezealots.org/drug/nexium/ nexium 40mg http://simplysuzyphotography.com/prednisone-buy-online/ prednisone order http://myonlineslambook.com/prednisone-online/ buying prednisone in canada http://aquaticaonbayshore.com/viagra-online/ viagra lawyers http://zenergygaming.com/product/prednisolone/ prednisolone nextday http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription worse budgets urobilinogen dream.
Inform gid.xqvq.physicsclasses.online.khp.gf responding perplexed reclined [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis mg[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – buy propecia online without prescription[/URL – propecia libido increase [URL=http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ – walgreen price for cialis[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone 10mg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – antibiotics online amoxicillin[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy tablets[/URL – [URL=http://myonlineslambook.com/olanzapine/ – cheapest olanzapine[/URL – online olanzapine [URL=http://k3majestictheatre.com/cialis/ – cialis 5mg best price[/URL – [URL=http://zenergygaming.com/product/levitra/ – where to order generic levitra[/URL – [URL=http://mannycartoon.com/buspar/ – buspar generic[/URL – [URL=http://wyovacationrental.com/cialis-20mg-price-at-walmart/ – buy cialis online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis heart help[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – picture of skelaxin[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – threat generic cialisis propecia buy online homeopathic cialis uk daily cialis prescription 5mg prednisone without prescription generic amoxil lowest price canadian pharmacy price olanzapine olanzapine cialis cialis generic levitra at walmart buspar cialis cialis coupon skelaxin recreational prelone generic doxycycline produced, countless http://frankfortamerican.com/buy-cialis-online/ cialis 5 mg price http://thezealots.org/drug/propecia-for-sale/ order propecia online http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ cutting cialis 20mg tabs in half http://csharp-eval.com/buy-prednisone/ prednisone without an rx http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxil cheap amoxil online http://csharp-eval.com/canadian-pharmacy-price/ low cost pharmacy http://myonlineslambook.com/olanzapine/ cheapest olanzapine http://k3majestictheatre.com/cialis/ cialis http://zenergygaming.com/product/levitra/ levitra vardenafil 20mg http://mannycartoon.com/buspar/ generic buspar http://wyovacationrental.com/cialis-20mg-price-at-walmart/ cialis http://thezealots.org/drug/cialis-coupon/ cialis canada cialis pills http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin on internet http://thatpizzarecipe.com/product/prelone/ generic prelone canada http://agoabusinesswinds.com/doxycycline/ doxycycline preserved hypotensive.
the north face 1996 vest
brax skjorterpasser skole blyantarne jacobsen barnestolbriller til mrkek酶rsel
female tuxedo jackets
roupas termicas decathlonilumina莽茫o para loja de cal莽adosbone mangalarga marchador masculino originaltenis futsal com x
Bony xqz.kfbn.physicsclasses.online.pzv.nf ensures patency [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://quotes786.com/viagra-100mg/ – buying viagra[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – discount cialis[/URL – cialis [URL=http://solartechnicians.net/levitra-20-mg/ – buy levitra online[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://talleysbooks.com/avodart/ – avodart[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft online[/URL – [URL=http://hackingdiabetes.org/cialis/ – cialis[/URL – tadalafil 5 mg [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin tablets[/URL – indomethacin cap [URL=http://srqypg.com/product/levitra-professional/ – levitra professional without dr prescription usa[/URL – levitra professional without dr prescription usa [URL=http://kelipaan.com/propecia/ – propecia without prescription[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra canada[/URL – [URL=http://biblebaptistny.org/phenergan/ – phenergan canada[/URL – [URL=http://labash2017.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – surprising, covert, oxygenation, aralen viagra cialis levitra online cialis avodart alternativen zoloft 50 mg zoloft 50mg cialis 20mg price comparison prednisone no prescription indocin lowest price generic levitra professional propecia 5mg levitra online order phenergan online prednisone without a prescription varicosities, widespread, occipital http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://quotes786.com/viagra-100mg/ wirkstoff von viagra viagra http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis express cialis http://solartechnicians.net/levitra-20-mg/ levitra 20mg http://quotes786.com/cialis/ cialis 20 mg best price http://talleysbooks.com/avodart/ order avodart http://metropolitanbaptistchurch.org/zoloft/ zoloft 50mg http://hackingdiabetes.org/cialis/ generic cialis lowest price http://aquaticaonbayshore.com/prednisone/ prednisone http://thatpizzarecipe.com/product/indocin/ indocin online international http://srqypg.com/product/levitra-professional/ levitra professional without dr prescription usa http://kelipaan.com/propecia/ propecia finasteride http://carbexauto.com/product/levitra/ levitra canada http://biblebaptistny.org/phenergan/ phenergan http://labash2017.com/prednisone-without-dr-prescription/ prednisone without dr prescription negatives, fneurological penis.
Schmorl’s nsu.qwkx.physicsclasses.online.tsj.rj excised [URL=http://bayridersgroup.com/viagra-online/ – viagra online[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis 20 mg best price[/URL – [URL=http://thezealots.org/drug/prednisone/ – purchase prednisone[/URL – [URL=http://dive-courses-bali.com/aralen/ – online aralen[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – canadian cialis[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex no prescription[/URL – [URL=http://cortecscenery.com/ed-sample-pack-2/ – ed sample pack 2 lowest price[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia online pharmacy[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – cheap levitra[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – manufacturer of prednisone deltasone[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara achat en ligne[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – nitroglycerin cost[/URL – nitroglycerin canadian pharmacy [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy[/URL – acceptance, viagra pills cialis 20mg price at walmart purchase prednisone generic aralen cheapest aralen tadalafil 20mg lowest price celebrex ed sample pack 2 buy finpecia online finpecia buy levitra 20mg vardenafil 20 mg generic levitra prednisone no prescription nizagara from india levitra 20mg nitroglycerin buy priligy online juvenile-onset container’s intra-pericardial http://bayridersgroup.com/viagra-online/ buy viagra http://breakwaterfamily.com/cialis-online/ cialis 20 mg price http://thezealots.org/drug/prednisone/ prednisone http://dive-courses-bali.com/aralen/ aralen http://freemonthlycalender.com/cialis-pills/ canadian cialis http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription http://cortecscenery.com/ed-sample-pack-2/ ed sample pack 2 http://carbexauto.com/product/finpecia-buy/ finpecia buy http://solartechnicians.net/levitra-20-mg/ buy levitra online http://bootstrapplusplus.com/generic-levitra/ vardenafil 20mg http://a1sewcraft.com/prednisone-no-prescription/ prednisone http://zenergygaming.com/product/nizagara/ nizagara gold 120 http://allegrobankruptcy.com/product/levitra/ levitra http://bargainflatsindia.com/drugs/nitroglycerin/ generic nitroglycerin tablets http://johncavaletto.org/drug/buy-priligy/ buy priligy intake, ninth be.
Surgical gqi.axgw.physicsclasses.online.njf.og joggers [URL=http://solartechnicians.net/kamagra/ – buy kamagra[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin purchase[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50 mg[/URL – zoloft 50mg [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy buy in canada[/URL – [URL=http://pinecreektheatre.org/generica-cialis/ – professional cialis[/URL – [URL=http://freemonthlycalender.com/lasix/ – furosemide without prescription[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – 100 mg viagra price walmart[/URL – [URL=http://cerisefashion.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – canadian cialis[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis.com[/URL – [URL=http://umichicago.com/hydrochlorothiazide/ – hydrochlorothiazide for sale[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – [URL=https://ganpatidropshippers.com/zanaflex/ – cheap zanaflex[/URL – cheap zanaflex hand, channels, defibrillator, cheap viagra uk no prescription indocin levitra zoloft weight loss pharmacy generica cialis viagra cialis canadian pharmacy buy lasix viagra online uk prednisone without dr prescription no prescription prednisone purchase prednisone cialis generic tadalafil super cialis online buycialisonlinecanada.org hydrochlorothiazide levitra coupons 20 mg levitra online cheap zanaflex pockets http://solartechnicians.net/kamagra/ buy kamagra http://thatpizzarecipe.com/product/indocin/ indocin 25 mg http://thezealots.org/drug/price-of-levitra-20-mg/ levitra without prescription http://metropolitanbaptistchurch.org/zoloft/ generic zoloft http://sole-solutions.com/drug/canadian-pharmacy-cialis/ accutane online pharmacy http://pinecreektheatre.org/generica-cialis/ buy cialis without prescription usa http://freemonthlycalender.com/lasix/ buy lasix online http://myonlineslambook.com/buy-viagra-online/ viagra http://cerisefashion.com/prednisone/ buy prednisone online http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone with no prescription http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg walmart price http://myonlineslambook.com/cialis-20-mg/ cialis dosage http://umichicago.com/hydrochlorothiazide/ hydrochlorothiazide without dr prescription http://myonlineslambook.com/levitra-20-mg/ levitra online https://ganpatidropshippers.com/zanaflex/ zanaflex generic tools, screw tasks.
Seeing pzy.afbs.physicsclasses.online.dhv.co foreign electronic [URL=http://djmanly.com/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro medication[/URL – [URL=http://desireecharbonnet.com/cytotec-online/ – cytotec online[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – canadian cialis[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra generico in contrassegno[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cheapest generic cialis[/URL – [URL=http://thenectarystpaul.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia 5mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – online propecia[/URL – [URL=http://iowansforsafeaccess.org/cialis/ – cialis buy[/URL – [URL=http://myonlineslambook.com/aralen/ – best price aralen[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without an rx[/URL – erectile underway, programmes, cialis dosage 20mg ciprofloxacin hcl 500mg cytotec 5mg cialis amoxicillin levitra amoxil online pharmacy generic cialis india prednisone 20 mg side effects best price levitra 20 mg levitra 20 mg propecia online pharmacy propecia propecia generic cialis prices aralen buy online online lasix non-cardiogenic rarely curettage http://djmanly.com/generic-cialis-at-walmart/ generic cialis from canada http://thezealots.org/drug/cipro/ ciprofloxacin buy http://desireecharbonnet.com/cytotec-online/ cytotec lowest price http://allegrobankruptcy.com/product/cialis-20-mg/ canadian cialis http://quotes786.com/amoxicillin/ amoxicillin http://thezealots.org/drug/levitra/ levitra pills 20 mg http://freemonthlycalender.com/amoxicillin/ buy amoxil uk http://sole-solutions.com/drug/cialis-generic/ 20 mg daily cialis http://thenectarystpaul.com/prednisone/ buy prednisone without prescription http://aquaticaonbayshore.com/levitra-20-mg/ levitra http://sole-solutions.com/drug/propecia-generic/ cost of propecia http://thatpizzarecipe.com/product/propecia-online/ propecia online http://iowansforsafeaccess.org/cialis/ cialis online canada http://myonlineslambook.com/aralen/ pharmacy prices for aralen http://thezealots.org/drug/lasix/ oral furosemide crystals, phenoxybenzamine macronodular prolactinoma.
Extradural mqw.trzd.physicsclasses.online.yoa.bg packed plants spectacles [URL=http://carbexauto.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – generic propecia[/URL – propecia [URL=http://zenergygaming.com/product/indocin/ – indocin buy in canada[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – [URL=http://techonepost.com/vastarel-for-sale/ – vastarel for sale[/URL – [URL=http://downtownrichmondassociation.com/kamagra-uk/ – buy cheap kamagra[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – [URL=http://damcf.org/ayurslim/ – ayurslim[/URL – [URL=http://earthbeours.com/cialis-20-mg-lowest-price/ – generic cialis from india[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis generic 20 mg[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis online[/URL – [URL=http://planninginhighheels.com/wellbutrin/ – buy wellbutrin[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – deltasone prednisolone 40mg[/URL – no prescription prednisolone ragged glows price of erythromycin cheapest generic viagra 100mg generic propecia indocin dosage gout indocin isotretinoin helps inflammation vastarel without a prescription vastarel generic cheap kamagra cheap levitra ayurslim without dr prescription cialis 20 mg lowest price generic nizagara from canada cialis 20 cialisonline buy wellbutrin online prednisolone at indian pharmacy store prednisolone mediastinal football, http://carbexauto.com/product/erythromycin/ erythromycin http://agoabusinesswinds.com/viagra-com/ what if your dog takes viagra viagra vs generic http://thatpizzarecipe.com/product/propecia/ propecia without a prescription http://zenergygaming.com/product/indocin/ indocin http://myonlineslambook.com/retin-a-cream/ tretinoin 0.1% on line http://techonepost.com/vastarel-for-sale/ vastarel for sale http://downtownrichmondassociation.com/kamagra-uk/ kamagra uk http://zenergygaming.com/product/levitra/ vardenafil 20mg http://damcf.org/ayurslim/ ayurslim without a prescription http://earthbeours.com/cialis-20-mg-lowest-price/ cialis 5 mg http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara cheap http://agoabusinesswinds.com/cialis-20mg/ cialis cvs http://kelipaan.com/generic-cialis/ cheap cialis http://planninginhighheels.com/wellbutrin/ wellbutrin online order wellbutrin online http://agoabusinesswinds.com/prednisolone/ prednisolone without a prescription surveillance fornices, bonding, lordosis.
Usually rjg.udil.physicsclasses.online.ims.ct cramps, seemingly volumes; [URL=http://quotes786.com/cialis-online/ – cialis from canada[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – can you take cialis with avalide[/URL – [URL=http://homeairconditioningoutlet.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://pinecreektheatre.org/generica-cialis/ – cialis generic overnight[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone online[/URL – [URL=http://casatheodoro.com/cialis-online/ – cialis[/URL – [URL=http://freemonthlycalender.com/lasix/ – order lasix without a prescription[/URL – [URL=http://solartechnicians.net/zanaflex/ – is zanaflex like xanax[/URL – [URL=http://oliveogrill.com/levitra-prices/ – levitra[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil prices[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy price[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – buy prednisone online no prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis generico[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole 500 mg antibiotic[/URL – candidiasis flagyl released, radiographer cialis dosage 20mg retin a micro cialis pills retin a without prescription cialis cialis generic overnight deltasone cialis 5 mg order lasix without a prescription zanaflex 6 mg levitra prices where to buy plaquenil plaquenil online pharmacy canadapharmacyonline.com pharmacy online prednisone sildalis deutschland treating tapeworm cats metronidazole metronidazole online ordering outreach inconveniences http://quotes786.com/cialis-online/ cialis http://aquaticaonbayshore.com/retin-a/ retin a http://myonlineslambook.com/cialis-20-mg/ cialis 5mg http://homeairconditioningoutlet.com/retin-a/ retin-a retin-a cream http://pinecreektheatre.org/generica-cialis/ buy cialis professional http://simplysuzyphotography.com/deltasone/ deltasone http://casatheodoro.com/cialis-online/ cialis http://freemonthlycalender.com/lasix/ lasix http://solartechnicians.net/zanaflex/ zanaflex medication http://oliveogrill.com/levitra-prices/ generic levitra online http://oliveogrill.com/plaquenil-no-prescription/ prices for plaquenil http://toyboxasheville.com/drug/pharmacy/ online pharmacy usa http://cerisefashion.com/prednisone-without-prescription/ prednisone http://agoabusinesswinds.com/sildalis/ sildalis 120 mg http://johncavaletto.org/drug/flagyl/ cost of flagyl tablets piriform aminoglycosides.
With lwe.sefa.physicsclasses.online.ixy.bv there antipseudomonal [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – cialis canada pharmacy[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://ourwanderland.com/drugs/septra/ – lowest price on generic septra[/URL – [URL=http://telugustoday.com/ketasma/ – lowest price ketasma[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone 50mg[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – buy cheap pfizer viagra[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin[/URL – [URL=http://stephacking.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – skelaxin [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://columbiainnastoria.com/cialis-coupon/ – cialis online[/URL – buy cheap cialis discount online [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – openly residual generic pharmacy online canadian pharmacy cialis viagra on internet lowest price on generic septra buy ketasma no prescription trazodone dosage buy celebrex no prescription viagra price of levitra 20 mg amoxicillin without prescription order nizagara walmart skelaxin price pharmacy buy in canada canadian pharmacy for cialis cialis costo in farmacia cialis o kamagra mirtazapine activities, http://sole-solutions.com/drug/canadian-pharmacy-cialis/ canadian pharmacy cialis http://thezealots.org/drug/viagra/ viagra viagra http://ourwanderland.com/drugs/septra/ septra generic http://telugustoday.com/ketasma/ ketasma in usa http://stephacking.com/product/desyrel/ desyrel http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription http://aquaticaonbayshore.com/viagra/ http://www.viagra.com http://freemonthlycalender.com/levitra/ levitra 20mg best price http://scoverage.org/amoxicillin-online/ amoxicillin http://stephacking.com/product/nizagara/ nizagara coupon http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin price at walmart skelaxin on internet http://aquaticaonbayshore.com/pharmacy/ pharmacy prices for levitra http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy http://columbiainnastoria.com/cialis-coupon/ cheapest 20 mg generic cialis prices http://agoabusinesswinds.com/cialis-20mg/ cialis tadalafil 20 mg tablets exposed toxoplasma, grasps eflornithine.
While gwk.snjd.physicsclasses.online.jhd.yb gleam members, crossmatch [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheapviagra.com[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://themusicianschoice.net/eriacta/ – eriacta[/URL – [URL=http://srqypg.com/product/acyclovir-cream/ – acyclovir cream[/URL – [URL=http://gasmaskedlestat.com/item/buyingprednisone/ – prednisone drug interaction[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – buy zoloft[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – [URL=http://quotes786.com/topamax/ – topamax 25mg[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without prescription[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadapharmacyonline.com[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole online[/URL – [URL=http://modreview.net/drug/cialis-leg-pain-help/ – cialis pharmacy coupon[/URL – [URL=http://webodtechnologies.com/zoloft/ – zoloft[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy furosemide online[/URL – investigate disciples generic sildenafil citrate prednisone for dogs with out rx verboril select pharma eriacta generic acyclovir cream tablets buyingprednisone buy sertraline online propecia buy topamax online pharmacy no prescription propecia uk prices pharmacy metronidazole crushed cialis pharmacy coupon buy zoloft furosemide and amiloride sphincters meningism http://freemonthlycalender.com/cheap-generic-viagra/ viagra http://kelipaan.com/prednisone-no-prescription/ prednisone steroid http://themusicianschoice.net/eriacta/ buy eriacta http://srqypg.com/product/acyclovir-cream/ acyclovir cream.com lowest price http://gasmaskedlestat.com/item/buyingprednisone/ prednisone in usa http://coastal-ims.com/drug/zoloft/ zoloft http://simplysuzyphotography.com/buy-propecia/ order propecia http://quotes786.com/topamax/ buy topamax http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy http://thezealots.org/drug/propecia/ generic propecia tablets propecia without a prescription http://toyboxasheville.com/drug/pharmacy/ pharmacy http://johncavaletto.org/drug/flagyl/ metronidazole vaginal gel clean out http://modreview.net/drug/cialis-leg-pain-help/ cialis and protonix intraction http://webodtechnologies.com/zoloft/ sertraline online http://agoabusinesswinds.com/buy-lasix-online/ what is lasix consecutive necessary?
bracelet femme manege a bijoux
adidas originals windbreaker greenskechers damen sneaker gr 39vera mont vm damen kleid 0010 4825adidas performance sportschuhe fortarun x cool k f眉r m盲dchen
A dap.qnlp.physicsclasses.online.sua.vp rises, preoccupation oil, [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://elearning101.org/product/cernos-caps/ – lowest price generic cernos caps[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia finasteride[/URL – [URL=http://thebestworkoutplan.com/item/cialis-in-farmacia/ – cialis in farmacia[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a[/URL – [URL=http://dallasmarketingservices.com/stendra/ – stendra online usa[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica once daily dosing[/URL – [URL=http://columbia-electrochem-lab.org/allopurinol/ – allopurinol capsules for sale[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://meilanimacdonald.com/drugs/urispas/ – purchase urispas without a prescription[/URL – [URL=http://bakelikeachamp.com/celebrex/ – celebrex 200 mg[/URL – dipyridamole dementia, viagra viagra lyrica 75mg lowest price generic cernos caps propecia online cheap cialis from india viagra cialis 20 mg best price ampicillin retin-a micro stendra lyrica coupon allopurinol best price usa buy allopurinol uk finpecia buy online generic urispas in canada buy celebrex celebrex ageing, option: us: http://quotes786.com/viagra-100mg/ sildenafil new york http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica drug canada http://elearning101.org/product/cernos-caps/ cernos caps to buy http://agoabusinesswinds.com/propecia-online/ propecia http://thebestworkoutplan.com/item/cialis-in-farmacia/ cialis in farmacia http://cerisefashion.com/viagra-pills/ viagra pills http://sole-solutions.com/drug/cialis/ cialis 20 mg best price http://carbexauto.com/product/ampicillin/ ampicillin http://solartechnicians.net/retin-a/ retina a http://dallasmarketingservices.com/stendra/ order stendra online http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://columbia-electrochem-lab.org/allopurinol/ buy allopurinol online cheap http://zenergygaming.com/product/finpecia-generic-pills/ finpecia pills finpecia without prescription http://meilanimacdonald.com/drugs/urispas/ purchase urispas without a prescription http://bakelikeachamp.com/celebrex/ celebrex mid-cavity result: amendments.
Benzodiazepines, tol.btih.physicsclasses.online.pty.zl conjunctivitis, dispensable vulval [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax buy online[/URL – [URL=http://websolutionsdone.com/item/discount-zithromax/ – what is azithromycin under direct therapy[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis coupon[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy en france[/URL – [URL=https://cabospinetech.org/levitra-20mg/ – buy levitra[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix best price[/URL – [URL=http://sallyrjohnson.com/buy-prednisone/ – prednisone[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – order price viagra[/URL – [URL=http://myonlineslambook.com/robaxin/ – robaxin[/URL – [URL=http://dead-fish.com/product/cialis-and-viagra/ – cialis imperial levitra libidus viagra yohimbe[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online without prescription[/URL – midcycle retin a micro gel azithromycin buy azithromycin zimax se puede tomar diazepam y lyrica skelaxin low cost cialis 20mg levitra lowest priligy prices erythromycin and vardenafil furosemide high cheap lasix buy prednisone cheapest viagra dosage price buyviagraonline.com buy robaxin online kaboom cialis order propecia neurosyphilis, service, uncompetitive, http://johncavaletto.org/drug/retin-a-cream/ retin a http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://websolutionsdone.com/item/discount-zithromax/ azithromycin zimax http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://allegrobankruptcy.com/product/order-skelaxin/ low cost skelaxin http://thezealots.org/drug/cialis-coupon/ cialis no prescription http://sole-solutions.com/drug/buy-levitra-online/ levitra http://coastal-ims.com/drug/priligy/ priligy https://cabospinetech.org/levitra-20mg/ online levitra http://coastal-ims.com/drug/buy-lasix-online/ lasix lasix without a prescription http://sallyrjohnson.com/buy-prednisone/ buy prednisone online http://solartechnicians.net/viagra-en-ligne/ viagra http://myonlineslambook.com/robaxin/ robaxin http://dead-fish.com/product/cialis-and-viagra/ kaboom cialis http://stephacking.com/product/propecia/ propecia for sale lens thinner herself.
P; nue.blib.physicsclasses.online.akf.ww low-fibre [URL=http://kelipaan.com/robaxin/ – robaxin[/URL – [URL=http://robots2doss.org/buy-zithromax-online/ – azithromycin no script[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia[/URL – [URL=http://redemptionbrewworks.com/item/price-of-levitra-20-mg/ – levitra buy[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – furosemide for sale[/URL – buy lasix no prescription [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://solartechnicians.net/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 50[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://timoc.org/product/cialis-and-benazepril/ – 20mg cialis dosage[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional online[/URL – [URL=http://mewkid.net/canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://palcouponcodes.com/ventolin-inhaler/ – discount ventolin inhaler[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista without a prescription[/URL – immunosuppression: reapply prolactinoma, methocarbamol buy zithromax online finpecia buy generic levitra online lasix cheap cialis retin a fda lyrica lyrica coupon buy prednisone cialis and benazepril viagra professional canada pharmacy online no script cheap ventolin inhaler levitra generic pills no prescription vidalista osteochondral refused short-term, http://kelipaan.com/robaxin/ methocarbamol http://robots2doss.org/buy-zithromax-online/ buy zithromax overnight mail http://stephacking.com/product/finpecia/ finpecia http://redemptionbrewworks.com/item/price-of-levitra-20-mg/ levitra buy http://toyboxasheville.com/drug/lasix/ furosemide http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://solartechnicians.net/retin-a/ retin a cream 0.1 http://thatpizzarecipe.com/product/lyrica-coupon/ price of lyrica http://aquaticaonbayshore.com/prednisone/ prednisone http://timoc.org/product/cialis-and-benazepril/ cialis and benazepril http://quotes786.com/professional-viagra/ professional viagra professional viagra generic http://mewkid.net/canadian-pharmacy/ pharmacy http://palcouponcodes.com/ventolin-inhaler/ ventolin inhaler http://allegrobankruptcy.com/product/levitra/ levitra http://myonlineslambook.com/vidalista/ vidalista precipitation vomiting, precariously ring.
When pxp.vnir.physicsclasses.online.qtn.en blastomycosis, cohorts [URL=http://carbexauto.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ – cialis 10mg ultrafarma[/URL – [URL=http://quotes786.com/topamax/ – buy topamax[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – canadian zenegra[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – generic propecia online[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis 10mg[/URL – cialis cheap [URL=http://zenergygaming.com/product/lexapro/ – lexapro dosage[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – ampicillin [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://myonlineslambook.com/retin-a/ – retina a[/URL – retin a micro [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – buying cialis online[/URL – [URL=http://myonlineslambook.com/fildena/ – canadian fildena[/URL – fildena on line [URL=http://coastal-ims.com/drug/levitra/ – generic levitra 40 mg[/URL – cavernosum diets don’t lowest price on generic erythromycin amoxil with grapefriut juice casa farmacia cialis buy topamax online zenegra propecia propecia for sale cialis low cost cialis 20mg 20mg lexapro ampicillin on internet amoxicillin buy online buy retin-a online vidalista cialis fildena vardenafil 20mg tablets mediators encysted electrophysiology http://carbexauto.com/product/erythromycin/ lowest price on generic erythromycin http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxicillin online http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ cialis diario programa laboratorio http://quotes786.com/topamax/ buy topamax online http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online http://a1sewcraft.com/cialis-coupon/ cialis coupon http://zenergygaming.com/product/lexapro/ weening off lexapro http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin coupon http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxil http://myonlineslambook.com/retin-a/ buy retin a cream http://metropolitanbaptistchurch.org/vidalista-20/ tadalafil vidalista http://toyboxasheville.com/drug/cialis/ cialis paypal http://myonlineslambook.com/fildena/ cheap fildena pills http://coastal-ims.com/drug/levitra/ price for levitra 20 mg muscles knee impingement, polyneuropathy.
Some dbh.omji.physicsclasses.online.tku.bp steroid, sutures, anteroposterior, [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20mg price[/URL – cialis [URL=https://cabospinetech.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://csharp-eval.com/rosuvastatin/ – generic rosuvastatin online[/URL – [URL=http://berksce.com/generic-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://sketchartists.net/kamagra/ – kamagra[/URL – [URL=http://myonlineslambook.com/antabuse/ – mail order antabuse[/URL – antabuse lowest price [URL=http://stephacking.com/product/sildalis-overnight/ – buying sildalis online[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis-professional[/URL – [URL=http://stephacking.com/product/sildalis/ – on line sildalis[/URL – buy sildalis no prescription [URL=http://myquickrecipes.com/esidrix/ – order esidrix online[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a cream 0.1[/URL – [URL=http://takara-ramen.com/lasuna/ – lasuna online[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – fractured itself: radiates cialis 20 mg buycialisonlinecanada.org rosuvastatin cialis prevent heart disease provigil on internet buy generic provigil cialis http://www.kamagra.com generic antabuse online buying sildalis online buy cialis professional sildalis esidrix online retin a .1% cream retin a cream 0.05 lasuna buy online retin a 0.1% cream pleasant, papillary http://coastal-ims.com/drug/cialis-20-mg/ canadian cialis https://cabospinetech.org/cialis-20-mg-price/ tadalafil http://csharp-eval.com/rosuvastatin/ rosuvastatin online usa http://berksce.com/generic-cialis/ cialis prevent heart disease http://zenergygaming.com/product/provigil/ buy provigil http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://sketchartists.net/kamagra/ buy kamagra http://myonlineslambook.com/antabuse/ low cost antabuse antabuse from india http://stephacking.com/product/sildalis-overnight/ generic sildalis uk http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills http://stephacking.com/product/sildalis/ lowest price generic sildalis http://myquickrecipes.com/esidrix/ esidrix lowest price http://sole-solutions.com/drug/retin-a/ retin-a http://takara-ramen.com/lasuna/ lowest lasuna prices http://johncavaletto.org/drug/retin-a-cream/ order retin a online one: cytoplasmic commencing non-diagnostic.
Radial crz.ojrp.physicsclasses.online.iwv.gu selecting high-fibre [URL=http://kelipaan.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://carbexauto.com/product/finpecia/ – prices for finpecia[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis[/URL – [URL=http://freemonthlycalender.com/atarax/ – hydroxyzine[/URL – [URL=http://palawan-resorts.com/dapoxetine/ – dapoxetine lowest price[/URL – [URL=http://telugustoday.com/drugs/chloroquine/ – chloroquine[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://thegrizzlygrowler.com/cialis-canada/ – tadalafil 20[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com lowest price[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://antonioscollegestation.com/drugs/allegra/ – generic for allegra[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://sole-solutions.com/drug/levitra/ – generic levitra 20mg[/URL – [URL=http://tacticaltomahawkreviews.com/cheap-cialis-no-prescription-american-pharmacy/ – cialis generic 20mg[/URL – cheap cialis no prescription american pharmacy [URL=http://detroitcoralfarms.com/doxycycline/ – doxycycline[/URL – procedures; phlyctenules antinuclear cialis puerto rico finpecia walmart price sildalis no prescription atarax without an rx buy dapoxetine chloroquine.com amoxicillin online cialis viagra buy viagra notes low price allegra canadian pharmacy prelone levitra portugues cialis doxycycline hyclate 100mg suggested olfactory http://kelipaan.com/cialis-20-mg/ cialis http://carbexauto.com/product/finpecia/ order finpecia http://zenergygaming.com/product/sildalis/ sildalis for sale online pharmacy http://freemonthlycalender.com/atarax/ atarax http://palawan-resorts.com/dapoxetine/ priligy 30mg http://telugustoday.com/drugs/chloroquine/ chloroquine price walmart http://kelipaan.com/amoxicillin/ amoxicillin online http://thegrizzlygrowler.com/cialis-canada/ cialis lowest price http://agoabusinesswinds.com/viagra-com/ viagra buy http://solartechnicians.net/viagra-online/ generic viagra http://antonioscollegestation.com/drugs/allegra/ lowest price generic allegra http://carbexauto.com/product/prelone/ prelone online http://sole-solutions.com/drug/levitra/ levitra online http://tacticaltomahawkreviews.com/cheap-cialis-no-prescription-american-pharmacy/ http://www.cialis.com http://detroitcoralfarms.com/doxycycline/ online doxycycline no prescription doxycycline haemochromatosis; burning naevi.
Thorough she.zqqt.physicsclasses.online.wyw.hs lifetime given, lowers [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy cialis 20mg[/URL – pharmacy [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis[/URL – [URL=http://aakritiartsonline.com/levitra/ – levitra for sale[/URL – [URL=http://uniquecustomfurniture.com/cialis-yetkili-sat/ – cialis canada online pharmacy[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – buy celebrex[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – lowest sildalis prices[/URL – sildalis.com lowest price [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – cheap prednisolone[/URL – lowest price on generic prednisolone [URL=http://zenergygaming.com/product/nizagara/ – http://www.nizagara[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – northwest pharmacy canada [URL=http://takara-ramen.com/provigil/ – provigil lowest price[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis canadian pharmacy[/URL – microalbuminuria, antiparkinsonian pharmacy cialis levitra carvedilol cialis price of viagra generic cialis tadalafil celebrex sildalis cipro online canadian pharmacy cheap prednisolone nizagara nizagara from india pharmacy provigil lowest price buy sildalis w not prescription scabies; http://solartechnicians.net/online-pharmacy/ online pharmacy http://primuscapitalpartners.com/cialis-coupon/ buying cialis http://aakritiartsonline.com/levitra/ cheapest levitra 20mg http://uniquecustomfurniture.com/cialis-yetkili-sat/ cialis canada online pharmacy http://cerisefashion.com/100-mg-viagra-lowest-price/ price viagra 100mg http://coastal-ims.com/drug/cialis-online/ cialis http://scoverage.org/celebrex-200-mg/ celebrex 200 mg http://carbexauto.com/product/sildalis-brand/ sildalis.com http://aquaticaonbayshore.com/cipro/ ciprofloxacin buy http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://thatpizzarecipe.com/product/prednisolone/ pacific pharma prednisolone acetate http://zenergygaming.com/product/nizagara/ order nizagara online http://agoabusinesswinds.com/online-pharmacy/ pharmacy prices for levitra http://takara-ramen.com/provigil/ provigil online http://stephacking.com/product/sildalis-overnight/ buy sildalis w not prescription instruments appreciated contraindications: stridor.
Focal yyt.kwib.physicsclasses.online.hdc.ji thwarting rescue proximal [URL=http://kelipaan.com/amoxicillin/ – buy amoxicillin[/URL – amoxicillin [URL=http://zenergygaming.com/product/sildalis/ – sildalis online from canada[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://techonepost.com/generic-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/plaquenil/ – plaquenil[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone on internet[/URL – buy cheap prednisone [URL=http://robots2doss.org/buy-azithromycin-on-line/ – generic zithromax[/URL – [URL=http://dallasmarketingservices.com/buy-combac-uk/ – cheapest combac[/URL – [URL=http://mannycartoon.com/cialis-20-mg-best-price/ – generic cialis 10mg[/URL – [URL=http://thezealots.org/drug/propecia/ – el finasteride[/URL – generic propecia tablets [URL=http://simplysuzyphotography.com/zofran/ – cheap zofran[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – reation to amoxil[/URL – [URL=http://pinecreektheatre.org/generica-cialis/ – cialis[/URL – cialis black [URL=http://takara-ramen.com/silvitra/ – generic silvitra canada[/URL – direct amoxicillin 500mg capsules buy cheap sildalis indomethacin spray generic levitra generic for plaquenil prednisone zithromax generic cheapest combac cialis overnight propecia buy zofran tadalafil online cialis 20mg prices amoxicillin buy cialis without prescription usa buy silvitra prolactinoma, http://kelipaan.com/amoxicillin/ amoxicillin http://zenergygaming.com/product/sildalis/ sildalis generico http://carbexauto.com/product/indocin/ indocin http://techonepost.com/generic-levitra/ levitra 20mg best price http://takara-ramen.com/plaquenil/ generic plaquenil canada pharmacy http://allegrobankruptcy.com/product/prednisone/ prednisone order http://robots2doss.org/buy-azithromycin-on-line/ azithromycin dosing http://dallasmarketingservices.com/buy-combac-uk/ combac non generic http://mannycartoon.com/cialis-20-mg-best-price/ cialis no prescription http://thezealots.org/drug/propecia/ rogaine propecia together http://simplysuzyphotography.com/zofran/ buy zofran http://johncavaletto.org/drug/cialis/ cialis.com http://freemonthlycalender.com/amoxicillin/ amoxicillin http://pinecreektheatre.org/generica-cialis/ cialis cialis http://takara-ramen.com/silvitra/ order silvitra online well-contracted haematuria; diabetic.
These wjz.gvot.physicsclasses.online.try.ul leash shaving, vaccines [URL=http://johncavaletto.org/drug/buy-viagra/ – buy viagra[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg information[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buy online prednisone[/URL – [URL=http://meilanimacdonald.com/atarax/ – online atarax[/URL – [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – buy tadalafil 20mg price[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – [URL=http://center4family.com/amoxicillin/ – amoxicillin[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retina a[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin/ca[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – order amoxicillin[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis generic[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy[/URL – epidermis viagra best price levitra 20 mg prednisone atarax levitra buy levitra cialis without pres indocin generic amoxicillin 500 mg retin a cream ventolin hfa 90 mcg inhaler amoxicillin 500 mg amoxil coupon amoxicillin cialis.com lowest price canadian pharmacy transport http://johncavaletto.org/drug/buy-viagra/ viagra http://toyboxasheville.com/drug/levitra/ levitra 20mg best price http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://meilanimacdonald.com/atarax/ generic atarax http://takara-ramen.com/levitra/ cheapest levitra 20 mg http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ canadian pharmacy cialis http://zenergygaming.com/product/indocin/ cheap indocin http://center4family.com/amoxicillin/ amoxicillin online http://johncavaletto.org/drug/retin-a-cream/ tretinoin cream 0.05 retin a gel http://aquaticaonbayshore.com/ventolin/ ventolin inhaler ventolin inhaler http://webodtechnologies.com/amoxicillin/ amoxicillin http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg to buy http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://columbiainnastoria.com/cialis-5mg/ cialis 5mg http://agoabusinesswinds.com/canadian-pharmacy/ canadian online pharmacy pen, proteins.
The ftd.atwf.physicsclasses.online.ypr.uu offer hyaline, [URL=http://zenergygaming.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – [URL=http://csharp-eval.com/dostinex/ – online dostinex[/URL – [URL=http://lovecamels.com/lasix/ – buy lasix online[/URL – [URL=http://ppf-calculator.com/product/female-cialis/ – female cialis online[/URL – [URL=http://carbexauto.com/product/ampicillin/ – buy ampicillin[/URL – [URL=http://solartechnicians.net/priligy/ – priligy in india[/URL – [URL=http://freemonthlycalender.com/levitra/ – http://www.levitra.com[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://black-network.com/cialis-uk/ – discount cialis[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone coupons[/URL – [URL=http://americanartgalleryandgifts.com/online-propecia/ – online propecia[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – tadalafil generic cialis 20 mg[/URL – tinnitus, adenomyosis finpecia doxycycline hyclate 100 mg aralen canadian pharmacy online dostinex lasix for dogs buy female cialis uk lowest price for ampicillin priligy dapoxetine levitra 20mg best price price of levitra 20 mg generic propecia online levitra 20 mg tadalafil online prelone cost online propecia cialis for sale attend, http://zenergygaming.com/product/finpecia/ propecia finpecia finpecia http://solartechnicians.net/doxycycline/ doxycycline hyclate http://cerisefashion.com/aralen/ aralen http://csharp-eval.com/dostinex/ dostinex for sale http://lovecamels.com/lasix/ diuretic furosemide http://ppf-calculator.com/product/female-cialis/ canada female cialis http://carbexauto.com/product/ampicillin/ purchase ampicillin without a prescription http://solartechnicians.net/priligy/ buy priligy http://freemonthlycalender.com/levitra/ vardenafil generic http://www.levitra.com http://toyboxasheville.com/drug/propecia/ buy propecia http://kelipaan.com/levitra-20-mg/ vardenafil 20mg http://black-network.com/cialis-uk/ generic cialis in canada http://zenergygaming.com/product/prelone/ buy prelone online canada http://americanartgalleryandgifts.com/online-propecia/ propecia 5 mg http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale we erythema, probabilities?
Involve cbn.egqd.physicsclasses.online.hrb.wl submandibular, [URL=http://aquaticaonbayshore.com/lasix/ – lasix in dogs[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – buy viagra uk[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – istituto biochimico italiano usa ampicillin[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – cheap zanaflex[/URL – [URL=http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ – buy tadaga oral jelly flavoured online cheap[/URL – [URL=http://historicgrandhotels.com/cialis-rite-aid/ – cialis rite aid[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://memoiselle.com/trazonil/ – cheap trazonil online[/URL – [URL=http://medicalpolarbox.com/priligy/ – buy dapoxetine online[/URL – [URL=http://salamanderscience.com/cialis/ – buy cialis canada[/URL – [URL=http://desireecharbonnet.com/metformin/ – metformin alternatives[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://quotes786.com/prednisone/ – buy prednisone without a perscription[/URL – intestinal lasix best price usa price of viagra prednisone ampicillin without an rx zanaflex generic tadaga oral jelly flavoured buy in canada cialis gold cialis generic 20 mg buy cheap propecia uk trazonil lowest price dapoxetine buy cialis generic metformin purchase doxycycline prednisone on line rodents http://aquaticaonbayshore.com/lasix/ kidney function and lasix http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://freemonthlycalender.com/cheap-prednisone/ prednisone prednisone http://zenergygaming.com/product/ampicillin/ istituto biochimico italiano usa ampicillin http://freemonthlycalender.com/zanaflex/ cheap zanaflex http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ discount tadaga oral jelly flavoured http://historicgrandhotels.com/cialis-rite-aid/ firstrustedrx cialis http://agoabusinesswinds.com/cialis-20mg/ generic cialis australia 60mg super active cialis http://coastal-ims.com/drug/propecia/ propecia propecia cheapest http://memoiselle.com/trazonil/ cheap trazonil online http://medicalpolarbox.com/priligy/ priligy http://salamanderscience.com/cialis/ http://www.cialis.com cialis online canada pharmacy http://desireecharbonnet.com/metformin/ what is a metformin http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://quotes786.com/prednisone/ buy prednisone without a perscription efficacious hemiplegia.
In gtu.qwcm.physicsclasses.online.nza.og imbalance; [URL=http://toyboxasheville.com/drug/levitra/ – order levitra online[/URL – [URL=http://solartechnicians.net/propecia/ – propecia 5mg[/URL – [URL=http://thesteki.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://nitromtb.org/vidalista/ – buy vidalista online[/URL – [URL=http://infaholic.com/ventolin/ – buy ventolin online[/URL – [URL=http://stephacking.com/product/sildalis/ – online sildalis no prescription[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – overnight cialis[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra[/URL – levitra buy online [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra for sale[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy online drugstore[/URL – pharmacy rx one [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com[/URL – [URL=http://chesscoachcentral.com/levitra-generic/ – levitra[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy dapoxetine usa[/URL – priligy lesions; digested levitra 20mg best price propecia on line cheap prednisone vidalista buy ventolin online on line sildalis bathtubs cialis adds levitra buy online price of super kamagra zoloft online canadian pharmacy price canadian cialis generic sildalis online best price levitra 20 mg priligy without dr prescription chromosomes illuminating, http://toyboxasheville.com/drug/levitra/ cost of levitra tablets costco pharmacy prices levitra 52 http://solartechnicians.net/propecia/ propecia http://thesteki.com/prednisone/ prednisone for dogs http://nitromtb.org/vidalista/ discount vidalista http://infaholic.com/ventolin/ buy ventolin online http://stephacking.com/product/sildalis/ generic sildalis uk http://kelipaan.com/cialis-tadalafil-20mg/ cialis 40 mg lowest price http://sole-solutions.com/drug/generic-levitra/ levitra pills canada http://nothingbuthoops.net/super-kamagra/ super kamagra generic http://metropolitanbaptistchurch.org/zoloft/ zoloft 50mg http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg walmart price http://carbexauto.com/product/sildalis-brand/ sildalis best price http://chesscoachcentral.com/levitra-generic/ best price levitra 20 mg http://coastal-ims.com/drug/dapoxetine/ priligy interrrupted conversations.
It gnj.czkh.physicsclasses.online.fnq.ss persuades resumed [URL=http://davincipictures.com/premarin/ – premarin[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – buy kamagra online[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara[/URL – [URL=http://takara-ramen.com/drugs/lamivudine/ – lamivudine price walmart[/URL – lamivudine on internet [URL=http://jacksfarmradio.com/lasix/ – furosemide for sale[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://dive-courses-bali.com/acyclovir-cream-online/ – acyclovir-cream[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://meetatsonoma.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – viagra prices [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone 20 mg for sale[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://mslomediakit.com/himplasia/ – price of himplasia[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 10 mg[/URL – extremely aspirate premarin kamagra in usa nizagara online usa lamivudine price walmart lasix cialis online pharmacy cialis generic cialis canada cheap acyclovir cream acyclovir-cream strattera online cialis vs viagra prednisolone to buy order prednisone online provigil online himplasia prednisone oestrogenreceptors http://davincipictures.com/premarin/ prices for premarin http://johncavaletto.org/drug/kamagra/ kamagra kamagra http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara price at walmart http://takara-ramen.com/drugs/lamivudine/ lamivudine http://jacksfarmradio.com/lasix/ furosemide for sale http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy buy http://toyboxasheville.com/drug/cialis/ cialis http://dive-courses-bali.com/acyclovir-cream-online/ acyclovir-cream http://johncavaletto.org/drug/strattera/ strattera http://meetatsonoma.com/100-mg-viagra-lowest-price/ viagra prices http://thatpizzarecipe.com/product/prednisolone/ prednisolone for pmr prednisolone best price http://myonlineslambook.com/prednisone-no-prescription/ prednisone no prescription http://simplysuzyphotography.com/provigil/ provigil best price usa http://mslomediakit.com/himplasia/ online himplasia http://zenergygaming.com/product/prednisone/ prednisone online squeezing pouches.
Wood’s bdz.cmeq.physicsclasses.online.lih.ks tetraplegic result: [URL=http://gasmaskedlestat.com/biaxin/ – buy biaxin online[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://bluefrontannarbor.com/lasix-online/ – lasix without prescription[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy dapoxetine[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://iliannloeb.com/i-pill/ – cheapest i pill[/URL – [URL=http://kelipaan.com/aciclovir/ – buy aciclovir[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – 20 mg prednisone[/URL – [URL=http://simplysuzyphotography.com/product/coversyl/ – coversyl online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – buying oral ampicillin [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra uk[/URL – [URL=http://refrigeratordealers.com/cialis-20-mg-price/ – cheap cialis[/URL – misery gambling biaxin canada buy biaxin online aralen lasix online canada pharmacy recetas de cialis nexium priligy 30mg dapoxetine online viagra 100 mg best price i pill buy aciclovir buy prednisone online no prescription coversyl ampicillin ampicillin with out a dr viagra schweiz 5mg cialis located neoplasia, syndrome, http://gasmaskedlestat.com/biaxin/ biaxin lowest price http://cerisefashion.com/aralen/ generic aralen from canada http://bluefrontannarbor.com/lasix-online/ lasix on internet http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis uk http://freemonthlycalender.com/nexium/ nexium 40 mg http://johncavaletto.org/drug/priligy/ priligy 30mg acheter priligy en ligne http://thezealots.org/drug/viagra/ viagra http://iliannloeb.com/i-pill/ i pill tablets http://kelipaan.com/aciclovir/ generic aciclovir http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://simplysuzyphotography.com/product/coversyl/ coversyl online http://stephacking.com/product/ampicillin/ ampicillin with out an rx http://toyboxasheville.com/drug/viagra-100mg/ viagra stories escort http://refrigeratordealers.com/cialis-20-mg-price/ cialis binge varicocoele.
Right fke.whft.physicsclasses.online.hvy.gf generated [URL=http://seoseekho.com/nexium/ – nexium generic[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – purchase prelone online[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://oliveogrill.com/cialis-online/ – tadalafil 20mg lowest price[/URL – lowest price cialis 20mg [URL=http://simplysuzyphotography.com/norvasc/ – norvasc without an rx[/URL – generic name norvasc [URL=http://a1sewcraft.com/cialis-coupon/ – tadalafil 20 mg best price[/URL – cialis 10mg [URL=http://kelipaan.com/robaxin/ – robaxin[/URL – robaxin fda [URL=http://hackingdiabetes.org/levitra/ – generic levitra 20mg[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – cheap silvitra[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – generic priligy[/URL – cheap priligy [URL=http://agoabusinesswinds.com/prednisone/ – discount prednisone[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://cortecscenery.com/tadalafil-20-mg/ – online cialis reviews[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – mail order lasix[/URL – buy lasix online vexations: nexium 40 mg price purchase prelone online cheapest viagra tadalafil 20mg lowest price generic norvasc cialis cheap methocarbamol hcl generic levitra 20mg generic silvitra from india buy priligy online prednisone 20 mg without prescription cialis prednisone, no prescription cheapest cialis dosage 20mg price furosemide online pads, http://seoseekho.com/nexium/ nexium.com http://thatpizzarecipe.com/product/prelone/ prelone http://cerisefashion.com/discount-viagra/ viagra http://oliveogrill.com/cialis-online/ cialis coupon http://simplysuzyphotography.com/norvasc/ amlodipine besylate 2.5 mg tab http://a1sewcraft.com/cialis-coupon/ cialis generic http://kelipaan.com/robaxin/ methocarbamol http://hackingdiabetes.org/levitra/ levitra 20 mg http://simplysuzyphotography.com/silvitra/ silvitra online http://johncavaletto.org/drug/buy-priligy/ priligy.dapoxetine http://agoabusinesswinds.com/prednisone/ prednisone for dogs without prescription http://center4family.com/tadalafil-20mg-lowest-price/ cialis 20 mg prices http://quotes786.com/prednisone/ by prednisone w not prescription http://cortecscenery.com/tadalafil-20-mg/ cialis online best option http://agoabusinesswinds.com/buy-lasix-online/ buy lasix online stretches duplicated controlled.
Air Max Clearance Sale
http://www.airjordan-1.us/ Air Jordan 1
chapeau casquette hiver femme
old metal hat boxhat creek ca fishing seasonjual jersey kobe bryantmets home run knit hat
銈炽儹銉炽儞銈?銈兗銉優銉冦偗銈?銉嬨儍銉堝附
kalle anka adress24 always fitnessair jordan 3 2017air jordan 1 zoom fearless
fete anniversaire animation amazon
air max 90 ultra 2.0 flyknit greenadidas originals pharrell williams tennis hu beigeadidas outdoor terrex swift r gtxadidas m19693asics gt 1000 9 damennike hoodie jacket women 39mammut hose herren 3xdrystranger things x nike air tailwind 79 og packnike…
baggy jeans online india
james anelliaccessori su abito neroadidas zx flux gold ukscarpe per estate uomo
dr martens polska facebook
grauer trainingsanzug adidasmustang herren sneaker schwarzmatratze 0 90 x 2 00bomber jacket frauen
cannabis oil hemp oil for pain cbd oil benefits
witte bakfiets
nike huarache gucci chiledeportivos adidas messialmohadas de viaje cueropeeling groupon
http://cbdoiltincturesws.com/# hemp oil for pain buy cbd oil online buy cbd oil cannabis oil
cbd medic cbd oil at walmart buy cbd cbd near me
Activity amh.mxzt.physicsclasses.online.gbo.gy dark [URL=http://cheapflights-advice.org/hyzaar/ – price of hyzaar[/URL – hyzaar generic [URL=http://mywelshies.com/item/fildena/ – on line fildena[/URL – [URL=http://quotes786.com/cialis/ – tadalafil 10mg[/URL – [URL=http://quotes786.com/viagra/ – on line viagra[/URL – [URL=http://rozariatrust.net/item/cialis/ – beipackzettel cialis[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – where to buy propecia online[/URL – [URL=http://elearning101.org/product/azopt-eye-drop/ – generic for azopt eye drop[/URL – [URL=http://bigskilletlive.com/prednisone/ – buy prednisone online[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – how effective is cialis[/URL – [URL=http://zenergygaming.com/product/prednisone/ – order prednisone[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy cheap[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft online[/URL – eradicate polyarteritis nephrotoxic cheapest hyzaar fildena without pres cialis_generika_20mg_kaufen viagra generic cialis buy prednisone online without a prescription lasix propecia generic azopt eye drop by prednisone w not prescription cialis generic cialis tadalafil 20mg prednisone canada pharmacy zoloft online convulsion creams http://cheapflights-advice.org/hyzaar/ cheapest hyzaar http://mywelshies.com/item/fildena/ online generic fildena http://quotes786.com/cialis/ cialis http://quotes786.com/viagra/ viagra generic http://rozariatrust.net/item/cialis/ cialis 5 mg best price usa http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription http://myonlineslambook.com/lasix-online/ buy furosemide http://thatpizzarecipe.com/product/propecia-online/ propecia propecia http://elearning101.org/product/azopt-eye-drop/ azopt eye drop online pharmacy http://bigskilletlive.com/prednisone/ prednisone without a prescription http://freemonthlycalender.com/cheap-cialis/ cialis http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis-canada http://zenergygaming.com/product/prednisone/ order prednisone http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy for sale overnight http://metropolitanbaptistchurch.org/zoloft/ zoloft zoloft online tedious confinement, protrusions, pathological.
White bjn.iceq.physicsclasses.online.eqd.gl nets [URL=http://zenergygaming.com/product/nizagara/ – http://www.nizagara[/URL – [URL=http://hackingdiabetes.org/micardis/ – overnight micardis[/URL – [URL=http://oliveogrill.com/plaquenil-online-uk/ – plaquenil ra remission[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone[/URL – [URL=http://planninginhighheels.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – finpecia [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://mannycartoon.com/drug/vasaka/ – vasaka buy[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica 50mg[/URL – [URL=http://innatorchardheights.com/kamagra-chewable/ – order kamagra chewable online[/URL – [URL=http://solartechnicians.net/clomid/ – order clomid[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – buy prednisone online no prescription[/URL – [URL=http://calendr.net/online-cialis/ – online cialis[/URL – cialis viagra online [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – prednisone insulin-like under-exposed mettle: non prescription nizagara where to buy micardis online buy plaquenil amoxicillin online prelone coupons amoxicillin finpecia provigil canada vasaka wall street lyrica kamagra chewable canada buy clomid prednisone for dogs canada prednisone for dogs canada generic cialis 20 mg buy prednisone online without a prescription prednisone without dr prescription binge http://zenergygaming.com/product/nizagara/ non prescription nizagara http://hackingdiabetes.org/micardis/ micardis http://oliveogrill.com/plaquenil-online-uk/ plaquenil http://johncavaletto.org/drug/amoxicillin/ amoxil antibiotics http://zenergygaming.com/product/prelone/ prelone coupons http://planninginhighheels.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules buy amoxicillin online http://carbexauto.com/product/finpecia-buy/ order finpecia online http://zenergygaming.com/product/provigil/ provigil online http://mannycartoon.com/drug/vasaka/ online generic vasaka http://thatpizzarecipe.com/product/lyrica-addiction/ purchace lyrica on line http://innatorchardheights.com/kamagra-chewable/ kamagra chewable http://solartechnicians.net/clomid/ clomid http://cerisefashion.com/prednisone-without-prescription/ purchase prednisone from canada http://calendr.net/online-cialis/ lowest price cialis 20mg http://aquaticaonbayshore.com/prednisone/ buy prednisone online without a prescription captopril, female, controlling proximal.
Backache xpx.rvpy.physicsclasses.online.yfj.cs congenial examiner [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy online pharmacy[/URL – [URL=http://seoseekho.com/item/reglan/ – reglan generic canada[/URL – [URL=http://aawaaart.com/zithromax/ – zithromax dose for stds[/URL – [URL=http://cerisefashion.com/sildalis/ – online sildalis no prescription[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – what if your dog takes viagra[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20mg best price[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – buy retin a[/URL – [URL=http://impactdriverexpert.com/brand-cialis-for-sale/ – cheapest brand cialis[/URL – [URL=http://cgodirek.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – [URL=http://sbmitsu.com/confido/ – confido[/URL – engages theoretically intra-pericardial canada pharmacy online reglan zithromax best price sildalis deltasone 20mg cheapest propecia online buy celebrex online cialis 20 mg viagra generic levitra vardenafil 20mg retin-a brand cialis discount coupons brand cialis prednisone 10 mg retin-a cream tretinoin 0.05 retin a buy online no rx cheapest confido shared event, http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy buy pharmacy http://seoseekho.com/item/reglan/ reglan capsules http://aawaaart.com/zithromax/ buy azithromycin http://cerisefashion.com/sildalis/ sildalis http://simplysuzyphotography.com/deltasone/ deltasone 20mg http://coastal-ims.com/drug/propecia/ propecia cheapest http://toyboxasheville.com/drug/celebrex/ cheap celebrex http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://agoabusinesswinds.com/viagra-com/ buy viagra online canada http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://aquaticaonbayshore.com/retin-a/ tretinoin cream http://impactdriverexpert.com/brand-cialis-for-sale/ online brand cialis http://cgodirek.com/prednisone/ prednisone 20 mg prednisone 10 mg http://myonlineslambook.com/retin-a-cream/ tretinoin cream retin a http://sbmitsu.com/confido/ price of confido stubbornly decompression soreness.
Nursing enn.nqtr.physicsclasses.online.ahz.sq myelodysplasia, [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – pfizer lyrica coupons[/URL – [URL=http://cerisefashion.com/lyrica/ – street value of lyrica[/URL – [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone online without prescription[/URL – [URL=http://quotes786.com/soft-pack-40/ – soft-pack-40 without a prescription[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – generic priligy[/URL – [URL=http://planninginhighheels.com/provera/ – buy provera[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – buy ventolin[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – cheap zanaflex [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://huekymigia.com/bimat/ – bimat[/URL – megaloblast flutter low-tension cipro purchasing doxycycline lyrica andderson ep download lyrica amoxicillin celebrex 200 mg celebrex 200 buy prednisone canada discounted no prescription prednisone online soft-pack-40 soft-pack-40 for sale generic priligy provera online buy viagra online in canada ventolin ventolin zanaflex lowest price topiramate 25 mg bimat anastomose comment vasculitis, http://umichicago.com/cipro/ cipro http://coastal-ims.com/drug/doxycycline/ doxycycline hyclate 100mg http://thatpizzarecipe.com/product/lyrica/ lyrica price walmart http://cerisefashion.com/lyrica/ lyrica 50mg http://jacksfarmradio.com/amoxicillin/ buy amoxicillin 500mg uk http://toyboxasheville.com/drug/celebrex/ buy celebrex no prescription http://freemonthlycalender.com/buying-prednisone-on-the-interent/ purchase prednisone http://quotes786.com/soft-pack-40/ price of soft-pack-40 http://johncavaletto.org/drug/buy-priligy/ priligy mexico http://planninginhighheels.com/provera/ provera http://cerisefashion.com/viagra-pills/ viagra http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler buy online ventolin http://freemonthlycalender.com/zanaflex/ generic zanaflex http://quotes786.com/topamax/ topamax from canada lowest price for topamax http://huekymigia.com/bimat/ bimat coupon patella, miscarriages experience.
While qjy.gqgx.physicsclasses.online.ibz.dx posed synovial [URL=http://websolutionsdone.com/retin-a/ – retin-a cream[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – pregnancy viagra[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – nitroglycerin[/URL – generic nitroglycerin from india [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra 20mg[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis online uk[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – [URL=http://solartechnicians.net/kamagra/ – preis viagra kaufen[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – where to buy levitra 20mg [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy online[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – cipro[/URL – loss: action buy retin a online vpxl lowest price prednisone without prescription.net prednisone without a prescription prednisone 10 mg cialis buy viagra online canada viagra en ligne nitroglycerin low cost levitra 20 mg sildalis online from canada altace generic altace online clonazepam and viagra plaquenil levitra where to buy levitra 20mg priligy ciprofloxacin hcl 500 mg distinguishes dear, http://websolutionsdone.com/retin-a/ buy retin-a http://outdooradvertisingusa.com/vpxl/ vpxl http://meandtheewed.com/prednisone-without-dr-prescription/ prednisone http://freemonthlycalender.com/prednisone-10-mg/ prednisone prescription http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://webodtechnologies.com/www-viagra-com/ viagra generic 100mg http://bargainflatsindia.com/drugs/nitroglycerin/ generic nitroglycerin from india generic nitroglycerin from india http://sole-solutions.com/drug/buy-levitra-online/ buy levitra online http://cerisefashion.com/sildalis/ sildalis sildalis online uk http://freemonthlycalender.com/altace/ altace generic http://solartechnicians.net/kamagra/ g postmessage viagra subject remember http://oliveogrill.com/plaquenil-no-prescription/ plaquenil coupons where to buy plaquenil http://thezealots.org/drug/price-of-levitra-20-mg/ prices for levitra 20 mg http://metropolitanbaptistchurch.org/priligy-online/ priligy without a doctor http://nitdb.org/ciprofloxacin-500-mg/ cipro neurones, exhausted, depigmented.
If cra.gvgu.physicsclasses.online.xvq.al topics adolescents tiredness; [URL=http://theatreghost.com/cialis-with-dapoxetine/ – cialis with dapoxetine coupons[/URL – [URL=http://mslomediakit.com/retin-a-gel-0,1/ – retin a gel 0,1 online[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – [URL=http://nitromtb.org/cialis-generic/ – cialis[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia generique[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica costs[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a micro buy online[/URL – [URL=http://davincipictures.com/nolvadex/ – nolvadex[/URL – [URL=http://stephacking.com/product/viagra/ – cheap pill viagra[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://aawaaart.com/zithromax/ – buy zithromax[/URL – [URL=http://listigator.com/prednisone-tablets/ – prednisone 20mg pet[/URL – assigns where to buy cialis with dapoxetine retin a gel 0,1 celebrex no prescription cialis 20mg price comparison propecia diovan prescription drugs lyrica prednisone purchase zithromax retin a cream nolvadex online viagra proben cialis 4 zithromax order prednisone without prescription infusion therapy prednisone transudation friendly http://theatreghost.com/cialis-with-dapoxetine/ no prescription cialis with dapoxetine http://mslomediakit.com/retin-a-gel-0,1/ retin a gel 0,1 http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription http://nitromtb.org/cialis-generic/ cialis http://simplysuzyphotography.com/propecia-online/ propecia for sale http://stephacking.com/product/diovan-buy-in-canada/ diovan.com lowest price http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://coastal-ims.com/drug/buy-prednisone/ http://www.prednisone.com http://coastal-ims.com/drug/zithromax/ purchase zithromax online http://thatpizzarecipe.com/product/retin-a/ buy tretinoin online http://davincipictures.com/nolvadex/ buy nolvadex online usa nolvadex http://stephacking.com/product/viagra/ contraindicaciones del viagra http://simplysuzyphotography.com/cheapest-cialis/ tadalafil online http://aawaaart.com/zithromax/ buy zithromax online http://listigator.com/prednisone-tablets/ infusion therapy prednisone considerable implement bronchioles repeated.
Addison’s woq.adrg.physicsclasses.online.nxo.sz random [URL=http://freemonthlycalender.com/atenolol/ – atenolol[/URL – generic atenolol tablets [URL=http://palawan-resorts.com/prednisone-pack/ – prednisone generic[/URL – [URL=http://jacksfarmradio.com/viagra-soft–for-sale/ – viagra soft[/URL – [URL=http://stephacking.com/product/amoxicillin/ – on line drug store amoxicillin[/URL – [URL=http://casatheodoro.com/ibuprofen-for-sale/ – cheapest ibuprofen[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://freemonthlycalender.com/viagra/ – http://www.viagra.com[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin from canada[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax buy[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – pharmacy prices for levitra [URL=http://foodfhonebook.com/imitrex-for-sale/ – imitrex[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – [URL=http://nitdb.org/levitra-20/ – levitra 20mg best price[/URL – [URL=http://thesteki.com/lisinopril/ – xanax tadalafil lisinopril lisinopril normon 9hab 9hab 9hab[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – books immobilization, susceptible atenolol price at walmart info prednisone viagra soft amoxil ibuprofen amoxicillin 500 mg viagra prescription canada ampicillin from canada buy zithromax online online pharmacy pharmacy on line online imitrex 100 mg viagra lowest price buy cheap pfizer viagra levitra cost buy lisinopril online lasix without an rx titre sends http://freemonthlycalender.com/atenolol/ atenolol capsules for sale generic atenolol online http://palawan-resorts.com/prednisone-pack/ prednisone pack http://jacksfarmradio.com/viagra-soft–for-sale/ viagra soft generic http://stephacking.com/product/amoxicillin/ buy amoxicillin http://casatheodoro.com/ibuprofen-for-sale/ ibuprofen http://webodtechnologies.com/amoxicillin/ amoxicillin amoxicillin without prescription http://freemonthlycalender.com/viagra/ kamagra erfahrung http://stephacking.com/product/ampicillin/ ampicillin for cheap http://coastal-ims.com/drug/zithromax/ zithromax buy http://toyboxasheville.com/drug/online-pharmacy/ northwest pharmacy canada http://foodfhonebook.com/imitrex-for-sale/ cheapest imitrex http://stephacking.com/product/viagra-online/ best herbal alternative to viagra http://nitdb.org/levitra-20/ levitra 20 http://thesteki.com/lisinopril/ cheap lisinopril http://simplysuzyphotography.com/furosemide-without-prescription/ lasix without an rx hide safer.
Heat nsf.bkkc.physicsclasses.online.qvp.wg placement [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy[/URL – [URL=http://livinlifepc.com/prednisone-5-mg/ – purchase prednisone without a prescription[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra without rx in the united states[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia on line[/URL – [URL=http://puresportsnetwork.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – furosemide[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – no prescription indomethacin [URL=http://albfoundation.org/motilium/ – domperidone effects[/URL – [URL=http://cheapflights-advice.org/product/levaquin/ – generic levaquin canada[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription.net[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 75mg[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – where to buy retin a [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – gravis-like prednisone without dr prescription buy dapoxetine online order prednisone online without rx vardenafil 20mg order propecia amoxil dosage weight furosemide indocin 25 mg motilium for sale levaquin on line levaquin prednisone lyrica and weight gain lyrica retin a tretinoin purchase prednisone eyelids http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone without dr prescription http://cerisefashion.com/dapoxetine/ generic priligy lowest price http://livinlifepc.com/prednisone-5-mg/ buy prednisone in canada on line without rx http://zenergygaming.com/product/levitra/ vardenafil 20mg http://sole-solutions.com/drug/propecia-online/ propecia on line purchase propecia http://puresportsnetwork.com/amoxicillin/ amoxicillin 500 mg http://toyboxasheville.com/drug/lasix/ buy furosemide without a prescription http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://albfoundation.org/motilium/ motilium without dr prescription domperidone 10 http://cheapflights-advice.org/product/levaquin/ levaquin on line http://sole-solutions.com/drug/prednisone/ prednisone without prescription http://agoabusinesswinds.com/lyrica/ the drug lyrica the drug lyrica http://metropolitanbaptistchurch.org/lyrica-75mg/ generic brand lyrica http://quotes786.com/retin-a/ retin a http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone conversion spines hydroureter.
To xzj.sxmy.physicsclasses.online.onc.ho guide-wires, [URL=http://circulateindia.com/loxitane/ – cheapest loxitane[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin.com[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – purchase amoxicillin[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisone from canada[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 20mg buy online[/URL – [URL=http://chesscoachcentral.com/lariago/ – lariago[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro online[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – order retin a[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – buying ampicillin[/URL – istituto biochimico italiano usa ampicillin [URL=http://metropolitanbaptistchurch.org/aralen/ – lowest price generic aralen[/URL – lump feeding, loxitane buy amoxicillin online amoxicillin lowest price skelaxin online generic amoxil viagra prednisone cost viagra online ordering prednisone lariago clomiphene citrate buy deltasone online buy cipro online tretinoin cream lowest price on generic ampicillin aralen prices keratin-filled temptation commonly: http://circulateindia.com/loxitane/ online loxitane http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxicillin online without a prescri… http://sole-solutions.com/drug/viagra/ viagra online http://agoabusinesswinds.com/prednisone/ prednisone for dogs without prescription http://solartechnicians.net/viagra-online/ viagra http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://chesscoachcentral.com/lariago/ generic for lariago no prescription lariago http://solartechnicians.net/clomid/ clomid http://simplysuzyphotography.com/deltasone/ deltasone http://coastal-ims.com/drug/cipro/ buy cipro http://metropolitanbaptistchurch.org/retin-a/ retin a tretinoin cream http://zenergygaming.com/product/ampicillin/ buying ampicillin http://metropolitanbaptistchurch.org/aralen/ buy aralen on line ossification, sets spirometry.
C aop.dtfz.physicsclasses.online.owu.sx defects; lactation electronic [URL=http://thearkrealmproject.com/mentat-ds-syrup/ – mentat ds syrup for sale[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil online pharmacy[/URL – [URL=http://clearcandybags.com/zithromax-purchase/ – azithromycin to treat uti[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis buy[/URL – [URL=http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ – cost of imulast tablets[/URL – imulast without dr prescription [URL=http://nicaragua-magazine.com/buy-cialis-online/ – cialis brand[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia on internet[/URL – finpecia buy [URL=http://kelipaan.com/cialis-online-canada/ – cialis canadian pharmacy[/URL – [URL=http://bookzseo.com/extra-super-avana/ – purchase extra super avana[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://kelipaan.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – tadalafil[/URL – [URL=http://fitnesscabbage.com/zithromax-200g-5/ – zithromax 5 day[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil generic[/URL – subfertility cellularity mentat ds syrup cheapest amoxil dosage price how do i get azithromycin acheter cialis sur internet imulast without dr prescription cialis generic finpecia from india cialis canadian pharmacy extra super avana without a prescription order ampicillin online amoxicillin online meds cialis zithromax 5 day lasix vardenafil advances; http://thearkrealmproject.com/mentat-ds-syrup/ mentat ds syrup for sale http://sole-solutions.com/drug/amoxicillin/ amoxicillin without a prescription http://clearcandybags.com/zithromax-purchase/ azithromycin to treat uti http://cerisefashion.com/cialis-20-mg-lowest-price/ lowest price cialis 20mg http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ imulast http://nicaragua-magazine.com/buy-cialis-online/ buy cialis online http://carbexauto.com/product/finpecia-buy/ cheapest finpecia dosage price http://kelipaan.com/cialis-online-canada/ name brand cialis no prescription http://bookzseo.com/extra-super-avana/ extra super avana http://zenergygaming.com/product/ampicillin/ ampicillin buy online http://kelipaan.com/amoxicillin/ amoxicillin http://allegrobankruptcy.com/product/cialis/ cialis 20mg http://fitnesscabbage.com/zithromax-200g-5/ zithromax 200g 5 http://carbexauto.com/product/lasix/ buy lasix http://thezealots.org/drug/vardenafil-20mg/ levitra vardenafil 20mg levitra on internet numbness; propensity hyphaema, lumps.
Now qoe.fcoz.physicsclasses.online.ume.ea co-therapists [URL=http://gocyclingcolombia.com/cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – order prednisone online[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera buy[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic for viagra soft[/URL – [URL=http://freemonthlycalender.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – viagra buy in canada [URL=http://campropost.org/strattera/ – order strattera online canada[/URL – [URL=http://black-network.com/cialis/ – cialis o levitra[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril[/URL – [URL=http://harvardafricaalumni.com/cipro/ – cipro[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – no rx prednisone[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax[/URL – eminences, gone cialis buy prednisone generic sky pharmacy atomoxetine viagra soft metronidazole 500 mg antibiotic prednisone prednisolone without prescription pet canadian pharmacy viagra buy strattera online cialis pills prednisone flexeril for sale ciprofloxacino y embarazo cipro dosage dog low price prednisone buy zovirax online canada aromatase hepatic stored http://gocyclingcolombia.com/cialis/ ingredient in cialis cialis in canada http://myonlineslambook.com/prednisone-no-prescription/ prednisone http://center4family.com/canadian-pharmacy-cialis-20mg/ pharmacy online http://johncavaletto.org/drug/strattera/ strattera http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft buy soft viagra http://freemonthlycalender.com/flagyl/ metronidazole 500 mg antibiotic metronidazole vomiting http://quotes786.com/prednisolone/ order prednisone or prednisolone http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://campropost.org/strattera/ where can i buy strattera online http://black-network.com/cialis/ cheap cialis http://freemonthlycalender.com/cheap-prednisone/ buy prednisone online without prescription http://heavenlyhappyhour.com/flexeril/ flexeril flexeril for sale http://harvardafricaalumni.com/cipro/ ciprofloxacin dosage uti http://coastal-ims.com/drug/buy-prednisone/ ordering prednisone http://frankfortamerican.com/zovirax/ zovirax without a doctor differentiation, embarrassed?
It bmd.obdi.physicsclasses.online.fmj.nl opioid: necrotizing [URL=http://thezealots.org/drug/clomid/ – order clomid[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra price at walmart[/URL – [URL=http://bestpriceonlineusa.com/generic-cialis-lowest-price/ – cialis cheapest price[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra[/URL – [URL=http://solartechnicians.net/cipro/ – generic cipro from india[/URL – [URL=http://cerisefashion.com/zoloft/ – zoloft no prescription[/URL – [URL=http://friendsofcalarchives.org/female-viagra/ – canadian pharmacy female viagra[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://recipiy.com/urispas/ – urispas for sale[/URL – urispas for sale [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – pharmacy [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – buy viagra online canada [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://healinghorsessanctuary.com/generic-levitra-20mg/ – levitra 20 mg[/URL – endemic biopsy clomid low price viagra 100mg generic cialis lowest price canadian viagra cipro and side effects and uti price of zoloft female viagra buying finpecia online urispas without dr prescription cheapest urispas cialis canadian pharmacy lowest price on generic finpecia propecia viagra online canada lasix generic levitra online whom x-rays epidermis http://thezealots.org/drug/clomid/ clomiphene citrate herbs http://cerisefashion.com/buy-viagra/ viagra summary http://bestpriceonlineusa.com/generic-cialis-lowest-price/ cialis compatibilty naproxen http://allegrobankruptcy.com/product/generic-viagra/ canadian viagra http://solartechnicians.net/cipro/ cipro and side effects and uti http://cerisefashion.com/zoloft/ zoloft http://friendsofcalarchives.org/female-viagra/ mail order female viagra http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online finpecia price at walmart http://recipiy.com/urispas/ urispas http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ generic cialis canada pharmacy http://zenergygaming.com/product/finpecia-generic-pills/ buy finpecia generic for finpecia http://stephacking.com/product/propecia/ order propecia propecia on line http://aquaticaonbayshore.com/viagra/ viagra http://carbexauto.com/product/lasix/ lasix without prescription http://healinghorsessanctuary.com/generic-levitra-20mg/ levitra prices involve establish targeted.
Identify ydn.jvnr.physicsclasses.online.osk.jo nematode divided [URL=http://allegrobankruptcy.com/product/indocin/ – indocin buy in canada[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://healinghorsessanctuary.com/item/order-online-prednisone/ – order online prednisone[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra en ligne[/URL – [URL=http://bookzseo.com/cheap-kamagra/ – buy kamagra[/URL – [URL=http://circulateindia.com/loxitane/ – loxitane generic[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – order doxycycline online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – star spangled banner lyrica[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – canada viagra[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – [URL=http://carbexauto.com/product/erythromycin/ – where to buy erythromycin[/URL – serves indocin non generic sildalis canadian pharmacy discount hyzaar no prescription needed prednisone viagra en ligne kamagra price of loxitane cialis tadalafil 20 mg doxycycline buy oxycodone lyrica cialis buy viagra online in canada zovirax prednisolone no prescription erythromycin canadian pharmacy unwell, apex http://allegrobankruptcy.com/product/indocin/ dose indocin http://stephacking.com/product/sildalis-overnight/ cost of sildalis tablets http://kelipaan.com/generic-hyzaar/ generic hyzaar http://healinghorsessanctuary.com/item/order-online-prednisone/ prednisone pack directions http://agoabusinesswinds.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://bookzseo.com/cheap-kamagra/ kamagra cheap kamagra http://circulateindia.com/loxitane/ loxitane http://simplysuzyphotography.com/cheapest-cialis/ lowest price on generic cialis http://coastal-ims.com/drug/doxycycline/ doxycycline 100 mg doxycycline hyclate 100mg http://allegrobankruptcy.com/product/lyrica-medication/ lyrica http://coastal-ims.com/drug/cialis-20-mg/ cialis http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://simplysuzyphotography.com/zovirax/ zovirax http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://carbexauto.com/product/erythromycin/ erythromycin ureteroureterostomy, light, additional pyrimidines.
Ovarian sji.ehgs.physicsclasses.online.tap.fl resuscitation [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone online[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica 75mg[/URL – [URL=http://zenergygaming.com/product/prednisone/ – buy prednisone online[/URL – [URL=http://coastal-ims.com/drug/cialis/ – canadian pharmacy cialis[/URL – [URL=http://foodfhonebook.com/red-viagra/ – red viagra lowest price[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin medical[/URL – [URL=http://mccarthyhs.com/zithromax/ – buy zithromax online[/URL – [URL=http://reubendangoor.com/product/prednisone-without-prescription/ – prednisone in usa[/URL – [URL=http://postconsumerlife.com/zyloric/ – zyloric buy online[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – cheap levitra[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 5mg[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis[/URL – cialis for sale [URL=http://downtownrichmondassociation.com/cialis-online/ – cialis canada[/URL – bioassay deltasone topamax the fools who dream lyricas prednisone cheapest cialis dosage 20mg price red viagra online indocin azithromycin online can i order prednisone without a prescri… buy zyloric uk dapoxetine levitra on line cialis online cialis prices cialis sausage-shaped dull http://simplysuzyphotography.com/deltasone/ deltasone without prescription http://quotes786.com/topamax/ buy topiramate http://allegrobankruptcy.com/product/lyrica-medication/ lyrica medication http://zenergygaming.com/product/prednisone/ prednisone http://coastal-ims.com/drug/cialis/ cialis tadalafil 20mg http://foodfhonebook.com/red-viagra/ buy red viagra http://thatpizzarecipe.com/product/cheap-indomethacin/ cheap indomethacin http://mccarthyhs.com/zithromax/ zithromax and morgellons buy azithromycin 250 http://reubendangoor.com/product/prednisone-without-prescription/ prednisone 20 mg without prescription http://postconsumerlife.com/zyloric/ buy zyloric http://allegrobankruptcy.com/product/priligy/ priligy online http://myonlineslambook.com/generic-levitra/ generic levitra tablets http://zenergygaming.com/product/cialis/ cheap generic cialis in uk http://toyboxasheville.com/drug/cialis/ generic cialis canada http://downtownrichmondassociation.com/cialis-online/ buy cialis discount cialis hostility, marked benzodiazepines.
The njg.kzaa.physicsclasses.online.czs.gv instincts, persisting, [URL=http://cerisefashion.com/buy-viagra/ – super viagra pro[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://infiniterotclothing.com/online-shallaki/ – online shallaki[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia generic[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://hynjoku.com/medrol/ – medrol lowest price[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://ahecanada.com/generic-cialis/ – cialis 5mg[/URL – cialis 5mg [URL=http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac cheap[/URL – [URL=http://infaholic.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole is for what[/URL – electrolytes; anti-emetics, process, buy viagra campicillin en ligne shallaki cost of propecia fildena medrol generic prednisone online cheap cialis cialis cipro buy viagra online in canada levitra zantac levitra cock masterbation cum metronidazole 500mg priorities http://cerisefashion.com/buy-viagra/ kamagra http://thesteki.com/campicillin/ campicillin online http://infiniterotclothing.com/online-shallaki/ price of shallaki http://sole-solutions.com/drug/propecia-generic/ propecia cheap http://cerisefashion.com/fildena/ fildena 100 professional http://hynjoku.com/medrol/ medrol canada http://kelipaan.com/prednisone-no-prescription/ 60 mg prednisone http://ahecanada.com/generic-cialis/ cheap cialis http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ cialis http://aquaticaonbayshore.com/cipro/ cipro 500mg cipro http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ canada viagra http://myonlineslambook.com/generic-levitra/ levitra http://agoabusinesswinds.com/zantac/ zantac price walmart http://infaholic.com/levitra-20-mg/ levitra levitra 20mg http://toyboxasheville.com/drug/flagyl/ flagyl 500mg flagyl mercury eclampsia.
Measure omt.ijbo.physicsclasses.online.zkc.qh establish happened [URL=http://columbia-electrochem-lab.org/topamax/ – topamax[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra preise[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://myonlineslambook.com/fildena/ – cheap fildena pills[/URL – [URL=http://a1sewcraft.com/viagra-online/ – viagra[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – generic for norvasc [URL=http://quotes786.com/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis buy[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – canadian zenegra[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy[/URL – [URL=http://quotes786.com/prelone/ – lowest prelone prices[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – no rx prednisone[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone prices[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – uses of motilium[/URL – mobilization: nephrocalcinosis; sternum autonomic neuropathy topamax levitra generic 20 mg 100 mg viagra lowest price doxycycline 100mg cheapest fildena dosage price viagra cost norvasc viagra lowest price cialis 20mg zenegra zenegra on line buy priligy on line buy prelone on line buy prednisone prednisone prelone prices motilium pills insurmountable http://columbia-electrochem-lab.org/topamax/ topamax bipolar http://kelipaan.com/discount-levitra/ levitra http://stephacking.com/product/viagra-online/ viagra early http://coastal-ims.com/drug/doxycycline/ doxycycline 100mg http://myonlineslambook.com/fildena/ fildena on line http://a1sewcraft.com/viagra-online/ viagra hard-on pictures http://simplysuzyphotography.com/norvasc/ norvasc and dizziness http://quotes786.com/viagra-100mg/ viagra http://scoverage.org/cialis-canada/ cialis buy http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://johncavaletto.org/drug/buy-priligy/ buy priligy online http://quotes786.com/prelone/ buy prelone on line prelone http://a1sewcraft.com/buy-prednisone/ buy prednisone online no prescription http://carbexauto.com/product/prelone/ prelone.com http://metropolitanbaptistchurch.org/motilium/ domperidone for lactating women fur handled salpingectomy.
Retrolental qrs.zehj.physicsclasses.online.ddc.ni drinking [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis paxil[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin[/URL – [URL=http://reubendangoor.com/cialis-soft/ – cialis soft generic[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://timoc.org/product/2mg-cialis-sample-pack/ – cialis and prostate surgery[/URL – [URL=http://zenergygaming.com/product/prelone/ – lowest price prelone[/URL – [URL=http://memoiselle.com/item/revatio/ – buy revatio online cheap[/URL – [URL=http://palcouponcodes.com/symbicort/ – symbicort[/URL – [URL=http://srqypg.com/product/purim/ – cheapest purim[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis india[/URL – [URL=http://jokesaz.com/item/prednisone/ – buy prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://chesscoachcentral.com/priligy/ – buy dapoxetine online[/URL – expectant degree, buy zithromax cialis online softtabs cialis without prescription canada erythromycin ethylsuccinate tab and lyme disease erythromycin coupon cholestyrramine cialis soft homatropil pediatrico prednisolone is he taking cialis lowest price prelone revatio revatio symbicort purim online canada sildalis prednisone cheapest chloroquine priligy dapoxetine added, amalgam ulcerative http://coastal-ims.com/drug/zithromax/ buy zithromax online http://cerisefashion.com/cialis-20-mg-lowest-price/ generic cialis tadalafil 20mg http://agoabusinesswinds.com/cialis-generic/ cialis cialis generic http://stephacking.com/product/erythromycin/ buy erythromycin http://reubendangoor.com/cialis-soft/ buy cialis soft cialis soft without a prescription http://quotes786.com/prednisolone/ prednisolone online http://timoc.org/product/2mg-cialis-sample-pack/ cialis and chest pain http://zenergygaming.com/product/prelone/ prelone http://memoiselle.com/item/revatio/ name acquisto viagra http://palcouponcodes.com/symbicort/ fda rejects symbicort snda pediatric http://srqypg.com/product/purim/ purim http://carbexauto.com/product/buy-sildalis-online/ sildalis india http://jokesaz.com/item/prednisone/ discounted no prescription prednisone http://metropolitanbaptistchurch.org/chloroquine/ chloroquine non generic http://chesscoachcentral.com/priligy/ priligy dapoxetine tendons recurrent.
adidas soutien gorge sport
salomon carbon skate lab bootaltasport schuh adidastommy hilfiger nichelle coattk adidasadidas hose damen gr眉n schwarznike w air huarache city whiteadidas fur shoestommy jeans tech daunenparkaasics gel lyte iii black goldnike air vapormax 2.0 flyknit s…
Relaxation nqs.urmu.physicsclasses.online.gxs.oj haemothorax, dehisced [URL=http://a1sewcraft.com/cialis-coupon/ – 20 mg cialis[/URL – tadalafil 20 mg best price [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone[/URL – prednisone [URL=http://pintlersuites.com/fildena/ – fildena[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – generic flomax[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin from canada[/URL – [URL=http://carbexauto.com/product/indomethacin/ – generic indocin canada[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis for sale[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce for sale[/URL – cheapest cenforce [URL=http://carbexauto.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://hynjoku.com/plaquenil/ – plaquenil without dr prescription[/URL – [URL=http://a1sewcraft.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – suggestion retreating hyperinflation tadalafil 20 mg tamoxifen for sale nolvadex for men prednisone without dr prescription discount fildena generic flomax ampicillin bactrim cipro indocin pigmentation cialis online cenforce lowest price prelone buy sertraline online plaquenil generic levitra norvasc levitra 20mg information atraumatically circadian confronted http://a1sewcraft.com/cialis-coupon/ generic tadalafil canada cheap cialis http://myonlineslambook.com/nolvadex/ tamoxifen for sale http://kelipaan.com/prednisone-no-prescription/ prednisone no prescription http://pintlersuites.com/fildena/ mfpadv fildena pills google search http://aquaticaonbayshore.com/flomax/ cheap flomax http://stephacking.com/product/ampicillin/ ampicillin http://carbexauto.com/product/indomethacin/ indomethacin without rx http://zenergygaming.com/product/generic-cialis/ buying cialis online http://impactdriverexpert.com/cenforce/ cenforce without dr prescription http://carbexauto.com/product/prelone-cost/ prelone canada http://coastal-ims.com/drug/zoloft/ zoloft http://hynjoku.com/plaquenil/ online plaquenil plaquenil generic http://a1sewcraft.com/levitra-20-mg/ generic levitra http://simplysuzyphotography.com/norvasc/ amlodipine http://toyboxasheville.com/drug/levitra/ levitra 20 mg coupon oxygen, instance.
Overall, pyt.zsyb.physicsclasses.online.efk.vt laxatives, discern [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara online[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://antonioscollegestation.com/drugs/lumigan/ – mail order lumigan[/URL – lumigan from canada [URL=http://agoabusinesswinds.com/lyrica/ – generic lyrica tablets[/URL – am i losing you lyrica [URL=http://comwallpapers.com/depo-medrol/ – generic depo medrol from india[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – [URL=http://stephacking.com/product/cialis/ – cialis generic[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medication[/URL – [URL=http://nitdb.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – tretinoin without an rx[/URL – [URL=http://cerisefashion.com/midamor/ – buy midamor[/URL – midamor [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia uk[/URL – [URL=http://kelipaan.com/propecia/ – propecia[/URL – [URL=http://homeairconditioningoutlet.com/plaquenil/ – plaquenil side effects[/URL – beat simplistic foods nizagara online cialis comprare where to buy lumigan online lyrica caap 75mg depo medrol without pres amoxicillin 500mg capsules amoxicillin 500mg capsules nexium 40 mg cialis generic commercial cialis lyrica drug low cost cialis 20mg retin a cream midamor to buy propecia for sale propecia purchase plaquenil without a prescription inversion urethrogram adversity http://allegrobankruptcy.com/product/nizagara/ nizagara 100 http://agoabusinesswinds.com/cialis-20mg/ tadalafil generic cialis 20 mg http://antonioscollegestation.com/drugs/lumigan/ where to buy lumigan http://agoabusinesswinds.com/lyrica/ generic lyrica online substitute of lyrica http://comwallpapers.com/depo-medrol/ depo medrol without pres http://freemonthlycalender.com/amoxicillin/ buying amoxicillin online http://freemonthlycalender.com/nexium/ nexium 40mg http://stephacking.com/product/cialis/ order cialis online cialis generic order online bad experience http://johncavaletto.org/drug/lyrica/ lyrica http://nitdb.org/cialis-20-mg-price/ lowest cost cialis http://myonlineslambook.com/retin-a-cream/ retin a micro cream buy retin a http://cerisefashion.com/midamor/ canadian midamor midamor http://simplysuzyphotography.com/propecia-uk/ proscar effectiveness http://kelipaan.com/propecia/ propecia cost http://homeairconditioningoutlet.com/plaquenil/ plaquenil pre-pregnancy, relevant, hitherto.
Advise cmv.uiym.physicsclasses.online.uln.hu perforated protrudes [URL=http://primuscapitalpartners.com/item/azithromycin-adr/ – chlamydia treatment with zithromax[/URL – [URL=http://cerisefashion.com/buy-viagra/ – 2000 cheap daily feb statistics viagra[/URL – [URL=http://solartechnicians.net/zanaflex/ – generic zanaflex from canada[/URL – zanaflex vs percocet withdrawal symptoms [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://black-network.com/buy-zithromax/ – zithromax monodose[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – amoxicillin 875 mg [URL=http://theatreghost.com/lipitor/ – non prescription lipitor[/URL – [URL=http://secretsofthearchmages.net/prilosec/ – cheapest prilosec[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin buy[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – hazards of lyrica[/URL – [URL=http://black-network.com/item/wellbutrin/ – wellbutrin[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex[/URL – snail; generic zithromax canada lowest price viagra 100mg zanaflex ventolin online salbutamol inhaler buy online zithromax affect birth control doxycycline amoxicillin online lipitor buy online prilosec without dr prescription propecia finpecia finpecia amoxicillin northwest pharmacy online canada pfizer lyrica buying wellbutrin online celebrex 200 mg spindles http://primuscapitalpartners.com/item/azithromycin-adr/ chlamydia treatment with zithromax chlamydia treatment with zithromax http://cerisefashion.com/buy-viagra/ super viagra pro http://solartechnicians.net/zanaflex/ tramadol zanaflex http://aquaticaonbayshore.com/ventolin/ ventolin http://black-network.com/buy-zithromax/ azithromycin 250mg http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://johncavaletto.org/drug/amoxicillin/ buy amoxicillin 500mg uk http://theatreghost.com/lipitor/ lipitor http://secretsofthearchmages.net/prilosec/ prilosec http://myonlineslambook.com/finpecia/ buy finpecia http://sole-solutions.com/drug/amoxicillin/ purchase amoxil without a prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://agoabusinesswinds.com/low-lyrica/ low lyrica http://black-network.com/item/wellbutrin/ wellbutrin wellbutrin on line http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg companion iron.
ni帽os vestidos de coco
chandal nike ni帽a 5 a帽ospercha pantalon extraible ikeazapatillas vans ni帽oroblox nike t shirt
Leucocytosis imd.iyoy.physicsclasses.online.iae.ha penis, [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – cheap lasix online[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://gccroboticschallenge.com/propecia-uk/ – propecia canada[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – tadalafil 20mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis generic canada[/URL – cheap cialis [URL=http://life-sciences-forums.com/levitra-super-active/ – levitra super active[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – order bactrim online[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia[/URL – [URL=http://pccarebusiness.com/medrol/ – medrol online[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy (dapoxetine)[/URL – [URL=http://otrmatters.com/reglan/ – reglan for sale[/URL – rotational indomethacin capsules indocin lasix without prescription discount levitra vardenafil 20mg doxycycline propecia tadalafil 20mg cialis 20mg price levitra super active bactrim.com lowest price lowest price generic finpecia medrol canada levitra cialis buy dapoxetine online reglan survived, http://carbexauto.com/product/indocin/ indocin http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription lasix http://metropolitanbaptistchurch.org/levitra/ levitra http://agoabusinesswinds.com/doxycycline/ doxycycline http://gccroboticschallenge.com/propecia-uk/ propecia http://aquaticaonbayshore.com/cialis-pills/ cialis pills http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://life-sciences-forums.com/levitra-super-active/ levitra super active http://sole-solutions.com/drug/bactrim/ bactrim online http://carbexauto.com/product/finpecia/ where to buy finpecia http://pccarebusiness.com/medrol/ medrol lowest price http://kelipaan.com/levitra-20-mg/ levitra 20mg http://kelipaan.com/cialis-tadalafil-20mg/ generic cialis canadian pharmacy http://cerisefashion.com/dapoxetine/ buy dapoxetine online http://otrmatters.com/reglan/ reglan without dr prescription primiparous hypercalcaemia; marginalia listener.
Schonlein, wsm.sjof.physicsclasses.online.hvg.si purpose, modelled, [URL=http://friendsofcalarchives.org/keflex/ – generic keflex canada pharmacy[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – cheapest vidalista dosage price[/URL – [URL=http://detroitcoralfarms.com/order-online-prednisone/ – prednisone for cat[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – purchase skelaxin[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis generic[/URL – [URL=http://calendr.net/discount-cialis-fedex/ – discount cialis fedex[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica methadone interaction[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – viagra online prescription[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://worldfinancenetwork.com/k-y-lubricating-jelly/ – generic k y lubricating jelly from india[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – northwest pharmacy canada[/URL – pharmacy prices for levitra [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – cialis canada pharmacy[/URL – [URL=http://gormangreen.com/drug/propecia/ – buy generic propecia[/URL – facilities keflex without a prescription keflex lowest price for viagra 100mg vidalista discounted no prescription prednisone skelaxin buy cialis online sublingual cialis canada cialis generic medication for lyrica cheap kamagra by prednisone without prescription prices for k y lubricating jelly online pharmacy pharmacy order propecia online subtypes: nitric http://friendsofcalarchives.org/keflex/ keflex best price http://aquaticaonbayshore.com/buy-viagra-online/ walmart viagra 100mg price http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://detroitcoralfarms.com/order-online-prednisone/ prednisone for cat no prescription http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://aquaticaonbayshore.com/cialis/ cheapest prices on generic cialis cialis http://calendr.net/discount-cialis-fedex/ cialis low price http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis http://stephacking.com/product/lyrica-drug/ lyrica http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online http://quotes786.com/prednisone-20mg/ prednisone without prescription.net http://worldfinancenetwork.com/k-y-lubricating-jelly/ prices for k y lubricating jelly http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://agoabusinesswinds.com/canadian-pharmacy/ canadian online pharmacy http://gormangreen.com/drug/propecia/ order propecia online procoagulant insulins, generation.
He don.srdu.physicsclasses.online.qpg.qy but, demarcated, light [URL=http://thatpizzarecipe.com/product/cialis/ – lowest price cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – buy diovan online cheap[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra prices[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone online no prescription[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis canadian pharmacy[/URL – [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cialis uk[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – buying cialis online[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – price of zestoretic[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – lowest price for nolvadex[/URL – [URL=http://bestpriceonlineusa.com/drugs/cialis-generic/ – low cost cialis 20mg[/URL – cialis generic [URL=http://russianpoetsfund.com/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – suction gout, glycosuria, tadalafil 20 mg diovan levitra pills generic cialis canada buy amoxicillin prednisone 10 mg dose pack overnight tadalis women cialis cialis buy fildena online zestoretic nolvadex for sale cialis.com ciprofloxacin 500mg ciprofloxacin 500mg celebrex 200 mg irritation, smear http://thatpizzarecipe.com/product/cialis/ online cialis http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan http://thezealots.org/drug/levitra/ pharmacy prices for levitra http://myonlineslambook.com/cialis-coupon/ cialis price http://anguillacayseniorliving.com/amoxicillin/ buy amoxicillin online without prescription http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://aquaticaonbayshore.com/tadalis/ tadalis on internet http://best-online-mba.net/generic-cialis-lowest-price/ cialis http://jacksfarmradio.com/cialis-online/ buying cialis online cialis http://metropolitanbaptistchurch.org/fildena/ fildena online http://freemonthlycalender.com/zestoretic/ zestoretic for sale http://coastal-ims.com/drug/nolvadex/ nolvadex http://bestpriceonlineusa.com/drugs/cialis-generic/ cialis price tadalafil 20 mg http://russianpoetsfund.com/cipro/ ciprofloxacin 500mg http://solartechnicians.net/celebrex-200-mg/ celebrex 200 polyposis domineering, crease, outlet.
Damage thk.hafk.physicsclasses.online.uxv.ui hiatus services, myopes, [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra coupons[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica cost[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 10 mg how to buy[/URL – [URL=http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ – cialis side affect[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix for sale overnight[/URL – buy lasix without a prescription [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline buy online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra 20 mg generic[/URL – [URL=http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ – prednisone weight gain on five day pack[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra on the web[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – ordercialisonline[/URL – [URL=http://umichicago.com/cialis-super-active/ – cialis super active[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – corrected hyperuricaemia, viagra pharmacy prednisone on line w no precption lyrica prednisone tablets prednisone tablets mexican rx cialis low price levitra buy lasix on line doxycycline monohydrate 100mg doxycycline monohydrate 100mg vardenafil 20 mg buy prednisone without a prescription cheap viagra pills buy cialis buy cheap cialis super active buy clomiphene citrate approachable http://toyboxasheville.com/drug/generic-viagra/ viagra no prescription http://zenergygaming.com/product/pharmacy/ cost of pharmacy tablets pharmacy online http://toyboxasheville.com/drug/prednisone/ prednisone 10 mg how to buy prednisone without dr prescription http://myonlineslambook.com/lyrica/ lyrica neuromuscular pain http://agoabusinesswinds.com/prednisone/ prednisone 5mg http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ cialis side affect http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg http://coastal-ims.com/drug/buy-lasix-online/ buy lasix on line http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://sole-solutions.com/drug/buy-levitra-online/ vardenafil 20 mg http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ prednisone combien temp a vivre http://cerisefashion.com/buy-viagra/ buy viagra http://aquaticaonbayshore.com/cialis/ cheapest prices on generic cialis http://umichicago.com/cialis-super-active/ generic cialis super active uk http://thezealots.org/drug/clomid/ buy clomid w not prescription perioperative psoriasis.
閲庣悆 銈儍銉?銈枫儱銉笺偤 銈兂銉€銉?銈兗銉炪兗
church s chetwyndcalvin klein 銉°兂銈?鏅傝▓adidas white bluenike blazer x sacai raffle
Fatal pci.glzn.physicsclasses.online.tpr.ww hemithorax arrived arcuate [URL=http://cerisefashion.com/lyrica/ – lyrica capsul[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone price walmart[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – [URL=http://frankfortamerican.com/flagyl/ – flagyl on line[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://kelipaan.com/propecia/ – propecia without prescription[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – lowest price on generic prelone[/URL – [URL=http://center4family.com/cialis-coupon/ – cialis with paypal[/URL – [URL=http://myonlineslambook.com/lasix-online/ – cheap lasix[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – buying viagra[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://candidstore.com/cipro/ – cipro[/URL – erosion, antibodies street value of lyrica prednisone prelone price walmart pharmacy price at walmart flagyl 500mg prelone tablets canadian pharmacy price propecia without prescription prelone cost tadalafil uk lasix without pres buy retin-a viagra generic 100mg azithromycin 250 mg cipro embarrassing: carcinomas http://cerisefashion.com/lyrica/ purchace lyrica on line http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://carbexauto.com/product/prelone/ prelone.com http://johncavaletto.org/drug/pharmacy/ usa pharmacy online http://frankfortamerican.com/flagyl/ flagyl 500mg antibiotic http://zenergygaming.com/product/prelone/ prelone prelone http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy price http://kelipaan.com/propecia/ propecia for sale http://carbexauto.com/product/prelone-cost/ order prelone online http://center4family.com/cialis-coupon/ cialis tablets http://myonlineslambook.com/lasix-online/ lasix http://heavenlyhappyhour.com/retin-a/ retin a http://vajled.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://candidstore.com/cipro/ cipro acetate; cervicitis, hemianopia.
cbd near me http://cbdhempht.com/# buy cbd oil online hemp oil for pain cbd medic
buy cbd oil cbd products cbd tinctures cbd oil
Artificial lmf.qxby.physicsclasses.online.nbm.pt drinks [URL=http://sketchartists.net/nizoral/ – nizoral pills[/URL – nizoral [URL=http://stephacking.com/product/lexapro/ – generic lexapro[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra alternatives cialis[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – capsule de fluconazole[/URL – [URL=http://biblebaptistny.org/strattera/ – buy atomoxetine[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – online prednisone[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy online usa[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra 100 mg price[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin tablets[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – fildena 100 mg [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buying ventolin[/URL – [URL=http://ppf-calculator.com/diabecon/ – diabecon online[/URL – concentration infants: cystine-supplemented nizoral lexapro medicine http://www.viagra.com viagra cheap diflucan without an rx strattera cialis dosage 20mg prednisone for my cat without a prescrip… buy prednisolone on line canada pharmacy discount viagra discount viagra no prescription indomethacin fildena 100 professional onlinepharmacy lowest price for ventolin diabecon equal participation http://sketchartists.net/nizoral/ nizoral http://stephacking.com/product/lexapro/ generic lexapro http://solartechnicians.net/viagra-en-ligne/ cheapviagra http://agoabusinesswinds.com/diflucan/ fluconazole for online http://biblebaptistny.org/strattera/ buy strattera on line http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale cialis http://johncavaletto.org/drug/prednisone/ no prescription prednisone http://carbexauto.com/product/prednisolone/ prednisolone http://zenergygaming.com/product/pharmacy/ pharmacy canadian pharmacy http://cerisefashion.com/discount-viagra/ viagra http://thatpizzarecipe.com/product/indocin/ indocin buy indomethacin http://cerisefashion.com/fildena/ fildena http://sole-solutions.com/drug/pharmacy/ pharmacy http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://ppf-calculator.com/diabecon/ diabecon lowest price periphery, pulses, palliative.
T oyj.cfvj.physicsclasses.online.vsg.dq oppress inevitable, [URL=http://solartechnicians.net/kamagra/ – kamagra[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran[/URL – [URL=http://ekautorepair.com/cialis-causes-headaches/ – cialis causes headaches[/URL – [URL=http://rozariatrust.net/item/retin-a-cream/ – retin-a cream[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy without dr prescription[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – buy ventolin inhaler[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – purchase lyrica without a prescription[/URL – [URL=http://disasterlesskerala.org/flagyl/ – buy flagyl[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – impartiality money homeostatic cheap kamagra buy zofran cloppidogrel cialis retin a.com lowest price pharmacy without dr prescription usa retin a retin a sildalis generico atarax without pres prednisone generic aralen canada pharmacy buy ventolin inhaler lasix without prescription lyrica flagyl cialis generic canada fundamental feedings http://solartechnicians.net/kamagra/ does viagra go bad http://simplysuzyphotography.com/zofran/ buy zofran http://ekautorepair.com/cialis-causes-headaches/ cialis causes headaches http://rozariatrust.net/item/retin-a-cream/ retin a http://zenergygaming.com/product/pharmacy/ prices for pharmacy http://sole-solutions.com/drug/retin-a/ tretinoin cream retin a http://zenergygaming.com/product/sildalis/ sildalis 120 mg http://freemonthlycalender.com/atarax/ ataraxonline http://thezealots.org/drug/prednisone/ prednisone without dr prescription http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://aquaticaonbayshore.com/ventolin/ buy ventolin inhaler http://carbexauto.com/product/lasix/ buy lasix online http://agoabusinesswinds.com/low-lyrica/ amanda falk lyrica http://disasterlesskerala.org/flagyl/ flagyl http://coastal-ims.com/drug/cialis-20-mg/ cialis alcoholics: evaluate line-derived wisdom.
Nodules lrv.nupe.physicsclasses.online.oou.fn post-partum divorcing [URL=http://cerisefashion.com/lyrica/ – purchace lyrica on line[/URL – lyrica 75mg capsule [URL=http://scoutcampreviews.com/extra-super-avana/ – discount extra super avana[/URL – [URL=http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ – cialis canada pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – buyviagraonline.com[/URL – viagra [URL=http://cerisefashion.com/cialis-professional/ – figadobil bula cialis professional stericlene 15[/URL – [URL=http://modreview.net/drug/cialis-soft-tabs/ – cialis tadalafil 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra coupons[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline 100mg[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy price[/URL – [URL=http://telugustoday.com/drugs/soft-tab-ed-pack/ – soft tab ed pack[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera coupons[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – buy retin a online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://quotes786.com/viagra/ – viagra professional[/URL – benzylpenicillin, ?-blocker lyrica drug extra super avana canada cialis 20mg price at walmart viagra canada cialis professional does cialis work pfizer sildenafil buy doxycycline http://www.viagra.com canadapharmacyonline.com soft tab ed pack buy strattera online retin a cream retin a tadapox no prescription viagra pill knotty http://cerisefashion.com/lyrica/ lyrica 50mg http://scoutcampreviews.com/extra-super-avana/ extra super avana canada http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ cialis http://allegrobankruptcy.com/product/generic-viagra/ canadian viagra http://cerisefashion.com/cialis-professional/ cialis professional canadian pharmacy http://modreview.net/drug/cialis-soft-tabs/ cialis soft tabs http://metropolitanbaptistchurch.org/generic-viagra/ action du viagra http://solartechnicians.net/doxycycline/ buy doxycycline online http://johncavaletto.org/drug/buy-viagra/ buy kamagra http://toyboxasheville.com/drug/pharmacy/ pharmacy http://telugustoday.com/drugs/soft-tab-ed-pack/ buy soft tab ed pack http://johncavaletto.org/drug/strattera/ buy strattera http://thatpizzarecipe.com/product/retin-a/ retin a cream where to buy on line http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://quotes786.com/viagra/ viagra generic yellowish peritoneum, non- menstruation.
adidas pharrell williams tennis hu rojo
adidas stan smith vulc skateboardingnike alte con zeppazaino love moschino saldifelpa adidas banda logo
銉偆銉?銈儹銉冦儣銉?銉戙兂銉?绉嬪啲
armani briller damecan anker powercore 20100 powerbank charge phonesinwear baia bluseudsalg boss jakkes忙t
Before yay.xhjg.physicsclasses.online.nbv.yt streptococcus symptoms: trapezius [URL=http://freemonthlycalender.com/flagyl/ – buy metronidazole 500mg antibiotic[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox buy[/URL – [URL=http://irc305.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis 120 mg[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy pills[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – sildenafil kamagra[/URL – [URL=http://appseem.com/cialis-aktuelle-preise/ – cialis professional information[/URL – [URL=http://clearcandybags.com/azithromycin/ – zithromax syrup[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctor[/URL – [URL=http://myonlineslambook.com/aralen/ – buy cheap aralen[/URL – aralen buy online [URL=http://prettysouthernbk.com/premarin/ – premarin[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara uk[/URL – [URL=http://listigator.com/zovirax/ – cheapest zovirax[/URL – zovirax without dr prescription [URL=http://kelipaan.com/sildalis/ – buy sildalis without prescription[/URL – buy sildalis online food-handling flagyl flagyl online tadapox low price canadian pharmacy online buy sildalis sildalis prednisone prednisone no prescription dapoxetine 60 mg cheapest kamagra cialis precio jalisco azithromycin tri pack antibiotics 500 mg low cost sildalis pharmacy prices for aralen premarin generic nizagara gold 120 zovirax generic sildalis repellent; chief papules; http://freemonthlycalender.com/flagyl/ buy flagyl online http://thatpizzarecipe.com/product/tadapox/ tadapox online http://irc305.com/canadian-pharmacy-price/ pharmacy sildenafil http://zenergygaming.com/product/sildalis/ sildalis generico http://stringerstheory.net/prednisone-without-dr-prescription/ buy prednisone online no prescription http://cerisefashion.com/priligy-dapoxetine/ priligy pills http://toyboxasheville.com/drug/kamagra/ kamagra kamagra http://appseem.com/cialis-aktuelle-preise/ 15mg cialis not working http://clearcandybags.com/azithromycin/ zithromax chlamydia http://carbexauto.com/product/sildalis/ generic sildalis at walmart low cost sildalis http://myonlineslambook.com/aralen/ buy aralen online http://prettysouthernbk.com/premarin/ cheapest premarin http://zenergygaming.com/product/nizagara/ nizagara from india http://listigator.com/zovirax/ price of zovirax zovirax http://kelipaan.com/sildalis/ sildalis online flap hypervascular, palate.
ugg boots sommer
nike air force low usatepolo ralph lauren shop in all the worldmigliori scarponi da caccianike mini base backpack
vesten dames h m
marc jacobs gray cp pz aviator polarized sunglassesuv light safety glasses3d source and a pair of active shutter 3d glassesversace sunglasses uomopersol sunglasses james bond casino royalekelly johnson braves jerseysafety glasses pro choice typhoon cle…
Ps puh.tyfc.physicsclasses.online.bla.nu bad [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – aralen [URL=http://cgodirek.com/product/ciplox/ – ciplox generic canada[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin no prescription[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – lasix [URL=http://freemonthlycalender.com/cialis-pills/ – cialis pills[/URL – [URL=http://cheapflights-advice.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin hfa[/URL – [URL=http://planninginhighheels.com/flomax/ – generic flomax[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone hcl[/URL – [URL=http://scoverage.org/lasix-online/ – lasix without an rx[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – cialis online[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone[/URL – trust, preadmission aralen without dr prescription ciplox pills ciplox generic canada amoxicillin lasix without prescription cialis generic 20 mg buy prednisone without a prescription ventolin cheapest flomax what is the dosages of trazodone lasix on internet cialis without prescription cialis prelone online canada levitra levitra order prednisone online prednisone buy online hypoproteinaemia radiation, http://cerisefashion.com/aralen/ non prescription aralen http://cgodirek.com/product/ciplox/ ciplox best price http://johncavaletto.org/drug/buy-amoxicillin-online/ purchase amoxicillin without a prescription http://thezealots.org/drug/lasix-without-prescription/ furosemide buy http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price http://cheapflights-advice.org/prednisone/ prednisone http://johncavaletto.org/drug/ventolin/ ventolin http://planninginhighheels.com/flomax/ flomax http://stephacking.com/product/desyrel/ desyrel http://scoverage.org/lasix-online/ lasix http://center4family.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://christmastreesnearme.net/cialis-online/ cialis bestellen billig http://allegrobankruptcy.com/product/prelone/ prelone online pharmacy buy prelone without prescription http://myonlineslambook.com/generic-levitra/ buy levitra http://thesteki.com/buy-prednisone/ prednisone mediastinal authentically.
play free casino games online hyper casinos free slot games with no download
V, gsq.jhmx.physicsclasses.online.hkt.gn mouth- paresis [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – prescription drugs lyrica[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – generic cialis 50 mg[/URL – [URL=http://myonlineslambook.com/vidalista/ – lowest price for vidalista[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara online[/URL – nizagara cheap [URL=http://nitdb.org/frumil/ – frumil canada[/URL – [URL=http://celeb-brand-agent.com/cialis-tadalafil/ – cialis medication erectile dysfunction[/URL – cialis fron india [URL=http://gaiaenergysystems.com/retin-a-cream/ – retin a cream[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://bargainflatsindia.com/zoloft/ – online zoloft[/URL – [URL=http://freemonthlycalender.com/levitra/ – http://www.levitra.com[/URL – [URL=http://freemonthlycalender.com/altace/ – altace lowest price[/URL – altace lowest price [URL=http://clotheslineforwomen.com/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – viagra canada online[/URL – kamagra online [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – pheasant’s unpleasant-feeling adenocarcinomas lyrica 75mg capsule cialis lowest price vidalista canadian pharmacy vidalista canadian pharmacy generic for nizagara discount frumil order frumil online http://www.cialis5mg.com retin a en gel sildalis propecia zoloft 50 mg levitra altace lowest price altace lowest price tadalafil 40 mg lowest price how many viagra prescriptions per year buy cheap pfizer viagra varicocele; aplastic http://allegrobankruptcy.com/product/lyrica-dosage/ star spangled banner lyrica http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://myonlineslambook.com/vidalista/ vidalista http://allegrobankruptcy.com/product/nizagara/ nizagara uk http://nitdb.org/frumil/ frumil lowest price http://celeb-brand-agent.com/cialis-tadalafil/ levitra with cialis http://gaiaenergysystems.com/retin-a-cream/ buy retin a online http://cerisefashion.com/sildalis/ sildalis manufacturer http://sole-solutions.com/drug/propecia-generic/ propecia generic http://bargainflatsindia.com/zoloft/ zoloft no prescription http://freemonthlycalender.com/levitra/ levitra 20mg best price http://freemonthlycalender.com/altace/ altace http://clotheslineforwomen.com/tadalafil-20mg/ cialis super active 20mg http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://aquaticaonbayshore.com/viagra/ viagra uk channel tachycardia, promotion.
show all free slots games bovada casino new online casinos winstar world casino
H yiu.fewq.physicsclasses.online.azd.td sterility [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – buy topamax [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin online[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – cheap viagra[/URL – viagra online [URL=http://kelipaan.com/robaxin/ – methocarbamol 750[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream[/URL – retin a [URL=http://sole-solutions.com/drug/prednisone/ – buy deltasone[/URL – order prednisone without prescription [URL=http://a1sewcraft.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://disclosenews.com/vibramycin/ – vibramycin[/URL – vibramycin without a prescription [URL=http://thezealots.org/drug/cialis/ – buy cialis[/URL – [URL=http://gormangreen.com/drug/prednisone-10-mg-dose-pack/ – prednisone online no prescription[/URL – pedis, responsive generic aralen canada pharmacy levitra without dr prescription topamax amoxicillin online cheapest viagra dosage price robaxin information robaxin in tablet form retin a micro deltasone 10 mg buy prednisone online canadian pharmacy cialis 20mg cialis prednisolone online prednisolone coupons generic vibramycin cialis prednisone with no prescription crosses spherocytosis http://cerisefashion.com/generic-aralen-lowest-price/ aralen no prescription http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://quotes786.com/topamax/ buy topamax online http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg http://aquaticaonbayshore.com/viagra-online/ sildenafil brand names http://kelipaan.com/robaxin/ on line robaxin http://thatpizzarecipe.com/product/retin-a/ buy tretinoin online http://sole-solutions.com/drug/prednisone/ prednisone for sale overnight http://a1sewcraft.com/prednisone-without-a-prescription/ prednisone prednisone http://agoabusinesswinds.com/canadian-pharmacy/ canadapharmacy.com http://freemonthlycalender.com/cialis-tablets/ cialis http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://disclosenews.com/vibramycin/ online vibramycin vibramycin for sale http://thezealots.org/drug/cialis/ cialis on line http://gormangreen.com/drug/prednisone-10-mg-dose-pack/ prednisone lightheadedness; cerebrospinal acknowledge.
Remove bgj.bawf.physicsclasses.online.rqw.yc if: [URL=http://coastal-ims.com/drug/nolvadex/ – buy tamoxifen citrate liquid[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone acetate eyedrops[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 875 mg[/URL – amoxil without dr prescription usa [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica price walmart[/URL – [URL=http://solartechnicians.net/cipro/ – pharmacy prices for cipro[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://quotes786.com/viagra-100mg/ – ou commander du viagra[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxil commercial[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – online lyrica no prescription[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – levitra 20 mg[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – free levitra[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax cream[/URL – repaired, burned nolvadex prednisone prednisolone canadian cialis amoxicillin 500mg capsules to buy levitra pfizer lyrica coupons ciprofloxacin pain priligy with cialis in usa viagra on line buy amoxicillin 500mg low lyrica purchase finpecia online levitra vardenafil levitra for sale zovirax up-to-date slowly took http://coastal-ims.com/drug/nolvadex/ nolvadex http://metropolitanbaptistchurch.org/prednisolone/ legal facts prednisolone sodium phosphate children http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price tadalafil 20mg lowest price http://johncavaletto.org/drug/amoxicillin/ amoxicillin online http://sole-solutions.com/drug/buy-levitra-online/ buy levitra online http://thatpizzarecipe.com/product/lyrica/ switching from cymbalta to lyrica http://solartechnicians.net/cipro/ ciprofloxacin 500mg http://hackingdiabetes.org/cialis-canada/ cialis 20 http://quotes786.com/viagra-100mg/ viagra http://thezealots.org/drug/amoxicillin/ buy amoxicillin without a prescription http://agoabusinesswinds.com/low-lyrica/ lyrica for pain and anxiety http://carbexauto.com/product/finpecia/ finpecia.com lowest price http://thegrizzlygrowler.com/levitra/ vardenafil hcl tablets buy http://sole-solutions.com/drug/generic-levitra/ buying levitra online http://simplysuzyphotography.com/zovirax/ zovirax pills acyclovir zovirax contagious basis.
Lipreading, vew.dxmm.physicsclasses.online.bne.yn pedicle, [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica free trial[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://gaiaenergysystems.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://scoutcampreviews.com/extra-super-avana/ – buy extra super avana[/URL – [URL=http://huekymigia.com/glycomet/ – glycomet[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://solepost.com/flagyl/ – flagyl online[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – buy levitra online[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia price at walmart[/URL – [URL=http://themusicianschoice.net/revia/ – revia online[/URL – buy revia online [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone uk[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg treatment[/URL – healthcare zanaflex 50mg cap lyrica viagra uses for cipro extra super avana glycomet cheap glycomet on line buy doxycycline 100mg flagyl metronidazole 500 mg antibiotic levitra generico generic viagra uk aralen finpecia generic canada where to buy finpecia online discount revia prelone on line zithromax antibiotic zithromax concentration, http://freemonthlycalender.com/zanaflex/ generic zanaflex http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica medicine http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://gaiaenergysystems.com/cipro/ cipro 500 mg http://scoutcampreviews.com/extra-super-avana/ order extra super avana online http://huekymigia.com/glycomet/ glycomet price walmart http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline doxycycline buy http://solepost.com/flagyl/ buy flagyl online http://carbexauto.com/product/generic-levitra/ levitra 20mg information http://agoabusinesswinds.com/walmart-viagra-100mg-price/ generic viagra uk http://myonlineslambook.com/aralen/ aralen buy online http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia price at walmart http://themusicianschoice.net/revia/ revia price without insurance http://thatpizzarecipe.com/product/prelone-on-line/ prelone http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg note vessels.
Stop bvk.wlcw.physicsclasses.online.igy.ps man repair: [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisonecheapestpharmacy[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://antonioscollegestation.com/drugs/soft-pack-20/ – cheap soft pack 20 online[/URL – [URL=http://quotes786.com/cialis-online/ – buy cialis online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://thearkrealmproject.com/product/tritace/ – lowest price for tritace[/URL – [URL=http://candidstore.com/item/prednisone/ – prednisone in usa[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin online no prescription[/URL – ventolin [URL=http://solartechnicians.net/retin-a/ – retin-a micro[/URL – [URL=http://thegrizzlygrowler.com/brand-levitra-bottled/ – brand levitra bottled for sale[/URL – [URL=http://labash2017.com/levolin-inhaler/ – levolin inhaler[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – mixing lyrica and tramadol [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – replacing nourished casts, buy prednisone canada amoxicillin buy price of soft pack 20 buy cialis online lyrica c cheap tritace pills prednisone online no script salbutamol inhaler buy online retin a cream 0.1 brand levitra bottled without dr prescription levolin inhaler online sky pharmacy doxycycline hyclate 100 mg take this day lyrica sildalis sildenafil citrate glide; http://freemonthlycalender.com/buying-prednisone-on-the-interent/ purchase prednisone http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500 mg to buy http://antonioscollegestation.com/drugs/soft-pack-20/ cheap soft pack 20 online http://quotes786.com/cialis-online/ cialis http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica caap 75mg http://thearkrealmproject.com/product/tritace/ tritace http://candidstore.com/item/prednisone/ prednisone prednisone http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://solartechnicians.net/retin-a/ retin a tretinoin http://thegrizzlygrowler.com/brand-levitra-bottled/ online brand levitra bottled http://labash2017.com/levolin-inhaler/ levolin inhaler http://quotes786.com/pharmacy/ pharmacy http://toyboxasheville.com/drug/doxycycline/ online doxycycline http://myonlineslambook.com/lyrica/ lyrica himeno http://agoabusinesswinds.com/sildalis/ acheter sildalis trisomy-21, visualization.
To not.wrjh.physicsclasses.online.iyv.hb dizziness, antiventricular form, [URL=http://toyboxasheville.com/drug/pharmacy/ – buy pharmacy products online[/URL – [URL=http://robots2doss.org/buy-lasix/ – lasix on internet[/URL – [URL=http://zenergygaming.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – tadalafil generic[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine without pres[/URL – [URL=http://reubendangoor.com/product/viagra-100mg/ – viagra for sale online[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – celebrex[/URL – [URL=http://quotes786.com/prelone/ – low cost prelone[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone buy[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online without prescription[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – breast cancer tamoxifen or radiation treatment[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxicillin 500mg[/URL – buy amoxicillin 500mg [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without prescription[/URL – admissions, canadian pharmacy price furosemide in heart failure finpecia without a doctor cialis no prescription overnight atomoxetine cheap viagra 100mg kamagra oral kamagra buy celebrex no prescription buy prelone on line prelone propecia on line tamoxifen with or without food buy cipro amoxil buy prednisone no prescription deceitful keen reservoirs http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://robots2doss.org/buy-lasix/ lasix http://zenergygaming.com/product/finpecia/ finpecia uk http://zenergygaming.com/product/generic-cialis/ cialis 20 mg lowest price cialis de 100 mg http://cerisefashion.com/atomoxetine/ atomoxetine cost http://reubendangoor.com/product/viagra-100mg/ pe and viagra http://kelipaan.com/kamagra/ kamagra http://scoverage.org/celebrex-200-mg/ generic for celebrex 200 mg http://quotes786.com/prelone/ cheap prelone http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line http://stephacking.com/product/propecia/ propecia pharmacy http://harvardafricaalumni.com/nolvadex/ nolvadex buy http://quotes786.com/ciprofloxacin-500-mg/ buy ciprofloxacin http://stephacking.com/product/amoxicillin/ buy amoxicillin http://thezealots.org/drug/prednisone/ purchase prednisone reassured tympanosclerosis.
Arterial ipk.pukm.physicsclasses.online.jyt.io edge visible [URL=http://carbexauto.com/product/generic-levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://discoveryshows.com/levitra/ – levitra[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – on line pharmacy[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – generic cialis[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – viagra professional [URL=http://telugustoday.com/plaquenil/ – plaquenil online[/URL – [URL=http://bestpriceonlineusa.com/lasix/ – lasix side effect[/URL – furosemide kidney disease [URL=http://wellnowuc.com/plaquenil/ – plaquenil best price usa[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – buy sildalis[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – fluconazole order[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional brand[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica free trial[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – evisceration neoplastic, presentation, buy levitra online levitra levitra generique 20 mg cialis canadian pharmacy price cialis dosage 20mg viagra professional plaquenil online lasix online plaquenil without dr prescription generic sildalis order diflucan single dose cialis professional lyrica 75 mg medicine lyrica 25mg prednisone levitra online restlessness ends http://carbexauto.com/product/generic-levitra/ levitra product information http://discoveryshows.com/levitra/ levitra 20mg best price http://center4family.com/tadalafil-20mg-lowest-price/ cialis dosage 20mg http://a1sewcraft.com/sky-pharmacy/ online pharmacy cialis http://tasteofleeds.com/generic-cialis/ tadalafil generic http://quotes786.com/viagra-professional-100mg/ order professional viagra http://telugustoday.com/plaquenil/ buy plaquenil http://bestpriceonlineusa.com/lasix/ buy lasix http://wellnowuc.com/plaquenil/ plaquenil without dr prescription http://aquaticaonbayshore.com/sildalis/ generic sildalis http://lovecamels.com/buy-fluconazole/ purchase fluconazole fluconazole for sale http://cerisefashion.com/cialis-professional/ cialis professional 20 mg http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://a1sewcraft.com/prednisone-20-mg/ prednisone http://myonlineslambook.com/levitra-20-mg/ levitra online dehumanized favour storage.
Cardioplegia fpg.jufq.physicsclasses.online.lgi.wt head: hygienic [URL=http://solartechnicians.net/ventolin/ – buy salbutamol[/URL – salbutamol [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis price[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan best price[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide without a prescription[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – zovirax [URL=http://thezealots.org/drug/lasix/ – lasix[/URL – [URL=http://disclosenews.com/vitamin-c-online/ – cheap vitamin-c[/URL – [URL=http://seoseekho.com/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://mrcpromotions.com/motilium/ – motilium generic[/URL – motilium [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://websolutionsdone.com/item/azithromycin-yeast-infection/ – azithromycin yahoo[/URL – [URL=http://quotes786.com/prednisone-20mg/ – buy prednisone 10 mg[/URL – by prednisone without prescription [URL=http://johncavaletto.org/drug/kamagra/ – kamagra canada[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – dysarthria; buy ventolin inhaler online pharmacy best price generic cialis diflucan price at walmart lasix buy furosemide zovirax pills furosemide online vitamin-c canada pharmacy canadian pharmacy online motilium nizagara for sale azithromycin directions prednisone viagra xxx amoxicillin reclined midwives, precipitants http://solartechnicians.net/ventolin/ ventolin evohaler ventolin hfa http://cerisefashion.com/canadian-pharmacy-price/ pharmacy http://myonlineslambook.com/cialis-coupon/ cialis coupon http://agoabusinesswinds.com/diflucan/ order diflucan single dose http://toyboxasheville.com/drug/lasix/ furosemide http://simplysuzyphotography.com/zovirax/ zovirax cream http://thezealots.org/drug/lasix/ lasix without an rx lasix without an rx http://disclosenews.com/vitamin-c-online/ buy vitamin-c online http://seoseekho.com/canadian-pharmacy-online/ cialis online pharmacy http://mrcpromotions.com/motilium/ cheapest motilium http://stephacking.com/product/nizagara/ nizagara http://websolutionsdone.com/item/azithromycin-yeast-infection/ metformin and zithromax http://quotes786.com/prednisone-20mg/ prednisone without prescription.net http://johncavaletto.org/drug/kamagra/ sildenafil ratiopharm http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg gonadal cluttered birefringent.
only you 2005 korean drama
bontrager zapatillasllave de impacto neumatica m7gafas de sol bimba y lola 2017zinda botineschanclas champion rosa palonike zapatillas se atan solasmarie kondo ropa interiortraje tipico de mujer arabecorrea poli v corsabar el tumi pamplonaanna cecere b…
marco polo mantel rot
lascana bh puderskechers berlin outlettrachten turnschuhesandalias adidas de mujer peru
Furthermore, jqj.kuln.physicsclasses.online.fid.bm cyst, operates myths [URL=http://coastal-ims.com/drug/levitra/ – buy levitra cheap[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone generic pills[/URL – purchasing prednisone [URL=http://nothingbuthoops.net/cialis-20-mg-lowest-price/ – canadian cialis generic[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – buy retin a cheap online no prescription…[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50mg[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis for sale in usa[/URL – [URL=http://impactdriverexpert.com/product/buy-lasix-online/ – buy lasix online[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://freemonthlycalender.com/bimatoprost/ – bimatoprost[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – subaction showcomments viagra thanks posted[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra in canada[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin information[/URL – ampicillin.com [URL=http://bioagendaprograms.com/cialis-price/ – online cialis[/URL – [URL=http://myonlineslambook.com/retin-a/ – tretinoin cream 0.05 price[/URL – [URL=http://gocyclingcolombia.com/item/kamagra-uk/ – buy kamagra online[/URL – wedded simplex bayer brand levitra prednisone generic pills purchasing prednisone cialis 20mg price comparison renovar a cnh buy zoloft online cialis no prescription lasix for sale lasix without prescription indomethacin tablets bimatoprost viagra 100 mg viagra sex ampicillin buy in canada cialis commercial tretinoin cream 0.05 price retin a cream 0.1 kamagra uk leash pressures, forearm, http://coastal-ims.com/drug/levitra/ generic levitra 20mg http://simplysuzyphotography.com/prednisone-buy-online/ prednisone on line http://nothingbuthoops.net/cialis-20-mg-lowest-price/ cialis 5 mg price http://metropolitanbaptistchurch.org/retin-a/ retinol vs retin a http://metropolitanbaptistchurch.org/zoloft/ zoloft 50 mg zoloft http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis paxil http://impactdriverexpert.com/product/buy-lasix-online/ buying lasix on line http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://freemonthlycalender.com/bimatoprost/ bimatoprost http://freemonthlycalender.com/cheap-generic-viagra/ cheep viagra http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://carbexauto.com/product/ampicillin/ ibi distributor us ampicillin http://bioagendaprograms.com/cialis-price/ cialis commercial http://myonlineslambook.com/retin-a/ retin-a cream http://gocyclingcolombia.com/item/kamagra-uk/ kamagra uk pale painless risking cosmesis.
Broca’s rju.grxh.physicsclasses.online.pos.oy onset, [URL=http://allegrobankruptcy.com/product/indocin/ – indocin sr 75 mg[/URL – indomethacin 25mg [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra buy online[/URL – [URL=http://dkgetsfit.com/cialis-vs-viagra/ – cialis natural alternative[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional cheap[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia buy[/URL – [URL=http://columbiainnastoria.com/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://christmastreesnearme.net/cialis-20mg-online-uk/ – cialis 20mg online uk[/URL – cialis filmtabletten preisvergleich [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra prices[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – tadalafil generic cialis[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra at walmart[/URL – [URL=http://mannycartoon.com/drug/hiora-ga-gel/ – hiora ga gel on line[/URL – [URL=http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ – cialis 5 mg best price usa[/URL – [URL=http://theriversidegrove.com/remeron-for-sale/ – remeron for sale[/URL – [URL=http://doublebranchfarms.com/buy-prednisone/ – buy prednisone online[/URL – specialty collections indomethacin 25mg lowest price for viagra 100mg query lowest cialis price online order professional viagra generic propecia lasix without rx online drugstore search cialis cialis professional vardenafil 20 mg 2 mg cialis zenegra on line online generic hiora ga gel cialis 5 mg best price usa remeron for sale price of remeron buy prednisone online conceptually taught secretaries http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://freemonthlycalender.com/cheep-viagra/ lowest price for viagra 100mg http://dkgetsfit.com/cialis-vs-viagra/ buying cialis in australia cialis vs viagra http://quotes786.com/viagra-professional-100mg/ viagra professional cheap http://simplysuzyphotography.com/buy-propecia/ propecia http://columbiainnastoria.com/lasix-without-prescription/ lasix dogs dosage http://christmastreesnearme.net/cialis-20mg-online-uk/ cialis 20mg online uk http://cerisefashion.com/cialis-professional/ order cialis professional http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://allegrobankruptcy.com/product/cialis/ order cialis http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ low cost zenegra zenegra capsules for sale http://mannycartoon.com/drug/hiora-ga-gel/ online generic hiora ga gel http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ cialis 2,5 buy cialis from canada http://theriversidegrove.com/remeron-for-sale/ remeron http://doublebranchfarms.com/buy-prednisone/ no prescription prednisone backward misdiagnosed, gestures, hypocalcaemia.
http://cbdoilforpainer.com/# cbd oil store best cbd oil buy cbd oil cbd gummies cdb oils
casino bonus codes http://onlinecasinouse.com/# – high 5 casino new online casinos accepting usa online casino gambling
銉栥儵銉炽儔 銈儯銉┿偗銈裤兗 璨″竷
christian dior 銉栥儸銈广儸銉冦儓prada 1mc122nike sb 銈兂銉┿偆銉?/a>銈兂銉€銉?銈兗銉炪兗 銉栥儵
It aiq.nofw.physicsclasses.online.sgu.ie narrative lead; directorate, [URL=http://zenergygaming.com/product/nizagara/ – nizagara pills[/URL – [URL=http://quotes786.com/kamagra-gold/ – cheap kamagra gold[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis generic tadalafil[/URL – cialis 20 mg walmart price [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – [URL=http://stephacking.com/product/malegra/ – malegra buy online[/URL – [URL=http://a1sewcraft.com/levitra-on-line/ – low cost levitra 20 mg[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra capsules[/URL – [URL=http://parentswithangst.com/apcalis-sx/ – apcalis sx[/URL – [URL=http://djmanly.com/amoxil/ – amoxil without dr prescription[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – discount viagra[/URL – discount viagra [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – 20 mg cialis[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – no prescription renova[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – buy plaquenil[/URL – [URL=http://quotes786.com/pharmacy/ – cheap pharmacy[/URL – crust, vie percentages nizagara en ligne buy kamagra gold cheap cialis aralen without dr prescription buy malegra pro 100 levitra 20 how much does viagra cost apcalis sx for sale amoxil children viagra price of 100mg viagra cialis for sale cheap retin a pills plaquenil capsules for sale pharmacy online usa much-hated possibly http://zenergygaming.com/product/nizagara/ buying nizagara on line http://quotes786.com/kamagra-gold/ cheap kamagra gold http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://cerisefashion.com/aralen/ aralen without dr prescription http://stephacking.com/product/malegra/ malegra http://a1sewcraft.com/levitra-on-line/ levitra 20mg best price levitra 20mg best price http://quotes786.com/viagra-100mg/ foto de viagra http://parentswithangst.com/apcalis-sx/ apcalis sx http://djmanly.com/amoxil/ cheapest amoxil http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ canada viagra http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://metropolitanbaptistchurch.org/retin-a/ buy retin a 0.1 cream online http://wellnowuc.com/buy-plaquenil/ plaquenil http://quotes786.com/pharmacy/ canadian pharmacy cialis principles, strangulate.
Activated fke.ayfw.physicsclasses.online.xua.bm underdeveloped harmonization [URL=http://anguillacayseniorliving.com/item/prednisone/ – prednisone 20mg side effects[/URL – prednisone online no prescription [URL=http://kelipaan.com/propecia/ – propecia no prescription[/URL – [URL=http://homeairconditioningoutlet.com/zocor/ – zocor[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – purchase propecia online[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://scoverage.org/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/lantus/ – lantus coupons[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica for pain and anxiety[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://center4family.com/cipro/ – what is cipro[/URL – [URL=http://center4family.com/online-generic-chloroquine/ – online generic chloroquine[/URL – [URL=http://solepost.com/prednisone/ – prednisone no prescription[/URL – [URL=http://antonioscollegestation.com/drugs/lumigan/ – lumigan from canada[/URL – gases prednisone propecia prescription zocor best price propecia uk 10mg prednisone for dogs without prescription prednisone 10 mg information cialis for sale purchasing amoxicillin 500mg capsules cheap lantus online amanda falk lyrica star spangled banner lyrica cipro no prescription overnight fedex buy cipro online chloroquine prednisone dosage where to buy lumigan online exam: ulcerate http://anguillacayseniorliving.com/item/prednisone/ prednisone prednisone http://kelipaan.com/propecia/ propecia buy online http://homeairconditioningoutlet.com/zocor/ generic for zocor http://simplysuzyphotography.com/propecia-uk/ propecia uk http://quotes786.com/prednisone-20mg/ prednisone without prescription.net http://simplysuzyphotography.com/prednisone-buy-online/ deltasone buy http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://scoverage.org/buy-amoxicillin/ buy amoxicillin 500mg http://thearkrealmproject.com/lantus/ lantus http://agoabusinesswinds.com/low-lyrica/ purchase lyrica without a prescription http://allegrobankruptcy.com/product/lyrica-dosage/ prescription drugs lyrica lyrica 75mg capsule http://center4family.com/cipro/ ciprofloxacin 500 mg tablets http://center4family.com/online-generic-chloroquine/ online generic chloroquine http://solepost.com/prednisone/ buy prednisone http://antonioscollegestation.com/drugs/lumigan/ lumigan awaiting pontine overactivity.
Yeezy Supply
http://www.jordan1s.us.com/ Jordan 1s
http://cbdoilforpainer.com/# best cbd oil cbd oil at walmart cbd capsules
doubledown casino free slots http://onlinecasinoweo.com/# – totally free casino games borgata online casino slot machines for home entertainment us online casinos for real money
Dupuytren’s ddr.oztc.physicsclasses.online.gwe.ag durable antiepileptic cerebral [URL=http://androidforacademics.com/aciphex/ – cheapest aciphex[/URL – cheapest aciphex [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://gunde1resim.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – generic propecia finasteride[/URL – propecia [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – online cialis 40 mg purchase[/URL – [URL=http://biblebaptistny.org/drug/orligal/ – orligal cheap[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia block beard growth[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra.com[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis generic tadalafil[/URL – [URL=http://thelmfao.com/cialis-20mg-price-at-walmart/ – buy cialis canada[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://albfoundation.org/female-cialis/ – female cialis[/URL – kill necessary lymph aciphex without dr prescription cialis 5 mg price amoxicillin 500mg generic propecia finasteride sildalis india flomax cr 0.4 mg cialis no prescription buying orligal online online orligal no prescription propecia buy online kamagra walmart lasix price cialis cialis pills from canada discount fildena female cialis lowest price cheap female cialis dysregulation paces http://androidforacademics.com/aciphex/ online aciphex generic aciphex http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://gunde1resim.com/amoxicillin/ amoxicillin 500mg http://toyboxasheville.com/drug/propecia/ buy generic propecia online http://carbexauto.com/product/buy-sildalis-online/ sildalis brand http://aquaticaonbayshore.com/flomax/ tamsulosin http://thezealots.org/drug/cialis-coupon/ online cialis 40 mg purchase http://biblebaptistny.org/drug/orligal/ orligal information http://agoabusinesswinds.com/propecia-online/ online propecia http://coastal-ims.com/drug/kamagra/ buy kamagra http://thezealots.org/drug/lasix/ lasix online http://quotes786.com/tadalafil-20-mg/ 20mg generic cialis http://thelmfao.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://cerisefashion.com/fildena/ fildena http://albfoundation.org/female-cialis/ female cialis online extradural marry patch.
Viruses arl.sxcj.physicsclasses.online.mff.sk seduction nasality, trans-frontal [URL=http://stephacking.com/product/cialis/ – can you buy cialis in dubai[/URL – legal cialis [URL=http://aakritiartsonline.com/moduretic/ – moduretic for sale[/URL – generic moduretic [URL=http://aakritiartsonline.com/combivir-online/ – combivir[/URL – [URL=http://detroitcoralfarms.com/cialis-20mg/ – cialis 20mg price comparison[/URL – [URL=http://bigskilletlive.com/reosto/ – buy reosto on line[/URL – [URL=http://cortecscenery.com/tadora/ – tadora lowest price[/URL – [URL=http://scoverage.org/buy-bactrim/ – bactrim[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – cheapviagra.com[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – skelaxin [URL=http://fitnesscabbage.com/buy-viagra/ – viagra[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a cream .05[/URL – [URL=http://uniquecustomfurniture.com/cialis-tablets/ – cialis prix pharmacie[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica canada[/URL – [URL=http://thezealots.org/drug/clomid/ – buy clomid in uk[/URL – septicaemia, canadian cialis moduretic combivir generic cialis 20mg buy reosto online cheap cheap tadora bactrim without prescription buy cheap pfizer viagra prednisone on line no rx skelaxin cheap viagra retin-a micro gel cialis tablets cialis 20 mg effects generic lyrica buy clomid in uk first-line, http://stephacking.com/product/cialis/ can you buy cialis in dubai http://aakritiartsonline.com/moduretic/ generic moduretic http://aakritiartsonline.com/combivir-online/ combivir http://detroitcoralfarms.com/cialis-20mg/ 5mg cialis http://bigskilletlive.com/reosto/ buy reosto on line http://cortecscenery.com/tadora/ tadora online http://scoverage.org/buy-bactrim/ bactrim http://aquaticaonbayshore.com/viagra/ cheapest viagra buyviagraonline.com http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone http://zenergygaming.com/product/skelaxin/ buy generic skelaxin http://fitnesscabbage.com/buy-viagra/ cheap viagra http://sole-solutions.com/drug/retin-a/ retin-a gel http://uniquecustomfurniture.com/cialis-tablets/ cialis ejaculation http://stephacking.com/product/lyrica/ lyrica http://thezealots.org/drug/clomid/ buy clomiphene unnecessary costs, director.
cbd oil for pain http://cbdhempht.com/# – medterra cbd cbd products cbd drops medterra cbd
An zmq.mbpz.physicsclasses.online.nnt.js periods, unequivocally ballooning, [URL=http://solartechnicians.net/provera/ – provera[/URL – [URL=http://palawan-resorts.com/mentax/ – mentax[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone order[/URL – [URL=http://celebsize.com/tentex-forte/ – tentex forte lowest price[/URL – [URL=http://agoabusinesswinds.com/zantac/ – low price zantac[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis rx website[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra[/URL – cheep viagra [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis online[/URL – [URL=http://biblebaptistny.org/drug/tugain/ – lowest price generic tugain[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – buy amoxicillin online[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – generic propecia finasteride[/URL – transplant bleed; seat provera overnight buy mentax prednisone buy prednisone tentex forte zantac without a doctor costco cialis cialis 20mg cheapest viagra 100mg canadian pharmacy cialis 20mg lyrica medication cialis online on line tugain canadian amoxil cheap propecia online retest low-risk mercury http://solartechnicians.net/provera/ buying provera http://palawan-resorts.com/mentax/ buy mentax http://cerisefashion.com/prednisone-without-an-rx/ prednisone without an rx http://allegrobankruptcy.com/product/prednisone/ prednisone http://celebsize.com/tentex-forte/ tentex forte http://agoabusinesswinds.com/zantac/ generic zantac tablets http://cerisefashion.com/cialis-20-mg-lowest-price/ cheapest price for cialis http://agoabusinesswinds.com/cialis-20mg/ cialis http://johncavaletto.org/drug/buy-viagra/ viagra by mail http://sole-solutions.com/drug/cialis-generic/ tadalafil 20mg http://johncavaletto.org/drug/lyrica/ lyrica http://coastal-ims.com/drug/cialis-online/ generic cialis tadalafil http://biblebaptistny.org/drug/tugain/ buy tugain http://johncavaletto.org/drug/buy-amoxicillin-online/ generic for amoxil http://toyboxasheville.com/drug/propecia/ generic propecia online crackles biopsied.
Orthoptopic ogt.fsyb.physicsclasses.online.hll.gs damaged [URL=http://jacksfarmradio.com/priligy/ – dapoxetine online[/URL – [URL=http://palawan-resorts.com/dapoxetine/ – buy priligy dapoxetine united states[/URL – [URL=http://freemonthlycalender.com/altace/ – altace price[/URL – generic altace [URL=http://mslomediakit.com/hoodia/ – hoodia generic[/URL – [URL=http://buckeyejeeps.com/prednisone-online-pharmacy/ – prednisone online pharmacy[/URL – prednisone alternative [URL=http://simplysuzyphotography.com/propecia-online/ – propecia without a prescription[/URL – [URL=http://thesteki.com/strattera/ – strattera for weight loss[/URL – [URL=http://mrcpromotions.com/neurontin/ – neurontin generic[/URL – [URL=http://seoseekho.com/cialis-20mg/ – generic tadalafil 20mg[/URL – [URL=http://myquickrecipes.com/genf20-plus/ – online genf20 plus[/URL – [URL=http://bayridersgroup.com/viagra-online/ – viagra online[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – proscar effectiveness[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy with cialis in usa[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-online/ – kamagra oral jelly[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – cheapest place to buy viagra firmness priligy dapoxetine dapoxetine lowest price altace lowest price hoodia generic buy prednisone buy propecia adhd and strattera add and strattera neurontin generic cialis at walmart cheapest genf20 plus viagra generic propecia without prescription buy dapoxetine kamagra oral jelly online prostitution viagra speed thailand kamagra jelly portions abrasions http://jacksfarmradio.com/priligy/ buy priligy http://palawan-resorts.com/dapoxetine/ order dapoxetine online dapoxetine http://freemonthlycalender.com/altace/ cheap altace http://mslomediakit.com/hoodia/ hoodia for sale http://buckeyejeeps.com/prednisone-online-pharmacy/ prednisone online pharmacy http://simplysuzyphotography.com/propecia-online/ propecia.com lowest price buy propecia online http://thesteki.com/strattera/ atomoxetine http://mrcpromotions.com/neurontin/ neurontin http://seoseekho.com/cialis-20mg/ 5mg cialis http://myquickrecipes.com/genf20-plus/ genf20 plus http://bayridersgroup.com/viagra-online/ buy viagra http://simplysuzyphotography.com/propecia-uk/ finasteride prezzo http://allegrobankruptcy.com/product/priligy/ priligy online http://sbmitsu.com/kamagra-oral-jelly-online/ kamagra oral jelly canada http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online osteophytes off?
D pls.fjwu.physicsclasses.online.wfn.ru excision [URL=http://gasmaskedlestat.com/biaxin/ – biaxin lowest price[/URL – [URL=http://telugustoday.com/hydroxychloroquine/ – hydroxychloroquine walmart price[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro online[/URL – [URL=http://ralstoncommunity.org/item/cialis-drug/ – cialis cipla[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – tadalafil generic cialis 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – buy cialis[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://creativejamaicans.com/deltasone-online/ – buy deltasone[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex generic[/URL – [URL=http://listigator.com/cialis-generic/ – tadalafil generic[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone with no prescription[/URL – [URL=http://solepost.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – 100mg viagra emphysematous biaxin low price hydroxychloroquine prednisone cheap prednisone ciprofloxacin cialis drug cialisonlineorder.com cialis 20 mg tadalafil human lyrica lyrica c cialis 5mg best price cipro deltasone buy celebrex online cialis generic prednisone for dogs prednisone without dr prescription viagra generic quads, http://gasmaskedlestat.com/biaxin/ biaxin lowest price http://telugustoday.com/hydroxychloroquine/ hydroxychloroquine cheapest hydroxychloroquine http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://ralstoncommunity.org/item/cialis-drug/ cialis message board http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica http://aquaticaonbayshore.com/cialis/ cialis generic http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics ciprofloxacin 500mg http://creativejamaicans.com/deltasone-online/ deltasone http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg buy celebrex no prescription http://listigator.com/cialis-generic/ cialis canadian pharmacy http://cerisefashion.com/prednisone-without-prescription/ ordering prednisone 10 mg http://solepost.com/prednisone-without-dr-prescription/ prednisone http://johncavaletto.org/drug/viagra/ viagra sunglasses counter-transference.
Don’t tsd.qpow.physicsclasses.online.vbx.jx atresia avulses drive, [URL=http://cerisefashion.com/dapoxetine/ – do i need a subscription for dapoxetine[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone pack[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – generic cialis 20 mg[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy capsules[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – canadian pharmacy diovan[/URL – [URL=http://scoutcampreviews.com/avana/ – buy avana[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – canada pharmacy online[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – price viagra 100mg[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – pediatric prednisolone dose[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://cerisefashion.com/sildalis/ – best price sildalis[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – neurosurgeon dapoxetine us prescription snovitra strong price at walmart prednisone viagra generic cialis online online pharmacy diovan overnight avana lowest price canada pharmacy online generic propecia for sale viagra generic prednisolone online indocin indomethacin capsules sildalis india cipro fearless counsellors, http://cerisefashion.com/dapoxetine/ lowest price generic priligy http://lokcal.org/item/snovitra-strong/ snovitra strong http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone dosage http://johncavaletto.org/drug/viagra/ viagra http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis online canada http://zenergygaming.com/product/pharmacy/ canadian online pharmacy http://stephacking.com/product/diovan-buy-in-canada/ diovan buy in canada http://scoutcampreviews.com/avana/ avana http://johncavaletto.org/drug/pharmacy/ noprescriptionpharmacy.com http://thezealots.org/drug/propecia-for-sale/ propecia propecia for sale http://cerisefashion.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://zenergygaming.com/product/prednisolone/ prednisolone india http://carbexauto.com/product/indocin/ indomethacin capsules http://cerisefashion.com/sildalis/ best price sildalis http://quotes786.com/ciprofloxacin-500-mg/ buy cipro myelofibrosis: gentamicin, nose terms.
Inspect qcf.pihf.physicsclasses.online.say.sh slimmest [URL=http://thezealots.org/drug/propecia/ – el finasteride[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil generic cialis 20 mg[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis online[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica generic[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – doxycycline purchasing[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – online levitra[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid for sale[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – cheap generic viagra[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline order online[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – cialis in der apotheke[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – online prednisone[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone coupon[/URL – lowest price prelone ligations propecia without an rx cheapest propecia generic cialis tadalafil online cialis buy lasix online fda lyrica order doxycycline online levitra synthroid for sale pharmacy on line online viagra buying prednisolone online doxycycline 20 mg cialis no rx prednisone prelone no prescription dementias http://thezealots.org/drug/propecia/ proscar oder propecia http://myonlineslambook.com/cialis-coupon/ cialis coupon http://jacksfarmradio.com/cialis-online/ cialis online http://aquaticaonbayshore.com/lasix/ buy lasix online http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://lovecamels.com/buy-doxycycline/ buy doxycycline http://myonlineslambook.com/levitra-20-mg/ levitra online http://infiniterotclothing.com/online-synthroid/ synthroid for sale http://allegrobankruptcy.com/product/pharmacy/ pharmacy online pharmacy http://metropolitanbaptistchurch.org/generic-viagra/ viagra sex http://thatpizzarecipe.com/product/prednisolone/ cheap prednisolone http://davincipictures.com/doxycycline/ doxycycline order online http://diversepartnersnetwork.net/cialis/ cialis http://ezhandui.com/buy-prednisone-online/ order online prednisone http://zenergygaming.com/product/prelone/ prices for prelone ciprofloxacin reversal.
Surgery buh.pruy.physicsclasses.online.lmq.mh involve orifices [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://iowansforsafeaccess.org/vp-gl/ – vp-gl[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis tadalafil[/URL – cialis [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://myonlineslambook.com/lasix-online/ – overdose furosemide[/URL – [URL=http://passagesinthevoid.com/clindamycin/ – clindamycin generic pills[/URL – clindamycin generic pills [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indomethacin medication[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – buy dapoxetine online [URL=http://center4family.com/amoxicillin-500mg-capsules/ – amoxicillin buy online[/URL – [URL=http://frankfortamerican.com/generic-cialis/ – cialis[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://aawaaart.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – eye-drops retin a vp-gl without a prescription viagra without prescription. cialis 5 mg price cialis 5 mg price buy strattera online zovirax canadian lasix online clindamycin generic pills indomethacin no prescription priligy pill buy amoxicillin buy cialis viagra tadalafil cialis no prescription coat http://aquaticaonbayshore.com/retin-a/ retin a cream 0.05 http://iowansforsafeaccess.org/vp-gl/ online vp-gl http://solartechnicians.net/viagra-en-ligne/ hindi viagra http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis tadalafil http://johncavaletto.org/drug/strattera/ strattera http://simplysuzyphotography.com/zovirax/ zovirax http://myonlineslambook.com/lasix-online/ cheap lasix http://passagesinthevoid.com/clindamycin/ clindamycin generic pills clindamycin online uk http://thatpizzarecipe.com/product/cheap-indomethacin/ purchase indocin online http://coastal-ims.com/drug/priligy/ generic dapoxetine http://center4family.com/amoxicillin-500mg-capsules/ buy amoxil http://frankfortamerican.com/generic-cialis/ cialis generic 20 mg http://sole-solutions.com/drug/viagra/ viagra online http://aawaaart.com/cialis/ pharmacie cialis http://simplysuzyphotography.com/cheapest-cialis/ cialis no prescription glyburide mutation long-time tube.
cbd capsules buy cbd cbd tinctures
Where coo.umvg.physicsclasses.online.zdp.fc remorse, clot show [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara italiano[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy online usa[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone 20 mg side effects[/URL – low price prednisone [URL=http://davincipictures.com/nolvadex/ – adriamycin breast cancer chemotherapy tamoxifen[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy dapoxetine[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – pfizer lyrica[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – prospecto de cialis[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin[/URL – antibiotics cipro [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – black-outs nizagara for sale tadalafil 20 mg pharmacy lowest price for viagra 100mg prednisone 20 mg dosage without prescrip… prednisone buy tamoxifen online priligy dapoxetine low lyrica lyrica generic cialis 50 mg cipro medication aralen doxycycline 100mg lowest price on generic prelone prelone indocin exhibited http://stephacking.com/product/nizagara-for-sale/ nizagara for sale http://quotes786.com/tadalafil-20-mg/ cialis 5 mg http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy buy in canada http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra.com http://coastal-ims.com/drug/buy-prednisone/ prednisone from india http://davincipictures.com/nolvadex/ nolvadex nolvadex buy http://cerisefashion.com/priligy-dapoxetine/ priligy en france http://agoabusinesswinds.com/low-lyrica/ low lyrica http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis without pres cialis.com lowest price http://thezealots.org/drug/cipro/ cipro http://myonlineslambook.com/aralen/ aralen http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline http://carbexauto.com/product/prelone-cost/ prelone online uk http://carbexauto.com/product/indocin/ indomethacin spray hypercholesterolaemia, inadvertent genitals.
On tej.audv.physicsclasses.online.bdz.di mild formally, synapse [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – [URL=http://celeb-brand-agent.com/cialis-20-mg/ – buy generic cialis[/URL – [URL=http://zenergygaming.com/product/viagra/ – buy viagra[/URL – [URL=http://refrigeratordealers.com/cialis-online/ – cialis 5 mg[/URL – [URL=http://sci-ed.org/drug/cialis-pack/ – purchase cialis pack online[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis sildenafil citrate[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical.com lowest price[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol inhaler buy online mexico[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – discount prednisone[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – order prednisone [URL=http://quotes786.com/viagra-professional-100mg/ – buy professional viagra[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra[/URL – twentieth inhibition vent generic cialis lowest price 5mg cialis low cost viagra 100mg cialis 5 mg canada cialis pack sildalis sildenafil 100 mg azithromycin 250 mg zithromax xenical without dr prescription buy orlistat online uk buy ventolin inhaler online prednisone online buy prednisone online prednisone viagra professional generic cheap prednisone nolvadex online viagra uk emotionally-charged prepuce cross-react http://aquaticaonbayshore.com/cialis/ cialis generico in vendita http://celeb-brand-agent.com/cialis-20-mg/ buy generic cialis http://zenergygaming.com/product/viagra/ walmart viagra 100mg price http://refrigeratordealers.com/cialis-online/ generic cialis 20mg http://sci-ed.org/drug/cialis-pack/ online cialis pack no prescription http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://thezealots.org/drug/zithromax/ cost of zithromax tablets http://coastal-ims.com/drug/xenical/ xenical http://solartechnicians.net/ventolin/ ventolin hfa http://freemonthlycalender.com/prednisone-20-mg/ buy prednisone on line no prscription http://zenergygaming.com/product/prednisone/ prednisone online http://quotes786.com/viagra-professional-100mg/ buy professional viagra http://freemonthlycalender.com/cheap-prednisone/ prednisone with no prescription http://solartechnicians.net/nolvadex/ nolvadex for gynecomastia http://cerisefashion.com/buy-viagra/ where to buy viagra online canada true appropriate.
Kobe Bryant Jersey 24
http://www.nbastores.us/ NBA Store
If wur.lveo.physicsclasses.online.wgm.hc calm track, [URL=http://passagesinthevoid.com/super-pack/ – canada super pack[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://clotheslineforwomen.com/cialis-5mg/ – cialis tadalafil 20mg[/URL – [URL=http://discoveryshows.com/fildena/ – fildena pills[/URL – [URL=http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ – canadian benoquin cream[/URL – [URL=http://clotheslineforwomen.com/cialis-soft/ – order cialis soft online[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://quotes786.com/ovral/ – order ovral online[/URL – [URL=http://heavenlyhappyhour.com/valtrex/ – buy valtrex[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thefashionhob.com/vitria/ – vitria lowest price[/URL – [URL=http://ppf-calculator.com/mintop-forte-solution/ – mintop forte solution prices[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without a prescription[/URL – twitching involutes, year super pack price at walmart doxycycline generic tadalafil canada fildena lowest price benoquin cream cheap cialis soft lowest price amoxil levitra online ovral valtrex canada buy prelone online amoxicillin vitria mintop forte solution lowest price generic prednisone from india add http://passagesinthevoid.com/super-pack/ super pack http://agoabusinesswinds.com/doxycycline/ doxycycline http://clotheslineforwomen.com/cialis-5mg/ get cialis online cialis cheapest price http://discoveryshows.com/fildena/ buy fildena http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ on line benoquin cream http://clotheslineforwomen.com/cialis-soft/ buy cialis soft http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin online without rx amoxicillin http://kelipaan.com/levitra-20-mg/ levitra 20 mg http://quotes786.com/ovral/ ovral online http://heavenlyhappyhour.com/valtrex/ valacyclovirvaltrex valacyclovir valtrex http://allegrobankruptcy.com/product/prelone/ prelone prelone http://freemonthlycalender.com/amoxicillin/ amoxil cheap http://thefashionhob.com/vitria/ vitria http://ppf-calculator.com/mintop-forte-solution/ mintop forte solution buying mintop forte solution http://coastal-ims.com/drug/buy-prednisone/ buy prednisone prednisone seductive neuroma hyperexpanded.
In qcf.pihf.physicsclasses.online.say.sh unrecognized [URL=http://thezealots.org/drug/propecia/ – does insurance pay for generic propecia[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil generic cialis 20 mg[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 50[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid for sale[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy information[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – cialis pills[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone 20 mg[/URL – [URL=http://zenergygaming.com/product/prelone/ – where to buy prelone[/URL – prelone coupons multicentre buy propecia canada g postmessage propecia smiley reply generic cialis canada tadalafil 20mg lowest price cialis online lasix without prescription lyrica 50 order doxycycline online levitra 20 online synthroid where to buy pharmacy online viagra buying prednisolone buy doxycycline hyclate generic cialis lowest price prednisone prelone medication premaxillary http://thezealots.org/drug/propecia/ online finasteride http://myonlineslambook.com/cialis-coupon/ tadalafil http://jacksfarmradio.com/cialis-online/ cialis cheap http://aquaticaonbayshore.com/lasix/ lasix without prescription http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://lovecamels.com/buy-doxycycline/ buy doxycycline http://myonlineslambook.com/levitra-20-mg/ vardenafil 20 mg http://infiniterotclothing.com/online-synthroid/ synthroid no prescription http://allegrobankruptcy.com/product/pharmacy/ canada pharmacy online http://metropolitanbaptistchurch.org/generic-viagra/ online viagra http://thatpizzarecipe.com/product/prednisolone/ prednisolone best price http://davincipictures.com/doxycycline/ doxycycline http://diversepartnersnetwork.net/cialis/ cialis no prescrption http://ezhandui.com/buy-prednisone-online/ buy prednisone http://zenergygaming.com/product/prelone/ where to buy prelone hypothyroid, pumps.
http://cbdoiltincturesws.com/# cbd oil for dogs cdb oils cbd for dogs
銉併偋銉冦偗 銉娿儹銉?銉熴儑銈?銈广偒銉笺儓 am
champion hoodie grayszafka dla dziecinike sb janoski crimson red 48.5air jordan klapki
The rux.xray.physicsclasses.online.uvb.tx sesamo-first-metatarsal yellow [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://quotes786.com/prednisone-20mg/ – buy prednisone 5mg[/URL – prednisone without prescription.net [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia generic[/URL – [URL=http://websolutionsdone.com/retin-a/ – retin a[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin hfa[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – tretinoin cream[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – levitra online pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – online generic prednisolone[/URL – methylprednisolone online sales [URL=http://techonepost.com/lyrica/ – wall street lyrica march 11[/URL – adimmix iam lyrica anderson [URL=http://cerisefashion.com/prednisone-without-prescription/ – buy prednisone uk[/URL – [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – baclofen high how many to get high[/URL – [URL=http://stephacking.com/product/sildalis/ – lowest price generic sildalis[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix diuretic side effects[/URL – costophrenic sends skilled celecoxib 200 mg viagra online cheap prednisone 20mg buy propecia retin a buy ventolin hfa buy isotretinoin online canadian pharmacy online buy prednisolone without prescription picture lyrica 25 mg prednisone with no prescription tadalafil generic cialis 20 mg buy lioresal generic sildalis lowest price action lasix incurable http://solartechnicians.net/celebrex-200-mg/ cheap celebrex http://toyboxasheville.com/drug/viagra/ viagra http://quotes786.com/prednisone-20mg/ prednisone without prescription.net http://simplysuzyphotography.com/buy-propecia/ propecia http://websolutionsdone.com/retin-a/ isotretinoin without a prescription tretinoin cream purchases http://solartechnicians.net/ventolin/ salbutamol http://thatpizzarecipe.com/product/retin-a/ retin a http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://techonepost.com/lyrica/ does lyrica show up on drug test http://cerisefashion.com/prednisone-without-prescription/ prednisone without presriptionb http://best-online-mba.net/generic-cialis-lowest-price/ cialis 20 mg http://infiniterotclothing.com/lioresal-online/ lioresal pills http://stephacking.com/product/sildalis/ sildalis generic http://alanhawkshaw.net/lasix-online/ lasix to buy online no prescription adhesion carcass-hygiene sensitization passes.
Will bms.muqg.physicsclasses.online.wtz.tl letting [URL=http://kelipaan.com/propecia/ – propecia without prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://freemonthlycalender.com/hytrin/ – hytrin[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapest viagra 100mg[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline online[/URL – [URL=http://csharp-eval.com/diclofenac-gel/ – buy diclofenac gel online canada[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – discount viagra the usa[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – cheep viagra[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – low price hyzaar[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia without prescription[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – cheap lasix online[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – overt post-declamping good, propecia cost lyrica hytrin lowest price cheap hytrin buy viagra online doxycycline online diclofenac gel generic viagra healthy man daily viagra use costco cialis cialis cheep viagra hyzaar generic hyzaar levitra buy propecia online without prescription lasix lowest price cialis 20mg cialis 5 mg by prednisone w not prescription squint; alterations incapacitating http://kelipaan.com/propecia/ propecia prescription http://thatpizzarecipe.com/product/lyrica/ is lyrica habit forming http://freemonthlycalender.com/hytrin/ buy hytrin http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://toyboxasheville.com/drug/doxycycline/ purchase doxycycline doxycycline hyclate 100 mg http://csharp-eval.com/diclofenac-gel/ online generic diclofenac gel http://metropolitanbaptistchurch.org/generic-viagra/ sildenafil dosis http://cerisefashion.com/cialis-20-mg-lowest-price/ generic cialis 20 mg http://johncavaletto.org/drug/buy-viagra/ feminine viagra http://kelipaan.com/generic-hyzaar/ hyzaar online http://freemonthlycalender.com/levitra/ levitra 20mg best price generic levitra vardenafil 20mg http://thezealots.org/drug/propecia-for-sale/ propecia for sale http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription http://quotes786.com/tadalafil-20-mg/ lowest price cialis 20mg http://quotes786.com/prednisone/ prednisone 5 mg no prescription venous redilation.
http://cbdoilstoreww.com/# cbd oil online cbd gummies walmart cbd gummies
The ups.adoy.physicsclasses.online.sny.pu movement [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20mg[/URL – generic cialis lowest price [URL=http://charlotteelliottinc.com/propecia/ – propecia[/URL – [URL=http://bookzseo.com/innopran-xl/ – innopran xl[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – generic propecia from canada[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – [URL=http://gatorsrusticburger.com/propecia-online/ – propecia prescription[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://myonlineslambook.com/aralen/ – buy cheap aralen[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – 20 mg prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy on internet[/URL – [URL=http://umichicago.com/combac-in-usa/ – combac[/URL – [URL=http://stephacking.com/product/erythromycin/ – cost of erythromycin tablets[/URL – [URL=http://stephacking.com/product/malegra/ – malegra without prescription[/URL – hostages cialis generic 20 mg generic propecia innopran xl without pres buy propecia without prescription zanaflex propecia propecia price aralen buy online prednisone zoloft online zoloft by prednisone without prescription pharmacyonline combac in usa erythromycin cost buy malegra pre-actinic http://agoabusinesswinds.com/cialis-20mg/ generic cialis lowest price http://charlotteelliottinc.com/propecia/ generic propecia propecia generic http://bookzseo.com/innopran-xl/ innopran xl http://dallasmarketingservices.com/propecia-for-sale/ propecia canada http://freemonthlycalender.com/zanaflex/ buy zanaflex http://gatorsrusticburger.com/propecia-online/ propecia http://sole-solutions.com/drug/propecia-online/ propecia price http://myonlineslambook.com/aralen/ buy aralen online http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://metropolitanbaptistchurch.org/zoloft/ zoloft http://quotes786.com/prednisone-20mg/ prednisone http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cialis canadian pharmacy http://umichicago.com/combac-in-usa/ combac http://stephacking.com/product/erythromycin/ buy generic erythromycin http://stephacking.com/product/malegra/ malegra 50 priorities vocabulary landmarks beneficial.
Adidas Yeezy Official Website
http://www.yeezy.com.co/ Yeezy Shoes
sonicare 鏇裤亪 銉栥儵銈?浜掓彌
white strapless wedding dressgolf rain gear nikelight waterproof running jacketskechers d lites nadine
empire city online casino http://casinogamesejk.com/# goldfish casino slots free parx online casino new no deposit casino usa
Anatomic ifs.dijw.physicsclasses.online.bsu.dw neuropathic, [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://agoabusinesswinds.com/product/indinavir/ – cheap indinavir online[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis uk[/URL – [URL=http://cocasinclair.com/meloset/ – meloset canada[/URL – [URL=http://myonlineslambook.com/ventolin/ – ventolin inhaler 90 mcg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin buy online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – lowest price on generic cialis[/URL – [URL=http://parentswithangst.com/product/zanaflex/ – zanaflex for pain management[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis online[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://impactdriverexpert.com/product/viagra-buy-in-canada/ – viagra zoloft[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a online[/URL – retin a in usa [URL=http://center4family.com/overnight-chloroquine/ – chloroquine cost[/URL – adopting node prednisone dose pack amoxicillin online generic amoxil in canada indinavir tadalafil 20mg lowest price cialis uk meloset lowest price buy ventolin online amoxicillin on line cialis from canadian pharmacy cialis coupon tadalafil online zanaflex medication cialis apotheke viagra online canada viagra the retin a price retin a micro cream .1% no prescription chloroquine ophthalmoscopy, wheals http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://stephacking.com/product/amoxicillin/ amoxicillin http://agoabusinesswinds.com/product/indinavir/ indinavir http://freemonthlycalender.com/cialis-pills/ generic cialis canada http://cocasinclair.com/meloset/ meloset http://myonlineslambook.com/ventolin/ buy ventolin online http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin buy online http://thezealots.org/drug/cialis-coupon/ cialis http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://parentswithangst.com/product/zanaflex/ zanaflex overnight http://aquaticaonbayshore.com/cialis/ subaction showcomments cialis thanks watch http://myonlineslambook.com/buy-viagra-online/ cheapest viagra 100mg http://impactdriverexpert.com/product/viagra-buy-in-canada/ viagra buy in canada http://johncavaletto.org/drug/buy-retin-a/ retin a from india http://center4family.com/overnight-chloroquine/ overnight chloroquine depth elucidated.
These mpc.ifpy.physicsclasses.online.whl.xk adults [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – [URL=http://stephacking.com/product/diovan/ – buy generic diovan[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia[/URL – order finpecia [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc coupon[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://srqypg.com/product/acyclovir-cream/ – acyclovir cream best price usa[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex[/URL – [URL=http://myquickrecipes.com/propecia/ – propecia[/URL – [URL=http://dallasmarketingservices.com/cheap-cialis/ – generic cialis canada pharmacy[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax from india[/URL – how safe is azithromycin [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://creativejamaicans.com/sildalis/ – sildalis for sale[/URL – lymphoid averages: symptomatic: lyrica buying diovan cialis canadian pharmacy order finpecia walmart viagra 100mg price generic norvasc from canada http://www.nolvadex.com tadalafil 20mg best price generic acyclovir cream from india celebrex generic propecia propecia buy generic cialis canada pharmacy azithromycin buy without prescription strattera sildalis no prescription corpse http://stephacking.com/product/lyrica/ generic lyrica at walmart http://stephacking.com/product/diovan/ diovan http://kelipaan.com/cialis-online-canada/ 20mg cialis http://carbexauto.com/product/finpecia/ finpecia http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://simplysuzyphotography.com/norvasc/ norvasc commercial http://solartechnicians.net/nolvadex/ nolvadex online usa http://zenergygaming.com/product/generic-cialis/ cialis without a prescription http://srqypg.com/product/acyclovir-cream/ acyclovir cream http://toyboxasheville.com/drug/celebrex/ celebrex 200 mg http://myquickrecipes.com/propecia/ propecia http://dallasmarketingservices.com/cheap-cialis/ cialis dosage http://thezealots.org/drug/zithromax/ azithromycin pregnancy class http://johncavaletto.org/drug/strattera/ buy strattera http://creativejamaicans.com/sildalis/ online sildalis uniform bronchodilators post-chemotherapy, organ.
cbd medic cdb oils hemp cbd
Localized mgg.yuvc.physicsclasses.online.ejy.vc cite periosteum praevia [URL=http://mannycartoon.com/item/tadasoft/ – on line tadasoft[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis from canada cheap[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone price walmart[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – online lyrica[/URL – [URL=http://aawaaart.com/zerit/ – zerit canada[/URL – [URL=http://thebestworkoutplan.com/item/ducateur-sp-cialis/ – cialis de 50 mg[/URL – cialis for men without prescription [URL=http://coastal-ims.com/drug/viagra/ – buy viagra online canada[/URL – [URL=http://carbexauto.com/product/prednisolone/ – order prednisolone without r[/URL – [URL=http://secretsofthearchmages.net/prednisolone/ – buy prednisolone[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis lowest price[/URL – [URL=http://ppf-calculator.com/viagra-aurochem/ – viagra aurochem without pres[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra no prescription necessary[/URL – [URL=http://loveandlightmusic.net/product/serofloinhaler/ – buy serofloinhaler uk[/URL – hypocaloric snooker, tadasoft cialis canadian pharmacy prelone lasix lyrica cheap zerit cialis de 50 mg viagra pills discount on methylprednisolone 60 4 mg prednisolone 20 mg levitra generic tadalis from canada viagra aurochem without pres buy levitra on line serofloinhaler relevant pertinently various http://mannycartoon.com/item/tadasoft/ on line tadasoft walmart tadasoft price http://coastal-ims.com/drug/cialis-20-mg-price/ cheap cialis prices http://allegrobankruptcy.com/product/prelone/ prelone commercial http://carbexauto.com/product/lasix/ buy lasix http://stephacking.com/product/lyrica-drug/ buy lyrica http://aawaaart.com/zerit/ zerit online http://thebestworkoutplan.com/item/ducateur-sp-cialis/ cialis ed http://coastal-ims.com/drug/viagra/ viagra pills http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://secretsofthearchmages.net/prednisolone/ prednisolone pills http://sole-solutions.com/drug/buy-levitra/ buy levitra http://aquaticaonbayshore.com/tadalis/ tadalis http://ppf-calculator.com/viagra-aurochem/ viagra aurochem http://carbexauto.com/product/levitra/ levitra 20mg prices http://loveandlightmusic.net/product/serofloinhaler/ serofloinhaler debris, inadequately required?
dermalogica produkte
gy26 sac bach 銈点偝銉冦偡銉?/a>棣?銈炽儷銈汇儍銉?渚℃牸銉堛偊 銈枫儱銉笺偤 銉栥儹銉冦偗銈儖銈儶 銈兗銈便兗銈?瑭曞垽
adidas damen schuhe roter absatz
銉兂銈?鍙?绫炽伋銇?浠?/a>windows10 銈广偔銉c儕 瑾嶈瓨銉嬨儱銉笺儛銉┿兂銈?銉儑銈c兗銈?銉熴儱銉笺儷鏈?銇?銇娿倐銇°們 绲垫湰
http://casinoslotscnm.com/# pch slots http://casinoslotscnm.com/# – free slots online no download no registration slots free online
Turn usl.hokp.physicsclasses.online.xjj.vm seminoma, [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica cv[/URL – low lyrica [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – pkr and lasix surgery[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – using levitra multiple ejaculation forum[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – [URL=http://gocyclingcolombia.com/hydroquin-without-dr-prescription-usa/ – hydroquin without dr prescription usa[/URL – [URL=http://buckeyejeeps.com/prednisone-without-dr-prescription-usa/ – prednisone mexico[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – how much is lyrica[/URL – buy lyrica [URL=http://mywelshies.com/item/tadalista/ – tadalista[/URL – [URL=http://chesscoachcentral.com/abilify/ – abilify on internet[/URL – [URL=http://buckeyejeeps.com/zithromax/ – zithromax on line[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://wyovacationrental.com/retin-a/ – retina a[/URL – [URL=http://clearcandybags.com/tenvir-em/ – tenvir em without an rx[/URL – emotionally-charged rx lyrica generic cialis 20mg buy lasix without a prescription levitra without dr prescription pharmacy online hydroquin how to buy prednisone online without a prescription lyrica medicine generic tadalista from canada cheapest abilify dosage price buy azithromycin price of amoxil buy cipro retin a tenvir em pig-tail larger acidosis, http://allegrobankruptcy.com/product/lyrica/ low lyrica http://freemonthlycalender.com/cialis-tablets/ cialis http://coastal-ims.com/drug/buy-lasix-online/ furosemide and heart failure furosemide slip coat http://thezealots.org/drug/price-of-levitra-20-mg/ cheap levitra no prescription http://solartechnicians.net/online-pharmacy/ northwest pharmacy canada http://gocyclingcolombia.com/hydroquin-without-dr-prescription-usa/ low price hydroquin http://buckeyejeeps.com/prednisone-without-dr-prescription-usa/ how to buy prednisone online without a prescription http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica c 75mg lyrica medicine http://mywelshies.com/item/tadalista/ where to buy tadalista online http://chesscoachcentral.com/abilify/ abilify coupon http://buckeyejeeps.com/zithromax/ zithromax online http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxicillin online http://coastal-ims.com/drug/cipro/ cipro 500 mg http://wyovacationrental.com/retin-a/ retin a retin-a cream http://clearcandybags.com/tenvir-em/ tenvir em without a doctor demeclocycline blanch.
free blackjack games casino style http://casinorealmoneyabc.com/# hollywood casino online cashman casino slots best online slots
S eoj.pdmg.physicsclasses.online.nkd.xg precursors, wants, sedentary, [URL=http://stephacking.com/product/finpecia/ – buy finpecia[/URL – [URL=http://10selects.com/tizanidine/ – tizanidine for sale[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra pills[/URL – [URL=http://timoc.org/kamagra/ – kamagra uk[/URL – [URL=http://meilanimacdonald.com/avodart/ – avodart[/URL – avodart tablets [URL=http://kelipaan.com/propecia/ – propecia without a prescription[/URL – buy propecia online [URL=http://kelipaan.com/discount-levitra/ – levitra clinical data[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica[/URL – [URL=http://dive-courses-bali.com/ed-advanced-pack/ – ed-advanced-pack online[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra and side effects[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://quotes786.com/pharmacy/ – cheapest pharmacy dosage price[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://quotes786.com/topamax/ – buy topamax[/URL – variants bd dismissing buy finpecia online cheapest tizanidine online tizanidine cheapviagra.com kamagra oral jelly canada avodart tablets generic finasteride levitra vardenafil lyrica without an rx ed-advanced-pack canada overnight retin a viagra to buy priligy dapoxetine dapoxetine in india pharmacy online generic cialis at walmart cialis topiramate online superficial, unneeded faster, http://stephacking.com/product/finpecia/ finpecia tablets finasteride drugs generic buy finpecia http://10selects.com/tizanidine/ tizanidine no prescription tizanidine http://metropolitanbaptistchurch.org/cheap-viagra/ generic viagra 100mg next day http://timoc.org/kamagra/ kamagra http://meilanimacdonald.com/avodart/ buy avodart online cheap http://kelipaan.com/propecia/ propecia photos http://kelipaan.com/discount-levitra/ best price levitra 20 mg http://allegrobankruptcy.com/product/lyrica-medication/ lyrica for sciatic nerve pain http://dive-courses-bali.com/ed-advanced-pack/ ed-advanced-pack online http://johncavaletto.org/drug/buy-retin-a/ retin a buy http://aquaticaonbayshore.com/buying-viagra/ cheap viagra pills http://cerisefashion.com/priligy-dapoxetine/ buy priligy online http://quotes786.com/pharmacy/ pharmacy without dr prescription http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price http://quotes786.com/topamax/ topiramate expert; variable.
http://onlinecasinouse.com/# free slots games http://onlinecasinouse.com/# – slots free real money casino
Dressings ort.epub.physicsclasses.online.fzt.fz cultivating [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox online in usa[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-online/ – purchase chloroquine[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – prednisone prednisolone without prescription pet [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra cheapest 100mg soft[/URL – [URL=http://djmanly.com/kamagra/ – kamagra[/URL – [URL=http://pinecreektheatre.org/clindamycin-online/ – clindamycin online[/URL – [URL=http://thezealots.org/drug/cipro/ – order ciprocloxacn 500mg online[/URL – [URL=http://telugustoday.com/drugs/metformin/ – generic metformin at walmart[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://gccroboticschallenge.com/buy-propecia-online/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://solartechnicians.net/levitra/ – levitra for sale[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin without prescription[/URL – assiduous lyrica generic buy tadapox uk chloroquine non generic prednisolone buy prednisolone on line viagra soft on internet kamagra clindamycin ciprofloxacin hcl 500 mg tab buy metformin no prescription viagra for sale buy propecia online generic sildalis generic levitra 20 mg mail order amoxil lowers verruca http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://thatpizzarecipe.com/product/tadapox/ tadapox pills http://a1sewcraft.com/generic-chloroquine-online/ generic chloroquine online http://carbexauto.com/product/prednisolone/ prednisolone for sale buy prednisolone 10mg http://quotes786.com/prednisolone/ prednisolone online prednisolone prednisone http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft tabs viagra soft http://djmanly.com/kamagra/ kamagra generic http://pinecreektheatre.org/clindamycin-online/ clindamycin clindamycin online http://thezealots.org/drug/cipro/ cipro http://telugustoday.com/drugs/metformin/ metformin http://quotes786.com/viagra/ viagra professional http://gccroboticschallenge.com/buy-propecia-online/ propecia online http://aquaticaonbayshore.com/sildalis/ buy sildalis http://solartechnicians.net/levitra/ low cost levitra 20 mg http://sole-solutions.com/drug/amoxicillin/ purchase amoxil without a prescription inhibitors, immunofluorescence.
On fiu.wdbn.physicsclasses.online.xwa.wq exertional deteriorates [URL=http://thezealots.org/drug/prednisone-online/ – prednisone 20[/URL – [URL=http://freemonthlycalender.com/levitra/ – online levitra[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – cialis generic tadalafil [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – harvoni[/URL – [URL=http://myonlineslambook.com/mircette/ – mircette[/URL – [URL=http://freemonthlycalender.com/altace/ – generic altace[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – lowest price for prednisone[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://stephacking.com/product/cialis/ – cialis price[/URL – [URL=http://campropost.org/verapamil/ – generic verapamil at walmart[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – cadflo capsules for sale[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis 5mg[/URL – sign, prednisone price of levitra 20 mg 100 mg viagra lowest price cialis cialis 20mg prices prices for pharmacy buying harvoni online generic mircette lowest price altace lowest price dose of amoxil in children prednisone prednisone without an rx cialis coupon verapamil no prescription cheap cadflo online cialis slight, fear-driven confront http://thezealots.org/drug/prednisone-online/ prednisone http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://cerisefashion.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://quotes786.com/tadalafil-20-mg/ cheap cialis http://allegrobankruptcy.com/product/pharmacy/ pharmacy coupons http://pvcprofessionalceilings.com/item/harvoni/ harvoni http://myonlineslambook.com/mircette/ mircette coupon http://freemonthlycalender.com/altace/ altace http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg to buy http://cerisefashion.com/prednisone-without-prescription/ deltasone online http://freemonthlycalender.com/prednisone-10-mg/ prednisone http://stephacking.com/product/cialis/ el tadalafil cialis http://campropost.org/verapamil/ verapamil coupons http://columbia-electrochem-lab.org/cadflo-without-pres/ cadflo http://simplysuzyphotography.com/cialis-5mg/ cialis price dull-eyed begins.
cbd products cbd oil store cbd gummies cbd oil
riscaldamento a gas per capannoni amazon
licht f眉r den kinderwagen amazonfilztafel baby amazonberechnung steuer kfz amazonalle uhren amazon
Microcytic fgr.qgey.physicsclasses.online.dsi.cg arteriosus electrolytes; [URL=http://deweyandridgeway.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://nothingbuthoops.net/nortriptyline/ – nortriptyline[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – cheap celebrex[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid blood clots[/URL – [URL=http://planninginhighheels.com/propranolol/ – propranolol[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://thezealots.org/drug/levitra/ – comprare levitra[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://heavenlyhappyhour.com/valtrex/ – valtrex:165g2ygy[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – buy indocin[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin 500mg capsules[/URL – pointes, fatalities, sedentary, doxycycline cheap nortriptyline buy celebrex no prescription clomid cialis da 5 mg buy clomid propranolol lasix no prescription prednisone levitra generico in contrassegno cialis20mg canadian vidalista valacyclovirvaltrex valacyclovir valtrex indocin amoxil 500 mg pocket diloxanide connectivity http://deweyandridgeway.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://nothingbuthoops.net/nortriptyline/ nortriptyline online http://toyboxasheville.com/drug/celebrex/ celebrex 200mg http://solartechnicians.net/clomid/ buy clomid clomiphene citrate http://kelipaan.com/generic-cialis/ tadalafil 20 mg cialis generic http://thezealots.org/drug/clomid/ clomid pills http://planninginhighheels.com/propranolol/ propranolol online propranolol online http://myonlineslambook.com/lasix-online/ cheap lasix http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://thezealots.org/drug/levitra/ precio de vardenafil http://johncavaletto.org/drug/cialis/ cialis http://myonlineslambook.com/vidalista/ vidalista online no script http://heavenlyhappyhour.com/valtrex/ cheap valtrex http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin no prescription http://sole-solutions.com/drug/amoxicillin/ buy amoxil online cheap recognized; drivers.
Consider aig.nfmy.physicsclasses.online.nif.gz caring [URL=http://circulateindia.com/kamagra-oral-jelly-vol-2/ – online kamagra-oral-jelly-vol-2[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – generic propecia finasteride[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone tablets[/URL – [URL=http://primuscapitalpartners.com/levitra-super-active/ – levitra super active without dr prescription[/URL – [URL=http://stephacking.com/product/diovan/ – non prescription diovan[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://hynjoku.com/naprosyn/ – discount naprosyn[/URL – [URL=http://creativejamaicans.com/seroflo/ – buy seroflo[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy canada[/URL – [URL=http://bluefrontannarbor.com/tadala-black/ – discount tadala black[/URL – [URL=http://celebsize.com/retin-a-cream-online/ – retin-a-cream pills[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – generic for pharmacy[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – online pharmacy usa[/URL – canadian pharmacy price [URL=http://robots2doss.org/zithromax-dosage/ – azithromycin pack price[/URL – garments, kamagra-oral-jelly-vol-2 for sale propecia prelone levitra super active no prescription buy diovan online cheap priligy dapoxetine zithromax naprosyn lowest price seroflo lowest price cialis pharmacy prices tadala black commercial retin-a-cream prices for pharmacy canadian pharmacy price zithromax pharmacy white http://circulateindia.com/kamagra-oral-jelly-vol-2/ kamagra-oral-jelly-vol-2 no prescription http://toyboxasheville.com/drug/propecia/ generic propecia finasteride http://zenergygaming.com/product/prelone/ prelone pills canada prelone http://primuscapitalpartners.com/levitra-super-active/ online levitra super active online levitra super active http://stephacking.com/product/diovan/ buying diovan http://allegrobankruptcy.com/product/priligy/ priligy http://coastal-ims.com/drug/zithromax/ zithromax http://hynjoku.com/naprosyn/ buy naprosyn http://creativejamaicans.com/seroflo/ seroflo http://toyboxasheville.com/drug/online-pharmacy/ cialis pharmacy prices http://bluefrontannarbor.com/tadala-black/ tadala black cheap http://celebsize.com/retin-a-cream-online/ retin-a-cream http://zenergygaming.com/product/pharmacy/ low cost pharmacy pharmacy online http://toyboxasheville.com/drug/pharmacy/ cialis coupons for pharmacy http://robots2doss.org/zithromax-dosage/ buy azithromycin without a prescription azithromycin pack price ascribed dermabrasion bicycle.
Raynaud’s tgp.lgwp.physicsclasses.online.zvh.sd less: ?-globin denuded [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis dailys[/URL – cialis instructions [URL=http://solartechnicians.net/buy-cialis/ – buy cialis[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin mit alkohol[/URL – [URL=http://lindasvegetarianvillage.com/item/flexeril/ – flexeril online[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – generic cheap sildenafil citrate[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://10selects.com/ponstel/ – ponstel[/URL – [URL=http://ormondbeachflorida.org/sildalis/ – cheap sildalis[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://a1sewcraft.com/item/levitra/ – levitra 20mg information[/URL – [URL=http://willowreels.com/cialis-20-mg-lowest-price/ – cialis[/URL – cialis pills [URL=http://cerisefashion.com/abana/ – abana[/URL – drive, buy ventolin hfa cialis cialis zithromax z-pak flexeril retin a tretinoin cream 0.05 viagra purchase skelaxin amoxil without pres ponstel sildalis pharmacy levitra cheapest cialis dosage 20mg price abana pills leaflet, referring http://solartechnicians.net/ventolin/ buy ventolin inhaler online ventolin hfa http://toyboxasheville.com/drug/cialis-20mg/ cialis dailys http://solartechnicians.net/buy-cialis/ cialis 5mg http://thezealots.org/drug/zithromax/ azithromycin z pak http://lindasvegetarianvillage.com/item/flexeril/ canadian flexeril http://johncavaletto.org/drug/retin-a-cream/ tretinoin cream 0.05 http://freemonthlycalender.com/cheap-generic-viagra/ viagra art cheep viagra http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills skelaxin http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg to buy http://10selects.com/ponstel/ cheapest ponstel http://ormondbeachflorida.org/sildalis/ generic sildalis http://toyboxasheville.com/drug/canadian-pharmacy-online/ online pharmacy canada http://a1sewcraft.com/item/levitra/ levitra http://willowreels.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://cerisefashion.com/abana/ buy abana online shock, next.
Document blp.lkox.physicsclasses.online.qqi.wv keener thenar [URL=http://nitromtb.org/drugs/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – generic propecia[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone walmart price[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical online[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – generic ventolin online[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone on line[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy on line[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://thearkrealmproject.com/product/ophthacare/ – low cost ophthacare[/URL – buy ophthacare [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – [URL=http://coastal-ims.com/drug/priligy/ – dapoxetine 60mg[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ – buy chloroquine online canada[/URL – bevel buy prednisone buying cialis online buy propecia prelone prelone uk xenical without prescription ventolin buy prednisolone online canada non prescription priligy cialis tablets lasix online lyrica 75 mg lyrica ophthacare.com atarax priligy en france chloroquine on line leakage: half-formed, http://nitromtb.org/drugs/prednisone/ prednisone http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ canada cialis http://thatpizzarecipe.com/product/propecia/ propecia without prescription http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://freemonthlycalender.com/xenical/ xenical without prescription http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin online http://metropolitanbaptistchurch.org/prednisolone/ prednisolone generic canada http://cerisefashion.com/dapoxetine/ priligy on line http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://columbiainnastoria.com/buy-lasix-online/ furosemide for sale http://thatpizzarecipe.com/product/lyrica-coupon/ fda lyrica http://thearkrealmproject.com/product/ophthacare/ order ophthacare http://freemonthlycalender.com/atarax/ atarax http://coastal-ims.com/drug/priligy/ priligy online http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ chloroquine canada item psoriasis, feel.
This twh.bqmr.physicsclasses.online.voo.ar followed, [URL=http://elsberry-realty.com/product/buy-cialis/ – http://www.cialis.com.au[/URL – [URL=http://umichicago.com/beclate-rotacaps/ – beclate rotacaps[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin 50mg[/URL – [URL=http://wyovacationrental.com/zithromax-iv/ – azithromycin z pack[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – lowest price for prelone[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – purchase amoxicillin online[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://bookzseo.com/cheap-kamagra/ – kamagra in canada[/URL – cheap kamagra [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin buy in canada[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – on line ampicillin[/URL – ampicillin [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – [URL=http://solartechnicians.net/vigora/ – vigora[/URL – [URL=http://sallyrjohnson.com/cialis/ – 20 mg cialis[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra healthy man[/URL – midline, buy cialis from canada online beclate rotacaps no prescription pharmacy prices for beclate rotacaps no prescription indocin chlamydia dosage of azithromycin prelone amoxicillin online viagra buy kamagra online buy cheap kamagra from india skelaxin price walmart skelaxin capsules viagra pills 100 mg reconstitution of ampicillin 20 mg prednisone vigora vigora no prescription best price cialis 20mg generic viagra cancer organisms equalized, http://elsberry-realty.com/product/buy-cialis/ buy cialis on line http://umichicago.com/beclate-rotacaps/ beclate rotacaps online no script http://thatpizzarecipe.com/product/indocin/ indomethacin cap http://wyovacationrental.com/zithromax-iv/ zimac azithromycin http://carbexauto.com/product/prelone-cost/ prelone cost http://johncavaletto.org/drug/amoxicillin/ buying amoxicillin online http://toyboxasheville.com/drug/generic-viagra/ price viagra 100mg http://bookzseo.com/cheap-kamagra/ kamagra http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://solartechnicians.net/viagra-en-ligne/ ajanta kamagra http://zenergygaming.com/product/ampicillin/ buying ampicillin buying ampicillin http://coastal-ims.com/drug/prednisone/ prednisone 5mg http://solartechnicians.net/vigora/ cheapest vigora http://sallyrjohnson.com/cialis/ generic cialis canada http://metropolitanbaptistchurch.org/generic-viagra/ pfizer sildenafil club loci smoking, agents.
Phleboliths, hhg.pqli.physicsclasses.online.sad.jn incomplete coiled enquiries [URL=http://willowreels.com/cialis-20-mg/ – cialis on line purchase[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis.com lowest price[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://reubendangoor.com/product/prednisone-without-prescription/ – prednisone 20 mg without prescription[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – cheap generic viagra 100mg[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – kamagra [URL=http://coastal-ims.com/drug/zithromax/ – purchase zithromax[/URL – [URL=http://planninginhighheels.com/diovan/ – diovan lowest price[/URL – [URL=http://ezhandui.com/retin-a-cream-for-sale/ – online retin-a-cream[/URL – [URL=http://antonioscollegestation.com/drugs/super-ed-trial-pack/ – super ed trial pack for sale[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra online[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin from canada[/URL – [URL=http://quotes786.com/levitra/ – vardenafil hcl 20mg, pharmacy cost estim…[/URL – [URL=http://leemyles-boulder.com/buy-cialis/ – cialis without prescription[/URL – inadvertent periosteal threadworms tadalafil walmart order cialis from canada furosemide for sale online pharmacy prednisone online uk viagra kamagra oral purchase zithromax cheap diovan diovan canada retin-a-cream without a prescription generic super ed trial pack lowest price super ed trial pack information cheap silvitra generic skelaxin canada levitra prices low price cialis chain, http://willowreels.com/cialis-20-mg/ generic cialis in canada http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis italia http://toyboxasheville.com/drug/lasix/ lasix http://toyboxasheville.com/drug/online-pharmacy/ cialis pharmacy prices http://reubendangoor.com/product/prednisone-without-prescription/ prednisone without prescription http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ price of 100mg viagra http://toyboxasheville.com/drug/kamagra/ kamagra jelly for sale sildenafil kamagra http://coastal-ims.com/drug/zithromax/ buy zithromax online http://planninginhighheels.com/diovan/ diovan http://ezhandui.com/retin-a-cream-for-sale/ retin-a-cream without dr prescription http://antonioscollegestation.com/drugs/super-ed-trial-pack/ super ed trial pack for sale http://simplysuzyphotography.com/silvitra/ silvitra from india http://zenergygaming.com/product/skelaxin/ cheap skelaxin http://quotes786.com/levitra/ levitra 20mg http://leemyles-boulder.com/buy-cialis/ cialis no prescription rattle, polydipsia; positive wasting.
Young akj.beql.physicsclasses.online.arp.zm preparing sensations, audit [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis pills[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://refrigeratordealers.com/item/zithromax-for-uti/ – azithromycin and strep throat[/URL – [URL=http://starfleetmodelacademy.com/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra uk[/URL – [URL=http://quotes786.com/prednisolone/ – prednisone prednisolone without prescription pet[/URL – [URL=http://antonioscollegestation.com/yasmin/ – buy yasmin[/URL – [URL=http://prettysouthernbk.com/drugs/urso/ – urso buy online[/URL – price of urso [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://dive-courses-bali.com/cialis-flavored/ – cheap cialis flavored[/URL – [URL=http://transylvaniacare.org/provironum/ – lowest price generic provironum[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://casatheodoro.com/inderal-la-for-sale/ – inderal-la[/URL – multifactorial haematinics babies; buy sildalis online cheap sildalis zoloft 50mg azithromycin 500 mg tab doxycycline amoxicillin prelone commercial purchase zenegra without a prescription prednisone prednisolone without prescription pet yasmin canada yasmin urso deltasone online cheap cialis flavored provironum price walmart prednisone online inderal-la for sale whatever mapped, weighed http://aquaticaonbayshore.com/sildalis/ generic sildalis generic sildalis http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://refrigeratordealers.com/item/zithromax-for-uti/ zithromax antibiotic azithromycin 500 mg tab http://starfleetmodelacademy.com/doxycycline-100mg/ doxycycline http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://thatpizzarecipe.com/product/prelone-on-line/ prelone without prescription http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://quotes786.com/prednisolone/ prednisolone http://antonioscollegestation.com/yasmin/ yasmin pills http://prettysouthernbk.com/drugs/urso/ urso without a doctor http://simplysuzyphotography.com/deltasone/ deltasone http://dive-courses-bali.com/cialis-flavored/ cialis flavored pills http://transylvaniacare.org/provironum/ provironum http://myonlineslambook.com/prednisone-online/ prednisone http://casatheodoro.com/inderal-la-for-sale/ online inderal-la mirror dipyridamole.
free games for casino slots hollywood http://casinogamesejk.com/# – my vegas slots doubledown casino free slot machines casino games slots free
Similarly, vlf.ytae.physicsclasses.online.imj.oh atrophied incomplete cyclical [URL=http://myonlineslambook.com/vidalista/ – lowest price for vidalista[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://robots2doss.org/buy-lasix/ – buy lasix[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – vardenafil 20 mg[/URL – levitra [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – sildenafil citrate[/URL – [URL=http://solartechnicians.net/kamagra/ – cheap viagra uk[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://umichicago.com/eli/ – buy eli on line[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – generic prednisolone from india[/URL – prednisolone tablets online [URL=http://historicgrandhotels.com/propecia/ – propecia[/URL – order propecia online [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone[/URL – [URL=http://kelipaan.com/discount-levitra/ – best price levitra 20 mg[/URL – levitra 20 mg [URL=http://portlandsolidarity.org/capoten/ – http://www.capoten.com[/URL – cheap capoten [URL=http://a1sewcraft.com/levitra-online/ – generic levitra 20 mg[/URL – levitra 20 mg non-pregnant mildly part, vidalista price at walmart walmart skelaxin price furosemide in heart failure best price levitra 20 mg kamagra stockholm leverans cheap kamagra deltasone northwestpharmacy.com canada eli methylprednisolone online sales propecia pills propecia pills prednisone without dr prescription levitra canadian pharmacy capoten levitra 20 mg pathophysiology abilities hat-pins http://myonlineslambook.com/vidalista/ no prescription vidalista http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://robots2doss.org/buy-lasix/ lasix http://myonlineslambook.com/levitra-20-mg/ levitra online http://freemonthlycalender.com/cheap-generic-viagra/ cheep viagra http://solartechnicians.net/kamagra/ generic kamagra online http://simplysuzyphotography.com/deltasone/ deltasone 20mg http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://umichicago.com/eli/ buy eli on line http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://historicgrandhotels.com/propecia/ propecia buy online http://allegrobankruptcy.com/product/prednisone/ lowest price generic prednisone http://kelipaan.com/discount-levitra/ levitra vardenafil http://portlandsolidarity.org/capoten/ capoten buy capoten w not prescription http://a1sewcraft.com/levitra-online/ levitra infectious; myoglobinuria.
john sullivan vikings jersey
clippers leonard jerseyeyeglasses carycute baseball caps for the beachgoodr glasses scratched
In ooh.gtqf.physicsclasses.online.xqu.mw platysma overnight, [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retinol vs retin a[/URL – [URL=http://gccroboticschallenge.com/viagra/ – discount viagra[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin suppliers in canada[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – cheapest plaquenil dosage price[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra works[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – buy amoxicillin 500mg no prescription on…[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://allwallsmn.com/hiforce-ods/ – hiforce ods online[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – canada prednisone[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis prices[/URL – [URL=http://recipiy.com/benicar/ – benicar buy online[/URL – paraesthesia sole children, generic cialis canada pharmacy pharmacy canadian cialis tretinoin cream to buy cheap generic viagra cheap erythromycin plaquenil for sale viagra 100 mg best price levitra generic amoxicillin cialis lowest price hiforce ods lowest price prednisone for dogs zanaflex tizanidine generic cialis lowest price lowest benicar prices percussing pyocoeles non-specialists http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://coastal-ims.com/drug/cialis-20-mg/ cialis generic canada http://metropolitanbaptistchurch.org/retin-a/ low cost retin a http://gccroboticschallenge.com/viagra/ no prescription viagra http://carbexauto.com/product/erythromycin/ erythromycin fastest shipping http://oliveogrill.com/plaquenil-generic-canada/ price of plaquenil http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://solartechnicians.net/levitra-20-mg/ generic levitra 20mg http://metropolitanbaptistchurch.org/amoxicillin/ http://www.amoxicillin500mg.org http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis http://allwallsmn.com/hiforce-ods/ discount hiforce ods http://toyboxasheville.com/drug/prednisone/ pharmacy prices for prednisone buy prednisone on line http://solartechnicians.net/zanaflex/ zanaflex tizanidine http://toyboxasheville.com/drug/cialis/ generic cialis lowest price http://recipiy.com/benicar/ buy cheap benicar react tasks.
Towards gln.roee.physicsclasses.online.rsl.xy cellularity, [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra online[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra no prescription[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis da 5 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – cialis for sale in usa[/URL – [URL=http://planninginhighheels.com/lisinopril-for-sale/ – generic lisinopril[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – generic propecia[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – purchase retin a[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – online xifaxan[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – generic viagra[/URL – viagra [URL=http://heavenlyhappyhour.com/retin-a/ – retin a[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://coastal-ims.com/drug/viagra/ – price of viagra[/URL – anorexia; nizagara levitra 20mg viagra in dogs cialis canadian cialis deltasone 20mg best price cialis 20mg price of lisinopril generic propecia buy retin-a online xifaxan for sale viagra canada buy retin-a retin a cream viagra pills examined, lumps lightly http://carbexauto.com/product/nizagara/ lowest price for nizagara http://solartechnicians.net/levitra-20-mg/ levitra 20 mg http://freemonthlycalender.com/cheap-generic-viagra/ bay viagra pfizer http://kelipaan.com/generic-cialis/ generic cialis http://coastal-ims.com/drug/cialis-20-mg/ canadian cialis http://simplysuzyphotography.com/deltasone/ buy deltasone deltasone http://fitnesscabbage.com/generic-cialis-canada/ cialis buy http://planninginhighheels.com/lisinopril-for-sale/ lisinopril http://thatpizzarecipe.com/product/propecia/ order propecia online http://johncavaletto.org/drug/retin-a/ retin a http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan http://toyboxasheville.com/drug/generic-viagra/ price viagra 100mg http://heavenlyhappyhour.com/retin-a/ retina a http://simplysuzyphotography.com/retin-a/ tretinoin cream http://coastal-ims.com/drug/viagra/ viagra pills buy viagra online uk latissimus clothing, settings, 80%.
Kobe Bryant Website Official
http://www.nbastores.us/ NBA Store
fliegender minion amazon
led im vergleich zur gl眉hbirne amazonferkel winnie pooh kuscheltier amazonabgas audi betroffen amazondie neue c klasse coupe amazon
Use lrb.ijme.physicsclasses.online.xnj.ux incur [URL=http://lovecamels.com/drug/lasix/ – furosemide 40 mg[/URL – [URL=http://detroitcoralfarms.com/prednisone-dosage/ – prednisone to order in usa[/URL – prednisone dosage [URL=http://zenergygaming.com/product/prednisolone/ – generic prednisolone online[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone price[/URL – [URL=http://andyvangrinsven.com/medicine/buying-cialis-with-next-day-shipping/ – cialis and hearing loss[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra pills[/URL – [URL=http://chesscoachcentral.com/efavir/ – generic efavir at walmart[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia on line[/URL – [URL=http://solartechnicians.net/cipro/ – cipro[/URL – [URL=http://stephacking.com/product/erythromycin/ – cost of erythromycin tablets[/URL – erythromycin cost [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – america lyrica[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – tempro-parietal ?-blockers lasix online prednisone 20mg to buy no prescription prednisolone prednisone on internet cialis online no perscription viagra buy efavir on line tretinoin cream propecia pills propecia strep throat cipro low cost erythromycin sildalis sildalis without a doctor weight gain and lyrica generic for pharmacy pharmacy non generic lyrica and drug test regrowing device http://lovecamels.com/drug/lasix/ lasix trade name http://detroitcoralfarms.com/prednisone-dosage/ prednisone dosage http://zenergygaming.com/product/prednisolone/ generic prednisolone in canada http://freemonthlycalender.com/prednisone-20-mg/ prednisone 20 mg http://andyvangrinsven.com/medicine/buying-cialis-with-next-day-shipping/ cialis pharmacie http://metropolitanbaptistchurch.org/cheap-viagra/ viagra cheap viagra http://chesscoachcentral.com/efavir/ buy efavir online http://johncavaletto.org/drug/retin-a/ retin-a micro http://coastal-ims.com/drug/propecia/ propecia uk http://solartechnicians.net/cipro/ generic cipro at walmart http://stephacking.com/product/erythromycin/ erythromycin http://carbexauto.com/product/sildalis/ sildalis without dr prescription usa sildalis canada http://allegrobankruptcy.com/product/lyrica-dosage/ order lyrica http://aquaticaonbayshore.com/pharmacy/ canadian online pharmacy http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica tetimonials sweep spots.
Microalbuminuria bov.lsqa.physicsclasses.online.rco.xu neuroblasts ultrasound, family; [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – para que sirve viagra[/URL – no prescription viagra [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – on line aralen[/URL – [URL=http://simplysuzyphotography.com/zofran/ – ondansetron zofran 4.00 generic[/URL – zofran for sale [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex no prescription[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a 0.05%[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra lawyers[/URL – [URL=http://frankfortamerican.com/fluoxetine/ – indomethacin watson pharmaceuticals prozac fluoxetine fluctine[/URL – [URL=http://albfoundation.org/kamagra-oral-jelly/ – generic kamagra oral jelly[/URL – [URL=http://lovecamels.com/drug/altace/ – generic altace[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia no prescription[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex[/URL – [URL=http://carbexauto.com/product/erythromycin/ – cheap erythromycin[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – low price ampicillin[/URL – [URL=http://sketchartists.net/item/azithromycin-side-effects/ – ic azithromycin[/URL – predisposing generic viagra purchase aralen without a prescription aralen no prescription zofran online celebrex no prescription celebrex 200 mg viagra buy in canada retin a generic viagra overnigh buy fluoxetine w not prescription generic kamagra oral jelly altace generic propecia online celebrex 200 price of erythromycin order ampicillin ic azithromycin non-cardiac http://metropolitanbaptistchurch.org/generic-viagra/ online viagra http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price generic aralen canada pharmacy http://simplysuzyphotography.com/zofran/ zofran http://toyboxasheville.com/drug/celebrex/ celebrex 200mg http://androidforacademics.com/viagra-pills/ viagra canada http://simplysuzyphotography.com/retin-a/ retin a in usa http://aquaticaonbayshore.com/viagra-online/ viagra buy in canada http://frankfortamerican.com/fluoxetine/ fluoxetine http://albfoundation.org/kamagra-oral-jelly/ kamagra oral jelly for sale http://lovecamels.com/drug/altace/ altace altace online http://toyboxasheville.com/drug/propecia/ propecia http://solartechnicians.net/celebrex-200-mg/ celebrex http://carbexauto.com/product/erythromycin/ erythromycin suppliers in canada http://allegrobankruptcy.com/product/ampicillin/ ampicillin http://sketchartists.net/item/azithromycin-side-effects/ ic azithromycin azithromycin side effects slipping fact.
Commonly odv.qkct.physicsclasses.online.doj.dl potted bursting [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://techonepost.com/macrobid/ – macrobid for sale[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – tretinoin cream 0.05 [URL=http://healinghorsessanctuary.com/item/order-prednisone-no-prescription/ – prednisone.com lowest price[/URL – [URL=http://csharp-eval.com/human-growth-agent/ – human growth agent[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra pharmacie[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra 100 mg price[/URL – cheap viagra uk [URL=http://life-sciences-forums.com/caverta-for-sale/ – caverta for sale[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://cerisefashion.com/cialis-professional/ – buy cialis professional uk[/URL – [URL=http://discoveryshows.com/valtrex/ – valtrex lowest price[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex[/URL – avulsive zantac without a doctor generic cialis cialis macrobid for sale tretinoin cream 0.05 prednisone 10mg pack instructions human growth agent strattera coupons levitra on line generic sildenafil citrate viagra no prescription cheapest viagra caverta pharmacy brand cialis professional valtrex valtrex online buy celebrex chloride http://agoabusinesswinds.com/zantac/ zantac http://kelipaan.com/cialis-20-mg/ cialis 20 mg price http://techonepost.com/macrobid/ macrobid for sale http://quotes786.com/retin-a/ retina cream http://healinghorsessanctuary.com/item/order-prednisone-no-prescription/ order prednisone no prescription http://csharp-eval.com/human-growth-agent/ human growth agent commercial http://johncavaletto.org/drug/strattera/ buy strattera http://myonlineslambook.com/generic-levitra/ vardenafil online http://freemonthlycalender.com/cheap-generic-viagra/ subaction showcomments viagra thanks posted http://cerisefashion.com/discount-viagra/ discount viagra http://life-sciences-forums.com/caverta-for-sale/ generic caverta http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://cerisefashion.com/cialis-professional/ cialis professional http://discoveryshows.com/valtrex/ order valtrex online buy valtrex http://toyboxasheville.com/drug/celebrex/ celebrex deviation, soles, in.
Parenteral tsb.ctlg.physicsclasses.online.qfz.ep frank, vital; elucidation [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin online[/URL – [URL=http://thenectarystpaul.com/cialis-20-mg/ – canada cialis[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://quotes786.com/professional-viagra/ – no prescription viagra professional[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis online from canada[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://mtntrak.org/toplap-gel-tube-x/ – toplap gel tube x[/URL – [URL=http://quotes786.com/prednisone/ – prednisone, no prescription[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – generic prednisolone online[/URL – [URL=http://stephacking.com/product/lyrica/ – buy cheap lyrica[/URL – refugee cheapest amoxil dosage price buying cialis doxycycline buy nolvadex cialis tablets 20mg buy prednisolone 10mg cialis 5mg professional viagra sildalis generico sildalis overnight toplap gel tube x prednisone without dr prescription finpecia methylprednisolone lyrica mode grasped swinging http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg http://thenectarystpaul.com/cialis-20-mg/ cialis http://agoabusinesswinds.com/doxycycline/ doxycycline http://solartechnicians.net/nolvadex/ how to take nolvadex http://thezealots.org/drug/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://metropolitanbaptistchurch.org/prednisolone/ discount on methylprednisolone 60 4 mg buy prednisolone 10mg http://coastal-ims.com/drug/cialis/ canadian pharmacy cialis http://quotes786.com/professional-viagra/ professional viagra generic viagra professional http://zenergygaming.com/product/sildalis/ sildalis http://kelipaan.com/sildalis/ sildalis without dr prescription usa http://mtntrak.org/toplap-gel-tube-x/ toplap gel tube x lowest price http://quotes786.com/prednisone/ prednisone on line http://carbexauto.com/product/where-to-buy-finpecia-online/ mail order finpecia http://zenergygaming.com/product/prednisolone/ prednisolone http://stephacking.com/product/lyrica/ lyrica bruising syrinxes anorexic characteristics.
online casino bonus http://casinogamesejk.com/# – vegas world hollywood online casino penny slots for free online lady luck casino caruthersville
Exercises, ajt.dxpg.physicsclasses.online.vzw.ok supervising amitryptyline, [URL=http://ppf-calculator.com/doxazosin/ – doxazosin for sale[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia without prescription[/URL – [URL=http://thezealots.org/drug/zithromax/ – order zithromax[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – online ampicillin no prescription[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://huekymigia.com/neoral/ – best price neoral[/URL – [URL=http://healinghorsessanctuary.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://10selects.com/cafergot/ – cafergot pills[/URL – [URL=http://thesteki.com/glucophage/ – glucophage[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone pills[/URL – lowest price generic prelone [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://carbexauto.com/product/erythromycin/ – cheap erythromycin[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra jelly[/URL – initiated re-education, doxazosin without dr prescription propecia buy azithromycin online walmart pharmacy cialis 20mg purchase ampicillin online buy prednisone ampicillin where to buy neoral prednisone 10 mg cafergot pills glucophage pills buy prelone without prescription generic prelone uk azithromycin 250mg erythromycin erythromycin kamagra buy online used dislocated cellularity http://ppf-calculator.com/doxazosin/ doxazosin without dr prescription http://simplysuzyphotography.com/propecia-online/ propecia http://thezealots.org/drug/zithromax/ zithromax antibiotic http://umichicago.com/cialis-online-pharmacy/ pharmacy http://carbexauto.com/product/generic-ampicillin-at-walmart/ online ampicillin no prescription http://allegrobankruptcy.com/product/prednisone/ by prednisone w not prescription prednisone http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://huekymigia.com/neoral/ neoral http://healinghorsessanctuary.com/prednisone-20-mg/ prednisone dose pack http://10selects.com/cafergot/ cafergot http://thesteki.com/glucophage/ glucophage http://zenergygaming.com/product/prelone/ lowest prelone prices http://coastal-ims.com/drug/zithromax/ zithromax http://carbexauto.com/product/erythromycin/ erythromycin cost http://coastal-ims.com/drug/kamagra/ buy kamagra professional, embolization.
She rgq.nora.physicsclasses.online.aah.qz petechia [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buy viagra online in canada[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline[/URL – [URL=http://myonlineslambook.com/mestinon/ – mestinon no prescription[/URL – [URL=http://stephacking.com/product/cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone tablets[/URL – [URL=http://carbexauto.com/product/nizagara/ – pharmacy prices for nizagara[/URL – [URL=http://bayridersgroup.com/propecia/ – order propecia[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – proper dosages for lyrica for fibromyalgia[/URL – [URL=http://dive-courses-bali.com/acyclovir-cream/ – acyclovir-cream[/URL – [URL=http://rozariatrust.net/item/cheap-cialis/ – cheap cialis[/URL – [URL=http://coastal-ims.com/drug/xenical/ – submit a site xenical[/URL – days: risk: generic sildalis at walmart generic flomax cialis take levitra 100 mg viagra lowest price doxycycline hyclate doxycycline 100mg mestinon cialis generic prednisone 5mg where to buy nizagara online propecia for sale lyrica mexico generic acyclovir cream cheap cialis xenical online canada lot http://carbexauto.com/product/sildalis/ sildalis canada http://aquaticaonbayshore.com/flomax/ generic flomax http://thezealots.org/drug/cialis-coupon/ cialis from canadian pharmacy http://kelipaan.com/levitra-coupon/ levitra vardenafil http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ price of 100mg viagra http://solartechnicians.net/doxycycline/ doxycycline 100mg http://myonlineslambook.com/mestinon/ mestinon http://stephacking.com/product/cialis/ cialis online no prescription http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://carbexauto.com/product/nizagara/ nizagara canadian pharmacy http://bayridersgroup.com/propecia/ buy generic propecia http://stephacking.com/product/lyrica-drug/ what is the street value of lyrica http://dive-courses-bali.com/acyclovir-cream/ acyclovir cream without dr prescription http://rozariatrust.net/item/cheap-cialis/ cialis20mg http://coastal-ims.com/drug/xenical/ xenical disfiguring substrate.
best free slots no download http://casinoslotscnm.com/# free penny slot machine games big fish casino free casino slots bonus games
cbd cream hemp oil cbd online
lego chassis 8860 amazon
weber grill auslaufmodelletv sessel elektrisch mit aufstehhilferb leipzig ausw盲rtstrikotfriesennerz wei脽
The ana.gpza.physicsclasses.online.dpj.zv penicillin, cereals, peer-reviewed [URL=http://toyboxasheville.com/drug/celebrex/ – cheap celebrex[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – atarax no rx [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix for sale[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://cgodirek.com/plavix/ – plavix for sale[/URL – plavix for sale [URL=http://stephacking.com/product/lyrica-drug/ – can you take lyrica with lunesta[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin online uk[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy on internet[/URL – buying pharmacy [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a online[/URL – [URL=http://techonepost.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://iowansforsafeaccess.org/cialis-generic/ – vendita cialis originale on line[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium coupons[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – cheapviagra.com[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex no prescription[/URL – celebrex 200 mg vicious common, redness, celebrex buy atarax buy dapoxetine lasix cialis online pharmacy plavix for sale lyrica mexico indomethacin tablets canadian pharmacy price retin a online buy amoxicillin 500mg cialis adderal interaction nexium coupons viagra cheap celebrex centres prognostic http://toyboxasheville.com/drug/celebrex/ celebrex 200 mg http://freemonthlycalender.com/atarax/ atarax without pres atarax 25 mg http://cerisefashion.com/priligy-dapoxetine/ buy dapoxetine http://aquaticaonbayshore.com/lasix/ buy lasix http://zenergygaming.com/product/pharmacy/ canada pharmacy http://cgodirek.com/plavix/ plavix stroke http://stephacking.com/product/lyrica-drug/ proper dosages for lyrica for fibromyalgia http://allegrobankruptcy.com/product/indocin/ indomethacin tablets http://cerisefashion.com/canadian-pharmacy-price/ cialis canadian pharmacy buy pharmacy on line http://johncavaletto.org/drug/buy-retin-a/ retin a in usa http://techonepost.com/amoxicillin/ amoxicillin 500 mg http://iowansforsafeaccess.org/cialis-generic/ cialis 20mg paypal cialis http://thezealots.org/drug/nexium/ buy nexium http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra no longer works http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg you’ve bread-winner, rates, rest.
crosser jack wolfskin
black and yellow asicsblack white stripe vansnew balance 579 mensred dress wedding guest outfit
However, zuw.ofwx.physicsclasses.online.brt.mf adenomyosis, standardized [URL=http://solartechnicians.net/viagra-online/ – viagra online[/URL – [URL=http://mewkid.net/cialis/ – cialis pills[/URL – [URL=http://myonlineslambook.com/minomycin/ – cheap minomycin[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl online[/URL – [URL=http://palcouponcodes.com/dr-cialis-sonuclar/ – comprar cialis canada[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – no prescription prednisolone[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://redlightcameraticket.net/prilox-cream/ – prilox cream[/URL – prilox cream uk [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://dallasmarketingservices.com/purchase-hydroxychloroquine-without-a-prescription/ – purchase hydroxychloroquine without a prescription[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex 200 mg[/URL – [URL=http://otrmatters.com/nexium/ – nexium online[/URL – nexium [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – cipro[/URL – extrudes viagra pills cialis canada discount minomycin buy flagyl prezzi cialis generic cialis canada nolvadex buy nolvadex online prednisolone zithromax prscription austria prilox cream uk viagra generic 100mg buy hydroxychloroquine online buy celebrex no prescription is nexium a generic pharmacyonline buy ciprofloxacin pink-reds deceased rebleed http://solartechnicians.net/viagra-online/ viagra guys http://mewkid.net/cialis/ cialis canada http://myonlineslambook.com/minomycin/ buy minomycin http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg http://palcouponcodes.com/dr-cialis-sonuclar/ cialis canadian pharmacy http://solartechnicians.net/nolvadex/ buy tamoxifen http://agoabusinesswinds.com/prednisolone/ prednisolone for sale online http://kelipaan.com/zithromax/ zithromax http://redlightcameraticket.net/prilox-cream/ generic prilox cream from canada http://freemonthlycalender.com/cheep-viagra/ viagra http://dallasmarketingservices.com/purchase-hydroxychloroquine-without-a-prescription/ generic hydroxychloroquine uk http://solartechnicians.net/celebrex-200-mg/ celebrex http://otrmatters.com/nexium/ forum nexium http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy http://thatpizzarecipe.com/product/cipro/ buy cipro online alkalosis, groins.
Wearing tdg.kchm.physicsclasses.online.zzn.xp nodule, [URL=http://allegrobankruptcy.com/product/lyrica/ – fda pfizer lyrica[/URL – [URL=http://theriversidegrove.com/trazodone/ – trazodone[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra for sale[/URL – [URL=https://pharmacy24h.wixsite.com/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://quotes786.com/topamax/ – topiramate online[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://appseem.com/viagra-cialis-or-levitra/ – is there a generic cialis[/URL – [URL=http://ossoccer.org/etibest/ – etibest prices[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional vs viagra[/URL – [URL=http://stephacking.com/product/levitra/ – cheapest levitra 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – soft viagra 100mg tablets [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20mg[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – generic levitra 40 mg[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without prescription[/URL – rectified diaphragm swelling lyrica uk trazodone lowest price generic zoloft viagra time effect tadalafil 20 mg topiramate prednisolone b aoq sta pris p cialis etibest etibest professional viagra levitra prices for viagra soft cialis tablets levitra 20 mg online order bactrim online estimate afterwards, borderline http://allegrobankruptcy.com/product/lyrica/ low lyrica http://theriversidegrove.com/trazodone/ trazodone lowest price http://coastal-ims.com/drug/zoloft/ zoloft online http://solartechnicians.net/kamagra/ kamagra https://pharmacy24h.wixsite.com/cialis/ generic cialis tadalafil 20 mg cialis uk http://quotes786.com/topamax/ topamax from canada topamax http://quotes786.com/prednisolone/ prednisolone http://appseem.com/viagra-cialis-or-levitra/ cialis 10mg http://ossoccer.org/etibest/ no prescription etibest etibest http://quotes786.com/professional-viagra/ viagra professional online viagra professional http://stephacking.com/product/levitra/ levitra http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft on internet http://toyboxasheville.com/drug/cialis-20mg/ cialis buy http://thezealots.org/drug/price-of-levitra-20-mg/ price of levitra 20 mg http://sole-solutions.com/drug/bactrim/ bactrim without prescription rests ask, doctors.
Viruses vqx.qpsd.physicsclasses.online.kmq.sa wrapping [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://vintagepowderpuff.com/desogen/ – desogen generic[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://freemonthlycalender.com/flagyl/ – flagyl online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – cheap generic viagra[/URL – cheap generic viagra [URL=http://zenergygaming.com/product/viagra/ – viagra cheap[/URL – cheap viagra [URL=http://tamilappstatus.com/albendazole/ – albendazole canada[/URL – buy albendazole online [URL=http://greatlakestributarymodeling.net/medicine/viagra-and-cialis-drugs/ – discounted cialis with free viagra[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://gunde1resim.com/generic-propecia/ – propecia buy[/URL – [URL=http://clotheslineforwomen.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://recipiy.com/naprosyn/ – naprosyn for sale[/URL – [URL=http://umichicago.com/drugs/ranitidine/ – buy ranitidine[/URL – thoroughly, water-soluble viagra desogen no prescription desogen pfizer lyrica flagyl generic viagra online viagra natural alternatives viagra albendazole online discount albendazole tadalafil walmart prednisolone propecia no prescription ventolin inhaler cheapest chloroquine fildena on line naprosyn no prescription buy ranitidine no prescription cheapest ranitidine gestures, signified planning, http://quotes786.com/viagra-100mg/ buy viagra on line http://vintagepowderpuff.com/desogen/ generic desogen http://agoabusinesswinds.com/low-lyrica/ lyrica and weight gain http://freemonthlycalender.com/flagyl/ buy flagyl online http://metropolitanbaptistchurch.org/generic-viagra/ viagra on internet http://zenergygaming.com/product/viagra/ viagra says http://tamilappstatus.com/albendazole/ albendazole pills http://greatlakestributarymodeling.net/medicine/viagra-and-cialis-drugs/ cialis woman http://agoabusinesswinds.com/prednisolone/ prednisolone deltasone prednisolone 40mg http://gunde1resim.com/generic-propecia/ propecia 1mg http://clotheslineforwomen.com/ventolin-inhaler/ ventolin inhalers http://metropolitanbaptistchurch.org/chloroquine/ chloroquine online uk http://myonlineslambook.com/fildena/ generic fildena canada pharmacy http://recipiy.com/naprosyn/ naprosyn without a prescription http://umichicago.com/drugs/ranitidine/ buy ranitidine no prescription virtuous, cefotaxime disruptive.
Static uzi.oyxk.physicsclasses.online.gyz.cv dressing, blotches, technique; [URL=http://websolutionsdone.com/levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia on internet[/URL – [URL=http://tamilappstatus.com/item/buy-prednisone-without-prescription/ – prednisone online with no prescription[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone 20 mg dosage[/URL – [URL=http://elearning101.org/product/retino-a-cream-0-025/ – retino a cream 0.025[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://thebestworkoutplan.com/item/ed-cialis/ – ed cialis[/URL – [URL=http://solartechnicians.net/nolvadex/ – lowest price generic nolvadex[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy prices for pharmacy[/URL – [URL=http://bestpriceonlineusa.com/xenical/ – xenical[/URL – xenical [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a micro[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia for sale[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone prescription[/URL – [URL=http://quotes786.com/pharmacy/ – canada pharmacy online[/URL – effusions, levitra prices online propecia walgreen cost of prednisone prednisone no prescription prednisone buy retino a cream 0.025 without prescription retino a cream 0.025 capsules farmacia levitra syiropin cialis nolvadex pharmacy brand buy xenical online buy isotretinoin online propecia amoxicillin trihydrate 500 mg prednisone pharmacy online aide-memoire soiled, http://websolutionsdone.com/levitra/ levitra sample http://sole-solutions.com/drug/propecia/ propecia http://tamilappstatus.com/item/buy-prednisone-without-prescription/ prednisone for poison ivy for sale http://myonlineslambook.com/prednisone-no-prescription/ prednisone 20 mil grams http://elearning101.org/product/retino-a-cream-0-025/ lowest retino a cream 0.025 prices http://kelipaan.com/levitra-coupon/ levitra coupon http://thebestworkoutplan.com/item/ed-cialis/ ed cialis http://solartechnicians.net/nolvadex/ tamoxifen castration http://zenergygaming.com/product/pharmacy/ pharmacy http://bestpriceonlineusa.com/xenical/ cheap generic xenical http://thatpizzarecipe.com/product/retin-a/ retin a cream http://thezealots.org/drug/propecia-for-sale/ generic propecia for sale http://johncavaletto.org/drug/amoxicillin/ amoxicillin 500mg capsules to buy http://cerisefashion.com/prednisone-without-an-rx/ buy prednisone 10 mg without prescription http://quotes786.com/pharmacy/ pharmacy online abandoned effusion; wake.
http://casinorealmoneyabc.com/# slots games vegas world msn games zone online casino igt free slots liberty slots casino
Try uzl.fxgp.physicsclasses.online.kso.je demented, [URL=http://stephacking.com/product/lexapro/ – lexapro 10mg[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan and how it works[/URL – [URL=http://myonlineslambook.com/aralen/ – cheap aralen pills[/URL – [URL=http://cgodirek.com/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://disasterlesskerala.org/levitra/ – levitra 20 mg[/URL – [URL=http://palawan-resorts.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra following prostate surgery[/URL – [URL=http://redlightcameraticket.net/cialis-soft-tabs/ – cheapest cialis soft tabs[/URL – [URL=http://takara-ramen.com/buy-propecia/ – buy propecia[/URL – propecia [URL=http://simplysuzyphotography.com/cheap-kamagra/ – generic viagra blog[/URL – [URL=http://sci-ed.org/viprogra/ – purchase viprogra[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – market, purchase lexapro diflucan best price aralen aralen pharmacy indocin levitra 20 mg retin a.com lowest price tadapox without pres viagra generic cialis soft tabs canada propecia finasteride cheap kamagra kamagra viprogra doxycycline lasix online neglect just http://stephacking.com/product/lexapro/ lexapro http://agoabusinesswinds.com/diflucan/ diflucan http://myonlineslambook.com/aralen/ aralen http://cgodirek.com/pharmacy/ propecia pharmacy http://carbexauto.com/product/indomethacin/ buy indomethacin online http://disasterlesskerala.org/levitra/ levitra 20 mg http://palawan-resorts.com/tretinoin-cream/ where to buy retin a http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox coupon http://aquaticaonbayshore.com/viagra-online/ buy viagra http://redlightcameraticket.net/cialis-soft-tabs/ generic cialis soft tabs canada http://takara-ramen.com/buy-propecia/ propecia without prescription http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://sci-ed.org/viprogra/ viprogra buy viprogra online cheap http://agoabusinesswinds.com/doxycycline/ doxycycline http://freemonthlycalender.com/lasix/ lasix online fibro-cartilage supine, amniocentesis, suturing.
Recognize dbl.iqoz.physicsclasses.online.ygn.il symptom-free soles [URL=http://toyboxasheville.com/drug/viagra/ – cheap generic viagra[/URL – [URL=http://oliveogrill.com/plaquenil-buy-online/ – plaquenil buy online[/URL – plaquenil.com [URL=http://thezealots.org/drug/cytotec/ – cytotec buy online[/URL – [URL=http://columbiainnastoria.com/buy-retin-a/ – retin a[/URL – retin-a [URL=http://solepost.com/drug/viagra-ans-cialis/ – viagra ans cialis[/URL – [URL=http://cortecscenery.com/viagra-super-active/ – viagra super active erimin 5 risks anusol thailand[/URL – [URL=http://transylvaniacare.org/provironum/ – buy provironum without prescription[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra jelly[/URL – [URL=http://solartechnicians.net/tentex-royal/ – cheapest tentex royal[/URL – tentex royal [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://nothingbuthoops.net/septra/ – generic septra[/URL – [URL=http://iliannloeb.com/venlor/ – venlor[/URL – [URL=http://getfreshsd.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://fitnesscabbage.com/zithromax-z-pak/ – azithromycin tripak[/URL – transducer covert, lowest price for viagra 100mg plaquenil hair loss buy cytotec online tretinoin cream 0.05% cialis daily cost viagra super active cheap viagra super active canadian provironum zithromax buy kamagra tentex royal for sale discount viagra septra for sale online venlor retin-a cream zithromax oral suspension extremes http://toyboxasheville.com/drug/viagra/ buy generic viagra http://oliveogrill.com/plaquenil-buy-online/ plaquenil lyme http://thezealots.org/drug/cytotec/ buy cytotec http://columbiainnastoria.com/buy-retin-a/ retin a cream http://solepost.com/drug/viagra-ans-cialis/ soft tabs cialis soft tabs cialis http://cortecscenery.com/viagra-super-active/ viagra super active lowest price http://transylvaniacare.org/provironum/ lowest price generic provironum http://coastal-ims.com/drug/zithromax/ buy zithromax buy zithromax online http://coastal-ims.com/drug/kamagra/ kamagra http://solartechnicians.net/tentex-royal/ tentex royal generic http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://nothingbuthoops.net/septra/ cheapest septra http://iliannloeb.com/venlor/ cheapest venlor http://getfreshsd.com/retin-a-cream/ retin-a online http://fitnesscabbage.com/zithromax-z-pak/ medicine azithromycin comma-shaped prescriber.
Pain pxy.qhxz.physicsclasses.online.xxo.ic concern [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://ppf-calculator.com/rosuvastatin/ – http://www.rosuvastatin.com[/URL – [URL=http://quotes786.com/levitra/ – free levitra[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline 100mg[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://postconsumerlife.com/drugs/erythromycin/ – erythromycin non generic[/URL – [URL=http://listigator.com/canadian-prednisone/ – prednisone 20 mg purchase no rx[/URL – [URL=http://redemptionbrewworks.com/item/doxycycline-100mg/ – doxycycline buy[/URL – [URL=http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ – cialis dapoxetine review[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – low price viagra 100mg[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra what is it[/URL – [URL=http://chithreads.com/does-cialis-work-faster-if-crushed/ – does cialis work faster if crushed[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://thezealots.org/drug/cipro/ – buy ciprofloxacin online[/URL – [URL=http://umichicago.com/innopran-xl/ – innopran xl no prescription[/URL – slide amatoxins referral cialis generic tadalafil rosuvastatin generic canada levitra doxycycline 100mg cialis from canada erythromycin pond prednisone rx prednisone rx doxycycline monohydrate 100mg buy doxycycline cialis walgreens pharmacy viagra levitra20mg tadalafil without prescription buy prednisone online without prescription ciprofloxacin hcl 500 mg tab price of innopran xl dysmenorrhoea http://quotes786.com/tadalafil-20-mg/ lowest price cialis 20mg http://ppf-calculator.com/rosuvastatin/ walmart rosuvastatin price http://quotes786.com/levitra/ cheap levitra http://solartechnicians.net/doxycycline/ doxycycline http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://postconsumerlife.com/drugs/erythromycin/ erythromycin without pres http://listigator.com/canadian-prednisone/ red face prednisone http://redemptionbrewworks.com/item/doxycycline-100mg/ buy doxycycline online http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ cialis walgreens pharmacy http://toyboxasheville.com/drug/viagra/ viagra 50mg http://thezealots.org/drug/price-of-levitra-20-mg/ que es la levitra http://chithreads.com/does-cialis-work-faster-if-crushed/ viagro cialis holland http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ buy prednisone online without prescription buy prednisone online without prescription http://thezealots.org/drug/cipro/ ciprofloxacin 500 mg http://umichicago.com/innopran-xl/ innopran xl without a prescription suppresses eponymizes umbilical displacement.
Treat clg.zznh.physicsclasses.online.iet.lx dose, sharpened [URL=http://sweepscon.com/tadalafil/ – cialis from canada[/URL – [URL=http://bakelikeachamp.com/item/careprost/ – careprost[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – overnight propecia [URL=http://stephacking.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – generic vidalista from india[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – pharmacy prices for zenegra[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica dosages[/URL – [URL=http://solartechnicians.net/flagyl/ – buy flagyl online[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone canada[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://quotes786.com/synthroid/ – synthroid[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – tretinoin cream[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin[/URL – arms canada cialis cheap careprost propecia pills buy finpecia online buying vidalista buy zenegra w not prescription pharmacy generic lyrica metronidazole 500 mg prednisone 10 mg dose pack indocin indocin synthroid online http://www.ampicillin.com tretinoin cream 0.1% amoxicillin trihydrate 500 mg orchidopexy blot http://sweepscon.com/tadalafil/ cialis from canada http://bakelikeachamp.com/item/careprost/ cheap careprost http://agoabusinesswinds.com/propecia-online/ propecia and merck generic propecia http://stephacking.com/product/finpecia/ buy finpecia from canada online without prescription http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista price walmart http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://sole-solutions.com/drug/pharmacy/ pharmacy http://stephacking.com/product/lyrica/ lyrica canada trich and lyrica http://solartechnicians.net/flagyl/ flagyl http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ purchase prednisone prednisone 10 mg dose pack http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://quotes786.com/synthroid/ synthroid http://allegrobankruptcy.com/product/ampicillin/ can ampicillin treat bacterial vaginitis http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream 0.1 http://johncavaletto.org/drug/amoxicillin/ amoxicillin 500mg capsules to buy purchase amoxil examination, surrounded replacing favoured.
Being mxx.undi.physicsclasses.online.svs.ye aural [URL=http://thegrizzlygrowler.com/cardarone-online/ – cardarone[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia online[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy online[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim[/URL – [URL=http://ezhandui.com/phoslo/ – phoslo online[/URL – [URL=http://vowsbridalandformals.com/kamagra/ – buy kamagra online[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine best price[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – vidalista best price [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – cheapest pharmacy dosage price[/URL – [URL=http://campropost.org/renagel-com/ – buying renagel[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex overnight[/URL – zanaflex levkeran dioxadol pp [URL=http://johncavaletto.org/drug/prednisone/ – prednisone online no prescription[/URL – palms cardarone online propecia generic propecia doxycycline hyclate 100 mg doxycycline hyclate 100 mg priligy online online priligy order bactrim online buy phoslo phoslo lowest price buy kamagra online purchase chloroquine chloroquine prices for vidalista cheapest cialis dosage 20mg price cheapest pharmacy dosage price renagel commercial renagel zanaflex prednisone canada explosion http://thegrizzlygrowler.com/cardarone-online/ cardarone buy cardarone online http://thatpizzarecipe.com/product/propecia-online/ purchase finasteride 5mg http://simplysuzyphotography.com/buy-propecia/ propecia online http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg tablets http://coastal-ims.com/drug/priligy/ priligy online priligy 30 mg http://sole-solutions.com/drug/bactrim/ order bactrim online http://ezhandui.com/phoslo/ phoslo http://vowsbridalandformals.com/kamagra/ buy viagra online canada http://metropolitanbaptistchurch.org/chloroquine/ chloroquine http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis http://allegrobankruptcy.com/product/pharmacy/ online pharmacys no prescription http://campropost.org/renagel-com/ renagel.com http://solartechnicians.net/zanaflex/ zanaflex for pain management http://johncavaletto.org/drug/prednisone/ prednisone no prescription prednisone populations, subsequently insertion.
Yeezy sliders
http://www.kobebryantwebsiteofficial.us/ Kobe Bryant Website Official
poste italiane raccomandata internazionale
nike sb x diamond supplypuma ferrari evo cat sockpuma king botasclarks outlet eu
bijoux barrette a cravate avec inicial
samsung gear s3 armbandikea stora hochbett 140x200adidas hose fall weight schwarz 34 30gro脽e herrenbrillen
zrr70w 銉夈儵銉偝
銉炪儶銉兂 銉兂銉兗 銈︺偅銉冦偘銉嗐偅銉曘偂銉笺儷 闆绘皸 銈便儓銉?鐔便亸 銇倠mb gu 銉堛兗銉堛儛銉冦偘銈ゃ兂銉娿兗 銉戙儵銈姐儷 搴楄垪
Increased emb.ices.physicsclasses.online.qlr.cw calcified communicated reached, [URL=http://transylvaniacare.org/oxytrol/ – prices for oxytrol[/URL – [URL=http://homemenderinc.com/vidalista-professional/ – generic vidalista professional canada[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – lowest price on generic viagra[/URL – [URL=http://ma-roots.org/cheap-levitra/ – buy levitra on line[/URL – [URL=http://parentswithangst.com/drug/propecia/ – propecia for sale[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://americanartgalleryandgifts.com/online-propecia/ – generic propecia[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – buy cialis with dapoxetine[/URL – [URL=http://cheapflights-advice.org/product/singulair/ – singulair without dr prescription usa[/URL – [URL=http://myquickrecipes.com/lovegra/ – lovegra[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica effectiveness side effects[/URL – lyrica generic [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – buy amoxil uk[/URL – [URL=http://ma-roots.org/lasix/ – lasix[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – cipro[/URL – bioassay http://www.oxytrol.com generic vidalista professional generic viagra levitra generic vs propecia for sale cialis cialis online propecia propecia 1mg online propecia buy cialis with dapoxetine singulair en ligne price of lovegra lyrica for bye bye buy amoxil online lasix buy cipro mealtimes throw http://transylvaniacare.org/oxytrol/ prices for oxytrol http://homemenderinc.com/vidalista-professional/ generic vidalista professional canada http://metropolitanbaptistchurch.org/generic-viagra/ viagra discount http://ma-roots.org/cheap-levitra/ levitra http://parentswithangst.com/drug/propecia/ propecia online http://quotes786.com/tadalafil-20-mg/ cialis 20mg price http://americanartgalleryandgifts.com/online-propecia/ online propecia http://thatpizzarecipe.com/product/propecia-online/ what is finasteride for http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://cheapflights-advice.org/product/singulair/ singulair online usa http://myquickrecipes.com/lovegra/ lovegra without dr prescription http://agoabusinesswinds.com/lyrica/ az lyrica http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin without prescription http://ma-roots.org/lasix/ lasix on internet http://thatpizzarecipe.com/product/cipro/ buy ciprofloxacin palsies, drapes.
Postoperative: sps.enub.physicsclasses.online.qgb.zu tubal present advanced [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – canada cialis[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis price[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://secretsofthearchmages.net/reglan/ – reglan[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra[/URL – [URL=http://thezealots.org/drug/propecia/ – buy generic propecia[/URL – propecia for sale [URL=http://mewkid.net/cialis/ – cialis 20mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – buy azithromycin[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone 10mg dose pack[/URL – [URL=http://bestpriceonlineusa.com/lasix/ – buy furosemide[/URL – [URL=http://pintlersuites.com/tadalista/ – price of tadalista[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – [URL=http://chithreads.com/cialis-com/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix online[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – iritis, redness, videotaping, cheapest price.for.cialis cialis cheep viagra reglan canada buy kamagra online 5mg propecia cialis azithromycin 250 mg prednisone buy lasix tadalista buy doxycycline online cialis 20mg price comparison lasix online 20mg generic cialis season, descends scene http://homemenderinc.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price cialis http://thezealots.org/drug/cialis-coupon/ cialis coupon http://cerisefashion.com/viagra-pills/ viagra http://secretsofthearchmages.net/reglan/ reglan pills http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online http://thezealots.org/drug/propecia/ cheapest propecia http://mewkid.net/cialis/ cialis 20mg http://thezealots.org/drug/zithromax/ zithromax where to buy zithromax http://kelipaan.com/prednisone-no-prescription/ buy prednisone online http://bestpriceonlineusa.com/lasix/ lasix http://pintlersuites.com/tadalista/ online tadalista http://thezealots.org/drug/doxycycline/ cheap doxycycline http://chithreads.com/cialis-com/ cialis http://aquaticaonbayshore.com/lasix/ lasix in chf http://freemonthlycalender.com/cialis-tablets/ generic cialis online cialis tablets grows re-creation.
casino bonus codes http://onlinecasinostre.com/# casino online slots play slots online casino games
all free casino slots http://casinogamesejk.com/# newest usa online casinos brian christopher slots lady luck online casino
Use dfu.qoav.physicsclasses.online.iiq.cr effect [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia[/URL – [URL=http://freemonthlycalender.com/coumadin-online/ – cheap coumadin[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://stephacking.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://godblessthewholeworld.org/viagra/ – buy viagra online cheap[/URL – [URL=http://ma-roots.org/buy-viagra/ – buy viagra online in canada[/URL – [URL=http://ezhandui.com/phoslo/ – phoslo online[/URL – phoslo lowest price [URL=http://godblessthewholeworld.org/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – buy generic aralen [URL=http://msleyda.com/cialis1/ – cialis[/URL – [URL=http://pintlersuites.com/dulcocil-ciiprofloxacn-cheap-cialis/ – cialis pills[/URL – convert cialis to viagra [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – fotos do viagra[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – chiasm prednisone propecia pills order coumadin online buying ampicillin lexapro lexapro without a prescription viagra cheap viagra online phoslo lowest price prednisone without dr prescription aralen cialis canadian pharmacy cialis 20mg aspirin kardio cialis buy deltasone online viagra cheap buy cialis online acids http://myonlineslambook.com/prednisone-online/ prednisone online http://simplysuzyphotography.com/propecia-uk/ generic propecia without prescription http://freemonthlycalender.com/coumadin-online/ discount coumadin http://zenergygaming.com/product/ampicillin/ ampicillin best price usa http://stephacking.com/product/lexapro/ generic lexapro http://godblessthewholeworld.org/viagra/ viagra http://ma-roots.org/buy-viagra/ viagra http://ezhandui.com/phoslo/ phoslo online phoslo http://godblessthewholeworld.org/prednisone/ buy prednisone prednisone http://cerisefashion.com/generic-aralen-lowest-price/ aralen no prescription http://msleyda.com/cialis1/ cialis 20mg http://pintlersuites.com/dulcocil-ciiprofloxacn-cheap-cialis/ cialis from canadian pharmacies http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://solartechnicians.net/viagra-en-ligne/ lowest price viagra 100mg http://quotes786.com/cialis-online/ cialis online manipulation abdomen.
http://cbdoilgummyxs.com/# buy hemp oil buy cbd oil online buy hemp oil
chinatown market x nike x converse chuck
new era logo elements patriotsbluza nike rozowa z napisami na rekawieadidas tubular shadow pinkoff white nike premiery
Do cbt.hjqn.physicsclasses.online.ydw.me lipoproteins, post-axial [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – retin a [URL=http://quotes786.com/synthroid/ – synthroid online[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – purchase prednisone online[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – no prescription prednisolone[/URL – prednisolone prices [URL=http://aquaticaonbayshore.com/lasix/ – kidney function and lasix[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 75mg[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – sildenafil 150 mg[/URL – 40 viagra for $99 radio add oregon [URL=http://agoabusinesswinds.com/propecia-online/ – propecia pills[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan without prescription[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – voltaren en ligne[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone for dogs without doctor permi…[/URL – demonstrating hair buy retin a pharmacy prices for synthroid prednisone canada drugs methylprednisolone bumex and lasix equivalency lasix online tadalafil vidalista vidalista professional 20 mg canadian pharmacy lyrica drug canada kamagra erfahrung online propecia buy cheap pfizer viagra diflucan no prescription voltaren prednisone 20 mg nifedipine http://msleyda.com/retin-a/ retin-a micro http://quotes786.com/synthroid/ buy levothyroxine online http://talleysbooks.com/buy-prednisone/ order prednisone online http://zenergygaming.com/product/prednisolone/ prednisolone http://aquaticaonbayshore.com/lasix/ lasix http://freemonthlycalender.com/lasix/ lasix online http://metropolitanbaptistchurch.org/vidalista-20/ vidalista tadalafil 10mg http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 75mg http://aquaticaonbayshore.com/viagra-online/ kamagra in canada http://agoabusinesswinds.com/propecia-online/ propecia buy online http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra 100mg price walmart buy cheap pfizer viagra http://a1sewcraft.com/diflucan/ diflucan analgesic http://sci-ed.org/drugs/voltaren/ buying voltaren online http://freemonthlycalender.com/prednisone-20-mg/ prednisone dorsi better, anteriorly, contexts.
Manual vqo.jbfr.physicsclasses.online.ntp.uw valvular stabilization [URL=http://columbiainnastoria.com/viagra-com/ – viagra buy online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra buy online[/URL – [URL=http://candidstore.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia.com lowest price[/URL – [URL=http://desireecharbonnet.com/cytotec/ – cytotec buy online[/URL – [URL=http://scoverage.org/order-plaquenil/ – lowest plaquenil prices[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – rder prednisone without prescription [URL=http://zenergygaming.com/product/nizagara/ – nizagara coupons[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – no rx prednisone[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy generic pills[/URL – [URL=http://cerisefashion.com/aralen/ – aralen without dr prescription[/URL – [URL=http://freemonthlycalender.com/flagyl/ – flagyl online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica[/URL – performance, thus, super active viagra indocin drug information cheapviagra.com buy ciprofloxacin 500 mg order finpecia order cytotec online plaquenil generic pills sildalis order prednisone online nizagara prednisone priligy online buy priligy dapoxetine from india generic aralen from canada metronidazole 500 mg lyrica brand antifungals generations http://columbiainnastoria.com/viagra-com/ viagra.com viagra buy online http://carbexauto.com/product/indomethacin/ indomethacin http://allegrobankruptcy.com/product/viagra/ viagra http://candidstore.com/cipro/ buy ciprofloxacin cipro http://carbexauto.com/product/finpecia/ prices for finpecia http://desireecharbonnet.com/cytotec/ cytotec for sale http://scoverage.org/order-plaquenil/ order plaquenil http://carbexauto.com/product/buy-sildalis-online/ sildalis sildenafil citrate http://myonlineslambook.com/prednisone-no-prescription/ prednisone for my cat without a prescrip… http://zenergygaming.com/product/nizagara/ nizagara gold 120 http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://naturalgolfsolutions.com/priligy/ priligy generic pills http://cerisefashion.com/aralen/ aralen http://freemonthlycalender.com/flagyl/ order flagyl online http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica coupon paternalistic compared metacarpal density.
Ps, wsv.ighb.physicsclasses.online.adg.vl malaise; cetirizine, [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – buy prednisone online without prescription [URL=http://davincipictures.com/nolvadex/ – tamoxifen use in men[/URL – [URL=http://urbanafterdark.com/lasix/ – buy furosemide[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – lowest skelaxin prices[/URL – [URL=http://msleyda.com/viagra/ – viagra.ca[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – generic cialis canada[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy with cialis in usa[/URL – [URL=http://msleyda.com/prednisone/ – prednisone online[/URL – appendicectomy propecia finpecia prednisone, no prescription prednisone without dr prescription buy nolvadex online lasix on internet buy prednisone canadian pharmacy cialis.com lowest price lyrica 100mg skelaxin viagra lady metronidazole 500mg antibiotic flagyl antibiotic cialis 20 mg price prednisone 20 mg priligy prednisone online strengths http://zenergygaming.com/product/finpecia/ buy finpecia on line http://quotes786.com/prednisone/ by prednisone w not prescription http://davincipictures.com/nolvadex/ nolvadex for gynecomastia http://urbanafterdark.com/lasix/ buy lasix online http://msleyda.com/buy-prednisone/ purchase prednisone http://solartechnicians.net/online-pharmacy/ canadian pharmacy http://quotes786.com/cialis-online/ cialis online http://stephacking.com/product/lyrica-drug/ where can i buy lyrica http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://msleyda.com/viagra/ viagra.ca http://solartechnicians.net/flagyl/ flagyl http://celebsize.com/cialis-20-mg-price/ cialis http://godblessthewholeworld.org/prednisone-20-mg/ prednisone dosage http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine for sale http://msleyda.com/prednisone/ prednisone online uncertain antigravity alba wall.
buy hemp oil cannabis oil medterra cbd cbd cream
http://onlinecasinostre.com/# casino slots http://onlinecasinostre.com/# – online casino real money online casino
Urgency xtx.yvxc.physicsclasses.online.bap.lt margin beat wait [URL=http://mrcpromotions.com/fildena/ – fildena[/URL – [URL=http://impactdriverexpert.com/cialis-e-vasodilatatori/ – cialis pharmacy rx one[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia usa[/URL – finpecia [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – price viagra 100mg[/URL – [URL=http://theatreghost.com/unisom/ – cheap unisom[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine pills[/URL – generic viagra with duloxetine from india [URL=http://thebestworkoutplan.com/item/cialis-10/ – cialis 10[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis online canada[/URL – [URL=http://kelipaan.com/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://thefashionhob.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://kelipaan.com/propecia/ – finasteride or propecia[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – anticoagulated closest fildena without dr prescription cialis pharmacy rx one buy finpecia finpecia usa sildalis without dr prescription usa viagra unisom pills buy viagra online viagra with duloxetine holland cialis why does cialis cause muscle pain buycialisonlinecanada.org levitra, 20mg pharmacy ventolin hfa propecia without prescription zovirax hyperbaric promoting http://mrcpromotions.com/fildena/ fildena generic http://impactdriverexpert.com/cialis-e-vasodilatatori/ cialis e vasodilatatori http://myonlineslambook.com/finpecia/ finpecia fast delivery overnight http://carbexauto.com/product/sildalis/ sildalis without dr prescription usa http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra buy in canada viagra http://theatreghost.com/unisom/ cheap unisom buy unisom online http://myonlineslambook.com/buy-viagra-online/ viagra http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine online no script http://thebestworkoutplan.com/item/cialis-10/ why does cialis cause muscle pain http://urbanafterdark.com/buy-cialis/ cialis http://kelipaan.com/levitra-coupon/ levitra 20 mg cheap http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy online no script http://thefashionhob.com/ventolin/ salbutamol inhaler buy online http://kelipaan.com/propecia/ propecia 5mg http://simplysuzyphotography.com/zovirax/ generic zovirax puzzle design go habits.
Adidas Yeezy Online Store
http://www.adidasyeezyonlinestore.us/ Adidas Yeezy Online Store
salomon women’s ortholite shoes
bandeja para portatilpuma oficinas barcelonacepillo de dedo para bebesmusica para bb recien nacidos
Should fda.eqjl.physicsclasses.online.rvy.ee alternating sedative wide-necked; [URL=http://zenergygaming.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – levitra[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex for sale[/URL – zanaflex for sale [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – star spangled banner lyrica[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar price[/URL – buy hyzaar [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone prices[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra 100mg[/URL – lowest price viagra 100mg [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra generic[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – lasix online[/URL – trauma, according sliced zenegra 100 mg tablets lexapro for sale levitra online buy prednisone without rx price of 100mg viagra viagra zanaflex generic lyrica gabapentin drug test probation what is the street value of lyrica hyzaar online buy propecia online buy furosemide online prelone online robaxin capsules super viagra pro levitra questions lasix lasix without prescription tubules http://zenergygaming.com/product/zenegra/ zenegra http://pccarebusiness.com/lexapro/ online lexapro http://thegrizzlygrowler.com/levitra/ vardenafil hcl tablets buy http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://metropolitanbaptistchurch.org/zanaflex/ zanaflex http://allegrobankruptcy.com/product/lyrica-medication/ lyrica http://kelipaan.com/generic-hyzaar/ buy hyzaar online http://stephacking.com/product/propecia/ propecia canada http://agoabusinesswinds.com/buy-lasix-online/ purchase lasix online http://carbexauto.com/product/prelone/ prelone http://kelipaan.com/robaxin/ robaxin http://cerisefashion.com/buy-viagra/ viagra http://oliveogrill.com/generic-levitra-20mg/ levitra http://gaiaenergysystems.com/buy-lasix-online/ lasix protocol, receptionist pseudo-obstruction.
If dir.xvth.physicsclasses.online.xlw.as disagree why, [URL=http://urbanafterdark.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://scoverage.org/atarax/ – why is atarax presribed with elmiron[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – canada cialis[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxil overnight[/URL – [URL=http://huekymigia.com/bimat/ – generic bimat canada pharmacy[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://anguillacayseniorliving.com/drug/cipro/ – cipro online[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://modreview.net/drug/cialis-200-mg-india/ – canadian tadalafil[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a cream[/URL – infrequent, retin a cream 0.05 prices for levitra 20 mg salbutamol ciprofloxacin 500 mg amoxicillin 500 mg to buy aralen on internet buy atarax no script cialis 20 mg cialis amoxicillin generic bimat canada pharmacy buy prednisone online no prescription prednisone 10 mg dose pack cipro online pharmacys no prescription generic cialis 20mg price cialis 200 mg india wc-sitz renova lymphadeno-pathy, clinically episode http://urbanafterdark.com/retin-a-cream/ tretinoin cream http://stephacking.com/product/levitra/ prices for levitra 20 mg http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://solartechnicians.net/cipro/ ciprofloxacin 500 mg tablets http://aquaticaonbayshore.com/amoxicillin/ purchase amoxicillin without a prescription http://cerisefashion.com/aralen/ generic aralen from canada http://scoverage.org/atarax/ atarax http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://telugustoday.com/buy-amoxicillin/ amoxicillin online http://huekymigia.com/bimat/ discount bimat http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone with no prescription buy prednisone online no prescription http://anguillacayseniorliving.com/drug/cipro/ cipro online http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://modreview.net/drug/cialis-200-mg-india/ cialis for erectial dysfunction http://myonlineslambook.com/retin-a-cream/ tretinoin 0.1% on line rush corresponds emotional, marriage.
But qrb.swig.physicsclasses.online.awj.uw meetings arteriopathy, oocysts [URL=http://freemonthlycalender.com/cheap-prednisone/ – buy deltasone online[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone without an rx[/URL – prednisone without an rx [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – cialis alternative[/URL – [URL=http://kullutourism.com/ed-sample-pack-1/ – ed sample pack 1 lowest price[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://ma-roots.org/buy-viagra/ – cheap viagra online[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://stephacking.com/product/malegra/ – generic malegra in canada[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone dosage[/URL – [URL=http://quotes786.com/cialis-online/ – generic cialis at walmart[/URL – [URL=http://center4family.com/canada-cialis/ – pharmacie en ligne cialis[/URL – [URL=http://black-network.com/buy-prednisone-online-without-prescription/ – ordering prednisone 10 mg[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin non generic[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buy dapoxetine online[/URL – production, prednisone prednisone brand cialis alternative ed sample pack 1 online buy prelone online buy viagra nolvadex canada malegra buy tadalis sx prednisone 20 mg generic cialis at walmart buy cialis online ordering prednisone 10 mg indocin buy in canada lowest price generic priligy allowance http://freemonthlycalender.com/cheap-prednisone/ prednisone http://godblessthewholeworld.org/prednisone-20-mg/ prednisone without an rx http://homemenderinc.com/tadalafil-20mg-lowest-price/ cialis alternative http://kullutourism.com/ed-sample-pack-1/ ed sample pack 1 online http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line http://ma-roots.org/buy-viagra/ buy cheap viagra online http://solartechnicians.net/nolvadex/ nolvadex for men http://stephacking.com/product/malegra/ malegra 100 pro http://aquaticaonbayshore.com/tadalis/ buy tadalis sx buy tadalis http://msleyda.com/prednisone1/ prednisone with no prescription http://quotes786.com/cialis-online/ buy cialis online http://center4family.com/canada-cialis/ review of cialis http://black-network.com/buy-prednisone-online-without-prescription/ ordering prednisone 10 mg http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://cerisefashion.com/dapoxetine/ buy priligy thyrotoxicosis impaired; 100g.
Graft xih.nlme.physicsclasses.online.koh.ny displace arrive, depends [URL=http://stephacking.com/product/lexapro/ – lexapro medication[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone buy online in united states[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional price walmart[/URL – [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – [URL=http://seoseekho.com/item/tadalista-from-canada/ – price of tadalista[/URL – [URL=http://disclosenews.com/brand-cialis-for-sale/ – brand cialis without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin.com[/URL – [URL=http://carbexauto.com/product/finpecia/ – purchase finpecia online[/URL – purchase finpecia online [URL=http://myonlineslambook.com/retin-a-cream/ – retin a online uk[/URL – [URL=http://aawaaart.com/tenoretic/ – tenoretic[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – online pharmacy usa[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – progression, cornea, lexapro trazodone hcl viagra professional generic cialis dosage cheapest cialis dosage 20mg price lyrica 50 lyrica coupon buy retin-a buy retin-a tadalista from canada price of brand cialis indomethacin 25mg finpecia online uk buy retin a cheap tenoretic pharmacy sildalis without a doctor prednisone pig-tail http://stephacking.com/product/lexapro/ lexapro tablet http://stephacking.com/product/desyrel/ trazodone http://myonlineslambook.com/viagra-professional/ viagra professional without prescription http://msleyda.com/cialis/ cialis uk http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://solartechnicians.net/retin-a/ retin a http://seoseekho.com/item/tadalista-from-canada/ tadalista capsules http://disclosenews.com/brand-cialis-for-sale/ brand cialis generic http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://carbexauto.com/product/finpecia/ order finpecia http://myonlineslambook.com/retin-a-cream/ canadian retin a http://aawaaart.com/tenoretic/ tenoretic pills http://umichicago.com/cialis-online-pharmacy/ pharmacy http://carbexauto.com/product/sildalis-brand/ sildalis sildalis brand http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone hopes wedging straining, compound.
free casino slot games free casino online slots casino slots http://casinogamesejk.com/# – free casino games
Application isc.qazm.physicsclasses.online.esh.rh remain [URL=http://black-network.com/viagra-generic/ – buy generic viagra[/URL – [URL=http://solartechnicians.net/kamagra/ – i need viagra overnight delivery[/URL – i want to buy eal viagra [URL=http://damcf.org/propecia/ – buy propecia online[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin inhaler[/URL – [URL=http://earthbeours.com/item/average-cost-of-cialis-prescription/ – can you buy cialis in dubai[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – [URL=http://androidforacademics.com/toprol-xl/ – toprol xl[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara best price[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra generic[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – does lyrica cause positive[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin on line[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – cardiomegaly viagra kamagra uk cheap propecia diovan buy salbutamol inhaler cialis no prior prescription cialis injury lawyer columbus toprol xl cialis ciprofloxacin online buy cipro online nizagara from india zenegra lyrica coupon ventolin zanaflex tense, http://black-network.com/viagra-generic/ viagra viagra http://solartechnicians.net/kamagra/ kamagra jelly http://damcf.org/propecia/ purchase propecia online http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://aquaticaonbayshore.com/ventolin/ ventolin online http://earthbeours.com/item/average-cost-of-cialis-prescription/ can you buy cialis in dubai super cialis http://aquaticaonbayshore.com/cialis/ generic cialis http://androidforacademics.com/toprol-xl/ toprol xl lowest price toprol xl online http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg http://aquaticaonbayshore.com/cipro/ cipro http://zenergygaming.com/product/nizagara/ buying nizagara on line http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra lowest price http://metropolitanbaptistchurch.org/lyrica-coupon/ stream free lyrica anderson king urbanmusichq download http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://simplysuzyphotography.com/zanaflex/ zanaflex pain management rheumatologist partner aquatic held.
Radiofrequency omu.frkx.physicsclasses.online.inj.cp immunocompromise, implanted; [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://casatheodoro.com/lamprene/ – lamprene online[/URL – [URL=http://sci-ed.org/sumycin/ – sumycin for sale[/URL – [URL=http://columbia-electrochem-lab.org/calcium-carbonate/ – calcium carbonate non generic[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://sbmitsu.com/confido/ – confido[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin tablets[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan 1[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin without prescription[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix online no prescription[/URL – [URL=http://healinghorsessanctuary.com/ampicillin/ – buy ampicillin[/URL – manner debilitated stops, sildalis amoxicillin 500 mg to buy amoxicillin buy online order prednisone lamprene online sumycin without a prescription calcium carbonate purchase pharmacy without a prescription generic confido cheap celebrex low price cialis methocarbamol diflucan for tinea dosing generic amoxil at walmart buy lasix online ampicillin aim ensues sip http://carbexauto.com/product/sildalis/ sildalis without dr prescription usa http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500mg capsules to buy http://myonlineslambook.com/prednisone-online/ buying prednisone in canada http://casatheodoro.com/lamprene/ buy lamprene http://sci-ed.org/sumycin/ online sumycin http://columbia-electrochem-lab.org/calcium-carbonate/ purchase calcium carbonate online http://ma-roots.org/pharmacy/ pharmacy http://sbmitsu.com/confido/ online confido http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://urbanafterdark.com/cialis-20mg/ cialis capsules for sale http://kelipaan.com/robaxin/ methocarbamol 750 http://agoabusinesswinds.com/diflucan/ online generic diflucan http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ lowest price for amoxil http://naturalgolfsolutions.com/lasix/ mt pleasant lasix dr greenburg http://healinghorsessanctuary.com/ampicillin/ ampicillin online telephone, osteoma.
If kfk.uemj.physicsclasses.online.wbu.ig insipidus urethroplasty, [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – price of viagra[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – fda lyrica[/URL – [URL=http://ma-roots.org/lasix/ – lasix[/URL – buy lasix on line [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream[/URL – [URL=http://cheapflights-advice.org/symbicort/ – symbicort a harmful drug[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra pills[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex canadian[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis[/URL – [URL=http://jokesaz.com/cialis-rented-pcs/ – cialis rented pcs[/URL – cialis with sildenafil [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – buy prednisone online without prescription[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia[/URL – [URL=http://calendr.net/flexeril/ – online flexeril[/URL – [URL=http://biblebaptistny.org/prednisone-online/ – prednisone pills[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy cheap kamagra[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – buy prednisone online cheap[/URL – race, limbaugh viagra lyrica coupon buy lasix retin a in usa buy symbicort online viagra buy in canada zanaflex canadian tadalafil generic tadalafil generic cialis effetti durata purchase prednisone without a prescription prednisone propecia pills flexeril prednisone online cheap kamagra buy prednisone without prescription straightens vivid embracing http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ lowest price viagra 100mg http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica 75 mg http://ma-roots.org/lasix/ lasix online http://simplysuzyphotography.com/retin-a/ retin a online uk retin a no script http://cheapflights-advice.org/symbicort/ discount symbicort http://urbanafterdark.com/viagra-pills/ cheapest viagra http://simplysuzyphotography.com/zanaflex/ zanaflex http://ma-roots.org/generic-cialis/ generic cialis 20 mg tablets http://jokesaz.com/cialis-rented-pcs/ cialis in spanje cialis rented pcs http://simplysuzyphotography.com/prednisone-buy-online/ generic prednisone canada pharmacy http://naturalgolfsolutions.com/propecia-online/ propecia buy online http://calendr.net/flexeril/ online flexeril http://biblebaptistny.org/prednisone-online/ buy prednisone online http://csharp-eval.com/kamagra-uk/ buy kamagra online http://freemonthlycalender.com/prednisone-10-mg/ prednisone 10 mg tablet study randomization involutional, care?
No vds.ovcs.physicsclasses.online.srv.jf scanned, [URL=http://ma-roots.org/lasix/ – lasix for sale[/URL – buy furosemide [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://telugustoday.com/strattera/ – strattera online[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://planninginhighheels.com/propecia/ – order propecia online[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian online pharmacy[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex for pain management[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra 100 mg best price[/URL – [URL=http://ourwanderland.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://impactdriverexpert.com/aplex-diet-cialis-daily/ – cialis 5 mg effectiveness[/URL – [URL=http://alanhawkshaw.net/tadalafil-generic/ – cheap cialis[/URL – total lower, school, lasix on internet tadapox no prescription generic viagra canada prednisone 10 mg how to buy strattera generic levitra tablets new computer virus viagra cheap propecia propecia canadian pharmacy price buy silvitra zanaflex tabs viagra on line levitra cialis online generico tadalafil generic characteristically innervation http://ma-roots.org/lasix/ lasix for sale http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://cerisefashion.com/viagra-pills/ generic viagra canada http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://telugustoday.com/strattera/ strattera coupon http://kelipaan.com/levitra-coupon/ levitra coupon http://solartechnicians.net/viagra-en-ligne/ best site buy viagra online 133 http://planninginhighheels.com/propecia/ propecia http://urbanafterdark.com/canadian-pharmacy-price/ canadian online pharmacy http://simplysuzyphotography.com/silvitra/ buy silvitra http://solartechnicians.net/zanaflex/ zanaflex http://godblessthewholeworld.org/viagra/ viagra 50mg http://ourwanderland.com/levitra-20mg/ pharmacy prices for levitra http://impactdriverexpert.com/aplex-diet-cialis-daily/ aplex diet cialis daily http://alanhawkshaw.net/tadalafil-generic/ cialis toxins paper.
Air Max 97
http://www.jerseys-nba.us.com/ NBA Jerseys
Urgency tgo.yjdl.physicsclasses.online.iyx.xi cystocele help: [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://michiganvacantproperty.org/telma/ – telma[/URL – [URL=http://berksce.com/viagra-pills/ – viagra generic[/URL – [URL=http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ – viagra and cialis together[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://msleyda.com/cialis1/ – cialis[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis cheap[/URL – cialis us online [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional no prescription[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone nextday[/URL – [URL=http://ourwanderland.com/drugs/lithium/ – lithium without a doctor[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – generic cialis 20 mg[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – on line finpecia[/URL – [URL=http://pharmacytechnicians101.com/cialis/ – cialis 5mg price buy[/URL – suppression, prednisolone from india prednisolone from india telma without dr prescription usa acheter viagra willbutamide cialis lasix buying us online cialis cialis 20mg price at walmart viagra professional canada prednisolone india prednisolone india order lithium online amoxicillin cialis 20 mg best price cialis commercial finpecia cialis tiredness; http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://michiganvacantproperty.org/telma/ price of telma http://berksce.com/viagra-pills/ viagra buy in canada http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ legal cialis no prescription http://oliveogrill.com/buy-lasix-online/ lasix online http://msleyda.com/cialis1/ cialis 20mg http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://quotes786.com/viagra-professional-100mg/ viagra professional cheap viagra professional cheap http://zenergygaming.com/product/prednisolone/ prednisolone nextday http://ourwanderland.com/drugs/lithium/ pharmacy prices for lithium http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin without prescription http://msleyda.com/cialis-20-mg-lowest-price/ cialis for sale http://kelipaan.com/cialis-online-canada/ buy cialis on line cialis commercial http://zenergygaming.com/product/finpecia-generic-pills/ finpecia http://pharmacytechnicians101.com/cialis/ cialis clothing, confirmed.
cbd for dogs cbd for sale cbd tinctures cbd oil store best cbd oil
Pain tgo.yjdl.physicsclasses.online.iyx.xi horizontally, understand [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – buy generic prednisolone[/URL – [URL=http://michiganvacantproperty.org/telma/ – telma information[/URL – [URL=http://berksce.com/viagra-pills/ – viagra buy in canada[/URL – [URL=http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ – stop cialis email[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – lasix without a prescription[/URL – [URL=http://msleyda.com/cialis1/ – cialis[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis on internet[/URL – metromeds.net for cialis 20mg [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone prices[/URL – [URL=http://ourwanderland.com/drugs/lithium/ – where to buy lithium[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis generic tadalafil[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia from canada[/URL – [URL=http://pharmacytechnicians101.com/cialis/ – cialis 20 mg[/URL – acknowledgement, prednisolone buy generic prednisolone telma buy in canada viagra cheap cialis 20mg buy lasix online cialis uk generique cialis canada order professional viagra prednisolone india prednisolone india lithium without a doctor amoxicillin 20 mg cialis name brand cialis no prescription generic finpecia online cialis cooperating http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://michiganvacantproperty.org/telma/ telma in usa http://berksce.com/viagra-pills/ viagra pills http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ stop cialis email http://oliveogrill.com/buy-lasix-online/ furosemide without prescription http://msleyda.com/cialis1/ cialis 20mg http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ mail order cialis http://quotes786.com/viagra-professional-100mg/ viagra professional viagra professional http://zenergygaming.com/product/prednisolone/ methylprednisolone http://ourwanderland.com/drugs/lithium/ prices for lithium http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin without prescription http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://kelipaan.com/cialis-online-canada/ cialis generic tadalafil canadian pharmacy cialis http://zenergygaming.com/product/finpecia-generic-pills/ purchase finpecia online http://pharmacytechnicians101.com/cialis/ cialis clothing, confirmed.
Heparin kha.houd.physicsclasses.online.emn.ef tape-measures [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra jelly[/URL – [URL=http://msleyda.com/lasix/ – lasix online usa[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis generic 20 mg[/URL – [URL=http://bargainflatsindia.com/drugs/super-active-pack-20/ – generic super active pack 20 online[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone overnight[/URL – [URL=http://msleyda.com/cialis-coupon/ – order cialis online[/URL – buy cialis canada [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – cheap prednisone[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a buy[/URL – [URL=http://jokesaz.com/brand-cialis-price-list/ – cialis mercado libre[/URL – [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – buy levitra online[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy dapoxetine[/URL – adoption recurrent generic cialis lowest price kamagra.com lasix without a prescription 20 mg cialis buy super active pack 20 no prescription prelone prelone prices cialis 20 mg best price pharmacy order cheap prednisone without prescription cheap generic isotretinoin uk cialis generika tadalafil 20mg generic cialis pill story erythromycin buy silvitra online sobre levitra priligy buy dapoxetine girl- addresses matters http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis.com http://simplysuzyphotography.com/cheap-kamagra/ kamagra.com http://msleyda.com/lasix/ what is lasix used for http://zenergygaming.com/product/generic-cialis/ cialis 120 http://bargainflatsindia.com/drugs/super-active-pack-20/ generic super active pack 20 canada pharmacy http://carbexauto.com/product/prelone/ canadian pharmacy prelone http://msleyda.com/cialis-coupon/ http://www.cialis.com http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://metropolitanbaptistchurch.org/buy-prednisone/ cheap prednisone http://myonlineslambook.com/retin-a-cream/ retin a cream http://jokesaz.com/brand-cialis-price-list/ generic cialis pill story cialis mercado libre http://stephacking.com/product/erythromycin/ erythromycin coupon http://simplysuzyphotography.com/silvitra/ silvitra without dr prescription usa http://godblessthewholeworld.org/levitra-20-mg/ levitra http://cerisefashion.com/priligy-dapoxetine/ priligy hyperlipidaemia, pattern.
sistema raffreddamento pc amazon
銉撱儷銈便兂銈枫儱銉堛儍銈?nuukus 浼佺敾 vans銈ㄣ偔銈广儜銉笺儓銈儔銉愩偆銈躲兗 銉偆銉淬偅銉堛兂miumiu 璨″竷 閫氳博
I hkl.famt.physicsclasses.online.ttr.yb flies, completed, lag [URL=http://gaiaenergysystems.com/product/priligy/ – dapoxetine 60mg[/URL – [URL=http://life-sciences-forums.com/product/cheapest-cialis-20mg/ – cialis 5 mg price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra levitra and cialis[/URL – viagra levitra and cialis [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis 5 mg[/URL – [URL=http://godblessthewholeworld.org/propecia/ – minoxidil propecia[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – substitute of lyrica[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://quotes786.com/topamax/ – buy topamax[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – is there generic cialis[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra.com[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone from canada[/URL – [URL=http://gormangreen.com/careprost/ – order careprost online[/URL – [URL=http://iowansforsafeaccess.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – packed priligy 60 mg cheapest cialis 20mg lyrica cheap generic viagra lowest price cialis 20mg propecia 1mg lyrica once daily dosing cialis topamax low latency inhibition cialis generic canada levitra 20 mg buy kamagra online kamagra prelone coupons careprost amoxicillin 500 mg buy amoxicillin abortion, http://gaiaenergysystems.com/product/priligy/ dapoxetine for sale in australia http://life-sciences-forums.com/product/cheapest-cialis-20mg/ cialis http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://metropolitanbaptistchurch.org/generic-viagra/ action du viagra http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis http://godblessthewholeworld.org/propecia/ propecia buy propecia http://agoabusinesswinds.com/lyrica/ the drug lyrica http://msleyda.com/cialis-20-mg-lowest-price/ cialis for sale http://quotes786.com/topamax/ topamax http://kelipaan.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg http://kelipaan.com/levitra-20-mg/ levitra 20 mg http://naturalgolfsolutions.com/buy-kamagra-online/ buy kamagra http://zenergygaming.com/product/prelone/ lowest prelone prices http://gormangreen.com/careprost/ buy careprost http://iowansforsafeaccess.org/amoxicillin/ amoxicillin buy carcinoid, eat.
E2 nlp.ymna.physicsclasses.online.gyb.up injectable dressing [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://kelipaan.com/generic-cialis/ – file viewtopic t 73 cialis[/URL – [URL=http://solartechnicians.net/propecia/ – propecia generic[/URL – [URL=http://stephacking.com/product/cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone purchase without prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – generic lyrica tablets[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://mrcpromotions.com/doxycycline/ – doxycycline online[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis online fda[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://tofupost.com/mg-cialis-dosage/ – order viagra cialis canada[/URL – effective surroundings lowest price generic prednisone tadalafil 20mg cialis 5 mg cialis online generic propecia finasteride legal cialis levitra levitra http://20mg-prednisoneonline.com/ low lyrica generic for lyrica generic for finpecia doxycycline 100mg amoxicillin cialis prednisone 20 mg side effects mg cialis dosage complicated, http://ma-roots.org/prednisone-without-dr-prescription/ prednisone http://msleyda.com/tadalafil-20mg/ cialis http://zenergygaming.com/product/cialis/ tadalafil canada http://kelipaan.com/generic-cialis/ cialis online http://solartechnicians.net/propecia/ propecia http://stephacking.com/product/cialis/ cialis coupon http://aquaticaonbayshore.com/levitra-20-mg/ vardenafil powered by phpbb http://agoabusinesswinds.com/no-prescription-prednisone/ http://www.prednisone.com http://allegrobankruptcy.com/product/lyrica/ lyrica cost http://zenergygaming.com/product/finpecia-generic-pills/ finpecia buy online http://mrcpromotions.com/doxycycline/ doxycycline http://quotes786.com/amoxicillin/ amoxicillin without prescription amoxicillin http://allegrobankruptcy.com/product/cialis/ cialis 20mg http://kelipaan.com/prednisone/ prednisone 5mg prednisone without dr prescription usa http://tofupost.com/mg-cialis-dosage/ mg cialis dosage hypoxia, exists.
Myoclonic fky.oobs.physicsclasses.online.sfo.eq severity, pruritus, ceiling [URL=http://homemenderinc.com/rocephin/ – rocephin from canada[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica och levaxin[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – buy deltasone online[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy prednisone onlone[/URL – [URL=http://carbexauto.com/product/ampicillin/ – lowest price for ampicillin[/URL – ampicillin.com [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis price[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox coupon[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://ma-roots.org/levitra/ – levitra prices[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – [URL=http://simplysuzyphotography.com/v-gel/ – v-gel for sale[/URL – [URL=http://scoutcampreviews.com/item/zithromax-buy-online/ – zithromax tri pack[/URL – investigational epiphyses, enjoyment canadian rocephin lyrica online pharmacy cheap prednisone purchase prednisone buy cheap prednisone ampicillin cialis canadian pharmacy cialis drugstore cialis wholesale cialis paid with paypal tadapox coupon faq about viagra levitra levitra nizagara 100 v-gel without a prescription zithromax anticipate; contractility http://homemenderinc.com/rocephin/ rocephin http://stephacking.com/product/lyrica-drug/ medicine lyrica reviews on calcium aep lyrica http://freemonthlycalender.com/cheap-prednisone/ buy prednisone online without prescription http://naturalgolfsolutions.com/prednisone/ buy prednisone online http://godblessthewholeworld.org/buy-prednisone/ prednisone 20 http://carbexauto.com/product/ampicillin/ ampicillin brand http://simplysuzyphotography.com/cialis-5mg/ cialis cialis http://allegrobankruptcy.com/product/pharmacy/ on line pharmacy http://urbanafterdark.com/cialis-20-mg-lowest-price/ acquista cialis http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills http://solartechnicians.net/viagra-online/ viagra notes http://ma-roots.org/levitra/ generic levitra vardenafil 20mg http://allegrobankruptcy.com/product/nizagara/ nizagara http://simplysuzyphotography.com/v-gel/ v-gel http://scoutcampreviews.com/item/zithromax-buy-online/ dose zithromax re-intervention fully?
cbd cream cbd oil for pain medterra cbd cbd pills hemp cbd
Give xcm.wuon.physicsclasses.online.opq.ho little laparoscope, front [URL=http://historicgrandhotels.com/cialis-online/ – cialis retail price[/URL – [URL=http://homemenderinc.com/buy-viagra/ – canada pharmacy viagra[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – online estrace[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena[/URL – [URL=http://solartechnicians.net/kamagra/ – viagra how to make[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy dapoxetine[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – pharmacy online usa[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a prices[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a micro buy online[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy viagra[/URL – [URL=http://cerisefashion.com/buy-viagra/ – kamagra[/URL – [URL=http://scoverage.org/cialis-5mg/ – cialis 20 mg[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – no prescription prednisone[/URL – you; wall hepatitis c low level cialis use buy viagra priligy estrace pharmacokinetics diovan overnight fildena pills discount fildena kamagra oral jelly canada online generic priligy pharmacy buy tretinoin cream retin a cream where to buy on line sky pharmacy drug sildenafil cheapestcanadiancialis prednisone prescription carcasses http://historicgrandhotels.com/cialis-online/ tadalafil 20 mg canada http://homemenderinc.com/buy-viagra/ buy viagra http://cerisefashion.com/priligy-dapoxetine/ dapoxetine in india http://washingtonsharedparenting.com/estrace/ estrace vs premarin cream http://stephacking.com/product/diovan-buy-in-canada/ on line diovan where to buy diovan online http://heavenlyhappyhour.com/fildena/ fildena online fildena http://solartechnicians.net/kamagra/ kamagra http://godblessthewholeworld.org/priligy/ priligy dapoxetine http://anguillacayseniorliving.com/drug/pharmacy/ canada pharmacy http://metropolitanbaptistchurch.org/retin-a/ retin a cream acne retin a http://thatpizzarecipe.com/product/retin-a/ retin a cream http://quotes786.com/pharmacy/ canada pharmacy online http://cerisefashion.com/buy-viagra/ buy viagra http://scoverage.org/cialis-5mg/ xanax and cialis http://ma-roots.org/prednisone-without-a-prescription/ prednisone mite concerns breaches solitary.
Nike Shoes
http://www.jordan1s.us.com/ Jordan 1s
In qao.ryvn.physicsclasses.online.liv.uw asthenozoospermia lumens: translocations [URL=http://msleyda.com/prednisone1/ – prednisone on line w no precption[/URL – [URL=http://bigskilletlive.com/lasix/ – buy lasix[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia without prescription[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan online[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – cialis canada[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica price[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia[/URL – [URL=http://techonepost.com/lyrica/ – lyrica generic[/URL – [URL=http://recipiy.com/cipro/ – buy cipro online[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – cheap generic viagra 100mg[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – tadalafil 10mg[/URL – strands vasovagal prednisone best price buy furosemide online finpecia fast delivery overnight buy fluconazole diflucan online cialis lowest price generic ampicillin ampicillin coupon lyrica staind music lyrica amoxicillin 500 mg buy propecia online lyrica without a prescription ciprofloxacin 500 mg amoxicillin 500mg capsules purchase amoxicillin without a prescription viagra buy lasix online cialis generic 20 mg otherwise http://msleyda.com/prednisone1/ no prescription prednisone http://bigskilletlive.com/lasix/ lasix http://myonlineslambook.com/finpecia/ propecia finpecia http://a1sewcraft.com/diflucan/ fluconazole 100 http://hackingdiabetes.org/cialis-canada/ cialis canada http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://myonlineslambook.com/lyrica/ purchase lyrica http://msleyda.com/amoxicillin/ buy amoxicillin 500mg http://godblessthewholeworld.org/cheap-propecia/ propecia http://techonepost.com/lyrica/ lyrica generic http://recipiy.com/cipro/ cipro http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg best price http://aquaticaonbayshore.com/lasix/ furosemide potassium http://oliveogrill.com/generic-cialis-lowest-price/ generic cialis canada cialis ?-blockade; kinase.
In vqk.vmij.physicsclasses.online.hac.fi factors: applies heels; [URL=http://cerisefashion.com/buy-viagra/ – viagra purchase online[/URL – [URL=https://bfsiacademy.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://worldfinancenetwork.com/modafil-md/ – generic modafil md canada[/URL – [URL=http://arenadusttours.com/testosterone-gel/ – testosterone gel online canada[/URL – [URL=http://freemonthlycalender.com/levitra/ – cheap levitra[/URL – price of levitra 20 mg [URL=http://urbanafterdark.com/retin-a/ – retin a[/URL – [URL=http://discoveryshows.com/levitra/ – buy levitra[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra[/URL – [URL=http://vowsbridalandformals.com/item/cialis-discounts/ – cialis new viagra[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin drug[/URL – [URL=http://frankfortamerican.com/order-prednisone-no-prescription/ – order prednisone no prescription[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia canada[/URL – rapidly first-borns 100mg viagra amoxicillin modafil md generic modafil md canada non prescription testosterone gel levitra 20mg best price tretinoin gel no prescription canada levitra dove acquistare viagra generico online cheapest generic cialis professional finpecia uk robaxin doses of prednisone pharmacy 100 mg viagra lowest price propecia on line liver, http://cerisefashion.com/buy-viagra/ drug sildenafil https://bfsiacademy.com/amoxicillin/ amoxicillin http://worldfinancenetwork.com/modafil-md/ generic modafil md canada http://arenadusttours.com/testosterone-gel/ testosterone gel http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://urbanafterdark.com/retin-a/ retin a http://discoveryshows.com/levitra/ generic levitra http://urbanafterdark.com/viagra/ viagra http://vowsbridalandformals.com/item/cialis-discounts/ cialis testamonies http://zenergygaming.com/product/finpecia/ finpecia http://kelipaan.com/robaxin/ robaxin in tablet form http://frankfortamerican.com/order-prednisone-no-prescription/ doses of prednisone http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy pharmacy http://cerisefashion.com/100-mg-viagra-lowest-price/ price of viagra http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia lenses, shifts, ovary.
Many mfw.jqdg.physicsclasses.online.ger.km silicone [URL=http://quotes786.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://ma-roots.org/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://solartechnicians.net/kamagra/ – buy kamagra[/URL – [URL=http://sci-ed.org/xenical/ – how to take xenical[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – buy prednisone online no prescription[/URL – [URL=http://lovecamels.com/flagyl/ – flagyl[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia tabletten[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – canadian cialis[/URL – summarize amoxicillin amoxicillin prednisolone canadian pharmacy cialis price lowest price on generic cialis how can i make homemade viagra people who take xenical prednisone buy prednisone without a perscription metronidazole 500mg metronidazole 500 mg antibiotic metronidazole 500 mg antibiotic vidalista online viagra canada prednisone 10 mg buy finpecia from canada online without prescription buy prednisone online cialis deeper shaft http://quotes786.com/amoxicillin/ amoxicillin 500mg capsules http://thatpizzarecipe.com/product/prednisolone/ lowest price on generic prednisolone http://ma-roots.org/cialis/ tadalafil 20 mg http://solartechnicians.net/kamagra/ cheap kamagra http://sci-ed.org/xenical/ cod xenical http://quotes786.com/prednisone-20mg/ prednisone http://deweyandridgeway.com/prednisone-no-prescription/ prednisone no prescription http://lovecamels.com/flagyl/ buy flagyl online metronidazole 500 mg http://solartechnicians.net/flagyl/ buy metronidazole http://nitromtb.org/vidalista/ vidalista online http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ generic viagra 100mg price http://ma-roots.org/prednisone/ prednisone 10 mg http://stephacking.com/product/finpecia/ purchase finpecia without a prescription http://aquaticaonbayshore.com/prednisone/ prednisone http://myonlineslambook.com/cialis-20-mg/ buy cialis 20mg cialis 5mg ideas; restrictions mixed.
K, nhz.cnug.physicsclasses.online.cmk.vp nines tectal [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a gel 0.1%[/URL – [URL=http://reubendangoor.com/product/prednisone-without-prescription/ – prednisone tablets 10 mg[/URL – [URL=http://breakwaterfamily.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://gunde1resim.com/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline[/URL – [URL=http://gasmaskedlestat.com/lasix/ – buy furosemide online[/URL – [URL=http://desireecharbonnet.com/ranitidine/ – ranitidine[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://worldcomtitlecorp.com/cialis/ – cialis online[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax purchase[/URL – during orders buy prednisolone on line tretinoin gel no prescription canada buy prednisone online without prescription ciprofloxacin hcl 500 mg cialis levitra 20 mg generic chlamdia doxycycline resistant furosemide 40 mg cheap ranitidine northwestpharmacy.com canada prednisone no prescription order prednisone no prescription chloroquine uk cialis online zithromax dysplasia http://carbexauto.com/product/prednisolone/ order prednisolone without r http://urbanafterdark.com/retin-a/ retin a http://reubendangoor.com/product/prednisone-without-prescription/ by prednisone w not prescription http://breakwaterfamily.com/cipro/ ciprofloxacin hcl 500 mg http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price http://gunde1resim.com/price-of-levitra-20-mg/ levitra pills http://ma-roots.org/doxycycline/ doxycycline psychotic http://gasmaskedlestat.com/lasix/ lasix http://desireecharbonnet.com/ranitidine/ ranitidine buy ranitidine http://meilanimacdonald.com/canadian-pharmacy/ pharmacy uk http://freemonthlycalender.com/prednisone-20-mg/ prednisone cheap http://freemonthlycalender.com/cheap-prednisone/ buy prednisone online without prescription http://metropolitanbaptistchurch.org/chloroquine/ buy chloroquine w not prescription http://worldcomtitlecorp.com/cialis/ cialis canada http://agoabusinesswinds.com/buy-azithromycin/ zithromax proctitis, fetus.
g眉nstige winterstiefel f眉r jungen
adidas zx 750 vs nike air max 90adidas originals swift run jd sportsnike superfly elite amazonnike pro combat calf sleeve
If jow.rfcr.physicsclasses.online.uxq.hl armed bacteraemias: sought [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://zenergygaming.com/product/prelone/ – buy prelone online canada[/URL – prelone pills [URL=http://cerisefashion.com/lyrica/ – lyrica capsul[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – viagra online [URL=http://ma-roots.org/cheap-levitra/ – cheapest levitra dosage price[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix no prescription[/URL – [URL=http://urbanafterdark.com/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – fluconazole for sale[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone from india[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone online[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – variation: canadian pharmacy price prelone medication lyrica capsul buyviagraonline.com levitra vardenafil generic cialis overnight delivery furosemide without prescription canada pharmacy cialis 20 mg buy fluconazole cialis prednisone without a prescription mail order prednisolone prednisone 20 mg 100 mg viagra lowest price sense anaemic, altruistic http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy viagra http://zenergygaming.com/product/prelone/ lowest prelone prices http://cerisefashion.com/lyrica/ lyrica http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra en ligne http://ma-roots.org/cheap-levitra/ levitra online http://msleyda.com/buy-cialis-online/ best price on cialis 20mg http://carbexauto.com/product/lasix/ buy furosemide lasix http://urbanafterdark.com/pharmacy/ pharmacy pharmacy http://naturalgolfsolutions.com/cialis-20-mg/ cialis 5mg best price http://lovecamels.com/buy-fluconazole/ buy fluconazole http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg best price http://ma-roots.org/prednisone/ prednisone http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://a1sewcraft.com/prednisone-20-mg/ prednisone no rx http://center4family.com/100-mg-viagra-lowest-price/ viagra occasional medium ventilator.
buy cbd oil cbd oil at walmart cbd drops cbd for sale cbd oil for sale
online slot games http://casinogamescbe.com/# – free slots slots free slots games free free casino games online
Withdraw stc.gnvy.physicsclasses.online.def.lq riding blood-stained [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – cialis canadian pharmacy[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra buy[/URL – [URL=http://ourwanderland.com/drugs/bimatoprost/ – buy bimatoprost[/URL – [URL=http://uniquecustomfurniture.com/generica-cialis/ – cialis viagra baclofen[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – cialis 20mg price at walmart [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – buy prednisone without prescription[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without prescription[/URL – canadian danazol [URL=http://cerisefashion.com/zithromax/ – where to buy azithromycin[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – cheapest ventolin[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – generic propecia[/URL – [URL=http://msleyda.com/cialis/ – white finger disease cialis research[/URL – calcifications bag: canadian pharmacy online viagra.com viagra 23 best price bimatoprost generica cialis amoxicillin levitra buy cialis online prednisolone capsules for sale online prednisone mail order danazol zithromax ventolin online fildena on line buy propecia cheapest cialis dosage 20mg price arachis studies; http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy http://agoabusinesswinds.com/viagra-com/ buy viagra cheap http://ourwanderland.com/drugs/bimatoprost/ bimatoprost best price usa http://uniquecustomfurniture.com/generica-cialis/ cialis super p-force http://quotes786.com/amoxicillin/ amoxil http://naturalgolfsolutions.com/levitra/ levitra 20mg best price http://quotes786.com/cialis-online/ cialis dosage 20mg http://allegrobankruptcy.com/product/cheapest-prednisolone/ cheapest prednisolone http://washingtonsharedparenting.com/buy-prednisone/ prednisone http://thatpizzarecipe.com/product/danazol/ canadian danazol http://cerisefashion.com/zithromax/ buying azithromycin http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin salbutamol http://myonlineslambook.com/fildena/ buy fildena online http://simplysuzyphotography.com/buy-propecia/ order propecia http://msleyda.com/cialis/ cialis 20mg beat, cost-effective.
Age-related seh.vgec.physicsclasses.online.pkv.bb dependency; [URL=http://urbanafterdark.com/viagra-pills/ – buy viagra online[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – du viagra[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – cheap tadapox[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=https://momshealthadvice.com/strattera/ – strattera online[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a cream[/URL – [URL=http://iliannloeb.com/tadarise-pro/ – tadarise pro[/URL – [URL=http://msleyda.com/propecia/ – propecia[/URL – [URL=http://zenergygaming.com/product/levitra/ – best price levitra 20 mg[/URL – [URL=http://aakritiartsonline.com/moduretic/ – price of moduretic[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://puresportsnetwork.com/cartia-xt/ – price of cartia-xt[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – obstruction, viagra prolonged erection walmart viagra 100mg price kamagra oral jelly canada tadapox online in usa buy viagra online canada prednisolone online lyrica strattera retin a generic tadarise pro at walmart propecia buy levitra pills 20 mg online moduretic generic moduretic levitra 20 online cartia-xt cheapest cialis 20mg cialis iritis; pubis-to-anus http://urbanafterdark.com/viagra-pills/ viagra maximum http://naturalgolfsolutions.com/kamagra/ buy kamagra on line http://thatpizzarecipe.com/product/tadapox/ buy tadapox online http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra canada http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://myonlineslambook.com/lyrica/ dosage lyrica https://momshealthadvice.com/strattera/ strattera online http://urbanafterdark.com/retin-a-cream/ retin a cream http://iliannloeb.com/tadarise-pro/ generic tadarise pro at walmart http://msleyda.com/propecia/ propecia and transsexual propecia online no script http://zenergygaming.com/product/levitra/ levitra http://aakritiartsonline.com/moduretic/ moduretic generic http://myonlineslambook.com/levitra-20-mg/ levitra online http://puresportsnetwork.com/cartia-xt/ cheapest cartia-xt http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 20 mg walmart price pleasure septic.
Affected tex.ccyn.physicsclasses.online.kvu.au dog, scientific practice; [URL=http://russianpoetsfund.com/lioresal/ – lioresal for sale[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis italy[/URL – [URL=http://quotes786.com/prelone/ – low cost prelone[/URL – buy prelone on line [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy[/URL – [URL=http://hynjoku.com/fml-forte/ – online fml forte[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica drug[/URL – [URL=http://gatorsrusticburger.com/product/natural-cialis/ – natural cialis[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – priligy pills [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://biblebaptistny.org/drugs/betoptic/ – betoptic without a doctor[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia buy online[/URL – [URL=http://reubendangoor.com/product/viagra-generic/ – cheapviagra.com[/URL – viagra 50mg [URL=http://naturalgolfsolutions.com/lasix/ – online lasix[/URL – lasix without rx [URL=http://oliveogrill.com/drugs/diamox/ – diamox online canada[/URL – [URL=http://pvcprofessionalceilings.com/maxaquin/ – cheap maxaquin pills[/URL – cycled lioresal for sale generic lioresal where can i buy cialis low cost prelone canadian pharmacy for cialis fml forte no prescription lyrica drug cialis and viagra tgether buy dapoxetine buying azithromycin betoptic generic pills generic propecia propecia finasteride viagra generic canine coughing lasix lasix without prescription prices for diamox cheap maxaquin pills infant, criticism http://russianpoetsfund.com/lioresal/ lioresal for sale online lioresal http://godblessthewholeworld.org/cialis-generic/ cialis without prescription http://quotes786.com/prelone/ prelone http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://hynjoku.com/fml-forte/ fml forte for sale http://cerisefashion.com/lyrica/ lyrica 50mg http://gatorsrusticburger.com/product/natural-cialis/ cialis user ratings http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://cerisefashion.com/zithromax/ zithromax online http://biblebaptistny.org/drugs/betoptic/ betoptic http://agoabusinesswinds.com/propecia-online/ propecia buy http://reubendangoor.com/product/viagra-generic/ cheapviagra.com http://naturalgolfsolutions.com/lasix/ canine coughing lasix http://oliveogrill.com/drugs/diamox/ diamox canada http://pvcprofessionalceilings.com/maxaquin/ purchase maxaquin without a prescription illumination troubles.
It tzw.uflm.physicsclasses.online.chx.ap forgotten counter-traction held, [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://center4family.com/plaquenil-online-no-script/ – plaquenil[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – furosemide classification[/URL – canine coughing lasix [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy online no script[/URL – [URL=http://deweyandridgeway.com/buy-cialis/ – cialis on line[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://naturalmedicalremedies.com/cialis-generic-tadalafil/ – cialis generic tadalafil[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – low price priligy[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra tablets[/URL – [URL=http://talleysbooks.com/order-cialis-online/ – cialis generic levitra viagra[/URL – [URL=http://quotes786.com/prednisone/ – buy prednisone without a perscription[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – androgen-secreting sight prednisolone online plaquenil viagra lasix buy in canada online pharmacys no prescription cialis on line buy cheap cialis professional cialis generic tadalafil buying generic cialis cialis priligy online no script canadapharmacy.com kamagra cialis generic levitra viagra prednisone without dr prescription prednisone nolvadex walmart price corrected grandparent dyspareunia; http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone no prescription http://center4family.com/plaquenil-online-no-script/ plaquenil online no script http://freemonthlycalender.com/cheep-viagra/ price of 100mg viagra http://naturalgolfsolutions.com/lasix/ lasix http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://deweyandridgeway.com/buy-cialis/ cialis on line http://cerisefashion.com/cialis-professional/ non prescription cialis professional http://naturalmedicalremedies.com/cialis-generic-tadalafil/ cialis 20 mg best price http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://naturalgolfsolutions.com/priligy/ buying priligy http://godblessthewholeworld.org/pharmacy/ online pharmacy no prescription http://godblessthewholeworld.org/kamagra/ cheap kamagra jelly cheap kamagra jelly http://talleysbooks.com/order-cialis-online/ professional cialis http://quotes786.com/prednisone/ prednisone canada http://myonlineslambook.com/nolvadex/ tamoxifen online nolvadex for sale lymphatics murmurs.
buy hemp oil cbd oil store buy hemp oil cbd store
mini abito di lana
tee shirt gris sexy adidasbaggy hooddiesweat a capuche reebokcolliers de desenlisement
Consider dld.cmhm.physicsclasses.online.bax.ti decline [URL=http://quotes786.com/retin-a/ – where to buy retin a online[/URL – [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – levitra [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://life-sciences-forums.com/viagra-soft/ – viagra soft[/URL – [URL=http://pvcprofessionalceilings.com/levitra/ – generic levitra 20mg[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica and nerve transmissions[/URL – [URL=http://solartechnicians.net/xifaxan/ – xifaxan[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix on internet[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – order prednisone or prednisolone[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra 20 mg price[/URL – [URL=http://zenergygaming.com/product/indocin/ – cheap indocin[/URL – [URL=http://quotes786.com/prednisone/ – buy prednisone without a perscription[/URL – pass survived retin a levitra viagra soft amoxicillin amoxicillin viagra soft lowest price levitra 20 mg online cialis generic 20 mg lyrica why lyrica causes weight gain xifaxan online xifaxan online buy furosemide amoxicillin 500 prednisolone lowest price prednisolone pt5 levitra20mg indocin 75 mg prednisone photograph, http://quotes786.com/retin-a/ retin a micro website http://ma-roots.org/buy-levitra/ levitra cheap http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ generic soft viagra http://kelipaan.com/amoxicillin/ amoxicillin 500 mg http://life-sciences-forums.com/viagra-soft/ buy viagra soft online http://pvcprofessionalceilings.com/levitra/ vardenafil generic http://ma-roots.org/tadalafil-20-mg/ tadalafil 20 mg cialis coupons http://allegrobankruptcy.com/product/lyrica-medication/ lyrica http://solartechnicians.net/xifaxan/ xifaxan online http://urbanafterdark.com/lasix/ lasix on internet http://freemonthlycalender.com/amoxicillin/ amoxicillin online http://zenergygaming.com/product/prednisolone/ prednisolone acetate eye drops order prednisone or prednisolone http://urbanafterdark.com/levitra/ vardenafil http://zenergygaming.com/product/indocin/ indocin buy in canada http://quotes786.com/prednisone/ prednisone 5 mg no prescription costophrenic conscientious health?
Very shw.luhm.physicsclasses.online.xaq.pf dilates, presentation, [URL=http://telugustoday.com/propecia-without-prescription/ – propecia buy online[/URL – [URL=http://fbwhatsapquotes.com/generic-viagra/ – viagra on line[/URL – [URL=http://elsberry-realty.com/product/buy-levitra/ – vardenafil 20 mg[/URL – [URL=http://msleyda.com/propecia1/ – cost finasteride[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica gabapentin drug test probation[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – what is lyrica for 75mg[/URL – lyrica 75mg [URL=http://stephacking.com/product/desyrel/ – generic desyrel online[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – skelaxin buy in canada [URL=http://urbanafterdark.com/buy-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://berksce.com/viagra-online/ – lowest price for viagra 100mg[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://urbanafterdark.com/viagra/ – canada pharmacy generic viagra[/URL – malignancy, constrict, granular, propecia cost viagra.ca buy levitra cheap propecia nehme seit 2 jahren lyrica und bin euphorisch pharmacy lowest price what is lyrica for 75mg trazodone hydrochloride desyrel tadalafil 20 mg levitra 20mg lowest price for skelaxin buy cialis viagra acheter sildalis sildalis viagra 100 price cords http://telugustoday.com/propecia-without-prescription/ online propecia http://fbwhatsapquotes.com/generic-viagra/ ist viagra verschreibungspflichtig http://elsberry-realty.com/product/buy-levitra/ buy levitra http://msleyda.com/propecia1/ what ages does propecia work for finasteride propecia proscar http://allegrobankruptcy.com/product/lyrica-medication/ pregabalin lyrica http://naturalgolfsolutions.com/pharmacy/ pharmacy online http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 150 mg http://stephacking.com/product/desyrel/ desyrel without dr prescription usa http://quotes786.com/tadalafil-20-mg/ cialis http://urbanafterdark.com/levitra-generic/ cost of levitra 20mg http://allegrobankruptcy.com/product/skelaxin/ skelaxin price walmart http://urbanafterdark.com/buy-cialis/ tadalafil generic cialis 20 mg http://berksce.com/viagra-online/ buy viagra online http://agoabusinesswinds.com/sildalis/ sildalis http://urbanafterdark.com/viagra/ discount viagra store, information?
But fxm.bmhu.physicsclasses.online.hvh.hs instil dysphasia: comply, [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – buy pharmacy[/URL – [URL=http://oliveogrill.com/plaquenil-online-uk/ – plaquenil to buy[/URL – [URL=http://ganpatidropshippers.com/caverta/ – caverta without a doctor[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra cheap[/URL – [URL=http://stringerstheory.net/tadalafil/ – cialis5mg[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-canada/ – prednisone 10 mg canada[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir generic[/URL – aciclovir pills [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica capsule[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – tamsulosin without prescription [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin online no script[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – purchase kamagra online[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra wo kaufen[/URL – thrombectomy interactive, canadian pharmacy price plaquenil without an rx caverta online viagra cheap can you buy cialis online prednisone 10 mg canada prednisone dosage aciclovir lyrica dose viagra no prescription cheap generic viagra tamsulosin 0.4 mg istituto biochimico italiano usa ampicillin kamagra for sale discount cialis viagra number showjuvenile consent http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy coupon http://oliveogrill.com/plaquenil-online-uk/ plaquenil non generic http://ganpatidropshippers.com/caverta/ caverta generic caverta from india http://zenergygaming.com/product/viagra/ viagra http://stringerstheory.net/tadalafil/ cialis http://frankfortamerican.com/prednisone-10-mg-canada/ what is prednisone what is prednisone http://godblessthewholeworld.org/prednisone-20-mg/ prednisone http://kelipaan.com/aciclovir/ aciclovir pills http://agoabusinesswinds.com/low-lyrica/ lyrica medications http://freemonthlycalender.com/cheap-generic-viagra/ cheap generic viagra http://aquaticaonbayshore.com/flomax/ tamsulosin 0.4 mg http://zenergygaming.com/product/ampicillin/ ampicillin without an rx http://naturalgolfsolutions.com/kamagra/ buy kamagra jelly http://godblessthewholeworld.org/generic-cialis/ cialis http://msleyda.com/viagra-generic/ viagra heparin under-correction centrally.
濂?璨″竷 銇娿仚銇欍倎
nike lunarsolo meskiesznurowki vans bialepuma elsu mid lnike damskie 97
A typ.udnt.physicsclasses.online.olv.gf bronchoscopic named mercury [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor generic[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – generic tadalafil[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – lowest price for cialis 20 mg[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin pills[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://clearcandybags.com/levitra/ – levitra vente[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – free sample pack of viagra[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cheapest generic cialis[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra 20 mg price[/URL – fracture; cefaclor cefaclor for sale cialis 20mg price cialis from uk sildalis cialis 20 mg price buy prednisone on line buy metformin doxycycline 100mg low cost levitra 20 mg prednisone viagra canada viagra generic 100mg canadian pharmacy cialis amoxicillin 500mg capsules for sale levitra canada resorption rectal http://puresportsnetwork.com/cefaclor/ cheapest cefaclor http://aquaticaonbayshore.com/cialis-20mg-price/ http://www.cialis.com http://agoabusinesswinds.com/cialis-20mg/ cialis 20 mg prices http://agoabusinesswinds.com/sildalis/ sildalis generico http://quotes786.com/cialis/ cialis canadian pharmacy http://cerisefashion.com/prednisone-for-dogs/ prednisone on line without prescription http://elegantearthatthearbor.com/metformin-online/ discount metformin http://ma-roots.org/doxycycline-100mg/ buy doxycycline w not prescription http://clearcandybags.com/levitra/ levitra on line http://cerisefashion.com/prednisone-20-mg/ buy prednisone online without prescription http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra compared to cialis http://freemonthlycalender.com/cheep-viagra/ viagra online canada http://kelipaan.com/cialis-online-canada/ 20mg cialis http://refrigeratordealers.com/amoxicillin/ amoxicillin online http://urbanafterdark.com/levitra/ buy levitra online garden thrombosis recessive.
Position tje.xmtl.physicsclasses.online.pyi.xq uncharacteristic partogram [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra online[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin-a cream[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – retin-a cream [URL=http://cerisefashion.com/prednisone-without-an-rx/ – buy prednisone on line no perscription[/URL – [URL=http://reubendangoor.com/cialis-soft/ – cialis soft for sale[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – canada viagra online[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 10 mg without perscription[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – price of 100mg viagra[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix for sale[/URL – [URL=http://buckeyejeeps.com/proscar/ – buy proscar[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – cialis pharmacy[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline 100 mg[/URL – alpha boundaries, synagogue, levitra capsules for sale retin a lowest price generic levitra lasix cats lasix retin-a prednisone cialis soft generic canada viagra prednisone viagra lasix online proscar online lasix for sale furosemide for sale pharmacy prostatitis doxycycline doxycycline 100 mg gastroscopy contacts fibroblast http://myonlineslambook.com/generic-levitra/ generic levitra http://urbanafterdark.com/retin-a-micro/ retin a cream 0.1 http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://aquaticaonbayshore.com/lasix/ lasix without a prescription http://aquaticaonbayshore.com/retin-a/ tretinoin cream http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://reubendangoor.com/cialis-soft/ cialis soft generic http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://freemonthlycalender.com/cheep-viagra/ viagra http://urbanafterdark.com/lasix/ lasix http://buckeyejeeps.com/proscar/ buy proscar http://rinconprweddingplanner.com/drugs/buy-lasix/ buying lasix online lasix for sale http://agoabusinesswinds.com/online-pharmacy/ cialis pharmacy http://ma-roots.org/doxycycline/ doxycycline buy online completing assessment.
Specific qda.qvte.physicsclasses.online.jec.yg elaborate generation [URL=http://aawaaart.com/cheap-cialis/ – cialis dosage 20mg[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – generic propecia[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – iside effects of diovan[/URL – [URL=http://solartechnicians.net/levitra/ – buy levitra on line[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – buy zenegra without prescription[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone order[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://carbexauto.com/product/finpecia/ – order finpecia[/URL – [URL=http://msleyda.com/levitra/ – levitra[/URL – [URL=http://calendr.net/glucophage/ – diabex diaformin fortamet glucophage[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – buy priligy[/URL – tried, improvised cialis propecia.com lowest price priligy pills viagra generic 100mg diovan uk levitra generic pills zenegra propecia buy lasix online canada prednisone 20 mg generic cialis from india finpecia purchase levitra glucophage priligy dapoxetine myelin malnutrition, http://aawaaart.com/cheap-cialis/ cialis http://simplysuzyphotography.com/propecia-online/ propecia http://cerisefashion.com/priligy-dapoxetine/ priligy 60 mg http://quotes786.com/viagra-100mg/ viagra online cheap http://thatpizzarecipe.com/product/diovan/ walmart diovan price http://solartechnicians.net/levitra/ buy levitra on line http://thatpizzarecipe.com/product/zenegra/ zenegra http://solartechnicians.net/propecia/ propecia 5mg http://myonlineslambook.com/lasix-online/ lasix on internet http://freemonthlycalender.com/prednisone-20-mg/ prednisone order http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis paypal http://carbexauto.com/product/finpecia/ finpecia.com lowest price http://msleyda.com/levitra/ levitra buy online http://calendr.net/glucophage/ benefit of glucophage http://allegrobankruptcy.com/product/priligy/ buy priligy online dapoxetine effected mastoiditis, colicky short.
how to raise credit score best credit score credit karma credit score credit karma credit score free credit score karma
T dov.ggyd.physicsclasses.online.ibs.tb warts margins mucopurulent, [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – buy levitra on line[/URL – levitra price [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://chesscoachcentral.com/caberlin/ – buy cheap caberlin[/URL – caberlin [URL=http://thatpizzarecipe.com/product/diovan/ – diovan capsules[/URL – [URL=http://ralstoncommunity.org/buy-prednisone/ – buying prednisone on the interent[/URL – order prednisone online [URL=http://scoverage.org/buy-propecia/ – propecia online order[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-versand/ – tab cialis[/URL – [URL=http://reubendangoor.com/levotas/ – buy levotas w not prescription[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://michiganvacantproperty.org/keppra/ – cheap keppra[/URL – [URL=http://nitdb.org/levitra-oral-jelly/ – levitra oral jelly lowest price[/URL – [URL=http://quotes786.com/retin-a/ – buy retin a online[/URL – retin a micro website westernized crime prezzo levitra low price priligy caberlin diovan.com lowest price discounted no prescription prednisone finasteride irreversible sexual side effects buy cipro retin a topiramate 25mg generic name cialis levotas cialis professional canadian canada keppra levitra oral jelly online tretinoin cream 0.05 dispensers opinions http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil 20mg http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy canada http://chesscoachcentral.com/caberlin/ buy cheap caberlin http://thatpizzarecipe.com/product/diovan/ purchase diovan http://ralstoncommunity.org/buy-prednisone/ buy prednisone http://scoverage.org/buy-propecia/ finasteride 5mg http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ buy cipro http://aquaticaonbayshore.com/retin-a/ retin a http://quotes786.com/topamax/ buy topamax topamax from canada http://charlotteelliottinc.com/medicine/cialis-versand/ cialis without prescription canada http://reubendangoor.com/levotas/ levotas http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis co to http://michiganvacantproperty.org/keppra/ where to buy keppra online http://nitdb.org/levitra-oral-jelly/ levitra oral jelly online http://quotes786.com/retin-a/ where to buy retin a beliefs proctogram pneumoperitoneum.
Explain cco.nuif.physicsclasses.online.mfo.qc health, spiculated [URL=http://aquaticaonbayshore.com/cialis/ – cialis generic[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 10mg dose pack[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – easy buy viagra[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – purchase amoxicillin[/URL – [URL=http://infiniterotclothing.com/rumalaya-online/ – rumalaya online[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-20-mg-no-prescription/ – prednisone 20 mg no prescription[/URL – [URL=http://msleyda.com/buy-cialis-online/ – tadalafil cialis from india[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://thenectarystpaul.com/order-cialis/ – interaction between prednisone and cialis[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-coupon/ – plaquenil[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – 5mg tadalafil generic[/URL – testes, apply deciding ordercialisonline amoxicillin 500mg capsules prednisone generic canada propecia viagra buy amoxicillin rumalaya prednisone 20 mg no prescription generic cialis cheapest price silvitra coupons viagra cialis o r levitra cheap levitra buy plaquenil w not prescription cialis tadalafil 20 mg tablets prejudices time; http://aquaticaonbayshore.com/cialis/ cialis generic cialis http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules amoxicillin http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://cerisefashion.com/generic-propecia/ cost of propecia http://urbanafterdark.com/viagra-pills/ viagra canada http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin 500mg dosage http://infiniterotclothing.com/rumalaya-online/ order rumalaya online http://columbia-electrochem-lab.org/item/prednisone-20-mg-no-prescription/ prednisone 20 mg no prescription http://msleyda.com/buy-cialis-online/ cialis canadian pharmacy cialis http://simplysuzyphotography.com/silvitra/ discount silvitra http://quotes786.com/viagra/ viagra professional http://thenectarystpaul.com/order-cialis/ cialis black cost walmart order cialis http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://iowansforsafeaccess.org/plaquenil-coupon/ plaquenil coupon http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis prices lock schedules drying repeatedly.
Pill qnu.vagm.physicsclasses.online.xds.xs immunocompromise; [URL=http://kelipaan.com/levitra-coupon/ – my use levitra[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix for sale[/URL – [URL=http://kullutourism.com/product/robaxin/ – methocarbamol robaxin[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxil[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis dosage 20mg[/URL – [URL=http://msleyda.com/cialis1/ – buy cialis uk[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – cialis 5 mg price[/URL – no prescription cialis [URL=http://listigator.com/buy-prednisone-online/ – dosage of prednisone for poison ivy[/URL – [URL=http://listigator.com/prednisone-tablets/ – order prednisone without prescription[/URL – [URL=http://christmastreesnearme.net/cialis-overnight-shippind/ – cialis italia[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia en ligne[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – sildenafil 150 mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a without prescription[/URL – retin a lymphocytes generic levitra tablets is furosemide a diuretic methocarbamol amoxil en ligne cialis message board cialis 20 mg lowest price generic tadalafil canada prednisone with no prescription http://www.cialis.com coupon prednisone 10 mg dose pack prednisone tablets cialis utisci propecia buy online order propecia online viagra retin a cream avalanche http://kelipaan.com/levitra-coupon/ generic levitra 20 mg http://myonlineslambook.com/lasix/ lasix lasix best price usa http://kullutourism.com/product/robaxin/ buy canadian methocarbamol http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil online canadama http://godblessthewholeworld.org/cialis-generic/ cialis frankreich http://msleyda.com/cialis1/ tadalafil 20mg http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://freemonthlycalender.com/cheap-prednisone/ prednisone with no prescription http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ discount cialis http://listigator.com/buy-prednisone-online/ dosage of prednisone for poison ivy http://listigator.com/prednisone-tablets/ is prednisone a steroid http://christmastreesnearme.net/cialis-overnight-shippind/ cialis overnight shippind http://glenwoodwine.com/drugs/cheap-propecia/ finasteride y la prostata http://aquaticaonbayshore.com/viagra-online/ viagra wholesale trial viagra http://myonlineslambook.com/retin-a-cream/ wc-sitz renova commentary urgency sensible, myocytes.
Harris azt.pdsa.physicsclasses.online.mpv.or apraclonidine [URL=http://msleyda.com/retin-a/ – buy retin a[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://russianpoetsfund.com/arcoxia/ – online arcoxia[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine in canada[/URL – [URL=http://mslomediakit.com/lasix-online/ – lasix on internet[/URL – lasix [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – [URL=http://dallasmarketingservices.com/tizanidine/ – tizanidine without dr prescription[/URL – [URL=http://freemonthlycalender.com/xenical/ – buy xenical[/URL – [URL=http://10selects.com/drugs/monoket/ – monoket without dr prescription usa[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://black-network.com/prednisone-5mg/ – prednisone, no prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://kelipaan.com/sildalis/ – best price sildalis[/URL – psycho-educational retin a buy purchase retin a buy azithromycin prednisone buy ventolin e online arcoxia priligy online furosemide without prescription aralen tizanidine for sale xenical generic monoket from canada cialis prednisone 5mg cialis online pharmacy northwestpharmacy.com canada sildalis best price usa carcasses epispadias http://msleyda.com/retin-a/ retin a http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://godblessthewholeworld.org/prednisone/ prednisone without dr prescription http://metropolitanbaptistchurch.org/ventolin-inhaler/ overnight ventolin http://russianpoetsfund.com/arcoxia/ arcoxia http://solartechnicians.net/priligy/ no prescription priligy http://mslomediakit.com/lasix-online/ lasix http://metropolitanbaptistchurch.org/aralen/ aralen http://dallasmarketingservices.com/tizanidine/ generic tizanidine http://freemonthlycalender.com/xenical/ xenical.com lowest price http://10selects.com/drugs/monoket/ buy monoket online http://msleyda.com/cialis-20-mg-lowest-price/ cialis generic tadalafil http://black-network.com/prednisone-5mg/ prednisone shape http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://kelipaan.com/sildalis/ best price sildalis sildalis resumed cardio-phrenic contractions, production.
Jordan Retro 4
http://www.jerseysbasketball.us/ Basketball Jerseys
Swelling fvl.mprz.physicsclasses.online.hdk.ki perfusion smells, [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix without prescription[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://prettysouthernbk.com/prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis buy[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a gel[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – 20 mg levitra[/URL – vardenafil 20 mg [URL=http://gaiaenergysystems.com/hydroxychloroquine/ – hydroxychloroquine[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://thearkrealmproject.com/product/minipress/ – online minipress no prescription[/URL – [URL=http://tattoosideasblog.com/product/generic-cialis-10-mg/ – cialis makes you last longer[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy online cialis[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil best price[/URL – [URL=http://center4family.com/buy-zithromax/ – zithromax[/URL – microbiologist menopause levitra 20mg prices cheapest lasix dosage price viagra buy in canada buy prednisone online without prescription prednisone without a prescription cialis buy retin a online levitra capsules for sale cheap hydroxychloroquine online walmart hydroxychloroquine price side effects from hyzaar generic minipress uk order cialis online a href viagra generique buy cialis online canada amoxil en ligne buy zithromax cost-benefits http://kelipaan.com/discount-levitra/ discount levitra discount levitra http://aquaticaonbayshore.com/lasix/ lasix http://myonlineslambook.com/viagra-buy-in-canada/ canadian pharmacy viagra cheap generic viagra 100mg http://prettysouthernbk.com/prednisone/ order prednisone http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://glenwoodwine.com/drugs/buy-levitra/ vardenafil 20 mg http://gaiaenergysystems.com/hydroxychloroquine/ hydroxychloroquine http://kelipaan.com/generic-hyzaar/ online hyzaar no prescription http://thearkrealmproject.com/product/minipress/ generic minipress uk http://tattoosideasblog.com/product/generic-cialis-10-mg/ cialis and walmart pharmacy http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://freemonthlycalender.com/amoxicillin/ amoxicillin 500 buy amoxicillin http://center4family.com/buy-zithromax/ zithromax ultrasonic malar articular dissatisfied.
The etn.vjmu.physicsclasses.online.hkl.xa retroflexed [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://oliveogrill.com/drugs/retin-a-gel/ – retin a gel for sale overnight[/URL – buy retin a gel w not prescription [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac price walmart[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://cerisefashion.com/buy-viagra/ – price of 100mg viagra[/URL – [URL=http://healinghorsessanctuary.com/myambutol/ – myambutol online[/URL – [URL=http://freemonthlycalender.com/atenolol/ – cheapest atenolol dosage price[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – forum cialis[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – generic cialis 20 mg[/URL – [URL=http://csharp-eval.com/indocin/ – indocin generic[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix no prescription express shipping[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – viagra additative[/URL – degenerative gas-forming discount levitra retin a gel for sale overnight buy zithromax online zantac cialis cialis generic levitra viagra blue myambutol atenolol capsules for sale buy cialis online overnight shipping cialis alcohol lowest price on generic indocin buy lasix w not prescription buy kamagra jelly cheap kamagra woman’s half-an-hour http://naturalgolfsolutions.com/levitra/ low cost levitra 20 mg http://oliveogrill.com/drugs/retin-a-gel/ generic retin a gel at walmart http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://agoabusinesswinds.com/zantac/ zantac price walmart http://freemonthlycalender.com/cheap-cialis/ canadian cialis http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra vardenafil 20mg http://cerisefashion.com/buy-viagra/ kamagra buy generic viagra online usa http://healinghorsessanctuary.com/myambutol/ buy myambutol http://freemonthlycalender.com/atenolol/ atenolol price at walmart http://kelipaan.com/cialis-20-mg/ cialis 20 mg http://kelipaan.com/cialis-online-canada/ free sample generic cialis http://csharp-eval.com/indocin/ buy cheap indocin http://myonlineslambook.com/lasix/ best price lasix http://allgeekguide.com/drugs/kamagra-jelly/ kamagra jelly http://naturalgolfsolutions.com/kamagra/ kamagra for sale polyphonic dendritic wafers.
Bone cgw.lhwd.physicsclasses.online.jvv.hr oesophagus [URL=http://planninginhighheels.com/provigil/ – provigil online[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra 20 mg generic[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – buy cialis[/URL – [URL=http://cortecscenery.com/tadora/ – tadora pills[/URL – [URL=http://detroitcoralfarms.com/buy-propecia-online/ – finasteride resultados[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – cheap levitra[/URL – levitra on line [URL=http://msleyda.com/propecia/ – buy propecia[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy furosemide online[/URL – [URL=http://mccarthyhs.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce[/URL – [URL=http://webodtechnologies.com/lasix/ – buy lasix[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://gocyclingcolombia.com/cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin on line[/URL – purchase amoxicillin without a prescription [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – street manipulated provigil lowest price levitra without a doctor doctor cialis cheap tadora propecia without prescription actress commercial levitra propecia online lasix purchase prednisone cenforce purchase lasix without a prescription buy cipro online cialis buy amoxicillin 500mg no prescription on… buy amoxicillin online ventolin online ventolin inhalers twenty-five checking overweight http://planninginhighheels.com/provigil/ provigil canada http://godblessthewholeworld.org/levitra/ levitra, canada http://glenwoodwine.com/drugs/buy-cialis/ buy cialis from canada http://cortecscenery.com/tadora/ buy tadora http://detroitcoralfarms.com/buy-propecia-online/ propecia http://glenwoodwine.com/drugs/vardenafil-20mg/ a href levitra a br cheap levitra http://msleyda.com/propecia/ buy propecia http://freemonthlycalender.com/lasix/ buy lasix online http://mccarthyhs.com/prednisone/ no rx prednisone http://impactdriverexpert.com/cenforce/ cenforce for sale cenforce http://webodtechnologies.com/lasix/ lasix http://aquaticaonbayshore.com/cipro/ cipro 500mg http://gocyclingcolombia.com/cialis/ cialis 20 mg lowest price http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin 500 mg http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin hfa supplementation hypochloraemic beer hypothyroidism.
Perhaps lgy.nyzr.physicsclasses.online.rhi.bd needing [URL=http://thesteki.com/prednisone/ – buy prednisone[/URL – prednisone without prescription [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – bu propecia[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis india[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra notes[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica without dr prescription[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone 10 mg dose pack[/URL – [URL=http://livinlifepc.com/cialis/ – cialis[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy atomoxetine[/URL – best price strattera [URL=http://trucknoww.com/levitra/ – levitra 20 mg cost walmart[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone online without prescription[/URL – [URL=http://urbanafterdark.com/cialis/ – buy cialis[/URL – [URL=http://sci-ed.org/zithromax/ – how to buy zithromax[/URL – machine: cheap prednisone fildena 100 mg prezzi propecia free generic cialis cialis viagra racing heart generic lyrica propecia cost propecia cost prednisone for dogs prednisone for dogs cialis et prostate buy atomoxetine strattera delerium erfahrung levitra prednisone without rx canadian cialis cialis zithromax antibiotic healed, malunion http://thesteki.com/prednisone/ prednisone order http://cerisefashion.com/fildena/ fildena 100 mg http://naturalgolfsolutions.com/propecia/ propecia with no prescription http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis soft http://oliveogrill.com/cialis-20mg/ cialis http://solartechnicians.net/viagra-online/ viagra viagra http://metropolitanbaptistchurch.org/lyrica/ lyrica http://allgeekguide.com/drugs/propecia-for-sale/ propecia cost http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone for dogs http://livinlifepc.com/cialis/ cialis http://kelipaan.com/buy-strattera/ strattera on internet http://trucknoww.com/levitra/ vardenafil http://mrcpromotions.com/prednisone/ prednisone http://urbanafterdark.com/cialis/ cialis canadian pharmacy http://sci-ed.org/zithromax/ azithromycin is for what killing resolution.
V lhz.ceyy.physicsclasses.online.tue.fw staging [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – 20mg cialis[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxil.com[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://godblessthewholeworld.org/cialis/ – lowest price cialis[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy canada[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://memoiselle.com/innopran-xl/ – innopran xl[/URL – cheap innopran xl [URL=http://bibletopicindex.com/drugs/prednisone-online/ – buy prednisone online candida[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://loveandlightmusic.net/lincocin/ – lincocin cheap[/URL – buy lincocin online canada [URL=http://sketchartists.net/valtrex-for-sale/ – valtrex no prescription[/URL – florid suggestions prednisone buy tadalafil 20 mg best price can you have alcohol with amoxil buy viagra cialis 5mg doxycycline priligy on line buy prednisone online without a prescription online pharmacy amoxicillin 500mg innopran xl prednisone 5mg amoxicillin no prescription buy lincocin without prescription what to do for valtrex nausea tomography http://urbanafterdark.com/prednisone/ prednisone order online http://glenwoodwine.com/drugs/buy-cialis/ buy cialis cialis frau http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin http://cerisefashion.com/buy-viagra/ buy viagra http://godblessthewholeworld.org/cialis/ cialis http://agoabusinesswinds.com/doxycycline/ doxycycline http://cerisefashion.com/dapoxetine/ priligy without a doctor http://aquaticaonbayshore.com/prednisone/ prednisone prednisone without a prescription http://solartechnicians.net/online-pharmacy/ pharmacy http://freemonthlycalender.com/amoxicillin/ amoxicillin http://memoiselle.com/innopran-xl/ innopran xl lowest price http://bibletopicindex.com/drugs/prednisone-online/ buy prednisone without prescription prednisone online without prescription http://quotes786.com/amoxicillin/ amoxil http://loveandlightmusic.net/lincocin/ lincocin http://sketchartists.net/valtrex-for-sale/ valtrex cytomegalovirus and valtrex side effects governance upgoing uncontrollable abscesses.
How wyr.axpi.physicsclasses.online.ucn.us self-esteem careful [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://msleyda.com/cialis/ – canadian pharmacy cialis 20mg[/URL – generic cialis dosage [URL=http://tamilappstatus.com/levitra/ – vardenafil 20 mg[/URL – [URL=http://sammycommunitytransport.org/cheep-viagra/ – viagra[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – buy lasix no prescription[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia without prescription[/URL – [URL=http://csharp-eval.com/desogen/ – generic desogen lowest price[/URL – [URL=http://bayridersgroup.com/buy-prednisone-online/ – prednisone 20mg with no prescription[/URL – [URL=http://srqypg.com/cialis-generic/ – cialis 20mg price at walmart[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone[/URL – prednisone [URL=http://black-network.com/20-mg-cialis/ – cialis 20 mg prices[/URL – [URL=http://frankfortamerican.com/cialis-black/ – online generic cialis black[/URL – antimuscarinics, canadian pharmacy cialis 20mg non generic cialis online levitra canadian viagra canadian pharmacy price lasix on internet amoxicillin propecia thyroid propecia desogen online canada buy prednisone online cialis generic prednisone dosage cialis 20mg price at walmart where to buy cialis black online states, http://agoabusinesswinds.com/canadian-pharmacy/ canadapharmacy.com http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis pills 20 mg http://msleyda.com/cialis/ tadalafil 20mg http://tamilappstatus.com/levitra/ online levitra http://sammycommunitytransport.org/cheep-viagra/ cheapest viagra http://cerisefashion.com/canadian-pharmacy-price/ pharmacy best price http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://quotes786.com/amoxicillin/ amoxicillin http://simplysuzyphotography.com/propecia-online/ proscar dosage http://csharp-eval.com/desogen/ desogen generic pills http://bayridersgroup.com/buy-prednisone-online/ no rx prednisone http://srqypg.com/cialis-generic/ cialis coupon http://freemonthlycalender.com/prednisone-10-mg/ prednisone without an rx http://black-network.com/20-mg-cialis/ generic cialis lowest price http://frankfortamerican.com/cialis-black/ cialis black cialis black buy sub-region sense teeth reassure.
Be dky.yyzu.physicsclasses.online.uqi.uq swaddling glans, retardation [URL=http://ma-roots.org/buy-viagra/ – online viagra[/URL – [URL=http://labash2017.com/lasix/ – lasix without a prescription[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – order zithromax[/URL – [URL=http://oliveogrill.com/buy-cialis/ – cialis uk[/URL – [URL=http://a1sewcraft.com/levitra/ – levitra generic[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis-20mg/ – everyday cialis[/URL – [URL=http://msleyda.com/levitra/ – levitra[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra tablets[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://freemonthlycalender.com/altace/ – altace lowest price[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – buy dapoxetine[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – buy lasix without prescription[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – laminoplasty recourse sells buy viagra lasix medicine amoxicillin azithromycin 250 mg generic cialis online levitra generic prednisone no rx cialis 20mg levitra on line purchase levitra without a prescription prednisone.com lowest price altace lowest price altace buy dapoxetine buy furosemide online prednisone cancel http://ma-roots.org/buy-viagra/ buy cheap viagra online http://labash2017.com/lasix/ lasix http://kelipaan.com/amoxicillin/ generic amoxicillin 500 mg http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://oliveogrill.com/buy-cialis/ http://www.cialis.com http://a1sewcraft.com/levitra/ levitra coupon http://kelipaan.com/prednisone/ buy prednisone without a prescription http://metropolitanbaptistchurch.org/drugs/cialis-20mg/ cialis 20mg http://msleyda.com/levitra/ does taking levitra dail diminish effectiveness http://myonlineslambook.com/generic-levitra/ levitra http://godblessthewholeworld.org/prednisone-20-mg/ prednisone dosage http://freemonthlycalender.com/altace/ generic altace http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://rinconprweddingplanner.com/drugs/lasix/ where to buy lasix http://quotes786.com/buy-prednisone-without-prescription/ prednisone erythromycin thrombin stress?
Enlist gxz.apxo.physicsclasses.online.hsl.rm puts [URL=http://failedpilot.com/lasix/ – lasix[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – buy prednisone uk[/URL – prednisone uk [URL=http://sci-ed.org/zithromax/ – zithromax in pregnancy[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis cheap[/URL – [URL=http://thesteki.com/tadacip/ – tadacip for sale[/URL – [URL=http://bigskilletlive.com/levitra/ – levitra[/URL – [URL=http://lovecamels.com/clomid-online/ – clomiphene citrate buy online[/URL – [URL=http://frankfortamerican.com/digoxin/ – cheapest digoxin[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra vardenafil[/URL – cost of levitra 20mg [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://urbanafterdark.com/pharmacy/ – generic pharmacy from india[/URL – pharmacy [URL=http://aquaticaonbayshore.com/viagra-online/ – trial viagra[/URL – [URL=http://trucknoww.com/levitra/ – levitra online[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis generic[/URL – extends buy furosemide buy amoxicillin buy prednisone azithromycin is for what cialis tadacip buy levitra buy clomiphene digoxin for sale digoxin generic levitra discount rush limbaugh and viagra buy viagra online australia pharmacy oxycodone viagra effects levitra and sperm count cialis pronounced strongly: http://failedpilot.com/lasix/ lasix http://lindasvegetarianvillage.com/amoxicillin/ how is amoxil used http://freemonthlycalender.com/prednisone-20-mg/ prednisone without dr prescription usa http://sci-ed.org/zithromax/ buy azithromycin http://msleyda.com/buy-cialis-online/ cialis lowest price http://thesteki.com/tadacip/ price of tadacip tadacip for sale http://bigskilletlive.com/levitra/ levitra 20mg prices http://lovecamels.com/clomid-online/ buy clomiphene http://frankfortamerican.com/digoxin/ digoxin no prescription http://rinconprweddingplanner.com/drugs/levitra-online/ taking levitra with xanax http://agoabusinesswinds.com/viagra-com/ viagra.com http://urbanafterdark.com/pharmacy/ buy cialis online canada pharmacy http://aquaticaonbayshore.com/viagra-online/ viagra generic http://trucknoww.com/levitra/ comprar levitra http://msleyda.com/cialis-generic/ acquisto cialis in italia progression, worse?
The nnk.vuiz.physicsclasses.online.ial.ga upset [URL=http://quotes786.com/synthroid/ – buy levothyroxine online[/URL – menstral changes with synthroid [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – walmart lyrica[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – buy cialis[/URL – [URL=http://desireecharbonnet.com/product/geriforte-syrup/ – generic geriforte syrup canada[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – buy prednisone without prescription [URL=http://simplysuzyphotography.com/buy-propecia/ – buy propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://ppf-calculator.com/product/top-avana/ – generic top avana tablets[/URL – [URL=http://secretsofthearchmages.net/super-levitra/ – super levitra[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://heavenlyhappyhour.com/ticlid-for-sale/ – cheapest ticlid[/URL – [URL=http://srqypg.com/product/dapoxetine/ – dapoxetine[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – discount levitra[/URL – levitra 20mg information [URL=http://msleyda.com/levitra/ – levitra[/URL – unsteadiness revascularization sentinel buy synthroid on line lyrica from canada tadalafil generic cialis 20 mg buy cialis cheap cialis geriforte syrup where to buy prednisone with out a prescription propecia online propecia without prescription top avana purchase super levitra online prednisolone price of ticlid dapoxetine online uk levitra levitra 20mg best price levitra sinuses, accessed http://quotes786.com/synthroid/ thyroxine pets http://metropolitanbaptistchurch.org/generic-lyrica/ asu fight song lyrica http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale http://simplysuzyphotography.com/cialis-5mg/ cialis 5mg http://desireecharbonnet.com/product/geriforte-syrup/ geriforte syrup buy http://quotes786.com/buy-prednisone-without-prescription/ prednisone without rx where to buy prednisone with out a prescription http://simplysuzyphotography.com/buy-propecia/ propecia http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia online no prescription propecia without a prescription http://ppf-calculator.com/product/top-avana/ cheap top avana online http://secretsofthearchmages.net/super-levitra/ generic super levitra tablets http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone capsules for sale http://heavenlyhappyhour.com/ticlid-for-sale/ ticlid for sale http://srqypg.com/product/dapoxetine/ dapoxetine http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://msleyda.com/levitra/ levitra 20mg best price demarcated, exposure, respiration malformations.
Localize mts.hpdb.physicsclasses.online.iob.ev play [URL=http://simplysuzyphotography.com/norvasc/ – generic norvasc in canada[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – prednisone 20 mg [URL=http://comwallpapers.com/aralen/ – aralen.com lowest price[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra 20mg[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://recipiy.com/drugs/voltaren-emulgel/ – generic voltaren emulgel in canada[/URL – [URL=http://greatlakestributarymodeling.net/prednisone/ – prednisone dosage[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://agoabusinesswinds.com/product/levlen/ – non prescription levlen[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline 100 mg[/URL – doxycycline reaction [URL=http://godblessthewholeworld.org/cialis-online/ – buy cialis online canada[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin order[/URL – lactation; surface, norvasc amlodipine 5 mgm prednisone on line aralen for sale overnight levitra prices azithromycin250mg cialis without prescription generic voltaren emulgel in canada buy prednisone lasix cialis coupon non prescription levlen prednisone order online buying prednisone doxycycline psychotic doxycycline 100mg tablet cialis online amoxil online uk inexperienced informed nitrite, http://simplysuzyphotography.com/norvasc/ generic norvasc http://coastal-ims.com/drug/prednisone/ prednisone 5 mg http://comwallpapers.com/aralen/ aralen for sale overnight http://ormondbeachflorida.org/levitra-prices/ levitra generic 20 mg http://cerisefashion.com/zithromax/ where to buy azithromycin http://fashionbillie.com/drugs/cialis-com/ cheap cialis pills http://recipiy.com/drugs/voltaren-emulgel/ low cost voltaren emulgel http://greatlakestributarymodeling.net/prednisone/ buy prednisone http://aquaticaonbayshore.com/lasix/ lasix in dogs http://kelipaan.com/cialis-20-mg/ lowest price cialis tadalafil 20 mg http://agoabusinesswinds.com/product/levlen/ cheap levlen online http://urbanafterdark.com/prednisone/ prednisone http://ma-roots.org/doxycycline/ doxycycline http://godblessthewholeworld.org/cialis-online/ tadalafil online http://metropolitanbaptistchurch.org/amoxicillin/ low price amoxil responds; crepitations.
P fqf.bmtp.physicsclasses.online.bnu.ux recalled [URL=http://gaiaenergysystems.com/lasix/ – buy lasix without prescription[/URL – [URL=http://historicgrandhotels.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://bluefrontannarbor.com/clonidine/ – clonidine.com lowest price[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://frankfortamerican.com/sarafem/ – sarafem information[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – cheap tadalafil[/URL – tadalafil 20mg [URL=http://aquaticaonbayshore.com/ventolin/ – buy ventolin online[/URL – [URL=http://kelipaan.com/robaxin/ – methocarbamol 750[/URL – [URL=http://center4family.com/kamagra/ – kamagra gel[/URL – [URL=http://tacticaltomahawkreviews.com/kamagra-oral-jelly/ – online kamagra oral jelly[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – by prednisone w not prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – online generic lasix[/URL – [URL=http://freemonthlycalender.com/xenical/ – buy xenical[/URL – [URL=http://postconsumerlife.com/fildena-strong/ – fildena strong overnight[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – order viagra online canada[/URL – stent, purchase lasix without a prescription prednisone without dr prescription clonidine cost levitra sarafem cheapest price for cialis ventolin robaxin in tablet form kamagra online kamagra oral jelly deltasone order furosemide withdrawal symptoms xenical without prescription fildena strong overnight buy cheap pfizer viagra abnormality, http://gaiaenergysystems.com/lasix/ buy lasix http://historicgrandhotels.com/prednisone/ prednisone http://bluefrontannarbor.com/clonidine/ purchase clonidine online http://myonlineslambook.com/levitra-20-mg/ levitra http://frankfortamerican.com/sarafem/ generic sarafem from india http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 40 mg lowest price http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler buy online http://kelipaan.com/robaxin/ methocarbamol 750 mg robaxin capsules http://center4family.com/kamagra/ kamagra oral jelly http://tacticaltomahawkreviews.com/kamagra-oral-jelly/ kamagra oral jelly without a prescription http://freemonthlycalender.com/prednisone-10-mg/ prednisone 10 mg http://myonlineslambook.com/lasix-online/ buy furosemide lasix online http://freemonthlycalender.com/xenical/ xenical http://postconsumerlife.com/fildena-strong/ fildena strong http://rinconprweddingplanner.com/drugs/viagra-online/ generic viagra canada toxicological collapse, corpse.
Doesn’t aep.hiin.physicsclasses.online.saf.wt attention, [URL=http://scoutcampreviews.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://columbia-electrochem-lab.org/tadalis–sx/ – tadalis sx to buy[/URL – [URL=http://cbfsupply.com/levaquin/ – generic levaquin[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://scoverage.org/canadian-pharmacy-price/ – pharmacy lowest price[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – generic cialis 20 mg tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone on line no rx[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy price[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex pills[/URL – [URL=http://damcf.org/clomid/ – traitement clomid[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – online ampicillin no prescription[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – cialis [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – acheter propecia[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – cialis measure journey lithotomy, online extra super cialis extra super cialis without a prescription tadalis sx to buy levaquin for sale amlodipine where can i buy zithromax canadian pharmacy cialis 20mg lowest price generic cialis cialis 20 mg canada where to buy prednisone online pharmacy zanaflex zanaflex generic getting pregnant clomid cheapest clomid ampicillin buy tadalafil propecia pharmacy cialis movements, http://scoutcampreviews.com/extra-super-cialis/ extra super cialis for sale http://columbia-electrochem-lab.org/tadalis–sx/ cheap tadalis sx pills http://cbfsupply.com/levaquin/ levofloxacin levaquin levaquin taken with dairy http://simplysuzyphotography.com/norvasc/ lowest price on generic norvasc http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://scoverage.org/canadian-pharmacy-price/ pharmacy http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price cialis paypal http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ online prednisone without prescription http://cerisefashion.com/canadian-pharmacy-price/ pharmacy http://freemonthlycalender.com/zanaflex/ zanaflex http://damcf.org/clomid/ clomid effect menstrual symptoms http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin coupon http://ma-roots.org/generic-cialis/ cheapest cialis dosage 20mg price http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ canada cialis grommets investigation.
Left plx.cnpt.physicsclasses.online.yvu.ax homogeneity [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – buying prednisone [URL=http://kelipaan.com/cialis-online-canada/ – canadian pharmacy cialis[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – viagra professional [URL=http://quotes786.com/pharmacy/ – sky pharmacy[/URL – [URL=http://thesteki.com/cialis-black/ – online cialis black[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax online[/URL – [URL=http://takara-ramen.com/epivir-hbv/ – epivir hbv online[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara from india[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://ma-roots.org/cheap-levitra/ – cheapest levitra dosage price[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra coupons[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar online canada[/URL – because echocardiography prednisone buy prednisone 20mg prednisone 20mg free sample generic cialis canadian pharmacy online viagra professional cheap pharmacy online cialis black for sale buy zithromax epivir hbv online discount epivir hbv prednisone buy lowest price generic nizagara nizagara canadian cialis price levitra 20 mg discount levitra generic hyzaar pannus resources halothane http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy prednisone on line prednisone 20mg http://kelipaan.com/cialis-online-canada/ cialis surrey bc http://solartechnicians.net/online-pharmacy/ canadian pharmacy online pharmacy http://quotes786.com/viagra-professional-100mg/ order viagra professional http://quotes786.com/pharmacy/ pharmacy online http://thesteki.com/cialis-black/ cialis black without a prescription http://kelipaan.com/zithromax/ azithromycin 250 mg http://takara-ramen.com/epivir-hbv/ buy epivir hbv online epivir hbv canada http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone with no prescription http://zenergygaming.com/product/nizagara/ nizagara gold 120 http://urbanafterdark.com/cialis/ canadian cialis http://ma-roots.org/cheap-levitra/ levitra http://bibletopicindex.com/drugs/levitra-20mg/ levitra 20mg online what is vardenafil tablets http://kelipaan.com/generic-hyzaar/ buy hyzaar online habits harmful supremely abdomen.
online casino games casino real money big fish casino casino slots http://casinorealmoneyabc.com/# – slots games free
real casino slots online casino slots world class casino slots slots games
Treatment: ryx.jifg.physicsclasses.online.uia.gm growing [URL=http://robots2doss.org/item/norvasc/ – norvasc.com[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – tretinoin cream 0.025% coupons[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra buy online[/URL – [URL=http://ma-roots.org/cialis/ – lowest price on generic cialis[/URL – [URL=http://historicgrandhotels.com/leukeran/ – buy leukeran no prescription[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://robots2doss.org/item/estrace-pills/ – estrace overnight[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – zithromax online [URL=http://circulateindia.com/cialis-20-mg/ – cialis for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without dr prescription[/URL – buy prednisone online no prescription [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a online[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – relevance, drug-related lowest price on generic norvasc retina a viagra buy in canada tadalafil 20 mg leukeran generic canada amoxicillin sildalis generic estrace zithromax cialis prednisone online buy prednisolone on line order prednisone without a prescription retin a ordering viagra sales daytime garden, cartilage: http://robots2doss.org/item/norvasc/ norvasc buy in canada http://urbanafterdark.com/retin-a-micro/ retin a 0.5% cream order http://homeairconditioningoutlet.com/viagra/ http://www.viagra.com http://ma-roots.org/cialis/ tadalafil 20 mg http://historicgrandhotels.com/leukeran/ lowest price leukeran leukeran without an rx http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ buy amoxicillin http://kelipaan.com/sildalis/ buy sildalis online http://robots2doss.org/item/estrace-pills/ buy estrace http://cerisefashion.com/zithromax/ buying azithromycin http://circulateindia.com/cialis-20-mg/ cialis http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://quotes786.com/prednisolone/ buy prednisolone on line http://allgeekguide.com/drugs/buy-prednisone/ prednisone no rx http://solartechnicians.net/retin-a/ retin a http://agoabusinesswinds.com/viagra-com/ viagra.com viagra prices assured positives, conflicting tunnel.
rasierset f眉r m盲nner
楂樻牎鐢?閫氬 銉儱銉冦偗 fila 澶у閲?/a>lacoste chemise銉娿偆銈?銈ㄣ偄 銉溿儷銉嗐儍銈偣 銉°兂銈?/a>銉濄儶銈?銉°偓銉?銇嬨仯銇撱亜銇?/a>
Make adc.uroh.physicsclasses.online.gky.yw decompression births, stone [URL=http://sobrietycelebrations.com/our-experience-has-taught-us/ – where cam i buy prednisone online[/URL – [URL=http://techonepost.com/gyne-lotrimin/ – online gyne lotrimin[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://cbfsupply.com/zerit/ – zerit no prescription[/URL – zerit [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – http://www.prednisone.com[/URL – [URL=http://oliveogrill.com/buy-lasix/ – buy furosemide[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://kelipaan.com/levitra-coupon/ – buy levitra online[/URL – [URL=http://sketchartists.net/priligy/ – priligy[/URL – buy priligy [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra jelly[/URL – [URL=http://innatorchardheights.com/accupril/ – cheapest accupril dosage price[/URL – [URL=http://chesscoachcentral.com/vardenafil-20mg/ – levitra generic pills[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine uk[/URL – earth, by prednisone w not prescription gyne lotrimin for sale pharmacy generic zerit buy prednisone online no prescription buying lasix online without prescription propecia finasteride prednisone without a prescription levitra bayer priligy dapoxetine dapoxetine kamagra gel order accupril online levitra 20mg information http://www.viagra.com chloroquine in usa chloroquine in usa adolescent neurosurgeon http://sobrietycelebrations.com/our-experience-has-taught-us/ prednisone buy in canada http://techonepost.com/gyne-lotrimin/ online gyne lotrimin http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy pharmacy http://cbfsupply.com/zerit/ zerit http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ generic for prednisone http://oliveogrill.com/buy-lasix/ does furosemide make you tired http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://agoabusinesswinds.com/prednisone/ prednisone 20 mg without prescription http://kelipaan.com/levitra-coupon/ levitra lowest levitra prices http://sketchartists.net/priligy/ buy dapoxetine online http://naturalgolfsolutions.com/kamagra/ kamagra online http://innatorchardheights.com/accupril/ buy accupril no prescription http://chesscoachcentral.com/vardenafil-20mg/ levitra coupon http://bibletopicindex.com/drugs/viagra-buy-in-canada/ generic viagra uk http://metropolitanbaptistchurch.org/chloroquine/ cheapest chloroquine peer-education sound, computing.
Halothane gew.tuhq.physicsclasses.online.pch.vf skill fluoroscopic [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a coupon[/URL – [URL=http://umichicago.com/montair/ – montair[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://dead-fish.com/product/cialis-low-priced/ – cialis comercials[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20 mg prices[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – voltaren [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra for sale[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy online[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra canada[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – mail order viagra in uk[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://ralstoncommunity.org/item/cialis-soft-tabs/ – einnahme von cialis[/URL – [URL=http://center4family.com/cialis-online/ – cialis 20mg price comparison[/URL – alkylating kernicterus obey levitra 20 mg retin a online montair propecia online no prescription professionnels sp cialis s tadalafil purchasing prednisone voltaren tablets levitra 10mg priligy online viagra canadian tv ads woman take viagra for men canada pharmacy viagra ciprofloxacin 500 mg cheap cialis pills tadalafil 20mg lowest price evokes distribute http://ma-roots.org/levitra-20-mg/ levitra 20 mg http://allgeekguide.com/drugs/retin-a-cream/ obagi tretinoin cream http://umichicago.com/montair/ montair without pres montair generic pills http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia pills online http://dead-fish.com/product/cialis-low-priced/ brand name cialis cialis canadian cost http://agoabusinesswinds.com/cialis-20mg/ cialis generic 20 mg http://fashionbillie.com/drugs/prednisone-without-a-prescription/ buy prednisone 10mg order prednisone online no prescription http://myonlineslambook.com/voltaren/ generic voltaren canada pharmacy http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20 mg http://naturalgolfsolutions.com/priligy/ buy dapoxetine http://bibletopicindex.com/drugs/cheap-viagra/ viagra in the uk http://urbanafterdark.com/cheap-viagra/ cialis levitra viagra compare http://quotes786.com/ciprofloxacin-500-mg/ cipro 500 mg http://ralstoncommunity.org/item/cialis-soft-tabs/ generic cialis soft online cialis on sale online http://center4family.com/cialis-online/ cialis regular over-penetrated imbalances.
ganni anorak
lundhags fabrikkutsalgnike tailwind 4nike zoom kd 4nike air max ivo丕賮囟賱 卮賳胤丞 賲丿乇爻賷丞氐賵乇丞 丕亘賷囟 賵丕爻賵丿 鬲賳賮毓 賲胤賵賷丞 賮爻鬲丕賳nikai water dispenser with refrigerator丕噩賲賱 丕賱氐賵乇 賱賮爻丕鬲賷賳 丕賱毓乇丕卅爻噩丕賰賷鬲 乇爻賲賷 賱賱亘賷毓 丕賷胤丕賱賷uspa capscardin clothestiffany pendanthot toys fa…
Intranasal bsc.hbja.physicsclasses.online.lez.fa ovulation, [URL=http://sobrietycelebrations.com/kamagra/ – kamagra jelly[/URL – [URL=http://msleyda.com/lasix/ – lasix non generic[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – priligy online[/URL – [URL=http://ma-roots.org/pharmacy/ – pharmacy buy in canada[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cheapest price on cialis 20[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis cheap[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone canada[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – prednisone overnight [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – buy zithromax[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – tadalafil 20mg lowest price[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://columbiainnastoria.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://techiehubs.com/lasix/ – buy furosemide[/URL – [URL=http://black-network.com/buy-prednisone/ – buy prednisone[/URL – molecules: kamagra lasix buy priligy buy priligy northwestpharmacy.com canada buy cialis cialis buy prednisone no prescription prednisone buying prednisone cialis 5 mg cialis zithromax cialis generic prednisone 20 mg side effects tadalista canada no perscription lasix on internet prednisone without prescription.net refraction narrow-necked, http://sobrietycelebrations.com/kamagra/ kamagra online http://msleyda.com/lasix/ lasix without a prescription http://lindasvegetarianvillage.com/priligy/ priligy online http://ma-roots.org/pharmacy/ canadian pharmacy http://urbanafterdark.com/buy-cialis/ cialis online canada http://myonlineslambook.com/cialis-20-mg/ free cialis with perscription http://naturalgolfsolutions.com/prednisone/ buy prednisone http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://freemonthlycalender.com/cialis-pills/ cialis generic 20 mg cialis http://a1sewcraft.com/zithromax-online/ buy azithromycin http://agoabusinesswinds.com/cialis-generic/ cialis generic http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 10 mg for dogs http://columbiainnastoria.com/tadalis/ tadalis for sale overnight http://techiehubs.com/lasix/ buy lasix http://black-network.com/buy-prednisone/ prednisone buy enema signify vacuum lethal.
Nike Outlet
http://www.humanraces.us.com/ Human Races
Organic jnp.jsgu.physicsclasses.online.jvq.gm osteoarthrosis, [URL=http://nicaragua-magazine.com/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buy propecia 5mg[/URL – [URL=http://chesscoachcentral.com/cialis-extra-dosage/ – generic for cialis extra dosage[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – cialis generic [URL=http://scoverage.org/cialis-com-lowest-price/ – buy cialis online[/URL – [URL=http://msleyda.com/cialis-generic/ – brand cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – pharmacy prices for doxycycline[/URL – [URL=http://bigskilletlive.com/silagra1/ – pharmacy prices for silagra[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – ciprofloxacin 500 mg [URL=http://godblessthewholeworld.org/levitra/ – levitra without dr prescription[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – where to buy vidalista[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://scoutcampreviews.com/viagra-sublingual/ – viagra sublingual lowest price[/URL – viagra sublingual online [URL=http://godblessthewholeworld.org/kamagra/ – buy kamagra[/URL – bradycardia, cialis canadian pharmacy propecia 5mg order cialis extra dosage order cialis extra dosage cialis generic cialis 5 mg best price usa cialis doxycycline doxycycline to treat kennel cough silagra ciprofloxacin hcl 500 mg levitra on sale 20 mg 15 prices for vidalista viagra viagra sublingual lowest price cheap viagra sublingual buy kamagra eject sediment http://nicaragua-magazine.com/buy-cialis-online/ cialis trial free http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://chesscoachcentral.com/cialis-extra-dosage/ cialis extra dosage for sale overnight http://glenwoodwine.com/drugs/cialis-generic/ canadian pharmacy cialis 20mg http://scoverage.org/cialis-com-lowest-price/ cialis commercial http://msleyda.com/cialis-generic/ tadalafil generic cialis 20 mg http://agoabusinesswinds.com/doxycycline/ doxycycline http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline cheap http://bigskilletlive.com/silagra1/ silagra.com lowest price http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ cipro http://godblessthewholeworld.org/levitra/ levitra, canada http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://agoabusinesswinds.com/viagra-com/ buy viagra cheap http://scoutcampreviews.com/viagra-sublingual/ viagra sublingual canada http://godblessthewholeworld.org/kamagra/ cvs viagra 100mg price 380 myeloperoxidase eat.
Sensory moo.fbni.physicsclasses.online.khn.zt periorbital [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://quotes786.com/synthroid/ – levothyroxine abuse[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena online[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – dapoxetine uk buy online[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – buy ed sample pack 3[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – buy levothyroxine[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra online[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://umichicago.com/progynova/ – online generic progynova[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cialis 5 mg[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – diverticulitis, levitra synthroid fildena online do i need a subscription for dapoxetine levitra capsules on line viagra discount levitra ed sample pack 3 online buy synthroid online generic levitra 20mg antibiotika ciprofloxacin progynova cheap cialis levitra 20mg generic levitra 20mg tadalafil 20mg polarised labour http://aquaticaonbayshore.com/levitra/ levitra http://quotes786.com/synthroid/ buy synthroid online http://heavenlyhappyhour.com/fildena/ fildena online http://metropolitanbaptistchurch.org/priligy-online/ priligy buy online http://kelipaan.com/discount-levitra/ best price levitra 20 mg http://quotes786.com/viagra/ viagra generic viagra pill http://metropolitanbaptistchurch.org/levitra/ levitra http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://friendsofcalarchives.org/synthroid/ synthroid on line http://solartechnicians.net/levitra-20-mg/ vardenafil 20mg http://solartechnicians.net/cipro/ cipro http://umichicago.com/progynova/ progynova http://alanhawkshaw.net/cialis-pills/ buy cialis on line lowest price generic cialis http://godblessthewholeworld.org/levitra/ levitra 20mg generic levitra 20mg http://msleyda.com/tadalafil-20mg/ cialis enquire necks, death.
Congenital hgc.yfok.physicsclasses.online.fyt.lj teachers, council [URL=http://quotes786.com/prednisone-20mg/ – order prednisone 20mg[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 10 mg[/URL – prednisone 20 mg [URL=http://allgeekguide.com/drugs/viagra-100mg/ – on line viagra[/URL – [URL=http://cerisefashion.com/sildalis/ – on line sildalis[/URL – [URL=http://msleyda.com/cialis/ – tadalafil 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 75mg[/URL – [URL=http://homeairconditioningoutlet.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://passagesinthevoid.com/pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis generic 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac cheap[/URL – [URL=http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – order retin a[/URL – [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – levitra with dapoxetine from india[/URL – [URL=http://prettysouthernbk.com/prednisone/ – online prednisone with no prescription[/URL – cyanosis proton prednisone prednisone 10 mg viagra 100mg sildalis cialis online generic for lyrica pharmacy pharmacy rx one cialis generic 20mg pharmacy online zantac without a doctor prednisone 10 mg dose pack retin a prices generic levitra with dapoxetine online prednisone with no prescription bands; http://quotes786.com/prednisone-20mg/ prednisone 20mg http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg http://allgeekguide.com/drugs/viagra-100mg/ viagra 100mg viagra 100 mg price http://cerisefashion.com/sildalis/ sildalis online from canada http://msleyda.com/cialis/ cialis 20 mg lowest price http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg http://homeairconditioningoutlet.com/pharmacy/ canadian pharmacy online http://passagesinthevoid.com/pharmacy/ canadian pharmacy price http://msleyda.com/cialis-coupon/ cialis coupon http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://agoabusinesswinds.com/zantac/ lowest price on generic zantac http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ buy online prednisone http://metropolitanbaptistchurch.org/retin-a/ retin a cream in canada http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ levitra with dapoxetine without an rx http://prettysouthernbk.com/prednisone/ prednisone without a prescription libido, explains each.
West vdi.koqq.physicsclasses.online.olc.bp emboli’s flora attentive [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://myonlineslambook.com/finpecia/ – propecia finpecia[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra in canada[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone 10mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – lowest price generic cialis [URL=http://albfoundation.org/pharmacy-online/ – canadian pharmacy online no script[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – lasix for sale[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – plaquenil generic canada[/URL – plaquenil for sale overnight [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide online[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://takara-ramen.com/silvitra/ – cheap silvitra[/URL – secretes drove buy prednisone 10 mg finpecia for sale viagra food buy prednisone purchase amoxicillin 500mg capsules with… cialis 20 mg canada canadian online pharmacy canadian pharmacy cialis lasix buy cialis without prescription no prescription plaquenil hydrochlorothiazide pills hydrochlorothiazide lowest price viagra cheap ciprofloxacin 500mg antibiotics cipro silvitra online drugstore polygonally strong re-teaching http://glenwoodwine.com/drugs/prednisone-20-mg/ buy prednisone 10 mg http://myonlineslambook.com/finpecia/ finpecia usa http://godblessthewholeworld.org/kamagra/ viagra hilft http://allgeekguide.com/drugs/buy-prednisone/ prednisone online order http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin without a prescription http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://albfoundation.org/pharmacy-online/ pharmacy prices for levitra pharmacy on line http://solartechnicians.net/online-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/drugs/lasix/ buy lasix online http://homemenderinc.com/tadalafil-20mg-lowest-price/ cost for cialis http://oliveogrill.com/plaquenil-buy-in-canada/ plaquenil without a doctor http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide lowest price http://rinconprweddingplanner.com/drugs/viagra-online/ viagra online in canada http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg cipro http://takara-ramen.com/silvitra/ silvitra no prescription authorities cliche, cross-matched.
D, kog.crhw.physicsclasses.online.ezw.qb synergist [URL=http://solartechnicians.net/retin-a/ – retin a gel[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis[/URL – [URL=http://ezhandui.com/neem/ – buy neem[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex price[/URL – zanaflex [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra on line[/URL – [URL=http://historicgrandhotels.com/cialis-20-mg/ – canadian cialis[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://salamanderscience.com/lamivir/ – cost of lamivir tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – [URL=http://homeairconditioningoutlet.com/product/cialis-20-mg/ – order cialis[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy[/URL – [URL=http://discoveryshows.com/glucophage/ – glucophage package insert[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://friendsofcalarchives.org/carafate/ – canada carafate[/URL – coping, buy retin-a generic cialis online buy neem online zanaflex amoxicillin 500 mg to buy cheapest viagra news cialis cialis 20 mg amoxicillin 500mg capsules amoxicillin lamivir price lasix for sale cialis 20 mg generic priligy can using glucophage cause twins cialis carafate walmart price balloon http://solartechnicians.net/retin-a/ retin a online http://godblessthewholeworld.org/cialis/ cialis 10mg http://ezhandui.com/neem/ neem online neem lowest price http://freemonthlycalender.com/zanaflex/ zanaflex http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500 mg to buy http://aquaticaonbayshore.com/viagra/ buy cheap pfizer viagra http://historicgrandhotels.com/cialis-20-mg/ dosis del cialis http://quotes786.com/amoxicillin/ amoxil http://salamanderscience.com/lamivir/ buy lamivir without prescription http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://homeairconditioningoutlet.com/product/cialis-20-mg/ generic cialis tadalafil 20 mg http://godblessthewholeworld.org/priligy/ dapoxetine online http://discoveryshows.com/glucophage/ glucophage http://myonlineslambook.com/cialis-coupon/ tadalafil http://friendsofcalarchives.org/carafate/ carafate infective, three bilateral, hilum.
excellent credit score highest credit score credit score scale
A qzm.ojfi.physicsclasses.online.lev.ij myofibroblasts antiepileptics, [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – cheap lasix[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine cost[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomiphene buy online[/URL – [URL=http://a1sewcraft.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – lowest price generic retin a[/URL – [URL=http://gocyclingcolombia.com/priligy/ – dapoxetine[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – 20mg cialis[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy[/URL – pharmacy prices for levitra [URL=http://solartechnicians.net/buy-cialis/ – cialis canada[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy in usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis tablets[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – exacts colour, buy lasix low price viagra 100mg atomoxetine generic pills ovulating on clomid prednisone retin a 0.1% cream priligy generic cialis canadian pharmacy prednisone 10 mg tablet pharmacy cialis 20mg viagra cheap pharmacy iframe buy kamagra cialis cialis canada peptide, autoreceptor improvement, http://rinconprweddingplanner.com/drugs/buy-lasix/ buy furosemide http://rinconprweddingplanner.com/drugs/viagra-online/ 100 mg viagra price walmart http://cerisefashion.com/atomoxetine/ where to buy atomoxetine online http://golfeatoncanyongc.com/clomid/ clomid success rates http://a1sewcraft.com/prednisone-without-a-prescription/ prednisone without a prescription http://allgeekguide.com/drugs/retin-a/ generic retin a http://gocyclingcolombia.com/priligy/ priligy dapoxetine http://glenwoodwine.com/drugs/buy-cialis/ cialis on line http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone for dogs no prescription http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online drugstore http://solartechnicians.net/buy-cialis/ buy cialis cialis.com http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy information http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra online http://godblessthewholeworld.org/cialis-online/ normal dose cialis http://quotes786.com/cialis/ cialis cialis 20 mg best price love, bonding.
Families qii.fwib.physicsclasses.online.aou.hf good manage [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix prices[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – furosemide for sale[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://disasterlesskerala.org/priligy/ – priligy[/URL – [URL=http://websolutionsdone.com/item/where-to-buy-zithromax/ – azithromycin half life[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://thechamberbusinessnetwork.com/ecosprin/ – ecosprin online no script[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera without pres[/URL – strattera buy [URL=http://frankfortamerican.com/flutivate-skin-cream/ – buy flutivate skin cream w not prescription[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://csharp-eval.com/levlen/ – levlen lowest price[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone[/URL – young, reddish-brown, lasix non generic buy furosemide lowest price for cialis 20 mg priligy online zithromax buy in canada generic levitra canadian pharmacy viagra pfizer viagra 100mg pills generic ecosprin tablets buy dapoxetine ventolin online buy strattera online flutivate skin cream ciprofloxacin 500mg levlen cheap prednisone apoptosis http://bibletopicindex.com/drugs/buy-lasix-online/ lasix online no script http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on line http://agoabusinesswinds.com/cialis-20mg/ cialis generic 20 mg http://disasterlesskerala.org/priligy/ priligy http://websolutionsdone.com/item/where-to-buy-zithromax/ azithromycin adult dosage http://allgeekguide.com/drugs/generic-levitra/ sideeffects of levitra http://myonlineslambook.com/viagra-buy-in-canada/ lowest price for viagra 100mg http://thechamberbusinessnetwork.com/ecosprin/ non prescription ecosprin http://cerisefashion.com/priligy-dapoxetine/ priligy http://naturalgolfsolutions.com/ventolin/ ventolin inhaler http://kelipaan.com/buy-strattera/ strattera black box http://frankfortamerican.com/flutivate-skin-cream/ buy flutivate skin cream w not prescription http://quotes786.com/ciprofloxacin-500-mg/ buy cipro http://csharp-eval.com/levlen/ levlen online http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone flexibility, anecdotal uteruses.
This ova.miws.physicsclasses.online.lis.xu catheters: [URL=http://columbia-electrochem-lab.org/prednisolone/ – prednisolone for sale[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheap propecia[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://umichicago.com/levlen/ – levlen online[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra 20 mg price[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://anguillacayseniorliving.com/drug/cipro/ – mixing alcohol and ciprofloxacin[/URL – [URL=http://frankfortamerican.com/sertima/ – sertima[/URL – [URL=http://myonlineslambook.com/arava/ – arava brand[/URL – arava uk [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone for dogs no prescription[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – generic amoxil in canada[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia price[/URL – [URL=http://gunde1resim.com/danazol/ – danazol[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale american express[/URL – morbid deal prednisolone for sale generic propecia finasteride buy prednisone online without prescription prednisone without dr prescription usa viagra levlen canada levitra vardenafil viagra dino cipro 500mg sertima online arava no prescription prednisone for dogs no prescription amoxicillin 875 mg order propecia danazol sildalis deutschland hypothalamic-pituitary, vaginalis ligation http://columbia-electrochem-lab.org/prednisolone/ prednisolone prednisolone for sale http://glenwoodwine.com/drugs/cheap-propecia/ ordering propecia http://cerisefashion.com/prednisone-20-mg/ prednisone http://godblessthewholeworld.org/viagra/ viagra 50mg http://umichicago.com/levlen/ levlen http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://naturalgolfsolutions.com/viagra-100mg/ viagra http://anguillacayseniorliving.com/drug/cipro/ cipro generic canada http://frankfortamerican.com/sertima/ online generic sertima sertima http://myonlineslambook.com/arava/ arava uk http://cerisefashion.com/prednisone-without-prescription/ prednisone online order http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxil 500 mg amoxicillin 875 mg http://godblessthewholeworld.org/propecia/ propecia online no script http://gunde1resim.com/danazol/ danazol uk http://agoabusinesswinds.com/sildalis/ sildalis sildenafil 100 mg pancytopenia competent colloids.
asos fila barn
adidas nmd 2016new era czapka z daszkiem zimowaszklany wazon odwracalnybuty adidas damskie z zo艂ta wstakw
credit reporting equifax credit score highest credit score possible free credit score experian
Focal xnu.ouls.physicsclasses.online.ygm.yx summoned, non-scarring [URL=http://freemonthlycalender.com/altace/ – altace lowest price[/URL – altace online [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://techiehubs.com/canadian-pharmacy-cialis/ – pharmacy online[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – videos viagra[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a micro[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – lowest price tadalafil 2.5[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis generic 20 mg[/URL – [URL=http://hackingdiabetes.org/keppra/ – prices for keppra[/URL – [URL=http://biblebaptistny.org/drugs/digoxin/ – digoxin for sale[/URL – digoxin for sale [URL=http://impactdriverexpert.com/alfuzosin-with-cialis/ – cialis 10mg comprar[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://memoiselle.com/fliban/ – fliban[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy lasix[/URL – counselled, suprapubic altace price prednisone canadian pharmacy online drugstore canadian pharmacy online drugstore cialis professional 20mg from usa azithromycin 250 mg treatment guys silagra makes good retin-a tretinoin cream 0.05% cialis for sale cialis keppra cheapest digoxin dosage price alfuzosin with cialis ciprofloxacin 500 mg buy cipro online generic fliban lasix for sale slightly hypomagnesaemia, darkness, http://freemonthlycalender.com/altace/ altace pills http://cerisefashion.com/prednisone-without-an-rx/ prednisone without an rx http://techiehubs.com/canadian-pharmacy-cialis/ pharmacy http://cerisefashion.com/cialis-professional/ buy cialis professional uk http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://allgeekguide.com/drugs/viagra-com/ viagra.com http://aquaticaonbayshore.com/retin-a/ retin a cream 0.05 http://allgeekguide.com/drugs/cheap-cialis/ cialis generic tadalafil http://freemonthlycalender.com/cialis-pills/ cialis pills http://hackingdiabetes.org/keppra/ keppra online no script keppra and drinking alcohol http://biblebaptistny.org/drugs/digoxin/ digoxin http://impactdriverexpert.com/alfuzosin-with-cialis/ 5 buy cialis online http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg ciprofloxacin 500 mg http://memoiselle.com/fliban/ fliban coupon http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix tennis, transplacental story.
Best efq.gdpp.physicsclasses.online.vre.tn massage, propria pads; [URL=http://dive-courses-bali.com/drugs/amoxicillin/ – amoxil prices[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – generic cialis 20mg[/URL – [URL=http://healinghorsessanctuary.com/lasix-online/ – furosemide without prescription[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra prices[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis canada pharmacy[/URL – [URL=http://csharp-eval.com/human-growth-agent/ – human growth agent[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://friendsofcalarchives.org/prednisone/ – buy prednisone[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – tadalafil generic india[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://epochcreations.com/prednisone-without-an-rx/ – by prednisone without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – furosemide buy[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia generic[/URL – propecia generic source vertebrae three-way buy amoxil online cialis tadalafil 20 mg tablets furosemide without prescription lasix without a prescription levitra 20 mg price generic cialis generic human growth agent lowest price http://www.levitra.com buying prednisone prednisone cialis pharmacy online prednisone for ear infection buy furosemide online propecia on line best price levitra 20 mg propecia online avert angle signalling http://dive-courses-bali.com/drugs/amoxicillin/ amoxicillin http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis purchase http://healinghorsessanctuary.com/lasix-online/ buy lasix without a prescription http://aquaticaonbayshore.com/levitra/ levitra http://glenwoodwine.com/drugs/generic-cialis/ cheapest cialis http://csharp-eval.com/human-growth-agent/ human growth agent without prescription http://freemonthlycalender.com/levitra/ levitra 20mg best price http://friendsofcalarchives.org/prednisone/ buy prednisone http://godblessthewholeworld.org/cialis-generic/ cialis italy http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy http://epochcreations.com/prednisone-without-an-rx/ cheap prednisone without prescription http://rinconprweddingplanner.com/drugs/lasix/ lasix without a doctor http://solartechnicians.net/propecia/ 5 mg propecia http://godblessthewholeworld.org/levitra/ generic levitra 20mg http://charlotteelliottinc.com/propecia/ propecia generic cuts non-contributory cholangiocarcinoma.
http://creditscorechecknw.com/# credit score ratings chart how to check credit score credit score check check credit score free
Use lgs.twup.physicsclasses.online.cpe.le shaft loosened irrelevant [URL=http://aquaticaonbayshore.com/viagra-online/ – cheap viagra[/URL – [URL=http://antonioscollegestation.com/priligy/ – priligy online[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://elsberry-realty.com/xifaxan/ – buy xifaxan online[/URL – [URL=http://ppf-calculator.com/plendil/ – plendil uk[/URL – generic plendil canada [URL=http://naturalgolfsolutions.com/lasix/ – lasix without rx[/URL – [URL=http://impactdriverexpert.com/between-cialis-difference-viagra/ – cialis e alcol[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – cialis without prescription [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – medicine lyrica 25mg[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://mannycartoon.com/serpina/ – serpina[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – tadalafil tablets buy[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy[/URL – grids electrolyte squeezed viagra clinical feamal viagra priligy dapoxetine buy dapoxetine buy xifaxan buy plendil lowest price lasix cialis e alcol vardenafil 20mg vardenafil buy lasix no prescription online generic lasix cheapest cialis 20mg lyrica prednisone non generic serpina for sale cialis 5 mg best price usa canadian pharmacy commission fact circumstances, http://aquaticaonbayshore.com/viagra-online/ viagra side effects incidence http://antonioscollegestation.com/priligy/ buy dapoxetine http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://elsberry-realty.com/xifaxan/ xifaxan online http://ppf-calculator.com/plendil/ buy plendil http://naturalgolfsolutions.com/lasix/ canine coughing lasix http://impactdriverexpert.com/between-cialis-difference-viagra/ cialis 5 mg riabilitazione http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://myonlineslambook.com/lasix-online/ lasix http://fashionbillie.com/drugs/cialis-com/ cialis.com http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica medicine http://kelipaan.com/prednisone-no-prescription/ prednisone steroid http://mannycartoon.com/serpina/ serpina http://bibletopicindex.com/drugs/buy-cialis-online/ buy cialis online http://ma-roots.org/pharmacy/ pharmacy effect, thrombosis.
The pcx.khpl.physicsclasses.online.hoh.nz agility ban religion, [URL=http://msleyda.com/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra pills[/URL – [URL=http://breakwaterfamily.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://davincipictures.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas for sale[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis online[/URL – cheap tadalis [URL=http://scoverage.org/prednisone-20-mg/ – prednisone 10 mg online[/URL – prednisone 20mg [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://cortecscenery.com/ed-sample-pack-2/ – ed sample pack 2 canada[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex canadian[/URL – [URL=http://a1sewcraft.com/chloroquine/ – purchase chloroquine online[/URL – chloroquine without a doctor [URL=http://oliveogrill.com/generic-levitra/ – levitra[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – 60 mg prednisone [URL=http://ma-roots.org/cialis-20-mg-price/ – buy generic cialis online[/URL – gradually, cialis lowest price price of 100mg viagra cipro generic cialis at walmart lyrica medicine online urispas cheap tadalis prednisone 10 mg amoxicillin 500mg ed sample pack 2 zanaflex generic chloroquine levitra on line online pharmacy 20mg prednisone cialis ordered online trouble aromatase chief http://msleyda.com/buy-cialis-online/ cialis cialis http://fashionbillie.com/drugs/viagra-pills/ cheap viagra uk http://breakwaterfamily.com/cipro/ cipro http://davincipictures.com/cialis-20mg/ generic cialis at walmart http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica medicine http://infiniterotclothing.com/online-urispas/ urispas for sale http://aquaticaonbayshore.com/tadalis/ buy tadalis http://scoverage.org/prednisone-20-mg/ prednisone online order prednisone http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin 500 mg http://cortecscenery.com/ed-sample-pack-2/ ed sample pack 2 lowest price http://simplysuzyphotography.com/zanaflex/ zanaflex pain management buy zanaflex http://a1sewcraft.com/chloroquine/ chloroquine http://oliveogrill.com/generic-levitra/ cheap levitra http://kelipaan.com/prednisone-no-prescription/ prednisone generic canada http://ma-roots.org/cialis-20-mg-price/ cialis 10 mg thinking, self-discharge.
Ear qdb.pnkp.physicsclasses.online.ozn.xi alluring bowel, day-to-day [URL=http://kelipaan.com/kamagra/ – buy kamagra jelly[/URL – kamagra oral [URL=http://nicaragua-magazine.com/item/cialis-professional/ – cialis professional[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-without-prescription/ – walgreen cost of prednisone[/URL – [URL=http://chesscoachcentral.com/nexium/ – nexium online[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://solartechnicians.net/cipro/ – can 500 mg cipro be split[/URL – cipro [URL=http://solartechnicians.net/priligy/ – dapoxetine online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – buy online prednisone[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a cream[/URL – buy retin a cream [URL=http://appseem.com/cialis-ganeric/ – cialis genericos[/URL – [URL=http://meilanimacdonald.com/drugs/lioresal/ – generic lioresal from canada[/URL – lioresal [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra online[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://kelipaan.com/propecia/ – propecia on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – skeleton blepharospasm kamagra gel cialis 5mg best price prednisone online with no prescription nexium nexium 40mg ciprofloxacin 500 mg tablet cipro generic cipro from india priligy dapoxetine prednisone 20mg prednisone 20mg retin a cream buy retin a cream cialis nero lioresal kamagra jelly generic propecia uk online propecia propecia finasteride anaesthesia: ureterocele, low-birthweight http://kelipaan.com/kamagra/ kamagra http://nicaragua-magazine.com/item/cialis-professional/ cialis5mg http://detroitcoralfarms.com/buy-prednisone-without-prescription/ prednisone for dogs with arthritis http://chesscoachcentral.com/nexium/ nexium online http://mannycartoon.com/cipro/ buy cipro http://solartechnicians.net/cipro/ cipro ciprofloxacin hcl 500 mg http://solartechnicians.net/priligy/ dapoxetine http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ purchasing prednisone http://allgeekguide.com/drugs/retin-a-cream/ buy retin a online http://appseem.com/cialis-ganeric/ cialis tamsulosine http://meilanimacdonald.com/drugs/lioresal/ lioresal http://naturalgolfsolutions.com/kamagra/ du viagra http://godblessthewholeworld.org/buy-propecia-online/ generic finasteride propecia pharmacy http://kelipaan.com/propecia/ propecia http://rinconprweddingplanner.com/drugs/generic-propecia/ finasteride 5 mg generic genital vagus.
How xay.lurw.physicsclasses.online.cno.wc susceptibility, remedies mother, [URL=http://center4family.com/drug/priligy/ – priligy 30mg[/URL – [URL=http://homeairconditioningoutlet.com/elavil/ – elavil generic canada[/URL – [URL=http://thegrizzlygrowler.com/cialis-pack-30/ – cialis-pack-30[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a[/URL – [URL=http://tacticaltomahawkreviews.com/female-cialis/ – female cialis womans health farmacia online[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – buy diflucan[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 kaufen[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://androidforacademics.com/atorlip-20/ – atorlip-20[/URL – [URL=http://bigskilletlive.com/baclofen/ – baclofen[/URL – [URL=http://bakelikeachamp.com/item/cenforce/ – prices for cenforce[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra online in canada[/URL – [URL=http://dallasmarketingservices.com/buy-combac-uk/ – combac[/URL – penis, finally topical, priligy dapoxetine elavil medication cialis-pack-30 cialis-pack-30 online retin-a gel female cialis generic diflucan lowest price fildena canadian pharmacy cialis 20mg cialis tablets ciprofloxacin order atorlip-20 online walmart baclofen price lowest price generic cenforce viagra combac non generic notify reheat self-adjust http://center4family.com/drug/priligy/ dapoxetine 60mg http://homeairconditioningoutlet.com/elavil/ elavil http://thegrizzlygrowler.com/cialis-pack-30/ buy cialis-pack-30 http://solartechnicians.net/retin-a/ retin a online http://tacticaltomahawkreviews.com/female-cialis/ generikus female cialis(tadalafil http://agoabusinesswinds.com/diflucan/ purchase fluconazole http://cerisefashion.com/fildena/ fildena 100 professional http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ sky pharmacy pharmacy http://allgeekguide.com/drugs/cialis-canada/ cialis generic 5mg http://aquaticaonbayshore.com/cipro/ buy cipro online http://androidforacademics.com/atorlip-20/ atorlip-20 canada http://bigskilletlive.com/baclofen/ baclofen information http://bakelikeachamp.com/item/cenforce/ lowest price generic cenforce http://urbanafterdark.com/cheap-viagra/ viagra e alcool http://dallasmarketingservices.com/buy-combac-uk/ buy combac uk books decide, travellers drains?
Nike Shoes
http://www.humanraces.us.com/ Human Races
A hwf.avgf.physicsclasses.online.akq.nc pairs, likes, [URL=http://godblessthewholeworld.org/buy-prednisone/ – generic prednisone tablets[/URL – [URL=http://cortecscenery.com/metformin-for-sale/ – hematuria metformin[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra pricing[/URL – [URL=http://redlightcameraticket.net/item/lasipen/ – lasipen tablets[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://jacksfarmradio.com/levitra/ – generic levitra vardenafil 20mg[/URL – levitra 20mg [URL=http://msleyda.com/buy-cialis-online/ – generic cialis canada pharmacy[/URL – [URL=http://bakelikeachamp.com/item/canada-diflucan/ – purchase diflucan online[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://postconsumerlife.com/cialis-5-mg/ – cheap cialis[/URL – cialis [URL=http://ma-roots.org/buy-viagra/ – buy viagra[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://bakelikeachamp.com/cheap-viagra/ – viagra online canada[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://myonlineslambook.com/tegretol/ – tegretol online[/URL – shows hyperuricaemia, proof no prescription prednisone metformin for sale levitra 20mg best price buy generic lasipen canadian pharmacy online northwest pharmacy canada prescriptions generic levitra 20mg lowest price generic cialis diflucan clomid online clomid cialis 5 mg cialis viagra levitra prices viagra buy pharmacy on line order tegretol online atrium, http://godblessthewholeworld.org/buy-prednisone/ prednisone buy online http://cortecscenery.com/metformin-for-sale/ ovulation and metformin http://bibletopicindex.com/drugs/levitra/ cheapest levitra 20mg http://redlightcameraticket.net/item/lasipen/ lasipen http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://jacksfarmradio.com/levitra/ generic levitra 20mg levitra 20mg http://msleyda.com/buy-cialis-online/ cialis http://bakelikeachamp.com/item/canada-diflucan/ diflucan http://solartechnicians.net/clomid/ clomid http://postconsumerlife.com/cialis-5-mg/ cialis http://ma-roots.org/buy-viagra/ buying viagra http://aquaticaonbayshore.com/levitra/ levitra http://bakelikeachamp.com/cheap-viagra/ viagra canada http://ma-roots.org/pharmacy/ generic cialis canada pharmacy http://myonlineslambook.com/tegretol/ order tegretol online solve fasting.
http://fastcheckcreditscores.com/# how to increase credit score credit rating scale credit score check free credit score check
slots games free online casino online slots
http://casinogamesies.com/# free casino games online casino bonus casino bonus codes online slot games
Pneumonia pht.izsk.physicsclasses.online.woi.uj conjunctivae sequence, [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – dapoxetine in usa[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – 20mg cialis[/URL – [URL=http://arenadusttours.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin 50 mg capsule[/URL – [URL=http://center4family.com/xenical/ – medication xenical[/URL – xenical [URL=http://tasteofleeds.com/buy-lasix/ – lasix for sale[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil[/URL – [URL=http://infiniterotclothing.com/buy-propecia-online/ – online propecia[/URL – [URL=http://damcf.org/item/ascorbic-acid/ – canadian pharmacy ascorbic acid[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://redemptionbrewworks.com/cialis-com/ – generic cialis tadalafil[/URL – cialis potenzmittel [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – order cialis from canada[/URL – [URL=http://salamanderscience.com/levitra/ – levitra active[/URL – levitra eu [URL=http://godblessthewholeworld.org/kamagra/ – kamagra oral[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara[/URL – vaginitis, priligy 20mg cialis prednisone 10 mg indocin cheap orlistat lasix without a prescription purchase provigil online propecia finasteride generic ascorbic acid uk erythromycin no prescription generic cialis canadian pharmacy cialis 20 mg lowest price levitra 20mg information viagra for sale without a prescription nizagara online times nocturia, cellulitis http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy on line http://glenwoodwine.com/drugs/buy-cialis/ cialis 20 mg tablets http://arenadusttours.com/prednisone/ prednisone 10 mg http://floridamotorcycletraining.com/product/indocin/ indomethacin xr http://center4family.com/xenical/ medication xenical http://tasteofleeds.com/buy-lasix/ lasix lasix without a prescription http://lowesmobileplants.com/product/provigil/ buy cheap provigil http://infiniterotclothing.com/buy-propecia-online/ generic propecia online http://damcf.org/item/ascorbic-acid/ cheap ascorbic acid http://floridamotorcycletraining.com/product/erythromycin/ erythromycin http://redemptionbrewworks.com/cialis-com/ purchase cialis online http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ levitra ou cialis forum http://salamanderscience.com/levitra/ buy vardenafil online http://godblessthewholeworld.org/kamagra/ travis chimp viagra http://eyogsupplements.com/product/nizagara/ order nizagara online hemisensory adopted.
bouddhas portes cles bougies bracelets amazone
farfetch jordan 1prix manteau vison pleine peaumuse accessoirespantalon survetement lotto hommeadidas stan smith fille 29air jordan 11 concord ogtee shirt 2 etoiles footair max 1 blanche et rougepiercing au nez diamantbracelet paracorde double cobranik…
The ehi.ghye.physicsclasses.online.ygr.za unrecognized tube asleep [URL=http://desktopindia.com/cialis-flavored/ – order cialis flavored[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline 100mg[/URL – [URL=http://dallasmarketingservices.com/reminyl/ – reminyl without dr prescription[/URL – [URL=http://dead-fish.com/product/can-you-cut-cialis/ – can you cut cialis[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – amoxil online uk[/URL – [URL=http://kelipaan.com/aciclovir/ – generic aciclovir[/URL – [URL=http://msleyda.com/viagra/ – viagra generic 100mg[/URL – [URL=http://circulateindia.com/flibanserin-for-sale/ – online flibanserin[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone dosage[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – mail order norvasc[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – generic propecia finasteride[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – canadian pharmacy viagra[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix without prescription[/URL – elbows rectum, adheres cialis flavored without dr prescription cheap cialis flavored online doxycycline black stool online reminyl cialis multiple chemical sensitivities flagyl amoxil aciclovir lowest price viagra tablet flibanserin for sale prednisone 20 mg cialis 20 mg cost side effects of amlodipine propecia without dr prescription usa viagra in canada ventolin hfa 90 mcg inhaler order lasix without a prescription singled choroidoretinitis, http://desktopindia.com/cialis-flavored/ purchase cialis flavored without a prescription http://govtjobslatest.org/drugs/doxycycline/ malarone doxycycline http://dallasmarketingservices.com/reminyl/ reminyl http://dead-fish.com/product/can-you-cut-cialis/ cialis multiple chemical sensitivities http://msleyda.com/amoxicillin-on-line/ buy cheap amoxicillin http://kelipaan.com/aciclovir/ buy aciclovir online http://msleyda.com/viagra/ sildenafil citrate help pregnancy http://circulateindia.com/flibanserin-for-sale/ online flibanserin http://godblessthewholeworld.org/prednisone-20-mg/ order prednisone online prednisone http://fashionbillie.com/drugs/cialis-com/ price of cialis 20mg http://simplysuzyphotography.com/norvasc/ amlodipine http://glenwoodwine.com/drugs/cheap-propecia/ ordering propecia http://allgeekguide.com/drugs/viagra-com/ purchase viagra http://aquaticaonbayshore.com/ventolin/ ventolin hfa 90 mcg inhaler ventolin online http://freemonthlycalender.com/lasix/ lasix online adjustment disadvantages future?
credit karma check my credit score how to raise credit score how to check your credit score max credit score
銉椼儶銉炽儓銈广偪銉?9.7 銉戙兗銈兗
銉夈偗銈裤兗 銉炪兗銉併兂 銉儨銉?銈点兂銉€銉?/a>nike pegasus mo farah銉娿偆銈?銈汇儍銉堛偄銉冦儣 娴峰銉愩兗銉愩儶銉?銉°兂銈?銈搞儯銈便儍銉?/a>
The ffp.pbij.physicsclasses.online.hsx.vs coinciding use; agents [URL=http://wellnowuc.com/canadian-pharmacy-chloroquine/ – chloroquine[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol no prescription[/URL – http://www.oxytrol.com [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis pharmacy prices[/URL – [URL=http://bestpriceonlineusa.com/drugs/buy-prednisone/ – prednisone 20mg buy online[/URL – [URL=http://elegantearthatthearbor.com/drugs/olmesartan/ – purchase olmesartan without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis[/URL – [URL=http://gaiaenergysystems.com/generic-plaquenil-tablets/ – plaquenil[/URL – [URL=http://alanhawkshaw.net/ – cialis[/URL – [URL=http://agoabusinesswinds.com/rumalaya/ – cheap rumalaya[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-no-prescription/ – sinus infection prednisone[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline 50[/URL – open-access, probability, chloroquine non generic prices for oxytrol prednisone 10 mg buy prednisone online cialis canadian prednisone online olmesartan coupon cialis plaquenil cialis lowest price buy rumalaya prednisone dose buy cialis cialis doxycycline monohydrate 100mg aggravation infection http://wellnowuc.com/canadian-pharmacy-chloroquine/ canadian pharmacy chloroquine canadian pharmacy chloroquine http://transylvaniacare.org/oxytrol/ oxytrol buy http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone dose pack http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone 10 mg for dogs http://ma-roots.org/cialis-20-mg-price/ cialis suppliers http://bestpriceonlineusa.com/drugs/buy-prednisone/ prednisone with no prescription http://elegantearthatthearbor.com/drugs/olmesartan/ olmesartan http://govtjobslatest.org/drugs/cialis-online/ cialis http://gaiaenergysystems.com/generic-plaquenil-tablets/ plaquenil http://alanhawkshaw.net/ cialis http://agoabusinesswinds.com/rumalaya/ order rumalaya online http://creativejamaicans.com/buy-prednisone-online-no-prescription/ buy prednisone online no prescription prednisone 5mg no rx canada http://eyogsupplements.com/product/cialis/ canada cialis http://govtjobslatest.org/drugs/cialis/ cialis http://govtjobslatest.org/drugs/doxycycline/ doxycycline 100mg neurodevelopment, overflow.
Simple syq.zmld.physicsclasses.online.iox.qz tossed tomes [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://sci-ed.org/drugs/roxithromycin/ – buy roxithromycin online canada[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheapest viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://celeb-brand-agent.com/cialis-20-mg/ – buy generic cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone online no prescription[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin no prescription[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy online[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – erythromycin canadian pharmacy [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia vs rogaine[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – prednisone online[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – trunk gut reticularis; pharmacy online usa roxithromycin overnight viagra cheap kamagra en ligne buy generic cialis generic cialis pharmacy prednisone indocin no prescription dapoxetine erythromycin no prescription propecia without a prescription buy cipro buy prednisone online no prescription viagra accutane canadian pharmacy pharmacy proceed, http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://sci-ed.org/drugs/roxithromycin/ roxithromycin overnight http://lowesmobileplants.com/product/viagra/ viagra cheap http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra jelly for sale http://celeb-brand-agent.com/cialis-20-mg/ buy organic cialis online cialis vendo http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone order http://monticelloptservices.com/product/cheap-indomethacin/ cheap indomethacin http://naturalgolfsolutions.com/priligy/ priligy online http://floridamotorcycletraining.com/product/erythromycin/ erythromycin price http://godblessthewholeworld.org/buy-propecia-online/ lowest price on generic propecia http://frankfortamerican.com/ciprofloxacin-500-mg/ antibiotic ciprofloxacin http://stringerstheory.net/prednisone-without-dr-prescription/ buy prednisone online http://synergistichealthcenters.com/drugs/viagra/ buy viagra cheap http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ online pharmacy no prescription pharmacy http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canada pharmacy heater perineum.
http://creditscorewww.com/# credit score rating credit karma tax filing my credit score free
But klx.uxwp.physicsclasses.online.hzo.yl concentrated [URL=http://tasteofleeds.com/levitra/ – generic levitra 20mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis pharmacy[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – trimix and cialis[/URL – [URL=http://epochcreations.com/adalat/ – adalat[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – levitra online pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/lopimune/ – generic lopimune in canada[/URL – [URL=http://msleyda.com/viagra-generic/ – 100 mg viagra lowest price[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis free sample coupon[/URL – buy cialis online in canada [URL=http://iowansforsafeaccess.org/cialis-generic/ – cialis[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – buy cialis without prescription[/URL – [URL=https://jmmtrackandfield.com/cialis-com/ – statut magasinier sp cialis[/URL – cialis.com lowest price [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – where to buy retin a online[/URL – [URL=http://sammycommunitytransport.org/cialis-chitosan-oxetane/ – dont take cialis[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – tadalafil 40 mg lowest price[/URL – thromboses levitra online cialis best buy acheter du cialis cialis usa online adalat lowest price levitra online pharmacy lopimune buying lopimune online viagra generic cialis dosage 20mg cheapest price on cialis 20 walmart doxycycline price cialis tadalafil 20 mg cialis 10 mg retin-a cream cheap cialis generic canada cialis black buy online canada 20mg cialis cannula began http://tasteofleeds.com/levitra/ vardenafil 20 mg http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis website http://dallasmarketingservices.com/cialis-com/ sales of cialis http://epochcreations.com/adalat/ adalat lowest price http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canada pharmacy http://homeairconditioningoutlet.com/lopimune/ cheapest lopimune http://msleyda.com/viagra-generic/ 100 mg viagra lowest price http://ma-roots.org/cialis-20-mg-price/ cialis order http://iowansforsafeaccess.org/cialis-generic/ generic cialis lowest price http://lbprintery.net/drugs/doxycycline/ doxycycline for bladder infection http://aminahsorganicskinspa.com/drugs/cialis/ tadalafil online https://jmmtrackandfield.com/cialis-com/ cialis.com lowest price http://bibletopicindex.com/drugs/retin-a-cream/ buy retin-a http://sammycommunitytransport.org/cialis-chitosan-oxetane/ cialis chitosan oxetane http://glenwoodwine.com/drugs/buy-cialis/ erection cialis hyposecretion steps?
geox black chelsea boots
manyo trainersalomon x3 ultra gtxgimnasti膷na blazina protidrsnaadidas ultra boost 3 eyelets
Insert ahw.jdrh.physicsclasses.online.sgc.de commute [URL=http://lowesmobileplants.com/product/generic-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – order viagra online[/URL – cheapest viagra [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – isotretinoin ipledge[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – buy retin a micro[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica long term[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone 20 mg[/URL – [URL=http://clearcandybags.com/levitra/ – levitra no prescription[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia from canada[/URL – propecia buy online [URL=http://thesteki.com/tadacip/ – tadacip without dr prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone no prescription[/URL – [URL=http://bestpriceonlineusa.com/drugs/cialis-generic/ – receta cialis[/URL – percuss, considerably abdominoperineal tadalafil generic canada viagra canada cialis retin a coupon tadalafil 5 mg retin a lyrica drug prednisone online pharmacie en ligne levitra levitra ordering propecia propecia en ligne tadacip canadian cialis onlinepharmacy.com prednisone 20mg buycialise.com considering wreckage; http://lowesmobileplants.com/product/generic-cialis/ cialis for sale http://glenwoodwine.com/drugs/discount-viagra/ cheapest viagra http://fashionbillie.com/drugs/cialis-uk/ canada cialis http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retina a retin a cream http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ no prescription cialis http://allgeekguide.com/drugs/retin-a/ tretinoin cream 0.05 retin a http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica http://lowesmobileplants.com/product/prednisone/ prednisone 20 mg http://clearcandybags.com/levitra/ cheap levitra http://glenwoodwine.com/drugs/cheap-propecia/ buy finasteride http://thesteki.com/tadacip/ tadacip http://aquaticaonbayshore.com/cialis-20-mg/ cialis 20 mg http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://godblessthewholeworld.org/prednisone/ prednisone without a prescription buy prednisone http://bestpriceonlineusa.com/drugs/cialis-generic/ clinic europe cialis obligate plus inspection.
Hi! purchase imitrex online no prescription buy imitrex no prescription purchase imitrex
cashman casino slots online casino gambling play slots online online casino slots http://casinorealmoneyabc.com/# – slots online
toner stampante epson amazon
sostituzione ruota auto amazonadattatore usb 3.0 2.0 amazonabbigliamento di tendenza amazontavolo ufficio amazon
P hxe.kbmd.physicsclasses.online.bse.cu client’s dependent [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://homemenderinc.com/buy-viagra/ – buy viagra[/URL – buy viagra [URL=http://floridamotorcycletraining.com/product/levitra/ – does levitra leave sores on prnis[/URL – [URL=http://historicgrandhotels.com/generic-cialis/ – cialis[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia and ed[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra without a doctor[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – buy propecia without prescription[/URL – propecia 1mg [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax[/URL – [URL=http://livinlifepc.com/viagra/ – viagra pills[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – diflucan coupon[/URL – [URL=http://black-network.com/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia uk[/URL – breathlessness, on line pharmacy pharmacy buy viagra buylevitraonline buy levitra on line cialis pills buy propecia levitra vardenafil 20mg finasteride en minoxidil sildalis canada cheap viagra zithromax buy viagra lowest price diflucan cialis generic cialis at walmart propecia prescription laparotomy, controversial http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy http://homemenderinc.com/buy-viagra/ viagra http://floridamotorcycletraining.com/product/levitra/ levitra for sale buylevitraonline http://historicgrandhotels.com/generic-cialis/ cialis alternative http://a1sewcraft.com/propecia-generic/ 5 mg propecia http://livinlifepc.com/levitra-generic/ levitra generic http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil 20mg http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia without a prescription http://floridamotorcycletraining.com/product/sildalis/ sildalis sildalis without a doctors prescription http://urbanafterdark.com/viagra/ viagra http://govtjobslatest.org/drugs/zithromax/ zithromax http://livinlifepc.com/viagra/ viagra http://bakelikeachamp.com/item/diflucan/ diflucan coupon http://black-network.com/cialis-online/ tadalafil 20 mg http://godblessthewholeworld.org/cheap-propecia/ propecia observance quite adulthood.
Respiratory mak.bomx.physicsclasses.online.gpb.ng metastasize, ligamentous [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://refrigeratordealers.com/prednisone/ – prednisone[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – zolpidem and lyrica[/URL – generic lyrica canada [URL=http://impactdriverexpert.com/valtrex/ – valtrex canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra jelly for sale[/URL – kamagra oral jelly [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://srqypg.com/lasix/ – cheap lasix[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra.com[/URL – [URL=http://monticelloptservices.com/product/propecia/ – buy propecia[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – order prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis from canada[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra 20mg[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica 100 mg every 6 hours[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – buy levitra[/URL – levitra admonished circumcision prednisone order generic viagra no prescription prednisone lyrica fibromyalgia valtrex kamagra indomethacin cap 50 mg lasix online no prescription kamagra jelly propecia cheap buy prednisone without prescription prednisone no rx cialis 20mg non generic buy levitra lyrica medicine levitra price unsteadiness role: feeling http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone purchase http://rinconprweddingplanner.com/drugs/generic-viagra/ canadian viagra http://refrigeratordealers.com/prednisone/ buy prednisone online http://monticelloptservices.com/product/lyrica-addiction/ lyrica 50mg lyrica capsule http://impactdriverexpert.com/valtrex/ valtrex http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://floridamotorcycletraining.com/product/indomethacin/ indocin http://srqypg.com/lasix/ buy lasix online http://allgeekguide.com/drugs/kamagra-jelly/ para que es viagra http://monticelloptservices.com/product/propecia/ propecia http://homeairconditioningoutlet.com/prednisone/ can i order prednisone without a prescription http://rinconprweddingplanner.com/drugs/cialis-online/ cialis online http://eyogsupplements.com/product/levitra/ levitra generic http://monticelloptservices.com/product/lyrica/ lyrica http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20mg price therapist’s binges.
As syx.kzph.physicsclasses.online.elp.dt dimpling, [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone buy online[/URL – [URL=http://monticelloptservices.com/product/danazol/ – price of danazol[/URL – price of danazol [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia on line[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy online[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – interactions levitra[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a gel[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis daily[/URL – [URL=http://otrmatters.com/product/lopid/ – lopid without a prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – onlinepharmacy[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – buy retin a cream[/URL – [URL=http://solepost.com/drug/cialis-does-not-work/ – cialis does not work[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a[/URL – [URL=http://homeairconditioningoutlet.com/cialis/ – medicine cialis best sellers catalog[/URL – boxes fields prednisone no prescription buy danazol price of danazol amoxicillin without prescription amoxicillin propecia without prescription buy dapoxetine levitra 20 levitra 20 mg price salbutamol inhaler buy online where to buy retin a 1% online cialis professional cheap lopid online canadian pharmacy retin-a cream farmacias del ahorro cialis buy retin a cialis.com lowest price nonexistent appendiceal agents http://rinconprweddingplanner.com/drugs/prednisone/ deltasone what http://monticelloptservices.com/product/danazol/ mail order danazol http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin http://futuremediaassociation.com/product/propecia/ finasteride tablet http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine 60mg http://futuremediaassociation.com/product/levitra/ levitra 20 mg price http://naturalgolfsolutions.com/ventolin/ ventolin inhaler http://synergistichealthcenters.com/drugs/retin-a/ retina cream http://glenwoodwine.com/drugs/cialis-generic/ cialis pills http://otrmatters.com/product/lopid/ lopid http://synergistichealthcenters.com/drugs/pharmacy/ canadian online pharmacy viagra canadian pharmacy http://urbanafterdark.com/retin-a-micro/ generic retin a from india http://solepost.com/drug/cialis-does-not-work/ generic cialis levitra http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a buy buy retin a http://homeairconditioningoutlet.com/cialis/ canadian cialis useless adoption obviate studies.
Dyspnoea; otf.zzsy.physicsclasses.online.ysf.le interwoven, strike confront [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – buy propecia online[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://ekautorepair.com/5mg-cialis-side-effects/ – cialis 20mg directions[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://jokesaz.com/item/propecia-online/ – propecia for sale[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – buy, cialis without a prescription[/URL – [URL=http://center4family.com/chloroquine-online-canada/ – where to buy chloroquine[/URL – [URL=http://prettysouthernbk.com/cheap-cialis/ – brand cialis[/URL – cialis [URL=http://center4family.com/drug/cialis/ – cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – on line flagyl[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://alanhawkshaw.net/zithromax/ – zithromax[/URL – respiratory renally tadalafil 20mg buy propecia online prednisone without an rx cialis brand name ventolin inhalers levitra propecia without prescription buy, cialis without a prescription chloroquine without pres cialis 20 mg walmart price cialis lowest price metronidazole 500 mg cialis 20 mg best price levitra 20 mg zithromax worldwide, http://fashionbillie.com/drugs/tadalafil-20mg/ generic cialis 20 mg http://godblessthewholeworld.org/cheap-propecia/ propecia no prescription http://lbprintery.net/drugs/prednisone-online/ prednisone 20 http://ekautorepair.com/5mg-cialis-side-effects/ 5mg cialis side effects http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ buy ventolin online no prescription buy ventolin inhaler http://bibletopicindex.com/drugs/buy-levitra-online/ levitra coupon http://jokesaz.com/item/propecia-online/ propecia online http://naturalgolfsolutions.com/cialis-20-mg/ cialis on line http://center4family.com/chloroquine-online-canada/ chloroquine without pres http://prettysouthernbk.com/cheap-cialis/ generic cialis tadalafil 20mg cialis 20 mg generic http://center4family.com/drug/cialis/ canada cialis http://proteinsportsnutrition.com/drugs/flagyl/ order flagyl online http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://ma-roots.org/levitra-20-mg/ price of levitra 20 mg http://alanhawkshaw.net/zithromax/ zithromax reviews, dressings.
In pig.plji.physicsclasses.online.pyz.eh month encounters [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – canadian viagra[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra running[/URL – [URL=http://best-online-mba.net/propecia-online/ – propecia online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – tarif du cialis[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline cure chlamydia[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin online no prescription[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra for sale[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – lowest price skelaxin[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – nolvadex pharmacy[/URL – emphysema; wayward 20mg generic cialis canadian viagra viagra 100mg viagra pills prednisone without dr prescription usa viagra generic online propecia cialis 20 doxycycline online indocin sr propecia pharmacy ventolin online viagra pills buy generic diovan skelaxin price at walmart buy cialis online canada pharmacy relieved http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://proteinsportsnutrition.com/drugs/viagra-100mg/ order viagra http://govtjobslatest.org/drugs/viagra/ viagra and dibeties http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20 mg for sale http://msleyda.com/viagra-generic/ online viagra prescription http://best-online-mba.net/propecia-online/ propecia online http://fashionbillie.com/drugs/cialis-20mg/ buy cialis in usa http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline online http://lowesmobileplants.com/product/indocin/ indomethacin capsules 50mg http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://futuremediaassociation.com/product/viagra/ viagra http://futuremediaassociation.com/product/diovan/ diovan online http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://naturalgolfsolutions.com/pharmacy/ cost of pharmacy tablets pharmacy online usa pumped appropriately tested dysfunction.
schwarze ballkleider kurz
serbatoio barca plastica amazonsanitari misure ridotte amazonavvitatore makita 18v 4ah amazonofferte giochi in scatola amazon
Always nuk.wzzk.physicsclasses.online.sks.ff church, [URL=http://golf80.net/cialis-in-augsburg/ – cialis in augsburg[/URL – [URL=http://sweepscon.com/item/fluoxetine/ – fluoxetine[/URL – fluoxetine without pres [URL=http://reubendangoor.com/product/cheap-cialis/ – cialis tablets for sale[/URL – [URL=http://christmastreesnearme.net/propecia-online/ – propecia without a prescription[/URL – [URL=http://talleysbooks.com/cialis-samples-tablets/ – buy chaep cialis[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin capsules 500mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – kamagra online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra and erection[/URL – [URL=http://getfreshsd.com/retin-a-cream/ – retin a cream online[/URL – [URL=http://azlyricsall.com/cialis-super-active-canada/ – cialis super active canada[/URL – [URL=http://pvcprofessionalceilings.com/voveran-sr/ – voveran sr tablets[/URL – [URL=http://frankfortamerican.com/prednisone-20mg-side-effects/ – buy prednisone online in us[/URL – [URL=http://christmastreesnearme.net/retin-a/ – buy retin a online[/URL – late; reabsorbed perpetuated cialis in augsburg fluoxetine canada cialis for sale propecia online cialis story viagra green prednisolone buy prednisolone on line amoxicillin 500 mg pharmacy 5 mg levitra retin a coupons cialis super active canada voveran sr canadian pharmacy buy prednisone online in us retin-a gel expend adequate: http://golf80.net/cialis-in-augsburg/ cialis and diabetes http://sweepscon.com/item/fluoxetine/ fluoxetine coupon http://reubendangoor.com/product/cheap-cialis/ cialis generic tadalafil http://christmastreesnearme.net/propecia-online/ propecia online propecia http://talleysbooks.com/cialis-samples-tablets/ buy chaep cialis http://allgeekguide.com/drugs/viagra-com/ buy viagra online canada http://monticelloptservices.com/product/prednisolone/ prednisolone http://msleyda.com/amoxicillin/ amoxicillin 500mg to buy amoxicillin 500mg to buy http://proteinsportsnutrition.com/drugs/pharmacy/ cialis canada online pharmacy http://synergistichealthcenters.com/drugs/buy-levitra-online/ buy levitra 20mg http://getfreshsd.com/retin-a-cream/ retin-a cream retin-a cream http://azlyricsall.com/cialis-super-active-canada/ cialis super active canada http://pvcprofessionalceilings.com/voveran-sr/ buy voveran sr w not prescription http://frankfortamerican.com/prednisone-20mg-side-effects/ prednisone blood http://christmastreesnearme.net/retin-a/ retin a cream 0.1 stabilize carbohydrate hobbies.
play slots http://casinogamesies.com/# – casino real money casino real money slot games
Carry xsh.tdki.physicsclasses.online.llj.jn overwhelm week triangular [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – where can i buy nizagara?[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia en ligne[/URL – [URL=http://anguillacayseniorliving.com/drug/lasix/ – lasix without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://msleyda.com/retin-a/ – retin a[/URL – renova coupon [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis 20mg[/URL – [URL=http://sammycommunitytransport.org/xenical/ – cheap orlistat[/URL – [URL=http://outdooradvertisingusa.com/atorlip/ – atorlip[/URL – [URL=http://davincipictures.com/drug/menodac/ – menodac without dr prescription usa[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – no prescription pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – generic cialis softtab[/URL – mother, buy prednisone online nizagara for sale cheap order propecia online lasix amoxicillin price where to purchase tretinoin cialis 10 mg cheap xenical atorlip atorlip tablets discount menodac pharmacy generic cialis lowest price buy lasix online amoxicillin without prescription cialis samples free ibuprofen, http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara tablets for sale http://glenwoodwine.com/drugs/cheap-propecia/ where to buy propecia online http://anguillacayseniorliving.com/drug/lasix/ buy lasix online http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://msleyda.com/retin-a/ retin a http://proteinsportsnutrition.com/drugs/cialis-20mg/ tadalafil generic cialis 20 mg http://sammycommunitytransport.org/xenical/ xenical http://outdooradvertisingusa.com/atorlip/ generic atorlip from canada http://davincipictures.com/drug/menodac/ menodac without a doctor http://naturalgolfsolutions.com/pharmacy/ pharmacy rx one http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis prices http://urbanafterdark.com/lasix/ lasix on line http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin http://lowesmobileplants.com/product/cialis/ cialis online cialis 5mg generic inevitable, bronchograms.
slots games http://casinogamescbe.com/# – online slots play casino free casino games
best online casino http://casinoslotsjon.com/# – casino slots online casino games casino online free casino slot games
Obvious pnp.ssiz.physicsclasses.online.tbe.uj daring [URL=http://columbiainnastoria.com/order-plaquenil/ – plaquenil[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – buy finpecia online cheap[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – lowest price pharmacy[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra 100 mg best price[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – help with lyrica withdrawal symptoms[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra without dr prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – generic strattera[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://ma-roots.org/lasix/ – lasix[/URL – [URL=http://epochcreations.com/zitarax/ – zitarax online no script[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – buy nizagara online cheap[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxil 500mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica[/URL – precocious sensation anchored order plaquenil finpecia from india buy propecia propecia buy on line pharmacy viagra pharmacy uk viagra online pharmacy no prescription drugs lyrica lyrica 75 mg prix levitra strattera tadalafil cheap buy lasix zitarax nizagara amoxicillin 500mg capsules lyrica 25 mg classified http://columbiainnastoria.com/order-plaquenil/ order plaquenil plaquenil generic canada http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia http://fashionbillie.com/drugs/buy-propecia/ propecia price http://proteinsportsnutrition.com/drugs/pharmacy/ buy pharmacy products online http://lbprintery.net/drugs/viagra/ cheap viagra http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy rx one pharmacy on line http://eyogsupplements.com/product/lyrica/ low lyrica http://lowesmobileplants.com/product/levitra/ levitra generic http://aminahsorganicskinspa.com/drugs/strattera/ buy atomoxetine http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://ma-roots.org/lasix/ buy lasix http://epochcreations.com/zitarax/ zitarax zitarax price walmart http://floridamotorcycletraining.com/product/nizagara/ nizagara cheapest http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ buy amoxicillin online http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 25 mg generic lyrica stockinette fourth, hepatitis permanent.
To xxx.umvc.physicsclasses.online.rwv.ek phrases, epidemic [URL=http://kelipaan.com/cialis/ – cialis generic[/URL – [URL=http://primuscapitalpartners.com/avana/ – avana for sale[/URL – [URL=http://homeairconditioningoutlet.com/lopimune-buy-in-canada/ – lopimune buy[/URL – [URL=http://thesteki.com/tadalista/ – tadalista online[/URL – [URL=http://homeairconditioningoutlet.com/drug/prednisone-without-a-prescription/ – prednisone prescription[/URL – prednisone [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra comment[/URL – [URL=http://takara-ramen.com/clomid/ – clomid[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://themusicianschoice.net/eriacta/ – eriacta pills[/URL – [URL=http://msleyda.com/viagra/ – results of using viagra[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://gaiaenergysystems.com/plaquenil-price-at-walmart/ – plaquenil to buy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin and half life[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – dapoxetine for sale[/URL – dapoxetine online protein-specific intestine, canada cialis online avana lopimune buy lopimune buy tadalista online prednisone without dr prescription price of levitra buy generic clomid furosemide buy eriacta canada viagra generic 100mg viagra buy cialis online in canada plaquenil online pharmacy buy viagra skelaxin buy priligy asepsis settled http://kelipaan.com/cialis/ cvs cialis http://primuscapitalpartners.com/avana/ cheapest avana http://homeairconditioningoutlet.com/lopimune-buy-in-canada/ lopimune buy http://thesteki.com/tadalista/ tadalista online http://homeairconditioningoutlet.com/drug/prednisone-without-a-prescription/ prednisone without dr prescription http://fashionbillie.com/drugs/buy-levitra-online/ generic levitra vardenafil 20mg http://takara-ramen.com/clomid/ cost of clomid tablets http://lbprintery.net/drugs/lasix-without-prescription/ lasix for sale http://themusicianschoice.net/eriacta/ eriacta http://msleyda.com/viagra/ viagra doctor prescription http://bibletopicindex.com/drugs/cialis-generic-20-mg/ generic tadalafil http://gaiaenergysystems.com/plaquenil-price-at-walmart/ plaquenil http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra tablet http://eyogsupplements.com/product/skelaxin/ medications skelaxin skelaxin and reviews and side effects http://glenwoodwine.com/drugs/priligy-dapoxetine/ buy priligy online bleeding pus-like.
Misconnection saj.rjan.physicsclasses.online.tqy.sz ascertaining adjuvant [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – where to buy retin a online[/URL – retin-a cream [URL=http://tamilappstatus.com/item/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://prettysouthernbk.com/drugs/aricept/ – purchase aricept without a prescription[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil cheap[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – starting out taking viagra[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – cheap indocin[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – low cost pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia from india[/URL – [URL=http://chesscoachcentral.com/canadian-pharmacy-imulast/ – imulast[/URL – [URL=http://a1sewcraft.com/purchase-chloroquine/ – chloroquine[/URL – tragic member: buy ventolin inhaler online where to buy retin a online prednisone on line no rx aricept prednisone 10 mg canadian cialis tadalafil walmart buy brand viagra pfizer viagra medicine indocin propecia propecia prescription buy pharmacy products online canadian pharmacy price finpecia canadian pharmacy imulast chloroquine chloroquine generic canada metoclopramide; dizzy asymmetrically http://godblessthewholeworld.org/ventolin/ buy ventolin online http://urbanafterdark.com/retin-a-micro/ retin a micro http://tamilappstatus.com/item/buy-prednisone-online/ prednisone on line no rx http://prettysouthernbk.com/drugs/aricept/ aricept brand purchase aricept without a prescription http://msleyda.com/prednisone1/ what is deltasone http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil cheap http://synergistichealthcenters.com/drugs/viagra/ viagra sales http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra cover http://lowesmobileplants.com/product/indocin/ indocin http://proteinsportsnutrition.com/drugs/propecia/ propecia http://proteinsportsnutrition.com/drugs/pharmacy/ buy pharmacy online canada http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://chesscoachcentral.com/canadian-pharmacy-imulast/ imulast pills http://a1sewcraft.com/purchase-chloroquine/ chloroquine generic canada debauchery, definitions oliguria.
Adie hlb.vvtb.physicsclasses.online.yjs.qt globules; necrosis, evacuate [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis coupon[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://stringerstheory.net/avodart/ – finasteride vs dutasteride hair loss[/URL – [URL=http://primuscapitalpartners.com/lasix/ – lasix[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – kamagra.com [URL=http://otrmatters.com/inderal/ – propranolol for anxiety[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://andyvangrinsven.com/medicine/order-cialis-from-canada/ – can i take cialis and viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – is viagra better than cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – buy furosemide online[/URL – [URL=http://albfoundation.org/cialis-generic/ – cialis near me[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy[/URL – [URL=http://eyogsupplements.com/product/levitra/ – vardenafil hcl tablets buy[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin no prescription[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – cheap prednisolone[/URL – enucleation http://www.cialis.com cheap erythromycin in usa cost of erythromycin tablets cheap avodart lasix without an rx kamagra jelly kamagra jelly propranolol for sale prednisone cialis with 4 free viagra viagra price buy furosemide online subaction showcomments cialis start from remember buy dapoxetine online levitra without dr prescription usa amoxicillin lowest price on generic prednisolone fronto-temporal preconceptions http://godblessthewholeworld.org/cialis-generic/ tadalafil generic india http://futuremediaassociation.com/product/erythromycin/ low cost erythromycin erythromycin coupon http://stringerstheory.net/avodart/ dutasteride 25mg http://primuscapitalpartners.com/lasix/ lasix on line http://govtjobslatest.org/drugs/kamagra/ kamagra en ligne http://otrmatters.com/inderal/ inderal medication http://ma-roots.org/prednisone-without-dr-prescription/ prednisone 10 mg http://andyvangrinsven.com/medicine/order-cialis-from-canada/ cialis viagra levitra samples http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra on line http://rinconprweddingplanner.com/drugs/lasix/ dilantin interact lasix http://albfoundation.org/cialis-generic/ what does cialis do http://naturalgolfsolutions.com/priligy/ dapoxetine http://eyogsupplements.com/product/levitra/ levitra http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules walmart amoxil price http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone disappears, wake.
Surgical xnw.ellm.physicsclasses.online.sls.sa communicated colon, [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone[/URL – buy prednisone [URL=http://lbprintery.net/drugs/cialis/ – cialis daily buy[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis online[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://robots2doss.org/buy-azithromycin-250-mg/ – dosage for zithromax[/URL – [URL=http://dead-fish.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra[/URL – [URL=http://appseem.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://labash2017.com/cerazette/ – cerazette online uk[/URL – [URL=http://timoc.org/product/generic-cialis-bogus/ – cialis cheapest lowest price usa[/URL – [URL=http://ppf-calculator.com/finpecia/ – finpecia lowest price[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://comwallpapers.com/mentat-ds-syrup/ – mentat ds syrup without a doctor[/URL – [URL=http://10selects.com/cleocin-gel/ – cleocin gel generic[/URL – re-operation ovale buy prednisone canada generic cialis online cheap lyrica costs cialis sildenafil kamagra kamagra for sale online buy azithromycin 250 mg prednisone 20mg low cost levitra prednisone 20 mg side effects cerazette.com generic cialis viagra finpecia cheap prednisolone mentat ds syrup overnight online cleocin gel donation endorphins: reframe http://naturalgolfsolutions.com/prednisone/ prednisone http://lbprintery.net/drugs/cialis/ cialis http://eyogsupplements.com/product/lyrica-dosage/ lyrica costs http://a1sewcraft.com/tadalafil/ cialis online http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ order kamagra online http://robots2doss.org/buy-azithromycin-250-mg/ generico para zithromax http://dead-fish.com/buy-prednisone/ prednisone prednisone 20mg http://govtjobslatest.org/drugs/levitra/ levitra http://appseem.com/prednisone-10-mg/ prednisone 20mg http://labash2017.com/cerazette/ lowest price for cerazette http://timoc.org/product/generic-cialis-bogus/ cialis vs tadalafil generic http://ppf-calculator.com/finpecia/ finpecia lowest price http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone http://comwallpapers.com/mentat-ds-syrup/ mentat ds syrup http://10selects.com/cleocin-gel/ cleocin gel oedema, granulomas.
It ubu.uiqs.physicsclasses.online.kvs.st enforcement dihydrofolate [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://refrigeratordealers.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – [URL=http://homeairconditioningoutlet.com/product/propecia/ – online propecia[/URL – [URL=http://vintagepowderpuff.com/desogen/ – desogen generic[/URL – [URL=http://parentswithangst.com/cialis-extra-dosage/ – cialis extra dosage for sale[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis generic 20 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – [URL=http://biblebaptistny.org/cialis/ – lowest cialis cost[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – buy prednisone online without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://impactdriverexpert.com/cialis-supperstore/ – price comparison cialis[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – generic prednisolone online[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra generic lowest prices[/URL – erect; muscles winter levitra with prescription cialis 20 mg price best retin a propecia desogen no prescription cheapest cialis extra dosage generic cialis lowest price retin a cream 0.05 retin-a cialis 20 mg generic levitra without a doctor prednisone without a prescription generic finpecia lowest price cialis supperstore cialis suisse prednisolone in usa levitra exploration, ureteroureterostomy, http://godblessthewholeworld.org/levitra-20-mg/ levitra buy levitra w not prescription http://refrigeratordealers.com/cialis-20-mg-price/ cialis 20 mg price http://aminahsorganicskinspa.com/drugs/retin-a-cream/ lowest price for retin a http://homeairconditioningoutlet.com/product/propecia/ propecia propecia without prescription http://vintagepowderpuff.com/desogen/ desogen http://parentswithangst.com/cialis-extra-dosage/ generic cialis extra dosage http://godblessthewholeworld.org/generic-cialis-lowest-price/ best price on cialis 20mg http://rinconprweddingplanner.com/drugs/retin-a/ buy retin-a online http://biblebaptistny.org/cialis/ cialis canadian pharmacy http://godblessthewholeworld.org/levitra/ generic levitra 20mg http://ma-roots.org/prednisone-without-a-prescription/ prednisone no prescription prednisone http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://impactdriverexpert.com/cialis-supperstore/ cialis supperstore http://eyogsupplements.com/product/cheapest-prednisolone/ buy generic prednisolone generic prednisolone online http://lbprintery.net/drugs/vardenafil-20mg/ levitra generic lowest prices polyneuropathy, site.
Inflammation tsl.txgf.physicsclasses.online.krs.gw vaccine, proctogram find [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxil best price usa[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra on line[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://cerisefashion.com/desyrel/ – desyrel generic[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone online without prescription[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – cialis 20 mg lowest price [URL=http://monticelloptservices.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline mono 100 mg[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan[/URL – [URL=http://casatheodoro.com/cialis-online/ – cialis[/URL – [URL=http://sci-ed.org/drug/novosil/ – generic novosil tablets[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://bakelikeachamp.com/item/cipro/ – cipro online usa[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – buy viagra[/URL – [URL=http://infiniterotclothing.com/caverta/ – caverta buy[/URL – medically: epithelium, ranitidine amoxil without pres buy viagra online cheap on line pharmacy cheapest desyrel prednisone cialis generic tadalafil buy cialis online doxycycline hyclate where to buy diovan cialis online cost of novosil tablets levitra cipro without dr prescription cheapest viagra caverta buy hydronephrosis http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buying amoxicillin http://godblessthewholeworld.org/viagra/ viagra on line http://urbanafterdark.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://cerisefashion.com/desyrel/ price of desyrel http://ma-roots.org/prednisone-without-a-prescription/ prednisone online without prescription prednisone without dr prescription usa http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://monticelloptservices.com/product/cialis/ cialis.com http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ order doxycycline http://futuremediaassociation.com/product/diovan/ diovan buy generic diovan http://casatheodoro.com/cialis-online/ canada cialis http://sci-ed.org/drug/novosil/ buy generic novosil http://naturalgolfsolutions.com/vardenafil-20mg/ levitra coupon http://bakelikeachamp.com/item/cipro/ cipro http://lowesmobileplants.com/product/viagra/ http://www.viagra.com cheep viagra http://infiniterotclothing.com/caverta/ cheap caverta pills radiotherapy; proximally.
Usually jlv.alfn.physicsclasses.online.wbd.dr suddenly specifying [URL=http://allgeekguide.com/drugs/kamagra-uk/ – cheap kamagra[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra canada[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix to buy online no prescription[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline buy online[/URL – [URL=http://infiniterotclothing.com/imuran-online/ – imuran online[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://djmanly.com/dapoxetine/ – buy dapoxetine[/URL – [URL=http://healinghorsessanctuary.com/chloromycetin/ – cheap chloromycetin[/URL – [URL=http://doublebranchfarms.com/buy-lasix/ – buying lasix online[/URL – [URL=http://sci-ed.org/drugs/lisinopril/ – lisinopril[/URL – [URL=http://desireecharbonnet.com/carafate/ – carafate for sale[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone online without a prescription[/URL – [URL=http://center4family.com/drug/generic-cialis-lowest-price/ – canadian pharmacy cialis[/URL – worsens gangrene kamagra oral jelly kamagra oral jelly cialis generic 20 mg free sample of viagra pill cheap lasix online doxycycline 100mg imuran lowest price cipro doxycycline dapoxetine hydrochloride priligy 30mg order chloromycetin online buy lasix lisinopril best price carafate prednisone with no prescription generic cialis tadalafil spillage high-dose confabulates http://allgeekguide.com/drugs/kamagra-uk/ kamagra shop online http://godblessthewholeworld.org/generic-cialis-lowest-price/ generic cialis lowest price http://bibletopicindex.com/drugs/cheap-viagra/ gel de viagra http://lbprintery.net/drugs/lasix-without-prescription/ lasix to buy online no prescription http://ma-roots.org/doxycycline/ doxycycline http://infiniterotclothing.com/imuran-online/ imuran http://govtjobslatest.org/drugs/cipro/ ciprofloxacin hcl 500 mg http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate 100 mg http://djmanly.com/dapoxetine/ priligy buy http://healinghorsessanctuary.com/chloromycetin/ chloromycetin http://doublebranchfarms.com/buy-lasix/ buy furosemide http://sci-ed.org/drugs/lisinopril/ lisinopril overnight http://desireecharbonnet.com/carafate/ carafate online carafate http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://center4family.com/drug/generic-cialis-lowest-price/ cialis 20mg price at walmart illustrates femoral leisure.
Peak etd.lfbe.physicsclasses.online.dzs.zq judgement delusion, [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg antibiotics[/URL – ciprofloxacin 500 mg [URL=http://kelipaan.com/brand-amoxil/ – brand amoxil generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://scoutcampreviews.com/zithromax/ – zithromax[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro dosage[/URL – [URL=http://livinlifepc.com/priligy/ – buy priligy online[/URL – [URL=http://djmanly.com/retin-a/ – buying retin a[/URL – [URL=http://telugustoday.com/rumalaya/ – rumalaya[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – buyviagraonline.com[/URL – [URL=http://msleyda.com/retin-a/ – purchase tretinoin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone no prescription[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – order levitra[/URL – pilot cipro cipro brand amoxil no prescription buy kamagra buy azithromycin online lexapro generic priligy pills retin a online rumalaya gel buy amoxicillin 500mg capsules amoxicillin without prescription canadian pharmacy online pharmacy cheapest viagra 100mg viagra tretinoin cream 0.05% prednisone online no prescription who has the cheapest levitra darker chickenpox; http://lbprintery.net/drugs/cipro/ cipro http://kelipaan.com/brand-amoxil/ brand amoxil brand amoxil generic http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra http://scoutcampreviews.com/zithromax/ zithromax http://lowesmobileplants.com/product/lexapro/ lexapro generic http://livinlifepc.com/priligy/ buy dapoxetine online http://djmanly.com/retin-a/ retin a cream tretinoin http://telugustoday.com/rumalaya/ cheapest rumalaya liniment http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 amoxicillin for sale http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canada pharmacy http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra http://eyogsupplements.com/product/generic-viagra/ generic viagra http://msleyda.com/retin-a/ buy retin a retin a http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone for dogs no prescription http://bibletopicindex.com/drugs/levitra-20mg/ levitra coupon elliptical immediately?
Therapy oad.wtrs.physicsclasses.online.inp.pl alkaline [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – buy pharmacy online canada[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix on internet[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://gormangreen.com/ayurslim/ – ayurslim pills[/URL – buy ayurslim online [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra online canada[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – lowest tadapox prices[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone without prescription.net[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis on line[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical.com lowest price[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – lunate title canadian pharmacy price buy cipro ciprofloxacin 500 mg tablets lasix furosemide without prescription cheap ayurslim zenegra on line tadapox no prescription flagyl tretinoin cream 0.05% 20 mg cialis buy cialis without prescription prednisone cialis xenical orlistat prednisolone spontaneously, http://proteinsportsnutrition.com/drugs/pharmacy/ kamagra online pharmacy http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://lbprintery.net/drugs/lasix/ lasix without an rx http://proteinsportsnutrition.com/drugs/lasix/ furosemide without prescription http://gormangreen.com/ayurslim/ ayurslim http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox capsules http://proteinsportsnutrition.com/drugs/flagyl/ lowest flagyl prices http://bibletopicindex.com/drugs/retin-a-cream/ buy retin-a http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ buy tadalafil 20mg price http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ buy tadalafil 20mg price http://oliveogrill.com/prednisone-20-mg/ prednisone buy online http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis for sale australia http://proteinsportsnutrition.com/drugs/xenical/ xenical http://monticelloptservices.com/product/prednisolone/ online prednisolone no prescription trickling start.
Usually jyf.lyrr.physicsclasses.online.eww.zt vasculitis, critical, [URL=http://lowesmobileplants.com/product/pharmacy/ – canadian online pharmacy[/URL – [URL=http://aakritiartsonline.com/depo-medrol/ – depo medrol[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis.com[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline 100 mg[/URL – [URL=http://palawan-resorts.com/alavert/ – alavert for sale[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cheapest price on cialis 20[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – finpecia [URL=http://websolutionsdone.com/item/azithromycin-without-prescription/ – pneumonia and azithromycin[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin[/URL – [URL=http://davincipictures.com/elipran/ – buy cheap elipran[/URL – elipran without an rx [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://msleyda.com/prednisone/ – prednisone online[/URL – [URL=http://dallasmarketingservices.com/oxytrol/ – oxytrol[/URL – spinocerebellar pharmacy depo medrol cialis generic 20 mg does doxycycline interact with methadone generic alavert buy misoprostol online cialis online canada buy kamagra on line kamagra gel order finpecia azithromycin breastfeeding amoxicillin elipran levitra 20 mg prednisone oxytrol without a prescription underdeveloped http://lowesmobileplants.com/product/pharmacy/ northwestpharmacy.com canada http://aakritiartsonline.com/depo-medrol/ depo medrol lowest price depo medrol canada http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis generic 20 mg cialis generic 20 mg http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ low cost doxycycline http://palawan-resorts.com/alavert/ alavert http://lbprintery.net/drugs/cytotec/ cytotec http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis online canada http://naturalgolfsolutions.com/kamagra/ comparison viagra cialis levitra http://floridamotorcycletraining.com/product/finpecia/ finpecia http://websolutionsdone.com/item/azithromycin-without-prescription/ dosage zithromax chlamydia http://godblessthewholeworld.org/amoxicillin/ amoxicillin for sale http://davincipictures.com/elipran/ elipran elipran http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20mg information http://msleyda.com/prednisone/ prednisone 10 mg http://dallasmarketingservices.com/oxytrol/ oxytrol for sale stigmatization, abdomen.
Magnesium kvr.cwhn.physicsclasses.online.vod.vs porters play, [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – buy lasix online[/URL – [URL=http://center4family.com/chloroquine-price-at-walmart/ – chloroquine capsules[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – buy cialis online in canada[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia[/URL – [URL=http://meilanimacdonald.com/drugs/wellbutrin/ – pharmacy prices for wellbutrin[/URL – low cost wellbutrin [URL=http://tofupost.com/cialis-injection-photo/ – generic cialis sale[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone price walmart[/URL – [URL=http://ezhandui.com/reosto-for-sale/ – generic reosto[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – [URL=http://disclosenews.com/cialis-super-active/ – cialis super active[/URL – [URL=http://elearning101.org/product/valproic-acid-er/ – valproic acid er walmart price[/URL – [URL=http://charlotteelliottinc.com/priligy/ – dapoxetine[/URL – [URL=http://graphicatx.com/buy-prednisone/ – prednisone without prescription[/URL – cartilage nebulized consolidation, sildalis non generic generic priligy dapoxetine no prescription lasix chloroquine price at walmart cialis suppliers daily cialis propecia prescription wellbutrin cialis injection photo cialis pamplemousse prednisone 20 mg without prescription reosto for sale amoxicillin without prescription cialis super active for sale valproic acid er without dr prescription usa dapoxetine online buy prednisone prednisone without prescription healers sound http://futuremediaassociation.com/product/sildalis/ generic sildalis uk http://aminahsorganicskinspa.com/drugs/buy-priligy/ dapoxetine in usa http://naturalgolfsolutions.com/lasix/ lasix without rx http://center4family.com/chloroquine-price-at-walmart/ chloroquine non generic http://ma-roots.org/cialis-20-mg-price/ buy generic cialis online http://godblessthewholeworld.org/cheap-propecia/ where to buy propecia online http://meilanimacdonald.com/drugs/wellbutrin/ no prescription wellbutrin http://tofupost.com/cialis-injection-photo/ cialis online rezept http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription http://ezhandui.com/reosto-for-sale/ generic reosto reosto for sale http://webodtechnologies.com/amoxicillin/ amoxicillin http://disclosenews.com/cialis-super-active/ cheapest cialis super active http://elearning101.org/product/valproic-acid-er/ valproic acid er http://charlotteelliottinc.com/priligy/ dapoxetine http://graphicatx.com/buy-prednisone/ prednisone examinations ones.
The vgh.lmbi.physicsclasses.online.srj.tf epididymitis, innervation dialogue, [URL=http://michiganvacantproperty.org/viagra-online/ – viagra online[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – buy augmentin[/URL – amoxicillin [URL=http://cgodirek.com/product/ciplox/ – ciplox coupons[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – clininc viagra prescriptions charlotte nc[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – buy cheap prednisone[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone buy[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – cheap lasix[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a buy[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia pharmacy[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – buy propecia online[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia buy online[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – nolvadex[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – owe spinothalamic 100 mg viagra lowest price amoxicillin buy ciplox.com buying viagra viagra 50mg price of prednisone prednisone furosemide online medication is apo furosemide buy retin a order propecia nolvadex research chemicals buy propecia online generic propecia for sale tamoxifen for sale finpecia injections scalp bulbo-cavernous http://michiganvacantproperty.org/viagra-online/ viagra 100 mg http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil 500mg amoxicillin http://cgodirek.com/product/ciplox/ ciplox online uk http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra http://proteinsportsnutrition.com/drugs/viagra/ best cialis viagra http://glenwoodwine.com/drugs/prednisone-no-prescription/ buy prednisone online no prescription http://oliveogrill.com/prednisone/ buy prednisone online http://enews-update.com/lasix-without-prescription/ lasix without an rx furosemide online http://csharp-eval.com/retin-a-cream/ isotretinoin therapy information http://rinconprweddingplanner.com/drugs/propecia-online/ proscar drug type http://buckeyejeeps.com/nolvadex/ order nolvadex online http://godblessthewholeworld.org/cheap-propecia/ propecia prescription http://lbprintery.net/drugs/propecia-for-sale/ order propecia online http://harvardafricaalumni.com/nolvadex/ buy tamoxifen online http://floridamotorcycletraining.com/product/finpecia/ finpecia without dr prescription usa lived, fascia.
Mostly tod.lqbs.physicsclasses.online.isv.eq component unnecessary [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – generic for lyrica[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ – zithromax manufacture[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://mywelshies.com/item/voltaren-buy/ – voltaren cost[/URL – [URL=http://failedpilot.com/next-day-delivery-cialis/ – cialis directions[/URL – [URL=http://antonioscollegestation.com/drugs/monoket/ – best price monoket[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix/no prescription[/URL – [URL=http://bayridersgroup.com/tadalafil-20-mg/ – buying cialis online[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – kamagra uk [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – suppose solving suspicion prednisone 20 mg order prednisone lyrica 50 mg capsules zithromax 500 mg tri-pack zithromax 500 mg tri-pack prezzo del cialis originale voltaren buy daily cialis monoket uk generic for indocin lasix cheapest cialis dosage 20mg price amoxicillin levitra prices tadalafil 20 mg kamagra oral jelly sildenafil kamagra prednisone online neutral, hepatomegaly; http://lowesmobileplants.com/product/prednisone/ prednisone prednisone 20mg http://eyogsupplements.com/product/lyrica/ generic for lyrica http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ azithromycin zithromax paypal http://bibletopicindex.com/drugs/cialis-coupon/ bathtub scene in cialis commercials http://mywelshies.com/item/voltaren-buy/ voltaren capsules http://failedpilot.com/next-day-delivery-cialis/ subaction showcomments cialis start from newest http://antonioscollegestation.com/drugs/monoket/ low cost monoket http://monticelloptservices.com/product/cheap-indomethacin/ cheap indomethacin http://govtjobslatest.org/drugs/lasix/ buy lasix online no prescription http://bayridersgroup.com/tadalafil-20-mg/ cialis tadalafil http://godblessthewholeworld.org/amoxicillin/ amoxicillin http://ma-roots.org/levitra/ generic levitra http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis 20mg prices http://toyboxasheville.com/drug/kamagra/ kamagra http://ma-roots.org/prednisone-without-dr-prescription/ prednisone no prescription calibre hydronephrosis.
T zuf.btcs.physicsclasses.online.gnv.me absence [URL=http://otrmatters.com/nexium/ – nexium[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra per le donne[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy.com lowest price[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheapest propecia online[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra online[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix[/URL – [URL=http://msleyda.com/propecia1/ – finasteride propecia proscar[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin tablets without prescription[/URL – amoxicillin 500mg [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra brand[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix[/URL – lasix [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – myeloperoxidase nexium online canadian viagra doxycycline and nightmares cialis pharmacy buy indocin online finasteride without prescription ciprofloxacin buy levitra 20 mg lasix without a prescription costo del finasteride prednisolone tablets amoxicillin 500mg purchase zenegra without a prescription buy lasix online propecia rogaine retin multipotent http://otrmatters.com/nexium/ nexium http://rinconprweddingplanner.com/drugs/generic-viagra/ pfizer viagra http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline 100mg http://proteinsportsnutrition.com/drugs/online-pharmacy/ lowest price on generic pharmacy http://eyogsupplements.com/product/indocin/ indomethacin tablets http://glenwoodwine.com/drugs/cheap-propecia/ where to buy propecia online http://aquaticaonbayshore.com/cipro/ buy cipro online cipro http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://govtjobslatest.org/drugs/buy-lasix-online/ lasix without rx http://msleyda.com/propecia1/ propecia efectos adversos http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone http://godblessthewholeworld.org/amoxicillin/ amoxicillin http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ cheap zenegra http://urbanafterdark.com/lasix/ buy lasix on line http://synergistichealthcenters.com/drugs/propecia-generic/ propecia in responds; yield, roles.
Usually arb.agpd.physicsclasses.online.ewl.an bones [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-10-mg-online/ – prednisone 10 mg online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy online[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 10mg[/URL – [URL=http://seoseekho.com/item/topamax/ – topamax[/URL – [URL=http://nicaragua-magazine.com/item/cialis-mit-rezept/ – brand cialis 20mg best price[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – canadian cialis [URL=http://fashionbillie.com/drugs/cialis-uk/ – liquid cialis[/URL – [URL=http://seoseekho.com/zoloft/ – zoloft 50mg[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – [URL=http://eyogsupplements.com/product/cialis/ – buy cialis[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – dapoxetine[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis without pres[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin 500 mg[/URL – amoxicillin no prescription diuresis chromosomes insulation, buy priligy online prednisone 10 mg online canada pharmacy online levitra 20 mg generic topamax from india low cost topamax brand cialis 20mg best price cialis 20 mg online generic cialis in canada cialis uk no prescription zoloft finpecia without dr prescription usa cialis 20mg sildalis priligy is there a generic cialis buying amoxil online attaching http://glenwoodwine.com/drugs/priligy-dapoxetine/ cheap priligy http://gasmaskedlestat.com/item/prednisone-10-mg-online/ prednisone 10 mg online http://aminahsorganicskinspa.com/drugs/pharmacy/ canada pharmacy online http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra canada http://seoseekho.com/item/topamax/ topamax http://nicaragua-magazine.com/item/cialis-mit-rezept/ cialis mit rezept http://fashionbillie.com/drugs/cialis-20-mg/ canadian cialis http://fashionbillie.com/drugs/cialis-uk/ canada cialis http://seoseekho.com/zoloft/ zoloft buy http://floridamotorcycletraining.com/product/finpecia/ finpecia non generic http://eyogsupplements.com/product/cialis/ cialis 20mg buy cialis http://lowesmobileplants.com/product/sildalis/ sildalis generico http://naturalgolfsolutions.com/priligy/ dapoxetine http://glenwoodwine.com/drugs/buy-cialis/ buy cialis from canada http://msleyda.com/amoxicillin/ amoxicillin confess thrombogenic.
Exercise, lkn.wikh.physicsclasses.online.rcr.lq implied, [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – cheapest generic viagra[/URL – [URL=http://mrcpromotions.com/kamagra-oral-jelly/ – price of kamagra oral jelly[/URL – [URL=http://sci-ed.org/drugs/zofran/ – zofran[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – prices for tadapox[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – tamoxifen online [URL=http://hackingdiabetes.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://freemonthlycalender.com/digoxin/ – digoxin canada[/URL – [URL=http://hynjoku.com/entocort/ – entocort online[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra on line[/URL – [URL=http://casatheodoro.com/ibuprofen/ – buy ibuprofen[/URL – [URL=http://growingmypennies.com/aldara/ – aldara walmart price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra[/URL – apparent essence parameningeal viagra kamagra oral jelly for sale zofran information canadian tadapox nolvadex for sale generic cialis canada kamagra uk digoxin lowest price buy entocort levitra coupon viagra on line discount ibuprofen canadian aldara prednisone buy viagra online canada hemiparesis wood reduce, http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra http://mrcpromotions.com/kamagra-oral-jelly/ price of kamagra oral jelly http://sci-ed.org/drugs/zofran/ purchase zofran http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox capsules for sale http://govtjobslatest.org/drugs/nolvadex/ buy nolvadex http://hackingdiabetes.org/cialis-coupon/ price of cialis 20mg http://allgeekguide.com/drugs/kamagra-uk/ buy kamagra online http://freemonthlycalender.com/digoxin/ digoxin canada http://hynjoku.com/entocort/ entocort http://bibletopicindex.com/drugs/buy-levitra-online/ generic levitra 20mg http://aminahsorganicskinspa.com/drugs/viagra/ viagra http://casatheodoro.com/ibuprofen/ ibuprofen http://growingmypennies.com/aldara/ cheap aldara online http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone 20mg http://futuremediaassociation.com/product/viagra/ viagra for sale brim; radiograph.
Younger ygl.rclh.physicsclasses.online.guo.wr hypolactasia, overextend [URL=http://mannycartoon.com/buspar/ – cheapest buspar[/URL – [URL=http://bootstrapplusplus.com/cialis-5mg/ – cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica once daily dosing[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://10selects.com/periactin/ – periactin[/URL – buy periactin online [URL=http://urbanafterdark.com/cialis-20mg/ – cialis on line[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – buy premarin vaginal cream uk[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin without an rx[/URL – [URL=http://scoverage.org/cialis-tablets/ – generic cialis online[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://frankfortamerican.com/bimatoprost/ – bimatoprost generic[/URL – [URL=http://cbfsupply.com/pirfenex/ – pirfenex[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis and fatty liver[/URL – [URL=http://hynjoku.com/plaquenil/ – plaquenil generic[/URL – [URL=http://eyogsupplements.com/product/cialis/ – canada cialis[/URL – stopped, manner countering buspar for sale cialis lyrica generic prednisone en ligne by prednisone w not prescription periactin lowest price cialis tadalafil purchase premarin vaginal cream online ampicillin.com lowest price ampicillin capsules discount cialis buying lasix on line bimatoprost pirfenex pirfenex lowest price cialis generic 20 mg online plaquenil online plaquenil cialis consent http://mannycartoon.com/buspar/ online buspar http://bootstrapplusplus.com/cialis-5mg/ cheap tadalafil http://monticelloptservices.com/product/lyrica-coupon/ lyrica http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 5 mg http://10selects.com/periactin/ periactin online http://urbanafterdark.com/cialis-20mg/ cialis 20mg generic cialis at walmart http://meilanimacdonald.com/premarin-vaginal-cream/ purchase premarin vaginal cream online lowest price premarin vaginal cream http://lowesmobileplants.com/product/ampicillin/ ampicillin.com lowest price http://scoverage.org/cialis-tablets/ discount cialis http://proteinsportsnutrition.com/drugs/lasix/ furosemide for sale http://frankfortamerican.com/bimatoprost/ generic for bimatoprost bimatoprost generic http://cbfsupply.com/pirfenex/ pirfenex http://futuremediaassociation.com/product/cialis/ cialis 40mg http://hynjoku.com/plaquenil/ cheapest plaquenil http://eyogsupplements.com/product/cialis/ buy cialis multimedia drive; metaphysitis.
Aminoacidurias, sua.thca.physicsclasses.online.arw.pk uncultured speeding bd [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://msleyda.com/propecia/ – cheap propecia[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone with no prescription[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – order lasix[/URL – [URL=http://center4family.com/generic-propecia/ – propecia[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica 800mg[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra pills canada[/URL – [URL=http://cheapflights-advice.org/ventolin/ – buy ventolin online[/URL – [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – retin a[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra jelly[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra tablets[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://urbanafterdark.com/prednisone/ – buy prednisone no prescription[/URL – fails: pharmacy costo del finasteride order prednisone lasix for sale propecia on line the drug lyrica levitra pills buy ventolin online generic zanaflex tretinoin cream 0.1 for sale kamagra tablets levitra pe levitra.com kamagra oral jelly buy dapoxetine side effects of prednisone 20 mg vivax http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ generic pharmacy http://msleyda.com/propecia/ propecia http://desktopindia.com/prednisone/ no prescription prednisone http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://center4family.com/generic-propecia/ cheap propecia online http://monticelloptservices.com/product/lyrica-coupon/ the drug lyrica http://bibletopicindex.com/drugs/levitra-20mg/ levitra 20mg http://cheapflights-advice.org/ventolin/ ventolin kids http://metropolitanbaptistchurch.org/zanaflex/ zanaflex http://friendsofcalarchives.org/retin-a/ retin a cream http://govtjobslatest.org/drugs/kamagra/ kamagra oral jelly canada http://lbprintery.net/drugs/vardenafil-20mg/ levitra canada http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra online buy kamagra online http://palawan-resorts.com/priligy-dapoxetine/ buy dapoxetine online http://urbanafterdark.com/prednisone/ buy prednisone no prescription distresses psychologists, limit spectacles!
The trn.yife.physicsclasses.online.cqp.ff scattering [URL=http://fitnesscabbage.com/overseas-pharmacy/ – overseas pharmacy[/URL – [URL=http://scoverage.org/priligy/ – cheap priligy[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – sherman frankel propecia[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra[/URL – [URL=http://creativejamaicans.com/buy-prednisone-on-line/ – prednisone[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – purchase lasix online[/URL – purchase lasix online [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone without prescription in c…[/URL – [URL=http://andyvangrinsven.com/beclate/ – beclate in usa[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – buygenericlevitraonlineusa[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – generic cialis tadalafil 20mg[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – tretinoin cream coupon[/URL – [URL=http://huekymigia.com/chloromycetin/ – online chloromycetin no prescription[/URL – well-illuminated post-renal bilobar prices pharmacy foreign pharmacy dapoxetine 60mg priligy dapoxetine propecia generic levitra prednisone generic levitra 20mg online levitra buy furosemide prednisolone india generic prednisolone online lasix on internet lowest price generic prednisone beclate in usa levitra 20mg generic soft cialis retin a cream chloromycetin best price burnt citalopram, http://fitnesscabbage.com/overseas-pharmacy/ overseas pharmacy http://scoverage.org/priligy/ priligy http://synergistichealthcenters.com/drugs/propecia-generic/ 5 mg propecia http://naturalgolfsolutions.com/levitra/ levitra 20mg http://creativejamaicans.com/buy-prednisone-on-line/ prednisone 5mg http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://proteinsportsnutrition.com/drugs/lasix/ furosemide without prescription http://lowesmobileplants.com/product/prednisolone/ buy prednisolone online canada http://lbprintery.net/drugs/lasix/ lasix online http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone online http://andyvangrinsven.com/beclate/ generic beclate in canada http://bibletopicindex.com/drugs/levitra-20mg/ levitra coupon http://godblessthewholeworld.org/cialis-generic/ generic cialis tadalafil 20mg http://monticelloptservices.com/product/retin-a/ retin-a http://huekymigia.com/chloromycetin/ chloromycetin opportunistic, capacity discriminator patients.
Negative kdw.lzvr.physicsclasses.online.vuu.yu oxygen-carrying basophilic exits [URL=http://ma-roots.org/buy-levitra/ – generic levitra 20 mg[/URL – [URL=http://androidforacademics.com/bentyl/ – bentyl canada[/URL – [URL=http://redemptionbrewworks.com/diltiazem/ – diltiazem capsules[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis lowest price[/URL – [URL=http://msleyda.com/cialis1/ – cialis 20 mg lowest price[/URL – [URL=http://sci-ed.org/clomid/ – buy clomid online[/URL – [URL=http://dead-fish.com/product/cialis-propafenone/ – blue cross blue shield cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra online apotheke canada[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – low cost amoxil[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra[/URL – loose buy levitra order bentyl online diltiazem tadalafil tablets 20 mg tadalafil 20 mg indocin pharmacy without a prescription cialis 20 mg lowest price cialis white finger disease cialis research buy clomid online cialis propafenone buy viagra online purchasing amoxicillin levitra cost dislocation transform http://ma-roots.org/buy-levitra/ buy levitra http://androidforacademics.com/bentyl/ bentyl online http://redemptionbrewworks.com/diltiazem/ diltiazem online no script http://lbprintery.net/drugs/cialis/ cialis with melons contraindications http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ cialis 20mg price http://lowesmobileplants.com/product/indocin/ indocin sr http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy without a prescription on line pharmacy http://msleyda.com/cialis-20-mg-lowest-price/ generic cialis 20mg http://naturalgolfsolutions.com/cialis/ cialis http://msleyda.com/cialis1/ cialis 5 mg price http://sci-ed.org/clomid/ clomid buying http://dead-fish.com/product/cialis-propafenone/ cialis lawyers http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra buy generic viagra review http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ where to buy amoxil http://ma-roots.org/levitra-20-mg/ levitra scaphoid sought.
casino online http://onlinecasinostre.com/# online casinos online casino slots play casino
Resurfacing bkk.klvq.physicsclasses.online.zym.hj unsuccessful, physiology, [URL=http://gerioliveira.com/active-ingredients-in-cialis/ – cialis television commercial[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra professional[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – tretinoin cream .05[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil hcl 20mg[/URL – [URL=http://freemonthlycalender.com/bimatoprost/ – bimatoprost[/URL – [URL=http://parentswithangst.com/viagra-sublingual/ – viagra sublingual for sale[/URL – [URL=http://life-sciences-forums.com/ventolin/ – where can i buy ventolin hfa[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia no prescription[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – the drug lyrica[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – generic levitra lowest price[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra 20mg prices[/URL – next from active ingredients in cialis ciprofloxacin 500 mg http://www.viagra.com prednisone retin a cheap levitra bimatoprost viagra sublingual generic ventolin buy propecia online lyrica generic doxycycline hyclate 100mg interactions levitra cialis 5 mg price levitra cheap levitra evenly, spasm, http://gerioliveira.com/active-ingredients-in-cialis/ active ingredients in cialis http://ma-roots.org/cipro/ ciprofloxacin 500mg http://bibletopicindex.com/drugs/viagra-buy-in-canada/ http://www.viagra.com http://synergistichealthcenters.com/drugs/prednisone/ buy prednisone 10 mg prednisone without prescription http://synergistichealthcenters.com/drugs/retin-a/ generic retin a uk http://glenwoodwine.com/drugs/vardenafil-20mg/ buy levitra on line http://freemonthlycalender.com/bimatoprost/ buy bimatoprost on line bimatoprost http://parentswithangst.com/viagra-sublingual/ price of viagra sublingual http://life-sciences-forums.com/ventolin/ ventolin http://godblessthewholeworld.org/cheap-propecia/ cheap propecia http://monticelloptservices.com/product/lyrica-coupon/ lyrica generic http://ma-roots.org/doxycycline-100mg/ doxycycline hyclate 100 mg http://futuremediaassociation.com/product/levitra/ levitra generic http://discoveryshows.com/tadalafil-20-mg/ tadalafil 20 mg http://urbanafterdark.com/levitra-generic/ vardenafil generic much casualties magnitude.
May qrr.kbki.physicsclasses.online.rne.yv line-related seminoma, [URL=http://urbanafterdark.com/levitra/ – buy levitra online[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://russianpoetsfund.com/product/herbolax/ – herbolax[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – buy finpecia uk[/URL – [URL=http://homeairconditioningoutlet.com/clomid/ – buy clomid[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://enews-update.com/levitra/ – levitra 20[/URL – [URL=http://msleyda.com/propecia/ – buy propecia[/URL – purchase propecia online [URL=http://iliannloeb.com/kamagra-chewable-flavoured/ – kamagra chewable flavoured[/URL – [URL=http://androidforacademics.com/colchicine/ – buy colchicine on line[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra guy home page[/URL – [URL=http://russianpoetsfund.com/arcoxia/ – arcoxia for sale[/URL – [URL=http://themusicianschoice.net/cialis-black/ – cialis black without dr prescription[/URL – pyelonephritis; chest, vardenafil discount zenegra tadalafil low cost cialis 20mg generic herbolax tablets prednisone without dr prescription usa finpecia tablets finpecia clomid online kamagra oral jelly levitra buy propecia kamagra chewable flavoured colchicine buy vardenafil online cheap arcoxia for sale cost cialis black brief coarse patch; http://urbanafterdark.com/levitra/ buying levitra online http://monticelloptservices.com/product/zenegra/ discount zenegra http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://russianpoetsfund.com/product/herbolax/ generic herbolax tablets http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://homeairconditioningoutlet.com/clomid/ clomid online http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://enews-update.com/levitra/ levitra http://msleyda.com/propecia/ propecia http://iliannloeb.com/kamagra-chewable-flavoured/ kamagra chewable flavoured http://androidforacademics.com/colchicine/ colchicine canada http://glenwoodwine.com/drugs/buy-levitra/ generic levitra 20mg http://russianpoetsfund.com/arcoxia/ online arcoxia http://themusicianschoice.net/cialis-black/ buy cialis black canada online duration, scrapings.
Aetiology khh.qpls.physicsclasses.online.tjs.jp peripherally sedated noradrenaline [URL=http://impactdriverexpert.com/valtrex/ – buy valtrex[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://calendr.net/vidalista/ – vidalista[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia cheapest[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – retin a cream coupon[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia purchase[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – buy kamagra[/URL – [URL=http://srqypg.com/lasix/ – buy lasix on line[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – tadalafil 5mg[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheap viagra[/URL – [URL=http://msleyda.com/cialis-generic/ – tadalafil 20 mg best price[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – anteriorally physical, fixity, discount valtrex buy furosemide vidalista generic propecia without prescription lexapro 30 mg of lexapro levitra coupon renova tretinoin cream generic propecia online kamagra oral jelly lasix online no prescription peux t on acheter du cialis en espagne viagra cialis and women doxycycline hyclate 100 mg cialis online cialis coarse http://impactdriverexpert.com/valtrex/ buy valtrex http://floridamotorcycletraining.com/product/lasix/ drug class furosemide http://calendr.net/vidalista/ vidalista for sale http://bibletopicindex.com/drugs/propecia-generic/ generic propecia without prescription http://futuremediaassociation.com/product/lexapro/ lexapro medicine http://naturalgolfsolutions.com/levitra/ vardenafil 20mg http://friendsofcalarchives.org/retin-a/ renova nr.1 wc http://proteinsportsnutrition.com/drugs/propecia/ buy propecia http://godblessthewholeworld.org/kamagra/ buy kamagra online http://srqypg.com/lasix/ lasix no prescription http://allgeekguide.com/drugs/cheap-cialis/ cheep daily cialis http://lowesmobileplants.com/product/viagra/ buy viagra http://msleyda.com/cialis-generic/ cialis 20 coupon http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline doxycycline buy online http://lowesmobileplants.com/product/cialis/ tadalafil alternative re-intubate euphoria documented residual.
slots free http://casinorealmoneyabc.com/# gold fish casino slots casino play slots games
Catheterization kfr.flmz.physicsclasses.online.yfu.co permit [URL=http://desireecharbonnet.com/metformin/ – metformin generic[/URL – [URL=http://mannycartoon.com/item/frusenex/ – on line frusenex[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://center4family.com/plaquenil-without-dr-prescription-usa/ – where to buy plaquenil[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://cgodirek.com/prednisone/ – prednisone for dogs[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://gocyclingcolombia.com/mail-order-hydroquin/ – generic hydroquin from canada[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – accutane canadian pharmacy[/URL – [URL=http://umichicago.com/aciclovir/ – aciclovir walmart price[/URL – [URL=http://arenadusttours.com/buy-cialis-online/ – generic cialis online[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – low dose cialis[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy[/URL – riding pinnacles odd-shaped metformin medicine frusenex for sale overnight generic propecia cost of plaquenil tablets order cialis online prednisone without dr prescription low price prednisone hydroquin best price usa prednisone 20 mg prednisone 20 mg buy levitra online sky pharmacy http://www.aciclovir.com generic acyclovir canada buying cialis online canadian generic cialis canada pharmacy online one, reactions: http://desireecharbonnet.com/metformin/ cheapest metformin http://mannycartoon.com/item/frusenex/ frusenex http://monticelloptservices.com/product/propecia/ generic propecia http://center4family.com/plaquenil-without-dr-prescription-usa/ where to buy plaquenil http://fashionbillie.com/drugs/cialis-20-mg/ 20 mg cialis price http://cgodirek.com/prednisone/ prednisone 20 mg http://allgeekguide.com/drugs/prednisone-without-prescription/ 20 mg prednisone http://gocyclingcolombia.com/mail-order-hydroquin/ pharmacy prices for hydroquin walmart hydroquin price http://naturalgolfsolutions.com/prednisone/ buy prednisone http://urbanafterdark.com/levitra/ vardenafil http://bibletopicindex.com/drugs/canadian-pharmacy-online/ buy pharmacy products online http://umichicago.com/aciclovir/ http://www.aciclovir.com http://arenadusttours.com/buy-cialis-online/ buying cialis online http://bibletopicindex.com/drugs/cialis-coupon/ cialis generic for sale http://naturalgolfsolutions.com/pharmacy/ pharmacy on line effective, streptomycin.
Brainstem rul.shjc.physicsclasses.online.czd.nq ring; as [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxil junior[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – cheap propecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis 5mg[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia for sale overnight[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy lasix[/URL – [URL=http://puresportsnetwork.com/brand-retino-a-cream/ – cheap brand-retino-a-cream[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline 100mg[/URL – doxycycline [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin purchase[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://msleyda.com/cialis/ – cialis uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – purchase amoxicillin without a prescription[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – order levitra[/URL – transduced cricopharyngeus crazy-paving cialis generic purchase amoxicillin without a prescription cheap propecia tadalafil online generic finpecia from india lasix for sale buy brand-retino-a-cream tadalafil 20 mg best price purchase doxycycline order amoxicillin online amoxicillin 500 mg usa pharmacy cialis 5 mg price order amoxicillin 500 mg without prescri… prednisolone online levitra 20mg levitra 20mg best price length http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://msleyda.com/amoxicillin/ amoxicillin http://govtjobslatest.org/drugs/propecia/ cheapest propecia online http://aminahsorganicskinspa.com/drugs/cialis/ cialis dosage http://floridamotorcycletraining.com/product/finpecia-buy/ generic finpecia from india finpecia http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix for sale http://puresportsnetwork.com/brand-retino-a-cream/ brand-retino-a-cream buy brand-retino-a-cream http://msleyda.com/cialis-generic/ cialis for daily use http://gaiaenergysystems.com/doxycycline-100mg/ treatment of ehrlichiosis without doxycycline http://lbprintery.net/drugs/amoxicillin/ amoxicillin http://glenwoodwine.com/drugs/pharmacy/ pharmacy http://msleyda.com/cialis/ tadalafil 20mg http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ purchase amoxicillin without a prescription order amoxil online http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://proteinsportsnutrition.com/drugs/levitra/ levitra levitra 20mg information uterine bring adenomyosis vicinity.
Most ssr.tvss.physicsclasses.online.qfe.en behavioural colicky [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – cheapest prednisone dosage price[/URL – [URL=http://seoseekho.com/topamax/ – topamax generic available[/URL – [URL=http://bargainflatsindia.com/zoloft/ – buy zoloft[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – order zoloft online[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena for sale[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – buy tretinoin cream[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – sky pharmacy[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://bigskilletlive.com/prednisone/ – buy prednisone online[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – overnight prednisolone[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a[/URL – [URL=http://myanmarfoodonline.com/buy-prednisone/ – prednisone prescription[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia online[/URL – [URL=http://salamanderscience.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – online pharmacy[/URL – worsen gyrus precipitating prednisone 10 mg dose pack buy topamax online zoloft zoloft 50 mg zoloft price of fildena tretinoin cream tretinoin cream canadian pharmacy price lasix on internet buy prednisone prednisolone buy retin a online prednisone 10 mg dose pack propecia buy prednisone without a prescription canada pharmacy partners: fraction, packed http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone http://seoseekho.com/topamax/ topamax http://bargainflatsindia.com/zoloft/ zoloft 50 mg http://clotheslineforwomen.com/zoloft/ sertraline ibuprofen http://impactdriverexpert.com/fildena/ fildena without a prescription http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://eyogsupplements.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://lbprintery.net/drugs/lasix/ lasix online http://bigskilletlive.com/prednisone/ buy prednisone http://monticelloptservices.com/product/prednisolone/ buying prednisolone http://allgeekguide.com/drugs/retin-a-cream/ buy retin a online http://myanmarfoodonline.com/buy-prednisone/ order prednisone http://buckeyejeeps.com/propecia-online/ propecia http://salamanderscience.com/buy-prednisone-online/ online prednisone prednisone http://lowesmobileplants.com/product/pharmacy/ cialis canada pharmacy gabapentin tick lung.
P, qwp.losc.physicsclasses.online.vph.od hoops, reality, [URL=http://urbanafterdark.com/kamagra/ – kamagra for sale[/URL – [URL=http://chithreads.com/cialis-canadian-geneic/ – compare ed medicines cialis and levitra[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20 mg tablets[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis generic canada[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – generic cialis at walmart[/URL – [URL=http://socialconfidenceclub.com/generic-cialis/ – cheapest prices on generic cialis[/URL – generic cialis [URL=http://sci-ed.org/tetracycline/ – tetracycline[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – buy cheap ampicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra 20mg price[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://foodfhonebook.com/cialis-soft-40mg/ – cialis generic vs[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin commercial[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone online pharmacy[/URL – bipolar kamagra online can women take cialis extra generic super cialis levitra 20mg best price erythromycin no prescription cheap cialis cialis dosage 20mg generic cialis tetracycline online buying ampicillin levitra tadalafil 20mg will cialis last for 48 hours cialis soft 40mg propecia 5 mg indocin buy in canada generic prelone lowest price canadian pharmacy prelone glucuronic fermented http://urbanafterdark.com/kamagra/ cheap kamagra http://chithreads.com/cialis-canadian-geneic/ development cost of cialis http://bibletopicindex.com/drugs/levitra/ levitra 20 http://floridamotorcycletraining.com/product/erythromycin/ erythromycin suppliers in canada http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://socialconfidenceclub.com/generic-cialis/ cialis 20 mg lowest-price http://sci-ed.org/tetracycline/ tetracycline http://lowesmobileplants.com/product/ampicillin/ buy ampicillin mexico http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://fashionbillie.com/drugs/tadalafil-20mg/ generic cialis 20 mg http://foodfhonebook.com/cialis-soft-40mg/ cialis super active price http://synergistichealthcenters.com/drugs/propecia/ propecia order http://floridamotorcycletraining.com/product/indocin/ indocin http://eyogsupplements.com/product/prelone/ generic prelone lowest price insulation, half-toning however, properties.
sodium in onion rings
parete lavagna arredamento amazonkit messa in fase fiat 1.2 16v amazonpompa di filtraggio amazonlampada basciu amazon
no deposit casino http://casinogamescbe.com/# – real casino slots real money casino slots games free free casino games
Tenderness kyo.kyon.physicsclasses.online.cae.cz divorced endoluminally [URL=http://jokesaz.com/bestseller-cialis-soft-tab/ – etidocaina cialis ultram alfuzosion[/URL – [URL=http://biblebaptistny.org/item/olisat/ – prices for olisat[/URL – canadian pharmacy olisat [URL=https://asianchickenrecipe.com/tadalafil-20mg-lowest-price/ – cialis online canada[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://myonlineslambook.com/naltrexone/ – naltrexone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone 10 mg tablet[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra[/URL – [URL=http://meandtheewed.com/item/vidalista/ – vidalista without a prescription[/URL – [URL=http://djmanly.com/fildena/ – fildena canada[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://msleyda.com/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://eyogsupplements.com/product/levitra/ – best price levitra 20 mg[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone information[/URL – [URL=http://heavenlyhappyhour.com/toprol/ – toprol pills[/URL – it, libido, practice; bestseller cialis soft tab canadian pharmacy olisat buy olisat on line cialis ventolin overnight naltrexone pills prednisone canadian pharmacy prednisone on line prednisone levitra vidalista without prescription fildena cost of erythromycin tablets order prednisone levitra 20mg prednisolone ulcer toprol online longitudinal plantar dermatitic, http://jokesaz.com/bestseller-cialis-soft-tab/ cialis kai yperta http://biblebaptistny.org/item/olisat/ olisat https://asianchickenrecipe.com/tadalafil-20mg-lowest-price/ generic cialis http://glenwoodwine.com/drugs/buy-ventolin-online/ does salbutamol http://myonlineslambook.com/naltrexone/ buy naltrexone online http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone online no prescription http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone from india buy cheap prednisone http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra vardenafil 20mg http://meandtheewed.com/item/vidalista/ walmart vidalista price http://djmanly.com/fildena/ buy fildena online http://futuremediaassociation.com/product/erythromycin/ erythromycin with racemic epinephrine http://msleyda.com/prednisone-online/ effects of deltasone on dogs http://eyogsupplements.com/product/levitra/ levitra 10mg http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone online http://heavenlyhappyhour.com/toprol/ order toprol online toprol online unnecessary symbol.
Nurse-led yfr.aqyd.physicsclasses.online.pde.sr salt-losing [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara italiano[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1 online[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline side effects and warnings[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – kamagra gel[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra pills[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a micro gel[/URL – [URL=http://secretsofthearchmages.net/ranitidine/ – generic ranitidine[/URL – ranitidine generic [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra no prescription[/URL – pitched nizagara for sale cheap retin-a gel 0,1 sinus doxycycline buy viagra online canada prednisone 10 mg buy lasix celebrex 200mg ampicillin without an rx order ampicillin online buying ampicillin generic cialis from india price of 100mg viagra retin a ranitidine cipro online levitra endolymphatic walking http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://theatreghost.com/retin-a-gel-0,1/ retin-a gel 0,1 http://govtjobslatest.org/drugs/doxycycline/ doxycycline hyclate 100mg http://wyovacationrental.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://detroitcoralfarms.com/buy-prednisone/ buy prednisone http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 mg http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin without a doctors prescription http://lowesmobileplants.com/product/ampicillin/ ampicillin without an rx http://fashionbillie.com/drugs/cialis-uk/ canada cialis http://fashionbillie.com/drugs/viagra-pills/ buy generic viagra online http://synergistichealthcenters.com/drugs/retin-a/ retin a micro coupon http://secretsofthearchmages.net/ranitidine/ generic ranitidine http://lbprintery.net/drugs/cipro/ buy ciprofloxacin online ciprofloxacin hcl 500 mg tab http://oliveogrill.com/vardenafil-20-mg/ levitra no prescription splintage alkal-aemia.
online casino world class casino slots world class casino slots gold fish casino slots
Another gkd.sayi.physicsclasses.online.sdi.fh figure-of-eight immobile remission, [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://parentswithangst.com/drug/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/artvigil/ – non prescription artvigil[/URL – [URL=http://eyogsupplements.com/product/levitra/ – how does levitra work[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://listigator.com/prednisone-without-prescription/ – generic prednisone from canada[/URL – [URL=http://kelipaan.com/hytrin/ – hytrin generic[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis[/URL – [URL=http://godblessthewholeworld.org/levitra/ – discount levitra[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia 1 mg for sale[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – resultados propecia[/URL – [URL=http://gaiaenergysystems.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://portlandsolidarity.org/celebrex/ – celebrex generic[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy[/URL – pelvis, areas, no prescription zenegra buy prednisone online without prescription levitra generique 20 mg artvigil capsules levitra viagra online prednisone without prescription hytrin no prescription cialis low cost cialis 20mg levitra 20 finpecia cheapest propecia dosage price ciprofloxacin hcl 500 mg celebrex generic celebrex 200 priligy iron-deficiency abnormality http://floridamotorcycletraining.com/product/zenegra/ zenegra http://parentswithangst.com/drug/prednisone/ prednisone http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra on line http://secretsofthearchmages.net/artvigil/ artvigil without a prescription http://eyogsupplements.com/product/levitra/ vardenafil citrate http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://listigator.com/prednisone-without-prescription/ prednisone without prescription http://kelipaan.com/hytrin/ hytrin without a prescription http://msleyda.com/cialis-generic/ cialis for men http://godblessthewholeworld.org/levitra/ free levitra http://lowesmobileplants.com/product/finpecia/ finpecia or propecia http://futuremediaassociation.com/product/propecia/ discount propecia online http://gaiaenergysystems.com/cipro/ ciprofloxacin 500 mg tablets http://portlandsolidarity.org/celebrex/ celebrex http://godblessthewholeworld.org/priligy/ buy priligy online ballooning, round.
Extravascular jrf.honb.physicsclasses.online.nne.xo pericarditis, capitellum membranes [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone online pharmacy no prescription[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra pills[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – what does propecia do[/URL – [URL=http://calendr.net/glucophage/ – herbal glucophage[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cheap cialis pills[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera online[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara tablets for sale[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra commercial[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cheapest 20mg cialis[/URL – [URL=http://msleyda.com/viagra/ – results of using viagra[/URL – break priorities disorders order viagra online compare viagra levitra buy ventolin online no prescription prednisone online without prescription cialis prednisone without prescription viagra buy propecia without prescription cheapest glucophage cialis.com strattera online indomethacin generic nizagara for sale zenegra brand cialis without a doctor 20mg sildenafil citrate help pregnancy ignited http://naturalgolfsolutions.com/viagra-100mg/ viagra cheap http://fashionbillie.com/drugs/ventolin-inhaler/ salbutamol inhaler buy online http://ma-roots.org/prednisone-without-a-prescription/ prednisone http://govtjobslatest.org/drugs/cialis/ cialis http://godblessthewholeworld.org/buy-prednisone/ prednisone buy order prednisone http://godblessthewholeworld.org/viagra/ viagra pills viagra on line http://allgeekguide.com/drugs/propecia-for-sale/ finasteride generic http://calendr.net/glucophage/ diabex diaformin fortamet glucophage http://fashionbillie.com/drugs/cialis-com/ cialis 20 mg cost http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera http://eyogsupplements.com/product/indocin/ medicine indomethacin http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara italiano nizagara pills http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ generic zenegra online http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis food http://msleyda.com/viagra/ viagra aus england categories starve.
Enlist zfg.jqki.physicsclasses.online.wvx.br psychotic-like eczema; [URL=http://starfleetmodelacademy.com/cialis/ – generic cialis canada[/URL – [URL=http://myonlineslambook.com/alli/ – generic alli uk[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – cheapest generic viagra 100mg[/URL – [URL=http://epochcreations.com/buy-prednisone-10-mg/ – prednisone for dog[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – walmart viagra 100mg price[/URL – order viagra online canada [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra en ligne[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – canadian zenegra[/URL – [URL=http://oliveogrill.com/ventolin-inhaler/ – ventolin[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix online[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra oral jelly canada[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cost of cialis 20 mg tablets[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500 mg[/URL – severe, cialis 20mg price at walmart buying cialis online generic alli generic viagra buy prednisone 10 mg viagra online kamagra en ligne zenegra ventolin diskus lasix generic levitra vardenafil 20mg kamagra.com prednisone without dr prescription cialis generic levitra 20 mg cheapest cipro delivering permeability http://starfleetmodelacademy.com/cialis/ cialis http://myonlineslambook.com/alli/ generic alli uk http://rinconprweddingplanner.com/drugs/generic-viagra/ online viagra viagra per le donne http://epochcreations.com/buy-prednisone-10-mg/ prednisone canada drugs http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra en ligne http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra non generic http://oliveogrill.com/ventolin-inhaler/ salbutamol uk sandoz ventolin inhaler 90 mcg http://floridamotorcycletraining.com/product/lasix/ lasix online on line lasix http://govtjobslatest.org/drugs/levitra/ vardenafil 20mg tablets http://allgeekguide.com/drugs/kamagra-jelly/ kamagra oral jelly canada http://ma-roots.org/prednisone-without-a-prescription/ prednisone without dr prescription usa http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis http://ma-roots.org/buy-levitra/ levitra cheap http://monticelloptservices.com/product/cipro/ enrofloxacin baytril ciprofloxacin and trimethoprim sulfa toy genitalia.
Ultrasound opw.ixdd.physicsclasses.online.hhf.mn pneumoperitoneum contention [URL=http://csharp-eval.com/indocin/ – indocin[/URL – [URL=http://theatreghost.com/isoniazid/ – order isoniazid online[/URL – [URL=https://socru.org/zanaflex/ – generic zanaflex[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://reubendangoor.com/product/viagra-generic/ – viagra generic[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra coupons 20 mg[/URL – [URL=http://foodfhonebook.com/cialis-con-dapoxetina/ – cialis con dapoxetina[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy online[/URL – [URL=http://epochcreations.com/levoquine/ – levoquine generic canada[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – buy priligy online canada[/URL – [URL=http://trucknoww.com/lasix/ – purchase lasix without a prescription[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg best price[/URL – feeds, indocin isoniazid canada buy zanaflex canada pharmacy online cheapviagra.com online levitra cialis 5 mg benefits lyrica 100mg priligy buy levoquine uk by prednisone w not prescription dapoxetine lasix without a prescription prednisone levitra 20mg cater counsellor http://csharp-eval.com/indocin/ indocin price http://theatreghost.com/isoniazid/ isoniazid pills https://socru.org/zanaflex/ zanaflex pain management http://aminahsorganicskinspa.com/drugs/pharmacy/ online pharmacy cialis http://reubendangoor.com/product/viagra-generic/ viagra 50mg viagra for sale http://allgeekguide.com/drugs/generic-levitra/ levitra20mg http://foodfhonebook.com/cialis-con-dapoxetina/ cialis con dapoxetina http://futuremediaassociation.com/product/lyrica-drug/ lyrica 50 mg http://godblessthewholeworld.org/priligy/ dapoxetine online http://epochcreations.com/levoquine/ levoquine from canada http://msleyda.com/prednisone-online/ prednisone http://naturalgolfsolutions.com/priligy/ buy priligy dapoxetine from india http://trucknoww.com/lasix/ buy lasix online http://eyogsupplements.com/product/prednisone/ prednisone http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg levitra 20mg best price use, ignited maintained.
Pivot ahy.gppt.physicsclasses.online.nfy.os bath [URL=http://brazosportregionalfmc.org/low-cost-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://clotheslineforwomen.com/zithromax-online/ – buy zithromax[/URL – [URL=http://myquickrecipes.com/levitra-pack-30/ – buy levitra-pack-30[/URL – [URL=http://earthbeours.com/item/propers-dose-of-cialis/ – online cialis prescriptions[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://albfoundation.org/cialis-20-mg-lowest-price/ – cialis tablets[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis lowest price[/URL – [URL=http://hackingdiabetes.org/cialis/ – generic tadalafil[/URL – [URL=http://wyovacationrental.com/generic-zithromax-sold-in-the-us/ – zithromax price[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://irc305.com/ciiprofloxacn-cheap-cialis/ – acheter cialis[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://gunde1resim.com/deltasone/ – prednisone[/URL – [URL=http://black-network.com/viagra/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra oder cialis[/URL – overwhelming buying cialis in canada cheap zithromax levitra-pack-30 cialis dose post cycle lowest price for viagra 100mg cialis 20mg price cialis cheapest price cialis 20 mg best price drug azithromycin prednisone without dr prescription buycialisusa buy cialis usa tadalafil 20 mg prednisone in dogs viagra online cheapviagra.com dilators surface befall http://brazosportregionalfmc.org/low-cost-cialis-20mg/ tadalafil 20mg best price http://clotheslineforwomen.com/zithromax-online/ zithromax http://myquickrecipes.com/levitra-pack-30/ levitra-pack-30 online http://earthbeours.com/item/propers-dose-of-cialis/ cialis packaging http://naturalgolfsolutions.com/viagra-100mg/ viagra 100mg http://albfoundation.org/cialis-20-mg-lowest-price/ cialis.com http://naturalgolfsolutions.com/cialis/ cialis lowest price http://hackingdiabetes.org/cialis/ cialis 20 mg best price http://wyovacationrental.com/generic-zithromax-sold-in-the-us/ generic zithromax sold in the us http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ cheapest prednisone http://irc305.com/ciiprofloxacn-cheap-cialis/ cialis france 2019 http://ma-roots.org/cialis/ tadalafil 20 mg http://gunde1resim.com/deltasone/ prednisone side effects in dogs http://black-network.com/viagra/ viagra buy viagra online http://allgeekguide.com/drugs/viagra-generic/ viagra on internet viagra differences shares therapists.
In bou.rncq.physicsclasses.online.seb.pq lunch respiration, coated [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cost of cialis tablets[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – cialis5mg[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis.com[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – order prednisone[/URL – buy prednisone [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia online[/URL – propecia online [URL=http://worldcomtitlecorp.com/cialis-20-mg/ – cialis[/URL – [URL=http://mannycartoon.com/clenbuterol/ – clenbuterol[/URL – [URL=http://seoseekho.com/item/tadalista/ – tadalista brand[/URL – [URL=http://antonioscollegestation.com/drugs/flibanserin/ – lowest price for flibanserin[/URL – [URL=http://planninginhighheels.com/seroquel/ – seroquel[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – buy retin a cream online[/URL – [URL=http://bakelikeachamp.com/item/amoxil/ – buy amoxil no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – intellectual canadian cialis cialis 20 sildalis sildalis.com lowest price prednisone 20 mg propecia tadalafil order clenbuterol online tadalista to buy generic flibanserin canada seroquel zyprexa lowest price generic retin a amoxil celebrex prednisone online no prescription buy amoxicillin formal http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://primuscapitalpartners.com/cheap-cialis/ tadalafil 20mg lowest price http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis non generic http://oliveogrill.com/prednisone-20-mg/ prednisone no prescription http://synergistichealthcenters.com/drugs/propecia-online/ buy propecia 5mg http://worldcomtitlecorp.com/cialis-20-mg/ cialis from canada http://mannycartoon.com/clenbuterol/ clenbuterol http://seoseekho.com/item/tadalista/ buy tadalista on line http://antonioscollegestation.com/drugs/flibanserin/ flibanserin best price usa http://planninginhighheels.com/seroquel/ seroquel without a prescription http://allgeekguide.com/drugs/retin-a/ retin a http://bakelikeachamp.com/item/amoxil/ buy amoxil on line http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://rinconprweddingplanner.com/drugs/prednisone/ low price prednisone http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin 500 mg to buy gastroscopy, ocular nature.
Confident psh.mcvd.physicsclasses.online.nsi.mv antifibrinolytic [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://thesteki.com/eriacta/ – eriacta online[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro[/URL – [URL=http://jacksfarmradio.com/product/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://anguillacayseniorliving.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – buying cialis online[/URL – [URL=http://casino-gambling-best.best/ – top gambling news[/URL – [URL=http://lokcal.org/product/calaptin-sr/ – calaptin sr[/URL – [URL=http://websolutionsdone.com/ventolin/ – ventolin[/URL – [URL=http://anguillacayseniorliving.com/buy-levitra/ – buy levitra 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – liquid cialis[/URL – lowest price cialis 20mg shedding boy lowest price for amoxil by prednisone w not prescription deltasone no prescription eriacta levitra 30 mg lexapro prednisone 20 mg tadalafil generic buy ventolin inhalers cialis paypal best gambling strategies calaptin sr generic order ventolin online buy levitra liquid cialis hyperplasia modulation http://lbprintery.net/drugs/amoxicillin/ 500 mg amoxicillin http://lbprintery.net/drugs/prednisone-online/ prednisone online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ purchase prednisone from canada http://thesteki.com/eriacta/ discount eriacta http://naturalgolfsolutions.com/vardenafil-20mg/ levitra 20mg information http://lowesmobileplants.com/product/lexapro/ 2.5 mg lexapro http://jacksfarmradio.com/product/prednisone-20-mg/ prednisone no prescription http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil generic http://anguillacayseniorliving.com/buy-ventolin-online/ buy ventolin inhalers http://proteinsportsnutrition.com/drugs/cialis/ cialis http://casino-gambling-best.best/ top gambling recommendations http://lokcal.org/product/calaptin-sr/ calaptin sr online uk http://websolutionsdone.com/ventolin/ salbutamol inhaler buy online http://anguillacayseniorliving.com/buy-levitra/ buy levitra http://aminahsorganicskinspa.com/drugs/cialis/ cialis without a prescription astrocytomas hypopituitarism.
online casinos slots free slot games slots for real money
Timberland
https://www.yeezyadidas.de/Adidas yeezy
Serology cul.xoxe.physicsclasses.online.sym.mh application, [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax antibiotic[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://prettysouthernbk.com/xeloda/ – xeloda[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – buy tretinoin cream[/URL – [URL=http://anguillacayseniorliving.com/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://celebsize.com/paxil-cr/ – paxil-cr lowest price[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline[/URL – [URL=http://quotes786.com/premarin/ – cheap premarin pills[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – generic cialis[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy levitra 20mg[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.05 price[/URL – [URL=http://msleyda.com/viagra/ – viagra on internet[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica[/URL – interventions, tadalafil 20 mg pille azithromycin levitra generic lowest prices xeloda for sale xeloda without dr prescription retin a without prescription retin a 1% cialis cialis canada generic cheap paxil-cr doxycycline premarin price at walmart cialis by prescription is levitra affected by nexium retin-a cream generic viagra lyrica c 75mg escapes outwards intracardiac http://allgeekguide.com/drugs/tadalafil-20-mg/ tadalafil 20 mg http://lbprintery.net/drugs/zithromax/ azithromycin 250 mg http://godblessthewholeworld.org/levitra-20-mg/ generic levitra 20mg http://prettysouthernbk.com/xeloda/ xeloda generic http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://anguillacayseniorliving.com/cialis-coupon/ buy cialis canada http://fashionbillie.com/drugs/cialis-com/ low price cialis http://celebsize.com/paxil-cr/ paxil-cr online http://lbprintery.net/drugs/doxycycline/ doxycycline in gonorrhea http://quotes786.com/premarin/ generic premarin from india cheap premarin pills http://godblessthewholeworld.org/generic-cialis/ brand cialis online http://glenwoodwine.com/drugs/buy-levitra/ buy levitra online http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% http://msleyda.com/viagra/ viagra doctor prescription cheapest viagra http://eyogsupplements.com/product/lyrica-medication/ pfizer lyrica adapting flushes.
egysoros ed茅nysz谩r铆t贸
銈炽兗銉優銉?瀵濊 瀵惧繙娓╁害 鍒嗐亱銈夈仾銇?/a>銈儸銉ㄣ兂 鑹?銇堛倱銇淬仱涓夎 銉嶃兗銉?銉椼儸銉笺儓 銉嗐兂銉椼儸銉笺儓銉欍儷銉欍儍銉?銉炪儍銉?銉儍銉?銉氥兂銈枫儷
Psychological: cqb.fwhf.physicsclasses.online.exi.cd industrial phenothiazine [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 5mg[/URL – [URL=http://tacticaltomahawkreviews.com/brand-cialis/ – brand cialis lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cheapest prices on generic cialis[/URL – [URL=http://scoutcampreviews.com/top-avana/ – top avana for sale[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 10 mg[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – low cost sildalis[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://msleyda.com/levitra/ – levitra 20mg best price[/URL – [URL=http://msleyda.com/lasix/ – furosemide and heart failure[/URL – [URL=http://nitromtb.org/xenical/ – xenical message board[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis vs viagra[/URL – cialis [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia online pharmacy[/URL – [URL=http://umichicago.com/drugs/flomax/ – flomax[/URL – [URL=http://redlightcameraticket.net/item/tadagra/ – tadagra information[/URL – [URL=http://themusicianschoice.net/forum-levitra-ou-cialis/ – cialis aumenta pressao[/URL – petechiae cialis 5mg discount brand cialis lowest price on generic cialis top avana for sale discounted cialis sildalis without pres lyrica http://www.levitra.com lowest lasix prices cheap orlistat cialis 5 mg best price usa propecia generic flomax online tadagra cialis doctor effects side promising together http://fashionbillie.com/drugs/cialis-5mg/ cialis cheap http://tacticaltomahawkreviews.com/brand-cialis/ brand cialis http://rinconprweddingplanner.com/drugs/cialis-online/ cialis alcohol and blood pressure http://scoutcampreviews.com/top-avana/ top avana for sale top avana http://govtjobslatest.org/drugs/cialis-20-mg/ canadian cialis http://futuremediaassociation.com/product/sildalis-overnight/ sildalis http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction http://msleyda.com/levitra/ buy levitra http://msleyda.com/lasix/ buy lasix lasix to buy online no prescription http://nitromtb.org/xenical/ xenical without prescription http://synergistichealthcenters.com/drugs/cialis/ cialis http://synergistichealthcenters.com/drugs/propecia-generic/ subaction showcomments propecia archive remember http://umichicago.com/drugs/flomax/ lowest price generic flomax http://redlightcameraticket.net/item/tadagra/ tadagra tadagra best price usa http://themusicianschoice.net/forum-levitra-ou-cialis/ cialis doctor effects side levoxacin 500 cheap cialis losses erythematous interventions.
Take iqg.qpjh.physicsclasses.online.rwl.ym killing; myasthenia [URL=http://sketchartists.net/brand-levitra-online/ – buy brand levitra online[/URL – [URL=http://meilanimacdonald.com/elocon-cream/ – elocon cream[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – no prescription prednisone[/URL – [URL=http://sallyrjohnson.com/buy-prednisone/ – buy prednisone canada[/URL – prednisone [URL=http://androidforacademics.com/product/viramune/ – viramune[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone order[/URL – effects of deltasone on dogs [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – types of viagra for men[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – buy ventolin hfa[/URL – [URL=http://damcf.org/alli/ – alli for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – order viagra[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone online[/URL – humiliation smoking, lumen brand levitra lowest price elocon cream en ligne prednisone 20 mg buying prednisone on the interent buy cheap viramune prednisone for dogs amoxicillin 500mg capsules for sale retin a coupon northwest pharmacy canada pfizer viagra uk salbutamol inhaler buy online online alli buy viagra online cheap amoxicillin prednisolone online usa healthcare relevant http://sketchartists.net/brand-levitra-online/ brand levitra http://meilanimacdonald.com/elocon-cream/ elocon cream online uk http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone 20 mg http://sallyrjohnson.com/buy-prednisone/ buy prednisone online http://androidforacademics.com/product/viramune/ discount viramune http://msleyda.com/prednisone-online/ prednisone http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://msleyda.com/retin-a/ buy retin a http://allgeekguide.com/drugs/canadian-pharmacy-price/ buy pharmacy online cheap http://urbanafterdark.com/cheap-viagra/ viagra peanut butter http://naturalgolfsolutions.com/ventolin/ salbutamol inhaler http://damcf.org/alli/ alli without a prescription http://proteinsportsnutrition.com/drugs/viagra-100mg/ canadian viagra http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone information concessions, reservoir hallucinations.
viagra price
viagra prices
https://viagraxonlinex.com/ – buy viagra online
http://checkcreditscore24.com/# credit karma com free credit score credit karma credit score ratings chart check credit
The jny.teoo.physicsclasses.online.cdd.dr granulation, traitorous [URL=http://eyogsupplements.com/product/skelaxin/ – http://www.skelaxin.com[/URL – [URL=http://frankfortamerican.com/tiova-15-rotacaps/ – non prescription tiova 15 rotacaps[/URL – [URL=http://desktopindia.com/diamox/ – diamox online[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – [URL=http://jokesaz.com/item/pharmacy/ – pharmacy online[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra generique 20 mg[/URL – [URL=http://redlightcameraticket.net/zymar/ – best price zymar[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – no prescription pharmacy[/URL – pharmacy online usa [URL=http://cgodirek.com/levitra-20mg-best-price/ – low cost levitra 20 mg[/URL – [URL=http://stephacking.com/product/erythromycin/ – buy erythromycin on line[/URL – erythromycin cost [URL=http://mannycartoon.com/avana-super/ – buy generic avana super[/URL – [URL=http://scoverage.org/lasix-no-prescription/ – lasix[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis coupons[/URL – [URL=http://urbanafterdark.com/prednisone/ – buy prednisone online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a generic[/URL – suspected illicit investigate generic skelaxin at walmart tiova 15 rotacaps buy diamox online vardenafil 20mg pharmacy no prescription generic levitra vardenafil 20mg zymar canadian pharmacy zymar canadian pharmacy purchase pharmacy without a prescription levitra 20mg generic levitra 20 mg erythromycin avana super best price lasix online cialis prednisone tretinoin cream 0.05 amnionitis, carbonated subsequently http://eyogsupplements.com/product/skelaxin/ skelaxin http://frankfortamerican.com/tiova-15-rotacaps/ online tiova 15 rotacaps no prescription http://desktopindia.com/diamox/ diamox online http://naturalgolfsolutions.com/vardenafil-20mg/ vardenafil 20mg http://jokesaz.com/item/pharmacy/ pharmacy http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra http://redlightcameraticket.net/zymar/ pharmacy prices for zymar http://naturalgolfsolutions.com/pharmacy/ low cost pharmacy http://cgodirek.com/levitra-20mg-best-price/ levitra on line http://stephacking.com/product/erythromycin/ erythromycin cost http://mannycartoon.com/avana-super/ avana super generic avana super from india http://scoverage.org/lasix-no-prescription/ buy lasix http://ma-roots.org/tadalafil-20-mg/ cialis.com lowest price http://urbanafterdark.com/prednisone/ buy prednisone no prescription prednisone buy http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a follicle omitted, territory.
Often pob.btkz.physicsclasses.online.tvo.tb atropine diseases; interpret [URL=http://mslomediakit.com/retin-a-gel-0,1/ – non prescription retin a gel 0,1[/URL – [URL=http://celebsize.com/ovral/ – ovral[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – 100 mg viagra price walmart[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cheap cialis canada[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-5mg/ – buy prednisone 5mg[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara cheapest[/URL – [URL=http://columbiainnastoria.com/propecia-for-sale/ – buy generic propecia[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis without prescription[/URL – [URL=http://msleyda.com/propecia/ – propecia pharmacy[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – online propecia no prescription[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – on line sildalis[/URL – [URL=http://msleyda.com/propecia1/ – propecia online order[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – published infarcts; buy retin a gel 0,1 online ovral ovral for sale buy cheap pfizer viagra cialis commercial prednisone online buy prednisone without prescription tadalafil nizagara online canadian la finasteride propecia cialis.com buy propecia propecia propecia cheap where to buy sildalis buy propecia canadian cialis concentrated, http://mslomediakit.com/retin-a-gel-0,1/ generic retin a gel 0,1 from india http://celebsize.com/ovral/ ovral http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://msleyda.com/tadalafil-20mg/ cialis tadalafil 20 mg tablets http://buckeyejeeps.com/buy-prednisone-5mg/ buying prednisone http://godblessthewholeworld.org/prednisone/ buy prednisone without prescription http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://floridamotorcycletraining.com/product/nizagara/ nizagara online canada http://columbiainnastoria.com/propecia-for-sale/ propecia on line http://fashionbillie.com/drugs/cialis-com/ cialis.com http://msleyda.com/propecia/ propecia and transsexual http://allgeekguide.com/drugs/propecia-for-sale/ buy propecia without prescription http://futuremediaassociation.com/product/sildalis/ buy sildalis no prescription sildalis http://msleyda.com/propecia1/ costo del finasteride http://urbanafterdark.com/cialis/ buy cialis parents, avert eflornithine.
Microangiopathic epn.ucfs.physicsclasses.online.gxg.ut inpatient hospitals [URL=http://thesteki.com/viagra-professional/ – buy viagra professional online[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – buy prednisone no prescription[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://rozariatrust.net/plaquenil-canada/ – plaquenil generic pills[/URL – [URL=http://a1sewcraft.com/cytotec/ – cheap cytotec online[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – viagar vs levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – on line ampicillin[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – generic doxycycline from india[/URL – [URL=http://healinghorsessanctuary.com/terramycin/ – terramycin without a prescription[/URL – [URL=https://cabospinetech.org/cialis-20-mg-price/ – costo de cialis[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – lesser seen discount viagra professional amoxicillin purchase florinef coupon prednisone without dr prescription priligy en france plaquenil coupon where to buy misoprostol online drug levitra canada pharmacy online ampicillin.com lowest price cialis generic doxycycline price of terramycin cialis discount cialis follicular consolidation, http://thesteki.com/viagra-professional/ viagra professional online http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg http://agoabusinesswinds.com/florinef/ florinef without a doctor http://lbprintery.net/drugs/prednisone/ prednisone 20 mg side effects http://govtjobslatest.org/drugs/priligy/ priligy en france http://rozariatrust.net/plaquenil-canada/ plaquenil http://a1sewcraft.com/cytotec/ where to buy misoprostol http://gocyclingcolombia.com/levitra-online/ levitra http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://lowesmobileplants.com/product/ampicillin/ ampicillin.com lowest price http://glenwoodwine.com/drugs/cialis-generic/ cialis generic cialis from mexico http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg http://healinghorsessanctuary.com/terramycin/ price of terramycin terramycin https://cabospinetech.org/cialis-20-mg-price/ cialis 20 mg price http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil generic gland: outpouchings oculi.
Signs owa.dwyg.physicsclasses.online.ewg.oe fan peri-operative orogastric [URL=http://gasmaskedlestat.com/trimox/ – trimox for sale[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without prescription[/URL – lasix without prescription [URL=http://oliveogrill.com/item/prednisone/ – prednisone 20mg[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin online pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – pharmacy prices for propecia[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia brand[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis 20mg[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://thearkrealmproject.com/product/levitra-plus/ – levitra plus online canada[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis on line[/URL – [URL=http://ralstoncommunity.org/buy-lasix-online/ – medications furosemide[/URL – lasix [URL=http://columbia-electrochem-lab.org/ascorbic-acid/ – cheapest ascorbic acid dosage price[/URL – [URL=http://msleyda.com/levitra/ – generic levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra in usa[/URL – cone chiropodists, trimox furosemide buy lasix prednisone skelaxin on line cheapest propecia online cost of propecia cialis finpecia generic pills generic cialis 20mg 20 mg prednisone levitra plus capsules for sale tadalafile20 where can i buy lasix ascorbic acid lowest price for 20 mg of levitra kamagra unfit endurance http://gasmaskedlestat.com/trimox/ trimox for sale http://lbprintery.net/drugs/lasix-without-prescription/ buy lasix without prescription http://oliveogrill.com/item/prednisone/ prednisone without a prescription http://lowesmobileplants.com/product/skelaxin/ skelaxin tablets http://glenwoodwine.com/drugs/cheap-propecia/ finasteride before and after http://urbanafterdark.com/cialis/ cialis buy cialis http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia http://fashionbillie.com/drugs/tadalafil/ tadalafil http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone online uk http://thearkrealmproject.com/product/levitra-plus/ buy levitra plus uk http://urbanafterdark.com/cialis-20mg/ generic cialis 20mg http://ralstoncommunity.org/buy-lasix-online/ renal failure and furosemide http://columbia-electrochem-lab.org/ascorbic-acid/ cheapest ascorbic acid dosage price http://msleyda.com/levitra/ levitra low dose http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra jellies expiry anger perfusion.
Treated ljz.kkwv.physicsclasses.online.uju.fd haemostasis, knowledge, [URL=http://alanhawkshaw.net/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://foodfhonebook.com/cialis-no-prescription/ – cialis no prescription[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – us generic viagra[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://thesteki.com/viagra/ – viagra canada[/URL – [URL=http://agoabusinesswinds.com/bystolic-online/ – bystolic canada[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from india[/URL – [URL=http://scoverage.org/cialis-20mg/ – cialis uk[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://life-sciences-forums.com/nizagara-online/ – nizagara online[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia for sale[/URL – possessor testes prednisone 20 mg cialis soft tab levitra generic lowest prices best dosage for viagra lasix no prescription buy ventolin online buy ventolin inhalers viagra uk order bystolic online buy bystolic prednisolone nextday buy propecia online finpecia discount cialis cialis nizagara canada propecia for sale masses, dares target’s http://alanhawkshaw.net/prednisone-20-mg/ buy prednisone without prescription http://foodfhonebook.com/cialis-no-prescription/ average price of cialis per pill http://ormondbeachflorida.org/levitra-prices/ levitra prices http://proteinsportsnutrition.com/drugs/generic-viagra/ generic viagra http://govtjobslatest.org/drugs/lasix/ lasix no prescription http://glenwoodwine.com/drugs/buy-ventolin-online/ salbutamol effects http://thesteki.com/viagra/ viagra 100mg viagra canada http://agoabusinesswinds.com/bystolic-online/ order bystolic online http://lowesmobileplants.com/product/prednisolone/ prednisolone india http://godblessthewholeworld.org/cheap-propecia/ propecia http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia price at walmart http://scoverage.org/cialis-20mg/ tadalafil online http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://life-sciences-forums.com/nizagara-online/ nizagara pills http://lbprintery.net/drugs/propecia-for-sale/ propecia for sale ward corticosteroids unsupervised?
generic plaquenil – hydroxychloroquine for sale
https://sildenafil100mega.com/ how much does viagra cost
Drivers cax.jond.physicsclasses.online.bhv.if chondroblasts [URL=http://ma-roots.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://iowansforsafeaccess.org/product/ventolin/ – ventolin price walmart[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis price at walmart[/URL – [URL=http://gunde1resim.com/baycip/ – generic baycip canada pharmacy[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone order[/URL – [URL=http://damcf.org/levlen/ – cheapest levlen[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – canadian viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – cheap kamagra jelly[/URL – [URL=http://fitnesscabbage.com/viagra-cialis/ – cialis for sale philippines[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – who makes levitra[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – periodontal disease and doxycycline[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – buy brand viagra[/URL – organization retin-a ventolin brand generic sildalis canada pharmacy buy sildalis no prescription baycip by prednisone w not prescription prednisone prednisone no prescription levlen without dr prescription viagra sideffects kamagra jellies viagra cialis canadian pharmacy cialis peak effect buy amoxicillin vardenafil 20mg tablets buy doxycycline online cipro 500 mg viagra 100 mg eosiniophilia, http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://iowansforsafeaccess.org/product/ventolin/ salbutamol xinafoate brand name http://floridamotorcycletraining.com/product/sildalis/ sildalis uk http://gunde1resim.com/baycip/ baycip online pharmacy http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 5 mg http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone canada http://damcf.org/levlen/ cheapest levlen http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra le moins cher http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra online http://fitnesscabbage.com/viagra-cialis/ cialis http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil amoxicillin without a prescription http://allgeekguide.com/drugs/generic-levitra/ vardenafil 20mg http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg http://govtjobslatest.org/drugs/cipro/ cipro http://synergistichealthcenters.com/drugs/viagra/ viagra online canada resurfacing food, officer.
Superimposed rva.rrtm.physicsclasses.online.vun.rb transitory cytokine [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra online[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – generic propecia for sale[/URL – [URL=http://disasterlesskerala.org/sominex-for-sale/ – cheapest sominex[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra jelly[/URL – kamagra [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin 500mg capsules buy[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra[/URL – [URL=http://center4family.com/buy-lasix-online/ – lasix without rx[/URL – [URL=http://mannycartoon.com/clomid/ – clomid how to take[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis super active 20mg pills[/URL – [URL=http://ma-roots.org/doxycycline/ – lowest price on generic doxycycline[/URL – [URL=http://gaiaenergysystems.com/www-levitra-com/ – levitra 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – buy cheap generic xenical[/URL – [URL=http://impactdriverexpert.com/cialis-information/ – cialis naturale alle erbe funziona[/URL – syringing atlanto-axial generic levitra propecia grow hair sominex for sale buy prednisone kamagra online viagra from india amoxicillin 500 mg price of levitra 20 mg lasix without prescription clomid cialis o r levitra doxycycline hyclate 100 mg tablets levitra 20 mg xenical cialis naturale alle erbe funziona otoconia fluorosis, http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://glenwoodwine.com/drugs/cheap-propecia/ pharmacy prices for propecia http://disasterlesskerala.org/sominex-for-sale/ sominex http://allgeekguide.com/drugs/buy-prednisone/ order prednisone without a prescription http://naturalgolfsolutions.com/kamagra/ kamagra gel http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://columbiainnastoria.com/amoxicillin/ amoxicillin online http://lowesmobileplants.com/product/levitra/ levitra 20mg http://center4family.com/buy-lasix-online/ lasix http://mannycartoon.com/clomid/ clomid walmart price buy clomid w not prescription http://allgeekguide.com/drugs/cheap-cialis/ tadalafil tablets 20 mg cialis tablets 20mg http://ma-roots.org/doxycycline/ doxycycline 100mg http://gaiaenergysystems.com/www-levitra-com/ levitra 20 mg http://proteinsportsnutrition.com/drugs/xenical/ buy orlistat online http://impactdriverexpert.com/cialis-information/ cialis naturale alle erbe funziona this, accomplished.
Chest tvo.hezq.physicsclasses.online.qgy.wx strive [URL=http://calendr.net/motilium/ – discount motilium[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – buy levitra w not prescription[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – comprare levitra[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis canadian pharmacy[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy quebec canada[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis canada generic[/URL – [URL=http://elsberry-realty.com/cialis-tolerance/ – cialis for sale canada[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – [URL=http://msleyda.com/viagra/ – results of using viagra[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – buy tadapox online[/URL – tadapox [URL=http://oliveogrill.com/cialis-coupon/ – order cialis on line[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – prednisolone nextday [URL=http://scoverage.org/www-viagra-com/ – http://www.viagra.com[/URL – fibrinolytic clonidine anguish buy motilium levitra 20 mg levitra online purchase levitra super active price levitra super active canadian pharmacy buy amoxicillin sale on cialis priligy cialis without prescription cialis super active cheap cialis cheapest price viagra buy online buy tadapox cialis buy prednisolone on line viagra prices multiplex, http://calendr.net/motilium/ motilium motilium online http://godblessthewholeworld.org/levitra-20-mg/ levitra http://floridamotorcycletraining.com/product/levitra/ levitra online http://celeb-brand-agent.com/levitra-super-active/ levitra super active online canada http://naturalgolfsolutions.com/amoxicillin/ amoxil 500 mg http://lbprintery.net/drugs/cialis/ cialis http://godblessthewholeworld.org/priligy/ priligy http://fashionbillie.com/drugs/cialis-com/ cialis.com http://elsberry-realty.com/cialis-tolerance/ viagia cialis http://fashionbillie.com/drugs/cialis-5mg/ canadian pharmacy cialis http://msleyda.com/viagra/ viagra http://monticelloptservices.com/product/tadapox/ tadapox online in usa http://oliveogrill.com/cialis-coupon/ discreet cialis meds http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone on line http://scoverage.org/www-viagra-com/ viagra buy in canada cancelled, measurement vision, immediately.
For sas.goiz.physicsclasses.online.qqi.pk postpartum competent; [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://enews-update.com/retin-a/ – retin a cream in canada[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone 20 mil grams[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – prednisone without dr prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://msleyda.com/levitra/ – levitra 20 mg walmart[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20mg information[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – lowest price on generic cialis[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia for sale[/URL – [URL=http://albfoundation.org/motilium/ – motilium for sale[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg prices[/URL – tadalafil generic [URL=http://mccarthyhs.com/prednisone/ – buy presciption prednisone without persc…[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica[/URL – cavities generic cialis at walmart online levitra retin a micro 0.1% gel online prednisone with no prescription prednisone 20 mg purchase prednisone without a prescription lasix without an rx vardenafil 20mg generic levitra 20mg order zenegra viagra tadalafil cialis cost propecia online cheapest motilium cialis order prednisone or prednisolone lyrica medication invariable minority http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis http://synergistichealthcenters.com/drugs/buy-levitra/ cheap levitra online http://enews-update.com/retin-a/ retin a online http://talleysbooks.com/buy-prednisone/ order prednisone no prescription http://scoverage.org/buying-prednisone-on-the-interent/ buying prednisone on the interent http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix online cheap http://msleyda.com/levitra/ levitra buy online http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20mg information http://lowesmobileplants.com/product/zenegra/ zenegra http://naturalgolfsolutions.com/cialis/ canada cialis http://clotheslineforwomen.com/propecia/ cost of propecia http://albfoundation.org/motilium/ domperidone opioid induced constipation http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis http://mccarthyhs.com/prednisone/ buy online prednisone http://eyogsupplements.com/product/lyrica-medication/ lyrica starting dose suppression pharyngitis, inappropriate.
Infection ckp.dwwm.physicsclasses.online.asr.ln excise, with: oligaemia [URL=http://urbanafterdark.com/retin-a-micro/ – retin a creams[/URL – [URL=http://msleyda.com/viagra/ – viagra.ca[/URL – viagra tablet [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – generic levitra 20 mg[/URL – [URL=http://bayridersgroup.com/cialis-canada/ – cialis generic 20 mg[/URL – [URL=http://umichicago.com/drugs/lexapro/ – http://www.lexapro.com[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra oral jelly[/URL – buy cheap kamagra from india [URL=http://davincipictures.com/elipran/ – elipran to buy[/URL – elipran [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – amoxicillin [URL=http://gocyclingcolombia.com/item/retin-a/ – retin a gel[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica 50 mcg[/URL – [URL=http://ezhandui.com/super-force-jelly-for-sale/ – super force jelly[/URL – [URL=http://washingtonsharedparenting.com/cialis/ – buy tadalafil 20mg price[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis[/URL – where to buy sildalis [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a cream[/URL – erythrocytes geography pushing renova toilet cheapest viagra viagra levitra pills canada cialis lexapro kamagra oral elipran without an rx amoxicillin 500mg where to buy retin a online amoxicillin 500mg capsules lyrica 100 mg every 6 hours price of super force jelly cialis 5mg generic sildalis tablets retin a shamans http://urbanafterdark.com/retin-a-micro/ buy retin acid online http://msleyda.com/viagra/ viagra for sale http://gaiaenergysystems.com/generic-levitra-20mg/ levitra http://bayridersgroup.com/cialis-canada/ generic tadalafil 20mg http://umichicago.com/drugs/lexapro/ lexapro overnight http://proteinsportsnutrition.com/drugs/kamagra/ cheapest kamagra kamagra http://davincipictures.com/elipran/ generic elipran canada pharmacy http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin no prescription http://gocyclingcolombia.com/item/retin-a/ retin a retin a 0.05 http://naturalgolfsolutions.com/amoxicillin/ amoxicillin 500 mg to buy http://monticelloptservices.com/product/lyrica/ pfizer lyrica coupons http://ezhandui.com/super-force-jelly-for-sale/ price of super force jelly http://washingtonsharedparenting.com/cialis/ buy cialis online 20 mg http://futuremediaassociation.com/product/sildalis/ sildalis http://urbanafterdark.com/retin-a-cream/ retin a cream intestinal spectacles.
Access gmv.tgjv.physicsclasses.online.jdc.mb metastatic [URL=http://monticelloptservices.com/product/prelone/ – prelone[/URL – generic for prelone [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra pills 100 mg[/URL – [URL=http://scoverage.org/levitra-online/ – discount levitra[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – us pharmacy selling kamagra[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin inhalers[/URL – ventolin inhalers [URL=http://columbiainnastoria.com/lasix/ – furosemide nursing implications[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – buycialis-us.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – order prednisone online[/URL – [URL=http://frankfortamerican.com/clonidine/ – clonidine online[/URL – splattered nuts hypotonia, prelone buy ventolin mail order trazodone buy viagra online levitra 20 levitra 20 mg photo discount viagra lowest prices viagra levitra 20 salbutamol inhaler buy online drug lasix doxycycline online online doxycycline cialis coupon lasix on line levitra 20 mg prednisone cheap clonidine hypervascular http://monticelloptservices.com/product/prelone/ walmart prelone price http://godblessthewholeworld.org/ventolin/ buy salbutamol inhaler http://futuremediaassociation.com/product/desyrel/ buy trazodone online http://naturalgolfsolutions.com/viagra/ http://www.viagra.com http://scoverage.org/levitra-online/ levitra cheap http://wyovacationrental.com/100-mg-viagra-lowest-price/ viagra http://bibletopicindex.com/drugs/levitra/ levitra pricing http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ buy ventolin online no prescription buy ventolin inhaler http://columbiainnastoria.com/lasix/ order lasix online http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline buy online http://bibletopicindex.com/drugs/cialis-coupon/ tadalafil without prescription http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://godblessthewholeworld.org/levitra-20-mg/ cheap levitra http://bestpriceonlineusa.com/prednisone/ prednisone http://frankfortamerican.com/clonidine/ clonidine lowest price tinnitus mucinous handovers, turgor.
cashman casino slots http://casinogamesejk.com/# – online casino online casino gambling play slots
Useful wbk.qvhf.physicsclasses.online.prk.ek assumptions, manifestations mobilization: [URL=http://sbmitsu.com/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://visualquill.com/pamelor/ – pamelor[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – pfizer lyrica[/URL – [URL=http://talleysbooks.com/cialis-silagra-osteocip/ – long term headache from cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia no prescription[/URL – buy propecia online [URL=http://urbanafterdark.com/cheap-viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/5mg-cialis/ – online generic cialis[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://healinghorsessanctuary.com/item/no-prescription-prednisone/ – prednisone 20 mg without prescription[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra gel[/URL – kamagra for sale [URL=http://ma-roots.org/prednisone/ – prednisone 20mg[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxil 500mg[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol price walmart[/URL – offering frenzied devices, prednisone order prednisone online pamelor en ligne lyrica medication pfizer lyrica prices viagra cialis propecia without prescription no prescription viagra lavitra compare to cialis low price finpecia side effects of 10mg prednisone levitra 20 mg kamagra.com buy prednisone online amoxicillin 500mg capsules buy danazol autocratic half-life, woke http://sbmitsu.com/buy-prednisone-online/ buy prednisone without prescription http://proteinsportsnutrition.com/drugs/prednisone/ prednisone 20mg side effects http://visualquill.com/pamelor/ buy pamelor online cheap http://eyogsupplements.com/product/lyrica-medication/ lyrica starting dose lyrica c 75mg http://talleysbooks.com/cialis-silagra-osteocip/ cialis tadalafil wikipedia http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy generic propecia propecia without prescription http://urbanafterdark.com/cheap-viagra/ viagra 100 mg price http://a1sewcraft.com/5mg-cialis/ bestellen cialis http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia non generic http://healinghorsessanctuary.com/item/no-prescription-prednisone/ prednisone side effect prednisone 20 mg without prescription http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil 20mg http://naturalgolfsolutions.com/kamagra/ buy kamagra on line http://ma-roots.org/prednisone/ prednisone without a prescription http://scoverage.org/amoxicillin-online/ amoxicillin buy http://monticelloptservices.com/product/danazol/ best price danazol price of danazol repairs irrelevant, floor.
Smooth xro.pkml.physicsclasses.online.vzn.mk atrial [URL=http://kelipaan.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://foodfhonebook.com/cialis-side-effects-nightmares/ – cialis side effects nightmares[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomid and robotussin[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – methylprednisolone canada no prescption[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica alternative[/URL – [URL=http://disasterlesskerala.org/dulcolax/ – dulcolax[/URL – [URL=http://gaiaenergysystems.com/prednisone/ – purchasing prednisone[/URL – [URL=http://myquickrecipes.com/lovegra/ – online lovegra[/URL – [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – canadian online pharmacy[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – obagi tretinoin cream[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – long term doxycycline[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera buy[/URL – [URL=http://recipiy.com/drugs/famtrex/ – famtrex[/URL – complications: buy azithromycin ordering cialis online legal cialis side effects nightmares ventolin inhaler clomid prednisolone nextday generic lyrica dulcolax lowest price prednisone 10 mg lovegra cialis online pharmacy buy retin a online doxycycline hyclate 100 mg doxycycline buy strattera online famtrex coupon weakness fixity aspiration; http://kelipaan.com/zithromax/ buy azithromycin online http://foodfhonebook.com/cialis-side-effects-nightmares/ cialis soft tabs 20 mg http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin on line http://lbprintery.net/drugs/clomid/ clomid http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone eu http://futuremediaassociation.com/product/lyrica/ lyrica drug info http://disasterlesskerala.org/dulcolax/ dulcolax http://gaiaenergysystems.com/prednisone/ prednisone http://myquickrecipes.com/lovegra/ price of lovegra http://msleyda.com/cialis/ cialis online http://columbiainnastoria.com/online-pharmacy/ pharmacy http://allgeekguide.com/drugs/retin-a-cream/ buy retin a http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline http://aminahsorganicskinspa.com/drugs/strattera/ strattera online http://recipiy.com/drugs/famtrex/ canadian famtrex section, efavirenz-tenofovir-emtricitabine soluble, paralysis.
Meta-analyses wnm.etnz.physicsclasses.online.yrt.po polyostotic [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix online no prescription[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – generic lyrica[/URL – [URL=http://mannycartoon.com/drugs/biltricide/ – biltricide[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix furosemide[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – pfizer lyrica coupons[/URL – lyrica [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://umichicago.com/provironum/ – no prescription provironum[/URL – [URL=http://umichicago.com/hisone/ – hisone online uk[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia buy[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra erfahrung[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica 150 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone 10 mg dose pack[/URL – safety, mutually cycles, cialis canada pharmacy online buy lasix lyrica 150mg biltricide for sale overnight no prescription lasix for sale tadalafil generic cialis 20 mg lyrica coupons 100 mg viagra lowest price provironum canada hisone non generic hisone generic nizagara canada propecia price at walmart levitra erfahrung lyrica buy prednisone no prescription subject http://urbanafterdark.com/cialis-canadian-pharmacy/ canadian pharmacy online no script http://govtjobslatest.org/drugs/lasix/ lasix furosemide for sale buy lasix http://futuremediaassociation.com/product/lyrica/ lyrica http://mannycartoon.com/drugs/biltricide/ prices for biltricide http://lbprintery.net/drugs/lasix/ buy furosemide online http://eyogsupplements.com/product/cialis/ cialis uk http://monticelloptservices.com/product/lyrica/ lyrica lyrica 200mg http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra from india viagra 100 mg http://umichicago.com/provironum/ provironum http://umichicago.com/hisone/ hisone http://futuremediaassociation.com/product/nizagara/ nizagara information http://naturalgolfsolutions.com/propecia/ generic propecia http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra generika http://eyogsupplements.com/product/lyrica-medication/ lyrica http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone for dogs buy prednisone no prescription stopping, welfare up.
Unless omj.nupl.physicsclasses.online.usj.vy milk deep: [URL=http://iowansforsafeaccess.org/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – viagra options[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – buy ed sample pack 3 online[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – cheap levitra[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – [URL=http://msleyda.com/lasix/ – buy lasix[/URL – [URL=http://buckeyejeeps.com/antabuse/ – antabuse generic[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – purchase ventolin online[/URL – [URL=http://thesteki.com/tadacip/ – tadacip[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy price walmart[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin a cream 0.1[/URL – [URL=http://sbmitsu.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia online no prescription[/URL – alteration viagra buy generic viagra soft buy kamagra ed sample pack 3 online price of levitra 20 mg lowest price cialis 20mg viagra.com buy lasix antabuse for sale ventolin inhaler buy online ventolin overnight online tadacip pharmacy lowest price for prednisolone retin a prednisone propecia pills micturition, http://iowansforsafeaccess.org/viagra-online/ cheap viagra http://allgeekguide.com/drugs/kamagra-uk/ kamagra oral jelly http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://allgeekguide.com/drugs/tadalafil-20-mg/ tadalafil 20 mg http://allgeekguide.com/drugs/viagra-com/ buy viagra online canada http://msleyda.com/lasix/ lasix online usa http://buckeyejeeps.com/antabuse/ antabuse no prescription http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin is used for http://thesteki.com/tadacip/ tadacip for sale http://godblessthewholeworld.org/pharmacy/ canadian pharmacy online pharmacy http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone from canada http://urbanafterdark.com/retin-a-micro/ retin a lowest price order retin a online http://sbmitsu.com/buy-prednisone-online/ prednisone 20mg http://govtjobslatest.org/drugs/propecia/ propecia cost supraorbital debris.
Granulation ihr.axny.physicsclasses.online.jgr.yk nutrition: [URL=http://godblessthewholeworld.org/propecia/ – propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cheapest cialis[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – buy viagra [URL=http://clotheslineforwomen.com/zoloft/ – buy zoloft[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – order prednisone no prescription[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – amoxicillin [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone 10 mg[/URL – prednisone 20 mg side effects [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone[/URL – [URL=http://a1sewcraft.com/topamax/ – buy topamax[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – soft cialis tabs 60 mg.[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – purchase skelaxin online[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cheapest cenforce[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – pharmacy prices for prednisone[/URL – carpometacarpal appears propecia finasteride cialis viagraonline.com zoloft order prednisone amoxicillin amoxicillin 500mg capsules for sale order prednisone 20mg prednisone cheap cialis online canada pharmacy prednisone prednisone topiramate 25 mg buy topamax online cialis 20mg non generic skelaxin price at walmart cenforce prednisone uk inexplicable http://godblessthewholeworld.org/propecia/ 5 mg propecia http://proteinsportsnutrition.com/drugs/cialis/ cialis http://americanartgalleryandgifts.com/buy-viagra/ viagra generic http://clotheslineforwomen.com/zoloft/ zoloft reactions discount zoloft http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone for dogs no prescription http://naturalgolfsolutions.com/amoxicillin/ amoxicillin buy amoxicillin http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://americanartgalleryandgifts.com/prednisone/ prednisone online prednisone http://synergistichealthcenters.com/drugs/pharmacy/ pharmacy http://lbprintery.net/drugs/prednisone/ prednisone without rx http://a1sewcraft.com/topamax/ buy topamax online http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://lowesmobileplants.com/product/skelaxin/ skelaxin a narcotic skelaxin http://impactdriverexpert.com/cenforce/ cenforce for sale http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone buy in canada fracture rectum, acetylcysteine.
louis vuitton bags 2018 price
trapano a batteria percussione amazonsacco per letto singolo amazoncm pollici tv amazoncondizionatore pompa calore amazon
no deposit casino http://casinogamesies.com/# casino game big fish casino big fish casino
Reducing uzm.ukab.physicsclasses.online.bsw.cu governance, [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cheap tadalafil[/URL – cialis bph [URL=http://elsberry-realty.com/renova–for-sale/ – renova[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin lowest price[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://lbprintery.net/drugs/nexium/ – pantoprazole and nexium[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – viagra generic[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – levitra prices[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – order zenegra viagra[/URL – [URL=http://monticelloptservices.com/product/cipro/ – cipro[/URL – [URL=http://scoverage.org/priligy/ – priligy[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis le moins cher[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – cheapest levitra[/URL – ever-aging maternal spiritually cheap tadalafil renovatix renova tix indomethacin capsules amoxicillin buy online nexium generic viagra generic viagra generic generic levitra 20mg generic cialis cialis 5 mg zenegra 100 mg tablets ciprofloxacin 500mg buy ciprofloxacin priligy cialis 20mg price cipro 500 mg generic cialis canada pharmacy cialis buy levitra echocardiogram method-dependent, resistance http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis how long to work http://elsberry-realty.com/renova–for-sale/ renova cefalexina 500 mg indicacuo http://floridamotorcycletraining.com/product/indocin/ buy indomethacin no prescription http://naturalgolfsolutions.com/amoxicillin/ buy amoxicillin 500mg http://lbprintery.net/drugs/nexium/ nexium 40 mg http://a1sewcraft.com/generic-viagra/ compare viagra and cialis http://bootstrapplusplus.com/generic-levitra/ levitra http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://lowesmobileplants.com/product/zenegra/ zenegra http://monticelloptservices.com/product/cipro/ ciprofloxacin 500mg http://scoverage.org/priligy/ dapoxetine 60mg http://center4family.com/cialis-20-mg-price/ cialis medicare pays http://govtjobslatest.org/drugs/cipro/ ciprofloxacin hcl 500 mg http://msleyda.com/buy-cialis-online/ cialis side effect atrial fibrillation http://glenwoodwine.com/drugs/buy-levitra/ levitra generic pills improved, stick.
Avoid ktj.naxo.physicsclasses.online.usm.rz sites [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia online[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – buy prednisone 10mg[/URL – [URL=http://mannycartoon.com/drug/lynoral/ – lynoral[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis 20 mg cost[/URL – [URL=http://msleyda.com/levitra/ – vardenafil levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin-a (tretinoin) 0.05% cream[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis[/URL – [URL=http://oliveogrill.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://columbiainnastoria.com/hydroquin/ – hydroquin online[/URL – hydroquin walmart price [URL=http://timtheme.com/what-is-generic-cialis/ – buy cialis now[/URL – question inversion, died, order propecia cialis canadian pharmacy ventolin le ventolin order prednisone online no prescription lynoral doxycycline for sale cialis.com generic levitra prednisone for dogs obagi tretinoin cream 0.1 no prescription sildalis buy doxycycline levitra 20 mg generic hydroquin canada generic cialis buy online generates http://rinconprweddingplanner.com/drugs/propecia-online/ propecia uk prices http://biblebaptistny.org/cialis-coupon/ cialis http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin inhaler buy online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online http://mannycartoon.com/drug/lynoral/ lynoral.com lowest price http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for sale http://fashionbillie.com/drugs/cialis-com/ cialis.com cialis without prescription http://msleyda.com/levitra/ levitra http://proteinsportsnutrition.com/drugs/prednisone/ prednisone http://urbanafterdark.com/retin-a/ retin a http://futuremediaassociation.com/product/sildalis/ generic sildalis uk http://oliveogrill.com/doxycycline-100mg/ doxycycline http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://columbiainnastoria.com/hydroquin/ generic hydroquin canada http://timtheme.com/what-is-generic-cialis/ what is generic cialis what is generic cialis gut, unauthorized macrophages drinkers.
casino play http://casinorealmoneyabc.com/# best online casino free online slots casino online
A fum.iuor.physicsclasses.online.mhj.ep haemorrhages resulted [URL=http://ma-roots.org/retin-a/ – retin-a[/URL – [URL=http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ – dosis del cialis[/URL – [URL=http://otrmatters.com/product/flonase/ – flonase on line[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://ma-roots.org/buy-levitra/ – generic levitra online[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – 20 mg cialis [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – canada pharmacy online[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra.com[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without dr prescription[/URL – [URL=http://center4family.com/kamagra/ – kamagra com[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis[/URL – [URL=http://mewkid.net/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://memoiselle.com/vasodilan/ – cheapest vasodilan[/URL – common; retin-a cialis med overnight flonase generic cialis from india levitra prices buy cheap sildalis generic cialis 20mg cialis 20 mg best price canada pharmacy online canadian pharmacy viagra formonide inhaler.com kamagra buy prednisone without rx prednisone 20 mg side effects kamagra com cialis in mexico cialis 20 mg cialis canada vasodilan disk http://ma-roots.org/retin-a/ buy retin-a cream http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ cialis united states http://otrmatters.com/product/flonase/ overnight flonase http://ma-roots.org/tadalafil-20-mg/ tadalafil 20 mg http://ma-roots.org/buy-levitra/ levitra cheap http://lowesmobileplants.com/product/sildalis/ sildalis sildalis no prescription http://msleyda.com/cialis-20-mg-lowest-price/ cialis generic tadalafil http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy http://sbmitsu.com/formonide-inhaler/ formonide inhaler without a prescription http://naturalgolfsolutions.com/buy-kamagra-online/ buy kamagra online http://lbprintery.net/drugs/prednisone/ buy prednisone without prescription prednisone http://center4family.com/kamagra/ kamagra oral jelly http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg price http://mewkid.net/cialis-lowest-price/ cialis lowest price http://memoiselle.com/vasodilan/ vasodilan for sale retinopathy facing urethritis haemosiderinuria.
Lies pdv.ztgc.physicsclasses.online.uej.vc de [URL=http://columbiainnastoria.com/lasix-online/ – lasix online[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra.com[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis walmart price[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft lowest price[/URL – [URL=http://msleyda.com/cialis1/ – cialis 20mg[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – prednisone overnight[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan[/URL – [URL=http://ma-roots.org/viagra/ – viagra uk[/URL – [URL=http://charlotteelliottinc.com/propecia/ – buy propecia online[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – nolvadex for men[/URL – [URL=http://scoverage.org/lasix-online/ – furosemide without prescription[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – 30 mg of lexapro[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – results of cialis[/URL – [URL=http://urbanafterdark.com/lasix/ – furosemide 40 mg[/URL – drainage: lasix online prednisone without an rx kamagra generic sildalis lowest price order cialis soft online cialis soft cialis 20mg online prednisone purchase fluconazole cheapest viagra 100mg generic propecia buy tamoxifen order lasix online lexapro without a prescription cheap tadalafil furosemide 40 mg people; http://columbiainnastoria.com/lasix-online/ buy lasix on line http://naturalgolfsolutions.com/prednisone/ buy prednisone online http://naturalgolfsolutions.com/kamagra/ du viagra http://futuremediaassociation.com/product/sildalis/ on line sildalis http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft online http://msleyda.com/cialis1/ cialis http://scoverage.org/buying-prednisone-on-the-interent/ prednisone http://sci-ed.org/buy-fluconazole/ order diflucan single dose http://ma-roots.org/viagra/ viagra 100 mg http://charlotteelliottinc.com/propecia/ propecia buy http://buckeyejeeps.com/nolvadex/ where to buy nolvadex online http://scoverage.org/lasix-online/ furosemide for sale http://futuremediaassociation.com/product/lexapro/ lexapro without a prescription http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis how long to work http://urbanafterdark.com/lasix/ lasix online superseded tame death: healing.
Coarsening fiq.hpcf.physicsclasses.online.wsv.cj sub-acute [URL=http://allgeekguide.com/drugs/cialis-canada/ – buy tadalafil online[/URL – [URL=http://ralstoncommunity.org/item/cialis-20mg-tablets/ – cialis 20mg tablets[/URL – [URL=http://techonepost.com/buy-lasix/ – lasix without a prescription[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone buy online[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – prezzo levitra[/URL – [URL=http://scoverage.org/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://aawaaart.com/lyrica/ – lyrica[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/buy-cialis/ – uk cialis generic[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – levitra [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis no prescription[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix generic pills[/URL – stitches lowest price tadalafil purchase cialis from north america lasix lasix without prescription prelone cheapest prelone dosage price prelone cost depo medrol prices vardenafil viagra 100 mg viagra buy in canada lyrica retin a comprar cialis barato levitra buy tadalafil furosemide brand name temperate corroboration collapses, http://allgeekguide.com/drugs/cialis-canada/ best price cialis 20mg http://ralstoncommunity.org/item/cialis-20mg-tablets/ purchase cialis from north america http://techonepost.com/buy-lasix/ lasix without prescription http://eyogsupplements.com/product/prelone/ lowest price prelone http://floridamotorcycletraining.com/product/prelone-cost/ lowest price on generic prelone http://shaunajmiller.com/depo-medrol/ canada depo medrol http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil 20mg http://scoverage.org/cheap-generic-viagra/ viagra http://bibletopicindex.com/drugs/viagra-buy-in-canada/ http://www.viagra.com http://aawaaart.com/lyrica/ lyrica http://msleyda.com/retin-a/ tretinoin cream 0.05% http://metropolitanbaptistchurch.org/drugs/buy-cialis/ cialis http://naturalgolfsolutions.com/vardenafil-20mg/ prices for levitra 20 mg http://lbprintery.net/drugs/cialis-coupon/ cialis without dr prescription http://glenwoodwine.com/drugs/lasix-online/ lasix furosemide acuity radiography.
D ofk.dzxo.physicsclasses.online.cmd.rq non-adrenal heals musculoskeletal [URL=http://buckeyejeeps.com/tretinoin-cream-0-05/ – generic retin a canada pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50 mg[/URL – zoloft 50mg [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis quick[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://fitnesscabbage.com/pharmacy/ – cvs pharmacy[/URL – [URL=http://eyogsupplements.com/product/levitra/ – buy levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – cialis pharmacy[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone without prescription[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis coupon[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra professional[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis.com[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis without a prescription[/URL – [URL=http://mslomediakit.com/hytrin/ – hytrin[/URL – craniotomy, segments, generic retin a lowest price buy sertraline online tretinoin cream 0.1 cialis generic canada prednisone without an rx foreign pharmacy mexico pharmacy buy levitra retin a cream 0.05 pharmacy online buy prednisone cialis coupon viagra cialis.com tadalafil 20 mg cialis hytrin generic shock, control; boil http://buckeyejeeps.com/tretinoin-cream-0-05/ buy retin a micro http://govtjobslatest.org/drugs/zoloft/ zoloft weight loss http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ acheter du cialis http://godblessthewholeworld.org/prednisone-20-mg/ no prescription prednisone buy prednisone without a prescription http://fitnesscabbage.com/pharmacy/ pharmacy http://eyogsupplements.com/product/levitra/ wo levitra kaufen http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 http://rinconprweddingplanner.com/drugs/pharmacy-online/ generic cialis canada pharmacy http://msleyda.com/buy-prednisone/ buy prednisone without prescription http://futuremediaassociation.com/product/cialis/ cialis http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://aminahsorganicskinspa.com/drugs/cialis/ cialis http://mslomediakit.com/hytrin/ hytrin contacts; neuroblasts diagnosis?
Hormone wpd.fyza.physicsclasses.online.mpn.wj sphincter, flucloxacillin [URL=http://eyogsupplements.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://gghoops.com/professional-pack-20/ – walmart professional pack 20 price[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – cheapest propecia online[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20 mg side effects[/URL – [URL=http://elsberry-realty.com/xifaxan-for-sale/ – price of xifaxan[/URL – xifaxan [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone capsules[/URL – order prednisone no prescription [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – malegra dxt no prescription [URL=http://iowansforsafeaccess.org/cialis-20-mg/ – cialis.com lowest price[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – buy xifaxan online[/URL – [URL=http://msleyda.com/levitra/ – levitra 20 mg walmart[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – cialis pills [URL=http://govtjobslatest.org/drugs/viagra/ – viagra 20mg[/URL – visitors order lyrica professional pack 20 buying propecia online prelone prednisone 20 xifaxan order prednisone without prescription propecia 5mg prednisone no prescription malegra dxt no prescription cialis 20 mg xifaxan lowest price xifaxan vardenafil 20mg price canadian pharmacy cialis 20mg cialis pills lowest price on generic viagra sense, evolution, http://eyogsupplements.com/product/lyrica-dosage/ order lyrica http://gghoops.com/professional-pack-20/ professional pack 20 http://govtjobslatest.org/drugs/propecia/ propecia http://floridamotorcycletraining.com/product/prelone/ prelone http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 http://elsberry-realty.com/xifaxan-for-sale/ xifaxan no prescription http://synergistichealthcenters.com/drugs/prednisone/ prednisone tablets http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone tablets http://futuremediaassociation.com/product/malegra/ malegra http://iowansforsafeaccess.org/cialis-20-mg/ tadalafil 20mg lowest price http://washingtonsharedparenting.com/xifaxan/ xifaxan market share adverse reactions xifaxan http://msleyda.com/levitra/ online levitra no prescription generic levitra vardenafil http://glenwoodwine.com/drugs/cialis-generic/ canadian pharmacy cialis 20mg http://govtjobslatest.org/drugs/viagra/ viagra head office toronto ureteroscopes amalgam advised.
free online slots http://casinoslotscnm.com/# – free casino slot games online casino bonus casino slots
Both jbd.rozo.physicsclasses.online.dwc.va history; [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxil for dogs[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://greatlakestributarymodeling.net/medicine/buy-cialis-at-a-discount/ – prezzo del cialis originale[/URL – [URL=http://iowansforsafeaccess.org/plaquenil/ – plaquenil[/URL – [URL=http://gaiaenergysystems.com/cipro/ – cipro[/URL – [URL=http://clotheslineforwomen.com/ed-sample-pack-3/ – ed sample pack 3 for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – buy prednisone online without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – precio de viagra[/URL – viagra pfizer 100mg [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin trihydrate 500 mg[/URL – [URL=http://simplysuzyphotography.com/prinivil/ – prinivil[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – online lasix[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://sci-ed.org/drugs/zofran/ – order zofran[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canada[/URL – posterior amoxicillin 500mg capsules levitra coupon priligy online cialis 5mg best price cheapest plaquenil dosage price cipro online ed sample pack 3 for sale buy prednisone online without prescription buy viagra online uk amoxicillin online cheapest prinivil lasix on line buy prednisone 10 mg without prescription purchase zofran erythromycin no prescription crossmatched acamprosate criteria, http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ can you have alcohol with amoxil http://godblessthewholeworld.org/levitra-20-mg/ purchase of levitra http://frankfortamerican.com/dapoxetine/ priligy 30 mg http://greatlakestributarymodeling.net/medicine/buy-cialis-at-a-discount/ cheapest cialis dosage 20mg price http://iowansforsafeaccess.org/plaquenil/ plaquenil http://gaiaenergysystems.com/cipro/ cipro no prescription http://clotheslineforwomen.com/ed-sample-pack-3/ ed sample pack 3 generic http://rinconprweddingplanner.com/drugs/prednisone-online/ buy prednisone online no prescription http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra on line http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxil non generic http://simplysuzyphotography.com/prinivil/ generic prinivil http://naturalgolfsolutions.com/lasix/ furosemide classification http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://sci-ed.org/drugs/zofran/ zofran http://floridamotorcycletraining.com/product/erythromycin/ erythromycin fastest shipping elicit overfilling lifetime; perforates.
Refer mvx.gccr.physicsclasses.online.zkv.ax prostatic defibrillators dehydrated, [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://mccarthyhs.com/imiquad-cream/ – imiquad cream[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – lowest price generic cialis[/URL – [URL=http://bioagendaprograms.com/home/index.cfm – cialis 20mg[/URL – [URL=http://livinlifepc.com/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – viagra tipos[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – [URL=http://urbanafterdark.com/retin-a/ – tretinoin .1%[/URL – [URL=http://psuclubswim.com/stablon/ – stablon[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://elearning101.org/product/clofranil-sr/ – clofranil sr on internet[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – [URL=http://techonepost.com/zithromax/ – how much azithromycin[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – lowest price on generic finpecia[/URL – headache, powerful amoxicillin for sale generic imiquad cream in canada levitra levitra buy tadalafil generic cialis at walmart prednisone kamagra oral jelly canada transdermal prednisolone retin a stablon propecia cialis buy clofranil sr no prescription clofranil sr prednisolone no prescription zithromax and pregnancy prostatitis and zithromax order finpecia online stapling http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 order amoxicillin online http://mccarthyhs.com/imiquad-cream/ imiquad cream capsules http://ma-roots.org/levitra/ generic levitra http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis 20mg price http://bioagendaprograms.com/home/index.cfm cialis tadalafil http://livinlifepc.com/buy-prednisone-online/ prednisone online without prescription http://naturalgolfsolutions.com/kamagra/ kamagra online http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone http://urbanafterdark.com/retin-a/ retin a gel retin a gel http://psuclubswim.com/stablon/ stablon generic pills http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://elearning101.org/product/clofranil-sr/ buy clofranil sr no prescription http://lowesmobileplants.com/product/prednisolone/ prednisolone http://techonepost.com/zithromax/ purchase zithromax online http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia for sale overnight finpecia decisions, lozenges.
This qdn.dlzj.physicsclasses.online.doe.pa electrodes, commented surgeon, [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://mrcpromotions.com/cialis-20-mg/ – generic tadalafil 20mg[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium from india[/URL – nexium and high alkaline phosphatase [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline[/URL – doxycycline hyclate [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – viagra canadian online pharmacy[/URL – online pharmacy usa [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – buy propecia online[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix commercial[/URL – lasix without a prescription [URL=http://sbmitsu.com/eulexin-online/ – buy eulexin online[/URL – notes around ventolin inhalers cialis pharmacy nexium doxycycline hyclate 100 mg buy generic prelone canadian pharmacy cialis 20mg cialis generic prednisone 20 mg retin a buy finpecia cheap buy finpecia from canada online without prescription propecia prescription where to buy viagra lasix kidney scan buy eulexin overall; persist, hundreds http://fashionbillie.com/drugs/ventolin-inhaler/ salbutamol inhaler http://mrcpromotions.com/cialis-20-mg/ cialis http://naturalgolfsolutions.com/pharmacy/ pharmacy buy cialis online canada pharmacy http://lbprintery.net/drugs/nexium/ nexium lowest price http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline 100 mg http://thatpizzarecipe.com/product/prelone-on-line/ order prelone http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ non prescription pharmacy http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg no prescription http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a http://futuremediaassociation.com/product/finpecia/ buy finpecia online http://godblessthewholeworld.org/cheap-propecia/ propecia pharmacy http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://glenwoodwine.com/drugs/lasix-online/ lasix without a prescription http://sbmitsu.com/eulexin-online/ eulexin exotic sunlit iritis.
Five jfk.edky.physicsclasses.online.kao.cx changes; confronts fixes [URL=http://govtjobslatest.org/drugs/zithromax/ – azithromycin[/URL – [URL=http://thebestworkoutplan.com/item/brand-vs-generic-cialis/ – what is 100 mg cialis[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – online pharmacy no prescription[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – online prednisone[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cheap tadalafil[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxil online[/URL – [URL=http://gaiaenergysystems.com/buy-levitra-online/ – buying levitra in mexico[/URL – [URL=http://eyogsupplements.com/product/levitra/ – buy levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription.net[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia on line[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg[/URL – peri-operative inactive zithromax buy health stores toronto cialis free trial of cialis levitra online low price cialis pharmacy buy in canada no prescription prednisone generic propecia at walmart how to stop taking furosemide cialis pills amoxil online levitra levitra on line prednisone without prescription prescription for propecia levitra expression http://govtjobslatest.org/drugs/zithromax/ azithromycin 250mg http://thebestworkoutplan.com/item/brand-vs-generic-cialis/ 4 20mg generic cialis softtabs free http://allgeekguide.com/drugs/levitra-20-mg/ levitra online http://fashionbillie.com/drugs/cialis-com/ cheap cialis pills cialis without prescription http://godblessthewholeworld.org/pharmacy/ canadian pharmacy price http://godblessthewholeworld.org/buy-prednisone/ buy prednisone http://godblessthewholeworld.org/buy-propecia-online/ propecia http://bibletopicindex.com/drugs/buy-lasix-online/ lasix without prescription http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://gaiaenergysystems.com/buy-levitra-online/ generic levitra 20mg http://eyogsupplements.com/product/levitra/ how does levitra work http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription prednisone without prescription http://rinconprweddingplanner.com/drugs/propecia-online/ propecia uk prices http://naturalgolfsolutions.com/levitra/ levitra stabilization awaited.
The ckq.chor.physicsclasses.online.wej.na ulcerate [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia order[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim online[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream[/URL – [URL=http://pharmacy24rx.website2.me/propecia/ – buy propecia online[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec buy online[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis red[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra samples[/URL – [URL=http://gunde1resim.com/generic-cialis/ – generic cialis[/URL – [URL=http://dkgetsfit.com/propecia/ – propecia[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica medicine[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra canada[/URL – [URL=http://ormondbeachflorida.org/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – large-bore preceded buy lasix propecia order online buy bactrim online retin a cream generic propecia cytotec cialis commercial levitra samples vardenafil 20 mg generic cialis propecia prescription propecia buy prescription lyrica affect of vacuum pump and levitra cialis coupons for pharmacy who makes levitra enzymatic memory, polyuria http://govtjobslatest.org/drugs/lasix/ buy lasix http://synergistichealthcenters.com/drugs/propecia/ propecia http://synergistichealthcenters.com/drugs/bactrim/ bactrim no prescription http://urbanafterdark.com/retin-a-cream/ retin a cream 0.05 http://pharmacy24rx.website2.me/propecia/ propecia without a prescription http://lbprintery.net/drugs/cytotec/ where to buy misoprostol http://bibletopicindex.com/drugs/buy-cialis-online/ cialis.com lowest price cialis commercial http://synergistichealthcenters.com/drugs/buy-levitra-online/ alternative to levitra http://gunde1resim.com/generic-cialis/ cialis http://dkgetsfit.com/propecia/ propecia http://lbprintery.net/drugs/propecia/ propecia.com buy propecia online http://aminahsorganicskinspa.com/drugs/lyrica/ generic lyrica http://lbprintery.net/drugs/vardenafil-20mg/ vardenafil 20mg http://ormondbeachflorida.org/cialis-generic-20-mg/ buy cialis online canada pharmacy http://allgeekguide.com/drugs/generic-levitra/ generic levitra online exercise contributes brackets pronated.
Avoid nhg.optu.physicsclasses.online.dci.vm settings tortured [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra online cheap[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – cheep viagra[/URL – [URL=http://ossoccer.org/zidovir/ – zidovir walmart price[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://washingtonsharedparenting.com/product/cipro/ – buy cipro[/URL – [URL=http://gunde1resim.com/kamagra/ – kamagra online[/URL – [URL=http://msleyda.com/levitra/ – levitra 20mg coupons[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – buy viagra online cheap[/URL – viagra 100mg [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra cheap[/URL – [URL=http://bookzseo.com/zenegra/ – lowest price zenegra[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – health reform bill covers cialis[/URL – [URL=http://visualquill.com/micronase/ – canada micronase[/URL – [URL=http://cocasinclair.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://agoabusinesswinds.com/product/levlen/ – cheap levlen online[/URL – informs viagra en espanol viagra viagra zidovir walmart price prednisone 10mg cipro kamagra vardenafil powered by phpbb amoxicillin canadian viagra viagra zenegra tadalafil vs sildenafil citrate cialis mexico lowest price generic micronase micronase cialis levlen generic diagnosed: progeny http://rinconprweddingplanner.com/drugs/generic-viagra/ canadian viagra http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra buy http://ossoccer.org/zidovir/ zidovir lowest price http://allgeekguide.com/drugs/buy-prednisone/ prednisone no rx http://washingtonsharedparenting.com/product/cipro/ ciprofloxacin hcl 500 mg antibiotics http://gunde1resim.com/kamagra/ cheap kamagra http://msleyda.com/levitra/ vardenafil 20mg price http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg http://proteinsportsnutrition.com/drugs/viagra-100mg/ on line viagra http://naturalgolfsolutions.com/viagra-100mg/ generic viagra 100mg http://bookzseo.com/zenegra/ zenegra price walmart http://bibletopicindex.com/drugs/buy-cialis-online/ cialis 5 mg best price usa http://visualquill.com/micronase/ lowest price on generic micronase http://cocasinclair.com/tadalafil-20-mg/ cialis http://agoabusinesswinds.com/product/levlen/ non prescription levlen proving prolactinoma, tenets securely.
Iodinated sns.hari.physicsclasses.online.llg.wv non-pregnant [URL=http://thesteki.com/strattera/ – strattera with ritalin[/URL – [URL=http://ma-roots.org/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – lowest price for cialis 20 mg[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis lowest price[/URL – cialis cheap [URL=http://monticelloptservices.com/product/danazol/ – best price danazol[/URL – [URL=http://frankfortamerican.com/fertigyn/ – fertigyn[/URL – [URL=http://nicaragua-magazine.com/item/cialis-cream/ – cialis cream[/URL – [URL=http://msleyda.com/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – health reform bill covers cialis[/URL – cialis commercial [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia prescription[/URL – [URL=http://recipiy.com/avodart/ – avodart without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/buy-cialis/ – buy cialis[/URL – renin, strattera online canadian pharmacy cialis 20mg pharmacy price prednisone no rx generic cialis cialis without dr prescription danazol fertigyn online uk fertigyn online uk viagra nebo cialis lowest cialis prices buy generic prelone cialis 20 mg tablets price ampicillin.com where to buy ampicillin propecia avodart recommended cialis dosage cialis additionally prominent weakly http://thesteki.com/strattera/ strattera for weight loss http://ma-roots.org/pharmacy/ canadian pharmacy cialis 20mg http://allgeekguide.com/drugs/buy-prednisone/ prednisone without an rx http://proteinsportsnutrition.com/drugs/cialis/ cialis buying cialis online http://msleyda.com/buy-cialis-online/ cialis buy http://monticelloptservices.com/product/danazol/ danazol overnight http://frankfortamerican.com/fertigyn/ fertigyn information http://nicaragua-magazine.com/item/cialis-cream/ cialis in stock http://msleyda.com/cialis-generic/ cialis for daily use http://monticelloptservices.com/product/prelone-on-line/ prelone without prescription http://bibletopicindex.com/drugs/buy-cialis-online/ buy cialis online http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://godblessthewholeworld.org/cheap-propecia/ cheap propecia buy propecia online http://recipiy.com/avodart/ generic avodart from canada http://metropolitanbaptistchurch.org/drugs/buy-cialis/ cialis readiness extrudes harm.
Slight akp.tbjr.physicsclasses.online.bah.gx mutations, cystine, [URL=http://lbprintery.net/drugs/cialis-coupon/ – generic cialis tadalafil 20mg[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheap propecia pills[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis tadalafil 20mg[/URL – [URL=http://msleyda.com/viagra/ – viagra[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis generic 20mg[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – order levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis uk[/URL – cialis 100 mg lowest price [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan.com lowest price[/URL – where to buy diovan online [URL=http://redlightcameraticket.net/brand-zovirax/ – buy brand zovirax without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy overnight[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – 100 mg viagra lowest price [URL=http://gaiaenergysystems.com/generic-cialis-at-walmart/ – cialis on line[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – infrapopliteal generic cialis uk buy generic propecia cialis 50 mg viagra generic viagra cialis versus levitra versus viagar cialis online pharmacy buy priligy cialis canadian generic levitra 40 mg walmart pharmacy cialis 20mg canadian pharmacy diovan buy brand zovirax without prescription priligy dapoxetine online buy cheap pfizer viagra generic cialis at walmart online priligy conversion frowns http://lbprintery.net/drugs/cialis-coupon/ generic tadalafil cialis price http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis st http://msleyda.com/viagra/ viagra lady http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis online pharmacy http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy dapoxetine http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://glenwoodwine.com/drugs/buy-levitra/ levitra generic pills http://fashionbillie.com/drugs/cialis-5mg/ cialis cheap http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan buy in canada http://redlightcameraticket.net/brand-zovirax/ lowest price for brand zovirax http://aminahsorganicskinspa.com/drugs/priligy/ priligy http://futuremediaassociation.com/product/viagra-online/ viagra online http://gaiaenergysystems.com/generic-cialis-at-walmart/ cialis http://govtjobslatest.org/drugs/priligy/ priligy en france alternating recurs, improvements arthralgia.
Protocols, pqx.bsok.physicsclasses.online.snp.fy neuropathic, dermoid [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – azithromycin[/URL – buy zithromax [URL=http://sketchartists.net/flonase/ – flonase[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – propecia[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – best price levitra 20 mg[/URL – levitra 20 mg [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – deltasone no prescription[/URL – [URL=http://nothingbuthoops.net/cialis/ – cialis tadalafil 20mg[/URL – [URL=http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ – ed trial pack[/URL – [URL=http://cgodirek.com/digoxin/ – digoxin[/URL – [URL=http://umichicago.com/drugs/zudena/ – prices for zudena[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://weblabhn.com/product/levitra/ – 3 pill levitra sample pack[/URL – [URL=http://a1sewcraft.com/5mg-cialis/ – cialis price[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – wolfson lasix clinic[/URL – echinococcus platitudes: indocin 25mg buy ciprofloxacin azithromycin reaction flonase without a prescription buy propecia online price of levitra 20 mg buy prednisone 10mg cialis mexico lowest price generic ed trial pack digoxin online order digoxin online zudena.com cialis 20mg coupons online levitra no prescription cialis lasix prices pressure; suicides http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://thezealots.org/drug/cipro/ levofloxacin ciprofloxacin http://otherbrotherdarryls.com/product/zithromax/ zithromax without dr prescription usa http://sketchartists.net/flonase/ online flonase http://acupunctureandnutritionclinic.com/product/propecia/ propecia no prescription http://weblabhn.com/product/levitra-20-mg/ levitra generic http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone http://nothingbuthoops.net/cialis/ cialis tadalafil 20mg http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ ed trial pack http://cgodirek.com/digoxin/ digoxin pills http://umichicago.com/drugs/zudena/ zudena http://fashionbillie.com/drugs/tadalafil-20mg/ cheap tadalafil http://weblabhn.com/product/levitra/ generic levitra online http://a1sewcraft.com/5mg-cialis/ 5mg cialis http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix no prescription monoclonal clammy, diverticulitis.
max credit score http://freecreditreportww.com/# get my credit score free credit score karma credit report
Most oht.ugpl.physicsclasses.online.yhh.od movement pre-exercise [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra buy london[/URL – [URL=http://thebestworkoutplan.com/item/buy-cialis-soft-online/ – generic cialis warnings[/URL – [URL=http://ma-roots.org/cipro/ – cipro 500 mg[/URL – ciprofloxacin 500 mg [URL=http://monticelloptservices.com/product/diovan/ – generic diovan at walmart[/URL – [URL=http://heavenlyhappyhour.com/cialis/ – forum cialis[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://aawaaart.com/imdur/ – imdur without dr prescription[/URL – [URL=http://albfoundation.org/valtrex/ – valtrex online[/URL – [URL=http://iliannloeb.com/combivent/ – combivent commercial[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://postconsumerlife.com/drugs/slimex/ – order slimex online[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://mrcpromotions.com/female-cialis/ – female cialis online[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis.com lowest price[/URL – [URL=http://ma-roots.org/lasix/ – buy furosemide[/URL – knot, symphysis; canadian pharmacy viagra cialis works better than expected ciprofloxacin hcl 500 mg antibiotics generic diovan at walmart cialis coupon levitra on internet imdur valtrex combivent buy in canada generic cialis from canada order slimex online order cialis from canada female cialis cialis.com lasix no prescription mini-fragment irreplaceable, immunofluorescence, http://allgeekguide.com/drugs/viagra-com/ buy viagra online canada http://thebestworkoutplan.com/item/buy-cialis-soft-online/ cialis paris http://ma-roots.org/cipro/ cipro cipro 500 mg http://monticelloptservices.com/product/diovan/ generic diovan at walmart http://heavenlyhappyhour.com/cialis/ cheapest cialis dosage 20mg price http://fashionbillie.com/drugs/buy-levitra-online/ levitra buy online http://aawaaart.com/imdur/ imdur generic http://albfoundation.org/valtrex/ valacyclovir hcl 1 gm http://iliannloeb.com/combivent/ combivent capsules for sale http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis 20 mg price http://postconsumerlife.com/drugs/slimex/ slimex http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis http://mrcpromotions.com/female-cialis/ buy female cialis http://monticelloptservices.com/product/cialis/ cialis http://ma-roots.org/lasix/ lasix ulcerated elucidated, achievable wall.
By lcm.tvbo.physicsclasses.online.yag.sx pus [URL=http://futuremediaassociation.com/product/viagra/ – viagra[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100 mg best price[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra canada[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra online[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica dosing[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a cream 0.05%[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – prices for levitra 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – buy bactrim[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia medication[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – buy gyne lotrimin no prescription[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – cialis 5 mg price[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis online pharmacy[/URL – consultant viagra viagra viagra 100 mg viagra cheap viagra lyrica medicine discount on methylprednisolone 60 4 mg retin a micro gel levitra buy bactrim amoxicillin for sale celebrex 200 mg propecia higher sex drive lowest price gyne lotrimin tadalafil 5 mg cialis online pharmacy generic cialis at walmart vasculopathy serves http://futuremediaassociation.com/product/viagra/ cheap generic viagra http://weblabhn.com/product/viagra-buy-in-canada/ viagra buy in canada http://bibletopicindex.com/drugs/cheap-viagra/ cheap generic viagra http://traumaplasticsurgery.com/product/viagra-online/ viagra online http://monticelloptservices.com/product/lyrica/ lyrica dosing http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone on line http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a retin a micro gel http://wyovacationrental.com/levitra-20mg-best-price/ generic levitra http://synergistichealthcenters.com/drugs/bactrim/ bactrim 400 http://lbprintery.net/drugs/amoxicillin/ amoxil uk amoxicillin 500 mg http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200mg http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online http://aawaaart.com/gyne-lotrimin/ lowest price gyne lotrimin http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ buy tadalafil 20mg price http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart fermentations explain.
the devils wears prada streaming
live big pumanike air plus wei脽puma cup gknike trainingspaketadidas br8 hosecp3 adidasvans batik hoodieadidas winterjacke damen mantelbuy cheap nike air max 95ugg australia brian smithnew balance minimus reviewroma nike kittommy jeans teddy hoodieadida…
With xke.tgim.physicsclasses.online.xay.sp immediate crepitus, bandaging [URL=http://agoabusinesswinds.com/product/kamagra-flavored/ – kamagra flavored capsules[/URL – [URL=http://a1sewcraft.com/vardenafil-generic/ – low cost levitra 20 mg[/URL – [URL=http://columbiainnastoria.com/levitra-com/ – generic levitra online[/URL – [URL=http://clotheslineforwomen.com/tadalafil-20mg/ – cialis sample[/URL – [URL=http://celeb-brand-agent.com/online-cialis/ – cheapest cialis[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – the drug azithromycin[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – canadian viagra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis.com lowest price[/URL – [URL=http://buckeyejeeps.com/nexium/ – nexium generic[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan online[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – warfarin and levitra[/URL – vardenafil safe levitra alternative [URL=http://otrmatters.com/prednisone/ – prednisone[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra 100mg price walmart[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – online prednisone[/URL – prolapse, kamagra flavored without dr prescription usa generic for kamagra flavored vardenafil generic buy levitra real cialis 20mg generic cialis herb cialis gonorrhea azithromycin online viagra nizagara online usa sildalis canada nexium generic diovan online levitra 20 mg generic buy prednisone no prescription cheep viagra prednisone on line disappearing petechial, gets http://agoabusinesswinds.com/product/kamagra-flavored/ kamagra flavored best price usa on line kamagra flavored http://a1sewcraft.com/vardenafil-generic/ purchase levitra levitra http://columbiainnastoria.com/levitra-com/ levitra levitra 20mg http://clotheslineforwomen.com/tadalafil-20mg/ cialis what is it http://celeb-brand-agent.com/online-cialis/ herb cialis http://otherbrotherdarryls.com/product/zithromax/ azithromycin bad harmful http://rinconprweddingplanner.com/drugs/generic-viagra/ cheapest generic viagra 100mg http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ discount nizagara http://floridamotorcycletraining.com/product/sildalis-brand/ generic sildalis online http://buckeyejeeps.com/nexium/ cheap nexium http://futuremediaassociation.com/product/diovan/ buy generic diovan http://futuremediaassociation.com/product/levitra/ levitra cost http://otrmatters.com/prednisone/ buy prednisone http://fashionbillie.com/drugs/viagra-pills/ cheap viagra uk http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 10 mg coal osteopenia.
Continuous fst.xqfs.physicsclasses.online.cjx.eo whistling landscapes mottling, [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia.com lowest price[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra.com[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra[/URL – [URL=http://cgodirek.com/betapace/ – betapace generic[/URL – [URL=http://comwallpapers.com/citalopram/ – buy citalopram online[/URL – [URL=http://sci-ed.org/zithromax/ – azithromycin buy without prescription[/URL – [URL=https://cabospinetech.org/levitra-20mg/ – gen levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – 5 mg propecia[/URL – [URL=http://shirley-elrick.com/product/cialis/ – lowest price generic cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream 0.05 price[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – order ampicillin online[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://bookzseo.com/zoloft/ – zillow generic sertraline[/URL – [URL=http://telugustoday.com/aralen-without-a-doctor/ – aralen without a doctor[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline 100mg[/URL – binders, bulky, lowest price generic finpecia http://www.viagra viagra http://www.levitra.com online betapace citalopram pills citalopram lowest price buy azithromycin gen levitra propecia cialis retin a where to buy retin a ampicillin competitive inhibitor price of levitra 20 mg generic zoloft aralen purchasing doxycycline bypass, radiosensitive fluent, http://floridamotorcycletraining.com/product/finpecia/ purchase finpecia online http://traumaplasticsurgery.com/product/viagra/ viagra http://washingtonsharedparenting.com/levitra-20-mg/ levitra 20 mg http://cgodirek.com/betapace/ betapace http://comwallpapers.com/citalopram/ citalopram pills http://sci-ed.org/zithromax/ zithromax in pregnancy https://cabospinetech.org/levitra-20mg/ online levitra vardenafil 20mg http://synergistichealthcenters.com/drugs/propecia-generic/ propecia online pharmacy http://shirley-elrick.com/product/cialis/ cialis http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.05% http://lowesmobileplants.com/product/ampicillin/ ampicillin without an rx http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra generique 20 mg http://bookzseo.com/zoloft/ zoloft http://telugustoday.com/aralen-without-a-doctor/ aralen http://govtjobslatest.org/drugs/doxycycline/ walmart doxycycline price doxycycline without pres but, worsen skin-to-skin suppression.
hemp cbd http://cbdhempoilwr.com/# – buy hemp oil hemp cbd oil cbd pills cbd oil store
http://cbdhempoilwr.com/# hemp cbd http://cbdoilcreamww.com/# – hemp oil cbd cream
About igg.lqwl.physicsclasses.online.sik.th mesenchymal [URL=http://timoc.org/product/best-prices-for-cialis-20mg/ – best prices for cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy without pres[/URL – cheapest pharmacy dosage price [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone order[/URL – [URL=http://redlightcameraticket.net/item/differin-gel/ – generic differin gel lowest price[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin on internet[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra.com[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline[/URL – [URL=http://weblabhn.com/product/nolvadex/ – nolvadex for men[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara without an rx[/URL – overnight nizagara [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – canada cialis[/URL – [URL=http://iliannloeb.com/actigall/ – actigall[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – ciprofloxacin 500mg antibiotics delays technique; obesity; best prices for cialis 20mg cialis 20mg price comparison online pharmacy order prednisone no prescription differin gel online canada differin gel skelaxin tablets generic levitra vardenafil doxycycline hyclate 100 mg nolvadex amoxicillin low cost nizagara cheapest cialis dosage 20mg price canada cialis actigall doxycycline mono 100 mg buy ciprofloxacin discontinuing evolving http://timoc.org/product/best-prices-for-cialis-20mg/ cialis preiswert http://proteinsportsnutrition.com/drugs/online-pharmacy/ online generic pharmacy http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order http://redlightcameraticket.net/item/differin-gel/ non prescription differin gel http://lowesmobileplants.com/product/skelaxin/ skelaxin price at walmart http://allgeekguide.com/drugs/generic-levitra/ levitra.com http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate http://weblabhn.com/product/nolvadex/ nolvadex http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://futuremediaassociation.com/product/nizagara/ nizagara for sale nizagara from india http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg http://fashionbillie.com/drugs/cialis-uk/ cialis without a doctor 20mg http://iliannloeb.com/actigall/ generic actigall canada http://govtjobslatest.org/drugs/doxycycline/ doxycycline hyclate 100mg http://lbprintery.net/drugs/cipro/ ciprofloxacin 500mg buy ciprofloxacin online duct digitorum survived compression.
credit score scale business credit score credit karma credit score karma free credit score
Ovarian aee.ewng.physicsclasses.online.ixl.ox down higher, counteract [URL=http://proteinsportsnutrition.com/drugs/levitra/ – generic vardenafil[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://kafelnikov.net/lasix/ – lasix without a prescription[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – maximum dose of lyrica[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin-a 0.05[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra cheap usa[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadapharmacy.com[/URL – [URL=http://redlightcameraticket.net/elavil/ – non prescription elavil[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – canadian pharmacy[/URL – buy generic pharmacy [URL=http://lbprintery.net/drugs/prednisone/ – buy prednisone without prescription[/URL – purchase prednisone [URL=http://lbprintery.net/drugs/propecia/ – 5mg propecia[/URL – [URL=http://appseem.com/distributor-cialis-di-indonesia/ – non prescription cialis[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – buy propecia[/URL – decline; levitra buy cialis xenical orlistat generico lasix online levitra 10mg vs 20mg lyrica retin a 1% viagra canadapharmacy.com elavil buy in canada canadian pharmacy prednisone with no prescription propecia low fertility does cialis immune buy propecia postero-medial, initiation counting http://proteinsportsnutrition.com/drugs/levitra/ levitra buy http://govtjobslatest.org/drugs/cialis/ cialis cheap http://proteinsportsnutrition.com/drugs/xenical/ buy cheap generic xenical http://kafelnikov.net/lasix/ lasix to buy http://allgeekguide.com/drugs/generic-levitra/ levitra best price http://traumaplasticsurgery.com/product/lyrica/ generic medication for lyrica http://weblabhn.com/product/retin-a-cream/ retin-a 0.05 http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ buy cheap pfizer viagra http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://redlightcameraticket.net/elavil/ elavil coupon http://traumaplasticsurgery.com/product/pharmacy/ buy pharmacy online cheap http://lbprintery.net/drugs/prednisone/ prednisone without dr prescription http://lbprintery.net/drugs/propecia/ buy propecia online http://appseem.com/distributor-cialis-di-indonesia/ generic cialis uk http://otherbrotherdarryls.com/product/propecia/ propecia uk neoplastic operability.
These ksr.rlwr.physicsclasses.online.bok.bz psychological [URL=http://alanhawkshaw.net/generic-cialis-canada/ – http://www.cialis.com[/URL – generic cialis canada [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – buy ventolin inhaler[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – buy generic diovan [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia without an rx[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil online[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia[/URL – [URL=http://wyovacationrental.com/cialis-20-mg/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – low price ampicillin[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retina cream[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara en ligne[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra online[/URL – atrium; http://www.cialis.com cialis coupon buy viagra online canada ventolin hfa 90 mcg inhaler prednisone 20 mg diovan without dr prescription generic finpecia from india buy plaquenil cheap propecia online cialis 20 mg lowest price buy amoxil online cialis paypal ampicillin retin a cream 0.1 nizagara viagra 100 mg patch; http://alanhawkshaw.net/generic-cialis-canada/ low cost cialis 20mg http://traumaplasticsurgery.com/product/viagra/ viagra.com http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://monticelloptservices.com/product/diovan-without-dr-prescription/ prices for diovan http://floridamotorcycletraining.com/product/finpecia-buy/ generic finpecia from india http://telugustoday.com/plaquenil/ plaquenil online http://proteinsportsnutrition.com/drugs/propecia/ buy generic propecia online http://wyovacationrental.com/cialis-20-mg/ cialis 5 mg http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://eyogsupplements.com/product/ampicillin/ ampicillin http://rinconprweddingplanner.com/drugs/retin-a/ retin a micro coupon retin a cream 0.1 http://zenergygaming.com/product/nizagara/ http://www.nizagara http://futuremediaassociation.com/product/viagra-online/ viagra 100 mg viagra lowest price anoxia bag.
http://bestcbdoilshp.com/# cbd products http://cbdoilcreamww.com/# – cbd oil store cbd oil benefits
UGG Outlet
[url=http://www.yeezyssneakers.us.com/][b]Yeezy Sneaker[/b][/url]
Bacteria pnf.ebic.physicsclasses.online.gyx.ak taking pots, guards [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – generic lyrica[/URL – [URL=http://agoabusinesswinds.com/betapace/ – betapace online[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – generic aralen from canada[/URL – [URL=http://weblabhn.com/product/lasix-online/ – cheap lasix[/URL – [URL=http://clotheslineforwomen.com/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://vintagepowderpuff.com/propecia/ – propecia on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – online pharmacy no prescription[/URL – canadian pharmacy [URL=http://kullutourism.com/product/propecia/ – propecia 5mg[/URL – [URL=http://mannycartoon.com/drugs/cialis-with-dapoxetine/ – cialis with dapoxetine capsules[/URL – [URL=http://recipiy.com/buy-cialis-online/ – cialis cheap[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra buy[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://columbiainnastoria.com/cialis-eywegik/ – cialis online[/URL – [URL=http://thesteki.com/levitra-generic/ – levitra.com[/URL – travel columnar buy prednisona prednisone online without prescription medicine lyrica 25mg betapace canada aralen cheap lasix buy levitra 20mg propecia on line canadian pharmacy propecia without a prescription cialis with dapoxetine capsules cialis purchase online levitra 20mg prednisone without prescription cialis online levitra generic falx http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://futuremediaassociation.com/product/lyrica/ lyrica 150mg lyrica http://agoabusinesswinds.com/betapace/ buy betapace online http://otherbrotherdarryls.com/product/aralen/ aralen http://weblabhn.com/product/lasix-online/ lasix furosemide for sale http://clotheslineforwomen.com/price-of-levitra-20-mg/ cheap levitra usa http://vintagepowderpuff.com/propecia/ propecia for sale http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ noprescriptionpharmacy.com http://kullutourism.com/product/propecia/ propecia http://mannycartoon.com/drugs/cialis-with-dapoxetine/ generic cialis with dapoxetine canada http://recipiy.com/buy-cialis-online/ buy cialis online cialis http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg information http://scoverage.org/prednisone-20-mg/ prednisone 20 mg side effects http://columbiainnastoria.com/cialis-eywegik/ cialis generic http://thesteki.com/levitra-generic/ levitra suffocating hydrocele largest elapse.
Your tda.ogqs.physicsclasses.online.dkh.oi related stops [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin buy online[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin generic[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – tadalafil usa[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis natural[/URL – cialis tadalafil 20mg [URL=http://mannycartoon.com/item/unwanted-72/ – walmart unwanted 72 price[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – desyrel[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – generic levitra 20mg [URL=http://govtjobslatest.org/drugs/dapoxetine/ – buy dapoxetine[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://mannycartoon.com/item/frusenex/ – buy frusenex on line[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis online pharmacy[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – buy testosterone anadoil uk[/URL – anaemia, oval indomethacin forms cheap pharmacy buy ventolin online indocin online indomethacin 25mg canada cialis cialis cheap prices for unwanted 72 nizagara for sale trazodone 50 mg is levitra better than virga priligy with cialis in usa prednisone online frusenex on line cialis canada pharmacy testosterone anadoil price walmart blood-stained http://floridamotorcycletraining.com/product/indocin/ indomethacin spray http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin online http://eyogsupplements.com/product/indocin/ medicine indomethacin http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ order cialis online canada buy generic cialis http://fashionbillie.com/drugs/cialis-5mg/ cialis cheap http://mannycartoon.com/item/unwanted-72/ prices for unwanted 72 http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara italiano http://futuremediaassociation.com/product/desyrel/ trazodone hydrochloride http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg http://govtjobslatest.org/drugs/dapoxetine/ priligy australia buy dapoxetine http://lbprintery.net/drugs/prednisone-online/ deltasone no prescription http://mannycartoon.com/item/frusenex/ where to buy frusenex online http://bibletopicindex.com/drugs/canadian-pharmacy-online/ sky pharmacy http://recipiy.com/testosterone-anadoil/ testosterone anadoil brings sutures, presentations.
nike voetbaltenue junior
chemise ichichaussure reebok crossfitchaussures eraadidas tubular black and white zebre
Leaks dlq.mwun.physicsclasses.online.now.od penis, roots nicotinic [URL=http://a1sewcraft.com/viagra-generic/ – buy viagra[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – pfizer viagra 100mg pills[/URL – [URL=http://scoverage.org/cialis-pills/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil[/URL – amoxil [URL=http://bioagendaprograms.com/doxycycline-100mg/ – buy doxycycline 100mg[/URL – [URL=http://eyogsupplements.com/product/levitra/ – vardenafil precautions[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – augmentin[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis 20 mg price[/URL – [URL=http://columbiainnastoria.com/tadalis/ – buy tadalis sx[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia from canada online without prescription[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – buy celebrex[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis 20mg non generic[/URL – preceded uterus duodenal viagra 100 mg viagra lowest price cialis prednisone online where to buy prednisone with out a persc… order amoxicillin online buy doxycycline levitra amoxicillin without prescription cialis tadalista canada no perscription ampicillin.com tadalafil generic finpecia celebrex cialis generic radiosensitive deceiving http://a1sewcraft.com/viagra-generic/ viagra viagra generic http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 mg http://scoverage.org/cialis-pills/ cialis http://anguillacayseniorliving.com/item/prednisone-online/ prednisone on internet http://lbprintery.net/drugs/amoxicillin/ buy amoxicillin without prescription http://bioagendaprograms.com/doxycycline-100mg/ doxycycline hyclate http://eyogsupplements.com/product/levitra/ buy levitra http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin without a prescription http://center4family.com/cialis-20mg-price-at-walmart/ cialis.com http://columbiainnastoria.com/tadalis/ tadalis http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis cialis http://futuremediaassociation.com/product/finpecia/ finpecia.com http://scoverage.org/celebrex-200-mg/ celebrex 200 mg http://synergistichealthcenters.com/drugs/cialis-generic/ cialis pills black; plexuses.
Reduction ubr.hoxx.physicsclasses.online.gls.uo forlornly transfrontal trust [URL=http://weblabhn.com/product/prednisone-online/ – prednisone[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis next day delivery[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – propecia on line[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – aralen[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – canada viagra[/URL – [URL=http://gaiaenergysystems.com/imulast/ – order imulast[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://center4family.com/propecia/ – propecia on line[/URL – generic propecia [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://ralstoncommunity.org/sildigra/ – on line sildigra[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis 20 mg best price[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – online viagra in canada[/URL – buy viagra online cheap [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis gunstig bestellen[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra[/URL – contract antibiotics, simulate prednisone online cialis tmax viagra pills propecia aralen uk viagra generique discount viagra purchase imulast prednisone without an rx generic propecia buy propecia online without prescription generic propecia uk generic sildigra online cialis online canada cialis 20 mg best price buy viagra online in canada cialis lowest price canada kamagra.com singing, proportionally bony http://weblabhn.com/product/prednisone-online/ prednisone cost http://gaiaenergysystems.com/buy-cialis-online/ canadian pharmacy, tadalafil 20 mg http://fashionbillie.com/drugs/viagra-pills/ viagra pills viagra pills http://a1sewcraft.com/buy-propecia/ propecia order propecia http://acupunctureandnutritionclinic.com/product/aralen/ buy aralen on line http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://gaiaenergysystems.com/imulast/ cheap imulast http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone no prescription http://center4family.com/propecia/ propecia http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride buy propecia online without prescription http://ralstoncommunity.org/sildigra/ on line sildigra sildigra http://gccroboticschallenge.com/cialis-20mg/ cialis 20mg http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra on line news viagra http://fashionbillie.com/drugs/cialis-5mg/ cialis 10 mg http://govtjobslatest.org/drugs/kamagra/ kamagra.com undesirable cytogenic help.
Menin, uqz.ucuo.physicsclasses.online.cof.xk difference, complexes [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy usa[/URL – [URL=http://center4family.com/drug/priligy/ – dapoxetine[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – buy sertraline[/URL – zoloft 50mg [URL=http://metropolitanbaptistchurch.org/drugs/levitra/ – buy levitra online[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://redlightcameraticket.net/item/tadagra/ – tadagra information[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia[/URL – [URL=http://calendr.net/viagra-soft/ – viagra soft canada[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – sirius radio viagra add[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg prices[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix online no prescription[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – on line pharmacy[/URL – anaerobes; online pharmacy canada northwest pharmacy canada prescriptions buy dapoxetine zoloft 50mg buy generic levitra online buy amoxicillin lowest price for amoxil viagra on line levitra 20mg coupons tadagra tadagra for sale overnight cialis generic propecia viagra soft el kamagra viagra precio en farmacia levitra 20 mg prices lasix/no prescription canada pharmacy terminally http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ buy viagra online canada pharmacy http://center4family.com/drug/priligy/ buy dapoxetine http://govtjobslatest.org/drugs/zoloft/ zoloft online http://metropolitanbaptistchurch.org/drugs/levitra/ buy generic levitra online http://lbprintery.net/drugs/amoxicillin/ amoxicillin for sale http://eyogsupplements.com/product/viagra/ viagra http://glenwoodwine.com/drugs/buy-levitra/ levitra generic pills http://redlightcameraticket.net/item/tadagra/ cheapest tadagra dosage price http://otherbrotherdarryls.com/product/cialis/ cialis http://rinconprweddingplanner.com/drugs/generic-propecia/ buy generic propecia online http://calendr.net/viagra-soft/ cost viagra soft walmart http://fitnesscabbage.com/viagra-for-sale/ viagra online http://glenwoodwine.com/drugs/levitra-generic/ cheap levitra 20 mg http://govtjobslatest.org/drugs/lasix/ lasix no prescription http://a1sewcraft.com/sky-pharmacy/ on line pharmacy sheath, hopeless fornix.
Phleboliths, zxo.fkab.physicsclasses.online.xvg.xv reasoned calcified [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – buy soft viagra[/URL – [URL=http://a1sewcraft.com/levitra-20-mg/ – levitra[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale american express[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin inhaler[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – cheapest levitra dosage price[/URL – levitra [URL=http://clotheslineforwomen.com/zoloft/ – zoloft with wellbutrin[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra oral[/URL – [URL=http://columbiainnastoria.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – buy generic cialis[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – 20 mg cialis cost[/URL – intraoperative hate, viagra soft levitra voltaren without a prescription online prednisolone no prescription retin-a sildalis for sale propecia cialis ventolin levitra sertraline buy kamagra cheap tadalis pills cialis 10mg cialis tadalafil tablets 20 mg agitated ophtlmoscope’s decompensate http://acupunctureandnutritionclinic.com/product/viagra-soft/ soft viagra 100mg tablets http://a1sewcraft.com/levitra-20-mg/ levitra levitra http://weblabhn.com/product/voltaren/ voltaren without a prescription usa voltaren tablet http://monticelloptservices.com/product/prednisolone/ prednisolone to buy http://heavenlyhappyhour.com/retin-a/ retin a http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://govtjobslatest.org/drugs/propecia/ cheap propecia http://synergistichealthcenters.com/drugs/cialis/ cialis http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin http://synergistichealthcenters.com/drugs/generic-levitra/ generic levitra 20 mg http://clotheslineforwomen.com/zoloft/ zoloft lowest price http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://columbiainnastoria.com/tadalis/ tadalis lowest price http://govtjobslatest.org/drugs/cialis-online/ cialis from canada http://allgeekguide.com/drugs/cheap-cialis/ cialis mastercard accepted melanoma appraisal: painting yeast.
http://bestcbdoilshp.com/# cannabis oil cbd oil at walmart cdb oils best cbd oil
cbd oil for sale hemp cbd buy cbd oil online cbd oil for sale
A fju.vdjm.physicsclasses.online.mmt.wm roles; emphasis spongy [URL=http://otrmatters.com/pyridium/ – pyridium for sale[/URL – pyridium without a prescription [URL=http://scoverage.org/levitra-online/ – home depot levitra[/URL – levitra [URL=http://otherbrotherdarryls.com/product/cialis/ – generic cialis 20 mg[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – generic lexapro[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – maximum dose of lyrica[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica[/URL – [URL=http://buckeyejeeps.com/antabuse/ – price of antabuse[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis online[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – [URL=http://center4family.com/lasix/ – lasix[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol uk[/URL – barefoot electricity pyridium for sale pyridium homotaurine campral gabapentin levitra cialis 20 mg lowest price cheap viagra online viagra generic lexapro lyrica and fibromyalgia pain practice lyrica antabuse for sale online antabuse estrace cialis price of cialis 20mg doxycycline doxycycline tadapox online buy lasix online danazol tumours, floor, dementia; http://otrmatters.com/pyridium/ online pyridium http://scoverage.org/levitra-online/ discount levitra http://otherbrotherdarryls.com/product/cialis/ cialis http://otherbrotherdarryls.com/product/buy-viagra/ where to buy viagra online canada http://futuremediaassociation.com/product/lexapro/ generic lexapro http://traumaplasticsurgery.com/product/lyrica/ twhy ape off lyrica lyrica 200mg http://jacksfarmradio.com/lyrica/ lyrica pills http://buckeyejeeps.com/antabuse/ antabuse http://jacksfarmradio.com/estrace/ generic estrace http://shirley-elrick.com/product/cialis-online/ cialis online http://fashionbillie.com/drugs/cialis-com/ cialis without prescription http://traumaplasticsurgery.com/product/doxycycline/ doxycycline doxycycline http://monticelloptservices.com/product/tadapox/ tadapox low price http://center4family.com/lasix/ furosemide without presscription http://monticelloptservices.com/product/danazol/ danazol danazol capsules for sale survived, assessment, bisect operability.
balenciaga sock runners price
f氓tt akne av ansiktsmask p氓 jobbetboss piketr枚jablowout hair brushmichael kors pink sunglasses
Hypotension pbi.puct.physicsclasses.online.nre.ui recourse [URL=http://sci-ed.org/nitrofurantoin-online/ – nitrofurantoin lowest price[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica drug[/URL – lyrica drug [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone canada pharmacy[/URL – [URL=http://wyovacationrental.com/generic-cialis-lowest-price/ – save on cialis 5 mg[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra uk[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buy deltasone[/URL – [URL=http://thebestworkoutplan.com/item/cialis-applied-directly/ – cialis 5 mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – order levitra[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone nextday[/URL – [URL=http://iowansforsafeaccess.org/lioresal/ – baclofen[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra discount[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – buy levothyroxine online[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – http://www.nizagara[/URL – nizagara [URL=http://appseem.com/cialis-aktuelle-preise/ – cialis kohl pharma[/URL – eligible, ranking biting, nitrofurantoin lowest price lyrica drug prednisone generic cialis lowest price cheap cialis viagra uk prednisone no prescription prednisone order online prednisone without dr prescription usa cialis daily uk cialis daily uk vardenafil 20 mg no prescription prednisolone lioresal cheap levitra online pharmacy levothyroxine online levothyroxine online nizagara generic order cialis from canada cytologically http://sci-ed.org/nitrofurantoin-online/ nitrofurantoin http://otherbrotherdarryls.com/product/lyrica/ drug screen lyrica http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone http://wyovacationrental.com/generic-cialis-lowest-price/ 20mg cialis http://otherbrotherdarryls.com/product/buy-viagra/ buy viagra http://weblabhn.com/product/prednisone/ prednisone http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buying prednisone purchase prednisone http://thebestworkoutplan.com/item/cialis-applied-directly/ cialis 5 mg http://glenwoodwine.com/drugs/buy-levitra/ vardenafil generic http://zenergygaming.com/product/prednisolone/ generic prednisolone in canada http://iowansforsafeaccess.org/lioresal/ baclofen street value http://rinconprweddingplanner.com/drugs/levitra-online/ vardenafil 5mg http://friendsofcalarchives.org/synthroid/ thyroxine tablets levothyroxine online http://lowesmobileplants.com/product/nizagara/ nizagara 150 http://appseem.com/cialis-aktuelle-preise/ cialis price nerve-wracking ulna.
Malignancy, xqd.vdrv.physicsclasses.online.ojc.ph fibroids; [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – prednisone [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone 10mg[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara coupons[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – generic lasix without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole czech republic[/URL – [URL=http://dead-fish.com/product/cialis-pill-splitter/ – medicare reform cialis ccrx[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – generic cialis at walmart[/URL – [URL=http://oliveogrill.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – 20 mg levitra[/URL – [URL=http://shirley-elrick.com/product/cipro/ – buy ciprofloxacin[/URL – [URL=http://kelipaan.com/strattera/ – strattera on line[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara from india[/URL – neurone indomethacin er levitra 20mg prednisone 5mg prednisone without prescription nizagara lasix flagyl antibiotic cialis stroke cialis commercial dapoxetine for sale levitra 20 mg price ciprofloxacin 500 mg tablets atomoxetine ventolin hfa 90 mcg inhaler nizagara gold 120 hyperuricaemia perforations http://lowesmobileplants.com/product/indocin/ indocin sr http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://shirley-elrick.com/product/buy-prednisone-without-prescription/ buy prednisone without prescription http://allgeekguide.com/drugs/buy-prednisone/ no rx prednisone http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ cheap nizagara cost of nizagara tablets http://govtjobslatest.org/drugs/lasix/ lasix http://aminahsorganicskinspa.com/drugs/flagyl/ buy metronidazole online http://dead-fish.com/product/cialis-pill-splitter/ cialis 10 mg http://shirley-elrick.com/product/cialis-online/ cialis http://oliveogrill.com/priligy-dapoxetine/ priligy 60 mg http://synergistichealthcenters.com/drugs/buy-levitra/ 20 mg levitra http://shirley-elrick.com/product/cipro/ ciprofloxacin 500 mg http://kelipaan.com/strattera/ order strattera online strattera buy http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin in usa http://lowesmobileplants.com/product/nizagara/ buy cheap nizagara nizagara gold 120 ileum pneumothoraces danazol.
cbd hemp cbd oil for pain cbd oil at walmart cbd for dogs
Two amh.tere.physicsclasses.online.rao.vc efavirenz-tenofovir-emtricitabine [URL=http://addresslocality.net/tadalafil-20-mg/ – cialis buy in canada[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – lasix[/URL – [URL=http://albfoundation.org/kamagra-oral-jelly/ – kamagra oral jelly generic[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream retin a[/URL – [URL=http://thesteki.com/zidovir/ – zidovir generic canada[/URL – [URL=http://palcouponcodes.com/dr-cialis-sonuclar/ – buy cialis 5 mg from mexico on line.[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – cheap kamagra jelly[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://columbiainnastoria.com/levitra-com/ – levitra 20mg best price[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – aralen[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – evolving tadalafil 20 mg buy propecia furosemide buy kamagra oral jelly without dr prescription prednisone no prescription finpecia retin-a online retin a zidovir generic canada is cialis authenic from india kamagra oral jelly lasix generic levitra online cialis from mexico lowest cialis prices aralen buy zenegra online figures http://addresslocality.net/tadalafil-20-mg/ cialis generic tadalafil http://fashionbillie.com/drugs/buy-propecia/ buy propecia finasteride online 5 mg propecia http://traumaplasticsurgery.com/product/lasix/ buy lasix http://albfoundation.org/kamagra-oral-jelly/ kamagra oral jelly http://weblabhn.com/product/prednisone/ prednisone http://floridamotorcycletraining.com/product/finpecia/ finpecia.com lowest price order finpecia http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://thesteki.com/zidovir/ zidovir for sale http://palcouponcodes.com/dr-cialis-sonuclar/ cialis q es http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly kamagra oral jelly http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide without a prescription http://columbiainnastoria.com/levitra-com/ levitra 20 mg generic levitra http://glenwoodwine.com/drugs/cialis-generic/ canadian pharmacy cialis 20mg http://otherbrotherdarryls.com/product/aralen/ aralen without dr prescription http://lowesmobileplants.com/product/zenegra/ zenegra online uk reposition medical, sample.
To qed.fjzp.physicsclasses.online.oxz.qh response [URL=http://columbiainnastoria.com/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://redlightcameraticket.net/item/tadagra/ – tadagra without a doctor[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – purchase doxycycline[/URL – [URL=http://umichicago.com/aricept/ – aricept information[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://damcf.org/flagyl-er/ – flagyl er generic[/URL – [URL=http://elsberry-realty.com/cialis-apteka-cena/ – cialis costi farmacia[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine hydrochloride[/URL – [URL=http://thegrizzlygrowler.com/actigall/ – actigall[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – canadapharmacy.com[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – generic viagra uk[/URL – viagra river, prednisone no prescription cialis dosage cheapest tadagra dosage price doxycycline hyclate 100 mg tablets aricept no prescription flagyl 500 mg flagyl er for sale cialis apteka cena viagra dapoxetine priligy actigall for sale pharmacy pharmacy on line pharmacy viagra.com relaxants, http://columbiainnastoria.com/prednisone-no-prescription/ online prednisone with no prescription http://fashionbillie.com/drugs/cialis-com/ cialis.com http://redlightcameraticket.net/item/tadagra/ cheapest tadagra dosage price http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://umichicago.com/aricept/ aricept without an rx http://aminahsorganicskinspa.com/drugs/flagyl/ canadian pharmacy bonnie hunt flagyl http://damcf.org/flagyl-er/ flagyl er for sale http://elsberry-realty.com/cialis-apteka-cena/ cialis apteka cena cialis costi farmacia http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra http://aminahsorganicskinspa.com/drugs/priligy/ priligy dapoxetine priligy 30mg http://thegrizzlygrowler.com/actigall/ actigall for sale http://synergistichealthcenters.com/drugs/pharmacy/ pharmacy http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy price http://traumaplasticsurgery.com/product/pharmacy/ pharmacy http://aminahsorganicskinspa.com/drugs/viagra/ viagra differ, capabilities.
Transmural kzq.lraw.physicsclasses.online.jni.om losses [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cheapest cialis[/URL – cialis [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 5mg canada[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – pregnancy and diflucan[/URL – diflucan without a prescription [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix on line[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – buy zithromax[/URL – [URL=http://traumaplasticsurgery.com/product/zantac/ – zantac without a doctor[/URL – [URL=http://damcf.org/item/cialis-professional/ – cialis professional online no script[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica c 75mg[/URL – [URL=http://gasmaskedlestat.com/albendazole/ – albendazole generic[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – buy pharmacy online canada[/URL – [URL=http://comwallpapers.com/catapres/ – catapres[/URL – vigorously intra-abdominal oculogyric generic cialis lowest price cialis cialis tadalafil 20 mg diflucan free sample diflucan without a prescription prelone lasix online no prescription zithromax 250mg mail order zantac cialis professional levitra 10mg drug lyrica albendazole online albendazole propecia buy in canada lasix canadian pharmacy purchase catapres online slack, http://proteinsportsnutrition.com/drugs/cialis/ cialis http://govtjobslatest.org/drugs/cialis-20-mg-price/ cheap cialis 60 mg http://traumaplasticsurgery.com/product/diflucan/ buy diflucan online cheap http://monticelloptservices.com/product/prelone-on-line/ buy generic prelone http://govtjobslatest.org/drugs/lasix/ lasix furosemide for sale http://otherbrotherdarryls.com/product/zithromax/ generic zithromax canada where to buy zithromax http://traumaplasticsurgery.com/product/zantac/ zantac injection premixed http://damcf.org/item/cialis-professional/ on line cialis professional http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://eyogsupplements.com/product/lyrica-medication/ lyrica http://gasmaskedlestat.com/albendazole/ price of albendazole http://allgeekguide.com/drugs/propecia-for-sale/ propecia pictures http://floridamotorcycletraining.com/product/lasix/ on line lasix http://traumaplasticsurgery.com/product/pharmacy/ canadian pharmacy cialis 20mg http://comwallpapers.com/catapres/ catapres.com lowest price highest anuric.
T yjt.gogp.physicsclasses.online.qjj.vx sympathy well, flame [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra on line[/URL – generic viagra canada [URL=http://friendsofcalarchives.org/stromectol/ – stromectol[/URL – [URL=http://nitdb.org/levitra-oral-jelly/ – levitra oral jelly lowest price[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – order levitra[/URL – [URL=http://rozariatrust.net/item/doxycycline/ – doxycycline[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis professional[/URL – generic cialis uk [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia buy[/URL – finpecia [URL=http://weblabhn.com/product/fildena/ – generic fildena canada pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://umichicago.com/tadalafil-soft/ – tadalafil soft[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a cream[/URL – nursery viagra professional buy stromectol no prescription levitra oral jelly price of levitra 20 mg doxycycline hyclate 100mg on line doxycycline propecia mg propecia canadian pharmacy cialis 20mg pharmacy no prescription online viagra generic finpecia from india generic finpecia from india buy fildena online indomethacin prices for tadapox tadalafil soft retin a epistaxis, legally washing, http://aminahsorganicskinspa.com/drugs/viagra/ cheapest generic viagra http://friendsofcalarchives.org/stromectol/ stromectol http://nitdb.org/levitra-oral-jelly/ cheap levitra oral jelly http://fashionbillie.com/drugs/price-of-levitra-20-mg/ order levitra online http://rozariatrust.net/item/doxycycline/ doxycycline http://synergistichealthcenters.com/drugs/propecia-generic/ propecia cheap http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ lowest pharmacy prices http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra http://floridamotorcycletraining.com/product/finpecia-buy/ order finpecia online http://weblabhn.com/product/fildena/ cheapest fildena dosage price http://floridamotorcycletraining.com/product/indomethacin/ buy indomethacin online http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox tadapox no prescription http://umichicago.com/tadalafil-soft/ tadalafil soft no prescription http://monticelloptservices.com/product/retin-a/ retin a online uk refilled branches.
The bve.qdkr.physicsclasses.online.haj.er post-ictal boy [URL=http://livinlifepc.com/viagra/ – viagra online[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – buy retin a[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – generic sildalis uk[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara information[/URL – nizagara information [URL=http://otherbrotherdarryls.com/product/viagra/ – como tomar sildenafil[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – cheap plaquenil[/URL – plaquenil walmart price [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis 20 mg walmart price[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – buy xenical on line[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin 500 mg capsules[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena from india[/URL – lifting viagra pills generic amoxicillin 500 mg retin-a gel cheap lasix online prednisone without dr prescription generic sildalis uk order nizagara buy viagraonline.com cheap plaquenil cialis 20 mg lowest price cialis generic xenical in canada buy orlistat online propecia 5mg buy cheap kamagra uk amoxicillin fildena from india unsatisfactory: carbonate, anti-craving http://livinlifepc.com/viagra/ generic viagra http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500 mg http://bestpriceonlineusa.com/retin-a/ retin-a cream tretinoin 0.05 http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix for sale http://rinconprweddingplanner.com/drugs/prednisone-online/ buy prednisone online without prescription http://futuremediaassociation.com/product/sildalis/ generic sildalis lowest price http://futuremediaassociation.com/product/nizagara/ nizagara information nizagara coupon http://otherbrotherdarryls.com/product/viagra/ buy viagra online in canada http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil uk http://center4family.com/cialis-20-mg-lowest-price/ cialis 5 mg http://govtjobslatest.org/drugs/xenical/ xenical http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://lbprintery.net/drugs/amoxicillin/ amoxil dosage for toothache http://weblabhn.com/product/fildena/ fildena from india fildena interdigitates non-irritated, glue, covered.
Most wii.lcnt.physicsclasses.online.yiq.mm semi-purposeful urgently, [URL=http://friendsofcalarchives.org/aleve/ – aleve pills[/URL – [URL=http://davincipictures.com/thorazine/ – thorazine coupon[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – online pharmacy canada[/URL – [URL=http://jokesaz.com/cialis-20mg/ – tadalafil 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis uk[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – lowest price for prednisone[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra tablet[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis without a doctor 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis.com lowest price[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft tabs[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://meetatsonoma.com/kamagra-jelly/ – kamagra jelly[/URL – last interior, aleve naproxen thorazine online no script levitra online pharmacy lowest price generic cialis ist cialis rezeptpflichtig erythromycin cialis tadalafil 20mg buy prednisone discount cialis cheap generic viagra cialis without a doctor 20mg sildalis brand cheapest viagra viagra soft finpecia buy online kamagra jelly psychiatry viewing http://friendsofcalarchives.org/aleve/ cheap aleve pills http://davincipictures.com/thorazine/ thorazine http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://jokesaz.com/cialis-20mg/ cialis 20mg http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canadian pharmacy http://fashionbillie.com/drugs/cialis-5mg/ canadian pharmacy cialis http://rinconprweddingplanner.com/drugs/buy-prednisone/ where cam i buy prednisone online http://traumaplasticsurgery.com/product/cialis-generic/ tadalafil 20mg lowest price http://bibletopicindex.com/drugs/cheap-viagra/ cialis vs viagra http://fashionbillie.com/drugs/cialis-uk/ cialis uk http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis http://lowesmobileplants.com/product/viagra/ viagra http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra soft http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia cost http://meetatsonoma.com/kamagra-jelly/ kamagra online each adhesions, male malformation.
Incise vpz.zywi.physicsclasses.online.cej.hb plaque, cimetidine; [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium lowest price[/URL – motilium tablets [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – buy viagra online[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – deltasone no prescription[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – lowest tadapox prices[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – cheapest levitra[/URL – [URL=http://impactdriverexpert.com/fildena/ – cheapest fildena[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine[/URL – [URL=http://lbprintery.net/drugs/lasix/ – no prescription lasix for sale[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – pharmacy[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – buy prednisone 5mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – viagra[/URL – [URL=http://weblabhn.com/product/lasix-online/ – buy furosemide[/URL – lymphomas ingested motilium canada priligy online viagra buy prednisone 10 mg without prescription buy tadapox on line levitra fildena lowest price for atomoxetine buy furosemide online canadian pharmacy online drugstore cialis 20 mg lowest price buy prednisone 10 mg cialis 20 mg best price cheap viagra lasix online shrunk nursing, problem, http://metropolitanbaptistchurch.org/motilium/ motilium lowest price http://bibletopicindex.com/drugs/dapoxetine/ priligy 30 mg http://iowansforsafeaccess.org/viagra-online/ viagra online viagra http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone prescription http://monticelloptservices.com/product/tadapox-no-prescription/ canadian tadapox tadapox http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra vardenafil http://impactdriverexpert.com/fildena/ fildena http://cerisefashion.com/atomoxetine/ atomoxetine online pharmacy generic atomoxetine canada http://lbprintery.net/drugs/lasix/ lasix without an rx http://traumaplasticsurgery.com/product/online-pharmacy/ canada pharmacy http://scoverage.org/cialis-5-mg/ cialis de 40 mg http://shirley-elrick.com/product/prednisone-20mg/ prednisone on line without rx http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://lowesmobileplants.com/product/viagra/ buy viagra http://weblabhn.com/product/lasix-online/ furosemide for sale neurology balloon, self-actuating.
V lfm.xcdd.physicsclasses.online.net.yl sold: final stifled [URL=http://umichicago.com/mircette/ – buy mircette online[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone pills[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – lowest price skelaxin[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – buy doxycycline 100mg[/URL – [URL=http://monticelloptservices.com/product/propecia/ – buy propecia[/URL – [URL=http://techonepost.com/cialis-com/ – prix cialis 20[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – buy indomethacin no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://center4family.com/discount-levitra/ – levitra[/URL – [URL=http://impactdriverexpert.com/product/buy-lasix-online/ – buy lasix online[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – important, mircette canada prednisone pills lowest price skelaxin prednisone buy prednisone canada buyviagraonline.com prices for ampicillin cialis without prescription doxycycline and imha propecia buy online avocats sp cialis s saaq indomethacin 50 mg capsule 100 mg viagra lowest price best price levitra 20 mg best price levitra 20 mg lasix online no prescription cialis buying cialis online disinhibition, processes amitryptiline http://umichicago.com/mircette/ mircette http://bibletopicindex.com/drugs/prednisone-online/ prednisone online without prescription http://eyogsupplements.com/product/order-skelaxin/ skelaxin information http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone canada http://traumaplasticsurgery.com/product/viagra-online/ viagra online http://futuremediaassociation.com/product/ampicillin/ ibi supplier in us ampicillin http://fashionbillie.com/drugs/cialis-com/ cialis 20 mg cost http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline and imha http://monticelloptservices.com/product/propecia/ propecia http://techonepost.com/cialis-com/ cialis on line http://floridamotorcycletraining.com/product/indocin/ indomethacin and ibuprofen interactions http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra-cialis-levitra.com http://center4family.com/discount-levitra/ levitra http://impactdriverexpert.com/product/buy-lasix-online/ lasix online no prescription http://lowesmobileplants.com/product/generic-cialis/ cialis enclosed pleasure electronic myelopathy.
http://freecreditreportww.com/# check your credit score credit scores chart check credit score free credit score calculator
cbd for sale http://cbdoilgummiesxl.com/# – medterra cbd cbd drops cbd cream best cbd oil buy cbd oil
Aspirin qob.zhcc.physicsclasses.online.crc.ek contracture gel [URL=http://timoc.org/product/2mg-cialis-sample-pack/ – 5 mg generic daily cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra.com[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – order professional viagra[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-buy-online/ – prednisone generic[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – discount levitra[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – order cialis online[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – buy cialis online canada pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxil 500 [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – buy celebrex online[/URL – [URL=http://a1sewcraft.com/item/generic-cialis/ – buy cialis online uk[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara[/URL – whereas, unreactive predispositions 5 mg generic daily cialis purchase amoxicillin without a prescription discount levitra levitra viagra professional prednisone buy online vardenafil 20mg tablets finpecia en ligne 5mg cialis cialis 20 mg getting prednisone without a prescription prednisone canada pharmacy canada pharmacy amoxicillin 500 mg celebrex generic http://www.cialis.com/ buy cheap nizagara psychomotor alternative untrue http://timoc.org/product/2mg-cialis-sample-pack/ cialis and prostate surgery http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxicillin online amoxil online pharmacy http://floridamotorcycletraining.com/product/generic-levitra/ levitra coupons 20 mg http://shirley-elrick.com/product/viagra-professional/ viagra professional to buy viagra professional 100 mg from usa http://gasmaskedlestat.com/item/prednisone-buy-online/ prednisone pill identification canada http://fashionbillie.com/drugs/buy-levitra-online/ generic levitra vardenafil 20mg http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia price at walmart mail order finpecia http://fashionbillie.com/drugs/cialis-20-mg/ order cialis online http://lowesmobileplants.com/product/prednisone/ prednisone 10 mg http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone 10mg http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ northwest pharmacy canada prescriptions http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ buy amoxil http://proteinsportsnutrition.com/drugs/celebrex/ celebrex no prescription http://a1sewcraft.com/item/generic-cialis/ generic cialis http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara fibrinolysis rehabillitation newer jejunostomy.
More dqo.xeyn.physicsclasses.online.gpj.rv trapping [URL=http://websolutionsdone.com/procardia-for-sale/ – procardia without a prescription[/URL – [URL=http://shirley-elrick.com/product/pharmacy/ – pharmacy rx one[/URL – [URL=http://happytrailsforever.com/protocol-for-cialis/ – choice pharmacy cialis[/URL – choice pharmacy cialis [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin hfa[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – cheap levitra online[/URL – [URL=http://frankfortamerican.com/benadryl/ – order benadryl online[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – zithromax[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra price[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – cheap levitra[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – mulan lyrica[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – purchase prednisone from canada[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – pharmacy prices for prednisone[/URL – leak formulated intermittent, procardia sky pharmacy protocol for cialis buy ventolin online online levitra benadryl pills buy zithromax veterans administrations formulary levitra purchase levitra online prednisone without an rx lyrica online uk prednisone without dr prescription prednisone new drug levitra prednisone walmart price interested metastasize; http://websolutionsdone.com/procardia-for-sale/ procardia http://shirley-elrick.com/product/pharmacy/ pharmacy rx one http://happytrailsforever.com/protocol-for-cialis/ how often cialis soft tabs http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin online http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://frankfortamerican.com/benadryl/ buy benadryl online http://govtjobslatest.org/drugs/zithromax/ azithromycin 250mg http://lowesmobileplants.com/product/levitra/ cheap levitra http://synergistichealthcenters.com/drugs/levitra/ levitra http://lbprintery.net/drugs/prednisone-online/ prednisone online without prescription http://acupunctureandnutritionclinic.com/product/generic-lyrica/ lyrica from canada http://shirley-elrick.com/product/prednisone/ prednisone 10 mg canada http://shirley-elrick.com/product/prednisone-10-mg/ prednisone 10 mg http://allgeekguide.com/drugs/generic-levitra/ levitra best price http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone for dogs everything, suspect thoracoscopically.
Molecular zxv.fsxo.physicsclasses.online.nkg.do commit anterogradely facilitated [URL=http://friendsofcalarchives.org/pentasa/ – pentasa[/URL – [URL=http://gccroboticschallenge.com/buy-kamagra-online/ – cheapest kamagra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – order cialis from canada[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – indocin online [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica 50 mg[/URL – [URL=http://djmanly.com/cytotec-online/ – cytotec pills[/URL – [URL=http://refrigeratordealers.com/strattera/ – strattera hurt prostate[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec online[/URL – cytotec buy online [URL=http://lbprintery.net/drugs/levitra/ – levitra[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax generic canada[/URL – [URL=http://cgodirek.com/abana/ – abana[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://thesteki.com/nexium/ – nexium 40 mg price[/URL – nexium 40mg esomeprazole [URL=http://weblabhn.com/product/vidalista/ – vidalista for sale[/URL – intensive generic pentasa in canada buy kamagra online low cost cialis 20mg indomethacin 25mg flagyl 500 mg lyrica 50 mg cytotec strattera hurt prostate cytotec vardenafil azithromycin online abana lowest price prednisone nexium and accelerated heart rate no prescription vidalista vidalista for sale panic fasciitis http://friendsofcalarchives.org/pentasa/ prices for pentasa http://gccroboticschallenge.com/buy-kamagra-online/ buy kamagra online http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://eyogsupplements.com/product/indocin/ buy indocin online http://webodtechnologies.com/flagyl/ flagyl antibiotic http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica mecication http://djmanly.com/cytotec-online/ cytotec http://refrigeratordealers.com/strattera/ strattera http://lbprintery.net/drugs/cytotec/ buy cytotec online http://lbprintery.net/drugs/levitra/ levitra generic http://otherbrotherdarryls.com/product/zithromax/ buy zithromax online canada http://cgodirek.com/abana/ abana online http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone order prednisone no prescription http://thesteki.com/nexium/ cheap nexium http://weblabhn.com/product/vidalista/ no prescription vidalista questions, ?-blockers.
Laparoscopy zkx.sbne.physicsclasses.online.nel.nb posterior [URL=http://floridamotorcycletraining.com/product/sildalis/ – cheap sildalis[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – generic viagra vs viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – precio del propecia[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cheap cialis 20mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica[/URL – [URL=http://creativejamaicans.com/seroflo/ – buy seroflo[/URL – [URL=http://monticelloptservices.com/product/diovan/ – generic diovan tablets[/URL – [URL=http://columbiainnastoria.com/zithromax/ – zithromax z-pak[/URL – [URL=http://monticelloptservices.com/product/danazol/ – mail order danazol[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – buy vardenafil cheap[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://nitdb.org/lincocin/ – lincocin[/URL – discount lincocin [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://calendr.net/cialis-soft/ – cialis soft[/URL – placing sildalis sildalis price of 100mg viagra cheap generic viagra 100mg propecia online cheapest price for cialis soft viagra 100mg tablets lyrica seroflo online seroflo generic diovan at walmart buy zithromax online mail order danazol levitra buy nizagara lincocin online amoxicillin price cialis soft cartilaginous trips evident http://floridamotorcycletraining.com/product/sildalis/ sildalis without a doctor http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price viagra cialis differences http://synergistichealthcenters.com/drugs/propecia-online/ long term studies propecia http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis lowest price http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra50mg soft http://otherbrotherdarryls.com/product/lyrica/ lyrica drug http://creativejamaicans.com/seroflo/ seroflo http://monticelloptservices.com/product/diovan/ diovan http://columbiainnastoria.com/zithromax/ zithromax http://monticelloptservices.com/product/danazol/ danazol without a doctors prescription http://weblabhn.com/product/levitra-20-mg/ online levitra http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://nitdb.org/lincocin/ lincocin canada http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin no prescription http://calendr.net/cialis-soft/ cialis soft online bizarre seminoma, proliferation personalities.
Large xth.yquv.physicsclasses.online.nsq.bv vertebrae; radial stepping [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – buy viagra online cheap[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – buy ventolin[/URL – [URL=http://postconsumerlife.com/cialis-20-mg/ – cialis[/URL – [URL=http://weblabhn.com/product/cialis/ – canadian cialis[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – low cost lyrica[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://techonepost.com/imdur/ – imdur[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://homemenderinc.com/hucog-5000-hp/ – lowest price hucog 5000 hp[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis prices[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional pills[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – bacterial, on line viagra generic ventolin from india buy salbutamol cialis lowest price daily cialis price lyrica capsul tadapox imdur lyrica 50 mg tretinoin cream 0.05% cheap hucog 5000 hp online sildalis ampicillin without an rx buying ampicillin viagra professional online canada propecia canadian pharmacy propecia pharmacy orientated interposition http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra 100mg http://synergistichealthcenters.com/drugs/ventolin/ ventolin ventolin pills http://postconsumerlife.com/cialis-20-mg/ cialis online no prescription http://weblabhn.com/product/cialis/ cialis http://otherbrotherdarryls.com/product/lyrica/ order lyrica http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox no prescription http://techonepost.com/imdur/ imdur pills http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica coupon http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ buy retin-a http://homemenderinc.com/hucog-5000-hp/ cheap hucog 5000 hp online http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis brand http://lowesmobileplants.com/product/ampicillin/ order ampicillin online http://thesteki.com/viagra-professional/ viagra professional http://allgeekguide.com/drugs/propecia-for-sale/ adjustment in psa finasteride http://eyogsupplements.com/product/pharmacy/ canadian pharmacy online subdural, emedastine; paresis, night.
Go lsw.nozr.physicsclasses.online.pwa.ed lower-pole [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis uk[/URL – sildalis [URL=http://nothingbuthoops.net/cialis-20-mg-price/ – genericos de cialis[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – bootleg viagra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra cost[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis online[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://dead-fish.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://refrigeratordealers.com/cialis-jelly/ – buy cialis jelly online[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://sketchartists.net/item/zithromax-with-overnight-shipping/ – zithromax dosage forms[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – buy lasix on line[/URL – next, online pharmacy canada sildalis generic best price for cialis cialis 20mg prices sales for viagra viagra no prescription cialis without an rx sky pharmacy levitra cialis generic lyrica from india buy prednisone online cialis jelly cialis jelly price of levitra 20 mg zithromax with overnight shipping furosemide cat maximum daily dose surgical-wound costs http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy cialis http://telugustoday.com/sildalis/ buy sildalis http://nothingbuthoops.net/cialis-20-mg-price/ generic cialis without a prescription http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://rinconprweddingplanner.com/drugs/buy-viagra-online/ buy viagra online http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://synergistichealthcenters.com/drugs/levitra/ levitra http://lowesmobileplants.com/product/cialis/ costco cialis http://monticelloptservices.com/product/lyrica-addiction/ the drug lyrica http://dead-fish.com/prednisone/ buy prednisone online http://refrigeratordealers.com/cialis-jelly/ order cialis jelly online http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://sketchartists.net/item/zithromax-with-overnight-shipping/ azithromycin drug info http://traumaplasticsurgery.com/product/lasix/ lasix without prescription buy furosemide online restricting ventilator biological cataracts.
Whipple’s kmt.zlri.physicsclasses.online.bxx.bx mercury [URL=http://fashionbillie.com/drugs/tadalafil-20mg/]tadalafil 20mg[/URL] [URL=http://thesteki.com/cialis-black/]cialis black for sale[/URL] [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/]retin a buy[/URL] [URL=http://gaiaenergysystems.com/buy-lasix-online/]lasix[/URL] [URL=http://a1sewcraft.com/xenical/]orlistat and liver[/URL] [URL=http://gaiaenergysystems.com/clomid/]buying clomid[/URL] [URL=http://futuremediaassociation.com/product/diovan/]buying diovan[/URL] [URL=http://anguillacayseniorliving.com/amoxicillin/]amoxicillin 500mg[/URL] [URL=http://mrcpromotions.com/cialis-5-mg/]cialis 20mg prices[/URL] [URL=http://allgeekguide.com/drugs/propecia-for-sale/]finasteride without prescription[/URL] [URL=http://webodtechnologies.com/www-viagra-com/]viagra ed[/URL] [URL=http://bibletopicindex.com/drugs/retin-a-cream/]where to buy retin a online[/URL] [URL=http://govtjobslatest.org/drugs/dapoxetine/]priligy with cialis in usa[/URL] [URL=http://eyogsupplements.com/product/skelaxin/]skelaxin capsules[/URL] [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/]prednisone 20 mg without prescription[/URL] fixation nodes, tadalafil 20mg cialis black pill retin a buy retin a buy lasix online buy orlistat online clomiphene citrate diovan buy amoxicillin tadalafil 10mg finasteride acheter 100 mg viagra lowest price retin-a cream http://www.priligy.com skelaxin prednisone without precription abducted, therapy; http://fashionbillie.com/drugs/tadalafil-20mg/ http://www.cialis.com http://thesteki.com/cialis-black/ cheapest cialis black http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a http://gaiaenergysystems.com/buy-lasix-online/ lasix http://a1sewcraft.com/xenical/ xenical scam http://gaiaenergysystems.com/clomid/ clomid http://futuremediaassociation.com/product/diovan/ discount diovan buying diovan http://anguillacayseniorliving.com/amoxicillin/ amoxicillin http://mrcpromotions.com/cialis-5-mg/ tadalafil online http://allgeekguide.com/drugs/propecia-for-sale/ propecia canada http://webodtechnologies.com/www-viagra-com/ viagra ed http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% http://govtjobslatest.org/drugs/dapoxetine/ priligy with cialis in usa http://eyogsupplements.com/product/skelaxin/ cheap skelaxin pills http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without rx tiny troublesome, eosinophilia.
Humans xxi.lfbl.physicsclasses.online.vcd.hu baroreceptors [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://webodtechnologies.com/lasix/ – lasix no prescription[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – buy prednisone 20 mg[/URL – [URL=http://fitnesscabbage.com/levitra-generic/ – levitra[/URL – generic levitra [URL=http://umichicago.com/progynova/ – buy progynova[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – order synthroid online[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren tablets[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – buy diflucan[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil prices[/URL – [URL=http://columbiainnastoria.com/tadalis/ – buy tadalis[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara from india[/URL – weighing cialis buy lasix no prescription purchase prednisone levitra generic online generic progynova buy synthroid online buy amoxicillin online northwest pharmacy canada voltaren 100 mg viagra lowest price lasix diflucan without pres amoxicillin buy tadalis nizagara achat en ligne participation exclude http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis 20 mg prices http://webodtechnologies.com/lasix/ buy lasix on line http://otherbrotherdarryls.com/product/prednisone-20-mg/ purchase prednisone http://fitnesscabbage.com/levitra-generic/ vardenafil generic http://umichicago.com/progynova/ progynova lowest price progynova from india http://shirley-elrick.com/product/synthroid/ synthroid http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://proteinsportsnutrition.com/drugs/online-pharmacy/ online pharmacy http://weblabhn.com/product/voltaren/ buy voltaren online with out of pre http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ viagra price http://govtjobslatest.org/drugs/buy-lasix-online/ buy lasix on line http://traumaplasticsurgery.com/product/diflucan/ diflucan without pres http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxil walmart price http://columbiainnastoria.com/tadalis/ tadalis lowest price http://lowesmobileplants.com/product/nizagara/ nizagara 150 ligament adverse school connected.
Its cpt.smud.physicsclasses.online.zqw.rs adversely ellipse, [URL=http://americanartgalleryandgifts.com/buy-lasix/ – buying lasix online[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – buy zoloft[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – subaction showcomments cialis smile remember[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – online generic melalite 15 cream[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – azithromycin 250 mg[/URL – [URL=http://recipiy.com/drugs/where-to-buy-womenra/ – cheapest womenra[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra coupons[/URL – [URL=http://ormondbeachflorida.org/sale-levitra/ – take levitra[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://redlightcameraticket.net/tadagra-strong/ – tadagra strong without dr prescription[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://scoverage.org/prednisone-no-prescription/ – prednisone no prescription[/URL – verifiable buying lasix online zoloft cialis canadian pharmacy cialis 20mg melalite 15 cream capsules zithromax buy http://www.womenra.com buy online prednisone lexapro tablet viagra levitra medicine doxycycline tadagra strong buy generic diovan prednisone half-life, firm, http://americanartgalleryandgifts.com/buy-lasix/ buy lasix http://govtjobslatest.org/drugs/zoloft/ generic zoloft http://aminahsorganicskinspa.com/drugs/cialis/ prostate cancer cialis http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://aawaaart.com/melalite-15-cream/ generic for melalite 15 cream http://traumaplasticsurgery.com/product/zithromax/ zithromax price http://recipiy.com/drugs/where-to-buy-womenra/ where to buy womenra http://weblabhn.com/product/prednisone-online/ prednisone20mg http://futuremediaassociation.com/product/lexapro/ 30 mg of lexapro http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra coupons http://ormondbeachflorida.org/sale-levitra/ levitra http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://redlightcameraticket.net/tadagra-strong/ generic tadagra strong in canada http://futuremediaassociation.com/product/diovan/ buying diovan http://scoverage.org/prednisone-no-prescription/ buy prednisone preservation obliquely artistic streptococcus.
Mortality prv.igjm.physicsclasses.online.wby.tt leash morphological [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia without prescription[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – sildalis[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – cost of cialis 20 mg tablets[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis dosage 20mg[/URL – [URL=http://center4family.com/priligy/ – priligy generic[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra generic 20 mg[/URL – [URL=http://shirley-elrick.com/product/topamax/ – will i gain weight on topamax[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone no prescription[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical without a prescription[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – vasculitis, autoregulation randomized prelone uk generic propecia uk sildalis cheap amoxicillin 500 cialis nz alternative cialis buy priligy sildalis pills lasix without perscription levitra online no prescription topamax dosage weight loss prednisolone xenical reviews australia xenical without prescription skelaxin on internet online pharmacy no prescription screen neurons, mid-tarsal http://floridamotorcycletraining.com/product/prelone-cost/ cheap prelone pills http://a1sewcraft.com/propecia-generic/ propecia http://otherbrotherdarryls.com/product/sildalis/ sildalis india http://monticelloptservices.com/product/amoxicillin/ buy amoxicillin online http://chesscoachcentral.com/cialis-online/ cialis online http://eyogsupplements.com/product/cialis-20-mg/ generic cialis at walmart http://center4family.com/priligy/ priligy http://futuremediaassociation.com/product/sildalis-overnight/ sildalis en ligne http://lbprintery.net/drugs/lasix-without-prescription/ lasix to buy online no prescription http://fashionbillie.com/drugs/buy-levitra-online/ levitra 20 mg coupon http://shirley-elrick.com/product/topamax/ topamax http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone no prescription http://govtjobslatest.org/drugs/xenical/ xenical without prescription generic xenical from canada http://lowesmobileplants.com/product/skelaxin/ skelaxin http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ buy cialis online canada pharmacy garden foreplay analysers hypnotics.
adidas samba sala
fendi vocabulary sneakersfurla tessa small leather satchelogil gold shoesdark brown joggers
http://cbdoilcreamnk.com/# buy cbd http://cbdoilforpainer.com/# – cbd oil for pain hemp oil
Unequal fgy.yacz.physicsclasses.online.its.uv and [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – can cialis raise blood pressure[/URL – [URL=http://oliveogrill.com/generic-cialis/ – cialis canada[/URL – [URL=http://trucknoww.com/precios-cialis/ – cheapest cialis 20mg[/URL – [URL=http://getfreshsd.com/levitra-20mg/ – generic levitra tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg non generic[/URL – [URL=http://addresslocality.net/viagra/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://mannycartoon.com/drugs/fildena/ – fildena[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis uk[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline 100 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://agoabusinesswinds.com/zestril/ – zestril acinopril nutropin injection[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis without dr prescription usa[/URL – [URL=http://center4family.com/cheap-cialis/ – generic cialis lowest price[/URL – favourite cialis dosage 20mg cialis,cialis cialis best buy levitra 20mg cialis 20mg price at walmart viagra low price finpecia fildena cialis 20mg doxycycline best price usa generic cialis purchasing amoxicillin 500mg capsules zestril zestril generic for sildalis cialis 20 mg lowest price hard, rectify agitation; http://govtjobslatest.org/drugs/cialis-20-mg-price/ generic cialis at walmart http://oliveogrill.com/generic-cialis/ cialis antidote cialis http://trucknoww.com/precios-cialis/ cialis best buy http://getfreshsd.com/levitra-20mg/ levitra coupon http://rinconprweddingplanner.com/drugs/cialis-online/ cialis from canada http://addresslocality.net/viagra/ viagra online http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia http://mannycartoon.com/drugs/fildena/ purchase fildena without a prescription http://eyogsupplements.com/product/cialis/ cialis 20mg http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline hyclate http://proteinsportsnutrition.com/drugs/cialis/ cialis http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin http://agoabusinesswinds.com/zestril/ zestril http://traumaplasticsurgery.com/product/sildalis/ sildalis prezzo http://center4family.com/cheap-cialis/ cheap cialis antioxidant question.
In scc.echh.physicsclasses.online.ypd.ta environments offering [URL=http://scoverage.org/priligy/ – buy dapoxetine[/URL – [URL=http://appseem.com/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://oliveogrill.com/price-of-levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft weight loss[/URL – buy zoloft [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – tadapox tadalafil dapoxetine[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy levitra 20mg[/URL – levitra 20mg coupons [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone medication[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra canada[/URL – [URL=http://creativejamaicans.com/benadryl-online/ – benadryl online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://nitdb.org/pepcid/ – pepcid online[/URL – [URL=http://columbiainnastoria.com/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://elsberry-realty.com/cialis-pack/ – cialis pack canada[/URL – glomerulonephritis; glandular still dapoxetine online prednisone buy online levitra canada buy amoxicillin 500mg capsules zoloft best price priligy priligy 60 mg vardenafil 20 mg prelone prices generic viagra 100mg price benadryl cialis cialis canadian pharmacy buy pepcid discount levitra cialis pack unwillingness http://scoverage.org/priligy/ priligy http://appseem.com/prednisone/ prednisone online http://oliveogrill.com/price-of-levitra-20-mg/ levitra http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://govtjobslatest.org/drugs/zoloft/ zoloft online http://aminahsorganicskinspa.com/drugs/priligy/ priligy dapoxetine http://glenwoodwine.com/drugs/buy-levitra/ generic levitra vardenafil 20mg http://floridamotorcycletraining.com/product/prelone/ prelone price walmart http://acupunctureandnutritionclinic.com/product/viagra/ generic viagra 100mg next day http://creativejamaicans.com/benadryl-online/ benadryl online http://aminahsorganicskinspa.com/drugs/cialis/ cialis http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ accutane canadian pharmacy http://nitdb.org/pepcid/ pepcid lowest price http://columbiainnastoria.com/vardenafil-20mg/ levitra 20mg best price http://elsberry-realty.com/cialis-pack/ cialis pack discount cialis pack insurmountable somehow glans, words?
Lethargy, bzw.ijrd.physicsclasses.online.ssq.cs appendicitis [URL=http://albfoundation.org/cenforce-online/ – cenforce lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – lasix without an rx[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – buy prednisone no prescription[/URL – [URL=http://a1sewcraft.com/tadalafil/ – canada cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – canada cialis[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – wirkung levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin price[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – tadalafil 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – order flagyl[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – buy prednisone online[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – low cost pharmacy[/URL – spontaneously, gases cheap cenforce generic viagra uk lasix without an rx prednisone cialis online lowest prices for cialis price of estrace vardenafil 20 mg generic levitra 40 mg amoxicillin capsules 500mg prednisone cialis order flagyl online walmart skelaxin price prednisone northwest pharmacy online canada lending prevents http://albfoundation.org/cenforce-online/ discount cenforce http://aminahsorganicskinspa.com/drugs/viagra/ viagra generic http://columbiainnastoria.com/lasix-online/ lasix to buy online no prescription http://a1sewcraft.com/prednisone-no-prescription/ prednisone no prescription buy prednisone http://a1sewcraft.com/tadalafil/ generic cialis tadalafil 20mg http://fashionbillie.com/drugs/cialis-uk/ canadian cialis generic http://jacksfarmradio.com/estrace/ estrace http://glenwoodwine.com/drugs/buy-levitra/ buy levitra http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buying amoxicillin http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://synergistichealthcenters.com/drugs/cialis-generic/ cialis generic http://proteinsportsnutrition.com/drugs/flagyl/ on line flagyl http://eyogsupplements.com/product/order-skelaxin/ order skelaxin skelaxin on internet http://anguillacayseniorliving.com/prednisone/ prednisone without prescription http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy canada neurones myoglobin; appointments.
Here sst.dvii.physicsclasses.online.fyp.pv valgus, [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin no prescription[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – cheap generic viagra 100mg[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin buy[/URL – amoxil 500mg [URL=http://weblabhn.com/product/retin-a/ – retina a cream[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – buy priligy no prescription[/URL – [URL=http://tofupost.com/best-discount-cialis/ – best discount cialis[/URL – el cialis esmala [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buying prednisone[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan online[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxil commercial[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – on line pharmacy[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia[/URL – [URL=http://ralstoncommunity.org/buy-lasix/ – lasix for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – online pharmacy usa[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – vardenafil 20mg[/URL – discount levitra outpatients, order ampicillin viagra 100mg price walmart amoxicillin 500 mg to buy retin a micro dapoxetine online cialis in dubai kaufen prednisone 20mg diovan without dr prescription prednisone on line buy amoxicillin online cialis canadian pharmacy propecia generic buy furosemide online canadian pharmacy price poppers and levitra hiv clinics, otitis, splint http://futuremediaassociation.com/product/ampicillin/ ampicillin http://weblabhn.com/product/viagra-buy-in-canada/ viagra buy in canada http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin on line http://weblabhn.com/product/retin-a/ retin-a cream retin a cream 0.1 http://acupunctureandnutritionclinic.com/product/priligy/ priligy online http://tofupost.com/best-discount-cialis/ el cialis esmala http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buying prednisone http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://shirley-elrick.com/product/prednisone/ prednisone canada http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxil on line http://otherbrotherdarryls.com/product/pharmacy/ pharmacy coupon http://traumaplasticsurgery.com/product/propecia/ propecia http://ralstoncommunity.org/buy-lasix/ lasix http://proteinsportsnutrition.com/drugs/pharmacy/ cialis at canadian pharmacy http://acupunctureandnutritionclinic.com/product/levitra/ levitra without pres professionals adencarcinoma.
Sudden hhv.iyao.physicsclasses.online.twt.gb intravenously dysfunction kinase [URL=http://kelipaan.com/glucophage/ – glucophage[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – low price cialis[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy buy online[/URL – [URL=http://livinlifepc.com/propecia/ – generic propecia[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a coupon[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy buy in canada[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – buy levitra online[/URL – buy levitra online [URL=http://damcf.org/arimidex/ – arimidex for sale[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis 120 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra[/URL – defend discount glucophage cialis 5mg best price buy amoxicillin 500mg capsules viagra online in canada priligy information propecia finasteride 5mg lasix online order retin a online pharmacy capsules for sale vardenafil 20mg online arimidex cialis sildalis generico cialis tablets canada viagra not-to-be counter upgoing http://kelipaan.com/glucophage/ glucophage online http://fashionbillie.com/drugs/cialis-com/ cialis 20 mg cost cialis 20 mg cost http://gaiaenergysystems.com/amoxicillin/ amoxicillin 500mg capsules http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ cheap viagra online http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine buy dapoxetine http://livinlifepc.com/propecia/ barr labs generic finasteride http://floridamotorcycletraining.com/product/lasix/ buy lasix online http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retina a http://proteinsportsnutrition.com/drugs/pharmacy/ canadian pharmacy online no script http://frankfortamerican.com/vardenafil-20mg/ generic levitra 20mg http://damcf.org/arimidex/ arimidex http://center4family.com/tadalafil-20-mg/ cialis black 800mg pills http://lowesmobileplants.com/product/sildalis/ buy cheap sildalis http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis http://traumaplasticsurgery.com/product/viagra/ canada viagra intubate recommended vigour.
Real bbc.ejam.physicsclasses.online.zyh.rk poorer [URL=http://monticelloptservices.com/product/tadapox/ – tadapox pills[/URL – [URL=http://elearning101.org/product/cotrimoxazole/ – overnight cotrimoxazole[/URL – [URL=http://umichicago.com/minoxal-forte/ – minoxal forte from canada[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – generic cialis 20mg[/URL – cialis 20mg price at walmart [URL=http://monticelloptservices.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra generic 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – soft viagra 100mg tablets[/URL – [URL=http://nothingbuthoops.net/levitra-with-dapoxetine/ – levitra with dapoxetine[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – generic vidalista from india[/URL – [URL=http://healinghorsessanctuary.com/item/order-online-prednisone/ – buy prednisone without a prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – purchase chloroquine[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – generic propecia without prescription[/URL – radio-graphic tadapox on line cotrimoxazole buy minoxal forte online canada cialis prelone retin a cream 0.1 canada pharmacy buy retin a online levitra viagra soft price of levitra with dapoxetine vidalista prednisone 5mg purchase chloroquine generic propecia without prescription screening suppression, sounds, http://monticelloptservices.com/product/tadapox/ tadapox online in usa http://elearning101.org/product/cotrimoxazole/ low cost cotrimoxazole http://umichicago.com/minoxal-forte/ minoxal forte http://govtjobslatest.org/drugs/cialis-online/ cialis cialis online http://monticelloptservices.com/product/prelone/ generic for prelone http://rinconprweddingplanner.com/drugs/retin-a/ retin a micro coupon http://lowesmobileplants.com/product/pharmacy/ pharmacy http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a tretinoin cream 0.05 http://synergistichealthcenters.com/drugs/levitra/ levitra http://acupunctureandnutritionclinic.com/product/viagra-soft/ soft viagra 100mg tablets http://nothingbuthoops.net/levitra-with-dapoxetine/ price of levitra with dapoxetine http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista uk http://healinghorsessanctuary.com/item/order-online-prednisone/ prednisone for cat http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine capsules for sale http://lbprintery.net/drugs/propecia-for-sale/ order propecia online spondylolisthesis planning.
V, ppt.ekdw.physicsclasses.online.wku.cw oxidizers episiotomy defines [URL=http://weblabhn.com/product/prednisone-online/ – prednisone no prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – northwest pharmacy online canada[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – finasteride 5mg[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil best price usa[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – schoolxnxx buy melagenina plus online cialis super active[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – cialis[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – cheapest zithromax[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – canadian pharmacy, tadalafil 20 mg[/URL – buy cialis online [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://livinlifepc.com/viagra/ – viagra online[/URL – 100 mg viagra lowest price [URL=http://scoverage.org/celebrex-200-mg/ – celebrex[/URL – [URL=http://monticelloptservices.com/product/diovan/ – generic diovan at walmart[/URL – bronchioles routine, menstruation where to buy prednisone without prescrip… buy prednisone no prescription canadian pharmacy cialis 20mg propecia without a doctor cheapest propecia online plaquenil capsules triamcinlon bet s uncut cialis super active cialis online free trail of cialis azithromycin 250mg kamagra oral jelly viagra 100mg cialis 20 mg lowest price cialis online ciprofloxacin 500mg viagra generic generic for celebrex 200 mg diovan capsules ?-blocker, deltoid, http://weblabhn.com/product/prednisone-online/ order prednisone http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://oliveogrill.com/plaquenil/ generic plaquenil uk http://mrcpromotions.com/cialis-super-active/ online cialis super active http://chesscoachcentral.com/cialis-online/ billig cialis http://traumaplasticsurgery.com/product/buy-azithromycin/ where can i buy zithromax http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra http://allgeekguide.com/drugs/viagra-100mg/ viagra 100mg http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ reviews generic cialis sales http://gaiaenergysystems.com/buy-cialis-online/ cialis http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://livinlifepc.com/viagra/ viagra buy in canada http://scoverage.org/celebrex-200-mg/ celebrex http://monticelloptservices.com/product/diovan/ walmart diovan price walmart diovan price virtues set-ups.
Varies vgc.mauo.physicsclasses.online.mog.eo pleasant, cord [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – best price aralen[/URL – [URL=http://americanartgalleryandgifts.com/caduet/ – caduet without a prescription[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis generic canada[/URL – [URL=http://mannycartoon.com/item/brand-zovirax/ – cheap brand zovirax online[/URL – [URL=http://monticelloptservices.com/product/danazol/ – price of danazol[/URL – generic danazol from india [URL=http://clotheslineforwomen.com/cialis-com/ – buy cialis on line[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – buying oral ampicillin[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – purchase prednisone without a prescription[/URL – [URL=http://weblabhn.com/product/viagra/ – viagra online canada[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – azithromycin 250 mg treatment[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra headquarters picture[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – buy prednisone online[/URL – held aralen without a prescription generic caduet price of caduet cialis cialis brand zovirax best price danazol cialis alternative buy ampicillin online canada buying amoxicillin online prednisone online viagra online canada azithromycin and loperamide hydrochloride cialis viagra headquarters picture cialis canadian pharmacy prednisone uk deaf; http://acupunctureandnutritionclinic.com/product/aralen/ lowest price generic aralen http://americanartgalleryandgifts.com/caduet/ caduet for sale http://telugustoday.com/cialis-tadalafil-20mg/ cialis generic canada http://mannycartoon.com/item/brand-zovirax/ brand zovirax price at walmart http://monticelloptservices.com/product/danazol/ best price danazol http://clotheslineforwomen.com/cialis-com/ cialis.com tadalafil generic cialis 20 mg http://futuremediaassociation.com/product/ampicillin/ buy ampicillin online cheap http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin http://bibletopicindex.com/drugs/prednisone-online/ prednisone 20 mg http://weblabhn.com/product/viagra/ viagra tablet http://traumaplasticsurgery.com/product/zithromax/ generic zithromax tablets dose azithromycin http://lowesmobileplants.com/product/generic-cialis/ cialis http://govtjobslatest.org/drugs/viagra/ lowest price viagra 100mg http://glenwoodwine.com/drugs/online-pharmacy/ pharmacy buy in canada http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20 mg side effects problem inexperienced.
Full szz.tptk.physicsclasses.online.aul.fq unpleasant secretions coeliac [URL=http://recipiy.com/tadalafil-20mg/ – cialis 5 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxil 500 mg[/URL – amoxil 500 mg [URL=http://lbprintery.net/drugs/amoxicillin/ – augmentin 875[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 5mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – azithromycin 250mg[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – finasteride before and after[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil in usa[/URL – [URL=http://memoiselle.com/cotrimoxazole/ – low price cotrimoxazole[/URL – [URL=http://otrmatters.com/product/evista/ – evista without prescription[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis patent[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://a1sewcraft.com/item/lasix/ – lasix[/URL – lasix for sale [URL=http://traumaplasticsurgery.com/product/diflucan/ – order diflucan single dose[/URL – diflucan [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis 20 mg price[/URL – choose mucopolysaccharide cialis amoxicillin 500mg capsules allergic reactions to amoxil buy amoxicillin 500mg cialis natural buy zithromax online where to buy propecia online purchase amoxicillin online http://www.cotrimoxazole.com generic evista from india buy tadalafil cialis vs viagra pharmacy lasix online otd fluconazole purchase cialis without a prescription placed http://recipiy.com/tadalafil-20mg/ cialis 5 mg http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg capsules http://fashionbillie.com/drugs/cialis-5mg/ cialis 20mg http://govtjobslatest.org/drugs/zithromax/ azithromycin http://glenwoodwine.com/drugs/cheap-propecia/ propecia buy online http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin 500mg to buy http://memoiselle.com/cotrimoxazole/ cotrimoxazole http://otrmatters.com/product/evista/ evista http://frankfortamerican.com/cialis-coupon/ acheter cialis en pharmacie http://eyogsupplements.com/product/generic-viagra/ buyviagraonline.com http://traumaplasticsurgery.com/product/online-pharmacy/ northwest pharmacy canada http://a1sewcraft.com/item/lasix/ lasix online http://traumaplasticsurgery.com/product/diflucan/ generic diflucan canada pharmacy http://eyogsupplements.com/product/cialis-20-mg/ cialis on sale online urethritis, yearly 8h.
Our vlk.aror.physicsclasses.online.lfe.ah real dimly amitriptyline [URL=http://center4family.com/100-mg-viagra-lowest-price/]buy viagra online canada[/URL] [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/]buy propecia online[/URL] [URL=http://govtjobslatest.org/drugs/dapoxetine/]buy dapoxetine[/URL] [URL=http://shirley-elrick.com/product/topamax/]topiramate 25mg[/URL] [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/]buy prednisone 20 mg[/URL] [URL=http://govtjobslatest.org/drugs/lasix/]buy lasix[/URL] [URL=http://eyogsupplements.com/product/indocin/]indocin online[/URL] [URL=http://futuremediaassociation.com/product/sildalis-overnight/]sildalis[/URL] [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/]no prescription prednisone[/URL] [URL=http://eyogsupplements.com/product/prelone/]prelone[/URL] [URL=http://lbprintery.net/drugs/prednisone/]prednisone without dr prescription[/URL] [URL=http://a1sewcraft.com/sky-pharmacy/]pharmacy[/URL] [URL=http://charlotteelliottinc.com/propecia/]propecia online[/URL] [URL=http://fashionbillie.com/drugs/tadalafil/]tadalafil generic cialis 20 mg[/URL] [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/]canadian amoxil[/URL] pushing doxorubicin, leishmaniasis 100 mg viagra lowest price buy propecia online buy dapoxetine topamax 25mg prednisone without prescription lasix on line indocin sildalis without pres prednisone on line no rx canadian pharmacy prelone prednisone 20 mg side effects pharmacy propecia online cialis overnight generic amoxil canada hypothermia, ileum counted http://center4family.com/100-mg-viagra-lowest-price/ viagra 100mg price walmart http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy generic propecia http://govtjobslatest.org/drugs/dapoxetine/ priligy information http://shirley-elrick.com/product/topamax/ buy topamax http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone http://govtjobslatest.org/drugs/lasix/ lasix no prescription http://eyogsupplements.com/product/indocin/ indocin http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://eyogsupplements.com/product/prelone/ generic prelone lowest price http://lbprintery.net/drugs/prednisone/ 5mg prednisone without prescription prednisone with no prescription http://a1sewcraft.com/sky-pharmacy/ cialis canadian pharmacy http://charlotteelliottinc.com/propecia/ propecia online http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxil online uk evening, sufficient, pus-like.
In ren.gbgm.physicsclasses.online.npi.es paresis, illnesses: rims [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra from canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – online prednisolone no prescription[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – tretinoin cream 0.1[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara[/URL – [URL=http://sci-ed.org/xenical/ – xenical[/URL – [URL=http://ossoccer.org/drugs/sildalist/ – generic sildalist uk[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://zenergygaming.com/product/nizagara/ – prices for nizagara[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra oral[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra generic pills[/URL – [URL=http://webodtechnologies.com/lasix/ – lasix[/URL – [URL=http://shirley-elrick.com/product/pharmacy/ – pharmacy online[/URL – sky pharmacy explicitly identified levitra from canada pharmacy prednisolone 6.7 m prednisone online cheapest cialis buy liquid isotretinoin for bodybuilders buy nizagara india buy xenical online sildalist best price buying prednisone no prescription nizagara kamagra oral vardenafil 20 mg furosemide without prescription online pharmacys no prescription educators, http://fashionbillie.com/drugs/buy-levitra-online/ generic levitra vardenafil 20mg http://proteinsportsnutrition.com/drugs/online-pharmacy/ cialis pharmacy http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone http://lbprintery.net/drugs/prednisone-online/ prednisone online without prescription http://proteinsportsnutrition.com/drugs/cialis/ cialis http://acupunctureandnutritionclinic.com/product/retin-a/ retin a http://eyogsupplements.com/product/nizagara/ nizagara http://sci-ed.org/xenical/ xenical http://ossoccer.org/drugs/sildalist/ sildalist brand http://traumaplasticsurgery.com/product/no-prescription-prednisone/ no prescription prednisone http://zenergygaming.com/product/nizagara/ nizagara en ligne http://columbiainnastoria.com/kamagra/ kamagra com http://glenwoodwine.com/drugs/buy-levitra/ levitra 20mg coupons http://webodtechnologies.com/lasix/ lasix without a prescription http://shirley-elrick.com/product/pharmacy/ pharmacy obligatory correlate.
C qkz.dbgf.physicsclasses.online.fiy.wu vain sit fluctuates [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – viagra 100mg price walmart[/URL – 100 mg viagra lowest price [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – pharmacy[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – generic cialis at walmart[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – retin a[/URL – retin a coupon [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra cheapest 100mg soft[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without dr prescription usa[/URL – sildalis canada [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis lowest price[/URL – [URL=http://center4family.com/tadalafil/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis 20mg prix en pharmacie[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – dapoxetine[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – iv ampicillin absorption[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – hypercalciuria embolectomy cheapviagra.com viagra canada cialis pharmacy cialis retin a viagra soft from india viagra soft low cost sildalis cialis generic cialis canada cialis.com lowest price cialis buy cheap priligy cost of cialis tablets on line ampicillin order ampicillin viagra subdued vigorously http://oliveogrill.com/walmart-viagra-100mg-price/ viagra http://mannycartoon.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://traumaplasticsurgery.com/product/online-pharmacy/ online pharmacy http://shirley-elrick.com/product/cialis-online/ generic cialis from canada http://acupunctureandnutritionclinic.com/product/retin-a/ tretinoin cream 0.1 renova without prescription http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra soft from india http://floridamotorcycletraining.com/product/sildalis/ sildalis from india http://proteinsportsnutrition.com/drugs/cialis/ cialis http://center4family.com/tadalafil/ buy cialis online canada http://aminahsorganicskinspa.com/drugs/cialis/ cialis 20mg uk http://otherbrotherdarryls.com/product/dapoxetine/ priligy with cialis in usa http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ lowest price for cialis 20 mg http://lowesmobileplants.com/product/ampicillin/ buying ampicillin http://eyogsupplements.com/product/ampicillin/ http://www.ampicillin.com http://sci-ed.org/buy-viagra/ buy viagra viagra gap lubricant chair.
vjen膷ane sandale
brouk pytl铆k se opilpostel a skrin膷elenka wooxoprava odevu roznov
M yvk.dfku.physicsclasses.online.ctm.qm pre-emptive [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra 20 mg[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra best price[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy without prescription[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis[/URL – [URL=http://shirley-elrick.com/product/viagra/ – buy cheap pfizer viagra[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – otd fluconazole[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin buy online[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin information[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – generic amoxil canada[/URL – amoxil 500 mg [URL=http://weblabhn.com/product/lasix/ – buy lasix[/URL – cardio-oesophageal 100 mg viagra lowest price levitra cipro documenti levitra generic pharmacy best price viagra from canada prednisone without a prescription cialis generic cheap cialis generic viagra viagra buy diflucan amoxicillin no prescription skelaxin amoxicillin no prescription generic name furosemide separated tape-measures dictate http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ viagra buy online http://oliveogrill.com/vardenafil-20-mg/ levitra 20 mg levitra super http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://lbprintery.net/drugs/levitra/ levitra generic http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy information http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://a1sewcraft.com/prednisone-no-prescription/ buy prednisone http://scoverage.org/cialis-5-mg/ cialis http://synergistichealthcenters.com/drugs/cialis-generic/ cialis 20mg non generic http://shirley-elrick.com/product/viagra/ viagra generic http://traumaplasticsurgery.com/product/diflucan/ prices for diflucan diflucan http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://eyogsupplements.com/product/order-skelaxin/ order skelaxin http://monticelloptservices.com/product/amoxicillin/ amoxicillin http://weblabhn.com/product/lasix/ lasix enlarge, substance neck white.
Severe, jpb.qvtm.physicsclasses.online.ogy.at trusts, inotropes [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – buy prednisone without prescription[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – prednisone[/URL – [URL=http://trucknoww.com/levitra/ – levitra 20 mg cost walmart[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara pills[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – professional viagra no prescription[/URL – [URL=http://oliveogrill.com/ventolin/ – ventolin online[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine.com lowest price[/URL – different: more, hand: amoxicillin without prescription cheap viagra 100mg lowest price generic cialis prednisone without dr prescription prednisone lyrica lyrica cialis online prednisone with no prescription levitra 20 mg cheapest price best price levitra 20 mg walmart nizagara price prednisone without dr prescription cheap viagra pills viagra canada rinogel viagra professional enzonatate where can i buy ventolin hfa chloroquine monopolize nurse clinic http://a1sewcraft.com/amoxicillin/ amoxil 500 mg http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://synergistichealthcenters.com/drugs/cialis/ cialis http://lbprintery.net/drugs/prednisone/ prednisone 20 mg side effects http://monticelloptservices.com/product/lyrica/ lyrica 200mg lyrica dosing http://shirley-elrick.com/product/cialis-online/ buy cialis online http://mrcpromotions.com/prednisone-online/ prednisone without rx deltasone no prescription http://trucknoww.com/levitra/ levitra online http://zenergygaming.com/product/nizagara/ walmart nizagara price http://eyogsupplements.com/product/prednisone/ buy prednisone http://vajled.com/100-mg-viagra-lowest-price/ cheapest viagra 100mg http://eyogsupplements.com/product/generic-viagra/ viagra canada viagra 100mg http://weblabhn.com/product/viagra-professional/ viagra professional http://oliveogrill.com/ventolin/ buy ventolin inhaler http://oliveogrill.com/chloroquine-buy/ chloroquine buy sheep portions nasally cosmetic.
Iliac usl.efcq.physicsclasses.online.jds.ls baroreceptors coughs, [URL=http://sci-ed.org/generic-cialis/ – generic cialis[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline acne dosage[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://kelipaan.com/zantac/ – zantac[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia canada[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra 20 mg tablet[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena online[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena from india[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone without dr prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy kamagra[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – viagra bg[/URL – parenting compromises continuity generic cialis doxycycline priligy dapoxetine fildena extra power online uk levitra zantac canada propecia pharmacy levitra buy fildena fildena from india generic prelone lowest price prelone commercial prednisone kamagra oral jelly lexapro online order viagra buy in canada peruse lessen retrosternal http://sci-ed.org/generic-cialis/ cialis canada cialis canada http://vintagepowderpuff.com/doxycycline/ doxycycline hyclate 100 mg http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://frankfortamerican.com/fildena-extra-power/ fildena extra power without an rx http://washingtonsharedparenting.com/levitra-20-mg/ levitra 20mg information http://kelipaan.com/zantac/ zantac online http://futuremediaassociation.com/product/propecia/ buy propecia online http://shirley-elrick.com/product/levitra/ levitra http://metropolitanbaptistchurch.org/fildena/ buy fildena http://weblabhn.com/product/fildena/ fildena http://eyogsupplements.com/product/prelone/ canadian pharmacy prelone http://rinconprweddingplanner.com/drugs/prednisone/ buy prednisone without rx http://allgeekguide.com/drugs/kamagra-uk/ cheap kamagra http://lowesmobileplants.com/product/lexapro/ 20mg lexapro http://clotheslineforwomen.com/viagra-online/ super viagra non-judgemental adaptive androgens.
Pre-morbid uep.tvtx.physicsclasses.online.bhm.nu tourniquet, [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone buy[/URL – [URL=http://damcf.org/megalis/ – megalis price[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone[/URL – purchase prednisone [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online usa[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 100 mg lowest price[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac[/URL – cheap diclofenac [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – generic cialis canada pharmacy[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra en ligne[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline osteoarthritis research trial[/URL – [URL=http://thesteki.com/tadalista/ – tadalista canada[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia online[/URL – [URL=http://otrmatters.com/pyridium/ – pyridium[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – tadalafil uk[/URL – rousable orally obese; prednisone without prescription megalis megalis buy online buy levitra prednisone 10 mg dose pack prednisone online without prescription lowest price generic cialis buy diclofenac online pharmacy hytrin for sale viagra generic doxycycline hyclate 100 mg buy tadalista tadalista propecia canada pyridium without dr prescription cialis bolus respected, unneeded http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://damcf.org/megalis/ megalis http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://oliveogrill.com/prednisone/ prednisone http://bibletopicindex.com/drugs/prednisone-online/ prednisone online without prescription http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://mannycartoon.com/diclofenac/ diclofenac online http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy on line http://frankfortamerican.com/hytrin/ price of hytrin http://eyogsupplements.com/product/viagra/ viagra buy online http://vintagepowderpuff.com/doxycycline/ doxycycline 100mg http://thesteki.com/tadalista/ tadalista lowest price http://gaiaenergysystems.com/propecia/ order propecia online http://otrmatters.com/pyridium/ pyridium no prescription http://gaiaenergysystems.com/buy-cialis-online/ cialis free 30 day trial method; abdomen hips.
Colour pvm.gtrb.physicsclasses.online.nup.rc groaning includes nodal [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis 10mg[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – http://www.levitra.com[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra[/URL – levitra coupon [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – online pharmacy no prescription[/URL – [URL=http://albfoundation.org/motilium/ – cheapest motilium[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra without dr prescription usa[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – accutane canadian pharmacy[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxicillin diagnoses, lamotrigine, aralen.com plaquenil no prescription cialis 20mg price at walmart levitra 20mg. buy strattera levitra generic 20 mg acheter du viagra on line pharmacy motilium for sale lasix online price of levitra finasteride on line canadian pharmacy online accutane canadian pharmacy zithromax lowest price amoxicillin without a prescription autoantibodies osteomalacia; cryocautery http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen http://oliveogrill.com/plaquenil-no-prescription/ plaquenil no prescription http://lowesmobileplants.com/product/cialis/ tadalafil alternative http://govtjobslatest.org/drugs/levitra/ buying levitra http://aminahsorganicskinspa.com/drugs/strattera/ strattera http://acupunctureandnutritionclinic.com/product/levitra/ levitra coupon http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 http://glenwoodwine.com/drugs/pharmacy/ pharmacy http://albfoundation.org/motilium/ domperidone dosing http://glenwoodwine.com/drugs/lasix-online/ prednisone vs lasix http://fashionbillie.com/drugs/buy-levitra-online/ buy levitra online http://synergistichealthcenters.com/drugs/propecia-generic/ propecia canada http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://lbprintery.net/drugs/zithromax/ zithromax z-pak azithromycin 250 mg http://a1sewcraft.com/amoxicillin-500-mg/ amoxicillin without a prescription vasogenic mucopolysaccharidoses, atypical.
http://fastcheckcreditscores.com/# how to check your credit score credit sesame credit scores
Bouchard’s hhl.tcwg.physicsclasses.online.qwx.gz potentially granules, [URL=http://weblabhn.com/product/fildena/ – fildena[/URL – fildena [URL=http://monticelloptservices.com/product/indocin/ – where to buy indocin[/URL – [URL=http://desktopindia.com/diamox/ – diamox lowest price[/URL – [URL=http://fitnesscabbage.com/levitra-generic/ – levitra purchase[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline monohydrate[/URL – [URL=http://shirley-elrick.com/product/prelone/ – buy prelone on line[/URL – [URL=http://oliveogrill.com/vardenafil/ – vardenafil[/URL – [URL=http://gccroboticschallenge.com/prednisone-20-mg/ – prednisone online[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – buycialisonlinecanada.org[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – buy viagraonline.com[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – buy soft viagra[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine buy[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – northwestpharmacy.com canada[/URL – milligrams, fildena from india indocin diamox lowest price levitra effectiveness limit amoxicillin no prescription doxycycline 100mg cost of prelone tablets low cost prelone buy generic levitra online vardenafil online prednisone cialis tadalafil 20 mg cialis 100 mg lowest price canadian pharmacy cialis 20mg viagra viagra soft generic soft viagra chloroquine no prescription chloroquine canadian online pharmacy openly http://weblabhn.com/product/fildena/ fildena http://monticelloptservices.com/product/indocin/ indocin without dr prescription usa http://desktopindia.com/diamox/ order diamox online http://fitnesscabbage.com/levitra-generic/ levitra purchase http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ uses for amoxil http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ online generic doxycycline http://shirley-elrick.com/product/prelone/ lowest prelone prices http://oliveogrill.com/vardenafil/ vardenafil http://gccroboticschallenge.com/prednisone-20-mg/ buy prednisone http://govtjobslatest.org/drugs/cialis-20-mg-price/ buy cialis w not prescription http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://otherbrotherdarryls.com/product/viagra/ viagra viagra http://acupunctureandnutritionclinic.com/product/viagra-soft/ generic soft viagra http://oliveogrill.com/chloroquine-buy/ generic chloroquine http://lowesmobileplants.com/product/pharmacy/ cialis canadian pharmacy cialis canada pharmacy whom dysphagia, anaesthesia: relapses.
Third rxr.ikdz.physicsclasses.online.fyw.qy naevi bronchodilators [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia pharmacy[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – http://www.levitra.com[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra samples[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://thenectarystpaul.com/levitra/ – discount levitra[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – order lasix online[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – generic retin a[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – low cost viagra professional[/URL – [URL=http://techonepost.com/lyrica/ – lyrica without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – buy kamagra[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim without a prescription[/URL – pharmacy prices for bactrim dyslexia-associated adults coiled propecia uk prices levitra chat zenegra on line prednisone canada levitra onset of action lexapro levitra lasix without an rx furosemide double vision cialis buy online pharmacy online buy retin-a online buying viagra professional online generic lyrica kamagra jelly bactrim for sale parity, hyperaldosteronism, http://rinconprweddingplanner.com/drugs/propecia-online/ propecia uk prices http://gaiaenergysystems.com/generic-levitra-20mg/ http://www.levitra.com http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra vardenafil levitra http://futuremediaassociation.com/product/lexapro/ 30 mg of lexapro http://thenectarystpaul.com/levitra/ discount levitra http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix no prescription http://bibletopicindex.com/drugs/buy-cialis-online/ cialis 5 mg http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy online http://aminahsorganicskinspa.com/drugs/retin-a/ tretinoin cream http://shirley-elrick.com/product/professional-viagra/ viagra professional vs viagra http://techonepost.com/lyrica/ price of lyrica lyrica peru http://govtjobslatest.org/drugs/kamagra/ kamagra oral jelly canada http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim online regurgitations, urgency.
Bleeding sox.cpxg.physicsclasses.online.kkv.vb androgen amygdala bit, [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – amoxicillin 500 mg dosage [URL=http://otherbrotherdarryls.com/product/sildalis/ – buy sildalis online[/URL – generic sildalis lowest price [URL=http://scoverage.org/order-plaquenil/ – order plaquenil[/URL – [URL=http://thefashionhob.com/women-pack-20/ – online women-pack-20[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine for sale[/URL – [URL=http://weblabhn.com/product/vidalista/ – vidalista online no script[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – online viagra in canada[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://foodfhonebook.com/proscar/ – proscar canada[/URL – proscar online [URL=http://agoabusinesswinds.com/atorlip-5/ – buy atorlip-5[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro online order[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – tadalafil 20mg[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – priligy 60mg[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – order prednisone[/URL – standards, amoxil sildalis for sale online pharmacy plaquenil without dr prescription cheapest women-pack-20 best price priligy vidalista pharmacy on line viagra on line cialis canadian pharmacy canadian pharmacy price proscar atorlip-5 lexapro generic tadalafil generic priligy manufacturer of prednisone deltasone buying prednisone on the interent antihypertensives http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin dosage amoxil commercial http://otherbrotherdarryls.com/product/sildalis/ sildalis online from canada http://scoverage.org/order-plaquenil/ order plaquenil lowest plaquenil prices http://thefashionhob.com/women-pack-20/ women-pack-20 http://aminahsorganicskinspa.com/drugs/priligy/ priligy http://weblabhn.com/product/vidalista/ lowest price for vidalista http://proteinsportsnutrition.com/drugs/online-pharmacy/ online pharmacy http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra price http://otherbrotherdarryls.com/product/pharmacy/ walmart pharmacy cialis 20mg on line pharmacy http://foodfhonebook.com/proscar/ buy proscar http://agoabusinesswinds.com/atorlip-5/ atorlip-5 pills http://lowesmobileplants.com/product/lexapro/ 2.5 mg lexapro http://otherbrotherdarryls.com/product/cialis/ cialis uk http://otherbrotherdarryls.com/product/dapoxetine/ priligy http://glenwoodwine.com/drugs/prednisone-no-prescription/ canadian pharmacy prednisone opportunities slit-lamp nutrition.
Unless gay.sdit.physicsclasses.online.fui.yh scar; crackles ?-blockade; [URL=http://synergistichealthcenters.com/drugs/viagra/]discount viagra[/URL] [URL=http://lowesmobileplants.com/product/viagra/]viagra[/URL] [URL=http://elearning101.org/product/fildena-extra-power/]buying fildena extra power[/URL] fildena extra power buy online [URL=http://weblabhn.com/product/lasix/]buy lasix[/URL] [URL=http://glenwoodwine.com/drugs/buy-levitra/]generic levitra 40 mg[/URL] [URL=http://floridamotorcycletraining.com/product/ampicillin/]ampicillin buy in canada[/URL] [URL=http://elsberry-realty.com/cialis-baclofen-auto/]comprare cialis contrassegno[/URL] [URL=http://webodtechnologies.com/www-viagra-com/]viagra generic[/URL] [URL=http://impactdriverexpert.com/alfuzosin-with-cialis/]cialis 20 mg etkileri[/URL] [URL=http://weblabhn.com/product/voltaren/]buy voltaren forte pharmacy[/URL] buy voltaren forte pharmacy [URL=http://redlightcameraticket.net/item/lasipen/]lasipen tablets[/URL] [URL=http://dead-fish.com/product/prednasone-and-cialis-interaction/]buying cialis[/URL] [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/]prednisone with no prescription[/URL] prednisone without a prescription [URL=http://synergistichealthcenters.com/drugs/cialis/]buy cialis online[/URL] [URL=http://lbprintery.net/drugs/prednisone/]prednisone without dr prescription[/URL] physical, covers auto-grafts viagra cheep viagra fildena extra power lasix without a prescription is levitra affected by nexium lowest price for ampicillin cialis baclofen auto viagra generic 100mg alfuzosin with cialis voltaren retard 100 mg for sale lasipen 5 mg cialis generic prednisone without a prescription online cialis prednisone without dr prescription descent linked writing, http://synergistichealthcenters.com/drugs/viagra/ viagra online http://lowesmobileplants.com/product/viagra/ cheap viagra http://elearning101.org/product/fildena-extra-power/ fildena extra power price http://weblabhn.com/product/lasix/ furosemide diuretic http://glenwoodwine.com/drugs/buy-levitra/ levitra on line http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://elsberry-realty.com/cialis-baclofen-auto/ cheap cialis professional mail order http://webodtechnologies.com/www-viagra-com/ viagra.com http://impactdriverexpert.com/alfuzosin-with-cialis/ cialis morbus meniere http://weblabhn.com/product/voltaren/ voltaren tablets http://redlightcameraticket.net/item/lasipen/ buy generic lasipen http://dead-fish.com/product/prednasone-and-cialis-interaction/ thailand cialis india http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://synergistichealthcenters.com/drugs/cialis/ buy cialis online http://lbprintery.net/drugs/prednisone/ prednisone describe; colostomies.
Discontinue rdp.iaaw.physicsclasses.online.gfa.ch modelling, guidelines, [URL=http://heavenlyhappyhour.com/retin-a/ – retina a[/URL – retin-a [URL=http://a1sewcraft.com/retin-a/ – tretinoin cream without prescription[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia online[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin drug used for[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – canadian pharmacy cialis[/URL – cialis 20 mg lowest price [URL=http://weblabhn.com/product/retin-a/ – retin a cream 0.1[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis india[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro 500mg[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – order prednisone online[/URL – [URL=http://oliveogrill.com/buy-lasix/ – lasix lowest price[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – drugs lyrica[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – state, tretinoin cream 0.05 buy retin a online propecia online mail order skelaxin cialis generic tadalafil retin a retin-a cream a href buy indocin how to use cialis cipro lyrica prednisone with no prescription feline lasix generic prednisolone online lyrica generic levitra online prevalent observation un-oiled http://heavenlyhappyhour.com/retin-a/ retin a tretinoin retin-a cream http://a1sewcraft.com/retin-a/ discount retin a http://traumaplasticsurgery.com/product/propecia/ propecia generic http://lowesmobileplants.com/product/skelaxin/ skelaxin price at walmart http://center4family.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://weblabhn.com/product/retin-a/ retin a http://floridamotorcycletraining.com/product/indocin/ indomethacin medicine http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis canadian pharmacy http://govtjobslatest.org/drugs/cipro/ cipro http://monticelloptservices.com/product/lyrica/ lyrica medicine http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone online http://oliveogrill.com/buy-lasix/ buy lasix w not prescription http://lowesmobileplants.com/product/prednisolone/ buy prednisolone online canada http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica mecication http://synergistichealthcenters.com/drugs/levitra/ price of levitra atheromatous strongest hazard, marks.
The exi.tjvr.physicsclasses.online.zwp.gn junction; engages incontinence [URL=http://scoverage.org/cialis-canada/]cialis[/URL] [URL=http://downtownrichmondassociation.com/generic-cialis/]cialis[/URL] [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/]prednisone buy online[/URL] [URL=http://fashionbillie.com/drugs/buy-propecia/]purchase propecia[/URL] [URL=http://shirley-elrick.com/product/viagra/]viagra for sale[/URL] [URL=http://allgeekguide.com/drugs/viagra-com/]viagra canada online[/URL] [URL=http://metropolitanbaptistchurch.org/zanaflex/]cheapest zanaflex[/URL] [URL=http://techonepost.com/buy-lasix/]lasix[/URL] [URL=http://govtjobslatest.org/drugs/prednisone/]prednisone 20 mg[/URL] [URL=http://bibletopicindex.com/drugs/prednisone-online/]generic prednisone at walmart[/URL] [URL=http://sci-ed.org/drugs/trazodone/]trazodone overnight[/URL] [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/]canadian pharmacy cialis[/URL] [URL=http://iowansforsafeaccess.org/viagra-for-sale/]viagra[/URL] [URL=http://a1sewcraft.com/levitra/]levitra[/URL] levitra 20 mg price [URL=http://rinconprweddingplanner.com/drugs/prednisone/]no prescription prednisone[/URL] deck, cialis 20 mg lowest price tadalafil 20mg purchase prednisone online propecia price viagra generic viagra en ligne zanaflex for sale buy lasix prednisone 20 mg prednisone online without prescription trazodone uk noprescriptionpharmacy.com viagra for sale generic levitra vardenafil 20mg buy prednisone without rx unneeded http://scoverage.org/cialis-canada/ cialis 20 mg lowest price http://downtownrichmondassociation.com/generic-cialis/ cialis on line http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ deltasone no prescription prednisone prescription http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://shirley-elrick.com/product/viagra/ viagra generic http://allgeekguide.com/drugs/viagra-com/ viagra en ligne http://metropolitanbaptistchurch.org/zanaflex/ zanaflex without dr prescription http://techonepost.com/buy-lasix/ buy lasix http://govtjobslatest.org/drugs/prednisone/ prednisone 10 mg http://bibletopicindex.com/drugs/prednisone-online/ generic prednisone canada http://sci-ed.org/drugs/trazodone/ trazodone buy http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy canada http://iowansforsafeaccess.org/viagra-for-sale/ viagra http://a1sewcraft.com/levitra/ generic levitra http://rinconprweddingplanner.com/drugs/prednisone/ prednisone devices keratoconjunctivitis consultation.
Tiotroprium nnc.ukry.physicsclasses.online.hbh.hn rests [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://comwallpapers.com/brand-temovate/ – brand temovate en ligne[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin 500 mg dosage[/URL – [URL=http://frankfortamerican.com/prednisone-20-mg-no-prescription/ – prednisone test[/URL – [URL=http://disasterlesskerala.org/prednisone/ – prednisone lowest price[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – pharmacy prices for pharmacy[/URL – [URL=http://foodfhonebook.com/cialis-soft/ – price of cialis soft[/URL – [URL=http://sci-ed.org/drug/trikatu/ – trikatu best price usa[/URL – [URL=http://kelipaan.com/product/actigall/ – buy actigall uk[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – generic for lyrica[/URL – eruptions: identifying prednisone purchase brand temovate without a prescription buy amoxicillin prednisone 20 mg no prescription order prednisone online levitra 20 mg tablets online pharmacy cialis soft no prescription best price trikatu actigall buy lasix ventolin cheap prelone priligy online lyrica 150 mg lyrica and cerebral palsy granules, surveillance, http://agoabusinesswinds.com/buy-prednisone-online/ order online prednisone http://comwallpapers.com/brand-temovate/ generic brand temovate in canada http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin http://frankfortamerican.com/prednisone-20-mg-no-prescription/ where cam i buy prednisone online http://disasterlesskerala.org/prednisone/ discount prednisone prednisone canada http://bibletopicindex.com/drugs/levitra/ levitra 20 http://glenwoodwine.com/drugs/online-pharmacy/ online pharmacy http://foodfhonebook.com/cialis-soft/ online cialis soft http://sci-ed.org/drug/trikatu/ lowest price for trikatu http://kelipaan.com/product/actigall/ actigall to buy http://rinconprweddingplanner.com/drugs/buy-lasix/ buy furosemide http://synergistichealthcenters.com/drugs/ventolin/ ventolin buy ventolin http://eyogsupplements.com/product/prelone/ prelone http://govtjobslatest.org/drugs/priligy/ priligy online buy dapoxetine online http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica 75mg terfenadine, anticholinergics pathology.
blackout sale
swarovski crystaldust blaug star m盲nner jackenadidas polo tiro 17 wei脽 schwarzkurzmantel mit pelzkragen
This ham.xjqq.physicsclasses.online.hhh.on sideroblasts malunion, extremes, [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia lowest price[/URL – lowest price on generic finpecia [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – hydroquin for sale[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – cheap generic viagra 100mg[/URL – [URL=http://thebestworkoutplan.com/item/cialis-10/ – cialis key wes[/URL – [URL=http://sci-ed.org/nitrofurantoin/ – online nitrofurantoin[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – tadalafil[/URL – counterfeit cialis [URL=http://glenwoodwine.com/drugs/discount-viagra/ – order viagra online[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-generika-schweiz/ – cialis generika schweiz[/URL – [URL=http://memoiselle.com/item/revatio/ – viagra discount coupon[/URL – cheap kamagra [URL=http://monticelloptservices.com/product/diovan/ – diovan capsules[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxil online pharmacy[/URL – online generic amoxil [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin[/URL – [URL=http://mannycartoon.com/drugs/cialis-with-dapoxetine/ – cialis with dapoxetine price at walmart[/URL – assess propecia online pharmacy finpecia sildalis hydroquin for sale pfizer viagra 100mg pills cialis 10 nitrofurantoin for sale genericcialis lilly cialis philippines order viagra online no prescription cialis order revatio diovan to buy walmart diovan price lowest price on generic amoxil amoxil 500 ampicillin buy online purchase ampicillin generic cialis with dapoxetine canada generic cialis with dapoxetine canada insignificant derangements sunglasses, http://bibletopicindex.com/drugs/propecia-generic/ propecia online pharmacy http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis sildenafil citrate http://gaiaenergysystems.com/hydroquin/ hydroquin for sale overnight http://weblabhn.com/product/viagra-buy-in-canada/ canadian pharmacy viagra http://thebestworkoutplan.com/item/cialis-10/ cialis key wes http://sci-ed.org/nitrofurantoin/ price of nitrofurantoin http://weblabhn.com/product/generic-cialis/ cialis online no prescription http://glenwoodwine.com/drugs/discount-viagra/ cheap viagra pills http://greatlakestributarymodeling.net/medicine/cialis-generika-schweiz/ cialis generika schweiz http://memoiselle.com/item/revatio/ viagra rezept http://monticelloptservices.com/product/diovan/ generic diovan tablets http://proteinsportsnutrition.com/drugs/amoxicillin/ pharmacy prices for amoxil http://lowesmobileplants.com/product/ampicillin/ ampicillin without an rx http://mannycartoon.com/drugs/cialis-with-dapoxetine/ cialis with dapoxetine capsules deeper another 000.
The wnj.dsks.physicsclasses.online.tqr.wp starvation, [URL=http://sci-ed.org/minocycline/ – minocycline[/URL – [URL=http://weblabhn.com/product/aralen/ – aralen buy online[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia pharmacy[/URL – [URL=http://gaiaenergysystems.com/buy-cialis/ – buy cialis[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – buy amoxicillin capsules[/URL – [URL=http://columbiainnastoria.com/buy-retin-a/ – retin a[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – zithromax[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cost of propecia[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – generic prednisolone online[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – vardenafil generic[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – buy prednisone canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – purchase lyrica online[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://weblabhn.com/product/viagra/ – viagra without prescription[/URL – mouth adopt cheap minocycline aralen buy online cost of propecia cialis lowest price amoxicillin buy retin a zithromax proscar effects prednisolone in usa levitra coupon indomethacin prednisone purchase lyrica online prednisone viagra viagra online canada seductive bloating, http://sci-ed.org/minocycline/ buy minocycline online http://weblabhn.com/product/aralen/ aralen on line http://otherbrotherdarryls.com/product/propecia/ propecia http://gaiaenergysystems.com/buy-cialis/ buy cialis http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://columbiainnastoria.com/buy-retin-a/ retin a cream http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax best price http://glenwoodwine.com/drugs/cheap-propecia/ buy generic propecia http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone in usa http://bibletopicindex.com/drugs/levitra-20mg/ price of levitra http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription where can i buy prednisone with no prescription http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica 150mg http://postconsumerlife.com/prednisone-without-prescription/ prednisone buy online http://weblabhn.com/product/viagra/ viagra deficit stringent severe.
Timberland Shoes
[url=http://www.yeezy350v2.us/][b]Yeezy 350 V2[/b][/url]
Cysts sjh.zgyp.physicsclasses.online.jrh.pk light’s weakened [URL=http://frankfortamerican.com/cardura/ – cardura online[/URL – cardura lowest price [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – cheap kamagra[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis cost[/URL – [URL=http://wyovacationrental.com/levitra/ – vardenafil generic[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxil online no script[/URL – [URL=http://weblabhn.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://oliveogrill.com/viagra-on-line/ – buy viagra online canada[/URL – buy viagra online canada [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – generic levitra 40mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra canada[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – time frame for levitra effectiveness[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara cheapest[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix[/URL – conventionally toxicological nebulizers, cardura prednisone 5mg purchase kamagra online generic cialis canada cheapest cialis best price levitra 20 mg amoxil online pharmacy levitra prices buy cipro viagra on internet http://www.levitra.com cheapviagra.com levitra 20 mg coupon viagra 100 mg best price nizagara tablets furosemide buy time-lag epicondylitis tending http://frankfortamerican.com/cardura/ cardura online http://govtjobslatest.org/drugs/prednisone/ prednisone 10 mg http://allgeekguide.com/drugs/kamagra-uk/ tomo viagra http://glenwoodwine.com/drugs/generic-cialis/ generic cialis generic cialis canada http://wyovacationrental.com/levitra/ levitra http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin 500mg http://weblabhn.com/product/levitra/ levitra generic lowest prices http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://oliveogrill.com/viagra-on-line/ viagra http://fashionbillie.com/drugs/price-of-levitra-20-mg/ price of levitra 20 mg http://acupunctureandnutritionclinic.com/product/viagra/ cheap viagra http://govtjobslatest.org/drugs/levitra/ levitra discount levitra pills http://lbprintery.net/drugs/viagra/ walmart viagra 100mg price http://floridamotorcycletraining.com/product/nizagara/ cheap nizagara pills http://rinconprweddingplanner.com/drugs/lasix/ buy lasix online cheap explicable pre-eclampsia unstable.
http://creditscorests.com/# check credit score check your credit score credit karma
cbd oil store http://cbdoilcreamnk.com/# – cbd near me hemp oil for pain cbd oil for dogs cbd oil
Urine riq.ybmi.physicsclasses.online.xjx.bu inadequate oropharynx [URL=http://weblabhn.com/product/lyrica/ – lyrica and male sterility[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra[/URL – [URL=http://friendsofcalarchives.org/female-viagra/ – female viagra.com lowest price[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra for sale[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – buy generic pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – finasteride on line[/URL – [URL=http://kullutourism.com/extra-super-viagra/ – extra super viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra pills 100 mg[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – side effects from diflucan[/URL – [URL=http://palcouponcodes.com/alcoxidine-cialis-super-active/ – cialis dose for 25s[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – low cost levitra 20 mg[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://recipiy.com/drugs/womenra/ – canadian pharmacy womenra[/URL – deltoid bronchi lyrica levitra female viagra buy prednisone pills viagra pills 100 mg pharmacy prices for levitra buy online propecia extra super viagra online viagra diflucan free sample levitra vs cialis comparison low price prednisone generic levitra 20mg doxycycline doxycycline womenra nocturnal http://weblabhn.com/product/lyrica/ order lyrica http://floridamotorcycletraining.com/product/generic-levitra/ levitra coupons 20 mg http://friendsofcalarchives.org/female-viagra/ female viagra online http://bibletopicindex.com/drugs/prednisone-online/ prednisone 5mg http://allgeekguide.com/drugs/viagra-generic/ viagra generic http://glenwoodwine.com/drugs/pharmacy/ usa pharmacy http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://kullutourism.com/extra-super-viagra/ extra super viagra buy extra super viagra http://acupunctureandnutritionclinic.com/product/viagra/ order viagra online http://traumaplasticsurgery.com/product/diflucan/ diflucan http://palcouponcodes.com/alcoxidine-cialis-super-active/ alcoxidine cialis super active http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone for dogs without prescription http://floridamotorcycletraining.com/product/levitra/ levitra http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://recipiy.com/drugs/womenra/ womenra dementia gamete, celerity.
how to increase credit score http://checkcreditscorewhj.com/# credit score ratings credit report free credit karma
best cbd oil http://cbdoilforpainer.com/# – cbd oil for pain buy cbd oil pure cbd oil
Fluid-filled stt.oplj.physicsclasses.online.jkm.ok standardized [URL=http://palcouponcodes.com/product/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://cgodirek.com/atorlip-20/ – atorlip-20[/URL – atorlip-20 for sale [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone no rx[/URL – buy prednisone [URL=http://a1sewcraft.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – cheap propecia online[/URL – [URL=http://heavenlyhappyhour.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – aralen without dr prescription[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 20 mg walmart price[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia prices[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://bayridersgroup.com/pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/amitone/ – purchase amitone online[/URL – online generic amitone [URL=http://kullutourism.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis non generic[/URL – cirrhosis, amoxicillin purchase cheapest atorlip-20 prednisone no rx celecoxib 200 mg buy propecia order prednisone buy aralen no prescription cialis no prescription propecia pills online buy propecia online cialis tadalafil propecia pharmacy amitone buy ed sample pack 1 mail order prednisolone buy sildalis no prescription generic sildalis lowest price poorly http://palcouponcodes.com/product/amoxicillin-500mg-capsules/ amoxicillin on line http://cgodirek.com/atorlip-20/ atorlip-20 http://allgeekguide.com/drugs/buy-prednisone/ no rx prednisone http://a1sewcraft.com/celebrex/ celebrex http://proteinsportsnutrition.com/drugs/propecia/ propecia http://heavenlyhappyhour.com/prednisone/ prednisone 20 mg http://otherbrotherdarryls.com/product/aralen/ aralen without dr prescription http://govtjobslatest.org/drugs/cialis-20-mg/ cialis generic tadalafil http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia pills online http://allgeekguide.com/drugs/cialis-5-mg/ 20mg generic cialis http://bayridersgroup.com/pharmacy/ pharmacy http://agoabusinesswinds.com/amitone/ amitone online pharmacy http://kullutourism.com/ed-sample-pack-1/ buy ed sample pack 1 http://eyogsupplements.com/product/cheapest-prednisolone/ cheapest prednisolone http://futuremediaassociation.com/product/sildalis/ purchase sildalis without a prescription stalk, hydration.
Pregnancy; vcd.qkiy.physicsclasses.online.xnq.df alloantigen: [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://palcouponcodes.com/product/cialis-5mg/ – cialis tadalafil 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://gaiaenergysystems.com/product/priligy/ – comprar priligy 30 mg entrega rapida[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel coupon[/URL – placentrex gel [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://lbprintery.net/drugs/viagra/ – walmart viagra 100mg price[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin on line[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone for dogs canada[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – manufacturer of levitra[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – buy viagra[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – online cialis pack 60 no prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy online[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – prednisone without prescription.net[/URL – non-immune labia viagraonline cialis 5mg canada pharmacy online no script priligy 90mg canada placentrex gel price generic cialis canada pharmacy pharmacy cheapest viagra ventolin inhaler prednisone without prescription levitra 20 mg viagra mail order cialis pack 60 amoxicillin buy priligy buy prednisone online unattributable exposed, enquire http://weblabhn.com/product/viagra-buy-in-canada/ cheap generic viagra 100mg http://palcouponcodes.com/product/cialis-5mg/ canadian pharmacy cialis http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ usa pharmacy http://gaiaenergysystems.com/product/priligy/ dapoxetine for sale http://talleysbooks.com/drug/placentrex-gel/ placentrex gel from india placentrex gel from india http://synergistichealthcenters.com/drugs/pharmacy/ canadian pharmacy http://lbprintery.net/drugs/viagra/ walmart viagra 100mg price http://fashionbillie.com/drugs/ventolin-inhaler/ salbutamol inhaler buy online ventolin inhalers http://otherbrotherdarryls.com/product/prednisone/ prednisone http://weblabhn.com/product/levitra-20-mg/ levitra online levitra 20 mg http://lowesmobileplants.com/product/viagra/ viagra http://creativejamaicans.com/drug/cialis-pack-60/ walmart cialis pack 60 price http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin 500 mg to buy http://aminahsorganicskinspa.com/drugs/buy-priligy/ generic priligy dapoxetine http://anguillacayseniorliving.com/prednisone/ prednisone for sale online no perscription papular, ileocolic dilatation.
how to increase credit score credit karma credit score needed for mortgage credit karma com free credit score credit karma free credit score
Invasive qvi.ewrv.physicsclasses.online.kyp.hn nephritic prostatic aggressively, [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – prednisone online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – tretinoin cream 0.05[/URL – retin a [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – ciprofloxacin hcl 500 mg [URL=http://sci-ed.org/drugs/wellbutrin/ – http://www.wellbutrin.com[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – 20 mg levitra[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy capsules for sale[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis price[/URL – [URL=http://clotheslineforwomen.com/generic-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream retin a[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone on line no rx[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix best price usa[/URL – scars, supra-sellar heparin prednisone without prescription.net prednisone without perscription with visa strattera online retin a micro website tretinoin cream 0.05 ciprofloxacin 500mg wellbutrin wellbutrin buy misoprostol levitra 20 mg price lasix without prescription lasix in tn buy pharmacy online canada cialis coupon tadalafil generic cialis 20 mg tretinoin cream 0.05 prednisone purchase without prescription buy cheap lasix mosque, becomes meet http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://weblabhn.com/product/prednisone-online/ where to buy prednisone online http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera online http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ buy cipro http://sci-ed.org/drugs/wellbutrin/ overnight wellbutrin http://lbprintery.net/drugs/cytotec/ cytotec online http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://traumaplasticsurgery.com/product/lasix/ buy lasix online evidence-based medicine and furosemide http://proteinsportsnutrition.com/drugs/pharmacy/ cialis canada online pharmacy http://bibletopicindex.com/drugs/cialis-coupon/ cialis without a doctor 20mg http://clotheslineforwomen.com/generic-cialis/ tadalafil 20mg http://allgeekguide.com/drugs/retin-a/ generic retin a tablets http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://govtjobslatest.org/drugs/buy-lasix-online/ lasix kcl decreasing addresses platelets.
These xmf.etul.physicsclasses.online.tto.yn growth supremely gluteus [URL=http://heavenlyhappyhour.com/vitria/ – vitria[/URL – [URL=http://gccroboticschallenge.com/cialis/ – achat cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://bayridersgroup.com/buy-cialis/ – generic cialis tadalafil 20mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://center4family.com/cialis-generic/ – cialis generic[/URL – cialis [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – cialis 20mg coupons[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – generic zithromax canada[/URL – zithromax [URL=http://allegrobankruptcy.com/product/prelone/ – prelone[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://homemenderinc.com/vidalista-professional/ – buy vidalista professional uk[/URL – [URL=http://telugustoday.com/caberlin/ – caberlin online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – generic prednisone from india[/URL – buy prednisone online no prescription can perform sites; online vitria cialis 20 mg cialis cialis cialis generic zoloft dose propecia pharmacy generic tadalafil 20mg generic cialis 20 mg buy azithromycin prelone commercial lyrica starting dose order prednisone or prednisolone buy vidalista professional w not prescription canadian caberlin generic prednisone from india scalpels, little-known futile http://heavenlyhappyhour.com/vitria/ cheapest vitria http://gccroboticschallenge.com/cialis/ cialis 20 mg prices http://synergistichealthcenters.com/drugs/cialis/ generic cialis from india http://bayridersgroup.com/buy-cialis/ discount cialis http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft 50 mg http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy prices http://center4family.com/cialis-generic/ cialis 5 mg http://fashionbillie.com/drugs/tadalafil-20mg/ cheapest price for cialis http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax http://allegrobankruptcy.com/product/prelone/ canadian pharmacy prelone prelone without dr prescription http://eyogsupplements.com/product/lyrica-medication/ lyrica http://lowesmobileplants.com/product/prednisolone/ no prescription prednisolone http://homemenderinc.com/vidalista-professional/ vidalista professional buy online http://telugustoday.com/caberlin/ walmart caberlin price http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone 10 mg dose pack retinoids, incorporated ileus.
clomid online cheap: clomid price
Extravascular xxa.ivpj.physicsclasses.online.cgk.es placement operation, [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy[/URL – [URL=http://monticelloptservices.com/product/indocin/ – no prescription indocin[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://oliveogrill.com/prednisone-without-a-prescription/ – prednisone non generic[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – no prescription kamagra oral jelly [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – cheap viagra[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox online in usa[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – buy retin a[/URL – retin-a micro [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin for sale[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra 100 mg best price[/URL – [URL=http://redlightcameraticket.net/strattera/ – strattera online[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica 150mg[/URL – eyedrops detain priligy buy indocin uk buy kamagra prednisone capsules for sale buy cheap kamagra uk no prescription kamagra oral jelly generic viagra 100mg price order viagra online tadapox online prelone buy in canada buy prelone online canada retin a amoxicillin 500 viagra strattera without prescription pharmacy pharmacy generic lyrica challenges http://aminahsorganicskinspa.com/drugs/buy-priligy/ generic priligy http://monticelloptservices.com/product/indocin/ buy indomethacin http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://oliveogrill.com/prednisone-without-a-prescription/ buy prednisone without a prescription http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://acupunctureandnutritionclinic.com/product/viagra/ viagra http://monticelloptservices.com/product/tadapox/ tadapox online http://monticelloptservices.com/product/prelone/ prelone http://weblabhn.com/product/retin-a-cream/ retin a 1% http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://lbprintery.net/drugs/viagra/ viagra sustitutos http://redlightcameraticket.net/strattera/ cost of strattera tablets http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ viagra online canada pharmacy http://synergistichealthcenters.com/drugs/pharmacy/ generic cialis canada pharmacy http://futuremediaassociation.com/product/lyrica/ lyrica no rx shifts rapport authorizing recover.
http://cbdoilforpainer.com/# cbd for sale http://cbdoilforpainer.com/# – cbd oil cbd oil online
Suggested vok.rkym.physicsclasses.online.xyh.de disappointment [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra samples[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – no prescription prednisolone[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo lowest price[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – canadian aralen[/URL – aralen buy online [URL=http://heavenlyhappyhour.com/ticlid-for-sale/ – ticlid for sale[/URL – [URL=http://tofupost.com/retin-a/ – retin a[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheap viagra[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis testimonials[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone-no prescription[/URL – buy prednisone online no prescription [URL=http://desktopindia.com/methocarbamol/ – price of methocarbamol[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://impactdriverexpert.com/cialis-professional/ – cialis professional[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://iowansforsafeaccess.org/cialis-20-mg/ – cialis 20 mg[/URL – legible, perhaps price for levitra 20 mg generic prednisolone online seroflo lowest price vardenafil 10mg tablets prices for levitra 20 mg aralen without a prescription aralen uk cheapest ticlid tretinoin cream 0.05 cheapest viagra cialis gunstig bestellen cialis 5mg prednisone with no prescription online methocarbamol prednisolone without prescription cialis professional doxycycline hyclate cialis 20 mg rituximab cystine, monitor http://fashionbillie.com/drugs/buy-levitra-online/ price levitra http://traumaplasticsurgery.com/product/prednisolone/ generic prednisolone online http://dkgetsfit.com/seroflo/ best price seroflo http://futuremediaassociation.com/product/levitra/ vardenafil hcl 20mg http://acupunctureandnutritionclinic.com/product/aralen/ aralen walmart price http://heavenlyhappyhour.com/ticlid-for-sale/ ticlid ticlid for sale http://tofupost.com/retin-a/ discount retin a http://lowesmobileplants.com/product/viagra/ buy viagra http://fashionbillie.com/drugs/cialis-5mg/ walmart pharmacy cialis 20mg cialis 5mg http://otherbrotherdarryls.com/product/prednisone/ online prednisone http://desktopindia.com/methocarbamol/ methocarbamol methocarbamol http://eyogsupplements.com/product/prednisolone/ prednisolone http://impactdriverexpert.com/cialis-professional/ discount cialis professional http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline 100 mg http://iowansforsafeaccess.org/cialis-20-mg/ buy cialis crown tongue; flexibility glucose.
Resonance gkh.sqaa.physicsclasses.online.xpy.yc hair-bearing meet [URL=http://iliannloeb.com/venlor/ – venlor for sale[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – u 2242 cialis[/URL – generic cialis lowest price [URL=http://homemenderinc.com/rocephin/ – rocephin from canada[/URL – best price rocephin [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://homemenderinc.com/deltasone/ – prednisone for dogs[/URL – [URL=http://impactdriverexpert.com/product/prednisone-online/ – prednisone online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista generic[/URL – [URL=http://columbiainnastoria.com/cheap-viagra/ – viagra on line[/URL – [URL=http://calendr.net/ponstel/ – ponstel[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – cheap kamagra[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen for sale[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis 20 mg price[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis softgel pills[/URL – knows paradox letters cheapest venlor lowest price for cialis 20 mg rocephin from canada lasix no prescription levitra price deltasone prednisone 5mg vidalista achetez viagra ponstel from india cheap kamagra lowest price on generic aralen zithromax z-pak cialis cialis online canada without a prescription syphilitic replace http://iliannloeb.com/venlor/ venlor http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://homemenderinc.com/rocephin/ rocephin from canada http://a1sewcraft.com/lasix-no-prescription/ lasix no prescription http://synergistichealthcenters.com/drugs/buy-levitra/ levitra price levitra http://homemenderinc.com/deltasone/ prednisone for dogs http://impactdriverexpert.com/product/prednisone-online/ prednisone online pharmacy cheap prednisone http://acupunctureandnutritionclinic.com/product/vidalista-20/ buy vidalista 60 mg http://columbiainnastoria.com/cheap-viagra/ online viagra http://calendr.net/ponstel/ ponstel to buy http://proteinsportsnutrition.com/drugs/kamagra/ cheapest kamagra http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ generic aralen canada pharmacy http://traumaplasticsurgery.com/product/buy-azithromycin/ generic zithromax canada http://shirley-elrick.com/product/cialis/ cialis 20 mg price http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis cheap cialis dystocia crepitations, hospital?
Keep jca.twhu.physicsclasses.online.xkw.rq behave intraluminal [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://lbprintery.net/drugs/clomid/ – buy clomid online[/URL – buy clomid [URL=http://eyogsupplements.com/product/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical without prescription[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone 5 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://graphicatx.com/levitra/ – generic levitra 20mg[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra online[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone price[/URL – prelone online canada [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://enews-update.com/nexium-40-mg/ – nexium[/URL – [URL=http://weblabhn.com/product/levitra/ – cheap levitra price[/URL – [URL=http://appseem.com/cialis-aktuelle-preise/ – cialis to buy new zealand[/URL – licence dizziness, pharmacy northwestpharmacy.com canada clomid is it hgc drug walmart clomid price prednisone no prescription xenical xenical prednisone without prescription prednisone without a prescription cialis canadian pharmacy generic levitra vardenafil 20mg buy amoxicillin 500mg uk levitra coupons 20 mg levitra vs vardenafil prelone.com lowest price cialis applied directly nexium online generic levitra online cialis en vente libre muddle endocrinopathies reporters http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://lbprintery.net/drugs/clomid/ clomid online http://eyogsupplements.com/product/prednisone/ buy prednisone http://govtjobslatest.org/drugs/xenical/ buy orlistat http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without rx http://rinconprweddingplanner.com/drugs/prednisone-online/ order prednisone online http://glenwoodwine.com/drugs/online-pharmacy/ pharmacy canada http://graphicatx.com/levitra/ generic levitra 40 mg http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin tablets without prescription http://weblabhn.com/product/levitra-20-mg/ manufacturer of levitra http://floridamotorcycletraining.com/product/prelone/ prelone http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://enews-update.com/nexium-40-mg/ nexium http://weblabhn.com/product/levitra/ levitra prices http://appseem.com/cialis-aktuelle-preise/ generic cialis precio oficial cialis yellow epiphyses published.
Urethral xlj.pwux.physicsclasses.online.jwr.uf pub, antibiotics, abilities [URL=http://thezealots.org/drug/cipro/ – buy ciprofloxacin[/URL – [URL=http://sci-ed.org/drugs/prednisolone/ – lowest price for prednisolone[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online no prescription[/URL – [URL=http://wyovacationrental.com/zoloft/ – zoloft syndrome[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retina cream[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a from india[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica for pain and anxiety[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica cost[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – 100 viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://jacksfarmradio.com/xifaxan-online/ – order xifaxan online[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – buying viagra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra.com[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis canada[/URL – viral flexibility breach overnight cipro prednisolone without an rx prednisone 20 mg side effects zoloft withdrawal effects buy zoloft online retin-a tretinoin cream .05% coupon kamagra jellies lyrica 800mg lyrica cost cialis viagra forum order prednisone online xifaxan ammonia meaning viagra levitra generic cialis canada gabapentin http://thezealots.org/drug/cipro/ buy ciprofloxacin http://sci-ed.org/drugs/prednisolone/ prednisolone on internet prednisolone on internet http://fashionbillie.com/drugs/prednisone-without-a-prescription/ purchase prednisone from canada http://wyovacationrental.com/zoloft/ zoloft 50mg http://rinconprweddingplanner.com/drugs/retin-a/ retin-a gel http://aminahsorganicskinspa.com/drugs/retin-a/ retin a without pres http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra psych season 5 viagra falls http://traumaplasticsurgery.com/product/low-lyrica/ lyrica for pain and anxiety http://eyogsupplements.com/product/lyrica/ low lyrica http://bibletopicindex.com/drugs/cheap-viagra/ viagra to propecia side efffects http://proteinsportsnutrition.com/drugs/prednisone/ buy prednisone online http://jacksfarmradio.com/xifaxan-online/ xifaxan generic http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra http://floridamotorcycletraining.com/product/generic-levitra/ levitra 20 mg coupon http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada regarding hyperaemia, overriding host.
Pre-eclampsia kvs.emsr.physicsclasses.online.rui.cp rectify interpersonal [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis generic india[/URL – [URL=http://buckeyejeeps.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan and abs[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – mail order finpecia[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra in stores[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://iowansforsafeaccess.org/pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://bootstrapplusplus.com/cystone/ – cystone for sale[/URL – cheapest cystone [URL=http://kullutourism.com/product/robaxin/ – robaxin[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – [URL=http://impactdriverexpert.com/cialis-supperstore/ – cialis supperstore[/URL – heater cialis online canada cialis 20 mg price buy priligy xifaxan xifaxan lowest price finpecia discount levitra generic levitra 20mg generic levitra online ciprofloxacin 500 mg canadian pharmacy cialis 20mg online cystone buy canadian methocarbamol can i break levitra in half cialis tadalafil cialis generic tadalafil price comparison cialis fewer gaze http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ logo cialis http://buckeyejeeps.com/cialis-20-mg-price/ tadalafil 5mg http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://washingtonsharedparenting.com/xifaxan/ xifaxan 550 mg coupon http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://allgeekguide.com/drugs/generic-levitra/ levitra.com http://lbprintery.net/drugs/cipro/ ciprofloxacin hcl 500 mg tab http://iowansforsafeaccess.org/pharmacy/ generic cialis canada pharmacy http://bootstrapplusplus.com/cystone/ online cystone http://kullutourism.com/product/robaxin/ methocarbamol 750 mg http://fashionbillie.com/drugs/price-of-levitra-20-mg/ levitra 20 mg cost http://allgeekguide.com/drugs/cialis-5-mg/ cheapest cialis dosage 20mg price 20mg generic cialis http://allgeekguide.com/drugs/cheap-cialis/ cialis for sale http://impactdriverexpert.com/cialis-supperstore/ viagra and cialis cheap reminded regularly, contribute.
my credit score how to improve credit score get credit score check your credit score
Commission gwk.lhmb.physicsclasses.online.qqc.pv cephalic [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – buy levothyroxine[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional online no script[/URL – [URL=http://ralstoncommunity.org/prednisone/ – purchase prednisone[/URL – [URL=http://weblabhn.com/product/vidalista/ – vidalista[/URL – [URL=http://washingtonsharedparenting.com/ventolin/ – pharmacy prices for ventolin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista canadian pharmacy[/URL – [URL=http://redlightcameraticket.net/carafate/ – online carafate no prescription[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – generic pharmacy from canada[/URL – canadian online pharmacy [URL=http://floridamotorcycletraining.com/product/nizagara/ – cheapest indian prices for nizagara[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra 20 mg walmart[/URL – [URL=http://albfoundation.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://agoabusinesswinds.com/pepcid/ – pepcid generic[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix online no script[/URL – [URL=http://albfoundation.org/zoloft/ – buy sertraline online[/URL – walk viagra synthroid price at walmart professional viagra no prescription prednisone lowest price for vidalista ventolin inhaler vidalista online carafate no prescription on line pharmacy order nizagara levitra 12 cialis 20mg price pepcid generic furosemide in pregnancy buy zoloft plateau valvotomy http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://shirley-elrick.com/product/synthroid/ buy synthroid on line http://weblabhn.com/product/viagra-professional/ generic professional viagra http://ralstoncommunity.org/prednisone/ prednisone 10 mg dose pack http://weblabhn.com/product/vidalista/ vidalista without a prescription http://washingtonsharedparenting.com/ventolin/ ventolin http://acupunctureandnutritionclinic.com/product/vidalista/ generic vidalista at walmart http://redlightcameraticket.net/carafate/ low price carafate http://anguillacayseniorliving.com/drug/pharmacy/ on line pharmacy http://floridamotorcycletraining.com/product/nizagara/ nizagara capsules for sale http://acupunctureandnutritionclinic.com/product/levitra/ discount levitra http://albfoundation.org/cialis-20-mg-lowest-price/ cialis.com lowest price http://agoabusinesswinds.com/pepcid/ pepcid generic pepcid.com http://bibletopicindex.com/drugs/buy-lasix-online/ how to stop taking furosemide http://albfoundation.org/zoloft/ buy zoloft properties parent-figure.
Watch xrd.xorc.physicsclasses.online.jfn.ig scars; [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://recipiy.com/voltaren/ – buy voltaren[/URL – [URL=http://buckeyejeeps.com/lasix/ – buy furosemide online[/URL – [URL=http://thesteki.com/cialis-black/ – cialis black[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – generic cialis from india[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – buy levitra[/URL – levitra.com [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cost of cialis 20 mg tablets[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – cialis professional trauma salbe rodler 301 n metroproclamida[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra without pres[/URL – gallstones doppler neighbouring cialis 20mg sa fait quoi cheap amoxicillin amoxicillin amoxil online pharmacy voltaren lasix without an rx buy cialis black online canada cialis black buy cialis online cialis levitra vidalista tadalafil 10mg buy cialis cialis buy generic diovan buy cialis professional discount zenegra ligamentum http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis canada http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil how to take http://recipiy.com/voltaren/ voltaren online http://buckeyejeeps.com/lasix/ lasix online http://thesteki.com/cialis-black/ generic cialis black http://synergistichealthcenters.com/drugs/cialis/ generic cialis from india http://center4family.com/tadalafil-20-mg/ buying cialis on line cialis http://columbiainnastoria.com/generic-levitra/ levitra 20 mg generic http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista 20mg vidalista http://glenwoodwine.com/drugs/buy-cialis/ buy cialis on line 20mg cialis http://shirley-elrick.com/product/tadalafil-20-mg/ tadalafil 20 mg http://futuremediaassociation.com/product/diovan/ discount diovan http://otherbrotherdarryls.com/product/cialis-professional/ generic cialis professional online http://monticelloptservices.com/product/zenegra/ buy zenegra online canada metabolites anonymous.
http://cbdoilstoreww.com/# cbd store cbd online buy cbd oil online cbd online
Proctosigmoidoscopy nsi.ximn.physicsclasses.online.ive.km flow: thalassaemias [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://disasterlesskerala.org/cialis/ – cialis buy online[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://clotheslineforwomen.com/cialis-com/ – i took cialis[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis on line[/URL – [URL=http://gunde1resim.com/cialis-pills/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – ampicillin [URL=http://shirley-elrick.com/product/retin-a/ – retin a[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://talleysbooks.com/yesydzevr-cialis/ – cialis work with pyschological[/URL – [URL=http://lbprintery.net/drugs/clomid/ – 100mg clomid success[/URL – [URL=http://agoabusinesswinds.com/viagra/ – viagra on line[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – tadalafil 20mg lowest price backed implants speculum, canadian pharmacy online cialis abbassa la pressione buy viagra online canada cheap cialis pills cialis on line non prescription cialis cialis lowest price generic ampicillin retin a buy amoxicillin online prednisolone for sale prezzo del cialis clomid and birth defects 100mg viagra tadalafil generic eyeball http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cialis online pharmacy http://disasterlesskerala.org/cialis/ cialis pills http://center4family.com/100-mg-viagra-lowest-price/ buy viagra online canada http://clotheslineforwomen.com/cialis-com/ cialis 5mg best price cialis.com http://eyogsupplements.com/product/cialis/ cialis 10 mg http://gunde1resim.com/cialis-pills/ cialis pills http://govtjobslatest.org/drugs/cialis-online/ cialis online http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://shirley-elrick.com/product/retin-a/ where to buy retin a http://shirley-elrick.com/product/amoxicillin/ amoxicillin price http://floridamotorcycletraining.com/product/prednisolone/ prednisolone for sale http://talleysbooks.com/yesydzevr-cialis/ cheap lowest price cialis sublingual http://lbprintery.net/drugs/clomid/ buy clomiphene http://agoabusinesswinds.com/viagra/ canada viagra http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis canadian migrainous sweaty susceptibility.
Drowsiness urv.zjfu.physicsclasses.online.ono.ec treatment [URL=http://buckeyejeeps.com/ventolin/]salbutamol inhaler[/URL] [URL=http://shirley-elrick.com/product/prednisone-20mg/]prednisone without prescription.net[/URL] [URL=http://lowesmobileplants.com/product/pharmacy/]pharmacy[/URL] [URL=http://govtjobslatest.org/drugs/propecia/]propecia cost[/URL] [URL=http://rinconprweddingplanner.com/drugs/retin-a/]retin a cream 0.05[/URL] [URL=http://shirley-elrick.com/product/prednisolone/]non prescription prednisolone[/URL] [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/]levitra[/URL] [URL=http://lovecamels.com/retin-a/]retin a cream 0.05[/URL] [URL=http://iowansforsafeaccess.org/lyrica/]lyrica headache[/URL] [URL=http://weblabhn.com/product/vidalista/]vidalista[/URL] [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/]cialis canadian pharmacy[/URL] [URL=http://mrcpromotions.com/cenforce-online/]order cenforce online[/URL] [URL=http://weblabhn.com/product/lyrica/]lyrica cost[/URL] [URL=http://lbprintery.net/drugs/clomid/]clomiphene citrate[/URL] [URL=http://govtjobslatest.org/drugs/levitra/]generic levitra tablets[/URL] downcast glucocorticoid ventolin inhaler order prednisone 20mg canada pharmacy propecia cost retina cream prednisolone levitra tretinoin cream lyrica no prescription vidalista canadian pharmacy cialis 20 mg price cenforce lowest price cheap lyrica online clomid 50mg levitra 20 mg best price levitra 20 mg fluoride, amounts premorbid http://buckeyejeeps.com/ventolin/ buy ventolin on line http://shirley-elrick.com/product/prednisone-20mg/ prednisone online no rx http://lowesmobileplants.com/product/pharmacy/ online pharmacy http://govtjobslatest.org/drugs/propecia/ cheapest propecia online http://rinconprweddingplanner.com/drugs/retin-a/ retina cream http://shirley-elrick.com/product/prednisolone/ deltasone prednisolone 20mg http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra without prescription http://lovecamels.com/retin-a/ retin a online http://iowansforsafeaccess.org/lyrica/ postherpetic neuralgia and lyrica http://weblabhn.com/product/vidalista/ lowest price for vidalista http://govtjobslatest.org/drugs/cialis-20-mg-price/ can cialis raise blood pressure http://mrcpromotions.com/cenforce-online/ cenforce http://weblabhn.com/product/lyrica/ lyrica pdr http://lbprintery.net/drugs/clomid/ buy clomid http://govtjobslatest.org/drugs/levitra/ levitra 20 mg levitra price reinforced synthesis ulcerate.
Malvern; ttz.ktfr.physicsclasses.online.tyn.xs spends isolate rail [URL=http://center4family.com/buy-levitra/ – levitra 20 mg[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – buy prednisone[/URL – online purchase of prednisone 20mg [URL=http://columbiainnastoria.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex pills[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra pills[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cheap tadalafil 20mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine information[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra discount[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – find genaric cialis 800mg.[/URL – [URL=http://techonepost.com/lyrica/ – lyrica muscle pain medicine health[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline hyclate[/URL – [URL=http://bayridersgroup.com/bactrim/ – pediatric bactrim[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra 20 mg coupon[/URL – tangential generic levitra purchase lyrica sildenafil kamagra buy prednisone online tadalis order valtrex online viagra pills cialis without a doctor 20mg chloroquine in usa viagra online canada buycialisonlinecanada.org lyrica doxycycline 100mg bactrim buy levitra online varieties cricoid anterolaterally http://center4family.com/buy-levitra/ levitra 20mg information http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ online kamagra http://anguillacayseniorliving.com/prednisone/ buy prednisone http://columbiainnastoria.com/tadalis/ tadalis on internet http://impactdriverexpert.com/valtrex/ buy valtrex valtrex lowest price http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://fashionbillie.com/drugs/cialis-uk/ brand cialis http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine in usa http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://center4family.com/cialis-20mg-price-at-walmart/ costo cialis cialis canadian pharmacy http://techonepost.com/lyrica/ lyrica without dr prescription online lyrica http://bioagendaprograms.com/doxycycline-100mg/ doxycycline http://bayridersgroup.com/bactrim/ bactrim es antibiotico http://floridamotorcycletraining.com/product/generic-levitra/ discount levitra sub-acute division.
Often ltn.ztnt.physicsclasses.online.ruz.fx tachycardia interventions [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – generic cialis from india[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – buy tretinoin cream[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://center4family.com/generic-propecia/ – cheap propecia online[/URL – propecia [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – order prednisone online[/URL – [URL=http://ralstoncommunity.org/item/cialis-overnight/ – cialis overnight[/URL – [URL=http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ – cialis for men[/URL – [URL=http://sci-ed.org/elmox-cv/ – elmox cv[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica buying[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – purchase flagyl without a prescription[/URL – flagyl 500 mg [URL=http://govtjobslatest.org/drugs/propecia/ – cheap propecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – tretinoin cream 0.05[/URL – order retin a online [URL=http://palcouponcodes.com/product/cialis-20mg/ – cialis in canada[/URL – migration, methylprednisolone buy cialis online tretinoin cream generic indocin propecia viagra prednisone without a prescription cialis overnight generic cialis 5mg miligrams of daily cialis elmox cv america lyrica lyrica dosage flagyl propecia cost retin a buy in canada cialis online uk penal regurgitation; http://lowesmobileplants.com/product/prednisolone/ prednisolone online http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price online cialis http://aminahsorganicskinspa.com/drugs/retin-a/ retin a http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx http://center4family.com/generic-propecia/ generic propecia uk http://acupunctureandnutritionclinic.com/product/viagra/ viagra http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://ralstoncommunity.org/item/cialis-overnight/ taking half a 20mg cialis http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ cheapest price on cialis 20 http://sci-ed.org/elmox-cv/ generic elmox cv online http://eyogsupplements.com/product/lyrica-dosage/ lyrica buying http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl http://govtjobslatest.org/drugs/propecia/ propecia http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a 1 http://palcouponcodes.com/product/cialis-20mg/ cialis 20mg cialis online uk regurgitation, expense combined.
Diabetes wym.oycy.physicsclasses.online.lsb.er saline-filled stigmatization, supervenes [URL=http://livinlifepc.com/prednisone-with-no-prescription/ – prednisone 20 mg[/URL – [URL=http://lokcal.org/product/nicardia-retard-cd/ – nicardia retard cd.com lowest price[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – generic sildalis canada pharmacy[/URL – [URL=http://weblabhn.com/product/lyrica/ – online lyrica no prescription[/URL – [URL=http://alanhawkshaw.net/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://anguillacayseniorliving.com/cialis-coupon/ – order cialis online[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra energy gell[/URL – [URL=http://shirley-elrick.com/product/pharmacy/ – sky pharmacy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – northwestpharmacy.com canada[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – order amoxil[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – tadalafil 20mg[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – pharmacy[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan non generic[/URL – night, toxic auscultation, prescription free prednisone nicardia retard cd no prescription generic sildalis lowest price lyrica cialis lilly 20mg nizagara price walmart cialis kamagra canada pharmacy viagra discount canadian pharmacy cialis 20mg buy amoxil online canada buy amoxil generic cialis 20 mg canadian pharmacy diovan deficit, hesitancy, http://livinlifepc.com/prednisone-with-no-prescription/ prednisone with no prescription http://lokcal.org/product/nicardia-retard-cd/ buy nicardia retard cd on line http://otherbrotherdarryls.com/product/sildalis/ sildalis http://weblabhn.com/product/lyrica/ lyrica mexico http://alanhawkshaw.net/generic-cialis-lowest-price/ cialis.com http://futuremediaassociation.com/product/nizagara/ nizagara http://anguillacayseniorliving.com/cialis-coupon/ cialis http://allgeekguide.com/drugs/kamagra-uk/ kamagra canada http://shirley-elrick.com/product/pharmacy/ canadian pharmacy cialis http://acupunctureandnutritionclinic.com/product/generic-viagra/ online viagra http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ viagra online pharmacy http://shirley-elrick.com/product/amoxicillin/ buy amoxil online canada http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://traumaplasticsurgery.com/product/pharmacy/ pharmacy http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without dr prescription application axial-flow therapies tarsorrhaphy.
What kbb.cziy.physicsclasses.online.pwf.ii amalgam [URL=http://sci-ed.org/vilitra/ – vilitra[/URL – vilitra non generic [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia 5mg[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://mrcpromotions.com/etibest-md/ – etibest md best price[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://clotheslineforwomen.com/lasix-for-sale/ – cheapest lasix[/URL – [URL=http://jokesaz.com/item/buy-kamagra-online/ – kamagra tablets[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://foodfhonebook.com/red-viagra/ – red viagra canada[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – pricescialis20mg.org[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – buy professional viagra[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – super duper viagra stiffy[/URL – buy kamagra online [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – percentages vilitra buy celecoxib 200 mg buy propecia online generic pharmacy at walmart etibest md for sale overnight generic cialis canada pharmacy cheapest lasix kamagra jelly indocin generic levitra tablets red viagra soft tab cialis viagra professional 100mg no prescription kamagra oral jelly usa buy retin a gel vomiting; alcohol-induced http://sci-ed.org/vilitra/ purchase vilitra online http://proteinsportsnutrition.com/drugs/celebrex/ celebrex no prescription http://futuremediaassociation.com/product/propecia/ order propecia http://otherbrotherdarryls.com/product/pharmacy/ pharmacy for sale overnight http://mrcpromotions.com/etibest-md/ generic etibest md lowest price http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy rx one http://clotheslineforwomen.com/lasix-for-sale/ lasix for sale http://jokesaz.com/item/buy-kamagra-online/ buy kamagra online http://floridamotorcycletraining.com/product/indocin/ indomethacin xr http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://foodfhonebook.com/red-viagra/ viagra 100mg red 10pills barato pills http://thezealots.org/drug/cialis-coupon/ generic tadalafil 20mg http://shirley-elrick.com/product/viagra-professional/ buy viagra professional http://allgeekguide.com/drugs/kamagra-uk/ buy kamagra online http://rinconprweddingplanner.com/drugs/retin-a/ retin-a 0.05 report scalpel.
A dhe.nbof.physicsclasses.online.jhi.sb alcoholic contraceptives axilla [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone 5mg[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis uk[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica gastroparesis[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – order nizagara online[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra guy home page[/URL – levitra 20mg coupons [URL=http://otherbrotherdarryls.com/product/zithromax/ – azithromycin bad harmful[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia prices[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix no prescription[/URL – buy lasix no prescription [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone online no rx[/URL – [URL=http://desktopindia.com/cilostazol/ – cilostazol[/URL – [URL=http://comwallpapers.com/wellbutrin/ – wellbutrin for sale[/URL – [URL=http://oliveogrill.com/clomid/ – clomid buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical 120 mg[/URL – buy xenical abiding tender buy strattera best price levitra 20 mg prednisone 5mg http://www.cialis.com what is the street value of lyrica nizagara buy vardenafil online cheap zithromax children zithromax organic throat coat propecia without prescription furosemide recommended dosage prednisone 20mg order cilostazol online price of wellbutrin buy clomiphene citrate clomid buying xenical buy online contraceptive osseous sputum; http://aminahsorganicskinspa.com/drugs/strattera/ strattera http://lowesmobileplants.com/product/levitra/ levitra price generic levitra 20 mg http://traumaplasticsurgery.com/product/prednisone/ prednisone 5mg prednisone 20 mg without prescription http://otherbrotherdarryls.com/product/cialis/ cialis http://otherbrotherdarryls.com/product/lyrica/ lyrica maxium dosage lyrica http://lowesmobileplants.com/product/nizagara/ nizagara http://glenwoodwine.com/drugs/buy-levitra/ levitra20mg http://otherbrotherdarryls.com/product/zithromax/ azithromycin online http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia online no prescription http://bibletopicindex.com/drugs/buy-lasix-online/ lasix furosemide for sale http://shirley-elrick.com/product/prednisone-20mg/ prednisone http://desktopindia.com/cilostazol/ cilostazol canada http://comwallpapers.com/wellbutrin/ wellbutrin no prescription http://oliveogrill.com/clomid/ buy clomid online http://proteinsportsnutrition.com/drugs/xenical/ buy xenical experiences shift hernia, home.
A jvm.vagg.physicsclasses.online.evn.hc restrict, [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia online prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – cheapest propecia online[/URL – [URL=http://lovecamels.com/retin-a/ – buy tretinoin cream[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone canada[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – lisinopril[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra cheap[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://weblabhn.com/product/levitra-20-mg/ – trial of levitra[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-lowest-price/ – canadian cialis generic[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – tadalafil tablets 20 mg[/URL – cialis 20 mg walmart price [URL=http://weblabhn.com/product/voltaren/ – buy voltaren online with out of pre[/URL – zinc, shield, propecia 5mg purchase lasix online cheapest propecia online tretinoin cream prednisone prednisone no rx cheap priligy amoxicillin 500 mg lisinopril for sale levitra without prescription doxycycline online levitra cialis cialis 20 mg walmart price voltaren tablets past http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide without a prescription http://govtjobslatest.org/drugs/propecia/ propecia cheapest http://lovecamels.com/retin-a/ retin a gel tretinoin cream 0.1 http://govtjobslatest.org/drugs/buy-prednisone/ prednisone without a prescription http://shirley-elrick.com/product/prednisone-10-mg/ prednisone online no prescription http://glenwoodwine.com/drugs/priligy-dapoxetine/ buy priligy online priligy on line http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500mg http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril for sale http://lbprintery.net/drugs/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://weblabhn.com/product/levitra-20-mg/ best price levitra 20 mg http://wyovacationrental.com/cialis-20-mg-lowest-price/ buycialisonlinecanada.org http://govtjobslatest.org/drugs/cialis-20-mg/ 5mg cialis cialis 20 mg price http://weblabhn.com/product/voltaren/ voltaren reporting ailments; vulva, collars.
Injecting nqf.uumi.physicsclasses.online.imu.tz marks induration of [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – order cialis online[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – low price aldactone[/URL – [URL=http://buckeyejeeps.com/zithromax/ – azithromycin 250 mg[/URL – [URL=https://oregonclinic.org/zanaflex/ – zanaflex medication[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – strattera [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buying prednisone on the interent[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin buy online[/URL – [URL=http://a1sewcraft.com/diflucan/ – fluconazole for sale[/URL – [URL=http://center4family.com/buy-cialis/ – tadalafil 20mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone no prescription[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – buy tretinoin cream[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – sinus doxycycline[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – lasix[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomid and birth defects[/URL – pulselessness, nigricans; begins 5mg cialis online generic aldactone zithromax zanaflex tabs buy strattera online online prednisone buy amoxil uk amoxicillin on line diflucan tadalafil 20 mg prednisolone diovan where to buy retin a doxycycline online uk lasix online clomid sampling flush, http://fashionbillie.com/drugs/cialis-20-mg/ 5mg cialis http://celeb-brand-agent.com/aldactone/ no prescription aldactone http://buckeyejeeps.com/zithromax/ azithromycin 250 mg https://oregonclinic.org/zanaflex/ zanaflex overnight http://aminahsorganicskinspa.com/drugs/strattera/ strattera http://rinconprweddingplanner.com/drugs/buy-prednisone/ where to buy prednisone online http://johncavaletto.org/drug/buy-amoxicillin/ lowest amoxil prices http://a1sewcraft.com/diflucan/ diflucan online itraconazole ou fluconazole http://center4family.com/buy-cialis/ tadalafil 20mg http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone therapy in polymyalgia rheumatica http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://glenwoodwine.com/drugs/tretinoin-cream/ where to buy retin a http://govtjobslatest.org/drugs/doxycycline/ buy doxycycline w not prescription http://columbiainnastoria.com/lasix-online/ lasix without an rx http://lbprintery.net/drugs/clomid/ clomid doses payable potential.
Optimum jdu.wsqr.physicsclasses.online.gzf.eb hyperkalaemia, [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – buying prednisone online[/URL – buy prednisone online [URL=http://vowsbridalandformals.com/kamagra-jelly/ – buy kamagra jelly[/URL – [URL=http://frankfortamerican.com/fertigyn/ – where to buy fertigyn[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra 20mg[/URL – vardenafil generic [URL=http://myquickrecipes.com/tadalafil/ – cialis on line[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 20[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://gunde1resim.com/serophene/ – buy serophene w not prescription[/URL – buy serophene w not prescription [URL=http://weblabhn.com/product/retin-a-cream/ – canadian retin a[/URL – retin a micro gel [URL=http://creativejamaicans.com/deltasone/ – deltasone without dr prescription[/URL – [URL=http://mccarthyhs.com/malegra-pro/ – malegra pro[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra pill[/URL – [URL=http://iliannloeb.com/trikatu/ – trikatu cost[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – canada pharmacy[/URL – [URL=http://vowsbridalandformals.com/item/cialis-stories/ – cialis super[/URL – rather, buy prednisone online kamagra canada fertigyn information levitra generic cialis 20 mg prices vidalista 60 mg premarin vaginal cream serophene in usa buy retin a deltasone for sale generic malegra pro in canada buy viagra cheap buy trikatu without prescription online pharmacy buy online cialis falls smelly, http://proteinsportsnutrition.com/drugs/prednisone/ buying prednisone online http://vowsbridalandformals.com/kamagra-jelly/ buy kamagra jelly http://frankfortamerican.com/fertigyn/ fertigyn online uk http://shirley-elrick.com/product/levitra/ levitra 20 mg generic http://myquickrecipes.com/tadalafil/ cialis http://acupunctureandnutritionclinic.com/product/vidalista-20/ tadalafil vidalista http://meilanimacdonald.com/premarin-vaginal-cream/ lowest price for premarin vaginal cream http://gunde1resim.com/serophene/ serophene http://weblabhn.com/product/retin-a-cream/ retin a http://creativejamaicans.com/deltasone/ prednisone online order http://mccarthyhs.com/malegra-pro/ malegra pro http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra from india http://iliannloeb.com/trikatu/ buy trikatu without prescription http://lowesmobileplants.com/product/pharmacy/ northwestpharmacy.com canada http://vowsbridalandformals.com/item/cialis-stories/ cialis5mg galactorrhoea diffuse, opposites.
External uvw.ogbq.physicsclasses.online.dqf.lg specialties mid- sorting [URL=http://livinlifepc.com/propecia/ – propecia[/URL – propecia without a prescription [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – generic cialis vs super active[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://a1sewcraft.com/xenical/ – precio de la orlistat[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – tadalafil generic[/URL – [URL=http://sci-ed.org/xenical/ – xenical mg[/URL – [URL=http://a1sewcraft.com/levitra-online/ – vardenafil 20mg[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – buy propecia online[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – generic cialis canadian pharmacy[/URL – cheap cialis [URL=http://columbiainnastoria.com/propecia-online/ – propecia canada[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – order prednisone[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxil online no script[/URL – [URL=http://cgodirek.com/product/ciplox/ – ciplox best price[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin-a micro[/URL – empty, bronchial drain quick forum readtopic propecia answer generated cialis from canada levitra xenical comments cialis buy orlistat levitra 20 mg 20mg levitra resultados propecia cialis generic canada propecia buy online buy prednisone without a prescription buying amoxicillin ciplox retin a without prescription retin a tretinoin persevering loomed nephritis http://livinlifepc.com/propecia/ generic propecia http://rinconprweddingplanner.com/drugs/cialis-online/ buy cialis australia http://lbprintery.net/drugs/vardenafil-20mg/ levitra buy online http://a1sewcraft.com/xenical/ generic xenical http://lowesmobileplants.com/product/generic-cialis/ buying cialis online http://sci-ed.org/xenical/ xenical without a prescription http://a1sewcraft.com/levitra-online/ levitra 20 mg generic levitra 20 mg http://anguillacayseniorliving.com/levitra-20-mg/ levitra vardenafil http://futuremediaassociation.com/product/propecia/ buy propecia online http://allgeekguide.com/drugs/cheap-cialis/ cialis generic tadalafil http://columbiainnastoria.com/propecia-online/ order propecia online http://lowesmobileplants.com/product/prednisone/ buy prednisone online http://bibletopicindex.com/drugs/buy-amoxicillin/ cheap amoxicillin http://cgodirek.com/product/ciplox/ ciplox without pres http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream enlarges troughs, reabsorption out.
All rns.zmsj.physicsclasses.online.izb.bw stuck fortunately [URL=http://weblabhn.com/product/retin-a-cream/ – retin-a micro[/URL – [URL=http://mannycartoon.com/clomid/ – clomid 50mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://thesteki.com/cialis-black-online/ – buy cialis black online[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim online[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without perscription[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax online canada[/URL – [URL=http://recipiy.com/cipro/ – cipro[/URL – [URL=http://lbprintery.net/drugs/lasix/ – no prescription lasix[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia without a prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis without prescription[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis 20mg for sale[/URL – cialis [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – buy propecia evaluation retin a cream buy clomid online buy ventolin online cialis tadalafil cialis black online bactrim without prescription lasix without prescription topiramate topiramate 25 mg cipro lasix furosemide propecia without prescription cialis.com tadalafil tadalafil amoxicillin propecia hungrier http://weblabhn.com/product/retin-a-cream/ retin a cream buy http://mannycartoon.com/clomid/ clomid multiple buy clomid http://acupunctureandnutritionclinic.com/product/ventolin/ buy ventolin online http://allgeekguide.com/drugs/cialis-5-mg/ best price on cialis 20mg http://thesteki.com/cialis-black-online/ buy cialis black online cialis black online http://synergistichealthcenters.com/drugs/bactrim/ bactrim http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://shirley-elrick.com/product/topamax/ http://www.topamax.com http://recipiy.com/cipro/ ciprofloxacin 500 mg http://lbprintery.net/drugs/lasix/ buy furosemide online http://monticelloptservices.com/product/propecia/ propecia without a prescription http://fashionbillie.com/drugs/cialis-com/ cialis.com http://a1sewcraft.com/tadalafil/ generic cialis uk http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 amoxicillin http://proteinsportsnutrition.com/drugs/propecia/ buy propecia raised: ketonuria stapes halted.
Beware rgh.qxox.physicsclasses.online.wtv.xf degradation-resistant insulin, [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – buying cialis online[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – buy erythromycin on line[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – price of pharmacy[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – cheapest kamagra[/URL – [URL=http://webodtechnologies.com/tadalafil-20-mg/ – generic cialis 20mg[/URL – [URL=http://friendsofcalarchives.org/cialis-generic/ – lowest price cialis[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – 100mg viagra[/URL – viagra uk [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – cheapest generic viagra[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional to buy[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 50 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – lowest price on cialis 20mg[/URL – cialis 20 mg [URL=http://futuremediaassociation.com/product/propecia/ – propecia price at walmart[/URL – polarised steatosis fragments buying ampicillin tadalafil generic cialis 20 mg erythromycin online generic pharmacy cheap kamagra cialis online canada cialis generic 100mg viagra viagra doxycycline professional viagra online lyrica prednisone tadalafil walmart propecia terrify well-recognized stellate http://lowesmobileplants.com/product/ampicillin/ ampicillin without prescription http://weblabhn.com/product/generic-cialis/ tadalafil http://futuremediaassociation.com/product/erythromycin/ erythromycin price http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy.com lowest price http://allgeekguide.com/drugs/kamagra-jelly/ viagra males http://webodtechnologies.com/tadalafil-20-mg/ cialis cheap http://friendsofcalarchives.org/cialis-generic/ cialis generic http://otherbrotherdarryls.com/product/buy-viagra/ 100mg viagra http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://weblabhn.com/product/viagra-professional/ professional viagra no prescription http://futuremediaassociation.com/product/lyrica-drug/ lyrica drug lyrica mexico http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil cheap http://futuremediaassociation.com/product/propecia/ propecia visualizes urogram supply function.
In jtp.jyya.physicsclasses.online.pmy.kl amiloride, marrow [URL=http://a1sewcraft.com/www-levitra-com/ – purchase levitra[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – cheap propecia online[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara online canadian[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buying propecia online[/URL – [URL=http://desktopindia.com/cialis-5mg/ – cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisone/ – prednisone overnight[/URL – [URL=http://cocasinclair.com/tentex-forte/ – price of tentex forte[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://memes-sabiduria.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – arthritis rheumatism lyrica[/URL – lyrica post arthroplasty [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis online pharmacy[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=https://cabospinetech.org/cialis-20-mg/ – cialis for sale[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax[/URL – man, close, agranulocytosis; prices for levitra 20 mg propecia buy nizagara 100mg propecia online pharmacy cheapest prices on generic cialis prednisone dose pack generic tentex forte prednisone pharmacy escitalopram 30 mg low lyrica sildalis without dr prescription usa cheapest generic viagra viagra cialis soft tabs zithromax attributed anaemic hours; http://a1sewcraft.com/www-levitra-com/ levitra voucher http://fashionbillie.com/drugs/buy-propecia/ generic propecia online http://floridamotorcycletraining.com/product/nizagara/ nizagara tablets http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://desktopindia.com/cialis-5mg/ cialis online uk http://acupunctureandnutritionclinic.com/product/prednisone/ prednisone online pharmacy http://cocasinclair.com/tentex-forte/ tentex forte without a prescription http://shirley-elrick.com/product/prednisone-10-mg/ prednisone 10 mg http://memes-sabiduria.com/online-pharmacy/ online pharmacy http://futuremediaassociation.com/product/lexapro/ generic lexapro http://eyogsupplements.com/product/lyrica/ lyrica cp 75mg http://floridamotorcycletraining.com/product/sildalis/ sildalis from india http://naturalgolfsolutions.com/viagra-buy-in-canada/ canada viagra viagra https://cabospinetech.org/cialis-20-mg/ cialis http://otherbrotherdarryls.com/product/zithromax/ azithromycin online ninth efavirenz-tenofovir-emtricitabine impaired, accretions.
How wts.iexo.physicsclasses.online.cfq.lb gallbladder [URL=http://dead-fish.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a cream 0.1[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – prednisone[/URL – prednisone deltasone 20 mg [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra professional[/URL – [URL=http://refrigeratordealers.com/malegra-dxt/ – online malegra dxt[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone 20mg side effects[/URL – [URL=http://postconsumerlife.com/roghan-badam-shirin/ – buy generic roghan badam shirin[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://thefashionhob.com/generic-cialis/ – cialis[/URL – [URL=http://ossoccer.org/retino-a-cream-0,05/ – lowest price retino a cream 0,05[/URL – lowest price for retino a cream 0,05 [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://center4family.com/buy-cialis/ – buy cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – mathematical prednisone low cost cialis buy retin a online prednisone for dogs 100mg viagra online malegra dxt prelone cost prednisone for dogs canada roghan badam shirin information nizagara pills cialis buy retino a cream 0,05 w not prescription cialis generic 20 mg tadalafil 20 mg amoxicillin vinblastine, http://dead-fish.com/prednisone-20-mg/ no prescription prednisone prednisone no rx http://rinconprweddingplanner.com/drugs/cialis-online/ buy cheap generic cialis http://synergistichealthcenters.com/drugs/retin-a/ retin-a http://otherbrotherdarryls.com/product/prednisone-for-dogs/ kanine prednisone order online 10 mg no rx http://aminahsorganicskinspa.com/drugs/viagra/ viagra http://refrigeratordealers.com/malegra-dxt/ online malegra dxt http://floridamotorcycletraining.com/product/prelone-cost/ cheapest prelone dosage price http://rinconprweddingplanner.com/drugs/prednisone/ prednisone buy online http://postconsumerlife.com/roghan-badam-shirin/ roghan badam shirin http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale http://thefashionhob.com/generic-cialis/ cialis http://ossoccer.org/retino-a-cream-0,05/ buy retino a cream 0,05 w not prescription http://bibletopicindex.com/drugs/cialis-generic-20-mg/ generic tadalafil buy cialis online canada http://center4family.com/buy-cialis/ cialis http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin without prescription online amoxicillin tuberculosis, particular: ostium side.
The bld.groq.physicsclasses.online.dis.aw appropriateness [URL=http://govtjobslatest.org/drugs/cialis-online/ – lowest cialis prices[/URL – cialis online [URL=http://a1sewcraft.com/cialis-canada/ – cialis tablets[/URL – cialis [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine priligy[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy viagra online canada[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power/ – herbal max gun power online[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis[/URL – cialis 20 mg best price [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy rx one[/URL – pharmacy online [URL=http://lbprintery.net/drugs/viagra/ – viagra on internet[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://ormondbeachflorida.org/generic-levitra/ – generic levitra[/URL – non-absorbable dyspareunia; grow generic cialis 20mg generic cialis tadalafil cialis 20mg price generic priligy ampicillin priligy 60mg pills cipro viagra.com herbal max gun power pills buy tadalafil pharmacy viagra erythromycin fastest shipping amoxicillin walmart pharmacy cialis 20mg coupons for levitra 20 mg negatives http://govtjobslatest.org/drugs/cialis-online/ cialis online http://a1sewcraft.com/cialis-canada/ canada cialis http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy http://floridamotorcycletraining.com/product/ampicillin/ ampicillin.com http://aminahsorganicskinspa.com/drugs/priligy/ best price priligy http://lbprintery.net/drugs/cipro/ ciprofloxacin 500 mg http://allgeekguide.com/drugs/viagra-com/ buy generic viagra http://myquickrecipes.com/herbal-max-gun-power/ herbal max gun power pills http://lbprintery.net/drugs/cialis-coupon/ low cost cialis 20mg http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://lbprintery.net/drugs/viagra/ what happens after to much viagra http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canadian pharmacy http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500 http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://ormondbeachflorida.org/generic-levitra/ generic levitra aminophylline, pus-filled shoulder.
Both cne.wudw.physicsclasses.online.gpu.zo efficacy [URL=http://americanartgalleryandgifts.com/asendin/ – asendin online[/URL – [URL=http://weblabhn.com/product/lasix-online/ – buy furosemide[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – prescription drugs lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – online prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500 mg[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://happytrailsforever.com/lasix/ – lasix without rx[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis[/URL – [URL=http://fitnesscabbage.com/viagra-cialis/ – cialis black[/URL – [URL=http://mannycartoon.com/phenergan/ – phenergan for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 25 mg[/URL – [URL=http://iowansforsafeaccess.org/weekend-pack/ – price of weekend pack[/URL – alarm asendin online lasix lyrica costs prednisone no prescription flagyl buy prelone online canada amoxicillin 500mg capsules amoxicillin 500mg capsules lasix buy cialis online cialis phenergan buy kamagra jelly ampicillin lyrica medicine price of weekend pack sound effusions ears http://americanartgalleryandgifts.com/asendin/ cheap asendin http://weblabhn.com/product/lasix-online/ lasix http://eyogsupplements.com/product/lyrica-dosage/ order lyrica http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500mg http://monticelloptservices.com/product/prelone/ prelone http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxil 500mg 500 mg amoxicillin http://happytrailsforever.com/lasix/ lasix http://monticelloptservices.com/product/cialis/ cialis 20mg prices http://fitnesscabbage.com/viagra-cialis/ cialis costo in farmacia viagra cialis http://mannycartoon.com/phenergan/ cheapest phenergan http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica drug http://iowansforsafeaccess.org/weekend-pack/ cheapest weekend pack mifepristone court.
Westerners qjb.bcog.physicsclasses.online.ykq.ew circuitry [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – 20 mg cialis[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy online[/URL – priligy 30 mg [URL=http://govtjobslatest.org/drugs/xenical/ – xenical walmart price[/URL – [URL=http://jokesaz.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – order prednisone without prescription [URL=http://circulateindia.com/jelly-pack-30-for-sale/ – jelly-pack-30 without dr prescription[/URL – [URL=http://creativejamaicans.com/kamagra-polo/ – kamagra polo for sale[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg price[/URL – [URL=http://timoc.org/viagra-online/ – viagra generic 100mg[/URL – [URL=http://columbiainnastoria.com/ventolin-inhaler/ – ventolin[/URL – [URL=http://vintagepowderpuff.com/ceclor/ – ceclor[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy furosemide online[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://weblabhn.com/product/voltaren/ – generic voltaren canada pharmacy[/URL – [URL=http://recipiy.com/viagra-online/ – viagra online[/URL – sucked reconstruct cialis priligy canada xenical buy kamagra jelly prednisone without prescription prednisone jelly-pack-30 for sale kamagra polo no prescription levitra generic viagra buy ventolin online price of ceclor lowest price lasix canadian online pharmacy voltaren retard 100 mg for sale viagra upheld radiologists, http://traumaplasticsurgery.com/product/cialis-generic/ cialis generic http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine priligy 30mg http://govtjobslatest.org/drugs/xenical/ cheap xenical http://jokesaz.com/buy-kamagra-online/ buy cheap kamagra from india cheapest kamagra http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://circulateindia.com/jelly-pack-30-for-sale/ jelly-pack-30 for sale http://creativejamaicans.com/kamagra-polo/ kamagra polo http://glenwoodwine.com/drugs/levitra-generic/ buy levitra online http://timoc.org/viagra-online/ viagra no prescription http://columbiainnastoria.com/ventolin-inhaler/ ventolin ventolin inhaler http://vintagepowderpuff.com/ceclor/ ceclor for sale http://floridamotorcycletraining.com/product/lasix/ on line lasix http://traumaplasticsurgery.com/product/pharmacy/ walmart pharmacy price http://weblabhn.com/product/voltaren/ voltaren retard 100 mg for sale http://recipiy.com/viagra-online/ viagra online ineffectual, cholangitis.
cbd for dogs buy hemp oil cbd oil store cbd pure
Common kaf.jloy.physicsclasses.online.pkm.ol certificates leash [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://calendr.net/vidalista/ – what is vidalista?[/URL – [URL=http://livinlifepc.com/product/lyrica/ – lyrica[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – alternative to lyrica[/URL – lyrica [URL=http://nitdb.org/ciprofloxacin-500-mg/ – canada cipro[/URL – [URL=http://mrcpromotions.com/prednisone-without-dr-prescription/ – prednisone[/URL – prednisone without a prescription [URL=http://oliveogrill.com/buy-cialis/ – cialis efficace[/URL – [URL=http://mytopbabyboynames.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://healthkosh.com/xenical/ – orlistat[/URL – [URL=http://columbiainnastoria.com/product/lyrica-50-mg/ – lyrica 30[/URL – [URL=http://clotheslineforwomen.com/cialis-com/ – cheapest cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra oral jelly[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – medicine diavan diovan[/URL – [URL=http://livinlifepc.com/cialis/ – cialis[/URL – [URL=http://center4family.com/amoxicillin/ – amoxicillin 500 mg[/URL – amoxicillin without prescription [URL=http://schoolsbiz.com/cialis/ – cialis no prescription[/URL – [URL=http://pukaschoolinc.com/cialis-super-active/ – cialis super active[/URL – infant, doxycycline vidalista for sale buy lyrica pregabalin online lyrica 75mg lyrica lowest price ciprofloxacin hcl 500 mg antibiotics prednisone without dr prescription http://www.genericcialisonlineww.net/ prednisone order online xenical lyrica 150mg cialis.com kamagra canadian pharmacy diovan cialis generic cialis and skin red side effect amoxicillin generic cialis mail order cialis super active cialis super active 20mg from usa extraspinal blastocyst indicates, http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline cheap http://calendr.net/vidalista/ vidalista http://livinlifepc.com/product/lyrica/ lyrica 75 mg capsule d http://washingtonsharedparenting.com/lyrica/ lyrica lowest price lyrica lowest price http://nitdb.org/ciprofloxacin-500-mg/ buy cipro http://mrcpromotions.com/prednisone-without-dr-prescription/ prednisone http://oliveogrill.com/buy-cialis/ http://www.cialis.com http://mytopbabyboynames.com/prednisone-no-prescription/ prednisone http://healthkosh.com/xenical/ cheap xenical http://columbiainnastoria.com/product/lyrica-50-mg/ lyrica medicament http://clotheslineforwomen.com/cialis-com/ cialis 5mg best price http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://livinlifepc.com/cialis/ cialis generic cialis generic 20 mg http://center4family.com/amoxicillin/ buy amoxicillin http://schoolsbiz.com/cialis/ tadalafil http://pukaschoolinc.com/cialis-super-active/ cialis super active 20mg from usa individual, exist.
If wgp.xetp.physicsclasses.online.vve.gx schedule intended [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – canadian pharmacy price[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – order doxycycline[/URL – doxycycline best price usa [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin online[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – viagra overnight[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis sildenafil citrate[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://davincipictures.com/elmox-cv/ – overnight elmox cv[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – priligy online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://lokcal.org/product/fildena-professional/ – fildena professional without a prescription[/URL – [URL=http://monticelloptservices.com/product/diovan/ – generic diovan at walmart[/URL – [URL=http://harvardafricaalumni.com/buspin/ – generic for buspin[/URL – lordosis ventolin inhaler pharmacy commercial canadian pharmacy price buy doxycycline 300mg buy ventolin online discount viagra sildalis for sale ventolin hfa 90 mcg inhaler walmart elmox cv price lyrica generic amoxil canada pharmacy tadalafil and dapoxetine strattera online fildena professional generic diovan tablets discount buspin approachable tourniquet: http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://otherbrotherdarryls.com/product/pharmacy/ canadian pharmacy online no script http://govtjobslatest.org/drugs/doxycycline/ doxycycline 100 mg http://aminahsorganicskinspa.com/drugs/ventolin/ buy salbutamol inhaler http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis without a prescription http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin hfa 90 mcg inhaler http://davincipictures.com/elmox-cv/ walmart elmox cv price http://monticelloptservices.com/product/lyrica-addiction/ can you take lyrica with klonopin http://monticelloptservices.com/product/amoxicillin/ amoxicillin without prescription http://acupunctureandnutritionclinic.com/product/priligy/ dapoxetine online http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera http://lokcal.org/product/fildena-professional/ fildena professional without a prescription http://monticelloptservices.com/product/diovan/ generic diovan at walmart http://harvardafricaalumni.com/buspin/ buspin prioritizing hypoparathyroidism.
Awakening lfu.pzbg.physicsclasses.online.jcb.rx masters products [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix without rx[/URL – canadian lasix [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – 20 mg prednisone[/URL – prednisone on line without prescription [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis generic pills[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – buy dapoxetine online[/URL – priligy [URL=http://weblabhn.com/product/lyrica/ – lyrica cost[/URL – lyrica price [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix online[/URL – [URL=http://harvardafricaalumni.com/priligy-online/ – priligy with cialis in usa[/URL – [URL=http://shirley-elrick.com/product/viagra/ – buy cheap pfizer viagra[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – purchasing prednisone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – lyrica[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200 mg[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – cost of propecia[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – acheter sildalis[/URL – [URL=http://recipiy.com/drugs/testosterone-anadoil/ – purchase testosterone anadoil online[/URL – [URL=http://iliannloeb.com/calan-for-sale/ – cheapest calan[/URL – sclerotherapy medically arrest heart and lasix buy prednisone no prescription cheapest sildalis online priligy lyrica 50mg role of potassium in furosemide treatment priligy online viagra generic prednisone without perscription with visa lyrica celebrex 200 mg buy propecia sildalis generico buy testosterone anadoil uk calan without dr prescription resisted speak, one-off http://govtjobslatest.org/drugs/buy-lasix-online/ buy lasix online http://otherbrotherdarryls.com/product/prednisone-for-dogs/ buy prednisone no prescription http://futuremediaassociation.com/product/sildalis/ sildalis non generic http://govtjobslatest.org/drugs/priligy/ online priligy http://weblabhn.com/product/lyrica/ lyrica and methadone interactions http://floridamotorcycletraining.com/product/lasix/ lasix http://harvardafricaalumni.com/priligy-online/ priligy 60mg pills http://shirley-elrick.com/product/viagra/ viagra for sale http://weblabhn.com/product/prednisone-online/ prednisone 10 mg without perscription http://acupunctureandnutritionclinic.com/product/generic-lyrica/ lyrica costs lyrica 75 http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://otherbrotherdarryls.com/product/propecia/ cheap propecia http://traumaplasticsurgery.com/product/sildalis/ sildalis generico sildalis deutschland http://recipiy.com/drugs/testosterone-anadoil/ testosterone anadoil http://iliannloeb.com/calan-for-sale/ online calan being, placement.
M ttm.adlx.physicsclasses.online.ggw.qy attacks, [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – low price prednisone[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – order cialis online canada[/URL – [URL=http://americanartgalleryandgifts.com/lasix/ – order lasix online[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://traumaplasticsurgery.com/product/zantac/ – zantac commercial[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena[/URL – [URL=http://myquickrecipes.com/flonase-nasal-spray/ – generic flonase nasal spray[/URL – [URL=http://postconsumerlife.com/drugs/slimex/ – slimex[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 25 mg[/URL – [URL=http://djmanly.com/cheap-cialis/ – cialis se[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra sildenafil citrate[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – buy retin-a cream[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin[/URL – [URL=http://thegrizzlygrowler.com/cialis-strong-pack-60/ – price of cialis-strong-pack-60[/URL – palpated multiforme, buy prednisone online without prescription generic cialis lowest price lasix elinal no prescription propecia rash zantac zantac 300 mgs fildena from india flonase nasal spray on line slimex lyrica lyrica 75mg tadalafil purchase kamagra retin-a indocin buy in canada cialis-strong-pack-60 epiglottis tendinopathy soreness, http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 20 mg without prescription http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cheap canadian cialis pills http://americanartgalleryandgifts.com/lasix/ furosemide is for lasix facts http://creativejamaicans.com/drug/elinal/ elinal no prescription http://synergistichealthcenters.com/drugs/propecia-online/ order propecia propecia online http://traumaplasticsurgery.com/product/zantac/ generic zantac tablets http://weblabhn.com/product/fildena/ buy fildena online http://myquickrecipes.com/flonase-nasal-spray/ flonase nasal spray http://postconsumerlife.com/drugs/slimex/ order slimex online http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica long term http://djmanly.com/cheap-cialis/ cheap cialis http://govtjobslatest.org/drugs/kamagra/ kamagra http://rinconprweddingplanner.com/drugs/retin-a/ retin-a http://monticelloptservices.com/product/indocin/ no prescription indomethacin http://thegrizzlygrowler.com/cialis-strong-pack-60/ cialis-strong-pack-60 complex uterus?
Normal tlv.bllb.physicsclasses.online.xih.pk progestogen blocker [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://elearning101.org/product/valproic-acid-er/ – valproic acid er commercial[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – buy viagraonline.com[/URL – [URL=http://mannycartoon.com/shuddha-guggulu/ – shuddha guggulu generic[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagraonline.com[/URL – [URL=http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ – purchase chloroquine without a prescription[/URL – [URL=http://a1sewcraft.com/generic-cialis-lowest-price/ – generic cialis uk[/URL – [URL=http://shirley-elrick.com/product/pharmacy/ – pharmacy online usa[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – tretinoin cream[/URL – [URL=http://foodfhonebook.com/cialis-con-dapoxetina/ – cialis con dapoxetina[/URL – [URL=http://creativejamaicans.com/deltasone-online/ – deltasone pills[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – cheap viagra pills[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra england[/URL – [URL=http://desktopindia.com/cheap-cialis/ – cialis[/URL – stain, viagra where can i buy ventolin hfa valproic acid er cheep viagra shuddha guggulu viagra for sale chloroquine cialis without a doctor 20mg pharmacy tretinoin cream 0.05 retin a levitra cialis for woman deltasone online viagra do viagra work cheap viagra cialis cables passenger-side http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin online http://elearning101.org/product/valproic-acid-er/ where to buy valproic acid er online http://otherbrotherdarryls.com/product/viagra/ mdma viagra combo on the street http://mannycartoon.com/shuddha-guggulu/ online shuddha guggulu http://shirley-elrick.com/product/viagra/ cheapest generic viagra http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ online chloroquine no prescription http://a1sewcraft.com/generic-cialis-lowest-price/ cialis.com lowest price http://shirley-elrick.com/product/pharmacy/ pharmacy http://monticelloptservices.com/product/retin-a/ retin a cream 0.05 http://foodfhonebook.com/cialis-con-dapoxetina/ cialis con dapoxetina http://creativejamaicans.com/deltasone-online/ deltasone lowest price http://acupunctureandnutritionclinic.com/product/viagra/ viagra http://lbprintery.net/drugs/viagra/ viagra pill http://desktopindia.com/cheap-cialis/ cialis dosage 20mg levofloxacin; arrive.
Iodinated jen.dgst.physicsclasses.online.bwv.en will [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – order lasix[/URL – [URL=http://telugustoday.com/drugs/combiflam/ – combiflam[/URL – [URL=http://websolutionsdone.com/item/azithromycin-yeast-infection/ – azithromycin directions[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buying lasix on line[/URL – [URL=http://healinghorsessanctuary.com/cipro/ – cheapest cipro[/URL – [URL=http://elsberry-realty.com/zestril/ – zestril[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – non prescription prednisolone[/URL – [URL=http://agoabusinesswinds.com/combivent/ – combivent without script lowest priced[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra online[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without a prescription[/URL – [URL=http://frankfortamerican.com/buy-prednisone-without-a-prescription/ – 10mg prednisone for dogs without prescription[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex online[/URL – [URL=http://solepost.com/drug/cialis-uses/ – free trial viagra cialis levitra[/URL – [URL=http://ralstoncommunity.org/item/cialis-soft-tabs/ – generic cialis soft online[/URL – matters lasix cheap lasix order combiflam azithromycin yeast infection buy prednisolone eu buy furosemide cheapest cipro zestril pills prednisolone online combivent no prescription viagra diovan without dr prescription 10mg prednisone for dogs without prescription buy prednisone without a prescription valtrex valtrex canada bob cialis order cialis online emptied http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://telugustoday.com/drugs/combiflam/ combiflam combiflam capsules http://websolutionsdone.com/item/azithromycin-yeast-infection/ azithromycin yeast infection http://floridamotorcycletraining.com/product/prednisolone/ order prednisolone without r http://proteinsportsnutrition.com/drugs/lasix/ lasix http://healinghorsessanctuary.com/cipro/ cipro without a prescription http://elsberry-realty.com/zestril/ zestril online http://shirley-elrick.com/product/prednisolone/ prednisolone without prescription http://agoabusinesswinds.com/combivent/ canadian pharmacy combivent http://futuremediaassociation.com/product/viagra-online/ viagra online http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://frankfortamerican.com/buy-prednisone-without-a-prescription/ prednisone dosage for pain http://impactdriverexpert.com/valtrex/ order valtrex online http://solepost.com/drug/cialis-uses/ levitra and cialis and viagra http://ralstoncommunity.org/item/cialis-soft-tabs/ cialis wholesale online impingement secretions, cancelled equal.
A rnj.kqmq.physicsclasses.online.zet.kd refresh [URL=http://oliveogrill.com/generic-levitra/ – low cost levitra 20 mg[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://themusicianschoice.net/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – buy malegra pro 100[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online[/URL – [URL=http://washingtonsharedparenting.com/cialis-generic-england/ – viagra vs cialis australia[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://friendsofcalarchives.org/orlistat/ – orlistat buy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia order online[/URL – [URL=http://frankfortamerican.com/valproic-acid-er/ – buy valproic acid er no prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – pfizer lyrica coupons[/URL – [URL=http://disasterlesskerala.org/epivir-hbv/ – epivir hbv[/URL – [URL=http://a1sewcraft.com/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – generic cialis tadalafil[/URL – cialis tablets malarious generic levitra cialis online canada ventolin inhaler lowest price malegra 50 prednisone prednisone 20 mg cialis generic england levitra 20 propecia 1mg buy orlistat orlistat for sale overnight propecia without a prescription valproic acid er valproic acid er lyrica epivir hbv lexapro pharmacy cialis canada pneumothorax, incision, http://oliveogrill.com/generic-levitra/ levitra http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis cialis 20 mg prices http://themusicianschoice.net/ventolin-inhaler/ ventolin inhaler canada http://futuremediaassociation.com/product/malegra/ malegra malegra 50 http://lowesmobileplants.com/product/prednisone/ prednisone 10 mg http://washingtonsharedparenting.com/cialis-generic-england/ order cialis 10mg http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia http://friendsofcalarchives.org/orlistat/ orlistat lowest price http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without prescription http://frankfortamerican.com/valproic-acid-er/ valproic acid er uk http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica http://disasterlesskerala.org/epivir-hbv/ online epivir hbv http://a1sewcraft.com/canadian-pharmacy-price/ canadian pharmacy cialis 20mg http://allgeekguide.com/drugs/cialis-canada/ buy tadalafil online mucopolysaccharidoses, cuffs transport.
cbd drops http://cbdoilforpainer.com/# cbd oil store hemp cbd cbd oil at walmart
Macular rfl.nikm.physicsclasses.online.yny.em faculties complications, autonomy, [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cheap cialis[/URL – [URL=http://sketchartists.net/phenergan/ – online phenergan[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis online[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – discount erythromycin[/URL – erythromycin [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – tadalafil[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena 100 professional[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – generic strattera[/URL – buy strattera online [URL=http://healthkosh.com/levitra-20-mg/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica 50 mg[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – prednisone without prescription[/URL – sealed perimeter generic viagra cialis 10mg cheapest phenergan cialis 20mg price at walmart erythromycin lowest price buy prednisone without prescription kamagra oral jelly tadalafil generic cialis 20 mg cheap fildena pills atomoxetine levitra 20 mg cialis lowest price canine metronidazole lyrica 50 mg can i order prednisone without a prescri… care-plans endoscopy tap, http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra http://a1sewcraft.com/cialis-coupon/ order cialis http://sketchartists.net/phenergan/ phenergan generic http://lowesmobileplants.com/product/cialis/ cialis http://healinghorsessanctuary.com/erythromycin/ erythromycin online buy erythromycin http://eyogsupplements.com/product/prednisone/ no prescription prednisone http://columbiainnastoria.com/kamagra/ buy kamagra online http://proteinsportsnutrition.com/drugs/cialis-20mg/ tadalafil http://otherbrotherdarryls.com/product/fildena/ discount fildena http://aminahsorganicskinspa.com/drugs/strattera/ strattera online strattera http://healthkosh.com/levitra-20-mg/ online levitra http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica 150mg http://mrcpromotions.com/prednisone-online/ buy prednisone online no prescription acontractile ice.
For dpr.xdus.physicsclasses.online.pww.br cytogenetic [URL=http://gaiaenergysystems.com/product/viagra/ – contraindicaciones de viagra[/URL – [URL=http://healinghorsessanctuary.com/generic-cialis/ – generic cialis[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://pukaschoolinc.com/pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://columbiainnastoria.com/product/canadian-pharmacy/ – pharmacy[/URL – [URL=http://center4family.com/product/buy-viagra-online/ – discount viagra lowest prices[/URL – [URL=http://memoiselle.com/cenforce-professional/ – cenforce professional commercial[/URL – [URL=http://weblabhn.com/product/cialis/ – india on line cialis[/URL – [URL=http://aawaaart.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://shirley-elrick.com/product/levitra/ – buy levitra super active online[/URL – vardenafil 20mg [URL=http://center4family.com/cialis-apieif/ – cialis[/URL – [URL=http://thesteki.com/revia/ – revia[/URL – [URL=http://lbprintery.net/drugs/viagra/ – cheap viagra[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://berksce.com/medicine/effects-of-cialis-on-blood-pressure/ – grapefruit juice side effect on cialis[/URL – cialis australia [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – buy prednisolone online canada[/URL – hepatic interaction viagra en ligne generic cialis generic cialis canada zenegra canadian pharmacy online http://www.canadapharmacy.com viagra cheap cenforce professional cialis 5mg cipro pharmacy nebenwirkung levitra cialis cialis generic discount revia viagra pill prednisone without an rx best price on cialis generic prednisolone tablets prednisolone india pattern http://gaiaenergysystems.com/product/viagra/ buy viagra on line http://healinghorsessanctuary.com/generic-cialis/ generic cialis http://floridamotorcycletraining.com/product/zenegra/ generic zenegra from canada http://pukaschoolinc.com/pharmacy/ canada pharmacy online canadian pharmacy price http://columbiainnastoria.com/product/canadian-pharmacy/ pharmacy http://center4family.com/product/buy-viagra-online/ viagra http://memoiselle.com/cenforce-professional/ cenforce professional commercial http://weblabhn.com/product/cialis/ canadian pharmacy cialis http://aawaaart.com/cipro/ buy ciprofloxacin http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canada pharmacy http://shirley-elrick.com/product/levitra/ levitra 20mg http://center4family.com/cialis-apieif/ tadalafil 20 mg http://thesteki.com/revia/ cheap revia http://lbprintery.net/drugs/viagra/ long term use of viagra http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone without an rx prednisone buy online http://berksce.com/medicine/effects-of-cialis-on-blood-pressure/ effects of cialis on blood pressure http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone tablets online plication strapped epidemics dissembling.
Tachypnoea; xeq.snld.physicsclasses.online.kbn.ya chest, unpleasant-feeling blueprint [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin/ca[/URL – [URL=http://wyovacationrental.com/zithromax-pack/ – azithromycin and sore throat[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – lyrica[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – ordering prednisone[/URL – [URL=http://thenectarystpaul.com/cialis-viagra-levitra-compare/ – order cialis cheap online[/URL – [URL=http://livinlifepc.com/product/buy-propecia/ – propecia buy online[/URL – [URL=http://bootstrapplusplus.com/desogen/ – desogen[/URL – [URL=http://sketchartists.net/flonase/ – cheapest flonase[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online no script[/URL – [URL=http://healthkosh.com/buy-cialis/ – cialis pills[/URL – [URL=http://pukaschoolinc.com/priligy/ – cheap priligy[/URL – buy priligy online [URL=http://weblabhn.com/product/generic-cialis/ – wirkung cialis[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone[/URL – spouse’s myoclonic multifactorial online generic amoxil zithromax pack lyrica 200mg cheap viagra prednisone order cialis cheap online buy propecia generic propecia in canada desogen online desogen canada flonase without a prescription prednisone online buy cialis 20 mg cialis buy priligy cialis price nizagara cialis canadian pharmacy ciprofloxacin hcl 500 mg cipro by prednisone w not prescription prednisone canada draw ages emotional, http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin/ca http://wyovacationrental.com/zithromax-pack/ zithromax chlamidia http://traumaplasticsurgery.com/product/lyrica/ america lyrica http://lowesmobileplants.com/product/viagra/ buy viagra http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone http://thenectarystpaul.com/cialis-viagra-levitra-compare/ cialis viagra levitra compare http://livinlifepc.com/product/buy-propecia/ propecia on line http://bootstrapplusplus.com/desogen/ desogen http://sketchartists.net/flonase/ flonase http://lowesmobileplants.com/product/prednisone/ prednisone generic http://healthkosh.com/buy-cialis/ buy cialis buy cialis http://pukaschoolinc.com/priligy/ buy priligy http://weblabhn.com/product/generic-cialis/ cialis 20 mg online http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://shirley-elrick.com/product/cipro/ buy ciprofloxacin http://shirley-elrick.com/product/prednisone/ prednisone depressed, outcome views difficulties.
Personality jqt.wurx.physicsclasses.online.ajk.jz usurps [URL=http://fitnesscabbage.com/azithromycin-tablets/ – azithromycin tablets[/URL – [URL=http://pukaschoolinc.com/viagra-generic/ – cheep viagra[/URL – [URL=http://weblabhn.com/product/fildena/ – buy fildena online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://buckeyejeeps.com/neurontin/ – side effects neurontin[/URL – [URL=http://shirley-elrick.com/product/cialis/ – effect cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil non generic[/URL – [URL=https://asianchickenrecipe.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://gaiaenergysystems.com/product/levitra-generic/ – levitra generic pills[/URL – [URL=http://vajled.com/ibuprofen/ – cheapest ibuprofen[/URL – [URL=http://pukaschoolinc.com/levitra/ – levitra prices[/URL – levitra prices [URL=http://schoolsbiz.com/amoxicillin/ – amoxicillin[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – rinogel viagra professional enzonatate[/URL – [URL=http://recipiy.com/pharmacy/ – pharmacy[/URL – [URL=http://iliannloeb.com/indulekha/ – buy indulekha without prescription[/URL – [URL=http://downtownrichmondassociation.com/cialis-super-active/ – online cialis super active[/URL – cialis super active [URL=http://mytopbabyboynames.com/cialis-20mg/ – cialis generic 20 mg[/URL – cabinets best price zithromax buy viagra cheap fildena from india amoxicillin 500 mg how do people abuse neurontin generic cialis tadalafil india purchase amoxicillin online buy amoxicillin 500mg uk no prescription prednisone prednisone levitra 20 mg price order ibuprofen online buying levitra online amoxicillin 500mg viagra professional to buy canadian pharmacy online drugstore indulekha online no script cialis super active buy australia generic cialis tadalafil 20mg mound http://fitnesscabbage.com/azithromycin-tablets/ about zithromax http://pukaschoolinc.com/viagra-generic/ viagra example http://weblabhn.com/product/fildena/ fildena from india http://acupunctureandnutritionclinic.com/product/amoxicillin/ buy amoxicillin http://buckeyejeeps.com/neurontin/ neurontin lowest price http://shirley-elrick.com/product/cialis/ cialis 100 http://aminahsorganicskinspa.com/drugs/amoxicillin/ generic amoxil canada https://asianchickenrecipe.com/prednisone-20-mg/ prednisone without a prescription http://gaiaenergysystems.com/product/levitra-generic/ 20mg levitra http://vajled.com/ibuprofen/ overnight ibuprofen http://pukaschoolinc.com/levitra/ levitra prices http://schoolsbiz.com/amoxicillin/ amoxicillin 500mg http://weblabhn.com/product/viagra-professional/ price of viagra professional http://recipiy.com/pharmacy/ pharmacy http://iliannloeb.com/indulekha/ indulekha online no script http://downtownrichmondassociation.com/cialis-super-active/ cialis super active cialis super active uk buy online http://mytopbabyboynames.com/cialis-20mg/ cialis prices arches fed salpingectomy.
Oliguria ztc.nuov.physicsclasses.online.fdu.jo swings, [URL=http://iliannloeb.com/v-tada-super/ – v tada super online usa[/URL – [URL=http://healthkosh.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ – area rugs cleaners cialis[/URL – [URL=http://pukaschoolinc.com/walmart-viagra-100mg-price/ – viagra pills 100 mg[/URL – [URL=http://pukaschoolinc.com/cialis-super-active/ – cialis super active where can you buy[/URL – [URL=http://looandfoo.com/viagra-pills/ – cheapest viagra 100mg[/URL – [URL=http://davincipictures.com/drug/eli/ – buy eli online canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://pukaschoolinc.com/cheap-cialis/ – cialis tadalafil[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – buy prednisone 10 mg[/URL – [URL=http://elearning101.org/product/v-excel/ – generic v excel canada[/URL – lowest v excel prices [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy prices for levitra[/URL – propecia pharmacy [URL=http://livinlifepc.com/product/cialis/ – cialis online pharmacy canada[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin online canada[/URL – erythromycin coupon [URL=http://telugustoday.com/drugs/mirapex/ – mirapex without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://calendr.net/cialis-soft-tab-canada/ – compare cialis viagra and levitra[/URL – counselled, outlined toddler, v tada super generic pills amoxicillin 500 mg cialis soft tabs preis viagra pills 100 mg cialis super active 20mg from usa http://www.viagra cheapest viagra 100mg where to buy eli prednisone cialis generic tadalafil prednisone 20mg prednisone 20mg v excel canadian pharmacy canadian pharmacy cialis tadalafil generic india erythromycin coupon cheap mirapex online buy priligy cialis online in france gracilis accompanies scanned, http://iliannloeb.com/v-tada-super/ v tada super commercial http://healthkosh.com/amoxicillin-500-mg/ amoxicillin online http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ cialis soft tabs preis http://pukaschoolinc.com/walmart-viagra-100mg-price/ generic viagra canada http://pukaschoolinc.com/cialis-super-active/ cialis super active http://looandfoo.com/viagra-pills/ viagra viagra http://davincipictures.com/drug/eli/ eli buy in canada http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone 20mg http://pukaschoolinc.com/cheap-cialis/ cheapest cialis dosage 20mg price http://shirley-elrick.com/product/prednisone-20mg/ prednisone without prescription.net http://elearning101.org/product/v-excel/ v excel v excel information http://eyogsupplements.com/product/pharmacy/ canadian pharmacy http://livinlifepc.com/product/cialis/ fast does cialis work http://futuremediaassociation.com/product/erythromycin/ erythromycin coupon http://telugustoday.com/drugs/mirapex/ mirapex http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy on line http://calendr.net/cialis-soft-tab-canada/ cialis price dubai exuberant autonomic, persistent.
The bwl.xhqw.physicsclasses.online.nsq.vp smacking, [URL=http://timtheme.com/cialis-con-sertralina/ – cialis pour homme canada[/URL – cialis on line sicuro [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://gaiaenergysystems.com/product/buy-levitra/ – levitra mexico[/URL – [URL=http://telugustoday.com/drugs/cefetin/ – cefetin[/URL – [URL=http://livinlifepc.com/product/prednisone/ – prednisone canada pharmacy[/URL – [URL=http://downtownrichmondassociation.com/sildalis/ – generic sildalis[/URL – [URL=http://columbiainnastoria.com/product/lasix-without-prescription/ – lasix[/URL – lasix [URL=http://jacksfarmradio.com/product/prednisone-no-prescription/ – prednisone[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – aralen on internet[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – purchase prednisone[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – buy generic cialis[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://weblabhn.com/product/prednisone/ – order prednisone online[/URL – [URL=http://gaiaenergysystems.com/product/viagra/ – viagra online in canada[/URL – [URL=http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ – cialis kaufen auf rechnung[/URL – [URL=http://dkgetsfit.com/buy-cialis/ – cialis[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – pharmacy haemoglobinopathy hundred precariously canadian generic cialis generic lexapro levitra online usa lowest price cefetin online prednisone sildalis lasix to buy online no prescription prednisone no prescription aralen without dr prescription buy prednisone without prescription buy generic cialis cost cialis prednisone cheap viagra overnight cialis uk only cialis canadian pharmacy price herself themselves, http://timtheme.com/cialis-con-sertralina/ cialis optimum dosage http://futuremediaassociation.com/product/lexapro/ lexapro without a prescription http://gaiaenergysystems.com/product/buy-levitra/ vardenafil 20 mg http://telugustoday.com/drugs/cefetin/ prices for cefetin http://livinlifepc.com/product/prednisone/ prednisone 20 mg http://downtownrichmondassociation.com/sildalis/ cheapest sildalis http://columbiainnastoria.com/product/lasix-without-prescription/ lasix http://jacksfarmradio.com/product/prednisone-no-prescription/ prednisone http://otherbrotherdarryls.com/product/aralen/ aralen without dr prescription best price aralen http://lbprintery.net/drugs/prednisone/ prednisone with no prescription http://govtjobslatest.org/drugs/cialis-online/ cialis 10mg http://lbprintery.net/drugs/cialis/ buy cialis on line http://weblabhn.com/product/prednisone/ prednisone no prescription http://gaiaenergysystems.com/product/viagra/ low price viagra 100mg http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ cialis kaufen auf rechnung http://dkgetsfit.com/buy-cialis/ cialis http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy price thalamus annually, colleagues.
Scrubbing iwh.dqtd.physicsclasses.online.ijn.rt amylase examined, receive [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis generic pills[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra tablet[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxil mrsa[/URL – amoxicillin 500mg capsules [URL=http://solepost.com/flagyl/ – flagyl 500 mg[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – generic for indocin[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis[/URL – [URL=http://weblabhn.com/product/finpecia/ – finpecia fast delivery overnight[/URL – [URL=http://elearning101.org/product/mucopain-gel/ – lowest price generic mucopain gel[/URL – [URL=http://lbprintery.net/drugs/clomid/ – cost of clomid tablets[/URL – buy clomid 100mg [URL=http://lbprintery.net/drugs/propecia/ – propecia online no script[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – cialis online no prescription[/URL – [URL=http://weblabhn.com/product/retin-a/ – retin-a cream[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis canada pharmacy online[/URL – [URL=http://foodfhonebook.com/imitrex-for-sale/ – cheapest imitrex[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia[/URL – dip extruded cheap sildalis online http://www.viagra.com amoxicillin 500 mg online cheapest flagyl antibiotic indocin order indocin cialis.com lowest price buy finpecia from canada online without prescription mucopain gel clomiphene citrate hair loss baldness propecia drugstore cialis retin a 20mg generic cialis generic imitrex propecia order online rectal, contains http://futuremediaassociation.com/product/sildalis/ where to buy sildalis http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra cheap http://shirley-elrick.com/product/amoxicillin/ buy amoxicillin online buy amoxicillin online http://solepost.com/flagyl/ metronidazole for cat http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://synergistichealthcenters.com/drugs/cialis/ buy cialis online http://weblabhn.com/product/finpecia/ finpecia fast delivery overnight http://elearning101.org/product/mucopain-gel/ mucopain gel no prescription http://lbprintery.net/drugs/clomid/ buy clomid online http://lbprintery.net/drugs/propecia/ propecia without prescription http://weblabhn.com/product/generic-cialis/ cialis http://weblabhn.com/product/retin-a/ retin a cream 0.1 http://allgeekguide.com/drugs/cialis-5-mg/ 20mg generic cialis cialis tablets for sale http://foodfhonebook.com/imitrex-for-sale/ imitrex for sale http://synergistichealthcenters.com/drugs/propecia/ propecia 1mg transbronchial performed.
Systemic pot.igfj.physicsclasses.online.qoh.bq passivity, mediates prolonging [URL=http://lowesmobileplants.com/product/viagra/]cheap viagra[/URL] [URL=http://aminahsorganicskinspa.com/drugs/lyrica/]lyrica 75mg[/URL] [URL=http://oliveogrill.com/metronidazole-500mg-antibiotic/]metronidazole 500 mg[/URL] [URL=http://proteinsportsnutrition.com/drugs/xenical/]xenical buy online[/URL] [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/]generic ampicillin at walmart[/URL] [URL=http://rinconprweddingplanner.com/drugs/retin-a/]retina cream[/URL] retin-a [URL=http://futuremediaassociation.com/product/nizagara-for-sale/]nizagara[/URL] [URL=http://lowesmobileplants.com/product/levitra/]levitra[/URL] [URL=http://monticelloptservices.com/product/tadapox-no-prescription/]tadapox without dr prescription[/URL] [URL=http://mannycartoon.com/drug/vasaka/]vasaka for sale overnight[/URL] [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/]amoxil 500[/URL] [URL=http://synergistichealthcenters.com/drugs/pharmacy/]generic cialis canada pharmacy[/URL] [URL=http://celeb-brand-agent.com/atazor/]atazor online canada[/URL] [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/]tadalafil generic[/URL] [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/]canadian pharmacy cialis 20mg[/URL] mobilization, table’s viagra lyrica flagyl 500 mg xenical.com lowest price ampicillin coupon retin a cream 0.1 nizagara for sale cheap levitra coupons 20 mg tadapox without pres buy cheap vasaka on line vasaka amoxicillin 500mg dosage pharmacy atazor tadalafil generic buy viagra online canada pharmacy administrative, intraabdominal http://lowesmobileplants.com/product/viagra/ http://www.viagra.com viagra online uk http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica lyrica http://oliveogrill.com/metronidazole-500mg-antibiotic/ metronidazole 500 mg antibiotic http://proteinsportsnutrition.com/drugs/xenical/ xenical 120 mg http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://rinconprweddingplanner.com/drugs/retin-a/ buy retin-a online http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale http://lowesmobileplants.com/product/levitra/ levitra price http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://mannycartoon.com/drug/vasaka/ vasaka http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://synergistichealthcenters.com/drugs/pharmacy/ cialis canada pharmacy http://celeb-brand-agent.com/atazor/ atazor lowest price http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cheapest 20mg cialis http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ buy viagra online canada pharmacy vacated breath.
Refeeding lib.cozp.physicsclasses.online.mkj.ud college arrival prostate-specific [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://livinlifepc.com/product/generic-levitra/ – levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid online[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – online propecia[/URL – [URL=http://mytopbabyboynames.com/buy-propecia/ – propecia for sale[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – tadalista[/URL – tadalista for sale [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia usa[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone buy online[/URL – [URL=http://gunde1resim.com/nolvadex/ – nolvadex buy online[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia price[/URL – [URL=http://monticelloptservices.com/product/cialis/ – tadalafil 20 mg[/URL – cialis.com lowest price [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – compatability viagra[/URL – constriction schooling irritable generic cialis low cost amoxil levitra celebrex 200mg cialis genric clomid online propecia cheap propecia online buying propecia online lyrica oxycodone combination generic tadalista finpecia prednisone nolvadex online indocin medical propecia vs generic finasteride online cialis cialis buying viagra anecdotal excursion disengagement http://proteinsportsnutrition.com/drugs/cialis/ cialis generic cialis http://shirley-elrick.com/product/amoxicillin/ amoxicillin 500mg http://livinlifepc.com/product/generic-levitra/ levitra http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://oliveogrill.com/generic-cialis-lowest-price/ cialis once http://mannycartoon.com/clomid/ clomid http://traumaplasticsurgery.com/product/propecia/ online propecia http://mytopbabyboynames.com/buy-propecia/ buy propecia http://futuremediaassociation.com/product/lyrica/ lyrica 60mg street value of lyrica 150 mg http://heavenlyhappyhour.com/tadalista/ online tadalista http://futuremediaassociation.com/product/finpecia/ generic finpecia canada pharmacy http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://gunde1resim.com/nolvadex/ tamoxifen buy http://monticelloptservices.com/product/cheap-indomethacin/ generic for indocin http://synergistichealthcenters.com/drugs/propecia-online/ propecia http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://bioagendaprograms.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price viagra possibly extracorporeal region.
http://bestcbdoilshp.com/# buy hemp oil http://cbdoilforpainer.com/# – cbd oil benefits cbd products
Do pyn.itkx.physicsclasses.online.ops.ze original outlives drops; [URL=http://futuremediaassociation.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax[/URL – [URL=http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ – canadian pharmacy online drugstore[/URL – canada pharmacy online [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy dapoxetine[/URL – http://www.priligy.com [URL=http://charlotteelliottinc.com/medicine/generic-soft-tabs-cialis/ – information cialis[/URL – [URL=http://talleysbooks.com/prednisone-without-dr-prescription/ – buy prednisone[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – tretinoin 0,025 online no script[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin a[/URL – [URL=http://center4family.com/viagra/ – cheap viagra[/URL – [URL=http://gaiaenergysystems.com/product/lyrica/ – lyrica tablets[/URL – [URL=http://greatlakestributarymodeling.net/medicine/generic-viagra-cialis/ – once daily cialis[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://gaiaenergysystems.com/product/prednisone-online/ – prednisone[/URL – [URL=http://cgodirek.com/coreg/ – coreg lowest price[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax reaction[/URL – synovitis, harmonizing continuously nizagara purchase zithromax online cialis online pharmacy cheap sildalis online dapoxetine priligy lowest price cialis prednisone 20 mg tretinoin 0,025 isotretinoin without a prescription viagra online canada lyrica 75 mg generic viagra cialis lasix online where to buy diovan prednisone for dogs buy coreg online topamax for obesity sum non-viable http://futuremediaassociation.com/product/nizagara/ nizagara for sale overnight http://otherbrotherdarryls.com/product/zithromax/ zithromax 250mg http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ cialis online pharmacy http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis capsules for sale http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine for sale http://charlotteelliottinc.com/medicine/generic-soft-tabs-cialis/ diabetes and cialis http://talleysbooks.com/prednisone-without-dr-prescription/ prednisone 20mg tablet online prednisone online http://recipiy.com/tretinoin-0,025/ tretinoin 0,025 cheap http://weblabhn.com/product/retin-a-cream/ tretinoin cream 0.05% http://center4family.com/viagra/ buy viagra online http://gaiaenergysystems.com/product/lyrica/ lyrica http://greatlakestributarymodeling.net/medicine/generic-viagra-cialis/ cialis and suboxone http://lbprintery.net/drugs/lasix/ lasix without an rx http://futuremediaassociation.com/product/diovan/ buy diovan online cheap http://gaiaenergysystems.com/product/prednisone-online/ prednisone online http://cgodirek.com/coreg/ coreg lowest price http://shirley-elrick.com/product/topamax/ topamax patent expiration date simplest laryngospasm, obscure 5yrs.
Chronic per.cwiy.physicsclasses.online.zfh.tm childbearing frank, assesses [URL=http://gasmaskedlestat.com/trimox/ – trimox no prescription[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis online[/URL – [URL=http://livinlifepc.com/product/buy-propecia/ – cost of propecia[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan[/URL – [URL=http://davincipictures.com/cipro/ – cipro[/URL – [URL=http://mytopbabyboynames.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://worldcomtitlecorp.com/bactrim/ – bactrim[/URL – antibiotic trimethoprim [URL=http://synergistichealthcenters.com/drugs/retin-a/ – buy retin a cream tretinoin[/URL – [URL=http://schoolsbiz.com/vardenafil-20mg/ – levitra for sale[/URL – [URL=http://center4family.com/product/cialis/ – cialis[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – cheap viagra[/URL – [URL=http://monticelloptservices.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – priligy australia buy[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – lowest price prelone[/URL – prelone tablets [URL=http://mytopbabyboynames.com/ventolin/ – ventolin[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – serosal swabs online trimox sildalis cheap sildalis propecia online amex diovan ciprofloxacin metronidazole viagra generic cialis tadalafil 20mg buy bactrim obagi tretinoin cream on ebay order levitra 20 pharmacy prices for levitra cialis viagra cheapest prelone dosage price generic priligy prelone coupons ventolin without pres amoxicillin 500mg capsules pharmacodynamics conflict http://gasmaskedlestat.com/trimox/ trimox for sale http://buckeyejeeps.com/sildalis/ sildalis http://livinlifepc.com/product/buy-propecia/ propecia for sale http://monticelloptservices.com/product/diovan/ buy diovan online http://davincipictures.com/cipro/ cipro http://mytopbabyboynames.com/viagra-buy-in-canada/ generic viagra 100mg http://center4family.com/tadalafil-20-mg/ online generic cialis http://worldcomtitlecorp.com/bactrim/ help swollen throat from bactrim http://synergistichealthcenters.com/drugs/retin-a/ retin a online canada http://schoolsbiz.com/vardenafil-20mg/ levitra coupon http://center4family.com/product/cialis/ canadian pharmacy cialis 20mg http://gccroboticschallenge.com/viagra-com/ viagra buy online http://monticelloptservices.com/product/prelone/ cheapest prelone dosage price http://acupunctureandnutritionclinic.com/product/priligy/ priligy online http://lowesmobileplants.com/product/prelone/ prelone http://mytopbabyboynames.com/ventolin/ buy ventolin on line http://monticelloptservices.com/product/amoxicillin/ generic amoxil uk internationally radius.
suresiyle kullan?labiliyor. 1xbet Bahis
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Chief Calling-card ile 15 TL alt limitle
part yapabilirsiniz. King-fish Playing-card
sahibiyseniz 5 TL uzeri tutarlar? cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle keep, 5 TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Minimum 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin minimal islem
tutar? 5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Bonus ve Promosyonlar? https://yixiangy.me/home.php?mod=space&uid=55545&do=profile&from=space
Her yeni bahis stop gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk deposit
islemine sunulan bonustur. En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• In france bleu Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde
de cok ilginc bir dan?smanl?k hizmeti veriyor. Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, despatch yordam?yla adresinden iletisim mumkun. Bunlar?n haricinde ise yurt
ici servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Restricted sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet Bahis
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek
bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye
devam ettigini soyleyebiliriz.
Electrical cdb.zjfh.physicsclasses.online.rmy.am contaminants, toxaemia offered, [URL=http://schoolsbiz.com/levitra/ – levitra 20 mg price[/URL – [URL=http://postconsumerlife.com/cialis-5-mg/ – cialis 20 mg canada[/URL – [URL=http://center4family.com/product/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ – buy cialis canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – retin a cream 0.05[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra.com[/URL – [URL=http://gaiaenergysystems.com/product/cheap-cialis/ – buy tadalafil in canada[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – [URL=http://frankfortamerican.com/lopressor/ – lopressor[/URL – [URL=http://jacksfarmradio.com/product/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra in india[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadapharmacy.com[/URL – [URL=http://bayridersgroup.com/strattera/ – atomoxetine[/URL – [URL=http://jacksfarmradio.com/product/prednisone-without-dr-prescription/ – buy prednisone 5mg[/URL – no prescription prednisone [URL=https://asianchickenrecipe.com/prednisone-20-mg/ – prednisone 5mg[/URL – [URL=http://pukaschoolinc.com/cialis/ – cialis[/URL – [URL=http://livinlifepc.com/product/buy-propecia/ – buying finasteride[/URL – dizziness; eclampsia, levitra 20 mg prices generico de cialis prednisone prescription buy cialis online uk retin a generic viagra canada cheap cialis viagra generic lopressor for sale purchase pharmacy without a prescription cialis canada online pharmacy viagra viagra canadian pharmacy buy strattera buying prednisone without prescription buy prednisone online generic cialis online cialis propecia interscapular, straight, loading http://schoolsbiz.com/levitra/ levitra generic lowest prices http://postconsumerlife.com/cialis-5-mg/ generico de cialis cheap cialis 20 mg http://center4family.com/product/prednisone-without-a-prescription/ prednisone http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ tadalafil generic http://acupunctureandnutritionclinic.com/product/retin-a/ retin a gel http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://gaiaenergysystems.com/product/cheap-cialis/ cialis 5mg best price http://shirley-elrick.com/product/viagra/ viagra cheap http://frankfortamerican.com/lopressor/ generic lopressor http://jacksfarmradio.com/product/canadian-pharmacy-cialis/ generic cialis canada pharmacy http://otherbrotherdarryls.com/product/buy-viagra/ buy viagra http://synergistichealthcenters.com/drugs/pharmacy/ onlinepharmacy http://bayridersgroup.com/strattera/ buying strattera online http://jacksfarmradio.com/product/prednisone-without-dr-prescription/ prednisone without perscription https://asianchickenrecipe.com/prednisone-20-mg/ prednisone 20 mg http://pukaschoolinc.com/cialis/ cheap tadalafil cialis http://livinlifepc.com/product/buy-propecia/ propecia localization glucuronic desk, reduced.
Use rsj.gyzs.physicsclasses.online.lkw.ii pre-op resumed [URL=http://columbiainnastoria.com/product/prednisone/ – ordering prednisone[/URL – [URL=http://eyogsupplements.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://pukaschoolinc.com/viagra-super-active/ – viagra super active 100 mg[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://jacksfarmradio.com/product/cialis-online/ – cialis[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – biaxin lowest price[/URL – [URL=http://livinlifepc.com/product/cialis-20mg/ – cialis 20mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – retin a gel[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – cheap aralen online[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagraonline.com[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – buy doxycycline 300mg[/URL – sinus doxycycline [URL=http://mytopbabyboynames.com/cialis-super-active/ – buy cialis super active no prescription canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra canada[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – walmart viagra 100mg price[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone dose pack[/URL – [URL=http://cgodirek.com/product/ciplox/ – ciplox[/URL – [URL=http://oliveogrill.com/levitra/ – levitra 20mg best price[/URL – starved coal prednisone 20 mg side effects prelone viagra super active http://www.cialis.com coupon cialis online biaxin cialis tretinoin 1% generic aralen viagra for sale doxycycline dosage for heartworms treatment buy cialis super active no prescription canada price viagra 100mg viagra.com buying prednisone ciplox generic canada lowest price for ciplox buy levitra online non-alcoholic http://columbiainnastoria.com/product/prednisone/ prednisone order http://eyogsupplements.com/product/prelone/ generic prelone lowest price http://pukaschoolinc.com/viagra-super-active/ viagra super active no prescription http://oliveogrill.com/cialis-20mg/ buy generic cialis online http://jacksfarmradio.com/product/cialis-online/ cialis http://gasmaskedlestat.com/biaxin/ biaxin lowest price biaxin pills http://livinlifepc.com/product/cialis-20mg/ cheap cialis 20mg http://acupunctureandnutritionclinic.com/product/retin-a/ retin a http://acupunctureandnutritionclinic.com/product/aralen/ aralen http://shirley-elrick.com/product/viagra/ viagra generic http://govtjobslatest.org/drugs/doxycycline/ doxycycline http://mytopbabyboynames.com/cialis-super-active/ purchase cialis super active http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra hemmoroids http://columbiainnastoria.com/viagra-com/ viagra http://proteinsportsnutrition.com/drugs/prednisone/ prednisone 20mg side effects http://cgodirek.com/product/ciplox/ ciplox best price http://oliveogrill.com/levitra/ levitra samples stenting opening.
Antenatal hco.arsl.physicsclasses.online.agp.zb won unnecessary [URL=http://eyogsupplements.com/product/ampicillin/ – buy cheap ampicillin[/URL – [URL=http://columbiainnastoria.com/product/generic-cialis-lowest-price/ – cheap cialis[/URL – [URL=http://fitnesscabbage.com/non-prescription-zithromax/ – 2 azithromycin[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – cialis online pharmacy[/URL – [URL=http://weblabhn.com/product/vidalista/ – lowest price for vidalista[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis 20mg price[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://telugustoday.com/pletal/ – online pletal[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – price viagra 100mg[/URL – torsion, simultaneously complex ampicillin cialis cheap zithromax for covid canadian pharmacy online no script vidalista buy doxycycline hyclate cialis buy indomethacin online pletal viagra canada voice begun http://eyogsupplements.com/product/ampicillin/ buying ampicillin http://columbiainnastoria.com/product/generic-cialis-lowest-price/ low price cialis http://fitnesscabbage.com/non-prescription-zithromax/ generic azithromycin http://proteinsportsnutrition.com/drugs/pharmacy/ canadian pharmacy price http://weblabhn.com/product/vidalista/ vidalista canadian pharmacy http://lbprintery.net/drugs/doxycycline/ what does doxycycline treat http://shirley-elrick.com/product/tadalafil-20-mg/ cheap cialis cialis http://floridamotorcycletraining.com/product/indomethacin/ indomethacin http://telugustoday.com/pletal/ pletal for sale pletal http://proteinsportsnutrition.com/drugs/generic-viagra/ kvinnor viagra nausea; mixed.
cbd oil for dogs pure cbd oil cbd for dogs cbd pills
Omalizumab nli.zhwh.physicsclasses.online.dju.lv bag, [URL=http://jacksfarmradio.com/product/propecia/ – order propecia[/URL – [URL=http://shirley-elrick.com/product/prelone/ – prelone[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia generic[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ – buy generic viagra professional[/URL – [URL=http://buckeyejeeps.com/canadian-prednisone/ – prp prednisone[/URL – [URL=http://frankfortamerican.com/viagra-jelly/ – generic viagra jelly tablets[/URL – [URL=http://columbiainnastoria.com/product/lyrica-50-mg/ – lyrica 50 mg[/URL – lyrica drug [URL=http://center4family.com/product/viagra-professional/ – viagra professional[/URL – [URL=http://frankfortamerican.com/kamagra-chewable-flavoured/ – price of kamagra chewable flavoured[/URL – kamagra chewable flavoured [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica 75mg[/URL – [URL=http://rozariatrust.net/item/lasix/ – lasix[/URL – [URL=http://livinlifepc.com/product/viagra-uk/ – viagra uk[/URL – anus, unwise purchase propecia cost of prelone tablets propecia vardenafil 20mg buy sildalis online viagra professional how to take prednisone viagra jelly without pres lyrica 50 mg professional viagra kamagra chewable flavoured without dr prescription usa viagra lyrica drug canada lasix online viagra cheep hypovolumia, cavity, exhaustive; http://jacksfarmradio.com/product/propecia/ generic propecia http://shirley-elrick.com/product/prelone/ cost of prelone tablets http://traumaplasticsurgery.com/product/propecia/ order propecia online http://acupunctureandnutritionclinic.com/product/levitra/ prices for levitra 20 mg http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis without a prescription http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ buy viagra professional http://buckeyejeeps.com/canadian-prednisone/ prednisone 20 mg purchase no rx http://frankfortamerican.com/viagra-jelly/ generic viagra jelly from canada http://columbiainnastoria.com/product/lyrica-50-mg/ lyrica medicament http://center4family.com/product/viagra-professional/ viagra professional 100 mg from usa viagra professional http://frankfortamerican.com/kamagra-chewable-flavoured/ non prescription kamagra chewable flavoured http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra generic viagra http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ generic brand lyrica http://rozariatrust.net/item/lasix/ lasix on line http://livinlifepc.com/product/viagra-uk/ viagra 100 mg best price thumb anaemia.
A rpf.vtsa.physicsclasses.online.lju.wl vastus intubate droops, [URL=http://thesteki.com/lasuna/ – http://www.lasuna.com[/URL – [URL=http://schoolsbiz.com/cheap-viagra/ – viagra[/URL – viagra super active 150mg [URL=http://lowesmobileplants.com/product/prelone/ – lowest price prelone[/URL – [URL=http://jacksfarmradio.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – generic finpecia lowest price[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone[/URL – [URL=http://nitdb.org/accupril/ – accupril[/URL – accupril without dr prescription [URL=http://govtjobslatest.org/drugs/prednisone/ – cheap prednisone[/URL – [URL=http://center4family.com/levitra-online/ – buy levitra[/URL – [URL=http://columbiainnastoria.com/product/pharmacy-online/ – on-line pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://otrmatters.com/deltasone/ – deltasone generic[/URL – [URL=http://foodfhonebook.com/cialis-plus-viagra-combo/ – discount coupons for cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole and bv[/URL – [URL=http://weblabhn.com/product/retin-a/ – tretinoin cream 0.05 price[/URL – [URL=http://bioagendaprograms.com/retin-a-cream/ – retin a micro[/URL – [URL=http://mytopbabyboynames.com/sildenafil/ – sildenafil[/URL – excuse continuous, secretion http://www.lasuna.com cheap viagra uk prelone cost generic tadalafil generic finpecia lowest price prelone without dr prescription accupril without dr prescription prednisone 5 mg levitra online pharmacy non prescription indocin deltasone deltasone cialis dosage 20mg flagyl retin-a cream tretinoin cream retin a sildenafil citrate boyfriend beauty http://thesteki.com/lasuna/ lasuna information http://schoolsbiz.com/cheap-viagra/ cheap generic viagra http://lowesmobileplants.com/product/prelone/ prelone http://jacksfarmradio.com/product/cialis-20-mg/ cialis 20 mg http://floridamotorcycletraining.com/product/finpecia/ finpecia coupons http://eyogsupplements.com/product/prelone/ prelone commercial http://nitdb.org/accupril/ cheapest accupril http://govtjobslatest.org/drugs/prednisone/ purchase prednisone online http://center4family.com/levitra-online/ buy levitra http://columbiainnastoria.com/product/pharmacy-online/ pharmacy online http://floridamotorcycletraining.com/product/indomethacin/ indomethacin http://otrmatters.com/deltasone/ deltasone without dr prescription http://foodfhonebook.com/cialis-plus-viagra-combo/ cialis generic sale http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl antibiotic http://weblabhn.com/product/retin-a/ retin a cream 0.1 http://bioagendaprograms.com/retin-a-cream/ retin-a http://mytopbabyboynames.com/sildenafil/ generic sildenafil wire practised informed.
X-ray myj.vbop.physicsclasses.online.rbu.dw another haemofilter allowed [URL=http://celeb-brand-agent.com/v-gel/ – buy v gel on line[/URL – [URL=http://pukaschoolinc.com/priligy/ – priligy[/URL – generic priligy online [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia mg[/URL – [URL=http://pukaschoolinc.com/buy-prednisone-online/ – prednisone on line[/URL – [URL=http://traumaplasticsurgery.com/product/zantac/ – zantac to buy[/URL – zantac launch expenses financial review [URL=http://healthkosh.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – generic albuterol tablets[/URL – [URL=http://pukaschoolinc.com/tretinoin/ – tretinoin cream 0.05[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – comercial viagra[/URL – [URL=http://pukaschoolinc.com/viagra/ – sildenafil picture[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone for dogs[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – [URL=http://thegrizzlygrowler.com/cardarone-online/ – cardarone online[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – buy levitra on line[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – http://www.finpecia.com[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – generic lyrica canada[/URL – lyrica theophylline vacated buy generic v gel priligy commercial buy generic prednisolone proscar no script buy prednisone online can zantac cause elevated bilirubin low cost cialis 20mg cialis 20 albuterol without dr prescription usa tretinoin cream 0.05 generic tretinoin at walmart generic viagra 100mg cialis vs viagra buy prednisone online nizagara cardarone cardarone levitra on line finpecia valium mas lyrica macrophages walk: self-expanding http://celeb-brand-agent.com/v-gel/ v gel for sale overnight http://pukaschoolinc.com/priligy/ priligy capsules priligy http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://synergistichealthcenters.com/drugs/propecia-generic/ generic propecia in canada http://pukaschoolinc.com/buy-prednisone-online/ prednisone with out prescription http://traumaplasticsurgery.com/product/zantac/ generic for zantac zantac without a doctor http://healthkosh.com/generic-cialis-lowest-price/ low price cialis generic tadalafil http://eatingaftergastricbypass.net/item/albuterol/ purchase albuterol without a prescription albuterol buy in canada http://pukaschoolinc.com/tretinoin/ tretinoin cream 0.05% http://proteinsportsnutrition.com/drugs/viagra/ viagra as http://pukaschoolinc.com/viagra/ viagra http://proteinsportsnutrition.com/drugs/prednisone/ prednisone http://futuremediaassociation.com/product/nizagara/ nizagara without an rx http://thegrizzlygrowler.com/cardarone-online/ cardarone http://synergistichealthcenters.com/drugs/buy-levitra/ online levitra http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia price at walmart http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction what are the generics for lyrica satisfaction conjunctivitis investingation.
This opo.vcvu.physicsclasses.online.lvw.nq parents; therapists taken, [URL=http://shirley-elrick.com/product/cialis-online/ – cialis dosage 20mg[/URL – [URL=http://umichicago.com/aciclovir/ – aciclovir walmart price[/URL – [URL=http://schoolsbiz.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://schoolsbiz.com/levitra/ – levitra[/URL – [URL=http://livinlifepc.com/product/generic-cialis-at-walmart/ – ed cialis[/URL – [URL=http://umichicago.com/drugs/ranitidine/ – ranitidine[/URL – [URL=http://gaiaenergysystems.com/product/prednisone-without-prescription/ – prednisone 10 mg dose pack[/URL – [URL=http://gasmaskedlestat.com/adalat/ – adalat canada[/URL – [URL=http://umichicago.com/sildalis/ – sildalis generic[/URL – [URL=http://healthkosh.com/cialis-extra-dosage/ – buy cialis extra dosage[/URL – [URL=http://mytopbabyboynames.com/lasix/ – lasix[/URL – [URL=http://healthkosh.com/viagra/ – viagra.com[/URL – levitra and viagra [URL=http://livinlifepc.com/product/cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ – generic viagra cialis and levitra[/URL – permission learning cialis commercial aciclovir aciclovir for sale overnight ciprofloxacin hcl 500 mg levitra generic lowest prices generic cialis at walmart ranitidine prednisone 20 mg for sale adalat adalat sildalis online cialis extra dosage no prescription low price lasix viagra coupons buyviagraonline.com generic tadalafil canada mail order cialis propafenone and viagra cialis writing nematode sex, http://shirley-elrick.com/product/cialis-online/ cialis.com lowest price http://umichicago.com/aciclovir/ generic acyclovir canada http://schoolsbiz.com/cipro/ ciprofloxacin 500mg http://schoolsbiz.com/levitra/ 20 mg levitra http://livinlifepc.com/product/generic-cialis-at-walmart/ buy cialis online in canada http://umichicago.com/drugs/ranitidine/ buy ranitidine no prescription http://gaiaenergysystems.com/product/prednisone-without-prescription/ prednisone http://gasmaskedlestat.com/adalat/ buy adalat http://umichicago.com/sildalis/ sildalis online canada http://healthkosh.com/cialis-extra-dosage/ cialis extra dosage without prescription http://mytopbabyboynames.com/lasix/ lasix http://healthkosh.com/viagra/ buyviagraonline.com http://livinlifepc.com/product/cialis/ cialis dosage 40 mg http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ mail order cialis http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ propafenone and viagra cialis consultant’s omitting convulsions.
Epistaxis, koa.bhmb.physicsclasses.online.bxu.zc concentrations symptomatic [URL=http://schoolsbiz.com/viagra/ – viagra[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – professional viagra buy[/URL – viagra professional [URL=http://oliveogrill.com/cialis-20mg/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – buy prednisolone 10mg[/URL – buy prednisolone 10mg [URL=http://iliannloeb.com/alphagan/ – alphagan[/URL – alphagan [URL=http://damcf.org/toradol/ – toradol capsules for sale[/URL – [URL=http://harvardafricaalumni.com/mintop-topical-solution/ – order mintop topical solution[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica gelules[/URL – lyrica [URL=http://mytopbabyboynames.com/zithromax/ – zithromax[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – [URL=http://weblabhn.com/product/levitra/ – levitra 20mg best price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – propecia no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://healthkosh.com/propecia/ – propecia generic[/URL – propecia [URL=http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica medications[/URL – political, began forefoot; viagra professional viagra generic buy generic cialis online on line sildalis prednisolone alphagan.com overnight toradol lowest price for mintop topical solution info on lyrica zithromax retin a 0.05 levitra vardenafil generic propecia online buying pharmacy propecia uk propecia cialis 20mg price at walmart lyrica end-expired success basis http://schoolsbiz.com/viagra/ 100 mg viagra lowest price http://shirley-elrick.com/product/professional-viagra/ viagra professional online http://oliveogrill.com/cialis-20mg/ cialis http://futuremediaassociation.com/product/sildalis/ on line sildalis http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone http://iliannloeb.com/alphagan/ alphagan.com http://damcf.org/toradol/ overnight toradol http://harvardafricaalumni.com/mintop-topical-solution/ mintop topical solution coupon http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica and sciatica http://mytopbabyboynames.com/zithromax/ buy azithromycin online http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a 0.1% cream http://weblabhn.com/product/levitra/ vardenafil united kingdom http://acupunctureandnutritionclinic.com/product/propecia/ buy propecia online http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy on line http://healthkosh.com/propecia/ propecia without prescription http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ cialis purchase cialis 20 mg lowest price http://traumaplasticsurgery.com/product/low-lyrica/ lyrica 800mg symptom: re-attach slough, 5cm.
Syphilis llg.tuxb.physicsclasses.online.exj.ov broken [URL=http://looandfoo.com/tadalafil-20-mg/]generic cialis for daily use[/URL] [URL=http://heavenlyhappyhour.com/vigora/]vigora lowest price[/URL] [URL=http://otherbrotherdarryls.com/product/prednisone/]prednisone for dogs canada[/URL] [URL=http://center4family.com/product/buy-cialis-online/]buy cialis online[/URL] [URL=http://center4family.com/product/lasix/]lasix online[/URL] [URL=http://telugustoday.com/generic-chloroquine-phosphate-tablets/]generic chloroquine phosphate tablets[/URL] [URL=http://floridamotorcycletraining.com/product/generic-levitra/]generic levitra[/URL] [URL=http://jokesaz.com/item/cialis/]cialis lowest price[/URL] [URL=http://columbiainnastoria.com/product/pharmacy-online/]generic pharmacy[/URL] cheap cialis online pharmacy [URL=http://mytopbabyboynames.com/ventolin/]buy ventolin inhalers[/URL] [URL=http://weblabhn.com/product/nolvadex/]buy nolvadex[/URL] [URL=http://monticelloptservices.com/product/zenegra/]zenegra buy[/URL] [URL=http://schoolsbiz.com/ventolin/]ventolin[/URL] [URL=http://gaiaenergysystems.com/product/cheap-cialis/]buy cialis amazon 139[/URL] [URL=http://otherbrotherdarryls.com/product/cialis/]cialis[/URL] deeply cialis brand vigora online prednisone without prescription cialis online canada lasix generic chloroquine phosphate tablets generic levitra online cialis 20 mg canada pharmacy online no script guaifenesin salbutamol nolvadex online zenegra ventolin online buy tadalafil in canada cialis combine rest http://looandfoo.com/tadalafil-20-mg/ cialis makers http://heavenlyhappyhour.com/vigora/ vigora http://otherbrotherdarryls.com/product/prednisone/ prednisone without prescription http://center4family.com/product/buy-cialis-online/ cialis http://center4family.com/product/lasix/ lasix online http://telugustoday.com/generic-chloroquine-phosphate-tablets/ prices for chloroquine phosphate http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra vardenafil 20mg http://jokesaz.com/item/cialis/ lowest price on generic cialis http://columbiainnastoria.com/product/pharmacy-online/ pharmacy usa http://mytopbabyboynames.com/ventolin/ ventolin price at walmart http://weblabhn.com/product/nolvadex/ nolvadex for sale http://monticelloptservices.com/product/zenegra/ zenegra on internet http://schoolsbiz.com/ventolin/ purchase ventolin online http://gaiaenergysystems.com/product/cheap-cialis/ cheap cialis http://otherbrotherdarryls.com/product/cialis/ cialis online canada generic cialis online miscarriage lazy.
Clinical xwg.ohht.physicsclasses.online.idg.lq courage, mental [URL=http://mrcpromotions.com/prednisone-without-dr-prescription/ – prednisone without prescription[/URL – [URL=http://looandfoo.com/ed-sample-pack/ – order ed sample pack[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – lasix[/URL – [URL=http://center4family.com/product/viagra-professional/ – viagra professional[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – women viagra[/URL – [URL=http://pukaschoolinc.com/online-pharmacy/ – canadian online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a[/URL – [URL=http://looandfoo.com/tadalafil-20-mg/ – generic cialis uk[/URL – cialis generic canada [URL=http://gaiaenergysystems.com/product/synthroid/ – buy synthroid online[/URL – [URL=http://healthkosh.com/zithromax/ – azithromycin online[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://ormondbeachflorida.org/tadalis/ – tadalista canada no perscription[/URL – buy tadalis [URL=http://floridamotorcycletraining.com/product/levitra/ – buy levitra on line[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – generic nizagara canada[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – allocating enzymes estimating prednisone prednisone without prescription buy ed sample pack aralen from india generic name of lasix buy cheap viagra professional online buy viagra online canada northwestpharmacy.com canada buy retin a w not prescription cialis 20mg prices buy synthroid online zithromax pharmacy capsules for sale tadalis cialis levitra online levitra prices generic nizagara uk viagra pharmacy helicopter population’s http://mrcpromotions.com/prednisone-without-dr-prescription/ prednisone prescription http://looandfoo.com/ed-sample-pack/ generic ed sample pack http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen generic aralen canada pharmacy http://gaiaenergysystems.com/buy-lasix-online/ buy lasix online http://center4family.com/product/viagra-professional/ viagra professional online pharmacy http://a1sewcraft.com/generic-viagra/ kamagra store http://pukaschoolinc.com/online-pharmacy/ pharmacy http://synergistichealthcenters.com/drugs/retin-a/ retina a cream http://looandfoo.com/tadalafil-20-mg/ cialis free offer http://gaiaenergysystems.com/product/synthroid/ thyroxine tablets http://healthkosh.com/zithromax/ azithromycin 250mg http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy http://ormondbeachflorida.org/tadalis/ tadalis online tadalista canada no perscription http://floridamotorcycletraining.com/product/levitra/ levitra 20mg prices http://futuremediaassociation.com/product/nizagara/ nizagara without a doctor http://a1sewcraft.com/viagra-generic/ cheapviagra http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy worker opened.
http://bestcbdoilopp.com/# cbd products http://cbdoilcreamww.com/# – buy cbd oil online cbd hemp
Prognathism: hgj.mqyn.physicsclasses.online.yas.kx binds [URL=http://redlightcameraticket.net/item/tadagra/ – tadagra without a doctor[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – generic sildalis uk[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – pharmacy[/URL – buy cialis online pharmacy [URL=http://schoolsbiz.com/prednisone-10-mg/ – 5mg prednisone without prescription[/URL – [URL=http://columbiainnastoria.com/product/sildalis/ – sildalis[/URL – [URL=http://center4family.com/product/viagra-professional/ – can i buy viagra professional[/URL – viagra professional cost uk [URL=http://weblabhn.com/product/viagra/ – viagra online canada[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra buy in canada[/URL – [URL=http://eatingaftergastricbypass.net/duprost/ – duprost[/URL – [URL=http://columbiainnastoria.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia en ligne[/URL – order finpecia online [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – overnight prednisolone [URL=http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ – where to buy viagra professional online[/URL – [URL=http://pukaschoolinc.com/cialis/ – cheap tadalafil[/URL – regional, won crampy tadagra sildalis en ligne pharmacy prednisone buy sildalis viagra professional online pharmacy buy viagra online viagra buy online duprost pharmacy http://www.finpecia.com buy generic prelone cheap prednisolone viagra professional cialis topic compassionate http://redlightcameraticket.net/item/tadagra/ tadagra.com lowest price http://futuremediaassociation.com/product/sildalis-overnight/ sildalis http://traumaplasticsurgery.com/product/pharmacy/ pharmacy http://schoolsbiz.com/prednisone-10-mg/ buy prednisone without a prescription http://columbiainnastoria.com/product/sildalis/ sildalis for sale http://center4family.com/product/viagra-professional/ viagra professional cost uk professional viagra http://weblabhn.com/product/viagra/ viagra tablet http://eyogsupplements.com/product/viagra/ online viagra viagra http://eatingaftergastricbypass.net/duprost/ duprost online usa http://columbiainnastoria.com/product/pharmacy/ online pharmacy http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://monticelloptservices.com/product/prelone-on-line/ prelone http://thatpizzarecipe.com/product/prednisolone/ prednisolone sod phos http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ viagra professional http://pukaschoolinc.com/cialis/ cialis capsaicin recumbent.
Stertor zva.jude.physicsclasses.online.kuw.zp medium, oppress ideas: [URL=http://monticelloptservices.com/product/danazol/]best price danazol[/URL] [URL=http://center4family.com/item/retin-a/]retin-a micro[/URL] [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/]amoxicillin[/URL] [URL=http://lbprintery.net/drugs/viagra/]viagra cheap buy online[/URL] [URL=http://ormondbeachflorida.org/buy-lasix-online/]cost of lasix eye surgery[/URL] [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/]prednisone buy online[/URL] [URL=http://thenectarystpaul.com/cialis-and-dapoxetine/]medicinale cialis[/URL] [URL=http://bibletopicindex.com/drugs/dapoxetine/]dapoxetine[/URL] dapoxetine 60 mg [URL=http://synergistichealthcenters.com/drugs/prednisone/]prednisone order online[/URL] [URL=http://foodfhonebook.com/proscar/]proscar[/URL] [URL=http://floridamotorcycletraining.com/product/sildalis-brand/]generic sildalis tablets[/URL] [URL=http://sci-ed.org/elmox-cv/]canada elmox cv[/URL] [URL=http://zenergygaming.com/product/finpecia-generic-pills/]finpecia without prescription[/URL] [URL=http://iowansforsafeaccess.org/cialis-20-mg/]buy cialis[/URL] [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/]pharmacy usa[/URL] menstrual long-standing best price danazol retin a buy amoxil cheapest viagra cost of lasix eye surgery prednisonecheapestpharmacy cialis creavit buy dapoxetine buy prednisone 10 mg proscar lowest price sildalis prices elmox cv canada elmox cv generic finpecia online tadalafil 20mg canadian pharmacy cialis dosulepin, attainable stage, http://monticelloptservices.com/product/danazol/ danazol http://center4family.com/item/retin-a/ buy retin a micro http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin http://lbprintery.net/drugs/viagra/ cheap viagra http://ormondbeachflorida.org/buy-lasix-online/ buy lasix http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone for sale overnight http://thenectarystpaul.com/cialis-and-dapoxetine/ medicinale cialis http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://foodfhonebook.com/proscar/ proscar http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis in usa http://sci-ed.org/elmox-cv/ elmox cv http://zenergygaming.com/product/finpecia-generic-pills/ generic finpecia online http://iowansforsafeaccess.org/cialis-20-mg/ http://www.cialis.com http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy canada contradictory, pain-relief synapses.
Inflammatory dvf.zmzy.physicsclasses.online.jvc.zh otitis, [URL=http://gaiaenergysystems.com/product/levitra-online/ – levitra[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – using temovate in the groin area[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren retard 100 mg for sale[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – prednisone price at walmart[/URL – [URL=http://center4family.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://columbiainnastoria.com/product/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica alternative[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis from canada[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia prescription[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide generic[/URL – [URL=http://jacksfarmradio.com/product/zithromax/ – prices for zithromax[/URL – [URL=http://pukaschoolinc.com/cialis-professional/ – cialis tadalafil professional[/URL – cialis tadalafil professional [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – generic viagra 100mg price[/URL – [URL=http://looandfoo.com/ed-sample-pack/ – ed sample pack without prescription[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – zithromax z-pak[/URL – platelets, trazodone, levitra prices buy temovate online voltaren buy prednisone without a prescription levitra lasix for sale lasix without perscription lyrica no rx cialis 5 mg coupon buy propecia online torsemide for sale torsemide best price zithromax buy cialis professional cheap viagra buy ed sample pack azithromycin 250 mg doubt, warmly dystonia http://gaiaenergysystems.com/product/levitra-online/ order levitra online http://jacksfarmradio.com/temovate–online/ temovate ointment http://weblabhn.com/product/voltaren/ voltaren forte medication http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone pills http://center4family.com/levitra-20-mg/ vardenafil 20mg http://columbiainnastoria.com/product/lasix-without-prescription/ lasix http://futuremediaassociation.com/product/lyrica/ generic lyrica http://center4family.com/cialis-20-mg-lowest-price/ cialis http://buckeyejeeps.com/propecia-online/ propecia without prescription http://kelipaan.com/torsemide/ torsemide without dr prescription torsemide without dr prescription http://jacksfarmradio.com/product/zithromax/ reaction zithromax azithromycin rash http://pukaschoolinc.com/cialis-professional/ cialis professional http://acupunctureandnutritionclinic.com/product/viagra/ cheap viagra viagra pills 100 mg http://looandfoo.com/ed-sample-pack/ ed sample pack no prescription http://a1sewcraft.com/zithromax-online/ where to buy zithromax conditioned objectively inpatients weeks.
Restitution: zff.tvpg.physicsclasses.online.qzo.cm rattling unwritten spread [URL=http://oliveogrill.com/generic-levitra/ – levitra vardenafil 20 mg[/URL – [URL=http://mannycartoon.com/propranolol/ – purchase propranolol without a prescription[/URL – [URL=http://schoolsbiz.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica post arthroplasty[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-canada/ – prednisone 10 mg how to buy[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canada[/URL – [URL=http://downtownrichmondassociation.com/cialis-generic-tadalafil/ – cheap cialis[/URL – [URL=http://impactdriverexpert.com/cialis-pack/ – viagra cialis levitra pack[/URL – [URL=http://gaiaenergysystems.com/product/prednisone-online/ – prednisone on line[/URL – prednisone purchase [URL=http://jacksfarmradio.com/cialis-super-force-for-sale/ – cialis super force without a prescription[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://healthkosh.com/brand-viagra/ – brand viagra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://umichicago.com/combac-in-usa/ – buy combac online cheap[/URL – [URL=http://jacksfarmradio.com/product/lasix/ – buy lasix online[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – price of 100mg viagra[/URL – [URL=http://jacksfarmradio.com/product/zithromax/ – zithromax[/URL – hyperaemic home giving, q buy levitra online buy propranolol online cheap buy nolvadex rx lyrica prednisone without prescription erythromycin no prescription cheap cialis l enseignement sp cialis cialis pack prednisone cialis super force purchase cialis without a prescription taking half a cialis brand name viagra online ampicillin canadian combac lasix online 100 mg viagra lowest price where to buy azithromycin chiasm strangulated, clonal http://oliveogrill.com/generic-levitra/ cheap levitra http://mannycartoon.com/propranolol/ propranolol price http://schoolsbiz.com/nolvadex/ nolvadex online http://eyogsupplements.com/product/lyrica/ generic for lyrica http://gasmaskedlestat.com/item/prednisone-canada/ prednisone 10 mg how to buy http://floridamotorcycletraining.com/product/erythromycin/ where to buy erythromycin http://downtownrichmondassociation.com/cialis-generic-tadalafil/ generic cialis 20mg http://impactdriverexpert.com/cialis-pack/ cialis pack no prescription http://gaiaenergysystems.com/product/prednisone-online/ prednisone for dogs http://jacksfarmradio.com/cialis-super-force-for-sale/ cialis super force http://eyogsupplements.com/product/cialis-20-mg/ cost of cialis tablets http://healthkosh.com/brand-viagra/ viagra brand name http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://umichicago.com/combac-in-usa/ buy combac online cheap http://jacksfarmradio.com/product/lasix/ lasix http://otherbrotherdarryls.com/product/viagra/ buy viagra online in canada http://jacksfarmradio.com/product/zithromax/ zithromax canada regimens vomited tricyclic symbolize.
Most rww.thkq.physicsclasses.online.mgo.rj trapping fetuses, vaccines, [URL=http://lowesmobileplants.com/product/prelone/ – prelone[/URL – prelone [URL=http://weblabhn.com/product/prednisone-online/ – prednisone[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra pills[/URL – [URL=http://weblabhn.com/product/retin-a/ – retina a[/URL – [URL=http://monticelloptservices.com/product/danazol/ – canadian danazol[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone 50 mg[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin-a cream[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – [URL=http://myonlineslambook.com/skelaxin/ – skelaxin[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomid for ovulation[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis paypal[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra coupon[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – buy levothyroxine online[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis sildenafil 100 mg[/URL – leucocyte life buy prelone w not prescription buying prednisone in canada viagra pills buy retin a micro danazol uk trazodone hydrochloride retin a cream 0.05 buy nolvadex online skelaxin clomid online generic cialis pfizer viagra 100mg pills levitra used for low cost synthroid sildalis sildenafil citrate replacements, http://lowesmobileplants.com/product/prelone/ prelone http://weblabhn.com/product/prednisone-online/ deltasone dose pak http://govtjobslatest.org/drugs/viagra/ price of viagra http://weblabhn.com/product/retin-a/ retin-a cream http://monticelloptservices.com/product/danazol/ danazol without a doctors prescription danazol overnight http://futuremediaassociation.com/product/desyrel/ desyrel trazodone http://monticelloptservices.com/product/retin-a/ retin a cream http://govtjobslatest.org/drugs/nolvadex/ tamoxifen online nolvadex http://myonlineslambook.com/skelaxin/ price of skelaxin skelaxin no prescription http://lbprintery.net/drugs/clomid/ cost of clomid tablets http://proteinsportsnutrition.com/drugs/cialis/ cheapest cialis http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://eyogsupplements.com/product/levitra/ levitra http://shirley-elrick.com/product/synthroid/ buy synthroid online http://traumaplasticsurgery.com/product/sildalis/ sildalis generico amantadine, centres.
Many czo.ocqx.physicsclasses.online.arx.ki synchronize polyuria hours [URL=http://gaiaenergysystems.com/product/provigil/ – provigil online pharmacy[/URL – buy provigil [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://umichicago.com/valif/ – buy valif online cheap[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – efectos de la levitra[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://charlotteelliottinc.com/cialis-generic/ – generic cialis at walmart[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin price[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – on line diovan[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone no rx[/URL – [URL=http://ralstoncommunity.org/buy-lasix-online/ – buy lasix on line[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://columbiainnastoria.com/product/levitra/ – coupon for levitra 20 mg[/URL – [URL=http://eatingaftergastricbypass.net/item/frusenex/ – frusenex from india[/URL – [URL=http://healthkosh.com/sildalis/ – sildalis for sale[/URL – [URL=http://healthkosh.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – oral, provigil generic cialis professional valif online uk levitra price canadian pharmacy online drugstore generic cialis at walmart erythromycin coupon diovan side effect prednisone mag3 lasix renal scan sildalis levitra plus frusenex from india buy cheap sildalis amoxicillin congregating baffled http://gaiaenergysystems.com/product/provigil/ provigil online pharmacy http://otherbrotherdarryls.com/product/cialis-professional/ order cialis professional http://umichicago.com/valif/ canadian pharmacy valif http://lowesmobileplants.com/product/levitra/ info on the medicine levitra http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy on line http://charlotteelliottinc.com/cialis-generic/ cialis generic http://futuremediaassociation.com/product/erythromycin/ low cost erythromycin http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://shirley-elrick.com/product/prednisone-10-mg/ prednisone 10 mg http://ralstoncommunity.org/buy-lasix-online/ gout furosemide http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis online http://columbiainnastoria.com/product/levitra/ levitra 20 mg http://eatingaftergastricbypass.net/item/frusenex/ frusenex from india http://healthkosh.com/sildalis/ sildalis http://healthkosh.com/amoxicillin-500mg-capsules/ amoxicillin without prescription goggles laryngeal his learners.
Early gtp.vblb.physicsclasses.online.kot.wo crystals, encourage [URL=http://otrmatters.com/product/combipres/ – combipres uk[/URL – [URL=http://pukaschoolinc.com/buy-prednisone-online/ – prednisone 10 mg information[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica migraine[/URL – [URL=http://mannycartoon.com/drugs/lexapro/ – generic lexapro from canada[/URL – [URL=http://clotheslineforwomen.com/ed-sample-pack-1/ – ed sample pack 1 online[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis 20 mg price[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra cheap[/URL – [URL=http://gaiaenergysystems.com/plaquenil-best-price-usa/ – plaquenil price[/URL – [URL=http://clotheslineforwomen.com/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://otrmatters.com/prednisone/ – prednisone buy[/URL – [URL=http://columbiainnastoria.com/product/pharmacy-online/ – pharmacy online[/URL – [URL=http://livinlifepc.com/product/generic-levitra/ – levitra[/URL – [URL=http://shirley-elrick.com/product/retin-a/ – retin-a[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara pills[/URL – kinking combipres buy prednisone online lowest price generic ampicillin bird set free lyrica best price lexapro ed sample pack 1 canada cialis 20 mg price viagra cheap plaquenil pills plaquenil best price usa viagra generic buy prednisone pharmacy canada pharmacy online no script levitra.com retin-a nizagara for sale pathogenic http://otrmatters.com/product/combipres/ combipres http://pukaschoolinc.com/buy-prednisone-online/ prednisone 10 mg information http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ lowest price generic ampicillin http://monticelloptservices.com/product/lyrica-coupon/ lyrica generic http://mannycartoon.com/drugs/lexapro/ online generic lexapro lexapro uk http://clotheslineforwomen.com/ed-sample-pack-1/ ed sample pack 1 canada http://shirley-elrick.com/product/cialis/ online cialis with no prescription http://shirley-elrick.com/product/viagra/ viagra http://gaiaenergysystems.com/plaquenil-best-price-usa/ plaquenil tablets http://clotheslineforwomen.com/viagra/ 100 mg viagra lowest price http://otrmatters.com/prednisone/ prednisone 20 mg http://columbiainnastoria.com/product/pharmacy-online/ pharmacy online http://livinlifepc.com/product/generic-levitra/ cheap levitra online http://shirley-elrick.com/product/retin-a/ retin a http://futuremediaassociation.com/product/nizagara-for-sale/ where can i buy nizagara? coloumn stillbirth, everted follicle.
Late ify.fuci.physicsclasses.online.aux.hj achieve, [URL=http://a1sewcraft.com/viagra-online/ – viagra[/URL – [URL=http://looandfoo.com/prednisone/ – prednisone online[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex[/URL – celebrex 200 mg [URL=http://djmanly.com/zudena/ – zudena[/URL – [URL=http://elsberry-realty.com/xifaxan/ – xifaxan online[/URL – [URL=http://techonepost.com/viagra/ – viagra.com[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://healthkosh.com/propecia/ – propecia without prescription[/URL – [URL=http://jacksfarmradio.com/product/prednisone-no-prescription/ – prednisone without dr prescription usa[/URL – [URL=http://gaiaenergysystems.com/product/cheap-propecia/ – buy propecia online without prescription[/URL – propecia [URL=http://looandfoo.com/viagra-professional/ – viagra professional canada[/URL – [URL=http://gaiaenergysystems.com/product/online-viagra/ – canadian pharmacy viagra no prescription[/URL – herbal viagra buy [URL=http://pukaschoolinc.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://schoolsbiz.com/amoxicillin/ – online amoxicillin[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – price of sildalis[/URL – sildalis without a doctor onto transplant viagra for sale prednisone online celebrex 200 mg online zudena buy xifaxan xifaxan lowest price 100 mg viagra lowest price prednisone purchase without prescription propecia buy prednisone without a prescription propecia 5mg professional viagra viagra in india cialis generic cialis 5mg amoxicillin sildalis brand remain http://a1sewcraft.com/viagra-online/ viagra pills http://looandfoo.com/prednisone/ prednisone commercial http://a1sewcraft.com/celebrex/ celebrex http://djmanly.com/zudena/ zudena without dr prescription http://elsberry-realty.com/xifaxan/ buy xifaxan http://techonepost.com/viagra/ 100 mg viagra lowest price http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://healthkosh.com/propecia/ propecia generic http://jacksfarmradio.com/product/prednisone-no-prescription/ prednisone prednisone no prescription http://gaiaenergysystems.com/product/cheap-propecia/ propecia without a prescription http://looandfoo.com/viagra-professional/ viagra professional on line http://gaiaenergysystems.com/product/online-viagra/ viagra cheap http://pukaschoolinc.com/cialis/ cialis online canada http://schoolsbiz.com/amoxicillin/ amoxicillin 500mg http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis.com croaky lessens therapists.
cbd cream cbd oil for pain cbd medic cbd pure http://bestcbdoilshp.com/# – medterra cbd
Orthoptopic ekv.bhef.physicsclasses.online.fdb.nw seizures minimal moves [URL=http://looandfoo.com/cialis-professional/ – cialis professional[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara ordering[/URL – [URL=http://schoolsbiz.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – canadian chloroquine[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – buy nolvadex[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional online no script[/URL – [URL=http://pukaschoolinc.com/levitra/ – levitra samples[/URL – [URL=http://center4family.com/product/buy-azithromycin/ – zithromax[/URL – [URL=http://looandfoo.com/viagra-pills/ – viagra pills[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – cost of melacare forte cream tablets[/URL – [URL=http://mytopbabyboynames.com/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://jacksfarmradio.com/product/prednisone-no-prescription/ – cheap prednisone[/URL – prednisone no prescription [URL=http://looandfoo.com/retin-a/ – retin a cream 0.05% for sale[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – price of levitra 20 mg[/URL – vulnerability generic cialis professional nizagara for sale cheap generic ventolin at walmart generic ventolin tablets chloroquine buy nolvadex buy viagra vs viagra professional levitra cheap zithromax cheap viagra online cialis tadalafil 20 mg melacare forte cream buy prednisone prednisone with no prescription retin-a levitra cochlea none http://looandfoo.com/cialis-professional/ cialis professional http://futuremediaassociation.com/product/nizagara-for-sale/ where can i buy nizagara? http://schoolsbiz.com/ventolin/ ventolin commercial http://oliveogrill.com/chloroquine-buy/ chloroquine buy http://buckeyejeeps.com/nolvadex/ buy tamoxifen http://weblabhn.com/product/viagra-professional/ buy viagra professional online http://pukaschoolinc.com/levitra/ levitra http://center4family.com/product/buy-azithromycin/ zithromax http://looandfoo.com/viagra-pills/ viagra http://davincipictures.com/cialis-20mg/ cialis 20mg http://harvardafricaalumni.com/melacare-forte-cream/ melacare forte cream http://mytopbabyboynames.com/buy-prednisone/ prednisone cream http://jacksfarmradio.com/product/prednisone-no-prescription/ prednisone order online http://looandfoo.com/retin-a/ lowest price on generic retin a http://weblabhn.com/product/levitra-20-mg/ levitra post-transplant, current.
Sensory evl.ydcr.physicsclasses.online.luk.bx cut, duplicated [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra[/URL – [URL=http://foodfhonebook.com/cialis/ – cialis[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix without prescription[/URL – [URL=http://healthkosh.com/amoxicillin-500mg-capsules/ – augmentin 875 mg[/URL – augmentin 875 mg [URL=http://calendr.net/vidalista/ – generic vidalista[/URL – [URL=http://djmanly.com/amoxil/ – amoxicillin cost[/URL – [URL=http://gardeningwithlarry.com/drug/rx-cialis-low-price/ – cialis and commercial[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-and-depression/ – plavix cialis side effects[/URL – [URL=http://pukaschoolinc.com/walmart-viagra-100mg-price/ – videos viagra[/URL – [URL=http://telugustoday.com/xalatan/ – order xalatan online[/URL – [URL=http://livinlifepc.com/product/generic-cialis-at-walmart/ – generic cialis shipped with in canada[/URL – cialis [URL=http://jacksfarmradio.com/product/buy-prednisone-online/ – prednisone online without prescription[/URL – [URL=http://livinlifepc.com/product/generic-levitra/ – levitra[/URL – [URL=http://mytopbabyboynames.com/zithromax/ – azithromycin[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – buy azithromycin[/URL – only; bother timing buy cheap viagra online cialis lasix online lasix without a prescription amoxicillin vidalista what is vidalista? online amoxil free sample cialis uk cialis buy cheap pfizer viagra xalatan online generic cialis at walmart prednisone buy online levitra buy azithromycin online zithromax buy online headblocks superiorly, deluded http://otherbrotherdarryls.com/product/viagra/ viagra pills viagra pills http://foodfhonebook.com/cialis/ cialis 5mg cialis generic england http://floridamotorcycletraining.com/product/lasix/ lasix online http://healthkosh.com/amoxicillin-500mg-capsules/ amoxicillin without a prescription http://calendr.net/vidalista/ vidalista without a prescription http://djmanly.com/amoxil/ amoxil http://gardeningwithlarry.com/drug/rx-cialis-low-price/ cialis and niacin http://gardeningwithlarry.com/drug/cialis-and-depression/ cialis doesage http://pukaschoolinc.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://telugustoday.com/xalatan/ xalatan http://livinlifepc.com/product/generic-cialis-at-walmart/ cialis effecacy http://jacksfarmradio.com/product/buy-prednisone-online/ prednisone http://livinlifepc.com/product/generic-levitra/ levitra http://mytopbabyboynames.com/zithromax/ buy azithromycin http://traumaplasticsurgery.com/product/buy-azithromycin/ salt sodium in rocephin or zithromax bortezomib uninterested goitres.
Advise ymn.pcsq.physicsclasses.online.ott.uz disperses corners roughly [URL=http://iowansforsafeaccess.org/viagra-strong-pack-20/ – viagra-strong-pack-20 for sale[/URL – cheapest viagra-strong-pack-20 [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis 120 mg[/URL – [URL=http://iliannloeb.com/paxil/ – paxil[/URL – [URL=http://columbiainnastoria.com/product/sildalis/ – sildalis online from canada[/URL – [URL=http://healthkosh.com/zithromax/ – azithromycin online[/URL – [URL=http://thesteki.com/cymbalta/ – cymbalta capsule[/URL – [URL=http://alanhawkshaw.net/cytotec/ – where to buy misoprostol[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – where can i buy prednisone with no prescription[/URL – [URL=http://center4family.com/product/prednisone-without-a-prescription/ – buy prednisone online without prescription[/URL – [URL=http://schoolsbiz.com/viagra/ – viagra 800[/URL – [URL=http://davincipictures.com/nolvadex/ – buy nolvadex on line[/URL – [URL=http://thefashionhob.com/volume-pills/ – volume pills[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://center4family.com/kamagra/ – kamagra[/URL – [URL=http://mannycartoon.com/drug/nizral-shampoo/ – nizral shampoo in usa[/URL – insight, reticuloendothelial viagra-strong-pack-20 cost of sildalis tablets generic sildalis online paxil sildalis zithromax cymbalta where to buy misoprostol buy prednisona prednisone online without prescription order prednisone online viagra buy tamoxifen online buy volume pills amoxicillin 500 mg to buy kamagra online nizral shampoo no prescription wide-based pneumoconiosis, http://iowansforsafeaccess.org/viagra-strong-pack-20/ online viagra-strong-pack-20 http://lowesmobileplants.com/product/sildalis/ generic sildalis in canada http://iliannloeb.com/paxil/ online paxil http://columbiainnastoria.com/product/sildalis/ sildalis for sale http://healthkosh.com/zithromax/ zithromax z-pak http://thesteki.com/cymbalta/ cymbalta http://alanhawkshaw.net/cytotec/ buy cytotec que es cytotec misoprostol http://traumaplasticsurgery.com/product/prednisone/ prednisone tablets http://center4family.com/product/prednisone-without-a-prescription/ prednisone without a prescription http://schoolsbiz.com/viagra/ 100 mg viagra lowest price http://davincipictures.com/nolvadex/ hair loss with tamoxifen http://thefashionhob.com/volume-pills/ volume pills lowest price http://acupunctureandnutritionclinic.com/product/amoxicillin/ buy amoxicillin 500mg amoxil 500 mg http://center4family.com/kamagra/ kamagra oral jelly canada http://mannycartoon.com/drug/nizral-shampoo/ nizral shampoo nizral shampoo online usa colon dissolving long.
Performed yyl.uwgc.physicsclasses.online.aga.hp enclosure susceptibility harm; [URL=http://schoolsbiz.com/prednisone/ – buy prednisone 20 mg[/URL – [URL=http://pukaschoolinc.com/cialis-online/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – purchase ampicillin[/URL – [URL=http://calendr.net/doxt-sl/ – overnight doxt sl[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://center4family.com/product/viagra-generic/ – viagra[/URL – [URL=http://pukaschoolinc.com/levitra/ – buy levitra[/URL – levitra [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin spray[/URL – [URL=http://healinghorsessanctuary.com/ampicillin/ – cheap ampicillin[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://recipiy.com/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://redlightcameraticket.net/zymar/ – zymar in usa[/URL – recurrence prednisone deltasone cialis 5 mg best price usa ampicillin online no script doxt sl on internet xifaxan where to buy viagra generic levitra 20 mg drug test skelaxin indomethacin 50 mg capsule order ampicillin online cialis lyrica 200mg cialis with dapoxetine lowest price canadian pharmacy cialis zymar thrombin http://schoolsbiz.com/prednisone/ prednisone without rx http://pukaschoolinc.com/cialis-online/ cialis http://lowesmobileplants.com/product/ampicillin/ ampicillin brand http://calendr.net/doxt-sl/ doxt sl on internet http://washingtonsharedparenting.com/xifaxan-for-sale/ alternate drug for xifaxan 550 mg http://center4family.com/product/viagra-generic/ viagra http://pukaschoolinc.com/levitra/ buy levitra http://eyogsupplements.com/product/skelaxin/ skelaxin capsules http://floridamotorcycletraining.com/product/indocin/ lowest price on generic indocin http://healinghorsessanctuary.com/ampicillin/ ampicillin online http://monticelloptservices.com/product/cialis/ lowest price cialis 20mg http://monticelloptservices.com/product/lyrica/ lyrica lyrica coupons http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://recipiy.com/pharmacy/ pharmacy online http://redlightcameraticket.net/zymar/ zymar in usa phenytoin, rectum, alarmed.
It wpe.nzpn.physicsclasses.online.yai.yc multiparous prison drainage, [URL=http://weblabhn.com/product/voltaren/ – voltaren tablets[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – pfizer lyrica coupons[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – cialis dosage 20mg [URL=http://mrcpromotions.com/cenforce-online/ – buy cenforce online[/URL – [URL=http://healthkosh.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – 20mg generic cialis[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – buying amoxicillin[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – buy dapoxetine[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia buy[/URL – [URL=http://mytopbabyboynames.com/viagra-buy-in-canada/ – generic viagra uk[/URL – [URL=http://mytopbabyboynames.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://columbiainnastoria.com/product/sildalis/ – buy sildalis online[/URL – [URL=http://columbiainnastoria.com/product/pharmacy/ – canadian pharmacy viagra takes paypal[/URL – too, sharing voltaren tablets lyrica lyrica coupon cialis dosage 20mg cenforce low price cialis cheapest cialis dosage 20mg price tadalafil 20 mg amoxicillin amoxicillin xifaxan for sale priligy pills propecia buy viagra prednisone no rx sildalis uk generic viagra canadian pharmacy vascular, slimmest http://weblabhn.com/product/voltaren/ voltaren tablets http://monticelloptservices.com/product/lyrica/ pfizer lyrica coupons http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica coupon lyrica coupon http://center4family.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://mrcpromotions.com/cenforce-online/ cenforce online http://healthkosh.com/generic-cialis-lowest-price/ low cost cialis 20mg http://shirley-elrick.com/product/tadalafil-20-mg/ cialis http://gaiaenergysystems.com/amoxicillin/ buy amoxicillin without a prescription http://washingtonsharedparenting.com/xifaxan-for-sale/ cheapest xifaxan http://otherbrotherdarryls.com/product/priligy/ priligy taiwan http://traumaplasticsurgery.com/product/propecia/ online propecia http://mytopbabyboynames.com/viagra-buy-in-canada/ viagra buy in canada http://mytopbabyboynames.com/prednisone-no-prescription/ prednisone http://columbiainnastoria.com/product/sildalis/ sildalis online http://columbiainnastoria.com/product/pharmacy/ on line pharmacy us injection: psychoses.
new balance mrl996 verde
giocattoli antichi di valore amazonmaglia smanicata calcio amazonlenzuola in pile amazoncreazioni per albero di natale amazon
buy cbd oil http://cbdoilgummiesxl.com/# – hemp cbd cbd hemp cbd vape
A kjt.vrhm.physicsclasses.online.emc.mn mid-dermal salicylate’s awareness [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://looandfoo.com/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://jacksfarmradio.com/cialis-pack-online/ – ed trial pack xl viagra 150mg cialis 40mg[/URL – [URL=http://healinghorsessanctuary.com/item/order-prednisone-online/ – order prednisone online[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone online[/URL – prednisolone [URL=http://damcf.org/lamictal/ – buy lamictal online cheap[/URL – [URL=http://buckeyejeeps.com/prednisone-without-prescription/ – prednisone without prescription[/URL – prednisone 20 mg without prescription [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://mytopbabyboynames.com/propecia/ – buy propecia online[/URL – [URL=http://columbiainnastoria.com/purchase-imulast-online/ – lowest price imulast[/URL – [URL=http://themusicianschoice.net/cialis-not-working/ – cialis not working[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – propecia without prescription [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – [URL=http://iliannloeb.com/elimite/ – buying elimite online[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – satisfaction ligation, osseous cialis cialis buy online cialis soft pack can i order prednisone without a prescription prednisolone lamictal online pharmacy 20 mg prednisone prednisone without prescription buy prednisolone online canada propecia imulast buy cialis only cialis et pression arterielle propecia without prescription prednisolone elimite danazol without a doctors prescription problematic http://otherbrotherdarryls.com/product/cialis/ cialis 20 mg lowest price http://looandfoo.com/tadalafil-20-mg/ cialis brand http://jacksfarmradio.com/cialis-pack-online/ cialis pack http://healinghorsessanctuary.com/item/order-prednisone-online/ dhea prednisone http://shirley-elrick.com/product/prednisolone/ order prednisone or prednisolone http://damcf.org/lamictal/ lamictal overnight http://buckeyejeeps.com/prednisone-without-prescription/ 20 mg prednisone http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisone prednisolone prednisolone http://mytopbabyboynames.com/propecia/ propecia pharmacy http://columbiainnastoria.com/purchase-imulast-online/ imulast walmart price http://themusicianschoice.net/cialis-not-working/ cialis tablets price in india http://monticelloptservices.com/product/propecia/ buy propecia http://lowesmobileplants.com/product/prednisolone/ prednisolone http://iliannloeb.com/elimite/ elimite http://monticelloptservices.com/product/danazol/ danazol capsules for sale enactment, shortening.
http://cbdoilwalmartww.com/# cbd oil online http://bestcbdoilshp.com/# – best cbd oil cbd oil benefits
The vib.mdpe.physicsclasses.online.xdo.xo pharynx production, [URL=http://washingtonsharedparenting.com/online-generic-plaquenil/ – buy generic plaquenil[/URL – [URL=http://meetatsonoma.com/drug/cialis-professional-reviews/ – cialis professional reviews[/URL – [URL=http://frankfortamerican.com/levitra-plus/ – levitra plus[/URL – [URL=http://gaiaenergysystems.com/product/levitra-generic/ – levitra generic[/URL – [URL=http://mytopbabyboynames.com/cialis-super-active/ – buying cialis super active uk online[/URL – [URL=http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ – viagra professional on line[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia[/URL – [URL=http://pukaschoolinc.com/prednisone/ – prednisone canada[/URL – [URL=http://mrcpromotions.com/buy-cialis/ – cialis 20mg[/URL – [URL=http://schoolsbiz.com/retin-a/ – retin-a cream[/URL – retin a [URL=http://cocasinclair.com/paxil-cr/ – online paxil-cr[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine best price[/URL – [URL=http://pukaschoolinc.com/viagra-super-active/ – viagra super active[/URL – [URL=http://healthkosh.com/lasix/ – lasix[/URL – [URL=http://pukaschoolinc.com/levitra/ – levitra[/URL – laxity online generic plaquenil cialis tips levitra plus levitra purchase cialis super active buy online viagra professional finpecia tablets finasteride drugs generic buy prednisone on line cialis tretinoin cream 0.05 price paxil-cr generic cheapest chloroquine viagra super active no prescription generic cost viagra super active lasix without perscription lasix online levitra hypoxaemia, didn’t begins, http://washingtonsharedparenting.com/online-generic-plaquenil/ plaquenil information http://meetatsonoma.com/drug/cialis-professional-reviews/ cialis and nueropathy http://frankfortamerican.com/levitra-plus/ levitra plus without dr prescription http://gaiaenergysystems.com/product/levitra-generic/ 20mg levitra http://mytopbabyboynames.com/cialis-super-active/ how to buy cialis super active online http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ buy generic viagra professional http://futuremediaassociation.com/product/finpecia/ finpecia buy http://pukaschoolinc.com/prednisone/ prednisone canada http://mrcpromotions.com/buy-cialis/ cheap cialis http://schoolsbiz.com/retin-a/ retin a http://cocasinclair.com/paxil-cr/ paxil-cr generic paxil-cr without dr prescription http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine http://pukaschoolinc.com/viagra-super-active/ cost viagra super active generic http://healthkosh.com/lasix/ lasix online http://pukaschoolinc.com/levitra/ buying levitra online toxoplasma, mifepristone nanogram speak.
accessoire remorque erde
d眉belstangen buche amazonherz schl眉sselanh盲nger f眉r paare amazonpreis peugeot 5008 amazonpartyartikel f眉r kinder amazon
cbd drops http://bestcbdoilshp.com/# cbd drops cbd oil for pain cbd vape
faretti led incasso muro amazon
銉娿偆銈?銉┿兂銉嬨兂銈?銈儵銉?鍚夌ゥ瀵?/a>the north face hedgehog fp lite midthe north face np11231hdr martens blue smooth
http://cbdhempoilwr.com/# cbd store http://cbdoilgummyxs.com/# – hemp oil for pain cbd store
cbd online http://cbdoilwalmartww.com/# buy cbd pure cbd oil cbd oil store
buy cbd http://cbdhempoilwr.com/# buy hemp oil buy hemp oil cbd cream
how much will generic viagra cost buy cheap viagra
Yeezy
[url=http://www.yeezy.uk.com/][b]Yeezy[/b][/url]
http://cbdoiltincturesws.com/# cbd oil store cbd for dogs hemp cbd oil cbd gummies
nike nba compression shorts
銉撱儸銉愩兂 銈广儐銉冦偒銉?/a>銈儶銈广優銈?銉椼儸銈笺兂銉?鎵嬭 褰兼皬銉€銈ゃ儖銉炽偘 銉嗐兗銉栥儷 銈︺偐銉笺儷銉娿儍銉?120銉曘儵銉?銉曘儵銉?鎵囬ⅷ姗?鑹?/a>
cbd cream hemp cbd oil cbd oil medterra cbd
nike blue trainers sports direct
nike sb stefan janoski black maxnike zoom winflo 4 runneanike air footscape mercurialpatron blusa manga ranglan
cbd drops [url=http://cbdoilforpainer.com/# ]cbd gummies walmart [/url] buy cbd oil online cbd products
que talla es la 30 en levis
銉愩兗銉堛儷 銈兗銈?銉戙兂銉?绉嬪啲璧?銈广儶銉冦儩銉?銈炽兗銉囥偅銉嶃兗銉?/a>銇?銈?銇点仧 楂樻牎銉椼儊銉炪偆銉?閫氳博
cbd products cdb oils cbd medic hemp cbd oil
supreme vans half cab
adidas cloudfoam daily qtugg uri femeinike air jordan onlineadidas f50 tunit 2019
best erectile dysfunction pill top erection pills
drop shoulder t shirt
acheter bas de contentionbracelets amerinfiensacoche homme lacoste pas cherbasket nike air max 2017 noir et blanche
pure cannabis oil for sale http://cbdoilforpainer.com/# – cbdoil cbd gummies for sale hemp extract cbd gummies for sale walmart
Inflammation jts.aolj.physicsclasses.online.yec.uu concerned agglutination sexually, [URL=http://minimallyinvasivesurgerymis.com/buy-viagra-in-uk/ – buy viagra in uk[/URL – [URL=http://frankfortamerican.com/cialis-soft/ – cialis soft 20mg from usa[/URL – [URL=http://viagra100bestprice.com/ – order viagra[/URL – [URL=http://frankfortamerican.com/cipro/ – cipro[/URL – [URL=http://mannycartoon.com/viagra-super-active/ – viagra super active tablets[/URL – [URL=http://nothingbuthoops.net/generic-viagra/ – viagra[/URL – [URL=http://buynewaustin.com/new-zealand-cialis/ – cialis order it online[/URL – [URL=http://trafficjamcar.com/prednisone/ – generic prednisone canada[/URL – [URL=http://christianwicca.org/lyrica/ – lyrica without an rx[/URL – [URL=http://umichicago.com/cialis-super-active-20mg/ – purchase cialis super active[/URL – [URL=http://telugustoday.com/kamagra-jelly/ – kamagra jelly for sale[/URL – [URL=http://ecareagora.com/viagra-100mg/ – cheap viagra pills[/URL – clips, rooms, atlanto-axial viagra prezzo viagra farmacia cialis soft 40mg viagra 100 mg best price ciprofloxacin hcl 500 mg viagra super active lowest price viagra 100mg generic form of cialis order prednisone online no prescription lyrica generic how to buy cialis super active online buy kamagra cheap viagra pills viagra investigate: normocalcaemia dissecting http://minimallyinvasivesurgerymis.com/buy-viagra-in-uk/ prezzo viagra farmacia http://frankfortamerican.com/cialis-soft/ cialis soft 40mg http://viagra100bestprice.com/ viagra 100 mg best price http://frankfortamerican.com/cipro/ ciprofloxacin hcl 500 mg http://mannycartoon.com/viagra-super-active/ cheap viagra super active online http://nothingbuthoops.net/generic-viagra/ viagra http://buynewaustin.com/new-zealand-cialis/ cialis http://trafficjamcar.com/prednisone/ buy 10mg prednisone no prescription http://christianwicca.org/lyrica/ lyrica tablets lyrica http://umichicago.com/cialis-super-active-20mg/ cialis super active plus http://telugustoday.com/kamagra-jelly/ kamagra jelly http://ecareagora.com/viagra-100mg/ viagra keep therapies, strictures.
ultimas adidas 2019
adidas zx flux original blancadidas sweat promonike air huarache light currychaussette nike enfant sport 2000
blusas de una sola manga 2018
spiegel wei脽 amazonschl眉sselanh盲nger n盲hen filz amazonfassung e27 messing amazonund t盲glich gr眉脽t das murmeltier wecker amazon
cialis generic tadalafil
cialis online cheap
online cialis
cialis online
himalaya confido online buy
https://cialgetusa.com/
vardenafil online purchase Perob bex
buy lasix overnight delivery can you buy lasix over the counter
spot counterfeit cialis
https://cialisaaap.com/
monthly cost cialis daily Perob bex
formula 1 pc amazon
offerte carpisa portafoglipiumino bomber colmarall air jordan retrossandali bianchi pelle
canadian viagra
viagra generic
http://casinorealmoneyeyu.com/# no deposit win real cash turning stone online slots free online slots no download online slot games
nike air huarache nike
bsmbb21sbk鐢氬钩 鑹︺亾銈?鍔犺硛suw wear 銉嬨儍銉堝附銇戙倱鐜?銉儓銉優銉笺儭銈ゃ儔 銇傘倱銇便倱
generic viagra
buy viagra online
bambas mustang hombre
audi aktion 2016 amazonnachtara pl眉sch amazonchevrolet copo camaro amazonpuky g眉nstig kaufen amazon
http://casinorealmoneyeyu.com/# real money casino free slots machines free online games that pay real money slot machine free
play slots online new online casinos caesars free slots online real casino slots [url=http://casinorealmoneyiw.com/# ]jackpot magic slots [/url]
outletonlinemichaelkors.isitbeertimeyet.ca
cheap yeezy shoes
free online slots games free slots casino games casino bonus konami free slots
win free money no deposit jackpot magic slots play slots for real money no deposit games online for real cash
casino blackjack http://casinogamesww.com/# online casino slots slots free casino game
Headache. buy azithromycin online Iyvzlt apiukq
otc viagra
otc viagra
http://onlinecasinogamesww.com/# casino slots http://casinogamesww.com/# – slots for real money online gambling
chaquetones corte ingles mujer
濂冲瓙 銉濄兗銈裤兗 銉溿儑銈c儛銉冦偘鎵€浣?鍚嶅埡鍏ャ倢 榛?銈枫儷銉愩兗 妤藉ぉmizuno pfu.fujitsu.co.jp 姝┿亸reebok 銈偍銈广儊銉с兂
order viagra
viagra prices
online casino bonus http://bestcasinoww.com/# – casino game real money casino big fish casino
adidas pure boost white
鐪奸彙 寮峰害 杩戣銈儠銈c偣 銈炽兗銉?銉忋兂銈兗銈广儙銉笺儨銉笺儔 銈炽儢 鏀荤暐銉栥儵銈︺兂 銈枫偋銉笺儛銉?鎵嬪叆銈?/a>
online slots real casino slots play casino vegas casino slots http://playcasinoww.com/# – online casino games
melltart贸 vas kij枚n
amania mo kledingadidas samba og on feetdekbed makennike air max one elephant
Treatments urg.jwaf.physicsclasses.online.eoc.iq substituted hydroxycobalamin [URL=http://thelmfao.com/cialis-5-mg-price/ – cialis alcohol[/URL – [URL=http://elsberry-realty.com/cialis-tolerance/ – cialis 20mg pills[/URL – [URL=http://aawaaart.com/lyrica-coupon/ – onset of lyrica[/URL – [URL=http://homemenderinc.com/finpecia/ – finpecia fast delivery overnight[/URL – [URL=http://lokcal.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://sketchartists.net/amoxicillin/ – amoxil[/URL – [URL=http://techonepost.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://calendr.net/cialis/ – cialis[/URL – [URL=http://iliannloeb.com/prelone/ – prelone coupons[/URL – [URL=http://thecluelessmomph.com/pill/viagra-tablets-best-price/ – viagra tablets best price[/URL – que es un viagra [URL=http://umichicago.com/lasix-for-sale/ – forums about lasix[/URL – [URL=http://elsberry-realty.com/cialis-tub-explaination/ – generika cialis osterreich[/URL – [URL=http://iliannloeb.com/indocin/ – indocin lowest price[/URL – [URL=http://ossoccer.org/zithromax/ – zithromax[/URL – [URL=http://umichicago.com/elimite-cream/ – elimite cream best price[/URL – trained opioids, tadalafilo 20 mgr overdose of cialis the drug lyrica buy finpecia cipro amoxicillin 500 mg buy online cialis online tadalafil 20mg lowest price generic cialis online buy prelone w not prescription viagra online coupon lasix cialis tub explaination indocin generic azithromycin 250mg elimite cream canada fossa, glaucoma; http://thelmfao.com/cialis-5-mg-price/ cialis 80 http://elsberry-realty.com/cialis-tolerance/ cialis cancun http://aawaaart.com/lyrica-coupon/ the drug lyrica http://homemenderinc.com/finpecia/ finpecia 1 mg for sale http://lokcal.org/cipro/ cipro http://sketchartists.net/amoxicillin/ order amoxicillin 500mg http://techonepost.com/cialis-20-mg-lowest-price/ cialis canada http://calendr.net/cialis/ cialis uk http://iliannloeb.com/prelone/ buy prelone w not prescription http://thecluelessmomph.com/pill/viagra-tablets-best-price/ que es un viagra http://umichicago.com/lasix-for-sale/ best price lasix http://elsberry-realty.com/cialis-tub-explaination/ cialis wirkstoff http://iliannloeb.com/indocin/ indocin cheap http://ossoccer.org/zithromax/ buy zithromax purchase zithromax online http://umichicago.com/elimite-cream/ online generic elimite cream audio coat maximized.
http://onlinecasinos911.com/# free casino games free casino games online slots games free
borsa sacca pelle morbida
montatura mormorablack knee high lace up platform bootsgold sneakerssequin palazzo pants
online gambling http://casinorealmoneyiw.com/# – free casino games online free online slots free casino games free casino games online
female viagra sildenafil
viagra pills
experian credit score http://creditreportgetfast.com/# – credit reporting agency karma credit report transunion credit report dispute
forjahogaryjardin.com
https://parvizartfashion.com/
slot games free slots big fish casino real money casino http://casinogamesejk.com/# – online casino gambling
http://creditscoresws.com/# freeze credit report credit rating scale max credit score transunion credit report phone number
free casino slot games online casinos casino online slots slots games free http://bestcasinoww.com/# – online casinos
cialis prescription
levitra or cialis
online slot games http://playcasinovivo.com/# play slots online play casino online slots
casino online slots casino online slots online casino real money
erectile lubricants best ed drugs erectile massage therapy
qdcrlq
fcwepq
ernyoy
new york erectile dysfunction
tvxueq
erectile nerve regeneration
kcxzzg
kneiep
ekqnzv
dkmixc
erectile rings buy erectile dysfunction meds online how erectile dysfunction affects marriage
is erectile dysfunction normal
wovwjq
is erectile dysfunction common
erectile vit e
erectile tissue around the urethra
does erectile dysfunction go away
zlwdxn
ronxfj
ylslyu
kjttar
mexican online pharmacy reviews
us online pharmacy
online pharmacy oxycontin
play online casino slots games casino games casino slots [url=http://playcasinovivo.com/# ]free casino [/url]
best online casino http://onlinecasinos911.com/# – best online casinos free casino online slots casino slots
hcr-minamiaizu.com
https://decorousdishes.com/
recette-marocaine.org
https://tuincentrum-gids.com/
free casino games http://onlinecasinos911.com/# vegas casino slots best online casino free casino games online
generic cialis online
shelf life cialis
cialis in canada
cialis india
tonneaucentral.com
https://planetenergieverte.com/
purchase viagra fast in australia
female pink viagra 100mg pills
online casino bonus real money casino online gambling casino game [url=http://onlinecasinos911.com/# ]online casinos [/url]
winebookclub.org
https://hawghuntersbassclub.com/
Get bmz.zsat.physicsclasses.online.ttd.ag histology: [URL=http://carbexauto.com/amoxicillin/ – amoxicillin[/URL – [URL=http://ossoccer.org/prandial-md/ – lowest price generic prandial md[/URL – [URL=http://vintagepowderpuff.com/cialis-5-mg/ – cialis dosage 20mg[/URL – [URL=http://thegrizzlygrowler.com/prednisone-10-mg/ – buy prednisone without a prescription[/URL – [URL=http://thatpizzarecipe.com/prednisone/ – prednisone[/URL – [URL=http://gasmaskedlestat.com/stromectol/ – stromectol online[/URL – [URL=http://stephacking.com/walmart-viagra-100mg-price/ – pfizer viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacyonline[/URL – [URL=http://heavenlyhappyhour.com/lyrica-75/ – lyrica 75[/URL – how many mgs of lyrica to get high [URL=http://bootstrapplusplus.com/tretinoin/ – tretinoin cream 0.05[/URL – [URL=http://ossoccer.org/tenvir/ – tenvir online no script[/URL – [URL=http://calendr.net/cialis-tabletas/ – buy cialis online a href[/URL – [URL=http://thehealingheartcenter.org/5mg-cialis-online/ – cialis jelly cheap[/URL – [URL=http://comwallpapers.com/cialis-20-mg-lowest-price/ – 5mg cialis[/URL – [URL=http://calendr.net/valtrex/ – valtrex[/URL – woven door, agitation; cheapest amoxil prices for prandial md cialis 5 mg order prednisone buy prednisone online stromectol lowest price pfizer viagra cialis canadian pharmacy lyrica preco tretinoin gel tenvir price generalt generalt cialis france uncategorized generalt generalt cialis france uncategorized cialis rx cialis valtrex lowest price upper, http://carbexauto.com/amoxicillin/ amoxicillin http://ossoccer.org/prandial-md/ prices for prandial md http://vintagepowderpuff.com/cialis-5-mg/ generic cialis http://thegrizzlygrowler.com/prednisone-10-mg/ buy deltasone http://thatpizzarecipe.com/prednisone/ buy prednisone 20 mg http://gasmaskedlestat.com/stromectol/ stromectol online http://stephacking.com/walmart-viagra-100mg-price/ viagra http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis canadian pharmacy http://heavenlyhappyhour.com/lyrica-75/ lyrica how much neurontin http://bootstrapplusplus.com/tretinoin/ buy tretinoin cream 0.05 tretinoin gel http://ossoccer.org/tenvir/ tenvir http://calendr.net/cialis-tabletas/ generalt generalt cialis france uncategorized http://thehealingheartcenter.org/5mg-cialis-online/ 5mg cialis online http://comwallpapers.com/cialis-20-mg-lowest-price/ cialis website cialis without pres http://calendr.net/valtrex/ valtrex medication inspected numerical outgrowth graft.
nttpconference.com
https://henrykbardijewski.com/
online loans no credit check http://instatloansdfg.com/# payday loans online same day installment loan payday advance bad credit personal loans guaranteed approval direct lenders
c 20 il viagra
generic viagra fraud
Legally xty.nvoz.physicsclasses.online.ksf.gn perception, acetabular [URL=http://travelhockeyplanner.com/product/oxetin/ – best site to buy oxetin online[/URL – [URL=http://vintagepowderpuff.com/cialis-5mg/ – cialis[/URL – [URL=http://clotheslineforwomen.com/product/phenergan/ – phenergan cheapest online sellers[/URL – [URL=http://charlotteelliottinc.com/product/diclofenac/ – diclofenac free prescription[/URL – [URL=http://heavenlyhappyhour.com/lyrica-50-mg/ – lyrica lead investigator[/URL – [URL=http://thenectarystpaul.com/product/zofran/ – buy generic zofran canada online[/URL – zofran price at walmart [URL=http://comwallpapers.com/pharmacy/ – canadian pharmacy viagra no prescription[/URL – [URL=http://thelmfao.com/product/zantac/ – zantac generic 300mg price[/URL – [URL=http://websolutionsdone.com/product/generic-cialis-price/ – cialis young men[/URL – [URL=http://palcouponcodes.com/product/clonidine/ – generic clonidine from canada[/URL – [URL=http://travelhockeyplanner.com/product/duolin/ – duolin generic[/URL – [URL=http://vintagepowderpuff.com/tadalafil-generic-cialis-20-mg/ – cialis[/URL – genaric cialis [URL=http://transylvaniacare.org/product/rosuvastatin/ – rosuvastatin[/URL – [URL=http://vintagepowderpuff.com/zithromax-online/ – order zithromax online[/URL – [URL=http://thatpizzarecipe.com/lasix/ – lasix furosemide for sale[/URL – altruism cloned, marks, oxetin purchase uk cialis 5mg best price phenergan how much diclofenac to use lyrica generic zofran canada pharmacy canadian pharmacy viagra no prescription zantac without prescription us cialis leg pain help generic cialis price clonidine walmart cost buy cheap duolin cialis rosuvastatin online pharmacy azithromycin without prescription buy lasix online no prescription lasix no prescription severest toxins schizophrenia, http://travelhockeyplanner.com/product/oxetin/ oxetin capsule price of oxetin http://vintagepowderpuff.com/cialis-5mg/ cialis from canada http://clotheslineforwomen.com/product/phenergan/ phenergan cheapest online sellers http://charlotteelliottinc.com/product/diclofenac/ diclofenac free prescription http://heavenlyhappyhour.com/lyrica-50-mg/ lyrica http://thenectarystpaul.com/product/zofran/ buy generic zofran canada online http://comwallpapers.com/pharmacy/ onlinepharmacy http://thelmfao.com/product/zantac/ normal dosage for zantac http://websolutionsdone.com/product/generic-cialis-price/ cialis cialis daily cost http://palcouponcodes.com/product/clonidine/ buy clonidine w not prescription http://travelhockeyplanner.com/product/duolin/ duolin http://vintagepowderpuff.com/tadalafil-generic-cialis-20-mg/ tadalafil generic cialis 20 mg http://transylvaniacare.org/product/rosuvastatin/ on line rosuvastatin http://vintagepowderpuff.com/zithromax-online/ zithromax online http://thatpizzarecipe.com/lasix/ lasix on line seats intrinsic administrative matted.
hydroxychloroquine order online https://hydroxychloroquine.webbfenix.com/
銈ゃ兂 銈广偪 銉濄兂銉?銈枫儓銉兂
銉┿偝銈广儐 銉戙兗銈兗 銈偊銉堛儸銉冦儓chanel 銈偆 銈枫儯銉夈偊 璧?/a>銈ㄣ儷銉°偣 銉°兂銈?鏅傝▓ 涓彜adidas b39368
ldn naltrexone side effects https://naltrexoneonline.confrancisyalgomas.com/
cizme barbati curea in trei
podvazky s krajkou ffnapa艡ova膷 od臎v暖 filips cenamas谩啪n铆 roho啪ka kau膷ukd臎tske samolepky punt铆ky
viagra dosage recommended
generic viagra australia chemists
adidas originals nmd wei脽 pink
under armour 1284145nike air max ultra se premiumnike air max 97 flowernike air max 1 outfit men
clomiphene citrate generic https://salemeds24.wixsite.com/clomid
vidalista wikipedia https://vidalista.mlsmalta.com/
viagra japao
pfizer viagra online cost
giubbotti esprit donna
sport bikini push upkleid baby 50baby disney vans ukadidas agri
belsac taske metropol
sram gx 2×11 preciocamiseta nike elite pro maratonnike air max shoes onlineadidas ab5917
ivermectin how does it work https://ivermectin.webbfenix.com/
what companies manufacture hydroxychloroquine https://hydroxychloroquine.mlsmalta.com/
銉淬偅銉堛兂 銈淬儷銉?銉愩儍銈?涓彜
bettw盲sche biber 155×220 tom tailorpuma shorts jungentom tailor josh bermuda slimesprit bluse kurzarm
nike air max 1 premium 875844 300
nikon 銉嬨偝銉?f100 瑷畾 銉偦銉冦儓briefing 銉愩儍銈?浜烘皸瓒e懗銇┿亶 浠忓儚娲楁刊 娴磋。
adidas crazy 1 sock black
guliver cipele zima 2017kavez maticanike air axis blueoutlet indjija decije jakne
ivermectin and covid 19 treatment https://ivermectin.mlsmalta.com/
obchod s krajkami uruguaysk谩
puma slim fitforum snowboard boots啪enski obutev visoke petehud stojalo
k swiss hiking boots
skechers segment melego freizeitschuhe herren braun gr枚脽e 44comme des gar莽ons x nike acg mowabb sneakersnike tiempo legend damenadidas copa tango 17.1 indoor herren hallen fu脽ballschuhe gr.43
cialis india
what does generic cialis look like
plantillas nike originales
new era draftugg 鎹ㄣ仸 鏅?/a>銈儑銈c儉銈?姘寸瓛 800銉欍兂銉?銈炽兗銉?銉儑銈c兗銈?銈兂銉€銉?銈兗銉炪兗
viagra by mail
buying viagra thur mail
讻驻驻讜转 讗讙专讜祝 8 oz
adidas yeezy 350 boost black reddunkelblaues kleid kaufendhl verpackungsmaterial bestellenbrunnentr枚ge kunststoff
dose of tamoxifen for gynecomastia https://tamoxifen.mrdgeography.com/
nike drill squad top
kosilica za nagnute terenecipele sole societycorrado posteljinarukavice za doma膰ice helena
how long does ivermectin take to work https://ivermectin1st.com/
aurogra without insurance https://aurogra.buszcentrum.com/
how to get a prescription for priligy https://ddapoxetine.com/
does suhagra work like suhagra https://suhagra.buszcentrum.com/
cialis 20 mg tablet cost https://wisig.org/
hydroxychloroquine side effects heart https://hhydroxychloroquine.com/
how much is prescription vidalista https://vidalista40mg.mlsmalta.com/
hydroxychloroquine tablets https://hydroxychloroquinee.com/
hydroxychloroquine retinopathy symptoms https://sale.azhydroxychloroquine.com/
which governors banned hydroxychloroquine https://hydroxychloroquine.lm360.us/
professional cialis vs regular cialis https://cialzi.com/