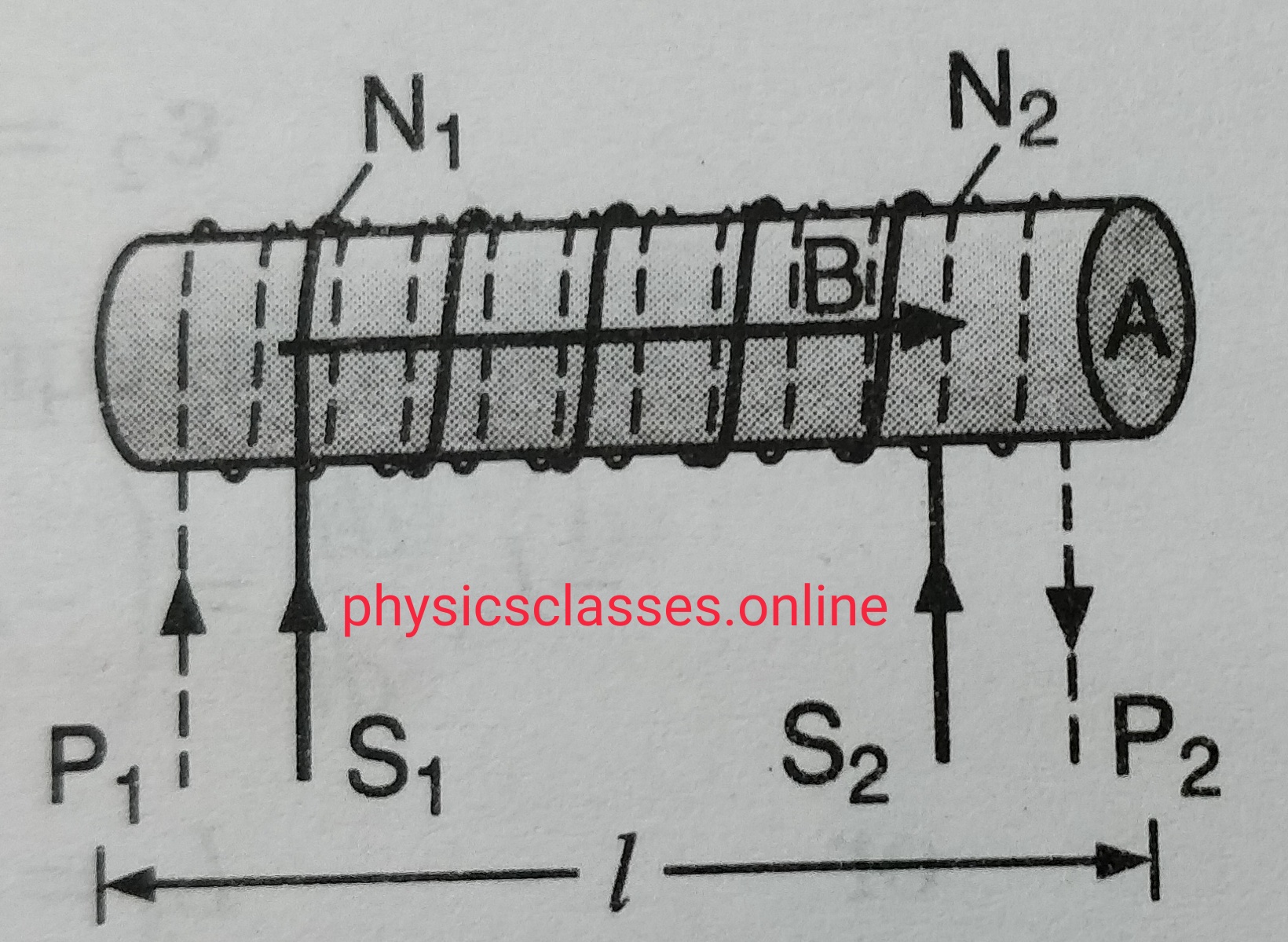
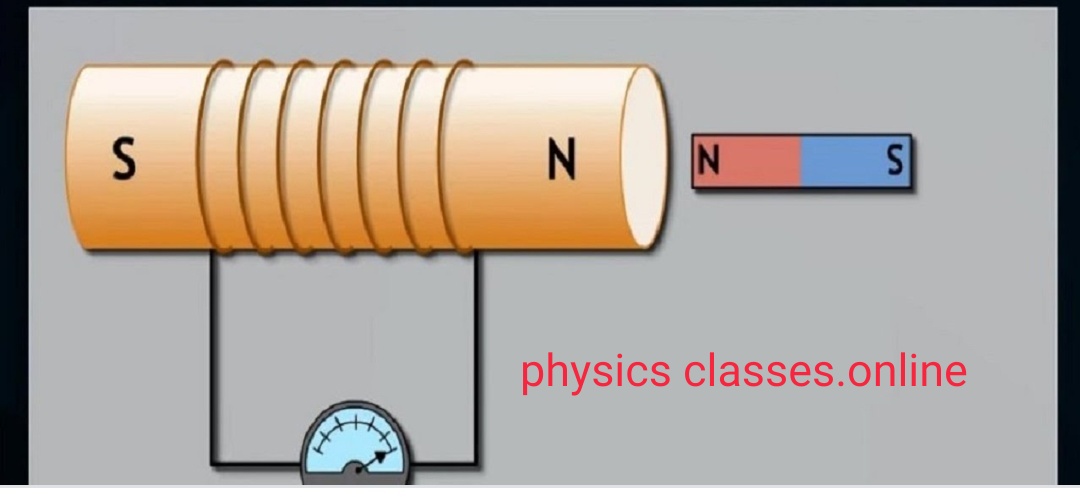
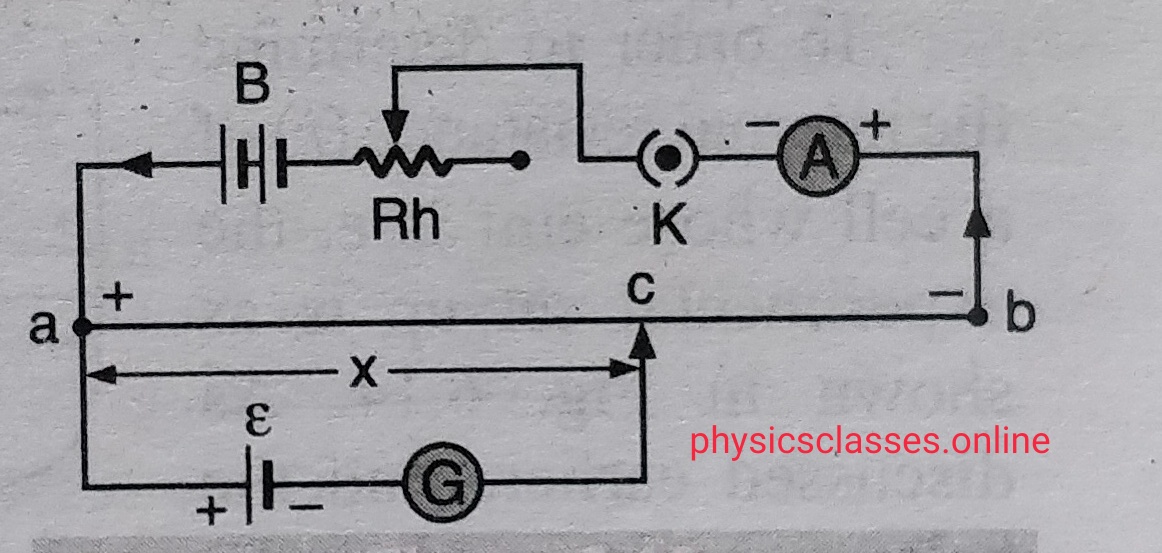
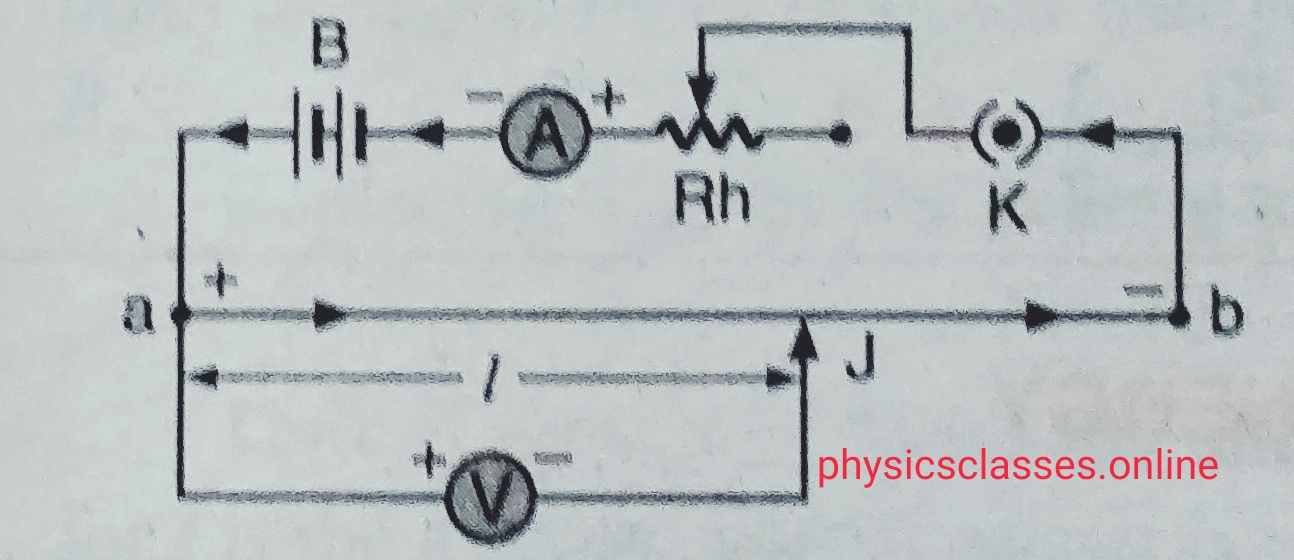
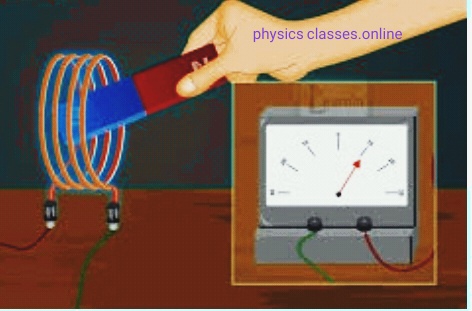
Mutual induction- In this topic students will study what is mutual induction and coefficient of mutual induction / mutual inductance? And what is the unit of mutual inductance Mutual induction- Let us consider two coils placed near to each other closely . One of the coil carries the battery is the primary coil and the […]
Define 1 Ampere This topic only explain the term definition of Ampere ( which is explain in different-different type . Students can learn it according to there needs. ) Ampere is the basic unit of electric current . It is named after Andre-Marie -Ampere a French scientist born in 1775 . He also known as […]
ELECTRIC CURRENT or CURRENT ELECTRICITY electric current – Electric current – When electric charges is in motion , they constitute what is called an electric current . electric current is defined as the rate of flow of charge through an area of the conductor . if Q is the charge flows through a conductor […]
SELF-INDUCTION OF LONG SOLENOID SELF-INDUCTION OF LONG SOLENOID this topic is important for the class 12th board examination Self-inductance of long air-cored solenoid question may asked as – what do you mean by the term self-induction ? Find expression for the self-inductance of long air cored solenoid . Self-inductance of long air-cored solenoid – Suppose […]
Explain the term self-induction of a coil Self – Induction – It is the property of an electric circuit or coil by virtue of which it opposes any change of flux or current in it by inducing a current in itself is called self- induction. In another words we can say “self-induction is the inertia […]
What is electric current What is electric current ? what is its unit ? define Ampere. Electric current-When electric charges is in motion , they constitute what is called an electric current . electric current is defined as the rate of flow of charge through an area of the conductor . if Q is the […]
Faraday’s law of electromagnetic induction Electromagnetic induction – As we know when electric current passes through a conductor then magnetic field developed across the conductor , first discovered by Oersted . But Michael Faraday found its converse is also possible i.e. Whenever magnetic field changes around a coil ( and hence magnetic flux linked across […]
USES OF POTENTIOMETER Uses of potentiometer – Measurement of emf of cell- Let , E is the emf of driver cell and , E1 is the emf of cell to be measured Here potential gradient K= [ {E / (R+r)} r]/l . Let l1 is the length of the wire from […]
POTENTIOMETER THIS TOPIC EXPLAIN ABOUT THE POTENTIOMETER Potentiometer – An instrument used to measure accurately the EMF or potential difference is called potentiometer. Principle– Its working based on the principle that the potential drop across a conductor is directly proportional to the length of the conductor , if constant current passes through the conductor having […]
In moving coil galvanometer we will learn about the working theory of a galvanometer and its conversion from galvanometer to ammeter and voltmeter To read the complete topic click here- Moving Coil Galvanometer