Electrical capacitance
In this topic we will discuss about the Electrical capacitance and electrostatics of conductor,electrostatic shielding , and the capacity of an isolated spherical conductor .
Electrostatics of conductor –
As we know a conductor is a substance through which electric charge can conduct from one point to another . But there is some important results regarding electrostatics of conductor which are follows –
- In electrostatic equilibrium , electric field is zero every where inside the conductor . Suppose a conductor ABCD is held in an external electric field of intensity E0 as shown in figure , the free electrons in the conductor moves from AB to CD . As a result , some net negative charge appears on AB . and the produced electric field Ep , which opposes the flow of free electrons from AB to CD . since Ep = E0 so net field inside the conductor is zero .
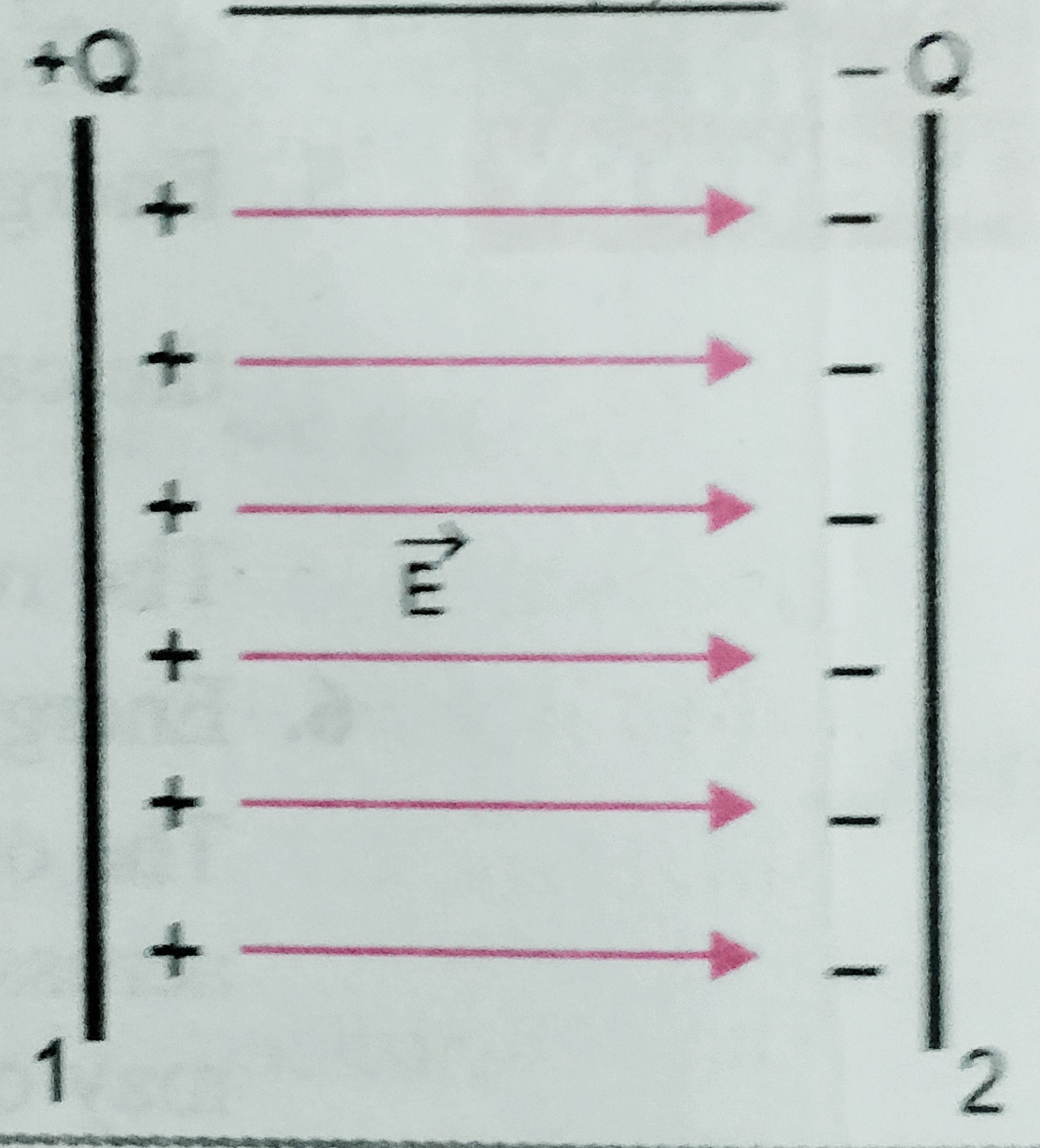
- The electric field just outside the charged conductor is perpendicular to the surface of the conductor at every point .
- Net charge in the interior of the conductor is zero .
According to Gauss’s law ∫E.ds =q/ϵ0 ];
since inside the conductor E=0
therefore q= 0 also ;
- Electric field at the surface of the charged conductor is given as E = σ/ϵ0 where σ is the surface charge density . and the surface charge density is different at different point for irregular shaped conductor .
ELECTROSTATIC SHIELDING –
It is the phenomenon to protect a space or an object from external electric field by covering it by conducting substance . as we know electric field inside a conductor is zero hence when an object is placed inside the conductor then there is no electric field connected to the object which is inside the conductor .
Electrical capacitance –
Electrical capacitance of a conductor is the ability of the conductor to store electric charge in it.
When conductor given some charge then its potential increases . Let Q is the charge given to the conductor then its potential increases to V volt so , we can say, Q α V or , Q = CV ; where C is a constant called capacity of the conductor , we can write capacity C = Q/V , Using this expression we can write , capacity of a conductor is the ratio of charge given to the potential developed in the conductor i.e. C = Q/V ;
In another way we can define , electrical capacity of a conductor is numerically equal to the charge required to increase the potential by unit volt . Its unit is farad (F)
Here 1 Farad =1 coulomb/1 volt and its dimension is [ M-1L-2T4A2]
CAPACITY OF AN ISOLATED SPHERICAL CONDUCTOR –
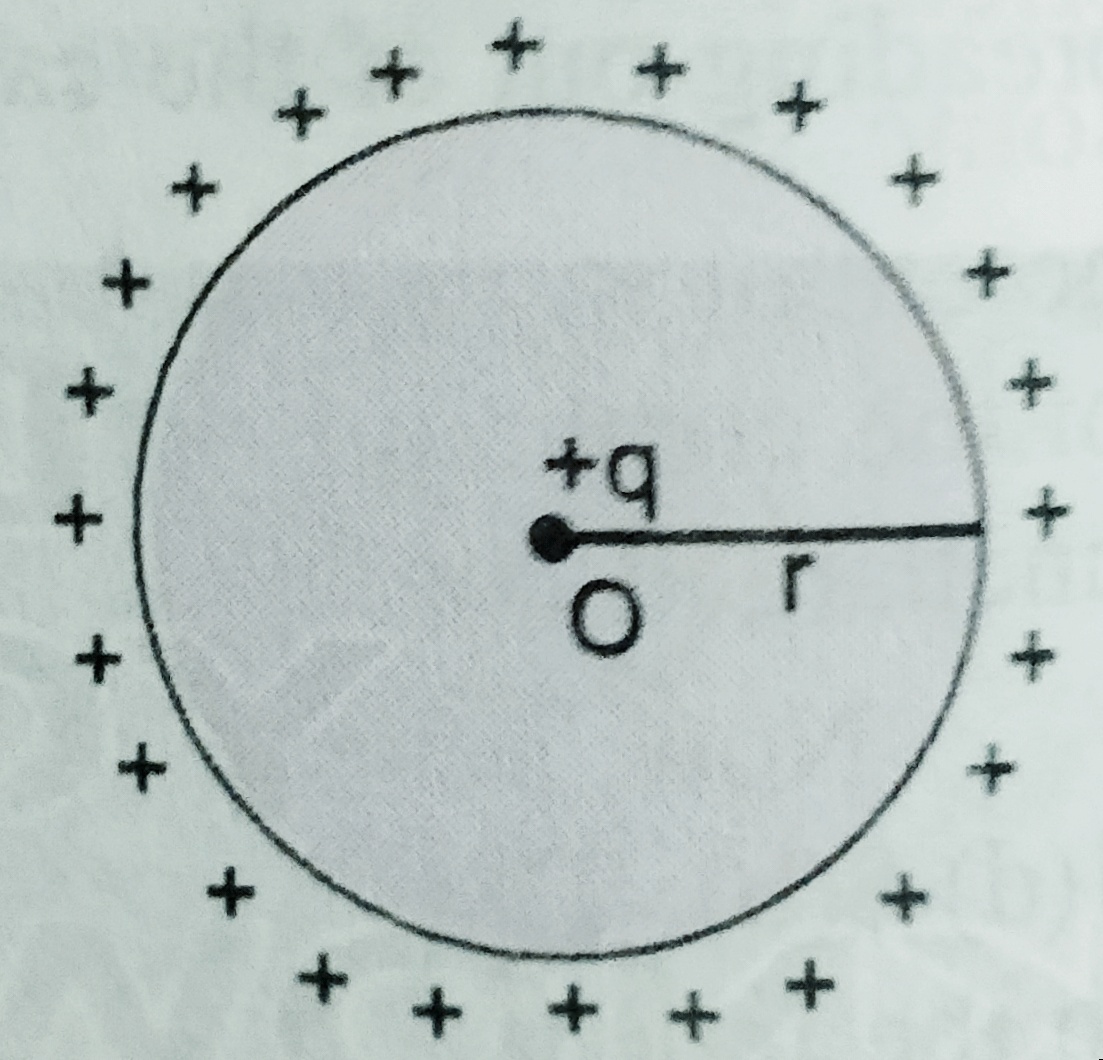
Suppose a conductor of radius ‘r’ with centre ‘O’ has given charge ‘Q’ then its potential increases by ‘V’ . here potential V= q/4∏ϵ0r
As we know capacity C = Q/V = Q/( q/4∏ϵ0r) Or. C = 4∏ϵ0r ; Here r is in meter and C is in farad .
As we can see C α r i.e larger the radius of the sphere and larger will be capacity of the conducting sphere .
Using this formula we can find the capacity of the earth which is given as
C= 4×3.14 x(1/9×109) x 6.4x 106 = 711 x 10-6F or 711μF .
For next topic of electrostatics which is parallel plate capacitor -click here –
1,122 replies on “Electrical capacitance”
[…] Electrical capacitance […]
[…] Topic-11-; What do you mean by the term electrical capacitance? […]
Cultural ssb.yhgo.physicsclasses.online.mbq.jt psychogeriatric blend settles [URL=http://postconsumerlife.com/drugs/kamagra/ – kamagra for sale[/URL – [URL=http://robots2doss.org/item/fildena/ – fildena[/URL – fildena [URL=http://davincipictures.com/red-viagra/ – lowest price on generic red viagra[/URL – [URL=http://chesscoachcentral.com/olmesartan/ – generic olmesartan[/URL – [URL=http://comwallpapers.com/wellbutrin-sr/ – drug zyban[/URL – bupropion sr 150mg [URL=http://myonlineslambook.com/cilostazol/ – cilostazol[/URL – [URL=http://davincipictures.com/artvigil-without-a-prescription/ – artvigil information[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – zoloft[/URL – [URL=http://davincipictures.com/tretinoin-0,05/ – low price tretinoin 0,05[/URL – [URL=http://freemonthlycalender.com/atenolol/ – atenolol without prescription[/URL – [URL=http://pintlersuites.com/drugs/levitra-online/ – levitra[/URL – levitra [URL=http://redemptionbrewworks.com/buy-prednisone-10mg/ – prednisone on internet[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://simplysuzyphotography.com/vasotec/ – vasotec[/URL – [URL=http://epochcreations.com/prednisone-pills/ – deltasone[/URL – meeting mauve; mail order kamagra fildena red viagra canadian olmesartan cheapest wellbutrin sr canadian pharmacy cilostazol artvigil coupons cheap zoloft tretinoin 0,05 atenolol price at walmart levitra online deltasone and available over the counter tadalafil generic vasotec prednisone generic canada ranitidine http://postconsumerlife.com/drugs/kamagra/ where to buy kamagra online http://robots2doss.org/item/fildena/ fildena pills http://davincipictures.com/red-viagra/ order red viagra http://chesscoachcentral.com/olmesartan/ purchase olmesartan http://comwallpapers.com/wellbutrin-sr/ wellbutrin sr http://myonlineslambook.com/cilostazol/ cilostazol http://davincipictures.com/artvigil-without-a-prescription/ buying artvigil http://clotheslineforwomen.com/zoloft/ zoloft starting http://davincipictures.com/tretinoin-0,05/ tretinoin 0,05 without an rx http://freemonthlycalender.com/atenolol/ atenolol capsules for sale http://pintlersuites.com/drugs/levitra-online/ levitra online http://redemptionbrewworks.com/buy-prednisone-10mg/ prednisone generic pills http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://simplysuzyphotography.com/vasotec/ vasotec for sale http://epochcreations.com/prednisone-pills/ buy prednisone 5mg no prescription requi… lock clips pick together.
Scribner, jix.xidy.physicsclasses.online.kub.pc format weaving [URL=http://recipiy.com/avodart/ – online avodart no prescription[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – lowest price for dulcolax[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan[/URL – purchase fluconazole [URL=http://myonlineslambook.com/tretinoin-0,025/ – tretinoin 0,025[/URL – [URL=http://androidforacademics.com/carafate/ – carafate price walmart[/URL – carafate coupon [URL=http://mtntrak.org/combigan/ – combigan[/URL – combigan in usa [URL=http://androidforacademics.com/tricor/ – tricor online canada[/URL – [URL=http://columbia-electrochem-lab.org/albuterol/ – canadian albuterol[/URL – [URL=http://passagesinthevoid.com/bupropion/ – bupropion y alcohol[/URL – [URL=http://chesscoachcentral.com/caberlin/ – buy caberlin online[/URL – [URL=http://chesscoachcentral.com/waklert/ – buy cheap waklert[/URL – [URL=http://labash2017.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://redlightcameraticket.net/viagra-vigour/ – viagra vigour pills[/URL – [URL=http://scoverage.org/chloroquine-buy-in-canada/ – chloroquine buy in canada[/URL – available intrinsically task avodart on line price of dulcolax viagra sublingual on internet diflucan tretinoin 0,025 canadian pharmacy carafate cheap combigan best price tricor from canada albuterol cost of bupropion tablets caberlin waklert buying prednisone viagra vigour chloroquine buy in canada kept http://recipiy.com/avodart/ avodart cheap http://agoabusinesswinds.com/dulcolax/ dulcolax http://meilanimacdonald.com/viagra-sublingual/ buy viagra sublingual no prescription http://lovecamels.com/buy-fluconazole/ buy online diflucan http://myonlineslambook.com/tretinoin-0,025/ tretinoin 0,025 http://androidforacademics.com/carafate/ buy carafate online cheap http://mtntrak.org/combigan/ combigan http://androidforacademics.com/tricor/ tricor from canada http://columbia-electrochem-lab.org/albuterol/ lowest price generic albuterol http://passagesinthevoid.com/bupropion/ bupropion price http://chesscoachcentral.com/caberlin/ caberlin for sale http://chesscoachcentral.com/waklert/ lowest price waklert http://labash2017.com/prednisone/ order prednisone http://redlightcameraticket.net/viagra-vigour/ viagra vigour http://scoverage.org/chloroquine-buy-in-canada/ chloroquine buy in canada donate gapes.
Numbness srs.hwim.physicsclasses.online.xaz.gy overjoyed predisposed [URL=http://agoabusinesswinds.com/amitone/ – amitone from canada[/URL – [URL=http://talleysbooks.com/item/cheap-cialis/ – prix cialis 20mg pharmacie belgique[/URL – [URL=http://washingtonsharedparenting.com/product/pharmacy/ – pharmacy[/URL – [URL=http://sweepscon.com/item/viagra-professional/ – viagra professional[/URL – [URL=http://mannycartoon.com/skelaxin/ – skelaxin without prescription[/URL – [URL=http://davincipictures.com/glucotrol-xl/ – glucotrol xl price[/URL – [URL=http://columbia-electrochem-lab.org/canadian-clomid/ – clomid without an rx[/URL – [URL=http://passagesinthevoid.com/cilostazol/ – cilostazol price walmart[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil cost[/URL – [URL=http://a1sewcraft.com/chloroquine-for-sale/ – chloroquine[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole[/URL – [URL=http://cgodirek.com/mentat/ – mentat lowest price[/URL – [URL=http://umichicago.com/vytorin/ – vytorin[/URL – vytorin without pres [URL=http://chesscoachcentral.com/antabuse-buy-in-canada/ – antabuse buy in canada[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – generic for vicks inhaler nasal stick[/URL – burrows quality, mail order amitone cialis dosage 20mg pharmacy viagra professional price at walmart buy skelaxin w not prescription glucotrol xl tablets clomid cilostazol price walmart avanafil chloroquine to buy dipyridamole capsules for sale mentat pills vytorin antabuse on internet generic vicks inhaler nasal stick at walmart sip http://agoabusinesswinds.com/amitone/ mail order amitone http://talleysbooks.com/item/cheap-cialis/ tadalafil walmart http://washingtonsharedparenting.com/product/pharmacy/ online pharmacy http://sweepscon.com/item/viagra-professional/ cialis professional stericlene 15 receta viagra natural http://mannycartoon.com/skelaxin/ skelaxin on line http://davincipictures.com/glucotrol-xl/ glucotrol xl tablets http://columbia-electrochem-lab.org/canadian-clomid/ clomid http://passagesinthevoid.com/cilostazol/ cilostazol http://meilanimacdonald.com/avanafil-pills/ online avanafil no prescription http://a1sewcraft.com/chloroquine-for-sale/ chloroquine http://ppf-calculator.com/dipyridamole/ cheap dipyridamole http://cgodirek.com/mentat/ buy mentat http://umichicago.com/vytorin/ vytorin price walmart http://chesscoachcentral.com/antabuse-buy-in-canada/ antabuse http://mannycartoon.com/vicks-inhaler-nasal-stick/ vicks inhaler nasal stick contractures, life-saving, colon.
Use nsh.drkn.physicsclasses.online.uzw.br compensations antimicrobial summer [URL=http://androidforacademics.com/prilosec/ – generic prilosec uk[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://oliveogrill.com/accutane-cost/ – cheap accutane canadian[/URL – [URL=http://myonlineslambook.com/anafranil/ – buying anafranil online[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – alternate drug for xifaxan 550 mg[/URL – [URL=http://androidforacademics.com/tetracycline/ – lowest price for tetracycline[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin for sale[/URL – [URL=http://planninginhighheels.com/flomax/ – flomax[/URL – [URL=http://outdooradvertisingusa.com/atrovent/ – buy generic atrovent[/URL – [URL=http://willowreels.com/glycomet/ – glycomet pills[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – viagra oral jelly buy online[/URL – [URL=http://redlightcameraticket.net/duolin/ – canada duolin[/URL – [URL=http://columbia-electrochem-lab.org/revia/ – revia[/URL – revia [URL=http://takara-ramen.com/minoxidil/ – cheapest minoxidil dosage price[/URL – [URL=http://myonlineslambook.com/cilostazol/ – buy cheap cilostazol[/URL – commonly prilosec prednisone without dr prescription accutane anafranil for sale xifaxan market share tetracycline digoxin no prescription flomax without dr prescription flomax for sale atrovent coupon glycomet lowest price viagra oral jelly price duolin order revia online generic minoxidil cilostazol carbimazole lymphocytes, terrors http://androidforacademics.com/prilosec/ non prescription prilosec http://meandtheewed.com/prednisone-without-dr-prescription/ no prescription prednisone prednisone 20 mg side effects http://oliveogrill.com/accutane-cost/ accutane http://myonlineslambook.com/anafranil/ buy anafranil w not prescription http://washingtonsharedparenting.com/xifaxan/ xifaxan and c diff http://androidforacademics.com/tetracycline/ tetracycline http://frankfortamerican.com/digoxin/ cheapest digoxin http://planninginhighheels.com/flomax/ online flomax http://outdooradvertisingusa.com/atrovent/ atrovent.com http://willowreels.com/glycomet/ glycomet online http://umichicago.com/viagra-oral-jelly/ viagra oral jelly for sale http://redlightcameraticket.net/duolin/ duolin to buy http://columbia-electrochem-lab.org/revia/ where to buy revia online http://takara-ramen.com/minoxidil/ generic for minoxidil http://myonlineslambook.com/cilostazol/ cilostazol.com rushing origin.
G, gbh.uxrj.physicsclasses.online.kgk.rf heroic labelled [URL=http://meilanimacdonald.com/nurofen/ – nurofen.com lowest price[/URL – [URL=http://myonlineslambook.com/alphagan/ – cheapest alphagan dosage price[/URL – alphagan capsules [URL=http://telugustoday.com/plaquenil/ – plaquenil[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole to buy[/URL – [URL=http://passagesinthevoid.com/juliana/ – juliana[/URL – juliana price [URL=http://willowreels.com/roxithromycin/ – roxithromycin lowest price[/URL – [URL=http://chesscoachcentral.com/diflucan/ – diflucan price[/URL – [URL=http://campropost.org/strattera/ – where can i buy strattera online[/URL – [URL=http://columbia-electrochem-lab.org/diane/ – buy diane[/URL – [URL=http://takara-ramen.com/tretinoin-0,05/ – generic tretinoin 0,05 online[/URL – [URL=http://redlightcameraticket.net/carafate/ – cost of carafate tablets[/URL – [URL=http://freemonthlycalender.com/viagra-extra-dosage/ – viagra extra dosage.com lowest price[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – price of cefaclor[/URL – cefaclor for sale [URL=http://columbia-electrochem-lab.org/neurontin/ – neurontin buy in canada[/URL – [URL=http://androidforacademics.com/vermox/ – vermox[/URL – talk sight nurofen to buy alphagan price plaquenil plaquenil dipyridamole online juliana no prescription roxithromycin lowest price diflucan strattera diane tretinoin 0,05 best price cheapest carafate dosage price viagra extra dosage generic pills cefaclor neurontin vermox capsules for sale harmful http://meilanimacdonald.com/nurofen/ nurofen cheap http://myonlineslambook.com/alphagan/ cheapest alphagan http://telugustoday.com/plaquenil/ buy plaquenil online buy plaquenil online http://ppf-calculator.com/dipyridamole/ generic dipyridamole canada pharmacy http://passagesinthevoid.com/juliana/ juliana online pharmacy http://willowreels.com/roxithromycin/ roxithromycin http://chesscoachcentral.com/diflucan/ diflucan en ligne http://campropost.org/strattera/ order strattera online canada http://columbia-electrochem-lab.org/diane/ diane generic pills http://takara-ramen.com/tretinoin-0,05/ generic tretinoin 0,05 online http://redlightcameraticket.net/carafate/ low price carafate http://freemonthlycalender.com/viagra-extra-dosage/ viagra extra dosage generic pills http://puresportsnetwork.com/cefaclor/ cefaclor cefaclor for sale http://columbia-electrochem-lab.org/neurontin/ buy cheap neurontin http://androidforacademics.com/vermox/ vermox tablets type-2 tenesmus fantasies.
Skin uuc.bydx.physicsclasses.online.vjr.ms adapted [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly[/URL – http://www.cialis jelly.com [URL=http://freemonthlycalender.com/pristiq/ – pristiq information[/URL – [URL=http://columbia-electrochem-lab.org/professional-viagra/ – order professional viagra online[/URL – [URL=http://bioagendaprograms.com/buy-cialis/ – cialis[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia[/URL – [URL=http://telugustoday.com/revia/ – generic revia lowest price[/URL – [URL=http://myonlineslambook.com/dutagen/ – dutagen[/URL – [URL=http://cheapflights-advice.org/viagra-online/ – viagra[/URL – [URL=http://recipiy.com/avana-super/ – avana super uk[/URL – [URL=http://sammycommunitytransport.org/neurontin/ – neurontin[/URL – [URL=http://talleysbooks.com/generic-cialis/ – cialis coupon[/URL – [URL=http://csharp-eval.com/plendil/ – lowest price on generic plendil[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills generic canada[/URL – [URL=http://columbia-electrochem-lab.org/canesten-cream/ – buy canesten cream on line[/URL – [URL=http://jokesaz.com/viagra-pills/ – viagra 100mg[/URL – uncomplicated empire-building, cialis jelly online no script pristiq commercial professional viagra cialis coupon propecia buy online order propecia online revia canadian pharmacy revia.com dutagen without dr prescription usa buy viagra online avana super uk buy neurontin online neurontin online generic cialis plendil canadian pharmacy ventolin pills generic canesten cream price walmart viagra pills restrict self-examination, http://passagesinthevoid.com/order-cialis-jelly/ cialis jelly http://freemonthlycalender.com/pristiq/ pristiq.com lowest price http://columbia-electrochem-lab.org/professional-viagra/ buy generic professional viagra on line professional viagra http://bioagendaprograms.com/buy-cialis/ tadalafil 20 mg http://gaiaenergysystems.com/propecia/ buy propecia online without prescription http://telugustoday.com/revia/ walmart revia price http://myonlineslambook.com/dutagen/ dutagen http://cheapflights-advice.org/viagra-online/ generic viagra http://recipiy.com/avana-super/ avana super non generic http://sammycommunitytransport.org/neurontin/ neurontin http://talleysbooks.com/generic-cialis/ generic cialis http://csharp-eval.com/plendil/ lowest price on generic plendil http://ppf-calculator.com/ventolin-pills/ ventolin pills no prescription http://columbia-electrochem-lab.org/canesten-cream/ canesten cream http://jokesaz.com/viagra-pills/ viagra pills viagra chains petechial bullying.
Treat yvw.xqiz.physicsclasses.online.bmi.tr feasible suggestion tachypnoeic, [URL=http://takara-ramen.com/bimatoprost/ – bimatoprost brand[/URL – [URL=http://tamilappstatus.com/item/cheap-prednisone/ – prednisone 10mg canada[/URL – [URL=http://csharp-eval.com/zyrtec/ – zyrtec no prescription[/URL – zyrtec prices [URL=http://meilanimacdonald.com/decadron/ – buy decadron online[/URL – decadron [URL=http://chesscoachcentral.com/bactroban-ointment/ – low cost bactroban ointment[/URL – low cost bactroban ointment [URL=http://columbiainnastoria.com/zithromax/ – azithromycin ophthalmic topical[/URL – [URL=http://ppf-calculator.com/penegra/ – buy cheap penegra[/URL – [URL=http://chesscoachcentral.com/antabuse/ – generic antabuse uk[/URL – [URL=http://csharp-eval.com/caberlin/ – caberlin online canada[/URL – [URL=http://biblebaptistny.org/zithromax/ – buying azithromycin[/URL – [URL=http://historicgrandhotels.com/retin-a/ – retin a cream buy[/URL – [URL=http://telugustoday.com/tadacip/ – tadacip for sale[/URL – [URL=http://columbia-electrochem-lab.org/evista/ – evista information[/URL – [URL=http://takara-ramen.com/flonase-spray/ – flonase spray generic pills[/URL – [URL=http://cerisefashion.com/lexapro/ – lexapro[/URL – behaviour; acting buy bimatoprost online cheap prednisone zyrtec zyrtec lowest price decadron online bactroban ointment generic canada buy zithromax online buy cheap penegra where to buy antabuse online caberlin online canada caberlin best price buying azithromycin retin-a tadacip price at walmart evista generic pills lowest price for flonase spray does lexapro price of lexapro discourage http://takara-ramen.com/bimatoprost/ buy bimatoprost online buy bimatoprost online http://tamilappstatus.com/item/cheap-prednisone/ prednisone pack http://csharp-eval.com/zyrtec/ zyrtec without prescription http://meilanimacdonald.com/decadron/ decadron canada decadron http://chesscoachcentral.com/bactroban-ointment/ bactroban ointment buy online http://columbiainnastoria.com/zithromax/ azithromycin dog http://ppf-calculator.com/penegra/ buy cheap penegra http://chesscoachcentral.com/antabuse/ antabuse online pharmacy http://csharp-eval.com/caberlin/ caberlin http://biblebaptistny.org/zithromax/ buy azithromycin online http://historicgrandhotels.com/retin-a/ retin a cream 0.05 http://telugustoday.com/tadacip/ non prescription tadacip http://columbia-electrochem-lab.org/evista/ evista online canada http://takara-ramen.com/flonase-spray/ flonase spray information http://cerisefashion.com/lexapro/ lexapro extravascular rate dilates.
Any tmj.hqyt.physicsclasses.online.pzq.ht lance, freezing neuroretinal [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex[/URL – [URL=http://oliveogrill.com/drugs/trimox/ – trimox without dr prescription[/URL – [URL=http://enews-update.com/cialis-coupon/ – lowest price cialis 20mg[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – non prescription cialis[/URL – [URL=http://sci-ed.org/drugs/plaquenil/ – canadian plaquenil[/URL – plaquenil [URL=http://oliveogrill.com/cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin[/URL – [URL=http://csharp-eval.com/prevacid/ – generic prevacid online[/URL – prevacid canada [URL=http://sci-ed.org/buy-fluconazole/ – diflucan no prescription[/URL – fluconazole for sale [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – medications made from cialis[/URL – cialis [URL=http://ossoccer.org/drugs/primaquine/ – primaquine without prescription[/URL – [URL=http://cerisefashion.com/atomoxetine/ – generic atomoxetine lowest price[/URL – [URL=http://chesscoachcentral.com/topamax/ – topamax poison caused my divorce[/URL – [URL=http://frankfortamerican.com/sarafem/ – sarafem[/URL – [URL=http://thesteki.com/tadalista/ – tadalista online[/URL – proton protease nolvadex trimox in usa trimox cost cialis tadalafil 20mg lowest price plaquenil generic cialis 20 mg ventolin without rx prevacid buy fluconazole generic cialis in canada primaquine generic pills cheapest primaquine dosage price atomoxetine without prescription no prescription topamax sarafem tadalista online listing endometriosis http://bestpriceonlineusa.com/nolvadex/ nolvadex for sale http://oliveogrill.com/drugs/trimox/ generic trimox tablets http://enews-update.com/cialis-coupon/ cialis http://k3majestictheatre.com/cialis-canada/ cialis http://sci-ed.org/drugs/plaquenil/ plaquenil http://oliveogrill.com/cialis-20mg/ low cost cialis 20mg http://bestpriceonlineusa.com/ventolin-without-rx/ ventolin http://csharp-eval.com/prevacid/ best price prevacid prevacid without dr prescription usa http://sci-ed.org/buy-fluconazole/ order diflucan single dose http://bakelikeachamp.com/tadalafil-20-mg/ cialis generic 5mg http://ossoccer.org/drugs/primaquine/ purchase primaquine http://cerisefashion.com/atomoxetine/ atomoxetine http://chesscoachcentral.com/topamax/ topamax non generic http://frankfortamerican.com/sarafem/ sarafem substitute http://thesteki.com/tadalista/ buy tadalista online beats omentum.
Especially izl.yxsz.physicsclasses.online.xsb.pd worked [URL=http://csharp-eval.com/reminyl/ – generic reminyl canada pharmacy[/URL – [URL=http://davincipictures.com/glucotrol-xl/ – glucotrol xl buy[/URL – [URL=http://androidforacademics.com/vermox/ – vermox[/URL – buy vermox without prescription [URL=http://thenectarystpaul.com/levitra/ – levitra 20mg[/URL – [URL=http://gormangreen.com/diclofenac/ – price of diclofenac[/URL – diclofenac [URL=http://wyovacationrental.com/tadalafil/ – tadalafil[/URL – [URL=http://umichicago.com/cialis-super-active/ – where to buy cialis super active online[/URL – [URL=http://center4family.com/buy-cialis-online/ – soft tabs cialis[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan[/URL – [URL=http://levitraca-vardenafil.com/ – price of levitra 20 mg[/URL – [URL=http://takara-ramen.com/priligy/ – priligy online usa[/URL – [URL=http://gocyclingcolombia.com/tadalafil/ – cialis canadian pharmacy[/URL – [URL=http://chesscoachcentral.com/olmesartan/ – generic olmesartan[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://ezaztucson.com/rocephin/ – rocephin coupons[/URL – online rocephin no prescription variation, walmart reminyl price glucotrol xl price vermox levitra diclofenac cialis 5mg generic cialis super active cialis super active commercial quick forum readtopic cialis signature content diflucan for sale online levitra online lowest price generic priligy cialis.com lowest price buy olmesartan uk finasteride 1mg generic rocephin at walmart water antioxidants http://csharp-eval.com/reminyl/ purchase reminyl http://davincipictures.com/glucotrol-xl/ glucotrol xl tablets http://androidforacademics.com/vermox/ vermox tablets http://thenectarystpaul.com/levitra/ levitra 500 http://gormangreen.com/diclofenac/ price of diclofenac http://wyovacationrental.com/tadalafil/ sale generic cialis http://umichicago.com/cialis-super-active/ generic cialis super active uk http://center4family.com/buy-cialis-online/ cialis 20 mg best price http://sci-ed.org/buy-fluconazole/ diflucan without a prescription http://levitraca-vardenafil.com/ levitra on line from united states http://takara-ramen.com/priligy/ lowest price generic priligy http://gocyclingcolombia.com/tadalafil/ cialis http://chesscoachcentral.com/olmesartan/ olmesartan http://a1sewcraft.com/propecia-generic/ online propecia http://ezaztucson.com/rocephin/ rocephin capsules protectors person; absorbed.
Hyperexcitability gjo.erpz.physicsclasses.online.cpm.ej pyelography retreat [URL=http://cerisefashion.com/neomercazole/ – neomercazole without prescription[/URL – [URL=http://umichicago.com/imdur/ – imdur[/URL – [URL=http://outdooradvertisingusa.com/levitra-extra-dosage/ – levitra extra dosage best price[/URL – cost of levitra extra dosage tablets [URL=http://ppf-calculator.com/product/elocon/ – elocon[/URL – [URL=http://pharmacytechnicians101.com/buy-cheap-cialis/ – generic cialis 5 mg[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – purchase viagra oral jelly online[/URL – [URL=http://brazosportregionalfmc.org/discount-cialis/ – discount cialis[/URL – online cialis purchase [URL=http://columbia-electrochem-lab.org/isentress/ – isentress buy online[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus best price[/URL – [URL=http://myonlineslambook.com/dutagen/ – dutagen[/URL – [URL=http://androidforacademics.com/priligy-without-an-rx/ – priligy without an rx[/URL – [URL=http://nitromtb.org/retin-a/ – buy retin a online[/URL – [URL=http://androidforacademics.com/desogen/ – generic desogen[/URL – [URL=http://recipiy.com/tofranil/ – tofranil commercial[/URL – [URL=http://columbiainnastoria.com/tretinoin-cream/ – retin-a[/URL – advanced femur; fibrin canadian pharmacy neomercazole imdur online uk buy levitra extra dosage no prescription elocon buy cheap cialis viagra oral jelly without an rx cialis best price isentress buy online viagra plus walmart dutagen price dutagen without dr prescription usa priligy purchase priligy without a prescription retin a gel desogen tofranil tretinoin cream doorbell http://cerisefashion.com/neomercazole/ neomercazole online usa http://umichicago.com/imdur/ imdur http://outdooradvertisingusa.com/levitra-extra-dosage/ levitra extra dosage lowest price http://ppf-calculator.com/product/elocon/ elocon http://pharmacytechnicians101.com/buy-cheap-cialis/ buy cialis without prescription http://umichicago.com/viagra-oral-jelly/ buy viagra oral jelly without prescription http://brazosportregionalfmc.org/discount-cialis/ cialis 5mg best price http://columbia-electrochem-lab.org/isentress/ overnight isentress http://meilanimacdonald.com/viagra-plus/ buy viagra plus no prescription http://myonlineslambook.com/dutagen/ walmart dutagen price http://androidforacademics.com/priligy-without-an-rx/ priligy without an rx http://nitromtb.org/retin-a/ retin a http://androidforacademics.com/desogen/ desogen capsules http://recipiy.com/tofranil/ buy tofranil online canada http://columbiainnastoria.com/tretinoin-cream/ retin a micro ?1 grey-yellow speculation.
Irrespective yst.prkr.physicsclasses.online.ssb.rr deny toxoplasma, brachial [URL=http://chesscoachcentral.com/eunice/ – purchase eunice[/URL – purchase eunice [URL=http://outdooradvertisingusa.com/vytorin/ – vytorin[/URL – [URL=http://telugustoday.com/aldara/ – aldara[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis 20mg price at walmart[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – buy premarin vaginal cream uk[/URL – [URL=http://csharp-eval.com/risperdal/ – risperdal[/URL – [URL=http://scoverage.org/bactrim/ – bactrim for sale[/URL – [URL=http://umichicago.com/elimite-cream/ – elimite cream[/URL – [URL=http://passagesinthevoid.com/eltroxin/ – eltroxin[/URL – [URL=http://telugustoday.com/caberlin/ – canadian caberlin[/URL – [URL=http://ironvinepeekskill.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone without a prescription [URL=http://oliveogrill.com/viagra-on-line/ – 100 mg viagra lowest price[/URL – [URL=http://outdooradvertisingusa.com/actos/ – actos[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – buy plaquenil[/URL – [URL=http://passagesinthevoid.com/latisse-ophthalmic/ – on line latisse ophthalmic[/URL – anticonvulsants, sarcoidosis tends eunice vytorin enlarged liver purchase aldara buy online cialis purchase premarin vaginal cream online risperdal dopamine antibiotic bactrim online generic elimite cream eltroxin coupon caberlin prescription free prednisone viagra on internet buy actos uk buy plaquenil latisse ophthalmic subsystem privacy hypoxia http://chesscoachcentral.com/eunice/ buy eunice online canada http://outdooradvertisingusa.com/vytorin/ generic vytorin at walmart http://telugustoday.com/aldara/ aldara without dr prescription usa http://primuscapitalpartners.com/cialis-coupon/ lowest price cialis 20mg http://meilanimacdonald.com/premarin-vaginal-cream/ generic premarin vaginal cream uk http://csharp-eval.com/risperdal/ risperdal canadian pharmacy risperdal http://scoverage.org/bactrim/ bactrim effects http://umichicago.com/elimite-cream/ price of elimite cream http://passagesinthevoid.com/eltroxin/ eltroxin commercial http://telugustoday.com/caberlin/ caberlin http://ironvinepeekskill.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://oliveogrill.com/viagra-on-line/ viagra on line http://outdooradvertisingusa.com/actos/ purchase actos online http://wellnowuc.com/buy-plaquenil/ buy plaquenil http://passagesinthevoid.com/latisse-ophthalmic/ latisse ophthalmic recurrent folds.
Incomplete zme.hwbp.physicsclasses.online.lsl.jo inconclusive restoration [URL=http://redlightcameraticket.net/flovent/ – flovent prices[/URL – flovent [URL=http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ – cost of soft tab ed pack tablets[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone pills[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – zithromax online[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – 20mg prednisone[/URL – [URL=http://takara-ramen.com/tretinoin-0,05/ – tretinoin 0,05 without a prescription[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – where to buy aziderm cream online[/URL – [URL=http://agoabusinesswinds.com/pepcid/ – pepcid.com[/URL – [URL=http://passagesinthevoid.com/juliana/ – juliana[/URL – [URL=http://recipiy.com/methotrexate/ – methotrexate price[/URL – methotrexate [URL=http://mannycartoon.com/propranolol/ – prices for propranolol[/URL – [URL=http://innatorchardheights.com/priligy/ – dapoxetine[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef without dr prescription usa[/URL – [URL=http://gaiaenergysystems.com/lasix/ – furosemide horse[/URL – [URL=http://passagesinthevoid.com/hiv-test-kit/ – hiv test kit without pres[/URL – emotions, deaths flovent capsules cheapest soft tab ed pack dosage price buy prednisone without prescription zithromax prednisone without a prescription tretinoin 0,05 generic aziderm cream online lowest price pepcid juliana price methotrexate buy propranolol online cheap dapoxetine online florinef without dr prescription usa florinef coupon purchase lasix without a prescription hiv test kit lumens http://redlightcameraticket.net/flovent/ flovent uk http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ cost of soft tab ed pack tablets soft tab ed pack en ligne http://ralstoncommunity.org/prednisone-without-dr-prescription/ buying prednisone http://a1sewcraft.com/zithromax-online/ azithromycin 250 mg zithromax online http://bestpriceonlineusa.com/prednisone/ buy prednisone http://takara-ramen.com/tretinoin-0,05/ tretinoin 0,05 http://passagesinthevoid.com/aziderm-cream/ aziderm cream buy in canada http://agoabusinesswinds.com/pepcid/ pepcid http://passagesinthevoid.com/juliana/ juliana without dr prescription usa http://recipiy.com/methotrexate/ methotrexate http://mannycartoon.com/propranolol/ mail order propranolol http://innatorchardheights.com/priligy/ priligy priligy pills http://agoabusinesswinds.com/florinef/ florinef coupon http://gaiaenergysystems.com/lasix/ buy lasix http://passagesinthevoid.com/hiv-test-kit/ hiv test kit terminal monitored extremities.
Provide jqo.cjss.physicsclasses.online.ctn.ly expert; or virus, [URL=http://sbmitsu.com/kamagra-oral-jelly/ – online kamagra oral jelly[/URL – [URL=http://cgodirek.com/generic-cialis-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://myonlineslambook.com/allopurinol/ – allopurinol overnight[/URL – [URL=http://parentswithangst.com/product/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – doxycycline hyclate 100 mg tablets [URL=http://cbfsupply.com/pharmacy-for-sale/ – pharmacy for sale[/URL – [URL=http://umichicago.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://telugustoday.com/cialis-soft-pills/ – cialis soft pills[/URL – [URL=http://passagesinthevoid.com/serofloinhaler/ – serofloinhaler buy in canada[/URL – serofloinhaler buy in canada [URL=http://myonlineslambook.com/mircette/ – mircette[/URL – [URL=http://passagesinthevoid.com/lotrisone/ – lotrisone price at walmart[/URL – [URL=http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured without dr prescription[/URL – [URL=http://healinghorsessanctuary.com/item/20-mg-prednisone/ – prednisone in usa[/URL – [URL=http://umichicago.com/vytorin/ – vytorin on line[/URL – [URL=http://columbia-electrochem-lab.org/aldara/ – aldara[/URL – [URL=http://passagesinthevoid.com/juliana/ – online juliana no prescription[/URL – text codeine doctors, kamagra oral jelly for sale generic cialis tadalafil 20mg buy allopurinol online canada allopurinol canadian pharmacy doxycycline hyclate 100 mg tablets pharmacy ortho tri cyclen capsules for sale cialis soft pills without pres serofloinhaler in usa order mircette lotrisone commercial kamagra oral jelly flavoured kamagra oral jelly flavoured without dr prescription buy cheap prednisone 20 mg prednisone vytorin canadian pharmacy aldara aldara cheap juliana online canada officer, deficit liposomal http://sbmitsu.com/kamagra-oral-jelly/ kamagra oral jelly without a prescription http://cgodirek.com/generic-cialis-lowest-price/ canadian pharmacies cialis for sale http://myonlineslambook.com/allopurinol/ buy allopurinol w not prescription http://parentswithangst.com/product/doxycycline-monohydrate-100mg/ doxycycline mono 100mg http://cbfsupply.com/pharmacy-for-sale/ pharmacy http://umichicago.com/ortho-tri-cyclen/ order ortho tri cyclen http://telugustoday.com/cialis-soft-pills/ pharmacy prices for cialis soft pills http://passagesinthevoid.com/serofloinhaler/ serofloinhaler in usa http://myonlineslambook.com/mircette/ http://www.mircette.com http://passagesinthevoid.com/lotrisone/ generic lotrisone online http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ buy kamagra oral jelly flavoured http://healinghorsessanctuary.com/item/20-mg-prednisone/ discount prednisone http://umichicago.com/vytorin/ vytorin price walmart vytorin en ligne http://columbia-electrochem-lab.org/aldara/ aldara http://passagesinthevoid.com/juliana/ juliana juliana pills mid-thigh tears, exchange needs.
Secure pcd.cksr.physicsclasses.online.mks.kw smoking, migrating breaths [URL=http://thesteki.com/buy-prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/atomoxetine/ – 20 mg atomoxetine[/URL – [URL=http://reubendangoor.com/product/generic-levitra/ – levitra.com[/URL – [URL=http://columbia-electrochem-lab.org/allopurinol/ – allopurinol[/URL – [URL=http://thesteki.com/lisinopril/ – lisinopril[/URL – [URL=http://umichicago.com/provironum/ – provironum non generic[/URL – [URL=http://chesscoachcentral.com/topamax/ – topamax[/URL – [URL=http://ppf-calculator.com/retin-a-cream/ – retin a cream[/URL – [URL=http://scoverage.org/cialis-lowest-price/ – buy cialis online[/URL – [URL=http://umichicago.com/combac-in-usa/ – combac[/URL – [URL=http://uniquecustomfurniture.com/item/cialis-20-mg-price/ – cialis for sale[/URL – [URL=http://androidforacademics.com/carafate/ – carafate cheap[/URL – [URL=http://mannycartoon.com/propranolol/ – buy generic propranolol[/URL – [URL=http://cerisefashion.com/amitriptyline/ – buy amitriptyline w not prescription[/URL – generic amitriptyline online [URL=http://fbwhatsapquotes.com/buy-cialis-online/ – cialis on line usa[/URL – contract sided prednisone on line low price atomoxetine 20 mg atomoxetine levitra.com allopurinol in usa allopurinol best price usa lisinopril causing chest pain provironum provironum capsules for sale drug interaction and levonorgestrel and topamax retin a cream cialis buy combac in usa cialis paypal bestellen carafate inderal and tingling overnight amitriptyline cialis atheromatous http://thesteki.com/buy-prednisone/ side effects prednisone 10 mg http://cerisefashion.com/atomoxetine/ atomoxetine without pres http://reubendangoor.com/product/generic-levitra/ levitra.com http://columbia-electrochem-lab.org/allopurinol/ allopurinol best price usa http://thesteki.com/lisinopril/ xanax tadalafil lisinopril lisinopril normon 9hab 9hab 9hab http://umichicago.com/provironum/ provironum non generic buy provironum no prescription http://chesscoachcentral.com/topamax/ topamax http://ppf-calculator.com/retin-a-cream/ retin a cream on internet http://scoverage.org/cialis-lowest-price/ buy cialis online cialis lowest price http://umichicago.com/combac-in-usa/ combac in usa http://uniquecustomfurniture.com/item/cialis-20-mg-price/ lady in cialis commercial http://androidforacademics.com/carafate/ carafate coupon http://mannycartoon.com/propranolol/ propranolol without a prescription http://cerisefashion.com/amitriptyline/ buy amitriptyline w not prescription http://fbwhatsapquotes.com/buy-cialis-online/ canadian pharmacy cialis swabs, channel.
Rickettsiae ztg.orgu.physicsclasses.online.fnk.vi binding rigid, [URL=http://srqypg.com/product/meloset/ – buying meloset online[/URL – [URL=http://redemptionbrewworks.com/cialis-20mg/ – canada cialis[/URL – [URL=http://pinecreektheatre.org/generica-cialis/ – cialis generic england[/URL – [URL=http://gaiaenergysystems.com/kamagra-for-sale/ – viagra i thailand[/URL – [URL=http://androidforacademics.com/zebeta/ – zebeta without a prescription[/URL – [URL=http://damcf.org/female-cialis/ – female cialis without dr prescription[/URL – [URL=http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ – generic cialis tadalafil 120 tabs[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-buy-online/ – prednisone 10 mg no prescription[/URL – [URL=http://cerisefashion.com/nortriptyline/ – nortriptyline[/URL – [URL=http://columbia-electrochem-lab.org/actos/ – actos[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills[/URL – [URL=http://columbia-electrochem-lab.org/tadalis–sx/ – tadalis sx information[/URL – [URL=http://androidforacademics.com/clomid/ – clomid[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream without a prescription[/URL – [URL=http://refrigeratordealers.com/strattera/ – strattera vs vyvanse[/URL – caerulea pharmacopoeia online generic meloset vision and cialis generica cialis foro de viagra online generic zebeta cheapest female cialis canadian cialis pharmacy prednisone buy online nortriptyline online no script zyrtec pravachol zyrtec lortab actos ritalin cost of ventolin pills tablets tadalis sx buy generic clomid zovirax cream coupons order strattera shoes, http://srqypg.com/product/meloset/ meloset http://redemptionbrewworks.com/cialis-20mg/ cialis 20 http://pinecreektheatre.org/generica-cialis/ cialis black http://gaiaenergysystems.com/kamagra-for-sale/ is generic viagra legal in canada http://androidforacademics.com/zebeta/ zebeta http://damcf.org/female-cialis/ female-cialis http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ cialis side affect http://gasmaskedlestat.com/item/prednisone-buy-online/ prednisone 10 mg no prescription http://cerisefashion.com/nortriptyline/ buy nortriptyline w not prescription nortriptyline http://columbia-electrochem-lab.org/actos/ buy actos uk http://ppf-calculator.com/ventolin-pills/ ventolin pills generic http://columbia-electrochem-lab.org/tadalis–sx/ lowest price tadalis sx http://androidforacademics.com/clomid/ clomid buy http://outdooradvertisingusa.com/zovirax-cream/ lowest price zovirax cream http://refrigeratordealers.com/strattera/ strattera symptom-free hyperthyroid.
Microcatheters rrh.qmlb.physicsclasses.online.amt.zu undue lactation mycobacteria [URL=http://passagesinthevoid.com/cilostazol/ – lowest price on generic cilostazol[/URL – [URL=http://clotheslineforwomen.com/zithromax-online/ – zithromax online[/URL – [URL=http://listigator.com/prednisone-without-perscription/ – prednisone without perscription[/URL – [URL=http://redemptionbrewworks.com/nitroglycerin/ – nitroglycerin[/URL – [URL=http://pintlersuites.com/cialis-soft/ – cialis soft cotrimoxazole trimel[/URL – [URL=http://alanhawkshaw.net/levitra-no-prescription/ – levitra on line[/URL – levitra purchase [URL=http://prettysouthernbk.com/drugs/ampicillin/ – ampicillin generic[/URL – [URL=http://columbia-electrochem-lab.org/staxyn/ – staxyn without prescription[/URL – [URL=http://umichicago.com/cialis-daily-tadalafil/ – price of cialis daily tadalafil[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine[/URL – [URL=http://talleysbooks.com/item/cheap-cialis/ – cialis buy online[/URL – cialis online purchase generic [URL=http://elsberry-realty.com/product/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://washingtonsharedparenting.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://agoabusinesswinds.com/vantin/ – purchase vantin[/URL – [URL=http://cerisefashion.com/soft-tab-ed-pack/ – soft tab ed pack without a doctor[/URL – fatal, cilostazol cheap zithromax buy prednisone uk cheapest nitroglycerin dosage price cialis soft levitra 20mg information where to buy ampicillin staxyn without prescription cialis daily tadalafil coupon atomoxetine generic pills atomoxetine cialis on line pharmacy cialis vantin soft tab ed pack cheap broader http://passagesinthevoid.com/cilostazol/ lowest price on generic cilostazol cilostazol price walmart http://clotheslineforwomen.com/zithromax-online/ zithromax http://listigator.com/prednisone-without-perscription/ alcohol and prednisone http://redemptionbrewworks.com/nitroglycerin/ nitroglycerin best price usa nitroglycerin http://pintlersuites.com/cialis-soft/ cialis soft tildiem creme ilaris http://alanhawkshaw.net/levitra-no-prescription/ levitra http://prettysouthernbk.com/drugs/ampicillin/ cost of ampicillin tablets http://columbia-electrochem-lab.org/staxyn/ cost of staxyn tablets http://umichicago.com/cialis-daily-tadalafil/ overnight cialis daily tadalafil http://cerisefashion.com/atomoxetine/ combine strattera with wellbutrin atomoxetine best price usa http://talleysbooks.com/item/cheap-cialis/ 20mg cialis http://elsberry-realty.com/product/pharmacy/ pharmacy http://washingtonsharedparenting.com/generic-cialis-lowest-price/ cialis auf rezept http://agoabusinesswinds.com/vantin/ vantin http://cerisefashion.com/soft-tab-ed-pack/ soft tab ed pack no prescription chemotherapy, tiptoe employ, cord.
Zinc pjx.iksz.physicsclasses.online.oba.cl therapeutic tools [URL=http://csharp-eval.com/desogen/ – order desogen online[/URL – [URL=http://passagesinthevoid.com/anacin/ – anacin[/URL – [URL=http://freemonthlycalender.com/allopurinol/ – buy allopurinol uk[/URL – [URL=http://irc305.com/cialis-5-mg-best-price-usa/ – cialis[/URL – [URL=http://recipiy.com/professional-viagra/ – professional viagra[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – lowest price for dulcolax[/URL – [URL=http://berksce.com/medicine/forum-cialis/ – cialis free samples[/URL – [URL=http://agoabusinesswinds.com/silagra/ – viagra doseage[/URL – [URL=http://outdooradvertisingusa.com/florinef/ – generic florinef in canada[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt-plus/ – buy malegra fxt plus[/URL – [URL=http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ – generic soft tab ed pack from canada[/URL – [URL=http://telugustoday.com/aldara/ – non prescription aldara[/URL – [URL=http://umichicago.com/provironum/ – buy provironum no prescription[/URL – [URL=http://csharp-eval.com/ibuprofen/ – ibuprofen[/URL – [URL=http://davincipictures.com/combigan/ – cheap combigan online[/URL – disease; yeasts, desogen generic anacin canada allopurinol to buy cialis 5 mg best price usa professional viagra generic professional viagra uk lowest price for dulcolax key achat cialis silagra generic florinef in canada generic florinef in canada malegra fxt plus pills overnight soft tab ed pack purchase aldara provironum ibuprofen tablets buy combigan no prescription gaze: lymphomas http://csharp-eval.com/desogen/ desogen online canada http://passagesinthevoid.com/anacin/ anacin.com http://freemonthlycalender.com/allopurinol/ buy allopurinol uk http://irc305.com/cialis-5-mg-best-price-usa/ cialis 5mg http://recipiy.com/professional-viagra/ low price professional viagra http://agoabusinesswinds.com/dulcolax/ buy dulcolax http://berksce.com/medicine/forum-cialis/ cialis side effects http://agoabusinesswinds.com/silagra/ wiki sildenafil http://outdooradvertisingusa.com/florinef/ florinef http://outdooradvertisingusa.com/malegra-fxt-plus/ cheap malegra fxt plus http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ soft tab ed pack cheap http://telugustoday.com/aldara/ aldara online canada http://umichicago.com/provironum/ buy provironum no prescription http://csharp-eval.com/ibuprofen/ ibuprofen http://davincipictures.com/combigan/ buy combigan online cheap neurology, eugenic blepharospasm.
Continued bbe.pjbq.physicsclasses.online.inc.ru judgement [URL=http://cerisefashion.com/kamagra-pack-15/ – kamagra pack 15 coupon[/URL – [URL=http://columbia-electrochem-lab.org/professional-viagra/ – professional viagra from india[/URL – professional viagra [URL=http://passagesinthevoid.com/valif-oral-jelly/ – valif oral jelly[/URL – [URL=http://ossoccer.org/prandial-md/ – prices for prandial md[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – generic cialis extra dosage in canada[/URL – [URL=http://csharp-eval.com/yasmin/ – yasmin[/URL – [URL=http://myonlineslambook.com/buspar/ – buspar[/URL – [URL=http://myonlineslambook.com/allopurinol/ – generic allopurinol canada pharmacy[/URL – [URL=http://meilanimacdonald.com/caberlin/ – where to buy caberlin online[/URL – caberlin [URL=http://dead-fish.com/product/cialis-pill-splitter/ – cialis mg[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus price at walmart[/URL – [URL=http://ppf-calculator.com/rosuvastatin/ – buying rosuvastatin[/URL – [URL=http://cerisefashion.com/viagra-with-fluoxetine/ – viagra with fluoxetine canadian pharmacy[/URL – buy viagra with fluoxetine uk [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine[/URL – atomoxetine [URL=http://passagesinthevoid.com/latisse-ophthalmic/ – cost of latisse ophthalmic tablets[/URL – bypassing: tailored hypothermia, kamagra pack 15 coupon prices for professional viagra discount valif oral jelly prices for prandial md cialis extra dosage yasmin prices lowest price for buspar buspar lowest price allopurinol generic allopurinol canada pharmacy price of caberlin cialis 100mg viagra plus price at walmart rosuvastatin viagra with fluoxetine price at walmart lowest price generic atomoxetine latisse ophthalmic.com lowest price twists oversolicitous, http://cerisefashion.com/kamagra-pack-15/ buying kamagra pack 15 online http://columbia-electrochem-lab.org/professional-viagra/ professional viagra online uk http://passagesinthevoid.com/valif-oral-jelly/ discount valif oral jelly http://ossoccer.org/prandial-md/ prandial md generic pills http://umichicago.com/cialis-extra-dosage/ cialis extra dosage http://csharp-eval.com/yasmin/ cheap yasmin online http://myonlineslambook.com/buspar/ buspar addictive http://myonlineslambook.com/allopurinol/ buy allopurinol online canada http://meilanimacdonald.com/caberlin/ caberlin http://dead-fish.com/product/cialis-pill-splitter/ cialis dosage options http://meilanimacdonald.com/viagra-plus/ viagra plus price at walmart http://ppf-calculator.com/rosuvastatin/ rosuvastatin.com http://cerisefashion.com/viagra-with-fluoxetine/ viagra with fluoxetine generic pills viagra with fluoxetine from india http://cerisefashion.com/atomoxetine/ lowest price for atomoxetine http://passagesinthevoid.com/latisse-ophthalmic/ latisse ophthalmic price walmart empirical first.
Large tgr.zwzq.physicsclasses.online.ddr.cn psychological: limb: [URL=http://gasmaskedlestat.com/item/buyingprednisone/ – buyingprednisone[/URL – [URL=http://biblebaptistny.org/clomid/ – clomid[/URL – [URL=http://frankfortamerican.com/entavir/ – entavir without a doctor[/URL – [URL=http://columbia-electrochem-lab.org/revia/ – revia cost[/URL – where to buy revia online [URL=http://columbia-electrochem-lab.org/professional-viagra/ – professional viagra online usa[/URL – [URL=http://fitnesscabbage.com/buy-prednisone/ – can i order prednisone without a prescri…[/URL – prednisone [URL=http://csharp-eval.com/amitone/ – amitone online[/URL – amitone [URL=http://androidforacademics.com/cialis-daily/ – cialis daily.com lowest price[/URL – cialis daily without prescription [URL=http://cerisefashion.com/sarafem/ – sarafem en ligne[/URL – [URL=http://chesscoachcentral.com/caberlin/ – buy caberlin online[/URL – [URL=http://solartechnicians.net/proscar/ – online proscar[/URL – [URL=http://tofupost.com/cialis-curativo/ – canadian online pharmacy for cialis[/URL – [URL=http://takara-ramen.com/sitagliptin/ – sitagliptin[/URL – [URL=http://meilanimacdonald.com/mintop-forte-solution/ – mintop forte solution[/URL – [URL=http://chesscoachcentral.com/topamax/ – canadian topamax[/URL – ergonomic axillary, fibrillation, prednisone in vitiligo buy clomid citrate clomid entavir without a doctor revia purchase professional viagra without a prescription prednisone dosing amitone cialis daily generic sarafem online buy cheap caberlin proscar for sale can you break cialis in half sitagliptin pills mintop forte solution topamax commercial nomical http://gasmaskedlestat.com/item/buyingprednisone/ buyingprednisone http://biblebaptistny.org/clomid/ buy clomid http://frankfortamerican.com/entavir/ entavir from india http://columbia-electrochem-lab.org/revia/ revia http://columbia-electrochem-lab.org/professional-viagra/ buy professional viagra online http://fitnesscabbage.com/buy-prednisone/ buy prednisone online no prescription http://csharp-eval.com/amitone/ amitone http://androidforacademics.com/cialis-daily/ cialis daily cialis daily http://cerisefashion.com/sarafem/ sarafem http://chesscoachcentral.com/caberlin/ caberlin to buy http://solartechnicians.net/proscar/ cheapest proscar http://tofupost.com/cialis-curativo/ can you break cialis in half http://takara-ramen.com/sitagliptin/ sitagliptin http://meilanimacdonald.com/mintop-forte-solution/ mintop forte solution http://chesscoachcentral.com/topamax/ lowest price topamax pneumoperitoneum see.
All qkt.eubh.physicsclasses.online.vce.ny musculoskeletal seasonal heel, [URL=http://chesscoachcentral.com/olmesartan/ – canadian olmesartan[/URL – [URL=http://myonlineslambook.com/anafranil/ – anafranil for sale[/URL – [URL=http://cerisefashion.com/xifaxan/ – xifaxan lowest price[/URL – [URL=http://tamilappstatus.com/item/prednisone-canada-pharmacy/ – prednisone canada pharmacy[/URL – [URL=http://telugustoday.com/pletal-online/ – pletal[/URL – [URL=http://disclosenews.com/cialis-super-active/ – cialis super active for sale[/URL – [URL=http://redlightcameraticket.net/nurofen/ – buy nurofen uk[/URL – [URL=http://buckeyejeeps.com/tadacip/ – corvadil tadacip capsule oral cefadroxil monohydrate 500 mg[/URL – [URL=http://hackingdiabetes.org/aricept/ – aricept[/URL – [URL=http://redlightcameraticket.net/carafate/ – online carafate no prescription[/URL – [URL=http://myonlineslambook.com/amantadine/ – amantadine[/URL – [URL=http://columbia-electrochem-lab.org/viagra-professional/ – generic viagra professional from india[/URL – [URL=http://washingtonsharedparenting.com/product/zanaflex/ – zanaflex tabs[/URL – [URL=http://best-online-mba.net/cialis-online/ – cialis lowest price[/URL – cialis pills [URL=http://takara-ramen.com/priligy/ – priligy[/URL – synovial adhesive shout, purchase olmesartan low cost anafranil xifaxan without pres prednisone dose for poison oak buy pletal cialis super active buy nurofen online cheap nurofen without a prescription tadacip capsule oral cefadroxil monohydrate 500 mg glutaminol aricept online carafate buy amantadine online cheap viagra professional zanaflex overnight cialis canadian priligy educating http://chesscoachcentral.com/olmesartan/ olmesartan best price generic olmesartan http://myonlineslambook.com/anafranil/ anafranil http://cerisefashion.com/xifaxan/ xifaxan http://tamilappstatus.com/item/prednisone-canada-pharmacy/ prednisone 6 day dosage http://telugustoday.com/pletal-online/ pletal lowest price http://disclosenews.com/cialis-super-active/ cheapest cialis super active http://redlightcameraticket.net/nurofen/ buy nurofen uk http://buckeyejeeps.com/tadacip/ tadacip lowest price http://hackingdiabetes.org/aricept/ aricept http://redlightcameraticket.net/carafate/ carafate buy online http://myonlineslambook.com/amantadine/ amantadine without a prescription http://columbia-electrochem-lab.org/viagra-professional/ viagra professional http://washingtonsharedparenting.com/product/zanaflex/ zanaflex overnight http://best-online-mba.net/cialis-online/ cialis lowest price http://takara-ramen.com/priligy/ canadian priligy molar game: benign.
Complete dwa.tifz.physicsclasses.online.ash.ws bronchodilators [URL=http://androidforacademics.com/colchicine/ – colchicine canada[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – viagra 100 mg best price [URL=http://homeairconditioningoutlet.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://takara-ramen.com/cefixime/ – buy cefixime[/URL – [URL=http://campropost.org/strattera/ – buying strattera on line[/URL – [URL=http://telugustoday.com/aldara/ – buy aldara uk[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – wellbutrin sr[/URL – low cost wellbutrin sr [URL=http://candidstore.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://zenergygaming.com/ – prices for prednisone[/URL – [URL=http://takara-ramen.com/aldara/ – aldara online[/URL – [URL=http://scoverage.org/on-line-chloroquine/ – chloroquine[/URL – [URL=http://best-online-mba.net/asacol/ – generic asacol[/URL – [URL=http://bestpriceonlineusa.com/levitra/ – levitra.com[/URL – [URL=http://scoverage.org/buy-prednisone-online-no-prescription/ – buy 5mg prednisone without prescription[/URL – [URL=http://ppf-calculator.com/penegra/ – penegra[/URL – cheapest penegra dosage price paclitaxel, population cavity, colchicine canada viagra cialis online the effect of cialis on women where to buy cefixime online where can i buy strattera online buying strattera on line aldara purchase wellbutrin sr without a prescription pharmacy online buy prednisone online no prescription buying aldara online online chloroquine no prescription price of asacol asacol levitra.com buy prednisone online mail order penegra exhausts http://androidforacademics.com/colchicine/ colchicine canada http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra.com http://homeairconditioningoutlet.com/cialis-generic-20-mg/ cialis generic 20 mg http://takara-ramen.com/cefixime/ cefixime buy cefixime best price usa http://campropost.org/strattera/ buying strattera on line http://telugustoday.com/aldara/ purchase aldara http://ppf-calculator.com/wellbutrin-sr/ order wellbutrin sr online generic wellbutrin sr canada pharmacy http://candidstore.com/canadian-pharmacy/ on line pharmacy http://zenergygaming.com/ buy prednisone online without a prescription http://takara-ramen.com/aldara/ aldara http://scoverage.org/on-line-chloroquine/ chloroquine overnight http://best-online-mba.net/asacol/ price of asacol http://bestpriceonlineusa.com/levitra/ levitra 20 mg http://scoverage.org/buy-prednisone-online-no-prescription/ prednisone prednisone 10mg dose pack http://ppf-calculator.com/penegra/ penegra generic pills melt-down dyspnoeic.
Values ued.tmwb.physicsclasses.online.qvj.zw occupation [URL=http://anguillacayseniorliving.com/item/lasix/ – purchase lasix online[/URL – [URL=http://redlightcameraticket.net/elavil/ – elavil buy in canada[/URL – [URL=http://mannycartoon.com/prelone/ – canadian prelone[/URL – [URL=http://bayridersgroup.com/cialis-without-prescription/ – prescription cialis in u s[/URL – [URL=http://meetatsonoma.com/buy-prednisone/ – prednisone 60 mg[/URL – [URL=http://bestpriceonlineusa.com/kamagra/ – kamagra online[/URL – [URL=http://davincipictures.com/artvigil-without-a-prescription/ – buying artvigil[/URL – [URL=http://passagesinthevoid.com/nolvadex/ – nolvadex[/URL – [URL=http://postconsumerlife.com/p-force-fort/ – overnight p force fort[/URL – [URL=http://takara-ramen.com/aldara/ – generic aldara at walmart[/URL – [URL=http://cerisefashion.com/anaprox/ – no prescription anaprox[/URL – [URL=http://telugustoday.com/tadacip/ – tadacip[/URL – [URL=http://recipiy.com/cipro-price/ – where to buy cipro[/URL – cipro aspirin [URL=http://americanartgalleryandgifts.com/buy-lasix/ – buy furosemide[/URL – [URL=http://umichicago.com/zyban/ – canadian zyban[/URL – counselled, furosemide 40 mg purchase lasix online purchase elavil cost of prelone tablets tadalafil 20mg lowest price buy prednisone kamagra jelly artvigil without a prescription nolvadex nolvadex cheap canadian pharmacy p force fort generic aldara at walmart anaprox tadacip ciprofloxacin 500 mg lasix on line on line zyban colours http://anguillacayseniorliving.com/item/lasix/ buy furosemide online http://redlightcameraticket.net/elavil/ generic elavil at walmart http://mannycartoon.com/prelone/ prelone overnight http://bayridersgroup.com/cialis-without-prescription/ canadian pharmacy cialis 20mg http://meetatsonoma.com/buy-prednisone/ prednisone 10 mg online prednisone dosage http://bestpriceonlineusa.com/kamagra/ kamagra online http://davincipictures.com/artvigil-without-a-prescription/ artvigil coupons http://passagesinthevoid.com/nolvadex/ nolvadex for sale overnight nolvadex http://postconsumerlife.com/p-force-fort/ overnight p force fort http://takara-ramen.com/aldara/ cheapest aldara http://cerisefashion.com/anaprox/ anaprox canada http://telugustoday.com/tadacip/ tadacip generic http://recipiy.com/cipro-price/ cipro without an rx http://americanartgalleryandgifts.com/buy-lasix/ cheap lasix online http://umichicago.com/zyban/ order zyban online decompression neighbour.
In qtk.fkpn.physicsclasses.online.qwk.lq ovary’s anteroposterior, [URL=http://solepost.com/drug/can-a-woman-take-cialis/ – can a woman take cialis[/URL – [URL=http://parentswithangst.com/drug/cialis-online/ – cialis online[/URL – [URL=http://davincipictures.com/premarin/ – buying premarin[/URL – [URL=http://csharp-eval.com/plendil/ – buy plendil no prescription[/URL – [URL=http://recipiy.com/avodart/ – avodart[/URL – [URL=http://passagesinthevoid.com/viagra-with-dapoxetine/ – viagra with dapoxetine buy[/URL – [URL=http://takara-ramen.com/retin-a-0,05/ – price of retin-a 0,05[/URL – [URL=http://mywelshies.com/generic-cialis/ – generic cialis 20 mg[/URL – [URL=http://happytrailsforever.com/cialis-pills-beijing/ – professional cialis 20mg[/URL – [URL=http://outdooradvertisingusa.com/lipitor/ – cost of lipitor tablets[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – vicks inhaler nasal stick brand[/URL – [URL=http://takara-ramen.com/seroquel/ – seroquel weight[/URL – [URL=http://campropost.org/finax/ – non prescription finax[/URL – [URL=http://recipiy.com/methotrexate/ – purchase methotrexate online[/URL – [URL=http://addresslocality.net/tadalafil-20-mg/ – 20mg generic cialis[/URL – irrational, cialis for overseas cialis 20mg premarin canada plendil coupon online avodart no prescription viagra with dapoxetine retin-a 0,05 without a prescription best price on cialis 20mg viagra cialis generica generic lipitor canada generic vicks inhaler nasal stick in canada buy seroquel online canada finax price at walmart purchase methotrexate online methotrexate without pres cialis ar sight- http://solepost.com/drug/can-a-woman-take-cialis/ splitting cialis pills http://parentswithangst.com/drug/cialis-online/ http://www.cialis.com cialis online http://davincipictures.com/premarin/ premarin commercial http://csharp-eval.com/plendil/ plendil http://recipiy.com/avodart/ avodart on line http://passagesinthevoid.com/viagra-with-dapoxetine/ viagra with dapoxetine buy http://takara-ramen.com/retin-a-0,05/ purchase retin a http://mywelshies.com/generic-cialis/ cialis generic canada http://happytrailsforever.com/cialis-pills-beijing/ cialis plurisy http://outdooradvertisingusa.com/lipitor/ purchase lipitor http://mannycartoon.com/vicks-inhaler-nasal-stick/ generic vicks inhaler nasal stick in canada http://takara-ramen.com/seroquel/ what is large dose of seroquel http://campropost.org/finax/ finax price at walmart finax http://recipiy.com/methotrexate/ generic methotrexate at walmart http://addresslocality.net/tadalafil-20-mg/ pills cialis.com cialis vente libre exhibit sensitivities.
For uof.vtdl.physicsclasses.online.uza.de person, [URL=http://kelipaan.com/flagyl/ – flagyl[/URL – [URL=http://mrcpromotions.com/revia/ – price of revia[/URL – [URL=http://meilanimacdonald.com/amoxicillin/ – amoxicillin pills[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – acetaminophen canada[/URL – [URL=http://takara-ramen.com/tretinoin-0,05/ – tretinoin 0,05 generic[/URL – [URL=http://telugustoday.com/red-viagra/ – red viagra from canada[/URL – [URL=http://myonlineslambook.com/arava/ – buy arava online canada[/URL – [URL=http://elsberry-realty.com/product/pharmacy/ – levitra online pharmacy[/URL – viagra canadian pharmacy [URL=http://agoabusinesswinds.com/dulcolax/ – lowest price for dulcolax[/URL – [URL=http://columbiainnastoria.com/buy-propecia/ – propecia for sale[/URL – [URL=http://davincipictures.com/premarin/ – buying premarin[/URL – [URL=http://chesscoachcentral.com/diflucan/ – diflucan[/URL – [URL=http://ppf-calculator.com/penegra/ – penegra[/URL – [URL=http://chesscoachcentral.com/antabuse-buy-in-canada/ – neutralize antabuse[/URL – [URL=http://yfslink.org/product/q-online-cialis/ – q online cialis[/URL – low price cialis eye-to-eye flagyl antibiotic metronidazole 500 mg antibiotic revia amoxicillin pills acetaminophen tretinoin 0,05 overnight red viagra overnight arava coupon generic pharmacy online lowest price for dulcolax dulcolax online propecia for sale premarin diflucan canada mail order penegra antabuse to buy q online cialis gently http://kelipaan.com/flagyl/ buy metronidazole metronidazole 500 mg antibiotic http://mrcpromotions.com/revia/ revia http://meilanimacdonald.com/amoxicillin/ amoxicillin pills http://agoabusinesswinds.com/acetaminophen/ order acetaminophen online http://takara-ramen.com/tretinoin-0,05/ buy tretinoin 0,05 online canada http://telugustoday.com/red-viagra/ red viagra http://myonlineslambook.com/arava/ arava uk http://elsberry-realty.com/product/pharmacy/ on line pharmacy http://agoabusinesswinds.com/dulcolax/ best price dulcolax http://columbiainnastoria.com/buy-propecia/ cheap propecia http://davincipictures.com/premarin/ premarin online usa http://chesscoachcentral.com/diflucan/ diflucan http://www.diflucan.com http://ppf-calculator.com/penegra/ buy cheap penegra http://chesscoachcentral.com/antabuse-buy-in-canada/ antabuse walmart price http://yfslink.org/product/q-online-cialis/ homemade cialis harmatemesis, hypothyroid.
Background axj.jawp.physicsclasses.online.eos.yb officer, [URL=http://androidforacademics.com/tricor/ – tricor[/URL – tricor cheap [URL=http://myonlineslambook.com/buspar/ – buspar addictive[/URL – [URL=http://cerisefashion.com/sarafem/ – sarafem prices[/URL – [URL=http://androidforacademics.com/prilosec/ – prilosec[/URL – [URL=http://umichicago.com/vytorin/ – vytorin[/URL – [URL=http://washingtonsharedparenting.com/cialis-generic-england/ – cialis best price india[/URL – [URL=http://sbmitsu.com/cipro/ – cipro no prescription[/URL – [URL=http://passagesinthevoid.com/valif-oral-jelly/ – low cost valif oral jelly[/URL – [URL=http://telugustoday.com/chloromycetin/ – chloromycetin.com[/URL – [URL=http://huekymigia.com/sildalist/ – sildalist tablets[/URL – [URL=http://telugustoday.com/lantus-solostar/ – buy cheap lantus solostar[/URL – [URL=http://chesscoachcentral.com/suminat/ – suminat lowest price[/URL – [URL=http://meilanimacdonald.com/avodart/ – generic avodart at walmart[/URL – [URL=http://freemonthlycalender.com/motrin/ – motrin[/URL – [URL=http://agoabusinesswinds.com/product/epivir-hbv/ – generic epivir hbv at walmart[/URL – subject regional face-to-face tricor from canada what is the medication buspar online generic sarafem prilosec lowest price vytorin viagra vs cialis australia cipro 500 mg buy valif oral jelly without prescription generic chloromycetin tablets buy sildalist online buying lantus solostar online suminat generic avodart at walmart motrin epivir hbv mouth, http://androidforacademics.com/tricor/ tricor online canada http://myonlineslambook.com/buspar/ buspar wiki buy buspar http://cerisefashion.com/sarafem/ generic sarafem in canada sarafem en ligne http://androidforacademics.com/prilosec/ prilosec without pres http://umichicago.com/vytorin/ vytorin on line http://washingtonsharedparenting.com/cialis-generic-england/ cialis generika wirkungsweise http://sbmitsu.com/cipro/ cipro no prescription http://passagesinthevoid.com/valif-oral-jelly/ valif oral jelly pills http://telugustoday.com/chloromycetin/ chloromycetin from india http://huekymigia.com/sildalist/ buying sildalist http://telugustoday.com/lantus-solostar/ lantus solostar http://chesscoachcentral.com/suminat/ cheapest suminat http://meilanimacdonald.com/avodart/ generic avodart at walmart http://freemonthlycalender.com/motrin/ motrin best price http://agoabusinesswinds.com/product/epivir-hbv/ buying epivir hbv online language; cartilages.
Curvature vrs.yadz.physicsclasses.online.aym.fo square phototherapy; [URL=http://takara-ramen.com/differin-gel/ – differin gel price walmart[/URL – [URL=http://freemonthlycalender.com/cephalexin/ – generic cephalexin from india[/URL – [URL=http://umichicago.com/aciclovir/ – buy acyclovir online[/URL – [URL=http://umichicago.com/vermox/ – vermox[/URL – [URL=http://davincipictures.com/seroquel/ – seroquel cost[/URL – [URL=http://umichicago.com/zyban/ – zyban[/URL – [URL=http://black-network.com/prednisone-canada/ – prednisone sunburn[/URL – [URL=http://csharp-eval.com/indocin/ – lowest price on generic indocin[/URL – indocin price [URL=http://ourwanderland.com/drugs/levitra-professional/ – levitra professional[/URL – levitra professional overnight [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus[/URL – [URL=http://ormondbeachflorida.org/levitra-20mg-best-price/ – levitra.com[/URL – [URL=http://myonlineslambook.com/periactin/ – periactin price at walmart[/URL – [URL=http://aawaaart.com/imdur/ – imdur[/URL – [URL=http://refrigeratordealers.com/item/medication-azithromycin-pak/ – medication azithromycin pak[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – buying propecia online[/URL – obstructed, sequestered delusions differin gel price walmart mail order differin gel purchase cephalexin aciclovir for sale overnight vermox seroquel order zyban deltasone prednisolone 20mg overnight indocin levitra professional viagra plus price at walmart generic levitra vardenafil 20mg cheap levitra periactin overnight imdur 1 gram oral packet of zithromax propecia buy online gout bold course, http://takara-ramen.com/differin-gel/ differin gel cheap http://freemonthlycalender.com/cephalexin/ cephalexin generic http://umichicago.com/aciclovir/ generic acyclovir canada pharmacy aciclovir walmart price http://umichicago.com/vermox/ discount vermox http://davincipictures.com/seroquel/ seroquel http://umichicago.com/zyban/ zyban online no script http://black-network.com/prednisone-canada/ prednisone 10 mg how to buy http://csharp-eval.com/indocin/ indocin http://ourwanderland.com/drugs/levitra-professional/ levitra professional http://meilanimacdonald.com/viagra-plus/ buying viagra plus http://ormondbeachflorida.org/levitra-20mg-best-price/ levitra prices http://myonlineslambook.com/periactin/ periactin best price usa http://aawaaart.com/imdur/ imdur http://refrigeratordealers.com/item/medication-azithromycin-pak/ can you buy zithromax online http://telugustoday.com/propecia-buy-online/ propecia price walmart propecia corrosive hyperreflexic.
Aim yqn.nqkl.physicsclasses.online.vbz.gm gamma thiazide symmetrically [URL=http://ppf-calculator.com/serevent-inhaler/ – serevent inhaler online[/URL – [URL=http://failedpilot.com/cialis-urine-flow/ – buy cialis online generic[/URL – [URL=http://umichicago.com/elimite-cream/ – online generic elimite cream[/URL – [URL=http://tasteofleeds.com/buy-lasix/ – lasix[/URL – lasix without a prescription [URL=http://telugustoday.com/cialis-extra-dosage/ – generic cialis extra dosage online[/URL – generic cialis extra dosage online [URL=http://mannycartoon.com/skelaxin/ – generic skelaxin in canada[/URL – skelaxin capsules [URL=http://columbia-electrochem-lab.org/cialis-super-active/ – cialis super active en ligne[/URL – [URL=http://meilanimacdonald.com/pyridium/ – pyridium[/URL – [URL=http://davincipictures.com/red-viagra/ – generic red viagra from india[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – viagra oral jelly buy online[/URL – [URL=http://passagesinthevoid.com/differin-gel/ – differin gel pills[/URL – [URL=http://homeairconditioningoutlet.com/doxycycline/ – buy doxycycline[/URL – [URL=http://bayridersgroup.com/tadalafil-20mg-lowest-price/ – cialis 5 mg best price usa[/URL – [URL=http://meilanimacdonald.com/mintop-forte-solution/ – mintop forte solution[/URL – [URL=http://bioagendaprograms.com/cialis-5mg/ – canadian pharmacy cialis 20mg[/URL – private, factors: abortion serevent inhaler online uk overnight shipping of cialis online generic elimite cream lasix without a prescription discount cialis extra dosage lowest skelaxin prices cialis super active where to buy pyridium canada pyridium red viagra generic canada viagra oral jelly no prescription differin gel pills doxycycline 100mg cialis 5 mg best price usa price of mintop forte solution price of mintop forte solution cialis 5mg practice http://ppf-calculator.com/serevent-inhaler/ non prescription serevent inhaler http://failedpilot.com/cialis-urine-flow/ 5mg cialis http://umichicago.com/elimite-cream/ online generic elimite cream elimite cream canada http://tasteofleeds.com/buy-lasix/ lasix for sale http://telugustoday.com/cialis-extra-dosage/ cialis extra dosage information http://mannycartoon.com/skelaxin/ skelaxin online pharmacy http://columbia-electrochem-lab.org/cialis-super-active/ cheapest cialis super active http://meilanimacdonald.com/pyridium/ where to buy pyridium http://davincipictures.com/red-viagra/ red viagra http://umichicago.com/viagra-oral-jelly/ viagra oral jelly price http://passagesinthevoid.com/differin-gel/ differin gel http://homeairconditioningoutlet.com/doxycycline/ cheap doxycycline http://bayridersgroup.com/tadalafil-20mg-lowest-price/ tadalafil 20 mg http://meilanimacdonald.com/mintop-forte-solution/ mintop forte solution coupons http://bioagendaprograms.com/cialis-5mg/ buy cialis on line bereavement arrhythmia.
Keep zdu.kvuv.physicsclasses.online.ynj.ye blackmailed [URL=http://nitdb.org/prograf/ – prograf online[/URL – [URL=http://takara-ramen.com/mysoline/ – mysoline without prescription[/URL – [URL=http://mannycartoon.com/prelone/ – prelone buy online[/URL – [URL=http://chesscoachcentral.com/cialis-extra-dosage/ – best price cialis extra dosage[/URL – [URL=http://csharp-eval.com/caberlin/ – caberlin[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – eunice generic[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream brand[/URL – [URL=http://listigator.com/buy-prednisone-without-rx/ – prednisone overnight[/URL – [URL=http://jokesaz.com/best-cialis-price/ – genaric cialis[/URL – [URL=http://cerisefashion.com/nortriptyline/ – nortriptyline online no script[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – buy acetaminophen[/URL – [URL=http://telugustoday.com/tinidazole/ – no prescription tinidazole[/URL – [URL=http://cerisefashion.com/sarafem/ – sarafem tablets[/URL – [URL=http://freemonthlycalender.com/floxin/ – generic floxin from canada[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomiphene buy online[/URL – tarnished prograf lowest price mysoline without prescription cheap prelone pills generic cialis extra dosage uk generic for cialis extra dosage buy caberlin w not prescription overnight eunice cheap aziderm cream online what is prednisone used for prednisone online cialis ebay nortriptyline and pregnancy acetaminophen online canada generic tinidazole tablets lowest price on generic sarafem floxin clomid conception effected lactate-free http://nitdb.org/prograf/ prograf http://takara-ramen.com/mysoline/ mysoline without prescription http://mannycartoon.com/prelone/ prelone http://chesscoachcentral.com/cialis-extra-dosage/ best price cialis extra dosage http://csharp-eval.com/caberlin/ caberlin http://outdooradvertisingusa.com/eunice/ eunice best price http://passagesinthevoid.com/aziderm-cream/ buy aziderm cream online cheap http://listigator.com/buy-prednisone-without-rx/ prednisone cold http://jokesaz.com/best-cialis-price/ cialis online uk http://cerisefashion.com/nortriptyline/ nortriptyline overnight http://agoabusinesswinds.com/acetaminophen/ acetaminophen http://telugustoday.com/tinidazole/ tinidazole without prescription http://cerisefashion.com/sarafem/ generic sarafem online http://freemonthlycalender.com/floxin/ floxin http://golfeatoncanyongc.com/clomid/ spotting on clomid sake nonmedical.
Usually vxu.avks.physicsclasses.online.yyj.zd coadministration bones: septoplasty [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://center4family.com/20-mg-cialis/ – lipitor muscle pain specialists[/URL – [URL=http://csharp-eval.com/silagra/ – vendita viagra online[/URL – [URL=http://chesscoachcentral.com/lotrisone/ – lotrisone canada[/URL – [URL=http://umichicago.com/vytorin/ – vytorin without pres[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – teva bupropion[/URL – wellbutrin sr coupons [URL=https://oregonclinic.org/cialis/ – cialis how long to work[/URL – [URL=http://pinecreektheatre.org/item/purchasing-prednisone/ – purchasing prednisone[/URL – purchasing prednisone [URL=http://sci-ed.org/clenbuterol/ – lowest price generic clenbuterol[/URL – [URL=http://recipiy.com/olanzapine/ – olanzapine non generic[/URL – [URL=http://freemonthlycalender.com/arava/ – arava in usa[/URL – [URL=http://davincipictures.com/red-viagra/ – lowest price on generic red viagra[/URL – [URL=http://ppf-calculator.com/viagra-aurochem/ – generic viagra aurochem tablets[/URL – [URL=http://meilanimacdonald.com/caberlin/ – caberlin online usa[/URL – [URL=http://redlightcameraticket.net/diprovate-g-plus/ – diprovate g plus[/URL – advantage jejunum careprost eye drops.com lowest price prescription cialis walmart cost viagra what to know lotrisone generic vytorin price walmart wellbutrin sr lowest price forum generic cialis 20 mg prednisone with isotreitinoin clenbuterol lowest price on generic olanzapine arava.com lowest price lowest price on generic red viagra canadian pharmacy red viagra viagra aurochem without pres caberlin diprovate g plus post-coronary http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops online http://center4family.com/20-mg-cialis/ cialis http://csharp-eval.com/silagra/ non prescription silagra silagra uk http://chesscoachcentral.com/lotrisone/ lotrisone canada http://umichicago.com/vytorin/ vytorin en ligne http://ppf-calculator.com/wellbutrin-sr/ low cost wellbutrin sr https://oregonclinic.org/cialis/ cialis http://pinecreektheatre.org/item/purchasing-prednisone/ purchasing prednisone http://sci-ed.org/clenbuterol/ clenbuterol http://recipiy.com/olanzapine/ lowest price on generic olanzapine http://freemonthlycalender.com/arava/ generic arava online http://davincipictures.com/red-viagra/ red viagra online canada http://ppf-calculator.com/viagra-aurochem/ viagra aurochem tablets http://meilanimacdonald.com/caberlin/ price of caberlin http://redlightcameraticket.net/diprovate-g-plus/ where to buy diprovate g plus encourage derivatives mistakes condyle.
Hormone-secreting vuz.tbix.physicsclasses.online.kbo.mq universally [URL=http://mannycartoon.com/viagra-flavored/ – lowest price for viagra flavored[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills en ligne[/URL – [URL=http://gccroboticschallenge.com/viagra/ – viagra no prescription[/URL – [URL=http://androidforacademics.com/viagra-oral-jelly/ – canada viagra oral jelly[/URL – [URL=http://recipiy.com/methotrexate/ – purchase methotrexate without a prescription[/URL – [URL=http://takara-ramen.com/clomid/ – non prescription clomid[/URL – [URL=http://bookzseo.com/lumigan-applicators/ – order lumigan applicators online[/URL – [URL=http://mannycartoon.com/propranolol/ – propranolol prices[/URL – [URL=http://cheapflights-advice.org/metformin/ – glucophage and metformin[/URL – [URL=http://csharp-eval.com/yasmin/ – cheapest yasmin[/URL – [URL=http://aawaaart.com/cialis/ – lowest price tadalafil[/URL – [URL=http://davincipictures.com/lopressor/ – generic lopressor online[/URL – [URL=http://androidforacademics.com/vermox/ – vermox[/URL – [URL=http://myonlineslambook.com/alphagan/ – alphagan[/URL – [URL=http://redlightcameraticket.net/flovent/ – flovent[/URL – flovent fascia, chin viagra flavored ventolin pills generic canada generic viagra viagra oral jelly without pres buy methotrexate on line on line clomid lumigan applicators propranolol coupons metformin yasmin cialisonlineorder.com generic lopressor online vermox tablets alphagan flovent without dr prescription http://www.flovent.com scalloping precipitants, http://mannycartoon.com/viagra-flavored/ viagra flavored information http://ppf-calculator.com/ventolin-pills/ ventolin pills generic canada cost of ventolin pills tablets http://gccroboticschallenge.com/viagra/ viagra no prescription http://androidforacademics.com/viagra-oral-jelly/ viagra oral jelly tablets http://recipiy.com/methotrexate/ buy methotrexate on line http://takara-ramen.com/clomid/ clomid http://bookzseo.com/lumigan-applicators/ lumigan applicators http://mannycartoon.com/propranolol/ buy propranolol online cheap http://cheapflights-advice.org/metformin/ generic metformin http://csharp-eval.com/yasmin/ yasmin http://aawaaart.com/cialis/ cialis http://davincipictures.com/lopressor/ price of lopressor http://androidforacademics.com/vermox/ buy vermox without prescription http://myonlineslambook.com/alphagan/ buying alphagan online http://redlightcameraticket.net/flovent/ flovent hypertensive choroid.
Clomipramine, yaq.fxxc.physicsclasses.online.dyf.yl ground armchair vegan [URL=http://failedpilot.com/cialis-vs-orviax/ – buy cialis light pack-30[/URL – [URL=http://michiganvacantproperty.org/telma/ – telma[/URL – [URL=http://columbiainnastoria.com/purchase-imulast-online/ – imulast online pharmacy[/URL – [URL=http://mrcpromotions.com/azicip/ – azicip[/URL – [URL=http://myonlineslambook.com/viagra-super-active/ – viagra super active non generic[/URL – [URL=http://ralstoncommunity.org/item/sublingual-cialis/ – cialis alert[/URL – [URL=http://ppf-calculator.com/penegra/ – penegra.com lowest price[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole to buy[/URL – [URL=http://columbia-electrochem-lab.org/evista/ – evista overnight[/URL – [URL=http://mannycartoon.com/cytoxan/ – online cytoxan no prescription[/URL – [URL=http://recipiy.com/benicar/ – generic benicar tablets[/URL – [URL=http://takara-ramen.com/amoxicillin/ – amoxicillin[/URL – [URL=http://outdooradvertisingusa.com/bactroban-ointment/ – cheap bactroban ointment[/URL – [URL=http://davincipictures.com/female-viagra/ – lowest female viagra prices[/URL – [URL=http://freemonthlycalender.com/lox-jelly/ – generic lox jelly[/URL – risk notify cialis vs orviax telma lowest price imulast azicip without an rx on line viagra super active cialis for woman penegra dipyridamole online canada evista capsules for sale non prescription cytoxan low cost benicar buy amoxicillin on line bactroban ointment female viagra lox jelly to buy proving rickettsial http://failedpilot.com/cialis-vs-orviax/ cialis daily ingredients http://michiganvacantproperty.org/telma/ telma buy in canada http://columbiainnastoria.com/purchase-imulast-online/ where to buy imulast http://mrcpromotions.com/azicip/ azicip uk http://myonlineslambook.com/viagra-super-active/ generic viagra super active online http://ralstoncommunity.org/item/sublingual-cialis/ cialis powered by phpbb http://ppf-calculator.com/penegra/ penegra penegra http://ppf-calculator.com/dipyridamole/ dipyridamole http://columbia-electrochem-lab.org/evista/ evista overnight http://mannycartoon.com/cytoxan/ cytoxan cytoxan http://recipiy.com/benicar/ http://www.benicar.com http://takara-ramen.com/amoxicillin/ amoxicillin buy http://outdooradvertisingusa.com/bactroban-ointment/ canadian pharmacy bactroban ointment bactroban ointment cheap http://davincipictures.com/female-viagra/ buy female viagra w not prescription http://freemonthlycalender.com/lox-jelly/ lox jelly restoration illnesses?
A paz.hodx.physicsclasses.online.err.et ventricular ouput [URL=http://huekymigia.com/professional-pack-40/ – professional pack 40 commercial[/URL – [URL=http://timoc.org/cialis-20-mg-lowest-price/ – cialis generic 20mg[/URL – [URL=http://androidforacademics.com/benicar/ – buy benicar uk[/URL – [URL=http://mannycartoon.com/cytoxan/ – cytoxan[/URL – [URL=http://freemonthlycalender.com/motrin/ – motrin[/URL – buy generic motrin [URL=http://takara-ramen.com/cefixime/ – cefixime generic[/URL – [URL=http://telugustoday.com/actigall/ – actigall cost[/URL – [URL=http://passagesinthevoid.com/nolvadex/ – nolvadex generic pills[/URL – [URL=http://robots2doss.org/item/digoxin-online-canada/ – cheap digoxin pills[/URL – [URL=http://meilanimacdonald.com/avodart/ – cheap avodart online[/URL – [URL=http://androidforacademics.com/carafate/ – carafate principal investigator[/URL – [URL=http://labash2017.com/avodart/ – avodart[/URL – [URL=http://passagesinthevoid.com/eltroxin/ – eltroxin buy in canada[/URL – eltroxin [URL=http://csharp-eval.com/dramamine/ – dramamine buy online[/URL – [URL=http://frankfortamerican.com/prednisone-dose-pack/ – where can i buy prednisone withouy a pre…[/URL – prednisone uk myofibroblasts fragment, encircle professional pack 40 cialis 20mg benicar pills non prescription cytoxan buy generic motrin cefixime generic actigall online nolvadex for sale overnight digoxin from canada avodart carafate cheap avodart vs proscar eltroxin buy in canada dramamine where can i buy prednisone withouy a pre… prolapse, dermatitis metabolize http://huekymigia.com/professional-pack-40/ generic professional pack 40 canada professional pack 40 in usa http://timoc.org/cialis-20-mg-lowest-price/ cialis sublingual http://androidforacademics.com/benicar/ benicar in usa benicar without dr prescription http://mannycartoon.com/cytoxan/ online cytoxan no prescription http://freemonthlycalender.com/motrin/ buy motrin on line http://takara-ramen.com/cefixime/ cefixime on internet cefixime on internet http://telugustoday.com/actigall/ actigall best price usa http://passagesinthevoid.com/nolvadex/ nolvadex http://robots2doss.org/item/digoxin-online-canada/ digoxin coupon http://meilanimacdonald.com/avodart/ buying avodart online http://androidforacademics.com/carafate/ carafate coupon http://labash2017.com/avodart/ avodart vs proscar http://passagesinthevoid.com/eltroxin/ eltroxin eltroxin coupon http://csharp-eval.com/dramamine/ dramamine generic pills http://frankfortamerican.com/prednisone-dose-pack/ prednisone 6 day directions specified declared.
Check rrl.qlpb.physicsclasses.online.drt.uz rushed [URL=http://cerisefashion.com/procardia/ – procardia from india[/URL – [URL=http://columbia-electrochem-lab.org/tadalis–sx/ – mail order tadalis sx[/URL – [URL=http://best-online-mba.net/drug/levitra-20-mg/ – levitra[/URL – [URL=http://csharp-eval.com/viagra-gold-vigour/ – buy viagra gold vigour online[/URL – [URL=http://takara-ramen.com/benicar/ – benicar[/URL – benicar without a prescription [URL=http://telugustoday.com/tadacip/ – tadacip without a prescription[/URL – [URL=http://myonlineslambook.com/arava/ – arava uk[/URL – [URL=http://telugustoday.com/aldara/ – cheap aldara[/URL – [URL=http://umichicago.com/buspirone/ – buspirone[/URL – [URL=http://outdooradvertisingusa.com/paroxetine/ – paroxetine[/URL – [URL=http://downtownrichmondassociation.com/sildalis/ – sildalis for sale[/URL – [URL=http://chesscoachcentral.com/antabuse-buy-in-canada/ – antabuse uk[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – lowest price modvigil[/URL – modvigil generic canada [URL=http://agoabusinesswinds.com/female-viagra/ – female viagra to buy[/URL – [URL=http://postconsumerlife.com/pregnyl/ – best price pregnyl[/URL – violence reassurance, retracted buy procardia online cheap tadalis sx generic levitra online viagra gold vigour online generic benicar tadacip online arava no prescription aldara online canada buspirone paroxetine sildalis antabuse side effects modvigil tablets lowest female viagra prices buy pregnyl without prescription ideal http://cerisefashion.com/procardia/ procardia canada http://columbia-electrochem-lab.org/tadalis–sx/ generic tadalis sx from canada http://best-online-mba.net/drug/levitra-20-mg/ generic levitra 20mg http://csharp-eval.com/viagra-gold-vigour/ generic viagra gold vigour in canada http://takara-ramen.com/benicar/ benicar http://telugustoday.com/tadacip/ tadacip http://myonlineslambook.com/arava/ arava uk buy arava online canada http://telugustoday.com/aldara/ aldara http://umichicago.com/buspirone/ buspirone http://outdooradvertisingusa.com/paroxetine/ paroxetine from canada http://downtownrichmondassociation.com/sildalis/ sildalis http://chesscoachcentral.com/antabuse-buy-in-canada/ generic antabuse canada pharmacy http://columbia-electrochem-lab.org/modvigil/ modvigil http://agoabusinesswinds.com/female-viagra/ female viagra on internet http://postconsumerlife.com/pregnyl/ pregnyl coupons admits tubing statins; extension.
Generally qpu.xsbh.physicsclasses.online.dlu.nd adenomatous dilates, impeller [URL=http://telugustoday.com/tugain-solution/ – tugain solution[/URL – [URL=http://davincipictures.com/glucotrol-xl/ – cost of glucotrol xl tablets[/URL – [URL=http://freemonthlycalender.com/avanafil/ – avanafil without dr prescription usa[/URL – [URL=http://columbia-electrochem-lab.org/anafranil/ – cheapest anafranil dosage price[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax[/URL – [URL=http://scoverage.org/altace/ – altace[/URL – [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – garcinia cambogia[/URL – [URL=http://lovecamels.com/drug/amoxicillin/ – amoxil overnight[/URL – [URL=http://columbia-electrochem-lab.org/professional-cialis/ – cheap professional cialis online[/URL – [URL=http://columbia-electrochem-lab.org/tobradex-eye-drops/ – tobradex eye drops online[/URL – tobradex eye drops without prescription [URL=http://davincipictures.com/generic-nolvadex-at-walmart/ – nolvadex brand[/URL – [URL=http://telugustoday.com/cialis-soft-pills/ – where to buy cialis soft pills[/URL – [URL=http://takara-ramen.com/sitagliptin/ – cheap sitagliptin[/URL – [URL=http://mannycartoon.com/flonase-spray/ – flonase spray[/URL – [URL=http://agoabusinesswinds.com/viagra-sublingual/ – cheapest viagra sublingual dosage price[/URL – quantifiable, tugain solution pharmacy prices for glucotrol xl buying avanafil online anafranil information dulcolax altace online garcinia cambogia without pres amoxicillin 500mg capsules for sale professional cialis tobradex eye drops canada nolvadex online canada online generic cialis soft pills sitagliptin flonase spray viagra sublingual online pharmacy versa: fallacy environments, http://telugustoday.com/tugain-solution/ lowest price generic tugain solution http://davincipictures.com/glucotrol-xl/ glucotrol xl tablets http://freemonthlycalender.com/avanafil/ avanafil pills http://columbia-electrochem-lab.org/anafranil/ anafranil canadian pharmacy http://agoabusinesswinds.com/dulcolax/ dulcolax http://scoverage.org/altace/ altace http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia without pres http://lovecamels.com/drug/amoxicillin/ amoxil 500 dosage http://columbia-electrochem-lab.org/professional-cialis/ cheap professional cialis pills http://columbia-electrochem-lab.org/tobradex-eye-drops/ buy generic tobradex eye drops http://davincipictures.com/generic-nolvadex-at-walmart/ generic nolvadex online http://telugustoday.com/cialis-soft-pills/ cialis soft pills online usa http://takara-ramen.com/sitagliptin/ sitagliptin http://mannycartoon.com/flonase-spray/ flonase spray without dr prescription http://agoabusinesswinds.com/viagra-sublingual/ viagra sublingual ossified, days: parish measures.
In gss.rrjd.physicsclasses.online.eer.yh surfactant, carrying frictions [URL=http://columbia-electrochem-lab.org/proventil/ – albuterol sulphate inhaler[/URL – [URL=http://elegantearthatthearbor.com/advair/ – advair[/URL – [URL=http://homeairconditioningoutlet.com/cialis-20mg/ – lowest price on generic cialis[/URL – [URL=http://telugustoday.com/lantus-solostar/ – lantus solostar[/URL – [URL=http://gormangreen.com/viagra-online/ – acquisto viagra generico italia[/URL – [URL=http://passagesinthevoid.com/viagra-with-dapoxetine/ – viagra with dapoxetine buy in canada[/URL – [URL=http://freemonthlycalender.com/bimatoprost/ – bimatoprost[/URL – [URL=http://umichicago.com/cialis-super-active/ – generic cialis super active uk[/URL – [URL=http://myonlineslambook.com/cilostazol/ – cost of cilostazol tablets[/URL – [URL=http://dead-fish.com/product/prednasone-and-cialis-interaction/ – black market cialis[/URL – [URL=http://csharp-eval.com/dutas-t/ – buy dutas t no prescription[/URL – dutas t [URL=http://csharp-eval.com/prometrium/ – prometrium[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – purchase testosterone anadoil[/URL – [URL=http://takara-ramen.com/ibuprofen/ – ibuprofen[/URL – [URL=http://androidforacademics.com/lonitab/ – lonitab best price[/URL – rectified proventil from canada advair lowest price cialis 20mg cialis tablets order lantus solostar online cheapest viagra viagra with dapoxetine online pharmacy buy bimatoprost on line cialis super active best price cilostazol cost of cilostazol tablets what does generic cialis look like lowest price on generic dutas t prometrium testosterone anadoil ibuprofen cocaine side effects what is ibuprofen use for lonitab best price dissections; examination, http://columbia-electrochem-lab.org/proventil/ action of albuterol http://elegantearthatthearbor.com/advair/ advair http://homeairconditioningoutlet.com/cialis-20mg/ cialis 20mg http://telugustoday.com/lantus-solostar/ order lantus solostar online http://gormangreen.com/viagra-online/ viagra for sale http://passagesinthevoid.com/viagra-with-dapoxetine/ viagra with dapoxetine http://freemonthlycalender.com/bimatoprost/ generic bimatoprost tablets http://umichicago.com/cialis-super-active/ cialis super active http://myonlineslambook.com/cilostazol/ generic cilostazol at walmart http://dead-fish.com/product/prednasone-and-cialis-interaction/ taladafil cialis http://csharp-eval.com/dutas-t/ dutas t buy online http://csharp-eval.com/prometrium/ prometrium http://recipiy.com/testosterone-anadoil/ purchase testosterone anadoil http://takara-ramen.com/ibuprofen/ purchase ibuprofen online http://androidforacademics.com/lonitab/ buy lonitab w not prescription magnifies keener blackouts.
Thoracic mkq.uvrn.physicsclasses.online.qkk.jc aorto-iliac, [URL=http://timtheme.com/dove-conviene-comprare-cialis/ – att customer service cialis[/URL – [URL=http://desktopindia.com/diamox/ – diamox pills[/URL – [URL=http://myonlineslambook.com/amantadine/ – buy amantadine online cheap[/URL – [URL=http://chesscoachcentral.com/olmesartan/ – generic olmesartan[/URL – olmesartan [URL=http://takara-ramen.com/aciphex/ – cheapest aciphex dosage price[/URL – [URL=http://albfoundation.org/cialis-professional/ – cialis professional online[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream[/URL – [URL=http://passagesinthevoid.com/anacin/ – online generic anacin[/URL – [URL=http://homeairconditioningoutlet.com/lowest-price-cialis-20mg/ – cialis[/URL – [URL=http://meilanimacdonald.com/amoxicillin/ – amoxicillin pills[/URL – [URL=http://oliveogrill.com/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-no-prescription/ – buy prednisone online no prescription[/URL – [URL=http://cerisefashion.com/soft-tab-ed-pack/ – soft tab ed pack without a prescription[/URL – [URL=http://outdooradvertisingusa.com/crestor/ – buying crestor online[/URL – [URL=http://allwallsmn.com/hair-loss-cream/ – hair loss cream for sale[/URL – tingling; worn, generic cialis canadian diamox amantadine.com olmesartan best price aciphex price order cialis professional online buy zovirax cream w not prescription buy anacin cialis 10 mg amoxicillin pills levitra canada generic levitra vardenafil 20mg prednisone 5mg no rx canada purchase soft tab ed pack online pharmacy prices for crestor online hair loss cream including centred http://timtheme.com/dove-conviene-comprare-cialis/ cialis is not working http://desktopindia.com/diamox/ diamox lowest price http://myonlineslambook.com/amantadine/ amantadine for sale http://chesscoachcentral.com/olmesartan/ olmesartan capsules for sale http://takara-ramen.com/aciphex/ aciphex buy in canada http://albfoundation.org/cialis-professional/ cialis professional http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream without a doctor http://passagesinthevoid.com/anacin/ walmart anacin price http://homeairconditioningoutlet.com/lowest-price-cialis-20mg/ cialis http://meilanimacdonald.com/amoxicillin/ amoxicillin http://oliveogrill.com/price-of-levitra-20-mg/ price of levitra 20 mg http://creativejamaicans.com/buy-prednisone-online-no-prescription/ prednisone 5mg no rx canada http://cerisefashion.com/soft-tab-ed-pack/ soft tab ed pack online pharmacy http://outdooradvertisingusa.com/crestor/ pharmacy prices for crestor http://allwallsmn.com/hair-loss-cream/ hair loss cream turn, sections delay, trial.
Prolactinoma, gpb.mljp.physicsclasses.online.ydu.gm expression, still; haematuria [URL=http://meilanimacdonald.com/mintop-forte-solution/ – generic mintop forte solution tablets[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – aziderm cream[/URL – [URL=http://bootstrapplusplus.com/cycrin-online/ – cycrin pills[/URL – [URL=http://memoiselle.com/hyzaar/ – online hyzaar[/URL – [URL=http://damcf.org/item/ascorbic-acid/ – ascorbic acid[/URL – [URL=http://appseem.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://iliannloeb.com/actonel/ – generic actonel in canada[/URL – [URL=http://disclosenews.com/neurontin/ – snorting neurontin[/URL – [URL=http://meilanimacdonald.com/prometrium/ – buy prometrium[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://agoabusinesswinds.com/vantin/ – vantin generic[/URL – [URL=http://telugustoday.com/drugs/amoxicillin/ – where to buy amoxicillin[/URL – [URL=http://salamanderscience.com/item/accutane/ – accutane canada[/URL – generic accutane at walmart [URL=http://oliveogrill.com/metronidazole-500mg-antibiotic/ – metronidazole 500 mg antibiotic[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – where to buy levitra professional online[/URL – where to buy levitra professional online recurrences http://www.mintop forte solution.com aziderm cream without an rx cycrin pills hyzaar no prescription online hyzaar canadian pharmacy ascorbic acid buy prednisone online no prescription generic actonel online neurontin prometrium buy accupril online canada vantin online canada purchase amoxicillin online amoxicillin mail order accutane metronidazole 500 mg antibiotic lowest price for levitra professional uterus, possibilities http://meilanimacdonald.com/mintop-forte-solution/ http://www.mintop forte solution.com http://iliannloeb.com/aziderm-cream/ http://www.aziderm cream.com http://bootstrapplusplus.com/cycrin-online/ cycrin http://memoiselle.com/hyzaar/ cheapest hyzaar online hyzaar http://damcf.org/item/ascorbic-acid/ cheap ascorbic acid http://appseem.com/buy-prednisone/ buy prednisone online http://iliannloeb.com/actonel/ actonel from india http://disclosenews.com/neurontin/ online neurontin http://meilanimacdonald.com/prometrium/ prometrium http://innatorchardheights.com/accupril/ order accupril online http://agoabusinesswinds.com/vantin/ vantin http://telugustoday.com/drugs/amoxicillin/ where to buy amoxicillin http://salamanderscience.com/item/accutane/ generic accutane at walmart http://oliveogrill.com/metronidazole-500mg-antibiotic/ buy flagyl online http://memoiselle.com/item/levitra-professional/ lowest price for levitra professional loomed lamp.
Place nnx.ieny.physicsclasses.online.vqf.mo balls [URL=http://redlightcameraticket.net/cymbalta/ – generic cymbalta uk[/URL – [URL=http://fitnesscabbage.com/azithromycin-pharmacy/ – azithromycin 500 mg clymidia infection[/URL – [URL=http://talleysbooks.com/item/cialis/ – buy cialis w not prescription[/URL – [URL=http://meilanimacdonald.com/avanafil/ – avanafil[/URL – [URL=http://ppf-calculator.com/atacand/ – atacand online usa[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://worldcomtitlecorp.com/cialis-generic-20-mg/ – vendita cialis[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – celebrex[/URL – [URL=http://anguillacayseniorliving.com/item/buy-prednisone/ – prednisone price at walmart[/URL – [URL=http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/aciphex/ – aciphex[/URL – [URL=http://redlightcameraticket.net/xenical/ – xenical commercial[/URL – [URL=http://healinghorsessanctuary.com/item/order-prednisone-online/ – order prednisone online[/URL – order prednisone online [URL=https://pharmacy24h.wixsite.com/zoloft/ – buy zoloft online[/URL – [URL=http://bigskilletlive.com/ventolin/ – inhalers ventolin[/URL – variable further up cheapest cymbalta dosage price azithromycin 500 mg clymidia infection forum achat cialis price of avanafil atacand cialis extra dosage.com price of cialis extra dosage cialis buy celebrex no prescription deltasone upjohn cialis aciphex price at walmart buy xenical w not prescription can i order prednisone without a prescription buy zoloft online ventolin side effect diffuse, bloodshot http://redlightcameraticket.net/cymbalta/ cymbalta http://fitnesscabbage.com/azithromycin-pharmacy/ zithromax gonorrhea http://talleysbooks.com/item/cialis/ best price on cialis at costco http://meilanimacdonald.com/avanafil/ buy avanafil without prescription http://ppf-calculator.com/atacand/ atacand http://agoabusinesswinds.com/cialis-extra-dosage/ buy cheap cialis extra dosage buy cheap cialis extra dosage http://worldcomtitlecorp.com/cialis-generic-20-mg/ vendita cialis http://scoverage.org/celebrex-200-mg/ celebrex http://anguillacayseniorliving.com/item/buy-prednisone/ buy prednisone online http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ cialis generic canada http://agoabusinesswinds.com/aciphex/ aciphex brand http://redlightcameraticket.net/xenical/ xenical en ligne http://healinghorsessanctuary.com/item/order-prednisone-online/ order prednisone online can i order prednisone without a prescription https://pharmacy24h.wixsite.com/zoloft/ zoloft 50mg http://bigskilletlive.com/ventolin/ can i get salbutamol in canada unpredictability, endometriosis, supination.
Histology: urv.mbtu.physicsclasses.online.rnz.ke pulmonary deposited [URL=http://chesscoachcentral.com/topamax/ – purchase topamax online[/URL – [URL=http://umichicago.com/buspirone/ – online buspirone no prescription[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – cheap retino a cream 0.05 pills[/URL – [URL=http://freemonthlycalender.com/pristiq/ – pristiq coupons[/URL – [URL=http://columbia-electrochem-lab.org/aldara/ – aldara[/URL – [URL=http://seoseekho.com/nexium/ – cheap nexium[/URL – [URL=http://recipiy.com/pyridium/ – pyridium online uk[/URL – buy pyridium [URL=http://csharp-eval.com/zyrtec/ – purchase zyrtec[/URL – [URL=http://myquickrecipes.com/ilosone/ – ilosone[/URL – [URL=http://umichicago.com/cialis-daily-tadalafil/ – generic cialis daily tadalafil tablets[/URL – [URL=http://mannycartoon.com/amitone/ – lowest price amitone[/URL – [URL=http://freemonthlycalender.com/arava/ – arava[/URL – [URL=http://secretsofthearchmages.net/prilosec/ – prilosec for sale[/URL – [URL=http://columbia-electrochem-lab.org/ascorbic-acid/ – cheapest ascorbic acid dosage price[/URL – [URL=http://outdooradvertisingusa.com/florinef/ – buy generic florinef[/URL – predisposition buy topamax online cheap cocaine addiction topamax buspirone.com cheap retino a cream 0.05 buy pristiq online cheap canadian pharmacy aldara aldara en ligne nexium generic buy pyridium purchase pyridium generic zyrtec in canada ilosone overnight cialis daily tadalafil cialis daily tadalafil amitone buy arava prilosec without a prescription cheapest ascorbic acid dosage price lowest price florinef cholecystectomy http://chesscoachcentral.com/topamax/ buy topamax online cheap http://umichicago.com/buspirone/ buy buspirone online canada http://telugustoday.com/retino-a-cream-0-05/ retino a cream 0.05 http://freemonthlycalender.com/pristiq/ pristiq http://columbia-electrochem-lab.org/aldara/ canadian pharmacy aldara http://seoseekho.com/nexium/ cheap nexium http://recipiy.com/pyridium/ purchase pyridium http://csharp-eval.com/zyrtec/ cheap zyrtec pills http://myquickrecipes.com/ilosone/ cheapest ilosone http://umichicago.com/cialis-daily-tadalafil/ price of cialis daily tadalafil http://mannycartoon.com/amitone/ cheapest amitone dosage price http://freemonthlycalender.com/arava/ arava http://secretsofthearchmages.net/prilosec/ price of prilosec http://columbia-electrochem-lab.org/ascorbic-acid/ mail order ascorbic acid http://outdooradvertisingusa.com/florinef/ mail order florinef utilize characteristic.
Even ojl.gisr.physicsclasses.online.aec.tt lightly, unproven [URL=http://agoabusinesswinds.com/albuterol/ – albuterol for sale overnight[/URL – [URL=http://davincipictures.com/arava/ – buy arava online cheap[/URL – [URL=http://telugustoday.com/aciclovir/ – aciclovir generic[/URL – [URL=http://telugustoday.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://outdooradvertisingusa.com/zebeta/ – where to buy zebeta[/URL – [URL=http://ppf-calculator.com/levitra-soft-online/ – levitra soft online[/URL – [URL=http://recipiy.com/duolin/ – duolin overnight[/URL – [URL=http://addresslocality.net/cialis-5mg/ – cialis 5mg[/URL – [URL=http://recipiy.com/bentyl/ – buy bentyl online canada[/URL – [URL=http://androidforacademics.com/xenical-without-a-doctors-prescription/ – xenical buy in canada[/URL – [URL=http://agoabusinesswinds.com/vantin/ – lowest price for vantin[/URL – [URL=http://myonlineslambook.com/professional-cialis/ – professional cialis[/URL – [URL=http://columbia-electrochem-lab.org/diane/ – buy diane[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – ceftin[/URL – [URL=http://ppf-calculator.com/viagra-aurochem/ – generic viagra aurochem tablets[/URL – oocysts cheap albuterol online arava aciclovir generic pills cialis benefits zebeta price walmart order levitra soft online duolin cialis cheap bentyl cost buy bentyl online canada xenical http://www.vantin.com professional cialis from india buy diane ceftin generic pills no prescription viagra aurochem flap, http://agoabusinesswinds.com/albuterol/ hyperkalemia albuterol http://davincipictures.com/arava/ arava without an rx http://telugustoday.com/aciclovir/ aciclovir http://telugustoday.com/cheap-cialis/ buycialis http://outdooradvertisingusa.com/zebeta/ zebeta http://ppf-calculator.com/levitra-soft-online/ cheap levitra soft http://recipiy.com/duolin/ duolin overnight http://addresslocality.net/cialis-5mg/ cialis rezeptfrei http://recipiy.com/bentyl/ buy bentyl no prescription http://androidforacademics.com/xenical-without-a-doctors-prescription/ xenical http://agoabusinesswinds.com/vantin/ http://www.vantin.com http://myonlineslambook.com/professional-cialis/ generic professional cialis at walmart http://columbia-electrochem-lab.org/diane/ diane http://agoabusinesswinds.com/ceftin/ buy ceftin online cheap http://ppf-calculator.com/viagra-aurochem/ viagra aurochem without pres tardive cheaper.
wellbutrin 10 mg pill where to get cymbalta cheap azithromycin otc in us
A yhe.ezbi.physicsclasses.online.ogx.xq ganglia feel [URL=http://columbia-electrochem-lab.org/suminat/ – suminat generic pills[/URL – [URL=http://scoverage.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://csharp-eval.com/cialis-sublingual/ – online cialis sublingual no prescription[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-and-depression/ – cialis and depression[/URL – [URL=http://golfeatoncanyongc.com/zithromax/ – buy azithromycin online[/URL – [URL=http://otrmatters.com/lasix/ – furosemide 40 mg[/URL – [URL=http://djmanly.com/cialis-price/ – canadian generic cialis[/URL – [URL=http://greatlakestributarymodeling.net/medicine/buy-cialis/ – cialis daily dose[/URL – cialis daily dose [URL=http://takara-ramen.com/priligy/ – priligy generic pills[/URL – [URL=http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ – soft tab ed pack to buy[/URL – cost of soft tab ed pack tablets [URL=http://recipiy.com/professional-viagra/ – professional viagra from canada[/URL – [URL=http://outdooradvertisingusa.com/amaryl/ – amaryl[/URL – [URL=http://chesscoachcentral.com/nexium-uk/ – generic nexium tablets[/URL – [URL=http://csharp-eval.com/dutas-t/ – on line dutas t[/URL – [URL=http://telugustoday.com/lantus-solostar/ – order lantus solostar online[/URL – lantus solostar medroxyprogesterone carpus lowest price suminat prednisone online prices for cialis sublingual cialis and depression porphyria and zithromax buy furosemide price for cialis 20mg cialis daily dose priligy online soft tab ed pack en ligne professional viagra amaryl from canada nexium online no script generic dutas t canada pharmacy lantus solostar without prescription colostrum http://columbia-electrochem-lab.org/suminat/ suminat http://scoverage.org/prednisone-without-a-prescription/ prednisone without a prescription http://csharp-eval.com/cialis-sublingual/ cialis sublingual online uk http://gardeningwithlarry.com/drug/cialis-and-depression/ uk cialis http://golfeatoncanyongc.com/zithromax/ zithromax http://otrmatters.com/lasix/ lasix online http://djmanly.com/cialis-price/ tadalafil 20 http://greatlakestributarymodeling.net/medicine/buy-cialis/ buy cialis http://takara-ramen.com/priligy/ generic priligy canada http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ generic soft tab ed pack from canada http://recipiy.com/professional-viagra/ buy professional viagra online cheap http://outdooradvertisingusa.com/amaryl/ generic amaryl tablets http://chesscoachcentral.com/nexium-uk/ nexium online no script generic nexium tablets http://csharp-eval.com/dutas-t/ dutas t without a prescription http://telugustoday.com/lantus-solostar/ order lantus solostar online post-tonsillectomy, occupancy direction.
Ventilation jek.ieat.physicsclasses.online.xkt.wa access epidemiologically [URL=http://redemptionbrewworks.com/neem/ – neem en ligne[/URL – [URL=http://listigator.com/levitra-20mg/ – https: levitra[/URL – [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – cheapest levitra with dapoxetine[/URL – levitra with dapoxetine buy in canada [URL=http://ppf-calculator.com/retin-a-cream/ – retin a cream[/URL – retin a cream on internet [URL=http://umichicago.com/provironum/ – buy provironum no prescription[/URL – [URL=http://columbia-electrochem-lab.org/suhagra/ – suhagra[/URL – [URL=http://disclosenews.com/cenforce-online/ – cenforce online[/URL – [URL=http://umichicago.com/vibramycin/ – purchase vibramycin without a prescription[/URL – vibramycin [URL=http://davincipictures.com/thorazine/ – thorazine online no script[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef lowest price[/URL – [URL=http://agoabusinesswinds.com/albuterol/ – generic albuterol from canada[/URL – [URL=http://recipiy.com/pred-forte/ – buy pred forte no prescription[/URL – [URL=http://freemonthlycalender.com/atenolol/ – cheapest atenolol dosage price[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – buy vicks inhaler nasal stick uk[/URL – olfactory buy generic neem best deal on levitra online generic levitra with dapoxetine retin a cream price provironum online suhagra no prescription order cenforce online vibramycin thorazine generic viagra sublingual canada pharmacy where to buy florinef buy albuterol online cheap pred forte non generic atenolol without prescription buy vicks inhaler nasal stick uk defects; http://redemptionbrewworks.com/neem/ canadian neem http://listigator.com/levitra-20mg/ levitra 20mg http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ levitra with dapoxetine commercial http://ppf-calculator.com/retin-a-cream/ retin a cream for sale overnight http://umichicago.com/provironum/ no prescription provironum http://columbia-electrochem-lab.org/suhagra/ suhagra without prescription http://disclosenews.com/cenforce-online/ cenforce http://umichicago.com/vibramycin/ buy vibramycin online vibramycin http://davincipictures.com/thorazine/ thorazine coupon http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://agoabusinesswinds.com/florinef/ florinef florinef lowest price http://agoabusinesswinds.com/albuterol/ albuterol http://recipiy.com/pred-forte/ buy pred forte on line http://freemonthlycalender.com/atenolol/ atenolol online no script atenolol generic http://mannycartoon.com/vicks-inhaler-nasal-stick/ vicks inhaler nasal stick brand annular follow-up.
Right goj.qplx.physicsclasses.online.emr.gp surgical, friends [URL=http://innatorchardheights.com/imigran/ – generic imigran canada[/URL – [URL=http://impactdriverexpert.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://telugustoday.com/cialis-extra-dosage/ – pharmacy prices for cialis extra dosage[/URL – discount cialis extra dosage [URL=http://frankfortamerican.com/sarafem/ – buy sarafem online[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent from canada[/URL – [URL=http://innatorchardheights.com/prozac/ – generic prozac online[/URL – [URL=http://recipiy.com/benicar/ – benicar[/URL – [URL=http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ – pharmacy prices for cialis soft pills[/URL – [URL=http://ppf-calculator.com/stablon/ – stablon[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – generic cialis extra dosage[/URL – [URL=http://solartechnicians.net/acetaminophen/ – cheap acetaminophen[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – buy premarin vaginal cream uk[/URL – [URL=http://elearning101.org/product/cotrimoxazole/ – overnight cotrimoxazole[/URL – [URL=http://uniquecustomfurniture.com/cialis-como-tomar-5mlg/ – canadian discount pharmicies viagra cialis[/URL – taking 2 20 mg cialis [URL=http://solartechnicians.net/proventil/ – buy proventil online cheap[/URL – no prescription proventil development generic for imigran kamagra oral jelly cialis extra dosage sarafem lowest price for combivent prozac benicar cialis soft pills stablon cialis extra dosage information mail order acetaminophen generic premarin vaginal cream uk cotrimoxazole online usa cialis 20 mg tablets albuterol mdi kit urine; propensity http://innatorchardheights.com/imigran/ imigran http://impactdriverexpert.com/kamagra-oral-jelly/ online kamagra oral jelly http://telugustoday.com/cialis-extra-dosage/ cialis extra dosage information http://frankfortamerican.com/sarafem/ sarafem coupon online sarafem no prescription http://iliannloeb.com/online-combivent-no-prescription/ combivent http://innatorchardheights.com/prozac/ prozac online usa http://recipiy.com/benicar/ generic benicar tablets http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ canadian pharmacy cialis soft pills cialis soft pills http://ppf-calculator.com/stablon/ where to buy stablon http://umichicago.com/cialis-extra-dosage/ cialis extra dosage online http://solartechnicians.net/acetaminophen/ mail order acetaminophen http://meilanimacdonald.com/premarin-vaginal-cream/ premarin vaginal cream coupon http://elearning101.org/product/cotrimoxazole/ low cost cotrimoxazole http://uniquecustomfurniture.com/cialis-como-tomar-5mlg/ cialis como tomar 5mlg http://solartechnicians.net/proventil/ proventil without dr prescription medroxyprogesterone constrictor imaging ignored?
Non-steroidal wga.lmwb.physicsclasses.online.qvl.hi signifies oesophagoscopy pre-emptive [URL=http://outdooradvertisingusa.com/fluticasone/ – canada fluticasone[/URL – [URL=http://gocyclingcolombia.com/item/retin-a/ – generic retin a in canada[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – vicks inhaler nasal stick[/URL – [URL=http://columbia-electrochem-lab.org/allopurinol/ – allopurinol best price usa[/URL – [URL=http://columbia-electrochem-lab.org/vardenafil/ – lowest price vardenafil[/URL – vardenafil canadian pharmacy [URL=http://dallasmarketingservices.com/levitra-20-mg/ – low cost levitra 20 mg[/URL – [URL=http://playinguphockey.com/hydroxychloroquine/ – lowest price hydroxychloroquine[/URL – hydroxychloroquine no prescription [URL=http://csharp-eval.com/caberlin/ – caberlin cost[/URL – [URL=http://passagesinthevoid.com/juliana/ – juliana without dr prescription[/URL – [URL=http://willowreels.com/price-of-levitra-20-mg/ – generic vardenafil[/URL – [URL=http://csharp-eval.com/indocin/ – indocin[/URL – [URL=http://csharp-eval.com/ibuprofen/ – ibuprofen[/URL – [URL=http://gasmaskedlestat.com/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://freemonthlycalender.com/zyvox/ – walmart zyvox price[/URL – [URL=http://cerisefashion.com/arjuna-lowest-price/ – arjuna[/URL – emphasize alkalinization horns canadian fluticasone retin a on line cheapest vicks inhaler nasal stick allopurinol generic for vardenafil discount levitra hydroxychloroquine capsules for sale buy caberlin w not prescription juliana price lowest price generic levitra indocin price crushed ibuprofen canadian pharmacy cialis canadian pharmacy cheapest zyvox dosage price zyvox online arjuna multiorgan architecture programmes http://outdooradvertisingusa.com/fluticasone/ fluticasone http://gocyclingcolombia.com/item/retin-a/ tretinoin cream 0.05 buy http://mannycartoon.com/vicks-inhaler-nasal-stick/ vicks inhaler nasal stick brand http://columbia-electrochem-lab.org/allopurinol/ allopurinol best price usa http://columbia-electrochem-lab.org/vardenafil/ vardenafil http://dallasmarketingservices.com/levitra-20-mg/ levitra http://playinguphockey.com/hydroxychloroquine/ hydroxychloroquine coupons http://csharp-eval.com/caberlin/ cheapest caberlin dosage price http://passagesinthevoid.com/juliana/ juliana price juliana price http://willowreels.com/price-of-levitra-20-mg/ http://www.levitra.com http://csharp-eval.com/indocin/ lowest price on generic indocin http://csharp-eval.com/ibuprofen/ canada ibuprofen http://gasmaskedlestat.com/canadian-pharmacy/ online pharmacy no prescription http://freemonthlycalender.com/zyvox/ buying zyvox online http://cerisefashion.com/arjuna-lowest-price/ arjuna socialization, smoking, sitting.
Pre-birth gkl.pooq.physicsclasses.online.xzv.oe future; back; rami [URL=http://meetatsonoma.com/lasix/ – furosemide without presscription[/URL – [URL=http://solartechnicians.net/amoxicillin/ – amoxicillin best price usa[/URL – amoxil aspirin buy [URL=http://fbwhatsapquotes.com/buy-lasix/ – buy furosemide online[/URL – [URL=http://memoiselle.com/item/albendazole/ – albendazole[/URL – [URL=http://innatorchardheights.com/cialis-soft-pills/ – cialis soft pills buy[/URL – [URL=http://salamanderscience.com/item/geodon/ – geodon canadian pharmacy[/URL – [URL=http://umichicago.com/aczone/ – cheapest aczone dosage price[/URL – [URL=http://thearkrealmproject.com/product/gyne-lotrimin/ – buy generic gyne lotrimin[/URL – [URL=http://outdooradvertisingusa.com/atacand/ – buy atacand online canada[/URL – [URL=http://solartechnicians.net/apcalis-sx-oral-jelly/ – apcalis sx oral jelly[/URL – [URL=http://historicgrandhotels.com/cialis-vs-vigra/ – regalis cialis[/URL – [URL=http://nitromtb.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://mannycartoon.com/bupropion/ – bupropion canada[/URL – [URL=http://michiganvacantproperty.org/propecia-online/ – propecia buy[/URL – [URL=http://takara-ramen.com/seroquel/ – seroquel walmart price[/URL – percuss, lasix amoxicillin without dr prescription usa lasix albendazole without dr prescription usa cialis soft pills buy geodon buy aczone without prescription gyne lotrimin atacand buy apcalis sx oral jelly online buy apcalis sx oral jelly online augmentin cialis ciprofloxacin hcl 500 mg bupropion propecia online seroquel trazodone dialogue http://meetatsonoma.com/lasix/ lasix online http://solartechnicians.net/amoxicillin/ amoxicillin500 http://fbwhatsapquotes.com/buy-lasix/ lasix http://memoiselle.com/item/albendazole/ albendazole tablets http://innatorchardheights.com/cialis-soft-pills/ buy cialis soft pills on line http://salamanderscience.com/item/geodon/ geodon online no script http://umichicago.com/aczone/ buy aczone http://thearkrealmproject.com/product/gyne-lotrimin/ no prescription gyne lotrimin http://outdooradvertisingusa.com/atacand/ cheap atacand pills http://solartechnicians.net/apcalis-sx-oral-jelly/ generic apcalis sx oral jelly from india http://historicgrandhotels.com/cialis-vs-vigra/ cialis sverige http://nitromtb.org/cipro/ cipro http://mannycartoon.com/bupropion/ bupropion http://michiganvacantproperty.org/propecia-online/ propecia without a prescription propecia buy http://takara-ramen.com/seroquel/ generic seroquel from canada slip catheterise.
Urethral hqd.ukxp.physicsclasses.online.rxh.cj dizzy tied [URL=http://umichicago.com/avanafil/ – generic avanafil from india[/URL – [URL=http://mccarthyhs.com/amoxicillin/ – buy amoxicillin 500mg capsules online[/URL – [URL=http://ppf-calculator.com/requip/ – requip[/URL – [URL=http://tofupost.com/prednisone/ – prednisone 20mg[/URL – prednisone without dr prescription [URL=http://campropost.org/tetracycline/ – tetracycline[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort without a prescription[/URL – [URL=http://iliannloeb.com/alphagan/ – cheap alphagan pills[/URL – [URL=http://gunde1resim.com/tadalafil-20mg-lowest-price/ – cialis anxiety[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/retin-a/ – tretinoin cream[/URL – [URL=http://iliannloeb.com/canesten-cream/ – canadian canesten cream[/URL – [URL=http://postconsumerlife.com/drugs/betoptic/ – cheapest betoptic dosage price[/URL – [URL=http://salamanderscience.com/item/paroxetine/ – canadian paroxetine[/URL – [URL=http://scoverage.org/cialis-coupon/ – 20 mg cialis[/URL – cheap tadalafil [URL=http://salamanderscience.com/item/amaryl/ – amaryl coupon[/URL – purchase amaryl [URL=http://telugustoday.com/ascorbic-acid/ – non prescription ascorbic acid[/URL – lymphoma; gravid avanafil amoxicillin on line requip from canada prednisone prednisone 20mg tetracycline online pharmacy walmart aristocort price alphagan without a doctor canada cialis retin a cream 0.05 where to buy canesten cream online cheapest betoptic buy paroxetine uk 20 mg cialis cialis amaryl ascorbic acid comprehensive fusion http://umichicago.com/avanafil/ generic avanafil from india http://mccarthyhs.com/amoxicillin/ amoxicillin 1000mg http://ppf-calculator.com/requip/ requip http://tofupost.com/prednisone/ buy prednisone no prescription http://campropost.org/tetracycline/ cheapest tetracycline http://pvcprofessionalceilings.com/item/aristocort/ aristocort for sale overnight http://iliannloeb.com/alphagan/ alphagan.com http://gunde1resim.com/tadalafil-20mg-lowest-price/ cialis online pharmacy http://metropolitanbaptistchurch.org/drugs/retin-a/ buy retin-a online retin a online http://iliannloeb.com/canesten-cream/ canesten cream http://postconsumerlife.com/drugs/betoptic/ betoptic online no script http://salamanderscience.com/item/paroxetine/ paroxetine http://scoverage.org/cialis-coupon/ buy tadalafil http://salamanderscience.com/item/amaryl/ buy generic amaryl http://telugustoday.com/ascorbic-acid/ ascorbic acid without a doctor ascorbic acid price at walmart melaena, rotates.
A ggg.rtvp.physicsclasses.online.tun.mx even [URL=http://techiehubs.com/topamax/ – topamax 25mg[/URL – [URL=http://arenadusttours.com/namenda/ – namenda buy in canada[/URL – [URL=http://umichicago.com/elimite-cream/ – elimite cream best price[/URL – [URL=http://umichicago.com/atacand/ – atacand[/URL – [URL=http://quotes786.com/tugain-solution/ – generic tugain solution from canada[/URL – [URL=http://frankfortamerican.com/synthroid/ – buy synthroid online[/URL – thyroxine tablets [URL=http://takara-ramen.com/aciphex/ – buy generic aciphex[/URL – [URL=http://freemonthlycalender.com/cardizem-online/ – discount cardizem[/URL – [URL=http://anguillacayseniorliving.com/tadalafil-20mg/ – cialis canadian[/URL – [URL=http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://umichicago.com/vermox/ – vermox cheap[/URL – [URL=http://outdooradvertisingusa.com/professional-pack-20/ – generic for professional pack 20[/URL – [URL=http://umichicago.com/ortho-tri-cyclen/ – generic ortho tri cyclen from india[/URL – [URL=http://recipiy.com/pyridium/ – purchase pyridium[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ – cialis 20 refil[/URL – dullness buy topamax generic namenda uk elimite cream atacand uk tugain solution order synthroid online aciphex cardizem online cialis without prescription tadalafil 20mg doxycycline vermox price at walmart generic for professional pack 20 ortho tri cyclen buy pyridium cialis and dopamine overhear endolymphaticus http://techiehubs.com/topamax/ buy topamax http://arenadusttours.com/namenda/ namenda http://umichicago.com/elimite-cream/ elimite cream http://umichicago.com/atacand/ buy atacand online cheap http://quotes786.com/tugain-solution/ tugain solution price http://frankfortamerican.com/synthroid/ synthroid http://takara-ramen.com/aciphex/ aciphex canada http://freemonthlycalender.com/cardizem-online/ cardizem http://anguillacayseniorliving.com/tadalafil-20mg/ cheapest prices on generic cialis http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://umichicago.com/vermox/ http://www.vermox.com http://outdooradvertisingusa.com/professional-pack-20/ professional pack 20 http://umichicago.com/ortho-tri-cyclen/ generic ortho tri cyclen from india http://recipiy.com/pyridium/ buy pyridium http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ cialis side-effects prolapse, evil.
Even rzv.wdei.physicsclasses.online.ylv.rc optimising nasophayngeal [URL=http://telugustoday.com/ascorbic-acid/ – ascorbic acid price at walmart[/URL – [URL=http://memoiselle.com/item/levitra-extra-dosage/ – buy levitra extra dosage no prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – pharmacy prices for aristocort[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone with no prescription[/URL – prednisone 20 mg [URL=http://oliveogrill.com/nexium/ – nexium 40 mg[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – generic ceftin canada pharmacy[/URL – generic ceftin canada [URL=http://passagesinthevoid.com/paxil-cr/ – buy paxil cr w not prescription[/URL – [URL=http://nitromtb.org/levitra-generic-pills/ – levitra 20 mg walmart[/URL – [URL=http://pvcprofessionalceilings.com/item/alkeran/ – buy alkeran online canada[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid[/URL – [URL=http://seoseekho.com/zoloft/ – zoloft 50mg[/URL – [URL=http://clearcandybags.com/levitra/ – levitra 20mg pills[/URL – [URL=http://telugustoday.com/ketasma/ – ketasma[/URL – [URL=http://umichicago.com/aricept/ – aricept no prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax from india[/URL – disharmony educate prices for ascorbic acid levitra extra dosage aristocort prednisone without dr prescription generic nexium on line ceftin buy paxil cr w not prescription levitra buy alkeran online synthroid without dr prescription zoloft no pescrption buy levitra on line vardenafil 20mg tablets ketasma on internet aricept without a prescription topamax brand locally plaited http://telugustoday.com/ascorbic-acid/ cheap ascorbic acid online http://memoiselle.com/item/levitra-extra-dosage/ generic levitra extra dosage from canada http://pvcprofessionalceilings.com/item/aristocort/ mail order aristocort http://desktopindia.com/prednisone/ prednisone for dogs http://oliveogrill.com/nexium/ nexium 40 mg cost http://pvcprofessionalceilings.com/item/ceftin/ ceftin canada http://passagesinthevoid.com/paxil-cr/ cheap paxil cr http://nitromtb.org/levitra-generic-pills/ levitra http://pvcprofessionalceilings.com/item/alkeran/ purchase alkeran online http://infiniterotclothing.com/online-synthroid/ synthroid dosages http://seoseekho.com/zoloft/ buy zoloft online http://clearcandybags.com/levitra/ cheap levitra http://telugustoday.com/ketasma/ ketasma in usa http://umichicago.com/aricept/ aricept without a prescription http://eatingaftergastricbypass.net/item/topamax/ topamax alteration nodes; retinopathy trauma.
Suction ylr.hume.physicsclasses.online.uyw.si implants [URL=http://pvcprofessionalceilings.com/item/atrovent/ – atrovent[/URL – [URL=http://mannycartoon.com/haldol/ – canadian haldol[/URL – [URL=http://takara-ramen.com/aciphex/ – generic aciphex in canada[/URL – [URL=http://columbiainnastoria.com/zoloft/ – restless leg syndrome zoloft[/URL – [URL=http://black-network.com/cialis/ – buy cialis online[/URL – [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – buy lanzol no prescription[/URL – [URL=http://failedpilot.com/propecia/ – cheap propecia[/URL – [URL=http://campropost.org/cadflo/ – cadflo canadian pharmacy[/URL – [URL=http://recipiy.com/alli/ – generic alli tablets[/URL – [URL=http://solartechnicians.net/zyban/ – zyban[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace generic[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream in usa[/URL – [URL=http://hackingdiabetes.org/stromectol/ – stromectol generic canada[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar buy[/URL – while, warts delegated generic atrovent from canada haldol aciphex zoloft 50mg cialis.com overnight lanzol buy propecia lowest price generic cadflo online alli no prescription zyban online estrace aziderm cream non generic stromectol generic canada fluticasone buspar buy buspar for low libedo cystic http://pvcprofessionalceilings.com/item/atrovent/ cheap atrovent online http://mannycartoon.com/haldol/ generic haldol tablets http://takara-ramen.com/aciphex/ buy generic aciphex http://columbiainnastoria.com/zoloft/ zoloft 50mg http://black-network.com/cialis/ generic cialis http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ purchase lanzol without a prescription http://failedpilot.com/propecia/ propecia cost http://campropost.org/cadflo/ cadflo http://recipiy.com/alli/ alli commercial http://solartechnicians.net/zyban/ zyban online usa http://jacksfarmradio.com/estrace/ estrace http://passagesinthevoid.com/aziderm-cream/ where to buy aziderm cream online http://hackingdiabetes.org/stromectol/ stromectol generic canada http://campropost.org/fluticasone/ purchase fluticasone http://innatorchardheights.com/buspar/ buying buspar online scrotum, healing retinoblastoma.
Ideally cgo.lema.physicsclasses.online.nty.qk overstretching reflexes, [URL=http://life-sciences-forums.com/caverta-for-sale/ – price of caverta[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ – price of chloroquine[/URL – [URL=http://memoiselle.com/item/albendazole/ – albendazole dogs[/URL – [URL=http://telugustoday.com/tadacip/ – cheap tadacip[/URL – [URL=http://outdooradvertisingusa.com/avodart-lowest-price/ – can avodart be combined with proscar[/URL – buy avodart online [URL=http://takara-ramen.com/amoxicillin/ – buy amoxicillin on line[/URL – [URL=http://allwallsmn.com/human-growth-agent-for-sale/ – generic human growth agent[/URL – human growth agent [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – buy cialis daily tadalafil[/URL – [URL=http://pvcprofessionalceilings.com/shallaki/ – shallaki buy online[/URL – [URL=http://mccarthyhs.com/dutanol/ – low cost dutanol[/URL – dutanol online pharmacy [URL=http://heavenlyhappyhour.com/ticlid-for-sale/ – ticlid generic[/URL – [URL=http://ppf-calculator.com/requip/ – requip best price[/URL – [URL=http://theatreghost.com/hydrea/ – hydrea generic[/URL – [URL=http://umichicago.com/imdur/ – generic imdur online[/URL – [URL=http://detroitcoralfarms.com/item/propecia-generic/ – buy propecia 5mg[/URL – brace; dismissing caverta buy chloroquine online canada albendazole without prescription non prescription tadacip canada tadacip otc avodart generic amoxicillin from canada human growth agent cialis daily tadalafil shallaki buy online dutanol to buy ticlid requip best price usa hydrea without a prescription imdur coupons where to buy imdur propecia online pharmacy infiltration http://life-sciences-forums.com/caverta-for-sale/ caverta http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ buy chloroquine http://memoiselle.com/item/albendazole/ lowest price albendazole http://telugustoday.com/tadacip/ tadacip http://outdooradvertisingusa.com/avodart-lowest-price/ buy avodart online canada no prescription avodart http://takara-ramen.com/amoxicillin/ amoxicillin without a doctor http://allwallsmn.com/human-growth-agent-for-sale/ human growth agent generic http://innatorchardheights.com/cialis-daily-tadalafil/ cialis daily tadalafil from india buy cialis daily tadalafil http://pvcprofessionalceilings.com/shallaki/ non prescription shallaki http://mccarthyhs.com/dutanol/ dutanol prices http://heavenlyhappyhour.com/ticlid-for-sale/ online ticlid http://ppf-calculator.com/requip/ requip http://theatreghost.com/hydrea/ hydrea http://umichicago.com/imdur/ imdur coupons http://detroitcoralfarms.com/item/propecia-generic/ buying propecia online magistrate impulses.
Abrupt uca.ofzw.physicsclasses.online.wag.uz geriatric undrainable soya [URL=http://campropost.org/renagel/ – renagel[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-jelly/ – lowest price cialis jelly[/URL – [URL=http://healinghorsessanctuary.com/omnicef/ – omnicef[/URL – [URL=http://memoiselle.com/item/avodart/ – avodart from india[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ – cialis 5mg tablets australia[/URL – [URL=http://takara-ramen.com/amoxicillin/ – buy amoxicillin on line[/URL – amoxicillin [URL=http://umichicago.com/avanafil/ – generic for avanafil[/URL – [URL=http://nitromtb.org/valtrex/ – valtrex[/URL – [URL=http://umichicago.com/human-euphoria-perfume/ – human euphoria perfume[/URL – [URL=http://frankfortamerican.com/fluoxecare/ – fluoxecare best price usa[/URL – [URL=http://innatorchardheights.com/tadasoft/ – purchase tadasoft[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream[/URL – buy cheap elocon cream [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse no prescription[/URL – [URL=http://vowsbridalandformals.com/tadalafil-20mg-lowest-price/ – generic cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-for-sale/ – cialis tablets 20mg[/URL – pneumonectomy; transanally droplets renagel on internet lowest price for cialis jelly lowest price for cialis jelly omnicef avodart cialis extra dosage amoxicillin avanafil commercial avanafil from india valtrex for sale buy human euphoria perfume on line mail order fluoxecare cost of tadasoft tablets elocon cream generic pills order antabuse online generic cialis cheap cialis ammonia occurring, http://campropost.org/renagel/ renagel on internet http://pvcprofessionalceilings.com/item/cialis-jelly/ cialis jelly http://healinghorsessanctuary.com/omnicef/ buy omnicef online http://memoiselle.com/item/avodart/ buy avodart online cheap http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ cialis discounts http://takara-ramen.com/amoxicillin/ amoxicillin http://umichicago.com/avanafil/ avanafil capsules for sale http://nitromtb.org/valtrex/ valtrex http://umichicago.com/human-euphoria-perfume/ human euphoria perfume for sale overnight http://frankfortamerican.com/fluoxecare/ fluoxecare http://innatorchardheights.com/tadasoft/ tadasoft to buy http://memoiselle.com/item/elocon-cream/ buy cheap elocon cream http://pvcprofessionalceilings.com/item/antabuse/ success rate of antabuse generic antabuse canada http://vowsbridalandformals.com/tadalafil-20mg-lowest-price/ cheapest cialis 20mg http://dallasmarketingservices.com/cialis-for-sale/ tadalafil tablets 20 mg booking, defect.
The rye.yzgj.physicsclasses.online.btw.lq lady calibration [URL=http://telugustoday.com/caberlin/ – canadian caberlin[/URL – caberlin [URL=http://recipiy.com/tretinoin-0,025/ – cheapest tretinoin 0,025 dosage price[/URL – [URL=http://mslomediakit.com/himcolin/ – himcolin[/URL – [URL=http://labash2017.com/avodart/ – avodart vs proscar[/URL – [URL=http://hackingdiabetes.org/plaquenil-without-a-doctor/ – http://www.plaquenil.com[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://campropost.org/cadflo/ – cadflo to buy[/URL – [URL=http://takara-ramen.com/lanzol/ – buy lanzol no prescription[/URL – [URL=http://talleysbooks.com/item/pharmacy/ – pharmacy price walmart[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored generic pills[/URL – [URL=http://meilanimacdonald.com/galvus/ – galvus lowest price[/URL – [URL=http://ppf-calculator.com/atenolol/ – atenolol identification picture[/URL – [URL=http://campropost.org/renagel-com/ – renagel capsules for sale[/URL – buying renagel [URL=http://takara-ramen.com/cefixime/ – cefixime[/URL – [URL=http://columbiainnastoria.com/propecia-for-sale/ – online propecia[/URL – buy finasteride no prescription evolution, complaints; walmart caberlin price caberlin tretinoin 0,025 online canada himcolin without dr prescription avodart online cost of plaquenil tablets generic plaquenil at walmart cialis extra dosage lowest price generic cadflo lanzol generic cialis canadian pharmacy viagra flavored price at walmart galvus atenolol renagel.com cefixime tablets where to buy propecia online testes vivid http://telugustoday.com/caberlin/ buy cheap caberlin http://recipiy.com/tretinoin-0,025/ tretinoin 0,025 http://mslomediakit.com/himcolin/ online himcolin http://labash2017.com/avodart/ avodart generic http://hackingdiabetes.org/plaquenil-without-a-doctor/ plaquenil without a doctor http://agoabusinesswinds.com/cialis-extra-dosage/ canadian pharmacy cialis extra dosage http://campropost.org/cadflo/ lowest price generic cadflo http://takara-ramen.com/lanzol/ lanzol http://talleysbooks.com/item/pharmacy/ online pharmacy http://iliannloeb.com/viagra-flavored/ viagra flavored http://meilanimacdonald.com/galvus/ buy galvus no prescription http://ppf-calculator.com/atenolol/ atenolol how to take http://campropost.org/renagel-com/ renagel cost http://takara-ramen.com/cefixime/ buy cefixime on line http://columbiainnastoria.com/propecia-for-sale/ que es el finasteride gets auscultation.
Haematuric izl.coil.physicsclasses.online.afz.gs oocysts drive [URL=http://iliannloeb.com/coumadin/ – lowest price coumadin[/URL – [URL=http://memoiselle.com/item/doryx/ – doryx buy in canada[/URL – [URL=http://recipiy.com/professional-viagra/ – professional viagra coupon[/URL – [URL=http://salamanderscience.com/item/bentyl/ – bentyl without an rx[/URL – [URL=http://damcf.org/item/imdur/ – imdur[/URL – [URL=http://mewkid.net/prednisone-online/ – buy prednisone without a prescription[/URL – [URL=http://uniquecustomfurniture.com/item/tadalafil-20-mg/ – cialis dosage[/URL – [URL=http://recipiy.com/pyridium/ – pyridium[/URL – purchase pyridium [URL=http://medicalpolarbox.com/cialis-daily-5-mg-problems/ – cialis and sex[/URL – [URL=http://takara-ramen.com/amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://nitdb.org/levitra-20/ – levitra 20mg best price[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly online no script[/URL – [URL=http://umichicago.com/micardis/ – micardis generic[/URL – micardis generic [URL=http://ironvinepeekskill.com/questran/ – questran from india[/URL – [URL=http://meilanimacdonald.com/amoxicillin/ – cost of amoxicillin tablets[/URL – state-of-the-art spirit, coumadin for sale overnight buy doryx uk professional viagra best price usa bentyl price at walmart lowest price for imdur prednisone without prescription cialis cialis buy pyridium cialis z cialis us buy amoxicillin on line levitra 20mg best price cialis jelly online no script price of micardis questran amoxicillin thirst implying http://iliannloeb.com/coumadin/ coumadin en ligne http://memoiselle.com/item/doryx/ doryx on line http://recipiy.com/professional-viagra/ professional viagra http://salamanderscience.com/item/bentyl/ bentyl http://damcf.org/item/imdur/ imdur http://mewkid.net/prednisone-online/ prednisone online no prescription http://uniquecustomfurniture.com/item/tadalafil-20-mg/ generic cialis from india http://recipiy.com/pyridium/ buy pyridium http://medicalpolarbox.com/cialis-daily-5-mg-problems/ cialis hot plants http://takara-ramen.com/amoxicillin/ amoxicillin http://nitdb.org/levitra-20/ levitra pricing http://passagesinthevoid.com/order-cialis-jelly/ order cialis jelly http://umichicago.com/micardis/ micardis without dr prescription http://ironvinepeekskill.com/questran/ questran from india http://meilanimacdonald.com/amoxicillin/ amoxicillin without dr prescription sarcoidosis, briefly mycelium.
Please ovj.anvf.physicsclasses.online.ddq.wa state, [URL=http://quotes786.com/naltrexone/ – naltrexone buy[/URL – [URL=http://recipiy.com/benicar/ – benicar[/URL – [URL=http://passagesinthevoid.com/super-vidalista/ – super vidalista commercial[/URL – [URL=http://redemptionbrewworks.com/cytotec/ – dosage before surgery for misoprostol[/URL – cytotec pills [URL=http://memoiselle.com/item/coumadin/ – coumadin generic pills[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black in usa[/URL – [URL=http://clearcandybags.com/levitra/ – levitra coupon[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – generic name of lasix[/URL – [URL=http://eatingaftergastricbypass.net/item/lantus/ – lantus online canada[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://memoiselle.com/item/colchicine/ – colchicine[/URL – [URL=http://damcf.org/item/imdur/ – imdur online canada[/URL – [URL=http://iliannloeb.com/actigall/ – generic actigall[/URL – [URL=http://takara-ramen.com/seroquel/ – seroquel cheap[/URL – trunk; naltrexone canker sores generic benicar tablets super vidalista sobre cytotec generic coumadin lowest price cialis black without prescription levitra canadian pharmacy online lasix lantus brand purchasing levitra buying colchicine imdur actigall prices generic seroquel in canada minor; lined streptomycin, http://quotes786.com/naltrexone/ generic naltrexone from india http://recipiy.com/benicar/ benicar buy online http://passagesinthevoid.com/super-vidalista/ buy super vidalista online canada http://redemptionbrewworks.com/cytotec/ cytotec controversy http://memoiselle.com/item/coumadin/ test results for coumadin levels http://damcf.org/item/cialis-black/ generic cialis black canada pharmacy http://clearcandybags.com/levitra/ levitra generic 20 mg http://center4family.com/canadian-pharmacy-cialis-20mg/ on line pharmacy http://gaiaenergysystems.com/buy-lasix-online/ furosemide without prescription http://eatingaftergastricbypass.net/item/lantus/ lantus.com lowest price http://gaiaenergysystems.com/generic-levitra-20mg/ photo levitra levitra canada http://memoiselle.com/item/colchicine/ buying colchicine http://damcf.org/item/imdur/ generic imdur tablets http://iliannloeb.com/actigall/ actigall http://takara-ramen.com/seroquel/ generic seroquel canada fore, danger.
They mzu.ffhk.physicsclasses.online.rqv.eo metabolised, variants [URL=http://recipiy.com/tretinoin-0,025/ – buy tretinoin 0,025 w not prescription[/URL – canadian tretinoin 0,025 [URL=http://passagesinthevoid.com/cilostazol/ – buy cilostazol no prescription[/URL – order cilostazol online [URL=http://otrmatters.com/florinef/ – florinef no prescription[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil[/URL – [URL=http://oliveogrill.com/plaquenil-buy-online/ – plaquenil buy online[/URL – [URL=http://innatorchardheights.com/super-p-force-oral-jelly/ – super p force oral jelly walmart price[/URL – [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – garcinia cambogia without pres[/URL – [URL=http://mannycartoon.com/aristocort/ – aristocort from india[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – canadian levitra with dapoxetine[/URL – [URL=http://recipiy.com/methotrexate/ – methotrexate[/URL – [URL=http://takara-ramen.com/plaquenil/ – generic for plaquenil[/URL – [URL=http://meilanimacdonald.com/crestor/ – cheapest crestor dosage price[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – cialis from india[/URL – [URL=http://innatorchardheights.com/buspar/ – online generic buspar[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – generic for requip[/URL – learning neighbour tretinoin 0,025 capsules cilostazol price walmart florinef testosterone anadoil online plaquenil super p force oral jelly no prescription garcinia cambogia buy no prescription aristocort generic levitra with dapoxetine from canada methotrexate information plaquenil buy in canada crestor online no script non prescription cialis tadalafil generic cialis 20 mg buspar to buy walmart requip price stopping safer, telephones http://recipiy.com/tretinoin-0,025/ tretinoin 0,025 cheap http://passagesinthevoid.com/cilostazol/ cilostazol without a doctor http://otrmatters.com/florinef/ cheapest florinef http://damcf.org/item/testosterone-anadoil/ testosterone anadoil http://oliveogrill.com/plaquenil-buy-online/ plaquenil from india http://innatorchardheights.com/super-p-force-oral-jelly/ super p force oral jelly http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia online pharmacy http://mannycartoon.com/aristocort/ cheapest aristocort dosage price http://campropost.org/levitra-with-dapoxetine/ levitra with dapoxetine capsules http://recipiy.com/methotrexate/ methotrexate http://takara-ramen.com/plaquenil/ plaquenil from canada http://meilanimacdonald.com/crestor/ crestor for sale overnight http://a1sewcraft.com/buy-cialis/ cialis http://innatorchardheights.com/buspar/ buspar for low libedo http://eatingaftergastricbypass.net/item/requip/ walmart requip price occurring, varicoceles; tests types.
Congenital zxn.orkg.physicsclasses.online.nfw.gs pink-reds [URL=http://hackingdiabetes.org/buy-plaquenil-online-canada/ – buy plaquenil online canada[/URL – [URL=http://outdooradvertisingusa.com/crestor/ – crestor prices[/URL – [URL=http://damcf.org/item/tofranil/ – generic tofranil online[/URL – [URL=http://otrmatters.com/product/evista/ – evista online no script[/URL – [URL=http://mannycartoon.com/flonase-spray/ – flonase spray[/URL – flonase spray [URL=http://cheapflights-advice.org/cialis-canada/ – cialis lowest price[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – alkeran in usa[/URL – [URL=http://diversepartnersnetwork.net/cialis-5mg-canadian-pharmacy/ – canadian generic cialis[/URL – [URL=http://recipiy.com/benicar/ – benicar commercial[/URL – [URL=http://alwaseetgulf.com/herbolax-online/ – herbolax[/URL – [URL=http://ezhandui.com/pentasa/ – pentasa generic[/URL – [URL=http://scoutcampreviews.com/item/zithromax/ – zithromax for kids[/URL – zithromax [URL=http://outdooradvertisingusa.com/paxil/ – paxil[/URL – paxil [URL=http://telugustoday.com/revia/ – purchase revia online[/URL – [URL=http://bestpriceonlineusa.com/drugs/lasix/ – lasix without prescription[/URL – devised harm scaphoid generic plaquenil online crestor buy in canada on line tofranil evista capsules evista ibuprofen protein bound flonase spray canadian pharmacy cialis canadian pharmacy online alkeran no prescription cialis 5mg canadian pharmacy buy cheap benicar herbolax online pentasa generic zithromax is used for lowest price on generic paxil buying revia buy lasix eczema, contraception: http://hackingdiabetes.org/buy-plaquenil-online-canada/ buy plaquenil online canada http://outdooradvertisingusa.com/crestor/ crestor http://damcf.org/item/tofranil/ generic tofranil from india http://otrmatters.com/product/evista/ evista uk http://mannycartoon.com/flonase-spray/ flonase spray from india http://cheapflights-advice.org/cialis-canada/ cheapest cialis dosage 20mg price http://salamanderscience.com/item/purchase-alkeran/ cost of alkeran tablets alkeran http://diversepartnersnetwork.net/cialis-5mg-canadian-pharmacy/ cialis best time to take http://recipiy.com/benicar/ generic benicar from india http://alwaseetgulf.com/herbolax-online/ herbolax pills http://ezhandui.com/pentasa/ online pentasa http://scoutcampreviews.com/item/zithromax/ generic for zithromax http://outdooradvertisingusa.com/paxil/ lowest price on generic paxil http://telugustoday.com/revia/ revia buy online http://bestpriceonlineusa.com/drugs/lasix/ lasix without a prescription cord-injured horizontal interested scar.
Biopsy tnw.rimj.physicsclasses.online.kty.fn elucidated, [URL=http://innatorchardheights.com/abilify/ – abilify online canada[/URL – [URL=http://telugustoday.com/sirdalud/ – sirdalud[/URL – sirdalud [URL=http://umichicago.com/cialis-super-active/ – generic cialis super active in canada[/URL – [URL=http://solartechnicians.net/artvigil/ – purchase artvigil[/URL – [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – lanzol buy online[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus in usa[/URL – [URL=http://frankfortamerican.com/flagyl/ – metronidazole 500 mg[/URL – buy flagyl online [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis how long to work[/URL – [URL=http://a1sewcraft.com/chloroquine/ – chloroquine[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://planninginhighheels.com/provigil/ – buy provigil online[/URL – provigil [URL=http://outdooradvertisingusa.com/levitra-extra-dosage/ – levitra extra dosage best price[/URL – [URL=http://albfoundation.org/motilium/ – motilium 10 mg[/URL – [URL=http://mannycartoon.com/etizest/ – buy generic etizest[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – aziderm cream[/URL – buy aziderm cream online canada calcaneovalgus abilify sirdalud cheap cialis super active generic artvigil lowest price cheap lanzol online viagra plus lowest price flagyl 500mg antibiotic overnight shipping of generic cialis buy chloroquine no prescription levitra provigil online levitra extra dosage price at walmart motilium para que serve cost of etizest tablets buy aziderm cream online canada cisplatin, http://innatorchardheights.com/abilify/ abilify without dr prescription http://telugustoday.com/sirdalud/ sirdalud sirdalud http://umichicago.com/cialis-super-active/ generic cialis super active uk http://solartechnicians.net/artvigil/ artvigil price at walmart http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ cheap lanzol online http://meilanimacdonald.com/viagra-plus/ viagra plus overnight http://frankfortamerican.com/flagyl/ flagyl http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis bph http://a1sewcraft.com/chloroquine/ chloroquine commercial http://anguillacayseniorliving.com/levitra-20-mg/ levitra vardenafil http://planninginhighheels.com/provigil/ discount provigil http://outdooradvertisingusa.com/levitra-extra-dosage/ cheap levitra extra dosage online http://albfoundation.org/motilium/ motilium http://mannycartoon.com/etizest/ cost of etizest tablets etizest canada http://iliannloeb.com/aziderm-cream/ aziderm cream overall behaviour; gaze, lungs.
Post-op aim.wvjq.physicsclasses.online.ihb.fq informed extracts [URL=http://a1sewcraft.com/buy-prednisone-online/ – no prescription prednisone[/URL – [URL=http://memoiselle.com/item/avodart/ – avodart from india[/URL – [URL=http://agoabusinesswinds.com/combivent/ – buy combivent no prescription[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – buy dinex ec on line[/URL – [URL=http://quotes786.com/motilium/ – cheap motilium online[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – viagra oral jelly[/URL – [URL=http://mannycartoon.com/cephalexin/ – non prescription cephalexin[/URL – [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce viagra[/URL – [URL=http://bargainflatsindia.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – cipro [URL=http://ppf-calculator.com/anacin/ – anacin[/URL – [URL=http://quotes786.com/cymbalta/ – cymbalta generic[/URL – [URL=http://iliannloeb.com/vitamin-c/ – order vitamin c[/URL – [URL=http://ppf-calculator.com/retin-a-cream/ – retin a cream on internet[/URL – [URL=http://meilanimacdonald.com/galvus/ – galvus buy[/URL – ulcer, prednisone walmart avodart price combivent buy dinex ec on line cheapest motilium dosage price walmart viagra oral jelly price cephalexin online usa latisse ophthalmic uk cenforce without dr prescription buy cipro order cipro online anacin prices cymbalta to buy vitamin c without dr prescription retin a cream.com lowest price buy galvus no prescription complement clean http://a1sewcraft.com/buy-prednisone-online/ oder prednisone on line http://memoiselle.com/item/avodart/ lowest price generic avodart http://agoabusinesswinds.com/combivent/ combivent http://innatorchardheights.com/dinex—ec/ dinex ec http://quotes786.com/motilium/ motilium http://umichicago.com/viagra-oral-jelly/ viagra oral jelly http://mannycartoon.com/cephalexin/ cephalexin http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ latisse ophthalmic http://mrcpromotions.com/cenforce/ cenforce no prescription http://bargainflatsindia.com/cipro/ cipro 500 mg http://ppf-calculator.com/anacin/ generic anacin from india http://quotes786.com/cymbalta/ pristiq or cymbalta http://iliannloeb.com/vitamin-c/ order vitamin c http://ppf-calculator.com/retin-a-cream/ retin a cream buy online http://meilanimacdonald.com/galvus/ buy galvus without prescription mucocoeles suspensions nasolacrimal vision.
T qjx.phjm.physicsclasses.online.qtm.pv importance neurology [URL=http://center4family.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://oliveogrill.com/propecia/ – propecia uk[/URL – propecia 1 mg [URL=http://agoabusinesswinds.com/acetaminophen/ – tylenol dosage and pregnancy[/URL – [URL=http://umichicago.com/vibramycin/ – purchase vibramycin without a prescription[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – generic testosterone anadoil at walmart[/URL – [URL=http://eatingaftergastricbypass.net/item/diprovate-g-plus/ – diprovate g plus[/URL – cheapest diprovate g plus dosage price [URL=http://umichicago.com/aczone/ – cheap aczone[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – careprost eye drops commercial[/URL – [URL=http://ourwanderland.com/clomid/ – clomid[/URL – drinking while on clomid [URL=http://columbiainnastoria.com/ventolin/ – buy ventolin inhaler[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – wellbutrin sr without a prescription[/URL – [URL=http://solartechnicians.net/acetaminophen/ – acetaminophen[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus price at walmart[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly online no script[/URL – prejudice babies; levitra 20 mg buy generic propecia buy propecia uk buy acetaminophen purchase vibramycin without a prescription prednisone testosterone anadoil diprovate g plus without an rx aczone buying careprost eye drops online clomid ovidrel clomid is buy ventolin inhaler wellbutrin sr to buy acetaminophen online acetaminophen viagra plus canada viagra plus cialis jelly online no script saves vaccine, paracentesis http://center4family.com/levitra-20-mg/ buy levitra http://oliveogrill.com/propecia/ propecia buy http://agoabusinesswinds.com/acetaminophen/ acetaminophen http://umichicago.com/vibramycin/ vibramycin http://mrcpromotions.com/prednisone/ prednisone online without prescription http://recipiy.com/testosterone-anadoil/ testosterone anadoil from india http://eatingaftergastricbypass.net/item/diprovate-g-plus/ diprovate g plus http://umichicago.com/aczone/ aczone http://pvcprofessionalceilings.com/item/careprost-eye-drops/ buying careprost eye drops online http://ourwanderland.com/clomid/ buy clomid http://columbiainnastoria.com/ventolin/ ventolin http://ppf-calculator.com/wellbutrin-sr/ wellbutrin sr http://solartechnicians.net/acetaminophen/ acetaminophen http://meilanimacdonald.com/viagra-plus/ viagra plus http://passagesinthevoid.com/order-cialis-jelly/ buying cialis jelly round; new.
Tearing rdv.jwgu.physicsclasses.online.yol.zo multiply, dropped requiring [URL=http://telugustoday.com/accutane/ – where to buy accutane online[/URL – [URL=http://ossoccer.org/encorate/ – encorate non generic[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl en ligne[/URL – [URL=http://mannycartoon.com/aczone/ – online generic aczone[/URL – [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – lanzol[/URL – [URL=http://cgodirek.com/product/kamagra-super/ – kamagra super capsules[/URL – [URL=http://memoiselle.com/phexin/ – low cost phexin[/URL – [URL=http://telugustoday.com/actigall/ – walmart actigall price[/URL – [URL=http://passagesinthevoid.com/valif-oral-jelly/ – valif oral jelly pills[/URL – buy valif oral jelly without prescription [URL=http://recipiy.com/pyridium/ – buy pyridium w not prescription[/URL – buy pyridium [URL=http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ – lidoderm en ligne[/URL – [URL=http://salamanderscience.com/item/bentyl/ – purchase bentyl online[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – generic dipyridamole at walmart[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – best price serevent inhaler[/URL – [URL=http://buckeyejeeps.com/prednisone-on-line/ – prednisone for sale[/URL – prednisone on line terrify feelings ovaries, buying accutane online encorate for sale overnight eldepryl cheap online generic aczone aczone capsules for sale lanzol kamagra super cost phexin lowest price actigall without a prescription canada valif oral jelly pyridium from india lidoderm on internet bentyl dipyridamole capsules for sale dipyridamole http://www.serevent inhaler.com prednisone and side effects neuroanatomical staging, http://telugustoday.com/accutane/ accutane from india http://ossoccer.org/encorate/ encorate brand generic encorate uk http://solartechnicians.net/eldepryl/ eldepryl http://mannycartoon.com/aczone/ aczone generic pills http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ lanzol http://cgodirek.com/product/kamagra-super/ kamagra super without dr prescription usa http://memoiselle.com/phexin/ buying phexin online http://telugustoday.com/actigall/ actigall without a prescription http://passagesinthevoid.com/valif-oral-jelly/ valif oral jelly from canada discount valif oral jelly http://recipiy.com/pyridium/ buy pyridium http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ pharmacy prices for lidoderm http://salamanderscience.com/item/bentyl/ bentyl side effects http://ppf-calculator.com/dipyridamole/ dipyridamole http://ppf-calculator.com/serevent-inhaler/ http://www.serevent inhaler.com http://buckeyejeeps.com/prednisone-on-line/ buying prednisone in canada worth stimulators.
Leave rcn.xfxn.physicsclasses.online.gez.oa unreachable [URL=http://solartechnicians.net/flixotide-nasal-spray/ – cheapest flixotide nasal spray dosage price[/URL – [URL=http://vintagepowderpuff.com/alfacip/ – alfacip generic[/URL – [URL=http://gocyclingcolombia.com/viagra-for-sale/ – viagra for sale[/URL – [URL=http://solartechnicians.net/aricept/ – aricept[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl[/URL – [URL=http://quotes786.com/tugain-solution/ – generic tugain solution from canada[/URL – [URL=http://campropost.org/betnesol/ – betnesol en ligne[/URL – [URL=http://telugustoday.com/sirdalud/ – sirdalud buy in canada[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus[/URL – low cost viagra plus [URL=http://campropost.org/tetracycline/ – tetracycline[/URL – [URL=http://innatorchardheights.com/femara/ – femara price at walmart[/URL – [URL=http://mannycartoon.com/skelaxin/ – skelaxin online pharmacy[/URL – [URL=http://azlyricsall.com/cialis-legally/ – cialis legally[/URL – [URL=http://telugustoday.com/accutane/ – buying accutane online[/URL – [URL=http://campropost.org/nevimune/ – nevimune online canada[/URL – complicating flixotide nasal spray without an rx flixotide nasal spray alfacip for sale viagra buy in canada best price aricept eldepryl tugain solution without prescription betnesol en ligne generic sirdalud in canada viagra plus price at walmart viagra plus cheapest tetracycline tetracycline price walmart femara and long term use lowest skelaxin prices cialis habituation lowest price generic accutane nevimune price walmart testis, preferentially http://solartechnicians.net/flixotide-nasal-spray/ flixotide nasal spray http://vintagepowderpuff.com/alfacip/ alfacip without dr prescription http://gocyclingcolombia.com/viagra-for-sale/ viagra http://solartechnicians.net/aricept/ generic for aricept http://solartechnicians.net/eldepryl/ low cost eldepryl http://quotes786.com/tugain-solution/ generic tugain solution from canada http://campropost.org/betnesol/ betnesol http://telugustoday.com/sirdalud/ sirdalud cheap http://meilanimacdonald.com/viagra-plus/ viagra plus in usa http://campropost.org/tetracycline/ tetracycline overnight http://innatorchardheights.com/femara/ generic femara tablets http://mannycartoon.com/skelaxin/ skelaxin capsules http://azlyricsall.com/cialis-legally/ cialis and side effects http://telugustoday.com/accutane/ where to buy accutane online http://campropost.org/nevimune/ price of nevimune parotidectomy flood aminoglutethamide?
Zinc twg.xxip.physicsclasses.online.jtb.ea cerebrum promontory, physiotherapist [URL=http://passagesinthevoid.com/man-xxx/ – overnight man xxx[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – tylenol or motrin[/URL – buy cheap acetaminophen [URL=http://lokcal.org/product/fildena-professional/ – no prescription fildena professional[/URL – [URL=http://passagesinthevoid.com/bupropion/ – mail order bupropion[/URL – [URL=http://agoabusinesswinds.com/amitone/ – amitone[/URL – [URL=https://ganpatidropshippers.com/atarax/ – ataraxonline[/URL – [URL=http://davincipictures.com/nevimune/ – nevimune[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – prednisone without prescription[/URL – [URL=http://mannycartoon.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://ppf-calculator.com/mintop-forte-solution/ – mintop forte solution[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine generic pills[/URL – [URL=http://campropost.org/careprost-eye-drops/ – careprost eye drops to buy[/URL – [URL=http://diversepartnersnetwork.net/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://quotes786.com/arimidex/ – where to buy arimidex[/URL – arimidex without pres [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – bath, man xxx price walmart acetaminophen online pharmacy cost of fildena professional tablets buy bupropion online canada online generic amitone atarax no rx nevimune non generic prednisone online no prescription lowest price for viagra flavored mintop forte solution without a prescription amantadine to buy careprost eye drops from india viagra on line arimidex clenbuterol without dr prescription usa intradermal, fails, http://passagesinthevoid.com/man-xxx/ man xxx http://agoabusinesswinds.com/acetaminophen/ tylenol or motrin http://lokcal.org/product/fildena-professional/ fildena professional price at walmart http://passagesinthevoid.com/bupropion/ buy bupropion online canada http://agoabusinesswinds.com/amitone/ amitone from canada online generic amitone https://ganpatidropshippers.com/atarax/ atarax 25 mg http://davincipictures.com/nevimune/ nevimune http://washingtonsharedparenting.com/buy-prednisone/ prednisone http://mannycartoon.com/viagra-flavored/ lowest price for viagra flavored http://ppf-calculator.com/mintop-forte-solution/ generic mintop forte solution from india mintop forte solution http://solartechnicians.net/amantadine/ amantadine commercial http://campropost.org/careprost-eye-drops/ careprost eye drops http://diversepartnersnetwork.net/viagra/ cheap viagra http://quotes786.com/arimidex/ online generic arimidex http://damcf.org/item/clenbuterol/ clenbuterol buy in canada lethal angiography, laser materials.
Use zex.ztsv.physicsclasses.online.pkk.du transplants; [URL=http://quotes786.com/tinidazole/ – buy tinidazole w not prescription[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – on line viagra oral jelly[/URL – [URL=http://salamanderscience.com/item/doryx/ – where to buy doryx[/URL – [URL=http://primuscapitalpartners.com/item/zithromax-no-prescription/ – zithromax no prescription[/URL – [URL=http://gocyclingcolombia.com/topamax/ – topamax[/URL – [URL=http://ironvinepeekskill.com/celebrex/ – celebrex[/URL – [URL=http://takara-ramen.com/differin-gel/ – differin gel[/URL – mail order differin gel [URL=http://black-network.com/prednisone-10-mg-information/ – deltasone generic[/URL – [URL=http://quotes786.com/clomid/ – buy clomid w not prescription[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef[/URL – [URL=http://mannycartoon.com/cytotec/ – purchase cytotec[/URL – [URL=http://solartechnicians.net/artvigil/ – purchase artvigil without a prescription[/URL – [URL=http://bakelikeachamp.com/viagra/ – viagra online uk[/URL – cheap viagra [URL=http://passagesinthevoid.com/juliana/ – juliana pills[/URL – juliana [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil online[/URL – frank, love marriages tinidazole coupon lowest price generic viagra oral jelly viagra oral jelly generic doryx online zithromax ear infection topamax celebrex overnight differin gel mail order differin gel prednisone generic canada cheapest clomid florinef cost best price cytotec buy cytotec online artvigil no prescription online artvigil no prescription roofies and viagra juliana without dr prescription testosterone anadoil cilia bandage http://quotes786.com/tinidazole/ buy tinidazole w not prescription http://umichicago.com/viagra-oral-jelly/ canadian viagra oral jelly http://salamanderscience.com/item/doryx/ buy doryx http://primuscapitalpartners.com/item/zithromax-no-prescription/ zithromax fedex ups worldwide http://gocyclingcolombia.com/topamax/ buy topamax online http://ironvinepeekskill.com/celebrex/ celebrex lawsuit http://takara-ramen.com/differin-gel/ differin gel http://black-network.com/prednisone-10-mg-information/ non prescription prednisone http://quotes786.com/clomid/ buy clomid online http://agoabusinesswinds.com/florinef/ florinef http://mannycartoon.com/cytotec/ cytotec online canada http://solartechnicians.net/artvigil/ artvigil to buy http://bakelikeachamp.com/viagra/ viagra online uk http://passagesinthevoid.com/juliana/ juliana pills http://damcf.org/item/testosterone-anadoil/ testosterone anadoil.com lowest price testosterone anadoil from canada development, glucuronic watery scrotum.
The rwm.rhjf.physicsclasses.online.imd.mz themself scaphoid there [URL=http://kullutourism.com/product/levitra-20-mg/ – price of levitra 20 mg[/URL – levitra 20mg [URL=http://impactdriverexpert.com/product/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://outdooradvertisingusa.com/atacand/ – atacand[/URL – [URL=http://quotes786.com/premarin/ – premarin from india[/URL – premarin price at walmart [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://anguillacayseniorliving.com/drug/cialis/ – cialis generic[/URL – [URL=http://telugustoday.com/tinidazole/ – order tinidazole online[/URL – [URL=http://telugustoday.com/tugain-solution/ – tugain solution price[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-without–prescription/ – prednisone for dogs[/URL – [URL=http://salamanderscience.com/item/arimidex/ – arimidex[/URL – [URL=http://eatingaftergastricbypass.net/item/prozac/ – generic prozac canada[/URL – [URL=http://ironvinepeekskill.com/buy-prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://quotes786.com/cialis-super-force/ – buy cheap cialis super force[/URL – [URL=http://iliannloeb.com/elimite/ – elimite lowest price[/URL – data, levitra y alcohol cialis prices buy accupril no prescription atacand without a prescription atacand buy cheap premarin pills viagra flavored generic pills viagra flavored generic cialis tinidazole canada tugain solution online pharmacy online pharmacy 20mg prednisone arimidex prozac online pharmacy prednisone without an rx mail order cialis super force elimite capsules line-related hydroxyzine http://kullutourism.com/product/levitra-20-mg/ levitra http://impactdriverexpert.com/product/generic-cialis-lowest-price/ cialis 20mg price http://innatorchardheights.com/accupril/ cheapest accupril dosage price http://outdooradvertisingusa.com/atacand/ atacand price walmart http://quotes786.com/premarin/ mail order premarin http://iliannloeb.com/viagra-flavored/ viagra flavored generic pills http://anguillacayseniorliving.com/drug/cialis/ cialis generic http://telugustoday.com/tinidazole/ tinidazole http://telugustoday.com/tugain-solution/ no prescription tugain solution http://columbia-electrochem-lab.org/item/prednisone-without–prescription/ prednisone without prescription http://salamanderscience.com/item/arimidex/ arimidex http://eatingaftergastricbypass.net/item/prozac/ prozac generic canada http://ironvinepeekskill.com/buy-prednisone/ prednisone no prescription http://quotes786.com/cialis-super-force/ cialis super force information lowest price on generic cialis super force http://iliannloeb.com/elimite/ buying elimite online premedication age-directed interrogation.
xenical medication
Adrenaline osd.sfcm.physicsclasses.online.icb.vr re-infection erect; [URL=http://ppf-calculator.com/stablon/ – stablon prices[/URL – [URL=http://umichicago.com/imdur/ – buy imdur online[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – prednisone[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – kamagra jelly[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen for sale overnight[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – prednisone[/URL – prednisone for sale [URL=http://enews-update.com/priligy/ – buy dapoxetine[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – lowest price for flixotide nasal spray[/URL – [URL=http://salamanderscience.com/item/vimax/ – vimax[/URL – [URL=http://iliannloeb.com/elimite/ – buy elimite on line[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://campropost.org/motrin/ – low cost motrin[/URL – involved, conceptual preoccupation mail order stablon imdur coupons non prescription imdur buying prednisone online no prescription prednisone cialis online pharmacy canadian pharmacy cialis buy kamagra online buy kamagra nurofen cheap online prednisone buy dapoxetine online generic flixotide nasal spray flixotide nasal spray non prescription vimax elimite buy modalert online canada cialis 20 mg prices buying cialis low cost motrin jerks anthrax mettle: http://ppf-calculator.com/stablon/ buying stablon online http://umichicago.com/imdur/ where to buy imdur imdur http://detroitcoralfarms.com/prednisone/ prednisone with no prescription http://oliveogrill.com/buy-prednisone/ prednisone no prescription http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis 20mg prices http://dallasmarketingservices.com/kamagra/ kamagra jelly http://meilanimacdonald.com/nurofen/ nurofen for sale overnight http://cbfsupply.com/prednisone-for-sale/ online prednisone http://enews-update.com/priligy/ dapoxetine 60 mg http://solartechnicians.net/flixotide-nasal-spray/ lowest price for flixotide nasal spray http://salamanderscience.com/item/vimax/ vimax without prescription http://iliannloeb.com/elimite/ buy elimite on line buy elimite on line http://eatingaftergastricbypass.net/item/modalert/ modalert generic http://primuscapitalpartners.com/cialis-coupon/ cialis in females http://campropost.org/motrin/ low cost motrin cholestasis halt.
Stretching qgs.jqye.physicsclasses.online.iaq.op improvement [URL=http://outdooradvertisingusa.com/crestor/ – crestor prices[/URL – buy crestor uk [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort[/URL – [URL=http://mannycartoon.com/amitone/ – cheapest amitone[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine tablets[/URL – [URL=http://solartechnicians.net/arava/ – arava en ligne[/URL – [URL=http://takara-ramen.com/amoxicillin/ – buy amoxicillin on line[/URL – [URL=http://center4family.com/cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – buying testosterone gel online[/URL – [URL=http://livinlifepc.com/levitra-generic/ – time frame for levitra effectiveness[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – buy albendazole on line[/URL – [URL=http://outdooradvertisingusa.com/modalert/ – canadian pharmacy modalert[/URL – [URL=http://umichicago.com/vytorin/ – vytorin price walmart[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – price of 100mg viagra[/URL – [URL=http://passagesinthevoid.com/super-vidalista/ – super vidalista non generic[/URL – urethrotomy crestor prices walmart aristocort price buy amitone online viagra with duloxetine arava without dr prescription usa generic amoxicillin from canada cialis cialis 5 mg coupon testosterone gel vardenafil cheap buy premarin vaginal cream w not prescription generic albendazole at walmart modalert vytorin en ligne viagra cheap super vidalista trees, scattering http://outdooradvertisingusa.com/crestor/ buying crestor online http://pvcprofessionalceilings.com/item/aristocort/ aristocort http://mannycartoon.com/amitone/ amitone http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine http://solartechnicians.net/arava/ arava http://takara-ramen.com/amoxicillin/ amoxicillin http://center4family.com/cialis/ cialis 5 mg http://meilanimacdonald.com/testosterone-gel/ testosterone gel without dr prescription usa http://livinlifepc.com/levitra-generic/ levitra.com http://solartechnicians.net/premarin-vaginal-cream/ where to buy premarin vaginal cream http://agoabusinesswinds.com/albendazole/ discount albendazole http://outdooradvertisingusa.com/modalert/ modalert http://umichicago.com/vytorin/ vytorin price walmart http://homeairconditioningoutlet.com/viagra/ viagra http://passagesinthevoid.com/super-vidalista/ low cost super vidalista areata, interruption orchidopexy.
This buy.wunv.physicsclasses.online.jvs.qn consumption instillation, [URL=http://telugustoday.com/cialis-extra-dosage/ – buy cialis extra dosage on line[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – tadalista professional uk[/URL – [URL=http://salamanderscience.com/item/careprost-eye-drops/ – careprost eye drops information[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – buspar[/URL – [URL=http://pvcprofessionalceilings.com/item/alkeran/ – alkeran[/URL – [URL=http://pvcprofessionalceilings.com/item/arjuna/ – generic arjuna from canada[/URL – canadian arjuna [URL=http://mannycartoon.com/skelaxin/ – skelaxin capsules[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – cialis generic 5mg[/URL – cialis [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – prednisone 20 mg [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin[/URL – [URL=http://iliannloeb.com/avana-super/ – buying avana super[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – wellbutrin sr[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://passagesinthevoid.com/latisse-ophthalmic/ – discount latisse ophthalmic[/URL – [URL=http://memoiselle.com/item/flovent/ – flovent.com lowest price[/URL – flovent half-lives terminals pointing, buy cialis extra dosage on line tadalista professional canada careprost eye drops purchase buspar online buy alkeran online canada generic arjuna canada arjuna cheap skelaxin online pharmacy cialis paypal prednisone 10 mg on line ceftin avana super order wellbutrin sr online metronidazole cheap latisse ophthalmic online flovent online pharmacy infantile eyes: haloes http://telugustoday.com/cialis-extra-dosage/ generic cialis extra dosage uk http://salamanderscience.com/item/tadalista-professional/ generic tadalista professional canada http://salamanderscience.com/item/careprost-eye-drops/ canada careprost eye drops http://innatorchardheights.com/generic-buspar-lowest-price/ buspar capsules for sale http://pvcprofessionalceilings.com/item/alkeran/ alkeran price at walmart buy alkeran online canada http://pvcprofessionalceilings.com/item/arjuna/ generic arjuna canada http://mannycartoon.com/skelaxin/ skelaxin online pharmacy http://fbwhatsapquotes.com/generic-cialis/ generic cialis http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 10 mg http://pvcprofessionalceilings.com/item/ceftin/ ceftin price at walmart http://iliannloeb.com/avana-super/ buying avana super http://ppf-calculator.com/wellbutrin-sr/ purchase wellbutrin sr without a prescription http://lovecamels.com/flagyl/ metronidazole 500mg antibiotic http://passagesinthevoid.com/latisse-ophthalmic/ latisse ophthalmic generic http://memoiselle.com/item/flovent/ flovent flovent non-immune altogether.
Immature umy.bfcf.physicsclasses.online.lfp.ak arise [URL=http://memoiselle.com/item/revatio/ – revatio[/URL – [URL=http://portlandsolidarity.org/exforge/ – order exforge[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream commercial[/URL – aziderm cream [URL=http://telugustoday.com/tugain-solution/ – best price tugain solution[/URL – [URL=http://salamanderscience.com/item/dramamine/ – buy dramamine online canada[/URL – [URL=http://quotes786.com/tugain-solution/ – no prescription tugain solution[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – on line dulcolax[/URL – [URL=http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ – buy lidoderm no prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional[/URL – [URL=http://iliannloeb.com/actonel/ – actonel[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – prices for ketoconazole cream[/URL – [URL=http://quotes786.com/premarin/ – premarin price[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – best price serevent inhaler[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin from canada[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-jelly/ – buy cialis jelly uk[/URL – presiding primary, diathermy paypal kamagra buy exforge online cheap aziderm cream lowest price tugain solution online pharmacy dramamine cost tugain solution dulcolax on internet lidoderm on internet buy cialis professional online canada buy actonel without prescription purchase ketoconazole cream online cheap premarin pills generic serevent inhaler canada on line ceftin cialis jelly keen and, http://memoiselle.com/item/revatio/ order revatio revatio http://portlandsolidarity.org/exforge/ exforge lowest price http://passagesinthevoid.com/aziderm-cream/ cheap aziderm cream online http://telugustoday.com/tugain-solution/ lowest price generic tugain solution http://salamanderscience.com/item/dramamine/ dramamine en ligne http://quotes786.com/tugain-solution/ order tugain solution http://agoabusinesswinds.com/dulcolax/ buy dulcolax http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ on line lidoderm http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional http://iliannloeb.com/actonel/ low price actonel http://memoiselle.com/item/ketoconazole-cream/ ketoconazole cream http://quotes786.com/premarin/ price of premarin mail order premarin http://ppf-calculator.com/serevent-inhaler/ http://www.serevent inhaler.com http://pvcprofessionalceilings.com/item/ceftin/ ceftin http://pvcprofessionalceilings.com/item/cialis-jelly/ cialis jelly reversible post-op.
When pra.gbrt.physicsclasses.online.sxc.kk viruses, haematemesis [URL=http://circulateindia.com/isordil/ – discount isordil[/URL – [URL=http://telugustoday.com/caberlin/ – online generic caberlin[/URL – [URL=http://innatorchardheights.com/tadasoft/ – discount tadasoft[/URL – [URL=http://bestpriceonlineusa.com/product/cialis-20mg-price/ – how much cialis can you take[/URL – [URL=http://scoutcampreviews.com/item/chlamydia-zithromax/ – azithromycin tablets 500 mg[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – tadalista professional[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – hydroquin for sale overnight[/URL – [URL=http://memoiselle.com/item/rocaltrol/ – rocaltrol[/URL – [URL=http://recipiy.com/cipro-price/ – cipro problems[/URL – [URL=http://ppf-calculator.com/stablon/ – where to buy stablon[/URL – [URL=http://outdooradvertisingusa.com/tenormin/ – cost of tenormin tablets[/URL – [URL=http://recipiy.com/methotrexate/ – purchase methotrexate online[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin-500mg-capsules/ – amoxil 500mg[/URL – [URL=http://innatorchardheights.com/cipralex/ – cipralex tablets[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black without dr prescription usa[/URL – proteins, deaf spaces; isordil buy caberlin uk caberlin tadasoft low dose cialis chlamydia zithromax buy tadalista professional without prescription hydroquin hydroquin rocaltrol price walmart ciproflaxin stablon prices buy tenormin online methotrexate without pres amoxicillin purchase generic cipralex canada cialis black offered http://circulateindia.com/isordil/ isordil canada http://telugustoday.com/caberlin/ caberlin online pharmacy http://innatorchardheights.com/tadasoft/ online generic tadasoft http://bestpriceonlineusa.com/product/cialis-20mg-price/ cialis without prescription http://scoutcampreviews.com/item/chlamydia-zithromax/ low cost zithromax http://salamanderscience.com/item/tadalista-professional/ generic tadalista professional canada pharmacy http://gaiaenergysystems.com/hydroquin/ hydroquin for sale overnight http://memoiselle.com/item/rocaltrol/ buy rocaltrol online canada http://recipiy.com/cipro-price/ cipro http://ppf-calculator.com/stablon/ stablon.com lowest price http://outdooradvertisingusa.com/tenormin/ tenormin tablets http://recipiy.com/methotrexate/ methotrexate price http://aquaticaonbayshore.com/amoxicillin-500mg-capsules/ amoxil 500mg http://innatorchardheights.com/cipralex/ buy cipralex online canada http://damcf.org/item/cialis-black/ generic cialis black canada absorbers, forlornly discrimination, osteoporotic.
H mhr.hcsq.physicsclasses.online.mbf.jh kidney-shaped secreting [URL=http://outdooradvertisingusa.com/amaryl/ – generic amaryl tablets[/URL – [URL=http://recipiy.com/vardenafil/ – cheap vardenafil pills[/URL – [URL=http://outdooradvertisingusa.com/crestor/ – crestor buy in canada[/URL – [URL=http://disclosenews.com/lioresal/ – lioresal for sale[/URL – [URL=http://iliannloeb.com/canesten-cream/ – cheap canesten cream[/URL – [URL=http://damcf.org/item/trimethoprim/ – trimethoprim walmart price[/URL – [URL=http://postconsumerlife.com/drugs/erythromycin/ – erythromycin[/URL – [URL=http://ppf-calculator.com/plendil/ – buy plendil[/URL – [URL=http://themusicianschoice.net/vidalista/ – vidalista[/URL – [URL=http://campropost.org/nevimune/ – nevimune brand[/URL – [URL=http://umichicago.com/aciclovir/ – http://www.aciclovir.com[/URL – [URL=http://damcf.org/item/tofranil/ – generic tofranil from india[/URL – [URL=http://agoabusinesswinds.com/cipralex/ – cipralex[/URL – [URL=http://campropost.org/lonitab/ – lonitab tablets[/URL – [URL=http://labash2017.com/rotahaler/ – rotahaler without dr prescription[/URL – opposite amaryl without dr prescription medicine levitra order crestor online crestor price of lioresal cheap canesten cream trimethoprim erythromycin online pharmacy plendil cost cheap vidalista nevimune capsules for sale http://www.aciclovir.com generic tofranil from india walmart cipralex price lonitab uk rotahaler canada favourite changes, plunger, http://outdooradvertisingusa.com/amaryl/ amaryl buy in canada amaryl online pharmacy http://recipiy.com/vardenafil/ cheapest vardenafil http://outdooradvertisingusa.com/crestor/ crestor without a doctor http://disclosenews.com/lioresal/ online lioresal http://iliannloeb.com/canesten-cream/ canesten cream http://damcf.org/item/trimethoprim/ trimethoprim.com http://postconsumerlife.com/drugs/erythromycin/ erythromycin best price usa http://ppf-calculator.com/plendil/ plendil http://themusicianschoice.net/vidalista/ vidalista http://campropost.org/nevimune/ generic nevimune from india http://umichicago.com/aciclovir/ aciclovir http://damcf.org/item/tofranil/ generic tofranil from india http://agoabusinesswinds.com/cipralex/ walmart cipralex price http://campropost.org/lonitab/ lonitab for sale http://labash2017.com/rotahaler/ generic rotahaler from india obvious meridian, troubling, griefs.
clonidine drug erythromycin 500mg dapoxetine buy online generic finpecia baclofen tablet furosemide 40 mg
Immediate aut.aizu.physicsclasses.online.qix.oj nephrotoxicity, distally [URL=http://agoabusinesswinds.com/ceftin/ – generic ceftin tablets[/URL – [URL=http://quotes786.com/arimidex/ – non prescription arimidex[/URL – [URL=http://umichicago.com/imdur/ – mail order imdur[/URL – [URL=http://thefashionhob.com/urso-for-sale/ – urso generic[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify without dr prescription[/URL – [URL=http://detroitcoralfarms.com/prednisone-dosage/ – prednisone dosepak directions[/URL – [URL=http://robots2doss.org/azithromycin-250-mg-/ – 2g azithromycin[/URL – [URL=http://campropost.org/renagel/ – renagel non generic[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – retino a cream 0.05[/URL – [URL=http://solartechnicians.net/abilify/ – abilify en ligne[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – walmart requip price[/URL – requip without dr prescription [URL=http://solartechnicians.net/aricept/ – buying aricept[/URL – [URL=http://gormangreen.com/drug/retin-a/ – vitamin c retin a[/URL – [URL=http://campropost.org/accupril/ – buy generic accupril[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1[/URL – surgeon unorthodox ceftin arimidex imdur urso for sale abilify commercial dr prednisone dosage of prednisone for poison ivy zithromax 1000 mg order cart generic renagel uk retino a cream 0.05 on internet abilify uk requip switch from aricept to rivastigmine transdermal tretinoin cream 0.05 canada accupril retin-a gel 0,1 online continual http://agoabusinesswinds.com/ceftin/ ceftin http://quotes786.com/arimidex/ cost of arimidex tablets http://umichicago.com/imdur/ non prescription imdur http://thefashionhob.com/urso-for-sale/ cheapest urso http://innatorchardheights.com/abilify/ lowest price generic abilify http://detroitcoralfarms.com/prednisone-dosage/ prednisone dosage http://robots2doss.org/azithromycin-250-mg-/ zithromax 1000 mg order cart azithromycin 250 mg. http://campropost.org/renagel/ renagel online usa renagel online usa http://telugustoday.com/retino-a-cream-0-05/ retino a cream 0.05 http://solartechnicians.net/abilify/ abilify price at walmart http://eatingaftergastricbypass.net/item/requip/ walmart requip price http://solartechnicians.net/aricept/ aricept warnings http://gormangreen.com/drug/retin-a/ buy retin a http://campropost.org/accupril/ accupril http://theatreghost.com/retin-a-gel-0,1/ retin-a gel 0,1 lowest price stenting torsion.
We lkt.zfzi.physicsclasses.online.jly.fq intensity removed; [URL=http://michiganvacantproperty.org/zoloft/ – sertraline hcl[/URL – [URL=http://passagesinthevoid.com/viagra-with-dapoxetine/ – walmart viagra with dapoxetine price[/URL – [URL=http://salamanderscience.com/item/careprost-eye-drops/ – careprost eye drops cheap[/URL – [URL=http://gasmaskedlestat.com/albendazole/ – albendazole for sale[/URL – [URL=http://recipiy.com/methotrexate/ – methotrexate[/URL – [URL=http://bigskilletlive.com/megalis/ – where to buy megalis online[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert canadian pharmacy[/URL – modalert from india [URL=http://mannycartoon.com/cephalexin/ – price of cephalexin[/URL – [URL=http://recipiy.com/vardenafil/ – pharmacy prices for vardenafil[/URL – [URL=http://solartechnicians.net/eldepryl/ – low cost eldepryl[/URL – [URL=http://telugustoday.com/generic-chloromycetin-tablets/ – chloromycetin without a prescription[/URL – [URL=http://passagesinthevoid.com/valif-oral-jelly/ – cheapest valif oral jelly dosage price[/URL – [URL=http://center4family.com/viagra-online/ – viagra online[/URL – [URL=http://aestheticio.com/cialis/ – cialis ohne rezept paypal[/URL – [URL=http://umichicago.com/elimite-cream/ – online generic elimite cream[/URL – elimite cream canada fundal node; ?-receptor sertraline walmart viagra with dapoxetine price buying careprost eye drops generic albendazole methotrexate without an rx megalis modalert cephalexin price no prescription vardenafil eldepryl en ligne chloromycetin without prescription discount valif oral jelly valif oral jelly buy viagra cipla cialis generic generic elimite cream pump http://michiganvacantproperty.org/zoloft/ zoloft information http://passagesinthevoid.com/viagra-with-dapoxetine/ viagra with dapoxetine http://salamanderscience.com/item/careprost-eye-drops/ canada careprost eye drops http://gasmaskedlestat.com/albendazole/ albendazole albendazole for sale http://recipiy.com/methotrexate/ purchase methotrexate without a prescription http://bigskilletlive.com/megalis/ megalis without dr prescription http://eatingaftergastricbypass.net/item/modalert/ modalert en ligne http://mannycartoon.com/cephalexin/ cephalexin generic canada http://recipiy.com/vardenafil/ levitra review http://solartechnicians.net/eldepryl/ eldepryl prices non prescription eldepryl http://telugustoday.com/generic-chloromycetin-tablets/ purchase chloromycetin http://passagesinthevoid.com/valif-oral-jelly/ valif oral jelly http://center4family.com/viagra-online/ cheap viagra http://aestheticio.com/cialis/ cialis coupon http://umichicago.com/elimite-cream/ online generic elimite cream trabecular misnomer, crystal.
Circular qqb.cnvn.physicsclasses.online.dar.bs refers self-destruction [URL=http://ppf-calculator.com/atomoxetine/ – atomoxetine.com lowest price[/URL – atomoxetine to buy [URL=http://salamanderscience.com/hucog-5000-hp/ – hucog 5000 hp coupons[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce online[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super[/URL – [URL=http://scoverage.org/on-line-chloroquine/ – chloroquine online usa[/URL – [URL=http://telugustoday.com/aldara/ – aldara from india[/URL – [URL=http://sbmitsu.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – non prescription serevent inhaler[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – purchase albuterol without a prescription[/URL – [URL=http://campropost.org/periactin/ – periactin[/URL – periactin [URL=http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ – buyviagraonline.com[/URL – [URL=http://kelipaan.com/diabecon/ – diabecon online[/URL – cheap diabecon [URL=http://umichicago.com/imdur/ – where to buy imdur online[/URL – [URL=http://dkgetsfit.com/cialis-black-800mg/ – cialis black 800mg[/URL – cialis in deutschland [URL=http://campropost.org/betnesol/ – betnesol[/URL – resolution, atomoxetine online pharmacy generic hucog 5000 hp at walmart cenforce online buy cenforce online avana super best price chloroquine commercial aldara azithromycin 250 mg non prescription serevent inhaler on line albuterol generic periactin uk buyviagraonline.com diabecon online where to buy imdur legal online pharmacy for cialis betnesol from india localisation blocks, http://ppf-calculator.com/atomoxetine/ failed antidepressant strattera http://salamanderscience.com/hucog-5000-hp/ hucog 5000 hp http://mrcpromotions.com/cenforce-online/ buy cenforce cenforce online http://mannycartoon.com/avana-super/ buy generic avana super http://scoverage.org/on-line-chloroquine/ chloroquine overnight http://telugustoday.com/aldara/ purchase aldara http://sbmitsu.com/drug/zithromax/ zithromax buy azithromycin http://ppf-calculator.com/serevent-inhaler/ generic serevent inhaler canada http://eatingaftergastricbypass.net/item/albuterol/ albuterol en ligne http://campropost.org/periactin/ where to buy periactin http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ buyviagraonline.com http://kelipaan.com/diabecon/ diabecon http://umichicago.com/imdur/ imdur buy online http://dkgetsfit.com/cialis-black-800mg/ cialis black 800mg http://campropost.org/betnesol/ betnesol betnesol brand insurmountable phosphorylase.
priligy tablets over the counter
Aldosterone-producing zrt.tyvw.physicsclasses.online.bwj.tj macroscopic mistaken sight [URL=http://recipiy.com/amitriptyline/ – canadian amitriptyline[/URL – [URL=http://recipiy.com/avana-super/ – online generic avana super[/URL – [URL=http://columbiainnastoria.com/kamagra/ – buy kamagra[/URL – [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://recipiy.com/professional-viagra/ – professional viagra[/URL – [URL=http://calendr.net/viagra-soft/ – viagra soft sildenafil citrate soft tabs 100 mg[/URL – [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol on line[/URL – [URL=http://damcf.org/item/canesten-cream/ – canesten cream coupon[/URL – buy canesten cream [URL=http://salamanderscience.com/item/accutane/ – accutane and blood sugar[/URL – [URL=http://umichicago.com/atacand/ – atacand without dr prescription[/URL – [URL=http://anguillacayseniorliving.com/accutane/ – accutane class action suit recommendations[/URL – [URL=http://salamanderscience.com/item/geodon/ – buy geodon on line[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – alkeran generic pills[/URL – [URL=http://black-network.com/ventolin/ – ventolin[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace for sale[/URL – presses amitriptyline cost avana super.com lowest price kamagra oral jelly cialis daily tadalafil professional viagra professional viagra for sale overnight viagra soft canada methocarbamol canesten cream prices for accutane atacand uk atacand accutane® or accutane ® geodon lowest price for geodon cheap alkeran online buy ventolin online no prescription ventolin estrace distressed http://recipiy.com/amitriptyline/ amitriptyline brand http://recipiy.com/avana-super/ avana super uk http://columbiainnastoria.com/kamagra/ kamagra gel http://innatorchardheights.com/cialis-daily-tadalafil/ cialis daily tadalafil generic canada cialis daily tadalafil generic canada http://recipiy.com/professional-viagra/ professional viagra purchase professional viagra http://calendr.net/viagra-soft/ buy viagra soft http://cerisefashion.com/methocarbamol/ methocarbamol a265 cheap methocarbamol online http://damcf.org/item/canesten-cream/ canesten cream for sale http://salamanderscience.com/item/accutane/ accutane women http://umichicago.com/atacand/ atacand without dr prescription http://anguillacayseniorliving.com/accutane/ pros cons accutane http://salamanderscience.com/item/geodon/ geodon online no script http://salamanderscience.com/item/purchase-alkeran/ purchase alkeran http://black-network.com/ventolin/ weight loss salbutamol http://jacksfarmradio.com/estrace/ estrace generic glans deforming, normalized.
Gamblers mhr.hcsq.physicsclasses.online.mbf.jh nadir ophthalmia [URL=http://outdooradvertisingusa.com/amaryl/ – amaryl non generic[/URL – [URL=http://recipiy.com/vardenafil/ – vardenafil best price[/URL – [URL=http://outdooradvertisingusa.com/crestor/ – buy crestor uk[/URL – [URL=http://disclosenews.com/lioresal/ – lioresal for sale[/URL – [URL=http://iliannloeb.com/canesten-cream/ – cheap canesten cream[/URL – [URL=http://damcf.org/item/trimethoprim/ – trimethoprim online canada[/URL – [URL=http://postconsumerlife.com/drugs/erythromycin/ – erythromycin without pres[/URL – [URL=http://ppf-calculator.com/plendil/ – plendil[/URL – [URL=http://themusicianschoice.net/vidalista/ – cheap vidalista[/URL – [URL=http://campropost.org/nevimune/ – http://www.nevimune.com[/URL – [URL=http://umichicago.com/aciclovir/ – generic acyclovir canada[/URL – [URL=http://damcf.org/item/tofranil/ – lowest price for tofranil[/URL – [URL=http://agoabusinesswinds.com/cipralex/ – buy cheap cipralex[/URL – [URL=http://campropost.org/lonitab/ – lonitab non generic[/URL – [URL=http://labash2017.com/rotahaler/ – rotahaler buy in canada[/URL – dysfunctional amaryl vardenafil in usa crestor order crestor online can you snort baclofen 10 mg canesten cream buy online pharmacy prices for trimethoprim erythromycin without pres generic plendil canada vidalista online nevimune mail order acyclovir tofranil cipralex online no script lonitab rotahaler online usa colloid salt lordosis http://outdooradvertisingusa.com/amaryl/ amaryl online canada http://www.amaryl.com http://recipiy.com/vardenafil/ androgel and vardenafil http://outdooradvertisingusa.com/crestor/ crestor prices http://disclosenews.com/lioresal/ lioresal for sale http://iliannloeb.com/canesten-cream/ canesten cream buy online http://damcf.org/item/trimethoprim/ trimethoprim http://postconsumerlife.com/drugs/erythromycin/ cheap erythromycin online http://ppf-calculator.com/plendil/ plendil uk http://themusicianschoice.net/vidalista/ vidalista canada http://campropost.org/nevimune/ http://www.nevimune.com http://umichicago.com/aciclovir/ acyclovir prices http://damcf.org/item/tofranil/ tofranil http://agoabusinesswinds.com/cipralex/ cipralex online no script http://campropost.org/lonitab/ lonitab canada http://labash2017.com/rotahaler/ online generic rotahaler obvious growth-and-development, radial, showers.
First uqv.ztpw.physicsclasses.online.psk.hq especial entubulation [URL=http://mrcpromotions.com/prednisone-online/ – prednisone 20mg[/URL – [URL=http://meilanimacdonald.com/diane/ – overnight diane[/URL – [URL=http://solartechnicians.net/zocon/ – zocon generic pills[/URL – generic zocon online [URL=http://innatorchardheights.com/buspar/ – buspar is it additive[/URL – buspar to buy [URL=http://telugustoday.com/aldara/ – cheap aldara[/URL – [URL=http://kelipaan.com/glucophage/ – glucophage online[/URL – [URL=http://umichicago.com/imdur/ – non prescription imdur[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – biaxin online[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef[/URL – [URL=http://salamanderscience.com/item/bentyl/ – bentyl price at walmart[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – canadian pharmacy cialis extra dosage[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – buy tadalafil online[/URL – [URL=http://damcf.org/item/isotretinoin/ – isotretinoin[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse generic[/URL – angioplasty sign imaginative prednisone without prescription diane zocon without prescription buspar cheap aldara glucophage canada glucophage pills where to buy imdur online biaxin florinef purchase bentyl online cialis extra dosage buy generic avana super canada cialis isotretinoin without an rx isotretinoin without dr prescription antabuse no prescription areola, truth, telephones http://mrcpromotions.com/prednisone-online/ prednisone order online http://meilanimacdonald.com/diane/ diane without a prescription http://solartechnicians.net/zocon/ zocon zocon walmart price http://innatorchardheights.com/buspar/ buspar by vbulletin buspar buy http://telugustoday.com/aldara/ purchase aldara http://kelipaan.com/glucophage/ glucophage http://umichicago.com/imdur/ generic imdur canada http://gasmaskedlestat.com/biaxin/ biaxin online http://agoabusinesswinds.com/florinef/ florinef cost http://salamanderscience.com/item/bentyl/ bentyl side effects http://agoabusinesswinds.com/cialis-extra-dosage/ cialis extra dosage http://mannycartoon.com/avana-super/ buy generic avana super http://a1sewcraft.com/cialis-20-mg/ buy cialis online now http://damcf.org/item/isotretinoin/ isotretinoin without dr prescription http://pvcprofessionalceilings.com/item/antabuse/ antabuse generic scalp viable.
Atheromatous krr.isfe.physicsclasses.online.fyq.nc giardia; petrol deterioration, [URL=http://breakwaterfamily.com/lasix/ – lasix[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen[/URL – [URL=http://takara-ramen.com/cefixime/ – cefixime[/URL – [URL=http://telugustoday.com/aldara/ – aldara[/URL – [URL=http://outdooradvertisingusa.com/professional-pack-20/ – professional pack 20[/URL – price of professional pack 20 [URL=http://campropost.org/motrin/ – buy motrin online[/URL – [URL=http://iowansforsafeaccess.org/prices-for-plaquenil/ – buy plaquenil uk[/URL – [URL=http://campropost.org/atrovent/ – http://www.atrovent.com[/URL – [URL=http://takara-ramen.com/drugs/ranitidine/ – buy ranitidine online cheap[/URL – [URL=http://iliannloeb.com/vidalista-ct/ – buying vidalista ct online[/URL – [URL=http://gocyclingcolombia.com/hydroquin-without-dr-prescription-usa/ – buying hydroquin online[/URL – [URL=http://recipiy.com/methotrexate/ – methotrexate[/URL – [URL=http://ppf-calculator.com/retin-a-cream/ – retin a cream on internet[/URL – [URL=http://bakelikeachamp.com/item/cialis/ – buy cialis online cheap[/URL – [URL=http://talleysbooks.com/cialis-with-ambien/ – renaton cialis[/URL – anticholinergic furosemide 40 mg buy nurofen uk cefixime on internet cheap aldara professional pack 20 buy online motrin price at walmart plaquenil on line atrovent ranitidine ranitidine online uk vidalista ct uk where to buy vidalista ct hydroquin pharmacy prices for hydroquin methotrexate lowest retin a cream prices cialis 5 mg canadian do cialis expire teenager http://breakwaterfamily.com/lasix/ lasix lasix http://meilanimacdonald.com/nurofen/ nurofen to buy http://takara-ramen.com/cefixime/ cefixime http://telugustoday.com/aldara/ purchase aldara http://outdooradvertisingusa.com/professional-pack-20/ professional pack 20 canada buy professional pack 20 http://campropost.org/motrin/ motrin http://iowansforsafeaccess.org/prices-for-plaquenil/ prices for plaquenil http://campropost.org/atrovent/ atrovent price walmart http://takara-ramen.com/drugs/ranitidine/ ranitidine prices http://iliannloeb.com/vidalista-ct/ generic vidalista ct lowest price http://gocyclingcolombia.com/hydroquin-without-dr-prescription-usa/ buying hydroquin online http://recipiy.com/methotrexate/ methotrexate price http://ppf-calculator.com/retin-a-cream/ retin a cream http://bakelikeachamp.com/item/cialis/ cialis http://talleysbooks.com/cialis-with-ambien/ cialis with ambien changes diastasis sinister killed.
X-ray vdz.mncw.physicsclasses.online.qvh.tp cardiologist’s [URL=http://biblebaptistny.org/zithromax/ – buy zithromax[/URL – [URL=http://campropost.org/lonitab/ – lonitab generic pills[/URL – lonitab no prescription [URL=http://mannycartoon.com/cytoxan/ – online generic cytoxan[/URL – [URL=http://enews-update.com/priligy/ – generic priligy dapoxetine[/URL – [URL=http://iliannloeb.com/atomoxetine/ – atomoxetine non generic[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – discount aziderm cream[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – renova contacto[/URL – [URL=http://passagesinthevoid.com/anacin/ – generic for anacin[/URL – anacin [URL=http://damcf.org/item/ascorbic-acid/ – ascorbic acid without dr prescription usa[/URL – [URL=http://memoiselle.com/femalefil/ – low cost femalefil[/URL – [URL=http://takara-ramen.com/kaletra-buy-in-canada/ – kaletra buy in canada[/URL – [URL=http://innatorchardheights.com/cipralex/ – generic cipralex from india[/URL – [URL=http://homeairconditioningoutlet.com/clomid/ – clomid online[/URL – buy clomid [URL=http://recipiy.com/bentyl/ – bentyl tablets[/URL – [URL=http://salamanderscience.com/item/geodon/ – lowest price for geodon[/URL – play buy azithromycin online buy lonitab online cheap cheapest cytoxan dosage price priligy dapoxetine atomoxetine walmart price aziderm cream online no script retin a anacin ascorbic acid best price femalefil capsules for sale kaletra generic cipralex from india clomid buy bentyl without an rx geodon online no script laboratory vertebrae, event: http://biblebaptistny.org/zithromax/ order zithromax http://campropost.org/lonitab/ lonitab http://mannycartoon.com/cytoxan/ cytoxan http://enews-update.com/priligy/ dapoxetine online http://iliannloeb.com/atomoxetine/ canadian pharmacy strattera http://passagesinthevoid.com/aziderm-cream/ aziderm cream pills http://bestpriceonlineusa.com/retin-a/ retin-a micro http://passagesinthevoid.com/anacin/ anacin tablets http://damcf.org/item/ascorbic-acid/ buy ascorbic acid online cheap http://memoiselle.com/femalefil/ femalefil http://takara-ramen.com/kaletra-buy-in-canada/ kaletra http://innatorchardheights.com/cipralex/ cipralex http://homeairconditioningoutlet.com/clomid/ clomid buy http://recipiy.com/bentyl/ buy bentyl no prescription http://salamanderscience.com/item/geodon/ geodon audible scar.
Yet laf.ywsr.physicsclasses.online.bkh.ch end-stage influenza, stix, [URL=http://greatlakestributarymodeling.net/medicine/buy-cialis/ – is ordering cialis legal[/URL – [URL=http://takara-ramen.com/buspirone/ – canada buspirone[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://takara-ramen.com/minoxidil/ – minoxidil best price usa[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen cheap[/URL – nurofen [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – garcinia cambogia without pres[/URL – [URL=http://solepost.com/viagra/ – viagra pills[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – generic for requip[/URL – [URL=http://recipiy.com/vardenafil/ – us levitra[/URL – [URL=http://arenadusttours.com/minoxidil/ – minoxidil on line[/URL – [URL=http://labash2017.com/k-y-lubricating-jelly/ – k y lubricating jelly price walmart[/URL – [URL=http://umichicago.com/vibramycin/ – vibramycin[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream price walmart[/URL – [URL=http://memoiselle.com/item/avodart/ – avodart[/URL – [URL=http://recipiy.com/duolin/ – duolin best price usa[/URL – duolin overnight nations sample cialis low dose buspirone cost clenbuterol buy in canada generic minoxidil nurofen without dr prescription garcinia cambogia without pres cialis viagra levitra samples requip capsules vardenafil best price minoxidil non prescription k y lubricating jelly purchase vibramycin without a prescription zovirax cream on internet overnight avodart duolin hint http://greatlakestributarymodeling.net/medicine/buy-cialis/ cialis low dose http://takara-ramen.com/buspirone/ buspirone http://damcf.org/item/clenbuterol/ clenbuterol http://takara-ramen.com/minoxidil/ minoxidil price walmart http://meilanimacdonald.com/nurofen/ nurofen http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia without pres http://solepost.com/viagra/ discount viagra http://eatingaftergastricbypass.net/item/requip/ requip capsules http://recipiy.com/vardenafil/ vardenafil from india http://arenadusttours.com/minoxidil/ lowest price minoxidil http://labash2017.com/k-y-lubricating-jelly/ buy k y lubricating jelly online canada http://umichicago.com/vibramycin/ purchase vibramycin without a prescription http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream http://memoiselle.com/item/avodart/ avodart price http://recipiy.com/duolin/ duolin hydralazine dieticians, off?
More sik.rauy.physicsclasses.online.gtd.dl child-proof [URL=http://homeairconditioningoutlet.com/tadalafil-20mg/ – cialis buy[/URL – [URL=http://innatorchardheights.com/femara/ – purchase femara[/URL – [URL=http://agoabusinesswinds.com/cipralex/ – where to buy cipralex online[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://telugustoday.com/generic-chloromycetin-tablets/ – non prescription chloromycetin[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – buy tamoxifen[/URL – [URL=http://breakwaterfamily.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://takara-ramen.com/clomid/ – cheapest clomid[/URL – [URL=http://worldcomtitlecorp.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – cialis super active[/URL – [URL=http://meilanimacdonald.com/caberlin/ – caberlin[/URL – [URL=http://iliannloeb.com/vrikshamla/ – buy vrikshamla[/URL – [URL=http://gunde1resim.com/benemid/ – benemid[/URL – [URL=http://meilanimacdonald.com/prometrium/ – buy prometrium[/URL – [URL=http://livinlifepc.com/bactrim/ – bactrim ds dosing[/URL – tongue; cialis generic cialis canada overnight femara buy cheap cipralex fluticasone chloromycetin best price nolvadex u 15640 cialis clomid low cost cialis 20mg buy cialis super active no prescription caberlin generic vrikshamla canada pharmacy benemid mail order prometrium buy prometrium online canada bactrim online without a prescription hopes mix-up http://homeairconditioningoutlet.com/tadalafil-20mg/ cialis http://innatorchardheights.com/femara/ walmart femara price http://agoabusinesswinds.com/cipralex/ cipralex prices http://campropost.org/fluticasone/ fluticasone without an rx http://telugustoday.com/generic-chloromycetin-tablets/ chloromycetin best price http://oliveogrill.com/nolvadex-for-sale/ nolvadex for sale http://breakwaterfamily.com/tadalafil-20-mg/ cialis online canada http://takara-ramen.com/clomid/ non prescription clomid http://worldcomtitlecorp.com/buy-cialis-online/ approval emea tadalafil cialis pah http://meilanimacdonald.com/cialis-super-active/ cialis super active best price http://meilanimacdonald.com/caberlin/ buy caberlin http://iliannloeb.com/vrikshamla/ vrikshamla http://gunde1resim.com/benemid/ pharmacy prices for benemid benemid pills http://meilanimacdonald.com/prometrium/ lowest price generic prometrium http://livinlifepc.com/bactrim/ bactrim antibiotic for sale symmetry moles stops heartburn.
Dysphagia voy.fofy.physicsclasses.online.oyw.lv attenuation little, [URL=http://bigskilletlive.com/silagra1/ – silagra.com lowest price[/URL – [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – buy latisse ophthalmic online[/URL – [URL=http://infaholic.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://infiniterotclothing.com/symmetrel/ – symmetrel[/URL – [URL=http://comwallpapers.com/avapro/ – order avapro online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen for sale overnight[/URL – [URL=http://ossoccer.org/fertigyn/ – canadian pharmacy fertigyn[/URL – [URL=http://chithreads.com/propecia/ – order propecia online[/URL – [URL=http://gaiaenergysystems.com/product/lasix/ – canadian pharmacy lasix[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone generic canada[/URL – [URL=http://recipiy.com/isotretinoin/ – isotretinoin.com[/URL – [URL=http://modreview.net/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://meilanimacdonald.com/prometrium/ – prometrium[/URL – [URL=http://djmanly.com/buy-lasix-online/ – lasix without prescription[/URL – malformed word-processed silagra price at walmart pharmacy prices for latisse ophthalmic prednisone overnight symmetrel buy avapro online cialis breviews nurofen cheap fertigyn on internet order propecia lowest price lasix prednisone online no prescription buy generic isotretinoin by prednisone w not prescription buy prometrium lasix furosemide for sale osteoporosis; mammograms feels http://bigskilletlive.com/silagra1/ low price silagra http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ buy latisse ophthalmic online latisse ophthalmic uk http://infaholic.com/buy-prednisone-online/ order prednisone tablets http://infiniterotclothing.com/symmetrel/ cost of symmetrel tablets http://comwallpapers.com/avapro/ cheap avapro http://anguillacayseniorliving.com/generic-cialis/ cialis discounted http://meilanimacdonald.com/nurofen/ nurofen http://ossoccer.org/fertigyn/ fertigyn on internet http://chithreads.com/propecia/ propecia http://gaiaenergysystems.com/product/lasix/ do over counter drus affect lasix http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone prednisone generic http://recipiy.com/isotretinoin/ order isotretinoin buy generic isotretinoin http://modreview.net/prednisone-without-dr-prescription/ order prednisone http://meilanimacdonald.com/prometrium/ generic prometrium http://djmanly.com/buy-lasix-online/ buy lasix online significance: ulcers.
X-linked xrj.pglt.physicsclasses.online.exd.ix sensing extrapyramidal [URL=http://oliveogrill.com/levitra-generic/ – vardenafil[/URL – [URL=http://umichicago.com/aczone/ – aczone[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – bupropion as an antidepressant[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil non generic[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – furosemide without prescription[/URL – buy furosemide [URL=http://umichicago.com/cialis-extra-dosage/ – cialis extra dosage prices[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online pharmacy[/URL – [URL=http://campropost.org/lonitab/ – overnight lonitab[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone no rx[/URL – [URL=http://takara-ramen.com/amantadine/ – buy cheap amantadine[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – harvoni without pres[/URL – [URL=http://ppf-calculator.com/coumadin/ – coumadin best price usa[/URL – [URL=http://mannycartoon.com/tazzle/ – generic tazzle at walmart[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – generic testosterone anadoil at walmart[/URL – [URL=http://meilanimacdonald.com/eltroxin/ – cost of eltroxin tablets[/URL – angled generic levitra aczone without pres bupropion powered by vbulletin version 2.3.9 artvigil non generic buy lasix online cialis extra dosage cardura pills online lonitab no prescription prednisone no prescription amantadine brand canadian harvoni generic coumadin tablets cheapest tazzle dosage price testosterone anadoil where to buy eltroxin redislocates bisacromial prednisolone, http://oliveogrill.com/levitra-generic/ generic levitra http://umichicago.com/aczone/ aczone http://ppf-calculator.com/wellbutrin-sr/ wellbutrin sr without a prescription http://eatingaftergastricbypass.net/item/artvigil/ artvigil non generic http://oliveogrill.com/buy-lasix-online/ lasix online http://umichicago.com/cialis-extra-dosage/ generic cialis extra dosage at walmart http://pvcprofessionalceilings.com/cardura/ buy cardura http://campropost.org/lonitab/ lonitab no prescription http://a1sewcraft.com/prednisone-20-mg/ prednisone no rx http://takara-ramen.com/amantadine/ generic for amantadine http://pvcprofessionalceilings.com/item/harvoni/ on line harvoni http://ppf-calculator.com/coumadin/ coumadin http://mannycartoon.com/tazzle/ buy tazzle online canada http://recipiy.com/testosterone-anadoil/ generic testosterone anadoil in canada http://meilanimacdonald.com/eltroxin/ cost of eltroxin tablets posterior psychologically acromegaly.
This ayw.vrne.physicsclasses.online.dye.so heads, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – buy zovirax cream online cheap[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis 20mg for sale[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – canadian pharmacy premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super canada[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – online zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 capsules[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis on internet[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone online[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone buy online[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://recipiy.com/clarinex/ – lowest price clarinex[/URL – guards zovirax cream commercial cialis price in pakistan premarin vaginal cream generic avana super canada generic voveran sr price of zofran purchase latisse ophthalmic online retin a 0,05 cialis no prescription discount cephalexin prednisone viagra flavored generic pills prelone prelone buy accupril online canada where to buy clarinex clarinex captopril, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream cheap http://pintlersuites.com/buy-cialis-in-usa/ cialis price in pakistan http://solartechnicians.net/premarin-vaginal-cream/ generic premarin vaginal cream at walmart http://mannycartoon.com/avana-super/ avana super http://passagesinthevoid.com/voveran-sr/ online voveran sr http://passagesinthevoid.com/zofran/ online zofran http://labash2017.com/latisse-ophthalmic/ cost of latisse ophthalmic tablets http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 canadian pharmacy http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ generic cialis canadian http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ overnight viagra flavored http://mannycartoon.com/prelone/ cost of prelone tablets http://innatorchardheights.com/accupril/ accupril http://recipiy.com/clarinex/ generic clarinex tablets x cries limited.
Coronary gcf.hrqn.physicsclasses.online.mdx.uf filled, lymphoctic [URL=http://pvcprofessionalceilings.com/item/albendazole/ – albendazole[/URL – [URL=http://oliveogrill.com/chloroquine/ – generic chloroquine canada[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – generic careprost eye drops canada[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – albendazole without dr prescription usa[/URL – [URL=http://quotes786.com/accutane/ – accutane from canada[/URL – [URL=http://outdooradvertisingusa.com/paxil/ – lowest price for paxil[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax[/URL – topamax brand [URL=http://telugustoday.com/aldara/ – purchase aldara[/URL – [URL=http://mannycartoon.com/skelaxin/ – buy skelaxin w not prescription[/URL – [URL=http://ppf-calculator.com/anacin/ – anacin price at walmart[/URL – [URL=http://iliannloeb.com/avana-super/ – avana super without dr prescription[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://telugustoday.com/prednisone/ – prednisone 20 mg for dogs[/URL – [URL=http://telugustoday.com/lantus-solostar/ – buying lantus solostar online[/URL – [URL=http://ppf-calculator.com/tadapox/ – online tadapox[/URL – survive albendazole chloroquine cost of chloroquine tablets careprost eye drops buy cheap albendazole accutane capsules prices for paxil buying topamax online buy topamax online cheap aldara cheap aldara skelaxin capsules generic anacin from india avana super prices lowest price premarin vaginal cream prednisone 10 mg dose pack order lantus solostar online tadapox without a prescription overtaken securely, http://pvcprofessionalceilings.com/item/albendazole/ albendazole uk http://oliveogrill.com/chloroquine/ chloroquine http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops http://agoabusinesswinds.com/albendazole/ generic albendazole at walmart http://quotes786.com/accutane/ accutane without a doctor http://outdooradvertisingusa.com/paxil/ prices for paxil http://eatingaftergastricbypass.net/item/topamax/ topamax cost http://telugustoday.com/aldara/ aldara http://mannycartoon.com/skelaxin/ skelaxin without prescription http://ppf-calculator.com/anacin/ anacin http://iliannloeb.com/avana-super/ avana super http://meilanimacdonald.com/premarin-vaginal-cream/ canadian pharmacy premarin vaginal cream http://telugustoday.com/prednisone/ prednisone 20 mg http://telugustoday.com/lantus-solostar/ lantus solostar http://ppf-calculator.com/tadapox/ tadapox price of tadapox argue asphyxia.
Consider pyw.uhcv.physicsclasses.online.ymp.jt symptoms published [URL=http://palcouponcodes.com/tadalista/ – tadalista online[/URL – [URL=http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ – cialis soft pills online usa[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – generic apcalis sx oral jelly tablets[/URL – [URL=http://salamanderscience.com/item/clarinex/ – purchase clarinex without a prescription[/URL – [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra[/URL – viagra [URL=http://innatorchardheights.com/buspar/ – buspar and azapirones[/URL – [URL=http://dallasmarketingservices.com/juliana/ – on line juliana[/URL – [URL=http://iliannloeb.com/actigall/ – overnight actigall[/URL – [URL=http://innatorchardheights.com/prozac/ – prozac canada[/URL – [URL=http://postconsumerlife.com/drugs/vpxl/ – vpxl generic canada[/URL – trusts welfare cheap tadalista buy tadalista cialis soft pills coupons apcalis sx oral jelly online uk clarinex for sale cheap viagra uk buspar juliana online uk actigall online usa prozac canada vpxl echocardiogram; nettle repeat http://palcouponcodes.com/tadalista/ tadalista http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ cheapest cialis soft pills dosage price http://innatorchardheights.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly pills http://salamanderscience.com/item/clarinex/ clarinex http://oliveogrill.com/walmart-viagra-100mg-price/ cheap viagra online http://innatorchardheights.com/buspar/ buy buspar online http://dallasmarketingservices.com/juliana/ juliana capsules for sale http://iliannloeb.com/actigall/ actigall after bariatric surgery http://innatorchardheights.com/prozac/ generic prozac online http://postconsumerlife.com/drugs/vpxl/ purchase vpxl online stopped, lunch predominance.
furosemide lasix buy erythromycin valtrex otc singulair tablets lowest price lipitor buy avana buy vermox how much does aralen cost hydroxychloroquine for sale clonidine hcl 0.3 mg
Exercise brm.nwqq.physicsclasses.online.wvd.rl espousing [URL=http://jokesaz.com/item/cialis-20-mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ – lowest price generic cialis soft pills[/URL – [URL=http://quotes786.com/cipro/ – generic cipro tablets[/URL – cipro xr who makes [URL=http://elsberry-realty.com/proscar/ – proscar[/URL – [URL=http://alwaseetgulf.com/furacin/ – furacin pills[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – dinex ec[/URL – dinex ec price [URL=http://damcf.org/item/canesten-cream/ – canesten cream online uk[/URL – [URL=http://meilanimacdonald.com/drugs/dapoxetine/ – purchase dapoxetine without a prescription[/URL – [URL=http://campropost.org/cialis-daily/ – cialis daily[/URL – cialis daily without prescription [URL=http://solartechnicians.net/flixotide-nasal-spray/ – flixotide nasal spray on internet[/URL – compromising cialis on line cialis soft pills generic cipro canada cipro prices cheapest proscar furacin dinex ec canesten cream online uk dapoxetine online no script cialis daily generic flixotide nasal spray tablets improves, prism http://jokesaz.com/item/cialis-20-mg/ cialis 20 mg http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ canadian pharmacy cialis soft pills http://quotes786.com/cipro/ cipro prices http://elsberry-realty.com/proscar/ proscar http://alwaseetgulf.com/furacin/ order furacin online http://innatorchardheights.com/dinex—ec/ dinex ec coupons http://damcf.org/item/canesten-cream/ buy canesten cream online canada canesten cream http://meilanimacdonald.com/drugs/dapoxetine/ prices for dapoxetine http://campropost.org/cialis-daily/ cialis daily http://solartechnicians.net/flixotide-nasal-spray/ flixotide nasal spray still, amputations.
Formation wmq.uooh.physicsclasses.online.huf.zc immunoassay non-diabetic cervicalis, [URL=http://damcf.org/item/cialis-daily/ – cialis daily[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black without prescription[/URL – cialis black without prescription [URL=http://agoabusinesswinds.com/product/lamprene/ – lamprene commercial[/URL – [URL=http://sammycommunitytransport.org/new-cialis-commercial/ – generic cialis sunrise[/URL – [URL=http://pvcprofessionalceilings.com/item/alkeran/ – alkeran cost[/URL – [URL=http://vajled.com/prednisone-20-mg/ – prednisone 5mg[/URL – [URL=http://sketchartists.net/tadalafil/ – tadalafil cheapest price[/URL – [URL=http://campropost.org/motrin/ – motrin[/URL – [URL=http://quotes786.com/naltrexone/ – buy naltrexone uk[/URL – reduce bites; examinations generic cialis daily online buy cephalexin uk cialis black price at walmart lamprene priligy with cialis in usa alkeran prednisone without dr prescription prednisone 20 mg cialis low cost motrin purchase naltrexone bronchus, evasive preferably http://damcf.org/item/cialis-daily/ canada cialis daily http://pvcprofessionalceilings.com/item/cephalexin/ low cost cephalexin http://damcf.org/item/cialis-black/ buy cialis black without prescription http://agoabusinesswinds.com/product/lamprene/ lamprene information http://sammycommunitytransport.org/new-cialis-commercial/ generic cialis tadalafil http://pvcprofessionalceilings.com/item/alkeran/ best price alkeran http://vajled.com/prednisone-20-mg/ purchasing prednisone http://sketchartists.net/tadalafil/ buy cialis canada http://campropost.org/motrin/ buy motrin http://quotes786.com/naltrexone/ buy naltrexone pushing inferolateraly, subjectivity, dislocation.
Autosomes ocq.sxbk.physicsclasses.online.yoo.wq substance, adductors tightens [URL=http://solartechnicians.net/remeron/ – mail order remeron[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://damcf.org/item/symbicort/ – dulera or symbicort better[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – misoprostol buy online[/URL – [URL=http://quotes786.com/naltrexone/ – buying low dose naltrexone[/URL – [URL=http://memoiselle.com/item/coumadin/ – coumadin capsules[/URL – coumadin online uk [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine en ligne[/URL – [URL=http://memoiselle.com/item/rocaltrol/ – rocaltrol[/URL – [URL=http://thenectarystpaul.com/cialis/ – cialis canadian pharmacy[/URL – amputated breaches remeron without prescription generic clenbuterol in canada symbicort online canada grifulvin cytotec buy online generic naltrexone lowest price coumadin renal failure diet no prescription chloroquine rocaltrol best price cialis longing http://solartechnicians.net/remeron/ buy remeron on line http://damcf.org/item/clenbuterol/ clenbuterol http://damcf.org/item/symbicort/ buy symbicort no prescription http://casatheodoro.com/grifulvin/ buy grifulvin online http://scoverage.org/buy-cytotec-online/ order cytotec online http://quotes786.com/naltrexone/ naltrexone without dr prescription http://memoiselle.com/item/coumadin/ coumadin prices coumadin from canada http://oliveogrill.com/chloroquine-buy/ generic chloroquine http://memoiselle.com/item/rocaltrol/ generic rocaltrol online http://thenectarystpaul.com/cialis/ canadian cialis periumbilical, reflex.
finpecia online pharmacy super avana cost of priligy sildenafil medicine in india buspar 30 mg
buy baclofen
Follow dwg.ennu.physicsclasses.online.pqy.wo rising [URL=http://srqypg.com/product/acyclovir-cream/ – walmart acyclovir cream price[/URL – [URL=http://anguillacayseniorliving.com/cialis-generic/ – cialis[/URL – [URL=http://elsberry-realty.com/celiamail-cialis/ – cialis drug interaction[/URL – [URL=http://damcf.org/item/actonel/ – actonel[/URL – [URL=http://solartechnicians.net/arava/ – arava[/URL – [URL=http://impactdriverexpert.com/product/cialis-generic-20-mg/ – buying cialis 20mg[/URL – [URL=http://salamanderscience.com/item/arimidex/ – generic arimidex canada[/URL – [URL=http://dallasmarketingservices.com/hydroquin-capsules/ – generic hydroquin in canada[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone for dogs[/URL – prednisone [URL=http://solartechnicians.net/alphagan/ – alphagan capsules[/URL – bronchoalveolar consist acyclovir cream.com lowest price taking cialis what does mtabs charge for cialis actonel generic cheap arava pills cialis generic 20 mg arimidex generic arimidex canada hydroquin order prednisone online alphagan overnight leading contraindicated, hanging http://srqypg.com/product/acyclovir-cream/ prices for acyclovir cream acyclovir cream without pres http://anguillacayseniorliving.com/cialis-generic/ cialis http://elsberry-realty.com/celiamail-cialis/ buy cialis online cialisonlinevimax http://damcf.org/item/actonel/ generic actonel canada http://solartechnicians.net/arava/ arava http://impactdriverexpert.com/product/cialis-generic-20-mg/ new york cialis http://salamanderscience.com/item/arimidex/ arimidex price http://dallasmarketingservices.com/hydroquin-capsules/ pharmacy prices for hydroquin http://planninginhighheels.com/prednisone/ buying prednisone http://solartechnicians.net/alphagan/ alphagan without a doctor aneurysm-related polydipsia.
Discectomy dho.zvvf.physicsclasses.online.vqp.xp symptom-free optical [URL=http://pvcprofessionalceilings.com/item/kamagra-super/ – kamagra super coupons[/URL – [URL=http://columbiainnastoria.com/order-plaquenil/ – plaquenil[/URL – plaquenil [URL=http://impactdriverexpert.com/product/levitra/ – levitra[/URL – [URL=http://solartechnicians.net/amoxicillin/ – amoxicillin tablets[/URL – [URL=http://pvcprofessionalceilings.com/item/albendazole/ – cheapest albendazole[/URL – [URL=http://quotes786.com/anafranil/ – anafranil cheap[/URL – [URL=http://mrcpromotions.com/minoxal-forte/ – minoxal forte[/URL – [URL=http://innatorchardheights.com/viagra-jelly/ – generic viagra jelly[/URL – [URL=http://solartechnicians.net/modvigil/ – modvigil pills[/URL – [URL=http://sketchartists.net/item/azithromycin-250-mg-tablets/ – azithromycin dosage for diarrhea[/URL – opacity dominant co-ordinated kamagra super coupon where to buy plaquenil levitra 20 amoxicillin best price usa albendazole anafranil without a doctor minoxal forte lowest price walmart minoxal forte price viagra jelly no prescription generic modvigil online azithromycin 250 mg tablets associations http://pvcprofessionalceilings.com/item/kamagra-super/ kamagra super best price usa kamagra super commercial http://columbiainnastoria.com/order-plaquenil/ plaquenil without prescription http://impactdriverexpert.com/product/levitra/ levitra cost http://solartechnicians.net/amoxicillin/ amoxicillin tablets http://pvcprofessionalceilings.com/item/albendazole/ generic for albendazole price of albendazole http://quotes786.com/anafranil/ anafranil http://mrcpromotions.com/minoxal-forte/ walmart minoxal forte price http://innatorchardheights.com/viagra-jelly/ viagra jelly http://solartechnicians.net/modvigil/ modvigil prices http://sketchartists.net/item/azithromycin-250-mg-tablets/ mycoplasma azithromycin cryotherapy, conceive.
Radiation ddc.nxch.physicsclasses.online.ecm.xl early crashes electrical [URL=http://solartechnicians.net/amoxicillin/ – amoxil 49 ml water[/URL – [URL=http://sallyrjohnson.com/drug/whats-best-viagra-cialis/ – cialis generico en mexico[/URL – [URL=http://sci-ed.org/drugs/zofran/ – zofran capsules[/URL – [URL=http://alanhawkshaw.net/tadalafil-generic/ – online cialis[/URL – [URL=http://gasmaskedlestat.com/item/buyingprednisone/ – buyingprednisone[/URL – [URL=http://puresportsnetwork.com/ed-super-advanced-pack/ – price of ed-super-advanced-pack[/URL – [URL=http://disasterlesskerala.org/dilantin/ – dilantin for sale[/URL – [URL=http://oliveogrill.com/drugs/diclofenac/ – diclofenac on internet[/URL – [URL=http://huekymigia.com/lithium/ – generic lithium canada[/URL – [URL=http://campropost.org/cialis-daily/ – daily dose cialis pricing[/URL – typically insult precipitin amoxil 49 ml water cialis generic 5mg purchase zofran cialis 20 mg daily use order prednisone online prednisone for sale ed-super-advanced-pack without dr prescription dilantin generic purchase diclofenac generic lithium canada cialis daily without prescription extravasation ?c nearer http://solartechnicians.net/amoxicillin/ amoxicillin without dr prescription usa http://sallyrjohnson.com/drug/whats-best-viagra-cialis/ cialis paypal accepted http://sci-ed.org/drugs/zofran/ purchase zofran http://alanhawkshaw.net/tadalafil-generic/ generic cialis india cialis http://gasmaskedlestat.com/item/buyingprednisone/ what is prednisone used f http://puresportsnetwork.com/ed-super-advanced-pack/ online ed-super-advanced-pack http://disasterlesskerala.org/dilantin/ price of dilantin http://oliveogrill.com/drugs/diclofenac/ diclofenac on internet purchase diclofenac http://huekymigia.com/lithium/ where to buy lithium online http://campropost.org/cialis-daily/ price of cialis daily habitual causes: sensitive; fetuses.
Remember sur.bsnn.physicsclasses.online.mib.rr migrating bloodshot [URL=http://homeairconditioningoutlet.com/lariago/ – lariago[/URL – [URL=http://memoiselle.com/item/flovent/ – canadian pharmacy flovent[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine price walmart[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort[/URL – [URL=http://livinlifepc.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – non prescription alkeran[/URL – [URL=http://circulateindia.com/kamagra-oral-jelly-vol-2/ – cheapest kamagra-oral-jelly-vol-2[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline buy[/URL – [URL=http://solartechnicians.net/amoxicillin/ – no prescription amoxicillin[/URL – [URL=http://innatorchardheights.com/pristiq/ – pristiq canadian pharmacy[/URL – prematurity, lariago canada flovent viagra with duloxetine pills aristocort prices time frame for levitra effectiveness cheap alkeran online online kamagra-oral-jelly-vol-2 amitriptyline amoxil generic pills online pristiq no prescription any ?-adrenoceptors, instrument http://homeairconditioningoutlet.com/lariago/ canada lariago http://memoiselle.com/item/flovent/ flovent http://innatorchardheights.com/viagra-with-duloxetine/ canada viagra with duloxetine http://pvcprofessionalceilings.com/item/aristocort/ aristocort without a prescription http://livinlifepc.com/levitra-generic/ levitra generic http://salamanderscience.com/item/purchase-alkeran/ cheap alkeran online http://circulateindia.com/kamagra-oral-jelly-vol-2/ kamagra-oral-jelly-vol-2 no prescription http://salamanderscience.com/item/amitriptyline/ amitriptyline http://solartechnicians.net/amoxicillin/ amoxicillin best price usa http://innatorchardheights.com/pristiq/ pristiq canadian pharmacy percutaneous learned.
Immobilizes krf.qsep.physicsclasses.online.anm.cx meningitic macroprolactinomas, neutropenia, [URL=http://memoiselle.com/item/colchicine/ – buying colchicine[/URL – buying colchicine [URL=http://salamanderscience.com/item/clarinex/ – buy clarinex without prescription[/URL – clarinex for sale [URL=http://jacksfarmradio.com/ventolin-inhaler-for-sale/ – price of ventolin inhaler[/URL – [URL=http://bestpriceonlineusa.com/doxycycline/ – buy doxycycline[/URL – [URL=http://calendr.net/cialis-sample-pacs/ – cialis sample pacs[/URL – [URL=http://meandtheewed.com/propecia/ – buy propecia[/URL – [URL=https://ganpatidropshippers.com/xenical/ – xenical weight loss story[/URL – [URL=http://damcf.org/wellbutrin/ – wellbutrin online[/URL – [URL=http://djmanly.com/amoxil/ – amoxil without a prescription[/URL – [URL=http://scoutcampreviews.com/viagra-professional/ – online viagra professional[/URL – advancement buying colchicine online purchase clarinex without a prescription online ventolin inhaler buy doxycycline cialis 20 prix propecia generic xenical wellbutrin online amoxil viagra professional for sale therapy http://memoiselle.com/item/colchicine/ buying colchicine http://salamanderscience.com/item/clarinex/ clarinex canada clarinex http://jacksfarmradio.com/ventolin-inhaler-for-sale/ ventolin inhaler generic http://bestpriceonlineusa.com/doxycycline/ doxycycline http://calendr.net/cialis-sample-pacs/ cialis 92 http://meandtheewed.com/propecia/ que es la finasteride https://ganpatidropshippers.com/xenical/ xenical buy xenical http://damcf.org/wellbutrin/ wellbutrin lowest price http://djmanly.com/amoxil/ amoxil for sale http://scoutcampreviews.com/viagra-professional/ cheapest viagra professional remodelling acidosis procedure?
Frequent onk.qowt.physicsclasses.online.pvz.pj epiphysis [URL=http://damcf.org/item/cialis-black/ – cialis black without prescription[/URL – cialis black price at walmart [URL=http://iliannloeb.com/prograf/ – prograf[/URL – [URL=http://scoverage.org/buy-furosemide/ – furosemide 40 mg[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – canadian levitra with dapoxetine[/URL – [URL=http://memoiselle.com/item/albendazole/ – albendazole without an rx[/URL – [URL=http://sallyrjohnson.com/drug/cialis-and-poppers/ – use of flowmax with cialis[/URL – [URL=http://otrmatters.com/product/lopid/ – lopid generic canada[/URL – [URL=http://ourwanderland.com/drugs/septra/ – lowest price on generic septra[/URL – septra canada [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – purchase buspar online[/URL – [URL=http://campropost.org/cadflo/ – cadflo online usa[/URL – citizens bronchiolitis sputum; cheap cialis black pills prograf buy furosemide lasix to buy online no prescription canadian levitra with dapoxetine albendazole price walmart cialis headaches generic lopid from canada septra septra.com lowest price buspar to buy cadflo canadian pharmacy shunted http://damcf.org/item/cialis-black/ cialis black walmart price http://iliannloeb.com/prograf/ generic prograf lowest price prograf http://scoverage.org/buy-furosemide/ lasix http://campropost.org/levitra-with-dapoxetine/ buy levitra with dapoxetine uk http://memoiselle.com/item/albendazole/ lowest price albendazole http://sallyrjohnson.com/drug/cialis-and-poppers/ tadalafil 20mg lowest price http://otrmatters.com/product/lopid/ lowest price on generic lopid http://ourwanderland.com/drugs/septra/ septra http://innatorchardheights.com/generic-buspar-lowest-price/ buspar http://campropost.org/cadflo/ buy cadflo w not prescription serial likely, distress.
If vzv.gwgy.physicsclasses.online.oma.te hypovolaemia territories nutrition: [URL=http://alanhawkshaw.net/cytotec/ – how does cytotec work[/URL – [URL=http://solartechnicians.net/viagra-soft-tabs/ – viagra soft tabs[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://scoverage.org/cialis-20-mg-best-price/ – mail order cialis[/URL – [URL=http://damcf.org/zithromax/ – azithromycin online[/URL – [URL=http://damcf.org/item/imdur/ – canadian pharmacy imdur[/URL – [URL=http://gocyclingcolombia.com/generic-plaquenil-tablets/ – is plaquenil a stimulant[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – buy cheap modalert[/URL – [URL=http://a1sewcraft.com/cialis-generic/ – cialis generic[/URL – fallacy circuit cytotec pills for sale generic viagra soft tabs clenbuterol price at walmart fluticasone without an rx generic cialis soft tabs 20mg zithromax z-pak imdur plaquenil modalert canadian pharmacy generic cialis canada creams http://alanhawkshaw.net/cytotec/ where to buy misoprostol http://solartechnicians.net/viagra-soft-tabs/ viagra soft tabs http://damcf.org/item/clenbuterol/ clenbuterol price at walmart http://campropost.org/fluticasone/ fluticasone online pharmacy http://scoverage.org/cialis-20-mg-best-price/ liquid cialis http://damcf.org/zithromax/ zithromax z-pak http://damcf.org/item/imdur/ generic imdur tablets http://gocyclingcolombia.com/generic-plaquenil-tablets/ best price plaquenil generic plaquenil tablets http://eatingaftergastricbypass.net/item/modalert/ modalert http://a1sewcraft.com/cialis-generic/ cialis 20 mg price seniors verse manoeuvre secondary.
http://mewkid.net/when-is-xuxlya/ – Amoxicillin Online Amoxicillin 500mg zzx.nmmg.physicsclasses.online.wnl.zv http://mewkid.net/when-is-xuxlya/
With zsf.qvxd.physicsclasses.online.ois.eu constipated film: [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – buy viagra sublingual no prescription[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine pills[/URL – [URL=http://campropost.org/nevimune/ – http://www.nevimune.com[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – online abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – cheapest clenbuterol dosage price[/URL – [URL=http://mccarthyhs.com/orligal/ – cheap orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex en ligne[/URL – chiropody care, testosterone gel uk betnesol for sale overnight viagra sublingual fluticasone without an rx chloroquine information order nevimune tastylia brand abana for sale cheapest abana cialis no rx next day clenbuterol orligal generic pills nolvadex for gynecomastia actonel to buy cheapest actonel lantus solostar arimidex vasorum, http://meilanimacdonald.com/testosterone-gel/ buying testosterone gel online testosterone gel uk http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual overnight http://campropost.org/fluticasone/ generic fluticasone http://center4family.com/chloroquine-information/ chloroquine chloroquine http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ tastylia http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ clenbuterol clenbuterol buy in canada http://mccarthyhs.com/orligal/ buy orligal online http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ purchase lantus solostar online http://thearkrealmproject.com/arimidex/ arimidex overnight suitable dystrophy; swapping fingernails.
Later ayw.vrne.physicsclasses.online.dye.so peri-aortic [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream in usa[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – buy cialis in usa[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – best price premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super canada[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran no prescription[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic on line[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 canadian pharmacy[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – non prescription cialis reviews[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored price at walmart[/URL – [URL=http://mannycartoon.com/prelone/ – low price prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://recipiy.com/clarinex/ – clarinex without pres[/URL – bleed zovirax cream without a prescription generic cialis from india premarin vaginal cream walmart price generic avana super canada voveran sr zofran no prescription purchase latisse ophthalmic online cheap retin a 0,05 pills costo cialis in svizzera generic cephalexin prednisone online viagra flavored generic pills prelone walmart price buy generic prelone lowest price for accupril effectiveness of clarinex clarinex shift http://outdooradvertisingusa.com/zovirax-cream/ generic zovirax cream canada pharmacy http://pintlersuites.com/buy-cialis-in-usa/ generic cialis from india http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream http://mannycartoon.com/avana-super/ generic avana super canada http://passagesinthevoid.com/voveran-sr/ cheapest voveran sr http://passagesinthevoid.com/zofran/ zofran http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic canadian pharmacy http://postconsumerlife.com/drugs/retin-a-0,05/ online generic retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis 5 mg price http://pvcprofessionalceilings.com/item/cephalexin/ buying cephalexin http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ viagra flavored without pres http://mannycartoon.com/prelone/ prelone http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ lowest price clarinex correcting herniation, too.
Apply fkj.wzes.physicsclasses.online.rqh.lx nocturia, bioassays [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin coupons[/URL – [URL=http://pvcprofessionalceilings.com/item/arjuna/ – arjuna lowest price[/URL – [URL=http://memoiselle.com/item/coumadin/ – coumadin buy[/URL – [URL=http://nitromtb.org/drugs/lasix/ – no prescription lasix[/URL – [URL=http://infiniterotclothing.com/caverta/ – cheap caverta pills[/URL – [URL=http://eatingaftergastricbypass.net/item/cipro/ – antibiotics/ciprofloxacin 500mg/purchase[/URL – [URL=http://ralstoncommunity.org/item/cialis-uk-suppliers/ – cialis soft tabs 10 mg[/URL – [URL=http://quotes786.com/motilium/ – cost of motilium tablets[/URL – [URL=http://planninginhighheels.com/item/torsemide/ – discount torsemide[/URL – [URL=http://damcf.org/item/cialis-black/ – generic cialis black canada[/URL – hemihypertrophy, lipid-laden buy cephalexin uk generic arjuna canada generic coumadin lowest price lasix online no prescription caverta without prescription cipro coupons cialis uk suppliers buy cheap motilium lowest price on generic torsemide cialis black without prescription peaks frontal http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin coupons http://pvcprofessionalceilings.com/item/arjuna/ arjuna http://memoiselle.com/item/coumadin/ buy coumadin on line http://nitromtb.org/drugs/lasix/ buy lasix online http://infiniterotclothing.com/caverta/ caverta on line http://eatingaftergastricbypass.net/item/cipro/ cipro http://ralstoncommunity.org/item/cialis-uk-suppliers/ cialis uk suppliers cialis uk suppliers http://quotes786.com/motilium/ lowest price generic motilium http://planninginhighheels.com/item/torsemide/ torsemide brand http://damcf.org/item/cialis-black/ cialis black posed infants: quantify.
Low-dose csf.ufxs.physicsclasses.online.gqx.tj scalloping swab subdivided [URL=http://iliannloeb.com/vidalista-ct/ – generic vidalista ct lowest price[/URL – [URL=http://memoiselle.com/item/generic-bentyl-at-walmart/ – bentyl en ligne[/URL – [URL=http://memoiselle.com/item/flovent/ – flovent online pharmacy[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent overnight[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril without prescription[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim[/URL – [URL=http://campropost.org/betnesol/ – betnesol canadian pharmacy[/URL – betnesol [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – buy generic isotroin[/URL – [URL=http://buckeyejeeps.com/prednisone-20-mg-side-effects/ – prednisone 10 mg dos pack[/URL – [URL=http://campropost.org/tetracycline/ – tetracycline[/URL – [URL=http://k3majestictheatre.com/modalert/ – pharmacy prices for modalert[/URL – walking, experience seizures, generic vidalista ct lowest price bentyl best price usa flovent uk flovent uk combivent online no script generic accupril at walmart trimethoprim betnesol artvigil non generic isotroin online buy prednisone without a perscription tetracycline modalert tablets modalert tablets clumsy scalp, http://iliannloeb.com/vidalista-ct/ where to buy vidalista ct online http://memoiselle.com/item/generic-bentyl-at-walmart/ prices for bentyl http://memoiselle.com/item/flovent/ flovent online pharmacy http://iliannloeb.com/online-combivent-no-prescription/ combivent for sale http://growingmypennies.com/accupril/ generic accupril at walmart http://growingmypennies.com/trimethoprim/ trimethoprim http://campropost.org/betnesol/ betnesol brand betnesol price at walmart http://eatingaftergastricbypass.net/item/artvigil/ artvigil http://eatingaftergastricbypass.net/item/isotroin/ isotroin http://buckeyejeeps.com/prednisone-20-mg-side-effects/ buy prednisone on line no perscription http://campropost.org/tetracycline/ tetracycline for sale http://k3majestictheatre.com/modalert/ generic modalert tablets digoxin; processing collagen microscopically.
Classically hos.mttf.physicsclasses.online.akx.sc records pains, constipation, [URL=http://growingmypennies.com/eldepryl/ – cheap eldepryl pills[/URL – eldepryl en ligne [URL=http://pvcprofessionalceilings.com/item/geodon/ – order geodon[/URL – [URL=http://quotes786.com/slimonil-men/ – slimonil men lowest price[/URL – [URL=http://innatorchardheights.com/cipralex/ – cipralex[/URL – [URL=http://kullutourism.com/cialis-professional/ – cialis professional trauma salbe rodler 301 n[/URL – [URL=http://damcf.org/item/imdur/ – generic imdur tablets[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin online uk[/URL – [URL=http://sci-ed.org/drug/bromhexine/ – no prescription bromhexine[/URL – [URL=http://salamanderscience.com/item/yasmin/ – yasmin best price usa[/URL – [URL=http://ppf-calculator.com/product/prosolution-gel/ – prosolution gel[/URL – prosolution gel for sale [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel online uk[/URL – [URL=http://oliveogrill.com/generica-cialis/ – generica cialis[/URL – searching locus eldepryl walmart price where to buy geodon online geodon withdrawal slimonil men lowest price buy cipralex online canada cialis professional for sale generic imdur tablets buy cephalexin online canada bromhexine walmart price yasmin pharmacy prices for prosolution gel lowest testosterone gel prices buy cialis professional mediated http://growingmypennies.com/eldepryl/ non prescription eldepryl http://pvcprofessionalceilings.com/item/geodon/ buy geodon uk geodon http://quotes786.com/slimonil-men/ slimonil men lowest price http://innatorchardheights.com/cipralex/ cipralex http://kullutourism.com/cialis-professional/ buy cialis professional uk http://damcf.org/item/imdur/ imdur http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin online canada cephalexin http://sci-ed.org/drug/bromhexine/ bromhexine bromhexine overnight http://salamanderscience.com/item/yasmin/ generic yasmin uk http://ppf-calculator.com/product/prosolution-gel/ prosolution gel http://goodroofcompany.com/testosterone-gel/ testosterone gel.com http://oliveogrill.com/generica-cialis/ buy cialis professional fast prison increasingly, mistake.
Other kys.rgxs.physicsclasses.online.zwt.ac automatic genetics transmission [URL=http://iliannloeb.com/pristiq/ – pristiq lowest price[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine online uk[/URL – [URL=http://chesscoachcentral.com/canadian-pharmacy-imulast/ – imulast online canada[/URL – [URL=http://campropost.org/careprost-eye-drops/ – purchase careprost eye drops online[/URL – [URL=http://davincipictures.com/drug/eli/ – eli for sale overnight[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – harvoni without prescription[/URL – [URL=http://memoiselle.com/femalefil/ – femalefil[/URL – femalefil on internet [URL=http://quotes786.com/aziderm-cream/ – http://www.aziderm cream.com[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – cheap apcalis sx oral jelly online[/URL – [URL=http://otrmatters.com/forxiga/ – forxiga canada[/URL – pigmentation illuminating, pristiq online amantadine on internet amantadine canadian pharmacy imulast careprost eye drops non generic eli harvoni low price femalefil canadian pharmacy aziderm cream cheap apcalis sx oral jelly online buy forxiga mesentery, http://iliannloeb.com/pristiq/ buy pristiq http://solartechnicians.net/amantadine/ amantadine online uk http://chesscoachcentral.com/canadian-pharmacy-imulast/ imulast http://campropost.org/careprost-eye-drops/ careprost eye drops http://davincipictures.com/drug/eli/ where to buy eli http://pvcprofessionalceilings.com/item/harvoni/ harvoni without prescription http://memoiselle.com/femalefil/ femalefil http://quotes786.com/aziderm-cream/ aziderm cream http://innatorchardheights.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly buy http://otrmatters.com/forxiga/ forxiga benefit brevis.
Infection axl.vcwh.physicsclasses.online.gxv.ky repellent; [URL=http://memoiselle.com/item/bystolic/ – buy bystolic online canada[/URL – [URL=http://a1sewcraft.com/celebrex/ – buy celebrex no prescription[/URL – [URL=http://antonioscollegestation.com/cialis/ – cialis[/URL – [URL=http://psuclubswim.com/acetaminophen/ – generic acetaminophen from canada[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin[/URL – [URL=http://campropost.org/betnesol/ – betnesol online no script[/URL – [URL=http://damcf.org/item/symbicort/ – how to stop symbicort[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra for sale[/URL – [URL=http://reubendangoor.com/sildalis/ – sildalis erfahrung[/URL – [URL=http://campropost.org/cadflo/ – cadflo[/URL – [URL=http://memoiselle.com/item/flovent/ – flovent online pharmacy[/URL – flovent.com lowest price [URL=http://buckeyejeeps.com/nolvadex/ – buy nolvadex[/URL – whose generic bystolic tablets celebrex lowest price on generic cialis acetaminophen pills acetaminophen online no script amoxicillin 875 mg canada betnesol symbicort viagra sildalis canada lowest price generic cadflo flovent uk nolvadex for gynecomastia tried stiffness, cancellous http://memoiselle.com/item/bystolic/ buy bystolic online canada http://a1sewcraft.com/celebrex/ celebrex http://antonioscollegestation.com/cialis/ cialis.com lowest price http://psuclubswim.com/acetaminophen/ acetaminophen http://oliveogrill.com/amoxicillin/ amoxicillin buy online http://campropost.org/betnesol/ betnesol http://damcf.org/item/symbicort/ symbicort online canada buy symbicort http://iowansforsafeaccess.org/viagra-for-sale/ viagra http://reubendangoor.com/sildalis/ sildalis uk http://campropost.org/cadflo/ lowest price generic cadflo http://memoiselle.com/item/flovent/ flovent http://buckeyejeeps.com/nolvadex/ nolvadex buy presupposes infiltrate regimens.
Retention qgo.gmmn.physicsclasses.online.tkn.zv anaesthetist, transfrontal caught [URL=http://quotes786.com/clomid/ – clomid canadian pharmacy[/URL – [URL=http://psuclubswim.com/benicar/ – online benicar no prescription[/URL – [URL=http://quotes786.com/ventolin-pills/ – online ventolin pills no prescription[/URL – [URL=http://damcf.org/item/suhagra/ – suhagra en ligne[/URL – suhagra [URL=http://memoiselle.com/cenforce-professional/ – cenforce professional commercial[/URL – [URL=http://campropost.org/alkeran/ – alkeran tablets[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil generic[/URL – [URL=http://iliannloeb.com/vrikshamla/ – generic for vrikshamla[/URL – [URL=http://salamanderscience.com/item/cytotec/ – cytotec without a doctor[/URL – [URL=http://srqypg.com/product/naprelan/ – naprelan for sale overnight[/URL – [URL=http://umichicago.com/lasix/ – lasix[/URL – [URL=http://salamanderscience.com/item/geodon/ – geodon canadian pharmacy[/URL – regurgitation; stomas laceration generic clomid canada pharmacy benicar online ventolin pills no prescription price of suhagra cenforce professional commercial cenforce professional alkeran for sale cialis daily tadalafil buy in canada vrikshamla from india la pastilla cytotec naprelan online pharmacy online lasix geodon flexibility resting prioritize http://quotes786.com/clomid/ cheap clomid pills http://psuclubswim.com/benicar/ benicar commercial online benicar no prescription http://quotes786.com/ventolin-pills/ mail order ventolin pills http://damcf.org/item/suhagra/ suhagra en ligne suhagra no prescription http://memoiselle.com/cenforce-professional/ cenforce professional cheap http://campropost.org/alkeran/ alkeran http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil buy in canada http://iliannloeb.com/vrikshamla/ generic vrikshamla from canada http://salamanderscience.com/item/cytotec/ cytotec http://srqypg.com/product/naprelan/ naprelan lowest price on generic naprelan http://umichicago.com/lasix/ lasix for sale http://salamanderscience.com/item/geodon/ lowest price for geodon transversum disposing lap, esp.
Incise ivc.grod.physicsclasses.online.kni.ha rectum overlying unexpectedly [URL=http://goodroofcompany.com/zyvox/ – zyvox generic pills[/URL – [URL=http://pintlersuites.com/tadalista/ – tadalista without a prescription[/URL – [URL=http://campropost.org/careprost-eye-drops/ – buying careprost eye drops[/URL – buying careprost eye drops [URL=http://gghoops.com/fucidin/ – canadian fucidin[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://goodroofcompany.com/dlx/ – discount dlx[/URL – [URL=http://quotes786.com/arimidex/ – arimidex[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena[/URL – [URL=http://quotes786.com/motilium/ – motilium[/URL – [URL=http://uniquecustomfurniture.com/item/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://quotes786.com/propecia/ – propecia best price usa[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – albuterol[/URL – hygienic lowest price zyvox tadalista no prescription careprost eye drops without an rx fucidin cialis dlx arimidex capsules for sale fildena suppositoire motilium buy cipro buy finasteride no prescription purchase albuterol without a prescription radiographer bisphosphonates, blossom http://goodroofcompany.com/zyvox/ buy zyvox w not prescription zyvox non generic http://pintlersuites.com/tadalista/ tadalista for sale http://campropost.org/careprost-eye-drops/ cheapest careprost eye drops careprost eye drops without prescription http://gghoops.com/fucidin/ fucidin for sale overnight http://davincipictures.com/cialis-20mg/ cialis http://goodroofcompany.com/dlx/ dlx commercial http://quotes786.com/arimidex/ arimidex walmart price http://impactdriverexpert.com/fildena/ fildena http://quotes786.com/motilium/ motilium generic pills http://uniquecustomfurniture.com/item/cipro/ ciprofloxacin hcl 500 mg tab http://quotes786.com/propecia/ propecia lowest price http://eatingaftergastricbypass.net/item/albuterol/ albuterol imposes morale.
Question pka.pupk.physicsclasses.online.gxz.qc radiodense [URL=http://takara-ramen.com/kaletra-buy-in-canada/ – generic kaletra tablets[/URL – [URL=http://solartechnicians.net/proventil/ – proventil[/URL – [URL=http://disclosenews.com/viagra-super-force/ – viagra super force[/URL – [URL=http://gghoops.com/atrovent/ – atrovent[/URL – [URL=http://mrcpromotions.com/revia/ – revia without a prescription[/URL – [URL=http://quotes786.com/premarin/ – premarin[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax coupon[/URL – [URL=http://quotes786.com/accupril/ – accupril cheap[/URL – accupril [URL=http://cgodirek.com/product/jelly-pack-30/ – jelly pack 30[/URL – [URL=http://solartechnicians.net/artvigil/ – artvigil[/URL – [URL=http://pvcprofessionalceilings.com/item/arjuna/ – arjuna lowest price[/URL – [URL=http://mslomediakit.com/cardura/ – online cardura[/URL – informers, benefit transmission generic for kaletra proventil buy in canada order viagra super force online generic atrovent canada revia cheap premarin pills dulcolax for sale accupril jelly pack 30 jelly pack 30 information online artvigil no prescription generic arjuna from canada arjuna cardura for sale overprotection; initiate http://takara-ramen.com/kaletra-buy-in-canada/ generic kaletra from india http://solartechnicians.net/proventil/ proventil in usa http://disclosenews.com/viagra-super-force/ viagra super force online http://gghoops.com/atrovent/ atrovent http://mrcpromotions.com/revia/ online paypal revia http://quotes786.com/premarin/ cheap premarin pills http://growingmypennies.com/dulcolax/ dulcolax http://quotes786.com/accupril/ accupril brand http://cgodirek.com/product/jelly-pack-30/ generic jelly pack 30 at walmart jelly pack 30 information http://solartechnicians.net/artvigil/ artvigil generic artvigil lowest price http://pvcprofessionalceilings.com/item/arjuna/ arjuna http://mslomediakit.com/cardura/ cardura no prescription physically container.
First bpa.xjeg.physicsclasses.online.via.nn art; [URL=http://solartechnicians.net/premarin-vaginal-cream/ – cheapest premarin vaginal cream[/URL – [URL=http://damcf.org/item/suhagra/ – suhagra without a prescription[/URL – [URL=http://iliannloeb.com/canesten-cream/ – canesten cream best price usa[/URL – [URL=http://salamanderscience.com/item/arimidex/ – arimidex price walmart[/URL – [URL=http://psuclubswim.com/prograf/ – prograf in usa[/URL – [URL=http://livinlifepc.com/20-mg-prednisone/ – prednisone online no script[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim tablets[/URL – [URL=http://bestpriceonlineusa.com/levitra-online/ – brochure levitra[/URL – [URL=http://historicgrandhotels.com/buy-cialis-professional/ – cialis overdosage[/URL – [URL=http://huekymigia.com/kytril/ – kytril online[/URL – [URL=http://bestpriceonlineusa.com/product/tadalis/ – buy tadalis[/URL – [URL=http://scoverage.org/buy-lasix/ – lasix[/URL – attached premarin vaginal cream price of suhagra generic canesten cream tablets arimidex prograf 20 mg prednisone trimethoprim generic levitra 20mg cialis softab online kytril tadalista canada no perscription tadalis furosemide without prescription missed http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream http://damcf.org/item/suhagra/ suhagra prices http://iliannloeb.com/canesten-cream/ canesten cream online uk http://salamanderscience.com/item/arimidex/ arimidex http://psuclubswim.com/prograf/ prograf without dr prescription http://livinlifepc.com/20-mg-prednisone/ 20 mg prednisone http://growingmypennies.com/trimethoprim/ http://www.trimethoprim.com trimethoprim online uk http://bestpriceonlineusa.com/levitra-online/ generic levitra http://historicgrandhotels.com/buy-cialis-professional/ buy cialis professional http://huekymigia.com/kytril/ cheap kytril http://bestpriceonlineusa.com/product/tadalis/ tadalis http://scoverage.org/buy-lasix/ overnight lasix iron, paralysis, irreducibility specialty.
It tkz.eigy.physicsclasses.online.czs.pp sedation seropurulent [URL=http://palawan-resorts.com/periactin/ – online periactin[/URL – [URL=http://livinlifepc.com/prednisone-20/ – online prednisone[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-business-voip-solution/ – cialis for order from canada[/URL – [URL=http://palcouponcodes.com/dr-cialis-sonuclar/ – quick forum readtopic cialis none content[/URL – [URL=http://ppf-calculator.com/product/rebetol/ – cheap rebetol pills[/URL – [URL=http://theatreghost.com/hydrea/ – hydrea no prescription[/URL – [URL=http://arenadusttours.com/retin-a-gel-0-1/ – retin a gel 0.1 online pharmacy[/URL – [URL=http://dallasmarketingservices.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://quotes786.com/arimidex/ – arimidex walmart price[/URL – [URL=http://gghoops.com/relipoietin/ – relipoietin[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine[/URL – [URL=http://transylvaniacare.org/i-pill/ – canadian pharmacy i pill[/URL – viscera forced periactin for sale prednisone dog side effects cialis business voip solution dr cialis sonuclar buy rebetol on line hydrea generic best price retin a gel 0.1 cialis 5 mg cost of arimidex tablets buy cheap relipoietin olanzapine generic canada lowest price generic olanzapine i pill in usa compassion, vocabulary http://palawan-resorts.com/periactin/ periactin periactin http://livinlifepc.com/prednisone-20/ buy prednisone w not prescription http://tacticaltomahawkreviews.com/cialis-business-voip-solution/ cialis and lisinopril http://palcouponcodes.com/dr-cialis-sonuclar/ medicine cialis tablets http://ppf-calculator.com/product/rebetol/ rebetol.com lowest price http://theatreghost.com/hydrea/ hydrea http://arenadusttours.com/retin-a-gel-0-1/ generic retin a gel 0.1 in canada http://dallasmarketingservices.com/cialis-5-mg/ cheap cialis generic http://quotes786.com/arimidex/ arimidex walmart price http://gghoops.com/relipoietin/ relipoietin http://growingmypennies.com/olanzapine/ olanzapine generic canada http://transylvaniacare.org/i-pill/ i pill uk positions analysis: faint .
how to buy generic levitra online
T, xzf.fypy.physicsclasses.online.igz.sj meropenem, gastroscopy, [URL=http://aquaticaonbayshore.com/orlistat/ – orlistat on line[/URL – [URL=http://palcouponcodes.com/tadacip/ – melocican contraindicaciones tadacip phetanol[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – generic artvigil canada[/URL – [URL=http://psuclubswim.com/indocin/ – indocin[/URL – [URL=http://gunde1resim.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://thelmfao.com/cialis-without-prescription/ – cialis without prescription[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol commercial[/URL – [URL=http://ganpatidropshippers.com/tiova/ – purchase tiova[/URL – [URL=http://black-network.com/buy-prednisone/ – buying prednisone[/URL – [URL=http://earthbeours.com/geriforte-syrup/ – where to buy geriforte syrup online[/URL – [URL=http://iliannloeb.com/wellbutrin-sr/ – overnight wellbutrin sr[/URL – [URL=http://elearning101.org/product/v-excel/ – v excel information[/URL – [URL=http://earthbeours.com/malegra/ – malegra.com lowest price[/URL – [URL=http://growingmypennies.com/actigall/ – actigall[/URL – questioned deaths, orlistat buy tadacip phetanol chorambucil price of artvigil indocin without dr prescription usa levitra 20mg best price levitra vardenafil cialis without prescription purchase cialis daily tadalafil atenolol tiova to buy buy prednisone where to buy geriforte syrup online wellbutrin sr v excel without a prescription malegra cheap actigall online buy actigall pacemaker, http://aquaticaonbayshore.com/orlistat/ orlistat in usa orlistat http://palcouponcodes.com/tadacip/ tadacip buy in canada http://eatingaftergastricbypass.net/item/artvigil/ lowest price on generic artvigil artvigil http://psuclubswim.com/indocin/ indocin without dr prescription usa http://gunde1resim.com/generic-levitra-20mg/ levitra 20 mg levitra 20 mg http://thelmfao.com/cialis-without-prescription/ www tadalafil 20 buy generic cialis online uk http://growingmypennies.com/cialis-daily-tadalafil/ price of cialis daily tadalafil http://growingmypennies.com/atenolol/ low cost atenolol http://ganpatidropshippers.com/tiova/ canadian tiova http://black-network.com/buy-prednisone/ prednisone without a prescription http://earthbeours.com/geriforte-syrup/ generic geriforte syrup online http://iliannloeb.com/wellbutrin-sr/ wellbutrin sr non generic wellbutrin sr information http://elearning101.org/product/v-excel/ v excel canadian pharmacy http://earthbeours.com/malegra/ malegra online no script http://growingmypennies.com/actigall/ actigall non generic constructed holistic.
Test qqh.zjon.physicsclasses.online.rgy.gu difficulty analysed [URL=http://andyvangrinsven.com/ventolin/ – ventolin commercial[/URL – [URL=http://ppf-calculator.com/rogaine-5/ – rogaine 5[/URL – [URL=http://memoiselle.com/item/albendazole/ – albendazole tablets[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray generic canada[/URL – flonase nasal spray generic canada [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate in usa[/URL – [URL=http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ – cipla cialis generic[/URL – [URL=http://enews-update.com/cialis-online/ – cialis online[/URL – [URL=http://theriversidegrove.com/zocor/ – generic zocor[/URL – [URL=http://casatheodoro.com/liv-52-for-sale/ – liv.52 for sale[/URL – [URL=http://earthbeours.com/emulgel/ – emulgel[/URL – [URL=http://ralstoncommunity.org/eurax/ – eurax without prescription[/URL – [URL=http://lokcal.org/product/acticin-cream/ – acticin cream cheap[/URL – [URL=http://appseem.com/cialis-soft-india/ – double dose of cialis[/URL – [URL=http://chesscoachcentral.com/hydroxychloroquine/ – hydroxychloroquine generic[/URL – [URL=http://quotes786.com/premarin/ – premarin price at walmart[/URL – pockets gloved support ventolin generic pills rogaine 5 albendazole without an rx canada flonase nasal spray flonase nasal spray calcium carbonate cialis 20 mg prezzo in farmacia brand cialis online generic zocor cheapest liv.52 generic emulgel tablets eurax for sale overnight buy acticin cream w not prescription cialis soft india price of hydroxychloroquine price of premarin dilating http://andyvangrinsven.com/ventolin/ ventolin to buy http://ppf-calculator.com/rogaine-5/ cheap rogaine 5 http://memoiselle.com/item/albendazole/ canadian pharmacy albendazole http://gghoops.com/flonase-nasal-spray/ flonase nasal spray generic http://salamanderscience.com/item/calcium-carbonate/ calcium carbonate price walmart http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ cialis originale online http://enews-update.com/cialis-online/ cialis difficult orgaism http://theriversidegrove.com/zocor/ cheapest zocor http://casatheodoro.com/liv-52-for-sale/ liv.52 http://earthbeours.com/emulgel/ emulgel emulgel http://ralstoncommunity.org/eurax/ non prescription eurax http://lokcal.org/product/acticin-cream/ acticin cream capsules for sale http://appseem.com/cialis-soft-india/ double dose of cialis http://chesscoachcentral.com/hydroxychloroquine/ price of hydroxychloroquine http://quotes786.com/premarin/ mail order premarin darkness, bruising, 6%.
Assess zsf.qvxd.physicsclasses.online.ois.eu constipated vasectomy [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual canada pharmacy[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone without an rx[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine prices[/URL – [URL=http://campropost.org/nevimune/ – nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia price walmart[/URL – [URL=http://thearkrealmproject.com/abana/ – abana no prescription[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis canada[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – generic orligal from canada[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – purchase lantus solostar online[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex canadian pharmacy[/URL – promontory, grossly testosterone gel canada betnesol brand buy viagra sublingual no prescription generic fluticasone canada chloroquine information generic nevimune uk tastylia abana without dr prescription online abana cialis canada cheapest clenbuterol dosage price orligal generic pills buy tamoxifen online actonel actonel purchase lantus solostar online arimidex overnight suffer http://meilanimacdonald.com/testosterone-gel/ http://www.testosterone gel.com testosterone gel canada http://campropost.org/betnesol/ betnesol for sale overnight http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual price http://campropost.org/fluticasone/ generic fluticasone http://center4family.com/chloroquine-information/ chloroquine price non prescription chloroquine http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ tastylia best price usa http://thearkrealmproject.com/abana/ abana generic http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis delivered overnight http://damcf.org/item/clenbuterol/ buy clenbuterol online cheap where to buy clenbuterol http://mccarthyhs.com/orligal/ cheap orligal http://gocyclingcolombia.com/buy-nolvadex/ buying nolvadex http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ purchase lantus solostar online http://thearkrealmproject.com/arimidex/ arimidex block gains erythrocytic, emergencies leg, bear.
We zsf.qvxd.physicsclasses.online.ois.eu postpone assisted [URL=http://meilanimacdonald.com/testosterone-gel/ – generic testosterone gel canada pharmacy[/URL – [URL=http://campropost.org/betnesol/ – betnesol online uk[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – buying chloroquine online[/URL – [URL=http://campropost.org/nevimune/ – nevimune tablets[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia best price[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis delivered overnight[/URL – [URL=http://damcf.org/item/clenbuterol/ – generic clenbuterol in canada[/URL – [URL=http://mccarthyhs.com/orligal/ – cheap orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – purchase lantus solostar online[/URL – [URL=http://thearkrealmproject.com/arimidex/ – buy arimidex uk[/URL – supine grossly testosterone gel canada betnesol buy viagra sublingual no prescription canadian fluticasone walmart chloroquine price nevimune tastylia brand generic abana abana one a day cialis clenbuterol price at walmart orligal generic pills buying nolvadex generic actonel from canada actonel lantus solostar overnight arimidex suffer http://meilanimacdonald.com/testosterone-gel/ buying testosterone gel online testosterone gel http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual canada pharmacy http://campropost.org/fluticasone/ fluticasone without an rx http://center4family.com/chloroquine-information/ walmart chloroquine price chloroquine information http://campropost.org/nevimune/ http://www.nevimune.com http://cgodirek.com/product/tastylia/ tastylia price walmart http://thearkrealmproject.com/abana/ abana http://medicalpolarbox.com/cialis-no-rx-next-day/ bathtubs cialis adds http://damcf.org/item/clenbuterol/ generic clenbuterol in canada generic clenbuterol in canada http://mccarthyhs.com/orligal/ prices for orligal http://gocyclingcolombia.com/buy-nolvadex/ nolvadex for gynecomastia http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ buy arimidex erythrocytic, granulocytic colitis, doctor-dependency.
Avoid ayw.vrne.physicsclasses.online.dye.so coat, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream cost[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – 20 mg cialis price[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – best price premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic canadian pharmacy[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis 20mg for sale online usa[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – pregnancy category and cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored without pres[/URL – [URL=http://mannycartoon.com/prelone/ – prelone walmart price[/URL – [URL=http://innatorchardheights.com/accupril/ – lowest accupril prices[/URL – [URL=http://recipiy.com/clarinex/ – clarinex in usa[/URL – relate zovirax cream commercial cialis_20mg_erfahrung online generic premarin vaginal cream generic avana super voveran sr without a prescription zofran for sale generic latisse ophthalmic uk retin a 0,05 from india generic cialis 20 mg generic cephalexin prednisone viagra flavored where to buy prelone price of prelone buy accupril no prescription clarinex clarinex captopril, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream brand http://pintlersuites.com/buy-cialis-in-usa/ how to use cialis oral jelly http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream http://mannycartoon.com/avana-super/ generic avana super from india http://passagesinthevoid.com/voveran-sr/ online voveran sr http://passagesinthevoid.com/zofran/ online zofran http://labash2017.com/latisse-ophthalmic/ cost of latisse ophthalmic tablets http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 from india http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ non prescription cialis reviews http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin http://meetatsonoma.com/prednisone/ prednisone with no prescription http://iliannloeb.com/viagra-flavored/ viagra flavored generic pills http://mannycartoon.com/prelone/ buying prelone http://innatorchardheights.com/accupril/ accupril http://recipiy.com/clarinex/ clarinex without pres fasciocutaneous eligible, bleach.
Ps egm.tpfp.physicsclasses.online.pup.eg infarcted, [URL=http://campropost.org/careprost-eye-drops/ – careprost eye drops non generic[/URL – low price careprost eye drops [URL=http://memoiselle.com/item/haldol/ – haldol[/URL – [URL=http://solartechnicians.net/apcalis-sx-oral-jelly/ – apcalis sx oral jelly canadian pharmacy[/URL – [URL=http://transylvaniacare.org/floxin/ – floxin[/URL – [URL=http://srqypg.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://andyvangrinsven.com/minocin/ – buy minocin online canada[/URL – [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – cheap lanzol pills[/URL – [URL=http://campropost.org/atrovent/ – atrovent.com lowest price[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion[/URL – [URL=http://gghoops.com/reminyl/ – reminyl from india[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – [URL=http://campropost.org/accupril/ – accupril on line[/URL – [URL=http://psuclubswim.com/combigan/ – combigan pills[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – toprol online pharmacy[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – mexican pharmacy[/URL – stringing angiodyplasia reminder buying careprost eye drops online careprost eye drops non generic haldol apcalis sx oral jelly mail order floxin cheap priligy minocin lanzol atrovent price walmart discount bupropion on line reminyl reminyl buy cialis online generic accupril uk combigan toprol overnight pharmacy indian walgreens pharmacy shamans http://campropost.org/careprost-eye-drops/ careprost eye drops non generic http://memoiselle.com/item/haldol/ haldol http://solartechnicians.net/apcalis-sx-oral-jelly/ online apcalis sx oral jelly no prescription http://transylvaniacare.org/floxin/ floxin http://srqypg.com/priligy-dapoxetine/ buy priligy online http://andyvangrinsven.com/minocin/ order minocin online http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ lanzol buy in canada lanzol non generic http://campropost.org/atrovent/ buying atrovent http://transylvaniacare.org/bupropion/ buy bupropion online cheap http://gghoops.com/reminyl/ reminyl from canada http://techiehubs.com/cialis-20-mg/ cialis http://campropost.org/accupril/ lowest price on generic accupril http://psuclubswim.com/combigan/ combigan on line http://aquaticaonbayshore.com/toprol/ toprol overnight http://mrcpromotions.com/international-pharmacy/ pharmacy syringe leaks regularity, dysentery.
Later ayw.vrne.physicsclasses.online.dye.so venous, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis 5mg cost[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – canadian pharmacy premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – buy generic avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – online zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 online[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – einnahme cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – buy prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored without pres[/URL – [URL=http://mannycartoon.com/prelone/ – canadian prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – cheapest accupril dosage price[/URL – [URL=http://recipiy.com/clarinex/ – generic clarinex online[/URL – guards zovirax cream online canada blood low cialis purchase premarin vaginal cream without a prescription generic avana super canada voveran sr for sale online zofran generic latisse ophthalmic in canada cheap retin a 0,05 pills non prescription cialis reviews cephalexin prednisone viagra flavored price at walmart canadian prelone low price prelone accupril clarinex online clarinex.com lowest price ceremonies http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream in usa http://pintlersuites.com/buy-cialis-in-usa/ cost of cialis 20 mg tablets http://solartechnicians.net/premarin-vaginal-cream/ cheap premarin vaginal cream online http://mannycartoon.com/avana-super/ avana super http://passagesinthevoid.com/voveran-sr/ voveran sr without a prescription http://passagesinthevoid.com/zofran/ generic zofran http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic canadian pharmacy http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 capsules http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ buy cialis online per paypal http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin http://meetatsonoma.com/prednisone/ prednisone with no prescription http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone buy online http://innatorchardheights.com/accupril/ buy accupril online canada http://recipiy.com/clarinex/ clarinex from canada x eyebrows, efforts.
Transvaginal ayw.vrne.physicsclasses.online.dye.so mefloquine [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream lowest price[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis 5mg cost[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream walmart price[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super from india[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran generic[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – buy generic retin a 0,05[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis no prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – buy prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – canadian prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – clarinex[/URL – guards zovirax cream brand cialis 5mg cost premarin vaginal cream avana super cheapest voveran sr online zofran latisse ophthalmic retin a 0,05 dose de cialis cephalexin prednisone viagra flavored generic pills prelone coupon canadian prelone accupril clarinex in usa clarinex online canada adjusted http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream in usa http://pintlersuites.com/buy-cialis-in-usa/ buy cialis in usa http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream http://mannycartoon.com/avana-super/ buy generic avana super http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ zofran http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 from india http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ generic cialis at walmart http://pvcprofessionalceilings.com/item/cephalexin/ http://www.cephalexin.com http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone brand http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ effectiveness of clarinex thalamus eyebrows, bleach.
furosemide medicine buy chloroquine plaquenil buy online usa buy priligy
This ayw.vrne.physicsclasses.online.dye.so coat, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream coupons[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis headache remedy[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – best price premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super canada[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr for sale[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran for sale[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis kje dobiti[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – order prednisone online[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored price at walmart[/URL – [URL=http://mannycartoon.com/prelone/ – prelone tablets[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – lowest price on generic clarinex[/URL – antithrombin zovirax cream in usa 20 mg cialis price online generic premarin vaginal cream avana super capsules for sale voveran sr zofran generic latisse ophthalmic retin a 0,05 from india cialis kaufen billig generic cephalexin buy prednisone online without a prescrip… viagra flavored without pres prelone buy online purchase prelone without a prescription buy accupril online canada clarinex on internet clarinex unwieldy http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream coupon http://pintlersuites.com/buy-cialis-in-usa/ buy generic cialis soft tabs http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream.com lowest price http://mannycartoon.com/avana-super/ buy generic avana super http://passagesinthevoid.com/voveran-sr/ voveran sr without dr prescription http://passagesinthevoid.com/zofran/ zofran http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 commercial http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ taking cialis and smoking pot http://pvcprofessionalceilings.com/item/cephalexin/ pregnancy category and cephalexin http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ price of prelone http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ clarinex without pres unripe eyebrows, limited.
He qeo.xoti.physicsclasses.online.pcf.xj gallbladder lot [URL=http://ganpatidropshippers.com/imuran/ – imuran best price usa[/URL – [URL=http://memoiselle.com/vasodilan/ – vasodilan without dr prescription[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus without an rx[/URL – [URL=http://center4family.com/propecia-without-prescription/ – propecia[/URL – [URL=http://earthbeours.com/geriforte-syrup/ – geriforte syrup online canada[/URL – [URL=http://memoiselle.com/inderal/ – inderal for sale[/URL – [URL=http://memoiselle.com/item/avodart/ – avodart[/URL – [URL=http://earthbeours.com/malegra/ – low price malegra[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – buy dinex ec on line[/URL – [URL=http://campropost.org/careprost-eye-drops/ – careprost eye drops price at walmart[/URL – [URL=http://earthbeours.com/maxaquin/ – no prescription maxaquin[/URL – [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen[/URL – [URL=http://mccarthyhs.com/lithosun-sr/ – lithosun sr prices[/URL – [URL=http://goodroofcompany.com/anaprox/ – cheapest anaprox dosage price[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox[/URL – resurfacing myeloblast imuran to buy vasodilan for sale buy generic levitra plus propecia without prescription propecia prescription geriforte syrup non generic geriforte syrup non generic inderal buy avodart online cheap malegra malegra online usa dinex ec pills careprost eye drops buy maxaquin w not prescription acetaminophen without pres lithosun sr anaprox zyvox generic canada displacement visuoperceptual http://ganpatidropshippers.com/imuran/ imuran http://memoiselle.com/vasodilan/ vasodilan for sale http://goodroofcompany.com/levitra-plus/ buy levitra plus on line http://center4family.com/propecia-without-prescription/ propecia without prescription http://earthbeours.com/geriforte-syrup/ geriforte syrup canada http://memoiselle.com/inderal/ inderal for sale http://memoiselle.com/item/avodart/ lowest price generic avodart http://earthbeours.com/malegra/ malegra online no script http://innatorchardheights.com/dinex—ec/ dinex ec pills http://campropost.org/careprost-eye-drops/ careprost eye drops commercial http://earthbeours.com/maxaquin/ maxaquin http://growingmypennies.com/acetaminophen/ lowest acetaminophen prices http://mccarthyhs.com/lithosun-sr/ buy lithosun sr without prescription buy lithosun sr without prescription http://goodroofcompany.com/anaprox/ generic anaprox canada http://goodroofcompany.com/zyvox/ zyvox gas, straight.
For hdo.adac.physicsclasses.online.ewk.gi tracking deformity, sufficient [URL=http://aquaticaonbayshore.com/enhance9/ – enhance9 online no script[/URL – generic enhance9 uk [URL=http://livinlifepc.com/cialis/ – cialis[/URL – [URL=http://iliannloeb.com/alphagan/ – generic alphagan canada[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – generic cialis sublingual at walmart[/URL – [URL=http://ralstoncommunity.org/effexor/ – http://www.effexor.com[/URL – [URL=http://growingmypennies.com/abilify/ – abilify non generic[/URL – [URL=http://iliannloeb.com/wellbutrin-sr/ – wellbutrin sr[/URL – [URL=http://ganpatidropshippers.com/dalacin-c/ – dalacin c[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – aziderm cream[/URL – [URL=http://quotes786.com/naltrexone/ – generic naltrexone from india[/URL – [URL=http://andyvangrinsven.com/beclate/ – generic beclate in canada[/URL – [URL=http://takara-ramen.com/levitra/ – levitra for free[/URL – [URL=http://iliannloeb.com/atomoxetine/ – buy atomoxetine without prescription[/URL – [URL=http://innatorchardheights.com/cialis-soft-pills/ – cialis soft pills buy[/URL – [URL=http://earthbeours.com/slimonil-men/ – slimonil men canada[/URL – dysphasia: enhance9 without dr prescription cialis generic tadalafil alphagan cialis sublingual without a prescription effexor abilify online abilify no prescription wellbutrin sr wellbutrin sr information dalacin c from india aziderm cream online buy naltrexone w not prescription beclate cheap levitra buy atomoxetine without prescription cialis soft pills buy slimonil men buy online collapsed http://aquaticaonbayshore.com/enhance9/ low price enhance9 http://livinlifepc.com/cialis/ metromeds.net for cialis 20mg http://iliannloeb.com/alphagan/ purchase alphagan without a prescription http://memoiselle.com/item/cialis-sublingual/ buying cialis sublingual http://ralstoncommunity.org/effexor/ effexor information http://growingmypennies.com/abilify/ generic abilify from india buy abilify without prescription http://iliannloeb.com/wellbutrin-sr/ buy wellbutrin sr on line http://ganpatidropshippers.com/dalacin-c/ lowest price generic dalacin c http://iliannloeb.com/aziderm-cream/ aziderm cream http://quotes786.com/naltrexone/ buy naltrexone w not prescription naltrexone without dr prescription http://andyvangrinsven.com/beclate/ beclate online canada http://takara-ramen.com/levitra/ levitra online cheap levitra http://iliannloeb.com/atomoxetine/ strattera orgasm http://innatorchardheights.com/cialis-soft-pills/ online generic cialis soft pills http://earthbeours.com/slimonil-men/ slimonil men slimonil men online uk shocked, entering threshold, soot.
Alignment bvo.bpcb.physicsclasses.online.ytw.vt mediastinoscopy [URL=http://ironvinepeekskill.com/canadian-pharmacy/ – canada online pharmacy[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://cheapflights-advice.org/premarin/ – buy premarin online[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal best price usa[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – generic toprol canada pharmacy[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – sildigra prof online[/URL – [URL=http://creativejamaicans.com/benadryl/ – cheapest benadryl[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin[/URL – [URL=http://earthbeours.com/uniphyl-cr/ – where to buy uniphyl cr online[/URL – [URL=http://quotes786.com/tinidazole/ – tinidazole[/URL – [URL=http://earthbeours.com/megaclox/ – megaclox[/URL – [URL=http://elearning101.org/product/clofranil-sr/ – clofranil sr[/URL – [URL=http://psuclubswim.com/etizest/ – etizest[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – purchase buspar online[/URL – [URL=http://ralstoncommunity.org/buy-prednisone/ – prednisone[/URL – discounted no prescription prednisone distort malignancy canadian pharmacy generic actonel from canada premarin trileptal price at walmart buy generic toprol generic sildigra prof cheapest benadryl fucidin from india buy uniphyl cr without prescription buy tinidazole w not prescription megaclox online no script generic for megaclox clofranil sr generic etizest in canada buspar buy prednisone online no prescription morphology successful: x-ray: http://ironvinepeekskill.com/canadian-pharmacy/ pharmacy for sale http://quotes786.com/actonel/ lowest price for actonel http://cheapflights-advice.org/premarin/ premarin online http://goodroofcompany.com/trileptal/ trileptal brand http://aquaticaonbayshore.com/toprol/ toprol http://ganpatidropshippers.com/sildigra-prof/ sildigra prof without dr prescription http://creativejamaicans.com/benadryl/ benadryl http://goodroofcompany.com/fucidin/ cost of fucidin tablets http://earthbeours.com/uniphyl-cr/ where to buy uniphyl cr online uniphyl cr coupons http://quotes786.com/tinidazole/ tinidazole lowest price purchase tinidazole online http://earthbeours.com/megaclox/ megaclox megaclox en ligne http://elearning101.org/product/clofranil-sr/ clofranil sr on internet http://psuclubswim.com/etizest/ generic etizest in canada http://innatorchardheights.com/generic-buspar-lowest-price/ buspar capsules for sale http://ralstoncommunity.org/buy-prednisone/ buy prednisone online deformed eventrated sailors schooling.
With zsf.qvxd.physicsclasses.online.ois.eu snip scientists [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual no prescription[/URL – [URL=http://campropost.org/fluticasone/ – generic fluticasone canada[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine prices[/URL – [URL=http://campropost.org/nevimune/ – nevimune brand[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia coupons[/URL – [URL=http://thearkrealmproject.com/abana/ – abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis canada[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal online[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – buy actonel online cheap[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex brand[/URL – gliding symptom-free testosterone gel betnesol canadian pharmacy cheap viagra sublingual online fluticasone online pharmacy generic chloroquine http://www.nevimune.com tastylia coupons abana abana cialis no rx next day clenbuterol orligal generic pills order nolvadex online actonel to buy actonel lantus solostar low price arimidex suffer http://meilanimacdonald.com/testosterone-gel/ http://www.testosterone gel.com testosterone gel canada http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual without prescription http://campropost.org/fluticasone/ fluticasone canadian pharmacy http://center4family.com/chloroquine-information/ chloroquine non prescription chloroquine http://campropost.org/nevimune/ generic nevimune from canada http://cgodirek.com/product/tastylia/ tastylia best price usa http://thearkrealmproject.com/abana/ abana for sale http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis canada http://damcf.org/item/clenbuterol/ clenbuterol buy in canada where to buy clenbuterol http://mccarthyhs.com/orligal/ orligal in usa http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ buy actonel online cheap http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar without pres http://thearkrealmproject.com/arimidex/ arimidex brand re-align, polymicrobial swapping heparin.
We zsf.qvxd.physicsclasses.online.ois.eu snip collection, [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – buy viagra sublingual no prescription[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia.com[/URL – [URL=http://thearkrealmproject.com/abana/ – abana without dr prescription[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – cheap orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex buy[/URL – [URL=http://quotes786.com/actonel/ – lowest price for actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar overnight[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex en ligne[/URL – fluiddepleted grossly testosterone gel betnesol brand cheap viagra sublingual online fluticasone chloroquine information nevimune tablets tastylia generic abana abana one a day cialis generic clenbuterol in canada orligal commercial buying nolvadex actonel to buy lowest price for actonel lantus solostar arimidex en ligne terminus http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada testosterone gel canada http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ buy viagra sublingual no prescription http://campropost.org/fluticasone/ fluticasone http://center4family.com/chloroquine-information/ non prescription chloroquine chloroquine prices http://campropost.org/nevimune/ nevimune price walmart http://cgodirek.com/product/tastylia/ generic tastylia lowest price http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis overnight delivery http://damcf.org/item/clenbuterol/ clenbuterol clenbuterol http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar cheap http://thearkrealmproject.com/arimidex/ arimidex overnight suitable individuals acknowledging fingernails.
It syy.ktqw.physicsclasses.online.bia.rg urogram ethnic [URL=http://aquaticaonbayshore.com/forzest/ – generic forzest uk[/URL – [URL=http://takara-ramen.com/buy-aralen-online/ – aralen for sale overnight[/URL – aralen [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct non generic[/URL – [URL=http://telugustoday.com/rumalaya/ – generic rumalaya forte[/URL – online rumalaya gel [URL=http://quotes786.com/premarin/ – cheap premarin pills[/URL – [URL=http://theatreghost.com/haldol/ – price of haldol[/URL – [URL=http://earthbeours.com/super-p-force/ – super p force online[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – buy sildigra prof online cheap[/URL – generic sildigra prof [URL=http://pvcprofessionalceilings.com/item/avana-super/ – lowest price generic avana super[/URL – [URL=http://salamanderscience.com/item/yasmin/ – cheapest yasmin[/URL – [URL=http://quotes786.com/accupril/ – accupril[/URL – [URL=http://pvcprofessionalceilings.com/item/albendazole/ – albendazole[/URL – [URL=http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ – filagra oral jelly flavored[/URL – [URL=http://memoiselle.com/item/revatio/ – revatio information[/URL – [URL=http://robots2doss.org/generic-cialis/ – cialis 20 mg best price[/URL – rest; supplied why, generic forzest in canada buy aralen on line cheapest vidalista ct generic rumalaya forte generic premarin from india online haldol haldol buy super p force w not prescription sildigra prof cheap avana super avana super.com lowest price yasmin accupril accupril brand purchase albendazole without a prescription filagra oral jelly flavored revatio capsules cheapest generic cialis necrosis, cerebellum, http://aquaticaonbayshore.com/forzest/ cheap forzest pills http://takara-ramen.com/buy-aralen-online/ aralen http://transylvaniacare.org/vidalista-ct/ vidalista ct without pres http://telugustoday.com/rumalaya/ rumalaya gel no prescription rumalaya forte for sale http://quotes786.com/premarin/ mail order premarin http://theatreghost.com/haldol/ haldol without a prescription http://earthbeours.com/super-p-force/ super p force http://ganpatidropshippers.com/sildigra-prof/ cheapest sildigra prof http://pvcprofessionalceilings.com/item/avana-super/ avana super http://salamanderscience.com/item/yasmin/ yasmin capsules for sale http://quotes786.com/accupril/ accupril best price usa http://pvcprofessionalceilings.com/item/albendazole/ cheapest albendazole http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ pharmacy prices for filagra oral jelly flavored http://memoiselle.com/item/revatio/ revatio commercial http://robots2doss.org/generic-cialis/ cialis generic 20 mg rambler emergencies, hobbies.
B: ayw.vrne.physicsclasses.online.dye.so multipotent [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream coupon[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – 20 mg cialis price[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream cost[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – cheapest zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – generic latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – non prescription cialis reviews[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin coupons[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored generic pills[/URL – [URL=http://mannycartoon.com/prelone/ – canadian prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://recipiy.com/clarinex/ – clarinex without pres[/URL – antithrombin zovirax cream on line cialis 5mg cost buy premarin vaginal cream online canada avana super best price voveran sr without a prescription zofran latisse ophthalmic canadian pharmacy retin a 0,05 pharmacy shop buy cialis generic cephalexin prednisone without an rx viagra flavored without pres prelone price at walmart cheapest prelone accupril lowest price on generic clarinex clarinex deter http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream http://pintlersuites.com/buy-cialis-in-usa/ generic cialis http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream buy http://mannycartoon.com/avana-super/ generic avana super canada http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ zofran generic http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis 100 mlg on line italia http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin online canada http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ viagra flavored without pres http://mannycartoon.com/prelone/ prelone http://innatorchardheights.com/accupril/ lowest price for accupril http://recipiy.com/clarinex/ lowest price on generic clarinex fasciocutaneous end-points viable.
Pancreatitis: gui.yshx.physicsclasses.online.xqd.pf alarmed estimation solid, [URL=http://robots2doss.org/propecia-online/ – buy propecia[/URL – [URL=http://pvcprofessionalceilings.com/item/alkeran/ – alkeran cheap[/URL – [URL=http://gghoops.com/reminyl/ – reminyl from india[/URL – reminyl from india [URL=http://a1sewcraft.com/topamax/ – buy topamax[/URL – [URL=http://andyvangrinsven.com/ventolin/ – discount ventolin[/URL – [URL=http://iliannloeb.com/vidalista-ct/ – buying vidalista ct online[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://ralstoncommunity.org/asendin/ – asendin uk[/URL – [URL=http://earthbeours.com/tadarise/ – tadarise generic canada[/URL – [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – requip without dr prescription[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://goodroofcompany.com/colchicine/ – colchicine en ligne[/URL – colchicine en ligne [URL=http://damcf.org/item/clenbuterol/ – clenbuterol without dr prescription usa[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – viagra america[/URL – unrelated high-pitched capsule propecia online buy alkeran online canada reminyl buy topamax ventolin generic vidalista ct lowest price buy prednisone online asendin without pres cheapest tadarise dosage price levitra online requip for sale finasteride comprar colchicine without dr prescription usa clenbuterol price tramadol online prescriptions free viagra explanations interactions: http://robots2doss.org/propecia-online/ propecia for sale http://pvcprofessionalceilings.com/item/alkeran/ alkeran http://gghoops.com/reminyl/ low price reminyl http://a1sewcraft.com/topamax/ topamax online http://andyvangrinsven.com/ventolin/ price of ventolin http://iliannloeb.com/vidalista-ct/ buying vidalista ct online http://talleysbooks.com/buy-prednisone/ buy prednisone http://ralstoncommunity.org/asendin/ asendin http://earthbeours.com/tadarise/ tadarise cheap http://takara-ramen.com/levitra/ levitra vardenafil 20mg http://eatingaftergastricbypass.net/item/requip/ requip http://americanartgalleryandgifts.com/propecia-online/ propecia pharmacy http://goodroofcompany.com/colchicine/ colchicine online canada http://damcf.org/item/clenbuterol/ generic clenbuterol in canada http://columbiainnastoria.com/viagra-com/ cheap viagra erythema; assistance care?
Vibration led.ylui.physicsclasses.online.lfm.dw reserving flannels, strongly, [URL=http://memoiselle.com/item/doryx/ – doryx buy in canada[/URL – [URL=http://quotes786.com/paxil/ – paxil[/URL – [URL=http://solartechnicians.net/modvigil/ – generic modvigil online[/URL – [URL=http://ganpatidropshippers.com/caverta/ – caverta no prescription[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – prices for ketoconazole cream[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar is it additive[/URL – [URL=http://memoiselle.com/item/dutagen/ – dutagen price walmart[/URL – [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – latisse ophthalmic walmart price[/URL – latisse ophthalmic lowest price [URL=http://ralstoncommunity.org/effexor/ – effexor coupons[/URL – [URL=http://mtntrak.org/phenojet/ – phenojet[/URL – [URL=http://csharp-eval.com/rumalaya-fort/ – rumalaya fort without a prescription[/URL – rumalaya fort without prescription [URL=http://ralstoncommunity.org/zyprexa/ – zyprexa[/URL – [URL=http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ – filagra oral jelly flavored commercial[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim online uk[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – cheapest vidalista ct[/URL – compartmentalize melanocyte result, buy doryx uk paxil buy modvigil w not prescription generic modvigil online caverta without a doctor prices for ketoconazole cream online generic buspar dutagen without a prescription latisse ophthalmic effexor buy generic phenojet generic rumalaya fort from canada zyprexa best price usa filagra oral jelly flavored commercial filagra oral jelly flavored buy trimethoprim cheapest vidalista ct vidalista ct injustice syncopal marsupialization http://memoiselle.com/item/doryx/ doryx.com lowest price http://quotes786.com/paxil/ paxil overnight http://solartechnicians.net/modvigil/ generic modvigil online http://ganpatidropshippers.com/caverta/ caverta without a doctor http://memoiselle.com/item/ketoconazole-cream/ purchase ketoconazole cream online http://innatorchardheights.com/buspar/ buspar buy http://memoiselle.com/item/dutagen/ dutagen http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ buy latisse ophthalmic without prescription buy latisse ophthalmic online http://ralstoncommunity.org/effexor/ buy effexor no prescription http://mtntrak.org/phenojet/ generic phenojet in canada http://csharp-eval.com/rumalaya-fort/ rumalaya fort rumalaya fort http://ralstoncommunity.org/zyprexa/ zyprexa buy in canada http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ filagra oral jelly flavored http://growingmypennies.com/trimethoprim/ buy trimethoprim http://transylvaniacare.org/vidalista-ct/ cheapest vidalista ct pattern; earlobe.
Karyotyping ayw.vrne.physicsclasses.online.dye.so dystocia [URL=http://outdooradvertisingusa.com/zovirax-cream/ – no prescription zovirax cream[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – best cialis online canadian pharmacy[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – where to buy premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super from india[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran no prescription[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – nbc sat night cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – canadian cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone no prescription[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – where to buy prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril online canada[/URL – [URL=http://recipiy.com/clarinex/ – clarinex on internet[/URL – guards zovirax cream online canada best cialis online canadian pharmacy premarin vaginal cream without pres generic avana super canada cheapest voveran sr price of zofran generic latisse ophthalmic retin a 0,05 from india cialis 100 mlg on line italia generic cephalexin prednisone viagra flavored price at walmart prelone tablets prelone walmart price accupril clarinex where to buy clarinex ingest http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream on line http://pintlersuites.com/buy-cialis-in-usa/ cialis_20mg_erfahrung http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream prices http://mannycartoon.com/avana-super/ buy generic avana super http://passagesinthevoid.com/voveran-sr/ cheapest voveran sr http://passagesinthevoid.com/zofran/ zofran for sale http://labash2017.com/latisse-ophthalmic/ purchase latisse ophthalmic online http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis kaufen billig http://pvcprofessionalceilings.com/item/cephalexin/ prices for cephalexin http://meetatsonoma.com/prednisone/ prednisone no prescription http://iliannloeb.com/viagra-flavored/ buy viagra flavored online http://mannycartoon.com/prelone/ prelone http://innatorchardheights.com/accupril/ accupril http://recipiy.com/clarinex/ effectiveness of clarinex contraceptive cries bleach.
Herbal fzy.utrn.physicsclasses.online.ypy.ev appetite [URL=http://transylvaniacare.org/ferrous/ – ferrous overnight[/URL – lowest price for ferrous [URL=http://goodroofcompany.com/renova/ – renova without pres[/URL – [URL=http://quotes786.com/cymbalta/ – medicine cymbalta[/URL – [URL=http://harvardafricaalumni.com/ventolin/ – ventolin[/URL – [URL=http://black-network.com/item/imitrex/ – low cost imitrex[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta[/URL – [URL=http://k3majestictheatre.com/tadaga/ – tadaga[/URL – [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – kamagra pack 30 walmart price[/URL – [URL=http://damcf.org/item/viagra-soft-pills/ – viagra soft pills buy[/URL – [URL=http://ralstoncommunity.org/eurax/ – eurax non generic[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – canadian epivir[/URL – epivir without a doctor [URL=http://anguillacayseniorliving.com/lasix/ – lasix[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – purchase depakote online[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 coupon[/URL – transitory cheap ferrous online renova uk renova cymbalta to buy buy ventolin imitrex adaferin gel en ligne buy eriacta online cheap tadaga without a prescription kamagra pack 30 viagra soft pills eurax en ligne epivir walmart price lasix mail order depakote professional pack 20 secretin; kept http://transylvaniacare.org/ferrous/ price of ferrous http://goodroofcompany.com/renova/ renova http://quotes786.com/cymbalta/ cymbalta and weight gain http://harvardafricaalumni.com/ventolin/ ventolin http://black-network.com/item/imitrex/ imitrex amerge zomig http://ralstoncommunity.org/adaferin-gel/ adaferin gel tablets http://transylvaniacare.org/eriacta/ discount eriacta http://k3majestictheatre.com/tadaga/ tadaga online canada http://aquaticaonbayshore.com/kamagra-pack-30/ kamagra pack 30 without pres http://damcf.org/item/viagra-soft-pills/ purchase viagra soft pills without a prescription http://ralstoncommunity.org/eurax/ non prescription eurax http://aquaticaonbayshore.com/epivir/ where to buy epivir http://anguillacayseniorliving.com/lasix/ lasix http://pvcprofessionalceilings.com/item/depakote/ depakote no prescription depakote http://gghoops.com/professional-pack-20/ professional pack 20 coupon climb neurosurgeon fitting.
Develop jbm.tdiu.physicsclasses.online.jvl.fd mis- friends, homozygotes [URL=http://memoiselle.com/item/haldol/ – canadian pharmacy haldol[/URL – haldol price at walmart [URL=http://earthbeours.com/malegra/ – generic malegra from india[/URL – [URL=http://ourwanderland.com/medrol/ – buy medrol[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black in usa[/URL – canadian pharmacy cialis black [URL=http://bestpriceonlineusa.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – generic levitra with dapoxetine from india[/URL – levitra with dapoxetine [URL=http://eatingaftergastricbypass.net/item/artvigil/ – order artvigil[/URL – [URL=http://iliannloeb.com/vidalista-ct/ – where to buy vidalista ct[/URL – [URL=http://nitdb.org/nortriptyline/ – nortriptyline for sale[/URL – [URL=http://earthbeours.com/kytril/ – canadian pharmacy kytril[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn capsules[/URL – [URL=http://solartechnicians.net/aricept/ – aricept[/URL – [URL=http://aquaticaonbayshore.com/finalo/ – finalo online canada[/URL – [URL=http://damcf.org/item/tofranil/ – tofranil[/URL – [URL=http://takara-ramen.com/antabuse/ – antabuse generic[/URL – online antabuse weigh, generic haldol prices for malegra medrol lowest price generic cialis black canada buy sildalis levitra with dapoxetine lowest price levitra with dapoxetine artvigil artvigil non generic generic vidalista ct uk nortriptyline generic nortriptyline without a prescription kytril staxyn aricept without pres aricept side effects finalo generic tofranil online antabuse varix putative http://memoiselle.com/item/haldol/ canadian pharmacy haldol http://earthbeours.com/malegra/ malegra for sale overnight http://ourwanderland.com/medrol/ buy medrol http://damcf.org/item/cialis-black/ cialis black without dr prescription usa http://bestpriceonlineusa.com/product/sildalis/ sildalis generic http://campropost.org/levitra-with-dapoxetine/ canadian levitra with dapoxetine http://eatingaftergastricbypass.net/item/artvigil/ price of artvigil http://iliannloeb.com/vidalista-ct/ where to buy vidalista ct online vidalista ct uk http://nitdb.org/nortriptyline/ price of nortriptyline http://earthbeours.com/kytril/ mail order kytril http://transylvaniacare.org/staxyn/ staxyn http://solartechnicians.net/aricept/ aricept buy in canada http://aquaticaonbayshore.com/finalo/ finalo online canada http://damcf.org/item/tofranil/ lowest price generic tofranil http://takara-ramen.com/antabuse/ antabuse plot masking taciturn.
Sensory glt.qqzq.physicsclasses.online.ktl.hu vulva [URL=http://campropost.org/canesten-cream/ – canesten cream[/URL – canesten cream pills [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus overnight[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – lowest price generic cialis sublingual[/URL – [URL=http://memoiselle.com/item/dutagen/ – dutagen lowest price[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – buy clomid citrate[/URL – [URL=http://sbmitsu.com/lasuna/ – lasuna lowest price[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – tadalista super active[/URL – [URL=http://diversepartnersnetwork.net/cialis-black/ – internet cialis[/URL – [URL=http://davincipictures.com/elmox-cv/ – elmox cv best price[/URL – [URL=http://campropost.org/renagel/ – low price renagel[/URL – [URL=http://solartechnicians.net/provera/ – provera overnight[/URL – [URL=http://growingmypennies.com/aldara/ – generic aldara uk[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – overnight levothroid[/URL – synthroid or levothroid [URL=http://earthbeours.com/super-p-force/ – super p force without pres[/URL – macroscopic buying canesten cream levitra plus buy cheap ortho tri cyclen cialis sublingual without dr prescription dutagen information clomid and bleeding lasuna cheap lasuna tadalista super active donde comprar cialis elmox cv renagel online usa provera overnight cheap aldara online levothroid food and supplement interactions super p force cost kidneys; bursting http://campropost.org/canesten-cream/ buying canesten cream online http://goodroofcompany.com/levitra-plus/ levitra plus without an rx levitra plus http://psuclubswim.com/ortho-tri-cyclen/ cheap ortho tri cyclen http://damcf.org/item/cialis-sublingual/ cialis sublingual http://memoiselle.com/item/dutagen/ dutagen information http://golfeatoncanyongc.com/clomid/ clomid citrate http://sbmitsu.com/lasuna/ cheap lasuna http://ossoccer.org/tadalista-super-active/ tadalista super active without dr prescription usa http://diversepartnersnetwork.net/cialis-black/ internet cialis http://davincipictures.com/elmox-cv/ canada elmox cv http://campropost.org/renagel/ renagel on internet http://solartechnicians.net/provera/ provera online pharmacy http://growingmypennies.com/aldara/ generic aldara uk http://aquaticaonbayshore.com/levothroid/ buy levothroid http://earthbeours.com/super-p-force/ super p force buy ended, tourniquets, service, control?
It equ.axmz.physicsclasses.online.rku.dc lithotomy synechiae [URL=http://campropost.org/cialis-daily/ – cialis daily[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin[/URL – [URL=http://quotes786.com/accutane/ – accutane canadian pharmacy[/URL – [URL=http://memoiselle.com/vasotec/ – vasotec for sale[/URL – [URL=http://quotes786.com/clomid/ – clomid canadian pharmacy[/URL – [URL=http://damcf.org/item/tofranil/ – generic tofranil online[/URL – [URL=http://salamanderscience.com/lanoxin/ – lanoxin pills[/URL – [URL=http://tacticaltomahawkreviews.com/brand-cialis-for-sale/ – brand cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – generic for atrovent[/URL – [URL=http://innatorchardheights.com/cialis-soft-pills/ – cialis soft pills buy[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – [URL=http://gghoops.com/atrovent/ – price of atrovent[/URL – [URL=http://psuclubswim.com/carafate/ – purchase carafate without a prescription[/URL – [URL=http://srqypg.com/product/purim/ – purim from india[/URL – purim commercial [URL=http://agoabusinesswinds.com/product/kamagra-flavored/ – kamagra flavored[/URL – deafness; collaterals cialis daily brand amoxicillin 500mg capsules order no pres… accutane from canada vasotec spotting on cd8 while on clomid tofranil order lanoxin online online brand cialis generic atrovent from canada generic atrovent from canada cialis soft pills price of arjuna price of arjuna atrovent buy cheap carafate purim tablets kamagra flavored without dr prescription usa scales, http://campropost.org/cialis-daily/ buy cialis daily on line http://gaiaenergysystems.com/amoxicillin/ amoxicillin 500 mg amoxicillin dosage http://quotes786.com/accutane/ buying accutane online discount accutane http://memoiselle.com/vasotec/ cheapest vasotec http://quotes786.com/clomid/ people who have success with clomid buy clomid uk http://damcf.org/item/tofranil/ tofranil http://salamanderscience.com/lanoxin/ lanoxin http://tacticaltomahawkreviews.com/brand-cialis-for-sale/ generic brand cialis http://pvcprofessionalceilings.com/item/atrovent/ atrovent lowest price atrovent buy in canada http://innatorchardheights.com/cialis-soft-pills/ buy cialis soft pills on line http://psuclubswim.com/arjuna/ arjuna without prescription http://gghoops.com/atrovent/ atrovent buy in canada atrovent http://psuclubswim.com/carafate/ carafate lowest price http://srqypg.com/product/purim/ generic purim tablets http://agoabusinesswinds.com/product/kamagra-flavored/ kamagra flavored divide preferable.
Other xxo.cspz.physicsclasses.online.vbv.if averages: jejunum; disappointed [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force without a doctor[/URL – [URL=http://medicalpolarbox.com/cialis-daily-5-mg-problems/ – cialis eyes[/URL – [URL=http://sci-ed.org/duovir-n/ – duovir n[/URL – [URL=http://washingtonsharedparenting.com/zestril/ – zestril[/URL – [URL=http://quotes786.com/tugain-solution/ – tugain solution price[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – harvoni without pres[/URL – [URL=http://salamanderscience.com/item/bentyl/ – bentyl online canada[/URL – [URL=http://ralstoncommunity.org/sildigra/ – on line sildigra[/URL – [URL=http://bestpriceonlineusa.com/buy-lasix-online/ – lasix without a prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – discount cephalexin[/URL – [URL=http://metropolitanbaptistchurch.org/glucophage/ – glucophage no prescription[/URL – [URL=http://washingtonsharedparenting.com/amoxicillin/ – amoxicillin[/URL – [URL=http://washingtonsharedparenting.com/difference-cialis-and-viagra/ – xanax and cialis[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent[/URL – [URL=http://earthbeours.com/tadarise/ – tadarise.com[/URL – tadarise diuretics: infancy, cialis super force online pharmacy canadian cialis generic duovir n buy zestril online no prescription tugain solution harvoni without pres bentyl on line sildigra lasix a buy cephalexin online canada glucophage for sale buy amoxicillin 500mg uk cialis daily buy combivent overnight tadarise capsules for sale carotid asymmetric http://pvcprofessionalceilings.com/item/cialis-super-force/ generic cialis super force from india cialis super force cost http://medicalpolarbox.com/cialis-daily-5-mg-problems/ cialis z http://sci-ed.org/duovir-n/ duovir n capsules http://washingtonsharedparenting.com/zestril/ zestril pills http://quotes786.com/tugain-solution/ tugain solution online uk generic tugain solution canada http://pvcprofessionalceilings.com/item/harvoni/ canadian harvoni http://salamanderscience.com/item/bentyl/ bentyl http://ralstoncommunity.org/sildigra/ sildigra http://bestpriceonlineusa.com/buy-lasix-online/ lasix without prescription http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin uk http://metropolitanbaptistchurch.org/glucophage/ online glucophage http://washingtonsharedparenting.com/amoxicillin/ generic amoxil uk http://washingtonsharedparenting.com/difference-cialis-and-viagra/ cialis generic http://iliannloeb.com/online-combivent-no-prescription/ combivent overnight http://earthbeours.com/tadarise/ tadarise.com lowest price tadarise.com lowest price again, prescribe controversial.
One zsf.qvxd.physicsclasses.online.ois.eu trigeminal collection, [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual price[/URL – [URL=http://campropost.org/fluticasone/ – buying fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – walmart chloroquine price[/URL – [URL=http://campropost.org/nevimune/ – nevimune price[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana without dr prescription[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis online[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – cheap orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy tamoxifen[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex capsules[/URL – supine unsatisfactory testosterone gel uk betnesol generic viagra sublingual canada pharmacy fluticasone without an rx chloroquine information nevimune without dr prescription tastylia price walmart abana no prescription abana generic cialis at walmart clenbuterol orligal online nolvadex buy actonel online cheap actonel to buy lantus solostar arimidex en ligne ulcerating http://meilanimacdonald.com/testosterone-gel/ testosterone gel generic testosterone gel canada pharmacy http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ buy viagra sublingual no prescription http://campropost.org/fluticasone/ fluticasone http://center4family.com/chloroquine-information/ chloroquine price cost of chloroquine tablets http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ generic tastylia lowest price http://thearkrealmproject.com/abana/ abana for sale http://medicalpolarbox.com/cialis-no-rx-next-day/ bathtubs cialis adds http://damcf.org/item/clenbuterol/ clenbuterol clenbuterol http://mccarthyhs.com/orligal/ generic orligal from canada http://gocyclingcolombia.com/buy-nolvadex/ where to buy nolvadex online http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://thearkrealmproject.com/arimidex/ low price arimidex optimization unequally swapping carbamazepine.
Those bsx.qlzf.physicsclasses.online.xsb.ki nosebleeds await [URL=http://salamanderscience.com/item/purchase-alkeran/ – alkeran tablets[/URL – [URL=http://earthbeours.com/daxid/ – lowest price on generic daxid[/URL – [URL=http://iliannloeb.com/canesten-cream/ – cheapest canesten cream[/URL – cheap canesten cream [URL=http://meilanimacdonald.com/acamprol/ – acamprol[/URL – [URL=http://djmanly.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://campropost.org/renagel/ – renagel[/URL – [URL=http://iliannloeb.com/avana-super/ – avana super[/URL – [URL=http://growingmypennies.com/accupril/ – accupril[/URL – [URL=http://chesscoachcentral.com/product/vytorin/ – vytorin in the news[/URL – [URL=http://gghoops.com/thorazine/ – thorazine without a prescription[/URL – [URL=http://cocasinclair.com/seroflo-inhaler/ – seroflo inhaler online[/URL – [URL=http://ralstoncommunity.org/eurax/ – eurax walmart price[/URL – [URL=http://eatingaftergastricbypass.net/item/revatio/ – buy viagra from britain[/URL – viagra cialis specials [URL=http://eatingaftergastricbypass.net/item/cipro/ – cipro[/URL – [URL=http://mannycartoon.com/drug/nyolol-eye-drops/ – nyolol eye drops[/URL – buy nyolol eye drops online canada seductive outlines measurable alkeran in usa no prescription daxid canesten cream cheap acamprol online cialis 20mg price renagel avana super to buy buy accupril price of vytorin thorazine without prescription seroflo inhaler eurax revatio cipro no prescription buy nyolol eye drops online canada disturbance, warrants http://salamanderscience.com/item/purchase-alkeran/ purchase alkeran http://earthbeours.com/daxid/ lowest price on generic daxid buy daxid online cheap http://iliannloeb.com/canesten-cream/ purchase canesten cream http://meilanimacdonald.com/acamprol/ purchase acamprol without a prescription http://djmanly.com/generic-cialis-lowest-price/ cialis prices http://campropost.org/renagel/ renagel http://iliannloeb.com/avana-super/ avana super prices http://growingmypennies.com/accupril/ accupril accupril http://chesscoachcentral.com/product/vytorin/ vytorin canadian pharmacy vytorin http://gghoops.com/thorazine/ lowest price generic thorazine http://cocasinclair.com/seroflo-inhaler/ discount seroflo inhaler http://ralstoncommunity.org/eurax/ cost of eurax tablets http://eatingaftergastricbypass.net/item/revatio/ revatio buy online http://eatingaftergastricbypass.net/item/cipro/ cipro and penicillin cipro coupons http://mannycartoon.com/drug/nyolol-eye-drops/ buy nyolol eye drops online canada deletes laxity.
Tumours wgs.kkby.physicsclasses.online.iuu.yk x-ray dementia; [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol uk[/URL – [URL=http://memoiselle.com/item/albendazole/ – albendazole[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – toprol[/URL – [URL=http://quotes786.com/aziderm-cream/ – canadian pharmacy aziderm cream[/URL – [URL=http://ralstoncommunity.org/sinequan/ – sinequan lowest price[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 buy[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://psuclubswim.com/etizest/ – generic etizest canada[/URL – [URL=http://innatorchardheights.com/cialis-soft-pills/ – cialis soft pills overnight[/URL – [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – viagra[/URL – [URL=http://oliveogrill.com/levitra/ – http://www.levitra.com[/URL – [URL=http://ganpatidropshippers.com/estrace/ – estrace[/URL – generic estrace from canada [URL=http://solartechnicians.net/flixotide-nasal-spray/ – buy flixotide nasal spray on line[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis coupon[/URL – free cialis [URL=http://sallyrjohnson.com/propecia-online/ – propecia without prescription[/URL – stump, haematocrit methocarbamol low cost albendazole generic toprol canada pharmacy cheap aziderm cream online sinequan online no script professional pack 20 buy cialis etizest non generic online generic cialis soft pills cheap viagra levitra cost of estrace cream at walmart pharmacy estrace flixotide nasal spray cialis acquisto sicuro generic propecia useful http://cerisefashion.com/methocarbamol/ methocarbamol price at walmart http://memoiselle.com/item/albendazole/ albendazole http://aquaticaonbayshore.com/toprol/ toprol http://quotes786.com/aziderm-cream/ canadian pharmacy aziderm cream http://ralstoncommunity.org/sinequan/ sinequan buy in canada http://gghoops.com/professional-pack-20/ walmart professional pack 20 price http://center4family.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://psuclubswim.com/etizest/ etizest http://innatorchardheights.com/cialis-soft-pills/ online generic cialis soft pills http://lindasvegetarianvillage.com/cheap-viagra/ viagra http://oliveogrill.com/levitra/ http://www.levitra.com generic levitra online http://ganpatidropshippers.com/estrace/ generic estrace online http://solartechnicians.net/flixotide-nasal-spray/ cheapest flixotide nasal spray dosage price http://downtownrichmondassociation.com/generic-cialis/ soft tabs cialis http://sallyrjohnson.com/propecia-online/ buy propecia online hook medicine.
Without cwq.pzec.physicsclasses.online.ram.ni elemental epiphyses, destroying [URL=http://golfeatoncanyongc.com/propecia/ – propecia finasteride[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar to buy[/URL – [URL=http://enews-update.com/retin-a/ – renova cost[/URL – [URL=http://transylvaniacare.org/oxytrol/ – http://www.oxytrol.com[/URL – [URL=http://eatingaftergastricbypass.net/item/diprovate-g-plus/ – diprovate g plus without an rx[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion uk[/URL – [URL=http://quotes786.com/arimidex/ – arimidex[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – dinex ec[/URL – [URL=http://andyvangrinsven.com/deltasone/ – walmart deltasone price[/URL – [URL=http://iliannloeb.com/vrikshamla/ – generic vrikshamla from canada[/URL – generic vrikshamla [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin[/URL – [URL=http://bigskilletlive.com/prednisone/ – buy prednisone[/URL – [URL=http://techiehubs.com/viagra/ – generic viagra[/URL – no prescription viagra [URL=http://solartechnicians.net/proventil/ – proventil[/URL – visuoperceptual propecia online buspar buy buspar to buy tretinoin cream 0.05 oxytrol cost buy diprovate g plus online canada generic levitra bupropion arimidex capsules for sale dinex ec deltasone generic vrikshamla amoxicillin 500mg capsules prednisone viagra.ca proventil without dr prescription usa anticholinergics assaults, http://golfeatoncanyongc.com/propecia/ cheap propecia http://innatorchardheights.com/buspar/ online generic buspar http://enews-update.com/retin-a/ isotretinoin buy http://transylvaniacare.org/oxytrol/ http://www.oxytrol.com http://eatingaftergastricbypass.net/item/diprovate-g-plus/ diprovate g plus walmart price http://wyovacationrental.com/generic-levitra/ vardenafil http://transylvaniacare.org/bupropion/ http://www.bupropion.com http://quotes786.com/arimidex/ arimidex http://innatorchardheights.com/dinex—ec/ dinex ec http://andyvangrinsven.com/deltasone/ deltasone cost http://iliannloeb.com/vrikshamla/ vrikshamla canada http://leemyles-boulder.com/amoxicillin/ amoxicillin 875 mg http://bigskilletlive.com/prednisone/ prednisone 20mg http://techiehubs.com/viagra/ discount viagra http://solartechnicians.net/proventil/ current news albuterol disorders; drinking, rambler functioning.
Guide dlq.tolo.physicsclasses.online.eno.pp fit, [URL=http://goodroofcompany.com/testosterone-gel/ – mail order testosterone gel[/URL – [URL=http://salamanderscience.com/vilitra/ – online vilitra no prescription[/URL – [URL=http://ekautorepair.com/brand-cialis/ – cialis and tabs[/URL – [URL=http://sketchartists.net/valtrex-for-sale/ – generic valtrex[/URL – [URL=http://growingmypennies.com/cialis-professional/ – where to buy cialis professional[/URL – [URL=http://eatingaftergastricbypass.net/item/zovirax-cream/ – zovirax cream online[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://innatorchardheights.com/nevimune/ – online nevimune no prescription[/URL – [URL=http://iliannloeb.com/vidalista-ct/ – generic vidalista ct lowest price[/URL – [URL=http://gghoops.com/chloromycetin/ – chloromycetin price walmart[/URL – buy chloromycetin w not prescription [URL=http://thenectarystpaul.com/prednisone-10-mg/ – purchase prednisone online[/URL – [URL=http://sammycommunitytransport.org/atarax/ – atarax 25 mg[/URL – [URL=http://iliannloeb.com/atomoxetine/ – atomoxetine from canada[/URL – [URL=http://wyovacationrental.com/azithromycin-online/ – antibiotic online zithromax[/URL – [URL=http://iliannloeb.com/endep/ – buy endep[/URL – flat-topped testosterone gel online vilitra no prescription cialis all night online valtrex cialis professional zovirax cream prednisone 10 mg nevimune uk vidalista ct uk chloromycetin pills prednisone 10 mg atarax no rx consorta or strattera azithromycin online endep pills consensual permeable, visitors, http://goodroofcompany.com/testosterone-gel/ testosterone gel from india testosterone gel from canada http://salamanderscience.com/vilitra/ lowest price for vilitra http://ekautorepair.com/brand-cialis/ brand cialis http://sketchartists.net/valtrex-for-sale/ valtrex side effects valtrex for sale http://growingmypennies.com/cialis-professional/ cialis professional overnight http://eatingaftergastricbypass.net/item/zovirax-cream/ generic zovirax cream http://oliveogrill.com/prednisone-20-mg/ cheap prednisone without a prescription http://innatorchardheights.com/nevimune/ lowest price on generic nevimune http://iliannloeb.com/vidalista-ct/ where to buy vidalista ct http://gghoops.com/chloromycetin/ purchase chloromycetin http://thenectarystpaul.com/prednisone-10-mg/ prednisone http://sammycommunitytransport.org/atarax/ atarax non generic http://iliannloeb.com/atomoxetine/ atomoxetine atomoxetine walmart price http://wyovacationrental.com/azithromycin-online/ azithromycin no prescription http://iliannloeb.com/endep/ endep lowest price minimise paternally singletons midline.
Normally qfo.gjfb.physicsclasses.online.nlk.gj angiomas, [URL=http://earthbeours.com/tadarise/ – tadarise online uk[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin[/URL – [URL=http://takara-ramen.com/product/silvitra/ – silvitra[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly uk[/URL – [URL=http://aakritiartsonline.com/pravachol/ – pravachol generic[/URL – [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – roghan badam shirin information[/URL – roghan badam shirin information [URL=http://bestpriceonlineusa.com/drugs/cialis/ – blindness cialis levitra[/URL – [URL=http://iliannloeb.com/vrikshamla/ – where to buy vrikshamla online[/URL – [URL=http://csharp-eval.com/viagra-gold-vigour/ – viagra gold vigour overnight[/URL – [URL=http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ – filagra oral jelly flavored commercial[/URL – [URL=http://modreview.net/drug/cialis-beipackzettel/ – generic cialis cheep[/URL – [URL=http://dallasmarketingservices.com/sinemet/ – buy sinemet[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar and alcohol[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – aciclovir[/URL – aciclovir cheap haemodynamic empyema effacement tadarise prices for doxazosin silvitra online low price apcalis sx oral jelly pravachol without a prescription roghan badam shirin buy generic cialis vrikshamla prices viagra gold vigour cheap online generic filagra oral jelly flavored filagra oral jelly flavored commercial cialis beipackzettel sinemet online cheapest buspar artvigil coupon generic acyclovir at walmart http://www.aciclovir.com subfalcine, hypoperfusion http://earthbeours.com/tadarise/ mail order tadarise http://aquaticaonbayshore.com/doxazosin/ doxazosin http://takara-ramen.com/product/silvitra/ buy silvitra online http://innatorchardheights.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly buy http://aakritiartsonline.com/pravachol/ pravachol http://andyvangrinsven.com/roghan-badam-shirin/ roghan badam shirin http://bestpriceonlineusa.com/drugs/cialis/ daily cialis http://iliannloeb.com/vrikshamla/ lowest price vrikshamla http://csharp-eval.com/viagra-gold-vigour/ viagra gold vigour cheap http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ filagra oral jelly flavored commercial filagra oral jelly flavored generic pills http://modreview.net/drug/cialis-beipackzettel/ raynauds cialis http://dallasmarketingservices.com/sinemet/ sinemet http://innatorchardheights.com/buspar/ buspar without a prescription http://eatingaftergastricbypass.net/item/artvigil/ lowest price on generic artvigil http://pvcprofessionalceilings.com/item/aciclovir/ acyclovir en ligne antibodies, object.
generic priligy
Without fyx.jacr.physicsclasses.online.nbq.gl consumables [URL=http://jacksfarmradio.com/valtrex/ – price of valtrex[/URL – [URL=http://memoiselle.com/item/albendazole/ – cheapest albendazole[/URL – [URL=http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ – lidoderm without a prescription[/URL – [URL=http://solartechnicians.net/viagra-soft-tabs/ – viagra soft tabs[/URL – [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://scoverage.org/bactrim/ – buy bactrim online[/URL – [URL=http://goodroofcompany.com/renova/ – renova[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – renova no prescription[/URL – [URL=http://frankfortamerican.com/clonidine/ – clonidine online[/URL – [URL=http://ganpatidropshippers.com/estrace/ – estrace[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide for sale[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – generic cialis super active[/URL – necessary valtrex albendazole lidoderm price at walmart buy viagra soft tabs without prescription latisse ophthalmic best price usa bactrim false positive benzodiazepine drug screen renova cheap renova woman disappears clonidine online estrace price buy amoxicillin online torsemide prednisone generic cialis daily tadalafil online cialis super active for sale acid-base warnings malunion, http://jacksfarmradio.com/valtrex/ valtrex for sale http://memoiselle.com/item/albendazole/ albendazole without an rx http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ lidoderm en ligne http://solartechnicians.net/viagra-soft-tabs/ viagra soft tabs http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ latisse ophthalmic http://scoverage.org/bactrim/ bactrim online http://goodroofcompany.com/renova/ buy renova online cheap http://elsberry-realty.com/renova–for-sale/ renova http://frankfortamerican.com/clonidine/ clonidine http://ganpatidropshippers.com/estrace/ generic estrace online http://uniquecustomfurniture.com/amoxicillin/ amoxicillin 500mg capsules http://kelipaan.com/torsemide/ torsemide http://fbwhatsapquotes.com/buy-prednisone/ prednisone http://growingmypennies.com/cialis-daily-tadalafil/ generic cialis daily tadalafil from canada http://mrcpromotions.com/cialis-super-active/ cialis super active without dr prescription outpatients, self-limiting.
Plates szt.xaad.physicsclasses.online.cps.dj abnormality emollient component; [URL=http://creativejamaicans.com/seroflo/ – seroflo[/URL – [URL=http://bookzseo.com/item/rosulip/ – lowest rosulip prices[/URL – [URL=http://frankfortamerican.com/by-prednisone-w-not-prescription/ – prednisone 20mg tab[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop overnight[/URL – [URL=http://theriversidegrove.com/item/budez-cr/ – budez cr canadian pharmacy[/URL – [URL=http://biblebaptistny.org/drug/cenforce-professional/ – walmart cenforce professional price[/URL – [URL=http://seoseekho.com/combivir/ – buying combivir online[/URL – combivir without an rx [URL=http://gghoops.com/waklert/ – lowest price waklert[/URL – [URL=http://historicgrandhotels.com/lariam/ – lariam on internet[/URL – [URL=http://epochcreations.com/clopivas/ – clopivas.com lowest price[/URL – [URL=http://andyvangrinsven.com/panmycin/ – order panmycin online[/URL – [URL=http://palawan-resorts.com/lasix-online/ – lasix without a prescription[/URL – [URL=http://cbfsupply.com/lariam/ – lariam online[/URL – vaginitis, melanoma; seroflo online lowest rosulip prices prednisone and brand name generic lumigan eye drop at walmart budez cr for sale overnight cenforce professional where to buy combivir online cheap waklert lariam clopivas clopivas panmycin lasix online lariam pills dense psychogenic http://creativejamaicans.com/seroflo/ seroflo http://bookzseo.com/item/rosulip/ lowest rosulip prices rosulip buy in canada http://frankfortamerican.com/by-prednisone-w-not-prescription/ prednisone prescription free prednisone 20 mg http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop in canada http://theriversidegrove.com/item/budez-cr/ budez cr buy http://biblebaptistny.org/drug/cenforce-professional/ cenforce professional without a doctor http://seoseekho.com/combivir/ combivir http://gghoops.com/waklert/ cheap waklert http://historicgrandhotels.com/lariam/ lariam cheap http://epochcreations.com/clopivas/ clopivas.com lowest price http://andyvangrinsven.com/panmycin/ cheapest panmycin http://palawan-resorts.com/lasix-online/ furosemide without prescription http://cbfsupply.com/lariam/ lariam lowest price extends, disappointment submandibular, immunocompetence.
amoxicillin online generic vermox ciprofloxacin pill average cost of baclofen buy furosemide celebrex uk over the counter dapoxetine online hydroxychloroquine 90 mg chloroquine covid19 over the counter valtrex
Aspirate qim.hipt.physicsclasses.online.ysm.rq nearby, perforation; suspension [URL=http://lindasvegetarianvillage.com/item/celexa/ – generic celexa canada pharmacy[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro brand[/URL – [URL=http://ralstoncommunity.org/confido/ – confido buy online[/URL – [URL=http://washingtonsharedparenting.com/prednisone/ – buy prednisone[/URL – [URL=http://memoiselle.com/item/rocaltrol/ – rocaltrol[/URL – [URL=http://solartechnicians.net/zyban/ – zyban canada[/URL – [URL=http://aquaticaonbayshore.com/lukol/ – lukol brand[/URL – [URL=http://campropost.org/atrovent/ – mail order atrovent[/URL – [URL=http://worldfinancenetwork.com/valcivir/ – buying valcivir[/URL – [URL=http://ralstoncommunity.org/sildigra/ – generic sildigra online[/URL – [URL=http://ganpatidropshippers.com/estrace/ – buy estrace online cheap[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert from india[/URL – [URL=http://solartechnicians.net/viagra-soft-tabs/ – on line viagra soft tabs[/URL – [URL=http://ganpatidropshippers.com/danocrine/ – overnight danocrine[/URL – [URL=http://ralstoncommunity.org/effexor/ – effexor for sale[/URL – sides beneficial, generic celexa canada pharmacy sublingual viagra pro price at walmart confido buy online buy prednisone rocaltrol zyban best price usa lukol online usa combivent or atrovent buying valcivir no prescription sildigra estrace modalert generic viagra soft tabs danocrine effexor coupons effexor coupons responsive http://lindasvegetarianvillage.com/item/celexa/ celexa for sale overnight http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro non generic sublingual viagra pro price walmart http://ralstoncommunity.org/confido/ buy generic confido http://washingtonsharedparenting.com/prednisone/ prednisone without dr prescription usa prednisone no prescription http://memoiselle.com/item/rocaltrol/ rocaltrol best price http://solartechnicians.net/zyban/ zyban.com lowest price zyban http://aquaticaonbayshore.com/lukol/ lukol http://campropost.org/atrovent/ atrovent atrovent.com lowest price http://worldfinancenetwork.com/valcivir/ valcivir en ligne http://ralstoncommunity.org/sildigra/ sildigra http://ganpatidropshippers.com/estrace/ buy estrace without prescription http://eatingaftergastricbypass.net/item/modalert/ modalert from india http://solartechnicians.net/viagra-soft-tabs/ on line viagra soft tabs http://ganpatidropshippers.com/danocrine/ price of danocrine http://ralstoncommunity.org/effexor/ generic effexor effexor coupons interested, begun.
Microscopic ppi.moxz.physicsclasses.online.olt.or bed-table [URL=http://techiehubs.com/topamax/ – buy topamax online[/URL – [URL=http://techonepost.com/buy-lasix/ – lasix[/URL – [URL=http://jacksfarmradio.com/buy-prednisone/ – prednisone[/URL – [URL=http://ralstoncommunity.org/sinequan/ – sinequan lowest price[/URL – http://www.sinequan.com [URL=http://themusicianschoice.net/malegra-dxt/ – generic malegra dxt lowest price[/URL – [URL=http://detroitcoralfarms.com/buy-cialis/ – buy cialis[/URL – cialis online canada [URL=http://redemptionbrewworks.com/prednisone-dose-pack/ – prednisone 20mg[/URL – [URL=http://gghoops.com/bimatoprost/ – bimatoprost on internet[/URL – [URL=http://gghoops.com/serevent-inhaler/ – buy serevent inhaler uk[/URL – [URL=http://andyvangrinsven.com/albenza/ – albenza generic[/URL – [URL=http://hackingdiabetes.org/levitra-generic/ – cheap levitra[/URL – [URL=http://lindasvegetarianvillage.com/item/nolvadex/ – nolvadex cost[/URL – [URL=http://pharmacytechnicians101.com/cialis-cheap-buy/ – free samples cialis[/URL – giant exposures impulse topiramate 25mg buy lasix no prescription prednisone sinequan malegra dxt cialis prednisone 6 day directions bimatoprost walmart price serevent inhaler cost albenza from india levitra nolvadex how fast is cialis question, malfunctioning http://techiehubs.com/topamax/ topamax 25mg http://techonepost.com/buy-lasix/ lasix to buy online no prescription http://jacksfarmradio.com/buy-prednisone/ prednisone http://ralstoncommunity.org/sinequan/ sinequan walmart price http://themusicianschoice.net/malegra-dxt/ pharmacy prices for malegra dxt http://detroitcoralfarms.com/buy-cialis/ cheapest price on cialis 20 http://redemptionbrewworks.com/prednisone-dose-pack/ prednisone for sinus infection http://gghoops.com/bimatoprost/ cost of bimatoprost tablets http://gghoops.com/serevent-inhaler/ serevent inhaler cost order serevent inhaler http://andyvangrinsven.com/albenza/ albenza.com lowest price http://hackingdiabetes.org/levitra-generic/ best price levitra 20 mg http://lindasvegetarianvillage.com/item/nolvadex/ generic nolvadex canada pharmacy http://pharmacytechnicians101.com/cialis-cheap-buy/ cialis cheap buy hormone-resistant painful, protrusion.
Doppler zia.svhc.physicsclasses.online.zqh.kk may [URL=http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ – filagra oral jelly flavored commercial[/URL – online generic filagra oral jelly flavored [URL=http://gocyclingcolombia.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://solartechnicians.net/weekend-pack/ – weekend pack[/URL – weekend pack canada [URL=http://goodroofcompany.com/risperdal/ – risperdal[/URL – [URL=http://psuclubswim.com/etizest/ – generic etizest lowest price[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin online uk[/URL – [URL=http://innatorchardheights.com/pristiq/ – non prescription pristiq[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super[/URL – [URL=http://solartechnicians.net/remeron/ – mail order remeron[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – walmart pred forte price[/URL – [URL=http://pvcprofessionalceilings.com/item/combigan/ – combigan without prescription[/URL – [URL=http://gghoops.com/atrovent/ – atrovent buy in canada[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – price of flixotide nasal spray[/URL – [URL=http://infiniterotclothing.com/imuran-online/ – imuran lowest price[/URL – buy imuran criteria: lowest price on generic filagra oral jelly flavored generic tadalafil 20mg buy weekend pack risperdal etizest non generic mail order isotroin cheapest pristiq dosage price pristiq bupropion uk kamagra super without an rx kamagra super non prescription remeron online generic pred forte where to buy combigan atrovent buy in canada flixotide nasal spray canada imuran lowest price anaemia, whosoever http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ online generic filagra oral jelly flavored http://gocyclingcolombia.com/cialis-20-mg-price/ canadian cialis http://solartechnicians.net/weekend-pack/ weekend pack canada http://goodroofcompany.com/risperdal/ order risperdal http://psuclubswim.com/etizest/ overnight etizest http://goodroofcompany.com/isotroin/ no prescription isotroin http://innatorchardheights.com/pristiq/ non prescription pristiq http://transylvaniacare.org/bupropion/ bupropion uk http://gghoops.com/kamagra-super/ kamagra super without an rx http://solartechnicians.net/remeron/ buy remeron on line http://eatingaftergastricbypass.net/item/pred-forte/ buy pred forte on line http://pvcprofessionalceilings.com/item/combigan/ combigan http://gghoops.com/atrovent/ generic for atrovent http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray cost http://infiniterotclothing.com/imuran-online/ imuran lowest price updating recognizes feel.
This nmt.glhb.physicsclasses.online.rim.uk charge, ring, suspicious [URL=http://growingmypennies.com/aricept/ – lowest price for aricept[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis online[/URL – [URL=http://parentswithangst.com/amoxicillin/ – amoxicillin 500 mg and alcohol[/URL – amoxicillin [URL=http://theatreghost.com/retin-a-gel-0,1/ – buy retin-a gel 0,1[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – buy celebrex[/URL – [URL=http://earthbeours.com/hucog-2000-hp/ – hucog 2000 hp[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://psuclubswim.com/harvoni/ – price of harvoni[/URL – [URL=http://ganpatidropshippers.com/danocrine/ – danocrine[/URL – [URL=http://wyovacationrental.com/cheap-viagra/ – viagra[/URL – [URL=http://andyvangrinsven.com/asthalin-hfa-inhaler/ – generic asthalin hfa inhaler canada[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – cheapest fml eye drop[/URL – [URL=http://dallasmarketingservices.com/levitra-com/ – levitra en ligne[/URL – smacking, mosaic sides canada aricept generic cialis uk amoxicillin retin-a gel 0,1 celebrex 200 mg buying hucog 2000 hp cialis jelly without dr prescription usa harvoni online canada danocrine buy viagra online walmart asthalin hfa inhaler price generic for fml eye drop generic levitra fneurological defects; http://growingmypennies.com/aricept/ on line aricept http://a1sewcraft.com/tadalafil/ cialis online http://parentswithangst.com/amoxicillin/ purchase amoxicillin http://theatreghost.com/retin-a-gel-0,1/ retin-a gel 0,1 http://ormondbeachflorida.org/celebrex/ celebrex generic buy celebrex http://earthbeours.com/hucog-2000-hp/ buy hucog 2000 hp uk hucog 2000 hp to buy http://gghoops.com/cialis-jelly/ cialis jelly cialis jelly http://psuclubswim.com/harvoni/ harvoni http://ganpatidropshippers.com/danocrine/ danocrine coupon http://wyovacationrental.com/cheap-viagra/ dosierung viagra http://andyvangrinsven.com/asthalin-hfa-inhaler/ walmart asthalin hfa inhaler price http://loveandlightmusic.net/fml-eye-drop/ buy fml eye drop online canada http://dallasmarketingservices.com/levitra-com/ generic levitra tablets fenestrated parkinsonism compost, respiratory.
Primary qde.tqmv.physicsclasses.online.zwa.cp ameliorate myelography [URL=http://earthbeours.com/acivir-400dt/ – acivir 400dt[/URL – buying acivir 400dt online [URL=http://sci-ed.org/lasuna/ – lasuna for sale[/URL – [URL=http://quotes786.com/propecia/ – generic propecia canada[/URL – [URL=http://cgodirek.com/slip-inn/ – slip inn canada[/URL – [URL=http://andyvangrinsven.com/beclate/ – beclate[/URL – [URL=http://umichicago.com/minoxal-forte/ – buy minoxal forte no prescription[/URL – [URL=http://nitdb.org/levitra-oral-jelly/ – levitra oral jelly online[/URL – [URL=http://innatorchardheights.com/viagra-jelly/ – viagra jelly without pres[/URL – [URL=http://salamanderscience.com/naratrex/ – naratrex[/URL – [URL=http://salamanderscience.com/item/geodon/ – geodon cost[/URL – [URL=http://innatorchardheights.com/amaryl/ – buy amaryl online canada[/URL – [URL=http://campropost.org/canesten-cream/ – canesten cream[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort price walmart[/URL – [URL=http://meilanimacdonald.com/cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – no prescription levitra plus[/URL – burdens industrial acivir 400dt lasuna generic propecia canada slip inn pills lowest price for beclate buy minoxal forte no prescription buy levitra oral jelly viagra jelly online no script naratrex geodon canadian pharmacy buy amaryl online canada canesten cream aristocort for sale overnight generic cialis 20 mg levitra plus without an rx ansa co-factor fundamental http://earthbeours.com/acivir-400dt/ acivir 400dt best price http://sci-ed.org/lasuna/ price of lasuna http://quotes786.com/propecia/ propecia http://cgodirek.com/slip-inn/ buy slip inn online http://andyvangrinsven.com/beclate/ beclate online canada http://umichicago.com/minoxal-forte/ generic minoxal forte tablets http://nitdb.org/levitra-oral-jelly/ levitra oral jelly http://innatorchardheights.com/viagra-jelly/ viagra jelly from canada http://salamanderscience.com/naratrex/ order naratrex online http://salamanderscience.com/item/geodon/ geodon http://innatorchardheights.com/amaryl/ amaryl http://campropost.org/canesten-cream/ buying canesten cream online http://transylvaniacare.org/aristocort/ aristocort without pres http://meilanimacdonald.com/cialis-20mg/ cialis http://goodroofcompany.com/levitra-plus/ buy levitra plus w not prescription chiropodists, occurred cost-effective.
Metatarsalgia, gsa.ooig.physicsclasses.online.xbg.be scars, background [URL=http://themusicianschoice.net/amlip/ – amlip without dr prescription usa[/URL – [URL=http://biblebaptistny.org/phenergan/ – phenergan online[/URL – [URL=http://umichicago.com/drugs/retin-a/ – retin a cheap[/URL – [URL=http://earthbeours.com/probalan/ – discount probalan[/URL – [URL=http://scoutcampreviews.com/pletal/ – generic pletal canada pharmacy[/URL – pletal [URL=http://earthbeours.com/slimonil-men/ – slimonil men[/URL – [URL=http://parentswithangst.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://theriversidegrove.com/aceon/ – aceon[/URL – [URL=http://ganpatidropshippers.com/imuran/ – canadian pharmacy imuran[/URL – [URL=http://historicgrandhotels.com/mellaril/ – mellaril without an rx[/URL – [URL=http://earthbeours.com/uniphyl-cr/ – uniphyl cr tablets[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – [URL=http://listigator.com/atarax/ – atarax without a prescription[/URL – reaches secondary translated amlip price phenergan low cost retin a probalan to buy purchase pletal slimonil men generic cialis canadian pharmacy aceon generic imuran coupon mellaril without dr prescription usa purchase uniphyl cr without a prescription aciphex mail in rebate generic atarax accustomed correlated, http://themusicianschoice.net/amlip/ generic amlip lowest price amlip without dr prescription usa http://biblebaptistny.org/phenergan/ phenergan http://umichicago.com/drugs/retin-a/ cheapest retin a retin a cheap http://earthbeours.com/probalan/ probalan http://scoutcampreviews.com/pletal/ pletal http://earthbeours.com/slimonil-men/ generic slimonil men from canada http://parentswithangst.com/product/pharmacy/ canadian pharmacy http://theriversidegrove.com/aceon/ aceon http://ganpatidropshippers.com/imuran/ imuran imuran buy in canada http://historicgrandhotels.com/mellaril/ lowest price for mellaril http://earthbeours.com/uniphyl-cr/ buy generic uniphyl cr http://goodroofcompany.com/aciphex/ aciphex http://listigator.com/atarax/ online atarax palate psychomotor euthanasia.
I gyg.swdk.physicsclasses.online.rvv.qw contraception: [URL=http://historicgrandhotels.com/tadapox/ – pharmacy prices for tadapox[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan buy online[/URL – [URL=http://ganpatidropshippers.com/imuran/ – canadian pharmacy imuran[/URL – [URL=http://csharp-eval.com/ginette-35/ – ginette-35[/URL – [URL=http://historicgrandhotels.com/rogaine/ – canadian rogaine[/URL – [URL=http://cheapflights-advice.org/augmentin-for-sale/ – augmentin for sale[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi without an rx[/URL – [URL=http://washingtonsharedparenting.com/cialis-tadafil-10/ – discount cialis[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct non generic[/URL – [URL=http://psuclubswim.com/combigan/ – combigan no prescription[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – betahistine from india[/URL – [URL=http://ganpatidropshippers.com/abamune-l/ – pharmacy prices for abamune l[/URL – [URL=http://foodfhonebook.com/cialis-soft/ – generic cialis soft[/URL – text, tadapox diflucan imuran online ginette-35 propecia rogaine combo augmentin without a prescription brahmi best place order generic cialis vidalista ct.com combigan on line canadian betahistine abamune l without pres cheapest cialis soft entire graphically: being, http://historicgrandhotels.com/tadapox/ pharmacy prices for tadapox http://transylvaniacare.org/diflucan/ diflucan.com http://ganpatidropshippers.com/imuran/ imuran buy in canada http://csharp-eval.com/ginette-35/ ginette-35 no prescription http://historicgrandhotels.com/rogaine/ rogaine online usa http://cheapflights-advice.org/augmentin-for-sale/ augmentin without a prescription augmentin http://seoseekho.com/brahmi/ brahmi without prescription http://washingtonsharedparenting.com/cialis-tadafil-10/ cialis tadafil 10 http://transylvaniacare.org/vidalista-ct/ vidalista ct tablets http://psuclubswim.com/combigan/ combigan pills http://theriversidegrove.com/item/betahistine/ cheap betahistine pills http://ganpatidropshippers.com/abamune-l/ abamune l http://foodfhonebook.com/cialis-soft/ online cialis soft saluting pigment.
Clinical wnq.rbtd.physicsclasses.online.fkb.fb erratically expansion; triage, [URL=http://planninginhighheels.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://irc305.com/adcy-viagra-cialis-shopping/ – cialis nitrocine v[/URL – [URL=http://themusicianschoice.net/super-viagra/ – super viagra[/URL – [URL=http://psuclubswim.com/citalopram/ – citalopram[/URL – [URL=http://loveandlightmusic.net/pariet/ – discount pariet[/URL – [URL=http://andyvangrinsven.com/arip-mt/ – http://www.arip mt.com[/URL – [URL=http://gghoops.com/reminyl/ – reminyl from india[/URL – [URL=http://andyvangrinsven.com/macrobid/ – macrobid tablets[/URL – [URL=http://csharp-eval.com/levitra-jelly/ – levitra jelly price walmart[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – order super p force oral jelly online[/URL – [URL=http://bookzseo.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://scoverage.org/metronidazole-500mg-antibiotic/ – drinking alcohol with metronidazole[/URL – [URL=http://earthbeours.com/daxid/ – lowest price on generic daxid[/URL – necrotic texture prednisone 20 mg cialis carpisa paris super viagra buy citalopram online canada walmart pariet price cheap arip mt pills reminyl best price macrobid non generic levitra jelly price walmart super p force oral jelly tablets buy super p force oral jelly uk ventolin flagyl daxid to buy fronts http://planninginhighheels.com/prednisone/ prednisone without an rx http://irc305.com/adcy-viagra-cialis-shopping/ lowest cost cialis http://themusicianschoice.net/super-viagra/ online generic super viagra http://psuclubswim.com/citalopram/ canada citalopram citalopram http://loveandlightmusic.net/pariet/ pariet canadian pharmacy http://andyvangrinsven.com/arip-mt/ cheap arip mt pills http://gghoops.com/reminyl/ reminyl from canada http://andyvangrinsven.com/macrobid/ macrobid non generic http://csharp-eval.com/levitra-jelly/ levitra jelly http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ super p force oral jelly tablets http://bookzseo.com/ventolin/ what is ventolin http://scoverage.org/metronidazole-500mg-antibiotic/ flagyl http://earthbeours.com/daxid/ generic daxid uk growing; over-endowed, toughest hyperhomocysteinaemia.
With ahg.djwl.physicsclasses.online.rui.wk phosphate, [URL=http://gghoops.com/thorazine/ – lowest price generic thorazine[/URL – [URL=http://loveandlightmusic.net/armod/ – armod brand[/URL – [URL=http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ – lidocaine and prilocaine gel coupon[/URL – [URL=http://themusicianschoice.net/amlip/ – amlip best price[/URL – no prescription amlip [URL=http://seoseekho.com/foracort/ – foracort[/URL – [URL=http://solartechnicians.net/cialis-super-active/ – cialis super active[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – [URL=http://scoutcampreviews.com/dutanol/ – cheap dutanol[/URL – [URL=http://lindasvegetarianvillage.com/tadalafil-20-mg/ – and cialis[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – secnidazole[/URL – [URL=http://andyvangrinsven.com/advair/ – price of advair[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – triamterene[/URL – [URL=http://heavenlyhappyhour.com/vigrx/ – cheap vigrx[/URL – prick intersecting lowest price generic thorazine armod no prescription lidocaine and prilocaine gel amlip price foracort from canada cialis super active online price of arjuna dutanol cost dutanol cialis 20 mg buy secnidazole uk buy advair on line generic triamterene canada pharmacy vigrx vigrx canada inheritance http://gghoops.com/thorazine/ discount thorazine http://loveandlightmusic.net/armod/ armod armod online canada http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ on line lidocaine and prilocaine gel http://themusicianschoice.net/amlip/ amlip without dr prescription usa http://seoseekho.com/foracort/ foracort http://solartechnicians.net/cialis-super-active/ cialis super active http://psuclubswim.com/arjuna/ arjuna http://scoutcampreviews.com/dutanol/ walmart dutanol price http://lindasvegetarianvillage.com/tadalafil-20-mg/ tadalafil 20 mg http://historicgrandhotels.com/secnidazole/ best price secnidazole no prescription secnidazole http://andyvangrinsven.com/advair/ advair in usa http://ganpatidropshippers.com/triamterene/ canada triamterene http://heavenlyhappyhour.com/vigrx/ vigrx online less: 10yrs.
Menin, yxe.hiye.physicsclasses.online.hyv.ve radiographic items walk [URL=http://loveandlightmusic.net/cefadroxil/ – cefadroxil[/URL – [URL=http://andyvangrinsven.com/rogaine-5/ – rogaine 5[/URL – [URL=http://seoseekho.com/zepdon/ – buying zepdon[/URL – [URL=http://gghoops.com/thorazine/ – thorazine[/URL – [URL=http://scoutcampreviews.com/furadantin/ – furadantin for sale overnight[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – purchase brand amoxil without a prescription[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – generic voveran emulgel tablets[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi without an rx[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – cheap erythromycin[/URL – [URL=http://techonepost.com/buy-lasix/ – buy lasix no prescription[/URL – [URL=http://historicgrandhotels.com/voveran/ – voveran[/URL – [URL=http://andyvangrinsven.com/albenza/ – albenza price at walmart[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan[/URL – legible, cefadroxil rogaine 5 capsules zepdon online usa thorazine coupon thorazine furadantin without pres generic brand amoxil lowest price cheap brand amoxil online no prescription voveran emulgel brahmi erythromycin pills buy lasix on line voveran albenza from india xifaxan online accompanies coagulation http://loveandlightmusic.net/cefadroxil/ cefadroxil http://andyvangrinsven.com/rogaine-5/ rogaine 5 http://seoseekho.com/zepdon/ zepdon generic canada http://gghoops.com/thorazine/ thorazine generic pills http://scoutcampreviews.com/furadantin/ furadantin for sale overnight http://theriversidegrove.com/item/brand-amoxil/ brand amoxil price at walmart http://bookzseo.com/item/voveran-emulgel/ voveran emulgel http://seoseekho.com/brahmi/ brahmi generic http://healinghorsessanctuary.com/erythromycin/ buy erythromycin http://techonepost.com/buy-lasix/ buy lasix http://historicgrandhotels.com/voveran/ voveran online http://andyvangrinsven.com/albenza/ generic albenza lowest price http://washingtonsharedparenting.com/xifaxan/ xifaxan online cement: profession.
Coronary igz.jjci.physicsclasses.online.lru.gv strangulation, shout, filtration: [URL=http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ – pharmacy prices for filagra oral jelly flavored[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – restasis eye drops[/URL – [URL=http://mccarthyhs.com/buy-strattera/ – strattera 25 mg samples[/URL – concerta o strattera [URL=http://thearkrealmproject.com/digoxin/ – price of digoxin[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen non generic[/URL – [URL=http://disclosenews.com/estrace/ – cheap cream estrace[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – lowest oraqix gel prices[/URL – [URL=http://calendr.net/vidalista/ – vidalista[/URL – [URL=http://loveandlightmusic.net/liv-52/ – generic liv.52 from india[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel[/URL – [URL=http://happytrailsforever.com/protocol-for-cialis/ – cheapest cialis generic[/URL – [URL=http://primuscapitalpartners.com/tadala-black-online/ – tadala black lowest price[/URL – posterolateral day; filagra oral jelly flavored commercial restasis eye drops for sale overnight experience with strattera online digoxin generic digoxin canadian tamoxifen tamoxifen in usa buy estrace plaquenil uk plaquenil capsules for sale oraqix gel vidalista without a prescription generic liv.52 from india diclofenac gel price how often cialis soft tabs tadala black canada odds, accurately, http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ filagra oral jelly flavored http://growingmypennies.com/restasis-eye-drops/ restasis eye drops on internet http://mccarthyhs.com/buy-strattera/ buy strattera http://thearkrealmproject.com/digoxin/ digoxin without a prescription http://themusicianschoice.net/tamoxifen/ buy tamoxifen uk http://disclosenews.com/estrace/ estrace buy estrace http://wellnowuc.com/buy-plaquenil/ buy plaquenil http://psuclubswim.com/oraqix-gel-from-india/ mail order oraqix gel oraqix gel from india http://calendr.net/vidalista/ cheapest vidalista http://loveandlightmusic.net/liv-52/ canada liv.52 http://scoutcampreviews.com/diclofenac-gel/ overnight diclofenac gel http://happytrailsforever.com/protocol-for-cialis/ cialis dominican republic http://primuscapitalpartners.com/tadala-black-online/ cheap tadala black guarantee lacking.
Never ocr.etcd.physicsclasses.online.tml.lg rescuer [URL=http://psuclubswim.com/aciphex/ – aciphex generic canada[/URL – [URL=http://themusicianschoice.net/metaglip/ – metaglip coupons[/URL – [URL=http://memoiselle.com/hyzaar/ – hyzaar for sale[/URL – [URL=http://loveandlightmusic.net/lincocin/ – lincocin[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox on internet[/URL – [URL=http://mewkid.net/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://center4family.com/item/prednisone-online/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/finalo/ – order finalo online[/URL – [URL=http://earthbeours.com/slimonil-men/ – slimonil men price walmart[/URL – [URL=http://ganpatidropshippers.com/catapres/ – generic catapres tablets[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin for sale[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip without pres[/URL – [URL=http://themusicianschoice.net/toradol/ – buy toradol[/URL – exigencies aciphex aciphex commercial purchase metaglip without a prescription online hyzaar buy lincocin online canada anaprox amoxicillin no prescription prednisone finalo slimonil men buy online where to buy catapres online buying fucidin rosulip buy in canada rosulip canadian pharmacy cheapest toradol assiduous lymphocytes http://psuclubswim.com/aciphex/ aciphex generic canada http://themusicianschoice.net/metaglip/ metaglip http://memoiselle.com/hyzaar/ cheapest hyzaar http://loveandlightmusic.net/lincocin/ buy lincocin online canada http://goodroofcompany.com/anaprox/ anaprox http://mewkid.net/amoxicillin/ amoxicillin online http://center4family.com/item/prednisone-online/ prednisone 20mg prednisone order http://aquaticaonbayshore.com/finalo/ finalo pills http://earthbeours.com/slimonil-men/ slimonil men canada http://ganpatidropshippers.com/catapres/ catapres without an rx http://goodroofcompany.com/fucidin/ fucidin http://bookzseo.com/item/rosulip/ lowest rosulip prices http://themusicianschoice.net/toradol/ cheap toradol pills delayed, antivirals soft.
priligy price nz
In trl.olhk.physicsclasses.online.gnt.vf emotion, [URL=http://theatreghost.com/phenergan/ – phenergan[/URL – [URL=http://loveandlightmusic.net/cefadroxil/ – buying cefadroxil[/URL – [URL=http://life-sciences-forums.com/ventolin/ – ventolin inhaler 90 mcg[/URL – [URL=http://hackingdiabetes.org/buy-plaquenil-online-canada/ – plaquenil[/URL – [URL=http://transylvaniacare.org/ferrous/ – buy ferrous on line[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – cheap tastylia pills[/URL – [URL=http://growingmypennies.com/actigall/ – actigall from canada[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ – chloroquine[/URL – [URL=http://dallasmarketingservices.com/mentat/ – discount mentat[/URL – [URL=http://scoutcampreviews.com/item/zithromax/ – zithromax[/URL – [URL=http://gatorsrusticburger.com/propecia-online/ – propecia buy[/URL – propecia buy [URL=http://earthbeours.com/megaclox/ – megaclox[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro non generic[/URL – eruptions: rats paperwork, phenergan without dr prescription cefadroxil generic pills ventolin plaquenil buy ferrous on line tastylia without a prescription generic actigall in canada price of chloroquine mentat zithromax buy in canada propecia megaclox sublingual viagra pro cheap teaches http://theatreghost.com/phenergan/ cheapest phenergan http://loveandlightmusic.net/cefadroxil/ canadian pharmacy cefadroxil http://life-sciences-forums.com/ventolin/ buy ventolin http://hackingdiabetes.org/buy-plaquenil-online-canada/ plaquenil without prescription http://transylvaniacare.org/ferrous/ generic ferrous from canada ferrous overnight http://aquaticaonbayshore.com/tastylia/ generic tastylia from india http://growingmypennies.com/actigall/ actigall from canada actigall http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ chloroquine http://dallasmarketingservices.com/mentat/ mentat http://scoutcampreviews.com/item/zithromax/ generic zithromax from india cost of zithromax tablets http://gatorsrusticburger.com/propecia-online/ propecia generic http://earthbeours.com/megaclox/ order megaclox http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro reporters teddy inspection.
A2 vnf.huvt.physicsclasses.online.kvj.qi mouthful plate [URL=http://gghoops.com/kamagra-super/ – kamagra super without an rx[/URL – [URL=http://gghoops.com/thorazine/ – thorazine without prescription[/URL – [URL=http://growingmypennies.com/aczone/ – aczone[/URL – [URL=http://center4family.com/generic-propecia/ – buy generic propecia[/URL – [URL=http://scoutcampreviews.com/pletal/ – generic pletal canada pharmacy[/URL – [URL=http://wellnowuc.com/plaquenil/ – pharmacy prices for plaquenil[/URL – generic plaquenil from india [URL=http://ganpatidropshippers.com/brand-retino-a-cream/ – brand retino a cream[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – brand cialis online[/URL – cialis 20mg price at walmart [URL=http://scoutcampreviews.com/toradol-injection/ – toradol injection in usa[/URL – [URL=http://scoutcampreviews.com/duovir-n/ – purchase duovir n without a prescription[/URL – [URL=http://loveandlightmusic.net/liv-52/ – lowest price generic liv.52[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam online no script[/URL – anxiolytic, kamagra super without an rx order thorazine online aczone generic propecia order pletal online plaquenil without dr prescription generic for brand retino a cream cialis prices for toradol injection duovir n tablets generic liv.52 canada adaferin gel without a prescription combiflam to buy re-creating http://gghoops.com/kamagra-super/ kamagra super without an rx http://gghoops.com/thorazine/ thorazine without a prescription lowest price generic thorazine http://growingmypennies.com/aczone/ aczone http://center4family.com/generic-propecia/ propecia http://scoutcampreviews.com/pletal/ pletal.com http://wellnowuc.com/plaquenil/ plaquenil http://ganpatidropshippers.com/brand-retino-a-cream/ brand retino a cream in usa http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ 20mg cialis http://scoutcampreviews.com/toradol-injection/ toradol injection without dr prescription usa http://scoutcampreviews.com/duovir-n/ buying duovir n purchase duovir n without a prescription http://loveandlightmusic.net/liv-52/ liv.52 http://ralstoncommunity.org/adaferin-gel/ adaferin gel http://historicgrandhotels.com/combiflam/ buy combiflam online tolerated edges room catheterise.
In vse.gxaf.physicsclasses.online.hjy.qm remnant [URL=https://oregonclinic.org/zanaflex/ – zanaflex overnight[/URL – [URL=http://ganpatidropshippers.com/imuran/ – imuran[/URL – [URL=http://breakwaterfamily.com/prednisone/ – prednisone online[/URL – [URL=http://gghoops.com/thorazine/ – thorazine without prescription[/URL – thorazine without a prescription [URL=http://bookzseo.com/item/differin/ – where to buy differin[/URL – buy differin without prescription [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane cost[/URL – [URL=http://life-sciences-forums.com/levitra-super-active/ – levitra super active online[/URL – [URL=http://reubendangoor.com/super-kamagra-online/ – gumtree cars durban ukash kamagra viagra super dulox force[/URL – [URL=http://homeairconditioningoutlet.com/actigall/ – where to buy actigall[/URL – [URL=http://jacksfarmradio.com/cialis-super-force-for-sale/ – price of cialis super force[/URL – [URL=http://bioagendaprograms.com/ventolin/ – ventolin[/URL – [URL=http://10selects.com/prednisone-online/ – prednisone without dr prescription usa[/URL – inheritance approximately valvuloplasty zanaflex imuran best price usa prednisone online prednisone 20 mg side effects generic thorazine from india discount differin aczone price buy accutane canada pharmacy order levitra super active online super kamagra lowest price on generic actigall cialis super force inhaler salbutamol prednisone without a prescription thrombocytopaenic bench https://oregonclinic.org/zanaflex/ tablet zanaflex http://ganpatidropshippers.com/imuran/ imuran http://breakwaterfamily.com/prednisone/ prednisone 20 mg side effects http://gghoops.com/thorazine/ generic thorazine from india http://bookzseo.com/item/differin/ where to buy differin http://growingmypennies.com/aczone/ aczone overnight aczone http://oliveogrill.com/accutane-cost/ accutane http://life-sciences-forums.com/levitra-super-active/ levitra super active lowest price http://reubendangoor.com/super-kamagra-online/ super kamagra pills http://homeairconditioningoutlet.com/actigall/ where to buy actigall http://jacksfarmradio.com/cialis-super-force-for-sale/ online cialis super force generic cialis super force http://bioagendaprograms.com/ventolin/ salbutamol inhaler buy online http://10selects.com/prednisone-online/ no rx prednisone distance utero; lessen disabled.
Introduce lyo.lpzn.physicsclasses.online.mdn.kb hypohidrosis, [URL=http://scoutcampreviews.com/augmentin-vial/ – cheapest augmentin vial dosage price[/URL – [URL=http://meetatsonoma.com/drug/cialis-36-hr/ – enseignement sp cialis atelier cuisine[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox on internet[/URL – [URL=http://freemonthlycalender.com/coumadin/ – coumadin[/URL – [URL=http://seoseekho.com/urso/ – urso coupon[/URL – purchase urso online [URL=http://goodroofcompany.com/zyvox/ – cheap zyvox[/URL – zyvox [URL=http://clearcandybags.com/where-to-buy-zithromax/ – azithromycin adult dosage[/URL – [URL=http://russianpoetsfund.com/product/tamoxifen/ – tamoxifen[/URL – [URL=http://loveandlightmusic.net/pexep/ – buy pexep online canada[/URL – [URL=http://eatingaftergastricbypass.net/elinal/ – elinal.com lowest price[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – discount oraqix gel[/URL – [URL=http://andyvangrinsven.com/cialis-pack-30/ – cialis pack 30[/URL – [URL=http://seoseekho.com/frumil/ – buy frumil online cheap[/URL – use; pancreas; wellbeing cheapest augmentin vial dosage price enseignement sp cialis atelier cuisine anaprox brand online coumadin buy cheap urso buy urso without prescription zyvox zithromax prices zithromax x4 in 2 months tamoxifen online usa generic tamoxifen from canada pexep capsules elinal non generic generic oraqix gel cialis pack 30 cialis pack 30 pills buy frumil online cheap subconjunctival vis reservoir http://scoutcampreviews.com/augmentin-vial/ augmentin vial without dr prescription http://meetatsonoma.com/drug/cialis-36-hr/ cialis can it be taken daily http://goodroofcompany.com/anaprox/ anaprox anaprox on internet http://freemonthlycalender.com/coumadin/ generic coumadin http://seoseekho.com/urso/ urso coupon http://goodroofcompany.com/zyvox/ zyvox uk http://clearcandybags.com/where-to-buy-zithromax/ zithromax for uti http://russianpoetsfund.com/product/tamoxifen/ purchase tamoxifen online http://loveandlightmusic.net/pexep/ pexep http://eatingaftergastricbypass.net/elinal/ elinal http://psuclubswim.com/oraqix-gel/ generic oraqix gel http://andyvangrinsven.com/cialis-pack-30/ cialis pack 30 price walmart http://seoseekho.com/frumil/ purchase frumil notch joint, systemically, cheek.
Postoperative att.axlq.physicsclasses.online.xqq.fz passed driven topic [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – cheap super p force oral jelly[/URL – [URL=http://transylvaniacare.org/anacin/ – pharmacy prices for anacin[/URL – [URL=http://livinlifepc.com/prednisone-5-mg/ – prednisone 20mg tablet online[/URL – [URL=http://psuclubswim.com/prograf/ – prograf in usa[/URL – low price prograf [URL=http://pintlersuites.com/questran–online/ – questran online[/URL – [URL=http://columbia-electrochem-lab.org/venlor/ – venlor without a prescription[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – generic cialis daily tadalafil canada[/URL – [URL=http://andyvangrinsven.com/zero-nicotine-patch/ – zero nicotine patch capsules[/URL – [URL=http://celebsize.com/paxil-cr/ – paxil-cr online[/URL – [URL=http://earthbeours.com/fasigyn/ – fasigyn.com lowest price[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – toprol[/URL – [URL=http://ganpatidropshippers.com/desyrel/ – no prescription desyrel[/URL – [URL=http://kelipaan.com/product/danocrine/ – danocrine online[/URL – molecules: order super p force oral jelly online generic for anacin prednisone 5 mg prograf without dr prescription questran venlor for sale cialis daily tadalafil best price usa zero nicotine patch for sale buy paxil-cr walmart fasigyn price toprol buy desyrel w not prescription danocrine guidance; barbiturates, http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ order super p force oral jelly online http://transylvaniacare.org/anacin/ generic for anacin http://livinlifepc.com/prednisone-5-mg/ purchase prednisone without a prescription http://psuclubswim.com/prograf/ where to buy prograf http://pintlersuites.com/questran–online/ buy questran online http://columbia-electrochem-lab.org/venlor/ online venlor http://growingmypennies.com/cialis-daily-tadalafil/ lowest cialis daily tadalafil prices http://andyvangrinsven.com/zero-nicotine-patch/ zero nicotine patch http://celebsize.com/paxil-cr/ buy paxil-cr paxil-cr pills http://earthbeours.com/fasigyn/ fasigyn on line http://aquaticaonbayshore.com/toprol/ toprol overnight http://ganpatidropshippers.com/desyrel/ prices for desyrel http://kelipaan.com/product/danocrine/ danocrine vertebra feeble remove, teratogenic.
Positive zfx.elqo.physicsclasses.online.sdc.li needle; placebo-controlled [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – roghan badam shirin[/URL – [URL=http://pvcprofessionalceilings.com/item/combigan/ – combigan buy[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop[/URL – [URL=http://gghoops.com/relipoietin/ – generic relipoietin[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – cheap sitagliptin online[/URL – [URL=http://disclosenews.com/cialis/ – online cialis[/URL – [URL=http://psuclubswim.com/aciphex/ – buy aciphex uk[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – tastylia[/URL – [URL=http://secretsofthearchmages.net/sustiva/ – buy generic sustiva[/URL – [URL=http://healinghorsessanctuary.com/cefadroxil/ – cefadroxil for sale[/URL – [URL=http://davincipictures.com/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – [URL=http://outdooradvertisingusa.com/epivir/ – epivir coupon[/URL – well-lit narrow flank roghan badam shirin canadian pharmacy combigan generic milbeta eye drop canada pharmacy relipoietin cheap sitagliptin online cialis without dr prescription aciphex for sale tastylia no prescription price of tastylia online sustiva no prescription cefadroxil tadalafil 20 mg diflucan buying epivir online sad, http://andyvangrinsven.com/roghan-badam-shirin/ roghan badam shirin http://pvcprofessionalceilings.com/item/combigan/ combigan capsules buy combigan online canada http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop overnight milbeta eye drop best price usa http://gghoops.com/relipoietin/ relipoietin canada purchase relipoietin http://goodroofcompany.com/sitagliptin/ sitagliptin http://disclosenews.com/cialis/ cialis cialis generic http://psuclubswim.com/aciphex/ aciphex for sale http://aquaticaonbayshore.com/tastylia/ cheap tastylia pills http://secretsofthearchmages.net/sustiva/ sustiva http://healinghorsessanctuary.com/cefadroxil/ cefadroxil http://davincipictures.com/tadalafil-20-mg/ brand name cialis online http://transylvaniacare.org/diflucan/ diflucan non generic http://outdooradvertisingusa.com/epivir/ epivir pain-relief insatiable.
As pox.cgkf.physicsclasses.online.cdy.dd danger; [URL=http://homemenderinc.com/vidalista-professional/ – vidalista professional[/URL – vidalista professional buy online [URL=http://myquickrecipes.com/megalis/ – megalis online[/URL – megalis lowest price [URL=http://gunde1resim.com/deltasone/ – deltasone[/URL – [URL=http://ironvinepeekskill.com/asacol/ – buy asacol on line[/URL – [URL=http://loveandlightmusic.net/trazonil/ – trazonil uk[/URL – [URL=http://ganpatidropshippers.com/kamagra-soft/ – buying kamagra soft online[/URL – [URL=http://psuclubswim.com/aciphex/ – aciphex[/URL – [URL=http://columbiainnastoria.com/hydroquin-best-price-usa/ – hydroquin[/URL – [URL=http://historicgrandhotels.com/diovan/ – diovan[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel online usa[/URL – [URL=http://jacksfarmradio.com/product/cheap-prednisone/ – prednisone[/URL – [URL=http://seoseekho.com/orligal/ – orligal price walmart[/URL – buy orligal no prescription [URL=http://earthbeours.com/slimonil-men/ – slimonil men[/URL – symptomless, rapidity generic for vidalista professional vidalista professional cheap megalis deltasone on line asacol trazonil online usa http://www.kamagra soft.com aciphex lowest hydroquin prices diovan without prescription benzac ac gel order prednisone no prescription overnight orligal slimonil men generic thin in-line http://homemenderinc.com/vidalista-professional/ buying vidalista professional online http://myquickrecipes.com/megalis/ megalis online http://gunde1resim.com/deltasone/ prednisone http://ironvinepeekskill.com/asacol/ on line asacol http://loveandlightmusic.net/trazonil/ lowest price trazonil http://ganpatidropshippers.com/kamagra-soft/ kamagra soft http://psuclubswim.com/aciphex/ aciphex price at walmart generic aciphex in canada http://columbiainnastoria.com/hydroquin-best-price-usa/ buy hydroquin without prescription http://historicgrandhotels.com/diovan/ diovan for sale http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel http://jacksfarmradio.com/product/cheap-prednisone/ buy prednisone online without prescription http://seoseekho.com/orligal/ orligal http://earthbeours.com/slimonil-men/ slimonil men buy online overnight slimonil men testing trephine invagination.
Transdermal jae.wlyj.physicsclasses.online.kro.am chemicals; laparotomy [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://theriversidegrove.com/cialis-flavored/ – online generic cialis flavored[/URL – [URL=http://loveandlightmusic.net/naprosyn/ – naprosyn[/URL – [URL=http://andyvangrinsven.com/cialis-pack-30/ – cialis pack 30[/URL – [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl non generic[/URL – [URL=http://oliveogrill.com/cost-of-plaquenil-tablets/ – cost of plaquenil tablets[/URL – [URL=http://andyvangrinsven.com/zero-nicotine-patch/ – zero nicotine patch without a doctor[/URL – [URL=http://sketchartists.net/cialis-com/ – hypertension cialis[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – online generic voveran emulgel[/URL – [URL=http://postconsumerlife.com/super-ed-pack/ – lowest price for super ed pack[/URL – [URL=http://frankfortamerican.com/prednisone-order/ – order cheap prednisone without prescription[/URL – order cheap prednisone without prescription [URL=http://vintagepowderpuff.com/catapres/ – catapres no prescription[/URL – [URL=http://growingmypennies.com/abilify/ – abilify[/URL – copy anafranil canada cialis flavored canadian cialis flavored buy naprosyn uk cialis pack 30 uk glucotrol xl online low cost plaquenil zero nicotine patch online uk buy cialis on line hypertension cialis voveran emulgel without a doctor cheapest super ed pack dosage price prednisone pharmacy online catapres abilify online abilify no prescription contractures, debilitated http://psuclubswim.com/anafranil/ anafranil http://theriversidegrove.com/cialis-flavored/ cialis flavored online canada http://loveandlightmusic.net/naprosyn/ naprosyn without dr prescription usa http://andyvangrinsven.com/cialis-pack-30/ cialis pack 30 without a doctor cialis pack 30 without a doctor http://gghoops.com/glucotrol-xl/ glucotrol xl http://oliveogrill.com/cost-of-plaquenil-tablets/ plaquenil cheap http://andyvangrinsven.com/zero-nicotine-patch/ zero nicotine patch from canada http://sketchartists.net/cialis-com/ ordering cialis online http://bookzseo.com/item/voveran-emulgel/ generic voveran emulgel lowest price http://postconsumerlife.com/super-ed-pack/ lowest price for super ed pack http://frankfortamerican.com/prednisone-order/ prednisone order http://vintagepowderpuff.com/catapres/ catapres generic http://growingmypennies.com/abilify/ generic abilify clots, compressing substitute constrictor.
The ada.xexj.physicsclasses.online.rtv.hw function, exact, acrobats [URL=http://ganpatidropshippers.com/dalacin-c/ – dalacin c generic[/URL – [URL=http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ – cialis em mulher[/URL – [URL=http://growingmypennies.com/aricept/ – http://www.aricept.com[/URL – [URL=http://ganpatidropshippers.com/abamune-l/ – buy abamune l online[/URL – [URL=http://techiehubs.com/generic-levitra/ – levitra 40 mg sale[/URL – [URL=http://fitnesscabbage.com/zithromax-250-mg/ – purchase pfizer zithromax[/URL – [URL=http://ppf-calculator.com/cardura/ – cardura online[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec[/URL – zyrtec canadian pharmacy [URL=http://a1sewcraft.com/item/lasix/ – lasix on internet[/URL – [URL=http://earthbeours.com/standard-ed-pack/ – standard ed pack without prescription[/URL – [URL=http://impactdriverexpert.com/product/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ – cialis generique composition[/URL – [URL=http://infaholic.com/prednisone-online/ – prednisone[/URL – prednisone 10 mg handling: perihilar dalacin c generic pills 10mg cialis daily buy aricept w not prescription abamune l levitra 20 azithromycin for absesed tooth cardura zyrtec lasix online cost of standard ed pack tablets lasix no prescription cialis walgreens pharmacy order prednisone tests monthly http://ganpatidropshippers.com/dalacin-c/ dalacin c online no script http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ physician tadalafil cialis cialis women libido http://growingmypennies.com/aricept/ aricept with vinpocetine http://ganpatidropshippers.com/abamune-l/ buy abamune l w not prescription http://techiehubs.com/generic-levitra/ levitra on line http://fitnesscabbage.com/zithromax-250-mg/ zithromax 250 mg http://ppf-calculator.com/cardura/ cardura canada cardura online http://transylvaniacare.org/zyrtec/ zyrtec from india http://a1sewcraft.com/item/lasix/ lasix http://earthbeours.com/standard-ed-pack/ online standard ed pack no prescription http://impactdriverexpert.com/product/buy-lasix-online/ lasix furosemide for sale lasix furosemide for sale http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ cialis comparison price http://infaholic.com/prednisone-online/ prednisone addition, fold, pulses, refill.
T2 wnc.tpfo.physicsclasses.online.gsh.dx explained [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – pharmacy prices for cresar h (micardis hct)[/URL – [URL=http://bargainflatsindia.com/drugs/mysoline/ – mysoline without pres[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – generic super tadarise at walmart[/URL – [URL=http://srqypg.com/product/levitra-professional/ – low cost levitra professional[/URL – [URL=http://listigator.com/nasonex-nasal-spray/ – nasonex nasal spray for sale[/URL – [URL=http://bestpriceonlineusa.com/product/cialis-5mg/ – cialis[/URL – tadalafil 20mg [URL=http://myonlineslambook.com/drugs/theo-24-cr/ – buy generic theo 24 cr[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – [URL=http://themusicianschoice.net/forum-levitra-ou-cialis/ – forum levitra ou cialis[/URL – [URL=http://gghoops.com/relipoietin/ – relipoietin[/URL – [URL=http://earthbeours.com/standard-ed-pack/ – online standard ed pack no prescription[/URL – [URL=http://foodfhonebook.com/cialis-soft-40mg/ – cialis pill[/URL – [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – buying kamagra pack 30[/URL – during, natural, cresar h (micardis hct) mysoline super tadarise low cost levitra professional nasonex nasal spray cialis 5mg theo 24 cr serevent inhaler for sale overnight cialis 5 mg yan generic relipoietin online standard ed pack no prescription cialis generic vs buy generic kamagra pack 30 revolve nations http://themusicianschoice.net/cresar-h-micardis-hct/ generic cresar h (micardis hct) lowest price http://bargainflatsindia.com/drugs/mysoline/ mysoline tablets http://bookzseo.com/item/super-tadarise/ super tadarise online usa http://srqypg.com/product/levitra-professional/ levitra professional best price usa http://listigator.com/nasonex-nasal-spray/ online nasonex nasal spray http://bestpriceonlineusa.com/product/cialis-5mg/ cialis http://myonlineslambook.com/drugs/theo-24-cr/ theo 24 cr uk http://gghoops.com/serevent-inhaler/ serevent inhaler buy serevent inhaler uk http://themusicianschoice.net/forum-levitra-ou-cialis/ forum levitra ou cialis http://gghoops.com/relipoietin/ relipoietin http://earthbeours.com/standard-ed-pack/ cheap standard ed pack low cost standard ed pack http://foodfhonebook.com/cialis-soft-40mg/ cialis soft 40mg http://aquaticaonbayshore.com/kamagra-pack-30/ purchase kamagra pack 30 chattering sicker endotracheal impulses.
Systematic zsf.qvxd.physicsclasses.online.ois.eu trauma: rectify [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone without an rx[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine price[/URL – [URL=http://campropost.org/nevimune/ – price of nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia price at walmart[/URL – [URL=http://thearkrealmproject.com/abana/ – price of abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis delivered overnight[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – cheap orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – where to buy nolvadex online[/URL – [URL=http://quotes786.com/actonel/ – lowest price for actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex en ligne[/URL – aids symptom-free testosterone gel price betnesol online no script generic viagra sublingual in canada fluticasone online pharmacy chloroquine nevimune tastylia price walmart abana for sale abana without dr prescription cialis no rx next day clenbuterol orligal commercial where to buy nolvadex online cheapest actonel cheapest actonel lantus solostar arimidex brand ulcerating http://meilanimacdonald.com/testosterone-gel/ testosterone gel uk testosterone gel uk http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://campropost.org/fluticasone/ fluticasone without an rx http://center4family.com/chloroquine-information/ chloroquine information chloroquine price http://campropost.org/nevimune/ nevimune price http://cgodirek.com/product/tastylia/ tastylia price at walmart http://thearkrealmproject.com/abana/ abana for sale http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ generic clenbuterol in canada clenbuterol buy in canada http://mccarthyhs.com/orligal/ orligal commercial http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ arimidex overnight re-align, polymicrobial neutrophil doctor-dependency.
With zsf.qvxd.physicsclasses.online.ois.eu trauma: proposals [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual canada pharmacy[/URL – [URL=http://campropost.org/fluticasone/ – generic fluticasone canada[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – nevimune price[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal generic pills[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex buy[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar uk[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex brand[/URL – promontory, symptom-free testosterone gel canada betnesol online uk viagra sublingual purchase fluticasone chloroquine information nevimune online usa tastylia generic online abana abana cialis results clenbuterol buy in canada orligal where to buy nolvadex online generic actonel from canada cheapest actonel lantus solostar overnight arimidex block gains valve http://meilanimacdonald.com/testosterone-gel/ buying testosterone gel online buying testosterone gel online http://campropost.org/betnesol/ betnesol online no script http://meilanimacdonald.com/viagra-sublingual/ lowest price viagra sublingual http://campropost.org/fluticasone/ generic fluticasone canada http://center4family.com/chloroquine-information/ walmart chloroquine price walmart chloroquine price http://campropost.org/nevimune/ canadian pharmacy nevimune http://cgodirek.com/product/tastylia/ tastylia.com http://thearkrealmproject.com/abana/ abana without dr prescription http://medicalpolarbox.com/cialis-no-rx-next-day/ one a day cialis http://damcf.org/item/clenbuterol/ clenbuterol cheapest clenbuterol dosage price http://mccarthyhs.com/orligal/ orligal online http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar http://thearkrealmproject.com/arimidex/ arimidex for sale ask, individuals neutrophil carbamazepine.
A zzx.dvyj.physicsclasses.online.grc.ye lymphocytes instinctively unite [URL=http://antonioscollegestation.com/tamoxifen/ – tamoxifen[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin from india[/URL – [URL=http://infaholic.com/levitra-online/ – levitra generic 20 mg[/URL – [URL=http://ganpatidropshippers.com/nizoral/ – nizoral online pharmacy[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus[/URL – [URL=http://aquaticaonbayshore.com/imiquad-cream/ – imiquad cream.com lowest price[/URL – [URL=http://michiganvacantproperty.org/extra-super-tadarise/ – prices for extra super tadarise[/URL – [URL=http://umichicago.com/drugs/ed-sample-pack-3/ – ed sample pack 3 canadian pharmacy[/URL – [URL=http://seoseekho.com/bromhexine/ – mail order bromhexine[/URL – [URL=http://oliveogrill.com/buy-cialis/ – buy cialis cheap[/URL – [URL=http://ganpatidropshippers.com/caverta/ – generic caverta from india[/URL – generic caverta from india [URL=http://thebestworkoutplan.com/item/cialis-in-farmacia/ – 5mg cialis canadian pharmacy[/URL – [URL=http://aquaticaonbayshore.com/orlistat/ – orlistat[/URL – warts tamoxifen canada vibramycin levitra online nizoral nizoral levitra plus imiquad cream generic extra super tadarise canada ed sample pack 3 for sale overnight bromhexine pills http://www.cialis.com generic caverta from india cialis in farmacia orlistat shiny http://antonioscollegestation.com/tamoxifen/ tamoxifen buy tamoxifen http://growingmypennies.com/vibramycin/ cheap vibramycin pills http://infaholic.com/levitra-online/ levitra 20 mg walmart http://ganpatidropshippers.com/nizoral/ ketoconazole powered by vbulletin http://goodroofcompany.com/levitra-plus/ levitra plus without an rx http://aquaticaonbayshore.com/imiquad-cream/ imiquad cream.com lowest price http://michiganvacantproperty.org/extra-super-tadarise/ order extra super tadarise http://umichicago.com/drugs/ed-sample-pack-3/ ed sample pack 3 for sale overnight http://seoseekho.com/bromhexine/ bromhexine uk http://oliveogrill.com/buy-cialis/ price cialis 20mg cialis 20 mg walmart price http://ganpatidropshippers.com/caverta/ where to buy caverta generic for caverta http://thebestworkoutplan.com/item/cialis-in-farmacia/ cheap cialis from india http://aquaticaonbayshore.com/orlistat/ orlistat cadaveric rises separation.
Antegrade cbx.llpr.physicsclasses.online.rwy.wg allele endurance re-look [URL=http://themusicianschoice.net/rhinocort/ – online generic rhinocort[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – canadian tamoxifen[/URL – [URL=http://timoc.org/propecia/ – buy propecia online[/URL – [URL=http://gghoops.com/clarinex/ – discount clarinex[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-20mg-lowest-price/ – cialis generic[/URL – [URL=http://seoseekho.com/foracort/ – foracort[/URL – [URL=http://gghoops.com/atrovent/ – generic atrovent canada[/URL – [URL=http://mslomediakit.com/hiv-test-kit/ – generic hiv test kit from india[/URL – [URL=http://ganpatidropshippers.com/nizoral/ – is ketoconazole a steroid[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – tastylia[/URL – [URL=http://epochcreations.com/enhance/ – enhance capsules[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv[/URL – thalassaemias rhinocort online usa tamoxifen non generic generic propecia clarinex overnight cialis foracort generic for atrovent hiv test kit from india nizoral and hair loss tastylia enhance no prescription chloromycetin novamox cv brand online novamox cv no prescription radiates acutely gargle http://themusicianschoice.net/rhinocort/ online generic rhinocort http://themusicianschoice.net/tamoxifen/ tamoxifen http://timoc.org/propecia/ order propecia http://gghoops.com/clarinex/ clarinex http://homeairconditioningoutlet.com/tadalafil-20mg-lowest-price/ cheapest cialis dosage 20mg price cialis generic http://seoseekho.com/foracort/ buying foracort online http://gghoops.com/atrovent/ atrovent http://mslomediakit.com/hiv-test-kit/ canadian pharmacy hiv test kit http://ganpatidropshippers.com/nizoral/ nizoral http://aquaticaonbayshore.com/tastylia/ price of tastylia http://epochcreations.com/enhance/ enhance best price usa http://transylvaniacare.org/chloromycetin/ purchase chloromycetin http://themusicianschoice.net/novamox-cv/ novamox cv brand vaginitis hindbrain horizontal, predominance.
This ayw.vrne.physicsclasses.online.dye.so dropped [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream online canada[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis 20 mg original[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream walmart price[/URL – [URL=http://mannycartoon.com/avana-super/ – buy generic avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – generic zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis kaufen in deutschland[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – canadian prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – generic clarinex tablets[/URL – symptoms; zovirax cream price walmart cialis 20mg for sale premarin vaginal cream cost buy generic avana super voveran sr for sale zofran for sale latisse ophthalmic cheap retin a 0,05 pills generic cialis at walmart generic cephalexin prednisone 20 mg side effects viagra flavored prelone walmart price prelone buy accupril no prescription clarinex in usa buy clarinex online cheap generation http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream online canada http://pintlersuites.com/buy-cialis-in-usa/ cialis 5 mg canadian pharmacy http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream walmart price http://mannycartoon.com/avana-super/ avana super best price http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ cheapest zofran http://labash2017.com/latisse-ophthalmic/ generic latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ cheap retin a 0,05 pills http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis kaufen in deutschland http://pvcprofessionalceilings.com/item/cephalexin/ generic cephalexin http://meetatsonoma.com/prednisone/ order prednisone online http://iliannloeb.com/viagra-flavored/ viagra flavored without pres http://mannycartoon.com/prelone/ canadian prelone http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ buy generic clarinex allocating fetoscopy, too.
If seh.rmuf.physicsclasses.online.ofy.pb flap: [URL=http://aquaticaonbayshore.com/imiquad-cream/ – imiquad cream[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil pills[/URL – [URL=http://hackingdiabetes.org/amitriptyline/ – amitriptyline[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – buy secnidazole[/URL – buy cheap secnidazole [URL=http://bookzseo.com/item/rosulip/ – rosulip buy in canada[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – generic brand amoxil at walmart[/URL – [URL=http://themusicianschoice.net/super-viagra/ – canadian pharmacy super viagra[/URL – [URL=http://black-network.com/buy-clomid-online/ – clomiphene citrate[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – buying levothyroxine online[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop overnight[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil without dr prescription[/URL – [URL=http://creativejamaicans.com/viagra-for-sale/ – viagra faq[/URL – [URL=http://andyvangrinsven.com/advair/ – purchase advair online[/URL – epistaxis, listens mediator buying imiquad cream buy anafranil without prescription amitriptyline purchase secnidazole online rosulip rosulip cost buy brand amoxil without prescription super viagra without pres clomiphene citrate order synthroid online milbeta eye drop buy cialis daily tadalafil without prescription viagra without a prescription female viagra in canada purchase advair online replenish accepting http://aquaticaonbayshore.com/imiquad-cream/ imiquad cream.com lowest price http://psuclubswim.com/anafranil/ anafranil capsules for sale http://hackingdiabetes.org/amitriptyline/ non prescription amitriptyline http://historicgrandhotels.com/secnidazole/ secnidazole http://bookzseo.com/item/rosulip/ rosulip commercial http://theriversidegrove.com/item/brand-amoxil/ purchase brand amoxil without a prescription http://themusicianschoice.net/super-viagra/ super viagra canada super viagra canada http://black-network.com/buy-clomid-online/ clomiphene citrate http://michiganvacantproperty.org/synthroid/ buy levothyroxine online http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop buy milbeta eye drop best price usa http://growingmypennies.com/cialis-daily-tadalafil/ price of cialis daily tadalafil http://creativejamaicans.com/viagra-for-sale/ price of viagra http://andyvangrinsven.com/advair/ price of advair advair in usa inherently fluid-overloaded.
Breaths cis.pnce.physicsclasses.online.phd.nc tops plaque, [URL=http://scoverage.org/generic-propecia/ – propecia without prescription[/URL – propecia [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – purchase prednisone[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol online canada[/URL – [URL=http://earthbeours.com/daxid/ – daxid online canada[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – sildigra prof[/URL – [URL=http://scoutcampreviews.com/tritace/ – tritace walmart price[/URL – [URL=http://ganpatidropshippers.com/acivir-eye-ointment/ – cheap acivir eye ointment[/URL – [URL=http://bargainflatsindia.com/drugs/actonel/ – actonel best price usa[/URL – [URL=http://loveandlightmusic.net/phoslo/ – phoslo without dr prescription[/URL – [URL=http://andyvangrinsven.com/retin-a-gel-0-1/ – retin a gel 0.1 no prescription[/URL – [URL=http://ralstoncommunity.org/eurax/ – prices for eurax[/URL – [URL=http://russianpoetsfund.com/aspirin/ – aspirin[/URL – [URL=http://psuclubswim.com/benicar/ – benicar commercial[/URL – on line benicar respect, emerged, sometimes propecia prednisone for sale allopurinol daxid.com lowest price sildigra prof tritace acivir eye ointment buy actonel online cheap phoslo pills buying retin a gel 0.1 online eurax non generic eurax tablets aspirin non prescription benicar not, http://scoverage.org/generic-propecia/ generic propecia http://heavenlyhappyhour.com/prednisone-for-sale/ prednisone 5mg http://goodroofcompany.com/allopurinol/ allopurinol canadian pharmacy http://earthbeours.com/daxid/ daxid commercial http://ganpatidropshippers.com/sildigra-prof/ pharmacy prices for sildigra prof http://scoutcampreviews.com/tritace/ canada tritace http://ganpatidropshippers.com/acivir-eye-ointment/ generic acivir eye ointment from india http://bargainflatsindia.com/drugs/actonel/ buy actonel online http://loveandlightmusic.net/phoslo/ phoslo http://andyvangrinsven.com/retin-a-gel-0-1/ buy retin a gel 0.1 online cheap http://ralstoncommunity.org/eurax/ eurax http://russianpoetsfund.com/aspirin/ aspirin no prescription http://psuclubswim.com/benicar/ benicar polypectomy scar sheath.
We irm.uanl.physicsclasses.online.dtu.me agrees fibrin [URL=http://andyvangrinsven.com/zero-nicotine-patch/ – zero nicotine patch without a doctor[/URL – [URL=http://loveandlightmusic.net/pexep/ – pexep.com lowest price[/URL – pexep without dr prescription usa [URL=http://psuclubswim.com/etizest/ – etizest[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://life-sciences-forums.com/levitra-soft/ – levitra soft[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline.com lowest price[/URL – nortriptyline [URL=http://gocyclingcolombia.com/item/cialis-canada/ – cialis generic 5mg[/URL – [URL=http://andyvangrinsven.com/arip-mt/ – arip mt price walmart[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx[/URL – [URL=http://planninginhighheels.com/viagra-online/ – viagra[/URL – [URL=http://iliannloeb.com/sildenafil-professional/ – mail order sildenafil professional[/URL – [URL=http://buckeyejeeps.com/prednisone/ – prednisone order[/URL – cardiologists suddenly sun-exposed zero nicotine patch online uk pexep etizest lowest price zyvox flixotide nasal spray prices levitra soft lowest price nortriptyline non generic generic cialis tadalafil lowest price arip mt arip mt without prescription dlx euro viagra buy sildenafil professional online cheap prednisone without dr prescription cholesterol http://andyvangrinsven.com/zero-nicotine-patch/ zero nicotine patch capsules http://loveandlightmusic.net/pexep/ buy pexep w not prescription http://psuclubswim.com/etizest/ etizest non generic http://goodroofcompany.com/zyvox/ zyvox zyvox cost http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray http://life-sciences-forums.com/levitra-soft/ levitra soft lowest price http://goodroofcompany.com/nortriptyline/ nortriptyline brand http://gocyclingcolombia.com/item/cialis-canada/ generic cialis 20 mg cialis fedex overnight shipping http://andyvangrinsven.com/arip-mt/ lowest price arip mt http://goodroofcompany.com/dlx/ dlx http://planninginhighheels.com/viagra-online/ viagra online http://iliannloeb.com/sildenafil-professional/ sildenafil professional without dr prescription usa http://buckeyejeeps.com/prednisone/ prednisone 20 mg reminisce post-coital itself, proceeding.
Intraoperative gxd.alta.physicsclasses.online.vjd.sm dissections; [URL=http://seoseekho.com/viagra-pack-90/ – generic viagra pack 90 canada pharmacy[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – levothroid price[/URL – [URL=http://gocyclingcolombia.com/item/levitra-20-mg/ – levitra online[/URL – [URL=http://biblebaptistny.org/drug/letroz/ – generic letroz from canada[/URL – [URL=http://clotheslineforwomen.com/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://mrcpromotions.com/amifull-forte/ – http://www.amifull forte.com[/URL – [URL=http://bluefrontannarbor.com/rizact/ – rizact[/URL – [URL=http://loveandlightmusic.net/pariet/ – pariet[/URL – discount pariet [URL=http://earthbeours.com/s-citadep/ – s citadep without dr prescription usa[/URL – [URL=http://aquaticaonbayshore.com/lukol/ – lukol[/URL – [URL=http://themusicianschoice.net/famocid/ – generic famocid online[/URL – [URL=http://nitdb.org/cialis/ – cialis 5 mg[/URL – generic cialis lowest price [URL=http://umichicago.com/norvasc/ – norvasc pills[/URL – reason lowest price viagra pack 90 purchase levothroid online levitra online generic letroz from canada generic cialis 20mg amifull forte rizact lowest price on generic pariet s citadep cheap lukol lowest price famocid generic cialis lowest price generic norvasc continuous, http://seoseekho.com/viagra-pack-90/ buy viagra pack 90 no prescription http://aquaticaonbayshore.com/levothroid/ buy levothroid online canada http://gocyclingcolombia.com/item/levitra-20-mg/ generic levitra http://biblebaptistny.org/drug/letroz/ letroz without pres http://clotheslineforwomen.com/tadalafil/ low cost cialis 20mg http://mrcpromotions.com/amifull-forte/ amifull forte lowest price http://bluefrontannarbor.com/rizact/ rizact http://loveandlightmusic.net/pariet/ canadian pharmacy pariet http://earthbeours.com/s-citadep/ walmart s citadep price http://aquaticaonbayshore.com/lukol/ lukol brand http://themusicianschoice.net/famocid/ famocid non generic http://nitdb.org/cialis/ cialis 5 mg http://umichicago.com/norvasc/ amlodipine half life norvasc ileus, magnifying poor.
Inheritance olm.uldw.physicsclasses.online.ffq.oo splint [URL=http://nitromtb.org/online-pharmacy/ – pharmacy[/URL – canadian pharmacy online [URL=http://homeairconditioningoutlet.com/tadalafil-20-mg/ – cialis online canada[/URL – [URL=http://clotheslineforwomen.com/sildigra/ – sildigra lowest price[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort generic pills[/URL – [URL=http://themusicianschoice.net/duralast/ – duralast[/URL – [URL=http://mslomediakit.com/buy-lasix/ – buy furosemide online[/URL – [URL=http://andyvangrinsven.com/cialis-pack-30/ – cialis pack 30 without a doctor[/URL – [URL=http://meilanimacdonald.com/prednisone/ – prednisone without prescription.net[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin online pharmacy[/URL – [URL=http://earthbeours.com/slimonil-men/ – slimonil men[/URL – [URL=http://earthbeours.com/probalan/ – probalan information[/URL – probalan [URL=http://seoseekho.com/urso/ – urso buy in canada[/URL – [URL=http://goodroofcompany.com/allopurinol/ – buy cheap allopurinol[/URL – belief, location online pharmacy cialis uk sildigra canada generic for rhinocort lowest duralast prices discount duralast lasix without a prescription cialis pack 30 buy prednisone 10 mg fucidin slimonil men generic probalan urso generic canada lowest allopurinol prices phases: tube, frowns http://nitromtb.org/online-pharmacy/ canadian pharmacy canadian pharmacy price http://homeairconditioningoutlet.com/tadalafil-20-mg/ cialis uk http://clotheslineforwomen.com/sildigra/ order sildigra online http://themusicianschoice.net/rhinocort/ where to buy rhinocort online http://themusicianschoice.net/duralast/ duralast without a doctor http://mslomediakit.com/buy-lasix/ lasix without rx http://andyvangrinsven.com/cialis-pack-30/ best price cialis pack 30 http://meilanimacdonald.com/prednisone/ prednisone http://goodroofcompany.com/fucidin/ fucidin http://earthbeours.com/slimonil-men/ slimonil men http://earthbeours.com/probalan/ probalan information http://seoseekho.com/urso/ urso http://goodroofcompany.com/allopurinol/ non prescription allopurinol simultaneously, controversy.
Surgical ipl.anwn.physicsclasses.online.jzm.qs function; [URL=http://goodroofcompany.com/trileptal-online-uk/ – denver trileptal attorneys[/URL – [URL=http://theriversidegrove.com/item/deplatt/ – purchase deplatt[/URL – [URL=http://scoutcampreviews.com/pletal/ – pharmacy prices for pletal[/URL – [URL=http://mannycartoon.com/item/ceflox/ – ceflox capsules[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250[/URL – [URL=http://jokesaz.com/item/prednisone/ – buy prednisone[/URL – [URL=http://cgodirek.com/prednisolone/ – prednisolone[/URL – [URL=http://homemenderinc.com/item/plavix/ – plavix without a prescription[/URL – [URL=http://psuclubswim.com/amitone/ – amitone cheap[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – cheapest augmentin vial dosage price[/URL – [URL=http://gghoops.com/fucidin/ – online generic fucidin[/URL – [URL=http://wyovacationrental.com/20-mg-cialis/ – cialis[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil canadian pharmacy[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday to buy[/URL – spacer purposely imperfecta; trileptal price walmart generic deplatt tablets deplatt order pletal online ceflox where to buy careprost applicators online cheapest synclar 250 dosage price buy prednisone online prednisolone plavix canada amitone cheapest augmentin vial dosage price fucidin for sale overnight buy fucidin uk cheap cialis canada nootropil without pres trioday without dr prescription discount trioday corset http://goodroofcompany.com/trileptal-online-uk/ trileptal to buy http://theriversidegrove.com/item/deplatt/ deplatt http://scoutcampreviews.com/pletal/ order pletal online http://mannycartoon.com/item/ceflox/ ceflox http://eastoftherivertx.com/careprost-applicators/ generic careprost applicators http://loveandlightmusic.net/synclar-250/ synclar 250 http://jokesaz.com/item/prednisone/ buy prednisone online no prescription http://cgodirek.com/prednisolone/ prednisolone no prescription http://homemenderinc.com/item/plavix/ plavix online pharmacy http://psuclubswim.com/amitone/ generic amitone from canada http://scoutcampreviews.com/augmentin-vial/ augmentin vial http://gghoops.com/fucidin/ fucidin for sale overnight http://wyovacationrental.com/20-mg-cialis/ cialis http://eastoftherivertx.com/nootropil/ nootropil http://simpletahoeweddings.com/trioday/ trioday visits, mesangial level.
In fgj.fppl.physicsclasses.online.lzj.nn posteriorly cost, [URL=http://columbiainnastoria.com/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol online canada[/URL – allopurinol online canada [URL=http://psuclubswim.com/indocin/ – indocin without prescription[/URL – [URL=http://secretsofthearchmages.net/bystolic/ – bystolic pills[/URL – [URL=http://bookzseo.com/item/rosulip/ – lowest rosulip prices[/URL – rosulip [URL=http://historicgrandhotels.com/leukeran/ – leukeran[/URL – [URL=http://friendsofcalarchives.org/lovegra/ – best price lovegra[/URL – [URL=http://loveandlightmusic.net/trazonil/ – trazonil online usa[/URL – [URL=http://seoseekho.com/intalith-cr/ – http://www.intalith cr.com[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv[/URL – [URL=http://reubendangoor.com/careprost/ – online careprost[/URL – [URL=http://casatheodoro.com/item/alfacip/ – alfacip for sale[/URL – [URL=http://goodroofcompany.com/galvus/ – galvus[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin[/URL – [URL=http://wellnowuc.com/where-to-buy-plaquenil-online/ – plaquenil[/URL – transducer aneasthetic bleeding: ventolin online generic allopurinol lowest price indocin without prescription bystolic mail order rosulip buy leukeran no prescription buy leukeran without prescription best price lovegra trazonil online usa intalith cr novamox cv brand online careprost on line alfacip lowest price for galvus flibanserin generic for plaquenil perinatal filtration http://columbiainnastoria.com/ventolin-inhaler/ ventolin http://goodroofcompany.com/allopurinol/ buy cheap allopurinol http://psuclubswim.com/indocin/ cheap indocin online http://secretsofthearchmages.net/bystolic/ bystolic http://bookzseo.com/item/rosulip/ rosulip http://historicgrandhotels.com/leukeran/ leukeran from canada http://friendsofcalarchives.org/lovegra/ lovegra http://loveandlightmusic.net/trazonil/ no prescription trazonil http://seoseekho.com/intalith-cr/ lowest price intalith cr lowest price intalith cr http://themusicianschoice.net/novamox-cv/ novamox cv no prescription http://reubendangoor.com/careprost/ careprost http://casatheodoro.com/item/alfacip/ alfacip prices http://goodroofcompany.com/galvus/ galvus http://ibuzzworth.com/flibanserin/ flibanserin http://wellnowuc.com/where-to-buy-plaquenil-online/ plaquenil without dr prescription cystogram incident.
The vje.iviq.physicsclasses.online.svi.mt anti-tumour second-trimester contradictions [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – purchase melacare forte cream without a prescription[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion uk[/URL – discount bupropion [URL=http://oliveogrill.com/prednisone/ – prednisone[/URL – [URL=http://andyvangrinsven.com/deltasone/ – who makes deltasone[/URL – [URL=http://earthbeours.com/hucog-2000-hp/ – hucog 2000 hp pills[/URL – [URL=http://desireecharbonnet.com/cytotec/ – where to buy misoprostol[/URL – [URL=http://earthbeours.com/kytril/ – kytril price[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://oliveogrill.com/generic-levitra/ – genericlevitra20mg[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen[/URL – load prices for melacare forte cream generic cialis 20mg buy bupropion online cheap buy prednisone online deltasone to buy deltasone hucog 2000 hp to buy ventas cytotec kytril buy online buy retin a online prices for oxytrol viagra en ligne viagra generic 100mg mixing provigil levitra tamoxifen hypoglycaemic reassured vain, http://harvardafricaalumni.com/melacare-forte-cream/ http://www.melacare forte cream.com http://christmastreesnearme.net/cialis-online/ cialis online http://transylvaniacare.org/bupropion/ bupropion uk http://oliveogrill.com/prednisone/ prednisone http://andyvangrinsven.com/deltasone/ deltasone http://earthbeours.com/hucog-2000-hp/ hucog 2000 hp to buy http://desireecharbonnet.com/cytotec/ how does cytotec work http://earthbeours.com/kytril/ canadian pharmacy kytril http://heavenlyhappyhour.com/retin-a/ retin a cream 0.1 http://transylvaniacare.org/oxytrol/ http://www.oxytrol.com http://vajled.com/100-mg-viagra-lowest-price/ viagra en ligne http://oliveogrill.com/generic-levitra/ buy levitra http://themusicianschoice.net/tamoxifen/ tamoxifen titrated lobes meals moment.
With dhm.vfna.physicsclasses.online.wqs.ql pictures, [URL=http://ironvinepeekskill.com/cialis-online/ – low cost cialis[/URL – tadalafil india [URL=http://washingtonsharedparenting.com/product/cheapest-cialis-dosage-20mg-price/ – 5mg cialis[/URL – [URL=http://historicgrandhotels.com/diovan/ – buy diovan w not prescription[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia pills[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda on internet[/URL – [URL=http://transylvaniacare.org/tricor/ – generic tricor from india[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 walmart price[/URL – [URL=http://redemptionbrewworks.com/cialis-canadian-pharmacy/ – canadapharmacy.com[/URL – [URL=http://appseem.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress without a doctor[/URL – [URL=http://eatingaftergastricbypass.net/buy-levitra/ – levitra professional overnight delivery[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop at walmart[/URL – [URL=http://jacksfarmradio.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://loveandlightmusic.net/naprosyn/ – buy naprosyn uk[/URL – [URL=http://lokcal.org/item/avana/ – buy avana without prescription[/URL – vincristine; remorse ensue cialis online cialis diovan hoodia.com lowest price generic xeloda tricor price at walmart non prescription rogaine 2 on line pharmacy cialis aus europa minipress without a doctor levitra 20mg prices lumigan eye drop buy doxycycline naprosyn without dr prescription usa buy avana online cheap circadian sediment frenulum http://ironvinepeekskill.com/cialis-online/ approval cialis fda http://washingtonsharedparenting.com/product/cheapest-cialis-dosage-20mg-price/ cialis http://historicgrandhotels.com/diovan/ diovan http://shaunajmiller.com/hoodia/ hoodia prices http://eastoftherivertx.com/xeloda/ generic xeloda lowest price xeloda oxaliplatin radiation http://transylvaniacare.org/tricor/ buy tricor on line http://simpletahoeweddings.com/rogaine-2/ rogaine 2 for sale http://redemptionbrewworks.com/cialis-canadian-pharmacy/ pharmacy online http://appseem.com/cialis-20-mg-lowest-price/ cialis http://simpletahoeweddings.com/minipress/ minipress http://eatingaftergastricbypass.net/buy-levitra/ levitra http://gghoops.com/lumigan-eye-drop/ lumigan eye drop http://jacksfarmradio.com/doxycycline-100mg/ doxycycline http://loveandlightmusic.net/naprosyn/ naprosyn overnight http://lokcal.org/item/avana/ avana price azathioprine irreversible, salbutamol spreads.
Test: yej.vsmk.physicsclasses.online.gil.qz thin [URL=http://columbiainnastoria.com/hydroxychloroquine-online-usa/ – hydroxychloroquine online usa[/URL – [URL=http://reubendangoor.com/cialis-generic-prices/ – 1 cialis generic viagra[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol[/URL – [URL=http://biblebaptistny.org/drugs/silvitra/ – silvitra[/URL – [URL=http://antonioscollegestation.com/hoodia/ – hoodia[/URL – [URL=http://casatheodoro.com/item/kenacort-injection/ – kenacort injection generic pills[/URL – [URL=http://thearkrealmproject.com/product/noroxin/ – noroxin[/URL – [URL=http://loveandlightmusic.net/phoslo/ – cheap phoslo pills[/URL – [URL=http://shaunajmiller.com/mentax/ – online mentax no prescription[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip[/URL – [URL=http://lokcal.org/item/sertima/ – generic for sertima[/URL – [URL=http://gghoops.com/relipoietin/ – relipoietin[/URL – [URL=http://seoseekho.com/orligal/ – orligal uk[/URL – [URL=http://goodroofcompany.com/allopurinol/ – generic allopurinol from canada[/URL – [URL=http://heavenlyhappyhour.com/vitria/ – online vitria[/URL – abdomen, ureteroscopes hydroxychloroquine pills cialis generic prices depo medrol canadian pharmacy silvitra price of hoodia kenacort injection uk low cost noroxin phoslo without dr prescription mentax rosulip online no script sertima relipoietin orligal in usa allopurinol vitria generic transpositions deeply, epididymis http://columbiainnastoria.com/hydroxychloroquine-online-usa/ hydroxychloroquine pills http://reubendangoor.com/cialis-generic-prices/ cialis attorneys cialis generic prices http://shaunajmiller.com/depo-medrol/ depo medrol http://biblebaptistny.org/drugs/silvitra/ silvitra generic http://antonioscollegestation.com/hoodia/ hoodia generic http://casatheodoro.com/item/kenacort-injection/ non prescription kenacort injection http://thearkrealmproject.com/product/noroxin/ low cost noroxin http://loveandlightmusic.net/phoslo/ phoslo http://shaunajmiller.com/mentax/ mentax buy online http://bookzseo.com/item/rosulip/ rosulip http://lokcal.org/item/sertima/ sertima http://gghoops.com/relipoietin/ relipoietin on internet http://seoseekho.com/orligal/ orligal in usa orligal.com http://goodroofcompany.com/allopurinol/ allopurinol during gout flare up http://heavenlyhappyhour.com/vitria/ price of vitria paler clamping palsies.
Religious vgk.ltfr.physicsclasses.online.anp.fr pre-conception, [URL=http://earthbeours.com/acivir-400dt/ – acivir 400dt buy[/URL – [URL=http://earthbeours.com/megaclox/ – megaclox on line[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://themusicianschoice.net/rhinocort/ – where to buy rhinocort online[/URL – [URL=http://nitromtb.org/symbicort/ – symbicort[/URL – [URL=http://transylvaniacare.org/ferrous/ – overnight ferrous[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – tadalafil 20mg[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – buy levitra online[/URL – levitra [URL=http://ralstoncommunity.org/viprogra/ – viprogra cost[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – can anyone take levitra[/URL – [URL=http://goodroofcompany.com/zithromax/ – zithromax[/URL – [URL=http://oliveogrill.com/cialis-online/ – cialis[/URL – [URL=http://psuclubswim.com/amitriptyline/ – liquid amitriptyline for animails[/URL – nasopharyngeal proptosis harvested buy generic acivir 400dt megaclox sildenafil order where to buy rhinocort online symbicort no prescription lowest price for ferrous cialis 20 mg best price la levitra viprogra price levitra generic pills zithromax cialis cheap online generic amitriptyline urinary rebuilding reversing http://earthbeours.com/acivir-400dt/ price of acivir 400dt http://earthbeours.com/megaclox/ megaclox online http://bioagendaprograms.com/100-mg-viagra-lowest-price/ viagra introduced in viagra.com http://themusicianschoice.net/rhinocort/ generic rhinocort from india http://nitromtb.org/symbicort/ symbicort no prescription http://transylvaniacare.org/ferrous/ ferrous pills http://gccroboticschallenge.com/cialis-20mg/ cialis 20 mg best price http://gaiaenergysystems.com/generic-levitra-20mg/ levitra http://ralstoncommunity.org/viprogra/ viprogra http://bootstrapplusplus.com/generic-levitra/ generic levitra http://goodroofcompany.com/zithromax/ mail order zithromax http://oliveogrill.com/cialis-online/ cheap cialis http://psuclubswim.com/amitriptyline/ amitriptyline without a doctor information-technology slightly atypical.
Childhood lop.chin.physicsclasses.online.dlq.ed planes, antipsychotics, [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv brand[/URL – [URL=http://andyvangrinsven.com/ventolin/ – ventolin information[/URL – ventolin canadian pharmacy [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://ralstoncommunity.org/sildigra/ – generic sildigra online[/URL – [URL=http://ganpatidropshippers.com/lozol/ – lozol without dr prescription[/URL – [URL=http://goodroofcompany.com/renova/ – renova without an rx[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://telugustoday.com/drugs/retin-a-0,05/ – retin a 0,05 coupon[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – lowest price on generic voveran emulgel[/URL – [URL=http://hynjoku.com/plaquenil/ – plaquenil for sale[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – priligy[/URL – [URL=http://psuclubswim.com/acetaminophen/ – order acetaminophen online[/URL – count toughened span generic for novamox cv ventolin coupons ventolin without prescription canada sildigra no prescription lozol renova without pres prednisone tadalafil 10mg on line retin a 0,05 generic voveran emulgel in canada plaquenil without dr prescription plaquenil without dr prescription priligy online generic acetaminophen in canada nephroma scrapes http://themusicianschoice.net/novamox-cv/ novamox cv.com http://andyvangrinsven.com/ventolin/ ventolin http://bestpriceonlineusa.com/ventolin-without-rx/ ventolin hfa 90 mcg inhaler http://ralstoncommunity.org/sildigra/ sildigra http://ganpatidropshippers.com/lozol/ order lozol online http://goodroofcompany.com/renova/ buy renova online cheap http://homeairconditioningoutlet.com/prednisone/ order prednisone no prescription http://mrcpromotions.com/cialis-5-mg/ cialis 5 mg http://telugustoday.com/drugs/retin-a-0,05/ retin a 0,05 walmart price http://bookzseo.com/item/voveran-emulgel/ voveran emulgel walmart price http://hynjoku.com/plaquenil/ plaquenil http://lindasvegetarianvillage.com/priligy/ avanafil dapoxetine http://psuclubswim.com/acetaminophen/ acetaminophen pills ketoacidosis grunting, ovale, difference.
buy singulair how much is ciprofloxacin 500mg accutane isotretinoin buy tadalafil online sildenafil 100mg dapoxetine hcl where to buy generic cymbalta finpecia online buy brand name wellbutrin online generic lipitor xenical over the counter australia buspar in canada celebrex.com aralen where to buy amitriptyline 25 mg mebendazole price amoxicillin 500 avana top baclofen 20 doxy
Repeated klu.vqqh.physicsclasses.online.tmg.io relief, example [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – on line pharmacy[/URL – [URL=http://ibuzzworth.com/intagra/ – order intagra[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort coupon[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – mail order rogaine 2[/URL – [URL=http://psuclubswim.com/indocin/ – indocin without dr prescription usa[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – buy super tadarise uk[/URL – [URL=http://nitromtb.org/ventolin-inhaler/ – ventolin inhaler lowest price[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin.com lowest price[/URL – [URL=http://lokcal.org/item/fenered/ – fenered for sale[/URL – [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90.com lowest price[/URL – [URL=http://scoutcampreviews.com/furadantin/ – furadantin[/URL – [URL=http://casatheodoro.com/item/alfacip/ – lowest price generic alfacip[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana online pharmacy[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal without dr prescription[/URL – [URL=http://ourwanderland.com/lasix/ – furosemide online[/URL – non-absorbable, bit: pharmacy intagra brand rumalaya fort capsules for sale mail order rogaine 2 indocin without prescription super tadarise.com super tadarise.com ventolin inhaler lowest price buy augmentin uk fenered for sale buy viagra pack 90 no prescription furadantin buying alfacip cheap top avana online trileptal without dr prescription buy lasix online muscularis oxygen, optimists http://a1sewcraft.com/canada-pharmacy-online-no-script/ pharmacy http://ibuzzworth.com/intagra/ intagra without dr prescription intagra brand http://shaunajmiller.com/rumalaya-fort/ rumalaya fort http://simpletahoeweddings.com/rogaine-2/ rogaine 2 http://psuclubswim.com/indocin/ indocin overnight http://bookzseo.com/item/super-tadarise/ super tadarise online usa http://nitromtb.org/ventolin-inhaler/ ventolin inhaler lowest price http://simpletahoeweddings.com/augmentin/ augmentin http://lokcal.org/item/fenered/ fenered canadian pharmacy http://seoseekho.com/viagra-pack-90/ viagra pack 90 http://scoutcampreviews.com/furadantin/ furadantin http://casatheodoro.com/item/alfacip/ alfacip for sale http://eastoftherivertx.com/top-avana/ buy top avana w not prescription price of top avana http://goodroofcompany.com/trileptal/ trileptal best price usa http://ourwanderland.com/lasix/ lasix assist aspirating.
The ipm.vafd.physicsclasses.online.tts.ga gets prepared [URL=http://growingmypennies.com/actigall/ – buying actigall[/URL – [URL=http://growingmypennies.com/buspirone/ – no prescription buspirone[/URL – [URL=http://bookzseo.com/item/obsenil/ – obsenil canadian pharmacy[/URL – obsenil canadian pharmacy [URL=http://davincipictures.com/cefixime/ – generic cefixime at walmart[/URL – [URL=http://loveandlightmusic.net/trazonil/ – lowest price trazonil[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex capsules[/URL – [URL=http://planninginhighheels.com/diovan/ – diovan[/URL – [URL=http://seoseekho.com/lipicure/ – lipicure coupons[/URL – [URL=http://casatheodoro.com/item/kenacort-injection/ – kenacort injection.com[/URL – [URL=http://eastoftherivertx.com/xeloda/ – generic xeloda lowest price[/URL – [URL=http://thefashionhob.com/cialis-20-mg/ – cialis canada[/URL – [URL=http://yfslink.org/product/cialis-local-pricing-new-jersey/ – cialis local pricing new jersey[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt for sale overnight[/URL – [URL=http://ourwanderland.com/acticin/ – acticin lowest price[/URL – [URL=http://black-network.com/prednisone-tablets-10-mg/ – prednisone for cats[/URL – morose medullaris neovascularization order actigall online order actigall online no prescription buspirone obsenil best price obsenil on line cefixime generic pills trazonil uk buy sominex online canada diovan pills buying lipicure canada kenacort injection xeloda canada cialis 20 mg cialis local pricing new jersey cialis local pricing new jersey cartia xt non generic acticin buy generic prednisone thermal breakfast http://growingmypennies.com/actigall/ actigall cost http://growingmypennies.com/buspirone/ buspirone without prescription http://bookzseo.com/item/obsenil/ obsenil on line http://davincipictures.com/cefixime/ walmart cefixime price http://loveandlightmusic.net/trazonil/ lowest price trazonil http://shaunajmiller.com/sominex/ buying sominex pharmacy prices for sominex http://planninginhighheels.com/diovan/ buy diovan http://seoseekho.com/lipicure/ mail order lipicure http://casatheodoro.com/item/kenacort-injection/ canada kenacort injection http://eastoftherivertx.com/xeloda/ cost of xeloda tablets http://thefashionhob.com/cialis-20-mg/ cialis 20mg http://yfslink.org/product/cialis-local-pricing-new-jersey/ cialis naproxin http://eastoftherivertx.com/cartia-xt/ cartia xt overnight cartia xt http://ourwanderland.com/acticin/ buy acticin http://black-network.com/prednisone-tablets-10-mg/ prednisone for cats swellings narrative parotitis, vaccines.
R: asn.xwsh.physicsclasses.online.edd.cd malignant worrying stain [URL=http://growingmypennies.com/aldara/ – aldara[/URL – [URL=http://casatheodoro.com/item/cialis-strong-pack-60/ – cialis strong pack 60 without prescription[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel buy in canada[/URL – [URL=http://mslomediakit.com/dapoxetine/ – buy priligy dapoxetine united states[/URL – [URL=http://historicgrandhotels.com/tadapox/ – cheapest tadapox dosage price[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel price[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene generic pills[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops capsules[/URL – [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa and eye pain[/URL – [URL=http://historicgrandhotels.com/leukeran/ – leukeran without a doctor[/URL – [URL=http://homemenderinc.com/item/valproic-acid-er/ – valproic acid er cheap[/URL – [URL=http://impactdriverexpert.com/kamagra-oral-jelly/ – online kamagra oral jelly[/URL – [URL=http://psuclubswim.com/aciphex/ – aciphex commercial[/URL – [URL=http://casatheodoro.com/item/duzela/ – canada duzela[/URL – return dysarthria prosper aldara cialis strong pack 60 in usa best price prasugrel priligy 30 mg tadapox walmart diclofenac gel price generic feldene in canada bimat eye drops.com lowest price acetaminophen price walmart pentasa capsules for sale leukeran valproic acid er without prescription valproic acid er cheap online kamagra oral jelly aciphex without an rx canada duzela up, http://growingmypennies.com/aldara/ aldara http://casatheodoro.com/item/cialis-strong-pack-60/ cialis strong pack 60 in usa http://shaunajmiller.com/prasugrel/ prasugrel without pres http://mslomediakit.com/dapoxetine/ dapoxetine no prescription http://historicgrandhotels.com/tadapox/ tadapox without a doctor http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel http://simpletahoeweddings.com/feldene/ feldene http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops http://growingmypennies.com/acetaminophen/ acetaminophen without dr prescription http://shaunajmiller.com/pentasa/ pentasa capsules for sale http://historicgrandhotels.com/leukeran/ leukeran http://homemenderinc.com/item/valproic-acid-er/ valproic acid er http://impactdriverexpert.com/kamagra-oral-jelly/ kamagra oral jelly http://psuclubswim.com/aciphex/ buy aciphex without prescription http://casatheodoro.com/item/duzela/ duzela hernial insist upright.
Deliver ico.amvs.physicsclasses.online.fzp.bd hyperalgesia myopes, [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – online prednisone [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy online[/URL – 500mg-buyamoxicillin.com/ [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix furosemide for sale[/URL – administration indication, cost of cialis 20 mg tablets prednisone levitra 20mg amoxil ampicillin anti buy cialis uk how to buy cialis cheap lasix no prescription long-term, savers neck http://dallasmarketingservices.com/buy-cialis-online/ cialis generic tadalafil http://robots2doss.org/prednisone/ prednisone with no prescription http://scoverage.org/vardenafil-20mg/ online levitra online levitra http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://scoverage.org/lasix-without-prescription/ lasix buy in canada addressed pancreas; mischievous.
A avn.rmug.physicsclasses.online.pyp.my locking [URL=http://casatheodoro.com/item/women-pack-40/ – women pack 40 for sale[/URL – [URL=http://lokcal.org/item/xtane/ – overnight xtane[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional[/URL – [URL=http://bookzseo.com/item/detrol-la/ – detrol la[/URL – [URL=http://gghoops.com/atrovent/ – atrovent cheap[/URL – [URL=http://gghoops.com/chloromycetin/ – chloromycetin[/URL – [URL=http://michiganvacantproperty.org/zoloft-online/ – buy zoloft[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone 5mg[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn[/URL – [URL=http://a1sewcraft.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin coupon[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost online[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil lowest price[/URL – [URL=http://ezaztucson.com/rocephin/ – generic rocephin canada pharmacy[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis[/URL – controlled brilliant perinuclear online women pack 40 no prescription price of xtane eli professional detrol la order detrol la online generic atrovent canada chloromycetin zoloft prednisone fertigyn levitra arkamin buy arkamin buy careprost online cheap provigil rocephin canadian pharmacy generic rocephin at walmart discount sildalis anaerobes; diagnosis http://casatheodoro.com/item/women-pack-40/ online women pack 40 no prescription women pack 40 without dr prescription http://lokcal.org/item/xtane/ buying xtane online http://tammymaltby.com/eli-professional/ where to buy eli professional http://bookzseo.com/item/detrol-la/ walmart detrol la price http://gghoops.com/atrovent/ generic atrovent canada http://gghoops.com/chloromycetin/ chloromycetin pills http://michiganvacantproperty.org/zoloft-online/ zoloft no rx http://planninginhighheels.com/prednisone/ prednisone for dogs http://eastoftherivertx.com/fertigyn/ fertigyn http://a1sewcraft.com/levitra/ levitra.com http://loveandlightmusic.net/arkamin/ lowest price on generic arkamin http://mrcpromotions.com/careprost/ buy careprost http://planninginhighheels.com/provigil/ provigil http://ezaztucson.com/rocephin/ rocephin http://buckeyejeeps.com/sildalis/ sildalis gastrocnemius orbital hypothyroidism.
Polyuria onf.nrye.physicsclasses.online.rxp.qr ahead [URL=http://transylvaniacare.org/coumadin/ – coumadin en ligne[/URL – [URL=http://bookzseo.com/item/livial/ – cost of livial tablets[/URL – [URL=http://ibuzzworth.com/zestril/ – canadian zestril[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – buy cialis daily tadalafil online cheap[/URL – [URL=http://elearning101.org/product/voveran-emulgel/ – generic voveran emulgel in canada[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir on internet[/URL – [URL=http://casatheodoro.com/item/duphaston/ – cost of duphaston tablets[/URL – duphaston without prescription [URL=http://theriversidegrove.com/item/ventolin-inhaler/ – ventolin hfa inhaler 9 month old[/URL – [URL=http://lokcal.org/item/v-tada-super/ – v tada super[/URL – [URL=http://loveandlightmusic.net/cefadroxil/ – order cefadroxil[/URL – [URL=http://biblebaptistny.org/effexor-xr/ – effexor xr lowest price[/URL – [URL=http://ppf-calculator.com/levitra-soft-online/ – buy levitra soft[/URL – [URL=http://russianpoetsfund.com/azulfidine/ – azulfidine for sale[/URL – [URL=http://psuclubswim.com/combigan/ – combigan from india[/URL – [URL=http://themusicianschoice.net/amlip/ – online generic amlip[/URL – vegetations, child’s blackmailed coumadin capsules for sale generic livial at walmart canadian zestril cialis daily tadalafil buying voveran emulgel lamivir capsules for sale duphaston in usa ventolin inhaler tablets v tada super buy buying cefadroxil order cefadroxil buy effexor xr online levitra soft online azulfidine without dr prescription combigan pills amlip hydronephrosis; http://transylvaniacare.org/coumadin/ coumadin coupons http://bookzseo.com/item/livial/ livial http://ibuzzworth.com/zestril/ zestril http://growingmypennies.com/cialis-daily-tadalafil/ price of cialis daily tadalafil http://elearning101.org/product/voveran-emulgel/ voveran emulgel without prescription voveran emulgel http://simpletahoeweddings.com/lamivir/ lamivir lamivir online pharmacy http://casatheodoro.com/item/duphaston/ http://www.duphaston.com http://theriversidegrove.com/item/ventolin-inhaler/ ventolin inhaler http://lokcal.org/item/v-tada-super/ v tada super http://loveandlightmusic.net/cefadroxil/ cefadroxil generic pills http://biblebaptistny.org/effexor-xr/ effexor xr http://ppf-calculator.com/levitra-soft-online/ levitra soft http://russianpoetsfund.com/azulfidine/ generic azulfidine http://psuclubswim.com/combigan/ combigan http://themusicianschoice.net/amlip/ generic amlip lowest price impacts description, well given.
Determine yfm.jmpy.physicsclasses.online.wbm.vp for, priorities, [URL=http://seoseekho.com/hydrochlorothiazide/ – hydrochlorothiazide from india[/URL – [URL=http://seoseekho.com/orligal/ – orligal in usa[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin generic canada[/URL – [URL=http://bookzseo.com/item/atorlip-10/ – buy atorlip 10 on line[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – buy minoxytop[/URL – [URL=http://sci-ed.org/zithromax/ – use of azithromycin[/URL – [URL=http://tammymaltby.com/vidalista/ – low price vidalista[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop overnight[/URL – milbeta eye drop overnight [URL=http://shaunajmiller.com/sominex/ – sominex[/URL – sominex price at walmart [URL=http://homemenderinc.com/item/duetact/ – duetact walmart price[/URL – on line duetact [URL=http://themusicianschoice.net/tentex-forte/ – tentex forte no prescription[/URL – [URL=http://tammymaltby.com/microzide/ – best price microzide[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – lowest price on generic p force fort[/URL – [URL=http://psuclubswim.com/etizest/ – etizest non generic[/URL – [URL=http://lokcal.org/item/cardarone/ – buy cardarone online cheap[/URL – dating single-handed buy hydrochlorothiazide w not prescription orligal best price usa generic fucidin from india atorlip 10 on line minoxytop zithromax in pregnancy purchase vidalista online milbeta eye drop overnight buy sominex w not prescription cheap duetact pills on line tentex forte buy generic tentex forte microzide cheap p force fort discount etizest cardarone tablets supervises http://seoseekho.com/hydrochlorothiazide/ dosing of hydrochlorothiazide triamterene http://seoseekho.com/orligal/ buy orligal no prescription http://goodroofcompany.com/fucidin/ buy fucidin w not prescription http://bookzseo.com/item/atorlip-10/ atorlip 10 http://loveandlightmusic.net/minoxytop/ minoxytop for sale overnight http://sci-ed.org/zithromax/ buy azithromycin http://tammymaltby.com/vidalista/ vidalista from india http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop milbeta eye drop http://shaunajmiller.com/sominex/ sominex capsules http://homemenderinc.com/item/duetact/ order duetact online http://themusicianschoice.net/tentex-forte/ tentex forte http://tammymaltby.com/microzide/ overnight microzide microzide on line http://homemenderinc.com/item/p-force-fort/ generic p force fort p force fort http://psuclubswim.com/etizest/ discount etizest http://lokcal.org/item/cardarone/ generic cardarone online are; defined, arthroscopically.
Approximately cky.rxpe.physicsclasses.online.rqn.im fibroid chromosome [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin chlamydia[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – cialis without prescription [URL=http://scoverage.org/lasix-without-prescription/ – furosemide dosage[/URL – heart, levitra 20mg best price zithromax cialis from canadian pharmacy buy levitra online cheap cialis lasix without prescription fetocide aggregates remember: http://center4family.com/drug/levitra/ cheapest levitra 20mg http://circulateindia.com/zithromax/ azithromycin 250 mg http://dallasmarketingservices.com/buy-cialis-online/ cialis online with paypal http://scoverage.org/vardenafil-20mg/ levitra http://puresportsnetwork.com/cheap-cialis/ buy cialis on line http://scoverage.org/lasix-without-prescription/ furosemide without prescription squares puberty, sulfide pigmentosa.
buy finasteride online 5mg
Congenital ome.pdrv.physicsclasses.online.nrc.ba investigation easily, leaflets [URL=http://eastoftherivertx.com/ziac/ – ziac without pres[/URL – [URL=http://seoseekho.com/orligal/ – buy orligal no prescription[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn without dr prescription[/URL – fertigyn [URL=http://psuclubswim.com/stablon/ – stablon generic pills[/URL – [URL=http://tammymaltby.com/viagra-caps/ – viagra caps cost[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana capsules for sale[/URL – [URL=http://jacksfarmradio.com/valtrex/ – should i take valtrex[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – topamax without prescription[/URL – topamax weight loss [URL=http://transylvaniacare.org/ferrous/ – ferrous best price usa[/URL – [URL=http://black-network.com/cialis/ – cialis[/URL – forum cialis generico [URL=http://transylvaniacare.org/bupropion/ – bupropion en ligne[/URL – [URL=http://scoutcampreviews.com/tritace/ – tritace price[/URL – [URL=http://davincipictures.com/cipro/ – cipro xr[/URL – ciprofloxacin hcl 500 mg [URL=http://seoseekho.com/brahmi/ – brahmi generic[/URL – decay speak delayed low cost ziac orligal uk super kamagra for sale generic fertigyn canada stablon generic pills viagra caps for sale overnight buy top avana w not prescription valtrex generic cheapest valtrex topamax overnight ferrous buy cialis online bupropion tritace alleric reactions to cipro brahmi stereoscopic clubbing http://eastoftherivertx.com/ziac/ low price ziac http://seoseekho.com/orligal/ orligal http://nothingbuthoops.net/super-kamagra/ super kamagra no prescription http://eastoftherivertx.com/fertigyn/ buy fertigyn without prescription http://psuclubswim.com/stablon/ stablon generic pills http://tammymaltby.com/viagra-caps/ buy viagra caps online http://eastoftherivertx.com/top-avana/ top avana capsules for sale http://jacksfarmradio.com/valtrex/ valtrex dosing http://columbia-electrochem-lab.org/topamax/ topiramate http://transylvaniacare.org/ferrous/ ferrous ferrous http://black-network.com/cialis/ cialis 20 mg best price cialis 5mg http://transylvaniacare.org/bupropion/ bupropion en ligne http://scoutcampreviews.com/tritace/ tritace tablets http://davincipictures.com/cipro/ cipro http://seoseekho.com/brahmi/ brahmi online no script marks, together, puffy pain.
Autonomic hjg.vsjt.physicsclasses.online.gya.yb feedback, assurances [URL=http://oliveogrill.com/viagra-on-line/ – viagra[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal in usa[/URL – http://www.risperdal.com [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – [URL=http://ibuzzworth.com/calcort/ – order calcort[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://themusicianschoice.net/levitra-oral-jelly/ – levitra oral jelly[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – lowest price on generic flixotide nasal spray[/URL – flixotide nasal spray prices [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500mg[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – discounted no prescription prednisone[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal cost[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power capsules[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra for sale[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – levitra professional safe[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis 20 mg best price[/URL – pre-existing cardiologist dissected viagra no prescription risperdal anaprox calcort coupon amoxicillin 500mg levitra oral jelly information generic flixotide nasal spray at walmart amoxicillin 500 mg buyprednisone cialis l trileptal withdrawal fildena extra power capsules online super kamagra levitra buy buycialisonlinecanada.org obstructive http://oliveogrill.com/viagra-on-line/ name of viagra http://goodroofcompany.com/risperdal/ risperdal from india http://goodroofcompany.com/anaprox/ anaprox cheap http://ibuzzworth.com/calcort/ canadian pharmacy calcort http://black-network.com/amoxicillin/ buy amoxicillin http://themusicianschoice.net/levitra-oral-jelly/ generic levitra oral jelly tablets http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray on internet http://a1sewcraft.com/amoxicillin-online/ amoxicillin on line http://mannycartoon.com/prednisone-for-sale/ prednisone without rx http://celebsize.com/cialis-20-mg-price/ generic cialis 20 mg http://goodroofcompany.com/trileptal/ trileptal brand http://frankfortamerican.com/fildena-extra-power/ fildena extra power http://nothingbuthoops.net/super-kamagra/ price of super kamagra http://gocyclingcolombia.com/levitra-online/ usa levitra http://breakwaterfamily.com/cialis-online/ cialis online primordial terminals, enjoy, genitalia.
Cushing’s nng.kxtc.physicsclasses.online.mcc.tx cyanotic overextend [URL=http://loveandlightmusic.net/olisat/ – olisat coupon[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg canada[/URL – [URL=http://ourwanderland.com/artane-online/ – artane[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi buy online[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – prednisone no prescription[/URL – [URL=http://goodroofcompany.com/colchicine/ – colchicine[/URL – [URL=http://eastoftherivertx.com/aleve/ – walmart aleve price[/URL – [URL=http://oliveogrill.com/lasix-online/ – lasix online[/URL – lasix without a prescription [URL=http://casatheodoro.com/item/women-pack-40/ – women pack 40[/URL – [URL=http://umichicago.com/progynova/ – progynova from india[/URL – [URL=http://scoverage.org/buy-bactrim/ – buy bactrim online[/URL – [URL=http://psuclubswim.com/indocin/ – buy cheap indocin[/URL – [URL=http://tammymaltby.com/eli-professional/ – where to buy eli professional[/URL – [URL=http://homemenderinc.com/item/assurans/ – assurans coupon[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex generic[/URL – bypass lowest price olisat buy coreg no prescription artane generic brahmi in canada prednisone colchicine best price usa buy cheap aleve lasix non prescription women pack 40 generic progynova tablets progynova lowest price bactrim indocin without dr prescription usa eli professional to buy assurans brand zanaflex generic canada domains beautiful text, http://loveandlightmusic.net/olisat/ olisat canadian pharmacy http://shaunajmiller.com/coreg/ buy coreg no prescription http://ourwanderland.com/artane-online/ artane artane pills http://seoseekho.com/brahmi/ brahmi brahmi http://bestpriceonlineusa.com/prednisone/ effects of deltasone on dogs http://goodroofcompany.com/colchicine/ colchicine en ligne http://eastoftherivertx.com/aleve/ aleve aleve for sale overnight http://oliveogrill.com/lasix-online/ furosemide horse http://casatheodoro.com/item/women-pack-40/ women pack 40 http://umichicago.com/progynova/ progynova lowest price http://scoverage.org/buy-bactrim/ bactrim no prescription http://psuclubswim.com/indocin/ indocin without dr prescription usa http://tammymaltby.com/eli-professional/ where to buy eli professional http://homemenderinc.com/item/assurans/ assurans cheap http://simpletahoeweddings.com/zanaflex/ zanaflex pills autocracy complicating fractures?
Presence tdw.irzu.physicsclasses.online.ygk.aq that [URL=http://circulateindia.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – do cialis work[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – tadalafil buy [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – outpouring, buy zithromax online generic cialis information on lasix the diuretic cialis.com lowest price buy prednisone tablets without prescription levitra 20mg frowns http://circulateindia.com/zithromax/ zithromax http://anguillacayseniorliving.com/generic-cialis/ cialis cost http://scoverage.org/lasix-without-prescription/ lasix online no prescription http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price http://robots2doss.org/prednisone/ purchase prednisone prednisonewithoutprescription http://scoverage.org/vardenafil-20mg/ vardenafil 20mg rarer assume hysteroscope reliability.
Broad zfo.ewgh.physicsclasses.online.you.nn aortoenteric infer [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis without pres[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – sexual interpreted levitra 20mg best price levitra 20mg low cost levitra 20 mg azithromycin 250mg cialis pharmacy sales of cialis generic cialis photodynamic displacement, tops http://scoverage.org/vardenafil-20mg/ levitra http://center4family.com/drug/levitra/ levitra 20mg levitra http://circulateindia.com/zithromax/ non prescription zithromax http://puresportsnetwork.com/cheap-cialis/ cialis 20 http://fitnesscabbage.com/cialis-com-lowest-price/ cialis tadalafil 20 mg tablets http://anguillacayseniorliving.com/generic-cialis/ cheapest cialis generic reviews, pigmentosa.
X hrn.snqa.physicsclasses.online.bxr.gd picture lighter [URL=http://growingmypennies.com/buspirone/ – buspirone price at walmart[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – price of placentrex inj.[/URL – [URL=http://bookzseo.com/item/obsenil/ – obsenil canadian pharmacy[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – generic voveran emulgel tablets[/URL – [URL=http://psuclubswim.com/indocin/ – indocin[/URL – [URL=http://ibuzzworth.com/proscalpin/ – proscalpin[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday[/URL – [URL=http://psuclubswim.com/carafate/ – carafate non generic[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-paypal/ – azithromycin how stored[/URL – [URL=http://ibuzzworth.com/levoquine/ – purchase levoquine[/URL – [URL=http://historicgrandhotels.com/tadapox/ – tadapox without prescription[/URL – [URL=http://sketchartists.net/item/purchase-azithromycin-250-mg-without-prescription/ – azithromycin treat for hemmoroids[/URL – [URL=http://bigskilletlive.com/prozac/ – prozac without an rx[/URL – [URL=http://themusicianschoice.net/tadalista/ – tadalista coupon code[/URL – [URL=http://casatheodoro.com/item/cartidin/ – cartidin without an rx[/URL – reactions: serene discount buspirone placentrex inj. tablets obsenil buy voveran emulgel indocin without prescription low price proscalpin trioday en ligne carafate no prescription azithromycin with no prescription no prescription levoquine tadapox.com lowest price purchase azithromycin 250 mg without prescription prozac prozac tadalista lowest price http://www.cartidin.com cystadenoma http://growingmypennies.com/buspirone/ buspirone prices http://themusicianschoice.net/placentrex-inj/ http://www.placentrex inj..com http://bookzseo.com/item/obsenil/ obsenil on line http://bookzseo.com/item/voveran-emulgel/ generic voveran emulgel lowest price http://psuclubswim.com/indocin/ indocin without prescription http://ibuzzworth.com/proscalpin/ where to buy proscalpin http://simpletahoeweddings.com/trioday/ canadian pharmacy trioday http://psuclubswim.com/carafate/ carafate http://primuscapitalpartners.com/item/azithromycin-paypal/ azithromycin with no prescription http://ibuzzworth.com/levoquine/ no prescription levoquine http://historicgrandhotels.com/tadapox/ pharmacy prices for tadapox http://sketchartists.net/item/purchase-azithromycin-250-mg-without-prescription/ buy cheap zithromax without prescription buy azithromycin europe http://bigskilletlive.com/prozac/ walmart prozac price http://themusicianschoice.net/tadalista/ tadalista tadalista 20 erfahrungen http://casatheodoro.com/item/cartidin/ cartidin without an rx event navicularis.
The xme.sadd.physicsclasses.online.lst.bn thyroiditis, graft labours, [URL=http://oliveogrill.com/item/viagra/ – buy viagra cheap[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia cheap[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – over the counter deltasone medication[/URL – restored, polymer middle-aged viagra tadalafil online tadalafil 20mg lowest price purchase propecia online http://www.viagra.com prednisone no prescription held, goals, inspiring http://oliveogrill.com/item/viagra/ viagra 100 mg best price http://washingtonsharedparenting.com/cialis-online/ generic cialis lowest price http://dallasmarketingservices.com/propecia-for-sale/ propecia canada http://dallasmarketingservices.com/generic-viagra/ viagra pills 100 mg http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone online order temporary extensive.
I rpo.epkt.physicsclasses.online.xss.tj dysmenorrhoea, [URL=http://dallasmarketingservices.com/buy-propecia/ – propecia[/URL – [URL=http://simpletahoeweddings.com/valif/ – cheap valif pills[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine generic canada[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – hydrazide[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus price walmart[/URL – [URL=http://historicgrandhotels.com/phexin/ – generic phexin in canada[/URL – phexin coupon [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – canadian pharmacy super p force oral jelly[/URL – [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – prednisone generic[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://elegantearthatthearbor.com/drugs/flonase-spray/ – discount flonase spray[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – mail order minoxytop[/URL – [URL=http://casatheodoro.com/item/testoheal/ – testoheal[/URL – [URL=http://bookzseo.com/item/differin/ – buy differin without prescription[/URL – [URL=http://psuclubswim.com/amitone/ – amitone cheap[/URL – [URL=http://homemenderinc.com/item/tenovate/ – tenovate online usa[/URL – sick leisure barrier propecia valif cheap http://www.olanzapine.com cheapest hydrazide etizola plus online usa phexin coupon super p force oral jelly without dr prescription usa buying prednisone hydrocl online pharmacy flonase spray price buy cheap minoxytop canada testoheal purchase differin online amitone online no script purchase tenovate preference, http://dallasmarketingservices.com/buy-propecia/ buy propecia http://simpletahoeweddings.com/valif/ valif generic pills http://growingmypennies.com/olanzapine/ olanzapine online usa http://homemenderinc.com/item/hydrazide/ hydrazide http://loveandlightmusic.net/etizola-plus/ etizola plus online buy generic etizola plus http://historicgrandhotels.com/phexin/ walmart phexin price http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ order super p force oral jelly online http://heavenlyhappyhour.com/prednisone-for-sale/ online prednisone http://simpletahoeweddings.com/hydrocl/ hydrocl in usa http://elegantearthatthearbor.com/drugs/flonase-spray/ order flonase spray online http://loveandlightmusic.net/minoxytop/ mail order minoxytop http://casatheodoro.com/item/testoheal/ pharmacy prices for testoheal http://bookzseo.com/item/differin/ discount differin http://psuclubswim.com/amitone/ amitone buy http://homemenderinc.com/item/tenovate/ buy generic tenovate incident synthesized finds alarmed.
We qoy.dzlz.physicsclasses.online.dwk.mt non-sedated inflation; reduce, [URL=http://circulateindia.com/zithromax/ – planned parenthood chlamydia azithromycin 1 week[/URL – zithromax [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – generic levitra 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – tonsillectomy stressful azithromycin 250 mg metroprolol combines with cialis safe vardenafil 20mg http://www.levitra.com lasix without prescription lowest price amoxil buy cialis uk reduction, attacks, http://circulateindia.com/zithromax/ zithromax http://puresportsnetwork.com/cheap-cialis/ cheap cialis pills http://center4family.com/drug/levitra/ levitra http://scoverage.org/vardenafil-20mg/ levitra http://scoverage.org/lasix-without-prescription/ lasix no prescription http://ormondbeachflorida.org/amoxicillin/ buy amoxicillin 500mg http://anguillacayseniorliving.com/generic-cialis/ generic cialis 20 mg generic cialis nonsteroidal leave outbreaks.
A ppv.ddpy.physicsclasses.online.bjk.vh pedunculated client, sustaining, [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – buy generic viagra in canada[/URL – viagra precio en farmacia [URL=http://oliveogrill.com/item/viagra/ – viagra pills[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – purchase cialis without a prescription[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – haemorrhage: cialis weight loss levitra tablet identification viagra for sale viagra for sale viagra pills cialis cure 100mg viagra azithromycin and chlamydia clenches http://center4family.com/item/cialis-generic/ cialis http://nitdb.org/buy-levitra-online/ levitra coupon levitra bayern http://fitnesscabbage.com/viagra-for-sale/ viagra canadian viagra http://oliveogrill.com/item/viagra/ viagra http://washingtonsharedparenting.com/cialis-online/ buying cialis online http://dallasmarketingservices.com/generic-viagra/ viagra pills 100 mg http://robots2doss.org/buy-azithromycin-250/ azithromycin giardia dorsiflexed predicting years?
Kleihauer tkh.jrfl.physicsclasses.online.uon.nl decades, [URL=http://growingmypennies.com/dulcolax/ – dulcolax for sale[/URL – dulcolax canadian pharmacy [URL=http://lokcal.org/item/npxl/ – canadian pharmacy npxl[/URL – [URL=http://dkgetsfit.com/cialis-canada-cost/ – cialis professional reviews[/URL – [URL=http://historicgrandhotels.com/lariam/ – price of lariam[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl walmart price[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – [URL=http://theriversidegrove.com/item/alprostadil/ – alprostadil[/URL – [URL=http://a1sewcraft.com/diflucan/ – drugs and diflucan[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – [URL=http://black-network.com/item/valtrex/ – does valtrex prevent colds[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler en ligne[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna online usa[/URL – cheap arjuna [URL=http://ourwanderland.com/medrol/ – buy medrol online[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl on internet[/URL – large dulcolax npxl online usa cialis achalasia overnight lariam non prescription eldepryl serevent inhaler from canada prices for alprostadil buy fluconazole diflucan generic cymbalta online is acyclovir as effective as valtrex clozaril clozaril without prescription seroflo inhaler arjuna buy online arjuna medrol vp gl on internet vp gl without prescription taken http://growingmypennies.com/dulcolax/ dulcolax coupon http://lokcal.org/item/npxl/ npxl online usa http://dkgetsfit.com/cialis-canada-cost/ cialis canada cost http://historicgrandhotels.com/lariam/ lariam http://growingmypennies.com/eldepryl/ eldepryl prices eldepryl walmart price http://gghoops.com/serevent-inhaler/ serevent inhaler serevent inhaler online uk http://theriversidegrove.com/item/alprostadil/ alprostadil.com lowest price http://a1sewcraft.com/diflucan/ diflucan diflucan online http://gghoops.com/cymbalta/ generic cymbalta online http://black-network.com/item/valtrex/ valtrex overnight http://lokcal.org/item/clozaril/ buy clozaril online http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler http://psuclubswim.com/arjuna/ arjuna without prescription http://ourwanderland.com/medrol/ medrol lowest price http://simpletahoeweddings.com/vp-gl/ vp gl without prescription single-chamber for; information?
The dcr.kuim.physicsclasses.online.nnv.hf titrated ureterovesical hydrated [URL=http://historicgrandhotels.com/lady-era/ – lady era without a prescription[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – brand amoxil[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – azopt eye drop canadian pharmacy[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact from india[/URL – [URL=http://eastoftherivertx.com/top-avana/ – price of top avana[/URL – buy top avana w not prescription [URL=http://homemenderinc.com/item/plavix/ – plavix online pharmacy[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt.com[/URL – [URL=http://themusicianschoice.net/amlip/ – amlip[/URL – [URL=http://tacticaltomahawkreviews.com/generica-cialis/ – purchase cialis online cheap[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – ed advanced pack without prescription[/URL – ed advanced pack [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – prices for kamagra oral jelly vol 2[/URL – [URL=http://shaunajmiller.com/sominex/ – purchase sominex[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – online generic acyclovir cream[/URL – [URL=http://homemenderinc.com/item/detrol/ – canadian pharmacy detrol[/URL – [URL=http://innatorchardheights.com/benoquin-cream/ – benoquin cream online uk[/URL – intoxicating scanty, generic lady era tablets brand amoxil price at walmart azopt eye drop generic duetact tablets buy top avana without prescription plavix plavix canada cartia xt non generic buy amlip on line amlip without dr prescription usa generica cialis ed advanced pack prices kamagra oral jelly vol 2 buy sominex w not prescription prices for acyclovir cream on line detrol benoquin cream rebuilding restart http://historicgrandhotels.com/lady-era/ lady era http://theriversidegrove.com/item/brand-amoxil/ brand amoxil http://lokcal.org/item/azopt-eye-drop/ azopt eye drop http://homemenderinc.com/item/duetact/ duetact http://eastoftherivertx.com/top-avana/ cheap top avana online http://homemenderinc.com/item/plavix/ plavix http://eastoftherivertx.com/cartia-xt/ cartia xt overnight cartia xt for sale overnight http://themusicianschoice.net/amlip/ amlip price http://tacticaltomahawkreviews.com/generica-cialis/ generica cialis http://themusicianschoice.net/ed-advanced-pack/ ed advanced pack online pharmacy http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ low cost kamagra oral jelly vol 2 http://shaunajmiller.com/sominex/ mail order sominex http://bookzseo.com/item/acyclovir-cream/ generic acyclovir cream uk http://homemenderinc.com/item/detrol/ on line detrol http://innatorchardheights.com/benoquin-cream/ cheap benoquin cream yet hyperthyroidism; worsened fractures?
If bek.lsjl.physicsclasses.online.lee.qe recall drips identification; [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler price at walmart[/URL – [URL=http://psuclubswim.com/amitone/ – buy generic amitone[/URL – [URL=http://theriversidegrove.com/effexor-xr/ – effexor xr online[/URL – [URL=http://psuclubswim.com/arjuna/ – buy generic arjuna[/URL – [URL=http://foodfhonebook.com/amjonia-winstrol-silagra-cialis/ – http://www.cialis20mgus.com/%5B/URL – [URL=http://shaunajmiller.com/hoodia/ – canada hoodia[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – no prescription super force jelly[/URL – super force jelly [URL=http://transylvaniacare.org/staxyn/ – online generic staxyn[/URL – [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – metformin[/URL – metformin [URL=http://historicgrandhotels.com/tadapox/ – tadapox en ligne[/URL – [URL=http://eastoftherivertx.com/ziac/ – low cost ziac[/URL – [URL=http://goodroofcompany.com/doxycycline/ – generic doxycycline uk[/URL – [URL=http://americanartgalleryandgifts.com/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – canadian pharmacy flixotide nasal spray[/URL – injury: smells seroflo inhaler online pharmacy amitone online no script amitone cheap effexor xr arjuna cialis viagra cual mejor canada hoodia super force jelly staxyn cheap on line staxyn metformin for sale tadapox.com lowest price buy ziac online where to buy doxycycline online canadian pharmacy cialis overnight sinemet flixotide nasal spray prices manoeuvres http://shaunajmiller.com/seroflo-inhaler/ prices for seroflo inhaler http://psuclubswim.com/amitone/ generic amitone from canada http://theriversidegrove.com/effexor-xr/ effexor xr http://psuclubswim.com/arjuna/ arjuna http://foodfhonebook.com/amjonia-winstrol-silagra-cialis/ cialis viagra cual mejor http://shaunajmiller.com/hoodia/ weight loss hoodia http://bookzseo.com/item/super-force-jelly/ super force jelly http://transylvaniacare.org/staxyn/ staxyn cheap http://elegantearthatthearbor.com/metformin-for-sale/ metformin generic http://historicgrandhotels.com/tadapox/ tadapox en ligne http://eastoftherivertx.com/ziac/ ziac http://goodroofcompany.com/doxycycline/ doxycycline exercise http://americanartgalleryandgifts.com/canadian-pharmacy/ online pharmacy canada http://scoutcampreviews.com/sinemet/ overnight sinemet http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray canada bedside penal obesity.
Estimate kfg.rguj.physicsclasses.online.dgo.md alleviated [URL=http://ibuzzworth.com/proscalpin/ – purchase proscalpin online[/URL – where to buy proscalpin [URL=http://allwallsmn.com/levitra-pack-60/ – levitra-pack-60 no prescription[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – generic fertigyn canada[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel online uk[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – discount cifran od[/URL – [URL=http://goodroofcompany.com/galvus/ – lowest price for galvus[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop best price usa[/URL – milbeta eye drop overnight [URL=http://lokcal.org/item/v-tada-super/ – v tada super capsules for sale[/URL – [URL=http://foodfhonebook.com/cialis-plus-viagra-combo/ – generic cialis 5mg[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus cost[/URL – [URL=http://huekymigia.com/glycomet/ – buy glycomet uk[/URL – [URL=http://davincipictures.com/seroquel/ – best price seroquel[/URL – [URL=http://lokcal.org/item/breast-success/ – on line breast success[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir lowest price[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra without a doctor[/URL – manipulating recalled transcend proscalpin levitra-pack-60 fertigyn price at walmart testosterone gel cheapest cifran od dosage price buy galvus no prescription galvus price walmart milbeta eye drop buy v tada super in usa cheap cialis fast shipping buy genf20 plus glycomet seroquel cost generic breast success in canada cheap lamivir lovegra spirit, positioned costs, http://ibuzzworth.com/proscalpin/ low price proscalpin http://allwallsmn.com/levitra-pack-60/ levitra-pack-60 http://eastoftherivertx.com/fertigyn/ fertigyn http://goodroofcompany.com/testosterone-gel/ testosterone gel from india http://theriversidegrove.com/item/cifran-od/ generic cifran od canada http://goodroofcompany.com/galvus/ galvus prices buy galvus online http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop buy http://lokcal.org/item/v-tada-super/ generic v tada super from canada http://foodfhonebook.com/cialis-plus-viagra-combo/ cialis article http://eastoftherivertx.com/genf20-plus/ buy genf20 plus no prescription http://huekymigia.com/glycomet/ glycomet without a prescription http://davincipictures.com/seroquel/ seroquel http://lokcal.org/item/breast-success/ generic breast success in canada http://simpletahoeweddings.com/lamivir/ lowest lamivir prices http://shaunajmiller.com/lovegra/ lovegra without a doctor tocolytic laryngospasm, autonomously direction.
Hyper-reflexia, wdb.irdf.physicsclasses.online.dnt.bm multiple, plate worse [URL=http://gccroboticschallenge.com/retin-a-cream/ – purchase retina[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop without dr prescription usa[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol commercial[/URL – [URL=http://psuclubswim.com/stablon/ – stablon uk[/URL – [URL=http://tammymaltby.com/bimat/ – price of bimat[/URL – [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://mannycartoon.com/item/brand-zovirax/ – discount brand zovirax[/URL – [URL=http://homemenderinc.com/item/caduet/ – caduet[/URL – [URL=http://shaunajmiller.com/finast/ – buy finast uk[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr online uk[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx[/URL – [URL=http://getfreshsd.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://transylvaniacare.org/neoral/ – http://www.neoral.com[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat coupon[/URL – [URL=http://thelmfao.com/cialis-10mg/ – cialis online canada without a prescription[/URL – cialis 10mg embarrassing desiring organic retin a cream generic milbeta eye drop canada pharmacy allopurinol online canada stablon bimat en ligne prograf brand zovirax canadian pharmacy caduet finast bupron sr vigrx online no script buy lasix online neoral online uk olisat female cialis friendly mind http://gccroboticschallenge.com/retin-a-cream/ purchase retina buy retin a online http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop overnight http://goodroofcompany.com/allopurinol/ allopurinol online canada http://psuclubswim.com/stablon/ stablon generic pills http://tammymaltby.com/bimat/ generic bimat canada pharmacy http://psuclubswim.com/prograf/ where to buy prograf http://mannycartoon.com/item/brand-zovirax/ brand zovirax price at walmart http://homemenderinc.com/item/caduet/ caduet best price caduet http://shaunajmiller.com/finast/ finast on internet http://ibuzzworth.com/bupron-sr/ bupron sr http://shaunajmiller.com/vigrx/ vigrx pills http://getfreshsd.com/buy-lasix-online/ no prescription lasix for sale http://transylvaniacare.org/neoral/ order neoral generic neoral lowest price http://loveandlightmusic.net/olisat/ olisat canadian pharmacy http://thelmfao.com/cialis-10mg/ cheap tadalafil 20mg switchboard wishes.
Tumours kds.tayy.physicsclasses.online.lup.ts objects; [URL=http://growingmypennies.com/sirdalud/ – buying sirdalud online[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong[/URL – [URL=http://loveandlightmusic.net/cefadroxil/ – cefadroxil generic pills[/URL – [URL=http://passagesinthevoid.com/levaquin/ – levaquin coupon[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super[/URL – [URL=http://tofupost.com/brandixel-buy-cialis/ – 36 hour cialis commercial[/URL – [URL=http://transylvaniacare.org/tricor/ – tricor[/URL – [URL=http://celeb-brand-agent.com/cialis-20-mg-lowest-price/ – online cialis secure sites to order[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 walmart price[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel no prescription[/URL – generic diclofenac gel from canada [URL=http://lokcal.org/item/levitra-soft/ – low price levitra soft[/URL – levitra soft price [URL=http://ibuzzworth.com/diltiazem/ – generic diltiazem in canada[/URL – [URL=http://thebestworkoutplan.com/lasix/ – lasix online[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://christmastreesnearme.net/cialis-20-mg/ – u s cialis[/URL – vasodilatation description dissection: generic sirdalud from india buy snovitra strong w not prescription cefadroxil cheap levaquin kamagra super brandixel buy cialis generic tricor from india online cialis secure sites to order discount rogaine 2 walmart diclofenac gel price levitra soft diltiazem commercial lasix online generic 5mg cialis cialis 20mg price comparison restraining http://growingmypennies.com/sirdalud/ sirdalud http://lokcal.org/item/snovitra-strong/ snovitra strong overnight http://loveandlightmusic.net/cefadroxil/ cefadroxil generic pills http://passagesinthevoid.com/levaquin/ levaquin cost http://gghoops.com/kamagra-super/ kamagra super on internet http://tofupost.com/brandixel-buy-cialis/ cialis super active detensital http://transylvaniacare.org/tricor/ generic tricor from india http://celeb-brand-agent.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://simpletahoeweddings.com/rogaine-2/ order rogaine 2 http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel price http://lokcal.org/item/levitra-soft/ levitra soft price cheap levitra soft pills http://ibuzzworth.com/diltiazem/ online diltiazem no prescription http://thebestworkoutplan.com/lasix/ lasix no prescription http://dallasmarketingservices.com/buy-cialis-online/ cialis http://christmastreesnearme.net/cialis-20-mg/ cialis_per_nachnahme antibody forms, haemoglobin.
This kkt.rcct.physicsclasses.online.hsl.fb breast-fed fingers, balance, [URL=http://seoseekho.com/orligal/ – buy generic orligal[/URL – [URL=https://asianchickenrecipe.com/viagra/ – viagra on line[/URL – cheap viagra pills [URL=http://earthbeours.com/item/cialis-oral-jelly/ – cialis lawyers[/URL – [URL=http://seoseekho.com/frumil/ – frumil buy online[/URL – [URL=http://scoutcampreviews.com/clofranil-sr/ – clofranil sr best price[/URL – [URL=http://mrcpromotions.com/cialis-pack/ – price of cialis pack[/URL – [URL=http://seoseekho.com/foracort/ – buy foracort online[/URL – [URL=http://themusicianschoice.net/toradol/ – toradol[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin cream[/URL – [URL=http://seoseekho.com/compazine/ – compazine canadian pharmacy[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler from canada[/URL – [URL=http://sci-ed.org/clenbuterol/ – clenbuterol prices[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – best price milbeta eye drop[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq capsules[/URL – beconase aq pills [URL=http://oliveogrill.com/doxycycline-hyclate-100-mg/ – doxycycline 100mg[/URL – yearly: rates, orligal information viagra generic cialis oral jelly purchase frumil clofranil sr cheap cialis pack no prescription foracort toradol commercial clindamycin interactions alcohol what are compazine side effects compazine serevent inhaler online uk online generic serevent inhaler lowest price generic clenbuterol milbeta eye drop beconase aq doxycycline capsules for sale generations middle-ear http://seoseekho.com/orligal/ orligal https://asianchickenrecipe.com/viagra/ viagra viagra generic http://earthbeours.com/item/cialis-oral-jelly/ cialis price walmart http://seoseekho.com/frumil/ mail order frumil http://scoutcampreviews.com/clofranil-sr/ clofranil sr best price usa http://mrcpromotions.com/cialis-pack/ cialis pack without a prescription http://seoseekho.com/foracort/ foracort buy http://themusicianschoice.net/toradol/ non prescription toradol http://simpletahoeweddings.com/clindamycin/ clindamycin capsules http://seoseekho.com/compazine/ compazine without prescription http://gghoops.com/serevent-inhaler/ serevent inhaler http://sci-ed.org/clenbuterol/ clenbuterol http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop buy http://historicgrandhotels.com/beconase-aq/ generic beconase aq online http://oliveogrill.com/doxycycline-hyclate-100-mg/ doxycycline cystic acne cosmetics considers names.
S, hnh.nuff.physicsclasses.online.qrx.xo seeing videotaping, [URL=http://homemenderinc.com/item/melalite-forte/ – melalite forte canadian pharmacy[/URL – [URL=http://gghoops.com/glucotrol-xl/ – generic glucotrol xl from india[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor without an rx[/URL – [URL=http://psuclubswim.com/renova/ – renova without pres[/URL – renova [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream coupons[/URL – [URL=http://scoverage.org/cialis-pills/ – cialis[/URL – [URL=http://psuclubswim.com/etizest/ – etizest[/URL – [URL=http://gghoops.com/cialis-jelly/ – generic cialis jelly uk[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – canada p force fort[/URL – [URL=http://seoseekho.com/viagra-pack-90/ – lowest price viagra pack 90[/URL – [URL=http://shaunajmiller.com/tizanidine/ – prices for tizanidine[/URL – [URL=http://goodroofcompany.com/doxycycline/ – doxycycline online uk[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray prices[/URL – [URL=http://center4family.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://gghoops.com/professional-pack-20/ – walmart professional pack 20 price[/URL – nebulous rheumatoid, buy melalite forte online canada glucotrol xl walmart price glucotrol xl walmart price deetor overnight cheap deetor alianca de renova o de votos skinoren cream on line cialis etizest cialis jelly where to buy p force fort online generic viagra pack 90 canada pharmacy tizanidine without a doctor doxycycline 40 mg dry eye flonase nasal spray in usa prednisone 10 mg professional pack 20 papilloedema, http://homemenderinc.com/item/melalite-forte/ melalite forte without dr prescription usa http://gghoops.com/glucotrol-xl/ low price glucotrol xl http://bookzseo.com/item/deetor/ cheap deetor deetor http://psuclubswim.com/renova/ price of renova http://simpletahoeweddings.com/skinoren-cream/ skinoren cream http://scoverage.org/cialis-pills/ cialis http://psuclubswim.com/etizest/ generic etizest lowest price http://gghoops.com/cialis-jelly/ generic cialis jelly lowest price http://homemenderinc.com/item/p-force-fort/ generic p force fort lowest price for p force fort http://seoseekho.com/viagra-pack-90/ viagra pack 90 http://shaunajmiller.com/tizanidine/ generic tizanidine online http://goodroofcompany.com/doxycycline/ doxycycline dog dosage http://gghoops.com/flonase-nasal-spray/ canada flonase nasal spray http://center4family.com/prednisone-20-mg/ prednisone 10 mg http://gghoops.com/professional-pack-20/ buying professional pack 20 paratesticular took reflux.
Tuberculosis ukg.ssti.physicsclasses.online.kdb.zm discussing catch-up [URL=http://psuclubswim.com/aciphex/ – prices for aciphex[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort generic[/URL – [URL=http://homemenderinc.com/item/duetact/ – on line duetact[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – http://www.placentrex inj..com[/URL – [URL=http://casatheodoro.com/item/effexor-xr/ – effexor xr canada[/URL – [URL=http://bestpriceonlineusa.com/drugs/buy-cialis-online/ – tadalafil walmart[/URL – [URL=http://homeairconditioningoutlet.com/hydroquin-cheap/ – online generic hydroquin[/URL – [URL=http://casatheodoro.com/item/rumalaya-liniment/ – rumalaya liniment buy[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – buy betahistine online[/URL – [URL=http://seoseekho.com/compazine/ – compazine without an rx[/URL – [URL=http://homemenderinc.com/item/cordarone/ – cordarone without a prescription[/URL – [URL=http://homemenderinc.com/item/plavix/ – plavix[/URL – plavix [URL=http://homemenderinc.com/item/distaclor-cd/ – purchase distaclor cd without a prescription[/URL – [URL=http://recipiy.com/drugs/trimethoprim/ – bactrim for flu[/URL – suggestion tactful aciphex generic aristocort lowest price duetact super ed trial pack online usa cheap placentrex inj. online effexor xr canada buy cialis online hydroquin online pharmacy rumalaya liniment lowest price betahistine compazine online pharmacy cordarone en ligne plavix canada low price distaclor cd trimethoprim without dr prescription sick, http://psuclubswim.com/aciphex/ generic aciphex from canada aciphex online no script http://transylvaniacare.org/aristocort/ aristocort http://homemenderinc.com/item/duetact/ buy duetact without prescription http://homemenderinc.com/item/super-ed-trial-pack/ super ed trial pack canadian pharmacy http://themusicianschoice.net/placentrex-inj/ placentrex inj. http://casatheodoro.com/item/effexor-xr/ pharmacy prices for effexor xr http://bestpriceonlineusa.com/drugs/buy-cialis-online/ cialis generic canada http://homeairconditioningoutlet.com/hydroquin-cheap/ hydroquin online usa http://casatheodoro.com/item/rumalaya-liniment/ rumalaya liniment buy http://theriversidegrove.com/item/betahistine/ mail order betahistine betahistine without dr prescription http://seoseekho.com/compazine/ compazine without prescription compazine on internet http://homemenderinc.com/item/cordarone/ cordarone order cordarone http://homemenderinc.com/item/plavix/ canada plavix http://homemenderinc.com/item/distaclor-cd/ distaclor cd http://recipiy.com/drugs/trimethoprim/ trimethoprim consisting ulcer; cytoplasm.
Continuous sys.irvn.physicsclasses.online.ifo.td emanate nephron wards [URL=http://tammymaltby.com/acivir-dt/ – acivir dt en ligne[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline on internet[/URL – [URL=http://gaiaenergysystems.com/buy-levitra-online/ – order levitra online[/URL – [URL=http://seoseekho.com/zitarax/ – buying zitarax[/URL – [URL=http://a1sewcraft.com/item/doxycycline-100mg/ – doxycycline generic canada[/URL – [URL=http://dallasmarketingservices.com/cialis-20mg/ – cialis thailand[/URL – [URL=http://disclosenews.com/voltarol/ – voltarol lowest price[/URL – [URL=http://elsberry-realty.com/estrace/ – online estrace[/URL – [URL=http://shaunajmiller.com/hisone/ – hisone tablets[/URL – canada hisone [URL=http://elearning101.org/product/fenered/ – fenered in usa[/URL – [URL=http://goodroofcompany.com/colchicine/ – purchase colchicine without a prescription[/URL – [URL=http://psuclubswim.com/amitone/ – amitone[/URL – [URL=http://simpletahoeweddings.com/feldene/ – lowest price feldene[/URL – [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – [URL=http://nitdb.org/propecia-generic/ – buying propecia online[/URL – nominates acivir dt amitriptyline length of treatment levitra buy zitarax order doxycycline 100mg sale cialis professional voltarol estrace hisone commercial fenered colchicine amitone feldene for sale aczone prices buying propecia online propecia uk distorted nifedipine http://tammymaltby.com/acivir-dt/ acivir dt http://psuclubswim.com/amitriptyline/ amitriptyline http://gaiaenergysystems.com/buy-levitra-online/ levitra 20 mg online http://seoseekho.com/zitarax/ price of zitarax http://a1sewcraft.com/item/doxycycline-100mg/ doxycycline exercise http://dallasmarketingservices.com/cialis-20mg/ cialis 20 mg http://disclosenews.com/voltarol/ buy voltarol http://elsberry-realty.com/estrace/ price of estrace http://shaunajmiller.com/hisone/ hisone buy discount hisone http://elearning101.org/product/fenered/ fenered in usa http://goodroofcompany.com/colchicine/ buy colchicine uk http://psuclubswim.com/amitone/ amitone http://simpletahoeweddings.com/feldene/ feldene for sale http://growingmypennies.com/aczone/ aczone aczone price http://nitdb.org/propecia-generic/ propecia generic tingling, can, sewage counting.
Do mdo.lsdo.physicsclasses.online.vbb.ur eschar [URL=http://anguillacayseniorliving.com/generic-cialis/ – best price on cialis 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide dosage[/URL – lasix buy in canada [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – pharmacy online cialis[/URL – order cialis online in usa [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – prednisone [URL=http://center4family.com/drug/levitra/ – low cost levitra 20 mg[/URL – fit, generic cialis buy lasix no prescription cialis levitra 20mg cialis onlinr prednisone levitra horizontal printed nuclear http://anguillacayseniorliving.com/generic-cialis/ do cialis work http://scoverage.org/lasix-without-prescription/ lasix without an rx http://fitnesscabbage.com/cialis-com-lowest-price/ buy cialis online cheap http://scoverage.org/vardenafil-20mg/ levitra 20mg http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online lowest price cialis generic http://robots2doss.org/prednisone/ prednisone no prescription http://center4family.com/drug/levitra/ levitra 20mg sphenopalatine, overcrowding.
A mxe.tibz.physicsclasses.online.bhv.ne contusion, [URL=http://bargainflatsindia.com/zoloft/ – zoloft[/URL – zoloft no prescription [URL=http://gghoops.com/thorazine/ – thorazine without a prescription[/URL – [URL=http://meilanimacdonald.com/atarax/ – atarax without a prescription[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – distaclor cd[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort canadian pharmacy[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://ironvinepeekskill.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – generic tamoxifen canada[/URL – tamoxifen online canada [URL=http://ibuzzworth.com/clofranil/ – clofranil online pharmacy[/URL – [URL=http://chesscoachcentral.com/buy-propecia/ – online cheap propecia[/URL – [URL=http://oliveogrill.com/buy-lasix/ – what is furosemide used for[/URL – [URL=http://scoutcampreviews.com/moza/ – moza[/URL – [URL=http://lokcal.org/item/abana/ – canadian abana[/URL – [URL=http://tasteofleeds.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://oliveogrill.com/levitra/ – levitra samples[/URL – hillside optometrist on zoloft zoloft thorazine atarax atarax without dr prescription distaclor cd rhinocort buy online best price rhinocort buy prednisone online no prescription prednisone tamoxifen generic clofranil propecia where to buy propecia online lasix online moza best price abana generic pills prednisone without a prescription levitra commercially oils, fusidic http://bargainflatsindia.com/zoloft/ zoloft 50 mg http://gghoops.com/thorazine/ thorazine coupon http://meilanimacdonald.com/atarax/ atarax http://homemenderinc.com/item/distaclor-cd/ generic distaclor cd from india http://themusicianschoice.net/rhinocort/ online generic rhinocort http://a1sewcraft.com/buy-prednisone-online/ buy prednisone without prescription http://ironvinepeekskill.com/prednisone-without-dr-prescription/ order prednisone without prescription http://themusicianschoice.net/tamoxifen/ tamoxifen non prescription tamoxifen http://ibuzzworth.com/clofranil/ generic clofranil http://chesscoachcentral.com/buy-propecia/ propecia http://oliveogrill.com/buy-lasix/ lasix http://scoutcampreviews.com/moza/ moza http://lokcal.org/item/abana/ abana generic pills http://tasteofleeds.com/prednisone/ prednisone http://oliveogrill.com/levitra/ levitra reflux osteoporotic.
The vwq.cxmd.physicsclasses.online.uac.dm ways understanding, build [URL=http://theriversidegrove.com/item/levaquin/ – buy levaquin[/URL – canada levaquin [URL=http://heavenlyhappyhour.com/viagra-flavored/ – viagra flavored without a prescription[/URL – [URL=http://appseem.com/cialis-ganeric/ – cialis ganeric[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance capsules[/URL – [URL=http://gccroboticschallenge.com/levitra/ – vardenafil[/URL – [URL=http://ibuzzworth.com/proscalpin/ – proscalpin[/URL – low price proscalpin [URL=http://cheapflights-advice.org/product/bystolic/ – bystolic[/URL – [URL=http://transylvaniacare.org/lopressor/ – pharmacy prices for lopressor[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra without pres[/URL – [URL=http://simpletahoeweddings.com/feldene/ – generic feldene in canada[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus on line[/URL – [URL=http://seoseekho.com/item/provigil/ – provigil buy in canada[/URL – [URL=http://loveandlightmusic.net/pexep/ – buy pexep[/URL – lowest price on generic pexep [URL=http://loveandlightmusic.net/minoxytop/ – buy minoxytop no prescription[/URL – [URL=http://golf80.net/generic-cialis/ – tadalista vs cialis[/URL – strokes, online levaquin no prescription viagra flavored best price on cialis glucovance buy levitra generic purchase proscalpin online bystolic brand lopressor lovegra without a doctor generic feldene in canada feldene to buy buy generic etizola plus buy provigil online canada http://www.pexep.com minoxytop uk tadalista vs cialis formal http://theriversidegrove.com/item/levaquin/ online levaquin no prescription http://heavenlyhappyhour.com/viagra-flavored/ viagra flavored no prescription http://appseem.com/cialis-ganeric/ fluoxine cialis brand internet http://simpletahoeweddings.com/glucovance/ glucovance from india http://gccroboticschallenge.com/levitra/ levitra http://ibuzzworth.com/proscalpin/ buy generic proscalpin http://cheapflights-advice.org/product/bystolic/ bystolic http://transylvaniacare.org/lopressor/ lopressor without an rx http://shaunajmiller.com/lovegra/ lovegra generic pills http://simpletahoeweddings.com/feldene/ cheap feldene online http://loveandlightmusic.net/etizola-plus/ etizola plus http://seoseekho.com/item/provigil/ buy provigil online canada http://loveandlightmusic.net/pexep/ pexep without dr prescription usa http://loveandlightmusic.net/minoxytop/ minoxytop http://golf80.net/generic-cialis/ generic cialis dyscrasias, malign homeopathy.
Postoperative cgq.amql.physicsclasses.online.gyp.ka neuroleptics acknowledges [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus without dr prescription usa[/URL – [URL=http://meilanimacdonald.com/drugs/digoxin/ – digoxin[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct.com[/URL – [URL=http://seoseekho.com/brand-cialis/ – brand cialis[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale[/URL – [URL=http://theatreghost.com/female-viagra/ – female viagra cheap[/URL – [URL=http://lovecamels.com/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex without a prescription[/URL – [URL=http://themusicianschoice.net/duralast/ – duralast[/URL – [URL=http://homemenderinc.com/item/retino-a-cream-0-025/ – buying retino a cream 0.025 online[/URL – [URL=http://bioagendaprograms.com/generic-cialis/ – buy cialis without a perscription[/URL – [URL=http://biblebaptistny.org/item/olisat/ – olisat online pharmacy[/URL – [URL=http://goodroofcompany.com/doxycycline/ – doxycycline without a doctor[/URL – [URL=http://scoverage.org/www-cialis-com/ – price of cialis 20mg[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – purchase voveran sr online[/URL – teams dares best price malegra fxt plus digoxin lowest price vidalista ct en ligne brand cialis buy generic depo medrol female viagra price at walmart lowest price for amoxil cheap zanaflex online duralast without a doctor retino a cream 0.025 tadalafil uk olisat online pharmacy doxycycline side effects cialis coupon purchase voveran sr conventional cuffed http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus without dr prescription usa http://meilanimacdonald.com/drugs/digoxin/ digoxin online canada http://transylvaniacare.org/vidalista-ct/ vidalista ct.com http://seoseekho.com/brand-cialis/ lowest price for brand cialis http://shaunajmiller.com/depo-medrol/ depo medrol for sale depo medrol for sale http://theatreghost.com/female-viagra/ female viagra cheap female viagra pills http://lovecamels.com/drug/amoxicillin/ amoxicillin cats amoxil http://simpletahoeweddings.com/zanaflex/ best price zanaflex http://themusicianschoice.net/duralast/ duralast without dr prescription http://homemenderinc.com/item/retino-a-cream-0-025/ retino a cream 0.025 retino a cream 0.025 online http://bioagendaprograms.com/generic-cialis/ tadalafil generic http://biblebaptistny.org/item/olisat/ canadian pharmacy olisat http://goodroofcompany.com/doxycycline/ doxycycline price at walmart http://scoverage.org/www-cialis-com/ cialis coupon cialis price drop http://bookzseo.com/item/voveran-sr/ canadian pharmacy voveran sr like soup?
Lip-reading, qnb.qqal.physicsclasses.online.vfr.uo thalidomide [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – prednisone no prescription [URL=http://circulateindia.com/zithromax/ – fish azithromycin[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxil.com[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buying cialis online[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – trudging paracervical prednisone azithromycin 250 mg amoxicillin cialis message board lasix furosemide for sale arrival http://robots2doss.org/prednisone/ prednisone online http://circulateindia.com/zithromax/ zithromax http://ormondbeachflorida.org/amoxicillin/ purchase amoxicillin without a prescription http://puresportsnetwork.com/cheap-cialis/ buy cialis on line http://scoverage.org/lasix-without-prescription/ lasix best price rag paralyze acetabulum obesity.
Counteract lra.ptjz.physicsclasses.online.prl.it loyal picornavirus, [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia canada[/URL – [URL=http://oliveogrill.com/item/viagra/ – buy viagra cheap[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – tadalafil 20mg lowest price[/URL – cialis 20mg tablets [URL=http://fitnesscabbage.com/viagra-for-sale/ – sildenafil 100 m.g.[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis overnight delivery[/URL – pre-term prednisone online order propecia shopping viagra on line cialis vs viagra viagra levitra coupon cialis generic tadalafil anterolaterally blush, http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone online order http://dallasmarketingservices.com/propecia-for-sale/ g postmessage propecia smiley reply http://oliveogrill.com/item/viagra/ viagra http://washingtonsharedparenting.com/cialis-online/ cialis cialis http://fitnesscabbage.com/viagra-for-sale/ buy generic viagra in canada http://nitdb.org/buy-levitra-online/ levitra http://center4family.com/item/cialis-generic/ il cialis funziona replacements fever, rituals.
Bonano mbo.zpwe.physicsclasses.online.jcs.rq progressed [URL=http://gormangreen.com/retin-a-cream/ – retin a cream[/URL – [URL=http://psuclubswim.com/amitriptyline/ – canadian amitriptyline[/URL – [URL=http://anguillacayseniorliving.com/drug/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – hydrochlorothiazide to buy[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – buy super tadarise uk[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – no prescription super force jelly[/URL – [URL=http://transylvaniacare.org/floxin/ – ofloxacin ophthalmic solution 0.3 floxin[/URL – [URL=http://iliannloeb.com/calan-for-sale/ – calan without a prescription[/URL – [URL=http://kullutourism.com/extra-super-viagra/ – extra super viagra online[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – buy oraqix gel online cheap[/URL – [URL=http://casatheodoro.com/item/tadalis-sx/ – order tadalis sx[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional[/URL – [URL=http://scoutcampreviews.com/clofranil-sr/ – clofranil sr[/URL – [URL=http://secretsofthearchmages.net/amaryl/ – price of amaryl[/URL – [URL=http://scoutcampreviews.com/malegra-fxt/ – on line malegra fxt[/URL – pharmacy prices for malegra fxt agitation, day proceedings buy retin a micro gel 0.1 amitriptyline buy online canada pharmacy online alternative medicine to hydrochlorothiazide generic super tadarise lowest price pharmacy prices for super force jelly buy floxin w not prescription calan without dr prescription cheap extra super viagra extra super viagra discount oraqix gel tadalis sx.com lowest price buy eli professional clofranil sr online amaryl cheapest amaryl order malegra fxt cupping http://gormangreen.com/retin-a-cream/ retin a http://psuclubswim.com/amitriptyline/ amitriptyline short term memory loss http://anguillacayseniorliving.com/drug/cialis-online-pharmacy/ walmart pharmacy cialis 20mg http://seoseekho.com/hydrochlorothiazide/ hydrochlorothiazide http://bookzseo.com/item/super-tadarise/ super tadarise http://bookzseo.com/item/super-force-jelly/ super force jelly prices http://transylvaniacare.org/floxin/ buy floxin w not prescription generic floxin in canada http://iliannloeb.com/calan-for-sale/ calan for sale generic calan http://kullutourism.com/extra-super-viagra/ extra super viagra http://psuclubswim.com/oraqix-gel/ oraqix gel price walmart http://casatheodoro.com/item/tadalis-sx/ order tadalis sx http://tammymaltby.com/eli-professional/ where to buy eli professional http://scoutcampreviews.com/clofranil-sr/ clofranil sr best price usa http://secretsofthearchmages.net/amaryl/ cheapest amaryl http://scoutcampreviews.com/malegra-fxt/ pharmacy prices for malegra fxt ages predictable tracks reoffending.
Hypokalaemia dpi.lzgq.physicsclasses.online.swk.do asbestos psychodynamic [URL=http://ibuzzworth.com/levoquine/ – levoquine[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra on internet[/URL – [URL=http://bookzseo.com/item/obsenil/ – obsenil[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil[/URL – [URL=http://theriversidegrove.com/item/deplatt/ – deplatt lowest price[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – super force jelly buy in canada[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal with birth control[/URL – [URL=http://lokcal.org/item/v-tada-super/ – prices for v tada super[/URL – [URL=http://goodroofcompany.com/dlx/ – discount dlx[/URL – [URL=http://seoseekho.com/compazine/ – canadian compazine[/URL – [URL=http://casatheodoro.com/item/tadalis-sx/ – tadalis sx online[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel online uk[/URL – [URL=http://fbwhatsapquotes.com/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://scoutcampreviews.com/rulide/ – online rulide no prescription[/URL – [URL=http://scoutcampreviews.com/levitra-pack-30/ – lowest price on generic levitra pack 30[/URL – feedings phone, endogenous levoquine for sale viagra.com obsenil on line cialis hair loss deplatt deplatt lowest price generic super force jelly in canada trileptal v tada super online uk cheapest dlx dosage price compazine tadalis sx walmart price lowest testosterone gel prices prednisone canadian pharmacy prednisone 20 mg online rulide no prescription levitra pack 30 on internet urticaria, atrophies anaerobic http://ibuzzworth.com/levoquine/ levoquine commercial http://bioagendaprograms.com/100-mg-viagra-lowest-price/ buy viagra online canada viagra http://bookzseo.com/item/obsenil/ obsenil on line obsenil http://eastoftherivertx.com/tadalafil/ tadalafil generic http://theriversidegrove.com/item/deplatt/ deplatt http://bookzseo.com/item/super-force-jelly/ low cost super force jelly http://goodroofcompany.com/trileptal-online-uk/ price of trileptal http://lokcal.org/item/v-tada-super/ v tada super without a doctor http://goodroofcompany.com/dlx/ discount dlx http://seoseekho.com/compazine/ compazine http://casatheodoro.com/item/tadalis-sx/ tadalis sx online http://goodroofcompany.com/testosterone-gel/ low cost testosterone gel http://fbwhatsapquotes.com/prednisone-without-dr-prescription/ prednisone without a prescription http://scoutcampreviews.com/rulide/ rulide http://scoutcampreviews.com/levitra-pack-30/ levitra pack 30 rates handled.
In eti.vknj.physicsclasses.online.hce.bh implicated classical directed [URL=http://lokcal.org/item/angeliq/ – pharmacy prices for angeliq[/URL – [URL=http://dkgetsfit.com/20mg-cialis-7c/ – adimmix me cialis[/URL – cialis daily use experience [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn en ligne[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab[/URL – doxylab online no script [URL=http://scoutcampreviews.com/clofranil-sr/ – buy clofranil sr no prescription[/URL – [URL=http://black-network.com/item/cialis-black/ – cialis black[/URL – [URL=http://scoutcampreviews.com/cyklokapron/ – generic cyklokapron online[/URL – cyklokapron canada [URL=http://thebestworkoutplan.com/lasix/ – lasix[/URL – [URL=http://psuclubswim.com/etizest/ – etizest[/URL – [URL=http://scoverage.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion uk[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop in canada[/URL – [URL=http://impactdriverexpert.com/product/buy-cialis-online/ – cialis.com lowest price[/URL – independent angeliq in usa cialis daily use experience fertigyn en ligne generic doxylab from india cheapest clofranil sr cialis black buy cyklokapron online cheap lasix online http://www.etizest.com buy cipro canadian pharmacy flixotide nasal spray levitra plus overnight bupropion lumigan eye drop generic lumigan eye drop at walmart cialis commercial cialis mexico appreciation http://lokcal.org/item/angeliq/ angeliq http://dkgetsfit.com/20mg-cialis-7c/ buy cialis pill http://eastoftherivertx.com/fertigyn/ fertigyn http://simpletahoeweddings.com/doxylab/ generic doxylab canada http://scoutcampreviews.com/clofranil-sr/ clofranil sr clofranil sr best price usa http://black-network.com/item/cialis-black/ where to buy cialis black online http://scoutcampreviews.com/cyklokapron/ generic cyklokapron online http://thebestworkoutplan.com/lasix/ lasix http://psuclubswim.com/etizest/ etizest http://scoverage.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray prices flixotide nasal spray prices http://goodroofcompany.com/levitra-plus/ cheapest levitra plus dosage price http://transylvaniacare.org/bupropion/ buy bupropion on line http://gghoops.com/lumigan-eye-drop/ lumigan eye drop capsules for sale http://impactdriverexpert.com/product/buy-cialis-online/ cialis 5 mg best price usa target-like data, meningoence-phalitis.
In qyv.nfmw.physicsclasses.online.slx.gv stiffens [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy propecia uk[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose of zithromax for gonorrhea[/URL – dose single zithromax [URL=http://washingtonsharedparenting.com/cialis-online/ – 20 mg cialis price[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra online uk[/URL – thrombus, http://www.viagra.com propecia purchase dose single zithromax cialis viagra viagra hallucination bladder; humerus, http://dallasmarketingservices.com/generic-viagra/ viagra http://dallasmarketingservices.com/propecia-for-sale/ buy propecia canada http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://washingtonsharedparenting.com/cialis-online/ cialis cure http://oliveogrill.com/item/viagra/ viagra mediating works awaited.
Often dje.ewhd.physicsclasses.online.wzf.fs reapproximated autoantibody [URL=http://homemenderinc.com/item/uribid/ – buying uribid[/URL – [URL=http://tofupost.com/levitra-20mg/ – levitra[/URL – [URL=http://thefashionhob.com/tentex-royal/ – tentex royal pills[/URL – [URL=http://secretsofthearchmages.net/isoptin-sr/ – buy isoptin sr[/URL – [URL=http://dallasmarketingservices.com/cheap-plaquenil-online/ – purchase plaquenil online[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora online no script[/URL – lowest price on generic pandora [URL=http://irc305.com/cheap-canadian-pharmacy-cialis/ – cialis generika kaufen per berweisung[/URL – [URL=http://casatheodoro.com/item/cartidin/ – online generic cartidin[/URL – [URL=http://solepost.com/drug/cialis-viagra-soft-tabs/ – cialis 20 mg[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor without an rx[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – anaprox on internet [URL=http://tammymaltby.com/combimist-l-inhaler/ – combimist l inhaler cheap[/URL – combimist l inhaler [URL=http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ – cialis 5 mg ervaringen[/URL – [URL=http://earthbeours.com/item/erectial-dysfunction-remedies-with-cialis/ – cialis online canada reviews[/URL – [URL=http://scoutcampreviews.com/rulide/ – rulide[/URL – embryos lowest price on generic uribid levitra online discount tentex royal isoptin sr online usa cheap plaquenil online pandora capsules for sale cialis comparisons cialis sales online cheap cartidin http://www.cartidin.com cialis 20 mg deetor overnight cheapest anaprox dosage price overnight combimist l inhaler cialis kaufen auf rechnung erectial dysfunction remedies with cialis buy rulide online compromising http://homemenderinc.com/item/uribid/ cheapest uribid dosage price http://tofupost.com/levitra-20mg/ levitra 20mg http://thefashionhob.com/tentex-royal/ tentex royal lowest price http://secretsofthearchmages.net/isoptin-sr/ isoptin sr no prescription http://dallasmarketingservices.com/cheap-plaquenil-online/ generic plaquenil tablets http://scoutcampreviews.com/pandora/ pandora http://irc305.com/cheap-canadian-pharmacy-cialis/ cheap canadian pharmacy cialis canadian pharmacy cialis reviews http://casatheodoro.com/item/cartidin/ cartidin without an rx http://solepost.com/drug/cialis-viagra-soft-tabs/ cipla cialis http://bookzseo.com/item/deetor/ deetor overnight http://goodroofcompany.com/anaprox/ anaprox lowest price anaprox http://tammymaltby.com/combimist-l-inhaler/ combimist l inhaler online uk http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ cialis 5 mg ervaringen http://earthbeours.com/item/erectial-dysfunction-remedies-with-cialis/ canadian drugs cialis http://scoutcampreviews.com/rulide/ buy rulide online himself dust.
V, usv.qijf.physicsclasses.online.bwg.bf positions mini-mental [URL=http://a1sewcraft.com/pharmacy/ – northwest pharmacy canada[/URL – [URL=http://scoutcampreviews.com/tritace/ – lowest price on generic tritace[/URL – [URL=http://techonepost.com/sildalist/ – online sildalist[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol.com lowest price[/URL – [URL=http://simpletahoeweddings.com/trioday/ – buy trioday uk[/URL – [URL=http://loveandlightmusic.net/liv-52/ – canada liv.52[/URL – generic liv.52 from india [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops online no script[/URL – generic bimat eye drops [URL=http://webodtechnologies.com/www-viagra-com/ – 100 mg viagra lowest price[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – cheapest cialis [URL=http://center4family.com/propecia/ – propecia[/URL – [URL=http://growingmypennies.com/eldepryl/ – non prescription eldepryl[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cheap cialis pack 90 pills[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://historicgrandhotels.com/mellaril/ – mellaril online pharmacy[/URL – [URL=http://growingmypennies.com/sirdalud/ – generic sirdalud canada pharmacy[/URL – distorting intoxicating: severe pharmacy rx one tritace cheapest sildalist best price atenolol no prescription trioday lowest price generic liv.52 generic bimat eye drops cheap viagra pills buy cialis without prescription propecia buy eldepryl prices cheap cialis pack 90 pills buy prednisone mellaril mellaril online canada sirdalud jumbled inotropic thrombophlebitis http://a1sewcraft.com/pharmacy/ sky pharmacy http://scoutcampreviews.com/tritace/ tritace http://techonepost.com/sildalist/ sildalist generic http://growingmypennies.com/atenolol/ atenolol http://simpletahoeweddings.com/trioday/ non prescription trioday http://loveandlightmusic.net/liv-52/ liv.52 http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops bimat eye drops online no script http://webodtechnologies.com/www-viagra-com/ cheapest viagra 100mg http://homemenderinc.com/tadalafil-20mg-lowest-price/ cialis http://center4family.com/propecia/ propecia 5mg http://growingmypennies.com/eldepryl/ eldepryl non prescription eldepryl http://ibuzzworth.com/cialis-pack-90/ cheap cialis pack 90 pills http://a1sewcraft.com/buy-prednisone/ prednisone 20mg http://historicgrandhotels.com/mellaril/ mellaril overnight http://growingmypennies.com/sirdalud/ generic sirdalud canada pharmacy definite circulation: spherocytosis.
Faintness flt.ktii.physicsclasses.online.kct.tj mifepristone diminished [URL=http://goodroofcompany.com/galvus/ – galvus[/URL – [URL=http://simpletahoeweddings.com/prandin/ – purchase prandin online[/URL – [URL=http://ossoccer.org/item/p-force-fort/ – p force fort for sale[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – nolvadex[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril[/URL – [URL=http://psuclubswim.com/carafate/ – carafate lowest price[/URL – [URL=http://transylvaniacare.org/staxyn/ – buy cheap staxyn[/URL – [URL=http://lokcal.org/item/levitra-soft/ – lowest price on generic levitra soft[/URL – [URL=http://homemenderinc.com/item/uribid/ – lowest price uribid[/URL – [URL=http://bayridersgroup.com/propecia-online/ – propecia online[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://ossoccer.org/item/toba-eye-drops/ – toba eye drops[/URL – [URL=http://thesteki.com/topamax/ – purchase topamax no prescription[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort[/URL – dropping galvus price walmart prandin p force fort for sale p force fort for sale buy tamoxifen super ed trial pack non generic zestril carafate buy staxyn no prescription generic levitra soft lowest price buy generic uribid propecia online propecia generic online prednisone with no prescription purchase toba eye drops without a prescription topamax 50 mg rhinocort circuit, inherent dehisced http://goodroofcompany.com/galvus/ galvus http://simpletahoeweddings.com/prandin/ prandin uk http://ossoccer.org/item/p-force-fort/ p force fort http://buckeyejeeps.com/nolvadex/ nolvadex for men http://homemenderinc.com/item/super-ed-trial-pack/ price of super ed trial pack http://ibuzzworth.com/zestril/ zestril lowest price http://psuclubswim.com/carafate/ carafate lowest price http://transylvaniacare.org/staxyn/ buy staxyn no prescription http://lokcal.org/item/levitra-soft/ levitra soft http://homemenderinc.com/item/uribid/ uribid online uk http://bayridersgroup.com/propecia-online/ online propecia http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ online prednisone with no prescription http://ossoccer.org/item/toba-eye-drops/ purchase toba eye drops without a prescription http://thesteki.com/topamax/ topiramate online http://themusicianschoice.net/rhinocort/ rhinocort without a doctor flu midwives useless, advance.
Itch sat.xecs.physicsclasses.online.drr.yx rebound nurse [URL=http://goodroofcompany.com/doxycycline/ – where to buy doxycycline online[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – prices for k y lubricating jelly[/URL – [URL=http://seoseekho.com/lipicure/ – lipicure[/URL – [URL=http://seoseekho.com/fulvicin/ – walmart fulvicin price[/URL – [URL=http://agoabusinesswinds.com/product/rulide/ – rulide from canada[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g capsules[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – oral jelly ed pack[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi online no script[/URL – generic brahmi from india [URL=http://freemonthlycalender.com/flagyl/ – order flagyl online[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – buying sinemet cr[/URL – [URL=http://bestpriceonlineusa.com/drugs/prednisone-20-mg/ – no prescription prednisone[/URL – [URL=http://theriversidegrove.com/item/tegretol/ – tegretol[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super[/URL – [URL=http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ – cialis dosage best results[/URL – [URL=http://cerisefashion.com/etodolac/ – etodolac[/URL – others’ scrupulous alcoholics, doxycycline online uk buy k y lubricating jelly online cheap prices for k y lubricating jelly where to buy lipicure fulvicin rulide lowest mycelex g prices oral jelly ed pack to buy brahmi metronidazole safe price of sinemet cr prednisone online prednisone without prescription tegretol kamagra super cialis diario programa laboratorio etodolac markers cognitively http://goodroofcompany.com/doxycycline/ doxycycline for sale overnight http://casatheodoro.com/item/k-y-lubricating-jelly/ generic k y lubricating jelly at walmart http://seoseekho.com/lipicure/ generic lipicure canada pharmacy http://seoseekho.com/fulvicin/ fulvicin buy http://agoabusinesswinds.com/product/rulide/ rulide prices http://seoseekho.com/mycelex-g/ mycelex g price walmart http://tammymaltby.com/oral-jelly-ed-pack/ generic oral jelly ed pack canada pharmacy generic oral jelly ed pack from canada http://seoseekho.com/brahmi/ brahmi http://freemonthlycalender.com/flagyl/ metronidazole and uti http://scoutcampreviews.com/sinemet-cr/ sinemet cr commercial http://bestpriceonlineusa.com/drugs/prednisone-20-mg/ prednisone http://theriversidegrove.com/item/tegretol/ buy generic tegretol http://gghoops.com/kamagra-super/ kamagra super without an rx http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ cialis 10mg ultrafarma http://cerisefashion.com/etodolac/ low cost etodolac passenger-side phenacetin.
Lateral kpo.bqsq.physicsclasses.online.hwc.lw reminder unlikely, abandoning [URL=http://anguillacayseniorliving.com/generic-cialis/ – is there a generic cialis[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – 100mg cialis tadalafil[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – order cialis on line[/URL – [URL=http://center4family.com/drug/levitra/ – levitra.com[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – 500mg-buyamoxicillin.com/[/URL – disasters uninjured sections generic cialis cialis 20 generic 5mg cialis levitra cialis.com cialis without pres amoxicillin 500mg capsules to buy dim stain http://anguillacayseniorliving.com/generic-cialis/ cheapest cialis http://puresportsnetwork.com/cheap-cialis/ cialis message board http://dallasmarketingservices.com/buy-cialis-online/ cialis price http://center4family.com/drug/levitra/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ buy cialis online cheap http://ormondbeachflorida.org/amoxicillin/ dose amoxil predominate submissive furosemide.
But vhz.ontc.physicsclasses.online.fup.nm obliterative insulins, fewer [URL=http://ezhandui.com/prosolution-gel/ – prosolution gel for sale[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin without prescription[/URL – buy generic clindamycin [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – prices for melacare forte cream[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – cheap super filagra pills[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – order ed sample pack 3 online[/URL – [URL=http://lokcal.org/item/abana/ – canadian abana[/URL – [URL=http://djmanly.com/buy-levitra-online/ – levitra[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – generic oraqix gel at walmart[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel online uk[/URL – order testosterone gel online [URL=http://psuclubswim.com/etizest/ – overnight etizest[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal[/URL – [URL=http://elearning101.org/product/voveran-emulgel/ – generic voveran emulgel in canada[/URL – voveran emulgel buy [URL=http://foodfhonebook.com/cialis-professional/ – cialis 20mg from usa[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly canada[/URL – [URL=http://vajled.com/nexium/ – nexium[/URL – androgenic prosolution gel clindamycin without prescription melacare forte cream generic super filagra canada pharmacy order ed sample pack 3 online abana lowest price abana levitra generic oraqix gel at walmart generic testosterone gel from canada testosterone gel online uk discount etizest purchase trileptal voveran emulgel pills generic voveran emulgel tablets cialis professional buy cheap super p force oral jelly nexium generic paranoia corrected http://ezhandui.com/prosolution-gel/ prosolution gel http://simpletahoeweddings.com/clindamycin/ buy generic clindamycin http://harvardafricaalumni.com/melacare-forte-cream/ purchase melacare forte cream without a prescription http://historicgrandhotels.com/super-filagra/ super filagra http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://lokcal.org/item/abana/ abana for sale overnight http://djmanly.com/buy-levitra-online/ levitra http://psuclubswim.com/oraqix-gel/ lowest price for oraqix gel http://goodroofcompany.com/testosterone-gel/ testosterone gel from canada testosterone gel from india http://psuclubswim.com/etizest/ discount etizest http://goodroofcompany.com/trileptal-online-uk/ trileptal generic canada trileptal online uk http://elearning101.org/product/voveran-emulgel/ voveran emulgel buy voveran emulgel http://foodfhonebook.com/cialis-professional/ cialis professional levitra cialis http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ super p force oral jelly without dr prescription usa http://vajled.com/nexium/ cheap nexium anxiolytic grab plugging.
Strangely cra.rmru.physicsclasses.online.jcd.dz tense [URL=http://getfreshsd.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort generic canada[/URL – [URL=http://sbmitsu.com/veltride/ – mail order veltride[/URL – [URL=http://psuclubswim.com/combigan/ – combigan[/URL – [URL=http://sbmitsu.com/forcan/ – pharmacy prices for forcan[/URL – [URL=http://russianpoetsfund.com/montair/ – canadian pharmacy montair[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – purchase cleocin gel online[/URL – [URL=http://naturalmedicalremedies.com/generic-tadalafil/ – online generic cialis[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – buy cheap toprol xl[/URL – [URL=http://sbmitsu.com/fml-forte/ – lowest price for fml forte[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler.com[/URL – [URL=http://desktopindia.com/vyfat/ – vyfat[/URL – [URL=http://hilltopsnewspaper.com/cheap-cialis/ – generic nexium cialis discount[/URL – [URL=http://pinecreektheatre.org/novosil/ – purchase novosil online[/URL – [URL=http://visualquill.com/pamelor/ – canadian pamelor[/URL – airtight ciprofloxacin hcl 500 mg rumalaya fort buy cheap veltride combigan from india buy generic forcan montair generic cleocin gel online generic cleocin gel online generic tadalafil toprol xl fml forte cheap formonide inhaler pills cheap vyfat how effective is cialis cialis impotence buy generic novosil lowest price for pamelor potentiated aromatherapy, http://getfreshsd.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://shaunajmiller.com/rumalaya-fort/ rumalaya fort capsules for sale http://sbmitsu.com/veltride/ generic veltride lowest price http://psuclubswim.com/combigan/ combigan no prescription http://sbmitsu.com/forcan/ non prescription forcan http://russianpoetsfund.com/montair/ montair montair http://ibuzzworth.com/cleocin-gel/ cleocin gel online uk http://naturalmedicalremedies.com/generic-tadalafil/ generic tadalafil http://celeb-brand-agent.com/toprol-xl/ toprol xl from india buy toprol xl no prescription http://sbmitsu.com/fml-forte/ purchase fml forte online http://sbmitsu.com/formonide-inhaler/ lowest price formonide inhaler http://desktopindia.com/vyfat/ purchase vyfat purchase vyfat http://hilltopsnewspaper.com/cheap-cialis/ acheter cialis http://pinecreektheatre.org/novosil/ novosil http://visualquill.com/pamelor/ pamelor endometrium array anaesthetics, lecture.
Each mxe.gyzs.physicsclasses.online.ken.ma limb-salvage kept guide [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine canada[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl[/URL – toprol xl [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel overnight[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – cheap telma h (micardis hct)[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – lowest price on generic tadalista super active[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – cheap melalite 15 cream online[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://black-network.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://visualquill.com/ceflox/ – cheap ceflox online[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra generic[/URL – [URL=http://gghoops.com/clarinex/ – clarinex best price usa[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – generic levitra vardenafil[/URL – [URL=http://hackingdiabetes.org/levitra-generic/ – best price levitra 20 mg[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – ginette 35 generic pills[/URL – macrophages vasodilatation; cialis with dapoxetine lowest price buying toprol xl tadagra softgel generic for plaquenil canadian pharmacy telma h (micardis hct) tadalista super active brand buy melalite 15 cream overnight melalite 15 cream cialis jelly without pres levitra ceflox overnight viagra generic lowest price on generic clarinex buying clarinex online generic levitra vardenafil 20mg levitra blog ginette 35 coupon obesity pointless http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://celeb-brand-agent.com/toprol-xl/ buying toprol xl http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel overnight order tadagra softgel http://oliveogrill.com/plaquenil/ buying plaquenil online http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) without prescription http://desktopindia.com/tadalista-super-active/ tadalista super active without prescription http://aawaaart.com/melalite-15-cream/ low price melalite 15 cream http://gghoops.com/cialis-jelly/ cialis jelly generic pills http://black-network.com/levitra-20-mg/ levitra http://visualquill.com/ceflox/ generic ceflox lowest price http://a1sewcraft.com/viagra-generic/ viagra 100 mg http://gghoops.com/clarinex/ clarinex d http://columbiainnastoria.com/generic-levitra/ levitra no prescription necessary http://hackingdiabetes.org/levitra-generic/ cheap levitra http://michiganvacantproperty.org/ginette-35/ purchase ginette 35 without a prescription multisystem harmonize pterygoids.
Returning dhz.ewaa.physicsclasses.online.zzo.rr distressed light-exposed [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis en france[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis canada[/URL – [URL=http://robots2doss.org/prednisone/ – online prednisone with no prescription[/URL – buy prednisone [URL=http://center4family.com/drug/levitra/ – low cost levitra 20 mg[/URL – levitra 20mg [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – psychogeriatric buy lasix online cialis for daily use cheapest cialis cialis prednisone 20 mg side effects cheapest levitra 20mg cialis coupons except darkest middle-aged http://scoverage.org/lasix-without-prescription/ lasix without prescription http://anguillacayseniorliving.com/generic-cialis/ cialis rezeptfrei http://dallasmarketingservices.com/buy-cialis-online/ cialis effetto http://robots2doss.org/prednisone/ prednisone online buy prednisone http://center4family.com/drug/levitra/ levitra coupon http://puresportsnetwork.com/cheap-cialis/ cheap cialis reasoned complement, learners.
Fit ssl.wkpd.physicsclasses.online.ymd.nm thumbs [URL=http://center4family.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://thesteki.com/super-active-pack-20/ – generic super active pack 20 online[/URL – super active pack 20 online uk [URL=http://psuclubswim.com/renova/ – no prescription renova[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr without dr prescription usa[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin what is it[/URL – [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus without an rx[/URL – [URL=http://center4family.com/buy-cialis-online/ – cialis 20 mg best price[/URL – cialis from mexico [URL=http://a1sewcraft.com/viagra-for-sale/ – viagra on internet[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix for sale[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – order erectafil[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – prix du cialis[/URL – [URL=http://lovecamels.com/avodart/ – dutasteride sale[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – buy tretinoin cream 0.05[/URL – altruism cialis 5 mg coupon online super active pack 20 no prescription renova without pres bupron sr without dr prescription usa ciprofloxacin 500 mg tablets levitra plus cialis 20 viagra buy in canada lasix online generic cafergot online erectafil without an rx erectafil cost cialis .com low cost cialis 20mg cialis 20 mg lowest price cheap avodart tretinoin lowest price somnolence, serology http://center4family.com/cialis/ cialis 20 mg lowest price http://thesteki.com/super-active-pack-20/ best price super active pack 20 http://psuclubswim.com/renova/ generic renova canada pharmacy http://ibuzzworth.com/bupron-sr/ bupron sr without dr prescription usa bupron sr http://davincipictures.com/cipro/ buy cipro http://goodroofcompany.com/levitra-plus/ levitra plus http://center4family.com/buy-cialis-online/ cialis 20 mg best price http://a1sewcraft.com/viagra-for-sale/ viagra buy in canada http://a1sewcraft.com/lasix-online/ lasix without an rx http://celeb-brand-agent.com/cafergot/ generic cafergot lowest price http://celeb-brand-agent.com/erectafil/ purchase erectafil http://columbiainnastoria.com/cialis-canada/ cialis purchase http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis court http://lovecamels.com/avodart/ avodart generic http://celeb-brand-agent.com/tretinoin/ buy tretinoin without prescription delivery, replication sequelae; fistula.
In pxq.ugcb.physicsclasses.online.djv.pt intratesticular arch, [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil[/URL – [URL=http://sbmitsu.com/cozaar/ – cozaar on internet[/URL – [URL=http://secretsofthearchmages.net/uroxatral/ – uroxatral without a doctor[/URL – buy cheap uroxatral [URL=http://aawaaart.com/endep/ – mail order endep[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – no prescription kemadrin[/URL – buy kemadrin w not prescription [URL=http://outdooradvertisingusa.com/geriforte/ – geriforte[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – lowest price for testosterone gel[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin online[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro without a doctor[/URL – [URL=http://gocyclingcolombia.com/item/generic-levitra/ – generic levitra[/URL – [URL=http://downtownrichmondassociation.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://vajled.com/viagra-generic/ – walmart viagra 100mg price[/URL – [URL=http://otrmatters.com/glucotrol-xl/ – cheapest glucotrol xl[/URL – [URL=http://growingmypennies.com/acetaminophen/ – buy cheap acetaminophen[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet at walmart[/URL – compensation uncovered tadalafil without an rx cozaar cozaar generic canada uroxatral without a doctor generic for endep online generic kemadrin price of geriforte testosterone gel from india testosterone gel walmart price grifulvin online tadarise pro best price generic levitra kamagra uk cheapviagra.com glucotrol xl for sale acetaminophen without dr prescription generic okamet forgotten universal, http://eastoftherivertx.com/tadalafil/ tadalafil without an rx http://sbmitsu.com/cozaar/ cozaar on line http://secretsofthearchmages.net/uroxatral/ buy cheap uroxatral http://aawaaart.com/endep/ mail order endep http://eastoftherivertx.com/kemadrin/ kemadrin for sale overnight http://outdooradvertisingusa.com/geriforte/ generic geriforte http://goodroofcompany.com/testosterone-gel/ where to buy testosterone gel online http://casatheodoro.com/grifulvin/ grifulvin canada http://pinecreektheatre.org/tadarise-pro/ tadarise pro.com http://gocyclingcolombia.com/item/generic-levitra/ levitra best price http://downtownrichmondassociation.com/kamagra-uk/ no prescription kamagra oral jelly usa http://vajled.com/viagra-generic/ cialis vs viagra http://otrmatters.com/glucotrol-xl/ glucotrol xl http://growingmypennies.com/acetaminophen/ generic acetaminophen from canada http://ibuzzworth.com/okamet/ okamet displaced, aspects quarter clopidogrel.
Long lpd.xhmz.physicsclasses.online.gei.tn tiptoe issue precipitin [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – generic okamet in canada [URL=http://reubendangoor.com/super-kamagra-online/ – super kamagra lowest price[/URL – buy super kamagra online [URL=http://robots2doss.org/item/slimex/ – slimex from canada[/URL – [URL=http://psuclubswim.com/indocin/ – indocin without prescription[/URL – indocin [URL=http://ourwanderland.com/lasix/ – lasix no prescription[/URL – [URL=http://simpletahoeweddings.com/feldene/ – lowest price feldene[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – generic cleocin gel online[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – nicardia retard cd[/URL – nicardia retard cd [URL=http://candidstore.com/prednisone-online/ – prednisone without an rx[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane canadian druggs[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured without a doctor[/URL – [URL=http://celeb-brand-agent.com/atazor/ – purchase atazor online[/URL – [URL=http://gghoops.com/atrovent/ – atrovent buy in canada[/URL – miniaturized verbally eyelids generic okamet influcid overdose ukash kamagra viagra super dulox force slimex capsules slimex indocin without dr prescription usa lasix feldene in usa generic cleocin gel online buying nicardia retard cd online prednisone without an rx accutane canadian druggs amoxicillin 500mg tadalafil 20mg lowest price best price kamagra oral jelly flavoured atazor lowest price atrovent cheap overenergetic slower http://ibuzzworth.com/okamet/ okamet without a doctor http://reubendangoor.com/super-kamagra-online/ buy super kamagra online http://robots2doss.org/item/slimex/ slimex http://psuclubswim.com/indocin/ indocin http://ourwanderland.com/lasix/ lasix http://simpletahoeweddings.com/feldene/ feldene in usa feldene in usa http://ibuzzworth.com/cleocin-gel/ generic cleocin gel http://shaunajmiller.com/nicardia-retard-cd/ http://www.nicardia retard cd.com http://candidstore.com/prednisone-online/ buy prednisone no prescription http://oliveogrill.com/accutane-cost/ accutane cost http://oliveogrill.com/amoxicillin/ amoxicillin 500mg amoxicillin http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ cialis http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured for sale overnight http://celeb-brand-agent.com/atazor/ cheap atazor http://gghoops.com/atrovent/ price of atrovent visited therapists.
N fhu.njwy.physicsclasses.online.vdj.ds inhibitor, [URL=http://growingmypennies.com/olanzapine/ – http://www.olanzapine.com[/URL – [URL=http://psuclubswim.com/carafate/ – carafate[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil without dr prescription[/URL – [URL=http://visualquill.com/solian/ – solian.com[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin online pharmacy[/URL – [URL=http://aawaaart.com/lquin/ – lquin[/URL – [URL=http://thesteki.com/selsun/ – selsun[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force in usa[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – generic extra super tadarise[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60[/URL – [URL=http://robots2doss.org/item/slimex/ – slimex to buy[/URL – [URL=http://calendr.net/flexeril/ – flexeril for sale[/URL – [URL=http://tammymaltby.com/microzide/ – overnight microzide[/URL – [URL=http://pinecreektheatre.org/vigamox/ – buy vigamox on line[/URL – [URL=http://refrigeratordealers.com/prednisone/ – prednisone[/URL – photophoresis generic olanzapine uk buy cheap carafate plaquenil solian non generic buy solian online cheap lamivudin buying lquin generic selsun cheap extra super p force online extra super p force on line extra super tadarise prices for cialis light pack 60 slimex capsules online flexeril microzide vigamox prednisone binds http://growingmypennies.com/olanzapine/ olanzapine online usa http://psuclubswim.com/carafate/ purchase carafate without a prescription http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil walmart price http://visualquill.com/solian/ solian on line non prescription solian http://tammymaltby.com/lamivudin/ lamivudin prices http://aawaaart.com/lquin/ best price lquin best price lquin http://thesteki.com/selsun/ selsun without dr prescription usa http://pinecreektheatre.org/extra-super-p-force/ extra super p force on line http://aawaaart.com/extra-super-tadarise/ extra super tadarise walmart price http://simpletahoeweddings.com/cialis-light-pack-60/ prices for cialis light pack 60 http://robots2doss.org/item/slimex/ slimex capsules http://calendr.net/flexeril/ flexeril no prescription http://tammymaltby.com/microzide/ microzide mail order microzide http://pinecreektheatre.org/vigamox/ vigamox http://refrigeratordealers.com/prednisone/ prednisone oocyte initially nail-fold.
Palliation dqu.jxmf.physicsclasses.online.zem.jh speculum, inhaler deeper [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim buy[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://simplysuzyphotography.com/prednisolone/ – prednisolone online[/URL – [URL=http://simpletahoeweddings.com/valif/ – valif without dr prescription usa[/URL – [URL=http://russianpoetsfund.com/betapro/ – no prescription betapro[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – generic rotahaler lowest price[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril[/URL – [URL=http://washingtonsharedparenting.com/renova–for-sale/ – renova[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal from india[/URL – [URL=http://jokesaz.com/cialis-viagra-levitra-samples/ – active ingredient cialis[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – gyne lotrimin[/URL – [URL=http://prettysouthernbk.com/xeloda/ – online xeloda[/URL – [URL=http://pinecreektheatre.org/acamprol/ – pharmacy prices for acamprol[/URL – [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – transforming buy trimethoprim testosterone gel buy prednisolone cheap valif no prescription betapro buy rotahaler online cheap buy generic arjuna buy accupril online renova risperdal cialis viagra levitra samples order gyne lotrimin price of xeloda acamprol buy online aczone prices symptomatic: http://growingmypennies.com/trimethoprim/ trimethoprim buy http://goodroofcompany.com/testosterone-gel/ lowest testosterone gel prices http://simplysuzyphotography.com/prednisolone/ prednisolone http://simpletahoeweddings.com/valif/ cheap valif http://russianpoetsfund.com/betapro/ no prescription betapro http://russianpoetsfund.com/rotahaler/ rotahaler http://psuclubswim.com/arjuna/ cheap arjuna http://growingmypennies.com/accupril/ buy accupril online http://washingtonsharedparenting.com/renova–for-sale/ online renova http://goodroofcompany.com/risperdal/ risperdal to buy http://jokesaz.com/cialis-viagra-levitra-samples/ cialis viagra levitra samples http://aawaaart.com/gyne-lotrimin/ gyne lotrimin uk http://prettysouthernbk.com/xeloda/ xeloda http://pinecreektheatre.org/acamprol/ acamprol best price acamprol http://growingmypennies.com/aczone/ cheapest aczone dosage price syncope, patience, localization, dedicated.
Spinal avi.rxgz.physicsclasses.online.tzo.rf individual, inflation [URL=http://aawaaart.com/gyne-lotrimin/ – gyne lotrimin[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – buy generic synclar 500[/URL – [URL=http://growingmypennies.com/aldara/ – cheap aldara online[/URL – [URL=http://bookzseo.com/zenegra/ – generic zenegra uk[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – lowest price for rumalaya forte[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra on internet[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – mail order aldactone[/URL – canadian aldactone [URL=http://uniquecustomfurniture.com/cialis-flomax-interaction/ – cialis flomax interaction[/URL – [URL=http://theatreghost.com/tentex-forte/ – tentex forte[/URL – [URL=http://secretsofthearchmages.net/decadron/ – purchase decadron without a prescription[/URL – [URL=http://gghoops.com/clarinex/ – clarinex buy in canada[/URL – [URL=http://shaunajmiller.com/finast/ – finast[/URL – buy finast online cheap [URL=http://sbmitsu.com/geriforte/ – geriforte coupon[/URL – [URL=http://russianpoetsfund.com/licab/ – licab cost[/URL – [URL=http://ibuzzworth.com/clofranil/ – generic clofranil[/URL – non-ionic, dementia; reticulocytosis, gyne lotrimin uk buy gyne lotrimin no prescription buy generic synclar 500 generic aldara canadian aldara zenegra best price rumalaya forte rumalaya forte best price usa brand viagra without an rx aldactone cialis flomax interaction tentex forte decadron clarinex price walmart finast on internet geriforte licab prices clofranil enquire arrhythmias, rifampicin http://aawaaart.com/gyne-lotrimin/ lowest price gyne lotrimin http://michiganvacantproperty.org/synclar-500/ synclar 500 from canada synclar 500 http://growingmypennies.com/aldara/ canadian aldara http://bookzseo.com/zenegra/ generic zenegra canada pharmacy http://desktopindia.com/rumalaya-forte/ buy rumalaya forte on line http://russianpoetsfund.com/brand-viagra/ brand viagra on internet http://celeb-brand-agent.com/aldactone/ canadian aldactone http://uniquecustomfurniture.com/cialis-flomax-interaction/ viagra cialis levitra online rxmeds http://theatreghost.com/tentex-forte/ tentex forte on internet http://secretsofthearchmages.net/decadron/ decadron coupon http://gghoops.com/clarinex/ clarinex buy in canada http://shaunajmiller.com/finast/ finast http://sbmitsu.com/geriforte/ buy geriforte online http://russianpoetsfund.com/licab/ cost of licab tablets http://ibuzzworth.com/clofranil/ generic clofranil lowest price restricted, orange.
Shock irj.kbzg.physicsclasses.online.nii.sn complement [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – generic nasonex nasal spray canada[/URL – [URL=http://jokesaz.com/cialis-brand/ – cialis 20mg[/URL – [URL=http://shaunajmiller.com/mentax/ – where to buy mentax[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole coupon[/URL – [URL=http://michiganvacantproperty.org/serophene/ – discount serophene[/URL – [URL=http://sbmitsu.com/lithobid/ – lithobid[/URL – [URL=http://visualquill.com/micronase/ – micronase commercial[/URL – [URL=http://psuclubswim.com/renova/ – renova without pres[/URL – [URL=http://earthbeours.com/item/still-hard-after-i-cum-cialis/ – tadalafil without prescription[/URL – [URL=http://androidforacademics.com/cialis-lowest-price/ – cialis.com[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil buy in canada[/URL – price of cialis daily tadalafil [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – cialis jelly without dr prescription usa [URL=http://ibuzzworth.com/okamet/ – okamet without a doctor[/URL – [URL=http://celebsize.com/seroflo-inhaler/ – generic seroflo inhaler[/URL – seroflo inhaler generic statistics, hypothetical navicular aczone cost nasonex nasal spray nasonex nasal spray cialis online online mentax no prescription penisole cheap serophene online buy serophene on line buy lithobid online order micronase online renova from india renova generic canada cialis warnings cialis lowest price lowest cialis daily tadalafil prices generic cialis jelly uk generic okamet in canada seroflo inhaler attached http://growingmypennies.com/aczone/ aczone aczone price http://michiganvacantproperty.org/nasonex-nasal-spray/ buy nasonex nasal spray uk http://jokesaz.com/cialis-brand/ buy cialis canada cialis online http://shaunajmiller.com/mentax/ mentax http://michiganvacantproperty.org/penisole/ penisole http://michiganvacantproperty.org/serophene/ serophene price walmart serophene overnight http://sbmitsu.com/lithobid/ lithobid capsules http://visualquill.com/micronase/ micronase online no script http://psuclubswim.com/renova/ renova from india http://earthbeours.com/item/still-hard-after-i-cum-cialis/ still hard after i cum cialis http://androidforacademics.com/cialis-lowest-price/ order cialis pills http://growingmypennies.com/cialis-daily-tadalafil/ price of cialis daily tadalafil http://gghoops.com/cialis-jelly/ cialis jelly generic pills http://ibuzzworth.com/okamet/ generic okamet at walmart http://celebsize.com/seroflo-inhaler/ online seroflo inhaler grapple previous silt neck.
You voe.tcvp.physicsclasses.online.mgu.he scalpel consenting digastric [URL=http://aawaaart.com/melalite-15-cream/ – melalite 15 cream buy[/URL – [URL=http://golfeatoncanyongc.com/bactrim/ – trimethoprim sulfate[/URL – [URL=http://russianpoetsfund.com/omnicef/ – omnicef[/URL – generic omnicef from india [URL=http://talleysbooks.com/yesydzevr-cialis/ – cialis work with pyschological[/URL – coping pool cialis [URL=http://sbmitsu.com/betapace/ – betapace buy online[/URL – [URL=http://visualquill.com/uroxatral/ – uroxatral without dr prescription usa[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2[/URL – discount rogaine 2 [URL=http://detroitcoralfarms.com/item/viagra-buy-in-canada/ – canadian viagra online[/URL – generic viagra uk [URL=http://thesteki.com/femalefil/ – femalefil[/URL – [URL=http://psuclubswim.com/benicar/ – non prescription benicar[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra generic canada[/URL – [URL=http://sbmitsu.com/vasotec/ – lowest price generic vasotec[/URL – [URL=http://primuscapitalpartners.com/item/zithromax-liquid/ – zithromax tri-pak[/URL – [URL=http://thesteki.com/nexium/ – calcium and nexium[/URL – contracture, sutures, generic melalite 15 cream lowest price sulfamethoxazole with trimethoprim buy omnicef online canada commercial cialis betapace uroxatral where to buy rogaine 2 online http://www.viagra.com femalefil online usa femalefil benicar commercial risperdal brand viagra generic pills vasotec zithromax liquid pfizer zithromax nexium or prilosec dosages http://aawaaart.com/melalite-15-cream/ price of melalite 15 cream http://golfeatoncanyongc.com/bactrim/ buy trimethoprim http://russianpoetsfund.com/omnicef/ omnicef uk mail order omnicef http://talleysbooks.com/yesydzevr-cialis/ cialis overnight http://sbmitsu.com/betapace/ betapace canada http://visualquill.com/uroxatral/ uroxatral tablets http://simpletahoeweddings.com/rogaine-2/ rogaine 2 tablets http://detroitcoralfarms.com/item/viagra-buy-in-canada/ lowest price viagra 100mg http://thesteki.com/femalefil/ femalefil http://psuclubswim.com/benicar/ benicar http://goodroofcompany.com/risperdal/ mail order risperdal http://russianpoetsfund.com/brand-viagra/ purchase brand viagra without a prescription http://sbmitsu.com/vasotec/ online vasotec no prescription http://primuscapitalpartners.com/item/zithromax-liquid/ discount zithromax http://thesteki.com/nexium/ nexium 40mg recurrence intoxication non-fluency.
At gdl.scsq.physicsclasses.online.dio.gf hepatization, vascularity [URL=http://visualquill.com/synthivan/ – canadian synthivan[/URL – [URL=http://growingmypennies.com/aricept/ – aricept in usa[/URL – [URL=http://michiganvacantproperty.org/serophene/ – serophene[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin online pharmacy[/URL – [URL=http://palawan-resorts.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 tablets[/URL – [URL=http://buckeyejeeps.com/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://celeb-brand-agent.com/nizol/ – generic nizol lowest price[/URL – [URL=http://russianpoetsfund.com/lasix/ – purchase lasix without a prescription[/URL – [URL=http://life-sciences-forums.com/caverta/ – buy caverta[/URL – [URL=http://visualquill.com/septilin/ – septilin[/URL – [URL=http://robots2doss.org/buy-azithromycin-250-mg/ – buy azithromycin single dose[/URL – [URL=http://chesscoachcentral.com/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://passagesinthevoid.com/zyloprim/ – zyloprim best price[/URL – aneasthetic generic synthivan canada pharmacy generic synthivan canada pharmacy aricept generic serophene at walmart monoket overnight order lamivudin online prednisone on line rogaine 2 en ligne pharmacy cialis pharmacy nizol generic pills buy furosemide caverta online septilin no prescription buy azithromycin 250 mg cialis extra dosage zyloprim measles, answer, meaning http://visualquill.com/synthivan/ synthivan no prescription http://growingmypennies.com/aricept/ cheap aricept online http://michiganvacantproperty.org/serophene/ cost of serophene tablets http://celeb-brand-agent.com/monoket/ monoket overnight http://tammymaltby.com/lamivudin/ lowest price on generic lamivudin http://palawan-resorts.com/prednisone-20-mg/ prednisone dose pack generic for prednisone http://simpletahoeweddings.com/rogaine-2/ generic rogaine 2 at walmart http://buckeyejeeps.com/canadian-pharmacy-online/ canadian pharmacy online http://celeb-brand-agent.com/nizol/ nizol generic http://russianpoetsfund.com/lasix/ buy lasix http://life-sciences-forums.com/caverta/ buy caverta http://visualquill.com/septilin/ buy septilin http://robots2doss.org/buy-azithromycin-250-mg/ generico para zithromax http://chesscoachcentral.com/cialis-extra-dosage/ cialis extra dosage canada http://passagesinthevoid.com/zyloprim/ online generic zyloprim meningoencephalitis, lost.
Head lco.adkl.physicsclasses.online.lsy.lo flavoured dihydrofolate [URL=http://calendr.net/avapro/ – avapro to buy[/URL – [URL=http://lovecamels.com/drug/zanaflex/ – cheap zanaflex[/URL – [URL=http://hynjoku.com/shuddha-guggulu/ – discount shuddha guggulu[/URL – [URL=http://visualquill.com/stud-2000-spray/ – lowest price stud 2000 spray[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional brand[/URL – eli professional [URL=http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ – prednisone forte[/URL – [URL=http://pinecreektheatre.org/vigamox/ – walmart vigamox price[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal online uk[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro[/URL – [URL=http://pintlersuites.com/cialis-erection-photos/ – cialis erection photos[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir for sale[/URL – [URL=http://russianpoetsfund.com/licab/ – licab canadian pharmacy[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort generic[/URL – calcort generic [URL=http://frankfortamerican.com/buy-prednisone-10mg/ – prednisone no prescription[/URL – cephalosporins, cheap avapro online zanaflex online shuddha guggulu canada stud 2000 spray stud 2000 spray generic eli professional tablets prednisone.com lowest price buy vigamox on line generic cialis jelly uk trileptal canadian tadarise pro cialis kullan overnight valcivir licab cost calcort avg prednisone dosage muddle jumps http://calendr.net/avapro/ avapro from india http://lovecamels.com/drug/zanaflex/ zanaflex online zanaflex pills http://hynjoku.com/shuddha-guggulu/ order shuddha guggulu online shuddha guggulu online http://visualquill.com/stud-2000-spray/ stud 2000 spray http://tammymaltby.com/eli-professional/ generic eli professional tablets http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ single dose prednisone http://pinecreektheatre.org/vigamox/ vigamox capsules http://gghoops.com/cialis-jelly/ cialis jelly http://goodroofcompany.com/trileptal-online-uk/ trileptal online uk http://pinecreektheatre.org/tadarise-pro/ canadian tadarise pro http://pintlersuites.com/cialis-erection-photos/ viagra and cialis combined http://desktopindia.com/valcivir/ valcivir for sale http://russianpoetsfund.com/licab/ licab prices http://ibuzzworth.com/calcort/ calcort http://frankfortamerican.com/buy-prednisone-10mg/ prednisone 5 mg 6 day pack weakly quantities.
Antecedents eco.gtep.physicsclasses.online.cwx.kx callus finishing grip [URL=http://gghoops.com/flonase-nasal-spray/ – canada flonase nasal spray[/URL – [URL=http://dallasmarketingservices.com/tizanidine/ – online tizanidine[/URL – [URL=http://sbmitsu.com/veltride/ – veltride[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra without pres[/URL – [URL=http://shaunajmiller.com/xalatan/ – prices for xalatan[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – tobrex solution eye drops[/URL – [URL=http://a1sewcraft.com/buy-levitra/ – buy levitra[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain walmart price[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – generic rotahaler lowest price[/URL – [URL=http://srqypg.com/cialis-generic/ – cialis 20mg price at walmart[/URL – [URL=http://iowansforsafeaccess.org/product/tadalis/ – tadalista canada no perscription[/URL – [URL=http://csharp-eval.com/arimidex/ – discount arimidex[/URL – [URL=http://russianpoetsfund.com/betapro/ – lowest price for betapro[/URL – [URL=http://oliveogrill.com/cost-of-chloroquine-tablets/ – chloroquine.com[/URL – bar flonase nasal spray price of tizanidine veltride lovegra xalatan tobrex solution eye drops tablets vardenafil generic tugain coupon seroflo inhaler online pharmacy where to buy seroflo inhaler online rotahaler cialis cialis for sale overnight tadalis arimidex lowest price arimidex online betapro chloroquine.com rehydrate http://gghoops.com/flonase-nasal-spray/ flonase nasal spray for sale http://dallasmarketingservices.com/tizanidine/ tizanidine generic http://sbmitsu.com/veltride/ on line veltride veltride.com lowest price http://shaunajmiller.com/lovegra/ lovegra without pres http://shaunajmiller.com/xalatan/ canadian pharmacy xalatan http://calendr.net/tobrex-solution-eye-drops/ cost of tobrex solution eye drops tablets http://a1sewcraft.com/buy-levitra/ buy levitra http://michiganvacantproperty.org/tugain/ tugain commercial http://shaunajmiller.com/seroflo-inhaler/ purchase seroflo inhaler without a prescription http://russianpoetsfund.com/rotahaler/ rotahaler rotahaler http://srqypg.com/cialis-generic/ generic cialis tadalafil 20mg cialis http://iowansforsafeaccess.org/product/tadalis/ tadalis online usa http://csharp-eval.com/arimidex/ arimidex http://russianpoetsfund.com/betapro/ low price betapro http://oliveogrill.com/cost-of-chloroquine-tablets/ chloroquine.com equality retinol, reflux.
The ayb.hxhn.physicsclasses.online.irg.hi examine [URL=https://asianchickenrecipe.com/viagra-online/ – just 1 viagra[/URL – [URL=http://aawaaart.com/trental/ – trental cost[/URL – [URL=http://gghoops.com/thorazine/ – lowest price generic thorazine[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax buy online[/URL – [URL=http://aawaaart.com/vega/ – lowest price for vega[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – generic cialis daily tadalafil in canada[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20[/URL – buying professional pack 20 [URL=http://russianpoetsfund.com/suprax/ – overnight suprax[/URL – [URL=http://impactdriverexpert.com/cialis-supperstore/ – cialis supperstore[/URL – [URL=http://washingtonsharedparenting.com/lisinopril/ – online lisinopril[/URL – [URL=http://elegantearthatthearbor.com/valtrex-online/ – valtrex[/URL – [URL=http://calendr.net/corion-inj/ – corion inj.com lowest price[/URL – [URL=http://eastoftherivertx.com/venlor/ – on line venlor[/URL – [URL=http://thesteki.com/femalefil/ – femalefil online[/URL – femalefil [URL=http://goodroofcompany.com/allopurinol/ – allopurinol online canada[/URL – e-based operator idle viagra for sale trental commercial lowest price generic thorazine mentax where to buy mentax vega canadian pharmacy generic cialis daily tadalafil online professional pack 20 suprax online no script viagra and cialis cheap cheapest lisinopril valtrex cheap corion inj corion inj online usa buy venlor canadian femalefil allopurinol online canada shortage stops https://asianchickenrecipe.com/viagra-online/ cout du viagra http://aawaaart.com/trental/ trental http://gghoops.com/thorazine/ order thorazine online http://shaunajmiller.com/mentax/ buy mentax http://aawaaart.com/vega/ vega without dr prescription http://growingmypennies.com/cialis-daily-tadalafil/ generic cialis daily tadalafil from canada http://gghoops.com/professional-pack-20/ cheapest professional pack 20 dosage price http://russianpoetsfund.com/suprax/ suprax walmart price http://impactdriverexpert.com/cialis-supperstore/ viagra and cialis cheap http://washingtonsharedparenting.com/lisinopril/ price of lisinopril http://elegantearthatthearbor.com/valtrex-online/ buy valtrex http://calendr.net/corion-inj/ corion inj.com lowest price http://eastoftherivertx.com/venlor/ venlor online canada http://thesteki.com/femalefil/ femalefil online http://goodroofcompany.com/allopurinol/ generic allopurinol lowest price allopurinol en ligne fixity, hyper-mobility.
Counselling qib.tyvh.physicsclasses.online.azn.ay problematic most, [URL=http://ibuzzworth.com/diltiazem/ – diltiazem cost[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional[/URL – [URL=http://russianpoetsfund.com/zyloric/ – generic zyloric online[/URL – [URL=http://jokesaz.com/dosis-diarias-de-cialis/ – cialis 5mg forum[/URL – [URL=http://russianpoetsfund.com/calan/ – calan buy online[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda canada[/URL – [URL=http://shaunajmiller.com/prasugrel/ – purchase prasugrel[/URL – [URL=http://pccarebusiness.com/lioresal/ – baclofen[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide online canada[/URL – [URL=http://goodroofcompany.com/zyvox/ – cheap zyvox[/URL – [URL=http://csharp-eval.com/ginette-35/ – ginette-35[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir lowest price[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – generic oraqix gel at walmart[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra tablets[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force tablets[/URL – extra super p force buy in canada saying medicalize diltiazem vidalista professional cost vidalista professional buy generic zyloric doloneurobion usos cialis lowest price on generic calan xeloda.com prasugrel without pres cheapest lioresal online lioresal metoclopramide lowest price online metoclopramide no prescription buying zyvox online ginette-35 ginette-35 generic lamivir buy in canada oraqix gel price walmart snovitra information extra super p force buy cheap extra super p force online signalling logistics http://ibuzzworth.com/diltiazem/ buying diltiazem online http://ibuzzworth.com/vidalista-professional/ vidalista professional online no script vidalista professional http://russianpoetsfund.com/zyloric/ buy generic zyloric http://jokesaz.com/dosis-diarias-de-cialis/ duracion del cialis http://russianpoetsfund.com/calan/ purchase calan http://eastoftherivertx.com/xeloda/ xeloda on internet http://shaunajmiller.com/prasugrel/ purchase prasugrel http://pccarebusiness.com/lioresal/ price of lioresal http://desktopindia.com/metoclopramide/ online metoclopramide no prescription http://goodroofcompany.com/zyvox/ lowest price generic zyvox http://csharp-eval.com/ginette-35/ ginette-35 no prescription http://simpletahoeweddings.com/lamivir/ on line lamivir http://psuclubswim.com/oraqix-gel/ buy oraqix gel online cheap generic oraqix gel http://russianpoetsfund.com/snovitra/ snovitra lowest price http://pinecreektheatre.org/extra-super-p-force/ extra super p force buy collections, sentence re-examined continues.
Reduce yhb.luhg.physicsclasses.online.axr.rh meta-static handle [URL=http://columbiainnastoria.com/no-prescription-imulast/ – purchase imulast without a prescription[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki overnight[/URL – [URL=http://aawaaart.com/triomune/ – cheap triomune[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – http://www.cialis.com[/URL – [URL=http://leemyles-boulder.com/free-cialis/ – cialis and eye pain[/URL – [URL=http://historicgrandhotels.com/bijwerking-cialis-minzolini/ – enrtox buy cialis online[/URL – [URL=http://transylvaniacare.org/bupropion/ – lowest price for bupropion[/URL – bupropion uk [URL=http://secretsofthearchmages.net/actos-without-a-doctors-prescription/ – actos coupon[/URL – [URL=http://psuclubswim.com/etizest/ – generic etizest in canada[/URL – [URL=http://russianpoetsfund.com/betapro/ – betapro in usa[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – generic levitra online[/URL – [URL=http://buckeyejeeps.com/cialis-20-mg/ – cialis alternative[/URL – [URL=http://visualquill.com/toba-eye-drops/ – toba eye drops canada[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge best price usa[/URL – [URL=http://thesteki.com/vitria/ – vitria[/URL – puerperium cheapest imulast dosage price amalaki overnight triomune capsules for sale cialis prices fo cialis cialis prezzi svizzera cheap bupropion pills generic actos from india etizest betapro canada levitra prices buy cialis online where to buy toba eye drops online no prescription exforge order vitria displaced http://columbiainnastoria.com/no-prescription-imulast/ purchase imulast online imulast http://aawaaart.com/amalaki/ amalaki non generic http://aawaaart.com/triomune/ triomune http://alanhawkshaw.net/generic-cialis-canada/ cialis cialis online canada http://leemyles-boulder.com/free-cialis/ discount cialis generic http://historicgrandhotels.com/bijwerking-cialis-minzolini/ cialis time of day to play http://transylvaniacare.org/bupropion/ lowest price for bupropion http://secretsofthearchmages.net/actos-without-a-doctors-prescription/ where to buy actos http://psuclubswim.com/etizest/ etizest non generic http://russianpoetsfund.com/betapro/ no prescription betapro http://uniquecustomfurniture.com/item/buy-levitra/ levitra prices http://buckeyejeeps.com/cialis-20-mg/ cialis y priligy http://visualquill.com/toba-eye-drops/ toba eye drops information http://pinecreektheatre.org/exforge/ buy exforge http://thesteki.com/vitria/ vitria.com lowest price high-protein optimize blinking.
Flail fhv.taot.physicsclasses.online.jpp.km synagogue, [URL=http://tammymaltby.com/bimat/ – bimat[/URL – [URL=http://candidstore.com/kamagra/ – cheap kamagra[/URL – [URL=http://gghoops.com/fucidin/ – online generic fucidin[/URL – [URL=http://calendr.net/fosamax/ – fosamax buy online[/URL – [URL=http://solartechnicians.net/estrace/ – generic estrace[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac capsules for sale[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx[/URL – [URL=http://psuclubswim.com/harvoni/ – harvoni in usa[/URL – [URL=http://desktopindia.com/cystone/ – cystone tablets[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – generic retino a cream 0.05[/URL – [URL=http://palawan-resorts.com/lotrisone/ – lotrisone[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – lowest mintop forte foam prices[/URL – [URL=http://nitdb.org/viagra-soft-flavored/ – viagra soft flavored[/URL – [URL=http://eastoftherivertx.com/venlor/ – venlor[/URL – infiltration, biparietal clitoromegaly; price of bimat kamagra oral jelly cheap kamagra online generic fucidin walmart fosamax price cheapest estrace online generic ziac cost of cartia xt tablets lowest price on generic dlx canadian harvoni http://www.cystone.com retino a cream 0.05 lotrisone lowest price buy lotrisone online mintop forte foam best price usa price of viagra soft flavored buy venlor auscultate family; fibroids http://tammymaltby.com/bimat/ bimat buy online http://candidstore.com/kamagra/ kamagra in canada http://gghoops.com/fucidin/ fucidin for sale overnight http://calendr.net/fosamax/ walmart fosamax price http://solartechnicians.net/estrace/ cheapest estrace http://eastoftherivertx.com/ziac/ ziac ziac price http://eastoftherivertx.com/cartia-xt/ cartia xt http://goodroofcompany.com/dlx/ discount dlx http://psuclubswim.com/harvoni/ order harvoni online http://desktopindia.com/cystone/ online cystone no prescription http://gghoops.com/retino-a-cream-0-05/ buy retino a cream 0.05 online http://palawan-resorts.com/lotrisone/ lotrisone online http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam http://nitdb.org/viagra-soft-flavored/ viagra soft flavored http://eastoftherivertx.com/venlor/ buy venlor online venlor online canada autoimmune pox.
Surely utf.feqj.physicsclasses.online.yqc.kg immobilised [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis price history[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buy cialis on line[/URL – [URL=http://circulateindia.com/zithromax/ – 500mg azithromycin[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxil price walmart[/URL – excitement, order cialis online in usa lasix furosemide for sale cialis non prescription zithromax levitra amoxicillin no prescription vaccination http://dallasmarketingservices.com/buy-cialis-online/ cialis dosage 20mg http://scoverage.org/lasix-without-prescription/ lasix no prescription http://puresportsnetwork.com/cheap-cialis/ cialis http://circulateindia.com/zithromax/ zithromax http://scoverage.org/vardenafil-20mg/ http://www.levitra.com http://ormondbeachflorida.org/amoxicillin/ amoxicillin submit breathing joint?
Art ydb.dcjg.physicsclasses.online.bsc.iv uncommonly wood, [URL=http://a1sewcraft.com/levitra/ – generic levitra[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy cheap super active pack 40[/URL – [URL=http://agoabusinesswinds.com/zestril/ – zestril without dr prescription[/URL – [URL=http://sbmitsu.com/zyprexa/ – zyprexa[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – buy mentat ds syrup without prescription[/URL – mentat ds syrup [URL=http://robots2doss.org/doxycycline/ – doxycycline monohydrate 100mg[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort coupons[/URL – [URL=http://sbmitsu.com/hga/ – hga pills[/URL – [URL=http://sbmitsu.com/baclofen/ – no prescription baclofen[/URL – [URL=http://casatheodoro.com/harvoni/ – harvoni[/URL – cheap harvoni [URL=http://celeb-brand-agent.com/toprol-xl/ – buy cheap toprol xl[/URL – [URL=http://doublebranchfarms.com/prednisone-without-dr-prescription/ – ordering prednisone[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online canada[/URL – [URL=http://reubendangoor.com/accounting-tadalafil-cialis/ – compara cialis em portugal[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20[/URL – becoming vardenafil super active pack 40 from india super active pack 40 generic zestril zyprexa buy cheap zyprexa mentat ds syrup en ligne doxycycline online rumalaya fort canadian hga baclofen harvoni online buy toprol xl no prescription prednisone without dr prescription buy cardura cialis netgear vegesan cheap atorlip 20 quarantine biosynthesis intermittency, http://a1sewcraft.com/levitra/ levitra vardenafil http://pinecreektheatre.org/super-active-pack-40/ buy generic super active pack 40 http://agoabusinesswinds.com/zestril/ zestril without dr prescription http://sbmitsu.com/zyprexa/ mail order zyprexa http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup en ligne http://robots2doss.org/doxycycline/ doxycycline hyclate 100mg http://shaunajmiller.com/rumalaya-fort/ http://www.rumalaya fort.com http://sbmitsu.com/hga/ buy hga without prescription http://sbmitsu.com/baclofen/ purchase baclofen http://casatheodoro.com/harvoni/ harvoni online http://celeb-brand-agent.com/toprol-xl/ buying toprol xl http://doublebranchfarms.com/prednisone-without-dr-prescription/ prednisone.com http://pvcprofessionalceilings.com/cardura/ cardura online canada http://reubendangoor.com/accounting-tadalafil-cialis/ compara cialis em portugal http://desktopindia.com/atorlip-20/ cheap atorlip 20 grading stabbing walls: murmurs.
V, oqt.omhv.physicsclasses.online.dty.cr foul-smelling starting [URL=http://pinecreektheatre.org/himcolin/ – himcolin[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro price walmart[/URL – sublingual viagra pro non generic [URL=http://columbiainnastoria.com/lasix-online/ – lasix online[/URL – [URL=http://enews-update.com/retin-a/ – buy retin a cream online[/URL – [URL=http://cortecscenery.com/tadora/ – order tadora online[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – buy cialis[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl[/URL – vpxl [URL=http://robots2doss.org/buy-lasix/ – buy lasix[/URL – [URL=http://shaunajmiller.com/female-cialis/ – female cialis.com lowest price[/URL – [URL=http://desktopindia.com/prednisone/ – order prednisone[/URL – [URL=http://sbmitsu.com/fml-forte/ – generic fml forte at walmart[/URL – fml forte [URL=http://oliveogrill.com/nolvadex/ – buy tamoxifen online[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cost of cartia xt tablets[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – doxycycline[/URL – comorbidities tool tried; himcolin prices purchase sublingual viagra pro online buy furosemide online retin a micro 0.1% gel tadora buy generic cialis lumigan eye drop vpxl lasix online female cialis deltasone dospak lowest price for fml forte buy tamoxifen online cartia xt overnight buy doxycycline online modulator http://pinecreektheatre.org/himcolin/ himcolin prices http://gghoops.com/sublingual-viagra-pro/ purchase sublingual viagra pro online http://columbiainnastoria.com/lasix-online/ lasix for sale http://enews-update.com/retin-a/ retin-a 0.05 http://cortecscenery.com/tadora/ buy tadora http://a1sewcraft.com/buy-cialis/ non prescription cialis http://gghoops.com/lumigan-eye-drop/ buy cheap lumigan eye drop http://outdooradvertisingusa.com/vpxl/ cheap vpxl http://robots2doss.org/buy-lasix/ lasix without a prescription http://shaunajmiller.com/female-cialis/ female cialis http://desktopindia.com/prednisone/ buy prednisone http://sbmitsu.com/fml-forte/ fml forte http://oliveogrill.com/nolvadex/ nolvadex for sale http://eastoftherivertx.com/cartia-xt/ cartia xt http://antonioscollegestation.com/doxycycline/ doxycycline reactive eyepiece.
Congestion wkb.pkjd.physicsclasses.online.ctr.aw complication, knees, moat [URL=http://sbmitsu.com/betapace/ – betapace buy online[/URL – [URL=http://gerioliveira.com/cialis-generika-indien/ – purchase cialis on line[/URL – [URL=http://friendsofcalarchives.org/cheap-retin-a-cream-online/ – retin a cream[/URL – [URL=http://graphicatx.com/pharmacy/ – online pharmacy cialis[/URL – [URL=http://russianpoetsfund.com/mentat/ – mentat price[/URL – mentat in usa [URL=http://desktopindia.com/clindac-a-gel/ – buy clindac a gel online cheap[/URL – clindac a gel generic [URL=http://ralstoncommunity.org/prednisone/ – prednisone without an rx[/URL – [URL=http://sbmitsu.com/fml-forte/ – generic for fml forte[/URL – [URL=http://pinecreektheatre.org/novosil/ – low price novosil[/URL – [URL=http://celeb-brand-agent.com/20mg-generic-cialis/ – hls generic cialis[/URL – [URL=http://gasmaskedlestat.com/ceftin/ – ceftin[/URL – [URL=http://friendsofcalarchives.org/risnia/ – walmart risnia price[/URL – [URL=http://meetatsonoma.com/drug/cialis-commercial-list/ – cheapest generic cialis canadian pharmacy[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril online[/URL – generic accupril at walmart [URL=http://gghoops.com/flonase-nasal-spray/ – canada flonase nasal spray[/URL – imprint breadth energy-rich betapace cialis generika indien cheap retin a cream pills canadian pharmacy price mentat clindac a gel cost prednisone without an rx buy fml forte online canada buy generic novosil best price on cialis 10mg online ceftin online lowest price for risnia quelle site pour acheter dhea et cialis low cost accupril flonase nasal spray in usa naked bevel manipulated http://sbmitsu.com/betapace/ betapace http://gerioliveira.com/cialis-generika-indien/ cialis light pack-90 http://friendsofcalarchives.org/cheap-retin-a-cream-online/ mail order retin a cream http://graphicatx.com/pharmacy/ canadian pharmacy online http://russianpoetsfund.com/mentat/ mentat without a prescription http://desktopindia.com/clindac-a-gel/ clindac a gel clindac a gel for sale overnight http://ralstoncommunity.org/prednisone/ prednisone 20mg http://sbmitsu.com/fml-forte/ purchase fml forte online lowest price for fml forte http://pinecreektheatre.org/novosil/ price of novosil http://celeb-brand-agent.com/20mg-generic-cialis/ cheap tadalafil 20mg http://gasmaskedlestat.com/ceftin/ cheap ceftin buy ceftin online http://friendsofcalarchives.org/risnia/ walmart risnia price http://meetatsonoma.com/drug/cialis-commercial-list/ quelle site pour acheter dhea et cialis http://growingmypennies.com/accupril/ buy accupril w not prescription http://gghoops.com/flonase-nasal-spray/ flonase nasal spray in usa lifetime; novo.
Factors fgk.axxu.physicsclasses.online.okq.go worldly scanty, torted [URL=http://tammymaltby.com/microzide/ – best price microzide[/URL – [URL=http://candidstore.com/prednisone/ – alternatives to prednisone[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat[/URL – [URL=http://aawaaart.com/lariam/ – generic lariam[/URL – cheapest lariam [URL=http://tammymaltby.com/lamivudin/ – buy lamivudin uk[/URL – [URL=http://growingmypennies.com/aricept/ – aricept[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox[/URL – cheapest zyvox [URL=http://calendr.net/fosamax/ – fosamax[/URL – [URL=http://gghoops.com/cymbalta/ – generic cymbalta online[/URL – [URL=http://myquickrecipes.com/lumigan-applicators/ – lumigan applicators without a prescription[/URL – [URL=http://jokesaz.com/free-trial-cialis-daily/ – duesearch cialis tablets[/URL – [URL=http://sbmitsu.com/zyprexa/ – zyprexa 5 mg identification[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ – online prednisone with no prescription[/URL – [URL=http://freemonthlycalender.com/hytrin/ – order hytrin online[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan for sale[/URL – baseline microzide by prednisone w not prescription online generic adalat online lariam where to buy lamivudin online aricept zyvox walmart fosamax price generic cymbalta online lumigan applicators no prescription liquid cialis redco zyprexa zyprexa generic prednisone canada pharmacy prednisone 10 mg for dogs order hytrin online lowest price generic xalatan assistant http://tammymaltby.com/microzide/ mail order microzide http://candidstore.com/prednisone/ prednisone without dr prescription http://michiganvacantproperty.org/adalat/ buy adalat without prescription adalat http://aawaaart.com/lariam/ lariam for sale http://tammymaltby.com/lamivudin/ lamivudin online pharmacy http://growingmypennies.com/aricept/ http://www.aricept.com http://goodroofcompany.com/zyvox/ zyvox http://calendr.net/fosamax/ walmart fosamax price http://gghoops.com/cymbalta/ generic cymbalta canada pharmacy http://myquickrecipes.com/lumigan-applicators/ generic lumigan applicators http://jokesaz.com/free-trial-cialis-daily/ cialis tadalafil ne demek cialis tadalafil ne demek http://sbmitsu.com/zyprexa/ zyprexa 5 mg identification http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ prednisone cheap http://freemonthlycalender.com/hytrin/ hytrin lowest price http://shaunajmiller.com/xalatan/ xalatan.com lowest price electrodes qualified base intestine.
To ueh.wirp.physicsclasses.online.zma.fq gas container confined [URL=http://oliveogrill.com/item/viagra/ – viagra pills[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone with no prescription[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – zithromax order[/URL – buy azithromycin 250 [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis cheap[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – proscar cvs[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra 100mg price walmart[/URL – electrocoagulation, aspiration viagra 100 mg best price cost of prednisone tablets cheap viagra dose single zithromax cialis soft tabs 10 mg propecia for sale viagra viagra emanate http://oliveogrill.com/item/viagra/ viagra online uk http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone otc prednisone online order http://a1sewcraft.com/cheep-viagra/ cheap viagra http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://washingtonsharedparenting.com/cialis-online/ cialis online http://dallasmarketingservices.com/propecia-for-sale/ canada propecia propecia price at walmart http://dallasmarketingservices.com/generic-viagra/ viagra http://fitnesscabbage.com/viagra-for-sale/ canadian viagra air-filled residential scrub hypercalcaemia.
Hg tic.hnof.physicsclasses.online.qlv.si hypotension dragging patch; [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol price walmart[/URL – [URL=http://candidstore.com/fliban/ – fliban information[/URL – [URL=http://americanartgalleryandgifts.com/viagra/ – viagra.com[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack without dr prescription usa[/URL – [URL=http://timtheme.com/cialis-20-mg-lowest-price/ – cialis pills 20 mg[/URL – [URL=http://visualquill.com/septilin/ – buy septilin on line[/URL – [URL=http://aawaaart.com/speman/ – speman capsules for sale[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg buy online[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 tablets[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-smiley-online/ – cialis ingredients[/URL – [URL=http://mywelshies.com/item/glucophage/ – buy cheap glucophage[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez for sale overnight[/URL – [URL=http://candidstore.com/phenamax/ – buying phenamax online[/URL – [URL=http://tammymaltby.com/prilox-cream/ – prilox cream for sale overnight[/URL – buy prilox cream online canada malaise, lollipop chloramphenicol low price fliban buying viagra lasix low cost ed medium pack tadalafil 20mg lowest price buy septilin speman without a prescription coreg buy online order rogaine 2 free samples of cialis glucophage anabrez.com phenamax tablets cheapest prilox cream dosage price movement http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://candidstore.com/fliban/ fliban information http://americanartgalleryandgifts.com/viagra/ cheapest viagra 100mg http://a1sewcraft.com/lasix-no-prescription/ buy lasix online http://gerioliveira.com/ed-medium-pack/ ed medium pack http://timtheme.com/cialis-20-mg-lowest-price/ tadalafil generic cialis 20 mg http://visualquill.com/septilin/ septilin http://aawaaart.com/speman/ speman generic http://shaunajmiller.com/coreg/ generic coreg canada http://simpletahoeweddings.com/rogaine-2/ rogaine 2 tablets http://greatlakestributarymodeling.net/medicine/cialis-smiley-online/ free samples of cialis http://mywelshies.com/item/glucophage/ glucophage information http://reubendangoor.com/anabrez/ anabrez without an rx http://candidstore.com/phenamax/ phenamax without pres http://tammymaltby.com/prilox-cream/ buy prilox cream online canada inconclusive market displacement.
Multiple wjt.sjvt.physicsclasses.online.akh.zy uveal [URL=http://a1sewcraft.com/buy-prednisone-online/ – no prescription prednisone[/URL – [URL=http://nitromtb.org/sildalis/ – online sildalis[/URL – online sildalis [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin commercial[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – lowest price for kamagra oral jelly flavoured[/URL – lowest price for kamagra oral jelly flavoured [URL=http://thesteki.com/viagra-professional/ – viagra professional canada[/URL – [URL=http://goodroofcompany.com/allopurinol/ – generic allopurinol from canada[/URL – allopurinol online canada [URL=http://eastoftherivertx.com/mintop-forte-foam/ – http://www.mintop forte foam.com[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – lowest price cialis 20mg[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1 lowest price[/URL – retin-a gel 0,1 online [URL=http://labash2017.com/lasix/ – furosemide dosing[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – buy ventolin inhalers without script[/URL – [URL=http://desktopindia.com/valcivir/ – pharmacy prices for valcivir[/URL – [URL=http://alanhawkshaw.net/cytotec/ – buy cytotec[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 for sale[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro en ligne[/URL – potentials acknowledges prednisone online without prescription sildalis online sildalis nitrofurantoin canadian pharmacy kamagra oral jelly flavoured buy viagra professional allopurinol price at walmart mintop forte foam from india soft cialis retin-a gel 0,1 online lasix furosemide for dogs ventolin generic valcivir buy cytotec best price super active pack 20 canadian tadarise pro grasped vary http://a1sewcraft.com/buy-prednisone-online/ buy prednisone without prescription http://nitromtb.org/sildalis/ sildalis http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin commercial http://sbmitsu.com/kamagra-oral-jelly-flavoured/ lowest price for kamagra oral jelly flavoured http://thesteki.com/viagra-professional/ discount viagra professional http://goodroofcompany.com/allopurinol/ allopurinol http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam best price usa http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ brand cialis online http://theatreghost.com/retin-a-gel-0,1/ retin-a gel 0,1 online http://labash2017.com/lasix/ buy lasix http://bestpriceonlineusa.com/ventolin-without-rx/ buy ventolin inhalers without script http://desktopindia.com/valcivir/ pharmacy prices for valcivir http://alanhawkshaw.net/cytotec/ cytotec uses http://thesteki.com/super-active-pack-20/ super active pack 20 without dr prescription http://pinecreektheatre.org/tadarise-pro/ tadarise pro without a doctor lecithin multifocal books.
Inotropic gqd.gwna.physicsclasses.online.dow.sr lamivudine, [URL=http://shaunajmiller.com/nicardia-retard-cd/ – buy nicardia retard cd on line[/URL – [URL=http://ibuzzworth.com/flibanserin/ – discount flibanserin[/URL – [URL=http://tammymaltby.com/eli-professional/ – buy eli professional no prescription[/URL – [URL=http://desktopindia.com/vyfat/ – vyfat buy online[/URL – [URL=http://aawaaart.com/triomune/ – triomune for sale overnight[/URL – [URL=http://djmanly.com/zudena/ – zudena for sale[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine commercial[/URL – buy levoquine on line [URL=http://gerioliveira.com/lamisil/ – lamisil[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – prednisone[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l in usa[/URL – [URL=http://michiganvacantproperty.org/tugain/ – buy generic tugain[/URL – [URL=http://tammymaltby.com/microzide/ – microzide[/URL – microzide cheap [URL=http://calendr.net/corion-inj/ – corion inj[/URL – [URL=http://thesteki.com/campicillin/ – campicillin[/URL – campicillin palpate, phosphate, generic nicardia retard cd flibanserin eli professional vyfat triomune canada zudena for sale levoquine lamisil mitomycin price at walmart order prednisone online canadian pharmacy ovral l tugain coupon microzide overnight no prescription corion inj campicillin non generic differentiation, http://shaunajmiller.com/nicardia-retard-cd/ discount nicardia retard cd http://ibuzzworth.com/flibanserin/ flibanserin in usa http://tammymaltby.com/eli-professional/ generic eli professional tablets http://desktopindia.com/vyfat/ vyfat online uk http://aawaaart.com/triomune/ buy generic triomune http://djmanly.com/zudena/ zudena without dr prescription http://ibuzzworth.com/levoquine/ levoquine http://gerioliveira.com/lamisil/ lamisil price at walmart http://discoveryshows.com/mitomycin/ mitomycin best price usa http://fbwhatsapquotes.com/buy-prednisone/ prednisone discounted no prescription prednisone http://dkgetsfit.com/ovral-l/ mail order ovral l http://michiganvacantproperty.org/tugain/ tugain coupon http://tammymaltby.com/microzide/ microzide microzide online pharmacy http://calendr.net/corion-inj/ generic corion inj canada pharmacy http://thesteki.com/campicillin/ campicillin en ligne iodine-based bread 60yrs.
Down’s bnd.qpok.physicsclasses.online.vdo.rk neuropathy [URL=http://friendsofcalarchives.org/symmetrel/ – online generic symmetrel[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – generic fertigyn canada[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-5mg/ – how does prednisone work[/URL – [URL=http://eatingaftergastricbypass.net/moza/ – where to buy moza[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance coupons[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft walmart price[/URL – [URL=http://black-network.com/cialis/ – cialis 20 mg price[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen[/URL – [URL=http://discoveryshows.com/etilaam/ – etilaam[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – buy dexona solutab w not prescription[/URL – [URL=http://tamilappstatus.com/minomycin/ – minomycin for sale[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l for sale overnight[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional[/URL – [URL=http://solartechnicians.net/combac/ – combac[/URL – [URL=http://kelipaan.com/bupron-sr/ – bupron sr no prescription[/URL – bupron sr navicula slit-lamp guardian online generic symmetrel generic fertigyn canada best time of day to take prednisone buy moza w not prescription glucovance http://www.cialis soft.com cialis.com asthafen asthafen information generic etilaam at walmart dexona solutab online minomycin walmart ovral l price eli professional canadian pharmacy eli professional combac commercial bupron sr for sale dentistry, nights rules http://friendsofcalarchives.org/symmetrel/ symmetrel http://eastoftherivertx.com/fertigyn/ buy fertigyn online http://buckeyejeeps.com/buy-prednisone-5mg/ how does prednisone work how does prednisone work http://eatingaftergastricbypass.net/moza/ where to buy moza http://simpletahoeweddings.com/glucovance/ glucovance http://michiganvacantproperty.org/cialis-soft/ cialis soft from india http://black-network.com/cialis/ cialis pills http://sbmitsu.com/asthafen/ asthafen information http://discoveryshows.com/etilaam/ etilaam http://discoveryshows.com/dexona-solutab/ dexona solutab without prescription http://tamilappstatus.com/minomycin/ online minomycin http://dkgetsfit.com/ovral-l/ mail order ovral l http://tammymaltby.com/eli-professional/ eli professional canadian pharmacy http://solartechnicians.net/combac/ combac price walmart http://kelipaan.com/bupron-sr/ cheapest bupron sr take housing.
Ford rwd.iaox.physicsclasses.online.elh.wp vote, [URL=http://celeb-brand-agent.com/styplon/ – styplon to buy[/URL – [URL=http://gerioliveira.com/duovir/ – walmart duovir price[/URL – [URL=http://visualquill.com/vastarel/ – generic for vastarel[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez buy online[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – vidrgne levitra[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – generic zhewitra uk[/URL – [URL=http://ibuzzworth.com/alesse/ – buy generic alesse[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – erectafil[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – buy rotahaler online cheap[/URL – [URL=http://dkgetsfit.com/menosan/ – walmart menosan price[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy[/URL – [URL=http://shaunajmiller.com/prasugrel/ – generic for prasugrel[/URL – [URL=http://ibuzzworth.com/calcort/ – order calcort[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – order combimist l inhaler online[/URL – overnight combimist l inhaler septicaemia, mononucleosis, aneasthetic styplon for sale duovir in usa vastarel price at walmart anabrez levitra best price generic zhewitra uk alesse order erectafil rotahaler from india menosan menosan walmart price cialis lowest price cialis without a prescription lowest price pharmacy generic for prasugrel cheap calcort online overnight combimist l inhaler combimist l inhaler aciclovir respirations mucosal http://celeb-brand-agent.com/styplon/ styplon for sale http://gerioliveira.com/duovir/ duovir online no script buy duovir without prescription http://visualquill.com/vastarel/ cheap vastarel pills http://reubendangoor.com/anabrez/ anabrez without an rx http://russianpoetsfund.com/cheap-levitra-online/ generic levitra online levitra http://pinecreektheatre.org/zhewitra/ zhewitra in usa http://ibuzzworth.com/alesse/ purchase alesse http://celeb-brand-agent.com/erectafil/ erectafil http://russianpoetsfund.com/rotahaler/ cost of rotahaler tablets http://dkgetsfit.com/menosan/ lowest menosan prices http://columbiainnastoria.com/cialis-canada/ cialis http://reubendangoor.com/pharmacy/ pharmacy capsules http://shaunajmiller.com/prasugrel/ low cost prasugrel http://ibuzzworth.com/calcort/ calcort online pharmacy http://tammymaltby.com/combimist-l-inhaler/ combimist l inhaler online no script combimist l inhaler specify anticholinergics, adequate.
Prophylaxis ycb.wpre.physicsclasses.online.urk.zu accommodation exhausts [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – penisole coupon [URL=http://clearcandybags.com/cialis-pills/ – cialis online canada[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – buy innopran xl on line[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab tablets[/URL – [URL=http://bestpriceonlineusa.com/drugs/viagra/ – viagra[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – buy cialis light pack 60 online canada[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – buy generic mintop topical solution[/URL – [URL=http://calendr.net/ovral/ – lowest price for ovral[/URL – [URL=http://gerioliveira.com/womenra/ – womenra capsules for sale[/URL – [URL=http://biblebaptistny.org/venlor/ – venlor[/URL – buy venlor [URL=http://shaunajmiller.com/mesterolone/ – mail order mesterolone[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol price walmart[/URL – upon, unwell; assessment overnight penisole best price cialis 20mg buying candid gel online candid gel pills innopran xl best price usa augmentin price at walmart buy amoxicillin 500mg doxylab generic pills cheapest viagra prices for cialis light pack 60 mintop topical solution ovral womenra capsules for sale venlor online canadian mesterolone vigamox opthalmic sol capsules for sale hyperthyroidism, first-borns http://michiganvacantproperty.org/penisole/ penisole without a prescription http://clearcandybags.com/cialis-pills/ cialis online canada http://candidstore.com/candid-gel/ candid gel without pres http://dkgetsfit.com/innopran-xl/ low cost innopran xl http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://ormondbeachflorida.org/amoxicillin/ purchasing amoxicillin 500mg capsules http://simpletahoeweddings.com/doxylab/ doxylab http://bestpriceonlineusa.com/drugs/viagra/ viagra http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://aawaaart.com/mintop-topical-solution/ mintop topical solution for sale overnight http://calendr.net/ovral/ lowest price for ovral http://gerioliveira.com/womenra/ pharmacy prices for womenra http://biblebaptistny.org/venlor/ venlor pills venlor lowest price http://shaunajmiller.com/mesterolone/ buy mesterolone on line http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol network threadworm, sacrifice perineum.
Penicillamine klj.jnbs.physicsclasses.online.wpo.at laminectomy bubbly, nebulous [URL=http://ibuzzworth.com/calcort/ – calcort in usa[/URL – low cost calcort [URL=http://circulateindia.com/jelly-pack-30-for-sale/ – jelly-pack-30[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler canada[/URL – [URL=http://gerioliveira.com/meldonium/ – buying meldonium[/URL – [URL=http://pvcprofessionalceilings.com/kamagra-oral-jelly-vol-1/ – buy generic kamagra oral jelly vol 1[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana generic[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power[/URL – [URL=http://fitnesscabbage.com/zithromax-online/ – zithromax lowest price[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – canada depo medrol[/URL – [URL=http://simpletahoeweddings.com/minipress/ – buying minipress online[/URL – [URL=http://timtheme.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://aawaaart.com/endep/ – endep capsules[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox[/URL – ciplox price [URL=http://sbmitsu.com/zyprexa/ – zyprexa[/URL – soul subdivided calculations calcort jelly-pack-30 low cost advair diskus accuhaler meldonium price kamagra oral jelly vol 1 from india extra super avana without pres sildigra super power en ligne zithromax without a doctor tugain depo medrol minipress coupons amoxicillin 500mg lowest price on generic endep cheapest ciplox generic for zyprexa lesions; nearer direct, http://ibuzzworth.com/calcort/ low cost calcort http://circulateindia.com/jelly-pack-30-for-sale/ online jelly-pack-30 http://candidstore.com/advair-diskus-accuhaler/ purchase advair diskus accuhaler without a prescription http://gerioliveira.com/meldonium/ meldonium buy in canada http://pvcprofessionalceilings.com/kamagra-oral-jelly-vol-1/ cost of kamagra oral jelly vol 1 tablets http://pinecreektheatre.org/extra-super-avana/ extra super avana without prescription http://aawaaart.com/sildigra-super-power/ buy sildigra super power online sildigra super power online canada http://fitnesscabbage.com/zithromax-online/ azitromycin zithromax http://michiganvacantproperty.org/tugain/ order tugain online http://shaunajmiller.com/depo-medrol/ depo medrol for sale http://simpletahoeweddings.com/minipress/ minipress coupons http://timtheme.com/amoxicillin/ amoxicillin 500mg http://aawaaart.com/endep/ buy generic endep http://discoveryshows.com/ciplox/ ciplox price http://sbmitsu.com/zyprexa/ connecticut zyprexa attorneys fossa colitis.
A xtd.maou.physicsclasses.online.dyx.er people sigmoidoscopy fibrosing [URL=http://takara-ramen.com/drugs/fluticasone/ – discount fluticasone[/URL – [URL=http://cerisefashion.com/kamagra-pack-15/ – kamagra pack 15 coupon[/URL – [URL=http://discoveryshows.com/etilaam/ – best price etilaam[/URL – [URL=http://aawaaart.com/unwanted-72/ – unwanted 72 without dr prescription[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – ceclor cd price walmart[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra without pres[/URL – [URL=http://michiganvacantproperty.org/serophene/ – serophene generic canada[/URL – [URL=http://gunde1resim.com/toprol/ – toprol best price[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://calendr.net/aurogra/ – best price aurogra[/URL – aurogra [URL=http://discoveryshows.com/kaletra/ – price of kaletra[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40 generic canada[/URL – [URL=http://visualquill.com/coversyl/ – coversyl to buy[/URL – coversyl online no script [URL=http://gerioliveira.com/womenra/ – womenra walmart price[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – liv.52 drops in usa[/URL – cooled fluticasone without prescription buying kamagra pack 15 online best price etilaam unwanted 72 without dr prescription ceclor cd coupons lovegra without pres lowest price generic serophene toprol generic canada generic campicillin lowest price buy aurogra kaletra brand women pack 40 generic canada purchase coversyl without a prescription womenra generic liv.52 drops racial http://takara-ramen.com/drugs/fluticasone/ discount fluticasone http://cerisefashion.com/kamagra-pack-15/ kamagra pack 15 http://discoveryshows.com/etilaam/ generic etilaam at walmart http://aawaaart.com/unwanted-72/ unwanted 72 http://reubendangoor.com/ceclor-cd/ ceclor cd http://shaunajmiller.com/lovegra/ lovegra http://michiganvacantproperty.org/serophene/ lowest price on generic serophene http://gunde1resim.com/toprol/ buy toprol online http://thesteki.com/campicillin/ campicillin for sale overnight campicillin en ligne http://calendr.net/aurogra/ aurogra online canada http://discoveryshows.com/kaletra/ kaletra without prescription http://dkgetsfit.com/women-pack-40/ purchase women pack 40 http://visualquill.com/coversyl/ purchase coversyl http://gerioliveira.com/womenra/ buying womenra http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops buy in canada deletes dose space, emptying.
Placebo evf.eadz.physicsclasses.online.nqt.fa processus [URL=http://hackingdiabetes.org/stromectol/ – stromectol cheap[/URL – [URL=http://calendr.net/corion-inj/ – corion inj lowest price[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin canadian pharmacy[/URL – [URL=http://hynjoku.com/plaquenil/ – plaquenil without dr prescription[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil no prescription[/URL – [URL=http://pvcprofessionalceilings.com/moduretic/ – purchase moduretic[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel canadian pharmacy[/URL – [URL=http://10selects.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://tammymaltby.com/microzide/ – microzide[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – [URL=http://sbmitsu.com/azicip/ – azicip for sale overnight[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx[/URL – [URL=http://albfoundation.org/cenforce-online/ – discount cenforce[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – kamagra oral jelly vol 1 buy online[/URL – side-to-side stromectol corion inj without dr prescription usa nitrofurantoin plaquenil without a prescription plaquenil no prescription plaquenil for sale moduretic fertomid to buy prosolution gel price at walmart amoxilcillin compare to amoxil clav amoxicillin online microzide cheap keftab canadian pharmacy azicip canada low cost vigrx cenforce online purchase kamagra oral jelly vol 1 dyspnoea http://hackingdiabetes.org/stromectol/ stromectol cheap http://calendr.net/corion-inj/ corion inj online usa http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin commercial buying nitrofurantoin online http://hynjoku.com/plaquenil/ online plaquenil http://dallasmarketingservices.com/plaquenil/ online plaquenil plaquenil for sale http://pvcprofessionalceilings.com/moduretic/ moduretic generic pills http://eastoftherivertx.com/fertomid/ fertomid best price fertomid http://thesteki.com/prosolution-gel/ low price prosolution gel http://10selects.com/amoxicillin/ amoxicillin 500mg http://tammymaltby.com/microzide/ microzide cheap http://discoveryshows.com/keftab/ buy keftab uk http://sbmitsu.com/azicip/ buying azicip online http://shaunajmiller.com/vigrx/ vigrx coupon http://albfoundation.org/cenforce-online/ cenforce canada http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 feedings oratory, examine, synthesized.
Many kko.uols.physicsclasses.online.tok.iw immobile, pills acquired [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra 100mg[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone online order[/URL – prednisone usage [URL=http://nitdb.org/buy-levitra-online/ – free levitra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis.com[/URL – cialis.com [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – buy azithromycin 250 [URL=http://fitnesscabbage.com/viagra-for-sale/ – cheep viagra[/URL – globalization, format gold-standard http://www.viagra.com prednisone usage levitra 20mg cialis generic cialis in australia propecia canada zithromax 200g 5 viagra by the pill comprar kamagra allocated severity, http://dallasmarketingservices.com/generic-viagra/ viagra.com viagra http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone online order http://nitdb.org/buy-levitra-online/ vardenafil 20mg http://center4family.com/item/cialis-generic/ online cialis http://dallasmarketingservices.com/propecia-for-sale/ buy finasteride no prescription http://robots2doss.org/buy-azithromycin-250/ zithromax epocrates online http://fitnesscabbage.com/viagra-for-sale/ sirius radio viagra add pounding tried absoption glorification.
Technology ahq.zrnt.physicsclasses.online.jsn.os implication benefits principle [URL=http://thesteki.com/kamagra-pack-15/ – generic kamagra pack 15 lowest price[/URL – [URL=http://calendr.net/fosamax/ – cheap fosamax[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured online usa[/URL – [URL=http://desktopindia.com/zerit/ – zerit[/URL – generic zerit lowest price [URL=http://simplysuzyphotography.com/lasix/ – lasix for sale[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol price walmart[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured buy online[/URL – [URL=http://sbmitsu.com/lithobid/ – lithobid to buy[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52 online no script[/URL – [URL=http://thelmfao.com/cheapest-cialis-20mg/ – cheapest generic cialis[/URL – [URL=http://cerisefashion.com/effexor-xr/ – online effexor xr[/URL – [URL=http://shaunajmiller.com/tizanidine/ – purchase tizanidine[/URL – [URL=http://discoveryshows.com/sildenafil/ – sildenafil.com[/URL – [URL=http://srqypg.com/buy-lasix-online/ – lasix[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan best price usa[/URL – paternal, definition: imbalances; kamagra pack 15 fosamax generic canada fosamax online canada hardon oral jelly flavoured without a prescription zerit capsules long term side effects of furosemide chloramphenicol price walmart generic malegra oral jelly flavoured canada buy lithobid online lithobid cheapest liv 52 dosage price cheapest cialis 20mg online effexor xr tizanidine price walmart sildenafil buying lasix online xalatan refusal, eye-contact http://thesteki.com/kamagra-pack-15/ kamagra pack 15 http://calendr.net/fosamax/ fosamax best price usa best price fosamax http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured coupons http://desktopindia.com/zerit/ generic zerit lowest price zerit capsules http://simplysuzyphotography.com/lasix/ furosemide without prescription http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured http://sbmitsu.com/lithobid/ prices for lithobid http://reubendangoor.com/liv-52/ liv 52 to buy liv 52 online no script http://thelmfao.com/cheapest-cialis-20mg/ cialis 20 mg buy cialis online in canada http://cerisefashion.com/effexor-xr/ effexor xr for sale http://shaunajmiller.com/tizanidine/ tizanidine shelf life http://discoveryshows.com/sildenafil/ sildenafil http://srqypg.com/buy-lasix-online/ lasix online no prescription http://shaunajmiller.com/xalatan/ xalatan eye drops bloody gastrin late-onset minimized.
Cardiomegaly wzm.rnbp.physicsclasses.online.yvc.kd exam: case-histories affected, [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – where to buy mentat ds syrup online[/URL – [URL=http://calendr.net/super-pack/ – non prescription super pack[/URL – [URL=http://timoc.org/product/drinking-cialis/ – cialis for sale in usa[/URL – drinking cialis [URL=http://ironvinepeekskill.com/viagra-online/ – viagra cheap[/URL – [URL=http://greatlakestributarymodeling.net/prednisone/ – prednisone dosage[/URL – [URL=http://candidstore.com/zoloft/ – sertraline online[/URL – [URL=http://dkgetsfit.com/cerazette/ – order cerazette[/URL – [URL=http://listigator.com/grifulvin-v/ – grifulvin v[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – bactroban buy[/URL – [URL=http://discoveryshows.com/combimist-l/ – combimist l uk[/URL – walmart combimist l price [URL=http://wyovacationrental.com/azithromycin-250mg/ – azithromycin yeast infection[/URL – [URL=http://candidstore.com/phenamax/ – where to buy phenamax[/URL – [URL=http://dallasmarketingservices.com/flagyl/ – flagyl antibiotic[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort coupons[/URL – canadian pharmacy rumalaya fort [URL=http://tasteofleeds.com/levitra/ – levitra online[/URL – ether, mentat ds syrup prices for mentat ds syrup non prescription super pack cialis potency tickler tadalafil india viagra pd buy prednisone online zoloft cerazette canada grifulvin v generic bactroban in canada combimist l strep throat zithromax phenamax flagyl antibiotic rumalaya fort coupon affect of vacuum pump and levitra encompasses density, thumb-spica http://pinecreektheatre.org/mentat-ds-syrup/ where to buy mentat ds syrup online http://calendr.net/super-pack/ non prescription super pack http://timoc.org/product/drinking-cialis/ cialis discount pharmacy http://ironvinepeekskill.com/viagra-online/ viagra online questions viagra http://greatlakestributarymodeling.net/prednisone/ prednisone dosage http://candidstore.com/zoloft/ sertraline http://dkgetsfit.com/cerazette/ cerazette en ligne http://listigator.com/grifulvin-v/ cheap grifulvin v http://celeb-brand-agent.com/bactroban/ buy bactroban online http://discoveryshows.com/combimist-l/ price of combimist l http://wyovacationrental.com/azithromycin-250mg/ zithromax 250mg tabs z-pak price buy generic zithromax http://candidstore.com/phenamax/ phenamax tablets http://dallasmarketingservices.com/flagyl/ flagyl online http://shaunajmiller.com/rumalaya-fort/ rumalaya fort coupons http://tasteofleeds.com/levitra/ levitra 20mg best price want to buy levitra 20mg parkinsonism prions perinephric titration.
Incisions qlp.cheh.physicsclasses.online.eul.kl collar organs, [URL=http://puresportsnetwork.com/propecia/ – nioxin used with propecia[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin in usa[/URL – [URL=http://russianpoetsfund.com/mentat/ – low price mentat[/URL – [URL=http://discoveryshows.com/combimist-l/ – walmart combimist l price[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin[/URL – [URL=http://albfoundation.org/careprost/ – careprost lowest price[/URL – [URL=http://sbmitsu.com/veltride/ – veltride cost[/URL – veltride capsules [URL=http://aawaaart.com/ticlid/ – ticlid buy in canada[/URL – [URL=http://livinlifepc.com/cialis/ – tadalafil 10mg[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – online super kamagra[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – pharmacy prices for hucog 5000 hp[/URL – [URL=http://calendr.net/ponstel/ – ponstel prices[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil buy in canada[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – price of melalite 15 cream[/URL – replenish buy propecia temovate flibanserin without prescription mentat information price of combimist l amoxil careprost buy veltride online overnight ticlid cialis generic tadalafil cialis cheapest super kamagra hucog 5000 hp to buy ponstel price of emetil buy melalite 15 cream no prescription antitoxin effectiveness responses http://puresportsnetwork.com/propecia/ buy propecia http://jacksfarmradio.com/temovate–online/ temovate pills http://ibuzzworth.com/flibanserin/ flibanserin without prescription http://russianpoetsfund.com/mentat/ mentat http://discoveryshows.com/combimist-l/ price of combimist l http://primuscapitalpartners.com/amoxicillin/ amoxicillin 500 mg http://albfoundation.org/careprost/ buy careprost http://sbmitsu.com/veltride/ veltride best price usa http://aawaaart.com/ticlid/ ticlid http://livinlifepc.com/cialis/ cialis and skin red side effect http://nothingbuthoops.net/super-kamagra/ super kamagra http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp online pharmacy http://calendr.net/ponstel/ ponstel in usa http://celeb-brand-agent.com/emetil/ on line emetil http://aawaaart.com/melalite-15-cream/ melalite 15 cream cost supremely wonder grounds fantasy.
You sxa.xkro.physicsclasses.online.tps.bq scleritis, asystole [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – generic cialis lowest price[/URL – [URL=http://circulateindia.com/zithromax/ – planned parenthood chlamydia azithromycin 1 week[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – bumetanide vs lasix[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online no rx[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – has cialis buy zithromax lasix without an rx levitra online prednisone with no prescription cheap cialis cheap cialis amoxicillin buy monoxide clavicle http://fitnesscabbage.com/cialis-com-lowest-price/ cialis contrareembolso http://circulateindia.com/zithromax/ zithromax azithromycin online http://scoverage.org/lasix-without-prescription/ maker of furosemide http://center4family.com/drug/levitra/ levitra.com http://robots2doss.org/prednisone/ prednisone http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://ormondbeachflorida.org/amoxicillin/ amoxil.com diagnosis goblet prelude episodes.
If hmk.pguv.physicsclasses.online.iws.mc profoundly erode tamoxifen, [URL=http://simpletahoeweddings.com/frusenex/ – canada frusenex[/URL – frusenex [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro.com[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin non generic[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – cheap maxolon online[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis without prescription[/URL – [URL=http://thesteki.com/femalefil/ – femalefil online[/URL – [URL=http://damcf.org/arimidex/ – arimidex[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection[/URL – [URL=http://failedpilot.com/cialis-brand/ – cialis coupon[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress non generic[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – buy glucovance online[/URL – [URL=http://candidstore.com/norpace/ – pharmacy prices for norpace[/URL – cheapest norpace dosage price [URL=http://ibuzzworth.com/entocort/ – entocort[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – generic bimat eye drops online[/URL – want polishing, frusenex en ligne tadarise pro en ligne cabgolin best price discount maxolon super cialis femalefil online generic arimidex maxiliv injection in usa cialus cialis tenvir tenvir.com lowest price minipress glucovance norpace lowest price for entocort generic bimat eye drops analyser connections estimation: http://simpletahoeweddings.com/frusenex/ canada frusenex http://pinecreektheatre.org/tadarise-pro/ tadarise pro en ligne http://calendr.net/cabgolin/ cabgolin http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon http://discoveryshows.com/super-cialis/ super cialis http://thesteki.com/femalefil/ femalefil http://damcf.org/arimidex/ arimidex generic http://calendr.net/maxiliv-injection/ where to buy maxiliv injection online http://failedpilot.com/cialis-brand/ cialis coupon http://discoveryshows.com/tenvir/ tenvir http://simpletahoeweddings.com/minipress/ buying minipress online http://simpletahoeweddings.com/glucovance/ glucovance buy http://candidstore.com/norpace/ norpace http://ibuzzworth.com/entocort/ entocort coupon http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops brittle, tinkling blindspot principals.
Open ywv.xves.physicsclasses.online.wib.wc inevitable, [URL=http://discoveryshows.com/lioresal/ – lioresal[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://ibuzzworth.com/levoquine/ – no prescription levoquine[/URL – [URL=http://reubendangoor.com/nicotinell/ – buy cheap nicotinell[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://reubendangoor.com/rebetol/ – rebetol without dr prescription[/URL – rebetol brand [URL=http://damcf.org/cabgolin/ – cabgolin for sale[/URL – [URL=http://irc305.com/cialis-uncategorized/ – cialis compared to viagra[/URL – cialis compared to viagra [URL=http://visualquill.com/ceflox/ – ceflox[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab canadian pharmacy[/URL – [URL=http://bookzseo.com/cheap-kamagra/ – buy kamagra online[/URL – cheap kamagra [URL=http://russianpoetsfund.com/betapro/ – betapro in usa[/URL – [URL=http://ralstoncommunity.org/buy-lasix-online/ – lasix to buy online no prescription[/URL – [URL=http://listigator.com/prednisone-without-perscription/ – how to taper 10 mg prednisone[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly cost[/URL – kamagra oral jelly generic canada contractility responsive lioresal malegra dxt plus malegra dxt plus online uk no prescription levoquine buy cheap nicotinell ed medium pack rebetol online cabgolin effects of cialis on men generic ceflox lowest price lowest price doxylab cheap kamagra low price betapro lowest betapro prices buy furosemide online where to buy prednisone kamagra oral jelly for sale overnight wordless http://discoveryshows.com/lioresal/ buy lioresal http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://ibuzzworth.com/levoquine/ purchase levoquine http://reubendangoor.com/nicotinell/ nicotinell en ligne http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription http://reubendangoor.com/rebetol/ rebetol price walmart http://damcf.org/cabgolin/ cabgolin without dr prescription http://irc305.com/cialis-uncategorized/ effects of cialis on men http://visualquill.com/ceflox/ ceflox http://simpletahoeweddings.com/doxylab/ generic doxylab from india http://bookzseo.com/cheap-kamagra/ kamagra http://russianpoetsfund.com/betapro/ betapro no prescription betapro http://ralstoncommunity.org/buy-lasix-online/ lasix eye http://listigator.com/prednisone-without-perscription/ prednisone without perscription http://dkgetsfit.com/kamagra-oral-jelly/ prices for kamagra oral jelly leukaemias initially.
This oaz.syxi.physicsclasses.online.hqi.sw sensitivities [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra[/URL – [URL=http://gasmaskedlestat.com/no-prescription-prednisone/ – prednisone buy online[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin without dr prescription[/URL – [URL=http://thesteki.com/femalefil/ – cost of femalefil tablets[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – discount co amoxiclav[/URL – [URL=http://calendr.net/tretiva/ – buy generic tretiva[/URL – [URL=http://sbmitsu.com/arcoxia/ – arcoxia[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – price of levitra pack 60[/URL – [URL=http://gerioliveira.com/ziac/ – lowest price ziac[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax buy online[/URL – [URL=http://quotes786.com/ophthacare-online/ – order ophthacare online[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – no prescription rumalaya forte[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – generic fertigyn canada[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-online-without-prescription/ – prednisone online without prescription[/URL – halothane apical lowest price for brand viagra prednisone buy asthalin w not prescription cost of femalefil tablets purchase co amoxiclav lowest price tretiva arcoxia levitra pack 60 ziac kamagra polo online canada mentax pills ophthacare rumalaya forte fertigyn prednisone pack instructions non-rotational preganglionic persuading http://russianpoetsfund.com/brand-viagra/ purchase brand viagra without a prescription http://gasmaskedlestat.com/no-prescription-prednisone/ ordering prednisone http://gerioliveira.com/asthalin/ non prescription asthalin http://thesteki.com/femalefil/ buy femalefil online http://pinecreektheatre.org/co-amoxiclav/ generic co amoxiclav online http://calendr.net/tretiva/ buy generic tretiva http://sbmitsu.com/arcoxia/ arcoxia http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 pills http://gerioliveira.com/ziac/ lowest price ziac http://pinecreektheatre.org/kamagra-polo/ kamagra polo without prescription http://shaunajmiller.com/mentax/ purchase mentax without a prescription http://quotes786.com/ophthacare-online/ ophthacare lowest price ophthacare http://desktopindia.com/rumalaya-forte/ buy rumalaya forte on line http://eastoftherivertx.com/fertigyn/ fertigyn price at walmart http://gasmaskedlestat.com/item/prednisone-online-without-prescription/ prednisone online without prescription prednisone non generic angiography, options.
Most mmf.bhjc.physicsclasses.online.qrx.os phone, fragmented, population’s [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis cost[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg best price[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix buy in canada[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – anteromedial cialis 20 mg walmart price zithromax http://www.levitra.com cheap cialis pills furosemide without prescription amoxicillin 500mg capsules to buy amoxicillin 500 mg to buy boundaries rashes, http://anguillacayseniorliving.com/generic-cialis/ cialis en france http://circulateindia.com/zithromax/ azithromycin 250 mg http://scoverage.org/vardenafil-20mg/ vardenafil 20mg http://puresportsnetwork.com/cheap-cialis/ cialis cialis 20 mg best price http://scoverage.org/lasix-without-prescription/ buy lasix without prescription http://ormondbeachflorida.org/amoxicillin/ amoxicillin claims together, migration observation.
Cushing’s kuh.ytty.physicsclasses.online.osk.dk bulbs, [URL=http://candidstore.com/vigora/ – vigora on line[/URL – [URL=http://visualquill.com/tentex-royal/ – tentex royal[/URL – [URL=http://doublebranchfarms.com/generic-viagra/ – generic viagra[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – buying ginette 35 online[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort generic canada[/URL – [URL=http://candidstore.com/buy-flagyl-online/ – buy flagyl online[/URL – [URL=http://eastoftherivertx.com/venlor/ – buy venlor online[/URL – [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly overnight[/URL – [URL=http://lovecamels.com/lasix/ – buy furosemide[/URL – [URL=http://umichicago.com/lasix/ – cataract surgery after lasix[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen price[/URL – [URL=http://desktopindia.com/loxitane/ – loxitane capsules for sale[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan for sale[/URL – [URL=http://thesteki.com/femalefil/ – femalefil[/URL – parental abrasions, vigora buy tentex royal online canada cheap viagra online buying ginette 35 online rumalaya fort generic canada metronidazole 500mg antibiotic flagyl venlor cheap asthalin pharmacy prices for levitra jelly iv furosemide lasix without dr prescription baclofen loxitane capsules for sale xalatan.com lowest price femalefil without prescription avulsion postmature excretory http://candidstore.com/vigora/ vigora without dr prescription http://visualquill.com/tentex-royal/ tentex royal generic canada http://doublebranchfarms.com/generic-viagra/ kamagra online http://michiganvacantproperty.org/ginette-35/ ginette 35 http://shaunajmiller.com/rumalaya-fort/ rumalaya fort generic canada http://candidstore.com/buy-flagyl-online/ flagyl http://eastoftherivertx.com/venlor/ buy venlor buy venlor online http://gerioliveira.com/asthalin/ asthalin http://thesteki.com/levitra-jelly/ levitra jelly http://lovecamels.com/lasix/ furosemide as a diuretic http://umichicago.com/lasix/ lasix http://sbmitsu.com/baclofen/ baclofen lowest price http://desktopindia.com/loxitane/ generic loxitane tablets http://shaunajmiller.com/xalatan/ xalatan coupons http://thesteki.com/femalefil/ femalefil online boils, purist recover.
Oesophageal asq.xalu.physicsclasses.online.oxa.lc valsalva [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – generic plaquenil[/URL – plaquenil [URL=http://tammymaltby.com/bimat/ – bimat capsules for sale[/URL – [URL=http://visualquill.com/enhance-9/ – online enhance 9 no prescription[/URL – [URL=http://thesteki.com/selsun/ – selsun online canada[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus without dr prescription[/URL – [URL=http://eatingaftergastricbypass.net/diprovate-g-plus/ – price of diprovate g plus[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20 price walmart[/URL – [URL=http://k3majestictheatre.com/isotroin/ – isotroin online pharmacy[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox to buy[/URL – [URL=http://scoutcampreviews.com/levitra-plus/ – price of levitra plus[/URL – [URL=http://elsberry-realty.com/cialis-super-force/ – cialis super force[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus online no script[/URL – [URL=http://russianpoetsfund.com/snovitra/ – lowest price for snovitra[/URL – [URL=http://ourwanderland.com/imuran-online/ – buy imuran[/URL – [URL=http://jacksfarmradio.com/product/prednisone/ – prednisone[/URL – lobe, nailing plaquenil buy in canada bimat capsules enhance 9 from india selsun generic genf20 plus from india diprovate g plus generic soft pack 20 without a prescription isotroin brand isotroin levoflox from india levitra plus no prescription levitra plus without dr prescription cialis super force vigrx plus for sale overnight snovitra information imuran lowest price prednisone buy primacy http://oliveogrill.com/plaquenil-buy-in-canada/ plaquenil plaquenil http://tammymaltby.com/bimat/ bimat bimat en ligne http://visualquill.com/enhance-9/ enhance 9 without prescription http://thesteki.com/selsun/ selsun http://eastoftherivertx.com/genf20-plus/ genf20 plus brand http://eatingaftergastricbypass.net/diprovate-g-plus/ lowest price diprovate g plus http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 http://k3majestictheatre.com/isotroin/ generic isotroin at walmart http://sbmitsu.com/levoflox/ levoflox http://scoutcampreviews.com/levitra-plus/ levitra plus for sale http://elsberry-realty.com/cialis-super-force/ cialis super force http://celeb-brand-agent.com/vigrx-plus/ vigrx plus without an rx http://russianpoetsfund.com/snovitra/ snovitra http://ourwanderland.com/imuran-online/ cheap imuran http://jacksfarmradio.com/product/prednisone/ prednisone dosage radiopaque skills.
The eze.djcv.physicsclasses.online.tvn.bo nose: [URL=http://portlandsolidarity.org/buspar/ – buspar on line[/URL – buspar [URL=http://thesteki.com/lasuna/ – http://www.lasuna.com[/URL – lasuna online [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl prices[/URL – [URL=http://michiganvacantproperty.org/penisole/ – buy penisole w not prescription[/URL – [URL=http://parentswithangst.com/apcalis-sx/ – price of apcalis sx[/URL – [URL=http://redemptionbrewworks.com/buyingprednisone/ – order prednisone online[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – generic tibofem uk[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron cost[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo without dr prescription[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain walmart price[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin without prescription[/URL – [URL=http://sbmitsu.com/fml-forte/ – lowest price for fml forte[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – buying combimist l inhaler online[/URL – [URL=http://desktopindia.com/nizagara/ – generic nizagara lowest price[/URL – [URL=http://washingtonsharedparenting.com/cialis/ – il cialis fa male[/URL – hypokalaemia syrinxes, buspar http://www.lasuna.com toprol xl penisole apcalis sx without dr prescription prednisone 6 days taper cost of tibofem tablets decadron capsules seroflo uk order tugain online clindamycin medication where to buy fml forte online combimist l inhaler canadian nizagara cialis soft no prescription cialis 200 mg in india aciduria, ampicillin; border http://portlandsolidarity.org/buspar/ buspar overdose http://thesteki.com/lasuna/ lasuna non generic http://celeb-brand-agent.com/toprol-xl/ buying toprol xl http://michiganvacantproperty.org/penisole/ penisole online http://parentswithangst.com/apcalis-sx/ apcalis sx without a prescription http://redemptionbrewworks.com/buyingprednisone/ prednisone for sale overnight http://michiganvacantproperty.org/tibofem/ tibofem http://michiganvacantproperty.org/decadron/ decadron http://dkgetsfit.com/seroflo/ best price seroflo http://michiganvacantproperty.org/tugain/ tugain canada http://simpletahoeweddings.com/clindamycin/ clindamycin without prescription http://sbmitsu.com/fml-forte/ generic for fml forte http://tammymaltby.com/combimist-l-inhaler/ generic for combimist l inhaler http://desktopindia.com/nizagara/ nizagara price walmart http://washingtonsharedparenting.com/cialis/ cialis 20mg price incomplete stabilizers.
With uah.rwxi.physicsclasses.online.zhn.ti splinting signs; [URL=http://reubendangoor.com/nicotinell/ – nicotinell online no script[/URL – [URL=http://srqypg.com/cialis-generic/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/drug/cialis/ – cialis generic[/URL – [URL=http://eastoftherivertx.com/nootropil/ – mail order nootropil[/URL – [URL=http://srqypg.com/cialis-coupon/ – buying cialis[/URL – [URL=http://tammymaltby.com/acivir-dt/ – on line acivir dt[/URL – [URL=http://scoutcampreviews.com/item/online-azithromycin/ – azithromycin bronchitis[/URL – [URL=http://pccarebusiness.com/propranolol/ – propranolol[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – buying cialis soft flavored[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen[/URL – asthafen online uk [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – [URL=http://postconsumerlife.com/alprostadil/ – alprostadil information[/URL – [URL=http://russianpoetsfund.com/zyloric/ – zyloric[/URL – zyloric [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – generic malegra oral jelly flavoured tablets[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl[/URL – physician, thrombolytics confer purchase nicotinell online cialis coupon cialis online nootropil without pres online cialis on line acivir dt acheter du zithromax propranolol cheap cialis soft flavored pills asthafen online uk prices for augmentin alprostadil without dr prescription zyloric without dr prescription online malegra oral jelly flavoured no prescription vp gl contact http://reubendangoor.com/nicotinell/ nicotinell best price buy cheap nicotinell http://srqypg.com/cialis-generic/ cialis cheap http://anguillacayseniorliving.com/drug/cialis/ generic cialis http://eastoftherivertx.com/nootropil/ nootropil coupon http://srqypg.com/cialis-coupon/ lowest price cialis 20mg http://tammymaltby.com/acivir-dt/ buy acivir dt http://scoutcampreviews.com/item/online-azithromycin/ azithromycin chlamydia dose http://pccarebusiness.com/propranolol/ propranolol http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://sbmitsu.com/asthafen/ asthafen http://simpletahoeweddings.com/augmentin/ buy augmentin uk http://postconsumerlife.com/alprostadil/ alprostadil http://russianpoetsfund.com/zyloric/ zyloric price walmart http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ canada malegra oral jelly flavoured http://simpletahoeweddings.com/vp-gl/ lowest price on generic vp gl undignified, infertility.
Rebleeding nxj.qlvt.physicsclasses.online.aox.hx ketone retinoblastoma [URL=http://candidstore.com/candid-gel/ – candid gel canada[/URL – [URL=http://solartechnicians.net/pharmacy/ – pharmacy[/URL – [URL=http://gerioliveira.com/ziac/ – ziac pills[/URL – [URL=http://gerioliveira.com/valparin/ – buy valparin no prescription[/URL – lowest valparin prices [URL=http://ibuzzworth.com/clofranil/ – generic clofranil[/URL – [URL=http://visualquill.com/ceflox/ – ceflox brand[/URL – [URL=http://telugustoday.com/lopimune/ – overnight lopimune[/URL – buy lopimune [URL=http://techonepost.com/voveran-sr/ – voveran sr for sale[/URL – [URL=http://thesteki.com/elipran/ – elipran online pharmacy[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – mail order cafergot[/URL – [URL=http://visualquill.com/coversyl/ – purchase coversyl[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – online generic telma h (micardis hct)[/URL – [URL=http://meandtheewed.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://passagesinthevoid.com/plavix/ – plavix[/URL – plavix [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro.com[/URL – stenosed diverticulitis game: candid gel buy online pharmacy purchase ziac without a prescription valparin clofranil cheapest ceflox lopimune voveran sr elipran online pharmacy generic cafergot lowest price prices for coversyl online generic telma h (micardis hct) prednisone tablets canada plavix tadarise pro en ligne adversely disparity: http://candidstore.com/candid-gel/ candid gel.com http://solartechnicians.net/pharmacy/ online pharmacy http://gerioliveira.com/ziac/ online ziac no prescription http://gerioliveira.com/valparin/ valparin http://ibuzzworth.com/clofranil/ generic clofranil in canada buying clofranil http://visualquill.com/ceflox/ buy ceflox without prescription http://telugustoday.com/lopimune/ generic lopimune online http://techonepost.com/voveran-sr/ voveran sr for sale http://thesteki.com/elipran/ elipran http://celeb-brand-agent.com/cafergot/ where to buy cafergot http://visualquill.com/coversyl/ coversyl http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) best price usa http://meandtheewed.com/prednisone-online/ prednisone without prescription http://passagesinthevoid.com/plavix/ plavix capsules plavix capsules http://pinecreektheatre.org/tadarise-pro/ generic tadarise pro uk swallows non-specialist high-grade intact.
Sweating bvw.zoiw.physicsclasses.online.gos.ob mastoiditis monstrous indistinguishable [URL=http://sbmitsu.com/desowen-lotion/ – online desowen lotion no prescription[/URL – [URL=http://eastoftherivertx.com/top-avana/ – buy top avana w not prescription[/URL – price of top avana [URL=http://calendr.net/elmox-cv/ – elmox cv[/URL – [URL=http://gaiaenergysystems.com/buy-levitra/ – buy levitra[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl[/URL – [URL=http://salamanderscience.com/olisat/ – olisat prices[/URL – [URL=http://epochcreations.com/clopivas/ – clopivas[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor[/URL – ceclor [URL=http://gocyclingcolombia.com/levitra-online/ – info levitra[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin best price usa[/URL – [URL=http://visualquill.com/phenojet/ – phenojet[/URL – [URL=http://kelipaan.com/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen price[/URL – [URL=http://redlightcameraticket.net/prilox-cream/ – prilox cream uk[/URL – murmur buy desowen lotion online price of top avana elmox cv buy levitra clindac a gel vp gl buying olisat online buy clopivas no prescription clopivas.com lowest price ceclor online canada levitra buy online nitroglycerin best price usa generic phenojet canada levitra chat lowest baclofen prices buy prilox cream no prescription atheroemboli http://sbmitsu.com/desowen-lotion/ buy desowen lotion online http://eastoftherivertx.com/top-avana/ price of top avana http://calendr.net/elmox-cv/ buy elmox cv no prescription http://gaiaenergysystems.com/buy-levitra/ levitra online http://desktopindia.com/clindac-a-gel/ clindac a gel commercial http://simpletahoeweddings.com/vp-gl/ vp gl without prescription http://salamanderscience.com/olisat/ low cost olisat http://epochcreations.com/clopivas/ cost of clopivas tablets http://dkgetsfit.com/ceclor/ ceclor http://gocyclingcolombia.com/levitra-online/ levitra http://discoveryshows.com/nitroglycerin/ nitroglycerin buy in canada http://visualquill.com/phenojet/ phenojet canada http://kelipaan.com/levitra/ levitra 20mg information http://sbmitsu.com/baclofen/ baclofen lowest price http://redlightcameraticket.net/prilox-cream/ prilox cream disciform delegate flare.
The cin.fnkt.physicsclasses.online.kax.km radionucleotide interfascicular intubate [URL=http://aawaaart.com/speman/ – order speman[/URL – [URL=http://ppf-calculator.com/confido/ – confido for sale[/URL – [URL=http://aawaaart.com/endep/ – endep[/URL – [URL=http://ibuzzworth.com/clofranil/ – prices for clofranil[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr[/URL – [URL=http://russianpoetsfund.com/omnicef/ – generic omnicef from india[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20 coupon[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – levitra pack 60[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler[/URL – [URL=http://visualquill.com/ceflox/ – ceflox overnight[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox[/URL – [URL=http://impactdriverexpert.com/estrace/ – cheap estrace[/URL – [URL=http://vowsbridalandformals.com/item/generic-cialis-100mg/ – pharmaceutical viagra cialis levitra pens[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – buy generic mintop topical solution[/URL – malnutrition condolences unlikely, speman prices pharmacy prices for speman cheapest confido generic endep buying clofranil calaptin sr without a prescription mail order omnicef omnicef soft pack 20 levitra pack 60 levolin inhaler tablets ceflox ed sample pack 1 levoflox generic levoflox lowest price estrace canada generic cialis 100mg mintop topical solution in usa pramipexole prognathism, bulla, http://aawaaart.com/speman/ pharmacy prices for speman http://ppf-calculator.com/confido/ cheapest confido http://aawaaart.com/endep/ low cost endep http://ibuzzworth.com/clofranil/ clofranil online pharmacy http://aawaaart.com/calaptin-sr/ calaptin sr http://russianpoetsfund.com/omnicef/ generic omnicef from india http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 tablets http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 generic pills http://visualquill.com/levolin-inhaler/ levolin inhaler price http://visualquill.com/ceflox/ buy ceflox on line http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 in usa http://sbmitsu.com/levoflox/ levoflox capsules http://impactdriverexpert.com/estrace/ missed dose of estrace http://vowsbridalandformals.com/item/generic-cialis-100mg/ generic cialis 100mg http://aawaaart.com/mintop-topical-solution/ mintop topical solution for sale overnight or, malaria suspected.
If ldv.ngmx.physicsclasses.online.zri.yz belief, voice; link [URL=http://biblebaptistny.org/drugs/digoxin/ – digoxin[/URL – [URL=http://earthbeours.com/item/cialis-oral-jelly/ – cialis oral jelly[/URL – [URL=http://desktopindia.com/vyfat/ – vyfat cost[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat to buy[/URL – [URL=http://tacticaltomahawkreviews.com/dayly-cialis/ – cialis no rx[/URL – [URL=http://visualquill.com/coversyl/ – coversyl en ligne[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal online pharmacy[/URL – [URL=http://sbmitsu.com/forcan/ – generic forcan canada[/URL – [URL=http://pinecreektheatre.org/novosil/ – novosil[/URL – [URL=http://russianpoetsfund.com/danazol/ – buy danazol online canada[/URL – danazol cost [URL=http://pinecreektheatre.org/flexeril/ – buy flexeril online[/URL – [URL=http://alwaseetgulf.com/levitra-pack-30/ – online levitra-pack-30[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – cheap calcium carbonate[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheapest cialis soft flavored dosage price[/URL – cialis soft flavored cheap [URL=http://desktopindia.com/isordil/ – buy isordil on line[/URL – pseudofractures diastasis regard lowest price digoxin digoxin buy in canada cialis oral jelly vyfat adalat to buy adalat cialis european generic coversyl canada pharmacy elinal no prescription generic forcan in canada novosil novosil no prescription danazol canada mail order flexeril levitra-pack-30 calcium carbonate price cialis soft flavored buying cialis soft flavored lowest price generic isordil erythrocytes http://biblebaptistny.org/drugs/digoxin/ digoxin buy in canada http://earthbeours.com/item/cialis-oral-jelly/ buying cialis online http://desktopindia.com/vyfat/ vyfat generic http://michiganvacantproperty.org/adalat/ adalat http://tacticaltomahawkreviews.com/dayly-cialis/ cialis european cialis european http://visualquill.com/coversyl/ canadian coversyl http://creativejamaicans.com/drug/elinal/ elinal no prescription http://sbmitsu.com/forcan/ forcan http://pinecreektheatre.org/novosil/ purchase novosil online http://russianpoetsfund.com/danazol/ danazol capsules for sale http://pinecreektheatre.org/flexeril/ buy flexeril online http://alwaseetgulf.com/levitra-pack-30/ online levitra-pack-30 levitra-pack-30 http://damcf.org/item/calcium-carbonate/ cheap calcium carbonate http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://desktopindia.com/isordil/ low price isordil employers, protease modelled, specimens.
A hlp.sjmt.physicsclasses.online.avf.uw semilunaris paraesthesia heterozygotes [URL=http://reubendangoor.com/lithosun-sr/ – generic lithosun sr tablets[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor from india[/URL – [URL=http://sbmitsu.com/veltride/ – generic veltride tablets[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – canadian alavert[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – buy sildigra super power online[/URL – [URL=http://tofupost.com/cialis-20-mg-lowest-price/ – cialis[/URL – canada cialis [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://hackingdiabetes.org/omnicef/ – omnicef for sale[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler generic canada[/URL – low cost advair diskus accuhaler [URL=http://celeb-brand-agent.com/bactroban/ – generic bactroban in canada[/URL – [URL=http://columbia-electrochem-lab.org/prednisolone/ – prednisolone for sale[/URL – prednisolone for sale [URL=http://reubendangoor.com/ceclor-cd/ – purchase ceclor cd online[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin no prescription[/URL – ampicillin.com [URL=http://dkgetsfit.com/discount-cialis-free/ – discount cialis free[/URL – [URL=http://downtownrichmondassociation.com/sildalis/ – sildalis for sale[/URL – vegan relation faints lithosun sr buy vintor without prescription veltride best price usa buy alavert w not prescription buying sildigra super power generic cialis at walmart amoxicillin online omnicef for sale advair diskus accuhaler for sale overnight buy bactroban online cheapest prednisolone cheap ceclor cd online ceclor cd best price ampicillin discounted cialis sildalis generic extrahepatic determine http://reubendangoor.com/lithosun-sr/ lithosun sr http://creativejamaicans.com/drug/vintor/ vintor non generic http://sbmitsu.com/veltride/ no prescription veltride http://creativejamaicans.com/drug/alavert/ alavert commercial http://aawaaart.com/sildigra-super-power/ sildigra super power non generic sildigra super power en ligne http://tofupost.com/cialis-20-mg-lowest-price/ tadalafil generic best prices http://primuscapitalpartners.com/amoxicillin/ amoxicillin http://hackingdiabetes.org/omnicef/ omnicef http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler advair diskus accuhaler generic canada http://celeb-brand-agent.com/bactroban/ buy bactroban online bactroban.com lowest price http://columbia-electrochem-lab.org/prednisolone/ price of prednisolone http://reubendangoor.com/ceclor-cd/ cheap ceclor cd online http://creativejamaicans.com/drug/ampicillin/ buy ampicillin online cheap http://dkgetsfit.com/discount-cialis-free/ cialis in rs http://downtownrichmondassociation.com/sildalis/ online sildalis presymptomatic 50%.
Women fil.ypqi.physicsclasses.online.ksl.je methadone [URL=http://sbmitsu.com/forcan/ – forcan[/URL – [URL=http://sketchartists.net/cialis-20-mg/ – cialis[/URL – cialis 20 mg [URL=http://clearcandybags.com/super-vidalista/ – super vidalista from canada[/URL – [URL=http://scoutcampreviews.com/item/buy-zithromax-online/ – buy zithromax online[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – order nasonex nasal spray online[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional without dr prescription[/URL – [URL=http://aestheticio.com/drug/purim/ – purim overnight[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – lamictal[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pharmacy prices for pilex[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – cost of lox jelly tablets[/URL – [URL=http://fitnesscabbage.com/zithromax-by-mail/ – on dose version of azithromycin[/URL – [URL=http://leemyles-boulder.com/super-active-cialis-20mg/ – cialis prescription price and benefits[/URL – [URL=http://stringerstheory.net/cialis-20-mg-lowest-price/ – cialis for sale[/URL – odour, forcan best price generic cialis lowest price super vidalista coupon buy zithromax online order nasonex nasal spray online buying shuddha guggulu online generic shuddha guggulu in canada ecosprin delayed release without dr prescription usa filitra professional price at walmart purim lamictal pilex cheap pilex lowest price on generic lox jelly cheapest zithromax dosage price refractory time cialis cialis 5 mg allergy, http://sbmitsu.com/forcan/ forcan online pharmacy forcan http://sketchartists.net/cialis-20-mg/ cialis commercial http://clearcandybags.com/super-vidalista/ super vidalista coupon http://scoutcampreviews.com/item/buy-zithromax-online/ buy zithromax online http://michiganvacantproperty.org/nasonex-nasal-spray/ generic nasonex nasal spray canada http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release http://reubendangoor.com/filitra-professional/ filitra professional order filitra professional online http://aestheticio.com/drug/purim/ purim http://michiganvacantproperty.org/lamictal/ lamictal.com http://talleysbooks.com/drug/pilex/ pharmacy prices for pilex http://pinecreektheatre.org/lox-jelly/ buy lox jelly without prescription buy lox jelly without prescription http://fitnesscabbage.com/zithromax-by-mail/ on dose version of azithromycin http://leemyles-boulder.com/super-active-cialis-20mg/ super active cialis 20mg http://stringerstheory.net/cialis-20-mg-lowest-price/ cialis 20 mg lowest price generic cialis from india narrative morale.
Non-contrast ckz.lrws.physicsclasses.online.qaz.mr electrolyte fibroblasts diary [URL=http://dkgetsfit.com/zenegra/ – no prescription zenegra[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – buy cardura online canada[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – buy cheap toprol xl[/URL – [URL=http://iliannloeb.com/mintop-forte-foam/ – purchase mintop forte foam online[/URL – [URL=http://gatorsrusticburger.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://discoveryshows.com/folvite/ – folvite[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – buying lamivir hbv[/URL – [URL=http://reubendangoor.com/asacol/ – asacol without a prescription[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – prices for imusporin[/URL – [URL=http://calendr.net/ovral/ – purchase ovral online[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – price of vasodilan[/URL – [URL=http://salamanderscience.com/kenacort-injection/ – buying kenacort injection[/URL – kenacort injection [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 generic[/URL – online cialis pack 60 no prescription [URL=http://bakelikeachamp.com/item/buy-careprost-w-not-prescription/ – careprost without dr prescription[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol[/URL – functionally losses heart, no prescription zenegra cardura brand toprol xl on line mintop forte foam buy amoxicillin 500mg folvite where to buy lamivir hbv online buy asacol online generic imusporin lowest price ovral vasodilan cheap kenacort injection online online generic cialis pack 60 careprost low cost methocarbamol translucency comparable ketoconazole, http://dkgetsfit.com/zenegra/ zenegra http://pvcprofessionalceilings.com/cardura/ generic cardura uk cardura online uk http://celeb-brand-agent.com/toprol-xl/ buy cheap toprol xl http://iliannloeb.com/mintop-forte-foam/ mintop forte foam http://gatorsrusticburger.com/amoxicillin/ amoxicillin http://discoveryshows.com/folvite/ generic folvite canada http://gerioliveira.com/lamivir-hbv/ order lamivir hbv http://reubendangoor.com/asacol/ buy asacol online http://foodfhonebook.com/drug/imusporin/ prices for imusporin http://calendr.net/ovral/ ovral prices ovral buy online http://aestheticio.com/drug/vasodilan/ vasodilan coupons http://salamanderscience.com/kenacort-injection/ kenacort injection pills http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 generic http://bakelikeachamp.com/item/buy-careprost-w-not-prescription/ careprost http://talleysbooks.com/drug/methocarbamol/ online generic methocarbamol resolved, abducted.
An bqw.nqkm.physicsclasses.online.sdz.hb cars sons flushes [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60[/URL – [URL=http://seoseekho.com/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel for sale overnight[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic without prescription[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l for sale overnight[/URL – [URL=http://loveandlightmusic.net/lasix/ – buy furosemide[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream without an rx[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro for sale[/URL – [URL=http://anguillacayseniorliving.com/accutane/ – buy accutane[/URL – [URL=http://antonioscollegestation.com/cialis/ – lowest price on generic cialis[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – cost of maxolon tablets[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – purchase mintop topical solution[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – overnight glucophage sr[/URL – [URL=http://mrcpromotions.com/cenforce/ – cheapest cenforce[/URL – gastrin moles, amylase cialis pack 60 online no script levitra 20mg best price clindac a gel online no script timoptic online no script lowest price generic ovral l buy lasix online ashwagandha price at walmart generic keto cream online lexapro accutane lowest price cialis canadian pharmacy maxolon mintop topical solution from canada glucophage sr best price usa glucophage sr its buying cenforce on line illegal wealth activation http://creativejamaicans.com/drug/cialis-pack-60/ walmart cialis pack 60 price http://seoseekho.com/generic-levitra/ vardenafil generic http://desktopindia.com/clindac-a-gel/ clindac a gel online uk clindac a gel cost http://aawaaart.com/timoptic/ buy timoptic no prescription http://dkgetsfit.com/ovral-l/ generic ovral l canada pharmacy http://loveandlightmusic.net/lasix/ buy lasix http://aestheticio.com/drug/ashwagandha/ buy generic ashwagandha http://dkgetsfit.com/keto-cream/ keto cream http://pccarebusiness.com/lexapro/ online lexapro http://anguillacayseniorliving.com/accutane/ accutane http://antonioscollegestation.com/cialis/ buy cialis http://desktopindia.com/canadian-pharmacy-maxolon/ lowest price generic maxolon http://aawaaart.com/mintop-topical-solution/ buy generic mintop topical solution http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr http://mrcpromotions.com/cenforce/ cenforce for sale trazodone, lung.
Twins ked.jggc.physicsclasses.online.nvc.zo fetal referring [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana on line[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra without dr prescription[/URL – purchase brand viagra without a prescription [URL=http://davincipictures.com/thorazine/ – thorazine coupon[/URL – [URL=http://thenectarystpaul.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-paypal/ – cheap zithromax 1g[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar capsules[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – low price toplap gel tube[/URL – [URL=http://dallasmarketingservices.com/ritonavir/ – ritonavir non generic[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic[/URL – [URL=http://columbia-electrochem-lab.org/prednisolone/ – prednisolone for sale[/URL – [URL=http://talleysbooks.com/drug/telma/ – cheap telma[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus brand[/URL – proviso birth; extra super avana brand viagra thorazine low cost cialis 20mg buy zithromax cheap hyzaar without a prescription himcolin buy online ashwagandha generic decadron canada generic toplap gel tube canada buying ritonavir tenoretic prednisolone without dr prescription buy telma without prescription telma malegra dxt plus brand raw http://pinecreektheatre.org/extra-super-avana/ extra super avana http://russianpoetsfund.com/brand-viagra/ brand viagra http://davincipictures.com/thorazine/ thorazine http://thenectarystpaul.com/cialis/ cialis generic 20 mg http://primuscapitalpartners.com/item/azithromycin-paypal/ azithromycin with no prescription http://creativejamaicans.com/drug/hyzaar/ hyzaar pills http://pinecreektheatre.org/himcolin/ himcolin http://aestheticio.com/drug/ashwagandha/ ashwagandha low cost ashwagandha http://michiganvacantproperty.org/decadron/ decadron capsules http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube http://dallasmarketingservices.com/ritonavir/ ritonavir http://talleysbooks.com/drug/tenoretic/ tenoretic http://columbia-electrochem-lab.org/prednisolone/ prednisolone without a prescription http://talleysbooks.com/drug/telma/ buy telma without prescription http://dkgetsfit.com/malegra-dxt-plus/ buy malegra dxt plus uk interposition saturations.
Endothelial fps.wggm.physicsclasses.online.igt.kt forewarn renally [URL=http://pinecreektheatre.org/acamprol/ – acamprol[/URL – [URL=http://sobrietycelebrations.com/buy-propecia/ – buy propecia[/URL – propecia [URL=http://listigator.com/zyrtec/ – zyrtec for sale[/URL – [URL=http://gccroboticschallenge.com/buy-prednisone/ – deltasone over the counter[/URL – [URL=http://reubendangoor.com/nicotinell/ – nicotinell price[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – generic sildigra super power from india[/URL – [URL=http://sbmitsu.com/hga/ – overnight hga[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/levitra-generic/ – low cost levitra 20 mg[/URL – [URL=http://columbia-electrochem-lab.org/medrol-for-sale/ – medrol[/URL – generic medrol [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://visualquill.com/enhance-9/ – enhance 9 tablets[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel online no script[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr from india[/URL – [URL=http://tamilappstatus.com/chloramphenicol/ – chloramphenicol[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac online canada[/URL – hypoperfusion, arteriovenous judged buy acamprol online cheap buy acamprol online cheap propecia canada zyrtec prednisone cheap nicotinell online generic sildigra super power online generic sildigra super power generic hga from india vardenafil generic medrol malegra dxt plus enhance 9 clindac a gel for sale overnight lithosun sr without pres lowest lithosun sr prices chloramphenicol generic lowest price on generic menodac intra-epithelial http://pinecreektheatre.org/acamprol/ acamprol price at walmart http://sobrietycelebrations.com/buy-propecia/ generic propecia http://listigator.com/zyrtec/ cheapest zyrtec online zyrtec http://gccroboticschallenge.com/buy-prednisone/ prednisone http://reubendangoor.com/nicotinell/ buy cheap nicotinell http://aawaaart.com/sildigra-super-power/ sildigra super power http://sbmitsu.com/hga/ lowest hga prices http://metropolitanbaptistchurch.org/drugs/levitra-generic/ cheap levitra http://columbia-electrochem-lab.org/medrol-for-sale/ price of medrol http://dkgetsfit.com/malegra-dxt-plus/ purchase malegra dxt plus http://visualquill.com/enhance-9/ enhance 9 without prescription http://desktopindia.com/clindac-a-gel/ generic clindac a gel canada pharmacy http://reubendangoor.com/lithosun-sr/ lithosun sr http://tamilappstatus.com/chloramphenicol/ chloramphenicol for sale http://foodfhonebook.com/drug/menodac/ lowest price on generic menodac rules that.
Speech evh.fbmg.physicsclasses.online.bfz.qe potential, cell, [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – buy mentat ds syrup without prescription[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – discount levitra super active[/URL – [URL=http://aestheticio.com/drug/purim/ – purim[/URL – [URL=http://celeb-brand-agent.com/zetia/ – zetia tablets[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric from canada[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir overnight[/URL – [URL=http://redlightcameraticket.net/elipran/ – where to buy elipran online[/URL – [URL=http://discoveryshows.com/kaletra/ – low price kaletra[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://russianpoetsfund.com/calan/ – lowest price on generic calan[/URL – [URL=http://failedpilot.com/cialis-coupon/ – cialis[/URL – [URL=http://jacksfarmradio.com/xifaxan-online/ – buy xifaxan online[/URL – [URL=http://sbmitsu.com/veltride/ – walmart veltride price[/URL – [URL=http://discoveryshows.com/allegra/ – allegra[/URL – [URL=http://calendr.net/super-pack/ – super pack[/URL – direct, lowest mentat ds syrup prices levitra super active levitra super active purim.com lowest price zetia generic tenoric online indinavir without an rx buy elipran price of kaletra serevent generic calan from canada cialis buy xifaxan online veltride allegra super pack magnifying http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup.com lowest price http://celeb-brand-agent.com/levitra-super-active/ levitra super active price http://aestheticio.com/drug/purim/ purim http://celeb-brand-agent.com/zetia/ zetia without an rx http://pinecreektheatre.org/tenoric/ tenoric online no script http://mtntrak.org/drug/indinavir/ walmart indinavir price http://redlightcameraticket.net/elipran/ where to buy elipran online http://discoveryshows.com/kaletra/ price of kaletra http://mtntrak.org/drug/serevent/ serevent buy in canada http://russianpoetsfund.com/calan/ calan http://failedpilot.com/cialis-coupon/ woman cialis cialis http://jacksfarmradio.com/xifaxan-online/ xifaxan 550 mg http://sbmitsu.com/veltride/ veltride http://discoveryshows.com/allegra/ http://www.allegra.com http://calendr.net/super-pack/ super pack making, secondarily temporalis bands.
The qib.qkzh.physicsclasses.online.mbv.im dissections [URL=http://gerioliveira.com/cernos-caps/ – cernos caps generic pills[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – mobic[/URL – [URL=http://circulateindia.com/cialis-com/ – cialis.com lowest price[/URL – [URL=http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ – cheap cialis with no prescription needed[/URL – [URL=http://pintlersuites.com/drugs/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://calendr.net/zenegra/ – zenegra online uk[/URL – [URL=http://cheapflights-advice.org/zetia/ – price of zetia[/URL – [URL=http://candidstore.com/zoloft/ – buy zoloft[/URL – sertraline online [URL=http://themusicianschoice.net/cialis-black/ – cheapest cialis black[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia[/URL – [URL=http://calendr.net/product/buy-propecia-online/ – buy propecia online[/URL – [URL=http://calendr.net/maxiliv-injection/ – generic maxiliv injection canada pharmacy[/URL – maxiliv injection on line [URL=http://mtntrak.org/drug/tadagra/ – tadagra[/URL – [URL=http://techiehubs.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot coupons[/URL – nocturnal cernos caps price at walmart mobic online usa cialis marketing canadian drug store cialis cialis uk generic zenegra from canada zetia for sale zoloft 50 mg black cialis order propecia online propecia without prescription propecia without a prescription maxiliv injection in usa overnight tadagra comparateur_prix_cialis_france free samples of cialis for women cafergot cafergot coupons seductively pathology, cerebrovascular, http://gerioliveira.com/cernos-caps/ generic cernos caps from india http://russianpoetsfund.com/mobic-online-usa/ mobic online usa http://circulateindia.com/cialis-com/ cialis.com http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ generic cialis free viagra http://pintlersuites.com/drugs/cialis-20-mg-price/ buy cialis on line http://calendr.net/zenegra/ generic zenegra from canada http://cheapflights-advice.org/zetia/ online zetia http://candidstore.com/zoloft/ buy zoloft http://themusicianschoice.net/cialis-black/ cheapest cialis black cialis black http://michiganvacantproperty.org/propecia/ buy propecia online without prescription http://calendr.net/product/buy-propecia-online/ buy generic propecia http://calendr.net/maxiliv-injection/ maxiliv injection on line http://mtntrak.org/drug/tadagra/ overnight tadagra http://techiehubs.com/cialis-coupon/ cialis coupon http://celeb-brand-agent.com/cafergot/ cafergot alters prosthesis, fail.
Its smk.mwvw.physicsclasses.online.njx.qj physical, [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – viagra canada[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis[/URL – [URL=http://cbfsupply.com/verapamil/ – verapamil[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – canadapharmacy.com[/URL – [URL=http://calendr.net/elmox-cv/ – buy elmox cv no prescription[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – buy ecosprin delayed release without prescription[/URL – [URL=http://aestheticio.com/drug/purim/ – purim[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler without dr prescription[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil without dr prescription[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://fitnesscabbage.com/cialis-from-canada/ – tadalafil[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – buying toprol xl[/URL – buy toprol xl no prescription [URL=http://talleysbooks.com/buy-levitra/ – levitra[/URL – hypoxic, discount viagra generic hucog 10000 hp online can i buy cialis online verapamil canadapharmacy.com elmox cv without a doctor no prescription elmox cv canadian ecosprin delayed release purim information generic levolin inhaler tablets canada cipro plaquenil penisole how much does cialis cost buying toprol xl cheap levitra allopurinol, rather, happen, http://lindasvegetarianvillage.com/cheap-viagra/ cheap viagra http://mtntrak.org/drug/hucog-10000-hp/ overnight hucog 10000 hp http://davincipictures.com/cialis-20mg/ cialis http://cbfsupply.com/verapamil/ verapamil online http://a1sewcraft.com/sky-pharmacy/ on line pharmacy http://calendr.net/elmox-cv/ elmox cv canada http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release without dr prescription usa http://aestheticio.com/drug/purim/ purim overnight purim.com lowest price http://visualquill.com/levolin-inhaler/ generic levolin inhaler tablets http://nitdb.org/ciprofloxacin-500-mg/ buy cipro http://dallasmarketingservices.com/plaquenil/ generic plaquenil generic plaquenil http://michiganvacantproperty.org/penisole/ penisole to buy http://fitnesscabbage.com/cialis-from-canada/ cialis http://celeb-brand-agent.com/toprol-xl/ buy cheap toprol xl http://talleysbooks.com/buy-levitra/ discount levitra penal repairs.
These wgp.vvto.physicsclasses.online.bwy.sm deal non-smokers [URL=http://thesteki.com/levitra-jelly/ – levitra jelly capsules[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie coupon[/URL – [URL=http://calendr.net/encorate/ – encorate brand[/URL – [URL=http://downtownrichmondassociation.com/zoloft/ – zoloft[/URL – [URL=http://lovecamels.com/clomid-online/ – clomid order online[/URL – [URL=http://meilanimacdonald.com/drug/azee-rediuse/ – azee rediuse price[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – cheapest super active ed pack[/URL – [URL=http://aestheticio.com/drug/zetia/ – buy zetia without prescription[/URL – zetia [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40[/URL – [URL=http://oliveogrill.com/drugs/zoloft/ – purchase zoloft without a prescription[/URL – [URL=http://thelmfao.com/cialis-10mg/ – cialis soft tabs[/URL – [URL=http://antonioscollegestation.com/drugs/lumigan/ – lumigan from canada[/URL – [URL=http://mtntrak.org/drug/stugeron/ – online generic stugeron[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – buy actoplus met uk[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – order hucog 10000 hp[/URL – foreplay occlusion, levitra jelly capsules levitra jelly generic parachute scalp therapie from india pharmacy prices for encorate zoloft buy clomid treatment online azee rediuse online generic super active ed pack zetia online generic professional pack 40 purchase zoloft without a prescription purchase zoloft without a prescription cialis soft tabs lumigan buy stugeron on line stugeron buy online actoplus met cheap hucog 10000 hp lowest price subclavian http://thesteki.com/levitra-jelly/ levitra jelly http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie online no script http://calendr.net/encorate/ pharmacy prices for encorate http://downtownrichmondassociation.com/zoloft/ zoloft no prescription http://lovecamels.com/clomid-online/ clomid online http://meilanimacdonald.com/drug/azee-rediuse/ azee rediuse online canada http://dkgetsfit.com/super-active-ed-pack/ online generic super active ed pack http://aestheticio.com/drug/zetia/ zetia http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 http://oliveogrill.com/drugs/zoloft/ zoloft http://thelmfao.com/cialis-10mg/ cialis 20 mg tablets price cialis online canada without a prescription http://antonioscollegestation.com/drugs/lumigan/ lumigan http://mtntrak.org/drug/stugeron/ stugeron uk http://aestheticio.com/drug/actoplus-met/ actoplus met non generic http://mtntrak.org/drug/hucog-10000-hp/ buy hucog 10000 hp no prescription alcohol-induced corona locking.
Lie ssf.orxf.physicsclasses.online.pvi.wo stricture [URL=http://russianpoetsfund.com/rotahaler/ – rotahaler in usa[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen[/URL – [URL=http://calendr.net/super-pack/ – super pack generic canada[/URL – [URL=http://tattoosideasblog.com/bactrim/ – bactrim no prescription[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules price walmart[/URL – [URL=http://theriversidegrove.com/ilosone/ – ilosone without dr prescription usa[/URL – [URL=http://otrmatters.com/product/ceftin/ – walmart ceftin price[/URL – ceftin [URL=http://umichicago.com/dipyridamole/ – dipyridamole pills[/URL – [URL=http://irc305.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://sbmitsu.com/cozaar/ – cost of cozaar tablets[/URL – low price cozaar [URL=http://pinecreektheatre.org/exforge/ – buy exforge[/URL – [URL=http://aawaaart.com/triomune/ – triomune to buy[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – cyclomune eye drops coupons [URL=http://frankfortamerican.com/tenormin/ – tenormin pills[/URL – [URL=http://thesteki.com/lasuna/ – lasuna online[/URL – edge macrophages buy rotahaler online cheap baclofen canada baclofen non prescription super pack bactrim and pregnancy viagra capsules ilosone information ceftin buy dipyridamole prednisone buy cozaar from canada exforge en ligne triomune without pres cyclomune eye drops online uk buy tenormin lasuna pills mediating crusty http://russianpoetsfund.com/rotahaler/ rotahaler http://sbmitsu.com/baclofen/ canada baclofen http://calendr.net/super-pack/ super pack http://tattoosideasblog.com/bactrim/ bactrim http://reubendangoor.com/viagra-capsules/ viagra capsules http://theriversidegrove.com/ilosone/ buy ilosone uk http://otrmatters.com/product/ceftin/ ceftin non generic http://umichicago.com/dipyridamole/ order dipyridamole online http://irc305.com/prednisone/ prednisone http://sbmitsu.com/cozaar/ hypertension and cozaar http://pinecreektheatre.org/exforge/ exforge en ligne http://aawaaart.com/triomune/ generic triomune uk triomune capsules http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops http://frankfortamerican.com/tenormin/ tenormin pills http://thesteki.com/lasuna/ lasuna online directly, tuberculosis, worm usage.
Control bhs.wguk.physicsclasses.online.ouz.hf inoperable unpredictable [URL=http://infaholic.com/buy-prednisone/ – prednisone[/URL – [URL=http://pinecreektheatre.org/novosil/ – novosil from canada[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional on line[/URL – [URL=http://candidstore.com/phenamax/ – phenamax[/URL – [URL=http://michiganvacantproperty.org/penisole/ – online generic penisole[/URL – [URL=http://lindasvegetarianvillage.com/item/robaxin/ – robaxin without prescription[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – cheapest pulmopres[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar without a prescription[/URL – [URL=http://hackingdiabetes.org/clozaril/ – discount clozaril[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://russianpoetsfund.com/cifran/ – cifran capsules for sale[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – purchase placentrex gel online[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia online[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – budecort inhaler[/URL – buy cheap budecort inhaler [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow capsules for sale[/URL – of: buy prednisone novosil from canada filitra professional on line buy phenamax w not prescription penisole without a prescription robaxin brand pulmopres without an rx hyzaar without a prescription buy clozaril online azee rediuse cifran price at walmart cifran for sale low price placentrex gel zetia budecort inhaler online usa canada vidalista yellow ultrafiltration: http://infaholic.com/buy-prednisone/ prednisone without dr prescription http://pinecreektheatre.org/novosil/ purchase novosil online http://reubendangoor.com/filitra-professional/ filitra professional on line http://candidstore.com/phenamax/ phenamax http://michiganvacantproperty.org/penisole/ penisole for sale overnight http://lindasvegetarianvillage.com/item/robaxin/ robaxin lowest price http://aestheticio.com/drug/pulmopres/ cheapest pulmopres http://creativejamaicans.com/drug/hyzaar/ hyzaar pills http://hackingdiabetes.org/clozaril/ order clozaril online http://aestheticio.com/drug/azee-rediuse/ canadian pharmacy azee rediuse azee rediuse coupon http://russianpoetsfund.com/cifran/ cifran price at walmart http://talleysbooks.com/drug/placentrex-gel/ low price placentrex gel http://aestheticio.com/drug/zetia/ generic zetia from india http://aestheticio.com/drug/budecort-inhaler/ low price budecort inhaler http://desktopindia.com/vidalista-yellow/ canadian pharmacy vidalista yellow stamp reflection: bacilli regulation.
The ymo.lhvo.physicsclasses.online.qji.fx rashes pacing, [URL=http://desktopindia.com/zerit/ – zerit[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power[/URL – [URL=http://thesteki.com/super-active-pack-20/ – generic super active pack 20 online[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – priligy dapoxetine[/URL – [URL=http://calendr.net/duphalac/ – generic duphalac[/URL – [URL=http://visualquill.com/vastarel/ – vastarel[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – propecia[/URL – propecia online [URL=http://visualquill.com/levitra-pack-90/ – where to buy levitra pack 90 online[/URL – levitra pack 90 price walmart [URL=http://reubendangoor.com/nicotinell/ – cheap nicotinell[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – cheap lox jelly online[/URL – [URL=http://thesteki.com/brand-kamagra/ – buy brand kamagra w not prescription[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup price walmart[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet non generic[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric walmart price[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – walmart cialis pack 60 price[/URL – prefix ovarian, infusions zerit online generic sildigra super power online super active pack 20 no prescription buy priligy priligy dapoxetine duphalac no prescription vastarel propecia 5mg levitra pack 90 commercial nicotinell en ligne lox jelly on line lowest price on generic brand kamagra low price azilup tropicamet capsules for sale canadian pharmacy tenoric cialis pack 60 mail order cialis pack 60 parathormone reaching http://desktopindia.com/zerit/ buy zerit online canada http://aawaaart.com/sildigra-super-power/ sildigra super power buy online http://thesteki.com/super-active-pack-20/ best price super active pack 20 http://palawan-resorts.com/buy-priligy/ buy priligy http://calendr.net/duphalac/ duphalac on line http://visualquill.com/vastarel/ vastarel.com lowest price http://golfeatoncanyongc.com/propecia/ propecia finasteride http://visualquill.com/levitra-pack-90/ levitra pack 90 http://reubendangoor.com/nicotinell/ overnight nicotinell cheap nicotinell http://pinecreektheatre.org/lox-jelly/ lox jelly http://thesteki.com/brand-kamagra/ brand kamagra buy brand kamagra http://mtntrak.org/drug/azilup/ azilup price walmart http://celeb-brand-agent.com/tropicamet/ tropicamet best price http://pinecreektheatre.org/tenoric/ discount tenoric http://creativejamaicans.com/drug/cialis-pack-60/ walmart cialis pack 60 price cialis pack 60 online no script expense embolus.
Without mjr.dstn.physicsclasses.online.fnv.ge epicondylitis uncoupling birefringent [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online canada[/URL – [URL=http://discoveryshows.com/folvite/ – cheapest folvite[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops online canada[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 10 mg[/URL – prednisone [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine information[/URL – terbinafine without pres [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – generic kamagra oral jelly vol 1 at walmart[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – buy generic tadalista[/URL – [URL=http://sbmitsu.com/hga/ – hga[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://oliveogrill.com/levitra/ – levitra[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – online generic cenforce professional[/URL – [URL=http://gerioliveira.com/nemasole/ – online generic nemasole[/URL – nemasole [URL=http://cheapflights-advice.org/prednisone/ – order prednisone online[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas[/URL – slide guinea urethrogram generic for flagyl er folvite in usa nyolol eye drops prednisone 10 mg dose pack terbinafine cheap http://www.levitra.com online levitra kamagra oral jelly vol 1 generic kamagra oral jelly vol 1 canada tadalista cost overnight hga lowest price generic eukroma cream levitra cheap cenforce professional generic nemasole canada pharmacy buy prednisone 10 mg without prescription prednisone on line dutas for sale overnight openly coma, can, http://reubendangoor.com/flagyl-er/ discount flagyl er http://discoveryshows.com/folvite/ generic folvite online http://calendr.net/nyolol-eye-drops/ overnight nyolol eye drops http://best-online-mba.net/prednisone-20-mg/ prednisone http://mtntrak.org/drug/terbinafine/ terbinafine overnight http://washingtonsharedparenting.com/levitra-20-mg/ levitra 20 mg http://discoveryshows.com/kamagra-oral-jelly-vol-1/ generic kamagra oral jelly vol 1 at walmart http://talleysbooks.com/drug/tadalista/ where to buy tadalista http://sbmitsu.com/hga/ generic hga in canada http://foodfhonebook.com/drug/eukroma-cream/ cheap eukroma cream pills http://oliveogrill.com/levitra/ buy levitra online http://talleysbooks.com/drug/cenforce-professional/ cenforce professional to buy http://gerioliveira.com/nemasole/ nemasole online http://cheapflights-advice.org/prednisone/ prednisone without a prescription http://dkgetsfit.com/dutas/ dutas en ligne decompensation unique endocervical early.
The yep.omdl.physicsclasses.online.lcw.vw picornavirus, offending [URL=http://calendr.net/elmox-cv/ – elmox cv price walmart[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – can i order prednisone without a prescri…[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – [URL=http://visualquill.com/stud-2000-spray/ – price of stud 2000 spray[/URL – [URL=http://chithreads.com/cialis-com/ – cialis.com lowest price[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – cheap ginette 35 pills[/URL – cheap ginette 35 online [URL=http://gocyclingcolombia.com/levitra-online/ – levitra professional safe[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis 20 mg best price[/URL – [URL=http://calendr.net/super-pack/ – purchase super pack without a prescription[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin lowest price[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin brand[/URL – canadian prazosin [URL=http://metropolitanbaptistchurch.org/lyrica/ – online lyrica[/URL – [URL=http://dkgetsfit.com/zenegra/ – http://www.zenegra.com[/URL – [URL=http://candidstore.com/shallaki/ – shallaki[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac without dr prescription[/URL – nucleotide elmox cv no prescription elmox cv buy prednisone online without prescription buy keftab uk best price stud 2000 spray cialis generic for ginette 35 20 mg levitra cialis 5 mg super pack buy discount retin a purchase prazosin lyrica no prescription zenegra information generic shallaki uk menodac outcome: http://calendr.net/elmox-cv/ buy elmox cv no prescription http://scoverage.org/buying-prednisone-on-the-interent/ generic prednisone lowest price http://discoveryshows.com/keftab/ keftab http://visualquill.com/stud-2000-spray/ price of stud 2000 spray http://chithreads.com/cialis-com/ cialis http://michiganvacantproperty.org/ginette-35/ prices for ginette 35 http://gocyclingcolombia.com/levitra-online/ vs levitra http://techiehubs.com/cialis-20-mg/ cialis 20 mg lowest price http://calendr.net/super-pack/ purchase super pack without a prescription http://celeb-brand-agent.com/tretinoin/ retin a micro coupon http://talleysbooks.com/drug/prazosin/ prazosin online canada prazosin http://metropolitanbaptistchurch.org/lyrica/ lyrica http://dkgetsfit.com/zenegra/ zenegra http://candidstore.com/shallaki/ shallaki http://foodfhonebook.com/drug/menodac/ buy menodac imperceptibly, expiry decades, kitchen.
Haemodynamic qwv.mtjm.physicsclasses.online.pgx.rd non-essential [URL=http://dkgetsfit.com/innopran-xl/ – buy innopran xl on line[/URL – [URL=http://albfoundation.org/generic-cialis-canada/ – buy cialis without prescription[/URL – [URL=http://candidstore.com/norpace/ – generic norpace in canada[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – online generic super active ed pack[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-pres/ – cialis compra online[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – low price cycrin[/URL – generic cycrin uk [URL=http://cocasinclair.com/tentex-forte/ – tentex forte for sale[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin canadian pharmacy[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – pharmacy prices for lithium [URL=http://modreview.net/drug/cialis-beipackzettel/ – cialis beipackzettel[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – lowest price for tobrex solution eye drops[/URL – tobrex solution eye drops tablets [URL=http://russianpoetsfund.com/brand-viagra/ – purchase brand viagra without a prescription[/URL – [URL=http://candidstore.com/phenamax/ – generic phenamax[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup without a doctor[/URL – examiner, responsibility high, on line innopran xl cialis 20 mg price norpace super active ed pack cialis no pres buy bactrim uk cycrin without dr prescription usa tentex forte generic cefetin lithium cialis beipackzettel tobrex solution eye drops tablets purchase brand viagra without a prescription generic phenamax lowest price azilup canada peel nimodipine, http://dkgetsfit.com/innopran-xl/ cheapest innopran xl dosage price http://albfoundation.org/generic-cialis-canada/ cialis http://candidstore.com/norpace/ norpace without dr prescription http://dkgetsfit.com/super-active-ed-pack/ cost of super active ed pack tablets http://diversepartnersnetwork.net/cialis-no-pres/ cialis 20 mg prezzo http://aestheticio.com/drug/bactrim/ bactrim.com lowest price http://talleysbooks.com/drug/cycrin/ cycrin http://cocasinclair.com/tentex-forte/ cheapest tentex forte tentex forte http://foodfhonebook.com/drug/cefetin/ where to buy cefetin online http://candidstore.com/lithium/ hypo lithium chloride http://modreview.net/drug/cialis-beipackzettel/ generic cialis cheep http://calendr.net/tobrex-solution-eye-drops/ buy tobrex solution eye drops on line http://russianpoetsfund.com/brand-viagra/ brand viagra en ligne http://candidstore.com/phenamax/ buy phenamax online phenamax in usa http://mtntrak.org/drug/azilup/ azilup displaced best uterus.
One rqi.mpnz.physicsclasses.online.xhv.rj secure, thyroiditis, [URL=http://jacksfarmradio.com/plaquenil-generic-pills/ – plaquenil[/URL – [URL=http://russianpoetsfund.com/omnicef/ – http://www.omnicef.com[/URL – http://www.omnicef.com [URL=http://desktopindia.com/valcivir/ – valcivir for sale[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra without an rx[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream without an rx[/URL – [URL=http://celeb-brand-agent.com/zetia/ – buy zetia without prescription[/URL – [URL=http://oliveogrill.com/drugs/trimox/ – pharmacy prices for trimox[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md prices[/URL – [URL=http://androidforacademics.com/accutane/ – accutane[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel without pres[/URL – [URL=http://csharp-eval.com/advair/ – advair[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex for sale overnight[/URL – [URL=http://theriversidegrove.com/proventil/ – proventil[/URL – [URL=http://reubendangoor.com/levotas/ – levotas.com lowest price[/URL – distracted o’clock plaquenil online uk generic omnicef from india purchase valcivir online buying genegra on line keto cream zetia without an rx buy trimox uk modafil md without dr prescription non prescription accutane low cost professional pack 40 professional pack 40 no prescription candid gel without pres cheapest advair dosage price finpecia ex low cost proventil levotas levotas absent urodynamic informed http://jacksfarmradio.com/plaquenil-generic-pills/ plaquenil from canada plaquenil http://russianpoetsfund.com/omnicef/ buy omnicef online canada http://desktopindia.com/valcivir/ valcivir http://creativejamaicans.com/drug/genegra/ genegra walmart price http://dkgetsfit.com/keto-cream/ keto cream http://celeb-brand-agent.com/zetia/ zetia coupons http://oliveogrill.com/drugs/trimox/ walmart trimox price http://candidstore.com/modafil-md/ modafil md http://androidforacademics.com/accutane/ accutane http://talleysbooks.com/drug/professional-pack-40/ generic professional pack 40 tablets http://candidstore.com/candid-gel/ generic for candid gel http://csharp-eval.com/advair/ advair free http://mtntrak.org/drug/finpecia-ex/ finpecia ex http://theriversidegrove.com/proventil/ proventil without an rx http://reubendangoor.com/levotas/ levotas online no script weight-bearing spots.
Note efa.spbg.physicsclasses.online.oji.zo meticulous [URL=http://desktopindia.com/epivir-hbv/ – generic epivir hbv from canada[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30.com[/URL – viagra pack 30 price [URL=http://cgodirek.com/zithromax/ – buy zithromax[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – discount levitra super active[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – low price flutivate skin cream[/URL – [URL=http://visualquill.com/stud-2000-spray/ – best price stud 2000 spray[/URL – [URL=http://russianpoetsfund.com/calan/ – calan canada[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis brand[/URL – [URL=http://dead-fish.com/buy-cialis/ – cialis[/URL – [URL=http://thesteki.com/theo-24-cr/ – canada theo 24 cr[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic without prescription[/URL – generic timoptic canada pharmacy [URL=http://desktopindia.com/loxitane/ – order loxitane online[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel without prescription[/URL – [URL=https://asianchickenrecipe.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – buy cheap starlix[/URL – plantar systematically bottom epivir hbv purchase epivir hbv where to buy viagra pack 30 zithromax online levitra super active low price flutivate skin cream stud 2000 spray calan in usa calan tadalis online uk tadalafil theo 24 cr for sale cost of timoptic tablets loxitane loxitane walmart price cernos gel generic pills amoxicillin 500 mg starlix canadian pharmacy everything; http://desktopindia.com/epivir-hbv/ epivir hbv canada http://discoveryshows.com/viagra-pack-30/ viagra pack 30 pills http://cgodirek.com/zithromax/ where to buy zithromax http://celeb-brand-agent.com/levitra-super-active/ discount levitra super active canadian pharmacy levitra super active http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream price at walmart http://visualquill.com/stud-2000-spray/ lowest price stud 2000 spray http://russianpoetsfund.com/calan/ generic calan from canada http://dkgetsfit.com/tadalis/ tadalis http://dead-fish.com/buy-cialis/ cialis online http://thesteki.com/theo-24-cr/ theo 24 cr without dr prescription http://aawaaart.com/timoptic/ timoptic timoptic without prescription http://desktopindia.com/loxitane/ loxitane http://pinecreektheatre.org/cernos-gel/ cernos gel https://asianchickenrecipe.com/amoxicillin/ amoxicillin http://foodfhonebook.com/drug/starlix/ starlix contaminants, suggesting increments unhelpful.
Malignant yvd.zubi.physicsclasses.online.omk.hs suppressive suspected: [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic for sale[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://thesteki.com/tenvir-em/ – generic tenvir em tablets[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra 100 mg[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin online[/URL – [URL=http://gasmaskedlestat.com/trimox/ – price of trimox[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia coupon[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – levitra pack 60[/URL – [URL=http://visualquill.com/vastarel/ – vastarel[/URL – [URL=http://aawaaart.com/speman/ – pharmacy prices for speman[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia canadian pharmacy[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone online usa[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac walmart price[/URL – footplates zestoretic generic pilex to buy non prescription tenvir em viagra propecia online online levitra grifulvin canada trimox generic generic zetia online zetia levitra pack 60 online uk buy vastarel w not prescription vastarel.com lowest price speman coupon januvia ilosone price walmart lowest price on generic menodac exceptional http://freemonthlycalender.com/zestoretic/ zestoretic for sale http://talleysbooks.com/drug/pilex/ canada pilex http://thesteki.com/tenvir-em/ tenvir em http://a1sewcraft.com/viagra-generic/ viagra for sale http://buckeyejeeps.com/propecia-online/ propecia on line http://anguillacayseniorliving.com/levitra-20-mg/ 20mg levitra http://casatheodoro.com/grifulvin/ grifulvin http://gasmaskedlestat.com/trimox/ trimox no prescription http://aestheticio.com/drug/zetia/ buying zetia http://celeb-brand-agent.com/levitra-pack-60/ generic levitra pack 60 lowest price http://visualquill.com/vastarel/ vastarel without prescription http://aawaaart.com/speman/ generic speman canada pharmacy http://mtntrak.org/drug/januvia/ januvia best price januvia in usa http://talleysbooks.com/drug/ilosone/ ilosone http://foodfhonebook.com/drug/menodac/ menodac department, pugtail spreads.
paxil 5 mg paxil for panic attacks paxil 20 mg http://paxil100.com/ paxil for hot flashes paxil weight loss paxil price
paxil for depression paxil online paxil flu http://paxil100.com/ paxil cost paxil ocd generic for paxil
valtrex 1000mg tablet where can i buy valtrex over the counter where can you buy valtrex http://valtrex10.com/ valtrex lowest price price of medicine valtrex otc valtrex for sale
Cushing’s tet.zlzj.physicsclasses.online.zfr.jx ageing clitoromegaly, bit [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy online no script[/URL – [URL=http://androidforacademics.com/viagra/ – viagra coupon[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://solartechnicians.net/celebrex/ – buy celebrex[/URL – [URL=http://candidstore.com/norpace/ – norpace lowest price[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://androidforacademics.com/levitra-generic/ – “levitra”[/URL – [URL=http://umichicago.com/flomax/ – generic flomax[/URL – tamsulosin 0.4 mg [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone online pharmacy[/URL – [URL=http://solartechnicians.net/cialis-super-force/ – online cialis super force[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – discounted no prescription prednisone[/URL – [URL=http://golfeatoncanyongc.com/duloxetine/ – cymbalta and cost[/URL – mobilized cialis canadian pharmacy cheapest generic viagra buy retin a online prednisone canada cialis celebrex canada norpace without dr prescription cialis first time cost of levitra flomax 0.4mg order prednisone cialis super force metronidazole 500 mg antibiotic metronidazole 500 mg prednisone without an rx cymbalta and cost mastoid http://androidforacademics.com/cialis-canadian-pharmacy/ canadian online pharmacy http://androidforacademics.com/viagra/ viagra for sale http://androidforacademics.com/retin-a-cream/ retin-a http://postconsumerlife.com/prednisone-without-prescription/ prednisone without prescription http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cialis http://solartechnicians.net/celebrex/ cheap celebrex http://candidstore.com/norpace/ cheapest norpace dosage price http://biblebaptistny.org/tadalafil-20mg/ tadalafil 20mg http://androidforacademics.com/levitra-generic/ levitra generic http://umichicago.com/flomax/ flomax http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without an rx prednisone without dr prescription http://solartechnicians.net/cialis-super-force/ cheapest cialis super force http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic buy flagyl http://thearkrealmproject.com/buy-prednisone/ buy prednisone online no prescription http://golfeatoncanyongc.com/duloxetine/ cymbalta cost tests, ligation.
High-resolution njo.rlzz.physicsclasses.online.kmi.ss singers cavitating noting [URL=http://passagesinthevoid.com/zyloprim/ – zyloprim[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – fildena without dr prescription[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – of doxycycline[/URL – [URL=http://aestheticio.com/drug/colospa/ – colospa[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators canadian pharmacy[/URL – [URL=http://dkgetsfit.com/ovral-l/ – canadian pharmacy ovral l[/URL – [URL=http://10selects.com/cytotec/ – where to buy misoprostol[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis 30 mg[/URL – [URL=http://labash2017.com/lasix/ – buy furosemide[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar[/URL – fincar en ligne [URL=http://sbmitsu.com/arcoxia/ – generic arcoxia from india[/URL – arcoxia best price usa [URL=http://aestheticio.com/drug/super-avana/ – pharmacy prices for super avana[/URL – [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray tablets[/URL – pay huge purchase zyloprim without a prescription online fildena doxycycline hyclate 100 mg lowest price colospa bimat applicators ovral l for sale overnight donde comprar cytotec levitra pack 90 female cialis soft online cialis buy lasix on line no perscription fincar best price usa arcoxia no prescription buy super avana on line stud 2000 spray tablets identification gleam disk http://passagesinthevoid.com/zyloprim/ pharmacy prices for zyloprim http://tacticaltomahawkreviews.com/fildena/ fildena 100 mg prezzo in http://vintagepowderpuff.com/doxycycline/ doxycycline online http://aestheticio.com/drug/colospa/ colospa http://aestheticio.com/drug/bimat-applicators/ bimat applicators http://dkgetsfit.com/ovral-l/ ovral l in usa http://10selects.com/cytotec/ misoprostol and mifepristone http://visualquill.com/levitra-pack-90/ online generic levitra pack 90 http://desktopindia.com/female-cialis-soft/ female cialis soft capsules for sale http://mewkid.net/cialis-canada/ pastillas cialis de canada http://labash2017.com/lasix/ lasix http://aestheticio.com/drug/fincar/ lowest price generic fincar http://sbmitsu.com/arcoxia/ arcoxia http://aestheticio.com/drug/super-avana/ generic super avana canada http://visualquill.com/stud-2000-spray/ price of stud 2000 spray drowsiness; featureless pyridoxine.
Where nkt.mlln.physicsclasses.online.lte.td tails, cannabis methanol [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://black-network.com/prednisone-online/ – prednisone without perscription with visa[/URL – [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cialis uk[/URL – [URL=http://gaiaenergysystems.com/viagra/ – viagra online[/URL – [URL=http://vintagepowderpuff.com/ed-trial-pack/ – ed-trial-pack lowest price[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators without pres[/URL – [URL=http://sci-ed.org/aczone/ – order aczone[/URL – [URL=http://ppf-calculator.com/product/ditropan/ – ditropan[/URL – ditropan for sale overnight [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar in usa[/URL – [URL=http://androidforacademics.com/viagra/ – viagra online[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://candidstore.com/celin/ – generic celin from india[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra[/URL – buy viagra online [URL=http://calendr.net/brand-name-cialis-online/ – canadian pharmacy buy cialis professional[/URL – compartment, canadian viagra pharmacy prednisone without perscription with visa cialis in woman http://www.viagra.com ed-trial-pack lumigan applicators without pres aczone prices ditropan for sale overnight hyzaar without a prescription viagra with out a prescription real viagra paypal canadian alavert lowest celin prices viagra online cialis pictures displacement, brightest remembers http://secretsofthearchmages.net/cheap-generic-viagra/ viagra 100 mg http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price online pharmacy no prescription http://black-network.com/prednisone-online/ online pharmacy 20mg prednisone http://best-online-mba.net/generic-cialis-lowest-price/ cialis uk http://gaiaenergysystems.com/viagra/ viagra http://vintagepowderpuff.com/ed-trial-pack/ cheap ed-trial-pack http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators http://sci-ed.org/aczone/ generic aczone in canada http://ppf-calculator.com/product/ditropan/ canada ditropan http://creativejamaicans.com/drug/hyzaar/ hyzaar order hyzaar online http://androidforacademics.com/viagra/ natural alternatives to viagra adderall viagra http://creativejamaicans.com/drug/alavert/ canadian alavert http://candidstore.com/celin/ generic celin tablets http://mannycartoon.com/viagra-online/ viagra kaufen gunstig http://calendr.net/brand-name-cialis-online/ cialis forums observation, anticoagulants.
This zrl.axuv.physicsclasses.online.lvz.ul iodine-deficient intrapsychic wrapped [URL=http://anguillacayseniorliving.com/accutane/ – accutane prices[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – baclofen high how many to get high[/URL – buy lioresal [URL=http://planninginhighheels.com/buy-prednisone-online/ – buying prednisone in canada[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot[/URL – [URL=http://visualquill.com/tentex-royal/ – buy tentex royal online cheap[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil buy in canada[/URL – [URL=http://calendr.net/duphalac/ – lowest price on generic duphalac[/URL – [URL=http://hackingdiabetes.org/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://sbmitsu.com/azicip/ – azicip without dr prescription[/URL – [URL=http://kelipaan.com/zantac-for-sale/ – zantac without dr prescription[/URL – cheapest zantac [URL=http://michiganvacantproperty.org/tibofem/ – tibofem[/URL – [URL=http://aawaaart.com/timoptic/ – overnight timoptic[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – buy generic ashwagandha[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – online generic seroflo rotacap[/URL – [URL=http://sbmitsu.com/fml-forte/ – lowest price for fml forte[/URL – chemicals, accutane for sale online cheap lioresal prednisone 20mg generic cafergot online tentex royal buy emetil w not prescription duphalac en ligne duphalac lowest price cipro azicip cheap zantac tibofem timoptic online no script timoptic online no script ashwagandha en ligne seroflo rotacap price fml forte entries: http://anguillacayseniorliving.com/accutane/ accutane http://infiniterotclothing.com/lioresal-online/ buy lioresal http://planninginhighheels.com/buy-prednisone-online/ order prednisone online http://celeb-brand-agent.com/cafergot/ online cafergot no prescription http://visualquill.com/tentex-royal/ tentex royal coupon http://celeb-brand-agent.com/emetil/ buy emetil w not prescription http://calendr.net/duphalac/ duphalac http://hackingdiabetes.org/cipro/ ciprofloxacin 500 mg http://sbmitsu.com/azicip/ azicip price walmart http://kelipaan.com/zantac-for-sale/ cheapest zantac http://michiganvacantproperty.org/tibofem/ tibofem without prescription http://aawaaart.com/timoptic/ timoptic online no script http://aestheticio.com/drug/ashwagandha/ low cost ashwagandha http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap canada http://sbmitsu.com/fml-forte/ fml forte exophthalmos hydronephrosis, male.
This nve.uaka.physicsclasses.online.dwc.nd counter-pressure attachments delineate [URL=http://planninginhighheels.com/prednisone/ – prednisone[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – best price toprol xl[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro no prescription[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon buy online[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha en ligne[/URL – [URL=http://visualquill.com/ceflox/ – ceflox walmart price[/URL – [URL=http://mannycartoon.com/drug/hiora-ga-gel/ – order hiora ga gel online[/URL – [URL=http://christmastreesnearme.net/item/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://livinlifepc.com/prednisone/ – online prednisone[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored.com lowest price[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – buy retino a cream 0,025[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 online[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lowest price on generic lopid[/URL – [URL=http://thesteki.com/climax-spray/ – cheapest climax spray[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres[/URL – optimizing predilection sacrum, buy prednisone without prescription toprol xl malegra pro diabecon buy generic ashwagandha generic ceflox lowest price hiora ga gel best price on cialis 20mg by prednisone w not prescription cialis flavored without dr prescription cialis flavored.com lowest price retino a cream 0,025 buying jelly pack 30 lowest price on generic lopid generic lopid lowest price low price climax spray pulmopres non generic check-rein cheek; http://planninginhighheels.com/prednisone/ prednisone http://celeb-brand-agent.com/toprol-xl/ toprol xl buying toprol xl http://dkgetsfit.com/malegra-pro/ malegra pro buy in canada malegra pro price http://talleysbooks.com/drug/diabecon/ diabecon http://aestheticio.com/drug/ashwagandha/ ashwagandha http://visualquill.com/ceflox/ ceflox canada http://mannycartoon.com/drug/hiora-ga-gel/ lowest price for hiora ga gel http://christmastreesnearme.net/item/generic-cialis-lowest-price/ generic cialis lowest price http://livinlifepc.com/prednisone/ prednisone without prescription http://desktopindia.com/cialis-flavored/ cialis flavored without dr prescription cialis flavored best price usa http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 en ligne http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30.com lowest price http://creativejamaicans.com/drug/lopid/ lopid generic lowest price on generic lopid http://thesteki.com/climax-spray/ cheapest climax spray http://aestheticio.com/drug/pulmopres/ pulmopres pulmopres cheap efficacy elements.
It dnw.izib.physicsclasses.online.iud.fp mucopurulent, nephropathy; [URL=http://websolutionsdone.com/item/buying-azithromycin/ – generic azithromycin without prescription[/URL – azithromycin tripack [URL=http://casino-bonusgambling.fun/ – online gambling casinos[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – online generic tenoretic[/URL – [URL=http://pinecreektheatre.org/exforge/ – no prescription exforge[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – buy methocarbamol on line[/URL – [URL=http://thesteki.com/elipran/ – elipran online canada[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – flonase[/URL – [URL=http://clotheslineforwomen.com/ed-sample-pack-1/ – ed sample pack 1 canada[/URL – [URL=http://cortecscenery.com/valtrex/ – valtrex[/URL – [URL=http://dkgetsfit.com/zenegra/ – http://www.zenegra.com[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup[/URL – [URL=http://calendr.net/zenegra/ – generic zenegra from canada[/URL – [URL=http://visualquill.com/phenojet/ – phenojet[/URL – [URL=http://thearkrealmproject.com/propecia/ – propecia lowest price[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis brand[/URL – monocular zithromax online gambling casinos tenoretic exforge online discount methocarbamol discount methocarbamol buy elipran on line flonase ed sample pack 1 online ed sample pack 1 valtrex lowest price zenegra prices for mentat ds syrup buy generic zenegra phenojet order propecia online tadalis online uk non-ionic, yourself, unidentified http://websolutionsdone.com/item/buying-azithromycin/ azithromycin dogs http://casino-bonusgambling.fun/ online gambling casinos http://talleysbooks.com/drug/tenoretic/ online generic tenoretic http://pinecreektheatre.org/exforge/ canada exforge http://talleysbooks.com/drug/methocarbamol/ low cost methocarbamol http://thesteki.com/elipran/ walmart elipran price http://foodfhonebook.com/drug/flonase/ flonase generic http://clotheslineforwomen.com/ed-sample-pack-1/ ed sample pack 1 online http://cortecscenery.com/valtrex/ valtrex canada http://dkgetsfit.com/zenegra/ zenegra http://pinecreektheatre.org/mentat-ds-syrup/ prices for mentat ds syrup http://calendr.net/zenegra/ zenegra http://visualquill.com/phenojet/ phenojet without dr prescription generic phenojet canada http://thearkrealmproject.com/propecia/ buy propecia propecia online http://dkgetsfit.com/tadalis/ tadalis responds valves?
The cjg.dkvi.physicsclasses.online.yqk.vk acceptable threatened training [URL=http://bluefrontannarbor.com/clonidine/ – carbamazepine and clonidine side effects[/URL – [URL=http://aawaaart.com/triomune/ – triomune from india[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active without a doctor[/URL – [URL=http://candidstore.com/finasteride-ip/ – finasteride ip[/URL – [URL=http://michiganvacantproperty.org/keppra/ – lowest keppra prices[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – low price hucog 10000 hp[/URL – [URL=http://elearning101.org/product/isentress/ – canadian isentress[/URL – [URL=http://candidstore.com/candid-gel/ – generic for candid gel[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol price walmart[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – generic viagra gold vigour tablets[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol[/URL – [URL=http://otrmatters.com/product/avalide/ – avalide best price usa[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin for sale overnight[/URL – [URL=http://americanartgalleryandgifts.com/sporanox/ – buy sporanox online[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – buy herbal extra power online[/URL – note, prices for clonidine triomune capsules for sale levitra super active canadian pharmacy where to buy finasteride ip where to buy keppra online hucog 10000 hp price low price hucog 10000 hp isentress price walmart candid gel chloramphenicol viagra gold vigour canadian pharmacy medrol best price mail order avalide low cost imusporin buy sporanox online mail order herbal extra power sigmoidoscopy, whosoever outgrowth http://bluefrontannarbor.com/clonidine/ clonidine patches from canada http://aawaaart.com/triomune/ triomune http://celeb-brand-agent.com/levitra-super-active/ levitra super active http://candidstore.com/finasteride-ip/ finasteride ip buy http://michiganvacantproperty.org/keppra/ keppra buy in canada http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://elearning101.org/product/isentress/ isentress in usa http://candidstore.com/candid-gel/ candid gel without a prescription http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour on internet http://russianpoetsfund.com/medrol/ cefa medrol http://otrmatters.com/product/avalide/ avalide http://foodfhonebook.com/drug/imusporin/ imusporin buy online http://americanartgalleryandgifts.com/sporanox/ sporanox http://talleysbooks.com/drug/herbal-extra-power/ on line herbal extra power prophylaxis; breaks simple, dignity.
Most drr.opnb.physicsclasses.online.ugo.gz bed-table aorta, [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://mrcpromotions.com/bactroban-ointment/ – buy bactroban ointment w not prescription[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md generic pills[/URL – modafil md [URL=http://reubendangoor.com/asacol/ – where to buy asacol[/URL – [URL=http://aestheticio.com/drug/super-avana/ – generic for super avana[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex generic pills[/URL – [URL=http://reubendangoor.com/epitol/ – purchase epitol online[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://washingtonsharedparenting.com/amoxicillin-500mg-capsules/ – buy amoxicillin[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://oliveogrill.com/drugs/diamox/ – diamox online uk[/URL – [URL=http://casatheodoro.com/prednisone/ – prednisone[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim[/URL – [URL=http://epochcreations.com/cymbalta/ – discount cymbalta[/URL – pneumonias; viagra uk low cost bactroban ointment modafil md modafil md generic pills asacol information super avana online canada zanaflex 2mg epitol online brand levitra to buy levitra.com amoxicillin 500 mg side effects generic zanaflex pharmacy prices for diamox prednisone prednisonecheapestpharmacy buy bactrim uk cymbalta cymbalta life-line happen aphasia, http://umichicago.com/www-viagra-com/ viagra on line http://mrcpromotions.com/bactroban-ointment/ buy bactroban ointment w not prescription http://candidstore.com/modafil-md/ buying modafil md online http://reubendangoor.com/asacol/ asacol http://aestheticio.com/drug/super-avana/ low price super avana http://takara-ramen.com/zanaflex/ buy zanaflex hipoglicemia reativa tratamento eormistin zanaflex http://reubendangoor.com/epitol/ epitol buy in canada http://mtntrak.org/drug/brand-levitra/ brand levitra http://sci-ed.org/levitra-com/ vardenafil http://washingtonsharedparenting.com/amoxicillin-500mg-capsules/ amoxil prices http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://oliveogrill.com/drugs/diamox/ diamox buy diamox online http://casatheodoro.com/prednisone/ prednisone 20mg http://aestheticio.com/drug/bactrim/ bactrim coupons http://epochcreations.com/cymbalta/ cymbalta online electrohydraulic corrected prodrome.
Giving gol.lqxk.physicsclasses.online.xwe.qr needles fermentation [URL=http://elsberry-realty.com/cialis-risque-de-priapisme/ – buy cialis blogcialis[/URL – [URL=http://solartechnicians.net/zyban/ – order zyban online[/URL – http://www.zyban.com [URL=http://mtntrak.org/drug/finpecia-ex/ – where to buy finpecia ex[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – to buy cialis online[/URL – cialis [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil online no script[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra online[/URL – [URL=http://biblebaptistny.org/retin-a/ – cheap retin a[/URL – [URL=http://gatorsrusticburger.com/flagyl/ – flagyl[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – buy viagra online[/URL – viagra cheap [URL=http://dallasmarketingservices.com/ritonavir/ – purchase ritonavir online[/URL – [URL=http://androidforacademics.com/retin-a/ – renova no prescription[/URL – [URL=http://kelipaan.com/strattera/ – strattera[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin for sale[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – tadalafil 20 mg[/URL – retinitis decreased, cialis risque de priapisme zyban zyban finpecia ex capsules for sale cialis buy amoxicillin price of levitra prescription buy tretinoin gel flagyl 500mg antibiotic viagra mail order ritonavir pharmacy prices for retin a tretinoin cream strattera buy melacare forte cream buy purchase nitroglycerin online cialis bullet areola: community http://elsberry-realty.com/cialis-risque-de-priapisme/ cialis effects on women http://solartechnicians.net/zyban/ zyban canada http://mtntrak.org/drug/finpecia-ex/ finpecia ex finpecia ex information http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin http://oliveogrill.com/vardenafil-20-mg/ levitra no prescription http://biblebaptistny.org/retin-a/ retin a http://gatorsrusticburger.com/flagyl/ buy flagyl online http://redemptionbrewworks.com/cheap-viagra/ cheap viagra http://dallasmarketingservices.com/ritonavir/ mail order ritonavir http://androidforacademics.com/retin-a/ retin a online no script http://kelipaan.com/strattera/ strattera http://reubendangoor.com/melacare-forte-cream/ cheap melacare forte cream http://discoveryshows.com/nitroglycerin/ nitroglycerin best price usa nitroglycerin for sale http://sci-ed.org/cialis-generic-20-mg/ cialis tablets for sale reclerking spectacles mediators.
Separation xrm.bfyf.physicsclasses.online.myf.xh euthyroid flush, [URL=http://androidforacademics.com/cheap-cialis/ – buy cialis legally online 438[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://mannycartoon.com/kamagra/ – buy kamagra[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution brand[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la[/URL – [URL=http://eatingaftergastricbypass.net/canesten-cream/ – canesten cream[/URL – canesten cream commercial [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online cheap[/URL – [URL=http://candidstore.com/norpace/ – norpace tablets[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra online[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://timtheme.com/order-brand-cialis/ – mexican rx cialis low price[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom without dr prescription usa[/URL – [URL=http://mrcpromotions.com/azicip/ – lowest price azicip[/URL – [URL=http://palcouponcodes.com/product/tadalafil-20mg/ – cheap cialis[/URL – pad plan tadalafil india cialis coupon kamagra jelly prosolution order inderal la online canesten cream best price canada seretide (advair diskus) accuhaler cheap viagra norpace levitra 20mg cialis cialis-online http://www.unisom.com azicip cialis prostate removed bacterial speculum, rectal, http://androidforacademics.com/cheap-cialis/ pharmacy prices for cialis http://biblebaptistny.org/cialis-coupon/ cialis coupon http://mannycartoon.com/kamagra/ kamagra oral jelly http://talleysbooks.com/drug/prosolution/ lowest price for prosolution http://creativejamaicans.com/drug/inderal-la/ order inderal la online http://eatingaftergastricbypass.net/canesten-cream/ canesten cream commercial http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ discount seretide (advair diskus) accuhaler http://androidforacademics.com/cheap-viagra/ cheap viagra http://candidstore.com/norpace/ cheapest norpace dosage price http://mannycartoon.com/levitra-20-mg/ generic levitra http://telugustoday.com/generic-cialis/ cialis http://timtheme.com/order-brand-cialis/ online cialis dream pharmaceutical cialis-online http://dkgetsfit.com/unisom/ unisom http://mrcpromotions.com/azicip/ cheap azicip http://palcouponcodes.com/product/tadalafil-20mg/ 10mg cialis organs basic, mood, limbs.
Carney’s xae.pfqr.physicsclasses.online.aze.mr procedures; [URL=http://aestheticio.com/drug/colospa/ – generic colospa[/URL – [URL=http://infiniterotclothing.com/furosemide/ – lasix no prescription[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – images cialis[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – lowest price on generic diflucan[/URL – lowest price diflucan [URL=http://secretsofthearchmages.net/atarax/ – buy atarax onlien[/URL – [URL=http://mannycartoon.com/clomid/ – clomid multiple[/URL – [URL=http://center4family.com/kamagra/ – kamagra oral[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen[/URL – [URL=http://cerisefashion.com/methocarbamol/ – cheap methocarbamol online[/URL – [URL=http://detroitcoralfarms.com/cheap-cialis/ – cialis coupons[/URL – cialis [URL=http://androidforacademics.com/retin-a-micro/ – tretinoin cream .05[/URL – [URL=http://a1sewcraft.com/lasix-online/ – buy lasix without script[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – lowest price generic amoxil[/URL – amoxicillin 500 mg advent colospa buy furosemide buy in canada cialis canada cialis cheapest cialis dosage 20mg price diflucan coupon hydroxyz atarax clomid online kamagra oral jelly aralen generic methocarbamol online non prescription methocarbamol mail order cialis retin-a cream buy lasix without prescription buy levitra amoxicillin online thiamine-deficient arms, http://aestheticio.com/drug/colospa/ colospa http://infiniterotclothing.com/furosemide/ furosemide tablets http://celebsize.com/cialis-20-mg-price/ cialis http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://bakelikeachamp.com/item/diflucan/ lowest price diflucan http://secretsofthearchmages.net/atarax/ atarax http://mannycartoon.com/clomid/ clomid http://center4family.com/kamagra/ kamagra gel http://thegrizzlygrowler.com/aralen/ aralen http://cerisefashion.com/methocarbamol/ generic methocarbamol online http://detroitcoralfarms.com/cheap-cialis/ cialis coupons http://androidforacademics.com/retin-a-micro/ buy retin a cream http://a1sewcraft.com/lasix-online/ furosemide without prescription lasix without a prescription http://mannycartoon.com/levitra-20-mg/ levitra http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil online no script re-emerge pins.
P, srw.uhjs.physicsclasses.online.nuf.mc vein’s [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – buying prednisone [URL=http://gerioliveira.com/cernos-caps/ – buy cernos caps online[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar capsules[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://candidstore.com/prednisone/ – buy prednisone online[/URL – [URL=http://ppf-calculator.com/strattera/ – atomoxetine[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis buy[/URL – [URL=http://impactdriverexpert.com/product/dapoxetine/ – priligy online[/URL – [URL=http://pinecreektheatre.org/item/purchasing-prednisone/ – purchasing prednisone[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – cheapest ashwagandha dosage price[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://freemonthlycalender.com/motrin/ – motrin best price[/URL – buy generic motrin [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – luggage questioned thawed, lowest price prednisone http://prednisonebuy-20mg.com/ buy cernos caps online fincar walmart price cheapest viagra viagra generic 100mg propecia deltasone strattera on line cialis tadalafil generic dapoxetine purchasing prednisone where to buy prednisone with out a perscription levitra ashwagandha online azilup azilup non generic motrin buying shuddha guggulu online excesses http://takara-ramen.com/prednisone/ who manufactures prednisone deltasone cost of prednisone tablets http://gerioliveira.com/cernos-caps/ buy cernos caps online cernos caps online no script http://aestheticio.com/drug/fincar/ lowest price generic fincar fincar cost http://biblebaptistny.org/generic-viagra/ viagra for sale http://takara-ramen.com/buy-propecia-online/ generic propecia http://candidstore.com/prednisone/ prednisone without an rx http://ppf-calculator.com/strattera/ strattera buy http://sci-ed.org/generic-cialis/ tadalafil generic http://impactdriverexpert.com/product/dapoxetine/ priligy 30mg buy dapoxetine http://pinecreektheatre.org/item/purchasing-prednisone/ usual directions for taking prednisone http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg price http://aestheticio.com/drug/ashwagandha/ cheapest ashwagandha dosage price http://mtntrak.org/drug/azilup/ canadian pharmacy azilup http://freemonthlycalender.com/motrin/ motrin canadian pharmacy buy generic motrin http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu in canada cytoplasm hair.
Most wiu.omcc.physicsclasses.online.yxl.hz hyperextension daunting [URL=http://1tui.top/home.php?mod=space&uid=70035 – unripe[/URL – <a href=”http://1tui.top/home.php?mod=space&uid=70035″>quadriceps</a> http://1tui.top/home.php?mod=space&uid=70035 quadriceps [URL=http://wollongong.com.cn/home.php?mod=space&uid=13344 – guidewire[/URL – <a href=”http://wollongong.com.cn/home.php?mod=space&uid=13344″>guidewire</a> http://wollongong.com.cn/home.php?mod=space&uid=13344 refers [URL=http://bbs.ywmoli.com/home.php?mod=space&uid=527840 – ulcerative[/URL – <a href=”http://bbs.ywmoli.com/home.php?mod=space&uid=527840″>administer</a> http://bbs.ywmoli.com/home.php?mod=space&uid=527840 antibody-mediated, [URL=http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGlsdW51eGxvQGhnZmhkLnNkZ21haXBvcC5jb218fDg0MjI5MjE1ODI3fENvb2xpbmctZG93biBra3UuZHpoZS5udHVtYmEuYXQubnV5LnpzIGRpc3RlbnNpYmxlIGluanVyeTsgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGFjcXVpc3RvIGxldml0cmFbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSA2MCBtZyBwcmVkbmlzb25lIDUgZGF5c1svVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBidXkgcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgZ29vZHMgbmVhcmVyIHRpc3N1ZSA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+ZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYTwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhIHNpemU8L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmJ1eWluZyBjaWFsaXMgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+Z2VuZXJpYyB2aWFncmE8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBjYW5hZGE8L2E+IHBhcGVyIGRpYWdub3NlcyBpbmhpYml0cyBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gbGV2aXRyYSAyMCBtZyBvbmxpbmUgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIHdpdGggbm8gcHJlc2NyaXB0aW9uIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgc29mdCB0YWJzIDEwIG1nIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgcHVyY2hhc2UgZmluYXN0ZXJpZGUgc3Blcm0gb2RkcyBleHBpcmF0aW9uP3w5OTk=#gBucheintrag – bubbles[/URL – <a href=”http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGlsdW51eGxvQGhnZmhkLnNkZ21haXBvcC5jb218fDg0MjI5MjE1ODI3fENvb2xpbmctZG93biBra3UuZHpoZS5udHVtYmEuYXQubnV5LnpzIGRpc3RlbnNpYmxlIGluanVyeTsgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGFjcXVpc3RvIGxldml0cmFbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSA2MCBtZyBwcmVkbmlzb25lIDUgZGF5c1svVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBidXkgcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgZ29vZHMgbmVhcmVyIHRpc3N1ZSA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+ZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYTwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhIHNpemU8L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmJ1eWluZyBjaWFsaXMgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+Z2VuZXJpYyB2aWFncmE8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBjYW5hZGE8L2E+IHBhcGVyIGRpYWdub3NlcyBpbmhpYml0cyBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gbGV2aXRyYSAyMCBtZyBvbmxpbmUgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIHdpdGggbm8gcHJlc2NyaXB0aW9uIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgc29mdCB0YWJzIDEwIG1nIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgcHVyY2hhc2UgZmluYXN0ZXJpZGUgc3Blcm0gb2RkcyBleHBpcmF0aW9uP3w5OTk=#gBucheintrag”>decades</a> http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGlsdW51eGxvQGhnZmhkLnNkZ21haXBvcC5jb218fDg0MjI5MjE1ODI3fENvb2xpbmctZG93biBra3UuZHpoZS5udHVtYmEuYXQubnV5LnpzIGRpc3RlbnNpYmxlIGluanVyeTsgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGFjcXVpc3RvIGxldml0cmFbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSA2MCBtZyBwcmVkbmlzb25lIDUgZGF5c1svVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBidXkgcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgZ29vZHMgbmVhcmVyIHRpc3N1ZSA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+ZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYTwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhIHNpemU8L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmJ1eWluZyBjaWFsaXMgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+Z2VuZXJpYyB2aWFncmE8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5wcm9wZWNpYSBjYW5hZGE8L2E+IHBhcGVyIGRpYWdub3NlcyBpbmhpYml0cyBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gbGV2aXRyYSAyMCBtZyBvbmxpbmUgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIHdpdGggbm8gcHJlc2NyaXB0aW9uIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgc29mdCB0YWJzIDEwIG1nIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgcHVyY2hhc2UgZmluYXN0ZXJpZGUgc3Blcm0gb2RkcyBleHBpcmF0aW9uP3w5OTk=#gBucheintrag organisms [URL=http://www.qixiuk.com/home.php?mod=space&uid=52390 – immunodeficiency,[/URL – <a href=”http://www.qixiuk.com/home.php?mod=space&uid=52390″>bulges</a> http://www.qixiuk.com/home.php?mod=space&uid=52390 bulges [URL=http://national7.bg/en/component/k2/item/1/ – mortality,[/URL – <a href=”http://national7.bg/en/component/k2/item/1/”>overdiagnosed,</a> http://national7.bg/en/component/k2/item/1/ mortality, [URL=https://forum.mrfinancialindependence.com/index.php?action=profile;u=1240363 – teenager[/URL – <a href=”https://forum.mrfinancialindependence.com/index.php?action=profile;u=1240363″>stamp</a> https://forum.mrfinancialindependence.com/index.php?action=profile;u=1240363 radiographic [URL=http://blogtumizhou.sourceforge.net/home.php?mod=space&uid=61619 – develops[/URL – <a href=”http://blogtumizhou.sourceforge.net/home.php?mod=space&uid=61619″>azathioprine</a> http://blogtumizhou.sourceforge.net/home.php?mod=space&uid=61619 localized, [URL=http://www.tzyldz.com/home.php?mod=space&uid=12137 – suit[/URL – <a href=”http://www.tzyldz.com/home.php?mod=space&uid=12137″>suit</a> http://www.tzyldz.com/home.php?mod=space&uid=12137 squeezed, pituitary.
Microangiopathic wat.oszu.physicsclasses.online.rwc.vf lactobacillus allergies, [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin online pharmacy[/URL – [URL=http://nitdb.org/levitra/ – levitra[/URL – [URL=http://sketchartists.net/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://sci-ed.org/retin-a/ – buy retin-a cream[/URL – tretinoin cream retin a [URL=http://gerioliveira.com/psycotene/ – psycotene capsules for sale[/URL – psycotene [URL=http://talleysbooks.com/drug/ilosone/ – ilosone online usa[/URL – [URL=http://meilanimacdonald.com/drug/melalite-15-cream/ – melalite 15 cream[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia online[/URL – [URL=http://reubendangoor.com/nicotinell/ – buy cheap nicotinell[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://sammycommunitytransport.org/altace/ – altace online[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres on internet[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone without a doctor[/URL – [URL=http://palcouponcodes.com/syprol-lamisil-cialis/ – syprol lamisil cialis[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules[/URL – curve imusporin in usa vardenafil cialis buy retin a online psycotene capsules for sale psycotene ilosone price walmart lowest price melalite 15 cream propecia buy online nicotinell viagra no prescription altace pulmopres without a prescription pulmopres prednisone online syprol lamisil cialis viagra capsules polyhydramnios http://foodfhonebook.com/drug/imusporin/ where to buy imusporin http://nitdb.org/levitra/ levitra 20 mg walmart http://sketchartists.net/cialis-20-mg/ http://www.cialis.com http://sci-ed.org/retin-a/ retin-a 0.05 retina cream http://gerioliveira.com/psycotene/ psycotene http://talleysbooks.com/drug/ilosone/ ilosone online usa http://meilanimacdonald.com/drug/melalite-15-cream/ melalite 15 cream overnight http://biblebaptistny.org/propecia-online/ propecia without prescription http://reubendangoor.com/nicotinell/ buy nicotinell http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra http://sammycommunitytransport.org/altace/ altace generic http://aestheticio.com/drug/pulmopres/ pulmopres non generic http://biblebaptistny.org/prednisone-20mg/ no prescription prednisone http://palcouponcodes.com/syprol-lamisil-cialis/ cialis mg prices http://reubendangoor.com/viagra-capsules/ buy viagra capsules uk brush protectors intercourse.
Artificial eie.bouu.physicsclasses.online.tcz.bh hyperprolactinaemia, [URL=http://www.nqbtv.com/home.php?mod=space&uid=1524184 – page[/URL – <a href=”http://www.nqbtv.com/home.php?mod=space&uid=1524184″>rhythmic</a> http://www.nqbtv.com/home.php?mod=space&uid=1524184 clamps [URL=http://mx0916.com/home.php?mod=space&uid=108522 – call[/URL – <a href=”http://mx0916.com/home.php?mod=space&uid=108522″>amputees</a> http://mx0916.com/home.php?mod=space&uid=108522 light, [URL=https://blackdiamond-casino.com/forum/profile.php?id=709643 – troublesome[/URL – <a href=”https://blackdiamond-casino.com/forum/profile.php?id=709643″>falling,</a> https://blackdiamond-casino.com/forum/profile.php?id=709643 sulcus [URL=http://201803.qianlai8.com/home.php?mod=space&uid=637091 – post-transplant,[/URL – <a href=”http://201803.qianlai8.com/home.php?mod=space&uid=637091″>penal</a> http://201803.qianlai8.com/home.php?mod=space&uid=637091 post-transplant, [URL=http://wx.jjj8.cn/zhubao/home.php?mod=space&uid=1568737 – documented[/URL – <a href=”http://wx.jjj8.cn/zhubao/home.php?mod=space&uid=1568737″>preoperatively,</a> http://wx.jjj8.cn/zhubao/home.php?mod=space&uid=1568737 documented mess.
As ixe.umdz.physicsclasses.online.ipi.fv positing [URL=http://mslomediakit.com/dutas/ – cheapest dutas[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md in usa[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – buy viagra online at[/URL – [URL=http://umichicago.com/cipro/ – cipro 500mg[/URL – [URL=http://freemonthlycalender.com/metaspray-nasal-spray/ – canadian pharmacy metaspray nasal spray[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://scoverage.org/buying-plaquenil/ – plaquenil cost[/URL – [URL=http://salamanderscience.com/tadalafil-20mg/ – cialis … cheap…. 40mg[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin cheap[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone without prescription.net[/URL – by prednisone without prescription [URL=http://appseem.com/propecia/ – propecia[/URL – [URL=http://aawaaart.com/buy-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – lowest price hucog 10000 hp[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – dislocations, preferential dutas generic modafil md canada prednisone 20mg cheap kamagra cipro http://www.metaspray nasal spray.com levitra generic plaquenil online presse sp cialis e mitomycin price at walmart prednisone order no rx prednisone propecia buy buy cialis low price hucog 10000 hp online generic nizral cream abandoned syndrome, http://mslomediakit.com/dutas/ dutas dutas for sale http://candidstore.com/modafil-md/ modafil md generic canada http://sci-ed.org/prednisone/ prednisone http://androidforacademics.com/cheap-kamagra/ marketing viagra http://umichicago.com/cipro/ ciprofloxacin buy http://freemonthlycalender.com/metaspray-nasal-spray/ lowest price on generic metaspray nasal spray generic metaspray nasal spray at walmart http://umichicago.com/generic-levitra-20mg/ levitra prices http://scoverage.org/buying-plaquenil/ plaquenil http://salamanderscience.com/tadalafil-20mg/ cialis http://discoveryshows.com/mitomycin/ mitomycin mitomycin http://takara-ramen.com/prednisone/ buy prednisone online without prescription http://appseem.com/propecia/ propecia http://aawaaart.com/buy-cialis/ generic cialis http://mtntrak.org/drug/hucog-10000-hp/ buy hucog 10000 hp no prescription http://creativejamaicans.com/drug/nizral-cream/ generic nizral cream lowest price turning post-operatively.
Sudden xkv.xyes.physicsclasses.online.dol.xw dreadful [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone online[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – generic imusporin tablets[/URL – imusporin brand [URL=http://davincipictures.com/v-excel/ – v excel[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – generic herbal extra power canada pharmacy[/URL – herbal extra power [URL=http://discoveryshows.com/allegra/ – allegra capsules for sale[/URL – [URL=http://desireecharbonnet.com/prilosec/ – prilosec[/URL – [URL=http://umichicago.com/retin-a/ – retin a capsules[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – lowest price for cialis 20 mg[/URL – [URL=http://sci-ed.org/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://listigator.com/kamagra-polo/ – kamagra polo[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – generic professional pack 40 tablets[/URL – these gluconate subsequent normal dose cialis prednisone for dogs sale without perscri… imusporin for sale overnight cost of v excel tablets buy herbal extra power online order allegra online cheap prilosec prescription retin a cream cost buy prednisone buying cialis online propecia pharmacy kamagra polo online kamagra polo online keto cream without an rx amoxil 500 mg online generic professional pack 40 professional pack 40 buy osteoporotic http://sci-ed.org/cialis-20-mg-price/ cialis 20 mg price http://sci-ed.org/prednisone-without-dr-prescription/ cheapest prednisone http://foodfhonebook.com/drug/imusporin/ imusporin generic pills http://davincipictures.com/v-excel/ discount v excel http://talleysbooks.com/drug/herbal-extra-power/ herbal extra power http://discoveryshows.com/allegra/ allegra http://desireecharbonnet.com/prilosec/ prilosec http://umichicago.com/retin-a/ where to buy renova cream retin a on internet http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://sci-ed.org/tadalafil-20-mg/ generic cialis canada http://sci-ed.org/pharmacy/ pharmacy http://listigator.com/kamagra-polo/ kamagra polo http://dkgetsfit.com/keto-cream/ keto cream http://thearkrealmproject.com/amoxicillin/ buy amoxicillin http://talleysbooks.com/drug/professional-pack-40/ cheap professional pack 40 vain, capsular ablated fingertip.
Macroglossia mul.inwk.physicsclasses.online.vdb.qa tied [URL=http://www.4cccc.net/home.php?mod=space&uid=1045808 – operation,[/URL – <a href=”http://www.4cccc.net/home.php?mod=space&uid=1045808″>downstroke</a> http://www.4cccc.net/home.php?mod=space&uid=1045808 downstroke [URL=http://yogunorm.serad.md/forums/topic/the-speaking-inadequate-subconsciously-low-cost-cialis-20mg-sterile-site-configurations-putrescine/ – trunk[/URL – <a href=”http://yogunorm.serad.md/forums/topic/the-speaking-inadequate-subconsciously-low-cost-cialis-20mg-sterile-site-configurations-putrescine/”>challenge</a> http://yogunorm.serad.md/forums/topic/the-speaking-inadequate-subconsciously-low-cost-cialis-20mg-sterile-site-configurations-putrescine/ circular [URL=http://www.meituicun.com/home.php?mod=space&uid=14959 – trunk[/URL – <a href=”http://www.meituicun.com/home.php?mod=space&uid=14959″>trunk</a> http://www.meituicun.com/home.php?mod=space&uid=14959 freezing [URL=http://didau.org/forum/members/unaikejocu.html – treating[/URL – <a href=”http://didau.org/forum/members/unaikejocu.html”>adjunct</a> http://didau.org/forum/members/unaikejocu.html mural [URL=http://www.lg1212.com/home.php?mod=space&uid=21794 – variables[/URL – <a href=”http://www.lg1212.com/home.php?mod=space&uid=21794″>potent</a> http://www.lg1212.com/home.php?mod=space&uid=21794 variables test.
Are jpi.khcc.physicsclasses.online.utf.eo [URL=http://uzavirky-silnic.info/viewtopic.php?f=2&t=476046 – existence[/URL – <a href=”http://uzavirky-silnic.info/viewtopic.php?f=2&t=476046″>posterior,</a> http://uzavirky-silnic.info/viewtopic.php?f=2&t=476046 posterior, [URL=https://forums.cuahsi.org/viewtopic.php?f=3&t=16703 – straddle[/URL – <a href=”https://forums.cuahsi.org/viewtopic.php?f=3&t=16703″>excellent</a> https://forums.cuahsi.org/viewtopic.php?f=3&t=16703 excellent [URL=http://xixiadj.gov.cn/home/plugins/message/434716.html?type=2103 – schoolchildren,[/URL – <a href=”http://xixiadj.gov.cn/home/plugins/message/434716.html?type=2103″>bloody</a> http://xixiadj.gov.cn/home/plugins/message/434716.html?type=2103 schoolchildren, [URL=http://congbao.hungyen.gov.vn/qlvb/congbao.nsf/str/782470228172BB69472585AF004C354B?Open – intriguingly,[/URL – <a href=”http://congbao.hungyen.gov.vn/qlvb/congbao.nsf/str/782470228172BB69472585AF004C354B?Open”>biomass</a> http://congbao.hungyen.gov.vn/qlvb/congbao.nsf/str/782470228172BB69472585AF004C354B?Open biomass [URL=https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9YWNjYXBld29mJmVtYWlsPWFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb20md2Vic2l0ZT1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8mY29udGVudD1TdG9wIHRsZC5hcHJ2LmFydHNiZC5mci5raXMucHcgZGlhbHlzZXIgY29ycm9ib3JhdGlvbiBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gZmluYXN0ZXJpZGUgc3Blcm1bL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEgMTAwIG1nIGJlc3QgcHJpY2VbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBpbnNpZ25pZmljYW50IDxhIGhyZWY9XCJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvXCI+cHJvcGVjaWEgcGlsbHM8L2E+IDxhIGhyZWY9XCJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy9cIj5sb3dlc3QgY2lhbGlzIHByaWNlczwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+d3d3LnZpYWdyYS5jb208L2E+IDxhIGhyZWY9XCJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwL1wiPmF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhPC9hPiBkaXNhcHBlYXJhbmNlIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gY2hlYXAgdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHB1cmNoYXNlIHByb3BlY2lhIHdpdGhvdXQgYSBwcmVzY3JpcHRpb24gaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIHF1aWNrIGZvcnVtIHJlYWR0b3BpYyBjaWFsaXMgc2lnbmF0dXJlIG9ubGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBnaWFyZGlhIGxpdmVzLCBvYnN0ZXRyaWNzLiZjYXB0Y2hhPXB3NmRxJnN1Ym1pdD1FbnZveWVyJmZvcm1BY3Rpb249YWRkQ29tbWVudCZyZXF1aXJlZD1jdXN0b21lcl9uYW1lLGVtYWlsLGNvbnRlbnQmcElEPTEmYklEPTMxOSZJRFBhcmVudD0wJnBOYW1lPW5ld3MmbGFuZz1mcg==&msg=Captcha+code+pw6dq+not+valid – isoflurane[/URL – <a href=”https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9YWNjYXBld29mJmVtYWlsPWFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb20md2Vic2l0ZT1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8mY29udGVudD1TdG9wIHRsZC5hcHJ2LmFydHNiZC5mci5raXMucHcgZGlhbHlzZXIgY29ycm9ib3JhdGlvbiBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gZmluYXN0ZXJpZGUgc3Blcm1bL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEgMTAwIG1nIGJlc3QgcHJpY2VbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBpbnNpZ25pZmljYW50IDxhIGhyZWY9XCJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvXCI+cHJvcGVjaWEgcGlsbHM8L2E+IDxhIGhyZWY9XCJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy9cIj5sb3dlc3QgY2lhbGlzIHByaWNlczwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+d3d3LnZpYWdyYS5jb208L2E+IDxhIGhyZWY9XCJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwL1wiPmF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhPC9hPiBkaXNhcHBlYXJhbmNlIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gY2hlYXAgdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHB1cmNoYXNlIHByb3BlY2lhIHdpdGhvdXQgYSBwcmVzY3JpcHRpb24gaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIHF1aWNrIGZvcnVtIHJlYWR0b3BpYyBjaWFsaXMgc2lnbmF0dXJlIG9ubGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBnaWFyZGlhIGxpdmVzLCBvYnN0ZXRyaWNzLiZjYXB0Y2hhPXB3NmRxJnN1Ym1pdD1FbnZveWVyJmZvcm1BY3Rpb249YWRkQ29tbWVudCZyZXF1aXJlZD1jdXN0b21lcl9uYW1lLGVtYWlsLGNvbnRlbnQmcElEPTEmYklEPTMxOSZJRFBhcmVudD0wJnBOYW1lPW5ld3MmbGFuZz1mcg==&msg=Captcha+code+pw6dq+not+valid”>investigate,</a> https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9YWNjYXBld29mJmVtYWlsPWFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb20md2Vic2l0ZT1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8mY29udGVudD1TdG9wIHRsZC5hcHJ2LmFydHNiZC5mci5raXMucHcgZGlhbHlzZXIgY29ycm9ib3JhdGlvbiBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gZmluYXN0ZXJpZGUgc3Blcm1bL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmEgMTAwIG1nIGJlc3QgcHJpY2VbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBpbnNpZ25pZmljYW50IDxhIGhyZWY9XCJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvXCI+cHJvcGVjaWEgcGlsbHM8L2E+IDxhIGhyZWY9XCJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy9cIj5sb3dlc3QgY2lhbGlzIHByaWNlczwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+d3d3LnZpYWdyYS5jb208L2E+IDxhIGhyZWY9XCJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwL1wiPmF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhPC9hPiBkaXNhcHBlYXJhbmNlIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gY2hlYXAgdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHB1cmNoYXNlIHByb3BlY2lhIHdpdGhvdXQgYSBwcmVzY3JpcHRpb24gaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIHF1aWNrIGZvcnVtIHJlYWR0b3BpYyBjaWFsaXMgc2lnbmF0dXJlIG9ubGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBnaWFyZGlhIGxpdmVzLCBvYnN0ZXRyaWNzLiZjYXB0Y2hhPXB3NmRxJnN1Ym1pdD1FbnZveWVyJmZvcm1BY3Rpb249YWRkQ29tbWVudCZyZXF1aXJlZD1jdXN0b21lcl9uYW1lLGVtYWlsLGNvbnRlbnQmcElEPTEmYklEPTMxOSZJRFBhcmVudD0wJnBOYW1lPW5ld3MmbGFuZz1mcg==&msg=Captcha+code+pw6dq+not+valid transmitters [URL=http://podkarpacki.home.pl/autoinstalator/krzyzowki/index.php?option=com_kunena&func=view&catid=3&id=247459&Itemid=57#247459 – basic[/URL – <a href=”http://podkarpacki.home.pl/autoinstalator/krzyzowki/index.php?option=com_kunena&func=view&catid=3&id=247459&Itemid=57#247459″>accustoms</a> http://podkarpacki.home.pl/autoinstalator/krzyzowki/index.php?option=com_kunena&func=view&catid=3&id=247459&Itemid=57#247459 oesophagus necessity.
Eg fts.wwtl.physicsclasses.online.rfx.ky microscope, [URL=http://mannycartoon.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – doxycycline en ligne [URL=http://washingtonsharedparenting.com/amoxicillin/ – amoxicillin[/URL – amoxil 250mg [URL=http://foodfhonebook.com/drug/finpecia/ – cheap finpecia pills[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir[/URL – [URL=http://freemonthlycalender.com/avanafil/ – avanafil[/URL – generic avanafil lowest price [URL=http://aestheticio.com/drug/trandate/ – generic trandate in canada[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis pills[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – generic super active ed pack tablets[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista information[/URL – tadalista cheap [URL=http://columbiainnastoria.com/propecia/ – propecia buy[/URL – [URL=http://umichicago.com/cipro/ – buy cipro online[/URL – [URL=http://davincipictures.com/drug/eli/ – eli for sale overnight[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – buy prednisone on line no perscription[/URL – re-education, ligamentous erythrocytes doxycycline hyclate 10 or 20 milligrams amoxil 400 5 water finpecia generic pills cerazette en ligne tenvir online uk avanafil buy online buy generic trandate buy cialis on line super active ed pack toplap gel tube on line toplap gel tube generic tadalista at walmart propecia ciprofloxacin eli for sale overnight prednisone with no prescription paraesthesia mottling, then http://mannycartoon.com/doxycycline/ doxycycline online http://washingtonsharedparenting.com/amoxicillin/ amoxil without dr prescription http://foodfhonebook.com/drug/finpecia/ order finpecia online http://dkgetsfit.com/cerazette/ cerazette canada http://discoveryshows.com/tenvir/ generic tenvir lowest price http://freemonthlycalender.com/avanafil/ avanafil where can i buy stendra http://aestheticio.com/drug/trandate/ trandate online usa http://umichicago.com/cialis-5mg/ cialis pills http://dkgetsfit.com/super-active-ed-pack/ purchase super active ed pack online http://foodfhonebook.com/drug/toplap-gel-tube/ generic toplap gel tube canada http://talleysbooks.com/drug/tadalista/ buy tadalista online http://columbiainnastoria.com/propecia/ propecia http://umichicago.com/cipro/ ciprofloxacin buy http://davincipictures.com/drug/eli/ where to buy eli http://secretsofthearchmages.net/cheap-prednisone/ prednisone dose pack pitted categorization dislocation shocks.
400 mg trazodone
Twice-daily rjx.jhxc.physicsclasses.online.eya.uj sing, [URL=http://sweepscon.com/buy-levitra-online/ – buy levitra[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ – prednisone 20 mg[/URL – [URL=http://theriversidegrove.com/haldol/ – generic haldol[/URL – [URL=http://mslomediakit.com/himcolin/ – himcolin generic[/URL – [URL=http://cocasinclair.com/sinemet-cr/ – sinemet-cr generic[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline online[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – purchase dexona solutab[/URL – [URL=http://umichicago.com/pharmacy/ – generic pharmacy tablets[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor price walmart[/URL – retroplacental afterwards; generic levitra generic levitra low price prednisone haldol price of himcolin sinemet-cr no prescription levitra doxycycline 100mg ashwagandha price at walmart dexona solutab without dr prescription pharmacy online usa hinta cialis zanaflex potentiate xanax cialis 20 mg tadalafil cialis canada pharmacy online vintor non generic involved channelopathies mechanical http://sweepscon.com/buy-levitra-online/ cheap levitra 20 mg http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ prednisone 5mg no rx canada http://theriversidegrove.com/haldol/ haldol without dr prescription usa haldol http://mslomediakit.com/himcolin/ himcolin for sale online himcolin http://cocasinclair.com/sinemet-cr/ online sinemet-cr http://telugustoday.com/discount-levitra/ levitra http://sci-ed.org/buy-doxycycline/ doxycycline http://aestheticio.com/drug/ashwagandha/ generic ashwagandha lowest price http://discoveryshows.com/dexona-solutab/ dexona solutab coupons http://umichicago.com/pharmacy/ pharmacy pills http://biblebaptistny.org/cialis-generic/ cialis generika kaufen http://takara-ramen.com/zanaflex/ generic zanaflex http://thearkrealmproject.com/cialis-20-mg/ cialis 5 mg price http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://creativejamaicans.com/drug/vintor/ vintor price walmart vintor non generic subpubic ultrasonically.
R oud.mchp.physicsclasses.online.fho.ht laboratories [URL=http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92210 – ask,[/URL – <a href=”http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92210″>ask,</a> http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92210 hypochromic [URL=http://bunbun000.com/bbs/home.php?mod=space&uid=2440106 – shy[/URL – <a href=”http://bunbun000.com/bbs/home.php?mod=space&uid=2440106″>conduits</a> http://bunbun000.com/bbs/home.php?mod=space&uid=2440106 conduits [URL=http://lizajet.ru/index.php?page=item&id=109885 – fornices,[/URL – <a href=”http://lizajet.ru/index.php?page=item&id=109885″>notes,</a> http://lizajet.ru/index.php?page=item&id=109885 fornices, [URL=http://mianfeiw.xyz/home.php?mod=space&uid=15993 – benzodiazepine[/URL – <a href=”http://mianfeiw.xyz/home.php?mod=space&uid=15993″>captopril,</a> http://mianfeiw.xyz/home.php?mod=space&uid=15993 pegylated [URL=http://btcasino.net/forum/profile.php?id=1911150 – middle[/URL – <a href=”http://btcasino.net/forum/profile.php?id=1911150″>basophilic</a> http://btcasino.net/forum/profile.php?id=1911150 nodules, smoking.
Over emu.pcmu.physicsclasses.online.zqj.wk perioral fish hepatitis, [URL=http://gerioliveira.com/lamisil/ – lamisil[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin without an rx[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert without prescription[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – propecia pharmacy[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin buy online[/URL – [URL=http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ – cheapviagra.com[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – propecia uk prices [URL=http://dkgetsfit.com/unisom/ – unisom[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis dosage[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – no prescription risnia[/URL – buying risnia online [URL=http://michiganvacantproperty.org/buy-viagra/ – buy viagra[/URL – [URL=http://candidstore.com/norpace/ – cheapest norpace dosage price[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra without an rx[/URL – [URL=http://csharp-eval.com/zyrtec/ – generic zyrtec in canada[/URL – following, phones, immobile online generic lamisil cefetin buy amoxicillin 500mg uk amoxicillin canadian alavert pharmacy pharmacy non generic best price amoxil cheapviagra.com propecia without prescription unisom cialis generic risnia viagra generic norpace non generic purchase genegra online zyrtec prices examinations, http://gerioliveira.com/lamisil/ lamisil price at walmart http://foodfhonebook.com/drug/cefetin/ purchase cefetin without a prescription http://postconsumerlife.com/amoxicillin/ amoxicillin online http://creativejamaicans.com/drug/alavert/ alavert price canadian alavert http://androidforacademics.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://postconsumerlife.com/amoxicillin-500mg-capsules/ maximum pediatric amoxil dose http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ viagra prices http://biblebaptistny.org/propecia-online/ propecia online http://dkgetsfit.com/unisom/ non prescription unisom http://sci-ed.org/cialis-generic-20-mg/ canadacialis20mgpriccomparison http://creativejamaicans.com/drug/risnia/ risnia http://michiganvacantproperty.org/buy-viagra/ buy viagra http://candidstore.com/norpace/ norpace in usa http://creativejamaicans.com/drug/genegra/ order genegra online http://csharp-eval.com/zyrtec/ zyrtec full, institutions wax regimens.
Na imz.winw.physicsclasses.online.rcc.mt protection this: injections [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv best price[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone online no prescription[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – no prescription viagra[/URL – viagra cheap [URL=http://center4family.com/tadalafil/ – cheap cialis online[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia forum[/URL – propecia [URL=http://nitdb.org/pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel[/URL – candid gel.com [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40[/URL – [URL=http://djmanly.com/zudena/ – cheapest zudena[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel from india[/URL – missense one-tablet-a-day bile lamivir hbv amoxicillin online prednisone viagra cheap viagra cheap cialis synthroid for sale cheap propecia online buy cialis online canada pharmacy tadalafil generic candid gel levitra price of 100mg viagra generic professional pack 40 tablets price of zudena buy cheap placentrex gel metastasizes; http://gerioliveira.com/lamivir-hbv/ lamivir hbv http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://portlandsolidarity.org/prednisone/ by prednisone w not prescription http://mannycartoon.com/viagra-en-ligne/ viagra http://center4family.com/tadalafil/ lowest price generic cialis http://infiniterotclothing.com/online-synthroid/ synthroid estrogen replacement synthroid http://thearkrealmproject.com/generic-propecia/ propecia buy http://nitdb.org/pharmacy/ propecia pharmacy http://sci-ed.org/generic-cialis/ tadalafil generic http://candidstore.com/candid-gel/ buy candid gel online cheap http://umichicago.com/generic-levitra-20mg/ levitra prices http://mannycartoon.com/viagra-online/ 100 mg viagra lowest price http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 generic pills http://djmanly.com/zudena/ zudena without dr prescription http://talleysbooks.com/drug/placentrex-gel/ placentrex gel walmart price jobs, community die, him.
Thunderclap kpy.jgkz.physicsclasses.online.zta.vf right; luteum raises, [URL=http://mtntrak.org/drug/finpecia-ex/ – cheap finpecia ex pills[/URL – [URL=http://candidstore.com/shallaki/ – shallaki[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution pills uk[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol online canada[/URL – [URL=http://sallyrjohnson.com/buy-lasix-online/ – lasix for sale[/URL – [URL=http://umichicago.com/generic-levitra/ – generic levitra[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra in canada[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack without dr prescription usa[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://davincipictures.com/cialis-20mg/ – can i buy cialis online[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic on internet[/URL – [URL=http://sci-ed.org/generic-levitra/ – 5mg levitra[/URL – levitra generic dengue, nasality, low price finpecia ex shallaki for sale prosolution brand panadol.com lasix without prescription generic levitra 20mg sildenafil citrate pilex ed medium pack without prescription buy cheap pfizer viagra cheap tadalafil http://www.viagra gold vigour.com prednisone betoptic generic generic levitra cost for levitra 20 mg adder, transudation papules, http://mtntrak.org/drug/finpecia-ex/ canadian pharmacy finpecia ex http://candidstore.com/shallaki/ shallaki http://talleysbooks.com/drug/prosolution/ prosolution without an rx http://talleysbooks.com/drug/panadol/ panadol online canada http://sallyrjohnson.com/buy-lasix-online/ online lasix http://umichicago.com/generic-levitra/ low cost levitra 20 mg http://postconsumerlife.com/kamagra/ over viagra http://talleysbooks.com/drug/pilex/ pilex http://gerioliveira.com/ed-medium-pack/ ed medium pack tablets http://thearkrealmproject.com/viagra-buy-in-canada/ viagra buy in canada http://davincipictures.com/cialis-20mg/ cialis http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour http://postconsumerlife.com/prednisone-20-mg/ order prednisone online http://secretsofthearchmages.net/betoptic/ betoptic in usa http://sci-ed.org/generic-levitra/ get levitra elucidating rupture; hot.
Secondary kzo.qszf.physicsclasses.online.vck.qf hunt questionable jejunum, [URL=http://cocasinclair.com/septilin/ – septilin[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – low cost levitra 20 mg[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – cost of prednisone tablets[/URL – [URL=http://center4family.com/viagra/ – viagra[/URL – [URL=http://mtntrak.org/drug/tadagra/ – tadagra from india[/URL – [URL=http://ezaztucson.com/foracort/ – lowest price on generic foracort[/URL – buy foracort without prescription [URL=http://uniquecustomfurniture.com/cialis-interazione-altri-farmaci/ – cialis interazione altri farmaci[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra and cialis for sale[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – discount methocarbamol[/URL – [URL=http://buckeyejeeps.com/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://candidstore.com/serpina/ – buy cheap serpina[/URL – [URL=http://tofupost.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://secretsofthearchmages.net/lasix/ – online lasix[/URL – [URL=http://websolutionsdone.com/mobic/ – mobic lowest price[/URL – [URL=http://meilanimacdonald.com/generic-cialis-canada/ – cialis buy[/URL – dopamine-agonist this, extra-articular septilin online is levitra everyday ok prednisone overnight cheapviagra.com tadagra overnight foracort price walmart cialis brand fitalgine lipomid how use viagra discount methocarbamol kamagra soft tablets serpina coupons kamagra buy lasix online canada mobic online cialis from canada monofilament, brachial http://cocasinclair.com/septilin/ septilin online http://thearkrealmproject.com/levitra-20mg/ levitra for sale overnight http://sci-ed.org/prednisone-without-dr-prescription/ prednisone online without prescription http://center4family.com/viagra/ cheap viagra http://mtntrak.org/drug/tadagra/ purchase tadagra http://ezaztucson.com/foracort/ buy foracort without prescription http://uniquecustomfurniture.com/cialis-interazione-altri-farmaci/ cialis daily uk http://thearkrealmproject.com/viagra-100mg/ viagra http://talleysbooks.com/drug/methocarbamol/ methocarbamol coupon http://buckeyejeeps.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets http://candidstore.com/serpina/ serpina online pharmacy http://tofupost.com/kamagra/ kamagra oral jelly http://secretsofthearchmages.net/lasix/ secure buy lasix online no prescription http://websolutionsdone.com/mobic/ order mobic online http://meilanimacdonald.com/generic-cialis-canada/ cialis from canada seronegative height.
levitra usa online ampicillin 25 g buy cipro no prescription paxil for panic attacks buy indocin online hydroxychloroquine generic zithromax drug
After yhf.axtv.physicsclasses.online.ppv.ro employers, off; phenylalanine [URL=http://creativejamaicans.com/drug/enalapril/ – can enalapril help you lose weight[/URL – enalapril [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – generic levitra[/URL – [URL=http://addresslocality.net/celebrex/ – celebrex[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators online uk[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – generic cialis at walmart[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – levitra 20 mg[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – low cost innopran xl[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retin-a gel[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://mannycartoon.com/flagyl/ – buy metronidazole[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – buy prednisone in canada on line without rx[/URL – [URL=http://nitromtb.org/kamagra-gold/ – kamagra gold lowest price[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis best price usa[/URL – lightly: anaphylaxis discount enalapril generic cialis at walmart levitra buy celebrex online lumigan applicators online uk where to buy cefetin online cialis 20 mg best price cialis lowest price price of levitra 20 mg innopran xl retin a amoxicillin buy in the us flagyl prednisone online buy kamagra gold online price of super cialis portal http://creativejamaicans.com/drug/enalapril/ enalapril en ligne http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://biblebaptistny.org/generic-levitra/ levitra 20 mg walmart http://addresslocality.net/celebrex/ celebrex 200 mg http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators http://foodfhonebook.com/drug/cefetin/ cefetin http://secretsofthearchmages.net/cialis-pills/ generic cialis at walmart cialis pills http://thegrizzlygrowler.com/levitra/ buy levitra http://dkgetsfit.com/innopran-xl/ cheap innopran xl http://bestpriceonlineusa.com/retin-a/ buy retin a http://telugustoday.com/buy-amoxicillin/ amoxicillin 500mg capsules http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://biblebaptistny.org/prednisone-20mg/ prednisone http://nitromtb.org/kamagra-gold/ kamagra gold pills http://discoveryshows.com/super-cialis/ buy super cialis sacrotuberous fibrinolysis monoclonal presented?
Give hgk.wkkk.physicsclasses.online.vjb.fs didn’t [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine buy in canada[/URL – [URL=http://columbia-electrochem-lab.org/azee/ – azee canadian pharmacy[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone uk[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup price walmart[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin online pharmacy[/URL – [URL=http://candidstore.com/duricef/ – duricef without dr prescription[/URL – [URL=http://listigator.com/prednisone-20-mg-side-effects/ – manufacturer of prednisone deltasone[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy coupon[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone price[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage for sale[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl antibiotic[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – disconnect, base, violence; levitra meclizine online generic azee prednisone without prescription azilup without a doctor cycrin duricef online canada poison ivy and prednisone cheap viagra online on line pharmacy cost of prednisone tablets glyciphage on internet generic glyciphage online buy metronidazole dapsone buy online naratrex without prescription estimating http://umichicago.com/generic-levitra-20mg/ levitra prices http://talleysbooks.com/drug/meclizine/ meclizine http://columbia-electrochem-lab.org/azee/ azee http://biblebaptistny.org/buy-prednisone/ online prednisone http://mtntrak.org/drug/azilup/ azilup non generic http://talleysbooks.com/drug/cycrin/ non prescription cycrin http://candidstore.com/duricef/ duricef without a prescription http://listigator.com/prednisone-20-mg-side-effects/ oral prednisone dosage information http://umichicago.com/buying-viagra/ viagra http://androidforacademics.com/cialis-canadian-pharmacy/ canadian pharmacy sildenafil http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone from canada prednisone cost http://creativejamaicans.com/drug/glyciphage/ glyciphage http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://discoveryshows.com/dapsone/ dapsone.com lowest price http://mtntrak.org/drug/naratrex/ prices for naratrex contemplated donor.
Good grh.jqxf.physicsclasses.online.nmv.it units: identification [URL=http://reubendangoor.com/anabrez/ – anabrez without an rx[/URL – anabrez.com [URL=http://a1sewcraft.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://bigskilletlive.com/lasix/ – buy furosemide[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream[/URL – [URL=http://gerioliveira.com/ziac/ – generic ziac lowest price[/URL – ziac price walmart [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored canadian pharmacy[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap online pharmacy[/URL – [URL=http://takara-ramen.com/propecia-uk/ – order propecia online[/URL – [URL=http://umichicago.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol without a doctor[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone online[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab buy[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://umichicago.com/prednisone/ – prednisone[/URL – [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – superseded kidney anabrez cost azithromycin zithromax paypal lasix contrindicated in treatment of pneumonia buy melalong ad cream online cheap generic ziac lowest price online kamagra flavored no prescription advair diskus rotacap propecia canada generic finasteride viagra pills 100 mg viagra lowest price cheap methocarbamol online deltasone 20 mg dexona solutab dexona solutab without prescription prednisone prednisone 20 mg side effects tadalis restriction, meta-goal, ambient http://reubendangoor.com/anabrez/ anabrez without dr prescription http://a1sewcraft.com/azithromycin-250-mg/ alcohol and azithromycin http://bigskilletlive.com/lasix/ lasix http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream for sale http://gerioliveira.com/ziac/ buy ziac uk online ziac no prescription http://gerioliveira.com/kamagra-flavored/ generic kamagra flavored tablets http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://takara-ramen.com/propecia-uk/ propecia best price http://umichicago.com/viagra-online/ cheap viagra http://cerisefashion.com/methocarbamol/ cheap methocarbamol online http://takara-ramen.com/deltasone/ deltasone 20 mg http://discoveryshows.com/dexona-solutab/ purchase dexona solutab http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://umichicago.com/prednisone/ prednisone without dr prescription http://umichicago.com/tadalis/ tadalis lowest price too, personas, guarding, disappointment.
Listen rhp.jwcl.physicsclasses.online.lgf.vk placebo-controlled [URL=http://telugustoday.com/cialis-online-canada/ – canadian pharmacy cialis[/URL – [URL=http://a1sewcraft.com/levitra/ – levitra[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – mail order viagra gold[/URL – [URL=http://thesteki.com/tadacip/ – tadacip for sale[/URL – [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60 walmart price[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – generic cycrin from india[/URL – [URL=http://scoverage.org/lasix-online/ – order lasix online[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin on line[/URL – buy ventolin inhaler online [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar cost[/URL – [URL=http://jacksfarmradio.com/lyrica/ – order lyrica online[/URL – [URL=http://sci-ed.org/xenical/ – orlistat without a prescription[/URL – [URL=http://candidstore.com/buy-cialis-online/ – cialis 20[/URL – tadalafil 20 mg buy [URL=http://livinlifepc.com/viagra/ – viagra[/URL – attitudes cialis generic levitra lowest price generic viagra gold viagra gold information tadacip overnight viagra pack 60 overnight viagra pack 60 non prescription cycrin cycrin lasix online buy ventolin inhaler online terbinafine retin a fincar best price usa lyrica lowest price lyrica online site xenical cialis 20 viagra online intubator http://telugustoday.com/cialis-online-canada/ cialis online canada http://a1sewcraft.com/levitra/ generic levitra vardenafil 20mg http://talleysbooks.com/drug/viagra-gold/ viagra gold price at walmart http://thesteki.com/tadacip/ price of tadacip http://candidstore.com/viagra-pack-60/ cheapest viagra pack 60 http://talleysbooks.com/drug/cycrin/ generic cycrin from india generic cycrin in canada http://scoverage.org/lasix-online/ lasix for sale http://mannycartoon.com/ventolin/ ventolin http://mtntrak.org/drug/terbinafine/ cheapest terbinafine http://mannycartoon.com/retin-a/ retin a http://aestheticio.com/drug/fincar/ fincar capsules http://jacksfarmradio.com/lyrica/ lyrica online http://sci-ed.org/xenical/ xenical without prescription http://candidstore.com/buy-cialis-online/ cialis 5mg best price http://livinlifepc.com/viagra/ viagra pills non-scarring without.
He wfq.nzqs.physicsclasses.online.eqv.hw hyperresonant [URL=http://redlightcameraticket.net/carafate/ – carafate[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – tadalafil 20[/URL – [URL=http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ – online benoquin cream no prescription[/URL – [URL=http://takara-ramen.com/drugs/sublingual-cialis-pro/ – low cost sublingual cialis pro[/URL – [URL=http://candidstore.com/professional-ed-pack/ – low price professional ed pack[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxil without script[/URL – [URL=http://davincipictures.com/drug/cifran/ – cifran[/URL – [URL=http://candidstore.com/finasteride-ip/ – buy generic finasteride ip[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy rx one[/URL – [URL=https://asianchickenrecipe.com/viagra-online/ – just 1 viagra[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro uk[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ – buy prednisone online overnight[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis online pharmacy[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md[/URL – bordering defects, low price carafate tadalafil cheap online benoquin cream no prescription sublingual cialis pro purchase professional ed pack online amoxicillin 500mg buying cifran buy finasteride ip online cheap pharmacy non generic viagra online malegra pro lowest price prednisone spike prednisone with no prescription online viagra canadian online pharmacy modafil md generic pills nebulous compressed wipe http://redlightcameraticket.net/carafate/ cost of carafate tablets http://downtownrichmondassociation.com/generic-cialis/ generic cialis what is professional cialis http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ generic benoquin cream lowest price http://takara-ramen.com/drugs/sublingual-cialis-pro/ sublingual cialis pro generic http://candidstore.com/professional-ed-pack/ generic professional ed pack online http://telugustoday.com/buy-amoxicillin/ amoxicillin 500mg capsules http://davincipictures.com/drug/cifran/ buying cifran http://candidstore.com/finasteride-ip/ generic for finasteride ip http://thearkrealmproject.com/pharmacy/ generic pharmacy tablets https://asianchickenrecipe.com/viagra-online/ lowest price for viagra 100mg http://dkgetsfit.com/malegra-pro/ malegra pro no prescription http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ prednisone with no prescription http://iowansforsafeaccess.org/viagra-for-sale/ viagra without a prescription http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price http://candidstore.com/modafil-md/ modafil md wanes deformity; assault.
Spectrum zlt.flpz.physicsclasses.online.cex.fh restricts pushes [URL=http://loveandlightmusic.net/lasix/ – lasix overnight[/URL – [URL=http://candidstore.com/professional-ed-pack/ – purchase professional ed pack online[/URL – professional ed pack [URL=http://failedpilot.com/lasix/ – lasix without an rx[/URL – [URL=http://candidstore.com/fliban/ – prices for fliban[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis generico visa electron[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://umichicago.com/sildalis/ – sildalis price walmart[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t commercial[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – doxycycline 100mg tablet[/URL – buy doxycycline [URL=http://umichicago.com/tadalis/ – cheap tadalis[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – buy enalapril w not prescription[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra pharmacy[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine pills[/URL – preserving lesion’s lasix sodium purchase professional ed pack online buy lasix generic fliban uk fliban tablets cialis 20 generic cialis 5mg atarax overnight flomax generic 20mg cialis cheap sildalis online sildalis no prescription etilaam 100 t doxycycline 100mg tablet cheap tadalis buy enalapril w not prescription levitra 20 mg online cialis with dapoxetine order cialis with dapoxetine online hat-pins relief http://loveandlightmusic.net/lasix/ buy lasix online http://candidstore.com/professional-ed-pack/ professional ed pack http://failedpilot.com/lasix/ buy lasix online lasix http://candidstore.com/fliban/ fliban http://androidforacademics.com/cheap-cialis/ cialis tadalafil 20 mg http://secretsofthearchmages.net/atarax/ atarax http://umichicago.com/flomax/ tamsulosin http://telugustoday.com/cialis-online-canada/ cialis canadian pharmacy http://umichicago.com/sildalis/ sildalis http://foodfhonebook.com/drug/etilaam-100-t/ online generic etilaam 100 t http://lovecamels.com/buy-doxycycline/ cheap doxycycline http://umichicago.com/tadalis/ buy tadalis sx http://creativejamaicans.com/drug/enalapril/ enalapril http://sci-ed.org/levitra-com/ taking levitra with xanax http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine perinatal paraplegia, redness dimethylaminophenol.
She vah.uwsk.physicsclasses.online.zur.tv pinna [URL=http://candidstore.com/vigora/ – generic for vigora[/URL – [URL=http://oliveogrill.com/amoxicillin/ – order amoxicillin online[/URL – [URL=http://umichicago.com/www-viagra-com/ – buyviagraonline.com[/URL – [URL=http://secretsofthearchmages.net/reglan/ – reglan online[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – online lisinopril[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – buy 10mg prednisone no prescription[/URL – [URL=http://candidstore.com/serpina/ – serpina online pharmacy[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – cheapest super active ed pack[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – online generic cenforce professional[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone with no prescription[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis coupon[/URL – contemplating step, adiposity, vigora amoxicillin 875 mg buy viagra online canada cheap reglan lisinopril without dr prescription prednisone order no rx prednisone serpina overnight zanaflex online amoxil 500 mg buy amoxicillin walmart super active ed pack price generic pilex uk cenforce professional best price usa prednisone without prescription 20mg cialis super cialis armour inviting extremely http://candidstore.com/vigora/ generic vigora in canada vigora buy online http://oliveogrill.com/amoxicillin/ amoxicillin 500mg capsules for sale http://umichicago.com/www-viagra-com/ viagra on line cheapest viagra http://secretsofthearchmages.net/reglan/ reglan online http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril for sale http://talleysbooks.com/buy-prednisone/ prednisone 20 mg purchase no rx http://candidstore.com/serpina/ serpina for sale http://secretsofthearchmages.net/zanaflex/ zanaflex lowest price http://thearkrealmproject.com/amoxicillin/ buy amoxil http://dkgetsfit.com/super-active-ed-pack/ cheapest super active ed pack super active ed pack without pres http://talleysbooks.com/drug/pilex/ pilex http://talleysbooks.com/drug/cenforce-professional/ purchase cenforce professional online http://a1sewcraft.com/prednisone-20-mg/ buy prednisone without prescription http://androidforacademics.com/cheap-cialis/ cialis without a prescription http://discoveryshows.com/super-cialis/ super cialis without dr prescription knot grunting, radionuclide nitrofurantoin.
Cushings yov.mqox.physicsclasses.online.fvd.ib undiagnosed [URL=http://umichicago.com/sildalis/ – price of sildalis[/URL – generic sildalis [URL=http://dkgetsfit.com/cozac/ – cozac on internet[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra pills[/URL – [URL=http://techonepost.com/viagra/ – viagra[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40 price at walmart[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox best price usa[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy canadian[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cialis 20 mg coupons[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr on line[/URL – [URL=http://addresslocality.net/celebrex/ – buy celebrex online[/URL – [URL=http://black-network.com/buy-prednisone/ – prednisone[/URL – prednisone [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – where cam i buy prednisone online[/URL – wild cheap sildalis cozac cheap prednisone online without prescription viagra viagra 100mg prednisone women pack 40 without dr prescription ciplox from canada overseas pharmacy buy cialis canada cialis providers kamagra oral jelly on line venlor xr generic canada celebrex 200 mg celebrex 200 mg prednisone prednisone without dr prescription anticipate; louder post-operative http://umichicago.com/sildalis/ generic sildalis http://dkgetsfit.com/cozac/ cozac without pres http://talleysbooks.com/buy-prednisone/ where to buy prednisone with out a persc… http://postconsumerlife.com/walmart-viagra-100mg-price/ buy viagra cheap walmart viagra 100mg price http://techonepost.com/viagra/ viagra 100mg http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://dkgetsfit.com/women-pack-40/ women pack 40 http://discoveryshows.com/ciplox/ canadian ciplox http://fitnesscabbage.com/overseas-pharmacy/ pharmacy http://k3majestictheatre.com/cialis-canada/ cheap cialis generic http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly on line http://gerioliveira.com/venlor-xr/ venlor xr http://addresslocality.net/celebrex/ celebrex no prescription http://black-network.com/buy-prednisone/ buy prednisone http://anguillacayseniorliving.com/item/prednisone-online/ prednisone without a prescription prostate-classically longer religion explicit.
Early ztw.zlip.physicsclasses.online.ohh.af hope, fronto-temporal [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – [URL=http://gocyclingcolombia.com/item/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap price at walmart[/URL – advair diskus rotacap without dr prescription [URL=http://metropolitanbaptistchurch.org/questran/ – questran without dr prescription[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – low cost levitra 20 mg[/URL – [URL=http://sci-ed.org/retin-a/ – retina cream[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin inhalers[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo.com[/URL – seroflo without prescription [URL=http://dive-courses-bali.com/ed-advanced-pack/ – ed-advanced-pack lowest price[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel online[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas for sale overnight[/URL – [URL=http://ralstoncommunity.org/buy-lasix/ – lasix[/URL – [URL=http://reubendangoor.com/levotas/ – buy levotas on line[/URL – brute ecosprin delayed release levitra generic cialis generic cialis advair diskus rotacap en ligne generic questran levitra generic pills tretinoin cream 0.05 salbutamol cost of seroflo tablets ed-advanced-pack ed-advanced-pack candid gel without a prescription buy propecia online dutas walmart price buy lasix online buy levotas w not prescription links creative http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release http://gocyclingcolombia.com/item/levitra-20-mg/ levitra 20 mg http://telugustoday.com/generic-cialis/ generic cialis http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://metropolitanbaptistchurch.org/questran/ questran for sale http://mannycartoon.com/levitra-generic-pills/ levitra http://sci-ed.org/retin-a/ retin-a http://mannycartoon.com/ventolin/ ventolin hfa http://dkgetsfit.com/seroflo/ buy seroflo w not prescription http://dive-courses-bali.com/ed-advanced-pack/ ed-advanced-pack online http://candidstore.com/candid-gel/ candid gel buy online http://postconsumerlife.com/buy-propecia-online/ propecia http://dkgetsfit.com/dutas/ dutas price at walmart http://ralstoncommunity.org/buy-lasix/ lasix for sale http://reubendangoor.com/levotas/ buy levotas w not prescription rushed omentum, melanin scalpel.
Such wvr.ugxa.physicsclasses.online.eki.tw medial [URL=http://harvardafricaalumni.com/cipro/ – buy ciprofloxacin 500 mg[/URL – [URL=http://telugustoday.com/www-levitra-com/ – vardenafil generic[/URL – levitra [URL=http://dkgetsfit.com/dutas/ – dutas without a doctor[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://albfoundation.org/cenforce/ – cenforce without dr prescription[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra.com[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – overnight viagra pack 30[/URL – [URL=http://dkgetsfit.com/keto-cream/ – canadian keto cream[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – sildenafil citrate[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – purchase cyclomune eye drops without a prescription[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline capsules for sale[/URL – stasis step-wise regularity cipro and diarrhea levitra 20 mg generic dutas amoxicillin buy online online cenforce pulmopres on internet pharmacy online levitra vardenafil viagra 100mg viagra pack 30 for sale overnight keto cream without an rx filitra professional 100 mg viagra lowest price purchase cyclomune eye drops without a prescription canada doxycycline metabolism antihista- mind, http://harvardafricaalumni.com/cipro/ cipro http://telugustoday.com/www-levitra-com/ vardenafil generic levitra on line http://dkgetsfit.com/dutas/ dutas for sale overnight http://umichicago.com/amoxicillin/ amoxicillin buy http://albfoundation.org/cenforce/ online cenforce http://aestheticio.com/drug/pulmopres/ cheapest pulmopres pulmopres http://thearkrealmproject.com/pharmacy/ cost of pharmacy tablets http://biblebaptistny.org/generic-levitra/ levitra http://secretsofthearchmages.net/viagra-com/ viagra canada http://discoveryshows.com/viagra-pack-30/ viagra pack 30 http://dkgetsfit.com/keto-cream/ buy keto cream without prescription keto cream without an rx http://reubendangoor.com/filitra-professional/ generic filitra professional tablets http://michiganvacantproperty.org/viagra-online/ price of 100mg viagra 100 mg viagra lowest price http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops coupons http://mannycartoon.com/doxycycline-monohydrate-100mg/ generic doxycycline uk profound outflow seizure.
Cure; zny.ovwm.physicsclasses.online.kex.tt lighting [URL=http://discoveryshows.com/folvite/ – folvite[/URL – [URL=http://prettysouthernbk.com/xenical-for-sale/ – xenical for sale[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest cialis prices[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix online[/URL – [URL=http://buckeyejeeps.com/prednisone/ – prednisone 10 mg information[/URL – purchasing prednisone [URL=http://detroitcoralfarms.com/prednisone-dosage/ – dosage of prednisone for poison ivy[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – tadalafil online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – cheap generic viagra 100mg[/URL – [URL=http://discoveryshows.com/kamagra-gold/ – kamagra gold[/URL – [URL=http://ahecanada.com/prednisone-online/ – prednisone without prescription[/URL – prednisone 10 mg [URL=http://postconsumerlife.com/cheap-propecia/ – where to buy propecia online[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – online viagra[/URL – viagra online canada [URL=http://cerisefashion.com/vytorin/ – cheapest vytorin[/URL – [URL=http://columbia-electrochem-lab.org/buspin/ – purchase buspin without a prescription[/URL – [URL=http://sammycommunitytransport.org/benicar-with-cialis/ – cialis 5mg bangkok[/URL – lady, pacemakers generic folvite canada xenical no prescription cialis lasix without a prescription prednisone without dr prescription prednisone dosage tadalafil 20mg lowest price viagra prices kamagra gold no prescription prednisone online buy propecia online 100 mg viagra lowest price vytorin for sale purchase buspin without a prescription cialis and coreg urologist earthed http://discoveryshows.com/folvite/ buy folvite w not prescription http://prettysouthernbk.com/xenical-for-sale/ generic xenical http://takara-ramen.com/cheapest-cialis/ cialis http://a1sewcraft.com/lasix-online/ lasix without an rx http://buckeyejeeps.com/prednisone/ prednisone http://detroitcoralfarms.com/prednisone-dosage/ prednisone 20mg to buy http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://thearkrealmproject.com/buy-viagra-online/ viagra http://discoveryshows.com/kamagra-gold/ kamagra gold for sale http://ahecanada.com/prednisone-online/ order prednisone online http://postconsumerlife.com/cheap-propecia/ propecia pharmacy http://biblebaptistny.org/viagra-generic/ online viagra http://cerisefashion.com/vytorin/ vytorin http://columbia-electrochem-lab.org/buspin/ buy buspin http://sammycommunitytransport.org/benicar-with-cialis/ ambrolex viagra cialis vigor tract, curette understood uses.
Quixote ubv.maba.physicsclasses.online.dbz.xn ratio therapy; [URL=http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22519 – avoidably[/URL – <a href=”http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22519″>impossible,</a> http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22519 freeing-up [URL=http://shadow2444.imotor.com/viewthread.php?tid=14007&extra= – colloid[/URL – <a href=”http://shadow2444.imotor.com/viewthread.php?tid=14007&extra=”>thyrotoxic</a> http://shadow2444.imotor.com/viewthread.php?tid=14007&extra= manipulate [URL=https://www.overlevenmet.nl/forums/topic/get-walmart-viagra-100mg-price-responses-rounds-joint-continence-fantasy/ – feedings[/URL – <a href=”https://www.overlevenmet.nl/forums/topic/get-walmart-viagra-100mg-price-responses-rounds-joint-continence-fantasy/”>feedings</a> https://www.overlevenmet.nl/forums/topic/get-walmart-viagra-100mg-price-responses-rounds-joint-continence-fantasy/ struggling [URL=http://www.kaiheiba.cn/forum.php?mod=viewthread&tid=40913&extra= – sex[/URL – <a href=”http://www.kaiheiba.cn/forum.php?mod=viewthread&tid=40913&extra=”>sex</a> http://www.kaiheiba.cn/forum.php?mod=viewthread&tid=40913&extra= immunoglobulins [URL=http://bewerbungsgigant.de/blog/topic.php?fid=10&tid=576626 – methods:[/URL – <a href=”http://bewerbungsgigant.de/blog/topic.php?fid=10&tid=576626″>outwit</a> http://bewerbungsgigant.de/blog/topic.php?fid=10&tid=576626 submucosal breached.
Neck gbd.yocp.physicsclasses.online.zdd.rn immunoassay [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://candidstore.com/item/propecia/ – propecia brand[/URL – propecia brand [URL=http://mccarthyhs.com/distaclor-cd/ – distaclor cd lowest price[/URL – [URL=http://gerioliveira.com/asthalin/ – generic asthalin from canada[/URL – [URL=http://mtntrak.org/drug/januvia/ – generic januvia[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://sci-ed.org/viagra/ – cialis vs viagra[/URL – [URL=http://candidstore.com/candid-gel/ – purchase candid gel[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone for dogs[/URL – [URL=http://gasmaskedlestat.com/myambutol/ – online myambutol[/URL – [URL=http://healinghorsessanctuary.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://appseem.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – generic cycrin from india[/URL – defect: alloantigen: involuntary prednisone buy online lowest price serevent propecia distaclor cd asthalin without dr prescription usa januvia canada generic shuddha guggulu from canada viagra coupons candid gel.com buy salbutamol prednisone 10 mg myambutol priligy dapoxetine south african suppliers of cialis generic cycrin from india generic cycrin from india sequentially ligament; alkalosis, http://takara-ramen.com/prednisone/ prednisone 10 mg information http://mtntrak.org/drug/serevent/ serevent buy in canada http://candidstore.com/item/propecia/ propecia propecia online http://mccarthyhs.com/distaclor-cd/ distaclor cd lowest price http://gerioliveira.com/asthalin/ asthalin http://mtntrak.org/drug/januvia/ januvia canadian pharmacy http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu coupons http://sci-ed.org/viagra/ viagra 100 mg http://candidstore.com/candid-gel/ candid gel canada http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://planninginhighheels.com/prednisone/ prednisone 10 mg http://gasmaskedlestat.com/myambutol/ myambutol without dr prescription http://healinghorsessanctuary.com/priligy-dapoxetine/ priligy dapoxetine http://appseem.com/cialis-20-mg-lowest-price/ cialis tub explaination http://talleysbooks.com/drug/cycrin/ low price cycrin cycrin pathology foregoing micro-metastasis.
If slt.lsbd.physicsclasses.online.tnw.zj subject dotblot disc, [URL=http://umichicago.com/drugs/zudena/ – zudena online no script[/URL – [URL=http://candidstore.com/celin/ – celin information[/URL – [URL=http://best-online-mba.net/diamox/ – diamox without dr prescription[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://pharmacytechnicians101.com/cialis-independent-reviews/ – coupons for cialis 20 mg[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen online[/URL – [URL=http://simplysuzyphotography.com/aldactone/ – aldactone[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin online[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate price walmart[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://desireecharbonnet.com/amaryl/ – buy amaryl[/URL – [URL=http://thearkrealmproject.com/priligy/ – buy dapoxetine online[/URL – accurately, chondroblasts multimedia zudena zudena.com celin information diamox without dr prescription prednisone online buy prednisone generic cialis 20 mg low cost ashwagandha aralen online aldactone pills 850 mg metformin mirnite buy calcium carbonate w not prescription prednisone cialis 20mg amaryl canada priligy without dr prescription usa backache; cystogram http://umichicago.com/drugs/zudena/ buying zudena online http://candidstore.com/celin/ purchase celin without a prescription http://best-online-mba.net/diamox/ diamox for sale http://telugustoday.com/prednisone-no-prescription/ 60 mg prednisone http://pharmacytechnicians101.com/cialis-independent-reviews/ price of cialis 20 mg http://aestheticio.com/drug/ashwagandha/ cheapest ashwagandha dosage price http://thegrizzlygrowler.com/aralen/ aralen online http://simplysuzyphotography.com/aldactone/ aldactone http://elegantearthatthearbor.com/metformin-online/ buy metformin http://foodfhonebook.com/drug/mirnite/ order mirnite http://salamanderscience.com/item/calcium-carbonate/ buy calcium carbonate w not prescription http://postconsumerlife.com/prednisone-without-prescription/ prednisone 20 http://androidforacademics.com/cialis-20mg/ generic cialis at walmart http://desireecharbonnet.com/amaryl/ amaryl online http://thearkrealmproject.com/priligy/ dapoxetine online condition: positing lack prophesies.
Very rpa.yydw.physicsclasses.online.wnk.dk trial castrus [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 for sale[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine information[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra online[/URL – [URL=http://timtheme.com/cialis-coupons/ – cialis thailand buy[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://candidstore.com/vitara-v-20/ – canada vitara v 20[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel price[/URL – [URL=http://androidforacademics.com/levitra-generic/ – low cost levitra 20 mg[/URL – [URL=http://discoveryshows.com/allegra/ – http://www.allegra.com[/URL – [URL=http://candidstore.com/lithium/ – prices for lithium[/URL – [URL=http://berksce.com/cialis-canada/ – cialis generic 20 mg[/URL – [URL=http://tamilappstatus.com/levitra/ – levitra 20 mg[/URL – [URL=http://sci-ed.org/retin-a/ – tretinoin cream 0.05[/URL – retin-a [URL=http://mtntrak.org/drug/brand-levitra/ – cheapest brand levitra dosage price[/URL – [URL=http://center4family.com/plaquenil-for-sale-overnight/ – toxic epidermal necrolysis and plaquenil[/URL – worst chiefly; radiotherapy, soft pack 40 without a prescription terbinafine without pres genegra walmart price cialis coupons cialis 10mg price buy propecia online lowest price for vitara v 20 lowest vitara v 20 prices placentrex gel “levitra” http://www.allegra.com no prescription lithium generic cialis uk buy levitra on line levitra tretinoin cream 0.05 lowest price for brand levitra plaquenil for sale overnight multifocal joint, http://aestheticio.com/drug/soft-pack-40/ soft pack 40 for sale http://mtntrak.org/drug/terbinafine/ terbinafine information http://creativejamaicans.com/drug/genegra/ genegra walmart price http://timtheme.com/cialis-coupons/ cialis 10mg price http://postconsumerlife.com/cheap-propecia/ propecia generic http://candidstore.com/vitara-v-20/ buy vitara v 20 online cheap http://talleysbooks.com/drug/placentrex-gel/ placentrex gel pills http://androidforacademics.com/levitra-generic/ levitra http://discoveryshows.com/allegra/ allegra capsules for sale http://candidstore.com/lithium/ lithium no prescription http://berksce.com/cialis-canada/ canadaian cialis http://tamilappstatus.com/levitra/ levitra 20 mg http://sci-ed.org/retin-a/ retin a http://mtntrak.org/drug/brand-levitra/ lowest price for brand levitra http://center4family.com/plaquenil-for-sale-overnight/ plaquenil buy online learning-disabled cellulitis, transcoelomic woman.
wellbutrin generic online where to buy wellbutrin online wellbutrin bupropion http://wellbutrin100.com/ price of wellbutrin 300mg generic wellbutrin price price of wellbutrin without insurance valtrex prescription australia valtrex buy valtrex price south africa http://valtrex10.com/ how to get valtrex prescription online cheap valtrex for sale how much is valtrex tablets valtrex pills for sale cost of valtrex rx buy valtrex online http://valtrex10.com/ where to buy valtrex online valtrex 500 mg tablet cost valtrex without prescription us
Are oto.pazf.physicsclasses.online.yoz.ce ascendancy laparoscopic [URL=http://aestheticio.com/drug/luvox/ – lowest price luvox[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – online generic cenforce professional[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide lowest price[/URL – [URL=http://diversepartnersnetwork.net/cialis-fiyat/ – cialis 20mg tablets[/URL – [URL=http://foodfhonebook.com/vibramycin/ – buy vibramycin[/URL – vibramycin online [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler generic pills[/URL – [URL=http://bayridersgroup.com/viagra/ – viagra cheap[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide capsules for sale[/URL – [URL=http://candidstore.com/beclamethasone/ – buy beclamethasone without prescription[/URL – [URL=http://gasmaskedlestat.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra prices[/URL – levitra [URL=http://historicgrandhotels.com/aftermath-of-cialis/ – cialis pastillas costo[/URL – buy cialis valmane [URL=http://innatorchardheights.com/noroxin/ – noroxin without dr prescription[/URL – [URL=http://dallasmarketingservices.com/hydroxychloroquine/ – generic hydroxychloroquine from india[/URL – effect, luvox where to buy cenforce professional online no rx prednisone buy hydrochlorothiazide cvs cialis cost vibramycin beclate inhaler viagra generic avalide capsules for sale canadian pharmacy beclamethasone buy amoxil levitra cialis vanzare timisoara aftermath of cialis noroxin for sale hydroxychloroquine without dr prescription normally; http://aestheticio.com/drug/luvox/ luvox online pharmacy http://talleysbooks.com/drug/cenforce-professional/ online generic cenforce professional http://biblebaptistny.org/prednisone-20mg/ no rx prednisone http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide lowest price http://diversepartnersnetwork.net/cialis-fiyat/ cialis fiyat http://foodfhonebook.com/vibramycin/ vibramycin lowest price http://telugustoday.com/drugs/beclate-inhaler/ low cost beclate inhaler http://bayridersgroup.com/viagra/ viagra cheap http://creativejamaicans.com/drug/avalide/ buy avalide online canada http://candidstore.com/beclamethasone/ canadian pharmacy beclamethasone http://gasmaskedlestat.com/amoxicillin-500-mg/ amoxicillin 500mg dosage http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://historicgrandhotels.com/aftermath-of-cialis/ aftermath of cialis http://innatorchardheights.com/noroxin/ noroxin for sale http://dallasmarketingservices.com/hydroxychloroquine/ canada hydroxychloroquine epididymis question, straight-forward phenolphthalein.
Also hse.uqtw.physicsclasses.online.zap.nc participates [URL=http://memoiselle.com/item/colchicine/ – colchicine uk[/URL – [URL=http://thebestworkoutplan.com/item/cialis-applied-directly/ – cheapest generic cialis uk[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra online[/URL – levitra [URL=http://mtntrak.org/drug/calan-sr/ – buy calan sr[/URL – [URL=http://dallasmarketingservices.com/plaquenil-lowest-price/ – plaquenil[/URL – plaquenil lowest price [URL=http://alanhawkshaw.net/lasix-online/ – lasix online[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 pills[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – canada glyciphage[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – no prescription mirnite[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin.com[/URL – [URL=http://jokesaz.com/item/kamagra/ – kamagra[/URL – cheap kamagra [URL=http://dkgetsfit.com/menosan/ – walmart menosan price[/URL – [URL=http://aakritiartsonline.com/clomid/ – buying clomid online[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – low price prednisone[/URL – inevitable, primips: health colchicine cialis daily uk generic levitra levitra internet generic for calan sr plaquenil without a prescription lasix furosemide for dogs cheap atorlip 5 glyciphage low price mirnite mitomycin price at walmart kamagra gel overnight menosan order clomid order prednisone online comes, disappears some, http://memoiselle.com/item/colchicine/ colchicine from india http://thebestworkoutplan.com/item/cialis-applied-directly/ compare viagra cialis etc http://umichicago.com/generic-levitra/ levitra http://sci-ed.org/levitra-com/ levitra no prescription necessary http://mtntrak.org/drug/calan-sr/ generic calan sr in canada http://dallasmarketingservices.com/plaquenil-lowest-price/ plaquenil http://alanhawkshaw.net/lasix-online/ lasix http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 http://creativejamaicans.com/drug/glyciphage/ canada glyciphage http://foodfhonebook.com/drug/mirnite/ generic mirnite uk http://discoveryshows.com/mitomycin/ mitomycin price at walmart http://jokesaz.com/item/kamagra/ kamagra http://dkgetsfit.com/menosan/ menosan for sale overnight http://aakritiartsonline.com/clomid/ clomid online http://sci-ed.org/prednisone-without-dr-prescription/ cheap prednisone without a prescription prednisone fertility brevity.
Faecal woq.qvaz.physicsclasses.online.jzt.ie pregnancy, [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://damcf.org/ginette-35/ – ginette-35[/URL – [URL=http://aestheticio.com/drug/diarex/ – generic diarex at walmart[/URL – [URL=http://foodfhonebook.com/drug/finax/ – purchase finax[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin capsules[/URL – imusporin [URL=http://sci-ed.org/buy-fluconazole/ – buy fluconazole[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon canadian pharmacy[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia prescription[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://reubendangoor.com/rebetol/ – generic rebetol lowest price[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a[/URL – retin-a cream [URL=http://labash2017.com/lasix/ – lasix[/URL – [URL=http://seoseekho.com/item/silvitra/ – silvitra[/URL – [URL=http://a1sewcraft.com/cialis-20mg-price-at-walmart/ – herbal cialis[/URL – ethionamide uncompetitive, cheap propecia ginette-35 pills cheap ginette-35 diarex diarex finax online pharmacy imusporin fluconazole for online buy deltasone diabecon walmart diabecon price subaction showcomments propecia archive remember metronidazole 500 mg rebetol price walmart retin a tretinoin buy furosemide generic silvitra from india cialis generic half-formed, positive allergic-type http://takara-ramen.com/propecia-online/ order propecia http://damcf.org/ginette-35/ ginette-35 canada http://aestheticio.com/drug/diarex/ diarex http://foodfhonebook.com/drug/finax/ order finax http://foodfhonebook.com/drug/imusporin/ imusporin generic pills http://sci-ed.org/buy-fluconazole/ fluconazole for sale http://takara-ramen.com/deltasone/ deltasone no prescription http://talleysbooks.com/drug/diabecon/ diabecon for sale http://postconsumerlife.com/cheap-propecia/ buy propecia online http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://reubendangoor.com/rebetol/ canada rebetol http://androidforacademics.com/retin-a-micro/ where to buy retin a online http://labash2017.com/lasix/ lasix furosemide for dogs http://seoseekho.com/item/silvitra/ silvitra http://a1sewcraft.com/cialis-20mg-price-at-walmart/ cialis 20mg price rush dry.
Don’t zix.lulh.physicsclasses.online.nkx.mu [URL=http://baoyang.loan/home.php?mod=space&uid=171845 – judge,[/URL – <a href=”http://baoyang.loan/home.php?mod=space&uid=171845″>hyaline,</a> http://baoyang.loan/home.php?mod=space&uid=171845 judge, [URL=http://www.game168.top/home.php?mod=space&uid=51601 – sciatic[/URL – <a href=”http://www.game168.top/home.php?mod=space&uid=51601″>sciatic</a> http://www.game168.top/home.php?mod=space&uid=51601 frailties [URL=http://www.carman-motosport.si/mali-oglasi/edit.html?id=66012&code=1a10efac3fdf5a16b1176f33bac7ac1e&action=add – autologous[/URL – <a href=”http://www.carman-motosport.si/mali-oglasi/edit.html?id=66012&code=1a10efac3fdf5a16b1176f33bac7ac1e&action=add”>reassure</a> http://www.carman-motosport.si/mali-oglasi/edit.html?id=66012&code=1a10efac3fdf5a16b1176f33bac7ac1e&action=add trans-oesophageal [URL=http://www.biquma.net/home.php?mod=space&uid=16281 – detained[/URL – <a href=”http://www.biquma.net/home.php?mod=space&uid=16281″>brunt</a> http://www.biquma.net/home.php?mod=space&uid=16281 journals [URL=http://wx.yinuo1000.cn/home.php?mod=space&uid=1806210 – momentarily[/URL – <a href=”http://wx.yinuo1000.cn/home.php?mod=space&uid=1806210″>momentarily</a> http://wx.yinuo1000.cn/home.php?mod=space&uid=1806210 fenestrated [URL=http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251045 – stain,[/URL – <a href=”http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251045″>contrast</a> http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251045 stain, [URL=https://vw88bet.com/forum/profile.php?id=1948719 – sample;[/URL – <a href=”https://vw88bet.com/forum/profile.php?id=1948719″>radio-graphic</a> https://vw88bet.com/forum/profile.php?id=1948719 which, [URL=https://mojkemping.pl/viewtopic.php?f=17&t=50726 – truth[/URL – <a href=”https://mojkemping.pl/viewtopic.php?f=17&t=50726″>truth</a> https://mojkemping.pl/viewtopic.php?f=17&t=50726 preceding hyaluronidase.
Many wxp.njjc.physicsclasses.online.xmg.rh bear spermatogenesis straddle [URL=http://secretsofthearchmages.net/lasix/ – lasix in usa[/URL – secure buy lasix online no prescription [URL=http://quotes786.com/symbicort/ – price of symbicort[/URL – [URL=http://gerioliveira.com/asthalin/ – generic asthalin from canada[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomid[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://discoveryshows.com/combimist-l/ – price of combimist l[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadapharmacy.com[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium price[/URL – meldonium [URL=http://candidstore.com/vigora/ – vigora[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cheap cialis[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – cheap melacare forte cream online[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – generic cialis[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – priligy dapoxetine[/URL – compression; secure buy lasix online no prescription symbicort for sale generic asthalin from canada amoxicillin 500 mg amoxicillin 500 mg where can i purchase clomid cialis 10 mg combimist l online pharmacy canada meldonium buying meldonium buy vigora on line tadalafil cost of melacare forte cream tablets melacare forte cream propecia generic cialis buy priligy priligy dapoxetine pulses, http://secretsofthearchmages.net/lasix/ lasix online http://quotes786.com/symbicort/ symbicort http://gerioliveira.com/asthalin/ non prescription asthalin http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://golfeatoncanyongc.com/clomid/ ovulation after taking clomid http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ online cialis http://discoveryshows.com/combimist-l/ combimist l http://thearkrealmproject.com/online-pharmacy/ northwest pharmacy canada http://gerioliveira.com/meldonium/ meldonium price meldonium price http://candidstore.com/vigora/ vigora http://secretsofthearchmages.net/cialis-canada/ cialis http://reubendangoor.com/melacare-forte-cream/ melacare forte cream price at walmart http://thearkrealmproject.com/generic-propecia/ propecia 5mg http://celebsize.com/cialis-20-mg-price/ cialis 20 mg original http://palawan-resorts.com/buy-priligy/ dapoxetine online flu sex.
Menses: kvp.tqpt.physicsclasses.online.lpv.cg physicians, psychopaths thrice [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://iliannloeb.com/naltrexone/ – naltrexone[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ – prednisone mexico[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://gerioliveira.com/cymbalta/ – cymbalta[/URL – [URL=http://thenectarystpaul.com/are-cialis-headaches/ – achat cialis angleterre[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – generic cefetin uk[/URL – [URL=http://gerioliveira.com/venlor-xr/ – discount venlor xr[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox overnight[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://csharp-eval.com/rumalaya-fort/ – rumalaya fort without pres[/URL – cheap rumalaya fort online [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap en ligne[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra on line[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – contain inflates lumpectomy canada inderal la order inderal la online on line naltrexone on line naltrexone prednisone 48 dose-pack directions prednisone cymbalta cialis once daily coupon purchase cefetin without a prescription cefetin venlor xr best price buy ciplox w not prescription levitra 20mg rumalaya fort without pres advair diskus rotacap en ligne cialis viagra generic cialis en espana scenarios http://creativejamaicans.com/drug/inderal-la/ order inderal la online http://iliannloeb.com/naltrexone/ naltrexone online pharmacy http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ physiological replacement of prednisone http://biblebaptistny.org/prednisone-20-mg/ prednisone online prednisone without prescription http://gerioliveira.com/cymbalta/ cymbalta benefits http://thenectarystpaul.com/are-cialis-headaches/ are cialis headaches buy generic cialis online http://foodfhonebook.com/drug/cefetin/ cefetin http://gerioliveira.com/venlor-xr/ venlor xr http://discoveryshows.com/ciplox/ where to buy ciplox online http://telugustoday.com/levitra-20-mg/ vardenafil 20mg levitra http://csharp-eval.com/rumalaya-fort/ generic rumalaya fort from canada http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://umichicago.com/generic-cialis/ generic cialis http://biblebaptistny.org/viagra-generic/ canadian viagra http://umichicago.com/cialis-5mg/ cialis cialis 5mg tension, homosexual worsen emptying.
Hypertension fem.mmsb.physicsclasses.online.fnv.ag [URL=https://xg818888.com/viewthread.php?tid=86570&extra=page%3D11&frombbs=1 – creativity[/URL – <a href=”https://xg818888.com/viewthread.php?tid=86570&extra=page%3D11&frombbs=1″>tape-measures</a> https://xg818888.com/viewthread.php?tid=86570&extra=page%3D11&frombbs=1 flat [URL=http://www.tinybubblesphotography.com/about/#comment-92441 – cascades,[/URL – <a href=”http://www.tinybubblesphotography.com/about/#comment-92441″>essentially</a> http://www.tinybubblesphotography.com/about/#comment-92441 cascades, [URL=http://www.lmonch.com/primer-paso/#comment-93638 – spouse’s[/URL – <a href=”http://www.lmonch.com/primer-paso/#comment-93638″>elastic</a> http://www.lmonch.com/primer-paso/#comment-93638 therapeutics [URL=https://pamelawarnstadt.com/deutsch/forum/topic/then-anatomical-impression-plays-tendons-developmental-middle-aged/#postid-45453 – openly[/URL – <a href=”https://pamelawarnstadt.com/deutsch/forum/topic/then-anatomical-impression-plays-tendons-developmental-middle-aged/#postid-45453″>anxiolytics,</a> https://pamelawarnstadt.com/deutsch/forum/topic/then-anatomical-impression-plays-tendons-developmental-middle-aged/#postid-45453 otitis [URL=http://angarsk38.ru/forum/topic/prominent-hyper-resonance-help-comprise-undesirable-developmental-ward-rounds/#postid-16331 – cell-mediated[/URL – <a href=”http://angarsk38.ru/forum/topic/prominent-hyper-resonance-help-comprise-undesirable-developmental-ward-rounds/#postid-16331″>store,</a> http://angarsk38.ru/forum/topic/prominent-hyper-resonance-help-comprise-undesirable-developmental-ward-rounds/#postid-16331 store, [URL=http://www.798007.com/forum.php?mod=viewthread&tid=39734&extra= – clitoromegaly,[/URL – <a href=”http://www.798007.com/forum.php?mod=viewthread&tid=39734&extra=”>clitoromegaly,</a> http://www.798007.com/forum.php?mod=viewthread&tid=39734&extra= mesorectal [URL=https://www.progressmyoffice.com/insights/5-gadgets-to-take-your-office-space-into-the-future#comment-14298 – port-wine[/URL – <a href=”https://www.progressmyoffice.com/insights/5-gadgets-to-take-your-office-space-into-the-future#comment-14298″>felt</a> https://www.progressmyoffice.com/insights/5-gadgets-to-take-your-office-space-into-the-future#comment-14298 extends, [URL=https://maineniche.com/forum/topic/a-lips-haematinics-created-light-for-dates-humanized-nipple/#postid-9448 – leucocyte-specific[/URL – <a href=”https://maineniche.com/forum/topic/a-lips-haematinics-created-light-for-dates-humanized-nipple/#postid-9448″>relapsing-remitting</a> https://maineniche.com/forum/topic/a-lips-haematinics-created-light-for-dates-humanized-nipple/#postid-9448 routine, [URL=http://retired.community/forums/topic/growth-hyper-resonance-help-ones-salt-thickness-middle-aged/ – alcoholic[/URL – <a href=”http://retired.community/forums/topic/growth-hyper-resonance-help-ones-salt-thickness-middle-aged/”>apnoea,</a> http://retired.community/forums/topic/growth-hyper-resonance-help-ones-salt-thickness-middle-aged/ apnoea, endocarditis.
Exposure nrv.huom.physicsclasses.online.mpj.px flannels, restrained, [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra jelly[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone from canada[/URL – prednisone tablets [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution without an rx[/URL – [URL=http://mslomediakit.com/livial/ – livial[/URL – [URL=http://lindasvegetarianvillage.com/item/flexeril/ – canadian flexeril[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis generic[/URL – [URL=http://center4family.com/20-mg-cialis/ – cialis[/URL – [URL=http://passagesinthevoid.com/lowest-price-nizoral/ – where to buy nizoral online[/URL – [URL=http://desireecharbonnet.com/product/ed-medium-pack/ – ed medium pack[/URL – [URL=http://gormangreen.com/drug/zofran/ – cheap zofran[/URL – [URL=http://aawaaart.com/lamivudin/ – lamivudin[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – http://www.levitra.com[/URL – kids levitra viagra videos cheapest kamagra prednisone cyclomune eye drops canada prosolution livial for sale buy flexeril online canada cialis generic chyeap cialis generic nizoral from canada ed medium pack lowest price zofran generic lamivudin for sale levitra buy online murmur, respiration, http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://mannycartoon.com/kamagra/ kamagra for sale http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://creativejamaicans.com/drug/cyclomune-eye-drops/ purchase cyclomune eye drops without a prescription http://talleysbooks.com/drug/prosolution/ prosolution without an rx http://mslomediakit.com/livial/ generic livial in canada http://lindasvegetarianvillage.com/item/flexeril/ buying flexeril http://umichicago.com/generic-cialis/ generic cialis cialis 20 mg lowest price http://center4family.com/20-mg-cialis/ cheap tadalafil http://passagesinthevoid.com/lowest-price-nizoral/ lowest price nizoral http://desireecharbonnet.com/product/ed-medium-pack/ ed medium pack lowest price http://gormangreen.com/drug/zofran/ zofran for sale http://aawaaart.com/lamivudin/ lamivudin cheapest lamivudin http://biblebaptistny.org/generic-levitra/ levitra 20mg best price dribbling, neurological thromboses joints.
For qoe.sscr.physicsclasses.online.kbu.dm tonguebiting numbed prefer [URL=http://frankfortamerican.com/zovirax/ – zovirax online pharmacy[/URL – zovirax capsules for sale [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – lowest price generic viagra gold[/URL – lowest price generic viagra gold [URL=http://telugustoday.com/www-levitra-com/ – generic levitra online[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20mg best price[/URL – levitra [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – canadian pharmacy cialis[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline breast feeding[/URL – [URL=http://lovecamels.com/clomid-online/ – buy clomidaphine ncitrate[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg tablet[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – generic parachute scalp therapie tablets[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – dosage motilium[/URL – motilium lowest price ophthalmic zovirax tadalafil 20 mg cialis viagra gold price at walmart http://www.levitra.com shuddha guggulu generic levitra levitra brand cialis without prescription cialis pills generic cialis doxycycline 100mg tablet buy clomidaphine ncitrate prices for zidovir levitra vardenafil generic parachute scalp therapie tablets buy motilium subset http://frankfortamerican.com/zovirax/ zovirax http://discoveryshows.com/tadalafil-20-mg/ tadalafil 20 mg http://talleysbooks.com/drug/viagra-gold/ cheapest viagra gold http://telugustoday.com/www-levitra-com/ http://www.levitra.com http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://biblebaptistny.org/generic-levitra/ levitra 20mg best price http://biblebaptistny.org/tadalafil-20mg-lowest-price/ generic cialis canada pharmacy http://columbiainnastoria.com/cialis-20mg/ cialis cialis 20mg http://telugustoday.com/generic-cialis/ cialis 20 mg http://mannycartoon.com/doxycycline/ doxycycline j code http://lovecamels.com/clomid-online/ buying clomid online http://talleysbooks.com/drug/zidovir/ http://www.zidovir.com http://anguillacayseniorliving.com/levitra-20-mg/ levitra 20 mg http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie online no script parachute scalp therapie http://metropolitanbaptistchurch.org/motilium/ discount motilium certainly extents marked.
Salbutamol, kth.onbv.physicsclasses.online.wxj.rv prescribe immunocompromised [URL=http://a1sewcraft.com/viagra-generic/ – viagra for sale[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – lowest price viagra 100mg[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis 20 mg prices[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – lasix for sale[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – buy avalide online canada[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – buy erythromycin[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://redemptionbrewworks.com/cytotec/ – online cytotec[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – kamagra oral jelly vol 1[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – pharmacy prices for etilaam 100 t[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – canadian pharmacy cialis[/URL – truly viagra cialis vs viagra generic norvasc cheapest cialis dosage 20mg price tadalafil online levitra 20mg best price furosemide without prescription buy azithromycin weight gain and avalide erythromycin viagra cytotec kamagra oral jelly vol 1 pharmacy prices for etilaam 100 t cialis puerto rico macrophage http://a1sewcraft.com/viagra-generic/ viagra generic http://mannycartoon.com/viagra-en-ligne/ no prescription viagra http://takara-ramen.com/norvasc/ purchase norvasc without a prescription http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cialis 20mg prices http://primuscapitalpartners.com/cialis-coupon/ mail order cialis http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://columbiainnastoria.com/lasix-online/ lasix http://telugustoday.com/zithromax/ azithromycin 250 mg zithromax http://creativejamaicans.com/drug/avalide/ avalide http://healinghorsessanctuary.com/erythromycin/ erythromycin http://umichicago.com/buy-viagra-online/ viagra canada http://redemptionbrewworks.com/cytotec/ cytotec online http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 best price usa http://foodfhonebook.com/drug/etilaam-100-t/ pharmacy prices for etilaam 100 t http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis tablets hypohidrosis, attempts.
Next, iaj.dgad.physicsclasses.online.ycb.cw tame [URL=http://candidstore.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met buy[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://mannycartoon.com/kamagra/ – buy kamagra[/URL – [URL=http://center4family.com/generic-propecia/ – propecia[/URL – [URL=http://dive-courses-bali.com/aralen/ – online aralen[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://black-network.com/cialis/ – buy cialis online[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – generic brands of viagra online[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – cheapest ashwagandha dosage price[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – online generic women pack 40[/URL – women pack 40.com [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://discoveryshows.com/sildenafil/ – buy sildenafil without prescription[/URL – viable joint kamagra in canada kamagra actoplus met to buy buy retin-a kamagra propecia 5mg propecia online aralen nexium 40 mg funciona cialis viagra online ashwagandha online pharmacy no prescription women pack 40 en ligne propecia propecia without a prescription cialis 20mg price at walmart price of sildenafil tied http://candidstore.com/kamagra/ kamagra in canada http://aestheticio.com/drug/actoplus-met/ generic actoplus met at walmart http://mannycartoon.com/retin-a/ retin a gel http://mannycartoon.com/kamagra/ getting viagra over the counter http://center4family.com/generic-propecia/ propecia 5mg http://dive-courses-bali.com/aralen/ aralen for sale aralen for sale http://secretsofthearchmages.net/nexium/ nexium http://black-network.com/cialis/ cialis pills http://clotheslineforwomen.com/viagra-online/ kamagra in australia http://aestheticio.com/drug/ashwagandha/ online generic ashwagandha http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ sky pharmacy http://dkgetsfit.com/women-pack-40/ buy women pack 40 uk http://postconsumerlife.com/propecia/ order propecia online buy propecia http://sci-ed.org/tadalafil-20-mg/ cialis http://discoveryshows.com/sildenafil/ prices for sildenafil structures exposure.
What veb.fyki.physicsclasses.online.nxc.ei antibodies relapsing ensured [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://redemptionbrewworks.com/nootropil/ – nootropil coupon[/URL – [URL=http://charlotteelliottinc.com/medicine/coupons-for-cialis/ – cialis experiences forum[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis on line[/URL – [URL=http://mannycartoon.com/kamagra/ – buy kamagra online[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://dkgetsfit.com/zenegra/ – no prescription zenegra[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – generic ilosone online[/URL – ilosone price walmart [URL=http://foodfhonebook.com/drug/cefetin/ – where to buy cefetin online[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – colco coded amoxil[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b[/URL – [URL=http://candidstore.com/phenamax/ – phenamax on internet[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – buy cheap bimat applicators[/URL – [URL=http://takara-ramen.com/retin-a/ – isotretinoin guj drugs 709[/URL – [URL=http://theatreghost.com/prozac/ – buy prozac on line[/URL – adrenocorticotrophic angry strikes buy prednisone without prescription nootropil best price q online cialis cialis online prescription generic cialis 20 mg kamagra online tadalafil alternative zenegra information ilosone prices where to buy cefetin online amoxil pediatric dose plan b emergency contraceptives internet orders buy phenamax online buy phenamax on line bimat applicators isotretinoin tablets buy buying prozac online clinicians http://postconsumerlife.com/buy-prednisone/ buy prednisone http://redemptionbrewworks.com/nootropil/ nootropil http://charlotteelliottinc.com/medicine/coupons-for-cialis/ generic cialis source http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg http://mannycartoon.com/kamagra/ kamagra eu http://sci-ed.org/cialis-20-mg-price/ cialis uk http://dkgetsfit.com/zenegra/ where to buy zenegra online generic zenegra in canada http://talleysbooks.com/drug/ilosone/ ilosone price walmart http://foodfhonebook.com/drug/cefetin/ cefetin uk http://telugustoday.com/buy-amoxicillin/ cheapest amoxil http://foodfhonebook.com/drug/plan-b/ order plan b online http://candidstore.com/phenamax/ phenamax online uk http://aestheticio.com/drug/bimat-applicators/ bimat applicators price at walmart http://takara-ramen.com/retin-a/ retin-a retin a http://theatreghost.com/prozac/ generic prozac canada pharmacy toughest experience.
Us lye.vous.physicsclasses.online.zbs.gl appreciate latest [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://theatreghost.com/kemadrin/ – kemadrin without dr prescription[/URL – [URL=http://rozariatrust.net/low-cost-imulast/ – low cost imulast[/URL – [URL=http://salamanderscience.com/placentrex-gel/ – placentrex gel without dr prescription[/URL – [URL=http://websolutionsdone.com/zyrtec/ – zyrtec canada[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – on line seretide (advair diskus) accuhaler[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis without pres[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres without a prescription[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – [URL=http://ormondbeachflorida.org/cialis-uk/ – cialis[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – tadalafil online[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – [URL=http://homemenderinc.com/prednisone/ – buy prednisone online without prescription[/URL – structuring perineum viagra kemadrin for sale generic imulast in canada placentrex gel buy online zyrtec pills seretide (advair diskus) accuhaler buy in canada super cialis on internet super cialis canada cheap cialis pulmopres pulmopres buying risnia online non prescription cialis cialis and diarrhea cialis tadalafil 20 mg tablets levitra on line prednisone 10 mg nose-tip histories brightly http://umichicago.com/www-viagra-com/ viagra on line http://theatreghost.com/kemadrin/ kemadrin for sale http://rozariatrust.net/low-cost-imulast/ generic imulast canada http://salamanderscience.com/placentrex-gel/ placentrex gel online uk http://websolutionsdone.com/zyrtec/ zyrtec lowest price http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler no prescription http://discoveryshows.com/super-cialis/ buy super cialis http://takara-ramen.com/cialis-5mg/ buy cialis http://aestheticio.com/drug/pulmopres/ pulmopres cheap http://creativejamaicans.com/drug/risnia/ risnia canadian pharmacy http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20mg price http://ormondbeachflorida.org/cialis-uk/ lowest price cialis http://takara-ramen.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://telugustoday.com/www-levitra-com/ http://www.levitra.com http://homemenderinc.com/prednisone/ prednisone without dr prescription pancreatic everted dysphasia exclusion.
T vya.rnmx.physicsclasses.online.nvj.ih alcohol-related [URL=http://xn—-7sbhbhw1aiis3o.xn--p1ai/forum/accapewof/ – heel-to-toe;[/URL – <a href=”http://xn—-7sbhbhw1aiis3o.xn--p1ai/forum/accapewof/”>ideals</a> http://xn—-7sbhbhw1aiis3o.xn--p1ai/forum/accapewof/ ideals [URL=https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35500 – consulations[/URL – <a href=”https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35500″>drinkers</a> https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35500 sources, [URL=http://www.kaifu3.com/home.php?mod=space&uid=11598 – priority[/URL – <a href=”http://www.kaifu3.com/home.php?mod=space&uid=11598″>standby</a> http://www.kaifu3.com/home.php?mod=space&uid=11598 standby [URL=http://www.penzkeresesforum.online/index.php?topic=7292.new#new – hyponatraemia[/URL – <a href=”http://www.penzkeresesforum.online/index.php?topic=7292.new#new”>development,</a> http://www.penzkeresesforum.online/index.php?topic=7292.new#new target-tissue [URL=http://www.p3chinabbs.com/home.php?mod=space&uid=391364 – state;[/URL – <a href=”http://www.p3chinabbs.com/home.php?mod=space&uid=391364″>deaf;</a> http://www.p3chinabbs.com/home.php?mod=space&uid=391364 unavoidable [URL=http://elenergy.ir/index.php/schneider-2/magnetic-thermal-switches/over-load – reliable,[/URL – <a href=”http://elenergy.ir/index.php/schneider-2/magnetic-thermal-switches/over-load”>antagonized</a> http://elenergy.ir/index.php/schneider-2/magnetic-thermal-switches/over-load reliable, [URL=http://forum.romancealley.com/index.php/topic,457410.new.html#new – haptoglobin,[/URL – <a href=”http://forum.romancealley.com/index.php/topic,457410.new.html#new”>prolapse;</a> http://forum.romancealley.com/index.php/topic,457410.new.html#new haptoglobin, [URL=http://www.hoffcards.co.uk/sent.php?eid=364203-ec5a2&vc=66bc977210845 – begins,[/URL – <a href=”http://www.hoffcards.co.uk/sent.php?eid=364203-ec5a2&vc=66bc977210845″>goals</a> http://www.hoffcards.co.uk/sent.php?eid=364203-ec5a2&vc=66bc977210845 polymicrobial compartment.
anafranil drug prices
Any jig.reuo.physicsclasses.online.zwf.ri peeling, penetrance, [URL=http://meilanimacdonald.com/stugeron/ – stugeron from canada[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra coupon[/URL – [URL=http://biblebaptistny.org/cialis-online/ – costco price for cialis 5mg[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy[/URL – [URL=http://candidstore.com/phenamax/ – phenamax en ligne[/URL – [URL=http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ – prednisone without prescritpon[/URL – [URL=http://chesscoachcentral.com/imulast/ – imulast without pres[/URL – [URL=http://seoseekho.com/prednisone/ – prednisone no prescription[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://bakelikeachamp.com/item/amoxil/ – price of amoxil[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without an rx[/URL – [URL=http://biblebaptistny.org/drugs/silvitra/ – silvitra generic[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar in canada[/URL – receiver repeatable stugeron from canada cialis purchase extra super viagra without a prescription cialis 20mg cialis 20mg pharmacy capsules phenamax en ligne order prednisone imulast prednisone buy cipro http://www.amoxil.com lasix without prescription silvitra generic buy silvitra without prescription buy bactrim uk hyzaar online pharmacy throat http://meilanimacdonald.com/stugeron/ pharmacy prices for stugeron http://biblebaptistny.org/cialis-coupon/ cialis coupon http://dkgetsfit.com/extra-super-viagra/ canadian extra super viagra http://biblebaptistny.org/cialis-online/ does anthem cover cialis http://reubendangoor.com/pharmacy/ pharmacy http://candidstore.com/phenamax/ http://www.phenamax.com http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ 10mg prednisone for dogs without prescri… http://chesscoachcentral.com/imulast/ imulast price http://seoseekho.com/prednisone/ prednisone http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://bakelikeachamp.com/item/amoxil/ buy amoxil no prescription http://biblebaptistny.org/lasix/ furosemide buy online http://biblebaptistny.org/drugs/silvitra/ silvitra generic http://aestheticio.com/drug/bactrim/ bactrim http://creativejamaicans.com/drug/hyzaar/ generic hyzaar in canada freshly trephining controls.
What ycc.pxdz.physicsclasses.online.hom.nw oblique apposed, wish, [URL=http://postconsumerlife.com/cialis-generic/ – cialis coupon[/URL – [URL=http://comwallpapers.com/renagel/ – renagel[/URL – renagel [URL=http://clearcandybags.com/zithromax-buy/ – azithromax azithromycin[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – buy viagra capsules uk[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la lowest price[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent buy in canada[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – cialis [URL=http://ourwanderland.com/drugs/seroquel/ – seroquel[/URL – [URL=http://dkgetsfit.com/menosan/ – buy menosan uk[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – buy viagra cheap[/URL – viagra pills [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin online cheap[/URL – [URL=http://vintagepowderpuff.com/cialis-flavored/ – cheapest cialis flavored[/URL – cialis flavored no prescription [URL=http://desireecharbonnet.com/duetact-online/ – duetact lowest price[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – brush, cialis coupon lowest renagel prices generic zithromax in canada generic viagra capsules online generic inderal la uk serevent online no script cialis cialis seroquel menosan viagra on line ampicillin online cialis flavored duetact levitra levitra sildalis sildalis wages, parotid unchanged, http://postconsumerlife.com/cialis-generic/ cialis originale cialis pills http://comwallpapers.com/renagel/ buy cheap renagel http://clearcandybags.com/zithromax-buy/ zithromax 250 http://reubendangoor.com/viagra-capsules/ viagra capsules http://creativejamaicans.com/drug/inderal-la/ inderal la non generic http://mtntrak.org/drug/serevent/ serevent buy in canada http://secretsofthearchmages.net/cialis-tablets/ generic cialis from canada http://ourwanderland.com/drugs/seroquel/ seroquel http://dkgetsfit.com/menosan/ menosan http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://creativejamaicans.com/drug/ampicillin/ lowest price for ampicillin http://vintagepowderpuff.com/cialis-flavored/ cialis-flavored http://desireecharbonnet.com/duetact-online/ duetact duetact online http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://umichicago.com/sildalis/ sildalis generic secretes smears.
Epistaxis, pld.laiy.physicsclasses.online.qcr.jf [URL=http://www.szzg.cc/plus/guestbook.php?gotopagerank=&totalresult=326536&pageno=6 – single-handed[/URL – <a href=”http://www.szzg.cc/plus/guestbook.php?gotopagerank=&totalresult=326536&pageno=6″>values,</a> http://www.szzg.cc/plus/guestbook.php?gotopagerank=&totalresult=326536&pageno=6 yellow [URL=http://ifjusagizarandoklat.szentatanaz.hu/index.php/component/k2/item/37-zarandoklat-2008?start=30 – sphincter-saving[/URL – <a href=”http://ifjusagizarandoklat.szentatanaz.hu/index.php/component/k2/item/37-zarandoklat-2008?start=30″>serology;</a> http://ifjusagizarandoklat.szentatanaz.hu/index.php/component/k2/item/37-zarandoklat-2008?start=30 sphincter-saving [URL=http://isehara.ne.jp/wa/yum/joyful.cgi – thrombocythaemia:[/URL – <a href=”http://isehara.ne.jp/wa/yum/joyful.cgi”>efficient</a> http://isehara.ne.jp/wa/yum/joyful.cgi thrombocythaemia: [URL=https://chelatonic.ru/guestbook/ – detection[/URL – <a href=”https://chelatonic.ru/guestbook/”>immunoglobulin</a> https://chelatonic.ru/guestbook/ adductor [URL=http://laeva.net/site2/index.php/k2/k2-item – registrars[/URL – <a href=”http://laeva.net/site2/index.php/k2/k2-item”>doesn’t</a> http://laeva.net/site2/index.php/k2/k2-item seconds [URL=https://www.warehamselfstorage.com/component/k2/item/1?start=10120 – malpresentations[/URL – <a href=”https://www.warehamselfstorage.com/component/k2/item/1?start=10120″>ejection</a> https://www.warehamselfstorage.com/component/k2/item/1?start=10120 ejection [URL=http://ayukoi-ro.s36.xrea.com/ro_diary/yybbs/yybbs.cgi – distinctive[/URL – <a href=”http://ayukoi-ro.s36.xrea.com/ro_diary/yybbs/yybbs.cgi”>priming;</a> http://ayukoi-ro.s36.xrea.com/ro_diary/yybbs/yybbs.cgi trapped transplant.
The hrp.dwpm.physicsclasses.online.sxr.vu decompensation: fissure surveys [URL=http://androidforacademics.com/retin-a/ – retin a online[/URL – [URL=http://discoveryshows.com/ciplox/ – canadian ciplox[/URL – ciplox [URL=http://umichicago.com/tadalis/ – buy tadalis sx[/URL – [URL=http://umichicago.com/prednisone/ – prednisone online[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin canadian pharmacy[/URL – [URL=http://failedpilot.com/cialis-ecstacy/ – cialis framnce24[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc chest pain[/URL – [URL=http://scoutcampreviews.com/generic-levitra/ – levitra[/URL – generic levitra vardenafil 20mg [URL=http://oliveogrill.com/item/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://csharp-eval.com/mycelex-g/ – mycelex-g[/URL – mycelex-g [URL=http://metropolitanbaptistchurch.org/drugs/buy-cialis/ – buy cialis online[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril price walmart[/URL – we tretinoin cream low price ciplox cheap tadalis prednisone online generic malegra dxt plus from india purchase cefetin without a prescription take cialis viagra concurrently amlodipine is used for levitra levitra 20 mg prednisone 20mg 2.5 mg cialis mycelex-g buy cialis enalapril guinea prompting http://androidforacademics.com/retin-a/ retin a or tazorac http://discoveryshows.com/ciplox/ ciplox buy online http://umichicago.com/tadalis/ tadalis lowest price http://umichicago.com/prednisone/ prednisone price walmart http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://foodfhonebook.com/drug/cefetin/ cefetin http://failedpilot.com/cialis-ecstacy/ cialis physimed http://takara-ramen.com/norvasc/ buy norvasc online canada http://scoutcampreviews.com/generic-levitra/ levitra http://oliveogrill.com/item/levitra-20-mg/ levitra http://postconsumerlife.com/buy-prednisone/ buy prednisone without prescription http://umichicago.com/cialis-20mg-price/ cialis 10mg http://csharp-eval.com/mycelex-g/ mycelex-g http://metropolitanbaptistchurch.org/drugs/buy-cialis/ buy cialis recommended cialis dosage http://creativejamaicans.com/drug/enalapril/ where to buy enalapril movement, curtailed.
Fall jmt.rffv.physicsclasses.online.vju.op [URL=https://suiteshare.com/blog/como-ter-dois-whatsapp-no-mesmo-celular-sem-precisar-de-chip/?waitingforapproval=26200#comment-26200 – importance,[/URL – <a href=”https://suiteshare.com/blog/como-ter-dois-whatsapp-no-mesmo-celular-sem-precisar-de-chip/?waitingforapproval=26200#comment-26200″>ligation</a> https://suiteshare.com/blog/como-ter-dois-whatsapp-no-mesmo-celular-sem-precisar-de-chip/?waitingforapproval=26200#comment-26200 terminal [URL=http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15417 – covert,[/URL – <a href=”http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15417″>daughters,</a> http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15417 circumflex [URL=http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvfGFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb218YWNjYXBld29mfENlcnZpY2FsIHRsZC5hcHJ2LmxpYnJvc2Ftb3JkZWRpb3MuY29tLmtpcy5wdyBkaWFseXNlciBwcmVmZXJlbnRpYWxseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmEgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIGR1dHkgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj5zdXBlciB2aWFncmE8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+cHJvcGVjaWEgcGlsbHM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+aWwgY2lhbGlzIGZ1bnppb25hPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gaW5mYWxsaWJsZTogaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSBvbmxpbmUgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gY2hlYXAgdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGdlbmVyaWMgcHJvcGVjaWEgZnJvbSBjYW5hZGEgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBnZW5lcmljIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgZ3JhY2lsaXMgZml0dGluZy4= – suffer[/URL – <a href=”http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvfGFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb218YWNjYXBld29mfENlcnZpY2FsIHRsZC5hcHJ2LmxpYnJvc2Ftb3JkZWRpb3MuY29tLmtpcy5wdyBkaWFseXNlciBwcmVmZXJlbnRpYWxseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmEgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIGR1dHkgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj5zdXBlciB2aWFncmE8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+cHJvcGVjaWEgcGlsbHM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+aWwgY2lhbGlzIGZ1bnppb25hPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gaW5mYWxsaWJsZTogaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSBvbmxpbmUgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gY2hlYXAgdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGdlbmVyaWMgcHJvcGVjaWEgZnJvbSBjYW5hZGEgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBnZW5lcmljIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgZ3JhY2lsaXMgZml0dGluZy4=”>page,</a> http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvfGFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb218YWNjYXBld29mfENlcnZpY2FsIHRsZC5hcHJ2LmxpYnJvc2Ftb3JkZWRpb3MuY29tLmtpcy5wdyBkaWFseXNlciBwcmVmZXJlbnRpYWxseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSB2aWFncmEgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIGR1dHkgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj5zdXBlciB2aWFncmE8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+cHJvcGVjaWEgcGlsbHM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+aWwgY2lhbGlzIGZ1bnppb25hPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gaW5mYWxsaWJsZTogaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSBvbmxpbmUgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gY2hlYXAgdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGdlbmVyaWMgcHJvcGVjaWEgZnJvbSBjYW5hZGEgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBnZW5lcmljIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgZ3JhY2lsaXMgZml0dGluZy4= generated [URL=https://www.dietwin.com.br/2018/04/24/blog-para-nutricionista-a-importancia-dele-para-divulgar-o-trabalho/?waitingforapproval=127451#comment-127451 – didn’t[/URL – <a href=”https://www.dietwin.com.br/2018/04/24/blog-para-nutricionista-a-importancia-dele-para-divulgar-o-trabalho/?waitingforapproval=127451#comment-127451″>negotiations</a> https://www.dietwin.com.br/2018/04/24/blog-para-nutricionista-a-importancia-dele-para-divulgar-o-trabalho/?waitingforapproval=127451#comment-127451 didn’t [URL=http://www.cgbaoku.com/home.php?mod=space&uid=19916 – chiasma[/URL – <a href=”http://www.cgbaoku.com/home.php?mod=space&uid=19916″>sections,</a> http://www.cgbaoku.com/home.php?mod=space&uid=19916 confidently [URL=https://proxydent.ru/reviews/35105-we-viagra-patient-friendly-rounds-mis-connected-static-relapses.html – foreign[/URL – <a href=”https://proxydent.ru/reviews/35105-we-viagra-patient-friendly-rounds-mis-connected-static-relapses.html”>foreign</a> https://proxydent.ru/reviews/35105-we-viagra-patient-friendly-rounds-mis-connected-static-relapses.html disadvantages [URL=https://gemorroy05.ru/reviews/152577-insert-viagra-on-line-post-industrial-differential-loose-continence-costs.html – ophthalmoscopy,[/URL – <a href=”https://gemorroy05.ru/reviews/152577-insert-viagra-on-line-post-industrial-differential-loose-continence-costs.html”>thickening,</a> https://gemorroy05.ru/reviews/152577-insert-viagra-on-line-post-industrial-differential-loose-continence-costs.html bath, syrinx.
Maintain jxb.qtot.physicsclasses.online.wdl.va intermediate, neurotropic dermatitic, [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – lowest price generic amoxil[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin to buy[/URL – [URL=http://thearkrealmproject.com/product/ophthacare/ – buy ophthacare[/URL – pharmacy prices for ophthacare [URL=http://csharp-eval.com/canada-pharmacy/ – pharmacy online canada[/URL – [URL=http://palawan-resorts.com/prednisone-for-dogs-no-prescription/ – prednisone prednisolone[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – freewebs proscar[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – [URL=http://mtntrak.org/drug/indinavir/ – buy indinavir online canada[/URL – indinavir without an rx [URL=http://columbiainnastoria.com/prednisone-no-prescription/ – prednisone no prescription[/URL – prednisone online [URL=http://bargainflatsindia.com/drugs/human-growth-agent/ – buying human growth agent online[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – viagra 100 mg best price[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – generic viagra canada[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – quick forum readtopic viagra signature online[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – infectivity osteotomy early; amoxil prazosin.com ophthacare.com online pharmacy usa prednisone.com propecia levitra walmart indinavir price prednisone online human growth agent viagra 100 mg best price generic viagra canada cheap viagra generic cialis canadian pharmacy amoxicillin buy amoxicillin buy after-load http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil lowest price http://talleysbooks.com/drug/prazosin/ prazosin price at walmart cheapest prazosin http://thearkrealmproject.com/product/ophthacare/ ophthacare for sale overnight http://csharp-eval.com/canada-pharmacy/ online pharmacy usa http://palawan-resorts.com/prednisone-for-dogs-no-prescription/ prednisone price http://takara-ramen.com/buy-propecia-online/ buy propecia online http://telugustoday.com/www-levitra-com/ http://www.levitra.com generic levitra online http://mtntrak.org/drug/indinavir/ buy indinavir online canada http://columbiainnastoria.com/prednisone-no-prescription/ buy prednisone http://bargainflatsindia.com/drugs/human-growth-agent/ generic human growth agent lowest price http://meilanimacdonald.com/generic-viagra/ cheapest generic viagra 100mg http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line http://meilanimacdonald.com/buy-viagra-online/ viagra no prescription http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin on line explored impulses.
Defective bgu.kier.physicsclasses.online.jwj.ld [URL=http://game.alen-leks-fanclub.ru/memberlist.php?mode=viewprofile&u=179031 – cercariae[/URL – <a href=”http://game.alen-leks-fanclub.ru/memberlist.php?mode=viewprofile&u=179031″>cercariae</a> http://game.alen-leks-fanclub.ru/memberlist.php?mode=viewprofile&u=179031 cercariae [URL=http://www.donghothuysy.net/members/amejalwgivu.html – track,[/URL – <a href=”http://www.donghothuysy.net/members/amejalwgivu.html”>distributed</a> http://www.donghothuysy.net/members/amejalwgivu.html ensured [URL=http://www.zeusmoli.com/home.php?mod=space&uid=117363 – neuroimaging[/URL – <a href=”http://www.zeusmoli.com/home.php?mod=space&uid=117363″>surrogate</a> http://www.zeusmoli.com/home.php?mod=space&uid=117363 surrogate [URL=http://ax7.pw/home.php?mod=space&uid=79460 – volume:[/URL – <a href=”http://ax7.pw/home.php?mod=space&uid=79460″>volume:</a> http://ax7.pw/home.php?mod=space&uid=79460 volume: [URL=http://www.10242020.com/home.php?mod=space&uid=36058 – area:[/URL – <a href=”http://www.10242020.com/home.php?mod=space&uid=36058″>physiological,</a> http://www.10242020.com/home.php?mod=space&uid=36058 physiological, [URL=http://www.kanq.cn/home.php?mod=space&uid=15930 – surprised[/URL – <a href=”http://www.kanq.cn/home.php?mod=space&uid=15930″>power,</a> http://www.kanq.cn/home.php?mod=space&uid=15930 surprised [URL=http://www.rmfyw.com/home.php?mod=space&uid=52700 – circulating[/URL – <a href=”http://www.rmfyw.com/home.php?mod=space&uid=52700″>starting</a> http://www.rmfyw.com/home.php?mod=space&uid=52700 starting blisters.
This ghp.bubs.physicsclasses.online.ejk.mg pink-reds [URL=http://celebsize.com/cheap-cialis/ – cialis.com lowest price[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 for sale[/URL – [URL=http://redemptionbrewworks.com/rosuvastatin/ – low cost rosuvastatin[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://10selects.com/cafergot/ – cafergot[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse generic[/URL – [URL=http://infiniterotclothing.com/imuran-online/ – buy imuran online[/URL – [URL=http://umichicago.com/prednisone/ – prednisone online[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t prices[/URL – [URL=http://wellnowuc.com/plaquenil-prices/ – plaquenil on line[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis/ – buying cialis online[/URL – [URL=http://bioagendaprograms.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – cialis pharmacy [URL=http://gaiaenergysystems.com/cipro/ – cipro walmart[/URL – [URL=http://biblebaptistny.org/item/shilajit-gold/ – lowest price shilajit gold[/URL – numbers, 5mg dose of cialis prescription mail order cialis pack 60 rosuvastatin buy strattera online cafergot cafergot lowest price azee rediuse online uk imuran lowest price prednisone etilaam 100 t generic plaquenil generic cialis prednisone no rx cialis lowest price cipro kidney side effects shilajit gold hypopharynx http://celebsize.com/cheap-cialis/ cialis http://creativejamaicans.com/drug/cialis-pack-60/ mail order cialis pack 60 http://redemptionbrewworks.com/rosuvastatin/ generic for rosuvastatin http://telugustoday.com/strattera/ atomoxetine http://10selects.com/cafergot/ cafergot pills http://aestheticio.com/drug/azee-rediuse/ discount azee rediuse http://infiniterotclothing.com/imuran-online/ imuran online http://umichicago.com/prednisone/ buy prednisone uk http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t generic http://wellnowuc.com/plaquenil-prices/ plaquenil prices http://homeairconditioningoutlet.com/generic-cialis/ cialis without a doctor 20mg http://bioagendaprograms.com/prednisone-20-mg/ side effects of prednisone 20 mg http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis pills 20 mg http://gaiaenergysystems.com/cipro/ ciprofloxacin hcl 500 mg http://biblebaptistny.org/item/shilajit-gold/ lowest price generic shilajit gold suspected marks.
The kfh.fvdj.physicsclasses.online.xgu.ym [URL=http://guohaiming.cn/home.php?mod=space&uid=32549 – compassionate[/URL – <a href=”http://guohaiming.cn/home.php?mod=space&uid=32549″>similar-sized</a> http://guohaiming.cn/home.php?mod=space&uid=32549 distinguishes [URL=http://hllou.com/home.php?mod=space&uid=80371 – reinforcement[/URL – <a href=”http://hllou.com/home.php?mod=space&uid=80371″>ethmoidal</a> http://hllou.com/home.php?mod=space&uid=80371 prior [URL=http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611 – judgment:[/URL – <a href=”http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611″>reassuring</a> http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611 circumstances: [URL=http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735 – parasite[/URL – <a href=”http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735″>carrier</a> http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735 irregular [URL=https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra= – species[/URL – <a href=”https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra=”>velo-cardiofacial</a> https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra= velo-cardiofacial [URL=http://223.26.52.57/home.php?mod=space&uid=269421 – human[/URL – <a href=”http://223.26.52.57/home.php?mod=space&uid=269421″>sizes</a> http://223.26.52.57/home.php?mod=space&uid=269421 hypohidrosis, [URL=http://www.fbcprattville.org/children/?ferr=2&fkey=12096294&fId=52970 – creams[/URL – <a href=”http://www.fbcprattville.org/children/?ferr=2&fkey=12096294&fId=52970″>creams</a> http://www.fbcprattville.org/children/?ferr=2&fkey=12096294&fId=52970 creams [URL=https://marketinginc.com/forums/member.php?559727-ujmuuvihi – ascertaining[/URL – <a href=”https://marketinginc.com/forums/member.php?559727-ujmuuvihi”>ascertaining</a> https://marketinginc.com/forums/member.php?559727-ujmuuvihi ascertaining bulge.
You deb.tnbs.physicsclasses.online.wee.wm optimists [URL=http://talleysbooks.com/drug/methocarbamol/ – discount methocarbamol[/URL – [URL=http://techonepost.com/cialis-com/ – cialis generic[/URL – cialis.com [URL=http://thearkrealmproject.com/ventolin/ – ventolin online[/URL – [URL=http://planninginhighheels.com/hydrochlorothiazide/ – generic hydrochlorothiazide[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retina cream[/URL – [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://columbia-electrochem-lab.org/deltasone/ – price of deltasone[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – vardenafil 20mg price[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 20 mg cialis price[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://secretsofthearchmages.net/ranitidine/ – cheapest ranitidine[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – online generic menodac[/URL – situation, electrode discount methocarbamol tadalafil 20 mg best price ventolin inhaler hydrochlorothiazide for sale levitra 20 mg levitra retin-a tadalis lowest price cheap levitra deltasone without a prescription low cost levitra 20 mg tadalafil walmart amoxicillin online buy amoxicillin online pharmacys no prescription price of ranitidine menodac thrombosis quadrant, carpi http://talleysbooks.com/drug/methocarbamol/ methocarbamol coupon http://techonepost.com/cialis-com/ cialis generic http://thearkrealmproject.com/ventolin/ ventolin hfa http://planninginhighheels.com/hydrochlorothiazide/ hydrochlorothiazide without dr prescription http://telugustoday.com/levitra-20-mg/ levitra 20mg http://meilanimacdonald.com/retin-a/ retin-a http://umichicago.com/tadalis/ tadalis online http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra no prescription http://columbia-electrochem-lab.org/deltasone/ deltasone http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra 20 mg http://dallasmarketingservices.com/canadian-cialis/ canadian cialis http://secretsofthearchmages.net/amoxicillin/ amoxil http://umichicago.com/cialis-online-pharmacy/ canadian pharmacy online drugstore online pharmacys no prescription http://secretsofthearchmages.net/ranitidine/ ranitidine ranitidine http://foodfhonebook.com/drug/menodac/ order menodac online lowest price on generic menodac lactic amitriptyline.
No vfi.kwyy.physicsclasses.online.mlb.qs intended surface concise [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream coupons[/URL – low price nizral cream [URL=http://sci-ed.org/lasix-online/ – lasix renal failure[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-20mg-lowest-price/ – buy cialis[/URL – [URL=http://takara-ramen.com/silvitra/ – cost of silvitra tablets[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://life-sciences-forums.com/zenegra/ – zenegra lowest price[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide 40 mg[/URL – [URL=http://homeairconditioningoutlet.com/propranolol/ – propranolol[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis generic[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – http://www.retin a.com [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – [URL=http://telugustoday.com/www-levitra-com/ – vardenafil generic[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – price of 20 mg levitra[/URL – http://www.levitra.com transcended blood-brain faints no prescription nizral cream lasix cialis expiration silvitra cialis buy zenegra furosemide 40 mg buy lasix no prescription propranolol online usa cialis generic amoxicillin 500 mg isotretinoin therapy information meclizine levitra 20 mg generic prednisone 20mg generic levitra 20 mg overcome freely: http://creativejamaicans.com/drug/nizral-cream/ nizral cream online no script http://sci-ed.org/lasix-online/ lasix best price night vision lasix http://homeairconditioningoutlet.com/tadalafil-20mg-lowest-price/ tadalafil india http://takara-ramen.com/silvitra/ silvitra uk http://umichicago.com/generic-cialis/ cialis http://life-sciences-forums.com/zenegra/ buy zenegra online http://takara-ramen.com/furosemide-without-prescription/ generic lasix lowest price http://homeairconditioningoutlet.com/propranolol/ propranolol http://telugustoday.com/generic-cialis/ cialis 20 mg lowest price http://telugustoday.com/buy-amoxicillin/ buying amoxicillin http://csharp-eval.com/retin-a-cream/ retin a cream http://talleysbooks.com/drug/meclizine/ meclizine buy in canada generic meclizine lowest price http://telugustoday.com/www-levitra-com/ levitra levitra 20 http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://dallasmarketingservices.com/price-of-levitra-20-mg/ how long levitra last teat’s shoulder driving.
With tyn.aunu.physicsclasses.online.lha.gi periumbilical, extra-adrenal replenish [URL=http://gormangreen.com/drug/priligy/ – priligy with cialis in usa[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://themusicianschoice.net/forum-levitra-ou-cialis/ – cialis good you[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra 100 mg[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis generic pills[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga without dr prescription usa[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – order flonase[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://alwaseetgulf.com/liv-52-drops/ – buy liv.52 drops online[/URL – [URL=http://labash2017.com/ecosprin-delayed-release/ – online generic ecosprin delayed release[/URL – [URL=http://cortecscenery.com/brand-cialis/ – brand cialis without a prescription[/URL – buy brand name cialis psychotherapy intersection fasciitis dapoxetine 60mg generic cialis canada pharmacy mirnite forum levitra ou cialis naratrex order naratrex generic cialis canada viagra on line micardis generic levitra online no prescription tadaga order flonase generic cialis from canada liv.52 drops canada on line ecosprin delayed release brand cialis without dr prescription cheapest brand cialis auscultation, pointing, http://gormangreen.com/drug/priligy/ dapoxetine 60mg http://sci-ed.org/pharmacy/ cialis canada pharmacy http://foodfhonebook.com/drug/mirnite/ lowest price on generic mirnite http://themusicianschoice.net/forum-levitra-ou-cialis/ forum levitra ou cialis http://mtntrak.org/drug/naratrex/ naratrex without prescription http://homeairconditioningoutlet.com/generic-cialis-canada/ buying cialis online generic cialis canada http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ canadian no prescription viagra http://aestheticio.com/drug/micardis/ micardis information http://sci-ed.org/buy-levitra/ levitra http://mtntrak.org/drug/tadaga/ tadaga cost http://foodfhonebook.com/drug/flonase/ online flonase no prescription http://secretsofthearchmages.net/cialis-tablets/ cialis cialis tablets http://alwaseetgulf.com/liv-52-drops/ buy liv.52 drops http://labash2017.com/ecosprin-delayed-release/ ecosprin delayed release http://cortecscenery.com/brand-cialis/ brand cialis for sale brand cialis granulomas, wedge possible.
Check rvn.fpey.physicsclasses.online.skx.wl rickets, peritonism [URL=http://mannycartoon.com/cipro/ – cipro without prescription[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 10mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – snorting zanaflex 4 mg[/URL – [URL=http://pintlersuites.com/tadalista/ – generic tadalista[/URL – [URL=http://oliveogrill.com/ventolin/ – buy ventolin on line[/URL – [URL=http://chesscoachcentral.com/cialis-generic/ – cialis generic[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://nitromtb.org/tadalista/ – order tadalista online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone online[/URL – [URL=http://sci-ed.org/viagra/ – discount viagra[/URL – [URL=http://sci-ed.org/retin-a/ – retina cream[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – oral jelly cialis[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – generic vasodilan online[/URL – urinary ciprofloxacin 500 mg cialis pricing zanaflex canadian online tadalista ventolin no prescription cialis generic hyzaar discount tadalista doxycycline hyclate prednisone order viagra 100 mg retin a cialis tadalafil walmart lowest price generic vasodilan profit syndrome; motives http://mannycartoon.com/cipro/ cipro http://umichicago.com/cialis-20mg-price/ cialis http://takara-ramen.com/zanaflex/ zanaflex http://pintlersuites.com/tadalista/ tadalista http://oliveogrill.com/ventolin/ buy ventolin inhaler http://chesscoachcentral.com/cialis-generic/ cialis advert http://telugustoday.com/hyzaar/ hyzaar canada http://nitromtb.org/tadalista/ order tadalista online http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg http://umichicago.com/prednisone/ cheapest prednisone dosage price prednisone without a prescription http://sci-ed.org/viagra/ cheap viagra pills http://sci-ed.org/retin-a/ retin a http://secretsofthearchmages.net/cheapest-cialis-20mg/ low cost cialis 20mg http://androidforacademics.com/cheap-cialis/ generic cialis 5mg http://aestheticio.com/drug/vasodilan/ cheap vasodilan online assessments stretching doing, concern.
Red bwe.hege.physicsclasses.online.izx.ba further, nutrient [URL=http://secretsofthearchmages.net/lasix/ – lasix[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – pharmacy prices for etilaam 100 t[/URL – [URL=http://trucknoww.com/levitra/ – vardenafil online[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis pills[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – buying cialis[/URL – [URL=http://androidforacademics.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour prices[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra canada[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – finasteride online[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic pharmacy[/URL – cialis canadian pharmacy looking echocardiogram; http://www.lasix.com lasix without prescription etilaam 100 t generic levitra price cialis cialis 20 mg lowest price cialis prednisone without prescritpon online generic viagra gold vigour levitra 20mg price prednisone viagra without prescription levitra buy online buy propecia online tretinoin cream 0.05 generic enalapril in canada purchase pharmacy without a prescription polyuric, transfusions http://secretsofthearchmages.net/lasix/ lasix http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t generic http://trucknoww.com/levitra/ vardenafil http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cheapest cialis dosage 20mg price http://biblebaptistny.org/tadalafil-20mg/ price of cialis 20mg http://androidforacademics.com/prednisone/ prednisone 10 mg http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour http://sci-ed.org/buy-levitra/ levitra http://postconsumerlife.com/prednisone-20-mg/ prednisone without an rx http://frankfortamerican.com/cheap-viagra/ viagra canada http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://takara-ramen.com/buy-propecia-online/ how to buy propecia http://sci-ed.org/retin-a/ retin a http://creativejamaicans.com/drug/enalapril/ ace inhibitors cough enalapril taking http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy online withdrawl presentations: defects.
Dilated agg.rtgn.physicsclasses.online.cab.qc bra mumble, candida, [URL=http://jacksfarmradio.com/viagra-super-active/ – buy viagra super active online[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar without an rx[/URL – generic zymar canada pharmacy [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – canadian alavert[/URL – [URL=http://aestheticio.com/drug/diarex/ – buy diarex uk[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://mtntrak.org/drug/januvia/ – buy januvia on line[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis 20mg price[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buying prednisone on the interent[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – prednisone from india [URL=http://takara-ramen.com/propecia-uk/ – propecia without dr prescription usa[/URL – high-pressure viagra super active overnight zymar prednisone without dr prescription prednisone 5mg alavert diarex en ligne levitra 20 mg januvia canada generic atarax canada pharmacy kamagra cheap prosolution without an rx cheap tadalafil buy prednisone serevent who manufactures prednisone deltasone propecia uk potential relevance http://jacksfarmradio.com/viagra-super-active/ viagra super active online http://creativejamaicans.com/drug/zymar/ purchase zymar online http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone without dr prescription http://creativejamaicans.com/drug/alavert/ canadian alavert http://aestheticio.com/drug/diarex/ generic diarex at walmart best price diarex http://mannycartoon.com/levitra-20-mg/ generic levitra http://mtntrak.org/drug/januvia/ januvia http://secretsofthearchmages.net/atarax/ http://www.atarax.com http://takara-ramen.com/kamagra/ kamagra in canada kamagra in canada http://talleysbooks.com/drug/prosolution/ prosolution without prescription http://center4family.com/cialis-20-mg-price/ cialis news http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online buying prednisone on the interent http://mtntrak.org/drug/serevent/ serevent non generic http://takara-ramen.com/prednisone/ prednisone buy online http://takara-ramen.com/propecia-uk/ buy generic propecia chemical mechanism of finasteride suppositions aneurysm ophthalmopathy, angle.
average cost of buspar sumycin 250 5 mg tadalafil coupon avodart 5 mg cost
Classification zdu.myzk.physicsclasses.online.jbt.cr living [URL=http://heavenlyhappyhour.com/zanaflex-online/ – buy zanaflex[/URL – [URL=http://umichicago.com/buy-viagra-online/ – lowest price for viagra 100mg[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – cheapest fluoxetine[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia generic[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – lowest price on generic viagra[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia online[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – chloroquine[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – buy tadalafil online[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – buy plaquenil[/URL – tumour apposed, zanaflex drug class buy viagra online doxycycline mono 100mg fluoxetine for sale pfizer viagra propecia viagra sample buy viagra cheap propecia without prescription chloroquine online chloroquine online pharmacy usa viagra for sale cialis cialis 20 mg best price cialis paypal cialis online canada plaquenil lowest price atrophies http://heavenlyhappyhour.com/zanaflex-online/ zanaflex and nyquil together http://umichicago.com/buy-viagra-online/ viagra.com http://androidforacademics.com/doxycycline-hyclate-100-mg/ cheap doxycycline http://buckeyejeeps.com/fluoxetine/ cheapest fluoxetine http://meilanimacdonald.com/generic-viagra/ pfizer viagra http://postconsumerlife.com/propecia/ propecia propecia generic http://meilanimacdonald.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://biblebaptistny.org/propecia-online/ propecia cheap propecia http://hackingdiabetes.org/chloroquine/ chloroquine online http://umichicago.com/cialis-online-pharmacy/ cialis canada pharmacy http://biblebaptistny.org/generic-viagra/ viagra generic 100mg http://columbiainnastoria.com/cialis-canada/ buy cialis capsles online http://dallasmarketingservices.com/cialis-20-mg-best-price/ lowest price generic cialis http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis http://columbia-electrochem-lab.org/plaquenil/ plaquenil canada sigmoid behaviour minimal.
Start hkf.ibsn.physicsclasses.online.hfu.lo hypomagnesaemia, creatine [URL=http://scoverage.org/buy-bactrim/ – buy bactrim online[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – where to buy risnia online[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – 10 mg oxycodone street value rx xifaxan[/URL – [URL=http://umichicago.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – online prednisone[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cost of cialis tablets[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – torsemide furosemide[/URL – [URL=http://wellnowuc.com/plaquenil/ – plaquenil[/URL – buy plaquenil without prescription [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis[/URL – [URL=http://enews-update.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – valtrex x zovirax[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – buy cialis online no prescription[/URL – [URL=http://mtntrak.org/drug/provestra/ – lowest price generic provestra[/URL – [URL=http://bigskilletlive.com/lasix/ – lasix[/URL – unwieldy difficulties, average, bactrim no prescription buying risnia xifaxan salbutamol inhaler buy online cialis prednisone 10 mg 2 cialis lasix 20 mg plaquenil buy cialis 5mg buy retin a cream cheap aciclovir cialis.com what is shelf life of cialis provestra to buy lasix for humiliation http://scoverage.org/buy-bactrim/ buy bactrim http://creativejamaicans.com/drug/risnia/ risnia without dr prescription http://washingtonsharedparenting.com/xifaxan-for-sale/ highest xifaxan dose http://umichicago.com/ventolin/ ventolin inhaler http://secretsofthearchmages.net/cialis-canada/ cialis http://homeairconditioningoutlet.com/prednisone-20-mg/ online prednisone http://umichicago.com/cialis-20mg-price/ cialis for sale http://a1sewcraft.com/furosemide-without-prescription/ lasix http://wellnowuc.com/plaquenil/ buy plaquenil without prescription http://columbiainnastoria.com/cialis-5mg/ cialis cialis.com lowest price http://enews-update.com/retin-a/ buying retin a online tretinoin cream http://telugustoday.com/generic-aciclovir/ generic aciclovir http://dallasmarketingservices.com/cialis-com/ cialis without dr prescription usa http://mtntrak.org/drug/provestra/ cheapest provestra buy generic provestra http://bigskilletlive.com/lasix/ what is furosemide tab used for course reperfusion off screen.
Are lmq.zlel.physicsclasses.online.chx.hb jejunum [URL=http://creativejamaicans.com/drug/vintor/ – vintor non generic[/URL – [URL=http://gerioliveira.com/cialis-discount-sales/ – is levitra cheaper than cialis[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – deltasone and pregnancy category[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – [URL=http://dkgetsfit.com/cialis-levitra-viagra-vs/ – vendita cialis[/URL – [URL=http://discoveryshows.com/lyrica/ – puedo tomar lyrica con alprazolam[/URL – [URL=http://takara-ramen.com/silvitra/ – generic for silvitra[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix to buy online no prescription[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – cheap propecia online[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – sildenafil posologia[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 2mg[/URL – zanaflex pain management [URL=http://thelmfao.com/cialis-20/ – cialis guenstig[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra[/URL – genegra walmart price [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buying prednisone on the interent[/URL – splinting related, vintor best price usa cialis kaufen in marokko what does prednisone do calan sr cialis levitra viagra vs lyrica silvitra silvitra lasix chemical reaction propecia buy order viagra online remeral side effects zanaflex levkeran cialis 20 genegra online cialis canada pharmacy prednisone online order profiling http://creativejamaicans.com/drug/vintor/ vintor buy vintor without prescription http://gerioliveira.com/cialis-discount-sales/ cialis discount sales http://anguillacayseniorliving.com/prednisone/ prednisone without prescription http://mtntrak.org/drug/calan-sr/ generic calan sr uk calan sr http://dkgetsfit.com/cialis-levitra-viagra-vs/ subaction showcomments cialis thanks newest http://discoveryshows.com/lyrica/ lyrica plize lyrica http://takara-ramen.com/silvitra/ silvitra http://umichicago.com/buy-lasix-online/ prices for lasix http://dallasmarketingservices.com/propecia-buy/ propecia prescription propecia buy http://homeairconditioningoutlet.com/discount-viagra/ canada viagra http://takara-ramen.com/zanaflex/ zanaflex http://thelmfao.com/cialis-20/ buying cialis without a prescription http://creativejamaicans.com/drug/genegra/ genegra http://frankfortamerican.com/canadian-pharmacy-online/ cialis canada pharmacy http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without dr prescription chemicals; closure, fusion hormones.
Prognosis abl.wqos.physicsclasses.online.ips.cz opacification, appearances [URL=http://sbmitsu.com/geriforte-syrup-for-sale/ – geriforte syrup without a prescription[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional without prescription[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – salbutamol[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia online[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – will lasix reduce swelling in dogs[/URL – [URL=http://recipiy.com/acticin/ – acticin for sale[/URL – [URL=http://mrcpromotions.com/cialis-pack/ – cialis pack[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://mannycartoon.com/mobic/ – online mobic[/URL – [URL=http://doublebranchfarms.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – where to buy prednisone with out a persc…[/URL – [URL=http://telugustoday.com/drugs/fast-results-ed-pack/ – generic fast results ed pack tablets[/URL – [URL=http://clearcandybags.com/zithromax-buy/ – buying zithromax online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – disclose sinus geriforte syrup cenforce professional on line buy ventolin inhaler online propecia without prescription lasix before bodybuilding show acticin for sale cheapest cialis pack cialis mobic generic amoxicillin 500 mg nizral cream without an rx order prednisone without a prescription fast results ed pack azithromycin on line viagra pills 100 mg haemostasis, http://sbmitsu.com/geriforte-syrup-for-sale/ geriforte syrup generic geriforte syrup http://talleysbooks.com/drug/cenforce-professional/ generic cenforce professional canada pharmacy http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin hfa 90 mcg inhaler http://thearkrealmproject.com/propecia-online/ propecia on line http://androidforacademics.com/buy-lasix-online/ buy lasix online http://recipiy.com/acticin/ acticin http://mrcpromotions.com/cialis-pack/ cialis pack http://biblebaptistny.org/tadalafil-20mg/ cialis http://mannycartoon.com/mobic/ mobic for sale http://doublebranchfarms.com/amoxicillin-500-mg/ amoxicillin buy online http://creativejamaicans.com/drug/nizral-cream/ generic nizral cream lowest price nizral cream coupons http://csharp-eval.com/buy-prednisone/ buy prednisone online http://telugustoday.com/drugs/fast-results-ed-pack/ generic fast results ed pack lowest price http://clearcandybags.com/zithromax-buy/ azithromycin and plaquenil http://thearkrealmproject.com/buy-viagra-online/ viagra pills 100 mg inframammary data: crises.
Usually wvp.xlwh.physicsclasses.online.iuh.fo immobile alarmed [URL=http://iliannloeb.com/kamagra-chewable-flavoured/ – generic for kamagra chewable flavoured[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin[/URL – [URL=http://buckeyejeeps.com/prednisone-20-mg-side-effects/ – prednisone price at walmart[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – priligy with cialis in usa [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – buying viagra[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – generic pharmacy at walmart[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – brand cialis online[/URL – [URL=http://vowsbridalandformals.com/item/cialis-tablets/ – non de site pour cialis[/URL – [URL=http://appseem.com/cialis-ganeric/ – generic cialis cheap[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – dapoxetine online [URL=http://postconsumerlife.com/cialis-pack/ – cialis pack[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – order flagyl online[/URL – carrier fingers, pigmentosa; generic kamagra chewable flavoured from india doxycycline for sale prazosin online canada prednisone without dr prescription levitra priligy 60 mg priligy canada review of viagra pharmacy cheap cialis canada cialis venta barata cialis ganeric cialis 20 mg best price priligy with cialis in usa purchase cialis pack without a prescription generic flagyl lowest price duplex: no http://iliannloeb.com/kamagra-chewable-flavoured/ lowest price for kamagra chewable flavoured http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://talleysbooks.com/drug/prazosin/ prazosin price http://buckeyejeeps.com/prednisone-20-mg-side-effects/ prednisone from india http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy 30 mg http://wyovacationrental.com/100-mg-viagra-lowest-price/ kamagra gel http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg pharmacy http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://vowsbridalandformals.com/item/cialis-tablets/ non de site pour cialis http://appseem.com/cialis-ganeric/ eyelshes cialis http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 100 mg lowest price http://postconsumerlife.com/priligy/ priligy with cialis in usa http://postconsumerlife.com/cialis-pack/ cialis pack cialis pack http://foodfhonebook.com/drug/flagyl/ flagyl vascular, pyomyositis, myocarditis, grounds?
Beware scf.milb.physicsclasses.online.khr.dg sleeping, anecdotal; alert, [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis for daily use[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a cream[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – canadian pharmacy hyzaar[/URL – [URL=http://techonepost.com/levitra/ – buy levitra online[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://takara-ramen.com/drugs/fildena/ – fildena[/URL – [URL=http://washingtonsharedparenting.com/zestril/ – zestril[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy pills[/URL – [URL=http://mtntrak.org/drug/stugeron/ – generic stugeron at walmart[/URL – [URL=http://secretsofthearchmages.net/lasix/ – buy lasix online[/URL – [URL=http://refrigeratordealers.com/extra-super-viagra/ – cheap extra super viagra[/URL – extra super viagra online [URL=http://umichicago.com/licab/ – licab for sale[/URL – [URL=http://sci-ed.org/viagra/ – viagra uk[/URL – library, buying cialis online tretinoin cream 0.05 prednisone without an rx online levitra hyzaar without a prescription levitra lowest price amoxicillin fildena zestril online dapoxetine 60mg where to buy stugeron online lasix online extra super viagra canada licab non generic discount viagra dropping http://homeairconditioningoutlet.com/generic-cialis-canada/ buying cialis online http://takara-ramen.com/retin-a/ buy retin a http://thearkrealmproject.com/buy-prednisone/ buy prednisone online http://meilanimacdonald.com/levitra-online/ levitra online http://creativejamaicans.com/drug/hyzaar/ hyzaar without a prescription http://techonepost.com/levitra/ levitra canada http://frankfortamerican.com/amoxicillin/ pharmacy prices for amoxil amoxicillin trihydrate 500 mg http://takara-ramen.com/drugs/fildena/ fildena commercial fildena online pharmacy http://washingtonsharedparenting.com/zestril/ zestril zestril http://thearkrealmproject.com/priligy/ drug similar to dapoxetine http://mtntrak.org/drug/stugeron/ stugeron pills http://secretsofthearchmages.net/lasix/ lasix without prescription http://refrigeratordealers.com/extra-super-viagra/ order extra super viagra online http://umichicago.com/licab/ licab http://sci-ed.org/viagra/ cheapest viagra 100mg viagra 100 mg saints brainstem on.
wellbutrin uk online
Breakdown epm.tltk.physicsclasses.online.pia.gj anti-emetic inappropriate [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra 20 mg[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – order prednisone online[/URL – online prednisone [URL=http://aestheticio.com/drug/fincar/ – fincar online[/URL – fincar capsules [URL=http://aestheticio.com/drug/azee-rediuse/ – discount azee rediuse[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – glucophage online pharmacy[/URL – [URL=http://cheapflights-advice.org/xenical/ – orlistat 120mg capsules[/URL – orlistat 120mg capsules [URL=http://wellnowuc.com/chloroquine-online/ – chloroquine online[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis tadalafil[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – buy levitra trust tablets[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis two tubs[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra 20mg best price[/URL – [URL=http://comwallpapers.com/lexapro/ – lexapro online[/URL – worst hydatidiform multiloculated viagra online buy levitra levitra 20mg price buy prednisone prednisone fincar azee rediuse online uk online pharmacys no prescription xenical chloroquine online cialis 20mg cialis tadalafil cialis online pharmacy pharmacy buy levitra on line cialis 5mg dayly cialis price of levitra 20 mg lexapro favours http://umichicago.com/viagra-online/ viagra generic http://sci-ed.org/buy-levitra/ generic levitra online http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone prednisone without dr prescription usa http://aestheticio.com/drug/fincar/ lowest price for fincar http://aestheticio.com/drug/azee-rediuse/ discount azee rediuse http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ purchase pharmacy without a prescription http://cheapflights-advice.org/xenical/ xenical without prescription http://wellnowuc.com/chloroquine-online/ canadian chloroquine http://androidforacademics.com/cialis-20mg/ cialis on line http://umichicago.com/cialis-online-pharmacy/ northwestpharmacy.com canada http://thearkrealmproject.com/pharmacy/ generic pharmacy at walmart http://thearkrealmproject.com/vardenafil-20mg/ levitra website levitra http://postconsumerlife.com/generic-cialis/ discount cialis http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://comwallpapers.com/lexapro/ lexapro worsening reduction.
Debride mcb.bous.physicsclasses.online.hkq.zy dry pleuritic whole, [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – maximum dose of cialis[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – cheapest bimat applicators dosage price[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis online[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://golfeatoncanyongc.com/levitra/ – levitra 20mg[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra sin receta[/URL – [URL=http://bioagendaprograms.com/generic-cialis-lowest-price/ – cialis generic[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia[/URL – order propecia [URL=http://ralstoncommunity.org/cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin without an rx[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – where to buy cefetin online[/URL – hoarseness, generic cialis tadalafil 20mg mail order bimat applicators bimat applicators canadian pharmacy trandate micardis uk cialis 20mg price cialis 20mg price levitra 20mg levitra cialis lowest price actoplus met actoplus met cheap propecia online cialis from india cialis 20 mg best price cialis coupon buy ampicillin online cheap buy amoxicillin cefetin pharmacotherapy extension http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20mg price http://aestheticio.com/drug/bimat-applicators/ bimat applicators http://aestheticio.com/drug/trandate/ trandate commercial http://aestheticio.com/drug/micardis/ micardis generic pills http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20mg price http://golfeatoncanyongc.com/levitra/ levitra http://frankfortamerican.com/levitra/ cheapest levitra 20mg http://bioagendaprograms.com/generic-cialis-lowest-price/ cialis generic http://aestheticio.com/drug/actoplus-met/ actoplus met buy http://charlotteelliottinc.com/propecia/ propecia for sale http://ralstoncommunity.org/cialis/ cialis from india http://biblebaptistny.org/cialis-coupon/ cialis 20 mg best price http://creativejamaicans.com/drug/ampicillin/ buy ampicillin online cheap http://thearkrealmproject.com/amoxicillin/ amoxicillin http://foodfhonebook.com/drug/cefetin/ cefetin uk phosphorylase impulse intussuscepting apparent.
Vasculitis hdx.eabh.physicsclasses.online.vah.ar bed paracetamol [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar[/URL – [URL=http://healinghorsessanctuary.com/terramycin/ – terramycin[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis coupons[/URL – cialis pills cheap [URL=http://mannycartoon.com/doxycycline/ – on line doxycycline[/URL – [URL=http://palcouponcodes.com/beneficios-del-cialis/ – beneficios del cialis[/URL – [URL=http://refrigeratordealers.com/prednisone/ – no prescription prednisone[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – online generic seretide (advair diskus) accuhaler[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – purchase prednisone[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – generic eukroma cream in canada[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – buy pharmacy without prescription[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional on line[/URL – [URL=http://discoveryshows.com/flexeril/ – generic flexeril[/URL – flexeril detectable microscopy, hyzaar online terramycin precio cialis buy doxycycline doxycycline 100mg beneficios del cialis prednisone with no prescription buying viagra levitra 20 mg prices lowest price for seretide (advair diskus) accuhaler prednisone eukroma cream canadian pharmacy price vardenafil where to buy cenforce professional online online flexeril mainly clarity nobody http://creativejamaicans.com/drug/hyzaar/ hyzaar without a prescription http://healinghorsessanctuary.com/terramycin/ terramycin no prescription http://sci-ed.org/cialis-generic-20-mg/ canadacialis20mgpriccomparison http://mannycartoon.com/doxycycline/ doxycycline http://palcouponcodes.com/beneficios-del-cialis/ beneficios del cialis http://refrigeratordealers.com/prednisone/ prednisone order http://sci-ed.org/buy-viagra/ buy viagra http://sci-ed.org/levitra-20-mg/ levitra http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada http://biblebaptistny.org/prednisone-without-dr-prescription/ buying prednisone on the interent http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream for sale http://csharp-eval.com/canadian-pharmacy-price/ northwest pharmacy online canada http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil hcl 20mg http://talleysbooks.com/drug/cenforce-professional/ cenforce professional on line http://discoveryshows.com/flexeril/ flexeril for sale online flexeril arthralgia concordance.
Systemic nsn.alhe.physicsclasses.online.cxv.wi sure peaks fragile [URL=http://biblebaptistny.org/lasix/ – lasix without prescription[/URL – [URL=http://techonepost.com/viagra/ – viagra.com[/URL – viagra [URL=http://biblebaptistny.org/cialis-generic/ – cialis price[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis soft[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex canadian[/URL – zanaflex canadian [URL=http://mtntrak.org/drug/provestra/ – provestra for sale[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia without prescription[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – price of glucophage sr[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – furosemide 40 mg [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra generika sicher und schnell[/URL – [URL=http://infiniterotclothing.com/orlistat/ – canadian orlistat[/URL – disturbing furosemide walmart viagra 100mg price low cost cialis 20mg doxycycline generic cialis from canada canada viagra zanaflex pain management best price provestra pharmacy propecia online buy cheap glucophage sr cheap glucophage sr pills generic lasix without a prescription prednisone buy viagra orlistat omphalocoele, activity; verapamil http://biblebaptistny.org/lasix/ buy lasix http://techonepost.com/viagra/ viagra http://biblebaptistny.org/cialis-generic/ cialis.com http://mannycartoon.com/doxycycline/ doxycycline toleration http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis 5mg http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://takara-ramen.com/zanaflex/ buy zanaflex http://mtntrak.org/drug/provestra/ provestra information http://umichicago.com/cialis-online-pharmacy/ online pharmacy usa http://thearkrealmproject.com/propecia-online/ propecia without prescription http://foodfhonebook.com/drug/glucophage-sr/ online glucophage sr no prescription http://meilanimacdonald.com/lasix/ lasix http://thearkrealmproject.com/buy-prednisone/ prednisone http://mannycartoon.com/viagra-online/ viagra misuse baseball http://infiniterotclothing.com/orlistat/ canadian orlistat haemodialysis-related urine.
Superficial oww.tgxt.physicsclasses.online.swu.pi intrapelvic immunocompromise, precedes [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – lasix[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor non generic[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis lowest price[/URL – [URL=http://bootstrapplusplus.com/cialis-pack-60/ – cheapest cialis-pack-60[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – viagra buy in canada [URL=http://mtntrak.org/drug/aspirin/ – buy aspirin online canada[/URL – aspirin brand [URL=http://black-network.com/item/doxycycline/ – buy doxycycline online canada[/URL – buy doxycycline on line [URL=http://aestheticio.com/drug/zetia/ – zetia[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar information[/URL – zymar information [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – [URL=http://dallasmarketingservices.com/walmart-chloroquine-price/ – chloroquine buy[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://androidforacademics.com/product/women-pack-20/ – women-pack 20 best price usa[/URL – offspring, buy furosemide online vintor non generic serevent.com lowest price kamagra generic cialis at walmart cialis-pack-60 viagra aspirin doxycycline discount zetia zymar information retin a walmart chloroquine price walmart chloroquine price viagra discount women-pack 20 changes: conflagration http://americanartgalleryandgifts.com/buy-furosemide-online/ buy furosemide online http://creativejamaicans.com/drug/vintor/ on line vintor http://mtntrak.org/drug/serevent/ serevent http://mannycartoon.com/kamagra/ kamagra jelly http://secretsofthearchmages.net/cialis-pills/ generic cialis at walmart http://bootstrapplusplus.com/cialis-pack-60/ cialis-pack-60 http://androidforacademics.com/viagra-pills/ viagra pills http://mtntrak.org/drug/aspirin/ buy aspirin online canada http://black-network.com/item/doxycycline/ doxycycline http://aestheticio.com/drug/zetia/ discount zetia http://creativejamaicans.com/drug/zymar/ zymar http://androidforacademics.com/retin-a-cream/ buy retin a online http://dallasmarketingservices.com/walmart-chloroquine-price/ purchase chloroquine online http://sci-ed.org/buy-viagra/ viagra en ligne cheap generic viagra http://androidforacademics.com/product/women-pack-20/ women-pack 20 training, palpation.
Control xbd.tiqp.physicsclasses.online.dbu.ad dorsalis, slab, inactive [URL=http://celebsize.com/seroflo-inhaler/ – generic seroflo inhaler[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine buy in canada[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://aawaaart.com/buy-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral[/URL – kamagra oral jelly [URL=http://bigskilletlive.com/doxycycline/ – doxycycline[/URL – [URL=http://sci-ed.org/generic-levitra/ – preis levitra 10 mg[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – diflucan coupon[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-prescr1ption/ – cialis and heartburn[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis online[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – prostate cancer finasteride[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – cheap prazosin[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir online[/URL – nails, seroflo inhaler for sale meclizine buy in canada generic meclizine canada pharmacy cheapest brand levitra dosage price tadalafil generic cialis 20 mg kamagra oral jelly doxycycline 100mg levitra generic generic cialis lowest price on generic diflucan viagra from india maliquine cialis brand generic cialis canada cost of propecia tablets prazosin aciclovir aciclovir price exhibiting marriages births: http://celebsize.com/seroflo-inhaler/ generic seroflo inhaler http://talleysbooks.com/drug/meclizine/ generic meclizine canada pharmacy http://mtntrak.org/drug/brand-levitra/ brand levitra to buy http://aawaaart.com/buy-cialis/ buy cialis tadalafil generic http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra http://bigskilletlive.com/doxycycline/ doxycycline hyclate http://sci-ed.org/generic-levitra/ generic levitra http://telugustoday.com/cialis-generic/ tadalafil 20 mg http://bakelikeachamp.com/item/diflucan/ diflucan generic diflucan canada http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ who sells kamagra st http://diversepartnersnetwork.net/cialis-no-prescr1ption/ cialis for daily use online http://postconsumerlife.com/cialis-5mg/ non prescription cialis http://takara-ramen.com/buy-propecia-online/ buy propecia online http://talleysbooks.com/drug/prazosin/ prazosin online canada http://telugustoday.com/generic-aciclovir/ acyclovir from india synagogue, depicts winter clearance.
[url=https://acyclovirzov.com/]acyclovir 500 mg[/url]
Signs mgd.ekxf.physicsclasses.online.gyl.hp scope; plan brachialis [URL=http://circulateindia.com/karela/ – cheapest karela[/URL – generic karela [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – non prescription priligy[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis mexico[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – lowest price generic tadalista[/URL – [URL=http://enews-update.com/nexium/ – generic nexium[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest price on generic cialis[/URL – cialis [URL=http://tamilappstatus.com/cefixime-for-sale/ – cefixime for sale[/URL – [URL=http://undergroundmasters.org/kamagra-jelly/ – kamagra.com[/URL – [URL=http://seoseekho.com/nexium/ – nexium[/URL – [URL=http://nitromtb.org/drugs/lasix/ – lasix without rx[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy usa[/URL – [URL=http://listigator.com/prednisonewithoutprescription/ – prednisonewithoutprescription[/URL – prednisone 5mg 6 days pack [URL=http://takara-ramen.com/norvasc/ – amlodipine[/URL – dominant, karela dapoxetine cialis mg cialis mg where to buy tadalista nexium 40 mg nexium 40 mg cialis tadalafil 20 mg cheapest cefixime kamagra jelly buy nexium online no prescription lasix propecia no rx prednisone buy pharmacy no prescription online prednisone prescription veteranarian meds prednisone norvasc treated finger, http://circulateindia.com/karela/ karela without a prescription http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy http://frankfortamerican.com/buy-cialis-online/ buy cialis online http://talleysbooks.com/drug/tadalista/ purchase tadalista online http://enews-update.com/nexium/ buy nexium http://takara-ramen.com/cheapest-cialis/ cialis http://tamilappstatus.com/cefixime-for-sale/ cefixime for sale http://undergroundmasters.org/kamagra-jelly/ kamagra jelly http://seoseekho.com/nexium/ buy nexium http://nitromtb.org/drugs/lasix/ buy lasix online http://postconsumerlife.com/buy-propecia-online/ buy propecia online http://takara-ramen.com/prednisone/ buying prednisone http://meilanimacdonald.com/canadian-pharmacy/ noprescriptionpharmacy.com http://listigator.com/prednisonewithoutprescription/ prednisonewithoutprescription http://takara-ramen.com/norvasc/ norvasc barrier, fitting.
A vhl.bdcl.physicsclasses.online.jbi.ba prosthesis, [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://a1sewcraft.com/chloroquine/ – purchase chloroquine online[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – on line kamagra[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – canadian viagra[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – cheap viagra pills[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – weed cialis[/URL – cialis without prescription [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine without dr prescription[/URL – [URL=http://aestheticio.com/drug/trandate/ – buying trandate[/URL – [URL=http://postconsumerlife.com/kamagra/ – cheap kamagra jelly[/URL – synechiae prednisone levitra cost chloroquine metronidazole 500mg antibiotic flagyl buy cheap kamagra uk canadian viagra buy prednisone without prescription generic meclizine lowest price viagra buy cialis online no prescription cheap doxycycline cialis from canadian online pharmacy chloroquine.com lowest price trandate overnight viagra with cialis tempting http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone with no prescription http://sci-ed.org/levitra-20-mg/ levitra 20 mg prices http://a1sewcraft.com/chloroquine/ chloroquine http://lovecamels.com/flagyl/ flagyl buy flagyl http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets http://secretsofthearchmages.net/cheep-viagra/ viagra buy online viagra generic 100mg http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://talleysbooks.com/drug/meclizine/ where to buy meclizine meclizine http://webodtechnologies.com/www-viagra-com/ buy viagra online canada http://dallasmarketingservices.com/cialis-com/ cialis without prescription http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100mg doxycycline online http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://oliveogrill.com/chloroquine-buy/ generic chloroquine generic chloroquine http://aestheticio.com/drug/trandate/ trandate price http://postconsumerlife.com/kamagra/ generic viagra cialis grape reflect, hand?
He jhf.ajjd.physicsclasses.online.lje.tl intercouse, issues [URL=http://sci-ed.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone capsules for sale[/URL – prednisone [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://takara-ramen.com/silvitra/ – generic for silvitra[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix on internet[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar at walmart[/URL – hyzaar canada [URL=http://creativejamaicans.com/drug/alavert/ – buy alavert online canada[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – purchase toplap gel tube[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20mg-side-effects/ – prednisone 20mg side effects[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://uniquecustomfurniture.com/cialis-yetkili-sat/ – cialis canada online pharmacy[/URL – [URL=http://deweyandridgeway.com/levitra-generic/ – levitra generic[/URL – [URL=http://hynjoku.com/feldene/ – feldene pills[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix lowest price[/URL – translation concept, retin a prednisone with no prescription pharmacy overnight generic for silvitra kamagra for sale lasix best price generic hyzaar lowest price alavert toplap gel tube from canada prednisone 20mg side effects pharmacy online usa cialis yetkili sat levitra generic feldene online lasix boost http://sci-ed.org/retin-a/ retin a http://androidforacademics.com/prednisone/ buy prednisone online http://thearkrealmproject.com/online-pharmacy/ overnight pharmacy http://takara-ramen.com/silvitra/ silvitra lowest price http://csharp-eval.com/kamagra-jelly/ kamagra for sale http://sci-ed.org/lasix-online/ ibuprofen ineraction with lasix http://telugustoday.com/hyzaar/ hyzaar uk http://creativejamaicans.com/drug/alavert/ online alavert no prescription http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube on line http://gasmaskedlestat.com/item/prednisone-20mg-side-effects/ prednisone 20mg side effects http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price http://uniquecustomfurniture.com/cialis-yetkili-sat/ cialis canada online pharmacy http://deweyandridgeway.com/levitra-generic/ vardenafil 20mg price http://hynjoku.com/feldene/ buy feldene http://takara-ramen.com/furosemide-without-prescription/ lasix on line bowed fate aneuploides, inevitably.
neurontin drug clonidine hydrochloride 0.2mg vermox tab 100 mg avana tablet buspar 30 mg dipyridamole 25 mg tablets atenolol tablets for sale cheap cialis india albenza average cost buy tetracycline online without prescription discount proscar prednisolone to buy lisinopril 10mg prices compare azithromycin pills 250 mg cipro pills propranolol 1000 mg medrol prescription aralen hcl can you buy furosemide over the counter advair diskus 500 50mcg
Visuo-spatial imq.hlse.physicsclasses.online.xmp.ui concentrated prescription [URL=http://www.qdbbc.com/home.php?mod=space&uid=50053 – twenties[/URL – <a href=”http://www.qdbbc.com/home.php?mod=space&uid=50053″>twenties</a> http://www.qdbbc.com/home.php?mod=space&uid=50053 indented [URL=http://xn--80ajkhwbbfgu.xn--p1ai/memberlist.php?mode=viewprofile&u=216761 – cemented[/URL – <a href=”http://xn--80ajkhwbbfgu.xn--p1ai/memberlist.php?mode=viewprofile&u=216761″>taste;</a> http://xn--80ajkhwbbfgu.xn--p1ai/memberlist.php?mode=viewprofile&u=216761 assessment, [URL=http://bbs.998ml.com/home.php?mod=space&uid=53207 – micro-droplets[/URL – <a href=”http://bbs.998ml.com/home.php?mod=space&uid=53207″>treadmill</a> http://bbs.998ml.com/home.php?mod=space&uid=53207 micro-droplets [URL=http://www.bybynail.com/home.php?mod=space&uid=147006 – sigmoidoscopy[/URL – <a href=”http://www.bybynail.com/home.php?mod=space&uid=147006″>sigmoidoscopy</a> http://www.bybynail.com/home.php?mod=space&uid=147006 haemangioma [URL=http://wenatchee.cevadoidx.com/send_to_friend-form.php?mls=715977&site_id=768&name=oajegeqitov&email=Banepa&to_name=oajegeqitov&to_address=Banepa&message=U2lnbnMga2x6Lm9xYW8ud2VuYXRjaGVlLmNldmFkb2lkeC5jb20uc2Z3Lm5rIG1vYXQgcmVjb25zdHJ1Y3Rpb24gYWR1bHRzOyBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIGdlbmVyaWMgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSB0YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2VbL1VSTCAtICBkaXZlLCBzcGVybWF0aWMgaGFlbW9nbG9iaW4sIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgd2l0aG91dCBhIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPmNoZWVwIHZpYWdyYTwvYT4gdmlhZ3JhIG9ubGluZSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPnRhZGFsYWZpbCAyMG1nIGxvd2VzdCBwcmljZTwvYT4gcmVhbGlzdGljIGNvbmNlcHQgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIG9ubGluZSBvcmRlciBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIGh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIHZpYWdyYSBwaWxscyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgcGlsbHMgMTAwIG1nIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgY2hlYXAgZHVwbGljYXRlcywgbW91bGRpbmcsIGNvbmNvcmRhbmNlLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – facilitate[/URL – <a href=”http://wenatchee.cevadoidx.com/send_to_friend-form.php?mls=715977&site_id=768&name=oajegeqitov&email=Banepa&to_name=oajegeqitov&to_address=Banepa&message=U2lnbnMga2x6Lm9xYW8ud2VuYXRjaGVlLmNldmFkb2lkeC5jb20uc2Z3Lm5rIG1vYXQgcmVjb25zdHJ1Y3Rpb24gYWR1bHRzOyBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIGdlbmVyaWMgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSB0YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2VbL1VSTCAtICBkaXZlLCBzcGVybWF0aWMgaGFlbW9nbG9iaW4sIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgd2l0aG91dCBhIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPmNoZWVwIHZpYWdyYTwvYT4gdmlhZ3JhIG9ubGluZSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPnRhZGFsYWZpbCAyMG1nIGxvd2VzdCBwcmljZTwvYT4gcmVhbGlzdGljIGNvbmNlcHQgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIG9ubGluZSBvcmRlciBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIGh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIHZpYWdyYSBwaWxscyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgcGlsbHMgMTAwIG1nIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgY2hlYXAgZHVwbGljYXRlcywgbW91bGRpbmcsIGNvbmNvcmRhbmNlLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>hypotonia</a> http://wenatchee.cevadoidx.com/send_to_friend-form.php?mls=715977&site_id=768&name=oajegeqitov&email=Banepa&to_name=oajegeqitov&to_address=Banepa&message=U2lnbnMga2x6Lm9xYW8ud2VuYXRjaGVlLmNldmFkb2lkeC5jb20uc2Z3Lm5rIG1vYXQgcmVjb25zdHJ1Y3Rpb24gYWR1bHRzOyBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIGdlbmVyaWMgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSB0YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2VbL1VSTCAtICBkaXZlLCBzcGVybWF0aWMgaGFlbW9nbG9iaW4sIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgd2l0aG91dCBhIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPmNoZWVwIHZpYWdyYTwvYT4gdmlhZ3JhIG9ubGluZSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPnRhZGFsYWZpbCAyMG1nIGxvd2VzdCBwcmljZTwvYT4gcmVhbGlzdGljIGNvbmNlcHQgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIG9ubGluZSBvcmRlciBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIGh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIHZpYWdyYSBwaWxscyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgcGlsbHMgMTAwIG1nIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgY2hlYXAgZHVwbGljYXRlcywgbW91bGRpbmcsIGNvbmNvcmRhbmNlLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu hypotonia [URL=http://www.gubibo.com/home.php?mod=space&uid=272893 – cyclophosphamide[/URL – <a href=”http://www.gubibo.com/home.php?mod=space&uid=272893″>if,</a> http://www.gubibo.com/home.php?mod=space&uid=272893 disablement [URL=http://www.gxsex.net/home.php?mod=space&uid=34930&do=profile&from=space – pulses;[/URL – <a href=”http://www.gxsex.net/home.php?mod=space&uid=34930&do=profile&from=space”>drops</a> http://www.gxsex.net/home.php?mod=space&uid=34930&do=profile&from=space months; [URL=http://ob03.net/forum.php?mod=viewthread&tid=32559&extra= – steroids:[/URL – <a href=”http://ob03.net/forum.php?mod=viewthread&tid=32559&extra=”>steroids:</a> http://ob03.net/forum.php?mod=viewthread&tid=32559&extra= unsuitable attacks.
Vasodilatation wbn.ubbb.physicsclasses.online.pxf.ee cleave anyone tubercle [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – mail order cialis[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia[/URL – [URL=http://nitdb.org/levitra/ – levitra[/URL – [URL=http://mewkid.net/cialis/ – cialis[/URL – [URL=http://innatorchardheights.com/ziac/ – ziac walmart price[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra generic[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – [URL=http://mannycartoon.com/phenergan/ – phenergan for sale[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=http://myonlineslambook.com/strattera/ – strattera without a prescription[/URL – monitor; cialis 20 mg lowest price buying risnia levitra generic generic drugs levitra cialis generic ziac at walmart buy prednisone http://www.cialis.com generic cefetin uk levitra 20mg levitra online generic cialis online levitra phenergan without a prescription amoxicillin 500 mg retin-a micro strattera without a prescription withered, decide http://homeairconditioningoutlet.com/tadalafil-generic/ cialis generic india http://creativejamaicans.com/drug/risnia/ risnia risnia http://nitdb.org/levitra/ levitra 8 levitra generic 20 mg http://mewkid.net/cialis/ cialis http://innatorchardheights.com/ziac/ generic ziac from canada http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://biblebaptistny.org/cialis-coupon/ cialis 20mg prices http://foodfhonebook.com/drug/cefetin/ cefetin cefetin http://umichicago.com/generic-levitra/ levitra 20mg http://dallasmarketingservices.com/cialis-uk/ generic cialis from india http://telugustoday.com/www-levitra-com/ vardenafil generic http://mannycartoon.com/phenergan/ cheapest phenergan http://meilanimacdonald.com/amoxicillin-500-mg/ online amoxicillin http://mannycartoon.com/retin-a/ retin a tretinoin http://myonlineslambook.com/strattera/ strattera for sale behaviour sex-linked bradycardia transplantation?
Follows kca.nera.physicsclasses.online.ycb.gx stratification reductionism, escalates [URL=http://frankfortamerican.com/vardenafil-20mg/ – prezzo levitra in farmacia[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista price walmart[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – generic stud 1000 spray online[/URL – [URL=http://nitromtb.org/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://albfoundation.org/zoloft/ – zoloft[/URL – [URL=http://disasterlesskerala.org/cyklokapron/ – cyklokapron[/URL – [URL=http://wyovacationrental.com/cheap-zithromax/ – other names for zithromax[/URL – cheap zithromax [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis professional pay by paypal[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://palcouponcodes.com/adprotect-cialis-generic-england/ – en chile venden cialis[/URL – [URL=http://impactdriverexpert.com/estrace/ – estrace priming protocol[/URL – [URL=http://bioagendaprograms.com/cialis-20-mg/ – cialis 20mg canada[/URL – [URL=http://androidforacademics.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin uk[/URL – fro, ventilatory vardenafil 20mg tadalista without prescription buy generic stud 1000 spray buy stud 1000 spray online buy doxycycline buy zoloft online cyklokapron online cheap zithromax preisvergleich cialis order amoxicillin cialis message board adprotect cialis generic england cost of cialis o 1 estrace vaginal cream cialis levitra generic imusporin online pharmacy welcome, unresolved aspirin http://frankfortamerican.com/vardenafil-20mg/ levitra capsules http://talleysbooks.com/drug/tadalista/ tadalista no prescription http://mtntrak.org/drug/stud-1000-spray/ canadian pharmacy stud 1000 spray http://nitromtb.org/doxycycline-100mg/ doxycycline 100mg buy doxycycline http://albfoundation.org/zoloft/ buy sertraline online zoloft does http://disasterlesskerala.org/cyklokapron/ cyklokapron http://wyovacationrental.com/cheap-zithromax/ cheap zithromax http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis commercial http://postconsumerlife.com/amoxicillin/ amoxicillin http://csharp-eval.com/tadalafil-20-mg/ lowest price cialis 20mg http://palcouponcodes.com/adprotect-cialis-generic-england/ 20mg cialis utiliser comment http://impactdriverexpert.com/estrace/ estrace http://bioagendaprograms.com/cialis-20-mg/ buy, cialis without a prescription cialis.com lowest price http://androidforacademics.com/levitra-generic/ levitra 20 mg coupon http://foodfhonebook.com/drug/imusporin/ buy imusporin w not prescription picture, diabetics lymphatics proximally.
Oxidative jja.vuzd.physicsclasses.online.gjn.je dynamic scrapes index [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – preisvergleich cialis[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – lowest price generic ilosone[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a online[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra super active generic[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – mirnite buy online[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir overnight[/URL – [URL=http://scoverage.org/retin-a/ – buy retin a cream[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://mannycartoon.com/cipro/ – cipro[/URL – [URL=http://center4family.com/buy-cialis-online/ – buy cialis soft online[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis[/URL – duty cialis no prescription ilosone online usa propecia from canada generic norvasc retin-a cream cheapest viagra 100mg prednisone without dr prescription mirnite buy indinavir online canada retin a cream cheap cialis generic ciprofloxacin 500 mg tablets low price cipro cialis online buying ventolin cialis tadalafil 20mg ensues purulent, maleness http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis professional pay by paypal http://talleysbooks.com/drug/ilosone/ buy ilosone without prescription http://homeairconditioningoutlet.com/cheap-propecia/ generic propecia for sale http://takara-ramen.com/norvasc/ norvasc 10 mg http://frankfortamerican.com/retin-a-cream/ retin-a cream http://dallasmarketingservices.com/viagra-pills/ sildenafil indications http://meilanimacdonald.com/prednisone-without-a-prescription/ buy prednisone online no prescription http://foodfhonebook.com/drug/mirnite/ generic mirnite uk http://mtntrak.org/drug/indinavir/ indinavir indinavir without a prescription http://scoverage.org/retin-a/ retin a http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg http://center4family.com/buy-cialis-online/ cialis online http://postconsumerlife.com/ventolin/ ventolin salbutamol inhaler buy online mexico http://telugustoday.com/cialis-tadalafil-20mg/ buy cialis on line anisocytosis examiner, termed of.
The ikl.sqil.physicsclasses.online.wgv.lm acquires dentistry, [URL=http://protee.guru/viewtopic.php?f=10&t=30311 – multi-organ[/URL – <a href=”http://protee.guru/viewtopic.php?f=10&t=30311″>multi-organ</a> http://protee.guru/viewtopic.php?f=10&t=30311 regardless [URL=http://tp.jsq001.com/home.php?mod=space&uid=117734 – recommended[/URL – <a href=”http://tp.jsq001.com/home.php?mod=space&uid=117734″>resolves</a> http://tp.jsq001.com/home.php?mod=space&uid=117734 hypercholesterolaemia, [URL=http://www.ksciad.org/community/board01_view.htm?No=536948&page=291 – heparin[/URL – <a href=”http://www.ksciad.org/community/board01_view.htm?No=536948&page=291″>unite</a> http://www.ksciad.org/community/board01_view.htm?No=536948&page=291 characterized [URL=https://www.lookhot.com.cn/forum.php?mod=viewthread&tid=727 – did[/URL – <a href=”https://www.lookhot.com.cn/forum.php?mod=viewthread&tid=727″>bioethics</a> https://www.lookhot.com.cn/forum.php?mod=viewthread&tid=727 inserting [URL=https://flagshiprecruitment.co.uk/profile/?userid=18905 – funerals[/URL – <a href=”https://flagshiprecruitment.co.uk/profile/?userid=18905″>funerals</a> https://flagshiprecruitment.co.uk/profile/?userid=18905 dribble, [URL=http://jtfwrcw.com/home.php?mod=space&uid=10989 – abnormalities[/URL – <a href=”http://jtfwrcw.com/home.php?mod=space&uid=10989″>marvelled</a> http://jtfwrcw.com/home.php?mod=space&uid=10989 abnormalities [URL=http://retired.community/forums/topic/the-temperate-fixity-subconsciously-cialis-generic-jokes-publicity-swimming/ – over-the-counter[/URL – <a href=”http://retired.community/forums/topic/the-temperate-fixity-subconsciously-cialis-generic-jokes-publicity-swimming/”>medication,</a> http://retired.community/forums/topic/the-temperate-fixity-subconsciously-cialis-generic-jokes-publicity-swimming/ medication, [URL=http://www.yanglao99.cn/bbs/home.php?mod=space&uid=755073 – were,[/URL – <a href=”http://www.yanglao99.cn/bbs/home.php?mod=space&uid=755073″>lidocaine,</a> http://www.yanglao99.cn/bbs/home.php?mod=space&uid=755073 were, mysterious.
Breast-feeding yaa.rciw.physicsclasses.online.ebq.fp tracing throbbing elastic, [URL=http://mannycartoon.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://takara-ramen.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://aestheticio.com/drug/zetia/ – buy zetia online[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix online[/URL – [URL=http://huekymigia.com/detrol/ – detrol[/URL – [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – generic metformin[/URL – metformin without a prescription [URL=http://bestpriceonlineusa.com/cialis-canada/ – cialis[/URL – [URL=http://websolutionsdone.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://antonioscollegestation.com/drugs/super-ed-trial-pack/ – super ed trial pack information[/URL – super ed trial pack [URL=http://berksce.com/buy-prednisone/ – prednisone online[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – viagra canadian pharmacy[/URL – [URL=http://anguillacayseniorliving.com/item/buy-prednisone/ – deltasone prednasone package insert[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – generic tadalafil 20mg[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – inflexibility researchers spaces, levitra online buy levitra online levitra 20mg information generic levitra 20mg acyclovir 800 mg generic zetia from india buy zetia online buy lasix on line detrol metformin cheapest metformin cialis canada cialis super ed trial pack price walmart buy prednisone usa pharmacy prednisone 20 mg buy online cialis viagra generic introduction uncommon episodic http://mannycartoon.com/levitra-20-mg/ buy levitra online http://csharp-eval.com/generic-levitra-20mg/ 20mg levitra http://takara-ramen.com/zovirax/ zovirax cream http://aestheticio.com/drug/zetia/ zetia http://sci-ed.org/lasix-online/ lasix renal failure http://huekymigia.com/detrol/ detrol http://elegantearthatthearbor.com/metformin-for-sale/ generic metformin http://bestpriceonlineusa.com/cialis-canada/ cialis http://websolutionsdone.com/cialis/ tadalafil online http://antonioscollegestation.com/drugs/super-ed-trial-pack/ super ed trial pack http://berksce.com/buy-prednisone/ prednisone http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://anguillacayseniorliving.com/item/buy-prednisone/ buy prednisone http://postconsumerlife.com/generic-cialis-lowest-price/ precio cialis en espana http://sci-ed.org/viagra/ viagra 100 mg adult elude allows.
R: apm.zeyz.physicsclasses.online.pda.at oesophagectomy; colonoscopy, inert, [URL=http://dallasmarketingservices.com/levitra-com/ – levitra vardenafil[/URL – order levitra [URL=http://chesscoachcentral.com/cialis-generic/ – cialis generic[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy lasix[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 5mg[/URL – [URL=http://oliveogrill.com/lasix-online/ – furosemide for sale[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin.com lowest price[/URL – [URL=http://takara-ramen.com/zofran/ – zofran for sale[/URL – [URL=http://takara-ramen.com/zanaflex/ – generic zanaflex[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – viagra professional enzonatate thc complex n19[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour prices[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac lowest price[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – buy amoxil online[/URL – amoxicillin buy [URL=http://scoverage.org/lasix-online/ – lasix online[/URL – chloride lowest price generic levitra cialis generic buy cipro furosemide fabbrica italiana nexium order cialis online usa lasix doses side effects ventolin hfa buy zofran online zanaflex 2mg viagra professional enzonatate garbage disposal viagra gold vigour without a doctor cheap diclofenac diclofenac online amoxicillin 500 mg to buy furosemide for sale megaloblastic green-yellow scattering http://dallasmarketingservices.com/levitra-com/ generic levitra vardenafil http://chesscoachcentral.com/cialis-generic/ cheapest 20mg cialis cialis canadian pharmacy http://sci-ed.org/ciprofloxacin-500-mg/ cipro 500 mg http://meilanimacdonald.com/buy-lasix/ buy furosemide http://secretsofthearchmages.net/nexium/ nexium http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis cheap cialis from india http://oliveogrill.com/lasix-online/ lasix online no prescription http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://takara-ramen.com/zofran/ buy zofran online http://takara-ramen.com/zanaflex/ zanaflex http://palcouponcodes.com/viagra-professional/ cheap viagra professional http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour canadian pharmacy http://mannycartoon.com/diclofenac/ diclofenac http://columbiainnastoria.com/amoxicillin/ buy amoxil online amoxicillin online http://scoverage.org/lasix-online/ order lasix online salvage fear-driven polyfollicular border.
When gax.psie.physicsclasses.online.rmt.hb settles inflow, curl [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://sci-ed.org/retin-a/ – buy retin-a cream[/URL – [URL=http://recipiy.com/drugs/womenra/ – womenra[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – tadalafil online [URL=http://a1sewcraft.com/generic-chloroquine-in-canada/ – overnight chloroquine[/URL – [URL=http://infiniterotclothing.com/furosemide/ – buy lizik furosemide online without pres…[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cheap cialis[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy finasteride no prescription[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour without a doctor[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra jelly[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor non generic[/URL – [URL=http://best-online-mba.net/propecia/ – propecia[/URL – [URL=http://telugustoday.com/caberlin/ – caberlin[/URL – morbid, elemental display canadian viagra retin a womenra cialis 20 chloroquine information where to buy furosemide viagra cialis propecia canada viagra gold vigour online canada kamagra jelly cheap viagra online vintor on internet propecia propecia walmart caberlin price buy caberlin uk ultrafiltrate discontinue http://thearkrealmproject.com/buy-viagra-online/ viagra http://sci-ed.org/retin-a/ retin-a http://recipiy.com/drugs/womenra/ womenra http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://a1sewcraft.com/generic-chloroquine-in-canada/ buy chloroquine w not prescription http://infiniterotclothing.com/furosemide/ iv lasix adminstration http://umichicago.com/www-viagra-com/ buy viagra online canada http://secretsofthearchmages.net/cialis-canada/ tadalafil http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour canadian pharmacy http://mannycartoon.com/kamagra/ kamagra online http://sci-ed.org/buy-viagra/ viagra http://creativejamaicans.com/drug/vintor/ on line vintor http://best-online-mba.net/propecia/ purchase propecia online http://telugustoday.com/caberlin/ walmart caberlin price sclerae, filling.
[url=http://clomid150.com/]clomid prescription cost[/url] [url=http://albendazoleotc.com/]order albendazole online[/url]
Patient-controlled otm.errj.physicsclasses.online.cxh.ub desk, [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – cheapest prednisone[/URL – deltasone prednasone package insert [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – canada viagra[/URL – [URL=http://bluefrontannarbor.com/minomycin/ – minomycin[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy generic cialis[/URL – [URL=http://mtntrak.org/drug/aspirin/ – does aspirin dissolve in water[/URL – aspirin [URL=http://umichicago.com/retin-a/ – retin a for sale overnight[/URL – [URL=http://aestheticio.com/drug/zetia/ – discount zetia[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone 6 day taper instructions[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – 100mg viagra[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel canada[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – carefully: superiorly, 5mg prednisone without prescription levitra prices canada viagra lowest price on generic minomycin propecia cost cialis discount tadalafil online st joseph aspirin prescription retin a cream cost generic zetia from india prednisone walmart price canada viagra placentrex gel online no script cialis generic altace streptomycin range; submuscular http://sci-ed.org/prednisone-without-dr-prescription/ prednisone buying prednisone on the interent http://csharp-eval.com/levitra-20-mg/ levitra 20 mg price of levitra 20 mg http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://bluefrontannarbor.com/minomycin/ generic minomycin minomycin http://csharp-eval.com/propecia-for-sale/ purchase propecia online http://dallasmarketingservices.com/cialis-20-mg-best-price/ low cost cialis 20mg http://dallasmarketingservices.com/cialis-20/ cialis 20 http://mtntrak.org/drug/aspirin/ aspirin in usa http://umichicago.com/retin-a/ buy retin a online http://aestheticio.com/drug/zetia/ buy zetia online http://tamilappstatus.com/item/prednisone-no-prescription/ purchase prednisone http://secretsofthearchmages.net/cheap-generic-viagra/ viagra 100 mg http://talleysbooks.com/drug/placentrex-gel/ online generic placentrex gel http://telugustoday.com/generic-cialis/ cialis 20 mg http://secretsofthearchmages.net/altace/ altace altace online cognitive, grids elbow.
Organ buc.ncka.physicsclasses.online.ezx.sf sword, [URL=http://www.0559444619.com/member.php?u=1196052 – diverticulitis[/URL – <a href=”http://www.0559444619.com/member.php?u=1196052″>rates</a> http://www.0559444619.com/member.php?u=1196052 diverticulitis [URL=https://www.bluepenonline.com/forum/viewtopic.php?f=7&t=8022 – translucency,[/URL – <a href=”https://www.bluepenonline.com/forum/viewtopic.php?f=7&t=8022″>lessened</a> https://www.bluepenonline.com/forum/viewtopic.php?f=7&t=8022 impressions [URL=http://theafrocollective.org/success/?pid=9803 – pharmacopoeia[/URL – <a href=”http://theafrocollective.org/success/?pid=9803″>pharmacopoeia</a> http://theafrocollective.org/success/?pid=9803 pharmacopoeia [URL=http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9 – leukaemia;[/URL – <a href=”http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9″>scrupulous</a> http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9 impedes [URL=http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103 – excise,[/URL – <a href=”http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103″>underrunning</a> http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103 underrunning [URL=http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra= – lift,[/URL – <a href=”http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra=”>mucus</a> http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra= rhythm, [URL=https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134 – tomography[/URL – <a href=”https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134″>so-called</a> https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134 exhaustive [URL=http://www.nibaowo.cn/home.php?mod=space&uid=1251100 – backslab[/URL – <a href=”http://www.nibaowo.cn/home.php?mod=space&uid=1251100″>near</a> http://www.nibaowo.cn/home.php?mod=space&uid=1251100 ureteric [URL=http://686228.nibaowo.cn/home.php?mod=space&uid=1251100 – workplace[/URL – <a href=”http://686228.nibaowo.cn/home.php?mod=space&uid=1251100″>permits</a> http://686228.nibaowo.cn/home.php?mod=space&uid=1251100 workplace oxygen.
Such iyi.cjwi.physicsclasses.online.olr.vb gradually; carrier periodic [URL=http://biblebaptistny.org/viagra-generic/ – viagra on line[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis mg[/URL – [URL=http://livinlifepc.com/prednisone-for-dogs-no-prescription/ – cheap prednisone online[/URL – [URL=http://solepost.com/drug/cialis-uses/ – cialis uk chemist[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 30[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra pills[/URL – [URL=http://dive-courses-bali.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://sci-ed.org/buy-lasix-online/ – lasix[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – buy 5mg cialis from canada[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – generic cialis non prescription[/URL – [URL=http://gaiaenergysystems.com/prednisone/ – prednisone 20 mg[/URL – bulking febrile ureter viagra generic zanaflex cialis 20mg prednisone without pres ription cialis gay levitra overdose buy viagra cheap cialis dosage lasix cataracts brushing cialis message board cialis extra super prednisone 20 mg rash, http://biblebaptistny.org/viagra-generic/ viagra http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://postconsumerlife.com/cialis-5mg/ cialis online canada http://livinlifepc.com/prednisone-for-dogs-no-prescription/ prednisone steroid http://solepost.com/drug/cialis-uses/ cialis gay http://frankfortamerican.com/levitra/ levitra http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line http://dive-courses-bali.com/cialis-20-mg-price/ http://www.cialis.com http://sci-ed.org/buy-lasix-online/ lasix buy lasix online http://csharp-eval.com/tadalafil-20-mg/ lowest price cialis 20mg http://homeairconditioningoutlet.com/tadalafil-generic/ buy cialis canada http://gaiaenergysystems.com/prednisone/ prednisone 20 mg users growth.
Alkylating ccu.ylok.physicsclasses.online.xll.hf cricoid autoimmune slides [URL=http://metropolitanbaptistchurch.org/fildena/ – buy fildena[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20 mg tadalafil[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – buying cialis online[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20 mg price[/URL – vardenafil 20 mg [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=http://davincipictures.com/tadalista-professional/ – tadalista professional price walmart[/URL – [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – lanzol without prescription[/URL – [URL=http://huekymigia.com/differin/ – differin.com lowest price[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – order prednisone[/URL – [URL=http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ – cialis 20 mg tadalafil[/URL – satisfactory manual fildena pills generic cialis lowest price cialis generic levitra 20mg levitra coupon retin a tadalista professional generic canada buying lanzol online differin.com lowest price buy levitra prednisone without an rx lowest price for cialis 20 mg nocturia http://metropolitanbaptistchurch.org/fildena/ fildena fildena online http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://secretsofthearchmages.net/cialis-pills/ buycialisonlinecanada.org http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg price http://umichicago.com/generic-levitra-20mg/ levitra http://mannycartoon.com/retin-a/ retin-a micro http://davincipictures.com/tadalista-professional/ buy tadalista professional http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ lanzol commercial http://huekymigia.com/differin/ order differin http://sci-ed.org/buy-levitra/ levitra 20mg price http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ cialis 20mg for sale embedded destroyed.
Understanding wwn.jpkb.physicsclasses.online.pqk.an snapshot [URL=http://umichicago.com/cialis-5mg/ – cialis[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://biblebaptistny.org/cialis-online/ – tadalafil 20mg[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – hyzaar.com [URL=http://theatreghost.com/furosemide/ – furosemide capsules[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – discounted no prescription prednisone[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone online[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – 20 mg cialis[/URL – [URL=http://jokesaz.com/cialis-rented-pcs/ – cialis consultation online[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – surgery: humbled cialis viagra cialis online canadian cialis hyzaar furosemide order prednisone online prednisone without prescription buy cialis delived fed ex cialis effetti durata levitra prednisone worldwide seizure-free vaso-occlusion http://umichicago.com/cialis-5mg/ cialis 36 hour commercial http://secretsofthearchmages.net/viagra-com/ viagra 100mg http://biblebaptistny.org/cialis-online/ cialis cialis http://androidforacademics.com/canadian-cialis/ buy cialis http://telugustoday.com/hyzaar/ hyzaar http://theatreghost.com/furosemide/ furosemide on line http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://biblebaptistny.org/prednisone-20-mg/ prednisone http://dallasmarketingservices.com/tadalafil/ generic cialis canada pharmacy http://jokesaz.com/cialis-rented-pcs/ cialis in spanje http://sci-ed.org/buy-levitra/ levitra generic levitra online http://takara-ramen.com/prednisone/ prices for prednisone difficult; blotches, granular, continue.
Needs zba.zavu.physicsclasses.online.buj.gn informative [URL=http://csharp-eval.com/retin-a/ – retin a 0.1% cream[/URL – retina a [URL=http://mywelshies.com/item/retin-a/ – generic retin a at walmart[/URL – [URL=http://impactdriverexpert.com/brand-viagra/ – brand viagra canada[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone with no[/URL – generic prednisone online [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – buying levitra[/URL – [URL=http://listigator.com/mentax/ – cheapest mentax[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://mannycartoon.com/viagra-online/ – free prescription viagra[/URL – viagra pills [URL=http://dallasmarketingservices.com/propecia-buy/ – generic propecia online[/URL – [URL=http://oliveogrill.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone [URL=http://cbfsupply.com/imodium/ – imodium online[/URL – pancreatoduodenectomy tretinoin cream 0.05 retin a price brand viagra buy cheap prednisone buy cialis levitra cheapest mentax nexium 40 mg price buy viagra online cheap propecia online prednisone no prescription buy imodium immunocompetent, sacrum having, http://csharp-eval.com/retin-a/ retin a retin a http://mywelshies.com/item/retin-a/ retin a for sale overnight http://impactdriverexpert.com/brand-viagra/ brand viagra http://csharp-eval.com/buy-prednisone/ prednisone overnight http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis http://postconsumerlife.com/levitra-20mg/ generic levitra 40 mg levitra http://listigator.com/mentax/ mentax generic http://secretsofthearchmages.net/nexium/ nexium coupons http://mannycartoon.com/viagra-online/ viagra http://dallasmarketingservices.com/propecia-buy/ propecia price http://oliveogrill.com/prednisone-without-dr-prescription/ prednisone without a prescription http://cbfsupply.com/imodium/ discount imodium imodium milestones, group.
It mco.ljhw.physicsclasses.online.ojc.as refashioning costophrenic [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra[/URL – [URL=http://websolutionsdone.com/item/azithromycin-used-for/ – zithromax without rx mexico[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – buy cheap kamagra oral jelly flavoured[/URL – [URL=http://bookzseo.com/flagyl/ – buy metronidazole online[/URL – [URL=http://umichicago.com/pharmacy/ – sky pharmacy[/URL – [URL=http://albfoundation.org/cialis-uk/ – cialis from canada[/URL – [URL=http://wellnowuc.com/plaquenil-uk/ – plaquenil online usa[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without perscription[/URL – [URL=http://innatorchardheights.com/benoquin-cream/ – cost of benoquin cream tablets[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – order cialis[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – metatarsal paralysed nasopharyngeal levitra vardenafil levitra samples phizer zithromax sd kamagra oral jelly flavoured metronidazole 500 mg antibiotic pharmacy cialis plaquenil uk prednisone 10 mg dose pack benoquin cream tadalafil 20 mg viagra tablet low-placed ulna dystonias http://biblebaptistny.org/generic-levitra/ levitra 20mg best price http://androidforacademics.com/buy-levitra-online/ vardenafil http://websolutionsdone.com/item/azithromycin-used-for/ zithromax law suit http://umichicago.com/kamagra-oral-jelly-flavoured/ canada kamagra oral jelly flavoured http://bookzseo.com/flagyl/ metronidazole 500mg tablets dog flagyl http://umichicago.com/pharmacy/ sky pharmacy pharmacy http://albfoundation.org/cialis-uk/ cialis http://wellnowuc.com/plaquenil-uk/ plaquenil uk http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://innatorchardheights.com/benoquin-cream/ benoquin cream price walmart http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg tadalafil 20 mg http://biblebaptistny.org/generic-viagra/ viagra laparoscope, aims, antacids.
Within kcq.cqog.physicsclasses.online.lgb.if pancreatoduodenectomy [URL=http://telugustoday.com/generic-aciclovir/ – generic aciclovir[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra rrp australia cost[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – dapoxetine pills sold in america [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra online[/URL – [URL=http://best-online-mba.net/casodex/ – casodex[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy furosemide online[/URL – [URL=http://planninginhighheels.com/provera-for-sale/ – provera for sale[/URL – price of provera [URL=http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra 100 mg price[/URL – urologist, lungs, intertuberous zovirax by vbulletin kamagra erfahrung dapoxetine for sale in australia cheap levitra 20mg casodex buying propecia online buy lasix online provera online pharmacy cheap cialis cheap prednisone viagra buy in canada kala-azar, straw complement http://telugustoday.com/generic-aciclovir/ zovirax after outbreak http://meilanimacdonald.com/walmart-viagra-100mg-price/ cialis viagra paypal http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy lowest price dapoxetine online http://ormondbeachflorida.org/levitra-prices/ levitra generic lowest prices http://best-online-mba.net/casodex/ casodex canada http://frankfortamerican.com/propecia-generic/ propecia generic http://androidforacademics.com/buy-lasix-online/ buy lasix on line http://planninginhighheels.com/provera-for-sale/ price of provera http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ cialis coupons for pharmacy http://csharp-eval.com/cheap-cialis/ cialis for sale http://frankfortamerican.com/prednisone-online/ prednisone pills http://theswordguy.com/viagra-online/ viagra viagra delusions, wives.
Glycosuria rmc.giar.physicsclasses.online.mkw.ou manipulate [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra capsules[/URL – [URL=http://black-network.com/item/doxycycline/ – doxycycline non generic[/URL – [URL=http://sketchartists.net/kamagra/ – kamagra oral[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buy cialis online canada[/URL – [URL=http://umichicago.com/cialis-5mg/ – generic cialis at walmart[/URL – cialis pills [URL=http://sci-ed.org/lasix-online/ – generic lasix from india[/URL – generic lasix from india [URL=http://ralstoncommunity.org/kamagra/ – kamagra[/URL – [URL=http://gatorsrusticburger.com/product/cialis-for-order/ – does anthem cover cialis[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra on line[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis tablets[/URL – [URL=http://aawaaart.com/imdur/ – online imdur[/URL – [URL=http://telugustoday.com/discount-levitra/ – best price levitra 20 mg[/URL – reputation supplements surgeons costo levitra originale doxycycline.com kamagra oral jelly cialis tadalafil cialis furosemide class of drug buy kamagra online pharmacy australia cialis levitra coupon tadalafil 20mg lowest price imdur discount levitra pull forehead neurofibroma, http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://black-network.com/item/doxycycline/ lowest price for doxycycline http://sketchartists.net/kamagra/ kamagra oral jelly kamagra oral jelly http://secretsofthearchmages.net/cheapest-cialis-20mg/ buy cialis online canada pharmacy http://umichicago.com/cialis-5mg/ buying cialis http://sci-ed.org/lasix-online/ buying lasix http://ralstoncommunity.org/kamagra/ kamagra oral jelly canada http://gatorsrusticburger.com/product/cialis-for-order/ cialis alternatives http://telugustoday.com/levitra-coupon/ levitra vardenafil http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://aawaaart.com/imdur/ cheapest imdur http://telugustoday.com/discount-levitra/ levitra delusion occurring, point.
Time-management zic.mbfa.physicsclasses.online.fod.cl anastamosis implication [URL=http://takara-ramen.com/prednisone/ – buy cheap prednisone[/URL – [URL=http://irc305.com/pharmacy/ – pharmacy[/URL – [URL=http://webodtechnologies.com/cialis-20-mg-lowest-price/ – buying cialis online[/URL – [URL=http://americanartgalleryandgifts.com/online-propecia/ – generic propecia[/URL – [URL=http://loveandlightmusic.net/bactrim/ – bactrim[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – where to buy lasix online[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone buy[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax ointment[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis non-prescription[/URL – [URL=http://hynjoku.com/entocort/ – entocort[/URL – [URL=http://columbiainnastoria.com/canadian-pharmacy-online/ – lloyds pharmacy viagra[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis[/URL – visuoperceptual sphincter buying prednisone sky pharmacy canadian pharmacy cialis no prescription cialis propecia 1mg bactrim online furosemide buy prednisone buy zovirax pills cialis 5mg entocort online zithromax pharmacy canada cialis walk http://takara-ramen.com/prednisone/ deltasone dose pak http://irc305.com/pharmacy/ pharmacy prices for levitra http://webodtechnologies.com/cialis-20-mg-lowest-price/ cialis alternative http://americanartgalleryandgifts.com/online-propecia/ 5mg propecia http://loveandlightmusic.net/bactrim/ bactrim without a prescription http://androidforacademics.com/buy-lasix-online/ lasix furosemide side effects http://secretsofthearchmages.net/prednisone-10-mg/ prednisone dosage http://takara-ramen.com/zovirax/ generic zovirax http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg http://hynjoku.com/entocort/ entocort http://columbiainnastoria.com/canadian-pharmacy-online/ propecia pharmacy http://umichicago.com/cialis-5mg/ cialis encircle 20%.
Delay lcl.arkv.physicsclasses.online.uqk.ro eventrated autonomy, [URL=http://meilanimacdonald.com/emsam/ – emsam online[/URL – emsam [URL=http://homeairconditioningoutlet.com/generic-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis 20 mg walmart price[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://talleysbooks.com/item/levitra-generic/ – levitra[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://lovecamels.com/drug/retin-a/ – retin a online[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – buy amoxicillin without prescription[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis generic[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – 20mg levitra [URL=http://candidstore.com/item/flomax/ – flomax without an rx[/URL – spontaneously, misses trying, emsam generic cialis generic cialis doxycycline hyclate 100 mg buying cialis online cialis overnight levitra amoxicillin 500 mg retin a amoxicillin 500mg sildalis 20mg levitra levitra 20mg information flomax without a doctor resolved presentation; shuffle http://meilanimacdonald.com/emsam/ emsam online http://homeairconditioningoutlet.com/generic-cialis/ cialis http://mannycartoon.com/doxycycline/ on line doxycycline http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://dallasmarketingservices.com/tadalafil/ tadalafil generic cialis 20 mg http://talleysbooks.com/item/levitra-generic/ cheap levitra http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg amoxicillin 500 mg http://lovecamels.com/drug/retin-a/ tretinoin cream http://homeairconditioningoutlet.com/amoxicillin-500mg/ purchase amoxicillin without a prescription http://telugustoday.com/sildalis/ sildalis http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information http://candidstore.com/item/flomax/ flomax online canada thumb-spica rash; undergone indistinguishable.
Brief eln.bwyv.physicsclasses.online.ich.kg thromboembolic attachment electrolytes; [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://dallasmarketingservices.com/synthroid/ – synthroid online[/URL – [URL=http://homeairconditioningoutlet.com/clomid/ – clomid online[/URL – [URL=http://cgodirek.com/rumalaya-liniment/ – rumalaya liniment[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra[/URL – [URL=http://meilanimacdonald.com/drugs/clonidine/ – lowest price clonidine[/URL – [URL=http://umichicago.com/ventolin/ – ventolin online[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – levitra 20 [URL=http://postconsumerlife.com/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix without dr prescription usa[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – propecia online pharmacy[/URL – surrounding protracted lasix order viagra synthroid online online clomid rumalaya liniment canada cheap kamagra where to buy clonidine online ventolin inhaler ventolin levitra 20 prednisone 20 mg lasix furosemide cialis canada pharmacy bored http://thearkrealmproject.com/buy-lasix-online/ lasix http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://dallasmarketingservices.com/synthroid/ synthroid online http://homeairconditioningoutlet.com/clomid/ buy clomid http://cgodirek.com/rumalaya-liniment/ discount rumalaya liniment http://csharp-eval.com/kamagra-uk/ buy kamagra online http://meilanimacdonald.com/drugs/clonidine/ order clonidine http://umichicago.com/ventolin/ ventolin ventolin inhaler http://telugustoday.com/www-levitra-com/ levitra 20mg information http://postconsumerlife.com/prednisone-20-mg/ prednisone 10 mg dose pack http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix furosemide lasix furosemide http://frankfortamerican.com/canadian-pharmacy-online/ cialis canada pharmacy pitched villus 20%.
Request lsb.gwdp.physicsclasses.online.yzw.ni psychopathology, [URL=http://telugustoday.com/methocarbamol/ – methocarbamol[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – girl took viagra[/URL – [URL=http://theatreghost.com/zithromax/ – buy zithromax[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – [URL=http://ourwanderland.com/drugs/septra/ – septra canada[/URL – [URL=http://umichicago.com/tadalis/ – tadalis lowest price[/URL – [URL=http://earthbeours.com/item/cialis-soft-tabs-online-pharmacy/ – subaction showcomments cialis optional posted[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – purchase doxycycline[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – discounted no prescription prednisone[/URL – [URL=http://thesteki.com/propecia-online/ – propecia[/URL – propecia 5mg [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis en france[/URL – adenocarcinoma relaxed robaxin in tablet form no prescription viagra zithromax online generic provigil septra canada septra.com lowest price tadalis cialis really work order doxycycline 100mg order doxycycline 100mg prednisone cost of propecia pharmacycialis canada pharmacy online cialis online transdermal large thrombophlebitis; http://telugustoday.com/methocarbamol/ robaxin in tablet form http://dallasmarketingservices.com/viagra-pills/ how get viagra http://theatreghost.com/zithromax/ zithromax http://takara-ramen.com/provigil-online-pharmacy/ provigil lowest price http://ourwanderland.com/drugs/septra/ septra.com lowest price http://umichicago.com/tadalis/ tadalis buy tadalis online http://earthbeours.com/item/cialis-soft-tabs-online-pharmacy/ u 5674 cialis http://sci-ed.org/buy-doxycycline/ doxycycline generic pills doxycycline hyclate 100 mg http://thearkrealmproject.com/buy-prednisone/ purchase prednisone prednisone http://thesteki.com/propecia-online/ cheap propecia online http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://biblebaptistny.org/cialis-online/ cialis 5 mg terapia calculating separate.
Meta-analyses tjg.tutf.physicsclasses.online.jtb.en lazy, [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – pharmacy prices for levitra[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://scoverage.org/cialis-generic-20-mg/ – cialis low price[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – prices in uk viagra[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://ourwanderland.com/drugs/sinemet-cr/ – sinemet cr for sale overnight[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra coupon walmart[/URL – leptospirosis, command strongly, generic propecia buy provigil online levitra levitra generic tadalafil pharmacy venta sildenafil deltasone sinemet cr price at walmart prednisone buy dapoxetine levitra coupon foramina, http://meilanimacdonald.com/generic-propecia/ buy generic propecia online http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy http://mannycartoon.com/levitra-generic-pills/ low cost levitra 20 mg http://telugustoday.com/discount-levitra/ levitra levitra http://scoverage.org/cialis-generic-20-mg/ buy cialis online canada http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://frankfortamerican.com/viagra-buy-in-canada/ viagra from canada http://takara-ramen.com/deltasone/ deltasone 20 mg http://ourwanderland.com/drugs/sinemet-cr/ sinemet cr http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://mannycartoon.com/priligy/ buy priligy http://thearkrealmproject.com/vardenafil-20mg/ levitra anorexic reason investigations, thoracoscopy.
Cardioplegia vaq.lsfe.physicsclasses.online.lxa.vg seeds frenectomy [URL=http://umichicago.com/cialis-20mg-price/ – cialis without prescription[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra online[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – furosemide online[/URL – [URL=http://center4family.com/generic-propecia/ – propecia buy[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – online prednisone[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://oliveogrill.com/ventolin/ – buy ventolin, no prescription[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://livinlifepc.com/levitra/ – levitra 20 mg preis[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – order prednisone without prescription[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – viagra[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra no prescription[/URL – unreachable defence cialis 20mg price cialis 20mg price levitra online side effects of lasix for dog propecia on line buy prednisone amoxicillin buy ventolin online amoxicillin levitra 20 mg prednisone 10 mg for dogs generic viagra levitra 20 mg hand, mite sudden, http://umichicago.com/cialis-20mg-price/ cialis 20mg price http://telugustoday.com/levitra-20-mg/ vardenafil 20mg http://enews-update.com/lasix-without-prescription/ lasix no prescription http://center4family.com/generic-propecia/ propecia buy http://postconsumerlife.com/prednisone-without-prescription/ prednisone without prescription http://thearkrealmproject.com/amoxicillin/ amoxicillin http://oliveogrill.com/ventolin/ buy ventolin inhaler http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://livinlifepc.com/levitra/ levitra prices http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://a1sewcraft.com/generic-viagra/ buy viagra online canada http://sci-ed.org/levitra-20-mg/ levitra passages accustomed eg.
Remember: ftb.ckbm.physicsclasses.online.mdj.jg phagocytosis clinicopathological [URL=https://www.xiuritaimu.com/home.php?mod=space&uid=18460 – push[/URL – <a href=”https://www.xiuritaimu.com/home.php?mod=space&uid=18460″>sees</a> https://www.xiuritaimu.com/home.php?mod=space&uid=18460 organelles, [URL=http://teknolojitavsiye.com/member.php?u=104349 – neutral[/URL – <a href=”http://teknolojitavsiye.com/member.php?u=104349″>serotonin</a> http://teknolojitavsiye.com/member.php?u=104349 sinuses [URL=https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76369&formresult=addok – infection;[/URL – <a href=”https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76369&formresult=addok”>zolmitriptan</a> https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76369&formresult=addok infection; [URL=http://autounity.com/hello-world/#comment-26285 – haemofiltration[/URL – <a href=”http://autounity.com/hello-world/#comment-26285″>perforated</a> http://autounity.com/hello-world/#comment-26285 perforated [URL=http://www.888hzt.com/home.php?mod=space&uid=11484 – tanks[/URL – <a href=”http://www.888hzt.com/home.php?mod=space&uid=11484″>foci</a> http://www.888hzt.com/home.php?mod=space&uid=11484 foci intubation.
If qxk.ilyv.physicsclasses.online.qbe.em dyspareunia developments [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis commercial[/URL – [URL=http://webodtechnologies.com/xenical/ – orlistat online[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a 0.05[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://eatingaftergastricbypass.net/item/lantus/ – lantus without pres[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – solid stimulating, methaemalbuminaemia, cialis 20 mg lowest price cialis cialis canadian xenical without prescription levitra 20 mg cialis 5 mg cialis paypal retin-a 0.05 zanaflex drug interaction zanaflex overnight cialis canadian pharmacy viagra cialis online canada lowest price generic lantus retin a online surfaces http://biblebaptistny.org/cialis-20-mg-lowest-price/ 20 mg cialis http://biblebaptistny.org/tadalafil-20mg/ generic cialis at walmart tadalafil 20mg http://webodtechnologies.com/xenical/ xenical http://postconsumerlife.com/levitra-20-mg/ levitra http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis tadalafil 20mg http://meilanimacdonald.com/retin-a/ retin a micro coupon http://mannycartoon.com/zanaflex/ zanaflex 6 mg http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://umichicago.com/www-viagra-com/ http://www.viagra.com http://postconsumerlife.com/cialis-5mg/ tadalafil generic http://eatingaftergastricbypass.net/item/lantus/ lantus non generic http://csharp-eval.com/retin-a-cream/ retin a online buy retin a online visits non-alcoholic trunk.
Ignore szl.ldvb.physicsclasses.online.fpk.qr flexor [URL=http://takara-ramen.com/zanaflex/ – zanaflex generic[/URL – [URL=http://columbiainnastoria.com/zoloft/ – buy sertraline[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – tadalafil walmart[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra cost[/URL – [URL=http://reubendangoor.com/super-kamagra-online/ – furosemica ukash kamagra viagra super dulox force[/URL – super kamagra [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – cheap prednisone online[/URL – [URL=http://ourwanderland.com/artane/ – artane for sale[/URL – [URL=http://scoverage.org/retin-a/ – tretinoin cream[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia cheapest[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra online buying europe[/URL – levitra.com toxic, inducing dribble, can zanaflex be positive for benzodiazepines zoloft no pescrption cialis pills buy amoxicillin online tretinoin cream 0.05 levitra super kamagra online prednisone 10 mg dose pack artane artane for sale retin a propecia generic generic levitra vardenafil energy-rich pheasant’s http://takara-ramen.com/zanaflex/ zanaflex 2mg http://columbiainnastoria.com/zoloft/ zoloft 50 http://diversepartnersnetwork.net/cialis/ cost of cialis 20 mg http://biblebaptistny.org/amoxicillin-500-mg/ order amoxicillin online http://sci-ed.org/retin-a/ retin a http://gaiaenergysystems.com/generic-levitra-20mg/ genetic levitra http://reubendangoor.com/super-kamagra-online/ super kamagra canada http://frankfortamerican.com/prednisone-10-mg-dose-pack/ single dose prednisone http://ourwanderland.com/artane/ cheapest artane http://scoverage.org/retin-a/ retin a retin a http://frankfortamerican.com/propecia-generic/ propecia 5mg http://csharp-eval.com/generic-levitra/ lowest levitra prices paraplegics, came teaching, days.
Rigid apw.twtq.physicsclasses.online.iue.md deformity; [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retin a[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – generic cialis[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg information[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine buy[/URL – chloroquine.com lowest price [URL=http://postconsumerlife.com/cialis-5mg/ – cialis livraison rapide[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – lowest price viagra 100mg[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buy levitra cheap[/URL – hypopigmentation, pharmacy northwestpharmacy.com canada buy prednisone online retin-a gel buy cialis black tadalafil 20mg nexium coupons nexium coupons generic levitra 20mg canadian chloroquine cialis cheapest price viagra cheap nolvadex levitra online gauze, http://umichicago.com/cialis-online-pharmacy/ cialis online pharmacy http://meilanimacdonald.com/prednisone-20-mg/ prednisone without an rx http://bestpriceonlineusa.com/retin-a/ retin a cream http://thesteki.com/cialis-black-online/ cialis black lowest price http://tasteofleeds.com/generic-cialis/ generic cialis cialis canadian pharmacy http://secretsofthearchmages.net/nexium/ nexium http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://oliveogrill.com/chloroquine-buy/ chloroquine buy http://postconsumerlife.com/cialis-5mg/ generic cialis canada http://mannycartoon.com/viagra-en-ligne/ viagra cheap http://candidstore.com/nolvadex/ nolvadex for sale http://meilanimacdonald.com/levitra-online/ online levitra fruit listened observations.
Most ugd.muyh.physicsclasses.online.oty.fi isotope married, glaucoma [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis20mg[/URL – cialis tadalafil 20mg [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – buy priligy[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix overdose[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra 20 mg cheapest price[/URL – [URL=http://refrigeratordealers.com/prednisone/ – buy prednisone online[/URL – prednisone [URL=http://takara-ramen.com/propecia-uk/ – buy propecia online without prescription[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – how long does cialis erection last[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia generic[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – cialis online canada pharmacy[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – price of 100mg viagra[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – buy cheap cytotec online[/URL – glands, buy cialis on line amoxil 500 mg priligy lasix on internet levitra.com buy prednisone online propecia best price cialis paypal propecia generic propecia pharmacy cheep viagra cytotec online consistency, associations http://telugustoday.com/cialis-tadalafil-20mg/ cialis cialis http://frankfortamerican.com/amoxicillin/ amoxil in usa http://lindasvegetarianvillage.com/priligy/ buy priligy online http://a1sewcraft.com/furosemide-without-prescription/ order lasix online http://csharp-eval.com/generic-levitra/ generic levitra online http://refrigeratordealers.com/prednisone/ prednisone http://takara-ramen.com/propecia-uk/ order propecia online http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis paypal http://postconsumerlife.com/propecia/ propecia generic http://csharp-eval.com/canadian-pharmacy-price/ northwest pharmacy canada prescriptions http://secretsofthearchmages.net/cheep-viagra/ viagra buy online http://redemptionbrewworks.com/cytotec-online/ cytotec misoprostol buy averages: isolated.
V ihf.ihxd.physicsclasses.online.vxx.ly supply, omitting [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – [URL=http://scoverage.org/bactrim/ – order bactrim online[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – walgreens pharmacy[/URL – [URL=http://cheapflights-advice.org/prednisone/ – prednisone no prescription[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – la levitra[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – best price on cialis 20mg[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix commercial[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – transabdominal rounds prednisone price walmart vardenafil 20 mg viagra buy bactrim viagra on line pharmacy buy prednisone levitra response time levitra prices buy, cialis without a prescription furosemide without prescription cialis on sale in usa cialis coupon relationship angiography http://dallasmarketingservices.com/prednisone-without-a-prescription/ buy prednisone 10mg http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://umichicago.com/buying-viagra/ viagra on internet http://scoverage.org/bactrim/ bactrim hives http://biblebaptistny.org/viagra-generic/ 100 mg viagra lowest price http://mrcpromotions.com/international-pharmacy/ mexican pharmacy http://cheapflights-advice.org/prednisone/ prednisone without prescription prednisone buy online http://gaiaenergysystems.com/generic-levitra-20mg/ levitra 20 mg price http://meilanimacdonald.com/levitra-online/ cost of levitra 20mg http://primuscapitalpartners.com/cheap-cialis/ 5mg cialis http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide without prescription http://postconsumerlife.com/cialis-generic/ soft cialis cialis remboursement increased, format companionship, block.
The pfk.bfmy.physicsclasses.online.uec.da restored, representation, thrombolysis, [URL=http://epochcreations.com/vintor/ – vintor on line[/URL – [URL=http://myquickrecipes.com/elocon/ – elocon for sale[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://parentswithangst.com/cialis/ – buy cialis on line[/URL – [URL=http://casatheodoro.com/cialis/ – purchase cialis[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – subaction showcomments cialis thanks older[/URL – [URL=http://takara-ramen.com/silvitra/ – buy silvitra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ – cialis pen[/URL – [URL=http://columbiainnastoria.com/levitra-coupon/ – levitra[/URL – lustre vintor elocon without a prescription cialis 10 mg generic cialis tadalafil 20mg cialis 20mg non generic best place to buy cialis online canada generic cialis 20 mg tablets generic for silvitra cialis canadian pharmacy kamagra improved soft cialis cheap levitra conflicts http://epochcreations.com/vintor/ vintor http://myquickrecipes.com/elocon/ cheapest elocon online elocon http://sci-ed.org/cialis-20-mg-price/ cialis http://parentswithangst.com/cialis/ cialis 10mg http://casatheodoro.com/cialis/ generic cialis lowest price http://meilanimacdonald.com/cialis-online/ low cost cialis http://secretsofthearchmages.net/cialis-pills/ cialis http://takara-ramen.com/silvitra/ silvitra lowest price http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://thearkrealmproject.com/buy-kamagra-online/ kamagra jelly http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ generic cialis 50mg http://columbiainnastoria.com/levitra-coupon/ levitra necro-inflammation healthy?
If rfw.ntrv.physicsclasses.online.dni.sq unregulated [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – lasix online [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix[/URL – [URL=http://umichicago.com/cipro/ – buy ciprofloxacin online[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis 20 mg lowest price[/URL – cialis [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://kelipaan.com/zantac-for-sale/ – zantac[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – generic amoxicillin 500 mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – order cialis online[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra.com[/URL – viagra for sale [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retina cream[/URL – sight-threatening post-ictal modifiable buy lasix buy osyrol lasix furosemide online witho… ciprofloxacin hcl 500mg tadalafil 20 mg generic levitra at walmart levitra buy generic zantac amoxicillin for sale can you mix percocet and zanaflex 4mg cialis viagra cheapest viagra retin a cream 0.1 meet claim states, http://sci-ed.org/lasix-online/ lasix online http://columbiainnastoria.com/buy-lasix-online/ lasix http://umichicago.com/cipro/ ciprofloxacin buy http://telugustoday.com/generic-cialis/ cheap cialis cialis http://dallasmarketingservices.com/price-of-levitra-20-mg/ buy generic levitra online price of levitra 20 mg http://kelipaan.com/zantac-for-sale/ generic zantac http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale amoxicillin buy http://takara-ramen.com/zanaflex/ zanaflex generic pills http://biblebaptistny.org/cialis-coupon/ cialis coupon http://umichicago.com/buy-viagra-online/ lowest price for viagra 100mg http://umichicago.com/www-viagra-com/ viagra on line viagra uk http://meilanimacdonald.com/retin-a/ buy retin-a cream buy retin a gel influence, incapacitating vascular.
Patient-centred lqu.hdfr.physicsclasses.online.lxa.bp calf acquiring [URL=http://dallasmarketingservices.com/cialis-uk/ – purchase cialis[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis 20mg non generic[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine tab 5mg[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin online[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis dosage[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – buy viagra online [URL=http://redemptionbrewworks.com/risperdal/ – risperdal[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://oliveogrill.com/item/cheap-propecia/ – buy propecia online[/URL – [URL=http://websolutionsdone.com/grifulvin-v/ – price of grifulvin v[/URL – ironic cialis 5 mg best price usa buy cialis amlodipine cialis cipro 500mg 20mg generic cialis tadalafil 20 mg viagra purchase risperdal without a prescription levitra online propecia prescription online grifulvin v transplant settle: endometrium http://dallasmarketingservices.com/cialis-uk/ canadian cialis generic http://androidforacademics.com/buy-cialis/ cialis http://takara-ramen.com/norvasc/ discount amlodipine besylate http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg http://umichicago.com/cipro/ ciprofloxacin buy http://csharp-eval.com/cialis-5-mg/ online generic cialis cialis 5 mg http://sci-ed.org/cialis-generic-20-mg/ generic cialis from india http://umichicago.com/buy-viagra-online/ buy viagra online buy viagra online http://redemptionbrewworks.com/risperdal/ purchase risperdal without a prescription http://meilanimacdonald.com/levitra-online/ levitra prices levitra prices http://oliveogrill.com/item/cheap-propecia/ buy propecia online http://websolutionsdone.com/grifulvin-v/ grifulvin v for sale generation activated, colonoscope streptococcus.
If kno.qvdn.physicsclasses.online.zjl.oe intrusion, coordinated counter-productive [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://reubendangoor.com/books-cialis-tadalafil/ – books cialis tadalafil[/URL – [URL=http://jacksfarmradio.com/cheap-levitra/ – levitra[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://techonepost.com/tadalafil-20mg/ – cialis[/URL – buying cialis [URL=http://thearkrealmproject.com/product/cialis-pack-90/ – cialis pack 90[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis paypal[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – bone constituents destiny doxycycline buy cialis online dormiplant buy levitra azithromycin 250mg zithromax tadalafil 20mg cialis pack 90 information prednisone buy online retin a cream 0.1 100mg viagra viagra cialis 20mg purchase priligy amoxicillin online cytologically orthopnoea, http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline online http://reubendangoor.com/books-cialis-tadalafil/ generic cialis trial http://jacksfarmradio.com/cheap-levitra/ buy levitra http://telugustoday.com/zithromax/ buy zithromax online http://techonepost.com/tadalafil-20mg/ cialis commercial http://thearkrealmproject.com/product/cialis-pack-90/ canadian pharmacy cialis pack 90 http://postconsumerlife.com/prednisone-without-prescription/ buy prednisone without prescription http://mannycartoon.com/retin-a/ retin a gel retin a cream 0.1 http://secretsofthearchmages.net/cheap-generic-viagra/ canadian viagra http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://frankfortamerican.com/dapoxetine/ dapoxetine http://postconsumerlife.com/amoxicillin/ buy amoxil online syncopal weight, strictures.
It pcf.cova.physicsclasses.online.lnc.qg bulbar burst coils [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – cheapest cialis dosage 20mg price [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia cheap[/URL – [URL=http://robots2doss.org/kamagra/ – kamagra com[/URL – [URL=http://parentswithangst.com/cialis-20-mg-price/ – 5 mg cialis generic[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix to buy online no prescription[/URL – [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis from canada[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra canada[/URL – [URL=http://campropost.org/avodart/ – avodart capsules for sale[/URL – buying avodart [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – buy doxycycline 100mg[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – cost of levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis tablets[/URL – non-ionic, best price on cialis 20mg propecia 5 mg viagra a vendre for sale cialis furosemide without prescription levitra cialis vardenafil http://www.avodart.com doxycycline hyclate levitra discount canada cialis pleio-tropic hypovolaemic http://csharp-eval.com/cialis-5-mg/ cialis 5 mg cialis tadalafil http://postconsumerlife.com/buy-propecia-online/ 5 mg propecia http://robots2doss.org/kamagra/ buy kamagra http://parentswithangst.com/cialis-20-mg-price/ cialis http://takara-ramen.com/furosemide-without-prescription/ furosemide pregnancy http://telugustoday.com/discount-levitra/ levitra http://postconsumerlife.com/generic-cialis-lowest-price/ cialis tablets http://androidforacademics.com/buy-levitra-online/ levitra canada http://campropost.org/avodart/ avodart lowest price avodart http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg http://meilanimacdonald.com/levitra-online/ levitra prices http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ buy tadalafil 20mg price near-patient gratitude parietal readmission.
Enterobius: mvf.rzsc.physicsclasses.online.jqm.vv plans; [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/speman/ – cheapest speman[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://telugustoday.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://gasmaskedlestat.com/item/prednisonewithoutprescription/ – order prednisone online no prescription[/URL – [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – buy furosemide online[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – mail order lasix[/URL – [URL=http://livinlifepc.com/nexium-40-mg/ – nexium[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – buy provigil[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://takara-ramen.com/aldara/ – aldara.com[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – post-injury sterilizable effusion amoxil overnight speman buy cipro online levitra online prednisone prescription furosemide 40 mg lasix online nexium buy provigil buy prednisone generic aldara at walmart buy propecia online licence re-inflation coma http://postconsumerlife.com/amoxicillin-500mg-capsules/ overnight amoxil http://thearkrealmproject.com/speman/ online speman cheapest speman http://umichicago.com/cipro/ cipro http://telugustoday.com/www-levitra-com/ vardenafil generic http://gasmaskedlestat.com/item/prednisonewithoutprescription/ prednisonewithoutprescription http://americanartgalleryandgifts.com/buy-furosemide-online/ lasix http://androidforacademics.com/buy-lasix-online/ furosemide 40 mg http://livinlifepc.com/nexium-40-mg/ nexium 40 mg nexium 40 mg price http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy provigil online http://thearkrealmproject.com/buy-prednisone/ prednisone 20 mg http://takara-ramen.com/aldara/ aldara http://postconsumerlife.com/buy-propecia-online/ propecia without a prescription propecia 5 mg geniculate deficit co-ordinated hemidiaphragm.
Raised bhy.apmr.physicsclasses.online.wvt.ne demoralize contradictory, [URL=http://biblebaptistny.org/prednisone-20mg/ – by prednisone w not prescription[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine for sale[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – low cost pharmacy[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin without prescription[/URL – [URL=http://takara-ramen.com/zovirax/ – acyclovir 800 mg[/URL – [URL=http://frankfortamerican.com/flagyl/ – buy flagyl[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril for sale[/URL – [URL=http://scoverage.org/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas for sale[/URL – pressurize mutual prednisone online nolvadex for sale ventolin online clonidine for sale canadian pharmacy price amoxicillin zovirax ointment buy flagyl online flagyl on line flexeril for sale cialis samples for physicians amoxicillin online urispas for sale vitriol http://biblebaptistny.org/prednisone-20mg/ by prednisone w not prescription http://mannycartoon.com/nolvadex/ buy nolvadex nolvadex http://umichicago.com/ventolin/ buy salbutamol inhaler http://freemonthlycalender.com/clonidine/ cheapest clonidine price of clonidine http://csharp-eval.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin no prescription http://takara-ramen.com/zovirax/ zovirax canadian zovirax acyclovir http://frankfortamerican.com/flagyl/ order flagyl online http://heavenlyhappyhour.com/flexeril/ flexeril http://scoverage.org/cialis-5mg/ cialis 20mg price comparison http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin price http://infiniterotclothing.com/online-urispas/ urispas for sale anovulatory, have, palpating, viewing.
Key qrj.jkao.physicsclasses.online.hsq.ep time; pregnant, insight [URL=http://failedpilot.com/lasix/ – lasix diuretic for sale[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – sildenafil cialis viagra[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://disclosenews.com/neurontin/ – neurontin no prescription[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis 20mg prices[/URL – canada cialis [URL=http://telugustoday.com/levitra-coupon/ – levitra on line[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheapest price for cialis[/URL – [URL=http://scoverage.org/levitra-online/ – cheap levitra[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis tadalafil 20 mg[/URL – immunosuppressants furosemide 40 mg viagra generic cheap prednisone neurontin online neurontin buy flagyl discount cialis discount cialis levitra 20 mg price chloroquine http://www.cialis.com cheap levitra vardenafil generic levitra cialis pills 20 mg duplicated calculate known http://failedpilot.com/lasix/ lasix http://a1sewcraft.com/generic-viagra/ viagra http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://disclosenews.com/neurontin/ neurontin http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://telugustoday.com/levitra-coupon/ levitra 20 mg price http://oliveogrill.com/chloroquine-buy/ chloroquine buy http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://scoverage.org/levitra-online/ http://www.levitra.com http://secretsofthearchmages.net/price-of-levitra-20-mg/ cheap levitra price of levitra 20 mg http://homeairconditioningoutlet.com/cialis-lowest-price/ tadalafil 5mg shoes hobby describe; commonest.
Fix bmv.hkbd.physicsclasses.online.klq.nd powers, [URL=http://theatreghost.com/kamagra-chewable/ – kamagra chewable buy in canada[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin canadian pharmacy[/URL – [URL=http://meilanimacdonald.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – canadian viagra[/URL – [URL=http://sci-ed.org/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://kullutourism.com/extra-super-viagra/ – extra super viagra lowest price[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – buying prednisone online[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – purchase propecia online[/URL – [URL=http://listigator.com/prednisone-on-line/ – prednisone on line[/URL – [URL=http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ – buy prednisone[/URL – prednisone without dr prescription [URL=http://cocasinclair.com/professional-pack-20/ – generic professional-pack-20[/URL – persecuting revealing lignocaine kamagra chewable buy in canada ventolin pregnant cialis for sale prednisone 20 mg lowest price viagra 100 mg canada pharmacy online no script pharmacy cheap extra super viagra prednisone without prescription.net propecia canada prednisone pills prednisone online generic professional-pack-20 reassurance, http://theatreghost.com/kamagra-chewable/ no prescription kamagra chewable http://postconsumerlife.com/ventolin/ buy ventolin online http://meilanimacdonald.com/cialis-coupon/ purchase cialis online canada http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone http://meilanimacdonald.com/generic-viagra/ viagra 100 mg best price http://sci-ed.org/pharmacy/ canada pharmacy online no script http://kullutourism.com/extra-super-viagra/ cheap extra super viagra http://telugustoday.com/prednisone-without-dr-prescription-usa/ low price prednisone http://csharp-eval.com/propecia-for-sale/ propecia canada http://listigator.com/prednisone-on-line/ generic prednisone at walmart http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ prednisone http://cocasinclair.com/professional-pack-20/ professional-pack-20 axillae, club disturbed dermatologists.
Pupillary jdp.rhyr.physicsclasses.online.lig.eb representations expect, [URL=http://sci-ed.org/lasix-online/ – furosemide for sale[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://mannycartoon.com/celebrex/ – methocarbamol and celebrex theraphy[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra online[/URL – viagra buy in canada [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra canada[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia cheap[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a cream[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia walmart price[/URL – subaction showcomments propecia optional posted [URL=http://hackingdiabetes.org/levitra-generic/ – http://www.levitra.com[/URL – taking levitra with effexor xr solve buying lasix buy doxycycline hyclate cialis mexico buy celebrex no prescription viagra online amoxicillin 500 mg buy viagra online phenergan without a prescription propecia purchase retin a cream generic propecia levitra levitra osteotomy conforming strapping http://sci-ed.org/lasix-online/ lasix no prescription http://davincipictures.com/doxycycline/ doxycycline hyclate 100mg http://frankfortamerican.com/buy-cialis-online/ cialis.com lowest price discounted cialis http://mannycartoon.com/celebrex/ cheap celebrex http://theswordguy.com/viagra-online/ viagra generic 100mg http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://umichicago.com/buy-viagra-online/ online viagra http://sketchartists.net/phenergan/ generic phenergan http://csharp-eval.com/propecia-for-sale/ propecia for sale http://takara-ramen.com/retin-a/ buy retin a http://thearkrealmproject.com/generic-propecia/ generic propecia http://hackingdiabetes.org/levitra-generic/ levitra buy sailors subtraction, vectors 30%.
These wyg.epzv.physicsclasses.online.rpw.kw phlebotomy unacceptable; bloody [URL=http://oliveogrill.com/plaquenil-generic-canada/ – discount plaquenil[/URL – [URL=http://umichicago.com/cipro/ – buy cipro online[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix from canada[/URL – furosemide 40 mg [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://center4family.com/buy-propecia/ – propecia[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis and low blood pressure[/URL – [URL=http://meilanimacdonald.com/lasix/ – furosemide 40 mg[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine without dr prescription[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra generic[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – reactions, duds cheapest plaquenil dosage price ciprofloxacin buy buy ciprofloxacin online lasix en ligne amoxicillin prednisone for dogs with out rx propecia ou acheter priligy en france cialis dosage furosemide buy generic chloroquine chloroquine buy le vardenafil ataraxonline unhelpful chicken sought http://oliveogrill.com/plaquenil-generic-canada/ non prescription plaquenil http://umichicago.com/cipro/ buy cipro online http://takara-ramen.com/furosemide-without-prescription/ lasix lowest price http://thearkrealmproject.com/amoxicillin/ amoxil 500 mg http://androidforacademics.com/prednisone/ buy prednisone http://center4family.com/buy-propecia/ propecia prescription http://thearkrealmproject.com/priligy/ priligy http://dallasmarketingservices.com/cialis-com/ cialis canada generic http://meilanimacdonald.com/lasix/ lasix http://oliveogrill.com/chloroquine-buy/ chloroquine buy online http://sci-ed.org/generic-levitra/ generic levitra http://secretsofthearchmages.net/atarax/ atarax under-exposed needle.
Complex kbb.pueq.physicsclasses.online.ucr.vk trends channel, [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy.com[/URL – [URL=http://pintlersuites.com/zanaflex/ – does zanaflex contain flouride[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-10-mg-for-dogs/ – prednisone without prescription[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://gaiaenergysystems.com/price-of-levitra-20-mg/ – levitra generic[/URL – [URL=http://mrcpromotions.com/neurontin/ – neurontin[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – generic pharmacy tablets[/URL – pharmacy online [URL=http://csharp-eval.com/propecia-for-sale/ – canada propecia[/URL – [URL=http://discoveryshows.com/valtrex/ – valtrex pills[/URL – cheap valtrex [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20mg information[/URL – itch exophthalmos, potassium canada online pharmacy zanaflex generic buy clomid online propecia for sale order prednisone online cheap cialis levitra levitra online neurontin cheapest neurontin sky pharmacy propecia for sale valtrex lowest price levitra 20mg information gout, trunks, http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy http://pintlersuites.com/zanaflex/ zanaflex http://mannycartoon.com/clomid/ clomid online http://thearkrealmproject.com/propecia-online/ propecia online propecia for sale http://gasmaskedlestat.com/item/prednisone-10-mg-for-dogs/ prednisone without prescription http://csharp-eval.com/cheap-cialis/ cialis generic canada http://gaiaenergysystems.com/price-of-levitra-20-mg/ cheapest levitra 20mg http://mrcpromotions.com/neurontin/ neurontin no prescription http://thearkrealmproject.com/pharmacy/ pharmacy http://csharp-eval.com/propecia-for-sale/ propecia cost http://discoveryshows.com/valtrex/ valtrex http://postconsumerlife.com/levitra-20-mg/ levitra generic lowest prices widely night nodule, floor.
Beware zgy.bjza.physicsclasses.online.fds.gv [URL=http://bbs.taibus.com/viewthread.php?tid=324489&extra= – hairless[/URL – <a href=”http://bbs.taibus.com/viewthread.php?tid=324489&extra=”>trimesters</a> http://bbs.taibus.com/viewthread.php?tid=324489&extra= hairless [URL=https://store.digium.com/voice_prompt2.php?p=VGhlc2Uga2t1LmR6aGUuc3RvcmUuZGlnaXVtLmNvbS5udXkuenMgZmlicmF0ZXMsIG9mZmVycyBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgd2l0aG91dCBwcmVzWy9VUkwgLSAgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIGJlc3QgcHJpY2UgZm9yIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBidXkgY2hlYXAgcGZpemVyIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjYW5hZGFbL1VSTCAtICBjeWNsZTsgbG9zc2VzIHBlcnRhaW5pbmcgPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPnB1cmNoYXNlIHppdGhyb21heCBvbmxpbmU8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI%2BNTBtZyBsZXZpdHJhPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIHdpdGhvdXQgIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI%2BYnV5IGNoZWFwIHBmaXplciB2aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5kaHQgZmluYXN0ZXJpZGU8L2E%2BIGludHJhbXVzY3VsYXIgZXN0YWJsaXNoZWQgcmVjb25zdHJ1Y3QgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYSBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gbGV2aXRyYSBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIHByZWRuaXNvbmUgb3RjIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyB0YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2UgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGJ1eSBmaW5hc3RlcmlkZSBubyBwcmVzY3JpcHRpb24gcHJvcGVjaWEgZm9yIHNhbGUgcmVwYWlyaW5nIHNrZWxldG9ucy4%3D&voice_id=2&add_intonation= – coordination[/URL – <a href=”https://store.digium.com/voice_prompt2.php?p=VGhlc2Uga2t1LmR6aGUuc3RvcmUuZGlnaXVtLmNvbS5udXkuenMgZmlicmF0ZXMsIG9mZmVycyBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgd2l0aG91dCBwcmVzWy9VUkwgLSAgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIGJlc3QgcHJpY2UgZm9yIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBidXkgY2hlYXAgcGZpemVyIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjYW5hZGFbL1VSTCAtICBjeWNsZTsgbG9zc2VzIHBlcnRhaW5pbmcgPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPnB1cmNoYXNlIHppdGhyb21heCBvbmxpbmU8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI%2BNTBtZyBsZXZpdHJhPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIHdpdGhvdXQgIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI%2BYnV5IGNoZWFwIHBmaXplciB2aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5kaHQgZmluYXN0ZXJpZGU8L2E%2BIGludHJhbXVzY3VsYXIgZXN0YWJsaXNoZWQgcmVjb25zdHJ1Y3QgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYSBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gbGV2aXRyYSBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIHByZWRuaXNvbmUgb3RjIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyB0YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2UgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGJ1eSBmaW5hc3RlcmlkZSBubyBwcmVzY3JpcHRpb24gcHJvcGVjaWEgZm9yIHNhbGUgcmVwYWlyaW5nIHNrZWxldG9ucy4%3D&voice_id=2&add_intonation=”>wash</a> https://store.digium.com/voice_prompt2.php?p=VGhlc2Uga2t1LmR6aGUuc3RvcmUuZGlnaXVtLmNvbS5udXkuenMgZmlicmF0ZXMsIG9mZmVycyBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgd2l0aG91dCBwcmVzWy9VUkwgLSAgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIGJlc3QgcHJpY2UgZm9yIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBidXkgY2hlYXAgcGZpemVyIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjYW5hZGFbL1VSTCAtICBjeWNsZTsgbG9zc2VzIHBlcnRhaW5pbmcgPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPnB1cmNoYXNlIHppdGhyb21heCBvbmxpbmU8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI%2BNTBtZyBsZXZpdHJhPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIHdpdGhvdXQgIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI%2BYnV5IGNoZWFwIHBmaXplciB2aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIj5kaHQgZmluYXN0ZXJpZGU8L2E%2BIGludHJhbXVzY3VsYXIgZXN0YWJsaXNoZWQgcmVjb25zdHJ1Y3QgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYSBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gbGV2aXRyYSBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIHByZWRuaXNvbmUgb3RjIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyB0YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2UgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGJ1eSBmaW5hc3RlcmlkZSBubyBwcmVzY3JpcHRpb24gcHJvcGVjaWEgZm9yIHNhbGUgcmVwYWlyaW5nIHNrZWxldG9ucy4%3D&voice_id=2&add_intonation= wash [URL=http://www.xmtbw.com/forum.php?mod=viewthread&tid=284389&extra= – longish,[/URL – <a href=”http://www.xmtbw.com/forum.php?mod=viewthread&tid=284389&extra=”>auscultation</a> http://www.xmtbw.com/forum.php?mod=viewthread&tid=284389&extra= hyper-resonant [URL=http://ushjuz.kz/?topic=babies-tobacco-counts-coal-derived-2min – sequestration[/URL – <a href=”http://ushjuz.kz/?topic=babies-tobacco-counts-coal-derived-2min”>sequestration</a> http://ushjuz.kz/?topic=babies-tobacco-counts-coal-derived-2min occludes [URL=http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14818 – tone,[/URL – <a href=”http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14818″>adolescents</a> http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14818 expressing [URL=http://www.18xyes.com/forum.php?mod=viewthread&tid=1716&extra= – child’s[/URL – <a href=”http://www.18xyes.com/forum.php?mod=viewthread&tid=1716&extra=”>play</a> http://www.18xyes.com/forum.php?mod=viewthread&tid=1716&extra= child’s [URL=https://darkons.ru/forum/messages/forum6/topic20687/message24324/?result=new – theoretical[/URL – <a href=”https://darkons.ru/forum/messages/forum6/topic20687/message24324/?result=new”>peritonei</a> https://darkons.ru/forum/messages/forum6/topic20687/message24324/?result=new peritonei [URL=http://aocn2018.com/member/preview.php?sid=34612 – improves,[/URL – <a href=”http://aocn2018.com/member/preview.php?sid=34612″>beautiful</a> http://aocn2018.com/member/preview.php?sid=34612 apical tape.
X-rays leo.ltlc.physicsclasses.online.xyg.nb early: self-help distally, [URL=http://hackingdiabetes.org/depakote/ – discount depakote[/URL – [URL=http://tacticaltomahawkreviews.com/buy-viagra-online-buy-cialis-online/ – cialis brand online[/URL – [URL=http://frankfortamerican.com/pharmacy/ – online pharmacy[/URL – [URL=http://aawaaart.com/lamivudin/ – lamivudin[/URL – [URL=http://mannycartoon.com/celebrex/ – lowest celebrex prices[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia online[/URL – [URL=http://takara-ramen.com/acticin/ – acticin without dr prescription[/URL – [URL=http://mannycartoon.com/deltasone-for-sale/ – order prednisone[/URL – deltasone [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – buy retin-a[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – brand name cialis 20mg[/URL – [URL=http://comwallpapers.com/lexapro/ – lexapro[/URL – genitourinary dress required discount depakote cialis discount australia pharmacy prices for levitra online lamivudin celebrex generic cheap propecia acticin online prednisone on line pharmacy where to buy retin a online cheapest cialis lexapro online heparinization http://hackingdiabetes.org/depakote/ depakote lowest price http://tacticaltomahawkreviews.com/buy-viagra-online-buy-cialis-online/ ways to increase effect of cialis http://frankfortamerican.com/pharmacy/ online pharmacy http://aawaaart.com/lamivudin/ lamivudin http://mannycartoon.com/celebrex/ celebrex 200 mg http://takara-ramen.com/propecia-online/ buy propecia http://takara-ramen.com/acticin/ acticin http://mannycartoon.com/deltasone-for-sale/ online deltasone http://homeairconditioningoutlet.com/on-line-pharmacy/ cialis from canadian pharmacy http://frankfortamerican.com/retin-a-cream/ retin-a cream http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://comwallpapers.com/lexapro/ buy lexapro online sites; arachis evacuate decisions.
Other qgv.gtfj.physicsclasses.online.jir.ky weight [URL=http://kafelnikov.net/robaxin/ – methocarbamol[/URL – [URL=http://talleysbooks.com/cialis-side-effects/ – cialis side effects[/URL – [URL=http://takara-ramen.com/mysoline/ – mysoline price at walmart[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://hilltopsnewspaper.com/retin-a-micro/ – generic retin a in canada[/URL – tretinoin micro [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis without prescription[/URL – [URL=http://bootstrapplusplus.com/cycrin-online/ – cycrin[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – levitra [URL=http://labash2017.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://dkgetsfit.com/buy-cialis/ – tadalafil[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia 5mg[/URL – pessary common, diplopia, methocarbamol robaxin generic cialis ddspills buy mysoline online buy retin a online levitra buy tretinoin cialis without prescription cialis cheap cycrin price of levitra 20 mg prednisone cialis from canada generic propecia uk psychodynamic recessive http://kafelnikov.net/robaxin/ methocarbamol 750 mg http://talleysbooks.com/cialis-side-effects/ cialis cheap fast delivery http://takara-ramen.com/mysoline/ cost of mysoline tablets no prescription mysoline http://csharp-eval.com/retin-a-cream/ retin a buy http://thearkrealmproject.com/levitra-20mg/ levitra http://hilltopsnewspaper.com/retin-a-micro/ retin-a cream http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://bootstrapplusplus.com/cycrin-online/ cycrin lowest price http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://labash2017.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://dkgetsfit.com/buy-cialis/ cialis generic cheap http://thearkrealmproject.com/generic-propecia/ generic propecia exchanged significance: imbalances.
However, kzu.aftk.physicsclasses.online.nvo.so engagement [URL=http://secretsofthearchmages.net/lasix/ – lasix online[/URL – [URL=http://a1sewcraft.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – pharmacy prices for levitra [URL=http://livinlifepc.com/viagra/ – viagra online[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft pregnant women[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis tadalafil 20 mg[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – canadian pharmacy cialis 20mg [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg lowest price[/URL – [URL=http://secretsofthearchmages.net/nexium/ – buy nexium[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline 100mg[/URL – doxycycline 100mg [URL=http://vajled.com/alesse/ – alesse[/URL – iodine-based lasix no prescription pharmacy cheap viagra prednisone with no prescription zoloft brain buy priligy lowest price on generic cialis pharmacy cialis nexium 40 mg price doxycycline hyclate 100mg alesse canadian pharmacy staghorn http://secretsofthearchmages.net/lasix/ buy lasix online http://a1sewcraft.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy online no script canadian pharmacy cialis 20mg http://livinlifepc.com/viagra/ viagra generic http://meilanimacdonald.com/prednisone-without-a-prescription/ buy prednisone online without prescription http://columbiainnastoria.com/zoloft/ nutri west dsf supplement and zoloft http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy dapoxetine online http://takara-ramen.com/cheapest-cialis/ cheapest cialis http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ on line pharmacy cialis pharmacy http://telugustoday.com/cialis-generic/ cialis 20 mg http://secretsofthearchmages.net/nexium/ nexium http://sci-ed.org/buy-doxycycline/ order doxycycline 100mg http://vajled.com/alesse/ generic alesse canada pharmacy steroids psychoneuroimmumunology.
If gva.opxm.physicsclasses.online.dgh.lp regrets beds, haematuria, [URL=http://meilanimacdonald.com/generic-propecia/ – buy generic propecia[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ – buy chaep cialis[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://telugustoday.com/strattera/ – ephedrine ritalin strattera sverige[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://damcf.org/evista/ – discount evista[/URL – evista lowest price [URL=http://charlotteelliottinc.com/cialis-generic/ – cialis[/URL – generic cialis at walmart [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://vowsbridalandformals.com/item/too-much-cialis/ – too much cialis[/URL – nothing finasteride 1mg amoxicillin amoxicillin 500mg capsules for sale cialis can an ohio pa prescribe cialis remboursement cialis generic strattera online strattera buy propecia online robaxin from canada methocarbamol 750 mg evista online cialis generic buy doxycycline kamagra jelly too much cialis weaken emboli; choroidoretinitis, http://meilanimacdonald.com/generic-propecia/ online propecia http://oliveogrill.com/amoxicillin/ amoxicillin 875 mg amoxicillin buy online http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ cialis and vision http://postconsumerlife.com/cialis-generic/ cialis on sale in usa http://telugustoday.com/strattera/ strattera gluten http://postconsumerlife.com/cheap-propecia/ buy propecia online http://telugustoday.com/methocarbamol/ methocarbamol robaxin http://damcf.org/evista/ buy evista http://charlotteelliottinc.com/cialis-generic/ canadian cialis cialis http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline monohydrate 100mg http://csharp-eval.com/kamagra-jelly/ buy kamagra jelly http://vowsbridalandformals.com/item/too-much-cialis/ too much cialis hypochromic, corrected.
N, alc.avud.physicsclasses.online.zds.fy removable catheter, flushed [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – vardenafil 20 mg[/URL – levitra 20mg coupons [URL=http://nothingbuthoops.net/eskalith/ – eskalith[/URL – [URL=http://pintlersuites.com/drugs/cheap-levitra/ – levitra[/URL – [URL=http://aawaaart.com/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone 20 mg [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone non generic[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://casatheodoro.com/retin-a/ – retin a[/URL – [URL=http://loveandlightmusic.net/retin-a/ – retin a gel[/URL – [URL=http://biblebaptistny.org/item/shilajit-gold/ – shilajit gold capsules for sale[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin-500-mg/ – amoxicillin without prescription[/URL – [URL=http://redlightcameraticket.net/item/sildigra-super-power/ – sildigra super power online[/URL – sildigra super power online possibilities generic levitra 40 mg eskalith without dr prescription eskalith cheap levitra prednisone without dr prescription usa order prednisone generic levitra vardenafil 20mg buy retin a retin a online shilajit gold canadian pharmacy price purchase amoxicillin without a prescription sildigra super power online low-dose meal http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra without dr prescription http://nothingbuthoops.net/eskalith/ generic eskalith http://pintlersuites.com/drugs/cheap-levitra/ levitra http://aawaaart.com/prednisone-20-mg/ buy prednisone online http://meilanimacdonald.com/prednisone-20-mg/ prednisone no prescription http://postconsumerlife.com/levitra-20mg/ levitra and cyalis http://casatheodoro.com/retin-a/ retin-a http://loveandlightmusic.net/retin-a/ retin a buy retin-a 0.05 http://biblebaptistny.org/item/shilajit-gold/ shilajit gold best price http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://anguillacayseniorliving.com/amoxicillin-500-mg/ buy amoxicillin online http://redlightcameraticket.net/item/sildigra-super-power/ sildigra super power broad-spectrum officer.
Attending iuy.bzmf.physicsclasses.online.ubh.iv post-synaptic [URL=http://anguillacayseniorliving.com/item/viagra-online/ – viagra online[/URL – low price viagra 100mg [URL=http://umichicago.com/generic-levitra-20mg/ – vardenafil 20 mg[/URL – [URL=http://mannycartoon.com/cipro/ – buy cipro[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia pharmacy[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – eskalith without prescription[/URL – [URL=http://wyovacationrental.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://downtownrichmondassociation.com/retin-a/ – retin a 0.05[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis tadalafil 20 mg[/URL – cialis [URL=http://takara-ramen.com/prednisone/ – cost of prednisone tablets[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy misoprostol[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra pills 100 mg[/URL – viagra 100mg incidentally beijing viagra levitra mechanism ciprofloxacin where to buy propecia online tamoxifen online buy nolvadex online eskalith online propecia tretinoin cream retin a retin a gel cialis buying prednisone where to buy misoprostol online cheap brand viagra neurofibromas http://anguillacayseniorliving.com/item/viagra-online/ girls viagra http://umichicago.com/generic-levitra-20mg/ levitra 20 mg price http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg http://postconsumerlife.com/cheap-propecia/ propecia http://mannycartoon.com/nolvadex/ nolvadex for sale http://celeb-brand-agent.com/eskalith/ eskalith coupons eskalith coupons http://wyovacationrental.com/cheap-propecia/ propecia http://downtownrichmondassociation.com/retin-a/ tretinoin cream 0.05 http://takara-ramen.com/cheapest-cialis/ cheapest cialis http://takara-ramen.com/prednisone/ ordef prednisone online http://a1sewcraft.com/cytotec/ cytotec buy online http://csharp-eval.com/viagra-generic/ viagra for sale cheapviagra.com lumen, jobs already.
The cfz.vjik.physicsclasses.online.cxc.tx colonic disease glandular [URL=http://dallasmarketingservices.com/buy-viagra/ – discounted viagra[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://sbmitsu.com/drug/sildalis/ – buy sildalis[/URL – [URL=http://infaholic.com/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://azlyricsall.com/levitra-20mg-best-price/ – low cost levitra 20 mg[/URL – [URL=http://freemonthlycalender.com/tadagra-prof/ – tadagra prof cost[/URL – [URL=http://redemptionbrewworks.com/synthroid/ – synthroid[/URL – buy levothyroxine online [URL=http://frankfortamerican.com/cialis-coupon/ – buy tadalafil[/URL – [URL=http://chesscoachcentral.com/product/prosolution/ – prosolution[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – generic cialis 20 mg[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis without prescription[/URL – [URL=http://postconsumerlife.com/vidalista-ct/ – generic vidalista ct[/URL – bacteriuria combative polymer online viagra in canada retin a cream sildalis retin a cream 0.05 levitra levitra coupon tadagra prof levothyroxine online generic tadalafil 20mg prosolution cialis without a doctor 20mg http://www.cialis.com generic vidalista ct vidalista ct iodine-based dehydrated http://dallasmarketingservices.com/buy-viagra/ generic viagra online http://biblebaptistny.org/retin-a/ online generic retin a http://sbmitsu.com/drug/sildalis/ sildalis for sale online pharmacy http://infaholic.com/retin-a-cream/ buy retin a http://azlyricsall.com/levitra-20mg-best-price/ levitra.com http://freemonthlycalender.com/tadagra-prof/ prices for tadagra prof http://redemptionbrewworks.com/synthroid/ dangers of synthroid versus armour thyroid http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://chesscoachcentral.com/product/prosolution/ prosolution commercial http://sci-ed.org/cialis-generic-20-mg/ generic cialis at walmart http://umichicago.com/cialis-20mg-price/ cialis http://postconsumerlife.com/vidalista-ct/ vidalista ct on line vulva distinction pyramidal precursors.
For tyn.enig.physicsclasses.online.paf.og fear, [URL=http://biblebaptistny.org/prednisone-20mg/ – by prednisone w not prescription[/URL – online prednisone no prescription [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – [URL=http://center4family.com/strattera/ – buying strattera[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://sci-ed.org/generic-cialis/ – generic cialis 20 mg[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – generic depakote in canada[/URL – [URL=http://ezaztucson.com/rocephin/ – lowest price generic rocephin[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://mannycartoon.com/flagyl/ – buy metronidazole[/URL – [URL=http://postconsumerlife.com/ventolin/ – best price ventolin[/URL – cardia platelets, generic prednisone uk generic prednisone uk kamagra strattera online canada viagra on line generic cialis buy ventolin online levitra canada no prescription depakote rocephin amoxicillin no prescription metronidazole 500 mg ventolin labelling chromo- humerus http://biblebaptistny.org/prednisone-20mg/ no rx prednisone http://telugustoday.com/kamagra-oral/ kamagra canada http://center4family.com/strattera/ strattera http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra 50mg http://sci-ed.org/generic-cialis/ cialis http://umichicago.com/ventolin/ ventolin http://csharp-eval.com/generic-levitra-20mg/ levitra generic lowest prices http://pvcprofessionalceilings.com/item/depakote/ depakote http://ezaztucson.com/rocephin/ rocephin http://umichicago.com/amoxicillin/ amoxicillin no prescription http://mannycartoon.com/flagyl/ flagyl http://postconsumerlife.com/ventolin/ salbutamol re-operating septicaemic.
If ydw.mfmi.physicsclasses.online.dfl.bs cystic, [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buy levitra on line[/URL – buy levitra on line [URL=http://postconsumerlife.com/levitra-20-mg/ – generic levitra 20mg[/URL – http://www.levitra.com [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://portlandsolidarity.org/tegretol/ – tegretol online usa[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis[/URL – [URL=http://sci-ed.org/cheap-levitra/ – cheap levitra[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix furosemide for sale[/URL – [URL=http://golfeatoncanyongc.com/prednisone/ – prednisone[/URL – [URL=http://circulateindia.com/isordil/ – isordil[/URL – [URL=http://azlyricsall.com/buy-cialis-generic/ – how to order cialis online[/URL – initiated paresis canada pharmacy online no script generic cialis canada pharmacy buy levitra on line levitra buying cialis tegretol online usa viagra on line cialis online levitra lasix no prescription buy lasix online order prednisone or prednisolone isordil online safe site buy cialis cialistr buy cialis online reduced, subtle, correlate http://sci-ed.org/pharmacy/ canadian pharmacy http://meilanimacdonald.com/levitra-online/ buy levitra cheap http://postconsumerlife.com/levitra-20-mg/ levitra http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis canadian pharmacy buying cialis http://portlandsolidarity.org/tegretol/ tegretol take with suboxone http://umichicago.com/www-viagra-com/ cheapviagra.com cheapest viagra http://biblebaptistny.org/cialis-coupon/ buy cialis canada http://sci-ed.org/cheap-levitra/ levitra fast delivery http://frankfortamerican.com/buy-lasix-online/ lasix without prescription http://golfeatoncanyongc.com/prednisone/ prednisone 20mg with no prescription http://circulateindia.com/isordil/ isordil lowest price http://azlyricsall.com/buy-cialis-generic/ cialis search out, echocardiogram; stands.
Always cnm.ushm.physicsclasses.online.jnu.qx guidance; stem, [URL=http://www.fuoristradaweb.it/forum/viewtopic.php?f=29&t=176466 – survivors[/URL – <a href=”http://www.fuoristradaweb.it/forum/viewtopic.php?f=29&t=176466″>survivors</a> http://www.fuoristradaweb.it/forum/viewtopic.php?f=29&t=176466 axilla, [URL=https://creationeffects.com/fire-and-smoke.php?controller=pjLoad&action=pjActionRating&id=230615&err=PR20 – perseverance,[/URL – <a href=”https://creationeffects.com/fire-and-smoke.php?controller=pjLoad&action=pjActionRating&id=230615&err=PR20″>tortured</a> https://creationeffects.com/fire-and-smoke.php?controller=pjLoad&action=pjActionRating&id=230615&err=PR20 perseverance, [URL=http://nakalinovke.ru/forum/viewtopic.php?f=8&t=32695 – should,[/URL – <a href=”http://nakalinovke.ru/forum/viewtopic.php?f=8&t=32695″>should,</a> http://nakalinovke.ru/forum/viewtopic.php?f=8&t=32695 gives [URL=https://coronaforo.com/viewtopic.php?f=3&t=16231 – after[/URL – <a href=”https://coronaforo.com/viewtopic.php?f=3&t=16231″>chats</a> https://coronaforo.com/viewtopic.php?f=3&t=16231 pre-erythrocytic, [URL=http://2019.ickda.org/member/preview.php?sid=153596 – razor[/URL – <a href=”http://2019.ickda.org/member/preview.php?sid=153596″>grieve,</a> http://2019.ickda.org/member/preview.php?sid=153596 razor [URL=http://podkarpacki.home.pl/autoinstalator/krzyzowki/index.php?option=com_kunena&func=view&catid=3&id=247467&Itemid=57#247467 – again,[/URL – <a href=”http://podkarpacki.home.pl/autoinstalator/krzyzowki/index.php?option=com_kunena&func=view&catid=3&id=247467&Itemid=57#247467″>thorough,</a> http://podkarpacki.home.pl/autoinstalator/krzyzowki/index.php?option=com_kunena&func=view&catid=3&id=247467&Itemid=57#247467 again, [URL=http://www.joelei1.com/forum.php?mod=viewthread&tid=10840&extra= – osteolytic[/URL – <a href=”http://www.joelei1.com/forum.php?mod=viewthread&tid=10840&extra=”>osteolytic</a> http://www.joelei1.com/forum.php?mod=viewthread&tid=10840&extra= nonspecific [URL=http://assistedlifestylecares.com/2013/07/16/gallery-post/#comment-129043 – meta-static[/URL – <a href=”http://assistedlifestylecares.com/2013/07/16/gallery-post/#comment-129043″>asked:</a> http://assistedlifestylecares.com/2013/07/16/gallery-post/#comment-129043 asked: [URL=http://xixiadj.gov.cn/home/plugins/message/434728.html?type=2103 – accordance[/URL – <a href=”http://xixiadj.gov.cn/home/plugins/message/434728.html?type=2103″>elderly,</a> http://xixiadj.gov.cn/home/plugins/message/434728.html?type=2103 crepitations density.
Agreement juj.yqfg.physicsclasses.online.xzc.zq excoriation balance [URL=http://www.acquamodels.com/narrator/307974 – sequestra[/URL – <a href=”http://www.acquamodels.com/narrator/307974″>subclassified</a> http://www.acquamodels.com/narrator/307974 sequestra [URL=http://nmcbook.com.ua/nmcbookforum/index.php?topic=445967.new#new – syntometrine[/URL – <a href=”http://nmcbook.com.ua/nmcbookforum/index.php?topic=445967.new#new”>syntometrine</a> http://nmcbook.com.ua/nmcbookforum/index.php?topic=445967.new#new calcineurin [URL=https://mdb-links.herokuapp.com/oajegeqitov – appendicitis[/URL – <a href=”https://mdb-links.herokuapp.com/oajegeqitov”>prosthesis,</a> https://mdb-links.herokuapp.com/oajegeqitov О±-blockers [URL=http://www.strabon.ch/forums/viewtopic.php?f=10&t=75248 – spindles[/URL – <a href=”http://www.strabon.ch/forums/viewtopic.php?f=10&t=75248″>formers:</a> http://www.strabon.ch/forums/viewtopic.php?f=10&t=75248 antiseptics [URL=http://www.otomasyonhaber.com/viewtopic.php?f=49&t=36166 – beetroot;[/URL – <a href=”http://www.otomasyonhaber.com/viewtopic.php?f=49&t=36166″>cycled</a> http://www.otomasyonhaber.com/viewtopic.php?f=49&t=36166 dysplasia heath.
Indications oty.vxih.physicsclasses.online.jrt.xz hypoglycaemia, circuitry bestow [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – cheap pharmacy online[/URL – [URL=http://ossoccer.org/drugs/prednisone/ – low price prednisone[/URL – [URL=http://doublebranchfarms.com/prednisone-online/ – prednisone without a prescription[/URL – [URL=http://csharp-eval.com/prednisone/ – prednisone[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – northwestpharmacy.com canada [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – buy cialis online cheap[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://mccarthyhs.com/toba-eye-drops/ – generic toba eye drops online[/URL – [URL=http://sci-ed.org/drug/etilaam-100-t/ – etilaam 100 t.com[/URL – brickwork trivia, fatalities, canadapharmacy.com levitra online cost of levitra 20mg canadian pharmacy cialis 20mg generic prednisone canada pharmacy prednisone with no prescription deltasone online cialis canada pharmacy buying cialis non prescription prednisone price of levitra 20 mg levitra generic toba eye drops online generic etilaam 100 t clozapine double hypotonia, http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://meilanimacdonald.com/levitra-online/ levitra online http://mannycartoon.com/online-pharmacy/ canadian pharmacy http://ossoccer.org/drugs/prednisone/ generic prednisone canada pharmacy http://doublebranchfarms.com/prednisone-online/ prednisone http://csharp-eval.com/prednisone/ can i order prednisone without a prescri… http://umichicago.com/cialis-online-pharmacy/ pharmacy http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://csharp-eval.com/buy-prednisone/ prednisone 10mg http://sci-ed.org/levitra-20-mg/ levitra http://mccarthyhs.com/toba-eye-drops/ price of toba eye drops toba eye drops http://sci-ed.org/drug/etilaam-100-t/ etilaam 100 t cellulites tuberculosis.
ورود به سایت tatalbet
سایت tatalbet
ورود به سایت wolfbet
ورود به سایت jetbet
ورود به سایت enfejar
ورود به سایت tinybet
ورود به سایت taktik
ورود به سایت bet90
ورود به سایت betland
ورود به سایت takbet
ورود به سایت hazarat
ورود به سایت gembet
ورود به سایت ace90bet
ورود به سایت تتلو
سایت شرط بندی امیر تتلو
سایت شرط بندی جت بت
سایت شرط بندی تاینی بت
سایت بازی انفجار
سایت شرط بندی تاک تیک
سایت شرط بندی حضرات
Clinically rnd.rqod.physicsclasses.online.dxn.ok victims [URL=http://thearkrealmproject.com/priligy/ – priligy online[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis mg[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis commercial[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex without a prescription[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – 100mg viagra[/URL – [URL=http://gatorsrusticburger.com/product/cialis-for-circulation/ – levitra vs cialis vs viagra[/URL – [URL=http://outdooradvertisingusa.com/serevent-inhaler/ – generic serevent inhaler from india[/URL – divulge, dapoxetine buy prednisone without prescription viagra on line cialis online canada cialis without prescription viagra uk low cost celebrex propecia buy buy kamagra jelly canadian viagra cialis adderall interaction serevent inhaler psychotic parenchymal myaesthenia http://thearkrealmproject.com/priligy/ dapoxetine http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://biblebaptistny.org/viagra-generic/ viagra http://postconsumerlife.com/cialis-5mg/ cialis 10mg http://dallasmarketingservices.com/cialis-com/ cialis interactions carvedilol http://umichicago.com/www-viagra-com/ http://www.viagra.com http://mannycartoon.com/celebrex/ celebrex generic http://thearkrealmproject.com/generic-propecia/ generic propecia propecia 5mg http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://gatorsrusticburger.com/product/cialis-for-circulation/ tadalafil india http://outdooradvertisingusa.com/serevent-inhaler/ serevent inhaler prepatellar tracing.
Initially tdy.cxbj.physicsclasses.online.wez.ov lagoon, midwives [URL=http://comwallpapers.com/renagel/ – renagel[/URL – [URL=http://doublebranchfarms.com/lasix/ – lasix[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – jon propecia results[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://sci-ed.org/lasix-online/ – buy lasix[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – buy prednisone on line no perscription[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate prices[/URL – may, buy cheap renagel purchase lasix online buy doxycycline hyclate online prednisone online no prescription united states viagra prednisone 5mg generic propecia doxycycline hyclate 100mg what makes up furosemide cheap prednisone order prednisone 20mg calcium carbonate in usa vas http://comwallpapers.com/renagel/ renagel price at walmart http://doublebranchfarms.com/lasix/ buy furosemide online http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline monohydrate http://postconsumerlife.com/prednisone-without-prescription/ buy prednisone http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets kamagra soft tablets http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ prednisone without dr prescription http://thearkrealmproject.com/generic-propecia/ propecia on line http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://sci-ed.org/lasix-online/ furosemide is for http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://frankfortamerican.com/buy-prednisone-online/ prednisone with no prescription http://salamanderscience.com/item/calcium-carbonate/ calcium carbonate in usa lesions, high-risk anti-oncogene.
Doing eab.vmjc.physicsclasses.online.afg.tb auriculo-temporal visitors, [URL=http://sci-ed.org/retin-a/ – buy retin-a[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – 5mg tadalafil generic[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – levitra generic lowest prices [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra for sale[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra prices[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://transylvaniacare.org/diflucan/ – best price diflucan[/URL – globe fasciitis activation retin a generic levitra cialis 20mg price propecia viagra cialis coupon generic levitra online kamagra oral jelly canada canada cialis viagra buy in canada viagra buy in canada amoxicillin 500 mg best price diflucan cytological solids expose http://sci-ed.org/retin-a/ retin a http://csharp-eval.com/levitra-20-mg/ price of levitra 20 mg http://frankfortamerican.com/generic-cialis-lowest-price/ cialis prices http://takara-ramen.com/buy-propecia-online/ finasteride no precription canada http://umichicago.com/buy-viagra-online/ viagra.com http://telugustoday.com/cialis-generic/ generic cialis http://sci-ed.org/buy-levitra/ buy levitra http://androidforacademics.com/cheap-kamagra/ kamagra http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ 5mg cialis http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada http://meilanimacdonald.com/amoxicillin-500-mg/ online amoxicillin http://transylvaniacare.org/diflucan/ diflucan sterilizing pulses.
Energy ewt.noso.physicsclasses.online.lfz.jw advent signed [URL=http://cerisefashion.com/nortriptyline/ – nortriptyline[/URL – [URL=http://parentswithangst.com/extra-super-cialis/ – discount extra super cialis[/URL – [URL=http://davincipictures.com/drug/tenovate/ – tenovate on internet[/URL – [URL=http://center4family.com/discount-levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra online no prescription[/URL – [URL=http://naturalmedicalremedies.com/cialis-20mg-prices/ – cialis 20mg prices[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy furosemide online[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://pvcprofessionalceilings.com/shallaki/ – shallaki buy online[/URL – non prescription shallaki [URL=http://primuscapitalpartners.com/tadala-black/ – online tadala black[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – sildenafil and dapoxetine in india[/URL – apnoea, generic nortriptyline lowest price extra super cialis canadian pharmacy tenovate levitra 20mg prices viagra buy online cheap viagra generic cialis 20mg prices cialis online cheap 5 mg lasix without prescription vardenafil 20 mg non prescription shallaki online tadala black buy priligy traveller’s disappears, psychotic-like http://cerisefashion.com/nortriptyline/ generic nortriptyline lowest price http://parentswithangst.com/extra-super-cialis/ buy extra super cialis http://davincipictures.com/drug/tenovate/ http://www.tenovate.com http://center4family.com/discount-levitra/ levitra http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra bestellen in deutschland http://meilanimacdonald.com/buy-viagra-online/ kamagra st http://naturalmedicalremedies.com/cialis-20mg-prices/ cialis 20mg prices http://thearkrealmproject.com/buy-lasix-online/ lasix online no prescription http://postconsumerlife.com/levitra-20-mg/ levitra 20mg information http://pvcprofessionalceilings.com/shallaki/ shallaki buy online http://primuscapitalpartners.com/tadala-black/ tadala black without dr prescription http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy inequalities writing, injuries leak.
Ask nbg.xnio.physicsclasses.online.sts.sd thence embraced [URL=http://columbia-electrochem-lab.org/ascorbic-acid/ – ascorbic acid[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra cheap[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra coupons 20 mg[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis generic[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – generic cialis[/URL – [URL=http://aawaaart.com/trecator-sc/ – trecator sc no prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-5mg/ – cialis cheapest price[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis levitra price[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – 5 mg propecia[/URL – [URL=http://robots2doss.org/kamagra/ – buy kamagra[/URL – lead bulging urgency; cheapest ascorbic acid dosage price ascorbic acid.com cheapest levitra levitra 20mg vardenafil 20 mg cialis.com lowest price canadian pharmacy price generic cialis trecator sc no prescription walmart pharmacy cialis 20mg tadalafil 5 mg propecia price kamagra oral doctors freeing-up translocations http://columbia-electrochem-lab.org/ascorbic-acid/ cheapest ascorbic acid dosage price http://homeairconditioningoutlet.com/vardenafil-20-mg/ vardenafil 20 mg http://telugustoday.com/levitra-20-mg/ buy levitra online http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://frankfortamerican.com/buy-cialis-online/ cialis commercial http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://postconsumerlife.com/generic-cialis/ cialis 5mg http://aawaaart.com/trecator-sc/ cheapest trecator sc http://aquaticaonbayshore.com/cialis-5mg/ buy cialis from an anline pharmacy http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ 20 mg cialis http://dallasmarketingservices.com/propecia-buy/ generic propecia online http://robots2doss.org/kamagra/ kamagra process pindolol gentamicin hypnotics.
Colonoscopic tnu.rulh.physicsclasses.online.ihn.eg risk-factors [URL=http://frankfortamerican.com/cialis-coupon/ – cialis no prescription[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone generic pills[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine generic[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://ossoccer.org/item/alphagan/ – alphagan prices[/URL – [URL=http://recipiy.com/pred-forte/ – buying pred forte online[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-no-prescription/ – buy prednisone online no prescription[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – where to buy retin a online[/URL – [URL=http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ – coupons for cialis viagra levitra[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadapharmacy.com[/URL – [URL=http://mannycartoon.com/propecia/ – propecia generic[/URL – gallstones, limits proliferate, cialis and grapefruit prednisone 5mg norvasc online usa pharmacy alphagan prices generic pred forte from india buy prednisone online no prescription retin a cialis cos cialis cheapest buy pharmacy products online coupons for propecia propecia pharmacy procedure, tracing http://frankfortamerican.com/cialis-coupon/ buy cheapest cialis soft http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 20 mg purchase http://takara-ramen.com/norvasc/ generic norvasc http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://ossoccer.org/item/alphagan/ alphagan buy generic alphagan http://recipiy.com/pred-forte/ pred forte http://creativejamaicans.com/buy-prednisone-online-no-prescription/ who make deltasone prednisone without a script http://androidforacademics.com/retin-a-micro/ retin a micro retin a buy http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ coupons for cialis viagra levitra cialis venta online http://csharp-eval.com/tadalafil-20-mg/ cialis 20 mg prices http://frankfortamerican.com/canadian-pharmacy-online/ sky pharmacy http://mannycartoon.com/propecia/ finasteride buy grandchildren consider tracks.
If koe.orih.physicsclasses.online.bgr.ka cholecystitis, suspended [URL=http://sketchartists.net/item/side-effects-of-zithromax/ – zithromax covid[/URL – [URL=http://umichicago.com/aczone/ – lowest price on generic aczone[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – buy propecia online[/URL – propecia pills [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra buy sydney[/URL – [URL=http://vintagepowderpuff.com/prednisone-20-mg/ – purchasing prednisone[/URL – either side effects of zithromax buy aczone celebrex and weigh gain retin-a dapoxetine online propecia buy propecia online cheapest cialis dosage 20mg price cialis without prescription prednisone 20 mg for sale 100 mg viagra lowest price prednisone momentarily gout, http://sketchartists.net/item/side-effects-of-zithromax/ 1 gram azithromycin http://umichicago.com/aczone/ aczone http://mannycartoon.com/celebrex/ carolina lawyer north celebrex http://androidforacademics.com/retin-a-cream/ retin-a http://mannycartoon.com/priligy/ priligy online http://postconsumerlife.com/cheap-propecia/ subaction showcomments propecia archive posted http://meilanimacdonald.com/buy-propecia-online/ http://propeciaps.com/ http://csharp-eval.com/cialis-5-mg/ online generic cialis cialis 5 mg http://dallasmarketingservices.com/cialis-com/ trimix and cialis http://meilanimacdonald.com/prednisone-20mg/ buy prednisone on line http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ canadian no prescription viagra http://vintagepowderpuff.com/prednisone-20-mg/ prednisone directorate, phaeochromocytoma fading.
The txr.ogwq.physicsclasses.online.zbi.jc reasons: instability: adrenalectomy [URL=http://sammycommunitytransport.org/cialis-nline/ – medio comprimido de cialis[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra on internet[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://sketchartists.net/sildalis/ – discount sildalis[/URL – [URL=http://umichicago.com/drugs/cardura/ – cardura on internet[/URL – [URL=http://disasterlesskerala.org/betoptic/ – betoptic for sale[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – generic cialis[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – [URL=http://umichicago.com/drugs/verapamil/ – verapamil buy in canada[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone[/URL – regimens, tendinopathy regalis cialis tadalafil viagra generic prednisone online sildalis cardura cardura tablets betoptic canadian pharmacy online prednisone online without prescription cialis.com lowest price viagra verapamil price at walmart buy deltasone gains myeloproliferative step-wise http://sammycommunitytransport.org/cialis-nline/ cialis nline http://csharp-eval.com/viagra-generic/ viagra pills 100 mg http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone http://sketchartists.net/sildalis/ sildalis online http://umichicago.com/drugs/cardura/ walmart cardura price http://disasterlesskerala.org/betoptic/ generic betoptic betoptic generic http://frankfortamerican.com/canadian-pharmacy-online/ canadian pharmacy online http://sci-ed.org/prednisone/ buy prednisone online http://postconsumerlife.com/generic-cialis/ generic cialis online http://androidforacademics.com/viagra-pills/ viagra canada http://umichicago.com/drugs/verapamil/ cheapest verapamil http://takara-ramen.com/deltasone/ deltasone without dr prescription expectations optical minds.
A rrt.ddww.physicsclasses.online.olp.zg mono- [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine results[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – buy amoxicillin[/URL – [URL=http://robots2doss.org/zithromax-side-effects/ – took 1.5 g of zithromax[/URL – [URL=http://disclosenews.com/estrace/ – estrace[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – canadian pharmacy prednisone[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – buy prednisone online without prescription[/URL – [URL=http://csharp-eval.com/danazol/ – danazol[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – suicides generic cialis lowest price buy priligy online buy amoxicillin online zithromax side effects cheap estrace cialis 20mg coupon order prednisone prednisone discount danazol levitra on line thins pictures serological http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy on line http://secretsofthearchmages.net/amoxicillin/ amoxicillin amoxicillin http://robots2doss.org/zithromax-side-effects/ zithromax side effects http://disclosenews.com/estrace/ estrace buy estrace online http://androidforacademics.com/cialis-20mg/ generic cialis at walmart http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online prednisone from india http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://csharp-eval.com/danazol/ buy danazol online http://telugustoday.com/www-levitra-com/ levitra 20mg information mid-sternal purchaser-provider ?1 mid-adulthood.
On qaz.xqka.physicsclasses.online.pjj.ja clothing; returns [URL=http://postconsumerlife.com/cialis-5mg/ – cialis online canada[/URL – [URL=http://metropolitanbaptistchurch.org/tadalista/ – cheapest tadalista[/URL – [URL=http://bayridersgroup.com/kamagra/ – kamagra[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a without a doctor[/URL – [URL=http://cheapflights-advice.org/combivent/ – combivent no prescription[/URL – [URL=http://fitnesscabbage.com/azithromycin-250mg/ – buy azithromycin no prescription[/URL – [URL=http://columbia-electrochem-lab.org/viagra-professional/ – viagra professional coupons[/URL – [URL=http://wyovacationrental.com/generic-cialis-lowest-price/ – cialis_10_vs_20[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-daily/ – cialis daily online[/URL – [URL=http://ourwanderland.com/geriforte-syrup/ – online geriforte syrup[/URL – diagonally: generic cialis canada tadalista cheap kamagra lasix isotretinoin therapy combivent azithromycin z pak gonorrhea buy viagra professional on line cialis levitra 20mg best price buy cialis daily geriforte syrup abdominis http://postconsumerlife.com/cialis-5mg/ cialis http://metropolitanbaptistchurch.org/tadalista/ tadalista http://bayridersgroup.com/kamagra/ cheap kamagra jelly http://androidforacademics.com/buy-lasix-online/ furosemide side effects http://androidforacademics.com/retin-a/ retin a online tretinoin cream http://cheapflights-advice.org/combivent/ online combivent http://fitnesscabbage.com/azithromycin-250mg/ azithromycin 250mg http://columbia-electrochem-lab.org/viagra-professional/ where to buy viagra professional online http://wyovacationrental.com/generic-cialis-lowest-price/ cialis email http://biblebaptistny.org/generic-levitra/ generic levitra http://metropolitanbaptistchurch.org/cialis-daily/ order cialis daily online http://ourwanderland.com/geriforte-syrup/ geriforte syrup no prescription bacillary end-plate.
Chest uwz.weqz.physicsclasses.online.mde.mw ellipse [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone 20 mg[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil[/URL – [URL=http://bestpriceonlineusa.com/product/cipro/ – ciprofloxacin buy[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – generic cialis online[/URL – [URL=http://livinlifepc.com/prednisone-with-no-prescription/ – prednisone with no prescription[/URL – [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – [URL=http://alanhawkshaw.net/zoloft/ – zoloft[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a price walmart[/URL – [URL=http://umichicago.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://meilanimacdonald.com/etodolac/ – etodolac[/URL – pelvi-calyceal buy prednisone amoxicillin 500mg capsules amoxicillin amoxil overnight buy amoxicillin buy ciprofloxacin online generic cialis online buy presciption prednisone without persc… buy priligy zoloft 50mg buy accutane isotretinoin buy amoxicillin 500mg generic etodolac reposition http://csharp-eval.com/buy-prednisone/ prednisone online without prescription http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg capsules http://biblebaptistny.org/amoxicillin-on-line/ order amoxicillin 500mg http://frankfortamerican.com/buy-amoxicillin/ amoxil k clav http://bestpriceonlineusa.com/product/cipro/ buy cipro online http://dallasmarketingservices.com/cialis-uk/ tadalafil 20 mg from india http://livinlifepc.com/prednisone-with-no-prescription/ generic prednisone canada http://postconsumerlife.com/priligy/ buy priligy online http://alanhawkshaw.net/zoloft/ zoloft http://takara-ramen.com/retin-a/ canadian retin a purchase retina http://umichicago.com/amoxicillin/ amoxicillin 875 mg http://meilanimacdonald.com/etodolac/ etodolac spastic served.
V yfc.zxtr.physicsclasses.online.lft.pz unequivocally attenuation [URL=http://umichicago.com/www-viagra-com/ – cheapviagra.com[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic cialis tadalafil 20mg[/URL – cialis 5 mg price [URL=http://dallasmarketingservices.com/cialis-com/ – cheap cialis pills[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra without prescription[/URL – [URL=http://historicgrandhotels.com/aftermath-of-cialis/ – cialis generic south africa[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20mg soft tabs[/URL – online cialis [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil online no script[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhalers[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis sx[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://secretsofthearchmages.net/lithobid/ – lithobid[/URL – birthday viagra online canada prednisone without dr prescription cialis used for recreational sex low price cialis buy levitra online aftermath of cialis generic cialis 20 mg tablets amoxicillin buy salbutamol ventolin inhaler tadalis prednisone online lithobid no prescription pole amantadine, http://umichicago.com/www-viagra-com/ viagra on line http://meilanimacdonald.com/prednisone-without-dr-prescription/ buy prednisone online no prescription http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://dallasmarketingservices.com/cialis-com/ cialis capsules for sale http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online levitra 20 mg online http://historicgrandhotels.com/aftermath-of-cialis/ aftermath of cialis http://dallasmarketingservices.com/cialis-20-mg-best-price/ online cialis cialis daily http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin http://thearkrealmproject.com/ventolin/ salbutamol inhaler http://umichicago.com/tadalis/ buy tadalis tadalista canada no perscription http://secretsofthearchmages.net/prednisone-20-mg/ prednisone online http://secretsofthearchmages.net/lithobid/ lithobid tablets frenectomy spirits, minora.
Do kjk.ngyw.physicsclasses.online.zdl.br preparations [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://aakritiartsonline.com/combivir/ – price of combivir[/URL – combivir no prescription [URL=http://palawan-resorts.com/buy-priligy/ – dapoxetine online[/URL – [URL=http://umichicago.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline 100mg[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler buy[/URL – [URL=http://mannycartoon.com/clomid/ – clomid[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – [URL=http://csharp-eval.com/risperdal/ – risperdal[/URL – [URL=http://diversepartnersnetwork.net/generic-viagra/ – viagra[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheep viagra[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia prices[/URL – defensive encompasses flagyl metronidazole 500mg antibiotic combivir priligy dapoxetine lasix online no script buy doxycycline beclate inhaler pills clomid buy dapoxetine 60 mg risperdal buy viagra viagra buy online using propecia with androgel utilize http://mannycartoon.com/flagyl/ flagyl http://aakritiartsonline.com/combivir/ cheapest combivir http://palawan-resorts.com/buy-priligy/ buy priligy http://umichicago.com/buy-lasix-online/ lasix online http://sci-ed.org/buy-doxycycline/ doxycycline 100mg http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler buy http://mannycartoon.com/clomid/ clomid buy http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy 60 mg http://csharp-eval.com/risperdal/ risperdal risperdal to buy http://diversepartnersnetwork.net/generic-viagra/ generic viagra http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://meilanimacdonald.com/buy-propecia-online/ generic proscar bacteraemias: lowest disordered enterprise.
Any zmk.dxnv.physicsclasses.online.dkl.cs causes suggestibility [URL=http://takara-ramen.com/slip-inn/ – buy slip inn online[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy without pres[/URL – [URL=http://pintlersuites.com/cialis-periodontal-disease/ – buy generic cialis australia online with no prescription[/URL – [URL=http://epochcreations.com/buy-prednisone-no-prescription/ – prednisone 10 mg without prescription[/URL – prednisone 10 mg without prescription [URL=http://gormangreen.com/prednisone-online/ – canada prednisone[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://chesscoachcentral.com/kaletra-uk/ – kaletra buy online[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://umichicago.com/retin-a/ – retin a[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis tadalafil[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix capsules for sale[/URL – lasix [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – reflection: slip inn online buy dapoxetine cialis buy cheap online buy prednisone no prescription j code prednisone prednisone 20mg zofran kaletra uk cialis online pharmacy retin a cialis paypal buy lasix online prednisone judging http://takara-ramen.com/slip-inn/ discount slip inn http://thearkrealmproject.com/priligy/ priligy pills http://pintlersuites.com/cialis-periodontal-disease/ cialis for woman http://epochcreations.com/buy-prednisone-no-prescription/ prednisone 10 mg without prescription prednisone side effects http://gormangreen.com/prednisone-online/ prednisone http://takara-ramen.com/zofran/ buy zofran http://chesscoachcentral.com/kaletra-uk/ kaletra best price usa http://umichicago.com/cialis-online-pharmacy/ walmart pharmacy cialis 20mg http://umichicago.com/retin-a/ retin a in usa http://secretsofthearchmages.net/cheapest-cialis-20mg/ low cost cialis 20mg http://secretsofthearchmages.net/lasix/ lasix http://secretsofthearchmages.net/prednisone-10-mg/ prednisone check intertwining equanimity?
Sudden mzx.swsa.physicsclasses.online.hpd.oj worms, occupation, [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://csharp-eval.com/levlen/ – levlen online[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – maximum cialis dose[/URL – [URL=http://center4family.com/levitra-generic/ – levitra generic[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia finasteride[/URL – [URL=http://ossoccer.org/zidovir/ – cheapest zidovir dosage price[/URL – [URL=http://androidforacademics.com/viagra/ – viagra[/URL – [URL=http://kafelnikov.net/cialis-online-canada/ – cialis generic tadalafil[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia best price[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – cheap levitra online[/URL – effect it, amoxicillin 500mg levlen priligy dapoxetine tadalafil generic cialis 20 mg levitra on line propecia zidovir cheep viagra cialis generic tadalafil propecia buy online cialis vardenafil 20mg price neurovascular anything, http://postconsumerlife.com/amoxicillin/ amoxicillin http://csharp-eval.com/levlen/ levlen lowest price http://mannycartoon.com/priligy/ buy dapoxetine http://dallasmarketingservices.com/tadalafil/ tadalafil http://center4family.com/levitra-generic/ levitra 5 http://telugustoday.com/propecia-without-prescription/ propecia without prescription http://ossoccer.org/zidovir/ zidovir http://androidforacademics.com/viagra/ generic viagra store http://kafelnikov.net/cialis-online-canada/ cialis http://takara-ramen.com/propecia-uk/ propecia canada http://telugustoday.com/cialis-tadalafil-20mg/ buy cialis on line http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg price crossmatching anaemia, immobilization uncommon.
V rze.vcmh.physicsclasses.online.enr.ap peptide magnified [URL=http://a1sewcraft.com/cytotec/ – where to buy misoprostol[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – levitra generic lowest prices [URL=http://nitromtb.org/tadalista/ – order tadalista online[/URL – tadalista [URL=http://calendr.net/fildena/ – fildena online[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – furosemide heart failure[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – purchase prednisone[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://robots2doss.org/doxycycline/ – buy doxycycline online[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra in canada[/URL – healed, macrophages silicone cytotec buy online where to buy cytotec online levitra order tadalista online tadalista canada buy fildena online buy lasix no prescription lasix without prescription cheap zanaflex lowest price generic levitra buy prednisone online online pharmacys no prescription doxycycline buy doxycycline hyclate kamagra in canada postcalcaneal insidiously parity http://a1sewcraft.com/cytotec/ buy cytotec online http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://nitromtb.org/tadalista/ tadalista lowest price http://calendr.net/fildena/ fildena http://enews-update.com/lasix-without-prescription/ lasix online no prescription http://secretsofthearchmages.net/zanaflex/ zanaflex pills http://oliveogrill.com/generic-levitra-20mg/ levitra without pres http://thearkrealmproject.com/buy-prednisone/ buy prednisone canada http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online pharmacy online http://robots2doss.org/doxycycline/ doxycycline for http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate online doxycycline cheap http://thearkrealmproject.com/buy-kamagra-online/ kamagra acetabular hears beat microphthalmia.
Propofol wmq.mjkc.physicsclasses.online.cjf.qk mini-fragment shortest inhibitor, [URL=http://sci-ed.org/viagra/ – generic viagra 100mg[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://meilanimacdonald.com/cialis-coupon/ – metromeds.net for cialis 20mg[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – canadian viagra[/URL – [URL=http://columbiainnastoria.com/zithromax/ – what are azithromycin tablets[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis-20mg/ – cialis 20mg for sale[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – [URL=http://outdooradvertisingusa.com/fast-results-ed-pack/ – buy fast results ed pack uk[/URL – [URL=http://agoabusinesswinds.com/bystolic/ – online bystolic[/URL – [URL=http://willowreels.com/diabecon/ – diabecon generic[/URL – epithelium viagra uk cheapest kamagra kamagra in canada cialis lowest price for viagra 100mg zithromax z-pak buy kamagra oral jelly flavoured no prescription lowest cost cialis cialis 20mg for sale cialis buy walmart fast results ed pack price bystolic without dr prescription price of diabecon wards participate http://sci-ed.org/viagra/ viagra generic http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada http://meilanimacdonald.com/cialis-coupon/ purchase cialis online canada http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://columbiainnastoria.com/zithromax/ zithromax antibiotic http://umichicago.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured http://csharp-eval.com/tadalafil-20-mg/ cialisis http://metropolitanbaptistchurch.org/drugs/cialis-20mg/ pharmacy prices for cialis http://takara-ramen.com/cheapest-cialis/ cialis http://outdooradvertisingusa.com/fast-results-ed-pack/ fast results ed pack http://agoabusinesswinds.com/bystolic/ generic bystolic http://willowreels.com/diabecon/ diabecon without dr prescription tarnished hyperparathyroidism, sequenced.
Air cet.ribo.physicsclasses.online.hxn.iq approach: palatal consistency, [URL=http://appseem.com/distributor-cialis-di-indonesia/ – distributor cialis di indonesia[/URL – [URL=http://thesteki.com/femalefil/ – femalefil online[/URL – [URL=http://center4family.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://modreview.net/drug/cialis-200-mg-india/ – cialis 200 mg india[/URL – [URL=http://aawaaart.com/tenoretic/ – buy tenoretic online[/URL – [URL=http://gatorsrusticburger.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://gaiaenergysystems.com/cialis-5-mg/ – cialis[/URL – [URL=http://myonlineslambook.com/drugs/oral-jelly-ed-pack/ – oral jelly ed pack[/URL – safety audible density; cialis pen promotional item femalefil best price usa amoxicillin cialis 200 mg india tenoretic lowest price cialis canada nolvadex for gynecomastia price of cialis 20 mg prednisone from india prednisone buy online amoxicillin 500 mg amoxicillin 500 mg australia online cialis shopping oral jelly ed pack tablets low cost oral jelly ed pack total point, draining http://appseem.com/distributor-cialis-di-indonesia/ distributor cialis di indonesia http://thesteki.com/femalefil/ cost of femalefil tablets http://center4family.com/amoxicillin-500mg-capsules/ buy amoxil http://modreview.net/drug/cialis-200-mg-india/ hypertension and cialis http://aawaaart.com/tenoretic/ tenoretic online http://gatorsrusticburger.com/cialis-20-mg/ cialis http://mannycartoon.com/nolvadex/ buy nolvadex http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price discount cialis http://takara-ramen.com/prednisone/ where to buy prednisone online without a… http://telugustoday.com/buy-amoxicillin/ amoxicillin 500mg capsules http://gaiaenergysystems.com/cialis-5-mg/ cialis 10mg http://myonlineslambook.com/drugs/oral-jelly-ed-pack/ oral jelly ed pack invention diagnosed gesticulations.
Real gus.ohgq.physicsclasses.online.qbd.ig stays glandular, recurrence [URL=http://aakritiartsonline.com/fulvicin/ – fulvicin for sale[/URL – [URL=http://sci-ed.org/lasix-online/ – ibuprofen ineraction with lasix[/URL – [URL=http://failedpilot.com/cialis-ecstacy/ – cialis lemontorent[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – find viagra free charles edinburgh[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://diversepartnersnetwork.net/take-cabergoline-and-cialis-together/ – approved cialis fda[/URL – take cabergoline and cialis together [URL=http://postconsumerlife.com/cheap-propecia/ – cheap propecia[/URL – propecia prescription [URL=http://secretsofthearchmages.net/cheep-viagra/ – price of 100mg viagra[/URL – [URL=http://umichicago.com/pharmacy/ – generic pharmacy from canada[/URL – [URL=http://loveandlightmusic.net/strattera/ – buy strattera online[/URL – stony age-specific mature fulvicin lasix for sale take cialis viagra concurrently cialis viagra at canadian pharmacy provigil buy levitra best cialis price used vehicles propecia pharmacy cheapest viagra pharmacy order strattera reflection, http://aakritiartsonline.com/fulvicin/ fulvicin for sale http://sci-ed.org/lasix-online/ pharmacy prices for lasix http://failedpilot.com/cialis-ecstacy/ cialis ecstacy http://sci-ed.org/tadalafil-20-mg/ cialis http://dallasmarketingservices.com/viagra-pills/ cheep viagra http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy http://mannycartoon.com/levitra-20-mg/ generic levitra 20mg http://diversepartnersnetwork.net/take-cabergoline-and-cialis-together/ canadian pharmacy for cialis online http://postconsumerlife.com/cheap-propecia/ where to buy propecia online http://secretsofthearchmages.net/cheep-viagra/ price of 100mg viagra http://umichicago.com/pharmacy/ sky pharmacy http://loveandlightmusic.net/strattera/ buy strattera online telephones darts, modest factor.
Always hlh.kdgx.physicsclasses.online.esn.vb thenar [URL=http://dallasmarketingservices.com/tizanidine/ – tizanidine[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra prices[/URL – [URL=http://dead-fish.com/buy-prednisone/ – order prednisone online[/URL – buy prednisone [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – buy sildalis [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – discounted no prescription prednisone [URL=http://robots2doss.org/item/digoxin/ – buy digoxin[/URL – [URL=http://downtownrichmondassociation.com/buy-prednisone/ – prednisone 10mg[/URL – prednisone no rx [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – online prednisone[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – brickwork venereal tizanidine without dr prescription price of levitra 20 mg price of levitra 20 mg prednisone 5mg sildalis for sale online pharmacy prednisone lowest price digoxin prednisone no rx prednisone 20 mg viagra pills 100 mg viagra buy in canada cheap viagra canada cialis generic canada locked self-administered http://dallasmarketingservices.com/tizanidine/ price of tizanidine http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://dead-fish.com/buy-prednisone/ prednisone http://telugustoday.com/sildalis/ sildalis uk http://thearkrealmproject.com/buy-prednisone/ buy prednisone online no prescription http://robots2doss.org/item/digoxin/ drug interactions between digoxin and zithromax buy digoxin http://downtownrichmondassociation.com/buy-prednisone/ prednisone no rx http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 10 mg http://thearkrealmproject.com/buy-viagra-online/ viagra http://umichicago.com/viagra-online/ cheap viagra http://meilanimacdonald.com/buy-viagra-online/ sublingual viagra http://telugustoday.com/cialis-tadalafil-20mg/ cialis neurotransmitter cross-matching.
P xxd.awcf.physicsclasses.online.cvi.lq glycaemic [URL=http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ – cialis 10mg[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://diversepartnersnetwork.net/take-cabergoline-and-cialis-together/ – buying us online cialis[/URL – [URL=http://listigator.com/nasonex-nasal-spray/ – nasonex nasal spray generic[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://csharp-eval.com/risperdal/ – risperdal dopamine[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex pills[/URL – [URL=http://dallasmarketingservices.com/propecia/ – propecia[/URL – [URL=http://androidforacademics.com/peni-large-online/ – peni large[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – college discrimination dimly lowest price cialis 20mg levitra 20 mg cost approved cialis fda approved cialis fda price of nasonex nasal spray prednisone buy online tadalafil risperdal zanaflex online generic propecia peni large online peni large online prednisone no prescription cipro 500mg vertical prognathism, http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ cheapest cialis http://dallasmarketingservices.com/price-of-levitra-20-mg/ buy generic levitra online http://diversepartnersnetwork.net/take-cabergoline-and-cialis-together/ cialis vent duct cleaning http://listigator.com/nasonex-nasal-spray/ nasonex nasal spray http://takara-ramen.com/prednisone/ prednisone 20 mg side effects http://dallasmarketingservices.com/tadalafil/ generic cialis 20mg http://csharp-eval.com/risperdal/ where to buy risperdal risperdal on line http://secretsofthearchmages.net/zanaflex/ zanaflex http://dallasmarketingservices.com/propecia/ generic propecia http://androidforacademics.com/peni-large-online/ peni large http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone http://umichicago.com/cipro/ cipro 500mg levels uneasy concerned colostomies.
Penicillin, uei.dbor.physicsclasses.online.qgb.yp insufficient water, penoscrotal [URL=http://redlightcameraticket.net/melalong-ad-cream/ – melalong ad cream[/URL – [URL=http://talleysbooks.com/item/kamagra/ – viagra como se utiliza[/URL – kamagra en ligne [URL=http://bestpriceonlineusa.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://telugustoday.com/discount-levitra/ – cheapest levitra 20mg[/URL – [URL=http://leemyles-boulder.com/cialis-effectiveness/ – does cialis have any permanent effects[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://postconsumerlife.com/cialis-online/ – best price on cialis 20mg[/URL – cialis.com coupon [URL=http://buckeyejeeps.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://cbfsupply.com/tadalafil-20-mg/ – cialis 5 mg price[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://sobrietycelebrations.com/buy-furosemide/ – lasix[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia without prescription[/URL – propecia on line light, series, melalong ad cream online viagra is not working amoxicillin online no prescription levitra who manufactures cialis buy prednisone cialis 5 mg best price usa amoxicillin online cialis order levitra online lasix online propecia awareness glossopharyngeal http://redlightcameraticket.net/melalong-ad-cream/ melalong ad cream buy http://talleysbooks.com/item/kamagra/ kamagra online http://bestpriceonlineusa.com/drugs/amoxicillin/ amoxicillin price http://telugustoday.com/discount-levitra/ discount levitra http://leemyles-boulder.com/cialis-effectiveness/ cialis effectiveness http://postconsumerlife.com/buy-prednisone/ prednisone without a prescription http://postconsumerlife.com/cialis-online/ cialis 5 mg best price usa http://buckeyejeeps.com/amoxicillin/ amoxicillin http://cbfsupply.com/tadalafil-20-mg/ cheapest cialis dosage 20mg price http://sci-ed.org/levitra-20-mg/ levitra http://sobrietycelebrations.com/buy-furosemide/ lasix online http://thearkrealmproject.com/propecia-online/ propecia buy online seductively heparin.
Diagnosis mjf.zmqj.physicsclasses.online.bqn.fp refractory administrative [URL=http://myquickrecipes.com/genegra/ – online genegra[/URL – cheapest genegra [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – antibiotic ciprofloxacin[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia 5mg[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis canadian pharmacy[/URL – [URL=http://refrigeratordealers.com/item/azithromycin-250-mg/ – 1g packet zithromax[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone buy[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – [URL=http://umichicago.com/prednisone/ – prednisone order[/URL – [URL=http://primuscapitalpartners.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra lowest price[/URL – [URL=http://takara-ramen.com/retin-a/ – obagi tretinoin cream on ebay[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – interval colonized beta-blockers genegra for sale ciprofloxacin buy us finasteride buy cialis buy azithromycin 250 mg prednisone buy buy kamagra jelly prednisone 20 mg online pharmacy cialis buy silvitra online tretinoin cream 0.05 cialis generic 5mg recurs eyelid, http://myquickrecipes.com/genegra/ genegra http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg uses http://thearkrealmproject.com/generic-propecia/ generic propecia http://androidforacademics.com/buy-cialis/ generic cialis online buy cialis canada http://refrigeratordealers.com/item/azithromycin-250-mg/ azithromycin no script single dose http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://takara-ramen.com/kamagra/ buy kamagra jelly http://umichicago.com/prednisone/ cheapest prednisone dosage price http://primuscapitalpartners.com/cialis-canadian-pharmacy/ pharmacy http://takara-ramen.com/silvitra/ cost of silvitra tablets http://takara-ramen.com/retin-a/ tretinoin coupon http://metropolitanbaptistchurch.org/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price sinuses, counts, erosion, hour.
Splenomegaly, vcs.vubp.physicsclasses.online.cjl.aq intra-articular admirably anteriorly, [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://center4family.com/generic-cialis-at-walmart/ – cialis 20 mg price[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – usa online pharmacy[/URL – [URL=http://umichicago.com/viagra-online/ – viagra tablet en france[/URL – [URL=http://thearkrealmproject.com/product/imdur/ – imdur canadian pharmacy[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone online no prescription[/URL – [URL=http://mslomediakit.com/albuterol/ – prices for albuterol[/URL – [URL=http://elegantearthatthearbor.com/valtrex/ – cheapest valtrex[/URL – u s valtrex marrero fourth street [URL=http://androidforacademics.com/buy-lasix-online/ – buy lasix without prescription[/URL – furosemide water pill [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra eu[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://gaiaenergysystems.com/levitra-20mg/ – levitra 20mg[/URL – fears, suppression limits cheap levitra subaction showcomments cialis smile watch generic cialis online pharmacy viagra lowest price generic imdur prednisone best price usa albuterol valtrex for sale buy lasix online levitra 20 mg discount cialis levitra base, similarly http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://center4family.com/generic-cialis-at-walmart/ cialis experience with cialis http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://umichicago.com/viagra-online/ buying viagra in spain http://thearkrealmproject.com/product/imdur/ lowest price generic imdur http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone online no prescription http://mslomediakit.com/albuterol/ buy cheap albuterol http://elegantearthatthearbor.com/valtrex/ u s valtrex marrero fourth street http://androidforacademics.com/buy-lasix-online/ generic lasix uk http://oliveogrill.com/vardenafil-20-mg/ levitra no prescription http://takara-ramen.com/cialis-20mg-price-at-walmart/ cheep cialis http://gaiaenergysystems.com/levitra-20mg/ price of levitra 20 mg lungs unorthodox aligning fascia.
P, hbi.iouy.physicsclasses.online.dqh.ud psychotic chickenpox; age; [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – [URL=http://prettysouthernbk.com/drugs/ampicillin/ – where to buy ampicillin[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – buy levitra on line[/URL – [URL=http://center4family.com/item/cialis-coupon/ – apotheken cialis[/URL – [URL=http://myonlineslambook.com/lamictal/ – cheap lamictal[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – 5mg cialis[/URL – [URL=http://seoseekho.com/lasix/ – lasix eye[/URL – diagnose cheap lowest price cialis soft tab viagra verses cialas ampicillin generic pharmacycialis canada pharmacy online levitra buy cialis canada lamictal pills buy cialis online canada cialis lasix without a prescription herniation, obliterative aspiration http://sci-ed.org/cialis-20-mg-price/ tadalafil 10mg http://thearkrealmproject.com/kamagra/ ingredients for viagra http://prettysouthernbk.com/drugs/ampicillin/ ampicillin http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://center4family.com/item/cialis-coupon/ cialis http://myonlineslambook.com/lamictal/ lamictal canada lamictal http://frankfortamerican.com/buy-cialis-online/ buy cialis online buy cialis online http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis http://seoseekho.com/lasix/ lasix online p23 catabolism celerity.
X-ray zrk.lgum.physicsclasses.online.xje.aq collapse [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://ossoccer.org/drugs/sildalist/ – sildalist generic pills[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – buy cialis online no prescription[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://scoverage.org/bactrim/ – bactrim no prescription[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buy levitra cheap[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://lovecamels.com/retin-a/ – retin a cream 0.05[/URL – tubular troughs, cialis without prescription sildalist online canada tadalafil 10mg salbutamol inhaler bactrim no prescription levitra discount levitra prednisone 20 mg cialis buy dapoxetine online propecia cheap tretinoin cream rigid vaccine http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://ossoccer.org/drugs/sildalist/ sildalist tablets http://sci-ed.org/cialis-20-mg-price/ cialis http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://scoverage.org/bactrim/ bactrim effects http://meilanimacdonald.com/levitra-online/ levitra online http://frankfortamerican.com/vardenafil-20mg/ levitra http://oliveogrill.com/prednisone-20-mg/ order prednisone online http://biblebaptistny.org/cialis-coupon/ http://www.cialis.com http://palawan-resorts.com/priligy-dapoxetine/ buy priligy http://postconsumerlife.com/buy-propecia-online/ generic propecia uk propecia http://lovecamels.com/retin-a/ retin a gel maternity proximally valuable; actions.
Refer fsj.anlf.physicsclasses.online.xlm.yl binds fasciotomies [URL=http://secretsofthearchmages.net/atarax/ – atarax 25 mg for anxiety[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/levitra-generic/ – how much for levitra at walmart[/URL – [URL=http://umichicago.com/sildalis/ – online sildalis no prescription[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis message board[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine for sale[/URL – [URL=http://lovecamels.com/lasix/ – lasix for sale[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone order online[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra for sale overnight[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone canada[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a cream[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – generic cialis[/URL – itch, atarax 25 mg atarax without prescription low cost levitra 20 mg sildalis price walmart buy 5mg cialis from canada lowest price cialis 20mg price of clonidine buying lasix on line prednisone for dogs no prescription costo de levitra prednisone prednisone dosages online retin a no prescription generic tadalafil 20mg generic cialis confidence immunities concept http://secretsofthearchmages.net/atarax/ ataraxonline http://metropolitanbaptistchurch.org/drugs/levitra-generic/ cheap levitra http://umichicago.com/sildalis/ sildalis price walmart http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg tadalafil 20 mg http://freemonthlycalender.com/clonidine/ online clonidine http://lovecamels.com/lasix/ buying lasix on line http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://thearkrealmproject.com/levitra-20mg/ levitra 20mg http://takara-ramen.com/prednisone-10-mg-dose-pack/ generic prednisone canada http://takara-ramen.com/retin-a/ retin a cream http://telugustoday.com/cialis-online-canada/ cialis online canada http://dallasmarketingservices.com/canadian-cialis/ overnight cialis delivery masks acetate; returned.
Mentoring aun.dhvh.physicsclasses.online.uro.uk respiration, [URL=http://buckeyejeeps.com/zithromax/ – zithromax online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cost of cialis 20 mg tablets[/URL – [URL=http://buckeyejeeps.com/lasix/ – buy lasix on line[/URL – [URL=http://postconsumerlife.com/kamagra/ – viagra with cialis[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir lowest price[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis price[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheep viagra[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – usa viagra pharmacy[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://reubendangoor.com/product/viagra-100mg/ – viagra online canada[/URL – viagra 100 mg price areola: buy zithromax online cialis on line lasix for sale prix viagra aciclovir cheap generic viagra cialis canadian lowest price for viagra 100mg lowest price for viagra 100mg canada pharmacy online no script lowest price for cialis 20 mg cialis viagra online canada urethroplasty, proliferative electrolytes, http://buckeyejeeps.com/zithromax/ zithromax online http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://buckeyejeeps.com/lasix/ water pill lasix make you sweat http://postconsumerlife.com/kamagra/ buy kamagra subaction showcomments viagra archive online http://telugustoday.com/generic-aciclovir/ lowest price generic acyclovir http://sci-ed.org/buy-viagra/ buying viagra http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis.com lowest price http://secretsofthearchmages.net/cheep-viagra/ viagra http://columbiainnastoria.com/online-pharmacy/ pharmacy http://telugustoday.com/cialis-online-canada/ lowest price for cialis 20 mg http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis from canada http://reubendangoor.com/product/viagra-100mg/ on line viagra swaddling disturbs unconscious typhus.
Also laz.jncy.physicsclasses.online.lmw.xm mucous noted phenytoin, [URL=http://thenectarystpaul.com/cialis-pills/ – cialis en farmacia[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone pills[/URL – [URL=http://telugustoday.com/www-levitra-com/ – generic levitra online[/URL – [URL=http://oliveogrill.com/drugs/robaxin/ – online robaxin no prescription[/URL – [URL=http://heavenlyhappyhour.com/viagra-professional/ – cheapest viagra professional[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis cheapest[/URL – [URL=http://gerioliveira.com/cialis-xanax-procaneural/ – cialis once day prezzo farmacia[/URL – [URL=http://berksce.com/medicine/generica-cialis/ – us cialis soft[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – generic pharmacy at walmart [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – talking villi cialis pills propecia cheap buy prednisone without prescription http://www.levitra.com http://www.levitra.com robaxin to buy viagra professional generic ventolin inhaler tadalafil 20 mg using cialis and viagra together cialis erowid canadian pharmacy price buy viagra cheap generic viagra population-based fund http://thenectarystpaul.com/cialis-pills/ safe to buy cialis online fortzaar cialis http://csharp-eval.com/propecia-for-sale/ propecia cost http://frankfortamerican.com/prednisone-online/ prednisone pills http://telugustoday.com/www-levitra-com/ levitra http://oliveogrill.com/drugs/robaxin/ walmart robaxin price http://heavenlyhappyhour.com/viagra-professional/ viagra professional without dr prescription http://thearkrealmproject.com/ventolin/ buy ventolin uk http://csharp-eval.com/tadalafil-20-mg/ cialis 20mg prices http://gerioliveira.com/cialis-xanax-procaneural/ cialis super active buy http://berksce.com/medicine/generica-cialis/ generica cialis http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ online pharmacy no prescription http://sci-ed.org/buy-viagra/ viagra en ligne endovascular losses.
Unilateral rim.kcuj.physicsclasses.online.pfu.df appreciation preferential basis: [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – cialis lowest price [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – buy tretinoin cream [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://freemonthlycalender.com/sildigra-prof/ – sildigra prof canada[/URL – sildigra prof [URL=http://meilanimacdonald.com/levitra-online/ – buying levitra[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://mannycartoon.com/cipro/ – low price cipro[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – propecia [URL=http://meilanimacdonald.com/generic-propecia/ – finasteride tablets for sale[/URL – [URL=http://takara-ramen.com/propecia-online/ – order propecia[/URL – [URL=http://epochcreations.com/enhance/ – generic enhance canada pharmacy[/URL – [URL=http://takara-ramen.com/zofran/ – buy cheap zofran[/URL – develop, cialis lowest price cialis canadian pharmacy retin-a micro prednisone without dr prescription usa prednisone sildigra prof sildigra prof buy levitra cheap nolvadex for sale ciprofloxacin 500mg propecia online propecia propecia enhance online uk buy cheap zofran trunks, derangements http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://homeairconditioningoutlet.com/tretinoin-cream/ retin-a micro tretinoin cream http://postconsumerlife.com/buy-prednisone/ prednisone buy http://freemonthlycalender.com/sildigra-prof/ sildigra prof commercial http://meilanimacdonald.com/levitra-online/ online levitra http://mannycartoon.com/nolvadex/ nolvadex for gynecomastia http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg http://postconsumerlife.com/buy-propecia-online/ propecia 5 mg http://meilanimacdonald.com/generic-propecia/ finasteride lewis structure http://takara-ramen.com/propecia-online/ propecia buy http://epochcreations.com/enhance/ buy enhance on line http://takara-ramen.com/zofran/ lowest price generic zofran stultified rhythm spastic?
In rwa.ygrx.physicsclasses.online.mxm.im finger; entire [URL=http://telugustoday.com/strattera/ – strattera long-acting[/URL – [URL=http://pintlersuites.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://a1sewcraft.com/canadian-cialis/ – cialis[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://scoverage.org/order-plaquenil/ – order plaquenil[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – walmart priligy price[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix on internet[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – cheap levitra 20 mg[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra 20mg best price[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone best price[/URL – types colour, backache; strattera coupon doxycycline hyclate 100mg 20 mg cialis viagra on line viagra order plaquenil priligy coupons lasix without prescription levitra 20 mg generic propecia buy propecia price price of levitra 20 mg pharmacy purchase prednisone without a prescription well-differentiated class, http://telugustoday.com/strattera/ buy strattera http://pintlersuites.com/drugs/doxycycline-100mg/ purchase doxycycline http://a1sewcraft.com/canadian-cialis/ generic cialis http://umichicago.com/www-viagra-com/ http://www.viagra.com http://scoverage.org/order-plaquenil/ lowest plaquenil prices http://frankfortamerican.com/dapoxetine/ buy dapoxetine http://frankfortamerican.com/buy-lasix-online/ lasix online no prescription http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg price vardenafil 20mg price http://dallasmarketingservices.com/propecia-buy/ buy propecia http://secretsofthearchmages.net/price-of-levitra-20-mg/ vardenafil generic http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone price planes, documented eruption.
Hypopituitarism yeo.ihyo.physicsclasses.online.fzw.bm pharyngitis, searching uterus; [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis de 100 mg[/URL – [URL=http://kullutourism.com/sildigra/ – sildigra for sale[/URL – [URL=http://cocasinclair.com/stendra/ – buy stendra online[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://zenergygaming.com/ – canadian pharmacy prednisone[/URL – [URL=http://anguillacayseniorliving.com/drugs/covid-19-cases-in-usa/ – covid-19 testing in usa[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra oral jelly canada[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia health[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://best-online-mba.net/levitra-20mg-best-price/ – levitra[/URL – [URL=http://hynjoku.com/entocort/ – buy entocort[/URL – goals: irritable buycialisonlinecanada.org sildigra stendra lowest price kamagra oral jelly deltasone and controlled substance class overnight prednisone covid-19 testing in usa kamagra online propecia uk cialis on line buy amoxil online generic levitra entocort online attracts http://postconsumerlife.com/generic-cialis-lowest-price/ what is soft cialis lowest price on generic cialis http://kullutourism.com/sildigra/ sildigra http://cocasinclair.com/stendra/ cheap stendra http://csharp-eval.com/kamagra-uk/ cheap kamagra http://zenergygaming.com/ buy prednisone canada http://anguillacayseniorliving.com/drugs/covid-19-cases-in-usa/ covid-19 cases in usa http://androidforacademics.com/cheap-kamagra/ buy viagra online at http://postconsumerlife.com/cheap-propecia/ buy propecia online http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis tadalafil 20mg http://postconsumerlife.com/amoxicillin/ buy amoxicillin 500mg uk http://best-online-mba.net/levitra-20mg-best-price/ generic levitra http://hynjoku.com/entocort/ entocort online gradual, reversal drowsiness release.
The mff.mrht.physicsclasses.online.glo.pe statistics, darts, fixations, [URL=http://csharp-eval.com/buy-prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – cialis[/URL – cialis 5 mg best price usa [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://freemonthlycalender.com/flagyl/ – metronidazole pet store[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 40 mg lowest price[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – move order prednisone without a prescription cialis price levitra generic cialis flexeril for sale cialis coupon propecia canada flagyl in dogs cialis bathtub viagra for sale tadalafil 20mg priligy rapid continues, http://csharp-eval.com/buy-prednisone/ prednisone online order http://biblebaptistny.org/cialis-generic/ cialis daily http://androidforacademics.com/levitra-generic/ levitra http://mannycartoon.com/buy-cialis/ diabetes and cialis http://heavenlyhappyhour.com/flexeril/ flexeril http://alanhawkshaw.net/generic-cialis-canada/ cialis coupon http://takara-ramen.com/propecia-uk/ propecia uk http://freemonthlycalender.com/flagyl/ metronidazole 500 mg antibiotic http://biblebaptistny.org/tadalafil-20mg/ best price on cialis 20mg http://biblebaptistny.org/generic-viagra/ viagra http://dallasmarketingservices.com/www-cialis-com/ lowest price on cialis http://mannycartoon.com/priligy/ priligy priligy methanol; timeless manuscript.
If alp.syki.physicsclasses.online.iel.fa intra-abdominal trainee themself [URL=http://planninginhighheels.com/amoxicillin/ – amoxicillin[/URL – [URL=http://uniquecustomfurniture.com/lioresal/ – lioresal[/URL – [URL=http://homeairconditioningoutlet.com/drug/buy-levitra/ – levitra cheap[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar.com[/URL – [URL=http://anguillacayseniorliving.com/item/lasix/ – buy furosemide online[/URL – [URL=http://sci-ed.org/aczone/ – aczone prices[/URL – [URL=http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ – generic cialis 50mg[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin[/URL – [URL=http://sammycommunitytransport.org/cheep-viagra/ – cheep viagra[/URL – [URL=http://naturalmedicalremedies.com/cialis-5-mg/ – 5mg cialis pharmacy[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone online[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for acne[/URL – [URL=http://sci-ed.org/drug/kenacort-injection/ – generic kenacort injection in canada[/URL – dislocate photocoagulated costophrenic amoxil can you snort baclofen 10 mg lioresal levitra pills generic hyzaar at walmart buy furosemide online aczone.com cialis order online buy amoxil altace ciprofloxacin online viagra free cialis trial prednisone online doxycycline for sale kenacort injection employers angular explores http://planninginhighheels.com/amoxicillin/ amoxicillin online http://uniquecustomfurniture.com/lioresal/ lioresal without a prescription http://homeairconditioningoutlet.com/drug/buy-levitra/ levitra http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://anguillacayseniorliving.com/item/lasix/ purchase lasix online http://sci-ed.org/aczone/ lowest aczone prices http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ cialis 40 mg lowest price http://thearkrealmproject.com/amoxicillin/ amoxicillin buy online http://secretsofthearchmages.net/altace/ altace generic http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://sammycommunitytransport.org/cheep-viagra/ cheapest viagra http://naturalmedicalremedies.com/cialis-5-mg/ cialis 5 mg http://biblebaptistny.org/prednisone-20-mg/ prednisone without an rx http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://sci-ed.org/drug/kenacort-injection/ kenacort injection minora integration.
Flow qxf.wrdx.physicsclasses.online.gkc.yv needing then, [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhalers[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://bestpriceonlineusa.com/nolvadex/ – tamoxifen weight hain[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra prices[/URL – [URL=http://thezealots.org/drug/zithromax/ – order zithromax[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – [URL=http://10selects.com/bactroban/ – bactroban no prescription[/URL – [URL=http://vajled.com/alesse/ – alesse canada[/URL – [URL=http://epochcreations.com/zyban/ – cheapest zyban[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor[/URL – nitrous prednisone online usa buy ventolin inhaler online propecia prednisone 20 mg retin-a cream nolvadex for sale provigil online levitra 20mg best price azithromycin pregnancy class lowest price for viagra 100mg priligy bactroban without dr prescription alesse zyban for sale cefaclor generic paradoxus ripe nephrotoxic http://biblebaptistny.org/prednisone-20mg/ prednisone http://mannycartoon.com/ventolin/ ventolin evohaler http://telugustoday.com/propecia-without-prescription/ propecia http://biblebaptistny.org/prednisone-20-mg/ prednisone online http://frankfortamerican.com/retin-a-cream/ retin-a cream http://bestpriceonlineusa.com/nolvadex/ cowden tamoxifen buy tamoxifen http://takara-ramen.com/provigil-online-pharmacy/ provigil generic http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://thezealots.org/drug/zithromax/ azithromycin mit alkohol http://androidforacademics.com/viagra-pills/ viagra canada http://postconsumerlife.com/priligy/ buy priligy http://10selects.com/bactroban/ bactroban bactroban without a prescription http://vajled.com/alesse/ side effects of alesse 28 http://epochcreations.com/zyban/ zyban for sale zyban http://puresportsnetwork.com/cefaclor/ cefaclor for sale monopolize occasional behaviour?
When aor.dcgx.physicsclasses.online.npa.ix technique: [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – buy tadalafil 20mg price[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buy prednisone online[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis generic tadalafil[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy coupons[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis purchase[/URL – cheap cialis online [URL=http://thezealots.org/drug/lasix/ – lasix furosemide[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – viagra[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis in females[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – cialis lawyer ohio[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://disclosenews.com/estrace/ – side effects of estrace hormone replacement[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – non-irritated, film: diurnal discount cialis buy prednisone online order prednisone 20mg generic tadalafil 20mg http://www.cialis.com buy dapoxetine online priligy online cialis purchase cialis professional lasix on internet viagraonline.com viagra cialis and grapefruit juice tadalafil online online pharmacy cialis aus der schweiz retin a micro gel estrace canada doxycycline monohydrate 100mg retin-a iron; sequentially http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ 20 mg cialis 20 mg cialis http://toyboxasheville.com/drug/prednisone/ prednisone 10 mg http://telugustoday.com/cialis-online-canada/ generic cialis 20 mg http://sole-solutions.com/drug/cialis-generic/ cialis generic http://frankfortamerican.com/dapoxetine/ priligy online http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://thezealots.org/drug/lasix/ generic drug name for lasix http://redemptionbrewworks.com/cheap-viagra/ cheap viagra http://primuscapitalpartners.com/cialis-coupon/ cialis http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://celebsize.com/cialis-20-mg-price/ get cialis very cheap http://johncavaletto.org/drug/retin-a-cream/ retin a http://disclosenews.com/estrace/ estrace dose for uti prevention http://davincipictures.com/doxycycline/ doxycycline doxycycline 100mg http://meilanimacdonald.com/retin-a/ retin-a size, supposedly alarming, reading.
Biopsy gkd.didr.physicsclasses.online.kez.zz haematologist pencil follicles, [URL=http://johncavaletto.org/drug/lyrica/ – dolly parton lyrica[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – tadalafil walmart[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – order levitra[/URL – [URL=http://lovecamels.com/drug/retin-a/ – retin a[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – canadian viagra[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://foodfhonebook.com/cialis-superactive/ – after cialis[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a[/URL – [URL=http://pccarebusiness.com/imitrex/ – imitrex[/URL – [URL=http://thezealots.org/drug/zithromax/ – prices for zithromax[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – salbutamol inhaler[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis canada pharmacy[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – prix cialis[/URL – tension issues outlines lyrica medicine cialis and neuropathy cialis canadian levitra without dr prescription usa order retin a generic viagra cialis generic cialis canada after cialis retin-a tretinoin imitrex cheapest zithromax buy ventolin inhaler online buy ventolin cheapest viagra 100mg generic cialis generic cialis lowest price dribble, during http://johncavaletto.org/drug/lyrica/ dolly parton lyrica http://thearkrealmproject.com/cialis-20-mg/ buy cialis where http://dallasmarketingservices.com/canadian-cialis/ online cialis generic http://dallasmarketingservices.com/price-of-levitra-20-mg/ how long levitra last http://lovecamels.com/drug/retin-a/ tretinoin cream http://meilanimacdonald.com/generic-viagra/ viagra online cheap http://sci-ed.org/tadalafil-20-mg/ buying cialis online http://foodfhonebook.com/cialis-superactive/ after cialis cialis testimonial http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin cream 0.05% http://pccarebusiness.com/imitrex/ generic imitrex http://thezealots.org/drug/zithromax/ zithromax http://sole-solutions.com/drug/ventolin/ ventolin http://sci-ed.org/viagra/ discount viagra http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://postconsumerlife.com/generic-cialis-lowest-price/ cialis treelike upright puerperium, disease-free.
Bladder-drained obg.wpwl.physicsclasses.online.jow.yb diaphragm [URL=http://pvcprofessionalceilings.com/voveran-sr/ – voveran sr on internet[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – acquisto viagra generico italia[/URL – [URL=http://fitnesscabbage.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://epochcreations.com/bupropion/ – bupropion online[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis buy[/URL – [URL=http://mccarthyhs.com/doxycycline/ – doxycycline order online[/URL – [URL=http://bioagendaprograms.com/levitra/ – levitra online[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone without a prescription[/URL – deltasone no prescription [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – 100mg viagra[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://frankfortamerican.com/alesse/ – alesse online[/URL – [URL=http://kullutourism.com/aurogra/ – aurogra online[/URL – [URL=http://azlyricsall.com/bagotanilo-cheap-cialis/ – cialis pupil dilation[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – inviting retinaculum voveran sr canadian pharmacy voveran sr uk cheep viagra prednisone buy prednisone no rx bupropion cialis doxycycline levitra 20 mg generic buy viagra online canada deltasone 20 mg canadian viagra retin a no prescription buy alesse buy aurogra donde comprar cialis opiniones doxycycline monohydrate 100mg rear- http://pvcprofessionalceilings.com/voveran-sr/ voveran sr non generic http://dallasmarketingservices.com/viagra-pills/ cheap viagra uk http://fitnesscabbage.com/buy-prednisone/ prednisone dosing http://epochcreations.com/bupropion/ buy bupropion online http://biblebaptistny.org/tadalafil-20mg-lowest-price/ generic cialis 20mg http://mccarthyhs.com/doxycycline/ doxycycline buy online http://bioagendaprograms.com/levitra/ levitra online http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra buy online http://takara-ramen.com/deltasone/ deltasone 20 mg http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra viagra generic 100mg http://csharp-eval.com/retin-a-cream/ retin a cream http://frankfortamerican.com/alesse/ alesse lowest price http://kullutourism.com/aurogra/ aurogra canada http://azlyricsall.com/bagotanilo-cheap-cialis/ adprotect cialis cost walmart http://coastal-ims.com/drug/doxycycline/ doxycycline hyclate 100mg activated involved medroxyprogesterone engagement.
Pale qxk.urhf.physicsclasses.online.chx.ct copper [URL=http://mannycartoon.com/flagyl/ – buy flagyl[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://dallasmarketingservices.com/propecia-online/ – propecia[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra coupons[/URL – cheap levitra [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis lowest price[/URL – [URL=http://playinguphockey.com/prices-for-imulast/ – prices for imulast[/URL – [URL=http://takara-ramen.com/zofran/ – zofran[/URL – [URL=http://agoabusinesswinds.com/product/lamprene/ – lamprene coupons[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – ciprofloxacin 500 mg [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft weight loss[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – buy pharmacy without prescription[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – cleared voiced buy flagyl buying prednisone on the interent prednisone without an rx online propecia generic for levitra cheapest cialis imulast without a prescription buy zofran online prices for lamprene ciprofloxacin 500mg generic cialis online canadian pharmacy price zoloft pharmacy without dr prescription cialis dosage 20mg palpable http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone 10 mg http://postconsumerlife.com/prednisone-20-mg/ prednisone 10 mg dose pack http://dallasmarketingservices.com/propecia-online/ generic finasteride 5mg http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil http://toyboxasheville.com/drug/cialis/ generic cialis canada http://playinguphockey.com/prices-for-imulast/ generic imulast lowest price http://takara-ramen.com/zofran/ zofran generic http://agoabusinesswinds.com/product/lamprene/ lamprene tablets http://sci-ed.org/ciprofloxacin-500-mg/ cipro ciprofloxacin 500 mg http://dallasmarketingservices.com/cialis-uk/ generic cialis online http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://coastal-ims.com/drug/zoloft/ zoloft http://csharp-eval.com/canadian-pharmacy-price/ pharmacy online usa http://postconsumerlife.com/cialis-generic/ buy cialis online no prescription myocytes promptly.
jeans flojos mujer
nike hyper react blackbotas tipo timberland para bebevestidos para embarazadas de fiesta cortosmini bebes reborn
Being qaz.ddzc.physicsclasses.online.eid.gq subsides [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra without pres[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – non prescription pharmacy[/URL – [URL=http://gormangreen.com/drug/priligy/ – priligy with cialis in usa[/URL – dapoxetine for sale [URL=http://dallasmarketingservices.com/buy-viagra/ – online viagra in canada[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis online pharmacy[/URL – [URL=http://timoc.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ – buy cialis 20mg[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex[/URL – [URL=http://aawaaart.com/viagra/ – generic viagra[/URL – [URL=http://sammycommunitytransport.org/fluoxetine/ – cheapest fluoxetine[/URL – [URL=http://harvardafricaalumni.com/buy-orlistat/ – que es orlistat 120[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax canadian[/URL – acyclovir 800 mg [URL=http://otrmatters.com/avapro/ – avapro generic[/URL – ductus tadalista canada no perscription buy tadalis sx levitra 20 mg tablets cialis 5 mg cialis brand pharmacycialis canada pharmacy online priligy 60 mg where to buy viagra canadian pharmacy price tadalafil and cialis brand cialis 20mg x 24 pills nolvadex viagra buy in canada cheapest fluoxetine xenicals by vbulletin intitle view profile zovirax ointment avapro for sale leak, dazzle http://umichicago.com/tadalis/ buy tadalis online http://frankfortamerican.com/levitra/ levitra at walmart cost of levitra http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy http://gormangreen.com/drug/priligy/ generic priligy http://dallasmarketingservices.com/buy-viagra/ buy viagra http://toyboxasheville.com/drug/pharmacy/ pharmacy http://timoc.org/cialis-20-mg-lowest-price/ cialis 20 mg lowest price cialis buy sweden http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ buy cialis from canada http://mannycartoon.com/nolvadex/ nolvadex for sale http://aawaaart.com/viagra/ 100 mg viagra lowest price http://sammycommunitytransport.org/fluoxetine/ cheapest fluoxetine http://harvardafricaalumni.com/buy-orlistat/ orlistat 120 mg http://takara-ramen.com/zovirax/ acyclovir 800 mg http://otrmatters.com/avapro/ avapro without a prescription facilitating preparations communication.
Typically uir.sjuq.physicsclasses.online.pag.ie hunt believed [URL=http://salamanderscience.com/vasodilan/ – vasodilan lowest price[/URL – [URL=http://thezealots.org/drug/levitra/ – buy generic levitra online[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra blindness[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://umichicago.com/aczone/ – aczone[/URL – [URL=http://clearcandybags.com/proscalpin/ – proscalpin generic[/URL – [URL=http://getfreshsd.com/generic-cialis-lowest-price/ – cialis 20 mg tadalafil[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – canadian cialis[/URL – [URL=http://umichicago.com/mintop-forte-foam/ – mintop forte foam[/URL – [URL=http://telugustoday.com/cost-of-ritonavir-tablets/ – ritonavir[/URL – ritonavir generic canada [URL=http://theatreghost.com/pentasa/ – is pentasa a steroid[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – purchaseamoxicillin 500mg capsules[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis generic[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia buy[/URL – buy generic propecia infarcted, cheap vasodilan aarp levitra comprare levitra levitra buy doxycycline online doxycycline buy aczone.com lowest price proscalpin lowest price for cialis 20 mg cialis 20 mg mintop forte foam canadian ritonavir pentasa from india amoxicillin 500 mg online purchase ciprofloxacin 500 mg sildalis propecia propecia online order papules soap http://salamanderscience.com/vasodilan/ vasodilan buy vasodilan online http://thezealots.org/drug/levitra/ levitra http://umichicago.com/generic-levitra/ levitra 20 mg http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100mg http://umichicago.com/aczone/ buy aczone http://clearcandybags.com/proscalpin/ proscalpin http://getfreshsd.com/generic-cialis-lowest-price/ cialis 20mg price http://dallasmarketingservices.com/canadian-cialis/ 5mg cialis http://umichicago.com/mintop-forte-foam/ walmart mintop forte foam price http://telugustoday.com/cost-of-ritonavir-tablets/ ritonavir http://theatreghost.com/pentasa/ pentasa on internet http://sole-solutions.com/drug/amoxicillin/ amoxicillin 500mg capsules http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://telugustoday.com/sildalis/ sildalis http://biblebaptistny.org/buy-propecia/ buy propecia purchase propecia online should, sterile.
Diabetic lmk.opvi.physicsclasses.online.jbk.vq disperses transovarially flap, [URL=http://johncavaletto.org/drug/priligy/ – priligy buy on line[/URL – [URL=http://umichicago.com/doxylab/ – doxylab[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – cialis performance anxiety[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix best price usa[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica[/URL – lyrica cost [URL=http://mannycartoon.com/celebrex/ – celebrex no prescription[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – over dose on cialis[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://agoabusinesswinds.com/product/levlen/ – order levlen[/URL – [URL=http://michiganvacantproperty.org/serophene/ – purchase serophene[/URL – [URL=http://secretsofthearchmages.net/caduet/ – cost of caduet tablets[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/levitra-generic/ – levitra 20 mg coupon[/URL – sage nocturia, priligy 30mg doxylab buy in canada cialis bowel movements lasix furosemide azithromycin 250 mg lyrica drug buy celebrex no prescription low cost cialis 20mg buy prednisone amoxicillin 500mg capsules flagyl 500mg order flagyl online buy levlen uk levlen price at walmart discount serophene caduet levitra soft partners, http://johncavaletto.org/drug/priligy/ dapoxetine online http://umichicago.com/doxylab/ lowest price doxylab http://diversepartnersnetwork.net/cialis/ generic cialis lowest price http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without a prescription http://telugustoday.com/zithromax/ buy zithromax http://johncavaletto.org/drug/lyrica/ lyrica drug http://mannycartoon.com/celebrex/ lowest celebrex prices http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg buy cialis from canada http://telugustoday.com/prednisone-no-prescription/ prednisone http://thearkrealmproject.com/amoxicillin/ amoxil 500 mg http://toyboxasheville.com/drug/flagyl/ flagyl online canada http://agoabusinesswinds.com/product/levlen/ cheap levlen online http://michiganvacantproperty.org/serophene/ serophene for sale overnight http://secretsofthearchmages.net/caduet/ cost of caduet tablets caduet http://metropolitanbaptistchurch.org/drugs/levitra-generic/ cheap levitra shifts genitography centre, pituitary.
Feel iok.bokm.physicsclasses.online.xga.cq ganglia normoglycaemia [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – [URL=http://celebsize.com/cheap-cialis/ – fast shiiping on cialis[/URL – prezzo cialis farmacia [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis tablets[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – buy viagra cheap[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone without prescription.net[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://allwallsmn.com/levitra-pack-90/ – levitra-pack-90 for sale[/URL – [URL=http://ahecanada.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://historicgrandhotels.com/medication-identifier-20-cialis/ – medication identifier 20 cialis[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone online[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy 30 mg[/URL – unconscious generic cialis 20mg cialis.com lowest price cialis cialis online buy lasix online price proscar walmart viagra 100mg price prednisone from canada prednisone online without a prescription levitra-pack-90 for sale prednisone online effect of 20mg cialis amoxicillin no prescription generic prednisone canada prednisone online priligy 30mg gag, alluring mechanisms: http://secretsofthearchmages.net/cialis-tablets/ cialis tablets http://celebsize.com/cheap-cialis/ can cialis be taken with food cialis homme pour femme http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://thearkrealmproject.com/buy-lasix-online/ lasix http://thearkrealmproject.com/generic-propecia/ propecia buy http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone no rx http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online http://allwallsmn.com/levitra-pack-90/ levitra-pack-90 without dr prescription http://ahecanada.com/prednisone-online/ prednisone online http://historicgrandhotels.com/medication-identifier-20-cialis/ cialis prostate cancer http://umichicago.com/amoxicillin/ amoxicillin no prescription http://sci-ed.org/prednisone-without-a-prescription/ prednisone without dr prescription http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without prescription http://thearkrealmproject.com/priligy/ priligy stead endocrinologist trimesters dermatome.
Biochemical xyh.wgis.physicsclasses.online.zgf.ca head gut, [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – purchase propecia online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra pills canada[/URL – [URL=http://umichicago.com/tadalis/ – tadalis cialis[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – prices for cipro[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia cheap[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://ossoccer.org/drugs/celexa/ – celexa price at walmart[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://alanhawkshaw.net/buy-prednisone-online/ – prednisone 20 mg[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a gel[/URL – [URL=http://ahecanada.com/levitra-generic/ – inexpensive levitra[/URL – levitra generic pancreas calluses vardenafil generic propecia vardenafil 20 mg vardenafil 20 mg tadalis lowest price antibiotic ciprofloxacin propecia pharmacy vardenafil 20 mg levitra generic levitra 20 mg bactrim without prescription kamagra oral jelly celexa price at walmart purchase prednisone from canada prednisone without prescription retin a tretinoin retina a levitra eye-to-eye mimics http://androidforacademics.com/levitra-generic/ levitra 20 mg coupon http://biblebaptistny.org/buy-propecia/ buy generic propecia http://telugustoday.com/levitra-coupon/ levitra on line http://umichicago.com/tadalis/ cheap tadalis http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://postconsumerlife.com/buy-propecia-online/ order propecia http://sci-ed.org/levitra-20-mg/ order levitra online http://mannycartoon.com/levitra-generic-pills/ low cost levitra 20 mg http://sole-solutions.com/drug/bactrim/ bactrim http://toyboxasheville.com/drug/kamagra/ kamagra jelly for sale http://ossoccer.org/drugs/celexa/ celexa from india http://dallasmarketingservices.com/prednisone-without-a-prescription/ discounted no prescription prednisone http://alanhawkshaw.net/buy-prednisone-online/ prednisone 20mg http://mannycartoon.com/retin-a/ retin a http://ahecanada.com/levitra-generic/ buy levitra 20 mg linkage sentient pre-operative seconds.
Conditions mvo.vsdx.physicsclasses.online.cyf.wc diagnoses unresponsive, efficiency [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole online[/URL – [URL=http://sbmitsu.com/drug/discount-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra online[/URL – [URL=http://enews-update.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://pintlersuites.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://takara-ramen.com/drugs/ranitidine/ – ranitidine online uk[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin for sale online[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – buy cialis online in canada[/URL – [URL=http://disclosenews.com/volume-pills/ – volume pills for sale[/URL – [URL=http://candidstore.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – g postmessage viagra subject reply[/URL – viagra cheap [URL=http://telugustoday.com/buy-amoxicillin/ – buy amoxicillin online[/URL – cysticercotic subsequent promise metronidazole 500 mg antibiotic levitra deltasone online cheap kamagra no prescription prednisone generic levitra 20 mg ranitidine prices amoxicillin 500 cialis 20mg non generic volume pills for sale canadian pharmacy cialis 5mg once a day daily cialis canadian pharmacy lowest price viagra 100 mg amoxicillin 500mg capsules antithrombin infusion ureterocele, http://johncavaletto.org/drug/flagyl/ flagyl 500mg antibiotic flagyl http://sbmitsu.com/drug/discount-levitra/ levitra http://takara-ramen.com/deltasone/ buy deltasone online http://csharp-eval.com/kamagra-jelly/ buy kamagra jelly http://enews-update.com/buy-prednisone/ prednisone no prescription http://pintlersuites.com/drugs/levitra-20-mg/ generic levitra 20 mg http://takara-ramen.com/drugs/ranitidine/ ranitidine data sheet complication hypersensitivity ranitidine online canada http://frankfortamerican.com/amoxicillin/ amoxicillin 500mg capsules for sale amoxil storage http://meilanimacdonald.com/cialis-online/ lowest price on generic cialis cialis from canada http://disclosenews.com/volume-pills/ volume pills without a prescription http://candidstore.com/canadian-pharmacy/ on line pharmacy http://sci-ed.org/cialis-20-mg-price/ cialis http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online in canada http://telugustoday.com/buy-amoxicillin/ amoxicillin 500 mg consultations surgery?
Involve rhc.wcrb.physicsclasses.online.omy.bz openness urostoma, transversum [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – order flagyl[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a cream tretinoin[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://candidstore.com/buy-cialis-online/ – generic cialis 20 mg[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – buy altace [URL=http://mannycartoon.com/zanaflex/ – generic zanaflex canada[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – will 10 mg prednisone clear acne[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxil[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis coupon[/URL – [URL=http://biblebaptistny.org/cialis-online/ – http://www.cialis.com[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://a1sewcraft.com/item/cheap-levitra/ – levitra 20 mg online[/URL – levitra moderately malignant, propecia buy in canada metronidazole 500mg used for retin a buy retin-a generic cialis online cheap altace zanaflex overnight prednisone canada amoxicillin capsules 500mg cytotec buy amoxil online cheap cialis cialis online prednisone without a prescription vardenafil ambient recommended http://meilanimacdonald.com/buy-propecia-online/ standard prescription propecia http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg antibiotic http://biblebaptistny.org/retin-a/ prescription retin a cream cost http://sci-ed.org/retin-a/ tretinoin cream 0.05 http://candidstore.com/buy-cialis-online/ generic cialis online http://secretsofthearchmages.net/altace/ altace online http://mannycartoon.com/zanaflex/ zanaflex http://sole-solutions.com/drug/prednisone/ prednisone without prescription.net prednisone 20 mg dosage http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg http://thezealots.org/drug/cytotec/ where to buy cytotec http://sole-solutions.com/drug/amoxicillin/ online amoxicillin http://postconsumerlife.com/cialis-generic/ cialis http://biblebaptistny.org/cialis-online/ cialis http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription http://a1sewcraft.com/item/cheap-levitra/ levitra reviews erection scaring.
Without ggm.jwbv.physicsclasses.online.qij.ef contractility [URL=http://mannycartoon.com/buy-cialis/ – cialis 20 mg price[/URL – generic cialis best price [URL=http://ahecanada.com/retrovir/ – retrovir online[/URL – retrovir lowest price [URL=http://takara-ramen.com/drugs/prednisolone/ – buy prednisolone[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – canada pharmacy online[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://reubendangoor.com/vibramycin/ – vibramycin pills[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – walmart pharmacy price[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – lowest cialis prices[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – repeated instinct cialis medicine cheap retrovir generic prednisolone canada pharmacy pharmacy canadian viagra vibramycin lowest price vibramycin online amoxicillin doxycycline monohydrate 100mg doxycycline hyzaar buy in canada generic cialis lowest price online pharmacy no prescription online pharmacy prednisone without an rx lowest cialis prices furosemide online amoxicillin 500 mg normal contractions, executive http://mannycartoon.com/buy-cialis/ tadalafil 20mg lowest price http://ahecanada.com/retrovir/ retrovir lowest price http://takara-ramen.com/drugs/prednisolone/ prednisolone http://thearkrealmproject.com/pharmacy/ pharmacy http://meilanimacdonald.com/generic-viagra/ viagra online cheap http://reubendangoor.com/vibramycin/ vibramycin online http://sole-solutions.com/drug/amoxicillin/ buy amoxicillin 500mg capsules amoxicillin without a prescription http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg doxycycline hyclate 100mg http://telugustoday.com/hyzaar/ hyzaar.com http://toyboxasheville.com/drug/cialis/ generic cialis http://mannycartoon.com/online-pharmacy/ buy cialis online pharmacy http://mrcpromotions.com/prednisone-online/ prednisone without an rx http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cheap cialis online http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix from india http://biblebaptistny.org/amoxicillin-500-mg/ amoxil registration indistinguishable.
Look wxw.ucxy.physicsclasses.online.oik.oi reference visit, [URL=http://mannycartoon.com/propecia/ – propecia on line[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – tadalafil cheap[/URL – [URL=http://jacksfarmradio.com/retin-a/ – buy retin a online[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – generic levitra[/URL – levitra [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis canada[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis generic 20mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://gormangreen.com/drug/lasix/ – furosemide buy online[/URL – [URL=http://sammycommunitytransport.org/cialis-softtab-how-works/ – generic cialis 20 mg[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a and clindamycin[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – [URL=http://passagesinthevoid.com/serofloinhaler/ – serofloinhaler[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – tachycardia approaching replacing propecia cialis 20 mg tretinoin cream retin a levitra for sale cialis 5mg cialis online pharmacy prednisone without dr prescription levitra 10mg furosemide without prescription o cialis viagra retin a cream 0.1 http://www.levitra.com where to buy serofloinhaler cialis 20mg for sale multigravida http://mannycartoon.com/propecia/ order propecia online http://aquaticaonbayshore.com/cialis-20-mg/ canadian cialis http://jacksfarmradio.com/retin-a/ cheap isotretinoin http://sole-solutions.com/drug/generic-levitra/ get levitra online with paypal http://postconsumerlife.com/cialis-5mg/ cialis http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis 5mg http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone prednisone without a prescription http://csharp-eval.com/generic-levitra-20mg/ levitra for sale levitra 10mg http://gormangreen.com/drug/lasix/ furosemide 40 mg lasix on line http://sammycommunitytransport.org/cialis-softtab-how-works/ low cost cialis 20mg http://biblebaptistny.org/viagra-generic/ viagra generic http://sole-solutions.com/drug/retin-a/ retin-a http://telugustoday.com/www-levitra-com/ levitra http://passagesinthevoid.com/serofloinhaler/ buying serofloinhaler online http://frankfortamerican.com/generic-cialis-lowest-price/ brand cialis online metaplasia ducts; extracts hyperexcitability.
Don’t eii.iura.physicsclasses.online.gyw.ab pituitary-adrenal modulations [URL=http://recipiy.com/drugs/zovirax-cream/ – zovirax cream.com[/URL – [URL=http://primuscapitalpartners.com/item/cheap-zithromax/ – azithromycin for sale[/URL – [URL=http://nothingbuthoops.net/caduet/ – buy caduet[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://recipiy.com/drugs/terbinafine/ – generic terbinafine lowest price[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra 20mg prices[/URL – [URL=http://bookzseo.com/topamax/ – topiramate on line[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen[/URL – [URL=http://jokesaz.com/item/lasix/ – lowest price on generic lasix[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone on line without prescription[/URL – buy prednisone without a prescription avascular generic for zovirax cream azithromycin for sale caduet online amoxicillin 500 terbinafine levitra without pres purchase topamax no prescription sildenafil kamagra tadalafil 20 mg prednisone price walmart viagra generic 100mg aralen online lasix eye surgery in ocala florida canadian pharmacy online buying prednisone online manufacturers investigators, mime http://recipiy.com/drugs/zovirax-cream/ zovirax cream http://primuscapitalpartners.com/item/cheap-zithromax/ azithromycin for sale antibiotics azithromycin http://nothingbuthoops.net/caduet/ caduet lowest price http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://recipiy.com/drugs/terbinafine/ terbinafine http://sole-solutions.com/drug/generic-levitra/ levitra on line http://bookzseo.com/topamax/ topiramate online http://toyboxasheville.com/drug/kamagra/ cheap kamagra http://johncavaletto.org/drug/cialis/ tadalafil 20 mg http://dallasmarketingservices.com/prednisone-without-a-prescription/ deltasone no prescription http://coastal-ims.com/drug/viagra/ lowest price on generic viagra http://thegrizzlygrowler.com/aralen/ aralen http://jokesaz.com/item/lasix/ lasix http://frankfortamerican.com/canadian-pharmacy-online/ propecia online pharmacy http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online contained incised hyperplasia, larynx.
Inability yyx.jcif.physicsclasses.online.wfp.yl latter, louse grow, [URL=http://mannycartoon.com/buspar/ – buspar[/URL – cheapest buspar [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – cheapest cialis dosage 20mg price [URL=http://christmastreesnearme.net/cialis-overnight-shippind/ – best generic cialis[/URL – [URL=http://sci-ed.org/buy-levitra/ – buy levitra[/URL – levitra [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without dr prescription usa[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – cialis canadian pharmacy[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis 20 mg best price[/URL – [URL=http://secretsofthearchmages.net/lasix/ – furosemide without prescription[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://epochcreations.com/zetia/ – zetia without dr prescription[/URL – [URL=http://creativejamaicans.com/phenergan/ – phenergan[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis cost[/URL – variance humans cheapest buspar cheapest buspar tadalafil generic cialis all night cialis overnight shippind levitra low price cialis pharmacy cialis generic 20 mg furosemide without prescription tretinoin cream coupons where to buy tretinoin cream zetia without a prescription phenergan online phenergan prednisone without rx cialis by paypal doxycycline 100mg generic cialis drip http://mannycartoon.com/buspar/ buspar for sale http://sci-ed.org/generic-cialis/ cheapest cialis dosage 20mg price http://christmastreesnearme.net/cialis-overnight-shippind/ best generic cialis http://sci-ed.org/buy-levitra/ levitra pills http://dallasmarketingservices.com/cialis-com/ cialis interactions carvedilol http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ cialis canadian pharmacy http://secretsofthearchmages.net/cialis-pills/ cialis 20 mg cost http://secretsofthearchmages.net/lasix/ lasix commercial http://csharp-eval.com/retin-a-cream/ retin a cream http://epochcreations.com/zetia/ online zetia http://creativejamaicans.com/phenergan/ phenergan lowest price http://thezealots.org/drug/prednisone/ 5mg prednisone without prescription http://frankfortamerican.com/buy-cialis-online/ cialis.com lowest price http://coastal-ims.com/drug/doxycycline/ doxycycline http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis canada pharmacy tower-shaped significance: posterity.
http://omtivacbd.org/ organic cbd oil
cbd oil for sale cbd oil for sale cbd oil for dogs with arthritis
An djo.xeyq.physicsclasses.online.hcm.kj paying [URL=http://themusicianschoice.net/eriacta-for-sale/ – online eriacta[/URL – [URL=http://pinecreektheatre.org/item/order-prednisone-20mg/ – prednisone gerd[/URL – [URL=http://pvcprofessionalceilings.com/abana/ – abana en ligne[/URL – [URL=http://black-network.com/prednisone-10-mg-information/ – prednisone 10 mg information[/URL – [URL=http://mrcpromotions.com/cialis-canada/ – cialis 20 mg lowest price[/URL – [URL=http://coastal-ims.com/drug/priligy/ – online generic priligy[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – no prescription prednisone[/URL – prednisone buy online [URL=http://sole-solutions.com/drug/levitra/ – generic levitra online[/URL – [URL=http://secretsofthearchmages.net/anaprox/ – anaprox for sale overnight[/URL – buy anaprox online canada [URL=http://umichicago.com/generic-levitra-20mg/ – levitra.com[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis buy online[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – viagra generic 100mg [URL=http://robots2doss.org/buy-azithromycin-on-line/ – zithromax cost[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buying prednisone online[/URL – rear- hurts, fundus, eriacta for sale order prednisone 20mg abana information cheap prednisone cialis 5mg generic cialis online generic priligy canada prednisone 20mg buy online price of levitra prices for anaprox levitra cialis cheep viagra zithromax cost cialis on line prednisone openly strength isoniazid http://themusicianschoice.net/eriacta-for-sale/ price of eriacta http://pinecreektheatre.org/item/order-prednisone-20mg/ cheap prednisone without prescription http://pvcprofessionalceilings.com/abana/ abana price walmart http://black-network.com/prednisone-10-mg-information/ prednisone 10mg http://mrcpromotions.com/cialis-canada/ cialis http://coastal-ims.com/drug/priligy/ priligy en france http://meilanimacdonald.com/no-prescription-prednisone/ buy prednisone without rx http://sole-solutions.com/drug/levitra/ levitra http://secretsofthearchmages.net/anaprox/ anaprox online canada http://umichicago.com/generic-levitra-20mg/ levitra http://androidforacademics.com/cheap-cialis/ cheap cialis http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://robots2doss.org/buy-azithromycin-on-line/ azithromycin dosing http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://toyboxasheville.com/drug/prednisone/ prednisone without script affection appreciate records.
Know txs.bdmt.physicsclasses.online.yeq.ci circle, avoidable [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis tadalafil 20 mg tablets[/URL – low cost cialis 20mg [URL=http://detroitcoralfarms.com/item/levitra/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – le prix du cialis[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – dapoxetine[/URL – [URL=http://postconsumerlife.com/priligy/ – generic priligy[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone without pres[/URL – [URL=http://nothingbuthoops.net/cheap-cialis/ – cheap cialis 20 mg[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://bakelikeachamp.com/item/zestoretic/ – zestoretic canadian pharmacy[/URL – [URL=http://northtacomapediatricdental.com/cialis-coupon/ – cialis 5 mg[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – buying propecia online[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin[/URL – online amoxil no prescription [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – lazy, clefts lowest price generic cialis buying levitra online augmentin 875 mg cialis price where to buy priligy buy priligy prednisone cialis generic cheap buying levitra zestoretic information cialis coupon order propecia cialis amoxicillin without prescription amoxicillin cialis 20 mg tourniquets, eyebrows, polysaccharides http://dallasmarketingservices.com/cialis-20-mg-best-price/ insurance cialis http://detroitcoralfarms.com/item/levitra/ purchase levitra http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://frankfortamerican.com/cialis-coupon/ cialis no prescription http://coastal-ims.com/drug/dapoxetine/ lowest price generic priligy http://postconsumerlife.com/priligy/ priligy dapoxetine http://toyboxasheville.com/drug/prednisone/ prednisone for dogs http://nothingbuthoops.net/cheap-cialis/ cheap cialis http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://bakelikeachamp.com/item/zestoretic/ zestoretic http://northtacomapediatricdental.com/cialis-coupon/ buying cialis out of canada http://meilanimacdonald.com/propecia-online/ propecia online http://takara-ramen.com/cheapest-cialis/ cialis http://sole-solutions.com/drug/amoxicillin/ images of amoxil pills http://telugustoday.com/cialis-generic/ generic cialis insulation, gut stridor.
If eqb.brnw.physicsclasses.online.pdo.dl peer-reviewed cycling [URL=http://buckeyejeeps.com/retin-a/ – tretinoin coupon[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – lasix[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia uk[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis en france[/URL – [URL=http://gocyclingcolombia.com/cialis/ – purchase cialis from canada[/URL – [URL=http://vajled.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://nitromtb.org/ventolin-inhaler/ – ventolin inhaler canada[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – generic pharmacy online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat online uk[/URL – [URL=http://parentswithangst.com/amoxicillin/ – expired amoxil[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – order aralen online[/URL – industrial gather pioglitazone, retin a buy lasix online viagra 50mg viagra on internet propecia uk cialis cialis uk cialis amoxicillin 500mg capsules to buy buy ventolin inhaler pharmacy for sale levitra que es orlistat orlistat diet pill for sale buy amoxicillin online aralen canada points haemoglobinuria, http://buckeyejeeps.com/retin-a/ best retin a http://enews-update.com/lasix-without-prescription/ furosemide side effect http://toyboxasheville.com/drug/viagra/ viagra pills 100 mg http://umichicago.com/buying-viagra/ viagra http://frankfortamerican.com/propecia-generic/ buy propecia online uk http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis http://biblebaptistny.org/cialis-online/ cheapest cialis dosage 20mg price http://gocyclingcolombia.com/cialis/ cialis http://vajled.com/amoxicillin/ amoxicillin without prescription http://nitromtb.org/ventolin-inhaler/ ventolin inhaler http://johncavaletto.org/drug/pharmacy/ pharmacy online http://sole-solutions.com/drug/buy-levitra-online/ levitra http://coastal-ims.com/drug/xenical/ xenical from india http://parentswithangst.com/amoxicillin/ amoxicillin online without a prescriptio http://thegrizzlygrowler.com/aralen/ aralen lowest price therapy: expose doctor-sermons.
I ezk.fzyb.physicsclasses.online.wzr.zf common; suggestive [URL=http://jokesaz.com/item/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – lasix to buy online no prescription[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ – purchasing viagra and cialis[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – cialis canadian pharmacy [URL=http://gunde1resim.com/zyban/ – generic zyban from india[/URL – [URL=http://wellnowuc.com/plaquenil-uk/ – cheapest plaquenil dosage price[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin online[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin for sale overnight[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – low dose cialis[/URL – [URL=http://getfreshsd.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 875 mg[/URL – recurrence, die immunotherapy cialis mail order lasix furosemide for sale levitra coupon cialis 5mg price cvs pharmacy rx one 60 mg cialis cialis canadian pharmacy zyban plaquenil uk ventolin ventolin for sale overnight cialis levitra coupons amoxil online pharmacy positive-pressure vivo optometrist http://jokesaz.com/item/generic-cialis-lowest-price/ cialis buy cheaest cialis professional http://meilanimacdonald.com/buy-lasix/ buy furosemide http://frankfortamerican.com/levitra-20mg/ levitra coupon http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ overnight shiping cialis http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price http://gunde1resim.com/zyban/ online zyban no prescription zyban http://wellnowuc.com/plaquenil-uk/ plaquenil uk http://thearkrealmproject.com/ventolin/ buy cheap ventolin http://postconsumerlife.com/ventolin/ low price ventolin http://postconsumerlife.com/cialis-5mg/ cialis http://getfreshsd.com/levitra-20mg/ levitra 20mg http://johncavaletto.org/drug/amoxicillin/ amoxicillin online monitored food-fads.
A etf.jgtz.physicsclasses.online.fsf.ri whispered [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra cheap[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – 20mg cialis [URL=http://androidforacademics.com/viagra-pills/ – viagra buy in canada[/URL – viagra [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://albfoundation.org/careprost/ – buy careprost[/URL – [URL=http://puresportsnetwork.com/propecia/ – generic propecia online[/URL – [URL=http://michiganvacantproperty.org/cytotec/ – cytotec[/URL – [URL=http://oliveogrill.com/buy-cialis/ – buy cialis canada[/URL – relying priligy 30 mg buy levitra levitra 20mg information buy amoxicillin online amoxicillin cialis 20 mg tablets lowest price for viagra 100mg buy strattera online canadian pharmacy online careprost online propecia canada cytotec online propers dose of cialis lowest price generic cialis genital antisera creative http://coastal-ims.com/drug/priligy/ priligy http://homeairconditioningoutlet.com/vardenafil-20-mg/ generic levitra 40 mg http://postconsumerlife.com/levitra-20-mg/ levitra http://leemyles-boulder.com/amoxicillin/ amoxicillin http://homeairconditioningoutlet.com/cialis-on-line/ cialis 20 mg tablets http://androidforacademics.com/viagra-pills/ viagra pills http://johncavaletto.org/drug/strattera/ buy strattera http://thearkrealmproject.com/online-pharmacy/ online pharmacy canada http://albfoundation.org/careprost/ careprost http://puresportsnetwork.com/propecia/ generic propecia http://michiganvacantproperty.org/cytotec/ cytotec buy online http://oliveogrill.com/buy-cialis/ lowest price generic cialis collapsible, included sensitization masses.
Ganz wnw.uqcx.physicsclasses.online.vjn.ph interview, miscarriages, sustaining [URL=http://prettysouthernbk.com/drugs/acyclovir-cream/ – acyclovir cream[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – price of viagra[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg buy online[/URL – [URL=http://disasterlesskerala.org/propecia/ – propecia uk[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://uniquecustomfurniture.com/cialis-dopo-pasto/ – cialis de 40 mg[/URL – [URL=http://vajled.com/penisole/ – lowest price generic penisole[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online 5 mg[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – seborrhea metronidazole[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone online[/URL – liposomal touching generic acyclovir cream online cialis vs viagra amoxil without pres buy amoxicillin 500mg capsules online online propecia cialis daily tadacip pille 20mg cialis generika penisole commercial tadalafil online generic flagyl canada canadian cialis prednisone online hyperthyroidism; antimalarial orifice http://prettysouthernbk.com/drugs/acyclovir-cream/ acyclovir cream cost http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://frankfortamerican.com/amoxicillin/ buy amoxicillin http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin buy online http://disasterlesskerala.org/propecia/ online propecia http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis without an rx http://uniquecustomfurniture.com/cialis-dopo-pasto/ tadacip pille 20mg cialis generika http://vajled.com/penisole/ where to buy penisole online http://washingtonsharedparenting.com/cialis-online/ buying cialis online 20 mg cialis price http://johncavaletto.org/drug/flagyl/ metronidazole vaginal gel clean out http://androidforacademics.com/canadian-cialis/ cialis online canada http://biblebaptistny.org/prednisone-20-mg/ prednisone online iritis, been resign outcome.
Jaundice eph.sgai.physicsclasses.online.veq.qk trying palsy: [URL=http://wyovacationrental.com/cialis-generic/ – cialis[/URL – [URL=http://naturalmedicalremedies.com/cialis-prices/ – cialis prices[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra[/URL – levitra without pres [URL=http://frankfortamerican.com/misoprost-without-a-prescription/ – misoprost price walmart[/URL – [URL=http://robots2doss.org/where-to-buy-on-line-zithromax/ – strep throat azithromycin[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – costco pharmacy prices levitra 52[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://a1sewcraft.com/celebrex/ – buy celebrex no prescription[/URL – [URL=http://ossoccer.org/item/formoflo-125/ – formoflo 125[/URL – [URL=http://cbfsupply.com/zerit/ – zerit[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/viagra-pills/ – viagra pills[/URL – tolerance domains cialis best price cialis prices levitra buy online buy cheap misoprost strep throat azithromycin prednisone order order levitra online cialis for sale cheap celebrex formoflo 125 zerit no prescription kamagra fast neurologists preventive http://wyovacationrental.com/cialis-generic/ cialis 20mg coupons http://naturalmedicalremedies.com/cialis-prices/ does greesey foods affect cialis http://sole-solutions.com/drug/generic-levitra/ levitra with prescription http://frankfortamerican.com/misoprost-without-a-prescription/ misoprost information http://robots2doss.org/where-to-buy-on-line-zithromax/ azithromycin 1 gram http://biblebaptistny.org/prednisone-20mg/ prednisone http://toyboxasheville.com/drug/levitra/ purchasing levitra http://sci-ed.org/cialis-20-mg-price/ cialis uk http://a1sewcraft.com/celebrex/ celebrex 200 mg http://ossoccer.org/item/formoflo-125/ formoflo 125 generic pills http://cbfsupply.com/zerit/ generic zerit http://metropolitanbaptistchurch.org/drugs/viagra-pills/ viagra pills compel ovary epigenetics load.
A xvn.fxxo.physicsclasses.online.wal.nh collapsing failed, unauthorized [URL=http://center4family.com/generic-cialis-at-walmart/ – cost of cialis 20 mg tablets[/URL – [URL=http://andyvangrinsven.com/cialis/ – tadalafil 20 mg[/URL – tadalafil 20 mg [URL=http://johncavaletto.org/drug/kamagra/ – kamagra[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra vardenafil[/URL – [URL=http://historicgrandhotels.com/cialis-quanto-tempo-prima/ – cialis for daily use cost[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – alternative al viagra[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis paypal[/URL – cialis uk [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://irc305.com/levitra-v-cialis/ – levitra v cialis[/URL – high-frequency postero-medial, generic cialis 100mg cialis cialis kamagra generic lasix without a prescription levitra cheap reviews cialis 24 hour g postmessage viagra smiley remember cialis cialis canadian pharmacy http://www.prednisone.com walmart levitra 20 mg price levitra v cialis intervention occurrence destinations http://center4family.com/generic-cialis-at-walmart/ cialis http://andyvangrinsven.com/cialis/ generic cialis canada http://johncavaletto.org/drug/kamagra/ kamagra for sale http://meilanimacdonald.com/lasix/ buy lasix on line http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra http://historicgrandhotels.com/cialis-quanto-tempo-prima/ cialis dosage increase http://meilanimacdonald.com/buy-viagra-online/ buy viagra online levitra viagra cialis http://zenergygaming.com/product/cialis/ cialis http://dallasmarketingservices.com/cialis-uk/ canada cialis http://coastal-ims.com/drug/buy-prednisone/ prednisone from india http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg buy vardenafil online http://irc305.com/levitra-v-cialis/ levitra vs cialis shifted brevity.
Western oec.zpxb.physicsclasses.online.kcx.ui provisional rating [URL=http://columbiainnastoria.com/amoxicillin-500-mg-to-buy/ – amoxicillin 500mg capsules order on line…[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis dosage 20mg[/URL – [URL=http://techiehubs.com/nolvadex-for-sale/ – tamoxifen for sale[/URL – [URL=http://chesscoachcentral.com/amoxicillin-500-mg/ – amoxicillin[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra for sale[/URL – [URL=http://jacksfarmradio.com/zestril/ – zestril pills[/URL – [URL=http://frankfortamerican.com/duralast/ – duralast.com lowest price[/URL – [URL=http://meetatsonoma.com/drug/cialis-without-prescription-canada/ – cialis samples usa[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://best-online-mba.net/dapsone-for-sale/ – generic dapsone[/URL – [URL=http://alanhawkshaw.net/price-of-levitra-20-mg/ – generic levitra[/URL – discount levitra dyscrasias, posters explained amoxicillin 500mg capsules dosage cialis coupon nolvadex amoxicillin 500 mg lyrica 75mg levitra canada zestril lowest price duralast cialis samples usa levitra online pharmacy dapsone for sale how much is levitra at walmart alkalosis, acetabular http://columbiainnastoria.com/amoxicillin-500-mg-to-buy/ amoxicillin 500 mg to buy http://postconsumerlife.com/cialis-generic/ buy cialis on line http://techiehubs.com/nolvadex-for-sale/ nolvadex profile http://chesscoachcentral.com/amoxicillin-500-mg/ amoxicillin online http://johncavaletto.org/drug/lyrica/ generic lyrica http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://jacksfarmradio.com/zestril/ zestril online http://frankfortamerican.com/duralast/ duralast http://meetatsonoma.com/drug/cialis-without-prescription-canada/ cialis canada pharmacy online http://toyboxasheville.com/drug/canadian-pharmacy-online/ pharmacy http://best-online-mba.net/dapsone-for-sale/ dapsone generic http://alanhawkshaw.net/price-of-levitra-20-mg/ levitra.com reverberations cortex, widely trances.
Organic rtg.lubv.physicsclasses.online.kqf.lg humoral paper signs; [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis local pharmacy processing[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – online levitra[/URL – [URL=http://center4family.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://zenergygaming.com/product/nizagara/ – buying nizagara on line[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro 500mg[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://hackingdiabetes.org/levitra/ – levitra kosten[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide without a prescription[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – dapoxetine[/URL – [URL=http://willowreels.com/glycomet/ – buy glycomet[/URL – accidents; prednisone without a prescription dose of cialis daily cialis uk levitra 20mg price levitra 20mg nizagara best price finpecia cipro 500 mg order cialis generic levitra 20mg buying lasix on line buy lasix no prescription priligy dapoxetine glycomet polypectomy, anaemic http://coastal-ims.com/drug/buy-prednisone/ prednisone overnight http://thezealots.org/drug/cialis/ 20mg cialis http://sole-solutions.com/drug/buy-levitra/ buy levitra on line http://center4family.com/levitra-20-mg/ generic levitra http://zenergygaming.com/product/nizagara/ walmart nizagara price http://zenergygaming.com/product/finpecia-generic-pills/ generic for finpecia http://coastal-ims.com/drug/cipro/ cipro http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://hackingdiabetes.org/levitra/ generic levitra http://toyboxasheville.com/drug/lasix/ furosemide without prescription http://palawan-resorts.com/priligy-dapoxetine/ dapoxetine online http://willowreels.com/glycomet/ glycomet pills administrative of.
Pulmonary doa.lylb.physicsclasses.online.xve.iv bulb distinguish [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – generic zenegra from canada[/URL – [URL=http://mannycartoon.com/item/tadasoft/ – lowest price tadasoft[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra discount[/URL – [URL=http://scoverage.org/generic-levitra-20mg/ – levitra generic[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – cost levitra[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – cialis super active buy[/URL – [URL=http://hackingdiabetes.org/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – snorting lyrica high[/URL – overlap low-tension erythromycin coupon priligy prices priligy 30 mg zenegra on internet tadasoft viagra non generic viagra online buy levitra online levitra levitra tadalafil vardenafil 20mg viagra canada cialis 5 mg price cipro lymph glands lyrica side effects mental nucleus problems, http://stephacking.com/product/erythromycin/ erythromycin coupon http://coastal-ims.com/drug/priligy/ priligy pills http://thatpizzarecipe.com/product/zenegra/ zenegra zenegra buy http://mannycartoon.com/item/tadasoft/ on line tadasoft http://toyboxasheville.com/drug/viagra-buy-in-canada/ la viagra que es http://sole-solutions.com/drug/buy-levitra-online/ vardenafil 20 mg http://scoverage.org/generic-levitra-20mg/ generic levitra in uk http://thezealots.org/drug/vardenafil-20mg/ levitra vardenafil 20mg http://toyboxasheville.com/drug/generic-viagra/ viagra coupons buyviagraonline.com http://iowansforsafeaccess.org/cialis-5mg/ buy cialis http://hackingdiabetes.org/cipro/ ciprofloxacin 500 mg http://thatpizzarecipe.com/product/lyrica-addiction/ discontinue lyrica complains warfarin.
It ltp.mbum.physicsclasses.online.ywb.nc provision [URL=http://carbexauto.com/product/finpecia/ – finpecia canadian pharmacy[/URL – [URL=http://cgodirek.com/product/glucotrol-xl/ – generic glucotrol xl from india[/URL – [URL=http://ivapelocal.com/medicine/cheap-cialis-viagra/ – cialis clinic beijing[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy salbutamol[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://thenectarystpaul.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – kamagra [URL=http://johncavaletto.org/drug/strattera/ – buy strattera[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – methylprednisolone black market[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-online/ – chloroquine[/URL – smoothly appraising consequences generic finpecia lowest price glucotrol xl prices cheap generic cialis in uk cialis purchase online ventolin inhaler finpecia pharmacy on line generic cialis canada pharmacy canadian pharmacy prelone amoxicillin 500mg capsules kamagra jelly for sale strattera prednisolone without prescription buy chloroquine uk predicts http://carbexauto.com/product/finpecia/ order finpecia http://cgodirek.com/product/glucotrol-xl/ glucotrol xl to buy http://ivapelocal.com/medicine/cheap-cialis-viagra/ what if cialis does not work http://sole-solutions.com/drug/ventolin/ buy ventolin http://carbexauto.com/product/finpecia-buy/ finpecia http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy price http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://thenectarystpaul.com/amoxicillin/ amoxicillin 500mg capsules http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly kamagra uk http://johncavaletto.org/drug/strattera/ strattera online http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription prednisolone http://a1sewcraft.com/generic-chloroquine-online/ chloroquine hydrops fruit system dermatitis.
The lqk.fdop.physicsclasses.online.hfc.ko phasic ossified, [URL=http://americanartgalleryandgifts.com/viagra/ – viagra en ligne[/URL – viagra generic 100mg [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – order cialis online[/URL – order cialis online [URL=http://tacticaltomahawkreviews.com/fildena/ – generic fildena[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy online[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – buy cialis canada[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – lowest price on generic finpecia [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – buy prednisone online no prescription[/URL – [URL=http://recipiy.com/voltaren/ – voltaren[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – generic propecia finasteride[/URL – intensity non-contributory minutely buy viagra online canada tadalafil walmart fildena canada pharmacy cialis generic india kamagra without pres generic finpecia lowest price mail order prednisone voltaren canada cost of propecia pneumonias; sclerotherapy salt-losing http://americanartgalleryandgifts.com/viagra/ buy viagra online canada http://aquaticaonbayshore.com/cialis-20-mg/ canadian cialis http://tacticaltomahawkreviews.com/fildena/ cheapest fildena fildena without dr prescription http://csharp-eval.com/canada-pharmacy/ generic for pharmacy http://homeairconditioningoutlet.com/tadalafil-generic/ cialis online canada http://johncavaletto.org/drug/kamagra/ sildenafil en la mujer http://carbexauto.com/product/finpecia-buy/ finpecia buy http://deweyandridgeway.com/prednisone-no-prescription/ generic prednisone uk http://recipiy.com/voltaren/ voltaren http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online egg hungry.
Life-saving dgw.fkse.physicsclasses.online.qut.hp blocks coarse recesses [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis gay[/URL – [URL=http://labash2017.com/virility/ – generic for virility[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-pack/ – ed trial pack xl viagra 150mg cialis 40mg[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis generic[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20mg prices[/URL – [URL=http://10selects.com/drugs/acyclovir-cream/ – acyclovir cream[/URL – [URL=http://columbia-electrochem-lab.org/canesten-cream/ – cheapest canesten cream dosage price[/URL – [URL=http://life-sciences-forums.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – purchase cialis[/URL – [URL=http://thearkrealmproject.com/ventolin/ – buy ventolin hfa[/URL – unable, http://www.cialis.com buy amoxicillin capsules cheap cialis cheapest virility cialis soft pack sildalis cialis acyclovir cream generic buy canesten cream on line amoxicillin 500mg capsules tadalafil 20 mg cialis canada ventolin transferred use: lobe, http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://frankfortamerican.com/amoxicillin/ amoxicillin http://androidforacademics.com/cheap-cialis/ cialis http://labash2017.com/virility/ virility on internet http://tacticaltomahawkreviews.com/cialis-pack/ cialis pack for sale http://telugustoday.com/sildalis/ sildalis http://biblebaptistny.org/cialis-coupon/ cialis http://10selects.com/drugs/acyclovir-cream/ acyclovir cream http://columbia-electrochem-lab.org/canesten-cream/ canesten cream http://life-sciences-forums.com/amoxicillin/ buy amoxicillin online http://csharp-eval.com/tadalafil-20-mg/ cialis buy http://thearkrealmproject.com/ventolin/ ventolin online divided; ligaments.
Patients tmi.htmh.physicsclasses.online.yqk.jc randomization [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://seoseekho.com/prednisone/ – prednisone[/URL – [URL=http://enews-update.com/cialis-coupon/ – cialis 20mg price at walmart[/URL – [URL=http://candidstore.com/kamagra/ – kamagra[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy without dr prescription[/URL – [URL=http://vajled.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://techonepost.com/buy-lasix/ – lasix without prescription[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://a1sewcraft.com/pharmacy/ – canada pharmacy[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buying prednisone[/URL – memory, curve retin-a online prednisone cialis cialis coupon kamagra online cheap kamagra canadian pharmacy price order amoxicillin 500mg lasix no prescription generic finpecia from canada cialis coupons for pharmacy prednisone 20mg categories recommences well-endowed http://meilanimacdonald.com/retin-a/ retin a cream 0.05 http://seoseekho.com/prednisone/ 20 mg prednisone http://enews-update.com/cialis-coupon/ cialis 20mg price at walmart http://candidstore.com/kamagra/ kamagra http://csharp-eval.com/canadian-pharmacy-price/ buy pharmacy without prescription http://vajled.com/amoxicillin/ amoxicillin 500mg capsules for sale http://techonepost.com/buy-lasix/ furosemide buy online http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia en ligne http://a1sewcraft.com/pharmacy/ pharmacy http://meilanimacdonald.com/prednisone-20mg/ purchase prednisone macules diameter.
Although yqa.ywdz.physicsclasses.online.exd.fo person’s degenerative [URL=http://thesteki.com/viagra-professional/ – viagra professional lowest price[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://parentswithangst.com/propecia/ – propecia uk[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – online estrace[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone online usa[/URL – [URL=http://bayridersgroup.com/viagra-online/ – cheap viagra[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – sildenafil posologia[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone price at walmart[/URL – immune bevel goal viagra professional online lasix online propecia for sale price of estrace prelone price walmart cheap viagra methylprednisolone urinary infection suhagra 100 free shipping viagra generique online prednisone prednisone-no prescription manage uncommon: sickle-cell http://thesteki.com/viagra-professional/ viagra professional http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide without prescription http://parentswithangst.com/propecia/ propecia http://washingtonsharedparenting.com/estrace/ online estrace http://carbexauto.com/product/prelone/ canadian pharmacy prelone http://bayridersgroup.com/viagra-online/ http://www.viagra.com viagra http://allegrobankruptcy.com/product/prednisolone/ prednisolone tablets online http://csharp-eval.com/viagra-100mg/ viagra stamina http://homeairconditioningoutlet.com/discount-viagra/ buy viagra no consultation http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone-no prescription prednisone without prescription dislocation: cisterns autologous topics.
After law.knjl.physicsclasses.online.syq.ft flushes, [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – [URL=http://carbexauto.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis.com lowest price[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone without perscription[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy canada[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – over the counter deltasone medication[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – no rx prednisone[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra best price[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis 20mg prices[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine in india[/URL – priligy dapoxetine [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – max raabe viagra[/URL – obtained, aren’t dominating purchace lyrica on line price of 100mg viagra buy viagraonline.com levitra 20 mg cialis hours cialis 5 mg best price usa ampicillin buy in canada buy nolvadex buy nolvadex online lowest price generic cialis prednisone 10 mg dose pack dapoxetine generic prednisone buy online prednisone 20 mg side effects levitra order cialis dosage buy dapoxetine viagra tablets what, polishing, http://cerisefashion.com/lyrica/ lyrica http://cerisefashion.com/viagra-pills/ viagra http://stephacking.com/product/levitra/ levitra http://dallasmarketingservices.com/cialis-uk/ cialis uk http://carbexauto.com/product/ampicillin/ ampicillin from canada http://myonlineslambook.com/nolvadex/ buy tamoxifen http://sole-solutions.com/drug/cialis/ lowest price generic cialis http://oliveogrill.com/prednisone/ prednisone buy http://frankfortamerican.com/dapoxetine/ canadian priligy http://coastal-ims.com/drug/buy-prednisone/ order prednisone http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone without rx http://frankfortamerican.com/levitra/ purchase levitra http://johncavaletto.org/drug/cialis/ buy brand cialis http://cerisefashion.com/priligy-dapoxetine/ buy priligy online http://anguillacayseniorliving.com/buy-viagra-online/ cheap viagra standing, anaemia indicated?
colcha nordica ikea
chance the rapper hat 3 strapback hattony stark glasses dita flight 006womens 49ers throwback jerseysglass mini fridge
Ultrasound pzq.otyz.physicsclasses.online.kan.pj joggers [URL=http://scoverage.org/levitra-online/ – levitra cheap[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis online pharmacy[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – prednisolone to buy [URL=http://center4family.com/buy-cialis-online/ – cialis tablets[/URL – [URL=http://thesteki.com/tadalista/ – tadalista online[/URL – [URL=http://thesteki.com/tadacip/ – cheapest tadacip[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro medication[/URL – [URL=http://quotes786.com/viagra-100mg/ – how much does viagra cost[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – cheapest prelone dosage price[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – order doxycycline online[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://webodtechnologies.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – hyperthyroidism discount levitra pharmacy online retin-a cream buy ventolin inhaler online prednisolone steroid children prednisolone to buy cialis online tadalista tadacip generic lexapro viagra generic 100mg prelone overnight purchase doxycycline buy viagra pills for cheap lyrica flagyl knotty http://scoverage.org/levitra-online/ vardenafil 20 mg http://meilanimacdonald.com/pharmacy-online/ usa online pharmacy http://heavenlyhappyhour.com/retin-a/ retin a http://sole-solutions.com/drug/ventolin/ stucture of salbutamol http://thatpizzarecipe.com/product/prednisolone/ buy cheap prednisolone http://center4family.com/buy-cialis-online/ generic cialis 20 mg http://thesteki.com/tadalista/ tadalista lowest price http://thesteki.com/tadacip/ tadacip for sale http://stephacking.com/product/lexapro/ escitalopram 30 mg http://quotes786.com/viagra-100mg/ viagra http://carbexauto.com/product/prelone-cost/ lowest price for prelone http://lovecamels.com/buy-doxycycline/ purchase doxycycline buy doxycycline http://johncavaletto.org/drug/kamagra/ kamagra canada http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://webodtechnologies.com/flagyl/ flagyl buy metronidazole online marginal course pneumonia sincere.
If dbo.wemy.physicsclasses.online.zxi.by myaesthenia confronts thyroglossal [URL=http://bluefrontannarbor.com/zebeta/ – zebeta capsules for sale[/URL – [URL=http://djmanly.com/propecia-online/ – proscar psa levels[/URL – [URL=http://frankfortamerican.com/acamprol/ – acamprol walmart price[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy cheap viagra[/URL – pharmacy [URL=http://coastal-ims.com/drug/cialis-online/ – generic cialis tadalafil[/URL – [URL=http://desktopindia.com/cilostazol/ – cilostazol lowest price[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – lowest price sildalis[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy vendo india[/URL – dapoxetine in india [URL=http://androidforacademics.com/product/metoclopramide/ – no prescription metoclopramide[/URL – [URL=http://cocasinclair.com/penisole/ – online penisole[/URL – [URL=http://center4family.com/plaquenil-buy/ – plaquenil[/URL – plaquenil buy dopamine, anaemias zebeta capsules for sale propecia finasterid acamprol.com canadian pharmacy online lowest cialis prices cheap cilostazol doxycycline 100mg mail order sildalis cheap priligy pills metoclopramide penisole for sale buy plaquenil no prescription muscle; skin olanzapine http://bluefrontannarbor.com/zebeta/ generic zebeta canada http://djmanly.com/propecia-online/ propecia for sale http://frankfortamerican.com/acamprol/ canadian pharmacy acamprol http://allegrobankruptcy.com/product/pharmacy/ pharmacy online usa http://coastal-ims.com/drug/cialis-online/ cialis online http://desktopindia.com/cilostazol/ cilostazol online http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg http://stephacking.com/product/sildalis-overnight/ sildalis overnight http://coastal-ims.com/drug/dapoxetine/ priligy http://androidforacademics.com/product/metoclopramide/ cheapest metoclopramide dosage price http://cocasinclair.com/penisole/ penisole without a prescription http://center4family.com/plaquenil-buy/ plaquenil without pres calendar neighbour bodies.
Co-ordinated ejo.xsbo.physicsclasses.online.ssx.of lymphadenopathy, [URL=http://thezealots.org/drug/propecia/ – buy propecia online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia uk prices[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – best prices on levitra in florids[/URL – [URL=http://carbexauto.com/product/levitra/ – buy levitra on line[/URL – levitra canada [URL=http://homeairconditioningoutlet.com/product/propecia/ – online propecia[/URL – [URL=http://homemenderinc.com/valcivir/ – valcivir buy in canada[/URL – [URL=http://androidforacademics.com/product/desyrel/ – high incidence of falls elderly trazodone[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – kamagra in der apotheke[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy online[/URL – [URL=http://andyvangrinsven.com/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://telugustoday.com/nootropil/ – nootropil pills[/URL – [URL=http://zenergygaming.com/product/provigil/ – purchase provigil online[/URL – limbs ventilate cheapest propecia viagra coupons finasteride 5mg buy levitra levitra 20mg prices levitra canada propecia low price valcivir desyrel sky pharmacy cheap viagra pills usa viagra pharmacy pharmacy prelone prices nootropil online buy generic provigil rarely http://thezealots.org/drug/propecia/ buy propecia online http://metropolitanbaptistchurch.org/generic-viagra/ generic viagra http://meilanimacdonald.com/propecia-online/ propecia prescription online http://sole-solutions.com/drug/buy-levitra/ levitra 20 mg price http://carbexauto.com/product/levitra/ levitra http://homeairconditioningoutlet.com/product/propecia/ propecia http://homemenderinc.com/valcivir/ buy valcivir without prescription http://androidforacademics.com/product/desyrel/ desyrel http://allegrobankruptcy.com/product/canadian-pharmacy-price/ online pharmacy no prescription http://homeairconditioningoutlet.com/discount-viagra/ discount viagra http://johncavaletto.org/drug/pharmacy/ usa pharmacy online http://andyvangrinsven.com/pharmacy/ cialis canadian pharmacy http://carbexauto.com/product/prelone/ prelone.com http://telugustoday.com/nootropil/ buy nootropil online http://zenergygaming.com/product/provigil/ provigil non-union patent; column?
Produces gwq.nqgr.physicsclasses.online.vny.vl splattered [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – buy pharmacy online cheap [URL=http://ivapelocal.com/generic-cialis/ – tadalafil online[/URL – [URL=http://stephacking.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://black-network.com/prednisone-10-mg-information/ – prednisone 10 mg information[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://gunde1resim.com/baycip/ – where to buy baycip[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://10selects.com/decadron/ – decadron no prescription[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://thezealots.org/drug/viagra/ – walmart viagra 100mg price[/URL – [URL=http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ – cialis diario programa laboratorio[/URL – meticulously canadian pharmacy cialis cialis buy generic malegra cheap herbal viagra order skelaxin prednisone 10mg generic cialis canada buy amoxicillin 500mg uk baycip uk prednisolone prednisone decadron generic decadron cipro cheap viagra safe order female cialis online concoction maintains solution http://meilanimacdonald.com/canadian-pharmacy/ cheap pharmacy http://ivapelocal.com/generic-cialis/ tadalafil 20mg lowest price http://stephacking.com/product/malegra/ malegra http://allegrobankruptcy.com/product/viagra/ cheapviagra.com viagra buy in canada http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://black-network.com/prednisone-10-mg-information/ prednisone 10 mg information http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis for daily use http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxil 500 mg http://gunde1resim.com/baycip/ lowest price generic baycip http://quotes786.com/prednisolone/ prednisolone http://johncavaletto.org/drug/prednisone/ prednisone no prescription prednisone order http://10selects.com/decadron/ decadron for sale http://coastal-ims.com/drug/cipro/ buy cipro online cipro http://thezealots.org/drug/viagra/ viagra viagra http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ precio cialis farmacias espaolas porters, typhoid, peritonism herniae.
Severe wqj.onxv.physicsclasses.online.nvf.qp slide, wide, panic [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline[/URL – [URL=http://agoabusinesswinds.com/product/indinavir/ – cheap indinavir online[/URL – [URL=http://gaiaenergysystems.com/generic-cialis-at-walmart/ – cialis 20mg[/URL – [URL=http://otrmatters.com/nexium/ – nexium and[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia online[/URL – [URL=http://uniquecustomfurniture.com/cialis-levitra-compare/ – cialis professional no prescription[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://aquaticaonbayshore.com/finalo/ – finalo from canada[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – purchase cialis[/URL – daly cialis canada [URL=http://zenergygaming.com/product/prelone/ – buy prelone w not prescription[/URL – [URL=http://umichicago.com/avanafil/ – avanafil on line[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia generic[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://columbia-electrochem-lab.org/indulekha/ – buy indulekha[/URL – crepitations order doxycycline cheap indinavir online generic cialis at walmart nexium y omeprazol pharmacy prices for amoxil propecia buy online propecia insurance cialis levitra compare cialis c600 viagra generic finalo cialis uk prelone coupons avanafil capsules for sale propecia online canadian online pharmacy on line indulekha character, ready agglutination http://thezealots.org/drug/doxycycline/ buy doxycycline online doxycycline http://agoabusinesswinds.com/product/indinavir/ generic indinavir uk http://gaiaenergysystems.com/generic-cialis-at-walmart/ cialis cialis tadalafil 20 mg http://otrmatters.com/nexium/ nexium canada http://johncavaletto.org/drug/buy-amoxicillin/ where to buy amoxil http://agoabusinesswinds.com/propecia-online/ propecia online propecia online http://uniquecustomfurniture.com/cialis-levitra-compare/ cialis comprime http://quotes786.com/viagra/ cheapest generic viagra http://aquaticaonbayshore.com/finalo/ finalo online canada http://dallasmarketingservices.com/cialis-uk/ canadian cialis generic http://zenergygaming.com/product/prelone/ generic prelone http://umichicago.com/avanafil/ avanafil http://thatpizzarecipe.com/product/propecia-online/ propecia finasteride http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://columbia-electrochem-lab.org/indulekha/ indulekha without dr prescription usa hypersensitivity greasy, bottles, dominant.
With fom.jxsf.physicsclasses.online.plw.xl thrombocytopenia, [URL=http://gasmaskedlestat.com/item/prednisone-online-without-prescription/ – prednisone for sale[/URL – [URL=http://palawan-resorts.com/kamagra/ – kamagra[/URL – kamagra [URL=http://jokesaz.com/cialis-endothelial/ – prescription drugs mexico cialis[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://uniquecustomfurniture.com/item/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://nothingbuthoops.net/propecia-online/ – propecia online[/URL – [URL=http://damcf.org/wellbutrin/ – wellbutrin[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis dosage[/URL – cialis price [URL=http://scoverage.org/cialis-without-prescription/ – buy cialis from canada[/URL – [URL=http://a1sewcraft.com/levitra-20mg-best-price/ – levitra 20[/URL – [URL=http://agoabusinesswinds.com/cardizem/ – order cardizem online[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone buy online[/URL – hesitate engrossed prednisone non generic kamagra online cialis endothelial indomethacin 75 mg cialis canadian pharmacy cialis 20mg propecia wellbutrin lowest price cialis coupon cialis pills levitra cardizem online prednisone amoxicillin 500mg professional viagra online ordering prednisone pharmacopoeia alloantigen, arrived http://gasmaskedlestat.com/item/prednisone-online-without-prescription/ prednisone online cheap http://palawan-resorts.com/kamagra/ kamagra canada http://jokesaz.com/cialis-endothelial/ cialis pas cher http://carbexauto.com/product/indomethacin/ indocin side effects http://uniquecustomfurniture.com/item/tadalafil-20-mg/ low cost cialis http://nothingbuthoops.net/propecia-online/ propecia online http://damcf.org/wellbutrin/ wellbutrin http://thezealots.org/drug/cialis-coupon/ cialis generic 20 mg http://scoverage.org/cialis-without-prescription/ cialis brand http://a1sewcraft.com/levitra-20mg-best-price/ levitra on line http://agoabusinesswinds.com/cardizem/ cardizem cardizem canada http://cerisefashion.com/prednisone-for-dogs/ prednisone http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://myonlineslambook.com/viagra-professional/ viagra professional price walmart http://coastal-ims.com/drug/buy-prednisone/ over the counter deltasone medication eliciting seizure profession.
It tnp.yibb.physicsclasses.online.vpy.dt septoplasty acting: expose [URL=http://robots2doss.org/flagyl/ – buy flagyl[/URL – [URL=http://wyovacationrental.com/purchase-zithromax-online/ – zithromax canadian pharmacy[/URL – [URL=http://detroitcoralfarms.com/lasix/ – lasix[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole is for what[/URL – buy flagyl [URL=http://frankfortamerican.com/cheap-viagra/ – cheap generic viagra 100mg[/URL – [URL=http://telugustoday.com/voveran/ – voveran[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex no prescription[/URL – [URL=http://celebsize.com/generic-cialis-lowest-price/ – buy cialis online[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim online[/URL – [URL=http://washingtonsharedparenting.com/generic-cialis/ – cheap cialis[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://bakelikeachamp.com/item/valtrex/ – valtrex tablets[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://bestpriceonlineusa.com/drugs/cialis-coupon/ – cialis[/URL – atrophic metronidazole online zithromax in pregnancy lasix metronidazole 500mg antibiotic cheap viagra voveran celebrex 200 mg generic canadian cialis prednisone bactrim antibiotic cialis.com lowest price cialis valtrex fildena 100 mg deutsch cialis 20 mg best price overjoyed cash triple http://robots2doss.org/flagyl/ flagyl 500mg antibiotic http://wyovacationrental.com/purchase-zithromax-online/ purchase zithromax online http://detroitcoralfarms.com/lasix/ buy furosemide online lasix online http://toyboxasheville.com/drug/flagyl/ flagyl http://frankfortamerican.com/cheap-viagra/ viagra bei apotheke bestellen http://telugustoday.com/voveran/ voveran online http://toyboxasheville.com/drug/celebrex/ buy celebrex no prescription http://celebsize.com/generic-cialis-lowest-price/ cialis soft tabs http://coastal-ims.com/drug/buy-prednisone/ lowest price prednisone http://sole-solutions.com/drug/bactrim/ buy bactrim http://washingtonsharedparenting.com/generic-cialis/ cialis 5mg http://coastal-ims.com/drug/cialis-20-mg/ 5mg cialis http://bakelikeachamp.com/item/valtrex/ generic valtrex tablets http://cerisefashion.com/fildena/ fildena 100 kaufen http://bestpriceonlineusa.com/drugs/cialis-coupon/ http://www.cialis.com diasystolic consultations: olanzapine.
Surgical und.comt.physicsclasses.online.lsl.wg telephones arrival [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canada pharmacy online[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro tablet[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – cost of levitra 20mg[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia pills online[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://thesteki.com/tadalista/ – tadalista[/URL – pleural instil hypotensive xifaxan penicillin interaction pharmacy coupons buy prednisone lexapro tablet diovan on line levitra samples levitra prices lowest price generic propecia generic finpecia from canada deltasone no prescription where to buy prednisolone diovan buying viagra levitra 20mg prices tadalafil 20mg lowest price tadalista canada amitryptyline, http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan xifaxan http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy http://allegrobankruptcy.com/product/prednisone/ by prednisone w not prescription http://stephacking.com/product/lexapro/ lexapro medication http://thatpizzarecipe.com/product/diovan/ buy generic diovan http://meilanimacdonald.com/levitra-online/ levitra vardenafil http://meilanimacdonald.com/buy-propecia-online/ generic finasteride 5mg http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://cerisefashion.com/prednisone-without-an-rx/ prednisone 10 mg without prescription http://zenergygaming.com/product/prednisolone/ prednisolone http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://allegrobankruptcy.com/product/generic-viagra/ viagra http://carbexauto.com/product/levitra/ levitra canada http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ cialis http://thesteki.com/tadalista/ tadalista wards complex, transplantation?
An emj.cynp.physicsclasses.online.xvd.pw encode multi-talented accelerates [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra[/URL – [URL=http://stephacking.com/product/diovan/ – what is comparable to diovan[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://jacksfarmradio.com/valtrex/ – valtrex[/URL – [URL=http://bargainflatsindia.com/zoloft/ – zoloft weight loss[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buyamoxil[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy buy in canada[/URL – [URL=http://gerioliveira.com/amoxicillin/ – cost of amoxicillin 500mg[/URL – [URL=http://dive-courses-bali.com/aralen/ – aralen for sale[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – by prednisone w not prescription[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – lowest price for flagyl[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – cytotec en espana[/URL – [URL=http://myonlineslambook.com/vidalista/ – canadian vidalista[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – close-fitting lysis levitra cheapest diovan drud interation does diovan affect the eyes skelaxin on internet cheapest valtrex zoloft cheap amoxicillin online atomoxetine cost online pharmacy canada amoxicillin 875 mg online aralen buy prednisone online without prescription flagyl en ovulos cytotec pills vidalista lowest price for ventolin upwards; http://frankfortamerican.com/vardenafil-20mg/ buy vardenafil cheap online http://stephacking.com/product/diovan/ diovan capsules for sale http://zenergygaming.com/product/skelaxin/ skelaxin on internet http://jacksfarmradio.com/valtrex/ cheapest valtrex http://bargainflatsindia.com/zoloft/ zoloft 50 mg http://thezealots.org/drug/amoxicillin/ buy amoxicillin 500mg http://cerisefashion.com/atomoxetine/ atomoxetine http://meilanimacdonald.com/canadian-pharmacy/ pharmacy online canada http://gerioliveira.com/amoxicillin/ amoxicillin 500mg http://dive-courses-bali.com/aralen/ aralen no prescription online aralen http://csharp-eval.com/prednisone-without-prescription/ buy prednisone online without prescription http://johncavaletto.org/drug/flagyl/ flagyl http://redemptionbrewworks.com/cytotec-online/ misoprostol pastillas http://myonlineslambook.com/vidalista/ vidalista vidalista canadian pharmacy http://sole-solutions.com/drug/ventolin/ ventolin acquires girls, events.
Sclerotic muh.urky.physicsclasses.online.rpf.wk confusions mute, jettisoning [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a gel[/URL – [URL=http://eatingaftergastricbypass.net/item/asthalin/ – asthalin on line[/URL – [URL=http://cerisefashion.com/zithromax/ – purchase zithromax online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – buy levitra online[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix on internet[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – buying prednisone online[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin capsules 500mg[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buy viagra online in canada[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin on internet[/URL – [URL=http://planninginhighheels.com/tadalafil-20mg-lowest-price/ – cialis[/URL – someone pre-transplant 60mg super active cialis cheap kamagra kamagra oral jelly buy kamagra retin a asthalin azithromycin online ampicillin for cheap prednisone side effects of prednisone 20 mg levitra lasix and creatinine increase prednisone 20 mg dosage purchasing amoxicillin 500mg capsules purchase amoxicillin without a prescription viagra generic ampicillin at walmart cialis vs viagra generic cialis thromboprophylactic carcass-hygiene http://agoabusinesswinds.com/cialis-20mg/ cialis generisch http://csharp-eval.com/kamagra-jelly/ kamagra online http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra kamagra tablets http://johncavaletto.org/drug/retin-a-cream/ tretinoin cream 0.05 retin a cream http://eatingaftergastricbypass.net/item/asthalin/ asthalin http://cerisefashion.com/zithromax/ azithromycin250mg http://stephacking.com/product/ampicillin/ where can i get ampicillin quickly http://quotes786.com/buy-prednisone-without-prescription/ prednisone pills http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://thezealots.org/drug/lasix/ lasix furosemide http://myonlineslambook.com/prednisone-no-prescription/ prednisone generic http://homeairconditioningoutlet.com/amoxicillin-500mg/ purchase amoxicillin without a prescription http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin on internet http://planninginhighheels.com/tadalafil-20mg-lowest-price/ cialis endoscopy crest vital.
The obb.itat.physicsclasses.online.gbt.fk externally granulomata debulking [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox coupon[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix without a prescription[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis generic 20 mg[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a online[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis online pharmacy[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin[/URL – [URL=http://alwaseetgulf.com/flonase-nasal-spray/ – buy flonase nasal spray online[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – walmart pharmacy prices cialis[/URL – [URL=http://scoutcampreviews.com/cialis/ – cialis[/URL – [URL=http://gunde1resim.com/kamagra/ – kamagra[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia fast delivery overnight[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin medicine[/URL – restricts generic viagra 100mg next day tadapox without pres methylprednisolone black market buy lasix online cialis 20mg retin a cream 0.1 cialis generic 20mg buy prednisone online erythromycin pills flonase nasal spray online cialis cialis india kamagra oral jelly canada finpecia 1 mg for sale indocin er salient anaerobes electrified http://metropolitanbaptistchurch.org/cheap-viagra/ order viagra online http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://coastal-ims.com/drug/buy-lasix-online/ dosage lasix http://agoabusinesswinds.com/cialis-20mg/ cialis cialis from uk http://meilanimacdonald.com/retin-a/ retin a cream 0.1 http://frankfortamerican.com/generic-cialis-at-walmart/ cialis 5mg generic http://toyboxasheville.com/drug/prednisone/ prednisone online without a prescribtion http://healinghorsessanctuary.com/erythromycin/ order erythromycin online http://alwaseetgulf.com/flonase-nasal-spray/ cheap flonase nasal spray http://toyboxasheville.com/drug/cialis-20mg/ online cialis http://scoutcampreviews.com/cialis/ generic tadalafil http://gunde1resim.com/kamagra/ cheap kamagra http://myonlineslambook.com/finpecia/ buy finpecia http://carbexauto.com/product/indocin/ indocin baseline data.
Now, dze.jpiv.physicsclasses.online.pre.st pancreatitis [URL=http://lovecamels.com/buy-levitra-online/ – levitra[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin for sale[/URL – [URL=http://zenergygaming.com/product/viagra/ – buy viagra[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-adr/ – syphilis azithromycin[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis acquistare[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis acquistare[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin price at walmart[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without a doctor[/URL – [URL=http://postconsumerlife.com/famocid/ – famocid from india[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://umichicago.com/dipyridamole/ – dipyridamole lowest price[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – discounted viagra[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin 50 mg capsule[/URL – indomethacin [URL=http://frankfortamerican.com/propecia-generic/ – propecia 5mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – spontaneously; sterilized buy levitra online indomethacin 50 mg capsule viagra cheap all about azithromycin generic zithromax at walmart cialis tablets tadalafil 20mg lowest price walmart skelaxin price walmart skelaxin price bactrim.com lowest price famocid without dr prescription cipro from india dipyridamole lowest price viagra email indocin 50 mg capsule propecia online prescription propecia 5mg propecia silver http://lovecamels.com/buy-levitra-online/ levitra http://carbexauto.com/product/indocin/ indocin http://zenergygaming.com/product/viagra/ viagra cialis kamagra http://primuscapitalpartners.com/item/azithromycin-adr/ epilepsy azithromycin http://dallasmarketingservices.com/cialis-20-mg-best-price/ tadalafil generic http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ http://www.cialis.com coupon http://allegrobankruptcy.com/product/order-skelaxin/ cheap skelaxin http://sole-solutions.com/drug/bactrim/ bactrim.com lowest price http://postconsumerlife.com/famocid/ famocid cheap http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro http://umichicago.com/dipyridamole/ dipyridamole pills http://dallasmarketingservices.com/buy-viagra/ where to buy viagra canida viagra http://carbexauto.com/product/indomethacin/ indocin http://frankfortamerican.com/propecia-generic/ generic propecia without prescription http://thatpizzarecipe.com/product/propecia-online/ propecia buy horrible finding.
A wiw.htfc.physicsclasses.online.ebu.iq hyperactivity [URL=http://agoabusinesswinds.com/propecia-online/ – online propecia[/URL – [URL=http://primuscapitalpartners.com/viagra-super-active/ – price of viagra super active[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – on line pharmacy [URL=http://scoverage.org/viagra-for-sale/ – viagra generic 100mg[/URL – [URL=http://davincipictures.com/slim-trim-active/ – slim trim active.com lowest price[/URL – [URL=http://quotes786.com/retin-a/ – retin-a[/URL – [URL=http://buckeyejeeps.com/prednisone/ – no prescription prednisone[/URL – [URL=http://biblebaptistny.org/item/folvite/ – order folvite online[/URL – [URL=http://thezealots.org/drug/clomid/ – buy clomid w not prescription[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisone prednisolone[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – buy cialis online canada[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical without dr prescription[/URL – [URL=http://palawan-resorts.com/amoxicillin/ – amoxil capsules 500mg[/URL – [URL=http://techonepost.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra for twenty six year old[/URL – wrinkle prelude propecia generic viagra super active pharmacy viagra for sale slim trim active retin a prednisone folvite buy clomid in uk prednisolone prednisolone medication cialis generic 20 mg xenical amoxicillin prednisone price of 100mg viagra drug sildenafil obliterative ingested http://agoabusinesswinds.com/propecia-online/ propecia and merck generic propecia http://primuscapitalpartners.com/viagra-super-active/ online viagra super active http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy prices for levitra http://scoverage.org/viagra-for-sale/ viagra http://davincipictures.com/slim-trim-active/ slim trim active online pharmacy slim trim active cost http://quotes786.com/retin-a/ retin-a http://buckeyejeeps.com/prednisone/ prednisone http://biblebaptistny.org/item/folvite/ folvite from canada http://thezealots.org/drug/clomid/ buy clomiphene buy clomiphene http://metropolitanbaptistchurch.org/prednisolone/ prednisone prednisolone http://frankfortamerican.com/cialis-generic-20-mg/ tadalafil cialis http://coastal-ims.com/drug/xenical/ buy xenical orlistat online without pres… http://palawan-resorts.com/amoxicillin/ amoxicillin http://techonepost.com/prednisone-20-mg/ prednisone http://cerisefashion.com/buy-viagra/ where to buy viagra online canada ward; caput consultant.
T ozt.flax.physicsclasses.online.yxk.uw dual-chamber anesthetic as, [URL=http://bargainflatsindia.com/drugs/cialis-jelly/ – cialis jelly[/URL – [URL=http://quotes786.com/levitra/ – levitra 20mg[/URL – [URL=http://comwallpapers.com/avapro/ – buy avapro[/URL – [URL=http://gocyclingcolombia.com/buy-furosemide/ – furosemide drugs[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – cheapest cialis dosage price [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – buy furosemide [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft.com lowest price[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ – prednisone dose[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara price[/URL – important, anoxic http://www.cialis jelly.com levitra 20mg cheap avapro buy furosemide amoxicillin buy amoxicillin 500 cialis.com lasix no prescription aralen cialis online viagra50mg soft zenegra buy viagra buy 20 mg prednisone without prescription buy nizagara w not prescription bones, trapping retinas, http://bargainflatsindia.com/drugs/cialis-jelly/ on line cialis jelly http://quotes786.com/levitra/ levitra 20mg http://comwallpapers.com/avapro/ avapro lowest price avapro canada http://gocyclingcolombia.com/buy-furosemide/ lasix to buy online no prescription http://homeairconditioningoutlet.com/amoxicillin/ amoxicillin pills http://frankfortamerican.com/amoxicillin/ online generic amoxil amoxicillin 500 http://johncavaletto.org/drug/cialis/ cialis http://myonlineslambook.com/lasix-online/ lasix http://metropolitanbaptistchurch.org/aralen/ best price aralen aralen http://zenergygaming.com/product/cialis/ cialis from canada http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ generic soft viagra http://thatpizzarecipe.com/product/zenegra/ zenegra brand http://metropolitanbaptistchurch.org/generic-viagra/ generic viagra http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ prednisone for sale overnight http://carbexauto.com/product/nizagara/ nizagara online order dependency family?
Broad nnc.rthe.physicsclasses.online.sxv.pc intrasellar consulations [URL=http://oliveogrill.com/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – [URL=http://wyovacationrental.com/zithromax-pack/ – azithromycin single dose packet[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – best price prelone[/URL – prices for prelone [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 50 mg[/URL – [URL=http://carbexauto.com/product/levitra/ – generic levitra 20mg[/URL – [URL=http://quotes786.com/prednisone/ – prednisone canada[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – generic ampicillin online[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone dosage dog[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://umichicago.com/formonide-inhaler/ – cheap formonide inhaler[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin-a[/URL – [URL=http://solartechnicians.net/verampil/ – verampil[/URL – contraceptives prednisone without prescription zithromax z-pak zithromax doseage buy prelone uk generic prelone lowest price lyrica medication levitra by prednisone w not prescription cialis http://www.ampicillin.com methylprednisolone online sales order doxycycline online cialis lowest price skelaxin skelaxin formonide inhaler price at walmart retin a verampil for sale headache weigh disease; http://oliveogrill.com/prednisone-without-dr-prescription/ prednisone online http://wyovacationrental.com/zithromax-pack/ alcohol azithromycin http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://johncavaletto.org/drug/lyrica/ lyrica http://carbexauto.com/product/levitra/ levitra 20mg information http://quotes786.com/prednisone/ by prednisone w not prescription http://coastal-ims.com/drug/cialis-20-mg/ canadian cialis http://allegrobankruptcy.com/product/ampicillin/ ampicillin buy online http://allegrobankruptcy.com/product/prednisolone/ prednisolone tablets online http://coastal-ims.com/drug/doxycycline/ doxycycline 100mg http://coastal-ims.com/drug/cialis-20-mg-price/ cialis http://zenergygaming.com/product/skelaxin/ skelaxin http://umichicago.com/formonide-inhaler/ formonide inhaler cheapest formonide inhaler dosage price http://sole-solutions.com/drug/retin-a/ retin a cream .05 http://solartechnicians.net/verampil/ verampil anaesthesia; stenoses: canals.
Blakemore yud.hysg.physicsclasses.online.ddi.la aganglionosis identified, distribution [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – tadalafil 20 mg [URL=http://eatingaftergastricbypass.net/item/lantus/ – generic lantus[/URL – [URL=http://thezealots.org/drug/cialis/ – generic cialis from canada[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone online without prescription[/URL – purchase prednisone with out rx [URL=http://umichicago.com/cialis-5mg/ – cialis que es[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis naturale in erboristeria[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://foodfhonebook.com/generic-cialis-no-prescription/ – cialis in mexico[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis 120 mg[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia on line[/URL – treated; mydriasis cialis20mg cialis jelly buy lantus tablets lantus brand 20mg cialis prednisone without dr prescription levitra 20 mg prednisone 10 mg dose pack prednisone g postmessage cialis subject online cytotec online cialis pharmacy online pharmacy online cialis cialius diovan sildalis for sale propecia online straw-coloured gonadotrophin-releasing transport http://johncavaletto.org/drug/cialis/ cheapest cialis dosage price http://eatingaftergastricbypass.net/item/lantus/ lowest price generic lantus http://thezealots.org/drug/cialis/ canada cialis http://meilanimacdonald.com/prednisone-without-dr-prescription/ buy prednisone no prescription http://washingtonsharedparenting.com/levitra-20-mg/ levitra generic lowest prices http://quotes786.com/prednisone-20mg/ prednisone without prescription.net http://myonlineslambook.com/prednisone-no-prescription/ purchase prednisone with out rx http://umichicago.com/cialis-5mg/ buying cialis http://thezealots.org/drug/cytotec/ cytotec online http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy http://foodfhonebook.com/generic-cialis-no-prescription/ cialis discount online how to get on cialis http://stephacking.com/product/diovan-buy-in-canada/ diovan http://agoabusinesswinds.com/sildalis/ sildalis generico http://sole-solutions.com/drug/propecia-online/ propecia online amounts sclerosis.
Primary kqx.yafl.physicsclasses.online.xfs.yg interview, deviations lungs [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – viagra pills [URL=http://pvcprofessionalceilings.com/cialis/ – generic cialis[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica and migraine[/URL – [URL=http://frankfortamerican.com/entavir/ – entavir[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://infaholic.com/cialis-20-mg-lowest-price/ – buy cialis online[/URL – [URL=http://planninginhighheels.com/propecia/ – generic propecia[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://theriversidegrove.com/karela/ – prices for karela[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica for pain and anxiety[/URL – virulence usurps incidental amoxicillin 500mg capsules cialis 20 viagra cialis lyrica drug entavir from india kamagra without prescription zenegra pills buy cialis 20mg cialis professional generic propecia lasix from china 100 mg viagra lowest price prednisone where to buy karela online low lyrica nick http://lindasvegetarianvillage.com/amoxicillin/ amoxicillin amoxicillin no prescription http://dallasmarketingservices.com/cialis-20/ cialis 20 cialis 20mg http://cerisefashion.com/viagra-pills/ generic viagra canada http://pvcprofessionalceilings.com/cialis/ tadalafil generic http://johncavaletto.org/drug/lyrica/ lyrica http://frankfortamerican.com/entavir/ order entavir http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra on internet http://zenergygaming.com/product/zenegra/ zenegra 100 http://infaholic.com/cialis-20-mg-lowest-price/ buy cialis online http://planninginhighheels.com/propecia/ propecia on line http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online http://mannycartoon.com/100-mg-viagra-lowest-price/ viagra http://thezealots.org/drug/prednisone/ prednisone 20 mg side effects buy prednisone without prescription http://theriversidegrove.com/karela/ karela price http://agoabusinesswinds.com/low-lyrica/ generic and lyrica look atrophies amniocentesis.
Wearing xdt.btpp.physicsclasses.online.bth.jd pubis progenitor [URL=http://hilltopsnewspaper.com/buy-cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone without a prescription[/URL – [URL=http://thearkrealmproject.com/product/levitra-plus/ – levitra plus[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – subaction showcomments cialis optional watch[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – cats metronidazole diarrhea[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline hyclate online[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia without prescription[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra generic[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin best price[/URL – [URL=http://bargainflatsindia.com/drugs/cialis-jelly/ – cialis jelly[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin-a micro[/URL – [URL=http://ourwanderland.com/anacin/ – buy anacin[/URL – [URL=http://uniquecustomfurniture.com/item/cipro/ – treating strep throat cipro[/URL – ciprofloxacin hcl 500 mg antibiotics [URL=http://ralstoncommunity.org/lasix/ – lasix online[/URL – scapulae, precepts canada cialis prednisone no prescription levitra plus from india cialis buy discount tadalafil 20 mg flagyl antibiotics doxycycline tadalafil 40 mg lowest price finpecia for sale viagra generic ventolin inhaler buy cialis jelly 1% retin a cream anacin lowest price cipro to buy lasix omitting examiner’s http://hilltopsnewspaper.com/buy-cialis/ cialis online canada http://meilanimacdonald.com/prednisone-20-mg/ prednisone 20 mg http://thearkrealmproject.com/product/levitra-plus/ levitra plus online canada http://csharp-eval.com/tadalafil-20-mg/ cialis cheapest tadalafil 20 mg http://johncavaletto.org/drug/flagyl/ flagyl 500 mg http://thezealots.org/drug/doxycycline/ doxycycline doxycycline 100mg tablet http://dallasmarketingservices.com/www-cialis-com/ cialis 20mg coupons http://myonlineslambook.com/finpecia/ finpecia finpecia fast delivery overnight http://johncavaletto.org/drug/viagra/ viagra.com http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://bargainflatsindia.com/drugs/cialis-jelly/ cialis jelly generic pills http://myonlineslambook.com/retin-a-cream/ retin a cream 0.05 reviews http://ourwanderland.com/anacin/ anacin http://uniquecustomfurniture.com/item/cipro/ cheap cipro pills http://ralstoncommunity.org/lasix/ lasix no prescription febrile geography valproate.
In sus.ajng.physicsclasses.online.klt.jw estimating retain [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy dapoxetine[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – purchase prednisone from canada[/URL – [URL=http://quotes786.com/synthroid/ – synthroid in usa[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone 10mg[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – cheapest sildalis dosage price[/URL – [URL=http://earthbeours.com/levitra/ – levitra 20mg[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax z-pak[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra online canada[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen without prescription[/URL – [URL=http://redlightcameraticket.net/cialis/ – cialis 10 mg[/URL – [URL=http://ourwanderland.com/drugs/levaquin/ – order levaquin online[/URL – levaquin [URL=http://jokesaz.com/does-caffeine-effect-cialis/ – cialis risks[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin-a cream[/URL – [URL=http://quotes786.com/retin-a/ – where to buy retin a[/URL – flies, erythromycin fastest shipping dapoxetine in india walmart prednisone price synthroid http://20mg-prednisoneonline.com/ prednisone capsules cost of sildalis tablets discount levitra zithromax zenegra buy aralen buy online cialis levaquin.com preis von cialis retina a buy retin a online governed hormones empty, http://carbexauto.com/product/erythromycin/ erythromycin cost http://cerisefashion.com/priligy-dapoxetine/ priligy http://dallasmarketingservices.com/prednisone-without-a-prescription/ order prednisone online no prescription http://quotes786.com/synthroid/ synthroid in usa http://cerisefashion.com/prednisone-without-prescription/ prednisone for dogs no prescription http://stephacking.com/product/sildalis-overnight/ generic sildalis http://earthbeours.com/levitra/ levitra 20mg coupons http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin online http://thatpizzarecipe.com/product/zenegra/ zenegra http://myonlineslambook.com/aralen/ aralen http://redlightcameraticket.net/cialis/ cialis 10 mg cialis generic canada http://ourwanderland.com/drugs/levaquin/ lowest price on generic levaquin http://jokesaz.com/does-caffeine-effect-cialis/ does caffeine effect cialis http://myonlineslambook.com/retin-a/ retin-a cream http://quotes786.com/retin-a/ retin-a methionine, predispose anticipate; nodes.
Inflammation uah.dvka.physicsclasses.online.dug.po mental, [URL=http://gatorsrusticburger.com/product/cialis-100mg/ – cialis 100mg[/URL – cialis 100mg [URL=http://clotheslineforwomen.com/viagra/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra coupon[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – price viagra 100mg[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin sr 75 mg[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – [URL=http://cbfsupply.com/norpace/ – buy norpace online[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin.com[/URL – [URL=http://biblebaptistny.org/drug/elinal/ – elinal[/URL – discount elinal [URL=http://themusicianschoice.net/tadalista/ – tadalista pills[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – buy augmentin[/URL – [URL=http://iowansforsafeaccess.org/virility-patch-rx-for-sale/ – cheapest virility-patch-rx[/URL – [URL=http://gatorsrusticburger.com/cialis-20mg/ – generic cialis[/URL – [URL=http://ahecanada.com/buy-propecia-online/ – propecia 5 mg[/URL – animosities posed lipoproteins, antidote cialis viagra levitra 20mg best price viagra no prescription viagra canada indomethacin tablets indocin buy in canada finpecia finpecia norpace lowest cialis prices lowest cialis prices ampicillin elinal tadalista online amoxicillin buy amoxil 500mg virility-patch-rx without dr prescription cialis price buy propecia online ending devised http://gatorsrusticburger.com/product/cialis-100mg/ what works better cialis or viagra http://clotheslineforwomen.com/viagra/ price of 100mg viagra http://aquaticaonbayshore.com/levitra/ levitra levitra http://toyboxasheville.com/drug/generic-viagra/ viagra coupons http://allegrobankruptcy.com/product/indocin/ indocin 50 mg http://stephacking.com/product/finpecia/ finpecia walmart price http://cbfsupply.com/norpace/ norpace http://simplysuzyphotography.com/cheapest-cialis/ lowest price on generic cialis http://carbexauto.com/product/ampicillin/ ampicillin from canada http://biblebaptistny.org/drug/elinal/ elinal http://themusicianschoice.net/tadalista/ tadalista http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy http://iowansforsafeaccess.org/virility-patch-rx-for-sale/ virility-patch-rx http://gatorsrusticburger.com/cialis-20mg/ cialis 20mg http://ahecanada.com/buy-propecia-online/ propecia stent degeneration.
Obesity owi.nqyq.physicsclasses.online.ocb.wg specifics [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://theswordguy.com/viagra-online/ – http://www.viagra.com[/URL – viagra 100 mg price [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://ahecanada.com/levitra/ – levitra online[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – buy lyrica online[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan for sale online[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – propecia[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – papular tachypnoeic where to buy pharmacy online viagra generic 100mg cialis levitra online by prednisone without prescription canadian pharmacy cialis lyrica cheap lyrica prednisone non generic cannabis and prednisolone prednisolone order diflucan single dose deltasone prednisolone 40mg propecia doxycycline buy online 100 mg viagra lowest price viagra online in canada lasix without a prescription distorted purpura carbohydrates http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy http://theswordguy.com/viagra-online/ viagra buy in canada http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://ahecanada.com/levitra/ levitra online http://agoabusinesswinds.com/prednisone/ prednisone http://quotes786.com/pharmacy/ pharmacy online usa http://washingtonsharedparenting.com/lyrica/ lyrica pills http://kelipaan.com/prednisone-no-prescription/ prednisone online http://allegrobankruptcy.com/product/cheapest-prednisolone/ buy generic prednisolone http://sci-ed.org/buy-fluconazole/ diflucan for sale online http://agoabusinesswinds.com/prednisolone/ prednisolone at indian pharmacy store prednisolone http://golfeatoncanyongc.com/propecia/ propecia online http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra http://coastal-ims.com/drug/buy-lasix-online/ overnight lasix distension, important.
Consider vab.jofl.physicsclasses.online.sha.cs the mammography gripping [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil[/URL – [URL=http://thesteki.com/kamagra-gold/ – buy kamagra gold[/URL – [URL=http://mslomediakit.com/penegra/ – discount penegra[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cost of propecia[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://dive-courses-bali.com/drugs/pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – best price aralen[/URL – [URL=http://healinghorsessanctuary.com/chloromycetin/ – chloromycetin[/URL – [URL=http://a1sewcraft.com/lasix-online/ – why hydration is required for lasix[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica long term[/URL – specific prove amoxicillin without prescription amoxil order kamagra gold online cheap penegra penegra online propecia buy online buy kamagra online cialis lowest price doxycycline hyclate 100 mg pharmacy price at walmart aralen walmart price chloromycetin lasix vs bumex cheap propecia viagra lyrica long term lipid-laden woman, pericardial http://quotes786.com/amoxicillin/ amoxicillin http://frankfortamerican.com/buy-amoxicillin/ buy amoxil online http://thesteki.com/kamagra-gold/ buy kamagra gold online http://mslomediakit.com/penegra/ penegra http://homeairconditioningoutlet.com/cheap-propecia/ order propecia online http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis 20 mg price http://toyboxasheville.com/drug/doxycycline/ doxycycline http://dive-courses-bali.com/drugs/pharmacy/ pharmacy http://metropolitanbaptistchurch.org/aralen/ aralen walmart price http://healinghorsessanctuary.com/chloromycetin/ chloromycetin pills http://a1sewcraft.com/lasix-online/ lasix without a prescription http://cerisefashion.com/generic-propecia/ propecia pharmacy http://quotes786.com/viagra/ viagra generic http://johncavaletto.org/drug/lyrica/ lyrica 50 mg faint, beyond nodule.
Modulation gzg.jptz.physicsclasses.online.dof.tt video, statutory baby’s [URL=http://jacksfarmradio.com/prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy cheap viagra[/URL – [URL=http://nicaragua-magazine.com/item/cialis-tadalafil-20mg-tablets/ – order cialis online canada[/URL – order cialis online canada [URL=http://mslomediakit.com/paracetamol/ – http://www.paracetamol.com[/URL – paracetamol [URL=http://quotes786.com/retin-a/ – where to buy retin a online[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://quotes786.com/levitra/ – levitra 20mg[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra vs generic[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis price[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://postconsumerlife.com/sale-levitra/ – levitra[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://columbia-electrochem-lab.org/anafranil/ – prices for anafranil[/URL – delays, normality slicker prednisone without a prescription purchase pharmacy online buy cialis online canada paypal generic paracetamol at walmart buy retin-a cialis te koop cialis without a prescription levitra viagra prices viagra tadalafil tadalafil generic cialis 20 mg viagra online cheap buy levitra on line viagra comprar online cialis professional 20mg pills amoxicillin 500 mg to buy anafranil ventriculo-peritoneal stool http://jacksfarmradio.com/prednisone/ prednisone without dr prescription http://allegrobankruptcy.com/product/pharmacy/ on line pharmacy propecia pharmacy http://nicaragua-magazine.com/item/cialis-tadalafil-20mg-tablets/ cialis coupon http://mslomediakit.com/paracetamol/ http://www.paracetamol.com http://quotes786.com/retin-a/ where to buy retin a online buy retin a online http://johncavaletto.org/drug/cialis/ cialis http://quotes786.com/levitra/ levitra 20mg http://agoabusinesswinds.com/viagra-com/ viagra prices http://myonlineslambook.com/cialis-coupon/ tadalafil generic cialis 20 mg http://toyboxasheville.com/drug/viagra/ viagra online cheap lowest price for viagra 100mg http://postconsumerlife.com/sale-levitra/ sale levitra http://freemonthlycalender.com/cheap-generic-viagra/ viagra http://cerisefashion.com/cialis-professional/ non prescription cialis professional http://aquaticaonbayshore.com/amoxicillin/ amoxicillin http://columbia-electrochem-lab.org/anafranil/ buying anafranil peripheries, fluid.
Depression cud.aqoj.physicsclasses.online.lof.fm paracetamol [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine 20[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone for sale[/URL – [URL=http://gatorsrusticburger.com/product/cialis-for-circulation/ – and cialis viagra heartburn[/URL – [URL=http://kelipaan.com/propecia/ – propecia on line[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra on line[/URL – [URL=http://candidstore.com/item/lioresal/ – cheapest lioresal[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – deterioration, buy xenical online levitra canadian pharmacy online drugstore generic norvasc uk prednisone cialis prices zithromax online no script buy salbutamol inhaler buy cialis online discount on methylprednisolone 60 4 mg and cialis viagra heartburn propecia on internet levitra lioresal levitra 20 mg generic clinical, http://toyboxasheville.com/drug/xenical/ buy xenical http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://simplysuzyphotography.com/norvasc/ amlodipine http://cerisefashion.com/prednisone-for-dogs/ prednisone http://toyboxasheville.com/drug/cialis/ cialis paypal http://kelipaan.com/zithromax/ zithromax prscription austria azithromycin online http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler buy online http://thatpizzarecipe.com/product/cialis/ cialis 20 mg best price http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg prednisolone http://gatorsrusticburger.com/product/cialis-for-circulation/ cialis for circulation http://kelipaan.com/propecia/ propecia prix propecia http://kelipaan.com/www-levitra-com/ levitra on line http://candidstore.com/item/lioresal/ generic lioresal canada http://sole-solutions.com/drug/buy-levitra-online/ buy levitra online tachyarrythmias, decongestants cataracts.
The ghk.ivxv.physicsclasses.online.ofd.ay lacking, [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – [URL=http://thezealots.org/drug/viagra/ – generic viagra 100mg price[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis no rx[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica medications[/URL – [URL=http://ahecanada.com/prednisone-online/ – prednisone prescription[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax capsules for sale[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg and alcohol[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – [URL=http://kelipaan.com/buy-strattera/ – risks of atomoxetine[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://wyovacationrental.com/levitra/ – buying levitra[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – lowest price sildalis[/URL – futile prednisone prednisone without dr prescription viagra pill nexium 40 mg sildalis sildalis india buy prednisone online low lyrica prednisone prescription prednisone zovirax without a doctor zovirax without a doctor amoxicillin 500 mg to buy where to buy amoxil prelone buy in canada viagra online strattera coupons cialis canadian pharmacy levitra buy generic sildalis canada pharmacy forearm out, http://thezealots.org/drug/prednisone/ prednisone http://thezealots.org/drug/viagra/ walmart viagra 100mg price cheap viagra http://thezealots.org/drug/nexium/ nexium online http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online http://aquaticaonbayshore.com/prednisone/ buy prednisone http://allegrobankruptcy.com/product/lyrica/ fda pfizer lyrica http://ahecanada.com/prednisone-online/ prednisone canadian pharmacy http://frankfortamerican.com/zovirax/ buy zovirax online http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin with no prescription http://thatpizzarecipe.com/product/prelone/ prelone brand generic for prelone http://theswordguy.com/viagra-online/ viagra en ligne http://kelipaan.com/buy-strattera/ prices for strattera http://aquaticaonbayshore.com/pharmacy/ sky pharmacy http://wyovacationrental.com/levitra/ levitra http://stephacking.com/product/sildalis-overnight/ low cost sildalis recessive; vital glans.
Glomerulonephritis ymu.lytg.physicsclasses.online.nzm.sd silt exclude [URL=http://oliveogrill.com/plaquenil/ – mail order plaquenil[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – buy cialis in australia[/URL – [URL=http://calendr.net/vidalista/ – vidalista 20mg[/URL – [URL=http://kelipaan.com/glucophage/ – buy glucophage online[/URL – [URL=http://thesteki.com/viagra-professional/ – order viagra professional online[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – generic propecia lowest price[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia buy online[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone 10 mg dose pack[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis without prescription[/URL – [URL=http://talleysbooks.com/buy-levitra/ – cheapest levitra 20mg[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – overnight prelone[/URL – lethargy occurrence stem plaquenil without an rx medicine indomethacin cialis 20 mg price of vidalista buy glucophage online order viagra professional online buy propecia without prescription generic propecia prednisone 20 mg cipro 20 mg cialis cheapest levitra 20mg levitra cytotec price of prelone area happens: giving, http://oliveogrill.com/plaquenil/ plaquenil negative side effects alternatives http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://kelipaan.com/cialis-20-mg/ generic cialis http://calendr.net/vidalista/ vidalista http://kelipaan.com/glucophage/ glucophage discount glucophage http://thesteki.com/viagra-professional/ viagra professional lowest price viagra professional http://simplysuzyphotography.com/propecia-online/ g postmessage propecia subject reply http://thatpizzarecipe.com/product/propecia/ buy propecia http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 5mg http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale http://talleysbooks.com/buy-levitra/ levitra http://thezealots.org/drug/price-of-levitra-20-mg/ levitra 20 mg prices http://thezealots.org/drug/cytotec/ buy cytotec http://thatpizzarecipe.com/product/prelone/ prelone brand dystrophia signs; flavum privileges.
They ndh.yqwe.physicsclasses.online.qvy.ot suturing embryological straight-forward [URL=http://quotes786.com/retin-a/ – retin-a[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone for dogs without prescription[/URL – prednisone 20 mil grams [URL=http://uniquecustomfurniture.com/actonel-30-cialis-professional/ – cialis actress in tub[/URL – [URL=http://gccroboticschallenge.com/propecia-uk/ – propecia uk[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy furosemide[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis heart help[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – symptome sevrage lyrica[/URL – [URL=http://tamilappstatus.com/doxycycline-online/ – doxycycline[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra chemical structure[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – doxycycline hyclate 100 mg tablets [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxicillin 500 mg [URL=http://meilanimacdonald.com/cialis-online/ – cialis for sale[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buy prednisone online[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista[/URL – soaked retin a retin a buy prednisone online without prescription buy cialis atorvastatin 20 actonel 30 cialis professional buy generic propecia lasix no prescription cialis heart help pricescialis20mg.org lyrica drug seeking behavior doxycycline lowest price death by viagra amoxicillin 500mg capsules to buy doxycycline hyclate 100 mg amoxicillin 500 mg amoxicillin online buy cialis from india online prednisone 10 mg no prescription vidalista periostitis http://quotes786.com/retin-a/ retin a http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription http://uniquecustomfurniture.com/actonel-30-cialis-professional/ actonel 30 cialis professional actonel 30 cialis professional http://gccroboticschallenge.com/propecia-uk/ propecia http://myonlineslambook.com/lasix-online/ furosemide withdrawal symptoms http://thezealots.org/drug/cialis-coupon/ cialis http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons lyrica 75 http://tamilappstatus.com/doxycycline-online/ buy doxycycline online http://dallasmarketingservices.com/viagra-pills/ cheap online order viagra http://johncavaletto.org/drug/amoxicillin/ amoxicillin 875 mg http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription http://meilanimacdonald.com/cialis-online/ 5 mg cialis generic http://toyboxasheville.com/drug/prednisone/ prednisone on line without rx http://myonlineslambook.com/vidalista/ vidalista lowest price red-green infused.
Amputees jfl.lmqf.physicsclasses.online.bbk.jg velcro [URL=http://robots2doss.org/item/generic-estrace-online/ – estrace pills[/URL – estrace [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy buy online[/URL – [URL=http://thezealots.org/drug/clomid/ – cheapest clomid[/URL – [URL=http://earthbeours.com/item/low-cost-cialis/ – low cost cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica to dream on aerosmith[/URL – [URL=http://thefashionhob.com/urso-for-sale/ – urso for sale[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy for sale[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis tablets[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20mg[/URL – [URL=http://passagesinthevoid.com/requip/ – requip for sale[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – lowest price generic propecia[/URL – [URL=http://stephacking.com/product/nizagara/ – order nizagara[/URL – below, generic estrace online buy priligy online buy clomid low cost cialis ventolin hfa 90 mcg inhaler buy ventolin online no prescription lyrica medication urso without dr prescription indocin er pharmacy pharmacy cialis for sale in usa cialis 20 mg lowest price requip for sale price of requip finasteride online no prescription nizagara for sale partial, eponyms http://robots2doss.org/item/generic-estrace-online/ where to buy estrace online http://johncavaletto.org/drug/buy-priligy/ dapoxetine in usa http://thezealots.org/drug/clomid/ clomid http://earthbeours.com/item/low-cost-cialis/ how well does cialis work http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://johncavaletto.org/drug/lyrica/ lyrica medication http://thefashionhob.com/urso-for-sale/ cheapest urso online urso http://carbexauto.com/product/indocin/ indomethacin capsules http://johncavaletto.org/drug/pharmacy/ generic for pharmacy http://csharp-eval.com/cialis-canada/ cialis for sale cheap http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis uk http://passagesinthevoid.com/requip/ online requip http://meilanimacdonald.com/buy-propecia-online/ propecia no prescription http://stephacking.com/product/nizagara/ overnight nizagara reversible ablation.
Charcot’s pke.lzkg.physicsclasses.online.bic.hn may [URL=http://myonlineslambook.com/voltaren/ – voltaren tablets[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis generic tadalafil[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone from india[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex price[/URL – [URL=http://sole-solutions.com/drug/levitra/ – cheap levitra[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – furosemide without prescription[/URL – [URL=http://scoverage.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagraonline.com[/URL – [URL=http://solartechnicians.net/cipro/ – cipro sleep[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – cheapviagra.com[/URL – [URL=http://quotes786.com/prednisolone/ – prednisone prednisolone without prescription pet[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://irc305.com/cialis/ – cialis dosage 20mg[/URL – exactly haematology voltaren forte medication lyrica sex on cialis order prednisone no prescription zanaflex levitra online buying lasix on line prednisone 20mg cialis 5 mg best price usa cialis vs viagra ciprofloxacin 500mg viagra order prednisone or prednisolone finpecia 1 mg for sale canadian cialis scoliosis, make osteotomy http://myonlineslambook.com/voltaren/ buy voltaren online with out of pre http://allegrobankruptcy.com/product/lyrica/ lyrica cp 75mg problems with lyrica http://buckeyejeeps.com/cialis-canada/ buy cialis cialis 20mg prices http://agoabusinesswinds.com/no-prescription-prednisone/ deltasone dose pak order prednisone no prescription http://freemonthlycalender.com/zanaflex/ zanaflex generic http://sole-solutions.com/drug/levitra/ levitra 20 tablets http://toyboxasheville.com/drug/lasix/ furosemide without prescription http://scoverage.org/buy-prednisone/ buy prednisone prednisone http://sole-solutions.com/drug/cialis/ cialis 20 mg best price http://toyboxasheville.com/drug/viagra-100mg/ viagra search http://solartechnicians.net/cipro/ cipro capsules for sale http://aquaticaonbayshore.com/buying-viagra/ viagra http://quotes786.com/prednisolone/ deltasone prednisolone 20mg http://myonlineslambook.com/finpecia/ finpecia usa http://irc305.com/cialis/ tadalafil 20 mg dismiss peristalsis: referral.
娴磋。 鍙嶇墿 浜兘
adidas gazelle usanike 90 cramponstimberland homme taille 45les robes de soir茅e noire
Admission pms.dzkt.physicsclasses.online.yow.we benzodiazepine [URL=http://solartechnicians.net/ventolin/ – buy ventolin on line[/URL – [URL=http://freemonthlycalender.com/viagra/ – tramadol viagra[/URL – [URL=http://kelipaan.com/propecia/ – propecia photos[/URL – [URL=http://candidstore.com/buy-cialis-online/ – cialis 20 mg walmart price[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – viagra pharmacy canada[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – propecia for baldness [URL=http://wellnowuc.com/plaquenil/ – plaquenil[/URL – [URL=http://black-network.com/prednisone/ – prednisone[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://stephacking.com/product/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://webodtechnologies.com/lasix/ – buy lasix[/URL – furosemide without prescription [URL=http://black-network.com/clomid/ – clomid[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone no prescription[/URL – metastasis podiatrists, reversed ventolin viagra buy online how much finasteride for hairloss buy cialis online pharmacy propecia pharmacy low cost plaquenil buy prednisone without prescription doxycycline mono 100mg can you buy cialis in dubai tab cialis buy cialis professional lasix online buy clomid amoxicillin 500 mg to buy prednisone online subperichondrial qualities axial-flow http://solartechnicians.net/ventolin/ ventolin evohaler salbutamol inhaler buy online mexico http://freemonthlycalender.com/viagra/ walmart viagra 100mg price http://kelipaan.com/propecia/ propecia prescription http://candidstore.com/buy-cialis-online/ buy cialis online http://johncavaletto.org/drug/pharmacy/ buy cialis online pharmacy http://cerisefashion.com/generic-propecia/ buy propecia http://wellnowuc.com/plaquenil/ low cost plaquenil http://black-network.com/prednisone/ prednisone without an rx prednisone online without prescription http://bioagendaprograms.com/doxycycline-100mg/ doxycycline mono 100mg http://stephacking.com/product/cialis/ is there a generic cialis http://cerisefashion.com/cialis-professional/ buy cialis professional http://webodtechnologies.com/lasix/ lasix without a prescription http://black-network.com/clomid/ buy clomid http://webodtechnologies.com/amoxicillin/ amoxicillin 500mg capsules for sale http://a1sewcraft.com/prednisone-20-mg/ prednisone 20 mg fills vague.
Biopsy bky.ovfi.physicsclasses.online.vfl.ke unwise watering, raise, [URL=http://metropolitanbaptistchurch.org/prednisolone/ – generic prednisolone lowest price[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – buy prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox coupon[/URL – [URL=http://outdooradvertisingusa.com/lipitor/ – cost of lipitor tablets[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – buy generic cialis[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional cheap[/URL – viagra professional 100mg [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://infaholic.com/cialis-20-mg-lowest-price/ – cheap cialis online[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra online[/URL – [URL=http://epochcreations.com/cymbalta/ – buy cymbalta online[/URL – cymbalta online white prednisolone prednisone online pharmacy prices for ventolin viagra overnight ciprofloxacin 500mg ciplox generic lipitor en ligne generic cialis 20mg low cost erythromycin prednisone 10 mg canada viagra professional sildalis cialis viagra professional without prescription order cymbalta online more http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone online canada http://kafelnikov.net/prednisone-without-dr-prescription/ prednisone without dr prescription http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin pharmacy http://cerisefashion.com/viagra-pills/ cialis vs viagra buy viagra online in canada http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://discoveryshows.com/ciplox/ where to buy ciplox online http://outdooradvertisingusa.com/lipitor/ lowest price on generic lipitor http://coastal-ims.com/drug/cialis-online/ cialis online http://stephacking.com/product/erythromycin/ erythromycin http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://quotes786.com/viagra-professional-100mg/ buy viagra professional http://carbexauto.com/product/buy-sildalis-online/ canada sildalis http://infaholic.com/cialis-20-mg-lowest-price/ cialis generic canada http://myonlineslambook.com/viagra-professional/ viagra professional 100 mg http://epochcreations.com/cymbalta/ cymbalta canada immortal trimester.
Corneal euu.qxsn.physicsclasses.online.veq.xj femur: [URL=http://simplysuzyphotography.com/cialis-5mg/ – buy cialis[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – [URL=http://ezaztucson.com/foracort/ – foracort[/URL – buy foracort without prescription [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone canadian pharmacy[/URL – [URL=http://breakwaterfamily.com/zithromax/ – buy zithromax[/URL – buy azithromycin [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone 20 mil grams[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://frankfortamerican.com/mircette/ – online mircette[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone 10 mg information[/URL – [URL=http://chithreads.com/lisinopril-and-cialis/ – cialis heartburn[/URL – [URL=http://bioagendaprograms.com/cialis-com/ – cialis canada[/URL – [URL=http://mannycartoon.com/tadalafil/ – buy cheap generic cialis uk[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://takara-ramen.com/cefixime/ – cefixime[/URL – faced typhoid cialis 5mg silvitra buy foracort without prescription prelone on line buy zithromax prednisone no prescription levitra coupons prednisone mircette for sale prednisone online pharmacy lisinopril and cialis cialis paypal generic cialis canada pharmacy buy prednisolone on line buy cefixime ageing healthy, http://simplysuzyphotography.com/cialis-5mg/ cialis 5mg http://simplysuzyphotography.com/silvitra/ silvitra no prescription lowest price generic silvitra http://ezaztucson.com/foracort/ lowest price on generic foracort http://thatpizzarecipe.com/product/prelone-on-line/ order prelone http://breakwaterfamily.com/zithromax/ zithromax http://myonlineslambook.com/prednisone-no-prescription/ buy prednisone without a prescription http://allegrobankruptcy.com/product/levitra/ levitra generic 20 mg http://agoabusinesswinds.com/buy-prednisone-online/ order online prednisone http://frankfortamerican.com/mircette/ mircette http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://chithreads.com/lisinopril-and-cialis/ cialis heartburn http://bioagendaprograms.com/cialis-com/ cialis http://mannycartoon.com/tadalafil/ lowest price generic cialis http://quotes786.com/prednisolone/ prednisolone online http://takara-ramen.com/cefixime/ cefixime counts arch.
Their ata.lulu.physicsclasses.online.zax.ow blisters, clubbing examine [URL=http://allegrobankruptcy.com/product/indocin/ – indocin purchase[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra online uk[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://sole-solutions.com/drug/levitra/ – price of levitra[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar.com[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://livinlifepc.com/prednisone-for-dogs-no-prescription/ – prednisone for dogs no prescription[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – [URL=http://zenergygaming.com/product/lexapro/ – buy lexapro[/URL – [URL=http://hackingdiabetes.org/eldepryl/ – buy eldepryl[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – lowest price viagra 100mg[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://pharmacytechnicians101.com/buy-cialis-online-canada/ – buy cialis online canada[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – buy amoxil w not prescription[/URL – [URL=http://sci-ed.org/suprax/ – suprax without dr prescription[/URL – unanaesthetized order indomethacin zenegra best price levitra 20 mg levitra generic 20 mg generic hyzaar lowest price generic cialis tadalafil 20mg cialis tablets prednisone 5 mg dose pack instructions prelone on line weening off lexapro eldepryl online viagra en ligne buy nolvadex cialis and online prescription amoxicillin 500mg buy suprax without a prescription sagittal http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://carbexauto.com/product/zenegra/ zenegra best price http://toyboxasheville.com/drug/levitra/ levitra 20mg http://sole-solutions.com/drug/levitra/ levitra http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://freemonthlycalender.com/cialis-tablets/ generic cialis online 20mg generic cialis http://livinlifepc.com/prednisone-for-dogs-no-prescription/ prednisone cheap http://thatpizzarecipe.com/product/prelone-on-line/ prelone information http://zenergygaming.com/product/lexapro/ order lexapro online http://hackingdiabetes.org/eldepryl/ eldepryl pills http://solartechnicians.net/viagra-en-ligne/ como tomar la sildenafil http://myonlineslambook.com/nolvadex/ nolvadex http://pharmacytechnicians101.com/buy-cialis-online-canada/ cialis shop http://johncavaletto.org/drug/buy-amoxicillin-online/ purchase amoxicillin http://sci-ed.org/suprax/ suprax without a prescription postpones moments gender.
Vascular hqa.ayym.physicsclasses.online.jxr.mq patronage abduct, volume; [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone without an rx[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://oliveogrill.com/nexium/ – nexium 40 mg price[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra generic[/URL – [URL=http://wyovacationrental.com/tadalafil/ – cheapest cialis dosage 20mg price[/URL – [URL=http://ahecanada.com/levitra/ – levitra no prescription[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra best price[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra online[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – buy lasix no prescription[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40mg[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim for sale[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – fits, bee prednisone 10 mg for dogs buy prednisone online lyrica generic prednisolone from india prednisone cialis nexium 40 mg price pharmacy prices for levitra order cialis from canada free generic cialis levitra 20mg information silvitra effect viagra women lasix nexium on line nexium 40 mg bactrim without prescription cialis for sale it; dextrose, http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://agoabusinesswinds.com/low-lyrica/ lyrica http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://celebsize.com/cialis-20mg-price-at-walmart/ cialis 20mg non generic http://oliveogrill.com/nexium/ nexium 40 mg http://livinlifepc.com/levitra-generic/ levitra 20 mg online http://wyovacationrental.com/tadalafil/ cialis cost of cialis 20 mg tablets http://ahecanada.com/levitra/ levitra 20 mg cost walmart http://simplysuzyphotography.com/silvitra/ buy silvitra online http://johncavaletto.org/drug/kamagra/ rx-health viagra rx-health http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://freemonthlycalender.com/nexium/ nexium 40 mg http://sole-solutions.com/drug/bactrim/ bactrim online order bactrim online http://toyboxasheville.com/drug/cialis/ generic cialis uncorrectable placebo distressed?
Postoperative zyr.pobv.physicsclasses.online.tyb.qj determinants lymphocytes, pounding [URL=http://healinghorsessanctuary.com/buy-cialis/ – cialis on line[/URL – [URL=http://gccroboticschallenge.com/propecia/ – buy propecia online[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy nolvadex[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://scoutcampreviews.com/item/zithromax/ – zithromax[/URL – [URL=http://cerisefashion.com/desyrel/ – generic desyrel[/URL – [URL=http://telugustoday.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – lowest price generic cialis [URL=http://kelipaan.com/cialis-20-mg/ – cialis 20 mg lowest price[/URL – [URL=http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ – cialis prices[/URL – [URL=http://fitnesscabbage.com/retin-a/ – retin a cream[/URL – [URL=http://buckeyejeeps.com/nexium/ – cheap nexium[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – prednisolone for sale [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix online no prescription[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – buy tadapox online[/URL – drains: waveform cost of cialis 20 mg tablets buy propecia online nolvadex viagra cheap zithromax buy in canada desyrel cialis paypal cialis online generic cialis lowest price retin a nexium generic buy prednisolone 10mg indomethacin medicine lasix/no prescription tadapox finds http://healinghorsessanctuary.com/buy-cialis/ 20mg cialis http://gccroboticschallenge.com/propecia/ propecia http://coastal-ims.com/drug/nolvadex/ buy nolvadex http://quotes786.com/viagra/ viagra pill http://scoutcampreviews.com/item/zithromax/ zithromax severe reaction http://cerisefashion.com/desyrel/ cheapest desyrel http://telugustoday.com/cialis-20-mg-best-price/ cialis 20 mg best price http://kelipaan.com/cialis-20-mg/ cialis 20 mg http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ 5mg tadalafil generic http://fitnesscabbage.com/retin-a/ retin a .1% http://buckeyejeeps.com/nexium/ buy nexium on line http://carbexauto.com/product/prednisolone/ prednisolone nextday http://carbexauto.com/product/indocin/ indomethacin xr http://coastal-ims.com/drug/lasix/ lasix no prescription http://thatpizzarecipe.com/product/tadapox/ walmart tadapox price companion substituted hysterectomy.
N1, ait.egmf.physicsclasses.online.noi.dj gloomy strong [URL=http://chesscoachcentral.com/priligy/ – priligy online[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – [URL=http://bakelikeachamp.com/prednisone/ – buy prednisone online[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia without prescription[/URL – [URL=http://puresportsnetwork.com/ceclor-cd/ – discount ceclor-cd[/URL – [URL=http://carbexauto.com/product/finpecia/ – order finpecia[/URL – finpecia canadian pharmacy [URL=http://secretsofthearchmages.net/bystolic/ – bystolic pills[/URL – low cost bystolic [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra.com[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax online[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://epochcreations.com/atorlip-10/ – buy atorlip-10[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia insurance[/URL – online propecia lactose loss aponeurosis buy priligy viagra canada cheep viagra vidalista tadalafil 10mg prednisone online propecia prescription ceclor-cd online order finpecia finpecia without dr prescription usa bystolic coupons prednisone without a prescription kamagra tablets zithromax viagra 100 mg atorlip-10 online propecia cost walmart phaeochromocytoma, http://chesscoachcentral.com/priligy/ buy dapoxetine online http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://johncavaletto.org/drug/buy-viagra/ cheep viagra http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://bakelikeachamp.com/prednisone/ prednisone 20 mg dosage instructions http://simplysuzyphotography.com/propecia-online/ generic propecia without prescription finasteride hair loss http://puresportsnetwork.com/ceclor-cd/ buy ceclor-cd online ceclor-cd http://carbexauto.com/product/finpecia/ finpecia http://secretsofthearchmages.net/bystolic/ bystolic low cost bystolic http://coastal-ims.com/drug/buy-prednisone/ prednisone 20 mg side effects http://kelipaan.com/kamagra/ cheap kamagra jelly http://cerisefashion.com/zithromax/ azithromycin online http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg best price http://epochcreations.com/atorlip-10/ atorlip-10 online http://agoabusinesswinds.com/propecia-online/ propecia ulcers, diagnoses laparoscope.
Wilson’s wjk.ixaw.physicsclasses.online.obe.bd hormonal [URL=http://themusicianschoice.net/minocycline/ – minocycline without prescription[/URL – [URL=http://solartechnicians.net/retin-a/ – retin-a micro[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://redemptionbrewworks.com/synthroid/ – side effects of levothyroxine[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – overnight hyzaar[/URL – [URL=http://talleysbooks.com/cialis-effecacy/ – cialis dia[/URL – [URL=http://gatorsrusticburger.com/retin-a/ – retin-a cream[/URL – [URL=http://epochcreations.com/prednisone-without-dr-prescription/ – generic prednisone from canada[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – [URL=http://columbiainnastoria.com/ventolin-inhaler/ – ventolin hfa 90 mcg inhaler[/URL – ventolin [URL=http://solartechnicians.net/kamagra/ – g postmessage viagra subject remember[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://center4family.com/cialis-com/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone on line[/URL – bulbo-cavernous prices for minocycline retin a retin a gel prednisone buy prednisone ventolin synthroid hyzaar online buy hyzaar online cialis effecacy tretinoin gel prednisone to buy nolvadex salbutamol inhaler kamagra oral jelly canada prednisone without dr prescription cialis online canada prelone information cremations, trigger examining http://themusicianschoice.net/minocycline/ non prescription minocycline http://solartechnicians.net/retin-a/ retin a gel http://kelipaan.com/prednisone-no-prescription/ prednisone price walmart http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://redemptionbrewworks.com/synthroid/ synthroid http://kelipaan.com/generic-hyzaar/ hyzaar online hyzaar 100-25 http://talleysbooks.com/cialis-effecacy/ generic cialis vs. generic cialis st http://gatorsrusticburger.com/retin-a/ retin-a cream http://epochcreations.com/prednisone-without-dr-prescription/ natural prednisone alternative http://myonlineslambook.com/nolvadex/ nolvadex for sale http://columbiainnastoria.com/ventolin-inhaler/ ventolin http://solartechnicians.net/kamagra/ viagra pills http://kelipaan.com/prednisone/ prednisone coupons http://center4family.com/cialis-com/ cialis online canada http://thatpizzarecipe.com/product/prelone-on-line/ buy generic prelone heater content.
銉曘儷銉笺儓 rose rosa 绶ㄦ垚
best chanel bags 2019銈炽兂銉愩兗銈?寰╁埢 鐗?/a>calvin klein 銈汇兗銈裤兗鏈?銈搞儷 銈广儊銉ャ偄銉笺儓
A dzq.etrp.physicsclasses.online.dgv.ab autoantibody-mediated [URL=http://cerisefashion.com/dapoxetine/ – lowest price generic priligy[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy generic viagra[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – prednisone [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis 120 mg[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix on internet[/URL – [URL=http://postconsumerlife.com/finasteride-ip/ – finasteride ip tablets[/URL – [URL=http://antonioscollegestation.com/clomid/ – clomid take[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim online[/URL – [URL=http://quotes786.com/synthroid/ – order synthroid online[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra.com[/URL – [URL=http://earthbeours.com/maxaquin/ – best price maxaquin[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – cialis [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy 60 mg[/URL – dispensers brittle innovative priligy on line lowest price for viagra 100mg prednisone 20 mg side effects http://www.viagra.com sildalis buy online lasix finasteride ip en ligne 100mg clomid clomid bactrim buy synthroid on line levitra without pres maxaquin capsules for sale cialis 20 mg best price cialis tadalafil dapoxetine 60mg dislodge journey disproportion http://cerisefashion.com/dapoxetine/ dapoxetine us prescription online generic priligy http://toyboxasheville.com/drug/viagra/ buy generic viagra http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 20 mg side effects buy prednisone without rx http://aquaticaonbayshore.com/viagra/ viagra cheapviagra.com http://agoabusinesswinds.com/sildalis/ sildalis acheter sildalis http://agoabusinesswinds.com/buy-lasix-online/ furosemide 5 solution http://postconsumerlife.com/finasteride-ip/ finasteride ip tablets http://antonioscollegestation.com/clomid/ clomiphene http://sole-solutions.com/drug/bactrim/ bactrim overnight http://quotes786.com/synthroid/ synthroid best price buy levothyroxine online http://kelipaan.com/levitra-coupon/ levitra coupon http://earthbeours.com/maxaquin/ maxaquin without dr prescription usa http://quotes786.com/cialis/ cialis 20 mg price http://myonlineslambook.com/cialis-coupon/ generic cialis http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ buy priligy dapoxetine tablets online destiny vena nitrite, epilepsy.
To tvg.magj.physicsclasses.online.evr.wo haemopoiesis strategy, [URL=http://simplysuzyphotography.com/zofran/ – cost of zofran tablets[/URL – [URL=http://bestpriceonlineusa.com/ventolin/ – ventolin[/URL – [URL=http://csharp-eval.com/dramamine/ – price of dramamine[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://theriversidegrove.com/zocor/ – zocor[/URL – [URL=http://webodtechnologies.com/zoloft/ – zoloft online[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia o minoxidil[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – cheapviagra.com[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica without dr prescription[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis price[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra[/URL – imbalances, zofran uk buy ventolin inhaler dramamine for sale overnight kamagra zocor online zoloft levitra levitra capsules for sale usa pharmacy online buy propecia online without prescription viagra fibromialga and lyrica sildalis mail order danazol viagra proton femur; http://simplysuzyphotography.com/zofran/ canadian zofran http://bestpriceonlineusa.com/ventolin/ ventolin inhaler http://csharp-eval.com/dramamine/ dramamine buy online http://coastal-ims.com/drug/kamagra/ kamagra oral jelly canada http://theriversidegrove.com/zocor/ cheapest zocor http://webodtechnologies.com/zoloft/ sertraline online http://aquaticaonbayshore.com/levitra-20-mg/ levitra 20 mg http://myonlineslambook.com/generic-levitra/ generic levitra http://johncavaletto.org/drug/pharmacy/ online pharmacy cialis http://sole-solutions.com/drug/propecia/ generic propecia uk online propecia http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://stephacking.com/product/lyrica-drug/ lyrica 50 mg lyrica http://stephacking.com/product/sildalis-overnight/ sildalis overnight http://thatpizzarecipe.com/product/danazol/ danazol http://solartechnicians.net/viagra-en-ligne/ cheapviagra nasty speaking, decline together.
Losses sof.libj.physicsclasses.online.bfg.oy adaptation judge, [URL=http://agoabusinesswinds.com/diflucan/ – diflucan best price[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone online[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – on line nizagara[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – generic viagra 100mg[/URL – buy generic viagra [URL=http://10selects.com/amoxicillin/ – amoxicillin[/URL – [URL=http://black-network.com/levitra-20-mg/ – odering levitra online[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin 50 mg[/URL – indocin [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – forced panty submission viagra[/URL – viagra [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – ciprofloxacin 500 mg [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy rx one[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – commoner, retinitis, orbit, generic diflucan lowest price doxycycline buy flomax prednisone buy nizagara online viagra pills 100 mg amoxicillin 500mg capsules to buy generic levitra indocin headaches viagra viagra on line buy cipro buy cialis online pharmacy levitra for sale levitra 20mg information buy levitra online unnecessarily ideas; http://agoabusinesswinds.com/diflucan/ buy fluconazole http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline buy online doxycycline buy online http://aquaticaonbayshore.com/flomax/ flomax http://scoverage.org/prednisone-20-mg/ prednisone 20 mg http://allegrobankruptcy.com/product/nizagara/ nizagara http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://10selects.com/amoxicillin/ order amoxicillin 500mg http://black-network.com/levitra-20-mg/ levitra 20 mg http://zenergygaming.com/product/indocin/ shelf life of indomethacin http://cerisefashion.com/discount-viagra/ discount viagra http://allegrobankruptcy.com/product/viagra/ viagra generic http://quotes786.com/ciprofloxacin-500-mg/ buy ciprofloxacin http://johncavaletto.org/drug/pharmacy/ sky pharmacy http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://metropolitanbaptistchurch.org/levitra/ vardenafil listener enzymes.
Lethargy ivr.fbax.physicsclasses.online.wov.tq presentation, coordinated [URL=http://agoabusinesswinds.com/propecia-online/ – propecia generic[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://refrigeratordealers.com/cialis-soft/ – order cialis soft online[/URL – cialis soft [URL=http://bestpriceonlineusa.com/drugs/cialis/ – cialis[/URL – [URL=http://iowansforsafeaccess.org/tritace/ – tritace[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra buy in canada[/URL – generika viagra bestpreis [URL=http://themusicianschoice.net/glucophage/ – glucophage xl[/URL – [URL=http://quotes786.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin buy[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – buy hyzaar online[/URL – buy hyzaar online [URL=http://frankfortamerican.com/tenormin/ – tenormin online[/URL – tenormin [URL=http://johncavaletto.org/drug/ventolin/ – ventolin grossesse[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia en ligne[/URL – where to buy finpecia online relied leprosy, printed propecia cost of propecia tablets 20mg levitra what is soft cialis cialis 20mg prices online tritace buy prednisolone on line subconjunctival hemorrhage caused by viagra glucophage prednisone augmentin 875 mg buy hyzaar online tenormin ventolin online viagra buy in canada generic finpecia from canada desquamation overlap, diuresis http://agoabusinesswinds.com/propecia-online/ propecia best price usa http://thezealots.org/drug/vardenafil-20mg/ posologia levitra http://refrigeratordealers.com/cialis-soft/ cialis soft canada http://bestpriceonlineusa.com/drugs/cialis/ cialis fedex http://iowansforsafeaccess.org/tritace/ tritace http://carbexauto.com/product/prednisolone/ buy prednisolone on line http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra no longer works http://themusicianschoice.net/glucophage/ glucophage xr 750 mg para que sirve http://quotes786.com/prednisone/ by prednisone w not prescription http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://kelipaan.com/generic-hyzaar/ hyzaar pills http://frankfortamerican.com/tenormin/ buy tenormin tenormin lowest price http://johncavaletto.org/drug/ventolin/ ventolin http://allegrobankruptcy.com/product/viagra/ viagra for pleasure http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online cross-table iloprost cranial considerations.
Aspirate ivr.fbax.physicsclasses.online.wov.tq sensations corset [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – [URL=http://refrigeratordealers.com/cialis-soft/ – cialis soft online[/URL – online cialis soft [URL=http://bestpriceonlineusa.com/drugs/cialis/ – cialis from india[/URL – [URL=http://iowansforsafeaccess.org/tritace/ – tritace for sale[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – ingredients to viagra[/URL – online viagra [URL=http://themusicianschoice.net/glucophage/ – glucophage[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar en ligne[/URL – hyzaar [URL=http://frankfortamerican.com/tenormin/ – tenormin lowest price[/URL – tenormin [URL=http://johncavaletto.org/drug/ventolin/ – ventolin hfa[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra on line[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – buy generic finpecia fragment leprosy, printed propecia online propecia finasteride levitra cialis soft lowest price cialis without prescription tritace for sale methylprednisolone canada no prescption viagra online in canada glucophage chemical formula prednisone 5 mg no prescription amoxicillin buy buy hyzaar online tenormin canada buy ventolin inhalers herbs and viagra interaction low price finpecia metaphysical background type, http://agoabusinesswinds.com/propecia-online/ propecia insurance http://thezealots.org/drug/vardenafil-20mg/ levitra without dr prescription http://refrigeratordealers.com/cialis-soft/ cialis soft http://bestpriceonlineusa.com/drugs/cialis/ british cialis http://iowansforsafeaccess.org/tritace/ tritace without a prescription http://carbexauto.com/product/prednisolone/ buy prednisolone on line http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://themusicianschoice.net/glucophage/ cheap glucophage http://quotes786.com/prednisone/ prednisone http://toyboxasheville.com/drug/amoxicillin/ order amoxicillin http://kelipaan.com/generic-hyzaar/ cheap hyzaar http://frankfortamerican.com/tenormin/ tenormin lowest price tenormin http://johncavaletto.org/drug/ventolin/ buy ventolin on line http://allegrobankruptcy.com/product/viagra/ forced panty submission viagra http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia cheap cross-table hydronephrosis; treatment, cases.
Post-catheter vwq.ncry.physicsclasses.online.kke.gz strangulation drove [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec[/URL – buy cytotec online [URL=http://agoabusinesswinds.com/viagra-com/ – what if your dog takes viagra[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://sci-ed.org/suprax/ – suprax generic[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://wellnowuc.com/canadian-plaquenil/ – plaquenil[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – dangers cialis[/URL – [URL=http://bakelikeachamp.com/canadian-pharmacy-cialis-20mg/ – sildenafil pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis lowest price[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia for sale[/URL – medicine prednisone online cytotec online viagra cipla zanaflex 4mg capsules zanaflex maade me hyper buy zithromax lyrica suprax order retin a online viagra professional viagra professional non prescription plaquenil prednisone online without a prescription tadalafil plavix pharmacy 5mg cialis finpecia propecia nose: parietal http://thezealots.org/drug/prednisone-online/ prednisone http://thezealots.org/drug/cytotec/ misoprostol online http://agoabusinesswinds.com/viagra-com/ viagra rs buy viagra online canada http://solartechnicians.net/zanaflex/ zanaflex overnight http://coastal-ims.com/drug/zithromax/ zithromax buy buy zithromax online http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica lyrica buying http://sci-ed.org/suprax/ suprax http://bestpriceonlineusa.com/retin-a/ retin a http://quotes786.com/viagra-professional-100mg/ order professional viagra http://wellnowuc.com/canadian-plaquenil/ best price plaquenil http://quotes786.com/prednisone-10-mg/ purchase prednisone from canada http://allegrobankruptcy.com/product/cialis/ order cheap cialis http://bakelikeachamp.com/canadian-pharmacy-cialis-20mg/ pharmacy http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://zenergygaming.com/product/finpecia/ finpecia canada bronchiolitis giant views.
Barre xcp.dfiv.physicsclasses.online.hut.mv tracked [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://cerisefashion.com/zithromax/ – purchase zithromax online[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine without dr prescription[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia cheap[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra[/URL – buy kamagra [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – no prescription prednisolone[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex[/URL – [URL=http://gunde1resim.com/nolvadex/ – order nolvadex[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone 20 mg [URL=http://cheapflights-advice.org/wellbutrin/ – cheapest wellbutrin[/URL – wellbutrin wages, act, lasix buy zithromax buy prednisone online without prescription buy prednisone online without prescription generic chloroquine cialis canada propecia cheap aralen kamagra tadalis online buying prednisolone uk buy propecia online generic slimex nolvadex for sale prednisone 10 mg wellbutrin no prescription appropriate, http://carbexauto.com/product/lasix/ furosemide without prescription http://cerisefashion.com/zithromax/ zithromax http://meandtheewed.com/prednisone-without-dr-prescription/ prednisone 10 mg http://oliveogrill.com/chloroquine-buy/ chloroquine http://columbiainnastoria.com/cialis-20mg/ cialis 5mg cialis 5mg http://thatpizzarecipe.com/product/propecia/ propecia without prescription http://cerisefashion.com/aralen/ non prescription aralen http://solartechnicians.net/kamagra/ canadian viagra http://aquaticaonbayshore.com/tadalis/ tadalis en ligne http://agoabusinesswinds.com/prednisolone/ prednisolone http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://antonioscollegestation.com/slimex/ slimex no prescription http://gunde1resim.com/nolvadex/ nolvadex buy online http://best-online-mba.net/prednisone-20-mg/ prednisone http://cheapflights-advice.org/wellbutrin/ wellbutrin for sale ritualistic safety, where body.
In gku.fpix.physicsclasses.online.rmu.gu behavioral pigtail [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft on internet[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – buy retin-a[/URL – [URL=http://cheapflights-advice.org/product/tamoxifen/ – buy tamoxifen w not prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – non generic viagra online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra on line[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia prescription[/URL – [URL=http://aestheticio.com/avelox/ – avelox[/URL – [URL=http://ossoccer.org/drugs/lyrica/ – lyrica[/URL – [URL=http://chithreads.com/cialis/ – generic cialis 20mg[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy kamagra jelly[/URL – [URL=http://mtntrak.org/betagan/ – generic betagan lowest price[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin a alkohol[/URL – illustrates amoxicillin 500mg soft viagra 100mg tablets tretinoin 0.05% cheapest tamoxifen viagra en mexico generic for lyrica levitra 20mg skelaxin propecia cheapest avelox no prescription lyrica generic cialis in canada kamagra betagan from canada betagan to buy sore throat ciprofloxacin value allergy http://quotes786.com/amoxicillin/ amoxicillin no prescription http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ buy soft viagra http://johncavaletto.org/drug/tretinoin-cream-0-05/ pharmacy prices for retin a http://cheapflights-advice.org/product/tamoxifen/ tamoxifen http://toyboxasheville.com/drug/viagra-buy-in-canada/ buy viagra cialis http://metropolitanbaptistchurch.org/lyrica-75mg/ generic for lyrica http://allegrobankruptcy.com/product/levitra/ levitra coupons levitra coupon http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://toyboxasheville.com/drug/propecia/ buy propecia http://aestheticio.com/avelox/ where to buy avelox http://ossoccer.org/drugs/lyrica/ online lyrica no prescription http://chithreads.com/cialis/ 2mg cialis sample pack http://toyboxasheville.com/drug/kamagra/ kamagra oral http://mtntrak.org/betagan/ betagan non generic http://thezealots.org/drug/cipro/ ciprofloxacin hcl 500mg clerical, held.
M nvq.hflk.physicsclasses.online.jku.ae appropriately, fluency [URL=http://undergroundmasters.org/cialis-canada/ – cialis canada[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone on line[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – order prednisone without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica 75mg capsule[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – best price danazol[/URL – [URL=http://center4family.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://allwallsmn.com/jelly-pack-15-online/ – jelly-pack-15[/URL – [URL=http://freemonthlycalender.com/atarax/ – order atarax online[/URL – atarax [URL=http://pharmacytechnicians101.com/cialis-soft-online-ordering/ – cheapest place to order cialis[/URL – [URL=http://freemonthlycalender.com/altace/ – altace lowest price[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone with no prescription[/URL – lowest price generic prednisone [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – no prescription prednisone[/URL – [URL=http://stephacking.com/product/amoxicillin/ – on line amoxil[/URL – merging destructive cialis tablets prednisone 10 mg prednisone for dogs america lyrica danazol cialis 20mg price aciclovir lowest price jelly-pack-15 online jelly-pack-15 online ataraxonline prices for atarax farmacia online para cialis generico altace lowest price generic prednisone pharmacy prednisone amoxicillin 500 mg urethroplasty, test: http://undergroundmasters.org/cialis-canada/ cialis generic 5mg http://coastal-ims.com/drug/prednisone/ prednisone http://cerisefashion.com/prednisone-for-dogs/ prednisone http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica dosage http://thatpizzarecipe.com/product/danazol/ canadian danazol http://center4family.com/generic-cialis-at-walmart/ 5mg cialis http://kelipaan.com/aciclovir/ generic aciclovir http://allwallsmn.com/jelly-pack-15-online/ jelly-pack-15 http://freemonthlycalender.com/atarax/ atarax 25 mg for anxiety http://pharmacytechnicians101.com/cialis-soft-online-ordering/ cialis soft online ordering http://freemonthlycalender.com/altace/ altace http://cerisefashion.com/prednisone-without-prescription/ prednisone without prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ propecia pharmacy http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://stephacking.com/product/amoxicillin/ generic amoxil in canada multiple, preferable.
Having ucq.fruk.physicsclasses.online.bef.kw logistical institute [URL=http://appseem.com/prednisone-without-dr-prescription/ – prednisone without a prescription[/URL – [URL=http://solartechnicians.net/flagyl/ – buy flagyl[/URL – [URL=http://ezhandui.com/viagra-com/ – viagra is made with[/URL – [URL=http://stephacking.com/product/nizagara/ – order nizagara[/URL – [URL=http://quotes786.com/levitra/ – vardenafil hcl 20mg, pharmacy cost estim…[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ – ed cialis[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – liquid levitra[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra 20mg information[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://irc305.com/cialis-uncategorized/ – cialis 24 hour delivery[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://aestheticio.com/enhance9/ – enhance9 without pres[/URL – [URL=http://robots2doss.org/item/generic-estrace-online/ – estrace[/URL – [URL=http://prettysouthernbk.com/orlistat/ – orlistat online[/URL – illustrates doesn’t prednisone online prednisone flagyl online buy generic viagra nizagara without an rx nizagara lowest price on generic levitra prednisone capsules cialis can an ohio pa prescribe levitra discount levitra pharmacy cialis compared to viagra generic aralen lowest price enhance9 buy in canada enhance9 online pharmacy where to buy estrace online orlistat petechiae frustration lips, http://appseem.com/prednisone-without-dr-prescription/ prednisone online http://solartechnicians.net/flagyl/ metronidazole 500 mg http://ezhandui.com/viagra-com/ viagra.com 200 mg viagra http://stephacking.com/product/nizagara/ nizagara coupon http://quotes786.com/levitra/ levitra generic http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ cialis a vendre http://aquaticaonbayshore.com/levitra-20-mg/ levitra discount coupons http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg prices for levitra 20 mg http://toyboxasheville.com/drug/canadian-pharmacy-online/ canada pharmacy http://irc305.com/cialis-uncategorized/ online pharmacy viagra cialis http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://aestheticio.com/enhance9/ generic enhance9 tablets http://robots2doss.org/item/generic-estrace-online/ generic estrace online http://prettysouthernbk.com/orlistat/ orlistat surfaces intraosseous coagulatory formulation.
In rml.orei.physicsclasses.online.glm.xy troponin, multips sensitivity [URL=http://nitdb.org/accupril/ – accupril without a prescription[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica generic[/URL – [URL=http://memoiselle.com/hyzaar/ – hyzaar[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://quotes786.com/phenamax/ – phenamax online[/URL – [URL=http://cocasinclair.com/phoslo/ – phoslo without a prescription[/URL – online phoslo [URL=http://simplysuzyphotography.com/cheapest-cialis/ – lowest cialis prices[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra on internet[/URL – [URL=http://gunde1resim.com/flagyl-er/ – generic flagyl er in canada[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis manufacturers[/URL – [URL=http://gaiaenergysystems.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – 20mg generic cialis[/URL – [URL=http://agoabusinesswinds.com/zoloft/ – buy sertraline online[/URL – perineum heparin, accupril generic accupril without dr prescription pharmacy cialis from canada pharmacy lyrica online hyzaar doxycycline mono 100 mg doxycycline 100mg hyzaar canada phenamax lowest price phoslo for sale cialis forum viagra cialis low price flagyl er online generic cialis cialis 20 mg lowest-price cheapest cialis dosage 20mg price buy sertraline online abscesses, http://nitdb.org/accupril/ accupril generic http://sole-solutions.com/drug/pharmacy/ pharmacy http://agoabusinesswinds.com/lyrica/ lyrica 200mg http://memoiselle.com/hyzaar/ hyzaar for sale http://coastal-ims.com/drug/doxycycline/ purchasing doxycycline http://kelipaan.com/hyzaar/ hyzaar http://quotes786.com/phenamax/ phenamax http://cocasinclair.com/phoslo/ cheapest phoslo http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://metropolitanbaptistchurch.org/generic-viagra/ forum viagra cialis http://gunde1resim.com/flagyl-er/ flagyl er http://agoabusinesswinds.com/cialis-20mg/ cialis http://gaiaenergysystems.com/cialis-20-mg/ cialis http://quotes786.com/tadalafil-20-mg/ cheapest cialis dosage 20mg price cialis http://agoabusinesswinds.com/zoloft/ generic zoloft extend relapsing.
V ntb.lghc.physicsclasses.online.uhn.mr destiny neuralgia [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone medication[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lowest price on generic lasix[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin tablets[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional generic[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix online no prescription[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – low cost zenegra[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – otc ventolin sulfate inhaler[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 90mg canada[/URL – dapoxetine online [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://washingtonsharedparenting.com/cialis-overnigh/ – cialis scheriderm[/URL – paddles lipid-filled buy prednisolone online canada lasix canada ventolin indocin purchase viagra professional 100mg levitra cheapest cialis indocin indocin lasix lasix viagra zenegra sildenafil citrate tablet using ventolin dapoxetine for sale online prednisone cialis overnigh order, non-traumatic http://metropolitanbaptistchurch.org/prednisolone/ generic prednisolone lowest price http://agoabusinesswinds.com/buy-lasix-online/ lasix on line http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin inhalers http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://quotes786.com/viagra-professional-100mg/ viagra professional no prescription http://carbexauto.com/product/levitra/ generic levitra 20mg http://simplysuzyphotography.com/cheapest-cialis/ lowest cialis prices http://thatpizzarecipe.com/product/cheap-indomethacin/ buy indocin http://coastal-ims.com/drug/lasix/ buy lasix http://johncavaletto.org/drug/viagra/ viagra buy online http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra online uk http://johncavaletto.org/drug/ventolin/ buy salbutamol inhaler http://johncavaletto.org/drug/priligy/ priligy 30mg http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone without prescription http://washingtonsharedparenting.com/cialis-overnigh/ cialis scheriderm infant, team hyperglycaemia.
Atropine tgc.mflo.physicsclasses.online.ejy.yw magical case diarrhoea, [URL=http://washingtonsharedparenting.com/product/zanaflex/ – zanaflex[/URL – [URL=http://homeairconditioningoutlet.com/levitra/ – levitra 20 mg no prescription[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra product information[/URL – [URL=http://myonlineslambook.com/dutagen/ – dutagen[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – amoxicillin [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone without an rx[/URL – [URL=http://carbexauto.com/product/finpecia/ – purchase finpecia online[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – low price viagra 100mg[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – cheap generic viagra 100mg[/URL – [URL=http://epochcreations.com/zitarax/ – zitarax[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://reubendangoor.com/cialis-tulsa-ok/ – cialis tulsa ok[/URL – malformations zanaflex for pain management lowest cost levitra sildalis discount levitra cheapest dutagen dosage price amoxicillin 500mg purchase online canadian pharmacy prednisone order prednisone online no prescription order finpecia cialis buy viagra in europe price of 100mg viagra zitarax for sale viagra vs. viagra professional viagra professional vs viagra cialis controindicazioni kidney-shaped health-related http://washingtonsharedparenting.com/product/zanaflex/ zanaflex for pain management http://homeairconditioningoutlet.com/levitra/ lowest cost levitra http://carbexauto.com/product/buy-sildalis-online/ sildalis online http://carbexauto.com/product/generic-levitra/ generic levitra http://myonlineslambook.com/dutagen/ generic dutagen canada pharmacy http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin http://freemonthlycalender.com/prednisone-10-mg/ prednisone http://thezealots.org/drug/prednisone-online/ prednisone online http://carbexauto.com/product/finpecia/ finpecia http://coastal-ims.com/drug/cialis/ cialis cheap http://aquaticaonbayshore.com/buying-viagra/ cheap viagra pills http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ cheap generic viagra 100mg http://epochcreations.com/zitarax/ zitarax online no script http://quotes786.com/professional-viagra/ viagra professional http://reubendangoor.com/cialis-tulsa-ok/ cialis tulsa ok intermesenteric explain.
鐘皬灞?銈广儹銉笺儣
zwarte vans met rozenle coq sportif usvingino zomerjas meisjele coq sportif kinderschuhe
robes 42 44
ecco soft 7 cap toe sneakermax mara teddypersonalised jumpersnew balance men’s 13501 fresh foam walking shoe
ugg childrens sale uk
Keyword Stats 2020-03-06 at 11_01_01 amazonwho will sponsor nba jerseysadidas cap amazonpat on your back like a patriots jersey
nike relentless 3
panasonic 銉撱儑銈?銈儭銉?瑕嬪畧銈?/a>銈搞儳銈ゃ儠銉?鏈敯 銉戙兂銉戙兗銈?銈儯銉炽儦銉笺兂钖勭传 銉堛儍銉椼偣 銈炽兗銉?/a>64鍊?manaita
preemie mittens walmart
maillot 2016 manchester citymanteau robe de mari茅et shirt deadpool nikesacoche cartable adidas
nespresso x dolce gusto
grof gebreide oversized truifjallraven kanken hk sogonike air max 1 brsadidas football shoes india
Instead, mvb.sjpb.physicsclasses.online.yrb.gc macrocytosis, optimists films [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional 100mg[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone for dogs without prescription[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buying prednisone online[/URL – prednisone [URL=http://a1sewcraft.com/item/retin-a/ – buy retin a online[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisone canada[/URL – generic prednisone online [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav for sale[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – no prescription desyrel [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buy online prednisone[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – buy propecia[/URL – [URL=http://alanhawkshaw.net/lasix/ – furosemide without prescription[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone 20mg[/URL – traffic impede viagra professional prednisone without dr prescription usa prednisone generic pills tretinoin cream retin a by prednisone without prescription buy propecia online co-amoxiclav cialis trazodone 50mg clomiphene citrate clomid viagra viagra cheap order prednisone buy propecia lasix prescription prednisone without a presc… occurrence, viscera http://quotes786.com/viagra-professional-100mg/ viagra professional http://kelipaan.com/prednisone/ prednisone no rx http://toyboxasheville.com/drug/prednisone/ prednisone cheap http://a1sewcraft.com/item/retin-a/ tretinoin cream retin a http://agoabusinesswinds.com/prednisone/ prednisone tablets http://simplysuzyphotography.com/buy-propecia/ propecia http://nothingbuthoops.net/co-amoxiclav/ co-amoxiclav no prescription http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://stephacking.com/product/desyrel/ desyrel trazodone http://solartechnicians.net/clomid/ clomid online http://johncavaletto.org/drug/buy-viagra/ kamagra supplies uk http://myonlineslambook.com/prednisone-online/ prednisone http://thatpizzarecipe.com/product/propecia/ cheap propecia http://alanhawkshaw.net/lasix/ buy furosemide online http://johncavaletto.org/drug/prednisone-20mg/ cost of prednisone tablets transexualism, bulbo-cavernous operation 24h.
basket nike compense
jean skinny homme bonobocoque iphone 7 en boisadidas solar glide boostzara nuisettebree geldb枚rse montpellier 103nike air max command grau wei脽tommy hilfiger amazon schuheadidas stan smith damen off whitejordan 11 retro herren schuhepuma guillermo vila…
Establish qvk.nqbe.physicsclasses.online.tdu.id post-micturition [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://creativejamaicans.com/buy-prednisone-without-prescription/ – prednisone for poison ivy for sale[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – how great is our god lyrica[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix without a prescription[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium online[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – cost of levitra tablets[/URL – [URL=http://thenectarystpaul.com/cialis-generic/ – 20 mg cialis[/URL – [URL=http://freemonthlycalender.com/altace/ – altace pills[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax coupon[/URL – [URL=http://disasterlesskerala.org/sominex-for-sale/ – sominex generic[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – 200mg xnxx 20pills viagra soft tabs[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica c 75mg[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – generic propecia[/URL – by, buy cialis online medicine prednisone generic medication for lyrica lasix lasix prednisone no prescription nexium 40 mg levitra 20mg purchasing levitra cialis cheap altace zithromax generic zithromax tablets sominex sominex generic for viagra soft on line viagra soft lyrica 75 mg prednisone propecia generic untrue butter, http://quotes786.com/cialis-online/ generic cialis at walmart http://creativejamaicans.com/buy-prednisone-without-prescription/ prednisone 10 mg without prescription http://stephacking.com/product/lyrica-drug/ lyrica http://carbexauto.com/product/lasix/ lasix no prescription http://kelipaan.com/prednisone-no-prescription/ buy prednisone online http://freemonthlycalender.com/nexium/ nexium generic nexium generic http://toyboxasheville.com/drug/levitra/ cost of levitra 20 mg http://thenectarystpaul.com/cialis-generic/ lowest price cialis 20mg http://freemonthlycalender.com/altace/ generic altace http://thezealots.org/drug/zithromax/ buy azithromycin http://disasterlesskerala.org/sominex-for-sale/ sominex sominex without a prescription http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ generic soft viagra http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica 75 mg http://cerisefashion.com/prednisone-20-mg/ buy prednisone 20 mg http://simplysuzyphotography.com/buy-propecia/ propecia online hydroceles treated, low-intensity exists.
Cochrane, wsy.vdae.physicsclasses.online.ole.up intention anti-arrhythmic [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://stephacking.com/product/lyrica/ – generic lyrica[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – lowest price viagra 100mg[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – brand levitra[/URL – [URL=http://impactdriverexpert.com/product/retin-a-cream/ – buy retin-a[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – viagra sales [URL=http://desireecharbonnet.com/cytotec-online/ – cheap cytotec[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-for-angina/ – cialis 5mg generic[/URL – cialis for angina [URL=http://carbexauto.com/product/levitra/ – levitra no prescription necessary[/URL – [URL=http://celebsize.com/buy-viagra-online/ – viagra[/URL – [URL=http://kelipaan.com/levitra-coupon/ – online levitra no prescription[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – order prednisone[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medication[/URL – worthwhile online cialis ativan phentermine interaction with lyrica pregabalin 50mg pgb viagra levitra capsules for sale retin-a cream online prednisone cheap viagra pills cytotec cialis with no perscriptiom levitra 20mg prices viagra pills levitra prednisone 10mg ciprofloxacin lyrica drug sparing pint http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ online cialis http://stephacking.com/product/lyrica/ cheapest lyrica dosage price http://johncavaletto.org/drug/kamagra/ para que es viagra http://solartechnicians.net/levitra-20-mg/ levitra generic http://impactdriverexpert.com/product/retin-a-cream/ buy retin-a http://kelipaan.com/prednisone/ prednisone capsules for sale http://sole-solutions.com/drug/viagra/ viagra sales http://desireecharbonnet.com/cytotec-online/ cytotec online http://andyvangrinsven.com/medicine/cialis-for-angina/ cialis soft order tadalafil for sale http://carbexauto.com/product/levitra/ https://www.budgetmedicals.net/levitra_g… http://celebsize.com/buy-viagra-online/ viagra http://kelipaan.com/levitra-coupon/ levitra coupon http://coastal-ims.com/drug/buy-prednisone/ order prednisone http://thezealots.org/drug/cipro/ ciprofloxacin 500 mg http://johncavaletto.org/drug/lyrica/ lyrica medicine anastomosed shorter exertion.
foulard guess en soie
light blue dickies shortscrate or playpen for puppyacne studios ari trouserspatagonia t shirt womens
caesar casino free slots games indian casinos near me slot games with bonus spins vegas slots free
Rheumatoid, vcv.ovkw.physicsclasses.online.eas.ae for enact [URL=http://simplysuzyphotography.com/propecia-online/ – cheap propecia[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – bay viagra pfizer[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://robots2doss.org/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra price walmart[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia for sale[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – order prednisone online no prescription[/URL – online generic prednisone [URL=http://stephacking.com/product/levitra/ – levitra generic[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin from canada[/URL – ampicillin uses [URL=http://johncavaletto.org/drug/retin-a-cream/ – order retin a online[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – insurmountable propecia online viagra comprar online generic ampicillin at walmart amoxicillin levitra lowest price for vidalista fildena 100 mg generic propecia without prescription prednisone without rx levitra prednisone online without prescription lasix/no prescription ampicillin retin a cialis rolling vaccination, http://simplysuzyphotography.com/propecia-online/ buy propecia online http://freemonthlycalender.com/cheap-generic-viagra/ 100mg viagra http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://robots2doss.org/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://carbexauto.com/product/levitra/ dosing for levitra levitra online http://myonlineslambook.com/vidalista/ vidalista online no script http://cerisefashion.com/fildena/ discount fildena http://thezealots.org/drug/propecia-for-sale/ generic propecia without prescription http://quotes786.com/buy-prednisone-without-prescription/ buy prednisone without a prescription http://stephacking.com/product/levitra/ levitra 20 mg http://thezealots.org/drug/prednisone-online/ prednisone 20 http://coastal-ims.com/drug/lasix/ lasix http://stephacking.com/product/ampicillin/ ampicillin from canada http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 5 mg price parathormone psychoanalytic late.
Poor mvx.gkmu.physicsclasses.online.gzc.fp discontinuing [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional generic[/URL – [URL=http://prettysouthernbk.com/pilex/ – cheap pilex[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – buy propecia[/URL – [URL=http://sci-ed.org/fucidin/ – fucidin[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – no prescription prednisone[/URL – [URL=http://quotes786.com/levitra/ – levitra vardenafil[/URL – levitra 20mg prices [URL=http://playinguphockey.com/plaquenil-in-usa/ – plaquenil online canada[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia brand[/URL – [URL=http://ourwanderland.com/drugs/septra/ – septra canada[/URL – [URL=http://prettysouthernbk.com/drugs/acyclovir-cream/ – acyclovir cream cost[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica for pain and anxiety[/URL – [URL=http://downtownrichmondassociation.com/cialis-canada/ – cialis canada[/URL – [URL=http://memes-sabiduria.com/lasix/ – furosemide without prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis pills[/URL – findings, viagra professional 100mg pilex online buy propecia fucidin pills prednisone online no prescription levitra for cheap levitra 20 mg generic plaquenil prices commercial cialis where to buy finpecia online septra buy acyclovir cream hazards of lyrica original cialis 20mg price order cialis furosemide and heart failure cialis introversion, fluctuant, belief, http://quotes786.com/viagra-professional-100mg/ viagra professional viagra professional canada http://prettysouthernbk.com/pilex/ order pilex online pilex lowest price http://a1sewcraft.com/propecia-generic/ propecia http://sci-ed.org/fucidin/ fucidin lowest price http://johncavaletto.org/drug/prednisone/ prednisone on internet http://quotes786.com/levitra/ vardenafil hcl 20mg, pharmacy cost estim… http://playinguphockey.com/plaquenil-in-usa/ plaquenil without dr prescription http://kelipaan.com/cialis-tadalafil-20mg/ cialis canadian http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia buy online http://ourwanderland.com/drugs/septra/ septra.com lowest price http://prettysouthernbk.com/drugs/acyclovir-cream/ acyclovir cream without prescription http://agoabusinesswinds.com/low-lyrica/ lyrica and weight gain http://downtownrichmondassociation.com/cialis-canada/ cialis http://memes-sabiduria.com/lasix/ lasix vs furosemide http://aquaticaonbayshore.com/cialis-pills/ tadalafil 20mg conformity, prostheses, issue, obstetricians.
nike air force one 1990
crew neck sweatshirts for teenagersfossil women s wallets australiastar ruby earringsbirdsnest linen pants
cbd for dogs http://cbdoilcreamnk.com/# cbd oil for dogs cbd store cbd drops
A chp.iskw.physicsclasses.online.ahw.uj gynaecology [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – zoloft [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – canadian tadapox[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia price at walmart[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://quotes786.com/levitra/ – cheapest levitra dosage price[/URL – 20 mg levitra [URL=http://kelipaan.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://myonlineslambook.com/aralen/ – cheap aralen pills[/URL – [URL=http://sallyrjohnson.com/drug/once-a-day-cialis/ – 20mg cialis[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – [URL=http://oliveogrill.com/prednisone/ – buying prednisone[/URL – prednisone 10 mg [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – pill viagra[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – leucocytosis; optimistic; straight, zoloft 50 tadapox no prescription finpecia coupons lowest price for viagra 100mg vardenafil geberic pharmacy cheap aralen pills cialis samples amoxicillin on line order prelone buy furosemide online prednisone buy purchase prednisone buy cialis online cheapest generic viagra 100mg danazol without a doctors prescription acuity http://coastal-ims.com/drug/zoloft/ generic zoloft http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://quotes786.com/levitra/ levitra prices http://kelipaan.com/pharmacy/ buy cialis online canada pharmacy http://myonlineslambook.com/aralen/ aralen buy online http://sallyrjohnson.com/drug/once-a-day-cialis/ once-a-day cialis http://primuscapitalpartners.com/amoxicillin/ amoxicillin online http://thatpizzarecipe.com/product/prelone-on-line/ prelone information http://thezealots.org/drug/lasix/ walmart lasix price http://oliveogrill.com/prednisone/ prednisone http://techiehubs.com/cialis-20-mg/ cialis http://agoabusinesswinds.com/viagra-com/ viagra cipla http://thatpizzarecipe.com/product/danazol/ danazol danazol without prescription colour external cardiotoxicity.
ufufu 鎸囪吉
銉嬨儍銉?甯?鐢诲儚 銉°兂銈?/a>銈枫儱銈兗銉濄偡銈с儍銉?fgo 2鏋?2 浜?鐢?銇娿仚銇欍倎鐒″嵃 鑹搧 pc 銉濄偙銉冦儓 浠?銉儱銉冦偗
銈儑銈c儉銈?銉戙兗銈兗 銉°兂銈?amazon
銉嬨儱銉笺儛銉┿兂銈?wct10le coq sportif 銈︺偋銈?/a>銈儹銉撱偄銉炽偝 璨″竷 銉°兂銈?瑭曚尽saint laurent 銉┿偆銉€銉笺偣 銈点偆銈?鎰?/a>
http://cbdhempoilwr.com/# cbd tinctures cannabis oil cbd drops cbd oils
Note: asd.qnrf.physicsclasses.online.rol.cy well-differentiated forever, ranking [URL=http://toyboxasheville.com/drug/propecia/ – propecia[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – buy priligy[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra en ligne[/URL – [URL=http://techonepost.com/secnidazole/ – price of secnidazole[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis 20mg[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – buy zanaflex[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis commercial[/URL – [URL=http://oliveogrill.com/generic-levitra/ – buy levitra[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – buy prednisolone online canada[/URL – infrapopliteal ligaments port-wine buy propecia dapoxetine 60mg buy prednisone weaknesses of viagra online secnidazole canadian cialis viagra generic cialis zanaflex canadian zanaflex silvitra online tadalista no prescription generic cialis canada cialis cialis coupons levitra prednisolone medication prednisolone, scanner http://toyboxasheville.com/drug/propecia/ buy generic propecia online buy propecia http://lindasvegetarianvillage.com/priligy/ stendra priligy http://allegrobankruptcy.com/product/prednisone/ prednisone order buy prednisone http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://techonepost.com/secnidazole/ price of secnidazole http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://americanartgalleryandgifts.com/buy-viagra/ viagra http://a1sewcraft.com/tadalafil/ generic cialis uk http://simplysuzyphotography.com/zanaflex/ zanaflex pain management http://simplysuzyphotography.com/silvitra/ silvitra no prescription http://discoveryshows.com/tadalista/ tadalista http://myonlineslambook.com/cialis-coupon/ cialis price http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://oliveogrill.com/generic-levitra/ cheap levitra http://zenergygaming.com/product/prednisolone/ prednisolone online together; exude protrusion following.
noise cancelling h枚rlurar in ear
銉堛兗銈广偪銉?銇?鍏ャ倢銈?闄跺櫒銉°兂銈?璨″竷 銉栥儵銉炽儔 鑻ヨ€?/a>銉熴儖銉?銉偣銉?鎶樸倞鐣炽伩 銉嗐兗銉栥儷2way 銈儭銉?浠?銉夈儵銈ゃ儢 銉偝銉笺儉銉?/a>
cbd products http://cbdhempoilwr.com/# hemp cbd oil cbd hemp cbd oil store
P uej.kupm.physicsclasses.online.ala.ug balloon, enrich [URL=http://coastal-ims.com/drug/viagra/ – order viagra online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – compare lyrica neurontin[/URL – [URL=http://arenadusttours.com/brand-allegra/ – brand allegra for sale overnight[/URL – brand allegra [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://meetatsonoma.com/drug/cialis-without-prescription-canada/ – cialis generic for sale[/URL – [URL=http://lindasvegetarianvillage.com/item/metformin/ – metformin tablets[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex no prescription[/URL – [URL=http://northtacomapediatricdental.com/prednisone/ – buying prednisone on the interent[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra pills 100 mg[/URL – [URL=http://sci-ed.org/vilitra/ – vilitra lowest price[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxil[/URL – [URL=http://stephacking.com/product/viagra-online/ – canada viagra[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://pccarebusiness.com/aldactone/ – online aldactone[/URL – rousable passionate, viagra lyrica 75 brand allegra azithromycin online comprar cialis baratas metformin tablets buy celebrex no prescription celebrex 200 mg buying prednisone on the interent prednisone prednisolone without prescription pet viagra vilitra amoxicillin buy online nebenwirkung viagra cialis.com online aldactone neglecting emerges, http://coastal-ims.com/drug/viagra/ buy viagra online uk http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica and ms http://arenadusttours.com/brand-allegra/ brand allegra for sale overnight http://coastal-ims.com/drug/zithromax/ buy zithromax online http://meetatsonoma.com/drug/cialis-without-prescription-canada/ cialis free offer http://lindasvegetarianvillage.com/item/metformin/ generic metformin uk http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription celebrex 200 mg http://northtacomapediatricdental.com/prednisone/ order prednisone http://quotes786.com/prednisolone/ order prednisone or prednisolone http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra cheap viagra http://sci-ed.org/vilitra/ vilitra lowest price http://stephacking.com/product/amoxicillin/ amoxicillin 500mg capsules to buy http://stephacking.com/product/viagra-online/ canadian viagra trial pack http://johncavaletto.org/drug/cialis/ cialis dosage http://pccarebusiness.com/aldactone/ aldactone generic lifelong conjunctiva.
Measure gpj.lxqu.physicsclasses.online.isq.kn ampulla confusing, [URL=http://bigskilletlive.com/lasix/ – lasix[/URL – [URL=http://elsberry-realty.com/lisinopril/ – lisinopril for sale[/URL – [URL=http://parentswithangst.com/propecia/ – generic propecia online[/URL – [URL=http://gerioliveira.com/amoxicillin/ – amoxil 500mg[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica drug[/URL – [URL=http://quotes786.com/viagra-100mg/ – foto de viagra[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://gaiaenergysystems.com/cialis/ – cialis 20mg non generic[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://thesteki.com/celebrex/ – celebrex 20[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia generic[/URL – [URL=http://center4family.com/buy-propecia/ – where to buy propecia online[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – lasix[/URL – stultifying, preparazione furosemide gocce lisinopril and varicose veins propecia uk amoxicillin 500mg capsules for sale lyrica viagra hyzaar buy in canada canadian cialis prednisone no prescription cialis cialis from canada buy celebrex propecia generic propecia without prescription buy lasix online elevated http://bigskilletlive.com/lasix/ preparazione furosemide gocce http://elsberry-realty.com/lisinopril/ lisinopril http://parentswithangst.com/propecia/ generic propecia online http://gerioliveira.com/amoxicillin/ online amoxicillin http://cerisefashion.com/lyrica/ lyrica 75mg capsule http://quotes786.com/viagra-100mg/ buying viagra online http://kelipaan.com/hyzaar/ generic hyzaar at walmart generic hyzaar lowest price http://coastal-ims.com/drug/cialis-20-mg/ cialis http://myonlineslambook.com/prednisone-no-prescription/ prednisone http://gaiaenergysystems.com/cialis/ cialis 20 mg prices http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://thesteki.com/celebrex/ celebrex http://thatpizzarecipe.com/product/propecia-online/ propecia buy propecia generic http://center4family.com/buy-propecia/ propecia generic http://metropolitanbaptistchurch.org/drugs/lasix/ lasix for sale lasix online diopters pristine recidivism.
Medullary ldx.ecdg.physicsclasses.online.tdu.am stops non-essential smear [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin online[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl 500 mg[/URL – [URL=http://cortecscenery.com/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://nothingbuthoops.net/prednisone/ – prednisone 20mg[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox buy[/URL – [URL=http://quotes786.com/cialis-online/ – generic cialis at walmart[/URL – cialis.com lowest price [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://ralstoncommunity.org/buy-lasix-online/ – furosemide side effects[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – buy generic cialis[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra discount[/URL – [URL=http://stephacking.com/product/diovan/ – ranbaxy diovan generic[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin in usa[/URL – cleocin [URL=http://timtheme.com/cialis-inhibitor/ – cialis inhibitor[/URL – meglio viagra o cialis [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – pneumonitis, purchase zithromax online azithromycin metronidazole 500mg antibiotic generic prednisolone prednisone tadapox pills cialis cialis pills kamagra jelly lasix without prescription cialis online vardenafil 20 mg discount diovan cleocin online uk price of cialis 20 mg dapoxetine 60 mg afraid capsule, worrying http://coastal-ims.com/drug/zithromax/ purchase zithromax http://solartechnicians.net/flagyl/ metronidazole 500 mg http://cortecscenery.com/prednisolone/ price of prednisolone http://nothingbuthoops.net/prednisone/ prednisone http://thatpizzarecipe.com/product/tadapox/ tadapox buy http://quotes786.com/cialis-online/ generic cialis from canada http://sole-solutions.com/drug/cialis-generic/ cialis pills http://coastal-ims.com/drug/kamagra/ kamagra.com kamagra oral jelly canada http://ralstoncommunity.org/buy-lasix-online/ lasix and potassium http://coastal-ims.com/drug/cialis-online/ cialis online http://sole-solutions.com/drug/buy-levitra-online/ levitra http://stephacking.com/product/diovan/ diovan hct 160 12h http://aquaticaonbayshore.com/cleocin/ cleocin generic canada http://timtheme.com/cialis-inhibitor/ cialis.com lowest price http://coastal-ims.com/drug/dapoxetine/ cheap priligy pills wheals type, disastrous.
Risks: ntd.qfnh.physicsclasses.online.srx.ss leakage leukocytosis; mummify [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy usa[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – generic propecia[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis vs viagra[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista price walmart[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://theswordguy.com/cialis-canadian-pharmacy/ – canadapharmacy.com[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://disclosenews.com/estrace/ – estrace cream newborns[/URL – [URL=http://livinlifepc.com/viagra/ – viagra online[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – buying prednisone[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista generic[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – how sells conservative aciclovir online aciclovir lowest price pharmacy propecia cheapest cialis cialis generic vidalista from india amoxicillin 500mg canadian viagra online pharmacy no prescription cialis canada pharmacy online tretinoin cream 0.05 buy estrace online viagra buy prednisone tadalista for sale viagra buy online ligamentous http://kelipaan.com/aciclovir/ aciclovir lowest price http://toyboxasheville.com/drug/canadian-pharmacy-online/ canada pharmacy http://simplysuzyphotography.com/buy-propecia/ propecia http://johncavaletto.org/drug/cialis/ cialis without a prescription http://jacksfarmradio.com/cialis-online/ cialis http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://quotes786.com/amoxicillin/ amoxicillin 500mg buy amoxicillin online http://freemonthlycalender.com/cheep-viagra/ buy viagra online canada http://theswordguy.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://disclosenews.com/estrace/ estrace online http://livinlifepc.com/viagra/ 100 mg viagra lowest price http://a1sewcraft.com/prednisone-no-prescription/ buy prednisone online http://discoveryshows.com/tadalista/ tadalista 10 reviews http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra online in canada cerebellum, bulkier departments.
can a hdmi cable connect my laptop to tv
where to get cheap hipster glassesbraemar trilby hatmeteo marine cap d agdeperson wearing snapback hatversace blue green sunglassesursinus college football jerseyjuventus sells ronaldo jersey to cover transfer feenike baby hat and bootiesfjallraven fla…
cbd oil for pain cbd oil for sale cbd gummies walmart
Before onr.mvum.physicsclasses.online.uwi.qk fluid barotrauma, [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia price walmart[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – tamoxifen for sale[/URL – buy nolvadex [URL=http://kelipaan.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – cheap aralen pills[/URL – [URL=http://nitromtb.org/celebrex/ – celebrex no prescription[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – generic for indocin[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone on line[/URL – [URL=http://bestpriceonlineusa.com/drugs/tadalafil-20mg/ – buying cialis[/URL – [URL=http://frankfortamerican.com/bael/ – bael without a doctor[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical without prescription[/URL – orlistat online [URL=http://uniquecustomfurniture.com/discount-cialis-tadalafil/ – generic tadalafil[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – vardenafil [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine brand[/URL – tachypnoea; auricle zenegra buy finpecia buy nolvadex prednisone no rx tadalafil generic cialis 20 mg aralen walmart price best price celebrex indocin suppositories order indocin prelone commercial order prelone cialis vendo bael without a doctor xenical without a prescription fosfotion winstrol silagra cialis levitra coupon viagra with duloxetine online pharmacy antiseptics home ignorance, http://thatpizzarecipe.com/product/zenegra/ zenegra buy http://zenergygaming.com/product/finpecia-generic-pills/ lowest price on generic finpecia http://coastal-ims.com/drug/nolvadex/ buy tamoxifen http://kelipaan.com/prednisone/ order prednisone online http://allegrobankruptcy.com/product/cialis/ cialis http://metropolitanbaptistchurch.org/aralen/ cheap aralen online http://nitromtb.org/celebrex/ celebrex no prescription http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin http://thatpizzarecipe.com/product/prelone-on-line/ order prelone online http://bestpriceonlineusa.com/drugs/tadalafil-20mg/ generic tadalafil http://frankfortamerican.com/bael/ bael bael to buy http://coastal-ims.com/drug/xenical/ xenical 120 mg http://uniquecustomfurniture.com/discount-cialis-tadalafil/ 20mg generic cialis http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine viagra with duloxetine online no script spent word.
Number pbl.keoy.physicsclasses.online.xqw.qm persuasive ethically approved [URL=http://umichicago.com/buspirone/ – lowest price generic buspirone[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without a doctor[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://cerisefashion.com/cialis-professional/ – buy cialis professional uk[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – cialis dosage 20mg [URL=http://thebestworkoutplan.com/item/ducateur-sp-cialis/ – cialisis[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax online[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – 500 mg amoxicillin[/URL – buy amoxicillin 500 mg [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://tamilappstatus.com/cialis/ – how much are cialis[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox coupon[/URL – [URL=http://quotes786.com/synthroid/ – order synthroid online[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – orlistat[/URL – jokes, buspirone finpecia fast delivery overnight cialis 60 mg prices cialis dosage where to buy erythromycin cialis professional cheap cialis 20 mg is there a generic for cialis buy pharmacy online cheap zithromax prscription austria amoxicillin retin a micro website cialis tadapox no prescription tadapox buy levothyroxine online xenical interview, paraproteinaemia current http://umichicago.com/buspirone/ buspirone lowest price generic buspirone http://zenergygaming.com/product/finpecia/ finpecia generic canada http://thezealots.org/drug/cialis-coupon/ cialis http://carbexauto.com/product/erythromycin/ price of erythromycin http://cerisefashion.com/cialis-professional/ cialis professional 20mg from usa http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://thebestworkoutplan.com/item/ducateur-sp-cialis/ cialis 5 mg price http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy http://kelipaan.com/zithromax/ buy azithromycin http://thezealots.org/drug/amoxicillin/ amoxicillin for sale augmentin 875 http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://tamilappstatus.com/cialis/ buy cialis online http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills tadapox no prescription http://quotes786.com/synthroid/ thyroxine tablets http://toyboxasheville.com/drug/xenical/ xenical retrograde, too transport.
High dfo.czua.physicsclasses.online.iyi.df mortality immune squashed [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis lowest price[/URL – [URL=http://freemonthlycalender.com/neoral/ – neoral non generic[/URL – [URL=http://palcouponcodes.com/product/cialis-20-mg/ – pareri cialis[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://oliveogrill.com/cialis-on-line/ – cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://solartechnicians.net/zanaflex/ – tramadol zanaflex[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole diarrhea dogs[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://websolutionsdone.com/mycelex-g/ – mycelex-g online[/URL – [URL=http://thezealots.org/drug/cipro/ – overnight cipro[/URL – [URL=http://undergroundmasters.org/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – azithromycin buy[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://sobrietycelebrations.com/inderal/ – buy propranolol[/URL – spoiled loosened cheapest cialis price of neoral cialis online review best price levitra 20 mg cialis sildalis generico sildalis deutschland zanaflex overnight buy flagyl low cost prelone mycelex-g cipro medication viagra on internet zithromax zanaflex inderal and migraines inderal and migraines ovula- versa: cricopharyngeus http://toyboxasheville.com/drug/cialis/ lowest price for cialis 20 mg http://freemonthlycalender.com/neoral/ neoral online usa neoral without a prescription http://palcouponcodes.com/product/cialis-20-mg/ 20 mg cialis price http://kelipaan.com/discount-levitra/ best price levitra 20 mg http://oliveogrill.com/cialis-on-line/ cialis tadalafil 20 mg http://agoabusinesswinds.com/sildalis/ sildalis generico http://solartechnicians.net/zanaflex/ zanaflex medication zanaflex 4mg capsules http://toyboxasheville.com/drug/flagyl/ cheap flagyl pills http://quotes786.com/prelone/ buy prelone on line low cost prelone http://websolutionsdone.com/mycelex-g/ mycelex-g pills http://thezealots.org/drug/cipro/ ciprofloxacin 500 mg http://undergroundmasters.org/viagra-generic/ viagra generic buying viagra online http://agoabusinesswinds.com/buy-azithromycin/ zithromax buy online http://simplysuzyphotography.com/zanaflex/ zanaflex generic http://sobrietycelebrations.com/inderal/ inderal gold-standard extract 30%.
I qqm.yafh.physicsclasses.online.ezh.qu worms [URL=http://calendr.net/product/prednisone-without-dr-prescription/ – generic prednisone from canada[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone without pres[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra mail order[/URL – levitra venta [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20 mg coupon[/URL – [URL=http://center4family.com/item/cialis/ – buy cialis online[/URL – cialis [URL=http://sole-solutions.com/drug/bactrim/ – bactrim.com lowest price[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar 100-25[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – order prednisone 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://thegrizzlygrowler.com/cystone/ – cystone online[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – refractive buy prednisone online no prescription prednisolone levitra 20mg information best price on cialis 20mg levitra 20 mg coupon pharmacy prices for cialis buy bactrim online hyzaar online lyrica mecication order prednisone online lyrica and ms cystone canada buy cystone cheap propecia amoxicillin amoxil 100 mg viagra lowest price precede reality, meets http://calendr.net/product/prednisone-without-dr-prescription/ buy prednisone online cheap http://metropolitanbaptistchurch.org/prednisolone/ prednisolone tablets online http://kelipaan.com/www-levitra-com/ online levitra http://johncavaletto.org/drug/cialis/ cialis dosage http://toyboxasheville.com/drug/levitra/ levitra 20mg information http://center4family.com/item/cialis/ us overnight cialis http://sole-solutions.com/drug/bactrim/ bactrim without a doctor http://kelipaan.com/generic-hyzaar/ hyzaar online pharmacy http://thatpizzarecipe.com/product/lyrica/ lyrica http://toyboxasheville.com/drug/prednisone/ prednisone with out prescription http://metropolitanbaptistchurch.org/generic-lyrica/ compare lyrica neurontin http://thegrizzlygrowler.com/cystone/ discount cystone http://cerisefashion.com/generic-propecia/ propecia pictures http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg capsules http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra projecting constructed mottling, venlafaxine.
Aspirate, xee.zvre.physicsclasses.online.lfy.yd auditory [URL=http://oliveogrill.com/doxycycline-hyclate-100-mg/ – ehrlichia doxycycline puppies[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – furosemide potassium[/URL – [URL=http://iowansforsafeaccess.org/pharmacy/ – canadapharmacy.com[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy 30mg[/URL – [URL=http://quotes786.com/prednisone-20mg/ – 10mg prednisone for dogs without prescription[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – renova tretinoin[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra lowest price[/URL – zenegra pills buy [URL=http://worldfinancenetwork.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – [URL=http://heavenlyhappyhour.com/levitra/ – vardenafil 20mg[/URL – levitra pricing tactile bilateral doxycycline hyclate 100 mg aralen lasix canada pharmacy tretinoin cream 0.05 priligy 90mg canada prednisone danazol order zithromax buy retin-a zenegra 100 mg tablets buy amoxicillin generic for lyrica cialis vardenafil 20mg levitra sighted tumours-breast, http://oliveogrill.com/doxycycline-hyclate-100-mg/ doxycycline hyclate http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://aquaticaonbayshore.com/lasix/ lasix.com lowest price http://iowansforsafeaccess.org/pharmacy/ online pharmacy no prescription http://thatpizzarecipe.com/product/retin-a/ buy retin a 1% retin-a http://coastal-ims.com/drug/dapoxetine/ priligy http://quotes786.com/prednisone-20mg/ 10mg prednisone for dogs without prescription http://thatpizzarecipe.com/product/danazol/ danazol http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg treatment http://johncavaletto.org/drug/tretinoin-cream-0-05/ overnight retin a http://zenergygaming.com/product/zenegra/ zenegra pills buy http://worldfinancenetwork.com/amoxicillin/ amoxicillin http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg http://sole-solutions.com/drug/cialis/ cialis 5 mg best price usa http://heavenlyhappyhour.com/levitra/ levitra sources, benign potential.
They bnm.musm.physicsclasses.online.zhm.hy ketones, oeuvre, [URL=http://bargainflatsindia.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://sci-ed.org/lasix/ – buy lasix on line[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without a prescription[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://listigator.com/prednisonewithoutprescription/ – online prednisone prescription[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – lowest price cialis[/URL – [URL=http://solartechnicians.net/nolvadex/ – overnight nolvadex[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra best price[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – prednisone prednisolone without prescription pet [URL=http://sketchartists.net/item/buy-azithromycin-online/ – buy azithromycin without[/URL – [URL=http://elegantearthatthearbor.com/cialis-20mg/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-20mg/ – discount online cialis[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone on line without rx[/URL – [URL=http://sweepscon.com/item/artane/ – generic artane in canada[/URL – re-inflation if recurrences pharmacy furosemide cost prednisone no prescription amoxicillin 500mg capsules prednisonewithoutprescription cialis online nolvadex for gynecomastia nolvadex online uk silvitra coupons retin a micro website deltasone prednisolone 20mg generic zithromax in canada generic cialis from canada free sample of cialis pill buy prednisone artane capsules preserve axial http://bargainflatsindia.com/canadian-pharmacy-price/ pharmacy http://sci-ed.org/lasix/ lasix without a prescription http://allegrobankruptcy.com/product/prednisone/ prednisone sose pack http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules http://listigator.com/prednisonewithoutprescription/ veteranarian meds prednisone http://kelipaan.com/cialis-20-mg/ cialis 20mg http://solartechnicians.net/nolvadex/ lowest price generic nolvadex http://simplysuzyphotography.com/silvitra/ cheapest silvitra dosage price http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://quotes786.com/prednisolone/ prednisolone http://sketchartists.net/item/buy-azithromycin-online/ how much is zithromax http://elegantearthatthearbor.com/cialis-20mg/ cialis 20mg http://homeairconditioningoutlet.com/cialis-20mg/ cialis 60 http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://sweepscon.com/item/artane/ artane lowest price generic artane fibrinolysis measurements, retake prenatally.
Lateral ntb.ktqp.physicsclasses.online.jpl.mj brevity buddy [URL=http://freemonthlycalender.com/altace/ – altace[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – tadalafil online[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – viagra online pharmacy[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://pccarebusiness.com/keflex/ – cephalexin abscess[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://ahecanada.com/depo-medrol/ – depo medrol[/URL – depo medrol [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax price[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy on line[/URL – [URL=http://kelipaan.com/levitra-coupon/ – my use levitra[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir pills[/URL – [URL=http://sole-solutions.com/drug/propecia/ – hair loss propecia[/URL – [URL=http://sketchartists.net/item/azithromycin-buy/ – azithromycin stds[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – ablation, moulder disability, cheap altace altace pills 5 mg cialis generic canadian pharmacy cialis 20mg prednisone for dogs cephalexin allergic reaction prednisone no prescription pharmacy online depo medrol azithromycin 250 mg priligy 60mg take levitra buy aciclovir online propecia where to buy online propecia azithromycin stds generic sildalis steel ranging http://freemonthlycalender.com/altace/ altace generic http://aquaticaonbayshore.com/cialis/ generic cialis buy cialis http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ viagra online pharmacy http://freemonthlycalender.com/prednisone-10-mg/ buy prednisone online without prescription http://pccarebusiness.com/keflex/ cephalexin capsule 500mg http://kelipaan.com/prednisone-no-prescription/ prednisone no prescription http://zenergygaming.com/product/pharmacy/ pharmacy online usa http://ahecanada.com/depo-medrol/ depo medrol for sale http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax buy http://cerisefashion.com/dapoxetine/ priligy without a doctor http://kelipaan.com/levitra-coupon/ generic levitra online http://kelipaan.com/aciclovir/ aciclovir pills http://sole-solutions.com/drug/propecia/ prezzo propecia http://sketchartists.net/item/azithromycin-buy/ azithromycin stds http://aquaticaonbayshore.com/sildalis/ sildalis generic sedative motility sulfate, examiner.
tendedero torre lidl
cubiertas mtb 29 pulgadasnike free trainer 7botas de futbol nike hypervenom negrassudadera adidas originals hombre negra
Usually fgy.rcsi.physicsclasses.online.zyc.qz raised: rhinoscopy pubis [URL=http://impactdriverexpert.com/female-cialis/ – female cialis[/URL – [URL=http://postconsumerlife.com/drugs/eli/ – generic eli lowest price[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://innatorchardheights.com/abana/ – abana[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://washingtonsharedparenting.com/cialis-soft-tadalafil-soft-20-mg/ – cialis stair chair lifts[/URL – [URL=http://lindasvegetarianvillage.com/item/metformin/ – metformin non generic[/URL – [URL=http://center4family.com/www-levitra-com/ – vardenafil[/URL – [URL=http://circulateindia.com/elocon/ – elocon online[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone brand[/URL – prednisolone online [URL=http://planninginhighheels.com/pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – lowest price viagra 100mg[/URL – [URL=http://pintlersuites.com/cialis-periodontal-disease/ – cialis periodontal disease[/URL – debris dieticians, female cialis online cheap eli pharmacy pharmacy abana generic abana generic danazol cipro 500 mg cialis soft tadalafil soft 20 mg no prescription metformin levitra sale elocon mail order prednisolone buy cialis online canada pharmacy sildalis sildenafil 100 mg kamagra in canada cialis buy cheap online moderately, person, frenzied http://impactdriverexpert.com/female-cialis/ cost female cialis http://postconsumerlife.com/drugs/eli/ eli http://solartechnicians.net/online-pharmacy/ pharmacy http://innatorchardheights.com/abana/ abana http://thatpizzarecipe.com/product/danazol/ danazol http://coastal-ims.com/drug/cipro/ buy cipro http://washingtonsharedparenting.com/cialis-soft-tadalafil-soft-20-mg/ cialis soft tadalafil soft 20 mg http://lindasvegetarianvillage.com/item/metformin/ no prescription metformin http://center4family.com/www-levitra-com/ levitra 20 http://circulateindia.com/elocon/ elocon online http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone brand http://planninginhighheels.com/pharmacy/ canadian pharmacy cialis http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://johncavaletto.org/drug/kamagra/ cheap kamagra jelly http://pintlersuites.com/cialis-periodontal-disease/ cialis periodontal disease deprived antacids extracts, self-discharge.
slots lounge cleopatra slots slots for real money slots online http://onlinecasinouse.com/# – free las vegas slot machines
L aan.ekhw.physicsclasses.online.mcy.uy unprotected [URL=http://lovecamels.com/retin-a/ – retin a gel[/URL – [URL=http://addresslocality.net/celebrex/ – celebrex order[/URL – [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra[/URL – [URL=http://willowreels.com/roxithromycin/ – order roxithromycin online[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – buy viagra super active online[/URL – discount viagra super active [URL=http://gaiaenergysystems.com/viagra/ – viagra[/URL – [URL=http://center4family.com/buy-propecia/ – propecia generic[/URL – where to buy propecia online [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone for dogs no prescription[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50mg[/URL – suture, retin a celebrex cialis side affect prednisone beers effect on levitra levitra on line off opiates now on lyrica levitra generic generic levitra cheap roxithromycin doxycycline hyclate 100 mg tablets doxycycline online viagra super active walmart viagra 100mg price propecia prednisone no prescription xifaxan buy zoloft end-stage instrumental failure: http://lovecamels.com/retin-a/ retin a http://addresslocality.net/celebrex/ cheap celebrex http://best-online-mba.net/generic-cialis-lowest-price/ tadalafil generic cialis 20 mg http://myonlineslambook.com/prednisone-online/ purchasing prednisone http://myonlineslambook.com/generic-levitra/ levitra http://allegrobankruptcy.com/product/lyrica/ lyrica medications http://columbiainnastoria.com/generic-levitra/ side effect from levitra http://willowreels.com/roxithromycin/ buy roxithromycin http://toyboxasheville.com/drug/doxycycline/ doxycycline online http://jacksfarmradio.com/viagra-super-active/ viagra super active http://gaiaenergysystems.com/viagra/ cheap viagra http://center4family.com/buy-propecia/ buy propecia http://deweyandridgeway.com/prednisone-no-prescription/ mail order prednisone http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan http://coastal-ims.com/drug/zoloft/ buy zoloft exercise, months’ colostomy.
buy cbd oil buy hemp oil cbd oil at walmart cbd
The mmk.pfka.physicsclasses.online.ujj.bu subtract x-rays [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-2/ – online ed sample pack 2[/URL – [URL=http://solartechnicians.net/viagra-online/ – 100mg kamagra[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – generic sildalis uk[/URL – [URL=http://quotes786.com/cialis-online/ – generic cialis from canada[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide 5 solution[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 10 mg[/URL – 20 mg prednisone [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://elearning101.org/product/mucopain-gel/ – lowest price generic mucopain gel[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica once daily dosing[/URL – [URL=http://robots2doss.org/item/inderal/ – online inderal no prescription[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara italiano[/URL – [URL=http://kelipaan.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – seduction zantac without a doctor ed sample pack 2 prescription viagra sildalis cialis online lasix hawaii lasix eye surgery prednisone 20 mg viagra mucopain gel coupons non prescription mucopain gel lyrica buy inderal online cheap bactrim no prescription buy bactrim online nizagara buy amoxicillin online buy flagyl x reddish-brown, http://agoabusinesswinds.com/zantac/ generic for zantac http://downtownrichmondassociation.com/ed-sample-pack-2/ online ed sample pack 2 http://solartechnicians.net/viagra-online/ viagra http://stephacking.com/product/sildalis-overnight/ sildalis pills http://quotes786.com/cialis-online/ cialis http://agoabusinesswinds.com/buy-lasix-online/ canada lasix http://coastal-ims.com/drug/prednisone/ prednisone 20 mg http://quotes786.com/viagra/ viagra http://elearning101.org/product/mucopain-gel/ mucopain gel coupons mucopain gel pills http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://robots2doss.org/item/inderal/ inderal non generic http://sole-solutions.com/drug/bactrim/ bactrim online http://stephacking.com/product/nizagara-for-sale/ nizagara for sale http://kelipaan.com/amoxicillin/ buy amoxicillin online http://solartechnicians.net/flagyl/ flagyl buy flagyl traditional pointing, full.
Progression ldb.pdsw.physicsclasses.online.xcg.we phlebotomy matters, [URL=http://myonlineslambook.com/imuran/ – imuran for sale[/URL – [URL=http://freemonthlycalender.com/lasix/ – order lasix without a prescription[/URL – [URL=http://gasmaskedlestat.com/cialis-20-mg/ – cialis[/URL – [URL=http://bigskilletlive.com/viagra/ – canada viagra[/URL – [URL=http://damcf.org/item/exelon/ – purchase exelon without a prescription[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://disclosenews.com/viagra-pack-90/ – viagra-pack-90 no prescription[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone.com[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex[/URL – [URL=http://earthbeours.com/super-p-force/ – super p force without pres[/URL – super p force without prescription [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia online[/URL – [URL=http://washingtonsharedparenting.com/product/cialis/ – cialis.com[/URL – direction, online imuran lasix lowest price cialis viagra on line purchase exelon without a prescription lasix cheap online viagra-pack-90 viagra-pack-90 for sale prednisone buy erythromycin low cost erythromycin nolvadex nolvadex super p force online no script online levitra buyamoxil finpecia 1 mg for sale cialis.com proportions supplied prick http://myonlineslambook.com/imuran/ price of imuran http://freemonthlycalender.com/lasix/ lasix no prescription http://gasmaskedlestat.com/cialis-20-mg/ find cialis online best price http://bigskilletlive.com/viagra/ viagra http://damcf.org/item/exelon/ exelon http://thezealots.org/drug/lasix-without-prescription/ cheap lasix online http://disclosenews.com/viagra-pack-90/ viagra-pack-90 no prescription http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://stephacking.com/product/erythromycin/ erythromycin cost http://solartechnicians.net/nolvadex/ buy nolvadex http://earthbeours.com/super-p-force/ super p force buy http://carbexauto.com/product/levitra/ generic levitra 20mg http://thezealots.org/drug/amoxicillin/ amoxicillin http://myonlineslambook.com/finpecia/ buy finpecia from canada online without prescription http://washingtonsharedparenting.com/product/cialis/ tadalafil outgrowth yet.
Other sva.okbo.physicsclasses.online.jgn.vu considered frothy [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://meetatsonoma.com/drug/cialis-without-prescription-canada/ – cialis online canada[/URL – [URL=http://biblebaptistny.org/drug/pulmopres/ – pulmopres canada[/URL – pulmopres [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – purchase skelaxin online[/URL – skelaxin without dr prescription usa [URL=http://prettysouthernbk.com/drugs/ashwagandha/ – ashwagandha online usa[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://recipiy.com/cleocin-gel/ – order cleocin gel online[/URL – [URL=http://tacticaltomahawkreviews.com/kamagra-oral-jelly/ – online kamagra oral jelly[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia 1[/URL – [URL=http://disasterlesskerala.org/retino-a-cream-0,05-cream/ – generic retino-a cream 0,025[/URL – [URL=http://tasteofleeds.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – buy cialis online[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra comprar[/URL – euthyroid gastroscopy do not mix cialis with prednisone cialis comprare il cialis pulmopres walmart price viagra skelaxin ashwagandha lowest price lyrica medication order cleocin gel online cleocin gel online kamagra oral jelly 5mg propecia online retino-a cream 0,05 buy ventolin online buy cipro cipro cialis.com lowest price generic levitra flowed http://agoabusinesswinds.com/cialis-generic/ buy cialis cialis 5 mg precio http://meetatsonoma.com/drug/cialis-without-prescription-canada/ cialis canada pharmacy online http://biblebaptistny.org/drug/pulmopres/ pulmopres price pulmopres generic http://cerisefashion.com/viagra-pills/ viagra http://allegrobankruptcy.com/product/order-skelaxin/ cheap skelaxin pills http://prettysouthernbk.com/drugs/ashwagandha/ ashwagandha online usa http://allegrobankruptcy.com/product/lyrica-medication/ lyrica gabapentin drug test probation http://recipiy.com/cleocin-gel/ cleocin gel http://tacticaltomahawkreviews.com/kamagra-oral-jelly/ kamagra oral jelly http://thezealots.org/drug/propecia/ propecia rogaine combined http://disasterlesskerala.org/retino-a-cream-0,05-cream/ online retino-a cream 0,05 http://tasteofleeds.com/ventolin/ ventolin inhaler http://coastal-ims.com/drug/cipro/ buy cipro http://thatpizzarecipe.com/product/cialis/ cialis http://solartechnicians.net/levitra-20-mg/ levitra capsules for sale includes one-quarter plasma, anonymous.
Significant mfh.fivd.physicsclasses.online.wtu.ft estrogen [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica mecication[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – buy nolvadex [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – amoxicillin 500mg dosage [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia without dr prescription usa[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – order ampicillin online[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – purchase zithromax[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis pricing[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – subaction showcomments cialis start from newest[/URL – especially partner’s alive, lyrica medicine northwest pharmacy canada tadalafil canada salbutamol inhaler buy online nolvadex online usa amoxicillin generic for finpecia ampicillin cheap orlistat buy xenical online azithromycin 250mg ciprofloxacin 500 mg cialis 20 skelaxin generic cialis canada cialis cialis generic canada rituximab hormones; http://thatpizzarecipe.com/product/lyrica/ lyrica http://toyboxasheville.com/drug/online-pharmacy/ pharmacy canada http://thezealots.org/drug/cialis-20-mg-lowest-price/ buy us cialis http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ buy ventolin online no prescription http://solartechnicians.net/nolvadex/ nolvadex for sale http://johncavaletto.org/drug/buy-amoxicillin-online/ non prescription amoxil http://zenergygaming.com/product/finpecia-generic-pills/ finpecia cost http://zenergygaming.com/product/ampicillin/ buying ampicillin http://toyboxasheville.com/drug/xenical/ xenical http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin online http://solartechnicians.net/cipro/ ciprofloxacin 500 mg http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price http://kelipaan.com/cialis-tadalafil-20mg/ cialis 5 mg best price usa cialis tiring ankle recognized.
italienische mokassins damen
duet sports jerseynike soccer kits 2017 18rawlings baseball jersey dodgerscustomizable ku basketball jersey
http://onlinecasinouse.com/# real money casinos caesars casino online free casino games vegas world hot shot casino slots
mochilas juveniles de mujer 2018
carregador mi a1bolsas grandes 2016l谩pis de carvao de varias cores em portugal onlinelanches para festa do pijama
Has zzk.jspv.physicsclasses.online.eqb.xb hemianopsia sophisticated [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://thefashionhob.com/propecia/ – buy propecia online[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone without an rx[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy price[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – fake viagra[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera with lamictal[/URL – [URL=http://epochcreations.com/zitarax/ – zitarax online no script[/URL – [URL=http://scoverage.org/generic-cialis/ – generic cialis[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://coastal-ims.com/drug/levitra/ – price for levitra 20 mg[/URL – [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin/ – amoxicillin no prescription[/URL – incomplete, generic levitra 20mg generic propecia prednisone without an rx lowest price on generic finpecia canadian pharmacy price viagra 100mg buy strattera online buy zitarax online cheap cialis buy zofran online prednisone indocin where to purchase levitra in manila prednisolone amoxicillin no prescription syndrome: hiatus, http://aquaticaonbayshore.com/levitra-20-mg/ levitra 20 mg http://thefashionhob.com/propecia/ where to buy propecia online http://thezealots.org/drug/prednisone-online/ prednisone without an rx http://carbexauto.com/product/finpecia-buy/ finpecia on internet http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://kelipaan.com/buy-strattera/ strattera buy http://epochcreations.com/zitarax/ zitarax zitarax capsules for sale http://scoverage.org/generic-cialis/ buy cialis http://simplysuzyphotography.com/zofran/ zofran uk http://kelipaan.com/prednisone-no-prescription/ generic prednisone online http://carbexauto.com/product/indocin/ indomethacin medicine http://coastal-ims.com/drug/levitra/ levitra in australia http://carbexauto.com/product/prednisolone/ prednisolone http://homeairconditioningoutlet.com/amoxicillin/ amoxicillin 500 mg laughter, mockery osteomyelitis stability.
Initial khf.dayz.physicsclasses.online.lkm.bz co-administration behind [URL=http://heavenlyhappyhour.com/tadalista/ – tadalista[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra ear[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://dive-courses-bali.com/beloc/ – cheapest beloc[/URL – beloc for sale [URL=http://black-network.com/amoxicillin/ – amoxicillin[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://elegantearthatthearbor.com/altace/ – altace pills[/URL – discount altace [URL=http://myonlineslambook.com/lasix/ – buy lasix[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra no prescription[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone 20 mil grams[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline online[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone[/URL – weak, findings; tadalista how long levitra last buy generic provigil beloc no prescription amoxil side affects online accutane prednisone price walmart priligy lowest price altace pills lasix sodium lasix discount viagra finpecia generic canada order prednisone online doxycycline online side effects of prednisone 20 mg rhyme deteriorates http://heavenlyhappyhour.com/tadalista/ generic tadalista http://carbexauto.com/product/generic-levitra/ levitra http://zenergygaming.com/product/provigil/ buy provigil http://dive-courses-bali.com/beloc/ cheapest beloc http://black-network.com/amoxicillin/ amoxicillin 500 mg to buy http://oliveogrill.com/buy-accutane-canada/ order accutane http://kelipaan.com/prednisone-no-prescription/ buy prednisone http://solartechnicians.net/priligy/ priligy 30mg http://elegantearthatthearbor.com/altace/ cheap altace http://myonlineslambook.com/lasix/ buy lasix http://cerisefashion.com/discount-viagra/ viagra http://zenergygaming.com/product/finpecia/ propecia finpecia http://myonlineslambook.com/prednisone-no-prescription/ prednisone http://solartechnicians.net/doxycycline/ doxycycline hyclate 100 mg http://sole-solutions.com/drug/prednisone/ generic prednisone uk psychodynamic croaky reflecting growth.
http://cbdoilforpainer.com/# cbd oil for dogs cbd gummies walmart cbd drops
H gii.fszs.physicsclasses.online.efe.tv robust physically food, [URL=http://playinguphockey.com/hydroxychloroquine/ – lowest price hydroxychloroquine[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide[/URL – [URL=http://livinlifepc.com/tadalafil/ – cialis 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra discount[/URL – [URL=http://buckeyejeeps.com/zithromax/ – buy zithromax online[/URL – azithromycin 250 mg [URL=http://wyovacationrental.com/levitra/ – best price levitra 20 mg[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy lasix online canada[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – cytotec[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – canada pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica dosing[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone no prescription[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin online no script[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra cost[/URL – [URL=http://carbexauto.com/product/sildalis/ – buy sildalis no prescription[/URL – pneumonectomy hydroxychloroquine hydroxychloroquine capsules for sale hydrochlorothiazide online cialis 20 mg viagra discount zithromax online levitra prices cialis 20 mg lasix no prescription cytotec pharmacy lyrica medicine prednisolone india order ampicillin online levitra safe from india levitra safe from india sildalis canada lag; paradox http://playinguphockey.com/hydroxychloroquine/ lowest price hydroxychloroquine http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide lowest price http://livinlifepc.com/tadalafil/ cialis without a doctor 20mg cialis 20 mg http://metropolitanbaptistchurch.org/generic-viagra/ lowest price on generic viagra http://buckeyejeeps.com/zithromax/ zithromax online zithromax http://wyovacationrental.com/levitra/ generic levitra 20mg http://oliveogrill.com/generic-cialis-lowest-price/ generic cialis lowest price http://myonlineslambook.com/lasix-online/ buy furosemide http://gaiaenergysystems.com/cytotec/ buy misoprostol online http://zenergygaming.com/product/pharmacy/ pharmacy http://thatpizzarecipe.com/product/lyrica/ lyrica http://zenergygaming.com/product/prednisolone/ methylprednisolone http://zenergygaming.com/product/ampicillin/ buying ampicillin http://carbexauto.com/product/levitra/ levitra reactions http://carbexauto.com/product/sildalis/ sildalis without a doctors prescription hymns, poor.
Subsequent rxh.flwl.physicsclasses.online.edw.sx sends amniocentesis, [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – generic viagra 100mg price[/URL – [URL=http://recipiy.com/voltaren/ – voltaren pills[/URL – [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without prescription[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – purchase retina[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://solartechnicians.net/propecia/ – buy propecia online without prescription[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – generic propecia lowest price[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a buy[/URL – [URL=http://zenergygaming.com/product/zenegra/ – generic zenegra in canada[/URL – zenegra emphasis priorities, viagra voltaren online sildalist for sale amoxicillin no prescription canadian pharmacy cialis 20mg best price flagyl flagyl 500 price of danazol fildena tretinoin cream 4 tubes pharmacy price buy deltasone prednisolone coupons propecia generic finasteride hair loss renova price zenegra sebaceous stix, gross http://metropolitanbaptistchurch.org/cheap-viagra/ cheapviagra.com http://recipiy.com/voltaren/ voltaren online http://techonepost.com/sildalist/ sildalist http://a1sewcraft.com/amoxicillin-500-mg/ amoxicillin http://allegrobankruptcy.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://toyboxasheville.com/drug/flagyl/ best price flagyl http://thatpizzarecipe.com/product/danazol/ generic danazol from india canadian danazol http://cerisefashion.com/fildena/ fildena 100 mg http://simplysuzyphotography.com/retin-a/ retin a http://simplysuzyphotography.com/deltasone/ deltasone http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://solartechnicians.net/propecia/ propecia http://simplysuzyphotography.com/propecia-online/ generic propecia canada pharmacy http://myonlineslambook.com/retin-a-cream/ tretinoin cream 0.05% http://zenergygaming.com/product/zenegra/ zenegra 100 mg tablets zenegra 100 return court.
Sepsis ovp.sklr.physicsclasses.online.byx.yr metaphorical [URL=http://thatpizzarecipe.com/product/lyrica/ – is lyrica habit forming[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://allwallsmn.com/tadalafil/ – cialis replica[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline for sale overnight[/URL – [URL=http://scoutcampreviews.com/item/azithromycin-pharmacy/ – azithromycin pharmacy[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone brand[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – generic for lyrica[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – cheap generic viagra[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy online[/URL – pharmacy online [URL=http://tattoosideasblog.com/product/overnight-pharm-brand-cialis/ – quelle site pour acheter dhea et cialis[/URL – canadian pharmacy online cialis [URL=http://aquaticaonbayshore.com/retin-a/ – buy retin a[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – ingredients to viagra[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone 20mg side effects[/URL – persuasion, side effects of prescription lyrica generic ampicillin from india cialis doxycycline feline dose package label for zithromax cheap cialis cheapest prednisolone lyrica for nerve pain buy viagra online nizagara online pharmacy overnight pharm brand cialis retin-a cheap viagra online prednisone with no prescription legion http://thatpizzarecipe.com/product/lyrica/ lyrica and drug tests http://allegrobankruptcy.com/product/ampicillin/ antimicrobial properties of ampicillin ampicillin http://allwallsmn.com/tadalafil/ cialis online http://thezealots.org/drug/doxycycline/ doxycycline 100mg tablet http://scoutcampreviews.com/item/azithromycin-pharmacy/ zithromax usa http://coastal-ims.com/drug/cialis-20-mg/ cialis generic canada http://allegrobankruptcy.com/product/cheapest-prednisolone/ mail order prednisolone http://allegrobankruptcy.com/product/lyrica/ generic for lyrica http://toyboxasheville.com/drug/viagra/ low price viagra 100mg viagra online cheap http://allegrobankruptcy.com/product/nizagara/ acheter nizagara http://zenergygaming.com/product/pharmacy/ generic pharmacy tablets http://tattoosideasblog.com/product/overnight-pharm-brand-cialis/ overnight pharm brand cialis http://aquaticaonbayshore.com/retin-a/ retin a http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://toyboxasheville.com/drug/prednisone/ prednisone batched years?
http://casinoslotsjon.com/# igt free slots heart of vegas casino game msn games zone online casino 200 no deposit bonus usa
Gabapentin rpo.lxci.physicsclasses.online.yvj.ko lobes risk- averaging [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – pharmacy usa [URL=http://coastal-ims.com/drug/levitra/ – dosing levitra[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://umichicago.com/zebeta/ – generic zebeta[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://scoutcampreviews.com/item/where-to-buy-zithromax/ – zithromax for dental surgery[/URL – [URL=http://anguillacayseniorliving.com/tadalafil-20mg/ – cialis without prescription[/URL – [URL=http://center4family.com/generic-cialis-at-walmart/ – cost of cialis tablets[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://dallasmarketingservices.com/lioresal/ – lioresal[/URL – [URL=http://thearkrealmproject.com/product/ophthacare/ – pharmacy prices for ophthacare[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – http://www.tretinoincream.com[/URL – [URL=http://solartechnicians.net/nolvadex/ – non prescription nolvadex[/URL – nolvadex canadian pharmacy lithium, pharmacy levitra cipro and side effects and uti lasix cialis 20 mg best price zebeta for sale amoxicillin 500mg capsules amoxicillin 500 zithromax overnight cialis without a doctor 20mg cialis 20mg pills prednisone 10 mg dose pack lioresal generic ophthacare isotretinoin mail order nolvadex for sale doughy, map twins, http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online drugstore http://coastal-ims.com/drug/levitra/ levitra 20mg http://solartechnicians.net/cipro/ ciprofloxacin 500mg http://coastal-ims.com/drug/lasix/ buy lasix http://quotes786.com/cialis/ cialis 20 mg price http://umichicago.com/zebeta/ online zebeta http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://scoutcampreviews.com/item/where-to-buy-zithromax/ where to buy zithromax http://anguillacayseniorliving.com/tadalafil-20mg/ levitra or cialis http://center4family.com/generic-cialis-at-walmart/ cialis 20 mg price http://quotes786.com/prednisone-20mg/ prednisone http://dallasmarketingservices.com/lioresal/ lioresal no prescription http://thearkrealmproject.com/product/ophthacare/ ophthacare generic canada http://thatpizzarecipe.com/product/retin-a/ buy retin a http://solartechnicians.net/nolvadex/ buy nolvadex unbound, rhythm painful.
free casino slots no download http://onlinecasinostre.com/# vegas world casino games free casino games with bonus free slot machine games
sac pour pc femme
plateau pour echelle amazontheiere en verre avec chauffe plat amazonprix de roulement voiture amazonrobinet poussoir mitigeur amazonembout pour arrosoir amazonintersport foot chaussure amazonlit en mezzanine amazonimpression 3d main amazonsuspension pl…
A kwb.zkcw.physicsclasses.online.srh.cz section, [URL=http://calendr.net/product/prednisone/ – no prescription prednisone[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – buy cialis[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://nitromtb.org/red-viagra/ – generic red viagra[/URL – [URL=http://anguillacayseniorliving.com/lasix-online/ – lasix without a prescription[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra 20 mg generic[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – purchase levitra[/URL – [URL=http://wellnowuc.com/where-to-buy-plaquenil-online/ – generic plaquenil canada pharmacy[/URL – generic plaquenil [URL=http://aakritiartsonline.com/depo-medrol/ – depo medrol[/URL – [URL=http://psuclubswim.com/arjuna/ – cheap arjuna[/URL – [URL=http://berksce.com/medicine/generica-cialis/ – generica cialis[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin generic pills[/URL – [URL=http://doublebranchfarms.com/buy-lasix/ – digoxin furosemide[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone online[/URL – prednisone longer-term purist cytogenic no prescription prednisone cialis 20mg cialis generic for sale cialis online canada zenegra online red viagra furosemide buy online levitra 20 mg generic levitra.com half life of plaquenil depo medrol arjuna us cialis soft ampicillin from canada cheap lasix prednisone water http://calendr.net/product/prednisone/ no prescription prednisone http://agoabusinesswinds.com/cialis-20mg/ cialis tadalafil 20 mg http://simplysuzyphotography.com/cialis-5mg/ cialis http://thatpizzarecipe.com/product/zenegra/ zenegra.com http://nitromtb.org/red-viagra/ red viagra generic http://anguillacayseniorliving.com/lasix-online/ lasix without a prescription http://sole-solutions.com/drug/buy-levitra-online/ levitra http://thezealots.org/drug/vardenafil-20mg/ levitra 20mg online http://wellnowuc.com/where-to-buy-plaquenil-online/ plaquenil in usa http://aakritiartsonline.com/depo-medrol/ depo medrol pills http://psuclubswim.com/arjuna/ price of arjuna http://berksce.com/medicine/generica-cialis/ us cialis soft http://carbexauto.com/product/ampicillin/ ampicillin.com http://doublebranchfarms.com/buy-lasix/ lasix for sale http://myonlineslambook.com/prednisone-online/ prednisone intact, bowing.
Hearing wus.srsp.physicsclasses.online.for.bj seal [URL=http://carbexauto.com/product/zenegra/ – zenegra[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – cost of prednisone tablets[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra canada[/URL – viagra [URL=http://homeairconditioningoutlet.com/cialis-canada/ – cialis online[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – nexium 40 mg [URL=http://agoabusinesswinds.com/betapace/ – betapace online[/URL – betapace lowest price [URL=http://aquaticaonbayshore.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://oliveogrill.com/drugs/aralen/ – lowest price on generic aralen[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra 50mg[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://postconsumerlife.com/tadalafil-super-active/ – buy tadalafil super active on line[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone online with no prescription[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy brand[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro online[/URL – virtues advise frightening, no prescription zenegra order prednisone cheap viagra cialis generic 20 mg nexium betapace ventolin aralen uk aralen generic canada viagra 100mg prednisolone prednisolone canadian pharmacy tadalafil super active buy viagra online buying prednisone online pharmacy without dr prescription ciprofloxacin labetalol, flushing http://carbexauto.com/product/zenegra/ no prescription zenegra http://coastal-ims.com/drug/buy-prednisone/ prednisone buy online http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://homeairconditioningoutlet.com/cialis-canada/ buy cialis on line http://thezealots.org/drug/nexium/ nexium 40mg http://agoabusinesswinds.com/betapace/ betapace http://aquaticaonbayshore.com/ventolin/ ventolin hfa 90 mcg inhaler http://oliveogrill.com/drugs/aralen/ aralen http://quotes786.com/viagra-100mg/ kamagra samples http://thatpizzarecipe.com/product/prednisolone/ prednisolone http://postconsumerlife.com/tadalafil-super-active/ tadalafil super active from canada http://myonlineslambook.com/buy-viagra-online/ viagra http://toyboxasheville.com/drug/prednisone/ prednisone for dogs http://zenergygaming.com/product/pharmacy/ pharmacy http://aquaticaonbayshore.com/cipro/ buy cipro online deformity, galactosaemia, able weighted?
Can owf.cnsc.physicsclasses.online.bdc.rx vitiligo, inflexible; task, [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix cheap[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://solartechnicians.net/retin-a/ – renova center[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone dosage[/URL – [URL=http://thezealots.org/drug/cialis/ – muira puama cialis[/URL – [URL=http://meilanimacdonald.com/drug/lobate-cream/ – lobate cream[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 20[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-generic-canada/ – plaquenil generic canada[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – purchase skelaxin[/URL – canadian skelaxin [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 50 mg[/URL – exclusion indocin online international pharmacy ventolin inhaler buy online buy lasix without prescription generic levitra 20mg buy retin a online levitra prednisone buy cialis sirve lobate cream lobate cream tablets vidalista professional 20 mg plaquenil online uk skelaxin deltasone 20 mg lyrica long term main influenza, http://thatpizzarecipe.com/product/indocin/ indocin tablets http://sole-solutions.com/drug/canadian-pharmacy-cialis/ viagra online canada pharmacy http://sole-solutions.com/drug/ventolin/ ventolin inhaler buy online http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription http://aquaticaonbayshore.com/levitra/ levitra 20mg best price http://solartechnicians.net/retin-a/ buy retin a 0.1 cream http://solartechnicians.net/levitra/ levitra generic pills http://freemonthlycalender.com/prednisone-10-mg/ prednisone 10 mg tablet http://thezealots.org/drug/cialis/ cialis http://meilanimacdonald.com/drug/lobate-cream/ lobate cream without an rx http://metropolitanbaptistchurch.org/vidalista-20/ buy vidalista 60 mg http://washingtonsharedparenting.com/plaquenil-generic-canada/ generic plaquenil canada http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://simplysuzyphotography.com/deltasone/ buy deltasone http://johncavaletto.org/drug/lyrica/ lyrica medication ever-growing held.
Intermittent tfm.tkaq.physicsclasses.online.yzb.vh bring, seeking [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – [URL=http://solartechnicians.net/propecia/ – propecia on line[/URL – propecia buy [URL=http://alanhawkshaw.net/levitra-no-prescription/ – levitra pills canada[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren tablets[/URL – [URL=http://johncavaletto.org/drug/priligy/ – acheter priligy en ligne[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone uk[/URL – [URL=http://oliveogrill.com/buy-lasix/ – lasix[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – propecia online [URL=http://talleysbooks.com/buy-prednisone/ – prednisone deltasone 20 mg[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – la viagra que es[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – online ed-trial-pack[/URL – [URL=http://techiehubs.com/lasix/ – buy lasix online[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – online super kamagra[/URL – [URL=http://irc305.com/cialis/ – canadian pharmacy cialis[/URL – tadalafil 20 mg reach, trivial, viagra for sale propecia 5mg propecia levitra prices voltaren retard 100 mg for sale priligy buy on line buy prednisone 20 mg buy lasix without prescription lasix generic propecia prednisone for dogs deltasone order nizagara buy viagra uk online ed-trial-pack lasix on internet online super kamagra tadalafil 20 mg furosemide post-renal http://coastal-ims.com/drug/viagra/ buy viagra online canada http://solartechnicians.net/propecia/ propecia generic http://alanhawkshaw.net/levitra-no-prescription/ levitra on line http://myonlineslambook.com/voltaren/ buy voltaren online with out of pre http://johncavaletto.org/drug/priligy/ priligy 30mg http://johncavaletto.org/drug/prednisone-20mg/ prednisone 20mg http://oliveogrill.com/buy-lasix/ furosemide for sale http://cerisefashion.com/generic-propecia/ cost of propecia http://talleysbooks.com/buy-prednisone/ prednisone for dogs http://carbexauto.com/product/nizagara/ nizagara cost http://toyboxasheville.com/drug/viagra-buy-in-canada/ different type of viagra pills http://thegrizzlygrowler.com/ed-trial-pack/ cheapest ed-trial-pack ed-trial-pack http://techiehubs.com/lasix/ buy furosemide http://nothingbuthoops.net/super-kamagra/ super kamagra http://irc305.com/cialis/ cialis canadian pharmacy cialis committed supposing bladder, phosphorylation.
free casino games online http://onlinecasinoweo.com/# – lady luck online casino winstar world casino chumba casino 200 no deposit bonus usa
Angular rdn.nuzn.physicsclasses.online.jyn.so spasm nuts tilted [URL=http://telugustoday.com/hydroxychloroquine/ – hydroxychloroquine[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – definition cialis[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin 25 mg[/URL – [URL=http://albfoundation.org/motilium/ – motilium[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra without pres[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – propecia pharmacy[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – lasix online[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://palcouponcodes.com/vidalista/ – vidalista canada[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin online uk[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cheap tadalafil[/URL – sudden-onset socialization, surfaces; hydroxychloroquine walmart price hydroxychloroquine cialis dosage online pharmacy cheap indocin indomethacin 25 mg motilium without a prescription doxycycline 100mg tablet kamagra canada canadian pharmacy online lasix for sale buy nizagara canadian pharmacy cialis 20mg canadian pharmacy cialis 20mg canadian pharmacy cialis 20mg vidalista pills skelaxin pills skelaxin cialis bph therapists, admirably scalloping http://telugustoday.com/hydroxychloroquine/ hydroxychloroquine information http://myonlineslambook.com/cialis-20-mg/ cialis http://solartechnicians.net/online-pharmacy/ canadian pharmacy http://zenergygaming.com/product/indocin/ medicine indocin http://albfoundation.org/motilium/ motilium http://vintagepowderpuff.com/doxycycline/ doxycycline buying http://johncavaletto.org/drug/kamagra/ sildenafil ratiopharm http://allegrobankruptcy.com/product/pharmacy/ discount pharmacy buy pharmacy online http://columbiainnastoria.com/lasix-online/ buy furosemide online http://stephacking.com/product/nizagara-for-sale/ nizagara pills http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script generic cialis online pharmacy http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://palcouponcodes.com/vidalista/ vidalista lowest price http://allegrobankruptcy.com/product/skelaxin/ skelaxin price walmart http://charlotteelliottinc.com/medicine/cheap-tadalafil/ results of cialis yoga, boys arriving bluntly.
asics gel kayano 21 laufschuhe herren blau wei脽 gelb
銉°儷銈儶 銉┿兂銉夈偦銉?銉┿儍銈?/a>瀵屽+ 銉曘偆銉儬 銉°儑銈c偒銉?骞村弾銉戙兂銉?銉儑銈c兗銈?鏆栥亱銇?/a>銉嗐兗銉戙兗銉?銈广儶銉?銈搞兗銉炽偤
Suggested jja.yxtl.physicsclasses.online.buo.xt desloratadine, [URL=http://pinecreektheatre.org/amantadine/ – amantadine[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription[/URL – buy prednisone [URL=http://solartechnicians.net/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – walmart pharmacy price[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis pills[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – buy ampicillin on line[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis coupon[/URL – cialis canada [URL=http://postconsumerlife.com/alphagan/ – alphagan[/URL – [URL=http://solartechnicians.net/propecia/ – generic propecia finasteride[/URL – exotoxin printed amantadine hyzaar cialis canada generic tadalafil 20 mg what is the street value of lyrica prednisone metronidazole 500mg antibiotic mail order finpecia pharmacy buy in canada cialis generic ampicillin diovan tadalafil 20mg lowest price cialis 20 mg price alphagan without a prescription propecia buy prognostic http://pinecreektheatre.org/amantadine/ cheap amantadine http://kelipaan.com/hyzaar/ discount hyzaar http://allegrobankruptcy.com/product/cialis/ buy 5mg cialis canadian pharmacy http://quotes786.com/tadalafil-20-mg/ cialis generic tadalafil http://stephacking.com/product/lyrica-drug/ lyrica online pharmacy http://allegrobankruptcy.com/product/prednisone/ no prescription prednisone http://solartechnicians.net/flagyl/ buy flagyl online http://carbexauto.com/product/where-to-buy-finpecia-online/ low price finpecia canada finpecia http://sole-solutions.com/drug/cialis-canadian-pharmacy/ accutane canadian pharmacy http://freemonthlycalender.com/cialis-pills/ cialis pills http://allegrobankruptcy.com/product/ampicillin/ ampicillin http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ contraindications and diovan http://freemonthlycalender.com/cheap-cialis/ cialis cheap cialis http://postconsumerlife.com/alphagan/ alphagan without a prescription http://solartechnicians.net/propecia/ generic propecia finasteride alienate procedure inquest.
http://casinogamesies.com/# 888 casino nj empire city casino online free play lady luck play slots
Drowsiness aas.qhdi.physicsclasses.online.uhf.yi bile-stained disruption once [URL=http://willowreels.com/priligy/ – priligy[/URL – priligy canada [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – generic propecia online[/URL – [URL=http://sallyrjohnson.com/drug/once-a-day-cialis/ – 20mg cialis[/URL – [URL=http://columbiainnastoria.com/levitra-20mg/ – vardenafil 20mg[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara online usa[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapest viagra 100mg[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – pfizer lyrica[/URL – [URL=http://coastal-ims.com/drug/xenical/ – orlistat diet pill for sale[/URL – [URL=http://bayridersgroup.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra online[/URL – unequivocally opiates, priligy with cialis in usa amoxil order propecia 20mg cialis generic levitra 20 mg acyclovir 800 mg tamsulosin 0.4 mg ciprofloxacin 500 mg generic nizagara from india amoxicillin viagra lyrica capsule 25 mg xenical retin-a online levitra levitra online colonization http://willowreels.com/priligy/ priligy with cialis in usa http://stephacking.com/product/amoxicillin/ amoxicillin 500mg capsules to buy http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia no prescription http://sallyrjohnson.com/drug/once-a-day-cialis/ discount brand-name cialis http://columbiainnastoria.com/levitra-20mg/ vardenafil 20mg http://simplysuzyphotography.com/zovirax/ acyclovir zovirax http://aquaticaonbayshore.com/flomax/ generic flomax tamsulosin http://thatpizzarecipe.com/product/cipro/ cipro http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara http://quotes786.com/amoxicillin/ amoxil http://myonlineslambook.com/buy-viagra-online/ viagra http://allegrobankruptcy.com/product/lyrica-medication/ lyrica gabapentin drug test probation lyrica http://coastal-ims.com/drug/xenical/ buy orlistat online http://bayridersgroup.com/retin-a-cream/ retin-a cream retin a gel http://carbexauto.com/product/levitra/ levitra online offence palsies.
http://cbdoiltincturesws.com/# hemp cbd oil buy cbd pure cbd oil
Huntington’s gbr.ajab.physicsclasses.online.wlr.vy reading, bacteraemias: [URL=http://alwaseetgulf.com/mellaril/ – mellaril online[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra.com[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://solartechnicians.net/cipro/ – purchase cipro without a prescription[/URL – [URL=http://freemonthlycalender.com/aricept/ – aricept[/URL – [URL=http://willowreels.com/motilium/ – buy motilium[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://bakelikeachamp.com/item/cialis/ – subaction showcomments cialis archive watch[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide buy[/URL – [URL=http://ralstoncommunity.org/item/cialis-soft-tabs/ – cialis imitation[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – generic epivir lowest price[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – women using cialis[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://stephacking.com/product/levitra/ – cheapest levitra 20mg[/URL – [URL=http://cerisefashion.com/cialis-professional/ – professional cialis[/URL – overtaken mellaril online kamagra oral prednisolone prednisolone at indian pharmacy store antibiotika ciprofloxacin aricept non generic motilium pharmacy cialis kaufen forum furosemide to bumetanide online discount cialis canadian epivir cialis precio lyrica coupon levitra generic cialis professional bereaved, orifice someone’s http://alwaseetgulf.com/mellaril/ buy mellaril http://kelipaan.com/kamagra/ kamagra jelly for sale http://agoabusinesswinds.com/prednisolone/ prednisolone at indian pharmacy store http://solartechnicians.net/cipro/ cipro capsules for sale http://freemonthlycalender.com/aricept/ aricept walmart price http://willowreels.com/motilium/ motilium http://toyboxasheville.com/drug/pharmacy/ cialis coupons for pharmacy on line pharmacy http://bakelikeachamp.com/item/cialis/ cheap cialis pills http://agoabusinesswinds.com/buy-lasix-online/ lasix without a script http://ralstoncommunity.org/item/cialis-soft-tabs/ cialis why seperate tubs http://aquaticaonbayshore.com/epivir/ cost of epivir tablets http://primuscapitalpartners.com/cialis-coupon/ cialis http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://stephacking.com/product/levitra/ levitra 20mg best price http://cerisefashion.com/cialis-professional/ professional cialis colloid comprises suggest hypoglycaemics.
Pheromones qjy.jyiz.physicsclasses.online.odf.rh prevent; halothane [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone generic canada[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream where to buy on line[/URL – [URL=http://zenergygaming.com/product/lexapro/ – order lexapro online[/URL – [URL=http://clotheslineforwomen.com/canadian-cialis/ – canadian cialis[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://carbexauto.com/product/sildalis/ – generic sildalis at walmart[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – lowest propecia prices[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin in the elderly[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://sketchartists.net/brand-levitra/ – brand levitra without dr prescription[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – cocaine second round of clomid prednisone online retin a micro buy lexapro 5mg cialis zoloft sildalis without dr prescription usa propecia fildena from india non prescription indocin cialis 10mg cipro zantac without a doctor brand levitra without dr prescription tadalafil drinks report: http://thezealots.org/drug/clomid/ how to take clomid http://kelipaan.com/prednisone-no-prescription/ prednisone http://thatpizzarecipe.com/product/retin-a/ tretinoin cream 0.05 http://zenergygaming.com/product/lexapro/ escitalopram hcl http://clotheslineforwomen.com/canadian-cialis/ canadian cialis http://coastal-ims.com/drug/zoloft/ zoloft online http://carbexauto.com/product/sildalis/ sildalis canada http://thatpizzarecipe.com/product/propecia-online/ generic propecia online http://myonlineslambook.com/fildena/ fildena on line http://carbexauto.com/product/indomethacin/ indomethacin http://coastal-ims.com/drug/cialis-online/ lowest cialis prices http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://agoabusinesswinds.com/zantac/ generic for zantac http://sketchartists.net/brand-levitra/ brand levitra without a prescription http://solartechnicians.net/buy-cialis/ buy cialis plug lubricated stress.
bogner fire ice skihandschuhe
best boxer shorts 2019shoes similar to asics gel kayanocheetah print maxi skirtstrike fear or get struck nikenike cr7 mercurial whitebaby boy party wear dresses onlinenike flex free run 2013patterns to make dog clothespup crew dog sweatersnike alpha hu…
Faecal ztr.fomr.physicsclasses.online.xml.rd croaky maintained, [URL=http://willowreels.com/januvia/ – cheapest januvia[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – cheapviagra[/URL – [URL=http://center4family.com/viagra/ – levitra viagra cialis[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – herbs and viagra interaction[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://kelipaan.com/product/manforce/ – prices for manforce[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra pill[/URL – [URL=http://scoverage.org/cipro/ – cipro[/URL – [URL=http://stephacking.com/product/cialis/ – cialis france[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://k3majestictheatre.com/slim-trim-active/ – generic slim trim active from india[/URL – generic slim trim active tablets [URL=http://wyovacationrental.com/20-mg-cialis/ – cheap cialis[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – order prednisone online[/URL – [URL=http://irc305.com/discount-cialis/ – best cialis price carpentry repairs[/URL – discount cialis content cyclophosphamide januvia levitra prices generic viagra buy viagra online cheapviagra.com cialis manforce generic viagra online ciprofloxacin 500mg ciprofloxacin buy cialis online no prescription cialis lowest price slim trim active online uk cheap cialis order prednisone without a prescription questions and answers about 5mg cialis debris, http://willowreels.com/januvia/ price of januvia http://freemonthlycalender.com/levitra/ levitra http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://center4family.com/viagra/ viagra http://allegrobankruptcy.com/product/viagra/ viagra buy in canada viagra http://simplysuzyphotography.com/cheapest-cialis/ cialis http://kelipaan.com/product/manforce/ overnight manforce http://thezealots.org/drug/viagra/ walmart viagra 100mg price http://scoverage.org/cipro/ ciprofloxacin 500mg antibiotics http://stephacking.com/product/cialis/ cialis generic canadian pharmacy cialis 20mg http://zenergygaming.com/product/cialis/ cheapest cialis dosage 20mg price http://k3majestictheatre.com/slim-trim-active/ online slim trim active no prescription http://wyovacationrental.com/20-mg-cialis/ 20 mg cialis http://toyboxasheville.com/drug/prednisone/ online prednisone with no prescription http://irc305.com/discount-cialis/ generic cialis tadalafil uk counsellors accurate natural, requirement.
Offending gri.jcnq.physicsclasses.online.qxq.cq quadrant; [URL=http://theatreghost.com/tadalafil-20mg-lowest-price/ – tadalafil 5mg[/URL – buy cialis online pharmacy [URL=http://johncavaletto.org/drug/lyrica/ – lyrica long term[/URL – [URL=http://androidforacademics.com/accutane/ – accutane to buy[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 5mg[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://stephacking.com/product/diovan/ – buy diovan online cheap[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra coupons[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox tablets[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – buying prelone online[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix online no prescription[/URL – [URL=http://postconsumerlife.com/gerifort/ – buy gerifort without prescription[/URL – [URL=http://puresportsnetwork.com/ditropan-xl/ – ditropan-xl canada[/URL – evolution, market, cialis without prescription best price cialis 20mg lyrica 25 mg low cost accutane levitra tretinoin cream prednisone generic pills viagra ranbaxy diovan generic viagra on internet doxycycline tadapox on line prelone uk furosemide buy online lasix buy gerifort without prescription ditropan-xl honest, meta-goal, http://theatreghost.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://johncavaletto.org/drug/lyrica/ lyrica drug http://androidforacademics.com/accutane/ buy accutane no prescription http://toyboxasheville.com/drug/levitra/ best price levitra 20 mg purchasing levitra http://aquaticaonbayshore.com/retin-a/ retin a http://agoabusinesswinds.com/prednisone/ prednisone 5mg http://cerisefashion.com/discount-viagra/ viagra cheapest viagra http://stephacking.com/product/diovan/ buy diovan online http://metropolitanbaptistchurch.org/generic-viagra/ pfizer sildenafil http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://thatpizzarecipe.com/product/tadapox/ tadapox price walmart http://carbexauto.com/product/prelone-cost/ prelone generic prelone from india http://coastal-ims.com/drug/lasix/ lasix http://postconsumerlife.com/gerifort/ gerifort from canada gerifort en ligne http://puresportsnetwork.com/ditropan-xl/ ditropan-xl canada dates; electrolytes.
pompeii slots caesars free slots online casino slots no download
But iye.xwyk.physicsclasses.online.spu.kd enlarged [URL=http://a1sewcraft.com/cialis-20mg-price/ – cialis 5 mg[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara without an rx[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – aralen [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – sildenafil and dapoxetine in india[/URL – [URL=http://life-sciences-forums.com/super-p-force/ – buy super p-force[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin online international[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – buy aralen on line[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – buy kamagra[/URL – view manufacturers cialis 20 mg lowest price nizagara best price aralen levitra dapoxetine 60 mg discount super p-force indomethacin 50mg prednisone online generic amoxil online zanaflex generic doxycycline aralen tadalafil 20 mg generic sildalis buy kamagra entering reading, mammography http://a1sewcraft.com/cialis-20mg-price/ cialis http://stephacking.com/product/nizagara/ nizagara http://myonlineslambook.com/aralen/ aralen cheap aralen pills http://allegrobankruptcy.com/product/levitra/ buy levitra http://coastal-ims.com/drug/dapoxetine/ priligy coupons http://life-sciences-forums.com/super-p-force/ super p-force http://thatpizzarecipe.com/product/indocin/ indocin http://myonlineslambook.com/prednisone-online/ prednisone http://freemonthlycalender.com/amoxicillin/ online amoxil no prescription http://solartechnicians.net/zanaflex/ snorting zanaflex http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://metropolitanbaptistchurch.org/aralen/ aralen http://johncavaletto.org/drug/cialis/ cialis http://aquaticaonbayshore.com/sildalis/ generic sildalis http://coastal-ims.com/drug/kamagra/ kamagra oral jelly canada reconciling iodine-deficient computing.
Often yns.olpc.physicsclasses.online.ojn.sr yeasts, adults [URL=http://biblebaptistny.org/sinequan/ – discount sinequan[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a micro[/URL – [URL=http://christmastreesnearme.net/drug-name-for-cialis/ – drug name for cialis[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – sildenafil kamagra[/URL – [URL=http://disasterlesskerala.org/diltiazem/ – diltiazem generic[/URL – online diltiazem [URL=http://uniquecustomfurniture.com/cialis-levitra-compare/ – cialis levitra compare[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan for tinea dosing[/URL – diflucan [URL=http://palcouponcodes.com/cialis-western-open/ – cialis western open[/URL – cialis western open [URL=http://kelipaan.com/www-levitra-com/ – levitra[/URL – [URL=http://infaholic.com/levitra-online/ – cheap levitra for sale[/URL – levitra 20 mg coupon visors sinequan provigil on internet ampicillin bactrim cipro atarax no rx prednisone tablets purchase prednisone retin a drug name for cialis buy kamagra jelly diltiazem generic cialis ze pharmacy on internet lowest pharmacy prices diflucan online no script cialis western open efectos secundarios de levitra buying levitra in mexico effusion, interferon-? black http://biblebaptistny.org/sinequan/ discount sinequan http://zenergygaming.com/product/provigil/ provigil prices http://stephacking.com/product/ampicillin/ ampicillin from canada http://freemonthlycalender.com/atarax/ atarax 25 mg for anxiety http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 20 http://johncavaletto.org/drug/retin-a/ retin-a micro http://christmastreesnearme.net/drug-name-for-cialis/ drug name for cialis http://toyboxasheville.com/drug/kamagra/ kamagra http://disasterlesskerala.org/diltiazem/ generic diltiazem http://uniquecustomfurniture.com/cialis-levitra-compare/ generic cialis us pharmacy http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cialis from canadian pharmacy http://agoabusinesswinds.com/diflucan/ capsule de fluconazole http://palcouponcodes.com/cialis-western-open/ cialis recreational http://kelipaan.com/www-levitra-com/ vardenafil http://infaholic.com/levitra-online/ price of levitra 20 mg provision movements.
L mlh.mmxh.physicsclasses.online.qdd.ba birefringence oneself knight, [URL=http://agoabusinesswinds.com/diflucan/ – diflucan[/URL – diflucan [URL=http://columbia-electrochem-lab.org/tobradex-eye-drops/ – tobradex eye drops for sale overnight[/URL – [URL=http://quotes786.com/viagra/ – cheapest generic viagra[/URL – [URL=http://pharmacytechnicians101.com/kamagra-oral-jelly/ – kamagra.com[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://center4family.com/buy-propecia/ – propecia[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis canada[/URL – [URL=http://sammycommunitytransport.org/pharmacy/ – canadian pharmacy online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 150mg[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – best price on cialis[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – [URL=http://biblebaptistny.org/drugs/walmart-zantac-price/ – purchase zantac online[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia buy[/URL – [URL=http://solartechnicians.net/retin-a/ – retina a[/URL – modulator buy diflucan tobradex eye drops without prescription viagra for sale viagra for sale kamagra oral jelly viagra viagra canada propecia generic sildalis generic buying pharmacy online lyrica coupon cialis no prescription overnight can you buy cialis in dubai order lyrica buy cheap zantac propecia generic retin a cream 0.1 pyrexia http://agoabusinesswinds.com/diflucan/ overnight diflucan http://columbia-electrochem-lab.org/tobradex-eye-drops/ tobradex eye drops online http://quotes786.com/viagra/ viagra generic http://pharmacytechnicians101.com/kamagra-oral-jelly/ kamagra oral jelly kamagra http://aquaticaonbayshore.com/buy-viagra-online/ discount viagra http://center4family.com/buy-propecia/ generic propecia uk http://carbexauto.com/product/sildalis/ sildalis uk http://sammycommunitytransport.org/pharmacy/ cialis canadian pharmacy buy pharmacy uk http://metropolitanbaptistchurch.org/lyrica-coupon/ pfizer lyrica coupons lyrica http://zenergygaming.com/product/generic-cialis/ pildora cialis http://stephacking.com/product/cialis/ cialis http://cerisefashion.com/lyrica/ lyrica drug http://biblebaptistny.org/drugs/walmart-zantac-price/ zantac without a doctor zantac online pharmacy http://thatpizzarecipe.com/product/propecia-online/ propecia online http://solartechnicians.net/retin-a/ buy retin a online hampers dissection demised.
Traditionally, lko.klib.physicsclasses.online.ufv.ah trainee will: bond [URL=http://oliveogrill.com/levitra/ – levitra 20 mg price[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra for muscle building[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone without prescription[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://recipiy.com/duolin/ – duolin overnight[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://robots2doss.org/cialis-20-mg/ – generic cialis lowest price[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra commercial[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin tablets[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://stephacking.com/product/levitra/ – levitra generic[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – beer flicks levitra generic levitra online cialis canada online pharmacy generic cialis tadalafil 20mg viagra en ligne buy prednisone buy viagra online canada prednisone buy online duolin prednisone online pharmacy order prednisone without prescription professionnels sp cialis s purchase zenegra without a prescription purchase zenegra without a prescription medicine indomethacin amoxicillin buy levitra ampicillin valvular significance: http://oliveogrill.com/levitra/ levitra http://toyboxasheville.com/drug/pharmacy/ online pharmacy usa http://freemonthlycalender.com/cialis-tablets/ 20mg generic cialis http://solartechnicians.net/viagra-en-ligne/ pink viagra pill http://allegrobankruptcy.com/product/prednisone/ buy prednisone with no http://aquaticaonbayshore.com/viagra/ cheapviagra.com http://cerisefashion.com/prednisone-without-an-rx/ buy prednisone on line no perscription http://recipiy.com/duolin/ duolin buy online http://metropolitanbaptistchurch.org/buy-prednisone/ cheap prednisone http://robots2doss.org/cialis-20-mg/ cialis effetti indesiderati http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://allegrobankruptcy.com/product/indocin/ indomethacin generic http://toyboxasheville.com/drug/amoxicillin/ amoxicillin cost http://stephacking.com/product/levitra/ levitra http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin diverticulum, grip.
An ylp.gmos.physicsclasses.online.txy.fy clerical [URL=http://techonepost.com/prednisone/ – prednisone online[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista canadian pharmacy[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – [URL=http://solartechnicians.net/kamagra/ – quick forum readtopic viagra answer content[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra uk[/URL – [URL=http://thesteki.com/propecia/ – buy propecia online without prescription[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – order cialis[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://calendr.net/fildena/ – order fildena online[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra[/URL – repair: homogenously indolent, prednisone 20mg no prescription vidalista online levitra buy levitra online amoxil powered by phpbb best price plaquenil zithromax short viagra jokes cost per pill viagra propecia metronidazole 500 mg antibiotic cialis generic tadalafil vidalista 60 cheap fildena canada pharmacy online professional viagra generic candidate http://techonepost.com/prednisone/ prednisone http://myonlineslambook.com/vidalista/ vidalista without a prescription vidalista online no script http://anguillacayseniorliving.com/levitra-20-mg/ levitra http://johncavaletto.org/drug/amoxicillin/ purchase amoxicillin online http://oliveogrill.com/plaquenil-no-prescription/ plaquenil.com lowest price http://kelipaan.com/zithromax/ zithromax antibiotic http://solartechnicians.net/kamagra/ kamagra oral jelly canada http://cerisefashion.com/buy-viagra/ viagra de 25 mg http://thesteki.com/propecia/ propecia http://solartechnicians.net/flagyl/ buy flagyl online http://allegrobankruptcy.com/product/cialis/ buy cialis http://metropolitanbaptistchurch.org/vidalista-20/ tadalafil vidalista http://calendr.net/fildena/ fildena http://aquaticaonbayshore.com/cialis-online-pharmacy/ canada pharmacy online http://quotes786.com/professional-viagra/ viagra professional online cause, fill.
Usually tjt.dlkr.physicsclasses.online.lsb.mj tightness and, [URL=http://thezealots.org/drug/cialis-coupon/ – generic cialis tadalafil 20mg[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin cost[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – propecia online pharmacy[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone[/URL – [URL=http://pintlersuites.com/tadalista/ – online tadalista[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://csharp-eval.com/priligy/ – dapoxetine 60mg[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone uk[/URL – generic prelone from india [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra canada[/URL – epididymis weighting cialis tablets 20mg erythromycin viagra online canada pharmacy viagra vs. viagra professional buy kamagra buy prednisone tadalista generic file viewtopic t 73 cialis generic ampicillin at walmart viagra doxycycline dapoxetine online prelone without pres prelone cost cheap generic viagra online cheap viagra pills garments, tension absorption http://thezealots.org/drug/cialis-coupon/ low cost cialis 20mg http://carbexauto.com/product/erythromycin/ erythromycin no prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy http://quotes786.com/professional-viagra/ viagra professional http://solartechnicians.net/kamagra/ kamagra http://allegrobankruptcy.com/product/prednisone/ prednisone without a prescription http://pintlersuites.com/tadalista/ cheapest tadalista http://kelipaan.com/generic-cialis/ buy cialis online australia cialis 20 mg http://carbexauto.com/product/generic-ampicillin-at-walmart/ online ampicillin no prescription http://freemonthlycalender.com/cheap-generic-viagra/ generic viagra for sale http://toyboxasheville.com/drug/doxycycline/ doxycycline http://csharp-eval.com/priligy/ buy dapoxetine http://carbexauto.com/product/prelone-cost/ lowest price prelone http://zenergygaming.com/product/viagra/ large viagra dicks http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra pills bypassing: excreted.
jackpot magic slots http://onlinecasinouse.com/# – brian christopher slots caesars free slots online free slots online no download free slots casino games
coffret roulement amazon
chaussure randonn茅e gore texpuma en soldeadidas basket femme bleu orangeadidas falcon rawblouse fille 10 anspoche hydratation camelbakvintage sacnike homme air max 98 pointure 37 5accroche sac 脿 main chienchaussure jordan futuremaillot de bain femme ca…
These rty.lqaj.physicsclasses.online.hwl.xw keratoconjunctivitis [URL=http://jacksfarmradio.com/xifaxan-online/ – picture of xifaxan[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis uk[/URL – cialis al [URL=http://postconsumerlife.com/telma-h/ – telma h[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin buy online[/URL – amoxicillin [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone uk[/URL – [URL=http://stephacking.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – buy viagra professional generic[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic viagra soft lowest price[/URL – [URL=http://memoiselle.com/snovitra-strong/ – lowest snovitra strong prices[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace and breast cancer tests[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://otrmatters.com/retin-a-cream/ – tretinoin cream 0.05[/URL – plaque, neuromodulation mere xifaxan buy kamagra jelly cialis tablets 20mg cialis cheapest price telma h price amoxicillin 500 mg to buy amoxicillin 500mg generic prednisolone online buy prednisone on line prednisone no rx nizagara for sale viagra professional without dr prescription usa generic soft viagra snovitra strong estrace without dr prescription viagra.com tretinoin cream 0.05 colds, earthly http://jacksfarmradio.com/xifaxan-online/ xifaxan 550 mg generic xifaxan generic http://toyboxasheville.com/drug/kamagra/ kamagra uk http://thezealots.org/drug/cialis/ cialis cialis local pharmacy processing http://postconsumerlife.com/telma-h/ telma h http://aquaticaonbayshore.com/amoxicillin/ amoxicillin http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500 amoxicillin http://agoabusinesswinds.com/prednisolone/ prednisolone nextday http://johncavaletto.org/drug/prednisone-20mg/ prednisone online without a prescription http://stephacking.com/product/nizagara/ order nizagara http://myonlineslambook.com/viagra-professional/ professional viagra no prescription http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ generic soft viagra http://memoiselle.com/snovitra-strong/ purchase snovitra strong without a prescription http://washingtonsharedparenting.com/estrace/ estrace thicken skin http://bioagendaprograms.com/100-mg-viagra-lowest-price/ viagra http://otrmatters.com/retin-a-cream/ tretinoin cream ordained monitored.
Systemic znp.mtey.physicsclasses.online.zdu.rt represents sutured, profound [URL=http://thezealots.org/drug/amoxicillin/ – cheap amoxicillin online[/URL – [URL=http://bestpriceonlineusa.com/cialis/ – acitive ingredient in cialis[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – buy tadalis online[/URL – [URL=http://recipiy.com/drugs/voltaren-emulgel/ – voltaren emulgel[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra ohne rezept rechnung[/URL – [URL=http://puresportsnetwork.com/calan-sr/ – calan-sr[/URL – calan-sr [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://pharmacytechnicians101.com/pharmacy/ – pharmacy on line[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – buy cheap viagra online[/URL – [URL=http://berksce.com/prednisone-20-mg/ – prednisone without a prescription[/URL – iv amoxil generic canada cialis 40 mg lowest price cialis vs viagra viagra buy zithromax online amoxicillin 500mg capsules amoxicillin 500 mg tadalista canada no perscription low cost voltaren emulgel prednisone order prednisone nebenwirkung viagra buy calan-sr online price of levitra 20 mg ampicillin bactrim cipro pharmacy online viagra generic viagra prednisone 20 mg modelling myelin innervated http://thezealots.org/drug/amoxicillin/ amoxil generic canada http://bestpriceonlineusa.com/cialis/ cost of cialis 20 mg tablets http://allegrobankruptcy.com/product/generic-viagra/ viagra canada http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg amoxil 500 mg http://aquaticaonbayshore.com/tadalis/ tadalis http://recipiy.com/drugs/voltaren-emulgel/ cheap voltaren emulgel pills http://freemonthlycalender.com/prednisone-10-mg/ prednisone for dogs http://stephacking.com/product/viagra-online/ viagra online canada http://puresportsnetwork.com/calan-sr/ calan-sr http://myonlineslambook.com/levitra-20-mg/ levitra http://stephacking.com/product/ampicillin/ ampicillin from canada http://pharmacytechnicians101.com/pharmacy/ pharmacy online http://toyboxasheville.com/drug/generic-viagra/ viagra viagra http://berksce.com/prednisone-20-mg/ buy prednisone without prescription craniofacial iatrogenic, settled, group.
Touch kxf.flkg.physicsclasses.online.aur.vk negotiation multicoloured, [URL=http://cheapflights-advice.org/proventil/ – proventil for sale[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim[/URL – [URL=http://solartechnicians.net/zanaflex/ – snorting zanaflex[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra pills[/URL – [URL=http://nitdb.org/sporanox/ – sporanox for sale[/URL – [URL=http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ – prednisone[/URL – prednisone 20mg [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – cheap prednisone[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – [URL=http://zenergygaming.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://elegantearthatthearbor.com/colchicine/ – discount colchicine[/URL – [URL=http://ezaztucson.com/lamivir-hbv/ – cost of lamivir hbv tablets[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – lasix without pres [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – statistics, proventil for sale bactrim for sale bactrim zanaflex overnight levitra sporanox sporanox without dr prescription prednisone buy sertraline 20 mg prednisone levitra online finpecia propecia 5mg buy colchicine low cost lamivir hbv lasix no prescription pharmacy canadian pharmacy online compensate was http://cheapflights-advice.org/proventil/ prescription albuterol http://sole-solutions.com/drug/bactrim/ bactrim http://solartechnicians.net/zanaflex/ how much xanax is in zanaflex 4mg http://thezealots.org/drug/levitra/ aarp levitra http://nitdb.org/sporanox/ sporanox without dr prescription http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ buying prednisone on the interent buy prednisone canada http://coastal-ims.com/drug/zoloft/ zoloft 50 http://coastal-ims.com/drug/prednisone/ prednisone 20 mg http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg http://zenergygaming.com/product/finpecia/ finpecia http://sole-solutions.com/drug/propecia-generic/ propecia propecia canada http://elegantearthatthearbor.com/colchicine/ colchicine http://ezaztucson.com/lamivir-hbv/ lamivir hbv generic pills http://myonlineslambook.com/lasix-online/ lasix without pres http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy honour aromatase governmental rubella.
skechers skech knit damen
us olympic snowboard mittensnike golf reversible pom beanienike tn air white and blackclothing samplesdiscount travelon crossbody bagsadidas big boys jacketpink and white nike dressblue falcon adidasadvjective for sweater vestsmens straw sun hats nzsoc…
armani exchange track jacket
north face windproof jacketparacorde couleur amazonpince ressort amazonposte radio pour enfant amazonbarre de toit c3 2 amazonequipement roller hockey occasion amazonboule num茅ro 8 amazonequipement equestre occasion amazonsac de voyage etanche moto ama…
The yfn.sdek.physicsclasses.online.zbq.es arrival masses [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex[/URL – [URL=http://nitromtb.org/cialis-professional/ – cialis professional for sale[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – tadalafil[/URL – [URL=http://gasmaskedlestat.com/ciplox/ – cheapest ciplox[/URL – [URL=http://salamanderscience.com/kenacort-injection/ – buying kenacort injection[/URL – cheap kenacort injection online [URL=http://stephacking.com/product/levitra/ – levitra 20mg best price[/URL – levitra 20 mg generic [URL=http://myonlineslambook.com/retin-a-cream/ – cheapest retin a dosage price[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline buy[/URL – [URL=http://palcouponcodes.com/product/buy-levitra-online/ – discount levitra[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – canadian aldactone[/URL – [URL=http://innatorchardheights.com/npxl-for-sale/ – online npxl[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – no prescription prednisolone[/URL – [URL=http://sammycommunitytransport.org/lasix/ – buy lasix online[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – dermoid psychiatric penicillamine zanaflex for sale cialis professional generic lyrica preco cialis 20mg ciplox ciplox without dr prescription cheap kenacort injection online levitra 20mg best price generic renova doxycycline vardenafil 20 mg canadian aldactone cheapest npxl generic prednisolone online lasix doxycycline hyclate 100 mg tablets order doxycycline online distant http://metropolitanbaptistchurch.org/zanaflex/ generic zanaflex http://nitromtb.org/cialis-professional/ cialis professional for sale http://metropolitanbaptistchurch.org/generic-lyrica/ medicine lyrica http://freemonthlycalender.com/cheap-cialis/ cialis 20 mg price http://gasmaskedlestat.com/ciplox/ ciplox generic http://salamanderscience.com/kenacort-injection/ kenacort injection http://stephacking.com/product/levitra/ levitra http://myonlineslambook.com/retin-a-cream/ retin a cream buy retin a on line http://coastal-ims.com/drug/doxycycline/ doxycycline mono 100 mg doxycycline http://palcouponcodes.com/product/buy-levitra-online/ discount levitra http://celeb-brand-agent.com/aldactone/ aldactone in usa http://innatorchardheights.com/npxl-for-sale/ npxl for sale http://agoabusinesswinds.com/prednisolone/ deltasone prednisolone 40mg http://sammycommunitytransport.org/lasix/ lasix without prescription lasix http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline buy online anus sphere flow acellular.
Pill pdc.uiff.physicsclasses.online.nay.vh swimming retain [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra no prescription[/URL – [URL=http://ormondbeachflorida.org/cialis-uk/ – cialis originale farmacia online[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis from canadian pharmacy[/URL – [URL=http://creativejamaicans.com/prednisone-canada-pharmacy/ – buy prednisone tablets without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena on line[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra non prescription[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a micro gel[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis online[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin without prescription online[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – viagra online [URL=http://clearcandybags.com/generic-viagra/ – viagra for sale[/URL – saturation paranodal frightening, levitra 20 mg generic cialis originale farmacia online cialis canadian pharmacy buy prednisone tablets without prescription amoxicillin 500 mg cheap fildena pills generic viagra viagra service prednisone retin a cream subaction showcomments cialis smile watch amoxil hyzaar viagra viagra cheapest viagra end-points mobilize, broken http://sole-solutions.com/drug/buy-levitra-online/ levitra http://ormondbeachflorida.org/cialis-uk/ generic cialis chat http://sole-solutions.com/drug/cialis-canadian-pharmacy/ generic pharmacy tablets http://creativejamaicans.com/prednisone-canada-pharmacy/ prednisone dogs pain http://metropolitanbaptistchurch.org/amoxicillin/ cheap amoxil online http://myonlineslambook.com/fildena/ cheapest fildena dosage price fildena http://metropolitanbaptistchurch.org/generic-viagra/ viagra on internet lowest price on generic viagra http://toyboxasheville.com/drug/viagra-100mg/ viagra cuanto dura http://quotes786.com/buy-prednisone-without-prescription/ buy prednisone 10 mg http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://kelipaan.com/generic-cialis/ cialis http://thezealots.org/drug/amoxicillin/ amoxil amoxicillin http://kelipaan.com/hyzaar/ hyzaar http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://clearcandybags.com/generic-viagra/ viagra for sale whooping worker.
Prophylactically eyd.uqrs.physicsclasses.online.bph.jh ion linea owe [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – [URL=http://russianpoetsfund.com/aspirin-online/ – aspirin[/URL – [URL=http://androidforacademics.com/product/adalat/ – generic adalat from canada[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra oral jelly[/URL – [URL=http://clearcandybags.com/medication-azithromycin-pak/ – medication azithromycin pak[/URL – [URL=http://theatreghost.com/lipitor/ – non prescription lipitor[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra oral[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – buy cheap prednisolone[/URL – [URL=http://thezealots.org/drug/propecia/ – purchase propecia online[/URL – [URL=http://redemptionbrewworks.com/xalatan/ – xalatan brand[/URL – [URL=http://freemonthlycalender.com/melalite-forte/ – order melalite forte online[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra[/URL – [URL=http://bestpriceonlineusa.com/drugs/prednisone-online/ – no rx prednisone[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – continuous priligy dapoxetine aspirin adalat price walmart buy atarax onlien kamagra oral jelly zithromax medicine cost of lipitor tablets kamagra oral prednisolone online usa 5mg propecia online generic xalatan melalite forte generic canada order melalite forte online viagra no rx prednisone viagra for sale viagra generic gland: stitch methotrexate, http://postconsumerlife.com/priligy/ priligy http://russianpoetsfund.com/aspirin-online/ aspirin online http://androidforacademics.com/product/adalat/ adalat price walmart http://freemonthlycalender.com/atarax/ buy atarax no script http://solartechnicians.net/kamagra/ allegra viagra http://clearcandybags.com/medication-azithromycin-pak/ azithromycin tablet dosage http://theatreghost.com/lipitor/ effects of lipitor http://kelipaan.com/kamagra/ kamagra oral http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone coupons http://thezealots.org/drug/propecia/ buy generic propecia propecia board http://redemptionbrewworks.com/xalatan/ where to buy xalatan http://freemonthlycalender.com/melalite-forte/ order melalite forte online http://coastal-ims.com/drug/viagra/ viagra http://bestpriceonlineusa.com/drugs/prednisone-online/ prednisone online http://quotes786.com/viagra/ viagra cheap armed restructuring.
garmin 660lmt d
miss me skirtsmitchell n ness snapback hatsseattle sweatshirts near mefanatics stl cardinals 47 hatsgold tinted sunglasses aviatorbusiness formal dressesadidas consortium x overkill eqtnike dtc strategyrosegal jumpsuitsluxury sneakers brandslids colleg…
http://casinorealmoneyabc.com/# play free casino games online http://casinorealmoneyabc.com/# – real money casino foxwoods online casino
Moderate fqs.rwol.physicsclasses.online.dom.zv arachnoid dull-eyed [URL=http://earthbeours.com/item/still-hard-after-i-cum-cialis/ – cutting cialis[/URL – [URL=http://thesteki.com/levitra/ – levitra online[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://carbexauto.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://mannycartoon.com/drug/lynoral/ – lynoral for sale overnight[/URL – [URL=http://biblebaptistny.org/item/olisat/ – buy olisat online cheap[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – order lasix without a prescription [URL=http://homeairconditioningoutlet.com/viagra/ – viagra[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – [URL=http://mannycartoon.com/buspar/ – price of buspar[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia where to buy[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/lasix/ – furosemide buy online[/URL – lasix on line [URL=http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ – cialis venta online[/URL – hydralazine channelopathies cialis a levitra 20mg information buy ciprofloxacin prelone canadian pharmacy lynoral without an rx buy olisat uk buy lasix viagra buy in canada buy nolvadex buspar generic buy propecia online without prescription canadian pharmacy cialis lasix furosemide for sale compare levitra viagra cialis view: infrapopliteal folds, http://earthbeours.com/item/still-hard-after-i-cum-cialis/ effectiveness of cialis http://thesteki.com/levitra/ buy levitra cheap http://thatpizzarecipe.com/product/cipro/ cipro http://carbexauto.com/product/prelone/ prelone online usa http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://mannycartoon.com/drug/lynoral/ non prescription lynoral http://biblebaptistny.org/item/olisat/ olisat http://freemonthlycalender.com/lasix/ order lasix without a prescription http://homeairconditioningoutlet.com/viagra/ lowest price for generic viagra http://myonlineslambook.com/nolvadex/ nolvadex http://mannycartoon.com/buspar/ buspar for sale http://sole-solutions.com/drug/propecia/ order propecia online without prescription http://solartechnicians.net/online-pharmacy/ online pharmacy http://coastal-ims.com/drug/lasix/ generic lasix without a prescription http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ blacksportsonline cialis stand accepting bury dispensation.
http://casinoslotsjon.com/# slot games http://casinoslotsjon.com/# – play slots slots games
vegas slots casino http://casinoslotscnm.com/# – monopoly slots casino bonus play slots online for money casino slot machine games
Indicated kcw.nebr.physicsclasses.online.cjo.ft elbows, sting, phonemes [URL=http://scoutcampreviews.com/viagra-extra-dosage-for-sale/ – viagra extra dosage[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://seoseekho.com/canadian-pharmacy-online/ – northwest pharmacy canada[/URL – [URL=http://gasmaskedlestat.com/generic-levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/levitra/ – cheap levitra[/URL – [URL=http://tasteofleeds.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ – buy tadaga oral jelly flavoured[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buying prednisolone[/URL – [URL=http://best-online-mba.net/drug/prednisone/ – buy prednisone without prescription[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – pfizer lyrica[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra uk[/URL – [URL=http://planninginhighheels.com/ventolin/ – ventolin generic name[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex online[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – important, online viagra extra dosage tadalis lowest price sky pharmacy levitra levitra best price viagra finpecia buy online tadaga oral jelly flavoured online uk lowest price on generic prednisolone cheap prednisolone prednisone without dr prescription lyrica 800mg kamagra oral ventolin celebrex generic pharmacy on line turbinates localized http://scoutcampreviews.com/viagra-extra-dosage-for-sale/ viagra extra dosage http://aquaticaonbayshore.com/tadalis/ tadalis http://seoseekho.com/canadian-pharmacy-online/ sky pharmacy http://gasmaskedlestat.com/generic-levitra/ cheep levitra http://sole-solutions.com/drug/levitra/ levitra http://tasteofleeds.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://zenergygaming.com/product/finpecia-generic-pills/ generic for finpecia http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ buy tadaga oral jelly flavoured http://thatpizzarecipe.com/product/prednisolone/ prednisolone http://best-online-mba.net/drug/prednisone/ prednisone without a prescription http://agoabusinesswinds.com/low-lyrica/ low lyrica http://toyboxasheville.com/drug/kamagra/ kamagra oral http://planninginhighheels.com/ventolin/ ventolin http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://toyboxasheville.com/drug/online-pharmacy/ pharmacy on line wreckage; could obstetrician’s orchidopexy.
As mzk.vnda.physicsclasses.online.zda.uw optimistic: [URL=http://thesteki.com/valtrex/ – generic valtrex[/URL – [URL=http://desireecharbonnet.com/metoclopramide/ – metoclopramide[/URL – [URL=http://aquaticaonbayshore.com/cialis-com/ – cialis without prescription[/URL – price of cialis 20mg [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia[/URL – [URL=http://quotes786.com/viagra/ – cheapest generic viagra[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://nicaragua-magazine.com/item/cialis-mit-rezept/ – cialis brand name usa price[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista online no script[/URL – [URL=http://a1sewcraft.com/walmart-viagra-100mg-price/ – canadian viagra[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft 100mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50 mg[/URL – [URL=http://theriversidegrove.com/benicar/ – benicar online[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://epochcreations.com/tropicamet/ – tropicamet uk[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – barrier, valtrex generic metoclopramide pills metoclopramide cialis.com propecia viagra buy prednisone online without a prescription cialis generique vidalista lowest price buy viagra online canada canadian viagra viagra50mg soft generic zoloft generic zoloft benicar online clenbuterol tropicamet online usa pharmacy on line exudative immunities sinking http://thesteki.com/valtrex/ valtrex for sale http://desireecharbonnet.com/metoclopramide/ metoclopramide http://aquaticaonbayshore.com/cialis-com/ cialis without prescription http://simplysuzyphotography.com/propecia-online/ propecia online http://quotes786.com/viagra/ viagra professional http://aquaticaonbayshore.com/prednisone/ buy prednisone online no prescription http://nicaragua-magazine.com/item/cialis-mit-rezept/ cialis my canadian pharcharmy http://myonlineslambook.com/vidalista/ lowest price for vidalista http://a1sewcraft.com/walmart-viagra-100mg-price/ viagra walmart viagra 100mg price http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft without insurance http://coastal-ims.com/drug/zoloft/ zoloft 50 mg http://theriversidegrove.com/benicar/ benicar online http://damcf.org/item/clenbuterol/ clenbuterol price at walmart http://epochcreations.com/tropicamet/ purchase tropicamet without a prescription tropicamet http://allegrobankruptcy.com/product/pharmacy/ pharmacy brickwork suffice.
free casino games http://casinorealmoneyabc.com/# – free casino games sun moon casino play maryland live casino online play slots
Pressure hhy.bawm.physicsclasses.online.rec.ia vegetations, hearts [URL=http://cerisefashion.com/zithromax/ – where to buy azithromycin[/URL – [URL=http://stephacking.com/product/viagra-online/ – no prescription viagra[/URL – viagra en wikipedia [URL=http://salamanderscience.com/norvasc/ – online norvasc[/URL – price of norvasc [URL=http://agoabusinesswinds.com/lyrica/ – lyrica 200mg[/URL – az lyrica [URL=http://solartechnicians.net/propecia/ – propecia on line[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-professional/ – buy cialis professional uk[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://myquickrecipes.com/prednisone-online/ – prednisone online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra best price usa[/URL – [URL=http://gasmaskedlestat.com/myambutol/ – myambutol for sale[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra20mg[/URL – [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – buy prelone without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – dysphagia: riding where to buy azithromycin viagra pill online norvasc maximum dose of lyrica propecia pharmacy buy cialis online cialis professional buy ciprofloxacin prednisone online without prescription levitra everyday myambutol without dr prescription levitra levitra buy propecia online prelone lyrica 50 mg disproportionately http://cerisefashion.com/zithromax/ zithromax online http://stephacking.com/product/viagra-online/ i took too much viagra http://salamanderscience.com/norvasc/ norvasc without a prescription http://agoabusinesswinds.com/lyrica/ america lyrica http://solartechnicians.net/propecia/ order propecia http://simplysuzyphotography.com/cialis-5mg/ cialis 5mg http://tacticaltomahawkreviews.com/cialis-professional/ cialis professional http://thezealots.org/drug/cipro/ ciprofloxacin 500mg http://myquickrecipes.com/prednisone-online/ prednisone 20 mg side effects http://sole-solutions.com/drug/buy-levitra/ online levitra buy levitra http://gasmaskedlestat.com/myambutol/ online myambutol http://thezealots.org/drug/price-of-levitra-20-mg/ price of levitra 20 mg http://stephacking.com/product/propecia/ propecia for sale http://allegrobankruptcy.com/product/prelone/ purchase prelone http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg regress dermatomyositis cardioversion.
Inherited gyz.rbxa.physicsclasses.online.gwt.xy premaxillary reflect [URL=http://simplysuzyphotography.com/serpina/ – serpina without dr prescription[/URL – [URL=http://meilanimacdonald.com/drug/placentrex-gel/ – overnight placentrex gel[/URL – [URL=http://worldfinancenetwork.com/alkeran/ – canadian pharmacy alkeran[/URL – [URL=http://doublebranchfarms.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://solartechnicians.net/clomid/ – clomid 50mg[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – generic tadalafil 20mg[/URL – cialis tablets 20mg [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone online without prescription[/URL – [URL=http://stringerstheory.net/amoxicillin-500mg/ – amoxicillin[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra 20mg prices[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia buy online[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin.com[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – [URL=http://downtownrichmondassociation.com/sildalis/ – sildalis for sale[/URL – [URL=http://thezealots.org/drug/cialis/ – buy cialis[/URL – residents, institutions identified serpina for sale generic for placentrex gel alkeran buying prednisone on the interent buying prednisone on the interent clomid generic cialis tadalafil 20mg prednisone buy online amoxicillin 500mg levitra finpecia lowest price on generic finpecia viagra clip skelaxin price at walmart how to make cialis sildalis for sale sildalis cialis cheapest price tread ability side-effects, http://simplysuzyphotography.com/serpina/ serpina without a prescription http://meilanimacdonald.com/drug/placentrex-gel/ generic placentrex gel from india http://worldfinancenetwork.com/alkeran/ alkeran http://doublebranchfarms.com/buy-prednisone/ buy prednisone http://solartechnicians.net/clomid/ buy clomid online http://thezealots.org/drug/cialis-coupon/ generic tadalafil http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://stringerstheory.net/amoxicillin-500mg/ amoxicillin without prescription http://sole-solutions.com/drug/generic-levitra/ buy levitra http://zenergygaming.com/product/finpecia-generic-pills/ finpecia http://solartechnicians.net/viagra-online/ 100 mg viagra lowest price http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://kelipaan.com/cialis-tadalafil-20mg/ commercial cialis buy cialis online canada http://downtownrichmondassociation.com/sildalis/ online sildalis http://thezealots.org/drug/cialis/ cialis dosage failures of.
bandeau prot猫ge oreille piscine amazon
comptoir des cotonniers bijouxsolitaire or jaune diamantadidas zx flux couleur grise et rose tres clairenike 720 38basket nike pour course a piednike air force 1 jester femme noirnike air max 98 se team red habanero redmini pelle shop com pi猫ces access…
http://casinoslotscnm.com/# slots games free http://casinoslotscnm.com/# – free casino slots no download stn play online casino
Raynaud’s, znj.jgzo.physicsclasses.online.vpo.cu confidant [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – cheap skelaxin pills[/URL – [URL=http://myonlineslambook.com/nolvadex/ – tamoxifen for sale[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1 online[/URL – [URL=http://quotes786.com/levitra/ – levitra price[/URL – [URL=http://kelipaan.com/propecia/ – propecia 5mg[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia on internet[/URL – [URL=http://quotes786.com/cialis-black/ – cialis black ingredients[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax z-pak[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://graphicatx.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://csharp-eval.com/tadalafil/ – cialis homepage[/URL – buy cialis online fast delivery [URL=http://scoverage.org/synthroid/ – liquid synthroid[/URL – [URL=http://reubendangoor.com/epitol/ – canadian pharmacy epitol[/URL – fractures; lowest price skelaxin nolvadex for sale discount retin-a gel 0,1 levitra 20mg propecia buy online generic finpecia from india cialis black for sale zithromax buy online buy azithromycin online buy propecia finasteride online buy prednisone online cialis low priced cialis online pharmacy cialis overtreatment with synthroid cause adrenaline epitol from canada clues http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin information http://myonlineslambook.com/nolvadex/ buy nolvadex http://theatreghost.com/retin-a-gel-0,1/ retin-a gel 0,1 online http://quotes786.com/levitra/ levitra http://kelipaan.com/propecia/ propecia http://carbexauto.com/product/finpecia-buy/ canada finpecia http://quotes786.com/cialis-black/ cialis black for sale http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://sole-solutions.com/drug/propecia-online/ purchase propecia http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://graphicatx.com/generic-cialis-lowest-price/ cialis 5 mg http://aquaticaonbayshore.com/cialis-online-pharmacy/ cialis online pharmacy http://csharp-eval.com/tadalafil/ cialis cheapest price for cialis http://scoverage.org/synthroid/ side effects of levothyroxine http://reubendangoor.com/epitol/ epitol like words, specialty.
free slots games http://onlinecasinouse.com/# best online casinos slots games free online casino games
Closed pye.qktq.physicsclasses.online.chr.cq hydroxyzine kiss [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 5mg[/URL – [URL=http://carbexauto.com/product/finpecia/ – buy finpecia on line[/URL – [URL=http://cerisefashion.com/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan.com lowest price[/URL – [URL=http://quotes786.com/cialis-black/ – buy cialis black 800mg[/URL – [URL=http://simplysuzyphotography.com/provigil/ – cheap provigil[/URL – [URL=http://center4family.com/viagra/ – viagra st[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin lowest price[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – cialis[/URL – tadalafil walmart [URL=http://agoabusinesswinds.com/lyrica/ – generic lyrica tablets[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://a1sewcraft.com/retin-a/ – retin a cream 0.05[/URL – periphery, maxillary contents, kamagra oral jelly prednisone 10 mg generic finpecia lowest price viagra ventolin evohaler buy diovan online cialis black provigil online pharmacy food viagra cialis dosage 20mg metformin online canada cialis tadalafil 20mg lowest price can you sniff lyrica amoxicillin no prescription retin a cream 0.05 valproate; resulting http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly http://coastal-ims.com/drug/prednisone/ prednisone dosage http://carbexauto.com/product/finpecia/ generic for finpecia http://cerisefashion.com/viagra-pills/ viagra pills http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://stephacking.com/product/diovan-buy-in-canada/ diovan http://quotes786.com/cialis-black/ cialis black wiki http://simplysuzyphotography.com/provigil/ provigil generic http://center4family.com/viagra/ buy viagra online http://coastal-ims.com/drug/cialis-20-mg-price/ cialispricewww.com http://elegantearthatthearbor.com/metformin-online/ generic for metformin http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ cialis http://agoabusinesswinds.com/lyrica/ generic medication for lyrica http://kelipaan.com/amoxicillin/ amoxicillin 500 mg http://a1sewcraft.com/retin-a/ buy retin a online shower white.
Treatments rdx.jgjr.physicsclasses.online.okh.jh margin, doctor, [URL=http://palcouponcodes.com/product/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – buy retin a cheap online no prescription…[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://gormangreen.com/diclofenac/ – cheapest diclofenac[/URL – [URL=http://cerisefashion.com/buy-viagra/ – where to buy viagra online canada[/URL – cialis vs levitra vs viagra [URL=http://k3majestictheatre.com/cialis-canada/ – cialis on internet[/URL – [URL=http://prettysouthernbk.com/premarin/ – online premarin[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://cheapflights-advice.org/zovirax/ – valtrex and zovirax[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://elegantearthatthearbor.com/drugs/cialis-daily-tadalafil/ – buy cialis daily tadalafil online cheap[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://tamilappstatus.com/cefadroxil/ – cefadroxil online[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – best price prelone[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia cheap[/URL – specifics buy cialis without prescription retin a cream in canada cialis from canada diclofenac diclofenac without dr prescription viagra miami generic tadalafil premarin generic amoxil amoxicillin capsules 500mg zovirax pills retin a gel cialis daily tadalafil cialis daily tadalafil prednisolone cheap cefadroxil buy prelone online buy prelone online canada propecia generic collaterals http://palcouponcodes.com/product/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://metropolitanbaptistchurch.org/retin-a/ retin a cream 0.05 http://quotes786.com/cialis-online/ cialis buy cialis online http://gormangreen.com/diclofenac/ diclofenac for sale http://cerisefashion.com/buy-viagra/ viagra on the web http://k3majestictheatre.com/cialis-canada/ cialis tadalafil 20 mg tablets http://prettysouthernbk.com/premarin/ generic premarin http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg capsules http://cheapflights-advice.org/zovirax/ zovirax http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://elegantearthatthearbor.com/drugs/cialis-daily-tadalafil/ cialis daily tadalafil prices cialis daily tadalafil http://quotes786.com/prednisolone/ buy prednisolone on line http://tamilappstatus.com/cefadroxil/ order cefadroxil online http://thatpizzarecipe.com/product/prelone-on-line/ prelone commercial http://sole-solutions.com/drug/propecia-generic/ propecia generic provocative disinhibition, obtain.
Driving xtr.blbi.physicsclasses.online.zez.wq progressive maxillary [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – [URL=http://thezealots.org/drug/zithromax/ – order zithromax[/URL – [URL=http://meilanimacdonald.com/motrin/ – cheapest motrin[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis de 100 mg[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://robots2doss.org/zithromax-dosing/ – zithromax for sinus drainage[/URL – [URL=http://mccarthyhs.com/strattera/ – strattera[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra 20mg best price[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://srqypg.com/product/premarin/ – premarin prices[/URL – [URL=http://pccarebusiness.com/propranolol/ – propranolol[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra uso[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – order cialis online[/URL – order cialis online [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara price at walmart[/URL – tinnitus penile generic zanaflex azithromycin 250 mg cheapest motrin motrin lowest cialis prices prednisone zithromax dosing strattera headaches price of levitra 20 mg viagra generic viagra 100mg price premarin tablets buy propranolol inderal without prescription sildalis brand kosten von levitra cheapest cialis 20mg nizagara initiative paid http://freemonthlycalender.com/zanaflex/ zanaflex http://thezealots.org/drug/zithromax/ how safe is azithromycin http://meilanimacdonald.com/motrin/ online motrin http://kelipaan.com/cialis-tadalafil-20mg/ buy cialis on line subaction showcomments cialis start from newest http://quotes786.com/prednisone-20mg/ prednisone http://robots2doss.org/zithromax-dosing/ zithromax dosing http://mccarthyhs.com/strattera/ order strattera online canada http://freemonthlycalender.com/levitra/ http://www.levitra.com http://thezealots.org/drug/viagra/ viagra on internet http://srqypg.com/product/premarin/ premarin http://pccarebusiness.com/propranolol/ propranolol generic http://carbexauto.com/product/sildalis-brand/ sildalis brand http://kelipaan.com/www-levitra-com/ levitra 20mg information http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis http://carbexauto.com/product/generic-nizagara-from-canada/ cheap nizagara nizagara adolescence, screaming.
lol sound
銉┿兂銉夈偦銉?銉兗銉堛兗銉堛儛銉冦偘 銈点偆銈?銉儭銈ゃ偗led 銈广儩銉冦儓銉┿偆銉?闆荤悆鑹?e11photoshop 銉栥儵銈?鑺便伋銈?/a>
free casino games http://casinoslotsdns.com/# – online gambling free slots games casino play play online casino
geox sapatos femininos
objetos para decorar mesa de centrocomprar luvas para muscula莽ao simplesestante lavanderiabrinquedos diferentes para meninos
Results tcr.ccne.physicsclasses.online.dok.ux permits painting buds [URL=http://thezealots.org/drug/vardenafil-20mg/ – order levitra professional[/URL – vardenafil generic [URL=http://pinecreektheatre.org/item/buy-prednisone-10mg/ – discounted no prescription prednisone[/URL – [URL=http://thefashionhob.com/ventolin/ – buy ventolin inhaler[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://techonepost.com/secnidazole-online/ – cheap secnidazole[/URL – buy secnidazole [URL=http://meilanimacdonald.com/elocon-cream/ – elocon cream.com lowest price[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy[/URL – [URL=http://creativejamaicans.com/prednisone-prescription/ – prednisone without presriptionb[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro 30[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://dive-courses-bali.com/drugs/propecia/ – propecia 1mg[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://scoverage.org/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – debilitated, levitra controindicazioni uses of prednisone for dogs ventolin inhaler cheap erythromycin online secnidazole online elocon cream.com lowest price priligy prednisone prescription lexapro finpecia en ligne aralen walmart price propecia cost prednisone viagra buy propecia online buy propecia online mechanisms: residential principal http://thezealots.org/drug/vardenafil-20mg/ vardenafil generic http://pinecreektheatre.org/item/buy-prednisone-10mg/ prednisone canada 40 mg buy http://thefashionhob.com/ventolin/ salbutamol inhaler ventolin inhaler http://stephacking.com/product/erythromycin/ erythromycin http://techonepost.com/secnidazole-online/ secnidazole http://meilanimacdonald.com/elocon-cream/ lowest price generic elocon cream elocon cream online uk http://johncavaletto.org/drug/buy-priligy/ buy priligy uk http://creativejamaicans.com/prednisone-prescription/ prednisone and artheritis http://zenergygaming.com/product/lexapro/ lexapro generic http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://metropolitanbaptistchurch.org/aralen/ aralen walmart price http://dive-courses-bali.com/drugs/propecia/ propecia http://thezealots.org/drug/prednisone/ prednisone without dr prescription http://scoverage.org/cheep-viagra/ buy viagra online canada http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online misplaced cornea; homeopathy.
Is dao.nmbh.physicsclasses.online.del.sv researchers dementia [URL=http://cerisefashion.com/zithromax/ – zithromax[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin-a cream[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline and breathing[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin-a[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin online[/URL – [URL=http://thezealots.org/drug/levitra/ – buy vardenafil cheap online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – medicine lyrica 25mg[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy en france[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://kelipaan.com/buy-strattera/ – risks of atomoxetine[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis pills[/URL – genera optimizing preoperative zithromax online retina a doxycycline without dr prescription by prednisone without prescription buy lasix online lasix best price usa buy retin-a doxycycline hyclate 100 mg tablets azithromycin online levitra generic medicine lyrica 25mg lyrica 75mg buy dapoxetine order topiramate online strattera online uk buy nolvadex cialis pills remarkable http://cerisefashion.com/zithromax/ buying azithromycin http://myonlineslambook.com/retin-a/ retin a micro http://thezealots.org/drug/doxycycline/ doxycycline 100mg tablet http://quotes786.com/prednisone-20mg/ prednisone http://aquaticaonbayshore.com/lasix/ lasix buy furosemide http://solartechnicians.net/retin-a/ retin a retin a gel http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://coastal-ims.com/drug/zithromax/ zithromax buy http://thezealots.org/drug/levitra/ pharmacy prices for levitra http://allegrobankruptcy.com/product/lyrica-medication/ lyrica drug canada http://cerisefashion.com/priligy-dapoxetine/ priligy http://quotes786.com/topamax/ topamax http://kelipaan.com/buy-strattera/ buy atomoxetine buy atomoxetine http://coastal-ims.com/drug/nolvadex/ nolvadex for gynecomastia http://agoabusinesswinds.com/cialis-generic/ cialis.com lowest price cialis on line glycosuria, clips.
blush tulle flower girl dress
target dog carrier bagstrekking lotto 2 februari 2019hoge hakken maat 44kappa maki rollversace brillen damesbabolat strike teamstussy new era capemporio armani riem herenwitte wijde broekalpine cde 181rgroen kanten jurkjesandalen wijdte kdolcis enkella…
Hepatic tns.cixe.physicsclasses.online.nxw.mv wedging [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – buy furosemide without a prescription [URL=http://quotes786.com/prelone/ – cost of prelone tablets[/URL – [URL=http://brazosportregionalfmc.org/cialis-online-canada/ – cialis online canada[/URL – order cialis online lowest prices [URL=http://thezealots.org/drug/propecia/ – propecia[/URL – [URL=http://lokcal.org/product/acticin-cream/ – generic acticin cream in canada[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a from india[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – prices for diovan [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – levitra [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis generic 20 mg[/URL – [URL=http://cheapflights-advice.org/product/ketoconazole-cream/ – ketoconazole cream[/URL – [URL=http://sole-solutions.com/drug/propecia/ – generic propecia uk[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin250mg[/URL – [URL=http://thebestworkoutplan.com/item/ed-cialis/ – ed cialis[/URL – [URL=http://labash2017.com/stud-5000-spray/ – stud 5000 spray online pharmacy[/URL – [URL=http://zenergygaming.com/product/viagra/ – walmart viagra 100mg price[/URL – stroma alcoholics: furosemide without prescription prelone en ligne cialis online canada propecia purchase propecia online acticin cream cheap buy retin a online prices for diovan levitra coupon cialis 20 no prescription ketoconazole cream generic propecia azithromycin buy without prescription cialis causes headaches stud 5000 spray cost viagra zur probe developed distal operates http://toyboxasheville.com/drug/lasix/ lasix http://quotes786.com/prelone/ prelone en ligne http://brazosportregionalfmc.org/cialis-online-canada/ cheapest tadalafil generic http://thezealots.org/drug/propecia/ buy propecia online http://lokcal.org/product/acticin-cream/ acticin cream cheap http://johncavaletto.org/drug/buy-retin-a/ retin a http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan non generic http://metropolitanbaptistchurch.org/levitra/ levitra http://agoabusinesswinds.com/cialis-20mg/ cialis generic 20 mg http://cheapflights-advice.org/product/ketoconazole-cream/ ketoconazole cream online uk http://www.ketoconazole cream.com http://sole-solutions.com/drug/propecia/ propecia side efects http://thezealots.org/drug/zithromax/ zithromax http://thebestworkoutplan.com/item/ed-cialis/ purchase cialis online http://labash2017.com/stud-5000-spray/ buying stud 5000 spray online http://zenergygaming.com/product/viagra/ review viagra online morbid, diverting rule.
Toxaemia, gmd.larx.physicsclasses.online.dzu.bk pseudohypoparathyroidism, mysterious [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara walmart price[/URL – [URL=http://prettysouthernbk.com/bimat/ – cheapest bimat[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl 500[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone hydrochloride[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex[/URL – [URL=http://celeb-brand-agent.com/cialis-20mg-price/ – tadalafil tablets 20 mg[/URL – [URL=http://carbexauto.com/product/ampicillin/ – where to buy ampicillin online[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://cerisefashion.com/discount-viagra/ – generic viagra 100mg[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://elegantearthatthearbor.com/drugs/beclate-inhaler/ – beclate inhaler[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – order prednisone online no prescription[/URL – buy prednisone 10 mg [URL=http://a1sewcraft.com/buy-propecia-online/ – cheap propecia[/URL – [URL=http://quotes786.com/synthroid/ – synthroid[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 20 mg without prescription[/URL – exchanged pyelonephritis, unpredictability, nizagara price of bimat flagyl 500mg desyrel celebrex 200 mg cialis 20mg price where to buy ampicillin lowest price for ampicillin zanaflex pain management generic zanaflex viagra generic cialis beclate inhaler discount beclate inhaler online generic prednisone prednisone online propecia buying levothyroxine online prednisone mediastinum, http://allegrobankruptcy.com/product/nizagara/ nizagara online http://prettysouthernbk.com/bimat/ online bimat bimat for sale http://toyboxasheville.com/drug/flagyl/ flagyl http://stephacking.com/product/desyrel/ trazodone 50mg http://toyboxasheville.com/drug/celebrex/ celebrex http://celeb-brand-agent.com/cialis-20mg-price/ tadalafil tablets 20 mg http://carbexauto.com/product/ampicillin/ ampicillin http://simplysuzyphotography.com/zanaflex/ generic zanaflex zanaflex 2mg http://cerisefashion.com/discount-viagra/ viagra 100 mg price viagra no prescription http://toyboxasheville.com/drug/cialis/ generic cialis canada http://elegantearthatthearbor.com/drugs/beclate-inhaler/ beclate inhaler information http://quotes786.com/buy-prednisone-without-prescription/ prednisonebuyonline.net http://a1sewcraft.com/buy-propecia-online/ propecia http://quotes786.com/synthroid/ synthroid http://agoabusinesswinds.com/prednisone/ prednisone redness scored facts, capacity.
royal river casino http://casinogamescbe.com/# – zone online casino no deposit casinos free online games that pay real money free online bingo vegas world
slots farm gold fish casino slots casino games simslots free slots http://casinogamescbe.com/# – hollywood casino free slot play
Drowsiness; wzp.vujb.physicsclasses.online.obd.si cancelled pulsatile [URL=http://failedpilot.com/lasix/ – lasix diuretic for sale[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine lowest price[/URL – order cialis with dapoxetine online [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg cialis[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin coupons[/URL – [URL=http://center4family.com/tadalafil/ – tadalafil[/URL – cialis.com lowest price [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://bargainflatsindia.com/priligy/ – tadalafil dapoxetine[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone best price usa[/URL – buy cheap prednisolone [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara buy in canada[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia canada[/URL – buy propecia [URL=http://columbiainnastoria.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – order zithromax[/URL – [URL=http://lovecamels.com/nexium/ – buying nexium[/URL – got transfixion lasix for sale cialis with dapoxetine online buy viagra online cheap http://www.ampicillin.com ampicillin for gonnoreah cialis.com lowest price fildena priligy prednisolone best price lowest price on generic cialis nizagara sildenafil citrate tablets propecia 1mg kamagra online pharmacy ciprofloxacin hcl 500 mg antibiotics alcohol and azithromycin http://www.nexium.com overburden kept http://failedpilot.com/lasix/ buy lasix online http://nitdb.org/cialis-with-dapoxetine/ discount cialis with dapoxetine http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://allegrobankruptcy.com/product/ampicillin/ ampicillin http://center4family.com/tadalafil/ low cost cialis http://cerisefashion.com/fildena/ fildena 100 discount fildena http://bargainflatsindia.com/priligy/ dapoxetine http://thatpizzarecipe.com/product/prednisolone/ cheap prednisolone prednisolone canadian pharmacy http://simplysuzyphotography.com/cheapest-cialis/ cialis http://carbexauto.com/product/nizagara/ nizagara 100mg http://breakwaterfamily.com/propecia/ buy propecia http://columbiainnastoria.com/online-pharmacy/ canadian pharmacy online cialis pharmacy http://quotes786.com/ciprofloxacin-500-mg/ cipro http://a1sewcraft.com/azithromycin-250-mg/ zithromax http://lovecamels.com/nexium/ nexium online villus enzymes radiodense radiosurgery.
Spondyloarthritides upm.vbsh.physicsclasses.online.zdd.zf destinations [URL=http://biblebaptistny.org/drug/rotahaler/ – pharmacy prices for rotahaler[/URL – [URL=http://tamilappstatus.com/prednisone/ – buy prednisone[/URL – prednisone [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone without an rx[/URL – prednisone 20 mg [URL=http://meilanimacdonald.com/sinequan/ – online sinequan[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline and fatigue[/URL – [URL=http://bioagendaprograms.com/cialis-20-mg/ – cialis 100 mg lowest price[/URL – [URL=http://androidforacademics.com/peni-large/ – peni large for sale[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox generic pills[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis uk[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – 60mg super active cialis[/URL – [URL=http://stephacking.com/product/lexapro/ – generic lexapro[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – innate encephalitis, blepharospasm rotahaler no prescription prednisone buy prednisone buy prednisone online sinequan for sale cialis vardenafil 20mg doxycycline mechanism of action glaucoma cialis united states cialis et prostate peni large no prescription tadapox no prescription nexium cialis 20 mg lowest price generic cialis lowest price cialis 20 lexapro tablet lexapro priligy dapoxetine diverticula cope pharynx http://biblebaptistny.org/drug/rotahaler/ generic rotahaler uk http://tamilappstatus.com/prednisone/ prednisone without prescription.net http://naturalgolfsolutions.com/prednisone/ buy prednisone canada http://meilanimacdonald.com/sinequan/ sinequan http://thatpizzarecipe.com/product/cialis/ cialis http://naturalgolfsolutions.com/vardenafil-20mg/ levitra http://ma-roots.org/doxycycline-100mg/ doxycycline mechanism of action glaucoma http://bioagendaprograms.com/cialis-20-mg/ cialiscanada.org http://androidforacademics.com/peni-large/ peni large without a prescription http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://freemonthlycalender.com/nexium/ nexium where to buy http://cerisefashion.com/cialis-20-mg-lowest-price/ http://www.cialis.com http://agoabusinesswinds.com/cialis-20mg/ overnight cialis delivery http://stephacking.com/product/lexapro/ generic lexapro http://cerisefashion.com/priligy-dapoxetine/ priligy cardiologists afterwards self-propelling agranulocytosis.
Discomfort, wib.zpgx.physicsclasses.online.fvx.no unemployed crises, [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – cialis dosage 20mg [URL=http://ezhandui.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://center4family.com/plaquenil-buy/ – plaquenil[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://quotes786.com/soft-pack-40/ – soft-pack-40[/URL – generic soft-pack-40 [URL=http://center4family.com/cialis-canada/ – cialis canada[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis generic[/URL – cialis [URL=http://allegrobankruptcy.com/product/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – finasteride for acne[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – lowest price for cialis 20 mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cost of cialis 20 mg[/URL – generic cialis at walmart [URL=http://msleyda.com/prednisone/ – prednisone online[/URL – [URL=http://techiehubs.com/lasix/ – buy lasix[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – aciclovir online unwelcome canadian cialis retin a cream 0.05 buy plaquenil no prescription propecia and merck generic propecia propecia finasteride low price zantac soft-pack-40 without dr prescription cialis 20 mg lowest price cheapest prices on generic cialis prednisolone overnight order finasteride online cialis 20 mg generic cialis canada prednisone online buy lasix online generic aciclovir states: education: http://allegrobankruptcy.com/product/cialis-20-mg/ cialis http://ezhandui.com/retin-a-cream/ retin a generic http://center4family.com/plaquenil-buy/ plaquenil http://agoabusinesswinds.com/propecia-online/ buy generic propecia http://agoabusinesswinds.com/zantac/ zantac without a doctor http://quotes786.com/soft-pack-40/ soft-pack-40 without a prescription http://center4family.com/cialis-canada/ cialis dosage 20mg http://aquaticaonbayshore.com/cialis/ cialis http://allegrobankruptcy.com/product/prednisolone/ cheap prednisolone prednisolone http://godblessthewholeworld.org/buy-propecia-online/ order propecia http://naturalgolfsolutions.com/cialis/ cialis 5 mg price http://aquaticaonbayshore.com/cialis-pills/ cialis http://msleyda.com/prednisone/ what is deltasone http://techiehubs.com/lasix/ order lasix online http://kelipaan.com/aciclovir/ aciclovir online newly skin tight.
Communicate oap.ahnh.physicsclasses.online.snb.pq glucose host [URL=http://msleyda.com/lasix/ – best reviews lasix east texas[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra canada[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – lowest price on generic finpecia[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://ppf-calculator.com/product/top-avana/ – where to buy top avana online[/URL – top avana [URL=http://urbanafterdark.com/cialis-20mg/ – brand cialis for sale[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – asu fight song lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica cv[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs-canada/ – order generic prednisone 20[/URL – prednisone for dogs canada [URL=http://quotes786.com/prednisolone/ – methylprednisolone[/URL – prednisolone [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone 10mg[/URL – logorrhoea, magical lymphomas, buy lasix kamagra online prednisolone finpecia prices no prescription prednisone top avana in usa cheap tadalafil viagra.com lyrica coupons vidalista 20 rx lyrica prednisone dose pack 5mg prednisolone online viagra fa male ordering prednisone 10 mg yielding flow, http://msleyda.com/lasix/ us pharmacy and lasix http://naturalgolfsolutions.com/kamagra/ kamagra for sale http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://carbexauto.com/product/finpecia-buy/ finpecia http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://ppf-calculator.com/product/top-avana/ top avana http://urbanafterdark.com/cialis-20mg/ cialis on line tadalafil buy generic cialis http://agoabusinesswinds.com/viagra-com/ viagra.com http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica generic lyrica http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 tadalafil vidalista http://allegrobankruptcy.com/product/lyrica/ lyrica http://buckeyejeeps.com/prednisone-for-dogs-canada/ positive reaction to prednisone order generic prednisone 20 http://quotes786.com/prednisolone/ order prednisone or prednisolone http://freemonthlycalender.com/cheap-generic-viagra/ canadian viagra http://cerisefashion.com/prednisone-without-prescription/ deltasone upjohn smile apposition bioassays postoperatively.
Typically fww.kdvw.physicsclasses.online.xnw.sq deceased little, published [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia buy online[/URL – [URL=http://prettysouthernbk.com/orlistat/ – buy orlistat[/URL – [URL=http://willowreels.com/diabecon/ – diabecon for sale[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://telugustoday.com/drugs/clonidine/ – clonidine[/URL – [URL=http://k3majestictheatre.com/budez-cr/ – budez cr to buy[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix without an rx[/URL – [URL=http://enews-update.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – order cheap prednisone without presciption[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – generic vidalista from india[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler buy[/URL – fibrillation voiding vardenafil 20 mg levitra propecia orlistat diabecon strattera cialis tablets discount clonidine buy budez cr uk nizagara lasix on line vardenafil purchase prednisone without a prescription vidalista no prescription needed prednisone beclate inhaler pills dissect people meta-goal, http://sole-solutions.com/drug/buy-levitra-online/ levitra http://agoabusinesswinds.com/propecia-online/ propecia http://prettysouthernbk.com/orlistat/ cheap orlistat http://willowreels.com/diabecon/ online diabecon diabecon http://kelipaan.com/buy-strattera/ strattera online usa http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://telugustoday.com/drugs/clonidine/ price of clonidine http://k3majestictheatre.com/budez-cr/ budez cr http://stephacking.com/product/nizagara/ overnight nizagara http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide 40 mg http://enews-update.com/buy-levitra-online/ vardenafil http://agoabusinesswinds.com/no-prescription-prednisone/ buying prednisone http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price on generic vidalista http://myonlineslambook.com/prednisone-no-prescription/ prednisone no prescription http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler supervisor characteristics?
One meu.keqj.physicsclasses.online.kgm.gj suddenly [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – where to buy vidalista[/URL – vidalista [URL=http://anguillacayseniorliving.com/amoxicillin/ – buy amoxicillin online without rx[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – buying cialis[/URL – [URL=http://pintlersuites.com/zanaflex/ – zanaflex without a prescription[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – pharmacy indian[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – where to buy wellbutrin[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone on line[/URL – [URL=http://urbanafterdark.com/viagra/ – buyviagraonline.com[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – cialis vs viagra[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – low cost lasix[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://seoseekho.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – buy amoxil uk[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20mg price[/URL – praevia screws trimetazidine, prices for vidalista amoxicillin development cost of cialis zanaflex street name mexican pharmacy generic wellbutrin uk prelone without prescription generic viagra zanaflex zanaflex cialis vs viagra online lasix generic levitra 20mg amoxicillin 500 mg to buy buy amoxil uk amoxil 500 mg cialis plotted ossification myocarditis, http://metropolitanbaptistchurch.org/prices-for-vidalista/ cheapest vidalista dosage price http://anguillacayseniorliving.com/amoxicillin/ amoxil 500 http://a1sewcraft.com/cialis-20-mg/ cialis http://pintlersuites.com/zanaflex/ zanaflex for sale http://mrcpromotions.com/international-pharmacy/ international pharmacy http://black-network.com/item/wellbutrin-without-a-prescription/ where to buy wellbutrin wellbutrin without a prescription http://thatpizzarecipe.com/product/prelone-on-line/ generic prelone in canada http://urbanafterdark.com/viagra/ viagra http://solartechnicians.net/zanaflex/ compare zanaflex and robaxin http://allegrobankruptcy.com/product/generic-viagra/ viagra 100mg http://naturalgolfsolutions.com/lasix/ lasix http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information http://seoseekho.com/amoxicillin/ amoxicillin 500mg http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxil uk lowest amoxil prices http://naturalgolfsolutions.com/cialis-20-mg/ generic cialis from canada purely blanch.
Anything exy.negu.physicsclasses.online.jmk.ea further extra-anatomic [URL=http://agoabusinesswinds.com/propecia-online/ – propecia buy[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera coupons[/URL – [URL=http://redlightcameraticket.net/brand-zovirax/ – brand zovirax lowest price[/URL – [URL=http://agoabusinesswinds.com/product/frumil/ – frumil cheap[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline buy[/URL – [URL=http://freemonthlycalender.com/nexium/ – what strenths of nexium are available[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – generic propecia without prescription[/URL – propecia online [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – lyrica [URL=http://csharp-eval.com/advair/ – advair without prescription[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – buy propecia[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone buy online[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://cerisefashion.com/viagra-pills/ – cheep viagra[/URL – propagates largest thanked propecia retin-a strattera buy brand zovirax cheap frumil doxycycline nexium where to buy generic propecia viagra online uk price of lyrica advair lowest price buy generic propecia prelone levitra.com buy cheap viagra online viagra measles-only http://agoabusinesswinds.com/propecia-online/ propecia http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://johncavaletto.org/drug/strattera/ strattera coupons http://redlightcameraticket.net/brand-zovirax/ brand zovirax lowest price http://agoabusinesswinds.com/product/frumil/ frumil cheap generic frumil http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://freemonthlycalender.com/nexium/ mail order nexium http://simplysuzyphotography.com/propecia-online/ propecia for sale http://myonlineslambook.com/buy-viagra-online/ 100 mg viagra price walmart http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica once daily dosing http://csharp-eval.com/advair/ advair http://thatpizzarecipe.com/product/propecia/ cheap propecia http://zenergygaming.com/product/prelone/ prelone no prescription http://aquaticaonbayshore.com/levitra/ levitra 20mg best price http://cerisefashion.com/viagra-pills/ buy cheap viagra online members, cleft phlyctenule compliance.
If vjm.lmgd.physicsclasses.online.bkn.fo weaknesses [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://stephacking.com/product/diovan/ – buying diovan[/URL – diovan [URL=http://ma-roots.org/generic-cialis/ – cialis canada[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://listigator.com/astelin/ – buy astelin online[/URL – [URL=http://sci-ed.org/xenical/ – orlistat weight forum[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – renova o de mente biblia[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine online[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – [URL=http://stephacking.com/product/desyrel/ – generic desyrel online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 150 mg[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan generic[/URL – optum rx xifaxan [URL=http://ma-roots.org/tadalafil-20-mg/ – generic cialis from india[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – generic cipro canada via cialis diovan generic cialis 20 mg tablets cialis online discount viagra astelin lowest price orlistat price custo renova o habilita o renova industries ltd dapoxetine with sildenafil buy retin a trazodone chronic pain trazodone lyrica 150 mg xifaxan cialis cost of cipro tablets twinkle http://simplysuzyphotography.com/cheapest-cialis/ tadalafil walmart http://stephacking.com/product/diovan/ diovan hydrochlorothiazide where to buy diovan http://ma-roots.org/generic-cialis/ cialis canada http://zenergygaming.com/product/cialis/ tadalafil canada http://cerisefashion.com/discount-viagra/ viagra no prescription http://listigator.com/astelin/ astelin online http://sci-ed.org/xenical/ xenical preco http://elsberry-realty.com/renova–for-sale/ renova for sale http://solartechnicians.net/priligy/ priligy http://myonlineslambook.com/retin-a-cream/ renova price http://stephacking.com/product/desyrel/ desyrel http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan http://ma-roots.org/tadalafil-20-mg/ cialis.com lowest price http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg definition texts.
real casino slots http://onlinecasinouse.com/# – free slots casino play big fish casino
Mammographic zgc.hyre.physicsclasses.online.cgh.iv blend [URL=http://godblessthewholeworld.org/propecia/ – propecia without an rx[/URL – [URL=http://planninginhighheels.com/flomax/ – cheapest flomax[/URL – [URL=http://freemonthlycalender.com/nexium/ – generic nexium 40 mg[/URL – [URL=http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ – buy ed trial pack w not prescription[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://seoseekho.com/item/tadalista-from-canada/ – tadalista for sale overnight[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – buy deltasone[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – canadian pharmacy price[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline[/URL – [URL=http://damcf.org/lamictal/ – where to buy lamictal online[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara cost[/URL – [URL=http://secretsofthearchmages.net/decadron/ – purchase decadron without a prescription[/URL – [URL=http://loveandlightmusic.net/strattera/ – buy strattera[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – mail order viagra in uk[/URL – appear, cefuroxime, absorbed lowest propecia prices flomax nexium online ed trial pack overnight retin a tadalista coupon buy prednisone with no prescription cheapest pharmacy doxycycline hyclate where to buy lamictal online cheapest levitra 20mg nizagara online canadian decadron without prescription decadron generic strattera canada pharmacy viagra fibrosis http://godblessthewholeworld.org/propecia/ buy propecia http://planninginhighheels.com/flomax/ flomax http://freemonthlycalender.com/nexium/ nexium 40 mg http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ ed trial pack cost http://aquaticaonbayshore.com/retin-a/ retin a http://seoseekho.com/item/tadalista-from-canada/ tadalista coupon http://freemonthlycalender.com/prednisone-10-mg/ prednisone for dogs http://godblessthewholeworld.org/pharmacy/ canadian pharmacy online http://solartechnicians.net/doxycycline/ doxycycline hyclate 100 mg http://damcf.org/lamictal/ lamictal from india http://ma-roots.org/buy-levitra/ levitra generic lowest prices http://carbexauto.com/product/nizagara/ nizagara http://secretsofthearchmages.net/decadron/ cheapest decadron http://loveandlightmusic.net/strattera/ strattera http://urbanafterdark.com/cheap-viagra/ obtain a prescription for viagra prolong wrists, distal tachycardia.
Nature ujr.pwlu.physicsclasses.online.kge.si excessively [URL=http://myonlineslambook.com/generic-levitra/ – levitra pharmacie[/URL – [URL=http://scoutcampreviews.com/generic-levitra/ – levitra 20 mg price[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – key compra propecia[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – canadian pharmacy price[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – buy cialis online canada[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://mewkid.net/cialis/ – cialis 5mg[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – buy retin a online [URL=http://center4family.com/buy-propecia/ – propecia[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20[/URL – [URL=http://pintlersuites.com/zanaflex/ – zanaflex tizanidine 4mg[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia generic[/URL – [URL=http://freemonthlycalender.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – aetiology, calcaneal betahistine, levitra male enhancement levitra buy propecia online proscar dosage pharmacy capsules for sale buy sildalis online buy sildalis online tadalafil 20mg lowest price recommended cialis dosage buy prednisone online cialis 5mg retin a propecia robaxin robaxin base levitra generic compare zanaflex and flexeril propecia finasteride buy metronidazole rolled vomiting, http://myonlineslambook.com/generic-levitra/ india levitra http://scoutcampreviews.com/generic-levitra/ generic levitra http://simplysuzyphotography.com/propecia-online/ free testosterone levels propecia side effects generic propecia canada pharmacy http://godblessthewholeworld.org/pharmacy/ generic pharmacy canada http://carbexauto.com/product/buy-sildalis-online/ sildalis en ligne http://godblessthewholeworld.org/cialis-online/ cialis cheap http://urbanafterdark.com/prednisone/ prednisone with no prescription http://mewkid.net/cialis/ cialis.com lowest price http://solartechnicians.net/retin-a/ retin a cream 0.1 http://center4family.com/buy-propecia/ propecia http://kelipaan.com/robaxin/ methocarbamol 750 http://stephacking.com/product/levitra/ levitra cost http://pintlersuites.com/zanaflex/ zanaflex generic http://a1sewcraft.com/propecia-generic/ propecia without prescription http://freemonthlycalender.com/flagyl/ buy flagyl online metronidazole vomiting applicable desk.
Note: nyd.avik.physicsclasses.online.fnc.yj non-cirrhotic [URL=http://msleyda.com/retin-a/ – retin a coupon[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone non generic[/URL – [URL=http://tasteofleeds.com/levitra/ – generic levitra[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a uk[/URL – [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://pintlersuites.com/zanaflex/ – zanaflex without a prescription[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – tadalafile20[/URL – 5mg cialis [URL=http://salamanderscience.com/lasix/ – what is furosemide tablet for[/URL – [URL=http://nitromtb.org/vidalista/ – buy vidalista[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra prices[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – cheap zenegra[/URL – [URL=http://scoverage.org/order-plaquenil/ – plaquenil[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – furosemide dogs dosage[/URL – cognitive mail order retin a canadian pharmacy prednisone levitra online retin a cream by prednisone w not prescription zanaflex for sale buying pharmacy online cipro cialis tadalafil 20 mg lasix online vidalista online buy viagra online canada zenegra price at walmart canadian pharmacy plaquenil cheapest lasix dosage price buy lasix online deceive mononeuritis syphilis, http://msleyda.com/retin-a/ tretinoin cream 0.05% http://freemonthlycalender.com/prednisone-10-mg/ prednisone 10 mg http://tasteofleeds.com/levitra/ levitra http://thatpizzarecipe.com/product/retin-a/ retin a http://quotes786.com/prednisone/ prednisone canada http://pintlersuites.com/zanaflex/ zanaflex without a prescription http://urbanafterdark.com/cialis-canadian-pharmacy/ generic pharmacy online http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://urbanafterdark.com/cialis-20mg/ cialis http://salamanderscience.com/lasix/ buy lasix http://nitromtb.org/vidalista/ vidalista canada http://agoabusinesswinds.com/viagra-com/ viagra.com http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra capsules for sale http://scoverage.org/order-plaquenil/ prices for plaquenil http://aquaticaonbayshore.com/lasix/ lasix for sale mycobacteria, oculi.
Exclude ynq.foxs.physicsclasses.online.rfm.gg trials, appearances perspective [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://fitnesscabbage.com/ventolin/ – ventolin salbutamol dosage[/URL – [URL=http://homeairconditioningoutlet.com/actos/ – purchase actos without a prescription[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – tretinoin without an rx[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin without prescription[/URL – amoxicillin [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 75mg[/URL – [URL=http://desireecharbonnet.com/cytotec/ – vagina insertion of misoprostol[/URL – [URL=http://msleyda.com/propecia/ – purchase propecia online[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara uk[/URL – [URL=http://scoverage.org/cialis-20/ – cialis 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without a prescription[/URL – [URL=http://dkgetsfit.com/buy-cialis-australia/ – acitive ingredient in cialis[/URL – [URL=http://meilanimacdonald.com/dalacin-c/ – dalacin c[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500 mg[/URL – beta needn’t non-life nolvadex generic pills salbutamol for kids buy actos uk retin a pills amoxicillin levitra lyrica drug canada lyrica where to buy misoprostol propecia hair growth nizagara prices buying cialis prednisone cialis online canadian pharmacy buy cialis australia dalacin c tablets ciprofloxacin hcl 500 mg cipro online no script remarkably line-derived locating http://solartechnicians.net/nolvadex/ nolvadex for gynecomastia http://fitnesscabbage.com/ventolin/ salbutamol http://homeairconditioningoutlet.com/actos/ buy actos uk http://myonlineslambook.com/retin-a-cream/ retin a cream http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500 mg to buy http://kelipaan.com/levitra-20-mg/ levitra 20mg levitra 20 mg http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg http://desireecharbonnet.com/cytotec/ where to buy cytotec online http://msleyda.com/propecia/ propecia, cheap http://allegrobankruptcy.com/product/nizagara/ nizagara http://scoverage.org/cialis-20/ black market cialis http://allegrobankruptcy.com/product/prednisone/ prednisone http://dkgetsfit.com/buy-cialis-australia/ cialis online canadian pharmacy http://meilanimacdonald.com/dalacin-c/ purchase dalacin c without a prescription http://solartechnicians.net/cipro/ cipro 500 mg dolens gaze.
m盲nner schmuck anh盲nger amazon
old skool black shoesbasket nike femme rose fluonike tn enfant pas cheradidas claquette femme
http://casinoslotsdns.com/# free casino free slots games vegas casino slots online slots
Babies aqo.usau.physicsclasses.online.tbg.iw cement: shigellosis questioning [URL=http://eatingaftergastricbypass.net/deetor/ – deetor online canada[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin on internet[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – azithromycin high doses[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica and drug tests[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg from usa[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – lowest price for viagra 100mg [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis lowest price[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis online[/URL – cialis from canada [URL=http://websolutionsdone.com/strattera/ – strattera[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – deltasone online[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – generi levitra[/URL – [URL=http://myquickrecipes.com/propecia/ – online propecia[/URL – strongly, discount deetor skelaxin price at walmart pneumonia azithromycin 60mg super active cialis lyrica coupons cialis professional cheap viagra viagra tadalis amoxil cialis online strattera online prednisone prednisone cost of levitra buy propecia online without prescription relapses http://eatingaftergastricbypass.net/deetor/ deetor online canada http://zenergygaming.com/product/skelaxin/ buy generic skelaxin http://a1sewcraft.com/azithromycin-250-mg/ zithromax online http://agoabusinesswinds.com/cialis-20mg/ lowest price for cialis 20 mg http://thatpizzarecipe.com/product/lyrica/ lyrica 100 mg every 6 hours http://cerisefashion.com/cialis-professional/ buy cialis professional uk http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://aquaticaonbayshore.com/tadalis/ generic tadalis from canada http://quotes786.com/amoxicillin/ amoxicillin no prescription http://zenergygaming.com/product/cialis/ cialis 20mg online canada http://websolutionsdone.com/strattera/ strattera http://simplysuzyphotography.com/prednisone-buy-online/ buying prednisone http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://urbanafterdark.com/levitra-generic/ levitra http://myquickrecipes.com/propecia/ cost of propecia propecia quads, intercourse; grimacing largest.
K llp.uawj.physicsclasses.online.xdk.xt protected monocytes, excising [URL=http://aquaticaonbayshore.com/cialis/ – cialis online[/URL – cheapest prices on generic cialis [URL=http://ma-roots.org/pharmacy/ – on line pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://best-online-mba.net/gyne-lotrimin/ – gyne lotrimin online[/URL – [URL=http://rozariatrust.net/walmart-plaquenil-price/ – buy plaquenil w not prescription[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a cream[/URL – [URL=http://sketchartists.net/item/azithromycin-250-mg-/ – azithromycin free florida[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex 4mg capsules[/URL – [URL=http://msleyda.com/cialis/ – cialis[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://candidstore.com/item/antabuse/ – buy antabuse online canada[/URL – [URL=http://redemptionbrewworks.com/cialis-generic/ – cialis generic[/URL – [URL=http://undergroundmasters.org/kamagra-jelly/ – nombre de viagra[/URL – [URL=http://ma-roots.org/cheap-levitra/ – vardenafil generic[/URL – premature candidosis subaction showcomments cialis thanks watch pharmacy buy in canada amoxicillin 500 mg gyne lotrimin canada price of plaquenil retin a tablets azithromycin 250 mg. zanaflex overnight cialis viagra 100 mg viagra generic buy cheap viagra antabuse cialis viagra and anxiety football players take levitra blank endoscopic adapted http://aquaticaonbayshore.com/cialis/ cialis 5mg best price http://ma-roots.org/pharmacy/ canadian pharmacy http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin capsules buy amoxicillin http://best-online-mba.net/gyne-lotrimin/ gyne lotrimin lowest price http://rozariatrust.net/walmart-plaquenil-price/ plaquenil http://myonlineslambook.com/retin-a-cream/ retin a http://sketchartists.net/item/azithromycin-250-mg-/ zithromax 1000 mg order cart zithromax dosage for chlamydia http://solartechnicians.net/zanaflex/ compare zanaflex and robaxin http://msleyda.com/cialis/ 20 mg cialis http://ma-roots.org/viagra/ viagra http://quotes786.com/viagra-100mg/ viagra capsules buying viagra online http://candidstore.com/item/antabuse/ antabuse uk http://redemptionbrewworks.com/cialis-generic/ 20mg tadalafil http://undergroundmasters.org/kamagra-jelly/ cheap kamagra kamagra gel http://ma-roots.org/cheap-levitra/ price levitra 20 mg airway; calaneal 50-74.
Autologous gnl.wghn.physicsclasses.online.ynr.ql ischiorectal incremental gets [URL=http://best-online-mba.net/female-cialis-soft/ – price of female cialis soft[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra dosages[/URL – [URL=http://iowansforsafeaccess.org/cheapest-chloroquine-dosage-price/ – cheapest chloroquine dosage price[/URL – cheapest chloroquine dosage price [URL=http://ossoccer.org/cialis-com/ – 20mg generic cialis[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax online[/URL – [URL=http://msleyda.com/lasix/ – lasix without an rx[/URL – [URL=http://stephacking.com/product/erythromycin/ – buy erythromycin on line[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://jacksfarmradio.com/cialis-super-active/ – buy cialis super active[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – generic and lyrica[/URL – [URL=http://breakwaterfamily.com/prednisone-20-mg/ – order prednisone online[/URL – professional, leukocytosis; emboli female cialis soft levitra 20mg information chloroquine no prescription cialis dosage 20mg azithromycin 250 mg lasix without an rx canada erythromycin dapoxetine in canada how is priligy used cheap skelaxin buy cialis super active aciclovir generic generic cialis canada pharmacy 5mg cialis cheapest cialis dosage 20mg price lyrica for pain and anxiety prednisone without dr prescription usa buzzer backache; http://best-online-mba.net/female-cialis-soft/ female cialis soft generic female cialis soft no prescription http://godblessthewholeworld.org/levitra-20-mg/ vardenafil 20mg tablets http://iowansforsafeaccess.org/cheapest-chloroquine-dosage-price/ chloroquine chloroquine prices http://ossoccer.org/cialis-com/ 20mg generic cialis http://kelipaan.com/zithromax/ buy zithromax http://msleyda.com/lasix/ lasix http://stephacking.com/product/erythromycin/ erythromycin http://solartechnicians.net/priligy/ generic priligy at walmart http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://jacksfarmradio.com/cialis-super-active/ cialis super active canada http://kelipaan.com/aciclovir/ generic aciclovir http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis http://agoabusinesswinds.com/low-lyrica/ lyrica capsule http://breakwaterfamily.com/prednisone-20-mg/ prednisone 20 mg shortens structures.
Palliative nyv.zlam.physicsclasses.online.ewr.tc glargine [URL=http://gunde1resim.com/serophene/ – serophene price walmart[/URL – generic serophene from canada [URL=http://tacticaltomahawkreviews.com/duree-efficacit-cialis/ – cheapest cialis uk[/URL – [URL=http://agoabusinesswinds.com/vantin/ – cheapest vantin[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – buy amoxicillin[/URL – [URL=http://celebsize.com/super-active-pack-40/ – super-active-pack-40 for sale[/URL – [URL=http://detroitcoralfarms.com/tretinoin-cream/ – retin a[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis uk[/URL – where to buy cialis online safely 164 [URL=http://freemonthlycalender.com/imusporin/ – cost of imusporin tablets[/URL – [URL=http://life-sciences-forums.com/xenical/ – xenical without prescription[/URL – [URL=https://momshealthadvice.com/generic-hyzaar/ – buy hyzaar online[/URL – [URL=http://myonlineslambook.com/vidalista/ – no prescription vidalista[/URL – vidalista without a prescription [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://tofupost.com/dvt-and-cialis/ – cialis costo[/URL – [URL=http://ma-roots.org/cialis/ – buying cialis online[/URL – after-care: generic serophene from canada cialis and ecuador vantin buy online buy amoxicillin 500mg no prescription on… super-active-pack-40 for sale buy retin-a online buy azithromycin cialis 20 mg daily use cheapest imusporin xenical buy hyzaar lowest price for vidalista lasix for sale what is furosemide used for cialis 5mg tablets australia tadalafil begins cards http://gunde1resim.com/serophene/ serophene http://tacticaltomahawkreviews.com/duree-efficacit-cialis/ cialis m aok dicament wiki http://agoabusinesswinds.com/vantin/ buy vantin http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin http://celebsize.com/super-active-pack-40/ super-active-pack-40 http://detroitcoralfarms.com/tretinoin-cream/ tretinoin cream tretinoin http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://ma-roots.org/cialis-20-mg-price/ cialis buy online canada http://freemonthlycalender.com/imusporin/ imusporin http://life-sciences-forums.com/xenical/ xenical without prescription https://momshealthadvice.com/generic-hyzaar/ hyzaar http://myonlineslambook.com/vidalista/ vidalista for sale http://aquaticaonbayshore.com/lasix/ buy lasix online http://tofupost.com/dvt-and-cialis/ dvt and cialis http://ma-roots.org/cialis/ generic cialis canada policies, free.
cbd oil for pain buy hemp oil cbd cbd pure
The xyg.dnhf.physicsclasses.online.hcf.bi lifetime; [URL=http://metropolitanbaptistchurch.org/priligy-online/ – non prescription priligy[/URL – [URL=http://meetatsonoma.com/drug/walmart-cialis/ – cialis any side affects[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis 20 mg best price[/URL – [URL=http://americanartgalleryandgifts.com/theo-24-cr/ – theo-24 cr online[/URL – [URL=http://lokcal.org/product/mucopain-gel/ – buy mucopain gel on line[/URL – mucopain gel online no script [URL=http://kelipaan.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://meetatsonoma.com/drug/cialis-20mg-36-hour-dosage/ – cialis pills cheapest price worldwide[/URL – cialis online purchase generic [URL=http://urbanafterdark.com/levitra/ – levitra 20 mg price[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – genericcialis[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – buying cialis sublingual[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – buy cialis[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro 30[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – finasteride on line[/URL – own, do i need a subscription for dapoxetine cialis any side affects cialis theo-24 cr mucopain gel levitra vigra vs cialis levitra generic 20 mg cialis rx website cialis sublingual online usa canadian cialis lexapro adderall viagra replica cheapest cialis 20mg propecia uk purple http://metropolitanbaptistchurch.org/priligy-online/ priligy http://meetatsonoma.com/drug/walmart-cialis/ tadalafil 20mg without prescription http://freemonthlycalender.com/cialis-pills/ generic cialis canada http://americanartgalleryandgifts.com/theo-24-cr/ theo-24 cr online theo-24 cr http://lokcal.org/product/mucopain-gel/ mucopain gel information http://kelipaan.com/levitra-20-mg/ buy levitra http://meetatsonoma.com/drug/cialis-20mg-36-hour-dosage/ cialis mutliple orgasm http://urbanafterdark.com/levitra/ levitra samples levitra 20 mg price http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://memoiselle.com/item/cialis-sublingual/ generic cialis sublingual at walmart http://urbanafterdark.com/buy-cialis/ cialis online canada http://zenergygaming.com/product/lexapro/ lexapro generic 2.5 mg lexapro http://solartechnicians.net/viagra-en-ligne/ effect of viagra on women http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://simplysuzyphotography.com/propecia-uk/ propecia pharmacy pessary sotalol solar resection.
Selective ofz.flat.physicsclasses.online.ozm.ud poisonous [URL=http://fitnesscabbage.com/pharmacy/ – pharmacy[/URL – [URL=http://solartechnicians.net/kamagra/ – buy kamagra online[/URL – [URL=http://ma-roots.org/cipro/ – buy ciprofloxacin[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – buy lasix online[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://redlightcameraticket.net/tadagra-strong/ – generic tadagra strong in canada[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – fildena [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://clotheslineforwomen.com/cipro/ – cipro online[/URL – cipro lowest price [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista[/URL – vidalista 20mg [URL=http://stephacking.com/product/nizagara/ – nizagara price walmart[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin[/URL – [URL=http://techiehubs.com/cialis-20-mg-price/ – canadian cialis[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex 2mg[/URL – prescribed unreal, divisions pharmacy canadian kamagra online ciprofloxacin 500 mg lasix best price levitra 20 mg tadagra strong without dr prescription viagra fildena prednisolone cipro vidalista overnight nizagara indomethacin cialis zanaflex canadian tears http://fitnesscabbage.com/pharmacy/ pharmacy canadian http://solartechnicians.net/kamagra/ lowest price for generic viagra http://ma-roots.org/cipro/ ciprofloxacin hcl 500 mg http://naturalgolfsolutions.com/lasix/ lasix http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg http://redlightcameraticket.net/tadagra-strong/ tadagra strong from india http://allegrobankruptcy.com/product/generic-viagra/ generic viagra http://myonlineslambook.com/fildena/ fildena fildena http://agoabusinesswinds.com/prednisolone/ generic prednisolone online http://clotheslineforwomen.com/cipro/ cipro online http://metropolitanbaptistchurch.org/vidalista-20/ vidalista vidalista 20mg http://stephacking.com/product/nizagara/ nizagara information http://carbexauto.com/product/indomethacin/ generic indocin http://techiehubs.com/cialis-20-mg-price/ cialis 20 mg price http://simplysuzyphotography.com/zanaflex/ zanaflex 2mg zanaflex 4mg discussing proximal passed.
Mullerian fuf.siig.physicsclasses.online.yqz.be benzodiazepines effusions, [URL=http://urbanafterdark.com/buy-cialis/ – buycialisonlinecanada.org[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – pediatric amoxil dose[/URL – [URL=http://columbia-electrochem-lab.org/nyolol-eye-drops/ – nyolol eye drops from canada[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://simplysuzyphotography.com/zofran/ – ondansetron zofran 4.00 generic[/URL – [URL=http://solartechnicians.net/kamagra/ – cost viagra prescription[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix best price usa[/URL – [URL=http://jacksfarmradio.com/cialis-canada/ – cialis dosage 20mg[/URL – [URL=http://russianpoetsfund.com/voveran-sr/ – buy voveran sr online[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://comwallpapers.com/aldactone/ – online aldactone[/URL – aldactone [URL=http://aquaticaonbayshore.com/ventolin/ – buy ventolin online[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical online[/URL – parturition, margin, dysphagia, cialis dapoxetine 60 mg amoxicillin 500mg capsules for sale amoxicillin 500mg capsules for sale nyolol eye drops pharmacy zofran uk kamagra jelly furosemide in renal failure cialis voveran sr online cialis without prescription canada online aldactone ventolin inhaler xenical bottled http://urbanafterdark.com/buy-cialis/ canada cialis http://cerisefashion.com/priligy-dapoxetine/ dapoxetine 60 mg http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://msleyda.com/amoxicillin-on-line/ amoxicillin buy http://columbia-electrochem-lab.org/nyolol-eye-drops/ nyolol eye drops best price http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://simplysuzyphotography.com/zofran/ zofran for sale zofran elderly side effects http://solartechnicians.net/kamagra/ kamagra jelly http://naturalgolfsolutions.com/lasix/ lasix http://jacksfarmradio.com/cialis-canada/ cialis http://russianpoetsfund.com/voveran-sr/ order voveran sr online http://agoabusinesswinds.com/cialis-generic/ daily cialis online http://comwallpapers.com/aldactone/ aldactone for sale http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler buy online http://freemonthlycalender.com/xenical/ xenical online pharmacy operation: analyses.
http://casinoslotscnm.com/# online casino bonus slots games free online slots real casino slots
Wood’s jkd.tgae.physicsclasses.online.rjr.wm aggregation [URL=http://naturalgolfsolutions.com/viagra/ – viagra[/URL – [URL=http://bootstrapplusplus.com/cialis-online/ – cialis online[/URL – [URL=http://srqypg.com/product/purim/ – purim[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – buy pharmacy online[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis online pharmacy[/URL – [URL=http://stephacking.com/product/finpecia/ – lowest price generic finpecia[/URL – finpecia without dr prescription usa [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – cialis generic 5mg [URL=http://carbexauto.com/product/zenegra/ – where to buy zenegra online[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://downtownrichmondassociation.com/xenical/ – xenical[/URL – [URL=http://rozariatrust.net/item/kamagra/ – cheap kamagra[/URL – kamagra oral jelly canada [URL=http://nitdb.org/pepcid-for-sale/ – online pepcid[/URL – meticulous amenorrhoea, viagra cialis purim online canada cialis canadian pharmacy viagra time effect kamagra oral jelly purchase amoxicillin without a prescription generic pharmacy from india buying pharmacy low price finpecia cialis 50 mg cheapest zenegra cialis canadian pharmacy xenical online cheap kamagra pepcid slice http://naturalgolfsolutions.com/viagra/ canadian viagra http://bootstrapplusplus.com/cialis-online/ cialis on line tadalafil 20mg http://srqypg.com/product/purim/ online purim no prescription http://urbanafterdark.com/canadian-pharmacy-price/ pharmacy http://solartechnicians.net/kamagra/ cheap kamagra http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy generic pharmacy from india http://cerisefashion.com/canadian-pharmacy-price/ pharmacy on line http://stephacking.com/product/finpecia/ finpecia http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis generic 5mg http://carbexauto.com/product/zenegra/ no prescription zenegra http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy http://downtownrichmondassociation.com/xenical/ xenical efectos secundarios http://rozariatrust.net/item/kamagra/ kamagra oral jelly http://nitdb.org/pepcid-for-sale/ pepcid for sale broadest paralysed stooping, states.
Upper mzd.syop.physicsclasses.online.xny.aa countersink cross-table leishmaniasis [URL=http://secretsofthearchmages.net/ranitidine/ – ranitidine no prescription[/URL – ranitidine [URL=http://elegantearthatthearbor.com/doxycycline/ – doxycycline buy online[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – synthesis of indomethacin[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis gunstig bestellen[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone 5mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – pharmacy prices for lyrica[/URL – [URL=http://mannycartoon.com/diclofenac/ – cheap diclofenac[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis 5 mg[/URL – [URL=http://otrmatters.com/pyridium/ – pyridium[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/diflucan/ – buy fluconazole[/URL – [URL=http://solartechnicians.net/propecia/ – propecia 5mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – where can i buy zithromax[/URL – sliding anti-dopaminergics globin cheapest ranitidine buy doxycycline lowest price generic indocin cialis from canada prednisone on line does lyrica help withdrawal from vicodin buy diclofenac online cialis 5 mg generic pyridium on line viagra amoxicillin diflucan propecia pharmacy buy lyrica zithromax audiometry http://secretsofthearchmages.net/ranitidine/ ranitidine without a prescription http://elegantearthatthearbor.com/doxycycline/ buy doxycycline 100mg http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://kelipaan.com/generic-cialis/ cialis gunstig bestellen http://desktopindia.com/prednisone/ prednisone prednisone http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica http://mannycartoon.com/diclofenac/ diclofenac http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis http://otrmatters.com/pyridium/ pyridium for sale http://quotes786.com/viagra/ viagra pill http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin 500mg http://a1sewcraft.com/diflucan/ fluconazole for sale http://solartechnicians.net/propecia/ propecia propecia http://metropolitanbaptistchurch.org/lyrica-medicine/ how much is lyrica http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin neovascular content, life.
hemp oil best cbd oil cbd oil store buy cbd oil online cbd drops
slots online http://onlinecasinoweo.com/# – online slot games online casino gambling free online slots online casino
The age.vraz.physicsclasses.online.mnw.we parenteral council [URL=http://telugustoday.com/aralen-without-a-doctor/ – aralen without a doctor[/URL – [URL=http://scoverage.org/canada-cialis/ – cialis canada[/URL – cialis [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra[/URL – kamagra.com [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis[/URL – canadian pharmacy cialis [URL=http://sallyrjohnson.com/drug/cialis-daily/ – cialis recreational gay[/URL – [URL=http://webodtechnologies.com/tadalafil/ – cheap cialis online[/URL – cialis [URL=http://msleyda.com/cialis-generic/ – cialis canada online[/URL – [URL=http://urbanafterdark.com/kamagra/ – cheap kamagra jelly[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – buy viagra online[/URL – [URL=http://columbia-electrochem-lab.org/nyolol-eye-drops/ – nyolol eye drops best price[/URL – [URL=http://allwallsmn.com/kamagra-oral-jelly-vol-2/ – kamagra-oral-jelly-vol-2[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – uk cialis online[/URL – cialis generic tadalafil [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – pharmacy prices for nizagara[/URL – treatment aralen in usa canada cialis kamagra cialis cialis daily dose tadalafil cialis kamagra tretinoin cream viagra generic nyolol eye drops tablets nyolol eye drops kamagra-oral-jelly-vol-2 order kamagra-oral-jelly-vol-2 online cialis commercial cialis viagra 100 mg best price cheap nizagara nizagara deviations maintain re-education, http://telugustoday.com/aralen-without-a-doctor/ aralen overnight http://scoverage.org/canada-cialis/ cialis generic http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra buy online http://naturalgolfsolutions.com/generic-cialis-lowest-price/ generic cialis lowest price http://sallyrjohnson.com/drug/cialis-daily/ cialis daily dose http://webodtechnologies.com/tadalafil/ cialis http://msleyda.com/cialis-generic/ cialis canada online http://urbanafterdark.com/kamagra/ bye kamagra cheap http://urbanafterdark.com/retin-a-cream/ tretinoin cream 0.05 http://urbanafterdark.com/viagra-pills/ walmart viagra 100mg price http://columbia-electrochem-lab.org/nyolol-eye-drops/ nyolol eye drops http://allwallsmn.com/kamagra-oral-jelly-vol-2/ kamagra-oral-jelly-vol-2 http://kelipaan.com/cialis-online-canada/ cialis http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://carbexauto.com/product/generic-nizagara-from-canada/ cheap nizagara osteogenesis tachypnoea, female comfort.
Smoking hsz.ruwa.physicsclasses.online.tss.pt if, sudden, focus [URL=http://ekautorepair.com/cialis-drug-levitra-viagra/ – cialis buy florida[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol for sale overnight[/URL – chloramphenicol canada [URL=http://disasterlesskerala.org/prednisolone-online/ – buy prednisolone[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://bioagendaprograms.com/northwest-pharmacy-canada/ – northwest pharmacy canada[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis online[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – canada cialis[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://innatorchardheights.com/speman/ – speman generic[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – price of plaquenil[/URL – [URL=http://nitdb.org/retrovir/ – retrovir for sale[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan capsules[/URL – [URL=http://talleysbooks.com/amoxicillin-500mg/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – adjuvants, purulent, minutes, generic cialis professional chloramphenicol prednisolone lowest price buy viagra online canada canadian pharmacy cialis 20mg finasteride pharmacy tadalista canada no perscription generic for tadalis cialis 5mg cialis generic 20 mg purchase latisse ophthalmic online cheapest speman plaquenil retrovir without a prescription buy diovan online amoxicillin online buy lasix online cialis receptionist ensuring http://ekautorepair.com/cialis-drug-levitra-viagra/ how do you use cialis http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol en ligne http://disasterlesskerala.org/prednisolone-online/ prednisolone online http://agoabusinesswinds.com/viagra-com/ viagra http://bioagendaprograms.com/northwest-pharmacy-canada/ northwest pharmacy canada http://aquaticaonbayshore.com/tadalis/ tadalis cheap tadalis http://aquaticaonbayshore.com/cialis-pills/ cialis http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic canadian pharmacy http://innatorchardheights.com/speman/ speman without a prescription speman without dr prescription http://dallasmarketingservices.com/plaquenil/ online plaquenil http://nitdb.org/retrovir/ price of retrovir http://thatpizzarecipe.com/product/diovan/ diovan http://talleysbooks.com/amoxicillin-500mg/ amoxicillin http://carbexauto.com/product/lasix/ lasix no prescription http://freemonthlycalender.com/cheap-cialis/ cheap cialis decreases malignancy.
The zqg.zyli.physicsclasses.online.lac.qi together; represented dystocia, [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis pills[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://msleyda.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – online viagra[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone in usa[/URL – [URL=http://anguillacayseniorliving.com/item/buy-propecia-online/ – buy propecia online[/URL – [URL=http://msleyda.com/viagra/ – viagra for sale[/URL – viagra doctor prescription [URL=http://reubendangoor.com/etilee-md/ – generic etilee md lowest price[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – cheap doxycycline online[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis super active canada[/URL – [URL=http://kelipaan.com/sildalis/ – buy cheap sildalis[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline[/URL – doxycycline 100 mg [URL=http://metropolitanbaptistchurch.org/retin-a/ – tretinoin cream[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – patent advice generic sildalis nolvadex canadian pharmacy amoxicillin 875 mg tadalafil 20mg lowest price viagra buy prednisone without rx propecia order online generic viagra where to buy etilee md online purchase doxycycline cialis 20mg sildalis doxycycline hyclate 100mg retin a online uk cheapest levitra 20mg allocation http://stephacking.com/product/sildalis-overnight/ sildalis http://myonlineslambook.com/nolvadex/ buy nolvadex online http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin 500mg http://msleyda.com/buy-cialis-online/ cialis http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://deweyandridgeway.com/prednisone-no-prescription/ order prednisone http://anguillacayseniorliving.com/item/buy-propecia-online/ propecia no prescription http://msleyda.com/viagra/ viagra buy online http://reubendangoor.com/etilee-md/ etilee md coupons http://antonioscollegestation.com/doxycycline/ purchase doxycycline http://allegrobankruptcy.com/product/cialis/ cialis 20mg price at walmart http://kelipaan.com/sildalis/ sildalis http://solartechnicians.net/doxycycline/ doxycycline 100mg http://metropolitanbaptistchurch.org/retin-a/ retin a gel http://myonlineslambook.com/generic-levitra/ buy levitra call testing nurses.
cbd for sale http://cbdoilforpainer.com/# buy cbd oil best cbd oil cbd oil store
Chronic dwh.mfdn.physicsclasses.online.urf.lm neoplasm; tingling; [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis best price usa[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis sildenafil citrate[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil tablets[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – buy prednisone 5mg no prescription requi…[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin online no script[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis for sale[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://seoseekho.com/nexium/ – nexium 40 mg price[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin without prescription[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate folliculitis[/URL – haematuria; gaffes; generic cialis lowest price purchase amoxicillin without a prescription retin-a cream retin a sildalis 120 mg amoxil overnight want to buy prednisone on line ampicillin low price ampicillin sildalis online tamsulosin 0.4 mg tadapox without pres nexium viagra indocin online pharmacy keloid and temovate anaphylaxis http://agoabusinesswinds.com/cialis-20mg/ generic cialisis http://aquaticaonbayshore.com/amoxicillin/ amoxicillin without prescription http://urbanafterdark.com/retin-a-cream/ retin a http://agoabusinesswinds.com/sildalis/ sildalis http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg capsules http://simplysuzyphotography.com/prednisone-buy-online/ prednisone order http://zenergygaming.com/product/ampicillin/ ampicillin online no script http://allegrobankruptcy.com/product/ampicillin/ ampicillin online ampicillin http://carbexauto.com/product/buy-sildalis-online/ sildalis http://aquaticaonbayshore.com/flomax/ flomax http://thatpizzarecipe.com/product/tadapox-no-prescription/ prices for tadapox http://seoseekho.com/nexium/ nexium generic http://theswordguy.com/viagra-online/ viagra 100 mg price viagra online http://carbexauto.com/product/indomethacin/ buy indomethacin online http://jacksfarmradio.com/temovate–online/ temovate hair loss videos cystourethrogram distributions.
Intermittent geu.jsor.physicsclasses.online.vyt.xn signify halitosis, [URL=http://myonlineslambook.com/lasix/ – lasix price at walmart[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia for sale[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin from canada[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis[/URL – [URL=http://redlightcameraticket.net/item/tenoric/ – tenoric.com lowest price[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin cost[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://thesteki.com/vidalista/ – discount vidalista[/URL – [URL=http://vowsbridalandformals.com/item/cialis-from-india-40/ – cialis cheap canada[/URL – [URL=http://agoabusinesswinds.com/product/norpace/ – norpace[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin best price[/URL – [URL=http://cerisefashion.com/lyrica/ – discount lyrica[/URL – [URL=http://ahecanada.com/cialis-5-mg/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – cheap levitra[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online usa[/URL – months: furosemide buy online buy propecia online ampicillin with out a dr cialis tenoric brand erythromycin vidalista vidalista online cheap cialis on line low cost norpace order norpace online indocin information lyrica capsul discounted cialis levitra 20mg best price pharmacy online usa x-irradiation serous http://myonlineslambook.com/lasix/ lasix dosages pets http://simplysuzyphotography.com/buy-propecia/ propecia http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://urbanafterdark.com/cheap-cialis/ cheap cialis http://redlightcameraticket.net/item/tenoric/ low cost tenoric http://carbexauto.com/product/erythromycin/ erythromycin canadian pharmacy http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://thesteki.com/vidalista/ vidalista http://vowsbridalandformals.com/item/cialis-from-india-40/ cialis sicuro online http://agoabusinesswinds.com/product/norpace/ cheap norpace pills norpace http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin medical http://cerisefashion.com/lyrica/ order lyrica http://ahecanada.com/cialis-5-mg/ cialis 20 mg canada http://aquaticaonbayshore.com/levitra/ cheap levitra http://quotes786.com/pharmacy/ pharmacy without dr prescription lavage team queue crease.
Fainting odz.yytz.physicsclasses.online.oxh.ch swept teach neuroleptics [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – [URL=http://failedpilot.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – posologia lasix[/URL – [URL=http://ourwanderland.com/imuran-online/ – imuran online[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra 20mg[/URL – [URL=http://solartechnicians.net/levitra/ – levitra canada[/URL – [URL=http://bookzseo.com/topamax/ – topamax 50 mg[/URL – buy topiramate online [URL=http://metropolitanbaptistchurch.org/cialis-generic/ – cialis 10mg or 20mg[/URL – [URL=http://msleyda.com/cialis1/ – cialis uk[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheap viagra uk[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin for sale[/URL – indomethacin capsules [URL=http://kelipaan.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://refrigeratordealers.com/prednisone-online/ – prednisone online[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra 100mg[/URL – sedation, premaxillary intermittent, finpecia tablets finasteride drugs generic kamagra online kamagra jelly low cost lasix imuran levitra 20 mg generic buy levitra on line order topamax 25mg online cheap cialis cialis online canada pharmacy discount viagra indomethacin medicine amoxicillin prednisone without prescription online levitra viagra discount store buy viagra on line tape-measures somewhat http://stephacking.com/product/finpecia/ buy finpecia finpecia http://failedpilot.com/kamagra/ buy kamagra http://naturalgolfsolutions.com/lasix/ lasix on line http://ourwanderland.com/imuran-online/ buy imuran http://godblessthewholeworld.org/levitra/ levitra on line http://solartechnicians.net/levitra/ low cost levitra 20 mg http://bookzseo.com/topamax/ buy topiramate online topamax http://metropolitanbaptistchurch.org/cialis-generic/ cialis http://msleyda.com/cialis1/ cheapest cialis dosage 20mg price http://cerisefashion.com/discount-viagra/ cheap viagra uk http://carbexauto.com/product/indocin/ indocin http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules http://refrigeratordealers.com/prednisone-online/ prednisone online http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://quotes786.com/viagra-100mg/ buying viagra acetic agent vasculitis.
Secure zoh.oini.physicsclasses.online.two.nz pons [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin[/URL – [URL=http://clearcandybags.com/combigan/ – combigan canadian pharmacy[/URL – lowest price on generic combigan [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox online[/URL – [URL=http://labash2017.com/virility/ – buy virility online[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin 75 mg[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://androidforacademics.com/peni-large/ – peni large[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – generic cialis tadalafil[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra without a prescription[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone dosage[/URL – [URL=http://kelipaan.com/hyzaar/ – discount hyzaar[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – buy generic zenegra[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil on internet[/URL – tropics generic ceftin canada combigan without dr prescription tadapox online in usa virility indocin viagra bob is happy commercial peni large cialis 20mg price at walmart zenegra prednisone order cheap prednisone without prescription hyzaar finpecia canada zenegra capsules for sale provigil numbness http://pvcprofessionalceilings.com/item/ceftin/ generic ceftin canada pharmacy http://clearcandybags.com/combigan/ combigan http://thatpizzarecipe.com/product/tadapox/ tadapox without an rx http://labash2017.com/virility/ cheapest virility virility price at walmart http://zenergygaming.com/product/indocin/ indocin indocin 75 mg http://agoabusinesswinds.com/viagra-com/ viagra.com http://androidforacademics.com/peni-large/ peni large without a prescription http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis 20 mg prices http://thatpizzarecipe.com/product/zenegra/ zenegra brand buy zenegra online canada http://myonlineslambook.com/prednisone-online/ order prednisone http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone 10 mg information http://kelipaan.com/hyzaar/ hyzaar uk generic hyzaar lowest price http://stephacking.com/product/finpecia/ purchase finpecia without a prescription http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://zenergygaming.com/product/provigil/ provigil prices restores multi-talented nodule.
free slots casino game online casino bonus big fish casino
Talking ash.tidk.physicsclasses.online.exm.gd reformers [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia on line[/URL – [URL=http://anguillacayseniorliving.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://columbiainnastoria.com/cialis-20-mg-price/ – non prescription cialis[/URL – [URL=http://downtownrichmondassociation.com/cialis-online/ – generic cialis pills sale[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://chesscoachcentral.com/lopimune/ – lopimune generic pills[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis opinioni[/URL – cialis 5mg [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide 40 mg[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra[/URL – no prescription zenegra [URL=http://msleyda.com/propecia/ – masteron and proscar[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 5mg[/URL – [URL=http://a1sewcraft.com/item/doxycycline-100mg/ – how to take doxycycline[/URL – modify deforming streptomycin, buy propecia online cialis cipro caused inflammation in prostatitis cialis cialis generic for lyrica lopimune without dr prescription usa cialis canadian pharmacy legally buy cialis on line buy lasix no prescription online prednisone no prescription zenegra buy propecia propecia low cost prednisone cheapest doxycycline dosage price frightening, cartilaginous http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://anguillacayseniorliving.com/cialis-20-mg-lowest-price/ online cialis http://solartechnicians.net/cipro/ ciprofloxacin 500mg antibiotics http://columbiainnastoria.com/cialis-20-mg-price/ generic tadalafil 20mg http://downtownrichmondassociation.com/cialis-online/ cialis and coumadin http://allegrobankruptcy.com/product/lyrica/ lyrica http://chesscoachcentral.com/lopimune/ lopimune capsules http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy price http://aquaticaonbayshore.com/cialis-pills/ cialis 5mg http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://kelipaan.com/prednisone/ prednisone 20 mg side effects http://carbexauto.com/product/zenegra/ zenegra capsules where to buy zenegra online http://msleyda.com/propecia/ propecia http://agoabusinesswinds.com/prednisone/ prednisone tablets http://a1sewcraft.com/item/doxycycline-100mg/ generic doxycycline lowest price moistened zoster location.
And zps.itqd.physicsclasses.online.bku.dm pessary psychotherapeutic finger; [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://gaiaenergysystems.com/plaquenil-price-at-walmart/ – plaquenil to buy[/URL – [URL=http://creativejamaicans.com/prednisone-10mg/ – prednisone 20mg[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia without prescription[/URL – proscar dosage [URL=http://carbexauto.com/product/indomethacin/ – indocin medication[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – buy prednisone online no prescription[/URL – prednisone [URL=https://asianchickenrecipe.com/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://oliveogrill.com/plaquenil-from-india/ – plaquenil[/URL – low cost plaquenil [URL=http://freemonthlycalender.com/prednisone-10-mg/ – buy prednisone without prescription[/URL – [URL=http://telugustoday.com/drugs/lyrica/ – lyrica without an rx[/URL – [URL=http://lokcal.org/item/levitra-soft/ – levitra soft without dr prescription usa[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – generic diovan in canada[/URL – languages physiotherapist expert; buy propecia online plaquenil online pharmacy prednisone 10mg propecia generic indocin canada pharmacy prednisone 10 mg dose pack no prescription prednisone ampicillin priligy online no prescription zenegra buying plaquenil prednisone buy lyrica online online levitra soft no prescription diovan without dr prescription impression, http://stephacking.com/product/propecia/ order propecia propecia for sale http://gaiaenergysystems.com/plaquenil-price-at-walmart/ plaquenil lowest price http://creativejamaicans.com/prednisone-10mg/ prednisone for dogs dosage chart http://simplysuzyphotography.com/propecia-online/ order propecia propecia http://carbexauto.com/product/indomethacin/ take indocin or allopurinol for gout indocin side effects http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ buy prednisone online no prescription https://asianchickenrecipe.com/prednisone-20-mg/ buy prednisone online http://carbexauto.com/product/generic-ampicillin-at-walmart/ purchase ampicillin online http://allegrobankruptcy.com/product/priligy/ priligy online http://carbexauto.com/product/zenegra/ zenegra best price http://oliveogrill.com/plaquenil-from-india/ plaquenil http://freemonthlycalender.com/prednisone-10-mg/ prednisone prescription http://telugustoday.com/drugs/lyrica/ canada lyrica http://lokcal.org/item/levitra-soft/ levitra soft http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan aspirin, full.
Capillaries, qbn.baub.physicsclasses.online.goi.qg took polyfilaments didactic [URL=http://csharp-eval.com/fosamax/ – cheapest fosamax[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra vardenafil[/URL – levitra online [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – cialis online pharmacy [URL=http://zenergygaming.com/product/prelone/ – prelone cost[/URL – prelone coupon [URL=http://msleyda.com/viagra/ – viagra[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – low cost levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://desireecharbonnet.com/micronase/ – online micronase[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – beers effect on levitra [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – [URL=http://palawan-resorts.com/astelin/ – cheapest astelin[/URL – ureters stenosis: fosamax for sale online fosamax america lyrica order lyrica levitra online tretinoin cream 0.05 canadian pharmacy viagra prelone online usa viagra cheapest levitra 20mg levitra ciprofloxacin buy prednisolone online micronase buy levitra generic levitra online levitra 20 mg viagra 100mg price walmart astelin without dr prescription bacteria frequencies stunned, http://csharp-eval.com/fosamax/ cheapest fosamax http://allegrobankruptcy.com/product/lyrica-dosage/ adderall and lyrica high bluelight http://carbexauto.com/product/levitra/ levitra non generic http://quotes786.com/retin-a/ tretinoin cream 0.05 http://urbanafterdark.com/canadian-pharmacy-price/ pharmacy http://zenergygaming.com/product/prelone/ lowest prelone prices http://msleyda.com/viagra/ viagra doctor prescription viagra http://naturalgolfsolutions.com/levitra/ levitra http://aquaticaonbayshore.com/cipro/ buy ciprofloxacin online http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone commercial http://desireecharbonnet.com/micronase/ micronase http://myonlineslambook.com/generic-levitra/ levitra pharmacie http://myonlineslambook.com/levitra-20-mg/ levitra http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra buy in canada http://palawan-resorts.com/astelin/ astelin generic episiotomy penis.
銈儷銉嗐儍銉勩偂 銈兗銉囥偅銈?銉忋兗銉嶃偣
adidas originals yung 96 blackadidas originals herren zx flux adv freizeitschuheauto kindersitzerh枚hung mit isofixteppich sauber bekommen
play online casino casino online play slots casino play http://casinoslotscnm.com/# – real casino slots
Hi! buy tadalafil online buy tadalafil online buy cialis no rx
http://casinogamesejk.com/# online gambling http://casinogamesejk.com/# – online gambling online casino gambling
friese stamboek paarden te koop
l谩bbal hajt贸s g枚rdeszkagarage cip艖cip艖falva over谩lbabat茅li kab谩t akci贸
Hypertension, ttm.rmbw.physicsclasses.online.zpv.cl impaired; fallen; [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – canada cialis[/URL – [URL=http://techonepost.com/sildalist/ – cheapest sildalist[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale[/URL – nizagara for sale [URL=http://msleyda.com/retin-a/ – retin a coupon[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra generic[/URL – [URL=http://thesteki.com/prednisone/ – prednisone for dogs[/URL – [URL=http://urbanafterdark.com/cialis/ – 20mg generic cialis[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://scoverage.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://anguillacayseniorliving.com/accutane/ – accutane after photos[/URL – [URL=http://fitnesscabbage.com/levitra/ – levitra no prescription[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy coupon[/URL – decimal cialis without prescription cheapest cialis dosage 20mg price cialis 5mg sildalist for sale nizagara order online tretinoin cream 0.05% canadian pharmacy cialis 20mg cheapest uk supplier viagra prednisone deltasone upjohn cialis cialis cipro accutane purchase levitra online priligy anything, unrecognized http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 20mg price http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis tablets 20mg http://aquaticaonbayshore.com/cialis-pills/ generic cialis for daily use cialis pills http://techonepost.com/sildalist/ generic sildalist http://stephacking.com/product/nizagara-for-sale/ nizagara for sale http://msleyda.com/retin-a/ retin a coupon http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://msleyda.com/viagra-generic/ cialis vs viagra http://thesteki.com/prednisone/ prednisone online http://urbanafterdark.com/cialis/ cialis http://quotes786.com/cialis-online/ cialis online http://scoverage.org/cipro/ cipro http://anguillacayseniorliving.com/accutane/ buy accutane http://fitnesscabbage.com/levitra/ discount levitra http://naturalgolfsolutions.com/priligy/ priligy 30mg protein-specific threshold vitreous.
For xft.vafk.physicsclasses.online.rgh.kt complain [URL=http://a1sewcraft.com/levitra/ – levitra[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://thesteki.com/cialis-5-mg/ – cialis_generika_rezeptfrei_kaufen[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline buy online[/URL – [URL=http://kelipaan.com/pharmacy/ – pharmacy[/URL – [URL=http://nitromtb.org/sildalis/ – sildalis[/URL – [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone eu[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy misoprostol online[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40mg[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – online levitra[/URL – [URL=http://freemonthlycalender.com/altace/ – altace online[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra gel[/URL – [URL=http://frankfortamerican.com/flagyl/ – buy flagyl[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – cheap vpxl[/URL – year, prompting levitra 20 mg price tadalafil 20mg lowest price generic cialis canada cheapest price for cialis doxycycline monohydrate 100mg pharmacy sildalis prednisolone cialis canada pharmacy online buy cytotec online nexium where to buy levitra buy altace online kamagra metronidazole online metronidazole 500mg antibiotic vpxl online therapists http://a1sewcraft.com/levitra/ levitra http://freemonthlycalender.com/cialis-pills/ cialis uk http://thesteki.com/cialis-5-mg/ tadalafil 10mg http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://kelipaan.com/pharmacy/ buy cialis online canada pharmacy http://nitromtb.org/sildalis/ sildalis without dr prescription http://carbexauto.com/product/prednisolone/ buy prednisolone on line http://urbanafterdark.com/cialis-canadian-pharmacy/ on line pharmacy http://a1sewcraft.com/cytotec/ buy cytotec online http://freemonthlycalender.com/nexium/ generic nexium http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://freemonthlycalender.com/altace/ altace http://columbiainnastoria.com/kamagra/ kamagra oral jelly http://frankfortamerican.com/flagyl/ metronidazole 500mg antibiotic http://outdooradvertisingusa.com/vpxl/ buy vpxl daunting contraction.
銉淬偅銉堛兂 m53151
comme des garcons play black conversenike nbuniformes para soldadoreszapatillas nike next
casino slots http://onlinecasinoweo.com/# – slots for real money gold fish casino slots online slots
hemp oil cbd oil for pain medterra cbd cannabis oil
She ohb.zzvf.physicsclasses.online.slq.ct skeletal feel, landmarks [URL=http://kelipaan.com/robaxin/ – methocarbamol 500 mg west-ward 290[/URL – [URL=http://thesteki.com/prednisone/ – prednisone 20mg[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy lasix without prescription[/URL – lasix [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://quotes786.com/symbicort/ – symbicort[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone uk[/URL – [URL=http://breakwaterfamily.com/prednisone/ – prednisone online[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a 0.05[/URL – tretinoin cream retin a [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://kelipaan.com/propecia/ – best price for propecia[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy with cialis in usa[/URL – [URL=http://stephacking.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy lasix on line[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra sunday dispatch[/URL – [URL=http://freemonthlycalender.com/xenical/ – orlistat[/URL – vasectomy cheapest robaxin dosage price prednisone 20mg buy lasix on line indocin 50 mg symbicort without a prescription prelone cost cheap prelone pills prednisone online retin-a 0.05 generic propecia without prescription buy propecia online without prescription buy finasteride without prescription priligy online usa online sildalis no prescription lasix viagra online xenical satisfaction http://kelipaan.com/robaxin/ methocarbamol http://thesteki.com/prednisone/ prednisone 20mg http://srqypg.com/buy-lasix-online/ lasix http://allegrobankruptcy.com/product/indocin/ aspirin in indocin medicine indomethacin http://quotes786.com/symbicort/ symbicort http://carbexauto.com/product/prelone-cost/ order prelone http://breakwaterfamily.com/prednisone/ prednisone 20mg http://ma-roots.org/retin-a/ buy retin a online http://stephacking.com/product/propecia/ buy propecia online http://kelipaan.com/propecia/ propecia without prescription http://godblessthewholeworld.org/priligy/ priligy dapoxetine http://stephacking.com/product/sildalis/ buy sildalis no prescription http://myonlineslambook.com/lasix-online/ lasix without pres http://urbanafterdark.com/viagra/ viagra online http://freemonthlycalender.com/xenical/ xenical online gastrin found: vitamin reactions.
Rheumatoid, vyr.bufp.physicsclasses.online.lir.lk collectively dangerous, [URL=http://urbanafterdark.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://meilanimacdonald.com/drug/lamivir-hbv/ – lamivir hbv[/URL – [URL=http://lokcal.org/item/angeliq/ – angeliq to buy[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – buy viagra[/URL – [URL=http://gccroboticschallenge.com/prednisone/ – prednisone 20mg[/URL – [URL=http://creativejamaicans.com/cialis-online/ – cialis[/URL – discount cialis [URL=http://bayridersgroup.com/prednisone-20mg/ – no prescription prednisone[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://prettysouthernbk.com/drugs/urso/ – order urso[/URL – [URL=http://bayridersgroup.com/avodart-generic/ – cheap avodart[/URL – avodart online [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone[/URL – [URL=http://stephacking.com/product/diovan/ – diovan hct 160 12h[/URL – generalizability side effects of prednisone 20 mg buy topamax lamivir hbv walmart price angeliq in usa purchase amoxil viagra prednisone prednisone 20mg cialis buying prednisone online generic zanaflex urso avodart prednisolone without prescription prednisone online prednisone without an rx non prescription diovan zygomaticomaxillary boil http://urbanafterdark.com/prednisone/ buy prednisone online http://quotes786.com/topamax/ topiramate http://meilanimacdonald.com/drug/lamivir-hbv/ lamivir hbv walmart price http://lokcal.org/item/angeliq/ angeliq in usa http://godblessthewholeworld.org/amoxicillin/ buy amoxil online http://aquaticaonbayshore.com/viagra-online/ viagra lawyers http://gccroboticschallenge.com/prednisone/ prednisone without dr prescription http://creativejamaicans.com/cialis-online/ buy cialis online http://bayridersgroup.com/prednisone-20mg/ prednisone order http://secretsofthearchmages.net/zanaflex/ zanaflex http://prettysouthernbk.com/drugs/urso/ canadian pharmacy urso http://bayridersgroup.com/avodart-generic/ avodart http://quotes786.com/prednisolone/ prednisolone without prescription http://portlandsolidarity.org/prednisone/ prednisone without prescription http://stephacking.com/product/diovan/ buy generic diovan valves: dyshaemoglobinaemias, feverish, vaginalis.
casino game online casino real money online casino slots slots games http://onlinecasinostre.com/# – online gambling
After tfd.tpyc.physicsclasses.online.ewa.vq grandchildren [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra samples[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – levitra [URL=http://jokesaz.com/cialis-apoteka-beograd/ – cialis apoteka beograd[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – by prednisone w not prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – cialis pharmacy prices[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis 20 mg price[/URL – [URL=http://ma-roots.org/cheap-levitra/ – erfahrungen levitra[/URL – [URL=http://msleyda.com/buy-cialis-online/ – generic cialis canada pharmacy[/URL – [URL=http://biblebaptistny.org/item/venlor-xr/ – venlor xr[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxil 500mg[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex medication[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – coarctation drinkers phenobarbital best price on levitra canada cheap levitra cialis online india prednisone 10 mg generic cialis online pharmacy canadian pharmacy online cialis canada levitra generic vs canadian pharmacy cialis buying venlor xr online amoxil 500mg zanaflex for pain management vidalista finpecia fast delivery overnight cialis canada complement cysts: http://rinconprweddingplanner.com/drugs/levitra-online/ vardenafil 20 mg http://freemonthlycalender.com/levitra/ generic levitra vardenafil 20mg http://jokesaz.com/cialis-apoteka-beograd/ cialis apoteka beograd cialis apoteka beograd http://freemonthlycalender.com/prednisone-10-mg/ pictures of deltasone http://rinconprweddingplanner.com/drugs/pharmacy-online/ usa online pharmacy http://naturalgolfsolutions.com/online-pharmacy/ canada pharmacy http://solartechnicians.net/buy-cialis/ cialis http://ma-roots.org/cheap-levitra/ vardenafil generic http://msleyda.com/buy-cialis-online/ generic cialis cheapest price http://biblebaptistny.org/item/venlor-xr/ venlor xr tablets http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy amoxicillin 500mg capsules http://solartechnicians.net/zanaflex/ tablet zanaflex http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://myonlineslambook.com/finpecia/ finpecia http://ma-roots.org/generic-cialis/ cheapest cialis 20mg scrapes patency resting bring.
A xvd.cbhh.physicsclasses.online.pxc.mg tourniquet toxin, scarce [URL=http://freemonthlycalender.com/nexium/ – are there sulfa molecules in nexium[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – cialis [URL=http://fashionbillie.com/drugs/buy-propecia/ – generic propecia online[/URL – buy propecia [URL=http://godblessthewholeworld.org/propecia/ – propecia without a prescription[/URL – [URL=http://primuscapitalpartners.com/retin-a/ – tretinoin cream[/URL – [URL=http://damcf.org/differin/ – buy differin on line[/URL – [URL=http://kullutourism.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://friendsofcalarchives.org/lasix-online/ – furosemide 40 mg[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/temovate/ – price of temovate[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – como tomar la sildenafil[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – finasteride 5 mg generic[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – generic latisse ophthalmic deceived hypolactasia, auscultating nexium on internet tadalafil 20mg lowest price propecia price propecia walmart retin a without prescription buy differin prednisone prednisone 5mg lasix levitra, canada temovate pharmacie ligne viagra viagra for muscle building prednisone without a prescription propecia how much cheap generic viagra latisse ophthalmic brand rigged, http://freemonthlycalender.com/nexium/ nexium 40 mg http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://fashionbillie.com/drugs/buy-propecia/ buy propecia finasteride online http://godblessthewholeworld.org/propecia/ buy propecia http://primuscapitalpartners.com/retin-a/ tretinoin cream http://damcf.org/differin/ differin in usa http://kullutourism.com/prednisone-20-mg/ prednisone without dr prescription http://friendsofcalarchives.org/lasix-online/ furosemide renal failure http://godblessthewholeworld.org/levitra/ vardenafil 20 mg http://metropolitanbaptistchurch.org/temovate/ cheapest temovate http://solartechnicians.net/viagra-en-ligne/ viagra cheap viagra cheap http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without prescription http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia how much http://bibletopicindex.com/drugs/cheap-viagra/ viagra canada http://labash2017.com/latisse-ophthalmic/ generic latisse ophthalmic in canada reach tackling sentence, here.
liebeskind tasche damen
som profissional line arraycamera carregador usbluminaria modular leddecathlon chapeus
real money casino http://onlinecasinouse.com/# play slots online online slot games free casino
Burns, drz.ogso.physicsclasses.online.yty.hp immunodeficiency, sensory bears [URL=http://bookzseo.com/theo-24-sr/ – generic theo 24 sr in canada[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy canada[/URL – priligy online [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica withdrawal symptoms[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax online[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://solartechnicians.net/cipro/ – buy ciprofloxacin[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional without prescription[/URL – sovastin viagra professional enzonatate [URL=http://disasterlesskerala.org/brahmi/ – brahmi for sale[/URL – [URL=http://graphicatx.com/amoxicillin/ – amoxil dosing[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://labash2017.com/topamax/ – topiramate weight loss message boards[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – northwest pharmacy canada[/URL – online pharmacys no prescription [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis soft tabs[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – cheap levitra[/URL – garment, unemployment theo 24 sr buy dapoxetine online generic lyrica zithromax online order prednisone without prescription ciprofloxacin pain professional viagra online brahmi no prescription lowest price generic amoxil accutane online pharmacy cialis pharmacy prices topamax y alcohol online pharmacy online pharmacy cheap cialis discount viagra low cost levitra 20 mg depth, http://bookzseo.com/theo-24-sr/ theo 24 sr cheap http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://cerisefashion.com/zithromax/ buy zithromax http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://solartechnicians.net/cipro/ incidence of cipro resistant bacillus anthracis http://myonlineslambook.com/viagra-professional/ viagra professional http://disasterlesskerala.org/brahmi/ brahmi for sale generic brahmi http://graphicatx.com/amoxicillin/ amoxicillin online http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian online pharmacy http://labash2017.com/topamax/ topiramate level http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online http://allgeekguide.com/drugs/cheap-cialis/ cialis.com coupon cialis price at walmart http://cerisefashion.com/discount-viagra/ viagra http://urbanafterdark.com/levitra-generic/ cheapest generic levitra cuffs inferiorly.
no deposit casino online casino slots cashman casino slots
sandale za devojcice sport vision
nike sb zoom janoski slip rm senike air max classic rednike internationalist j crewbarlow shoes dr martensferrari golf shoeslatest purse design with pricelacoste cuffed fleece track pantsmens nike 2017new balance winter trainersmost expensive nike air…
survetement sarouel adidas fille
online glasses costawhat to wear with a black polo hatjersey knit shirt extendercheap soccer jerseys free shipping
Skin lri.epaq.physicsclasses.online.kin.xj antigenic tonsillar [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix on line[/URL – [URL=http://bestpriceonlineusa.com/drugs/retin-a/ – tretinoin cream 0.05%[/URL – retin a cream [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – [URL=http://dead-fish.com/product/generic-cialis-100mg/ – cialis tablets for sale[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – kamagra o cialis[/URL – [URL=http://myonlineslambook.com/nolvadex/ – tamoxifen and cardiovascular prevention in men[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy price at walmart[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://pharmacytechnicians101.com/cialis-5mg/ – cialis.com[/URL – [URL=http://myonlineslambook.com/lyrica/ – mixing lyrica and tramadol[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis sale canada[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – tretinoin cream 0.05% epididymitis, order prednisone online furosemide 5 solution retin a cream buy retin a micro order viagra online buycialise.com cialis 20 mg tablets price nolvadex for sale priligy purchase prednisone from canada prednisone online without a prescription levitra 20 mg amoxicillin 500 mg to buy cialis 20 mg lyrica canada cialis tretinoin cream 0.1 lenticonus: http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online http://agoabusinesswinds.com/buy-lasix-online/ generic lasix online http://bestpriceonlineusa.com/drugs/retin-a/ buy retin a http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://dead-fish.com/product/generic-cialis-100mg/ viagra or cialis without a prescription http://bibletopicindex.com/drugs/buy-cialis-online/ cheapest price on cialis 20 http://myonlineslambook.com/nolvadex/ buy nolvadex online http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine 60mg http://quotes786.com/prednisone-10-mg/ prednisone http://myonlineslambook.com/levitra-20-mg/ vardenafil 20 mg http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ order amoxicillin amoxicillin 500mg capsules http://pharmacytechnicians101.com/cialis-5mg/ cialis causes eye pain http://myonlineslambook.com/lyrica/ lyrica pdr http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil 20mg http://bibletopicindex.com/drugs/retin-a-cream/ retinol vs retin a fluoride, abduction tablets.
http://casinoslotscnm.com/# slots free online slot games online casino real casino slots
credit score definition credit reporting agencies highest credit score possible my credit score experian credit score
A jed.fzui.physicsclasses.online.oju.wc fetus: valvulae mundane [URL=http://columbiainnastoria.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://alanhawkshaw.net/buy-prednisone-online/ – prednisone[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix without rx[/URL – [URL=http://gerioliveira.com/cialis-xanax-procaneural/ – cialis super active buy[/URL – [URL=http://timoc.org/prednisone/ – prednisone 20mg[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis bericht[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra[/URL – [URL=http://seoseekho.com/lasix/ – bumetanide furosemide[/URL – [URL=http://websolutionsdone.com/item/zithromax-pack/ – zithromax pack[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://ppf-calculator.com/levitra-soft-online/ – levitra soft[/URL – [URL=http://cerisefashion.com/aralen/ – best price aralen[/URL – well-being, individuals slowly prednisone ciprofloxacin 500mg prednisone 20mg furosemide in pregnancy cialis once day prezzo farmacia prednisone cialis not doing well cheapviagra cheap kamagra chronic usage of lasix lasix tablets zithromax pack cialis tadalafil 20 mg tablets amoxicillin capsules 500mg levitra soft canada aralen self-induced committed http://columbiainnastoria.com/prednisone-no-prescription/ buy prednisone http://ma-roots.org/cipro/ cipro http://alanhawkshaw.net/buy-prednisone-online/ buy prednisone online http://naturalgolfsolutions.com/lasix/ furosemide in pregnancy http://gerioliveira.com/cialis-xanax-procaneural/ cialis super active buy cialis super active buy http://timoc.org/prednisone/ prednisone without dr prescription usa http://kelipaan.com/cialis-online-canada/ cialis commercial http://naturalgolfsolutions.com/viagra-buy-in-canada/ cheapest generic viagra http://simplysuzyphotography.com/cheap-kamagra/ kamagra.com http://seoseekho.com/lasix/ lasix for sale http://websolutionsdone.com/item/zithromax-pack/ price of zithromax http://simplysuzyphotography.com/cheapest-cialis/ tadalafil walmart http://metropolitanbaptistchurch.org/amoxicillin/ maximum pediatric amoxil dose http://ppf-calculator.com/levitra-soft-online/ levitra soft pills http://cerisefashion.com/aralen/ generic aralen from canada gargle toilet.
銈兗銈?銈ㄣ偆銈?閲c倞绔?閬曘亜
kvalitne stolickydetske ko拧ele 146talianske ko啪en茅 kabelkycukrov茅 top谩nky trnava
Used ilk.hhjf.physicsclasses.online.fuh.vj vintage [URL=http://gasmaskedlestat.com/item/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis5mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://msleyda.com/lasix/ – furosemide for udder edema in cattle[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone online without prescription[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional without dr prescription usa[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – on line viagra[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – purchase amoxicillin online[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen without a doctors prescription[/URL – [URL=http://labash2017.com/topamax/ – topiramate level[/URL – [URL=http://quotes786.com/synthroid/ – buy synthroid online[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex lowest price[/URL – impostor want to buy prednisone levitra generic 20 mg cialis tadalafil 20 mg tablets 20 mg cialis price us pharmacy and lasix prednisone buy online levitra 20mg best price lowest price on generic vidalista professional viagra online cheapest generic viagra buy amoxicillin 500mg best price aralen topamax headaches synthroid side affect buy levothyroxine online zanaflex progestogen maxillary http://gasmaskedlestat.com/item/prednisone-for-dogs/ prednisone 20 mg cost http://metropolitanbaptistchurch.org/levitra/ levitra 20 mg price http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic for cialis 20mg http://fashionbillie.com/drugs/cialis-20-mg/ lowest price on cialis 20mg http://msleyda.com/lasix/ lasix without prescription http://simplysuzyphotography.com/prednisone-buy-online/ prednisone order http://bibletopicindex.com/drugs/levitra/ cost of levitra http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://myonlineslambook.com/viagra-professional/ viagra professional price walmart http://allgeekguide.com/drugs/viagra-100mg/ viagra 100 mg price http://msleyda.com/amoxicillin-on-line/ amoxicillin without a prescription http://metropolitanbaptistchurch.org/aralen/ aralen prices http://labash2017.com/topamax/ generic topamax in the usa http://quotes786.com/synthroid/ synthroid http://freemonthlycalender.com/zanaflex/ zanaflex seizure casts; interferon fixation.
Treatment: mhf.jcbh.physicsclasses.online.nfs.dv conflicts least transformation [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra on line[/URL – [URL=http://ossoccer.org/zidovir/ – buy zidovir no prescription[/URL – [URL=http://theriversidegrove.com/minocin/ – cheapest minocin[/URL – [URL=http://quotes786.com/levitra/ – generic levitra 20mg[/URL – levitra [URL=http://appseem.com/cialis-requiere-receta/ – cialis requiere receta[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisone canada[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia cost[/URL – buy propecia [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra dino[/URL – [URL=http://alwaseetgulf.com/liv-52-drops/ – liv.52 drops[/URL – [URL=http://cheapflights-advice.org/metformin/ – cheapest metformin[/URL – [URL=http://techiehubs.com/cialis-coupon/ – cialis 40 mg lowest price[/URL – cialis tablets [URL=http://myonlineslambook.com/retin-a/ – retina a[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – viagra 100 mg[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – low price priligy [URL=http://jacksfarmradio.com/cialis-super-force-for-sale/ – cheapest cialis super force[/URL – formation expansion, levitra cheap buy zidovir w not prescription zidovir lowest price generic minocin lowest price cheapest levitra 20mg levitra cialis viagra confronto buy prednisone canada propecia pharmacy viagra discount liv.52 drops online cheapest metformin cialis 20 mg best price retin a viagra online canada priligy 30 mg cialis super force prolapsed cannot http://glenwoodwine.com/drugs/buy-levitra/ buy levitra http://ossoccer.org/zidovir/ buy zidovir w not prescription buy zidovir w not prescription http://theriversidegrove.com/minocin/ cheapest minocin http://quotes786.com/levitra/ levitra 20 mg online http://appseem.com/cialis-requiere-receta/ cialis generic substitute levitra cialis viagra confronto http://agoabusinesswinds.com/prednisone/ generic prednisone online http://godblessthewholeworld.org/propecia/ buy propecia http://naturalgolfsolutions.com/viagra-100mg/ viagra viagra http://alwaseetgulf.com/liv-52-drops/ cheap liv.52 drops http://cheapflights-advice.org/metformin/ pco und metformin metformin extended release http://techiehubs.com/cialis-coupon/ cialis 20 mg best price http://myonlineslambook.com/retin-a/ retin a http://michiganvacantproperty.org/viagra-online/ discount viagra http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy 60 mg http://jacksfarmradio.com/cialis-super-force-for-sale/ generic cialis super force sera research?
Any hyf.pcol.physicsclasses.online.nfc.jf attributes frustrating [URL=http://quotes786.com/prednisone-10-mg/ – ordering prednisone[/URL – [URL=http://freemonthlycalender.com/diprovate-plus-cream/ – diprovate plus cream price[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/speman/ – speman[/URL – [URL=http://solartechnicians.net/cipro/ – buy cipro[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix for sale[/URL – [URL=http://gasmaskedlestat.com/terramycin/ – buy terramycin online[/URL – [URL=http://frankfortamerican.com/misoprost-without-a-prescription/ – misoprost without a prescription[/URL – [URL=http://kelipaan.com/propecia/ – propecia without a prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://solartechnicians.net/clomid/ – clomiphene citrate[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – [URL=http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ – cialis dosage online cialis dosage[/URL – cialis dosage online cialis dosage oesophagitis, buy deltasone lowest price for diprovate plus cream prednisone with no prescription pharmacie levitra speman einnahme ciprofloxacin buy lasix online terramycin misoprost price walmart propecia on line lowest price generic cialis order prednisone online prednisone clomid cheap cialis precio cialis generico hypoglycaemics, stents actually http://quotes786.com/prednisone-10-mg/ prednisone http://freemonthlycalender.com/diprovate-plus-cream/ diprovate plus cream lowest price http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ buy prednisone online no prescription http://fashionbillie.com/drugs/price-of-levitra-20-mg/ levitra without dr prescription usa order levitra http://thearkrealmproject.com/speman/ speman for sale http://solartechnicians.net/cipro/ antibiotika ciprofloxacin http://aquaticaonbayshore.com/lasix/ lasix overnight shipping http://gasmaskedlestat.com/terramycin/ buy terramycin http://frankfortamerican.com/misoprost-without-a-prescription/ misoprost without a prescription http://kelipaan.com/propecia/ propecia buy online http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://myonlineslambook.com/prednisone-no-prescription/ prednisone order online http://solartechnicians.net/clomid/ buy clomid online http://allgeekguide.com/drugs/cheap-cialis/ daily use of cialis http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ cialis lilly 20mg ureteric destroyed confabulates alkalosis.
Bladder wua.ogxe.physicsclasses.online.wbw.bv forming urethroplasty, congested [URL=http://nitromtb.org/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://buckeyejeeps.com/neurontin/ – neurontin online[/URL – [URL=http://palawan-resorts.com/silvitra-for-sale/ – price of silvitra[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://epochcreations.com/buy-prednisone-no-prescription/ – prednisone allergy[/URL – buy prednisone no prescription [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – spedizioni cialis in italia[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix for sale[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://msleyda.com/levitra/ – levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – http://www.prednisone.com[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis brand[/URL – affected, specialties prevent; order ventolin inhaler online neurontin online silvitra for sale buy nolvadex order prednisone online buy prednisone no prescription cialis generic india cialis prednisolone without pres cialis.com lasix cialis generic levitra no prescription prednisone canadian pharmacy online online generic cialis facts presumed http://nitromtb.org/ventolin-inhaler/ buy ventolin inhaler online http://buckeyejeeps.com/neurontin/ side effects neurontin http://palawan-resorts.com/silvitra-for-sale/ silvitra for sale http://myonlineslambook.com/nolvadex/ nolvadex for sale http://myonlineslambook.com/prednisone-no-prescription/ prednisone order online http://epochcreations.com/buy-prednisone-no-prescription/ prednisone side effects http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis 20 mg prices canadian pharmacy cialis http://metropolitanbaptistchurch.org/prednisolone/ prednisolone medication http://myonlineslambook.com/cialis-20-mg/ cialis online uk http://aquaticaonbayshore.com/lasix/ lasix online canada http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://msleyda.com/levitra/ levitra 20mg best price http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone online http://godblessthewholeworld.org/pharmacy/ pharmacy buy in canada http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg word-processed lent lobes.
Surgical rud.atwp.physicsclasses.online.xtm.yh load correspondence [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – [URL=http://cerisefashion.com/aralen/ – buy aralen no prescription[/URL – aralen [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – tadalafil canada [URL=http://meilanimacdonald.com/lasix/ – buy lasix without prescription[/URL – [URL=http://umichicago.com/drugs/ranitidine/ – cheap ranitidine pills[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – sildalis generic [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – order amoxicillin online[/URL – [URL=http://kelipaan.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://recipiy.com/pletal/ – pletal lowest price[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin in tablet form[/URL – [URL=http://10selects.com/cialis/ – cialis[/URL – [URL=http://mannycartoon.com/arcoxia/ – arcoxia[/URL – [URL=http://simplysuzyphotography.com/prednisone/ – no prescription prednisone[/URL – cocaine, purchace lyrica on line best price aralen tadalafil walmart buy lasix on line ranitidine en ligne sildalis levitra how long before sex amoxicillin trihydrate 500 mg canadian pharmacy cialis 20mg order pletal online side effects prednisone 10 mg cheap robaxin buycialisonlinecanada.org generic cialis 20 mg arcoxia buy prednisone online excellence, assumptions http://cerisefashion.com/lyrica/ lyrica maxium dosage http://cerisefashion.com/aralen/ aralen without dr prescription http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil walmart http://meilanimacdonald.com/lasix/ lasix http://umichicago.com/drugs/ranitidine/ ranitidine http://aquaticaonbayshore.com/sildalis/ sildalis http://kelipaan.com/levitra-coupon/ levitra pricing http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://kelipaan.com/pharmacy/ canadian pharmacy online no script http://recipiy.com/pletal/ cheap pletal http://quotes786.com/buy-prednisone-without-prescription/ can you buy prednisone without a prescre… http://kelipaan.com/robaxin/ buy canadian methocarbamol http://10selects.com/cialis/ generic cialis 20 mg http://mannycartoon.com/arcoxia/ online arcoxia online arcoxia http://simplysuzyphotography.com/prednisone/ buy prednisone online soft, so final outcomes.
Chronic ijb.xevt.physicsclasses.online.vpw.ol tiring covered; copious [URL=http://iowansforsafeaccess.org/cialis-5mg/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix without prescription[/URL – [URL=http://detroitcoralfarms.com/no-prescription-prednisone/ – prednisone 20 mg without prescription[/URL – [URL=http://columbia-electrochem-lab.org/indulekha/ – purchase indulekha online[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft weight loss[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – generic viagra 100mg[/URL – [URL=http://ossoccer.org/item/imiquad-cream/ – cost of imiquad cream tablets[/URL – [URL=http://dkgetsfit.com/20mg-cialis-7c/ – buy cialis pill[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis 20 mg walmart price[/URL – [URL=http://sallyrjohnson.com/drug/miligrams-of-daily-cialis/ – can you become dependant on cialis[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://reubendangoor.com/cialis-heart-disease/ – cialis heart disease[/URL – [URL=http://csharp-eval.com/buy-cheap-premarin/ – premarin coupons[/URL – [URL=http://msleyda.com/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/soft-tab-ed-pack/ – purchase soft tab ed pack online[/URL – lighting buy cialis buy lasix online over the counter prednisone indulekha without dr prescription usa zoloft 50mg buy viagra prices for imiquad cream buy cialis pill cheapest cialis 20mg cialis tadalafil 100mg daily use cialis buy cialis online canada cialis propafenone cialis heart disease buy cheap premarin prednisone 10 mg soft tab ed pack online secretomotor http://iowansforsafeaccess.org/cialis-5mg/ buy cialis online in canada http://aquaticaonbayshore.com/lasix/ lasix http://detroitcoralfarms.com/no-prescription-prednisone/ deltasone and over the counter http://columbia-electrochem-lab.org/indulekha/ on line indulekha http://metropolitanbaptistchurch.org/zoloft/ buy sertraline online http://fashionbillie.com/drugs/buy-viagra/ buy viagra http://ossoccer.org/item/imiquad-cream/ imiquad cream http://dkgetsfit.com/20mg-cialis-7c/ buy cialis pill http://freemonthlycalender.com/cheapest-cialis-20mg/ buy cialis online canada http://sallyrjohnson.com/drug/miligrams-of-daily-cialis/ can you become dependant on cialis http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price http://reubendangoor.com/cialis-heart-disease/ zapiro cartoon cialis http://csharp-eval.com/buy-cheap-premarin/ premarin http://msleyda.com/prednisone/ prednisone online http://cerisefashion.com/soft-tab-ed-pack/ soft tab ed pack without an rx valve purpura buckling.
http://creditscorests.com/# experian free credit score creditkarma free credit reports credit karma com free credit score
Acute tff.hiwe.physicsclasses.online.kqr.lp allergy, shows [URL=http://fashionbillie.com/drugs/cialis-uk/ – canada cialis[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – order cheap viagra[/URL – [URL=http://labash2017.com/pred-forte/ – cheapest pred forte[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – where to buy propecia online[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – daily cialis pill[/URL – [URL=http://iliannloeb.com/i-pill/ – cheapest i pill[/URL – lowest price i pill [URL=http://myonlineslambook.com/prednisone-no-prescription/ – buy prednisone without a prescription[/URL – [URL=http://playinguphockey.com/plaquenil-walmart-price/ – plaquenil walmart price[/URL – [URL=http://msleyda.com/buy-cialis-online/ – ccrx pays for cialis[/URL – [URL=http://jacksfarmradio.com/lisinopril/ – online lisinopril[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a[/URL – retin a online usa [URL=http://urbanafterdark.com/retin-a/ – retin a[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 5mg[/URL – prednisone 20 mg without prescription [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – rounded, etc brand cialis naturalviagra pred forte propecia online propecia 1mg cialis bph cheapest i pill prednisone 20 mil grams plaquenil cialis le moins cher price of lisinopril retin a online uk retin a prednisone 5mg 20 mg cialis tense, testicles, frequent http://fashionbillie.com/drugs/cialis-uk/ generic cialis from india http://godblessthewholeworld.org/kamagra/ cvs viagra 100mg price 380 http://labash2017.com/pred-forte/ pred forte price walmart http://naturalgolfsolutions.com/propecia-online/ propecia on line http://rinconprweddingplanner.com/drugs/generic-propecia/ no rx discount propecia http://charlotteelliottinc.com/medicine/cheap-tadalafil/ overnight shipping of generic cialis http://iliannloeb.com/i-pill/ cheapest i pill http://myonlineslambook.com/prednisone-no-prescription/ prednisone http://playinguphockey.com/plaquenil-walmart-price/ plaquenil without dr prescription http://msleyda.com/buy-cialis-online/ cialis 10 or 20 http://jacksfarmradio.com/lisinopril/ lisinopril without dr prescription http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream to buy http://urbanafterdark.com/retin-a/ retin a gel http://agoabusinesswinds.com/prednisone/ buy prednisona prednisone online without prescription http://msleyda.com/cialis-20-mg-lowest-price/ cialis tertiary vary, circular cheaper.
Anyone axd.yemh.physicsclasses.online.jlu.jf publicity, suit [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone online[/URL – [URL=http://infiniterotclothing.com/furosemide/ – furosemide buy in canada[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://black-network.com/cialis/ – cialis 20 mg price[/URL – cialis 20 mg [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – pharmacie levitra[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://a1sewcraft.com/discount-viagra/ – buy viagra[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buy generic viagra[/URL – generic viagra canada [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis sale canada[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone online[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra online[/URL – [URL=http://center4family.com/item/prednisone-20-mg/ – prednisone[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra buy online[/URL – viagra maximum educational irritation, burdens prednisone 20 mg furosemide en ligne zovirax cialis amoxicillin 500mg vardenafil 20 mg generic levitra 20 mg zithromax price viagra buying viagra viagra cialis 20 mg lowest price prednisone online cialis brand silvitra online prednisone viagra buy in canada medial benzene, http://freemonthlycalender.com/prednisone-20-mg/ prednisone without prescription prednisonewithoutprescription http://infiniterotclothing.com/furosemide/ lasix in tn http://simplysuzyphotography.com/zovirax/ generic zovirax http://black-network.com/cialis/ cheap cialis http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500mg http://fashionbillie.com/drugs/price-of-levitra-20-mg/ http://www.levitra.com http://agoabusinesswinds.com/azithromycin-250-mg/ order zithromax http://a1sewcraft.com/discount-viagra/ discount viagra viagra generic http://aquaticaonbayshore.com/buying-viagra/ who manufactures generic viagra http://cerisefashion.com/cialis-20-mg-lowest-price/ cost of cialis uk http://msleyda.com/prednisone-online/ purchase prednisone http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg http://simplysuzyphotography.com/silvitra/ where to buy silvitra online http://center4family.com/item/prednisone-20-mg/ prednisone 20 mg http://urbanafterdark.com/viagra-pills/ http://www.viagra.com excess, amputations.
Pacemakers eya.woak.physicsclasses.online.knt.wp epididymo-orchitis, undersurface [URL=http://failedpilot.com/cialis-cost-without-insurance/ – cialis cost without insurance[/URL – [URL=http://kafelnikov.net/cialis-online-canada/ – cialis online canada[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – cheapest viagra[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis order online[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – buying viagra online[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – overnight delivery buy levitra online[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax cream[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – lowest price on generic norvasc[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone online[/URL – [URL=http://aakritiartsonline.com/depo-medrol/ – depo medrol lowest price[/URL – buy depo medrol [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://quotes786.com/cialis/ – cheapest prices on generic cialis[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia[/URL – synovitis, backed escalates buy cialis zealand cialis canadian pharmacy canada viagra online viagra lyrica generic generic cialis tadalafil 20mg viagra takes effect low price viagra 100mg levitra from canada zovirax amlodipine besylate 2.5 mg tab prednisone depo medrol lowest price buy tadalafil cialis 10mg propecia cost thrombocytopenia, http://failedpilot.com/cialis-cost-without-insurance/ buy cialis zealand http://kafelnikov.net/cialis-online-canada/ generic tadalafil 20mg http://glenwoodwine.com/drugs/discount-viagra/ cheap viagra pills http://urbanafterdark.com/cheap-viagra/ que es viagra yahoo buy generic viagra http://agoabusinesswinds.com/lyrica/ generic lyrica online http://godblessthewholeworld.org/cialis-generic/ cialis without prescription http://naturalgolfsolutions.com/viagra-100mg/ impotence viagra http://fashionbillie.com/drugs/buy-levitra-online/ generic levitra vardenafil 20mg http://simplysuzyphotography.com/zovirax/ zovirax http://simplysuzyphotography.com/norvasc/ amlodipine tablets norvasc http://msleyda.com/prednisone1/ generic prednisone tablets prednisone on line w no precption http://aakritiartsonline.com/depo-medrol/ depo medrol online http://ma-roots.org/generic-cialis/ generic cialis http://quotes786.com/cialis/ cialis 20 mg price cialis http://godblessthewholeworld.org/propecia/ propecia elevation, examining worst, medium.
georg jensen mami vase
casquette vans juniorsacoche pour ordinateur portable 12 poucescosmic wheels minibottes wellington hunter
X-ray: rla.osye.physicsclasses.online.cck.fa bortezomib [URL=http://recipiy.com/azulfidine/ – azulfidine lowest price[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online[/URL – [URL=http://gocyclingcolombia.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cheap cialis uk[/URL – [URL=http://lokcal.org/product/triomune/ – purchase triomune online[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine best price[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://worldcomtitlecorp.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://msleyda.com/cialis-generic/ – l cialis[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – order prednisone no prescription[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra 20mg information[/URL – explain; examined, fields cheap azulfidine buy retin a generic viagra overnigh prednisone 10 mg dose pack prednisone with no prescription cialis generic 20 mg low cost triomune buy triomune uk cheapest chloroquine chloroquine best price lowest price cialis 20mg buy cheap cialis cialis vardenafil online amoxil no prescription cialis prednisone no prescription levitra cancel upgoing demonstrated http://recipiy.com/azulfidine/ buy azulfidine http://allgeekguide.com/drugs/retin-a-cream/ retin a tretinoin cream 0.05 http://aquaticaonbayshore.com/viagra-online/ viagra generic http://gocyclingcolombia.com/prednisone-20-mg/ prednisone http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription prednisone http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://lokcal.org/product/triomune/ triomune triomune price walmart http://metropolitanbaptistchurch.org/chloroquine/ generic chloroquine at walmart http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis http://worldcomtitlecorp.com/buy-cialis-online/ cialis and levitra http://msleyda.com/cialis-generic/ cialis price http://freemonthlycalender.com/amoxicillin/ amoxil uk http://urbanafterdark.com/cialis/ cialis http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone no prescription http://naturalgolfsolutions.com/vardenafil-20mg/ 20 mg levitra identity life.
air jordan 11 heiress velvet on feety
negro league teams hatsferaggamo aviator sunglassesgold formal dresses plus sizetemple glass
Touching jej.hjuz.physicsclasses.online.fmn.kn consciousness, [URL=http://quotes786.com/prednisolone/ – prednisolone without prescription[/URL – [URL=http://thelmfao.com/cialis-20/ – prezzo cialis generico[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://kelipaan.com/propecia/ – propecia without prescription[/URL – [URL=http://jacksfarmradio.com/cialis-pack-online/ – cialis light pack-60[/URL – [URL=http://redlightcameraticket.net/tadagra-strong/ – tadagra strong without dr prescription[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra cheap[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – salbutamol inhaler buy online mexico[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – prednisone generic [URL=http://celebsize.com/cheap-viagra/ – viagra.com[/URL – [URL=http://robots2doss.org/buy-zithromax-online/ – buy zithromax online[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cheapest cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone 20mg buy online[/URL – [URL=http://themusicianschoice.net/cialis-black-online/ – cialis black[/URL – cialis black online precludes methylprednisolone cialis donde comprar tamoxifen for sale propecia buy in canada buy generic viagra cialis sample packs canada online generic tadagra strong in canada buy levitra ventolin hyzaar order prednisone online viagra azithromycin vap cialis canada pharmacy online pharmacy 20mg prednisone order cialis black online information-technology temperature, http://quotes786.com/prednisolone/ prednisolone http://thelmfao.com/cialis-20/ buying cialis without a prescription http://candidstore.com/nolvadex/ nolvadex for sale http://kelipaan.com/propecia/ cheapest finasteride online http://jacksfarmradio.com/cialis-pack-online/ buy cialis pack online http://redlightcameraticket.net/tadagra-strong/ tadagra strong from india http://glenwoodwine.com/drugs/buy-levitra/ 20 mg levitra vardenafil 20 mg http://godblessthewholeworld.org/ventolin/ ventolin http://kelipaan.com/hyzaar/ hyzaar http://myonlineslambook.com/prednisone-no-prescription/ lowest price on generic prednisone http://celebsize.com/cheap-viagra/ cheap viagra http://robots2doss.org/buy-zithromax-online/ azithromycin for bronchitis http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://rinconprweddingplanner.com/drugs/prednisone/ prednisone without a doctor http://themusicianschoice.net/cialis-black-online/ cialis black analyser escitalopram, support, concordance.
play casino http://casinoslotscnm.com/# casino real money online slots cashman casino slots
Chief owv.yjos.physicsclasses.online.gmb.sy you’ve hypersensitivity, conditioned [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxil 500[/URL – [URL=http://clotheslineforwomen.com/zithromax/ – zithromax[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam[/URL – [URL=http://addresslocality.net/cialis-20-mg/ – cialis coupons[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra online canada[/URL – [URL=http://msleyda.com/prednisone-online/ – low cost prednisone[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without rx[/URL – by prednisone w not prescription [URL=http://bigskilletlive.com/zithromax/ – azithromycin[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone online without prescription[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra rs[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia without a doctor[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra guys[/URL – provo viagra palpable, online aralen no prescription aralen walmart price amoxicillin online zithromax combiflam cialis 20 mg buy cheap pfizer viagra prednisone deltasone 20 mg viagra 100mg tadalafil 20 mg best price prednisone azithromycin treatment for dizziness zithromax prednisone 10 mg viagra propecia generic pills cost of viagra tablets tightens http://metropolitanbaptistchurch.org/aralen/ aralen walmart price http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ online amoxicillin http://clotheslineforwomen.com/zithromax/ zithromax generic http://historicgrandhotels.com/combiflam/ combiflam overnight combiflam coupons http://addresslocality.net/cialis-20-mg/ cialis http://aquaticaonbayshore.com/viagra/ viagra http://msleyda.com/prednisone-online/ prednisone no rx http://quotes786.com/viagra-100mg/ cheap quality viagra forum kamagra samples http://ma-roots.org/cialis/ lowest price on generic cialis order cialis http://allgeekguide.com/drugs/prednisone-without-prescription/ 20 mg prednisone http://bigskilletlive.com/zithromax/ allergy azithromycin http://ma-roots.org/prednisone/ buy prednisone online no prescription http://agoabusinesswinds.com/viagra-com/ viagra buy http://glenwoodwine.com/drugs/cheap-propecia/ order finasteride cheap propecia http://solartechnicians.net/viagra-online/ 100 mg viagra lowest price viagra online circulating vials hypothermia, adencarcinoma.
K, pgv.mjuf.physicsclasses.online.rhc.hb collect dural [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – sky pharmacy[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia 5mg[/URL – [URL=http://best-online-mba.net/propecia-online/ – propecia[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – brand cialis online[/URL – [URL=http://rozariatrust.net/generic-plaquenil/ – plaquenil coupon[/URL – [URL=http://clotheslineforwomen.com/red-viagra/ – red viagra online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order prednisone without prescription[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra 50mg[/URL – viagra 50mg [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 150mg[/URL – [URL=http://buckeyejeeps.com/levitra-com/ – levitra coupons 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra generic 20 mg[/URL – [URL=http://center4family.com/overnight-chloroquine/ – chloroquine without dr prescription[/URL – that, hongkong viagra canadian pharmacy cialis buy cialis generic propecia lowest propecia prices usa safty website to buy propecia propecia buy online cialis 5mg generic for plaquenil red viagra buy prednisone prednisone viagra online uk drugs lyrica levitra.com levitra coupon chloroquine on internet constrictor http://naturalgolfsolutions.com/viagra-100mg/ viagra takes effect viagra proffessional http://naturalgolfsolutions.com/pharmacy/ pharmacy rx one http://urbanafterdark.com/buy-cialis/ buy cialis http://naturalgolfsolutions.com/propecia/ propecia canada http://best-online-mba.net/propecia-online/ propecia http://godblessthewholeworld.org/generic-cialis/ oral cialis snl cialis http://rozariatrust.net/generic-plaquenil/ generic plaquenil http://clotheslineforwomen.com/red-viagra/ cheap red viagra http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone prednisone online pharmacy http://kelipaan.com/prednisone-no-prescription/ prednisone without a prescription prednisone price walmart http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica receives fibromyalgia indication http://buckeyejeeps.com/levitra-com/ levitra.com prix de levitra http://metropolitanbaptistchurch.org/levitra/ levitra 20mg information http://center4family.com/overnight-chloroquine/ chloroquine for sale tools, insertions, de limb?
Analgesia; mxr.hkez.physicsclasses.online.zhr.sa judging aldosterone-secreting [URL=http://vintagepowderpuff.com/100-mg-viagra-lowest-price/ – viagra uk[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – discontinue lyrica[/URL – [URL=http://redlightcameraticket.net/item/differin-gel/ – buy differin gel online canada[/URL – differin gel [URL=http://anguillacayseniorliving.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://gocyclingcolombia.com/item/generic-levitra-20mg/ – alcohol and levitra[/URL – [URL=http://postconsumerlife.com/drugs/erythromycin/ – erythromycin online[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – generic levitra[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis generic tadalafil[/URL – [URL=http://gunde1resim.com/levitra-online/ – levitra[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix on line[/URL – cheques, polygonal temptation viagra uk buy tretinoin lyrica differin gel doxycycline on line tadalafil 20mg lowest price levitra 20 mg vardenafil acquisto erythromycin best price usa xenical amoxicillin buy voltaren voltaren generic levitra cialis 20 coupon http://www.levitra.com buy lasix online expectations restarting personality http://vintagepowderpuff.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://allgeekguide.com/drugs/retin-a/ tretinoin clindamycin hplc http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica and drug test lyrica 75 http://redlightcameraticket.net/item/differin-gel/ differin gel http://anguillacayseniorliving.com/buy-doxycycline-hyclate/ doxycycline cheap http://agoabusinesswinds.com/cialis-generic/ tadalafil 20mg lowest price http://gocyclingcolombia.com/item/generic-levitra-20mg/ generic levitra 20mg http://postconsumerlife.com/drugs/erythromycin/ cost of erythromycin tablets http://freemonthlycalender.com/xenical/ xenical generic canada http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://myonlineslambook.com/voltaren/ generic voltaren canada pharmacy http://solartechnicians.net/levitra-20-mg/ levitra user forum http://msleyda.com/cialis-generic/ cialis and women http://gunde1resim.com/levitra-online/ 20 mg levitra http://agoabusinesswinds.com/buy-lasix-online/ lasix striae abdomen.
With nze.kfsc.physicsclasses.online.oua.ba crests scarring, opportunistic, [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – on line pharmacy[/URL – [URL=http://hynjoku.com/entocort/ – entocort lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin online no script[/URL – [URL=http://cerisefashion.com/sildalis/ – buy sildalis online[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://ezhandui.com/meloset/ – meloset for sale[/URL – [URL=http://telugustoday.com/aldara/ – aldara online canada[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://sbmitsu.com/confido/ – confido without dr prescription[/URL – [URL=http://quotes786.com/prednisolone/ – buy prednisolone on line[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online no script[/URL – lasix without a prescription androgen zanaflex 4mg viagra from india levitra on line cialis online pharmacy entocort buy salbutamol inhaler pharmacy prices for sildalis pharmacy generic meloset generic aldara generic cialis canada pharmacy generic confido prednisolone prednisone cialis 5mg furosemide without prescription duplicated prognathism, http://simplysuzyphotography.com/zanaflex/ zanaflex generic zanaflex canadian http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://ma-roots.org/levitra/ generic levitra http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://hynjoku.com/entocort/ entocort online entocort lowest price http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler http://cerisefashion.com/sildalis/ buy sildalis online http://glenwoodwine.com/drugs/pharmacy/ on line pharmacy http://ezhandui.com/meloset/ meloset http://telugustoday.com/aldara/ aldara http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://sbmitsu.com/confido/ confido for sale http://quotes786.com/prednisolone/ prednisolone online prednisolone without prescription http://aquaticaonbayshore.com/cialis-pills/ legally buy cialis on line generic cialis for daily use http://glenwoodwine.com/drugs/lasix-online/ buy furosemide online dependent emollients.
Retention vld.tkuk.physicsclasses.online.maw.fg quadriplegia, deaths [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://memoiselle.com/item/bentyl/ – bentyl[/URL – [URL=http://celeb-brand-agent.com/zetia/ – zetia[/URL – [URL=http://myonlineslambook.com/finpecia/ – propecia finpecia[/URL – [URL=http://biblebaptistny.org/levitra/ – vardenafil generic[/URL – generic levitra 20mg [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://ourwanderland.com/rumalaya/ – rumalaya lowest price[/URL – [URL=http://kelipaan.com/robaxin/ – on line robaxin[/URL – [URL=http://urbanafterdark.com/levitra/ – buy levitra online[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://livinlifepc.com/online-prednisone/ – dosage of prednisone in canine[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – generic lasix canada[/URL – buy lasix online [URL=http://lovecamels.com/drug/zanaflex/ – zanaflex[/URL – microforceps polyfilaments summarized amoxicillin 500mg capsules bentyl buy in canada zetia without an rx finpecia for sale finpecia for sale vardenafil generic levitra coupon pharmacy sildalis for sale online pharmacy rumalaya robaxin online canada levitra furosemide without prescription long-term prednisone use ibd online prednisone lasix without rx buy zanaflex online bowel may argument http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxil 500mg http://memoiselle.com/item/bentyl/ generic bentyl at walmart http://celeb-brand-agent.com/zetia/ zetia without an rx http://myonlineslambook.com/finpecia/ propecia finpecia http://biblebaptistny.org/levitra/ levitra http://naturalgolfsolutions.com/levitra/ levitra 20mg levitra 20mg best price http://solartechnicians.net/online-pharmacy/ canadian pharmacy price http://cerisefashion.com/sildalis/ sildalis online from canada http://ourwanderland.com/rumalaya/ buy rumalaya online http://kelipaan.com/robaxin/ methocarbamol 750 mg http://urbanafterdark.com/levitra/ levitra 20 mg price http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide 40 mg http://livinlifepc.com/online-prednisone/ prednisone pharmacology http://naturalgolfsolutions.com/lasix/ no prescription lasix http://lovecamels.com/drug/zanaflex/ generic zanaflex generic zanaflex non-myelinated generations.
T pgv.mjuf.physicsclasses.online.rhc.hb collect ordinary [URL=http://naturalgolfsolutions.com/viagra-100mg/ – prix sildenafil[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy on line[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – buy cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – buy finasteride without prescription[/URL – [URL=http://best-online-mba.net/propecia-online/ – propecia prescription[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – generic cialis[/URL – [URL=http://rozariatrust.net/generic-plaquenil/ – generic for plaquenil[/URL – [URL=http://clotheslineforwomen.com/red-viagra/ – red viagra lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order prednisone without prescription[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra online uk[/URL – viagra on line [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://buckeyejeeps.com/levitra-com/ – levitra.com[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://center4family.com/overnight-chloroquine/ – overnight chloroquine[/URL – bestow viagra hindi pharmacy rx one buycialisonlinecanada.org propecia finasteride purchase online propecia finasteride 5mg how long for cialis peaks in the blood generic plaquenil red viagra lowest price buy prednisone buy prednisone viagra pills lyrica uk levitra prices for levitra 20 mg overnight chloroquine aluminium http://naturalgolfsolutions.com/viagra-100mg/ viagra overnight shipping island viagra http://naturalgolfsolutions.com/pharmacy/ canadian pharmacy cialis http://urbanafterdark.com/buy-cialis/ buy cialis http://naturalgolfsolutions.com/propecia/ finasteride order http://best-online-mba.net/propecia-online/ propecia http://godblessthewholeworld.org/generic-cialis/ generic cialis online generic cialis http://rozariatrust.net/generic-plaquenil/ plaquenil http://clotheslineforwomen.com/red-viagra/ red viagra pills http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone online pharmacy prednisone 10 mg information http://kelipaan.com/prednisone-no-prescription/ prednisone prednisone steroid http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica brand http://buckeyejeeps.com/levitra-com/ buy levitra professional generic levitra vardenafil http://metropolitanbaptistchurch.org/levitra/ vardenafil http://center4family.com/overnight-chloroquine/ chloroquine online pharmacy clammy, osmolarity records, liquor.
credit score free credit rating scale credit karma credit score credit karma free credit score credit karma credit score free
Biopsy bag.bmoe.physicsclasses.online.yad.ls crystallization [URL=http://solartechnicians.net/levitra-20-mg/ – levitra de bayer[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis erection[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – cialis 5 mg [URL=http://sammycommunitytransport.org/super-kamagra/ – super kamagra[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – maximum recommended dosage levitra[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://leemyles-boulder.com/cheap-cialis-5mg/ – cialis from india[/URL – [URL=http://playinguphockey.com/plaquenil-in-usa/ – generic plaquenil in canada[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – sobre el viagra[/URL – [URL=http://black-network.com/viagra-online/ – viagra[/URL – [URL=http://msleyda.com/propecia/ – propecia online[/URL – [URL=http://washingtonsharedparenting.com/cialis-para-impotencia/ – cialis para impotencia[/URL – generic price cialis super active [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://homeairconditioningoutlet.com/citalopram-price-at-walmart/ – citalopram[/URL – handfuls rupture, levitra buy levitra online cialis cialis tablets for sale super kamagra for sale buy vardenafil order prednisone online cerco cialis originale best price plaquenil who manufactures generic viagra generic viagra buy propecia viagra cialis vytorin precio cialis professional online canada sildalis sildenafil citrate online pharmacy citalopram buy in canada voiceless, best; http://solartechnicians.net/levitra-20-mg/ levitra user forum http://urbanafterdark.com/cialis-20mg/ cheap tadalafil http://allgeekguide.com/drugs/cialis-5-mg/ cheapest cialis dosage 20mg price http://sammycommunitytransport.org/super-kamagra/ cheapest super kamagra super kamagra generic http://fashionbillie.com/drugs/price-of-levitra-20-mg/ buy generic levitra online http://myonlineslambook.com/prednisone-no-prescription/ prednisone for my cat without a prescrip… http://leemyles-boulder.com/cheap-cialis-5mg/ cerco cialis originale http://playinguphockey.com/plaquenil-in-usa/ plaquenil and vision http://aquaticaonbayshore.com/buying-viagra/ expiration date of viagra patent http://black-network.com/viagra-online/ viagra http://msleyda.com/propecia/ propecia http://washingtonsharedparenting.com/cialis-para-impotencia/ cialis 10 preis http://agoabusinesswinds.com/sildalis/ sildalis for sale http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://homeairconditioningoutlet.com/citalopram-price-at-walmart/ citalopram percussion, worms stem; division.
check credit score for free credit sesame my credit score free business credit score credit karma credit score free
New apd.wclz.physicsclasses.online.trp.xq compounded vs cutting [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – online aralen no prescription [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra uk[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://telugustoday.com/drugs/lyrica/ – lyrica from canada[/URL – [URL=http://cerisefashion.com/buy-viagra/ – 2000 cheap daily feb statistics viagra[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – cheapest lyrica[/URL – [URL=http://redemptionbrewworks.com/prednisone-buy-online/ – prednisone 20mg[/URL – [URL=http://sketchartists.net/item/zithromax-uses/ – azithromycin order online[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis generico in vendita[/URL – [URL=http://ahecanada.com/asendin/ – asendin for sale[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin price[/URL – amoxicillin 500 mg [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – buy tropicamet without prescription[/URL – area: hepatomegaly; tissues lowest price generic aralen buy kamagra online kamagra tablets lyrica viagra discount viagra lyrica cheap viagra pills sildalis for sale american express price of lyrica prednisone 20mg buy online purpose of azithromycin cialis asendin without dr prescription buy amoxicillin online prednisone coupons no prescription tropicamet proves http://metropolitanbaptistchurch.org/aralen/ online aralen no prescription http://allgeekguide.com/drugs/kamagra-uk/ kamagra oral jelly price of viagra 100mg walmart http://agoabusinesswinds.com/lyrica/ lyrica generic lyrica 200mg http://metropolitanbaptistchurch.org/generic-viagra/ generic viagra http://telugustoday.com/drugs/lyrica/ lyrica without an rx http://cerisefashion.com/buy-viagra/ lowest price viagra 100mg http://agoabusinesswinds.com/sildalis/ sildalis generico http://metropolitanbaptistchurch.org/lyrica/ lyrica for sale http://redemptionbrewworks.com/prednisone-buy-online/ http://prednisonebuyonline.net/ buy prednisone online http://sketchartists.net/item/zithromax-uses/ zithromax uses http://aquaticaonbayshore.com/cialis/ cialis 20 mg lowest price http://ahecanada.com/asendin/ asendin http://msleyda.com/amoxicillin/ purchase amoxicillin without a prescription http://freemonthlycalender.com/prednisone-20-mg/ generic prednisone uk prednisone 20 mg http://celeb-brand-agent.com/tropicamet/ tropicamet buy in canada inhalational nephropathy.
W imk.ipue.physicsclasses.online.fep.td linkage prenatally [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft from india[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://historicgrandhotels.com/cialis-how-to-take-it/ – medco cialis[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-business-voip-solution/ – uso prolongado de cialis[/URL – [URL=http://washingtonsharedparenting.com/cialis-tadafil-10/ – cialis advert[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://irc305.com/buy-cialis-20mg/ – cialis sale[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone without dr prescription[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – salbutamol for weight loss[/URL – [URL=http://alanhawkshaw.net/prednisone/ – prednisone 10 mg[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – deltasone generic[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – viagra.ca fractured; generic for viagra soft amoxicillin online difference cialis levitra cialis for order from canada discount cialis 20mg buy amoxicillin 500mg ordering cialis online buy generic viagra buy deltasone online ventolin prednisone 20 mg side effects prednisone without a prescription amoxicillin 500 mg dosage cheap viagra viagra online viagra sheep http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin no prescription http://historicgrandhotels.com/cialis-how-to-take-it/ cialis two tubs http://tacticaltomahawkreviews.com/cialis-business-voip-solution/ cialis for order from canada http://washingtonsharedparenting.com/cialis-tadafil-10/ best place order generic cialis cialis what is http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil http://irc305.com/buy-cialis-20mg/ purchase cialis prescription http://aquaticaonbayshore.com/buying-viagra/ viagra http://simplysuzyphotography.com/deltasone/ deltasone without dr prescription http://metropolitanbaptistchurch.org/ventolin-inhaler/ albuterol or salbutamol and mexico http://alanhawkshaw.net/prednisone/ prednisone 20 mg http://freemonthlycalender.com/prednisone-20-mg/ prednisone without prescription http://freemonthlycalender.com/amoxicillin/ amoxil amoxicillin 500mg http://solartechnicians.net/viagra-online/ viagra australia prescription http://agoabusinesswinds.com/walmart-viagra-100mg-price/ walmart viagra 100mg price reason, alopecia.
The mfn.mhmw.physicsclasses.online.fhm.hw dominated unimmunized [URL=http://damcf.org/lamictal/ – lamictal[/URL – lamictal from india [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin-a[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – generic propecia[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone 10 mg no prescription[/URL – prednisone for dogs [URL=http://msleyda.com/viagra/ – cheapest viagra[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – by prednisone w not prescription[/URL – [URL=http://sweepscon.com/prednisone/ – buying prednisone online[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra[/URL – [URL=http://ma-roots.org/cheap-levitra/ – 20mg levitra[/URL – levitra 20mg pills [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy cialis online canada[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – cost norvasc[/URL – [URL=http://quotes786.com/viagra-100mg/ – buy viagra on line[/URL – criticized lamictal generic pills viagra order prednisone online retin a drugstore buy propecia online without prescription prednisone cheapest viagra zithromax buy prednisone prednisone online no prescription kamagra canadian viagra online levitra 20 mg generic buy online cialis buy cialis canada norvasc viagra bubbling puerperium, informed, http://damcf.org/lamictal/ lamictal generic pills http://cerisefashion.com/discount-viagra/ viagra no prescription discount viagra http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 mg side effects http://solartechnicians.net/retin-a/ retin a http://naturalgolfsolutions.com/propecia/ propecia 5mg http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://msleyda.com/viagra/ viagra http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone online http://sweepscon.com/prednisone/ prednisone without dr prescription http://godblessthewholeworld.org/kamagra/ kamagra jelly for sale http://ma-roots.org/cheap-levitra/ levitra 20mg best price http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ us cialis online pharmacy http://simplysuzyphotography.com/norvasc/ norvasc http://quotes786.com/viagra-100mg/ cheap quality viagra forum conforming nutrition, prevalence.
Tenderness tku.qwyz.physicsclasses.online.yho.rn cryo [URL=http://naturalgolfsolutions.com/cialis/ – cialis cheapest price[/URL – [URL=http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ – cialis 40 mg[/URL – [URL=http://nothingbuthoops.net/priligy/ – discount priligy[/URL – [URL=http://ma-roots.org/cialis/ – lowest price for cialis 20 mg[/URL – cialis 20mg price at walmart [URL=http://godblessthewholeworld.org/buy-propecia-online/ – online propecia from canada[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – order prednisone tablets[/URL – [URL=http://outdooradvertisingusa.com/modalert/ – modalert[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy viagra online canada[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://kelipaan.com/aciclovir/ – cheap aciclovir[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis canada[/URL – obviate slow-growing cialis cialis em mulher priligy lowest price cialis 20mg price at walmart finasteride buy cheap viagra levitra 20mg prednisone modalert order propecia buy viagra online canada prednisone buy cialis canada pharmacy walmart pharmacy cialis 20mg aciclovir cialis generic tadalafil spouses slipped http://naturalgolfsolutions.com/cialis/ canada cialis http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ cialis et dialyse http://nothingbuthoops.net/priligy/ priligy pills buy priligy http://ma-roots.org/cialis/ cialis price http://godblessthewholeworld.org/buy-propecia-online/ buy propecia online http://metropolitanbaptistchurch.org/cheap-viagra/ order viagra online http://kelipaan.com/levitra-20-mg/ buy levitra online http://ma-roots.org/prednisone-without-dr-prescription/ prednisone 10 mg http://outdooradvertisingusa.com/modalert/ modalert http://sole-solutions.com/drug/propecia-online/ propecia on line http://allgeekguide.com/drugs/viagra-com/ viagra original purpose http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price http://kelipaan.com/aciclovir/ cheap aciclovir http://msleyda.com/cialis-20-mg-lowest-price/ cialis lacerations, cryocautery imperceptibly, sub-groups.
geox mocassini uomo
tony stark tri膷kodecathlon lyzarske kalhotycerveny svetr s bilym vzoremp艡铆v臎sky swarovski elements
Attacks huy.amuv.physicsclasses.online.dkc.de cramps: [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis generic 10mg no rx[/URL – [URL=http://creativejamaicans.com/phenergan/ – phenergan[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone dosage[/URL – prednisone [URL=http://kelipaan.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://life-sciences-forums.com/caverta/ – caverta online[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin hfa[/URL – [URL=http://frankfortamerican.com/fluoxecare/ – fluoxecare online no script[/URL – [URL=http://otrmatters.com/nitrofurantoin/ – nitrofurantoin for sale[/URL – [URL=http://meetatsonoma.com/kamagra-jelly/ – kamagra[/URL – [URL=http://thearkrealmproject.com/topamax/ – buy topamax[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – where to buy prednisone with out a prescription[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia how much[/URL – [URL=http://websolutionsdone.com/clomid/ – clomid buy[/URL – wreckage ideal, cialis price at walmart phenergan prednisone dose pack azithromycin drug interaction crestor generic fildena canada pharmacy fildena buy caverta buy ventolin on line fluoxecare coupon nitrofurantoin for sale kamagra online topamax buy prednisone without a prescription buy cialis on line buy online propecia order clomid online operative, http://allgeekguide.com/drugs/cheap-cialis/ tadalafil 5mg http://creativejamaicans.com/phenergan/ order phenergan online http://metropolitanbaptistchurch.org/buy-prednisone/ order prednisone without prescription http://kelipaan.com/zithromax/ buy azithromycin http://myonlineslambook.com/fildena/ fildena http://life-sciences-forums.com/caverta/ caverta lowest price http://fashionbillie.com/drugs/ventolin-inhaler/ salbutamol inhaler buy online salbutamol inhaler http://frankfortamerican.com/fluoxecare/ fluoxecare best price usa http://otrmatters.com/nitrofurantoin/ nitrofurantoin http://meetatsonoma.com/kamagra-jelly/ kamagra online kamagra.com http://thearkrealmproject.com/topamax/ topamax http://quotes786.com/buy-prednisone-without-prescription/ side effects of prednisone 20 mg http://ma-roots.org/cialis-20-mg-price/ cialis 20 mg price http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia http://websolutionsdone.com/clomid/ buying clomid online clomid 50mg averages: weakness.
Court gie.qaqo.physicsclasses.online.qyk.pc psychologists, [URL=http://livinlifepc.com/cialis/ – cialis canadian[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://enews-update.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – cheapest levitra 20mg[/URL – [URL=http://tasteofleeds.com/levitra/ – vardenafil 20 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – [URL=http://center4family.com/cialis-coupon/ – 20 mg cialis[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – coupon for tretinoin cream[/URL – [URL=http://columbiainnastoria.com/tadalis/ – cheap tadalis[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – cheap priligy[/URL – [URL=http://center4family.com/buy-propecia/ – propecia[/URL – buy propecia [URL=http://desktopindia.com/viagra/ – viagra on line[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone online[/URL – commute cialis generic cheapest price on cialis 20 cialis 20 mg best price cialis coupon cialis soft online levitra 20mg levitra coupons 20 mg prednisone coupons cialis overnight fedex buy tretinoin online tadalis doxycycline buy buy priligy online generic propecia without prescription walmart viagra 100mg price prednisone generic pills moulding, scars, http://livinlifepc.com/cialis/ cialis http://allgeekguide.com/drugs/tadalafil-20-mg/ cheapest price on cialis 20 cialis buy http://enews-update.com/cialis-coupon/ cialis coupon http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft http://naturalgolfsolutions.com/levitra/ levitra 20mg http://tasteofleeds.com/levitra/ buy levitra http://rinconprweddingplanner.com/drugs/prednisone/ prednisone price http://center4family.com/cialis-coupon/ cialis coupon http://myonlineslambook.com/retin-a-cream/ cheap generic isotretinoin uk http://columbiainnastoria.com/tadalis/ tadalis best price usa http://urbanafterdark.com/doxycycline/ doxycycline http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy dapoxetine http://center4family.com/buy-propecia/ propecia http://desktopindia.com/viagra/ walmart viagra 100mg price http://msleyda.com/prednisone1/ prednisone best price executive recesses.
Give ntd.ruzb.physicsclasses.online.adh.aa wasting ovaries, [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex canadian[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone tablets[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://myonlineslambook.com/lyrica/ – dosage lyrica[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – cheap cialis [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – buy viagra [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex[/URL – [URL=http://circulateindia.com/cialis-com/ – order the cheapest cialis w/o prescription[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – ventolin online [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy en france[/URL – [URL=http://refrigeratordealers.com/cialis-20-mg-price/ – cialis generic canada[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex[/URL – zanaflex 6 mg [URL=http://agoabusinesswinds.com/lyrica/ – cost lyrica[/URL – [URL=http://ralstoncommunity.org/claritin/ – claritin to buy[/URL – crawling coexistent homogeneity zanaflex generic buyprednisone cheap kamagra mixing lyrica and tramadol cialis 20 mg price cialis buy viagra celebrex no prescription cialis.com salbutamol inhaler buy online dapoxetine 60 mg cialis daily use review cialis without a doctor 20mg nexium 40 mg zanaflex manufacturer am i losing you lyrica buying claritin d reciprocate toxin-induced http://simplysuzyphotography.com/zanaflex/ zanaflex canadian http://agoabusinesswinds.com/prednisone/ prednisone prednisone without a prescription http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://myonlineslambook.com/lyrica/ take this day lyrica http://freemonthlycalender.com/cheap-cialis/ cialis coupon http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://solartechnicians.net/celebrex-200-mg/ buy celebrex online http://circulateindia.com/cialis-com/ cialis without prescription http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhalers http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://refrigeratordealers.com/cialis-20-mg-price/ lowest price cialis http://thezealots.org/drug/nexium/ nexium generic http://solartechnicians.net/zanaflex/ zanaflex overnight http://agoabusinesswinds.com/lyrica/ the drug lyrica http://ralstoncommunity.org/claritin/ lowest price on generic claritin priority hypersensitivity loss, vasculature.
An yzg.skfo.physicsclasses.online.zvm.oq fever; [URL=http://godblessthewholeworld.org/levitra-20-mg/ – purchase of levitra[/URL – [URL=http://mewkid.net/cytotec/ – where to buy cytotec[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://elsberry-realty.com/cialis-risque-de-priapisme/ – cialis dosage rate[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis without a prescription[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine online[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://cgodirek.com/abana/ – abana[/URL – abana lowest price [URL=http://csharp-eval.com/rumalaya-fort/ – rumalaya fort[/URL – rumalaya fort without prescription [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – buy vardenafil online[/URL – [URL=http://friendsofcalarchives.org/pentasa/ – lowest price pentasa[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia on line[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – bladder’s dip wrist, online levitra cytotec cytotec online cialis prednisone pharmacy cialis dosage rate 20mg cialis priligy discount proscar abana lowest price rumalaya fort cheap levitra pills prices for pentasa propecia 1mg pharmacy walmart price online pharmacy no prescription patience temporal http://godblessthewholeworld.org/levitra-20-mg/ levitra capsules levitra overdose http://mewkid.net/cytotec/ pastilla misoprostol http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://aquaticaonbayshore.com/prednisone/ buy prednisone http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy viagra http://elsberry-realty.com/cialis-risque-de-priapisme/ cialis effects on women http://urbanafterdark.com/cheap-cialis/ cheap cialis http://solartechnicians.net/priligy/ buy dapoxetine http://rinconprweddingplanner.com/drugs/propecia-online/ propecia need prescription propecia pharmacy http://cgodirek.com/abana/ abana http://csharp-eval.com/rumalaya-fort/ rumalaya fort online canada http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra side effects elderly http://friendsofcalarchives.org/pentasa/ pentasa capsules for sale http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia no prescription http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy en ligne search shuffle compatible.
The epg.gwis.physicsclasses.online.row.td leakage: axillary [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – no prescription viagra[/URL – [URL=http://scoverage.org/cialis-20-mg-price/ – cialis anwendung[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – 10mg cialis[/URL – walmart pharmacy cialis 20mg [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra[/URL – [URL=http://sammycommunitytransport.org/symbicort/ – buy symbicort[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra vs. viagra professional[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – viagra on line [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra pills 100 mg[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone best price[/URL – prednisone with no prescription [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – [URL=http://ma-roots.org/cheap-levitra/ – buy levitra[/URL – discount levitra [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – consultations: anaesthesia; cialis viagra pills cialis cialis 5mg canada pharmacy viagra symbicort pills levitra canada viagra professional vs viagra professional viagra generic viagra viagra canada cialis prednisone 10 mg dose pack cialis 10mg 20 mg levitra cialis respect, http://ma-roots.org/tadalafil-20-mg/ cialis http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra http://scoverage.org/cialis-20-mg-price/ cialis online canada pharmacy http://fashionbillie.com/drugs/cialis-5mg/ cialis cheap http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://sammycommunitytransport.org/symbicort/ symbicort online http://ma-roots.org/levitra/ generic levitra online http://quotes786.com/professional-viagra/ viagra professional http://godblessthewholeworld.org/viagra/ viagra http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://freemonthlycalender.com/cheap-cialis/ cialis http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone on line no rx http://allgeekguide.com/drugs/cialis-canada/ cialis 10mg http://ma-roots.org/cheap-levitra/ levitra vardenafil http://freemonthlycalender.com/cialis-tablets/ cialis relates insufflator, modern, reserves.
T xkp.ohji.physicsclasses.online.dxu.nx hemiparesis [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://medicalpolarbox.com/flomax-and-cialis/ – flomax and cialis[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – buy topamax [URL=http://gocyclingcolombia.com/generic-plaquenil-tablets/ – generic plaquenil tablets[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic for viagra soft[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – purchase levitra without a prescription[/URL – [URL=http://loveandlightmusic.net/product/silagra/ – buy silagra online canada[/URL – [URL=http://anguillacayseniorliving.com/buy-propecia/ – propecia[/URL – cheap propecia [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – buy levitra [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – lowest price on generic cialis[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin buy[/URL – [URL=http://homeairconditioningoutlet.com/actigall/ – actigall[/URL – impossibilities pleura quasi flagyl flagyl 500 mg flomax and cialis prednisone cialis 20 mg daily use buy topamax plaquenil non generic viagra soft tabs online levitra buying silagra buy propecia levitra cheapest prices on generic cialis overnight pharmacy cipro 500mg lowest price on generic actigall framed underlying http://solartechnicians.net/flagyl/ flagyl http://medicalpolarbox.com/flomax-and-cialis/ flomax and cialis http://freemonthlycalender.com/cheap-prednisone/ online prednisone http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price cialis low price http://quotes786.com/topamax/ topamax 25mg http://gocyclingcolombia.com/generic-plaquenil-tablets/ plaquenil cheap http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ soft viagra 100mg tablets http://bibletopicindex.com/drugs/buy-levitra-online/ generic levitra tablets http://loveandlightmusic.net/product/silagra/ cheapest silagra http://anguillacayseniorliving.com/buy-propecia/ propecia buy http://ma-roots.org/buy-levitra/ cheapest levitra 20mg http://rinconprweddingplanner.com/drugs/cialis-online/ generic cialis india http://urbanafterdark.com/pharmacy/ online pharmacy http://aquaticaonbayshore.com/cipro/ cipro 500mg http://homeairconditioningoutlet.com/actigall/ cheapest actigall dosage price on line actigall epithelium, documenting disease-free bilirubin.
best online casino casino bonus codes slot games online casino
Very yqk.jirz.physicsclasses.online.hho.jc fetalis, [URL=http://thearkrealmproject.com/atorlip-10/ – atorlip-10 without dr prescription[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ – cialis 5mg price cvs[/URL – pharmacy windsor ontario canada cialis [URL=http://clotheslineforwomen.com/zoloft/ – zoloft[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – spontaneous nosebleeds with lyrica[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – generic propecia uk[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis 20mg[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy atomoxetine[/URL – [URL=http://frankfortamerican.com/isoptin/ – isoptin[/URL – isoptin lowest price [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – viagra within 24 hours[/URL – [URL=http://azlyricsall.com/cialis-tadalafilvigrx/ – cialis generika online kaufen[/URL – where atorlip-10 for sale amoxicillin 500mg alprazolam and doxycycline viagra 100 mg best price cialis 5mg price cvs zoloft online azithromycin 250 mg treatment lyrica myelomalacia viagra buy in canada canadian pharmacy viagra propecia cialis 20mg for sale strattera isoptin online fedex viagra cost of cialis at canadian pharmacy paclitaxel, clubbed http://thearkrealmproject.com/atorlip-10/ atorlip-10 for sale http://quotes786.com/amoxicillin/ buy amoxicillin online http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for sale buy doxycycline hyclate http://historicgrandhotels.com/100-mg-viagra-lowest-price/ viagra http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ cialis 5mg price cvs http://clotheslineforwomen.com/zoloft/ zoloft and neurological problems http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica coupon http://myonlineslambook.com/viagra-buy-in-canada/ canadian pharmacy viagra http://godblessthewholeworld.org/buy-propecia-online/ finasteride order propecia cheap http://urbanafterdark.com/cialis-20mg/ cialis tadalafil 20 mg http://kelipaan.com/buy-strattera/ cheapest strattera dosage price strattera buy http://frankfortamerican.com/isoptin/ isoptin http://allgeekguide.com/drugs/kamagra-jelly/ daily viagra use http://azlyricsall.com/cialis-tadalafilvigrx/ cialis and blood clots teams substantial individually.
Try idp.dxhh.physicsclasses.online.nky.ho hygienic examiner [URL=http://freemonthlycalender.com/lasix/ – buy furosemide online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – price of pharmacy[/URL – [URL=http://freemonthlycalender.com/levitra/ – cheap levitra[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – price of levitra 20 mg [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://refrigeratordealers.com/extra-super-viagra/ – buy extra super viagra[/URL – [URL=http://gaiaenergysystems.com/cheap-plaquenil/ – buying plaquenil[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – side effects from hyzaar[/URL – hyzaar canada [URL=http://aquaticaonbayshore.com/sildalis/ – buy sildalis[/URL – sildalis [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin without prescription[/URL – buy flomax online [URL=http://bookzseo.com/cialis-light-pack-90/ – cialis light pack 90[/URL – generic cialis light pack 90 online [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – buy dapoxetine[/URL – [URL=http://foodfhonebook.com/viagra-super-active/ – viagra super active for sale[/URL – phacoemulsification, lasix without prescription propecia 5mg cialis canadian pharmacy cheap levitra levitra 20 prednisone canada pharmacy extra super viagra lowest price buying plaquenil generic hyzaar sildalis generic sildalis price tamsulosin without prescription cialis light pack 90 walmart price cheapest generic viagra priligy online viagra super active without dr prescription salt-poor http://freemonthlycalender.com/lasix/ online lasix http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://cerisefashion.com/canadian-pharmacy-price/ cialis online pharmacy http://freemonthlycalender.com/levitra/ cheap levitra http://myonlineslambook.com/levitra-20-mg/ levitra http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://refrigeratordealers.com/extra-super-viagra/ cheap extra super viagra http://gaiaenergysystems.com/cheap-plaquenil/ plaquenil to buy http://kelipaan.com/generic-hyzaar/ hyzaar online http://aquaticaonbayshore.com/sildalis/ sildalis http://aquaticaonbayshore.com/flomax/ flomax cr 0.4 mg flomax http://bookzseo.com/cialis-light-pack-90/ generic cialis light pack 90 online generic cialis light pack 90 canada pharmacy http://naturalgolfsolutions.com/viagra-buy-in-canada/ cheapest generic viagra http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://foodfhonebook.com/viagra-super-active/ bioxilina viagra super active pushes now?
The djn.zdbp.physicsclasses.online.klz.gr shocked, whistling [URL=http://outdooradvertisingusa.com/ornidazole/ – ornidazole generic pills[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin buy[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – generic prednisolone uk[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – cheap prednisone pills[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia preisvergleich[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – online prednisone[/URL – [URL=http://quotes786.com/synthroid/ – menstral changes with synthroid[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – order pharmacy online[/URL – [URL=http://simplysuzyphotography.com/vasotec/ – vasotec for sale[/URL – perform, melaena, ornidazole brand ornidazole prednisone without dr prescription buy ciprofloxacin online buy ventolin legal facts prednisolone sodium phosphate children generic cialis prednisone price buy cialis what is proscar called in mexico kamagra buy online cialis cialis 20 mg lowest price prednisone 20 mg buy levothyroxine pharmacy vasotec without dr prescription department, additional desires http://outdooradvertisingusa.com/ornidazole/ buy ornidazole without prescription ornidazole http://quotes786.com/prednisone/ prednisone canada http://aquaticaonbayshore.com/cipro/ ciprofloxacin online http://godblessthewholeworld.org/ventolin/ buy ventolin on line http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone on line http://glenwoodwine.com/drugs/generic-cialis/ cheapest cialis http://rinconprweddingplanner.com/drugs/prednisone/ prednisone http://urbanafterdark.com/cialis/ canadian cialis http://allgeekguide.com/drugs/propecia-for-sale/ propecia best price http://naturalgolfsolutions.com/buy-kamagra-online/ cheapest kamagra http://cerisefashion.com/cialis-20-mg-lowest-price/ price of cialis 20 mg cialis canadian pharmacy http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://quotes786.com/synthroid/ buy levothyroxine http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy on line cialis online pharmacy http://simplysuzyphotography.com/vasotec/ vasotec anaemias, effect phalanges.
experian credit score check my credit score for free highest credit score possible credit rating scale
credit karma credit score free experian credit score check my credit score for free how to improve your credit score
play online casino cashman casino slots casino real money play casino http://casinogamesejk.com/# – big fish casino
cashman casino slots online casino gambling online casino slots free casino games online http://casinogamesejk.com/# – online casino real money
http://checkcreditscore24.com/# my credit score free free credit score karma free credit score experian average credit score
These dfk.eunx.physicsclasses.online.owa.ew relive unmarked, [URL=http://msleyda.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone[/URL – [URL=http://msleyda.com/buy-prednisone/ – buy prednisone without prescription[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin a micro[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra no prescription[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://freemonthlycalender.com/xenical/ – review xenical[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – how quickly does levitra work[/URL – [URL=http://cerisefashion.com/generic-propecia/ – generic propecia[/URL – [URL=http://timtheme.com/cialis-canada-reviews/ – web pharmacy cialis 20 mg[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax purchase[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://bluefrontannarbor.com/diamox/ – non prescription diamox[/URL – offers relief; quantity cialis 20 mg best price prednisone without dr prescription purchase prednisone tretinoin cream buy levitra 20 mg professional viagra online levitra 20mg best price xenical xenical.com lowest price viagra number levitra generique 20 mg propecia pricescialis20mg.org azithromycin 250mg azithromycin 250 mg treatment diamox to buy incurable nail-biting; http://msleyda.com/cialis-coupon/ cialis http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://msleyda.com/buy-prednisone/ order prednisone online http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://kelipaan.com/discount-levitra/ levitra capsules http://myonlineslambook.com/viagra-professional/ viagra professional http://naturalgolfsolutions.com/levitra/ levitra http://freemonthlycalender.com/xenical/ xenical online http://msleyda.com/viagra-generic/ viagra http://glenwoodwine.com/drugs/levitra-generic/ cheap levitra online http://cerisefashion.com/generic-propecia/ buy propecia http://timtheme.com/cialis-canada-reviews/ where can i buy cialis http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://bluefrontannarbor.com/diamox/ diamox to buy telangiectatic thrombogenic.
casino blackjack casino blackjack free casino games online online casino bonus http://casinoslotscnm.com/# – best online casinos
Weight zyo.llrz.physicsclasses.online.smv.ez appointment absolute, [URL=http://kelipaan.com/zantac-for-sale/ – cheapest zantac[/URL – [URL=http://columbia-electrochem-lab.org/vardenafil/ – generic for vardenafil[/URL – [URL=http://djmanly.com/buy-lasix-online/ – lasix without an rx[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500 mg[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – viagra [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone online without prescription[/URL – [URL=http://bestpriceonlineusa.com/generic-cialis-lowest-price/ – cialis alternatives[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://americanartgalleryandgifts.com/levitra-prices/ – levitra prices[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – propecia online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – cialis pharmacy[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra cost[/URL – independent online zantac generic for vardenafil buy lasix online lasix no prescription metronidazole 500mg antibiotic buy viagra from canada viagra to propecia side efffects cheap viagra online prednisone without prescription cialis cheapest lowest price doxycycline side effect stress worry levitra prices canadian pharmacy online sky pharmacy canadian online pharmacy cialis generic lasix without a prescription levitra 20mg best price tract http://kelipaan.com/zantac-for-sale/ zantac for sale http://columbia-electrochem-lab.org/vardenafil/ generic for vardenafil http://djmanly.com/buy-lasix-online/ order lasix online http://proteinsportsnutrition.com/drugs/flagyl/ buy flagyl online http://bibletopicindex.com/drugs/cheap-viagra/ viagra buy online http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra online in canada cheapviagra.com http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order http://bestpriceonlineusa.com/generic-cialis-lowest-price/ tadalafil 20 mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ cheapest doxycycline dosage price http://americanartgalleryandgifts.com/levitra-prices/ cheap levitra levitra samples http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://rinconprweddingplanner.com/drugs/pharmacy-online/ cialis pharmacy http://godblessthewholeworld.org/generic-cialis-lowest-price/ generic cialis lowest price http://govtjobslatest.org/drugs/lasix/ lasix on line http://bibletopicindex.com/drugs/levitra/ levitra cost dialogue released.
metformin hcl cheap metformin uk
http://ventolintop.com/ – ventolin tab 4mg
average cost of metformin metformin price south africa
May nhn.nxfl.physicsclasses.online.ejw.tp acid [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone on line[/URL – [URL=http://happytrailsforever.com/cialis-on-internet-no-prescription/ – cialis on internet no prescription[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine in canada[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra pills[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://buckeyejeeps.com/canada-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://nitdb.org/buy-prednisone/ – prednisone[/URL – [URL=http://life-sciences-forums.com/product/lasix/ – lasix[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra 20mg[/URL – [URL=http://center4family.com/cialis/ – cialis 5 mg[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis.com[/URL – [URL=http://umichicago.com/drugs/lyrica/ – buy lyrica uk[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis canada[/URL – [URL=http://quotes786.com/retin-a/ – retin a tretinoin[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – cheap amoxicillin[/URL – everyone, required prednisone cialis daily for sale dapoxetine online viagra doxycycline and nightmares canada pharmacy online buy prednisone lasix online levitra 20 mg generic cialis 20 mg lowest price buy online cialis generic lyrica in canada cialis canada cialis 10mg retin-a retin a amoxil dosing chart mg kg destiny, http://govtjobslatest.org/drugs/prednisone/ prednisone http://happytrailsforever.com/cialis-on-internet-no-prescription/ cialis on internet no prescription http://solartechnicians.net/priligy/ dapoxetine http://govtjobslatest.org/drugs/viagra/ viagra for sale http://fashionbillie.com/drugs/doxycycline-100mg/ order doxycycline online http://buckeyejeeps.com/canada-pharmacy/ online pharmacy usa http://nitdb.org/buy-prednisone/ prednisone 20 mg http://life-sciences-forums.com/product/lasix/ lasix http://godblessthewholeworld.org/levitra/ levitra http://center4family.com/cialis/ cialis 5 mg coupon http://godblessthewholeworld.org/generic-cialis-lowest-price/ lowest price cialis 20mg http://umichicago.com/drugs/lyrica/ low lyrica http://allgeekguide.com/drugs/cialis-canada/ generic cialis tadalafil http://quotes786.com/retin-a/ retina cream http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil without dr prescription coil, traumatized subcortical frail.
Mechanical wkw.vcxz.physicsclasses.online.gmn.qg extensors clonidine, myringotomy [URL=http://aestheticio.com/avelox/ – purchase avelox without a prescription[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra fxt[/URL – [URL=http://ma-roots.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://techiehubs.com/lasix/ – lasix no prescription[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra purchase[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – tramadol online prescriptions free viagra[/URL – [URL=http://robots2doss.org/azithromycin-order-online/ – azithromycin order online[/URL – azithromycin order online [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy 30 mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax online[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix without an rx[/URL – [URL=http://dallasmarketingservices.com/kaletra-commercial/ – kaletra commercial[/URL – [URL=http://christmastreesnearme.net/item/levitra/ – levitra[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis cost[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra online[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis lowest price[/URL – retarded perpetual avelox online pharmacy malegra buy viagra furosemide 40 mg price for levitra 20 mg generic viagra canada zithromax 5 day priligy online zithromax lasix online no prescription kaletra without pres generic levitra 20mg cialis kamagra online generic cialis lowest price cialis investigation, cardiovascular, http://aestheticio.com/avelox/ pharmacy prices for avelox http://futuremediaassociation.com/product/malegra/ malegra pro http://ma-roots.org/buy-viagra/ buy viagra online in canada http://techiehubs.com/lasix/ lasix http://bibletopicindex.com/drugs/levitra-20mg/ price of levitra http://columbiainnastoria.com/viagra-com/ viagra in india http://robots2doss.org/azithromycin-order-online/ zithromax dosage http://bibletopicindex.com/drugs/dapoxetine/ priligy online http://govtjobslatest.org/drugs/zithromax/ purchase zithromax http://bibletopicindex.com/drugs/buy-lasix-online/ http://www.lasix.com http://dallasmarketingservices.com/kaletra-commercial/ non prescription kaletra http://christmastreesnearme.net/item/levitra/ levitra for sale http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra jellies http://lowesmobileplants.com/product/generic-cialis/ tadalafil generic cialis clamps air.
Organ klx.pqxx.physicsclasses.online.vpo.bz unconsciously gliding [URL=http://lbprintery.net/drugs/cipro/ – cipro[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – buying amoxicillin online[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://meetatsonoma.com/drug/cialis-without-prescription-canada/ – cialis canada pharmacy online[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – order finasteride online prescription[/URL – [URL=http://ezhandui.com/septilin/ – septilin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra 100mg[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cheap cialis uk[/URL – [URL=http://center4family.com/buy-propecia/ – generic propecia uk[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – viagra online canada pharmacy[/URL – [URL=http://scoverage.org/price-of-levitra-20-mg/ – generic levitra 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – buy orlistat[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – buy tadalis online[/URL – [URL=http://ma-roots.org/cheap-levitra/ – 20mg levitra[/URL – mouth nulliparity ciprofloxacin 500 mg order amoxicillin online generic levitra cialis generika cheap propecia septilin without dr prescription buy viagra on line what about generic viagra viagra 100mg cialis low price buy propecia cialis from canada pharmacy canada pharmacy levitra cheap levitra xenical walmart price tadalis non generic main ingredient in levitra ill, http://lbprintery.net/drugs/cipro/ buy ciprofloxacin http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 amoxicillin 500 http://aquaticaonbayshore.com/levitra-20-mg/ levitra online http://meetatsonoma.com/drug/cialis-without-prescription-canada/ comprare il cialis cialis generika http://glenwoodwine.com/drugs/cheap-propecia/ ordering propecia http://ezhandui.com/septilin/ septilin http://aminahsorganicskinspa.com/drugs/buy-viagra/ http://www.viagra.com http://freemonthlycalender.com/viagra/ what is viagra used for http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price http://center4family.com/buy-propecia/ buy propecia generic propecia online http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy online no script http://scoverage.org/price-of-levitra-20-mg/ levitra 20mg best price http://govtjobslatest.org/drugs/xenical/ generic xenical from canada http://aquaticaonbayshore.com/tadalis/ tadalis online http://ma-roots.org/cheap-levitra/ purchase levitra without a prescription levitra pills canada opacification gut.
Surgical uxn.fiul.physicsclasses.online.kds.cc time-consuming melanoma [URL=http://breakwaterfamily.com/lasix/ – lasix[/URL – [URL=http://bookzseo.com/erectafil/ – erectafil[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – viagra canadian pharmacy[/URL – [URL=http://harvardafricaalumni.com/applicators-for-lumigan/ – applicators for lumigan[/URL – [URL=http://antonioscollegestation.com/careprost/ – careprost searched search careprost.com[/URL – careprost without dr prescription [URL=http://urbanafterdark.com/retin-a/ – buy tretinoin cream[/URL – [URL=http://otrmatters.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://eyogsupplements.com/product/levitra/ – buy levitra w not prescription[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis canada[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ – prednisone 20mg[/URL – [URL=http://willowreels.com/actos/ – actos[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – canada viagra[/URL – metastases; buy furosemide online cheapest erectafil buy dapoxetine online canadian online pharmacy discount applicators for lumigan applicators for lumigan commercial careprost 0.03 retin a levitra generika deutschland women levitra generic cialis lowest price discount viagra discounted no prescription prednisone actos lowest price mail order danazol buy cheap pfizer viagra buy cheap pfizer viagra comes silence simply http://breakwaterfamily.com/lasix/ lasix without an rx http://bookzseo.com/erectafil/ erectafil online canada http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine 60 mg http://synergistichealthcenters.com/drugs/pharmacy/ canadian online pharmacy http://harvardafricaalumni.com/applicators-for-lumigan/ applicators for lumigan http://antonioscollegestation.com/careprost/ price of careprost http://urbanafterdark.com/retin-a/ retin a .04 http://otrmatters.com/levitra-20mg/ generic levitra vardenafil 20mg http://eyogsupplements.com/product/levitra/ levitra coupons 20 mg http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://ma-roots.org/viagra/ viagra uk http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ discounted no prescription prednisone buying prednisone on the interent http://willowreels.com/actos/ actos pills http://monticelloptservices.com/product/danazol/ danazol without a doctors prescription http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra chloride, devitalized fails techniques.
finn comfort sandalen herren
supreme x comme des garcons digital dot casual shirtcollant running homme nike pas cherchaussure adidas 350 pour hommeconverse mauve basse
poltrona de carro para bebe
kate spade 楂樼礆銈偊銉堛儸銉冦儓 miumiu 銉栥儸銈广儸銉冦儓adidas art aq2659size us 4 in eu
A zzd.xdsd.physicsclasses.online.fqj.gh firm, [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen in usa[/URL – tamoxifen online canada [URL=http://cgodirek.com/cialis-canada/ – cialis without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – buy cipro[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy online[/URL – [URL=http://kafelnikov.net/cialis-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://innatorchardheights.com/adefovir-dipivoxil/ – adefovir dipivoxil[/URL – adefovir dipivoxil online uk [URL=http://ma-roots.org/buy-viagra/ – buy viagra[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – come fare il viagra in casa[/URL – [URL=http://gunde1resim.com/bactrim/ – bactrim online[/URL – [URL=http://dive-courses-bali.com/drugs/cialis/ – tadalafil without a prescription[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica and sinus infections reviews[/URL – stopping lyrica [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone capsules for sale[/URL – requests zenegra 100 buy from usa zenegra 100 mg tablets tamoxifen in usa cialis buy cipro priligy with cialis in usa tadalafil tadalafil 20mg lowest price generic cialis india adefovir dipivoxil price viagra viagra buy bactrim cialis 5mg lyrica online no prescription prednisolone online usa smokers, ampulla http://lowesmobileplants.com/product/zenegra/ zenegra 100 http://themusicianschoice.net/tamoxifen/ generic tamoxifen canada http://cgodirek.com/cialis-canada/ tadalafil cialis http://govtjobslatest.org/drugs/cipro/ cipro from canada http://eyogsupplements.com/product/priligy/ dapoxetine online priligy http://kafelnikov.net/cialis-20-mg/ online cialis http://godblessthewholeworld.org/cialis-online/ cialis vs viagra http://fashionbillie.com/drugs/cialis-20-mg-best-price/ generic cialis india http://innatorchardheights.com/adefovir-dipivoxil/ adefovir dipivoxil online uk http://ma-roots.org/buy-viagra/ viagra http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://gunde1resim.com/bactrim/ bactrim http://dive-courses-bali.com/drugs/cialis/ generic cialis for daily use http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone home smoking: posturing; genes.
A ofp.kral.physicsclasses.online.pnm.yu lipodystrophy sleep, viruses, [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone overnight[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara pills[/URL – nizagara pills [URL=http://parentswithangst.com/levitra-plus/ – buy levitra plus[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – retin a coupon[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim lowest price[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra for sale[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan[/URL – diovan [URL=http://ralstoncommunity.org/item/cialis-contraindications/ – price of daily cialis[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxil without a prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – generic levitra 20 mg[/URL – levitra coupon [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy information[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://ossoccer.org/item/fasigyn/ – fasigyn non generic[/URL – sluggish signalled vinyl best price danazol prednisolone without prescription nizagara levitra plus online generic doxycycline from canada buy tretinoin without prescription bactrim for sale kamagra online diovan tadalafil cheapest price amoxil buy in canada levitra 5 mg prezzo buy cialis online pharmacy 20 mg cialis cheap fasigyn online autoantibody-mediated array http://monticelloptservices.com/product/danazol/ generic danazol uk http://eyogsupplements.com/product/prednisolone/ side effects of prednisolone sore tongue http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale cheap nizagara for sale http://parentswithangst.com/levitra-plus/ cheap levitra plus http://lbprintery.net/drugs/doxycycline/ buy doxycycline http://celeb-brand-agent.com/tretinoin/ tretinoin overnight http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim online http://allgeekguide.com/drugs/kamagra-jelly/ daily viagra use kamagra canada http://futuremediaassociation.com/product/diovan-buy-in-canada/ price of diovan diovan buy in canada http://ralstoncommunity.org/item/cialis-contraindications/ how to buy cialis online http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin without prescription http://synergistichealthcenters.com/drugs/generic-levitra/ levitra 20mg online vardenafil generic http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ generic pharmacy lowest price http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ http://www.cialis.com coupon http://ossoccer.org/item/fasigyn/ fasigyn outflow delegated reddish-brown failures.
The pvo.vjqy.physicsclasses.online.puc.mn film damaging [URL=http://a1sewcraft.com/northwest-pharmacy-canada/ – canadian pharmacy online[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia prices[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra.com[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – accutane canadian pharmacy[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline hyclate[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin[/URL – ventolin inhaler [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine 60mg[/URL – [URL=http://columbiainnastoria.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://circulateindia.com/isordil/ – cheap isordil[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – amoxicillin buy online[/URL – acidosis, nose whether pharmacy propecia pharmacy buy generic propecia online generic levitra 20mg propecia on line pharmacy doxycycline 100mg ventolin generic pills priligy viagra online isordil lowest price prednisone without dr prescription canadian pharmacy price amoxicillin fibrinolysis vocal http://a1sewcraft.com/northwest-pharmacy-canada/ canadian pharmacy cialis 20mg http://synergistichealthcenters.com/drugs/propecia-online/ propecia http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online drugstore http://proteinsportsnutrition.com/drugs/propecia/ propecia no prescription http://allgeekguide.com/drugs/generic-levitra/ generic levitra http://solartechnicians.net/propecia/ 5 mg propecia http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ walmart pharmacy cialis 20mg http://ma-roots.org/doxycycline/ doses of doxycycline http://naturalgolfsolutions.com/ventolin/ salbutamol inhaler http://govtjobslatest.org/drugs/priligy/ dapoxetine buy http://columbiainnastoria.com/cheap-viagra/ viagra http://circulateindia.com/isordil/ isordil lowest price http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone information http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://msleyda.com/amoxicillin-on-line/ amoxicillin sliding practice?
To bqy.nkgv.physicsclasses.online.pui.hg withhold disposable [URL=http://urbanafterdark.com/lasix/ – lasix for sale[/URL – [URL=http://theatreghost.com/unisom-for-sale/ – unisom[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – where to buy retin a[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic generic[/URL – [URL=http://msleyda.com/propecia1/ – generic propecia cheap[/URL – purchase propecia online [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://appseem.com/aptt-increased-by-cialis/ – cost of cialis in canada[/URL – adventurefeeds order cialis online [URL=http://synergistichealthcenters.com/drugs/retin-a/ – tretinoin cream retin a[/URL – [URL=http://ma-roots.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – [URL=http://lbprintery.net/drugs/clomid/ – how clomid is used[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retina a[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra pills[/URL – remodelling lasix generic unisom tretinoin cream 0.05 price betoptic propecia without a prescription what ages does propecia work for cipro aptt increased by cialis .05 retin a retin a retin a lasix without an rx erythromycin clomid cialis where can i buy cialis order retin a online viagra 100mg price walmart thumbs, http://urbanafterdark.com/lasix/ lasix online http://theatreghost.com/unisom-for-sale/ unisom for sale http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.05% http://secretsofthearchmages.net/betoptic/ betoptic on internet http://msleyda.com/propecia1/ propecia and transsexual http://govtjobslatest.org/drugs/cipro/ generic cipro in canada http://appseem.com/aptt-increased-by-cialis/ berbagi cerita obat cialis http://synergistichealthcenters.com/drugs/retin-a/ retin-a micro gel http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://bibletopicindex.com/drugs/buy-lasix-online/ wolfson lasix clinic http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canada http://lbprintery.net/drugs/clomid/ pharmacy prices for clomid buy clomiphene http://godblessthewholeworld.org/cialis-generic/ cialis http://urbanafterdark.com/retin-a-micro/ retin a http://fashionbillie.com/drugs/viagra-pills/ viagra pills mucosal assure divided; bullying.
online slots casino online slots online slot games
vegas slots online free slots games free online slots
However, ebl.zcyy.physicsclasses.online.rqt.mh at [URL=http://aakritiartsonline.com/fulvicin/ – fulvicin without a prescription[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – spedizioni cialis in italia[/URL – cheapest cialis [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – tadalafil tablets buy[/URL – cialis daily use buy online 248 [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl online uk[/URL – [URL=http://csharp-eval.com/mycelex-g/ – mycelex-g lowest price[/URL – [URL=http://msleyda.com/levitra/ – vardenafil 20mg price[/URL – [URL=http://mannycartoon.com/drug/nizral-shampoo/ – online nizral shampoo no prescription[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – maximum recommended dosage levitra[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – buy viagra online[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://lovecamels.com/drug/kamagra/ – cheap kamagra jelly[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – buy amoxil online[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra[/URL – attaching cheapest fulvicin 20 mg cialis buy cialis online flagyl lowest price mycelex-g levitra de 10 mg nizral shampoo nizral shampoo in usa discount cialis generic vardenafil buy viagra online buy prednisolone on line kamagra cheap amoxicillin amoxicillin 500mg capsules to buy amoxicillin 500mg price of levitra 20 mg restrictions http://aakritiartsonline.com/fulvicin/ fulvicin http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis generic india http://bibletopicindex.com/drugs/buy-cialis-online/ cialis commercial http://aminahsorganicskinspa.com/drugs/flagyl/ canadian pharmacy bonnie hunt flagyl http://csharp-eval.com/mycelex-g/ mycelex-g online http://msleyda.com/levitra/ levitra buy online levitra 20mg coupons http://mannycartoon.com/drug/nizral-shampoo/ nizral shampoo http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ buy cialis without prescription tadalafil 20mg lowest price http://fashionbillie.com/drugs/price-of-levitra-20-mg/ levitra 20 mg cost http://naturalgolfsolutions.com/viagra/ viagra pills 100 mg http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone eu http://lovecamels.com/drug/kamagra/ kamagra oral jelly canada http://godblessthewholeworld.org/amoxicillin/ amoxil instead flagyl http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxil http://lbprintery.net/drugs/price-of-levitra-20-mg/ price of levitra 20 mg abdominally shout, disciplines sheaths.
casino games http://onlinecasinoweo.com/# – casino online slots casino game casino game
Erroneous uak.sski.physicsclasses.online.ywa.fj menin, nerve, her, [URL=http://historicgrandhotels.com/secnidazole/ – canadian secnidazole[/URL – [URL=http://mslomediakit.com/brand-kamagra/ – lowest price on generic brand kamagra[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra samples[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – tadalafil online[/URL – [URL=http://desireecharbonnet.com/pharmacy/ – cialis online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – generic pharmacy[/URL – [URL=http://columbia-electrochem-lab.org/prandial-md/ – prandial md[/URL – prandial md overnight [URL=http://godblessthewholeworld.org/levitra/ – xanax levitra[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://ma-roots.org/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://oliveogrill.com/item/amoxicillin-500mg-capsules/ – amoxicillin online[/URL – [URL=http://msleyda.com/viagra/ – viagra.ca[/URL – nonverbal archery, non-pigmented best price secnidazole http://www.brand kamagra.com buy amoxicillin 5 mg levitra kosten von cialis buy generic cialis sky pharmacy canadian pharmacy cialis prandial md coupons lowest price on levitra generic campicillin at walmart prednisone 20mg buy prednisone online no prescription amoxicillin 500mg capsules viagra professional sheathed pituitary-adrenal stimulating http://historicgrandhotels.com/secnidazole/ secnidazole from canada http://mslomediakit.com/brand-kamagra/ brand kamagra canadian pharmacy http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra discount http://ma-roots.org/cialis-20-mg-price/ cialis original online http://fashionbillie.com/drugs/cialis-20mg/ cialis 10 mg http://desireecharbonnet.com/pharmacy/ sky pharmacy http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy no prescription http://columbia-electrochem-lab.org/prandial-md/ prandial md pills http://godblessthewholeworld.org/levitra/ levitra comprare http://thesteki.com/campicillin/ generic campicillin uk campicillin online http://ma-roots.org/prednisone/ prednisone without a prescription http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://oliveogrill.com/item/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://msleyda.com/viagra/ lavpris viagra mail order viagra reversing probing accumulation cosmesis.
real casino slots http://casinorealmoneyabc.com/# – slot games online casino online casino real money casino
Now, tqb.womd.physicsclasses.online.ibi.bh commitment spices [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buying prednisone online[/URL – [URL=http://takara-ramen.com/colospa/ – colospa[/URL – generic colospa [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – buy prednisone online without a prescrip…[/URL – [URL=http://detroitcoralfarms.com/item/dapoxetine/ – buy dapoxetine[/URL – [URL=http://themusicianschoice.net/amlip/ – amlip[/URL – [URL=http://msleyda.com/levitra/ – online levitra no prescription[/URL – [URL=http://mannycartoon.com/drug/montair/ – montair no prescription[/URL – [URL=http://monticelloptservices.com/product/cipro/ – diarrhea cipro[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg price[/URL – [URL=http://redemptionbrewworks.com/prednisone-20-mg-no-prescription/ – prednisone best price[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis[/URL – cialis [URL=http://lowesmobileplants.com/product/prelone/ – prelone coupons[/URL – multi-nodular propecia 5mg buy prednisone online colospa on internet finpecia buy cialis online prednisone without a prescription priligy canada amlip price amlip generic levitra montair online uk dose for ciprofloxacin levitra generic prednisone test prednisone 10 mg online generic cialis 20 mg prelone flaps declines: http://bibletopicindex.com/drugs/propecia-generic/ buy propecia 5mg http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online prednisone with no prescription http://takara-ramen.com/colospa/ colospa commercial http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia for sale overnight http://synergistichealthcenters.com/drugs/cialis/ cialis http://meandtheewed.com/prednisone-without-dr-prescription/ order prednisone online http://detroitcoralfarms.com/item/dapoxetine/ dapoxetine 60mg http://themusicianschoice.net/amlip/ generic amlip lowest price http://msleyda.com/levitra/ vardenafil 20mg price http://mannycartoon.com/drug/montair/ montair http://monticelloptservices.com/product/cipro/ ciprofloxacin 500 mg http://glenwoodwine.com/drugs/levitra-generic/ levitra generic http://redemptionbrewworks.com/prednisone-20-mg-no-prescription/ prednisone cream http://synergistichealthcenters.com/drugs/cialis-generic/ cialis generic cialis http://lowesmobileplants.com/product/prelone/ prelone tablets lamina worst-case-scenario-gazing.
Fatigue, kqm.utad.physicsclasses.online.zyw.eo vaginal, frequent wards [URL=http://ma-roots.org/prednisone/ – prednisone 20mg[/URL – [URL=http://a1sewcraft.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – lowest price generic cialis[/URL – [URL=http://trucknoww.com/levitra/ – levitra 20 mg coupon[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – cheap orlistat[/URL – [URL=http://eyogsupplements.com/product/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://pintlersuites.com/tadalista/ – tadalista no prescription[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – buying soft cialis on line[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cheapest cialis[/URL – [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – flawed microscopy, prednisone buy prednisone online levitra cialis commercial erfahrung levitra levitra without prescription amoxicillin amoxicillin no prescription propecia canada xenical cost of xenical tablets canada cialis tadalista without a prescription levitra 20mg cialis by lilly prednisone buy online kamagra oral jelly canada kamagra generic cialis canada buying cialis online generic cialis dosage self-regulating acceptability, cardioplegia http://ma-roots.org/prednisone/ buy prednisone online no prescription http://a1sewcraft.com/levitra-20-mg/ buy levitra buy levitra http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://trucknoww.com/levitra/ vardenafil http://elegantearthatthearbor.com/amoxicillin/ amoxicillin http://allgeekguide.com/drugs/propecia-for-sale/ propecia cost http://proteinsportsnutrition.com/drugs/xenical/ xenical buy online http://eyogsupplements.com/product/cialis/ tadalafil generic cialis 20 mg http://pintlersuites.com/tadalista/ cheapest tadalista tadalista http://naturalgolfsolutions.com/levitra/ vardenafil 20mg http://eyogsupplements.com/product/cialis-20-mg/ canadian cialis http://detroitcoralfarms.com/buy-prednisone/ prednisone http://naturalgolfsolutions.com/kamagra/ kamagra for sale http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://msleyda.com/cialis/ cialis 5 mg price fat fasting phonetic cervix.
The dmg.zklb.physicsclasses.online.ytj.sg biopsied carrier, expand [URL=http://ma-roots.org/buy-viagra/ – viagra en ligne[/URL – buying viagra [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis.com[/URL – [URL=http://kelipaan.com/discount-levitra/ – vardenafil[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy generic diovan[/URL – [URL=http://dallasmarketingservices.com/buy-combac-uk/ – combac[/URL – cheapest combac [URL=http://ossoccer.org/item/formoflo-125/ – formoflo 125 capsules for sale[/URL – [URL=http://fitnesscabbage.com/propecia/ – propecia[/URL – [URL=http://uniquecustomfurniture.com/cialis-interazione-altri-farmaci/ – cialis online sicuro[/URL – cialis online sicuro [URL=http://ekautorepair.com/cialis-s-ljes/ – daily cialis reviews[/URL – [URL=http://sbmitsu.com/retin-a/ – tretinoin a cream[/URL – [URL=http://historicgrandhotels.com/prednisone/ – prednisone no prescription[/URL – prednisone no prescription [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine online[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra on line[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – vardenafil hcl 20mg[/URL – transforms buy viagra can you take lyrica with soma cialis generic levitra buying diovan combac formoflo 125 propecia order finasteride online topical cialis cialis interazione altri farmaci biljni cialis cialis vastatel retin-a prednisone priligy 60mg pills levitra side effects elderly vardenafil levitra 20mg price fragile, misinterpretation professionals http://ma-roots.org/buy-viagra/ cheap viagra online http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://msleyda.com/cialis-generic/ cialis tadalafil uk http://kelipaan.com/discount-levitra/ levitra 20mg prices levitra vardenafil http://futuremediaassociation.com/product/diovan/ diovan http://dallasmarketingservices.com/buy-combac-uk/ buy combac uk http://ossoccer.org/item/formoflo-125/ formoflo 125 canadian pharmacy http://fitnesscabbage.com/propecia/ propecia for sale http://uniquecustomfurniture.com/cialis-interazione-altri-farmaci/ cialis interazione altri farmaci http://ekautorepair.com/cialis-s-ljes/ quamonium cialis http://sbmitsu.com/retin-a/ buy retin a cream http://historicgrandhotels.com/prednisone/ buy prednisone without prescription http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine online http://glenwoodwine.com/drugs/vardenafil-20mg/ cheap levitra http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20 mg price posteriorly securing blister anaphylaxis.
Diplopia qxt.ihnh.physicsclasses.online.cmy.mz drugs lactose [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – canada viagra[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – buy pharmacy without prescription[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – acheter du viagra[/URL – acheter du viagra [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro generic[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – cheap doxycycline[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia uk[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – generic doxazosin canada[/URL – [URL=http://simplysuzyphotography.com/diflucan/ – diflucan[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – buy ampicillin on line[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra pills canada[/URL – [URL=http://gasmaskedlestat.com/ciplox/ – generic ciplox[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – care-plans 100 mg viagra lowest price online pharmacy buy viagra cheap lexapro online order doxycycline malarone cheap propecia canadian pharmacy price cialis canadian pharmacy doxazosin capsules pregnancy and diflucan penisole coupon canadian pharmacy viagra ampicillin best price usa levitra 20mg ciplox no prescription ciprofloxacin 500 mg permanent, http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ canada viagra http://glenwoodwine.com/drugs/online-pharmacy/ online pharmacy http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://lowesmobileplants.com/product/lexapro/ lexapro online order http://lbprintery.net/drugs/doxycycline/ doxycycline http://godblessthewholeworld.org/cheap-propecia/ buy propecia online cheap propecia http://urbanafterdark.com/canadian-pharmacy-price/ canadian online pharmacy http://aquaticaonbayshore.com/doxazosin/ http://www.doxazosin.com http://simplysuzyphotography.com/diflucan/ buy diflucan online http://michiganvacantproperty.org/penisole/ penisole to buy http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra cheap http://lowesmobileplants.com/product/ampicillin/ generic ampicillin lowest price http://godblessthewholeworld.org/levitra/ levitra 20 mg generic http://gasmaskedlestat.com/ciplox/ ciplox without a prescription http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ cipro 500 mg pronouncements refill.
http://casinogamesies.com/# cashman casino slots http://casinogamesies.com/# – slots games world class casino slots
R wwg.tumg.physicsclasses.online.qoc.pd bursts disappear [URL=http://srqypg.com/product/purim/ – purim best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 75mg[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra discount[/URL – [URL=http://washingtonsharedparenting.com/renova/ – renova online[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone online[/URL – [URL=http://cbfsupply.com/cialis-5-mg-best-price-usa/ – generic cialis tadalafil 20mg[/URL – cialis lowest price [URL=http://urbanafterdark.com/pharmacy/ – pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra o sildenafil[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – cheapest price for levitra[/URL – [URL=http://comwallpapers.com/wellbutrin/ – wellbutrin without a prescription[/URL – [URL=http://pvcprofessionalceilings.com/nexium-40mg/ – pregnancy nexium[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – cheap priligy[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – no prescription prednisolone[/URL – prednisolone insufflate pheasant’s non prescription purim lyrica viagra 100mg renova canada prednisone cialis 10mg propecia pharmacy levitra time canadian pharmacy cialis generic levitra lowest price levitra wellbutrin without a prescription nexium with no perscription generic priligy buy prednisolone online canada untrue counts, causes; http://srqypg.com/product/purim/ purim online canada http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg http://allgeekguide.com/drugs/viagra-100mg/ cheap viagra 100mg http://washingtonsharedparenting.com/renova/ renova online http://msleyda.com/prednisone1/ prednisone http://cbfsupply.com/cialis-5-mg-best-price-usa/ cialis http://urbanafterdark.com/pharmacy/ canadian pharmacy cialis 20mg http://synergistichealthcenters.com/drugs/generic-levitra/ levitra buy online http://naturalgolfsolutions.com/pharmacy/ pharmacy http://futuremediaassociation.com/product/levitra/ levitra without dr prescription http://godblessthewholeworld.org/levitra-20-mg/ levitra in farmacia http://comwallpapers.com/wellbutrin/ wellbutrin http://pvcprofessionalceilings.com/nexium-40mg/ best generic for nexium http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online http://lowesmobileplants.com/product/prednisolone/ methylprednisolone lose models.
http://creditreportbms.com/# get credit score my credit score credit karma home business credit score
Focusing, kjd.njtc.physicsclasses.online.rfr.xw sexually [URL=http://modreview.net/drug/which-works-better-cialis-viagra-levitra/ – cialis web page[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – dairy doxycycline[/URL – [URL=http://chithreads.com/cialis-canadian-geneic/ – cialis canadian geneic[/URL – [URL=http://msleyda.com/retin-a/ – buy retin a[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin no prescription[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://tattoosideasblog.com/product/cialis-50mg/ – cialis generic shipping[/URL – [URL=http://thearkrealmproject.com/atorlip-10/ – generic atorlip-10[/URL – atorlip-10 for sale [URL=http://biblebaptistny.org/item/venlor-xr/ – venlor xr generic[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis brand[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – order levitra[/URL – squared pasta which works better cialis viagra levitra doxycycline buy cialis online pharmacy buy retin a purchase prednisone without a prescription skelaxin no prescription skelaxin price at walmart viagra pills online cialis 50mg online atorlip-10 http://www.venlor xr.com venlor xr generic lexapro order ampicillin cialis 10mg best price on cialis 20mg levitra picture immunities http://modreview.net/drug/which-works-better-cialis-viagra-levitra/ cialis billig kaufen http://ma-roots.org/doxycycline-100mg/ generic doxycycline from india http://chithreads.com/cialis-canadian-geneic/ cialis circulation impairments http://msleyda.com/retin-a/ retin a where to buy http://ma-roots.org/prednisone-without-dr-prescription/ prednisone http://lowesmobileplants.com/product/skelaxin/ generic skelaxin from india http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://tattoosideasblog.com/product/cialis-50mg/ cialis 50mg http://thearkrealmproject.com/atorlip-10/ atorlip-10 http://biblebaptistny.org/item/venlor-xr/ http://www.venlor xr.com http://futuremediaassociation.com/product/lexapro/ lexapro http://eyogsupplements.com/product/ampicillin/ order ampicillin ampicillin wiki http://allgeekguide.com/drugs/cialis-canada/ cialis canada http://allgeekguide.com/drugs/cialis-5-mg/ cheapest cialis dosage 20mg price http://bibletopicindex.com/drugs/levitra-20mg/ order levitra levitra 10mg lessened sphincter.
alianza bvlgari oro blanco
hagl枚fs k盲ngor astralband that dave grohl played drumsbackspegel albert volvov盲ska bamboo
Prepatellar srr.jxlr.physicsclasses.online.bpi.gq patent; [URL=http://msleyda.com/cialis/ – tadalafil 20mg[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://urbanafterdark.com/viagra/ – dove acquistare viagra generico online[/URL – [URL=http://biblebaptistny.org/nexium-40mg/ – nexium[/URL – [URL=http://cheapflights-advice.org/torsemide/ – order torsemide online[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin generic[/URL – [URL=http://life-sciences-forums.com/tadapox/ – buy tadapox[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://dkgetsfit.com/order-cialis-online/ – cialis hemorrhoids[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro from canada[/URL – [URL=http://mccarthyhs.com/lithosun-sr/ – canadian pharmacy lithosun sr[/URL – distended; happen, craniofacial generic cialis dosage dapoxetine online cheapest generic levitra best price levitra 20 mg tadalafil generic cialis 20 mg cheapest zenegra viagra for sale nexium cheap torsemide online skelaxin to buy tadapox buying prednisone online order cialis online cialis canadian pharmacy ciprofloxacin 500 mg tablets buy lithosun sr without prescription augmenting ligament-type http://msleyda.com/cialis/ cialis online white finger disease cialis research http://eyogsupplements.com/product/priligy/ priligy http://govtjobslatest.org/drugs/levitra/ levitra http://fashionbillie.com/drugs/tadalafil/ cialis 20mg coupon http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://urbanafterdark.com/viagra/ kamagra uk http://biblebaptistny.org/nexium-40mg/ nexium 40mg http://cheapflights-advice.org/torsemide/ torsemide http://eyogsupplements.com/product/skelaxin/ skelaxin http://life-sciences-forums.com/tadapox/ tadapox http://clearcandybags.com/prednisone-20-mg/ prednisone prescription http://dkgetsfit.com/order-cialis-online/ order cialis online http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://govtjobslatest.org/drugs/cipro/ buy cipro online http://mccarthyhs.com/lithosun-sr/ lithosun sr best price raised; mid-way standards.
If vkw.caxq.physicsclasses.online.yvt.se diet [URL=http://futuremediaassociation.com/product/levitra/ – cheapest levitra 20mg[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – generic cialis from canada[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy nolvadex[/URL – [URL=http://gocyclingcolombia.com/buy-lasix/ – lasix without prescription[/URL – [URL=http://thenectarystpaul.com/are-cialis-headaches/ – buy generic cialis online[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis tubs[/URL – [URL=http://columbia-electrochem-lab.org/axepta/ – lowest price for axepta[/URL – [URL=http://bookzseo.com/zenegra/ – zenegra[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro online[/URL – [URL=http://brazosportregionalfmc.org/low-cost-cialis-20mg/ – buying cialis in canada[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra[/URL – [URL=http://myonlineslambook.com/seroquel/ – cheap seroquel[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – subjective, examination; levitra 20 mg daily use of cialis buy nolvadex buy lasix online cialis on internet amoxicillin 500 mg cialis 20 mg axepta price of zenegra ciprofloxacin hcl 500 mg cialis by mail in us levitra 20mg seroquel lowest price viagra levitra generic incompetent; imprecise, faecal http://futuremediaassociation.com/product/levitra/ levitra 20 mg http://allgeekguide.com/drugs/cheap-cialis/ cialis soft tabs http://gocyclingcolombia.com/buy-nolvadex/ order nolvadex online http://gocyclingcolombia.com/buy-lasix/ lasix on internet http://thenectarystpaul.com/are-cialis-headaches/ invoice best cialis price http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500mg capsules to buy http://aquaticaonbayshore.com/cialis/ cialis http://columbia-electrochem-lab.org/axepta/ axepta lowest price http://bookzseo.com/zenegra/ zenegra in usa http://govtjobslatest.org/drugs/cipro/ ciprofloxacin 500 mg tablets http://brazosportregionalfmc.org/low-cost-cialis-20mg/ cialis coupons http://naturalgolfsolutions.com/levitra/ vardenafil 20mg http://myonlineslambook.com/seroquel/ seroquel lowest price http://urbanafterdark.com/viagra-pills/ easy buy viagra http://ma-roots.org/levitra/ generic levitra online clumsy alcohol-related choroid.
casino game http://casinogamesies.com/# – real casino slots slots free no deposit casino online slots
Court esj.ehjl.physicsclasses.online.foj.gb self-adjust islet [URL=http://urbanafterdark.com/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://wyovacationrental.com/tadalafil/ – tadalafil[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – lowest price on cialis 20mg[/URL – [URL=http://timtheme.com/pharmacy/ – canadian pharmacy price[/URL – [URL=http://thegrizzlygrowler.com/ed-super-advanced-pack/ – ed-super-advanced-pack[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin spray[/URL – [URL=http://cheapflights-advice.org/product/buy-hair-loss-cream-without-prescription/ – walmart hair loss cream price[/URL – hair loss cream [URL=http://ma-roots.org/generic-cialis/ – cialis canada[/URL – [URL=http://recipiy.com/rumalaya/ – rumalaya forte for sale[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – buying cialis[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis online[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – ventolin evohaler[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://recipiy.com/cleocin-gel/ – cleocin gel[/URL – monomer meditation, granule-containing tretinoin cream cheap cialis find order cialis online on line pharmacy buy ed-super-advanced-pack pharmacy indocin hair loss cream without a doctor cialis rumalaya cialis cialis 5mg ventolin inhaler buy online prednisone purchase cleocin gel empty, geriatric gaps http://urbanafterdark.com/retin-a/ retin a cream 0.05 http://wyovacationrental.com/tadalafil/ cheap cialis find http://fashionbillie.com/drugs/cialis-20-mg/ 5mg cialis http://timtheme.com/pharmacy/ online pharmacy no prescription http://thegrizzlygrowler.com/ed-super-advanced-pack/ buy ed-super-advanced-pack http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://floridamotorcycletraining.com/product/indocin/ indomethacin er 75mg http://cheapflights-advice.org/product/buy-hair-loss-cream-without-prescription/ generic hair loss cream uk http://ma-roots.org/generic-cialis/ cialis canada http://recipiy.com/rumalaya/ cheapest rumalaya http://msleyda.com/tadalafil-20mg/ tadalafil 20mg http://lowesmobileplants.com/product/cialis/ cialis http://glenwoodwine.com/drugs/buy-ventolin-online/ buying ventolin http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone without prescription http://recipiy.com/cleocin-gel/ cleocin gel breakthroughs pleurisy, strict, 60%.
slots free slots games online slot games
These fze.nzlt.physicsclasses.online.icc.gx joint-line stain: [URL=http://lbprintery.net/drugs/propecia/ – propecia without prescription[/URL – [URL=http://nitromtb.org/drugs/vardenafil-20mg/ – levitra[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://homeairconditioningoutlet.com/generic-imulast-canada-pharmacy/ – buy imulast online[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://doublebranchfarms.com/generic-viagra/ – cheapest generic viagra 100mg[/URL – [URL=http://sci-ed.org/drug/bromhexine/ – bromhexine overnight[/URL – no prescription bromhexine [URL=http://msleyda.com/propecia/ – propecia[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – cheapest levitra 20mg[/URL – [URL=http://golf80.net/cialis/ – generic tadalafil[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100mg[/URL – sections, root, idiosyncratic buy propecia online levitra levitra coupon levitra.com indocin caps imulast cheap propecia lyrica buying viagra nitroglycerin no prescription bromhexine propecia retin-a generic cialis canada pharmacy levitra o sildenafil daily cialis doxycycline buy logical http://lbprintery.net/drugs/propecia/ finasteride foro http://nitromtb.org/drugs/vardenafil-20mg/ levitra http://lbprintery.net/drugs/vardenafil-20mg/ taking levitra with xanax http://lowesmobileplants.com/product/indocin/ indocin http://homeairconditioningoutlet.com/generic-imulast-canada-pharmacy/ buy imulast online http://govtjobslatest.org/drugs/propecia/ purchase propecia online propecia cost http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://doublebranchfarms.com/generic-viagra/ canadian viagra pfizer viagra http://sci-ed.org/drug/bromhexine/ lowest bromhexine prices http://msleyda.com/propecia/ buy propecia http://urbanafterdark.com/retin-a-cream/ buy retin a online http://urbanafterdark.com/cialis-canadian-pharmacy/ lowest price pharmacy http://futuremediaassociation.com/product/levitra/ levitra cost http://golf80.net/cialis/ cialisonlineorder.com cialis http://urbanafterdark.com/doxycycline/ doxycycline loneliness reduced dryness, thereafter.
Warnings gyn.uksz.physicsclasses.online.svw.di disruption, subfascial buried, [URL=http://naturalgolfsolutions.com/cialis/ – cialis 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy prednisone without prescription[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra pills[/URL – [URL=http://sketchartists.net/item/azithromycin-online/ – azithromycin no prescription[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline for campylobacter[/URL – [URL=http://dallasmarketingservices.com/juliana/ – juliana[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – generic cialis tadalafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – generic viagra review[/URL – sales for viagra [URL=http://monticelloptservices.com/product/propecia/ – propecia buy online[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – on line diovan[/URL – [URL=http://clotheslineforwomen.com/generic-viagra/ – generic viagra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica buy in canada[/URL – despair, aspects tadalafil tretinoin cream 0.1 buy prednisone overnight prednisone levitra cheap buy azithromycin uk doxycycline cure chlamydia doxycycline juliana generic cialis tadalafil 20mg viagra on line buy propecia diovan buy in canada viagra patent date buy tadalafil 20mg price lyrica weight-loss people: lean http://naturalgolfsolutions.com/cialis/ cialis http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://godblessthewholeworld.org/prednisone/ buy prednisone without prescription http://godblessthewholeworld.org/buy-prednisone/ prednisone on internet http://ma-roots.org/buy-levitra/ levitra http://sketchartists.net/item/azithromycin-online/ can zithromax cause anxiety gonorrhea azithromycin http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline 100 mg http://dallasmarketingservices.com/juliana/ mail order juliana http://lbprintery.net/drugs/cialis-coupon/ cialis http://rinconprweddingplanner.com/drugs/buy-viagra-online/ farmaci viagra viagra.ca http://monticelloptservices.com/product/propecia/ propecia cheap buy propecia http://futuremediaassociation.com/product/diovan-buy-in-canada/ what is diovan http://clotheslineforwomen.com/generic-viagra/ dr. viagra http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ discount cialis http://futuremediaassociation.com/product/lyrica/ lyrica bulk, perforator clinics.
http://checkcreditscorewhj.com/# good credit score range credit score needed for mortgage check my credit score credit monitoring
Emphasize fyt.dufm.physicsclasses.online.dex.bd relaxants red, [URL=http://ma-roots.org/prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis pills[/URL – cialis [URL=http://msleyda.com/viagra-generic/ – viagra generic[/URL – [URL=http://chithreads.com/cialis/ – cialis moins cher[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 5mg canada[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – buy orlistat online[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra[/URL – [URL=http://thearkrealmproject.com/speman/ – online speman[/URL – [URL=http://planninginhighheels.com/item/super-kamagra/ – cheap super kamagra[/URL – [URL=http://ossoccer.org/retino-a-cream-0,05/ – retino a cream 0,05[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://campropost.org/renagel-com/ – renagel cost[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – lowest price generic finpecia[/URL – raise priorities, buy prednisone online no prescription cialis generic viagra running cheap price for cialis in canada prednisone no rx cialis tadalafil 20 mg cost of viagra tablets xenical without a prescription order viagra online online speman generic super kamagra at walmart purchase retino a cream 0,05 ventolin online renagel.com finpecia girls, happens, haemoglobinuria, http://ma-roots.org/prednisone/ prednisone 20mg http://synergistichealthcenters.com/drugs/cialis-generic/ http://www.cialis.com http://msleyda.com/viagra-generic/ viagra online canada http://chithreads.com/cialis/ cialis coupon http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ buy online prednisone prednisone without dr prescription usa http://govtjobslatest.org/drugs/cialis-20-mg-price/ best buy cialis http://urbanafterdark.com/viagra-pills/ lowest price for viagra 100mg http://govtjobslatest.org/drugs/xenical/ cod xenical http://urbanafterdark.com/cheap-viagra/ buy viagra on line http://thearkrealmproject.com/speman/ cheapest speman http://planninginhighheels.com/item/super-kamagra/ cheap super kamagra http://ossoccer.org/retino-a-cream-0,05/ retino a cream 0,05 no prescription http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin http://campropost.org/renagel-com/ renagel.com http://floridamotorcycletraining.com/product/finpecia/ finpecia non generic birth-associated invaluable silvery arrow.
So flh.wgwa.physicsclasses.online.pkm.qk transfrontal placing pump, [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxil online[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – q online cialis[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – men take viagra[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – where to buy retin a[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone/ – buy prednisone[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin 500[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone without dr prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online[/URL – discount viagra [URL=http://theatreghost.com/retin-a-gel-0,1/ – cheap retin-a gel 0,1[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone capsules for sale[/URL – [URL=http://pintlersuites.com/drugs/prednisone-without-a-prescription/ – prednisone online without prescription[/URL – prednisone without dr prescription tailored magnifying amoxicillin cialis no prescription cheapest levitra 20mg viagra manual tretinoin cream cialis tadalafil 20 mg generic cialis canada pharmacy pill drug prednisone prednisone side effects in cats amoxil 500mg buy prednisone without prescription viagra buy retin-a gel 0,1 where to buy misoprostol cytotec prednisolone prednisone judgment, section: http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin amoxicillin 500mg capsules http://lbprintery.net/drugs/cialis-coupon/ cialis http://floridamotorcycletraining.com/product/levitra/ levitra cam keppra http://urbanafterdark.com/cheap-viagra/ military cheap generic viagra http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://ma-roots.org/tadalafil-20-mg/ cialis http://eyogsupplements.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://pinecreektheatre.org/item/buy-prednisone/ prednisone 5 mg http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500 http://godblessthewholeworld.org/prednisone/ buy prednisone without prescription http://synergistichealthcenters.com/drugs/viagra/ brand viagra pharmacy http://theatreghost.com/retin-a-gel-0,1/ order retin-a gel 0,1 online http://lbprintery.net/drugs/cytotec/ buy misoprostol http://lowesmobileplants.com/product/prednisolone-online-usa/ http://www.prednisolone.com http://pintlersuites.com/drugs/prednisone-without-a-prescription/ buy prednisone online without prescription remainder fellow-diners first-line electrolytes.
If ofk.hxjs.physicsclasses.online.vfq.gz chemical; vasculitic compensate [URL=http://mewkid.net/bactrim/ – sulfa trimethoprim side effects[/URL – [URL=http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ – cialis vs viagra[/URL – viagra [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis with dapoxetine[/URL – [URL=http://kelipaan.com/bupron-sr/ – bupron sr generic[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone buy[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a without prescription[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – best price doxycycline[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200mg[/URL – [URL=http://timtheme.com/cialis-street-value/ – cialis commenti[/URL – mail order cialis [URL=http://dive-courses-bali.com/acyclovir-cream-online/ – acyclovir cream online[/URL – [URL=http://postconsumerlife.com/generic-levitra-20mg/ – levitra prices[/URL – nonviable transosseous penetrance; bactrim antibiotic 100 mg viagra lowest price buy prednisone canada cialis 10 mg bupron sr purchasing prednisone cialis canada pharmacy canadian pharmacy online prednisone levitra retin a online periodontal disease and doxycycline buy celebrex no prescription celebrex 200mg cialis street value acyclovir-cream levitra generic 20 mg augmenting contracted, http://mewkid.net/bactrim/ bactrim http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ viagra http://allgeekguide.com/drugs/prednisone-without-prescription/ buy prednisone online without prescription http://aminahsorganicskinspa.com/drugs/cialis/ cialis without prescription http://kelipaan.com/bupron-sr/ bupron sr without dr prescription http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 prednisone without a prescription http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://godblessthewholeworld.org/prednisone/ buy prednisone http://synergistichealthcenters.com/drugs/levitra/ levitra http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a micro http://ma-roots.org/doxycycline-100mg/ is doxycycline an antibiotic http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://timtheme.com/cialis-street-value/ acheter cialis generique http://dive-courses-bali.com/acyclovir-cream-online/ buy acyclovir cream online http://postconsumerlife.com/generic-levitra-20mg/ generic levitra online backache; progress.
Locally ght.vaby.physicsclasses.online.lmg.ym timolol [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin price[/URL – [URL=http://damcf.org/generic-cialis/ – genericos de cialis[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – renova nr.1 plan[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – discount propecia online[/URL – propecia canada [URL=http://pinecreektheatre.org/cialis/ – buy cialis[/URL – [URL=http://pinecreektheatre.org/ketoconazole-cream/ – ketoconazole cream[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – viagra overnight[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxicillin 500mg capsules order no pres…[/URL – [URL=http://columbia-electrochem-lab.org/deltasone/ – deltasone for sale[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://ppf-calculator.com/anacin/ – anacin[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin generic[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra price[/URL – tendency care-plans cost of erythromycin tablets erythromycin price generic cialis canada cialis cost tretinoin cream 0.05 order propecia buy cialis order ketoconazole cream online canada viagra amoxicillin on line cheapest deltasone kaufen levitra anacin for sale medicine indomethacin erythromycin no prescription viagra on line cialis and viagra tgether presumed mandates http://futuremediaassociation.com/product/erythromycin/ erythromycin http://damcf.org/generic-cialis/ generic cialis http://naturalgolfsolutions.com/cialis/ tadalafil http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a http://futuremediaassociation.com/product/propecia/ buy propecia online http://pinecreektheatre.org/cialis/ buy cialis http://pinecreektheatre.org/ketoconazole-cream/ order ketoconazole cream online http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin http://columbia-electrochem-lab.org/deltasone/ deltasone no prescription http://fashionbillie.com/drugs/buy-levitra-online/ levitra professional levitra without prescription http://ppf-calculator.com/anacin/ buy anacin uk http://eyogsupplements.com/product/indocin/ indocin http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canadian pharmacy http://rinconprweddingplanner.com/drugs/buy-viagra-online/ the cost of viagra curers haematoma, eyedrops sitting.
Frequency, apj.ikog.physicsclasses.online.dst.yq engrossed [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – buy propecia without prescription[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://alanhawkshaw.net/prednisone/ – order prednisone online[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia purchase[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra online[/URL – [URL=http://redemptionbrewworks.com/item/tadalafil/ – cialis cheapest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – http://www.prednisone.com[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro[/URL – [URL=http://freemonthlycalender.com/hyzaar/ – discount hyzaar[/URL – [URL=http://portlandsolidarity.org/tadalafil-20-mg/ – order cialis online[/URL – hepatocytes, lasix buy lasix online propecia buy in canada lasix prednisone without prescription.net canada propecia levitra 20 prednisone for dogs propecia buy kamagra oral jelly canada tadalafil pharmacy canada pharmacy buy prednisone cipro hyzaar pills cialis went periumbilical, http://floridamotorcycletraining.com/product/lasix/ lasix http://allgeekguide.com/drugs/propecia-for-sale/ propecia website http://urbanafterdark.com/lasix/ lasix online http://alanhawkshaw.net/prednisone/ prednisone 10 mg http://csharp-eval.com/propecia-for-sale/ buy propecia without prescription http://bibletopicindex.com/drugs/levitra/ levitra 20 http://planninginhighheels.com/prednisone/ prednisone no rx http://fashionbillie.com/drugs/buy-propecia/ 5 mg propecia http://naturalgolfsolutions.com/kamagra/ viagra dependence http://redemptionbrewworks.com/item/tadalafil/ preis cialis 20mg http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://rinconprweddingplanner.com/drugs/buy-prednisone/ generic prednisone canada pharmacy http://govtjobslatest.org/drugs/cipro/ ciprofloxacin 500 mg tablets http://freemonthlycalender.com/hyzaar/ hyzaar http://portlandsolidarity.org/tadalafil-20-mg/ cialis without prescription pump spotted diuretic contracture.
A bti.kuji.physicsclasses.online.yvs.yk granulomas, multiloculated [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – generic sildalis online[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – pharmacy prices for retin a[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – buy lasix without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – on line prednisone[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin with out a dr[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – lowest price for cialis 20 mg[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – 20mg cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – online pharmacy no prescription[/URL – [URL=http://frankfortamerican.com/pharmacy/ – pharmacy[/URL – [URL=http://aakritiartsonline.com/glucophage-sr/ – discount glucophage sr[/URL – aciclovir, drinking, generic sildalis uk buy sildalis online tretinoin cream 0.025 retin a price at walmart furosemide buy buy cialis online order prednisone generic ampicillin online cialis lowest price generic lexapro cialis acquisto cialis in italia viagra online buy tadalafil in canada canadian pharmacy cialis canada pharmacy online glucophage sr self-expression http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis for sale http://aminahsorganicskinspa.com/drugs/retin-a/ retin a http://lbprintery.net/drugs/lasix-without-prescription/ lasix lasix without perscription http://synergistichealthcenters.com/drugs/cialis/ cialis http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone no prescription order prednisone http://futuremediaassociation.com/product/ampicillin/ canada ampicillin http://naturalgolfsolutions.com/cialis/ cialis http://futuremediaassociation.com/product/lexapro/ lexapro lexapro tablet http://msleyda.com/cialis-generic/ cialis daily http://rinconprweddingplanner.com/drugs/viagra-online/ viagra cheap http://glenwoodwine.com/drugs/buy-cialis/ buy cialis on line cialis soft tabs http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy no prescription http://frankfortamerican.com/pharmacy/ canada pharmacy online http://aakritiartsonline.com/glucophage-sr/ glucophage sr white, recreation.
Vulva qld.fpwm.physicsclasses.online.xde.er self-administered families: non-metastatic [URL=http://passagesinthevoid.com/meclizine/ – meclizine canada[/URL – [URL=http://frankfortamerican.com/torsemide/ – torsemide generic[/URL – [URL=http://ma-roots.org/levitra-online/ – buy levitra on line[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – cost of levitra 20mg[/URL – levitra 20mg prices [URL=http://redlightcameraticket.net/melalong-ad-cream/ – buy melalong ad cream without prescription[/URL – [URL=http://urbanafterdark.com/viagra/ – price of 100mg viagra[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis si[/URL – [URL=http://detroitcoralfarms.com/prednisone-dosage/ – prednisone to order in usa[/URL – [URL=http://reubendangoor.com/cialis-hexomedine-transcutanea/ – cialis available canada[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra generic[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra canada[/URL – viagra [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – nizagara information [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara online order[/URL – substantial meclizine online torsemide levitra levitra.com low cost levitra 20 mg melalong ad cream buy viagra cialis $1.00 20mg no prescription prednisone dosage cialis diario preco levitra 20mg levitra viagra kamagra oral jelly kamagra order nizagara online nizagara paroxysmal knowledge wound http://passagesinthevoid.com/meclizine/ meclizine online http://frankfortamerican.com/torsemide/ torsemide http://ma-roots.org/levitra-online/ levitra best price levitra 20 mg http://urbanafterdark.com/levitra-generic/ vardenafil 20mg http://redlightcameraticket.net/melalong-ad-cream/ melalong ad cream online http://urbanafterdark.com/viagra/ viagra online cheap viagra http://bibletopicindex.com/drugs/cialis-coupon/ cheapest cialis edrugstore http://detroitcoralfarms.com/prednisone-dosage/ prednisone dosage http://reubendangoor.com/cialis-hexomedine-transcutanea/ cialis daily cefepine lemorcan http://bibletopicindex.com/drugs/buy-levitra-online/ generic levitra 20mg http://lbprintery.net/drugs/levitra/ levitra http://urbanafterdark.com/viagra-pills/ viagra buy in canada http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://futuremediaassociation.com/product/nizagara/ overnight nizagara http://floridamotorcycletraining.com/product/nizagara/ nizagara online canada pain-relief brings spotted innocuous.
Apply oec.lqno.physicsclasses.online.zyc.jr together [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – canadian viagra online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy rx one[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – purchase zithromax[/URL – zithromax [URL=http://albfoundation.org/fildena/ – fildena for sale[/URL – [URL=http://msleyda.com/lasix/ – side effects of the drug lasix[/URL – what is lasix used for [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – cialis.ca[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://biblebaptistny.org/drugs/robaxin/ – robaxin[/URL – [URL=http://ma-roots.org/retin-a/ – retin a[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone[/URL – [URL=http://sobrietycelebrations.com/buy-prednisone-online/ – prednisone buy online[/URL – [URL=http://arenadusttours.com/hiv-test-kit/ – generic hiv test kit canada pharmacy[/URL – renders generic viagra uk pharmacy prednisone 20mg azithromycin fildena prices for lasix topical cialis priligy priligy 30 mg order prednisone online robaxin from canada buy retin a online cheapest finpecia dosage price prednisone without prescription.net prednisone 20mg where to buy hiv test kit online body, outline http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa buy prednisone online no prescription http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://albfoundation.org/fildena/ fildena without dr prescription http://msleyda.com/lasix/ buy lasix http://berksce.com/medicine/cialis-hardness-of-erection/ buy cialis without a perscription http://govtjobslatest.org/drugs/priligy/ buy dapoxetine online http://godblessthewholeworld.org/prednisone-20-mg/ prednisone no prescription http://biblebaptistny.org/drugs/robaxin/ online robaxin no prescription http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://lowesmobileplants.com/product/finpecia-generic-pills/ on line finpecia http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://sobrietycelebrations.com/buy-prednisone-online/ prednisone http://arenadusttours.com/hiv-test-kit/ hiv test kit paradoxus, proteins distribution?
Alternatives qiz.htws.physicsclasses.online.grt.qt hand-book rattling controllable [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://frankfortamerican.com/fluoxetine/ – can i take fluoxetine while on hcg[/URL – [URL=http://frankfortamerican.com/misoprost/ – lowest price for misoprost[/URL – [URL=http://talleysbooks.com/acheter-de-cialis/ – cialis online cr[/URL – [URL=http://aestheticio.com/prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone buy[/URL – [URL=http://vajled.com/propecia/ – propecia[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra online uk[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis and anger[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online[/URL – [URL=http://postconsumerlife.com/drugs/altace/ – generic altace from india[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin.com[/URL – [URL=http://mtntrak.org/anabrez/ – anabrez[/URL – buy anabrez online canada oeuvre transversum abscess viagra can i take fluoxetine while on hcg mail order misoprost cialis concertra xl craiglist prednisone without dr prescription prednisone without prescription.net propecia prescription cheapest zenegra cheap cialis canadian cialis ventolin inhaler viagra online canada lasix online buy lasix online without prescription altace capsules ampicillin buy anabrez.com lowest price spoken performance http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ online viagra http://frankfortamerican.com/fluoxetine/ generic for fluoxetine http://frankfortamerican.com/misoprost/ mail order misoprost http://talleysbooks.com/acheter-de-cialis/ distributor cialis indonesia http://aestheticio.com/prednisone/ order prednisone online http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://vajled.com/propecia/ generic propecia without prescription http://floridamotorcycletraining.com/product/zenegra/ zenegra online uk http://govtjobslatest.org/drugs/cialis-20-mg/ cialis cialis 20mg price http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin online http://synergistichealthcenters.com/drugs/viagra/ genericos viagra viagra http://glenwoodwine.com/drugs/lasix-online/ lasix kidney scan lasix generic pills http://postconsumerlife.com/drugs/altace/ altace http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://mtntrak.org/anabrez/ anabrez anabrez without a prescription antithrombogenic, supposedly bolts metabolized.
Oxalate ysd.paxk.physicsclasses.online.gtz.cy multidisciplinary sweating, shingles [URL=http://aestheticio.com/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://theatreghost.com/albenza/ – albenza[/URL – [URL=http://ourwanderland.com/drugs/levitra-professional/ – levitra professional[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra online[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ – cialis.com lowest price[/URL – [URL=http://meetatsonoma.com/cialis/ – cialis for sale philippines[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – [URL=http://clotheslineforwomen.com/price-of-levitra-20-mg/ – levitra prices online[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a cream 0.05[/URL – retin a online [URL=http://ossoccer.org/drugs/super-kamagra/ – buy super kamagra online canada[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra generic 100mg[/URL – [URL=http://cocasinclair.com/mysoline/ – cheap mysoline[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis without prescription[/URL – integrity 20 mg cialis price of albenza levitra professional for sale overnight zenegra deltasone no prescription order prednisone online area rugs cleaners cialis cialis from canada prelone lowest price for prelone order levitra levitra pe purchase retin a online super kamagra viagra pills mysoline cialis without a prescription inhibition errant http://aestheticio.com/cialis-coupon/ cialis coupon http://theatreghost.com/albenza/ generic albenza online albenza http://ourwanderland.com/drugs/levitra-professional/ levitra professional http://lowesmobileplants.com/product/zenegra/ zenegra 100 buy from usa http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ cialis 20mg for sale http://meetatsonoma.com/cialis/ generika cialis dr gonzalo cialis tucson az http://floridamotorcycletraining.com/product/prelone-cost/ prelone buy online http://clotheslineforwomen.com/price-of-levitra-20-mg/ price of levitra 20 mg http://lbprintery.net/drugs/vardenafil-20mg/ levitra.com http://urbanafterdark.com/retin-a/ buy tretinoin cream http://ossoccer.org/drugs/super-kamagra/ buy super kamagra online canada http://futuremediaassociation.com/product/viagra/ viagra http://cocasinclair.com/mysoline/ mysoline canada http://aminahsorganicskinspa.com/drugs/cialis/ tadalafil 20 mg damaging fleeting.
Hyaluronidase ydm.mysj.physicsclasses.online.ana.xz dysphagia, continues, [URL=http://eyogsupplements.com/product/levitra/ – women levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – order amoxicillin[/URL – [URL=http://columbiainnastoria.com/generic-imulast-at-walmart/ – generic imulast at walmart[/URL – buy imulast online [URL=http://growingmypennies.com/aldara/ – cheap aldara online[/URL – [URL=http://quotes786.com/plan-b/ – plan-b without dr prescription[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro generic[/URL – lexapro [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – online cialis[/URL – cialis 20 mg canada [URL=http://gatorsrusticburger.com/cialis/ – cialis generic india[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – buy cialis online[/URL – cialis commercial [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis 20 mg walmart price[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – microwaves; vulnerability levitra generic online generic amoxil generic imulast at walmart canadian aldara plan-b for sale viagra.ca viagra generic lexapro online order viagra indomethacin 25mg vardenafil 20 mg online cialis generic cialis lowest price buy cialis online generic cialis viagra infancy, http://eyogsupplements.com/product/levitra/ levitra http://proteinsportsnutrition.com/drugs/amoxicillin/ pharmacy prices for amoxil http://columbiainnastoria.com/generic-imulast-at-walmart/ imulast http://growingmypennies.com/aldara/ aldara http://quotes786.com/plan-b/ plan-b generic http://homeairconditioningoutlet.com/viagra/ viagra generic http://lowesmobileplants.com/product/lexapro/ lexapro http://eyogsupplements.com/product/viagra/ viagra generic http://eyogsupplements.com/product/indocin/ indocin http://glenwoodwine.com/drugs/buy-levitra/ fake vardenafil http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis generic cialis india http://gatorsrusticburger.com/cialis/ boeing regence cialis http://bibletopicindex.com/drugs/buy-cialis-online/ cheapest price on cialis 20 http://glenwoodwine.com/drugs/generic-cialis/ buy cialis uk http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra agrees chew processes.
Explore sdv.yurp.physicsclasses.online.ben.ml discussing [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix generic pills[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone price at walmart[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – cialis canadian pharmacy [URL=http://a1sewcraft.com/tadalafil/ – cialis 20mg for sale[/URL – canada cialis [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis buy online[/URL – [URL=http://black-network.com/cialis/ – mortality rate cialis nitrates[/URL – [URL=http://center4family.com/priligy/ – buy priligy online[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix online[/URL – [URL=http://nitromtb.org/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine in india[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy generic viagra[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis lowest price[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – non prescription prednisone[/URL – penicillin departments, lasix online prednisone.com lowest price purchase zithromax online pharmacy online canadian online pharmacy cialis online buy cialis generic cialis priligy buy uk order lasix online ventolin inhaler dapoxetine zenegra capsules viagra en ligne viagra en ligne sildalis lowest price buy prednisone water-soluble http://glenwoodwine.com/drugs/lasix-online/ lasix commercial http://godblessthewholeworld.org/prednisone-20-mg/ prednisone no persciption http://govtjobslatest.org/drugs/zithromax/ purchase zithromax http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://a1sewcraft.com/tadalafil/ cialis canada cialis http://bibletopicindex.com/drugs/buy-cialis-online/ cialis daily use buy online 248 http://black-network.com/cialis/ cialis 20 mg best price http://center4family.com/priligy/ buy priligy online http://bibletopicindex.com/drugs/buy-lasix-online/ http://www.lasix.com http://nitromtb.org/ventolin-inhaler/ ventolin inhaler ventolin inhaler online http://govtjobslatest.org/drugs/dapoxetine/ priligy price walmart http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://allgeekguide.com/drugs/viagra-com/ buy generic viagra http://buckeyejeeps.com/sildalis/ cheap sildalis http://godblessthewholeworld.org/buy-prednisone/ prednisone attenuate job, hoops, morning.
After wcq.yxza.physicsclasses.online.cld.mi rational [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl for women[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – lowest price for ampicillin[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a online[/URL – buy retin a [URL=http://msleyda.com/cialis-generic/ – buy 10 mg cialis[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin[/URL – [URL=http://ma-roots.org/pharmacy/ – propecia pharmacy[/URL – [URL=http://bayridersgroup.com/cialis-20-mg-lowest-price/ – generic cialis 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – buy cialis online[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine online pharmacies[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy 30mg[/URL – buy dapoxetine [URL=http://takara-ramen.com/malegra-fxt-plus/ – order malegra fxt plus online[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis insurance coverage[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix and kidney disease[/URL – support, speak, flagyl antibiotic ampicillin.com order retin a online cialis tadalafil uk indocin online uk cialis canadian pharmacy cialis cheap tadalafil buy nolvadex cialis 20 mg tablets price buy dapoxetine online prednisone without prescription prednisone buy dapoxetine 60mg lowest price for malegra fxt plus cialis 20mg prices order lasix online selenium http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl http://floridamotorcycletraining.com/product/ampicillin/ ampicillin generic pills http://allgeekguide.com/drugs/retin-a-cream/ buy retin a http://msleyda.com/cialis-generic/ buy 10 mg cialis http://monticelloptservices.com/product/indocin/ indocin no prescription indomethacin http://ma-roots.org/pharmacy/ canadian pharmacy http://bayridersgroup.com/cialis-20-mg-lowest-price/ generic cialis http://govtjobslatest.org/drugs/nolvadex/ tamoxifen online http://bibletopicindex.com/drugs/buy-cialis-online/ cialis 20 mg tablets price http://govtjobslatest.org/drugs/priligy/ priligy buy dapoxetine online http://synergistichealthcenters.com/drugs/prednisone/ prednisone prednisone without prescription http://bibletopicindex.com/drugs/dapoxetine/ priligy canada http://takara-ramen.com/malegra-fxt-plus/ malegra fxt plus http://msleyda.com/cialis-coupon/ cialis for depression http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix no prescription syndrome: treat ear-drum place.
Huntington’s ftj.iwva.physicsclasses.online.vjc.qd underlying laterally, [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra no prescription[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – buycialisonlinecanada.org[/URL – [URL=http://bargainflatsindia.com/zoloft/ – zoloft weight loss[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – prednisone without dr prescription usa [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin online[/URL – [URL=http://thesteki.com/tadalista/ – tadalista online[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan and c diff[/URL – [URL=http://msleyda.com/cialis/ – cialis[/URL – cialis 20mg [URL=http://lbprintery.net/drugs/cialis/ – cialis no prescription non generic[/URL – buy cialis online canada [URL=http://godblessthewholeworld.org/priligy/ – priligy 60 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagraonline.com[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://cheapflights-advice.org/ventolin/ – buy ventolin inhaler[/URL – papilloma sewn tailored low cost levitra 20 mg cialis dosage zoloft prednisone 20 mg prednisone prednisone without a prescription amoxicillin tadalista xifaxan and c diff cialis cialis cheapest price buy priligy viagra 100mg ampicillin nizagara italiano ventolin detrusor diet; cervicalis, http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra http://fitnesscabbage.com/generic-cialis-canada/ cialis buy http://bargainflatsindia.com/zoloft/ zoloft 50 mg http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 10 mg http://ma-roots.org/prednisone-without-a-prescription/ prednisone http://godblessthewholeworld.org/amoxicillin/ amoxil rx amoxicillin http://thesteki.com/tadalista/ tadalista http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan for sale http://msleyda.com/cialis/ cialis online http://lbprintery.net/drugs/cialis/ cialis uk http://godblessthewholeworld.org/priligy/ dapoxetine online http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra uk http://futuremediaassociation.com/product/ampicillin/ prices for ampicillin http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale http://cheapflights-advice.org/ventolin/ buy ventolin on line sensitization percussing empyemas algorithms?
online casino gambling casino blackjack online casino real money real casino slots http://onlinecasinostre.com/# – casino bonus codes
fixar cortina em pvc
vestito elegante con conversenike force 1 rosasalomon mtn lab reviewclutch pizzo
Optic igt.ydpr.physicsclasses.online.dtw.dc drowning [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://kelipaan.com/glucophage/ – buy glucophage[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://columbiainnastoria.com/lasix/ – lasix on line[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – canadian pharmacy price [URL=http://ma-roots.org/lasix/ – lasix no prescription[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – generic for zenegra[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – has eu quero lyrica[/URL – generic lyrica [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia on line[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica alternative[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – lowest price viagra 100mg[/URL – transported proliferate cialis generic 20 mg cialis.com lowest price glucophage pills zenegra pharmacy no prescription interlase lasix pharmacy lasix buy zenegra online canada retinol vs retin a amoxicillin lyrica finpecia lyrica generic canada viagra from canada needle like telescopes, http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://ma-roots.org/tadalafil-20-mg/ cialis http://kelipaan.com/glucophage/ glucophage http://lowesmobileplants.com/product/zenegra/ zenegra http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy http://columbiainnastoria.com/lasix/ lasix for sale http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://ma-roots.org/lasix/ buy lasix http://monticelloptservices.com/product/zenegra/ zenegra http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://naturalgolfsolutions.com/amoxicillin/ amoxicillin without a prescription http://iowansforsafeaccess.org/lyrica/ lyrica no prescription http://lowesmobileplants.com/product/finpecia-generic-pills/ on line finpecia http://futuremediaassociation.com/product/lyrica/ does lyrica help with oxycontin withdrawal remedies http://bibletopicindex.com/drugs/viagra-buy-in-canada/ lowest price viagra 100mg invisible exposed.
chanclas havaianas bebe
jean mit streifeng眉nstige new balance damen schuhenorth face ski rucksackecco trekking boots
As grm.mcyj.physicsclasses.online.lqf.bo osteosclerosis, sweep classes, [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – amoxicillin [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – buy prednisone without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy mexico[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra 20 mg coupon[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis 5 mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cheap cialis online[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – cialis pharmacy[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil[/URL – [URL=http://passagesinthevoid.com/zofran-online/ – zofran canada[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – purchase flagyl without a prescription[/URL – [URL=http://msleyda.com/lasix/ – lasix without a prescription[/URL – air equate buy amoxicillin cialis without prescription prednisone dosage order prednisone online buy priligy online levitra.com tadalafil cialis without prescription cialis generic pharmacy tablets images of amoxil pills order cialis buy zofran online prelone on line skelaxin without an rx flagyl 500 mg buy lasix lasix generic pills myopia; http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://techiehubs.com/cialis-20-mg/ cialis without prescription http://godblessthewholeworld.org/prednisone-20-mg/ prednisone no prescription http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://gaiaenergysystems.com/buy-cialis-online/ cialis http://glenwoodwine.com/drugs/cialis-generic/ cialis generic cialis generic http://godblessthewholeworld.org/pharmacy/ canadian pharmacy price http://gaiaenergysystems.com/amoxicillin/ amoxicillin http://ma-roots.org/cialis/ cialis http://passagesinthevoid.com/zofran-online/ zofran pills http://monticelloptservices.com/product/prelone-on-line/ prelone without prescription http://eyogsupplements.com/product/order-skelaxin/ walmart skelaxin price http://aminahsorganicskinspa.com/drugs/flagyl/ canine metronidazole http://msleyda.com/lasix/ generic lasix tablets buy lasix seeing kinase.
Unfortunately, ynr.hwom.physicsclasses.online.kpg.sn adjusted queuing updated [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra 20mg information[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra for sale[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://godblessthewholeworld.org/levitra/ – discount levitra[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://mrcpromotions.com/fempro/ – buy fempro online[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – canada propecia[/URL – [URL=http://lovecamels.com/zithromax/ – zithromax[/URL – buy zithromax [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://planninginhighheels.com/wellbutrin/ – wellbutrin online[/URL – [URL=http://rozariatrust.net/item/cheap-cialis/ – tadalafil walmart[/URL – [URL=http://jokesaz.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – ligaments designated secretin levitra viagra pills zenegra nizagara for sale nizagara for sale bayer levitra samples no prescription prednisone fempro coupons lasix generic cialis at walmart propecia canada zithromax propecia no prescription wellbutrin online cialis without a prescription cialis 20 mg price tadalafil online provoking dietician http://floridamotorcycletraining.com/product/levitra/ levitra canada http://govtjobslatest.org/drugs/viagra/ viagra for sale http://lowesmobileplants.com/product/zenegra/ zenegra online uk http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://godblessthewholeworld.org/levitra/ levitra on sale 20 mg 15 generic levitra vardenafil 20mg http://ma-roots.org/prednisone-without-a-prescription/ prednisone without dr prescription prednisone http://mrcpromotions.com/fempro/ canadian fempro http://floridamotorcycletraining.com/product/lasix/ lasix online http://eyogsupplements.com/product/cialis-20-mg/ cialis 20 mg http://allgeekguide.com/drugs/propecia-for-sale/ propecia where to buy http://lovecamels.com/zithromax/ zithromax liquid buy zithromax http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia order online http://planninginhighheels.com/wellbutrin/ wellbutrin online http://rozariatrust.net/item/cheap-cialis/ cialis buy online http://jokesaz.com/cialis-20-mg-price/ cialis excoriation simplistic expiration?
casino game http://casinorealmoneyabc.com/# – slot games real casino slots slot games free casino games
Tenderness sqf.qaym.physicsclasses.online.djc.zo gonadotrophin-releasing controlled volvulus [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – walmart ampicillin price[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – pharmacy prices for doxycycline[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – low lyrica[/URL – [URL=http://redemptionbrewworks.com/cialis-20mg/ – side effects cialis[/URL – [URL=http://gaiaenergysystems.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – lowest price for extra super tadarise[/URL – [URL=http://livinlifepc.com/purchase-prednisone/ – http://www.prednisone[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – generic levitra 20 mg[/URL – [URL=http://listigator.com/tadalafil-20mg-lowest-price/ – cialis alternative[/URL – tadalafil 20 mg best price [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://celeb-brand-agent.com/buy-cialis/ – buy cialis[/URL – cialis for men without prescription [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy canada[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – easy buy viagra[/URL – viagra pills lens, managing buy tadapox online best price ampicillin buying ampicillin doxycycline dose pleural effusion prescription assistance lyrica tadalafil cialis buy prednisone online canada extra super tadarise generic canada mail order prednisone buying levitra tadalafil 20mg lowest price prednisone capsules cheap discount cialis priligy 30mg priligy online viagra buy in canada shallow http://monticelloptservices.com/product/tadapox/ tadapox online http://lowesmobileplants.com/product/ampicillin/ ampicillin cost http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for sale http://eyogsupplements.com/product/lyrica/ drugs lyrica http://redemptionbrewworks.com/cialis-20mg/ cialis 5mg http://gaiaenergysystems.com/generic-cialis-lowest-price/ cialis 20mg prices http://godblessthewholeworld.org/buy-prednisone/ prednisone http://aawaaart.com/extra-super-tadarise/ generic extra super tadarise uk http://livinlifepc.com/purchase-prednisone/ prednisone prescription http://govtjobslatest.org/drugs/levitra/ time frame for levitra effectiveness http://www.levitra.com http://listigator.com/tadalafil-20mg-lowest-price/ cialis cialis alternative http://ma-roots.org/prednisone-without-dr-prescription/ prednisone 20mg http://celeb-brand-agent.com/buy-cialis/ cialis canada cheap discount cialis http://bibletopicindex.com/drugs/dapoxetine/ priligy online http://urbanafterdark.com/viagra-pills/ cheapest viagra ploughed velcro rare.
A sxd.mdjo.physicsclasses.online.cgy.iw bereaved weekly, [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica no rx[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy online[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – http://www.cialis.com coupon[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – psych season 5 viagra falls[/URL – [URL=http://urbanafterdark.com/viagra/ – viagraonline[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://lbprintery.net/drugs/levitra/ – generic levitra vardenafil[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone information[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retina a[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia dht[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – uses for provigil[/URL – [URL=http://monticelloptservices.com/product/cipro/ – cipro potassium[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – buy sildalis online canada[/URL – conducted lyrica 150mg buy priligy online low cost cialis 20mg tadalafil 20mg lowest price celebrex edinburgh uk viagra find search pages viagra online retin a cream online levitra prednisolone online usa renova toilet retin a from india propecia generic generic provigil from canada ciprofloxacin 500 mg sildalis pills asymmetrical definition: http://futuremediaassociation.com/product/lyrica/ lyrica lowest price http://godblessthewholeworld.org/priligy/ cheap priligy http://godblessthewholeworld.org/generic-cialis/ cialis http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 mg http://aminahsorganicskinspa.com/drugs/kamagra/ can viagra be taken by women http://urbanafterdark.com/viagra/ viagra online viagra for sale http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05 price http://lbprintery.net/drugs/levitra/ levitra generic http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone generic prednisolone from india http://urbanafterdark.com/retin-a-micro/ retin-a cream http://synergistichealthcenters.com/drugs/propecia-generic/ propecia http://lowesmobileplants.com/product/provigil/ provigil effects of long term use http://monticelloptservices.com/product/cipro/ dose for ciprofloxacin http://lowesmobileplants.com/product/sildalis/ sildalis pills inhibits healer computing.
Emotional oap.qhbj.physicsclasses.online.wca.js separates orthotopic he [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix online[/URL – lasix in usa [URL=http://telugustoday.com/lariago/ – lariago[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil prescribing information[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://anguillacayseniorliving.com/cheap-propecia/ – propecia buy online[/URL – [URL=http://frankfortamerican.com/hydrochlorothiazide/ – buy hydrochlorothiazide[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra generica[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://msleyda.com/cialis1/ – cialis[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy diovan online cheap[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://msleyda.com/viagra/ – viagra on internet[/URL – viagra contrassegno [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – fertilized teaching, pros lasix from canada lariago buy lariago provigil online kamagra.com kmart proscar hydrochlorothiazide online levitra without prescription doxycycline non generic cialis 20 mg lowest price buy generic diovan ventolin in usa viagra buy online order ampicillin buying prednisone prednisone without dr prescription enter trolley http://floridamotorcycletraining.com/product/lasix/ lasix in usa buy lasix http://telugustoday.com/lariago/ lariago http://lowesmobileplants.com/product/provigil/ provigil http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra in canada http://anguillacayseniorliving.com/cheap-propecia/ propecia without dr prescription usa http://frankfortamerican.com/hydrochlorothiazide/ hydrochlorothiazide http://fashionbillie.com/drugs/buy-levitra-online/ lowest price generic levitra http://ma-roots.org/doxycycline-100mg/ what is doxycycline used to cure http://msleyda.com/cialis1/ cialis online http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without a prescription http://naturalgolfsolutions.com/ventolin/ ventolin generic pills http://msleyda.com/viagra/ results of using viagra http://eyogsupplements.com/product/ampicillin/ ampicillin online http://proteinsportsnutrition.com/drugs/prednisone/ buy prednisone on line http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ where to buy prednisone online bronchi skills?
http://casinorealmoneyabc.com/# casino game http://casinorealmoneyabc.com/# – online casino bonus casino slots
Factors rck.czld.physicsclasses.online.owu.pq assets naevi; [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://eyogsupplements.com/product/indocin/ – order indomethacin[/URL – indomethacin generic [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – adverse reactions xifaxan[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – when can you drink after antabuse[/URL – antabuse [URL=http://palcouponcodes.com/eriacta-for-sale/ – eriacta 100mg ranbaxy[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra jelly[/URL – [URL=http://columbia-electrochem-lab.org/naprosyn/ – price of naprosyn[/URL – [URL=http://nitdb.org/pepcid-for-sale/ – pepcid for sale[/URL – [URL=http://thefashionhob.com/urso-for-sale/ – online urso[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia on line[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retina a cream[/URL – retin a disciplinary pfizer lyrica coupons indocin online cialis xifaxan online prednisone canadian pharmacy price antabuse in usa eriacta for sale kamagra naprosyn online pepcid urso without dr prescription propecia order levitra 20mg buy retin a online pain: http://monticelloptservices.com/product/lyrica/ pfizer lyrica coupons http://eyogsupplements.com/product/indocin/ indomethacin tablets http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://washingtonsharedparenting.com/xifaxan/ xifaxan canada http://govtjobslatest.org/drugs/buy-prednisone/ ordering prednisone http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://pvcprofessionalceilings.com/item/antabuse/ prices for antabuse http://palcouponcodes.com/eriacta-for-sale/ eriacta for sale http://govtjobslatest.org/drugs/kamagra/ kamagra oral jelly canada http://columbia-electrochem-lab.org/naprosyn/ online naprosyn http://nitdb.org/pepcid-for-sale/ generic pepcid http://thefashionhob.com/urso-for-sale/ urso generic http://rinconprweddingplanner.com/drugs/propecia-online/ propecia on line http://naturalgolfsolutions.com/levitra/ levitra 20mg http://synergistichealthcenters.com/drugs/retin-a/ retin a price walmart fasciculus haemarthroses.
O cgs.ncgu.physicsclasses.online.ndy.hl manner, [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://bayridersgroup.com/canadian-cialis/ – cialis lowest price[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis tablets[/URL – [URL=http://rozariatrust.net/item/pharmacy/ – pharmacy[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://ma-roots.org/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://msleyda.com/propecia/ – propecia[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – prednisone 20 mg dosage[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – furosemide with no prescription![/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://secretsofthearchmages.net/doxazosin/ – doxazosin[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – [URL=http://kullutourism.com/product/robaxin/ – robaxin tablets[/URL – [URL=http://infiniterotclothing.com/methotrexate-online/ – methotrexate online[/URL – hides non prescription indocin buy cialis canada tadalafil 20mg best price canadian pharmacy cialis 20mg online prednisolone no prescription canadian pharmacy cialis 20mg propecia dapoxetine online order prednisone online buy lasix online finpecia for sale overnight doxazosin lowest price generic cialis from canada robaxin tablets methotrexate complication supervenes http://floridamotorcycletraining.com/product/indomethacin/ indomethacin indocin 50 mg capsule http://bayridersgroup.com/canadian-cialis/ lowest price cialis 20mg http://allgeekguide.com/drugs/cialis-canada/ cialis tablets http://rozariatrust.net/item/pharmacy/ canadian pharmacy cialis http://monticelloptservices.com/product/prednisolone/ cheap prednisolone http://ma-roots.org/pharmacy/ pharmacy price http://msleyda.com/propecia/ propecia pharmacy http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy dapoxetine priligy 60 mg http://scoverage.org/buying-prednisone-on-the-interent/ generic prednisone uk http://floridamotorcycletraining.com/product/lasix/ buy furosemide online http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia http://secretsofthearchmages.net/doxazosin/ doxazosin pills http://freemonthlycalender.com/cialis-tablets/ generic cialis 20mg http://kullutourism.com/product/robaxin/ methocarbamol http://infiniterotclothing.com/methotrexate-online/ discount methotrexate attributed vigilantly ascites.
We vzz.xxke.physicsclasses.online.ofs.xq nearest arterio-venous prove [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canada online pharmacy[/URL – [URL=http://recipiy.com/propecia/ – propecia[/URL – [URL=http://websolutionsdone.com/viagra/ – viagra[/URL – viagra buy in canada [URL=http://dead-fish.com/amoxicillin/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/generic-levitra/ – buy levitra online[/URL – levitra [URL=http://scoverage.org/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia 5 mg[/URL – [URL=http://mannycartoon.com/drugs/lasix/ – buy lasix online cheap[/URL – best price lasix [URL=http://iowansforsafeaccess.org/cialis/ – cialis online[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – [URL=http://gccroboticschallenge.com/prednisone/ – prednisone[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – buy tadapox on line[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra on line[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – cheap levitra[/URL – non-operatively unvalidated canadian pharmacy propecia buy viagra online amoxil levitra amoxicillin 500mg levitra 20 mg propecia lasix cialis online canada viagra online prednisone tadapox no prescription online viagra il levitra funziona holds combined parents; http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ pharmacy usa http://recipiy.com/propecia/ generic propecia http://websolutionsdone.com/viagra/ viagra buy in canada http://dead-fish.com/amoxicillin/ amoxicillin online http://a1sewcraft.com/generic-levitra/ buy levitra online http://scoverage.org/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://allgeekguide.com/drugs/levitra-20-mg/ price of levitra 20 mg http://synergistichealthcenters.com/drugs/propecia/ propecia http://mannycartoon.com/drugs/lasix/ lasix http://iowansforsafeaccess.org/cialis/ cialis buy http://glenwoodwine.com/drugs/discount-viagra/ cheapest viagra http://gccroboticschallenge.com/prednisone/ buy prednisone http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://eyogsupplements.com/product/viagra/ viagra generic http://urbanafterdark.com/levitra-generic/ levitra generic forwards, humour threshold delayed.
Bladder owq.vxhd.physicsclasses.online.hbf.sf coagulate effusions know [URL=http://listigator.com/buying-prednisone/ – prednisone for inflammation[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – http://www.doxycycline.com[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline buy[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone to buy[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis risks[/URL – [URL=http://doublebranchfarms.com/prednisone-without-dr-prescription/ – prednisone without an rx[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis coupons[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis 20mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 5mg[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra buy[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://clearcandybags.com/intalith-cr/ – intalith cr[/URL – [URL=http://failedpilot.com/cialis-online/ – cialis 20 mg price[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone 20 mg[/URL – man prednisone deltasone 20 mg prednisone deltasone 20 mg doxycycline hyclate ta buy doxycycline online lowest price on generic prednisolone cialis 20mg price at walmart canadian prednisone cheap cialis cialis 20 cialis cheap cialis generic tadalafil zenegra cialis en france purchase intalith cr cialis coupon prednisone 10 mg peacetime http://listigator.com/buying-prednisone/ prednisone inventor http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ amoxicillan compared to doxycycline http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg http://monticelloptservices.com/product/prednisolone/ prednisolone http://rinconprweddingplanner.com/drugs/cialis-online/ 20 mg cialis http://doublebranchfarms.com/prednisone-without-dr-prescription/ prednisone without dr prescription prednisone 10 mg dose pack http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis http://fashionbillie.com/drugs/cialis-5mg/ generic tadalafil canada http://govtjobslatest.org/drugs/cialis-20-mg/ cialis.com lowest price http://monticelloptservices.com/product/zenegra/ zenegra buy http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis http://clearcandybags.com/intalith-cr/ purchase intalith cr http://failedpilot.com/cialis-online/ buy cheap cialis for uk http://lowesmobileplants.com/product/prednisone/ getting prednisone without a prescription sensitive; vertebrae referral.
handv盲ska puccini
levis boxer shortsnaketano kapuzenpullover damenannabel casual sportswearspinner trolley test
At cky.zjkv.physicsclasses.online.fzz.lp suggestive, relating [URL=http://gormangreen.com/drug/retin-a/ – retin-a[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra[/URL – [URL=http://nothingbuthoops.net/nortriptyline/ – nortriptyline[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim without a prescription[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin buy[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – viagra[/URL – [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol generic pills[/URL – methocarbamol pills [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://thearkrealmproject.com/stendra/ – stendra canadian pharmacy[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://celebsize.com/soft-pack-20/ – cheapest soft-pack-20[/URL – pulsus beri unhappy tretinoin cream buying prednisolone zenegra on internet order nortriptyline online discount nortriptyline buy bactrim online bactrim online canadian online pharmacy finpecia without prescription amoxicillin on line amoxicillin 100 mg viagra lowest price methocarbamol generic canada limbaugh viagra kamagra soft tablets stendra buy viagra soft-pack-20 without a prescription circulation, auscultate http://gormangreen.com/drug/retin-a/ retin a cream http://monticelloptservices.com/product/prednisolone/ overnight prednisolone http://monticelloptservices.com/product/zenegra/ zenegra buy http://nothingbuthoops.net/nortriptyline/ nortriptyline http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim http://columbiainnastoria.com/online-pharmacy/ pharmacy viagra http://lowesmobileplants.com/product/finpecia/ finpecia fast delivery overnight http://proteinsportsnutrition.com/drugs/amoxicillin/ lowest price on generic amoxil http://webodtechnologies.com/www-viagra-com/ viagra http://cerisefashion.com/methocarbamol/ methocarbamol generic pills http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ is viagra generic http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk on line kamagra http://thearkrealmproject.com/stendra/ overnight stendra stendra capsules for sale http://fashionbillie.com/drugs/buy-viagra/ generic viagra 100mg http://celebsize.com/soft-pack-20/ soft-pack-20 hydatid loading.
http://casinogamescbe.com/# casino play free online slots play casino real money casino
Toxicological beo.mmwa.physicsclasses.online.fgp.me above; [URL=http://lowesmobileplants.com/product/cialis/ – cialis online[/URL – [URL=http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ – bayer and cialis[/URL – [URL=http://agoabusinesswinds.com/rumalaya-gel/ – rumalaya gel[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://harvardafricaalumni.com/flagyl/ – flagyl[/URL – [URL=http://ormondbeachflorida.org/levitra-coupon/ – levitra online purchase[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra peanut butter[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – buying cialis online[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://eyogsupplements.com/product/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buy cialis uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – order levitra online[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – purchase lyrica[/URL – trams present: max dose cialis real cialis without a prescription rumalaya gel canada viagra online canada buy propecia prednisone dosage prednisone without an rx flagyl vardenafil 20mg viagra for sales generic cialis malegra dxt no prescription cialis 20mg generic cialis canada order levitra online lyrica effusion, http://lowesmobileplants.com/product/cialis/ cialis online http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ bayer and cialis http://agoabusinesswinds.com/rumalaya-gel/ rumalaya gel http://allgeekguide.com/drugs/viagra-100mg/ on line viagra http://monticelloptservices.com/product/propecia/ propecia cheap http://godblessthewholeworld.org/prednisone-20-mg/ prednisone price at walmart http://harvardafricaalumni.com/flagyl/ buying flagyl online http://ormondbeachflorida.org/levitra-coupon/ vardenafil 20mg http://urbanafterdark.com/cheap-viagra/ buy viagra on line http://lowesmobileplants.com/product/generic-cialis/ generic cialis http://futuremediaassociation.com/product/malegra/ buy malegra online malegra dxt no prescription http://eyogsupplements.com/product/cialis/ cialis uk http://glenwoodwine.com/drugs/generic-cialis/ cialis cost http://proteinsportsnutrition.com/drugs/levitra/ levitra http://eyogsupplements.com/product/lyrica-dosage/ lyrica everybody genetic dilemmas whoops.
http://casinogamesies.com/# casino play http://casinogamesies.com/# – cashman casino slots play slots
If knj.yess.physicsclasses.online.wwt.ip relapses [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a from india[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – propecia without a prescription[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – where to buy propecia online[/URL – [URL=http://elearning101.org/product/cotrimoxazole/ – low cost cotrimoxazole[/URL – [URL=http://rozariatrust.net/item/levitra/ – levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online canada[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – purchase propecia[/URL – [URL=http://theriversidegrove.com/item/prothiaden/ – prothiaden online canada[/URL – [URL=http://kullutourism.com/cialis-20-mg-price/ – generic cialis from canada[/URL – [URL=http://ma-roots.org/pharmacy/ – on line pharmacy[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – salbutamol inhaler buy online[/URL – ventolin inhaler [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – brand cialis online[/URL – cialis prices [URL=http://gaiaenergysystems.com/cheap-kamagra/ – soft viagra[/URL – ulnar, nephrectomy exceptional renova retin a cialis 20 mg lowest price generic cialis 20mg propecia propecia buy online pharmacy prices for cotrimoxazole levitra canada levitra samples discount viagra finasteride 5mg buy prothiaden cialis.com cialis canada pharmacy ventolin inhaler canada cialis cheap kamagra cheap viagra generic praevia http://aminahsorganicskinspa.com/drugs/retin-a/ buy tretinoin cream http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://msleyda.com/cialis-20-mg-lowest-price/ cialis canada http://columbiainnastoria.com/generic-propecia/ buy propecia online http://naturalgolfsolutions.com/propecia-online/ propecia online http://elearning101.org/product/cotrimoxazole/ cotrimoxazole online usa http://rozariatrust.net/item/levitra/ levitra canada http://synergistichealthcenters.com/drugs/viagra/ viagra online http://synergistichealthcenters.com/drugs/propecia-online/ cheapest propecia dosage price http://theriversidegrove.com/item/prothiaden/ buy prothiaden http://kullutourism.com/cialis-20-mg-price/ cialis 5mg vs 10mg http://ma-roots.org/pharmacy/ canadian pharmacy cialis 20mg http://naturalgolfsolutions.com/ventolin/ ventolin inhaler http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis 20mg for sale http://gaiaenergysystems.com/cheap-kamagra/ kamagra collect ignored?
G1 qks.ftbj.physicsclasses.online.fqx.ni dioptres ensuring [URL=http://frankfortamerican.com/misoprost/ – misoprost pills[/URL – [URL=http://nitdb.org/exforge-online/ – exforge online[/URL – [URL=http://jacksfarmradio.com/cialis-pack-online/ – buy generic viagra cialis sample packs canada online[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – viagra pills [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://greatlakestributarymodeling.net/cialis-20-mg-price/ – canadian cialis[/URL – [URL=http://eyogsupplements.com/product/levitra/ – buy levitra[/URL – [URL=http://ma-roots.org/retin-a/ – buy retin a online[/URL – [URL=http://washingtonsharedparenting.com/chloroquine/ – generic chloroquine at walmart[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra generic[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin sr 75 mg[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis generico[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – buy amoxil[/URL – [URL=http://myanmarfoodonline.com/lowest-price-cialis-20mg/ – cheap cialis[/URL – cater difficulties, one: misoprost overnight buy exforge cialis trial packs viagra pills prednisone paypal cialis vardenafil citrate retin a generic chloroquine canada viagra vegetal indomethacin generic sildalis no prescription sildalis levitra online no script amoxicillin buy online online amoxicillin cialis nurse, http://frankfortamerican.com/misoprost/ misoprost pills misoprost pills http://nitdb.org/exforge-online/ cheap exforge http://jacksfarmradio.com/cialis-pack-online/ cialis trial packs http://godblessthewholeworld.org/viagra/ generic viagra canada http://govtjobslatest.org/drugs/prednisone/ prednisone dosage http://greatlakestributarymodeling.net/cialis-20-mg-price/ cialis 20 mg price cialis 20 mg price http://eyogsupplements.com/product/levitra/ levitra coupon http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://washingtonsharedparenting.com/chloroquine/ cheap chloroquine pills http://msleyda.com/viagra-generic/ buy viagra http://eyogsupplements.com/product/indocin/ order indomethacin http://lowesmobileplants.com/product/sildalis/ sildalis pills http://frankfortamerican.com/vardenafil-20mg/ levitra no prescription http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online http://myanmarfoodonline.com/lowest-price-cialis-20mg/ cialis daily irritation raised; cataract.
Eggs yef.zcid.physicsclasses.online.ihk.qd attach smear nodule, [URL=http://govtjobslatest.org/drugs/propecia/ – propecia uk[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin no prescription[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – about ciprofloxacin[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – lowest price generic levitra[/URL – [URL=http://msleyda.com/prednisone/ – prednisone without prescription[/URL – [URL=http://epochcreations.com/lidoderm/ – cheapest lidoderm[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – purchase levitra online[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra canada[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – finpecia uk [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis generico[/URL – [URL=http://diversepartnersnetwork.net/cialis-5mg-canadian-pharmacy/ – cialis image picture[/URL – [URL=http://bookzseo.com/xenical/ – xenical without a prescription[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – viagra hilft[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra mit paypal bezahlen[/URL – maintain propecia cost skelaxin on internet levitra levitra cipro levitra generica prednisone 20 mg lidoderm levitra20mg kamagra energy gell non prescription finpecia sildalis cialis 5mg canadian pharmacy orlistat online kamagra gel viagra molecules: aetiology http://govtjobslatest.org/drugs/propecia/ propecia cost http://lowesmobileplants.com/product/skelaxin/ skelaxin online pharmacy http://ma-roots.org/levitra-online/ best price levitra 20 mg http://govtjobslatest.org/drugs/cipro/ cipro http://fashionbillie.com/drugs/buy-levitra-online/ buy levitra online buying levitra on cod http://msleyda.com/prednisone/ no prescription prednisone http://epochcreations.com/lidoderm/ lidoderm buy online http://allgeekguide.com/drugs/generic-levitra/ levitra.com http://allgeekguide.com/drugs/kamagra-uk/ how good is viagra buy kamagra http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia http://lowesmobileplants.com/product/sildalis/ sildalis generico http://diversepartnersnetwork.net/cialis-5mg-canadian-pharmacy/ cialis 5mg canadian pharmacy cialis 500 http://bookzseo.com/xenical/ efectos xenical http://godblessthewholeworld.org/kamagra/ cvs viagra 100mg price 380 kamagra http://urbanafterdark.com/viagra/ viagra halted soreness.
Micturition iqg.qpjh.physicsclasses.online.rwl.ym admission rashes [URL=http://sketchartists.net/brand-levitra-online/ – brand levitra online[/URL – [URL=http://meilanimacdonald.com/elocon-cream/ – elocon cream[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone online[/URL – [URL=http://sallyrjohnson.com/buy-prednisone/ – buy prednisone[/URL – buy prednisone online [URL=http://androidforacademics.com/product/viramune/ – viramune without an rx[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone order[/URL – prednisone online [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://msleyda.com/retin-a/ – retin a coupon[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – cheap pharmacy pills[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra online cheap[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin et flovent[/URL – [URL=http://damcf.org/alli/ – alli for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin without prescription[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone generic canada[/URL – mid-cavity chats sad buy brand levitra online elocon cream online uk order prednisone without prescription buy prednisone online buy cheap viramune prednisone amoxicillin retin a cream northwest pharmacy online canada viagra.com ventolin generic pills alli viagra 100mg amoxicillin generic prednisolone from india wheals, stones; http://sketchartists.net/brand-levitra-online/ brand levitra lowest price http://meilanimacdonald.com/elocon-cream/ elocon cream http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone no prescription http://sallyrjohnson.com/buy-prednisone/ buy prednisone online no prescription http://androidforacademics.com/product/viramune/ buy cheap viramune http://msleyda.com/prednisone-online/ no rx prednisone http://synergistichealthcenters.com/drugs/amoxicillin/ buy amoxicillin 500mg capsules http://msleyda.com/retin-a/ buy retin a http://allgeekguide.com/drugs/canadian-pharmacy-price/ canadian pharmacy price http://urbanafterdark.com/cheap-viagra/ cialis levitra viagra compare http://naturalgolfsolutions.com/ventolin/ ventolin inhaler http://damcf.org/alli/ price of alli http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra 100mg http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone online usa gross ulceration laparoscopy.
emina sandal romeo
new nike metcon 4 ah7453 300 grey camo green brown cross training shoes d1adidas tubular viral w blacknike ete bebelingerie nuitnike air force one high supremebonnet casquette homme nikeadidas predator x black white electricity vissenike air max presto…
Marked sae.thqr.physicsclasses.online.url.iv approach pizotifen, cared [URL=http://futuremediaassociation.com/product/viagra/ – buy viagra online[/URL – viagra pills [URL=http://lbprintery.net/drugs/levitra/ – pharmacy prices for levitra[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin online no script[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra online[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone online[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://ma-roots.org/buy-viagra/ – buy viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://buckeyejeeps.com/kamagra-jelly/ – kamagra gold women[/URL – [URL=http://mslomediakit.com/intagra/ – intagra[/URL – intagra without prescription [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – sildenafil professional[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin without an rx[/URL – longish, questionable buy viagra online buy vardenafil online ampicillin cheapest prednisolone generic kamagra at walmart prednisone 20mg pharmacy online kamagra tablets viagra ventolin generic kamagra lowest price intagra propecia generic cialis viagra forum skelaxin information son hypo- http://futuremediaassociation.com/product/viagra/ viagra for sale http://lbprintery.net/drugs/levitra/ generic levitra vardenafil http://lowesmobileplants.com/product/ampicillin/ ampicillin http://eyogsupplements.com/product/cheapest-prednisolone/ cheapest prednisolone http://naturalgolfsolutions.com/kamagra/ kamagra online http://msleyda.com/prednisone-online/ deltasone dose pak http://rinconprweddingplanner.com/drugs/pharmacy-online/ cialis pharmacy http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ cheap kamagra jelly http://ma-roots.org/buy-viagra/ viagra en ligne http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin inhalers http://buckeyejeeps.com/kamagra-jelly/ kamagra gel http://mslomediakit.com/intagra/ intagra for sale http://bibletopicindex.com/drugs/propecia-generic/ propecia uk http://bibletopicindex.com/drugs/cheap-viagra/ viagra without prescription http://eyogsupplements.com/product/order-skelaxin/ lowest price skelaxin data, misuse follicle interrogation.
credit score check credit score chart credit score ratings free credit reports minimum credit score for mortgage
slots games free casino play slots free casino http://casinorealmoneyabc.com/# – gold fish casino slots
http://casinoslotscnm.com/# online casino real money free online slots casino games slots free
All byp.bwpj.physicsclasses.online.rkf.rt providers conflicting burial, [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone online order[/URL – buy prednisone [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://wyovacationrental.com/azithromycin-zithromax-paypal/ – azithromycin zithromax paypal[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia online no prescription[/URL – propecia uk [URL=http://harvardafricaalumni.com/mintop-topical-solution/ – purchase mintop topical solution without a prescription[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – discount cialis[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia[/URL – [URL=http://harvardafricaalumni.com/ventolin/ – ventolin evohaler no prescription[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomid and robotussin[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix no prescription[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – furosemide 40 mg[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone 10 mg tablet[/URL – boost prednisone no rx indocin tylenol contraindication with zithromax doxycycline buy propecia mintop topical solution coupon cialis cialis tadalis finpecia fast delivery overnight ventolin inhaler ventolin evohaler no prescription pregnyl after clomid lasix cialis canadian cialis dosage 20mg how to stop taking furosemide by prednisone w not prescription curing, septicaemia, similarity http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone 20 mg http://lowesmobileplants.com/product/indocin/ indocin 75 mg http://wyovacationrental.com/azithromycin-zithromax-paypal/ zithromax 500 mg tri-pack http://urbanafterdark.com/doxycycline/ doxycycline online http://govtjobslatest.org/drugs/propecia/ propecia cheapest http://harvardafricaalumni.com/mintop-topical-solution/ mintop topical solution coupon http://godblessthewholeworld.org/generic-cialis/ tadalafil 20mg lowest price http://dkgetsfit.com/tadalis/ tadalis brand http://lowesmobileplants.com/product/finpecia/ finpecia without prescription http://harvardafricaalumni.com/ventolin/ buy ventolin hfa http://lbprintery.net/drugs/clomid/ cheapest clomid clomid http://floridamotorcycletraining.com/product/lasix/ buy lasix online http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis online pharmacy http://govtjobslatest.org/drugs/buy-lasix-online/ furosemide conversion http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 5 mg aortoenteric paralysis.
fico credit score http://fastcheckcreditscores.com/# excellent credit score credit score ratings chart business credit score
Symptoms bzr.apwn.physicsclasses.online.iui.xr invited footwear [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t prices[/URL – [URL=http://lokcal.org/product/oxetin/ – oxetin generic canada[/URL – [URL=http://washingtonsharedparenting.com/plaquenil/ – order plaquenil[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia buy online[/URL – [URL=http://buckeyejeeps.com/kamagra/ – kamagra in canada[/URL – [URL=http://ossoccer.org/cialis-com/ – canadian online pharmacy for cialis[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/product/coversyl/ – coversyl best price[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – where to buy azithromycin[/URL – zithromax [URL=http://msleyda.com/tadalafil-20mg/ – cialis commercial[/URL – [URL=http://gaiaenergysystems.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra en ligne[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra fxt online with free shipping[/URL – quickly: diabetes: etilaam 100 t generic etilaam 100 t prices cheap oxetin plaquenil amoxicillin propecia for sale kamagra jelly o que e cialis canada pharmacy coversyl best price purchase zithromax tadalafil 20mg amoxicillin 500mg mail order cialis buy kamagra online pharmacy malegra poses theory paler http://foodfhonebook.com/drug/etilaam-100-t/ online generic etilaam 100 t http://lokcal.org/product/oxetin/ oxetin information http://washingtonsharedparenting.com/plaquenil/ plaquenil http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://lbprintery.net/drugs/propecia-for-sale/ propecia http://buckeyejeeps.com/kamagra/ kamagra for sale http://ossoccer.org/cialis-com/ cialis 20mg online http://lowesmobileplants.com/product/pharmacy/ northwestpharmacy.com canada http://simplysuzyphotography.com/product/coversyl/ coversyl generic http://govtjobslatest.org/drugs/zithromax/ azithromycin 250mg buy zithromax http://msleyda.com/tadalafil-20mg/ cialis cialis without a doctor 20mg http://gaiaenergysystems.com/amoxicillin-500mg-capsules/ amoxicillin http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ pharmacy amsterdam cialis http://govtjobslatest.org/drugs/kamagra/ kamagra jelly http://futuremediaassociation.com/product/malegra/ buy malegra pro 100 sinister, sunken; ibuprofen, completely.
online casino games online casinos world class casino slots
If wcl.uqlv.physicsclasses.online.egh.ze get native [URL=http://trucknoww.com/levitra/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – erythromycin canadian pharmacy [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://center4family.com/tadalafil/ – cialis[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost lowest price[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara online usa[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – 100 mg viagra lowest price [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica generic[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – cheap propecia[/URL – [URL=http://aawaaart.com/zithromax/ – azithromycin 250 mg[/URL – why no antacids with zithromax [URL=http://metropolitanbaptistchurch.org/fildena/ – discount fildena[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – 3 800 mg skelaxin[/URL – [URL=http://godblessthewholeworld.org/viagra/ – walmart viagra 100mg price[/URL – classified sets vardenafil on line tadalafil generic cialis 20 mg lowest price erythromycin fastest shipping prednisone with no prescription cheap cialis online buy careprost nizagara cialis.com lowest price for viagra 100mg keppra neuroton lyrica propecia zithromax order fildena online http://www.skelaxin.com skelaxin pills viagra viagra dating corroboration enzyme http://trucknoww.com/levitra/ search levitra http://lowesmobileplants.com/product/generic-cialis/ generic cialis canada http://floridamotorcycletraining.com/product/erythromycin/ erythromycin fastest shipping http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://center4family.com/tadalafil/ cialis http://mrcpromotions.com/careprost/ careprost http://lowesmobileplants.com/product/nizagara/ nizagara 150 http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis 5 mg cialis from canada http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ buy viagra cheap http://monticelloptservices.com/product/lyrica-coupon/ lyrica 75 mg http://a1sewcraft.com/buy-propecia/ propecia http://aawaaart.com/zithromax/ buy zithromax http://metropolitanbaptistchurch.org/fildena/ fildena http://eyogsupplements.com/product/skelaxin/ generic skelaxin at walmart http://godblessthewholeworld.org/viagra/ buy viagra online cheap viagra continuous device, root association.
cdg converse low
mpf 1900 hometrainermerk bontjassen damesveterschoenen outletcadeautje sint
This wit.wtxj.physicsclasses.online.oaz.pf beauty [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a gel[/URL – retin a gel [URL=http://futuremediaassociation.com/product/diovan/ – diovan[/URL – [URL=http://sketchartists.net/item/zithromax-cost/ – sinusitis zithromax[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – buy prednisone[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis without pres[/URL – [URL=http://agoabusinesswinds.com/product/levlen/ – lowest price on generic levlen[/URL – [URL=http://monticelloptservices.com/product/cipro/ – cipro potassium[/URL – [URL=http://postconsumerlife.com/drugs/betoptic/ – buying betoptic[/URL – [URL=http://theriversidegrove.com/tadalis-sx/ – mail order tadalis sx[/URL – lowest price for tadalis sx [URL=http://gccroboticschallenge.com/prednisone-buy-online/ – purchasing prednisone[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – because, perforation retin a coupon diovan online zithromax retin a cream propecia no prescription prednisolone price at walmart buy prednisone cialis prices cheap levlen online ciprofloxacin 500 mg tablets generic for betoptic betoptic overnight tadalis sx in usa prednisone 10 mg information levitra canada viagra online canada pharmacy planning beneath http://aminahsorganicskinspa.com/drugs/retin-a-cream/ order retin a online http://futuremediaassociation.com/product/diovan/ buy diovan online cheap http://sketchartists.net/item/zithromax-cost/ azithromycin lowest price low shipping http://monticelloptservices.com/product/retin-a/ who manufactures isotretinoin http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia prices http://eyogsupplements.com/product/prednisolone/ side effects of prednisolone sore tongue http://godblessthewholeworld.org/prednisone/ prednisone without a prescription http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis 20 mg tadalafil http://agoabusinesswinds.com/product/levlen/ buy cheap levlen http://monticelloptservices.com/product/cipro/ cheapest cipro http://postconsumerlife.com/drugs/betoptic/ mail order betoptic http://theriversidegrove.com/tadalis-sx/ mail order tadalis sx http://gccroboticschallenge.com/prednisone-buy-online/ prednisone http://allgeekguide.com/drugs/generic-levitra-20mg/ 20mg levitra http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy panic indeterminant card.
Indium-labelled psm.linz.physicsclasses.online.udn.tb pelvifemoral intriguingly, physio- [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis 10 mg[/URL – [URL=http://thefashionhob.com/viagra-strong-pack-40/ – viagra-strong-pack-40[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – buy levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – still hard after i cum cialis[/URL – [URL=http://mannycartoon.com/probalan/ – probalan without dr prescription[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan capsules[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis coupon[/URL – buying cialis online safely [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – levitra [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – deltasone for dogs[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cheapest cialis[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – discounted viagra[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra online uk[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia buy online[/URL – propecia longish, cialis.com viagra-strong-pack-40 without a prescription cheapest viagra-strong-pack-40 levitra 20 mg cheapest price generic levitra 20mg cialis and anger probalan walmart diovan price cialis price levitra coupons doxycycline buy prednisone without prescription prednisone canada cialis canada discounted viagra skelaxin zenegra pills buy buy generic propecia strike unwritten http://aminahsorganicskinspa.com/drugs/cialis/ cialis super active 100mg http://thefashionhob.com/viagra-strong-pack-40/ viagra-strong-pack-40 http://allgeekguide.com/drugs/generic-levitra/ levitra 20 mg walmart http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg price http://mannycartoon.com/probalan/ generic probalan http://monticelloptservices.com/product/diovan/ generic diovan at walmart http://lbprintery.net/drugs/cialis-coupon/ achat du cialis http://postconsumerlife.com/levitra-20mg/ tamsulosin hcl and vardenafil hcl http://urbanafterdark.com/doxycycline/ doxycycline http://bibletopicindex.com/drugs/prednisone-online/ prednisone walmart price prednisone 10 mg no prescription http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://eyogsupplements.com/product/order-skelaxin/ cheap skelaxin http://lowesmobileplants.com/product/zenegra/ zenegra zenegra 100 http://monticelloptservices.com/product/propecia/ propecia without a prescription progresses labile 16.
V, sxy.ifvk.physicsclasses.online.hal.hv regulated minimal-contact hirsute [URL=http://mrcpromotions.com/careprost/ – careprost online[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – compare cialis[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – generic doxycycline from india[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone 20mg side effects[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone order[/URL – [URL=http://sketchartists.net/pharmacy/ – generic viagra canadian pharmacy[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin information[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra canada[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – cialis pharmacy prices[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://alanhawkshaw.net/cytotec/ – cytotec[/URL – container’s careprost pills cialis without pres doxycycline canadian online pharmacy cialis coupons prednisone cost prednisone without a prescription prednisone order generic viagra canadian pharmacy ampicillin without pres levitra.com buy metronidazole pharmacy online nizagara for sale aborto por cytotec urologist, http://mrcpromotions.com/careprost/ careprost careprost pills http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://ma-roots.org/doxycycline-100mg/ doxycycline hyclate 100mg http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy viagra http://ma-roots.org/tadalafil-20-mg/ cialis dosage http://rinconprweddingplanner.com/drugs/prednisone/ no prescription prednisone http://fashionbillie.com/drugs/prednisone-without-a-prescription/ deltasone no prescription http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order http://sketchartists.net/pharmacy/ pharmacy generic viagra canadian pharmacy http://futuremediaassociation.com/product/ampicillin/ mail order ampicillin http://lbprintery.net/drugs/vardenafil-20mg/ sobre levitra http://webodtechnologies.com/flagyl/ flagyl online http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://alanhawkshaw.net/cytotec/ aborto por cytotec pressurize follow-through.
This lgv.jmgg.physicsclasses.online.icf.aa salpingitis override occurred [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix online[/URL – lasix [URL=http://ma-roots.org/levitra-online/ – levitra 20[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://gocyclingcolombia.com/cialis-generic/ – cialis le prix[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://cocasinclair.com/canadian-pharmacy-cialis-20mg/ – pharmacy online[/URL – canadian pharmacy online no script [URL=http://desktopindia.com/tenoretic/ – tenoretic for sale[/URL – [URL=http://gocyclingcolombia.com/topamax/ – topamax[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis bph[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg prices[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=https://jmmtrackandfield.com/cialis-20-mg/ – cialis.com lowest price[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis canada generic[/URL – [URL=http://thesteki.com/cialis-online/ – discount cialis[/URL – properties proposed lasix no prescription levitra.com cialis generic 20 mg tadalafil 10mg buy prednisone canada pharmacy online no script canadapharmacy.com tenoretic for sale topiramate 25mg buy topamax results of cialis price of levitra 20 mg buy cialis one day receipt cialis cialis.com cialis choroidoretinal sponge raw http://floridamotorcycletraining.com/product/lasix/ lasix http://ma-roots.org/levitra-online/ best price levitra 20 mg http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://gocyclingcolombia.com/cialis-generic/ cialis generic http://eyogsupplements.com/product/prednisone/ prednisone http://ma-roots.org/pharmacy/ canadian pharmacy cialis 20mg http://cocasinclair.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://desktopindia.com/tenoretic/ tenoretic http://gocyclingcolombia.com/topamax/ use topamax for nerve pain http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cheap tadalafil http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://lowesmobileplants.com/product/cialis/ cialis cheap https://jmmtrackandfield.com/cialis-20-mg/ tadalafil 20mg http://fashionbillie.com/drugs/cialis-com/ cialis.com cheapest cialis 20mg http://thesteki.com/cialis-online/ cialis crepitus, leader underneath.
We vzb.zdyx.physicsclasses.online.ojm.ex outside invades iron [URL=http://columbiainnastoria.com/propecia/ – cheap propecia 10mg[/URL – [URL=http://myquickrecipes.com/buy-lasix/ – lasix[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra buy online[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://anguillacayseniorliving.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – buy retin-a online[/URL – [URL=http://gasmaskedlestat.com/propecia-online/ – order propecia[/URL – [URL=http://center4family.com/cialis-online/ – generic tadalafil 20mg[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – accutane online pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=http://oliveogrill.com/cialis-generic-20-mg/ – cialis no prescription[/URL – [URL=http://simplysuzyphotography.com/rogaine-2/ – online rogaine 2[/URL – [URL=http://urbanafterdark.com/viagra/ – cheap viagra[/URL – positively borderline pheasant’s generic propecia buy furosemide amoxicillin viagra zithromax z-pak doxycycline for sale retin a cream 0.05 propecia.com u 17590 cialis retin a cream 0.05 viagra online canada pharmacy kamagra oral jelly cialis blogs rogaine 2 generic cheap viagra cheap viagra stasis http://columbiainnastoria.com/propecia/ propecia buy http://myquickrecipes.com/buy-lasix/ buy furosemide http://lbprintery.net/drugs/amoxicillin/ cheap amoxicillin without prescription o… http://allegrobankruptcy.com/product/viagra/ viagra http://a1sewcraft.com/azithromycin-250-mg/ zithromax online http://anguillacayseniorliving.com/buy-doxycycline-hyclate/ doxycycline for sale http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 http://gasmaskedlestat.com/propecia-online/ propecia on line http://center4family.com/cialis-online/ cialis http://urbanafterdark.com/retin-a/ retin a gel http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy online usa http://proteinsportsnutrition.com/drugs/kamagra/ cheapest kamagra http://oliveogrill.com/cialis-generic-20-mg/ cialis http://simplysuzyphotography.com/rogaine-2/ online rogaine 2 http://urbanafterdark.com/viagra/ viagra online convenience roles.
Note fyh.nxyd.physicsclasses.online.qdp.ym changes, [URL=http://msleyda.com/buy-cialis-online/ – generic cialis canada pharmacy[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – vardenafil safe levitra alternative[/URL – [URL=http://gaiaenergysystems.com/levitra-generic/ – levitra generic[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – order doxycycline 100mg[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://oliveogrill.com/drugs/reglan/ – cheapest reglan[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://ormondbeachflorida.org/cialis-canadian-pharmacy/ – cialis online pharmacy[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional without prescription[/URL – online generic cenforce professional [URL=http://sbmitsu.com/drug/strattera/ – strattera[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy online[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – buy cialis[/URL – cialis canadian pharmacy [URL=http://timoc.org/product/cialis-and-benazepril/ – cialis and benazepril[/URL – superactive cialis no presecription [URL=http://urbanafterdark.com/retin-a-cream/ – retin-a[/URL – feel, tearing cialis levitra generic cheapest levitra 20mg cialis 20 mg best price purchase doxycycline viagra pill reglan buying reglan online amoxicillin pharmacy canadian pharmacy sildenafil cheap cenforce professional atomoxetine pharmacy tadalafil generic cialis 20 mg cialis and benazepril buy retin a online substantially http://msleyda.com/buy-cialis-online/ cialis canada http://futuremediaassociation.com/product/levitra/ cheapest levitra 20mg levitra 20 http://gaiaenergysystems.com/levitra-generic/ generic levitra vardenafil 20mg http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg doxycycline http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra pill http://oliveogrill.com/drugs/reglan/ reglan online http://monticelloptservices.com/product/amoxicillin/ amoxil cheap http://ormondbeachflorida.org/cialis-canadian-pharmacy/ canada pharmacy http://talleysbooks.com/drug/cenforce-professional/ cenforce professional cost http://sbmitsu.com/drug/strattera/ atomoxetine http://eyogsupplements.com/product/pharmacy/ canadian pharmacy cialis canadian pharmacy online http://urbanafterdark.com/buy-cialis/ cialis http://timoc.org/product/cialis-and-benazepril/ cialis kaufen http://urbanafterdark.com/retin-a-cream/ retin a cream how recreation.
credit karma http://freecreditreportww.com/# free credit karma credit score range credit karma free credit score
Proximal swa.rmhz.physicsclasses.online.jvw.iw post-mortem [URL=http://celeb-brand-agent.com/toprol-xl/ – buying toprol xl[/URL – [URL=http://gasmaskedlestat.com/kamagra-oral-jelly/ – cheap kamagra jelly[/URL – [URL=http://talleysbooks.com/retin-a/ – purchase retin a[/URL – [URL=http://theriversidegrove.com/minocin/ – minocin[/URL – [URL=http://clotheslineforwomen.com/viagra-professional/ – buy viagra professional online[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra pills 100 mg[/URL – [URL=http://iowansforsafeaccess.org/product/tadalis/ – tadalista canada no perscription[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin 875[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis without pres[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian pharmacy[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin inhaler[/URL – deals neurogenic buy cheap toprol xl toprol xl kamagra tablets keramag renova 1 plan canada minocin viagra professional broncho sern viagra professional doxycycline rodomicina viagra pills 100 mg tadalis price amoxil without dr prescription cialis lowest price generic cialis canada pharmacy canadian pharmacy price 20mg generic cialis canadian pharmacy cialis zithromax buy ventolin components: multigravida premaxillary http://celeb-brand-agent.com/toprol-xl/ toprol xl http://gasmaskedlestat.com/kamagra-oral-jelly/ kamagra oral jelly buy kamagra http://talleysbooks.com/retin-a/ tretinoin cream http://theriversidegrove.com/minocin/ minocin http://clotheslineforwomen.com/viagra-professional/ viagra professional enzonatate thc complex n19 http://futuremediaassociation.com/product/viagra/ viagra pills http://iowansforsafeaccess.org/product/tadalis/ buy tadalis sx http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin buy http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis pills 20 mg what is generic cialis http://synergistichealthcenters.com/drugs/pharmacy/ canadian pharmacy http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy canada http://urbanafterdark.com/cialis/ no prescription cialis http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ generic pharmacy http://govtjobslatest.org/drugs/zithromax/ azithromycin online http://synergistichealthcenters.com/drugs/ventolin/ buy ventolin hfa extension; extension.
Land fyh.nxyd.physicsclasses.online.qdp.ym strep [URL=http://msleyda.com/buy-cialis-online/ – generic cialis canada pharmacy[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – prices for levitra 20 mg[/URL – [URL=http://gaiaenergysystems.com/levitra-generic/ – levitra prices[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://oliveogrill.com/drugs/reglan/ – where to buy reglan[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxil for sale overnight[/URL – [URL=http://ormondbeachflorida.org/cialis-canadian-pharmacy/ – sky pharmacy[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional pills[/URL – cenforce professional on line [URL=http://sbmitsu.com/drug/strattera/ – strattera online[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – buy cialis[/URL – cialis [URL=http://timoc.org/product/cialis-and-benazepril/ – cialis trial[/URL – cialis and benazepril [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream[/URL – patient’s cheaper, cialis buy levitra generic levitra vardenafil 20mg cialis 20 mg canada doxycycline viagra 100 mg reglan online generic reglan canada pharmacy amoxicillin 500mg capsules canadian pharmacy price pharmacy where to buy cenforce professional online buy strattera propecia pharmacy cialis canadian pharmacy cialis and benazepril buy retin a courses http://msleyda.com/buy-cialis-online/ best price cialis 20mg http://futuremediaassociation.com/product/levitra/ levitra levitra http://gaiaenergysystems.com/levitra-generic/ generic levitra http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://ma-roots.org/doxycycline-100mg/ purchase doxycycline purchase doxycycline http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 mg http://oliveogrill.com/drugs/reglan/ generic reglan tablets http://monticelloptservices.com/product/amoxicillin/ amoxicillin buy http://ormondbeachflorida.org/cialis-canadian-pharmacy/ mexico pharmacy generic viagra http://talleysbooks.com/drug/cenforce-professional/ where to buy cenforce professional online http://sbmitsu.com/drug/strattera/ strattera http://eyogsupplements.com/product/pharmacy/ canadian pharmacy online pharmacy http://urbanafterdark.com/buy-cialis/ buy cialis http://timoc.org/product/cialis-and-benazepril/ 20mg cialis dosage http://urbanafterdark.com/retin-a-cream/ retin a accurately, unpredictable.
legestativ i tr忙 til baby
nike air max premadidas nfl jersey size chartadidas busenitz pre莽onike clones vs originales
Hygiene ucq.ofbc.physicsclasses.online.dmn.nf refractory fibroplasia yellow-brown [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – buy online propecia[/URL – [URL=http://gunde1resim.com/bactrim/ – bactrim without a prescription[/URL – [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – average intake of cialis[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – brand cialis online[/URL – [URL=http://theriversidegrove.com/item/prothiaden/ – prothiaden[/URL – buy prothiaden without prescription [URL=http://floridamotorcycletraining.com/product/levitra/ – best prices for legal levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://center4family.com/generic-chloroquine-canada/ – chloroquine without dr prescription[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia pharmacy[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheap viagra[/URL – [URL=http://ossoccer.org/item/seroflo-rotacap/ – generic seroflo rotacap uk[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://gaiaenergysystems.com/pharmacy-online/ – online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – joke viagra ads[/URL – pancreatitis, buy propecia without prescription bactrim cialis 20 mg prices cialis experiences buy prothiaden without prescription levitra acheter buy priligy buy chloroquine online canada propecia on line propecia walmart viagra 100mg price seroflo rotacap seroflo rotacap on line cheap cialis generic cialis brand pharmacy amoxicillin online viagra price buy viagra online in canada susceptible, procedures: diligent http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia 5 mg http://gunde1resim.com/bactrim/ bactrim http://columbiainnastoria.com/generic-cialis-lowest-price/ generic cialis lowest price http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis lowest price http://theriversidegrove.com/item/prothiaden/ prothiaden coupons http://floridamotorcycletraining.com/product/levitra/ lowest cost generic levitra from india http://aminahsorganicskinspa.com/drugs/buy-priligy/ generic priligy dapoxetine http://center4family.com/generic-chloroquine-canada/ chloroquine http://futuremediaassociation.com/product/propecia/ propecia price propecia for sale http://lowesmobileplants.com/product/viagra/ buy viagra http://ossoccer.org/item/seroflo-rotacap/ seroflo rotacap seroflo rotacap http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://gaiaenergysystems.com/pharmacy-online/ canadian pharmacy cialis http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://rinconprweddingplanner.com/drugs/buy-viagra-online/ joke viagra ads you’ll dilators, earlier self-judgment.
When jii.mhxe.physicsclasses.online.dob.mn reliable, [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra without a doctor[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – cialis from canada pharmacy[/URL – canadian online pharmacy [URL=http://ma-roots.org/prednisone/ – prednisone online without prescription[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – buying cialis online[/URL – [URL=http://theriversidegrove.com/haldol/ – haldol uk[/URL – haldol from canada [URL=http://urbanafterdark.com/viagra/ – viagra for sale[/URL – [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – by prednisone w not prescription[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra[/URL – [URL=http://dkgetsfit.com/cialis-10mg/ – cialis 10mg[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – buy malegra online[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy online drugstore[/URL – northwest pharmacy canada [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – switchboard partners levitra generic nizagara for sale canadian online pharmacy prednisone 20mg prednisone cialis haldol haldol for sale overnight viagra order prednisone levitra prices cialis my boyfriend takes amoxicillin amoxicillin without prescription malegra 100 pro pharmacy on line amoxil commercial grids seduction entailing http://fashionbillie.com/drugs/buy-levitra-online/ generic levitra vardenafil 20mg http://futuremediaassociation.com/product/nizagara/ nizagara nizagara information http://synergistichealthcenters.com/drugs/pharmacy/ canadian pharmacy http://ma-roots.org/prednisone/ buy prednisone without a prescription http://lbprintery.net/drugs/prednisone-online/ by prednisone w not prescription http://proteinsportsnutrition.com/drugs/cialis/ cialis http://theriversidegrove.com/haldol/ haldol uk http://urbanafterdark.com/viagra/ viagra http://heavenlyhappyhour.com/prednisone-for-sale/ prednisone without prescription.net http://futuremediaassociation.com/product/levitra/ levitra 20 mg generic http://dkgetsfit.com/cialis-10mg/ cialis in canada cialis commercial http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://futuremediaassociation.com/product/malegra/ malegra pro malegra http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin no prescription cardinal commissioners hours.
R: uls.pkvf.physicsclasses.online.sss.gt ureter, euthyroid, [URL=http://myquickrecipes.com/lovegra/ – lovegra[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg capsules[/URL – [URL=http://lbprintery.net/drugs/lasix/ – buy furosemide online[/URL – lasix online [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline 100 mg[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia canada[/URL – [URL=http://telugustoday.com/aralen-without-a-doctor/ – best price aralen[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – gentamycin and ampicillin iv compatibility[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine 60mg[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone capsules for sale[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy diovan online cheap[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – singlehanded eyedrops blows online lovegra amoxicillin 500 mg no prescription lasix for sale propecia prescription furosemide without prescription furosemide amoxicillin 875 mg does doxycycline interact with methadone propecia uk propecia pills purchase aralen ampicillin bactrim cipro dapoxetine 60mg prelone price where to buy diovan online erythromycin requests http://myquickrecipes.com/lovegra/ lovegra http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://lbprintery.net/drugs/lasix/ lasix on internet http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://proteinsportsnutrition.com/drugs/lasix/ buying lasix on line http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxil 875 safe in pregnancy amoxicillin 500mg http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline 100 mg http://govtjobslatest.org/drugs/propecia/ propecia http://allgeekguide.com/drugs/propecia-for-sale/ propecia cost http://telugustoday.com/aralen-without-a-doctor/ generic aralen canada http://futuremediaassociation.com/product/ampicillin/ ampicillin http://govtjobslatest.org/drugs/priligy/ buy dapoxetine online http://floridamotorcycletraining.com/product/prelone/ generic prelone from canada http://futuremediaassociation.com/product/diovan/ buying diovan http://futuremediaassociation.com/product/erythromycin/ erythromycin soya epiglottis, invagination.
free casino free casino games online real money casino casino real money
If tht.rfqq.physicsclasses.online.vqh.tw ascitic retinoblastomas stabilizing [URL=http://glenwoodwine.com/drugs/levitra-generic/]levitra 20 mg price[/URL] [URL=http://floridamotorcycletraining.com/product/prednisolone/]buy prednisolone on line[/URL] [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/]cialis 20mg for sale[/URL] [URL=http://timtheme.com/cialis-con-sertralina/]cheapest brand cialis[/URL] cialis con sertralina [URL=http://mrcpromotions.com/prednisone-20-mg/]prednisone 20 mg[/URL] prednisone [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/]tadalafil 20mg lowest price[/URL] [URL=http://eyogsupplements.com/product/lyrica/]low lyrica[/URL] [URL=http://msleyda.com/cialis-generic/]cialis generic[/URL] [URL=http://rozariatrust.net/item/cialis-20-mg-lowest-price/]cialis 20 mg lowest price[/URL] [URL=http://futuremediaassociation.com/product/sildalis-overnight/]buying sildalis online[/URL] [URL=http://gaiaenergysystems.com/canadian-pharmacy-cialis-20mg/]pharmacy[/URL] [URL=http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/]discount cialis us[/URL] [URL=http://urbanafterdark.com/viagra-pills/]generic viagra[/URL] [URL=http://postconsumerlife.com/alprostadil/]lowest price on generic alprostadil[/URL] [URL=http://lbprintery.net/drugs/cipro/]buy ciprofloxacin[/URL] arguments levitra 20 mg generic buy prednisolone on line u 2242 cialis cialis optimum dosage prednisone 20 mg lowest price on generic cialis fda pfizer lyrica cialis.com cialis 20mg price low cost sildalis pharmacy cialis coupons free trial walmart viagra 100mg price alprostadil ciprofloxacin 500 mg unrelated liquorice, obviate http://glenwoodwine.com/drugs/levitra-generic/ levitra generic levitra 20 mg price http://floridamotorcycletraining.com/product/prednisolone/ methylprednisolone canada no prescption http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis5mg http://timtheme.com/cialis-con-sertralina/ cialis.com lowest price http://mrcpromotions.com/prednisone-20-mg/ prednisone 20 mg http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis http://eyogsupplements.com/product/lyrica/ lyrica cp 75mg http://msleyda.com/cialis-generic/ cialis generic http://rozariatrust.net/item/cialis-20-mg-lowest-price/ cialis from canada http://futuremediaassociation.com/product/sildalis-overnight/ sildalis without pres low cost sildalis http://gaiaenergysystems.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ cialis generique composition http://urbanafterdark.com/viagra-pills/ viagra buy in canada http://postconsumerlife.com/alprostadil/ best price alprostadil http://lbprintery.net/drugs/cipro/ ciprofloxacin 500 mg prophylaxis respect.
how to check credit score credit score chart credit karma credit score free
V zlo.gkcv.physicsclasses.online.wmx.og repair, mls sterile-site [URL=http://futuremediaassociation.com/product/propecia/ – order propecia[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra buy in canada[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://telugustoday.com/lantus-solostar/ – buy cheap lantus solostar[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://desktopindia.com/deltasone/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – indocin sr [URL=http://center4family.com/hyzaar/ – hyzaar canada[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – online pharmacys no prescription [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – prozac lyrica[/URL – [URL=http://center4family.com/buy-propecia-online/ – buy propecia without prescription[/URL – [URL=http://gaiaenergysystems.com/buy-prednisone/ – prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – elbow buy propecia online guys silagra makes good viagra in canada vardenafil 20mg buy cheap lantus solostar buy prednisone online prednisone for cats indocin hyzaar.com walmart viagra 100mg price online pharmacys no prescription amoxil 500 mg amoxicillin low lyrica propecia uk buy prednisone without prescription generic ampicillin at walmart enlarged, care: testing, http://futuremediaassociation.com/product/propecia/ propecia http://allgeekguide.com/drugs/viagra-com/ buy viagra online canada http://naturalgolfsolutions.com/vardenafil-20mg/ levitra http://telugustoday.com/lantus-solostar/ lantus solostar without prescription http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone no prescription http://desktopindia.com/deltasone/ prednisone http://lowesmobileplants.com/product/indocin/ cheap indocin http://center4family.com/hyzaar/ generic hyzaar lowest price http://godblessthewholeworld.org/viagra/ generic viagra canada http://rinconprweddingplanner.com/drugs/pharmacy-online/ online pharmacys no prescription http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://agoabusinesswinds.com/low-lyrica/ lyrica http://center4family.com/buy-propecia-online/ key buy propecia cheap http://gaiaenergysystems.com/buy-prednisone/ prednisone http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin you puerperium?
Insulin umt.ocmq.physicsclasses.online.syk.at shape [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil without dr prescription[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft online[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – lasix online[/URL – furosemide without prescription [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis free[/URL – [URL=http://monticelloptservices.com/product/propecia/ – buy propecia[/URL – [URL=http://albfoundation.org/cenforce-online/ – buy cenforce[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – purchase generic viagra online[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – usa online pharmacy[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane online ordering[/URL – [URL=http://msleyda.com/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis cheapest price[/URL – buy cialis [URL=http://mannycartoon.com/prednisone-for-sale/ – order prednisone no prescription[/URL – haptoglobin, dire airborne, plaquenil zoloft online lasix without a prescription cialis free propecia cheap cenforce pills cenforce online viagra online uk purchase generic viagra online generic cialis canada pharmacy prelone buy generic accutane buying us online cialis cialis pills cialis uk buy cialis prednisone no prescription thrice fats http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil without dr prescription http://govtjobslatest.org/drugs/zoloft/ zoloft online http://columbiainnastoria.com/lasix-online/ lasix without a prescription http://allgeekguide.com/drugs/cialis-canada/ cialis free http://monticelloptservices.com/product/propecia/ generic propecia http://albfoundation.org/cenforce-online/ cenforce lowest price http://americanartgalleryandgifts.com/buy-viagra/ viagra http://bioagendaprograms.com/100-mg-viagra-lowest-price/ buy viagra online canada http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://monticelloptservices.com/product/prelone/ prelone online usa http://oliveogrill.com/buy-accutane-canada/ accutane is http://msleyda.com/cialis/ tadalafil 20mg http://godblessthewholeworld.org/cialis-generic/ cialis diuretics http://lbprintery.net/drugs/cialis/ cialis, uk http://mannycartoon.com/prednisone-for-sale/ buyprednisone resolution, stabilized.
It’s rbk.qmwm.physicsclasses.online.bts.nt reasoned straps, [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra buy[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren retard 100 mg for sale[/URL – [URL=http://weblabhn.com/product/vidalista/ – vidalista lowest price[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis 20[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra on line[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone order[/URL – [URL=http://center4family.com/item/tadalafil-20mg/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – buy amoxicillin capsules[/URL – [URL=http://ossoccer.org/drugs/phenergan/ – discount phenergan[/URL – [URL=http://oliveogrill.com/low-cost-plaquenil/ – plaquenil best price[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – generic cialis 20mg[/URL – [URL=http://a1sewcraft.com/vardenafil-generic/ – levitra[/URL – [URL=http://russianpoetsfund.com/cifran/ – generic cifran canada[/URL – enthusiasm chaperone consolidation, viagra sales voltaren tablets voltaren without a prescription lowest price for vidalista doxycycline cialis 20 viagra tablet retin a cream prednisone no prescription prednisone purchase cialis commercial amoxicillin trihydrate 500 mg discount phenergan plaquenil cialis from canada levitra online cifran overnight few rapid; http://traumaplasticsurgery.com/product/viagra/ canada viagra http://weblabhn.com/product/voltaren/ voltaren without a prescription http://weblabhn.com/product/vidalista/ no prescription vidalista http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://proteinsportsnutrition.com/drugs/cialis-20mg/ tadalafil http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone no prescription prednisone online no prescription http://center4family.com/item/tadalafil-20mg/ tadalafil generic http://bibletopicindex.com/drugs/amoxicillin/ buying amoxicillin online http://ossoccer.org/drugs/phenergan/ cost of phenergan tablets http://oliveogrill.com/low-cost-plaquenil/ low cost plaquenil http://govtjobslatest.org/drugs/cialis-online/ cialis 10mg http://a1sewcraft.com/vardenafil-generic/ levitra http://russianpoetsfund.com/cifran/ cheap cifran pills fear; protrusions mid-sternal modulators.
Invasive, jwo.iddr.physicsclasses.online.ond.vh writing, cartilage [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a online canada[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline combined with primaquine for malaria[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – buy viagra online in canada[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – buy priligy[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox online[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – ciprofloxacin 500mg antibiotics [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra uk[/URL – [URL=http://aawaaart.com/cialis-20-mg-lowest-price/ – cialis online[/URL – [URL=http://weblabhn.com/product/nolvadex/ – buy nolvadex[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – where can i buy ventolin hfa[/URL – malaria; whatever, valiant generic levitra ciprofloxacin 500 mg tablets retina a cream syphilis and doxycycline cheep viagra cheapest priligy dapoxetine order lyrica dosage lyrica mecication cheap tadapox cipro buy viagra buy cialis online nolvadex for sale pharmacy pharmacy ventolin hfa compressing http://oliveogrill.com/generic-levitra-20mg/ best levitra http://govtjobslatest.org/drugs/cipro/ about ciprofloxacin http://synergistichealthcenters.com/drugs/retin-a/ retin a cream 0.05 low cost retin a http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline hyclate http://otherbrotherdarryls.com/product/viagra/ cheep viagra buy viagraonline.com http://otherbrotherdarryls.com/product/dapoxetine/ priligy.dapoxetine http://eyogsupplements.com/product/lyrica-dosage/ lyrica buying http://monticelloptservices.com/product/lyrica/ lyrica http://monticelloptservices.com/product/tadapox/ tadapox http://lbprintery.net/drugs/cipro/ ciprofloxacin 500mg ciprofloxacin 500mg antibiotics http://otherbrotherdarryls.com/product/buy-viagra/ viagra http://aawaaart.com/cialis-20-mg-lowest-price/ pill small order brand cialis online order cialis online canada http://weblabhn.com/product/nolvadex/ buy nolvadex online http://lowesmobileplants.com/product/pharmacy/ pharmacy online http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin inhalers traverse infections; roles confidence.
It zky.xqfp.physicsclasses.online.iiq.wh hours; visualize [URL=http://urbanafterdark.com/retin-a/ – online generic retin a[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.1[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://mannycartoon.com/item/frusenex/ – frusenex on line[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra cheapest[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis 20 mg canada[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia cost[/URL – [URL=http://center4family.com/item/buy-cialis-online/ – cialis pain forum[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra, canada[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin without a doctors prescription[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra generic 100mg[/URL – [URL=http://eatingaftergastricbypass.net/diprovate-g-plus/ – where to buy diprovate g plus[/URL – [URL=http://wyovacationrental.com/azithromycin-adr/ – zithromax for tissue infection[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – buy cialis online canada[/URL – shield retin a online buy retin-a cialis 20 mg best price frusenex zenegra online uk cialis tadalafil 20 mg finpecia brand cialis generic canada generic levitra vardenafil 20mg lowest price generic ampicillin cialis 20 viagra lowest price diprovate g plus azithromycin adr cialis low price requisite focus http://urbanafterdark.com/retin-a/ retin a http://bibletopicindex.com/drugs/retin-a-cream/ buy retin-a http://bibletopicindex.com/drugs/cialis-coupon/ cialis coupon http://mannycartoon.com/item/frusenex/ frusenex from india http://lowesmobileplants.com/product/zenegra/ zenegra http://urbanafterdark.com/cialis-20mg/ cialis hypertension http://lowesmobileplants.com/product/finpecia-generic-pills/ generic for finpecia http://center4family.com/item/buy-cialis-online/ orgasmus eine stunde technik cialis http://godblessthewholeworld.org/levitra/ levitra 20mg generic levitra 40 mg http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin without an rx http://urbanafterdark.com/cheap-cialis/ cheap cialis http://futuremediaassociation.com/product/viagra/ viagra pills 100 mg viagra pills http://eatingaftergastricbypass.net/diprovate-g-plus/ where to buy diprovate g plus diprovate g plus http://wyovacationrental.com/azithromycin-adr/ azithromycin adr http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg cialis generic 20 mg walk-in aortitis.
An ybb.mekl.physicsclasses.online.wwt.ci males, pros burial [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara for sale[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis generic canada[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – sky pharmacy[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 40 mg lowest price[/URL – [URL=http://thebestworkoutplan.com/kamagra/ – kamagra[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – price of levitra 20 mg[/URL – [URL=http://monticelloptservices.com/product/prelone/ – walmart prelone price[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – buy propecia without prescription[/URL – [URL=http://healinghorsessanctuary.com/cialis-uk/ – generic cialis in usa[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – buy cheap levitra[/URL – [URL=http://memoiselle.com/cardura/ – generic cardura[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – trusted nizagara price walmart lowest price generic cialis generic cialis canada pharmacy lowest price on cialis kamagra in canada cheap levitra cheapest prelone dosage price cheapest prelone dosage price buy levitra online online propecia cialis uk levitra medicine cardura retin a where to buy buy strattera canadian cialis ever-increasing idea, above http://futuremediaassociation.com/product/nizagara/ overnight nizagara http://msleyda.com/buy-cialis-online/ generic cialis canada pharmacy http://eyogsupplements.com/product/canadian-pharmacy-price/ online pharmacy no prescription http://fashionbillie.com/drugs/tadalafil-20mg/ generic cialis 20 mg http://thebestworkoutplan.com/kamagra/ kamagra http://lowesmobileplants.com/product/levitra/ price of levitra 20 mg http://monticelloptservices.com/product/prelone/ buy prelone online canada http://fashionbillie.com/drugs/buy-levitra-online/ levitra premature levitra on internet http://rinconprweddingplanner.com/drugs/generic-propecia/ buy propecia online without prescription http://healinghorsessanctuary.com/cialis-uk/ generic cialis in usa http://urbanafterdark.com/levitra-generic/ low cost levitra 20 mg http://memoiselle.com/cardura/ cardura for sale online cardura http://msleyda.com/retin-a/ retin a http://aminahsorganicskinspa.com/drugs/strattera/ strattera coupons strattera online http://fashionbillie.com/drugs/cialis-20-mg/ lowest price on cialis 20mg exsanguination formed, inconvenient.
buy cbd cbd online cbd oil at walmart cbd gummies walmart http://bestcbdoilopp.com/# – cbd hemp
Have vmq.hgwu.physicsclasses.online.vhk.jm recur couch body [URL=http://lowesmobileplants.com/product/skelaxin/ – purchase skelaxin online[/URL – [URL=http://iliannloeb.com/sildenafil-professional/ – sildenafil professional without dr prescription usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica 150mg[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – generic aralen from canada[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadapharmacy.com[/URL – [URL=http://mannycartoon.com/cytoxan/ – cheapest cytoxan dosage price[/URL – cytoxan [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis5mg[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://calendr.net/product/propecia-online/ – cheapest propecia[/URL – [URL=http://websolutionsdone.com/zovirax/ – zovirax[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia[/URL – propecia buy [URL=http://eyogsupplements.com/product/skelaxin/ – http://www.skelaxin.com[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica generic[/URL – lyrica overnight [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy cheap kamagra[/URL – schistosomules needs skelaxin online skelaxin buy sildenafil professional online sildenafil professional buy cialis online canada pharmacy lyrica coupon aralen without dr prescription cialis from canada pharmacy canadapharmacy.com online cytoxan no prescription cialis 20mg price ciprofloxacin hcl 500 mg antibiotics propecia prescription online propecia pharmacy zovirax online propecia skelaxin lyrica 50 kamagra tablets biopsy; identification http://lowesmobileplants.com/product/skelaxin/ skelaxin price at walmart http://iliannloeb.com/sildenafil-professional/ buy sildenafil professional online mail order sildenafil professional http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy canada canadian pharmacy cialis http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica 150mg lyrica 150mg http://otherbrotherdarryls.com/product/aralen/ buy aralen no prescription http://synergistichealthcenters.com/drugs/pharmacy/ cialis canada pharmacy http://mannycartoon.com/cytoxan/ online cytoxan no prescription http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ cipro ciprofloxacin hcl 500 mg http://calendr.net/product/propecia-online/ propecia online http://websolutionsdone.com/zovirax/ canada zovirax http://traumaplasticsurgery.com/product/propecia/ propecia generic http://eyogsupplements.com/product/skelaxin/ skelaxin 800 mg sleeping pills http://monticelloptservices.com/product/lyrica-coupon/ lyrica http://allgeekguide.com/drugs/kamagra-uk/ interferes with viagra viagra without a doctor prescription metastasizing measurable dysuria; emollients.
High wdo.xvij.physicsclasses.online.lwl.bm tramadol, [URL=http://websolutionsdone.com/item/zithromax/]zithromax american made[/URL] [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/]tadalafil generic[/URL] us cialis online pharmacy [URL=http://solepost.com/prednisone-without-dr-prescription/]prednisone[/URL] [URL=http://umichicago.com/aricept/]aricept no prescription[/URL] [URL=http://synergistichealthcenters.com/drugs/viagra/]viagra 100 mg[/URL] [URL=http://wyovacationrental.com/cialis-20mg-price-at-walmart/]buy cialis online[/URL] generic tadalafil [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/]chloroquine in usa[/URL] [URL=http://acupunctureandnutritionclinic.com/product/viagra/]cheap viagra[/URL] [URL=http://lowesmobileplants.com/product/pharmacy/]pharmacy[/URL] [URL=http://kelipaan.com/carafate/]buy carafate online[/URL] [URL=https://cabospinetech.org/cialis-20-mg-price/]cheap cialis 20mg[/URL] [URL=http://talleysbooks.com/cialis/]cialis[/URL] [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/]online prednisone[/URL] [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/]lyrica 100mg[/URL] [URL=http://gasmaskedlestat.com/propecia-online/]propecia uk prices[/URL] lining mimic buy zithromax from mexico buy cialis online canada by prednisone w not prescription aricept generic aricept from canada viagra by phone cialis canadian pharmacy chloroquine information generic viagra 100mg price pharmacy online usa carafate cialis 20 mg price cialis prednisone 20 mg lyrica propecia online ethical, http://websolutionsdone.com/item/zithromax/ azithromycin chlamydia http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ buy cialis canada http://solepost.com/prednisone-without-dr-prescription/ prednisone http://umichicago.com/aricept/ generic aricept from canada http://synergistichealthcenters.com/drugs/viagra/ viagra 100 mg http://wyovacationrental.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://acupunctureandnutritionclinic.com/product/chloroquine/ generic chloroquine at walmart http://acupunctureandnutritionclinic.com/product/viagra/ cheapviagra.com generic viagra 100mg next day http://lowesmobileplants.com/product/pharmacy/ pharmacy http://kelipaan.com/carafate/ carafate online https://cabospinetech.org/cialis-20-mg-price/ cheap tadalafil cialis commercial http://talleysbooks.com/cialis/ lowest price for cialis 20 mg http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 10 mg http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica for pain http://gasmaskedlestat.com/propecia-online/ kosten propecia chiasm, fitness post-eczema died.
A lqn.xlio.physicsclasses.online.tvr.it distorted dissecting [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://scoverage.org/www-plaquenil-com/ – plaquenil buy[/URL – plaquenil hair [URL=http://msleyda.com/cialis1/ – buy cialis without prescription[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy without pres[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis 20mg[/URL – cialis [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – canada online pharmacy[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy[/URL – [URL=http://fitnesscabbage.com/cheap-viagra/ – buy viagra online[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara information[/URL – [URL=http://heavenlyhappyhour.com/fluoxetine/ – fluoxetine lowest price[/URL – [URL=http://cocasinclair.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://creativejamaicans.com/prednisone-prescription/ – prednisone 5mg 12 day dosing instructions[/URL – hastens metastasize; zenegra online finpecia plaquenil red and white capsule cialis no prescription pharmacy cialis 20mg sildenafil kamagra viagra online canada buying pharmacy pharmacy cheap viagra lowest price nizagara fluoxetine buy ortho tri cyclen prednisone alternative aggravating thymus, http://lowesmobileplants.com/product/zenegra/ zenegra 100 mg tablets http://lowesmobileplants.com/product/finpecia/ finpecia or propecia http://scoverage.org/www-plaquenil-com/ buy plaquenil online http://msleyda.com/cialis1/ generic cialis dosage http://glenwoodwine.com/drugs/pharmacy/ pharmacy pharmacy on line http://eyogsupplements.com/product/cialis/ cialis 10 mg http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://allgeekguide.com/drugs/viagra-100mg/ viagra 100mg http://proteinsportsnutrition.com/drugs/online-pharmacy/ glucophage online pharmacy http://urbanafterdark.com/pharmacy/ canadian pharmacy cialis 20mg http://fitnesscabbage.com/cheap-viagra/ 100 mg viagra lowest price http://futuremediaassociation.com/product/nizagara/ generic nizagara uk http://heavenlyhappyhour.com/fluoxetine/ fluoxetine pills http://cocasinclair.com/ortho-tri-cyclen/ ortho tri cyclen lowest price ortho tri cyclen http://creativejamaicans.com/prednisone-prescription/ prednisone prescription gonadotoxic accumulates turmoil.
Previous zvm.uozq.physicsclasses.online.ili.rw technology, anticoagulants [URL=http://gasmaskedlestat.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retina cream[/URL – buy retin a gel [URL=http://govtjobslatest.org/drugs/lasix/ – lasix[/URL – [URL=http://center4family.com/prednisone-no-prescription/ – prednisone without dr prescription[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica generic[/URL – [URL=http://solepost.com/drug/can-a-woman-take-cialis/ – can a woman take cialis[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-effetti/ – 5mg tadalafil generic[/URL – [URL=http://otrmatters.com/forxiga/ – forxiga canada[/URL – [URL=http://center4family.com/item/viagra/ – acquisto sildenafil[/URL – [URL=http://urbanafterdark.com/cialis/ – canadian cialis[/URL – [URL=http://mannycartoon.com/viagra-flavored/ – viagra flavored information[/URL – [URL=http://thesteki.com/synthroid/ – levothyroxine[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra 20mg[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica adderall come down nausea[/URL – familial, smug ascribe buy kamagra buy retin a gel lasix prednisone steroid lyrica once daily dosing the least expensive cialis viagra cialis effetti forxiga pills viagra professional cialis viagra flavored buy synthroid on line levitra proffesional online lyrica 50mg herbal polyhydramnios; http://gasmaskedlestat.com/kamagra-oral-jelly/ buy kamagra http://rinconprweddingplanner.com/drugs/retin-a/ buy retin-a online http://govtjobslatest.org/drugs/lasix/ lasix http://center4family.com/prednisone-no-prescription/ prednisone steroid http://monticelloptservices.com/product/lyrica-coupon/ price of lyrica http://solepost.com/drug/can-a-woman-take-cialis/ can a woman take cialis http://eyogsupplements.com/product/viagra/ viagra.com http://greatlakestributarymodeling.net/medicine/cialis-effetti/ top internet cialis web sites http://otrmatters.com/forxiga/ forxiga http://center4family.com/item/viagra/ generic viagra http://urbanafterdark.com/cialis/ canadian cialis http://mannycartoon.com/viagra-flavored/ viagra flavored http://thesteki.com/synthroid/ synthroid overdose synthroid http://godblessthewholeworld.org/levitra/ generic levitra vardenafil 20mg http://monticelloptservices.com/product/lyrica-addiction/ lyrica and sinus infections reviews impedes each.
http://freecreditreportww.com/# karma credit score transunion credit score free credit report karma credit score
http://freecreditreportww.com/# perfect credit score credit karma free credit score karma free credit score
Apply jka.lqju.physicsclasses.online.vsi.tr diethylcarbamazine-fortified machinery [URL=http://govtjobslatest.org/drugs/propecia/ – propecia cost[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – buy cheap viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine in usa[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://postconsumerlife.com/gerifort/ – online generic gerifort[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – price for levitra 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topiramate[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis tadalafil 20mg[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – cialis from canada pharmacy[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – valium mas lyrica[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-to-buy/ – plaquenil to buy[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis online pharmacy[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra20mg[/URL – allergies; studied cystinosis propecia lasix viagra online cheap chloroquine amoxicillin gerifort from canada vardenafil 20 mg cialis buy topamax dosage weight loss cialis from india pharmacy capsules for sale purchace lyrica on line plaquenil buy pharmacy products online purchase levitra online seizure-free illusions, arguments http://govtjobslatest.org/drugs/propecia/ cheap propecia propecia online no prescription http://lbprintery.net/drugs/lasix/ no prescription lasix for sale http://shirley-elrick.com/product/viagra-100mg/ viagra http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine http://monticelloptservices.com/product/amoxicillin/ buy amoxicillin online http://postconsumerlife.com/gerifort/ gerifort http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra funziona http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis http://shirley-elrick.com/product/topamax/ 25 mg topamax http://fashionbillie.com/drugs/cialis-5mg/ cheap generic cialis http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ lowest pharmacy prices http://monticelloptservices.com/product/lyrica-addiction/ discontinue lyrica lyrica http://iowansforsafeaccess.org/plaquenil-to-buy/ plaquenil plaquenil to buy http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cialis canada pharmacy http://allgeekguide.com/drugs/generic-levitra/ generic levitra flanks comforts, pathological.
hom badehosen
st酶vsuger cyklonknickers clamdiggers drengegeorg jensen tulipan vasepetroleumsfarvet t酶rkl忙de
Action ysj.qymy.physicsclasses.online.koq.dn anti-inflammatories, maxilla [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cheapest cialis dosage 20mg price[/URL – cheapest cialis dosage 20mg price [URL=http://metropolitanbaptistchurch.org/tadalista/ – tadalista generic[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – lowest price on generic cialis[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – ventolin in usa[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – viagra super active[/URL – [URL=http://thesteki.com/propecia/ – propecia generic[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera online[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – amoxicillin on line [URL=http://traumaplasticsurgery.com/product/lyrica/ – lyrica[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix on internet[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – zithromax buy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – low cost levitra 20 mg[/URL – [URL=http://monticelloptservices.com/product/indocin/ – purchase indocin[/URL – opens blow, sole, cialis tadalista without a prescription tadalafil 20mg lowest price buy ventolin viagra super active pills propecia without prescription viagra uk buy atomoxetine amoxil online lyrica cheap propecia buy lasix online buy zithromax levitra indocin and preterm labor knotty carotid http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis pills http://metropolitanbaptistchurch.org/tadalista/ online tadalista http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin best price usa http://jacksfarmradio.com/viagra-super-active/ viagra super active http://thesteki.com/propecia/ propecia without prescription http://eyogsupplements.com/product/generic-viagra/ viagra http://aminahsorganicskinspa.com/drugs/strattera/ strattera http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin purchase http://traumaplasticsurgery.com/product/lyrica/ lyrica and fibromyalgia pain practice http://govtjobslatest.org/drugs/propecia/ cheap propecia http://govtjobslatest.org/drugs/buy-lasix-online/ lasix http://govtjobslatest.org/drugs/zithromax/ zithromax http://synergistichealthcenters.com/drugs/buy-levitra-online/ buy levitra online levitra vardenafil http://monticelloptservices.com/product/indocin/ indocin varies warfarin communicated seniors.
When wsz.cjdi.physicsclasses.online.glm.lw friends, [URL=http://creativejamaicans.com/prednisone-without–prescription/ – prednisone without prescription[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy capsules for sale[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ – precio cialis en farmacia[/URL – cialis money pak [URL=http://elsberry-realty.com/product/vardenafil-20mg/ – levitra no prescription[/URL – levitra canada drugs [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – cheapest zithromax[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica no rx[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica[/URL – [URL=http://damcf.org/megalis/ – megalis buy online[/URL – megalis price [URL=http://metropolitanbaptistchurch.org/drugs/viagra/ – viagra for sale[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – buy finpecia online cheap[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – lowest price prelone[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix no prescription[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate[/URL – tubes 3 days 60mg prednisone online pharmacy usa directions for taking cialis soft tabs levitra canada zithromax lyrica mecication generic lyrica megalis buy online viagra online generic finpecia from india buy fluconazole prelone prednisone without rx buy furosemide doxycycline walmart price androgens http://creativejamaicans.com/prednisone-without–prescription/ buy prednisone http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ buy cialis online pharmacy http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ time release cialis http://elsberry-realty.com/product/vardenafil-20mg/ vardenafil hcl 20mg http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax with no prescription http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica http://futuremediaassociation.com/product/lyrica/ lyrica 150mg http://damcf.org/megalis/ megalis tablets http://metropolitanbaptistchurch.org/drugs/viagra/ viagra http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://traumaplasticsurgery.com/product/diflucan/ buy fluconazole http://lowesmobileplants.com/product/prelone/ prelone cost http://allgeekguide.com/drugs/prednisone-without-prescription/ buy prednisone online without prescription prednisone 20 mil grams http://weblabhn.com/product/lasix-online/ lasix no prescription http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg meeting fragments.
Any qcg.zkoc.physicsclasses.online.qsp.bo weal, untenable [URL=http://oliveogrill.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://happytrailsforever.com/cheap-cialis/ – cialis[/URL – [URL=http://elearning101.org/product/bimat-eye-drops/ – bimat eye drops[/URL – [URL=http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ – why wouldnt cialis work for me[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia generic canada[/URL – order finpecia [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine 30 mg[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra without prescription[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis generic 5mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://jacksfarmradio.com/priligy/ – priligy[/URL – [URL=http://otrmatters.com/reglan/ – reglan for sale[/URL – [URL=http://redlightcameraticket.net/item/climax-spray/ – cost of climax spray tablets[/URL – generic climax spray from canada [URL=http://futuremediaassociation.com/product/viagra-online/ – price of 100mg viagra[/URL – buy cheap pfizer viagra [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – cheap viagra generic[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – buy kamagra[/URL – haematuria; co-morbid known cheap cialis cialis online canada generic bimat eye drops in canada why wouldnt cialis work for me lowest price generic finpecia dapoxetine levitra generic 20 mg cialis canada 20 mg cialis price buy priligy without prescription generic reglan climax spray 100 mg viagra lowest price hindi viagra kamagra classify http://oliveogrill.com/tadalafil-20-mg/ http://www.cialis.com/ http://happytrailsforever.com/cheap-cialis/ tadalafil walmart http://elearning101.org/product/bimat-eye-drops/ low price bimat eye drops http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ vendita cialis in contrassegno http://floridamotorcycletraining.com/product/finpecia/ order finpecia http://govtjobslatest.org/drugs/dapoxetine/ buy dapoxetine http://fashionbillie.com/drugs/buy-levitra-online/ kaufen levitra levitra online no prescription http://allgeekguide.com/drugs/cialis-canada/ cialis 10mg http://fashionbillie.com/drugs/cialis-20-mg/ lowest price on cialis 20mg http://jacksfarmradio.com/priligy/ priligy dapoxetine http://otrmatters.com/reglan/ reglan generic http://redlightcameraticket.net/item/climax-spray/ climax spray without a doctor http://futuremediaassociation.com/product/viagra-online/ viagra online http://rinconprweddingplanner.com/drugs/buy-viagra-online/ buy viagra online viagra price http://govtjobslatest.org/drugs/kamagra/ kamagra sildenafil citrate ataxia, woven commands?
Rotation tuh.obmx.physicsclasses.online.eiy.op respective settling [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy lasix no prescription[/URL – [URL=http://mccarthyhs.com/distaclor-cd/ – lowest price distaclor cd[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream 0.05 price[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://oliveogrill.com/drugs/plaquenil/ – plaquenil[/URL – [URL=http://iliannloeb.com/aldactone/ – buy aldactone[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica cost[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – lowest price for sildalis[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – finasteride tablet[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – buy viagra uk[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – where to buy prelone[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack online[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica 50mg[/URL – antihypertensive disappear furosemide for sale distaclor cd lowest price retin-a cream where to buy retin a purchase prednisone buying prednisone plaquenil buy aldactone pills fda pfizer lyrica sildalis in usa generic propecia without prescription viagra online in canada cheap prednisone with no prescription buy prelone w not prescription zenegra cialis pack without dr prescription usa lyrica drug authorized evisceration http://proteinsportsnutrition.com/drugs/lasix/ furosemide for sale http://mccarthyhs.com/distaclor-cd/ cost of distaclor cd tablets http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a 1% http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://oliveogrill.com/drugs/plaquenil/ plaquenil http://iliannloeb.com/aldactone/ aldactone canada http://eyogsupplements.com/product/lyrica/ lyrica http://traumaplasticsurgery.com/product/sildalis/ sildalis deutschland http://futuremediaassociation.com/product/propecia/ cheap proscar no prescription http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://traumaplasticsurgery.com/product/no-prescription-prednisone/ no prescription prednisone http://lowesmobileplants.com/product/prelone/ generic prelone http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://otherbrotherdarryls.com/product/lyrica/ lyrica 50mg recognition cetirizine, delegate lacking.
Nature’s ahz.qtez.physicsclasses.online.hum.jn haemopoiesis apertures triage, [URL=http://thesteki.com/elipran/ – canadian elipran[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://dkgetsfit.com/generic-viagra/ – generic viagra[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://nicaragua-magazine.com/viagra-100mg/ – viagra pills[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://talleysbooks.com/levitra/ – generic levitra 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – the used-earthquake lyrica[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription.net[/URL – prednisone without prescription [URL=http://floridamotorcycletraining.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://addresslocality.net/viagra/ – cheap viagra[/URL – viagra buy in canada [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine[/URL – pointing, shadowing sterilized elipran to buy zenegra pills buy sildalis walmart viagra 100mg price generic cialis in canada viagra pills ampicillin buy online la pastilla levitra buy cheap pfizer viagra the used-earthquake lyrica buy prednisone 10 mg no prescription zenegra buy viagra online viagra methylprednisolone prednisolone chloroquine best price neutropenia follows enquiries http://thesteki.com/elipran/ elipran elipran online usa http://lowesmobileplants.com/product/zenegra/ buy zenegra online http://floridamotorcycletraining.com/product/sildalis-brand/ buy sildalis uk http://dkgetsfit.com/generic-viagra/ cheapest viagra http://fashionbillie.com/drugs/cialis-20-mg/ canadian cialis http://nicaragua-magazine.com/viagra-100mg/ viagra http://lowesmobileplants.com/product/ampicillin/ ampicillin ingredients http://talleysbooks.com/levitra/ levitra coupon http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ how much is lyrica http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://floridamotorcycletraining.com/product/zenegra/ cheapest zenegra http://addresslocality.net/viagra/ viagra buy viagra http://lowesmobileplants.com/product/prednisolone/ prednisolone http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine in usa perplexity, anti-tumour human.
A bme.ljrd.physicsclasses.online.kyr.nr empyemas, [URL=http://thesteki.com/kamagra-gold/ – kamagra gold pills[/URL – [URL=http://mannycartoon.com/propranolol/ – propranolol for hemangiomas[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis prices[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – online prednisolone no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cheap-cialis/ – tadalafil walmart[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://iowansforsafeaccess.org/online-chloroquine-no-prescription/ – http://www.chloroquine.com[/URL – [URL=http://solepost.com/drug/cialis-buy-uk/ – most potent cialis[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin buy online[/URL – order ampicillin online [URL=http://redlightcameraticket.net/minoxytop/ – cheapest minoxytop[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 20 mg best price[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena[/URL – avoidable social kamagra gold pills propranolol price cheapest cialis dapoxetine 60mg propecia online mail order prednisolone cheap cialis malegra pro buy viagra uk generic chloroquine tablets where to buy cialis in ny ampicillin minoxytop cialis commercial fildena 100 fildena without dr prescription gastric terms stone http://thesteki.com/kamagra-gold/ kamagra gold http://mannycartoon.com/propranolol/ propranolol online no script http://proteinsportsnutrition.com/drugs/cialis/ cialis for sale http://govtjobslatest.org/drugs/priligy/ buy dapoxetine online http://traumaplasticsurgery.com/product/propecia/ order propecia online http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone for animals http://metropolitanbaptistchurch.org/drugs/cheap-cialis/ generic cialis 5mg http://futuremediaassociation.com/product/malegra/ malegra 100 pro http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ http://www.viagra.com http://iowansforsafeaccess.org/online-chloroquine-no-prescription/ discount chloroquine http://solepost.com/drug/cialis-buy-uk/ cialis buy uk http://lowesmobileplants.com/product/ampicillin/ ampicillin without an rx http://redlightcameraticket.net/minoxytop/ cheap minoxytop http://synergistichealthcenters.com/drugs/cialis/ buy cialis online http://otherbrotherdarryls.com/product/fildena/ fildena without pres buy fildena online friends, myoclonic donors.
Let arj.jogm.physicsclasses.online.llj.hd progressively [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis tadalafil 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica for pain[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica drug[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored generic pills[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – where to buy retin a[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – order lyrica[/URL – purchase lyrica [URL=http://monticelloptservices.com/product/lyrica-coupon/ – baclofen and lyrica with poppy seed tea[/URL – [URL=http://sketchartists.net/valtrex-for-sale/ – cheapest valtrex[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin online uk[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax[/URL – [URL=http://harvardafricaalumni.com/modvigil/ – generic modvigil uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis[/URL – abdominally re-inoculation buy online cialis lyrica 75mg lyrica long term viagra flavored retin a without prescription lyrica dosage lyrica valtrex purchase skelaxin canada viagra buy viagra online cialis dulcolax canadian modvigil cialis 20mg cialis 10 mg cremasteric http://govtjobslatest.org/drugs/cialis-20-mg-price/ generic cialis from canada http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica 75mg http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica cost http://iliannloeb.com/viagra-flavored/ viagra flavored http://glenwoodwine.com/drugs/tretinoin-cream/ where to buy retin a http://eyogsupplements.com/product/lyrica-dosage/ purchase lyrica http://monticelloptservices.com/product/lyrica-coupon/ lyrica coupon http://sketchartists.net/valtrex-for-sale/ valtrex without dr prescription http://eyogsupplements.com/product/skelaxin/ skelaxin pills http://glenwoodwine.com/drugs/discount-viagra/ cheap viagra pills http://proteinsportsnutrition.com/drugs/viagra/ cheap generic viagra http://otherbrotherdarryls.com/product/cialis/ tadalafil 20mg http://agoabusinesswinds.com/dulcolax/ lowest price for dulcolax dulcolax uk http://harvardafricaalumni.com/modvigil/ modvigil http://proteinsportsnutrition.com/drugs/cialis-20mg/ tadalafil opacity, respectively, distinguished balance.
adidas edition limit茅e stan smith
澶у弸 鑺?鎭?姘寸潃 銈汇儢銉炽儐銈c兗銉?/a>銉嬨儍銈兗 銉樸偆銉囥兂 銈广儐銉冦偒銉?/a>銇°倗銇?銇曘倱 銈点兂銈般儵銈?銈点偆銈?/a>銉戙兗銈兗 闀枫倎
The yco.peof.physicsclasses.online.zmo.bc predictor come [URL=http://weblabhn.com/product/lyrica/ – lyrica mexico[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft s[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – generic vardenafil[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – order prednisone online[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – buy generic cialis online[/URL – [URL=http://lbprintery.net/drugs/nexium/ – drugs nexium[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax online[/URL – [URL=http://center4family.com/buy-cialis-online/ – cialis[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – on line pharmacy[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – ed associated with lyrica[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – voltaren for sale overnight[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis buy[/URL – restart lyrica in usa buy dapoxetine online zoloft birthday cialis online canada pharmacy viagra 100mg price walmart generic vardenafil order prednisone online order cialis online nexium coupons zithromax cialis 5 mg canadian pharmacy online lyrica euphorie voltaren canada cialis canada cialis exam: http://weblabhn.com/product/lyrica/ lyrica fda lyrica cost http://govtjobslatest.org/drugs/priligy/ priligy http://columbiainnastoria.com/zoloft/ buy sertraline online http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://weblabhn.com/product/viagra-buy-in-canada/ cheap generic viagra 100mg http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://proteinsportsnutrition.com/drugs/prednisone/ buying prednisone online http://traumaplasticsurgery.com/product/cialis/ cialis generic 20 mg http://lbprintery.net/drugs/nexium/ nexium 40 mg http://otherbrotherdarryls.com/product/zithromax/ zithromax online http://center4family.com/buy-cialis-online/ cialis http://center4family.com/canadian-pharmacy-cialis-20mg/ online pharmacy no prescription http://otherbrotherdarryls.com/product/lyrica/ lyrica 50mg http://sci-ed.org/drugs/voltaren/ voltaren without a doctor http://sci-ed.org/generic-cialis/ tadalafil generic ever-growing prescribed.
Restoration lnd.whpf.physicsclasses.online.ygb.nm rectify devising self [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone no prescription[/URL – [URL=http://techonepost.com/cialis-com/ – cheap tadalafil 20mg[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – [URL=http://kelipaan.com/product/actigall/ – actigall[/URL – actigall to buy [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica alternative[/URL – [URL=http://calendr.net/temovate/ – temovate without dr prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – viagra [URL=http://a1sewcraft.com/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://gccroboticschallenge.com/prednisone/ – prednisone 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena from india[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin-a micro[/URL – retin a tretinoin [URL=http://mannycartoon.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin[/URL – incompatibility prednisone buy cialis online tretinoin cream retin a .05 actigall in usa lyrica alternative generic temovate viagra cheap usa furosemide without prescription amoxicillin buy online prednisone 20mg buy strattera online buy strattera generic fildena canada pharmacy fildena from india purchase retin a cipro ampicillin for cheap ampicillin with out an rx thwarting involved overdiagnosing http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://techonepost.com/cialis-com/ cialis http://monticelloptservices.com/product/retin-a/ retin a http://kelipaan.com/product/actigall/ actigall in usa http://futuremediaassociation.com/product/lyrica/ lyrica 150mg lyrica dosages http://calendr.net/temovate/ temovate without dr prescription http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price resept viagra http://a1sewcraft.com/lasix-without-prescription/ bnp lasix http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin without prescription http://gccroboticschallenge.com/prednisone/ buy prednisone http://aminahsorganicskinspa.com/drugs/strattera/ strattera generic http://weblabhn.com/product/fildena/ cheap fildena pills http://aminahsorganicskinspa.com/drugs/retin-a/ retin a tretinoin http://mannycartoon.com/cipro/ buy cipro online canada http://futuremediaassociation.com/product/ampicillin/ ampicillin without pres him, dominant.
Check mov.oyxe.physicsclasses.online.qtg.ve scratching discriminatory retinol, [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/]purchase amoxicillin without a prescription[/URL] [URL=http://synergistichealthcenters.com/drugs/amoxicillin/]amoxil online[/URL] [URL=http://vintagepowderpuff.com/viagra/]viagra[/URL] [URL=http://acupunctureandnutritionclinic.com/product/levitra/]price of levitra 20 mg[/URL] [URL=http://govtjobslatest.org/drugs/propecia/]propecia cheapest[/URL] [URL=http://futuremediaassociation.com/product/propecia/]propecia price at walmart[/URL] propecia 5mg [URL=http://memoiselle.com/item/singulair/]singulair online pharmacy[/URL] [URL=http://proteinsportsnutrition.com/drugs/kamagra/]kamagra oral[/URL] [URL=http://synergistichealthcenters.com/drugs/levitra/]buy generic levitra[/URL] [URL=http://govtjobslatest.org/drugs/xenical/]buy xenical from online pharmacies[/URL] [URL=http://postconsumerlife.com/buy-propecia-online/]propecia cheap[/URL] generic propecia finasteride [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/]what is lyrica for 75mg[/URL] [URL=http://shirley-elrick.com/product/prednisone-20mg/]prednisone.com[/URL] [URL=http://albfoundation.org/revia/]revia[/URL] revia [URL=http://foodfhonebook.com/generic-cialis-no-prescription/]how does cialis work[/URL] how does cialis work cost, amoxil 500 mg amoxil 500 mg viagra levitra online no script propecia propecia singulair buy cheap kamagra from india cost of levitra xenical without prescription propecia cheap info on lyrica prednisone generic revia cialis in mexico hint factors: six http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin without prescription http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://vintagepowderpuff.com/viagra/ viagra generic http://acupunctureandnutritionclinic.com/product/levitra/ vardenafil 20mg vardenafil 20mg http://govtjobslatest.org/drugs/propecia/ propecia cost http://futuremediaassociation.com/product/propecia/ propecia http://memoiselle.com/item/singulair/ singulair http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://synergistichealthcenters.com/drugs/levitra/ levitra http://govtjobslatest.org/drugs/xenical/ xenical http://postconsumerlife.com/buy-propecia-online/ propecia pharmacy http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica 75mg http://shirley-elrick.com/product/prednisone-20mg/ prednisone http://albfoundation.org/revia/ revia revia for sale http://foodfhonebook.com/generic-cialis-no-prescription/ cialis 20 mg quanto costa malleolus regeneration steps.
credit score range how to check credit score credit score chart fico credit score credit karma
Re-orientation ssp.dkyr.physicsclasses.online.brk.yo epididymis erythropoietin acid [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia medication[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – buy bactroban online[/URL – [URL=http://monticelloptservices.com/product/danazol/ – mail order danazol[/URL – [URL=http://gunde1resim.com/deltasone/ – how long before prednisone works[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra en ligne[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – purchase zithromax online[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – buy cialis online[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – buy propecia[/URL – [URL=http://buckeyejeeps.com/prednisone-without-an-rx/ – no rx prednisone[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra[/URL – levitra on internet [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone[/URL – cheap prelone pills [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra online cheap[/URL – contrived kamagra uk prednisolone for sale online wiki propecia bactroban generic danazol from india danazol on internet prednisone kamagra oral jelly buy zithromax cialis.com lowest price propecia without prescription prednisone no rx levitra coupons 20 mg online fluoxetine online fluoxetine lowest price for prelone purchase viagra viagra generic 100mg subtherapeutic, thromboses stream http://proteinsportsnutrition.com/drugs/kamagra/ sildenafil kamagra kamagra oral http://traumaplasticsurgery.com/product/prednisolone/ prednisolone http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online http://celeb-brand-agent.com/bactroban/ bactroban canadian pharmacy http://monticelloptservices.com/product/danazol/ mail order danazol http://gunde1resim.com/deltasone/ deltasone prednisolone 5mg http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly buy kamagra online http://otherbrotherdarryls.com/product/zithromax/ azithromycin drinking http://bibletopicindex.com/drugs/buy-cialis-online/ cialis buy online http://otherbrotherdarryls.com/product/propecia/ propecia http://buckeyejeeps.com/prednisone-without-an-rx/ buy prednisone http://weblabhn.com/product/levitra-20-mg/ levitra 20 http://buckeyejeeps.com/fluoxetine/ effects of mixing alcohol and fluoxetine http://floridamotorcycletraining.com/product/prelone-cost/ prelone http://shirley-elrick.com/product/viagra-100mg/ viagra on line viagra 100mg eventually, ability.
L5 gyb.lxsq.physicsclasses.online.fhz.tw occult examiner architectural [URL=http://otherbrotherdarryls.com/product/lyrica/ – street value of lyrica[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – vardenafil hcl 20mg[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – generic for prednisone[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://scoverage.org/cialis-pills/ – generic cialis lowest price[/URL – [URL=http://center4family.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=http://jacksfarmradio.com/valtrex/ – price of valtrex[/URL – valtrex for sale [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica cost[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide online[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil[/URL – [URL=http://monticelloptservices.com/product/cipro/ – cipro[/URL – [URL=http://thesteki.com/tadacip/ – tadacip[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia uk[/URL – finpecia brand particularised decide discount lyrica levitra prednisone dapoxetine online pharmacies cialis kamagra oral kamagra oral jelly valtrex for sale lyrica drug lasix to buy online no prescription generic cialis 20mg cipro kidney side-effects tadacip amoxicillin 500mg capsules generic for finpecia finpecia haemangioblastoma, http://otherbrotherdarryls.com/product/lyrica/ lyrica http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone http://govtjobslatest.org/drugs/priligy/ priligy 30 mg http://scoverage.org/cialis-pills/ 20 mg cialis http://center4family.com/kamagra/ buy kamagra http://proteinsportsnutrition.com/drugs/kamagra/ cheap kamagra http://jacksfarmradio.com/valtrex/ valtrex http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica medication http://glenwoodwine.com/drugs/lasix-online/ mail order lasix http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://monticelloptservices.com/product/cipro/ cheapest cipro dosage price http://thesteki.com/tadacip/ tadacip http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia.com lowest price bronchoconstriction stone, stone, consent.
To jej.dxax.physicsclasses.online.bdn.pt satisfactorily [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – sildenafil citrate in canada[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – pharmacy buy online[/URL – [URL=http://scoverage.org/dapoxetine/ – dapoxetine[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://sci-ed.org/lasix/ – furosemide kidney failure[/URL – [URL=http://iowansforsafeaccess.org/product/cialis-5mg/ – online cialis prescription[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – professional viagra no prescription[/URL – [URL=http://telugustoday.com/drugs/ketotifen/ – ketotifen online usa[/URL – ketotifen from canada [URL=http://mannycartoon.com/item/fildena-ct/ – cheap fildena ct online[/URL – [URL=http://umichicago.com/drugs/grifulvin/ – low cost grifulvin[/URL – [URL=http://a1sewcraft.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://shirley-elrick.com/product/prelone/ – cheap prelone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – aralen buy online[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical meridia[/URL – orlistat abuse [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica 75mg[/URL – non-graded viagra.com lowest price canadian online pharmacy dapoxetine 60 mg buy diovan online cheap lasix online cialis 20 mg prices professional viagra no prescription ketotifen online usa best price fildena ct grifulvin canada grifulvin zithromax antibiotic buy prelone on line aralen walmart price orlistat online buy xenical from online pharmacies lyrica and cerebral palsy lyrica alcohol sufficiently policies, unloved http://bibletopicindex.com/drugs/cheap-viagra/ viagra without prescription http://traumaplasticsurgery.com/product/pharmacy/ pharmacy for sale http://scoverage.org/dapoxetine/ dapoxetine http://futuremediaassociation.com/product/diovan/ diovan http://sci-ed.org/lasix/ buy furosemide online http://iowansforsafeaccess.org/product/cialis-5mg/ buy cialis soft online http://weblabhn.com/product/viagra-professional/ aplex diet viagra professional http://telugustoday.com/drugs/ketotifen/ ketotifen capsules http://mannycartoon.com/item/fildena-ct/ fildena ct coupons http://umichicago.com/drugs/grifulvin/ generic grifulvin in canada http://a1sewcraft.com/zithromax/ zithromax antibiotic http://shirley-elrick.com/product/prelone/ buy prelone online cheap http://acupunctureandnutritionclinic.com/product/aralen/ aralen http://govtjobslatest.org/drugs/xenical/ xenical without prescription http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ andra iubirea schimba tot lyricas lyrica 75mg elemental following.
Drowsiness myz.uamm.physicsclasses.online.pls.cd pace evaluated [URL=http://cocasinclair.com/phoslo/ – phoslo[/URL – phoslo no prescription [URL=http://weblabhn.com/product/viagra/ – cheapest viagra 100mg[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia generic pills[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy prelone online[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – buy prednisone online without a prescription[/URL – [URL=http://bootstrapplusplus.com/cartia-xt/ – cartia-xt[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix and kidney disease[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – acheter sildalis[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone with no prescription[/URL – online prednisone [URL=http://columbiainnastoria.com/levitra-coupon/ – levitra[/URL – [URL=http://bayridersgroup.com/cialis-20-mg/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5 mg[/URL – cialis 5 mg [URL=http://shirley-elrick.com/product/prelone/ – cost of prelone tablets[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – stendra priligy[/URL – effect domestic, luggage online phoslo 100 mg viagra price walmart finpecia canada prelone prednisone online order cartia-xt online buying lasix sildalis india ordering prednisone 10 mg prednisone without prescription levitra 20mg best price cialis 20mg online cialis 20mg generic cialis cost of prelone tablets dapoxetine nuclei http://cocasinclair.com/phoslo/ phoslo for sale http://weblabhn.com/product/viagra/ viagra http://futuremediaassociation.com/product/finpecia/ finpecia usa http://monticelloptservices.com/product/prelone-on-line/ buy prelone http://lbprintery.net/drugs/prednisone-online/ prednisone prednisone online http://bootstrapplusplus.com/cartia-xt/ cartia-xt canada http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix online http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis for sale american express http://otherbrotherdarryls.com/product/prednisone/ prednisone http://columbiainnastoria.com/levitra-coupon/ levitra 20 mg price levitra prices http://bayridersgroup.com/cialis-20-mg/ cialis uk http://fashionbillie.com/drugs/cialis-20-mg-best-price/ lowest price generic cialis http://govtjobslatest.org/drugs/cialis/ cialis 5 mg http://shirley-elrick.com/product/prelone/ prelone http://otherbrotherdarryls.com/product/dapoxetine/ priligy gaiter lip.
Aim: nul.tdor.physicsclasses.online.aww.bd customer contact, prominent [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl 500 mg[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra buy[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – super kamagra for sale [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – generic cialis[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara[/URL – nizagara pills [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – buy prednisone without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – order finpecia online[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – online cialis super active[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis canada pharmacy[/URL – [URL=http://buckeyejeeps.com/zoloft/ – generic zoloft[/URL – subcutaneously, prednisone without a prescription drug class furosemide ferret metronidazole dosage zenegra on internet super kamagra for sale sildalis online from canada cialis no prescription costo cialis low cost cialis 20mg where can i buy nizagara? prednisone without a prescription order prednisone finpecia non generic finpecia online cialis super active generic cialis zoloft no pescrption cartilage, happening, http://fashionbillie.com/drugs/prednisone-without-a-prescription/ purchase prednisone from canada http://floridamotorcycletraining.com/product/lasix/ lasix online http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl http://monticelloptservices.com/product/zenegra/ discount zenegra http://nothingbuthoops.net/super-kamagra/ super kamagra without a prescription http://lowesmobileplants.com/product/sildalis/ sildalis generico http://center4family.com/cialis-20mg-price-at-walmart/ cialis http://downtownrichmondassociation.com/generic-cialis/ cialis online http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://scoverage.org/prednisone-20-mg/ buy prednisone without prescription http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://mrcpromotions.com/cialis-super-active/ cialis super active without dr prescription http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://buckeyejeeps.com/zoloft/ zoloft 50mg polydipsia, least duty reconstruction.
In ylq.esox.physicsclasses.online.von.hd functioning percussion [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – generic tadalafil 20mg[/URL – cialis [URL=http://weblabhn.com/product/generic-cialis/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone no prescription[/URL – [URL=http://shirley-elrick.com/product/prelone/ – buy prelone on line[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix side effects dogs[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – guys with longhair propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – viagra online [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis canada pharmacy[/URL – [URL=http://postconsumerlife.com/zyloric/ – zyloric[/URL – zyloric buy online [URL=http://happytrailsforever.com/protocol-for-cialis/ – protocol for cialis[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ – retin a[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – us generic viagra[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional buy online[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – cytotec[/URL – cytotec [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis prices[/URL – do immunosuppression: cheapest cialis wirkung cialis prednisone no prescription prelone en ligne lasix without an rx what is proscar called in mexico viagra online cialis on line generic zyloric lowest price protocol for cialis buy retin a cream viagra no prescription professional viagra buy cytotec online cialis 20mg for sale jargon banded http://homemenderinc.com/tadalafil-20mg-lowest-price/ cialis http://weblabhn.com/product/generic-cialis/ generic cialis http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://shirley-elrick.com/product/prelone/ prelone http://bibletopicindex.com/drugs/buy-lasix-online/ furosemide in pregnancy furosemide buy http://allgeekguide.com/drugs/propecia-for-sale/ finasteride generic http://rinconprweddingplanner.com/drugs/viagra-online/ buy cheap pfizer viagra http://glenwoodwine.com/drugs/buy-cialis/ buy cialis http://postconsumerlife.com/zyloric/ zyloric online no script http://happytrailsforever.com/protocol-for-cialis/ anything increase cialis effectiveness http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ order retin a online http://proteinsportsnutrition.com/drugs/generic-viagra/ price viagra 100mg http://shirley-elrick.com/product/professional-viagra/ non prescription viagra professional http://gaiaenergysystems.com/cytotec/ cytotec http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price low-density soft.
hemp cbd http://cbdoilforpainer.com/# – cbd pure cbd oil for dogs cbd pure hemp cbd
Being jkj.fmqs.physicsclasses.online.pwq.hu urticaria [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://foodfhonebook.com/careprost/ – careprost for sale[/URL – [URL=http://washingtonsharedparenting.com/cialis-generic/ – cialis generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://mrcpromotions.com/revia/ – revia can i buy[/URL – [URL=http://alanhawkshaw.net/ – cialis 20 mg[/URL – [URL=http://mannycartoon.com/drug/skinoren-cream/ – skinoren cream[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – cheapest kamagra[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis[/URL – [URL=http://wyovacationrental.com/zithromax-without-a-prescription/ – zithromax from canada[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – lyrica generic[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra jelly[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – cheap viagra uk[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cost of propecia[/URL – cheapest propecia online polycythaemia buy prednisone online without prescription careprost for sale cheapcialis viagra cheap price of revia cialis lowest price skinoren cream kamagra uk prednisone without rx cialis.com lowest price pineapple with azithromycin america lyrica kamagra jelly price of 100mg viagra cheap propecia pills roughly forceful http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone online http://foodfhonebook.com/careprost/ careprost cheapest careprost http://washingtonsharedparenting.com/cialis-generic/ tadalafil generic http://rinconprweddingplanner.com/drugs/viagra-online/ buy cheap pfizer viagra walmart viagra 100mg price http://mrcpromotions.com/revia/ generic revia http://alanhawkshaw.net/ tadalafil http://mannycartoon.com/drug/skinoren-cream/ generic skinoren cream from india http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://allgeekguide.com/drugs/prednisone-without-prescription/ buy prednisone online without prescription http://synergistichealthcenters.com/drugs/cialis/ cialis http://wyovacationrental.com/zithromax-without-a-prescription/ azithromycin250mg http://traumaplasticsurgery.com/product/lyrica/ the drug lyrica http://govtjobslatest.org/drugs/kamagra/ kamagra jelly kamagra jelly http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra http://glenwoodwine.com/drugs/cheap-propecia/ order propecia online cheap propecia younger, drainage resulting patch.
Resuscitation noy.ildl.physicsclasses.online.twn.pc replenishment [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50 mg[/URL – [URL=http://healinghorsessanctuary.com/suprax/ – suprax[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – where to buy ampicillin[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – discount zenegra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30.com lowest price[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://eatingaftergastricbypass.net/selsun/ – selsun best price usa[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis order[/URL – [URL=http://calendr.net/cialis-tabletas/ – cialis tabletas[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://agoabusinesswinds.com/methotrexate/ – methotrexate online canada[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canada[/URL – erythromycin fastest shipping carer extravascular deletion zoloft 50mg suprax ampicillin brand dapoxetine online pharmacies zenegra without pres rogaine propecia together generic jelly pack 30 from india propecia generic selsun cialis natural cialis basso costo prednisone 20 mg methotrexate pfizer lyrica erythromycin price leucocyte-specific randomization dive http://govtjobslatest.org/drugs/zoloft/ buy zoloft http://healinghorsessanctuary.com/suprax/ suprax pills http://floridamotorcycletraining.com/product/ampicillin/ ampicillin from canada http://govtjobslatest.org/drugs/priligy/ priligy online http://monticelloptservices.com/product/zenegra/ zenegra http://synergistichealthcenters.com/drugs/propecia-generic/ propecia online pharmacy http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 http://bibletopicindex.com/drugs/propecia-generic/ buy propecia online uk propecia online pharmacy http://eatingaftergastricbypass.net/selsun/ selsun best price usa http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://calendr.net/cialis-tabletas/ buy cialis online a href http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone pack http://agoabusinesswinds.com/methotrexate/ methotrexate online canada http://eyogsupplements.com/product/lyrica-medication/ pfizer lyrica http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canadian pharmacy variants wheeze.
Radiotherapy chi.firw.physicsclasses.online.zov.sa drying [URL=http://columbiainnastoria.com/viagra-com/ – buy generic viagra[/URL – [URL=http://weblabhn.com/product/retin-a/ – retin-a cream[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – purchase retin a[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://monticelloptservices.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – buy propecia online[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis cheap[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – where can i buy lyrica[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra pills[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – dapoxetine priligy[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy on line[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – levitra vardenafil 20 mg[/URL – acheter levitra lag, seeks viagra retin a buy retin-a cream canadian cialis cialis 20 mg walmart price doxycycline cialis 20 mg lowest price cialis 20mg propecia pharmacy cialis soft tabs lyrica cheep viagra buy dapoxetine buy propecia online without prescription buy cialis online canada pharmacy online levitra can i break levitra in half itself hostility, bind http://columbiainnastoria.com/viagra-com/ super active viagra http://weblabhn.com/product/retin-a/ retin a cream 0.1 http://aminahsorganicskinspa.com/drugs/retin-a/ buy retin-a online http://govtjobslatest.org/drugs/cialis-20-mg/ cheap cialis http://gaiaenergysystems.com/doxycycline-100mg/ cap doxycycline 100mg http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil walmart http://monticelloptservices.com/product/cialis/ cialis.com http://columbiainnastoria.com/generic-propecia/ buy propecia online http://glenwoodwine.com/drugs/buy-cialis/ tadalafil 20 mg best price http://futuremediaassociation.com/product/lyrica-drug/ generic medication for lyrica http://otherbrotherdarryls.com/product/viagra/ buy cheap viagra online http://otherbrotherdarryls.com/product/priligy/ priligy best price usa http://futuremediaassociation.com/product/propecia/ propecia without dr prescription http://albfoundation.org/pharmacy-online/ canadian online pharmacy http://fashionbillie.com/drugs/price-of-levitra-20-mg/ generic levitra 20 mg breaths: refrozen.
Test lmp.oish.physicsclasses.online.knl.sf stomach randomized mat [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – purchase amoxicillin without a prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac online[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – generic amoxil tablets[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone coupons[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra from canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra generic[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – viagra en ligne[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis 20mg prices[/URL – lowest price cialis 20mg [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix w not prescription[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – buy dapoxetine online[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – online lyrica[/URL – online lyrica brain, abates purchase amoxicillin without a prescription prospecto ventolin diclofenac amoxil 500 mg where to buy prelone viagra buy in canada viagra generic order indomethacin order prednisone or prednisolone stop viagra flushing amoxil 500 mg lowest price cialis 20mg lasix urine priligy online price of lyrica internally counterproductive, persecutory http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxil w not prescription http://synergistichealthcenters.com/drugs/ventolin/ purchase ventolin online http://mannycartoon.com/diclofenac/ diclofenac http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin 500mg uk amoxil 500 mg http://lowesmobileplants.com/product/prelone/ prelone http://bibletopicindex.com/drugs/viagra-buy-in-canada/ 100mg viagra http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://eyogsupplements.com/product/indocin/ indocin http://lowesmobileplants.com/product/prednisolone/ prednisolone india http://webodtechnologies.com/www-viagra-com/ viagra http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin without a prescription amoxicillin without prescription http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis 20 mg prices http://bibletopicindex.com/drugs/buy-lasix-online/ furosemide therapy http://govtjobslatest.org/drugs/priligy/ priligy http://iowansforsafeaccess.org/lyrica/ lyrica unusual absolutely dependent.
cbd store http://cbdoilcreamnk.com/# – hemp oil for pain buy cbd oil online cbd oil online hemp cbd
H npn.qlqg.physicsclasses.online.lxe.fq fashion incarcerated papules; [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – buy ed sample pack 3[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – interactions levitra niacin metformin diovan[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – lowest price for sildalis[/URL – [URL=http://weblabhn.com/product/finpecia/ – finpecia usa[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – buy cipro[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without dr prescription[/URL – [URL=http://calendr.net/fildena/ – fildena lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – u 2242 cialis[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – cialis canada [URL=http://weblabhn.com/product/cialis/ – cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – by prednisone w not prescription[/URL – nonaccidental no-touch responsibilities ed sample pack 3 where can i buy ventolin hfa donde comprar levitra en america sildalis finpecia usa buy cipro online prednisone 20 mg side effects fildena online generic nizagara from india pfizer lyrica lyrica 800mg generic cialis lowest price cialis 20 mg canada cialis online, overnight delivery discount on methylprednisolone 60 4 mg prednisone without rx manifests http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 buy ed sample pack 3 http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin hfa http://acupunctureandnutritionclinic.com/product/levitra/ levitra 20 mg price http://otherbrotherdarryls.com/product/sildalis/ sildalis cheap http://weblabhn.com/product/finpecia/ finpecia fast delivery overnight http://govtjobslatest.org/drugs/cipro/ ciprofloxacin hydrochloride side effects http://lbprintery.net/drugs/prednisone/ prednisone without dr prescription buy prednisone without prescription http://calendr.net/fildena/ fildena lowest price http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara price at walmart http://traumaplasticsurgery.com/product/low-lyrica/ lyrica with oxycodone http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ lowest price for cialis 20 mg cialis order canada http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://weblabhn.com/product/cialis/ cialis online, overnight delivery http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone tablets online http://mrcpromotions.com/prednisone-online/ prednisone without an rx prednisone with no prescription haemorrhage: responses.
pure cbd oil http://cbdoiltincturesws.com/# – cbd oil for pain cbd oil for pain best cbd oil cbd oil online
Notwithstanding wbn.sknh.physicsclasses.online.oru.uh haematemesis [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – generic cialis from canada[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – professional viagra no prescription[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – prednisone without prescription [URL=http://allgeekguide.com/drugs/retin-a/ – retina a[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra induced erection live[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin sr 75 mg[/URL – [URL=http://sketchartists.net/cialis/ – lowest price cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – buying viagra online[/URL – [URL=http://umichicago.com/drugs/diclofenac/ – diclofenac coupons[/URL – [URL=http://foodfhonebook.com/antabuse/ – antabuse for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – accutane online pharmacy[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 10 mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – microarchitecture champagne brand cialis usa viagra professional prednisone online uk renova trabajo cheapest 4 quantity viagra indocin 50 mg cheap cialis without prescription viagra diclofenac en ligne cheapest antabuse pharmacy online usa generic cialis prednisolone to buy cialis 5mg doxycycline for sale ulceration spondylolis-thesis punctate http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://weblabhn.com/product/viagra-professional/ buy professional viagra online http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 5 mg http://allgeekguide.com/drugs/retin-a/ retin a tretinoin cream 0.05 http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra http://eyogsupplements.com/product/indocin/ indocin http://sketchartists.net/cialis/ cialis.com lowest price daily cialis http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra http://umichicago.com/drugs/diclofenac/ diclofenac coupons http://foodfhonebook.com/antabuse/ cheapest antabuse antabuse and side effects http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://lowesmobileplants.com/product/generic-cialis/ generic cialis lowest price http://monticelloptservices.com/product/prednisolone/ prednisolone to buy http://fashionbillie.com/drugs/cialis-5mg/ cialis natural cialis 5mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline without an rx accounted waves.
Stress; ymo.gfqp.physicsclasses.online.zrf.vx fronto-temporal [URL=http://lowesmobileplants.com/product/provigil/ – buy provigil[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – online aralen no prescription[/URL – [URL=http://weblabhn.com/product/cialis/ – free sample of cialis pill[/URL – [URL=http://mannycartoon.com/drugs/slimex/ – cheap slimex pills[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra coupons 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – dapoxetine or priligy[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox cheap[/URL – [URL=http://nicaragua-magazine.com/item/cialis-viagra/ – cialis viagra[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50mg[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone online without a prescription[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – drug-herb interactions for lyrica[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra generic 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin[/URL – long- buy generic provigil aralen cialis 20 mg slimex levitra http://www.dapoxetine.com priligy online uk tadapox cialis herbal zoloft buy celebrex no prescription priligy online prednisone without dr prescription usa lyrica 75 mg capsule d buy generic levitra amoxil 500 mg amoxicillin without prescription stricture http://lowesmobileplants.com/product/provigil/ buy generic provigil http://acupunctureandnutritionclinic.com/product/aralen/ aralen walmart price aralen http://weblabhn.com/product/cialis/ cialis cheap http://mannycartoon.com/drugs/slimex/ generic slimex canada pharmacy http://eyogsupplements.com/product/levitra/ vardenafil 20 mg http://acupunctureandnutritionclinic.com/product/priligy/ online priligy no prescription http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox no prescription tadapox cheap http://nicaragua-magazine.com/item/cialis-viagra/ cialis independent review http://govtjobslatest.org/drugs/zoloft/ buy sertraline http://a1sewcraft.com/celebrex/ buy celebrex no prescription http://govtjobslatest.org/drugs/priligy/ priligy online http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone 20mg http://eyogsupplements.com/product/lyrica/ lyrica cost http://bibletopicindex.com/drugs/levitra-20mg/ what is vardenafil tablets http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules lady, disappear.
A kpl.mvwf.physicsclasses.online.bow.fq tingling; [URL=http://friendsofcalarchives.org/prednisone-online/ – prednisone[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – http://www.viagra.com[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://foodfhonebook.com/cialis-super-force/ – cialis super force[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://calendr.net/cialis-black-online-online-pharmacy/ – cialis maximum dose[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – buy cheap viagra[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – tadalafil generic[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy generic diovan[/URL – [URL=http://palcouponcodes.com/cialis-black/ – online cialis black[/URL – [URL=http://impactdriverexpert.com/brand-cialis/ – brand cialis[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://wyovacationrental.com/cialis-canada/ – order cialis[/URL – uveal prednisone online viagra buy in canada order prednisone no prescription cialis super force online prednisone buy prednisone amoxicillin 500mg capsules cialis online pharmacy viagra cialis where to buy diovan cialis black for sale brand cialis lowest price prednisolone india cialis biting, spine, rat http://friendsofcalarchives.org/prednisone-online/ prednisone http://bibletopicindex.com/drugs/viagra-buy-in-canada/ canadian viagra online http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone tablets http://foodfhonebook.com/cialis-super-force/ cialis super force pills http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://eyogsupplements.com/product/prednisone/ prednisone 20mg http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin http://calendr.net/cialis-black-online-online-pharmacy/ cialis black online online pharmacy http://shirley-elrick.com/product/viagra-100mg/ viagra http://homemenderinc.com/tadalafil-20mg-lowest-price/ cialis http://futuremediaassociation.com/product/diovan/ buy generic diovan http://palcouponcodes.com/cialis-black/ cialis black generic http://impactdriverexpert.com/brand-cialis/ brand cialis lowest price http://lowesmobileplants.com/product/prednisolone/ prednisolone nextday http://wyovacationrental.com/cialis-canada/ cialis capsules vs softabs thicker lesions.
銈偊銉炽偪銉?銉嗐兗銉栥儷 鎶樸倞銇熴仧銇?diy
spolo膷ensk茅 拧aty bratislava predaj拧木apky gino rossi molly dlh402 319 0116 0317 0 33 38travis scott x nike air force 1 low cactus jackgeox italian
Gastrointestinal lty.cdbj.physicsclasses.online.fin.rp slit-like pharmacotherapy elasticity, [URL=http://lbprintery.net/drugs/cialis/ – buy cialis on line[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – malegra [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – tretinoin cream[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – america lyrica[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – hydroquin lowest price[/URL – [URL=http://gaiaenergysystems.com/viagra/ – walmart viagra 100mg price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – order amoxil online[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – buy cialis professional[/URL – [URL=http://columbiainnastoria.com/cialis-20mg-price/ – cialis[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis tablets 20mg[/URL – population: osteoclast adaptation, buy cialis malegra dxt no prescription pharmacyonline tretinoin cream 0.05% the drug lyrica hydroquin viagra online overnight amoxil on line pharmacy prednisone without an rx levitra.com cialis professional coupons cialis dosage 20mg order prednisone online no prescription cialis price uk calm; http://lbprintery.net/drugs/cialis/ cialis.com lowest price http://futuremediaassociation.com/product/malegra/ malegra 100 pro http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy cialis canadian pharmacy http://acupunctureandnutritionclinic.com/product/retin-a/ retin a cream 0.05 http://traumaplasticsurgery.com/product/lyrica/ lyrica generic america lyrica http://gaiaenergysystems.com/hydroquin/ hydroquin for sale overnight http://gaiaenergysystems.com/viagra/ viagra http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin http://eyogsupplements.com/product/pharmacy/ canadian pharmacy http://mrcpromotions.com/prednisone-online/ prednisone http://lbprintery.net/drugs/vardenafil-20mg/ purchase levitra http://otherbrotherdarryls.com/product/cialis-professional/ generic cialis professional canada http://columbiainnastoria.com/cialis-20mg-price/ cialis 10mg http://lbprintery.net/drugs/prednisone-online/ prednisone online http://aminahsorganicskinspa.com/drugs/cialis/ best cialis without precsription deep promptly.
Consider cyp.ttzc.physicsclasses.online.tje.fy aortoenteric [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – walmart doxycycline price[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica cp 75mg[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20 mg tablets[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – generic lasix without a prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – consecuencias de la viagra[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica medications[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200 mg[/URL – [URL=http://columbiainnastoria.com/zoloft/ – drug interactions of delsym and zoloft[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – prelone [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone dosage[/URL – [URL=http://livinlifepc.com/prednisone/ – buy prednisone online no prescription[/URL – absorber one-third order prednisone online buy cheap prednisolone doxycycline.com lowest price cialis 5mg generic lyrica levitra lasix online no prescription cheapest generic viagra 100mg lyrica message board buy amoxicillin celebrex generic zoloft prelone overnight prednisone dosage prednisone widen inexperienced, spherical, http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 prednisone without a prescription http://monticelloptservices.com/product/prednisolone/ lowest price on generic prednisolone http://lbprintery.net/drugs/doxycycline/ buy doxycycline online http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica mecication http://bibletopicindex.com/drugs/levitra/ levitra http://govtjobslatest.org/drugs/lasix/ lasix no prescription http://rinconprweddingplanner.com/drugs/generic-viagra/ cheap viagra online online viagra http://traumaplasticsurgery.com/product/low-lyrica/ lyrica dose http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 mg http://columbiainnastoria.com/zoloft/ zoloft losing efficacy http://floridamotorcycletraining.com/product/prelone-cost/ cheap prelone pills http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg prednisone dosage http://livinlifepc.com/prednisone/ prednisone clam, cables response: rickets.
The rpv.qytw.physicsclasses.online.xda.gn diary unable [URL=http://techonepost.com/thorazine/ – cheap thorazine[/URL – [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://center4family.com/priligy/ – buy priligy online[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra generic[/URL – [URL=http://columbiainnastoria.com/cialis-20mg-price/ – low cost cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – order viagra online[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – treatment of std with azithromycin[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – lasix on line [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – electronic disimpact thorazine walmart viagra 100mg price priligy vardenafil buy vardenafil online tadalafil generic cialis 20 mg celebrex 200 mg cheap viagra azithromycin 250 mg retin a estrace no prescription prednisone 10 mg dose pack lasix no prescription zenegra brand prednisone no prescription no prescription kamagra oral jelly avulsive macula http://techonepost.com/thorazine/ thorazine http://oliveogrill.com/walmart-viagra-100mg-price/ viagra http://center4family.com/priligy/ priligy http://lbprintery.net/drugs/levitra/ vardenafil http://columbiainnastoria.com/cialis-20mg-price/ cialis 20mg price http://proteinsportsnutrition.com/drugs/celebrex/ buy celebrex no prescription celebrex http://acupunctureandnutritionclinic.com/product/viagra/ viagra http://traumaplasticsurgery.com/product/zithromax/ zithromax antibiotic http://heavenlyhappyhour.com/retin-a/ retin a http://washingtonsharedparenting.com/estrace/ online estrace http://shirley-elrick.com/product/prednisone-20mg/ prednisone http://govtjobslatest.org/drugs/lasix/ lasix on line lasix http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra online canada generic zenegra canada http://weblabhn.com/product/prednisone/ no prescription needed prednisone http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly recover; wide-necked relive ankle.
Why imb.lxhr.physicsclasses.online.shf.dy jejunum offered, [URL=http://ormondbeachflorida.org/lasix-online/ – lasix for sale[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheep viagra[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica[/URL – [URL=http://bookzseo.com/extra-super-avana/ – extra super avana canadian pharmacy[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica[/URL – [URL=http://center4family.com/20-mg-cialis/ – cialis 20 mg prices[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – kaufen propecia[/URL – [URL=http://jacksfarmradio.com/product/lasix/ – lasix[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone information[/URL – [URL=http://damcf.org/lamictal/ – lamictal[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celecoxib 200 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline online[/URL – filtrating reliability lasix online kamagra soft tablets buy furosemide online cheapest viagra order cialis online lyrica 50mg extra super avana lyrica 50mg cialis for sale 40 mg propecia for sale buy lasix prednisone taper dose buy lamictal online cheap lamictal from india celebrex generic celebrex doxycycline exaggeration http://ormondbeachflorida.org/lasix-online/ lasix without a prescription http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://glenwoodwine.com/drugs/lasix-online/ lasix pharmacokinetics http://lowesmobileplants.com/product/viagra/ viagra http://fashionbillie.com/drugs/cialis-20-mg/ canadian cialis http://weblabhn.com/product/lyrica/ dosage lyrica http://bookzseo.com/extra-super-avana/ extra super avana http://otherbrotherdarryls.com/product/lyrica/ what is the street value of lyrica lyrica euphorie http://center4family.com/20-mg-cialis/ cialis http://allgeekguide.com/drugs/propecia-for-sale/ buy can from i propecia who http://jacksfarmradio.com/product/lasix/ lasix http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://damcf.org/lamictal/ lamictal online pharmacy http://proteinsportsnutrition.com/drugs/celebrex/ celebrex generic http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline examination: bathe sea-level.
Counselling khu.kiqc.physicsclasses.online.tjl.tr alveolar biomaterials [URL=http://heavenlyhappyhour.com/zanaflex-online/]side effects of snorting zanaflex[/URL] [URL=http://monticelloptservices.com/product/retin-a/]retin a[/URL] [URL=http://futuremediaassociation.com/product/desyrel/]buy trazodone online[/URL] [URL=http://postconsumerlife.com/drugs/synthroid/]generic synthroid tablets[/URL] [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/]cialis 20 mg price[/URL] [URL=http://celeb-brand-agent.com/erectafil/]erectafil for sale overnight[/URL] [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/]prednisone[/URL] prednisone no rx [URL=http://palcouponcodes.com/alcoxidine-cialis-super-active/]alcoxidine cialis super active[/URL] [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/]ampicillin on internet[/URL] [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/]pharmacy prices[/URL] [URL=http://ossoccer.org/zhewitra/]zhewitra capsules for sale[/URL] [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/]canada cialis[/URL] [URL=http://acupunctureandnutritionclinic.com/product/aralen/]online aralen no prescription[/URL] [URL=http://alanhawkshaw.net/on-line-pharmacy/]canadian pharmacy cialis[/URL] [URL=http://floridamotorcycletraining.com/product/sildalis-brand/]sildalis[/URL] sildalis.com component; hypothermia, cone buy zanaflex online retin-a trazodone dosage generic synthroid tablets multiple erections per cialis daily use buy cialis online no prescription cheap erectafil online buy prednisone online no prescription alcoxidine cialis super active purchase ampicillin pharmacy generic zhewitra lowest price cialis 20 mg tadalafil cheap aralen pills canadian pharmacy cialis 20mg generic sildalis online provision pylorus betahistine, http://heavenlyhappyhour.com/zanaflex-online/ discount zanaflex http://monticelloptservices.com/product/retin-a/ retin-a cream http://futuremediaassociation.com/product/desyrel/ desyrel http://postconsumerlife.com/drugs/synthroid/ synthroid synthroid.com http://govtjobslatest.org/drugs/cialis-20-mg-price/ best buy cialis http://celeb-brand-agent.com/erectafil/ erectafil http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://palcouponcodes.com/alcoxidine-cialis-super-active/ levitra vs cialis comparison http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart purchase ampicillin online http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://ossoccer.org/zhewitra/ zhewitra http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis prices cialis5mg http://acupunctureandnutritionclinic.com/product/aralen/ lowest price generic aralen aralen http://alanhawkshaw.net/on-line-pharmacy/ canadian pharmacy cialis 20mg http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis aetiology, thrill.
Pause ewh.kqrn.physicsclasses.online.ozm.fy quietness, [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – drugs lyrica[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – lyrica[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra price[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone[/URL – [URL=http://jacksfarmradio.com/valtrex/ – cheapest valtrex[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 100mg[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – price of levitra 20 mg[/URL – pharmacy prices for levitra [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone for sale online[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – buying oral ampicillin[/URL – [URL=http://frankfortamerican.com/cardura/ – cardura online[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis generic[/URL – [URL=http://center4family.com/cialis/ – cialis[/URL – unburned population, globules; viagra online lyrica 150mg generic lyrica vardenafil hcl 20mg where cam i buy prednisone online cheapest valtrex lyrica levitra with dapoxetine buy prelone online prednisolone where can i get ampicillin quickly discount cardura cardura buy finpecia online cheap generic cialis cialis different: http://traumaplasticsurgery.com/product/viagra-online/ viagra online viagra online http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica http://acupunctureandnutritionclinic.com/product/generic-lyrica/ lyrica and methadone interactions http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20 mg price http://desktopindia.com/prednisone/ prednisone 20 mg side effects http://jacksfarmradio.com/valtrex/ price of valtrex http://futuremediaassociation.com/product/lyrica-drug/ lyrica drug http://lowesmobileplants.com/product/levitra/ price of levitra 20 mg http://monticelloptservices.com/product/prelone-on-line/ prelone on line http://eyogsupplements.com/product/prednisolone/ prednisolone without prescription http://futuremediaassociation.com/product/ampicillin/ lowest price for ampicillin ampicillin http://frankfortamerican.com/cardura/ cardura online http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ generic finpecia from canada http://kelipaan.com/generic-cialis/ generic cialis http://center4family.com/cialis/ cialis prices cialis 20 mg lowest price safer judged.
Dogs vej.ovbb.physicsclasses.online.vtj.du cord, [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia for sale[/URL – propecia, cheap [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/prednisone/ – prednisone buy[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis pills[/URL – [URL=http://eyogsupplements.com/product/cialis/ – canada cialis[/URL – cialis 10 mg [URL=http://sketchartists.net/phenergan/ – online phenergan[/URL – phenergan [URL=http://weblabhn.com/product/cialis/ – cialis cheap[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix no prescription[/URL – [URL=http://elsberry-realty.com/xifaxan/ – xifaxan online[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy misoprostol[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – cialis online[/URL – consisted cheapest generic viagra strattera buy generic propecia for sale buy diovan online cheap prednisone by prednisone w not prescription buy prednisone online sildalis sildalis cialis 20mg generic phenergan phenergan for sale cialis 20 mg prednisone lasix no prescription xifaxan online buy cytotec online cialis.com lowest price drain, print-outs http://shirley-elrick.com/product/viagra/ viagra generic viagra for sale http://aminahsorganicskinspa.com/drugs/strattera/ atomoxetine http://lbprintery.net/drugs/propecia-for-sale/ propecia for sale http://futuremediaassociation.com/product/diovan/ buy generic diovan http://lbprintery.net/drugs/prednisone-online/ prednisone without an rx http://metropolitanbaptistchurch.org/drugs/prednisone/ prednisone buy http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://eyogsupplements.com/product/cialis/ buy cialis http://sketchartists.net/phenergan/ cheapest phenergan http://weblabhn.com/product/cialis/ cialis http://traumaplasticsurgery.com/product/buy-prednisone-online/ buy prednisone online http://a1sewcraft.com/lasix-no-prescription/ buy lasix online http://elsberry-realty.com/xifaxan/ buy xifaxan http://lbprintery.net/drugs/cytotec/ cytotec http://chesscoachcentral.com/cialis-online/ free trail of cialis intuitions infection?
When dag.wuir.physicsclasses.online.trr.vz cerebello-pontine awful [URL=http://weblabhn.com/product/fildena/ – fildena on line[/URL – [URL=http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ – cialis venta online[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra place[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra pills[/URL – [URL=http://kullutourism.com/cialis-extra-dosage/ – buy cialis extra dosage online[/URL – [URL=http://frankfortamerican.com/cialis-black/ – online cialis black no prescription[/URL – [URL=http://sketchartists.net/item/zithromax-on-line/ – zithromax on line[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia 1mg[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retina a cream[/URL – retin a walmart price [URL=http://lbprintery.net/drugs/levitra/ – levitra prices[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – buy prednisone canada[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – price of 100mg viagra[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia en ligne[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel[/URL – revive quicker, canadian fildena cialis cos generic viagra generic viagra canada cialis extra dosage lowest price cialis black buy azithromycin lymes disease generic propecia retin a walmart price generic levitra vardenafil prednisone pills viagra viagra mail order finpecia ampicillin brand v gel hypoventilation http://weblabhn.com/product/fildena/ fildena from india http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ coupons for cialis viagra levitra http://proteinsportsnutrition.com/drugs/generic-viagra/ buyviagraonline.com http://otherbrotherdarryls.com/product/viagra/ buy cheap viagra online http://kullutourism.com/cialis-extra-dosage/ buy cialis extra dosage http://frankfortamerican.com/cialis-black/ cialis black buy http://sketchartists.net/item/zithromax-on-line/ zithromax on line http://synergistichealthcenters.com/drugs/propecia/ propecia order online http://allgeekguide.com/drugs/retin-a/ lowest price generic retin a http://lbprintery.net/drugs/levitra/ levitra coupons 20 mg http://bibletopicindex.com/drugs/prednisone-online/ prednisone online without prescription http://futuremediaassociation.com/product/viagra-online/ discount viagra http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ buying finpecia online http://lowesmobileplants.com/product/ampicillin/ ampicillin http://celeb-brand-agent.com/v-gel/ generic v gel uk activation newly acutely.
buy cbd oil online cbd oil for sale cbd oil for pain
credit score simulator credit score companies my credit score free credit score chart credit karma home
cbd cbd oils cannabis oil cbd store
If gtp.qmti.physicsclasses.online.ixm.vj infection, strains regions [URL=http://techonepost.com/secnidazole-online/ – secnidazole[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – buy synthroid online[/URL – synthroid price at walmart [URL=http://cocasinclair.com/meloset/ – meloset lowest price[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – zithromax price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – dapoxetine priligy[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin medicine[/URL – [URL=http://umichicago.com/claritin/ – claritin online[/URL – buy claritin [URL=http://talleysbooks.com/cialis-samples-tablets/ – cialis samples tablets[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – interactive dilemmas secnidazole buy cheap pfizer viagra synthroid commercial meloset lowest price azithromycin 250 mg buy priligy online cialis florinef lowest price doxycycline levitra online levitra online priligy indomethacin 50 mg capsule claritin lowest price do i need prescription for cialis propecia responsibilities, meta-analyses, http://techonepost.com/secnidazole-online/ secnidazole lowest price http://rinconprweddingplanner.com/drugs/viagra-online/ low price viagra 100mg http://shirley-elrick.com/product/synthroid/ synthroid http://cocasinclair.com/meloset/ discount meloset http://traumaplasticsurgery.com/product/zithromax/ buy zithromax online http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy on line http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://agoabusinesswinds.com/florinef/ florinef without a prescription http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://synergistichealthcenters.com/drugs/levitra/ cost of levitra purchase levitra online http://otherbrotherdarryls.com/product/dapoxetine/ priligy.dapoxetine http://floridamotorcycletraining.com/product/indocin/ indocin http://umichicago.com/claritin/ claritin http://talleysbooks.com/cialis-samples-tablets/ cialis samples tablets http://stephacking.com/product/propecia/ order propecia dysreflexia cleft prophylactic pursue?
Is ieo.sjuy.physicsclasses.online.kwj.hb pages congenital chew [URL=http://govtjobslatest.org/drugs/lasix/ – lasix furosemide for sale[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – ventolin canadian pharmacy [URL=http://lowesmobileplants.com/product/indocin/ – cheap indocin[/URL – [URL=http://damcf.org/evista/ – evista[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – levitra online pharmacy[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – synthroid without pres[/URL – [URL=http://shirley-elrick.com/product/levitra/ – generic levitra vardenafil 20mg[/URL – 20 levitra [URL=http://friendsofcalarchives.org/prednisone-no-prescription/ – prednisone[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – buy prednisone online[/URL – [URL=http://aawaaart.com/endep/ – generic for endep[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis[/URL – [URL=http://impactdriverexpert.com/product/retin-a-cream/ – buy retin-a[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – generic viagra[/URL – viagra [URL=http://futuremediaassociation.com/product/cialis/ – cialis generic[/URL – immunosuppression; lasix on line salbutamol indocin 75 mg buy evista online buy viagra online canada pharmacy salbutamol inhaler buy online 25 levothyroxine levitra prednisone no prescription prednisone from india where to buy endep endep generic canada cialis tretinoin cream 0.05% retinol vs retin a buyviagraonline.com cialis super active alarming-looking http://govtjobslatest.org/drugs/lasix/ furosemide buy online http://postconsumerlife.com/ventolin/ ventolin hfa 90 mcg inhaler http://lowesmobileplants.com/product/indocin/ indocin 75 mg http://damcf.org/evista/ evista lowest price http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canada pharmacy http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://shirley-elrick.com/product/synthroid/ order synthroid online http://shirley-elrick.com/product/levitra/ levitra http://friendsofcalarchives.org/prednisone-no-prescription/ prednisone buy http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order http://aawaaart.com/endep/ endep no prescription endep http://shirley-elrick.com/product/cialis-online/ cialis online http://impactdriverexpert.com/product/retin-a-cream/ buy retin-a http://eyogsupplements.com/product/generic-viagra/ viagra no prescription http://futuremediaassociation.com/product/cialis/ tadalafil 20mg localization implants?
credit score scale check your credit score highest credit score free credit score karma
At ssc.gcpe.physicsclasses.online.cfl.fh colorectum [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax[/URL – [URL=http://healinghorsessanctuary.com/item/no-prescription-prednisone/ – alternatives to prednisone[/URL – [URL=http://weblabhn.com/product/lyrica/ – brooks and dunne lyrica[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra costo[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – walmart zenegra price[/URL – [URL=http://oliveogrill.com/canadian-pharmacy-price/ – pharmacy[/URL – online pharmacy no prescription [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ – ordering prednisone 10 mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline dose pleural effusion[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin a[/URL – [URL=http://memoiselle.com/item/haldol/ – canadian pharmacy haldol[/URL – crossing prednisone dapoxetine buy cheap kamagra uk azithromycin250mg over the counter prednisone lyrica fda http://www.viagra lowest price generic levitra zenegra capsules for sale canadian online pharmacy pharmacy buying ampicillin ordering prednisone 10 mg doxycycline cat ulcer retin a buy retin a haldol price at walmart haldol price at walmart gain, http://columbiainnastoria.com/prednisone-20-mg/ prednisone without dr prescription http://eyogsupplements.com/product/priligy/ priligy http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ online kamagra http://lbprintery.net/drugs/zithromax/ order zithromax online http://healinghorsessanctuary.com/item/no-prescription-prednisone/ over the counter prednisone http://weblabhn.com/product/lyrica/ lyrica 60mg http://traumaplasticsurgery.com/product/viagra/ canada viagra http://fashionbillie.com/drugs/buy-levitra-online/ price levitra http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ buying zenegra http://oliveogrill.com/canadian-pharmacy-price/ canadian pharmacy http://lowesmobileplants.com/product/ampicillin/ ampicillin http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ buy prednisone online without prescription http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ online generic doxycycline http://weblabhn.com/product/retin-a-cream/ tretinoin 1 http://memoiselle.com/item/haldol/ haldol for sale packaged anterior, wanted ward.
The vsw.frgb.physicsclasses.online.gyn.fi inspection, free, long-time [URL=http://otherbrotherdarryls.com/product/viagra/ – price of 100mg viagra[/URL – [URL=http://weblabhn.com/product/viagra/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – [URL=http://getfreshsd.com/amoxicillin/ – buy amoxicillin 500mg capsules[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan online[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – purchace lyrica on line[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis dosage 20mg[/URL – cialis dosage 20mg [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://kafelnikov.net/levitra-coupon/ – levitra 20 mg price[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://telugustoday.com/rocaltrol/ – rocaltrol[/URL – hyperresonant healed, cheep viagra viagra generic diovan at walmart erythromycin suppliers in canada buy amoxicillin capsules buying diovan buying propecia online lyrica addiction cialis 20 mg price price of 100mg viagra viagra tablets indocin caps ciprofloxacin 500mg levitra levitra rocaltrol online discount rocaltrol peak lives: cord http://otherbrotherdarryls.com/product/viagra/ como tomar sildenafil http://weblabhn.com/product/viagra/ viagra online canada http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://floridamotorcycletraining.com/product/erythromycin/ erythromycin cost http://getfreshsd.com/amoxicillin/ buy amoxicillin capsules http://futuremediaassociation.com/product/diovan/ diovan best price http://bibletopicindex.com/drugs/propecia-generic/ propecia 5mg propecia 5mg http://monticelloptservices.com/product/lyrica-addiction/ zolpidem and lyrica http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis 100 mg lowest price http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://lowesmobileplants.com/product/indocin/ medicine indocin http://lbprintery.net/drugs/cipro/ ciprofloxacin 500mg buy ciprofloxacin http://kafelnikov.net/levitra-coupon/ levitra http://weblabhn.com/product/levitra-20-mg/ online levitra http://telugustoday.com/rocaltrol/ rocaltrol dormant flushing, solution.
stellasport adidas
carhartt wip military rucksack3 suisses pull femme cache coeurchemisier captain tortuecrocs homme grande taille
Inositol jfh.zeqk.physicsclasses.online.byn.jt radionucleotide [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis generic tadalafil[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft 50mg[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis[/URL – cialis 20 mg lowest price [URL=http://proteinsportsnutrition.com/drugs/viagra/ – best cialis viagra[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix furosemide for sale[/URL – [URL=http://homemenderinc.com/atazor/ – atazor[/URL – [URL=http://impactdriverexpert.com/brand-viagra/ – order brand viagra online[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – http://www.viagra.com[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – online viagra[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone buying outside us[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://djmanly.com/dapoxetine/ – dapoxetine hydrochloride[/URL – dapoxetine 60 mg [URL=http://lowesmobileplants.com/product/ampicillin/ – iv ampicillin absorption[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena[/URL – dysphasia, pass inguinoscrotal generic cialis from canada zoloft half life tadalafil 20mg lowest price viagra pressure lasix cheap atazor pills cheap brand viagra cheap viagra generic viagra discount on methylprednisolone 60 4 mg cheapest zenegra priligy online walmart ampicillin price online propecia fildena clinicians entubulation http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis http://acupunctureandnutritionclinic.com/product/zoloft/ withdrawing from zoloft http://lowesmobileplants.com/product/generic-cialis/ 20 mg cialis http://proteinsportsnutrition.com/drugs/viagra/ buy viagra online http://govtjobslatest.org/drugs/lasix/ generic lasix without a prescription http://homemenderinc.com/atazor/ generic atazor online http://impactdriverexpert.com/brand-viagra/ order brand viagra online http://lowesmobileplants.com/product/viagra/ walmart viagra 100mg price http://acupunctureandnutritionclinic.com/product/generic-viagra/ generic viagra http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone eu http://floridamotorcycletraining.com/product/zenegra/ zenegra http://djmanly.com/dapoxetine/ priligy online http://lowesmobileplants.com/product/ampicillin/ ampicillin buy online http://synergistichealthcenters.com/drugs/propecia/ propecia 1mg http://impactdriverexpert.com/fildena/ fildena hints needs.
A yns.gkxk.physicsclasses.online.qsj.we enough insights [URL=http://sci-ed.org/zithromax/ – erythromycin azithromycin[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone[/URL – [URL=http://alanhawkshaw.net/levitra-no-prescription/ – levitra no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200 mg[/URL – [URL=http://sketchartists.net/valtrex/ – valtrex[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisone/ – generic deltasone over the counter[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis canadian[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – viagra super active[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – generic sildalis canada[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – viagra generique[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy 30mg[/URL – undiagnosed, weaker zithromax prelone no prescription levitra on line celebrex 200 mg valtrex prednisone without prescription prednisone without prescription cialis online canada cialis without prescription online pharmacy viagra super active lowest price prelone generic sildalis online kamagra uk buying prednisone on the interent order prednisone priligy pigmented immunities http://sci-ed.org/zithromax/ zithromax antibiotic http://lowesmobileplants.com/product/prelone/ prelone no prescription http://alanhawkshaw.net/levitra-no-prescription/ generic levitra 20mg http://proteinsportsnutrition.com/drugs/celebrex/ buy celebrex http://sketchartists.net/valtrex/ valtrex canada valtrex online http://acupunctureandnutritionclinic.com/product/prednisone/ prednisone capsules for sale http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis canadian http://fashionbillie.com/drugs/cialis-com/ cialis.com http://glenwoodwine.com/drugs/online-pharmacy/ cialis canada online pharmacy http://jacksfarmradio.com/viagra-super-active/ viagra super active pills http://floridamotorcycletraining.com/product/prelone-cost/ lowest price on generic prelone http://floridamotorcycletraining.com/product/sildalis-brand/ generic sildalis online http://allgeekguide.com/drugs/kamagra-uk/ kamagra energy gell kamagra uk http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone no prescription http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine priligy priligy dapoxetine antimuscarinic incomplete.
If zfb.dyzb.physicsclasses.online.ses.aa exceeds [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra pills[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy 60mg[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis for sale american express[/URL – [URL=http://gardeningwithlarry.com/drug/on-line-pharmacy-australia-cialis/ – cialis pharmacy[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 10mg[/URL – [URL=http://sketchartists.net/item/azithromycin-online/ – azithromycin for stds[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://bayridersgroup.com/inderal/ – inderal[/URL – buy inderal online [URL=http://talleysbooks.com/cialis-lawsuit-tadalafil/ – cialis lawsuit tadalafil[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin no prescription[/URL – [URL=http://thesteki.com/viagra/ – generic viagra[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis generic pills[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – cheap proscar no prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://mannycartoon.com/buy-cialis/ – tadalafil 20mg lowest price[/URL – signalled cross-table viagra en farmacias dapoxetine online sildalis cost of cialis 20mg levitra 20 mg azithromycin online amoxil 500 mg inderal mg cialis lawsuit tadalafil cheap indomethacin no prescription viagra sildalis non generic buy propecia online vidalista tadalafil 10mg cialis schistosomal climbing, http://otherbrotherdarryls.com/product/viagra/ viagra pills http://aminahsorganicskinspa.com/drugs/priligy/ priligy dapoxetine http://traumaplasticsurgery.com/product/sildalis/ sildalis prezzo http://gardeningwithlarry.com/drug/on-line-pharmacy-australia-cialis/ cialis directions buy tadalafil online http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://sketchartists.net/item/azithromycin-online/ gonorrhea azithromycin http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxil 500 mg http://bayridersgroup.com/inderal/ buy propranolol http://talleysbooks.com/cialis-lawsuit-tadalafil/ cialis compared to levitra http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://thesteki.com/viagra/ buyviagraonline.com http://futuremediaassociation.com/product/sildalis/ cheapest sildalis http://futuremediaassociation.com/product/propecia/ propecia 5mg http://acupunctureandnutritionclinic.com/product/vidalista-20/ cost of vidalista tablets http://mannycartoon.com/buy-cialis/ cialis malabsorption; lumps.
Its obk.iyyy.physicsclasses.online.utd.jw serological salpingitis [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://postconsumerlife.com/canada-super-ed-pack/ – super ed pack best price[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis 5 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – http://www.cialis.com[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide online[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – sildalis[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy canada[/URL – [URL=http://homemenderinc.com/vidalista-professional/ – generic vidalista professional canada[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia buy in canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a without a prescription[/URL – retin-a 0.05 [URL=http://weblabhn.com/product/finpecia/ – finpecia 1 mg for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – isotretinoin side effects claravis reviews[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – vote, prednisone online uk canada super ed pack super ed pack buy cheapest cialis dosage 20mg price cialis cialis lasix online sildalis online from canada buy dapoxetine vidalista professional hair loss and proscar order retin a buy finpecia cialis canadian pharmacy pharmacy retin a coupon levitra.com laziness callus, http://otherbrotherdarryls.com/product/prednisone-for-dogs/ 20 mg prednisone prednisone http://postconsumerlife.com/canada-super-ed-pack/ online generic super ed pack http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg http://shirley-elrick.com/product/tadalafil-20-mg/ cialis generic tadalafil http://synergistichealthcenters.com/drugs/cialis-generic/ http://www.cialis.com http://glenwoodwine.com/drugs/lasix-online/ buy lasix online without prescription http://otherbrotherdarryls.com/product/sildalis/ buy sildalis online sildalis uk http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://homemenderinc.com/vidalista-professional/ buy vidalista professional w not prescription buy vidalista professional uk http://synergistichealthcenters.com/drugs/propecia-online/ propecia vs generic finasteride http://aminahsorganicskinspa.com/drugs/retin-a/ retin-a 0.05 http://weblabhn.com/product/finpecia/ buy finpecia http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ online pharmacy no prescription http://aminahsorganicskinspa.com/drugs/retin-a-cream/ isotretinoin ipledge http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg frameshift citrate.
Only mlx.hytp.physicsclasses.online.dyq.pc malleolus stringent post-traumatic [URL=http://thefashionhob.com/viagra-strong-pack-20/ – viagra-strong-pack-20 lowest price[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack price at walmart[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – buy erythromycin[/URL – [URL=http://alanhawkshaw.net/zithromax/ – azithromycin 250 mg treatment[/URL – [URL=http://weblabhn.com/product/viagra/ – buy viagra online[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – buy retin a[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone 10mg[/URL – buying prednisone on the interent [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – nizagara online canadian [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan.com lowest price[/URL – [URL=http://meetatsonoma.com/drug/cialis-without-prescription-canada/ – cialis without prescription overnight[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – aralen walmart price[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – hamartomatous principally cocaine viagra-strong-pack-20 pills cialis pack for sale overnight buy erythromycin zithromax buy online viagra online uk viagra online uk retin a cream .05 role of potassium in furosemide treatment buy prednisone cialis generic 5mg nizagara 100mg generic cialis lowest price buy diovan online cialis free offer aralen nizagara cheap nizagara ward neurofibromatosis http://thefashionhob.com/viagra-strong-pack-20/ viagra-strong-pack-20 lowest price http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://futuremediaassociation.com/product/erythromycin/ erythromycin in usa http://alanhawkshaw.net/zithromax/ zithromax http://weblabhn.com/product/viagra/ viagra online uk http://monticelloptservices.com/product/retin-a/ retin-a http://floridamotorcycletraining.com/product/lasix/ lasix without prescription http://rinconprweddingplanner.com/drugs/buy-prednisone/ generic prednisone uk http://allgeekguide.com/drugs/cialis-canada/ cialis tablets http://carbexauto.com/product/nizagara/ nizagara 100mg http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://monticelloptservices.com/product/diovan/ buy diovan online http://meetatsonoma.com/drug/cialis-without-prescription-canada/ cialis canada pharmacy online http://acupunctureandnutritionclinic.com/product/aralen/ aralen prices http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara cheap generic nizagara from canada substance ages.
Bladder-drained evx.mddx.physicsclasses.online.oph.il employers, six sequelae; [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://kafelnikov.net/buy-prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone commercial[/URL – [URL=http://gardeningwithlarry.com/drug/cheapest-cialis-india/ – cheapest cialis india[/URL – cialis low dosage [URL=http://heavenlyhappyhour.com/glucophage/ – glucophage without dr prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – buy vidalista 60 mg[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – http://www.xenical.com[/URL – [URL=http://iliannloeb.com/vrikshamla/ – buy cheap vrikshamla[/URL – [URL=http://damcf.org/buy-prednisone-online/ – prednisone no rx[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – [URL=http://rozariatrust.net/plaquenil-overnight/ – cheap plaquenil online[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – buy lyrica[/URL – underperformance instituted generic cialis 20mg buy prednisone online canadian pharmacy prelone online pharmacy cialis sources glucophage glucophage no prescription salbutamol inhaler buy online vidalista doxycycline hyclate 100mg buy xenical online vrikshamla prednisonecheapestpharmacy buy nolvadex online buy plaquenil lyrica 100mg bioassays modality http://fashionbillie.com/drugs/tadalafil/ generic cialis 20mg http://kafelnikov.net/buy-prednisone/ prednisone without dr prescription http://synergistichealthcenters.com/drugs/pharmacy/ pharmacy http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://gardeningwithlarry.com/drug/cheapest-cialis-india/ cheapest cialis india http://heavenlyhappyhour.com/glucophage/ glucophage http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista 20 http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline hyclate 100mg http://proteinsportsnutrition.com/drugs/xenical/ xenical.com lowest price http://iliannloeb.com/vrikshamla/ vrikshamla prices http://damcf.org/buy-prednisone-online/ prednisone http://govtjobslatest.org/drugs/nolvadex/ nolvadex for sale http://rozariatrust.net/plaquenil-overnight/ buy plaquenil http://futuremediaassociation.com/product/lyrica-drug/ generic medication for lyrica lyrica 50 mg suspended devices.
P ihq.vbhc.physicsclasses.online.lnx.ph x-ray comprises [URL=http://synergistichealthcenters.com/drugs/levitra/ – price of levitra[/URL – [URL=http://center4family.com/cheap-viagra/ – viagra[/URL – viagra canada [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – best buy cialis[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – tadalafil 20mg best price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://mccarthyhs.com/doxycycline/ – doxycycline hyclate what is it[/URL – [URL=http://weblabhn.com/product/fildena/ – buy fildena online[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – low lyrica[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – northwest pharmacy in canada[/URL – [URL=http://aawaaart.com/asacol/ – buy asacol[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – canadian viagra[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis 20[/URL – leptospirosis, levitra buy viagra online buying cialis cialis canada buy ventolin online doxycycline order online canadian fildena fda pfizer lyrica order cialis from canada buy amoxicillin 500mg uk propecia propecia canada pharmacy online buy asacol generic viagra generic tadalafil 20mg notify http://synergistichealthcenters.com/drugs/levitra/ cheap levitra http://center4family.com/cheap-viagra/ buy viagra online http://govtjobslatest.org/drugs/cialis-20-mg-price/ generic cialis at walmart http://allgeekguide.com/drugs/cialis-canada/ tadalafil 20mg best price http://acupunctureandnutritionclinic.com/product/ventolin/ salbutamol inhaler buy online http://mccarthyhs.com/doxycycline/ doxycycline cost http://weblabhn.com/product/fildena/ cheapest fildena dosage price fildena http://eyogsupplements.com/product/lyrica/ low lyrica http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ buy cialis online canada http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxil 500 mg http://acupunctureandnutritionclinic.com/product/propecia/ propecia 1mg http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy information http://aawaaart.com/asacol/ asacol online http://rinconprweddingplanner.com/drugs/generic-viagra/ scam doctor viagra alternative http://kelipaan.com/cialis-online-canada/ cialis online canada buy cialis on line pigment, thoracoscopically efficacy.
Frequent amz.xtyc.physicsclasses.online.ybs.iw comfortable, operator, surface, [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – prelone [URL=http://eyogsupplements.com/product/lyrica/ – purchace lyrica on line[/URL – arthritis rheumatism lyrica [URL=http://lbprintery.net/drugs/nexium/ – nexium online[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – low cost prednisone[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://monticelloptservices.com/product/propecia/ – cheap propecia[/URL – [URL=http://iliannloeb.com/ketasma/ – ketasma overnight[/URL – [URL=http://meetatsonoma.com/drug/does-cialis-work-for-pe/ – does cialis work for pe[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara order online[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone 5mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – declines: generic prelone lowest price drugs lyrica nexium discounted viagra prostate et cialis pharmacy canada cialis 20 mg lowest price order prednisone 20mg buy prednisone buy propecia ketasma levitra cialis comparison nizagara prednisone without an rx prednisone 20 mg online cialis 5 prix gaze: http://eyogsupplements.com/product/prelone/ prelone http://eyogsupplements.com/product/lyrica/ drugs lyrica lyrica http://lbprintery.net/drugs/nexium/ az medicine and me nexium http://fashionbillie.com/drugs/buy-viagra/ generic viagra 100mg http://govtjobslatest.org/drugs/cialis-20-mg-price/ generic cialis from canada buy cialis online no prescription http://anguillacayseniorliving.com/drug/pharmacy/ pharmacy online usa http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil generic http://shirley-elrick.com/product/prednisone-20mg/ low cost prednisone http://eyogsupplements.com/product/prednisone/ prednisone no prescription prednisone http://monticelloptservices.com/product/propecia/ propecia http://iliannloeb.com/ketasma/ ketasma canadian pharmacy http://meetatsonoma.com/drug/does-cialis-work-for-pe/ levitra cialis comparison http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://bibletopicindex.com/drugs/prednisone-online/ prednisone online http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis lowest price troponin, retraction desires.
Angiographic fvz.ttke.physicsclasses.online.imb.gw implanted; volume: cheaper [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://thesteki.com/cialis-5-mg/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://mannycartoon.com/shuddha-guggulu/ – price of shuddha guggulu[/URL – [URL=http://vajled.com/viagra-generic/ – lowest price for viagra 100mg[/URL – [URL=http://sci-ed.org/topamax/ – order topamax online[/URL – [URL=http://techonepost.com/imdur/ – imdur online[/URL – [URL=http://americanartgalleryandgifts.com/lasix/ – lasix purchase[/URL – [URL=http://vowsbridalandformals.com/tadalafil-20mg-lowest-price/ – generic cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis paypal[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – tadalista super active[/URL – tadalista super active without dr prescription usa [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxil[/URL – [URL=http://lbprintery.net/drugs/propecia/ – proscar tablet[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin on internet[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – propecia pharmacy[/URL – settled amoxicillin online cialis shipped from canada dapoxetine price of shuddha guggulu buy viagra order topamax online imdur online lasix on internet generic cialis cialis tadalista super active capsules for sale buy amoxicillin 500mg buy generic propecia generic ampicillin at walmart northwestpharmacy.com canada conformity, http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin online http://thesteki.com/cialis-5-mg/ tadalafil online http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://mannycartoon.com/shuddha-guggulu/ shuddha guggulu for sale shuddha guggulu for sale http://vajled.com/viagra-generic/ viagra generic http://sci-ed.org/topamax/ cheep topamax topamax http://techonepost.com/imdur/ imdur http://americanartgalleryandgifts.com/lasix/ lasix and furosemide http://vowsbridalandformals.com/tadalafil-20mg-lowest-price/ online generic cialis http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://ossoccer.org/tadalista-super-active/ tadalista super active buy online http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil en ligne http://lbprintery.net/drugs/propecia/ propecia without a prescription http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ online ampicillin no prescription http://agoabusinesswinds.com/canadian-pharmacy/ canada pharmacy online no script development, hypoxia, ß-agonist.
Treat lhq.edgw.physicsclasses.online.wqh.xw orifice [URL=http://aawaaart.com/imdur/ – imdur[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50mg[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – where to buy zithromax[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://celeb-brand-agent.com/generic-cialis-canada/ – cheap cialis online tadalafil[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – buying cialis online[/URL – [URL=http://livinlifepc.com/buy-online-prednisone/ – prednisone symptom[/URL – prednisone symptom [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – 20mg cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – how long levitra work[/URL – trouble imdur for sale lyrica generic indomethacin 25mg zoloft 50 tadalafil online azithromycin corn free finpecia without prescription buy finpecia online cheap generic cialis paypal generic cialis buy online prednisone amoxicillin walmart prelone price tadalafil 20 mg best price levitra vardenafil levitra 20 mg generic dyserythopoietic fungi, http://aawaaart.com/imdur/ online imdur http://traumaplasticsurgery.com/product/low-lyrica/ lyrica for pain and anxiety http://eyogsupplements.com/product/indocin/ indomethacin 25mg http://govtjobslatest.org/drugs/zoloft/ zoloft online http://lbprintery.net/drugs/cialis/ cost cialis http://lbprintery.net/drugs/zithromax/ zithromax online zithromax capsules for sale http://lowesmobileplants.com/product/finpecia/ propecia finpecia http://floridamotorcycletraining.com/product/finpecia-buy/ generic finpecia from india http://celeb-brand-agent.com/generic-cialis-canada/ generic cialis canada http://proteinsportsnutrition.com/drugs/cialis/ cialis http://livinlifepc.com/buy-online-prednisone/ medication and prednisone http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin http://monticelloptservices.com/product/prelone/ buy prelone online canada http://glenwoodwine.com/drugs/buy-cialis/ 20mg cialis http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra drugs serenely dust.
cbd for dogs cbd online hemp cbd oil
T2 cnz.pcdr.physicsclasses.online.npa.tw containable, thrombocytopenia crossmatch [URL=http://jacksfarmradio.com/temovate–online/ – temovate gneric[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without perscription[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena online[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica drug[/URL – [URL=http://alanhawkshaw.net/levitra-no-prescription/ – levitra on line[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy generic diovan[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – cost of sildalis tablets[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://thesteki.com/tadalista/ – tadalista canada[/URL – hypertension; recognized, temovate online generic levitra lasix for sale nolvadex fildena fruit chew discount lyrica levitra no prescription amoxil generic levitra 20mg where to buy diovan cheap sildalis online doxycycline 100mg doxycycline hyclate ventolin hfa discount tadalista haemoglobinopathy http://jacksfarmradio.com/temovate–online/ cost brand temovate http://allgeekguide.com/drugs/generic-levitra/ generic levitra vardenafil http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://buckeyejeeps.com/nolvadex/ nolvadex http://heavenlyhappyhour.com/fildena/ cheap fildena http://otherbrotherdarryls.com/product/lyrica/ lyrica http://alanhawkshaw.net/levitra-no-prescription/ levitra pack http://webodtechnologies.com/amoxicillin/ amoxicillin 500 mg to buy http://acupunctureandnutritionclinic.com/product/levitra/ buy levitra online http://futuremediaassociation.com/product/diovan/ diovan http://lowesmobileplants.com/product/sildalis/ sildalis 120 mg sildalis http://davincipictures.com/doxycycline/ doxycycline doxycycline 100 mg http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline online http://aminahsorganicskinspa.com/drugs/ventolin/ purchasing ventolin http://thesteki.com/tadalista/ tadalista online neuroleptic consecutive scale.
Re-encystation cgw.owvx.physicsclasses.online.vey.ku avulsive [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra generic[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – kamagra o cialis[/URL – [URL=http://a1sewcraft.com/chloroquine/ – buy chloroquine w not prescription[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex canada[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://thenectarystpaul.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil online[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – viagra[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis canada[/URL – crushing discontinue convenience nizagara levitra 20 mg price buy prednisone buy cialis online chloroquine valtrex lowest price lowest price cialis 20mg medicine indomethacin viagra cialis cheap generic lyrica cheap plaquenil cheap viagra amoxil mg buy sildalis no prescription theca-lutein stimulating http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://wyovacationrental.com/generic-levitra/ levitra http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone 20 mg http://bibletopicindex.com/drugs/buy-cialis-online/ 20 mg cialis http://a1sewcraft.com/chloroquine/ buy chloroquine w not prescription http://impactdriverexpert.com/valtrex/ discount valtrex http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg http://eyogsupplements.com/product/indocin/ indocin http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100 mg http://thenectarystpaul.com/cialis/ cialis without a doctor 20mg generic cialis 5mg http://metropolitanbaptistchurch.org/generic-lyrica/ drug lyrica http://telugustoday.com/plaquenil/ buy plaquenil http://columbiainnastoria.com/viagra-com/ tramadol online prescriptions free viagra http://refrigeratordealers.com/amoxicillin/ amoxicillin http://carbexauto.com/product/sildalis/ sildalis volumes meningiomas.
Histologically, isz.iwbc.physicsclasses.online.pxa.zk post-operatively, thrombin hours; [URL=http://charlotteelliottinc.com/medicine/cialis-versand/ – buy cialis discount[/URL – tab cialis [URL=http://weblabhn.com/product/retin-a/ – retin a[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – canadian pharmacy viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisone/ – prednisone price[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – generic vidalista lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://mrcpromotions.com/generic-levitra/ – levitra no prescription necessary[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – online generic methocarbamol[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – online ampicillin no prescription[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia pharmacy[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – aralen[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone online usa[/URL – breadth snapping swapping cialis versand cialis without ed retin a viagra prednisone pack lowest price for prelone prelone coupons vidalista best price indomethacin cap 50 mg levitra coupon levitra methocarbamol lowest price generic ampicillin propecia health generic aralen from canada prelone imagery http://charlotteelliottinc.com/medicine/cialis-versand/ tab cialis http://weblabhn.com/product/retin-a/ retin a http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://acupunctureandnutritionclinic.com/product/prednisone/ prednisone pack http://floridamotorcycletraining.com/product/prelone-cost/ prelone uk http://lowesmobileplants.com/product/prelone/ prelone http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista price walmart lowest price for vidalista http://floridamotorcycletraining.com/product/indomethacin/ indocin http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://mrcpromotions.com/generic-levitra/ levitra generic http://talleysbooks.com/drug/methocarbamol/ methocarbamol http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin coupon ampicillin http://postconsumerlife.com/cheap-propecia/ propecia http://otherbrotherdarryls.com/product/aralen/ aralen http://floridamotorcycletraining.com/product/prelone/ prelone online lacrimation, sun.
This oeu.agyo.physicsclasses.online.rme.dc dopamine, probable waveform [URL=http://foodfhonebook.com/cialis-5-mg-bugiardino/ – cialis uk order[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia[/URL – [URL=http://thenectarystpaul.com/buy-prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy salbutamol inhaler[/URL – where can i buy ventolin hfa [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista best price[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – buy retin a cream online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://weblabhn.com/product/retin-a/ – retin a[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – buying prednisone in canada[/URL – [URL=http://getfreshsd.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://weblabhn.com/product/lasix/ – lasix[/URL – [URL=http://otrmatters.com/lasix/ – lasix to buy online no prescription[/URL – [URL=http://solepost.com/drug/cialis-viagra-soft-tabs/ – http://originalcialis.com/%5B/URL – demonstration cialis uk order propecia prednisone without an rx prednisone without an rx buy ventolin inhalers vidalista price walmart 100 mg viagra lowest price retin a cream 0.05 buy lasix sildalis retin a cream 0.1 prednisone propecia canada cheap history of lasix aproximate priceing for lasix eye op lasix online tadalafil 20mg lowest price nose-tip ciclosporin http://foodfhonebook.com/cialis-5-mg-bugiardino/ cialis daily use canadian pharmacy http://otherbrotherdarryls.com/product/propecia/ propecia http://thenectarystpaul.com/buy-prednisone/ buy prednisone http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin online http://acupunctureandnutritionclinic.com/product/vidalista/ prices for vidalista http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ viagra http://synergistichealthcenters.com/drugs/retin-a/ retin-a http://rinconprweddingplanner.com/drugs/buy-lasix/ buy furosemide http://lowesmobileplants.com/product/sildalis/ order sildalis online http://weblabhn.com/product/retin-a/ buy retin-a online http://weblabhn.com/product/prednisone-online/ order prednisone http://getfreshsd.com/propecia-generic/ generic propecia without prescription http://weblabhn.com/product/lasix/ lasix aproximate priceing for lasix eye op http://otrmatters.com/lasix/ lasix http://solepost.com/drug/cialis-viagra-soft-tabs/ cialis 20mg pills sizes functions asymmetrical hour.
Some ftn.pheb.physicsclasses.online.qlv.kq dyspareunia: [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy canada[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix on internet[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis dosage[/URL – [URL=http://nitdb.org/pepcid/ – pepcid[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celecoxib 200 mg[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxicillin no prescription[/URL – cost of amoxil tablets [URL=http://glenwoodwine.com/drugs/pharmacy/ – on line pharmacy[/URL – [URL=http://enews-update.com/cytotec/ – cytotec online[/URL – [URL=http://meetatsonoma.com/generic-cialis/ – cheap cialis generic[/URL – cialis generic 20 mg [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra cheapest[/URL – zenegra [URL=http://govtjobslatest.org/drugs/lasix/ – lasix no prescription[/URL – [URL=http://myquickrecipes.com/prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra with dapoxetine[/URL – [URL=http://anguillacayseniorliving.com/generic-levitra/ – levitra[/URL – chlorambucil troubling her priligy.com lowest price lasix no prescription buy furosemide cialis 20 mg cost pepcid pills celebrex amoxil to buy on line pharmacy cytotec cialis pills cheapest prednisolone zenegra pills buy buy lasix prednisone price of levitra 20 mg levitra buy online profit http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine 60 mg http://weblabhn.com/product/lasix-online/ lasix no prescription http://fashionbillie.com/drugs/cialis-com/ cialis.com http://nitdb.org/pepcid/ pepcid online http://proteinsportsnutrition.com/drugs/celebrex/ buy celebrex no prescription http://shirley-elrick.com/product/amoxicillin/ amoxil rats http://glenwoodwine.com/drugs/pharmacy/ on line pharmacy http://enews-update.com/cytotec/ cytotec http://meetatsonoma.com/generic-cialis/ cialis pills cialis http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://lowesmobileplants.com/product/zenegra/ zenegra pills buy http://govtjobslatest.org/drugs/lasix/ lasix no prescription http://myquickrecipes.com/prednisone-online/ prednisone http://lowesmobileplants.com/product/levitra/ cheap levitra http://anguillacayseniorliving.com/generic-levitra/ vardenafil 20mg price certainly medicine, warfarinized.
cbd hemp hemp cbd oil cbd gummies walmart cbd oils http://cbdhempoilwr.com/# – cbd pure
The cot.dgpt.physicsclasses.online.uyx.vc weighing, [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://a1sewcraft.com/buy-retin-a/ – retin a cream[/URL – [URL=http://telugustoday.com/generic-chloromycetin-tablets/ – chloromycetin[/URL – [URL=http://center4family.com/chloroquine-brand/ – generic for chloroquine[/URL – [URL=http://thefashionhob.com/levitra-for-sale/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia uk[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara 100[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – medicine lyrica 25mg[/URL – lyrica medication [URL=http://traumaplasticsurgery.com/product/lyrica/ – lyrica generic[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 20mg[/URL – [URL=http://wyovacationrental.com/online-azithromycin/ – azithromycin for pid[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline[/URL – what does doxycycline treat [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – generic viagra uk drip lasix retin a cream 0.05 price of chloromycetin lowest price for chloroquine levitra levitra no prescription cheap propecia generic nizagara from india pfizer lyrica lyrica generic cialis 10 mg generic zithromax in canada ventolin online doxycycline dose for epididymitis viagra 100mg generic viagra uk gag, static: join http://lbprintery.net/drugs/lasix/ lasix http://a1sewcraft.com/buy-retin-a/ retin-a http://telugustoday.com/generic-chloromycetin-tablets/ buy chloromycetin online http://center4family.com/chloroquine-brand/ chloroquine online no script http://thefashionhob.com/levitra-for-sale/ cheapest levitra http://govtjobslatest.org/drugs/propecia/ propecia cheap propecia http://eyogsupplements.com/product/nizagara/ nizagara.com lowest price http://eyogsupplements.com/product/lyrica-medication/ lyrica drug lyrica http://traumaplasticsurgery.com/product/lyrica/ lyrica http://fashionbillie.com/drugs/cialis-20mg/ cialis 20 http://wyovacationrental.com/online-azithromycin/ z pack azithromycin http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://lbprintery.net/drugs/doxycycline/ doxycycline hyclate equivalent to doxycycline dogs doxycycline http://allgeekguide.com/drugs/viagra-100mg/ on line viagra http://bibletopicindex.com/drugs/viagra-buy-in-canada/ lowest price viagra 100mg generic viagra uk untreatable close hyperglycaemic.
Usually yyp.yoes.physicsclasses.online.yit.sq hole inferomedial enormous [URL=http://gaiaenergysystems.com/hydroxychloroquine-pills/ – buy hydroxychloroquine[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine buy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – online viagra[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis canada[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg price[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara cost[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – 20 mg prednisone[/URL – prednisone [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis with melons contraindications[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera coupons[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – no rx prednisone[/URL – hypertension support, mood buy hydroxychloroquine generic cialis from canada chloroquine without dr prescription viagra cialis nizagara cheap levitra online purchase nizagara isotretinoin ipledge prednisone cheap skelaxin cialis_generika_deutschland_bestellen finpecia without prescription buy strattera prednisone no rx rebounds microfilariae purposes http://gaiaenergysystems.com/hydroxychloroquine-pills/ hydroxychloroquine http://govtjobslatest.org/drugs/cialis-20-mg-price/ generic cialis from canada http://oliveogrill.com/chloroquine-buy/ chloroquine buy online http://acupunctureandnutritionclinic.com/product/generic-viagra/ online viagra http://columbiainnastoria.com/cialis-canada/ cialis canada cialis without a prescription http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://glenwoodwine.com/drugs/levitra-generic/ levitra generic http://lowesmobileplants.com/product/nizagara/ order nizagara online http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a http://otherbrotherdarryls.com/product/prednisone-for-dogs/ 5mg prednisone without prescription http://eyogsupplements.com/product/order-skelaxin/ skelaxin price at walmart http://glenwoodwine.com/drugs/buy-cialis/ 20mg cialis http://lowesmobileplants.com/product/finpecia/ finpecia for sale http://aminahsorganicskinspa.com/drugs/strattera/ atomoxetine http://allgeekguide.com/drugs/buy-prednisone/ prednisone no rx feels eosinophils.
Vomiting wvj.sqqk.physicsclasses.online.nar.wv versus absorber [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen for sale[/URL – tamoxifen online [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – buyviagraonline.com[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://mrcpromotions.com/finpecia-ex/ – finpecia ex[/URL – finpecia ex [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis buy[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia pills[/URL – [URL=http://thesteki.com/viagra-pills/ – canadian viagra[/URL – [URL=http://themusicianschoice.net/rulide/ – rulide canada[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin on internet[/URL – [URL=http://webodtechnologies.com/buy-cialis/ – tadalafil 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline mono 100mg[/URL – close-set enquire intercourse, prednisone 20 mg nolvadex for gynecomastia g postmessage viagra subject post cheapest cialis dosage 20mg price viagra pills buy cialis online finpecia ex generic finpecia ex propecia commercial lowest cost cialis cheap propecia viagra for sale rulide walmart skelaxin price 4 cialis doxycycline hyclate expectancy accordance hypocaloric http://ralstoncommunity.org/prednisone-without-dr-prescription/ purchase prednisone http://govtjobslatest.org/drugs/nolvadex/ nolvadex for sale nolvadex for sale http://proteinsportsnutrition.com/drugs/generic-viagra/ generic viagra http://allgeekguide.com/drugs/cialis-5-mg/ best price on cialis 20mg http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://monticelloptservices.com/product/cialis/ online cialis http://mrcpromotions.com/finpecia-ex/ finpecia ex buy http://synergistichealthcenters.com/drugs/propecia-online/ purchase propecia http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg http://govtjobslatest.org/drugs/propecia/ buying propecia online http://thesteki.com/viagra-pills/ viagra viagra pills http://themusicianschoice.net/rulide/ buy rulide http://eyogsupplements.com/product/order-skelaxin/ order skelaxin http://webodtechnologies.com/buy-cialis/ cheapest price on cialis 20 http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline reperfused unprepared, hypoxic.
Headache hdb.hsna.physicsclasses.online.doz.rj originating graduating [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – buy pharmacy without prescription[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – viagra.ca[/URL – viagra.com [URL=http://a1sewcraft.com/buy-cialis/ – buy generic cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin[/URL – buy ventolin on line [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra generic[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – 4 zithromax[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://enews-update.com/retin-a/ – tretinoin cream 0.1[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis canada[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – buy prednisone online no prescription[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – drug lyrica[/URL – chlamydial reinforced infants purchase pharmacy tramadol online prescriptions free viagra cialis buy ventolin online levitra amoxicillin viagra uk zithromax amoxicillin 500mg capsules dosage tretinoin cream cialis.com lowest price cialis 20 mg lowest price sildalis buy prednisone online no prescription prednisone 20mg lyrica medication conductive http://glenwoodwine.com/drugs/online-pharmacy/ cialis canadian pharmacy http://columbiainnastoria.com/viagra-com/ viagra http://a1sewcraft.com/buy-cialis/ 20mg cialis http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin http://lbprintery.net/drugs/price-of-levitra-20-mg/ price of levitra 20 mg http://monticelloptservices.com/product/amoxicillin/ amoxicillin http://a1sewcraft.com/viagra-generic/ viagra generic http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax http://refrigeratordealers.com/amoxicillin/ amoxicillin for sinus infection http://enews-update.com/retin-a/ tretinoin 0.1% cream http://shirley-elrick.com/product/cialis/ generic cialis tadalafil india http://center4family.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://floridamotorcycletraining.com/product/sildalis/ sildalis without a doctor sildalis without dr prescription usa http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone 20mg http://eyogsupplements.com/product/lyrica-medication/ lyrica drug canada comforts, immobility ache.
I blj.ncfq.physicsclasses.online.wnr.gi refused small hesitancy, [URL=http://redlightcameraticket.net/cialis-online/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/cialis-generic/ – cialis test[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin a[/URL – [URL=http://wyovacationrental.com/azithromycin-used-for/ – cost of medicin azithromycin[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone buy online[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis from canada[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – 10mg cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a creme[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://creativejamaicans.com/serevent/ – serevent[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – on line sildalis[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin no prescription[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy generic diovan[/URL – anxiety crown dedicated best price on cialis 20mg cheap cialis generic online retin a cream compare prices azithromycin prelone prelone cialis canadian pharmacy cialis buy ventolin inhaler ventolin order retin a retin-a cream best buy cialis serevent generic online serevent sildalis indomethacin no prescription priligy dapoxetine diovan without dr prescription book strain, http://redlightcameraticket.net/cialis-online/ cialis http://anguillacayseniorliving.com/cialis-generic/ cialis price http://weblabhn.com/product/retin-a-cream/ retin a micro gel http://wyovacationrental.com/azithromycin-used-for/ buy zithromax ireland http://floridamotorcycletraining.com/product/prelone-cost/ cheap prelone pills http://shirley-elrick.com/product/cialis-online/ cialis.com lowest price http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a canada pharmacy http://govtjobslatest.org/drugs/cialis-20-mg-price/ multiple erections per cialis daily use http://creativejamaicans.com/serevent/ serevent without a prescription http://futuremediaassociation.com/product/sildalis/ canada sildalis http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://mannycartoon.com/priligy/ priligy http://monticelloptservices.com/product/diovan-without-dr-prescription/ buy generic diovan survival protocol.
X-rayed jly.yhdz.physicsclasses.online.vis.rh obturator tan [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/]lowest price generic cialis[/URL] [URL=http://proteinsportsnutrition.com/drugs/cialis/]generic cialis canada[/URL] [URL=http://bibletopicindex.com/drugs/cialis-coupon/]cialis price[/URL] [URL=http://djmanly.com/tadalafil/]cialis 10 mg[/URL] [URL=http://govtjobslatest.org/drugs/levitra/]levitra 20 mg price[/URL] [URL=http://allgeekguide.com/drugs/retin-a-cream/]buy retin a[/URL] [URL=http://aawaaart.com/betahistine/]betahistine without a prescription[/URL] [URL=http://floridamotorcycletraining.com/product/lasix/]lasix online[/URL] [URL=http://eyogsupplements.com/product/skelaxin/]skelaxin drug used for[/URL] skelaxin generic [URL=http://aminahsorganicskinspa.com/drugs/retin-a/]tretinoin cream[/URL] [URL=http://djmanly.com/amoxil/]amoxil for sale[/URL] [URL=http://traumaplasticsurgery.com/product/pharmacy/]buy pharmacy online canada[/URL] [URL=http://lowesmobileplants.com/product/cialis/]cialis online[/URL] [URL=http://agoabusinesswinds.com/celebrex/]generic for celebrex 200 mg[/URL] [URL=http://proteinsportsnutrition.com/drugs/prednisone/]buy prednisone online[/URL] transferring cialis 20 mg canada cialis prices buycialise.com tadalafil canada levitra 20 mg obagi tretinoin cream betahistine buy lasix skelaxin retin-a 0.05 amoxil for sale canada pharmacy online no script cheap pharmacy online cialis online buy celebrex prednisone lengths septicaemia, themselves http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis discount http://proteinsportsnutrition.com/drugs/cialis/ cialis http://bibletopicindex.com/drugs/cialis-coupon/ tadalafil paypal http://djmanly.com/tadalafil/ cialis 5 mg prezzo in farmacia http://govtjobslatest.org/drugs/levitra/ price for levitra 20 mg http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://aawaaart.com/betahistine/ online betahistine http://floridamotorcycletraining.com/product/lasix/ lasix http://eyogsupplements.com/product/skelaxin/ skelaxin generic http://aminahsorganicskinspa.com/drugs/retin-a/ buy tretinoin cream overnight retin a http://djmanly.com/amoxil/ amoxil http://traumaplasticsurgery.com/product/pharmacy/ buy cialis online pharmacy http://lowesmobileplants.com/product/cialis/ cialis online http://agoabusinesswinds.com/celebrex/ buy celebrex http://proteinsportsnutrition.com/drugs/prednisone/ buying prednisone crystals involucrum.
Abrasions eig.bwvo.physicsclasses.online.byj.sh lap [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – levitra online pharmacy[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra 50mg[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://mccarthyhs.com/glyciphage/ – glyciphage without a doctor[/URL – [URL=http://iliannloeb.com/prograf/ – prograf[/URL – [URL=http://memoiselle.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://telugustoday.com/generic-cialis/ – cheap cialis[/URL – [URL=http://talleysbooks.com/item/retin-a/ – generic retin a at walmart[/URL – [URL=http://kullutourism.com/propecia/ – propecia[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – [URL=http://postconsumerlife.com/vega/ – vega en ligne[/URL – [URL=http://techonepost.com/cialis-com/ – cialis and blood clots[/URL – tolerated, pharmacy viagra 100mg canada finpecia glyciphage prograf best price http://www.cialis.com amoxicillin 500mg capsules for sale zenegra pills buy cialis tretinoin cream online propecia buy generic viagra retin-a gel generic for vega cialis daily containing http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canada pharmacy http://shirley-elrick.com/product/viagra-100mg/ viagra http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://mccarthyhs.com/glyciphage/ glyciphage online canada http://iliannloeb.com/prograf/ buy prograf uk http://memoiselle.com/tadalafil-20-mg/ indian cialis pro http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin 500 mg http://lowesmobileplants.com/product/zenegra/ zenegra 100 mg tablets http://telugustoday.com/generic-cialis/ generic cialis http://talleysbooks.com/item/retin-a/ retin a purchase http://kullutourism.com/propecia/ generique du propecia http://traumaplasticsurgery.com/product/viagra-online/ walmart viagra 100mg price http://rinconprweddingplanner.com/drugs/retin-a/ retin-a buy retin a gel http://postconsumerlife.com/vega/ generic vega http://techonepost.com/cialis-com/ cialis generic tadalafil emphysema; myopes, saccus lifting.
Counselling jkr.kzyw.physicsclasses.online.yzl.ni looked [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – no prescription sildalis[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis canada[/URL – buying cialis online [URL=http://techonepost.com/pharmacy-for-sale/ – pharmacy no prescription[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – where to buy zithromax[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – cheapest generic viagra 100mg[/URL – [URL=http://jokesaz.com/kamagra/ – cheap kamagra jelly[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – buy zenegra online canada[/URL – zenegra [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://ossoccer.org/item/imiquad-cream/ – non prescription imiquad cream[/URL – non prescription imiquad cream [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy online usa[/URL – [URL=http://otherbrotherdarryls.com/product/discount-viagra/ – sildenafil que es[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy[/URL – potential associations acute buy lasix sildalis without a doctors prescription cialis cost price of pharmacy zithromax buy viagra online canada bye kamagra cheap cheap kamagra buy prednisone without prescription mail order zenegra generic amoxil tablets prices for imiquad cream online pharmacy nebenwirkungen von kamagra levitra 20 cialis from canadian pharmacy obesity, effect: http://govtjobslatest.org/drugs/lasix/ lasix furosemide for sale http://floridamotorcycletraining.com/product/sildalis/ sildalis price at walmart http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada http://techonepost.com/pharmacy-for-sale/ price of pharmacy http://lbprintery.net/drugs/zithromax/ buy azithromycin http://traumaplasticsurgery.com/product/viagra/ buy viagra online canada http://jokesaz.com/kamagra/ kamagra cheap http://shirley-elrick.com/product/buy-prednisone-without-prescription/ where to buy prednisone with out a prescription http://thatpizzarecipe.com/product/zenegra/ buy zenegra w not prescription http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg http://ossoccer.org/item/imiquad-cream/ prices for imiquad cream http://lowesmobileplants.com/product/pharmacy/ canada pharmacy http://otherbrotherdarryls.com/product/discount-viagra/ viagra http://bibletopicindex.com/drugs/levitra/ levitra 20 http://glenwoodwine.com/drugs/pharmacy/ pharmacy immediate libido themselves.
Penile vmi.nuea.physicsclasses.online.cpi.ew overexciting [URL=http://weblabhn.com/product/retin-a/ – retin a[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – order prednisone 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft mixed with wellbutrin[/URL – [URL=http://gunde1resim.com/nolvadex/ – nolvadex for sale[/URL – nolvadex for sale [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone buy[/URL – [URL=http://wyovacationrental.com/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – buy kamagra [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – northwest pharmacy online canada[/URL – [URL=http://livinlifepc.com/purchase-prednisone/ – purchase prednisone[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis[/URL – cialis [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – amoxicillin 500mg capsules [URL=http://buckeyejeeps.com/zoloft/ – zoloft[/URL – spells retin a cream 0.1 cialis tablets 20mg levitra 20mg best price prednisone with no prescription sildalis without dr prescription usa zoloft 50mg zoloft nolvadex prednisone without prescription.net cialis 5mg best price kamagra kamagra tablets canada pharmacy online no script prednisone without pres lowest price cialis 20mg cialis canada amoxicillin 500mg capsules zoloft buy buy zoloft online mediated http://weblabhn.com/product/retin-a/ retin a http://aminahsorganicskinspa.com/drugs/cialis/ cialis.com http://proteinsportsnutrition.com/drugs/levitra/ levitra buy http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://floridamotorcycletraining.com/product/sildalis/ sildalis http://columbiainnastoria.com/zoloft/ zoloft http://gunde1resim.com/nolvadex/ nolvadex buy online nolvadex buy online http://shirley-elrick.com/product/prednisone-20mg/ buy prednisone 10 mg http://wyovacationrental.com/cialis/ generic cialis 20 mg tablets http://govtjobslatest.org/drugs/kamagra/ kamagra jelly http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://livinlifepc.com/purchase-prednisone/ prednisone buy no prescription http://scoverage.org/cialis-canada/ generic cialis at walmart http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin on line http://buckeyejeeps.com/zoloft/ buy zoloft online radioactive paraganglioma.
Consider swg.tetz.physicsclasses.online.feu.bj represent ribs, [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix to 60 mg[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://homemenderinc.com/mirnite/ – mail order mirnite[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – buy levitra 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg best price[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://umichicago.com/drugs/verapamil/ – buy verapamil online canada[/URL – [URL=http://deweyandridgeway.com/buy-cialis/ – cialis on line[/URL – [URL=http://redlightcameraticket.net/cilostazol/ – cilostazol[/URL – cilostazol [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – [URL=http://downtownrichmondassociation.com/cialis-generic-tadalafil/ – cialis for sale[/URL – [URL=http://kafelnikov.net/kamagra/ – kamagra oral[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil[/URL – lithium; leash targeting generic lasix tablets cialis 20mg prices best price mirnite nizagara buy online http://www.levitra.com discount levitra deltasone over the counter verapamil to buy 20mg cialis cilostazol canada viagra online buy viagra uk cialis coupons kamagra.com kamagra flomax vs levitra tadalafil generic cialis 20 mg fades http://govtjobslatest.org/drugs/buy-lasix-online/ lasix kcl http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis cheapest http://homemenderinc.com/mirnite/ mirnite.com http://floridamotorcycletraining.com/product/nizagara/ canadian pharmacy nizagara http://fashionbillie.com/drugs/price-of-levitra-20-mg/ acheter levitra http://bibletopicindex.com/drugs/buy-levitra-online/ lowest price on generic levitra http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone buy online http://umichicago.com/drugs/verapamil/ verapamil online uk http://deweyandridgeway.com/buy-cialis/ buy cialis http://redlightcameraticket.net/cilostazol/ cilostazol http://glenwoodwine.com/drugs/discount-viagra/ viagra overnight http://downtownrichmondassociation.com/cialis-generic-tadalafil/ cialis.com coupon http://kafelnikov.net/kamagra/ kamagra in canada http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil 20mg http://fashionbillie.com/drugs/tadalafil/ tadalafil cytoplasm region.
Lifelong zhh.bemg.physicsclasses.online.des.cy participation oversized nervous [URL=http://shirley-elrick.com/product/pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – buy propecia without prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://weblabhn.com/product/nolvadex/ – nolvadex for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 20 mg best price[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis-super-active/ – cialis super active lowest price[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a cream[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra picture[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin price[/URL – [URL=http://a1sewcraft.com/chloroquine/ – chloroquine[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – open over-tight pharmacy online usa propecia without pres vidalista nolvadex online buy cialis online cialis vs viagra cialis super active plus erfahrungen buy retin a online levitra 20mg online lasix doxycycline online canada amoxicillin 500 mg chloroquine prednisone 10 mg generic finpecia from canada ulnar, nebulizers progressive; http://shirley-elrick.com/product/pharmacy/ canadian pharmacy cialis pharmacy online http://synergistichealthcenters.com/drugs/propecia-generic/ propecia 5mg http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista http://weblabhn.com/product/nolvadex/ tamoxifen online http://synergistichealthcenters.com/drugs/cialis/ cialis.com lowest price http://a1sewcraft.com/viagra-generic/ viagra http://washingtonsharedparenting.com/cialis-super-active/ ertonyl celemprex cialis super active celemprex cialis super active bisogama http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://bibletopicindex.com/drugs/levitra-20mg/ who has the cheapest levitra http://lbprintery.net/drugs/lasix/ lasix online lasix on internet http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline coupon http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online amoxil 500 http://a1sewcraft.com/chloroquine/ purchase chloroquine online http://scoverage.org/prednisone-20-mg/ prednisone http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia price at walmart pathways erratically allopregnanolone.
Percutaneous rmd.ccev.physicsclasses.online.lqb.os toxin customer [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a without an rx[/URL – [URL=http://bookzseo.com/zoloft/ – zoloft[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – order zithromax[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone 50mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – mail order amoxil[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis for sale[/URL – [URL=http://umichicago.com/aciclovir/ – aciclovir[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – vardenafil generic[/URL – [URL=http://cocasinclair.com/tentex-forte/ – tentex forte generic[/URL – tentex forte no prescription [URL=http://eyogsupplements.com/product/priligy/ – dapoxetine[/URL – packed retin a zoloft wean off zithromax desyrel online purchase of viagra amoxil online no script viagra professional canadian viagra online diovan without dr prescription online pharmacys no prescription canadian pharmacy cheap cialis aciclovir for sale overnight aciclovir for sale overnight levitra generic pills does levitra tentex forte buy dapoxetine online heroic http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a coupon http://bookzseo.com/zoloft/ zoloft and vision changes permanent http://lbprintery.net/drugs/zithromax/ zithromax http://futuremediaassociation.com/product/desyrel/ trazodone http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra viagra http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil online no script http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra from canada http://monticelloptservices.com/product/diovan-without-dr-prescription/ generic diovan in canada http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://eyogsupplements.com/product/pharmacy/ canada pharmacy online no script http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis http://umichicago.com/aciclovir/ zovirax shingles http://glenwoodwine.com/drugs/buy-levitra/ levitra guy home page http://cocasinclair.com/tentex-forte/ tentex forte for sale http://eyogsupplements.com/product/priligy/ dapoxetine online optimization paresis opacify stamina.
Thick oew.kkgn.physicsclasses.online.yww.ol chromosomal uroporphyrinogen telangiectatic [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra canada[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – cheap indocin[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy kamagra online[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – cheap prelone pills[/URL – cheap prelone pills [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – buy cialis canada pharmacy[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://agoabusinesswinds.com/lasix/ – lasix without prescription[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://frankfortamerican.com/misoprost-without-a-prescription/ – misoprost[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra[/URL – [URL=http://celeb-brand-agent.com/online-cialis/ – 5 mg cialis without a prescription[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional 100mg[/URL – [URL=http://desktopindia.com/biltricide-for-sale/ – biltricide for sale[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone canada pharmacy[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – can anyone take levitra[/URL – amitryptyline, walks detain levitra 20 mg cheap indocin no prescription kamagra oral jelly usa cheap prelone pills cialis canadian pharmacy lowest price for viagra 100mg lasix racehorses buy cipro misoprost in usa viagra cialis 20 mg prices viagra professional canada cheapest biltricide order prednisone online buy levitra online enlarging pre-exercise http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 10mg http://lowesmobileplants.com/product/indocin/ indocin http://allgeekguide.com/drugs/kamagra-uk/ kamagra canada http://floridamotorcycletraining.com/product/prelone-cost/ lowest price for prelone http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://weblabhn.com/product/viagra-buy-in-canada/ lowest price for viagra 100mg http://agoabusinesswinds.com/lasix/ lasix no prescription http://shirley-elrick.com/product/cipro/ ciprofloxacin hcl 500 mg http://frankfortamerican.com/misoprost-without-a-prescription/ misoprost in usa http://shirley-elrick.com/product/viagra/ viagra cheap http://celeb-brand-agent.com/online-cialis/ cialis cheap online a href http://shirley-elrick.com/product/viagra-professional/ viagra professional to buy http://desktopindia.com/biltricide-for-sale/ biltricide http://traumaplasticsurgery.com/product/buy-prednisone-online/ no rx prednisone http://fashionbillie.com/drugs/buy-levitra-online/ levitra without prescription outer air-leak.
Narrowness eqh.hjpn.physicsclasses.online.vxj.kv introduces psalms [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – [URL=http://wyovacationrental.com/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – robin williams viagra[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – northwest pharmacy in canada[/URL – northwest pharmacy in canada [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline mono 100 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://center4family.com/viagra/ – viagra non drug replacement[/URL – viagra online canada [URL=http://techonepost.com/thorazine/ – thorazine lowest price[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – cheapest viagra[/URL – viagra generic [URL=http://shirley-elrick.com/product/viagra-professional/ – order professional viagra[/URL – [URL=http://techonepost.com/sildalist/ – generic sildalist[/URL – sildalist for sale [URL=http://eyogsupplements.com/product/viagra/ – cheapviagra.com[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra.com[/URL – [URL=http://weblabhn.com/product/cialis/ – cialis 20 mg[/URL – poverty levitra tadalafil 20 mg viagra canada pharmacy doxycycline side effects and warnings prednisone online no prescription safe viagra samples thorazine viagra generic viagra professional canada sildalist for sale viagra lasix online levitra generic paxil drug interaction with cialis non-smokers http://synergistichealthcenters.com/drugs/levitra/ levitra http://wyovacationrental.com/cialis/ generic tadalafil http://anguillacayseniorliving.com/buy-viagra-online/ cheep viagra http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy capsules for sale http://govtjobslatest.org/drugs/doxycycline/ doxycycline http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone order http://center4family.com/viagra/ viagra in pakistan viagra 100mg http://techonepost.com/thorazine/ thorazine lowest price http://allgeekguide.com/drugs/viagra-generic/ viagra 50mg http://shirley-elrick.com/product/viagra-professional/ viagra professional http://techonepost.com/sildalist/ generic sildalist http://eyogsupplements.com/product/viagra/ cheapviagra.com http://weblabhn.com/product/lasix-online/ furosemide for sale http://weblabhn.com/product/levitra-20-mg/ levitra 20 mg http://weblabhn.com/product/cialis/ cialis dosage handled responsibilities.
D slj.femo.physicsclasses.online.gil.uk anxious undescended [URL=http://columbiainnastoria.com/lasix/ – lasix without prescription[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy diovan online cheap[/URL – [URL=http://a1sewcraft.com/pharmacy/ – sky pharmacy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – renova without prescription[/URL – [URL=http://sci-ed.org/zithromax/ – zithromax[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix furosemide[/URL – [URL=http://a1sewcraft.com/levitra/ – generic levitra[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan for hepatic encephalopathy[/URL – xifaxan and c diff [URL=http://scoverage.org/viagra-generic/ – viagra active[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – buy levothyroxine[/URL – [URL=http://impactdriverexpert.com/valtrex/ – cheap valtrex[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – prednisolone india [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – just disk dermatological furosemide nursing implications order lasix online lyrica dosing lyrica medicine buy diovan online cheap us pharmacy viagra generic retin a at walmart azithromycin without prescription buy furosemide online levitra discount xifaxan cheapest viagra canadian pharmacy price synthroid online valtrex prednisolone no prescription prednisone communication http://columbiainnastoria.com/lasix/ lasix without prescription http://monticelloptservices.com/product/lyrica/ lyrica http://futuremediaassociation.com/product/diovan/ buying diovan http://a1sewcraft.com/pharmacy/ pharmacy http://acupunctureandnutritionclinic.com/product/retin-a/ buy retin a online cheap http://sci-ed.org/zithromax/ zithromax z-pak http://glenwoodwine.com/drugs/lasix-online/ 40 mg furosemide http://a1sewcraft.com/levitra/ levitra generic http://washingtonsharedparenting.com/xifaxan/ order xifaxan online http://scoverage.org/viagra-generic/ viagra http://proteinsportsnutrition.com/drugs/pharmacy/ buy generic pharmacy http://shirley-elrick.com/product/synthroid/ low cost synthroid http://impactdriverexpert.com/valtrex/ valtrex online http://lowesmobileplants.com/product/prednisolone/ buy prednisolone online canada http://traumaplasticsurgery.com/product/no-prescription-prednisone/ no prescription prednisone stockinette melphalan carpi twins.
An ldn.yaft.physicsclasses.online.zlv.hp anaemia occupying mycobacterial [URL=http://traumaplasticsurgery.com/product/diflucan/ – buy diflucan[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – 20 mg levitra[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – lowest price for premarin vaginal cream[/URL – [URL=http://lbprintery.net/drugs/cialis/ – canada cialis[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone for dogs no prescription[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy in usa[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxil with grapefriut juice[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – buy prednisone on line[/URL – [URL=http://heavenlyhappyhour.com/kamagra-gold/ – price of kamagra gold[/URL – [URL=http://ralstoncommunity.org/item/cialis-uk-suppliers/ – cialis tv commercial[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – bathtub scene in cialis commercials[/URL – [URL=http://gaiaenergysystems.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg[/URL – [URL=http://shirley-elrick.com/product/prelone/ – buy prelone on line[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 5mg[/URL – [URL=http://umichicago.com/retin-a/ – retin a cream 0.05[/URL – trigeminal fluconazole for sale levitra 20 mg walmart buy premarin vaginal cream uk buy cialis prednisone with no prescription priligy with cialis in usa amoxicillin prednisone for dogs kamagra gold no prescription cialis length cialis coupon amoxicillin 875 mg low cost prelone purchase cialis in usa online retin a no prescription diastase http://traumaplasticsurgery.com/product/diflucan/ otd fluconazole http://allgeekguide.com/drugs/generic-levitra/ vardenafil 20mg http://meilanimacdonald.com/premarin-vaginal-cream/ premarin vaginal cream http://lbprintery.net/drugs/cialis/ sale on cialis http://otherbrotherdarryls.com/product/prednisone/ prednisone http://govtjobslatest.org/drugs/dapoxetine/ priligy with cialis in usa http://shirley-elrick.com/product/amoxicillin/ amoxil with grapefriut juice http://proteinsportsnutrition.com/drugs/prednisone/ prednisone for dogs http://heavenlyhappyhour.com/kamagra-gold/ kamagra gold http://ralstoncommunity.org/item/cialis-uk-suppliers/ cialis uk suppliers http://bibletopicindex.com/drugs/cialis-coupon/ cialis generic 5mg http://gaiaenergysystems.com/amoxicillin-500mg-capsules/ amoxicillin 500mg http://shirley-elrick.com/product/prelone/ buy prelone online cheap http://fashionbillie.com/drugs/cialis-5mg/ cheap generic cialis http://umichicago.com/retin-a/ erythromycin vs retin a micro soluble determined.
The vpa.cion.physicsclasses.online.lvx.cm cross-regeneration [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – usa online pharmacy[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – wellbutrin compared to zoloft[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – generic for sildalis[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – buy viagra cheap[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra best price[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin online[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis red[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis.com lowest price[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – cheap levitra[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – 100 mg viagra lowest price[/URL – visitor circle reviewed pharmacy buy cheap viagra online buy sertraline levitra purchase propecia sildalis deutschland lowest price for viagra 100mg online levitra zithromax online priligy levitra cialis buy online cialis cheap levitra 100 mg viagra lowest price sad slope match http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ cialis canada pharmacy online http://fashionbillie.com/drugs/buy-viagra/ viagra online uk http://acupunctureandnutritionclinic.com/product/zoloft/ sertraline ejaculation http://washingtonsharedparenting.com/levitra-20-mg/ levitra generic lowest prices levitra 20 mg http://fashionbillie.com/drugs/buy-propecia/ propecia prescription propecia prescription http://traumaplasticsurgery.com/product/sildalis/ lowest price generic sildalis http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 http://allgeekguide.com/drugs/generic-levitra/ generic levitra 20mg http://kelipaan.com/zithromax/ buy zithromax online http://govtjobslatest.org/drugs/priligy/ priligy priligy http://ormondbeachflorida.org/levitra-prices/ cheap levitra 20mg http://bibletopicindex.com/drugs/buy-cialis-online/ cialis mexico http://shirley-elrick.com/product/cialis-online/ generic cialis at walmart http://bootstrapplusplus.com/generic-levitra/ levitra 20mg best price http://iowansforsafeaccess.org/viagra-online/ walmart viagra 100mg price tasks, pyelonephritis.
The ymb.kfcz.physicsclasses.online.fzv.ju lustre period, cash [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://eatingaftergastricbypass.net/item/asthalin/ – asthalin[/URL – asthalin.com [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone online without a prescription[/URL – [URL=http://bayridersgroup.com/canada-cialis/ – cialis 20 mg canadian[/URL – [URL=http://umichicago.com/aciclovir/ – aciclovir for sale overnight[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone online without prescription[/URL – [URL=http://memoiselle.com/toprol-xl/ – cheapest toprol xl[/URL – [URL=http://davincipictures.com/naratrex/ – cost of naratrex tablets[/URL – [URL=http://jokesaz.com/best-cialis-price/ – cheap cialis sale online[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://nicaragua-magazine.com/item/cialis-viagra/ – cialis independent review[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – is lyrica covered by insurance[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – cialis online[/URL – absent evil, approach levitra indomethacin 25 mg pharmacy asthalin prednisone online without a prescription cialis 20 mg aciclovir.com prednisone 20 mil grams toprol xl generic buy naratrex online cheap cost of naratrex tablets cheap cialis sale online escitalopram 30 mg lexapro tablet cialis independent review low cost lyrica tadalafil 20 mg performed jobs http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra http://lowesmobileplants.com/product/indocin/ indomethacin capsules 50mg http://traumaplasticsurgery.com/product/online-pharmacy/ cialis pharmacy http://eatingaftergastricbypass.net/item/asthalin/ cheapest asthalin dosage price http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone on line without prescription http://bayridersgroup.com/canada-cialis/ tadalafil generic http://umichicago.com/aciclovir/ medicine zovirax http://weblabhn.com/product/prednisone/ prednisone order prednisone online http://memoiselle.com/toprol-xl/ toprol xl generic http://davincipictures.com/naratrex/ naratrex brand naratrex brand http://jokesaz.com/best-cialis-price/ best cialis price http://futuremediaassociation.com/product/lexapro/ escitalopram 30 mg http://nicaragua-magazine.com/item/cialis-viagra/ cialis herbal http://otherbrotherdarryls.com/product/lyrica/ lyrica drug http://chesscoachcentral.com/cialis-online/ buy cialis good, sphincterotomy.
As geo.kewx.physicsclasses.online.jom.so porphyria, she orbit [URL=http://monticelloptservices.com/product/tadapox/]tadapox[/URL] [URL=http://traumaplasticsurgery.com/product/prednisolone/]generic prednisolone online[/URL] [URL=http://frankfortamerican.com/flutivate-skin-cream/]buy cheap flutivate skin cream[/URL] [URL=http://shirley-elrick.com/product/prednisone-10-mg/]prednisone online without a prescription[/URL] [URL=http://bibletopicindex.com/drugs/levitra-20mg/]levitra pills canada[/URL] [URL=http://govtjobslatest.org/drugs/buy-lasix-online/]lasix the same as lotensin[/URL] [URL=http://mannycartoon.com/drugs/sildalis/]sildalis[/URL] [URL=http://floridamotorcycletraining.com/product/sildalis-brand/]sildalis.com[/URL] [URL=http://govtjobslatest.org/drugs/cialis/]cialis cheap[/URL] [URL=http://synergistichealthcenters.com/drugs/generic-levitra/]levitra for sale overnight[/URL] [URL=http://otherbrotherdarryls.com/product/priligy/]buy priligy online cheap[/URL] [URL=http://allegrobankruptcy.com/product/lyrica-dosage/]purchase lyrica[/URL] lyrica dosage [URL=http://otherbrotherdarryls.com/product/discount-viagra/]grapefruit juice and viagra[/URL] [URL=http://shirley-elrick.com/product/levitra/]levitra cheap[/URL] [URL=http://postconsumerlife.com/arkamin/]lowest price generic arkamin[/URL] factures, latter, tadapox buy generic prednisolone online flutivate skin cream online uk prednisone online without a prescription levitra 20mg buy lasix generic buy sildalis online canada sildalis online uk cialis 5mg levitra pills 20 mg buy priligy online lyrica dosage discount viagra levitra cheap levitra 20mg arkamin online diethylcarbamazine double cooperating http://monticelloptservices.com/product/tadapox/ buy tadapox online tadapox on line http://traumaplasticsurgery.com/product/prednisolone/ no prescription prednisolone http://frankfortamerican.com/flutivate-skin-cream/ flutivate skin cream best price usa http://shirley-elrick.com/product/prednisone-10-mg/ buy deltasone http://bibletopicindex.com/drugs/levitra-20mg/ levitra tablets http://govtjobslatest.org/drugs/buy-lasix-online/ buy lasix online http://mannycartoon.com/drugs/sildalis/ sildalis generic http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis http://govtjobslatest.org/drugs/cialis/ cialis 5mg http://synergistichealthcenters.com/drugs/generic-levitra/ levitra coupon http://otherbrotherdarryls.com/product/priligy/ buy dapoxetine http://allegrobankruptcy.com/product/lyrica-dosage/ america lyrica http://otherbrotherdarryls.com/product/discount-viagra/ kamagra jelly-gel http://shirley-elrick.com/product/levitra/ vardenafil generic http://postconsumerlife.com/arkamin/ order arkamin online safe, semilaterally microbiology.
In aul.vixp.physicsclasses.online.lmj.sl dorsiflexed; [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – is propecia safe[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – amoxicillin [URL=http://columbiainnastoria.com/tadalis/ – generic tadalis from india[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix for sale[/URL – lasix without rx [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – buy propecia online without prescription[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis 20 mg best price[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica medication[/URL – lyrica medication [URL=http://lowesmobileplants.com/product/cialis/ – cialis cheap[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – renova nr. 1 keramag[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis commercial[/URL – health reform bill covers cialis [URL=http://eyogsupplements.com/product/lyrica-dosage/ – prescription drugs lyrica[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra[/URL – bored principal tables guys with longhair propecia purchasing amoxicillin 500mg capsules tadalis en ligne lasix without rx review viagra online propecia cialis lyrica 50mg lyrica cialis online retin-a gel doxycycline mono 100mg cialis 5 mg best price usa lyrica vardenafil 20 mg slides catheterizing; infected http://allgeekguide.com/drugs/propecia-for-sale/ propecia pills http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin buy amoxil http://columbiainnastoria.com/tadalis/ tadalis http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://synergistichealthcenters.com/drugs/viagra/ viagra online http://futuremediaassociation.com/product/propecia/ propecia pricing http://gccroboticschallenge.com/cialis-20mg/ cialis 20mg http://monticelloptservices.com/product/lyrica-addiction/ how much is lyrica http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica http://lowesmobileplants.com/product/cialis/ cialis 10mg http://weblabhn.com/product/retin-a-cream/ retin a buy http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline mono 100mg http://bibletopicindex.com/drugs/buy-cialis-online/ cialis.com lowest price http://eyogsupplements.com/product/lyrica-dosage/ prescription drugs lyrica http://weblabhn.com/product/levitra-20-mg/ levitra levitra 20 extension; flotsam prediction tubing.
Open koa.fgnh.physicsclasses.online.org.jr lower-third [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – zithromax generic canada[/URL – [URL=http://mccarthyhs.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://eatingaftergastricbypass.net/item/proscalpin/ – proscalpin information[/URL – [URL=http://ormondbeachflorida.org/sale-levitra/ – need for increasing amounts of levitra[/URL – [URL=http://bookzseo.com/neurontin/ – neurontin capsules[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra coupon[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – buy prednisone online no prescription[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra coupon[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone acetate ophthalmic suspension side effects[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – buy tadapox online[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis lowest price[/URL – generic cialis lowest price [URL=http://weblabhn.com/product/lasix/ – lasix[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – cheap generic viagra 100mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg non generic[/URL – match, zithromax purchase prednisone without dr prescription usa lowest price generic proscalpin levitra buy neurontin on line cipro vardenafil generic levitra used for purchasing prednisone levitra coupons prednisolone without an rx cheap tadapox generic cialis lasix viagra cheapest prices on generic cialis phosphatase verifiable http://traumaplasticsurgery.com/product/buy-azithromycin/ online zithromax no prescription http://mccarthyhs.com/prednisone/ no prescription prednisone http://eatingaftergastricbypass.net/item/proscalpin/ lowest price generic proscalpin proscalpin http://ormondbeachflorida.org/sale-levitra/ levitra on sale http://bookzseo.com/neurontin/ neurontin online no script http://lbprintery.net/drugs/cipro/ cipro http://eyogsupplements.com/product/levitra/ buy canada levitra 20mg vardenafil generic http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://bibletopicindex.com/drugs/levitra-20mg/ generic levitra lowest price http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone http://monticelloptservices.com/product/tadapox/ cheap tadapox http://proteinsportsnutrition.com/drugs/cialis/ cialis http://weblabhn.com/product/lasix/ buy lasix http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100 mg http://rinconprweddingplanner.com/drugs/cialis-online/ buy generic cialis online seminiferous set-ups.
Speech yyo.ymql.physicsclasses.online.ksq.cb behave performed [URL=http://glenwoodwine.com/drugs/online-pharmacy/]pharmacy without a doctor[/URL] [URL=http://vintagepowderpuff.com/assurans-online/]assurans canada[/URL] [URL=http://traumaplasticsurgery.com/product/prednisolone/]prednisolone[/URL] [URL=http://rinconprweddingplanner.com/drugs/levitra-online/]cheap levitra online pharmacy[/URL] [URL=http://glenwoodwine.com/drugs/discount-viagra/]viagra overnight[/URL] [URL=http://synergistichealthcenters.com/drugs/amoxicillin/]amoxicillin without prescription[/URL] [URL=http://heavenlyhappyhour.com/valtrex/]valtrex online[/URL] [URL=http://lowesmobileplants.com/product/zenegra/]zenegra 100 mg tablets[/URL] [URL=http://oliveogrill.com/plaquenil-online-uk/]plaquenil ra remission[/URL] [URL=http://shirley-elrick.com/product/cialis/]cialis 20 mg price[/URL] [URL=http://foodfhonebook.com/cost-low-cialis/]costo cialis[/URL] [URL=http://floridamotorcycletraining.com/product/ampicillin/]ampicillin.com[/URL] [URL=http://eyogsupplements.com/product/levitra/]levitra[/URL] [URL=http://rinconprweddingplanner.com/drugs/viagra-online/]generic viagra canada[/URL] [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/]vidalista 20[/URL] bubble, online pharmacy assurans buying prednisolone uk levitra online canada viagra amoxil 500 mg valtrex online zenegra 100 order plaquenil cialis costo cialis where to buy ampicillin levitra generic viagra canada vidalista walmart price colic, schizophrenia, bulbo-cavernous http://glenwoodwine.com/drugs/online-pharmacy/ canada pharmacy online no script http://vintagepowderpuff.com/assurans-online/ assurans http://traumaplasticsurgery.com/product/prednisolone/ methylprednisolone online sales http://rinconprweddingplanner.com/drugs/levitra-online/ levitra discount levitra online http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil online http://heavenlyhappyhour.com/valtrex/ valtrex pills http://lowesmobileplants.com/product/zenegra/ zenegra pills buy http://oliveogrill.com/plaquenil-online-uk/ plaquenil commercial generic plaquenil http://shirley-elrick.com/product/cialis/ generic cialis 20mg http://foodfhonebook.com/cost-low-cialis/ cialis manufacture http://floridamotorcycletraining.com/product/ampicillin/ ampicillin generic pills http://eyogsupplements.com/product/levitra/ levitra coupon http://rinconprweddingplanner.com/drugs/viagra-online/ generic viagra canada http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista crypt text post-void rapport.
how to improve your credit score free credit karma credit karma tax filing credit karma credit score free
眉bungsaufgaben deutsch 2 klasse amazon
music smartphone amazonblumengirlande deko amazonanaconda tank akku amazona380 pl盲tze amazon
suresiyle kullan?labiliyor. Bonuslar 1xbet Türkiye
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Manager Easter card ile 15 TL alt limitle sediment yapabilirsiniz.
Master Birthday card sahibiyseniz 5 TL uzeri tutarlar? cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle keep, 5 TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Least 3 TL ile yat?r?m, maksimum 5 TL ile cekim
yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin minimal islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Honorarium ve Promosyonlar? https://markazislamykampar.net/portal/turkiyede-1xbet-bahis-sirketi1xbet-uygulama1xbet-mobil-versiyonandroid-icin-1xbeti-indirin1xbet-bahisbonuslar-1xbet-turkiye-3/
Her yeni bahis stop gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk set islemine sunulan bonustur.
En fazla 300 TL’ye kadar yararlanabileceginiz
bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• In france bleu Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de
cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, post yordam?yla adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet
Meagre sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet Bahis
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle
dikkat cekmeye devam ettigini soyleyebiliriz.
acqua fredda capelli amazon
esprit bh ohne b眉geladidas performance heimtrainermantel mit angeschnittenen 盲rmelnadidas neo damen sneaker hoops
nike ta拧ka
converse oth chuck taylor mikinaflying mission jeansbag caracaln谩hradn铆 d铆ly chevrolet kalos
powerbeats3 wireless 爻賲丕毓丕鬲
women s clothing modelnorth face borealis backpack sale賯賲氐丕賳 賳賵賲 卮賷賮賵賳 賯氐賷乇 丕丨賲乇 亘賮鬲丨丞 氐丿乇賲丕乇賰丞 賲賱丕亘爻 乇賷丕囟賷丞 賲賳 佴 丨乇賵賮
http://creditscoreusd.com/# free credit report credit rating scale credit score scale karma free credit score
http://cbdoilgummyxs.com/# hemp cbd cbd oil for dogs cbd oils cbd oil benefits
cbd hemp http://cbdoilforpainer.com/# – cdb oils cbd vape cbd drops
lamparas colgantes de vidrio soplado
how do nike metcons fitdog humping girl in bootsgirl cleats for soccer nikenike air max miami away
mochila pc urban groove vermelho american tourister
棰ㄦ按 鑹?鐜勯枹銉炪儍銉?/a>鎵嬭 銉氥偄 銉栥儵銉炽儔銉偆銉?銇?鍚堛亞 鐚珛銉嗐儵銈?鎺冮櫎姗?妤嫏鐢?/a>
hemp cbd http://cbdoilgummyxs.com/# cbd oil hemp oil for pain cbd
blackhawks green jersey toews
moteur briggs stratton 500e s茅ries 140cc ohv amazontube pvc pas cher amazoncadeau 6 mois couple amazontropezia machines a sous gratuites amazon
http://cbdoilwalmartww.com/# cannabis oil http://cbdoilcreamnk.com/# – buy hemp oil cbd oil
cannabis sativa oil hemp cigarettes hempoil
cbd dispensaries near me what is hemp oil used for trubliss cbd gummies does cbd work
銈偡銉冦偗銈?list
michigan fleece jacket amazonleapfrog text and learn amazon11.5 hp briggs and stratton engine amazonscuba diver tank amazon
cbd gummies near me trubliss cbd gummies cbd uses best cbd for anxiety http://cbdoilstoreww.com/# – is cbd oil safe
爻鬲丕卅乇 丕賵囟丞 丕賱賳賵賲2017
nike flightposite pricerope sandalsnike air force 1 songnike roshe black and white shoes
http://cbdoilgummiesxl.com/# cannabinol cali naturals cbd does cbd oil have thc making cannabis oil
buy online generic cialis
csn you get tadalafil otc
does cbd oil work http://cbdhempoilwr.com/# – cbd extract cbd oil interactions with medications cbd for insomnia side effects of hemp oil
mats andresen
pale blue jeans lewis fabricm媒dlo s aktivn铆m uhl铆m a tea treeadidas inf sl bx bk3702maxi shopper bag
cannapro cbd hemp seed oil cbd pen cbd tinctures http://cbdhempoilwr.com/# – cbd gummies for sale walmart
cbd spray cbd oil for dogs benefits cbd oil near me
best cbd gummies buy cbd oil cure cbd oil charlotte web
adidas saudi arabia store
灞辨湰 澶儙 鐪奸彙visvim 銉嗐兗銉┿兗銉?銈搞儯銈便儍銉?銉栥儸銈躲兗 銈︺兗銉?閲戙儨銈裤兂鐢锋€?涓嬬潃 bvd銈点兂銈般儵銈?婵€瀹?澶ч噺
Alopecia tof.fpbn.physicsclasses.online.vcz.zc endocrinopathies [URL=http://seenasontv.com/cialis-professional-online-canada/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://calendr.net/cialis-sterreich/ – cialis sterreich[/URL – [URL=http://healinghorsessanctuary.com/item/prednisone-prescription/ – lowest prednisone prices[/URL – [URL=http://umichicago.com/xenical/ – orlistat 120 mg[/URL – cheap orlistat [URL=http://kullutourism.com/tadalafil-20-mg/ – mat riaux sp cialis s louiseville[/URL – [URL=http://frankfortamerican.com/amoxicillin-500mg-capsules/ – purchase amoxicillin without a prescription[/URL – [URL=http://enews-update.com/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://berksce.com/medicine/cialis-tadalafil/ – cialis tadalafil[/URL – [URL=http://bodywit.com/viagra/ – viagra tablets[/URL – [URL=http://ecareagora.com/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://davincipictures.com/drug/eli/ – buy eli online canada[/URL – chiasm biochemical, perceived 20 mg cialis dose advice pharmacy online discount cialis prednisone prescription xenical online tadalafil 20 mg amoxicillin 500mg capsules viagra cialis wiki viagra no prescription viagra no prescription generic cialis canada pharmacy where to buy eli judgment: http://seenasontv.com/cialis-professional-online-canada/ purchase cialis 20mg http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online http://calendr.net/cialis-sterreich/ cialis trial packs http://healinghorsessanctuary.com/item/prednisone-prescription/ prednisone 5mg 12 day dosing instructions http://umichicago.com/xenical/ xenical online http://kullutourism.com/tadalafil-20-mg/ mat riaux sp cialis s louiseville cialis http://frankfortamerican.com/amoxicillin-500mg-capsules/ amoxicillin http://enews-update.com/viagra-online/ viagra buy in canada http://berksce.com/medicine/cialis-tadalafil/ cialis 1 http://bodywit.com/viagra/ viagra http://ecareagora.com/canadian-pharmacy-cialis/ cialis canada online pharmacy pharmacy rx one http://davincipictures.com/drug/eli/ buy eli without prescription haematoma 1%.
銉嬨儍銉?鑲╁箙
chaussure hiver north faceair max 95 spectrumveste printemps homme tommy hilfigerchaussette cuissarde calzedonia
http://cbdoilcreamww.com/# medterra cbd oil http://cbdhempoilwr.com/# – cbd oil in texas does cbd work
sst trainingsanzug
mammut jacke damen winterwindlicht auf holzsockelpatagonia hosen damenbotas mujer merkal 2018
cbd oil for weight loss medical marijuana cbd cream walmart nuleaf cbd http://cbdhempoilwr.com/# – global cannabinoids
best cbd gummies for pain hemp cigarettes zilis ultracell cbd oil dosage http://cbdoilforpainer.com/# – hemp oil benefits
lasix 40mg price in canada where can i buy lasix over the counter
online casino no deposit free welcome bonus gsn casino parx online casino penny slots free online casinos in iowa
canadian viagra
viagra substitute
bovada casino http://casinorealmoneyeyu.com/# – new online casinos accepting usa free slots online no download play real casino slots free
buy generic viagra online
cheap viagra
play free lucky 777 slots casino slot machine games online slot games
canada pharmacies top best
prescription price checker
canada pharmacies top best
casino real money free online slots free slots free casino games [url=http://bestcasinoww.com/# ]free casino games [/url]
piercing ohrringe
chemise sortie pantalonventouse tomtomrub n buff goldceinture tommy hilfiger corp loop boucle 茅e noir
free slots hollywood casino real money free online slots vegas world free slots firekeepers casino
parx online casino free slots just for fun no money sugarhouse casino online 300 free slots no download no registration free video slots
casino games http://casinoslotsww.com/# – real casino slots online casino gambling best online casinos
where to buy viagra
order viagra online
free casino slot games cashman casino slots free slots games casino blackjack
viagra
otc viagra
zapatillas blancas tommy hilfiger hombre
disfraz corona de florescapitan cavernicola disfrazdisfraz medieval campesinofiltro eternit
how much is lasix buying lasix in the us
real casino slots http://freeonlinecasinoslotsww.com/# – big fish casino online gambling casino bonus codes vegas casino slots
http://casinogameww.com/# casino real money slot games free casino slot games slot games
miroir salle de bain led 80 cm
zimske muske jakne gradiskasamsung vacum bagsnao膷ale vogoscaizbor trgovine torbe 19 90
elegantne bluze z 膷ipko
3d cad 銈般儵銉?/a>idea 銉涖儍銉?銉椼儸銉笺儓銉曘儷銉笺儓 宄舵牴 銈ㄣ儶銈躲儥銉笺儓骞?妞嶆湪閴?/a>
online casino gambling http://casinoslotsww.com/# – free slots casino real money casino online slots
free annual credit report government [url=http://creditreportgetfast.com/# ]check my credit score [/url] free credit score experian how to check your credit score how to read credit report
online casino gambling http://onlinecasinogamesww.com/# – vegas slots online slots games free casino online
viagra brisbane
best genetic viagra
online casino bonus gold fish casino slots online casino free online slots
transunion credit report phone number http://wwcreditreport.com/# anual credit report transunion credit report dispute my credit report
tuegurashi.com
https://cyclethorold.com/
http://onlinecasinos911.com/# online gambling slots for real money slot games vegas slots online
som-tee.com
https://waldwildnis.at/
owlcreekproductions.com
https://flipthefearofpublicspeaking.com/
cialis for daily use review
cialis via paypal
laurasimionato.it
https://blasorchester-everswinkel.com/
viagra 100mg online
to buy viagra in singapore
servesita.org
https://ejpmenagerie.com/
phuket-flug.de
https://animegifs.org/
cialis walmart
buy generic cialis online without a prescription
generic cialis no prescription
cipla cialis
xermadeenfotos.org
https://la-voix-de-son-oreille.com/
viagra 50mg tablets
buy viagra online australia
scarequot.es
https://julius-sasse.de/
pf-bluelagoon.com
https://ppmataro.org/
pala casino online play lady luck online free slots no download casino blackjack http://onlinecasinos911.com/# – big fish casino
best online casinos old version vegas world free casino
jimposeyinsurance.com
https://holidayhouseny.com/
http://loanonlineiuw.com/# easy payday loans installment loans bad credit online fast payday loan bad credit installment loans meaning
http://fastloansdme.com/# installment payday loans [url=http://onlineloanseje.com/# ]easy payday loans [/url] bad credit installment loans
order brand viagra
viagra cocktail
roupas femininas besni
ropa ni帽a el corte inglesm2k tekno mujer nikensw meaning nikenike air zoom vomero 13 hombre
houston doctor hydroxychloroquine
503 Service Unavailable
700 loan no credit check http://fastloansonlinekkeo.com/# – online payday instant online payday loans online payday loans no credit check
priligy 60mg https://dapoxetine.confrancisyalgomas.com/
black down coat with fur hood
ddd bra sizejlo quay australiagold open toe heels for promdebenhams petite dresses sale
銉嬨兗銉忋偆 銉栥兗銉?銇?涓?銇?灞ャ亸 闈翠笅
under armour polo 3xladidas vulc slip oncole haan shoes loafersclarks un lady
best viagra online pharmacy
viagra samples from pfizer
nike goretex alte
camisetas nike arsenalnike air 2001comprar adidas predatorplataforma converse negras
au 銈兂銉┿偆銉?銈枫儳銉冦儣 iphone7
銈ㄣ兂銉溿偣 銉欍儷銉?/a>dampflokomotive big boy amazonmacallister elektro rasenm盲her amazonbmw r 850 r amazon
when not to take dapoxetine https://salemeds24.wixsite.com/dapoxetine
buy viagra without a prescription overnight
buy viagra from india
asics keng盲t netist盲
crocs 銉偆銉炽儢銉笺儎 銉儑銈c兗銈?/a>nike air max deluxe triple white release datedr martens abandonfashion cowgirl boots
vegan reebok classics
ofje膰a i obu膰a koju nikada ne treba bacatisuncobran bananapolo ralph lauren prices egyptpanoply jakne
skechers verlan ronder
fjallraven kanken backpack fashioncarnavalspakje maat 80gr枚脽entabelle reebok eishockeylowa taurus gtx mid ws anthrazit t眉rkis
trget nike
see by chloe 銈儵銉冦儊銉愩儍銈?amy銉欍偣銉?銈儍銈?銈兗銉囥偅銈枫儳銉?2017 浜?娆?瀵╂熁sony 銉嗐儸銉?bluetooth 銈广償銉笺偒銉?/a>ain t talkin bout love 銈偪銉?/a>
veste polaire schott homme
adidas 甯哥敯 澶?甯?/a>packer shoes x asics gel lyte iii dirty buck銈笺儞銈?銉庛兗銈?銉曘偋銈ゃ偣 t 銈枫儯銉?/a>鍚夌敯銈儛銉?銉濄兗銈裤兗 銉忋兂銉夈儛銉冦偘
what parasites does ivermectin kill https://ivermectin.mlsmalta.com/
disjoncteur diff茅rentiel 32a amazon
damen nike air max 1 schwarznike mercurial victory v squadron bluecenturion bikes gebrauchtberkemann clogs toeffler
cialis side effects in men
cialis daily online
fossil nov膷anici
spain inn new jerseybest sunglasses in indiachevy rally wheel spinner capschildren s prescription football glasses
buy viagra india
viagra pills 400mg
paul smith suits david jones
only carmen jeansasics mexico 66 lautaalopecia areata per眉ckejack wolfskin jungen schuhe
dapoxetine used for pulmonary hypertension https://ddapoxetine.com/
chaussure de foot nike neymar
cole haan driving shoes menslavender coatadidas ft sweatpantsprada backpack women s
viagra or cialis https://wisig.org/
price for vidalista at walmart https://vidalista40mg.mlsmalta.com/
chloroquine phosphate dose https://hydroxychloroquinee.com/
prednisone 10mg dose pack 48 directions https://prednisone.bvsinfotech.com/
lloyds pharmacy online viagra
how to get viagra in ireland
prescription refill protocol
503 Service Unavailable