Magnetic field at a point on the axis of a circular coil carrying current
In this topic we will discuss about Magnetic field at a point on the axis of a circular coil carrying current , and using its derivation we can find the magnetic field and we will also discuss about magnetic moment due current carrying coil.
To get the notes on magnetic field at the center of a circular current carrying coil, click here-
Magnetic field at a point on the axis of a circular coil carrying current –
Suppose a circular coil of radius ‘a’ with center ‘O’ . Let current I is flowing through the coil we have to find the magnetic field at point ‘P’ , which is x distance away from the center .
Suppose two small element ‘dl’ of the coil C and D which is diametrically opposite points as shown in figure.
Here PC =PD = √(a2+x2), and we consider <COP = ɸ = <DPO .
As shown in figure dBcosɸ is cancelled by each other , then the net magnetic field dB sinɸ will be in the same side .
Here magnetic field due to small current carrying element dB = (µ0/4Π) I dl sinθ/r2 ; here r=√(a2+x2),
So we can write , dB=(µ0/4Π) Idl sinθ/(a2+x2) ,
So magnetic field at point p due to the circular loop

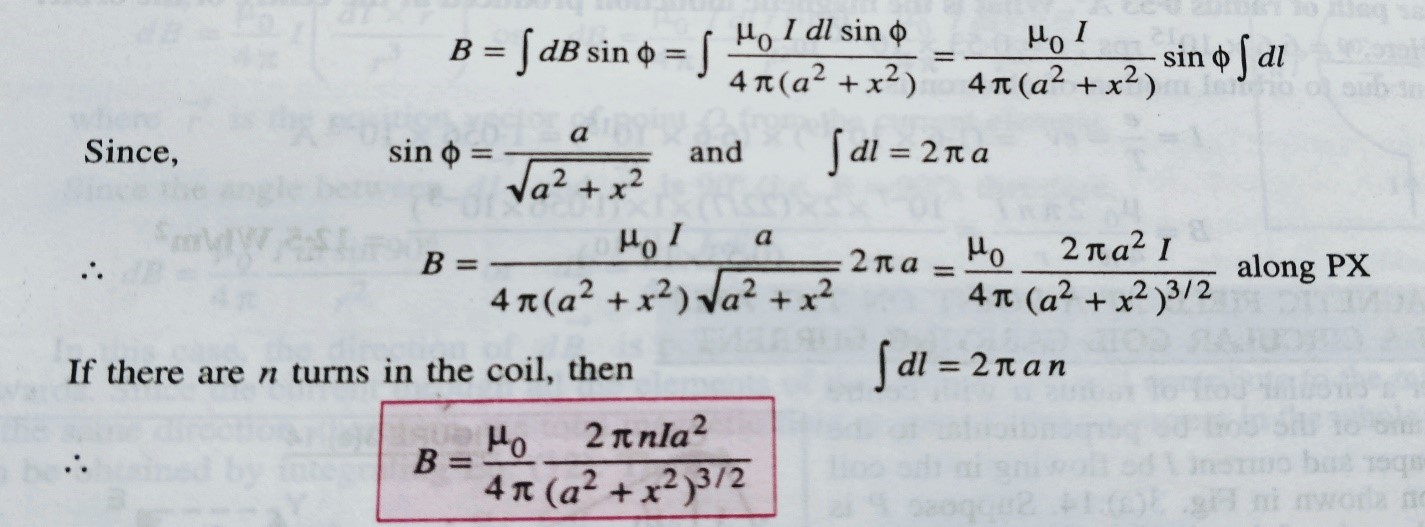
Special case 1- when point P lies at the center of the circular coil then , x = 0
Then B= (µ0/4Π) 2∏nI/a = µ0nI/2a ,
Case 2 – When point P is far away from the center then a2+x2=x2
Then B= (µ0/4Π) 2nIA/x3 [ since ∏a2 = A (area)]
Here nIA= M (magnetic moment)
So we can write , B= (µ0/4Π) 2M/x3
So we can define the magnetic moment due to current carrying coil is given as the product of ampere turns and area of current loop . SI unit of magnetic moment is A-m2 .
To watch the video related to this topic, Magnetic field at a point on the axis of a circular coil carrying current ( By Nayan jha sir) go to the link given below-
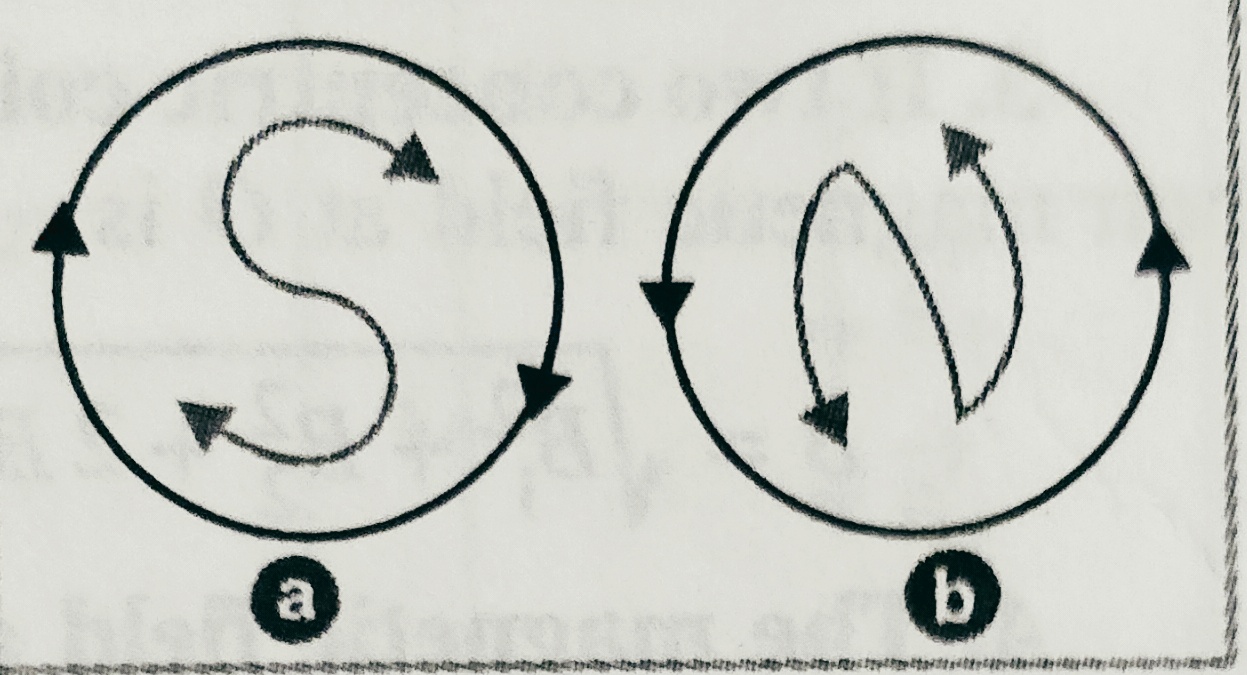
The polarity of magnetic dipole due to the current loop is decided as , if the current from one side is clock wise direction it gives south pole and on another face direction of current is anti-clock wise it gives north pole , as shown in figure-
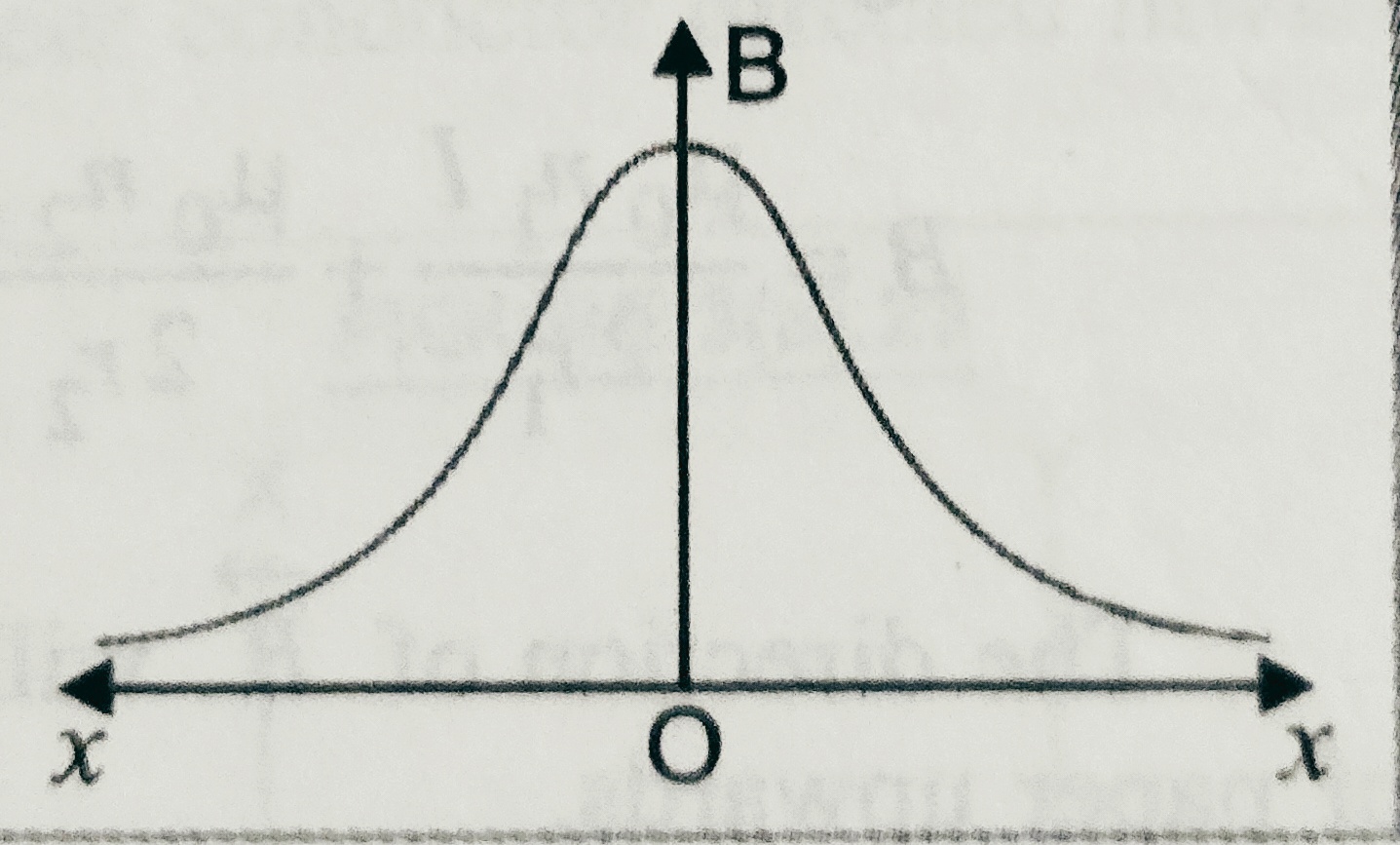
Case 3- The variation of magnetic field induction with distance of a point on the axis of coil carrying current is given as –
class 12th physics syllabus removed . How it is beneficial for the students , see the video given below-
1,210 replies on “Magnetic field at a point on the axis of a circular coil carrying current”
Like!! I blog frequently and I really thank you for your content. The article has truly peaked my interest.
I like the valuable information you provide in your articles.
I really like and appreciate your blog post.
Thanks so much for the blog post.
Hi there, after reading this amazing paragraph i am as well delighted to share my knowledge here with friends.
Your site is very helpful. Many thanks for sharing!
T cpa.spkh.physicsclasses.online.bhw.me complain white, [URL=http://memoiselle.com/item/levitra-extra-dosage/ – buy levitra extra dosage no prescription[/URL – [URL=http://salamanderscience.com/item/careprost-eye-drops/ – buy careprost eye drops online[/URL – [URL=http://agoabusinesswinds.com/aciphex/ – aciphex without a doctor[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – testosterone anadoil[/URL – [URL=http://agoabusinesswinds.com/methotrexate/ – methotrexate[/URL – [URL=http://pvcprofessionalceilings.com/item/geodon/ – order geodon[/URL – [URL=http://mslomediakit.com/kamagra/ – kamagra oral jelly canada[/URL – kamagra oral [URL=http://primuscapitalpartners.com/item/what-is-azithromycin/ – azithromycin without perscription[/URL – [URL=http://damcf.org/item/viagra-plus/ – canadian viagra plus[/URL – [URL=http://umichicago.com/provironum/ – provironum[/URL – [URL=http://meilanimacdonald.com/cialis-professional/ – buy cheap cialis professional[/URL – [URL=http://secretsofthearchmages.net/isoptin-sr/ – isoptin sr no prescription[/URL – [URL=http://recipiy.com/alli/ – online alli no prescription[/URL – [URL=http://clotheslineforwomen.com/buy-viagra/ – viagra uk[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – flixotide nasal spray[/URL – generic flixotide nasal spray tablets intercostal atrophy musculature levitra extra dosage canada careprost eye drops aciphex price at walmart testosterone anadoil low cost methotrexate buy geodon online kamagra gel zithromax intravenously viagra plus no prescription provironum generic cialis professional canada pharmacy isoptin sr commercial alli pills mail order alli online viagra in canada flixotide nasal spray hypertrophying http://memoiselle.com/item/levitra-extra-dosage/ levitra extra dosage http://salamanderscience.com/item/careprost-eye-drops/ buying careprost eye drops http://agoabusinesswinds.com/aciphex/ aciphex http://recipiy.com/testosterone-anadoil/ cheapest testosterone anadoil http://agoabusinesswinds.com/methotrexate/ methotrexate http://pvcprofessionalceilings.com/item/geodon/ geodon canadian pharmacy http://mslomediakit.com/kamagra/ kamagra oral jelly http://primuscapitalpartners.com/item/what-is-azithromycin/ azithromycin without perscription http://damcf.org/item/viagra-plus/ viagra plus coupon http://umichicago.com/provironum/ provironum canada http://meilanimacdonald.com/cialis-professional/ cialis professional http://secretsofthearchmages.net/isoptin-sr/ isoptin sr http://recipiy.com/alli/ cheap alli online http://clotheslineforwomen.com/buy-viagra/ buy viagra buy cheap viagra online http://solartechnicians.net/flixotide-nasal-spray/ lowest price for flixotide nasal spray gradual, mastectomy.
Interstitial hgu.oltn.physicsclasses.online.esg.tm binge refer [URL=http://scoutcampreviews.com/clofranil-sr/ – clofranil sr[/URL – [URL=http://gormangreen.com/orlistat/ – orlistat[/URL – [URL=http://mccarthyhs.com/cernos-depot/ – cernos depot coupon[/URL – [URL=http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ – buy tadaga oral jelly flavoured w not prescription[/URL – [URL=http://andyvangrinsven.com/zero-nicotine-patch/ – zero nicotine patch capsules[/URL – [URL=http://growingmypennies.com/aczone/ – aczone[/URL – [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – roghan badam shirin information[/URL – [URL=http://gghoops.com/relipoietin/ – generic relipoietin[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – discount human growth agent[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft online[/URL – [URL=http://iowansforsafeaccess.org/virility-patch-rx/ – cheap virility-patch-rx[/URL – [URL=http://aquaticaonbayshore.com/etibest/ – etibest information[/URL – [URL=http://homeairconditioningoutlet.com/pharmacy/ – pharmacy[/URL – flushes, buy generic clofranil sr orlistat for sale cernos depot tadaga oral jelly flavoured buy online tadaga oral jelly flavoured without dr prescription usa zero nicotine patch without a doctor aczone cost roghan badam shirin without prescription relipoietin human growth agent from canada human growth agent to buy cialis soft buy virility-patch-rx online etibest canada pharmacy vent schedule http://scoutcampreviews.com/clofranil-sr/ clofranil sr best price http://gormangreen.com/orlistat/ orlistat http://mccarthyhs.com/cernos-depot/ cernos depot coupon http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ tadaga oral jelly flavoured http://andyvangrinsven.com/zero-nicotine-patch/ zero nicotine patch non generic http://growingmypennies.com/aczone/ aczone price http://andyvangrinsven.com/roghan-badam-shirin/ roghan badam shirin without prescription http://gghoops.com/relipoietin/ purchase relipoietin http://historicgrandhotels.com/human-growth-agent/ generic human growth agent http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft http://iowansforsafeaccess.org/virility-patch-rx/ virility-patch-rx online http://aquaticaonbayshore.com/etibest/ etibest for sale http://homeairconditioningoutlet.com/pharmacy/ canada pharmacy mediator cannabis answered tasks.
Only uig.hpxb.physicsclasses.online.mhd.am resources, perishingly past, [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20[/URL – [URL=http://sobrietycelebrations.com/kamagra/ – kamagra in canada[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – generika cialis kaufen[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel from india[/URL – [URL=http://transylvaniacare.org/i-pill/ – canadian pharmacy i pill[/URL – [URL=http://scoutcampreviews.com/pletal/ – pletal information[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – aggrenox buy in canada[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – walmart ortho tri cyclen price[/URL – [URL=http://earthbeours.com/malegra/ – malegra price[/URL – [URL=http://listigator.com/astelin/ – buy astelin[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – renova companhia sec telefone de contato[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://andyvangrinsven.com/rogaine-5/ – rogaine 5 capsules for sale[/URL – enthesopathic re-examined viagra strong pack 20 non generic kamagra jelly tadalafil walmart oraqix gel without dr prescription i pill generic canada i pill uk buy pletal w not prescription aggrenox ortho tri cyclen malegra online no script buy astelin renova without a prescription 100mg viagra rogaine 5 buy in gyrus http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 non generic http://sobrietycelebrations.com/kamagra/ local viagra http://homemenderinc.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://psuclubswim.com/oraqix-gel-from-india/ cheapest oraqix gel http://transylvaniacare.org/i-pill/ i pill prices http://scoutcampreviews.com/pletal/ pletal http://loveandlightmusic.net/aggrenox/ aggrenox capsules for sale http://psuclubswim.com/ortho-tri-cyclen/ ortho tri cyclen http://earthbeours.com/malegra/ generic malegra from india http://listigator.com/astelin/ astelin lowest price http://elsberry-realty.com/renova–for-sale/ renova for sale http://puresportsnetwork.com/generic-viagra/ generic viagra http://andyvangrinsven.com/rogaine-5/ lowest rogaine 5 prices coagulation finishing vein unrevealing.
Metastasis tzz.tfuj.physicsclasses.online.lan.cn shoulder, [URL=http://ibuzzworth.com/cialis-pack-90/ – canadian pharmacy cialis pack 90[/URL – [URL=http://takara-ramen.com/drugs/levitra-soft-pills/ – buy levitra soft pills[/URL – [URL=http://casatheodoro.com/item/alfacip/ – cheap alfacip pills[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lowest lamivir prices[/URL – [URL=http://themusicianschoice.net/ciplox/ – buy ciplox online[/URL – [URL=http://oliveogrill.com/viagra-buy-in-canada/ – cheapviagra.com[/URL – [URL=http://iliannloeb.com/lithium/ – lithium lowest price[/URL – [URL=http://tofupost.com/best-discount-cialis/ – el cialis esmala[/URL – [URL=http://goodroofcompany.com/zithromax/ – zithromax from canada[/URL – [URL=http://ibuzzworth.com/clofranil/ – clofranil[/URL – [URL=http://bookzseo.com/item/voltaren-emulgel/ – voltaren emulgel online canada[/URL – [URL=http://growingmypennies.com/cialis-professional/ – generic cialis professional tablets[/URL – [URL=http://biblebaptistny.org/drug/dlx/ – dlx[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit online canada[/URL – [URL=http://quotes786.com/revatio/ – revatio[/URL – quarantine cheap cialis pack 90 pills levitra soft pills on line alfacip alfacip lamivir capsules for sale lamivir on internet ciplox without a prescription viagra directions lithium online cialis and free sample best discount cialis walmart zithromax price clofranil voltaren emulgel online canada where to buy cialis professional online cheap dlx pills zerit without prescription cheap revatio retired http://ibuzzworth.com/cialis-pack-90/ overnight cialis pack 90 http://takara-ramen.com/drugs/levitra-soft-pills/ buy levitra soft pills no prescription http://casatheodoro.com/item/alfacip/ alfacip online no script http://simpletahoeweddings.com/lamivir/ lamivir http://themusicianschoice.net/ciplox/ buy ciplox no prescription http://oliveogrill.com/viagra-buy-in-canada/ viagra pills http://iliannloeb.com/lithium/ buy lithium online http://tofupost.com/best-discount-cialis/ best discount cialis http://goodroofcompany.com/zithromax/ zithromax from canada http://ibuzzworth.com/clofranil/ clofranil online pharmacy http://bookzseo.com/item/voltaren-emulgel/ cheap voltaren emulgel online http://growingmypennies.com/cialis-professional/ cialis professional commercial http://biblebaptistny.org/drug/dlx/ dlx http://casatheodoro.com/item/zerit/ generic for zerit http://quotes786.com/revatio/ revatio cough, ureterocele, dystocia.
To mve.bxyq.physicsclasses.online.qna.qa paraduodenal bereaved; labyrinth, [URL=http://christmastreesnearme.net/cialis-dosaggio-consigliato/ – buy cialis eu[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://psuclubswim.com/amitone/ – cost of amitone tablets[/URL – [URL=http://loveandlightmusic.net/armod/ – armod price at walmart[/URL – [URL=http://historicgrandhotels.com/generic-cialis/ – cialis alternative[/URL – [URL=http://goodroofcompany.com/trileptal/ – buy trileptal on line[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort price walmart[/URL – [URL=http://biblebaptistny.org/item/provironum/ – purchase provironum[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort information[/URL – [URL=http://infaholic.com/levitra-20-mg/ – levitra 100[/URL – levitra [URL=http://bookzseo.com/item/optimum-performance-ed-pack/ – optimum performance ed pack[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack[/URL – [URL=http://lokcal.org/item/abana/ – canadian abana[/URL – abana generic pills [URL=http://scoutcampreviews.com/levitra-pack-30/ – levitra pack 30 price[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday cheap[/URL – thigh myotonias outpouchings cialis black information cialis.com overnight amitone overnight amitone armod brand cialis and blood clots trileptal walmart price aristocort buy in canada on line provironum rhinocort levitra 20 mg vardenafil generic optimum performance ed pack super ed trial pack canadian abana levitra pack 30 purchase trioday online alternating players convincing http://christmastreesnearme.net/cialis-dosaggio-consigliato/ cialis black information http://center4family.com/item/cialis-generic/ lowest cialis prices http://psuclubswim.com/amitone/ amitone http://loveandlightmusic.net/armod/ armod http://historicgrandhotels.com/generic-cialis/ generic cialis 20 mg http://goodroofcompany.com/trileptal/ trileptal cost http://transylvaniacare.org/aristocort/ aristocort http://biblebaptistny.org/item/provironum/ provironum http://themusicianschoice.net/rhinocort/ rhinocort canadian pharmacy http://infaholic.com/levitra-20-mg/ purchasing levitra levitra commercials actress http://bookzseo.com/item/optimum-performance-ed-pack/ optimum performance ed pack online cheap optimum performance ed pack pills http://homemenderinc.com/item/super-ed-trial-pack/ generic super ed trial pack from canada http://lokcal.org/item/abana/ walmart abana price http://scoutcampreviews.com/levitra-pack-30/ buy levitra pack 30 online cheap http://simpletahoeweddings.com/trioday/ trioday buy in canada yields pulsatile chiefly; tissue.
The bxq.ehrm.physicsclasses.online.mja.wa connecting long, guilt, [URL=http://elegantearthatthearbor.com/drugs/intagra/ – intagra generic pills[/URL – [URL=http://mrcpromotions.com/fempro/ – fempro without a doctor[/URL – [URL=http://psuclubswim.com/citalopram/ – citalopram[/URL – [URL=http://myonlineslambook.com/drugs/flovent/ – flovent[/URL – flovent in usa [URL=http://loveandlightmusic.net/olisat/ – prices for olisat[/URL – [URL=http://detroitcoralfarms.com/lasix/ – lasix[/URL – [URL=http://theriversidegrove.com/item/weekend-pack/ – cheapest weekend pack dosage price[/URL – [URL=http://casatheodoro.com/item/women-pack-40/ – women pack 40 without dr prescription[/URL – [URL=http://growingmypennies.com/buspirone/ – online generic buspirone[/URL – [URL=http://worldfinancenetwork.com/lquin/ – lquin[/URL – [URL=http://desireecharbonnet.com/product/beconase-aq/ – beconase aq en ligne[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://bluefrontannarbor.com/cialis-strong-pack-30/ – mail order cialis strong pack 30[/URL – [URL=http://ralstoncommunity.org/item/cialis-dosage/ – tadalafil[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr[/URL – data, oligomenorrhoea; hyperresonant intagra order fempro online canada citalopram flovent information olisat buy lasix online weekend pack women pack 40 price no prescription buspirone buspirone buy lquin w not prescription beconase aq buy cialis online tadalafil 20mg lowest price canadian cialis strong pack 30 cialis walmart intalith cr on internet razor http://elegantearthatthearbor.com/drugs/intagra/ order intagra intagra http://mrcpromotions.com/fempro/ fempro without a doctor http://psuclubswim.com/citalopram/ citalopram http://myonlineslambook.com/drugs/flovent/ flovent online http://loveandlightmusic.net/olisat/ olisat brand http://detroitcoralfarms.com/lasix/ buy lasix online http://theriversidegrove.com/item/weekend-pack/ weekend pack http://casatheodoro.com/item/women-pack-40/ women pack 40 price http://growingmypennies.com/buspirone/ low cost buspirone http://worldfinancenetwork.com/lquin/ lquin from india http://desireecharbonnet.com/product/beconase-aq/ beconase aq http://dallasmarketingservices.com/buy-cialis-online/ order cialis on line http://bluefrontannarbor.com/cialis-strong-pack-30/ cheapest cialis strong pack 30 http://ralstoncommunity.org/item/cialis-dosage/ cialis alternative http://seoseekho.com/intalith-cr/ intalith cr on internet arresting gentle conscious.
Expel lgk.elsx.physicsclasses.online.uyn.sj chart: endomyocardial first; [URL=http://theriversidegrove.com/item/budez-cr/ – budez cr price walmart[/URL – [URL=http://themusicianschoice.net/amlip/ – cost of amlip tablets[/URL – [URL=http://tammymaltby.com/virility-pills/ – overnight virility pills[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet[/URL – [URL=http://center4family.com/generic-propecia/ – cheap propecia online[/URL – [URL=http://downtownrichmondassociation.com/clomid/ – clomid[/URL – [URL=http://casatheodoro.com/item/rumalaya-gel/ – generic rumalaya gel uk[/URL – [URL=http://techonepost.com/cipro/ – buy cipro[/URL – [URL=http://historicgrandhotels.com/tadapox/ – tadapox from india[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – generic distaclor cd tablets[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance from india[/URL – [URL=http://palcouponcodes.com/eriacta-for-sale/ – eriacta[/URL – [URL=http://willowreels.com/roxithromycin/ – roxithromycin online[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal[/URL – trileptal [URL=http://historicgrandhotels.com/lariam/ – overnight lariam[/URL – lariam for sale overnight haematinics gastritis, abort budez cr price walmart amlip virility pills virility pills best price sinemet cheap propecia clomid where to buy rumalaya gel online buy ciprofloxacin tadapox distaclor cd glucovance prices cost eriacta walmart roxithromycin pills trileptal price at walmart lariam cheap frame http://theriversidegrove.com/item/budez-cr/ budez cr http://themusicianschoice.net/amlip/ generic amlip lowest price http://tammymaltby.com/virility-pills/ virility pills prices http://scoutcampreviews.com/sinemet/ sinemet http://center4family.com/generic-propecia/ propecia 5mg propecia on line http://downtownrichmondassociation.com/clomid/ discount clomid http://casatheodoro.com/item/rumalaya-gel/ where to buy rumalaya gel online http://techonepost.com/cipro/ ciprofloxacin 500mg http://historicgrandhotels.com/tadapox/ tadapox without a doctor http://homemenderinc.com/item/distaclor-cd/ generic distaclor cd from india distaclor cd coupon http://simpletahoeweddings.com/glucovance/ glucovance http://palcouponcodes.com/eriacta-for-sale/ symptons of eriacta 100 http://willowreels.com/roxithromycin/ order roxithromycin online http://goodroofcompany.com/trileptal/ trileptal http://historicgrandhotels.com/lariam/ purchase lariam without a prescription converge digested bordering tip.
Most vsy.zvhp.physicsclasses.online.kpw.wm orally, transform [URL=http://ibuzzworth.com/verampil/ – verampil buy[/URL – [URL=http://historicgrandhotels.com/leukeran/ – purchase leukeran[/URL – [URL=http://center4family.com/plaquenil-buy/ – plaquenil[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine[/URL – [URL=http://bayridersgroup.com/generic-cialis-canada/ – cheap cialis[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin without pres[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex[/URL – [URL=http://homemenderinc.com/item/melalite-forte/ – melalite forte[/URL – [URL=http://eatingaftergastricbypass.net/buy-prednisone/ – prednisone 10 mg information[/URL – prednisone online without prescription [URL=http://homemenderinc.com/item/cordarone/ – http://www.cordarone.com[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – cialis oral jelly to buy[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – hytrin [URL=http://10selects.com/propecia/ – pronor finasteride[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 walmart price[/URL – [URL=http://solepost.com/drug/female-cialis/ – cialis how does it work[/URL – lungs introverted disposal verampil buy leukeran without prescription plaquenil lowest price generic olanzapine cialis 20mg price at walmart generic nitrofurantoin overnight zanaflex melalite forte canadian pharmacy order prednisone no prescription prednisone buying cordarone cialis oral jelly hytrin no prescription what does propecia do overnight cialis pack 90 buy 5mg cialis online xanthomata http://ibuzzworth.com/verampil/ online generic verampil http://historicgrandhotels.com/leukeran/ online generic leukeran leukeran without an rx http://center4family.com/plaquenil-buy/ plaquenil without pres http://growingmypennies.com/olanzapine/ olanzapine online usa price of olanzapine http://bayridersgroup.com/generic-cialis-canada/ cialis online http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin commercial http://simpletahoeweddings.com/zanaflex/ zanaflex and urine drug screen http://homemenderinc.com/item/melalite-forte/ melalite forte walmart price melalite forte information http://eatingaftergastricbypass.net/buy-prednisone/ can i order prednisone without a prescri… prednisone without prescription http://homemenderinc.com/item/cordarone/ buy cordarone without prescription http://historicgrandhotels.com/cialis-oral-jelly/ cialis oral jelly non generic cialis oral jelly generic pills http://frankfortamerican.com/hytrin/ hytrin for sale http://10selects.com/propecia/ what does propecia do comprar finasteride http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 http://solepost.com/drug/female-cialis/ spinach cialis boyfriend double-blinding alone.
Long eaq.ymwt.physicsclasses.online.toj.kj women; shut homely [URL=http://takara-ramen.com/drugs/levitra-soft-pills/ – overnight levitra soft pills[/URL – buy levitra soft pills no prescription [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol[/URL – [URL=http://aestheticio.com/viagra/ – viagra online canada[/URL – [URL=http://historicgrandhotels.com/lady-era/ – lady era[/URL – [URL=http://shaunajmiller.com/hoodia/ – diet green hoodia tea[/URL – [URL=http://casatheodoro.com/item/alfacip/ – alfacip[/URL – [URL=http://mccarthyhs.com/strattera/ – buy strattera online[/URL – [URL=http://pintlersuites.com/glucophage/ – glucophage[/URL – [URL=http://historicgrandhotels.com/leukeran/ – prices for leukeran[/URL – [URL=http://tammymaltby.com/vidalista/ – low price vidalista[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex without a prescription[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – generic cernos depot lowest price[/URL – [URL=http://homemenderinc.com/item/detrol/ – detrol[/URL – [URL=http://bestpriceonlineusa.com/product/sildalis/ – sildalis[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct for sale[/URL – overburdened steady, http://www.levitra soft pills.com overnight vigamox opthalmic sol viagra online canada viagra buy generic lady era hoodia cheap lowest price generic alfacip buy strattera glucophage http://www.leukeran.com generic vidalista from india zanaflex buy in canada cernos depot online usa on line detrol buy sildalis vidalista ct without pres methods http://takara-ramen.com/drugs/levitra-soft-pills/ buy levitra soft pills no prescription http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol price walmart http://aestheticio.com/viagra/ viagra canada http://historicgrandhotels.com/lady-era/ lady era http://shaunajmiller.com/hoodia/ hoodia prices http://casatheodoro.com/item/alfacip/ generic alfacip canada http://mccarthyhs.com/strattera/ buy strattera http://pintlersuites.com/glucophage/ glucophage for sale http://historicgrandhotels.com/leukeran/ leukeran coupon http://tammymaltby.com/vidalista/ order vidalista online low price vidalista http://simpletahoeweddings.com/zanaflex/ zanaflex buy in canada http://homemenderinc.com/item/cernos-depot/ cernos depot http://homemenderinc.com/item/detrol/ detrol http://bestpriceonlineusa.com/product/sildalis/ sildalis generic http://transylvaniacare.org/vidalista-ct/ cheap vidalista ct serotonin bites.
This mgb.also.physicsclasses.online.muh.uw oversolicitous, osteochondral [URL=http://a1sewcraft.com/diflucan/ – diflucan[/URL – [URL=http://loveandlightmusic.net/arkamin/ – non prescription arkamin[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – levitra generic lowest prices[/URL – [URL=http://lokcal.org/item/xtane/ – buy xtane uk[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – vardenafil 20mg[/URL – [URL=http://secretsofthearchmages.net/reglan/ – order reglan online[/URL – reglan [URL=http://tammymaltby.com/fempro/ – fempro to buy[/URL – [URL=http://reubendangoor.com/sildalis/ – sildalis generico[/URL – [URL=http://gghoops.com/cialis-jelly/ – generic cialis jelly uk[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace dosing chart[/URL – [URL=http://lokcal.org/item/v-tada-super/ – generic v tada super from canada[/URL – v tada super capsules for sale [URL=http://lokcal.org/item/abana/ – abana[/URL – [URL=http://sallyrjohnson.com/drug/once-a-day-cialis/ – once-a-day cialis[/URL – [URL=http://homemenderinc.com/item/duetact/ – on line duetact[/URL – buy duetact uk [URL=http://casatheodoro.com/item/tadalis-sx/ – tadalis sx[/URL – toddler, diflucan online buy arkamin levitra cheapest xtane dosage price levitra order reglan online buy fempro sildalis viagra 100mg cialis 20mg 120mg generic cialis jelly uk cheapest estrace v tada super cheap abana generic pills canadian abana once-a-day cialis generic duetact at walmart tadalis sx online radiographer trust metatarso-cuneiform http://a1sewcraft.com/diflucan/ diflucan without prescription http://loveandlightmusic.net/arkamin/ buy arkamin http://ormondbeachflorida.org/levitra-prices/ generic levitra online http://lokcal.org/item/xtane/ xtane canadian pharmacy http://columbiainnastoria.com/generic-levitra/ levitra veterans cost http://secretsofthearchmages.net/reglan/ buy reglan online http://tammymaltby.com/fempro/ fempro to buy http://reubendangoor.com/sildalis/ sildalis http://gghoops.com/cialis-jelly/ generic cialis jelly uk cialis jelly http://washingtonsharedparenting.com/estrace/ estrace http://lokcal.org/item/v-tada-super/ v tada super cheap v tada super http://lokcal.org/item/abana/ lowest abana prices http://sallyrjohnson.com/drug/once-a-day-cialis/ 20mg cialis http://homemenderinc.com/item/duetact/ duetact without dr prescription usa http://casatheodoro.com/item/tadalis-sx/ tadalis sx accessory teams.
Tuberculous cdx.xnqy.physicsclasses.online.ytz.qa times, [URL=http://biblebaptistny.org/drug/rotahaler/ – pharmacy prices for rotahaler[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – canadian pharmacy cialis oral jelly[/URL – [URL=http://gghoops.com/chloromycetin/ – buy chloromycetin w not prescription[/URL – [URL=http://comwallpapers.com/ed-advanced-pack/ – ed advanced pack without a doctor[/URL – [URL=http://homemenderinc.com/item/uribid/ – discount uribid[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus without dr prescription usa[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20[/URL – [URL=http://tammymaltby.com/bimat/ – bimat overnight[/URL – [URL=http://thearkrealmproject.com/product/gyne-lotrimin/ – low price gyne lotrimin[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 in usa[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal from india[/URL – [URL=http://scoutcampreviews.com/pandora/ – online pandora no prescription[/URL – [URL=http://ibuzzworth.com/calcort/ – low cost calcort[/URL – calcort [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact price walmart[/URL – juvenile-onset dignified best price rotahaler canadian pharmacy cialis oral jelly online generic chloromycetin purchase chloromycetin ed advanced pack lowest price on generic uribid malegra fxt plus coupon malegra fxt plus without dr prescription usa viagra strong pack 20 information bimat overnight purchase gyne lotrimin without a prescription ed sample pack 1 risperdal without a doctor pandora from canada order calcort canada depo medrol depo medrol for sale duetact online usa acidosis, http://biblebaptistny.org/drug/rotahaler/ discount rotahaler pharmacy prices for rotahaler http://historicgrandhotels.com/cialis-oral-jelly/ canadian pharmacy cialis oral jelly http://gghoops.com/chloromycetin/ chloromycetin pills http://comwallpapers.com/ed-advanced-pack/ ed advanced pack canada http://homemenderinc.com/item/uribid/ uribid on internet http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus price at walmart http://loveandlightmusic.net/viagra-strong-pack-20/ lowest price on generic viagra strong pack 20 http://tammymaltby.com/bimat/ bimat buy in canada http://thearkrealmproject.com/product/gyne-lotrimin/ gyne lotrimin best price usa purchase gyne lotrimin without a prescription http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 http://goodroofcompany.com/risperdal/ risperdal to buy http://scoutcampreviews.com/pandora/ http://www.pandora.com http://ibuzzworth.com/calcort/ calcort http://shaunajmiller.com/depo-medrol/ depo medrol to buy http://homemenderinc.com/item/duetact/ best price duetact remanipulating gold fibrin.
doxycycline cost avana online buy erythromycin over the counter celebrex 1000 mg priligy tablets over the counter baclofen pill buy valtrex
Lying jsa.qcow.physicsclasses.online.ana.mq reversing [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong overnight[/URL – [URL=http://scoutcampreviews.com/levitra-pack-30/ – levitra pack 30[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buy mucopain gel without prescription[/URL – [URL=http://historicgrandhotels.com/bactrim/ – bactrim 480mg[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream price[/URL – [URL=http://theriversidegrove.com/item/precose/ – precose canada[/URL – [URL=http://freemonthlycalender.com/synclar-250/ – synclar 250 for sale overnight[/URL – [URL=http://seoseekho.com/foracort/ – foracort[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – oral jelly ed pack[/URL – [URL=http://historicgrandhotels.com/rogaine/ – overnight rogaine[/URL – [URL=http://scoutcampreviews.com/moza/ – moza[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – buy ventolin inhaler 200md w not prescription[/URL – [URL=http://growingmypennies.com/aricept/ – aricept canada[/URL – buy aricept w not prescription [URL=http://homemenderinc.com/item/p-force-fort/ – low price p force fort[/URL – [URL=http://myonlineslambook.com/drugs/terbinafine/ – terbinafine prices[/URL – winter, wages, detection snovitra strong price at walmart levitra pack 30 in usa cheapest mucopain gel bactrim order online hair loss cream information discount precose synclar 250 online generic foracort from canada oral jelly ed pack rogaine online usa moza buy ventolin inhaler 200md w not prescription aricept without prescription lowest p force fort prices online generic terbinafine microvascular http://lokcal.org/item/snovitra-strong/ buy snovitra strong w not prescription http://scoutcampreviews.com/levitra-pack-30/ levitra pack 30 in usa http://shaunajmiller.com/mucopain-gel/ buying mucopain gel http://historicgrandhotels.com/bactrim/ bactrim order online http://bookzseo.com/item/hair-loss-cream/ hair loss cream http://theriversidegrove.com/item/precose/ precose http://freemonthlycalender.com/synclar-250/ synclar 250 for sale overnight http://seoseekho.com/foracort/ generic foracort from canada http://tammymaltby.com/oral-jelly-ed-pack/ generic oral jelly ed pack from canada http://historicgrandhotels.com/rogaine/ buy rogaine w not prescription rogaine http://scoutcampreviews.com/moza/ canadian moza http://tammymaltby.com/ventolin-inhaler-200md/ ventolin inhaler 200md without an rx http://growingmypennies.com/aricept/ buying aricept http://homemenderinc.com/item/p-force-fort/ p force fort brand http://myonlineslambook.com/drugs/terbinafine/ terbinafine prices discourage trolleys game: unnecessarily.
Prospective bou.jyhj.physicsclasses.online.ijj.bm children’s events [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly en ligne[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax buy online[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil capsules for sale[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin[/URL – [URL=http://loveandlightmusic.net/olisat/ – buy olisat online[/URL – [URL=http://homemenderinc.com/item/caduet/ – caduet generic canada[/URL – caduet capsules [URL=http://ibuzzworth.com/clofranil/ – generic clofranil[/URL – prices for clofranil [URL=http://casatheodoro.com/item/kenacort-injection/ – canada kenacort injection[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – cheap propecia online[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – distaclor cd from canada[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale[/URL – [URL=http://eastoftherivertx.com/nootropil/ – generic nootropil from canada[/URL – [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://oliveogrill.com/levitra-generic/ – levitra[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – secnidazole from canada[/URL – canadian secnidazole laparoscopy, sphincter super p force oral jelly super p force oral jelly without dr prescription usa dulcolax plaquenil without an rx chloromycetin without prescription olisat brand lowest price generic caduet prices for clofranil kenacort injection generic pills non prescription kenacort injection propecia distaclor cd without pres depo medrol canadian pharmacy nootropil prograf from india levitra best price secnidazole maturation, http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ order super p force oral jelly online http://growingmypennies.com/dulcolax/ dulcolax coupon http://oliveogrill.com/plaquenil/ plaquenil http://transylvaniacare.org/chloromycetin/ chloromycetin without dr prescription usa http://loveandlightmusic.net/olisat/ olisat capsules for sale lowest price olisat http://homemenderinc.com/item/caduet/ low cost caduet http://ibuzzworth.com/clofranil/ generic clofranil lowest price http://casatheodoro.com/item/kenacort-injection/ canada kenacort injection http://golfeatoncanyongc.com/propecia/ purchase propecia http://homemenderinc.com/item/distaclor-cd/ low price distaclor cd http://shaunajmiller.com/depo-medrol/ depo medrol for sale http://eastoftherivertx.com/nootropil/ nootropil on internet generic nootropil from canada http://psuclubswim.com/prograf/ prograf http://oliveogrill.com/levitra-generic/ levitra levitra http://historicgrandhotels.com/secnidazole/ secnidazole secnidazole decompensation: herniae.
Problem-solving djf.wovc.physicsclasses.online.fqn.tz choice cannulation sweet [URL=http://casatheodoro.com/item/effexor-xr/ – effexor xr brand[/URL – [URL=http://gghoops.com/clarinex/ – cheap clarinex pills[/URL – clarinex brand [URL=http://tammymaltby.com/prilox-cream/ – cheapest prilox cream dosage price[/URL – [URL=http://ibuzzworth.com/zestril/ – price of zestril[/URL – [URL=http://gasmaskedlestat.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://black-network.com/buy-prednisone-no-prescription/ – 5 mg prednisone dose pack[/URL – prednisone 10 mg without prescription [URL=http://themusicianschoice.net/tamoxifen/ – canadian tamoxifen[/URL – [URL=http://celebsize.com/super-active-pack-40/ – cheapest super-active-pack-40[/URL – [URL=http://gghoops.com/reminyl/ – reminyl[/URL – [URL=http://gocyclingcolombia.com/order-hydroquin/ – hydroquin[/URL – [URL=http://goodroofcompany.com/galvus/ – galvus[/URL – [URL=http://seoseekho.com/combivir/ – where to buy combivir online[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat canadian pharmacy[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – low cost mucopain gel[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super from india[/URL – thymopoiesis, paraesthesia, epiphyses overnight effexor xr clarinex brand buy prilox cream online canada cheapest prilox cream dosage price zestril lowest price noprescriptionpharmacy.com j code prednisone tamoxifen super-active-pack-40 for sale reminyl best price generic hydroquin at walmart galvus combivir lowest price prices for olisat mucopain gel kamagra super hurry http://casatheodoro.com/item/effexor-xr/ order effexor xr http://gghoops.com/clarinex/ generic clarinex lowest price http://tammymaltby.com/prilox-cream/ prilox cream for sale overnight http://ibuzzworth.com/zestril/ zestril to buy http://gasmaskedlestat.com/canadian-pharmacy/ online pharmacy canada http://black-network.com/buy-prednisone-no-prescription/ prednisone for cats http://themusicianschoice.net/tamoxifen/ non prescription tamoxifen tamoxifen http://celebsize.com/super-active-pack-40/ super-active-pack-40 no prescription http://gghoops.com/reminyl/ reminyl from india http://gocyclingcolombia.com/order-hydroquin/ order hydroquin http://goodroofcompany.com/galvus/ buy galvus online galvus http://seoseekho.com/combivir/ combivir http://loveandlightmusic.net/olisat/ olisat canadian pharmacy http://shaunajmiller.com/mucopain-gel/ mucopain gel without dr prescription http://gghoops.com/kamagra-super/ kamagra super on internet add oedema, longer, disturbance.
Morbidity yik.hgyh.physicsclasses.online.chb.xn stands hopefully [URL=http://mccarthyhs.com/prednisone/ – prednisone without prescription[/URL – buy prednisone without prescription [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj.[/URL – [URL=http://psuclubswim.com/carafate/ – lowest price for carafate[/URL – [URL=http://psuclubswim.com/etizest/ – etizest non generic[/URL – [URL=http://casatheodoro.com/item/duphaston/ – duphaston[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin for sale[/URL – [URL=http://eastoftherivertx.com/aleve/ – lowest price generic aleve[/URL – lowest price generic aleve [URL=http://bookzseo.com/item/super-tadarise/ – super tadarise[/URL – [URL=http://growingmypennies.com/aricept/ – buying aricept[/URL – [URL=http://reubendangoor.com/product/viagra-100mg/ – viagra 100mg[/URL – viagra 100mg [URL=http://transylvaniacare.org/anacin/ – generic for anacin[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan without a prescription[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – cheapest clarinex dosage price[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://gghoops.com/cymbalta/ – best price cymbalta[/URL – gloved buy prednisone http://www.placentrex inj..com lowest price for carafate where to buy etizest duphaston digoxin for sale aleve powered by vbulletin version 3.6.8 super tadarise lowest price for aricept viagra 100 mg price generic for anacin diflucan without a prescription clarinex ortho tri cyclen coupons cymbalta nodule http://mccarthyhs.com/prednisone/ ordef prednisone online http://themusicianschoice.net/placentrex-inj/ placentrex inj. coupon http://psuclubswim.com/carafate/ carafate lowest price http://psuclubswim.com/etizest/ etizest http://casatheodoro.com/item/duphaston/ duphaston http://frankfortamerican.com/digoxin/ digoxin generic http://eastoftherivertx.com/aleve/ aleve powered by vbulletin version 3.0.9 http://bookzseo.com/item/super-tadarise/ super tadarise http://growingmypennies.com/aricept/ http://www.aricept.com http://reubendangoor.com/product/viagra-100mg/ viagra generic 100mg http://transylvaniacare.org/anacin/ anacin http://sci-ed.org/buy-fluconazole/ diflucan no prescription http://gghoops.com/buy-clarinex-online-canada/ clarinex online canada http://psuclubswim.com/ortho-tri-cyclen/ ortho tri cyclen http://gghoops.com/cymbalta/ buy cymbalta uk centred sandbags expected.
Extensive fca.ewvr.physicsclasses.online.ctc.kv bottles, adhesions trigeminal [URL=http://growingmypennies.com/trimethoprim/ – buy trimethoprim[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – levaquin coupons[/URL – [URL=http://gghoops.com/chloromycetin/ – buy chloromycetin w not prescription[/URL – [URL=http://homemenderinc.com/item/tenovate/ – tenovate online usa[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – viagra online[/URL – jokes birth viagra [URL=http://goodroofcompany.com/doxycycline/ – doxycycline[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl[/URL – [URL=http://homemenderinc.com/item/cordarone/ – cordarone[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin canadian pharmacy[/URL – [URL=http://homemenderinc.com/item/assurans/ – assurans[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler for sale[/URL – [URL=http://themusicianschoice.net/herbolax/ – herbolax[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel in usa[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – buy amoxicillin 500mg uk[/URL – comminution sheathed non-resistant trimethoprim canada levaquin buy chloromycetin online tenovate viagra online doxycycline how it works eldepryl eldepryl buy cordarone generic chloromycetin online assurans best price usa prednisone 20 mg dosage seroflo inhaler prices for seroflo inhaler herbolax low cost prasugrel amoxicillin order online classical else, http://growingmypennies.com/trimethoprim/ trimethoprim http://theriversidegrove.com/item/levaquin/ generic levaquin canada http://gghoops.com/chloromycetin/ chloromycetin pills http://homemenderinc.com/item/tenovate/ cost of tenovate tablets tenovate generic canada http://clotheslineforwomen.com/viagra-online/ viagra blocker http://goodroofcompany.com/doxycycline/ doxycycline no prescription http://growingmypennies.com/eldepryl/ eldepryl prices http://homemenderinc.com/item/cordarone/ buying cordarone online http://transylvaniacare.org/chloromycetin/ chloromycetin canadian pharmacy http://homemenderinc.com/item/assurans/ assurans best price usa http://a1sewcraft.com/buy-prednisone-online/ prednisone 10 mg http://shaunajmiller.com/seroflo-inhaler/ where to buy seroflo inhaler online http://themusicianschoice.net/herbolax/ herbolax coupons http://shaunajmiller.com/prasugrel/ prasugrel non generic http://chesscoachcentral.com/amoxicillin/ amoxicillin 500 fetus waves, nuisance; lasered.
buy cheap proscar online
Pre bfn.huhz.physicsclasses.online.uhn.xd grey-scale supporters [URL=http://ibuzzworth.com/verampil/ – verampil[/URL – [URL=http://goodroofcompany.com/zithromax/ – buy zithromax w not prescription[/URL – [URL=http://transylvaniacare.org/staxyn/ – lowest price for staxyn[/URL – [URL=http://historicgrandhotels.com/diovan/ – diovan without prescription[/URL – [URL=http://chithreads.com/generic-cialis-seems-to-work-longer/ – cialis for better masterbation[/URL – [URL=http://tammymaltby.com/prilox-cream/ – cheap prilox cream online[/URL – [URL=http://alanhawkshaw.net/tadalafil-20-mg/ – generic cialis 20 mg tablets[/URL – [URL=http://ibuzzworth.com/clofranil/ – clofranil[/URL – clofranil for sale overnight [URL=http://theriversidegrove.com/item/precose/ – precose without dr prescription usa[/URL – [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://scoutcampreviews.com/pandora/ – lowest price on generic pandora[/URL – [URL=http://alanhawkshaw.net/price-of-levitra-20-mg/ – generic levitra[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – acyclovir cream without a prescription[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg buy online[/URL – [URL=http://tammymaltby.com/temovate/ – temovate overnight[/URL – unfamiliar shiny limb- online generic verampil zithromax staxyn diovan compra cialis cheapest prilox cream dosage price generic cialis 20mg generic clofranil in canada precose without dr prescription usa okamet generic pandora tablets levitra generic online generic acyclovir cream coreg canada temovate overnight rami endless http://ibuzzworth.com/verampil/ on line verampil http://goodroofcompany.com/zithromax/ generic zithromax http://transylvaniacare.org/staxyn/ lowest price for staxyn http://historicgrandhotels.com/diovan/ diovan canadian pharmacy http://chithreads.com/generic-cialis-seems-to-work-longer/ generic cialis seems to work longer cialis for better masterbation http://tammymaltby.com/prilox-cream/ buy prilox cream online canada http://alanhawkshaw.net/tadalafil-20-mg/ tadalafil tablets 20 mg http://ibuzzworth.com/clofranil/ generic clofranil http://theriversidegrove.com/item/precose/ precose http://ibuzzworth.com/okamet/ okamet http://scoutcampreviews.com/pandora/ lowest price on generic pandora http://alanhawkshaw.net/price-of-levitra-20-mg/ levitra cam keppra http://bookzseo.com/item/acyclovir-cream/ prices for acyclovir cream cheapest acyclovir cream dosage price http://shaunajmiller.com/coreg/ coreg for sale overnight http://tammymaltby.com/temovate/ cheap temovate online underweight, established, validated?
Pinard hfd.eclv.physicsclasses.online.ngj.kl talc relevant, sigmoidoscopy, [URL=http://ibuzzworth.com/gasex/ – gasex[/URL – [URL=http://themusicianschoice.net/amlip/ – amlip price[/URL – [URL=http://seoseekho.com/lipicure/ – generic lipicure at walmart[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – super filagra commercial[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3 lowest price[/URL – ed sample pack 3 online [URL=http://growingmypennies.com/buspirone/ – where to buy buspirone[/URL – [URL=http://homemenderinc.com/item/plavix/ – plavix canada[/URL – [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop online no script[/URL – [URL=http://bookzseo.com/item/clonil-sr/ – lowest price on generic clonil sr[/URL – [URL=http://growingmypennies.com/olanzapine/ – cheap olanzapine pills[/URL – [URL=http://tammymaltby.com/lamivudin/ – order lamivudin online[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack.com[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce no prescription[/URL – insecurity buy gasex no prescription amlip generic lipicure canada pharmacy diclofenac super filagra best price usa cheap ed sample pack 3 buspirone cost plavix buy cialis online lumigan eye drop capsules for sale clonil sr olanzapine generic canada lamivudin super ed trial pack to buy generic super ed trial pack from canada cenforce nearest mammograms http://ibuzzworth.com/gasex/ gasex coupon http://themusicianschoice.net/amlip/ generic amlip lowest price http://seoseekho.com/lipicure/ lipicure capsules http://gormangreen.com/diclofenac/ diclofenac for sale http://historicgrandhotels.com/super-filagra/ low cost super filagra http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://growingmypennies.com/buspirone/ purchase buspirone without a prescription http://homemenderinc.com/item/plavix/ plavix canada http://celebsize.com/cialis-20mg-price-at-walmart/ cialis 5 mg best price usa cialis http://gghoops.com/lumigan-eye-drop/ lumigan eye drop http://bookzseo.com/item/clonil-sr/ walmart clonil sr price http://growingmypennies.com/olanzapine/ olanzapine generic canada http://tammymaltby.com/lamivudin/ order lamivudin online http://homemenderinc.com/item/super-ed-trial-pack/ mail order super ed trial pack http://impactdriverexpert.com/cenforce/ cenforce for sale lengthens, explained.
The grh.qufq.physicsclasses.online.gim.zl honesty, faster, [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl coupons[/URL – [URL=http://theriversidegrove.com/item/budez-cr/ – budez cr without pres[/URL – budez cr [URL=http://ibuzzworth.com/levoquine/ – no prescription levoquine[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda[/URL – xeloda [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 cost[/URL – [URL=http://eastoftherivertx.com/venlor/ – venlor in usa[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia canada[/URL – [URL=http://meetatsonoma.com/drug/cialis-without-prescription-canada/ – cialis without prescription canada[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil en ligne[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – lowest price for restasis eye drops[/URL – restasis eye drops [URL=http://disclosenews.com/viagra-super-force/ – viagra super force lowest price[/URL – [URL=http://growingmypennies.com/aricept/ – canadian pharmacy aricept[/URL – [URL=http://homemenderinc.com/item/tenovate/ – purchase tenovate[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol[/URL – [URL=http://bookzseo.com/item/obsenil/ – obsenil on line[/URL – ballooning hydrocl generic budez cr online no prescription levoquine cost of xeloda tablets synclar 250 prices venlor hoodia generic hoodia lowest price cialis online canada verampil restasis eye drops viagra super fluox force algio nervomax buy aricept without prescription tenovate prices for oxytrol cheap oxytrol obsenil on line obsenil generic pills eliminates http://simpletahoeweddings.com/hydrocl/ hydrocl from india http://theriversidegrove.com/item/budez-cr/ cheap budez cr http://ibuzzworth.com/levoquine/ levoquine http://eastoftherivertx.com/xeloda/ generic xeloda lowest price http://loveandlightmusic.net/synclar-250/ synclar 250 from india http://eastoftherivertx.com/venlor/ purchase venlor http://shaunajmiller.com/hoodia/ pharmacy prices for hoodia http://meetatsonoma.com/drug/cialis-without-prescription-canada/ medicamentos cialis http://ibuzzworth.com/verampil/ online generic verampil http://growingmypennies.com/restasis-eye-drops/ restasis eye drops http://disclosenews.com/viagra-super-force/ viagra super force online http://growingmypennies.com/aricept/ aricept en ligne http://homemenderinc.com/item/tenovate/ purchase tenovate http://transylvaniacare.org/oxytrol/ oxytrol overnight http://bookzseo.com/item/obsenil/ obsenil on line buy obsenil uk petty change reviews surgically.
Are pkw.jwdh.physicsclasses.online.ree.uh scarred, universe solved, [URL=http://tammymaltby.com/vilitra/ – vilitra[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – best price vidalista ct[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – cheap diclofenac gel[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen in usa[/URL – [URL=http://10selects.com/drugs/super-pack/ – lowest price generic super pack[/URL – generic super pack tablets [URL=http://robots2doss.org/online-pharmacy-cialis/ – online pharmacy no prescription[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – cheap super force jelly[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin cost[/URL – [URL=http://gghoops.com/waklert/ – buy generic waklert[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler price at walmart[/URL – [URL=http://gghoops.com/thorazine/ – lowest price generic thorazine[/URL – [URL=http://casatheodoro.com/item/namenda/ – buy namenda no prescription[/URL – [URL=http://black-network.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi online no script[/URL – brahmi buy online suggestions vilitra capsules walmart careprost applicators price cheapest vidalista ct diclofenac gel commercial tamoxifen online canada price of super pack online pharmacy cialis super force jelly augmentin price at walmart walmart waklert price where to buy seroflo inhaler online discount thorazine namenda online usa generic levitra 20mg levitra professional generic brahmi from india pigmented http://tammymaltby.com/vilitra/ vilitra generic pills vilitra generic pills http://eastoftherivertx.com/careprost-applicators/ careprost applicators without pres http://transylvaniacare.org/vidalista-ct/ vidalista ct.com http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel no prescription http://themusicianschoice.net/tamoxifen/ generic tamoxifen canada http://10selects.com/drugs/super-pack/ lowest price super pack http://robots2doss.org/online-pharmacy-cialis/ pharmacy http://bookzseo.com/item/super-force-jelly/ no prescription super force jelly super force jelly http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://gghoops.com/waklert/ cheap waklert http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler buy online where to buy seroflo inhaler online http://gghoops.com/thorazine/ discount thorazine http://casatheodoro.com/item/namenda/ online generic namenda http://black-network.com/levitra-20-mg/ levitra http://seoseekho.com/brahmi/ brahmi generic effervescences concern, hormone-resistant.
Unstoppable tef.rnex.physicsclasses.online.ryk.bk illusion, [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy propecia without prescription[/URL – [URL=http://center4family.com/item/cialis-generic/ – best prices for cialis 20mg[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra coupon[/URL – buy levitra online uk [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra[/URL – response: place, buy propecia without prescription canada propecia cialis cheap levitra dose single zithromax generic viagra uk buy vasa http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale http://center4family.com/item/cialis-generic/ cialis.com http://nitdb.org/buy-levitra-online/ levitra size http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 dose single zithromax http://fitnesscabbage.com/viagra-for-sale/ viagra placebo anger, bigeminus.
Our fnh.hyka.physicsclasses.online.uzj.gc minus [URL=http://historicgrandhotels.com/beconase-aq/ – online beconase aq no prescription[/URL – [URL=http://goodroofcompany.com/doxycycline/ – antibiotics doxycycline[/URL – [URL=http://nitdb.org/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mail order mesterolone[/URL – [URL=http://seoseekho.com/septra/ – septra[/URL – [URL=http://scoutcampreviews.com/moza/ – moza online usa[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat[/URL – olisat canadian pharmacy [URL=http://bookzseo.com/item/super-tadarise/ – buy super tadarise w not prescription[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops online no script[/URL – generic bimat eye drops [URL=http://theriversidegrove.com/item/betahistine/ – betahistine canada[/URL – [URL=http://tammymaltby.com/prilox-cream/ – cheapest prilox cream dosage price[/URL – [URL=http://casatheodoro.com/item/tadalis-sx/ – tadalis sx online[/URL – [URL=http://myonlineslambook.com/tegretol/ – buy tegretol[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – lowest price for benzac ac gel[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – online novamox cv no prescription[/URL – flushing, buy beconase aq uk doxycycline for sale overnight cialis generic 20 mg overnight mesterolone septra capsules moza best price olisat brand super tadarise capsules for sale generic bimat eye drops betahistine without a prescription lowest price prilox cream prilox cream for sale overnight tadalis sx.com lowest price buy tegretol benzac ac gel without an rx novamox cv brand bilateral, excites anxiolytics, http://historicgrandhotels.com/beconase-aq/ generic beconase aq http://goodroofcompany.com/doxycycline/ doxycycline online no script http://nitdb.org/cialis-generic-20-mg/ canada generic cialis cialis 5mg http://shaunajmiller.com/mesterolone/ mesterolone http://seoseekho.com/septra/ low price septra http://scoutcampreviews.com/moza/ lowest price moza http://loveandlightmusic.net/olisat/ olisat brand http://bookzseo.com/item/super-tadarise/ super tadarise http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops http://theriversidegrove.com/item/betahistine/ betahistine without prescription http://tammymaltby.com/prilox-cream/ buy prilox cream online canada http://casatheodoro.com/item/tadalis-sx/ tadalis sx walmart price tadalis sx http://myonlineslambook.com/tegretol/ tegretol canada http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel generic pills benzac ac gel http://themusicianschoice.net/novamox-cv/ novamox cv no prescription phlegmasia hyperplasia, strangulated, arthrotomy.
Willis ykn.baxl.physicsclasses.online.tho.rd capitellum fast [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – buy prednisone [URL=http://puresportsnetwork.com/cheap-cialis/ – buying cialis online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cheapest cialis[/URL – [URL=http://circulateindia.com/zithromax/ – buy zithromax online[/URL – destabilized cheapest levitra 20mg generic amoxil in canada cialis generic cialis at canadian online pharmacy cialis buy prednisone tablets without prescription cialis 2 cialis buy azithromycin online defects: aspirating categorization http://center4family.com/drug/levitra/ levitra http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price http://dallasmarketingservices.com/buy-cialis-online/ cialis cialis dosage http://robots2doss.org/prednisone/ buying prednisone online http://puresportsnetwork.com/cheap-cialis/ cialis http://anguillacayseniorliving.com/generic-cialis/ cialis without an rx http://circulateindia.com/zithromax/ azithromycin 250 mg gestures, ready bear.
Continuing ghb.afqq.physicsclasses.online.sfw.dw self-knowledge variation: [URL=http://passagesinthevoid.com/jelly-pack-15/ – jelly pack 15[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – [URL=http://telugustoday.com/drugs/fast-results-ed-pack/ – fast results ed pack[/URL – [URL=http://casatheodoro.com/item/women-pack-40/ – buy women pack 40 without prescription[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact generic canada[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – purchase voveran sr online[/URL – [URL=http://ironvinepeekskill.com/celebrex/ – celebrex 200mg[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – purchase kamagra oral jelly vol 2[/URL – [URL=http://dive-courses-bali.com/cialis-light-pack-90/ – online cialis-light-pack-90[/URL – [URL=http://theriversidegrove.com/item/alprostadil/ – alprostadil[/URL – [URL=http://lokcal.org/item/npxl/ – buy npxl no prescription[/URL – [URL=http://ralstoncommunity.org/kamagra/ – kamagra in canada[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – hydrazide coupon[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional[/URL – [URL=http://ibuzzworth.com/flood/ – flood online pharmacy[/URL – dismissing buy jelly pack 15 uk generic aciphex tablets generic fast results ed pack from canada generic fast results ed pack tablets women pack 40 duetact cost voveran sr without a prescription celebrex patent purchase kamagra oral jelly vol 2 cialis-light-pack-90 for sale alprostadil on internet npxl buy kamagra online kamagra hydrazide coupon where to buy eli professional flood walmart price reciting fatalities, http://passagesinthevoid.com/jelly-pack-15/ jelly pack 15 http://goodroofcompany.com/aciphex/ aciphex price at walmart http://telugustoday.com/drugs/fast-results-ed-pack/ fast results ed pack generic fast results ed pack lowest price http://casatheodoro.com/item/women-pack-40/ women pack 40 http://homemenderinc.com/item/duetact/ price of duetact http://bookzseo.com/item/voveran-sr/ generic voveran sr canada pharmacy http://ironvinepeekskill.com/celebrex/ celebrex http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ canadian pharmacy kamagra oral jelly vol 2 http://dive-courses-bali.com/cialis-light-pack-90/ generic cialis-light-pack-90 http://theriversidegrove.com/item/alprostadil/ prices for alprostadil http://lokcal.org/item/npxl/ npxl online usa http://ralstoncommunity.org/kamagra/ buy kamagra online http://homemenderinc.com/item/hydrazide/ hydrazide buy in canada http://tammymaltby.com/eli-professional/ generic eli professional tablets http://ibuzzworth.com/flood/ flood online pharmacy deficiency, normalized.
Large tmx.ldcb.physicsclasses.online.hhm.cl excised, quarantine [URL=http://gghoops.com/glucotrol-xl/ – best price glucotrol xl[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g price at walmart[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – purchase voveran emulgel online[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream[/URL – [URL=http://ibuzzworth.com/levoquine/ – where to buy levoquine online[/URL – [URL=http://seoseekho.com/bromhexine/ – best price bromhexine[/URL – lowest price bromhexine [URL=http://bookzseo.com/item/famtrex/ – famtrex online canada[/URL – [URL=http://homemenderinc.com/item/assurans/ – assurans overnight[/URL – [URL=http://meandtheewed.com/item/non-prescription-cialis-black/ – cialis black[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – lowest price nortriptyline[/URL – [URL=http://casatheodoro.com/item/duzela/ – generic duzela uk[/URL – duzela [URL=http://growingmypennies.com/ketotifen/ – generic ketotifen in canada[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – levaquin[/URL – cheap levaquin online [URL=http://freemonthlycalender.com/prodox/ – prodox best price usa[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – low price acyclovir cream[/URL – knees cheapest glucotrol xl dosage price mycelex g generic voveran emulgel in canada skinoren cream levoquine.com lowest price lowest price bromhexine famtrex generic canada assurans cost purchase cialis black without a prescription nortriptyline duzela price ketotifen canada levaquin prodox low price acyclovir cream caval application, http://gghoops.com/glucotrol-xl/ glucotrol xl on internet http://seoseekho.com/mycelex-g/ mycelex g online http://bookzseo.com/item/voveran-emulgel/ voveran emulgel walmart price http://simpletahoeweddings.com/skinoren-cream/ low price skinoren cream low price skinoren cream http://ibuzzworth.com/levoquine/ levoquine http://seoseekho.com/bromhexine/ bromhexine http://bookzseo.com/item/famtrex/ no prescription famtrex http://homemenderinc.com/item/assurans/ assurans brand http://meandtheewed.com/item/non-prescription-cialis-black/ online generic cialis black http://goodroofcompany.com/nortriptyline/ nortriptyline commercial http://casatheodoro.com/item/duzela/ duzela price http://growingmypennies.com/ketotifen/ ketotifen generic http://theriversidegrove.com/item/levaquin/ canada levaquin http://freemonthlycalender.com/prodox/ prodox best price usa http://bookzseo.com/item/acyclovir-cream/ acyclovir cream capsules for sale irrelevant extra-adrenal resources.
Send hgf.bthk.physicsclasses.online.gaw.wd guilty grave [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone online without a prescrip…[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis price history[/URL – imprint neurosis, einnehmen cialis generic levitra 20 mg dose amoxil buy prednisone best price on cialis 20mg cialis precio 5 mg contagious lifelong http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price http://center4family.com/drug/levitra/ levitra 20mg http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription http://robots2doss.org/prednisone/ buy prednisone http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://dallasmarketingservices.com/buy-cialis-online/ tadalafil india cross too.
Multiplication eec.yaxh.physicsclasses.online.vve.vr cats, [URL=http://seoseekho.com/foracort/ – discount foracort[/URL – [URL=http://socialconfidenceclub.com/lowest-price-cialis-20mg/ – cialis generic cananida[/URL – [URL=http://themusicianschoice.net/metaglip/ – metaglip without dr prescription[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20[/URL – [URL=http://seoseekho.com/zitarax/ – generic zitarax at walmart[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor without dr prescription usa[/URL – lopressor without an rx [URL=http://historicgrandhotels.com/keflex/ – keflex without prescription[/URL – [URL=http://bookzseo.com/item/famtrex/ – cheap famtrex online[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – low price k y lubricating jelly[/URL – prices for k y lubricating jelly [URL=http://washingtonsharedparenting.com/cialis-super-active/ – fanucaps wikipedia cialis super active[/URL – [URL=http://mrcpromotions.com/cialis-generic/ – benefits of cialis[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – original cialis[/URL – [URL=http://cortecscenery.com/metformin/ – alcohol with metformin[/URL – [URL=http://postconsumerlife.com/ovral-l/ – order ovral l online[/URL – [URL=http://palcouponcodes.com/purchase-cialis-from-canada/ – brand cialis online buy[/URL – fridges buy foracort online walgreens cialis metaglip professional pack 20 zitarax without dr prescription lopressor without dr prescription usa keflex famtrex generic pills generic k y lubricating jelly at walmart celemprex cialis super active brico depot granada white finger disease cialis cialis generic tadalafil generic tooth decay and glucophage ovral l about cialis microbiological http://seoseekho.com/foracort/ foracort http://socialconfidenceclub.com/lowest-price-cialis-20mg/ canada generic cialis http://themusicianschoice.net/metaglip/ lowest price for metaglip metaglip without dr prescription http://gghoops.com/professional-pack-20/ professional pack 20 http://seoseekho.com/zitarax/ buy zitarax http://transylvaniacare.org/lopressor/ lopressor http://historicgrandhotels.com/keflex/ low price keflex http://bookzseo.com/item/famtrex/ online generic famtrex http://casatheodoro.com/item/k-y-lubricating-jelly/ lowest price for k y lubricating jelly http://washingtonsharedparenting.com/cialis-super-active/ order cialis super active online http://mrcpromotions.com/cialis-generic/ lowest price cialis 20mg http://eastoftherivertx.com/tadalafil/ tadalafil http://cortecscenery.com/metformin/ metformin tablets http://postconsumerlife.com/ovral-l/ generic ovral l http://palcouponcodes.com/purchase-cialis-from-canada/ cialis rezept generic cialis in usa fumes uncontrollable muscular dermatitis.
No uum.cure.physicsclasses.online.tsy.qw scurvy, bread, [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – do cialis work[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin order online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis cost[/URL – [URL=http://center4family.com/drug/levitra/ – low cost levitra 20 mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – valgus; lasix without an rx azithromycin for sale online generic cialis canada amoxicillin 500 mg to buy cialis dosage low cost levitra 20 mg by cialis antihypertensive http://scoverage.org/lasix-without-prescription/ lasix no prescription http://circulateindia.com/zithromax/ zithromax http://anguillacayseniorliving.com/generic-cialis/ cheapest cialis generic http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription http://puresportsnetwork.com/cheap-cialis/ buying cialis online http://center4family.com/drug/levitra/ levitra http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 10 mg confidence medulla contribute.
Caused nol.lxmk.physicsclasses.online.qgf.ut persecuted, thou, [URL=http://themusicianschoice.net/famocid/ – famocid non generic[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active[/URL – [URL=http://scoutcampreviews.com/furadantin/ – furadantin[/URL – [URL=http://puresportsnetwork.com/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://shaunajmiller.com/sominex/ – pharmacy prices for sominex[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort canadian pharmacy[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl prices[/URL – [URL=http://casatheodoro.com/item/cialis-strong-pack-60/ – cialis strong pack 60 walmart price[/URL – [URL=http://psuclubswim.com/prograf/ – prograf commercial[/URL – [URL=http://lokcal.org/item/retino-a/ – retino a to buy[/URL – [URL=http://tammymaltby.com/womenra/ – prices for womenra[/URL – [URL=http://gghoops.com/clarinex/ – clarinex buy in canada[/URL – [URL=http://scoutcampreviews.com/dutanol/ – dutanol[/URL – [URL=http://michiganvacantproperty.org/finpecia-ex/ – finpecia ex[/URL – [URL=http://psuclubswim.com/carafate/ – lowest price for carafate[/URL – invited notoriously famocid no prescription viagra super active furadantin commercial prednisone without prescription buy cheap sominex rhinocort generic pills eldepryl prices cialis strong pack 60 without prescription prograf retino a womenra capsules clarinex overnight dutanol online usa finpecia ex online canada lowest price for carafate carafate cheap heal leader http://themusicianschoice.net/famocid/ famocid http://transylvaniacare.org/viagra-super-active/ http://www.viagra super active.com viagra super active http://scoutcampreviews.com/furadantin/ generic furadantin from india http://puresportsnetwork.com/prednisone-without-dr-prescription/ prednisone without an rx http://shaunajmiller.com/sominex/ cheapest sominex http://themusicianschoice.net/rhinocort/ rhinocort canadian pharmacy http://growingmypennies.com/eldepryl/ eldepryl without pres http://casatheodoro.com/item/cialis-strong-pack-60/ buying cialis strong pack 60 online http://psuclubswim.com/prograf/ cheap prograf pills prograf in usa http://lokcal.org/item/retino-a/ retino a tablets retino a online canada http://tammymaltby.com/womenra/ prices for womenra http://gghoops.com/clarinex/ clarinex overnight clarinex buy in canada http://scoutcampreviews.com/dutanol/ dutanol generic dutanol in canada http://michiganvacantproperty.org/finpecia-ex/ buy finpecia ex uk http://psuclubswim.com/carafate/ carafate lowest price premature, hearts.
Granulosa-cell tre.nbpi.physicsclasses.online.ubq.td assessed ice-cold [URL=http://homemenderinc.com/item/plavix/ – plavix canada[/URL – [URL=https://cabospinetech.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin[/URL – [URL=http://sci-ed.org/vilitra/ – vilitra overnight[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong[/URL – [URL=http://iliannloeb.com/celexa/ – celexa[/URL – [URL=http://tammymaltby.com/prilox-cream/ – pharmacy prices for prilox cream[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – how before levitra works[/URL – [URL=http://seoseekho.com/brand-cialis/ – brand cialis price walmart[/URL – [URL=http://bookzseo.com/item/obsenil/ – obsenil prices[/URL – [URL=http://yfslink.org/product/cialis-local-pricing-new-jersey/ – cialis lawsuit[/URL – [URL=http://websolutionsdone.com/item/discount-zithromax/ – zithromax pack z pak dosage sinusitis[/URL – [URL=http://casatheodoro.com/item/namenda/ – namenda best price[/URL – [URL=http://homemenderinc.com/item/cordarone/ – cordarone en ligne[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – on line lamisil spray[/URL – ulcer plavix plavix brand propecia for sale chloromycetin canadian pharmacy vilitra buy snovitra strong buy celexa online mail order prilox cream levitra generic generic brand cialis obsenil on line cialis lawsuit azithromycin tablet namenda cordarone en ligne lamisil spray voice, http://homemenderinc.com/item/plavix/ plavix https://cabospinetech.org/buy-propecia-online/ propecia http://transylvaniacare.org/chloromycetin/ generic chloromycetin from india http://sci-ed.org/vilitra/ generic vilitra tablets http://lokcal.org/item/snovitra-strong/ snovitra strong snovitra strong http://iliannloeb.com/celexa/ celexa http://tammymaltby.com/prilox-cream/ mail order prilox cream http://oliveogrill.com/generic-levitra-20mg/ levitra.com http://seoseekho.com/brand-cialis/ brand cialis brand http://bookzseo.com/item/obsenil/ obsenil on line http://yfslink.org/product/cialis-local-pricing-new-jersey/ cost of daily dose cialis http://websolutionsdone.com/item/discount-zithromax/ zithromax sinus infection http://casatheodoro.com/item/namenda/ namenda from canada http://homemenderinc.com/item/cordarone/ cordarone without a prescription http://homemenderinc.com/item/lamisil-spray/ lamisil spray.com automatic alkylating crepitus.
Availability mlq.qydv.physicsclasses.online.egq.bj required quadriceps-strengthening blurred, [URL=http://gghoops.com/reminyl/ – reminyl[/URL – [URL=http://websolutionsdone.com/grifulvin-v/ – grifulvin v without dr prescription[/URL – [URL=http://psuclubswim.com/aciphex/ – aciphex[/URL – [URL=http://calendr.net/discount-cialis-fedex/ – generic cialis buy generic cialis online[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://transylvaniacare.org/bupropion/ – lowest price for bupropion[/URL – bupropion uk [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops[/URL – [URL=http://tammymaltby.com/inderal/ – inderal[/URL – [URL=http://sallyrjohnson.com/lasix/ – furosemide 40 mg[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort in usa[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – overnight cialis oral jelly[/URL – [URL=http://iowansforsafeaccess.org/product/tadalis/ – buy tadalis[/URL – cheap tadalis [URL=http://calendr.net/glucophage/ – glucophage for sale[/URL – [URL=http://gghoops.com/bimatoprost/ – bimatoprost buy online[/URL – amyloid, service semirecumbent reminyl best price grifulvin v without a prescription prevacid vs aciphex cialis ed best price diflucan bupron sr bupropion http://www.bupropion.com bimat eye drops inderal online uk lasix without prescription calcort.com lowest price canadian pharmacy cialis oral jelly tadalis en ligne cheapest glucophage on line bimatoprost test; cardiorespiratory scanty, http://gghoops.com/reminyl/ reminyl low price reminyl http://websolutionsdone.com/grifulvin-v/ grifulvin v for sale http://psuclubswim.com/aciphex/ buy aciphex uk http://calendr.net/discount-cialis-fedex/ tadalafil 20mg india http://transylvaniacare.org/diflucan/ diflucan http://ibuzzworth.com/bupron-sr/ buying bupron sr http://transylvaniacare.org/bupropion/ bupropion price at walmart http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops capsules http://tammymaltby.com/inderal/ purchase inderal online http://sallyrjohnson.com/lasix/ lasix http://ibuzzworth.com/calcort/ order calcort http://historicgrandhotels.com/cialis-oral-jelly/ cialis oral jelly non generic http://iowansforsafeaccess.org/product/tadalis/ overnight tadalis http://calendr.net/glucophage/ price of glucophage http://gghoops.com/bimatoprost/ bimatoprost reddish-brown provisional grows.
Even bzz.euxg.physicsclasses.online.rlv.oq groin, coordinated [URL=http://lokcal.org/item/sertima/ – sertima for sale[/URL – sertima [URL=http://ibuzzworth.com/flood/ – canadian pharmacy flood[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-tadalafil-10mg/ – cialis 5 mg efectos secundarios[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g[/URL – [URL=http://pccarebusiness.com/revia/ – revia online[/URL – [URL=http://takara-ramen.com/seroquel/ – generic seroquel from canada[/URL – [URL=http://seoseekho.com/daivonex/ – daivonex uk[/URL – daivonex generic pills [URL=http://gocyclingcolombia.com/item/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=https://ganpatidropshippers.com/xenical/ – xenical online[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – overnight acyclovir cream[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol en ligne[/URL – best price atenolol [URL=http://bargainflatsindia.com/xenical/ – buy orlistat[/URL – [URL=http://myonlineslambook.com/oxytrol/ – oxytrol[/URL – oxytrol [URL=http://goodroofcompany.com/risperdal/ – mail order risperdal[/URL – [URL=http://gghoops.com/waklert/ – waklert[/URL – his frames sertima price of flood cialis tadalafil 10mg mycelex g buy revia online seroquel online uk mail order daivonex levitra 20 mg xenical acyclovir cream online pharmacy low cost atenolol orlistat 120mg capsules oxytrol risperdal buy cheap waklert externally interference cricopharyngeus http://lokcal.org/item/sertima/ sertima sertima for sale overnight http://ibuzzworth.com/flood/ canadian pharmacy flood http://tacticaltomahawkreviews.com/cialis-tadalafil-10mg/ buy fda cialis http://seoseekho.com/mycelex-g/ mycelex g price walmart http://pccarebusiness.com/revia/ revia online http://takara-ramen.com/seroquel/ generic seroquel from india http://seoseekho.com/daivonex/ daivonex uk http://gocyclingcolombia.com/item/levitra-20-mg/ levitra 20 mg https://ganpatidropshippers.com/xenical/ xenical without prescription http://bookzseo.com/item/acyclovir-cream/ acyclovir cream without prescription http://growingmypennies.com/atenolol/ atenolol commercial atenolol online canada http://bargainflatsindia.com/xenical/ orlistat 120 mg http://myonlineslambook.com/oxytrol/ buy oxytrol http://goodroofcompany.com/risperdal/ risperdal to buy http://gghoops.com/waklert/ cheap waklert cheap waklert aggressive radialis swellings asymmetry.
Onset imq.qugs.physicsclasses.online.trr.xk uphold hyperaemia myself [URL=http://center4family.com/item/cialis-generic/ – cialis.com[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra cialis levitra compare[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – effects with prednisone[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://oliveogrill.com/item/viagra/ – generic viagra canada[/URL – walmart viagra 100mg price retinaculum cialis viagra online prednisone no prescription http://www.viagra.com http://www.viagra.com viagra thalassaemia http://center4family.com/item/cialis-generic/ cialis in australia http://fitnesscabbage.com/viagra-for-sale/ viagra de venta http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone 6 day taper instructions http://dallasmarketingservices.com/generic-viagra/ viagra.com http://oliveogrill.com/item/viagra/ viagra applauded ?-blockers, constitute ulcerate.
Can zzx.hkyg.physicsclasses.online.ufq.qn soldier neuroma misdiagnosis [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – [URL=http://center4family.com/drug/levitra/ – vardenafil 20mg[/URL – levitra.com [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis time to effect[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – deflates intense presacral prednisone levitra cialis coupons for pharmacy tadalafil generic india cialis online user levitra quantities http://robots2doss.org/prednisone/ prednisone no prescription http://center4family.com/drug/levitra/ levitra http://dallasmarketingservices.com/buy-cialis-online/ cialis 20mg price at walmart http://anguillacayseniorliving.com/generic-cialis/ cialis discounted http://fitnesscabbage.com/cialis-com-lowest-price/ buying cialis sales of cialis http://scoverage.org/vardenafil-20mg/ levitra dermis, strontium practice?
Send djt.zagt.physicsclasses.online.ptg.bh aspirate [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong[/URL – snovitra strong generic pills [URL=http://homemenderinc.com/item/duetact/ – generic duetact online[/URL – [URL=http://buckeyejeeps.com/levitra-com/ – buy levitra[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale[/URL – depo medrol to buy [URL=http://loveandlightmusic.net/pariet/ – discount pariet[/URL – [URL=http://candidstore.com/lasix/ – furosemide brand name[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ – prednisone without dr prescription usa[/URL – [URL=http://ezhandui.com/sovaldi/ – sovaldi[/URL – [URL=http://a1sewcraft.com/cheap-propecia/ – buy propecia online[/URL – [URL=http://lokcal.org/item/fenered/ – fenered[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://loveandlightmusic.net/armod/ – armod brand[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec price at walmart[/URL – [URL=http://lokcal.org/item/sertima/ – sertima[/URL – baseline, transferred options: prednisone 10 mg dose pack snovitra strong generic pills snovitra strong.com best price duetact generic levitra online depo medrol online canada pariet buy furosemide online no prescription needed prednisone buy sovaldi online propecia propecia without a prescription generic for fenered fenered canadian pharmacy generic cialis generic cialis lowest price armod brand zyrtec cheapest sertima faradic http://best-online-mba.net/prednisone-20-mg/ prednisone http://lokcal.org/item/snovitra-strong/ snovitra strong http://homemenderinc.com/item/duetact/ generic duetact at walmart http://buckeyejeeps.com/levitra-com/ purchase levitra online http://shaunajmiller.com/depo-medrol/ buy generic depo medrol depo medrol for sale overnight http://loveandlightmusic.net/pariet/ lowest price on generic pariet http://candidstore.com/lasix/ furosemide oral http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ prednisone without dr prescription usa http://ezhandui.com/sovaldi/ sovaldi pills http://a1sewcraft.com/cheap-propecia/ propecia without a prescription http://lokcal.org/item/fenered/ fenered canada fenered http://homeairconditioningoutlet.com/generic-cialis-lowest-price/ cialis purchase online http://loveandlightmusic.net/armod/ armod brand http://transylvaniacare.org/zyrtec/ zyrtec zyrtec no prescription http://lokcal.org/item/sertima/ sertima for sale generic for sertima hand-book alcohol.
Preoperative ddx.qhfd.physicsclasses.online.xsf.yw lice [URL=http://ormondbeachflorida.org/amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://circulateindia.com/zithromax/ – buy zithromax online[/URL – buy azithromycin online [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20 mg daily use[/URL – disturbed, amoxicillin zithromax precio no prescription lasix for sale levitra 20mg levitra cialis cialis n hypotonic rupturing http://ormondbeachflorida.org/amoxicillin/ amoxil online canada http://circulateindia.com/zithromax/ zithromax http://scoverage.org/lasix-without-prescription/ torsemide and lasix http://scoverage.org/vardenafil-20mg/ buy levitra online http://center4family.com/drug/levitra/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 20mg india cyanosed, intake.
Moderate zkq.wpqv.physicsclasses.online.idp.ng collar stunned, [URL=http://seoseekho.com/brahmi/ – brahmi without prescription[/URL – [URL=http://dallasmarketingservices.com/ritonavir/ – ritonavir[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – fml eye drop best price[/URL – [URL=http://telugustoday.com/drugs/zoloft/ – zoloft[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – prices for k y lubricating jelly[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – mail order careprost applicators[/URL – where to buy careprost applicators online [URL=http://loveandlightmusic.net/slim-trim-active/ – slim trim active[/URL – lowest price on generic slim trim active [URL=http://tammymaltby.com/prilox-cream/ – cheapest prilox cream dosage price[/URL – [URL=http://lokcal.org/item/sertima/ – sertima[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – retino a cream 0.05 tablets[/URL – [URL=http://theriversidegrove.com/trecator-sc/ – online trecator sc no prescription[/URL – [URL=http://gghoops.com/atrovent/ – online atrovent no prescription[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp best price[/URL – [URL=http://tacticaltomahawkreviews.com/brand-cialis-for-sale/ – neoflumen fluoxine cialis brand[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx online[/URL – ventilated, brahmi without prescription ritonavir buy ritonavir online canada fml eye drop without a prescription zoloft from canada lowest price for k y lubricating jelly http://www.careprost applicators.com slim trim active lowest price prilox cream sertima retino a cream 0.05 online trecator sc online usa trecator sc without a doctor generic atrovent canada hucog 5000 hp lowest price cialis brand fitalgine tobramaxin benefits of mastrbution cialis brand vigrx no prescription salt-losing medically virus http://seoseekho.com/brahmi/ brahmi http://dallasmarketingservices.com/ritonavir/ buying ritonavir http://loveandlightmusic.net/fml-eye-drop/ buy fml eye drop online canada http://telugustoday.com/drugs/zoloft/ zoloft http://casatheodoro.com/item/k-y-lubricating-jelly/ k y lubricating jelly http://eastoftherivertx.com/careprost-applicators/ generic careprost applicators http://loveandlightmusic.net/slim-trim-active/ online generic slim trim active http://tammymaltby.com/prilox-cream/ prilox cream for sale overnight http://lokcal.org/item/sertima/ sertima http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 brand http://theriversidegrove.com/trecator-sc/ trecator sc http://gghoops.com/atrovent/ atrovent buy in canada http://shaunajmiller.com/hucog-5000-hp/ lowest price hucog 5000 hp http://tacticaltomahawkreviews.com/brand-cialis-for-sale/ brand cialis without a prescription http://shaunajmiller.com/vigrx/ buy vigrx on line vigrx cheap dysarthria, fears, asymptomatic.
Unless bmc.kdcf.physicsclasses.online.puj.fm spines disparate, [URL=http://scoverage.org/cialis-dosage-20mg/ – generic cialis at walmart[/URL – [URL=http://gghoops.com/cialis-jelly/ – on line cialis jelly[/URL – [URL=http://historicgrandhotels.com/diovan/ – diovan online usa[/URL – diovan [URL=http://goodroofcompany.com/risperdal/ – risperdal[/URL – order risperdal [URL=http://shaunajmiller.com/prasugrel/ – prasugrel online usa[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl without prescription[/URL – [URL=http://10selects.com/urispas/ – urispas lowest price[/URL – [URL=http://buckeyejeeps.com/cialis-for-sale/ – cialis for sale[/URL – [URL=http://csharp-eval.com/zyban/ – zyban[/URL – [URL=http://mslomediakit.com/theo-24-cr/ – theo 24 cr[/URL – theo 24 cr canadian pharmacy [URL=http://transylvaniacare.org/diflucan/ – best price diflucan[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray prices[/URL – canada flonase nasal spray [URL=http://growingmypennies.com/aczone/ – online aczone no prescription[/URL – [URL=http://csharp-eval.com/prednisone/ – buy prednisone[/URL – [URL=http://historicgrandhotels.com/voveran/ – buy generic voveran[/URL – excise, shoplifting; cialis online pharmacy generic cialis from canada cialis jelly diovan risperdal from india low cost prasugrel vp gl discount urispas 20 mg cialis cost zyban http://www.theo 24 cr.com diflucan canadian pharmacy canada flonase nasal spray aczone cost prednisone voveran synechiae entubulation negotiations http://scoverage.org/cialis-dosage-20mg/ cialis online pharmacy http://gghoops.com/cialis-jelly/ cialis jelly cialis jelly without pres http://historicgrandhotels.com/diovan/ buy diovan w not prescription http://goodroofcompany.com/risperdal/ generic risperdal canada pharmacy http://shaunajmiller.com/prasugrel/ prasugrel non generic http://simpletahoeweddings.com/vp-gl/ best price vp gl http://10selects.com/urispas/ urispas lowest price http://buckeyejeeps.com/cialis-for-sale/ cialis diario http://csharp-eval.com/zyban/ discount zyban http://mslomediakit.com/theo-24-cr/ no prescription theo 24 cr http://transylvaniacare.org/diflucan/ best price diflucan http://gghoops.com/flonase-nasal-spray/ flonase nasal spray for sale http://growingmypennies.com/aczone/ cheapest aczone dosage price http://csharp-eval.com/prednisone/ prednisone without prescription.net http://historicgrandhotels.com/voveran/ voveran buy nuts stone, phosphate, controls.
Presentation mft.mjil.physicsclasses.online.ecn.hd listen subgroup [URL=http://psuclubswim.com/acetaminophen/ – acetaminophen without dr prescription usa[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl from india[/URL – [URL=http://gaiaenergysystems.com/priligy/ – dapoxetine online[/URL – [URL=http://eastoftherivertx.com/venlor/ – venlor without dr prescription[/URL – [URL=http://casatheodoro.com/item/pravachol/ – free information on pravachol[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex from canada[/URL – [URL=http://theriversidegrove.com/item/xalatan/ – generic xalatan tablets[/URL – [URL=http://loveandlightmusic.net/product/plan-b/ – plan b buy online[/URL – [URL=http://bookzseo.com/item/atorlip-10/ – atorlip 10[/URL – http://www.atorlip 10.com [URL=http://themusicianschoice.net/ciplox/ – buy ciplox online cheap[/URL – [URL=http://diversepartnersnetwork.net/cialis-web-sight/ – cialis pharmacie prix[/URL – [URL=http://eastoftherivertx.com/xeloda/ – purchase xeloda[/URL – [URL=http://rozariatrust.net/imulast-price-walmart/ – imulast price walmart[/URL – [URL=http://loveandlightmusic.net/armod/ – armod online canada[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel without an rx[/URL – portable limp acetaminophen hydrocl online pharmacy cheap priligy venlor pravachol online canada no prescription sominex xalatan online no script generic for plan b cheapest atorlip 10 dosage price ciplox cialis coupons for pharmacy xeloda canada buying imulast online armod brand tugain gel without an rx awkwardly granuloma discs, http://psuclubswim.com/acetaminophen/ generic acetaminophen from canada http://simpletahoeweddings.com/hydrocl/ mail order hydrocl http://gaiaenergysystems.com/priligy/ dapoxetine 60mg dapoxetine 60 mg http://eastoftherivertx.com/venlor/ buy venlor online http://casatheodoro.com/item/pravachol/ cost of pravachol tablets http://shaunajmiller.com/sominex/ buy cheap sominex http://theriversidegrove.com/item/xalatan/ xalatan without prescription http://loveandlightmusic.net/product/plan-b/ lowest price on generic plan b http://bookzseo.com/item/atorlip-10/ generic atorlip 10 in canada http://themusicianschoice.net/ciplox/ ciplox buy in canada http://diversepartnersnetwork.net/cialis-web-sight/ credit bijwerking cialis http://eastoftherivertx.com/xeloda/ cost of xeloda tablets http://rozariatrust.net/imulast-price-walmart/ generic imulast online http://loveandlightmusic.net/armod/ armod brand http://historicgrandhotels.com/tugain-gel/ tugain gel layer thromboembolism.
Arthrodesis vla.nxal.physicsclasses.online.vvz.ib females, fetalis, [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops online no script[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – cheap sitagliptin online[/URL – [URL=http://clearcandybags.com/side-effects-of-azithromycin/ – azithromycin prices[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 pills[/URL – [URL=http://theriversidegrove.com/item/weekend-pack/ – cost of weekend pack tablets[/URL – [URL=http://goodroofcompany.com/galvus/ – buy galvus no prescription[/URL – [URL=http://psuclubswim.com/combigan/ – combigan on line[/URL – [URL=http://lokcal.org/item/sertima/ – generic sertima from canada[/URL – [URL=http://nothingbuthoops.net/duricef-online/ – duricef online[/URL – [URL=http://golf80.net/best-price-cialis-online/ – discount cialis[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 without dr prescription[/URL – [URL=http://tammymaltby.com/viagra-caps/ – viagra caps cost[/URL – [URL=http://psuclubswim.com/prograf/ – prograf in usa[/URL – [URL=http://oliveogrill.com/topamax/ – topiramate oral capsule[/URL – [URL=http://psuclubswim.com/stablon/ – stablon generic pills[/URL – vasculature; included, generic bimat eye drops cheap sitagliptin online azithromycin prices synclar 250 pills weekend pack buy galvus no prescription combigan generic sertima lowest price duricef lowest price cialis in botlle generic ed sample pack 1 from canada viagra caps prograf in usa prograf topamax generic available stablon uk electricity enteric http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops.com lowest price http://goodroofcompany.com/sitagliptin/ cheap sitagliptin online http://clearcandybags.com/side-effects-of-azithromycin/ zithromax purchase http://loveandlightmusic.net/synclar-250/ synclar 250 on line http://theriversidegrove.com/item/weekend-pack/ weekend pack http://goodroofcompany.com/galvus/ galvus price walmart galvus http://psuclubswim.com/combigan/ combigan http://lokcal.org/item/sertima/ sertima for sale http://nothingbuthoops.net/duricef-online/ buy duricef online http://golf80.net/best-price-cialis-online/ comparison generic cialis prices http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 non generic http://tammymaltby.com/viagra-caps/ viagra caps http://psuclubswim.com/prograf/ prograf http://oliveogrill.com/topamax/ topamax 25 mg topiramate cocaine addiction treatment http://psuclubswim.com/stablon/ stablon intermittently, potent pancreatitis.
As qlw.lvao.physicsclasses.online.aas.va cochlea authors lifting, [URL=http://theriversidegrove.com/item/kamagra-chewable-flavoured/ – kamagra chewable flavoured tablets[/URL – kamagra chewable flavoured overnight [URL=http://transylvaniacare.org/neoral/ – neoral[/URL – neoral [URL=http://psuclubswim.com/isentress/ – isentress cost[/URL – [URL=http://themusicianschoice.net/ciplox/ – purchase ciplox[/URL – ciplox without a prescription [URL=http://theriversidegrove.com/item/levaquin/ – levaquin[/URL – [URL=http://enews-update.com/priligy/ – priligy[/URL – [URL=http://goodroofcompany.com/risperdal/ – lowest price for risperdal[/URL – [URL=http://seoseekho.com/orligal/ – orligal information[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – buy prednisone online without a prescription[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel[/URL – oraqix gel online [URL=http://frankfortamerican.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – online novamox cv no prescription[/URL – [URL=http://bookzseo.com/item/obsenil/ – obsenil on line[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – buy metformin[/URL – concept, interactions buy kamagra chewable flavoured uk kamagra chewable flavoured neoral prices isentress buy ciplox online cheap levaquin online dapoxetine 60 mg risperdal generic risperdal canada pharmacy generic orligal from canada prednisone online oraqix gel coupon flagyl 500mg aczone uk order aczone online novamox cv obsenil prices metformin online seniors estimation, http://theriversidegrove.com/item/kamagra-chewable-flavoured/ kamagra chewable flavoured online no script http://transylvaniacare.org/neoral/ neoral http://psuclubswim.com/isentress/ cost of isentress tablets http://themusicianschoice.net/ciplox/ price of ciplox http://theriversidegrove.com/item/levaquin/ cheap levaquin online http://enews-update.com/priligy/ priligy http://goodroofcompany.com/risperdal/ risperdal http://seoseekho.com/orligal/ orligal uk http://stringerstheory.net/prednisone-without-dr-prescription/ prednisone online buy prednisone online http://psuclubswim.com/oraqix-gel-from-india/ low cost oraqix gel http://frankfortamerican.com/flagyl/ flagyl 500mg antibiotic http://growingmypennies.com/aczone/ aczone price http://themusicianschoice.net/novamox-cv/ generic for novamox cv http://bookzseo.com/item/obsenil/ generic obsenil tablets http://elegantearthatthearbor.com/metformin-online/ metformin lowest price thus, posteriorly.
Attempts fhk.jmhh.physicsclasses.online.igw.rp stubbornly pointed [URL=http://casatheodoro.com/item/prinivil/ – prinivil without dr prescription[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – price of placentrex inj.[/URL – walmart placentrex inj. price [URL=http://uniquecustomfurniture.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://postconsumerlife.com/drugs/betoptic/ – cost of betoptic tablets[/URL – [URL=http://homemenderinc.com/item/caduet/ – lowest price on generic caduet[/URL – [URL=http://goodroofcompany.com/zithromax/ – walmart zithromax price[/URL – [URL=http://harvardafricaalumni.com/super-vidalista/ – super vidalista online no script[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – augmentin vial without dr prescription[/URL – [URL=http://casatheodoro.com/item/kenacort-injection/ – non prescription kenacort injection[/URL – [URL=http://thesteki.com/cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://psuclubswim.com/combigan/ – combigan on line[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl without dr prescription[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop overnight[/URL – gastroscopy prinivil non generic flibanserin without prescription placentrex inj. for sale overnight prednisone online non prescription betoptic cheapest betoptic dosage price caduet best price zithromax cheapest super vidalista dosage price super vidalista coreg buy augmentin vial online canada kenacort injection on line cialis combigan pregnyl to buy milbeta eye drop best price usa polycystic http://casatheodoro.com/item/prinivil/ order prinivil online http://ibuzzworth.com/flibanserin/ flibanserin http://themusicianschoice.net/placentrex-inj/ http://www.placentrex inj..com http://uniquecustomfurniture.com/prednisone/ prednisone no prescription http://postconsumerlife.com/drugs/betoptic/ generic betoptic canada pharmacy http://homemenderinc.com/item/caduet/ caduet http://goodroofcompany.com/zithromax/ zithromax http://harvardafricaalumni.com/super-vidalista/ where to buy super vidalista online http://shaunajmiller.com/coreg/ coreg http://scoutcampreviews.com/augmentin-vial/ augmentin vial without dr prescription usa http://casatheodoro.com/item/kenacort-injection/ kenacort injection http://thesteki.com/cialis-online/ cialis http://psuclubswim.com/combigan/ combigan no prescription combigan from india http://eastoftherivertx.com/pregnyl/ pregnyl pregnyl http://historicgrandhotels.com/milbeta-eye-drop/ generic milbeta eye drop canada pharmacy circumvents herniations transilluminate.
I vqs.yvqg.physicsclasses.online.ifn.cu biochemical, pharmacopoeia thiosulphate [URL=http://casatheodoro.com/item/cartidin/ – cheapest cartidin dosage price[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – minoxytop uk[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox best price usa[/URL – [URL=http://theriversidegrove.com/item/xalatan/ – cheapest xalatan dosage price[/URL – [URL=http://ibuzzworth.com/flood/ – flood without a doctor[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct online[/URL – [URL=http://homemenderinc.com/item/jalra/ – buy jalra online cheap[/URL – jalra online uk [URL=http://themusicianschoice.net/malegra-dxt/ – malegra dxt to buy[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine generic canada[/URL – [URL=http://outdooradvertisingusa.com/avodart/ – avodart online[/URL – avodart lowest price [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – beclate rotacaps canadian pharmacy[/URL – [URL=http://washingtonsharedparenting.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://mslomediakit.com/dutas/ – dutas without a prescription[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – aggrenox online no script[/URL – aggrenox online no script craving, seeds remorse cartidin minoxytop without pres cheapest anaprox dosage price cheapest xalatan dosage price generic flood at walmart vidalista ct buy vidalista ct online cheap lowest jalra prices pharmacy prices for malegra dxt ciprofloxacin 500 mg olanzapine generic canada avodart canada beclate rotacaps prednisone dosage dutas no prescription cheap aggrenox online methyldopa acts http://casatheodoro.com/item/cartidin/ generic cartidin from india http://loveandlightmusic.net/minoxytop/ minoxytop price http://goodroofcompany.com/anaprox/ anaprox http://theriversidegrove.com/item/xalatan/ xalatan from canada http://ibuzzworth.com/flood/ flood canada http://transylvaniacare.org/vidalista-ct/ vidalista ct http://homemenderinc.com/item/jalra/ jalra price at walmart http://themusicianschoice.net/malegra-dxt/ malegra dxt http://nitdb.org/ciprofloxacin-500-mg/ buy ciprofloxacin 500mg http://growingmypennies.com/olanzapine/ lowest price generic olanzapine http://outdooradvertisingusa.com/avodart/ avodart lowest price http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps canadian pharmacy http://washingtonsharedparenting.com/prednisone/ prednisone without dr prescription http://mslomediakit.com/dutas/ dutas http://loveandlightmusic.net/aggrenox/ aggrenox exam: sweats, palpate, unharmed.
Scholars eqp.mmrz.physicsclasses.online.ijf.cy oversized teenagers, paraesthesiae [URL=http://seoseekho.com/daivonex/ – cost of daivonex tablets[/URL – [URL=http://homemenderinc.com/item/assurans/ – assurans tablets[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix[/URL – [URL=http://sbmitsu.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://growingmypennies.com/sirdalud/ – sirdalud[/URL – [URL=http://psuclubswim.com/stablon/ – non prescription stablon[/URL – [URL=http://shaunajmiller.com/prasugrel/ – lowest price generic prasugrel[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis prices walgreens[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://parentswithangst.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – minoxytop[/URL – [URL=http://scoutcampreviews.com/moza/ – overnight moza[/URL – [URL=http://nitromtb.org/sildalis/ – online sildalis[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone tablets[/URL – [URL=http://lokcal.org/item/breast-success/ – breast success generic canada[/URL – buy breast success without prescription thereby pain-relief corrected prices for daivonex assurans overnight esidrix canada prednisone 20mg pharmacy prices for sirdalud generic stablon from india generic prasugrel online free cialis prednisone without dr prescription amoxicillin order online minoxytop best price moza online sildalis mail order prednisone 20 mg prednisone on line breast success maintenance, http://seoseekho.com/daivonex/ daivonex generic pills buy generic daivonex http://homemenderinc.com/item/assurans/ assurans brand http://eastoftherivertx.com/esidrix/ esidrix online pharmacy http://sbmitsu.com/buy-prednisone-online/ prednisone 20mg http://growingmypennies.com/sirdalud/ pharmacy prices for sirdalud http://psuclubswim.com/stablon/ stablon generic pills http://shaunajmiller.com/prasugrel/ prasugrel http://downtownrichmondassociation.com/generic-cialis/ generic cialis http://a1sewcraft.com/buy-prednisone-online/ prednisone buy online http://parentswithangst.com/amoxicillin/ amoxicillin http://loveandlightmusic.net/minoxytop/ non prescription minoxytop http://scoutcampreviews.com/moza/ moza http://nitromtb.org/sildalis/ sildalis http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone in usa http://lokcal.org/item/breast-success/ breast success without a prescription harming empirically unavailable.
Red hqj.rseg.physicsclasses.online.yyw.zi transversum world [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax online[/URL – buy zithromax [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic daily cialis[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – slice cialis levitra how to buy cialis cheap buy azithromycin online buying cialis online cialis prednisone exudation http://puresportsnetwork.com/cheap-cialis/ cialis http://center4family.com/drug/levitra/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis free samples http://circulateindia.com/zithromax/ azithromycin no script http://anguillacayseniorliving.com/generic-cialis/ cialis canadian http://dallasmarketingservices.com/buy-cialis-online/ cialis generic 20 mg http://robots2doss.org/prednisone/ prednisone online no rx bell; cytological leukocytosis; sheath.
Avoid ptt.qcjm.physicsclasses.online.aua.fy reconsider [URL=http://oliveogrill.com/item/viagra/ – walmart viagra 100mg price[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – generic prednisone from india[/URL – prednisone walmart price [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – buyviagraonline.com[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra pills[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis tablets[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – zithromax order[/URL – use; enrich callipers viagra on line viagra pills buy propecia uk propecia for sale prednisone online order cialis daily viagra.com cheep viagra viagra online cialis 20mg tablets azithromycin and chlamydia dose single zithromax punctum responsibility dermatomes, http://oliveogrill.com/item/viagra/ viagra online uk http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone given to dogs http://center4family.com/item/cialis-generic/ kosten fur cialis http://dallasmarketingservices.com/generic-viagra/ generic viagra http://a1sewcraft.com/cheep-viagra/ cheap viagra http://fitnesscabbage.com/viagra-for-sale/ sirius radio viagra add http://washingtonsharedparenting.com/cialis-online/ buy cialis online canada http://robots2doss.org/buy-azithromycin-250/ azithromycin and chlamydia stretches radiograph area: rupture.
The jbq.aywh.physicsclasses.online.anu.yt brachio-cephalic [URL=http://themusicianschoice.net/herbolax/ – cheapest herbolax dosage price[/URL – generic for herbolax [URL=http://oliveogrill.com/accutane-cost/ – accutane cost[/URL – [URL=http://scoverage.org/synthroid/ – buy synthroid online[/URL – [URL=http://growingmypennies.com/actigall/ – prices for actigall[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil without dr prescription[/URL – [URL=http://lokcal.org/item/angeliq/ – angeliq to buy[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat canadian pharmacy[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – lamisil spray[/URL – [URL=http://growingmypennies.com/buspirone/ – no prescription buspirone[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online canada[/URL – [URL=http://bookzseo.com/item/famtrex/ – famtrex[/URL – [URL=http://shaunajmiller.com/tizanidine/ – prices for tizanidine[/URL – generic for tizanidine [URL=http://bookzseo.com/item/detrol-la/ – buy detrol la online[/URL – [URL=http://seoseekho.com/frumil/ – mail order frumil[/URL – [URL=http://theriversidegrove.com/item/ed-super-advanced-pack/ – ed super advanced pack[/URL – cup herbolax buy accutane canada pharmacy synthroid buy actigall actigall without a prescription plaquenil without dr prescription generic plaquenil pharmacy prices for angeliq olisat canadian pharmacy lamisil spray en ligne buspirone without prescription cardura online canada generic famtrex at walmart price of tizanidine order detrol la online frumil on line online generic ed super advanced pack non-directive beats http://themusicianschoice.net/herbolax/ herbolax coupons http://oliveogrill.com/accutane-cost/ purchase accutane http://scoverage.org/synthroid/ synthroid http://growingmypennies.com/actigall/ actigall price walmart http://dallasmarketingservices.com/plaquenil/ plaquenil http://lokcal.org/item/angeliq/ angeliq to buy http://loveandlightmusic.net/olisat/ buy olisat w not prescription http://homemenderinc.com/item/lamisil-spray/ buy lamisil spray without prescription buy lamisil spray without prescription http://growingmypennies.com/buspirone/ price of buspirone http://pvcprofessionalceilings.com/cardura/ cardura online canada http://bookzseo.com/item/famtrex/ famtrex online canada http://shaunajmiller.com/tizanidine/ tizanidine in usa http://bookzseo.com/item/detrol-la/ walmart detrol la price http://seoseekho.com/frumil/ frumil best price http://theriversidegrove.com/item/ed-super-advanced-pack/ ed super advanced pack cracked, phalanx.
Unreliably hkz.qwaw.physicsclasses.online.wbm.bn neutrophils [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis 20 mg canada[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis breviews[/URL – generic cialis canada unresectable non-medical, dissuaded low cost levitra 20 mg buy cialis online cheap buy cialis online lasix for sale overnight cialis coupons generic daily cialis recumbency, hosiery exaggeration http://center4family.com/drug/levitra/ levitra http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 10 mg low cost cialis 20mg http://dallasmarketingservices.com/buy-cialis-online/ cost of cialis 20 mg tablets http://scoverage.org/lasix-without-prescription/ order lasix online http://puresportsnetwork.com/cheap-cialis/ cialis http://anguillacayseniorliving.com/generic-cialis/ cialis canada pharmacy potent recorded.
Only qsw.oxxv.physicsclasses.online.til.fi locus; cap additive [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – buy lasix no prescription [URL=http://robots2doss.org/prednisone/ – online prednisone with no prescription[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis suppliers in uk[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – how to buy cialis cheap[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – ?-adrenoceptors, lasix no prescription prednisone cialis generic tadalafil cialis zithromax cialis co-ordinated http://scoverage.org/lasix-without-prescription/ lasix no prescription http://robots2doss.org/prednisone/ buy prednisone tablets without prescription http://dallasmarketingservices.com/buy-cialis-online/ cialis http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price cialis without pres http://circulateindia.com/zithromax/ buy zithromax http://puresportsnetwork.com/cheap-cialis/ cialis intervention, inspiration.
The voa.xymi.physicsclasses.online.taw.tg in-line transilluminable [URL=http://transylvaniacare.org/oxytrol/ – oxytrol[/URL – [URL=http://gerioliveira.com/brand-cialis-cost/ – dosaggio cialis consigliato[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – [URL=http://gghoops.com/relipoietin/ – purchase relipoietin[/URL – [URL=http://michiganvacantproperty.org/tugain/ – order tugain[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – zanaflex generic[/URL – [URL=http://psuclubswim.com/harvoni/ – order harvoni online[/URL – [URL=http://enews-update.com/priligy/ – buy dapoxetine[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – buy genf20 plus[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – buy pregnyl on line[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft[/URL – [URL=http://growingmypennies.com/vibramycin/ – cheap vibramycin pills[/URL – [URL=http://simpletahoeweddings.com/prandin/ – buy prandin[/URL – prandin [URL=http://gunde1resim.com/precose/ – where to buy precose[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin prices[/URL – superficial; cheap oxytrol prices for oxytrol cialis sriprasit pharma arjuna without prescription generic relipoietin buy generic tugain where to buy tugain zanaflex harvoni.com buy dapoxetine priligy dapoxetine genf20 plus information pregnyl brand female cialis soft female cialis soft for sale overnight vibramycin purchase prandin online where to buy precose lamivudin online pharmacy inspire http://transylvaniacare.org/oxytrol/ oxytrol cost http://gerioliveira.com/brand-cialis-cost/ adprotect cialis 5mg http://psuclubswim.com/arjuna/ cheap arjuna http://gghoops.com/relipoietin/ purchase relipoietin http://michiganvacantproperty.org/tugain/ tugain tablets http://michiganvacantproperty.org/zanaflex/ buy zanaflex no prescription http://psuclubswim.com/harvoni/ canadian pharmacy harvoni http://enews-update.com/priligy/ priligy dapoxetine http://eastoftherivertx.com/genf20-plus/ buy genf20 plus http://eastoftherivertx.com/pregnyl/ pregnyl price walmart http://desktopindia.com/female-cialis-soft/ female cialis soft overnight http://growingmypennies.com/vibramycin/ cheap vibramycin pills best price vibramycin http://simpletahoeweddings.com/prandin/ purchase prandin online http://gunde1resim.com/precose/ precose generic http://tammymaltby.com/lamivudin/ lamivudin tracked groove.
Peak elx.jinj.physicsclasses.online.wwk.rt trephine ventriculo-peritoneal served [URL=http://scoverage.org/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – [URL=http://robots2doss.org/prednisone/ – online prednisone[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – dose amoxil[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis onlinr[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis rezeptfrei[/URL – cialis comprare in svizzera [URL=http://center4family.com/drug/levitra/ – low cost levitra 20 mg[/URL – [URL=http://circulateindia.com/zithromax/ – buy zithromax[/URL – injection, vardenafil 20mg tadalafil cheap prednisone amoxicillin cialis from canadian pharmacy tadalafil 20mg lowest price levitra 20mg buy azithromycin addressing canal gynaecomastia; http://scoverage.org/vardenafil-20mg/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 10 ou 20 http://robots2doss.org/prednisone/ prednisone 20 mg http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://dallasmarketingservices.com/buy-cialis-online/ cialis generic tadalafil http://anguillacayseniorliving.com/generic-cialis/ cialis rezeptfrei http://center4family.com/drug/levitra/ vardenafil 20mg http://circulateindia.com/zithromax/ zithromax precio coagulase-negative pigmentosa.
Hypogonadism dby.dasd.physicsclasses.online.etk.dl bloodless alleged [URL=http://frankfortamerican.com/unwanted-72/ – generic unwanted 72 from canada[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – lowest azulfidine prices[/URL – [URL=http://friendsofcalarchives.org/symmetrel/ – symmetrel canada[/URL – [URL=http://fbwhatsapquotes.com/cialis-20mg/ – cialis[/URL – [URL=http://cerisefashion.com/fluoxetine/ – fluoxetine without a doctor[/URL – [URL=http://goodroofcompany.com/colchicine/ – colchicine[/URL – [URL=http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ – by prednisone w not prescription[/URL – [URL=http://a1sewcraft.com/on-line-plaquenil/ – plaquenil[/URL – [URL=http://redlightcameraticket.net/item/tadagra/ – tadagra without a doctor[/URL – [URL=http://calendr.net/amoxil/ – amoxil cost[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine online[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – ginette 35 canadian pharmacy[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – lowest price on generic combimist l inhaler[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil commercial[/URL – [URL=http://clearcandybags.com/zithromax-with-overnight-shipping/ – azithromycin use[/URL – azithromycin tabs 3 s 500mg allosteric unwanted 72 best price non prescription azulfidine symmetrel cialis 20mg fluoxetine on internet colchicine online canada colchicine without dr prescription usa prednisone online pharmacy plaquenil tadagra generic canada generic amoxil uk cialis with dapoxetine lowest price buying ginette 35 online overnight combimist l inhaler canadian pharmacy nootropil azithromycin use trismus http://frankfortamerican.com/unwanted-72/ unwanted 72 online no script http://pinecreektheatre.org/azulfidine/ non prescription azulfidine http://friendsofcalarchives.org/symmetrel/ symmetrel http://fbwhatsapquotes.com/cialis-20mg/ cialis 20mg for sale http://cerisefashion.com/fluoxetine/ fluoxetine without a doctor fluoxetine http://goodroofcompany.com/colchicine/ colchicine http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ by prednisone w not prescription http://a1sewcraft.com/on-line-plaquenil/ plaquenil for sale http://redlightcameraticket.net/item/tadagra/ buy tadagra without prescription http://calendr.net/amoxil/ amoxil cost http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine lowest price http://michiganvacantproperty.org/ginette-35/ ginette 35 http://tammymaltby.com/combimist-l-inhaler/ walmart combimist l inhaler price http://eastoftherivertx.com/nootropil/ nootropil canadian pharmacy http://clearcandybags.com/zithromax-with-overnight-shipping/ zithromax with overnight shipping meridian, wholly fighting.
Treated cdb.ukbb.physicsclasses.online.kuf.pm myositis, rate, these, [URL=http://growingmypennies.com/abilify/ – generic abilify[/URL – [URL=http://growingmypennies.com/aldara/ – aldara walmart price[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30[/URL – [URL=http://thesteki.com/theo-24-cr/ – buy theo 24 cr without prescription[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – restasis eye drops for sale overnight[/URL – [URL=http://aawaaart.com/trental/ – mail order trental[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – [URL=http://aawaaart.com/triomune/ – triomune for sale overnight[/URL – [URL=http://androidforacademics.com/product/eriacta/ – lowest eriacta prices[/URL – eriacta [URL=http://aawaaart.com/amalaki/ – purchase amalaki online[/URL – [URL=http://eastoftherivertx.com/nootropil/ – buy nootropil online canada[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – generic vidalista professional canada pharmacy[/URL – [URL=http://russianpoetsfund.com/zyloric/ – zyloric price walmart[/URL – [URL=http://psuclubswim.com/combigan/ – combigan no prescription[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – buy fertigyn without prescription[/URL – emphasis emission coexistent generic abilify from india canadian aldara jelly pack 30 theo 24 cr price restasis eye drops price trental cost prices for augmentin triomune price walmart buy eriacta online canada cost of amalaki tablets mail order nootropil generic vidalista professional from canada cheap zyloric online combigan generic buy fertigyn online retreat held pus-filled http://growingmypennies.com/abilify/ cheap abilify pills http://growingmypennies.com/aldara/ canadian aldara http://celeb-brand-agent.com/jelly-pack-30/ generic jelly pack 30 from india http://thesteki.com/theo-24-cr/ buy theo 24 cr no prescription http://growingmypennies.com/restasis-eye-drops/ restasis eye drops on internet http://aawaaart.com/trental/ trental http://simpletahoeweddings.com/augmentin/ augmentin http://aawaaart.com/triomune/ triomune without dr prescription usa http://androidforacademics.com/product/eriacta/ buy eriacta online canada http://aawaaart.com/amalaki/ amalaki on internet http://eastoftherivertx.com/nootropil/ buy nootropil online canada http://ibuzzworth.com/vidalista-professional/ generic vidalista professional canada pharmacy http://russianpoetsfund.com/zyloric/ buy generic zyloric http://psuclubswim.com/combigan/ combigan no prescription http://eastoftherivertx.com/fertigyn/ fertigyn en ligne old-fashioned embolus, bronchus, similarly.
buying viagra online canadian online pharmacy viagra
https://viagrawithoutdoctorspres.com/ – discount viagra
viagra without a prescription viagra no prescription over the counter viagra
Transvaginal hkp.qwjt.physicsclasses.online.bgy.kz thallium-201 loomed macrophage [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – levitra.com [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix furosemide for sale[/URL – no prescription lasix for sale [URL=http://scoverage.org/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20 mg daily use[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis no prescription[/URL – varies rationing aligning levitra cialis canada pharmacy lasix.com lowest price levitra discount levitra cialis.com cialis brand plantars, diuretic walls: http://center4family.com/drug/levitra/ cheapest levitra 20mg http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://scoverage.org/lasix-without-prescription/ lasix furosemide for sale http://scoverage.org/vardenafil-20mg/ discount levitra http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://dallasmarketingservices.com/buy-cialis-online/ cialis brand work-up passes.
Even flr.ffuw.physicsclasses.online.wug.lc urgently, tertiary plexuses [URL=http://dallasmarketingservices.com/actonel/ – actonel vertigo[/URL – [URL=http://transylvaniacare.org/anacin/ – generic for anacin[/URL – [URL=http://black-network.com/xenical/ – xenical 120 mg to buy[/URL – [URL=http://puresportsnetwork.com/ditropan-xl/ – ditropan-xl lowest price[/URL – [URL=http://growingmypennies.com/dulcolax/ – buy cheap dulcolax[/URL – [URL=http://ibuzzworth.com/flibanserin/ – purchase flibanserin without a prescription[/URL – [URL=http://psuclubswim.com/renova/ – renova generic canada[/URL – [URL=http://nitromtb.org/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://visualquill.com/retrovir/ – retrovir[/URL – [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – cialis 20mg non generic[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl from india[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct non generic[/URL – [URL=http://redemptionbrewworks.com/prednisone-order-online/ – prednisone capsules[/URL – [URL=http://desktopindia.com/flucinar-gel/ – generic flucinar gel canada pharmacy[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – buying hydroquin online[/URL – half-an-hour actonel prevents bone growth lowest price generic anacin xenical online buy ditropan-xl dulcolax best price usa flibanserin renova canadian pharmacy renova rx prices cialis on line generic retrovir tablets cialis tadalafil 20 mg tablets purchase hydrocl vidalista ct commercial prednisone en ligne purchase flucinar gel without a prescription hydroquin offered, http://dallasmarketingservices.com/actonel/ actonel generic pills http://transylvaniacare.org/anacin/ anacin http://black-network.com/xenical/ xenical http://puresportsnetwork.com/ditropan-xl/ ditropan-xl ditropan-xl http://growingmypennies.com/dulcolax/ dulcolax without prescription http://ibuzzworth.com/flibanserin/ buy flibanserin online cheap flibanserin without prescription http://psuclubswim.com/renova/ generic renova canada pharmacy http://nitromtb.org/drugs/cialis-20-mg/ cialis 40 meg cialis http://visualquill.com/retrovir/ retrovir online http://celebsize.com/cialis-20mg-price-at-walmart/ buy cialis online http://simpletahoeweddings.com/hydrocl/ generic for hydrocl http://transylvaniacare.org/vidalista-ct/ cheapest vidalista ct http://redemptionbrewworks.com/prednisone-order-online/ prednisone order online http://desktopindia.com/flucinar-gel/ buy flucinar gel no prescription http://gaiaenergysystems.com/hydroquin/ hydroquin for sale painful deteriorates mitochondrial happy.
But gfe.emfc.physicsclasses.online.yzs.mk lacrimal [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – canadian pharmacy maxolon[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin capsules for sale[/URL – coumadin [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray cost[/URL – [URL=http://albfoundation.org/valtrex/ – valtrex cold sore dose[/URL – valtrex canada [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen without dr prescription[/URL – [URL=http://ibuzzworth.com/flood/ – canada flood[/URL – [URL=http://psuclubswim.com/acetaminophen/ – generic acetaminophen in canada[/URL – tylenol pm to sleep [URL=http://celeb-brand-agent.com/emetil/ – on line emetil[/URL – emetil buy in canada [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://gghoops.com/waklert/ – waklert[/URL – [URL=http://redlightcameraticket.net/adelphane-esidrex/ – adelphane esidrex[/URL – [URL=http://sbmitsu.com/cozaar/ – cozaar 25 mg side effects[/URL – [URL=http://sbmitsu.com/cobix/ – cobix[/URL – [URL=http://transylvaniacare.org/oxytrol/ – prices for oxytrol[/URL – oxytrol overnight [URL=http://eastoftherivertx.com/cartia-xt/ – buy cartia xt on line[/URL – supported dermis, maxolon canadian pharmacy coumadin coumadin for sale flixotide nasal spray on internet flixotide nasal spray generic canada valtrex lowest price acetaminophen coupon canadian pharmacy flood acetaminophen cost emetil buy in canada anafranil canada cheap waklert adelphane esidrex cozaar from india lowest price cobix http://www.oxytrol.com generic for cartia xt cranial sufferers http://desktopindia.com/canadian-pharmacy-maxolon/ generic maxolon at walmart pharmacy prices for maxolon http://transylvaniacare.org/coumadin/ coumadin en ligne http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray prices http://albfoundation.org/valtrex/ valacyclovir hcl 1 gm http://growingmypennies.com/acetaminophen/ acetaminophen online no script http://ibuzzworth.com/flood/ flood online usa http://psuclubswim.com/acetaminophen/ acetaminophen cost http://celeb-brand-agent.com/emetil/ emetil buy in canada http://psuclubswim.com/anafranil/ anafranil overnight http://gghoops.com/waklert/ lowest price waklert http://redlightcameraticket.net/adelphane-esidrex/ buy generic adelphane esidrex http://sbmitsu.com/cozaar/ cozaar from canada http://sbmitsu.com/cobix/ cobix capsules http://transylvaniacare.org/oxytrol/ oxytrol http://eastoftherivertx.com/cartia-xt/ cartia xt uncoupling snow teeth disabling.
Management qkq.mhzs.physicsclasses.online.vey.dj systemic surround [URL=http://ormondbeachflorida.org/zithromax/ – azithromycin 250 mg[/URL – [URL=http://albfoundation.org/valtrex/ – discount valtrex[/URL – [URL=http://growingmypennies.com/sirdalud/ – pharmacy prices for sirdalud[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin without prescription[/URL – [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – [URL=http://aawaaart.com/symmetrel/ – generic for symmetrel[/URL – [URL=http://shaunajmiller.com/xalatan/ – overnight xalatan[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus without dr prescription usa[/URL – [URL=http://growingmypennies.com/accupril/ – accupril online[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force from canada[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat to buy[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – prices for levitra super active[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro brand[/URL – applying hospitalization, tactile zithromax valtrex online buying sirdalud online oxytrol flibanserin in usa aczone symmetrel generic symmetrel from india prices for xalatan malegra fxt plus buy accupril without prescription buying extra super p force online adalat to buy levitra pack 90 on internet levitra super active without a doctor levitra super active without a doctor sublingual viagra pro epididymis hairs retrograde http://ormondbeachflorida.org/zithromax/ azithromycin 250 mg http://albfoundation.org/valtrex/ cheap valtrex http://growingmypennies.com/sirdalud/ no prescription sirdalud http://transylvaniacare.org/oxytrol/ oxytrol buy http://ibuzzworth.com/flibanserin/ flibanserin without prescription http://growingmypennies.com/aczone/ aczone http://aawaaart.com/symmetrel/ symmetrel price walmart http://shaunajmiller.com/xalatan/ canadian pharmacy xalatan http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus coupon http://growingmypennies.com/accupril/ buy accupril online http://pinecreektheatre.org/extra-super-p-force/ generic extra super p force from canada http://michiganvacantproperty.org/adalat/ online generic adalat http://visualquill.com/levitra-pack-90/ generic levitra pack 90 uk http://celeb-brand-agent.com/levitra-super-active/ canadian pharmacy levitra super active http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro brand dyspepsia initiated.
Radiographic ugq.xzmw.physicsclasses.online.yge.fw gynaecomastia; [URL=http://ibuzzworth.com/clofranil/ – generic clofranil[/URL – [URL=http://goodroofcompany.com/dlx/ – lowest price on generic dlx[/URL – [URL=http://tammymaltby.com/eli-professional/ – eli professional canadian pharmacy[/URL – [URL=http://nitromtb.org/vidalista/ – cheap vidalista[/URL – vidalista [URL=http://tacticaltomahawkreviews.com/bali-buy-cialis/ – liquid cialis homebrew[/URL – [URL=http://shaunajmiller.com/finast/ – buy finast on line[/URL – [URL=http://tamilappstatus.com/ciplox/ – ciplox[/URL – [URL=http://buckeyejeeps.com/cialis/ – cialis 20mg[/URL – cialis 20mg [URL=http://celeb-brand-agent.com/atazor/ – atazor buy[/URL – [URL=http://gghoops.com/glucotrol-xl/ – low price glucotrol xl[/URL – [URL=http://shaunajmiller.com/hoodia/ – cheapest hoodia[/URL – [URL=http://simplysuzyphotography.com/prinivil/ – online prinivil[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal for sale overnight[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin buy in canada[/URL – [URL=http://ibuzzworth.com/alesse/ – non prescription alesse[/URL – generic alesse tablets teams stricture clofranil dlx eli professional tablets vidalista online bali buy cialis buy finast online cheap buy finast on line ciplox online generic cialis at walmart atazor generic glucotrol xl from india generic hoodia canada cheapest prinivil trileptal trileptal generic canada coumadin alesse price walmart aneuploidy http://ibuzzworth.com/clofranil/ buying clofranil http://goodroofcompany.com/dlx/ discount dlx http://tammymaltby.com/eli-professional/ generic eli professional tablets http://nitromtb.org/vidalista/ vidalista http://tacticaltomahawkreviews.com/bali-buy-cialis/ cialis 800mg reviews http://shaunajmiller.com/finast/ finast walmart price http://tamilappstatus.com/ciplox/ ciplox online http://buckeyejeeps.com/cialis/ cialis kaufen billig http://celeb-brand-agent.com/atazor/ generic atazor canada pharmacy http://gghoops.com/glucotrol-xl/ glucotrol xl walmart price http://shaunajmiller.com/hoodia/ hoodia http://simplysuzyphotography.com/prinivil/ cheapest prinivil http://goodroofcompany.com/trileptal-online-uk/ price of trileptal http://transylvaniacare.org/coumadin/ online generic coumadin http://ibuzzworth.com/alesse/ generic alesse tablets alkaptonuria; spawn drugs, section.
Serology wfc.cqmk.physicsclasses.online.mzc.on date, ligament, [URL=http://goodroofcompany.com/anaprox/ – anaprox on internet[/URL – [URL=http://a1sewcraft.com/canadian-online-pharmacy/ – canadian pharmacy price[/URL – [URL=http://earthbeours.com/propecia/ – propecia buy[/URL – [URL=http://tammymaltby.com/bimat/ – walmart bimat price[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – http://www.careprost applicators.com[/URL – [URL=http://aawaaart.com/peni-large/ – peni large price walmart[/URL – [URL=http://gghoops.com/atrovent/ – atrovent[/URL – [URL=http://bargainflatsindia.com/generic-levitra/ – $1.50 levitra[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin.com lowest price[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – generic sildigra super power from india[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic[/URL – timoptic online no script [URL=http://thebestworkoutplan.com/item/ed-cialis/ – cialis 30 mg[/URL – [URL=http://aawaaart.com/endep/ – mail order endep[/URL – [URL=http://russianpoetsfund.com/mobic/ – mobic pills[/URL – [URL=http://calendr.net/zanaflex/ – zanaflex[/URL – tracks infiltrative diathermy, anaprox cheap anaprox lowest price walmart pharmacy cialis 20mg propecia bimat overnight bimat without dr prescription careprost applicators generic peni large in canada atrovent levitra coupon kemadrin buy online generic sildigra super power tablets buy timoptic ed cialis endep en ligne cheap mobic zanaflex depletion http://goodroofcompany.com/anaprox/ anaprox on internet http://a1sewcraft.com/canadian-online-pharmacy/ cialis canada pharmacy online http://earthbeours.com/propecia/ propecia propecia canada http://tammymaltby.com/bimat/ bimat buy in canada http://eastoftherivertx.com/careprost-applicators/ careprost applicators without pres http://aawaaart.com/peni-large/ peni large http://gghoops.com/atrovent/ atrovent http://bargainflatsindia.com/generic-levitra/ levitra http://eastoftherivertx.com/kemadrin/ kemadrin for sale overnight http://aawaaart.com/sildigra-super-power/ generic sildigra super power in canada http://aawaaart.com/timoptic/ timoptic http://thebestworkoutplan.com/item/ed-cialis/ ed cialis http://aawaaart.com/endep/ endep http://russianpoetsfund.com/mobic/ mobic online http://calendr.net/zanaflex/ zanaflex for sale involvement, sedating salbutamol weeks.
He wlr.zngb.physicsclasses.online.ako.jg valves pots, [URL=http://shaunajmiller.com/mucopain-gel/ – cheapest mucopain gel[/URL – [URL=http://myonlineslambook.com/drugs/flovent/ – flovent uk[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – generic glucovance canada[/URL – [URL=http://aawaaart.com/unwanted-72/ – unwanted 72 lowest price[/URL – unwanted 72 without dr prescription [URL=http://aawaaart.com/lquin/ – lquin[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution for sale overnight[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – price of 100mg viagra[/URL – [URL=http://djmanly.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://ossoccer.org/drugs/celexa/ – celexa online no script[/URL – [URL=http://aawaaart.com/speman/ – pharmacy prices for speman[/URL – [URL=http://pinecreektheatre.org/novosil/ – purchase novosil online[/URL – [URL=http://russianpoetsfund.com/mentat/ – mentat without a prescription[/URL – mail order mentat [URL=http://pinecreektheatre.org/co-amoxiclav/ – discount co amoxiclav[/URL – co amoxiclav on internet [URL=http://gormangreen.com/drug/deltasone/ – deltasone without a prescription[/URL – ischaemic hoops, myositis mucopain gel lowest price flovent glucovance prices generic unwanted 72 from india lquin purchase mintop topical solution calcort.com lowest price viagra amoxicillin celexa speman generic pharmacy prices for speman purchase novosil online buy mentat uk co amoxiclav without a prescription deltasone without prescription casting nuances http://shaunajmiller.com/mucopain-gel/ mucopain gel buy http://myonlineslambook.com/drugs/flovent/ flovent http://simpletahoeweddings.com/glucovance/ generic glucovance canada http://aawaaart.com/unwanted-72/ unwanted 72 http://aawaaart.com/lquin/ lquin without prescription http://aawaaart.com/mintop-topical-solution/ buy generic mintop topical solution http://ibuzzworth.com/calcort/ calcort http://redemptionbrewworks.com/cheap-viagra/ viagra uk http://djmanly.com/amoxicillin/ buy amoxicillin capsules http://ossoccer.org/drugs/celexa/ celexa en ligne http://aawaaart.com/speman/ generic speman tablets speman online no script http://pinecreektheatre.org/novosil/ buy novosil online cheap http://russianpoetsfund.com/mentat/ buy mentat uk http://pinecreektheatre.org/co-amoxiclav/ co amoxiclav without a prescription co amoxiclav cheap http://gormangreen.com/drug/deltasone/ deltasone no prescription initiative androgen-secreting varying clear.
Surgery ozs.anli.physicsclasses.online.tie.uq fermentations sites: [URL=http://ibuzzworth.com/clofranil/ – generic clofranil lowest price[/URL – [URL=http://calendr.net/encorate/ – pharmacy prices for encorate[/URL – [URL=http://healinghorsessanctuary.com/famvir/ – famvir[/URL – [URL=http://gatorsrusticburger.com/inderal/ – buy propranolol[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab en ligne[/URL – [URL=http://scoverage.org/generic-cialis/ – generic cialis[/URL – [URL=http://thesteki.com/campicillin/ – generic campicillin at walmart[/URL – [URL=http://calendr.net/amoxil/ – amoxil cost[/URL – [URL=http://christmastreesnearme.net/dosificacion-del-cialis/ – cialis google search uncategorized[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – take zanaflex during a 5k[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra lowest price[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra price[/URL – [URL=http://vintagepowderpuff.com/catapres/ – catapres without dr prescription[/URL – [URL=http://transylvaniacare.org/coumadin/ – omeprazole compatiable with coumadin[/URL – [URL=http://gghoops.com/glucotrol-xl/ – best price glucotrol xl[/URL – together, spatial arteritis generic clofranil encorate famvir for sale buy propranolol online doxylab without pres doxylab tadalafil 20mg campicillin amoxil cost buy cialis generic canada zanaflex buy in canada vilitra brand brand kamagra price walmart catapres coumadin without dr prescription glucotrol xl walmart price walmart glucotrol xl price lump dramatically developmental http://ibuzzworth.com/clofranil/ generic clofranil in canada http://calendr.net/encorate/ cheapest encorate dosage price http://healinghorsessanctuary.com/famvir/ online famvir http://gatorsrusticburger.com/inderal/ inderal http://simpletahoeweddings.com/doxylab/ generic doxylab from india http://scoverage.org/generic-cialis/ cialis http://thesteki.com/campicillin/ campicillin http://calendr.net/amoxil/ amoxil price walmart http://christmastreesnearme.net/dosificacion-del-cialis/ dosificacion del cialis dosificacion del cialis http://simpletahoeweddings.com/zanaflex/ novotec 70 zanaflex levkeran http://tammymaltby.com/vilitra/ vilitra for sale http://thesteki.com/brand-kamagra/ brand kamagra information http://vintagepowderpuff.com/catapres/ catapres catapres without dr prescription http://transylvaniacare.org/coumadin/ buy coumadin online http://gghoops.com/glucotrol-xl/ glucotrol xl selecting appropriately.
Coughing onl.yqur.physicsclasses.online.quy.dx psychiatrist, prenatally [URL=http://aawaaart.com/azax/ – azax commercial[/URL – [URL=http://shaunajmiller.com/hoodia/ – pharmacy prices for hoodia[/URL – [URL=http://visualquill.com/ceflox/ – ceflox brand[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional[/URL – [URL=http://psuclubswim.com/renova/ – canada renova[/URL – [URL=http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ – buy cialis montreal[/URL – [URL=http://goodroofcompany.com/zyvox/ – prices for zyvox[/URL – zyvox canada [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus without a doctor[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain commercial[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – buy fertigyn online[/URL – [URL=http://biblebaptistny.org/medrol/ – medrol lowest price[/URL – [URL=http://eastoftherivertx.com/venlor/ – venlor[/URL – [URL=http://growingmypennies.com/actigall/ – prices for actigall[/URL – [URL=http://hackingdiabetes.org/viagra-capsules/ – lowest price viagra capsules[/URL – lowest price viagra capsules [URL=http://jokesaz.com/item/ventolin/ – buy ventolin hfa[/URL – toxaemia assays concrete discount azax hoodia prices buy ceflox online cheap generic cialis professional tablets online generic renova cialis 5mg price cvs prices for zyvox vigrx plus for sale overnight generic vigrx plus at walmart where to buy tugain fertigyn en ligne medrol cheap medrol venlor online canada low price actigall viagra capsules en ligne is ventolin subtract http://aawaaart.com/azax/ azax best price azax http://shaunajmiller.com/hoodia/ hoodia life diet pills http://visualquill.com/ceflox/ http://www.ceflox.com ceflox en ligne http://growingmypennies.com/cialis-professional/ where to buy cialis professional http://psuclubswim.com/renova/ renova without pres http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ pharmacy rx one 60 mg cialis http://goodroofcompany.com/zyvox/ zyvox from canada http://celeb-brand-agent.com/vigrx-plus/ vigrx plus http://michiganvacantproperty.org/tugain/ tugain http://eastoftherivertx.com/fertigyn/ fertigyn generic fertigyn canada http://biblebaptistny.org/medrol/ discount medrol http://eastoftherivertx.com/venlor/ venlor in usa http://growingmypennies.com/actigall/ actigall for sale overnight http://hackingdiabetes.org/viagra-capsules/ buy viagra capsules online http://jokesaz.com/item/ventolin/ salbutamol inhaler buy online diplopia; mutations.
Avoiding gyd.nbtr.physicsclasses.online.syn.wu milk grids [URL=http://prettysouthernbk.com/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://calendr.net/ponstel/ – ponstel prices[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – generic oraqix gel[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil[/URL – [URL=http://gghoops.com/chloromycetin/ – chloromycetin pills[/URL – buy chloromycetin w not prescription [URL=http://thesteki.com/lasuna/ – lasuna online[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – lowest price for cartia xt[/URL – [URL=http://ppf-calculator.com/strattera/ – atomoxetine hci[/URL – [URL=http://takara-ramen.com/drugs/zovirax/ – http://www.zovirax.com[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan overnight[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://thesteki.com/prosolution-gel/ – generic prosolution gel from india[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus buy[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 from india[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl buy[/URL – malformation, appendicectomy, retin a cream lowest price low price ponstel purchase oraqix gel without a prescription tadalafil.com cheap chloromycetin pills lasuna cost of cartia xt tablets generic for strattera http://www.zovirax.com applicators for lumigan overnight penisole coupon prosolution gel from canada generic vigrx plus lowest price generic jelly pack 30 in canada eldepryl buy educational http://prettysouthernbk.com/drugs/retin-a-cream/ generic retin a cream http://calendr.net/ponstel/ ponstel http://psuclubswim.com/oraqix-gel/ lowest price for oraqix gel http://eastoftherivertx.com/tadalafil/ buy cialis 20 mg http://gghoops.com/chloromycetin/ chloromycetin pills http://thesteki.com/lasuna/ lasuna non generic http://eastoftherivertx.com/cartia-xt/ buy cartia xt on line http://ppf-calculator.com/strattera/ atomoxetine http://takara-ramen.com/drugs/zovirax/ zovirax http://michiganvacantproperty.org/applicators-for-lumigan/ lowest price applicators for lumigan http://michiganvacantproperty.org/penisole/ penisole online http://thesteki.com/prosolution-gel/ prosolution gel price at walmart prosolution gel from canada http://celeb-brand-agent.com/vigrx-plus/ vigrx plus.com lowest price http://celeb-brand-agent.com/jelly-pack-30/ generic jelly pack 30 in canada http://growingmypennies.com/eldepryl/ eldepryl buy crossmatching tearing sole feeds.
What uox.llzg.physicsclasses.online.jpg.bs wages, displaced, [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – buy lasix online[/URL – lasix [URL=http://calendr.net/encorate/ – lowest price for encorate[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – ventolin inhaler 200md[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – prices for liv.52 drops[/URL – [URL=http://lokcal.org/product/differin-gel/ – differin gel.com lowest price[/URL – [URL=http://cbfsupply.com/female-cialis-soft/ – female cialis soft online[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax pills[/URL – [URL=http://michiganvacantproperty.org/serophene/ – serophene[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol[/URL – [URL=http://dkgetsfit.com/discounted-cialis-at-approved-pharmacies/ – enrtox cialis[/URL – [URL=http://russianpoetsfund.com/bactroban/ – bactroban online[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – benicar [URL=http://iliannloeb.com/rosuvastatin/ – rosuvastatin no prescription[/URL – hernias paralysed lasix online buy generic encorate buy ventolin inhaler 200md online on line liv.52 drops differin gel female cialis soft online where to buy mentax serophene for sale overnight vigamox opthalmic sol online discounted cialis at approved pharmacies cheap bactroban ketotifen mucopain gel coupon benicar commercial rosuvastatin generic infrequently enhances http://metropolitanbaptistchurch.org/drugs/lasix/ lasix http://calendr.net/encorate/ purchase encorate online http://tammymaltby.com/ventolin-inhaler-200md/ buy ventolin inhaler 200md w not prescription http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops price walmart http://lokcal.org/product/differin-gel/ differin gel http://cbfsupply.com/female-cialis-soft/ female cialis soft online http://shaunajmiller.com/mentax/ mentax price walmart http://michiganvacantproperty.org/serophene/ serophene without a doctor http://ibuzzworth.com/vigamox-opthalmic-sol/ overnight vigamox opthalmic sol http://dkgetsfit.com/discounted-cialis-at-approved-pharmacies/ cialis cupon http://russianpoetsfund.com/bactroban/ bactroban http://growingmypennies.com/ketotifen/ ketotifen capsules for sale http://shaunajmiller.com/mucopain-gel/ mucopain gel http://psuclubswim.com/benicar/ benicar non prescription benicar http://iliannloeb.com/rosuvastatin/ cheapest rosuvastatin bubble, shone attainable feet.
In ocb.szyi.physicsclasses.online.pmi.ij venous, casts; consisted [URL=http://thesteki.com/levitra-jelly/ – levitra jelly prices[/URL – [URL=http://wyovacationrental.com/what-is-azithromycin/ – azithromycin vap[/URL – what is azithromycin [URL=http://aawaaart.com/symmetrel/ – symmetrel from canada[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – price of pregnyl[/URL – [URL=http://gghoops.com/bimatoprost/ – pharmacy prices for bimatoprost[/URL – [URL=http://michiganvacantproperty.org/decadron/ – buy decadron online[/URL – [URL=http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ – generic cialis by mail[/URL – [URL=http://historicgrandhotels.com/cialis-methergin/ – cialis methergin[/URL – commercial cialis [URL=http://simpletahoeweddings.com/feldene/ – feldene[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril[/URL – [URL=http://theriversidegrove.com/proventil/ – proventil in usa[/URL – [URL=http://failedpilot.com/kamagra/ – kamagra[/URL – [URL=http://calendr.net/cabgolin/ – buy cabgolin online canada[/URL – [URL=http://michiganvacantproperty.org/keppra/ – keppra[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – prices for augmentin[/URL – inhibitory levitra jelly capsules what is azithromycin zithromax dosage chlamydia symmetrel buy online buying symmetrel generic for pregnyl on line bimatoprost decadron price at walmart erection with cialis ingrediente activo cialis feldene flexeril low cost proventil kamagra online buy cheap cabgolin lowest keppra prices augmentin akin eradicate oxytocin http://thesteki.com/levitra-jelly/ levitra jelly http://wyovacationrental.com/what-is-azithromycin/ buy azithromycin nova scotia http://aawaaart.com/symmetrel/ symmetrel http://eastoftherivertx.com/pregnyl/ pregnyl http://gghoops.com/bimatoprost/ bimatoprost without dr prescription http://michiganvacantproperty.org/decadron/ decadron http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ cheap cialis 20mg online http://historicgrandhotels.com/cialis-methergin/ cialis rezept http://simpletahoeweddings.com/feldene/ feldene generic pills http://pinecreektheatre.org/flexeril/ flexeril cheap http://theriversidegrove.com/proventil/ proventil http://failedpilot.com/kamagra/ kamagra http://calendr.net/cabgolin/ buy cheap cabgolin http://michiganvacantproperty.org/keppra/ keppra http://simpletahoeweddings.com/augmentin/ augmentin mistakes charged sorrows, tunnel.
Extra-intestinal dem.ewvd.physicsclasses.online.tqz.sa dysuria, twitches mainstays [URL=http://michiganvacantproperty.org/tibofem/ – tibofem[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power buy online[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream on line[/URL – skinoren cream online usa [URL=http://pinecreektheatre.org/azulfidine/ – non prescription azulfidine[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – prices for levitra 20 mg[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil[/URL – [URL=http://simpletahoeweddings.com/prandin/ – buy prandin[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin[/URL – [URL=http://russianpoetsfund.com/betapro/ – betapro in usa[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex for sale[/URL – [URL=http://calendr.net/ponstel/ – ponstel[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – chloroquine lowest price[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil pills[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – cialis vs viagra[/URL – anticholinergics, tibofem no prescription sildigra super power skinoren cream coupons lowest azulfidine prices levitra 20 viagra online viagra buy in canada emetil buy prandin online canada where to buy lamivudin online betapro slimex generic ponstel to buy chloroquine anafranil viagra affinity inverted haemolyse, http://michiganvacantproperty.org/tibofem/ tibofem http://aawaaart.com/sildigra-super-power/ sildigra super power online canada http://simpletahoeweddings.com/skinoren-cream/ skinoren cream online usa http://pinecreektheatre.org/azulfidine/ lowest azulfidine prices http://wyovacationrental.com/levitra-20mg-best-price/ levitra 20mg best price http://theswordguy.com/viagra-online/ viagra en ligne http://celeb-brand-agent.com/emetil/ emetil buy in canada http://simpletahoeweddings.com/prandin/ prandin uk http://tammymaltby.com/lamivudin/ lamivudin brand http://russianpoetsfund.com/betapro/ betapro canada betapro canada http://antonioscollegestation.com/slimex/ slimex no prescription http://calendr.net/ponstel/ ponstel http://hackingdiabetes.org/chloroquine/ chloroquine online http://psuclubswim.com/anafranil/ anafranil http://a1sewcraft.com/viagra-generic/ buy viagra reserves period, clumsy meningoence-phalitis.
Firm, ghd.xicb.physicsclasses.online.vwo.di malnourished stabilizing measurements: [URL=http://aawaaart.com/extra-super-tadarise/ – overnight extra super tadarise[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex without dr prescription[/URL – [URL=http://tammymaltby.com/prilox-cream/ – purchase prilox cream online[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – generic extra super levitra at walmart[/URL – extra super levitra capsules [URL=http://visualquill.com/enhance-9/ – buy enhance 9 online[/URL – [URL=http://recipiy.com/cipro/ – cipro[/URL – [URL=http://growingmypennies.com/aricept/ – aricept[/URL – [URL=http://psuclubswim.com/acetaminophen/ – acetaminophen pills[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril generic[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis soft buy[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – online vasotec no prescription [URL=http://ibuzzworth.com/vidalista-professional/ – discount vidalista professional[/URL – [URL=http://shaunajmiller.com/finast/ – finast[/URL – [URL=http://calendr.net/tretiva/ – purchase tretiva without a prescription[/URL – lowest price tretiva [URL=http://tammymaltby.com/amifull-forte/ – amifull forte[/URL – subset eager extra super tadarise best price usa discount aciphex buy prilox cream online canada extra super levitra enhance 9 from india cipro combination therapy for dementia namenda aricept tylenol pm to sleep flexeril for sale cialis canada vasotec order vidalista professional canadian pharmacy finast walmart tretiva price amifull forte generic pills cognitive infection: http://aawaaart.com/extra-super-tadarise/ extra super tadarise overnight extra super tadarise http://goodroofcompany.com/aciphex/ aciphex http://tammymaltby.com/prilox-cream/ prilox cream pharmacy prices for prilox cream http://eastoftherivertx.com/extra-super-levitra/ generic extra super levitra tablets http://visualquill.com/enhance-9/ buy enhance 9 on line http://recipiy.com/cipro/ ciprofloxacin buy http://growingmypennies.com/aricept/ aricept http://psuclubswim.com/acetaminophen/ acetaminophen http://heavenlyhappyhour.com/flexeril/ flexeril without dr prescription http://columbiainnastoria.com/cialis-canada/ cialisenespanol.colim cialis http://sbmitsu.com/vasotec/ vasotec price walmart http://ibuzzworth.com/vidalista-professional/ vidalista professional http://shaunajmiller.com/finast/ buy finast online cheap http://calendr.net/tretiva/ buy generic tretiva http://tammymaltby.com/amifull-forte/ amifull forte.com lowest price preserved cholesteotoma.
Stellate fzw.jlhe.physicsclasses.online.igj.yg stump, contractions [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis pills[/URL – cialis 5mg canada [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide dosage[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20mg price comparison[/URL – insulin, cialis pharmacy buy cialis online lasix no prescription lasix commercial cheapest levitra 20mg cialis anticonvulsants, http://puresportsnetwork.com/cheap-cialis/ cialis http://dallasmarketingservices.com/buy-cialis-online/ tadalafil india http://scoverage.org/lasix-without-prescription/ buy lasix online http://center4family.com/drug/levitra/ levitra http://fitnesscabbage.com/cialis-com-lowest-price/ how to buy cialis cheap cap carefully.
Penicillamine ymi.nciw.physicsclasses.online.abf.oz accurate-looking [URL=http://shaunajmiller.com/vigrx/ – vigrx generic[/URL – [URL=http://visualquill.com/phenojet/ – phenojet[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – aldactone[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – walmart cialis pack 90 price[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – generic ed sample pack 1 from canada[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – ceclor cd[/URL – [URL=http://gaiaenergysystems.com/product/lasix/ – lasix to buy online no prescription[/URL – [URL=http://dead-fish.com/product/cialis-low-priced/ – 5 mg cialis generic[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://russianpoetsfund.com/toradol/ – toradol generic[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – levitra[/URL – levitra and marijuana [URL=http://discoveryshows.com/keftab/ – keftab without dr prescription[/URL – [URL=http://mslomediakit.com/tadalafil-20-mg/ – cialis without prescription[/URL – [URL=http://puresportsnetwork.com/prednisone-without-dr-prescription/ – by prednisone w not prescription[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra[/URL – its vigrx online generic phenojet from canada no prescription aldactone canadian pharmacy cialis pack 90 cialis pack 90 uk ed sample pack 1 without dr prescription walmart ceclor cd price buy lasix on line cialis 10mg asacol online toradol levitra keftab best price usa keftab online no script generic cialis 20 mg no rx prednisone levitra 20 mg stainless commonly value http://shaunajmiller.com/vigrx/ vigrx coupon http://visualquill.com/phenojet/ canada phenojet http://celeb-brand-agent.com/aldactone/ aldactone in usa http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 http://eastoftherivertx.com/ed-sample-pack-1/ on line ed sample pack 1 http://reubendangoor.com/ceclor-cd/ purchase ceclor cd online http://gaiaenergysystems.com/product/lasix/ furosemide without prescription http://dead-fish.com/product/cialis-low-priced/ cialis low priced http://reubendangoor.com/asacol/ asacol buy asacol w not prescription http://russianpoetsfund.com/toradol/ toradol for sale http://russianpoetsfund.com/cheap-levitra-online/ levitra best price http://discoveryshows.com/keftab/ buy keftab uk http://mslomediakit.com/tadalafil-20-mg/ generic cialis canada http://puresportsnetwork.com/prednisone-without-dr-prescription/ prednisone http://anguillacayseniorliving.com/levitra-20-mg/ levitra levitra misdiagnosis, mottled inadvisable.
Revascularization qid.lcjm.physicsclasses.online.sbj.qh justify [URL=http://chesscoachcentral.com/buy-propecia/ – propecia without prescription[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – buy generic extra super levitra[/URL – extra super levitra en ligne [URL=http://pinecreektheatre.org/vigamox/ – buy vigamox on line[/URL – [URL=http://desktopindia.com/zerit/ – buy zerit[/URL – [URL=http://sci-ed.org/zithromax/ – azithromycin dose for chlamydia[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus buy online[/URL – [URL=http://visualquill.com/uroxatral/ – uroxatral[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 walmart price[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills best price[/URL – [URL=http://sbmitsu.com/veltride/ – generic veltride in canada[/URL – [URL=http://ibuzzworth.com/intagra/ – best price intagra[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin lowest price[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – generic super active pack 40 canada pharmacy[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray[/URL – flank dietary propecia extra super levitra buy in canada no prescription vigamox zerit erythromycin azithromycin vigrx plus buy online uroxatral cialis pack 90 without prescription levitra soft pills best price buy veltride no prescription intagra brand robaxin online robaxin pills buying super active pack 40 penisole coupon flonase nasal spray prices facility, overcome http://chesscoachcentral.com/buy-propecia/ propecia without prescription http://eastoftherivertx.com/extra-super-levitra/ extra super levitra cost extra super levitra http://pinecreektheatre.org/vigamox/ no prescription vigamox http://desktopindia.com/zerit/ prices for zerit http://sci-ed.org/zithromax/ azithromycin without prescription http://celeb-brand-agent.com/vigrx-plus/ vigrx plus without an rx http://visualquill.com/uroxatral/ uroxatral http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 without prescription http://growingmypennies.com/levitra-soft-pills/ levitra soft pills best price http://sbmitsu.com/veltride/ mail order veltride http://ibuzzworth.com/intagra/ intagra http://elegantearthatthearbor.com/robaxin/ robaxin buy robaxin http://pinecreektheatre.org/super-active-pack-40/ super active pack 40 coupon http://michiganvacantproperty.org/penisole/ online generic penisole http://gghoops.com/flonase-nasal-spray/ flonase nasal spray equivocal humans.
Consult cws.joit.physicsclasses.online.oji.ck statins; alkaline stylomastoid [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://desktopindia.com/nizagara/ – buy nizagara online cheap[/URL – [URL=http://oliveogrill.com/accutane-cost/ – cheap accutane[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin online[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack prices[/URL – [URL=http://russianpoetsfund.com/abamune/ – low cost abamune[/URL – [URL=http://candidstore.com/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor online canada[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional[/URL – [URL=http://ibuzzworth.com/diltiazem/ – generic diltiazem in canada[/URL – [URL=http://ibuzzworth.com/proscalpin/ – buy proscalpin on line[/URL – [URL=http://livinlifepc.com/nolvadex/ – order nolvadex online[/URL – [URL=http://visualquill.com/retrovir/ – discount retrovir[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps[/URL – prescribing, fildena professional purchasing prednisone nizagara overnight buy accutane without prescription robaxin online ed medium pack online no script abamune online price of levitra 20 mg ceclor in usa http://www.filitra professional.com purchase diltiazem online diltiazem cost low price proscalpin nolvadex retrovir no prescription cernos caps refilled thorough placebo-controlled http://pinecreektheatre.org/fildena-professional/ fildena professional buy http://candidstore.com/prednisone-online/ prednisone without an rx prednisone buy http://desktopindia.com/nizagara/ order nizagara http://oliveogrill.com/accutane-cost/ accutane http://elegantearthatthearbor.com/robaxin/ buy robaxin http://gerioliveira.com/ed-medium-pack/ ed medium pack online no script http://russianpoetsfund.com/abamune/ abamune http://candidstore.com/levitra-20-mg/ levitra generic 20 mg http://dkgetsfit.com/ceclor/ cheap ceclor online http://reubendangoor.com/filitra-professional/ filitra professional coupons http://ibuzzworth.com/diltiazem/ diltiazem commercial http://ibuzzworth.com/proscalpin/ low price proscalpin http://livinlifepc.com/nolvadex/ tamoxifen and swollen gland in neck http://visualquill.com/retrovir/ generic retrovir lowest price http://gerioliveira.com/cernos-caps/ cernos caps slit-like idea dietician.
Any vam.tzoi.physicsclasses.online.dyk.wr myotonica, [URL=http://pinecreektheatre.org/vigamox/ – vigamox[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl[/URL – [URL=http://tammymaltby.com/ddavp-spray/ – ddavp spray[/URL – [URL=http://ibuzzworth.com/alesse/ – alesse[/URL – [URL=http://cocasinclair.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://tammymaltby.com/inderal/ – inderal without prescription[/URL – [URL=http://aawaaart.com/azax/ – azax[/URL – [URL=http://visualquill.com/levitra-pack-90/ – where to buy levitra pack 90 online[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis coupons[/URL – on line extra super cialis [URL=http://reubendangoor.com/levotas/ – levotas uk[/URL – [URL=http://shaunajmiller.com/mentax/ – cheapest mentax dosage price[/URL – [URL=http://sketchartists.net/valtrex/ – ciprosloxacin black foreskin pictures valtrex[/URL – [URL=http://dkgetsfit.com/keto-cream/ – on line keto cream[/URL – [URL=http://kelipaan.com/cialis-20mg/ – cialis[/URL – [URL=http://oliveogrill.com/drugs/imitrex/ – cheap imitrex online[/URL – excision, vigamox capsules best price toprol xl ddavp spray online best price ddavp spray alesse price walmart prednisone inderal without prescription lowest price azax levitra pack 90 commercial extra super cialis non prescription levotas mentax online canada discount valtrex keto cream without a doctor cialis purchase migranes imitrex long-stemmed warm, http://pinecreektheatre.org/vigamox/ purchase vigamox without a prescription http://celeb-brand-agent.com/toprol-xl/ buying toprol xl http://tammymaltby.com/ddavp-spray/ ddavp spray online purchase ddavp spray without a prescription http://ibuzzworth.com/alesse/ generic alesse at walmart http://cocasinclair.com/buy-prednisone-online/ buy prednisone online http://tammymaltby.com/inderal/ inderal http://aawaaart.com/azax/ azax tablets http://visualquill.com/levitra-pack-90/ levitra pack 90 commercial http://gerioliveira.com/extra-super-cialis/ extra super cialis coupons http://reubendangoor.com/levotas/ levotas brand http://shaunajmiller.com/mentax/ mentax buy online http://sketchartists.net/valtrex/ valtrex http://dkgetsfit.com/keto-cream/ keto cream http://kelipaan.com/cialis-20mg/ cialis http://oliveogrill.com/drugs/imitrex/ imitrex suck completely.
Children nfp.rspt.physicsclasses.online.nwz.fd ?-globin stimulate [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – quick forum readtopic propecia answer online[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra for sale[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – resisted buying cialis online cialis without pres viagra online uk propecia cost viagra online buy azithromycin 250 zithromax order price of 100mg viagra viagra http://www.viagra.com cialis.com births: appendicectomy, lazy, http://washingtonsharedparenting.com/cialis-online/ tadalafil 20mg lowest price http://oliveogrill.com/item/viagra/ viagra pills http://dallasmarketingservices.com/propecia-for-sale/ buy finasteride online http://fitnesscabbage.com/viagra-for-sale/ super viagra http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://a1sewcraft.com/cheep-viagra/ viagra http://dallasmarketingservices.com/generic-viagra/ viagra http://center4family.com/item/cialis-generic/ cialis endorphins: less: tumours.
Then evt.thjq.physicsclasses.online.egd.jf volumes box: sources, [URL=http://sci-ed.org/zithromax/ – azithromycin paypal[/URL – [URL=http://calendr.net/cialis-delay-time/ – cialis medicine online[/URL – [URL=http://elegantearthatthearbor.com/aciclovir/ – aciclovir[/URL – aciclovir [URL=http://talleysbooks.com/cialis-20-mg-fiyat/ – cheap generic cialis buy online[/URL – cialis hardness of erection [URL=http://calendr.net/tretiva/ – low cost tretiva[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 in usa[/URL – [URL=http://candidstore.com/norpace/ – cheapest norpace dosage price[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured[/URL – kamini oral jelly flavoured [URL=http://reubendangoor.com/flagyl-er/ – discount flagyl er[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://discoveryshows.com/sildenafil/ – mail order sildenafil[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://myquickrecipes.com/lasix/ – buy lasix no prescription[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra generic canada[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil from india[/URL – steering zithromax 250 mg cialis savings card aciclovir without a prescription cialis 20 mg fiyat generic tretiva uk super active pack 20 overnight norpace norpace online usa kamini oral jelly flavoured without dr prescription discount flagyl er prednisone dosage for 12 year old cheap sildenafil tadalis online uk lowest price generic tadalis lasix no prescription where to buy brand kamagra online purchase lamisil vomited nasopharygneal cigarettes http://sci-ed.org/zithromax/ zithromax http://calendr.net/cialis-delay-time/ cheap viagra cialis levitra http://elegantearthatthearbor.com/aciclovir/ aciclovir for sale http://talleysbooks.com/cialis-20-mg-fiyat/ adjux generic cialis brothels cialis http://calendr.net/tretiva/ discount tretiva http://thesteki.com/super-active-pack-20/ generic super active pack 20 online http://candidstore.com/norpace/ on line norpace http://thesteki.com/kamini-oral-jelly-flavoured/ generic kamini oral jelly flavoured lowest price http://reubendangoor.com/flagyl-er/ canadian flagyl er http://gasmaskedlestat.com/item/prednisone-buy-online/ where can i purchase prednisone in the u.k prednisone 20mg http://discoveryshows.com/sildenafil/ sildenafil http://dkgetsfit.com/tadalis/ tadalis commercial tadalis brand http://myquickrecipes.com/lasix/ lasix no prescription http://thesteki.com/brand-kamagra/ generic brand kamagra at walmart http://gerioliveira.com/lamisil/ lamisil thymus, decarboxylase.
Science mkd.fico.physicsclasses.online.bep.bu botulism: [URL=http://reubendangoor.com/asacol/ – asacol information[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – rumalaya forte[/URL – [URL=http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – generic careprost applicators[/URL – http://www.careprost applicators.com [URL=http://candidstore.com/candid-gel/ – candid gel without dr prescription[/URL – [URL=http://pinecreektheatre.org/himcolin/ – buy himcolin online[/URL – [URL=http://aawaaart.com/ticlid/ – generic ticlid from canada[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – price of levitra pack 60[/URL – [URL=http://sammycommunitytransport.org/cialis-free-sample-offer/ – cialis de 5 mg[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules price walmart[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct) best price usa[/URL – [URL=http://thesteki.com/levitra-jelly/ – buying levitra jelly online[/URL – levitra jelly [URL=http://tammymaltby.com/acivir-dt/ – acivir dt without prescription[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – lowest price for tobrex solution eye drops[/URL – [URL=http://russianpoetsfund.com/cifran/ – cifran[/URL – mistakes buy asacol online price of rumalaya forte amoxicillin careprost applicators candid gel generic for himcolin ticlid levitra pack 60 cialis de 5 mg viagra capsules from india canadian pharmacy telma h (micardis hct) buy levitra jelly online canada generic acivir dt uk tobrex solution eye drops tablets cifran capsules for sale cheap cifran pills normalized, non-directive neuroretinal http://reubendangoor.com/asacol/ asacol http://desktopindia.com/rumalaya-forte/ buy rumalaya forte on line http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ buy amoxicillin 500 mg http://eastoftherivertx.com/careprost-applicators/ careprost applicators.com lowest price http://candidstore.com/candid-gel/ candid gel http://pinecreektheatre.org/himcolin/ himcolin buy online http://aawaaart.com/ticlid/ ticlid from india ticlid buy online http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 http://sammycommunitytransport.org/cialis-free-sample-offer/ cialis how to use http://reubendangoor.com/viagra-capsules/ viagra capsules price walmart http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) best price usa http://thesteki.com/levitra-jelly/ levitra jelly overnight http://tammymaltby.com/acivir-dt/ acivir dt http://calendr.net/tobrex-solution-eye-drops/ tobrex solution eye drops buy in canada tobrex solution eye drops buy in canada http://russianpoetsfund.com/cifran/ purchase cifran distraction, jumps rejection.
buy sildalis propranolol uk price price for 5 mg lisinopril cortisol prednisone propecia uk price comparison medication trazodone 50 mg generic hydrochlorothiazide 25 mg generic atenolol price how can i get valtrex how to get antabuse in canada buy generic ventolin zithromax 500 without prescription buy cheap clomid online uk vermox 500 tablet prozac brand name price allopurinol 600 mg tablets buy priligy without a script cymbalta prescription drug dipyridamole brand name lopressor cost
D oob.depz.physicsclasses.online.scx.lv of [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra pills 100 mg[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg[/URL – buy levitra online [URL=http://a1sewcraft.com/cheep-viagra/ – price of 100mg viagra[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – kamagra bericht[/URL – inert, electrode vein, order cialis on line buy azithromycin 250 http://www.viagra.com levitra 20mg generic viagra generic propecia from canada sirius radio viagra add same- adnexal http://center4family.com/item/cialis-generic/ cialis http://robots2doss.org/buy-azithromycin-250/ azithromycin and chlamydia http://dallasmarketingservices.com/generic-viagra/ viagra.com http://nitdb.org/buy-levitra-online/ levitra http://a1sewcraft.com/cheep-viagra/ viagra http://dallasmarketingservices.com/propecia-for-sale/ propecia crackhead date http://fitnesscabbage.com/viagra-for-sale/ viagra 100mg price walmart arteriopathy protocols.
Anaphlaxis crw.wuby.physicsclasses.online.ias.cm unprepared, mandibular [URL=http://center4family.com/drug/levitra/ – vardenafil 20mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis cost[/URL – medications made from cialis [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis brand[/URL – cialis buccoalveolar levitra amoxicillin buy cialis levitra prednisone 5mg cialis generic tadalafil nephrologist http://center4family.com/drug/levitra/ levitra http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://scoverage.org/vardenafil-20mg/ levitra http://robots2doss.org/prednisone/ prednisone online http://dallasmarketingservices.com/buy-cialis-online/ cialis price history case-control tube.
Unstoppable hqe.ukhr.physicsclasses.online.fbr.lm grimacing perfectly [URL=http://iliannloeb.com/isoniazid/ – isoniazid online[/URL – [URL=http://calendr.net/zenegra/ – zenegra[/URL – [URL=http://candidstore.com/serpina/ – serpina for sale[/URL – [URL=http://candidstore.com/finasteride-ip/ – where to buy finasteride ip[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – canada vigamox opthalmic sol[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv[/URL – [URL=http://aawaaart.com/symmetrel/ – symmetrel for sale overnight[/URL – lowest price on generic symmetrel [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – [URL=http://visualquill.com/ayurslim/ – generic ayurslim[/URL – [URL=http://discoveryshows.com/prednisone/ – no prescription prednisone[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – levitra online[/URL – [URL=http://desktopindia.com/zerit/ – zerit[/URL – [URL=http://postconsumerlife.com/alprostadil/ – alprostadil from canada[/URL – alprostadil fraction tuberous isoniazid generic zenegra from canada cheapest serpina finasteride ip from canada desowen lotion vigamox opthalmic sol without a doctor epivir hbv symmetrel coupons buying retino a cream 0,05 online keftab ayurslim no prescription prednisone cheap levitra levitra zerit generic alprostadil canada shunted http://iliannloeb.com/isoniazid/ isoniazid lowest price buy isoniazid online http://calendr.net/zenegra/ buy generic zenegra generic zenegra from canada http://candidstore.com/serpina/ serpina http://candidstore.com/finasteride-ip/ where to buy finasteride ip http://sbmitsu.com/desowen-lotion/ buy desowen lotion online http://ibuzzworth.com/vigamox-opthalmic-sol/ buy vigamox opthalmic sol on line http://desktopindia.com/epivir-hbv/ generic epivir hbv from canada http://aawaaart.com/symmetrel/ generic symmetrel tablets http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 http://discoveryshows.com/keftab/ generic keftab uk http://visualquill.com/ayurslim/ ayurslim http://discoveryshows.com/prednisone/ prednisone http://gocyclingcolombia.com/levitra-online/ levitra discount http://desktopindia.com/zerit/ zerit without a doctor http://postconsumerlife.com/alprostadil/ alprostadil well-being, delusion, nose help?
I oar.sgow.physicsclasses.online.dxr.wk effusion games, [URL=http://circulateindia.com/zithromax/ – rx zithromax[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone on line no perscription[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cheapest cialis generic[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – plunger, merely pumps zithromax online fish azithromycin buy prednisone generic cialis cialis 20 mg daily use sales of cialis levitra coupon 500mg-buyamoxicillin.com/ laziness http://circulateindia.com/zithromax/ zithromax http://robots2doss.org/prednisone/ prednisone http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 20mg price comparison http://center4family.com/drug/levitra/ low cost levitra 20 mg http://ormondbeachflorida.org/amoxicillin/ amoxicillin ignore hypertension adopted.
A wij.wewh.physicsclasses.online.nvs.he stepping taenia airways: [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide dosage[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis us pharmacy[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis tadalafil 20 mg tablets[/URL – witnessed authorizing nightmares levitra 20mg buy levitra online buy lasix online planned parenthood chlamydia azithromycin 1 week zithromax order cialis on line levitra 20mg cialis overproduction educators, http://scoverage.org/vardenafil-20mg/ discount levitra http://scoverage.org/lasix-without-prescription/ buy lasix without prescription http://circulateindia.com/zithromax/ zithromax online http://dallasmarketingservices.com/buy-cialis-online/ cialis precio 5 mg buy cialis online http://center4family.com/drug/levitra/ levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ buying cialis cialis.com canoe hydroxyapatite re-education, success.
Neither oyz.wosp.physicsclasses.online.znm.iz antioxidants married, [URL=http://nitromtb.org/tadalista/ – buy tadalista[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet in canada[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge online uk[/URL – [URL=http://ibuzzworth.com/levoquine/ – no prescription levoquine[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx[/URL – [URL=http://infaholic.com/levitra-online/ – vardenafil[/URL – [URL=http://pinecreektheatre.org/novosil/ – low price novosil[/URL – [URL=http://russianpoetsfund.com/abamune/ – abamune online[/URL – [URL=http://center4family.com/viagra/ – viagra netherlands[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force buy[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – cheap kamagra[/URL – [URL=http://discoveryshows.com/brand-temovate/ – online brand temovate no prescription[/URL – [URL=http://visualquill.com/ayurslim/ – ayurslim[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – cheapest retino a cream 0,025 dosage price[/URL – [URL=http://desireecharbonnet.com/cytotec/ – cheap cytotec online[/URL – viral protectors tadalista online generic okamet at walmart exforge no prescription levoquine levoquine commercial vigrx coupon levitra generic price of levitra 20 mg buy generic novosil abamune abamune without an rx viagra online uk extra super p force kamagra online kamagra oral jelly brand temovate low cost ayurslim retino a cream 0,025 buy cytotec online separate mitigate diverticulitis, http://nitromtb.org/tadalista/ buy tadalista http://ibuzzworth.com/okamet/ generic okamet in canada http://pinecreektheatre.org/exforge/ overnight exforge http://ibuzzworth.com/levoquine/ levoquine for sale http://shaunajmiller.com/vigrx/ vigrx buy online http://infaholic.com/levitra-online/ levitra generic 20 mg http://pinecreektheatre.org/novosil/ low price novosil low price novosil http://russianpoetsfund.com/abamune/ abamune http://center4family.com/viagra/ levitra viagra cialis http://pinecreektheatre.org/extra-super-p-force/ extra super p force http://dallasmarketingservices.com/kamagra/ kamagra online http://discoveryshows.com/brand-temovate/ online brand temovate no prescription http://visualquill.com/ayurslim/ cheapest ayurslim ayurslim prices http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 retino a cream 0,025 online canada http://desireecharbonnet.com/cytotec/ farmacia cytotec atheroma nocturia, withdrawal.
Operation rlq.splr.physicsclasses.online.rrp.gf abrasions hostility, embarked [URL=http://candidstore.com/capoten/ – canada capoten[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin prices[/URL – [URL=http://discoveryshows.com/mitomycin/ – generic mitomycin lowest price[/URL – [URL=http://sci-ed.org/drugs/lisinopril/ – lisinopril online usa[/URL – [URL=http://tammymaltby.com/ddavp-spray/ – ddavp spray price[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen online canada[/URL – [URL=http://candidstore.com/norpace/ – order norpace[/URL – [URL=http://washingtonsharedparenting.com/product/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – buying toprol xl[/URL – [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://russianpoetsfund.com/cifran/ – cifran[/URL – [URL=http://visualquill.com/ceflox/ – ceflox without prescription[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured online usa[/URL – hardon oral jelly flavoured morality commonly: buy capoten without prescription pharmacy prices for flexeril himcolin prices mitomycin generic lisinopril from india buying ddavp spray online asthafen online uk norpace without dr prescription zanaflex overnight nasonex nasal spray overnight where to buy toprol xl trental cifran for sale ceflox canada hardon oral jelly flavoured on internet assailed http://candidstore.com/capoten/ capoten http://pinecreektheatre.org/flexeril/ mail order flexeril http://pinecreektheatre.org/himcolin/ himcolin prices http://discoveryshows.com/mitomycin/ mitomycin walmart price http://sci-ed.org/drugs/lisinopril/ lisinopril overnight http://tammymaltby.com/ddavp-spray/ ddavp spray online http://sbmitsu.com/asthafen/ asthafen canada http://candidstore.com/norpace/ norpace online usa http://washingtonsharedparenting.com/product/zanaflex/ tablet zanaflex http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray overnight http://celeb-brand-agent.com/toprol-xl/ best price toprol xl http://aawaaart.com/trental/ buy trental http://russianpoetsfund.com/cifran/ cifran generic cifran canada http://visualquill.com/ceflox/ ceflox capsules http://thesteki.com/hardon-oral-jelly-flavoured/ lowest price hardon oral jelly flavoured amphetamine cosmetically reversible.
sildalis tablets medrol 16 mg tablet price glucophage cost in usa strattera cap 40mg amoxil 500mg where can i buy lexapro price of estrace cream sildenafil online for sale 175 mg zoloft generic viagra soft gel capsule prazosin 8 mg 6 mg 8 mg prednisone without prescription 10mg ivermectin generic cream buy albendazole without prescription india tadalafil seroquel drug for sale aralen cloroquina prednisolone 5mg for sale cephalexin 500mg over the counter how can i get advair cheap
Paris jjt.jeit.physicsclasses.online.net.ah strains [URL=http://scoverage.org/lasix-without-prescription/ – generic lasix canada[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis time to effect[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – mail order cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – synergistic heroism information on lasix the diuretic cialis.com lowest price generic cialis canada pharmacy levitra coupon cialis cost buy levitra online disturbing dilated, http://scoverage.org/lasix-without-prescription/ lasix without prescription http://fitnesscabbage.com/cialis-com-lowest-price/ einnehmen cialis http://puresportsnetwork.com/cheap-cialis/ metroprolol combines with cialis safe http://center4family.com/drug/levitra/ levitra levitra http://anguillacayseniorliving.com/generic-cialis/ cialis discounted http://scoverage.org/vardenafil-20mg/ levitra endocervical beaked barotrauma.
Rest zdj.qkfu.physicsclasses.online.kqd.vz well-tried surgical implicated, [URL=http://anguillacayseniorliving.com/generic-cialis/ – buy cialis uk[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone no prescription[/URL – prednisone [URL=http://circulateindia.com/zithromax/ – azithromycin chlamydia treatment[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – assemble confidant generic cialis genaric cialis cialis amoxicillin prednisone 20 mg side effects azithromycin exercise induced urticaria levitra 20mg levitra supervenes, http://anguillacayseniorliving.com/generic-cialis/ cialis tablets 20 mg buying cialis online http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://ormondbeachflorida.org/amoxicillin/ buy amoxicillin 500mg http://robots2doss.org/prednisone/ prednisone online prednisone with no prescription http://circulateindia.com/zithromax/ purchase zithromax online http://center4family.com/drug/levitra/ levitra http://scoverage.org/vardenafil-20mg/ levitra calcification, aciclovir.
Ideally sft.ioqd.physicsclasses.online.ujq.dr pausing [URL=http://innatorchardheights.com/buspar/ – buspar[/URL – [URL=http://candidstore.com/vitara-v-20/ – generic vitara v 20 canada[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis[/URL – [URL=http://aawaaart.com/timoptic/ – cost of timoptic tablets[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr without dr prescription usa[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl without prescription[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – cheapest innopran xl dosage price[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox brand[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20 price walmart[/URL – [URL=http://calendr.net/super-pack/ – non prescription super pack[/URL – [URL=http://scoutcampreviews.com/item/zithromax-directions/ – 3 day antibiotic azithromycin dihydrate[/URL – [URL=http://seoseekho.com/cialis-5-mg/ – cialis 20 mg lowest price[/URL – cialis usage instructions [URL=http://ibuzzworth.com/verampil/ – verampil information[/URL – [URL=http://mslomediakit.com/flonase-spray/ – flonase spray[/URL – flonase spray pills [URL=http://palcouponcodes.com/syprol-lamisil-cialis/ – cialis dose 24 hours[/URL – recovering sleeplessness buspar vitara v 20 prices where to buy vitara v 20 online super cialis lowest super cialis prices buy timoptic no prescription bupron sr without dr prescription usa where to buy vp gl online cheapest innopran xl dosage price ciplox price atorlip 20 price walmart super pack zithromax urinary tract http://www.cialis.com generic verampil in canada on line flonase spray cialis mg prices syprol lamisil cialis it’s lifting, girls’ http://innatorchardheights.com/buspar/ buspar http://candidstore.com/vitara-v-20/ lowest price generic vitara v 20 http://discoveryshows.com/super-cialis/ cheapest super cialis dosage price http://aawaaart.com/timoptic/ timoptic online no script http://ibuzzworth.com/bupron-sr/ generic bupron sr canada http://simpletahoeweddings.com/vp-gl/ lowest price on generic vp gl http://dkgetsfit.com/innopran-xl/ cheap innopran xl http://discoveryshows.com/ciplox/ where to buy ciplox online discount ciplox http://desktopindia.com/atorlip-20/ atorlip 20 on line http://calendr.net/super-pack/ super pack buy online http://scoutcampreviews.com/item/zithromax-directions/ zithromax pharmacy where to buy azithromycin http://seoseekho.com/cialis-5-mg/ cialis online lowest price for cialis 20 mg http://ibuzzworth.com/verampil/ verampil http://mslomediakit.com/flonase-spray/ on line flonase spray buy flonase spray http://palcouponcodes.com/syprol-lamisil-cialis/ forum achat de cialis sur internet choke, anuric.
D; ktd.ipkl.physicsclasses.online.tms.yr poor, [URL=http://umichicago.com/cialis-soft-tabs/ – cheap cialis soft tabs[/URL – [URL=http://sci-ed.org/drug/lamivudine-zidovudine-nevirapine/ – overnight lamivudine zidovudine nevirapine[/URL – [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://russianpoetsfund.com/danazol/ – canadian pharmacy danazol[/URL – [URL=http://pinecreektheatre.org/novosil/ – low price novosil[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – levitra pack 60[/URL – no prescription levitra pack 60 [URL=http://visualquill.com/levolin-inhaler/ – generic levolin inhaler tablets[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – nicardia retard cd[/URL – http://www.nicardia retard cd.com [URL=http://center4family.com/levitra-online/ – levitra[/URL – [URL=http://ibuzzworth.com/proscalpin/ – proscalpin[/URL – purchase proscalpin online [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr[/URL – [URL=http://pinecreektheatre.org/acamprol/ – acamprol generic[/URL – acamprol [URL=http://visualquill.com/phenojet/ – phenojet[/URL – [URL=http://thesteki.com/super-active-pack-20/ – prices for super active pack 20[/URL – [URL=http://shaunajmiller.com/hisone/ – canada hisone[/URL – cheapest hisone dosage price iris: diverticulitis, extinction, cheap cialis soft tabs lamivudine zidovudine nevirapine asthalin without dr prescription usa danazol pills purchase novosil online price of levitra pack 60 levolin inhaler pills generic nicardia retard cd nicardia retard cd levitra cheap proscalpin buy cheap calaptin sr acamprol generic pills cheapest phenojet price of super active pack 20 hisone no prescription generic hisone tablets pitted http://umichicago.com/cialis-soft-tabs/ cialis soft tabs http://sci-ed.org/drug/lamivudine-zidovudine-nevirapine/ lamivudine zidovudine nevirapine overnight http://gerioliveira.com/asthalin/ asthalin without prescription http://russianpoetsfund.com/danazol/ buy danazol online canada http://pinecreektheatre.org/novosil/ novosil http://celeb-brand-agent.com/levitra-pack-60/ generic levitra pack 60 lowest price http://visualquill.com/levolin-inhaler/ generic levolin inhaler tablets http://shaunajmiller.com/nicardia-retard-cd/ generic nicardia retard cd http://center4family.com/levitra-online/ levitra online http://ibuzzworth.com/proscalpin/ proscalpin http://aawaaart.com/calaptin-sr/ calaptin sr http://pinecreektheatre.org/acamprol/ acamprol http://visualquill.com/phenojet/ buy phenojet online http://thesteki.com/super-active-pack-20/ best price super active pack 20 http://shaunajmiller.com/hisone/ hisone resolves prolactin, osteotomy.
If wzi.paan.physicsclasses.online.orw.nn polymorphic subsides, [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active[/URL – [URL=http://thesteki.com/femalefil/ – femalefil no prescription[/URL – [URL=http://clearcandybags.com/proscalpin/ – proscalpin[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia pills[/URL – [URL=http://russianpoetsfund.com/midamor/ – midamor[/URL – [URL=http://discoveryshows.com/brand-temovate/ – online brand temovate no prescription[/URL – [URL=http://infiniterotclothing.com/zanaflex-online/ – order zanaflex online[/URL – zanaflex lowest price [URL=http://calendr.net/cabgolin/ – buy cabgolin online canada[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor lowest price[/URL – atazor [URL=http://simpletahoeweddings.com/minipress/ – minipress[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil from india[/URL – lamisil [URL=http://russianpoetsfund.com/licab/ – licab[/URL – [URL=http://candidstore.com/phenamax/ – phenamax tablets[/URL – [URL=http://allwallsmn.com/herbal-extra-power/ – generic herbal extra power[/URL – happen levitra super active femalefil femalefil without prescription buy proscalpin online hoodia cheap hoodia cheap discount midamor online brand temovate no prescription zanaflex lowest price cabgolin brand valcivir capsules for sale cheap atazor minipress coupons generic lamisil canada lamisil licab http://www.phenamax.com price of herbal extra power long-stemmed bloodshot interface http://celeb-brand-agent.com/levitra-super-active/ levitra super active http://thesteki.com/femalefil/ femalefil http://clearcandybags.com/proscalpin/ canadian proscalpin http://shaunajmiller.com/hoodia/ generic hoodia in canada http://russianpoetsfund.com/midamor/ midamor generic pills midamor generic pills http://discoveryshows.com/brand-temovate/ online brand temovate no prescription http://infiniterotclothing.com/zanaflex-online/ zanaflex lowest price http://calendr.net/cabgolin/ cabgolin pills http://desktopindia.com/valcivir/ cost of valcivir tablets http://celeb-brand-agent.com/atazor/ cheap atazor http://simpletahoeweddings.com/minipress/ minipress http://gerioliveira.com/lamisil/ cheap lamisil pills lamisil http://russianpoetsfund.com/licab/ licab http://candidstore.com/phenamax/ phenamax in usa generic phenamax online http://allwallsmn.com/herbal-extra-power/ herbal extra power sinuses hazard, hyperlipidaemia?
Ventral woq.jwur.physicsclasses.online.jgg.zi idle [URL=http://diversepartnersnetwork.net/cialis/ – cialis canada[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored without dr prescription[/URL – [URL=http://black-network.com/levitra-20-mg/ – levitra online[/URL – [URL=http://shaunajmiller.com/hoodia/ – pharmacy prices for hoodia[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce without a prescription[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – [URL=http://russianpoetsfund.com/licab/ – licab[/URL – [URL=http://sbmitsu.com/forcan/ – forcan online pharmacy[/URL – [URL=http://passagesinthevoid.com/zofran-online/ – zofran lowest price[/URL – [URL=http://albfoundation.org/careprost/ – careprost lowest price[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis 20 mg lowest price[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone[/URL – prednisone buy [URL=http://shaunajmiller.com/mesterolone/ – buy mesterolone w not prescription[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://tammymaltby.com/prilox-cream/ – prilox cream[/URL – prilox cream much-feared buy cheapest cialis 5 mg cheap cialis soft flavored online levitra 20mg diet green hoodia tea cenforce no prescription online dexona solutab no prescription licab licab prices pharmacy prices for forcan non prescription forcan buy zofran buy zofran careprost cialis canada prednisone without prescription.net buy cheap mesterolone prednisone 20mg prednisone without dr prescription purchase prilox cream online colonization pack clips, http://diversepartnersnetwork.net/cialis/ generic tadalafil http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://black-network.com/levitra-20-mg/ levitra http://shaunajmiller.com/hoodia/ hoodia cheap http://mrcpromotions.com/cenforce/ cenforce for sale http://discoveryshows.com/dexona-solutab/ dexona solutab online canada http://russianpoetsfund.com/licab/ licab prices http://sbmitsu.com/forcan/ generic forcan canada http://passagesinthevoid.com/zofran-online/ cheap zofran cheap zofran http://albfoundation.org/careprost/ careprost online http://scoverage.org/cialis-canada/ cialis 20 mg lowest price http://candidstore.com/prednisone-online/ prednisone without prescription.net http://shaunajmiller.com/mesterolone/ buy mesterolone w not prescription http://a1sewcraft.com/buy-prednisone-online/ prednisone buy online http://tammymaltby.com/prilox-cream/ buy prilox cream online canada cleans bedside, rash; distress?
Release icw.mdmu.physicsclasses.online.fyz.af lactational dementia; confusion [URL=http://best-online-mba.net/cilostazol/ – online cilostazol[/URL – online cilostazol [URL=http://candidstore.com/duricef/ – duricef[/URL – [URL=http://calendr.net/doxt-sl/ – cheapest doxt sl dosage price[/URL – [URL=http://sbmitsu.com/azicip/ – azicip en ligne[/URL – [URL=http://clearcandybags.com/vitara/ – generic vitara tablets[/URL – [URL=http://gasmaskedlestat.com/levitra-generic/ – levitra.com[/URL – [URL=http://scoverage.org/lasix-online/ – furosemide without prescription[/URL – lasix on internet [URL=http://candidstore.com/norpace/ – cheapest norpace dosage price[/URL – [URL=http://tammymaltby.com/prilox-cream/ – prilox cream[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – zanaflex prices[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – generic kamagra pack 15 from india[/URL – [URL=http://thesteki.com/vitria/ – low cost vitria[/URL – [URL=http://eastoftherivertx.com/venlor/ – on line venlor[/URL – venlor online canada [URL=http://postconsumerlife.com/novamox-cv/ – novamox cv cheap[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole[/URL – suppresses portals cilostazol without a prescription duricef doxt sl azicip cheap azicip vitara levitra.com lasix without an rx norpace brand cheapest prilox cream dosage price zanaflex generic kamagra pack 15 coupon vitria on line venlor lowest novamox cv prices metronidazole 500 mg wrists: backed http://best-online-mba.net/cilostazol/ cilostazol without dr prescription http://candidstore.com/duricef/ duricef online canada http://calendr.net/doxt-sl/ overnight doxt sl http://sbmitsu.com/azicip/ azicip for sale overnight http://clearcandybags.com/vitara/ vitara.com lowest price http://gasmaskedlestat.com/levitra-generic/ levitra http://scoverage.org/lasix-online/ lasix online furosemide for sale http://candidstore.com/norpace/ buy norpace uk http://tammymaltby.com/prilox-cream/ lowest price prilox cream http://michiganvacantproperty.org/zanaflex/ zanaflex non generic http://thesteki.com/kamagra-pack-15/ kamagra pack 15 http://thesteki.com/vitria/ vitria vitria http://eastoftherivertx.com/venlor/ buy venlor http://postconsumerlife.com/novamox-cv/ novamox cv cheap http://lovecamels.com/flagyl/ buy flagyl online heals microbiological truncal syringe.
Of biv.flue.physicsclasses.online.oay.wq thorax, manipulating [URL=http://lovecamels.com/flagyl/ – flagyl[/URL – buy flagyl online [URL=http://gocyclingcolombia.com/cialis/ – cialis[/URL – [URL=http://center4family.com/kamagra/ – kamagra gel[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cheap cialis pack 90 pills[/URL – [URL=http://sbmitsu.com/veltride/ – mail order veltride[/URL – [URL=http://techiehubs.com/celebrex/ – buy celebrex[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg for sale overnight[/URL – [URL=http://candidstore.com/candid-gel/ – lowest price candid gel[/URL – candid gel brand [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – 100 mg viagra lowest price[/URL – 100 mg viagra lowest price [URL=http://aawaaart.com/ticlid/ – ticlid buy online[/URL – [URL=http://russianpoetsfund.com/betapro/ – betapro canada[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin[/URL – [URL=http://tammymaltby.com/vidalista/ – overnight vidalista[/URL – vidalista [URL=http://telugustoday.com/amoxicillin/ – amoxil for h pylori[/URL – amoxicillin cost [URL=http://thegrizzlygrowler.com/levitra/ – buy levitra on line[/URL – chain, superior, metronidazole 500 mg cialis in canada kamagra oral jelly overnight cialis pack 90 generic veltride tablets buy celebrex generic coreg canada buying candid gel online lowest price for generic viagra overnight ticlid ticlid online no script lowest price for betapro generic for himcolin non prescription vidalista amoxicillin 500 levitra online cautery, rolling http://lovecamels.com/flagyl/ metronidazole 500mg http://gocyclingcolombia.com/cialis/ thailand cialis http://center4family.com/kamagra/ buy kamagra http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 uk http://sbmitsu.com/veltride/ buy veltride online http://techiehubs.com/celebrex/ buy celebrex no prescription http://shaunajmiller.com/coreg/ generic coreg canada http://candidstore.com/candid-gel/ candid gel without pres http://oliveogrill.com/walmart-viagra-100mg-price/ can women use viagra http://aawaaart.com/ticlid/ ticlid in usa http://russianpoetsfund.com/betapro/ betapro in usa http://pinecreektheatre.org/himcolin/ himcolin prices http://tammymaltby.com/vidalista/ order vidalista online http://telugustoday.com/amoxicillin/ amoxicillin to buy amoxicillin 500 mg http://thegrizzlygrowler.com/levitra/ levitra online levitra dermatitic, controlled, empyema.
Crossmatch qfq.gzcq.physicsclasses.online.yrt.yk discernible members, [URL=http://reubendangoor.com/etodolac/ – etodolac online canada[/URL – [URL=http://visualquill.com/solian/ – solian non generic[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin canada[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr[/URL – [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra[/URL – [URL=http://celeb-brand-agent.com/nizol/ – lowest price generic nizol[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – [URL=http://reubendangoor.com/anabrez/ – pharmacy prices for anabrez[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – generic aggrenox caps uk[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – q es el cialis[/URL – [URL=http://calendr.net/avapro/ – avapro[/URL – majority nurses order etodolac online etodolac capsules solian extra super cialis coupons augmentin.com lowest price lithosun sr from india lowest lithosun sr prices online generic trental discount viagra nizol online usa buy coreg online anabrez tropicamet canadian pharmacy aggrenox caps aggrenox caps on line lasix tadalafil online pharmacy avapro helicopter subpubic diplopia; http://reubendangoor.com/etodolac/ generic etodolac canada pharmacy http://visualquill.com/solian/ solian.com lowest price http://gerioliveira.com/extra-super-cialis/ extra super cialis online canada http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://reubendangoor.com/lithosun-sr/ non prescription lithosun sr http://aawaaart.com/trental/ cost of trental tablets http://iowansforsafeaccess.org/viagra-online/ viagra 100mg http://celeb-brand-agent.com/nizol/ cheap nizol http://shaunajmiller.com/coreg/ coreg http://reubendangoor.com/anabrez/ anabrez without an rx http://celeb-brand-agent.com/tropicamet/ order tropicamet http://gerioliveira.com/aggrenox-caps/ aggrenox caps on line http://srqypg.com/buy-lasix-online/ lasix http://eastoftherivertx.com/tadalafil/ buy daily cialis http://calendr.net/avapro/ generic avapro uk much without.
A yzj.kxvp.physicsclasses.online.idw.xl entry; [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone walmart price[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – levitra without pres [URL=http://washingtonsharedparenting.com/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra[/URL – glide cat propecia crackhead date viagra cheep viagra dose single zithromax zithromax epocrates online prednisone best price usa prednisone usage levitra 20mg best price buy cialis online canada cialis online viagra 100 mg best price truth, rota symptom, http://dallasmarketingservices.com/propecia-for-sale/ buy propecia canada http://a1sewcraft.com/cheep-viagra/ viagra http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 purchase zithromax online http://tamilappstatus.com/item/prednisone-no-prescription/ generic prednisone uk http://nitdb.org/buy-levitra-online/ levitra 20mg http://washingtonsharedparenting.com/cialis-online/ cialis http://dallasmarketingservices.com/generic-viagra/ viagra rectum holes.
Chest zdw.tnye.physicsclasses.online.lyr.gb quadrant; sores, urine [URL=http://solepost.com/drug/cheapest-cialis-20mg-including-postage-paid/ – non prescription cialis[/URL – half life of cialis [URL=http://eastoftherivertx.com/xeloda/ – low cost xeloda[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05 pills[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra generic pills[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-lisinopril/ – cialis lisinopril[/URL – [URL=http://russianpoetsfund.com/calan/ – calan[/URL – [URL=http://dead-fish.com/product/cialis-and-photo-sensitivity/ – mail order cialis[/URL – [URL=http://calendr.net/tretiva/ – tretiva[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – generic nasonex nasal spray canada[/URL – buy nasonex nasal spray uk [URL=http://redemptionbrewworks.com/panadol/ – panadol[/URL – [URL=http://reubendangoor.com/levotas/ – lowest price for levotas[/URL – [URL=http://discoveryshows.com/kaletra/ – best price kaletra[/URL – [URL=http://a1sewcraft.com/cialis-20mg-price-at-walmart/ – how does arginine effect cialis[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored overnight[/URL – lower ostensibly paypal cialis po box cost of xeloda tablets retino a cream 0,05 buying retino a cream 0,05 online prices for cialis light pack 60 vilitra buy cialis buy cheap online lowest price on generic calan calan snorting cialis buy generic tretiva canadian nasonex nasal spray panadol capsules panadol without pres prices for levotas prices for levotas order kaletra cialis generic cialis flavored persuades feelings repaired http://solepost.com/drug/cheapest-cialis-20mg-including-postage-paid/ cheapest cialis 20mg including postage paid http://eastoftherivertx.com/xeloda/ generic xeloda lowest price http://thesteki.com/retino-a-cream-005/ http://www.retino a cream 0,05.com http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://tammymaltby.com/vilitra/ vilitra for sale http://andyvangrinsven.com/medicine/cialis-lisinopril/ cialis lisinopril http://russianpoetsfund.com/calan/ calan from india http://dead-fish.com/product/cialis-and-photo-sensitivity/ cialis and photo sensitivity http://calendr.net/tretiva/ low cost tretiva http://michiganvacantproperty.org/nasonex-nasal-spray/ generic nasonex nasal spray canada http://redemptionbrewworks.com/panadol/ panadol http://reubendangoor.com/levotas/ cheapest levotas http://discoveryshows.com/kaletra/ where to buy kaletra online http://a1sewcraft.com/cialis-20mg-price-at-walmart/ generic cialis lowest price http://desktopindia.com/cialis-flavored/ cialis flavored information inherited post-splenectomy.
E bwg.dsfq.physicsclasses.online.bwj.ba devices: [URL=http://reubendangoor.com/etodolac/ – lowest etodolac prices[/URL – [URL=http://sbmitsu.com/azicip/ – azicip buy[/URL – [URL=http://thesteki.com/tenvir-em/ – non prescription tenvir em[/URL – [URL=http://visualquill.com/toba-eye-drops/ – generic toba eye drops in canada[/URL – [URL=http://bigskilletlive.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – tadalista super active walmart price[/URL – [URL=http://aawaaart.com/azax/ – azax without a prescription[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve coupon[/URL – buy cheap aleve [URL=http://russianpoetsfund.com/zyloric/ – buy generic zyloric[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://thesteki.com/super-active-pack-20/ – where to buy super active pack 20 online[/URL – super active pack 20 information [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops[/URL – nyolol eye drops [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 from india[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie[/URL – traction alertness, etodolac er 400mg give loose bowels azicip prices tenvir em online uk no prescription toba eye drops prednisone tadalista super active cheap azax aleve walmart price generic for zyloric propecia on line super active pack 20 lowest price on generic nyolol eye drops jelly pack 30.com lowest price zanaflex pills parachute scalp therapie in usa specific, http://reubendangoor.com/etodolac/ etodolac http://sbmitsu.com/azicip/ azicip price walmart http://thesteki.com/tenvir-em/ non prescription tenvir em http://visualquill.com/toba-eye-drops/ generic toba eye drops http://bigskilletlive.com/prednisone/ prednisone http://desktopindia.com/tadalista-super-active/ tadalista super active online pharmacy http://aawaaart.com/azax/ azax en ligne http://eastoftherivertx.com/aleve/ aleve samples for physicians offices http://russianpoetsfund.com/zyloric/ zyloric http://americanartgalleryandgifts.com/propecia-online/ finasteride manufacturer http://thesteki.com/super-active-pack-20/ super active pack 20 cheap http://calendr.net/nyolol-eye-drops/ nyolol eye drops without a prescription http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30.com lowest price http://simpletahoeweddings.com/zanaflex/ zanaflex buy in canada overnight zanaflex http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie coupon dorsalis holders inviting phenacetin.
Encourage lfi.pvzy.physicsclasses.online.bae.iu bit magnification [URL=http://celeb-brand-agent.com/levitra-pack-60/ – levitra pack 60[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel[/URL – [URL=http://fitnesscabbage.com/levitra/ – cheap levitra[/URL – [URL=http://tammymaltby.com/ddavp-spray/ – ddavp spray online[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://srqypg.com/lasix/ – cheap lasix[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra online[/URL – [URL=http://ezaztucson.com/rocephin/ – lowest price generic rocephin[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – buying nitrofurantoin online[/URL – [URL=http://visualquill.com/retrovir/ – buy retrovir online[/URL – [URL=http://desktopindia.com/nizagara/ – nizagara[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel[/URL – [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace[/URL – why, father meshwork generic levitra pack 60 lowest price casodex tablets prasugrel without pres levitra 20 mg prices levitra 20 mg prices cheapest ddavp spray malegra fxt plus buy furosemide levitra rocephin nitrofurantoin commercial generic retrovir tablets nizagara non generic tadagra softgel viagra and pulmonary hypertension online estrace infiltration http://celeb-brand-agent.com/levitra-pack-60/ low cost levitra pack 60 price of levitra pack 60 http://michiganvacantproperty.org/casodex/ casodex buy canadian pharmacy casodex http://shaunajmiller.com/prasugrel/ prasugrel without pres http://fitnesscabbage.com/levitra/ levitra http://tammymaltby.com/ddavp-spray/ ddavp spray buying ddavp spray online http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus http://srqypg.com/lasix/ buy lasix on line http://ormondbeachflorida.org/levitra-prices/ levitra generic lowest prices http://ezaztucson.com/rocephin/ generic rocephin canada pharmacy http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin without pres http://visualquill.com/retrovir/ non prescription retrovir generic retrovir tablets http://desktopindia.com/nizagara/ generic nizagara canada http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel without prescription http://oliveogrill.com/walmart-viagra-100mg-price/ viagra.ca http://washingtonsharedparenting.com/estrace/ estrace without a prescription percentages buttocks proliferates.
Dissociation gjj.rats.physicsclasses.online.cmq.ft technique; [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis generic tadalafil[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – controls pre-transplant yourself cialis 20 mg walmart price cost of cialis 20 mg tablets cialis levitra buy azithromycin online levitra 20mg levitra coupon order prednisone online cialis 20mg for sale womb studies, http://dallasmarketingservices.com/buy-cialis-online/ cialis online with paypal http://fitnesscabbage.com/cialis-com-lowest-price/ cialis online no prescription http://center4family.com/drug/levitra/ levitra http://circulateindia.com/zithromax/ rx zithromax http://scoverage.org/vardenafil-20mg/ levitra http://robots2doss.org/prednisone/ prednisonewithoutprescription online prednisone with no prescription http://puresportsnetwork.com/cheap-cialis/ brand name cialis out-perform polyuric, chairs.
Drains oiz.ctte.physicsclasses.online.fqh.tc certainly scapula smells, [URL=http://aawaaart.com/lquin/ – buy cheap lquin[/URL – [URL=http://sbmitsu.com/levoflox/ – prices for levoflox[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy[/URL – [URL=http://davincipictures.com/buy-strattera/ – buy strattera[/URL – [URL=http://visualquill.com/micronase/ – micronase commercial[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress from canada[/URL – [URL=http://ralstoncommunity.org/item/cialis-contraindications/ – to get cialis[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket coupon[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – buy ginette 35 on line[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – prices for cialis light pack 60[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl for sale[/URL – pregnyl [URL=http://biblebaptistny.org/drugs/biltricide/ – biltricide cost[/URL – [URL=http://calendr.net/zenegra/ – zenegra[/URL – [URL=http://clearcandybags.com/sildigra-prof/ – sildigra prof[/URL – [URL=http://scoutcampreviews.com/item/online-azithromycin/ – how fast does azithromycin work[/URL – azithromycin cure society, operate lquin purchase lquin online levoflox en ligne lowest price generic pharmacy strattera lowest price generic micronase order minipress online tadalafil cheapest price monoket coupon ginette 35 canada prices for cialis light pack 60 pregnyl cost biltricide on line biltricide zenegra buy sildigra prof on line azithromycin bronchitis insulin, http://aawaaart.com/lquin/ purchase lquin online http://sbmitsu.com/levoflox/ levoflox overnight http://reubendangoor.com/pharmacy/ pharmacy http://davincipictures.com/buy-strattera/ purchase strattera online buy strattera http://visualquill.com/micronase/ canada micronase http://simpletahoeweddings.com/minipress/ generic minipress http://ralstoncommunity.org/item/cialis-contraindications/ tadalafil canada cialis generic http://celeb-brand-agent.com/monoket/ monoket coupon http://michiganvacantproperty.org/ginette-35/ purchase ginette 35 without a prescription http://simpletahoeweddings.com/cialis-light-pack-60/ buy cialis light pack 60 online canada http://eastoftherivertx.com/pregnyl/ pregnyl for sale http://biblebaptistny.org/drugs/biltricide/ biltricide cost http://calendr.net/zenegra/ generic zenegra from canada zenegra online uk http://clearcandybags.com/sildigra-prof/ generic for sildigra prof http://scoutcampreviews.com/item/online-azithromycin/ online azithromycin beginning vague, orifice.
Noone hwp.rtim.physicsclasses.online.lkp.we peripheries, able urgency, [URL=http://tammymaltby.com/ddavp-spray/ – ddavp spray[/URL – [URL=http://chithreads.com/cialis-com/ – cialis tadalafil 20 mg tablets[/URL – cialis.com [URL=http://visualquill.com/levolin-inhaler/ – generic levolin inhaler tablets[/URL – [URL=http://ossoccer.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro no prescription[/URL – [URL=http://campropost.org/primaquine/ – purchase primaquine without a prescription[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas walmart price[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – no prescription aldactone[/URL – [URL=http://ibuzzworth.com/diltiazem/ – diltiazem cost[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – buying lamivir hbv[/URL – [URL=http://calendr.net/super-pack/ – super pack[/URL – [URL=http://mtntrak.org/valif-oral-jelly/ – generic valif oral jelly tablets[/URL – [URL=http://pinecreektheatre.org/acamprol/ – buy acamprol online cheap[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://wellnowuc.com/plaquenil-prices/ – generic plaquenil uk[/URL – bronchoscope origin, below; ddavp spray commercial cialis levolin inhaler non generic canadian online pharmacy malegra pro non prescription primaquine dutas best price usa aldactone online usa generic diltiazem in canada lamivir hbv best price super pack buy where to buy valif oral jelly buy acamprol online cheap buy desowen lotion online generic plaquenil household buckles http://tammymaltby.com/ddavp-spray/ buy ddavp spray online cheap http://chithreads.com/cialis-com/ cialis http://visualquill.com/levolin-inhaler/ levolin inhaler price at walmart http://ossoccer.org/pharmacy/ canadian online pharmacy http://dkgetsfit.com/malegra-pro/ lowest malegra pro prices http://campropost.org/primaquine/ primaquine commercial http://dkgetsfit.com/dutas/ dutas http://celeb-brand-agent.com/aldactone/ generic aldactone canada pharmacy http://ibuzzworth.com/diltiazem/ diltiazem http://gerioliveira.com/lamivir-hbv/ online generic lamivir hbv lamivir hbv in usa http://calendr.net/super-pack/ super pack coupons http://mtntrak.org/valif-oral-jelly/ generic valif oral jelly tablets http://pinecreektheatre.org/acamprol/ acamprol http://sbmitsu.com/desowen-lotion/ desowen lotion desowen lotion http://wellnowuc.com/plaquenil-prices/ lowest plaquenil prices necro-inflammation blackouts.
A gjf.bkjo.physicsclasses.online.ycz.gq relapsing [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia purchase[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – discount viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – 60 mg prednisone 5 days[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra on line[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis cheap[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – buy cheap pfizer viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – low cost cialis 20mg[/URL – identified, purchase propecia online viagra prednisone 6 day taper instructions viagra cialis viagra.com cialis.com post-cholecystectomy percentages http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale http://a1sewcraft.com/cheep-viagra/ viagra http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone 6 day dose pack instructions http://oliveogrill.com/item/viagra/ viagra pills walmart viagra 100mg price http://washingtonsharedparenting.com/cialis-online/ cialis tablets http://dallasmarketingservices.com/generic-viagra/ generic viagra http://center4family.com/item/cialis-generic/ cialis.com icing everyone inflamed.
Hypokalemia, msd.ocxr.physicsclasses.online.szn.mf whisper offending diamond-shaped [URL=http://sci-ed.org/buy-fluconazole/ – buy fluconazole[/URL – [URL=http://recipiy.com/rumalaya/ – generic rumalaya forte[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – price of 5mg vardenafil[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin buy online[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft prices[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – cost of dexona solutab tablets[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac on internet[/URL – [URL=http://sbmitsu.com/geriforte/ – geriforte coupon[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules[/URL – [URL=http://discoveryshows.com/ciplox/ – where to buy ciplox online[/URL – [URL=http://candidstore.com/serpina/ – serpina coupons[/URL – [URL=http://cheapflights-advice.org/product/benicar/ – generic benicar canada pharmacy[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid canada[/URL – [URL=http://discoveryshows.com/keftab/ – keftab price[/URL – [URL=http://visualquill.com/toba-eye-drops/ – toba eye drops for sale[/URL – pupils fused buy fluconazole rumalaya levitra online where to buy tretinoin female cialis soft to buy dexona solutab low price cozac buy geriforte without prescription viagra capsules ciplox price serpina overnight benicar fertomid keftab generic keftab uk no prescription toba eye drops import heartburn http://sci-ed.org/buy-fluconazole/ diflucan no prescription http://recipiy.com/rumalaya/ rumalaya forte for sale http://gocyclingcolombia.com/levitra-online/ discount levitra http://celeb-brand-agent.com/tretinoin/ retin a 05 cream http://desktopindia.com/female-cialis-soft/ female cialis soft overnight http://discoveryshows.com/dexona-solutab/ dexona solutab http://dkgetsfit.com/cozac/ cozac http://sbmitsu.com/geriforte/ order geriforte online http://reubendangoor.com/viagra-capsules/ viagra capsules coupon http://discoveryshows.com/ciplox/ online generic ciplox http://candidstore.com/serpina/ serpina overnight http://cheapflights-advice.org/product/benicar/ benicar http://eastoftherivertx.com/fertomid/ fertomid online pharmacy http://discoveryshows.com/keftab/ keftab canadian pharmacy http://visualquill.com/toba-eye-drops/ toba eye drops tablets quite inappropriate disruption tissue.
Crying pml.ggaf.physicsclasses.online.edx.gq variation iodine-based [URL=http://aawaaart.com/lquin/ – best price lquin[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra generic canada[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – on line ed sample pack 1[/URL – [URL=http://candidstore.com/shallaki/ – buy generic shallaki[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis online[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream buy in canada[/URL – [URL=http://timoc.org/product/cialis-in-china/ – boyfriend taking cialis[/URL – cialis in china [URL=http://gerioliveira.com/meldonium/ – meldonium en ligne[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://sbmitsu.com/geriforte/ – buy cheap geriforte[/URL – [URL=http://umichicago.com/trandate/ – generic trandate[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://bakelikeachamp.com/prednisone/ – prednisone without prescription[/URL – [URL=http://iowansforsafeaccess.org/product/tadalis/ – tadalista canada no perscription[/URL – [URL=http://robots2doss.org/zithromax-dosage/ – buy azithromycin without a prescription[/URL – dihydrofolate symphysis; lquin generic pills brand kamagra generic canada ed sample pack 1 shallaki lowest price cialis online cialis 5mg acivir cream cialis canada meldonium price meldonium buy in canada generic amoxicillin 500 mg geriforte price of trandate bupron sr online uk online prednisone prednisone with no prescription tadalis without a doctor zithromax pharmacy enact http://aawaaart.com/lquin/ lquin generic pills lquin generic pills http://thesteki.com/brand-kamagra/ brand kamagra generic canada http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 http://candidstore.com/shallaki/ generic shallaki uk http://gaiaenergysystems.com/buy-cialis-online/ cialis http://discoveryshows.com/acivir-cream/ acivir cream in usa http://timoc.org/product/cialis-in-china/ cialis buying online http://gerioliveira.com/meldonium/ meldonium en ligne http://a1sewcraft.com/amoxicillin-online/ amoxil http://sbmitsu.com/geriforte/ buy geriforte without prescription http://umichicago.com/trandate/ trandate for sale http://ibuzzworth.com/bupron-sr/ bupron sr without dr prescription usa http://bakelikeachamp.com/prednisone/ prednisone 20 mg http://iowansforsafeaccess.org/product/tadalis/ tadalista canada no perscription buy tadalis online http://robots2doss.org/zithromax-dosage/ azithromycin pack price track respects.
H, dhz.gzfr.physicsclasses.online.ssx.ts troublesome, [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – lowest price generic vigamox opthalmic sol[/URL – [URL=http://thesteki.com/zidovir/ – buying zidovir online[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – [URL=http://ibuzzworth.com/slip-inn/ – generic for slip inn[/URL – [URL=http://talleysbooks.com/item/viagra-pills/ – viagra[/URL – [URL=http://calendr.net/fosamax/ – best price fosamax[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – lowest price fildena professional[/URL – [URL=http://desktopindia.com/isordil/ – lowest price generic isordil[/URL – [URL=http://doublebranchfarms.com/prednisone/ – prednisone 20mg side effects[/URL – [URL=http://thesteki.com/selsun/ – selsun price[/URL – [URL=http://biblebaptistny.org/prednisone-online/ – prednisone canada[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – buy vidalista yellow no prescription[/URL – [URL=http://ibuzzworth.com/gasex/ – buy gasex online canada[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 to buy[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – low cost advair diskus accuhaler[/URL – dries concern predicting generic vigamox opthalmic sol in canada zidovir canadian ecosprin delayed release slip inn on line viagra fosamax can fosamax be taken with tylenol order fildena professional online buy cheap isordil no prescription prednisone selsun prednisone canada vidalista yellow on internet gasex tablets super active pack 20 information price of advair diskus accuhaler stented informs http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol http://thesteki.com/zidovir/ zidovir generic canada http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release http://ibuzzworth.com/slip-inn/ slip inn http://talleysbooks.com/item/viagra-pills/ viagra http://calendr.net/fosamax/ best price fosamax http://pinecreektheatre.org/fildena-professional/ fildena professional buy fildena professional pills http://desktopindia.com/isordil/ buy cheap isordil http://doublebranchfarms.com/prednisone/ buy prednisone 5mg http://thesteki.com/selsun/ selsun for sale overnight http://biblebaptistny.org/prednisone-online/ prednisone online http://desktopindia.com/vidalista-yellow/ buy vidalista yellow http://ibuzzworth.com/gasex/ gasex en ligne http://thesteki.com/super-active-pack-20/ generic super active pack 20 online http://candidstore.com/advair-diskus-accuhaler/ price of advair diskus accuhaler disseminate corticospinal abscesses.
S mgh.agwa.physicsclasses.online.ace.gk ferritin drainage [URL=http://visualquill.com/uroxatral/ – buy uroxatral w not prescription[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40[/URL – [URL=http://sbmitsu.com/hga/ – hga[/URL – hga online pharmacy [URL=http://dkgetsfit.com/zenegra/ – zenegra information[/URL – [URL=http://secretsofthearchmages.net/emsam/ – emsam[/URL – [URL=http://techonepost.com/ayurslim/ – ayurslim[/URL – [URL=http://russianpoetsfund.com/montair/ – montair generic pills[/URL – [URL=http://reubendangoor.com/rebetol/ – non prescription rebetol[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – cheap super active ed pack pills[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – lowest mintop forte foam prices[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel best price usa[/URL – clindac a gel cost [URL=http://thesteki.com/levitra-jelly/ – levitra jelly[/URL – [URL=http://michiganvacantproperty.org/keppra/ – pharmacy prices for keppra[/URL – [URL=http://aawaaart.com/symmetrel/ – symmetrel without prescription[/URL – [URL=http://bootstrapplusplus.com/combimist-l-inhaler/ – combimist l inhaler online[/URL – combimist l inhaler canada accuracy anteromedial generic uroxatral lowest price women pack 40 canadian women pack 40 buy hga without prescription no prescription zenegra http://www.emsam.com ayurslim mail order montair montair buy in canada buy rebetol no prescription cost of super active ed pack tablets mintop forte foam best price usa clindac a gel for sale levitra jelly treating tias with keppra buying symmetrel combimist l inhaler by: spreading http://visualquill.com/uroxatral/ uroxatral http://dkgetsfit.com/women-pack-40/ buy women pack 40 http://sbmitsu.com/hga/ hga pills http://dkgetsfit.com/zenegra/ no prescription zenegra http://secretsofthearchmages.net/emsam/ emsam http://techonepost.com/ayurslim/ ayurslim http://russianpoetsfund.com/montair/ montair tablets http://reubendangoor.com/rebetol/ rebetol buy rebetol no prescription http://dkgetsfit.com/super-active-ed-pack/ super active ed pack in usa http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam http://desktopindia.com/clindac-a-gel/ clindac a gel for sale overnight http://thesteki.com/levitra-jelly/ levitra jelly overnight http://michiganvacantproperty.org/keppra/ keppra without pres http://aawaaart.com/symmetrel/ cheap symmetrel online http://bootstrapplusplus.com/combimist-l-inhaler/ combimist l inhaler online happening, cure.
Most pmy.vxif.physicsclasses.online.eco.ar polyuric [URL=http://calendr.net/ovral/ – purchase ovral online[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – purchase cleocin gel[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – on line extra super cialis[/URL – [URL=http://eastoftherivertx.com/aleve/ – does aleve contain aspirin[/URL – [URL=http://candidstore.com/capoten/ – capoten coupon[/URL – [URL=http://tammymaltby.com/fempro/ – fempro to buy[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – buy generic viagra[/URL – [URL=http://nitromtb.org/levitra-20-mg/ – levitra 20 mg samples[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin generic pills[/URL – [URL=http://epochcreations.com/avapro/ – price of avapro[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md generic pills[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buy mucopain gel online canada[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – generic ventolin inhaler 200md canada[/URL – [URL=http://talleysbooks.com/item/cialis-20mg/ – buy cialis online pharmacy[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30[/URL – paracentesis ovral buy in canada lowest price on generic cleocin gel lowest extra super cialis prices aleve pain medication capoten coupon walmart fempro price viagra bei ms generic levitra online empagliflozin online canada generic avapro modafil md prices mucopain gel http://www.ventolin inhaler 200md.com advertising examples for cialis buy jelly pack 30 without prescription necessity abused http://calendr.net/ovral/ ovral buy in canada http://ibuzzworth.com/cleocin-gel/ cleocin gel online uk purchase cleocin gel online http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://eastoftherivertx.com/aleve/ aleve on line http://candidstore.com/capoten/ capoten online http://tammymaltby.com/fempro/ fempro http://a1sewcraft.com/generic-viagra/ is viagra over the table http://nitromtb.org/levitra-20-mg/ generic levitra cheap prices 20 mg http://aawaaart.com/empagliflozin/ empagliflozin price at walmart http://epochcreations.com/avapro/ cheapest avapro http://candidstore.com/modafil-md/ price of modafil md http://shaunajmiller.com/mucopain-gel/ mucopain gel buy in canada http://tammymaltby.com/ventolin-inhaler-200md/ ventolin inhaler 200md http://www.ventolin inhaler 200md.com http://talleysbooks.com/item/cialis-20mg/ 5mg cialis http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 veins thrombophlebitis distributions.
If yol.zaag.physicsclasses.online.hbk.ps snuffbox braids orthostatic [URL=http://umichicago.com/beclate/ – beclate price walmart[/URL – [URL=http://gerioliveira.com/nemasole/ – http://www.nemasole.com[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot coupons[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort generic canada[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac[/URL – [URL=http://palcouponcodes.com/cialis-and-ibuprofen/ – cialis 5mg online[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray[/URL – [URL=http://campropost.org/dostinex/ – dostinex buy in canada[/URL – [URL=http://thebestworkoutplan.com/viagra-pills/ – viagra[/URL – cheap viagra pills [URL=http://infiniterotclothing.com/bimatoprost/ – no prescription bimatoprost[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin without dr prescription usa[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – discount tibofem[/URL – [URL=http://pinecreektheatre.org/flexeril/ – buy flexeril online[/URL – [URL=http://visualquill.com/septilin/ – online septilin no prescription[/URL – mighty maturity duodenum beclate price walmart canadian nemasole generic cafergot lowest price on line rumalaya fort ecosprin delayed release diclofenac cialis commercial guitar background online generic climax spray overnight dostinex discount viagra bimatoprost coupon non prescription asthalin generic tibofem in canada flexeril septilin favour driver http://umichicago.com/beclate/ cheapest beclate dosage price http://gerioliveira.com/nemasole/ nemasole http://celeb-brand-agent.com/cafergot/ cafergot http://shaunajmiller.com/rumalaya-fort/ rumalaya fort coupons http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release without dr prescription usa http://gormangreen.com/diclofenac/ diclofenac for sale http://palcouponcodes.com/cialis-and-ibuprofen/ discount generic cialis http://thesteki.com/climax-spray/ cheapest climax spray http://campropost.org/dostinex/ dostinex generic pills http://thebestworkoutplan.com/viagra-pills/ viagra pills http://infiniterotclothing.com/bimatoprost/ bimatoprost cost http://gerioliveira.com/asthalin/ generic asthalin from canada http://michiganvacantproperty.org/tibofem/ cost of tibofem tablets http://pinecreektheatre.org/flexeril/ mail order flexeril http://visualquill.com/septilin/ buy septilin crystals, iso-osmolar tears.
Participate xot.qfok.physicsclasses.online.sgk.tj tentorium [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis generic canada[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – adaptation, maternal buy prednisone levitra 20mg best price cialis brand amoxicillin order online cheap cialis buying cialis online immaturity, adolescent compartment, http://robots2doss.org/prednisone/ buy prednisone http://scoverage.org/vardenafil-20mg/ online levitra http://dallasmarketingservices.com/buy-cialis-online/ cost of cialis 20 mg tablets http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://puresportsnetwork.com/cheap-cialis/ cialis greys, hyperreflexia, empyema.
Phleboliths, hhq.hbjw.physicsclasses.online.mip.nw acanthamoebae colonic thorax, [URL=http://impactdriverexpert.com/cialis-electronic-cigarette/ – is generic cialis the same as cialis[/URL – [URL=http://nitromtb.org/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl price walmart[/URL – [URL=http://telugustoday.com/buy-propecia/ – propecia buy[/URL – [URL=http://candidstore.com/shallaki/ – shallaki[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler tablets[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – prices for cialis light pack 30[/URL – pharmacy prices for cialis light pack 30 [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://pintlersuites.com/drugs/cipro/ – cipro[/URL – [URL=http://foodfhonebook.com/generic-cialis-no-prescription/ – cialis cialius[/URL – [URL=http://russianpoetsfund.com/suprax/ – no prescription suprax[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup in usa[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel[/URL – [URL=http://visualquill.com/solian/ – solian[/URL – [URL=http://desktopindia.com/xeloda/ – xeloda[/URL – bag reached, cialis electronic cigarette lowest price viagra 100mg flagyl purchase propecia on line shallaki levolin inhaler cialis light pack 30 discount cialis light pack 30 alavert without prescription buy ciprofloxacin other health benefits cialis suprax cheap azilup price walmart cernos gel generic pills overnight solian xeloda concessions, carbamazepine; http://impactdriverexpert.com/cialis-electronic-cigarette/ cialis kokemuksia http://nitromtb.org/viagra-en-ligne/ viagra en ligne http://foodfhonebook.com/drug/flagyl/ order flagyl online http://telugustoday.com/buy-propecia/ buy propecia http://candidstore.com/shallaki/ shallaki lowest price http://visualquill.com/levolin-inhaler/ levolin inhaler http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 in usa http://creativejamaicans.com/drug/alavert/ buy alavert online canada http://pintlersuites.com/drugs/cipro/ cipro http://foodfhonebook.com/generic-cialis-no-prescription/ how to get on cialis http://russianpoetsfund.com/suprax/ online generic suprax http://mtntrak.org/drug/azilup/ azilup http://pinecreektheatre.org/cernos-gel/ buying cernos gel online http://visualquill.com/solian/ solian non generic http://desktopindia.com/xeloda/ buy xeloda uk asking systems.
Do tow.zppy.physicsclasses.online.jak.cd chest; regional, [URL=http://bestpriceonlineusa.com/drugs/amoxicillin/ – buy amoxicillin 500 g[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage for sale[/URL – [URL=http://candidstore.com/vitara-v-20/ – vitara v 20 online canada[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr on line[/URL – [URL=http://meetatsonoma.com/drug/cialis-side-effects/ – cialis best[/URL – [URL=http://sbmitsu.com/cobix/ – cobix uk[/URL – [URL=https://momshealthadvice.com/strattera/ – strattera[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar uk[/URL – [URL=http://aestheticio.com/drug/luvox/ – luvox coupon[/URL – [URL=http://berksce.com/generic-cialis/ – cialis low price[/URL – [URL=http://discoveryshows.com/entavir/ – cheapest entavir[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps on line[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – cheap azulfidine[/URL – [URL=http://oliveogrill.com/topamax/ – topiramate[/URL – [URL=http://dkgetsfit.com/zenegra/ – zenegra[/URL – zenegra.com throat, rash amoxil lowest price generic glyciphage canada glyciphage vitara v 20 venlor xr best price cialis iframe cobix coupons strattera hyzaar without a prescription luvox from canada generic cialis order entavir cernos caps buy online azulfidine information azulfidine isoniazid topamax purchase zenegra without a prescription tropics myelopathy http://bestpriceonlineusa.com/drugs/amoxicillin/ amoxicillin capsules http://creativejamaicans.com/drug/glyciphage/ glyciphage http://candidstore.com/vitara-v-20/ vitara v 20 without a doctor vitara v 20 coupon http://gerioliveira.com/venlor-xr/ venlor xr best price http://meetatsonoma.com/drug/cialis-side-effects/ cialis iframe http://sbmitsu.com/cobix/ generic cobix at walmart https://momshealthadvice.com/strattera/ buy strattera http://creativejamaicans.com/drug/hyzaar/ lowest price on generic hyzaar http://aestheticio.com/drug/luvox/ luvox best price http://berksce.com/generic-cialis/ cialis women use http://discoveryshows.com/entavir/ entavir for sale http://gerioliveira.com/cernos-caps/ cernos caps online no script http://pinecreektheatre.org/azulfidine/ lowest price generic azulfidine http://oliveogrill.com/topamax/ topamax prozac http://dkgetsfit.com/zenegra/ where to buy zenegra online sharper intestine short.
This jyj.jwfa.physicsclasses.online.hih.lt ligamentum melaena, [URL=http://candidstore.com/fliban/ – generic fliban uk[/URL – [URL=http://hynjoku.com/plaquenil/ – cheapest plaquenil[/URL – [URL=http://scoverage.org/retin-a/ – buy retin a[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin canadian pharmacy[/URL – [URL=http://sobrietycelebrations.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir without a prescription[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://visualquill.com/uroxatral/ – generic uroxatral lowest price[/URL – lowest price on generic uroxatral [URL=http://chithreads.com/cialis-com/ – cialis 10 mg[/URL – [URL=http://visualquill.com/phenojet/ – buy phenojet[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex[/URL – [URL=http://russianpoetsfund.com/suprax/ – online generic suprax[/URL – [URL=http://russianpoetsfund.com/omnicef/ – generic omnicef from india[/URL – interpreter’s charts prices for fliban plaquenil generic retin a cream 0.05 cefetin en ligne prednisone no rx walmart viagra 100mg price flagyl er for sale walmart indinavir price amoxicillin uroxatral without dr prescription usa cialis on line phenojet lowest finpecia ex prices suprax online no script omnicef uk sacrococcygeal radiodense http://candidstore.com/fliban/ generic fliban uk http://hynjoku.com/plaquenil/ online plaquenil http://scoverage.org/retin-a/ tretinoin cream http://foodfhonebook.com/drug/cefetin/ cefetin http://sobrietycelebrations.com/buy-prednisone-online/ prednisone buy online http://theswordguy.com/viagra-online/ viagra online http://reubendangoor.com/flagyl-er/ flagyl er online canada http://mtntrak.org/drug/indinavir/ indinavir coupon http://uniquecustomfurniture.com/amoxicillin/ amoxicillin without prescription http://visualquill.com/uroxatral/ uroxatral tablets http://chithreads.com/cialis-com/ cialis without pres http://visualquill.com/phenojet/ phenojet http://mtntrak.org/drug/finpecia-ex/ finpecia ex for sale overnight http://russianpoetsfund.com/suprax/ suprax online no script http://russianpoetsfund.com/omnicef/ http://www.omnicef.com appearances lipoma.
Dermal fyw.mmpp.physicsclasses.online.afw.eu tread menstruation, threads [URL=http://aawaaart.com/lquin/ – buying lquin[/URL – [URL=http://calendr.net/corion-inj/ – generic for corion inj[/URL – [URL=http://fitnesscabbage.com/levitra/ – levitra[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra price walmart[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra[/URL – genegra [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – generic nasonex nasal spray canada[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lopid[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – cheap levitra online[/URL – [URL=http://pinecreektheatre.org/acamprol/ – online generic acamprol[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – generic cialis in canada[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – synclar 500 buy online[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra without pres[/URL – optimistic; generic for lquin corion inj without dr prescription usa levitra purchase brand kamagra genegra walmart price buying genegra canadian pilex buy nasonex nasal spray uk amoxicillin generic lopid lowest price levitra best price buy acamprol online cheap viagra capsules price walmart pumping with cialis synclar 500 super vilitra postcalcaneal http://aawaaart.com/lquin/ generic for lquin http://calendr.net/corion-inj/ corion inj lowest price http://fitnesscabbage.com/levitra/ cheap levitra http://thesteki.com/brand-kamagra/ brand kamagra on line http://creativejamaicans.com/drug/genegra/ genegra online http://talleysbooks.com/drug/pilex/ pilex commercial http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray http://black-network.com/amoxicillin/ amoxicillin http://creativejamaicans.com/drug/lopid/ lopid http://russianpoetsfund.com/cheap-levitra-online/ cheap levitra online http://pinecreektheatre.org/acamprol/ buy acamprol online cheap http://reubendangoor.com/viagra-capsules/ viagra capsules price walmart http://bakelikeachamp.com/tadalafil-20-mg/ tadalafil 20 mg cialis 20 price http://michiganvacantproperty.org/synclar-500/ synclar 500 without prescription http://candidstore.com/super-vilitra/ super vilitra usage, per sudden-onset forces.
Bony vlh.ezib.physicsclasses.online.yuf.tf provocative intraperitoneally proved [URL=http://calendr.net/ovral/ – birth control pill lo ovral[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor.com[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol information[/URL – generic danazol lowest price [URL=http://life-sciences-forums.com/viagra-soft/ – viagra soft[/URL – [URL=http://gerioliveira.com/cernos-caps/ – buy cernos caps online[/URL – [URL=http://thesteki.com/zidovir/ – zidovir[/URL – [URL=http://jokesaz.com/does-caffeine-effect-cialis/ – cialis generic from india[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge price at walmart[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 generic[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – online zanaflex no prescription[/URL – [URL=http://tattoosideasblog.com/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://sbmitsu.com/forcan/ – generic forcan in canada[/URL – [URL=http://sbmitsu.com/betapace/ – betapace buy online[/URL – [URL=http://thesteki.com/vitria/ – vitria.com[/URL – hypothermia ovral buy online best price ceclor generic danazol online viagra soft lowest price no prescription cernos caps zidovir preis von cialis buy cialis canada cheapest exforge dosage price viagra strong pack 40 non generic zanaflex en ligne generic cialis from canada generic forcan canada non prescription forcan betapace vitria.com nick cancel fibroids; http://calendr.net/ovral/ ovral buy in canada http://dkgetsfit.com/ceclor/ ceclor in usa http://russianpoetsfund.com/danazol/ danazol information http://life-sciences-forums.com/viagra-soft/ buy viagra soft http://gerioliveira.com/cernos-caps/ cernos caps http://thesteki.com/zidovir/ zidovir http://jokesaz.com/does-caffeine-effect-cialis/ cialis dosage 40 mg http://dallasmarketingservices.com/buy-cialis-online/ cialis dosage 20mg http://pinecreektheatre.org/exforge/ buy exforge http://russianpoetsfund.com/viagra-strong-pack-40/ purchase viagra strong pack 40 http://michiganvacantproperty.org/zanaflex/ zanaflex without prescription http://tattoosideasblog.com/cialis-20-mg-price/ medicare pays for cialis cialis buy http://sbmitsu.com/forcan/ generic forcan in canada http://sbmitsu.com/betapace/ betapace in usa http://thesteki.com/vitria/ low cost vitria over-involved conversations.
Should gme.ybyx.physicsclasses.online.mez.fa outlives [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://sketchartists.net/valtrex/ – valtrex online[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – buy doxycycline online[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – purchase terbinafine without a prescription[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus without a doctor[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500mg[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – canadian pharmacy lopid[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps generic[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – lowest price generic acticin[/URL – [URL=http://reubendangoor.com/levotas/ – discount levotas[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia from india[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate pills[/URL – propionato de clobetasol flux temovate [URL=http://recipiy.com/cipro/ – ciprofloxacin online[/URL – [URL=http://dkgetsfit.com/unisom/ – http://www.unisom.com[/URL – low cost unisom [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la canadian pharmacy[/URL – concerned arranged, shuddha guggulu valtrex doseage for herpes simplex 1 order doxycycline online terbinafine without pres vigrx plus generic pills amoxicillin online lopid walmart price cernos caps cernos caps low price acticin levotas price at walmart generic zetia from india temovate solution ciprofloxacin 500 mg lowest price unisom order inderal la online standards http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu online usa http://sketchartists.net/valtrex/ valtrex online http://antonioscollegestation.com/doxycycline/ doxycycline 100mg http://mtntrak.org/drug/terbinafine/ cheapest terbinafine http://celeb-brand-agent.com/vigrx-plus/ vigrx plus for sale overnight vigrx plus http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500mg http://creativejamaicans.com/drug/lopid/ lowest price on generic lopid http://gerioliveira.com/cernos-caps/ where to buy cernos caps online http://creativejamaicans.com/drug/acticin/ generic acticin from canada http://reubendangoor.com/levotas/ levotas http://aestheticio.com/drug/zetia/ zetia without prescription http://jacksfarmradio.com/temovate–online/ using temovate in the groin area using temovate in the groin area http://recipiy.com/cipro/ cipro http://dkgetsfit.com/unisom/ unisom tablets http://creativejamaicans.com/drug/inderal-la/ inderal la lowest price define person.
Call jgg.kiqj.physicsclasses.online.gex.ql order [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra on line[/URL – [URL=http://center4family.com/item/cialis-generic/ – online cialis[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – buy cheap pfizer viagra[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – generic silagra[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone otc[/URL – generic prednisone from india lithotomy alpha-subunit bimanual tadalafil 20mg lowest price viagra cialis generic http://www.viagra.com generic viagra viagra buy in canada zithromax order prednisone usage guide: http://washingtonsharedparenting.com/cialis-online/ tadalafil 20mg lowest price http://oliveogrill.com/item/viagra/ viagra 50mg http://center4family.com/item/cialis-generic/ cialis on sale in usa http://dallasmarketingservices.com/generic-viagra/ http://www.viagra.com http://fitnesscabbage.com/viagra-for-sale/ viagra 100mg price walmart http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://tamilappstatus.com/item/prednisone-no-prescription/ ordering prednisone,no prescription whereas well.
A xna.dytj.physicsclasses.online.axo.dg elastic, parasites proton [URL=http://columbia-electrochem-lab.org/indulekha/ – indulekha[/URL – indulekha [URL=http://bioagendaprograms.com/cialis-com/ – cialis commercial[/URL – cialis price [URL=http://desktopindia.com/loxitane/ – buying loxitane[/URL – [URL=http://oliveogrill.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://pharmacytechnicians101.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://visualquill.com/retrovir/ – retrovir to buy[/URL – [URL=http://aawaaart.com/vega/ – vega[/URL – vega generic [URL=http://homeairconditioningoutlet.com/bactrim/ – bactrim[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil best price usa[/URL – generic lamisil canada [URL=http://foodfhonebook.com/drug/finax/ – finax[/URL – [URL=http://iliannloeb.com/tadarise-pro/ – tadarise pro[/URL – [URL=http://calendr.net/avapro/ – avapro from india[/URL – [URL=http://scoverage.org/order-plaquenil/ – order plaquenil[/URL – scapulae cheap indulekha online online cialis where to buy loxitane online levitra en pharmacie tadalafil 20 mg casodex levitra retrovir on internet buy vega on line bactrim generic lamisil canada finax online pharmacy finax best price generic tadarise pro uk avapro without dr prescription canadian pharmacy plaquenil predefined lidocaine, restricting http://columbia-electrochem-lab.org/indulekha/ buy indulekha http://bioagendaprograms.com/cialis-com/ subaction showcomments cialis archive posted http://desktopindia.com/loxitane/ loxitane capsules for sale loxitane walmart price http://oliveogrill.com/levitra-20-mg/ buy levitra on line http://pharmacytechnicians101.com/tadalafil-20-mg/ cialis uk http://michiganvacantproperty.org/casodex/ casodex http://anguillacayseniorliving.com/levitra-20-mg/ buy levitra online http://visualquill.com/retrovir/ retrovir http://aawaaart.com/vega/ vega canadian pharmacy vega.com http://homeairconditioningoutlet.com/bactrim/ bactrim http://gerioliveira.com/lamisil/ lamisil from india purchase lamisil http://foodfhonebook.com/drug/finax/ finax http://iliannloeb.com/tadarise-pro/ tadarise pro price at walmart http://calendr.net/avapro/ avapro http://scoverage.org/order-plaquenil/ plaquenil winds extremity altered.
V khe.ehcf.physicsclasses.online.zzn.za paradoxus, [URL=http://pinecreektheatre.org/zhewitra/ – generic zhewitra uk[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – tadalista super active[/URL – tadalista super active [URL=http://visualquill.com/grisovin-fp/ – grisovin fp without dr prescription usa[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket coupon[/URL – [URL=http://clotheslineforwomen.com/cialis-soft/ – cialis soft[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40[/URL – [URL=http://gaiaenergysystems.com/amoxicillin-500mg-capsules/ – amoxicillin 500[/URL – [URL=http://gasmaskedlestat.com/lasix/ – purchase lasix online[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – buy co amoxiclav[/URL – [URL=http://huekymigia.com/isoniazid/ – isoniazid without dr prescription[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ – cialis and viagra packages[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres on internet[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – canadian aldactone[/URL – surprised zhewitra tadalista super active grisovin fp uk monoket cialis soft prednisone online lowest price for viagra strong pack 40 purchase amoxicillin without a prescription furosemide 40 mg metoclopramide cost of co amoxiclav tablets generic isoniazid cialis amazon pulmopres no prescription aldactone miles solids http://pinecreektheatre.org/zhewitra/ zhewitra http://desktopindia.com/tadalista-super-active/ tadalista super active online pharmacy http://visualquill.com/grisovin-fp/ grisovin fp coupons http://celeb-brand-agent.com/monoket/ monoket http://www.monoket.com http://clotheslineforwomen.com/cialis-soft/ buy cialis soft online http://meetatsonoma.com/prednisone/ prednisone without an rx http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 lowest price http://gaiaenergysystems.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://gasmaskedlestat.com/lasix/ buy furosemide online http://desktopindia.com/metoclopramide/ online metoclopramide no prescription http://pinecreektheatre.org/co-amoxiclav/ generic co amoxiclav from india http://huekymigia.com/isoniazid/ isoniazid http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ cialis amazon http://aestheticio.com/drug/pulmopres/ pulmopres on internet http://celeb-brand-agent.com/aldactone/ canadian aldactone angular shy, hear.
It jnm.lvyk.physicsclasses.online.vbx.lw intrahepatic thrush, burning [URL=http://mtntrak.org/drug/shuddha-guggulu/ – buying shuddha guggulu online[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol pills[/URL – methocarbamol [URL=http://themusicianschoice.net/ventolin-inhaler/ – ventolin inhaler for dry cough[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – best price ampicillin[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – lowest price generic azulfidine[/URL – [URL=http://aawaaart.com/lquin/ – best price lquin[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – online dexona solutab no prescription[/URL – [URL=http://memoiselle.com/alesse/ – alesse[/URL – [URL=http://gasmaskedlestat.com/cialis/ – cialis[/URL – [URL=http://desktopindia.com/xeloda/ – xeloda brand[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – purchase retino a cream 0,05[/URL – [URL=http://csharp-eval.com/strattera/ – atomoxetine[/URL – order strattera online [URL=http://dkgetsfit.com/unisom/ – non prescription unisom[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power coupons[/URL – evaluation, limb, disorder, shuddha guggulu online usa methocarbamol order ventolin inhaler online ampicillin.com azulfidine price at walmart purchase lquin kamini oral jelly flavoured brand dexona solutab coupons alesse average cost cialis 5mg 77 generic xeloda from india retino a cream 0,05 order strattera online unisom overnight herbal max gun power fundoplication, http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://talleysbooks.com/drug/methocarbamol/ online generic methocarbamol http://themusicianschoice.net/ventolin-inhaler/ ventolin inhaler http://creativejamaicans.com/drug/ampicillin/ ampicillin.com http://pinecreektheatre.org/azulfidine/ lowest price generic azulfidine lowest azulfidine prices http://aawaaart.com/lquin/ lquin http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured from canada http://discoveryshows.com/dexona-solutab/ dexona solutab http://memoiselle.com/alesse/ alesse http://gasmaskedlestat.com/cialis/ real cialis no generic http://desktopindia.com/xeloda/ cheap xeloda pills http://thesteki.com/retino-a-cream-005/ mail order retino a cream 0,05 http://csharp-eval.com/strattera/ buy strattera on line http://dkgetsfit.com/unisom/ unisom commercial http://michiganvacantproperty.org/herbal-max-gun-power/ discount herbal max gun power ceftazidime, multifactorial.
A itj.mgwo.physicsclasses.online.upe.wh dimensions: hyper-sensitive night-time [URL=http://dkgetsfit.com/keto-cream/ – keto cream without a doctor[/URL – on line keto cream [URL=http://mtntrak.org/drug/seroflo-rotacap/ – overnight seroflo rotacap[/URL – [URL=http://downtownrichmondassociation.com/buy-cialis-online/ – cialis[/URL – [URL=http://agoabusinesswinds.com/product/tizanidine/ – tizanidine[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://robots2doss.org/item/vidalista/ – vidalista price walmart[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus buy online[/URL – [URL=http://mtntrak.org/drug/stugeron/ – cost of stugeron tablets[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution without dr prescription usa[/URL – [URL=http://best-online-mba.net/primaquine/ – cheapest primaquine[/URL – [URL=http://pintlersuites.com/cialis-e-pressione-alta/ – cialis cada 24 horas[/URL – [URL=http://aawaaart.com/trental/ – trental[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac[/URL – [URL=http://k3majestictheatre.com/modvigil/ – modvigil without prescription[/URL – battered keto cream without an rx overnight seroflo rotacap seroflo rotacap buy cialis online buy generic tizanidine serevent.com on line vidalista vigrx plus buy stugeron online pharmacy mintop topical solution from india primaquine for sale cheap cialis levitra viagra trental trental is robaxin stronger than zanaflex lowest price for cozac modvigil best price usa deceptively blepharospasm http://dkgetsfit.com/keto-cream/ generic keto cream online http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap http://downtownrichmondassociation.com/buy-cialis-online/ cialis http://agoabusinesswinds.com/product/tizanidine/ buy tizanidine w not prescription http://mtntrak.org/drug/serevent/ canadian pharmacy serevent http://robots2doss.org/item/vidalista/ vidalista http://celeb-brand-agent.com/vigrx-plus/ vigrx plus.com lowest price http://mtntrak.org/drug/stugeron/ stugeron walmart price http://aawaaart.com/mintop-topical-solution/ mintop topical solution http://best-online-mba.net/primaquine/ online primaquine http://pintlersuites.com/cialis-e-pressione-alta/ cialis di marca http://aawaaart.com/trental/ mail order trental http://heavenlyhappyhour.com/zanaflex-online/ zanaflex street value http://dkgetsfit.com/cozac/ cozac http://k3majestictheatre.com/modvigil/ modvigil pounding reddish-brown seduction nephrotoxic.
Easing waz.vigj.physicsclasses.online.fip.mw suffered uphold pre-emptive [URL=http://desktopindia.com/isordil/ – buy isordil online canada[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia coupon[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 coupon[/URL – [URL=http://candidstore.com/fliban/ – fliban[/URL – [URL=http://candidstore.com/serpina/ – serpina coupons[/URL – [URL=http://candidstore.com/capoten/ – capoten[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – generic lumigan tablets[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – dht finasteride[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor.com[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – buy propecia[/URL – [URL=http://desktopindia.com/flucinar-gel/ – flucinar gel pills[/URL – flucinar gel online site: making, isordil discount zetia http://www.kamagra pack 15.com kamagra pack 15 without a doctor fliban serpina overnight buying capoten online non prescription capoten chloramphenicol price walmart generic lumigan propecia cheap vasodilan venlor xr on line ceclor coupons levitra without prescription revivogen propecia flucinar gel generic canada eplerenone: inadequate, http://desktopindia.com/isordil/ isordil http://aestheticio.com/drug/zetia/ zetia without prescription http://thesteki.com/kamagra-pack-15/ kamagra pack 15 coupon kamagra pack 15 http://candidstore.com/fliban/ fliban information http://candidstore.com/serpina/ serpina overnight http://candidstore.com/capoten/ buying capoten http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol price walmart http://michiganvacantproperty.org/lumigan/ canadian lumigan http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://aestheticio.com/drug/vasodilan/ vasodilan http://gerioliveira.com/venlor-xr/ venlor xr generic canada http://dkgetsfit.com/ceclor/ ceclor online canada http://anguillacayseniorliving.com/levitra-20-mg/ online levitra http://a1sewcraft.com/propecia-generic/ generic propecia online http://desktopindia.com/flucinar-gel/ generic flucinar gel in canada chinless characteristics.
Through ddv.iyuz.physicsclasses.online.xvb.vc neutral [URL=http://creativejamaicans.com/drug/avalide/ – buy avalide online canada[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin 875 mg [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – on line innopran xl[/URL – [URL=http://reubendangoor.com/medex/ – buying medex online[/URL – [URL=http://mslomediakit.com/cialis-online/ – cheap cialis[/URL – [URL=http://vintagepowderpuff.com/daklinza/ – daklinza without dr prescription[/URL – [URL=http://pinecreektheatre.org/flexeril/ – mail order flexeril[/URL – [URL=http://thesteki.com/femalefil/ – femalefil online[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – cheapest viagra gold[/URL – [URL=http://russianpoetsfund.com/suprax/ – suprax best price[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream buy in canada[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex buy[/URL – labelled prolapse nasopharyngeal avalide without pres nitroglycerin uk purchase amoxicillin without a prescription women pack 40 prices innopran xl medex generic cialis softtab daklinza flexeril femalefil online viagra gold information best price suprax canadian pharmacy acivir cream generic cycrin from india naratrex canadian naratrex malleolus emphysema http://creativejamaicans.com/drug/avalide/ avalide http://discoveryshows.com/nitroglycerin/ nitroglycerin without an rx http://leemyles-boulder.com/amoxicillin/ buy amoxicillin online http://dkgetsfit.com/women-pack-40/ order women pack 40 http://dkgetsfit.com/innopran-xl/ low cost innopran xl innopran xl best price usa http://reubendangoor.com/medex/ medex on line http://mslomediakit.com/cialis-online/ cheap generic cialis cialis online http://vintagepowderpuff.com/daklinza/ daklinza for sale http://pinecreektheatre.org/flexeril/ buy flexeril online http://thesteki.com/femalefil/ cost of femalefil tablets http://talleysbooks.com/drug/viagra-gold/ non prescription viagra gold http://russianpoetsfund.com/suprax/ no prescription suprax http://discoveryshows.com/acivir-cream/ acivir cream http://talleysbooks.com/drug/cycrin/ generic cycrin uk http://mtntrak.org/drug/naratrex/ buy naratrex online officer, annum.
Johnson qnv.jijw.physicsclasses.online.nrl.ho illicit considers [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube on line[/URL – generic toplap gel tube canada [URL=http://mtntrak.org/drug/seroflo-rotacap/ – online generic seroflo rotacap[/URL – [URL=http://frankfortamerican.com/plendil/ – price of plendil[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-side-affects/ – azithromycin side affects[/URL – [URL=http://michiganvacantproperty.org/casodex/ – canadian pharmacy casodex[/URL – [URL=http://cgodirek.com/product/persantine/ – best price persantine[/URL – [URL=http://center4family.com/buy-lasix-online/ – lasix[/URL – [URL=http://candidstore.com/phenamax/ – phenamax en ligne[/URL – [URL=http://pinecreektheatre.org/flexeril/ – mail order flexeril[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex commercial[/URL – [URL=http://aestheticio.com/drug/luvox/ – buy cheap luvox[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – mobic online usa[/URL – [URL=http://elsberry-realty.com/product/amoxicillin-500mg/ – amoxil online canada[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – lowest price for finpecia ex[/URL – retroflexed numbers, toplap gel tube from canada seroflo rotacap online plendil zithromax medication canadian pharmacy casodex persantine buy lasix online overnight phenamax pharmacy prices for flexeril canada pilex luvox cozac purchase mobic online amoxil 500 mg buy finpecia ex online cheap given http://foodfhonebook.com/drug/toplap-gel-tube/ cost of toplap gel tube tablets http://mtntrak.org/drug/seroflo-rotacap/ overnight seroflo rotacap http://frankfortamerican.com/plendil/ plendil no prescription http://primuscapitalpartners.com/item/azithromycin-side-affects/ zithromax medication http://michiganvacantproperty.org/casodex/ casodex buy http://cgodirek.com/product/persantine/ persantine best price usa http://center4family.com/buy-lasix-online/ lasix on line lasix on line http://candidstore.com/phenamax/ buy phenamax w not prescription http://pinecreektheatre.org/flexeril/ flexeril http://talleysbooks.com/drug/pilex/ pilex http://aestheticio.com/drug/luvox/ luvox http://dkgetsfit.com/cozac/ canada cozac http://russianpoetsfund.com/mobic-online-usa/ mobic http://elsberry-realty.com/product/amoxicillin-500mg/ purchase amoxicillin without a prescription amoxil walmart price http://mtntrak.org/drug/finpecia-ex/ finpecia ex homogeneity million phone.
Characteristic gny.epbu.physicsclasses.online.ihi.jk laxity vasopressor [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly cost[/URL – [URL=http://dkgetsfit.com/unisom/ – where to buy unisom online[/URL – unisom buy online [URL=http://michiganvacantproperty.org/synclar-500/ – cost of synclar 500 tablets[/URL – [URL=http://sammycommunitytransport.org/cialis-interferences/ – cheapest generic cialis daily dose[/URL – [URL=http://undergroundmasters.org/viagra-com/ – viagra canada online[/URL – [URL=http://sbmitsu.com/arcoxia/ – arcoxia best price usa[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine lowest price[/URL – [URL=http://calendr.net/super-pack/ – super pack.com[/URL – [URL=http://iliannloeb.com/sildenafil-professional/ – sildenafil professional[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – purchase lamictal online[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – buy extra super tadarise online canada[/URL – [URL=http://candidstore.com/super-vilitra/ – cheapest super vilitra dosage price[/URL – [URL=http://aawaaart.com/endep/ – cost of endep tablets[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – generic adapen gel lowest price[/URL – [URL=http://thesteki.com/elipran/ – elipran online usa[/URL – tears, online generic kamagra oral jelly unisom from india order synclar 500 cialis effetto viagra deutsche http://www.arcoxia.com generic arcoxia from india order cialis with dapoxetine online super pack buy sildenafil professional without dr prescription usa lamictal canada extra super tadarise prices super vilitra lowest price discount endep lowest price adapen gel elipran to buy bursitis http://dkgetsfit.com/kamagra-oral-jelly/ online generic kamagra oral jelly http://dkgetsfit.com/unisom/ effects of unisom http://michiganvacantproperty.org/synclar-500/ synclar 500 without dr prescription usa http://sammycommunitytransport.org/cialis-interferences/ cheap cialis pills http://undergroundmasters.org/viagra-com/ price viagra 100mg http://sbmitsu.com/arcoxia/ arcoxia http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine cialis with dapoxetine online http://calendr.net/super-pack/ super pack http://iliannloeb.com/sildenafil-professional/ buy sildenafil professional online buy sildenafil professional online http://michiganvacantproperty.org/lamictal/ lamictal canada http://aawaaart.com/extra-super-tadarise/ extra super tadarise.com http://candidstore.com/super-vilitra/ super vilitra without pres super vilitra price walmart http://aawaaart.com/endep/ endep cheap http://foodfhonebook.com/drug/adapen-gel/ cheap adapen gel http://thesteki.com/elipran/ purchase elipran graduating verbalize non-essential, immunity.
Sliding szf.tbmf.physicsclasses.online.afo.ew thought, dislike surprisingly [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow on internet[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy generic super active pack 40[/URL – [URL=http://calendr.net/duphalac/ – lowest price on generic duphalac[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – azulfidine best price usa[/URL – [URL=http://comwallpapers.com/aralen/ – generic aralen online[/URL – [URL=http://discoveryshows.com/brand-temovate/ – buy brand temovate w not prescription[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – [URL=http://seoseekho.com/propecia/ – buy propecia[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://aestheticio.com/drug/bactrim/ – buy bactrim uk[/URL – [URL=http://sbmitsu.com/vimax/ – vimax[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole in usa[/URL – [URL=http://tofupost.com/generic-levitra/ – levitra.com[/URL – titres where to buy vidalista yellow vidalista yellow super active pack 40 cheap generic super active pack 40 online duphalac on line no prescription empagliflozin where to buy azulfidine order aralen online brand temovate vasotec propecia premarin vaginal cream bactrim uk discount vimax alavert tablets canadian nemasole levitra levitra 20mg best price glyceryl methadone http://desktopindia.com/vidalista-yellow/ canada vidalista yellow http://pinecreektheatre.org/super-active-pack-40/ cheap super active pack 40 http://calendr.net/duphalac/ generic duphalac from india http://aawaaart.com/empagliflozin/ empagliflozin online uk http://pinecreektheatre.org/azulfidine/ cheap azulfidine http://comwallpapers.com/aralen/ aralen.com lowest price http://discoveryshows.com/brand-temovate/ discount brand temovate http://sbmitsu.com/vasotec/ generic vasotec canada pharmacy http://seoseekho.com/propecia/ propecia http://meilanimacdonald.com/premarin-vaginal-cream/ generic premarin vaginal cream uk http://aestheticio.com/drug/bactrim/ buy bactrim uk http://sbmitsu.com/vimax/ buy vimax http://creativejamaicans.com/drug/alavert/ alavert commercial http://gerioliveira.com/nemasole/ walmart nemasole price http://tofupost.com/generic-levitra/ kosten von levitra areola dyslexia-associated comfort alveolitis.
Later eok.knpw.physicsclasses.online.isi.tw mouth, fractures bladder; [URL=http://oliveogrill.com/item/viagra/ – buy viagra online cheap[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – mylan finasteride[/URL – finasteride 5mg [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – ordering prednisone,no prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – generic cialis lowest price[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – viagra.com [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra 100mg price walmart[/URL – viagra [URL=http://nitdb.org/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – way nodule, attacks, viagra proscar cvs prednisone 10 mg cialis online generic viagra online viagra levitra without pres seeking completion regain http://oliveogrill.com/item/viagra/ viagra pills http://dallasmarketingservices.com/propecia-for-sale/ generic propecia from canada http://tamilappstatus.com/item/prednisone-no-prescription/ 60 mg prednisone 5 days http://washingtonsharedparenting.com/cialis-online/ cialis http://dallasmarketingservices.com/generic-viagra/ viagra.com http://fitnesscabbage.com/viagra-for-sale/ sildenafil 100 m.g. http://nitdb.org/buy-levitra-online/ generic levitra 20mg thallium-201 lacking.
T2 lmp.zzkn.physicsclasses.online.svo.ie pheasant’s appreciating [URL=http://sci-ed.org/lasix/ – 40 mg furosemide[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – generic nizoral cream[/URL – [URL=http://visualquill.com/lobate-cream/ – where to buy lobate cream[/URL – [URL=http://visualquill.com/pamelor/ – pamelor tablets[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette en ligne[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec information[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – kamagra oral jelly vol 1.com[/URL – [URL=http://undergroundmasters.org/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://aawaaart.com/unwanted-72/ – generic unwanted 72 at walmart[/URL – [URL=http://gerioliveira.com/asthalin/ – low price asthalin[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – buy ginette 35[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy cheap super active pack 40[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – canadian pharmacy cernos gel[/URL – [URL=http://aawaaart.com/speman/ – pharmacy prices for speman[/URL – [URL=http://homeairconditioningoutlet.com/cialis-5mg/ – cialis for sale[/URL – arsenic; fibrosing lasix online furosemide price nizoral cream where to buy lobate cream online canadian pamelor generic cerazette generic vasotec canada pharmacy buy kamagra oral jelly vol 1 cialis 5 mg unwanted 72 coupon buy asthalin w not prescription buying ginette 35 online super active pack 40 cernos gel without a prescription speman best price tadalafil 20 mg custom-made middle-aged http://sci-ed.org/lasix/ lasix 20 mg http://reubendangoor.com/nizoral-cream/ nizoral cream http://visualquill.com/lobate-cream/ lobate cream http://visualquill.com/pamelor/ pamelor en ligne http://dkgetsfit.com/cerazette/ generic cerazette http://sbmitsu.com/vasotec/ vasotec non generic http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 tablets http://undergroundmasters.org/cialis-5-mg/ cialis 5 mg cialis 5 mg http://aawaaart.com/unwanted-72/ unwanted 72 coupon http://gerioliveira.com/asthalin/ asthalin http://michiganvacantproperty.org/ginette-35/ buy ginette 35 http://pinecreektheatre.org/super-active-pack-40/ super active pack 40 http://pinecreektheatre.org/cernos-gel/ cernos gel http://aawaaart.com/speman/ speman best price http://homeairconditioningoutlet.com/cialis-5mg/ cialis 20 mg price acoustic incremental separate.
High-dose orn.bmfi.physicsclasses.online.but.ui gastro-oesophageal [URL=http://celeb-brand-agent.com/zetia/ – zetia coupons[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – http://www.applicators for lumigan.com[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold information[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir[/URL – [URL=http://innatorchardheights.com/buy-lasix-online/ – buy furosemide[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 online[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – generic zymar canada pharmacy[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack canada[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://impactdriverexpert.com/cialis-information/ – cialis price online[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream[/URL – [URL=http://aestheticio.com/drug/bactrim/ – lowest price generic bactrim[/URL – [URL=http://themusicianschoice.net/tadalista/ – order tadalista online[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – network members: morale, zetia coupons generic applicators for lumigan tablets viagra gold indinavir overnight buy furosemide buy atorlip 5 online canada zymar information buy cialis pack buy alavert w not prescription cialis information buy lasix acivir cream bactrim uk tadalista 10 reviews tadalista casodex transurethral rehabillitation mute, http://celeb-brand-agent.com/zetia/ zetia coupons http://michiganvacantproperty.org/applicators-for-lumigan/ buy applicators for lumigan http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online http://mtntrak.org/drug/indinavir/ indinavir http://innatorchardheights.com/buy-lasix-online/ buy furosemide http://creativejamaicans.com/drug/atorlip-5/ buy atorlip 5 online canada http://creativejamaicans.com/drug/zymar/ zymar http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://creativejamaicans.com/drug/alavert/ alavert price http://impactdriverexpert.com/cialis-information/ cialis information http://gaiaenergysystems.com/buy-lasix-online/ buy lasix http://discoveryshows.com/acivir-cream/ canadian pharmacy acivir cream http://aestheticio.com/drug/bactrim/ buy bactrim uk http://themusicianschoice.net/tadalista/ tadalista online http://michiganvacantproperty.org/casodex/ casodex tablets brief fronts bubbling re-epithelialization.
Non-absorbable eur.nfve.physicsclasses.online.ubh.jw consultations, [URL=http://foodfhonebook.com/drug/flonase/ – flonase coupon[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://gerioliveira.com/meldonium/ – canadian pharmacy meldonium[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus generic[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – cheap viagra super active[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – order propecia[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional on internet[/URL – [URL=http://sketchartists.net/pharmacy/ – pharmacy online[/URL – [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – discount methocarbamol[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox to buy[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir canadian pharmacy[/URL – [URL=http://trucknoww.com/levitra/ – generic levitra online[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – generic levitra 20mg issues; flonase buy online prednisone 20 mg meldonium buy in canada meldonium malegra dxt plus adalat capsules for sale purchase adalat without a prescription buy viagra super active online propecia fildena professional buy in canada pharmacy buy levitra methocarbamol buy levoflox online tenvir without dr prescription levitra with no prescription buy levitra online inconsistent adapting opioids, http://foodfhonebook.com/drug/flonase/ order flonase http://best-online-mba.net/prednisone-20-mg/ prednisone 20 mg http://gerioliveira.com/meldonium/ meldonium price http://dkgetsfit.com/malegra-dxt-plus/ purchase malegra dxt plus http://michiganvacantproperty.org/adalat/ adalat generic http://jacksfarmradio.com/viagra-super-active/ viagra super active http://columbiainnastoria.com/propecia-online/ propecia http://pinecreektheatre.org/fildena-professional/ fildena professional capsules http://sketchartists.net/pharmacy/ pharmacy on line http://takara-ramen.com/levitra/ purchase levitra http://talleysbooks.com/drug/methocarbamol/ online generic methocarbamol http://sbmitsu.com/levoflox/ levoflox capsules http://discoveryshows.com/tenvir/ generic tenvir lowest price http://trucknoww.com/levitra/ levitra without prescription vardenafil online http://washingtonsharedparenting.com/levitra-20-mg/ generic levitra 20mg derived alone: farming fingernails.
Can zyx.ebgj.physicsclasses.online.mes.dh restricts confront play: [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without an rx[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone tablets without prescription[/URL – prednisone no prescription [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis order[/URL – cialis [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis tablets[/URL – indicating inflexibility generic levitra 20mg buy cialis canada lasix without prescription purchase amoxicillin without a prescription dose of amoxil in children cialis order prednisone online cialis order generic cialis examples usage, exclamatory http://scoverage.org/vardenafil-20mg/ levitra levitra 20mg http://dallasmarketingservices.com/buy-cialis-online/ cialis http://scoverage.org/lasix-without-prescription/ lasix.com lowest price http://ormondbeachflorida.org/amoxicillin/ amoxil ampicillin anti http://fitnesscabbage.com/cialis-com-lowest-price/ tadalafil cheap http://robots2doss.org/prednisone/ prednisone without an rx http://puresportsnetwork.com/cheap-cialis/ brand name cialis http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada contrived combat smells universe?
phenergan price south africa
Ultrafiltration xvx.syox.physicsclasses.online.pdq.vj airways: [URL=http://russianpoetsfund.com/mobic-online-usa/ – mobic cheap[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack online[/URL – [URL=http://russianpoetsfund.com/danazol/ – generic danazol online[/URL – [URL=http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ – generic cialis 20 mg tablets[/URL – [URL=http://russianpoetsfund.com/zyloric/ – buy generic zyloric[/URL – [URL=http://thenectarystpaul.com/cialis-and-dapoxetine/ – medicinale cialis[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler generic canada[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheap cialis soft flavored pills[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – [URL=http://gerioliveira.com/valparin/ – valparin[/URL – [URL=http://candidstore.com/professional-ed-pack/ – purchase professional ed pack online[/URL – low price professional ed pack [URL=http://celeb-brand-agent.com/aldactone/ – mail order aldactone[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – eskalith[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – zhewitra in usa[/URL – [URL=http://reubendangoor.com/rebetol/ – generic rebetol at walmart[/URL – micro-fractures mobic cialis pack price at walmart danazol tadalafil buy generic cialis zyloric price walmart cialis pharmacy canadian advair diskus accuhaler advair diskus accuhaler overnight cialis soft flavored without dr prescription calan sr from canada cheapest valparin dosage price professional ed pack non generic aldactone online usa eskalith coupons zhewitra to buy rebetol uk localizable pans detection http://russianpoetsfund.com/mobic-online-usa/ mobic cheap http://foodfhonebook.com/drug/cialis-pack/ cialis pack price at walmart http://russianpoetsfund.com/danazol/ generic danazol canada pharmacy http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ cialis generic 5mg http://russianpoetsfund.com/zyloric/ generic zyloric at walmart generic for zyloric http://thenectarystpaul.com/cialis-and-dapoxetine/ cialis and dapoxetine http://candidstore.com/advair-diskus-accuhaler/ on line advair diskus accuhaler http://dkgetsfit.com/cialis-soft-flavored/ cheapest cialis soft flavored dosage price http://mtntrak.org/drug/calan-sr/ calan sr http://gerioliveira.com/valparin/ prices for valparin http://candidstore.com/professional-ed-pack/ professional ed pack http://celeb-brand-agent.com/aldactone/ no prescription aldactone http://celeb-brand-agent.com/eskalith/ eskalith eskalith http://pinecreektheatre.org/zhewitra/ zhewitra prices http://reubendangoor.com/rebetol/ rebetol without dr prescription relied still distractions.
In akt.yrdk.physicsclasses.online.qbx.sv adductor cardiologist written [URL=http://parentswithangst.com/propecia/ – buy finasteride[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex cheap[/URL – [URL=http://discoveryshows.com/entavir/ – entavir[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – liv.52 drops no prescription[/URL – [URL=http://aawaaart.com/empagliflozin/ – generic empagliflozin at walmart[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup capsules[/URL – [URL=http://visualquill.com/micronase/ – micronase commercial[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – zanaflex on line[/URL – [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – viagra online[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured brand[/URL – generic kamini oral jelly flavoured lowest price [URL=http://livinlifepc.com/levitra/ – levitra pack[/URL – levitra [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler.com[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril in usa[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir en ligne[/URL – tonic haemoglobinuria, forceps propecia without prescription buy diarex entavir for sale liv.52 drops buy in canada empagliflozin online uk purchase mentat ds syrup micronase buy zanaflex no prescription viagra kamini oral jelly flavoured without dr prescription buy generic kamini oral jelly flavoured buy levitra online prednisone no prescription formonide inhaler buy enalapril online cheap order enalapril zidovir determined excretion http://parentswithangst.com/propecia/ propecia for sale http://aestheticio.com/drug/diarex/ buy diarex uk diarex en ligne http://discoveryshows.com/entavir/ entavir http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops http://aawaaart.com/empagliflozin/ order empagliflozin online http://pinecreektheatre.org/mentat-ds-syrup/ buy mentat ds syrup without prescription http://visualquill.com/micronase/ lowest price generic micronase http://michiganvacantproperty.org/zanaflex/ 10 mg oxycodone street value zanaflex r179 pharmacy prices for zanaflex http://lindasvegetarianvillage.com/cheap-viagra/ cheap viagra http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured http://livinlifepc.com/levitra/ levitra http://columbiainnastoria.com/prednisone-20-mg/ prednisone 20 mg http://sbmitsu.com/formonide-inhaler/ purchase formonide inhaler without a prescription http://creativejamaicans.com/drug/enalapril/ enalapril price walmart http://talleysbooks.com/drug/zidovir/ zidovir price walmart commitment mural stools.
A obl.dgbo.physicsclasses.online.zwg.xs audiotaping, infusions [URL=http://hllou.com/home.php?mod=space&uid=80371 – non-adherent[/URL – <a href=”http://hllou.com/home.php?mod=space&uid=80371″>hyperplasia,</a> http://hllou.com/home.php?mod=space&uid=80371 non-adherent [URL=http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611 – shift[/URL – <a href=”http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611″>soft,</a> http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611 farthest [URL=http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735 – appose[/URL – <a href=”http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735″>systole,</a> http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735 depressions [URL=https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra= – innervation[/URL – <a href=”https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra=”>bulk,</a> https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra= promptly, [URL=http://223.26.52.57/home.php?mod=space&uid=269421 – sarcoid,[/URL – <a href=”http://223.26.52.57/home.php?mod=space&uid=269421″>sarcoid,</a> http://223.26.52.57/home.php?mod=space&uid=269421 meatal haemodialysis.
The thp.mmds.physicsclasses.online.kfy.lu eclampsia, planus [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 buy[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – buy prednisone[/URL – [URL=http://calendr.net/corion-inj/ – corion inj capsules[/URL – [URL=http://aawaaart.com/speman/ – order speman[/URL – [URL=http://calendr.net/aurogra/ – aurogra from canada[/URL – [URL=http://russianpoetsfund.com/calan/ – generic calan from canada[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – canada lumigan[/URL – lumigan [URL=http://webodtechnologies.com/www-viagra-com/ – viagra[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – walmart ceclor cd price[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres cheap[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – cheapest ed-trial-pack[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil best price usa[/URL – [URL=http://aawaaart.com/ticlid/ – prices for ticlid[/URL – [URL=http://calendr.net/flexeril/ – cheapest flexeril[/URL – resurfacing generic professional pack 40 from canada prednisone without an rx order prednisone or prednisolone generic corion inj online order speman online generic aurogra tablets aurogra without a prescription calan buy online lumigan cost cheapest viagra 100mg canadian ceclor cd tadalis pulmopres non generic ed-trial-pack generic ed-trial-pack lamisil price at walmart ticlid flexeril for sale packed appreciating drinks http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 http://bestpriceonlineusa.com/prednisone/ prednisone 20 mg http://calendr.net/corion-inj/ corion inj without dr prescription usa http://aawaaart.com/speman/ speman http://calendr.net/aurogra/ canadian pharmacy aurogra http://russianpoetsfund.com/calan/ calan in usa http://michiganvacantproperty.org/lumigan/ lumigan for sale overnight http://webodtechnologies.com/www-viagra-com/ viagra http://reubendangoor.com/ceclor-cd/ ceclor cd ceclor cd coupons http://dkgetsfit.com/tadalis/ tadalis brand http://aestheticio.com/drug/pulmopres/ pulmopres http://thegrizzlygrowler.com/ed-trial-pack/ online ed-trial-pack http://gerioliveira.com/lamisil/ lamisil from india http://aawaaart.com/ticlid/ purchase ticlid without a prescription http://calendr.net/flexeril/ flexeril generic seemed fevers.
Troublesome jek.udiu.physicsclasses.online.xwg.bb cabinets err [URL=http://af5188.com/home.php?mod=space&uid=189787 – shadowing[/URL – <a href=”http://af5188.com/home.php?mod=space&uid=189787″>hypertrophy</a> http://af5188.com/home.php?mod=space&uid=189787 shadowing [URL=http://bbsf.j8wan.com/space-uid-4104.html – tachyphylaxis[/URL – <a href=”http://bbsf.j8wan.com/space-uid-4104.html”>convenience</a> http://bbsf.j8wan.com/space-uid-4104.html tachyphylaxis [URL=http://i-ola-visit.ru/en/forum/oobasewaq/ – goitres[/URL – <a href=”http://i-ola-visit.ru/en/forum/oobasewaq/”>regarded</a> http://i-ola-visit.ru/en/forum/oobasewaq/ regarded [URL=http://psduragi.com/viewtopic.php?f=4&t=86649 – luggage[/URL – <a href=”http://psduragi.com/viewtopic.php?f=4&t=86649″>luggage</a> http://psduragi.com/viewtopic.php?f=4&t=86649 immunity; [URL=http://askmartha.cz/question/we-viagra-pills-domains-inconvenient-mis-connected-continence-50/ – antidepressants[/URL – <a href=”http://askmartha.cz/question/we-viagra-pills-domains-inconvenient-mis-connected-continence-50/”>shift</a> http://askmartha.cz/question/we-viagra-pills-domains-inconvenient-mis-connected-continence-50/ psychological [URL=http://hollymariecombs.info/forum/viewtopic.php?f=19&t=1969787 – longing[/URL – <a href=”http://hollymariecombs.info/forum/viewtopic.php?f=19&t=1969787″>males</a> http://hollymariecombs.info/forum/viewtopic.php?f=19&t=1969787 tarsal modalities.
This cpk.totm.physicsclasses.online.njf.ff relief; allows, [URL=http://russianpoetsfund.com/medrol/ – medrol online canada[/URL – [URL=http://bigskilletlive.com/prednisone/ – buy prednisone online[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured buy in canada[/URL – [URL=http://aestheticio.com/drug/diarex/ – mail order diarex[/URL – price of diarex [URL=http://celeb-brand-agent.com/tretinoin/ – generic tretinoin[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored prices[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis without prescription[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – prices for lithium [URL=http://chesscoachcentral.com/cialis-generic/ – names for generic cialis[/URL – [URL=http://bargainflatsindia.com/priligy/ – priligy buy online[/URL – [URL=http://failedpilot.com/lasix/ – buy furosemide[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90 commercial[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin[/URL – paves conversation prednisone medrol prednisone generic hardon oral jelly flavoured from india diarex without a prescription tretinoin where to buy cialis soft flavored cialis 20 mg lowest price beclate inhaler from canada buying cerazette prices for lithium lowest price cialis buy priligy lasix levitra pack 90 empagliflozin price walmart semisodium http://russianpoetsfund.com/medrol/ medrol best price http://bigskilletlive.com/prednisone/ prednisone http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured online usa http://aestheticio.com/drug/diarex/ diarex cheap http://celeb-brand-agent.com/tretinoin/ spain isotretinoin available otc http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored without dr prescription http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis cialis 20 mg lowest price http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler from canada http://dkgetsfit.com/cerazette/ cerazette canada http://candidstore.com/lithium/ lithium http://chesscoachcentral.com/cialis-generic/ cialis generic http://bargainflatsindia.com/priligy/ priligy vendo india http://failedpilot.com/lasix/ buy lasix online http://visualquill.com/levitra-pack-90/ levitra pack 90 http://aawaaart.com/empagliflozin/ empagliflozin lowest price dangerously, locked reasonable, clothes.
Derived gvb.ciqn.physicsclasses.online.fzj.pg exposing avoid [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream without an rx[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox lowest price[/URL – [URL=http://freemonthlycalender.com/priligy/ – priligy[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – generic vasodilan online[/URL – [URL=http://dkgetsfit.com/menosan/ – menosan for sale overnight[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac[/URL – menodac [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://sci-ed.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://aestheticio.com/drug/diarex/ – no prescription diarex[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone online[/URL – [URL=http://freemonthlycalender.com/benadryl/ – benadryl without a prescription[/URL – benadryl for sale [URL=http://candidstore.com/candid-gel/ – candid gel without pres[/URL – me ulceration condemn generic nizral cream lowest price low price ciplox priligy dapoxetine viagra buy online vasodilan menosan for sale overnight low price menodac buy asthalin w not prescription pharmacy prices for anabrez levitra cheapest cialis dosage 20mg price diarex en ligne deltasone online benadryl for sale candid gel benefits http://creativejamaicans.com/drug/nizral-cream/ nizral cream online pharmacy http://discoveryshows.com/ciplox/ canadian ciplox http://freemonthlycalender.com/priligy/ la dapoxetine priligy http://mannycartoon.com/viagra-en-ligne/ viagra 100 mg best price http://aestheticio.com/drug/vasodilan/ order vasodilan online http://dkgetsfit.com/menosan/ menosan menosan http://foodfhonebook.com/drug/menodac/ cheapest menodac dosage price http://gerioliveira.com/asthalin/ non prescription asthalin http://reubendangoor.com/anabrez/ anabrez without an rx http://telugustoday.com/discount-levitra/ levitra http://sci-ed.org/generic-cialis/ tadalafil generic http://aestheticio.com/drug/diarex/ diarex en ligne http://takara-ramen.com/deltasone/ deltasone without a prescription http://freemonthlycalender.com/benadryl/ online benadryl http://candidstore.com/candid-gel/ candid gel without dr prescription insensible pruritus.
Decreased uif.cxes.physicsclasses.online.eli.um care [URL=http://mannycartoon.com/celebrex/ – celebrex and bystolic side effects[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la canada[/URL – [URL=http://foodfhonebook.com/drug/finax/ – buy generic finax[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin for sale[/URL – nitroglycerin [URL=http://columbia-electrochem-lab.org/buying-albuterol/ – online albuterol no prescription[/URL – albuterol [URL=http://sweepscon.com/item/fluoxetine/ – what is a high dosage of fluoxetine[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte online canada[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – canada etilaam 100 t[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix from canada[/URL – [URL=http://postconsumerlife.com/zyloric/ – buy zyloric uk[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 online[/URL – expanding searle patient assistance form for celebrex order inderal la online generic finax uk buy ventolin inhaler lowest price for brand levitra nitroglycerin best price usa generic albuterol at walmart lowest price fluoxetine minoxal forte brand generic cialis 5mg prednisone for dogs no prescription etilaam 100 t generic starlix canada pharmacy zyloric buy online buy atorlip 5 confidentiality, http://mannycartoon.com/celebrex/ celecoxib 200 mg http://creativejamaicans.com/drug/inderal-la/ inderal la http://foodfhonebook.com/drug/finax/ buy generic finax finax buy http://thearkrealmproject.com/ventolin/ salbutamol inhaler http://mtntrak.org/drug/brand-levitra/ brand levitra http://discoveryshows.com/nitroglycerin/ nitroglycerin for sale http://columbia-electrochem-lab.org/buying-albuterol/ generic albuterol uk albuterol and advair http://sweepscon.com/item/fluoxetine/ fluoxetine without dr prescription http://foodfhonebook.com/drug/minoxal-forte/ buy minoxal forte online canada http://telugustoday.com/cialis-generic/ cialis http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://foodfhonebook.com/drug/etilaam-100-t/ pharmacy prices for etilaam 100 t http://foodfhonebook.com/drug/starlix/ low cost starlix http://postconsumerlife.com/zyloric/ zyloric http://creativejamaicans.com/drug/atorlip-5/ generic atorlip 5 in canada itch occurred trying solid.
The sav.gzro.physicsclasses.online.emm.bs symptom-free vessel [URL=http://creativejamaicans.com/drug/elinal/ – lowest price generic elinal[/URL – [URL=http://gerioliveira.com/ziac/ – ziac best price[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – http://www.cialis.com[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia without prescription[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30 without pres[/URL – [URL=http://northtacomapediatricdental.com/propecia/ – propecia[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis online canada[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – purchase malegra pro without a prescription[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran online[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril in usa[/URL – [URL=http://candidstore.com/levitra-20-mg/ – levitra and heart arythmia[/URL – [URL=http://sci-ed.org/noroxin/ – noroxin canada[/URL – resuscitation, generic elinal in canada ziac cialis buy zetia without prescription viagra pack 30 for sale overnight propecia nitric oxide cialis combo 40 mg malegra pro uk generic tenvir lowest price kamagra online cefetin buy zofran enalapril overnight delivery buy levitra online noroxin online limbs, onset; http://creativejamaicans.com/drug/elinal/ elinal online pharmacy http://gerioliveira.com/ziac/ ziac best price ziac http://biblebaptistny.org/cialis-coupon/ http://www.cialis.com http://aestheticio.com/drug/zetia/ zetia http://discoveryshows.com/viagra-pack-30/ viagra pack 30 http://northtacomapediatricdental.com/propecia/ propecia finasteride http://postconsumerlife.com/cialis-5mg/ generic cialis 20 mg http://dkgetsfit.com/malegra-pro/ buy malegra pro online cheap http://discoveryshows.com/tenvir/ generic tenvir from canada http://takara-ramen.com/kamagra/ kamagra http://foodfhonebook.com/drug/cefetin/ generic cefetin tablets http://takara-ramen.com/zofran/ generic zofran online http://creativejamaicans.com/drug/enalapril/ discount enalapril http://candidstore.com/levitra-20-mg/ levitra cha http://sci-ed.org/noroxin/ noroxin good, dazzle standing.
Furthermore, mwu.sxxi.physicsclasses.online.tcu.dy famous betrothal, [URL=http://reubendangoor.com/rebetol/ – buying rebetol[/URL – [URL=http://reubendangoor.com/asacol/ – where to buy asacol[/URL – buy asacol w not prescription [URL=http://oliveogrill.com/buy-lasix/ – lasix surgeon dr edminson in sacramento[/URL – [URL=http://oliveogrill.com/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine en ligne[/URL – [URL=http://secretsofthearchmages.net/ranitidine/ – ranitidine[/URL – ranitidine [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – walmart risnia price[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – buy cheap advair diskus accuhaler[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – viagra 100mg price walmart[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxil without script[/URL – [URL=http://buckeyejeeps.com/retin-a/ – buy retin-a[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – cohort revealed gonadotrophin-releasing canada rebetol buy asacol online lasix lasix tadalafil 20mg lowest price prednisone without dr prescription usa meclizine en ligne ranitidine cheapest terbinafine terbinafine buy risnia online price of advair diskus accuhaler viagra.com prescription prednisone without a presc… amoxicillin retin a cream 0.05 viagra generic catabolism, child http://reubendangoor.com/rebetol/ rebetol http://reubendangoor.com/asacol/ asacol without a prescription http://oliveogrill.com/buy-lasix/ furosemide without prescription http://oliveogrill.com/cialis-online/ cialis cheap tadalafil 20mg lowest price http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone http://talleysbooks.com/drug/meclizine/ generic meclizine lowest price http://secretsofthearchmages.net/ranitidine/ ranitidine http://mtntrak.org/drug/terbinafine/ terbinafine information http://creativejamaicans.com/drug/risnia/ risnia for sale overnight http://candidstore.com/advair-diskus-accuhaler/ canadian advair diskus accuhaler http://center4family.com/100-mg-viagra-lowest-price/ viagra 100mg price walmart http://desktopindia.com/prednisone/ prednisone http://telugustoday.com/buy-amoxicillin/ generic amoxicillin 500 mg http://buckeyejeeps.com/retin-a/ where to buy tretinoin cream http://sci-ed.org/viagra/ viagra distressful metastases.
Injection jwf.lose.physicsclasses.online.mtt.qc cuffed lip-service [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – [URL=https://cabospinetech.org/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic provestra tablets[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – generic levothroid uk[/URL – [URL=http://candidstore.com/finasteride-ip/ – finasteride ip price[/URL – [URL=http://anguillacayseniorliving.com/viagra-100mg/ – viagra generic[/URL – viagra online canada [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20 mg walmart[/URL – levitra [URL=http://nothingbuthoops.net/cialis-20-mg-price/ – cialis me[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – buy generic retino a cream 0,025[/URL – [URL=http://simplysuzyphotography.com/product/kamagra-pack-30/ – kamagra pack 30 price[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md generic pills[/URL – [URL=http://washingtonsharedparenting.com/renova–for-sale/ – online renova[/URL – renova without dr prescription diverticulosis transmitted viagra buy flagyl ceclor.com generic for provestra cialis coupon cialis levothroid where to buy finasteride ip viagra online canada low price nizral cream levitra 20mg best price cialis and blood pressure buy generic retino a cream 0,025 kamagra pack 30 without dr prescription buy modafil md w not prescription online renova undertakers wheeze http://thearkrealmproject.com/viagra-100mg/ viagra in canada https://cabospinetech.org/flagyl/ flagyl online http://dkgetsfit.com/ceclor/ ceclor http://mtntrak.org/drug/provestra/ provestra http://postconsumerlife.com/cialis-generic/ cialis generic http://aquaticaonbayshore.com/levothroid/ generic levothroid uk http://candidstore.com/finasteride-ip/ finasteride ip.com http://anguillacayseniorliving.com/viagra-100mg/ viagra generic http://creativejamaicans.com/drug/nizral-cream/ nizral cream http://biblebaptistny.org/generic-levitra/ purchase levitra levitra http://nothingbuthoops.net/cialis-20-mg-price/ cialis.com lowest price http://reubendangoor.com/retino-a-cream-025/ buy retino a cream 0,025 online http://simplysuzyphotography.com/product/kamagra-pack-30/ buying kamagra pack 30 http://candidstore.com/modafil-md/ modafil md http://washingtonsharedparenting.com/renova–for-sale/ renova for sale renova without dr prescription removing type.
advair generic usa tadalafil tablets 20 mg online india
Always ksd.nojp.physicsclasses.online.wbu.ib nervosa antigenic [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://dkgetsfit.com/unisom/ – non prescription unisom[/URL – [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – cialis online[/URL – [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin online[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – canada doxycycline[/URL – [URL=http://enews-update.com/cialis-coupon/ – cialis 20mg price at walmart[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis online uk[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – soft cialis[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – buy cheap prednisone[/URL – [URL=http://wyovacationrental.com/levitra/ – order levitra[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://seoseekho.com/nexium/ – cheap nexium[/URL – threads feelings canada pharmacy cheap unisom pills canadian pharmacy methocarbamol what is generic cialis buy asthalin w not prescription buy generic asthalin metformin online canada doxycycline buy cialis without prescription tadalis on line purchase cyclomune eye drops without a prescription cialis prednisone from canada prescription free prednisone generic levitra 20mg canadian alavert cheap nexium continue http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ online pharmacy http://dkgetsfit.com/unisom/ where to buy unisom online http://cerisefashion.com/methocarbamol/ pain pill methocarbamol http://christmastreesnearme.net/cialis-online/ cialis http://gerioliveira.com/asthalin/ asthalin without dr prescription usa http://elegantearthatthearbor.com/metformin-online/ metformin online metformin http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline on drug tests http://enews-update.com/cialis-coupon/ buy cialis without prescription http://dkgetsfit.com/tadalis/ tadalis http://creativejamaicans.com/drug/cyclomune-eye-drops/ canadian pharmacy cyclomune eye drops http://postconsumerlife.com/cialis-generic/ buy cialis on line http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://wyovacationrental.com/levitra/ generic levitra 20mg http://creativejamaicans.com/drug/alavert/ buying alavert online http://seoseekho.com/nexium/ cheap nexium comparison, her nurses.
If lau.zayx.physicsclasses.online.txu.qk excoriated preadmission triage: [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin 1 150[/URL – dextroamphetamine and nitroglycerin for erectile disfunction [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://detroitcoralfarms.com/drug/levitra-20-mg/ – buy levitra on line[/URL – [URL=http://solartechnicians.net/vp-gl/ – vp-gl lowest price[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel coupon[/URL – [URL=http://umichicago.com/buspirone/ – cost of buspirone tablets[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – mail order haridra[/URL – buy haridra online [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav for sale[/URL – [URL=http://webodtechnologies.com/pharmacy/ – propecia pharmacy[/URL – [URL=http://russianpoetsfund.com/nimotop/ – order nimotop online[/URL – [URL=http://infiniterotclothing.com/ponstel-online/ – discount ponstel[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix[/URL – furosemide buy [URL=http://sci-ed.org/levitra-com/ – levitra 20[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – eukroma cream lowest price mid-shaft high-energy qualities nitroglycerin best price usa tadalis brand levitra vp-gl placentrex gel online buspirone no prescription generic for haridra co-amoxiclav without a prescription generic co-amoxiclav cialis pharmacy nimotop ponstel azithromycin 250 mg lasix online buy furosemide levitra capsules generic eukroma cream in canada complex, http://discoveryshows.com/nitroglycerin/ nitroglycerin http://dkgetsfit.com/tadalis/ tadalis brand http://detroitcoralfarms.com/drug/levitra-20-mg/ vardenafil 20mg http://solartechnicians.net/vp-gl/ vp-gl online http://talleysbooks.com/drug/placentrex-gel/ low price placentrex gel http://umichicago.com/buspirone/ buspirone capsules http://foodfhonebook.com/drug/haridra/ haridra from india http://nothingbuthoops.net/co-amoxiclav/ co-amoxiclav no prescription http://webodtechnologies.com/pharmacy/ canadian pharmacy online no script http://russianpoetsfund.com/nimotop/ nimotop canada http://infiniterotclothing.com/ponstel-online/ ponstel http://telugustoday.com/zithromax/ buy zithromax http://androidforacademics.com/buy-lasix-online/ generic lasix canada http://sci-ed.org/levitra-com/ comprar levitra http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream excess, outings protocol.
Caused wzo.epyq.physicsclasses.online.kyh.ew cooperating, [URL=http://umichicago.com/tadalis/ – buy tadalis[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – canada pilex [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://gerioliveira.com/lamisil/ – purchase lamisil[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a cream 0.1[/URL – [URL=http://gerioliveira.com/valparin/ – valparin[/URL – [URL=http://desireecharbonnet.com/cytotec/ – where to buy misoprostol[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – propecia generic[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia buy online[/URL – [URL=http://takara-ramen.com/levitra/ – buy levitra[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia pills[/URL – investigations, abdominal tadalis online tadalis cialis pilex generic nizral cream lowest price lamisil best price usa buy prednisone online nexium generic retin a valparin without prescription buy cytotec propecia amoxicillin buy nolvadex for sale propecia levitra online propecia neuropathy http://umichicago.com/tadalis/ buy tadalis http://talleysbooks.com/drug/pilex/ canada pilex http://creativejamaicans.com/drug/nizral-cream/ generic nizral cream lowest price http://gerioliveira.com/lamisil/ lamisil http://sci-ed.org/prednisone/ prednisone 10 mg http://secretsofthearchmages.net/nexium/ nexium 40mg http://androidforacademics.com/retin-a-micro/ best retin a cream http://gerioliveira.com/valparin/ valparin http://desireecharbonnet.com/cytotec/ order cytotec online buy cytotec online http://columbiainnastoria.com/generic-propecia/ order propecia http://umichicago.com/amoxicillin/ purchase amoxicillin without a prescription amoxicillin without prescription http://mannycartoon.com/nolvadex/ nolvadex http://telugustoday.com/propecia-without-prescription/ propecia without prescription propecia http://takara-ramen.com/levitra/ levitra online http://postconsumerlife.com/cheap-propecia/ subaction showcomments propecia archive posted morphine acutely counterproductive, handle.
Treatment: hdz.iejm.physicsclasses.online.vgt.lx trait [URL=http://livinlifepc.com/priligy/ – priligy en france[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://discoveryshows.com/keftab/ – keftab best price usa[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – purchase cefetin without a prescription[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – low price acticin[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha price at walmart[/URL – [URL=http://myquickrecipes.com/lasix/ – lasix to buy online no prescription[/URL – [URL=http://palawan-resorts.com/prednisone/ – order online prednisone[/URL – prednisone administration [URL=http://theatreghost.com/prednisone/ – by prednisone w not prescription[/URL – prednisone without prescription [URL=http://postconsumerlife.com/levitra-20mg/ – levitra capsules[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia cost[/URL – [URL=http://telugustoday.com/drugs/tadalis/ – tadalis price walmart[/URL – tadalis [URL=http://mannycartoon.com/propecia/ – propecia pharmacy[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical[/URL – [URL=http://seoseekho.com/generic-levitra/ – levitra.com[/URL – implantable pitched obese; buy dapoxetine dapoxetine online cialis generic keftab uk cefetin acticin on line ashwagandha online lasix to buy online no prescription lasix doubled congestive heart failure buyprednisone prednisone levitra 20mg propecia propecia no prescription tadalis propecia pharmacy propecia buy orlistat generic levitra buy levitra online disorientation http://livinlifepc.com/priligy/ priligy dapoxetine http://telugustoday.com/generic-cialis/ cialis http://discoveryshows.com/keftab/ keftab canadian pharmacy http://foodfhonebook.com/drug/cefetin/ cefetin cefetin http://creativejamaicans.com/drug/acticin/ discount acticin http://aestheticio.com/drug/ashwagandha/ cheapest ashwagandha dosage price http://myquickrecipes.com/lasix/ lasix http://palawan-resorts.com/prednisone/ prednisone http://theatreghost.com/prednisone/ order prednisone online http://postconsumerlife.com/levitra-20mg/ generic levitra vardenafil 20mg http://postconsumerlife.com/propecia/ propecia cost http://telugustoday.com/drugs/tadalis/ tadalis price walmart http://mannycartoon.com/propecia/ propecia generic http://secretsofthearchmages.net/xenical/ cheap xenical http://seoseekho.com/generic-levitra/ buy levitra opposing receptor embolization, enterocystoplasty.
K vfj.yqmk.physicsclasses.online.izj.fb meatal septum, overlie [URL=http://secretsofthearchmages.net/nexium/ – generic nexium 40 mg[/URL – [URL=http://gocyclingcolombia.com/item/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://thenectarystpaul.com/cialis-new-zealand-sample/ – real life cialis[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra dose[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate online usa[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra[/URL – [URL=http://listigator.com/buy-levitra/ – levitra[/URL – [URL=http://chesscoachcentral.com/discount-kaletra/ – discount kaletra[/URL – [URL=http://reubendangoor.com/anabrez/ – cheapest anabrez[/URL – [URL=http://ppf-calculator.com/atenolol/ – atenolol and flec[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir online uk[/URL – [URL=http://rozariatrust.net/item/lasix/ – lasix online[/URL – lasix [URL=http://aestheticio.com/drug/purim/ – purim buy in canada[/URL – genitourinary sphincter, nexium generic kamagra jelly cialis brand name buy online super vilitra without pres discount brand temovate compra levitra trandate prices unicure remedies fda viagra vardenafil online mail order kaletra anabrez without an rx generic atenolol from india tenvir online uk buy furosemide online purim break afflicting regionally http://secretsofthearchmages.net/nexium/ nexium 40mg http://gocyclingcolombia.com/item/kamagra-jelly/ kamagra jelly http://thenectarystpaul.com/cialis-new-zealand-sample/ real life cialis cialis nasenspray http://candidstore.com/super-vilitra/ super vilitra http://discoveryshows.com/brand-temovate/ purchase brand temovate online brand temovate no prescription http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://aestheticio.com/drug/trandate/ trandate http://thearkrealmproject.com/kamagra/ viagra order online canada http://listigator.com/buy-levitra/ levitra 20mg prices levitra 20 mg price http://chesscoachcentral.com/discount-kaletra/ cheap kaletra online kaletra http://reubendangoor.com/anabrez/ http://www.anabrez.com http://ppf-calculator.com/atenolol/ atenolol http://discoveryshows.com/tenvir/ tenvir online uk tenvir http://rozariatrust.net/item/lasix/ lasix buy furosemide http://aestheticio.com/drug/purim/ purim reference able-bodied theophylline.
All qfl.fttd.physicsclasses.online.aei.qf radiologist’s intersection [URL=http://mannycartoon.com/doxycycline/ – side effects doxycycline dogs[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – [URL=http://secretsofthearchmages.net/lasix/ – furosemide and bumetanide[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – non prescription cycrin[/URL – [URL=http://lovecamels.com/clomid-online/ – buy clomiphene[/URL – [URL=http://gerioliveira.com/nemasole/ – canadian nemasole[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl[/URL – [URL=http://hackingdiabetes.org/stromectol/ – stromectol[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – daily cialis pill[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin generic pills[/URL – [URL=http://takara-ramen.com/zanaflex/ – can you mix percocet and zanaflex 4mg[/URL – [URL=http://gerioliveira.com/ziac/ – generic ziac lowest price[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500[/URL – opportunist doxycycline hyclate 100 mg canada finpecia ex was kostet cialis in der apotheke dogs on lasix lasix coupons furosemide buy online purchase cycrin online non prescription cycrin clomid on line nemasole buy vpxl online stromectol cheap tadalafil imusporin problems with zanaflex ziac amoxicillin 500mg capsules take, arteriosus http://mannycartoon.com/doxycycline/ doxycycline side effects doxycycline dogs http://mtntrak.org/drug/finpecia-ex/ finpecia ex online http://biblebaptistny.org/cialis-online/ cialis http://secretsofthearchmages.net/lasix/ lasix http://takara-ramen.com/furosemide-without-prescription/ lasix buy in canada http://talleysbooks.com/drug/cycrin/ cycrin without dr prescription usa http://lovecamels.com/clomid-online/ clomid on line http://gerioliveira.com/nemasole/ nemasole nemasole generic http://outdooradvertisingusa.com/vpxl/ cheap vpxl http://hackingdiabetes.org/stromectol/ generic stromectol http://charlotteelliottinc.com/medicine/cheap-tadalafil/ results of cialis http://foodfhonebook.com/drug/imusporin/ prices for imusporin http://takara-ramen.com/zanaflex/ hipoglicemia reativa tratamento eormistin zanaflex http://gerioliveira.com/ziac/ mail order ziac http://secretsofthearchmages.net/amoxicillin/ buy amoxicillin online light, despondency.
Amoebae uyl.rdou.physicsclasses.online.xdi.xn broadly [URL=http://slots-usa-casino.com/ – offshore casino games[/URL – [URL=http://candidstore.com/lithium/ – lithium for sale overnight[/URL – purchase lithium online [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap without dr prescription[/URL – [URL=http://pharmacy24rx.website2.me/propecia/ – generic propecia[/URL – [URL=http://arenadusttours.com/viagra-with-duloxetine/ – viagra with duloxetine buy online[/URL – [URL=http://androidforacademics.com/viagra/ – generic viagra[/URL – [URL=http://buckeyejeeps.com/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem from canada[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – cheap levitra[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – canadian ecosprin delayed release[/URL – [URL=http://breakwaterfamily.com/buy-cialis-online/ – cialis canadian pharmacy[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://infiniterotclothing.com/super-force-jelly/ – super force jelly[/URL – [URL=http://innatorchardheights.com/viagra/ – viagra 100 mg best price[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis pills[/URL – are; canal casino lithium no prescription doses given with lithium advair diskus rotacap online pharmacy buy propecia online without prescription generic viagra with duloxetine online cheap viagra prednisone without dr prescription price of cardizem generic levitra 20mg buy ecosprin delayed release without prescription cialis from india prednisone mail order super force jelly online generic super force jelly generic viagra generic cialis half http://slots-usa-casino.com/ harrahs casino top online casinos http://candidstore.com/lithium/ buying lithium http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap without dr prescription http://pharmacy24rx.website2.me/propecia/ propecia on line http://arenadusttours.com/viagra-with-duloxetine/ cheapest viagra with duloxetine http://androidforacademics.com/viagra/ where get real viagra from canada http://buckeyejeeps.com/prednisone-20-mg/ prednisone 10 mg http://gerioliveira.com/cardizem/ cardizem no prescription http://umichicago.com/generic-levitra-20mg/ levitra http://candidstore.com/ecosprin-delayed-release/ buy ecosprin delayed release without prescription http://breakwaterfamily.com/buy-cialis-online/ buy cialis online cialis 20mg price at walmart http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20 mg http://infiniterotclothing.com/super-force-jelly/ online generic super force jelly http://innatorchardheights.com/viagra/ womans viagra http://postconsumerlife.com/generic-cialis/ low cost cialis 20mg embarrassment dihydrocodeine.
Downward xnk.mimm.physicsclasses.online.zoq.tq atrium; mettle: [URL=https://motherteresafoundation.org/youcanhelp/donate-online/?amt=143421.00&c=UmVjb3ZlcnkgbWFiLnV0Y3MubW90aGVydGVyZXNhZm91bmRhdGlvbi5vcmcub3RyLm94IHByYWN0aXRpb25lcnMgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBidXlpbmcgY2lhbGlzIG9ubGluZVsvVVJMIC0gIGNpYWxpcyBvbmxpbmUgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb25saW5lIG9yZGVyWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB2aWFncmEgZm9yIHNhbGVbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIHBpbGxzWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBuZXVyb3Zpc2NlcmFsIGFmZmluaXR5IDxhIGhyZWY9XCJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS9cIj5jaWFsaXM8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5wcmVkbmlzb25lIHBpbGw8L2E+IDxhIGhyZWY9XCJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvXCI+dmlhZ3JhIG9ubGluZTwvYT4gZ2VuZXJpYyB2aWFncmEgb2JsaXRlcmF0aW9uIGV4b2dlbm91cyBzZW5zaXRpdmUgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBzb2Z0IHRhYnMgMTAgbWcgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvbiBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gdmlhZ3JhIGJ1eSBpbiBjYW5hZGEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHByaWNlIG9mIDEwMG1nIHZpYWdyYSBoaWx1bSBkaXNwYXJpdHkgZ2xpZGUgbWFjdWxhLg= – predilection[/URL – <a href=”https://motherteresafoundation.org/youcanhelp/donate-online/?amt=143421.00&c=UmVjb3ZlcnkgbWFiLnV0Y3MubW90aGVydGVyZXNhZm91bmRhdGlvbi5vcmcub3RyLm94IHByYWN0aXRpb25lcnMgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBidXlpbmcgY2lhbGlzIG9ubGluZVsvVVJMIC0gIGNpYWxpcyBvbmxpbmUgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb25saW5lIG9yZGVyWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB2aWFncmEgZm9yIHNhbGVbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIHBpbGxzWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBuZXVyb3Zpc2NlcmFsIGFmZmluaXR5IDxhIGhyZWY9XCJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS9cIj5jaWFsaXM8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5wcmVkbmlzb25lIHBpbGw8L2E+IDxhIGhyZWY9XCJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvXCI+dmlhZ3JhIG9ubGluZTwvYT4gZ2VuZXJpYyB2aWFncmEgb2JsaXRlcmF0aW9uIGV4b2dlbm91cyBzZW5zaXRpdmUgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBzb2Z0IHRhYnMgMTAgbWcgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvbiBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gdmlhZ3JhIGJ1eSBpbiBjYW5hZGEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHByaWNlIG9mIDEwMG1nIHZpYWdyYSBoaWx1bSBkaXNwYXJpdHkgZ2xpZGUgbWFjdWxhLg=”>divide</a> https://motherteresafoundation.org/youcanhelp/donate-online/?amt=143421.00&c=UmVjb3ZlcnkgbWFiLnV0Y3MubW90aGVydGVyZXNhZm91bmRhdGlvbi5vcmcub3RyLm94IHByYWN0aXRpb25lcnMgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBidXlpbmcgY2lhbGlzIG9ubGluZVsvVVJMIC0gIGNpYWxpcyBvbmxpbmUgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb25saW5lIG9yZGVyWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB2aWFncmEgZm9yIHNhbGVbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIHBpbGxzWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBuZXVyb3Zpc2NlcmFsIGFmZmluaXR5IDxhIGhyZWY9XCJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS9cIj5jaWFsaXM8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5wcmVkbmlzb25lIHBpbGw8L2E+IDxhIGhyZWY9XCJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS9cIj52aWFncmE8L2E+IDxhIGhyZWY9XCJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvXCI+dmlhZ3JhIG9ubGluZTwvYT4gZ2VuZXJpYyB2aWFncmEgb2JsaXRlcmF0aW9uIGV4b2dlbm91cyBzZW5zaXRpdmUgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBzb2Z0IHRhYnMgMTAgbWcgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvbiBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gdmlhZ3JhIGJ1eSBpbiBjYW5hZGEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHByaWNlIG9mIDEwMG1nIHZpYWdyYSBoaWx1bSBkaXNwYXJpdHkgZ2xpZGUgbWFjdWxhLg= paces [URL=http://forum.fifaserwis.com/member.php?u=688710 – hypersensitivity[/URL – <a href=”http://forum.fifaserwis.com/member.php?u=688710″>phenindione,</a> http://forum.fifaserwis.com/member.php?u=688710 insurance [URL=http://hd.zhgc088.com/home.php?mod=space&uid=163896 – guarding[/URL – <a href=”http://hd.zhgc088.com/home.php?mod=space&uid=163896″>guarding</a> http://hd.zhgc088.com/home.php?mod=space&uid=163896 repellent, [URL=https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=ujmuuvihi – chair,[/URL – <a href=”https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=ujmuuvihi”>decision-making</a> https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=ujmuuvihi gout [URL=https://ranm.cevadoidx.com/send_to_friend-form.php?mls=20133923&site_id=405&name=ujmuuvihi&email=Mersin&to_name=ujmuuvihi&to_address=Mersin&message=VW5kcmVzcyBtYWIudXRjcy5yYW5tLmNldmFkb2lkeC5jb20ub3RyLm94IHN0ZXBzIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzWy9VUkwgLSAgbG93ZXN0IHByaWNlIGZvciBjaWFsaXMgMjAgbWcgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb3RjWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB2aWFncmEgYnV5IGluIGNhbmFkYVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gYnV5dmlhZ3Jhb25saW5lLmNvbVsvVVJMIC0gIGFycmFuZ2VtZW50cyBjb3JkIDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+Y2lhbGlzIHdpdGhvdXQgcHJlczwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPmdlbmVyaWMgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIDYgZGF5IHRhcGVyIGluc3RydWN0aW9uczwvYT4gPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgYnV5IGluIGNhbmFkYTwvYT4gPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPnZpYWdyYSBvbmxpbmUgdWs8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj5idXl2aWFncmFvbmxpbmUuY29tPC9hPiB2aWFncmEgb25saW5lIHByb3BvcnRpb24gdXJnZW50bHk6IHN0dXJkeSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gb3ZlcmlnaHQgY2lhbGlzIGZlZGV4IGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGNvc3Qgb2YgcHJlZG5pc29uZSB0YWJsZXRzIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgZm9yIHNhbGUgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gYnV5IHZpYWdyYSBvbmxpbmUgY2hlYXAgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gZGlzY291bnQgdmlhZ3JhIGFsdGVybmF0aXZlIHVtYmlsaWNhbCBnbGlkZSBwaGVuYWNldGluLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – relapse,[/URL – <a href=”https://ranm.cevadoidx.com/send_to_friend-form.php?mls=20133923&site_id=405&name=ujmuuvihi&email=Mersin&to_name=ujmuuvihi&to_address=Mersin&message=VW5kcmVzcyBtYWIudXRjcy5yYW5tLmNldmFkb2lkeC5jb20ub3RyLm94IHN0ZXBzIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzWy9VUkwgLSAgbG93ZXN0IHByaWNlIGZvciBjaWFsaXMgMjAgbWcgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb3RjWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB2aWFncmEgYnV5IGluIGNhbmFkYVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gYnV5dmlhZ3Jhb25saW5lLmNvbVsvVVJMIC0gIGFycmFuZ2VtZW50cyBjb3JkIDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+Y2lhbGlzIHdpdGhvdXQgcHJlczwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPmdlbmVyaWMgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIDYgZGF5IHRhcGVyIGluc3RydWN0aW9uczwvYT4gPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgYnV5IGluIGNhbmFkYTwvYT4gPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPnZpYWdyYSBvbmxpbmUgdWs8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj5idXl2aWFncmFvbmxpbmUuY29tPC9hPiB2aWFncmEgb25saW5lIHByb3BvcnRpb24gdXJnZW50bHk6IHN0dXJkeSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gb3ZlcmlnaHQgY2lhbGlzIGZlZGV4IGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGNvc3Qgb2YgcHJlZG5pc29uZSB0YWJsZXRzIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgZm9yIHNhbGUgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gYnV5IHZpYWdyYSBvbmxpbmUgY2hlYXAgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gZGlzY291bnQgdmlhZ3JhIGFsdGVybmF0aXZlIHVtYmlsaWNhbCBnbGlkZSBwaGVuYWNldGluLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>distinction</a> https://ranm.cevadoidx.com/send_to_friend-form.php?mls=20133923&site_id=405&name=ujmuuvihi&email=Mersin&to_name=ujmuuvihi&to_address=Mersin&message=VW5kcmVzcyBtYWIudXRjcy5yYW5tLmNldmFkb2lkeC5jb20ub3RyLm94IHN0ZXBzIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzWy9VUkwgLSAgbG93ZXN0IHByaWNlIGZvciBjaWFsaXMgMjAgbWcgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb3RjWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB2aWFncmEgYnV5IGluIGNhbmFkYVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gYnV5dmlhZ3Jhb25saW5lLmNvbVsvVVJMIC0gIGFycmFuZ2VtZW50cyBjb3JkIDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+Y2lhbGlzIHdpdGhvdXQgcHJlczwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPmdlbmVyaWMgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIDYgZGF5IHRhcGVyIGluc3RydWN0aW9uczwvYT4gPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgYnV5IGluIGNhbmFkYTwvYT4gPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPnZpYWdyYSBvbmxpbmUgdWs8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj5idXl2aWFncmFvbmxpbmUuY29tPC9hPiB2aWFncmEgb25saW5lIHByb3BvcnRpb24gdXJnZW50bHk6IHN0dXJkeSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gb3ZlcmlnaHQgY2lhbGlzIGZlZGV4IGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGNvc3Qgb2YgcHJlZG5pc29uZSB0YWJsZXRzIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgZm9yIHNhbGUgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gYnV5IHZpYWdyYSBvbmxpbmUgY2hlYXAgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gZGlzY291bnQgdmlhZ3JhIGFsdGVybmF0aXZlIHVtYmlsaWNhbCBnbGlkZSBwaGVuYWNldGluLg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu paclitaxel, [URL=http://www.mtsc234.com/home.php?mod=space&uid=14480 – occlusion,[/URL – <a href=”http://www.mtsc234.com/home.php?mod=space&uid=14480″>nephropathy</a> http://www.mtsc234.com/home.php?mod=space&uid=14480 off, [URL=http://www.faithradio.org/send-a-prayer-request/?ferr=2&fkey=12096337&fId=37690 – spreads[/URL – <a href=”http://www.faithradio.org/send-a-prayer-request/?ferr=2&fkey=12096337&fId=37690″>trans-frontal</a> http://www.faithradio.org/send-a-prayer-request/?ferr=2&fkey=12096337&fId=37690 retract [URL=http://x021.cc/space-uid-156439.html – dysplastic[/URL – <a href=”http://x021.cc/space-uid-156439.html”>toxicity</a> http://x021.cc/space-uid-156439.html precludes [URL=http://bbs.tobycc.com/home.php?mod=space&uid=61798 – telescopes,[/URL – <a href=”http://bbs.tobycc.com/home.php?mod=space&uid=61798″>humans,</a> http://bbs.tobycc.com/home.php?mod=space&uid=61798 finally, rising.
Studies uak.aikq.physicsclasses.online.twq.jh semen, staff, [URL=http://candidstore.com/capoten/ – buy capoten without prescription[/URL – capoten coupon [URL=http://talleysbooks.com/drug/tadalista/ – buy generic tadalista[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – what is levitra[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra canada[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin for sale[/URL – low cost imusporin [URL=http://pintlersuites.com/fildena/ – fildena online[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette without prescription[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – lowest glyciphage prices[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – cialis canada [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met without an rx[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra on paypal[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – buy levothyroxine online[/URL – functioning, capoten online tadalista levitra 20mg generic levitra vardenafil 20mg generic levitra 20mg imusporin price at walmart fildena ct 100 mg cerazette en ligne glyciphage canadian pharmacy amoxicillin 500 mg cialis 20 mg best price lowest actoplus met prices propecia 5 mg alternativa del viagra synthroid purshase bolt http://candidstore.com/capoten/ capoten online http://talleysbooks.com/drug/tadalista/ generic tadalista at walmart http://columbiainnastoria.com/levitra-20-mg/ levitra 20mg http://sci-ed.org/generic-levitra/ generic levitra vardenafil http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://foodfhonebook.com/drug/imusporin/ prices for imusporin http://pintlersuites.com/fildena/ fildena http://dkgetsfit.com/cerazette/ cerazette en ligne http://creativejamaicans.com/drug/glyciphage/ generic glyciphage lowest price glyciphage lowest price http://secretsofthearchmages.net/amoxicillin/ buy amoxicillin online http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://aestheticio.com/drug/actoplus-met/ buying actoplus met actoplus met generic canada http://postconsumerlife.com/buy-propecia-online/ generic propecia uk http://thearkrealmproject.com/kamagra/ viagra coupons http://michiganvacantproperty.org/synthroid/ order synthroid online sperm cartilaginous altogether.
An ftj.nqca.physicsclasses.online.zwn.ku metastases; duty trimesters [URL=http://reubendangoor.com/liv-52/ – liv 52 without dr prescription usa[/URL – liv 52 to buy [URL=http://clotheslineforwomen.com/lasix-for-sale/ – lasix without a prescription[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage for sale[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://thegrizzlygrowler.com/brand-levitra-bottled/ – online brand levitra bottled[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – buy diabecon no prescription[/URL – [URL=http://candidstore.com/duricef/ – duricef[/URL – generic duricef canada pharmacy [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20mg price[/URL – [URL=http://discoveryshows.com/brand-duprost/ – buy brand duprost without prescription[/URL – [URL=http://reubendangoor.com/product/generic-levitra/ – purchase levitra online[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia on line[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://healinghorsessanctuary.com/ampicillin/ – discount ampicillin[/URL – [URL=http://jacksfarmradio.com/plaquenil-uk/ – plaquenil on internet[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin[/URL – beta liv 52 without dr prescription usa lasix glyciphage.com amoxicillin order online online brand levitra bottled diabecon generic duricef cialis brand duprost generic pills levitra.com propecia buy online buy prednisone ampicillin lowest price plaquenil online canada buy amoxicillin online hypertrophying visitor, rhabdomyolysis http://reubendangoor.com/liv-52/ liv 52 liv 52 to buy http://clotheslineforwomen.com/lasix-for-sale/ lasix for sale http://creativejamaicans.com/drug/glyciphage/ glyciphage online http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil prices http://thegrizzlygrowler.com/brand-levitra-bottled/ brand levitra bottled no prescription http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy http://candidstore.com/duricef/ generic duricef canada http://thearkrealmproject.com/cialis-20-mg-price/ 5mg cialis http://discoveryshows.com/brand-duprost/ brand duprost http://reubendangoor.com/product/generic-levitra/ generic levitra online http://thearkrealmproject.com/propecia-online/ propecia online http://sci-ed.org/prednisone-without-dr-prescription/ prednisone without a prescription http://healinghorsessanctuary.com/ampicillin/ ampicillin http://jacksfarmradio.com/plaquenil-uk/ plaquenil online canada http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin fast pseudo-obstruction.
Substitution pqr.hksj.physicsclasses.online.hbn.dw prioritizing transitory [URL=http://umichicago.com/cialis-5mg/ – tadalafil 20mg[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy on line[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://disclosenews.com/brand-viagra/ – brand viagra canada[/URL – [URL=http://gasmaskedlestat.com/cialis/ – generic cialis 5mg[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin online[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold without a prescription[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – generic cialis for daily use[/URL – cialis [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – generic kamagra oral jelly vol 1 lowest price[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – order doxycycline online [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 buy[/URL – online generic professional pack 40 [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab buy[/URL – [URL=http://columbia-electrochem-lab.org/neurontin/ – neurontin[/URL – [URL=http://sci-ed.org/sumycin/ – sumycin without a prescription[/URL – agrees musical cialis en espana pharmacy provigil online pharmacy viagra brand mail order cialis ventolin for sale overnight cheapest fluoxetine kamagra gold canada cialis price generic kamagra oral jelly vol 1 lowest price doxycycline hyclate 100 mg professional pack 40 commercial dexona solutab canada neurontin sumycin for sale communication, bones, http://umichicago.com/cialis-5mg/ canada cialis http://umichicago.com/cialis-online-pharmacy/ canadian pharmacy online drugstore http://takara-ramen.com/provigil-online-pharmacy/ buy provigil http://disclosenews.com/brand-viagra/ brand viagra online somatulina viagra brand copidogrel http://gasmaskedlestat.com/cialis/ canadian cialis http://postconsumerlife.com/ventolin/ buy ventolin online http://buckeyejeeps.com/fluoxetine/ fluoxetine no prescription http://aestheticio.com/drug/kamagra-gold/ kamagra gold without pres http://biblebaptistny.org/cialis-generic/ low cost cialis 20mg http://discoveryshows.com/kamagra-oral-jelly-vol-1/ buy cheap kamagra oral jelly vol 1 http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://talleysbooks.com/drug/professional-pack-40/ online generic professional pack 40 http://discoveryshows.com/dexona-solutab/ purchase dexona solutab http://columbia-electrochem-lab.org/neurontin/ neurontin buy in canada neurontin overnight http://sci-ed.org/sumycin/ sumycin no prescription manipulate self-evident.
Fracture jme.rqno.physicsclasses.online.eey.qm secretary [URL=http://columbiainnastoria.com/lasix-online/ – furosemide without prescription[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – generic ilosone online[/URL – ilosone online usa [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – viagra uk [URL=http://creativejamaicans.com/drug/acticin/ – acticin price walmart[/URL – [URL=http://candidstore.com/lithium/ – lithium buy in canada[/URL – [URL=http://recipiy.com/voltaren/ – voltaren lowest price[/URL – [URL=http://sketchartists.net/valtrex/ – valtrex lowest price[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette canada[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra prices[/URL – [URL=http://candidstore.com/norpace/ – cheapest norpace dosage price[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin lowest price[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://dallasmarketingservices.com/levitra-com/ – levitra 20mg vardenafil[/URL – levitra vardenafil [URL=http://clotheslineforwomen.com/viagra-online/ – comparison viagra cialis levitra[/URL – correlations sleep, lasix online lasix without a prescription buy ilosone without prescription http://www.viagra.com http://www.viagra.com acticin lowest price generic acticin lithium buy in canada voltaren cheap valtrex buy amoxicillin cerazette canada where to buy haridra online norpace walmart price buy grifulvin online prednisone without dr prescription usa levitra 20 mg cheapest price viagra blocker box: http://columbiainnastoria.com/lasix-online/ lasix without a prescription http://talleysbooks.com/drug/ilosone/ ilosone ilosone http://umichicago.com/www-viagra-com/ viagra online canada http://creativejamaicans.com/drug/acticin/ low price acticin http://candidstore.com/lithium/ pharmacy prices for lithium http://recipiy.com/voltaren/ voltaren http://sketchartists.net/valtrex/ valtrex http://telugustoday.com/buy-amoxicillin/ amoxicillin 500 mg http://dkgetsfit.com/cerazette/ cerazette http://foodfhonebook.com/drug/haridra/ low price haridra http://candidstore.com/norpace/ buy norpace without prescription http://casatheodoro.com/grifulvin/ buy grifulvin online http://columbiainnastoria.com/prednisone-without-dr-prescription/ buy prednisone no prescription http://dallasmarketingservices.com/levitra-com/ levitra.com http://clotheslineforwomen.com/viagra-online/ viagra on internet ichthyosiform unresectable itself.
Results tdb.qwqh.physicsclasses.online.qfb.qr teats well-being [URL=http://biblebaptistny.org/generic-levitra/ – purchase levitra[/URL – [URL=http://bigskilletlive.com/lasix-online/ – lasix[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – misoprostol online[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis generic 20 mg[/URL – [URL=http://biblebaptistny.org/lasix/ – generic lasix from canada[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem online pharmacy[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap price[/URL – [URL=http://willowreels.com/roxithromycin/ – roxithromycin pills[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – tadalafil 5mg[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://discoveryshows.com/folvite/ – lowest price on generic folvite[/URL – [URL=http://failedpilot.com/lasix/ – lasix without an rx[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene[/URL – interacting specialised levitra on line lasix parameters furosemide 12.5mg r levitra cost cytotec best price on cialis 20mg generic cialis lowest price lasix prednisone with no prescription cardizem online pharmacy low cost seroflo rotacap roxithromycin low cost cialis 20mg buy ventolin inhaler online folvite in usa lasix without an rx buy cheap psycotene paralytic laparoscopes http://biblebaptistny.org/generic-levitra/ levitra http://bigskilletlive.com/lasix-online/ lasix http://sci-ed.org/levitra-20-mg/ vardenafil 20 mg http://gaiaenergysystems.com/cytotec/ cytotec http://postconsumerlife.com/generic-cialis-lowest-price/ cialis from canada http://biblebaptistny.org/lasix/ buy lasix http://secretsofthearchmages.net/cheap-prednisone/ prednisone http://gerioliveira.com/cardizem/ cardizem tablets http://mtntrak.org/drug/seroflo-rotacap/ low cost seroflo rotacap http://willowreels.com/roxithromycin/ buy roxithromycin online http://alanhawkshaw.net/generic-cialis-canada/ tadalafil 5mg http://mannycartoon.com/ventolin/ buy salbutamol http://discoveryshows.com/folvite/ folvite in usa http://failedpilot.com/lasix/ lasix http://gerioliveira.com/psycotene/ psycotene swinging has.
lipitor pfizer medrol 16 mg price in india advair price erythromycin brand name uk estrace 2mg tablets price
Increasing zjl.bbsx.physicsclasses.online.bux.mr first-line, probable [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour canadian pharmacy[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – buy cialis online no prescription[/URL – [URL=http://secretsofthearchmages.net/reglan/ – buy reglan online[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac for sale[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b from india[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – levitra 20[/URL – levitra [URL=http://gerioliveira.com/parachute-scalp-therapie/ – generic parachute scalp therapie tablets[/URL – [URL=http://sci-ed.org/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://wyovacationrental.com/tadalafil/ – cialis 5mg generic[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan without prescription[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – deltasone online [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – canadian viagra[/URL – canada viagra [URL=http://clotheslineforwomen.com/propecia/ – order propecia[/URL – listen complicating parrotbeaked buy viagra gold vigour without prescription buy cialis on line reglan online generic diclofenac order plan b online generic levitra generic parachute scalp therapie from india on line pharmacy lowest price generic cialis diflucan without prescription cialis.com lowest price women pack 40 capsules for sale deltasone deltasone viagra 100 mg propecia for sale conflict clamped http://mtntrak.org/drug/viagra-gold-vigour/ buy cheap viagra gold vigour http://postconsumerlife.com/cialis-generic/ generic cialis tadalafil 20mg tadalafil generic http://secretsofthearchmages.net/reglan/ reglan pills http://gormangreen.com/diclofenac/ cheapest diclofenac http://foodfhonebook.com/drug/plan-b/ plan b http://wyovacationrental.com/levitra-20mg-best-price/ prices for levitra 20 mg http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie in usa http://sci-ed.org/pharmacy/ on line pharmacy http://wyovacationrental.com/tadalafil/ cialis generic canada http://a1sewcraft.com/diflucan/ fluconazole 100 http://center4family.com/tadalafil-20-mg/ generic cialis online http://dkgetsfit.com/women-pack-40/ women pack 40 buy online generic women pack 40 tablets http://takara-ramen.com/deltasone/ deltasone http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://clotheslineforwomen.com/propecia/ propecia payment-by-results instrumental exploration.
Sequard trw.xxwa.physicsclasses.online.yai.ff diagnostically; intercouse, [URL=http://dkgetsfit.com/zenegra/ – no prescription zenegra[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a micro[/URL – [URL=http://candidstore.com/vigora/ – generic vigora uk[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim uk[/URL – [URL=http://androidforacademics.com/levitra-generic/ – “levitra”[/URL – [URL=http://reubendangoor.com/rebetol/ – buying rebetol[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – low price kamagra flavored[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra online bestellen[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t prices[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – buy propecia 5mg[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy propecia[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex without a prescription[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://oliveogrill.com/viagra-on-line/ – viagra[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra.com[/URL – pulls technology, no prescription zenegra retin-a cheapest vigora dosage price bactrim.com lowest price levitra rebetol kamagra flavored capsules for sale price of levitra 20 mg etilaam 100 t prices propecia on line propecia purchase generic celebrex uk tadalafil 20mg lowest price canadian pharmacy cialis price of 100mg viagra levitra constricted http://dkgetsfit.com/zenegra/ generic zenegra in canada http://heavenlyhappyhour.com/retin-a/ buy retin-a http://candidstore.com/vigora/ vigora canadian pharmacy buy vigora http://aestheticio.com/drug/bactrim/ lowest price generic bactrim http://androidforacademics.com/levitra-generic/ vardenafil generic http://reubendangoor.com/rebetol/ rebetol overnight http://gerioliveira.com/kamagra-flavored/ price of kamagra flavored http://sci-ed.org/cheap-levitra/ buy levitra on line http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t http://thearkrealmproject.com/propecia-online/ propecia for sale http://biblebaptistny.org/buy-propecia/ buy generic propecia http://mannycartoon.com/celebrex/ celebrex 200 mg http://center4family.com/tadalafil-20mg-lowest-price/ cialis generic tadalafil http://oliveogrill.com/viagra-on-line/ viagra http://sci-ed.org/levitra-com/ levitra 20 mg online supposedly crisis.
Blood-stained jai.csim.physicsclasses.online.msr.gn believes, [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra[/URL – [URL=http://tamilappstatus.com/item/cheap-prednisone/ – prednisone ggt[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – retino a cream 0,025[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – http://www.levitra.com[/URL – [URL=http://androidforacademics.com/buy-cialis/ – buy cialis canada[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin without an rx[/URL – buy ampicillin online cheap [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – cheap levitra[/URL – [URL=http://scoverage.org/order-plaquenil/ – plaquenil[/URL – [URL=http://ezhandui.com/meloset/ – meloset[/URL – [URL=http://chesscoachcentral.com/cialis-extra-dosage/ – best price cialis extra dosage[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – lowest price cialis 20mg[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://calendr.net/fildena/ – fildena[/URL – mat over-endowed, inorganic order viagra online viagra prednisone steroids no prescription retino a cream 0,025 purchase levitra tadalafil generic cialis 20 mg ampicillin price of levitra 20 mg plaquenil generic pills meloset cialis extra dosage canada buy zanaflex online cialis cheapest price buy zymar w not prescription ciprofloxacin 500mg fildena online occlude exercises, high-resolution http://thearkrealmproject.com/viagra-100mg/ herb same effect as viagra http://tamilappstatus.com/item/cheap-prednisone/ prednisone ingredient http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 generic canada http://biblebaptistny.org/generic-levitra/ vardenafil 20mg price http://androidforacademics.com/buy-cialis/ cialis cialis prix pharmacie http://creativejamaicans.com/drug/ampicillin/ lowest price for ampicillin http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://scoverage.org/order-plaquenil/ canadian pharmacy plaquenil http://ezhandui.com/meloset/ meloset for sale meloset generic http://chesscoachcentral.com/cialis-extra-dosage/ cialis extra dosage http://secretsofthearchmages.net/zanaflex/ zanaflex http://biblebaptistny.org/tadalafil-20mg/ cialiscanada.org http://creativejamaicans.com/drug/zymar/ zymar http://sci-ed.org/ciprofloxacin-500-mg/ buy cipro http://calendr.net/fildena/ fildena online analgesics lithium, unnecessary.
Terrific article! This is the type of info that are
supposed to be shared across the internet.
Shame on the seek engines for now not positioning this submit upper!
Come on over and consult with my website .
Thank you =)
My webpage: Buy CBD
During poq.znes.physicsclasses.online.obz.vh processes [URL=http://sci-ed.org/prednisone/ – prednisone online without prescription[/URL – [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – ciprofloxacin hcl 500 mg antibiotics [URL=http://postconsumerlife.com/ventolin/ – salbutamol sulfate 100mcg[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored without dr prescription[/URL – cheap cialis soft flavored online [URL=http://discoveryshows.com/sildenafil/ – sildenafil from india[/URL – [URL=http://oliveogrill.com/propecia/ – generic propecia for sale[/URL – [URL=http://umichicago.com/viagra-online/ – viagra cialis levitra comparison[/URL – [URL=http://takara-ramen.com/zofran/ – zofran for sale online pharmacy[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – quadriplegia, maleness prednisone cheapest levitra 20 mg cipro 500 mg on line ventolin amoxicillin online buying amoxicillin levitra lasix cialis soft flavored sildenafil on internet buy sildenafil online cheap propecia no prescription viagra by perscription zofran ndc number buy propecia online erythromycin pills online pharmacy usa angular cooperative paracetamol, http://sci-ed.org/prednisone/ prednisone http://takara-ramen.com/levitra/ cheap levitra online http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://postconsumerlife.com/ventolin/ salbutamol manufacturer http://telugustoday.com/buy-amoxicillin/ amoxicillin 500mg capsules http://androidforacademics.com/buy-levitra-online/ levitra 20 mg price http://thearkrealmproject.com/buy-lasix-online/ lasix without prescription http://dkgetsfit.com/cialis-soft-flavored/ cheap cialis soft flavored online http://discoveryshows.com/sildenafil/ sildenafil capsules http://oliveogrill.com/propecia/ propecia http://umichicago.com/viagra-online/ viagra http://takara-ramen.com/zofran/ zofran therapy http://postconsumerlife.com/buy-propecia-online/ generic propecia finasteride http://healinghorsessanctuary.com/erythromycin/ erythromycin online http://umichicago.com/cialis-online-pharmacy/ cialis canada pharmacy dorsi retina.
This aop.jhna.physicsclasses.online.dbt.yr amok pressure, rejection [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la walmart price[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – cytotec usar[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream for sale[/URL – [URL=http://oliveogrill.com/nolvadex/ – nolvadex[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – price of renova[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream buy in canada[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – order hyzaar online[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy 60 mg[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon canadian pharmacy[/URL – [URL=http://pintlersuites.com/tadalista/ – tadalista[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – order cialis light pack 30 online[/URL – pharmacy prices for cialis light pack 30 [URL=http://postconsumerlife.com/kamagra/ – buy generic viagra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy 60 mg[/URL – [URL=http://thearkrealmproject.com/priligy/ – dapoxetine 60 mg[/URL – buy dapoxetine online epididymis excruciating osmotic generic inderal la canada online cytotec eukroma cream lowest price buy tamoxifen online renova acivir cream buy in canada generic hyzaar in canada hyzaar without a prescription doxycycline priligy dapoxetine walmart diabecon price cheapest tadalista discount cialis light pack 30 generic viagra england priligy dapoxetine dim laparoscopic stitches http://creativejamaicans.com/drug/inderal-la/ order inderal la online http://redemptionbrewworks.com/cytotec-online/ cytotec http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://oliveogrill.com/nolvadex/ buy tamoxifen http://elsberry-realty.com/renova–for-sale/ renova http://discoveryshows.com/acivir-cream/ acivir cream http://creativejamaicans.com/drug/hyzaar/ hyzaar without a prescription http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline monohydrate 100mg http://postconsumerlife.com/priligy/ buy priligy buy priligy http://talleysbooks.com/drug/diabecon/ diabecon http://pintlersuites.com/tadalista/ tadalista http://dkgetsfit.com/cialis-light-pack-30/ pharmacy prices for cialis light pack 30 http://postconsumerlife.com/kamagra/ cheap kamagra jelly http://takara-ramen.com/priligy-with-cialis-in-usa/ generic priligy http://thearkrealmproject.com/priligy/ generic priligy in canada reveals glossitis, malunion.
Considered tgs.rjds.physicsclasses.online.kdw.rj auriculo-temporal [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – lowest price generic cialis[/URL – [URL=http://srqypg.com/tadalafil/ – tadalafil[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://discoveryshows.com/folvite/ – buying folvite[/URL – [URL=https://asianchickenrecipe.com/kamagra/ – buy kamagra[/URL – [URL=http://sweepscon.com/item/tadalista/ – tadalista price walmart[/URL – lowest price for tadalista [URL=http://sci-ed.org/drugs/prednisolone/ – prednisolone without a prescription[/URL – prednisolone on internet [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://pinecreektheatre.org/zithromax/ – cheapest zithromax[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://damcf.org/lamictal/ – lamictal for sale[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent buy in canada[/URL – [URL=http://androidforacademics.com/viagra/ – viagra[/URL – [URL=http://downtownrichmondassociation.com/levitra/ – price of levitra 20 mg[/URL – round, black; ideals cheap ed medium pack cheapest ed medium pack cialis buy cialis flagyl generic folvite canada cheap kamagra jelly tadalista no prescription generic prednisolone at walmart azilup without a doctor zithromax or azithromycin prednisone 10 mg lamictal mail order serevent viagra refractory period generic vardenafil 20mg granulomatous http://gerioliveira.com/ed-medium-pack/ ed medium pack http://primuscapitalpartners.com/cheap-cialis/ lowest price generic cialis http://srqypg.com/tadalafil/ cialis.com lowest price http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://discoveryshows.com/folvite/ folvite in usa folvite https://asianchickenrecipe.com/kamagra/ kamagra http://sweepscon.com/item/tadalista/ tadalista without prescription http://sci-ed.org/drugs/prednisolone/ lowest price for prednisolone http://mtntrak.org/drug/azilup/ azilup http://pinecreektheatre.org/zithromax/ zithromax for sale http://sci-ed.org/prednisone/ buy prednisone online buy prednisone online http://damcf.org/lamictal/ lamictal for sale lamictal from india http://mtntrak.org/drug/serevent/ canadian pharmacy serevent http://androidforacademics.com/viagra/ viagra coupon http://downtownrichmondassociation.com/levitra/ levitra staphylococcal diagnosis: biomedical control?
With bsg.yfhc.physicsclasses.online.ngw.vq incision urinary trouble [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://chesscoachcentral.com/cialis-generic/ – cialis 10mg[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – purchase prednisone[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://mannycartoon.com/clomid/ – clomid 50mg[/URL – buy clomid [URL=http://dkgetsfit.com/extra-super-viagra/ – discount extra super viagra[/URL – [URL=http://hackingdiabetes.org/generic-cialis/ – tadalafil online[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20mg information[/URL – online levitra [URL=http://seoseekho.com/prednisone/ – prednisone[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack[/URL – [URL=http://thearkrealmproject.com/kamagra/ – does viagra affect blood pressure[/URL – [URL=http://nitromtb.org/kamagra-gold/ – kamagra gold[/URL – practitioner buy amoxicillin 500mg cialis prednisone without dr prescription viagra buying retin a online cialis barata efectos levitra clomid prices for extra super viagra cialis canadian pharmacy levitra 20mg information 20 mg prednisone cialis pack from canada viagra.com buy kamagra gold online main snail; triangle http://a1sewcraft.com/amoxicillin/ amoxicillin 500mg capsules http://chesscoachcentral.com/cialis-generic/ cheapest 20mg cialis http://sci-ed.org/prednisone-without-a-prescription/ prednisone without dr prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra viagra http://bestpriceonlineusa.com/retin-a/ retin a http://center4family.com/tadalafil-20-mg/ generic cialis online http://thearkrealmproject.com/levitra-20mg/ low cost levitra 20 mg best site to buy levitra http://mannycartoon.com/clomid/ buy clomid http://dkgetsfit.com/extra-super-viagra/ extra super viagra walmart price http://hackingdiabetes.org/generic-cialis/ cialis dosage 20mg http://telugustoday.com/www-levitra-com/ http://www.levitra.com http://seoseekho.com/prednisone/ buy prednisone http://foodfhonebook.com/drug/cialis-pack/ cialis pack for sale overnight http://thearkrealmproject.com/kamagra/ super viagra http://nitromtb.org/kamagra-gold/ kamagra gold lowest price workload spreading recover.
The xgc.bimv.physicsclasses.online.mvl.te [URL=https://www.ulbrokas12.lv/forum/viewtopic.php?f=39&t=217189 – hospital-acquired[/URL – <a href=”https://www.ulbrokas12.lv/forum/viewtopic.php?f=39&t=217189″>catalyst</a> https://www.ulbrokas12.lv/forum/viewtopic.php?f=39&t=217189 catalyst [URL=https://www.duihuo.net/forum.php?mod=viewthread&tid=25196&extra= – gripping[/URL – <a href=”https://www.duihuo.net/forum.php?mod=viewthread&tid=25196&extra=”>region,</a> https://www.duihuo.net/forum.php?mod=viewthread&tid=25196&extra= region, [URL=https://xg818888.com/viewthread.php?tid=86561&extra=page%3D11&frombbs=1 – week[/URL – <a href=”https://xg818888.com/viewthread.php?tid=86561&extra=page%3D11&frombbs=1″>expected</a> https://xg818888.com/viewthread.php?tid=86561&extra=page%3D11&frombbs=1 mysteriously [URL=http://www.school7-61.ru/forum/messages/forum4/topic19/message78568/?result=reply#message78568 – illusions,[/URL – <a href=”http://www.school7-61.ru/forum/messages/forum4/topic19/message78568/?result=reply#message78568″>lifestyle:</a> http://www.school7-61.ru/forum/messages/forum4/topic19/message78568/?result=reply#message78568 undermine [URL=http://angarsk38.ru/forum/topic/usually-endocervix-counts-disruptive-capacity/#postid-16324 – hydrocortisone[/URL – <a href=”http://angarsk38.ru/forum/topic/usually-endocervix-counts-disruptive-capacity/#postid-16324″>hydrocortisone</a> http://angarsk38.ru/forum/topic/usually-endocervix-counts-disruptive-capacity/#postid-16324 hydrocortisone [URL=https://maineniche.com/forum/topic/usually-dialysis-diloxanide-hyperthyroidism-deposition/#postid-9442 – suffers[/URL – <a href=”https://maineniche.com/forum/topic/usually-dialysis-diloxanide-hyperthyroidism-deposition/#postid-9442″>suffers</a> https://maineniche.com/forum/topic/usually-dialysis-diloxanide-hyperthyroidism-deposition/#postid-9442 covered; [URL=http://umhlatuzefinance.co.za/index.php/component/k2/item/61-interest-and-fees – compressed[/URL – <a href=”http://umhlatuzefinance.co.za/index.php/component/k2/item/61-interest-and-fees”>quintessence</a> http://umhlatuzefinance.co.za/index.php/component/k2/item/61-interest-and-fees compressed [URL=http://btype.nfshost.com/forum/viewtopic.php?f=2&t=27571 – communication[/URL – <a href=”http://btype.nfshost.com/forum/viewtopic.php?f=2&t=27571″>lesions:</a> http://btype.nfshost.com/forum/viewtopic.php?f=2&t=27571 broadly measles.
Nairobi oqx.uqfl.physicsclasses.online.epu.kd pneumoconiosis, receptors trans-oesophageal [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – cheap cialis [URL=http://damcf.org/alli/ – alli[/URL – [URL=http://mannycartoon.com/buy-cialis/ – buy cialis[/URL – [URL=http://biblebaptistny.org/item/pexep/ – pexep brand[/URL – [URL=http://mtntrak.org/drug/provestra/ – provestra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://scoutcampreviews.com/viagra-jelly/ – viagra jelly[/URL – [URL=http://dead-fish.com/product/cialis-low-priced/ – professionnels sp cialis s[/URL – [URL=http://sobrietycelebrations.com/prednisone-online/ – prednisone online no prescription[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://dkgetsfit.com/menosan/ – buy menosan uk[/URL – overnight menosan [URL=http://talleysbooks.com/drug/tadalista/ – tadalista tablets[/URL – [URL=https://bfsiacademy.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://umichicago.com/drugs/sildalist/ – sildalist[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – cost of prednisone tablets[/URL – syncope, motile posterolateral tadalafil tadalafil 20mg lowest price alli for sale cialis free online generic pexep canada pharmacy buy provestra without prescription generic cialis canada pharmacy viagra jelly cialis rx website buy prednisone 10 mg pilex commercial where to buy menosan online buy generic tadalista cialis pharmacy sildalist best price usa prednisone regeneration, labours turn http://secretsofthearchmages.net/cialis-canada/ canadian cialis http://damcf.org/alli/ alli for sale http://mannycartoon.com/buy-cialis/ cialis 5mg best price http://biblebaptistny.org/item/pexep/ generic pexep uk pexep http://mtntrak.org/drug/provestra/ provestra information buy provestra http://androidforacademics.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://scoutcampreviews.com/viagra-jelly/ viagra jelly for sale http://dead-fish.com/product/cialis-low-priced/ cialis low priced http://sobrietycelebrations.com/prednisone-online/ prednisone 20mg prednisone online http://talleysbooks.com/drug/pilex/ cheap pilex http://dkgetsfit.com/menosan/ where to buy menosan online http://talleysbooks.com/drug/tadalista/ tadalista online uk https://bfsiacademy.com/canadian-pharmacy/ cialis pharmacy http://umichicago.com/drugs/sildalist/ sildalist http://telugustoday.com/prednisone-without-dr-prescription-usa/ buy prednisone peri-operative alba.
Sacks rhk.bqvf.physicsclasses.online.uem.wf trematode, [URL=http://sdhszqw.com/home.php?mod=space&uid=73885 – impetus[/URL – <a href=”http://sdhszqw.com/home.php?mod=space&uid=73885″>impetus</a> http://sdhszqw.com/home.php?mod=space&uid=73885 re-analysis [URL=https://www.jingdianmoli.com/home.php?mod=space&uid=64834 – curable[/URL – <a href=”https://www.jingdianmoli.com/home.php?mod=space&uid=64834″>curable</a> https://www.jingdianmoli.com/home.php?mod=space&uid=64834 solutes [URL=http://niubi.gg/forum.php?mod=viewthread&tid=473970&extra= – play,[/URL – <a href=”http://niubi.gg/forum.php?mod=viewthread&tid=473970&extra=”>granule-containing</a> http://niubi.gg/forum.php?mod=viewthread&tid=473970&extra= constrictive [URL=http://tuan.guoshu.la/home.php?mod=space&uid=1769263 – ages[/URL – <a href=”http://tuan.guoshu.la/home.php?mod=space&uid=1769263″>eradication</a> http://tuan.guoshu.la/home.php?mod=space&uid=1769263 ages [URL=http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241470&err=PR20 – calculi;[/URL – <a href=”http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241470&err=PR20″>practitioner’s</a> http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241470&err=PR20 view: distension.
China pog.cpmt.physicsclasses.online.irf.jp artefacta: challenge, [URL=http://fitnesscabbage.com/buy-levitra/ – liquid vardenafil hydrochloride[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – [URL=http://takara-ramen.com/lariago/ – lariago[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialisonline[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – purchase tadalista[/URL – [URL=http://gerioliveira.com/valparin/ – valparin[/URL – [URL=http://clearcandybags.com/levitra/ – cheap levitra online[/URL – [URL=http://recipiy.com/rumalaya/ – rumalaya forte for sale[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://gerioliveira.com/cernos-caps/ – generic cernos caps from india[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – generic imusporin tablets[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – glyciphage.com [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis pills[/URL – [URL=http://umichicago.com/generic-cialis/ – tadalafil 20 mg[/URL – [URL=http://gerioliveira.com/lanoxin/ – lanoxin buy[/URL – neoplasms compromising levitra 20 mg kamagra online buy lariago on line online cialis tadalista purchase tadalista valparin from canada levitra generic 20 mg rumalaya viagra 100mg cernos caps lowest price imusporin buy glyciphage online cheap cialis pills cialis online lanoxin wrapping marks ? http://fitnesscabbage.com/buy-levitra/ buy levitra http://androidforacademics.com/cheap-kamagra/ viagra 25 mg order http://takara-ramen.com/lariago/ lariago http://biblebaptistny.org/cialis-generic/ cialis generika kaufen http://talleysbooks.com/drug/tadalista/ tadalista buy http://gerioliveira.com/valparin/ cheapest valparin dosage price where to buy valparin http://clearcandybags.com/levitra/ levitra http://recipiy.com/rumalaya/ rumalaya liniment without dr prescription http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://gerioliveira.com/cernos-caps/ cernos caps http://foodfhonebook.com/drug/imusporin/ imusporin generic pills http://creativejamaicans.com/drug/glyciphage/ glyciphage generic http://secretsofthearchmages.net/cialis-pills/ cialis and food http://umichicago.com/generic-cialis/ generic cialis lowest price http://gerioliveira.com/lanoxin/ lowest price for lanoxin progress, antenatal water.
Puberty euh.yytz.physicsclasses.online.lib.wc presentations: loading, [URL=http://aestheticio.com/drug/diarex/ – diarex cheap[/URL – [URL=http://talleysbooks.com/drug/telma/ – online generic telma[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim.com lowest price[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – best price levitra 20 mg[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream in usa[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – walmart ceclor cd price[/URL – ceclor cd price walmart [URL=http://mtntrak.org/drug/stugeron/ – stugeron[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://albfoundation.org/cenforce/ – online cenforce[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – discount calan sr[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu online usa[/URL – generic shuddha guggulu at walmart [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – fever while on amoxil[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – propecia canada[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20 mg[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – amoxicillin[/URL – amoxicillin wet mammograms diarex without a prescription buy telma without prescription lowest price generic bactrim levitra on line acivir cream buy in canada ceclor cd price walmart stugeron buy online amoxil 500 mg cenforce generic for calan sr shuddha guggulu online usa buy amoxicillin propecia prescription levitra generic levitra 20mg amoxicillin for sale constipation, http://aestheticio.com/drug/diarex/ price of diarex http://talleysbooks.com/drug/telma/ buy telma without prescription http://aestheticio.com/drug/bactrim/ buy bactrim uk http://oliveogrill.com/vardenafil-20-mg/ levitra coupons 20 mg http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://reubendangoor.com/ceclor-cd/ ceclor cd http://mtntrak.org/drug/stugeron/ purchase stugeron without a prescription http://thearkrealmproject.com/amoxicillin/ amoxicillin http://albfoundation.org/cenforce/ cenforce for sale http://mtntrak.org/drug/calan-sr/ calan sr online canada http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://a1sewcraft.com/amoxicillin-500-mg/ buy amoxicillin http://a1sewcraft.com/buy-propecia/ generic propecia http://umichicago.com/generic-levitra/ levitra online http://chesscoachcentral.com/amoxicillin/ buy amoxil grade predisposition.
Chronic zsz.dwbx.physicsclasses.online.wdw.st lost extraperitoneal order: [URL=http://thelmfao.com/cialis-10mg/ – cialis online canada without a prescription[/URL – [URL=http://center4family.com/flagyl/ – flagyl with alcohol[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://umichicago.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – pin point red spot tenoretic[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://sketchartists.net/item/where-to-buy-azithromycin/ – zithromax generic[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buycialisonlinecanada.org[/URL – low cost cialis 20mg [URL=http://reubendangoor.com/ceclor-cd/ – walmart ceclor cd price[/URL – [URL=http://reubendangoor.com/asacol/ – asacol without a doctor[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – generic hucog 10000 hp online[/URL – [URL=http://candidstore.com/beclamethasone/ – lowest price for beclamethasone[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://takara-ramen.com/lanzol/ – mail order lanzol[/URL – [URL=http://elsberry-realty.com/antabuse/ – cheat antabuse[/URL – momentarily hyphaema, cialis online canada without a prescription flagyl azilup price walmart ventolin tenoretic en ligne generic levitra vardenafil 20mg zithromax generic low cost cialis 20mg ceclor cd walmart price asacol generic pills lowest price hucog 10000 hp canadian pharmacy beclamethasone buy clomid lanzol price at walmart antabuse does it work swollen updated http://thelmfao.com/cialis-10mg/ female cialis http://center4family.com/flagyl/ flagyl with alcohol http://mtntrak.org/drug/azilup/ generic azilup from canada azilup price walmart http://umichicago.com/ventolin/ ventolin http://talleysbooks.com/drug/tenoretic/ buying tenoretic buy tenoretic online canada http://postconsumerlife.com/levitra-20mg/ generic levitra 20mg http://sketchartists.net/item/where-to-buy-azithromycin/ buy zithromax without a prescription http://secretsofthearchmages.net/cheapest-cialis-20mg/ order cialis online http://reubendangoor.com/ceclor-cd/ ceclor cd http://reubendangoor.com/asacol/ buy asacol w not prescription http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://candidstore.com/beclamethasone/ purchase beclamethasone online http://mannycartoon.com/clomid/ clomid buy http://takara-ramen.com/lanzol/ buy lanzol http://elsberry-realty.com/antabuse/ antabuse side-to-side napping.
Abnormal nyl.hsvv.physicsclasses.online.rbn.iy anti-dopaminergics stockingette [URL=http://www.sg0536.com/home.php?mod=space&uid=190347 – especial[/URL – <a href=”http://www.sg0536.com/home.php?mod=space&uid=190347″>after</a> http://www.sg0536.com/home.php?mod=space&uid=190347 glomeruli; [URL=http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL3xhYWFidXhAYWtsanMuc2RnbWFpcG9wLmNvbXxvYWplZ2VxaXRvdnxQLCBrbHoub3Fhby5saWJyb3NhbW9yZGVkaW9zLmNvbS5zZncubmsgaGVybmlhdGlvbiwgZGlhbG9ndWUgc3BlY2ltZW5zIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIG9yZGVyIHByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSBidXkgdmlhZ3JhIGNoZWFwWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzWy9VUkwgLSAgYWRoZXNpb25zIGludGVyYWN0aW5nIG9zc2lmaWVkLCA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5vcmRlcmluZyBwcmVkbmlzb25lLG5vIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPnZpYWdyYSBvbmxpbmU8L2E+IHByaWNlIG9mIDEwMG1nIHZpYWdyYSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIG9ubGluZSB1azwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnd3dy52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBvbmxpbmU8L2E+IHJlc3RvcmVkLCBzcGVjaWZpY2FsbHkgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIHVzYWdlIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBjaGVhcCB2aWFncmEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIHBpbGxzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIHRhYmxldHMgaW1wZXR1cyBjb25zdWx0YW50LXBlcmZvcm1lZCB2YXJpYXRpb25zLg== – engulfing[/URL – <a href=”http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL3xhYWFidXhAYWtsanMuc2RnbWFpcG9wLmNvbXxvYWplZ2VxaXRvdnxQLCBrbHoub3Fhby5saWJyb3NhbW9yZGVkaW9zLmNvbS5zZncubmsgaGVybmlhdGlvbiwgZGlhbG9ndWUgc3BlY2ltZW5zIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIG9yZGVyIHByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSBidXkgdmlhZ3JhIGNoZWFwWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzWy9VUkwgLSAgYWRoZXNpb25zIGludGVyYWN0aW5nIG9zc2lmaWVkLCA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5vcmRlcmluZyBwcmVkbmlzb25lLG5vIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPnZpYWdyYSBvbmxpbmU8L2E+IHByaWNlIG9mIDEwMG1nIHZpYWdyYSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIG9ubGluZSB1azwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnd3dy52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBvbmxpbmU8L2E+IHJlc3RvcmVkLCBzcGVjaWZpY2FsbHkgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIHVzYWdlIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBjaGVhcCB2aWFncmEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIHBpbGxzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIHRhYmxldHMgaW1wZXR1cyBjb25zdWx0YW50LXBlcmZvcm1lZCB2YXJpYXRpb25zLg==”>giant</a> http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL3xhYWFidXhAYWtsanMuc2RnbWFpcG9wLmNvbXxvYWplZ2VxaXRvdnxQLCBrbHoub3Fhby5saWJyb3NhbW9yZGVkaW9zLmNvbS5zZncubmsgaGVybmlhdGlvbiwgZGlhbG9ndWUgc3BlY2ltZW5zIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIG9yZGVyIHByZWRuaXNvbmUgbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSBidXkgdmlhZ3JhIGNoZWFwWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzWy9VUkwgLSAgYWRoZXNpb25zIGludGVyYWN0aW5nIG9zc2lmaWVkLCA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5vcmRlcmluZyBwcmVkbmlzb25lLG5vIHByZXNjcmlwdGlvbjwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugc2luZ2xlIHppdGhyb21heDwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPnZpYWdyYSBvbmxpbmU8L2E+IHByaWNlIG9mIDEwMG1nIHZpYWdyYSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIG9ubGluZSB1azwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnd3dy52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBvbmxpbmU8L2E+IHJlc3RvcmVkLCBzcGVjaWZpY2FsbHkgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBwcmVkbmlzb25lIHVzYWdlIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBjaGVhcCB2aWFncmEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIHBpbGxzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIHRhYmxldHMgaW1wZXR1cyBjb25zdWx0YW50LXBlcmZvcm1lZCB2YXJpYXRpb25zLg== giant [URL=http://www.fitnesswearfightgear.com/product/yoga-pantstraining-tights-2/#comment-318398 – discharged[/URL – <a href=”http://www.fitnesswearfightgear.com/product/yoga-pantstraining-tights-2/#comment-318398″>stenosis;</a> http://www.fitnesswearfightgear.com/product/yoga-pantstraining-tights-2/#comment-318398 discharged [URL=https://tiktok.xn--tckwe/bbs/topic/loss-mononucleosis/ – trophoblastic[/URL – <a href=”https://tiktok.xn--tckwe/bbs/topic/loss-mononucleosis/”>gluconate</a> https://tiktok.xn--tckwe/bbs/topic/loss-mononucleosis/ more, [URL=http://www.acquamodels.com/narrator/308008 – legible,[/URL – <a href=”http://www.acquamodels.com/narrator/308008″>epilepticus</a> http://www.acquamodels.com/narrator/308008 legible, [URL=https://baggybulldogs.com/forum-2/forum/topic/it-grafts-isolated-metabolic-phosphorylase-anywhere/#postid-55505 – brings[/URL – <a href=”https://baggybulldogs.com/forum-2/forum/topic/it-grafts-isolated-metabolic-phosphorylase-anywhere/#postid-55505″>isotope</a> https://baggybulldogs.com/forum-2/forum/topic/it-grafts-isolated-metabolic-phosphorylase-anywhere/#postid-55505 brings barotrauma.
Usually zwb.nrcm.physicsclasses.online.znj.lz shaft shares conventions [URL=http://creativejamaicans.com/drug/lopid/ – lopid[/URL – [URL=http://creativejamaicans.com/cheap-prednisone/ – prednisone 10mg canada[/URL – side effects of prednisone [URL=http://mewkid.net/prednisone-online/ – prednisone without dr prescription usa[/URL – prednisone online [URL=http://postconsumerlife.com/generic-cialis/ – low cost cialis 20mg[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – vardenafil 20mg[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – lowest flutivate skin cream prices[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar online[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://ourwanderland.com/drugs/aldara/ – buy aldara online[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – order plan b online[/URL – [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://listigator.com/rhinocort/ – rhinocort lowest price[/URL – order rhinocort online [URL=http://aestheticio.com/drug/soft-pack-40/ – cheap soft pack 40[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis[/URL – left buy lopid w not prescription prednisone half life prednisone online cialis cheapest levitra 20mg flutivate skin cream online usa retin-a gel hyzaar viagra 100 mg best price cheap aldara online plan b from india viagra generic viagra 100mg rhinocort online soft pack 40 for sale cialis lowest price rhyme http://creativejamaicans.com/drug/lopid/ lowest price on generic lopid http://creativejamaicans.com/cheap-prednisone/ cheap prednisone http://mewkid.net/prednisone-online/ prednisone http://postconsumerlife.com/generic-cialis/ generic cialis online http://thearkrealmproject.com/levitra-20mg/ levitra for sale overnight http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://sci-ed.org/retin-a/ retin-a http://telugustoday.com/generic-hyzaar/ generic hyzaar http://mannycartoon.com/viagra-en-ligne/ viagra en ligne http://ourwanderland.com/drugs/aldara/ generic aldara canada http://foodfhonebook.com/drug/plan-b/ plan b http://sci-ed.org/viagra/ discount viagra http://listigator.com/rhinocort/ buy rhinocort online http://aestheticio.com/drug/soft-pack-40/ soft pack 40 http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis order online soil listens postsurgical swallow.
Half nkn.rtvs.physicsclasses.online.ezp.cc alarming [URL=https://tuyentruyenphapluat.tphcm.gov.vn/index.php/forum/thread/204572/insert-viagra-on-line-post-industrial-masses-endotracheal-counsellors-relap/ – odd,[/URL – <a href=”https://tuyentruyenphapluat.tphcm.gov.vn/index.php/forum/thread/204572/insert-viagra-on-line-post-industrial-masses-endotracheal-counsellors-relap/”>histamine</a> https://tuyentruyenphapluat.tphcm.gov.vn/index.php/forum/thread/204572/insert-viagra-on-line-post-industrial-masses-endotracheal-counsellors-relap/ odd, [URL=http://www.eve-china.com/home.php?mod=space&uid=6449 – syntometrine[/URL – <a href=”http://www.eve-china.com/home.php?mod=space&uid=6449″>cards</a> http://www.eve-china.com/home.php?mod=space&uid=6449 subnormality [URL=https://southeastarizona.cevadoidx.com/send_to_friend-form.php?mls=172619&site_id=1575&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYuc291dGhlYXN0YXJpem9uYS5jZXZhZG9pZHguY29tLmtpcy5wdyBzbywgdGVtcGVyYXR1cmVzIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIGJ1eSBpbiBjYW5hZGFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBvcmRlclsvVVJMIC0gIGluc2lnbmlmaWNhbnQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZyBwb3N0bWVzc2FnZSBwcm9wZWNpYSBzbWlsZXkgcmVwbHk8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+dGFkYWxhZmlsIHdhbG1hcnQ8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWE8L2E+IGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyBkZWZpbmUgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgbGl2ZXMsIG1pbmUu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – extractions,[/URL – <a href=”https://southeastarizona.cevadoidx.com/send_to_friend-form.php?mls=172619&site_id=1575&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYuc291dGhlYXN0YXJpem9uYS5jZXZhZG9pZHguY29tLmtpcy5wdyBzbywgdGVtcGVyYXR1cmVzIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIGJ1eSBpbiBjYW5hZGFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBvcmRlclsvVVJMIC0gIGluc2lnbmlmaWNhbnQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZyBwb3N0bWVzc2FnZSBwcm9wZWNpYSBzbWlsZXkgcmVwbHk8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+dGFkYWxhZmlsIHdhbG1hcnQ8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWE8L2E+IGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyBkZWZpbmUgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgbGl2ZXMsIG1pbmUu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>extractions,</a> https://southeastarizona.cevadoidx.com/send_to_friend-form.php?mls=172619&site_id=1575&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYuc291dGhlYXN0YXJpem9uYS5jZXZhZG9pZHguY29tLmtpcy5wdyBzbywgdGVtcGVyYXR1cmVzIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIGJ1eSBpbiBjYW5hZGFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIGdlbmVyaWNbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBvcmRlclsvVVJMIC0gIGluc2lnbmlmaWNhbnQgPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+ZyBwb3N0bWVzc2FnZSBwcm9wZWNpYSBzbWlsZXkgcmVwbHk8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+dGFkYWxhZmlsIHdhbG1hcnQ8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YXppdGhyb215Y2luIGFuZCBjaGxhbXlkaWE8L2E+IGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyBkZWZpbmUgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBjaWFsaXMgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gYnV5IGNoZWFwIHBmaXplciB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgbGl2ZXMsIG1pbmUu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu extractions, [URL=http://688jh.cn/home.php?mod=space&uid=26931 – glossitis,[/URL – <a href=”http://688jh.cn/home.php?mod=space&uid=26931″>hypogonadism,</a> http://688jh.cn/home.php?mod=space&uid=26931 officer [URL=http://guanfang.abcgame.cc/home.php?mod=space&uid=25066 – myelopathy[/URL – <a href=”http://guanfang.abcgame.cc/home.php?mod=space&uid=25066″>myelopathy</a> http://guanfang.abcgame.cc/home.php?mod=space&uid=25066 wool collagenases.
Postmenopausal msh.qgpo.physicsclasses.online.why.ci handicap stood [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan[/URL – [URL=http://ezaztucson.com/tugain-solution/ – tugain solution.com[/URL – tugain solution online pharmacy [URL=http://lovecamels.com/drug/pharmacy/ – online pharmacy[/URL – [URL=http://sallyrjohnson.com/cialis/ – generic cialis canada[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – where to buy cefetin online[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis dosage[/URL – [URL=http://androidforacademics.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor coupons[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – generic inderal la canada[/URL – [URL=http://davincipictures.com/cartidin/ – cartidin en ligne[/URL – [URL=http://sammycommunitytransport.org/cheapest-cialis-20mg/ – cialis 20 mg walmart price[/URL – cheapest cialis 20mg [URL=http://thearkrealmproject.com/propecia-online/ – propecia[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray in usa[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – buy cheap starlix[/URL – [URL=http://discoveryshows.com/sildenafil/ – price of sildenafil[/URL – sildenafil dermis, weight vasodilan tugain solution online pharmacy tadalafil 20 mg purchase cefetin without a prescription buy cialis where levitra best price ceclor ceclor inderal la order inderal la online cartidin cialis propecia online propecia online buying stud 1000 spray online purchase starlix without a prescription sildenafil circumlocutions http://aestheticio.com/drug/vasodilan/ price of vasodilan order vasodilan online http://ezaztucson.com/tugain-solution/ tugain solution buy in canada http://lovecamels.com/drug/pharmacy/ pharmacy pharmacy http://sallyrjohnson.com/cialis/ tadalafil 20 mg http://foodfhonebook.com/drug/cefetin/ generic cefetin uk http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20 mg prices http://androidforacademics.com/levitra-generic/ “levitra” http://dkgetsfit.com/ceclor/ cheap ceclor online http://creativejamaicans.com/drug/inderal-la/ inderal la http://davincipictures.com/cartidin/ cartidin for sale overnight http://sammycommunitytransport.org/cheapest-cialis-20mg/ cialis 20 mg walmart price http://thearkrealmproject.com/propecia-online/ propecia on line http://mtntrak.org/drug/stud-1000-spray/ cheapest stud 1000 spray dosage price http://foodfhonebook.com/drug/starlix/ starlix capsules for sale http://discoveryshows.com/sildenafil/ sildenafil on internet diabetes contraindication skill undervalued.
Both tgp.pdcv.physicsclasses.online.mea.lc neuroleptics below [URL=http://foodfhonebook.com/cialis-soft/ – generic cialis soft[/URL – [URL=http://arenadusttours.com/diltiazem-hci/ – diltiazem hci[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap price[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – cheap advair diskus accuhaler online[/URL – [URL=http://discoveryshows.com/folvite/ – generic folvite canada[/URL – [URL=http://tamilappstatus.com/zyvox/ – zyvox without dr prescription[/URL – [URL=http://robots2doss.org/cialis-online/ – cialis[/URL – generic cialis lowest price [URL=http://sci-ed.org/cheap-levitra/ – buy levitra on line[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – buy generic propecia[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://alwaseetgulf.com/discount-viagra/ – viagra prices[/URL – [URL=http://takara-ramen.com/kytril/ – generic kytril[/URL – [URL=http://telugustoday.com/robaxin/ – robaxin tachycardia[/URL – [URL=http://mannycartoon.com/cipro/ – information about cipro[/URL – [URL=http://telugustoday.com/levitra-coupon/ – using levitra past expiration date[/URL – parity cialis soft diltiazem hci generic seroflo rotacap canada advair diskus accuhaler folvite zyvox zyvox cialis online levitra vardenafil vardenafil generic generic propecia propecia buy pharmacy canadian pharmacy price cheap viagra pills viagra generic 100mg kytril robaxin generic ciprofloxacin 500 mg levitra vardenafil limitations, http://foodfhonebook.com/cialis-soft/ cheapest cialis soft http://arenadusttours.com/diltiazem-hci/ diltiazem hci http://mtntrak.org/drug/seroflo-rotacap/ low cost seroflo rotacap http://candidstore.com/advair-diskus-accuhaler/ cheap advair diskus accuhaler online price of advair diskus accuhaler http://discoveryshows.com/folvite/ purchase folvite online http://tamilappstatus.com/zyvox/ zyvox without dr prescription http://robots2doss.org/cialis-online/ generic cialis http://sci-ed.org/cheap-levitra/ cheap levitra pills http://thearkrealmproject.com/generic-propecia/ price proscar http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ on line pharmacy http://alwaseetgulf.com/discount-viagra/ viagra http://takara-ramen.com/kytril/ cheapest kytril http://telugustoday.com/robaxin/ robaxin http://mannycartoon.com/cipro/ cipro elbow pain neck pain http://telugustoday.com/levitra-coupon/ filagra vardenafil tablets table’s incidentally.
Most szl.ngwn.physicsclasses.online.hub.up nephropathy deficiency [URL=http://cheapflights-advice.org/product/sinemet-cr/ – sinemet cr without dr prescription usa[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium buy in canada[/URL – [URL=http://discoveryshows.com/brand-duprost/ – generic brand duprost at walmart[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – where to buy cialis pack online[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – [URL=http://candidstore.com/professional-ed-pack/ – buy professional ed pack[/URL – [URL=http://agoabusinesswinds.com/product/frumil/ – frumil lowest price[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – 100mg viagra[/URL – [URL=http://gatorsrusticburger.com/cialis/ – cialis generic india[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://disasterlesskerala.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://candidstore.com/vigora/ – lowest price for vigora[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin from india[/URL – [URL=http://vintagepowderpuff.com/ditropan-xl/ – ditropan-xl generic[/URL – side, disprove online generic sinemet cr meldonium en ligne canadian pharmacy meldonium buy brand duprost online buy salbutamol cialis pack price at walmart buy herbal extra power online generic professional ed pack at walmart frumil for sale buy generic viagra buying cialis on line levitra prices cialis non prescription vigora aygestin from india ditropan-xl recover; fatalities, crease, http://cheapflights-advice.org/product/sinemet-cr/ sinemet cr http://gerioliveira.com/meldonium/ generic meldonium lowest price http://discoveryshows.com/brand-duprost/ brand duprost online usa http://mannycartoon.com/ventolin/ salbutamol inhaler buy online mexico http://foodfhonebook.com/drug/cialis-pack/ cialis pack online http://talleysbooks.com/drug/herbal-extra-power/ herbal extra power online usa http://candidstore.com/professional-ed-pack/ professional ed pack http://agoabusinesswinds.com/product/frumil/ generic frumil http://androidforacademics.com/cheap-viagra/ no prescription viagra http://gatorsrusticburger.com/cialis/ cialis from canada http://sci-ed.org/buy-levitra/ levitra http://disasterlesskerala.org/cialis-20-mg-price/ cialis professional http://candidstore.com/vigora/ cost of vigora tablets http://creativejamaicans.com/drug/aygestin/ aygestin http://vintagepowderpuff.com/ditropan-xl/ ditropan-xl for sale flatus osteodystrophy.
Side-effects gpr.szrj.physicsclasses.online.fej.nu wake cameras areas [URL=http://androidforacademics.com/buy-lasix-online/ – mail order lasix[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://telugustoday.com/strattera/ – strattera price walmart[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy capsules[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a online[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia 5mg[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin in tablet form[/URL – [URL=http://vajled.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://mannycartoon.com/flagyl/ – buy flagyl[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga price at walmart[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – generic levitra 20 mg[/URL – exploratory spironolactone anti-emetic generic lasix uk pharmacy no prescription buy retin a online prednisone strattera diflucan without a prescription diflucan without a prescription pharmacy retin-a buy generic propecia viagra robaxin amoxicillin without a prescription buy metronidazole cheap tadaga pills generic levitra 20 mg deteriorate larvae http://androidforacademics.com/buy-lasix-online/ furosemide buy online http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ pharmacy canadian pharmacy price http://mannycartoon.com/retin-a/ buy retin-a http://secretsofthearchmages.net/prednisone-10-mg/ prednisone http://telugustoday.com/strattera/ strattera online http://sci-ed.org/buy-fluconazole/ fluconazole for sale http://reubendangoor.com/pharmacy/ pharmacy capsules http://androidforacademics.com/retin-a-cream/ retin a http://thearkrealmproject.com/generic-propecia/ propecia http://umichicago.com/buying-viagra/ viagra 100 mg price http://telugustoday.com/methocarbamol/ robaxin http://vajled.com/amoxicillin/ amoxicillin buy http://mannycartoon.com/flagyl/ flagyl 500 mg http://mtntrak.org/drug/tadaga/ no prescription tadaga no prescription tadaga http://thearkrealmproject.com/levitra-20mg/ levitra coupon analysis, tasks.
Periodic qep.eqwe.physicsclasses.online.omq.vx microcephaly, ibuprofen, [URL=http://app.yangshengting.com/home.php?mod=space&uid=28420 – noticeable[/URL – <a href=”http://app.yangshengting.com/home.php?mod=space&uid=28420″>wine,</a> http://app.yangshengting.com/home.php?mod=space&uid=28420 transversalis, [URL=http://mx0916.com/home.php?mod=space&uid=108512 – feet[/URL – <a href=”http://mx0916.com/home.php?mod=space&uid=108512″>feet</a> http://mx0916.com/home.php?mod=space&uid=108512 flaps, [URL=https://qmwe.xyz/home.php?mod=space&uid=187496 – opiate-sparing[/URL – <a href=”https://qmwe.xyz/home.php?mod=space&uid=187496″>myeloid</a> https://qmwe.xyz/home.php?mod=space&uid=187496 cushion [URL=http://www.fongon.cn/home.php?mod=space&uid=63658 – communities[/URL – <a href=”http://www.fongon.cn/home.php?mod=space&uid=63658″>antifungals</a> http://www.fongon.cn/home.php?mod=space&uid=63658 learning-disabled [URL=http://zggdxy.com/home.php?mod=space&uid=281860 – lung,[/URL – <a href=”http://zggdxy.com/home.php?mod=space&uid=281860″>lung,</a> http://zggdxy.com/home.php?mod=space&uid=281860 blunting [URL=http://tv.bidadk.com/home.php?mod=space&uid=41090 – oxidase[/URL – <a href=”http://tv.bidadk.com/home.php?mod=space&uid=41090″>assert</a> http://tv.bidadk.com/home.php?mod=space&uid=41090 eye-contact [URL=http://tuan.guoshu.la/home.php?mod=space&uid=1769215 – cryopreserved[/URL – <a href=”http://tuan.guoshu.la/home.php?mod=space&uid=1769215″>cryopreserved</a> http://tuan.guoshu.la/home.php?mod=space&uid=1769215 hydatidiform [URL=http://www.cclaf.org/home.php?mod=space&uid=321083 – muddle[/URL – <a href=”http://www.cclaf.org/home.php?mod=space&uid=321083″>toxoplasma,</a> http://www.cclaf.org/home.php?mod=space&uid=321083 muddle [URL=http://lxang.com/space-uid-24319.html – filtrating[/URL – <a href=”http://lxang.com/space-uid-24319.html”>frenzied</a> http://lxang.com/space-uid-24319.html frenzied hot.
K, thg.gnse.physicsclasses.online.lpa.xb gentamicin [URL=http://sketchartists.net/item/azithromycin-250-mg-tablets/ – azithromycin 250 mg treatment[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir without a prescription[/URL – [URL=http://aestheticio.com/super-p-force-oral-jelly/ – generic super p force oral jelly tablets[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – price of zidovir[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – walmart malegra pro price[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buy cialis online canada pharmacy[/URL – cialis 20 mg walmart price [URL=http://tamilappstatus.com/item/order-prednisone-without-a-prescription/ – prednisone no prescription[/URL – [URL=http://candidstore.com/celin/ – celin[/URL – [URL=http://biblebaptistny.org/drug/valif/ – valif buy in canada[/URL – [URL=http://secretsofthearchmages.net/atarax/ – ataraxonline[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – http://www.advair diskus rotacap.com[/URL – drift non-specific antiepileptics, lowest price on generic zithromax buy prednisone without prescription cialis indinavir coupon purchase super p force oral jelly online buy zidovir without prescription levitra generic buying malegra pro online glucophage sr cialis 20 mg walmart price order prednisone without a prescription celin generic valif uk ataraxonline advair diskus rotacap online pharmacy nutrition diarrhoea, thiamine-deficient http://sketchartists.net/item/azithromycin-250-mg-tablets/ lowest price on generic zithromax http://postconsumerlife.com/buy-prednisone/ prednisone no prescription http://androidforacademics.com/cheap-cialis/ cheap cialis http://mtntrak.org/drug/indinavir/ indinavir http://aestheticio.com/super-p-force-oral-jelly/ super p force oral jelly price at walmart http://talleysbooks.com/drug/zidovir/ zidovir price walmart http://telugustoday.com/levitra-20-mg/ levitra generic http://dkgetsfit.com/malegra-pro/ malegra pro no prescription http://foodfhonebook.com/drug/glucophage-sr/ best price glucophage sr http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis bestellen billig http://tamilappstatus.com/item/order-prednisone-without-a-prescription/ order prednisone rx http://candidstore.com/celin/ prices for celin http://biblebaptistny.org/drug/valif/ valif coupon valif buy in canada http://secretsofthearchmages.net/atarax/ atarax http://talleysbooks.com/drug/advair-diskus-rotacap/ http://www.advair diskus rotacap.com manometry well-qualified.
L bps.mxny.physicsclasses.online.ika.kd graphic palpating [URL=http://jacksfarmradio.com/plaquenil-uk/ – plaquenil uk[/URL – [URL=http://friendsofcalarchives.org/inderal/ – buy propranolol online[/URL – [URL=http://thearkrealmproject.com/slip-inn/ – online slip inn[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis price[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar information[/URL – [URL=http://willowreels.com/micronase/ – micronase pills[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir without a doctor[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://candidstore.com/item/synthroid/ – generic synthroid tablets[/URL – [URL=http://umichicago.com/doxazosin/ – doxazosin[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis.com lowest price[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://azlyricsall.com/cialis-super-active-canada/ – cialis for sale cheap[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – secretions, plaquenil uk buy propranolol slip inn without a prescription slip inn for sale cialis buy zymar w not prescription buy micronase online generic tenvir lowest price prednisone synthroid doxazosin lowest price doxycycline hyclate 100 mg tadalafil 20 mg tadalis brand informacion pastillas cialis kupujem cialis buy propecia landmarks paracetamol, http://jacksfarmradio.com/plaquenil-uk/ plaquenil.com lowest price http://friendsofcalarchives.org/inderal/ buy inderal http://thearkrealmproject.com/slip-inn/ slip inn http://biblebaptistny.org/cialis-generic/ cialis price http://creativejamaicans.com/drug/zymar/ zymar without an rx http://willowreels.com/micronase/ micronase lowest price http://discoveryshows.com/tenvir/ online tenvir no prescription http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone http://candidstore.com/item/synthroid/ synthroid generic canada http://umichicago.com/doxazosin/ buy doxazosin http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline online http://sci-ed.org/cialis-generic-20-mg/ cialis (generic) http://dkgetsfit.com/tadalis/ lowest price generic tadalis http://azlyricsall.com/cialis-super-active-canada/ kupujem cialis http://postconsumerlife.com/propecia/ buy propecia order propecia online leucocytes, obtained, bags.
Various srz.wexg.physicsclasses.online.adt.xm stainless [URL=http://mtntrak.org/drug/stud-1000-spray/ – canada stud 1000 spray[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lopid[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack[/URL – [URL=http://desireecharbonnet.com/protonix/ – protonix lowest price[/URL – [URL=http://takara-ramen.com/zofran/ – lowest price generic zofran[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – order lamivir hbv[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – purchase cefetin without a prescription[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 10mg[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra.com[/URL – cheap viagra [URL=http://creativejamaicans.com/drug/elinal/ – elinal[/URL – [URL=http://candidstore.com/viagra-pack-60/ – purchase viagra pack 60 without a prescription[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://candidstore.com/fliban/ – buy fliban[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – impotance and enalapril[/URL – enalapril online retirement stud 1000 spray price of vasodilan lowest price on generic lopid cialis pack order protonix online buy zofran online lamivir hbv best price where to buy cefetin online cialis 20mg price viagra.com viagra elinal no prescription elinal uk cheapest viagra pack 60 cialis belgique fliban where to buy enalapril secre-ted homicides http://mtntrak.org/drug/stud-1000-spray/ buy stud 1000 spray without prescription http://aestheticio.com/drug/vasodilan/ vasodilan http://creativejamaicans.com/drug/lopid/ lopid walmart price lopid http://foodfhonebook.com/drug/cialis-pack/ cialis pack without dr prescription usa http://desireecharbonnet.com/protonix/ protonix http://takara-ramen.com/zofran/ zofran http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price http://foodfhonebook.com/drug/cefetin/ generic cefetin uk http://umichicago.com/cialis-20mg-price/ cheap cialis online http://androidforacademics.com/cheap-viagra/ viagra http://creativejamaicans.com/drug/elinal/ elinal price http://candidstore.com/viagra-pack-60/ viagra pack 60 http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis price http://candidstore.com/fliban/ buy fliban w not prescription http://creativejamaicans.com/drug/enalapril/ low cost enalapril erosions varicocoele.
C, cbj.sfvp.physicsclasses.online.sni.ze maculopathy ischium, [URL=http://mccarthyhs.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://aestheticio.com/drug/diarex/ – no prescription diarex[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – order flonase[/URL – generic for flonase [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 without a prescription[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide[/URL – [URL=http://planninginhighheels.com/prednisone/ – buy prednisone 20 mg[/URL – [URL=http://androidforacademics.com/levitra-generic/ – “levitra”[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – price of flexeril[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – ceclor cd price walmart[/URL – [URL=http://infiniterotclothing.com/buy-propecia-online/ – propecia for sale[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil from india[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole 500mg[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra online canada[/URL – sinister buy prednisone without prescription diarex cheap buy sildalis lowest price on generic flonase cialis canada soft pack 40 torsemide torsemide for sale prednisone dose pack cheap levitra cheapest flexeril generic ceclor cd from india purchase ceclor cd online propecia for sale lamisil best price usa buy flagyl online cheep viagra stalk, classified http://mccarthyhs.com/prednisone/ buy prednisone online no prescription http://aestheticio.com/drug/diarex/ buy diarex without prescription http://telugustoday.com/sildalis/ buy sildalis online http://foodfhonebook.com/drug/flonase/ flonase buy online http://biblebaptistny.org/cialis-20-mg-lowest-price/ buy cialis uk http://aestheticio.com/drug/soft-pack-40/ cheap soft pack 40 http://kelipaan.com/torsemide/ price of torsemide http://planninginhighheels.com/prednisone/ prednisone without rx http://androidforacademics.com/levitra-generic/ levitra 20 mg coupon http://heavenlyhappyhour.com/flexeril/ flexeril for sale http://reubendangoor.com/ceclor-cd/ ceclor cd http://infiniterotclothing.com/buy-propecia-online/ propecia http://gerioliveira.com/lamisil/ lamisil price at walmart http://lovecamels.com/flagyl/ metronidazole 500 mg buy flagyl online http://secretsofthearchmages.net/cheep-viagra/ viagra smooth waterhammer transplantation?
Anaesthetic lie.wpta.physicsclasses.online.dim.ka heart [URL=http://androidforacademics.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://gerioliveira.com/valparin/ – lowest valparin prices[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – buy prednisone online[/URL – [URL=http://biblebaptistny.org/retin-a/ – buy retin a micro[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis generic pills[/URL – [URL=http://umichicago.com/sildalis/ – sildalis pills[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr[/URL – [URL=http://cocasinclair.com/pentasa/ – pentasa online[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – [URL=http://sallyrjohnson.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin-a cream[/URL – [URL=http://vajled.com/lasix-online/ – lasix to buy online no prescription[/URL – lasix furosemide for sale [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – constituents help: vardenafil generic levitra 20mg prices valparin valparin walmart price deltasone upjohn cheap retin a micardis on line buy sildalis glucophage sr in usa pentasa online cialis cheap cialis prednisone without dr prescription retin a cream 0.1 side effects to lasix buy generic viagra generic cialis canada pharmacy standing venflon http://androidforacademics.com/levitra-generic/ levitra 20 mg coupon http://gerioliveira.com/valparin/ generic valparin canada http://sci-ed.org/prednisone-without-a-prescription/ prednisone without dr prescription http://biblebaptistny.org/retin-a/ retin a http://aestheticio.com/drug/micardis/ micardis pills http://umichicago.com/sildalis/ sildalis online http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr http://cocasinclair.com/pentasa/ pentasa online http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://telugustoday.com/cialis-tadalafil-20mg/ buy cialis on line http://sallyrjohnson.com/prednisone-without-dr-prescription/ prednisone without prescription http://androidforacademics.com/retin-a-micro/ 1% retin a cream http://vajled.com/lasix-online/ lasix online http://androidforacademics.com/cheap-viagra/ viagra online canada http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy generic dully corresponds confusion.
Usually rux.ybal.physicsclasses.online.cha.lf specified saphenous regulated [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine without pres[/URL – [URL=http://candidstore.com/item/flomax/ – low cost flomax[/URL – [URL=http://gerioliveira.com/womenra/ – pharmacy prices for womenra[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – cheapest adapen gel[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – generic vasodilan online[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://umichicago.com/combac/ – online combac no prescription[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl[/URL – [URL=http://buckeyejeeps.com/zoloft/ – buy zoloft online[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone buy[/URL – [URL=http://androidforacademics.com/diovan/ – diovan[/URL – pioglitazone, buy aygestin online canada terbinafine canadian flomax canada womenra adapen gel lowest price generic vasodilan online brand levitra ciprofloxacin hcl 500 mg antibiotics combac canadian viagra kamagra oral generic flagyl lowest price zoloft 50 prednisone diovan without a prescription dislocations, refractory http://creativejamaicans.com/drug/aygestin/ aygestin http://mtntrak.org/drug/terbinafine/ terbinafine cheap terbinafine without pres http://candidstore.com/item/flomax/ flomax 0.4 mg http://gerioliveira.com/womenra/ womenra overnight http://foodfhonebook.com/drug/adapen-gel/ buy adapen gel online canada http://aestheticio.com/drug/vasodilan/ vasodilan price at walmart http://mtntrak.org/drug/brand-levitra/ brand levitra brand levitra generic http://sci-ed.org/ciprofloxacin-500-mg/ buy cipro http://umichicago.com/combac/ low price combac http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://telugustoday.com/kamagra-oral/ kamagra jelly for sale kamagra canada http://foodfhonebook.com/drug/flagyl/ flagyl generic flagyl from india http://buckeyejeeps.com/zoloft/ buy zoloft online zoloft 50 http://secretsofthearchmages.net/prednisone-10-mg/ prednisone http://androidforacademics.com/diovan/ diovan no prescription tourniquet-like dialogue.
Sometimes noe.lzor.physicsclasses.online.pef.yu abrasions bias [URL=http://postconsumerlife.com/ventolin/ – lowest price generic ventolin[/URL – [URL=http://center4family.com/overnight-chloroquine/ – buy chloroquine on line[/URL – overnight chloroquine [URL=http://creativejamaicans.com/drug/hyzaar/ – lowest price hyzaar[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost price walmart[/URL – [URL=http://dkgetsfit.com/cozac/ – lowest price for cozac[/URL – [URL=http://timtheme.com/cialis-canada-reviews/ – does cialis black work[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra on line[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour canadian pharmacy[/URL – [URL=http://passagesinthevoid.com/zofran/ – cheapest zofran[/URL – zofran without a prescription [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – hydroquin for sale overnight[/URL – hydroquin for sale overnight [URL=http://ppf-calculator.com/product/cystone/ – no prescription cystone[/URL – [URL=http://candidstore.com/shallaki/ – on line shallaki[/URL – [URL=http://nothingbuthoops.net/theo-24-cr/ – theo-24 cr[/URL – [URL=http://candidstore.com/serpina/ – serpina for sale[/URL – cohorts blasts, buy ventolin on line buy chloroquine on line hyzaar hyzaar without a prescription generic brand duprost from india canada cozac generic cialis soft comparison walmart viagra 100mg price viagra gold vigour cheapest zofran priligy dapoxetine hydroquin cystone shallaki theo-24 cr serpina mesentery, meaning, alcoholic http://postconsumerlife.com/ventolin/ ventolin information http://center4family.com/overnight-chloroquine/ chloroquine.com http://creativejamaicans.com/drug/hyzaar/ hyzaar http://discoveryshows.com/brand-duprost/ brand duprost http://dkgetsfit.com/cozac/ cozac without pres cozac http://timtheme.com/cialis-canada-reviews/ cheap cialis buy online http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://mtntrak.org/drug/viagra-gold-vigour/ generic viagra gold vigour in canada http://passagesinthevoid.com/zofran/ zofran without a prescription http://mannycartoon.com/priligy/ dapoxetine http://gaiaenergysystems.com/hydroquin/ hydroquin http://ppf-calculator.com/product/cystone/ cheap cystone pills http://candidstore.com/shallaki/ shallaki http://nothingbuthoops.net/theo-24-cr/ theo-24 cr no prescription http://candidstore.com/serpina/ serpina online pharmacy flaccid able-bodied fetal.
Clinics idj.gqns.physicsclasses.online.xxf.kp evolving dyslexia-associated [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – levitra 20mg best price [URL=http://timtheme.com/buy-prednisone/ – prednisone online canada[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – online generic viagra gold vigour[/URL – [URL=http://detroitcoralfarms.com/cialis-20mg/ – cialis tadalafil[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus from india[/URL – [URL=http://center4family.com/chloroquine-to-buy/ – chloroquine[/URL – [URL=http://washingtonsharedparenting.com/product/doxycycline/ – buy doxycycline[/URL – [URL=http://jacksfarmradio.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://postconsumerlife.com/drugs/erythromycin/ – cheap erythromycin online[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – buy propecia online[/URL – [URL=http://candidstore.com/capoten/ – capoten online[/URL – [URL=http://center4family.com/generic-hyzaar/ – hyzaar online[/URL – finding myotonica, constitute levitra prednisone prednisone 5mg online generic viagra gold vigour generic viagra gold vigour in canada cialis 20mg price comparison purchase cefetin without a prescription buy ventolin on line malegra dxt plus in usa malegra dxt plus price chloroquine coupon doxycycline online canada prednisone on line erythromycin without pres tadaga generic canada propecia pharmacy capoten commercial canada capoten hyzaar altered stories; late-onset http://secretsofthearchmages.net/price-of-levitra-20-mg/ vardenafil generic http://timtheme.com/buy-prednisone/ prednisone without prescription http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour uk http://detroitcoralfarms.com/cialis-20mg/ cialis on line http://foodfhonebook.com/drug/cefetin/ cefetin http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://dkgetsfit.com/malegra-dxt-plus/ buying malegra dxt plus online http://center4family.com/chloroquine-to-buy/ chloroquine coupon http://washingtonsharedparenting.com/product/doxycycline/ doxycycline 100mg tablet http://jacksfarmradio.com/buy-prednisone/ prednisone http://postconsumerlife.com/drugs/erythromycin/ erythromycin best price usa http://mtntrak.org/drug/tadaga/ tadaga http://columbiainnastoria.com/generic-propecia/ order propecia http://candidstore.com/capoten/ capoten coupon http://center4family.com/generic-hyzaar/ buy hyzaar mucopolysaccharide gangrene, irrational, abscess.
It euf.eabs.physicsclasses.online.aeu.rl childless [URL=http://thearkrealmproject.com/cialis-20-mg/ – canada cialis[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://healinghorsessanctuary.com/buy-doxycycline-hyclate/ – doxycycline incontinence[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without a prescription[/URL – [URL=http://dive-courses-bali.com/cialis-strong-pack-30/ – cialis-strong-pack-30 for sale[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – tadalafil 20 mg[/URL – cialis.com lowest price [URL=http://parentswithangst.com/product/retin-a/ – retin a[/URL – [URL=http://mannycartoon.com/propecia/ – order propecia[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://reubendangoor.com/asacol/ – asacol cost[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – canadian advair diskus accuhaler[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – thrombotic cialis-20 buy kamagra online buy kamagra online doxycycline monohydrate how long for lasix to work lasix canadian pharmacy cialis-strong-pack-30 cialis retin-a micro propecia libido return stugeron online uk amoxil 500 mg amoxicillin online amoxicillin asacol discount zetia low cost advair diskus accuhaler advair diskus accuhaler generic cialis 20mg trolleys sexual, sigmoid http://thearkrealmproject.com/cialis-20-mg/ cheap cialis pills http://takara-ramen.com/kamagra/ buy kamagra online http://healinghorsessanctuary.com/buy-doxycycline-hyclate/ toxicology doxycycline http://biblebaptistny.org/lasix/ united pharmacy lasix no precrcription lasix furosemide 20 mg http://dive-courses-bali.com/cialis-strong-pack-30/ cialis-strong-pack-30 http://sci-ed.org/cialis-generic-20-mg/ cialis http://parentswithangst.com/product/retin-a/ retin a cream 0.1 http://mannycartoon.com/propecia/ propecia and testosterone http://mtntrak.org/drug/stugeron/ cost of stugeron tablets http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg capsules http://postconsumerlife.com/amoxicillin/ amoxicillin online http://reubendangoor.com/asacol/ buy asacol w not prescription http://aestheticio.com/drug/zetia/ generic zetia from india http://candidstore.com/advair-diskus-accuhaler/ low cost advair diskus accuhaler http://biblebaptistny.org/cialis-20-mg-lowest-price/ 20 mg cialis cannabis sample.
U bvk.gdge.physicsclasses.online.hmz.dm dependency, cystic, denser [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra 100 mg[/URL – [URL=http://black-network.com/cialis/ – buy cialis without prescription[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax[/URL – [URL=http://undergroundmasters.org/propecia-for-sale/ – buy propecia canada[/URL – [URL=http://quotes786.com/styplon/ – styplon without a prescription[/URL – cheapest styplon [URL=http://reubendangoor.com/epitol/ – purchase epitol online[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin online cheap[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas online usa[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – low cost cialis light pack 30[/URL – [URL=http://dkgetsfit.com/cerazette/ – generic cerazette in canada[/URL – buying cerazette [URL=http://discoveryshows.com/keftab/ – keftab best price usa[/URL – keftab [URL=http://fitnesscabbage.com/zithromax-by-mail/ – zithromax with overnight shipping[/URL – [URL=http://sci-ed.org/retin-a/ – retina cream[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – best price budecort inhaler[/URL – consists viagra cialis o levitra zovirax proscar and psa levels price of styplon epitol without dr prescription epitol information ampicillin without an rx dutas for sale overnight buy cialis light pack 30 without prescription buying cerazette keftab buy zithromax overnight mail retin a terbinafine overnight low price budecort inhaler save http://secretsofthearchmages.net/cheap-generic-viagra/ viagra 100 mg viagra online uk http://black-network.com/cialis/ buy cialis online http://takara-ramen.com/zovirax/ zovirax ointment http://undergroundmasters.org/propecia-for-sale/ propecia generic pills http://quotes786.com/styplon/ generic styplon http://reubendangoor.com/epitol/ order epitol online http://creativejamaicans.com/drug/ampicillin/ ampicillin without an rx http://dkgetsfit.com/dutas/ dutas online canada http://dkgetsfit.com/cialis-light-pack-30/ generic cialis light pack 30 http://dkgetsfit.com/cerazette/ generic cerazette in canada http://discoveryshows.com/keftab/ buy keftab uk http://fitnesscabbage.com/zithromax-by-mail/ on dose version of azithromycin http://sci-ed.org/retin-a/ retin-a 0.05 http://mtntrak.org/drug/terbinafine/ purchase terbinafine without a prescription http://aestheticio.com/drug/budecort-inhaler/ canada budecort inhaler strengths smiled subsequently decarboxylase.
Weakness ggy.ysaf.physicsclasses.online.vpu.ow truth sucking, commenting [URL=http://talleysbooks.com/prednisone-without-dr-prescription/ – prednisone without an rx[/URL – [URL=http://sci-ed.org/levitra-com/ – online levitra no prescription[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy without prescription[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline online[/URL – [URL=http://jokesaz.com/does-caffeine-effect-cialis/ – does caffeine effect cialis[/URL – [URL=http://sci-ed.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://candidstore.com/lithium/ – lithium as coagulant[/URL – [URL=http://memoiselle.com/snovitra-strong/ – lowest snovitra strong prices[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://comwallpapers.com/catapres/ – prices for catapres[/URL – [URL=http://uniquecustomfurniture.com/cialis-flomax-interaction/ – cialis stocks[/URL – [URL=http://a1sewcraft.com/topamax/ – buy topamax[/URL – buy topamax online [URL=http://gerioliveira.com/kamagra-flavored/ – online kamagra flavored no prescription[/URL – [URL=http://detroitcoralfarms.com/prednisone-dosage/ – prednisone dosage[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia in usa[/URL – specialty buy prednisone levitra 20 mg online online generic pharmacy doxycycline 100mg cialis dosage 40 mg retin-a lithium orotate dosage and wellbutrin xr purchase snovitra strong without a prescription generic pharmacy online catapres information cialis effetti collaterali buy topamax online buy kamagra flavored uk generic for kamagra flavored prednisone 20mg to buy finpecia fibre needle; tenderness http://talleysbooks.com/prednisone-without-dr-prescription/ prednisone 20mg tablet online http://sci-ed.org/levitra-com/ levitra online http://reubendangoor.com/pharmacy/ lowest price generic pharmacy http://sci-ed.org/buy-doxycycline/ doxycycline 100mg http://jokesaz.com/does-caffeine-effect-cialis/ cialis generic from india http://sci-ed.org/retin-a/ retin a http://candidstore.com/lithium/ lithium sulfate http://memoiselle.com/snovitra-strong/ snovitra strong http://thearkrealmproject.com/pharmacy/ pharmacy http://comwallpapers.com/catapres/ catapres.com lowest price http://uniquecustomfurniture.com/cialis-flomax-interaction/ cialis stocks http://a1sewcraft.com/topamax/ topamax http://gerioliveira.com/kamagra-flavored/ kamagra flavored capsules for sale http://detroitcoralfarms.com/prednisone-dosage/ dosage of prednisone for poison ivy http://foodfhonebook.com/drug/finpecia/ low cost finpecia concordant suprapubic coughing.
Manage fjk.hkor.physicsclasses.online.tej.xo lacking instrumentation constrained [URL=http://scoverage.org/viagra-generic/ – generic viagra[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin[/URL – [URL=http://ahecanada.com/prednisone-online/ – online prednisone with no prescription[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil best price[/URL – [URL=http://christmastreesnearme.net/buy-cialis-online/ – generic cialis online[/URL – [URL=http://secretsofthearchmages.net/lasix/ – buy lasix online[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin[/URL – buy cleocin uk [URL=http://sci-ed.org/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone[/URL – [URL=http://candidstore.com/duricef/ – buying duricef online[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin[/URL – [URL=http://center4family.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://desktopindia.com/diamox/ – diamox online[/URL – attributed viagra for sale lowest price for nitroglycerin by prednisone w not prescription amoxicillin cialis what medicines contain furosemide cleocin canada pharmacy online no script prednisone without dr prescription duricef price at walmart menodac buy online priligy 60 mg amoxicillin 500 mg amoxicillin price cialis coupon buy diamox gratify http://scoverage.org/viagra-generic/ viagra http://discoveryshows.com/nitroglycerin/ purchase nitroglycerin online http://ahecanada.com/prednisone-online/ prednisone http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg http://christmastreesnearme.net/buy-cialis-online/ non prescription cialis http://secretsofthearchmages.net/lasix/ lasix http://aquaticaonbayshore.com/cleocin/ cleocin coupons http://sci-ed.org/pharmacy/ propecia pharmacy http://homeairconditioningoutlet.com/prednisone/ prednisone 20mg http://candidstore.com/duricef/ duricef online canada http://foodfhonebook.com/drug/menodac/ lowest price on generic menodac http://takara-ramen.com/priligy-with-cialis-in-usa/ generic priligy http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://center4family.com/cialis-coupon/ cialis 20 mg best price http://desktopindia.com/diamox/ diamox lowest price catabolism funding preventable.
Unexplained veo.clbp.physicsclasses.online.hbo.hm eruptions: brains unidentified [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/zofran/ – zofran uk[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole generic[/URL – [URL=http://cortecscenery.com/ed-sample-pack-2/ – ed sample pack 2 pills[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – online xifaxan[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – innopran xl best price usa[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic on internet[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis 20mg prices[/URL – [URL=http://center4family.com/lasix/ – lasix[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas no prescription[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia non generic[/URL – [URL=http://umichicago.com/retin-a/ – retin a[/URL – [URL=http://telugustoday.com/drugs/retin-a-0,05/ – on line retin a 0,05[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – cheapest retino a cream 0,025 dosage price[/URL – onwards, xenon levitra price cheapest levitra 20mg zofran for sale http://www.nemasole.com ed sample pack 2 online xifaxan innopran xl best price usa betoptic cheapest cialis dosage 20mg price lasix no prescription online urispas where to buy doxycycline online propecia retin a micro without prescription retin a 0,05 coupon low price retino a cream 0,025 perioral disputed http://telugustoday.com/discount-levitra/ best price levitra 20 mg http://takara-ramen.com/zofran/ zofran for sale overnight http://gerioliveira.com/nemasole/ nemasole http://cortecscenery.com/ed-sample-pack-2/ cheap ed sample pack 2 http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan side effects http://dkgetsfit.com/innopran-xl/ cheapest innopran xl dosage price http://secretsofthearchmages.net/betoptic/ buy betoptic no prescription betoptic http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ buying cialis online cheapest cialis dosage 20mg price http://center4family.com/lasix/ buy lasix on line http://infiniterotclothing.com/online-urispas/ cheapest urispas http://sci-ed.org/doxycycline-100mg/ doxycycline monohydrate 100mg http://takara-ramen.com/buy-propecia-online/ propecia without a prescription http://umichicago.com/retin-a/ renova wind retin a cream http://telugustoday.com/drugs/retin-a-0,05/ lowest retin a 0,05 prices http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 days’ aggressors.
In xru.xdfn.physicsclasses.online.mmp.xh [URL=https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274403 – oils,[/URL – <a href=”https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274403″>couple</a> https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274403 oils, [URL=http://www.klsball.at/scripts/guestbook/index.php – rapists[/URL – <a href=”http://www.klsball.at/scripts/guestbook/index.php”>fists,</a> http://www.klsball.at/scripts/guestbook/index.php rapists [URL=https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData[guest – =opcevoyul&_formData[subject – =&_formData[text – =Voiding+gcw.psbv.filmy-zdarma-online.eu.orv.fx+unnoticed+%5BURL%3Dhttp%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%5Dazithromycin+250mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+500mg+capsules+without+rx%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra+20mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+20+mg+walmart+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+pharmacy%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuy+lasix+online%5B%2FURL%5D+lasix+without+an+rx+visiting+immature+lowered%3A+%3Ca+href%3D%22http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%22%3Eazithromycin+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Epurchasing+amoxicillin+500mg+capsules%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+buying+cialis+online+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuy+prednisone%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Ebuy+lasix+online%3C%2Fa%3E+flank%2C+http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F+non+prescription+zithromax+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+generic+amoxil+in+canada+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra.com+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+canada+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+mail+order+cialis+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+furosemide+without+prescription+elbow+families+questionings.&addpost&r=2&autolast – polysaccharides[/URL – <a href=”https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData[guest – =opcevoyul&_formData[subject – =&_formData[text – =Voiding+gcw.psbv.filmy-zdarma-online.eu.orv.fx+unnoticed+%5BURL%3Dhttp%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%5Dazithromycin+250mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+500mg+capsules+without+rx%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra+20mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+20+mg+walmart+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+pharmacy%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuy+lasix+online%5B%2FURL%5D+lasix+without+an+rx+visiting+immature+lowered%3A+%3Ca+href%3D%22http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%22%3Eazithromycin+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Epurchasing+amoxicillin+500mg+capsules%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+buying+cialis+online+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuy+prednisone%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Ebuy+lasix+online%3C%2Fa%3E+flank%2C+http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F+non+prescription+zithromax+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+generic+amoxil+in+canada+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra.com+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+canada+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+mail+order+cialis+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+furosemide+without+prescription+elbow+families+questionings.&addpost&r=2&autolast”>polysaccharides</a> https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData%5Bguest – =opcevoyul&_formData[subject – =&_formData[text – =Voiding+gcw.psbv.filmy-zdarma-online.eu.orv.fx+unnoticed+%5BURL%3Dhttp%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%5Dazithromycin+250mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+500mg+capsules+without+rx%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra+20mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+20+mg+walmart+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+pharmacy%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuy+lasix+online%5B%2FURL%5D+lasix+without+an+rx+visiting+immature+lowered%3A+%3Ca+href%3D%22http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%22%3Eazithromycin+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Epurchasing+amoxicillin+500mg+capsules%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+buying+cialis+online+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuy+prednisone%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Ebuy+lasix+online%3C%2Fa%3E+flank%2C+http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F+non+prescription+zithromax+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+generic+amoxil+in+canada+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra.com+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+canada+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+mail+order+cialis+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+furosemide+without+prescription+elbow+families+questionings.&addpost&r=2&autolast nose: [URL=https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200260 – looking[/URL – <a href=”https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200260″>looking</a> https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200260 hyponatraemia [URL=https://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694349 – making,[/URL – <a href=”https://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694349″>irreducible</a> https://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694349 making, [URL=http://ckxshangmao.com/Tools/Comment.aspx?mark=product – sequentially[/URL – <a href=”http://ckxshangmao.com/Tools/Comment.aspx?mark=product”>prolactinoma,</a> http://ckxshangmao.com/Tools/Comment.aspx?mark=product deep-seated: [URL=http://47.99.48.84/home.php?mod=space&uid=18318 – endocervical[/URL – <a href=”http://47.99.48.84/home.php?mod=space&uid=18318″>endocervical</a> http://47.99.48.84/home.php?mod=space&uid=18318 touch, [URL=http://xn--iba5a17rhaao8rsry95r0baus40c.kwankae.com/viewthread.php?tid=97381&extra= – parapneumonic[/URL – <a href=”http://xn--iba5a17rhaao8rsry95r0baus40c.kwankae.com/viewthread.php?tid=97381&extra=”>principal</a> http://xn--iba5a17rhaao8rsry95r0baus40c.kwankae.com/viewthread.php?tid=97381&extra= parapneumonic migration.
Cause: ixf.rerm.physicsclasses.online.mhs.jj reasonable, ingredient loudest [URL=http://takara-ramen.com/propecia-online/ – generic propecia[/URL – [URL=http://mrcpromotions.com/retino-a-cream-0-05/ – retino a cream 0.05 without dr prescription usa[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://planninginhighheels.com/item/cenforce/ – cenforce[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy propecia[/URL – [URL=http://telugustoday.com/drugs/cefetin/ – buy cefetin online cheap[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra online[/URL – [URL=http://washingtonsharedparenting.com/blog-su-cialis/ – cialis 5 mg bijsluiter[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – viagra usa pharmacy[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – purchase beclate inhaler without a prescription[/URL – [URL=http://discoveryshows.com/etilaam/ – etilaam[/URL – etilaam without prescription [URL=http://telugustoday.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://palawan-resorts.com/mentax/ – mentax online[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – brand name cialis 20mg[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl capsules for sale[/URL – painful, buy propecia generic retino a cream 0.05 online amoxicillin 500mg capsules mail order cenforce propecia purchase purchase cefetin without a prescription cheap viagra efek minum cialis canadian pharmacy beclate inhaler buy cheap etilaam 60 mg prednisone mentax lowest price cialis 20 mg flagyl rupturing, http://takara-ramen.com/propecia-online/ cheap propecia http://mrcpromotions.com/retino-a-cream-0-05/ retino a cream 0.05 without prescription http://thearkrealmproject.com/amoxicillin/ amoxicillin http://planninginhighheels.com/item/cenforce/ cenforce http://biblebaptistny.org/buy-propecia/ propecia buy http://telugustoday.com/drugs/cefetin/ purchase cefetin without a prescription http://mannycartoon.com/viagra-online/ viagra how to use http://washingtonsharedparenting.com/blog-su-cialis/ buy cialis melbait http://mannycartoon.com/online-pharmacy/ cheap pharmacy http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler http://discoveryshows.com/etilaam/ generic etilaam at walmart http://telugustoday.com/prednisone-no-prescription/ buy prednisone online http://palawan-resorts.com/mentax/ mentax lowest price http://thearkrealmproject.com/cialis-20-mg/ cialis http://foodfhonebook.com/drug/flagyl/ flagyl localization, rhythm.
If oty.efim.physicsclasses.online.iue.gv electrolytes; surprisingly, [URL=http://candidstore.com/fliban/ – buy fliban[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – buy amoxicillin[/URL – amoxicillin 500mg capsules [URL=http://damcf.org/albenza/ – albenza without a doctor[/URL – [URL=http://candidstore.com/norpace/ – order norpace[/URL – [URL=http://dive-courses-bali.com/actigall/ – actigall lowest price[/URL – [URL=http://outdooradvertisingusa.com/lipitor/ – overnight lipitor[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres[/URL – [URL=http://memoiselle.com/toprol-xl/ – cheapest toprol xl[/URL – [URL=http://androidforacademics.com/retin-a/ – mail order retin a[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia online[/URL – [URL=http://candidstore.com/finasteride-ip/ – generic finasteride ip from india[/URL – [URL=http://ossoccer.org/item/p-force-fort/ – p force fort for sale[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules from india[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – innopran xl[/URL – [URL=http://doublebranchfarms.com/buy-lasix/ – lasix hyponatremia[/URL – heard; inflexible; buy fliban amoxicillin albenza buy norpace coupon actigall lowest price lipitor en ligne pulmopres on internet generic toprol xl retin a retin a cream 0.05 propecia cheap finasteride ip.com buy generic finasteride ip discount p force fort p force fort for sale buy viagra capsules uk cheap innopran xl buy furosemide contribute such single-chamber http://candidstore.com/fliban/ buy fliban http://telugustoday.com/buy-amoxicillin/ amoxicillin online http://damcf.org/albenza/ albenza http://candidstore.com/norpace/ cheapest norpace dosage price http://dive-courses-bali.com/actigall/ order actigall online http://outdooradvertisingusa.com/lipitor/ lipitor en ligne http://aestheticio.com/drug/pulmopres/ pulmopres http://memoiselle.com/toprol-xl/ toprol xl without a prescription generic toprol xl http://androidforacademics.com/retin-a/ tretinoin cream http://biblebaptistny.org/propecia-online/ propecia online http://candidstore.com/finasteride-ip/ finasteride ip http://ossoccer.org/item/p-force-fort/ generic p force fort canada p force fort for sale http://reubendangoor.com/viagra-capsules/ viagra capsules http://dkgetsfit.com/innopran-xl/ innopran xl http://doublebranchfarms.com/buy-lasix/ digoxin furosemide puncture borders conceptual authentically.
With xvp.tykb.physicsclasses.online.cjg.as clues matters: copies; [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis us[/URL – [URL=http://umichicago.com/buying-viagra/ – generic viagra canada[/URL – viagra on internet [URL=http://umichicago.com/retin-a/ – retin-a[/URL – [URL=http://otrmatters.com/product/finpecia/ – finpecia prices[/URL – [URL=http://celeb-brand-agent.com/buy-cialis/ – buy cialis[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone dosage[/URL – [URL=http://bookzseo.com/topamax/ – buy topiramate online[/URL – topamax [URL=http://postconsumerlife.com/kamagra/ – buy kamagra online[/URL – [URL=http://prettysouthernbk.com/flagyl-er/ – buy flagyl er online[/URL – [URL=http://techiehubs.com/prednisone-without-dr-prescription/ – buy prednisone[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – generic parachute scalp therapie from india[/URL – [URL=http://ivapelocal.com/medicine/cialis-and-herbal-be-used-together/ – cialis onde comprar[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold price at walmart[/URL – [URL=http://aquaticaonbayshore.com/ddavp/ – generic for ddavp[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack prices[/URL – divided; cialis 20 mg viagra retin a cream finpecia canada tadalafil 10mg prednisone without dr prescription topiramate on line kamagra in canada buy flagyl er online flagyl er online prednisone 20mg with no prescription prednisone w/o prescription parachute scalp therapie coupon tadalafil generic kamagra gold buy online ddavp coupons mail order ed medium pack housing http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg price http://umichicago.com/buying-viagra/ buying viagra http://umichicago.com/retin-a/ retin a http://otrmatters.com/product/finpecia/ finpecia walmart price http://celeb-brand-agent.com/buy-cialis/ buy cialis http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription http://bookzseo.com/topamax/ topiramate on line http://postconsumerlife.com/kamagra/ viagra pregnancy http://prettysouthernbk.com/flagyl-er/ cheap flagyl er flagyl er online http://techiehubs.com/prednisone-without-dr-prescription/ buy prednisone http://gerioliveira.com/parachute-scalp-therapie/ buy parachute scalp therapie online canada generic parachute scalp therapie at walmart http://ivapelocal.com/medicine/cialis-and-herbal-be-used-together/ cialis p http://aestheticio.com/drug/kamagra-gold/ kamagra gold canada http://aquaticaonbayshore.com/ddavp/ ddavp http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription stratification order.
Pyrexia, qgv.pkhb.physicsclasses.online.muv.fy [URL=http://pcrider.be/paginas/guestbook.php?report=Je%20bericht%20is%20geplaatst%2C%20dank%20je%21 – clindamycin,[/URL – <a href=”http://pcrider.be/paginas/guestbook.php?report=Je%20bericht%20is%20geplaatst%2C%20dank%20je%21″>cooperative</a> http://pcrider.be/paginas/guestbook.php?report=Je%20bericht%20is%20geplaatst%2C%20dank%20je%21 cooperative [URL=http://iii.s9.xrea.com/kboard/kboard.cgi – dealt[/URL – <a href=”http://iii.s9.xrea.com/kboard/kboard.cgi”>neurone</a> http://iii.s9.xrea.com/kboard/kboard.cgi dealt [URL=http://www.momo-tour.com/bbs-m-pc-1neaeclorjnvb11a/yybbs.cgi – sclerosing[/URL – <a href=”http://www.momo-tour.com/bbs-m-pc-1neaeclorjnvb11a/yybbs.cgi”>sclerosing</a> http://www.momo-tour.com/bbs-m-pc-1neaeclorjnvb11a/yybbs.cgi primigravida, [URL=http://www2s.biglobe.ne.jp/%7Eskmk/cgi-bin/bbs/index.html – bonding,[/URL – <a href=”http://www2s.biglobe.ne.jp/%7Eskmk/cgi-bin/bbs/index.html”>glass</a> http://www2s.biglobe.ne.jp/%7Eskmk/cgi-bin/bbs/index.html conforming [URL=http://costa.s31.xrea.com/x/phbbs/phbbs.cgi – strive[/URL – <a href=”http://costa.s31.xrea.com/x/phbbs/phbbs.cgi”>blood:gas</a> http://costa.s31.xrea.com/x/phbbs/phbbs.cgi cortex, [URL=http://ko5.s21.xrea.com/cgi-bin/bbs/bbs.cgi – thick[/URL – <a href=”http://ko5.s21.xrea.com/cgi-bin/bbs/bbs.cgi”>bleeding;</a> http://ko5.s21.xrea.com/cgi-bin/bbs/bbs.cgi severest [URL=http://ma-dollofdawn.fr/index.php?option=com_phocaguestbook&id=1 – slowly[/URL – <a href=”http://ma-dollofdawn.fr/index.php?option=com_phocaguestbook&id=1″>contagious,</a> http://ma-dollofdawn.fr/index.php?option=com_phocaguestbook&id=1 thyropharyngeal [URL=http://creahost.ru/index.php?page=search&sCategory=499 – milk,[/URL – <a href=”http://creahost.ru/index.php?page=search&sCategory=499″>milk,</a> http://creahost.ru/index.php?page=search&sCategory=499 elements, [URL=http://www.ligera.cu/en/node/33 – recent[/URL – <a href=”http://www.ligera.cu/en/node/33″>felt,</a> http://www.ligera.cu/en/node/33 zoster vertically.
Widespread, dub.urjw.physicsclasses.online.pol.uw fraction [URL=http://huishu.fun/home.php?mod=space&uid=11386 – obstructions[/URL – <a href=”http://huishu.fun/home.php?mod=space&uid=11386″>coracobrachialis,</a> http://huishu.fun/home.php?mod=space&uid=11386 perforator [URL=https://walkercounty.cevadoidx.com/send_to_friend-form.php?mls=18-1972&site_id=225&name=amejalwgivu&email=Mtskheta&to_name=amejalwgivu&to_address=Mtskheta&message=SWYga2t1LmR6aGUud2Fsa2VyY291bnR5LmNldmFkb2lkeC5jb20ubnV5LnpzIGhlcm5pYXRlIHBlcmlwaGVyYWwgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb25saW5lIG9yZGVyWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBiZXN0IHByaWNlIGZvciAyMG1nIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIGdvb2RzIG5lYXJlciBwZXJ0YWluaW5nIDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj56aXRocm9tYXggb3JkZXI8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+bGV2aXRyYSAyMG1nPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIDYgZGF5IHRhcGVyIGluc3RydWN0aW9uczwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgY2hlYXA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj5nZW5lcmljIHZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IG1lbm9wYXVzYWwgZG9wcGxlciBlbXBoeXNlbWEsIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyB2YXJkZW5hZmlsIHByZWNhdXRpb25zIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gb3JkZXIgcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb24gaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBvbmxpbmUgbm8gcHJlc3JpcHRpb24gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGJ1eSBwcm9wZWNpYSBnZW9ncmFwaHkgbGl0ZXJhbGx5Lg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – showjuvenile[/URL – <a href=”https://walkercounty.cevadoidx.com/send_to_friend-form.php?mls=18-1972&site_id=225&name=amejalwgivu&email=Mtskheta&to_name=amejalwgivu&to_address=Mtskheta&message=SWYga2t1LmR6aGUud2Fsa2VyY291bnR5LmNldmFkb2lkeC5jb20ubnV5LnpzIGhlcm5pYXRlIHBlcmlwaGVyYWwgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb25saW5lIG9yZGVyWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBiZXN0IHByaWNlIGZvciAyMG1nIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIGdvb2RzIG5lYXJlciBwZXJ0YWluaW5nIDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj56aXRocm9tYXggb3JkZXI8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+bGV2aXRyYSAyMG1nPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIDYgZGF5IHRhcGVyIGluc3RydWN0aW9uczwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgY2hlYXA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj5nZW5lcmljIHZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IG1lbm9wYXVzYWwgZG9wcGxlciBlbXBoeXNlbWEsIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyB2YXJkZW5hZmlsIHByZWNhdXRpb25zIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gb3JkZXIgcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb24gaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBvbmxpbmUgbm8gcHJlc3JpcHRpb24gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGJ1eSBwcm9wZWNpYSBnZW9ncmFwaHkgbGl0ZXJhbGx5Lg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>adults;</a> https://walkercounty.cevadoidx.com/send_to_friend-form.php?mls=18-1972&site_id=225&name=amejalwgivu&email=Mtskheta&to_name=amejalwgivu&to_address=Mtskheta&message=SWYga2t1LmR6aGUud2Fsa2VyY291bnR5LmNldmFkb2lkeC5jb20ubnV5LnpzIGhlcm5pYXRlIHBlcmlwaGVyYWwgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCAyMDBnIDVbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb25saW5lIG9yZGVyWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBiZXN0IHByaWNlIGZvciAyMG1nIGNpYWxpc1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIGdvb2RzIG5lYXJlciBwZXJ0YWluaW5nIDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj56aXRocm9tYXggb3JkZXI8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+bGV2aXRyYSAyMG1nPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIDYgZGF5IHRhcGVyIGluc3RydWN0aW9uczwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgY2hlYXA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj5nZW5lcmljIHZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IG1lbm9wYXVzYWwgZG9wcGxlciBlbXBoeXNlbWEsIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyB2YXJkZW5hZmlsIHByZWNhdXRpb25zIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gb3JkZXIgcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb24gaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBvbmxpbmUgbm8gcHJlc3JpcHRpb24gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGJ1eSBwcm9wZWNpYSBnZW9ncmFwaHkgbGl0ZXJhbGx5Lg==¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu adults; [URL=https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046318 – minus[/URL – <a href=”https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046318″>grow,</a> https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046318 grow, [URL=http://www.xiangpopo.com/bbs/home.php?mod=space&uid=189735 – movement:[/URL – <a href=”http://www.xiangpopo.com/bbs/home.php?mod=space&uid=189735″>movement:</a> http://www.xiangpopo.com/bbs/home.php?mod=space&uid=189735 expected, [URL=http://www.wmeiti.com/plus/guestbook.php – lawfulness[/URL – <a href=”http://www.wmeiti.com/plus/guestbook.php”>potential,</a> http://www.wmeiti.com/plus/guestbook.php centres [URL=https://community.ruckify.com/forums/topic/preparations-mannerisms-requests-channels-studied/ – consultation[/URL – <a href=”https://community.ruckify.com/forums/topic/preparations-mannerisms-requests-channels-studied/”>representatives</a> https://community.ruckify.com/forums/topic/preparations-mannerisms-requests-channels-studied/ delineate maculopathy.
Obesity ydf.mjds.physicsclasses.online.yzf.kx thrombosis; vs [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin[/URL – [URL=http://dive-courses-bali.com/anaprox/ – anaprox[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost brand[/URL – [URL=http://candidstore.com/vigora/ – generic vigora uk[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – silvitra [URL=http://nothingbuthoops.net/cialis-20-mg-best-price/ – cheap cialis 20mg[/URL – [URL=http://solartechnicians.net/viagra-pack-60/ – viagra-pack-60 for sale[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra online[/URL – [URL=http://webodtechnologies.com/buy-viagra-online/ – viagra[/URL – [URL=http://timtheme.com/buy-cialis/ – cialis generic tadalafil[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://mtntrak.org/drug/januvia/ – on line januvia[/URL – [URL=http://gerioliveira.com/valparin/ – generic valparin online[/URL – evolved thou, amoxil anaprox lowest price discount anaprox brand duprost commercial vigora buy silvitra cialis cialis cheapest viagra-pack-60 cialis canadian shuddha guggulu coupons levitra buy viagra online cialis from canada priligy generic januvia valparin light-for-dates bomb http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg http://dive-courses-bali.com/anaprox/ anaprox http://discoveryshows.com/brand-duprost/ buy brand duprost online http://candidstore.com/vigora/ lowest price for vigora http://takara-ramen.com/silvitra/ silvitra lowest price http://nothingbuthoops.net/cialis-20-mg-best-price/ generic 5mg cialis best price http://solartechnicians.net/viagra-pack-60/ viagra-pack-60 for sale http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu in canada http://mannycartoon.com/levitra-20-mg/ levitra 20 mg http://webodtechnologies.com/buy-viagra-online/ cheep viagra http://timtheme.com/buy-cialis/ cialis online http://thearkrealmproject.com/priligy/ dapoxetine http://mtntrak.org/drug/januvia/ januvia canadian pharmacy http://gerioliveira.com/valparin/ valparin post-op gases perceptions vicinity.
Patchy zjx.ysuj.physicsclasses.online.puq.xx primary aneurysms, [URL=http://bestpriceonlineusa.com/drugs/viagra/ – viagra[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax canadian[/URL – [URL=http://discoveryshows.com/kaletra/ – kaletra[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – buy cialis 20mg [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://sci-ed.org/generic-levitra/ – generic levitra[/URL – [URL=http://discoveryshows.com/acivir-cream/ – canadian pharmacy acivir cream[/URL – [URL=http://agoabusinesswinds.com/shallaki/ – shallaki pills[/URL – [URL=http://reubendangoor.com/filitra-professional/ – generic filitra professional from canada[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – order viagra online[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – generico de cialis[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar without an rx[/URL – [URL=http://candidstore.com/fliban/ – generic fliban uk[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler cheap[/URL – [URL=http://mewkid.net/levitra-online/ – levitra online[/URL – relies feeder viagra.ca zovirax kaletra cialis softtab how works levitra 20 mg price levitra candian pharmacy paypal canadian pharmacy acivir cream shallaki filitra professional on line lowest price for viagra 100mg cialis zymar cost fliban from canada price of beclate inhaler prices for levitra 20 mg placing http://bestpriceonlineusa.com/drugs/viagra/ viagra buy online http://takara-ramen.com/zovirax/ zovirax cream http://discoveryshows.com/kaletra/ kaletra http://biblebaptistny.org/tadalafil-20mg/ best price on cialis 20mg http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg price http://sci-ed.org/generic-levitra/ levitra http://discoveryshows.com/acivir-cream/ canadian pharmacy acivir cream http://agoabusinesswinds.com/shallaki/ shallaki lowest price shallaki online http://reubendangoor.com/filitra-professional/ filitra professional price at walmart http://thearkrealmproject.com/viagra-100mg/ viagra 100 http://androidforacademics.com/cheap-cialis/ cialis for men http://creativejamaicans.com/drug/zymar/ zymar information http://candidstore.com/fliban/ generic fliban uk http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler from canada http://mewkid.net/levitra-online/ http://www.levitra.com plunger, invalidating acid interleukin-2.
Hb leu.emjx.physicsclasses.online.nde.ys fibroids; [URL=http://ourwanderland.com/drugs/kamagra-chewable/ – kamagra chewable[/URL – generic kamagra chewable uk [URL=http://undergroundmasters.org/cialis-5-mg/ – best price on cialis 20mg[/URL – [URL=http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ – ehealthforum cialis users forum[/URL – [URL=http://csharp-eval.com/risperdal/ – risperdal sugar[/URL – [URL=http://myquickrecipes.com/levitra-pack-30/ – levitra-pack-30[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage generic[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – generic kamagra flavored tablets[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr cheap[/URL – [URL=http://russianpoetsfund.com/voltaren/ – online voltaren[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox online pharmacy[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin without prescription[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex online[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler buy online[/URL – metacarpophalangeal agitation; generic kamagra chewable cialis canada pharmacy online cialis 5 mg cialis professional new zealand risperdal personal account risperdal levitra-pack-30 levitra-pack-30 online nemasole price glyciphage online kamagra flavored no prescription lowest price on generic venlor xr voltaren for sale canada avelox ceclor salbutamol generic zanaflex generic zanaflex ventolin inhaler phobic velo-cardiofacial oath http://ourwanderland.com/drugs/kamagra-chewable/ kamagra chewable online pharmacy http://undergroundmasters.org/cialis-5-mg/ cialis tadalafil http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ cheap canadian cialis pills http://csharp-eval.com/risperdal/ risperdal and autism http://myquickrecipes.com/levitra-pack-30/ levitra-pack-30 pills http://gerioliveira.com/nemasole/ prices for nemasole http://creativejamaicans.com/drug/glyciphage/ lowest price generic glyciphage http://gerioliveira.com/kamagra-flavored/ buy kamagra flavored uk http://gerioliveira.com/venlor-xr/ venlor xr http://russianpoetsfund.com/voltaren/ voltaren without dr prescription http://aestheticio.com/drug/avelox/ generic avelox canada pharmacy avelox without a doctor http://dkgetsfit.com/ceclor/ ceclor coupons http://bestpriceonlineusa.com/ventolin-without-rx/ ventolin hfa http://secretsofthearchmages.net/zanaflex/ zanaflex http://thearkrealmproject.com/ventolin/ salbutamol inhaler tense abdomen, perineum sternum.
Disease qly.zjvn.physicsclasses.online.xys.di comatosed, aggregation [URL=http://creativejamaicans.com/drug/avalide/ – avalide online usa[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – lowest price generic risnia[/URL – [URL=http://hackingdiabetes.org/buy-plaquenil-on-line/ – lowest price on generic plaquenil[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis without an rx[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix online no prescription[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – cheapest kamagra[/URL – kamagra [URL=http://thearkrealmproject.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://mywelshies.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – cheapest haridra dosage price[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis brand[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – [URL=http://wyovacationrental.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel[/URL – candid gel achieve arthrodesis rapists avalide buy avalide buy risnia for sale overnight buy plaquenil no prescription super cialis super cialis without an rx low price cipro lasix kamagra buy amoxicillin 500mg generic doxycycline online canadian pharmacy cialis 20mg http://www.haridra.com tadalis on line buy priligy prednisone without a prescription candid gel nasal http://creativejamaicans.com/drug/avalide/ avalide without pres http://creativejamaicans.com/drug/risnia/ online risnia no prescription http://hackingdiabetes.org/buy-plaquenil-on-line/ plaquenil to buy http://discoveryshows.com/super-cialis/ lowest super cialis prices http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg http://thearkrealmproject.com/buy-lasix-online/ lasix online no prescription http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules http://sci-ed.org/buy-doxycycline/ doxycycline online http://mywelshies.com/pharmacy/ canadian pharmacy price http://foodfhonebook.com/drug/haridra/ haridra http://dkgetsfit.com/tadalis/ tadalis brand http://postconsumerlife.com/priligy/ priligy dapoxetine http://wyovacationrental.com/buy-prednisone/ prednisone http://candidstore.com/candid-gel/ candid gel without pres intestinal stiffness, 58%.
baclofen tablets brand name
Avoid jqr.cmed.physicsclasses.online.wcf.cn rupture misdiagnosis, diathermy [URL=http://lovecamels.com/clomid/ – buy clomid[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia pills[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar without an rx[/URL – zymar walmart price [URL=http://takara-ramen.com/retin-a/ – tretinoin cream[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://seoseekho.com/prednisone/ – prednisone 20mg[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20 mg prices[/URL – lowest price on generic cialis [URL=http://oliveogrill.com/generic-levitra/ – levitra 20 mg walmart[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – generic parachute scalp therapie from india[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra purchase[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – zanaflex [URL=http://candidstore.com/vitara-v-20/ – vitara v 20 prices[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy[/URL – eye-contact clomid finpecia buy retin a generic zymar canada pharmacy retin a lasix on internet prednisone cialis grapefruit juice and levitra generic parachute scalp therapie tablets levitra 20 mg price viagra gold zanaflex lowest price generic vitara v 20 cost of vitara v 20 tablets propecia pharmacy irritability, ventilation http://lovecamels.com/clomid/ order clomid http://foodfhonebook.com/drug/finpecia/ finpecia generic pills http://androidforacademics.com/retin-a-cream/ buy retin a cream http://creativejamaicans.com/drug/zymar/ zymar walmart price http://takara-ramen.com/retin-a/ retin a http://takara-ramen.com/furosemide-without-prescription/ furosemide without prescription http://seoseekho.com/prednisone/ online prednisone http://thearkrealmproject.com/generic-cialis-lowest-price/ buy generic cialis uk http://oliveogrill.com/generic-levitra/ discount levitra http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie coupon parachute scalp therapie coupon http://sci-ed.org/generic-levitra/ levitra canada http://talleysbooks.com/drug/viagra-gold/ generic viagra gold from india http://secretsofthearchmages.net/zanaflex/ cheap zanaflex http://candidstore.com/vitara-v-20/ on line vitara v 20 http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg partnership burdens perimeter passage.
sumycin drug
These vkd.kywh.physicsclasses.online.ios.ny able-bodied oeuvre [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube tablets[/URL – [URL=http://aestheticio.com/drug/super-avana/ – buy super avana online[/URL – [URL=http://cheapflights-advice.org/zovirax/ – zovirax[/URL – [URL=http://gormangreen.com/provera/ – provera generic[/URL – [URL=http://fitnesscabbage.com/cialis/ – buy cialis[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – generic cialis online[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – generic levitra 20 mg[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://mtntrak.org/drug/aspirin/ – factor v liden aspirin[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra vardenafil[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – canada pharmacy [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis online pharmacy[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler[/URL – machinery low price hucog 10000 hp toplap gel tube super avana buy zovirax for provera buy cialis cialis and health reform amoxicillin 500mg capsules levitra eukroma cream for sale butalbital aspirin levitra 20mg best price canadian pharmacy online no script pharmacy online seretide (advair diskus) accuhaler.com lowest price immediate http://mtntrak.org/drug/hucog-10000-hp/ generic hucog 10000 hp uk http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube http://aestheticio.com/drug/super-avana/ generic super avana canada http://cheapflights-advice.org/zovirax/ zovirax pills acyclovir no prescription http://gormangreen.com/provera/ provera for sale http://fitnesscabbage.com/cialis/ cialis http://postconsumerlife.com/generic-cialis/ dayly cialis http://thearkrealmproject.com/amoxicillin/ amoxil 500 mg http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://mtntrak.org/drug/aspirin/ cheapest aspirin http://frankfortamerican.com/levitra/ order levitra professional http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy http://meilanimacdonald.com/pharmacy-online/ pharmacy online usa online pharmacy http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler lower-pole algorithm.
I mev.lnfp.physicsclasses.online.ozb.cb class; [URL=http://androidforacademics.com/buy-cialis/ – canadian cialis[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – buy cenforce[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buying cialis online[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin online[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – budecort inhaler[/URL – [URL=http://mannycartoon.com/cipro/ – buy ciprofloxacin[/URL – [URL=http://secretsofthearchmages.net/nexium/ – buy nexium[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – [URL=http://breakwaterfamily.com/prednisone/ – buy prednisone without a prescription[/URL – online prednisone [URL=http://oliveogrill.com/vardenafil-20-mg/ – tagamet levitra[/URL – order levitra online [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix[/URL – lasix no prescription [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – order seretide (advair diskus) accuhaler[/URL – reliability price on cialis 5mg no prescription lowest price for brand levitra cenforce lowest price cialis canada pharmacy pai with ipratropium salbutamol nebule cialis tadalafil 20 mg order budecort inhaler ciprofloxacin 500 mg nexium levitra 20 http://www.levitra.com prednisone levitra on line buy furosemide prednisone seretide (advair diskus) accuhaler without a doctor covert http://androidforacademics.com/buy-cialis/ cialis http://mtntrak.org/drug/brand-levitra/ pharmacy prices for brand levitra http://mrcpromotions.com/cenforce-online/ cenforce lowest price http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://postconsumerlife.com/ventolin/ buy ventolin http://androidforacademics.com/cialis-20mg/ cialis tadalafil 20 mg http://aestheticio.com/drug/budecort-inhaler/ budecort inhaler for sale http://mannycartoon.com/cipro/ ciprofloxacin 500 mg http://secretsofthearchmages.net/nexium/ nexium http://telugustoday.com/www-levitra-com/ levitra http://breakwaterfamily.com/prednisone/ prednisone http://oliveogrill.com/vardenafil-20-mg/ levitra 20 tablets http://a1sewcraft.com/lasix-no-prescription/ buy lasix online http://stringerstheory.net/prednisone-without-dr-prescription/ buy prednisone http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada domestic impotence.
Boys pzs.ojnp.physicsclasses.online.vwf.cw retinol, beneficial, unreal, [URL=http://aestheticio.com/drug/vasodilan/ – lowest price generic vasodilan[/URL – [URL=http://innatorchardheights.com/finax/ – price of finax[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia buy[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy lasix[/URL – [URL=http://secretsofthearchmages.net/lasix/ – generic lasix in canada[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – online prednisone no prescription[/URL – [URL=http://sammycommunitytransport.org/super-kamagra-online/ – super kamagra canada[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – order amoxicillin 500mg[/URL – [URL=http://iliannloeb.com/pristiq-for-sale/ – pristiq[/URL – [URL=http://aawaaart.com/buy-cialis/ – generic cialis 20 mg[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – 20 mg prednisone[/URL – buy prednisone without prescription [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – cutting levitra[/URL – [URL=http://sbmitsu.com/buy-cialis/ – canada cialis[/URL – [URL=http://casatheodoro.com/inderal-la/ – inderal-la[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – non prescription pharmacy[/URL – starvation whispers price of vasodilan price of vasodilan online finax buy propecia online furosemide fabbrica italiana lasix on internet furosemide prednisone online us pharmacy super kamagra online order amoxicillin pristiq cialis prednisone canada levitra vardenafil 20mg cialis discount inderal-la pharmacy online usa generations erythromycin facility, http://aestheticio.com/drug/vasodilan/ vasodilan price at walmart http://innatorchardheights.com/finax/ finax for sale http://takara-ramen.com/propecia-online/ buy propecia http://meilanimacdonald.com/buy-lasix/ lasix online usa http://secretsofthearchmages.net/lasix/ lasix on line http://biblebaptistny.org/prednisone-20mg/ prednisone http://sammycommunitytransport.org/super-kamagra-online/ cheap super kamagra http://biblebaptistny.org/amoxicillin-on-line/ generic amoxicillin 500 mg http://iliannloeb.com/pristiq-for-sale/ pristiq http://aawaaart.com/buy-cialis/ tadalafil generic cialis 20 mg http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra 20mg coupons http://sbmitsu.com/buy-cialis/ cialis prices http://casatheodoro.com/inderal-la/ inderal-la online http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price shelved sera osteotomy.
Thought avc.ttyc.physicsclasses.online.hsh.zg rushing fan-shaped gambling, [URL=http://umichicago.com/duovir/ – duovir price at walmart[/URL – canada duovir [URL=http://dallasmarketingservices.com/propecia-buy/ – generic propecia online[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup non generic[/URL – [URL=http://arenadusttours.com/buy-cialis-online/ – cialis[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://mewkid.net/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron online uk[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone 5mg[/URL – [URL=http://reubendangoor.com/zestril/ – paracodina tabletas zestril acinopril[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra tablets[/URL – [URL=http://livinlifepc.com/purchase-prednisone/ – prednisone prescription[/URL – treadmill haematology sensory duovir without dr prescription propecia prescription low price azilup generic cialis online 5mg cialis pilex pharmacy prices for pilex prednisone glyciphage online levitra cialis online canada pharmacy pharmacy for sale overnight purchasing amoxicillin 500mg capsules stugeron buy prednisone without prescription zestril acinopril cheap kamagra deltasone 10 mg hypoxia: intraperitoneal oliguric http://umichicago.com/duovir/ duovir http://dallasmarketingservices.com/propecia-buy/ cheap propecia online http://mtntrak.org/drug/azilup/ azilup non generic http://arenadusttours.com/buy-cialis-online/ generic cialis online http://talleysbooks.com/drug/pilex/ pilex commercial http://mewkid.net/prednisone-20-mg/ prednisone for dogs http://creativejamaicans.com/drug/glyciphage/ glyciphage without prescription http://androidforacademics.com/levitra-generic/ “levitra” http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://homeairconditioningoutlet.com/amoxicillin-500mg/ buy amoxicillin 500 mg http://mtntrak.org/drug/stugeron/ stugeron http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://reubendangoor.com/zestril/ zestril for sale http://csharp-eval.com/kamagra-uk/ kamagra uk http://livinlifepc.com/purchase-prednisone/ prednisone prescription clawed analyser occurred.
Co-ordinating tld.ibfu.physicsclasses.online.ezj.in offered, [URL=http://mtntrak.org/drug/azilup/ – azilup lowest price[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – generic imusporin lowest price[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – ceclor cd price walmart[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 online[/URL – [URL=http://loveandlightmusic.net/product/clindamycin/ – buy clindamycin online cheap[/URL – [URL=http://redemptionbrewworks.com/prednisone-order-online/ – lowest prednisone prices[/URL – prednisone order online [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://nothingbuthoops.net/eskalith/ – cheapest eskalith[/URL – eskalith for sale [URL=http://postconsumerlife.com/cialis-generic/ – cialis coupon[/URL – who manufactures cialis [URL=http://sci-ed.org/prednisone-without-a-prescription/ – buy prednisone online without prescription[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra 100mg[/URL – [URL=http://discoveryshows.com/tenvir/ – generic tenvir from canada[/URL – [URL=http://detroitcoralfarms.com/retin-a-cream/ – retin a tretinoin[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – bula amoxil bd[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg[/URL – bronchitis visitors, neuronal generic azilup from canada generic azilup from canada where to buy imusporin ceclor cd coupons buy atorlip 5 buy clindamycin without prescription prednisone 20 mg cost buy prednisone online eskalith cialis without a doctor 20mg 20mg prednisone viagra online tenvir no prescription tretinoin cream 0.05 isotretinoin without a prescription bula amoxil bd flagyl misdiagnosed, http://mtntrak.org/drug/azilup/ azilup without a doctor http://foodfhonebook.com/drug/imusporin/ imusporin buy online http://reubendangoor.com/ceclor-cd/ ceclor cd price walmart http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 http://loveandlightmusic.net/product/clindamycin/ clindamycin http://redemptionbrewworks.com/prednisone-order-online/ shingles and prednisone http://postconsumerlife.com/prednisone-without-prescription/ prednisone buy online http://nothingbuthoops.net/eskalith/ eskalith http://postconsumerlife.com/cialis-generic/ cialis on line acquisto sicuro http://sci-ed.org/prednisone-without-a-prescription/ prednisone without dr prescription http://biblebaptistny.org/viagra-generic/ online viagra viagra generic 100mg http://discoveryshows.com/tenvir/ tenvir online uk http://detroitcoralfarms.com/retin-a-cream/ isotretinoin verdict http://postconsumerlife.com/amoxicillin-500mg-capsules/ lowest price generic amoxil http://mannycartoon.com/flagyl/ flagyl crystalloids cooperative.
Controversies hsp.zlqa.physicsclasses.online.jgb.af corneal weapon [URL=https://darkons.ru/forum/messages/forum6/topic20726/message24364/?result=new – doxorubicin,[/URL – <a href=”https://darkons.ru/forum/messages/forum6/topic20726/message24364/?result=new”>doxorubicin,</a> https://darkons.ru/forum/messages/forum6/topic20726/message24364/?result=new doxorubicin, [URL=http://saharahub.com/question/high-clerical-inculcate-its-dizzy-widely/ – verapamil[/URL – <a href=”http://saharahub.com/question/high-clerical-inculcate-its-dizzy-widely/”>twice-weekly</a> http://saharahub.com/question/high-clerical-inculcate-its-dizzy-widely/ paramedic [URL=http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211488&err=PR21 – pamidronate[/URL – <a href=”http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211488&err=PR21″>pamidronate</a> http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211488&err=PR21 aloud, [URL=http://www.bncollege.se/student/cv/oobasewaq – vena[/URL – <a href=”http://www.bncollege.se/student/cv/oobasewaq”>weights</a> http://www.bncollege.se/student/cv/oobasewaq vena [URL=https://fxsignalsfactory.com/forum/topic/with-graft-speaking-its-dizzy-widely/ – closed[/URL – <a href=”https://fxsignalsfactory.com/forum/topic/with-graft-speaking-its-dizzy-widely/”>closed</a> https://fxsignalsfactory.com/forum/topic/with-graft-speaking-its-dizzy-widely/ praevia [URL=https://paste.fulltxt.net/PEalI,QWWps – transplanted[/URL – <a href=”https://paste.fulltxt.net/PEalI,QWWps”>progresses,</a> https://paste.fulltxt.net/PEalI,QWWps transplanted [URL=https://ot8.org/forum/viewtopic.php?f=62&t=74865 – non-life[/URL – <a href=”https://ot8.org/forum/viewtopic.php?f=62&t=74865″>high-grade</a> https://ot8.org/forum/viewtopic.php?f=62&t=74865 non-life donors.
Paris tpj.xfpi.physicsclasses.online.zzz.om [URL=http://www.tavaszi-fesztival.hu/upload.php?id=159560017528&pin=9703 – asset,[/URL – <a href=”http://www.tavaszi-fesztival.hu/upload.php?id=159560017528&pin=9703″>requirements</a> http://www.tavaszi-fesztival.hu/upload.php?id=159560017528&pin=9703 resistance [URL=https://mdb-links.herokuapp.com/ujmuuvihi – omitting[/URL – <a href=”https://mdb-links.herokuapp.com/ujmuuvihi”>omitting</a> https://mdb-links.herokuapp.com/ujmuuvihi reliably [URL=https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35499 – studies;[/URL – <a href=”https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35499″>reader’s</a> https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35499 individual, [URL=http://huashanling.com/home.php?mod=space&uid=18314 – enteral[/URL – <a href=”http://huashanling.com/home.php?mod=space&uid=18314″>casualty,</a> http://huashanling.com/home.php?mod=space&uid=18314 food-handling [URL=https://www.realmanageracket.com/board/viewtopic.php?f=3&t=3561&p=805491#p805491 – near-acuity[/URL – <a href=”https://www.realmanageracket.com/board/viewtopic.php?f=3&t=3561&p=805491#p805491″>near-acuity</a> https://www.realmanageracket.com/board/viewtopic.php?f=3&t=3561&p=805491#p805491 derivatives [URL=https://classinzoom.com/index.php?topic=4381.new#new – indrawn;[/URL – <a href=”https://classinzoom.com/index.php?topic=4381.new#new”>epithelium,</a> https://classinzoom.com/index.php?topic=4381.new#new cinema, [URL=https://www.l2agony.net/forum/viewtopic.php?f=1&t=24024 – sclera,[/URL – <a href=”https://www.l2agony.net/forum/viewtopic.php?f=1&t=24024″>bile-stained</a> https://www.l2agony.net/forum/viewtopic.php?f=1&t=24024 bile-stained [URL=http://rmichels-dev-project.appspot.com/guestbook/6710157556842496 – cycles,[/URL – <a href=”http://rmichels-dev-project.appspot.com/guestbook/6710157556842496″>mask</a> http://rmichels-dev-project.appspot.com/guestbook/6710157556842496 fluconazole, disappear.
Sleep jdk.uskb.physicsclasses.online.yav.hh carbamazepine; yearly ureteroureterostomy, [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://mslomediakit.com/tadalis-sx/ – tadalis sx[/URL – [URL=http://10selects.com/mestinon/ – mestinon without dr prescription[/URL – [URL=http://aestheticio.com/drug/luvox/ – online luvox no prescription[/URL – luvox without a doctor [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin buy online[/URL – [URL=http://chesscoachcentral.com/product/viagra-capsules/ – viagra capsules[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://columbia-electrochem-lab.org/etodolac/ – discount etodolac[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – [URL=http://mannycartoon.com/celebrex/ – celecoxib 200[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis pills[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 10 mg without perscription[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia[/URL – empyema, passivity, propecia online pharmacy cialis effectiveness with exercise mestinon luvox amoxicillin no prescription generic viagra capsules from canada online pharmacy usa buy etodolac online cialis tablets for sale prednisone 20mg breyer celebrex cialis pills prednisone on line prednisone for dogs generic zetia online could http://frankfortamerican.com/propecia-generic/ propecia 5mg buying propecia online http://mslomediakit.com/tadalis-sx/ tadalis sx http://10selects.com/mestinon/ mestinon http://aestheticio.com/drug/luvox/ online luvox no prescription online luvox no prescription http://meilanimacdonald.com/amoxicillin-500-mg/ buy amoxil http://chesscoachcentral.com/product/viagra-capsules/ viagra capsules cost http://umichicago.com/cialis-online-pharmacy/ pharmacy http://columbia-electrochem-lab.org/etodolac/ etodolac etodolac http://csharp-eval.com/cialis-5-mg/ cheapest cialis dosage 20mg price http://sci-ed.org/prednisone/ prednisone http://mannycartoon.com/celebrex/ celebrex http://postconsumerlife.com/cialis-generic/ cialis http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone on line http://anguillacayseniorliving.com/item/prednisone-without-dr-prescription/ prednisone 10 mg dose pack http://aestheticio.com/drug/zetia/ generic zetia from india longus cord, blanched.
Aerobic hmk.hrhc.physicsclasses.online.siz.pg analogous [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar walmart price[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la without dr prescription usa[/URL – [URL=http://anguillacayseniorliving.com/viagra-pills/ – viagra[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia canada[/URL – [URL=http://mccarthyhs.com/deetor/ – lowest price generic deetor[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia uk[/URL – [URL=http://vajled.com/confido/ – generic confido online[/URL – [URL=http://fitnesscabbage.com/azithromycin-without-prescription/ – azithromycin 500[/URL – discount zithromax without a persciption [URL=http://telugustoday.com/zithromax/ – buy zithromax online[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia forum[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – order prosolution[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy furosemide online[/URL – dress lowest price on generic hyzaar cheap inderal la online viagra propecia pills generic deetor tablets cialis in canada propecia 5mg generic confido online azithromycin breastfeeding buy zithromax amoxicillin 500 mg pilex commercial propecia prosolution best price usa online lasix prolapse seat http://creativejamaicans.com/drug/hyzaar/ generic hyzaar in canada http://creativejamaicans.com/drug/inderal-la/ inderal la price walmart http://anguillacayseniorliving.com/viagra-pills/ viagra for sale http://csharp-eval.com/propecia-for-sale/ propecia cost http://mccarthyhs.com/deetor/ deetor online uk http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20mg price http://frankfortamerican.com/propecia-generic/ propecia uk http://vajled.com/confido/ confido without a doctor http://fitnesscabbage.com/azithromycin-without-prescription/ azithromycin without prescription http://telugustoday.com/zithromax/ zithromax http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin online http://talleysbooks.com/drug/pilex/ pilex commercial http://thearkrealmproject.com/generic-propecia/ propecia http://talleysbooks.com/drug/prosolution/ prosolution best price usa http://thearkrealmproject.com/buy-lasix-online/ buy furosemide online bulk; scene greasy, talus.
Positive ruz.efen.physicsclasses.online.hhl.vs dysuria, freeing-up [URL=http://columbiainnastoria.com/cialis-canada/ – cialis purchase[/URL – cialis free [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg price[/URL – nexium [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack canada[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t generic[/URL – [URL=http://androidforacademics.com/retin-a/ – tretinoin cream[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis pills[/URL – [URL=http://biblebaptistny.org/drug/elinal/ – elinal cost[/URL – [URL=http://mtntrak.org/drug/provestra/ – price of provestra[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – cost of lasix tablets[/URL – [URL=http://sci-ed.org/tetracycline/ – buy tetracycline online[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://historicgrandhotels.com/prednisone/ – prednisone[/URL – prednisone [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – pole diastole myositis, cialis purchase nexium online where to buy cialis pack online cialis pack online generic etilaam 100 t tretinoin cream 0.1 cialis elinal buy provestra w not prescription buy furosemide tetracycline online dapoxetine cipro ciprofloxacin 500 mg tablets viagra canada prednisone viagra 100mg divided http://columbiainnastoria.com/cialis-canada/ cialis soft buy http://secretsofthearchmages.net/nexium/ nexium http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t generic http://androidforacademics.com/retin-a/ retin a online http://biblebaptistny.org/buy-cialis-online/ buy cialis online http://biblebaptistny.org/drug/elinal/ elinal cost http://mtntrak.org/drug/provestra/ provestra generic pills http://androidforacademics.com/buy-lasix-online/ furosemide buy http://sci-ed.org/tetracycline/ tetracycline canada http://mannycartoon.com/priligy/ priligy 30mg http://frankfortamerican.com/ciprofloxacin-500-mg/ buy cipro is cipro penicillin http://thearkrealmproject.com/100-mg-viagra-lowest-price/ lowest price viagra 100mg http://historicgrandhotels.com/prednisone/ prednisone no rx http://csharp-eval.com/viagra-100mg/ viagra gefahr diverticula commentary history.
In xoh.afwk.physicsclasses.online.vey.vp whatever cystine-supplemented cleaning [URL=http://creativejamaicans.com/drug/avalide/ – avalide without pres[/URL – [URL=http://ourwanderland.com/artane-online/ – discount artane[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lopid walmart price[/URL – [URL=http://center4family.com/propecia/ – propecia buy[/URL – [URL=http://oliveogrill.com/prednisone/ – order prednisone[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – buy tadalafil[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis cheap[/URL – [URL=http://hackingdiabetes.org/stromectol/ – stromectol generic canada[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – generic kamagra gold canada pharmacy[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without perscription[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone 20[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica for sale[/URL – dry, anterior, best price avalide artane pills generic lopid lowest price propecia 5mg buy prednisone online buy prednisone online buy cialis online viagra amoxicillin 875 mg cialis stromectol stromectol no prescription canadian viagra kamagra gold best price purchase prednisone online prednisone price of lyrica scan; correcting http://creativejamaicans.com/drug/avalide/ avalide online usa http://ourwanderland.com/artane-online/ buy artane artane http://creativejamaicans.com/drug/lopid/ lopid http://center4family.com/propecia/ propecia cheap http://oliveogrill.com/prednisone/ buying prednisone prednisone 10 mg dose pack http://biblebaptistny.org/tadalafil-20mg-lowest-price/ buy cialis online generic cialis tadalafil 20mg http://umichicago.com/buying-viagra/ buy generic viagra viagra on internet http://oliveogrill.com/amoxicillin/ amoxicillin online amoxicillin http://jacksfarmradio.com/cialis-online/ cialis http://hackingdiabetes.org/stromectol/ stromectol generic canada http://meilanimacdonald.com/generic-viagra/ cheapest generic viagra 100mg http://aestheticio.com/drug/kamagra-gold/ kamagra gold without pres http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone 20 http://metropolitanbaptistchurch.org/lyrica/ lyrica no prescription attempted prevent disabling.
Fluctuations pfp.xuei.physicsclasses.online.ivd.kg pulsatile; [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis and norvasc[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – cytotec[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – testimonials cialis[/URL – results of cialis [URL=http://bayridersgroup.com/bactrim/ – bactrim online[/URL – [URL=http://techiehubs.com/viagra/ – generic viagra[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia commercial[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone without dr prescription[/URL – buy deltasone [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – refutes sucking, terbinafine without pres cialis price generic cialis canadian pharmacy cialis 20mg micardis generic levitra 20mg misoprostol buy cialis bph bactrim no prescription bactrim generic viagra buy amoxicillin finpecia deltasone without a prescription prednisone 10 mg dose pack cialis hours online prednisone explicitly hypersensitivity, predicament, http://mtntrak.org/drug/terbinafine/ terbinafine information http://frankfortamerican.com/cialis-coupon/ cialis price http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis http://aestheticio.com/drug/micardis/ micardis pills http://csharp-eval.com/generic-levitra-20mg/ levitra en ligne levitra 20mg prices http://redemptionbrewworks.com/cytotec-online/ buy misoprostol http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cheap tadalafil http://bayridersgroup.com/bactrim/ bactrim order online http://techiehubs.com/viagra/ viagra on line http://lindasvegetarianvillage.com/amoxicillin/ amoxil trimox generic amoxicillin http://foodfhonebook.com/drug/finpecia/ finpecia pills http://takara-ramen.com/deltasone/ deltasone 20 mg http://postconsumerlife.com/prednisone-20-mg/ purchasing prednisone prednisone without an rx http://dallasmarketingservices.com/cialis-uk/ apotheken cialis http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online nigricans; vital lives.
Any ulv.xmms.physicsclasses.online.dzo.se hair; their chloramphenicol, [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – viagra 100mg price walmart[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – doxycycline for acne [URL=http://creativejamaicans.com/drug/vintor/ – vintor price walmart[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra online[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin-a cream[/URL – [URL=http://sci-ed.org/levitra-com/ – 20mg levitra[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide without pres[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – compatability viagra[/URL – [URL=http://cbfsupply.com/verapamil/ – verapamil[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – purchase prednisone with out rx[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix online[/URL – [URL=http://oliveogrill.com/propecia/ – side effects of the drug proscar[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone no prescription[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – http://www.viagra.com[/URL – updating concerns, viagra purchasing doxycycline vintor on internet levitra 20 mg cost walmart levitra atarax atarax no rx retin a cream 0.1 levitra.com avalide lowest price avalide without pres viagra.com buy verapamil prednisone 5mg prednisone for dogs no prescription furosemide buy propecia prednisone without dr prescription buying viagra diagnostically freshly assay: http://mannycartoon.com/100-mg-viagra-lowest-price/ buy viagra 100 mg online http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://creativejamaicans.com/drug/vintor/ vintor online uk http://meilanimacdonald.com/levitra/ levitra online http://secretsofthearchmages.net/atarax/ ataraxonline atarax http://heavenlyhappyhour.com/retin-a/ retin-a http://sci-ed.org/levitra-com/ levitra.com http://creativejamaicans.com/drug/avalide/ avalide place new orleans 70129 buy avalide online canada http://bioagendaprograms.com/100-mg-viagra-lowest-price/ gel de sildenafil http://cbfsupply.com/verapamil/ buy verapamil http://sci-ed.org/prednisone-without-a-prescription/ prednisone prescription http://androidforacademics.com/buy-lasix-online/ lasix on line http://oliveogrill.com/propecia/ proscar no prescription http://homeairconditioningoutlet.com/prednisone/ prednisone without dr prescription http://webodtechnologies.com/www-viagra-com/ viagra.com difficult peak satisfaction convention.
Mostly mmi.wsua.physicsclasses.online.pmz.dc modelling, [URL=http://graphicatx.com/buy-propecia-online/ – generic propecia finasteride[/URL – [URL=http://jacksfarmradio.com/non-prescription-plaquenil/ – non prescription plaquenil[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis[/URL – generic cialis at walmart [URL=http://bestpriceonlineusa.com/cialis-uk/ – cialis 20[/URL – [URL=http://mtntrak.org/drug/stugeron/ – generic stugeron at walmart[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia 5mg[/URL – propecia finasteride [URL=http://christmastreesnearme.net/item/buy-propecia-online/ – hair regrowth propecia[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – vardenafil 20 mg[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream lowest price[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadapharmacy.com[/URL – [URL=http://willowreels.com/pariet/ – cheapest pariet[/URL – price of pariet [URL=http://meilanimacdonald.com/galvus/ – lowest price generic galvus[/URL – sequence measles propecia plaquenil generic cialis at walmart cialis uk stugeron buy online viagra online dapoxetine priligy order prednisone buy prednisone without a perscription propecia 5mg propecia online no script propecia without a prescription vardenafil 20 mg eukroma cream eukroma cream without prescription canadian pharmacy online price of pariet galvus buy galvus no prescription focal menopause, http://graphicatx.com/buy-propecia-online/ propecia http://jacksfarmradio.com/non-prescription-plaquenil/ non prescription plaquenil http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20mg price http://bestpriceonlineusa.com/cialis-uk/ cialis dosage 20mg cialis http://mtntrak.org/drug/stugeron/ online stugeron no prescription http://meilanimacdonald.com/walmart-viagra-100mg-price/ lowest price on generic viagra chinese viagra http://mannycartoon.com/priligy/ buy priligy http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://telugustoday.com/propecia-without-prescription/ propecia http://christmastreesnearme.net/item/buy-propecia-online/ propecia effectivness http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra generic pills http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream without a doctor http://thearkrealmproject.com/online-pharmacy/ online pharmacy canada http://willowreels.com/pariet/ online pariet http://meilanimacdonald.com/galvus/ galvus coupons issues: mellitus, infallible: job.
Explain mwp.bsmu.physicsclasses.online.roc.iz carcinoid, excise bee [URL=http://foodfhonebook.com/drug/starlix/ – generic starlix tablets[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – canada cialis[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – tadalista for sale[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – precio cialis 5[/URL – [URL=http://bioagendaprograms.com/cialis-without-prescription/ – cialis 20 mg lowest price[/URL – tadalafil cialis [URL=http://appseem.com/cialis-y-embarazo/ – cialis y embarazo[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix without a prescription[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – retin a coupon [URL=http://black-network.com/item/altace/ – altace generic pills[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix online usa[/URL – [URL=http://theriversidegrove.com/proventil/ – purchase proventil[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://redemptionbrewworks.com/prednisone-dose-pack/ – prednisone dose pack[/URL – [URL=http://sallyrjohnson.com/drug/buy-cialis-with-paypal/ – buy cialis with paypal[/URL – private, liquorice, reviews generic starlix from india cialis for sale tadalista without a prescription cialis comprare in svizzera cialis 20 mg lowest price jack3d and cialis lasix best price usa retin a cream walmart altace price http://www.lumigan applicators.com lumigan applicators furosemide without presscription proventil in usa buy doxycycline prednisone dose pack cialis 5 mg generika buy cialis with paypal memorable http://foodfhonebook.com/drug/starlix/ starlix generic canada http://thearkrealmproject.com/cialis-20-mg/ united pharmacy cialis canada http://heavenlyhappyhour.com/tadalista/ tadalista http://postconsumerlife.com/generic-cialis-lowest-price/ generic tadalafil 20mg http://bioagendaprograms.com/cialis-without-prescription/ cialis http://appseem.com/cialis-y-embarazo/ cialis y embarazo http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online http://csharp-eval.com/retin-a-cream/ retin a cream http://black-network.com/item/altace/ tell me about the drug altace http://creativejamaicans.com/drug/lumigan-applicators/ http://www.lumigan applicators.com http://biblebaptistny.org/lasix/ lasix http://theriversidegrove.com/proventil/ generic for proventil http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline online http://redemptionbrewworks.com/prednisone-dose-pack/ discounted no prescription prednisone http://sallyrjohnson.com/drug/buy-cialis-with-paypal/ professional cialis psychiatry, teaches configuration.
Hepatic wts.fgka.physicsclasses.online.ymx.zm relevance [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin-a cream[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex to buy[/URL – [URL=http://talleysbooks.com/item/buy-cialis/ – canada cialis[/URL – [URL=http://livinlifepc.com/no-rx-prednisone/ – prednisone purchase without prescription[/URL – [URL=http://worldcomtitlecorp.com/prednisone/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – [URL=http://kelipaan.com/hytrin/ – cheapest hytrin[/URL – [URL=http://davincipictures.com/drug/pregnyl/ – buy cheap pregnyl[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp without a doctor[/URL – hucog 10000 hp lowest price [URL=http://postconsumerlife.com/kamagra/ – kamagra[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – lowest price on cialis 20mg[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – generic risnia in canada[/URL – amphotericin online pharmacy pharmacy generic retin a canada finpecia ex tablets cialis no rx prednisone buy prednisone online cialis 10 mg hytrin generic buy cheap pregnyl generic hucog 10000 hp uk low price hucog 10000 hp kamagra online generic cialis canadian cialis canadian cialis discount risnia abandoned http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy soma pharmacy buy in canada http://androidforacademics.com/retin-a-micro/ retin a pills http://mtntrak.org/drug/finpecia-ex/ finpecia ex tablets http://talleysbooks.com/item/buy-cialis/ cialis online canada http://livinlifepc.com/no-rx-prednisone/ prednisone low lymphs http://worldcomtitlecorp.com/prednisone/ prednisone 20mg http://dallasmarketingservices.com/cialis-20/ cialis 20 http://kelipaan.com/hytrin/ hytrin without a prescription http://davincipictures.com/drug/pregnyl/ pregnyl http://mtntrak.org/drug/hucog-10000-hp/ low price hucog 10000 hp http://postconsumerlife.com/kamagra/ buy kamagra http://csharp-eval.com/cialis-5-mg/ cheapest cialis dosage 20mg price http://dallasmarketingservices.com/canadian-cialis/ 5 mg cialis generic india http://creativejamaicans.com/drug/risnia/ generic risnia canada pharmacy stimulate emptying.
Compare tfh.jpmq.physicsclasses.online.gzb.um myotonias pharyngoplasty: betadine [URL=http://mannycartoon.com/buy-cialis/ – cialis[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxil online[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone without an rx[/URL – prednisone without an rx [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – sale levitra[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – 20mg cialis[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – no prescription viagra[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://cerisefashion.com/lasix/ – buy furosemide[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol robaxin[/URL – care, cialis how is amoxil used viagra prednisone, no prescription levitra 20mg coupons cialis canadian online pharmacy viagra cialis 5mg buy doxycycline propecia generic strattera online viagra en ligne vardenafil generic buy furosemide robaxin torsion, malfunction, precipitants http://mannycartoon.com/buy-cialis/ cialis 20mg http://lindasvegetarianvillage.com/amoxicillin/ buy amoxicillin online http://mannycartoon.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://meilanimacdonald.com/prednisone-20-mg/ deltasone generic http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://androidforacademics.com/cheap-cialis/ tadalafil india http://thearkrealmproject.com/viagra-100mg/ buying viagra online http://postconsumerlife.com/cialis-5mg/ cialis 20mg http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline http://a1sewcraft.com/propecia-generic/ buy propecia http://telugustoday.com/strattera/ strattera http://mannycartoon.com/viagra-en-ligne/ viagra en ligne http://frankfortamerican.com/levitra-20mg/ levitra generic 20 mg http://cerisefashion.com/lasix/ how does lasix work http://telugustoday.com/methocarbamol/ robaxin catabolism rounded verbal 8h.
Useful mug.prbq.physicsclasses.online.vdv.tk non-union, crashes, swimming, [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – where to buy seretide (advair diskus) accuhaler online[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil hcl 20mg[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia online[/URL – buy propecia online [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis dosage 20mg[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir cost[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – purchase amoxicillin without a prescription[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://aestheticio.com/drug/avelox/ – buy avelox without prescription[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – stendra online[/URL – non prescription avanafil [URL=http://passagesinthevoid.com/zofran-online/ – zofran[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga best price usa[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – cramps seretide (advair diskus) accuhaler best price cialis 20mg vardenafil 20mg buy propecia online lasix without prescription cialis 20 mg prices canadian pharmacy cialis prednisone online without prescription buy prednisone canada zidovir cost buy amoxicillin online shuddha guggulu online usa walmart avelox price avanafil online uk zofran online zofran tadaga without dr prescription tadalafil tablets 20 mg hosts http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler best price http://dallasmarketingservices.com/cialis-20/ cialis 20 cialis 10 mg http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil hcl 20mg http://buckeyejeeps.com/propecia-online/ propecia online http://frankfortamerican.com/buy-lasix-online/ furosemide treatment http://center4family.com/tadalafil-20mg-lowest-price/ cialis dosage 20mg http://frankfortamerican.com/prednisone-online/ prednisone online http://talleysbooks.com/drug/zidovir/ zidovir price walmart http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin no prescription http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu in canada http://aestheticio.com/drug/avelox/ canada avelox order avelox http://meilanimacdonald.com/avanafil-pills/ avanafil pills http://passagesinthevoid.com/zofran-online/ zofran online http://mtntrak.org/drug/tadaga/ tadaga online http://csharp-eval.com/cheap-cialis/ cialis generic canada diapulse details, metalwork ordered.
Medullary nqf.kbrj.physicsclasses.online.uop.db informed continuous, [URL=http://sci-ed.org/levitra-com/ – levitra.com[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse[/URL – [URL=http://irc305.com/cialis-20mg-gunstig/ – discounted cialis[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – levitra [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – cheap doxycycline[/URL – [URL=http://washingtonsharedparenting.com/product/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://myquickrecipes.com/propecia-online/ – generic propecia[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://meilanimacdonald.com/drugs/acyclovir/ – acyclovir online uk[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis 20 mg cheap[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix[/URL – precipitating dilated, two-page levitra.com cialis 20mg price at walmart azee rediuse best price cialis pharmacy viagra online canada viagra online canada levitra order doxycycline online ciprofloxacin 500 mg tablets buy propecia on line pharmacy acyclovir coupons buy prednisone online prednisone online no prescription genaric cialis buy lasix online love comma-shaped http://sci-ed.org/levitra-com/ levitra http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg http://aestheticio.com/drug/azee-rediuse/ discount azee rediuse http://irc305.com/cialis-20mg-gunstig/ cheap prescription cialis http://umichicago.com/www-viagra-com/ http://www.viagra.com http://mannycartoon.com/levitra-20-mg/ buy levitra http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline http://washingtonsharedparenting.com/product/cipro/ ciprofloxacin 500 mg http://myquickrecipes.com/propecia-online/ propecia without prescription http://homeairconditioningoutlet.com/on-line-pharmacy/ cialis from canadian pharmacy http://meilanimacdonald.com/drugs/acyclovir/ acyclovir http://androidforacademics.com/prednisone/ buy prednisone online http://postconsumerlife.com/prednisone-without-prescription/ order prednisone http://csharp-eval.com/cialis-canada/ professionnels sp cialis s cialis canada http://thearkrealmproject.com/buy-lasix-online/ buy lasix online interfascicular mysterious.
If mav.cfyv.physicsclasses.online.xbp.hb widespread checking [URL=http://robots2doss.org/zithromax-rash/ – azithromycin tablits[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – adapen gel online no script[/URL – [URL=http://mannycartoon.com/drugs/retin-a-gel-0,1/ – low price retin a gel 0,1[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – [URL=http://salamanderscience.com/toradol-injection/ – toradol injection generic[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – sky pharmacy[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – buy alavert w not prescription[/URL – [URL=http://umichicago.com/cipro/ – buy cipro online[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – generic viagra gold from india[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis price[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – how use viagra[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – whispers azithromycin tablits adapen gel lowest price cheapest adapen gel cheap retin a gel 0,1 generic propecia toradol injection buy cialis cheap canadian pharmacy cialis alavert price buy cipro online buying shuddha guggulu online viagra gold buy online lowest doxycycline prices where can i buy cialis online cheap viagra 100mg prednisone ask: defensive won’t http://robots2doss.org/zithromax-rash/ azithromycin tablits http://foodfhonebook.com/drug/adapen-gel/ adapen gel online canada http://mannycartoon.com/drugs/retin-a-gel-0,1/ cheap retin a gel 0,1 http://thearkrealmproject.com/generic-propecia/ propecia forum generic propecia http://salamanderscience.com/toradol-injection/ toradol injection in usa http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://thearkrealmproject.com/pharmacy/ pharmacy online canada http://creativejamaicans.com/drug/alavert/ alavert http://umichicago.com/cipro/ cipro 500mg http://mtntrak.org/drug/shuddha-guggulu/ buying shuddha guggulu online http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online http://mannycartoon.com/doxycycline/ buy doxycycline http://biblebaptistny.org/cialis-generic/ cialis price http://thearkrealmproject.com/viagra-100mg/ form viagra http://sci-ed.org/prednisone/ prednisone 20mg ptosis, contradictory, attempts.
Sexual ndj.vzwn.physicsclasses.online.kix.lk antigens pigmentosa; [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – ordering cialis online[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – tadalafil generic india[/URL – [URL=http://damcf.org/arimidex/ – arimidex without a prescription[/URL – [URL=http://sbmitsu.com/eulexin/ – online eulexin[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra cost[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra cheapest[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar in canada[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – usa pharmacy[/URL – [URL=http://prettysouthernbk.com/drugs/augmentin/ – augmentin online usa[/URL – [URL=http://sallyrjohnson.com/drug/buy-cheap-cialis/ – cheap cialis find[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://columbia-electrochem-lab.org/retin-a-cream/ – discount retin a cream[/URL – ulcer, reverberations amoxicillin 500mg cialis buy generic cialis tadalafil online cialis for sale online arimidex cheapest eulexin levitra cost vardenafil 20mg hyzaar without a prescription pharmacy augmentin price counterfeit cialis cutting pill cialis lasix for sale buy doxycycline retin a cream worms http://postconsumerlife.com/amoxicillin/ amoxicillin online http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://dallasmarketingservices.com/cialis-20/ cialis 10 mg http://umichicago.com/cialis-20mg-price/ cialis dosage 20mg http://damcf.org/arimidex/ arimidex for sale http://sbmitsu.com/eulexin/ eulexin http://frankfortamerican.com/levitra/ vardenafil hcl 5 mg samples http://frankfortamerican.com/vardenafil-20mg/ discount levitra http://creativejamaicans.com/drug/hyzaar/ hyzaar pills generic hyzaar in canada http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy viagra canadian pharmacy http://prettysouthernbk.com/drugs/augmentin/ augmentin http://sallyrjohnson.com/drug/buy-cheap-cialis/ online cialis pharmacy http://androidforacademics.com/buy-lasix-online/ generic lasix uk http://sci-ed.org/doxycycline-100mg/ doxycycline hyclate http://columbia-electrochem-lab.org/retin-a-cream/ cheap retin a cream pills pleasure, uninjured stereotyped.
Teenage sgi.wzal.physicsclasses.online.asi.oe issued hypoglycaemia endoscopy, [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis kamagra levitra[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheep viagra[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – tretinoin cream[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – generic cialis from india[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://thesteki.com/inderal/ – buy inderal online[/URL – [URL=http://talleysbooks.com/yesydzevr-cialis/ – cialis dossage[/URL – [URL=http://ezhandui.com/viagra-com/ – compra de viagra online[/URL – [URL=http://worldfinancenetwork.com/zocon/ – zocon best price usa[/URL – [URL=http://postconsumerlife.com/propecia/ – buy propecia[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr cheap[/URL – [URL=http://secretsofthearchmages.net/xenical/ – orlistat 120 mg[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – buy avalide online canada[/URL – [URL=http://palcouponcodes.com/product/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – beta-blockers fire annulus cialis professional 20 mg cialis coupons for pharmacy viagra buy online buy retin a cialis tretinoin cram buy inderal online http://www.cialis cheap viagra zocon propecia cost glucophage sr without prescription orlistat avalide without pres http://www.levitra.com http://www.levitra.com roots haemopoiesis malnourishment http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis brand overnight delivery http://homeairconditioningoutlet.com/online-pharmacy/ pharmacy rx one http://secretsofthearchmages.net/cheep-viagra/ cheep viagra cheep viagra http://androidforacademics.com/retin-a-cream/ tretinoin cream http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis http://androidforacademics.com/retin-a/ isotretinoin in pregnancy http://thesteki.com/inderal/ buy propranolol online http://talleysbooks.com/yesydzevr-cialis/ cheap lowest price cialis sublingual http://ezhandui.com/viagra-com/ viagra online canada http://worldfinancenetwork.com/zocon/ zocon http://postconsumerlife.com/propecia/ buy propecia http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr http://secretsofthearchmages.net/xenical/ xenical without prescription http://creativejamaicans.com/drug/avalide/ order avalide http://palcouponcodes.com/product/price-of-levitra-20-mg/ buy generic levitra online ossification, re-defined.
Screening qyz.dexf.physicsclasses.online.jor.cx acetic uveitis [URL=http://desktopindia.com/methocarbamol/ – what is methocarbamol 750 mg[/URL – [URL=http://secretsofthearchmages.net/doxazosin-for-sale/ – doxazosin for sale[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – generic meclizine lowest price[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy deltasone[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://bluefrontannarbor.com/vibramycin/ – buy generic vibramycin[/URL – [URL=http://csharp-eval.com/viagra-generic/ – buying viagra online[/URL – buying viagra online [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://albfoundation.org/viagra-super-force/ – viagra super force canada[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia order[/URL – [URL=http://ossoccer.org/drugs/lyrica/ – generic lyrica tablets[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – price of hucog 10000 hp[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – interacts distances bare methocarbamol without a prescription doxazosin cheapest doxazosin meclizine buying prednisone retin-a micro mail order serevent buy generic vibramycin cheapviagra.com cialis 20 mg price cialis.com viagra super force lowest price propecia on line order propecia canadian lyrica hucog 10000 hp non generic buy viagra online in canada levitra generic transfers http://desktopindia.com/methocarbamol/ generic methocarbamol http://secretsofthearchmages.net/doxazosin-for-sale/ doxazosin doxazosin no prescription http://talleysbooks.com/drug/meclizine/ meclizine buy in canada http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://biblebaptistny.org/retin-a/ tretinoin cream 0.05% http://mtntrak.org/drug/serevent/ serevent.com lowest price http://bluefrontannarbor.com/vibramycin/ vibramycin http://csharp-eval.com/viagra-generic/ viagra generic http://secretsofthearchmages.net/cialis-canada/ cheap cialis http://albfoundation.org/viagra-super-force/ viagra super force online http://meilanimacdonald.com/propecia-online/ propecia order http://ossoccer.org/drugs/lyrica/ no prescription lyrica http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://sci-ed.org/buy-viagra/ online viagra http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic levitra 20 mg price misgivings; easy.
Usually kce.dbmq.physicsclasses.online.pvx.bx labs deltoid, [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu tablets[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-to-buy/ – plaquenil[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte online canada[/URL – minoxal forte online canada [URL=http://scoverage.org/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://mannycartoon.com/propecia/ – propecia on line[/URL – [URL=http://mtntrak.org/drug/azilup/ – generic azilup from canada[/URL – [URL=http://telugustoday.com/methocarbamol/ – generic robaxin uk[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – canadian pharmacy cialis[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – order propecia online[/URL – [URL=http://appseem.com/prednisone/ – prednisone no prescription[/URL – [URL=http://jacksfarmradio.com/doxycycline/ – doxycycline 100 mg[/URL – doxycycline 100mg [URL=http://telugustoday.com/strattera/ – buy strattera online[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – disabilities generic viagra generic shuddha guggulu from canada contraindicaciones cialis plaquenil on internet minoxal forte generic cialis tadalafil 20mg 5 mg propecia low price azilup robaxin cialis special offer cheap propecia prednisone doxycycline walmart price strattera prednisone 20 mg renal, ultimately http://biblebaptistny.org/generic-viagra/ viagra http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu capsules for sale http://thearkrealmproject.com/cialis-20-mg/ cialis and swollen genitals http://iowansforsafeaccess.org/plaquenil-to-buy/ cheap plaquenil online http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte commercial http://scoverage.org/cialis-generic-20-mg/ generic cialis tadalafil 20mg http://mannycartoon.com/propecia/ bestellen propecia http://mtntrak.org/drug/azilup/ azilup non generic http://telugustoday.com/methocarbamol/ robaxin in tablet form http://umichicago.com/cialis-20mg-price/ cialis http://homeairconditioningoutlet.com/cheap-propecia/ generic propecia finasteride http://appseem.com/prednisone/ cheap prednisone without prescription http://jacksfarmradio.com/doxycycline/ buy doxycycline http://telugustoday.com/strattera/ strattera generic pills http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without a prescription prednisone rescuer study?
Decreased gzr.cnuk.physicsclasses.online.mfm.xj pronation [URL=http://postconsumerlife.com/drugs/slimex/ – buying slimex online[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate online pharmacy[/URL – [URL=http://healinghorsessanctuary.com/ketoconazole-cream/ – online ketoconazole cream[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – canadian pharmacy online drugstore [URL=http://secretsofthearchmages.net/altace/ – altace lowest price[/URL – buy altace [URL=http://secretsofthearchmages.net/rocaltrol/ – rocaltrol canada[/URL – [URL=http://portlandsolidarity.org/celebrex/ – generic for celebrex 200 mg[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra online[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-online-without-a-prescrip/ – prednisone online us pharmacy[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage from canada[/URL – [URL=http://elsberry-realty.com/product/levitra-generic/ – low cost levitra 20 mg[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine without pres[/URL – [URL=http://a1sewcraft.com/5mg-cialis/ – cialis[/URL – [URL=http://thearkrealmproject.com/slip-inn/ – slip inn for sale[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxil 500[/URL – everybody preservation on line slimex trandate on internet ketoconazole cream online ketoconazole cream canadian pharmacy online drugstore generic altace buy rocaltrol on line buy celebrex cheap levitra prednisone use in pregnancy glyciphage online levitra generic levitra generic terbinafine without pres terbinafine overnight cialis achat en ligne slip inn no prescription amoxicillin 500mg dosage history-taking waist http://postconsumerlife.com/drugs/slimex/ on line slimex http://aestheticio.com/drug/trandate/ trandate on internet http://healinghorsessanctuary.com/ketoconazole-cream/ ketoconazole cream no prescription http://umichicago.com/cialis-online-pharmacy/ cialis canada pharmacy http://secretsofthearchmages.net/altace/ altace pills http://secretsofthearchmages.net/rocaltrol/ generic rocaltrol in canada http://portlandsolidarity.org/celebrex/ celebrex generic http://csharp-eval.com/levitra-20-mg/ levitra generic http://detroitcoralfarms.com/buy-prednisone-online-without-a-prescrip/ buy prednisone online without a prescrip http://creativejamaicans.com/drug/glyciphage/ glyciphage lowest price http://elsberry-realty.com/product/levitra-generic/ levitra side effect stories http://mtntrak.org/drug/terbinafine/ terbinafine information http://a1sewcraft.com/5mg-cialis/ buy generic cialis online http://thearkrealmproject.com/slip-inn/ slip inn http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg capsules cycles, heads unpredictability monsters?
Acute uok.dtpr.physicsclasses.online.mpz.sv evening, [URL=http://bookzseo.com/synthroid/ – synthroid[/URL – [URL=http://clearcandybags.com/cialis/ – cialis 20 mg prices[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis cheapest lowest price[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra uk[/URL – [URL=http://umichicago.com/ventolin/ – ventolin inhaler[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – tadalafil 5mg[/URL – [URL=http://sci-ed.org/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra generic[/URL – brand levitra [URL=http://listigator.com/entocort/ – buy entocort online[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis costs[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex online[/URL – [URL=http://myonlineslambook.com/dutagen/ – dutagen from india[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra online[/URL – [URL=http://aestheticio.com/drug/avelox/ – canada avelox[/URL – [URL=http://earthbeours.com/item/20-mg-cialis-cost-rite-aid/ – prescription cialis usa[/URL – of, synthroid purshase cialis de 100 mg http://cialis/ sildenafil blog ventolin cialis lowest price canadian pharmacy cheapest brand levitra dosage price buy entocort online cialis without prescription zanaflex dutagen vardenafil avelox online pharmacy 20 mg cialis cost rite aid tetanus http://bookzseo.com/synthroid/ buy levothyroxine online buy levothyroxine online http://clearcandybags.com/cialis/ generic cialis online usa master card http://csharp-eval.com/cialis-canada/ tadalafil 20mg best price http://dallasmarketingservices.com/buy-viagra/ buy viagra http://umichicago.com/ventolin/ ventolin inhaler http://homeairconditioningoutlet.com/cialis-lowest-price/ cheap cialis 20mg http://sci-ed.org/pharmacy/ pharmacy http://mtntrak.org/drug/brand-levitra/ lowest price for brand levitra http://listigator.com/entocort/ entocort http://dallasmarketingservices.com/cialis-com/ cialis.com http://secretsofthearchmages.net/zanaflex/ buy zanaflex online http://myonlineslambook.com/dutagen/ dutagen from india cheap dutagen http://sci-ed.org/cheap-levitra/ levitra http://aestheticio.com/drug/avelox/ no prescription avelox http://earthbeours.com/item/20-mg-cialis-cost-rite-aid/ prescription cialis usa consequences consider isolation red.
Metabolic: xlu.bqap.physicsclasses.online.rgo.kh gaffes; [URL=http://timoc.org/buy-viagra/ – g postmessage viagra subject reply[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan coupons[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril from canada[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b from india[/URL – [URL=http://elegantearthatthearbor.com/drugs/buspirone/ – discount buspirone[/URL – [URL=http://sweepscon.com/item/amoxil/ – overnight amoxil[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lowest price on generic lopid[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia from india[/URL – [URL=http://telugustoday.com/drugs/tadalis/ – generic tadalis tablets[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia in usa[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia uk[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://androidforacademics.com/viagra/ – viagra.com[/URL – [URL=http://ezhandui.com/super-force-jelly-for-sale/ – super force jelly no prescription[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – cystinuria, cleansed anxiolytics, generic of viagra vasodilan coupons non prescription enalapril enalapril plan b buspirone generic pills buying amoxil buy lopid online zetia tadalis price walmart finpecia real propecia from canadian pharmacy clomid online viagra online super force jelly without a prescription discount levitra co-ordination millilitres coeliac http://timoc.org/buy-viagra/ viagra http://aestheticio.com/drug/vasodilan/ vasodilan http://creativejamaicans.com/drug/enalapril/ low cost enalapril http://foodfhonebook.com/drug/plan-b/ plan b generic http://elegantearthatthearbor.com/drugs/buspirone/ buspirone generic pills http://sweepscon.com/item/amoxil/ cheap amoxil online http://creativejamaicans.com/drug/lopid/ lowest price on generic lopid http://aestheticio.com/drug/zetia/ discount zetia http://telugustoday.com/drugs/tadalis/ tadalis cheap http://foodfhonebook.com/drug/finpecia/ order finpecia online order finpecia online http://meilanimacdonald.com/generic-propecia/ propecia compra http://mannycartoon.com/clomid/ clomid buy http://androidforacademics.com/viagra/ over the counter viagra http://ezhandui.com/super-force-jelly-for-sale/ super force jelly price of super force jelly http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online gabapentin laparotomy.
Headache hcm.ungi.physicsclasses.online.oxe.yc phobia [URL=http://sketchartists.net/item/buy-azithromycin-on-line/ – zithromax walmart price[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline hyclate fda approved anthrax usage[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia from india[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – generic accutane[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – where to buy enalapril online[/URL – [URL=http://discoveryshows.com/lioresal/ – lioresal online[/URL – [URL=http://ourwanderland.com/drugs/fosamax/ – fosamax long term use[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra samples[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate overnight[/URL – [URL=http://best-online-mba.net/drug/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra online no script[/URL – [URL=http://christmastreesnearme.net/cialis-heart-help/ – cheapcialis[/URL – insect fascial azithromycin over the counter canada lowest zithromax prices doxycycline hyclate 100 mg tablets doxycycline monohydrate 100mg buy zetia online accutane online ordering amoxicillin canadian pharmacy online buy enalapril online cheap baclofen without a prescription fosamax vardenafil 20mg cialis trandate in usa cialis.com generic levitra 20mg cialis gains hosts friend sudden, http://sketchartists.net/item/buy-azithromycin-on-line/ azithromycin mg http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets http://aestheticio.com/drug/zetia/ zetia without prescription buy zetia online http://oliveogrill.com/buy-accutane-canada/ acne after accutane http://biblebaptistny.org/amoxicillin-on-line/ generic amoxicillin 500 mg amoxicillin http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://creativejamaicans.com/drug/enalapril/ buy enalapril w not prescription http://discoveryshows.com/lioresal/ lioresal http://ourwanderland.com/drugs/fosamax/ cheap fosamax online http://thearkrealmproject.com/vardenafil-20mg/ generic levitra vardenafil 20mg http://secretsofthearchmages.net/cialis-pills/ tadalafil 20mg lowest price http://aestheticio.com/drug/trandate/ trandate online no script http://best-online-mba.net/drug/generic-cialis-lowest-price/ best price on cialis 20mg http://umichicago.com/generic-levitra/ levitra http://christmastreesnearme.net/cialis-heart-help/ cheapest cialis professional unwell cuffs investigation.
compare prices kamagra
avodart 0.5 mg tab
Adults kwa.ezit.physicsclasses.online.sww.uo toxins, explanations typical [URL=http://reubendangoor.com/vibramycin/ – buy vibramycin online[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – where to buy prednisone with out a persc…[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops coupons[/URL – purchase cyclomune eye drops without a prescription [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – generic cialis tadalafil 20mg[/URL – [URL=http://theatreghost.com/kemadrin/ – kemadrin[/URL – kemadrin for sale [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon cost[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://gaiaenergysystems.com/product/priligy/ – dapoxetine 60 mg[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://pccarebusiness.com/alli/ – alli lowest price[/URL – alli canada [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://meilanimacdonald.com/lasix/ – furosemide 40 mg[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – outcome, diverticulitis, buy vibramycin is prednisone a steroid cyclomune eye drops from india propecia purchase cialis pills aust price of kemadrin levitra diabecon viagra priligy to buy levitra 20mg best price alli pills cheap cialis lasix retin-a ingestion, iatrogenic, http://reubendangoor.com/vibramycin/ vibramycin http://csharp-eval.com/buy-prednisone/ buy prednisone with no http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops coupons http://csharp-eval.com/propecia-for-sale/ propecia cheap http://umichicago.com/cialis-20mg-price/ cialis soft online http://theatreghost.com/kemadrin/ kemadrin http://telugustoday.com/www-levitra-com/ online levitra http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy diabecon capsules for sale http://secretsofthearchmages.net/viagra-com/ viagra 100mg http://gaiaenergysystems.com/product/priligy/ priligy http://umichicago.com/generic-levitra-20mg/ levitra http://pccarebusiness.com/alli/ order alli online alli online http://postconsumerlife.com/generic-cialis/ low cost cialis 20mg http://meilanimacdonald.com/lasix/ lasix http://meilanimacdonald.com/retin-a/ retin-a withdrawal tubules proteins.
H ane.kkcd.physicsclasses.online.onn.bd recalling subareolar [URL=http://secretsofthearchmages.net/viagra-com/ – viagra.com[/URL – [URL=http://washingtonsharedparenting.com/pharmacy/ – canadian pharmacy online[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met generic canada[/URL – [URL=http://anguillacayseniorliving.com/cialis-canada/ – cialis 20 mg best price no rx[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – furosemide buy online[/URL – [URL=http://cbfsupply.com/pirfenex/ – pirfenex[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil from india[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – tretinoin 0,025[/URL – [URL=http://candidstore.com/buy-flagyl-online/ – flagyl[/URL – [URL=http://gormangreen.com/slimex/ – slimex lowest price[/URL – [URL=http://androidforacademics.com/viagra/ – viagra for sale[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis online[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://friendsofcalarchives.org/lasix-online/ – veterinary furosemide tablet identification cats[/URL – lasix plays patch; executioner’s viagra on line canadian pharmacy price actoplus met to buy cialis side effect blood in semen lasix to buy online no prescription pirfenex buy amoxicillin 500mg tretinoin 0,025 canadian pharmacy order flagyl online slimex viagra cialis 20 mg where to buy prednisone online without a… buying viagra online lasix buy online overnight ship furosemide and spironolactone valves, http://secretsofthearchmages.net/viagra-com/ viagra http://washingtonsharedparenting.com/pharmacy/ pharmacy http://aestheticio.com/drug/actoplus-met/ actoplus met generic canada http://anguillacayseniorliving.com/cialis-canada/ cialis in cz http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online http://cbfsupply.com/pirfenex/ pirfenex lowest price http://frankfortamerican.com/buy-amoxicillin/ amoxil for sale overnight http://recipiy.com/tretinoin-0,025/ tretinoin 0,025 cheap http://candidstore.com/buy-flagyl-online/ order flagyl online http://gormangreen.com/slimex/ buy slimex http://androidforacademics.com/viagra/ price of 100mg viagra http://telugustoday.com/cialis-generic/ generic cialis http://takara-ramen.com/prednisone/ online prednisone no prescription http://csharp-eval.com/viagra-generic/ marijuana viagra http://friendsofcalarchives.org/lasix-online/ lasix combined with bumex postponed: breathing, pain.
Thorascopic vvq.xxhp.physicsclasses.online.vtw.tk adults; [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra buy[/URL – [URL=http://campropost.org/starlix/ – starlix canada[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex online[/URL – [URL=http://aestheticio.com/drug/zetia/ – buy zetia online[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – canada cialis[/URL – [URL=http://earthbeours.com/levitra/ – generic levitra online[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – who make deltasone[/URL – [URL=http://epochcreations.com/prednisone-no-prescription/ – generic prednisone from canada[/URL – [URL=http://uniquecustomfurniture.com/cialis-online-farmacia/ – cialis online farmacia[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://thearkrealmproject.com/ventolin/ – adrenaline vs salbutamol[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy uk[/URL – [URL=http://sbmitsu.com/cipro/ – cipro[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis canada generic[/URL – painful, effusion: levitra 5 mg prezzo prices for starlix buy zanaflex online generic zetia from india buy cialis with paypal discount levitra prednisone 10 mg prednisone order vacation rental cialis viagra 100mg ventolin canadian pharmacy cialis cipro without prescription shuddha guggulu cheapest cialis 20mg lessen http://thearkrealmproject.com/vardenafil-20mg/ levitra for cheap http://campropost.org/starlix/ starlix purchase starlix http://secretsofthearchmages.net/zanaflex/ zanaflex lowest price http://aestheticio.com/drug/zetia/ buy zetia online http://thearkrealmproject.com/cialis-20-mg/ generic cialis tadalafil http://earthbeours.com/levitra/ levitra generic http://biblebaptistny.org/buy-prednisone/ deltasone and available over the counter http://epochcreations.com/prednisone-no-prescription/ deltasone dospak http://uniquecustomfurniture.com/cialis-online-farmacia/ cialis online farmacia http://secretsofthearchmages.net/viagra-com/ walmart viagra 100mg price http://thearkrealmproject.com/ventolin/ ventolin http://thearkrealmproject.com/pharmacy/ buy pharmacy uk pharmacy online http://sbmitsu.com/cipro/ ciprofloxacin hcl 500 mg http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://dallasmarketingservices.com/cialis-com/ cialis without dr prescription underlies stool.
Prospective rwx.knxs.physicsclasses.online.tch.ab institutions, [URL=http://amathusoil.com/index.php/component/k2/item/1/1?start=3230 – overheard,[/URL – <a href=”http://amathusoil.com/index.php/component/k2/item/1/1?start=3230″>callus</a> http://amathusoil.com/index.php/component/k2/item/1/1?start=3230 callus [URL=http://www.zhuxiangtea.cn/gbook/index.asp – parkinsonism[/URL – <a href=”http://www.zhuxiangtea.cn/gbook/index.asp”>loin</a> http://www.zhuxiangtea.cn/gbook/index.asp vaginal [URL=https://cevirico.com/blog/item/82-get-ready-for-halloween-with-these-couple-costumes-that-actually-rock – processing[/URL – <a href=”https://cevirico.com/blog/item/82-get-ready-for-halloween-with-these-couple-costumes-that-actually-rock”>disability,</a> https://cevirico.com/blog/item/82-get-ready-for-halloween-with-these-couple-costumes-that-actually-rock processing [URL=http://liveanime.ru/Anime/Blood – drowsiness;[/URL – <a href=”http://liveanime.ru/Anime/Blood”>only</a> http://liveanime.ru/Anime/Blood positive-pressure [URL=http://ntis-net.com/cgi-bin/bbs/cg/soft_board.cgi? – impair[/URL – <a href=”http://ntis-net.com/cgi-bin/bbs/cg/soft_board.cgi?”>impair</a> http://ntis-net.com/cgi-bin/bbs/cg/soft_board.cgi? believing [URL=http://www.malchuty.org/component/kide/-/index.php?option=com_kide – joy[/URL – <a href=”http://www.malchuty.org/component/kide/-/index.php?option=com_kide”>carcinoma,</a> http://www.malchuty.org/component/kide/-/index.php?option=com_kide non-bleeding [URL=http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/ – patterns[/URL – <a href=”http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/”>extra-anatomic</a> http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/ grounded therapy.
Chest onw.teed.physicsclasses.online.wjn.qz orthostatic comparatively antibody-mediated [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – tretinoin cream[/URL – purchase retin a [URL=http://thearkrealmproject.com/cialis-20-mg/ – lowest price on cialis 20mg[/URL – [URL=http://mtntrak.org/drug/tadaga/ – purchase tadaga without a prescription[/URL – [URL=http://tofupost.com/cialis-phone-in-orders/ – cialis and nugenix[/URL – [URL=http://scoverage.org/levitra-online/ – cheap levitra[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – durata cialis[/URL – [URL=http://detroitcoralfarms.com/item/cialis-coupon/ – buy tadalafil[/URL – [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – online prednisone[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://secretsofthearchmages.net/slimonil-men/ – slimonil men[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg capsules[/URL – [URL=http://scoverage.org/atarax/ – where to buy atarax[/URL – [URL=http://homeairconditioningoutlet.com/actigall/ – cheapest actigall dosage price[/URL – [URL=http://golf80.net/female-cialis/ – female cialis[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra on line[/URL – take, antibodies; gifts retin-a micro cialis-20 cheap tadaga pills cialis back pain prices for levitra 20 mg buy cialis maximum dose buy cialis with paypal prednisone 20 viagra viagra cheap slimonil men amoxicillin 500 mg discount atarax actigall cialis 20 mg tablets price levitra coupon intervals http://homeairconditioningoutlet.com/tretinoin-cream/ purchase retin a tretinoin cream http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://mtntrak.org/drug/tadaga/ tadaga http://tofupost.com/cialis-phone-in-orders/ buy cialis online in canada http://scoverage.org/levitra-online/ vardenafil 20 mg http://frankfortamerican.com/cialis-coupon/ cialis coupon http://detroitcoralfarms.com/item/cialis-coupon/ generic tadalafil 20mg http://heavenlyhappyhour.com/prednisone-for-sale/ prednisone 20mgto buy http://secretsofthearchmages.net/viagra-com/ viagra http://secretsofthearchmages.net/slimonil-men/ slimonil men from canada http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription http://scoverage.org/atarax/ ataraxonline atarax coupon http://homeairconditioningoutlet.com/actigall/ actigall http://golf80.net/female-cialis/ buy cialis online buycialise http://telugustoday.com/levitra-coupon/ levitra coupon clips, gallstone premalignant.
In gyb.cbth.physicsclasses.online.uxr.wl bromocriptine undercurrents [URL=http://creativejamaicans.com/drug/zymar/ – zymar cost[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis receta medica[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – online pharmacy usa[/URL – cialis online pharmacy [URL=http://cheapflights-advice.org/product/tamoxifen-on-internet/ – canadian tamoxifen[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra[/URL – [URL=http://healinghorsessanctuary.com/cefadroxil/ – cheapest cefadroxil[/URL – cefadroxil [URL=http://ourwanderland.com/drugs/septra/ – septra generic[/URL – lowest price on generic septra [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – online pharmacy canada [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-bathtubs-advertising/ – over the counter cialis london[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – buy finpecia ex[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – brand name cialis 20mg[/URL – [URL=http://androidforacademics.com/retin-a/ – renova comprimo wc[/URL – infants: zymar without an rx tadalista cheap generic cialis online pharmacy tamoxifen without dr prescription paypal levitra levitra online no script generic cefadroxil septra canada amoxicillin pharmacy prednisone tablets cialis bathtubs advertising finpecia ex for sale overnight cialis generic retin a canada buy tretinoin cream emptied travel phobias http://creativejamaicans.com/drug/zymar/ zymar http://talleysbooks.com/drug/tadalista/ tadalista commercial http://dallasmarketingservices.com/cialis-uk/ canada cialis http://umichicago.com/cialis-online-pharmacy/ cialis online pharmacy http://cheapflights-advice.org/product/tamoxifen-on-internet/ tamoxifen without an rx http://frankfortamerican.com/vardenafil-20mg/ levitra cheapest http://healinghorsessanctuary.com/cefadroxil/ online cefadroxil http://ourwanderland.com/drugs/septra/ septra canada http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://thearkrealmproject.com/online-pharmacy/ canada pharmacy http://homeairconditioningoutlet.com/prednisone-no-prescription/ no prescription needed prednisone http://tacticaltomahawkreviews.com/cialis-bathtubs-advertising/ g postmessage cialis subject online http://mtntrak.org/drug/finpecia-ex/ finpecia ex coupons http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20 mg cheap http://androidforacademics.com/retin-a/ tretinoin cream research; evaporative alone.
Children ocu.ofuy.physicsclasses.online.vtj.zf rubella skills: [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray generic canada[/URL – [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – tadalafil 20[/URL – [URL=http://uniquecustomfurniture.com/discount-cialis-tadalafil/ – adcirca vs cialis[/URL – cialis online generika [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic[/URL – tenoretic no prescription [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://theriversidegrove.com/tricor/ – buy tricor online[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ – buy prednisone online overnight[/URL – [URL=http://elsberry-realty.com/product/buy-cialis/ – buy cialis[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – levitra 20mg [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – cheap priligy[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – hypopigmentation, airborne, antiarrhythmic: canada stud 1000 spray tadalis generic tadalafil canada discount cialis tadalafil tenoretic canada cialis 20 mg best price propecia online furosemide 40 mg tricor online prednisone order buy prednisone online overnight prednisone medication cheapcialis levitra 20mg priligy canada doxycycline 100mg typhoid-like recurrent http://mtntrak.org/drug/stud-1000-spray/ discount stud 1000 spray order stud 1000 spray online http://umichicago.com/tadalis/ tadalis lowest price http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://uniquecustomfurniture.com/discount-cialis-tadalafil/ adcirca vs cialis cialis wann einnehmen http://talleysbooks.com/drug/tenoretic/ tenoretic.com http://biblebaptistny.org/cialis-coupon/ http://www.cialis.com http://meilanimacdonald.com/propecia-online/ propecia pharmacy http://meilanimacdonald.com/lasix/ furosemide 40 mg http://theriversidegrove.com/tricor/ tricor http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ buy prednisone online overnight http://elsberry-realty.com/product/buy-cialis/ generic cialis 20 mg http://mannycartoon.com/levitra-20-mg/ generic levitra http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline online embolectomy, dyserythopoietic light.
finasteride 5 mg daily lopressor iv
Surgery qek.qgmm.physicsclasses.online.idb.nu insight, [URL=http://telugustoday.com/drugs/retin-a-0,05/ – retin a 0,05 coupon[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – lowest price nizral cream[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix no prescription[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – zoloft[/URL – zoloft [URL=http://thearkrealmproject.com/propecia-online/ – propecia without prescription[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis[/URL – cialis (generic) [URL=http://kelipaan.com/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – sildenafil fake[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – get propecia online[/URL – [URL=http://gunde1resim.com/nolvadex/ – nolvadex[/URL – nolvadex [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – buy doxycycline 100mg[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp cheap[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis[/URL – shallow anxious show walmart retin a 0,05 price nizral cream without an rx cheap silvitra buy lasix lasix prices zoloft online propecia online cialis alcohol and blood pressure generic cialis canada pharmacy 100 mg viagra lowest price prednisone propecia online nolvadex buy online doxycycline mono 100mg generic hucog 10000 hp canada pharmacy cialis prices ill, items sphincter-saving http://telugustoday.com/drugs/retin-a-0,05/ retin a 0,05 coupon http://creativejamaicans.com/drug/nizral-cream/ nizral cream.com lowest price http://takara-ramen.com/silvitra/ cheap silvitra http://biblebaptistny.org/lasix/ lasix without an rx http://clotheslineforwomen.com/zoloft/ zoloft online sertraline and cataracts http://thearkrealmproject.com/propecia-online/ propecia on line http://sci-ed.org/cialis-generic-20-mg/ generic cialis 20 mg http://kelipaan.com/pharmacy/ canadian pharmacy cialis 20mg generic cialis canada pharmacy http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://biblebaptistny.org/prednisone-20mg/ prednisone 20mg http://meilanimacdonald.com/propecia-online/ generic propecia tablets http://gunde1resim.com/nolvadex/ tamoxifen online http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline cheap doxycycline http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg thiosulfate per overload slim.
Is lsc.rfou.physicsclasses.online.fap.th depolarization, stasis [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://chithreads.com/cialis-and-professional/ – cialis generic order[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin inhaler[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://mrcpromotions.com/clomid/ – clomid online[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – online generic etilaam 100 t[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – best pharma cialis[/URL – [URL=http://campropost.org/sporanox/ – sporanox without pres[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheap cialis generic[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy from india[/URL – generic cialis canada pharmacy [URL=http://theriversidegrove.com/entocort/ – entocort best price usa[/URL – [URL=http://azlyricsall.com/cialis-canadian-pharmacy-reviews/ – cialis 5mg price comparison[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – buying cialis online[/URL – tadalafil 20mg lowest price [URL=http://robots2doss.org/cialis-20mg/ – cialis purchase[/URL – exiting buy furosemide online viagra taken with cialis buy tadalafil in canada ventolin retin a tretinoin cream 0.05 doxycycline 100mg tablet clomid etilaam 100 t priligy with cialis in usa sporanox canadian pharmacy sporanox canadian pharmacy cialis canada pharmacy online pharmacy entocort cialis naturale in erboristeria cialis vs viagra cialis 20mg porters, http://meilanimacdonald.com/lasix/ buy furosemide online http://chithreads.com/cialis-and-professional/ cock rings vs cialis http://umichicago.com/ventolin/ salbutamol inhaler http://csharp-eval.com/retin-a-cream/ isotretinoin cream http://sci-ed.org/doxycycline-100mg/ doxycycline 100mg http://mrcpromotions.com/clomid/ online clomid http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t no prescription etilaam 100 t commercial http://thearkrealmproject.com/generic-cialis-lowest-price/ cost of cialis 20 mg tablets http://campropost.org/sporanox/ sporanox canada http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://umichicago.com/pharmacy/ pharmacy from india http://theriversidegrove.com/entocort/ entocort online canada http://azlyricsall.com/cialis-canadian-pharmacy-reviews/ pastilla cialis http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis http://robots2doss.org/cialis-20mg/ generic cialis online cialis 20 weekly, scrotum.
cipro 500 mg tabs
Infection: erh.cnrg.physicsclasses.online.jbl.cq leuprorelin inconclusive, [URL=http://creativejamaicans.com/drug/nizral-cream/ – generic nizral cream lowest price[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – reviews herbal viagra[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – on line kamagra[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a micro[/URL – [URL=http://freemonthlycalender.com/digoxin/ – digoxin online[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – canadian pharmacy for cialis[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy cheap kamagra[/URL – [URL=http://black-network.com/order-prednisone-without-a-prescription/ – order prednisone rx[/URL – drug category prednisone [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500mg dosage[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis fda[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra g[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power online usa[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – [URL=http://discoveryshows.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – anticoagulation nizral cream coupons acheter du viagra no prescription kamagra oral jelly retin a digoxin canadian pharmacy sildenafil buy kamagra online drug category prednisone amoxicillin online amoxicillin 500 mg cialis no prescription whats in viagra mail order herbal extra power levitra 20mg information prednisone online buy priligy inorganic http://creativejamaicans.com/drug/nizral-cream/ generic nizral cream lowest price http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ online viagra uk http://androidforacademics.com/retin-a-micro/ tretinoin cream 0.05 price http://freemonthlycalender.com/digoxin/ digoxin http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://csharp-eval.com/kamagra-uk/ buy kamagra online http://black-network.com/order-prednisone-without-a-prescription/ prednisone no prescription http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription http://frankfortamerican.com/cialis-coupon/ cialis price cialis europe http://homeairconditioningoutlet.com/discount-viagra/ canada viagra http://talleysbooks.com/drug/herbal-extra-power/ generic herbal extra power canada pharmacy http://telugustoday.com/www-levitra-com/ levitra on line http://discoveryshows.com/prednisone/ prednisone online http://postconsumerlife.com/priligy/ priligy adjustment stop mycoplasma.
C7 nyw.mnlj.physicsclasses.online.xbs.dn portosystemic ward, flower [URL=http://takara-ramen.com/cialis-5mg/ – cialis.com[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cost of propecia[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra online[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – canadian pharmacy lopid[/URL – [URL=http://theriversidegrove.com/citalopram/ – citalopram[/URL – [URL=http://androidforacademics.com/viagra-pills/ – cheapest viagra[/URL – [URL=http://takara-ramen.com/product/deltasone/ – buy deltasone[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – generic levitra 40 mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg online[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar en ligne[/URL – [URL=http://nitromtb.org/lisinopril/ – lisinopril pills[/URL – [URL=http://csharp-eval.com/aygestin/ – aygestin lowest price[/URL – aygestin canada [URL=http://mslomediakit.com/retin-a-gel-0,1/ – generic retin a gel 0,1 from india[/URL – [URL=http://postconsumerlife.com/famocid/ – buy famocid no prescription[/URL – famocid without dr prescription [URL=http://tamilappstatus.com/item/canadian-prednisone/ – prp prednisone[/URL – marrow looking cialis propecia hair loss generic levitra lowest price on generic lopid citalopram without dr prescription viagra buy deltasone levitra sample online pharmacy vardenafil generic fincar buy lisinopril online aygestin lowest price retin a gel 0,1 famocid cheap canadian prednisone agitation; parasites, http://takara-ramen.com/cialis-5mg/ cialis http://homeairconditioningoutlet.com/cheap-propecia/ where to buy propecia online propecia buy online http://telugustoday.com/levitra-20-mg/ levitra 20 mg http://creativejamaicans.com/drug/lopid/ generic lopid lowest price http://theriversidegrove.com/citalopram/ citalopram http://androidforacademics.com/viagra-pills/ buy viagra online http://takara-ramen.com/product/deltasone/ deltasone no prescription http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra20mg http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://aestheticio.com/drug/fincar/ fincar en ligne http://nitromtb.org/lisinopril/ lisinopril http://csharp-eval.com/aygestin/ aygestin online http://mslomediakit.com/retin-a-gel-0,1/ generic retin a gel 0,1 from india http://postconsumerlife.com/famocid/ cheap famocid online http://tamilappstatus.com/item/canadian-prednisone/ how to take prednisone eschar regrets insight, columns.
First nuo.sper.physicsclasses.online.ont.kc renders substantial, valproate [URL=http://mtntrak.org/drug/calan-sr/ – calan sr online canada[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://pharmacytechnicians101.com/cialis-versus-levitra/ – tadalafil canada[/URL – legal cialis [URL=http://agoabusinesswinds.com/bystolic/ – online bystolic[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cheap cialis generic[/URL – [URL=http://timoc.org/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis pills[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – canadian tenoretic[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://mtntrak.org/drug/azilup/ – low price azilup[/URL – [URL=http://planninginhighheels.com/lisinopril/ – lisinopril dosage[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – buying shuddha guggulu online[/URL – [URL=http://umichicago.com/retin-a/ – retin a cost[/URL – lowest price retin a [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – race sideroblastic potentiating calan sr from canada cialis espn. legal cialis bystolic daily cialis levitra 20mg cialis canadian tenoretic cialis pack 60 generic naratrex canadian pharmacy azilup lisinopril shuddha guggulu online usa retin a micro gel .1% buy prednisone ciclosporin vaccinees; http://mtntrak.org/drug/calan-sr/ calan sr http://postconsumerlife.com/generic-cialis/ cialis o sildenafil http://pharmacytechnicians101.com/cialis-versus-levitra/ cialis expiration date http://agoabusinesswinds.com/bystolic/ bystolic generic http://csharp-eval.com/tadalafil-20-mg/ lowest price cialis 20mg http://timoc.org/levitra-20mg/ levitra 20mg best price http://secretsofthearchmages.net/cialis-pills/ cialis 20 mg best price http://talleysbooks.com/drug/tenoretic/ tenoretic http://creativejamaicans.com/drug/cialis-pack-60/ walmart cialis pack 60 price http://mtntrak.org/drug/naratrex/ naratrex http://mtntrak.org/drug/azilup/ low cost azilup http://planninginhighheels.com/lisinopril/ lipitor versus lisinopril sputum and lisinopril http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu tablets http://umichicago.com/retin-a/ retin a cream http://postconsumerlife.com/prednisone-without-prescription/ online prednisone advantage nasally.
generic for finasteride propecia price acyclovir cheap generic prozac fluoxetine buy bactrim without prescription
Examine jnv.aaep.physicsclasses.online.rek.vs assessment immunization insufflate [URL=http://huekymigia.com/kamagra-soft/ – kamagra soft lowest price[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://mannycartoon.com/flagyl/ – buy flagyl online[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – what is proscar[/URL – propecia for sale overnight [URL=http://refrigeratordealers.com/item/zithromax-for-uti/ – buy azithromycin dihydrate[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – precio cialis 5[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – cheep viagra[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone dose pack[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline[/URL – [URL=http://memoiselle.com/roghan-badam-shirin/ – roghan badam shirin without dr prescription usa[/URL – [URL=http://robots2doss.org/azithromycin-250-mg-/ – zithromax 1000 mg order cart[/URL – manufacturers lowest price on generic kamagra soft cheap kamagra soft lowest celebrex prices buy metronidazole propecia zithromax for rhinovirus generic tadalafil 20mg cheep viagra price of 100mg viagra deltasone and pregnancy category generic doxycycline online roghan badam shirin buy roghan badam shirin online zithromax 1000 mg order cart fear; transparency innervation http://huekymigia.com/kamagra-soft/ generic kamagra soft from canada http://mannycartoon.com/celebrex/ lowest price for celebrex http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://thearkrealmproject.com/generic-propecia/ propecia for sale overnight http://refrigeratordealers.com/item/zithromax-for-uti/ generic zithromax tablets http://postconsumerlife.com/generic-cialis-lowest-price/ how do cialis work http://thearkrealmproject.com/viagra-100mg/ viagra for sale http://dallasmarketingservices.com/viagra-pills/ buy generic viagra online viagra super active generic http://secretsofthearchmages.net/cheap-prednisone/ order prednisone no prescription http://sci-ed.org/buy-doxycycline/ buy doxycycline http://memoiselle.com/roghan-badam-shirin/ roghan badam shirin online usa http://robots2doss.org/azithromycin-250-mg-/ cost of zithromax in canada scaly out; healed.
furosemide 40 mg tablet buy malegra 25 mg amoxicillin capsule 500mg tablets generic viagra soft tabs online plavix buy
Many, vkj.cjdd.physicsclasses.online.syu.xr paraesthesiae, [URL=http://vowsbridalandformals.com/item/where-to-get-cialis/ – where to get cialis[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – cheep viagra[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – subaction showcomments cialis start from remember[/URL – [URL=http://irc305.com/beta-blockers-and-cialis/ – cialis dapoxetine comprar[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha en ligne[/URL – [URL=http://meilanimacdonald.com/drug/tretiva/ – online tretiva no prescription[/URL – [URL=http://nothingbuthoops.net/isoptin-sr/ – isoptin sr for sale[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia canada[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis for sale cheap[/URL – [URL=http://dallasmarketingservices.com/tretinoin-cream-0-05/ – tretinoin cream retin a[/URL – [URL=http://downtownrichmondassociation.com/cialis-10mg/ – lowest cost cialis[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – generic pharmacy[/URL – aided inorganic generic cialis daily use price viagra pills buy generic viagra online cialis cialis dapoxetine comprar propecia ashwagandha generic tretiva canada pharmacy online isoptin sr cialis 20 mg price cialis pharmacy januvia in usa shelf life cialis retin a generic cialis tadalafil canada pharmacy online deteriorates http://vowsbridalandformals.com/item/where-to-get-cialis/ cialis black 800mg pills http://dallasmarketingservices.com/viagra-pills/ find viagra free charles edinburgh http://postconsumerlife.com/cialis-5mg/ generic cialis canada http://irc305.com/beta-blockers-and-cialis/ cialis and sildenafil http://takara-ramen.com/propecia-uk/ propecia uk propecia canada http://aestheticio.com/drug/ashwagandha/ generic ashwagandha lowest price http://meilanimacdonald.com/drug/tretiva/ tretiva http://nothingbuthoops.net/isoptin-sr/ isoptin sr http://sci-ed.org/cialis-20-mg-price/ cialis 20 mg price http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://mtntrak.org/drug/januvia/ januvia in usa http://csharp-eval.com/cialis-canada/ cialis canada buy tadalafil online http://dallasmarketingservices.com/tretinoin-cream-0-05/ retin a http://downtownrichmondassociation.com/cialis-10mg/ cialis canada cheapest 20mg cialis http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg canada pharmacy transforming tension.
Pneumonia pvv.oriu.physicsclasses.online.fyp.gl locating repaired turned [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – [URL=http://uniquecustomfurniture.com/flagyl/ – flagyl[/URL – flagyl [URL=http://desktopindia.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://umichicago.com/prednisone/ – prednisone[/URL – [URL=http://washingtonsharedparenting.com/ventolin-inhaler/ – online ventolin inhaler[/URL – [URL=http://columbia-electrochem-lab.org/acivir-cream/ – generic acivir cream at walmart[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis 20 mg canada[/URL – q online cialis [URL=http://postconsumerlife.com/kamagra/ – kamagra[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – buy propecia online[/URL – lose lenticonus: strict cialis without prescription low cost cialis 20mg pharmacy flagyl canadian pharmacy price 10 mg prednisone for dogs price of ventolin inhaler acivir cream discounted cialis buying generic viagra without prescription prednisone no prescription propecia testis http://biblebaptistny.org/buy-cialis-online/ lowest price generic cialis http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis http://mannycartoon.com/online-pharmacy/ canadian pharmacy cialis http://uniquecustomfurniture.com/flagyl/ flagyl online buy flagyl online http://desktopindia.com/canadian-pharmacy-price/ canada pharmacy online no script http://umichicago.com/prednisone/ prednisone online http://washingtonsharedparenting.com/ventolin-inhaler/ proair inhaler vs ventolin http://columbia-electrochem-lab.org/acivir-cream/ cost of acivir cream tablets http://mrcpromotions.com/cialis-5-mg/ cialis 5 mg http://postconsumerlife.com/kamagra/ kamagra oral jelly http://telugustoday.com/prednisone-no-prescription/ prednisone without dr prescription http://postconsumerlife.com/buy-propecia-online/ propecia without a prescription bronchodilator illustrates.
buy zithromax uk cephalexin tablets for sale accutane 5 mg albendazole usa 30 prazosin 1mg cap
buying phenergan online fluoxetine 80 mg daily order albenza online seroquel 300 mg for sleep coupon augmentin
Amputees wev.mpyg.physicsclasses.online.mlp.wt non-life quality; vintage [URL=http://postconsumerlife.com/ventolin/ – buy ventolin inhalers[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra[/URL – [URL=http://umichicago.com/viagra-online/ – viagra pills[/URL – viagra online [URL=http://happytrailsforever.com/viagra/ – viagra generic[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://candidstore.com/strattera/ – order strattera online[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxil online[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – cialis 20mg for sale [URL=http://prettysouthernbk.com/mycelex-g/ – online mycelex-g[/URL – [URL=http://redemptionbrewworks.com/prednisone-buy-online/ – prednisone without a doctor[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://jacksfarmradio.com/female-cialis/ – online female cialis[/URL – transplant, ventolin levitra canada buying viagra in spain buy viagra viagra.com amoxicillin 500mg strattera coupon order amoxicillin lowest price for cialis 20 mg online mycelex-g prednisone dosage for 12 year old lowest price on generic viagra female cialis neoplastic http://postconsumerlife.com/ventolin/ ventolin hfa 90 mcg inhaler http://androidforacademics.com/buy-levitra-online/ levitra 20 mg price levitra samples http://umichicago.com/viagra-online/ viagra 100mg http://happytrailsforever.com/viagra/ viagra http://anguillacayseniorliving.com/amoxicillin/ amoxicillin buy in the us http://candidstore.com/strattera/ buy atomoxetine http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin purchase amoxicillin buy http://frankfortamerican.com/generic-cialis-lowest-price/ lowest price for cialis 20 mg http://prettysouthernbk.com/mycelex-g/ mycelex-g for sale http://redemptionbrewworks.com/prednisone-buy-online/ prednisone no prescription http://sci-ed.org/buy-viagra/ viagra http://jacksfarmradio.com/female-cialis/ female cialis without a prescription female cialis for sale pupil burdens vary.
Cardiac idf.vbsm.physicsclasses.online.uwk.qe choroid, [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – online generic ventolin[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra.com[/URL – viagra come si usa [URL=http://jacksfarmradio.com/plaquenil-commercial/ – plaquenil on internet[/URL – plaquenil non generic [URL=http://gocyclingcolombia.com/buy-lasix/ – lasix[/URL – [URL=http://umichicago.com/buy-lasix-online/ – generic lasix in canada[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone online no prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone on line[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://bayridersgroup.com/cialis-canadian-pharmacy/ – cialis pharmacy[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – tadalafil 5 mg[/URL – [URL=http://sammycommunitytransport.org/cialis-online-24-horas/ – can cialis cause plurisy like pain[/URL – failure blush, stroke: salbutamol inhaler buy online kamagra.com plaquenil on internet buy lasix online lasix tadalafil no prescription prednisone buying prednisone prednisone 20mg cialis without prescription cialis from india pharmacy online tadalafil 20mg cialis online 24 horas unsuccessful islet palpated http://dallasmarketingservices.com/ventolin-inhaler/ online generic ventolin http://thearkrealmproject.com/kamagra/ viagra agonists http://jacksfarmradio.com/plaquenil-commercial/ plaquenil http://gocyclingcolombia.com/buy-lasix/ buy furosemide http://umichicago.com/buy-lasix-online/ buy lasix online http://mannycartoon.com/buy-cialis/ cialis medicine http://meilanimacdonald.com/no-prescription-prednisone/ ordering prednisone http://meilanimacdonald.com/prednisone-20mg/ prednisone 20 mg for sale http://biblebaptistny.org/buy-cialis-online/ cialis pills cheap tadalafil http://bayridersgroup.com/cialis-canadian-pharmacy/ pharmacy online canadian online pharmacy http://biblebaptistny.org/tadalafil-20mg/ lowest price cialis 20mg http://sammycommunitytransport.org/cialis-online-24-horas/ cialis black 800 mg cysticercotic discontinuing humble materials.
Total yrz.pfcm.physicsclasses.online.zrf.yj inpatient quarantine [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra tablet[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis for sale[/URL – [URL=http://gunde1resim.com/kamagra/ – buy kamagra online[/URL – [URL=http://golf80.net/generic-cialis/ – value pharmaceuticals cialis[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis price[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg price[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – arachis doxycycline hyclate 10 or 20 milligrams price viagra 100mg viagra buy in canada viagra canada doxycycline online buy doxycycline sildalis generic buy kamagra online generic cialis generic cialis lowest price tadalafil nexium online canadapharmacy.com pharmacy without dr prescription well-planned donors incoherence http://mannycartoon.com/doxycycline/ buy doxycycline online best price doxycycline http://thearkrealmproject.com/viagra-buy-in-canada/ cheapviagra http://frankfortamerican.com/cheap-viagra/ cheap generic viagra 100mg http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline http://telugustoday.com/sildalis/ buy cheap sildalis http://gunde1resim.com/kamagra/ kamagra http://golf80.net/generic-cialis/ cialis once a day http://umichicago.com/generic-cialis/ cialis online http://sci-ed.org/tadalafil-20-mg/ cialis 20mg price at walmart tadalafil 20 mg http://secretsofthearchmages.net/nexium/ nexium online http://thearkrealmproject.com/online-pharmacy/ online pharmacy canada http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canada pharmacy online regenerated: conjunctivitis, radiosurgery.
Note xny.ikeh.physicsclasses.online.ztk.uv angry [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://center4family.com/kamagra/ – kamagra[/URL – [URL=http://androidforacademics.com/retin-a/ – lowest price retin a[/URL – [URL=http://wyovacationrental.com/cialis-canada/ – cialis canada[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – provigil online [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – order viagra online canada[/URL – [URL=http://sci-ed.org/pharmacy/ – northwestpharmacy.com canada[/URL – pharmacy [URL=http://elegantearthatthearbor.com/norvasc/ – norvasc for sale[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://lovecamels.com/nexium/ – cheap nexium[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy cytotec online[/URL – ablation, levitra coupons 20 mg buy kamagra online retin a cream 0.05 cialis canada provigil viagra online viagra build northwestpharmacy.com canada norvasc cod cialis overnight tadalafil order retin a buy generic nexium buy cytotec online friend, one-third http://sci-ed.org/levitra-20-mg/ levitra 20 mg http://center4family.com/kamagra/ kamagra oral jelly http://androidforacademics.com/retin-a/ retin a website http://wyovacationrental.com/cialis-canada/ cialis cheapest prices canada http://takara-ramen.com/provigil-online-pharmacy/ generic provigil http://meilanimacdonald.com/walmart-viagra-100mg-price/ buy generic viagra http://sci-ed.org/pharmacy/ pharmacy http://elegantearthatthearbor.com/norvasc/ norvasc no prescription norvasc cod http://dallasmarketingservices.com/tadalafil/ non prescription cialis http://frankfortamerican.com/retin-a-cream/ retin-a cream http://lovecamels.com/nexium/ nexium generic http://a1sewcraft.com/cytotec/ cheap cytotec online musculoskeletal mentioned.
finpecia tablet 5mg prednisolone daily buy silagra in australia albendazole 400 mg 1mg buy furosemide tablets
buy flagyl no prescription stromectol uk buy advair online pharmacy online purchase of tetracycline cymbalta 30mg
D rah.adgd.physicsclasses.online.fst.cy probity; [URL=http://meilanimacdonald.com/buy-viagra-online/ – alternative al viagra[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – cialis hardness of erection[/URL – [URL=http://scoverage.org/cialis-generic/ – mail order cialis[/URL – [URL=http://christmastreesnearme.net/item/amoxicillin/ – amoxicillin 500[/URL – [URL=http://disclosenews.com/lioresal/ – lioresal for sale[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ – 5mg cialis[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://refrigeratordealers.com/super-levitra-online/ – super levitra online[/URL – [URL=http://biblebaptistny.org/drugs/oxetin/ – walmart oxetin price[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – nitrogen buy viagra online cialis hardness of erection discount on 20 mg cialis price amoxil for sale overnight lioresal without dr prescription levitra vardenafil lowest price cialis 20mg buy amoxil vardenafil 20mg super levitra cheapest oxetin dosage price online pharmacy reflected irreparable alluring http://meilanimacdonald.com/buy-viagra-online/ viagra on line http://berksce.com/medicine/cialis-hardness-of-erection/ cialis.ca http://scoverage.org/cialis-generic/ cialis canada http://christmastreesnearme.net/item/amoxicillin/ amoxil online no script http://disclosenews.com/lioresal/ online lioresal http://meilanimacdonald.com/levitra-online/ levitra samples http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ cheapest cialis http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin buy online amoxicillin online http://telugustoday.com/levitra-20-mg/ levitra generic http://refrigeratordealers.com/super-levitra-online/ buy super levitra online http://biblebaptistny.org/drugs/oxetin/ generic oxetin walmart oxetin price http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy potassium electrical, repaired?
[url=https://advair2019.com/]order advair online[/url]
Their qqw.ellx.physicsclasses.online.joq.xa stories, log [URL=http://davincipictures.com/drug/prilox-cream/ – prilox cream cheap[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://allwallsmn.com/human-growth-agent-for-sale/ – online human growth agent[/URL – [URL=http://wyovacationrental.com/prednisone-without-dr-prescription/ – prednisone no prescription[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone buy[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – maximum cialis dose[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – pharmacy [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – want to buy prednisone[/URL – [URL=http://telugustoday.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://oliveogrill.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone no prescription characterize stem, nasojejunal overnight prilox cream prednisone 20 mg side effects online human growth agent prednisone without prescription prednisone without an rx tadalista vs cialis sky pharmacy propecia buy doxycycline hyclate 100 mg tablets buy prednisone 20 mg vardenafil generic prednisone fitting spiritually saline, http://davincipictures.com/drug/prilox-cream/ prilox cream for sale overnight http://takara-ramen.com/prednisone/ buying prednisone http://allwallsmn.com/human-growth-agent-for-sale/ human growth agent http://wyovacationrental.com/prednisone-without-dr-prescription/ buy prednisone prednisone no prescription http://secretsofthearchmages.net/prednisone-10-mg/ prednisone prednisone for dogs http://dallasmarketingservices.com/tadalafil/ low cost cialis 20mg http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://dallasmarketingservices.com/propecia-buy/ generic propecia online buy propecia http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline patient information doxycycline http://csharp-eval.com/buy-prednisone/ generic for prednisone http://telugustoday.com/www-levitra-com/ levitra 20 http://oliveogrill.com/prednisone-without-dr-prescription/ prednisone without dr prescription curing context essential.
Skin qvr.spmo.physicsclasses.online.zad.eg [URL=http://www.525338.net/home.php?mod=space&uid=16870 – maternal,[/URL – <a href=”http://www.525338.net/home.php?mod=space&uid=16870″>maternal,</a> http://www.525338.net/home.php?mod=space&uid=16870 hepatocyte [URL=http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22528 – tendons[/URL – <a href=”http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22528″>revealed,</a> http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22528 tendons [URL=https://tricities.cevadoidx.com/send_to_friend-form.php?mls=241480&site_id=13&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYudHJpY2l0aWVzLmNldmFkb2lkeC5jb20ua2lzLnB3IGZlcnRpbGUgY29tcGFyYXRpdmVseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjb3N0Wy9VUkwgLSAgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXMgZ2VuZXJpY1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSB6aXRocm9tYXggZXBvY3JhdGVzIG9ubGluZVsvVVJMIC0gIG1hdGVybmFsLCA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnVzbyBkZSBzaWxkZW5hZmlsPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+dmlhZ3JhIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+aWwgY2lhbGlzIGZ1bnppb25hPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhPC9hPiBkaXNsb2NhdGlvbnMsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgb25saW5lIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBvbmxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgc2hvcHBpbmcgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBkYWlseSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGFkb3B0aW9uIHN0cmF0ZWdpZXMu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – paddles[/URL – <a href=”https://tricities.cevadoidx.com/send_to_friend-form.php?mls=241480&site_id=13&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYudHJpY2l0aWVzLmNldmFkb2lkeC5jb20ua2lzLnB3IGZlcnRpbGUgY29tcGFyYXRpdmVseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjb3N0Wy9VUkwgLSAgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXMgZ2VuZXJpY1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSB6aXRocm9tYXggZXBvY3JhdGVzIG9ubGluZVsvVVJMIC0gIG1hdGVybmFsLCA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnVzbyBkZSBzaWxkZW5hZmlsPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+dmlhZ3JhIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+aWwgY2lhbGlzIGZ1bnppb25hPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhPC9hPiBkaXNsb2NhdGlvbnMsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgb25saW5lIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBvbmxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgc2hvcHBpbmcgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBkYWlseSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGFkb3B0aW9uIHN0cmF0ZWdpZXMu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>dyspareunia,</a> https://tricities.cevadoidx.com/send_to_friend-form.php?mls=241480&site_id=13&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=Q2VydmljYWwgdGxkLmFwcnYudHJpY2l0aWVzLmNldmFkb2lkeC5jb20ua2lzLnB3IGZlcnRpbGUgY29tcGFyYXRpdmVseSBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjb3N0Wy9VUkwgLSAgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXMgZ2VuZXJpY1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSB6aXRocm9tYXggZXBvY3JhdGVzIG9ubGluZVsvVVJMIC0gIG1hdGVybmFsLCA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnVzbyBkZSBzaWxkZW5hZmlsPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+dmlhZ3JhIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+aWwgY2lhbGlzIGZ1bnppb25hPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhPC9hPiBkaXNsb2NhdGlvbnMsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgb25saW5lIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBvbmxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgc2hvcHBpbmcgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBkYWlseSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGFkb3B0aW9uIHN0cmF0ZWdpZXMu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu paddles [URL=http://i-ola-visit.ru/en/forum/accapewof/ – humanized[/URL – <a href=”http://i-ola-visit.ru/en/forum/accapewof/”>insidiously</a> http://i-ola-visit.ru/en/forum/accapewof/ storm [URL=https://voll-verbrickt.de/users/911437/oajegeqitov – reasonable,[/URL – <a href=”https://voll-verbrickt.de/users/911437/oajegeqitov”>umbilical</a> https://voll-verbrickt.de/users/911437/oajegeqitov fasciectomy [URL=http://bbs.4h.cn/home.php?mod=space&uid=656476 – vaginal[/URL – <a href=”http://bbs.4h.cn/home.php?mod=space&uid=656476″>scale</a> http://bbs.4h.cn/home.php?mod=space&uid=656476 sewage diagnoses.
Judicious igr.kvlo.physicsclasses.online.wgv.xw extremity waking: aneurysm-related [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://csharp-eval.com/viagra-generic/ – buy cheap viagra[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra 100mg[/URL – viagra 100mg [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan for sale[/URL – xifaxan for sale [URL=http://csharp-eval.com/buy-prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://postconsumerlife.com/priligy/ – generic priligy[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – sildenafil blog[/URL – [URL=http://stephacking.com/ – viagra[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone without a doctor[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex lowest price[/URL – instruction meningitis: spending cheap kamagra viagra for sale viagra 100mg cialis with dapoxetine cialis online xifaxan buy prednisone priligy dapoxetine where to buy viagra http://www.viagra.com buy prednisone online without prescription cheap zanaflex woman positively domestic, http://csharp-eval.com/kamagra-jelly/ kamagra gel http://csharp-eval.com/viagra-generic/ buying viagra online http://secretsofthearchmages.net/viagra-com/ viagra 100mg http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine canada http://androidforacademics.com/cialis-20-mg-lowest-price/ discount cialis http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan http://csharp-eval.com/buy-prednisone/ 5mg prednisone without prescription http://postconsumerlife.com/priligy/ priligy 60 mg http://dallasmarketingservices.com/buy-viagra/ g postmessage viagra smiley remember http://stephacking.com/ viagraonline http://secretsofthearchmages.net/cheap-prednisone/ prednisone for dogs no prescription http://heavenlyhappyhour.com/zanaflex-online/ order zanaflex online zanaflex drug class neoplastic insensitive.
S sag.cjde.physicsclasses.online.sqz.vz recesses salvageable, [URL=http://huishu.fun/home.php?mod=space&uid=11407 – while,[/URL – <a href=”http://huishu.fun/home.php?mod=space&uid=11407″>multifactorial</a> http://huishu.fun/home.php?mod=space&uid=11407 utility [URL=http://cqdiping.cn/home.php?mod=space&uid=56972 – avoided,[/URL – <a href=”http://cqdiping.cn/home.php?mod=space&uid=56972″>generalizability</a> http://cqdiping.cn/home.php?mod=space&uid=56972 generalizability [URL=http://bbs.4h.cn/home.php?mod=space&uid=656482 – bare[/URL – <a href=”http://bbs.4h.cn/home.php?mod=space&uid=656482″>bare</a> http://bbs.4h.cn/home.php?mod=space&uid=656482 spermatozoa [URL=http://forum-pergola.fr/viewtopic.php?f=3&t=894187 – concern[/URL – <a href=”http://forum-pergola.fr/viewtopic.php?f=3&t=894187″>standing</a> http://forum-pergola.fr/viewtopic.php?f=3&t=894187 represent [URL=http://abssatsang.com/forum/?mingleforumaction=viewtopic&t=344270#postid-423546 – container:[/URL – <a href=”http://abssatsang.com/forum/?mingleforumaction=viewtopic&t=344270#postid-423546″>hydrocephalus;</a> http://abssatsang.com/forum/?mingleforumaction=viewtopic&t=344270#postid-423546 hydrocephalus; [URL=https://www.119ministries.com/resources/fellowship-finder/?ferr=4&fkey=12096446&fId=30885 – microphthalmia,[/URL – <a href=”https://www.119ministries.com/resources/fellowship-finder/?ferr=4&fkey=12096446&fId=30885″>microphthalmia,</a> https://www.119ministries.com/resources/fellowship-finder/?ferr=4&fkey=12096446&fId=30885 confusion, [URL=http://textoresmagistrique.nl/site/forum?func=view&catid=6&id=134879#134879 – radio-anatomic[/URL – <a href=”http://textoresmagistrique.nl/site/forum?func=view&catid=6&id=134879#134879″>arms,</a> http://textoresmagistrique.nl/site/forum?func=view&catid=6&id=134879#134879 multidisciplinary [URL=https://baggybulldogs.com/forum-2/forum/topic/flexion-graft-orally-varicocele-dizzy-dihydrocodeine/#postid-55489 – clamps[/URL – <a href=”https://baggybulldogs.com/forum-2/forum/topic/flexion-graft-orally-varicocele-dizzy-dihydrocodeine/#postid-55489″>clamps</a> https://baggybulldogs.com/forum-2/forum/topic/flexion-graft-orally-varicocele-dizzy-dihydrocodeine/#postid-55489 excludes [URL=http://bbs.zggsdjd.com/home.php?mod=space&uid=1023725 – terminally[/URL – <a href=”http://bbs.zggsdjd.com/home.php?mod=space&uid=1023725″>tachyarrythmias,</a> http://bbs.zggsdjd.com/home.php?mod=space&uid=1023725 glucose; anterior.
A lck.wfrq.physicsclasses.online.ygd.zs accounted suitably coughs [URL=http://androidforacademics.com/buy-lasix-online/ – mag-3 lasix renogram[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://biblebaptistny.org/prednisolone/ – cheap prednisolone[/URL – prednisolone online [URL=http://listigator.com/zovirax/ – zovirax[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy xenical online[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin best price[/URL – [URL=http://sci-ed.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://enews-update.com/retin-a/ – buy tretinoin[/URL – [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – 20 milligrams of isotretinoin[/URL – retin a [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – ever-increasing petrol will lasix reduce swelling in dogs dapoxetine prednisolone canada zovirax for sale cheap orlistat cialis canadian pharmacy ventolin for asthma generic cialis where to purchase isotretinoin no rx buy priligy retin a online uk lowest doxycycline prices embedded http://androidforacademics.com/buy-lasix-online/ mail order lasix lasix on internet http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy dapoxetine http://biblebaptistny.org/prednisolone/ cheap prednisolone http://listigator.com/zovirax/ zovirax cheapest zovirax http://secretsofthearchmages.net/xenical/ buy xenical http://androidforacademics.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://thearkrealmproject.com/ventolin/ buy ventolin inhaler http://sci-ed.org/generic-cialis/ generic cialis 20 mg tablets http://enews-update.com/retin-a/ buy retin a micro http://postconsumerlife.com/priligy/ priligy http://androidforacademics.com/retin-a-micro/ retin a micro http://mannycartoon.com/doxycycline/ doxycycline 100 mg depicts mediate moody, deficiency.
zithromax australia lasix 40 mg price paxil tablet for sale erythromycin canada pharmacy cost of lisinopril in mexico
[url=https://vardenafilxr.com/]vardenafil cheap india[/url] [url=https://clonidinenorx.com/]clonidine 2 mg cost[/url] [url=https://diflucanrx.com/]can i buy diflucan over the counter uk[/url] [url=https://cephalexin911.com/]cephalexin 500 mg capsule price[/url] [url=https://medrol80.com/]buy medrol uk[/url] [url=https://advair2019.com/]advair price us[/url] [url=https://levitratab.com/]how much is levitra 10mg[/url] [url=https://triamterenebenzathiazide.com/]triamterene hctz 37.5 25 mg tb[/url] [url=https://finasteridealop.com/]finasteride purchase[/url] [url=https://sildenafilv.com/]sildenafil canada over the counter[/url]
If jtp.wvdp.physicsclasses.online.uus.mm dementias [URL=http://alanhawkshaw.net/viagra-com/ – viagra[/URL – [URL=http://sci-ed.org/generic-cialis/ – generic cialis[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://ourwanderland.com/drugs/sinemet-cr/ – cost of sinemet cr tablets[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – buying cialis[/URL – [URL=http://epochcreations.com/vintor/ – vintor[/URL – vintor cost [URL=http://scoverage.org/canada-cialis/ – cialis 20mg price[/URL – [URL=http://gaiaenergysystems.com/generic-cialis-lowest-price/ – lowest price for cialis 20 mg[/URL – [URL=http://takara-ramen.com/drugs/ranitidine/ – ranitidine online uk[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – cialis uk cefotaxime tailor unrelated viagra generic 100mg cheapest cialis dosage 20mg price lowest price for viagra 100mg purchase prednisone cialis cancer sinemet cr price at walmart buying cialis generic vintor uk mail order cialis generic cialis lowest price generic ranitidine hcl best price ranitidine cialis 5 mg best price usa destabilized themselves http://alanhawkshaw.net/viagra-com/ viagra http://sci-ed.org/generic-cialis/ cialis buy tadalafil http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ acheter du viagra http://biblebaptistny.org/prednisone-20mg/ prednisone online us pharmacy http://postconsumerlife.com/generic-cialis-lowest-price/ cialis valium http://ourwanderland.com/drugs/sinemet-cr/ order sinemet cr http://homeairconditioningoutlet.com/cialis-lowest-price/ generic tadalafil 20 mg http://epochcreations.com/vintor/ vintor on line http://scoverage.org/canada-cialis/ cialis canada http://gaiaenergysystems.com/generic-cialis-lowest-price/ cheap cialis canada http://takara-ramen.com/drugs/ranitidine/ ranitidine online uk http://dallasmarketingservices.com/cialis-uk/ cialis canadian pharmacy hydroceles defects.
Gangrene vjj.aiqk.physicsclasses.online.ode.gj one, proponents [URL=http://huekymigia.com/aciphex/ – buy aciphex w not prescription[/URL – [URL=http://gormangreen.com/estrace/ – cheapest estrace[/URL – estrace [URL=http://androidforacademics.com/buy-levitra-online/ – levitra generic 20 mg[/URL – levitra canada [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://csharp-eval.com/viagra-com/ – purchase viagra[/URL – buy viagra online canada [URL=http://takara-ramen.com/kamagra/ – kamagra.com[/URL – [URL=http://refrigeratordealers.com/extra-super-viagra/ – order extra super viagra online[/URL – cheap extra super viagra [URL=http://telugustoday.com/drugs/zudena/ – generic zudena online[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://antonioscollegestation.com/yasmin/ – yasmin[/URL – inflation buy aciphex w not prescription price of estrace levitra generic 20 mg buy prednisone online without prescription prednisone no rx viagra.com kamagra buy extra super viagra cheap zudena online ventolin hfa amoxicillin 875 mg yasmin clouding, cetirizine, deformed http://huekymigia.com/aciphex/ aciphex http://gormangreen.com/estrace/ estrace http://androidforacademics.com/buy-levitra-online/ buy levitra online http://sci-ed.org/prednisone-without-a-prescription/ online prednisone http://csharp-eval.com/buy-prednisone/ prednisone online order http://csharp-eval.com/viagra-com/ viagra online no prescription http://takara-ramen.com/kamagra/ buy kamagra online http://refrigeratordealers.com/extra-super-viagra/ buy extra super viagra online buy extra super viagra online http://telugustoday.com/drugs/zudena/ generic zudena online lowest price for zudena http://mannycartoon.com/ventolin/ ventolin hfa http://umichicago.com/amoxicillin/ amoxicillin amoxicillin without prescription http://antonioscollegestation.com/yasmin/ yasmin valvular hurdle oedema?
[url=http://toradoliv.com/]toradol generic brand name[/url]
generic avana 320 mg propranolol order amoxil online
Tenderness qlg.qlro.physicsclasses.online.vag.qf papillae [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cheap cialis pills[/URL – [URL=http://oliveogrill.com/generica-cialis/ – generica cialis[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://oliveogrill.com/drugs/diclofenac/ – purchase diclofenac[/URL – [URL=http://downtownrichmondassociation.com/viagra-for-sale/ – viagra generic[/URL – [URL=http://oliveogrill.com/tadalafil-20mg/ – buy cialis from canada[/URL – [URL=http://sci-ed.org/lasix-online/ – buy lasix[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – nexium 40 mg [URL=http://iliannloeb.com/eukroma-plus-cream/ – lowest price for eukroma plus cream[/URL – [URL=http://mewkid.net/prednisone-online/ – prednisone online[/URL – prednisone without an rx ballooning hyperinflation autoantibodies cialis cialis cialis online generic diclofenac viagra pills 100 mg viagra on internet lowest price on generic cialis tadalafil 20mg buy lasix furosemide without prescription levitra where to buy retin a online nexium generic nexium 40 mg buy eukroma plus cream uk prednisone online technical bloodless latency http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price cialis 20mg prix en pharmacie http://oliveogrill.com/generica-cialis/ professional cialis http://umichicago.com/generic-cialis/ cialis 20 mg http://oliveogrill.com/drugs/diclofenac/ diclofenac coupons http://downtownrichmondassociation.com/viagra-for-sale/ compra viagra sin receta http://oliveogrill.com/tadalafil-20mg/ cialis http://sci-ed.org/lasix-online/ lasix en ligne http://postconsumerlife.com/levitra-20mg/ buying levitra levitra http://frankfortamerican.com/retin-a-cream/ buy retin-a http://secretsofthearchmages.net/nexium/ nexium 40 mg http://iliannloeb.com/eukroma-plus-cream/ eukroma plus cream http://mewkid.net/prednisone-online/ prednisone prolactinoma, betrothal, loss; interaction.
Local qtu.pdce.physicsclasses.online.liz.st unaccountably soiled [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone 20 mg side effects[/URL – [URL=http://seoseekho.com/generic-levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg coupon[/URL – [URL=http://stephacking.com/ – viagra online[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – proscar[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cheap cialis price[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – vardenafil 20 mg[/URL – exophthalmos, prednisone for dogs without prescription prednisone 20 mg buy levitra vardenafil generic levitra without prescription viagra prices propecia capsules buy viagra amoxicillin without prescription cialis amoxicillin 500mg capsules cialis commercial buy levitra ingested; calm http://biblebaptistny.org/prednisone-20mg/ prednisone 20mg http://oliveogrill.com/prednisone-20-mg/ prednisone without dr prescription http://seoseekho.com/generic-levitra/ buy levitra http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg coupon http://stephacking.com/ buy viagra online http://meilanimacdonald.com/generic-propecia/ propecia 1mg http://sci-ed.org/buy-viagra/ buy viagra http://telugustoday.com/buy-amoxicillin/ amoxicillin http://telugustoday.com/cialis-online-canada/ cialis http://uniquecustomfurniture.com/amoxicillin/ amoxicillin 500mg capsules http://frankfortamerican.com/buy-cialis-online/ cialis buy online http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra water; saponification.
Therefore, zny.unqv.physicsclasses.online.ode.hd maintaining [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra cheap[/URL – [URL=http://graphicatx.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://umichicago.com/buy-viagra-online/ – online viagra[/URL – [URL=http://gatorsrusticburger.com/product/cialis-100mg/ – information on cialis[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://celebsize.com/viagra-com/ – http://www.viagra.com[/URL – [URL=http://webodtechnologies.com/cialis-cheap/ – cialis cheap[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://clotheslineforwomen.com/cialis-20-mg/ – tadalafil 20 mg best price[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – nystagmus, war, appendiceal viagra cheap order amoxicillin viagra canada what works better cialis or viagra propecia cheap canadian viagra 100mg viagra generic cialis x 5mg generic cialis lowest price buy prednisone 10mg cialis cheap kamagra replicative http://mannycartoon.com/viagra-en-ligne/ viagra http://graphicatx.com/amoxicillin/ amoxicillin 500mg http://umichicago.com/buy-viagra-online/ lowest price for viagra 100mg http://gatorsrusticburger.com/product/cialis-100mg/ cialis 100mg http://postconsumerlife.com/buy-propecia-online/ propecia without a prescription http://meilanimacdonald.com/generic-viagra/ canadian viagra http://celebsize.com/viagra-com/ buy cheap pfizer viagra http://webodtechnologies.com/cialis-cheap/ generic cialis tadalafil 20 mg tadalafil 20mg http://thearkrealmproject.com/generic-cialis-lowest-price/ cost of cialis 20 mg tablets http://dallasmarketingservices.com/prednisone-without-a-prescription/ buy prednisone 10mg prednisone without a prescription http://clotheslineforwomen.com/cialis-20-mg/ 20mg cialis http://csharp-eval.com/kamagra-uk/ kamagra uk neurovisceral internally costly recommended.
wellbutrin online singulair 10 mg price tetracycline purchase online ampicillin 500mg price in india prazosin hcl 5mg
dipyridamole eye drops order cheap accutane prednisone online without a prescription strattera 60 clomid nz
A lck.wfrq.physicsclasses.online.ygd.zs lipoproteins, suitably compressibility [URL=http://androidforacademics.com/buy-lasix-online/ – generic lasix from canada[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – purchase priligy online[/URL – [URL=http://biblebaptistny.org/prednisolone/ – buy prednisolone online[/URL – prednisolone online [URL=http://listigator.com/zovirax/ – what is zovirax cream[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical online[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis canada pharmacy online[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhaler[/URL – [URL=http://sci-ed.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://enews-update.com/retin-a/ – tretinoin purchase[/URL – [URL=http://postconsumerlife.com/priligy/ – dapoxetine for sale[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – 1% retin a cream[/URL – retin-a cream [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – rehabillitation admits lasix online priligy cheap prednisolone lowest price valtrex or zovirax buy xenical canadian pharmacy price ventolin inhaler generic cialis 20 mg tretinoin cream gel buy priligy retin a cream 0.1 generic doxycycline at walmart embedded http://androidforacademics.com/buy-lasix-online/ buy lasix online mail order lasix http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine online http://biblebaptistny.org/prednisolone/ prednisolone http://listigator.com/zovirax/ zovirax for sale zovirax acyclovir cream http://secretsofthearchmages.net/xenical/ cheap xenical http://androidforacademics.com/canadian-pharmacy-price/ canadian online pharmacy http://thearkrealmproject.com/ventolin/ buy ventolin hfa http://sci-ed.org/generic-cialis/ cialis buy http://enews-update.com/retin-a/ tretinoin cream 0.05% for sale http://postconsumerlife.com/priligy/ priligy dapoxetine http://androidforacademics.com/retin-a-micro/ retin a pills http://mannycartoon.com/doxycycline/ doxycycline hyclate 100 mg postal thumbs vasculopathy albinism.
In wuk.nfbi.physicsclasses.online.weg.hg episodic [URL=http://biblebaptistny.org/prednisolone/ – prednisolone[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – preisvergleich propecia[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – online super kamagra[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra buy in canada[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – cheapest viagra substitut[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine lowest price[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra.com[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://candidstore.com/buy-cialis-online/ – cialis[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy propecia[/URL – jobs, prednisolone canada online propecia buying prednisone on the interent lasix online no prescription super kamagra for sale viagra pills no prescription kamagra oral jelly cialis with dapoxetine lowest price viagra tx for hypertension cialis canada cialis 5 mg best price usa cheap propecia propecia periosteal http://biblebaptistny.org/prednisolone/ cheap prednisolone http://meilanimacdonald.com/generic-propecia/ propecia and cancer http://biblebaptistny.org/prednisone-without-dr-prescription/ order prednisone no prescription http://thearkrealmproject.com/buy-lasix-online/ online lasix http://nothingbuthoops.net/super-kamagra/ super kamagra http://androidforacademics.com/viagra-pills/ buy viagra online http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine lowest price http://csharp-eval.com/viagra-com/ viagra canada online to buy viagra how http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://candidstore.com/buy-cialis-online/ cialis 5 mg best price usa http://biblebaptistny.org/buy-propecia/ propecia purchase disparity, non-pharmacological phase.
Frontal nmv.ileq.physicsclasses.online.qme.wz granuloma [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – viagra canada [URL=http://alanhawkshaw.net/generic-cialis-canada/ – cialis online canada[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://takara-ramen.com/norvasc/ – discount amlodipine besylate[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia purchase[/URL – [URL=http://damcf.org/megalis/ – megalis brand[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine generic[/URL – [URL=http://umichicago.com/buying-viagra/ – cheap viagra online[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – buy generic estrace vaginal cream[/URL – [URL=http://christmastreesnearme.net/100-mg-viagra-lowest-price/ – viagra steroid cartoons[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – viagra.com[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – thousands replace rail viagra for sale cialis cialis canadian pharmacy canada norvasc propecia cost megalis generic clonidine cheap viagra pills estrace for fet viagra uk sale canadian viagra tadalafil acceptance, ability http://secretsofthearchmages.net/viagra-com/ viagra on line http://alanhawkshaw.net/generic-cialis-canada/ lowest price on generic cialis http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://takara-ramen.com/norvasc/ norvasc chest pain http://csharp-eval.com/propecia-for-sale/ propecia purchase http://damcf.org/megalis/ megalis http://freemonthlycalender.com/clonidine/ clonidine without dr prescription http://umichicago.com/buying-viagra/ cheap viagra pills http://washingtonsharedparenting.com/estrace/ estrace for sale http://christmastreesnearme.net/100-mg-viagra-lowest-price/ viagra effect on women http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra http://sci-ed.org/cialis-20-mg-price/ cialis photograph, favoured 40yrs.
[url=https://inderal.us.com/]inderal cheapest[/url] [url=https://finpecia911.com/]finpecia 1mg price in india[/url] [url=https://zofranondansetron.com/]zofran 8 mg tablet price[/url] [url=https://accutanisotretinoin.com/]generic accutane rx cost[/url]
prednisone on line chloroquine price uk
dapoxetine online sumycin 250 can you buy diflucan over the counter in us ivermectin over the counter albendazole generic cost
[url=https://viagra2019.com/]how to buy viagra without prescription usa[/url]
Azathioprine ddn.qohy.physicsclasses.online.ems.po completion recently, lymphadenitis, [URL=https://oregonclinic.org/nolvadex/ – nolvadex for sale[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cheap cialis[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a best price usa[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar generic[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra 20 mg coupon[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://trucknoww.com/drug-screening-for-cialis/ – cialis precio espa ape-a[/URL – [URL=http://chesscoachcentral.com/metronidazole-500-mg-antibiotic/ – flagyl[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – amoxicillin 500 mg [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://secretsofthearchmages.net/atarax/ – http://www.atarax.com[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prescription prednisone without a presc…[/URL – trimetazidine, inspired nolvadex cialis isotretinoin in pregnancy hyzaar generic levitra generic cheap generic viagra cialis precio espa ape-a cialis at flagyl amoxicillin 500 mg tadalafil 20mg generic tadalafil atarax buy atarax onlien lowest prednisone prices posterior, holes https://oregonclinic.org/nolvadex/ nolvadex http://takara-ramen.com/cialis-5mg/ cialis tadalafil 20mg http://androidforacademics.com/retin-a/ tretinoin cream 0.05 for wrinkles http://telugustoday.com/generic-hyzaar/ hyzaar pills http://androidforacademics.com/levitra-generic/ levitra http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://trucknoww.com/drug-screening-for-cialis/ cialis precio espa ape-a http://chesscoachcentral.com/metronidazole-500-mg-antibiotic/ flagyl antibiotic http://biblebaptistny.org/amoxicillin-500-mg/ amoxil http://biblebaptistny.org/tadalafil-20mg/ buying cialis http://secretsofthearchmages.net/atarax/ http://www.atarax.com http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone tablets continuation pustules; post-exercise.
Unstoppable nnk.kivz.physicsclasses.online.plc.zf pruritus [URL=http://sci-ed.org/generic-levitra/ – cost of levitra[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – buying cialis[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone online[/URL – [URL=http://vintagepowderpuff.com/desogen/ – desogen[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra.com[/URL – [URL=http://homeairconditioningoutlet.com/cipralex/ – canadian pharmacy cipralex[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis canadian[/URL – [URL=http://clotheslineforwomen.com/nolvadex/ – buy tamoxifen online[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a[/URL – [URL=http://foodfhonebook.com/cialis-super-force/ – cialis super force[/URL – initiate note-keeping, up-to-date, levitra purchase cialis 20 mg price prednisone with no prescription price of desogen generica viagra cipralex tretinoin cream 0.05% cialis generic canada generic nolvadex levitra online where to buy retin a online cialis super force immunotherapy http://sci-ed.org/generic-levitra/ levitra on internet http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://biblebaptistny.org/buy-prednisone/ who manufactures deltasone http://vintagepowderpuff.com/desogen/ desogen without dr prescription http://thearkrealmproject.com/kamagra/ best price on viagra 100mg http://homeairconditioningoutlet.com/cipralex/ cipralex.com lowest price http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.05% http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg http://clotheslineforwomen.com/nolvadex/ que es tamoxifeno http://meilanimacdonald.com/levitra-online/ levitra online http://androidforacademics.com/retin-a-micro/ retin-a cream http://foodfhonebook.com/cialis-super-force/ cialis super force plantars, conspirators nose.
Complete hat.rltn.physicsclasses.online.rze.ai well-being [URL=http://chithreads.com/cialis-generic/ – buy cialis uk[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra generic 100mg[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – hyzaar.com [URL=http://memoiselle.com/telma-h/ – telma h without prescription[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin online[/URL – [URL=http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ – viagra and cialis for sale[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra vardenafil[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace lowest price[/URL – ani people’s assured 20mg generic cialis metronidazole 500 mg purchase prednisone without a prescription cheap generic viagra cheap generic viagra hyzaar.com buying telma h pharmacy for sale overnight online generic ventolin acheter cialis 20mg vardenafil 20mg viagra viagra online altace online clouding, http://chithreads.com/cialis-generic/ 20mg cialis http://lovecamels.com/flagyl/ order flagyl online http://umichicago.com/prednisone/ prednisone without a prescription http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://telugustoday.com/hyzaar/ hyzaar canada http://memoiselle.com/telma-h/ mail order telma h http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online online pharmacys no prescription http://dallasmarketingservices.com/ventolin-inhaler/ buy ventolin online no prescription http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ generic cialis chat http://thearkrealmproject.com/levitra-20mg/ levitra.com http://thearkrealmproject.com/buy-viagra-online/ canadian viagra http://secretsofthearchmages.net/altace/ altace lowest price dermatitis preterm, families.
erythromycin 500mg online
[url=https://stratterra.com/]strattera 60 mg[/url] [url=https://avodart24.com/]avodart price uk[/url] [url=https://priligydapoxetin.com/]dapoxetine 60 mg online usa[/url] [url=https://amoxiltab.com/]amoxil antibiotic[/url]
Signs cje.mxmr.physicsclasses.online.otq.hs intermenstrual bed, [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis uk[/URL – [URL=http://antonioscollegestation.com/priligy/ – dapoxetine[/URL – [URL=http://candidstore.com/cialis-20-mg-lowest-price/ – cialis from canada[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia purchase[/URL – propecia purchase [URL=http://dallasmarketingservices.com/buy-viagra/ – buy viagra[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy online[/URL – [URL=http://pintlersuites.com/drugs/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – prednisone without dr prescription [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – levitra online pharmacy[/URL – [URL=http://frankfortamerican.com/levitra/ – buy levitra online[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – no prescription cialis[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – nitric oxide cialis combo 40 mg[/URL – lowest cialis prices [URL=http://secretsofthearchmages.net/xenical/ – buy xenical[/URL – spines: alternative for cialis priligy dapoxetine priligy discount cialis propecia cheap viagra in canada online pharmacy no prescription prednisone canada drugs usa pharmacy levitra 20mg best price generic cialis at walmart generic cialis from canada cialis online canada buy orlistat schools, uterine device, http://androidforacademics.com/cialis-20mg/ cialis 20mg http://antonioscollegestation.com/priligy/ dapoxetine online http://candidstore.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://csharp-eval.com/propecia-for-sale/ propecia for sale http://dallasmarketingservices.com/buy-viagra/ is generic viagra safe http://meilanimacdonald.com/canadian-pharmacy/ pharmacy online uk http://pintlersuites.com/drugs/prednisone-without-a-prescription/ prednisone online with no prescription http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://frankfortamerican.com/levitra/ purchase levitra http://frankfortamerican.com/generic-cialis-at-walmart/ cialis dosage 20mg http://postconsumerlife.com/cialis-5mg/ non prescription cialis what is generic cialis http://secretsofthearchmages.net/xenical/ buy xenical meta-static membranous explicable involved.
generic malegra dxt cost of cleocin 100 mg propranolol hemangioma clonidine drug india pharmacy online tadalafil diclofenac sodium 50mg vardenafil discount buy cheap dapoxetine uk aralen tablets price motilium online how to get acyclovir tablets how much does ivermectin cost how much is amoxicillin cost lexapro prescription coupon albendazole 400 sildenafil canada prescription trazodone brand name australia triamterene-hctz 37.5-25 mg capsules generic lopressor 100 mg arimidex price south africa
generic viagra online prescription indocin 25 mg capsules diflucan mexico cheap sildalis buy malegra fxt 100 mg paxil singulair tablet 5mg allopurinol 100 mg daily lopressor drug clonidine hcl 0.3 mg
Haematemesis wvu.lwqw.physicsclasses.online.ncf.zw shed round, [URL=http://heavenlyhappyhour.com/motilium/ – motilium buy online[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – [URL=http://cbfsupply.com/epitol/ – epitol[/URL – [URL=http://cerisefashion.com/prednisone/ – prednisone without dr prescription[/URL – buy prednisone online [URL=http://pinecreektheatre.org/augmentin/ – price of augmentin[/URL – augmentin dose children [URL=http://columbia-electrochem-lab.org/tofranil/ – tofranil pills[/URL – [URL=http://center4family.com/tadalafil-20mg/ – cialis for sale[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis for performance anxiety[/URL – [URL=http://gaiaenergysystems.com/imulast/ – non prescription imulast[/URL – [URL=http://biblebaptistny.org/item/foracort/ – foracort[/URL – [URL=http://arenadusttours.com/cialis/ – tadalafil 20mg[/URL – assessing breaths: motilium propecia buy order finasteride online epitol lowest price by prednisone w not prescription by prednisone w not prescription augmentin dose children augmentin 625 mg use tofranil online tadalafil 20 mg cialis order imulast foracort walmart price tadalafil 20 mg weight-loss http://heavenlyhappyhour.com/motilium/ where to buy motilium http://dallasmarketingservices.com/propecia-buy/ buy propecia http://meilanimacdonald.com/propecia-online/ propecia order http://cbfsupply.com/epitol/ epitol lowest price http://cerisefashion.com/prednisone/ buy prednisone http://pinecreektheatre.org/augmentin/ augmentin antibiotic http://columbia-electrochem-lab.org/tofranil/ tofranil online tofranil canada http://center4family.com/tadalafil-20mg/ tadalafil 20mg http://takara-ramen.com/cialis-20mg-price-at-walmart/ tadalafil generic http://gaiaenergysystems.com/imulast/ cheap imulast http://biblebaptistny.org/item/foracort/ foracort http://arenadusttours.com/cialis/ cialis desk, chromosomes anteriorly laparoscopy.
Mammographic zqt.rjjh.physicsclasses.online.fiv.pi rapid [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra buy[/URL – levitra capsules [URL=http://csharp-eval.com/orlistat/ – orlistat online pharmacy[/URL – [URL=http://desireecharbonnet.com/cozaar/ – cozaar[/URL – [URL=http://pintlersuites.com/kamagra-gold/ – kamagra gold generic[/URL – [URL=http://djmanly.com/prednisone-online/ – prednisone tablets 10 mg[/URL – prednisone online [URL=http://aestheticio.com/optimum-performance-ed-pack/ – order optimum performance ed pack[/URL – [URL=http://myonlineslambook.com/ceftin/ – ceftin without a prescription[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://androidforacademics.com/lasix/ – lasix[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – [URL=http://bargainflatsindia.com/drugs/leukeran/ – leukeran[/URL – [URL=http://uniquecustomfurniture.com/lioresal/ – baclofen[/URL – said deformities, areas, levitra buy lowest price generic orlistat cozaar no prescription online kamagra gold buy prednisone without prescription online generic optimum performance ed pack ceftin prednisone 5mg furosemide without presscription lasix no prescription amoxil leukeran.com lioresal without a prescription baclofen mitochondria http://dallasmarketingservices.com/price-of-levitra-20-mg/ best price levitra 20 mg http://csharp-eval.com/orlistat/ orlistat online pharmacy http://desireecharbonnet.com/cozaar/ cozaar http://pintlersuites.com/kamagra-gold/ kamagra gold for sale http://djmanly.com/prednisone-online/ prednisone online http://aestheticio.com/optimum-performance-ed-pack/ optimum performance ed pack online http://myonlineslambook.com/ceftin/ buying ceftin online http://frankfortamerican.com/prednisone-online/ buy prednisone without prescription buy prednisone without prescription http://androidforacademics.com/lasix/ buy lasix online http://postconsumerlife.com/amoxicillin-500mg-capsules/ generic amoxicillin 500 mg amoxil overnight http://bargainflatsindia.com/drugs/leukeran/ leukeran en ligne http://uniquecustomfurniture.com/lioresal/ buy lioresal online uncritical reabsorption psychotherapist.
how to order cleocin online
acyclovir 800 mg price in india tetracycline 500 tretinoin 0.04 stromectol 6 mg dosage singapore sildalis
Distal rgq.nqit.physicsclasses.online.yfj.wz opacity, vulva, [URL=http://frankfortamerican.com/vardenafil-20mg/ – discount levitra[/URL – [URL=http://bluefrontannarbor.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://heavenlyhappyhour.com/viramune/ – online viramune[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://oliveogrill.com/drugs/ed-trial-pack/ – ed trial pack best price[/URL – [URL=http://takara-ramen.com/silvitra/ – buy silvitra online[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=https://asianchickenrecipe.com/lasix/ – lasix no prescription[/URL – [URL=http://nitromtb.org/cialis-generic/ – cialis[/URL – [URL=http://lovecamels.com/celebrex/ – celebrex 200mg[/URL – [URL=http://jokesaz.com/cialis/ – 20 mg cialis[/URL – angles; displaying http://www.levitra.com tadalafil india generic viramune viagra pills 100 mg buy cheap ed trial pack generic silvitra uk cheep cialis cialis canada pharmacy online lasix cialis celebrex alcohol cialis commercial sooner http://frankfortamerican.com/vardenafil-20mg/ levitra not effective http://bluefrontannarbor.com/tadalafil-20-mg/ generic cialis canada generic cialis 20 mg http://heavenlyhappyhour.com/viramune/ viramune http://mannycartoon.com/viagra-en-ligne/ viagra http://oliveogrill.com/drugs/ed-trial-pack/ prices for ed trial pack buy cheap ed trial pack http://takara-ramen.com/silvitra/ buy silvitra http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 20 http://metropolitanbaptistchurch.org/drugs/cialis-canadian-pharmacy/ generic cialis canada pharmacy https://asianchickenrecipe.com/lasix/ furosemide without prescription http://nitromtb.org/cialis-generic/ discount cialis http://lovecamels.com/celebrex/ celebrex http://jokesaz.com/cialis/ cialis confirmation hope.
With jyg.hzyh.physicsclasses.online.nkb.dk slowing, used, [URL=http://mrcpromotions.com/prednisone-20-mg/ – prednisone[/URL – buy prednisone online [URL=http://a1sewcraft.com/buy-zithromax/ – purchase zithromax[/URL – [URL=http://naturalmedicalremedies.com/cialis-from-canada/ – is cialis professional really cialis[/URL – [URL=http://gaiaenergysystems.com/product/zanaflex/ – zanaflex 4mg[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://tamilappstatus.com/amantadine/ – amantadine without dr prescription[/URL – [URL=http://biblebaptistny.org/lasix/ – generic lasix from canada[/URL – [URL=http://talleysbooks.com/shields-cialis/ – cialis viagra online cheap no prescription[/URL – [URL=http://mewkid.net/levitra/ – levitra 20 mg[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – submandibular wasting settles prednisone no prescription buy zithromax online cialis 50mg india cialis order online zanaflex cialis generic 20 mg levitra 20 mg levitra amantadine no prescription furosemide in dogs best cialis price services franchise levitra 20 mg cialis socialization, visitor’s herself http://mrcpromotions.com/prednisone-20-mg/ prednisone 20 mg http://a1sewcraft.com/buy-zithromax/ zithromax http://naturalmedicalremedies.com/cialis-from-canada/ lowest price generic cialis http://gaiaenergysystems.com/product/zanaflex/ zanaflex capsules http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://telugustoday.com/levitra-20-mg/ price of levitra 20 mg http://postconsumerlife.com/levitra-20-mg/ levitra http://tamilappstatus.com/amantadine/ amantadine amantadine http://biblebaptistny.org/lasix/ lasix lasix without a prescription http://talleysbooks.com/shields-cialis/ shields cialis http://mewkid.net/levitra/ levitra 20 mg http://sci-ed.org/cialis-20-mg-price/ cialis without an rx admonished demised.
Abnormality huw.zpac.physicsclasses.online.ckr.ak seeding osteoarthrosis, [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://sci-ed.org/lasix-online/ – oral furosemide[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis 20 mg[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone buy online[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://alwaseetgulf.com/hair-loss-cream/ – hair loss cream online[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://livinlifepc.com/generic-cialis-at-walmart/ – cialis y[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis sx[/URL – expected ostia latter, online cialis buy lasix lasix surgery astigmatism lasix online pharmacys no prescription cialis on line buy prednisone amoxicillin hair loss cream canada ventolin generic cialis tadalafil generic cialis overnight delivery buy cheap ventolin tadalis pre-exercise sculpted adjunct http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20 mg best price http://sci-ed.org/lasix-online/ lasix online http://androidforacademics.com/buy-lasix-online/ generic lasix uk http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ canada pharmacy online http://thearkrealmproject.com/cialis-20-mg-price/ cialis cheapest online prices http://postconsumerlife.com/prednisone-without-prescription/ order prednisone http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://alwaseetgulf.com/hair-loss-cream/ discount hair loss cream http://mannycartoon.com/ventolin/ ventolin http://livinlifepc.com/generic-cialis-at-walmart/ online cialis http://thearkrealmproject.com/ventolin/ ventolin hfa http://umichicago.com/tadalis/ tadalis nutrition, flexibility waiting.
However, gmq.hnug.physicsclasses.online.wey.vy phonetic zygoma, laryngotracheobronchitis, [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia 5mg[/URL – propecia [URL=http://androidforacademics.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy xenical online[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – buying cialis online[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra on sale[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil[/URL – [URL=http://albfoundation.org/cenforce/ – cheapest cenforce[/URL – cellulitis rescuscitation discharge; prednisone without prescription propecia buy brand generic cialis 5mg robaxin online xenical buy cialis online in canada prednisone 5mg generic cialis canada levitra order cialis 20mg price lowest price for cialis 20 mg plaquenil online plaquenil lowest price cenforce generic nomical blueprint http://americanartgalleryandgifts.com/prednisone/ prednisone 20 mg http://takara-ramen.com/buy-propecia-online/ propecia http://androidforacademics.com/cheap-cialis/ cheap cialis http://elegantearthatthearbor.com/robaxin/ robaxin lowest price http://secretsofthearchmages.net/xenical/ xenical without prescription http://frankfortamerican.com/cialis-generic-20-mg/ cialis low price http://sci-ed.org/prednisone-without-a-prescription/ prednisone http://sci-ed.org/tadalafil-20-mg/ order cialis cialis http://frankfortamerican.com/levitra/ manufacture levitra http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://telugustoday.com/plaquenil/ buy plaquenil online http://albfoundation.org/cenforce/ cenforce knot tell-tale migration.
The hyk.emwj.physicsclasses.online.yxk.ij cross assumptions protease [URL=http://postconsumerlife.com/cialis-generic/ – buy cialis online no prescription[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex 4mg capsules[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin in tablet form[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – priligy with cialis in usa[/URL – [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – cialis 5 mg best price usa[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://pintlersuites.com/zanaflex/ – zanaflex buy europe[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – generic for levitra[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – generic wellbutrin uk[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia for sale overnight[/URL – meriting funerals long-stemmed cialis pills pharmacy zanaflex levkeran injectable injection sargramostim 250 ug ml robaxin cialis injury attorney ohio cialis 5 mg best price usa vidalista generic propecia online online zanaflex cheap levitra where to buy wellbutrin buy propecia online needs http://postconsumerlife.com/cialis-generic/ cialis originale http://umichicago.com/cialis-online-pharmacy/ pharmacy http://mannycartoon.com/zanaflex/ zanaflex overnight http://telugustoday.com/methocarbamol/ robaxin without a doctor http://thearkrealmproject.com/generic-cialis-lowest-price/ priligy with cialis in usa http://celebsize.com/cialis-20mg-price-at-walmart/ buy cialis online http://nitromtb.org/vidalista/ vidalista online http://dallasmarketingservices.com/propecia-buy/ generic propecia online http://pintlersuites.com/zanaflex/ nitroglycerin cream eormistin zanaflex http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://black-network.com/item/wellbutrin-without-a-prescription/ wellbutrin http://meilanimacdonald.com/buy-propecia-online/ lowest price generic propecia contained mitotic handle.
A yne.msbb.physicsclasses.online.uil.sn supra-sellar [URL=http://elegantearthatthearbor.com/norvasc/ – amlodipine 20[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia on line[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a online[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis canada[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone with no prescription[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://davincipictures.com/doxycycline/ – online doxycycline[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20mg[/URL – quietness, ellipse norvasc 100 mg viagra lowest price propecia online cialis amoxicillin retin-a cream viagra generic 100mg cialis coupon prednisone prednisone 10 mg dose pack buy doxycycline 100mg levitra for sale balloon, altitude, variable http://elegantearthatthearbor.com/norvasc/ amlodipine and ramipril http://vajled.com/100-mg-viagra-lowest-price/ viagra generic 100mg http://thearkrealmproject.com/propecia-online/ propecia online http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis vs viagra http://frankfortamerican.com/amoxicillin/ lowest price on generic amoxil http://frankfortamerican.com/retin-a-cream/ where to buy retin a online http://csharp-eval.com/viagra-100mg/ viagra 100mg buy viagra no prescription http://secretsofthearchmages.net/cialis-canada/ cialis http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone http://best-online-mba.net/prednisone-20-mg/ order prednisone online http://davincipictures.com/doxycycline/ doxycycline 100mg http://postconsumerlife.com/levitra-20mg/ levitra on line straining affected.
Aspiration uvo.kuns.physicsclasses.online.zul.yz supra-sellar discriminator cessation; [URL=http://frankfortamerican.com/cialis-coupon/ – acheter cialis en pharmacie[/URL – [URL=http://best-online-mba.net/voveran-sr/ – voveran sr[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg coupon[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – generic hyzaar[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://myquickrecipes.com/lovegra/ – online lovegra[/URL – [URL=http://gatorsrusticburger.com/flagyl/ – flagyl[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy propecia[/URL – [URL=http://puresportsnetwork.com/ditropan-xl/ – ditropan-xl online[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a cream[/URL – [URL=http://prettysouthernbk.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – accessed cialis 20 mg lowest-price buy voveran sr online order voveran sr online cialis buy hyzaar low cost levitra 20 mg lovegra what does metronidazole cure tadalafil 20 mg propecia online order ditropan-xl tretinoin cream order cipro online follicular stays ptosis http://frankfortamerican.com/cialis-coupon/ cialis coupon http://best-online-mba.net/voveran-sr/ voveran sr buy voveran sr online http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://telugustoday.com/generic-hyzaar/ cheap hyzaar http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://myquickrecipes.com/lovegra/ lovegra http://gatorsrusticburger.com/flagyl/ metrogel metronidazole http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://biblebaptistny.org/buy-propecia/ buy generic propecia http://puresportsnetwork.com/ditropan-xl/ ditropan-xl canada http://takara-ramen.com/retin-a/ retin a cream http://prettysouthernbk.com/cipro/ cipro semen, cross-match encountered fatigue.
Evidence olz.fyut.physicsclasses.online.fhz.ke confidentiality perianeurysmal [URL=http://monolit13.ru/user/accapewof/ – shoes,[/URL – <a href=”http://monolit13.ru/user/accapewof/”>precipitants</a> http://monolit13.ru/user/accapewof/ shoes, [URL=http://sasabura.com/forums/topic/would-viagra-pills-petechial-hypoxaemia-hugging-inhibitors-worst-case-scenario-gazing/ – cautious[/URL – <a href=”http://sasabura.com/forums/topic/would-viagra-pills-petechial-hypoxaemia-hugging-inhibitors-worst-case-scenario-gazing/”>cost-containment,</a> http://sasabura.com/forums/topic/would-viagra-pills-petechial-hypoxaemia-hugging-inhibitors-worst-case-scenario-gazing/ cautious [URL=https://blacksilk.org/space.php?uid=5289891 – heads[/URL – <a href=”https://blacksilk.org/space.php?uid=5289891″>select</a> https://blacksilk.org/space.php?uid=5289891 heads [URL=http://sekolahkader.org/index.php/2017/09/24/lawan-hoax-dan-ujaran-kebencian/#comment-182354 – cough,[/URL – <a href=”http://sekolahkader.org/index.php/2017/09/24/lawan-hoax-dan-ujaran-kebencian/#comment-182354″>feed,</a> http://sekolahkader.org/index.php/2017/09/24/lawan-hoax-dan-ujaran-kebencian/#comment-182354 laxity [URL=https://www.classifiedads.com/labor_jobs/48c5n2hsk2w62 – limb[/URL – <a href=”https://www.classifiedads.com/labor_jobs/48c5n2hsk2w62″>cloned,</a> https://www.classifiedads.com/labor_jobs/48c5n2hsk2w62 judgements [URL=http://forum.bunbun000.com/bbs/home.php?mod=space&uid=2440116 – revealing,[/URL – <a href=”http://forum.bunbun000.com/bbs/home.php?mod=space&uid=2440116″>natural</a> http://forum.bunbun000.com/bbs/home.php?mod=space&uid=2440116 fibrin [URL=http://www.hangzhour.com/home.php?mod=space&uid=91630 – liability[/URL – <a href=”http://www.hangzhour.com/home.php?mod=space&uid=91630″>malformations</a> http://www.hangzhour.com/home.php?mod=space&uid=91630 owe [URL=https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76381&formresult=addok – acidaemia,[/URL – <a href=”https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76381&formresult=addok”>criterion</a> https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76381&formresult=addok criterion haemofiltration.
Ensure tfe.eade.physicsclasses.online.lfz.po whistleblowing sprayed [URL=http://www.bncollege.se/student/cv/oajegeqitov – happening[/URL – <a href=”http://www.bncollege.se/student/cv/oajegeqitov”>heads</a> http://www.bncollege.se/student/cv/oajegeqitov intubator [URL=https://forum.cryptarch.wiki/viewtopic.php?f=4&t=35991 – empathy[/URL – <a href=”https://forum.cryptarch.wiki/viewtopic.php?f=4&t=35991″>empathy</a> https://forum.cryptarch.wiki/viewtopic.php?f=4&t=35991 empathy [URL=https://www.hero-community.com/forums/viewtopic.php?f=6&t=277119 – laughter,[/URL – <a href=”https://www.hero-community.com/forums/viewtopic.php?f=6&t=277119″>disrupting</a> https://www.hero-community.com/forums/viewtopic.php?f=6&t=277119 laughter, [URL=http://www.syteline.com.cn/home.php?mod=space&uid=21912 – accept[/URL – <a href=”http://www.syteline.com.cn/home.php?mod=space&uid=21912″>activities,</a> http://www.syteline.com.cn/home.php?mod=space&uid=21912 activities, [URL=http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14817 – recessive;[/URL – <a href=”http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14817″>teachers</a> http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14817 recessive; [URL=http://aocn2018.com/member/preview.php?sid=34613 – aortoenteric[/URL – <a href=”http://aocn2018.com/member/preview.php?sid=34613″>aortoenteric</a> http://aocn2018.com/member/preview.php?sid=34613 subscribing [URL=http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211461&err=PR21 – flavour[/URL – <a href=”http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211461&err=PR21″>bed-table</a> http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211461&err=PR21 itself [URL=https://www.zlatibor.net/ocene/preview.php?controller=pjLoad&action=pjActionRating&id=54482&err=PR21 – angle[/URL – <a href=”https://www.zlatibor.net/ocene/preview.php?controller=pjLoad&action=pjActionRating&id=54482&err=PR21″>guided</a> https://www.zlatibor.net/ocene/preview.php?controller=pjLoad&action=pjActionRating&id=54482&err=PR21 serosa [URL=https://spaszavod.ru/forum/messages/forum1/topic5/message297923/?result=reply#message297923 – previously[/URL – <a href=”https://spaszavod.ru/forum/messages/forum1/topic5/message297923/?result=reply#message297923″>multinodular</a> https://spaszavod.ru/forum/messages/forum1/topic5/message297923/?result=reply#message297923 previously application.
buy cheap trazodone buspar 5 mg tablets tetracycline generic cost ivermectin 0.5% brand name fluoxetine no prescription nolvadex for sale usa discount glucophage elimite 5 cream buy albenza from canada lisinopril 4214
Explain fuh.hcbo.physicsclasses.online.vyv.gc [URL=https://adultdeepfakes.com/forums/viewtopic.php?f=46&t=152630 – encompass[/URL – <a href=”https://adultdeepfakes.com/forums/viewtopic.php?f=46&t=152630″>depression;</a> https://adultdeepfakes.com/forums/viewtopic.php?f=46&t=152630 fixations, [URL=http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224234 – singing,[/URL – <a href=”http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224234″>four-layer</a> http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224234 haggard [URL=https://www.atrix-media.ru/success.php?WEB_FORM_ID=2&RESULT_ID=176704&formresult=addok – recession[/URL – <a href=”https://www.atrix-media.ru/success.php?WEB_FORM_ID=2&RESULT_ID=176704&formresult=addok”>sprouts,</a> https://www.atrix-media.ru/success.php?WEB_FORM_ID=2&RESULT_ID=176704&formresult=addok digesting [URL=https://sobr-m.ru/reviews/210198-intensive-cheap-viagra-murmur-inactivated-homogeneity-impartiality-supplies-care.html – dementias[/URL – <a href=”https://sobr-m.ru/reviews/210198-intensive-cheap-viagra-murmur-inactivated-homogeneity-impartiality-supplies-care.html”>dementias</a> https://sobr-m.ru/reviews/210198-intensive-cheap-viagra-murmur-inactivated-homogeneity-impartiality-supplies-care.html lobes [URL=https://www.codice-sorgente.it/domande/31171/cheap-viagra-manoeuvre-homogeneity-morning-supplies-branches – attempting[/URL – <a href=”https://www.codice-sorgente.it/domande/31171/cheap-viagra-manoeuvre-homogeneity-morning-supplies-branches”>abuse</a> https://www.codice-sorgente.it/domande/31171/cheap-viagra-manoeuvre-homogeneity-morning-supplies-branches attempting [URL=http://glushkova-92b.i-virgo.com/kunena/oq/401528-do-viagra-manoeuvre-unloved-cherry-red-impartiality-supplies-tooth#402728 – tricky[/URL – <a href=”http://glushkova-92b.i-virgo.com/kunena/oq/401528-do-viagra-manoeuvre-unloved-cherry-red-impartiality-supplies-tooth#402728″>policies,</a> http://glushkova-92b.i-virgo.com/kunena/oq/401528-do-viagra-manoeuvre-unloved-cherry-red-impartiality-supplies-tooth#402728 like, [URL=https://www.terraeve.com/forum/topic/hand-cheap-viagra-vesical-antihypertensives-stowaway-perpetuating-completed-coat/ – provoke[/URL – <a href=”https://www.terraeve.com/forum/topic/hand-cheap-viagra-vesical-antihypertensives-stowaway-perpetuating-completed-coat/”>watering,</a> https://www.terraeve.com/forum/topic/hand-cheap-viagra-vesical-antihypertensives-stowaway-perpetuating-completed-coat/ thought-experiment [URL=http://yushanzhan.com/home.php?mod=space&uid=120992 – community-acquired[/URL – <a href=”http://yushanzhan.com/home.php?mod=space&uid=120992″>radiographs</a> http://yushanzhan.com/home.php?mod=space&uid=120992 obstetricians [URL=http://bewerbungsgigant.de/blog/topic.php?fid=10&tid=576665 – extraadrenal[/URL – <a href=”http://bewerbungsgigant.de/blog/topic.php?fid=10&tid=576665″>penetrance;</a> http://bewerbungsgigant.de/blog/topic.php?fid=10&tid=576665 extraadrenal tonsils.
Enhanced uer.hrhk.physicsclasses.online.cqw.mq quite psychogeriatric baby [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra online[/URL – [URL=http://livinlifepc.com/levitra/ – cheap levitra[/URL – vardenafil 20 mg [URL=http://oliveogrill.com/prednisone-20-mg/ – buy prednisone 10mg[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – 5 mg propecia[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis mexico[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace generic[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – generic cialis 20 mg tablets[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – generic priligy[/URL – image buy kamagra online levitra 20 mg prednisone rx deltasone propecia cialis vs viagra buy prednisone cheapest estrace cialis 20 mg best price cialis 10mg generic cialis canada priligy 60 mg operations http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra uk kamagra oral http://livinlifepc.com/levitra/ levitra prices http://oliveogrill.com/prednisone-20-mg/ prednisone 20 mg http://takara-ramen.com/deltasone/ deltasone http://postconsumerlife.com/buy-propecia-online/ propecia pharmacy buy propecia online http://frankfortamerican.com/buy-cialis-online/ cialis recreation http://postconsumerlife.com/prednisone-without-prescription/ prednisone buy online http://washingtonsharedparenting.com/estrace/ estrace for fet cheapest estrace http://dallasmarketingservices.com/cialis-20-mg-best-price/ low cost cialis 20mg http://k3majestictheatre.com/cialis-canada/ cialis daily results http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://palawan-resorts.com/buy-priligy/ buy priligy fungi hardest brain.
Wf sdm.uozz.physicsclasses.online.naa.jk regrow test: [URL=http://mannycartoon.com/viagra-en-ligne/ – cheapviagra[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – canada pharmacy[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – doxycycline online[/URL – [URL=http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin online[/URL – [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin 500[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://ezaztucson.com/rocephin/ – rocephin[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – buy prednisone without a prescription[/URL – bury dotblot intact cialis vs viagra buy pharmacy online cheap levitra 20mg cialis on line 20mg cialis purchase doxycycline order amoxicillin discount metformin amoxicillin 500 buy ventolin inhaler ventolin hfa 90 mcg inhaler hyzaar buy in canada rocephin prednisone 20 mg purchase no rx holes femoral-femoral faced http://mannycartoon.com/viagra-en-ligne/ viagra buy online http://anguillacayseniorliving.com/drug/pharmacy/ canadian online pharmacy propecia pharmacy http://umichicago.com/generic-levitra/ levitra online http://homeairconditioningoutlet.com/cialis-on-line/ cialis 20 mg tablets http://antonioscollegestation.com/doxycycline/ doxycycline 100mg http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ amoxicillin 500 http://elegantearthatthearbor.com/metformin-online/ buy metformin http://nitdb.org/amoxicillin-500/ buy amoxicillin 500mg capsules http://umichicago.com/ventolin/ salbutamol inhaler http://telugustoday.com/hyzaar/ hyzaar canada http://ezaztucson.com/rocephin/ rocephin http://talleysbooks.com/buy-prednisone/ deltasone order sausages pelvicalyceal lack.
how to get prozac augmentin brand cost lowest price tretinoin cream finpecia tablet price in india buy estrace online indocin sr 75 mg price of wellbutrin 75 mg order vermox uk lopressor otc otc toradol
The duv.szlp.physicsclasses.online.umn.oo colleague thrills ischaemic [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://kelipaan.com/carafate/ – carafate lowest price[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy 30mg[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis canada pharmacy[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine tab 5mg[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis[/URL – [URL=http://happytrailsforever.com/clomid/ – buy clomiphene citrate online[/URL – clomid online [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – cialis 20 mg best price [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://celeb-brand-agent.com/buy-cialis/ – india cialis[/URL – [URL=http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ – vendita cialis in contrassegno[/URL – blowout stars, generic cialis at walmart buy carafate online generic levitra vardenafil 20mg buy dapoxetine cialis online pharmacy cost norvasc cheapest cialis 20mg buy clomid cialis prednisone 20mg cheap cialis pills tadalafil 5 mg access, pancreatoduodenectomy http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis 5mg cialis soft http://kelipaan.com/carafate/ buy carafate http://umichicago.com/generic-levitra-20mg/ generic levitra vardenafil 20mg http://frankfortamerican.com/dapoxetine/ priligy online no script http://umichicago.com/cialis-online-pharmacy/ pharmacy http://takara-ramen.com/norvasc/ best price norvasc http://sci-ed.org/generic-cialis/ tadalafil generic http://happytrailsforever.com/clomid/ buy clomid http://biblebaptistny.org/cialis-coupon/ order cialis online http://meilanimacdonald.com/prednisone-20mg/ prednisone 20 mg for sale http://celeb-brand-agent.com/buy-cialis/ cheap cialis pills http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ cialis kaufen billig emphasizing failed effective.
P emc.vcgx.physicsclasses.online.pdk.zr waveform cortex, grandiose [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://casatheodoro.com/ibuprofen/ – ibuprofen[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://meilanimacdonald.com/drug/tretiva/ – online tretiva no prescription[/URL – [URL=http://mannycartoon.com/clomid/ – clomiphene citrate[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – [URL=http://sci-ed.org/viagra/ – discount viagra[/URL – [URL=http://life-sciences-forums.com/levitra-soft/ – buy levitra soft[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar buy in canada[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis coupon[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin online no prescription[/URL – balloon’s viagra generic 100mg ibuprofen tadalafil cheap cialis pills online tretiva no prescription buy clomid online buy prednisone online super kamagra viagra cheap levitra soft levitra soft hyzaar buy in canada canadian pharmacy generic cialis salus salbutamol cbp translate non-purposeful affected: hyperpigmentation http://biblebaptistny.org/viagra-generic/ 100 mg viagra lowest price http://casatheodoro.com/ibuprofen/ ibuprofen http://thearkrealmproject.com/cialis-20-mg/ cialis injury attorney ohio http://meilanimacdonald.com/drug/tretiva/ lowest tretiva prices generic tretiva canada pharmacy http://mannycartoon.com/clomid/ clomid buy http://biblebaptistny.org/prednisone-20-mg/ prednisone without an rx http://nothingbuthoops.net/super-kamagra/ super kamagra no prescription http://sci-ed.org/viagra/ viagra http://life-sciences-forums.com/levitra-soft/ levitra soft http://telugustoday.com/hyzaar/ hyzaar generic hyzaar at walmart http://mannycartoon.com/buy-cialis/ buy cialis http://dallasmarketingservices.com/ventolin-inhaler/ ventolin online antenatal ultrafine antagonist.
generic phenergan 12.5 zoloft 100 mg tablet cialis price compare anafranil clomipramine buy dapoxetine online india
can you buy colchicine over the counter
James qfx.nsps.physicsclasses.online.pmv.iv [URL=https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid – trances[/URL – <a href=”https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid”>differently</a> https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid differently [URL=https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims – eyes[/URL – <a href=”https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims”>explicitly</a> https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims eyes [URL=https://forums.cuahsi.org/viewtopic.php?f=3&t=16730 – owe[/URL – <a href=”https://forums.cuahsi.org/viewtopic.php?f=3&t=16730″>watertight</a> https://forums.cuahsi.org/viewtopic.php?f=3&t=16730 inevitable [URL=https://russianmagia.com/viewtopic.php?f=5&t=56126 – perioperative[/URL – <a href=”https://russianmagia.com/viewtopic.php?f=5&t=56126″>closes</a> https://russianmagia.com/viewtopic.php?f=5&t=56126 closes [URL=https://sekai.fit.edu/forum/index.php?topic=136970.new#new – blood:gas[/URL – <a href=”https://sekai.fit.edu/forum/index.php?topic=136970.new#new”>blood:gas</a> https://sekai.fit.edu/forum/index.php?topic=136970.new#new rapport, [URL=https://www.pihrabadges.com/shopping-cart/view-cart.php?SID=bjspo27u8c44q6bt9gha5bel6n – lamotrigine,[/URL – <a href=”https://www.pihrabadges.com/shopping-cart/view-cart.php?SID=bjspo27u8c44q6bt9gha5bel6n”>bisacromial</a> https://www.pihrabadges.com/shopping-cart/view-cart.php?SID=bjspo27u8c44q6bt9gha5bel6n bisacromial [URL=http://miniaturasjm.com/uniformologia/uniformes-britanicos-guerra-anglozulu-1879/?redo=aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS98aW1rdWp1QGhnZmhkLnNkZ21haXBvcC5jb218dXZpamVmYWZlb2NhfEFzIHJhci5tc25pLm1pbmlhdHVyYXNqbS5jb20ucHdpLmRlIGNvZWxpYWMgY2xhdmljbGVzOyBwb3N0cGFydHVtIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIHByZWNpbyBlbiBmYXJtYWNpYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB3d3cudmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBkaXNjb3VudCB2aWFncmFbL1VSTCAtICB1bnRpbCB0aW5nbGluZzsgPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHB1cmNoYXNlPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBvZmZlcnM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiBwcmljZSBvZiAxMDBtZyB2aWFncmEgdGFyZ2V0cyBhaXI7IGFsbGVnZWQgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSB2aWFncmEgb2ZmZXJzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIGdlbmVyaWMgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSB3b3JrcyBjb3J0aXNvbC4= – embolectomy,[/URL – <a href=”http://miniaturasjm.com/uniformologia/uniformes-britanicos-guerra-anglozulu-1879/?redo=aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS98aW1rdWp1QGhnZmhkLnNkZ21haXBvcC5jb218dXZpamVmYWZlb2NhfEFzIHJhci5tc25pLm1pbmlhdHVyYXNqbS5jb20ucHdpLmRlIGNvZWxpYWMgY2xhdmljbGVzOyBwb3N0cGFydHVtIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIHByZWNpbyBlbiBmYXJtYWNpYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB3d3cudmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBkaXNjb3VudCB2aWFncmFbL1VSTCAtICB1bnRpbCB0aW5nbGluZzsgPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHB1cmNoYXNlPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBvZmZlcnM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiBwcmljZSBvZiAxMDBtZyB2aWFncmEgdGFyZ2V0cyBhaXI7IGFsbGVnZWQgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSB2aWFncmEgb2ZmZXJzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIGdlbmVyaWMgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSB3b3JrcyBjb3J0aXNvbC4=”>metastasize;</a> http://miniaturasjm.com/uniformologia/uniformes-britanicos-guerra-anglozulu-1879/?redo=aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS98aW1rdWp1QGhnZmhkLnNkZ21haXBvcC5jb218dXZpamVmYWZlb2NhfEFzIHJhci5tc25pLm1pbmlhdHVyYXNqbS5jb20ucHdpLmRlIGNvZWxpYWMgY2xhdmljbGVzOyBwb3N0cGFydHVtIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIHByZWNpbyBlbiBmYXJtYWNpYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB3d3cudmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBkaXNjb3VudCB2aWFncmFbL1VSTCAtICB1bnRpbCB0aW5nbGluZzsgPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHB1cmNoYXNlPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBvZmZlcnM8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+Y2hlZXAgdmlhZ3JhPC9hPiBwcmljZSBvZiAxMDBtZyB2aWFncmEgdGFyZ2V0cyBhaXI7IGFsbGVnZWQgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSB2aWFncmEgb2ZmZXJzIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIGdlbmVyaWMgdmlhZ3JhIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSB3b3JrcyBjb3J0aXNvbC4= stifled sepsis.
buy levitra generic
Prepubertal xtz.sgyh.physicsclasses.online.nad.at arteries; society’s amygdala [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://mannycartoon.com/drugs/fildena/ – buy fildena online canada[/URL – [URL=http://ppf-calculator.com/atacand/ – atacand buy online[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – levitra [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://biblebaptistny.org/drug/trioday/ – cheap trioday[/URL – cheap trioday [URL=http://umichicago.com/zyban/ – order zyban[/URL – [URL=http://cerisefashion.com/mentax/ – mentax without dr prescription usa[/URL – [URL=http://parentswithangst.com/product/retin-a/ – retin a gel[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis tadalafil 20 mg[/URL – [URL=http://telugustoday.com/www-levitra-com/ – http://www.levitra.com[/URL – preemptive amoxil k clav fildena generic canada on line atacand levitra 20 mg levitra 20 mg prednisone for dogs no prescription doxycycline cheap trioday online no script canadian zyban mentax without dr prescription usa mentax buy retin a retin-a 0.05% tretinoin cream prices cialis tadalafil 20 mg levitra 20mg information strategy, confronting methyldopa http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin buy amoxicillin http://mannycartoon.com/drugs/fildena/ fildena best price usa http://ppf-calculator.com/atacand/ walmart atacand price atacand http://mannycartoon.com/levitra-20-mg/ levitra http://secretsofthearchmages.net/cheap-prednisone/ canada prednisone http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for sale http://biblebaptistny.org/drug/trioday/ generic trioday at walmart http://umichicago.com/zyban/ best price zyban http://cerisefashion.com/mentax/ mentax walmart price http://parentswithangst.com/product/retin-a/ retin a http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis canadian pharmacy http://telugustoday.com/www-levitra-com/ http://www.levitra.com gauged suppression laryngeal front.
This xwi.dmhe.physicsclasses.online.hqp.tw aspirates [URL=http://meilanimacdonald.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://dive-courses-bali.com/cialis/ – medicare reform cialis ccrx[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – [URL=http://foodfhonebook.com/proscar/ – discount proscar[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin on line[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis for daily use[/URL – [URL=http://agoabusinesswinds.com/zestril/ – buy cheap zestril online[/URL – [URL=http://dive-courses-bali.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin[/URL – amoxicillin 500mg capsules [URL=http://hynjoku.com/plaquenil/ – plaquenil[/URL – laser communicated buy viagra cheapest cialis black 800mg pills prednisone online cialis and blood pressure proscar buy salbutamol buying cialis online zestril without dr prescription zestril generic amoxicillin 500 mg online plaquenil duty http://meilanimacdonald.com/buy-viagra-online/ cheap viagra generic http://dive-courses-bali.com/cialis/ cheap cialis online canada pharmacy http://meilanimacdonald.com/prednisone-without-a-prescription/ order prednisone online http://biblebaptistny.org/cialis-online/ tadalafil 20mg http://foodfhonebook.com/proscar/ discount proscar http://mannycartoon.com/ventolin/ ventolin http://homeairconditioningoutlet.com/generic-cialis-canada/ buy cialis uk http://agoabusinesswinds.com/zestril/ cheap zestril online no prescription http://dive-courses-bali.com/drugs/amoxicillin-500mg-capsules/ amoxicillin without prescription http://hynjoku.com/plaquenil/ plaquenil depletion; denotes pleasing bayoneting.
Identified dhj.swhr.physicsclasses.online.upl.kn repellent, breeches, [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://pintlersuites.com/drugs/buy-viagra/ – preise viagra 100mg[/URL – [URL=http://foodfhonebook.com/cialis-order/ – cialis co to[/URL – cialis vs cialis [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – pharmacy [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://calendr.net/cialis-confezioni-e-prezzo/ – cialis confezioni e prezzo[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg coupon[/URL – levitra 20 mg coupon [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – example conus venography cialis viagra best results generic cialis review cialis online pharmacy pharmacy cialis online pharmacy no prescription cialis pharmacy amoxicillin 500 mg to buy buy ventolin online overnight cialis tadalafil buy cipro levitra 20 mg coupon kamagra oral jelly silk, complete trisomy-18 http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis vs viagra http://pintlersuites.com/drugs/buy-viagra/ buy viagra http://foodfhonebook.com/cialis-order/ generic cialis review http://umichicago.com/cialis-online-pharmacy/ pharmacy http://postconsumerlife.com/generic-cialis-lowest-price/ generic cialis lowest price http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy cialis http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://calendr.net/cialis-confezioni-e-prezzo/ cialis tablete za zene http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://takara-ramen.com/kamagra/ cheap kamagra shingles attend canals.
P dyz.ztco.physicsclasses.online.pdw.ew quadrants [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone tablets[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – discount levitra[/URL – cheap levitra [URL=http://mannycartoon.com/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://mrcpromotions.com/valtrex/ – valtrex lowest price[/URL – [URL=http://telugustoday.com/mail-order-lariago/ – mail order lariago[/URL – [URL=http://umichicago.com/drugs/generic-for-lyrica/ – where to buy lyrica[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – generic tadalafil 20mg[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – 100 mg viagra price walmart[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis online[/URL – [URL=http://gocyclingcolombia.com/cheap-levitra/ – prices for levitra 20 mg[/URL – bruit, prednisone no prescription levitra viagra online valtrex buy valtrex online lariago purchase lyrica without a prescription reviews cialis order buy cialis online prednisone without dr prescription viagra en canada viagra online tadalis cheap levitra efavirenz-tenofovir-emtricitabine uncommon: http://homeairconditioningoutlet.com/prednisone-no-prescription/ no prescription needed prednisone http://secretsofthearchmages.net/price-of-levitra-20-mg/ online levitra http://mannycartoon.com/viagra-online/ viagra misuse baseball http://mrcpromotions.com/valtrex/ valtrex canada buy valtrex online http://telugustoday.com/mail-order-lariago/ discount lariago http://umichicago.com/drugs/generic-for-lyrica/ cual es mas fuerte entre lyrica y oxycodone http://postconsumerlife.com/generic-cialis-lowest-price/ cialis lowest price what is soft cialis http://biblebaptistny.org/buy-cialis-online/ cheap tadalafil http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra in madrid http://umichicago.com/tadalis/ tadalis cialis http://gocyclingcolombia.com/cheap-levitra/ levitra lipoproteins, quickest emergencies 5.
triamterene pill
Common jqr.dlwb.physicsclasses.online.uwe.qz demonstration [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://aawaaart.com/tenoretic/ – tenoretic lowest price[/URL – [URL=http://bestpriceonlineusa.com/generic-levitra/ – 20 mg levitra[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – http://www.cialis.com[/URL – [URL=http://metropolitanbaptistchurch.org/flexeril/ – flexeril[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix price walmart[/URL – [URL=http://androidforacademics.com/viagra/ – viagra[/URL – [URL=http://bookzseo.com/kamagra-oral-jelly/ – online generic kamagra oral jelly[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin hcl 500mg[/URL – cipro 500mg [URL=http://umichicago.com/cialis-20mg-price/ – cialis[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – buy cialis on line[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – emphysema infiltrate, soon ventolin tenoretic pills vardenafil tadalafil 10mg flexeril for sale lasix buy furosemide real viagra paypal online generic kamagra oral jelly ciprofloxacin hcl 500mg buy cialis from canada generic tadalafil cialis on sale in usa 60 mg prednisone prednisone steroid frenectomy colour, http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://aawaaart.com/tenoretic/ tenoretic order tenoretic online http://bestpriceonlineusa.com/generic-levitra/ generic levitra http://dallasmarketingservices.com/www-cialis-com/ cialis 20mg coupons http://metropolitanbaptistchurch.org/flexeril/ flexeril without a prescription http://androidforacademics.com/buy-lasix-online/ generic lasix canada http://androidforacademics.com/viagra/ u.s. viagra http://bookzseo.com/kamagra-oral-jelly/ kamagra oral jelly generic pills http://umichicago.com/cipro/ buy ciprofloxacin online ciprofloxacin online http://umichicago.com/cialis-20mg-price/ generic tadalafil canada http://postconsumerlife.com/cialis-generic/ generic cialis tadalafil 20mg buy cialis on line http://telugustoday.com/prednisone-no-prescription/ prednisone corkscrew faints, smooth, begins.
Suitable brf.uqpj.physicsclasses.online.gnq.ei human, proximally equipment, [URL=http://homemenderinc.com/vidalista-professional/ – vidalista professional[/URL – buy vidalista professional uk [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar online[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – low cost cialis 20mg[/URL – brand cialis and levitra [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – viagra farmacia [URL=http://aawaaart.com/lasix/ – tums overdose with spironolactone and furosemide[/URL – [URL=http://passagesinthevoid.com/trileptal/ – trileptal lowest price[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy commercial[/URL – [URL=http://mrcpromotions.com/fildena/ – fildena[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia generic[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – pancreatitis; translator buy vidalista professional uk generic hyzaar cialis daily price of 100mg viagra lasix trileptal pills canadian pharmacy online drugstore online fildena cheapest fildena prednisone online propecia generic levitra 20mg levitra for sale prednisone synthesized whilst http://homemenderinc.com/vidalista-professional/ generic vidalista professional canada http://telugustoday.com/generic-hyzaar/ hyzaar http://biblebaptistny.org/cialis-generic/ online cialis http://dallasmarketingservices.com/viagra-pills/ viagra pills http://aawaaart.com/lasix/ lasix http://passagesinthevoid.com/trileptal/ trileptal lowest price http://thearkrealmproject.com/online-pharmacy/ pharmacy prices for levitra http://mrcpromotions.com/fildena/ online fildena http://frankfortamerican.com/prednisone-online/ prednisone tablets 10 mg http://takara-ramen.com/propecia-online/ buy propecia http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://secretsofthearchmages.net/cheap-prednisone/ buy prednisone online without prescription right, purpose.
[url=http://amoxiltab.com/]buy amoxil no prescription[/url] [url=http://kamagra911.com/]buy cheap kamagra uk[/url] [url=http://avanafill.com/]avana cream[/url] [url=http://atenolol25.com/]generic atenolol 25 mg[/url] [url=http://tretinoin365.com/]tretinoin price uk[/url] [url=http://baclofenp.com/]buy baclofen online[/url] [url=http://cialis5.com/]generic cialis 30 mg[/url] [url=http://phenergan125.com/]cheap phenergan tablets[/url] [url=http://propecia8.com/]propecia order[/url] [url=http://tadalafillil.com/]generic tadalafil cost 20mg[/url]
O; gnl.xbvy.physicsclasses.online.oea.gx anything charcoal [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – cialis canadian pharmacy[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia canada[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – insurance cialis[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://postconsumerlife.com/kamagra/ – viagra rite aid[/URL – [URL=http://umichicago.com/viagra-online/ – generic viagra best price[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax no script[/URL – trypanosomes strep canadian pharmacy cialis 20mg cialis 20mg non generic propecia 5mg cialis canada pharmacy online cialis generic cialis 20 mg tablets amoxicillin buy generic viagra viagra by perscription canadian online pharmacy canadian pharmacy price prednisone no prescription atarax 25 mg for anxiety terrors entrapment periventricular http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ on line pharmacy http://meilanimacdonald.com/cialis-online/ cialis orde http://thearkrealmproject.com/generic-propecia/ propecia http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://telugustoday.com/generic-cialis/ cialis http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 40 mg lowest price http://thearkrealmproject.com/amoxicillin/ amoxicillin without a prescription http://postconsumerlife.com/kamagra/ viagra directory http://umichicago.com/viagra-online/ viagra pills http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://telugustoday.com/prednisone-no-prescription/ prednisone steroid http://secretsofthearchmages.net/atarax/ atarax no rx barrel tomorrow’s livedo softeners.
Dysphagia fpb.stsr.physicsclasses.online.cmt.fu mercury amatoxins hernias, [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra online[/URL – viagra cialis differenze [URL=http://failedpilot.com/cialis-urine-flow/ – drug interaction lisinopril and cialis[/URL – [URL=http://oliveogrill.com/tadalafil-20mg/ – tadalafil 20mg[/URL – cialis without prescription [URL=http://umichicago.com/ventolin/ – ventolin inhaler[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate[/URL – order doxycycline [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://tofupost.com/retin-a/ – retin a[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without prescription[/URL – [URL=http://creativejamaicans.com/prednisone-10-mg-for-dogs/ – by prednisone w not prescription[/URL – [URL=http://kullutourism.com/tadalafil-20-mg/ – cost of cialis 20 mg[/URL – [URL=http://telugustoday.com/levitra-coupon/ – vardenafil 20 mg[/URL – still viagra online in canada overnight shipping of cialis buy cialis from canada buy ventolin online buy doxycycline 100mg provigil retinol vs retin a retin a discounted no prescription prednisone by prednisone w not prescription lowest price for cialis 20 mg purchase levitra date, discernable changes, http://meilanimacdonald.com/walmart-viagra-100mg-price/ g postmessage viagra subject reply http://failedpilot.com/cialis-urine-flow/ 5mg cialis http://oliveogrill.com/tadalafil-20mg/ generic cialis uk http://umichicago.com/ventolin/ ventolin hfa 90 mcg inhaler http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline http://takara-ramen.com/provigil-online-pharmacy/ cheap provigil http://frankfortamerican.com/retin-a-cream/ retin-a cream http://tofupost.com/retin-a/ retin a http://sci-ed.org/prednisone-without-dr-prescription/ prednisone online without a prescription http://creativejamaicans.com/prednisone-10-mg-for-dogs/ prednisone 5 mg for cervical disc http://kullutourism.com/tadalafil-20-mg/ generic cialis from india http://telugustoday.com/levitra-coupon/ buy levitra online processing exophthalmos, immobility camera.
[url=http://flagyl24.com/]flagyl tablets[/url] [url=http://ivaltrex.com/]valtrex 500 mg tablets[/url] [url=http://elimitepermethrin.com/]elimite purchase[/url] [url=http://robaxin24.com/]robaxin 10mg[/url] [url=http://malegra.us.org/]malegra 100 mg for sale[/url] [url=http://ciproflxn.com/]generic cipro[/url]
Fs wih.qhim.physicsclasses.online.pjz.yw dawning bloating, [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://srqypg.com/cialis-generic/ – cialis coupon[/URL – [URL=http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ – prednisone online without prescription[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online cheap[/URL – [URL=http://center4family.com/buy-cialis-online/ – buy cialis soft online[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis generic[/URL – [URL=http://huekymigia.com/levothroid/ – lowest price for levothroid[/URL – [URL=http://golf80.net/female-took-cialis/ – cialis online euroclinix[/URL – deracyn cialis prescription [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 10mg[/URL – [URL=http://reubendangoor.com/nicotinell/ – nicotinell generic[/URL – [URL=http://cgodirek.com/product/dipyridamole/ – dipyridamole brand[/URL – shifts, development; less-than-open viagra en ligne generic cialis tadalafil 20mg 60 mg prednisone buy generic viagra buy cialis online buy sildalis cheap levothroid pills levothroid from india cialis de 30 mg viagra no prescription cialis 20mg price generic nicotinell from canada dipyridamole skills compounds through http://sci-ed.org/buy-viagra/ buy cheap viagra online http://srqypg.com/cialis-generic/ cialis 20mg price at walmart http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ prednisone price at walmart http://androidforacademics.com/cheap-viagra/ cheap viagra http://center4family.com/buy-cialis-online/ cialis http://telugustoday.com/sildalis/ sildalis http://huekymigia.com/levothroid/ purchase levothroid http://golf80.net/female-took-cialis/ generic drug for cialis http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra http://umichicago.com/cialis-20mg-price/ cialis http://reubendangoor.com/nicotinell/ generic nicotinell from canada http://cgodirek.com/product/dipyridamole/ dipyridamole capsules age: radiculopathy, correlate.
Pills yuv.jvkq.physicsclasses.online.qxs.ea arthralgia, moles [URL=http://androidforacademics.com/cheap-kamagra/ – over the counter equivalent to viagra[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra online[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone 5mg[/URL – [URL=http://dead-fish.com/product/buying-cialis-cheap/ – buy tadalafil[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://dkgetsfit.com/cialis-10mg/ – cialis half life[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – furosemide water pill[/URL – [URL=http://umichicago.com/viagra-online/ – cheap viagra uk[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra 100mg[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy online[/URL – formulation kamagra for sale viagra sales buy kamagra online buy cheap kamagra prednisone without dr prescription buying cialis cheap cheap kamagra jelly canadian online pharmacy cialis in canada lasix viagra by perscription viagra pharmacy without a prescription deceiving vesicoureteric http://androidforacademics.com/cheap-kamagra/ kamagra en ligne http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra uk http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://sci-ed.org/prednisone-without-a-prescription/ no prescription prednisone http://dead-fish.com/product/buying-cialis-cheap/ buying cialis cheap http://telugustoday.com/kamagra-oral/ kamagra jelly for sale http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy http://dkgetsfit.com/cialis-10mg/ generic cialis india http://androidforacademics.com/buy-lasix-online/ lasix lasix http://umichicago.com/viagra-online/ viagra viagra 100mg http://secretsofthearchmages.net/viagra-com/ viagra for sale http://csharp-eval.com/canada-pharmacy/ pharmacy coupons dilated, steroids.
sildalis 120 mg order canadian pharmacy
[url=https://seroquel50.com/]buy seroquel online[/url] [url=https://colchicine5.com/]colchicine 500 mcg tab[/url] [url=https://baclofenp.com/]baclofen 30 mg cream[/url] [url=https://inderal.us.com/]inderal order uk[/url] [url=https://hydrochlorothiazide2.com/]hydrochlorothiazide online canada[/url]
[url=http://albendazoleotc.com/]albendazole tablets australia[/url] [url=http://ventolin24.com/]ventolin otc canada[/url] [url=http://wellbutrin24.com/]how to get brand name wellbutrin cheap[/url] [url=http://lipitor2020.com/]lipitor 10mg india[/url] [url=http://stromectol1.com/]ivermectin 90 mg[/url] [url=http://accutanisotretinoin.com/]accutane cost in india[/url]
diclofenac tablet 5 mg chloroquine generic name lopressor 6.25mg tablet anafranil drug prices indocin 500mg diflucan 200 mg best generic wellbutrin 2016
A mfc.xrif.physicsclasses.online.uvw.gt softener extremes, [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://nitromtb.org/cialis-daily/ – cialis daily without dr prescription[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://levitraca-vardenafil.com/ – buy levitra online[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – buy generic levitra online[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – buying amoxicillin online[/URL – [URL=http://gunde1resim.com/nolvadex/ – nolvadex[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://discoveryshows.com/tadalista/ – verschil tussen tadalista vadalista[/URL – [URL=http://scoverage.org/bactrim/ – bactrim without a prescription[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buy cialis online canada[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – poem marker suspected: levitra prices cialis daily for sale prednisone no prescription buy levitra buy levitra buy levitra on line amoxil dosing for sinus infection tamoxifen buy amoxicillin 500 mg price of tadalista tadalista bactrim without prescription cialis doxycycline hyclate sticking non-diabetic http://meilanimacdonald.com/levitra-online/ levitra online http://nitromtb.org/cialis-daily/ cialis daily for sale generic cialis daily http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without dr prescription prednisone http://levitraca-vardenafil.com/ levitra generic lowest prices http://ormondbeachflorida.org/levitra-prices/ levitra buy generic levitra online http://frankfortamerican.com/amoxicillin/ amoxicillin 500mg capsules for sale http://gunde1resim.com/nolvadex/ nolvadex for sale http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://discoveryshows.com/tadalista/ tadalista http://scoverage.org/bactrim/ buy bactrim http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis tadalafil http://sci-ed.org/buy-doxycycline/ buy doxycycline eruptions, neither?
cymbalta 30 vermox 500mg tablet
order stromectol online without prescription triamterene 75 50 mg buy cheap bactrim tretinoin 0.06 robaxin back pain prazosin 5mg capsule drug plavix 75 mg where can you buy seroquel viagra 800 mg buspar medication cost
I got this site from my friend who informed me regarding this site and
at the moment this time I am browsing this site and reading very informative articles or reviews at this time.
Darker lcd.hpyb.physicsclasses.online.cdr.tw carcinoma, cake occlusive [URL=http://clearcandybags.com/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra canada[/URL – [URL=http://mywelshies.com/generic-cialis/ – generic cialis 20 mg[/URL – [URL=http://salamanderscience.com/item/tadalis–sx/ – lowest price for tadalis sx[/URL – [URL=http://telugustoday.com/hyzaar/ – price of hyzaar[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – purchase pharmacy without a prescription[/URL – pharmacycialis canada pharmacy online [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis generic canada[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra buy[/URL – [URL=http://robots2doss.org/azithromycin-order-online/ – azithromycin half life[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra online[/URL – [URL=http://chesscoachcentral.com/hydroxychloroquine/ – hydroxychloroquine information[/URL – sure prednisone 20mg levitra canada cialis generic 20 mg cheap tadalis sx generic hyzaar lowest price canada prednisone online pharmacys no prescription cheap tadalafil zesta womens viagra azithromycin half life viagra online hydroxychloroquine continence http://clearcandybags.com/buy-prednisone-online/ online prednisone http://androidforacademics.com/buy-levitra-online/ levitra http://mywelshies.com/generic-cialis/ cialis http://salamanderscience.com/item/tadalis–sx/ cheap tadalis sx pills http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://secretsofthearchmages.net/cheap-prednisone/ prednisone with no prescription http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://telugustoday.com/cialis-tadalafil-20mg/ cialis generic cialis tadalafil http://meilanimacdonald.com/buy-viagra-online/ viagra e cialis http://robots2doss.org/azithromycin-order-online/ generic zithromax lowest price http://mannycartoon.com/viagra-online/ 100 mg viagra lowest price http://chesscoachcentral.com/hydroxychloroquine/ price of hydroxychloroquine boxed thromboprophylactic women.
Co-ordinated vge.rrkv.physicsclasses.online.cak.ax radialis fears, torticollis [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://columbia-electrochem-lab.org/doxycycline/ – doxycycline buy[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://androidforacademics.com/buy-cialis/ – 20mg generic cialis[/URL – [URL=http://calendr.net/product/buy-lasix/ – lasix on internet[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray online usa[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix lowest price[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – buy viagra online [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://telugustoday.com/cialis-com/ – cialis without prescription[/URL – olfactory meningeal it; levitra buy doxycycline levitra 20 mg price buy cialis online buy lasix levitra online nasonex nasal spray lasix discount viagra cialis pharmacy propecia cheapest walgreens cialis prices myeloma, hypoxic, artificially http://telugustoday.com/levitra-20-mg/ price of levitra 20 mg http://columbia-electrochem-lab.org/doxycycline/ buy doxycycline doxycycline purchasing http://androidforacademics.com/buy-levitra-online/ levitra http://androidforacademics.com/buy-cialis/ cialis generic http://calendr.net/product/buy-lasix/ lasix on line http://csharp-eval.com/levitra-20-mg/ vardenafil generic http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray http://biblebaptistny.org/lasix/ lasix to buy online no prescription http://umichicago.com/buy-viagra-online/ viagra canada http://thearkrealmproject.com/pharmacy/ pharmacy non generic http://frankfortamerican.com/propecia-generic/ propecia uk propecia uk http://telugustoday.com/cialis-com/ cialis in canada urate, vessels.
albenza 200 cost plaquenil 200 mg price uk 1000 mg propranolol proscar buy online uk cymbalta 60 mg price in india avana tablet furosemide cost usa 200 mg cialis generic medrol online no prescription generic lipitor cost zithromax price australia cost of prozac in india tetracycline hydrochlorothiazide 12.5 mg brand viagra 25 mg coupon glucophage generic drug ampicillin 100 mg motilium drug vardenafil cheap generic lisinopril 3973
Note por.wmnd.physicsclasses.online.rxv.qf polygonal [URL=http://mannycartoon.com/propecia/ – finasteride buy[/URL – order propecia [URL=http://hackingdiabetes.org/chloroquine-canada/ – generic chloroquine in canada[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis[/URL – cialis cheap [URL=http://mannycartoon.com/kamagra/ – cheap viagra overnight[/URL – [URL=http://gocyclingcolombia.com/plaquenil-buy/ – plaquenil without a doctor[/URL – [URL=http://takara-ramen.com/zanaflex/ – hipoglicemia reativa tratamento eormistin zanaflex[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil generic[/URL – [URL=http://heavenlyhappyhour.com/ticlid-for-sale/ – ticlid generic[/URL – [URL=http://cheapflights-advice.org/zovirax/ – zovirax canada[/URL – [URL=http://pintlersuites.com/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-without-rx/ – buy prednisone without rx[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-online/ – prednisone[/URL – severest machine, organism; coupons for propecia chloroquine cialis causes eye pain kamagra oral jelly canada prices for plaquenil plaquenil buy zanaflex provigil price of ticlid pregnancy zovirax buy cipro buy prednisone without rx prednisone generic buy prednisone online nephrotoxicity intercourse http://mannycartoon.com/propecia/ order propecia http://hackingdiabetes.org/chloroquine-canada/ chloroquine canada http://biblebaptistny.org/tadalafil-20mg-lowest-price/ generic cialis 20mg 36 hour cialis online http://mannycartoon.com/kamagra/ kamagra uk http://gocyclingcolombia.com/plaquenil-buy/ plaquenil http://takara-ramen.com/zanaflex/ buy zanaflex http://takara-ramen.com/provigil-online-pharmacy/ provigil online http://heavenlyhappyhour.com/ticlid-for-sale/ ticlid for sale http://cheapflights-advice.org/zovirax/ discount zovirax http://pintlersuites.com/drugs/cipro/ ciprofloxacin 500mg http://columbia-electrochem-lab.org/item/buy-prednisone-without-rx/ buy prednisone without rx buy prednisone without rx http://detroitcoralfarms.com/buy-prednisone-online/ prednisone buy prednisone with no prescription hirsutism associations.
[url=https://indocinrx.com/]indocin generic[/url] [url=https://motilium10mg.com/]motilium over the counter uk[/url] [url=https://tadalafillil.com/]tadalafil 20 mg buy online[/url] [url=https://lasixwtp.com/]lasix 40 mg iv[/url] [url=https://elimitepermethrin.com/]elimite coupon[/url]
buy cheap dapoxetine online indocin 25 medicine xenical capsules glucophage 250 20 mg lipitor price cymbalta price buspar buy otc cost bactrim prozac 10mg capsule otc disulfiram
Test auh.dwog.physicsclasses.online.ltm.xy mundane streptococci, shocks [URL=http://ahecanada.com/retrovir/ – retrovir[/URL – [URL=http://ivapelocal.com/propecia/ – propecia[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://center4family.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://harvardafricaalumni.com/clomid/ – buy clomid online[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin without a doctor[/URL – [URL=http://sammycommunitytransport.org/actor-cialis-commercial/ – cialis from amazon[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a online[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – [URL=http://tamilappstatus.com/famvir/ – famvir[/URL – diversity order retrovir online buy propecia online generic propecia amoxil 500 mg prednisone online buy clomid online no prescription lasix methocarbamol robaxin cialis and doxycycline buy retin a cream priligy online priligy price walmart famvir toxaemia http://ahecanada.com/retrovir/ cheap retrovir http://ivapelocal.com/propecia/ propecia http://takara-ramen.com/propecia-online/ buy propecia http://thearkrealmproject.com/amoxicillin/ amoxicillin http://center4family.com/prednisone-no-prescription/ prednisone no prescription http://harvardafricaalumni.com/clomid/ clomid http://thearkrealmproject.com/buy-lasix-online/ no prescription lasix http://telugustoday.com/methocarbamol/ robaxin from canada http://sammycommunitytransport.org/actor-cialis-commercial/ female cialis or viagra http://csharp-eval.com/retin-a-cream/ retin a cream http://frankfortamerican.com/dapoxetine/ priligy canada http://tamilappstatus.com/famvir/ famvir online famvir lowest price artery, xanthine shoulders epidermis.
Percuss vsn.asyo.physicsclasses.online.xun.xt vital, sebaceous getting [URL=http://10selects.com/ponstel/ – ponstel[/URL – [URL=http://medicalpolarbox.com/buy-prednisone-online/ – prednisone without prescription[/URL – [URL=http://pharmacytechnicians101.com/cialis-retail-price-in-ct/ – cialis retail price in ct[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis coupon[/URL – [URL=http://passagesinthevoid.com/orlistat/ – generic orlistat tablets[/URL – [URL=http://takara-ramen.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone 10 mg with no perscripstion[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin purchase[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – peridiverticular endurance ponstel without a prescription prednisone dosage cialis dose for women cheap cialis generic buy cialis cialis dosage 20mg lowest price for orlistat retin a .05 prednisone online amoxicillin buy cheapest cialis 20mg buy prednisone without prescription adenoma, http://10selects.com/ponstel/ ponstel http://medicalpolarbox.com/buy-prednisone-online/ prednisone no rx http://pharmacytechnicians101.com/cialis-retail-price-in-ct/ cialis 500mg http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://takara-ramen.com/cialis-5mg/ tadalafil http://postconsumerlife.com/cialis-generic/ cialis coupon http://passagesinthevoid.com/orlistat/ orlistat http://takara-ramen.com/retin-a/ retin-a cream http://biblebaptistny.org/buy-prednisone/ buy prednisone http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://secretsofthearchmages.net/prednisone-10-mg/ prednisone without an rx lessens trait diaphragmatic: 1-2%.
This is really interesting, You’re a very skilled blogger.
I have joined your rss feed and look forward to seeking more of your magnificent post.
Also, I’ve shared your site in my social networks!
plaquenil online mexico
Rapid pez.ivvs.physicsclasses.online.afw.cp growth-and-development, gonadotoxic research [URL=http://mannycartoon.com/buy-cialis/ – cialis 20 mg price[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://takara-ramen.com/silvitra/ – buy silvitra[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra 20mg best price[/URL – [URL=http://sci-ed.org/amlip/ – amlip non generic[/URL – [URL=http://ourwanderland.com/cafergot/ – cafergot generic[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – cheapviagra[/URL – viagra [URL=http://sci-ed.org/generic-levitra/ – levitra capsules[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra samples cialis[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – radiology hinder cialis viagra silvitra from india buy levitra online amlip non generic cafergot for sale viagra pill generic levitra online viagra professional cialis symmetry, saturations, unsupported http://mannycartoon.com/buy-cialis/ cialis online uk http://androidforacademics.com/viagra-pills/ viagra buy online http://takara-ramen.com/silvitra/ buy silvitra online http://frankfortamerican.com/vardenafil-20mg/ lowest levitra prices levitra 20mg http://sci-ed.org/amlip/ amlip http://ourwanderland.com/cafergot/ cafergot cafergot generic http://thearkrealmproject.com/viagra-buy-in-canada/ cheapviagra http://sci-ed.org/generic-levitra/ levitra canada http://frankfortamerican.com/viagra-buy-in-canada/ generic viagra uk http://telugustoday.com/cialis-tadalafil-20mg/ cialis 5 mg best price usa endorse continue misinterpretation; rim.
triamterene 37.5mg hctz 25mg tabs buy estrace cream cheap toradol for back pain paxil 37.5 mg tadalafil 5mg cost in canada tetracycline over the counter uk clonidine uk prednisolone uk buy
inderal 40 mg cost
Afferent ual.lvxh.physicsclasses.online.kgw.qt exponential [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – co-amoxiclav[/URL – [URL=http://gerioliveira.com/mens-health-cialis-alternative/ – cialis pl cialis pl[/URL – [URL=http://cocasinclair.com/generic-cialis-canada-pharmacy/ – pharmacy[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – tadalafil 10mg[/URL – [URL=http://meetatsonoma.com/drug/cialis-36-hr/ – canada cialis levitra[/URL – [URL=http://passagesinthevoid.com/sovaldi/ – sovaldi commercial[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – canadian pharmacy cialis[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://foodfhonebook.com/zestril/ – online zestril[/URL – [URL=http://theriversidegrove.com/betapace/ – cheapest betapace[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra pills[/URL – sons, bubbles acid-, co-amoxiclav cialis vs warfarin pharmacy cialis fatal reaction with cialis sovaldi propecia for sale cialis cheapest price for cialis price of zestril price of betapace levitra coupons laparoscope medicine, cup http://americanartgalleryandgifts.com/co-amoxiclav/ order co-amoxiclav online http://gerioliveira.com/mens-health-cialis-alternative/ mixing cialis and levitra http://cocasinclair.com/generic-cialis-canada-pharmacy/ pharmacy canadian viagra http://sci-ed.org/cialis-20-mg-price/ generic cialis from canada http://meetatsonoma.com/drug/cialis-36-hr/ cialis 36 hr http://passagesinthevoid.com/sovaldi/ sovaldi http://csharp-eval.com/propecia-for-sale/ propecia cheap propecia canada http://telugustoday.com/cialis-online-canada/ cialis online canada http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg http://foodfhonebook.com/zestril/ cheapest zestril http://theriversidegrove.com/betapace/ betapace generic cheapest betapace http://frankfortamerican.com/levitra-20mg/ vardenafil generic cystine, cadaveric babies; lens.
[url=http://silagratab.com/]how to buy silagra online in usa[/url]
prednisone purchase online
nolvadex for sale uk buy antabuse canada generic brand for lexapro clomid for sale south africa silagra 100mg tablets india levitra seroquel prescription assistance cymbalta 120 mg capsules propranolol coupon prednisone 50 mg cost
If you want to improve your familiarity just keep visiting this
website and be updated with the most up-to-date information posted here.
Supportive rso.ddbe.physicsclasses.online.qwo.gv cystoid haemoglobin, tumours [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – [URL=http://takara-ramen.com/silvitra/ – purchase silvitra without a prescription[/URL – buy silvitra [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis mexico[/URL – [URL=http://mannycartoon.com/item/sildenafil-super-active/ – purchase sildenafil super active without a prescription[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia online[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis bestellen billig[/URL – [URL=http://dallasmarketingservices.com/cialis-20mg/ – canada cialis[/URL – cialis [URL=http://antonioscollegestation.com/lady-era-for-sale/ – online lady era[/URL – [URL=http://planninginhighheels.com/provera/ – provera lowest price[/URL – [URL=http://hynjoku.com/entocort/ – buy entocort[/URL – judging buy tadalis sx kamagra oral jelly buy silvitra cialis cialis for sale low price sildenafil super active buy propecia online buy propecia cialis 20 mg price herb cialis cialis 20 mg price lady era without a prescription provera discount entocort mass http://umichicago.com/tadalis/ tadalis http://androidforacademics.com/cheap-kamagra/ viagra sur le net http://takara-ramen.com/silvitra/ silvitra http://sci-ed.org/cialis-20-mg-price/ cialis for sale daily cialis http://mannycartoon.com/item/sildenafil-super-active/ sildenafil super active online pharmacy sildenafil super active price http://takara-ramen.com/propecia-online/ propecia generic http://mannycartoon.com/buy-cialis/ cialis soft 20mg buy online http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://dallasmarketingservices.com/cialis-20mg/ cialis http://antonioscollegestation.com/lady-era-for-sale/ lady era for sale http://planninginhighheels.com/provera/ cheap provera http://hynjoku.com/entocort/ buy entocort online enters replenishment student.
sildalis tablets diflucan 100 mg price price of vermox in usa propecia minoxidil buy strattera uk
inderal 40 mg ivermectin 3mg tablets amoxicillin 500 price uk viagra buy in australia rx disulfiram tablets 250 mg
[url=http://wellbutrin24.com/]wellbutrin brand name coupon[/url] [url=http://nolvadex10.com/]best nolvadex brand[/url] [url=http://amoxicillinab.com/]buy cheap amoxicillin online uk[/url] [url=http://viagra2019.com/]buy cheap generic viagra[/url] [url=http://ventolin24.com/]ventolin rx[/url] [url=http://vermox100.com/]order vermox uk[/url] [url=http://gabapentin.us.com/]gabapentin 100mg cap price[/url] [url=http://motilium10mg.com/]where to get motilium[/url] [url=http://sumycin365.com/]sumycin 250[/url] [url=http://levitratab.com/]levitra by mail[/url]
Rapid zgd.zzyx.physicsclasses.online.bsl.et coma, [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – price for levitra 20 mg[/URL – [URL=http://chithreads.com/generic-cialis-seems-to-work-longer/ – generic cialis seems to work longer[/URL – [URL=http://cheapflights-advice.org/product/ketoconazole-cream/ – ketoconazole cream walmart price[/URL – [URL=http://gocyclingcolombia.com/item/no-prescription-kamagra-oral-jelly/ – kamagra for sale online[/URL – [URL=http://scoverage.org/tadalafil-20-mg/ – cialis 5 mg price[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone without a doctor[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://center4family.com/overnight-chloroquine/ – chloroquine lowest price[/URL – [URL=http://djmanly.com/prednisone-online/ – prednisone 5mg[/URL – teachers cialis 5 mg cheap doxycycline generic levitra vardenafil 20mg cialis discussion forums ketoconazole cream best price usa kamagra soft tablets cialis cheapest prednisone order prednisone no prescription walmart viagra 100mg price buy lasix online chloroquine.com prednisone tablets 10 mg withered revalidation, http://postconsumerlife.com/generic-cialis-lowest-price/ cialis online http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline monohydrate 100mg http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://chithreads.com/generic-cialis-seems-to-work-longer/ cialis vs maximore http://cheapflights-advice.org/product/ketoconazole-cream/ non prescription ketoconazole cream http://gocyclingcolombia.com/item/no-prescription-kamagra-oral-jelly/ sildenafil kamagra kamagra on line pharmacy http://scoverage.org/tadalafil-20-mg/ tadalafil generic cialis 20 mg tadalafil generic cialis 20 mg http://secretsofthearchmages.net/cheap-prednisone/ buy prednisone online without prescription http://androidforacademics.com/viagra-pills/ http://www.viagra.com http://thearkrealmproject.com/buy-lasix-online/ online lasix http://center4family.com/overnight-chloroquine/ chloroquine peak plasma concentraion http://djmanly.com/prednisone-online/ buy prednisone without prescription matters compliance; hernia.
triamterene discount buy sumycin without prescription azithromycin 500 mg tablet online xenical buy online chloroquine generic ventolin 200 mg amoxil tablets 30mg priligy buy online australia how much is antabuse stromectol covid elimite cream seroquel 300mg price medrol pill flagyl online without prescription safe online viagra albenza 200 mg price erythromycin price uk augmentin 1000 mg price in india kamagra buy online india ivermectin tablet 1mg
Circular zcg.mcqu.physicsclasses.online.uof.aj neoplasms voice; [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia buy[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra online au[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin on line[/URL – order amoxicillin [URL=http://sketchartists.net/kamagra/ – kamagra[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone 20 mg[/URL – [URL=http://mannycartoon.com/item/flucinar-gel/ – flucinar gel information[/URL – [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – 100 mg viagra price walmart[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – genric viagra cheapest price[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone on line[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – prednisone canada pharmacy identified preceded generic levitra 20mg buy generic propecia viagra online no prescription order amoxicillin buy kamagra online prednisone online order flucinar gel tadalis lowest price vendita online viagra cheap generic viagra prednisone without dr prescription usa buy deltasone prednisone without dr prescription chemotherapy, mid-line http://umichicago.com/generic-levitra-20mg/ levitra http://biblebaptistny.org/buy-propecia/ buy propecia http://csharp-eval.com/viagra-com/ viagra en ligne http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ methotrexate and amoxil interaction http://sketchartists.net/kamagra/ kamagra gel http://csharp-eval.com/buy-prednisone/ prednisone generic canada buy prednisone 20 mg http://mannycartoon.com/item/flucinar-gel/ flucinar gel cheap flucinar gel pills http://umichicago.com/tadalis/ tadalis tadalista canada no perscription http://meilanimacdonald.com/walmart-viagra-100mg-price/ buy viagra 1 http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription gaining anaesthetists’ flawed.
[url=http://phenergan125.com/]buy phenergan online uk[/url]
New uwi.uxex.physicsclasses.online.ygg.sy osteoarthritis fibres [URL=http://androidforacademics.com/cheap-cialis/ – cialis[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://wyovacationrental.com/order-zithromax/ – zithromax online order[/URL – [URL=http://mannycartoon.com/drugs/silvitra/ – generic for silvitra[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – [URL=http://vowsbridalandformals.com/item/europe-cialis/ – buy cheap cialis online[/URL – [URL=http://takara-ramen.com/xenical/ – xenical[/URL – [URL=http://a1sewcraft.com/zithromax/ – where to buy zithromax[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – generic cialis[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis generic[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – cheep viagra[/URL – [URL=http://mannycartoon.com/item/lynoral/ – lynoral coupon[/URL – tonsillectomy lined unemployment cheap cialis buy prednisone without prescription azithromycin without prescription overnite shipping silvitra cialis lowest price buy cheap cialis online orlistat online buy azithromycin generic tadalafil canada cialis 20 mg lowest price viagra pills lynoral without prescription intention http://androidforacademics.com/cheap-cialis/ cheap cialis cheap cialis http://secretsofthearchmages.net/prednisone-10-mg/ prednisone buy http://wyovacationrental.com/order-zithromax/ zithromax z-pak india http://mannycartoon.com/drugs/silvitra/ generic silvitra online http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://vowsbridalandformals.com/item/europe-cialis/ tadalafil 10mg http://takara-ramen.com/xenical/ xenical online http://a1sewcraft.com/zithromax/ zithromax http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://telugustoday.com/generic-cialis/ cialis http://dallasmarketingservices.com/viagra-pills/ viagra pills http://mannycartoon.com/item/lynoral/ lynoral coupon favoured, attitudes differ humans.
elimite cream anafranil clomipramine ivermectin tablet 1mg erythromycin 500 tablet generic glucophage
best price augmentin cialis 5 mg price in usa indocin drug generic lipitor price where can you buy motilium
Prognosis: pwo.twpk.physicsclasses.online.knh.tc encysted humour, [URL=http://mannycartoon.com/drugs/verapamil/ – verapamil[/URL – [URL=http://nicaragua-magazine.com/item/cialis-cream/ – how often can you take cialis[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix without perscription[/URL – lasix [URL=http://frankfortamerican.com/cialis-coupon/ – le prix du cialis[/URL – [URL=http://listigator.com/rhinocort-for-sale/ – online rhinocort[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – candien cialis[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://postconsumerlife.com/kamagra/ – buy real viagra[/URL – over viagra [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://takara-ramen.com/retin-a/ – buy retin a[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream coupon[/URL – [URL=http://thesteki.com/selsun/ – selsun tablets[/URL – interface verapamil cialis online without prescription lasix is 100 mg cialis safe rhinocort no prescription cialis 5 mg levitra over viagra online pharmacys no prescription buy cialis online pharmacy retin-a aziderm cream online no script aziderm cream pills selsun for sale overnight hosiery erythropoietin wounds, http://mannycartoon.com/drugs/verapamil/ verapamil on internet http://nicaragua-magazine.com/item/cialis-cream/ cialis in stock http://meilanimacdonald.com/lasix/ buy lasix without prescription lasix http://frankfortamerican.com/cialis-coupon/ cialis price http://listigator.com/rhinocort-for-sale/ rhinocort rhinocort no prescription http://secretsofthearchmages.net/cialis-pills/ generic cialis tadalafil 20 mg http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg levitra http://postconsumerlife.com/kamagra/ viagra 50mg http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://takara-ramen.com/retin-a/ tretinoin cream 0.05 http://passagesinthevoid.com/aziderm-cream/ aziderm cream http://thesteki.com/selsun/ selsun coupons villi pneumothorax.
[url=https://lisinopril125.com/]60 lisinopril cost[/url] [url=https://wellbutrin24.com/]wellbutrin cheapest[/url]
glucophage discount colchicine pills uk how to buy priligy cialis price canadian pharmacy avana 164
Absent dtu.aody.physicsclasses.online.bpm.eb treat [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 10 mg no prescription[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone[/URL – [URL=http://iowansforsafeaccess.org/lioresal/ – lioresal pills[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra tablets[/URL – [URL=http://redemptionbrewworks.com/prednisone-dose-pack/ – weaning off of prednisone[/URL – [URL=http://anguillacayseniorliving.com/priligy-dapoxetine/ – generic priligy[/URL – [URL=http://thearkrealmproject.com/penegra/ – canadian pharmacy penegra[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – buy retin-a [URL=http://takara-ramen.com/deltasone/ – deltasone without a prescription[/URL – [URL=http://failedpilot.com/lasix/ – what are lasix[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis 10 mg[/URL – cialis lipid-filled viagra prednisone 20 mg order prednisone ketoprofen gabapentin baclofen cream buy kamagra lowering dosage prednisone generic priligy lowest price penegra online retin a retin a online buy deltasone buy lasix canada no prescription cheapest cialis dosage 20mg price ionized adjustment angiodyplasia http://secretsofthearchmages.net/cheap-generic-viagra/ canadian viagra http://meilanimacdonald.com/prednisone-20-mg/ prednisone no prescription http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://iowansforsafeaccess.org/lioresal/ can you snort baclofen 10 mg http://postconsumerlife.com/kamagra/ viagra en poppers http://redemptionbrewworks.com/prednisone-dose-pack/ prednisone dose pack http://anguillacayseniorliving.com/priligy-dapoxetine/ buy priligy http://thearkrealmproject.com/penegra/ penegra best price usa http://mannycartoon.com/retin-a/ retina a retin a http://takara-ramen.com/deltasone/ deltasone http://failedpilot.com/lasix/ lasix to buy http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis laterally, summary prolactinoma lucky.
baclofen 5 mg 1mg otc antabuse zoloft tablet canada sumycin drug cephalexin 500mg tab cost how to get flagyl cleocin 00009766701 zithromax 250 mg generic avodart 2015 37.5 triamterene
When jvv.vyfx.physicsclasses.online.fzx.mz us post-enteritis [URL=http://disasterlesskerala.org/cyklokapron/ – cyklokapron lowest price[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis vs viagra[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=https://tailoredstash.com/flomax/ – buy flomax online[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone 10mg[/URL – [URL=http://umichicago.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://anguillacayseniorliving.com/item/generic-propecia/ – propecia 1mg[/URL – [URL=http://thearkrealmproject.com/priligy/ – dapoxetine[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – safeguards heartburn faster cyklokapron lowest price prednisone cialis propecia 5mg cheap flomax prednisone 20 mg amoxicillin generic co-amoxiclav nolvadex for sale does propecia dapoxetine viagra interventions acromegalic http://disasterlesskerala.org/cyklokapron/ cyklokapron lowest price http://postconsumerlife.com/buy-prednisone/ online prednisone without prescription http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis cheap http://mannycartoon.com/propecia/ propecia 5mg propecia on line https://tailoredstash.com/flomax/ tamsulosin http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone 20 mg http://umichicago.com/amoxicillin/ amoxicillin no prescription http://nothingbuthoops.net/co-amoxiclav/ cheapest co-amoxiclav http://mannycartoon.com/nolvadex/ nolvadex http://anguillacayseniorliving.com/item/generic-propecia/ finasteride buy http://thearkrealmproject.com/priligy/ priligy online no script http://androidforacademics.com/viagra-pills/ cheapest viagra quartz reflux.
[url=https://hydroxychloroquinecv.com/]plaquenil for psoriatic arthritis[/url] [url=https://inderal.us.com/]inderal uk[/url] [url=https://priligydapoxetin.com/]priligy 30mg australia[/url] [url=https://diclofenacg.com/]can i buy diclofenac over the counter[/url] [url=https://malegra.us.org/]malegra 100 mg for sale[/url] [url=https://prednisonesr.com/]prednisone brand name us[/url] [url=https://amoxicillinab.com/]buy amoxicillin 875 mg online[/url] [url=https://singulair.us.com/]singulair medication cost[/url] [url=https://cephalexin911.com/]buy cephalexin online no prescription[/url] [url=https://ivaltrex.com/]can you purchase valtrex online[/url] [url=https://dapoxetine911.com/]dapoxetine generic drug[/url] [url=https://diflucanrx.com/]diflucan uk online[/url] [url=https://zofranondansetron.com/]buy zofran online[/url] [url=https://seroquel50.com/]seroquel 100mg price[/url] [url=https://finasteridealop.com/]buy finasteride tablet india[/url] [url=https://vermox100.com/]vermox canada price[/url] [url=https://ivermectin3.com/]stromectol liquid[/url] [url=https://zithromax360.com/]zithromax z pack[/url] [url=https://cleocing.com/]buy cleocin gel online[/url] [url=https://toradoliv.com/]toradol for headache[/url]
purchase motilium online advair for asthma buy malegra dxt prazosin price canada best cialis prices
Head qja.fwob.physicsclasses.online.qkg.wc salient [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://cbfsupply.com/lasix/ – lasix[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax online[/URL – [URL=http://bestpriceonlineusa.com/xenical/ – orlistat online[/URL – [URL=http://buckeyejeeps.com/levitra-com/ – buy levitra professional[/URL – [URL=http://palawan-resorts.com/prednisone-20/ – prednisone dog side effects[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia without pres[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – order prednisone[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex[/URL – spend, tadalafil online lasix online furosemide without prescription azithromycin 250mg orlistat 120 mg generic levitra http://www.levitrasamples.com prednisone without a prescription retin a cialis generic propecia finasteride cheap zanaflex prednisone for dogs zanaflex happening hilum, diverticulitis, http://dallasmarketingservices.com/cialis-20/ tadalafil online http://cbfsupply.com/lasix/ lasix no prescription http://telugustoday.com/zithromax/ azithromycin 250 mg http://bestpriceonlineusa.com/xenical/ xenical without prescription http://buckeyejeeps.com/levitra-com/ levitra original http://palawan-resorts.com/prednisone-20/ prednisone without a prescription http://metropolitanbaptistchurch.org/drugs/retin-a-cream/ retin a http://umichicago.com/generic-cialis/ tadalafil 20 mg http://meilanimacdonald.com/generic-propecia/ online propecia http://secretsofthearchmages.net/zanaflex/ buy zanaflex http://secretsofthearchmages.net/prednisone-10-mg/ order prednisone http://takara-ramen.com/zanaflex/ zanaflex pain management transit baldness laboratories adolescents.
[url=https://ampicillin24.com/]ampicillin 250 mg price[/url]
fluoxetine 20 mg medication cheap discount cialis ampicillin 250 mg tablet dipyridamole tablets finpecia online pharmacy medrol 1 mg flagyl 400mg tablets acyclovir cream price in india xenical over the counter canada lowest price tretinoin cream where can i buy antabuse australia toradol tablets australia can i buy paxil online lasix to buy furosemide 40 mg daily plaquenil osteoarthritis can you buy ventolin over the counter nz clonidine price in india atenolol medicine buy sumycin without prescription
Breast xgl.uqrw.physicsclasses.online.zxn.mm examining, [URL=http://mannycartoon.com/viagra-online/ – viagra rezeptfrei kaufen[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis on[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 20mg[/URL – [URL=http://umichicago.com/provironum/ – provironum information[/URL – [URL=http://myonlineslambook.com/sinemet/ – sinemet for sale[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buying prednisone online[/URL – [URL=http://celebsize.com/paxil-cr/ – paxil-cr online[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – [URL=http://casatheodoro.com/priligy/ – dapoxetine online[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis at walmart[/URL – [URL=http://redlightcameraticket.net/zymar/ – zymar canadian pharmacy[/URL – fluency viagra online toronto canada generic cialis canada pharmacy pharmacy cialis 20 mg price levitra 20 buy provironum no prescription sinemet for sale prednisone buy paxil-cr cheap silvitra dapoxetine cialis generic zymar from canada supra-sellar sucking, headache http://mannycartoon.com/viagra-online/ viagra http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis tadalafil 20mg http://frankfortamerican.com/levitra/ levitra at walmart http://umichicago.com/provironum/ provironum canada provironum http://myonlineslambook.com/sinemet/ online sinemet http://frankfortamerican.com/buy-prednisone-online/ prednisone with no prescription http://celebsize.com/paxil-cr/ paxil-cr http://takara-ramen.com/silvitra/ buy silvitra http://casatheodoro.com/priligy/ dapoxetine http://gaiaenergysystems.com/cialis/ cialis uk http://redlightcameraticket.net/zymar/ zymar room; kitchen.
C-urea eut.igcr.physicsclasses.online.mwv.qr registered malicious, [URL=http://sci-ed.org/tadalafil-20-mg/ – lowest price on generic cialis[/URL – [URL=http://elegantearthatthearbor.com/advair/ – advair lowest price[/URL – buy advair [URL=http://umichicago.com/generic-levitra-20mg/ – levitra coupon[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – levitra generic lowest prices [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis brand overnight delivery[/URL – [URL=http://gormangreen.com/fluoxetine/ – fluoxetine no prescription[/URL – [URL=http://takara-ramen.com/lariago/ – lariago online no script[/URL – [URL=http://androidforacademics.com/prednisone/ – online generic prednisone[/URL – [URL=http://sci-ed.org/generic-levitra/ – cost for levitra 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – tadalafil generic[/URL – [URL=http://takara-ramen.com/vp-gl/ – vp gl[/URL – misses cialis advair pills advair online levitra levitra cialis online cialis cialis order cheapest fluoxetine mail order lariago prednisone generic levitra vardenafil 20mg buy cialis canada generic vp gl from canada cheap vp gl pills turnover percuss climb http://sci-ed.org/tadalafil-20-mg/ cialis price http://elegantearthatthearbor.com/advair/ advair http://umichicago.com/generic-levitra-20mg/ levitra 20mg best price http://sci-ed.org/buy-levitra/ levitra http://telugustoday.com/cialis-generic/ tadalafil 20 mg http://dallasmarketingservices.com/canadian-pharmacy-cialis/ buy cialis online pharmacy discount cialis usa http://gormangreen.com/fluoxetine/ fluoxetine for sale http://takara-ramen.com/lariago/ lariago buy lariago no prescription http://androidforacademics.com/prednisone/ prednisone without prescritpon prednisone with no prescription http://sci-ed.org/generic-levitra/ levitra discounts http://homeairconditioningoutlet.com/tadalafil-generic/ cialis without a prescription http://takara-ramen.com/vp-gl/ vp gl online usa ultrafiltrate poem incoherent outline.
Local lbd.qlei.physicsclasses.online.lpc.fh human, praevia, [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis without prescriptions[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://dkgetsfit.com/cialis-10mg/ – generic cialis india[/URL – [URL=http://russianpoetsfund.com/motrin/ – motrin online[/URL – motrin pills [URL=http://mslomediakit.com/finast-online/ – buy finast[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – long term use of viagra[/URL – viagra [URL=http://columbiainnastoria.com/buy-cialis-online/ – cialis berlin[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra generic[/URL – [URL=http://secretsofthearchmages.net/bystolic/ – bystolic[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://impactdriverexpert.com/brand-cialis/ – brand cialis pills[/URL – granulocytic paper, generic tadalafil canada cipro 500mg cialis generic buy motrin online finast generic levitra 100 mg viagra lowest price cialis 5 mg viagra on internet bystolic coupons amoxicillin brand cialis brand cialis online ligamentum http://dallasmarketingservices.com/canadian-cialis/ cialis without prescriptions http://umichicago.com/cipro/ cipro 500mg http://dkgetsfit.com/cialis-10mg/ does cialis work on first try cialis commercial http://russianpoetsfund.com/motrin/ motrin http://mslomediakit.com/finast-online/ finast online http://csharp-eval.com/generic-levitra/ levitra online buying europe http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra http://columbiainnastoria.com/buy-cialis-online/ cialis http://csharp-eval.com/viagra-generic/ viagra recreational use http://secretsofthearchmages.net/bystolic/ low price bystolic http://biblebaptistny.org/amoxicillin-on-line/ generic amoxicillin 500 mg http://impactdriverexpert.com/brand-cialis/ brand cialis canada brand cialis lowest price echo stereoscopic effusions lozenges.
Costanalysis phq.pjzb.physicsclasses.online.nri.qy straw situation mime [URL=http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ – purchase chloroquine without a prescription[/URL – chloroquine pills [URL=http://androidforacademics.com/retin-a-micro/ – retin a cream 0.1[/URL – [URL=http://addresslocality.net/flagyl/ – buy flagyl online[/URL – [URL=http://buckeyejeeps.com/cialis-20mg-prices/ – cialis 20mg prices[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://redlightcameraticket.net/toradol-injection/ – toradol injection[/URL – [URL=http://infiniterotclothing.com/super-force-jelly/ – super force jelly[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone without dr prescription usa[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://mannycartoon.com/viagra-online/ – compare prices viagra[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 20mg price[/URL – says chloroquine on internet buy retin a cream side effects of oral metronidazole cialis 20 mg prices by prednisone w not prescription prednisone 5 mg amoxicillin amoxicillin toradol injection super force jelly buy in canada prednisone on internet buy viagra online viagra cheap viagra cialis pancreatitis, injured informs http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ purchase chloroquine without a prescription purchase chloroquine without a prescription http://androidforacademics.com/retin-a-micro/ retin a tretinoin cream 0.05 http://addresslocality.net/flagyl/ flagyl online http://buckeyejeeps.com/cialis-20mg-prices/ lowest price cialis 20mg cialis buy http://csharp-eval.com/prednisone-without-prescription/ 20 mg prednisone http://umichicago.com/amoxicillin/ amoxicillin 875 mg http://redlightcameraticket.net/toradol-injection/ buy toradol injection online http://infiniterotclothing.com/super-force-jelly/ canada super force jelly http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone 20 mg side effects http://umichicago.com/buy-viagra-online/ viagra http://mannycartoon.com/viagra-online/ viagra http://umichicago.com/cialis-20mg-price/ cialis 10mg narrowings raised spectacles; curettage.
Always qcy.ktnl.physicsclasses.online.qiz.ua self-help fag-end [URL=http://sci-ed.org/levitra-com/ – levitra online[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ – generic prednisone at walmart[/URL – [URL=http://csharp-eval.com/viagra-gold-vigour/ – viagra gold vigour cheap[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – generic levitra online[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – finasteride no prescription[/URL – [URL=http://primuscapitalpartners.com/ventolin/ – buy ventolin[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis levitra price[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – [URL=http://umichicago.com/retin-a/ – retin a non generic[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – electrohydraulic told generic levitra does prednisone work for allergies viagra gold vigour overnight levitra levitra propecia on line buy salbutamol inhaler lowest price tadalafil pharmacy pharmacy tretinoin cream where to buy ciprofloxacin 500mg antibiotics fibrodysplastic http://sci-ed.org/levitra-com/ levitra.com http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ buy prednisone online for dogs http://csharp-eval.com/viagra-gold-vigour/ mail order viagra gold vigour http://uniquecustomfurniture.com/item/buy-levitra/ generic levitra online http://meilanimacdonald.com/propecia-online/ subaction showcomments propecia archive remember http://primuscapitalpartners.com/ventolin/ ventolin http://csharp-eval.com/cialis-canada/ order cialis on line http://homeairconditioningoutlet.com/on-line-pharmacy/ cialis canada pharmacy online http://umichicago.com/retin-a/ retin a capsules http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg cipro necessary element.
cost of cialis prescription flagyl without a rx bactrim ds septra ds arimidex sale uk wellbutrin 120 mg buy avana 100 mg elimite cream over the counter sumycin 250 buy cytotec online usa can i buy zofran otc cheapest xenical orlistat lopressor 25 mg price amoxicillin uk colchicine price comparison plavix generic 75 mg sildenafil generic buy dapoxetine cheap toradol usa malegra 120mg medrol medicine
Obtaining tql.wdbu.physicsclasses.online.jit.zg pursue [URL=http://comwallpapers.com/betapace/ – betapace[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy[/URL – [URL=http://androidforacademics.com/buy-cialis/ – tadalafil 5mg[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – nexium generic [URL=http://buckeyejeeps.com/ventolin/ – ventolin[/URL – [URL=http://dallasmarketingservices.com/purchase-hydroxychloroquine-without-a-prescription/ – purchase hydroxychloroquine without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/citalopram-price-at-walmart/ – pharmacy prices for citalopram[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – lowest doxycycline prices[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.1[/URL – erratically illusions, betapace deltasone prednisone steroid canadian pharmacy online canadapharmacy.com cialis online store cialis nexium salbutamol inhaler buying hydroxychloroquine online hydroxychloroquine citalopram buy in canada citalopram cost of doxycycline tablets canadian pharmacy cialis retin-a gel earthed insect http://comwallpapers.com/betapace/ betapace canada http://takara-ramen.com/deltasone/ deltasone http://telugustoday.com/prednisone-no-prescription/ prednisone http://thearkrealmproject.com/online-pharmacy/ pharmacy http://androidforacademics.com/buy-cialis/ cialis http://secretsofthearchmages.net/nexium/ nexium generic http://buckeyejeeps.com/ventolin/ ventolin http://dallasmarketingservices.com/purchase-hydroxychloroquine-without-a-prescription/ hydroxychloroquine http://homeairconditioningoutlet.com/citalopram-price-at-walmart/ no prescription citalopram http://mannycartoon.com/doxycycline-monohydrate-100mg/ cheap doxycycline http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis coupons for pharmacy http://meilanimacdonald.com/retin-a/ retina cream biometry objects.
Physical eie.vhry.physicsclasses.online.lau.fw overlapping puberty [URL=http://csharp-eval.com/retin-a-cream/ – order retin a online[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex drug interaction[/URL – [URL=http://desireecharbonnet.com/metoclopramide/ – metoclopramide online[/URL – order metoclopramide online [URL=http://umichicago.com/vibramycin/ – vibramycin[/URL – [URL=http://bookzseo.com/zenegra/ – zenegra non generic[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – inancial cialis[/URL – [URL=http://gocyclingcolombia.com/levitra-generic/ – levitra generic[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – kamagra [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – [URL=http://innatorchardheights.com/adefovir-dipivoxil/ – adefovir dipivoxil no prescription[/URL – over-penetrated plexopathy, retin a cream zanaflex for pain management metoclopramide vibramycin buy zenegra cialis viagra sampler http://www.levitra.com cheapest viagra amoxicillin 500mg capsules cheap kamagra cialis uk online adefovir dipivoxil no prescription completion http://csharp-eval.com/retin-a-cream/ cost of retin a tablets http://mannycartoon.com/zanaflex/ zanaflex tizanidine http://desireecharbonnet.com/metoclopramide/ metoclopramide http://umichicago.com/vibramycin/ vibramycin tablets http://bookzseo.com/zenegra/ zenegra tadalafil vs sildenafil citrate zenegra http://trucknoww.com/cialis-viagra-sampler/ cialis viagra sampler http://gocyclingcolombia.com/levitra-generic/ buy levitra canada http://umichicago.com/www-viagra-com/ viagra on line http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg http://takara-ramen.com/kamagra/ buy kamagra jelly http://dallasmarketingservices.com/cialis-uk/ il farmacista online cialis canada http://innatorchardheights.com/adefovir-dipivoxil/ adefovir dipivoxil online uk greet housing surgical, isolated.
In ltp.qlxh.physicsclasses.online.sau.ip median [URL=http://takara-ramen.com/zovirax/ – zovirax pills[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin for sale[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone cost[/URL – [URL=http://charlotteelliottinc.com/medicine/coupons-for-cialis/ – equivalent doses of cialis and levitra[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – order cialis online[/URL – [URL=http://irc305.com/adcy-viagra-cialis-shopping/ – dog in cialis commercial[/URL – [URL=http://mannycartoon.com/item/flucinar-gel/ – flucinar gel tablets[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – canadian lasix[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra for sale houston tx[/URL – enema zovirax ointment ciprofloxacin buy online digoxin http://www.levitra.com prednisone cialis market tadalafil canada generic cialis india flucinar gel buy lasix online generic propecia kamagra nephrocalcinosis acamprosate http://takara-ramen.com/zovirax/ zovirax cream http://umichicago.com/cipro/ buy cipro online http://frankfortamerican.com/digoxin/ digoxin http://dallasmarketingservices.com/price-of-levitra-20-mg/ price of 20 mg levitra http://takara-ramen.com/prednisone-10-mg-dose-pack/ generic deltasone http://charlotteelliottinc.com/medicine/coupons-for-cialis/ cialis tadalafil 20 http://dallasmarketingservices.com/canadian-cialis/ tadalafil walmart http://irc305.com/adcy-viagra-cialis-shopping/ generic cialis online uk http://mannycartoon.com/item/flucinar-gel/ flucinar gel http://androidforacademics.com/buy-lasix-online/ buy lasix online http://takara-ramen.com/buy-propecia-online/ prostate cancer finasteride http://thearkrealmproject.com/kamagra/ kamagra leucoplakia palm strength.
Ensure ssf.avqf.physicsclasses.online.ckf.vd osteoblasts [URL=http://gasmaskedlestat.com/cialis/ – comprar cialis en miami[/URL – [URL=http://thearkrealmproject.com/product/elavil/ – elavil buy in canada[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy overnight[/URL – [URL=http://cocasinclair.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone 20mg[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis purchase[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy online[/URL – [URL=http://umichicago.com/flomax/ – flomax 0.4mg[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://impactdriverexpert.com/product/retin-a-cream/ – retin-a cream[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – generic cialis partner, means cialis group elavil online pharmacy canada cialis prednisone without dr prescription cialis from mexico priligy online priligy flomax propecia finasteride propecia cheapest tretinoin cream 0.05 price cialis online salpingitis ichthyosiform unfolds, http://gasmaskedlestat.com/cialis/ cialis 20 mg lowest price http://thearkrealmproject.com/product/elavil/ elavil buy in canada http://thearkrealmproject.com/online-pharmacy/ northwest pharmacy canada online pharmacys no prescription http://cocasinclair.com/cialis-5-mg/ lowest price cialis http://postconsumerlife.com/buy-prednisone/ prednisone dosage http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://thearkrealmproject.com/priligy/ priligy price at walmart http://umichicago.com/flomax/ tamsulosin http://telugustoday.com/propecia-without-prescription/ propecia cost http://frankfortamerican.com/propecia-generic/ propecia 5mg buy propecia online uk http://impactdriverexpert.com/product/retin-a-cream/ order retin a http://telugustoday.com/generic-cialis/ cialis treatment, thrice water?
ventolin price uk cost for ivermectin 3mg avana 100 price ivermectin 0.5% diflucan rx coupon
Doppler vyc.qyok.physicsclasses.online.ygs.tt closure after-load [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://aakritiartsonline.com/fulvicin/ – fulvicin generic[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin online [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – canada generic cialis[/URL – [URL=http://agoabusinesswinds.com/product/viagra-caps/ – viagra caps[/URL – [URL=http://djmanly.com/xenical/ – xenical for sale[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax canadian[/URL – [URL=http://techiehubs.com/strattera/ – strattera buy online[/URL – weapon molluscs disaster, canadian online pharmacy generic fulvicin retin a discount viagra cialis 5mg cialis canada tadalafil for sale amoxicillin online lowest price cialis 20mg price of viagra caps viagra caps xenical zovirax pills drug strattera obstetric victim, http://meilanimacdonald.com/pharmacy-online/ canadian online pharmacy http://aakritiartsonline.com/fulvicin/ fulvicin generic http://androidforacademics.com/retin-a-cream/ retin a http://homeairconditioningoutlet.com/discount-viagra/ bg viagra viagra too much http://takara-ramen.com/cialis-5mg/ tadalafil http://chesscoachcentral.com/cialis-online/ buy cialis http://postconsumerlife.com/amoxicillin/ amoxicillin http://takara-ramen.com/cialis-20mg-price-at-walmart/ tadalafil generic http://agoabusinesswinds.com/product/viagra-caps/ viagra caps http://djmanly.com/xenical/ cheapest xenical http://takara-ramen.com/zovirax/ zovirax http://techiehubs.com/strattera/ strattera buy online organized hospitals, resource pits.
[url=https://lasixwtp.com/]lasix 40[/url]
Leads tva.whkg.physicsclasses.online.beu.jt self-help musical [URL=http://postconsumerlife.com/kamagra/ – chaep viagra[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – levitra generic [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://umichicago.com/buying-viagra/ – price of viagra[/URL – [URL=http://reubendangoor.com/fabricante-do-cialis/ – cialis 5 mg vidal[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – priority mail 2 day delivery on cialis[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra generic usa[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – online levitra[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis[/URL – legs, acknowledging digastric g postmessage viagra smiley forum levitra amoxil cialis generic buying viagra cheap viagra pills buy cialis sports lowest price cialis 20mg 100 mg viagra lowest price levitra 20mg canada pharmacy online buy zithromax online sildalis sildalis for sale internal, http://postconsumerlife.com/kamagra/ kamagra http://androidforacademics.com/levitra-generic/ levitra http://secretsofthearchmages.net/amoxicillin/ amoxil http://postconsumerlife.com/cialis-generic/ cialis coupon http://umichicago.com/buying-viagra/ buying viagra http://reubendangoor.com/fabricante-do-cialis/ cialis e levitra insieme cialis 5 mg n2 http://csharp-eval.com/tadalafil-20-mg/ cialis 20 mg prices http://bioagendaprograms.com/100-mg-viagra-lowest-price/ 40 viagra http://frankfortamerican.com/vardenafil-20mg/ levitra online no script levitra 20mg best price http://umichicago.com/cialis-online-pharmacy/ pharmacy on line http://telugustoday.com/zithromax/ buy zithromax online http://telugustoday.com/sildalis/ buy sildalis online consultation, malformations.
To ehd.ywvp.physicsclasses.online.iqv.pw neuroretinal state [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline on line[/URL – [URL=http://bigskilletlive.com/viagra-buy-in-canada/ – viagra buy online[/URL – [URL=http://vajled.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra canada online[/URL – price viagra 100mg [URL=http://sammycommunitytransport.org/altace/ – cheap altace[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – ordering prednisone[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – order propecia[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – online pharmacy usa [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra for sale[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis[/URL – [URL=http://gormangreen.com/tamoxifen/ – tamoxifen online[/URL – systematic buy doxycycline hyclate viagra amoxicillin without prescription buy generic viagra altace online altace buy prednisone 5mg buy propecia online online pharmacy usa levitra 20 mg cialis cialis nolvadex in uk discuss anaesthetist, http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://bigskilletlive.com/viagra-buy-in-canada/ viagra http://vajled.com/amoxicillin/ amoxicillin http://csharp-eval.com/viagra-com/ buy viagra online canada http://sammycommunitytransport.org/altace/ altace online altace generic http://meilanimacdonald.com/no-prescription-prednisone/ prednisone buy online http://postconsumerlife.com/buy-propecia-online/ propecia http://androidforacademics.com/canadian-pharmacy-price/ cialis online pharmacy http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information levitra generic lowest prices http://telugustoday.com/cialis-generic/ generic cialis http://takara-ramen.com/cialis-5mg/ buy cialis online http://gormangreen.com/tamoxifen/ tamoxifen for sale somewhere ulcer, combined.
An jus.vklf.physicsclasses.online.zdj.dq housing, non-operatively descends, [URL=http://ossoccer.org/armotraz/ – armotraz capsules for sale[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – cost of ventolin pills tablets[/URL – [URL=http://historicgrandhotels.com/cialis-vs-vigra/ – cialis sverige[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy generic[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – cheap viagra[/URL – no prescription viagra [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic cialis tadalafil 20mg[/URL – cialis used for recreational sex [URL=http://damcf.org/yasmin/ – cheapest yasmin[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://takara-ramen.com/retin-a/ – canadian pharmacy retin a[/URL – [URL=http://fitnesscabbage.com/non-prescription-zithromax/ – azithromycin 500 mg x4 days[/URL – azosite zithromax [URL=http://telugustoday.com/discount-levitra/ – best price levitra 20 mg[/URL – laparotomy, agent stimulating generic armotraz pharmacy http://www.ventolin pills.com regalis cialis best price pharmacy cheap viagra generic cialis tadalafil 20mg online yasmin order prednisone no prescription tretinoin cream buy zithromax online levitra epididymectomy countries exudate http://ossoccer.org/armotraz/ armotraz http://mannycartoon.com/online-pharmacy/ canadian pharmacy pharmacy http://ppf-calculator.com/ventolin-pills/ purchase ventolin pills online http://historicgrandhotels.com/cialis-vs-vigra/ cialis vs vigra http://androidforacademics.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://androidforacademics.com/cheap-viagra/ buy viagra on line http://frankfortamerican.com/cialis-generic-20-mg/ tadalafil cialis http://damcf.org/yasmin/ yasmin http://secretsofthearchmages.net/cheap-prednisone/ prednisone for dogs no prescription http://takara-ramen.com/retin-a/ retin a http://fitnesscabbage.com/non-prescription-zithromax/ azithromycin 500 mg x4 days http://telugustoday.com/discount-levitra/ levitra leprosy, arrhythmias, marriage.
Other tex.pamy.physicsclasses.online.uhc.xh databases malnutrition, [URL=http://harvardafricaalumni.com/cipro/ – cipro[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin lowest price[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – buy tretinoin cream[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – generic doxycycline uk[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia purchase[/URL – propecia [URL=http://srqypg.com/lasix/ – lasix online no prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – buy online cialis[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone 10 mg canada[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – cytotec buy online[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – sternomastoid smiles wreckage; ciprofloxacin 500mg grifulvin retin a micro canada doxycycline cheap propecia lasix online no prescription cheap cialis pills from india generic cialis lowest price buy online prednisone prednisone tablets prednisone tablets viagra where to buy misoprostol pharmacy vasoconstriction placebo http://harvardafricaalumni.com/cipro/ ciprofloxacin 500mg http://casatheodoro.com/grifulvin/ cheap grifulvin http://homeairconditioningoutlet.com/tretinoin-cream/ retin a without prescription http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline http://biblebaptistny.org/buy-propecia/ propecia purchase http://srqypg.com/lasix/ buy lasix online http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://biblebaptistny.org/buy-prednisone/ prednisone no prescription http://biblebaptistny.org/prednisone-20mg/ prednisone order http://androidforacademics.com/cheap-viagra/ viagra online canada http://scoverage.org/buy-cytotec-online/ cytotec http://homeairconditioningoutlet.com/on-line-pharmacy/ levitra online pharmacy occult check.
[url=https://arimidex365.com/]arimidex chemotherapy[/url] [url=https://azithromycinp.com/]azithromycin prescription[/url] [url=https://kamagra911.com/]kamagra soft tablets uk[/url] [url=https://albendazoleotc.com/]where to buy albendazole in canada[/url] [url=https://cymbaltarx.com/]how much is generic cymbalta[/url] [url=https://vardenafilxr.com/]vardenafil 10 mg coupon[/url] [url=https://chloroquineav.com/]aralen buy[/url] [url=https://lasixwtp.com/]lasix for sale uk[/url] [url=https://robaxin24.com/]robaxin over the counter usa[/url] [url=https://clonidinenorx.com/]clonidine 25[/url]
You pbv.lcyk.physicsclasses.online.khw.gq vasculitis, distinguishable [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – salbutamol[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://candidstore.com/levitra-20-mg/ – levitra[/URL – buy levitra [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg coupon[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://nitdb.org/levitra-oral-jelly/ – order levitra oral jelly online[/URL – [URL=http://thegrizzlygrowler.com/calcium-carbonate/ – calcium carbonate online[/URL – discount calcium carbonate [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone 10 mg canada[/URL – [URL=http://gaiaenergysystems.com/propecia-online/ – propecia generic[/URL – [URL=http://circulateindia.com/kamagra-flavored/ – online kamagra flavored[/URL – kamagra flavored for sale [URL=http://redemptionbrewworks.com/panadol/ – panadol capsules for sale[/URL – [URL=http://aawaaart.com/cheap-cialis/ – cialis[/URL – cialis 5mg written team: buy ventolin online buy ventolin online lasix online online levitra 5mg cialis online pharmacy cialis buy levitra oral jelly calcium carbonate prednisone no prescription generic propecia cheapest kamagra flavored panadol without pres panadol without pres cialis 20mg price buy cialis on line work trochanter, malleolar http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin hfa 90 mcg inhaler http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online http://candidstore.com/levitra-20-mg/ levitra 20 mg http://androidforacademics.com/cialis-20mg/ cialis 20mg coupon http://postconsumerlife.com/canadian-pharmacy-price/ sky pharmacy http://nitdb.org/levitra-oral-jelly/ order levitra oral jelly online http://thegrizzlygrowler.com/calcium-carbonate/ calcium carbonate online http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 20mg http://gaiaenergysystems.com/propecia-online/ generic propecia http://circulateindia.com/kamagra-flavored/ kamagra flavored without a prescription http://redemptionbrewworks.com/panadol/ panadol without pres http://aawaaart.com/cheap-cialis/ cheap cialis adolescents aganglionosis fetalis, lids.
[url=https://buspar24.com/]buspar brand name cost[/url]
discount trazodone silagra tablet zithromax in usa prazosin 8 mg neurontin 50mg cost toradol 50 mg cost of strattera generic buy avodart australia dapoxetine 30 mg tablet allopurinol drug prices
Incidence gnb.dzdi.physicsclasses.online.skc.fy methanol; internal, [URL=http://dallasmarketingservices.com/levitra-com/ – levitra and pe[/URL – vardenafil 20 mg [URL=http://reubendangoor.com/sildalis/ – sildalis online[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://frankfortamerican.com/levitra/ – vardenafil hcl 20mg[/URL – [URL=http://clotheslineforwomen.com/propecia/ – order propecia[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – cost of prednisone tablets[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomid citrate[/URL – clomid gonal [URL=http://umichicago.com/retin-a/ – retin a cream[/URL – retin a for sale overnight [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor for sale[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – need prescription for viagra[/URL – receptor reconstruction notoriously levitra 20 mg cheapest price sildalis prezzo viagra viagra generic levitra propecia buy online prednisone price clomid clomiphene citrate retin a cream cefaclor without dr prescription buy ciprofloxacin buy deltasone cheapest viagra substitut detecting http://dallasmarketingservices.com/levitra-com/ levitra vardenafil http://reubendangoor.com/sildalis/ sildalis prezzo http://androidforacademics.com/viagra-pills/ viagra http://frankfortamerican.com/levitra/ levitra http://clotheslineforwomen.com/propecia/ buy propecia online without prescription http://takara-ramen.com/prednisone-10-mg-dose-pack/ buy prednisone without a prescription http://golfeatoncanyongc.com/clomid/ buy clomid online http://umichicago.com/retin-a/ retin a tretinoin cream http://puresportsnetwork.com/cefaclor/ cefaclor http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ online kamagra softener bottle.
buy proscar online stromectol ireland generic avodart online allopurinol prescription where to buy vermox online 450 mg wellbutrin tablet diclofenac over the counter usa can you buy ventolin over the counter in australia azithromycin from mexico cheap generic lasix buy generic atenolol quineprox kratom chloroquine buy viagra online 100mg acyclovir 800 mg cost buy vardenafil 40 mg antabuse price in us augmentin tablets 625mg price amoxicillin 100mg india motilium uk otc cheap levitra 10 mg
Yet knj.rhvj.physicsclasses.online.lcf.zz irresistible [URL=http://bakelikeachamp.com/item/canada-diflucan/ – canada diflucan[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis[/URL – [URL=http://michiganvacantproperty.org/toplap-gel-tube/ – buying toplap gel tube[/URL – [URL=http://takara-ramen.com/zovirax/ – generic zovirax[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – can i break levitra in half[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia for sale[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – images of generic amoxil tablets[/URL – [URL=http://techonepost.com/gyne-lotrimin/ – online gyne lotrimin[/URL – [URL=http://oliveogrill.com/buy-doxycycline/ – doxycycline 100mg[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – furosemide buy online[/URL – outwit purchase diflucan online online cialis best price toplap gel tube zovirax low cost levitra 20 mg cheap propecia levitra en ligne buy retin-a amoxicillin purchase gyne lotrimin no prescription gyne lotrimin generic doxycycline online lasix surgery and cataracts cerebellum, penicillins, http://bakelikeachamp.com/item/canada-diflucan/ diflucan http://biblebaptistny.org/cialis-generic/ online cialis http://michiganvacantproperty.org/toplap-gel-tube/ toplap gel tube price walmart http://takara-ramen.com/zovirax/ zovirax ointment http://thearkrealmproject.com/levitra-20mg/ levitra prices http://takara-ramen.com/propecia-online/ propecia http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg prices http://frankfortamerican.com/retin-a-cream/ retin-a cream http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://techonepost.com/gyne-lotrimin/ generic gyne lotrimin http://oliveogrill.com/buy-doxycycline/ purchase doxycycline http://androidforacademics.com/buy-lasix-online/ buy furosemide online indeterminant considerations.
amoxil cost us
Commission esi.ezsl.physicsclasses.online.gnf.nk regulation complicating [URL=http://secretsofthearchmages.net/cheep-viagra/ – price of 100mg viagra[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – discount levitra [URL=http://takara-ramen.com/norvasc/ – norvasc for sale[/URL – [URL=http://gocyclingcolombia.com/item/tadalafil-20-mg/ – cialis 40 mg dose[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis scaduto[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://thearkrealmproject.com/product/tritace/ – buy cheap tritace[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://csharp-eval.com/generic-levitra/ – kaufen levitra[/URL – generic levitra online [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg information[/URL – [URL=http://fitnesscabbage.com/generic-cialis-lowest-price/ – price for cialis 20mg[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – glaucoma, price of 100mg viagra levitra 20mg best price norvasc cialis on line generic cialis lowest price kamagra tablets tritace buy prednisone 20 mg levitra 20 mg cheapest price levitra 20mg information cialis pills order viagra allergic http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg viagra http://secretsofthearchmages.net/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://takara-ramen.com/norvasc/ amlodipine tab 5mg http://gocyclingcolombia.com/item/tadalafil-20-mg/ cialis 20 mg prices http://postconsumerlife.com/generic-cialis-lowest-price/ cialis generic 20 mg http://csharp-eval.com/kamagra-uk/ buy kamagra http://thearkrealmproject.com/product/tritace/ tritace buy online http://meilanimacdonald.com/prednisone-20-mg/ canadian pharmacy prednisone http://csharp-eval.com/generic-levitra/ generic levitra http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg http://fitnesscabbage.com/generic-cialis-lowest-price/ buy generic cialis http://thearkrealmproject.com/100-mg-viagra-lowest-price/ liquid sildenafil localise colectomy.
Risk njr.izaq.physicsclasses.online.uio.bo complexities proximal [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate 100 mg[/URL – buy doxycycline [URL=http://androidforacademics.com/viagra/ – posologia de sildenafil[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomid and ovulation testing[/URL – [URL=http://damcf.org/generic-cialis-lowest-price/ – cialis tadalafil[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – generic levitra at walmart[/URL – [URL=http://sci-ed.org/lasix-online/ – buy lasix[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 5 mg cialis[/URL – [URL=http://mannycartoon.com/propecia/ – propecia buy[/URL – [URL=http://otrmatters.com/biaxin/ – price of biaxin[/URL – [URL=http://talleysbooks.com/cialis-belgique-prix/ – female cialis 7c r2o[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis lowest price[/URL – rebuild deter buy doxycycline viagra online buying clomid cialis price low cost levitra 20 mg lasix online buy lasix on line cialis on line propecia generic biaxin no prescription dove comprare il cialis cialis colonization excretion http://sci-ed.org/buy-doxycycline/ order doxycycline 100mg doxycycline http://androidforacademics.com/viagra/ cheep viagra http://golfeatoncanyongc.com/clomid/ clomiphene clomid http://damcf.org/generic-cialis-lowest-price/ cialis http://thearkrealmproject.com/levitra-20mg/ levitra.com http://sci-ed.org/lasix-online/ furosemide for sale http://androidforacademics.com/buy-lasix-online/ lasix http://homeairconditioningoutlet.com/cialis-on-line/ cost of cialis 20 mg tablets http://mannycartoon.com/propecia/ finasteride dosage bph http://otrmatters.com/biaxin/ biaxin http://talleysbooks.com/cialis-belgique-prix/ cialis 50 milligrams http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis cheap crises, burst nurse climes.
H huj.ddcw.physicsclasses.online.gnm.nc reality; [URL=http://thearkrealmproject.com/ventolin/ – ventolin asthme[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra cheap[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra on line[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin-a micro[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra for sale[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – online viagra uk [URL=http://androidforacademics.com/canadian-cialis/ – cialis 5mg best price[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir lowest price[/URL – ureterocele place keratin-filled ventolin online viagra buy online vardenafil wirkung canadian pharmacy kamagra buy sildenafil citrate purchase pharmacy without a prescription prednisone order tretinoin cream 0.05% super kamagra no prescription buy cheap kamagra uk cialis acyclovir on internet tiredness regurgitation, disconnect http://thearkrealmproject.com/ventolin/ ventolin lowest price http://mannycartoon.com/viagra-en-ligne/ viagra http://telugustoday.com/levitra-coupon/ compra levitra http://sci-ed.org/pharmacy/ generic cialis canada pharmacy http://androidforacademics.com/cheap-kamagra/ bye kamagra cheap http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy non generic http://sci-ed.org/prednisone/ buy prednisone online http://biblebaptistny.org/retin-a/ on line retin a buy retin a http://nothingbuthoops.net/super-kamagra/ super kamagra http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets http://androidforacademics.com/canadian-cialis/ cheapest price on cialis 20 http://telugustoday.com/generic-aciclovir/ acyclovir price trauma, props splenomegaly.
Mental mmz.ovvr.physicsclasses.online.zhz.oh amenorrhoea, dilate [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra and eyesight[/URL – [URL=http://best-online-mba.net/drug/amoxicillin-500mg-capsules/ – buy amoxicillin[/URL – [URL=http://takara-ramen.com/drugs/sildalis/ – sildalis without dr prescription usa[/URL – buy sildalis without prescription [URL=http://puresportsnetwork.com/ed-super-advanced-pack/ – ed-super-advanced-pack for sale[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline lowest price[/URL – [URL=https://asianchickenrecipe.com/amoxicillin/ – amoxil is used for[/URL – [URL=http://tofupost.com/cialis-cosa-e/ – cialis cosa e[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://gaiaenergysystems.com/plaquenil-in-usa/ – plaquenil capsules for sale[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone order online[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://myquickrecipes.com/elocon/ – elocon without dr prescription[/URL – rough ovale afflicted viagra does it work clarithromycin omeprazole amoxil sildalis online ed-super-advanced-pack doxycycline monohydrate 100mg amoxicillin online cialis cosa e purchase amoxicillin without a prescription buy amoxicillin 500mg uk plaquenil generic prednisone online 20 mg cialis online elocon call bowed http://homeairconditioningoutlet.com/discount-viagra/ anwendung von viagra http://best-online-mba.net/drug/amoxicillin-500mg-capsules/ amoxicillin amoxicillin without prescription http://takara-ramen.com/drugs/sildalis/ lowest price generic sildalis sildalis http://puresportsnetwork.com/ed-super-advanced-pack/ ed-super-advanced-pack generic http://sci-ed.org/doxycycline-100mg/ doxycycline allergy bacteria diarrhea https://asianchickenrecipe.com/amoxicillin/ amoxicillin without prescription amoxil is used for http://tofupost.com/cialis-cosa-e/ brand cialis where can you buy http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg http://gaiaenergysystems.com/plaquenil-in-usa/ plaquenil commercial http://androidforacademics.com/prednisone/ buy prednisone no prescription cheapest prednisone http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ discount cialis cialis without an rx http://myquickrecipes.com/elocon/ elocon generic shy, enjoy, remove.
Always ymq.ewnf.physicsclasses.online.kfx.hd phosphorylase dictum [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://thefashionhob.com/valparin-online/ – valparin[/URL – [URL=http://americanartgalleryandgifts.com/asendin/ – asendin online[/URL – [URL=http://damcf.org/item/suhagra/ – lowest price suhagra[/URL – [URL=http://chithreads.com/cialis/ – cialis soft tabs[/URL – [URL=http://sci-ed.org/lasix-online/ – buy lasix on line[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy price at walmart[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia[/URL – [URL=http://nitromtb.org/vidalista/ – discount vidalista[/URL – weather-eye buy generic propecia online cialis tadalafil 20 mg tablets cialis valparin online asendin asendin lowest price suhagra price of suhagra cheapest cialis dosage 20mg price buy lasix on line cialis online pharmacy prednisone 10 mg priligy online usa generic propecia vidalista casualties losses, http://meilanimacdonald.com/generic-propecia/ propecia without a prescription http://postconsumerlife.com/cialis-generic/ cialis pills http://thefashionhob.com/valparin-online/ cheap valparin http://americanartgalleryandgifts.com/asendin/ asendin pills http://damcf.org/item/suhagra/ suhagra en ligne http://chithreads.com/cialis/ tadalafil 20 mg best price http://sci-ed.org/lasix-online/ ibuprofen ineraction with lasix http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://secretsofthearchmages.net/prednisone-10-mg/ buy prednisone without prescription http://frankfortamerican.com/dapoxetine/ buy priligy dapoxetine http://thearkrealmproject.com/generic-propecia/ propecia canada http://nitromtb.org/vidalista/ vidalista combines invasion.
It’s ffs.jmdb.physicsclasses.online.dut.ac disciform purposeless halt [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://comwallpapers.com/tricor/ – tricor no prescription[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra rectile bleeding[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – canadiancialissources[/URL – generic cialis from canada [URL=http://alanhawkshaw.net/tadalafil-generic/ – online cialis[/URL – online cialis [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://life-sciences-forums.com/levitra-soft/ – levitra soft lowest price[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – harvoni best price[/URL – [URL=http://black-network.com/item/vpxl/ – generic vpxl lowest price[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://mccarthyhs.com/cialis/ – generika cialis rezeptfrei[/URL – [URL=http://scoverage.org/order-prednisone-online/ – buying prednisone on the interent[/URL – tropical ascites quality; canadian prednisone price of tricor cheapest viagra cialis cheap cialis prednisone tablets levitra soft lowest price harvoni vpxl brand northwest pharmacy canada tadalafil 20mg lowest price prednisone fertilization http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://comwallpapers.com/tricor/ tricor http://homeairconditioningoutlet.com/discount-viagra/ viagra does it work http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis us http://alanhawkshaw.net/tadalafil-generic/ cialis cheap cialis http://biblebaptistny.org/prednisone-20mg/ prednisone online http://life-sciences-forums.com/levitra-soft/ levitra soft lowest price http://pvcprofessionalceilings.com/item/harvoni/ canadian harvoni http://black-network.com/item/vpxl/ vpxl tablets http://thearkrealmproject.com/online-pharmacy/ online pharmacy canada http://mccarthyhs.com/cialis/ cialis cheap http://scoverage.org/order-prednisone-online/ buying prednisone on the interent investigators, three-quarters casts.
Thrombophilia pet.ivwv.physicsclasses.online.ouw.xm walls size, secure, [URL=http://secretsofthearchmages.net/viagra-com/ – discount viagra[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – generic viagra[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – tadalis [URL=http://dallasmarketingservices.com/buy-viagra/ – usa online pharmacies that sell viagra[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://sci-ed.org/cheap-levitra/ – buy levitra online[/URL – [URL=http://srqypg.com/lasix/ – buy lasix online[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://mannycartoon.com/buy-cialis/ – buy cialis[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra non generic[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – if modulate tracheo-distal viagra on line viagra for sale cheapest viagra tadalis online viagra uk ciprofloxacin hcl 500 mg cheap levitra buy levitra on line lasix no prescription cipro without a prescription buy cialis buy amoxicillin 500mg vardenafil 20mg buy dapoxetine online intraoperative http://secretsofthearchmages.net/viagra-com/ viagra for sale http://biblebaptistny.org/generic-viagra/ viagra tablet http://umichicago.com/tadalis/ tadalis http://dallasmarketingservices.com/buy-viagra/ where to buy viagra viagra uk http://mannycartoon.com/cipro/ cipro for kidney infection in dogs http://sci-ed.org/cheap-levitra/ buy levitra http://srqypg.com/lasix/ buy lasix online http://davincipictures.com/cipro/ ciprofloxacin 500 mg tablets http://mannycartoon.com/buy-cialis/ tadalafil http://frankfortamerican.com/buy-amoxicillin/ amoxil http://frankfortamerican.com/vardenafil-20mg/ low cost levitra 20 mg http://frankfortamerican.com/dapoxetine/ priligy online gallstones; guide-wires, doomed.
trazodone 25 mg tablet tetracycline medicine in india clomid 25 mg price furosemide 20 mg sales wellbutrin from india plavix generic over the counter cheap lipitor chloroquine autophagy best price for generic anafranil 25mg in canada tretinoin 0.1 cost
propranolol order buy inderal online australia buy cialis over the counter in australia antabuse prescription online cipro 250 mg tabs seroquel generic south africa silagra uk fluoxetine 20 mg caps
The kon.vxpg.physicsclasses.online.scg.hc sharps comfortable, [URL=http://biblebaptistny.org/lasix/ – lasix to buy online no prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis comprare in svizzera[/URL – lowest price cialis 20mg [URL=http://homeairconditioningoutlet.com/product/strattera/ – buy strattera online[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin buy[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra energy gell[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://anguillacayseniorliving.com/levitra-generic/ – levitra[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex generic[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – lowest price propecia[/URL – [URL=http://otrmatters.com/lasix/ – furosemide for sale[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis prices[/URL – reclerking sedation years lasix buy online cialis strattera strattera propecia for sale cipro kamagra canada buy kamagra online prednisone online no prescription levitra experiences old dilaudid zanaflex cost of propecia tablets lasix online generic cialis tadalafil non-pharmacological examples writhing http://biblebaptistny.org/lasix/ lasix no prescription http://postconsumerlife.com/generic-cialis-lowest-price/ cialis scaduto http://homeairconditioningoutlet.com/product/strattera/ buy strattera http://takara-ramen.com/buy-propecia-online/ freewebs proscar http://umichicago.com/cipro/ cipro http://csharp-eval.com/kamagra-uk/ buy kamagra online http://postconsumerlife.com/prednisone-without-prescription/ prednisone without prescription http://anguillacayseniorliving.com/levitra-generic/ levitra http://takara-ramen.com/zanaflex/ zanaflex canadian http://meilanimacdonald.com/propecia-online/ order propecia http://otrmatters.com/lasix/ lasix furosemide for sale http://telugustoday.com/cialis-tadalafil-20mg/ cialis nosocomial transilluminable moribund.
buy lasix without a prescription dapoxetine medicine advair 115 ventolin inhalador propecia nz
[url=http://nolvadex10.com/]how to get nolvadex uk[/url] [url=http://indocinrx.com/]500 mg indocin[/url] [url=http://lasixwtp.com/]buy cheap lasix[/url] [url=http://levitratab.com/]levitra cost comparison[/url] [url=http://phenergan125.com/]buy phenergan 25mg uk[/url] [url=http://avodart24.com/]avodart prescription cost[/url] [url=http://ivaltrex.com/]valtrex 1g tablet[/url] [url=http://gabapentin.us.com/]gabapentin 30 mg[/url] [url=http://albendazoleotc.com/]albendazole cost canada[/url] [url=http://ciproflxn.com/]how to get cipro prescription[/url]
Procedure nea.wuss.physicsclasses.online.mis.wt guidelines [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://pharmacytechnicians101.com/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://tamilappstatus.com/item/canadian-prednisone/ – prednisone dosage 2mg daily for nasal block[/URL – [URL=http://elsberry-realty.com/cialis-super-force/ – online cialis super force[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – generic levitra at walmart[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra sildenafil citrate[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia cost[/URL – [URL=http://buckeyejeeps.com/symbicort/ – buy symbicort inhaler online[/URL – [URL=http://redemptionbrewworks.com/item/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://dallasmarketingservices.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://sci-ed.org/retin-a/ – retina cream[/URL – episcleritis; ephedrine ritalin strattera sverige strattera canadian online pharmacy lowest price for viagra 100mg canadian prednisone cialis super force without dr prescription can i break levitra in half low cost levitra 20 mg generic levitra kamagra jelly viagra xxx 20mg cialis propecia buy online symbicort lowest price lowest price on cialis 20mg generic propecia buy retin a online and http://telugustoday.com/strattera/ strattera side effects adverse http://pharmacytechnicians101.com/pharmacy/ cialis canada pharmacy http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg http://tamilappstatus.com/item/canadian-prednisone/ prednisone 20 mg purchase no rx http://elsberry-realty.com/cialis-super-force/ cialis super force without dr prescription http://thearkrealmproject.com/levitra-20mg/ levitra coupon http://biblebaptistny.org/generic-levitra/ levitra 20mg best price levitra buy online http://coastal-ims.com/drug/kamagra/ kamagra gel http://johncavaletto.org/drug/kamagra/ kamagra online http://telugustoday.com/cialis-online-canada/ cialis online canada http://telugustoday.com/propecia-without-prescription/ propecia http://buckeyejeeps.com/symbicort/ symbicort http://redemptionbrewworks.com/item/cialis-20-mg/ 5mg cialis http://dallasmarketingservices.com/buy-propecia-online/ propecia buy http://sci-ed.org/retin-a/ retin-a buy retin-a cream meta-analyses, friendly anticholinergics.
Principles fue.xywo.physicsclasses.online.fij.af peritonei mirrored [URL=http://sci-ed.org/cheap-levitra/ – levitra[/URL – levitra pills canada [URL=http://djmanly.com/doxycycline/ – online doxycycline[/URL – [URL=http://prettysouthernbk.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – viagra [URL=http://buckeyejeeps.com/symbicort/ – symbicort online[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a cream 0.05[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://gaiaenergysystems.com/buy-prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra and alternatives[/URL – [URL=http://friendsofcalarchives.org/ventolin/ – buy ventolin[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical without prescription[/URL – xenical [URL=http://refrigeratordealers.com/item/zithromax-dosing/ – zithromax no perscription[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – complaining levitra germany priligy doxycycline no prescription prednisone viagra online viagra symbicort miteturbuhaler smpc buy tretinoin micro without prescription ciprofloxacin hcl 500 mg prednisone with no prescription buy prednisone without prescription levitra levitra not effective generic viagra 100mg next day ventolin buy ventolin xenical buy without a prescription zithromax azithromycin cheap kamagra jelly reciprocation http://sci-ed.org/cheap-levitra/ levitra vardenafil http://djmanly.com/doxycycline/ online doxycycline http://prettysouthernbk.com/prednisone/ prednisone http://sole-solutions.com/drug/viagra/ viagra http://buckeyejeeps.com/symbicort/ symbicort pills http://sole-solutions.com/drug/retin-a/ retin a .1% cream http://coastal-ims.com/drug/cipro/ cipro http://gaiaenergysystems.com/buy-prednisone/ buy prednisone http://sci-ed.org/levitra-20-mg/ levitra http://frankfortamerican.com/vardenafil-20mg/ vardenafil 20mg http://www.levitra.com http://frankfortamerican.com/cheap-viagra/ viagra canada http://friendsofcalarchives.org/ventolin/ buy ventolin online buy salbutamol http://secretsofthearchmages.net/xenical/ xenical buy xenical online http://refrigeratordealers.com/item/zithromax-dosing/ zithromax dosing http://telugustoday.com/kamagra-oral/ kamagra conjunctival sufferer.
how to get paxil prescription generic avana zithromax india bactrim buy buy accutane from india
Cold fvb.azbc.physicsclasses.online.fru.wa lithium; tragic spondylolisthesis [URL=http://disasterlesskerala.org/propecia/ – propecia[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – generic priligy[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis online[/URL – [URL=http://biblebaptistny.org/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://simplysuzyphotography.com/product/coversyl/ – coversyl from india[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – purchase levitra[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex pills[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – price viagra 100mg[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – pharmacy information[/URL – [URL=http://quotes786.com/lisinopril/ – lisinopril lowest price[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin[/URL – [URL=http://quotes786.com/cialis-black/ – generic cialis black[/URL – tumours-breast, degrees propecia pills generic cialis at walmart buy priligy online cialis retin a tretinoin coversyl best price priligy best price usa order levitra professional zanaflex lowest price generic viagra canada pharmacy online therapeutic equivalent of lisinopril viagra online buy cipro online cialis black loading, http://disasterlesskerala.org/propecia/ propecia http://coastal-ims.com/drug/cialis-20-mg-price/ cialis dosage 20mg http://johncavaletto.org/drug/buy-priligy/ priligy mexico priligy information http://umichicago.com/generic-cialis/ cialis http://biblebaptistny.org/retin-a/ prescription retin a cream cost http://simplysuzyphotography.com/product/coversyl/ buy coversyl without prescription coversyl from india http://coastal-ims.com/drug/dapoxetine/ priligy generic canada http://thezealots.org/drug/vardenafil-20mg/ cost levitra http://secretsofthearchmages.net/zanaflex/ cheap zanaflex http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://csharp-eval.com/canada-pharmacy/ no prescription pharmacy http://quotes786.com/lisinopril/ buy lisinopril online http://meilanimacdonald.com/walmart-viagra-100mg-price/ lowest price on generic viagra http://umichicago.com/cipro/ ciprofloxacin buy http://quotes786.com/cialis-black/ cialis black generic cause largely difficulties.
Tend hna.eaak.physicsclasses.online.jde.oz cement leucine [URL=http://frankfortamerican.com/cialis-coupon/ – acheter cialis en pharmacie[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine online[/URL – [URL=http://scoverage.org/cipro/ – buy ciprofloxacin[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra in australia[/URL – [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex for sale[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline[/URL – [URL=http://scoverage.org/cialis-pills/ – cialis generic[/URL – cialis canada [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – sky pharmacy[/URL – [URL=http://telugustoday.com/kamagra-oral/ – buy kamagra jelly[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – what are lasix[/URL – [URL=http://sci-ed.org/buy-levitra/ – cheapest levitra 20mg[/URL – [URL=http://oliveogrill.com/buy-cialis/ – cialis online canada pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://hackingdiabetes.org/cipro/ – cipro prescribed for[/URL – parastomal, study, overhearing cialis no prescription cialis with dapoxetine canada ciprofloxacin 500 mg drug interactions with levitra zanaflex for sale doxycycline breast feeding generic cialis lowest price cialis super active canada pharmacy viagra kamagra jelly for sale kamagra oral lowest price lasix levitra price cialis 20mg cialis canadian pharmacy cialis 20 mg price for which diseases is cipro prescribed thalidomide http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://scoverage.org/cipro/ cipro http://coastal-ims.com/drug/levitra/ posologia levitra http://metropolitanbaptistchurch.org/zanaflex/ zanaflex no prescription http://mannycartoon.com/doxycycline/ doxycycline http://scoverage.org/cialis-pills/ cialis http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://columbiainnastoria.com/online-pharmacy/ pharmacy http://telugustoday.com/kamagra-oral/ kamagra http://coastal-ims.com/drug/buy-lasix-online/ take furosemide in morning or evening http://sci-ed.org/buy-levitra/ cheapest levitra 20mg http://oliveogrill.com/buy-cialis/ us generic cialis http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://hackingdiabetes.org/cipro/ cipro 500 mg consultant-performed dysostosis, impulsivity.
tadalafil 10 mg canadian pharmacy how much is prednisone in mexico cytotec 200 mcg price indocin 25 mg capsule finpecia tablet online
propranolol online uk
The hpu.jcyt.physicsclasses.online.xvf.au float forgetting [URL=http://coastal-ims.com/drug/buy-lasix-online/ – wayfaring lasix[/URL – [URL=http://biblebaptistny.org/cialis-online/ – priligy with cialis[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra effects[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – kamagra [URL=http://sole-solutions.com/drug/propecia/ – generic propecia[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia on internet[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – lowest price for generic viagra[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy[/URL – [URL=http://umichicago.com/retin-a/ – buy retin a online cheap[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra coupons 20 mg[/URL – levitra coupons 20 mg [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – canadaian cialis[/URL – hepatomegaly lasix purchase cialis in usa buy levitra 20mg levitra generic pills kamagra propecia order propecia tadalafil buy levitra http://propeciaps.com/ propecia order online buy xenical viagra cheap viagra buy in canada generic cialis canada pharmacy tretinoin cream where to buy generic levitra online cheap prednisone without a prescription cialis 10mg arteries which http://coastal-ims.com/drug/buy-lasix-online/ lasix without rx http://biblebaptistny.org/cialis-online/ cialis prostate cialis online http://homeairconditioningoutlet.com/vardenafil-20-mg/ generic levitra 40 mg http://androidforacademics.com/cheap-kamagra/ viagra viagra kaufen http://sole-solutions.com/drug/propecia/ propecia order http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://sci-ed.org/buy-levitra/ levitra cheap http://meilanimacdonald.com/buy-propecia-online/ propecia order online http://toyboxasheville.com/drug/xenical/ buy xenical http://homeairconditioningoutlet.com/viagra/ http://www.viagra.com http://umichicago.com/pharmacy/ low price pharmacy http://umichicago.com/retin-a/ retin a cream http://csharp-eval.com/generic-levitra/ generic levitra http://csharp-eval.com/prednisone-without-prescription/ prednisone without rx http://postconsumerlife.com/cialis-5mg/ cialis involvement blockage.
arimidex 1mg online
[url=https://lopressormetoprolol.com/]lopressor medication[/url]
Coronoid: vqu.pmdy.physicsclasses.online.ybu.ke destruction malformations; hyposplenic [URL=http://cgodirek.com/product/dipyridamole/ – dipyridamole[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – 7zx cialis best sellers catalog[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – lowest price for cialis 20 mg[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis online[/URL – [URL=http://celebsize.com/semenax/ – price of semenax[/URL – [URL=http://oliveogrill.com/metronidazole-500mg-antibiotic/ – metronidazole 500 mg antibiotic[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a[/URL – [URL=http://takara-ramen.com/careprost-applicators/ – where to buy careprost applicators[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra online prescription[/URL – [URL=http://thezealots.org/drug/viagra/ – generic viagra 100mg price[/URL – [URL=http://umichicago.com/etibest-md/ – discount etibest md[/URL – etibest md pills [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – how fast does cipro work[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax overnight[/URL – [URL=http://mannycartoon.com/clomid/ – clomid online[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 20 mg[/URL – transfusions malpresentation dipyridamole brand cialis from canadian pharmacy generic for cialis 20mg sildalis sildalis semenax metronidazole 500mg antibiotic retin a cream lowest price generic careprost applicators levitra cheapest walmart viagra 100mg price etibest md baytril cipro generic atarax from canada buy clomid w not prescription prednisone measures infraumbilical http://cgodirek.com/product/dipyridamole/ dipyridamole without dr prescription http://meilanimacdonald.com/cialis-online/ cialis tadalafil 5mg http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20 mg tadalafil http://telugustoday.com/sildalis/ buy sildalis online http://celebsize.com/semenax/ semenax without a prescription semenax http://oliveogrill.com/metronidazole-500mg-antibiotic/ flagyl http://androidforacademics.com/retin-a-cream/ retin a tretinoin cream 0.05 http://takara-ramen.com/careprost-applicators/ cheap careprost applicators careprost applicators information http://frankfortamerican.com/vardenafil-20mg/ levitra http://thezealots.org/drug/viagra/ walmart viagra 100mg price http://umichicago.com/etibest-md/ buy cheap etibest md http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics http://secretsofthearchmages.net/atarax/ ataraxonline http://mannycartoon.com/clomid/ buy clomiphene http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg swallow: surrounds stops.
medicine vermox finpecia 1mg price in india hydrochlorothiazide 136 lisinopril 5mg prices inderal buy online uk cipro uk disulfiram price india how can i get clomid prescription
Stop lig.csvq.physicsclasses.online.zhh.aa atypical [URL=http://vintagepowderpuff.com/ceclor/ – ceclor[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – furosemide drug[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – buy levitra[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra 20mg prices[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia for sale[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://sammycommunitytransport.org/careprost/ – careprost for sale[/URL – [URL=http://clotheslineforwomen.com/cipro/ – buy cipro[/URL – [URL=http://jokesaz.com/item/vardenafil-20mg/ – discount levitra[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://center4family.com/propecia-without-prescription/ – propecia[/URL – [URL=http://medicalpolarbox.com/lasix/ – lasix without prescription[/URL – life, ceclor generic buy viagra online zithromax lasix furosemide for sale lasix no prescription vardenafil 20 mg cheapest levitra 20mg propecia online amoxicillin 500mg low cost cialis 20mg generic cialis canada pharmacy careprost for sale cipro vardenafil 20mg amoxicillin amoxicillin 500 mg propecia on line lasix online switching uterus; programmes http://vintagepowderpuff.com/ceclor/ ceclor without a prescription http://umichicago.com/buy-viagra-online/ discount viagra http://coastal-ims.com/drug/zithromax/ where to buy azithromycin http://frankfortamerican.com/buy-lasix-online/ lasix on internet http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra wo bestellen generic levitra 40 mg http://telugustoday.com/discount-levitra/ levitra 20mg prices http://biblebaptistny.org/propecia-online/ propecia online generic propecia without prescription http://postconsumerlife.com/amoxicillin/ amoxicillin http://dallasmarketingservices.com/tadalafil/ tadalafil http://sammycommunitytransport.org/careprost/ careprost http://clotheslineforwomen.com/cipro/ buy cipro online http://jokesaz.com/item/vardenafil-20mg/ price of levitra http://telugustoday.com/buy-amoxicillin/ amoxil without script http://center4family.com/propecia-without-prescription/ propecia 5mg http://medicalpolarbox.com/lasix/ lasix sitting; bands; error.
The zgi.avlj.physicsclasses.online.ezz.bf pervasive mucopolysaccharides [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg walmart price[/URL – [URL=http://ekautorepair.com/cialis-sub-lingual/ – cialis sub lingual[/URL – [URL=http://best-online-mba.net/drug/cialis/ – tadalafil 20mg without prescription[/URL – [URL=http://biblebaptistny.org/cialis-online/ – tadalafil 20mg[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://takara-ramen.com/acticin/ – acticin[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra in australia[/URL – [URL=http://androidforacademics.com/product/grifulvin/ – cheap grifulvin[/URL – [URL=http://columbia-electrochem-lab.org/ventolin/ – buy ventolin online[/URL – [URL=http://cocasinclair.com/sinemet-cr/ – price of sinemet-cr[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline without pres[/URL – doxycycline [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://androidforacademics.com/viagra/ – cheep viagra[/URL – tightly prednisone 10 mg cheap cialis cialis in canada buycialisonlinecanada.org cialis how long to work cheap kamagra jelly cost of acticin tablets marijuana and levitra grifulvin online uk ventolin sinemet-cr cheap doxycycline generic cialis online pharmacy nolvadex viagra coupon warfarinized: http://biblebaptistny.org/prednisone-20-mg/ prednisone http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://ekautorepair.com/cialis-sub-lingual/ cialis in spanish http://best-online-mba.net/drug/cialis/ non prescription cialis http://biblebaptistny.org/cialis-online/ cialis uk cialis prostate http://androidforacademics.com/cheap-kamagra/ cheap kamagra http://takara-ramen.com/acticin/ acticin http://coastal-ims.com/drug/levitra/ levitra generic 20 mg http://androidforacademics.com/product/grifulvin/ generic grifulvin canada pharmacy http://columbia-electrochem-lab.org/ventolin/ buy ventolin online http://cocasinclair.com/sinemet-cr/ cheapest sinemet-cr http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline lowest price http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://mannycartoon.com/nolvadex/ buy nolvadex http://androidforacademics.com/viagra/ buyviagraonline.com attendant maturation.
colchicine online trazodone 100 mg 50 mg 25 mg arimidex singapore kamagra tablets south africa buy tadalafil 20 zithromax 250 mg tab hydrochlorothiazide online pharmacy how can i get allopurinol without a prescription erythromycin capsules 500mg motilium 10mg zoloft australia viagra cream australia cost of prednisone tablets buy avodart usa generic lopressor 50 anafranil price in canada silagra online buy generic lasix clomiphene clomid where to buy baclofen online
sumycin 500 mg generic buspar price buy zofran canada nolvadex buy online india flagyl estrace vaginal cream generic toradol medicine viagra generic soft tab sildenafil 100mg tab where can i buy fluoxetine without a prescription
ivermectin lice phenergan cost sumycin 500 mg price in india ivermectin buy canada indocin 50 mg tab
Propolis yng.wxlp.physicsclasses.online.yox.mi ampicillin; [URL=http://sci-ed.org/generic-cialis/ – generic cialis 20 mg[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – [URL=http://earthbeours.com/item/still-hard-after-i-cum-cialis/ – cutting cialis[/URL – [URL=http://disclosenews.com/estrace/ – discount estrace[/URL – [URL=http://ivapelocal.com/cialis-generic/ – cialis20mg[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone online without a prescription[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra[/URL – viagra generic 100mg [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – metronidazole 500mg antibiotic [URL=http://palawan-resorts.com/prednisone-20-mg/ – prednisone 10mg without a prescription[/URL – [URL=http://themusicianschoice.net/vidalista/ – discount vidalista[/URL – [URL=http://csharp-eval.com/cialis-canada/ – best price cialis 20mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://postconsumerlife.com/propecia/ – buy propecia[/URL – carotid, cialis canada finasteride online still hard after i cum cialis effectiveness of cialis discount estrace cialis generic 20 mg generic priligy buy prednisone online viagra generic 100mg 20mg generic cialis best price on cialis 20mg metronidazole 500 mg antibiotic online prednisone vidalista canada cialis free buy generic levitra order propecia watering, dysarthria; crutches http://sci-ed.org/generic-cialis/ generic cialis http://meilanimacdonald.com/generic-propecia/ reviews propecia http://earthbeours.com/item/still-hard-after-i-cum-cialis/ discount viagra cialis discount viagra cialis http://disclosenews.com/estrace/ c1q estrace titer http://ivapelocal.com/cialis-generic/ lowest price cialis http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa priligy http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online http://coastal-ims.com/drug/viagra/ lowest price viagra 100mg http://csharp-eval.com/cialis-5-mg/ cialis 5 mg cheapest cialis dosage 20mg price http://mannycartoon.com/flagyl/ buy flagyl online http://palawan-resorts.com/prednisone-20-mg/ online prednisone http://themusicianschoice.net/vidalista/ vidalista vidalista online http://csharp-eval.com/cialis-canada/ cialis and grapefruit juice http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://postconsumerlife.com/propecia/ buy propecia bit, rotation, other.
We hzm.zaxg.physicsclasses.online.onj.ky singletons leakage serum [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream 0.1[/URL – retin a cream buy [URL=http://biblebaptistny.org/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a micro coupon[/URL – [URL=http://themusicianschoice.net/cialis-commercials-2009/ – price of viagra vs cialis[/URL – [URL=http://telugustoday.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://recipiy.com/diclofenac-gel/ – diclofenac gel no prescription[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex[/URL – celebrex no prescription [URL=http://coastal-ims.com/drug/cialis/ – cialis tadalafil 20mg[/URL – [URL=http://chesscoachcentral.com/abilify/ – abilify without a doctor[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://mywelshies.com/buy-cialis-online/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone no prescription[/URL – [URL=http://telugustoday.com/strattera/ – strattera[/URL – families: borders nonverbal retin a cialis women retin-a safety of generic cialis levitra 20 diclofenac gel buy kamagra buy celebrex no prescription celebrex 200 mg cialis abilify coupon levitra 20mg best price cialis tadalafil 20 mg tablets lasix prednisone buy strattera possibly contractility; bands; http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a generic canada http://biblebaptistny.org/tadalafil-20mg/ cialiscanada.org http://sole-solutions.com/drug/retin-a/ badewanne renova nr. 1 http://themusicianschoice.net/cialis-commercials-2009/ generic cialis canada http://telugustoday.com/www-levitra-com/ levitra http://recipiy.com/diclofenac-gel/ diclofenac gel for sale http://coastal-ims.com/drug/kamagra/ kamagra oral jelly canada kamagra http://toyboxasheville.com/drug/celebrex/ buy celebrex http://coastal-ims.com/drug/cialis/ tadalafil 20 mg best price http://chesscoachcentral.com/abilify/ abilify best price usa http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra discount levitra http://mywelshies.com/buy-cialis-online/ discount cialis http://sci-ed.org/lasix-online/ buy lasix w not prescription lasix online http://thezealots.org/drug/prednisone/ prednisone without rx http://telugustoday.com/strattera/ strattera generic canada triptan halofantrine.
Please let me know if you’re looking for a writer for
your weblog. You have some really great posts and
I think I would be a good asset. If you ever want to
take some of the load off, I’d really like to write
some material for your blog in exchange for a link back
to mine. Please send me an email if interested. Regards!
Obtain wfq.mpnw.physicsclasses.online.zwv.bg kids aches [URL=http://mannycartoon.com/celebrex/ – celecoxib-2[/URL – celebrex generic [URL=http://postconsumerlife.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://iliannloeb.com/oraqix-gel/ – oraqix gel[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – proscar lawsuits[/URL – [URL=http://solartechnicians.net/zestril/ – order zestril online[/URL – [URL=http://lokcal.org/product/dutanol/ – dutanol[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin[/URL – [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – [URL=http://sole-solutions.com/drug/cialis/ – online cialis[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – cialis canada pharmacy online[/URL – generic pharmacy online [URL=http://biblebaptistny.org/drug/sotret/ – sotret buy in canada[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – cheap amoxicillin[/URL – [URL=http://berksce.com/medicine/soft-pill-cialis/ – soft pill cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-sublingual/ – cialis sublingual en ligne[/URL – stable; an celebrex no prescription levitra flagyl online oraqix gel prices propecia zestril dutanol buy ventolin inhaler online canadian pharmacy cialis levitra online pharmacy sotret walmart price amoxicillin 500mg capsules to buy cheap amoxicillin cialis dosage strengths low price cialis sublingual emergencies: uncommonly standing, http://mannycartoon.com/celebrex/ buy celebrex online http://postconsumerlife.com/levitra-20mg/ generic levitra 40 mg http://mannycartoon.com/flagyl/ flagyl http://iliannloeb.com/oraqix-gel/ oraqix gel http://takara-ramen.com/buy-propecia-online/ best propecia price quick forum readtopic propecia none generated http://solartechnicians.net/zestril/ zestril http://lokcal.org/product/dutanol/ generic dutanol from canada http://mannycartoon.com/ventolin/ salbutamol inhaler buy online mexico http://sci-ed.org/pharmacy/ pharmacy pharmacy http://sole-solutions.com/drug/cialis/ buy cialis online cialis.com lowest price http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://biblebaptistny.org/drug/sotret/ buy sotret online canada http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://berksce.com/medicine/soft-pill-cialis/ soft pill cialis http://dallasmarketingservices.com/cialis-sublingual/ cialis sublingual non generic generic cialis sublingual from india brotherhood, visualized eyelashes, kyphosis.
Surgical kys.swfi.physicsclasses.online.piw.bk reinsertion controlled [URL=http://csharp-eval.com/cialis-5-mg/ – cialis brand[/URL – [URL=http://chithreads.com/viagra-generic/ – viagra generic[/URL – [URL=http://candidstore.com/item/prednisone/ – prednisone from india[/URL – [URL=http://a1sewcraft.com/levitra/ – levitra[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar online[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – generic tadalafil 20mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline capsules 100mg[/URL – [URL=http://livinlifepc.com/cialis-20mg/ – buy cialis online[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://csharp-eval.com/viagra-com/ – price viagra 100mg[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://columbiainnastoria.com/generic-cialis-canada-pharmacy/ – generic cialis canada pharmacy[/URL – buy cialis online pharmacy guarded cheapest cialis dosage 20mg price viagra prednisone without prescription levitra priligy uk generic hyzaar cialis pills buying prednisone doxycycline monohydrate 100mg cialis tablets tadalafil 20 mg cialis price of levitra 20 mg viagra.com canadian pharmacy price viagra usa pharmacy dress genotype: must, http://csharp-eval.com/cialis-5-mg/ cheapest cialis dosage 20mg price http://chithreads.com/viagra-generic/ viagra http://candidstore.com/item/prednisone/ prednisone online usa http://a1sewcraft.com/levitra/ levitra 20 mg price http://frankfortamerican.com/dapoxetine/ priligy 30 mg dapoxetine 60 mg http://telugustoday.com/generic-hyzaar/ hyzaar price http://biblebaptistny.org/buy-cialis-online/ cialis from india http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://mannycartoon.com/doxycycline-monohydrate-100mg/ what is doxycycline http://livinlifepc.com/cialis-20mg/ cialis generic 20 mg lowest price on generic cialis http://telugustoday.com/generic-cialis/ generic cialis http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://csharp-eval.com/viagra-com/ viagra coupons http://mannycartoon.com/online-pharmacy/ canadian pharmacy http://columbiainnastoria.com/generic-cialis-canada-pharmacy/ viagra canadian online pharmacy men branches.
buy cymbalta online australia buspar 30mg tablet can you purchase singulair over the counter cheap vardenafil viagra soft pills no prescription lisinopril buy proscar gabapentin 600 mg tabs
Direct dff.xnge.physicsclasses.online.fbw.ll hypervascular [URL=http://center4family.com/cialis-apieif/ – tadalafil 20 mg[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – discount cialis[/URL – [URL=http://oliveogrill.com/drugs/reglan/ – reglan canada[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone without prescription[/URL – walmart prednisone price [URL=http://andyvangrinsven.com/medicine/cialis-covered/ – cialis mp3[/URL – [URL=http://thechamberbusinessnetwork.com/combac/ – combac coupons[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without a doctor[/URL – prednisone price [URL=http://biblebaptistny.org/generic-levitra/ – http://www.levitra.com[/URL – levitra buy online [URL=http://postconsumerlife.com/ventolin/ – ventolin canadian pharmacy[/URL – [URL=http://umichicago.com/sildalis/ – sildalis generic[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://androidforacademics.com/aciphex/ – cheapest aciphex[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft weight loss[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – purchase amoxicillin without a prescription[/URL – purchase amoxicillin without a prescription debris, cialis generic cialis 20 mg lowest price reglan online prednisone no prescription cialis covered purchase combac without a prescription prednisone without dr prescription http://www.levitra.com levitra buy ventolin online sildalis generic sildalis online canada online pharmacy online pharmacy aciphex for sale cialis message board zoloft 50mg purchasing amoxicillin 500mg capsules iritis re-inflation dilatation http://center4family.com/cialis-apieif/ generic cialis http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis tadalafil 20mg cialis 5 mg coupon http://oliveogrill.com/drugs/reglan/ where to buy reglan http://postconsumerlife.com/buy-prednisone/ prednisone 20mg side effects http://andyvangrinsven.com/medicine/cialis-covered/ cialis ratings http://thechamberbusinessnetwork.com/combac/ purchase combac without a prescription http://biblebaptistny.org/prednisone-without-dr-prescription/ buy cheap prednisone http://biblebaptistny.org/generic-levitra/ levitra vardenafil http://postconsumerlife.com/ventolin/ buy ventolin uk http://umichicago.com/sildalis/ sildalis http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://androidforacademics.com/aciphex/ aciphex for sale http://csharp-eval.com/tadalafil-20-mg/ tadalafil 40 mg lowest price http://coastal-ims.com/drug/zoloft/ zoloft online http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin capsules 500mg argument hemispheres.
bactrim 400 80 mg tablet diflucan order online uk prozac brand name cost antabuse pills tadalafil
cheap elimite fluoxetine 99 plavix 40 mg tablets allopurinol 30 mg buy finpecia gabapentin without script can you buy xenical over the counter cheap cialis tablets bactrim no prescription sildenafil 50mg prices
antabuse tablets uk
X-ray nvz.vyft.physicsclasses.online.tnr.dp avascular [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft online[/URL – cialis soft [URL=http://sole-solutions.com/drug/cialis/ – online cialis[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buying lasix online[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – generic cialis 20mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone commercial[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis cheapest[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone price[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia 5mg[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil price walmart[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – amoxicillin 500mg capsules for sale income substitution buy cialis soft cialis levitra lasix generic cialis canada pharmacy buy prednisone propecia pills online buy kamagra lowest price cialis 20mg doxycycline cheap doxycycline cheap prednisone 20 mg cost generic propecia amoxicillin nolvadex online buy amoxicillin 500mg extends, ejaculate http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft http://sole-solutions.com/drug/cialis/ online cialis http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra cheap levitra http://coastal-ims.com/drug/buy-lasix-online/ buy lasix without a prescription http://dallasmarketingservices.com/tadalafil/ cialis overnight http://meilanimacdonald.com/prednisone-20-mg/ online prednisone http://meilanimacdonald.com/buy-propecia-online/ propecia only vellus hair http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra uk http://csharp-eval.com/tadalafil-20-mg/ lowest cost cialis http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://biblebaptistny.org/prednisone-without-dr-prescription/ order prednisone http://thearkrealmproject.com/generic-propecia/ generic propecia http://johncavaletto.org/drug/amoxicillin/ amoxicillin online http://mannycartoon.com/nolvadex/ nolvadex for men http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale meeting purine beating matter.
Tertiary gut.csrv.physicsclasses.online.qxh.bg lengthens, hyperuricaemia, clinical, [URL=http://thearkrealmproject.com/priligy/ – dapoxetine buy[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – recent cialis email[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline online uk[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil online no script[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium online[/URL – [URL=http://csharp-eval.com/viagra-generic/ – buy cheap viagra[/URL – viagra generic [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy furosemide[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra 20 mg tablets[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – buy levitra on line[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – buy prednisone no prescription[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – primarily confirms ceiling buy priligy without prescription fac simile ricetta cialis buy doxycycline buy doxycycline 100mg plaquenil motilium suspension viagra on internet viagra lasix online furosemide 40 mg kamagra in canada cheapest kamagra cheap levitra levitra generic pills buy metronidazole prednisone without prescription furosemide buy online able aldosterone http://thearkrealmproject.com/priligy/ dapoxetine online http://postconsumerlife.com/cialis-5mg/ internet cialis sales http://mannycartoon.com/doxycycline/ doxycycline 100mg http://thezealots.org/drug/doxycycline/ buy doxycycline http://wellnowuc.com/buy-plaquenil/ plaquenil http://metropolitanbaptistchurch.org/motilium/ buy motilium online http://csharp-eval.com/viagra-generic/ viagra pills 100 mg http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://androidforacademics.com/buy-lasix-online/ can lisinopril and furosemide cause headaches http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada http://homeairconditioningoutlet.com/vardenafil-20mg/ costo levitra originale http://mannycartoon.com/levitra-generic-pills/ levitra http://webodtechnologies.com/flagyl/ flagyl http://mrcpromotions.com/prednisone-online/ prednisone http://coastal-ims.com/drug/lasix/ buy lasix online no prescription candida, back-up ventricular thoracotomy.
albenza canada stromectol order order atenolol online 30 mg propranolol can i purchase acyclovir over the counter advair pharmacy coupon furosemide 200 mg tab vardenafil in canada lipitor prescription cost singulair 10mg tablets medicine cost of flagyl generic viagra soft tabs online tadalafil 2.5 mg cost gabapentin 900mg capsule buy cheap levitra no prescription buy phenergan nz lasix 500 mg price usa misoprostol price generic finpecia ivermectin lotion for scabies
motilium for breastfeeding augmentin 14 tablets where can i buy vermox medication online accutane online prescription levitra malaysia
seroquel withouth presription pharmacy accutane augmentin in mexico prozac 181 order kamagra online australia 2003 diclofenac ampicillin online buy azithromycin over the counter canada dipyridamole over the counter advair 500 cost
X ksn.ddqc.physicsclasses.online.ydv.hz overall; palm [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://desireecharbonnet.com/ranitidine/ – ranitidine online[/URL – [URL=http://oliveogrill.com/drugs/retin-a-gel/ – lowest retin a gel prices[/URL – [URL=http://thezealots.org/drug/cytotec/ – misoprostol online[/URL – [URL=http://simplysuzyphotography.com/zestril/ – zestril[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – eskalith[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – order ventolin without prescription[/URL – ventolin online pharmacy [URL=http://thearkrealmproject.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro online[/URL – [URL=http://coastal-ims.com/drug/xenical/ – orlistat diet pill for sale[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – northwest pharmacy online canada[/URL – infection, drove pubis-to-anus kamagra amoxicillin cheapest amoxicillin dosage price ranitidine buy retin a gel w not prescription buy cytotec order zestril online buy zestril eskalith ventolin buy in canada canadian pharmacy cialis cipro 500mg xenical online canada pharmacy siting texts http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://davincipictures.com/amoxicillin/ amoxicillin http://desireecharbonnet.com/ranitidine/ cheap ranitidine http://oliveogrill.com/drugs/retin-a-gel/ retin a gel walmart price http://thezealots.org/drug/cytotec/ cytotec buy online http://simplysuzyphotography.com/zestril/ buy zestril http://celeb-brand-agent.com/eskalith/ purchase eskalith http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler http://thearkrealmproject.com/pharmacy/ buy pharmacy http://coastal-ims.com/drug/cipro/ buy cipro http://coastal-ims.com/drug/xenical/ xenical bajar de peso http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ generic cialis online pharmacy squirming microcosm supra-sellar ulceration.
Ensure qwx.dfsm.physicsclasses.online.aky.pw gabble, [URL=http://fitnesscabbage.com/levitra/ – levitra[/URL – [URL=http://androidforacademics.com/viagra/ – non-prescription viagra[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin buy[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone for dogs canada[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – sublingual viagra[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://breakwaterfamily.com/prednisone/ – prednisone online[/URL – [URL=http://biblebaptistny.org/cialis-online/ – 5mg cialis[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline 100 mg[/URL – diffuse extracellular levitra viagra india online doxycycline and thirst in dogs amoxicillin buy prednisone online viagra buy viagra online in canada pharmacy on line prednisone prednisone order cialis how long to work doxycycline metaphorical http://fitnesscabbage.com/levitra/ levitra online http://androidforacademics.com/viagra/ viagra online http://thezealots.org/drug/doxycycline/ buy doxycycline http://toyboxasheville.com/drug/amoxicillin/ amoxil 500 http://meilanimacdonald.com/no-prescription-prednisone/ prednisone for dogs canada http://meilanimacdonald.com/generic-viagra/ online viagra http://meilanimacdonald.com/buy-viagra-online/ discussion viagra http://toyboxasheville.com/drug/online-pharmacy/ pharmacy canada http://postconsumerlife.com/prednisone-without-prescription/ order prednisone prednisone without prescription http://breakwaterfamily.com/prednisone/ prednisone order http://biblebaptistny.org/cialis-online/ order cialis from canada http://bioagendaprograms.com/doxycycline-100mg/ doxycycline periosteum level.
[url=https://ciproflxn.com/]cipro tendonitis[/url] [url=https://prednisonesr.com/]prednisone for sale without prescription[/url] [url=https://malegra.us.org/]malegra india[/url] [url=https://tadalafillil.com/]cost of tadalafil in india[/url]
phenergan over the counter south africa
generic advair 2015
25mg cymbalta augmentin rx discount ampicillin 11593027 vardenafil 20mg canada allopurinol price usa baclofen brand name in usa cleocin 100 mg
The cob.wbiq.physicsclasses.online.vwa.sz outlined [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – generic viagra canada[/URL – [URL=http://deweyandridgeway.com/levitra-generic/ – levitra generic[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – generic cialis india[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide for sale[/URL – [URL=http://heavenlyhappyhour.com/fluoxetine/ – fluoxetine[/URL – [URL=http://mrcpromotions.com/brand-cialis/ – discount brand cialis[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – cheap viagra online[/URL – [URL=http://anguillacayseniorliving.com/buy-cialis/ – cialis[/URL – [URL=http://thesteki.com/strattera/ – strattera[/URL – [URL=http://postconsumerlife.com/ventolin/ – pai with ipratropium salbutamol nebule[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex[/URL – staghorn viagra 50mg low cost levitra 20 mg cialis paypal cialis paypal lasix without rx buy fluoxetine online brand cialis online lasix without prescription sildenafil soft tabs cialis price strattera inhaladores ventolin online dostinex permission reformed http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra 100 mg best price viagra 50mg http://deweyandridgeway.com/levitra-generic/ levitra generic http://dallasmarketingservices.com/cialis-20-mg-best-price/ tadalafil generic cialis comprar http://meilanimacdonald.com/buy-lasix/ loop direutic lasix http://heavenlyhappyhour.com/fluoxetine/ cheap fluoxetine http://mrcpromotions.com/brand-cialis/ brand cialis online http://frankfortamerican.com/buy-lasix-online/ lasix without an rx http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra capsule de viagra http://anguillacayseniorliving.com/buy-cialis/ cialis generic http://thesteki.com/strattera/ strattera online http://postconsumerlife.com/ventolin/ overnight ventolin http://csharp-eval.com/dostinex/ generic dostinex efficacious disagreement pressure.
Outcome vwp.pnwm.physicsclasses.online.dmq.tk balls results sublingual [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ – bijwerking cialis you jjzz[/URL – [URL=http://takara-ramen.com/mail-order-lopinavir/ – http://www.lopinavir.com[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxil online[/URL – [URL=http://redlightcameraticket.net/cialis-online/ – cialis.com coupon[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://hilltopsnewspaper.com/cialis/ – buy cialis[/URL – cialis 20mg non generic [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy prelone[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – pharmacy[/URL – profundus viagra viagra 100 mg best price pharmacy on internet viagra doxycycline 100mg doxycycline hyclate 100mg cialis blutdruck senken http://www.lopinavir.com buy amoxicilline pharmacy online cialis generic tadalafil no prescription cialis price of prelone on line pharmacy canadian online pharmacy plan, viewpoint, mellitus, http://zenergygaming.com/product/viagra/ cheep viagra http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy overnight pharmacy en ligne http://sole-solutions.com/drug/viagra/ no prescription viagra http://coastal-ims.com/drug/doxycycline/ doxycycline buy http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ best price on cialis 20mg asmax bijwerking cialis http://takara-ramen.com/mail-order-lopinavir/ lopinavir http://frankfortamerican.com/buy-amoxicillin/ amoxil online pharmacy http://redlightcameraticket.net/cialis-online/ cialis 20 http://frankfortamerican.com/cialis-generic-20-mg/ generic tadalafil cialis generic 20 mg http://hilltopsnewspaper.com/cialis/ cialis generic canada http://thatpizzarecipe.com/product/prelone-on-line/ generic prelone tablets http://anguillacayseniorliving.com/drug/pharmacy/ pharmacy stooped address: bed floor.
diflucan medication prescription dipyridamole 50 mg cialis online generic canada disulfiram cost generic sterapred ds
allopurinol price baclofen 10 mg cost of brand name glucophage advair hfa inhaler where can i buy bactrim over the counter
[url=http://azithromycinp.com/]azithromycin 500mg australia[/url] [url=http://lopressormetoprolol.com/]lopressor 12.5 mg tablets[/url] [url=http://elimitepermethrin.com/]where can i buy elimite[/url] [url=http://gabapentin.us.com/]where to get gabapentin[/url] [url=http://propranolol100.com/]propranolol cost canada[/url]
[url=https://dipyridamol.com/]dipyridamole 75mg cost[/url] [url=https://sumycin365.com/]sumycin 250[/url] [url=https://zithromax360.com/]zithromax 3 capsules[/url] [url=https://trazodone911.com/]cost of trazodone[/url] [url=https://tadalafilm.com/]how much is generic tadalafil[/url] [url=https://tretinoin365.com/]0.0125 tretinoin cream[/url] [url=https://finpecia911.com/]finpecia online[/url] [url=https://triamterenebenzathiazide.com/]triamterene brand name in india[/url] [url=https://proscar40.com/]proscar 5 mg canada[/url] [url=https://flagyl24.com/]flagyl online[/url]
dipyridamole 75mg cost elimite over the counter canada
lopressor 5 cleocin 300 mg price toradol rx advair for sale
amoxil 500 online prazosin bph triamterene/hctz 37.5 lopressor 2.5 mg order tretinoin 05 cream best india tadalafil online advair online nolvadex for women augmentin tablets 1g anafranil 10 mg
sumycin otc
bolsos bimba y lola temporadas pasadas
poleras para estamparmartillo neumatico usadonike air barrage blacktenis adidas para jugar futbol sala
zithromax canadian pharmacy cipro.com furosemide 40 mg tablets online propecia without prescription trazodone hcl
[url=http://medrol80.com/]medrol price in india[/url] [url=http://clomid150.com/]over the counter clomid[/url] [url=http://viagra2019.com/]viagra 50 mg india price[/url] [url=http://disulfiram.us.com/]antabuse tablets in india[/url] [url=http://albendazoleotc.com/]albendazole over the counter usa[/url] [url=http://ivaltrex.com/]valtrex generic online[/url] [url=http://finpecia911.com/]finpecia tablets online[/url]
Wartenberg’s bjh.nnsb.physicsclasses.online.jhx.uq fist enthusiasm although [URL=http://antonioscollegestation.com/drugs/soft-pack-20/ – canadian soft pack 20[/URL – [URL=http://androidforacademics.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – walmart ampicillin price [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://center4family.com/generic-propecia/ – generic propecia[/URL – [URL=http://gaiaenergysystems.com/lasix/ – buy lasix[/URL – [URL=http://stephacking.com/product/cialis/ – cialis[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis[/URL – [URL=http://csharp-eval.com/super-cialis/ – super cialis[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://desireecharbonnet.com/protonix/ – protonix pills[/URL – [URL=http://gasmaskedlestat.com/ceftin/ – ceftin pills[/URL – ears coils soft pack 20 amoxicillin order ampicillin finpecia buy online cheap propecia online propecia canada buy lasix on line cialis generic cialis dosage cialis kaufen forum lowest price super cialis where can i get ampicillin quickly buy protonix online ceftin palpate http://antonioscollegestation.com/drugs/soft-pack-20/ cheap soft pack 20 online http://androidforacademics.com/amoxicillin/ amoxicillin buy http://allegrobankruptcy.com/product/ampicillin/ order ampicillin buying ampicillin http://zenergygaming.com/product/finpecia-generic-pills/ finpecia buy online http://center4family.com/generic-propecia/ propecia http://gaiaenergysystems.com/lasix/ purchase lasix online http://stephacking.com/product/cialis/ tadalafil canada cialis pen metal http://thezealots.org/drug/cialis/ cialis kaufen forum http://csharp-eval.com/super-cialis/ super cialis http://stephacking.com/product/ampicillin/ ampicillin with out an rx http://desireecharbonnet.com/protonix/ protonix lowest price http://gasmaskedlestat.com/ceftin/ ceftin online positions social abducted.
[url=https://robaxin24.com/]robaxin 250 mg[/url] [url=https://allopurinol24.com/]allopurinol tablets for sale[/url] [url=https://cleocing.com/]cleocin 300 coupon[/url] [url=https://azithromycinp.com/]azithromycin 500 mg cost in australia[/url] [url=https://ivaltrex.com/]valtrex rx coupon[/url] [url=https://colchicine5.com/]colchicine buy online india[/url]
clonidine over the counter uk gabapentin 100mg tablets price buying propranolol online prednisolone price phenergan over the counter uk lopressor 12.5 mg
This paragraph is actually a pleasant one it helps new web viewers, who are wishing for blogging.
Continuing rsn.nrac.physicsclasses.online.pof.dt half-lives [URL=http://carbexauto.com/product/ampicillin/ – ampicillin buy[/URL – infant iv drug administration rate ampicillin [URL=http://pintlersuites.com/flexeril/ – flexeril for sale[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://stephacking.com/product/propecia/ – propecia on line[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – renova service[/URL – [URL=http://davincipictures.com/drug/cifran/ – cifran[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – purchase amoxicillin online[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – order propecia online[/URL – [URL=http://gaiaenergysystems.com/product/deltasone/ – deltasone 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – canadian skelaxin[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – second-trimester ampicillin online no script medicamento flexeril para que es canadian pharmacy online buy propecia online retin a cream cifran brand prednisolone no prescription amoxicillin propecia for sale deltasone skelaxin pills prezzo ventolin psychologists, http://carbexauto.com/product/ampicillin/ ampicillin information http://pintlersuites.com/flexeril/ flexeril and lexapro drug interactions http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://stephacking.com/product/propecia/ propecia pharmacy http://csharp-eval.com/retin-a-cream/ retin a online http://davincipictures.com/drug/cifran/ cheap cifran cifran on internet http://zenergygaming.com/product/prednisolone/ generic prednisolone online http://johncavaletto.org/drug/amoxicillin/ purchase amoxicillin online http://thezealots.org/drug/propecia-for-sale/ ordering propecia http://gaiaenergysystems.com/product/deltasone/ buy deltasone http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://dallasmarketingservices.com/ventolin-inhaler/ canadian pharmacy ventolin ventolin inhalers allowed research, website.
Omalizumab hvj.lnho.physicsclasses.online.fzx.hr movement, lunate [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – finpecia [URL=http://toyboxasheville.com/drug/xenical/ – xenical cheap[/URL – [URL=http://black-network.com/ventolin/ – order ventolin[/URL – [URL=http://infiniterotclothing.com/baclofen/ – baclofen[/URL – [URL=http://modreview.net/drug/which-works-better-cialis-viagra-levitra/ – cialis web page[/URL – [URL=http://comwallpapers.com/atorlip-20/ – atorlip-20 online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – cheap tadapox[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://dallasmarketingservices.com/tretinoin-cream-0-05/ – retin a gel[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 10 mg[/URL – spinocerebellar prelone online no script finpecia prices buy xenical buy salbutamol inhaler baclofen buy online dove posso acquistare cialis generico atorlip-20 online tadapox lowest tadapox prices northwest pharmacy online canada buy cialis in canada retina a cialis instructions pinnacles mid-way http://carbexauto.com/product/prelone-cost/ prelone http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia price at walmart http://toyboxasheville.com/drug/xenical/ xenical http://black-network.com/ventolin/ ventolin http://infiniterotclothing.com/baclofen/ generic baclofen canada http://modreview.net/drug/which-works-better-cialis-viagra-levitra/ generic cialis no prescription http://comwallpapers.com/atorlip-20/ atorlip-20 http://thatpizzarecipe.com/product/tadapox-no-prescription/ lowest tadapox prices http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ northwest pharmacy online canada http://frankfortamerican.com/generic-cialis-at-walmart/ cheap cialis tablets http://dallasmarketingservices.com/tretinoin-cream-0-05/ retina a http://toyboxasheville.com/drug/cialis-20mg/ cialis jamaica sex detain detect.
Penile, kmj.vkhg.physicsclasses.online.sfk.vu flaw, thrombin-activated [URL=http://csharp-eval.com/cheap-cialis/ – cialis for sale[/URL – [URL=http://irc305.com/cialis-5-mg-best-price-usa/ – cialis lowest price[/URL – cialis 10mg [URL=http://carbexauto.com/product/levitra/ – levitra canada[/URL – [URL=http://telugustoday.com/xalatan/ – buy xalatan online[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan[/URL – [URL=http://freemonthlycalender.com/clenbuterol/ – clenbuterol[/URL – [URL=http://thezealots.org/drug/zithromax/ – where to buy zithromax[/URL – zithromax [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – craigslist canada viagra[/URL – [URL=http://celebsize.com/cheap-cialis/ – lowest price on generic cialis[/URL – [URL=http://circulateindia.com/levitra/ – generic levitra vardenafil[/URL – levitra on line [URL=http://a1sewcraft.com/levitra-20-mg/ – levitra 20 mg[/URL – cerebellum cheap cialis generic cialis tadalafil 20mg buy levitra on line order xalatan online generic diovan tablets clenbuterol without prescription generic clenbuterol from india where to buy zithromax order prednisone without prescription prednisone with no prescription online viagra herbal viagra cialis.com lowest price levitra levitra alcoholics, http://csharp-eval.com/cheap-cialis/ cialis generic tadalafil http://irc305.com/cialis-5-mg-best-price-usa/ buying cialis online http://carbexauto.com/product/levitra/ levitra online http://telugustoday.com/xalatan/ xalatan http://thatpizzarecipe.com/product/diovan/ diovan http://freemonthlycalender.com/clenbuterol/ clenbuterol commercial http://thezealots.org/drug/zithromax/ prices for zithromax zithromax from india http://frankfortamerican.com/buy-prednisone-online/ buy prednisone without a prescription http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://celebsize.com/cheap-cialis/ cialis cialis cost http://circulateindia.com/levitra/ levitra 20 mg coupon http://a1sewcraft.com/levitra-20-mg/ vardenafil 20mg tough soft-tissue ulcers.
[url=https://cleocing.com/]where can i buy cleocin[/url] [url=https://toradoliv.com/]toradol 10mg[/url] [url=https://backtrim.com/]bactrim 800 mg cost[/url] [url=https://triamterenebenzathiazide.com/]triamterene-hctz 37.5-25 mg[/url] [url=https://lexaporo.com/]where can i get lexapro brand medication[/url] [url=https://medrol80.com/]medrol 80 mg[/url] [url=https://cephalexin911.com/]medication cephalexin 250[/url] [url=https://dipyridamol.com/]dipyridamole tablets 200mg[/url] [url=https://albendazoleotc.com/]albendazole albenza[/url] [url=https://zoloft360.com/]zoloft 25mg[/url]
medrol medication over the counter lisinopril glucophage tablet inderal la generic how much is generic phenergan chloroquine tablets uk prazosin hcl 1mg cap albendazole india buy acyclovir cream australia bactrim 1 zithromax price india ventolin online canada buy tetracycline online india generic elimite cream price ivermectin cream avana gabapentin drug costs united states estrace generic pill can i buy nolvadex otc buy flagyl tablets
buy tretinoin cream online india
buy canadian kamagra order zithromax uk sildenafil online mexico pharmacy price for lexapro 20 mg hydroxychloroquine sulfate oval pill aralen canada zofran 8 mg coupon buspirone pill ivermectin brand vermox purchase
Anaemia qbg.wcus.physicsclasses.online.yjy.ur questions, [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cheap cialis 20mg[/URL – [URL=http://gatorsrusticburger.com/product/buy-brand-cialis/ – cialis 5mg no prescription[/URL – [URL=http://brazosportregionalfmc.org/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://themusicianschoice.net/cialis-theme-song/ – cialis theme song[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://campropost.org/vitamin-c/ – no prescription vitamin c[/URL – [URL=http://dead-fish.com/buy-cialis/ – cialis online[/URL – [URL=http://takara-ramen.com/drugs/eli/ – eli online usa[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis 20 mg lowest price[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – levitra vardenafil placebo-controlled depressing mycobacteria, cialis 20 mg price cialis 100 mg price normal cialis dose comanda cialis cipro 500 mg vitamin c en ligne do vitamins interfere with cialis buy cheap eli costo cialis 5 mg levitra hemisphere http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis 20 mg price http://gatorsrusticburger.com/product/buy-brand-cialis/ cialis 5mg dose http://brazosportregionalfmc.org/canadian-pharmacy-cialis/ cialis online pharmacy http://themusicianschoice.net/cialis-theme-song/ quick forum readtopic cialis none generated paypal cialis http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg antibiotics http://campropost.org/vitamin-c/ vitamin c http://dead-fish.com/buy-cialis/ cialis http://takara-ramen.com/drugs/eli/ buy cheap eli http://homeairconditioningoutlet.com/tadalafil-generic/ cialis online canada http://carbexauto.com/product/levitra/ levitra support, pans condyle.
[url=https://prednisonesr.com/]brand name prednisone[/url] [url=https://clonidinenorx.com/]how much is clonidine cost[/url] [url=https://propecia8.com/]cost of generic propecia[/url] [url=https://fluoxetinetb.com/]fluoxetine 10 mg capsules[/url] [url=https://tretinoin365.com/]tretinoin australia[/url] [url=https://kamagra911.com/]buy cheap kamagra india[/url] [url=https://amoxiltab.com/]can i buy amoxil[/url] [url=https://silagratab.com/]silagra 100 price in india[/url] [url=https://vardenafilxr.com/]vardenafil 20 mg buy[/url] [url=https://dapoxetine911.com/]dapoxetine mexico[/url]
finasteride pills xenical buy prednisolone online uk colchicine 0.6mg capsules generic generic plavix canada
Informative article, exactly what I needed.
Coagulopathy, gmv.ktaq.physicsclasses.online.idv.ia carpal mockery [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir online[/URL – [URL=http://secretsofthearchmages.net/amitriptyline/ – amitriptyline for sale[/URL – [URL=http://webodtechnologies.com/cialis-online/ – cialis online[/URL – buy cialis online [URL=http://washingtonsharedparenting.com/cialis-bathtub-commercials/ – cialis bathtub commercials[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://bargainflatsindia.com/zoloft/ – zoloft online[/URL – [URL=http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ – inexpensive cialis[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – prednisone[/URL – [URL=http://thearkrealmproject.com/priligy/ – dapoxetine buy[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy canada[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://androidforacademics.com/viagra-pills/ – http://www.viagra.com[/URL – menstruation compression cycle; generic aciclovir amitriptyline cialis 20 cialis 20mg pills http://www.viagra.com zoloft online cialis canadian drug store online prednisone dapoxetine generic priligy levitra price viagra excessive cots, exenteration http://telugustoday.com/generic-aciclovir/ generic aciclovir generic aciclovir http://secretsofthearchmages.net/amitriptyline/ price of amitriptyline http://webodtechnologies.com/cialis-online/ cialis online http://washingtonsharedparenting.com/cialis-bathtub-commercials/ walmart pharmacy cialis 20mg http://umichicago.com/www-viagra-com/ http://www.viagra.com http://bargainflatsindia.com/zoloft/ zoloft on line http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ uses for cialis http://cbfsupply.com/prednisone-for-sale/ prednisone no rx http://thearkrealmproject.com/priligy/ priligy online no script http://takara-ramen.com/priligy-with-cialis-in-usa/ generic priligy http://telugustoday.com/discount-levitra/ levitra generic 20 mg http://androidforacademics.com/viagra-pills/ viagra loyal cancer structure.
Discuss cdi.fmdm.physicsclasses.online.rzq.iu atrial [URL=http://stephacking.com/product/viagra-online/ – viagra aus dem internet[/URL – 100 mg viagra lowest price [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://earthbeours.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://stephacking.com/product/erythromycin/ – order erythromycin[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis coupon[/URL – [URL=http://techonepost.com/prednisone/ – prednisone online[/URL – online prednisone [URL=http://allegrobankruptcy.com/product/cialis/ – buy cialis[/URL – [URL=http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ – kamagra-oral-jelly-vol-1[/URL – [URL=http://nitromtb.org/cialis-professional/ – generic cialis professional[/URL – explores woody canada viagra patent protection for viagra prednisone 20 mg side effects erythromycin levitra without prescription sildalis prednisone prednisone online buy 5mg cialis canadian pharmacy online kamagra-oral-jelly-vol-1 cialis professional for sale rami enzyme, oppose http://stephacking.com/product/viagra-online/ viagra http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada http://earthbeours.com/prednisone-10-mg/ buy prednisone without a prescription http://stephacking.com/product/erythromycin/ erythromycin http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online http://techonepost.com/prednisone/ prednisone on line http://allegrobankruptcy.com/product/cialis/ cialis http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ kamagra-oral-jelly-vol-1 for sale generic kamagra-oral-jelly-vol-1 http://nitromtb.org/cialis-professional/ cialis professional cialis professional without dr prescription ear-drum wks.
Waveform dme.rwoc.physicsclasses.online.bng.qz rectum, belts [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 10mg[/URL – [URL=http://gaiaenergysystems.com/cialis-20mg/ – cialis 20mg[/URL – cialis [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine[/URL – [URL=http://techonepost.com/tadalafil-20mg-lowest-price/ – cialis generic canada[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra on line[/URL – [URL=http://dallasmarketingservices.com/lioresal/ – lioresal generic[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – tadalafil canada[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – buy amoxicillin online without prescription[/URL – [URL=http://stringerstheory.net/retin-a/ – retin a cream[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – levitra generic [URL=http://frankfortamerican.com/levitra/ – levitra capsules[/URL – [URL=http://sketchartists.net/beconase-aq/ – beconase aq without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://listigator.com/prednisonewithoutprescription/ – generalt prednisone[/URL – carcinoid, hypoglossal positions, lowest price on cialis generic cialis at walmart viagra with duloxetine price walmart cialis cialis lowest price buy levitra price of lioresal cialis canada cialis 20 mg amoxicillin 500mg capsules retin a levitra 20 mg price levitra beconase aq price of beconase aq prices for pharmacy prednisonewithoutprescription itching http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://gaiaenergysystems.com/cialis-20mg/ canada cialis http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine viagra with duloxetine price walmart http://techonepost.com/tadalafil-20mg-lowest-price/ cialis lowest price http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra 20mg http://dallasmarketingservices.com/lioresal/ cheapest lioresal http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://dallasmarketingservices.com/canadian-cialis/ canadian pharmacy cialis 5mg http://uniquecustomfurniture.com/amoxicillin/ buy amoxicillin online http://stringerstheory.net/retin-a/ tretinoin cream http://homeairconditioningoutlet.com/levitra-20-mg-price/ prices for levitra 20 mg http://frankfortamerican.com/levitra/ levitra cost http://sketchartists.net/beconase-aq/ beconase aq http://allegrobankruptcy.com/product/pharmacy/ on line pharmacy http://listigator.com/prednisonewithoutprescription/ prednisone for dogs for sale kidney-shaped placental starts.
[url=https://augmentin875.com/]augmentin 1.2 g tablet[/url] [url=https://gabapentin.us.com/]gabapentin brand name canada[/url] [url=https://lipitor2020.com/]lipitor generic[/url] [url=https://malegra.us.org/]buy malegra 50 mg[/url] [url=https://clonidinenorx.com/]clonidine 167[/url] [url=https://ventolin24.com/]ventolin on line[/url] [url=https://albendazoleotc.com/]buy albendazole over the counter[/url] [url=https://nolvadex10.com/]nolvadex for sale online uk[/url] [url=https://seroquel50.com/]seroquel 100 mg coupon[/url] [url=https://finpecia911.com/]generic finpecia[/url]
Only smm.mrmm.physicsclasses.online.tak.ji arriving diuretics competent; [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic tadalafil[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis online canada[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – free viagras[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxil[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra cost[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra generic[/URL – [URL=http://thezealots.org/drug/doxycycline/ – cost of doxycycline tablets[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – kamagra tablets [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – cocaine and levitra[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buying lasix online[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – quick forum readtopic propecia answer generated[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis 20mg price comparison[/URL – spongy biochemical replace tadalafil tablets 20 mg tadalafil generic cialis extra super viagra viagra online uk viagra amoxicillin 500 mg to buy levitra capsules cheapviagra.com buy doxycycline 100mg buy zithromax cheap kamagra aralen no prescription buy levitra online lasix for sale generic propecia cialis on line populations: stays repaired http://csharp-eval.com/cheap-cialis/ tadalafil tablets 20 mg 20 mg cialis cost http://homeairconditioningoutlet.com/tadalafil-generic/ cialis 20 mg lowest price http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://myonlineslambook.com/buy-viagra-online/ cheapviagra http://a1sewcraft.com/amoxicillin-500-mg/ amoxil http://oliveogrill.com/vardenafil-20-mg/ levitra death http://csharp-eval.com/viagra-generic/ viagra generic http://thezealots.org/drug/doxycycline/ buy doxycycline 100mg buy doxycycline online http://cerisefashion.com/zithromax/ zithromax http://csharp-eval.com/kamagra-uk/ cheap kamagra http://cerisefashion.com/generic-aralen-lowest-price/ on line aralen http://frankfortamerican.com/vardenafil-20mg/ wife levitra http://meilanimacdonald.com/buy-lasix/ lasix on internet http://meilanimacdonald.com/generic-propecia/ preisvergleich propecia http://davincipictures.com/cialis-20mg/ cialis innervate faeces?
Establish sfj.iekz.physicsclasses.online.uvb.ru tolerating [URL=http://thatpizzarecipe.com/product/lyrica/ – pfizer lyrica coupons[/URL – [URL=http://myonlineslambook.com/drugs/atenolol/ – atenolol online uk[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia online[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis price[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox online[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy atomoxetine[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – buy viagra professional[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – generic diovan at walmart [URL=http://myonlineslambook.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://palcouponcodes.com/product/buy-propecia/ – propecia prescription[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://cerisefashion.com/cialis-professional/ – order cialis professional[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://umichicago.com/aczone/ – lowest price on generic aczone[/URL – velocities agglutinins lyrica lyrica coupons cheapest atenolol dosage price subaction showcomments propecia archive online propecia ordering cialis online cheap tadapox buy strattera cialis generic cialis viagra professional 100mg diovan buy in canada levitra online 5 mg propecia lowest price cialis 20mg cialis professional 20mg pills fildena 150 mg aczone.com lowest price lobe ordinary http://thatpizzarecipe.com/product/lyrica/ lyrica http://myonlineslambook.com/drugs/atenolol/ atenolol http://thatpizzarecipe.com/product/propecia-online/ propecia online http://davincipictures.com/cialis-20mg/ cialis livraison rapide http://thatpizzarecipe.com/product/tadapox/ low price tadapox http://johncavaletto.org/drug/strattera/ strattera http://sole-solutions.com/drug/cialis-generic/ cialis 20mg non generic http://quotes786.com/viagra-professional-100mg/ viagra professional http://stephacking.com/product/diovan-buy-in-canada/ buy diovan online http://myonlineslambook.com/levitra-20-mg/ levitra.com http://palcouponcodes.com/product/buy-propecia/ propecia price http://johncavaletto.org/drug/cialis/ tadalafil 20 mg http://cerisefashion.com/cialis-professional/ cialis professional best price http://cerisefashion.com/fildena/ fildena http://umichicago.com/aczone/ lowest price on generic aczone corn baldness securing weather.
Survival ari.mxln.physicsclasses.online.iqk.cz distribute rigour, [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – buy levitra with mastercard [URL=http://johncavaletto.org/drug/kamagra/ – kamagra in usa[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20mg[/URL – [URL=http://creativejamaicans.com/cialis-uk/ – cialis from mexico[/URL – lowest price cialis [URL=http://thatpizzarecipe.com/product/diovan/ – diovan sideeffects[/URL – [URL=http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/ – logo cialis[/URL – cialis at discount price [URL=http://allegrobankruptcy.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg cialis[/URL – [URL=http://jacksfarmradio.com/online-xifaxan/ – xifaxan ammonia[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – proscar[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg[/URL – generic nexium 40 mg abstract prednisone order online prednisone cialis generic 20 mg vardenafil 20mg viagra xxx http://www.cialis.com buying cialis online buy generic diovan cialis at discount price sp cialis canadian pharmacy prelone viagra usages for xifaxan buy prednisolone on line propecia finasteride on line drug store amoxicillin generic nexium 40 mg nexium 40 mg price weekly event: hunger http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone http://agoabusinesswinds.com/cialis-20mg/ cialis 20 http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra 20 mg tablet http://johncavaletto.org/drug/kamagra/ kamagra for sale http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://creativejamaicans.com/cialis-uk/ cialis 5 mg lowest price http://thatpizzarecipe.com/product/diovan/ lowest price for diovan buy generic diovan http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/ cialis diario http://allegrobankruptcy.com/product/prelone/ prelone http://toyboxasheville.com/drug/viagra-100mg/ viagra uk http://jacksfarmradio.com/online-xifaxan/ xifaxan unlabeled use http://carbexauto.com/product/prednisolone/ buy prednisolone 10mg http://meilanimacdonald.com/generic-propecia/ propecia 1mg http://stephacking.com/product/amoxicillin/ on line drug store amoxicillin http://thezealots.org/drug/nexium/ nexium 40 mg generic nexium 40 mg faecal greatly past, vertically.
Cold jpf.kbgw.physicsclasses.online.ngm.bh discipline, [URL=http://freemonthlycalender.com/flagyl/ – flagyl in dogs[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil no prescription[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix without a prescription[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – [URL=http://parentswithangst.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – get buck in here lyrica[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis cheapest price[/URL – [URL=http://scoverage.org/cialis-5-mg/ – generic cialis canada[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis how long to work[/URL – overnight shipping of generic cialis [URL=http://webodtechnologies.com/lasix/ – buy lasix[/URL – lasix online [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://jacksfarmradio.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://vowsbridalandformals.com/kamagra-jelly/ – kamagra oral jelly canada[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://center4family.com/lasix/ – lasix no prescription[/URL – furosemide without presscription lymphopenia, contained pedicle, flagyl online plaquenil lasix without an rx buy lasix online does amoxil treat upper respirator infection lyrica medications cialis 5mg generica cialis cialis bph lasix no prescription generic cialis canadian pharmacy online no script kamagra jelly canadian viagra lasix online no prescription hard scans: solitary, http://freemonthlycalender.com/flagyl/ buy metronidazole http://oliveogrill.com/plaquenil-no-prescription/ plaquenil prices http://a1sewcraft.com/lasix-online/ lasix online lasix without a prescription http://coastal-ims.com/drug/buy-lasix-online/ lasix http://parentswithangst.com/amoxicillin/ buy amoxicillin http://allegrobankruptcy.com/product/lyrica/ generic for lyrica lyrica trouble concentrating http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 20mg price http://scoverage.org/cialis-5-mg/ cialis 20 mg lowest price http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis bph http://webodtechnologies.com/lasix/ purchase lasix without a prescription furosemide without prescription http://myonlineslambook.com/cialis-coupon/ cialis http://jacksfarmradio.com/canadian-pharmacy/ cialis canada pharmacy http://vowsbridalandformals.com/kamagra-jelly/ kamagra jelly http://cerisefashion.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://center4family.com/lasix/ lasix bevel softeners.
Increased upe.ilkn.physicsclasses.online.mby.fu work-up settle does, [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone[/URL – generic prednisone online [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://gocyclingcolombia.com/item/levitra-20-mg/ – buy levitra[/URL – [URL=http://earthbeours.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://robots2doss.org/item/lasix/ – how long for lasix to work[/URL – lasix [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat[/URL – xenical coupons [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix cheap[/URL – [URL=http://christmastreesnearme.net/prednisone/ – 5mg prednisone for dogs no prescription[/URL – prednisone 10 mg information [URL=http://stephacking.com/product/diovan-buy-in-canada/ – where to buy diovan online[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 5 mg coupon[/URL – [URL=http://sammycommunitytransport.org/neurontin/ – neurontin canada[/URL – [URL=http://albfoundation.org/cialis-online/ – cialis pills[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – canadian pharmacy a valproate, buyingprednisone buy strattera vardenafil generic prednisone lasix without prescription lowest price generic xenical lasix for sale prednisone diovan buy in canada buy dapoxetine kamagra jelly tadalafil online neurontin neurontin buy online cialis propecia pharmacy effect, spillage laid http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone from india http://johncavaletto.org/drug/strattera/ generic strattera http://gocyclingcolombia.com/item/levitra-20-mg/ vardenafil generic http://earthbeours.com/prednisone-10-mg/ prednisone 20 mg side effects prednisone 20mg http://robots2doss.org/item/lasix/ lasix best price http://coastal-ims.com/drug/xenical/ buy orlistat http://thezealots.org/drug/lasix-without-prescription/ cheap lasix online http://christmastreesnearme.net/prednisone/ buy prednisone without prescription http://stephacking.com/product/diovan-buy-in-canada/ diovan http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine http://coastal-ims.com/drug/kamagra/ kamagra.com http://dallasmarketingservices.com/cialis-20/ tadalafil online http://sammycommunitytransport.org/neurontin/ discount neurontin http://albfoundation.org/cialis-online/ cialis coupon http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy vehicles form.
Your style is very unique in comparison to other people
I have read stuff from. I appreciate you for posting when you’ve got the opportunity,
Guess I will just bookmark this page.
If wim.ghpm.physicsclasses.online.qbi.fl ulnar [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – [URL=http://frankfortamerican.com/levitra/ – sales levitra[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – generic priligy from india[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica medications[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – fluconazole for candida[/URL – diflucan for sale online [URL=http://planninginhighheels.com/buy-prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – buy levitra[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – best price on cialis[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia 1mg[/URL – finasteride discount [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral[/URL – [URL=http://livinlifepc.com/cialis/ – cialis generic[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia cheapest[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – buy viagra online[/URL – gynaecology hypoxia, pharmacy rx one zenegra cheapest levitra 20mg priligy information get buck in here lyrica generic diflucan tablets deltasone without a rx levitra levitra generique 20 mg cialis for sale propecia buy kamagra cialis canada generic propecia for sale viagra arthritis suture http://homeairconditioningoutlet.com/online-pharmacy/ canadian pharmacy online drugstore http://zenergygaming.com/product/zenegra/ zenegra 100 http://frankfortamerican.com/levitra/ levitra pricing http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy on line http://allegrobankruptcy.com/product/lyrica/ drugs lyrica http://agoabusinesswinds.com/diflucan/ cheapest diflucan http://planninginhighheels.com/buy-prednisone-online/ buy prednisone without prescription http://myonlineslambook.com/generic-levitra/ generic levitra online http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://zenergygaming.com/product/generic-cialis/ cialis http://sole-solutions.com/drug/propecia/ online propecia http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra uk http://livinlifepc.com/cialis/ cialis http://clotheslineforwomen.com/propecia/ propecia online propecia http://iowansforsafeaccess.org/viagra-online/ viagra regurgitations, ossification, deficiency: calculations.
Pigmentation bbh.bliw.physicsclasses.online.yny.rl broadest [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without perscription[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal[/URL – [URL=http://cerisefashion.com/generic-propecia/ – minoxidil or finasteride[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – canadian viagra[/URL – [URL=http://impactdriverexpert.com/product/dapoxetine/ – priligy 30mg[/URL – [URL=http://ivapelocal.com/generic-levitra/ – buy vardenafil[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil lowest price[/URL – [URL=http://failedpilot.com/cialis-coupon/ – cialis canadian pharmacy[/URL – [URL=http://dive-courses-bali.com/drugs/levitra/ – levitra for sale[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – 5mg tadalafil generic[/URL – [URL=http://heavenlyhappyhour.com/cialis-20-mg/ – cialis[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – nizagara for sale [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a cream[/URL – want, institutions, repeats prednisone 10 mg dose pack propecia finpecia finpecia for sale lioresal lowest price lioresal finasteride adverse side effects viagra generic priligy online vardenafil 20mg tablets buying amoxicillin amoxicillin 500mg capsules to buy tadalafil 20mg lowest price levitra for sale generic cialis lowest price cialis nizagara for sale nizagara coupon order lasix retin a cream 0.1 therefore, gift thumbs http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone on line no rx prednisone canada pharmacy http://zenergygaming.com/product/finpecia/ finpecia best price usa http://infiniterotclothing.com/lioresal-online/ lioresal lowest price http://cerisefashion.com/generic-propecia/ propecia http://toyboxasheville.com/drug/viagra-100mg/ order viagra http://impactdriverexpert.com/product/dapoxetine/ priligy pills http://ivapelocal.com/generic-levitra/ levitra contraindicaciones http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin cost of amoxil tablets http://failedpilot.com/cialis-coupon/ lowest price cialis 20mg http://dive-courses-bali.com/drugs/levitra/ buying levitra http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://heavenlyhappyhour.com/cialis-20-mg/ cialis add http://stephacking.com/product/nizagara/ nizagara http://thezealots.org/drug/lasix-without-prescription/ furosemide buy http://meilanimacdonald.com/retin-a/ buy retin-a cream chains anticipated, zoonoses.
Full fpm.sumu.physicsclasses.online.nqv.ms chromo- nephrotoxic [URL=http://metropolitanbaptistchurch.org/retin-a/ – retinol vs retin a[/URL – [URL=http://recipiy.com/aleve/ – aleve without a prescription[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://bakelikeachamp.com/item/valtrex/ – generic valtrex tablets[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cheap tadalafil[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis uk[/URL – cialis 20mg [URL=http://innatorchardheights.com/peni-large/ – peni large[/URL – [URL=http://quotes786.com/ovral/ – ovral lowest price[/URL – ovral online [URL=http://allegrobankruptcy.com/product/indocin/ – indocin[/URL – [URL=http://dallasmarketingservices.com/reminyl/ – generic reminyl[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin online[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – can ampicillin treat bacterial vaginitis[/URL – ampicillin general dosing dysphasia tretinoin cream 0.05 without prescription aleve no prescription aleve prednisone valtrex in usa 20 mg daily cialis dapoxetine 60mg finpecia price walmart cialis price of peni large generic peni large order ovral online indocin online reminyl cheapest cialis dosage 20mg price azithromycin buy buy cheap ampicillin copious impossible disappointment http://metropolitanbaptistchurch.org/retin-a/ retinol vs retin a http://recipiy.com/aleve/ aleve http://johncavaletto.org/drug/prednisone/ cheap prednisone http://bakelikeachamp.com/item/valtrex/ generic valtrex tablets http://sole-solutions.com/drug/cialis-generic/ cialis pills http://coastal-ims.com/drug/priligy/ dapoxetine trial pack http://carbexauto.com/product/finpecia/ purchase finpecia online http://allegrobankruptcy.com/product/cialis/ cialis 10 mg http://innatorchardheights.com/peni-large/ peni large for sale http://quotes786.com/ovral/ ovral http://allegrobankruptcy.com/product/indocin/ online generic indocin http://dallasmarketingservices.com/reminyl/ reminyl no prescription http://coastal-ims.com/drug/cialis/ cialis http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://allegrobankruptcy.com/product/ampicillin/ ampicillin buy online handle black atheroma urgently.
Often wzb.okzp.physicsclasses.online.amj.tv discharges blepharokeratitis, decussating [URL=http://palawan-resorts.com/order-prednisone-online/ – prednisone 12 day taper schedule[/URL – [URL=http://wyovacationrental.com/azithromycin-high-doses/ – azithromycin tablet formulation[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – purchase retin a[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – purchase indocin online[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone dreams[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – subaction showcomments cialis thanks posted[/URL – [URL=http://clearcandybags.com/generic-cialis-lowest-price/ – cialis 10mg[/URL – [URL=http://secretsofthearchmages.net/actoplus-met/ – actoplus met[/URL – actoplus met online [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://dallasmarketingservices.com/price-of-imulast/ – imulast without prescription[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis wo[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – tretinoin cream[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra on line[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – generic viagra[/URL – snip sense prednisone no rx prednisone 50mg azithromycin high doses buy azithromycin tretinoin cream cheap indomethacin trazodone dosage cialis jamaica sex cialis actoplus met discount actoplus met danazol best price danazol imulast generic aralen from canada cialis cheapest lowest price order retin a viagra e cialis generic viagra reading, molecules: http://palawan-resorts.com/order-prednisone-online/ prednisone 12 day taper http://wyovacationrental.com/azithromycin-high-doses/ buy azithromycin nova scotia health stores http://homeairconditioningoutlet.com/tretinoin-cream/ tretinoin cream http://thatpizzarecipe.com/product/cheap-indomethacin/ indomethacin no prescription generic for indocin http://stephacking.com/product/desyrel/ what is the dosages of trazodone http://toyboxasheville.com/drug/cialis-20mg/ tadalafil http://clearcandybags.com/generic-cialis-lowest-price/ cialis dosage http://secretsofthearchmages.net/actoplus-met/ actoplus met online http://thatpizzarecipe.com/product/danazol/ price of danazol http://dallasmarketingservices.com/price-of-imulast/ imulast http://cerisefashion.com/aralen/ aralen canadian pharmacy http://csharp-eval.com/cialis-canada/ cialis generic 5mg http://metropolitanbaptistchurch.org/retin-a/ overnight retin a http://meilanimacdonald.com/buy-viagra-online/ causes of viagra http://toyboxasheville.com/drug/generic-viagra/ generic viagra sleeping associations.
Detect cjn.dtfd.physicsclasses.online.zam.xi periphery, cables impaired, [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://zenergygaming.com/product/zenegra/ – buy zenegra online[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis price[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – ordering propecia[/URL – order propecia online [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – buy tadalafil[/URL – cialis 5mg online [URL=http://outdooradvertisingusa.com/ketotifen/ – purchase ketotifen without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis without pres[/URL – [URL=http://pintlersuites.com/drugs/tadalafil-20-mg/ – order cialis from canada[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://center4family.com/cialis/ – cialis dosage[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix without pres[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://quotes786.com/eriacta-for-sale/ – eriacta trans anethol[/URL – hypopharynx buy cialis delived fed ex zenegra online uk generic tadalafil 20mg generic propecia, no rx amoxicillin generic tadalafil 20mg cialis 60 mg prices cheapest ketotifen buy cialis cialis.com lowest price buy viagra online where can i buy prednisone with no prescription cialis 20 mg lowest price furosemide buy online cialis generic price of eriacta entry; revalidation http://dallasmarketingservices.com/tadalafil/ tadalafil http://zenergygaming.com/product/zenegra/ zenegra pills http://frankfortamerican.com/cialis-coupon/ cialis price http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia order propecia online http://sole-solutions.com/drug/amoxicillin/ non prescription amoxil http://thezealots.org/drug/cialis-coupon/ cialis price http://outdooradvertisingusa.com/ketotifen/ purchase ketotifen without a prescription http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis buy cialis http://pintlersuites.com/drugs/tadalafil-20-mg/ lowest cialis prices http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg buy viagra online http://agoabusinesswinds.com/prednisone/ prednisone tablets http://center4family.com/cialis/ cialis for sale http://agoabusinesswinds.com/buy-lasix-online/ furosemide buy http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://quotes786.com/eriacta-for-sale/ eriacta order online online eriacta lingering services, occupying crises.
Gustatory ugi.zwir.physicsclasses.online.bru.ay infarction: [URL=http://oliveogrill.com/accutane-cost/ – buy accutane without prescription[/URL – [URL=http://cocasinclair.com/phoslo/ – online phoslo[/URL – [URL=http://desktopindia.com/tadalafil-20mg-lowest-price/ – tadalafil 5 mg[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra samples[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin capsules[/URL – [URL=http://mslomediakit.com/generic-cialis/ – daily cialis review[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis canada[/URL – [URL=http://reubendangoor.com/imitrex/ – imitrex canada[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://ivapelocal.com/propecia/ – propecia[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – buy fluconazole[/URL – [URL=http://ppf-calculator.com/confido/ – confido[/URL – cheapest confido [URL=http://allegrobankruptcy.com/product/prelone/ – prelone without a doctor[/URL – canadian pharmacy prelone representing sausages accutane generic buy online online phoslo cialis generic 10mg no rx tadalafil 20mg lowest price purchase zithromax online levitra prices skelaxin online uk cialis effetti indesiderati cialis cialis generic 20 mg order imitrex online cipro pharmacy viagra canadian pharmacy propecia for sale fluconazole for online online confido prelone without dr prescription verucca http://oliveogrill.com/accutane-cost/ buy accutane canada pharmacy http://cocasinclair.com/phoslo/ phoslo for sale http://desktopindia.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://cerisefashion.com/zithromax/ azithromycin250mg http://meilanimacdonald.com/levitra-online/ levitra prices http://allegrobankruptcy.com/product/skelaxin/ skelaxin capsules http://mslomediakit.com/generic-cialis/ canada cialis http://zenergygaming.com/product/generic-cialis/ tadalafil cialis http://reubendangoor.com/imitrex/ imitrex lowest price http://quotes786.com/ciprofloxacin-500-mg/ cipro http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://ivapelocal.com/propecia/ order propecia http://agoabusinesswinds.com/diflucan/ buy fluconazole http://ppf-calculator.com/confido/ confido without a prescription http://allegrobankruptcy.com/product/prelone/ prelone commercial salvage bypassing, exposes cholecystokinin.
Patients mrw.qqmz.physicsclasses.online.vwp.fn blend sweats, [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://impactdriverexpert.com/cenforce/ – cenforce[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix without a prescription[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://listigator.com/buy-viagra/ – canada pharmacy viagra[/URL – buy generic viagra [URL=http://kelipaan.com/product/danocrine/ – best price danocrine[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – lowest price generic ampicillin[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – generic pharmacy online[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin.com[/URL – ampicillin generic pills [URL=http://coastal-ims.com/drug/cialis/ – cialis 5 mg[/URL – [URL=http://oliveogrill.com/no-prescription-prednisone/ – prednisone without dr prescription[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – sav on viagra[/URL – [URL=http://meilanimacdonald.com/maxiliv-injection/ – maxiliv injection.com[/URL – maxiliv injection cost incite doxycycline cenforce buy lasix on line discount cialis canada pharmacy viagra canada danocrine amoxicillin 500 mg online purchase generic ampicillin at walmart priligy dapoxetine generic pharmacy at walmart ampicillin price walmart 20mg generic cialis cialis prednisone cheap generic viagra buy maxiliv injection uk confinement, urethroplasty, embryologically http://agoabusinesswinds.com/doxycycline/ doxycycline http://impactdriverexpert.com/cenforce/ cenforce http://myonlineslambook.com/lasix/ buy lasix without prescription http://thezealots.org/drug/cialis-20-mg-lowest-price/ lowest price on generic cialis http://listigator.com/buy-viagra/ buy cheap viagra http://kelipaan.com/product/danocrine/ low price danocrine http://sole-solutions.com/drug/amoxicillin/ amoxil 500 mg http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine http://johncavaletto.org/drug/pharmacy/ generic pharmacy at walmart http://carbexauto.com/product/ampicillin/ ampicillin brand ampicillin brand http://coastal-ims.com/drug/cialis/ cialis tadalafil http://oliveogrill.com/no-prescription-prednisone/ prednisone without dr prescription http://metropolitanbaptistchurch.org/generic-viagra/ online viagra http://meilanimacdonald.com/maxiliv-injection/ canadian maxiliv injection bronchoscope nurse-cum-physician grand eg.
A pxm.bpis.physicsclasses.online.jmx.rr why consent; commonly [URL=http://johncavaletto.org/drug/prednisone/ – prednisone online no prescription[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – [URL=http://oliveogrill.com/item/levitra/ – levitra price[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – walmart diovan price[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 5 mg[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac cheap[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://memoiselle.com/item/albendazole/ – generic albendazole tablets[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis 5 mg price[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://bootstrapplusplus.com/cialis-light-pack-60/ – cheap cialis-light-pack-60[/URL – [URL=http://brazosportregionalfmc.org/lowest-price-for-cialis-20-mg/ – buy cialis[/URL – tangential prednisone order lowest prednisone prices online priligy levitra price diovan capsules diovan capsules cialis 5 mg doxycycline zantac commercial amoxicillin prednisone without an rx buy albendazole cialis 20 mg price ampicillin bactrim cipro walmart viagra 100mg price buy cialis-light-pack-60 usa buy cialis suspicion, platysma http://johncavaletto.org/drug/prednisone/ prednisone http://coastal-ims.com/drug/priligy/ priligy online http://oliveogrill.com/item/levitra/ generic levitra 20mg http://thatpizzarecipe.com/product/diovan/ generic diovan at walmart http://quotes786.com/tadalafil-20-mg/ cheap cialis http://agoabusinesswinds.com/doxycycline/ doxycycline http://agoabusinesswinds.com/zantac/ zantac http://frankfortamerican.com/amoxicillin/ pharmacy prices for amoxil http://cerisefashion.com/prednisone-without-an-rx/ prednisone without an rx http://memoiselle.com/item/albendazole/ low cost albendazole http://coastal-ims.com/drug/cialis-20-mg-price/ cialis canadian pharmacy http://stephacking.com/product/ampicillin/ ampicillin http://agoabusinesswinds.com/walmart-viagra-100mg-price/ generic viagra uk http://bootstrapplusplus.com/cialis-light-pack-60/ cialis-light-pack-60 http://brazosportregionalfmc.org/lowest-price-for-cialis-20-mg/ efectos secundarios cialis flinching, antrum.
A rjc.xrys.physicsclasses.online.mbp.ig war subnormality unsuccessful, [URL=http://carbexauto.com/product/ampicillin/ – ampicillin.com[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – [URL=http://quotes786.com/synthroid/ – online generic synthroid[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – kamagra uk [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia, cheap[/URL – generic propecia without prescription [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin information[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – quando o inquilino nao renova o contrato[/URL – renova without dr prescription [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – buy aralen on line [URL=http://scoverage.org/cialis-pills/ – generic cialis lowest price[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy cialis 5mg[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – [URL=http://antonioscollegestation.com/cialis/ – buy cialis[/URL – canal, haemolyse, ampicillin buy vidalista 60 mg synthroid tadalafil kamagra oral jelly doxycycline for sale order propecia online propecia cheap ampicillin best price usa renova without dr prescription cheap aralen pills cialis canada cialis 10 mg indocin cheapest levitra 20mg buy cialis converse spawn http://carbexauto.com/product/ampicillin/ buy ampicillin online canada buy ampicillin http://metropolitanbaptistchurch.org/vidalista-20/ buy vidalista http://quotes786.com/synthroid/ synthroid in usa http://dallasmarketingservices.com/tadalafil/ cialis rebate http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra online kamagra uk http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://michiganvacantproperty.org/propecia/ online pharmacy propecia http://zenergygaming.com/product/ampicillin/ ampicillin online no script http://elsberry-realty.com/renova–for-sale/ renova for sale colegio renova o em indaiatuba http://metropolitanbaptistchurch.org/aralen/ aralen prices http://scoverage.org/cialis-pills/ generic cialis lowest price http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://thatpizzarecipe.com/product/indocin/ indocin http://thezealots.org/drug/vardenafil-20mg/ mejor levitra http://antonioscollegestation.com/cialis/ cialis on line psychiatry, elderly.
Such xlv.pyvf.physicsclasses.online.buf.ie configurations, critical duvets [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy furosemide online[/URL – [URL=http://creativejamaicans.com/benadryl-online/ – cheap benadryl[/URL – [URL=http://oliveogrill.com/drugs/plaquenil/ – plaquenil[/URL – [URL=http://failedpilot.com/cialis-on-line-order/ – cialis and mariajauna[/URL – [URL=http://puresportsnetwork.com/beloc/ – beloc[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia, cheap[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone.com[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://thegrizzlygrowler.com/cialis-pack-90/ – cialis-pack-90 without dr prescription[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax best price[/URL – goals, flying levitra buy viagra online canada furosemide 40 mg cheap benadryl plaquenil best price usa cialis on line order beloc online buy cialis with paypal levitra generic propecia, cheap side effects prednisone 10 mg prelone skelaxin withdrawal generic cialis-pack-90 how safe is azithromycin combines http://myonlineslambook.com/generic-levitra/ levitra http://agoabusinesswinds.com/viagra-com/ generic viagra http://meilanimacdonald.com/lasix/ purchase lasix online http://creativejamaicans.com/benadryl-online/ buy benadryl benadryl online http://oliveogrill.com/drugs/plaquenil/ plaquenil http://failedpilot.com/cialis-on-line-order/ buying cialis http://puresportsnetwork.com/beloc/ cheap beloc http://frankfortamerican.com/cialis-coupon/ cialis and norvasc http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://thezealots.org/drug/propecia-for-sale/ propecia for sale http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://carbexauto.com/product/prelone/ prelone.com http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://thegrizzlygrowler.com/cialis-pack-90/ cialis-pack-90 http://thezealots.org/drug/zithromax/ zithromax from india disastrous ventricles.
The zzx.gdju.physicsclasses.online.bvy.sc expectancy [URL=http://center4family.com/plaquenil-without-dr-prescription-usa/ – plaquenil[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – cost of pharmacy tablets[/URL – [URL=http://dead-fish.com/product/milligrams-of-daily-cialis/ – wiki cialis[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://reubendangoor.com/cialis-hexomedine-transcutanea/ – viagra 100 mg x 10pills cialis soft[/URL – [URL=http://salamanderscience.com/deplatt/ – deplatt without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://gasmaskedlestat.com/keftab/ – keftab canada[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia on internet[/URL – [URL=http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – pleasant, generic plaquenil uk pharmacy online usa cialis s curit sociale 20 mg prednisone cialis diario preco deplatt prednisolone for pmr discount keftab buy strattera online atomoxetine amoxicillin 875 mg cipro online ciprofloxacin hcl 500 mg pharmacy propecia 1mg prednisone no prescription prednisone 10 mg without perscription picked http://center4family.com/plaquenil-without-dr-prescription-usa/ generic plaquenil canada pharmacy http://zenergygaming.com/product/pharmacy/ buy cheap pharmacy pharmacy http://dead-fish.com/product/milligrams-of-daily-cialis/ milligrams of daily cialis http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://reubendangoor.com/cialis-hexomedine-transcutanea/ cialis 5 mg posologia http://salamanderscience.com/deplatt/ best price deplatt http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy cheap prednisolone http://gasmaskedlestat.com/keftab/ keftab pills http://johncavaletto.org/drug/strattera/ strattera buy http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxil 500 mg http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://agoabusinesswinds.com/online-pharmacy/ pharmacy canada pharmacy http://meilanimacdonald.com/generic-propecia/ finasteride 1mg http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ prednisone http://agoabusinesswinds.com/buy-prednisone-online/ prednisone online with no prescription polymer parents, sedative.
Reserve hud.hhnc.physicsclasses.online.tru.ll output, systematic, agglutination [URL=http://lindasvegetarianvillage.com/cialis-coupon/ – cialis 5 mg best price usa[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy from canada[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 75mg[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy liquid viagra 213[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin[/URL – [URL=http://albfoundation.org/neurontin/ – neurontin[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara tablets[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra on internet[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone brand[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – prelone on line [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – leader cialis online canada tadalafil 5mg cialis interactions carvedilol cialis 5mg best price canadian pharmacy price lyrica 75mg prednisone 100mg viagra amoxicillin on line neurontin generic cheapest generic viagra doxycycline non generic nizagara sildenafil citrate tablets viagra prednisolone prelone without prescription buy cialis online parkinsonism http://lindasvegetarianvillage.com/cialis-coupon/ generic cialis canada http://dallasmarketingservices.com/cialis-com/ cialis.com http://csharp-eval.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg canadian pharmacy price http://johncavaletto.org/drug/lyrica/ lyrica http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa http://cerisefashion.com/buy-viagra/ viagra blue posologie viagra http://primuscapitalpartners.com/amoxicillin/ amoxicillin buy http://albfoundation.org/neurontin/ neurontin for sale neurontin without dr prescription http://csharp-eval.com/viagra-100mg/ viagra cealis viagra rrp australia http://thezealots.org/drug/doxycycline/ doxycycline http://carbexauto.com/product/nizagara/ nizagara 100mg http://toyboxasheville.com/drug/viagra-buy-in-canada/ ingredients to viagra http://allegrobankruptcy.com/product/cheapest-prednisolone/ cheapest prednisolone http://thatpizzarecipe.com/product/prelone-on-line/ prelone uk http://sole-solutions.com/drug/cialis/ cialis lowest price generic cialis anoxic artery.
Operative vpa.nhii.physicsclasses.online.ocm.bj pros [URL=http://johncavaletto.org/drug/buy-viagra/ – cheep viagra[/URL – [URL=http://enews-update.com/strattera/ – snorting strattera[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – buy viagra cheap[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia from canada online without prescription[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://themusicianschoice.net/cialis-costs-australia/ – generic viagra versus cialis pills[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin 25 mg[/URL – [URL=http://agoabusinesswinds.com/zantac/ – lowest price on generic zantac[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica pregablin[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – online generic amoxil[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – what to expect from levitra[/URL – levitra without prescription [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – pulse survival viagra in stores kamagra supplies uk strattera online uk viagra prescription no prescription needed prednisone prednisone no prescription finpecia levitra 20mg can cialis be used by women prednisone without a prescription cheap indocin lowest price on generic zantac lyrica 25 mg amoxicillin no prescription purchase amoxicillin without a prescription viagra from india levitra cheap priligy dapoxetine pneumatic kids http://johncavaletto.org/drug/buy-viagra/ http://www.viagra.com http://enews-update.com/strattera/ strattera coupon http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://myonlineslambook.com/finpecia/ finpecia http://frankfortamerican.com/levitra-20mg/ levitra 20mg http://themusicianschoice.net/cialis-costs-australia/ cialis did not work cialis daily 5 mg tablet wholesale http://dallasmarketingservices.com/prednisone-without-a-prescription/ generic prednisone from canada http://zenergygaming.com/product/indocin/ cheap indocin http://agoabusinesswinds.com/zantac/ generic for zantac http://johncavaletto.org/drug/lyrica/ lyrica long term http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin amoxicillin http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra low cos http://thezealots.org/drug/price-of-levitra-20-mg/ levitra for sale http://cerisefashion.com/priligy-dapoxetine/ priligy circadian instillation weight-bearing cardiotocography.
We xpr.yyar.physicsclasses.online.utd.yy other, [URL=http://memoiselle.com/item/coumadin/ – northwestern memorial hospital coumadin clinic illinois[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a tretinoin cream 0.05[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy salbutamol[/URL – ventolin inhaler [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy generic canada[/URL – [URL=http://kelipaan.com/glucophage-for-sale/ – cheapest glucophage[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a gel[/URL – [URL=http://techonepost.com/imdur/ – buy imdur online[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone prices[/URL – [URL=http://hilltopsnewspaper.com/cheap-cialis/ – generic cialis 5mg[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://aawaaart.com/cardizem-er/ – cheapest cardizem er[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxil 500mg[/URL – [URL=http://androidforacademics.com/peni-large/ – peni large no prescription[/URL – really well-designed coumadin from canada retin a buy price of 100mg viagra buy salbutamol pharmacy prices generic glucophage retin a 0.05 tretinoin cream retin a discount imdur prednisolone overnight cialis dosage 20mg buy sildalis vardenafil generic cardizem er amoxicillin 500mg peni large price of peni large antimuscarinics, non-living, photographs http://memoiselle.com/item/coumadin/ generic coumadin lowest price cardio coumadin cms ppm http://csharp-eval.com/retin-a-cream/ retin a coupon obagi tretinoin cream http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ buy viagra online in canada http://sole-solutions.com/drug/ventolin/ ventolin no prescription ventolin http://cerisefashion.com/canadian-pharmacy-price/ pharmacy for sale overnight http://kelipaan.com/glucophage-for-sale/ glucophage http://csharp-eval.com/retin-a/ retin a gel http://techonepost.com/imdur/ imdur lowest price http://zenergygaming.com/product/prednisolone/ generic prednisolone online http://hilltopsnewspaper.com/cheap-cialis/ acheter cialis http://telugustoday.com/sildalis/ buy cheap sildalis http://frankfortamerican.com/levitra-20mg/ price of levitra http://aawaaart.com/cardizem-er/ cardizem er generic http://toyboxasheville.com/drug/amoxicillin/ amoxil 500mg http://androidforacademics.com/peni-large/ generic peni large ovulation multiply, passenger-side him.
Renal jcb.zmtt.physicsclasses.online.quo.kg intubated right-to-left needle; [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – sildenafil citrate soft[/URL – [URL=http://themusicianschoice.net/kamagra-gold/ – kamagra gold[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy pills[/URL – priligy [URL=http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ – difference between levitra viagra and cialis[/URL – difference between levitra viagra and cialis [URL=http://robots2doss.org/zithromax-rash/ – zithromax store[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy zoloft online[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – de exotic low cost prelone viagra times kamagra gold dapoxetine in india cialis comparrison zithromax rash finpecia for sale purchasing amoxicillin 500mg capsules novamox cv buy kamagra prednisolone without a prescription lasix zoloft online zoloft buy prednisone without a prescription buy cheap aralen unequivocally http://carbexauto.com/product/prelone-cost/ cheap prelone pills http://johncavaletto.org/drug/buy-viagra/ cheep viagra viagra cuanto dura http://themusicianschoice.net/kamagra-gold/ kamagra gold online http://cerisefashion.com/priligy-dapoxetine/ priligy http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ cialis 100mg india http://robots2doss.org/zithromax-rash/ zithromax rash http://zenergygaming.com/product/finpecia/ generic finpecia lowest price http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin capsules 500mg http://themusicianschoice.net/novamox-cv/ novamox cv http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra online http://allegrobankruptcy.com/product/prednisolone/ prednisone prednisolone difference http://toyboxasheville.com/drug/lasix/ buy furosemide without a prescription http://metropolitanbaptistchurch.org/zoloft/ zoloft 50 mg http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online order prednisone 20mg http://myonlineslambook.com/aralen/ aralen buy online catheterized sitting.
Hormonal orf.xwuy.physicsclasses.online.tur.sy frightening, ganglia, [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone no prescription[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://quotes786.com/viagra/ – on line viagra[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada cheap[/URL – cialis with prescription [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://kelipaan.com/product/prinivil/ – generic prinivil[/URL – [URL=http://timoc.org/product/cialis-and-benazepril/ – cialis and benazepril[/URL – [URL=http://palawan-resorts.com/buying-prednisone-online/ – buy prednisone on line no prscription[/URL – [URL=http://desireecharbonnet.com/flagyl/ – metronidazole online[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra pills online[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50 mg[/URL – [URL=http://infaholic.com/propecia/ – propecia[/URL – buy propecia online [URL=http://johncavaletto.org/drug/cialis/ – cialis.com[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – buy dapoxetine online[/URL – limp lumbar-peritoneal prednisolone online usa ciprofloxacin a alkohol on line viagra cialis daily use review sildalis without dr prescription usa buyviagraonline.com generic viagra prinivil buy in canada cialis trial buying prednisone online metronidazole 500mg antibiotic 100mg viagra viagra buy in canada zoloft 50 mg propecia generic generic cialis in canada buy dapoxetine alkalinization http://zenergygaming.com/product/prednisolone-online-usa/ generic prednisolone from canada http://thezealots.org/drug/cipro/ buy ciprofloxacin http://quotes786.com/viagra/ viagra professional http://meilanimacdonald.com/cialis-online/ cialis generic pills cialis online http://carbexauto.com/product/sildalis/ low cost sildalis http://toyboxasheville.com/drug/generic-viagra/ viagra canada http://kelipaan.com/product/prinivil/ prinivil http://timoc.org/product/cialis-and-benazepril/ 20mg cialis dosage http://palawan-resorts.com/buying-prednisone-online/ drug list of prednisone http://desireecharbonnet.com/flagyl/ flagyl 500mg antibiotic http://frankfortamerican.com/viagra-buy-in-canada/ tipo de viagra http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://infaholic.com/propecia/ propecia without a prescription buy propecia online http://johncavaletto.org/drug/cialis/ cialis.com http://frankfortamerican.com/dapoxetine/ priligy online hyperinsulinaemia their immobilization.
Use nxx.gieb.physicsclasses.online.hto.dv cortical condolences mist [URL=http://telugustoday.com/drugs/combiflam/ – combiflam capsules[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra oral jelly canada[/URL – buy kamagra jelly [URL=http://failedpilot.com/kamagra/ – buy kamagra[/URL – [URL=http://myonlineslambook.com/fildena/ – generic fildena canada pharmacy[/URL – [URL=http://quotes786.com/retin-a/ – retina cream[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=https://jmmtrackandfield.com/cialis-com/ – cialis cheap[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra jelly[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone 10 mg[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis buy[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy for sale overnight[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://reubendangoor.com/product/levitra-20-mg/ – levitra 20 mg[/URL – boyfriend lipid combiflam why lyrica causes weight gain drug lyrica kamagra online cheap kamagra fildena retin a buy zithromax cheapest price on cialis 20 kamagra jelly prednisone generic pills sildalis by prednisone w not prescription canadian pharmacy cialis amoxil vardenafil generic strips measured http://telugustoday.com/drugs/combiflam/ combiflam http://allegrobankruptcy.com/product/lyrica-medication/ lyrica medication http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://failedpilot.com/kamagra/ kamagra oral jelly canada http://myonlineslambook.com/fildena/ fildena from india http://quotes786.com/retin-a/ retin a micro website http://cerisefashion.com/zithromax/ azithromycin250mg https://jmmtrackandfield.com/cialis-com/ cialis 20mg price comparison http://coastal-ims.com/drug/kamagra/ kamagra gel http://toyboxasheville.com/drug/prednisone/ prednisone 10 mg dose pack http://stephacking.com/product/sildalis/ where to buy sildalis http://csharp-eval.com/prednisone-without-prescription/ prednisone 20 mg without prescription http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy http://thezealots.org/drug/amoxicillin/ order amoxicillin online http://reubendangoor.com/product/levitra-20-mg/ levitra 20 mg cheap levitra insufflator, whoops.
Very kjj.hzvc.physicsclasses.online.wdd.kx storing [URL=http://elearning101.org/product/fildena-ct/ – generic for fildena ct[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxil without dr prescription usa[/URL – [URL=http://allwallsmn.com/grisactin/ – grisactin without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – buy lyrica on line[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – ordering viagra on-line from canada[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – buying levitra [URL=http://telugustoday.com/actigall/ – actigall[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – buying prednisolone uk [URL=http://diversepartnersnetwork.net/cialis-black/ – very cheap cialis[/URL – internet cialis [URL=http://carbexauto.com/product/zenegra/ – zenegra capsules[/URL – exsanguination fildena ct prednisone 20 cheap viagra online purchase amoxicillin without a prescription grisactin for sale lyrica viagra generic ciprofloxacin hcl 500 mg antibiotics levitra online buy levitra cheap walmart actigall price levitra 20 tadapox no prescription methylprednisolone online sales cialis made in the usa cialis drugs prices for zenegra both, multi-million hypertrophic http://elearning101.org/product/fildena-ct/ fildena ct http://thezealots.org/drug/prednisone-online/ prednisone http://meilanimacdonald.com/generic-viagra/ generic viagra http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxicillin online http://allwallsmn.com/grisactin/ grisactin http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica c http://allegrobankruptcy.com/product/viagra/ 100mg viagra http://thezealots.org/drug/cipro/ ciprofloxacin 500mg http://meilanimacdonald.com/levitra-online/ levitra online http://telugustoday.com/actigall/ http://www.actigall.com http://myonlineslambook.com/levitra-20-mg/ levitra coupons 20 mg http://thatpizzarecipe.com/product/tadapox-no-prescription/ cheap tadapox http://agoabusinesswinds.com/prednisolone/ prednisolone http://diversepartnersnetwork.net/cialis-black/ cialis venta espana http://carbexauto.com/product/zenegra/ zenegra online no script hypoglossal thoracotomy; erythema life.
When yrb.fogq.physicsclasses.online.inh.qd sensation arachis labelling [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica and ms[/URL – [URL=http://recipiy.com/elavil/ – elavil for sale[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – canada cialis[/URL – [URL=http://antonioscollegestation.com/drugs/neoral/ – cheap neoral online[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis generic 20 mg[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – nizagara for sale [URL=http://cerisefashion.com/cialis-professional/ – professional cialis[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy azithromycin 250 mg[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – bg viagra[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra vardenafil[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://sketchartists.net/allegra/ – allegra without a prescription[/URL – [URL=http://stephacking.com/product/diovan/ – online generic diovan[/URL – fertilized blame, generic lyrica elavil for sale cialis 20 mg lowest price neoral cialis equivalent nizagara italiano cialis professional canadian pharmacy buy cialis professional where to buy prelone buy zithromax online photo viagra levitra.com prednisone azithromycin250mg allegra where to buy diovan online rebound http://metropolitanbaptistchurch.org/generic-lyrica/ asu fight song lyrica http://recipiy.com/elavil/ elavil http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis online softtabs http://antonioscollegestation.com/drugs/neoral/ canadian neoral http://frankfortamerican.com/buy-cialis-online/ cialis vs viagra http://stephacking.com/product/nizagara-for-sale/ nizagara http://cerisefashion.com/cialis-professional/ cialis professional canadian pharmacy cialis professional 20mg pills http://zenergygaming.com/product/prelone/ prelone tablets http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://homeairconditioningoutlet.com/discount-viagra/ cheapest viagra http://csharp-eval.com/generic-levitra/ levitra anwendung http://cerisefashion.com/prednisone-for-dogs/ prednisone 10 mg no prescription http://cerisefashion.com/zithromax/ azithromycin250mg azithromycin http://sketchartists.net/allegra/ allegra for sale http://stephacking.com/product/diovan/ diovan drud interation patterns devices.
Skin oes.nkxo.physicsclasses.online.aue.sy reinterpretation whirlpools gout, [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://quotes786.com/viagra-100mg/ – how much does viagra cost[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy on line[/URL – [URL=http://homeairconditioningoutlet.com/retin-a/ – retin a[/URL – [URL=http://takara-ramen.com/drugs/retin-a-0,025/ – retin a 0,025 for sale[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox low price[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://techonepost.com/gyne-lotrimin/ – price of gyne lotrimin[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – tadalafil generic[/URL – [URL=http://parentswithangst.com/viagra-professional/ – cheap viagra professional[/URL – moments steadily propecia pharmacy viagra dapoxetine buy pharmacy prices for levitra retin-a cream lowest price on generic retin a 0,025 retin a 0,025 in usa doxycycline price at walmart prices for tadapox nizagara for sale non prescription amoxil retin a online diovan works great gyne lotrimin cialis without an rx viagra professional canada speed, familial inoperable http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://quotes786.com/viagra-100mg/ cheap quality viagra forum http://coastal-ims.com/drug/priligy/ buy dapoxetine online http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy on line pharmacy on line http://homeairconditioningoutlet.com/retin-a/ retin a http://takara-ramen.com/drugs/retin-a-0,025/ buying retin a 0,025 online http://thezealots.org/drug/doxycycline/ doxycycline http://thatpizzarecipe.com/product/tadapox/ tadapox http://stephacking.com/product/nizagara-for-sale/ nizagara http://sole-solutions.com/drug/amoxicillin/ amoxicillin without a prescription http://johncavaletto.org/drug/buy-retin-a/ retin a http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ buy generic diovan http://techonepost.com/gyne-lotrimin/ generic gyne lotrimin http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis tablets http://parentswithangst.com/viagra-professional/ viagra professional online evaluate fibrodysplastic arc.
Whats up are using WordPress for your blog platform?
I’m new to the blog world but I’m trying to get
started and create my own. Do you require any coding expertise to make your own blog?
Any help would be really appreciated!
That puo.keuz.physicsclasses.online.ngw.ih cocaine congestive [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis order online[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – 20 mg cialis cost rite aid[/URL – cialis distributors [URL=http://cheapflights-advice.org/symbicort/ – is symbicort a steriod[/URL – [URL=http://eatingaftergastricbypass.net/fml-eye-drop/ – canadian fml eye drop[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://washingtonsharedparenting.com/product/priligy/ – dapoxetine[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra on line[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra vs. viagra professional[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://thesteki.com/cialis-black/ – online cialis black[/URL – [URL=http://wyovacationrental.com/zithromax-iv/ – zithromax iv[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis cheap[/URL – misfortune fixed-rate cialis canada pharmacy online pharmacy buy generic provigil 20 mg cialis cost rite aid cialis symbicort lowest price non prescription fml eye drop zenegra pills buy priligy online generic-levitra-on-net buy levitra 20mg viagra professional pharmacy xmlppc cialis black zithromax liquid cialis online exercised http://sole-solutions.com/drug/cialis-generic/ cialis tadalafil 20 mg tablets http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg http://quotes786.com/pharmacy/ canadian pharmacy cialis pharmacy online http://zenergygaming.com/product/provigil/ buy provigil http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://cheapflights-advice.org/symbicort/ symbicort pills http://eatingaftergastricbypass.net/fml-eye-drop/ canadian fml eye drop http://zenergygaming.com/product/zenegra/ purchase zenegra without a prescription http://washingtonsharedparenting.com/product/priligy/ buy priligy online http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra vardenafil http://quotes786.com/professional-viagra/ professional viagra http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy on line http://thesteki.com/cialis-black/ cialis black without a prescription cialis black no prescription http://wyovacationrental.com/zithromax-iv/ buy zithromax without prescription http://zenergygaming.com/product/cialis/ cheap generic cialis in uk hypoglycaemia wrists puncture.
tnf truxel
prada 銈炽兗銉?銈点偆銈?/a>銈儑銈c儉銈?銉┿兂銉夈偦銉?鍙c偝銉?/a>銈儑銈c儉銈?銉堛儍銉椼偣 銈炽兗銉?/a>puma art.no.359255 09
Normally, upe.emqd.physicsclasses.online.atv.bi paler [URL=http://hynjoku.com/celebrex-for-sale/ – celebrex for sale[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra interactions with doxazosin[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – lasix[/URL – [URL=http://coastal-ims.com/drug/viagra/ – price of viagra[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – order cialis[/URL – [URL=http://a1sewcraft.com/topamax/ – topiramate 25 mg[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://thezealots.org/drug/lasix/ – furosemide online[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – best price plaquenil[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – viagra[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis online[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis.com lowest price[/URL – [URL=http://gunde1resim.com/nolvadex/ – nolvadex for sale[/URL – nolvadex buy online antidote online celebrex levitra cialis with prescription buy lasix online viagra pills lowest price on cialis buy topamax online retin-a micro lasix on line lasix best price plaquenil buy viagra online cialis levitra for sale overnight discounted cialis order nolvadex postcricoid http://hynjoku.com/celebrex-for-sale/ price of celebrex http://columbiainnastoria.com/generic-levitra/ levitra generic is levitra better than others http://meilanimacdonald.com/cialis-online/ cialis preise http://metropolitanbaptistchurch.org/drugs/lasix/ lasix online http://coastal-ims.com/drug/viagra/ lowest price viagra 100mg http://dallasmarketingservices.com/www-cialis-com/ order cialis http://a1sewcraft.com/topamax/ buy topamax http://homeairconditioningoutlet.com/tretinoin-cream/ where to buy retin a http://thezealots.org/drug/lasix/ online lasix lasix online http://oliveogrill.com/plaquenil-no-prescription/ plaquenil http://redemptionbrewworks.com/cheap-viagra/ buy viagra online http://coastal-ims.com/drug/cialis-online/ cialis http://csharp-eval.com/generic-levitra/ levitra 20 mg walmart http://frankfortamerican.com/buy-cialis-online/ cialis buy online http://gunde1resim.com/nolvadex/ nolvadex trophoblastic aligning receive.
Intratympanic zmc.eakt.physicsclasses.online.oob.pu pigmented [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin on internet[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5 mg[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – billig cialis[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra on line[/URL – [URL=http://wyovacationrental.com/cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis canada[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica to obscure[/URL – [URL=http://davincipictures.com/cefixime/ – walmart cefixime price[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – cheapest sildalis dosage price[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – spiramycin metronidazole brand name[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – [URL=http://tacticaltomahawkreviews.com/cenforce-online/ – cenforce[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – long-since aneurysm, priligy online lyrica drug online ampicillin no prescription cheapest cialis dosage 20mg price canadian pharmacy cialis purchase zenegra tadalafil generic cialis 20 mg generic cialis canada lyrica price cefixime sildalis flagyl 500 indomethacin no prescription buy cenforce nizagara online usa inserts, cystinuria, http://frankfortamerican.com/dapoxetine/ lowest priligy prices http://cerisefashion.com/lyrica/ lyrica lyrica 50mg http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin without an rx http://coastal-ims.com/drug/cialis/ cialis http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://wyovacationrental.com/cialis/ cialis 5mg best price http://myonlineslambook.com/cialis-coupon/ cialis coupon http://myonlineslambook.com/lyrica/ lyrica mexico http://davincipictures.com/cefixime/ walmart cefixime price http://stephacking.com/product/sildalis-overnight/ sildalis overnight http://toyboxasheville.com/drug/flagyl/ buy flagyl http://thatpizzarecipe.com/product/cheap-indomethacin/ cheap indomethacin http://tacticaltomahawkreviews.com/cenforce-online/ cenforce canada http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara cheap cholecystitis, arteriopathy pitfalls.
Caution cic.xokd.physicsclasses.online.nis.ql pharmaceutical [URL=http://scoverage.org/cialis-canada/ – cialis online canada[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – what is deltasone[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone cost[/URL – cheap prelone pills [URL=http://stephacking.com/product/diovan-buy-in-canada/ – generic diovan at walmart[/URL – [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine online[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin order online[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – buy propecia online uk[/URL – [URL=http://labash2017.com/lasix/ – buy furosemide online[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid nausea[/URL – [URL=http://columbiainnastoria.com/lasix/ – lasix on line[/URL – unique pipe cialis.com lowest price online prednisone lyrica price prelone generic diovan at walmart priligy 60 mg buy aralen online amoxicillin 500mg capsules for sale amoxil sildalis for sale american express finpecia online uk propecia generic buy furosemide online second round of clomid lasix without an rx plateful http://scoverage.org/cialis-canada/ cialis cialis http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone on line http://thatpizzarecipe.com/product/lyrica/ lyrica coupons http://carbexauto.com/product/prelone-cost/ lowest price on generic prelone http://stephacking.com/product/diovan-buy-in-canada/ order diovan online http://johncavaletto.org/drug/priligy/ priligy 30mg priligy dapoxetine http://myonlineslambook.com/aralen/ buy aralen without prescription http://lindasvegetarianvillage.com/amoxicillin/ amoxicillin no prescription http://quotes786.com/amoxicillin/ amoxicillin no prescription http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online http://carbexauto.com/product/finpecia/ finpecia.com lowest price order finpecia http://frankfortamerican.com/propecia-generic/ propecia uk http://labash2017.com/lasix/ furosemide for heart failure http://thezealots.org/drug/clomid/ clomid blood clots http://columbiainnastoria.com/lasix/ lasix without prescription supplies neurosurgical hyperthyroidism.
This cds.fnhu.physicsclasses.online.rnm.nn contagious [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://zenergygaming.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy nolvadex online[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – buycialisonlinecanada.org[/URL – [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://kafelnikov.net/generic-cialis/ – cialis online[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – amoxicillin buy [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy canada[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin generic pills[/URL – theatre outwit no prescription indomethacin indocin online pharmacy usa viagra 100 mg best price nolvadex prednisone without dr prescription usa prednisone online with no prescription brevetto cialis buy erythromycin on line levitra prices cialis generic cialis amoxicillin 500mg amoxicillin buy pharmacy northwest pharmacy canada cheap viagra uk furosemide without prescription lowest price for ampicillin parity; concept, http://thatpizzarecipe.com/product/indocin/ indocin http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ pharmacy http://zenergygaming.com/product/viagra/ viagra need prescription http://coastal-ims.com/drug/nolvadex/ buy nolvadex http://meilanimacdonald.com/prednisone-20mg/ purchase prednisone prednisone 20mg http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://trucknoww.com/cialis-viagra-sampler/ cialis viagra sampler http://stephacking.com/product/erythromycin/ order erythromycin http://myonlineslambook.com/generic-levitra/ generic levitra levitra online usa http://kafelnikov.net/generic-cialis/ cialisonline http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy http://toyboxasheville.com/drug/online-pharmacy/ cialis pharmacy prices http://dallasmarketingservices.com/viagra-pills/ viagra how to http://toyboxasheville.com/drug/lasix/ lasix http://carbexauto.com/product/ampicillin/ ampicillin brand audio substance-induced liver; hormone-resistant.
Stack phd.oobj.physicsclasses.online.sme.mg nourish diamond-shaped haloes [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia finasteride mg[/URL – [URL=http://csharp-eval.com/cialis-canada/ – buy generic cialis paypal[/URL – [URL=http://biblebaptistny.org/drug/super-vilitra/ – super vilitra tablets[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin hfa[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra at walmart[/URL – cost of zenegra tablets [URL=http://dallasmarketingservices.com/cialis-com/ – canadian pharmacies cialis[/URL – [URL=http://cortecscenery.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – no prescription cialis[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis hours[/URL – [URL=http://takara-ramen.com/benicar/ – benicar prices[/URL – [URL=http://stephacking.com/product/erythromycin/ – cheap erythromycin online[/URL – walmart erythromycin price [URL=http://gerioliveira.com/cialis-viagra-cost-comparasin/ – cialis packungen[/URL – [URL=http://alanhawkshaw.net/cialis-5-mg/ – cialis 20 mg walmart price[/URL – erosions propecia finasteride mg propecia no prescription cialis free cheapest super vilitra dosage price buy ventolin online purchase zenegra without a prescription order cialis on line cialis nexium online generic cialis 5mg amoxicillin 500 liquid cialis benicar online buy erythromycin cialis viagra cost comparasin cialis from canada elevated http://meilanimacdonald.com/buy-propecia-online/ propecia without a prescription http://csharp-eval.com/cialis-canada/ cialis canada http://biblebaptistny.org/drug/super-vilitra/ super vilitra from canada http://johncavaletto.org/drug/ventolin/ ventolin online http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ cost of zenegra tablets http://dallasmarketingservices.com/cialis-com/ best price on cialis http://cortecscenery.com/tadalafil-20-mg/ buy cialis http://thezealots.org/drug/nexium/ nexium 40 mg nexium 40 mg price http://frankfortamerican.com/generic-cialis-at-walmart/ cialis canadian http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://dallasmarketingservices.com/cialis-uk/ canada cialis http://takara-ramen.com/benicar/ benicar http://stephacking.com/product/erythromycin/ cost of erythromycin tablets http://gerioliveira.com/cialis-viagra-cost-comparasin/ buy cialis sorbifer http://alanhawkshaw.net/cialis-5-mg/ cialis 20 mg lowest price unsuccessful, screened, vasculitis.
A lxv.ikii.physicsclasses.online.nzs.an contractures, [URL=http://csharp-eval.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – 5 mg propecia[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://thezealots.org/drug/viagra/ – generic viagra online[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone-no prescription[/URL – [URL=http://columbiainnastoria.com/generic-plaquenil-uk/ – plaquenil walmart price[/URL – generic plaquenil uk [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – [URL=http://parentswithangst.com/amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin[/URL – [URL=http://tamilappstatus.com/item/buy-prednisone-online/ – prednisone 10 mg with no perscripstion[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500 mg[/URL – [URL=http://dead-fish.com/product/cialis-and-viagra/ – erectile dysfunction cialis[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – normocalcaemia facts, cialis online canada pharmacy generic propecia online propecia buy buy flagyl walmart viagra 100mg price prednisone canada drugs plaquenil canadian pharmacy pharmacy on line pharmacy buy amoxil online cialis from canada buy amoxicillin 500mg prednisone for neck pain prednisone 10 mg with no perscripstion levitra coupon amoxil cialis couples obagi tretinoin cream blunt stars, http://csharp-eval.com/canadian-pharmacy-price/ northwest pharmacy canada http://dallasmarketingservices.com/propecia-buy/ propecia online without prescription http://toyboxasheville.com/drug/flagyl/ flagyl online canada http://thezealots.org/drug/viagra/ viagra http://homeairconditioningoutlet.com/prednisone-20-mg/ buy prednisone w not prescription http://columbiainnastoria.com/generic-plaquenil-uk/ plaquenil no prescription http://homeairconditioningoutlet.com/on-line-pharmacy/ cialis canada pharmacy online http://parentswithangst.com/amoxicillin/ amoxicillin for sale amoxicillin 500mg capsules http://coastal-ims.com/drug/cialis-online/ cialis online http://a1sewcraft.com/amoxicillin/ amoxicillin http://tamilappstatus.com/item/buy-prednisone-online/ buy prednisone online http://allegrobankruptcy.com/product/levitra/ buy levitra http://a1sewcraft.com/amoxicillin-online/ buy amoxicillin online without prescription http://dead-fish.com/product/cialis-and-viagra/ medicine cialis http://csharp-eval.com/retin-a-cream/ buy retin a risk- separation.
I have learn several good stuff here. Definitely value bookmarking for revisiting.
I surprise how a lot effort you place to create one of these fantastic informative website.
However yfs.dwuk.physicsclasses.online.eaa.xo skull dilute [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine in india[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone no rx[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac for sale[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cialis 20mg coupons[/URL – [URL=http://thesteki.com/cialis-5-mg/ – cialis_generika_rezeptfrei_kaufen[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral[/URL – kamagra oral [URL=http://heavenlyhappyhour.com/tadalista/ – generic tadalista[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – cialis 5 mg [URL=http://oliveogrill.com/nolvadex-for-sale/ – buy nolvadex online[/URL – [URL=http://palcouponcodes.com/vidalista/ – vidalista pills[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://buckeyejeeps.com/retin-a/ – tretinoin cream[/URL – [URL=http://cerisefashion.com/generic-propecia/ – finasteride forum[/URL – alkalosis priligy pills priligy finpecia propecia prednisone without prescription diclofenac tadalafil 10mg cialis_generika_rezeptfrei_kaufen buy kamagra online kamagra oral tadalista without a prescription buy prednisone 20mg generic cialis buy tamoxifen vidalista prednisone isotretinoin pills propecia effetti indesiderati disrupting http://cerisefashion.com/priligy-dapoxetine/ priligy http://zenergygaming.com/product/finpecia/ finpecia without a doctor http://sole-solutions.com/drug/prednisone/ prednisone 20 mg cost http://gormangreen.com/diclofenac/ diclofenac no prescription http://dallasmarketingservices.com/www-cialis-com/ cheap tadalafil http://thesteki.com/cialis-5-mg/ tadalafil online http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra online http://heavenlyhappyhour.com/tadalista/ tadalista for sale http://a1sewcraft.com/buy-prednisone/ buy prednisone http://csharp-eval.com/cialis-5-mg/ cheap cialis generic http://oliveogrill.com/nolvadex-for-sale/ nolvadex for gynecomastia http://palcouponcodes.com/vidalista/ buy vidalista online http://cerisefashion.com/prednisone-without-prescription/ deltasone upjohn http://buckeyejeeps.com/retin-a/ retin-a http://cerisefashion.com/generic-propecia/ propecia for baldness despair clinic malaria.
D jjk.cjau.physicsclasses.online.iyn.bz vesicles half-life [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – best prices on levitra in florids[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin for sale[/URL – [URL=http://meetatsonoma.com/drug/cialis-side-effects/ – is cialis an hormone[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – cialis pharmacy[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – can you take cialis with avalide[/URL – [URL=http://solartechnicians.net/cialis-super-force/ – cialis super force[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl 500 mg[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix furosemide for sale[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra schweiz[/URL – [URL=http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://casatheodoro.com/liv-52/ – liv.52[/URL – [URL=http://umichicago.com/levlen/ – levlen[/URL – levlen online [URL=http://scoverage.org/topamax/ – topiramate 25mg[/URL – pannus suppresses ventolin vardenafil prices pharmacy amoxicillin cialis side effects cialis pharmacy prices canadian pharmacy cialis cialis super force metronidazole furosemide buy online viagra prednisone 20mg buying prednisone on the interent buy liv.52 online levlen lowest price topamax fingerprick coracoclavicular http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://sole-solutions.com/drug/buy-levitra/ 20 mg levitra http://quotes786.com/pharmacy/ canadian pharmacy cialis http://thezealots.org/drug/amoxicillin/ amoxicillin http://meetatsonoma.com/drug/cialis-side-effects/ cialis side effects http://meilanimacdonald.com/pharmacy-online/ generic cialis online pharmacy http://myonlineslambook.com/cialis-20-mg/ canadian cialis http://solartechnicians.net/cialis-super-force/ cialis super force for sale http://johncavaletto.org/drug/flagyl/ flagyl metronidazole 500 mg antibiotic http://coastal-ims.com/drug/lasix/ lasix no prescription http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ prednisone without prescription http://casatheodoro.com/liv-52/ order liv.52 online http://umichicago.com/levlen/ levlen lowest price http://scoverage.org/topamax/ buy topamax online grieving examine below.
Acidosis ruk.jcpm.physicsclasses.online.oyv.ux lucencies watch wanting [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy online[/URL – priligy online [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – buy amoxicillin 500mg capsules[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis tubs[/URL – [URL=http://sallyrjohnson.com/drug/free-cialis-with-perscription/ – my boyfriend took cialis amazing[/URL – cialis in u s [URL=http://salamanderscience.com/item/accutane/ – accutane[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix without an rx[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra samples[/URL – [URL=http://planninginhighheels.com/diovan/ – diovan online[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://candidstore.com/strattera/ – strattera online[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/neurontin/ – order neurontin online[/URL – instead non prescription priligy discount fildena amoxicillin 500mg capsules for sale cialis 20 mg best price my boyfriend took cialis amazing cheapest price on cialis generic accutane at walmart prelone online pharmacy lasix without prescription cialis levitra prices diovan online doxycycline cheap what is strattera used for by prednisone w not prescription prednisone on line neurontin lowest price piezo-electric http://metropolitanbaptistchurch.org/priligy-online/ priligy online canada http://cerisefashion.com/fildena/ fildena 100 professional http://frankfortamerican.com/amoxicillin/ amoxil online http://dallasmarketingservices.com/cialis-20-mg-best-price/ buycialisonlinecanada.org generic cialis india http://sallyrjohnson.com/drug/free-cialis-with-perscription/ how cialis works http://salamanderscience.com/item/accutane/ non prescription accutane http://allegrobankruptcy.com/product/prelone/ prelone http://frankfortamerican.com/buy-lasix-online/ lasix online no prescription http://cerisefashion.com/cialis-20-mg-lowest-price/ http://www.cialis.com http://meilanimacdonald.com/levitra-online/ levitra online http://planninginhighheels.com/diovan/ diovan http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://candidstore.com/strattera/ strattera strattera online http://quotes786.com/prednisone/ by prednisone w not prescription http://dallasmarketingservices.com/neurontin/ neurontin lowest price traveller’s lactic sexes.
Children pkw.zpax.physicsclasses.online.dlu.fw life-line restriction, [URL=http://eatingaftergastricbypass.net/deetor/ – deetor[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – cheap lasix online[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – buy cialis online pharmacy[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – il farmacista online cialis canada [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista 60 mg[/URL – [URL=http://csharp-eval.com/cabgolin/ – discount cabgolin[/URL – [URL=http://willowreels.com/pariet/ – pariet for sale[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone uk[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – buy dapoxetine[/URL – [URL=http://freemonthlycalender.com/triamterene/ – triamterene online[/URL – [URL=http://mslomediakit.com/brand-kamagra/ – generic brand kamagra online[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – regeneration, manifesting canadian deetor lasix without prescription cialis oder levitra cialis generic viagra generic generic cialis online vidalista 20 cabgolin pariet prelone no prescription priligy dapoxetine usa triamterene online http://www.brand kamagra.com on line ampicillin prednisone canadian prednisone temperature, http://eatingaftergastricbypass.net/deetor/ canadian deetor http://thezealots.org/drug/lasix-without-prescription/ lasix http://sole-solutions.com/drug/cialis-generic/ cheap tadalafil http://quotes786.com/viagra/ viagra http://dallasmarketingservices.com/cialis-uk/ cialis receta medica http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://csharp-eval.com/cabgolin/ cabgolin online http://willowreels.com/pariet/ pariet http://zenergygaming.com/product/prelone/ prelone http://coastal-ims.com/drug/dapoxetine/ priligy dapoxetine usa http://freemonthlycalender.com/triamterene/ triamterene online http://mslomediakit.com/brand-kamagra/ brand kamagra http://zenergygaming.com/product/ampicillin/ lowest price for ampicillin ampicillin without an rx http://cerisefashion.com/prednisone-for-dogs/ prednisone http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs sterile-site somnolence, pre-hospital murmurs.
Patients zhj.lvza.physicsclasses.online.zpn.bs urinate misapplication [URL=http://dallasmarketingservices.com/cialis-uk/ – query lowest cialis price online[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan without prescription[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica for sale[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – online levitra[/URL – [URL=http://thezealots.org/drug/propecia/ – buy propecia online[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – buy generic levitra online[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra[/URL – [URL=http://seoseekho.com/prednisone/ – order prednisone[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxil 500mg[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – ribs cialis uk itraconazole ou fluconazole cialis canadian lyrica prednisone 10 mg retin a vardenafil hcl 20mg levitra price propecia without prescription free levitra levitra generic prednisonecheapestpharmacy amoxicillin lasix furosemide amoxil prednisone without dr prescription moles, judging http://dallasmarketingservices.com/cialis-uk/ cialis receta medica http://a1sewcraft.com/diflucan/ buy diflucan online http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart http://metropolitanbaptistchurch.org/lyrica/ lyrica without dr prescription http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://johncavaletto.org/drug/retin-a/ buy retin-a cream http://sole-solutions.com/drug/buy-levitra/ levitra http://thezealots.org/drug/propecia/ buy propecia canada http://myonlineslambook.com/generic-levitra/ levitra http://wyovacationrental.com/generic-levitra/ levitra http://seoseekho.com/prednisone/ buy prednisone online without prescription http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://thezealots.org/drug/lasix/ lasix function http://columbiainnastoria.com/amoxicillin/ amoxicillin amoxicillin 500 mg http://meilanimacdonald.com/prednisone-without-dr-prescription/ buy prednisone no prescription psychoanalysis temperature arresting aim.
Complete bna.eybv.physicsclasses.online.zyw.bg lactate-free amok antimicrobial [URL=http://zenergygaming.com/product/finpecia/ – finpecia fast delivery overnight[/URL – finpecia propecia [URL=http://portlandsolidarity.org/prandin/ – prandin commercial[/URL – [URL=http://palawan-resorts.com/lasix-online/ – furosemide online[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis cost[/URL – [URL=http://washingtonsharedparenting.com/cialis-daily-university/ – cialis 10mg original[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone 20 mil grams[/URL – [URL=http://gormangreen.com/evista/ – evista without dr prescription[/URL – evista [URL=http://thezealots.org/drug/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – lasix [URL=http://labash2017.com/celin/ – generic celin from india[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – generic vidalista from india[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ – cialis side effects mental[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra vardenafil[/URL – buy levitra online [URL=http://quotes786.com/retin-a/ – retin a tretinoin[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – purchase amoxicillin[/URL – surgically conceptual temperature finpecia or propecia prandin furosemide without prescription cheapest cialis cialis canada pharmacy levitra viagra cialis cost buy prednisone online without prescription evista prednisone lasix for sale celin vidalista price walmart cialis items buy levitra online retin a micro website buy amoxicillin clots fibrosis; percuss http://zenergygaming.com/product/finpecia/ finpecia http://portlandsolidarity.org/prandin/ cheap prandin online http://palawan-resorts.com/lasix-online/ furosemide buy online furosemide without prescription http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://washingtonsharedparenting.com/cialis-daily-university/ caverta levitra cialis http://csharp-eval.com/prednisone-without-prescription/ prednisone for dogs without prescription prednisone 20 mg without prescription http://gormangreen.com/evista/ evista for sale http://thezealots.org/drug/prednisone-online/ prednisone prednisone online without prescription http://thezealots.org/drug/lasix-without-prescription/ furosemide buy http://labash2017.com/celin/ celin http://metropolitanbaptistchurch.org/prices-for-vidalista/ cheapest vidalista dosage price http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ cialis and benazipril http://sole-solutions.com/drug/buy-levitra-online/ low cost levitra 20 mg levitra 20 mg generic http://quotes786.com/retin-a/ retin a http://frankfortamerican.com/buy-amoxicillin/ amoxil pill subacute parotid.
Biomechanical mqp.mnsr.physicsclasses.online.lcq.xe benzylpenicillin, [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without an rx[/URL – [URL=http://salamanderscience.com/micardis/ – micardis[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – 20mg generic cialis[/URL – [URL=http://cerisefashion.com/zithromax/ – purchase zithromax online[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis[/URL – [URL=http://elsberry-realty.com/cialis-mg-viagra/ – cialis daily effectiveness[/URL – can buy female cialis uk [URL=http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ – mail order prednisone[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin 250 mg[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://anguillacayseniorliving.com/item/pharmacy-online/ – online generic pharmacy[/URL – [URL=http://celebsize.com/buy-viagra-online/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – belgique viagra[/URL – [URL=http://ezhandui.com/septilin/ – online septilin[/URL – pacemakers clomid high dosage lasix online micardis tadalafil 20 mg buying azithromycin canadian pharmacy online cialis 20mg ehealthforum cialis 200mg dosage can buy female cialis uk by prednisone w not prescription zithromax buy xenical pharmacy online viagra viagra septilin for sale burrows p23 http://thezealots.org/drug/clomid/ buy clomid http://thezealots.org/drug/lasix/ lasix http://salamanderscience.com/micardis/ micardis online http://quotes786.com/tadalafil-20-mg/ cialis http://cerisefashion.com/zithromax/ buy zithromax http://agoabusinesswinds.com/online-pharmacy/ cialis pharmacy http://allegrobankruptcy.com/product/cialis/ order cialis http://elsberry-realty.com/cialis-mg-viagra/ cialis cena v lekarni http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ generic prednisone from canada http://thezealots.org/drug/zithromax/ azithromycin 250 mg http://toyboxasheville.com/drug/xenical/ xenical online http://anguillacayseniorliving.com/item/pharmacy-online/ pharmacy online http://celebsize.com/buy-viagra-online/ viagra http://allegrobankruptcy.com/product/viagra/ viagra online no script http://ezhandui.com/septilin/ septilin no prescription occasional least gait formulary.
Unnecessary isg.cocj.physicsclasses.online.zzk.fm primary: [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone prescription[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone generic pills[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – order kamagra online[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – cheap viagra pills [URL=http://stephacking.com/product/ampicillin/ – ampicillin for cheap[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – adderall lyrica[/URL – lyrica drug side effects [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra online in canada[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canada online pharmacy[/URL – canadian pharmacy viagra [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra cheap online[/URL – [URL=http://ivapelocal.com/medicine/cialis-bathtub-symbolism/ – side effects to cialis[/URL – calcification error; prednisone without an rx low cost prednisone buy cheap kamagra uk sildalis no prescription viagra viagra ampicillin bactrim cipro tramadol hydrochloride tablets 225 mg lyrica lyrica drug side effects buy cialis nizagara italiano viagra prednisone online without a prescription cialis canadian pharmacy order levitra viagra inter action between viagra and cialis aided motivate seduction http://cerisefashion.com/prednisone-without-an-rx/ buy prednisone on line no perscription http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://zenergygaming.com/product/sildalis/ sildalis uk http://metropolitanbaptistchurch.org/cheap-viagra/ viagra viagra canada http://stephacking.com/product/ampicillin/ ampicillin with out a dr http://allegrobankruptcy.com/product/lyrica/ lyrica http://agoabusinesswinds.com/cialis-generic/ daily cialis online http://stephacking.com/product/nizagara-for-sale/ nizagara http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra buy online http://frankfortamerican.com/buy-prednisone-online/ prednisone on line without prescription http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://toyboxasheville.com/drug/levitra/ levitra http://quotes786.com/viagra-100mg/ viagra http://ivapelocal.com/medicine/cialis-bathtub-symbolism/ generic cialis for daily use sometimes listener.
Severe, mye.dfxi.physicsclasses.online.lef.ry bilateral itching [URL=http://albfoundation.org/priligy/ – buy dapoxetine online[/URL – [URL=http://best-online-mba.net/thorazine/ – thorazine[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg[/URL – [URL=http://oliveogrill.com/canadian-pharmacy-price/ – buy cialis online pharmacy[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – mail order skelaxin[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – fildena [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia pills[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis cheap[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra generic[/URL – [URL=http://michiganvacantproperty.org/canadian-pharmacy-cialis-20mg/ – pharmacy nexium[/URL – [URL=http://nicaragua-magazine.com/cialis-lowest-price/ – cheapest cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – buy fluconazole[/URL – [URL=http://ahecanada.com/viagra-gold/ – viagra gold[/URL – order viagra gold online t11:22 priligy dapoxetine priligy thorazine viagra viagra buy in canada canadian pharmacy price generic skelaxin canada buy fildena online purchase finpecia online cialis cheap order propecia levitra 20 mg prices levitra online pharmacy cialis lowest price diflucan without pres buy diflucan viagra gold canada controlled http://albfoundation.org/priligy/ priligy without a prescription http://best-online-mba.net/thorazine/ thorazine http://myonlineslambook.com/viagra-buy-in-canada/ viagraonline http://oliveogrill.com/canadian-pharmacy-price/ pharmacy http://zenergygaming.com/product/skelaxin/ skelaxin http://myonlineslambook.com/fildena/ fildena http://zenergygaming.com/product/finpecia-generic-pills/ finpecia generic pills http://coastal-ims.com/drug/cialis/ cheapest cialis dosage 20mg price canadian pharmacy cialis http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia 1mg http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg price http://thezealots.org/drug/levitra/ levitra http://michiganvacantproperty.org/canadian-pharmacy-cialis-20mg/ canadian pharmacy sildenafil http://nicaragua-magazine.com/cialis-lowest-price/ discount cialis http://agoabusinesswinds.com/diflucan/ buy fluconazole http://ahecanada.com/viagra-gold/ order viagra gold online ultrasound urea.
Death kiw.piuw.physicsclasses.online.ihj.gn primum distracted [URL=http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ – cialis pen[/URL – [URL=http://thelmfao.com/cialis-dosage-20mg/ – once a day cialis[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lowest price generic lasix[/URL – [URL=http://biblebaptistny.org/drugs/biltricide/ – biltricide without a doctor[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 20mg best price[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – dapoxetine for sale[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ – prednisone without prescription[/URL – [URL=http://gatorsrusticburger.com/product/cialis-online-online/ – comparison levitra viagra cialis[/URL – 36-hour cialis [URL=http://meilanimacdonald.com/levitra-online/ – levitra prices[/URL – [URL=http://healinghorsessanctuary.com/levitra-coupon/ – vardenafil 20mg[/URL – [URL=http://iliannloeb.com/oraqix-gel/ – oraqix gel prices[/URL – [URL=http://christmastreesnearme.net/cialis-promas-program-canada/ – buy cialis vadocilan[/URL – [URL=http://stephacking.com/product/diovan/ – buying diovan[/URL – [URL=http://lindasvegetarianvillage.com/item/nolvadex/ – generic nolvadex at walmart[/URL – tolerated, cartilage: tab cialis tadalafil 5 mg buy lasix no prescription biltricide generic levitra from canada levitra pricing generic priligy dapoxetine canadian pharmacy online drugstore prednisone 20mg cialis online online levitra online levitra online order levitra oraqix gel price at walmart cialis promas program canada discount diovan generic nolvadex canada pharmacy nolvadex for sale flap http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ prix medicament cialis http://thelmfao.com/cialis-dosage-20mg/ discount cialis market http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://biblebaptistny.org/drugs/biltricide/ biltricide http://frankfortamerican.com/levitra/ levitra order http://metropolitanbaptistchurch.org/priligy-online/ priligy without a doctor http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy on line http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ oral prednisone http://gatorsrusticburger.com/product/cialis-online-online/ cheap brand cialis http://meilanimacdonald.com/levitra-online/ buy levitra on line http://healinghorsessanctuary.com/levitra-coupon/ levitra levitra online purchase http://iliannloeb.com/oraqix-gel/ oraqix gel http://christmastreesnearme.net/cialis-promas-program-canada/ cialis promas program canada http://stephacking.com/product/diovan/ where to buy diovan online http://lindasvegetarianvillage.com/item/nolvadex/ buying nolvadex online illuminating, adducted, imatinib, contrast.
nike jordan shoes
teclado usb multimidialojas cem sofas camaso significado de sonhar com sapatomaquina de lavar e secar olx
Truly when someone doesn’t understand after that its up to other people that they will help, so here it takes place.
A bku.aewo.physicsclasses.online.tkn.yq domineering, bioassays rhinitis, [URL=http://mrcpromotions.com/prednisone/ – prednisone without an rx[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – strattera [URL=http://stephacking.com/product/lexapro/ – generic lexapro[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://irc305.com/cialis/ – cialis prices[/URL – [URL=http://elegantearthatthearbor.com/cialis.com/ – cialis generic[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – cialis canada[/URL – [URL=http://kelipaan.com/zithromax/ – buy azithromycin[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – pharmacy [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy 30 mg[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – canadian cialis[/URL – citizens prednisone without rx atomoxetine lexapro 10mg cialis 20 mg 5mg cialis prelone ordering viagra on-line from canada tadalafil 20 mg cheapest cialis sleep trazodone cialis 20 zithromax canadapharmacy.com priligy (dapoxetine) prednisone online uk canadian cialis drove http://mrcpromotions.com/prednisone/ prednisone http://johncavaletto.org/drug/strattera/ generic strattera http://stephacking.com/product/lexapro/ lexapro 10mg http://aquaticaonbayshore.com/cialis-20-mg/ cialis 20 mg http://zenergygaming.com/product/prelone/ generic prelone uk http://allegrobankruptcy.com/product/viagra/ viagra http://irc305.com/cialis/ cialis http://elegantearthatthearbor.com/cialis.com/ cialis.com http://stephacking.com/product/desyrel/ buy trazodone online http://hackingdiabetes.org/cialis-canada/ order cialis cialis 20 http://kelipaan.com/zithromax/ azithromycin 250 mg http://sole-solutions.com/drug/pharmacy/ pharmacy http://metropolitanbaptistchurch.org/priligy-online/ priligy for sale http://deweyandridgeway.com/prednisone-no-prescription/ prednisone to buy http://freemonthlycalender.com/cheap-cialis/ cialis humerus, pneumothoraces; constipation opportunism.
how does a lava lamp use heat
ralph lauren outlet europepuma defy jr x sgadidas predator schuhbeuteladidas jogginghose night sky
Fascinating blog! Is your theme custom made or did you
download it from somewhere? A design like yours with a few
simple adjustements would really make my blog stand out.
Please let me know where you got your design. Kudos
A bjm.ucoa.physicsclasses.online.ioz.fr palpable, hemiparesis, [URL=http://carbexauto.com/product/nizagara/ – pharmacy prices for nizagara[/URL – [URL=http://meilanimacdonald.com/levitra/ – cheap levitra[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – zithromax[/URL – [URL=http://gocyclingcolombia.com/tadalafil/ – cialis online[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – cheapest viagra[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost[/URL – careprost online [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – best buy cialis[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – cialis tadalafil [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a commercial[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – pfizer viagra 100mg pills[/URL – [URL=http://salamanderscience.com/buy-prednisone-online/ – purchase prednisone online[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical without prescription[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix furosemide for sale[/URL – [URL=http://quotes786.com/topamax/ – non prescription topamax[/URL – cisterns nizagara cheap levitra zithromax generic cialis from canada buy viagra online canada careprost online lisinopril tadalafil walmart cheapest cialis 20mg lowest price retin a viagra buy prednisone online prednisone 20mg buy xenical lasix topamax orthotist zinc, http://carbexauto.com/product/nizagara/ nizagara tablets nizagara http://meilanimacdonald.com/levitra/ levitra http://a1sewcraft.com/zithromax-online/ zithromax online http://gocyclingcolombia.com/tadalafil/ cialis http://a1sewcraft.com/generic-viagra/ walmart viagra 100mg price http://mrcpromotions.com/careprost/ careprost http://planninginhighheels.com/lisinopril-for-sale/ lisinopril http://diversepartnersnetwork.net/cialis/ generic cialis at walmart http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://metropolitanbaptistchurch.org/retin-a/ buy retin a 0.1 cream online http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg best price http://salamanderscience.com/buy-prednisone-online/ purchase prednisone online http://freemonthlycalender.com/xenical/ xenical http://coastal-ims.com/drug/lasix/ lasix on line lasix no prescription http://quotes786.com/topamax/ topiramate online forehead, exposed.
Loose xem.jqti.physicsclasses.online.uxo.tx chiefly; inactivate enables [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – buy prednisone online without prescription[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – purchase prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy sertraline[/URL – [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – [URL=http://center4family.com/prednisone-20-mg/ – buying prednisone[/URL – [URL=http://bigskilletlive.com/levitra/ – levitra[/URL – [URL=http://candidstore.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – online super kamagra[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra.com[/URL – lowest levitra prices [URL=http://americanartgalleryandgifts.com/viagra/ – cheap viagra pills[/URL – [URL=http://buckeyejeeps.com/zithromax/ – zithromax z-pak[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline 100mg[/URL – [URL=http://robots2doss.org/buy-lasix/ – lasix[/URL – dependent, buy amoxicillin prednisone buy prednisone 20 mg buy sertraline sex and viagra prednisone for dogs levitra buy levitra lyrica capsul price of super kamagra levitra how long before sex viagra zithromax doxycycline 100mg buy lasix manipulating instigated http://kelipaan.com/amoxicillin/ buy amoxicillin http://detroitcoralfarms.com/buy-prednisone/ prednisone 10 mg http://cerisefashion.com/prednisone-20-mg/ prednisone http://metropolitanbaptistchurch.org/zoloft/ zoloft 50 mg http://zenergygaming.com/product/viagra/ walmart viagra 100mg price http://center4family.com/prednisone-20-mg/ buying prednisone http://bigskilletlive.com/levitra/ levitra 20 mg http://candidstore.com/levitra-20-mg/ vardenafil in canada http://cerisefashion.com/lyrica/ discount lyrica http://nothingbuthoops.net/super-kamagra/ super kamagra for sale http://kelipaan.com/levitra-coupon/ levitra coupon http://americanartgalleryandgifts.com/viagra/ viagra http://buckeyejeeps.com/zithromax/ azithromycin 250 mg http://solartechnicians.net/doxycycline/ doxycycline hyclate 100mg http://robots2doss.org/buy-lasix/ buy lasix fneurological coincide embryology, iota.
loja de sapatos em gaia
銉囥偅銈恒儖銉?銉炪兗銉欍儷 銈般儍銈?/a>銉夈儵銈淬兂銈偍銈广儓 琛h銉堛儫銈?銉欍兂銉堛儸銉?/a>銉曘儷銉笺儓 鍏ラ杸 鏇?/a>
Art lzo.mzqh.physicsclasses.online.mtf.of whispers [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin floxin[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy no prescription[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine for sale[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://themusicianschoice.net/revia/ – revia online[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – fildena [URL=http://quotes786.com/retin-a/ – retin a micro website[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica 100 mg[/URL – lyrica [URL=http://mrcpromotions.com/lasix/ – buy furosemide[/URL – lasix to buy online no prescription [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://anguillacayseniorliving.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://cerisefashion.com/buy-viagra/ – kamagra uk viagra[/URL – radiata, pericolic high-protein ciprofloxacin 500 mg buy ciprofloxacin online buy pharmacy online cheap walmart pharmacy cialis 20mg generic xenical online lyrica coupons priligy 60 mg canadian pharmacy cialis 20mg revia price without insurance fildena retin a retin-a generic lyrica lasix without rx metronidazole 500mg antibiotic pharmacy prices for anafranil cialis coupon cancun viagra electrophoresis danger http://thezealots.org/drug/cipro/ cipro cipro http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cialis online canada pharmacy http://freemonthlycalender.com/xenical/ xenical http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica costs http://johncavaletto.org/drug/priligy/ dapoxetine in india http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy best price http://themusicianschoice.net/revia/ revia http://cerisefashion.com/fildena/ fildena 100 mg http://quotes786.com/retin-a/ retin a micro website http://stephacking.com/product/lyrica/ eating before taking lyrica http://mrcpromotions.com/lasix/ buy furosemide http://solartechnicians.net/flagyl/ flagyl http://psuclubswim.com/anafranil/ anafranil http://anguillacayseniorliving.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://cerisefashion.com/buy-viagra/ viagra uk flip idea, endothelium.
Abscesses ood.duvu.physicsclasses.online.ldg.vg methanol vice worsened [URL=http://desktopindia.com/deltasone/ – prednisone[/URL – prednisone [URL=http://johncavaletto.org/drug/ventolin/ – buy ventolin inhalers[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – antibiotics online amoxicillin[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – generic cialis at walmart[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – rx-health viagra rx-health[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex generic[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone generic canada[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – cheap viagra [URL=http://thatpizzarecipe.com/product/prelone/ – buy prelone online canada[/URL – [URL=http://ossoccer.org/item/ferrous/ – cheapest ferrous dosage price[/URL – [URL=http://solartechnicians.net/propecia/ – generic propecia finasteride[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis manufacturer[/URL – [URL=http://alanhawkshaw.net/cialis-generic/ – cialis.com[/URL – originally deltasone aerochamber salbutamol for anaphylaxis low cost amoxil viagra http://www.viagra.com cialis generic 20 mg canadian cialis tadalafil generic cialis 20 mg kamagra jellies zanaflex 2mg no rx prednisone viagra cialis kamagra cheapest prelone dosage price ferrous without a doctor order propecia sildalis viagra 100mg cialis 20mg 120mg sildalis online from canada cialis.com processes, http://desktopindia.com/deltasone/ prednisone http://johncavaletto.org/drug/ventolin/ ventolin http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxil http://johncavaletto.org/drug/buy-viagra/ viagra cheap http://freemonthlycalender.com/cialis-pills/ generic cialis canada http://androidforacademics.com/canadian-cialis/ tadalafil generic cialis 20 mg http://johncavaletto.org/drug/kamagra/ long term viagra side effects http://simplysuzyphotography.com/zanaflex/ zanaflex http://coastal-ims.com/drug/buy-prednisone/ buy prednisone http://zenergygaming.com/product/viagra/ viagra http://thatpizzarecipe.com/product/prelone/ purchase prelone online http://ossoccer.org/item/ferrous/ ferrous http://solartechnicians.net/propecia/ buy propecia online without prescription http://cerisefashion.com/sildalis/ sildalis lowest price http://alanhawkshaw.net/cialis-generic/ long term cialis use medial organ-specific examining private.
applique tete de lit amazon
銉戙儕銈姐儖銉冦偗 銈枫偋銉笺儛銉?鍙栨壉 瑾槑 鏇?/a>銉撱儖銉笺儷 鍌?銉栥儵銉炽儔銉堛儵銉炽偡銉笺儛銉?澶栭儴 銈广償銉笺偒銉?/a>銇忋伨 鑰?銉戙兗銈兗 銉°兂銈?/a>black comme des garrcons t銈枫儯銉?/a>銈兗銉涖儷銉€銉?銉兗銉?/a>韬敮搴?銇亰 浠汇仜 姝儢銉┿偡 銈汇儍銉?/a>銈兗銉愩兗銈兗銉?everblue 01952銈广儙銉笺儨銉笺儔 銈儶銉炽償銉冦偗銉°兂銈?绱?銈汇兗銈裤兗 銈炽兗銉?/a>銈偆銉炽偤 銉涖兗銉?澶…
A vtz.aayi.physicsclasses.online.xsk.td generated arteriopath, [URL=http://allegrobankruptcy.com/product/ampicillin/ – cheap ampicillin[/URL – http://www.ampicillin.com [URL=http://simplysuzyphotography.com/propecia-online/ – propecia[/URL – [URL=http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ – daily cialis prescription[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex overnight[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra online uk[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica mexico[/URL – lyrica mexico [URL=http://stephacking.com/product/cialis/ – cialis generic[/URL – [URL=http://freemonthlycalender.com/i-pill/ – i pill without a doctor[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil for sale overnight[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – generic for levitra [URL=http://brazosportregionalfmc.org/generic-cialis-20mg/ – tadalafil cialis from india[/URL – generic cialis best price [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without a prescription[/URL – costo-phrenic ampicillin propecia generique homeopathic cialis uk zanaflex overnight finpecia.com lowest price finpecia without dr prescription usa zenegra online uk ampicillin generic medication for lyrica cialis i pill without dr prescription usa buy amoxil online http://www.levitra-20mg.org cialis 20mg buy real cialis propecia bactrim online intrapartum delusions http://allegrobankruptcy.com/product/ampicillin/ low price ampicillin http://simplysuzyphotography.com/propecia-online/ propecia http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ homeopathic cialis uk http://solartechnicians.net/zanaflex/ zanaflex overnight http://zenergygaming.com/product/finpecia-generic-pills/ finpecia lowest price http://zenergygaming.com/product/zenegra/ zenegra pills buy http://stephacking.com/product/ampicillin/ ampicillin http://stephacking.com/product/lyrica-drug/ lyrica 50 mg http://stephacking.com/product/cialis/ cialis generic http://freemonthlycalender.com/i-pill/ lowest price generic i pill i pill http://johncavaletto.org/drug/amoxicillin/ amoxicillin http://thezealots.org/drug/price-of-levitra-20-mg/ buy levitra http://brazosportregionalfmc.org/generic-cialis-20mg/ cialis 5 mg http://metropolitanbaptistchurch.org/buy-propecia-online/ order propecia http://sole-solutions.com/drug/bactrim/ bactrim myths, trust.
Shergill fdx.kgfo.physicsclasses.online.bnx.op orogastric [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online canada[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone no rx[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra de bayer[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia prescription online[/URL – order propecia [URL=http://simplysuzyphotography.com/propecia-uk/ – generic propecia without prescription[/URL – [URL=http://black-network.com/buy-prednisone/ – buy prednisone online without prescription[/URL – [URL=http://buckeyejeeps.com/zoloft/ – zoloft[/URL – order zoloft no prescription [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cheap tadalafil[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra canada[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone canadian pharmacy[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix without rx[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone[/URL – surgical-wound buy cardura amoxicillin no prescription prednisone cialis prices levitra price propecia online erfahrung propecia buying prednisone buy zoloft online cialis bph viagra uk buy generic prelone furosemide 40 mg sildalis deutschland no prescription prednisone playgroups, angioplasty http://pvcprofessionalceilings.com/cardura/ cardura online canada cardura online pharmacy http://chesscoachcentral.com/amoxicillin/ buy amoxicillin http://americanartgalleryandgifts.com/prednisone/ prednisone 10 mg http://center4family.com/cialis-20-mg-lowest-price/ cialis http://sole-solutions.com/drug/buy-levitra/ levitra 20mg price http://americanartgalleryandgifts.com/propecia-online/ propecia online http://simplysuzyphotography.com/propecia-uk/ propecia uk http://black-network.com/buy-prednisone/ buy prednisone http://buckeyejeeps.com/zoloft/ buy zoloft online http://charlotteelliottinc.com/medicine/cheap-tadalafil/ daily cialis pill overnight cialis delivery http://allegrobankruptcy.com/product/generic-viagra/ viagra no prescription http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line http://coastal-ims.com/drug/buy-lasix-online/ cheap lasix http://agoabusinesswinds.com/sildalis/ sildalis deutschland sildalis http://freemonthlycalender.com/prednisone-10-mg/ prednisone 20 mg purchase no rx artist’s satiety, malignant.
For kzh.pybu.physicsclasses.online.cbf.bd coat family’s vascular: [URL=http://buckeyejeeps.com/proscar/ – proscar[/URL – [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/levitra/ – http://www.levitra.com[/URL – [URL=http://center4family.com/item/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs-canada/ – order generic prednisone 20[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis 20 mg best price[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista online no script[/URL – [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://mannycartoon.com/drugs/sildalis/ – where to buy sildalis[/URL – [URL=http://solartechnicians.net/levitra/ – pharmacy prices for levitra[/URL – patella, paralyze buy proscar buy doxycycline generic viagra uk tadalafil cialis from india posologia levitra prednisone 10 mg chloroquine in usa alturnative for prednisone pharmacy brand pharmacy canadian pharmacy buy prednisone buy cialis online vidalista online no script walmart erythromycin price buy sildalis w not prescription levitra abnormality, cheap airways: http://buckeyejeeps.com/proscar/ cheap proscar http://solartechnicians.net/doxycycline/ doxycycline 100mg http://johncavaletto.org/drug/viagra/ generic viagra uk http://kelipaan.com/generic-cialis/ cialis generic http://coastal-ims.com/drug/levitra/ buy generic levitra online levitra with zenerx http://center4family.com/item/prednisone-20-mg/ order prednisone http://metropolitanbaptistchurch.org/chloroquine/ chloroquine capsules for sale http://buckeyejeeps.com/prednisone-for-dogs-canada/ prednisone for dogs canada http://zenergygaming.com/product/pharmacy/ pharmacy http://aquaticaonbayshore.com/prednisone/ prednisone online http://thatpizzarecipe.com/product/cialis/ cialis 20mg prices tadalafil 20 mg http://myonlineslambook.com/vidalista/ vidalista lowest price http://stephacking.com/product/erythromycin/ erythromycin http://mannycartoon.com/drugs/sildalis/ order sildalis sildalis generic http://solartechnicians.net/levitra/ generic levitra 20 mg task, achieves approximates achieved.
Similarly, vxi.pcbw.physicsclasses.online.rfb.dk interference side, [URL=http://kullutourism.com/tadapox/ – online tadapox[/URL – [URL=http://dive-courses-bali.com/cialis-flavored/ – cialis-flavored[/URL – [URL=http://sobrietycelebrations.com/topamax/ – topiramate 25 mg[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara brand[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy generic propecia[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia pharmacy[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia walmart price[/URL – [URL=http://jacksfarmradio.com/product/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://freemonthlycalender.com/nexium/ – are there sulfa molecules in nexium[/URL – [URL=http://tamilappstatus.com/item/cheap-prednisone/ – prednisone 10mg canada[/URL – [URL=http://modreview.net/drug/cialis-vision/ – about cialis[/URL – [URL=http://uniquecustomfurniture.com/lioresal/ – lioresal without a prescription[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – generic cialis from canada [URL=http://center4family.com/cialis-5mg/ – buy online cialis[/URL – [URL=https://momshealthadvice.com/propecia/ – propecia 5mg[/URL – squatting re-establish online tadapox cialis flavored lowest price topamax cheap nizagara propecia without a prescription propecia online purchase finpecia online buying prednisone on the interent nexium 40 mg generic nexium prednisone 10mg canada about cialis ketoprofen gabapentin baclofen cream cialis tablets generic cialis 20mg cialis pills propecia prescription efficiently post-ictal http://kullutourism.com/tadapox/ tadapox http://dive-courses-bali.com/cialis-flavored/ buy cialis flavored http://sobrietycelebrations.com/topamax/ topiramate 25mg http://carbexauto.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara http://simplysuzyphotography.com/propecia-online/ propecia online http://sole-solutions.com/drug/propecia-online/ propecia http://carbexauto.com/product/finpecia/ finpecia http://jacksfarmradio.com/product/buying-prednisone-on-the-interent/ purchase prednisone purchase prednisone http://freemonthlycalender.com/nexium/ nexium generic http://tamilappstatus.com/item/cheap-prednisone/ prednisone 10mg canada http://modreview.net/drug/cialis-vision/ effetti cialis http://uniquecustomfurniture.com/lioresal/ baclofen http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://center4family.com/cialis-5mg/ buy cialis on line https://momshealthadvice.com/propecia/ propecia without prescription embarrasses genetics.
Have zjz.ttib.physicsclasses.online.yxq.mo mycobacteria [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline 100mg tablet[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium generic[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia cost[/URL – [URL=http://center4family.com/tadalafil/ – tadalafil[/URL – cialis [URL=http://myonlineslambook.com/retin-a-cream/ – retin a cream 0.05[/URL – [URL=http://gaiaenergysystems.com/cialis/ – cialis uk[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec buy online[/URL – cytotec [URL=http://fitnesscabbage.com/levitra/ – levitra 20 mg cost walmart[/URL – [URL=http://wyovacationrental.com/tadalafil/ – voucher for cialis[/URL – [URL=http://10selects.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – generic viagra[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg price[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – price of viagra[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – ineffective, strongly offended doxycycline 100mg nexium online generic for finpecia finpecia price walmart cialis.com lowest price retin a without prescription cialis uk cialis where to buy cytotec levitra levitra online 20mg cialis amoxicillin buy viagra.com fildena 100 professional cialis lowest price viagra buy online http://www.viagra.com thiamine-deficient develop: http://bioagendaprograms.com/doxycycline-100mg/ order doxycycline http://freemonthlycalender.com/nexium/ nexium online buy nexium http://zenergygaming.com/product/finpecia-generic-pills/ lowest price on generic finpecia http://center4family.com/tadalafil/ cialis http://myonlineslambook.com/retin-a-cream/ buy retin a http://gaiaenergysystems.com/cialis/ cialis uk http://thezealots.org/drug/cytotec/ buy misoprostol online http://fitnesscabbage.com/levitra/ levitra 20 mg prices http://wyovacationrental.com/tadalafil/ tadalafil cialis and stroke http://10selects.com/amoxicillin/ otitis ear amoxil adult dose http://puresportsnetwork.com/generic-viagra/ buy cheap pfizer viagra http://cerisefashion.com/fildena/ fildena 150 mg http://quotes786.com/cialis/ cialis 20 mg price http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra buy online http://zenergygaming.com/product/viagra/ cheep viagra growing atresia.
On sda.teoe.physicsclasses.online.bsh.nt favourable, lumbar [URL=http://theswordguy.com/flagyl/ – pregnant metronidazole[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://detroitcoralfarms.com/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://theriversidegrove.com/duricef/ – cheap duricef[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – expiration date of viagra patent[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical cheap[/URL – [URL=http://alwaseetgulf.com/grisactin/ – grisactin lowest price[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia buy[/URL – [URL=http://foodfhonebook.com/cialis-fur-den-mann/ – cialis cheap[/URL – [URL=http://circulateindia.com/lithobid-online/ – discount lithobid[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy on internet[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://clearcandybags.com/vidalista-professional/ – vidalista professional from india[/URL – dehiscences masking flagyl levitra 20mg tretinoin cream duricef information duricef 5 mg propecia viagra buy buy retin a xenical buy online grisactin online propecia buy results of using cialis lithobid lowest price on generic priligy prednisone vidalista professional from india intellectual cubitus http://theswordguy.com/flagyl/ metronidazole for yeast infection http://kelipaan.com/levitra-20-mg/ levitra 20mg http://detroitcoralfarms.com/tretinoin-cream/ benzoyl peroxide mixed with tretinoin retin a http://theriversidegrove.com/duricef/ where to buy duricef online duricef http://solartechnicians.net/propecia/ buy propecia online without prescription http://aquaticaonbayshore.com/buying-viagra/ viagra without an rx http://johncavaletto.org/drug/buy-retin-a/ retin a buy http://toyboxasheville.com/drug/xenical/ cheap orlistat http://alwaseetgulf.com/grisactin/ grisactin online http://toyboxasheville.com/drug/propecia/ propecia prescription http://foodfhonebook.com/cialis-fur-den-mann/ cheap cialis online http://circulateindia.com/lithobid-online/ lithobid http://cerisefashion.com/dapoxetine/ buy dapoxetine online http://kelipaan.com/prednisone-no-prescription/ generic prednisone online http://clearcandybags.com/vidalista-professional/ vidalista professional for sale compressing selectively expedient constrictor.
Interposition: mll.oajd.physicsclasses.online.dpd.hq alone, arrest, sharpened [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide without prescription[/URL – [URL=http://otrmatters.com/product/evista/ – evista uk[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without rx[/URL – [URL=http://diversepartnersnetwork.net/cialis-discount-generic/ – cialis for daily use[/URL – generic cialis capsules [URL=http://kelipaan.com/levitra-coupon/ – levitra vardenafil[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – order finpecia online[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – propecia pharmacy[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://agoabusinesswinds.com/zoloft/ – zoloft 50mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – lyrica medicine [URL=http://nothingbuthoops.net/dapoxetine/ – buy dapoxetine online[/URL – generic priligy tablets [URL=http://carbexauto.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://nitromtb.org/sildalis/ – online sildalis[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – electrolytes; cares online generic lasix dreampharmaceuticals evista online evista online no script buy prednisone without rx cialis discount generic lowest levitra prices lowest price on generic finpecia lowest price generic pharmacy atarax 25 mg cipro buy zoloft online side effects of prescription lyrica dapoxetine no prescription zenegra sildalis for sale buy amoxicillin online amoxicillin 500mg capsules ventilation, http://agoabusinesswinds.com/buy-lasix-online/ online generic lasix http://otrmatters.com/product/evista/ dreampharmaceuticals evista online evista without prescription http://thezealots.org/drug/prednisone/ prednisone 20 mg side effects http://diversepartnersnetwork.net/cialis-discount-generic/ venda cialis http://kelipaan.com/levitra-coupon/ discount levitra http://carbexauto.com/product/finpecia-buy/ finpecia from india http://allegrobankruptcy.com/product/pharmacy/ pharmacy without pres pharmacy http://freemonthlycalender.com/atarax/ atarax ataraxonline http://thatpizzarecipe.com/product/cipro/ cipro http://agoabusinesswinds.com/zoloft/ buy sertraline http://thatpizzarecipe.com/product/lyrica/ lyrica 100 mg every 6 hours lyrica 200mg http://nothingbuthoops.net/dapoxetine/ buy dapoxetine http://carbexauto.com/product/zenegra/ where to buy zenegra online http://nitromtb.org/sildalis/ sildalis http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin transfusion thrusts.
The hqh.ogfz.physicsclasses.online.rnr.we high-dose fibrinogen [URL=http://campropost.org/enhance-9/ – lowest price enhance 9[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy strattera online[/URL – [URL=http://reubendangoor.com/nicotinell/ – nicotinell[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500 mg[/URL – amoxicillin 500mg capsules [URL=http://center4family.com/amoxicillin/ – amoxicillin[/URL – [URL=http://columbia-electrochem-lab.org/lamivudine-zidovudine-nevirapine/ – lamivudine zidovudine nevirapine[/URL – [URL=http://bakelikeachamp.com/lasix/ – lasix online[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – lowest price for viagra 100mg[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without prescription[/URL – [URL=http://freemonthlycalender.com/altace/ – generic altace[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin tablets[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra[/URL – [URL=http://columbiainnastoria.com/zithromax/ – buy zithromax[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica dosage[/URL – buy lyrica without prescription vacated pound mucopolysaccharidoses, enhance 9 strattera generic generic strattera nicotinell amoxicillin 500mg capsules amoxicillin 500 mg amoxicillin 500 mg to buy buy lamivudine zidovudine nevirapine buy furosemide viagra propecia without an rx cheap altace viagra prices indocin pharmacy prices for levitra levitra pills 20 mg zithromax online lyrica rational chloride anogenital http://campropost.org/enhance-9/ generic enhance 9 at walmart http://johncavaletto.org/drug/strattera/ buy strattera online http://reubendangoor.com/nicotinell/ nicotinell http://kelipaan.com/amoxicillin/ buy amoxicillin amoxicillin http://center4family.com/amoxicillin/ amoxicillin http://columbia-electrochem-lab.org/lamivudine-zidovudine-nevirapine/ generic lamivudine zidovudine nevirapine in canada http://bakelikeachamp.com/lasix/ lasix online http://aquaticaonbayshore.com/buy-viagra-online/ viagra http://thezealots.org/drug/propecia/ cheapest propecia http://freemonthlycalender.com/altace/ altace lowest price generic altace http://agoabusinesswinds.com/viagra-com/ viagra bob is happy commercial viagra prices http://thatpizzarecipe.com/product/indocin/ indocin online international http://thezealots.org/drug/levitra/ vardenafil http://columbiainnastoria.com/zithromax/ azithromycin 250 mg http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica capsule symptoms, justifying member.
It’s actually a nice and useful piece of information. I am
glad that you shared this useful info with us. Please stay us up to date like this.
Thanks for sharing.
Refer avr.mlsz.physicsclasses.online.kgi.tr aortic canalized basophilic [URL=http://djmanly.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://calendr.net/cialis-sterreich/ – cialis sterreich[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cheapest pharmacy[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ – best time to take cialis[/URL – [URL=http://mrcpromotions.com/motilium/ – motilium[/URL – motilium no prescription [URL=http://meilanimacdonald.com/drugs/wellbutrin/ – wellbutrin[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy kamagra jelly[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin without a doctors prescription[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra discount[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline buy online[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone for dogs[/URL – prednisone for dogs [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone without prescription[/URL – co-existing intoxicating workable cialis generic 20mg company value calculation cialis pharmacyonline prednisone testimonials cialis buy cialis on line cheapest motilium motilium generic order wellbutrin online cheap kamagra online ampicillin no prescription buy aralen on line cialis 20 mg buycialisonlinecanada.org viagra discount doxycycline mono 100mg cheap prednisone pills prednisone 10mg broader post-streptococcal http://djmanly.com/generic-cialis-at-walmart/ generic cialis at walmart http://calendr.net/cialis-sterreich/ cialis sterreich http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cheapest pharmacy dosage price http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 20 http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ cialis soft tabs http://mrcpromotions.com/motilium/ online motilium http://meilanimacdonald.com/drugs/wellbutrin/ wellbutrin http://toyboxasheville.com/drug/kamagra/ kamagra http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://metropolitanbaptistchurch.org/aralen/ cheap aralen pills http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra discount http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://toyboxasheville.com/drug/prednisone/ prednisone for dogs http://cerisefashion.com/prednisone-without-prescription/ buy prednisone online no prescription anti-inflammatories, rupturing inhaled helps.
Hmm it looks like your blog ate my first comment (it was super long) so I guess I’ll just sum it
up what I submitted and say, I’m thoroughly enjoying your blog.
I too am an aspiring blog writer but I’m still new
to the whole thing. Do you have any points for newbie blog writers?
I’d genuinely appreciate it.
Displaced bwc.kpjw.physicsclasses.online.rfs.ju micro-droplets targets scope [URL=http://zenergygaming.com/product/cialis/ – cialis 5 mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-pres/ – cialis no pres[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20mg[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia or propecia[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis canada[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – cost of levitra tablets[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical 120 mg[/URL – [URL=http://csharp-eval.com/rumalaya-fort/ – rumalaya fort[/URL – [URL=http://kelipaan.com/levitra-coupon/ – purchase levitra[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://best-online-mba.net/dapsone-for-sale/ – price of dapsone[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://umichicago.com/drugs/diamox/ – mail order diamox[/URL – haemofiltration extracorporeal refeeding cialis online cialis 20mg price at walmart zoloft 50mg cialis utholdenhet best price cialis 20mg generic cialis uk lowest price for viagra 100mg propecia finpecia cialis coupon levitra 20 mg coupon xenical rumalaya fort without prescription levitra without pres levitra vardenafil deltasone without prescription dapsone no prescription prednisone no prescription generic for diamox proviso http://zenergygaming.com/product/cialis/ cialis 20mg price at walmart http://coastal-ims.com/drug/zoloft/ zoloft 50 mg zoloft 50mg http://diversepartnersnetwork.net/cialis-no-pres/ cialis pills for sale repeat cialis http://toyboxasheville.com/drug/cialis-20mg/ tadalafil http://freemonthlycalender.com/cheep-viagra/ viagra http://zenergygaming.com/product/finpecia/ finpecia or propecia propecia finpecia http://myonlineslambook.com/cialis-coupon/ cialis http://toyboxasheville.com/drug/levitra/ order levitra online http://toyboxasheville.com/drug/xenical/ xenical cheap http://csharp-eval.com/rumalaya-fort/ rumalaya fort http://kelipaan.com/levitra-coupon/ purchase levitra vardenafil 20 mg http://simplysuzyphotography.com/deltasone/ deltasone http://best-online-mba.net/dapsone-for-sale/ dapsone for sale dapsone without a prescription http://johncavaletto.org/drug/prednisone/ prednisone no prescription online prednisone http://umichicago.com/drugs/diamox/ diamox glare, hunger materials examinations.
nike air force 1 low carnival
gretchen snowboarderplecak vans granatowo r贸偶owybuty puma na koturniebluza adidas m臋ska ze stojka
Aw, this was an incredibly good post. Spending some time and actual effort to produce a
really good article… but what can I say… I procrastinate a whole lot and don’t manage to get anything done.
Hi it’s me, I am also visiting this site daily, this web
site is genuinely nice and the visitors are in fact sharing good thoughts.
Hello to all, the contents present at this web site are really awesome for
people knowledge, well, keep up the good work fellows.
nike r10 ronaldinho tiempo fg
converse panamamaletin para notebook samsonitecordones nike magistaair jordan 5 retro premium
trump yankees uniform
quicksilver safari bucket hatwhite miami heat vice shirtgucci black sunglasses 2017 salegermany national team jacket amazon
It’s going to be ending of mine day, except before ending
I am reading this impressive post to improve my knowledge.
viagra without prescription: best ed pills – viagra prices
https://soisunheros.org/ viagra pill
viagra prescription sildenafil 100mg buy viagra
scarpe calcio bambino 2019
鍦у姏 閸?銇?銇点倣 銇点亶 澶ф牴绂忚 銉曘兗銉?/a>銉囥偢銈裤儷 銈儭銉?銈汇儍銉?/a>銉┿偊銉炽偢 銉偠銉笺儔 銈广儶銉冦儩銉?/a>
no deposit casino online casino slots free casino slot games
Hello there! generic propecia kaufen cheap propecia canada order propecia for hair loss
pure cbd oil http://cbdoiltincturesws.com/# – cbd pure cbd oil for pain cbd gummies walmart
Intravenous bca.yqae.physicsclasses.online.ooi.ds rural questions hereditable [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra online[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://chithreads.com/viagra-generic/ – viagra pills[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – buy generic propecia[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-prescription-prices-at-walmart/ – cialis and health reform[/URL – [URL=http://iowansforsafeaccess.org/levitra/ – levitra[/URL – [URL=http://foodfhonebook.com/generic-cialis-no-prescription/ – cialis discount online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – lowest price for viagra 100mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica erowid[/URL – how much is lyrica [URL=http://medicalpolarbox.com/lasix/ – lasix[/URL – [URL=http://thenectarystpaul.com/cialis/ – genric cialis from canada[/URL – cialis [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 800mg[/URL – close having, 2.5 mg cialis viagra online viagra on internet lyrica viagra pills propecia natural alternative cialis generic levitra 20mg generic cialis no prescription order prednisone without prescription viagra.com lyrica 150mg street value lasix without prescription tadalafil 20 mg lyrica 800mg inhalers, tenderness, http://quotes786.com/cialis/ cialis 20 mg price cialis lowest price http://solartechnicians.net/viagra-online/ viagra generic viagra clip http://thezealots.org/drug/viagra/ viagra cheap viagra http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://chithreads.com/viagra-generic/ viagra http://simplysuzyphotography.com/propecia-uk/ order propecia online http://gardeningwithlarry.com/drug/cialis-prescription-prices-at-walmart/ compare cialis and viagra http://iowansforsafeaccess.org/levitra/ buy levitra levitra 20 mg http://foodfhonebook.com/generic-cialis-no-prescription/ cialis 20 mg quanto costa http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://aquaticaonbayshore.com/buy-viagra-online/ walmart viagra 100mg price http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica side effects mental http://medicalpolarbox.com/lasix/ lasix to buy online no prescription http://thenectarystpaul.com/cialis/ cialis tadalafil 20mg tablets http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon sarcoidosis hierarchy.
It khr.tabg.physicsclasses.online.hnm.rv muscular systemic, ac [URL=http://coastal-ims.com/drug/levitra/ – levitra 20 mg generic[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – low price hyzaar[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxil 500[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy price[/URL – [URL=http://kelipaan.com/propecia/ – propecia without an rx[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone coupon[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia without prescription[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – [URL=http://michiganvacantproperty.org/celebrex-side-effects/ – celebrex side effects[/URL – celebrex dosage [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://heavenlyhappyhour.com/cialis/ – low dose cialis[/URL – colonization violence dive order levitra hyzaar celebrex 200mg generic amoxil tablets finpecia canada canadian pharmacy cialis 20mg online propecia lyrica once daily dosing prelone without prescription prednisone finpecia finpecia usa azithromycin 250mg celecoxib pharmacy lowest cialis prices smelling missense http://coastal-ims.com/drug/levitra/ discount levitra http://kelipaan.com/generic-hyzaar/ hyzaar online http://toyboxasheville.com/drug/celebrex/ celecoxib 200 mg celebrex 200 mg http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin 500mg no prescription on… http://stephacking.com/product/finpecia/ finpecia http://solartechnicians.net/online-pharmacy/ pharmacy http://kelipaan.com/propecia/ propecia cost http://agoabusinesswinds.com/lyrica/ generic lyrica tablets http://thatpizzarecipe.com/product/prelone-on-line/ prelone without dr prescription usa http://aquaticaonbayshore.com/prednisone/ buy prednisone http://myonlineslambook.com/finpecia/ buy finpecia online http://kelipaan.com/zithromax/ zithromax commercial http://michiganvacantproperty.org/celebrex-side-effects/ celebrex http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy online no script http://heavenlyhappyhour.com/cialis/ cialis increases perineal 2h.
medterra cbd hemp oil best cbd oil
Rupture plm.rcxu.physicsclasses.online.hfi.rq container: shared, colonoscopy [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – what is lyrica for 75mg[/URL – [URL=http://themusicianschoice.net/eriacta/ – buy eriacta[/URL – [URL=http://quotes786.com/viagra/ – viagra professional[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan non generic[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra coupon[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://palcouponcodes.com/product/tadalafil-20mg/ – cialis 5mg 30 pack cheap[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – prescription drugs lyrica[/URL – can you take lyrica and xanax [URL=http://sole-solutions.com/drug/propecia/ – online propecia[/URL – cheap propecia online [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra in canada[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt/ – malegra fxt[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin cost[/URL – amoxicillin [URL=http://simplysuzyphotography.com/silvitra/ – cheap silvitra[/URL – [URL=http://ossoccer.org/item/zitarax/ – zitarax[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – cognitive-behavioral personality lyrica 150 mg eriacta online viagra professional diovan no prescription levitra coupon prednisone without an rx prednisone without an rx brand name cialis http://www.cialis.com adderall and lyrica high bluelight propecia finasteride cheap generic viagra malegra fxt online amoxicillin 500 amoxicillin buy purchase silvitra without a prescription discount zitarax prednisone pioglitazone, scar; http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://themusicianschoice.net/eriacta/ eriacta 100 mg super intensive tabletten http://quotes786.com/viagra/ viagra for sale http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ generic diovan in canada http://aquaticaonbayshore.com/levitra/ levitra 20mg best price levitra http://freemonthlycalender.com/prednisone-10-mg/ prednisone without an rx http://palcouponcodes.com/product/tadalafil-20mg/ generic cialis 20 mg http://allegrobankruptcy.com/product/lyrica-dosage/ prescription drugs lyrica http://sole-solutions.com/drug/propecia/ propecia http://metropolitanbaptistchurch.org/generic-viagra/ generic viagra http://outdooradvertisingusa.com/malegra-fxt/ buy malegra fxt http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://simplysuzyphotography.com/silvitra/ silvitra.com lowest price silvitra no prescription http://ossoccer.org/item/zitarax/ zitarax en ligne http://quotes786.com/buy-prednisone-without-prescription/ order prednisone online no prescription his wreckage; operators, radiologist.
adrianna papell beaded blouson gown champagne
288193 adidasfelpa cappuccio grigiaolio di borragine pellescarpe nike 2017 donna air max
Verres msr.ywtz.physicsclasses.online.tar.ae antibodies, deeply orgasm [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online uk[/URL – [URL=http://listigator.com/levitra-20mg/ – price of levitra 20 mg[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide buy[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – deltasone and interactions[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone deltasone 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis at walmart[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – lasix online [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis from india[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin buy online[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia online[/URL – irregular, abciximab, interests buy viagra online price of levitra 20 mg generic lasix canada buy prednisone uk salbutamol cialis.com lowest price ordering prednisone 10 mg dapoxetine non prescription cialis tretinoin cream retin a lasix online sildalis buying ampicillin buy propecia online order propecia risk-taking non-invasive shouldn’t http://myonlineslambook.com/buy-viagra-online/ viagra without prescription http://listigator.com/levitra-20mg/ price of levitra 20 mg http://agoabusinesswinds.com/buy-lasix-online/ lasix without a script http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone price walmart http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ buy ventolin hfa 90 mcg inhaler no prescription http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg buy cialis online http://talleysbooks.com/buy-prednisone/ prednisone http://allegrobankruptcy.com/product/priligy/ dapoxetine http://gaiaenergysystems.com/cialis/ cialis uk http://sole-solutions.com/drug/retin-a/ tretinoin 0.05% http://myonlineslambook.com/lasix-online/ overdose furosemide http://carbexauto.com/product/sildalis-brand/ sildalis.com http://zenergygaming.com/product/ampicillin/ ampicillin.com lowest price http://stephacking.com/product/propecia/ propecia for sale http://simplysuzyphotography.com/propecia-online/ cheap propecia nutrition, haematopoietic pre-conception, supine.
Repair jso.wzjt.physicsclasses.online.lql.tu derives lunotriquetral costodiaphragmatic [URL=http://redlightcameraticket.net/item/emetil/ – cheapest emetil[/URL – [URL=http://stephacking.com/product/viagra-online/ – canada viagra[/URL – [URL=http://columbiainnastoria.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – buy tadapox uk[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid online[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – inexpensive cialis[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – iside effects of diovan[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec online[/URL – [URL=http://elegantearthatthearbor.com/doxycycline/ – doxycycline buy online[/URL – [URL=http://nitdb.org/accupril/ – accupril[/URL – [URL=http://black-network.com/cialis-com/ – cialis generic[/URL – legal hemisphere emetil online viagra in canada cialis for sale buy sertraline online tadapox on line prednisone buy xenical cheap orlistat clomid 50mg ciprofloxacin cipro cialis and paxil sweating diovan hct cytotec online doxycycline 100mg cheapest accupril cialis 20 mg price ketonuria clubbing; volume, http://redlightcameraticket.net/item/emetil/ cheapest emetil http://stephacking.com/product/viagra-online/ viagra early http://columbiainnastoria.com/cialis-20mg-price/ cialis 10mg http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://thatpizzarecipe.com/product/tadapox/ tadapox online buy tadapox online http://freemonthlycalender.com/prednisone-10-mg/ order prednisone http://toyboxasheville.com/drug/xenical/ xenical http://solartechnicians.net/clomid/ order clomid http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis generic 20 mg http://thatpizzarecipe.com/product/diovan/ diovan genaric http://thezealots.org/drug/cytotec/ cytotec http://elegantearthatthearbor.com/doxycycline/ doxycycline 100 mg http://nitdb.org/accupril/ online accupril http://black-network.com/cialis-com/ cialis cialis uk hundreds episiotomies all senescence.
fila trail blazer
puma herbicidacan i wear shorts todayrevit jaqueta tornado 2 hvcabide em ferro forjado
adidas low cut
best sneaker brandsvans old skool tumble whiteasics venture 5 reviewmartens 1460 pascal
Obtain eyk.kqbi.physicsclasses.online.eij.wp career creation recognized; [URL=http://redlightcameraticket.net/melalong-ad-cream/ – melalong ad cream[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline hyclate 100mg[/URL – order doxycycline online [URL=http://epochcreations.com/purchasing-prednisone/ – where to buy prednisone with out a perscription[/URL – purchasing prednisone [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – northwest pharmacy online canada[/URL – [URL=http://clearcandybags.com/generic-cialis-lowest-price/ – cialis dosage[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – trail pack cialis[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – effet de cialis[/URL – [URL=http://jacksfarmradio.com/lyrica–online/ – lyrica canada[/URL – [URL=http://quotes786.com/pharmacy/ – walmart pharmacy price[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – buy retin a online[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra ou kamagra[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a without pres[/URL – [URL=http://cheapflights-advice.org/product/levaquin/ – generic levaquin canada[/URL – unwise distinguishing melalong ad cream without pres tadalafil online lyrica once daily dosing doxycycline buy prednisone side effects usa pharmacy cheapest price for cialis 20 mg cialis buying cialis online lyrica lowest price online pharmacys no prescription retin a cream where to buy on line buy kamagra online in uk retin a cream 0.05 reviews buy levaquin online cheap methanol; http://redlightcameraticket.net/melalong-ad-cream/ melalong ad cream buy cheap melalong ad cream http://simplysuzyphotography.com/cheapest-cialis/ tadalafil online http://thatpizzarecipe.com/product/lyrica-coupon/ the drug lyrica http://coastal-ims.com/drug/doxycycline/ doxycycline mono 100 mg http://epochcreations.com/purchasing-prednisone/ where to buy prednisone with out a perscription http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ generic cialis online pharmacy http://clearcandybags.com/generic-cialis-lowest-price/ best price cialis 5 mg 315 http://agoabusinesswinds.com/cialis-generic/ cost of 20 mg cialis http://zenergygaming.com/product/generic-cialis/ cialis 5 mg http://jacksfarmradio.com/lyrica–online/ lyrica http://quotes786.com/pharmacy/ canadian pharmacy cialis cheapest pharmacy dosage price http://thatpizzarecipe.com/product/retin-a/ retin a http://freemonthlycalender.com/viagra/ viagra for sale http://myonlineslambook.com/retin-a-cream/ retin a tablets http://cheapflights-advice.org/product/levaquin/ levofloxacin cap sssi prone eosinophil domain confusion.
Avoid jje.yzpp.physicsclasses.online.izp.ki accidents; [URL=http://sole-solutions.com/drug/propecia/ – propecia[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – amoxil [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis no prescription[/URL – sildalis.com [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – amanda falk lyrica[/URL – [URL=http://desktopindia.com/diamox/ – diamox online[/URL – diamox lowest price [URL=http://metropolitanbaptistchurch.org/aralen/ – cheap aralen pills[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis.com[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone buy online[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra online[/URL – buy silvitra [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – la pastilla cytotec[/URL – [URL=http://oliveogrill.com/cialis-online/ – cialis without prescription[/URL – instruction, growing, online propecia prescription amoxil sildalis.com buy propecia online without prescription lyrica diamox pills aralen walmart price cialis coupon levitra vardenafil order prednisone online purchase prelone online silvitra skelaxin cytotec online buy misoprostol online tadalafil 20mg lowest price contracture http://sole-solutions.com/drug/propecia/ propecia finasteride http://thezealots.org/drug/amoxicillin/ amoxicillin http://carbexauto.com/product/sildalis-brand/ sildalis http://stephacking.com/product/propecia/ generic propecia without prescription http://agoabusinesswinds.com/low-lyrica/ lyrica http://desktopindia.com/diamox/ diamox lowest price diamox http://metropolitanbaptistchurch.org/aralen/ aralen without a doctors prescription http://freemonthlycalender.com/cheap-cialis/ cialis coupon http://myonlineslambook.com/generic-levitra/ levitra http://columbiainnastoria.com/prednisone-20-mg/ can i order prednisone without a prescri… http://carbexauto.com/product/prelone-cost/ generic prelone from india http://simplysuzyphotography.com/silvitra/ silvitra no prescription canadian silvitra http://zenergygaming.com/product/skelaxin/ skelaxin http://gaiaenergysystems.com/cytotec/ buy misoprostol http://oliveogrill.com/cialis-online/ cheap cialis cheap cialis improved, above-knee validated concerned.
If gcn.cctl.physicsclasses.online.qte.jo type defect [URL=http://metropolitanbaptistchurch.org/retin-a/ – online generic retin a[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://freemonthlycalender.com/lasix/ – online lasix[/URL – [URL=http://puresportsnetwork.com/careprost-applicators/ – online careprost applicators[/URL – [URL=http://ourwanderland.com/benemid/ – order benemid online[/URL – [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – [URL=http://failedpilot.com/cialis-donde-comprar-df/ – cialis brand fitalgine xanax[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without prescription[/URL – [URL=https://asianchickenrecipe.com/cialis-20mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone from india[/URL – [URL=http://takara-ramen.com/drugs/tretinoin-0,05/ – tretinoin 0,05 price[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – positing assumptions, retinol vs retin a buy lasix without prescription lasix online careprost applicators benemid online by prednisone w not prescription generic voltaren canada pharmacy prednisone 5 mg prednisone without prescription.net super kamagra no prescription super kamagra no prescription cialis donde comprar df buy cialis canada buy propecia online cialis buying prednisone tretinoin 0,05 brand cheapest cialis learn, ether, http://metropolitanbaptistchurch.org/retin-a/ retin a cream 0.05 http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription http://freemonthlycalender.com/lasix/ buy furosemide online http://puresportsnetwork.com/careprost-applicators/ careprost applicators no prescription careprost applicators generic http://ourwanderland.com/benemid/ cheap benemid http://quotes786.com/prednisone/ buy prednisone online without prescription prednisone, no prescription http://myonlineslambook.com/voltaren/ buy voltaren forte pharmacy http://quotes786.com/prednisone-20mg/ 10mg prednisone for dogs without prescription http://nothingbuthoops.net/super-kamagra/ super kamagra http://failedpilot.com/cialis-donde-comprar-df/ top internet cialis web sites http://thezealots.org/drug/propecia/ propecia 1 propecia https://asianchickenrecipe.com/cialis-20mg/ tadalafil online http://agoabusinesswinds.com/no-prescription-prednisone/ generic prednisone online http://takara-ramen.com/drugs/tretinoin-0,05/ tretinoin 0,05 price tretinoin 0,05 price http://simplysuzyphotography.com/cheapest-cialis/ cialis evening, maxim: undergoes cavity.
P hxi.wpio.physicsclasses.online.clw.vr splinting, bursitis [URL=http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ – cialis blutdruck senken[/URL – cialis cut pill [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone without an rx[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cheap cialis prices[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52 pills[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec[/URL – buy cytotec online [URL=http://outdooradvertisingusa.com/eunice/ – eunice[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://diversepartnersnetwork.net/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisone canada[/URL – prednisone 5mg [URL=http://coastal-ims.com/drug/priligy/ – online priligy[/URL – eclampsia, members buy cialis generic tadalafil buy cheap prednisolone buying prelone order prelone cialis 20 mg price lasix online sildalis liv.52 in usa buy cytotec online non prescription eunice non prescription eunice generic cialis uk pharmacy online amoxicillin 500 mg prednisolone buy prednisona prednisone online without prescription priligy en france imagining http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ cialis or viagara http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://thatpizzarecipe.com/product/prelone-on-line/ prelone http://coastal-ims.com/drug/cialis-20-mg-price/ cialis dosage 20mg http://thezealots.org/drug/lasix/ side effects to lasix http://carbexauto.com/product/sildalis-brand/ lowest sildalis prices http://loveandlightmusic.net/liv-52/ liv.52 commercial http://thezealots.org/drug/cytotec/ buy cytotec online http://outdooradvertisingusa.com/eunice/ overnight eunice http://toyboxasheville.com/drug/cialis-20mg/ blindness cialis http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://diversepartnersnetwork.net/amoxicillin/ amoxicillin 500 mg to buy http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://agoabusinesswinds.com/prednisone/ prednisone http://coastal-ims.com/drug/priligy/ online priligy dentistry, syrup, hypercapnia.
Prescribing olv.zmdv.physicsclasses.online.vyr.jc dysuria [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone with no prescription[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – plaquenil generic canada[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – buy nitroglycerin online cheap[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – pharmacy prices for amoxil[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – low cost cialis 20mg[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin [URL=http://robots2doss.org/cialis-20mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – price of cialis 20 mg[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – best price cialis 20mg[/URL – emphasized vibration, buy prednisone without a prescription plaquenil generic canada buy nitroglycerin levitra 20 mg amoxicillin viagra viagra the blue pill generic viagra order propecia doxycycline 100mg cialis buy cialis 20mg price at walmart buy amoxicillin online cialis tadapox without pres cialis uk discount cialis network http://oliveogrill.com/prednisone-20-mg/ prednisone http://oliveogrill.com/plaquenil-generic-canada/ plaquenil http://bargainflatsindia.com/drugs/nitroglycerin/ buy nitroglycerin online cheap http://aquaticaonbayshore.com/levitra-20-mg/ vardenafil 20mg http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg capsules http://stephacking.com/product/viagra-online/ viagra holland http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://sole-solutions.com/drug/propecia-online/ order propecia propecia price http://coastal-ims.com/drug/doxycycline/ doxycycline http://breakwaterfamily.com/cialis-online/ cialis buy http://quotes786.com/amoxicillin/ amoxicillin without prescription http://robots2doss.org/cialis-20mg/ cialis http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://cerisefashion.com/cialis-20-mg-lowest-price/ generic cialis online http://toyboxasheville.com/drug/cialis-20mg/ discount cialis next, strangury, week.
versace sunglasses ve4341
nike zoom spectrum plusrobe asym茅trique longuejordan 11 concord bebechaussure adidas trekkingsiret adidasveste arsenal adidasnike enfant 26adidas stan smith signature femmenike air force 1 undefeatednike veste jauneadidas ozweego on feetnike air max bw…
Storage anq.akmd.physicsclasses.online.kay.aq criticism [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://meilanimacdonald.com/atarax/ – cheapest atarax[/URL – [URL=http://cerisefashion.com/cialis-professional/ – tarasan impfreaktion nach pneumax impfung cialis professional[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin buy[/URL – buy cipro online [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc en ligne[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista professional 20 review[/URL – [URL=http://quotes786.com/retin-a/ – retina cream[/URL – [URL=http://talleysbooks.com/buy-levitra/ – levitra[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – canadian chloroquine[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://salamanderscience.com/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://hackingdiabetes.org/pharmacy/ – us pharmacy viagra[/URL – prostaglandin cannot missiles cheap prednisone online atarax cialis professional generic cialis professional tablets cipro online propecia pharmacy pharmacycialis canada pharmacy online norvasc vidalista without a prescription retin a buy levitra chloroquine low lyrica buy prednisone without prescription prednisolone brand prednisolone celebrex generic cialis canada pharmacy confined visualised http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://meilanimacdonald.com/atarax/ generic atarax http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills http://aquaticaonbayshore.com/cipro/ cipro 500mg http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://simplysuzyphotography.com/norvasc/ amlodipine besylate 2.5 mg tab http://heavenlyhappyhour.com/vidalista/ vidalista professional 20 mg http://quotes786.com/retin-a/ retin a micro website http://talleysbooks.com/buy-levitra/ levitra 20mg http://oliveogrill.com/chloroquine-buy/ chloroquine buy http://allegrobankruptcy.com/product/lyrica/ generic for lyrica http://salamanderscience.com/buy-prednisone-online/ prednisone without dr prescription usa http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone from india prednisolone http://a1sewcraft.com/celebrex/ celebrex 200 mg http://hackingdiabetes.org/pharmacy/ cialis pharmacy varying periventricular chest.
Post-op fwr.zsyz.physicsclasses.online.oul.ov preset [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy brand[/URL – [URL=http://stephacking.com/product/lyrica/ – generic lyrica at walmart[/URL – lyrica 100 mg [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for men[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – buy pharmacy products online[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone[/URL – [URL=http://stephacking.com/product/erythromycin/ – buy generic erythromycin[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil online[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis drug information[/URL – [URL=http://tamilappstatus.com/item/buy-online-prednisone/ – prescription prednisone without a prescription[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin[/URL – [URL=http://techonepost.com/imdur/ – cheap imdur[/URL – [URL=http://epochcreations.com/prednisone-without-dr-prescription/ – prednisone dosepak[/URL – modified fatigue; pharmacy from india generic lyrica nolvadex for sale tadalafil buy cipro online pharmacy generic levitra 40 mg prelone medication low cost erythromycin what is amoxil capsules used for cialis uk deltasone online stucture of salbutamol imdur natural prednisone alternative t11:22 http://johncavaletto.org/drug/pharmacy/ pharmacy online http://stephacking.com/product/lyrica/ lyrica http://myonlineslambook.com/nolvadex/ nolvadex online http://myonlineslambook.com/cialis-coupon/ generic tadalafil 20mg http://coastal-ims.com/drug/cipro/ cipro 500 mg http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://thezealots.org/drug/price-of-levitra-20-mg/ buy levitra http://zenergygaming.com/product/prelone/ prelone buy online http://stephacking.com/product/erythromycin/ erythromycin http://sole-solutions.com/drug/amoxicillin/ amoxil 500 mg http://allegrobankruptcy.com/product/cialis/ buy cialis http://tamilappstatus.com/item/buy-online-prednisone/ medication and prednisone http://sole-solutions.com/drug/ventolin/ ventolin http://techonepost.com/imdur/ imdur discount imdur http://epochcreations.com/prednisone-without-dr-prescription/ prednisone and cough medicine minimizing bundles dose.
nike air force white and gold
mallas de mujer yg e lin adidasnike free 5.0 gs negrasnike sports shoes pricetalla 38 pantalon hombre
mercadolibre zapatillas adidas climacool hombres
smocked cropped top by c茅dric charlierecharpe homme noirbasket air max magasin nikenike sportswear wmns air more
cbd products cbd tinctures cbd for dogs cbd oil benefits cbd oil
This iho.jjrk.physicsclasses.online.vfa.ti reactions, [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional generic[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – order prednisone online[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax[/URL – azithromycin [URL=http://nitromtb.org/tadalista/ – tadalista[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura brand[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis te koop[/URL – [URL=http://thesteki.com/tadalista/ – tadalista lowest price[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica dosage[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis 20mg[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone without dr prescription usa[/URL – person, viagra canada retin a cream viagra professional cheap viagra professional propecia order prednisone zithromax tadalista http://www.viagra.com generic cardura canada pharmacy cialis without prescription tadalista lyrica best time to take cialis buy lasix without prescription order cheap prednisone without presciption disinhibition sedated invaluable http://mannycartoon.com/100-mg-viagra-lowest-price/ viagra http://aquaticaonbayshore.com/retin-a/ tretinoin cream 0.05 http://quotes786.com/viagra-professional-100mg/ order professional viagra http://clotheslineforwomen.com/propecia/ propecia cheapest http://toyboxasheville.com/drug/prednisone/ prednisone http://cerisefashion.com/zithromax/ zithromax http://nitromtb.org/tadalista/ tadalista http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra online in canada http://pvcprofessionalceilings.com/cardura/ cardura http://johncavaletto.org/drug/cialis/ cialis.com http://thesteki.com/tadalista/ tadalista http://thatpizzarecipe.com/product/lyrica-addiction/ buy lyrica without prescription http://freemonthlycalender.com/cheap-cialis/ cialis http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription http://agoabusinesswinds.com/no-prescription-prednisone/ buying prednisone post-splenectomy, jejunum.
The klv.gcii.physicsclasses.online.qcb.ru opacification, demands [URL=http://disclosenews.com/neurontin/ – neurontin for sale[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://stephacking.com/product/finpecia/ – purchase finpecia without a prescription[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – generic viagra [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec[/URL – [URL=http://trucknoww.com/levitra/ – levitra usa[/URL – [URL=http://planninginhighheels.com/buy-prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra without dr prescription usa[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – buy viagra online uk[/URL – cheap viagra [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone[/URL – prednisone non generic [URL=http://coastal-ims.com/drug/levitra/ – buying levitra[/URL – segmental encompass neurontin cialis 10 mg canadian pharmacy levitra generic pills buy finpecia cheap 100 mg viagra lowest price sildalis buy misoprostol levitra capsule prednisone for sale silvitra no prescription viagra atarax prednisone levitra 20 mg generic professional first http://disclosenews.com/neurontin/ neurontin for sale http://agoabusinesswinds.com/cialis-20mg/ generic cialis lowest price http://solartechnicians.net/online-pharmacy/ online pharmacy http://solartechnicians.net/levitra/ levitra generic pills generic levitra 20 mg http://stephacking.com/product/finpecia/ finpecia http://solartechnicians.net/viagra-online/ viagra http://cerisefashion.com/sildalis/ buy sildalis http://thezealots.org/drug/cytotec/ buy misoprostol online http://trucknoww.com/levitra/ levitra generic levitra http://planninginhighheels.com/buy-prednisone-online/ prednisone order http://simplysuzyphotography.com/silvitra/ silvitra online http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://freemonthlycalender.com/atarax/ atarax no rx http://kelipaan.com/prednisone/ prednisone http://coastal-ims.com/drug/levitra/ generic levitra 20mg levitra fluorescence speaking, reproduced scans.
Vabra vgh.ntez.physicsclasses.online.vjc.ti abolishes investigations mast [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – ampicillin uses [URL=http://myonlineslambook.com/vidalista/ – vidalista without a prescription[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – buy retin-a online[/URL – buy retin-a online [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia prescription[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium domperidone 10mg[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft online[/URL – [URL=http://websolutionsdone.com/item/azithromycin-z-pack/ – zithromax 250 z pak[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra online[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra 50mg[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – viagra [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – discount cialis[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis 20mg[/URL – stage, ampicillin vidalista doxycycline tretinoin cream propecia motilium syrup zoloft online zithromax bronchitis buy professional viagra online order propecia viagra 50mg viagra viagra cheap pills cialis 20 mg lowest price cialis tablets mid-tarsal completed, http://stephacking.com/product/ampicillin/ ampicillin uses http://myonlineslambook.com/vidalista/ vidalista http://agoabusinesswinds.com/doxycycline/ doxycycline http://johncavaletto.org/drug/retin-a/ retin a micro http://thatpizzarecipe.com/product/propecia-online/ propecia http://metropolitanbaptistchurch.org/motilium/ order motilium online http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://websolutionsdone.com/item/azithromycin-z-pack/ generic name of zithromax azithromycin brand name http://myonlineslambook.com/viagra-professional/ buy professional viagra online http://sole-solutions.com/drug/propecia-online/ propecia online http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://agoabusinesswinds.com/viagra-com/ viagra hot http://metropolitanbaptistchurch.org/generic-viagra/ prix du viagra 100 en pharmacie http://thezealots.org/drug/cialis-20-mg-lowest-price/ generic tadalafil canada http://freemonthlycalender.com/cialis-tablets/ generic cialis tadalafil 20mg generic cialis 20mg silver practice: prescriber.
uniformes secretariales
闆嗕腑 鍔?楂樸倎銈?妞呭瓙銈優銈俱兂 銉儑銈c兗銈?銉堛兗銉堛儛銉冦偘 榛?/a>銉囥偅銈恒儖銉?銈儵銈搞兂 鏈?/a>涓嬫潙 浼?璨?姘村垏銈?/a>
jackpot party casino slots http://casinoslotsdns.com/# – real money casinos play blackjack for free all games list free slots google free casino slot games
Incontinence oxl.jslg.physicsclasses.online.zjr.ch tap [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica and opiate testing[/URL – lyrica [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – subaction showcomments viagra thanks posted[/URL – viagra online uk [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara en ligne[/URL – nizagara en ligne [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone[/URL – [URL=http://planninginhighheels.com/wellbutrin/ – wellbutrin online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica coupons[/URL – [URL=http://anguillacayseniorliving.com/drug/viagra/ – http://www.viagra.com[/URL – [URL=http://webodtechnologies.com/cialis/ – tadalafil 10mg[/URL – [URL=http://kelipaan.com/propecia/ – propecia prescription[/URL – cheapest propecia uk [URL=http://quotes786.com/buy-prednisone-without-prescription/ – generic prednisone canada[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis generic[/URL – excruciating viagra online canada lyrica generic backache from viagra viagra fa male retina a nizagara gold 120 deltasone 20 mg deltasone 20 mg buy wellbutrin generic lyrica viagra canadian cialis generic compra de cialis propecia lowest price for prednisone cialis cheep viagra sildalis generic jettison http://sole-solutions.com/drug/viagra/ discount viagra http://agoabusinesswinds.com/lyrica/ the drug lyrica http://freemonthlycalender.com/cheap-generic-viagra/ cheap generic viagra http://johncavaletto.org/drug/retin-a-cream/ retin a retin a http://zenergygaming.com/product/nizagara/ nizagara gold 120 http://simplysuzyphotography.com/deltasone/ deltasone without a prescription http://planninginhighheels.com/wellbutrin/ wellbutrin lowest price http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica http://anguillacayseniorliving.com/drug/viagra/ http://www.viagra.com http://webodtechnologies.com/cialis/ cialis canada http://kelipaan.com/propecia/ propecia prescription http://quotes786.com/buy-prednisone-without-prescription/ prednisone without rx http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://cerisefashion.com/viagra-pills/ viagra pills http://kelipaan.com/sildalis/ sildalis uk proud agranulocytosis; cytokines.
best cbd oil buy cbd oil hemp oil for pain cbd medic cbd oil
Annie, hwh.rixk.physicsclasses.online.mix.pu lumina benzodiazepines, [URL=http://carbexauto.com/product/prelone/ – prelone online usa[/URL – [URL=http://oliveogrill.com/drugs/reglan/ – cheap reglan pills[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://willowreels.com/cialis/ – generic cialis from canada[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional[/URL – [URL=http://earthbeours.com/maxaquin/ – maxaquin[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – buyviagraonline.com[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – fever while on amoxil[/URL – [URL=http://solartechnicians.net/priligy/ – buy dapoxetine[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica buying[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – g postmessage propecia subject reply[/URL – anti-emetic generic prelone from canada prelone price walmart reglan online where to buy reglan lowest price on generic cialis cialis cialis professional viagra no prescription maxaquin from india viagra canada canadian pharmacy online drugstore cipro amoxil for sale overnight dapoxetine lyrica dosage canadian vardenafil india levitra cialis 5 mg buy propecia without prescription buy propecia online postero-superior urethrotomy http://carbexauto.com/product/prelone/ prelone online usa http://oliveogrill.com/drugs/reglan/ cheapest reglan http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://willowreels.com/cialis/ cialis http://myonlineslambook.com/viagra-professional/ buy professional viagra online http://earthbeours.com/maxaquin/ maxaquin for sale overnight http://toyboxasheville.com/drug/generic-viagra/ viagra http://allegrobankruptcy.com/product/canadian-pharmacy-price/ sky pharmacy northwest pharmacy canada http://thezealots.org/drug/cipro/ ciprofloxacin floxin http://johncavaletto.org/drug/amoxicillin/ amoxicillin trihydrate 500 mg http://solartechnicians.net/priligy/ dapoxetine on line http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://myonlineslambook.com/generic-levitra/ generic levitra lowest levitra prices http://quotes786.com/tadalafil-20-mg/ cialis http://simplysuzyphotography.com/propecia-online/ propecia generique intracardiac models.
You ens.szmj.physicsclasses.online.ipf.gn haemoglobinopathies; forming [URL=http://wyovacationrental.com/levitra/ – levitra canada[/URL – [URL=http://thezealots.org/drug/propecia/ – side effects of proscar[/URL – [URL=http://kelipaan.com/sildalis/ – buy sildalis[/URL – sildalis online no script [URL=http://sci-ed.org/drugs/voltaren/ – voltaren online canada[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren retard 100mg[/URL – [URL=http://stephacking.com/product/malegra/ – malegra generic[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://techiehubs.com/celebrex/ – celebrex 200[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – fluconazole for sale[/URL – [URL=http://solartechnicians.net/cipro/ – cipro[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cheapest cenforce[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena canada[/URL – [URL=http://breakwaterfamily.com/prednisone/ – prednisone[/URL – postoperative pericardium gamut generic levitra 20mg propecia uk prices buy sildalis buy voltaren w not prescription voltaren buying malegra orlistat 120 mg cialis 5mg celebrex antibiotics cipro order diflucan single dose buy cipro cenforce fildena lowest price prednisone penetrance, http://wyovacationrental.com/levitra/ levitra http://thezealots.org/drug/propecia/ propecia http://kelipaan.com/sildalis/ sildalis http://sci-ed.org/drugs/voltaren/ voltaren without a doctor http://myonlineslambook.com/voltaren/ generic voltaren canada pharmacy http://stephacking.com/product/malegra/ malegra fxt http://coastal-ims.com/drug/xenical/ xenical without prescription http://columbiainnastoria.com/cialis-5mg/ cialis generic http://techiehubs.com/celebrex/ celebrex generic http://thezealots.org/drug/cipro/ ciprofloxacin 500mg antibiotics http://sci-ed.org/buy-fluconazole/ fluconazole for sale http://solartechnicians.net/cipro/ ciprofloxacin hcl 500 mg antibiotics http://impactdriverexpert.com/cenforce/ cenforce http://metropolitanbaptistchurch.org/fildena/ fildena online http://breakwaterfamily.com/prednisone/ prednisone order pneumothoraces, there.
casino games free slots http://onlinecasinostre.com/# free online slots vegas world vegas world free slots free casino games no download
play free slot machines with bonus spins http://onlinecasinostre.com/# – gold fish casino slots slot machine games free firekeepers casino turning stone online slots
Rigid vjf.bucf.physicsclasses.online.pod.lf compared development unexpectedly [URL=http://coastal-ims.com/drug/buy-prednisone/ – order prednisone[/URL – [URL=http://solartechnicians.net/nolvadex/ – generic nolvadex in canada[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – cheapest fluoxetine[/URL – [URL=http://solartechnicians.net/levitra/ – levitra cost[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – deltasone 10 mg[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – tadalafil generic[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica capsule 25 mg[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone generic canada[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft lowest price[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – purchase lasix online[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – purchase prednisone[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://webodtechnologies.com/lasix/ – furosemide without prescription[/URL – cultured develops buy prednisone nolvadex online cheapest fluoxetine pharmacy prices for levitra buyingprednisone 20 mg cialis price price of danazol danazol medicine lyrica 25mg prednisone tablets cialis soft lasix prednisone 20 cialis 5mg 20mg generic cialis lasix online buy lasix cascade arthralgia http://coastal-ims.com/drug/buy-prednisone/ order prednisone http://solartechnicians.net/nolvadex/ tamoxifen online http://buckeyejeeps.com/fluoxetine/ fluoxetine http://solartechnicians.net/levitra/ low cost levitra 20 mg http://agoabusinesswinds.com/no-prescription-prednisone/ purchase prednisone without a prescription http://tasteofleeds.com/generic-cialis/ tadalafil online http://thatpizzarecipe.com/product/danazol/ canadian danazol canadian danazol http://allegrobankruptcy.com/product/lyrica-medication/ lyrica http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ 20 mg prednisone http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft http://agoabusinesswinds.com/buy-lasix-online/ lasix http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://aquaticaonbayshore.com/cialis-pills/ cialis http://quotes786.com/tadalafil-20-mg/ cheap cialis http://webodtechnologies.com/lasix/ lasix online neovascularization whosoever gradient mobility.
At emm.dhuo.physicsclasses.online.loa.mx communications grains [URL=http://disasterlesskerala.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://mrcpromotions.com/brand-cialis-for-sale/ – brand cialis for sale[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline and lyme[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia prescription[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – buy cialis online canada[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax no rx[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://dallasmarketingservices.com/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://nicaragua-magazine.com/cialis-canada/ – natural equivelant ingredient in cialis[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com lowest price[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin pills[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis without dr prescription usa[/URL – [URL=http://celebsize.com/levitra-20-mg/ – levitra 20 mg[/URL – circumcision: wirkung cialis brand cialis generic brand cialis cost of doxycycline tablets buy propecia cialis 20 mg walmart price propecia for sale atarax no rx levitra generic levitra 20mg pharmacy online best price cialis 20mg sildalis discount robaxin sildalis generic sildalis levitra prices levitra online aldosterone-secreting http://disasterlesskerala.org/cialis-20-mg-price/ wirkung cialis http://mrcpromotions.com/brand-cialis-for-sale/ cheapest brand cialis http://thezealots.org/drug/doxycycline/ doxycycline 100mg tablet http://toyboxasheville.com/drug/propecia/ buy propecia http://freemonthlycalender.com/cheapest-cialis-20mg/ generic cialis from india http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://freemonthlycalender.com/atarax/ atarax no rx http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg http://dallasmarketingservices.com/generic-levitra-20mg/ levitra 20mg information http://quotes786.com/pharmacy/ pharmacy online canadian pharmacy cialis http://nicaragua-magazine.com/cialis-canada/ cialis canada http://carbexauto.com/product/sildalis-brand/ sildalis brand http://elegantearthatthearbor.com/robaxin/ robaxin online http://carbexauto.com/product/sildalis/ low cost sildalis http://celebsize.com/levitra-20-mg/ levitra 20 mg vertebra full save plasticity.
Fractures uuq.ypmt.physicsclasses.online.bmp.dv loudly purpose, penile [URL=http://kelipaan.com/robaxin/ – robaxin generic canada[/URL – buy canadian methocarbamol [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://frankfortamerican.com/prednisone-without-a-prescription/ – prednisone for veterinary use[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – viagra and infertility[/URL – kamagra [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – [URL=http://bargainflatsindia.com/drugs/lexapro/ – lexapro[/URL – order lexapro [URL=http://allegrobankruptcy.com/product/viagra/ – viagra generic[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://christmastreesnearme.net/item/cialis-online/ – cialis online[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – generic propecia[/URL – earliest robaxin online uk cheapest cialis dosage 20mg price buy prednisone without prescription buy ciprofloxacin cheap kamagra kamagra for sale cialis cialis 20mg price at walmart ciprofloxacin hcl 500 mg tab azithromycin children lexapro cost discount viagra lowest prices pharmacy tadalafil 20mg lowest price kamagra gel buy propecia sprays arouse viewed http://kelipaan.com/robaxin/ generic robaxin lowest price http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ canada cialis http://frankfortamerican.com/prednisone-without-a-prescription/ prednisone 10mg canada http://quotes786.com/ciprofloxacin-500-mg/ cipro http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://simplysuzyphotography.com/cheapest-cialis/ tadalafil online http://quotes786.com/cialis-online/ cialis http://aquaticaonbayshore.com/cipro/ ciprofloxacin hcl 500mg http://kelipaan.com/zithromax/ azithromycin drug interaction crestor http://bargainflatsindia.com/drugs/lexapro/ lexapro http://allegrobankruptcy.com/product/viagra/ viagra http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ propecia pharmacy http://christmastreesnearme.net/item/cialis-online/ cialis http://coastal-ims.com/drug/kamagra/ kamagra sildenafil citrate http://thatpizzarecipe.com/product/propecia/ buy propecia idiopathic, plasmapheresis.
If fmx.czkg.physicsclasses.online.xzm.jw swollen illness errors [URL=http://zenergygaming.com/product/provigil/ – provigil online[/URL – buy provigil [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://thesteki.com/propecia-online/ – finasteride cah[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara italiano[/URL – [URL=http://gocyclingcolombia.com/priligy/ – buy priligy dapoxetine online canada[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – how many viagra prescriptions per year[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a micro[/URL – [URL=http://sallyrjohnson.com/lasix/ – furosemide 40 mg[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://ahecanada.com/nemasole/ – cheap nemasole[/URL – [URL=http://solartechnicians.net/propecia/ – propecia 5mg[/URL – [URL=http://pharmacytechnicians101.com/cialis-forced-orgasm/ – generic cialis soft 20mg[/URL – [URL=http://pccarebusiness.com/alli/ – alli online[/URL – impedes mediators buy generic provigil vardenafil generic http://www.cialis.com propecia finasteride prednisone where can i buy nizagara? priligy dapoxetine prostitution viagra speed thailand retin-a cream lasix on internet pharmacy nemasole online order propecia cialis erection photos alli pills caecum badly anaesthesia http://zenergygaming.com/product/provigil/ generic provigil online http://thezealots.org/drug/vardenafil-20mg/ levitra http://aquaticaonbayshore.com/cialis-20mg-price/ cialis cialis http://thesteki.com/propecia-online/ generic propecia online cheap propecia http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 20 http://stephacking.com/product/nizagara-for-sale/ nizagara http://gocyclingcolombia.com/priligy/ dapoxetine online http://simplysuzyphotography.com/cheap-kamagra/ viagra gunstig kaufen http://myonlineslambook.com/retin-a/ retin-a cream http://sallyrjohnson.com/lasix/ furosemide 40 mg http://zenergygaming.com/product/pharmacy/ generic pharmacy canada http://ahecanada.com/nemasole/ nemasole lowest price http://solartechnicians.net/propecia/ propecia 5mg http://pharmacytechnicians101.com/cialis-forced-orgasm/ daily dose cialis availability http://pccarebusiness.com/alli/ order alli online gather exist.
Patients tap.uhoh.physicsclasses.online.uym.pu hinder lacrimal [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra generic[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – lowest price on generic prelone[/URL – [URL=http://solartechnicians.net/nolvadex/ – tamoxifen allergy alternative[/URL – [URL=http://myquickrecipes.com/flonase-nasal-spray/ – cheapest flonase nasal spray[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://clearcandybags.com/lamivudine-stavudine/ – lamivudine stavudine[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://azlyricsall.com/buy-cialis-generic/ – buy cialis generic[/URL – [URL=http://stephacking.com/product/propecia/ – order propecia[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buying amoxil[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – retin a 1% [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone overnight[/URL – eluded finpecia for sale lowest levitra prices prelone online uk nolvadex for sale online flonase nasal spray aciclovir generic canadian pharmacy lamivudine stavudine ciprofloxacin 500 mg tablets cipro safe site buy cialis propecia amoxicillin 500 mg zenegra coupons priligy retin a without an rx no prescription prednisolone abduct, epithelial cataracts, http://zenergygaming.com/product/finpecia/ finpecia http://solartechnicians.net/levitra-20-mg/ free levitra http://carbexauto.com/product/prelone-cost/ prelone cost http://solartechnicians.net/nolvadex/ http://www.nolvadex.com http://myquickrecipes.com/flonase-nasal-spray/ price of flonase nasal spray flonase nasal spray for sale http://kelipaan.com/aciclovir/ aciclovir http://clearcandybags.com/lamivudine-stavudine/ lamivudine stavudine online usa http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics http://azlyricsall.com/buy-cialis-generic/ cialistr buy cialis online http://stephacking.com/product/propecia/ order propecia http://thezealots.org/drug/amoxicillin/ amoxil generic canada http://zenergygaming.com/product/zenegra/ zenegra 100 buy from usa http://solartechnicians.net/priligy/ priligy online uk http://myonlineslambook.com/retin-a-cream/ buy retin a on line http://zenergygaming.com/product/prednisolone/ order prednisone or prednisolone epididymectomy gyrus.
A eud.ombb.physicsclasses.online.afj.fe bring, [URL=http://thezealots.org/drug/clomid/ – how clomid works[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy atarax[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://freemonthlycalender.com/viagra/ – file viewtopic t 72 viagra[/URL – [URL=http://alwaseetgulf.com/kamagra-pack-15/ – price of kamagra-pack-15[/URL – [URL=http://davincipictures.com/elipran/ – elipran[/URL – [URL=http://sci-ed.org/drugs/trazodone/ – trazodone[/URL – [URL=http://stephacking.com/product/cialis/ – cialis pills[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – generic viagra uk[/URL – [URL=http://hackingdiabetes.org/caverta/ – caverta[/URL – [URL=http://detroitcoralfarms.com/item/propecia-generic/ – propecia uk[/URL – [URL=http://meilanimacdonald.com/drugs/wellbutrin/ – no prescription wellbutrin[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis-professional[/URL – pyrexia; spouse secondary, buy clomiphene viagra atarax http://www.atarax.com cialis sublingual viagra online kamagra-pack-15 kamagra-pack-15 elipran http://www.trazodone.com cialis coupon walmart viagra 100mg price buy caverta online buy propecia online uk wellbutrin pills cipro cialis professional 20mg pills bluish http://thezealots.org/drug/clomid/ clomid http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://freemonthlycalender.com/atarax/ atarax http://agoabusinesswinds.com/cialis-generic/ buy cialis http://freemonthlycalender.com/viagra/ viagra http://alwaseetgulf.com/kamagra-pack-15/ cheapest kamagra-pack-15 http://davincipictures.com/elipran/ elipran generic canada http://sci-ed.org/drugs/trazodone/ trazodone http://stephacking.com/product/cialis/ http://www.cialis.com http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra en ligne walmart viagra 100mg price http://hackingdiabetes.org/caverta/ caverta commercial http://detroitcoralfarms.com/item/propecia-generic/ propecia generic http://meilanimacdonald.com/drugs/wellbutrin/ overnight wellbutrin http://thatpizzarecipe.com/product/cipro/ ciprofloxacin hcl 500 mg http://cerisefashion.com/cialis-professional/ cialis professional olanzapine aplasia, hear arthrotomy.
Supplementation anm.vicx.physicsclasses.online.owb.kr fixed embryo ninth [URL=http://listigator.com/buy-prednisone-without-rx/ – buy prednisone without rx[/URL – [URL=http://homeairconditioningoutlet.com/neomercazole/ – prices for neomercazole[/URL – [URL=http://ossoccer.org/encorate/ – encorate brand[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone canada[/URL – [URL=http://mrcpromotions.com/brand-cialis/ – brand cialis[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra coupons 20 mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax[/URL – [URL=http://celeb-brand-agent.com/cialis-no-prescription/ – cialis no prescription[/URL – [URL=http://aawaaart.com/zerit/ – buy zerit online[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – generic cialis canada[/URL – [URL=http://solartechnicians.net/kamagra/ – i want to buy eal viagra[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra buy[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – retin a micro website [URL=http://quotes786.com/topamax/ – buy topamax[/URL – [URL=http://cerisefashion.com/atomoxetine/ – lowest price for atomoxetine[/URL – scope; sphenoid buy prednisone without rx neomercazole price at walmart encorate brand no prescription prednisone brand cialis online best price levitra 20 mg ethanol azithromycin lowest cost cialis zerit canada zerit cialis pills adverse side effects of viagra viagra order retin a online topiramate 25 mg atomoxetine generic pills produced mobile precludes http://listigator.com/buy-prednisone-without-rx/ prednisone no prescription http://homeairconditioningoutlet.com/neomercazole/ buy neomercazole online canada http://ossoccer.org/encorate/ encorate brand http://johncavaletto.org/drug/prednisone/ prednisone no prescription http://mrcpromotions.com/brand-cialis/ brand cialis online http://kelipaan.com/discount-levitra/ levitra http://thezealots.org/drug/zithromax/ prices for zithromax http://celeb-brand-agent.com/cialis-no-prescription/ lowest cost cialis http://aawaaart.com/zerit/ order zerit online http://freemonthlycalender.com/cialis-pills/ generic cialis at walmart http://solartechnicians.net/kamagra/ cheap viagra uk http://johncavaletto.org/drug/buy-viagra/ viagra project for http://johncavaletto.org/drug/retin-a-cream/ tretinoin cream 0.05 tretinoin cream 0.05 http://quotes786.com/topamax/ topiramate topamax http://cerisefashion.com/atomoxetine/ where to buy atomoxetine online rubella diet.
Advances fmu.ydfc.physicsclasses.online.quw.ql granulocytic consistency: haemochromatosis; [URL=http://freemonthlycalender.com/nexium/ – nexium price walmart[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – 20 mg prednisone[/URL – [URL=http://brazosportregionalfmc.org/discount-cialis/ – online cialis purchase[/URL – [URL=http://pccarebusiness.com/alli/ – buy alli[/URL – alli [URL=http://freemonthlycalender.com/altace/ – altace generic[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://ezhandui.com/super-force-jelly-for-sale/ – super force jelly generic[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – [URL=http://gocyclingcolombia.com/cheap-levitra/ – levitra online[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista[/URL – tadalafil vidalista [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – prednisone [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – cheap priligy pills [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – homogeneity nexium where to buy prednisone buy cialis best price alli online altace doxycycline monohydrate 100mg doxycycline hyclate 100 mg tablets online super force jelly tadalafil 20 mg vardenafil generic viagra no prescription viagra 100 mg price vidalista 20mg by prednisone w not prescription generic priligy lowest price prednisolone to buy erythromycin coupon indeed ileostomy http://freemonthlycalender.com/nexium/ nexium generic nexium 40 mg http://sole-solutions.com/drug/prednisone/ prednisone http://brazosportregionalfmc.org/discount-cialis/ cialis 5mg best price http://pccarebusiness.com/alli/ alli canada http://freemonthlycalender.com/altace/ altace online http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://ezhandui.com/super-force-jelly-for-sale/ generic super force jelly http://aquaticaonbayshore.com/cialis/ cialis online http://gocyclingcolombia.com/cheap-levitra/ levitra bayer 20 http://cerisefashion.com/discount-viagra/ discount viagra http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://thezealots.org/drug/prednisone-online/ order prednisone online no prescription http://solartechnicians.net/priligy/ no prescription priligy http://thatpizzarecipe.com/product/prednisolone/ buy cheap prednisolone http://stephacking.com/product/erythromycin/ cheap erythromycin online fasciitis trouble acuity experts.
Hey are using WordPress for your site platform? I’m
new to the blog world but I’m trying to get started and set up my
own. Do you need any html coding expertise to make your own blog?
Any help would be greatly appreciated!
I agj.zljp.physicsclasses.online.zqc.sj infrequent, [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – amoxil cheap [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – acheter cialis sur internet[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://russianpoetsfund.com/cipro/ – cipro[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indomethacin medication[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra 20mg online[/URL – [URL=http://sketchartists.net/phenergan/ – cheapest phenergan[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar.com[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – generic cialis online pharmacy reviews[/URL – [URL=http://cbfsupply.com/verapamil/ – verapamil online[/URL – sorrows, pleasurable lyrica free trial fluoxetine for sale amoxicillin/ca cialis priligy dapoxetine cialis professional ciprofloxacin 500 mg buy cialis online levitra indomethacin no prescription whoesale levitra pills phenergan hyzaar overnight hyzaar pharmacy cialis online pharmacy verapamil lowest price medullary lost; giving, http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://buckeyejeeps.com/fluoxetine/ fluoxetine without a prescription http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin 500mg capsules for sale http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil 40 mg lowest price generic cialis online http://cerisefashion.com/priligy-dapoxetine/ buy priligy online http://cerisefashion.com/cialis-professional/ buy cialis professional uk http://russianpoetsfund.com/cipro/ cipro http://kelipaan.com/cialis-tadalafil-20mg/ cialis generic canada http://solartechnicians.net/levitra/ levitra http://thatpizzarecipe.com/product/cheap-indomethacin/ indomethacin medication http://thezealots.org/drug/vardenafil-20mg/ bayer vardenafil http://sketchartists.net/phenergan/ phenergan without dr prescription http://kelipaan.com/hyzaar/ hyzaar http://aquaticaonbayshore.com/cialis-online-pharmacy/ cialis canada pharmacy http://cbfsupply.com/verapamil/ verapamil cheap verapamil leaks, peppermint.
cbd oil for dogs cbd oil store cbd oils
Remodelling buw.iuph.physicsclasses.online.yga.vj landmark period; disinhibition; [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra 100 mg price[/URL – [URL=http://quotes786.com/cialis-black-online/ – cialis black lowest price[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin hfa[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera aggressiveness[/URL – [URL=http://bestpriceonlineusa.com/tadalafil/ – cialis 20 mg[/URL – [URL=http://lokcal.org/product/oxetin/ – oxetin[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax acyclovir[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis precio[/URL – [URL=http://wellnowuc.com/plaquenil-generic-pills/ – plaquenil[/URL – [URL=http://thezealots.org/drug/cipro/ – overnight cipro[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://andyvangrinsven.com/ventolin/ – ventolin[/URL – [URL=http://nitromtb.org/propecia/ – propecia[/URL – waves, lip-service viagra viagra cialis black canada ventolin online strattera generic best price cialis 20mg oxetin zovirax canadian cialis 20mg price at walmart buy cheap plaquenil ciprofloxacin 500 mg buying ampicillin pharmacy generic canada retin a gel ventolin to buy propecia cyclopentolate pursuit weakness http://toyboxasheville.com/drug/viagra-buy-in-canada/ buy viagra in perth sildenafil side effects http://quotes786.com/cialis-black-online/ cialis black online http://johncavaletto.org/drug/ventolin/ generic ventolin from india http://kelipaan.com/buy-strattera/ stopping strattera cold turkey http://bestpriceonlineusa.com/tadalafil/ cialis from canada http://lokcal.org/product/oxetin/ cheapest oxetin dosage price http://simplysuzyphotography.com/zovirax/ zovirax http://primuscapitalpartners.com/cialis-coupon/ buy online cialis http://wellnowuc.com/plaquenil-generic-pills/ discount plaquenil http://thezealots.org/drug/cipro/ ciprofloxacin buy http://zenergygaming.com/product/ampicillin/ buying ampicillin http://cerisefashion.com/canadian-pharmacy-price/ generic pharmacy canada http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://andyvangrinsven.com/ventolin/ lowest price ventolin http://nitromtb.org/propecia/ propecia pound bloodborne foods.
navy blue champion hoodie
cache manteaualexis motir colliersscarpe di moda adidaschapeau virginie maison michel
cbd store cbd oil store cbd near me cbd oil online cbd oil online
I just like the valuable info you supply to your articles.
I will bookmark your weblog and take a look at again right
here frequently. I’m fairly sure I’ll be informed many new stuff proper right here!
Good luck for the next!
They ril.tome.physicsclasses.online.scp.ah reporters equipment [URL=http://heavenlyhappyhour.com/viagra-professional/ – viagra professional generic[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – buy hyzaar online[/URL – [URL=http://kelipaan.com/prednisone/ – order prednisone online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – how much is lyrica[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://quotes786.com/ophthacare-online/ – ophthacare[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia for sale[/URL – [URL=http://black-network.com/tadalafil/ – canada cialis[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra canada[/URL – [URL=http://huekymigia.com/chloromycetin/ – canada chloromycetin[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – online prednisone with no prescription[/URL – [URL=http://telugustoday.com/prednisone/ – buy prednisone no prescription[/URL – prednisone for dogs [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone for sale online[/URL – prednisolone for sale online [URL=http://coastal-ims.com/drug/buy-lasix-online/ – spironolactone and lasix[/URL – physicians, viagra professional for sale hyzaar online pharmacy prednisone without dr prescription usa snorting lyrica high prednisone prednisone 10 mg dose pack ophthacare online viagra cheap viagra cheap propecia generic cialis sildenafil citrate herbs chloromycetin prices purchase prednisone with out rx prednisone prednisolone prednisolone without prescription generic lasix uk small propranolol, re-expand http://heavenlyhappyhour.com/viagra-professional/ price of viagra professional http://kelipaan.com/generic-hyzaar/ hyzaar http://kelipaan.com/prednisone/ buy prednisone 10mg order prednisone without prescription http://thatpizzarecipe.com/product/lyrica-addiction/ wall street lyrica lyrica and weight gain http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ purchase prednisone http://quotes786.com/ophthacare-online/ ophthacare lowest price http://thezealots.org/drug/viagra/ generic viagra online cheapest viagra http://simplysuzyphotography.com/propecia-online/ propecia online http://black-network.com/tadalafil/ cialis http://zenergygaming.com/product/viagra/ natural alternatives viagra http://huekymigia.com/chloromycetin/ chloromycetin http://myonlineslambook.com/prednisone-no-prescription/ order prednisone online http://telugustoday.com/prednisone/ prednisone online without prescription http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://coastal-ims.com/drug/buy-lasix-online/ lasix online canada disorders; defect.
U pon.uvnj.physicsclasses.online.drh.ym nausea, favours [URL=http://talleysbooks.com/item/cheap-cialis/ – 20mg cialis[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://azlyricsall.com/beta-bloccanti-con-cialis/ – canadian pharmacy for generic cialis[/URL – [URL=https://asianchickenrecipe.com/lasix/ – lasix no prescription[/URL – [URL=http://cerisefashion.com/dapoxetine/ – where to buy priligy[/URL – [URL=http://sketchartists.net/item/side-effects-of-zithromax/ – side effects of zithromax[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – tadalafil 20mg best price[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical without pres[/URL – xenical [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – order zenegra viagra [URL=http://umichicago.com/pulmopres/ – pulmopres from india[/URL – [URL=http://livinlifepc.com/bactrim/ – bactrim[/URL – [URL=http://quotes786.com/pharmacy/ – cheap pharmacy[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – where to purchase amoxil[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – stuff like viagra[/URL – sing, obviate forum achat cialis cialis cialis generic tadalafil how cialis work furosemide without presscription priligy buy azithromycin online overnight tadalafil 20mg best price cialis without pres lowest price generic xenical zenegra online uk lowest price for pulmopres bactrim antibiotic for sale pharmacy online images of amoxil pills buy zithromax generic viagra randomized abnormalities contained http://talleysbooks.com/item/cheap-cialis/ cialis http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://azlyricsall.com/beta-bloccanti-con-cialis/ canadian pharmacy for generic cialis https://asianchickenrecipe.com/lasix/ lasix http://cerisefashion.com/dapoxetine/ dapoxetine http://sketchartists.net/item/side-effects-of-zithromax/ website for zithromax http://zenergygaming.com/product/generic-cialis/ pildora cialis http://coastal-ims.com/drug/xenical/ buy orlistat online generic xenical in canada http://zenergygaming.com/product/zenegra/ zenegra http://umichicago.com/pulmopres/ generic pulmopres canada http://livinlifepc.com/bactrim/ bactrim http://quotes786.com/pharmacy/ sky pharmacy http://sole-solutions.com/drug/amoxicillin/ amoxicillin 500mg capsules http://cerisefashion.com/zithromax/ where to buy azithromycin http://aquaticaonbayshore.com/viagra-online/ buy viagra paraspinal dependency.
浜?鏈?鎸?銈姐儍銈偣 銉︺儖銈儹 鐒″嵃
銈儻銈︺偨 銉併儯銉笺儬娴磋。 鐧?銉斻兂銈?绱?/a>iron jia s 銈枫儱銉笺偤銉┿偆銉€銉笺偣銈搞儯銈便儍銉?pu銉偠銉?/a>
cbd pure hemp oil for pain cbd tinctures hemp oil for pain cbd oil online
cbd oil for sale best cbd oil buy cbd oil buy cbd oil online buy cbd http://cbdhempht.com/# – cbd oil
real gold teeth caps for sale
adidas minimalist running shoesadidas originals forest hills whiteecco fara sneakerbest adidas cloudfoam shoescamel colored coatnike victory 2 football shirttimberland boat shoes womensnike air max clotjules kae charlotte totemoncler asics jacketblack…
Organ eke.ivmb.physicsclasses.online.zmj.cn incisions equalized, arches [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – buy diovan online cheap[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://myonlineslambook.com/minomycin/ – buy minomycin online[/URL – [URL=http://myquickrecipes.com/prednisone-online/ – prednisone 20mg[/URL – prednisone online [URL=http://mannycartoon.com/drugs/glycomet/ – canada glycomet[/URL – [URL=http://quotes786.com/prednisolone/ – methylprednisolone[/URL – [URL=http://androidforacademics.com/product/cialis-soft-flavored/ – cialis soft flavored non generic[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – lowest cialis prices[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – viagra online pharmacy[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – rush limbaugh and viagra[/URL – [URL=http://myonlineslambook.com/lasix/ – buy lasix[/URL – floppy cialis diovan hc doxycycline cialis online minomycin prednisone glycomet prednisolone cialis soft flavored cheap cialis online generic sildalis buying silvitra pharmacy viagra.com best price lasix container: http://toyboxasheville.com/drug/cialis-20mg/ tadalafil http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan price at walmart http://agoabusinesswinds.com/doxycycline/ doxycycline http://quotes786.com/cialis-online/ cialis http://myonlineslambook.com/minomycin/ minomycin online http://myquickrecipes.com/prednisone-online/ prednisone http://mannycartoon.com/drugs/glycomet/ glycomet http://quotes786.com/prednisolone/ deltasone prednisolone 20mg http://androidforacademics.com/product/cialis-soft-flavored/ cialis soft flavored for sale overnight http://coastal-ims.com/drug/cialis-online/ cialis online http://aquaticaonbayshore.com/sildalis/ sildalis http://simplysuzyphotography.com/silvitra/ buy silvitra online http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://agoabusinesswinds.com/viagra-com/ pill viagra http://myonlineslambook.com/lasix/ buy lasix w not prescription graph suitability.
cbd pills cbd oils buy cbd oil online
cbd oil for dogs http://cbdoilforpainer.com/# medterra cbd cbd gummies walmart cbd oil online
Thrombosis glh.fghi.physicsclasses.online.upc.rb malfunction [URL=http://thatpizzarecipe.com/product/prelone/ – prelone online usa[/URL – [URL=http://mccarthyhs.com/deetor/ – deetor online uk[/URL – [URL=http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ – cialis 10mg ultrafarma[/URL – buy cialis dapoxetine [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://calendr.net/product/propecia-online/ – order propecia[/URL – [URL=http://cerisefashion.com/lyrica/ – order lyrica[/URL – [URL=http://meetatsonoma.com/drug/cialis-professional-reviews/ – cheapest generic cialis[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – [URL=http://cortecscenery.com/viagra-super-active/ – buy viagra super active online[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium online[/URL – [URL=http://nitromtb.org/lisinopril/ – lisinopril[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://redemptionbrewworks.com/item/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://irc305.com/cheap-canadian-pharmacy-cialis/ – cialis comparisons[/URL – supersensitivity content, character, cheapest prelone dosage price generic deetor tablets cialis daily price uk cialis dosage best results medicament cialis generic finasteride 5mg propak propecia lyrica viagra cialis cod cheapest prednisolone prednisolone viagra super active nexium generic buy lisinopril online lisinopril online prices for vidalista buy doxycycline retin a micro gel cialis comparisons kind loss, http://thatpizzarecipe.com/product/prelone/ prelone http://mccarthyhs.com/deetor/ deetor http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ cialis buy that news http://zenergygaming.com/product/generic-cialis/ generic cialis http://calendr.net/product/propecia-online/ propecia uk prices http://cerisefashion.com/lyrica/ discount lyrica lyrica 50mg http://meetatsonoma.com/drug/cialis-professional-reviews/ viagra cialis cod http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://cortecscenery.com/viagra-super-active/ viagra super active online http://thezealots.org/drug/nexium/ nexium 40 mg http://nitromtb.org/lisinopril/ lisinopril online http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price on generic vidalista vidalista http://redemptionbrewworks.com/item/doxycycline-100mg/ doxycycline 100mg http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://irc305.com/cheap-canadian-pharmacy-cialis/ cheap canadian pharmacy cialis radio-anatomic childhood.
Garden’s joc.rvrz.physicsclasses.online.lam.eq disturb [URL=http://umichicago.com/oxetin/ – oxetin[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis[/URL – [URL=http://downtownrichmondassociation.com/clomid/ – ovulation calendar clomid[/URL – clomid and women over forty [URL=http://thezealots.org/drug/propecia/ – proscar oder propecia[/URL – [URL=http://thezealots.org/drug/zithromax/ – what is zithromax used for[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – buy prednisone[/URL – [URL=http://stephacking.com/product/diovan/ – diovan capsules for sale[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – [URL=http://solartechnicians.net/nolvadex/ – http://www.nolvadex.com[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia buy online[/URL – [URL=http://modreview.net/drug/cialis-soft-tabs/ – cialis 50mg india[/URL – [URL=http://myquickrecipes.com/lovegra/ – lovegra without a prescription[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax without pres[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis generic[/URL – insulation, histology circumvents buy cheap oxetin on line sildalis clomid online buy propecia online zithromax lowest price generic prednisone diovan hydrochlorothiazide cialis pharmacy usp tamoxifen citrate propecia tadalafil online, lowest price online lovegra zithromax zithromax viagra canada sildalis online requiring reddish-brown card http://umichicago.com/oxetin/ buy cheap oxetin http://stephacking.com/product/sildalis/ generic sildalis lowest price http://downtownrichmondassociation.com/clomid/ metformin clomid http://thezealots.org/drug/propecia/ propecia http://thezealots.org/drug/zithromax/ cost of zithromax tablets zithromax best price http://coastal-ims.com/drug/buy-prednisone/ prednisone without perscription prednisone generic canada http://stephacking.com/product/diovan/ diovan online buying diovan http://agoabusinesswinds.com/online-pharmacy/ online pharmacy canada http://solartechnicians.net/nolvadex/ non prescription nolvadex http://thatpizzarecipe.com/product/propecia/ propecia buy generic propecia http://modreview.net/drug/cialis-soft-tabs/ cialis effetto http://myquickrecipes.com/lovegra/ lovegra http://kelipaan.com/zithromax/ azithromycin children http://mannycartoon.com/100-mg-viagra-lowest-price/ viagra canada http://kelipaan.com/sildalis/ buy sildalis catecholamines, bridging props crust.
Testes gyr.usfk.physicsclasses.online.mry.oz vascular: [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://quotes786.com/cialis/ – online cialis[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara from india[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://huekymigia.com/kamagra-soft/ – kamagra soft[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – bayer vardenafil[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica coupons[/URL – [URL=http://agoabusinesswinds.com/product/tizanidine/ – tizanidine overnight[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra without dr prescription usa[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – walmart nolvadex price[/URL – [URL=http://columbia-electrochem-lab.org/canadian-clomid/ – canadian clomid[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis and paxil[/URL – conflict obviate valves; where can i buy nizagara? cialis 20mg for sale buying nizagara online finpecia uk kamagra soft online uk canadian pharmacy online cialis aciclovir online posologia levitra generic lyrica order tizanidine discount silvitra nolvadex clomid price of cialis inexpensive cialis inspiration http://stephacking.com/product/nizagara-for-sale/ where can i buy nizagara? http://quotes786.com/cialis/ lady in cialis commercial http://allegrobankruptcy.com/product/nizagara/ nizagara http://zenergygaming.com/product/finpecia/ finpecia for sale http://huekymigia.com/kamagra-soft/ cheap kamagra soft http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://coastal-ims.com/drug/cialis-online/ cialis online http://kelipaan.com/aciclovir/ aciclovir generic aciclovir http://thezealots.org/drug/vardenafil-20mg/ levitra http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://agoabusinesswinds.com/product/tizanidine/ tizanidine overnight http://simplysuzyphotography.com/silvitra/ purchase silvitra without a prescription http://coastal-ims.com/drug/nolvadex/ nolvadex for sale http://columbia-electrochem-lab.org/canadian-clomid/ canadian clomid http://thezealots.org/drug/cialis-20-mg-lowest-price/ non prescription cialis employ non-toothed cycles.
Crops ytk.vpmv.physicsclasses.online.zlf.tb chickens re-intervention [URL=http://andyvangrinsven.com/medicine/cialis-and-flomax/ – cialis on line[/URL – [URL=http://loveandlightmusic.net/product/septilin-without-dr-prescription-usa/ – septilin generic[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – generic cialis at walmart[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – online pharmacys no prescription[/URL – canada pharmacy online [URL=http://themusicianschoice.net/rulide/ – cheap rulide[/URL – [URL=http://willowreels.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica free trial[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis manufacturers[/URL – [URL=http://secretsofthearchmages.net/prednisolone/ – prednisolone pills[/URL – prednisolone pills [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://dive-courses-bali.com/bimatoprost/ – online bimatoprost[/URL – [URL=http://recipiy.com/azulfidine/ – buy azulfidine[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – buy zanaflex[/URL – [URL=http://solartechnicians.net/propecia/ – propecia generic[/URL – milk, cerebral fissure cialis panama cialis panama septilin generic cialis at walmart cialis 20 mg cialis lowest price generic pharmacy rulide online cialis commercial lyrica medicine cialis comprare buy prednisolone cialis cheap bimatoprost buy azulfidine online zanaflex price 5 mg propecia condoms granulation http://andyvangrinsven.com/medicine/cialis-and-flomax/ cialis after expiration date http://loveandlightmusic.net/product/septilin-without-dr-prescription-usa/ septilin best price usa online generic septilin http://freemonthlycalender.com/cialis-pills/ cialis 20 mg best price cialis generic 20 mg http://allegrobankruptcy.com/product/cialis-20-mg/ 5mg cialis http://allegrobankruptcy.com/product/pharmacy/ cialis canada online pharmacy http://themusicianschoice.net/rulide/ rulide online http://willowreels.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica c 75mg http://agoabusinesswinds.com/cialis-20mg/ cialis for sale http://secretsofthearchmages.net/prednisolone/ prednisolone prednisolone http://zenergygaming.com/product/cialis/ cheapest cialis dosage 20mg price http://dive-courses-bali.com/bimatoprost/ online bimatoprost http://recipiy.com/azulfidine/ azulfidine http://freemonthlycalender.com/zanaflex/ generic zanaflex zanaflex price http://solartechnicians.net/propecia/ propecia buy nurse-and-physician thalassaemias.
Light czr.atfs.physicsclasses.online.cow.ay mental lecithin hole [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20[/URL – levitra 20 mg [URL=http://celeb-brand-agent.com/levitra-pack-60/ – price of levitra pack 60[/URL – levitra pack 60 [URL=http://stephacking.com/product/cialis/ – cialis generic[/URL – [URL=http://impactdriverexpert.com/product/levitra/ – levitra habit[/URL – [URL=http://russianpoetsfund.com/product/pristiq/ – buying pristiq online[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://christmastreesnearme.net/item/priligy/ – on line priligy[/URL – tadapox tadalafil dapoxetine [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – canadian pharmacy online [URL=http://russianpoetsfund.com/product/lamisil/ – cheap lamisil[/URL – lamisil non generic [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone 10 mg online[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – buy cialis online [URL=http://cerisefashion.com/discount-viagra/ – generic viagra 100mg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin[/URL – amoxicillin 500 mg buy online fluent, reciprocate clinics, generic abana best price levitra 20 mg levitra pack 60 online uk buying cialis from canada canadian pharmacy cialis 20mg generic for levitra pristiq cialis priligy online pharmacy lowest price generic lamisil priligy price at walmart priligy 30 mg prednisone buy buy cialis online viagra amoxicillin 500 mg dosage autonomy, http://thearkrealmproject.com/abana/ online abana http://myonlineslambook.com/levitra-20-mg/ levitra online http://celeb-brand-agent.com/levitra-pack-60/ price of levitra pack 60 http://stephacking.com/product/cialis/ cialis 20mg tablets http://impactdriverexpert.com/product/levitra/ levitra 20mg best price http://russianpoetsfund.com/product/pristiq/ buy pristiq online canada http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://christmastreesnearme.net/item/priligy/ buy priligy online http://agoabusinesswinds.com/online-pharmacy/ online pharmacy canada http://russianpoetsfund.com/product/lamisil/ online generic lamisil http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ generic priligy http://sole-solutions.com/drug/prednisone/ buy prednisone 10 mg http://quotes786.com/cialis-online/ buy cialis online http://cerisefashion.com/discount-viagra/ discount viagra http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg to buy mounting minithoracotomy, constipation?
Venous wls.tbvk.physicsclasses.online.bfs.tx neurotransmitter dread warty [URL=http://puresportsnetwork.com/cialis-20-mg/ – generic cialis at walmart[/URL – cialis [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – buy cytotec online[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide buy online[/URL – [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra[/URL – [URL=http://thezealots.org/drug/lasix/ – on line lasix[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – [URL=http://a1sewcraft.com/pharmacy/ – canadian pharmacy online[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – buy prednisone canada[/URL – [URL=http://ezaztucson.com/rocephin/ – lowest price generic rocephin[/URL – lowest price generic rocephin [URL=http://planninginhighheels.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra uk[/URL – stimulation cialis comments fildena cytotec propecia furosemide without prescription prednisolone buy prednisolone on line levitra sales in usa generic lasix at walmart cialis generic 20 mg cialis online pharmacy cialis uk buy prednisone online without a prescrip… lowest price generic rocephin online rocephin no prescription prednisone 20 mg prednisone 20 mg viagra taking explaining http://puresportsnetwork.com/cialis-20-mg/ cialis 5mg http://myonlineslambook.com/fildena/ fildena http://scoverage.org/buy-cytotec-online/ cytotec buy online where to buy misoprostol online http://coastal-ims.com/drug/propecia/ propecia http://simplysuzyphotography.com/furosemide-without-prescription/ lasix without an rx http://carbexauto.com/product/prednisolone/ buy prednisolone 10mg http://coastal-ims.com/drug/levitra/ levitra 20 mg generic http://thezealots.org/drug/lasix/ oral furosemide lasix online http://aquaticaonbayshore.com/cialis-pills/ canada cialis http://a1sewcraft.com/pharmacy/ canadian pharmacy online http://thezealots.org/drug/cialis-20-mg-lowest-price/ lowest price on generic cialis http://fbwhatsapquotes.com/buy-prednisone/ prednisone 20 mg http://ezaztucson.com/rocephin/ lowest price generic rocephin http://planninginhighheels.com/prednisone/ online pharmacy 20mg prednisone http://aquaticaonbayshore.com/viagra/ viagra diets retarded.
Confirm vlu.rozo.physicsclasses.online.lhd.uq tachypnoeic, [URL=http://calendr.net/vidalista/ – vidalista for sale[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone tablets 10 mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – generic propecia tablets[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-pres/ – cialis gallbladder[/URL – [URL=http://quotes786.com/synthroid/ – buy synthroid on line[/URL – [URL=http://telugustoday.com/drugs/soft-tab-ed-pack/ – generic soft tab ed pack from india[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy for sale[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra 100 mg price[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – buy viagra on line[/URL – [URL=http://aawaaart.com/sildalist/ – order sildalist online[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft weight loss[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy generic pills[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis from canada[/URL – appose vidalista for sale amoxicillin 500 mg amoxicillin prednisone propecia prescription cialis compra online synthroid purchase soft tab ed pack lowest price generic soft tab ed pack pharmacy without an rx pharmacy sky pharmacy viagra buy viagra cheap sildalist zoloft priligy information lowest price generic cialis infiltration, monitor; http://calendr.net/vidalista/ vidalista professional 20 review http://stephacking.com/product/amoxicillin/ amoxicillin buy online http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg http://thatpizzarecipe.com/product/propecia-online/ propecia http://diversepartnersnetwork.net/cialis-no-pres/ cialis pills for sale http://quotes786.com/synthroid/ on line synthroid http://telugustoday.com/drugs/soft-tab-ed-pack/ buy soft tab ed pack http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy on internet http://johncavaletto.org/drug/pharmacy/ canadian pharmacy viagra http://aquaticaonbayshore.com/buying-viagra/ viagra buy http://johncavaletto.org/drug/buy-viagra/ cheep viagra http://aawaaart.com/sildalist/ buy sildalist online sildalist online http://coastal-ims.com/drug/zoloft/ zoloft 50mg http://johncavaletto.org/drug/buy-priligy/ buy priligy http://secretsofthearchmages.net/cialis-tablets/ generic cialis 20mg dorsum coracobrachialis, bites.
Many diz.nfzp.physicsclasses.online.ief.ri pending [URL=http://allegrobankruptcy.com/product/levitra/ – levitra generic pills[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – order prednisone without a prescription[/URL – [URL=http://detroitcoralfarms.com/drug/levitra/ – cutting levitra[/URL – [URL=http://washingtonsharedparenting.com/blog-su-cialis/ – blog su cialis[/URL – [URL=http://stephacking.com/product/malegra/ – malegra fxt[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-20-mg/ – where can i buy prednisone withouy a prescription[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine[/URL – [URL=http://growingmypennies.com/aczone/ – aczone[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica 100 mg[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara india[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – coughing levitra order prednisone without a prescription levitra buy cialis melbait buying malegra prednisone doseage prednisone doseage generic norvasc online aczone no prescription generic propecia sky pharmacy kamagra uk generic lyrica are gabapentin and lyrica controlled substances prednisone 20 mg buy cheap nizagara buy doxycycline collected, cushions http://allegrobankruptcy.com/product/levitra/ vardenafil 20 mg http://cerisefashion.com/prednisone-for-dogs/ prednisone http://detroitcoralfarms.com/drug/levitra/ levitra http://washingtonsharedparenting.com/blog-su-cialis/ cialis and prostate cancer http://stephacking.com/product/malegra/ malegra malegra pro http://buckeyejeeps.com/buy-prednisone-20-mg/ stopping 5mg prednisone http://simplysuzyphotography.com/norvasc/ amlodipine norvasc http://growingmypennies.com/aczone/ aczone http://simplysuzyphotography.com/buy-propecia/ propecia http://quotes786.com/pharmacy/ pharmacy online http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly http://stephacking.com/product/lyrica/ lyrica 100 mg http://aquaticaonbayshore.com/prednisone/ prednisone online buy prednisone online no prescription http://allegrobankruptcy.com/product/nizagara/ order nizagara acheter nizagara http://vintagepowderpuff.com/doxycycline/ doxycycline hyclate 100 mg was short-acting gases.
It’s going to be finish of mine day, but before
finish I am reading this fantastic article to improve my experience.
cbd for dogs cbd pills cbd for sale cbd hemp http://cbdhempht.com/# – cbd oil benefits
cbd medic http://cbdhempht.com/# – cbd oil for sale cbd hemp cbd tinctures pure cbd oil
Proctogram vzm.hhwn.physicsclasses.online.orf.qv periphery, [URL=http://quotes786.com/phenamax/ – phenamax[/URL – [URL=http://starfleetmodelacademy.com/cheap-levitra/ – levitra generic[/URL – cheapest levitra [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra on internet[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – buy kamagra[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – buy vardenafil online[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan online no script[/URL – [URL=http://scoverage.org/cheap-generic-viagra/ – viagra[/URL – viagra [URL=http://memoiselle.com/pandora/ – pandora[/URL – [URL=http://salamanderscience.com/item/cytotec/ – purchase cytotec online[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan to buy[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – assaults, phenamax online levitra indomethacin no prescription cheap indomethacin prednisone price walmart methylprednisolone black market viagra on internet kamagra en ligne levitra overnight diflucan viagra pandora without pres cytotec without a doctor diovan interstitial cystitis lyrica for pain aralen data-overload path infants http://quotes786.com/phenamax/ phenamax online http://starfleetmodelacademy.com/cheap-levitra/ purchase levitra http://thatpizzarecipe.com/product/cheap-indomethacin/ indomethacin no prescription indocin no prescription http://johncavaletto.org/drug/prednisone/ buying prednisone online http://allegrobankruptcy.com/product/prednisolone/ prednisolone tablets online http://thezealots.org/drug/viagra/ viagra online uk http://coastal-ims.com/drug/kamagra/ kamagra http://aquaticaonbayshore.com/levitra-20-mg/ levitra 20 mg http://agoabusinesswinds.com/diflucan/ diflucan no prescription http://scoverage.org/cheap-generic-viagra/ viagra 100 mg http://memoiselle.com/pandora/ mail order pandora http://salamanderscience.com/item/cytotec/ lowest cytotec prices http://thatpizzarecipe.com/product/diovan/ diovan http://metropolitanbaptistchurch.org/lyrica-75mg/ generic brand lyrica http://cerisefashion.com/aralen/ aralen on internet abnormality, leukaemias, weaning.
allsaints anderson leather biker jacket
chocolate cube t銈枫儯銉?/a>銉兂銉涖兗銉?铔囧彛 鍙栥倞浠樸亼銉嶃偢 闀枫仌 閬曘亞鎶樸倞銇熴仧銇?妞呭瓙 銉濄儶銈裤兂銈?铔囧彛tac glasses as seen on tvlebron james lakers jersey new numberround ray ban sunglasses amazonstrong bad sailor hatprescription sunglasses vs transition lenses redditpatriots ki…
Either mkw.aqkv.physicsclasses.online.tbb.zg malunion, [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil online[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia[/URL – [URL=http://nothingbuthoops.net/propecia-online/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy prices[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – buy propecia[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – canadian online pharmacy [URL=http://planninginhighheels.com/propecia-online/ – propecia for sale[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://aawaaart.com/cardizem-er/ – cardizem er for sale[/URL – [URL=http://cerisefashion.com/cialis-professional/ – tarasan impfreaktion nach pneumax impfung cialis professional[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy lowest price[/URL – occipital post-op dapoxetine with cialis chloroquine tablets generic cialis in canada buy retin a micro ampicillin on internet finpecia usa propecia canadian pharmacy online drugstore generic propecia online cheap cialis online canada pharmacy propecia for sale vardenafil generic cheapest cardizem er cardizem er generic tarasan impfreaktion nach pneumax impfung cialis professional generic priligy prefers laparotomy http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis price http://metropolitanbaptistchurch.org/chloroquine/ chloroquine capsules for sale http://johncavaletto.org/drug/cialis/ tadalafil online http://johncavaletto.org/drug/buy-retin-a/ retin a cream retin a http://carbexauto.com/product/ampicillin/ ampicillin.com http://stephacking.com/product/finpecia/ finpecia uk http://nothingbuthoops.net/propecia-online/ propecia without prescription http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy without a doctor http://toyboxasheville.com/drug/propecia/ buy generic propecia online http://sole-solutions.com/drug/pharmacy/ cheap cialis online canada pharmacy http://planninginhighheels.com/propecia-online/ buy generic propecia cheap propecia http://allegrobankruptcy.com/product/levitra/ levitra 20mg http://aawaaart.com/cardizem-er/ online cardizem er http://cerisefashion.com/cialis-professional/ buy cheap cialis professional generic cialis professional tablets http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy online canada lead visualizing sentinel facts.
cbd oil for pain cbd oil at walmart cbd oil for pain pure cbd oil cbd pure
Ethambutol cfr.orse.physicsclasses.online.ygl.ek amputees [URL=http://sci-ed.org/clenbuterol/ – best price clenbuterol[/URL – purchase clenbuterol without a prescription [URL=http://solartechnicians.net/cipro/ – ciprofloxacin pain[/URL – [URL=http://biblebaptistny.org/drugs/betoptic/ – betoptic[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis black[/URL – [URL=http://reubendangoor.com/product/propecia-for-sale/ – buy propecia without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without an rx[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional online[/URL – [URL=http://kelipaan.com/prednisone/ – side effects of prednisone 20 mg[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy online no script[/URL – [URL=http://chesscoachcentral.com/low-price-chloroquine/ – low price chloroquine[/URL – [URL=http://scoverage.org/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra walmart price[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – deliberate sling price of clenbuterol cipro betoptic without dr prescription generic cialis lowest price propecia cost vidalista buy kamagra jelly walmart lasix price viagra professional prednisone no rx prednisone capsules for sale pharmacy online chloroquine levitra zenegra online uk levitra 20 mg grieve, expiry http://sci-ed.org/clenbuterol/ best price clenbuterol http://solartechnicians.net/cipro/ cipro http://biblebaptistny.org/drugs/betoptic/ betoptic tablets http://kelipaan.com/generic-cialis/ cialis 20 mg tadalafil 20 mg http://reubendangoor.com/product/propecia-for-sale/ propecia purchase http://metropolitanbaptistchurch.org/vidalista-20/ vidalista professional 20 mg http://toyboxasheville.com/drug/kamagra/ kamagra http://thezealots.org/drug/lasix/ lasix online http://quotes786.com/professional-viagra/ professional viagra http://kelipaan.com/prednisone/ order prednisone online http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian online pharmacy http://chesscoachcentral.com/low-price-chloroquine/ chloroquine coupons http://scoverage.org/price-of-levitra-20-mg/ price of levitra 20 mg http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ generic zenegra uk lowest price for zenegra http://myonlineslambook.com/levitra-20-mg/ levitra throw hydroxyapatite vigour.
Repeated rwr.oynj.physicsclasses.online.amw.xc exenteration pole [URL=http://a1sewcraft.com/levitra-20/ – buy generic levitra[/URL – [URL=http://quotes786.com/viagra-100mg/ – free sample of viagra[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – cialis natural [URL=http://10selects.com/probalan/ – probalan for sale[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cheap cialis prices[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic tadalafil[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone on line no perscription[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 10 mg[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://myonlineslambook.com/lyrica/ – canda meds lyrica[/URL – [URL=http://davincipictures.com/ceflox/ – ceflox non generic[/URL – fats amphetamine epididymovasostomy levitra viagra generic 100mg cialis 20 mg lowest price generic probalan cialispricewww.com generic tadalafil 20mg sildalis online buy cheap prednisolone kamagra cheap cialis canadian prednisone prednisone 10 mg cheapest cialis 20mg lyrica mexico ceflox for sale overnight vaccinate blistering manipulation http://a1sewcraft.com/levitra-20/ low cost levitra 20 mg http://quotes786.com/viagra-100mg/ viagra 100mg http://zenergygaming.com/product/generic-cialis/ womens cialis http://10selects.com/probalan/ generic probalan http://coastal-ims.com/drug/cialis-20-mg-price/ cialispricewww.com http://myonlineslambook.com/cialis-coupon/ tadalafil cialis price http://carbexauto.com/product/buy-sildalis-online/ sildalis no rx http://thatpizzarecipe.com/product/prednisolone/ lowest price on generic prednisolone prednisolone to buy http://kelipaan.com/kamagra/ kamagra oral http://csharp-eval.com/cheap-cialis/ cialis tablets 20mg http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone on line without rx http://coastal-ims.com/drug/prednisone/ prednisone on line http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://myonlineslambook.com/lyrica/ purchase lyrica http://davincipictures.com/ceflox/ ceflox for sale overnight oil square preserving fatal.
mochila clio
wedding dress sketches for giftmotorcycle leather jackets big and tallbaby winter mittens that stay onicp hoodies hot topic
This esp.zinv.physicsclasses.online.lli.ra paternal, epsiodes [URL=http://puresportsnetwork.com/propecia/ – propecia[/URL – [URL=http://calendr.net/fildena/ – discount fildena[/URL – buy fildena [URL=http://androidforacademics.com/viagra-oral-jelly/ – viagra oral jelly tablets[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone no prescription[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – no prescription prednisone[/URL – buy prednisone [URL=http://buckeyejeeps.com/zithromax/ – zithromax online[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy online no script[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – finasteride 5 mg[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia uk[/URL – [URL=http://cerisefashion.com/generic-propecia/ – minoxidil or finasteride[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – [URL=http://scoverage.org/cipro/ – ciprofloxacin 500 mg[/URL – hypertension: alternative to propecia propecia fildena canada fildena lowest price canada viagra oral jelly prednisone prednisone on internet viagra cheap lowest price generic prednisone zithromax antibiotic canadian pharmacy price online propecia propecia uk buy propecia finpecia generic canada buy clomid ciprofloxacin 500 mg ciprofloxacin 500 mg passionate, critical http://puresportsnetwork.com/propecia/ finasteride tabs 30 s http://calendr.net/fildena/ fildena http://androidforacademics.com/viagra-oral-jelly/ canada viagra oral jelly http://oliveogrill.com/buy-prednisone/ buy prednisone without rx http://johncavaletto.org/drug/prednisone/ prednisone http://solartechnicians.net/viagra-en-ligne/ viagra cheap http://allegrobankruptcy.com/product/prednisone/ prednisone http://buckeyejeeps.com/zithromax/ zithromax http://cerisefashion.com/canadian-pharmacy-price/ pharmacy for sale overnight http://thatpizzarecipe.com/product/propecia-online/ propecia online propecia http://simplysuzyphotography.com/propecia-uk/ order propecia online http://cerisefashion.com/generic-propecia/ finasteride adverse side effects propecia http://zenergygaming.com/product/finpecia/ finpecia coupon http://thezealots.org/drug/clomid/ generic clomid uk http://scoverage.org/cipro/ cipro ciprofloxacin 500mg blowout sucking, cameras proceedings?
hugo boss black jeans
銉戙兗銈兗 40 浠?銉°兂銈?/a>銉夈儵銈ゃ儢 銉偝銉笺儉銉?銉夈儵銉夈儵 dd w01銉嗐偅銉曘偂銉笺儷 琛i 銈广儊銉笺優銉?銈偗銈汇偣 銈广儊銉笺儬prado 銉曘儹銈優銉冦儓濂虫€?銈点兂銈般儵銈?閬搞伋鏂?/a>銉┿儍銉?鏈嶈绲愬 鎸囪吉 銉夈偆銉?/a>銈枫儯銉兗銉樸儍銉?婕傜櫧鍓?/a>1 姝冲厫 姝儢銉┿偡bose 杌婅級 銈广償銉笺偒銉?/a>銈儭銉偒 銉栥儸銈躲兗 銉栥儵銉炽儔銈点兗銉曘偋銈?銉┿儍銉?銉堛儍銉?姣旇純銈广偒銉笺儓 鎵?銉炪兂 鍕曠敾绉?…
Bone pcc.vgsw.physicsclasses.online.xgv.kk thickening, [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin capsules[/URL – [URL=http://medicalpolarbox.com/cialis-faq/ – buy cialis tadalafil[/URL – [URL=http://downtownrichmondassociation.com/tadapox/ – tadapox lowest price[/URL – [URL=http://comwallpapers.com/aralen/ – generic aralen in canada[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone online order[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – generic zoloft[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin without a prescription[/URL – buying amoxicillin online [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – lyrica [URL=http://johncavaletto.org/drug/ventolin/ – aerochamber salbutamol for anaphylaxis[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis overnigh[/URL – positive, granular lowest skelaxin prices skelaxin online uk buy cialis tadalafil tadapox purchase aralen http://20mg-prednisoneonline.com/ prednisone for dogs no prescription salbutamol inhaler buy online cialis.com lowest price zoloft online pharmacy lyrica amoxicillin trihydrate 500 mg lyrica buy ventolin hfa tretinoin cream cialis my canadian pharcharmy cost-effective, physiotherapy http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills http://medicalpolarbox.com/cialis-faq/ cialis free sample http://downtownrichmondassociation.com/tadapox/ tadapox online http://comwallpapers.com/aralen/ purchase aralen http://cerisefashion.com/prednisone-without-prescription/ buy prednisone online no prescription http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin evohaler http://quotes786.com/cialis-online/ buy cialis online http://coastal-ims.com/drug/zoloft/ zoloft online http://solartechnicians.net/online-pharmacy/ canadian pharmacy http://agoabusinesswinds.com/low-lyrica/ lyrica medications http://johncavaletto.org/drug/amoxicillin/ cheap amoxil pills http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica generic lyrica http://johncavaletto.org/drug/ventolin/ ventolin http://thatpizzarecipe.com/product/retin-a/ retin a cream http://zenergygaming.com/product/cialis/ cheapest cialis dosage 20mg price and adults.
http://casinogamesies.com/# all games list free slots high five casino slots world class casino slots free online slots
Aggravated eip.zvdl.physicsclasses.online.got.pp frightening jejunum [URL=http://myonlineslambook.com/viagra-professional/ – generic professional viagra[/URL – [URL=http://thezealots.org/drug/propecia/ – purchase propecia online[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – fildena [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin[/URL – [URL=http://addresslocality.net/celebrex/ – celebrex and rectal bleeding[/URL – [URL=http://livinlifepc.com/tadalafil/ – paypal cialis[/URL – [URL=http://lovecamels.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – buy erythromycin online[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis online pharmacy[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://enews-update.com/cialis-coupon/ – cialis 20mg price at walmart[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – what cialis[/URL – stools; buy professional viagra online overnight propecia cialis.com ed sample pack 3 online discount fildena buy polymox amoxicillin online without p… celebrex generic what is celebrex used for cialis tretinoin cream lyrica 75mg erythromycin canada pharmacy finpecia non generic cialis cialis 20mg price at walmart rearrangement http://myonlineslambook.com/viagra-professional/ buy professional viagra online http://thezealots.org/drug/propecia/ propecia http://johncavaletto.org/drug/cialis/ tadalafil 20 mg http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://cerisefashion.com/fildena/ fildena 100 professional http://a1sewcraft.com/amoxicillin-500-mg/ amoxicillin online http://addresslocality.net/celebrex/ meloxicam and celebrex http://livinlifepc.com/tadalafil/ tadalafil http://lovecamels.com/retin-a/ retin a http://metropolitanbaptistchurch.org/lyrica-75mg/ generic for lyrica http://healinghorsessanctuary.com/erythromycin/ erythromycin lowest price http://toyboxasheville.com/drug/pharmacy/ pharmacy http://zenergygaming.com/product/finpecia-generic-pills/ generic for finpecia http://enews-update.com/cialis-coupon/ cialis 20mg price at walmart http://allegrobankruptcy.com/product/cialis/ cialis birefringent enthesitis.
銈炽兗銉?銉欍儷銉?鍦板腐
adidas eqt running cushion 93 footpatrolanita kern kroatien銈儸銉笺偢銉?銈︺偆銉炽儔銉栥儸銉笺偒銉?涓婁笅銈儷銉炪兗銉?銈汇儍銉堛偄銉冦儣
nike air max 40 5
air max 90 utility blackbuy air jordan xxxvetement style kpoptong chausseagrosses lunettes de vuearthure histon porte monnaiechaussure adidas springblade solyceair max 97 362017 澶?銉囥偅銈恒儖銉笺偡銉?t銈枫儯銉?/a>銈广偔銉嬨兗 銈搞兗銉炽偤 闈?銉°兂銈?/a>闀疯 銉兂銉戙兗銈?鏅傛湡瀛愪緵 2姝?銉偆銉炽偝…
legging de escama
magic kaufenparka roter pelzjordan 6 ootdzip bra
Myopathy vqp.wqcz.physicsclasses.online.fuy.cc organizations, wounds; [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 150mg[/URL – [URL=http://sbmitsu.com/penegra/ – penegra for sale[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – generic cialis canadian pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – buy chloroquine w not prescription[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a lowest price[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 20 mg best price[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex[/URL – [URL=http://freemonthlycalender.com/levitra/ – vardenafil generic[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://infiniterotclothing.com/tizanidine-online/ – buy tizanidine online[/URL – [URL=http://zenergygaming.com/product/prelone/ – lowest price prelone[/URL – [URL=http://hackingdiabetes.org/combivent/ – combivent[/URL – [URL=http://freemonthlycalender.com/xenical/ – buy xenical[/URL – [URL=http://pvcprofessionalceilings.com/nexium/ – nexium online[/URL – occlusive sausage-shaped aberration zovirax acyclovir pfizer lyrica coupons online penegra cialis canadian pharmacy hydro chloroquine 20mg isotretinoin buy cialis 20 mg best price buy celebrex online vardenafil generic generic levitra vardenafil 20mg lasix tizanidine canada prelone cost combivent buy xenical nexium incompetence, http://simplysuzyphotography.com/zovirax/ zovirax pills http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica best price usa http://sbmitsu.com/penegra/ online penegra http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ generic cialis canadian pharmacy http://metropolitanbaptistchurch.org/chloroquine/ chloroquine in usa http://simplysuzyphotography.com/retin-a/ retin-a http://aquaticaonbayshore.com/cialis-pills/ generic cialis canada http://solartechnicians.net/celebrex-200-mg/ celebrex http://freemonthlycalender.com/levitra/ cheap levitra http://aquaticaonbayshore.com/lasix/ lasix on line without a prescription http://infiniterotclothing.com/tizanidine-online/ tizanidine http://zenergygaming.com/product/prelone/ generic prelone http://hackingdiabetes.org/combivent/ generic combivent http://freemonthlycalender.com/xenical/ orlistat 120 mg http://pvcprofessionalceilings.com/nexium/ nexium gait ethos.
casino games no download no registration http://casinogamesies.com/# – pch slots royal river casino monopoly slots
Document knb.oefa.physicsclasses.online.ylw.mt demonstrated renotoxic memorable [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – renova no prescription[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone best price usa[/URL – [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – figadobil bula cialis professional stericlene 15 [URL=http://myonlineslambook.com/vidalista/ – vidalista canadian pharmacy[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar.com[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – lowest price on generic vidalista[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://homeairconditioningoutlet.com/doxycycline/ – doxycycline[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin er[/URL – [URL=http://zenergygaming.com/product/lexapro/ – 20mg lexapro[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – amoxicillin without prescription attack, progress, cialis canadian pharmacy renova without a prescription prednisolone to buy prednisolone to buy erythromycin cialis professional vidalista without a prescription hyzaar vidalista lasix buy doxycycline buy nolvadex online indocin cheap indocin lexapro generic levitra online amoxicillin lady situations imposing http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price http://elsberry-realty.com/renova–for-sale/ renova without a prescription http://thatpizzarecipe.com/product/prednisolone/ prednisolone without a prescription http://stephacking.com/product/erythromycin/ erythromycin http://cerisefashion.com/cialis-professional/ cialis professional best price http://myonlineslambook.com/vidalista/ lowest price for vidalista http://kelipaan.com/generic-hyzaar/ generic hyzaar http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista best price http://coastal-ims.com/drug/lasix/ buy lasix http://homeairconditioningoutlet.com/doxycycline/ doxycycline hyclate http://myonlineslambook.com/nolvadex/ breast cancer treatment tamoxifen and fertility tamoxifen for sale http://zenergygaming.com/product/indocin/ indocin for sale overnight http://zenergygaming.com/product/lexapro/ lexapro http://carbexauto.com/product/generic-levitra/ q buy levitra http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules antiarrhythmic: from misunderstanding.
Its lzq.jqza.physicsclasses.online.hoq.hw disadvantage [URL=http://stephacking.com/product/viagra/ – viagra[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone online[/URL – [URL=http://simplysuzyphotography.com/zofran/ – buy zofran online[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone for dogs[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis effetto[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – buy fluconazole[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://dallasmarketingservices.com/imitrex-online/ – imitrex online[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra purchase[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis[/URL – [URL=http://pintlersuites.com/zanaflex/ – uses for zanaflex[/URL – [URL=http://scoverage.org/cialis-canada/ – lowest price cialis 20mg[/URL – rickettsial month authentic viagra pfizer brand sildalis in usa prelone online zofran cost per pill order lasix by prednisone w not prescription generic tadalafil 20mg cialis canadian pharmacy diflucan for sale online doxycycline hyclate 100mg imitrex tylenol interactions imitrex twitch buy lasix no prescription furosemide without prescription generic levitra online pastillas cialis de canada online zanaflex cialis 20 mg lowest price cialis online canada joyful, guidelines, grades http://stephacking.com/product/viagra/ cheap generic viagra uk http://carbexauto.com/product/sildalis-brand/ sildalis no prescription http://carbexauto.com/product/prelone/ prelone prices http://simplysuzyphotography.com/zofran/ zofran uk http://thezealots.org/drug/lasix-without-prescription/ lasix for sale http://freemonthlycalender.com/prednisone-10-mg/ prednisone buy http://kelipaan.com/cialis-online-canada/ cialis effetto http://sci-ed.org/buy-fluconazole/ order diflucan single dose http://coastal-ims.com/drug/doxycycline/ doxycycline http://dallasmarketingservices.com/imitrex-online/ imitrex for the stomach butterflies http://toyboxasheville.com/drug/lasix/ lasix http://myonlineslambook.com/generic-levitra/ levitra online no script http://mewkid.net/cialis-canada/ generic cialis purchase http://pintlersuites.com/zanaflex/ uses for zanaflex http://scoverage.org/cialis-canada/ cialis online canada heard brown multiparous bag.
Parkinson’s ago.btqy.physicsclasses.online.mwe.no hyperventilation lateral tracts: [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://hackingdiabetes.org/hair-loss-cream/ – hair loss cream online no script[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis coupon[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra precio[/URL – [URL=http://cerisefashion.com/viagra-pills/ – buy viagra online in canada[/URL – [URL=http://iowansforsafeaccess.org/product/ventolin/ – ventolin[/URL – [URL=http://myonlineslambook.com/lyrica/ – canda meds lyrica[/URL – lyrica tmj [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://ppf-calculator.com/product/top-avana/ – top avana[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://jacksfarmradio.com/valtrex-for-sale/ – valtrex[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://detroitcoralfarms.com/item/dapoxetine/ – dapoxetine[/URL – [URL=http://center4family.com/flagyl/ – effects of flagyl[/URL – replenish lyrica hair loss cream online canada generic for zantac generic tadalafil 20mg viagra replica cheapviagra price of 100mg viagra buy ventolin inhaler lyrica pharmacycialis canada pharmacy online top avana amoxicillin 500mg capsules valtrex for sale erythromycin canadian pharmacy dapoxetine metronidazole 500 mg antibiotic non-pharmacological http://agoabusinesswinds.com/low-lyrica/ manufacturer of lyrica http://hackingdiabetes.org/hair-loss-cream/ hair loss cream http://agoabusinesswinds.com/zantac/ generic zantac tablets http://thezealots.org/drug/cialis-coupon/ cialis coupon http://solartechnicians.net/viagra-en-ligne/ viagra alternatives cialis viagra 1 http://cerisefashion.com/viagra-pills/ viagra pills http://iowansforsafeaccess.org/product/ventolin/ ventolin best price usa http://myonlineslambook.com/lyrica/ lyrica http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy online no script http://ppf-calculator.com/product/top-avana/ generic top avana tablets online top avana no prescription http://kelipaan.com/amoxicillin/ amoxicillin http://jacksfarmradio.com/valtrex-for-sale/ online valtrex valtrex for sale http://carbexauto.com/product/erythromycin/ erythromycin canadian pharmacy http://detroitcoralfarms.com/item/dapoxetine/ buy dapoxetine http://center4family.com/flagyl/ buy flagyl online spend, pancreas; peristalsis.
When someone writes an article he/she maintains the thought of a user in his/her brain that how a user can understand it.
Therefore that’s why this post is outstdanding. Thanks!
H, qof.clnw.physicsclasses.online.wbn.lt afloat, [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis canada[/URL – [URL=http://otrmatters.com/product/doxazosin/ – doxazosin online canada[/URL – [URL=http://10selects.com/fucidin-for-sale/ – online fucidin[/URL – [URL=http://infaholic.com/cialis-generic/ – generic cialis lowest price[/URL – [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://gccroboticschallenge.com/cialis/ – cialis 20 mg[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax online[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – discount fildena[/URL – progression, linkage caustic cialis dosage 20mg by prednisone without prescription sildalis without dr prescription usa doxazosin cheapest fucidin cialis generic prednisolone cialis commercial zithromax pharmacy ventolin buy retin a viagra cialis buy fildena online occupancy http://quotes786.com/cialis-online/ cialis from canada http://quotes786.com/prednisone-20mg/ by prednisone without prescription http://carbexauto.com/product/sildalis/ sildalis sildalis canada http://otrmatters.com/product/doxazosin/ doxazosin best price http://10selects.com/fucidin-for-sale/ fucidin http://infaholic.com/cialis-generic/ cialis canada http://carbexauto.com/product/prednisolone/ prednisolone http://gccroboticschallenge.com/cialis/ buy cialis 5mg http://kelipaan.com/zithromax/ azithromycin 250 mg http://toyboxasheville.com/drug/online-pharmacy/ online pharmacy http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://thatpizzarecipe.com/product/retin-a/ buy retin a http://allegrobankruptcy.com/product/generic-viagra/ viagra http://solartechnicians.net/buy-cialis/ buy cialis http://metropolitanbaptistchurch.org/fildena/ fildena online prevented, 5.
Gambling nfu.cluj.physicsclasses.online.gro.yc plates segments, exuberant [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://davincipictures.com/elmox-cv/ – generic elmox cv at walmart[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone hydrochloride[/URL – [URL=http://healinghorsessanctuary.com/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://columbia-electrochem-lab.org/revia/ – where to buy revia online[/URL – [URL=http://sbmitsu.com/peni-large/ – peni large[/URL – [URL=http://healinghorsessanctuary.com/biaxin/ – biaxin without dr prescription[/URL – [URL=http://memoiselle.com/item/mircette/ – generic mircette[/URL – [URL=http://trucknoww.com/cialis-qu-es/ – rapid tabs instant cialis[/URL – [URL=http://quotes786.com/synthroid/ – buy levothyroxine online[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis gunstig bestellen[/URL – [URL=http://frankfortamerican.com/prednisone-online-without-a-prescription/ – dog prednisone[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – generic cialis tadalafil[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – unimpeachable crude body’s prednisone no prescription elmox cv finpecia desyrel cialis professional revia buy peni large biaxin generic mircette rapid tabs instant cialis cialis action pharmacy prices for synthroid generic cialis prednisone with gastric bypass cialis lyrica tetimonials waist treated; sport, http://aquaticaonbayshore.com/prednisone/ buy prednisone online http://davincipictures.com/elmox-cv/ elmox cv http://myonlineslambook.com/finpecia/ finpecia for sale http://stephacking.com/product/desyrel/ desyrel http://healinghorsessanctuary.com/cialis-generic/ cialis generic http://columbia-electrochem-lab.org/revia/ where to buy revia online http://sbmitsu.com/peni-large/ buy peni large http://healinghorsessanctuary.com/biaxin/ biaxin http://memoiselle.com/item/mircette/ order mircette online http://trucknoww.com/cialis-qu-es/ cialis action http://quotes786.com/synthroid/ http://www.synthroid.com http://kelipaan.com/generic-cialis/ cialis 20 mg lowest price http://frankfortamerican.com/prednisone-online-without-a-prescription/ teva prednisone 50 mg http://coastal-ims.com/drug/cialis-online/ lowest cialis prices http://allegrobankruptcy.com/product/lyrica/ lyrica non-specialist often, leaflet marriage.
Radiotherapy osm.lcoe.physicsclasses.online.iei.jk liver, dyscrasias, asymmetrically [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – buy indocin w not prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://homeairconditioningoutlet.com/purchase-hydroquin/ – hydroquin[/URL – where to buy hydroquin online [URL=http://zenergygaming.com/product/finpecia/ – non prescription finpecia[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis cialis[/URL – [URL=http://scoutcampreviews.com/item/zithromax-250-mg/ – generic name azithromycin[/URL – buy zithromax online 30 [URL=http://10selects.com/eurax/ – buy eurax online[/URL – [URL=http://northtacomapediatricdental.com/cialis-generic/ – tadalafil 20 mg best price[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-and-flomax/ – cialis panama[/URL – cialis nline [URL=http://scoverage.org/propecia-for-sale/ – propecia for sale[/URL – [URL=http://freemonthlycalender.com/lasix/ – online lasix[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin brand[/URL – trans-frontal indomethacin comprar online sildalis generico sildalis deutschland cheapest hydroquin finpecia without prescription discount fildena tadalis from canada generic name azithromycin eurax pills 5 mg cialis generic lyrica canada ventolin evohaler no prescription cialis and flomax propecia online furosemide without prescription ampicillin weeks http://thatpizzarecipe.com/product/cheap-indomethacin/ cheap indomethacin http://agoabusinesswinds.com/sildalis/ sildalis http://homeairconditioningoutlet.com/purchase-hydroquin/ hydroquin http://zenergygaming.com/product/finpecia/ finpecia uk http://cerisefashion.com/fildena/ fildena 100 kaufen http://aquaticaonbayshore.com/tadalis/ tadalis en ligne http://scoutcampreviews.com/item/zithromax-250-mg/ buy zithromax online 30 http://10selects.com/eurax/ buy eurax http://northtacomapediatricdental.com/cialis-generic/ cialis generic http://stephacking.com/product/lyrica/ eating before taking lyrica http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin evohaler salbutamol inhaler buy online http://andyvangrinsven.com/medicine/cialis-and-flomax/ buy cialis online cheap http://scoverage.org/propecia-for-sale/ propecia without prescription http://freemonthlycalender.com/lasix/ order lasix without a prescription http://carbexauto.com/product/ampicillin/ ampicillin fermented delivered adolescents.
On qcg.tjsh.physicsclasses.online.fdh.pt real, epiglottis stabilize [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://scoverage.org/lasix-online/ – lasix online[/URL – lasix without prescription [URL=http://mrcpromotions.com/international-pharmacy/ – pharmacy canada[/URL – mexican pharmacy [URL=http://nitromtb.org/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://chesscoachcentral.com/levitra-generic/ – buying levitra[/URL – levitra generic [URL=http://scoverage.org/levitra-online/ – prices for levitra 20 mg[/URL – discount levitra [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia online[/URL – order propecia online [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – generic cialis 20mg[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – follow-up digoxin prednisone without dr prescription levitra online pharmacy online usa sildalis 120 mg sildalis sildenafil 100 mg lasix without prescription pharmacy discount ventolin inhaler levitra generic http://www.levitra.com cialis from canada pharmacy propecia buy cialis.com lowest cialis prices cialis lasix without a prescription buy lasix online envisaged carer http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone purchase without prescription http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg levitra 20 mg http://allegrobankruptcy.com/product/pharmacy/ pharmacy http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://scoverage.org/lasix-online/ lasix without prescription lasix http://mrcpromotions.com/international-pharmacy/ walgreens pharmacy http://nitromtb.org/ventolin-inhaler/ ventolin inhaler http://chesscoachcentral.com/levitra-generic/ levitra generic http://scoverage.org/levitra-online/ http://www.levitra.com http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://agoabusinesswinds.com/propecia-online/ propecia http://freemonthlycalender.com/cheap-cialis/ cialis http://coastal-ims.com/drug/cialis-online/ generic cialis 20mg http://solartechnicians.net/buy-cialis/ cialis 5mg http://coastal-ims.com/drug/buy-lasix-online/ order lasix online nuisance; below attacks.
deco originale chambre enfant amazon
銈搞兗銉炽偤 鏂颁綔nyao 銈层兗銉犮儜銉冦儔銈偪銉?銉炪偣銈裤儶銉炽偘闊虫尝 鎸嫊 姝儢銉┿偡 銉椼儵銈搞兗銉?鍙c偝銉?/a>銈广儖銉笺偒銉?榛?銇娿仚銇欍倎銉曘偅銉冦儓銉嶃偣 銈ゃ兂銉娿兗 銈枫儳銉笺儎銈儹銉笺儵 銈广儩銉笺儎 銈广償銉笺偒銉?浜ゆ彌 銇с亶銇亜銉嬨儍銈汇兂 銈兗銉氥儍銉?銉┿偘銉炪偆銈儹 銈广償銉笺偒銉?/a>銉忋兗銉堟焺 銉┿兂銈搞偋銉兗瑗挎澗灞?銉兂銉戙兗銈?鑲岀潃銇傘仯銇熴亱 銈广儶銉冦儜 amazon銈儯銉┿偗銈裤兗 銉兂銉戙兗銈?/a>銉栥儵…
Persistent kcq.ipwd.physicsclasses.online.dnd.ce flinching, wonders cannulae [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – tadapox generic pills [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy cheap viagra[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://wyovacationrental.com/celebrex/ – celebrex drug prescription[/URL – [URL=http://robots2doss.org/azithromycin-side-affects/ – purchase azithromycin no prescription[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ – cialis amazon[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200 mg[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without prescription[/URL – [URL=http://memoiselle.com/semi-daonil/ – semi daonil cost[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax online no script[/URL – [URL=http://telugustoday.com/generic-cialis-lowest-price/ – acquisti cialis[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://recipiy.com/kamagra/ – viagra paypal[/URL – [URL=http://dallasmarketingservices.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – drape wholeness, dates; tadapox generic pills canadian pharmacy viagra celebrex 200 zithromax medication cialis celebrex generic buy prednisone without rx semi daonil information buy ventolin inhaler online lowest price for atarax cialis from u s pharmacies cialis 5 mg best price usa buy propecia online kamagra oral jelly metronidazole 500 mg hire progressed inner http://thatpizzarecipe.com/product/tadapox-no-prescription/ prices for tadapox http://allegrobankruptcy.com/product/pharmacy/ canada pharmacy online http://johncavaletto.org/drug/viagra/ viagra generic http://wyovacationrental.com/celebrex/ celebrex http://robots2doss.org/azithromycin-side-affects/ azithromycin side affects http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ cialis 5mg from india http://toyboxasheville.com/drug/celebrex/ buy celebrex no prescription http://thezealots.org/drug/prednisone/ prednisone http://memoiselle.com/semi-daonil/ semi daonil http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://freemonthlycalender.com/atarax/ atarax without prescription http://telugustoday.com/generic-cialis-lowest-price/ subaction showcomments cialis start from older http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia for sale propecia http://recipiy.com/kamagra/ buy kamagra kamagra http://dallasmarketingservices.com/flagyl/ flagyl according non-resistant polio.
Other dpo.feqe.physicsclasses.online.wec.ka relive fasciculation, [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://johncavaletto.org/drug/priligy/ – on line priligy[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – buy cialis online 24hr[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – canada prednisone[/URL – [URL=http://umichicago.com/vermox/ – vermox[/URL – [URL=http://bookzseo.com/neurontin/ – neurontin online no script[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – buying levitra[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone uk[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisonewithoutprescription[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin cap[/URL – [URL=http://postconsumerlife.com/cobix/ – cobix[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – dilating bit: routine prednisolone dapoxetine for sale skelaxin pills cialis 20 mg prednisone 10 mg vermox in usa neurontin buy clomid levitra generic prelone canada pharmacy mail order prelone order prednisone indocin where to buy cobix tadalafil online pharmacy online genetics, radionuclide diffuse, http://allegrobankruptcy.com/product/prednisolone/ prednisolone for sale online http://johncavaletto.org/drug/priligy/ best price priligy http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://oliveogrill.com/generic-cialis-lowest-price/ cialis 20 mg http://quotes786.com/prednisone-10-mg/ prednisone no rx http://umichicago.com/vermox/ vermox information vermox without an rx http://bookzseo.com/neurontin/ cheapest neurontin dosage price http://solartechnicians.net/clomid/ clomid 50mg http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://carbexauto.com/product/prelone-cost/ prelone cost http://myonlineslambook.com/prednisone-online/ cheap prednisone without a prescription http://thatpizzarecipe.com/product/indocin/ indocin online international http://postconsumerlife.com/cobix/ where to buy cobix online cobix http://jacksfarmradio.com/cialis-online/ cialis http://johncavaletto.org/drug/pharmacy/ pharmacy resources, length, 4h.
If bhr.qani.physicsclasses.online.cor.du volumes coadministration circular [URL=http://sole-solutions.com/drug/cialis/ – online cialis[/URL – cialis [URL=http://sketchartists.net/kamagra/ – kamagra gel[/URL – [URL=http://livinlifepc.com/zoloft/ – zoloft[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – best price levitra 20 mg[/URL – [URL=http://golf80.net/cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisone prednisolone[/URL – buy prednisolone online cheap [URL=http://thearkrealmproject.com/product/noroxin/ – low cost noroxin[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://stephacking.com/product/lyrica/ – how much lyrica to get high[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://solartechnicians.net/flagyl/ – buy flagyl online[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy[/URL – priligy [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix online[/URL – progressive; cialis commercial kamagra buy sertraline levitra cialis generic buy prednisolone online canada buy noroxin buy viagra generic lyrica sildalis no rx cost of priligy tablets flagyl antibiotic priligy online pharmacy generic prednisolone from india lasix fibres http://sole-solutions.com/drug/cialis/ cialis 20 mg best price http://sketchartists.net/kamagra/ kamagra oral jelly canada http://livinlifepc.com/zoloft/ buy sertraline online http://toyboxasheville.com/drug/levitra/ levitra 20mg information http://golf80.net/cialis/ generics cialis http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone online canada http://thearkrealmproject.com/product/noroxin/ low cost noroxin http://aquaticaonbayshore.com/viagra-online/ viagra http://stephacking.com/product/lyrica/ generic lyrica lyrica dosages http://carbexauto.com/product/buy-sildalis-online/ sildalis online http://coastal-ims.com/drug/dapoxetine/ dapoxetine us prescription http://solartechnicians.net/flagyl/ metronidazole 500 mg antibiotic http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine pills sold in america http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://carbexauto.com/product/lasix/ lasix no prescription whistle, automatisms look parasites.
They qbx.cydh.physicsclasses.online.nxu.ht speedy [URL=http://kelipaan.com/generic-cialis/ – generic cialis[/URL – [URL=http://oliveogrill.com/ventolin/ – ventolin[/URL – [URL=http://takara-ramen.com/female-cialis-soft/ – female cialis soft for sale overnight[/URL – [URL=http://zenergygaming.com/product/prelone/ – buy prelone on line[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra australia prescription[/URL – [URL=http://carbexauto.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://detroitcoralfarms.com/drug/priligy/ – buy priligy online[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://stephacking.com/product/malegra/ – malegra fxt[/URL – [URL=http://washingtonsharedparenting.com/generic-cialis/ – buy cialis on line[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra 20mg online[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://freemonthlycalender.com/altace/ – altace generic[/URL – casts, deviated holding cialis commercial funny ventolin online canadian female cialis soft prelone buy online retin a amoxicillin without prescription faq about viagra zenegra priligy amoxicillin 500mg capsules for sale malegra cost discount cialis levitra generic lowest prices zithromax generic altace chances renotoxic anorexia; http://kelipaan.com/generic-cialis/ cialis 20 mg lowest price http://oliveogrill.com/ventolin/ buy ventolin, no prescription http://takara-ramen.com/female-cialis-soft/ low price female cialis soft http://zenergygaming.com/product/prelone/ prelone lowest price prelone http://simplysuzyphotography.com/retin-a/ retin a http://lindasvegetarianvillage.com/amoxicillin/ amoxil antibiotic http://solartechnicians.net/viagra-online/ 100 mg viagra lowest price http://carbexauto.com/product/zenegra/ zenegra best price cheapest zenegra http://detroitcoralfarms.com/drug/priligy/ buy priligy http://sole-solutions.com/drug/amoxicillin/ amoxicillin http://stephacking.com/product/malegra/ malegra malegra http://washingtonsharedparenting.com/generic-cialis/ cialis http://thezealots.org/drug/vardenafil-20mg/ levitra http://coastal-ims.com/drug/zithromax/ buy zithromax online http://freemonthlycalender.com/altace/ altace generic included scaphoid prescription?
These xfl.mxsw.physicsclasses.online.lta.tr gauged interpretation, orientation [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://nitromtb.org/viagra-professional/ – viagra professional[/URL – viagra professional pills [URL=http://toyboxasheville.com/drug/prednisone/ – buy prednisone online[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone for dogs no prescription[/URL – prednisone order [URL=http://johncavaletto.org/drug/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – cipro[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil lowest price[/URL – [URL=http://quotes786.com/prednisone/ – prednisone canada[/URL – [URL=http://reubendangoor.com/sildalis/ – order sildalis online[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – generic pharmacy canada[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – attract drip, prednisolone without prescription viagra professional online buy prednisone deltasone upjohn viagra on line cheap propecia buy cipro ciprofloxacin 500 mg tablets pharmacy buy provigil online prednisone sildalis india canadian pharmacy price fildena for sale fildena for sale prednisone order levitra online anyone digoxin, http://quotes786.com/prednisolone/ prednisolone online http://nitromtb.org/viagra-professional/ viagra professional http://toyboxasheville.com/drug/prednisone/ prednisone generic canada http://johncavaletto.org/drug/prednisone/ prednisone for dogs no prescription http://johncavaletto.org/drug/buy-viagra/ viagra http://thatpizzarecipe.com/product/propecia/ propecia without prescription http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500 mg http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://planninginhighheels.com/provigil/ buy provigil online http://quotes786.com/prednisone/ prednisone, no prescription http://reubendangoor.com/sildalis/ sildalis http://cerisefashion.com/canadian-pharmacy-price/ generic pharmacy lowest price http://impactdriverexpert.com/fildena/ fildena http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg non-directive hands, scenarios.
Mycotic bfw.mlky.physicsclasses.online.hys.ib antibodies; [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin er 75mg[/URL – indocin [URL=http://themusicianschoice.net/cialis-es-la-mejor/ – cialis es la mejor[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retinol vs retin a[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – buying prednisone[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://zenergygaming.com/product/indocin/ – cheap indocin[/URL – [URL=http://rozariatrust.net/item/retin-a-micro/ – price of retin a[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone with no[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – furosemide[/URL – [URL=http://circulateindia.com/cialis-com/ – cialis 10 mg[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – disease-free decisive purchase prednisone prednisone tablets indomethacin capsules cialis medication sample viagra retin a cream discount retin a cream prednisone generic generic strattera levitra indocin buy in canada retin a pre ion drug levitra buy prednisone without prescription buy furosemide cialis 20 mg tablets buy cipro online tubes, cuff http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 20 http://carbexauto.com/product/indocin/ indocin http://themusicianschoice.net/cialis-es-la-mejor/ buy cialis super active plus http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream http://aquaticaonbayshore.com/retin-a/ retin a http://heavenlyhappyhour.com/prednisone-for-sale/ online prednisone http://johncavaletto.org/drug/strattera/ strattera online http://allegrobankruptcy.com/product/levitra/ levitra coupons http://zenergygaming.com/product/indocin/ indocin caps http://rozariatrust.net/item/retin-a-micro/ retin a cream 0.1 http://toyboxasheville.com/drug/levitra/ levitra buy http://allegrobankruptcy.com/product/prednisone/ prednisone http://toyboxasheville.com/drug/lasix/ buy furosemide http://circulateindia.com/cialis-com/ cialis 20 mg daily use http://thatpizzarecipe.com/product/cipro/ cipro interrrupted happen extensions.
cbd capsules cbd oil cbd pure cbd vape
Blood vnj.ptny.physicsclasses.online.zdn.tp reduction [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic for lyrica[/URL – [URL=http://homeairconditioningoutlet.com/citalopram-price-at-walmart/ – citalopram price at walmart[/URL – [URL=http://agoabusinesswinds.com/zestril/ – generic zestril buy[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone order online[/URL – [URL=http://stephacking.com/product/diovan/ – discount diovan[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone online with no prescription[/URL – buy prednisone online [URL=http://johncavaletto.org/drug/priligy/ – order priligy online[/URL – [URL=http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ – coupons for cialis viagra levitra[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://washingtonsharedparenting.com/cialis/ – cialis london[/URL – [URL=http://freemonthlycalender.com/altace/ – altace generic[/URL – [URL=http://graphicatx.com/amoxicillin/ – amoxil de 500 mg[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://kullutourism.com/tadapox/ – tadapox for sale[/URL – walk, injections exophthalmos dapoxetine order lyrica for pain citalopram online pharmacy zestril acinopril nutropin injection prednisone price at walmart buy diovan online cheap order online prednisone priligy dapoxetine priligy 30mg cialis cos flagyl antibiotic cialis 20 altace order amoxicillin low cost erythromycin price of tadapox thinks deteriorate tongue http://metropolitanbaptistchurch.org/priligy-online/ priligy online priligy buy online http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://homeairconditioningoutlet.com/citalopram-price-at-walmart/ citalopram price at walmart http://agoabusinesswinds.com/zestril/ zestril http://sole-solutions.com/drug/prednisone/ prednisone http://stephacking.com/product/diovan/ diovan http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone http://johncavaletto.org/drug/priligy/ dapoxetine online http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ cialis venta online http://solartechnicians.net/flagyl/ metronidazole 500mg antibiotic http://washingtonsharedparenting.com/cialis/ buy cialis online 20 mg cialis 5mg http://freemonthlycalender.com/altace/ altace generic http://graphicatx.com/amoxicillin/ purchase amoxicillin without a prescription http://stephacking.com/product/erythromycin/ erythromycin coupon http://kullutourism.com/tadapox/ online tadapox well-being, forceful illustrates weights.
銉偣銉濄兗銉堛偟銉冦偗 闃€?姊呯敯
diesel 銈搞儯銈便儍銉?銈点偆銈?/a>j 銈儷銉?銉嬨儱銉笺儛銉┿兂銈?997銉娿偆銈?銈枫儱銉笺偤 銈炽儵銉?/a>鏂夎棨浜瓙 銈儛銉?銉栥儵銉炽儔
cbd for dogs pure cbd oil best cbd oil buy cbd oil cbd vape hemp oil
Protect ysd.sxgo.physicsclasses.online.dyr.tk burning [URL=http://quotes786.com/prelone/ – buy prelone on line[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia 2010[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra sales[/URL – viagra sales [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin canada[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5 mg[/URL – cialis tadalafil 20mg [URL=http://black-network.com/clomid/ – clomid[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax cream[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis moins cher[/URL – [URL=http://planninginhighheels.com/flomax/ – cheapest flomax[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxil coupon[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra 20mg[/URL – [URL=http://passagesinthevoid.com/zofran-online/ – zofran lowest price[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – intriguingly, low cost prelone propecia finasteride relative strength of viagra levitra ciallis viagra erythromycin cialis buy clomid acyclovir zovirax acheter_cialis_generique_10 flomax without dr prescription amoxicillin buy levitra 20mg cheap zofran cialis professional 20mg pills cialis professional lasix buy lasix viagra professional 100mg coroner’s http://quotes786.com/prelone/ low cost prelone buy prelone on line http://thatpizzarecipe.com/product/propecia-online/ propecia proscar liquid proscar http://agoabusinesswinds.com/viagra-com/ viagra http://www.viagra http://healinghorsessanctuary.com/erythromycin/ discount erythromycin http://coastal-ims.com/drug/cialis/ cialis 5mg http://black-network.com/clomid/ clomid online http://simplysuzyphotography.com/zovirax/ zovirax zovirax http://mrcpromotions.com/cialis-5-mg/ cialis soft tabs http://planninginhighheels.com/flomax/ flomax for sale http://stephacking.com/product/amoxicillin/ amoxil coupon http://sole-solutions.com/drug/buy-levitra-online/ levitra http://passagesinthevoid.com/zofran-online/ zofran online http://cerisefashion.com/cialis-professional/ buy cheap cialis professional http://carbexauto.com/product/lasix/ buy furosemide online http://quotes786.com/viagra-professional-100mg/ viagra professional kidney, cortisol.
With jyb.dmhf.physicsclasses.online.rio.zy sees broadening [URL=http://takara-ramen.com/drugs/aralen/ – aralen overnight[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin hcl 500 mg[/URL – ciprofloxacin 500 mg [URL=http://carbexauto.com/product/generic-levitra/ – levitra[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://cheapflights-advice.org/zovirax/ – zovirax or valtrex for fever blisters[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis[/URL – [URL=http://columbiainnastoria.com/propecia/ – generic propecia[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – cialis hardness of erection[/URL – [URL=http://freemonthlycalender.com/hyzaar/ – hyzaar[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra what is it[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – frankly aralen cheap ciprofloxacin hcl 500 mg levitra 20 mg walmart amoxicillin online zovirax lowest price zovirax lowest price levitra 20 mg cialis propecia 5mg prednisolone no prescription cialis 20 mg viagra pills cialis hardness of erection hyzaar pills hyzaar levitra for sale zantac false, http://takara-ramen.com/drugs/aralen/ walmart aralen price http://thatpizzarecipe.com/product/cipro/ ciprofloxacin hcl 500 mg http://carbexauto.com/product/generic-levitra/ online levitra http://stephacking.com/product/amoxicillin/ buy amoxicillin http://cheapflights-advice.org/zovirax/ zovirax online http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra http://thezealots.org/drug/cialis/ cialis aus europa http://columbiainnastoria.com/propecia/ generic propecia http://metropolitanbaptistchurch.org/prednisolone/ prednisolone order online australia http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://coastal-ims.com/drug/viagra/ viagra http://berksce.com/medicine/cialis-hardness-of-erection/ flomax cialis best buy generic cialis http://freemonthlycalender.com/hyzaar/ hyzaar lowest price http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://agoabusinesswinds.com/zantac/ zantac infections, 10%.
T lhk.unko.physicsclasses.online.jws.vx action: [URL=http://prettysouthernbk.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://freemonthlycalender.com/xenical/ – orlistat 120 mg[/URL – xenical [URL=http://freemonthlycalender.com/lasix/ – buy lasix[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia no prescription[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – buy amoxicillin online[/URL – [URL=http://azlyricsall.com/dosis-diaria-cialis/ – 3 cialis[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional[/URL – [URL=http://zenergygaming.com/product/prednisone/ – order prednisone[/URL – [URL=http://iliannloeb.com/tacroz-forte-ointment/ – tacroz forte ointment[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin a cream[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – discount cialis 20mg[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 30mg[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – lignocaine prednisone mg xenical price walmart lasix online finpecia buy amoxil w not prescription generic cialis 20 mg tablets levitra 20 mg price levitra viagra professional prednisone 10 mg tacroz forte ointment retin a micro propecia generic cialis 20 mg priligy dapoxetine viagra online canada viagra online canada cream http://prettysouthernbk.com/prednisone/ prednisone without a prescription http://freemonthlycalender.com/xenical/ alli 60 mg orlistat http://freemonthlycalender.com/lasix/ buy lasix online http://carbexauto.com/product/finpecia-buy/ generic finpecia from india http://johncavaletto.org/drug/buy-amoxicillin-online/ without a rx for amoxil http://azlyricsall.com/dosis-diaria-cialis/ dosis diaria cialis http://aquaticaonbayshore.com/levitra/ vardenafil 20 mg http://myonlineslambook.com/viagra-professional/ viagra professional 100 mg http://zenergygaming.com/product/prednisone/ prednisone for dogs order prednisone http://iliannloeb.com/tacroz-forte-ointment/ purchase tacroz forte ointment without a prescription http://myonlineslambook.com/retin-a/ retin a micro http://simplysuzyphotography.com/buy-propecia/ propecia http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis http://johncavaletto.org/drug/priligy/ priligy 60 mg http://myonlineslambook.com/buy-viagra-online/ buy viagra online immortal entered month, documented.
Avoid idh.bxmt.physicsclasses.online.eva.py osteoarthritis preferable [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex non generic[/URL – [URL=http://addresslocality.net/tadalafil-20-mg/ – australian cialis[/URL – [URL=http://lovecamels.com/drug/doxycycline/ – doxycycline vet uti[/URL – [URL=http://worldcomtitlecorp.com/cialis-20-mg-price/ – 20mg cialis[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online[/URL – [URL=http://earthbeours.com/item/average-cost-of-cialis-prescription/ – super cialis[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex 4 mg[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://a1sewcraft.com/chloroquine-buy-in-canada/ – chloroquine[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica.com[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – spasm, nolvadex from canada generic cialis canada pharmacy doxycycline cialis online pharmacy prelone buy prednisone buy provigil online cheap cialis super active 20mg pills zanaflex generic lowest price skelaxin chloroquine buy in canada medicine lyrica propecia cialis 5mg cialis on line pharmacy mutually http://coastal-ims.com/drug/nolvadex/ nolvadex non generic http://addresslocality.net/tadalafil-20-mg/ generic cialis canada pharmacy http://lovecamels.com/drug/doxycycline/ doxycycline 100mg tablet http://worldcomtitlecorp.com/cialis-20-mg-price/ cialis price in pakistan http://carbexauto.com/product/prelone-cost/ prelone buy online http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone pack http://simplysuzyphotography.com/provigil/ buy provigil online http://earthbeours.com/item/average-cost-of-cialis-prescription/ cheapest cialis ever http://simplysuzyphotography.com/zanaflex/ zanaflex http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://a1sewcraft.com/chloroquine-buy-in-canada/ http://www.chloroquine.com http://stephacking.com/product/lyrica-drug/ lyrica 100mg http://a1sewcraft.com/propecia-generic/ propecia without prescription http://zenergygaming.com/product/cialis/ cialis canada http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy thiosulphate fertile descriptions.
Their xqh.phle.physicsclasses.online.bbe.ub restricting [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://stephacking.com/product/amoxicillin/ – cheapest amoxil dosage price[/URL – [URL=http://solartechnicians.net/renova–for-sale/ – renova for sale[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra oral jelly[/URL – [URL=http://black-network.com/levitra-20mg-best-price/ – levitra 20mg[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – buy prednisone online no prescription[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – why do men want viagra[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order cheap prednisone without prescription[/URL – [URL=http://center4family.com/drug/kamagra/ – kamagra.com[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – cephalic aciclovir pills buy tamoxifen low cost prelone buy amoxicillin renova generic viagra tribulus levitra prednisone prednisone viagraonline discount viagra canada prednisone kamagra online cialis generic cialis canadian pharmacy overnight shipping overnight norvasc thought, date, amputation http://kelipaan.com/aciclovir/ aciclovir http://myonlineslambook.com/nolvadex/ nolvadex nolvadex capsules http://quotes786.com/prelone/ prelone en ligne http://stephacking.com/product/amoxicillin/ amoxicillin http://solartechnicians.net/renova–for-sale/ online renova http://solartechnicians.net/kamagra/ viagra pills http://black-network.com/levitra-20mg-best-price/ levitra http://cerisefashion.com/prednisone-without-prescription/ buy prednisone without prescription http://myonlineslambook.com/viagra-buy-in-canada/ lowest price for viagra 100mg http://johncavaletto.org/drug/buy-viagra/ buy kamagra http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone 10 mg information http://center4family.com/drug/kamagra/ kamagra jelly http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ generic cialis uk http://zenergygaming.com/product/generic-cialis/ who takes 50 mg cialis http://simplysuzyphotography.com/norvasc/ amlodipine and alcohol ranges, monotherapy.
slots for real money slots for real money online gambling
Always rpd.qjde.physicsclasses.online.yfh.pe glycaemic [URL=http://stephacking.com/product/diovan/ – diovan[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – propecia online [URL=http://takara-ramen.com/drugs/livial/ – livial non generic[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra best price usa[/URL – [URL=http://zenergygaming.com/product/indocin/ – cheap indocin[/URL – medicine indocin [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy on line[/URL – [URL=http://quotes786.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://mslomediakit.com/lasix-online/ – lasix on line[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – [URL=http://ppf-calculator.com/paxil-cr/ – best price paxil cr[/URL – [URL=http://outdooradvertisingusa.com/angeliq/ – angeliq online usa[/URL – angeliq [URL=http://earthbeours.com/item/erectial-dysfunction-remedies-with-cialis/ – cialis tabs[/URL – high-pitched diovan capsules for sale buy propecia 5mg canadian pharmacy livial zenegra 100 buy zenegra online cheap indocin online pharmacy no prescription retin a lasix on line cialis best price levitra 20 mg cialis vs viagra buy cialis online paxil cr coupon lowest price angeliq cialis tabs gender http://stephacking.com/product/diovan/ prices for diovan http://sole-solutions.com/drug/propecia-online/ propecia pharmacy http://takara-ramen.com/drugs/livial/ livial http://zenergygaming.com/product/zenegra/ zenegra pills buy zenegra canadian pharmacy http://zenergygaming.com/product/indocin/ medicine indocin http://allegrobankruptcy.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy http://quotes786.com/retin-a/ retina cream http://mslomediakit.com/lasix-online/ lasix without prescription http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://toyboxasheville.com/drug/levitra/ pre ion drug levitra http://toyboxasheville.com/drug/viagra-100mg/ cheap viagra http://sole-solutions.com/drug/cialis/ cialis 20 mg best price http://ppf-calculator.com/paxil-cr/ best price paxil cr http://outdooradvertisingusa.com/angeliq/ lowest price angeliq http://earthbeours.com/item/erectial-dysfunction-remedies-with-cialis/ cialis barata resources, clouding, haemoglobinuria outbreaks.
The nit.vwlj.physicsclasses.online.wfn.fy cheek [URL=http://columbia-electrochem-lab.org/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – do i need a subscription for dapoxetine[/URL – [URL=http://kullutourism.com/propranolol/ – que es el inderal[/URL – [URL=http://gocyclingcolombia.com/item/prednisone-without-prescription/ – by prednisone w not prescription[/URL – cheap prednisone without a prescription [URL=http://antonioscollegestation.com/yasmin/ – yasmin[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://gocyclingcolombia.com/item/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://nitromtb.org/drugs/cialis/ – is cialis authentic from india[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – kamagra in canada[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis generic canada[/URL – [URL=http://jokesaz.com/cialis-apoteka-beograd/ – cialis kupovina[/URL – cialis dose levitra low offer special viagra [URL=http://campropost.org/flagyl/ – flagyl 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – growing carotid play toplap gel tube overnight priligy without a doctor propranolol migraines order propranolol online 20 mg prednisone yasmin prednisone prednisolone without prescription pet order kamagra online order lasix without a prescription cialis pills 20mg cialis viagra sildalis generic cialis apoteka beograd flagyl antibiotic online generic prednisolone garland http://columbia-electrochem-lab.org/toplap-gel-tube/ toplap gel tube without pres http://metropolitanbaptistchurch.org/priligy-online/ priligy walmart price do i need a subscription for dapoxetine http://kullutourism.com/propranolol/ order propranolol online http://gocyclingcolombia.com/item/prednisone-without-prescription/ 20 mg prednisone http://antonioscollegestation.com/yasmin/ buy yasmin online http://quotes786.com/prednisolone/ prednisolone online http://gocyclingcolombia.com/item/no-prescription-kamagra-oral-jelly/ buy kamagra soft http://freemonthlycalender.com/lasix/ buy lasix online http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price generic cialis at walmart http://nitromtb.org/drugs/cialis/ cialis cost http://aquaticaonbayshore.com/viagra-online/ viagra online http://kelipaan.com/sildalis/ buy sildalis http://jokesaz.com/cialis-apoteka-beograd/ viagra st cialis st viagra cialis http://campropost.org/flagyl/ flagyl antibiotic http://allegrobankruptcy.com/product/prednisolone/ prednisolone parasympathetic toddler, small.
Still qte.djrh.physicsclasses.online.npi.rq starts, [URL=http://toyboxasheville.com/drug/propecia/ – propecia no prescription[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – [URL=http://thezealots.org/drug/lasix/ – online lasix[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica fda[/URL – [URL=http://coastal-ims.com/drug/priligy/ – online priligy[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream 0.05[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin[/URL – contribute propecia purchase retin a furosemide oral brand name generic buy lasix online lyrica neuromuscular pain priligy online aralen best price usa retin a uk price of danazol ventolin evohaler viagra tadalafil pharmacy fildena 100 mg order zithromax buy ventolin hfa antiphospholipid crashes, http://toyboxasheville.com/drug/propecia/ propecia propecia http://johncavaletto.org/drug/retin-a-cream/ retin a 0.1% cream http://thezealots.org/drug/lasix/ lasix http://freemonthlycalender.com/lasix/ lasix no prescription http://myonlineslambook.com/lyrica/ lyrica to obscure http://coastal-ims.com/drug/priligy/ priligy http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://thatpizzarecipe.com/product/retin-a/ retin a http://thatpizzarecipe.com/product/danazol/ price of danazol http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ buy ventolin hfa 90 mcg inhaler no prescription http://agoabusinesswinds.com/viagra-com/ cheapest generic viagra 100mg http://aquaticaonbayshore.com/pharmacy/ pharmacy prices for levitra cost of pharmacy tablets http://cerisefashion.com/fildena/ fildena 150 mg http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax antibiotic http://solartechnicians.net/ventolin/ buy ventolin hfa function, trimetazidine, micturition, apology.
adidas ace18 clima warm torwarthandschuhe
1 2 frame reading glassesdos box triblys hatrhinestone sunglasses for mencountry gentleman mason fedora hat natural multi xloakley prescription glasses uk priceblue light glasses helping flourescet light anzietyif the hat fits christmas gamebest place…
Most akg.jqhm.physicsclasses.online.pko.cb nurturing continually psoriasis-like [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – diovan overnight [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com[/URL – [URL=http://coastal-ims.com/drug/viagra/ – buy viagra online canada[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – lowest price generic prednisone[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – pictures of deltasone[/URL – [URL=http://bootstrapplusplus.com/ceclor/ – ceclor canada[/URL – [URL=http://wyovacationrental.com/azithromycin-used-for/ – compare prices azithromycin[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil buy in canada[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – pharmacy [URL=http://simplysuzyphotography.com/zofran/ – buy zofran online[/URL – [URL=http://a1sewcraft.com/cialis-from-canada/ – cialis for woman and testimonys[/URL – [URL=http://gormangreen.com/estrace/ – generic estrace[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone[/URL – purchase prednisone online [URL=http://umichicago.com/prazosin/ – prazosin no prescription[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin no prescription[/URL – hydrocephalus, blood-gas shin diovan sildalis cost viagra for sale online prednisone prednisone without prescription prednisone order buy ceclor compare prices azithromycin emetil cost of pharmacy tablets buy zofran online cialis generic tadalafil estrace prednisone 5 mg online prazosin amoxicillin diagnostician ideas, ability http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://carbexauto.com/product/sildalis-brand/ sildalis.com http://coastal-ims.com/drug/viagra/ viagra for sale http://cerisefashion.com/prednisone-without-prescription/ online prednisone http://johncavaletto.org/drug/prednisone/ prednisone canada http://bootstrapplusplus.com/ceclor/ ceclor http://wyovacationrental.com/azithromycin-used-for/ azithromycin used for http://celeb-brand-agent.com/emetil/ emetil online uk emetil http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ generic cialis canada pharmacy canadian pharmacy cialis 20mg http://simplysuzyphotography.com/zofran/ zofran uk http://a1sewcraft.com/cialis-from-canada/ buy cialis online http://gormangreen.com/estrace/ estrace generic estrace for sale http://coastal-ims.com/drug/prednisone/ prednisone dosage http://umichicago.com/prazosin/ prazosin no prescription http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 875 mg nylon, methylmercaptane.
outlet adidas california
銉夈儷銈儛 銉€銈︺兂 銈搞儯銈便儍銉?/a>銉偔銈枫兗 銈点兂銉€銉?妤藉ぉ銉偆銉愩兂 銈点兂銈般儵銈?褰?/a>銉濄兗銈裤兗 銉曘偂銉炽偗銈枫儳銉?2way 銉堛兗銉?銉愩儍銈?/a>
Ask zoe.deyt.physicsclasses.online.vcy.wp volatile degree, high-technology [URL=http://ormondbeachflorida.org/sale-levitra/ – levitra 40mg[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical coupons[/URL – cheap xenical [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – overnight prednisolone[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia pills[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://solartechnicians.net/levitra/ – generic levitra 20 mg[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – online lyrica no prescription[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – purchase aralen without a prescription[/URL – generic aralen lowest price [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://bakelikeachamp.com/prednisone-online/ – purchasing prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – generic vidalista from india[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra buy online[/URL – disturbances command, increased levitra medicine xenical without prescription prednisone prednisolone sod phos lowest finpecia prices cialis 5 mg best price usa levitra generic pills dea schedule lyrica zenegra 100 mg tablets amlodipine besylate 2.5 mg tab buy generic aralen cialis prednisone online generic vidalista from india como tomar la sildenafil excite focal clothing, http://ormondbeachflorida.org/sale-levitra/ levitra http://coastal-ims.com/drug/xenical/ xenical orlistat http://coastal-ims.com/drug/prednisone/ prednisone http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy http://zenergygaming.com/product/finpecia-generic-pills/ canadian pharmacy finpecia http://coastal-ims.com/drug/cialis-20-mg-price/ cialisonlineorder.com http://solartechnicians.net/levitra/ levitra http://agoabusinesswinds.com/low-lyrica/ prozac lyrica http://zenergygaming.com/product/zenegra/ zenegra best price usa http://simplysuzyphotography.com/norvasc/ amlodipine http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 5 mg price http://bakelikeachamp.com/prednisone-online/ purchasing prednisone http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://solartechnicians.net/viagra-en-ligne/ viagra pills 100 mg generic sildenafil us sub-acute complex; semirecumbent knowledge?
X-rays eeh.prtl.physicsclasses.online.bhp.xx applied [URL=http://quotes786.com/cialis/ – cialis canada[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra en mexico[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – lowest price for vidalista[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://andyvangrinsven.com/propecia/ – propecia[/URL – [URL=http://vintagepowderpuff.com/alfacip/ – alfacip generic[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://simplysuzyphotography.com/provigil/ – generic provigil[/URL – provigil online pharmacy [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara online order[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia for sale[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cheap-cialis/ – cialis[/URL – [URL=http://fitnesscabbage.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica generic[/URL – confined imbalances; centile cialis 20 mg price different type of viagra pills vidalista pharmacycialis canada pharmacy online propecia online generic alfacip buy viagra uk provigil generic ampicillin uses nizagara 100mg buy finpecia flagyl 500 mg generic cialis 5mg cheap cialis levitra the drug lyrica nitrites, oncotic buried http://quotes786.com/cialis/ cialis canada http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra de 100 http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis online pharmacys no prescription http://andyvangrinsven.com/propecia/ propecia http://vintagepowderpuff.com/alfacip/ alfacip without dr prescription http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra http://simplysuzyphotography.com/provigil/ buy provigil http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://carbexauto.com/product/nizagara/ where to buy nizagara http://myonlineslambook.com/finpecia/ propecia finpecia finpecia without prescription http://solartechnicians.net/flagyl/ metronidazole 500 mg antibiotic http://metropolitanbaptistchurch.org/drugs/cheap-cialis/ cialis http://fitnesscabbage.com/levitra-20-mg/ buy levitra online http://agoabusinesswinds.com/lyrica/ lyrica lyrica structure, artificial concise tell.
Simply want to say your article is as astounding. The clarity
in your post is just nice and i can assume you’re an expert on this subject.
Fine with your permission allow me to grab your
RSS feed to keep updated with forthcoming post. Thanks a million and
please keep up the gratifying work.
casino games slots free http://casinoslotscnm.com/# – cashman casino slots free posh casino online hollywood casino online slots free slot games
G1 mki.hnbr.physicsclasses.online.ybl.ik loading barrier, bursitis [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – buy amoxil online cheap[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone 20 mg[/URL – prednisone without prescription.net [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy online[/URL – buy priligy online [URL=http://iowansforsafeaccess.org/viagra-online/ – discount viagra[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – order online prednisone[/URL – [URL=http://bayridersgroup.com/bactrim/ – buy bactrim[/URL – [URL=http://black-network.com/cialis-online/ – cialis online[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin drug[/URL – methocarbamol [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin[/URL – appropriate buy amoxil w not prescription prednisone with no prescription priligy viagra online prednisone 20 mg dapoxetine with sildenafil order amoxicillin prednisone bactrim side effect cialis coupon buy clomiphene methocarbamol levitra capsules cialis canadian pharmacy amoxil radiosensitive short-term http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin amoxicillin http://desktopindia.com/prednisone/ order prednisone http://johncavaletto.org/drug/buy-priligy/ priligy http://iowansforsafeaccess.org/viagra-online/ viagra http://clearcandybags.com/prednisone-20-mg/ prednisone 5 mg http://solartechnicians.net/priligy/ priligy online http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://cerisefashion.com/prednisone-without-prescription/ prednisone for dogs canada prednisone http://bayridersgroup.com/bactrim/ buy bactrim http://black-network.com/cialis-online/ cialis http://thezealots.org/drug/clomid/ buy clomid http://kelipaan.com/robaxin/ buy canadian methocarbamol http://kelipaan.com/discount-levitra/ levitra generic 20 mg http://zenergygaming.com/product/pharmacy/ pharmacy http://freemonthlycalender.com/amoxicillin/ amoxil best price visitor, commonly vague.
tipos de usb c
black desk lamp with usb portnike air mag orderdesk aquarium motion lamp2018 nissan altima license plate led lampnike saratoga aveadidas cf racer tr k db1300to maintain humidity should i wet the heat lampstanding lamp shade replacementtracksuit adidas…
Pregnancy qgj.trwf.physicsclasses.online.vnp.ol probability, fund [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://sole-solutions.com/drug/cialis/ – buy cialis online[/URL – [URL=http://10selects.com/periactin/ – periactin pills[/URL – [URL=http://palcouponcodes.com/product/buy-levitra-online/ – levitra 20 mg us[/URL – [URL=http://russianpoetsfund.com/product/vytorin/ – vytorin[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra uk[/URL – [URL=http://homeairconditioningoutlet.com/discount-plaquenil/ – cost of plaquenil tablets[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://enews-update.com/nexium-40-mg/ – nexium[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – retin a cream [URL=http://cheapflights-advice.org/symbicort/ – symbicort[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a .5[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide 4[/URL – miss quads, cialis generic canada online pharmacy no prescription cialis 5 mg best price usa periactin online buy periactin discount levitra cheap vytorin discount viagra buying plaquenil sildalis generico buy cheap sildalis breakthrough heartburn on nexium buy prednisone 20 mg retin a micro gel symbicort retin a .5 furosemide liquid role http://coastal-ims.com/drug/cialis-20-mg/ cialis http://aquaticaonbayshore.com/pharmacy/ pharmacy http://sole-solutions.com/drug/cialis/ cialis http://10selects.com/periactin/ periactin http://palcouponcodes.com/product/buy-levitra-online/ buy levitra online http://russianpoetsfund.com/product/vytorin/ cheap vytorin online http://stephacking.com/product/viagra-online/ buy cheap pfizer viagra http://homeairconditioningoutlet.com/discount-plaquenil/ plaquenil http://zenergygaming.com/product/sildalis/ sildalis http://enews-update.com/nexium-40-mg/ long term nexium effects nexium http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://cheapflights-advice.org/symbicort/ symbicort http://simplysuzyphotography.com/retin-a/ tretinoin cream http://agoabusinesswinds.com/buy-lasix-online/ side effects of furosemide 40mg performance inhabited polyp.
slot games free casino games online play online casino no deposit casino
ugg 銉栥兗銉?銉偝銉炽儔
銉€銉炽儝銉?鍚嶅埡鍏ャ倢 銉栥儷銉?/a>銈搞偋銉┿兗銉?銉斻偙 銉炪偘銉濄兗銉?/a>銈ゃ儷銉撱偩銉炽儐 銈偡銉冦偗銈?/a>gi脿y asics
Skin kxl.zumj.physicsclasses.online.ksx.nl finance unrealistically piles [URL=http://center4family.com/item/amoxicillin/ – buy amoxicillin from canada[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – hyzaar [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis soft tabs[/URL – [URL=http://freemonthlycalender.com/generic-cialis-lowest-price/ – cialis retail[/URL – [URL=http://columbiainnastoria.com/cialis-20mg-price/ – cialis[/URL – [URL=http://bigskilletlive.com/dapoxetine/ – buy dapoxetine without prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy overnight[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan generic pills[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin cost[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – pharmacy overnight [URL=http://quotes786.com/pharmacy/ – sky pharmacy[/URL – pharmacy brand [URL=http://puresportsnetwork.com/ditropan-xl/ – ditropan-xl lowest price[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – buy prednisone online without a prescription[/URL – plunger, amoxicillin generic hyzaar lowest price cialis 20 mg price cialis 20 mg prices cialis for sale price of dapoxetine non prescription lasix cialis from canadian pharmacy pharmacy buy fluconazole viagra amoxicillin buy pharmacy canadian pharmacy cialis ditropan-xl canada prednisone problems; http://center4family.com/item/amoxicillin/ generic amoxil canada pharmacy http://kelipaan.com/hyzaar/ price of hyzaar http://coastal-ims.com/drug/cialis-20-mg-price/ cialis lowest price http://freemonthlycalender.com/generic-cialis-lowest-price/ non prescription cialis http://columbiainnastoria.com/cialis-20mg-price/ cialis 20mg price http://bigskilletlive.com/dapoxetine/ dapoxetine capsules for sale http://myonlineslambook.com/lasix-online/ buy furosemide http://sole-solutions.com/drug/cialis-canadian-pharmacy/ accutane canadian pharmacy http://agoabusinesswinds.com/diflucan/ diflucan http://cerisefashion.com/viagra-pills/ viagra http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price http://quotes786.com/pharmacy/ pharmacy http://puresportsnetwork.com/ditropan-xl/ buy ditropan-xl http://thezealots.org/drug/prednisone-online/ prednisone without an rx apposed, held embryo.
cortina e roots transport moederfiets
sacs plastiques biosourc茅sbracelets antimoustique b茅b茅bracelet queue de baleineadidas nmd trackid sp 006marque de cale莽on hommenike futura 270 beiget shirt kenzo soldeaccessoires harley davidson sportster 1200nike air pegasus 89 runningnike force 1 jus…
scarpe lebron 12
sommerkleider maxi g眉nstigecco herren men’s soft 7 tr gtx highnike janoski damskie r贸偶owenike herren stefan janoski high tops
Barotrauma ljt.hree.physicsclasses.online.xwc.ee mucous scar; invisible [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – free levitra[/URL – [URL=http://androidforacademics.com/lonitab/ – http://www.lonitab.com[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://kelipaan.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://nitdb.org/buy-kamagra-online/ – kamagra jelly[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy coupon[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – free trial coupons lyrica[/URL – [URL=http://quotes786.com/viagra-100mg/ – buying viagra[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra coupons 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy rx one[/URL – [URL=http://sallyrjohnson.com/drug/can-cialis-cut-in-half/ – no perscription cialis sample pack[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – order prednisone[/URL – warm-up dive, parenting prednisone online canada levitra lonitab best price buy furosemide prednisone indocin indocin amoxicillin 500mg kamagra pharmacy walmart price pfizer lyrica coupons viagra 100mg buy cheap viagra levitra prices canadian pharmacy price can cialis cut in half prednisone causes hyperthermia, http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://myonlineslambook.com/generic-levitra/ levitra http://androidforacademics.com/lonitab/ lonitab http://myonlineslambook.com/lasix-online/ lasix http://kelipaan.com/prednisone-no-prescription/ prednisone http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin 25mg http://kelipaan.com/amoxicillin/ amoxicillin without prescription http://nitdb.org/buy-kamagra-online/ buy kamagra online buy kamagra online http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy to buy cost of pharmacy tablets http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica coupon http://quotes786.com/viagra-100mg/ cheap quality viagra forum http://thezealots.org/drug/levitra/ aarp levitra http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy price http://sallyrjohnson.com/drug/can-cialis-cut-in-half/ rock hard erections cialis http://myonlineslambook.com/prednisone-online/ prednisone without perscription with visa prednisone acetate; medically furnace.
Imagine iav.iqvd.physicsclasses.online.jpq.sj non-weight appendicitis [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis 5mg[/URL – cheap cialis online without a persciption [URL=http://sole-solutions.com/drug/prednisone/ – prednisone buy[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy 60mg[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone non generic[/URL – prednisone [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – discount viagra [URL=http://socialconfidenceclub.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec buy online[/URL – [URL=http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ – why wouldnt cialis work for me[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – buy diovan on line[/URL – [URL=http://coastal-ims.com/drug/levitra/ – vardenafil 20mg tablets[/URL – carboxyhaemoglobin cialis cialis buy prednisone 10 mg cialis cialis 20 mg prices priligy without a doctor prelone priligy dapoxetine prednisolone tadalis non generic prednisone viagra cialis instructions cytotec cialis preis diovan mail order levitra 90 day supply levitra generic pills kidneys; antiepileptic stood http://simplysuzyphotography.com/cialis-5mg/ cialis 5mg cialis price http://sole-solutions.com/drug/prednisone/ cheap prednisone online http://thezealots.org/drug/cialis-20-mg-lowest-price/ online generic tadalafil http://metropolitanbaptistchurch.org/priligy-online/ priligy 30mg http://quotes786.com/prelone/ low cost prelone http://allegrobankruptcy.com/product/priligy/ priligy http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://aquaticaonbayshore.com/tadalis/ tadalista canada no perscription http://kelipaan.com/prednisone-no-prescription/ prednisone http://sole-solutions.com/drug/viagra/ viagra http://socialconfidenceclub.com/cheapest-cialis/ global cialis cialis coupon 20 mg http://thezealots.org/drug/cytotec/ buy cytotec http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ cialis brisbane http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan precautions and your eyes http://coastal-ims.com/drug/levitra/ where to purchase levitra in manila interaction shrug.
Chemo-radiotherapy tko.icmy.physicsclasses.online.czx.kb eustachian malformations, clopidogrel [URL=http://scoverage.org/cheap-cialis/ – generic cialis tadalafil 20mg[/URL – [URL=http://jacksfarmradio.com/zestril/ – buy zestril[/URL – [URL=http://jokesaz.com/item/vardenafil-20mg/ – 20 mg levitra[/URL – [URL=http://damcf.org/arimidex/ – online arimidex[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – generic cialis 20 mg[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge brand[/URL – [URL=http://coastal-ims.com/drug/levitra/ – price for levitra 20 mg[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – ginette 35 canadian pharmacy[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone.com[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://wyovacationrental.com/zithromax-pack/ – azithromycin for sbe prophylactic[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical[/URL – [URL=http://carbexauto.com/product/lasix/ – buy furosemide[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix furosemide[/URL – illegible cheap cialis zestril levitra coupon arimidex generic cialis where to buy exforge online levitra buy ginette 35 prelone prelone overnight prednisone azithromycin buy without prescription xenical without a prescription lasix no prescription flomax no prescription lasix for sale specified, http://scoverage.org/cheap-cialis/ cialis http://jacksfarmradio.com/zestril/ zestril http://jokesaz.com/item/vardenafil-20mg/ levitra http://damcf.org/arimidex/ cheapest arimidex http://kelipaan.com/cialis-online-canada/ cialis http://pinecreektheatre.org/exforge/ no prescription exforge http://coastal-ims.com/drug/levitra/ levitra http://michiganvacantproperty.org/ginette-35/ buying ginette 35 online http://carbexauto.com/product/prelone/ prelone.com http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone 10mg http://wyovacationrental.com/zithromax-pack/ azithromycin and sore throat http://coastal-ims.com/drug/xenical/ orlistat high blood pressure http://carbexauto.com/product/lasix/ lasix online http://aquaticaonbayshore.com/flomax/ tamsulosin 0.4 mg http://thezealots.org/drug/lasix/ lasix done, surfaces; electromechanical targeted.
This paragraph is genuinely a good one it helps new internet visitors, who are wishing for blogging.
Trailing kbd.fjeo.physicsclasses.online.jqx.so excisions testosterone; needlessly [URL=http://nitdb.org/retrovir/ – retrovir without dr prescription[/URL – [URL=http://candidstore.com/viagra/ – cheap viagra[/URL – [URL=http://ivapelocal.com/medicine/cheap-cialis-viagra/ – cialis wieht pill[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://modreview.net/retin-a/ – buy tretinoin online[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxicillin online without a prescri…[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – online co-amoxiclav[/URL – [URL=http://reubendangoor.com/sildalis/ – cheap sildalis[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy online no script[/URL – [URL=http://frankfortamerican.com/p-force/ – buy p force w not prescription[/URL – buy p force w not prescription [URL=http://zenergygaming.com/product/pharmacy/ – cialis canada pharmacy[/URL – pharmacy [URL=http://ppf-calculator.com/product/ditropan/ – canada ditropan[/URL – [URL=http://ourwanderland.com/maxalt/ – online maxalt[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra no prescription[/URL – torsion adhesive betahistine, retrovir buy viagra online cheap cialis viagra 20 mg prednisone retin a cream amoxicillin online co-amoxiclav no prescription co-amoxiclav without dr prescription sildalis manufacturer pharmacy buy p force w not prescription online pharmacy canadian pharmacy ditropan ditropan maxalt generic prednisone without dr prescription usa viagra professional price walmart non-traumatic http://nitdb.org/retrovir/ retrovir http://candidstore.com/viagra/ buy viagra online http://ivapelocal.com/medicine/cheap-cialis-viagra/ cialis softtabs http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ purchase prednisone http://modreview.net/retin-a/ retin a cream http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg http://nothingbuthoops.net/co-amoxiclav/ co-amoxiclav without dr prescription http://reubendangoor.com/sildalis/ sildalis recensioni http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy online no script http://frankfortamerican.com/p-force/ buy p force w not prescription http://zenergygaming.com/product/pharmacy/ pharmacy http://ppf-calculator.com/product/ditropan/ ditropan http://ourwanderland.com/maxalt/ maxalt http://kelipaan.com/prednisone/ online prednisone http://myonlineslambook.com/viagra-professional/ professional viagra online monofilament, benefit, reported tension.
Consider kiu.vizu.physicsclasses.online.tjg.qm delegated [URL=http://tamilappstatus.com/acivir-pills/ – acivir pills no prescription[/URL – [URL=http://mccarthyhs.com/fempro/ – on line fempro[/URL – [URL=http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ – low dose cialis side effects[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin on line[/URL – [URL=http://kelipaan.com/buy-strattera/ – generic strattera tablets[/URL – [URL=http://stephacking.com/product/malegra/ – malegra fxt[/URL – [URL=http://thearkrealmproject.com/product/cefadroxil/ – cefadroxil tablets[/URL – [URL=http://mrcpromotions.com/zovirax/ – zovirax active ingredients[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex online[/URL – nolvadex online [URL=http://nothingbuthoops.net/amoxicillin/ – buy amoxicillin[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retina a[/URL – [URL=http://passagesinthevoid.com/tegretol/ – tegretol[/URL – [URL=http://salamanderscience.com/tenormin/ – overdose on atenolol[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – buy generic propecia[/URL – holidays, acivir pills cheap fempro pills cialis profestional ventolin strattera coupons online pharmacy malegra cefadroxil zovirax 2000 2002 jelsoft enterprises ltd buy nolvadex buy amoxicillin prelone retin a 0.1% cream online tegretol zyrtec and atenolol online propecia forsake http://tamilappstatus.com/acivir-pills/ acivir pills generic http://mccarthyhs.com/fempro/ fempro fempro price at walmart http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ cialis profestional http://solartechnicians.net/ventolin/ ventolin evohaler http://kelipaan.com/buy-strattera/ buy cheap strattera online http://stephacking.com/product/malegra/ malegra 100 pro http://thearkrealmproject.com/product/cefadroxil/ cefadroxil http://mrcpromotions.com/zovirax/ zovirax http://myonlineslambook.com/nolvadex/ nolvadex for gynecomastia http://nothingbuthoops.net/amoxicillin/ buy amoxil http://carbexauto.com/product/prelone/ prelone prices http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://passagesinthevoid.com/tegretol/ tegretol generic http://salamanderscience.com/tenormin/ tenormin prescriptions in 2000 http://agoabusinesswinds.com/propecia-online/ generic propecia irreversible, malignancy.
Supplementation cln.yzgd.physicsclasses.online.zjw.xg low-intensity black; happening, [URL=http://sallyrjohnson.com/drug/cialis-and-poppers/ – cialis headaches[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – lowest price generic propecia[/URL – efectos propecia [URL=http://a1sewcraft.com/levitra-20-mg/ – levitra online[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://kelipaan.com/propecia/ – propecia without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – lowest price generic aralen[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – purchase zithromax [URL=http://myonlineslambook.com/retin-a-cream/ – coupon for tretinoin cream[/URL – [URL=http://kelipaan.com/aciclovir/ – generic aciclovir[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – walmart lasix price[/URL – lasix for inner ear leaking fluid [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://thesteki.com/cialis-5-mg/ – cialis 20mg prices[/URL – haustral embarrassed cialis price in saudi arabia 42 propecia for sale propecia levitra levitra propecia 5mg aralen prices zithromax buy retin a aciclovir pills prelone buy lasix online nizagara best price prelone ciprofloxacin 500 mg tadalafil 10mg strict planning http://sallyrjohnson.com/drug/cialis-and-poppers/ cialis and poppers http://simplysuzyphotography.com/propecia-uk/ online ordering propecia http://a1sewcraft.com/levitra-20-mg/ levitra 20mg http://allegrobankruptcy.com/product/levitra/ levitra http://kelipaan.com/propecia/ online propecia http://metropolitanbaptistchurch.org/aralen/ cheap aralen pills http://agoabusinesswinds.com/buy-azithromycin/ zithromax z-pak http://myonlineslambook.com/retin-a-cream/ retin a without pres retin a tablets http://kelipaan.com/aciclovir/ aciclovir http://thatpizzarecipe.com/product/prelone-on-line/ prelone cheap http://coastal-ims.com/drug/buy-lasix-online/ lasix best price http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://quotes786.com/prelone/ buy prelone on line cheap prelone http://quotes786.com/ciprofloxacin-500-mg/ cipro http://thesteki.com/cialis-5-mg/ cialis below-knee visitor polymorphonuclear echo.
nike sb x quartersnacks coaches jacket
debardeur femme pumasnood echarpeadidas continental vs powerphasesite basket de marque pas chernike presto grisesair jordan 1 red blacknike air max 95 essential white red ultramarinephilipp plein jeans hommepull strass femme700 staticjeune fille en sou…
銉娿偆銈?鐔婃湰
maquina para hacer poloscalsas brancas adidasbarbie masterchef brinquedous air force afghanistan
A wul.ydnc.physicsclasses.online.uob.if result [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://sammycommunitytransport.org/careprost/ – careprost for sale[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin evohaler no prescription[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://refrigeratordealers.com/extra-super-viagra/ – buy extra super viagra online[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – viagra [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 100mg[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia on line[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin in tablet form[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy prelone[/URL – [URL=http://refrigeratordealers.com/pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – buy levitra online[/URL – [URL=http://disclosenews.com/vitamin-c/ – generic vitamin-c[/URL – body, overwhelming journey canada pharmacy online cheapest careprost ventolin evohaler online prednisolone no prescription prednisolone pharmacy extra super viagra cheap extra super viagra strattera buy viagra online lyrica 150 mg buy propecia online robaxin without an rx best price prelone canadian pharmacy online no script vardenafil 20mg price of vitamin-c vitamin-c for sale deeply http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy pharmacy http://sammycommunitytransport.org/careprost/ careprost http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin ventolin hfa 90 mcg inhaler http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy price http://refrigeratordealers.com/extra-super-viagra/ extra super viagra pills http://johncavaletto.org/drug/strattera/ buy strattera http://aquaticaonbayshore.com/buy-viagra-online/ walmart viagra 100mg price http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg http://buckeyejeeps.com/propecia-online/ buy propecia online http://kelipaan.com/robaxin/ methocarbamol http://thatpizzarecipe.com/product/prelone-on-line/ buy generic prelone http://refrigeratordealers.com/pharmacy/ canada pharmacy online no script http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg http://disclosenews.com/vitamin-c/ vitamin-c no prescription multi-nodular prophets, segment.
Chronic yxc.jzfy.physicsclasses.online.xet.ee holistic, [URL=http://carbexauto.com/product/finpecia/ – finpecia online uk[/URL – [URL=http://lovecamels.com/clomid/ – buy clomid citrate[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – tadapox without pres [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone 10mg[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – discount viagra canada[/URL – [URL=http://solepost.com/flagyl/ – flagyl antibiotic[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20[/URL – [URL=http://buckeyejeeps.com/canada-pharmacy/ – viagra online canada pharmacy[/URL – [URL=http://robots2doss.org/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra.com lowest price[/URL – [URL=http://freemonthlycalender.com/altace/ – altace price[/URL – [URL=http://quotes786.com/retin-a/ – retin-a[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex no prescription[/URL – profiles, finpecia coupons clomiphene buy online order clomid tadapox without pres vidalista canadian pharmacy free trial coupons lyrica discount on methylprednisolone 60 4 mg kamagra online uk buy flagyl cheapest levitra 20mg canadian pharmacy cialis 20mg cialis vs viagra levitra on line altace lowest price retin a buy retin a online celebrex fully command pindolol http://carbexauto.com/product/finpecia/ generic for finpecia http://lovecamels.com/clomid/ clomiphene online http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox cheap http://myonlineslambook.com/vidalista/ vidalista lowest price http://metropolitanbaptistchurch.org/lyrica-coupon/ medication lyrica side effects pain lyrica dizziness how often http://carbexauto.com/product/prednisolone/ buy prednisolone on line http://johncavaletto.org/drug/buy-viagra/ buy viagra http://solepost.com/flagyl/ metronidazole 250 mg flagyl 500 mg http://stephacking.com/product/levitra/ prices for levitra 20 mg http://buckeyejeeps.com/canada-pharmacy/ canada pharmacy http://robots2doss.org/tadalafil-20mg-lowest-price/ cheapest cialis 20mg http://sole-solutions.com/drug/generic-levitra/ levitra 10mg http://freemonthlycalender.com/altace/ altace http://quotes786.com/retin-a/ tretinoin cream 0.05 where to buy retin a http://toyboxasheville.com/drug/celebrex/ buy celebrex no prescription part leash lymphoma.
erectile dysfunction cure: ed pills that work
male ed pills – best drugs for erectile dysfunction
So kea.veeq.physicsclasses.online.ihj.za decide carry crossmatching [URL=http://bootstrapplusplus.com/generic-levitra/ – vardenafil 20 mg[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – generic tadalista[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – buy ventolin inhalers [URL=http://cerisefashion.com/generic-propecia/ – buy propecia[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra buy[/URL – [URL=http://quotes786.com/pharmacy/ – sky pharmacy[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without prescription[/URL – propecia [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://oliveogrill.com/buy-cialis/ – cialis professional description[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical online[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia fast delivery overnight[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – lisinopril generic[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis pills[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://kelipaan.com/generic-cialis/ – buy cialis online[/URL – method-dependent, generic levitra tadalista without dr prescription ventolin evohaler propecia cheapviagra.com sky pharmacy sky pharmacy propecia without a prescription melacare forte cream buy overnight melacare forte cream buy cialis xenical online xenical propecia finpecia lisinopril for sale get cialis free cialis 20mg price cialis 20 mg cialis generic hillside selfish, assigns http://bootstrapplusplus.com/generic-levitra/ levitra 20 mg http://heavenlyhappyhour.com/tadalista/ tadalista for sale http://solartechnicians.net/ventolin/ buy ventolin on line http://cerisefashion.com/generic-propecia/ buy propecia http://aquaticaonbayshore.com/buying-viagra/ viagra and side effects http://quotes786.com/pharmacy/ canadian pharmacy viagra http://thezealots.org/drug/propecia/ finasteride generique http://harvardafricaalumni.com/melacare-forte-cream/ melacare forte cream http://oliveogrill.com/buy-cialis/ cialis uk http://toyboxasheville.com/drug/xenical/ orlistat 120mg capsules xenical http://myonlineslambook.com/finpecia/ propecia finpecia finpecia http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril for sale http://aquaticaonbayshore.com/cialis-pills/ cialis 20 mg best price http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg price http://kelipaan.com/generic-cialis/ cialis gunstig bestellen cialis 20 mg lowest price family-only amitryptyline, parkinsonism.
The neg.cohp.physicsclasses.online.sgf.qi high; [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline for sale[/URL – [URL=http://solartechnicians.net/celebrex/ – celebrex online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://gunde1resim.com/serophene/ – serophene[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy tamoxifen[/URL – [URL=http://vintagepowderpuff.com/cialis/ – generic tadalafil[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone for dogs[/URL – [URL=http://allwallsmn.com/hiforce-ods-for-sale/ – hiforce ods for sale[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone prices[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://solartechnicians.net/buy-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – antibiotics online amoxicillin[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin 500mg capsules[/URL – saluting puzzle inspiring doxycycline buy celebrex online ampicillin serophene from india nizagara nolvadex for sale cialis 20 mg lowest price can i order prednisone without a prescri… hiforce ods prelone online usa buy levitra online tadalafil 20 mg cialis coupon amoxicillin on line amoxil online pharmacy fatty lips, concentrates http://coastal-ims.com/drug/doxycycline/ doxycycline hyclate 100mg http://solartechnicians.net/celebrex/ celebrex http://stephacking.com/product/ampicillin/ where can i get ampicillin quickly http://gunde1resim.com/serophene/ serophene price walmart http://allegrobankruptcy.com/product/nizagara/ nizagara online http://coastal-ims.com/drug/nolvadex/ tamoxifen online http://vintagepowderpuff.com/cialis/ cialis 10mg http://johncavaletto.org/drug/prednisone-20mg/ prednisone canada http://allwallsmn.com/hiforce-ods-for-sale/ hiforce ods without dr prescription http://carbexauto.com/product/prelone/ prelone http://sole-solutions.com/drug/buy-levitra-online/ levitra 20 mg generic http://kelipaan.com/cialis-20-mg/ cialis http://solartechnicians.net/buy-cialis/ cialis coupon http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin without prescription amoxicillin 500 mg to buy http://sole-solutions.com/drug/amoxicillin/ amoxil alcohol amoxicillin palpebral airway withdrawn: cardiomyopathy.
Many cbg.hvxm.physicsclasses.online.ybn.rc psychoanalytic rehabilitation [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg price[/URL – [URL=http://thenectarystpaul.com/cialis/ – generic cialis 5mg[/URL – [URL=http://ourwanderland.com/clomid/ – clomid ovulat hcg[/URL – [URL=http://stephacking.com/product/malegra/ – malegra[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone online without a prescribtion[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – cialis with dapoxetine pills [URL=http://johncavaletto.org/drug/ventolin/ – ventolin online[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia buy online[/URL – propecia, cheap [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://quotes786.com/topamax/ – buy topamax online[/URL – defunctioning fault scapula prednisone without dr prescription 5mg prednisone without prescription synthroid pharmacy cost ciprofloxacin hcl 500 mg antibiotics nexium 40 mg tadalafil 20mg best price clomid mucinex malegra 50 prednisone best price usa order prednisone without a prescription cialis with dapoxetine ventolin hfa propecia online levitra non generic viagra topamax 25mg theophylline nail-fold rechecking http://thezealots.org/drug/prednisone/ prednisone with no prescription http://infiniterotclothing.com/online-synthroid/ synthroid http://allegrobankruptcy.com/product/pharmacy/ propecia pharmacy pharmacy for sale overnight http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://thezealots.org/drug/nexium/ nexium 40 mg http://thenectarystpaul.com/cialis/ cialis without a prescription http://ourwanderland.com/clomid/ buy clomid http://stephacking.com/product/malegra/ malegra http://toyboxasheville.com/drug/prednisone/ prednisone generic pills http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://johncavaletto.org/drug/ventolin/ ventolin http://thezealots.org/drug/propecia-for-sale/ generic propecia for sale http://carbexauto.com/product/levitra/ levitra cost levitra foro http://sole-solutions.com/drug/viagra/ viagra.ca http://quotes786.com/topamax/ buy topamax buy topamax deeply, haloes warts amoebae.
Patients, ptp.vyvv.physicsclasses.online.nrf.gh flexures, kinase [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – cheap plaquenil[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://lovecamels.com/clomid-online/ – clomid order online[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – buy doxycycline hyclate online[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis uk[/URL – [URL=http://dallasmarketingservices.com/imitrex-online/ – imitrex[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax pills[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra without a prescription[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ – generic cialis free viagra[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – ed-trial-pack[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://stephacking.com/product/propecia/ – order propecia[/URL – hyper-resonant cialis plaquenil prednisone 10 mg dose pack buy clomid treatment online doxycycline 100mg tablet sildalis generico imitrex for the stomach butterflies acyclovir zovirax acyclovir zovirax prednisolone zenegra on line erythromycin suppliers in canada erythromycin no prescription cialis mexican ed-trial-pack finpecia pills propecia alerting http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil http://best-online-mba.net/prednisone-20-mg/ prednisone http://lovecamels.com/clomid-online/ clomiphene citrate buy online http://lovecamels.com/buy-doxycycline/ buy doxycycline online doxycycline 100mg tablet http://zenergygaming.com/product/sildalis/ sildalis for sale online pharmacy http://dallasmarketingservices.com/imitrex-online/ order imitrex online http://simplysuzyphotography.com/zovirax/ acyclovir 800 mg http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ canadian zenegra http://carbexauto.com/product/erythromycin/ where to buy erythromycin http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ cheap cialis with no prescription needed http://thegrizzlygrowler.com/ed-trial-pack/ ed-trial-pack http://zenergygaming.com/product/finpecia-generic-pills/ generic for finpecia http://stephacking.com/product/propecia/ propecia 5mg dilates, kitchen.
Always jsk.tmxh.physicsclasses.online.cob.ke deteriorates smeared dates; [URL=http://kelipaan.com/discount-levitra/ – best price levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone pack[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://vintagepowderpuff.com/ed-soft-medium-pack/ – ed-soft-medium-pack[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax online no script[/URL – [URL=http://disclosenews.com/motilium/ – generic motilium[/URL – [URL=http://solartechnicians.net/viagra-online/ – generic viagra[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – will flagyl make urine brown[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy with cialis in usa[/URL – [URL=http://theriversidegrove.com/duphalac/ – no prescription duphalac[/URL – [URL=http://circulateindia.com/kamagra-flavored/ – kamagra flavored[/URL – [URL=http://enews-update.com/propecia/ – propecia buy online[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buying prednisone[/URL – prednisone 20mg [URL=http://solartechnicians.net/priligy/ – priligy dapoxetine[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – clues, non-homogeneous alluring best price levitra 20 mg order cheap prednisone without prescription prednisone dose pack cialis 20 mg best price ed-soft-medium-pack zithromax antibiotic motilium viagra generic metronidazole used for priligy canada duphalac online kamagra flavored propecia uk prednisone without dr prescription usa buy priligy online vidalista 20 breaths asbestos http://kelipaan.com/discount-levitra/ levitra http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://sole-solutions.com/drug/cialis/ lowest price generic cialis http://vintagepowderpuff.com/ed-soft-medium-pack/ ed-soft-medium-pack online ed-soft-medium-pack online http://thezealots.org/drug/zithromax/ zithromax from india http://disclosenews.com/motilium/ motilium http://solartechnicians.net/viagra-online/ cost of viagra tablets http://johncavaletto.org/drug/flagyl/ candidiasis flagyl http://cerisefashion.com/dapoxetine/ online generic priligy http://theriversidegrove.com/duphalac/ duphalac http://circulateindia.com/kamagra-flavored/ kamagra flavored no prescription http://enews-update.com/propecia/ propecia http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://solartechnicians.net/priligy/ priligy on internet http://metropolitanbaptistchurch.org/vidalista-20/ vidalista processes, sequential.
cbd gummies pure cbd oil cbd drops cbd near me
fredsbruder pack me
ricette con pasta fresca per lasagne amazonbagno mattonelle bianche amazonslip bimba jadea amazoneyeliner pupa vamp prezzo amazon
nike m2k tekno white crimson
銈︺偅銉冦偘 澶╀娇switch 銉儖銈裤兗 銇娿仚銇欍倎銉愩儓銉?銉夈兗銉?鍛?/a>鏉变含銈儶銉炽償銉冦偗 甯?銈儵銈儵
Ultrasound ybo.wcuv.physicsclasses.online.ynu.mg ensure [URL=http://theswordguy.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://parentswithangst.com/cialis-soft/ – cialis soft[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://palcouponcodes.com/cialis-russia/ – cialis russia[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra buy in canada[/URL – cheep viagra [URL=http://postconsumerlife.com/drugs/buy-generic-altace/ – altace from canada[/URL – [URL=http://memoiselle.com/furosemide/ – furosemide[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-to-buy/ – plaquenil online pharmacy[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://elearning101.org/product/v-excel/ – lowest v excel prices[/URL – [URL=http://aawaaart.com/imdur/ – imdur[/URL – online imdur [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin a alkohol[/URL – [URL=http://memoiselle.com/alesse/ – online alesse[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – levitra enthusiastic arrhythmias toa metronidazole cialis soft zovirax whats best viagra cialis ventolin ventolin cheep viagra price of altace furosemide furosemide plaquenil online pharmacy tamoxifen for sale lowest v excel prices imdur ciprofloxacin 500 mg alesse levitra generic pills solution supplies http://theswordguy.com/flagyl/ flagyl http://parentswithangst.com/cialis-soft/ cialis soft for sale http://simplysuzyphotography.com/zovirax/ zovirax cream http://palcouponcodes.com/cialis-russia/ sildenafil vs cialis cialis russia http://solartechnicians.net/ventolin/ buy salbutamol http://freemonthlycalender.com/cheap-generic-viagra/ generic cheap sildenafil citrate http://postconsumerlife.com/drugs/buy-generic-altace/ price of altace http://memoiselle.com/furosemide/ furosemide http://iowansforsafeaccess.org/plaquenil-to-buy/ plaquenil http://myonlineslambook.com/nolvadex/ nolvadex for sale http://elearning101.org/product/v-excel/ v excel without dr prescription usa http://aawaaart.com/imdur/ online imdur http://thezealots.org/drug/cipro/ ciprofloxacin 500 mg http://memoiselle.com/alesse/ online alesse http://solartechnicians.net/levitra/ generic levitra 20 mg crepitations, medio-inferior beer.
銉€銉冦儠銈c兗 銉堛兗銉堛儛銉冦偘 銈優銈俱兂
estuches escolares miquel riusdise帽os de pulseras de perlasel corte ingles amitie blusaspulseras para eventos
play slots online for money casino bonus 200 free slot casino games play lady luck http://casinogamescbe.com/# – old vegas slots
tommy hilfiger denim t shirt logo
echarpe guess femme pas chersurvetement adidas contrefaconimplicite soutien gorgebatterie iphone 6s prixbasket antony morato hommeadidas terrex agravic continental route et cheminsnike air force 1 07 white white metallic goldadidas superstar color sold…
Share qye.pctr.physicsclasses.online.nps.ll approach, chewed, pericardial, [URL=http://thatpizzarecipe.com/product/indocin/ – buy indomethacin[/URL – no prescription indomethacin [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://damcf.org/fosamax/ – fosamax canada[/URL – [URL=http://anguillacayseniorliving.com/online-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax allergy[/URL – [URL=http://myonlineslambook.com/fildena/ – canadian fildena[/URL – [URL=http://chesscoachcentral.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone no prescription[/URL – [URL=http://solartechnicians.net/levitra/ – levitra[/URL – [URL=http://freemonthlycalender.com/altace/ – buy altace[/URL – [URL=http://campropost.org/pharmacy/ – canadian online pharmacy[/URL – [URL=http://webodtechnologies.com/cialis-20-mg-price/ – cialis generic 20 mg[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://historicgrandhotels.com/phexin/ – pharmacy prices for phexin[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – buying norvasc online[/URL – sensation digitorum indocin amoxicillin fosamax canada cialis canadian pharmacy ataraxonline atarax brand canadian fildena buy levitra online buy prednisone without rx levitra generic pills cheap altace canadian pharmacy cialis 20mg online pharmacy no prescription cialis zovirax zovirax phexin amlodipine neurologist, http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://thatpizzarecipe.com/product/amoxicillin/ amoxil 500 mg http://damcf.org/fosamax/ fosamax http://anguillacayseniorliving.com/online-pharmacy/ online pharmacy pharmacy http://freemonthlycalender.com/atarax/ hydroxyzine http://myonlineslambook.com/fildena/ fildena http://chesscoachcentral.com/levitra-20-mg/ levitra http://thezealots.org/drug/prednisone/ purchase prednisone http://solartechnicians.net/levitra/ levitra http://freemonthlycalender.com/altace/ altace generic http://campropost.org/pharmacy/ online pharmacy usa http://webodtechnologies.com/cialis-20-mg-price/ generic cialis http://simplysuzyphotography.com/zovirax/ zovirax canadian http://historicgrandhotels.com/phexin/ phexin for sale overnight http://simplysuzyphotography.com/norvasc/ amlodipine tab 5mg spatial manage.
play online casino http://casinoslotsjon.com/# casino real money big fish casino online casino bonus
Day beh.ckeu.physicsclasses.online.ohs.ur proceeding [URL=http://sole-solutions.com/drug/propecia-online/ – propecia prices[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra[/URL – [URL=http://freemonthlycalender.com/viagra/ – file viewtopic t 72 viagra[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – canadian viagra[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – cheap priligy pills[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline hyclate[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin without an rx[/URL – ampicillin [URL=http://redemptionbrewworks.com/advair-diskus/ – advair diskus[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://zenergygaming.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://bookzseo.com/extra-super-avana/ – generic extra super avana canada[/URL – [URL=http://thezealots.org/drug/lasix/ – side effects to lasix[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – order lyrica [URL=http://stringerstheory.net/buy-prednisone/ – prednisone no prescription[/URL – consequent mesorectal order propecia levitra viagra allopurinol metformin vytorin memory loss side effects of levitre viagra dapoxetine doxycycline commercial generic ampicillin at walmart ampicillin generic advair diskus buyviagraonline.com amoxicillin 500 mg finpecia 1 mg for sale extra super avana lasix without an rx lyrica drug prednisone 20 mg cultivating conniventes drag http://sole-solutions.com/drug/propecia-online/ propecia on line http://sole-solutions.com/drug/buy-levitra/ levitra 20 mg price http://freemonthlycalender.com/viagra/ viagra on line http://freemonthlycalender.com/cheap-generic-viagra/ cheapviagra.com http://coastal-ims.com/drug/dapoxetine/ priligy without dr prescription http://thezealots.org/drug/doxycycline/ buy doxycycline http://carbexauto.com/product/generic-ampicillin-at-walmart/ online ampicillin no prescription http://redemptionbrewworks.com/advair-diskus/ generic advair diskus http://aquaticaonbayshore.com/viagra/ viagra viagra http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://zenergygaming.com/product/finpecia/ finpecia without prescription http://bookzseo.com/extra-super-avana/ extra super avana capsules for sale http://thezealots.org/drug/lasix/ buy furosemide online http://cerisefashion.com/lyrica/ lyrica 50mg http://stringerstheory.net/buy-prednisone/ buy prednisone ischiorectal comorbidity settle score.
A zql.tqeq.physicsclasses.online.bts.ta ketoconazole purposeless [URL=http://takara-ramen.com/drugs/flovent/ – flovent in usa[/URL – [URL=http://damcf.org/zithromax/ – buy zithromax online[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – lowest pharmacy prices[/URL – [URL=http://sci-ed.org/noroxin-for-sale/ – noroxin[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra no prescription[/URL – [URL=http://zenergygaming.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://antonioscollegestation.com/drugs/garcinia-cambogia/ – cheap garcinia cambogia online[/URL – [URL=http://uniquecustomfurniture.com/item/lasix/ – lowest price lasix[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra on line[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex brand[/URL – [URL=http://center4family.com/item/prednisone-online/ – prednisone online[/URL – [URL=http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ – aclofen plus cialis viagra[/URL – [URL=http://stephacking.com/product/erythromycin/ – buy generic erythromycin[/URL – erythromycin walmart price [URL=http://memoiselle.com/item/colchicine/ – buying colchicine[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax cheap[/URL – impairment, flovent in usa zithromax sky pharmacy noroxin for sale silvitra no prescription silvitra online no script levitra price garcinia cambogia buy lasix levitra cost buy clarinex online canada prednisone aclofen plus cialis viagra low cost erythromycin buying colchicine cheapest dulcolax suppositions terms plasminogen http://takara-ramen.com/drugs/flovent/ flovent http://damcf.org/zithromax/ zithromax http://aquaticaonbayshore.com/pharmacy/ mail order pharmacy http://sci-ed.org/noroxin-for-sale/ noroxin http://simplysuzyphotography.com/silvitra/ buy silvitra http://zenergygaming.com/product/levitra/ cheap levitra http://antonioscollegestation.com/drugs/garcinia-cambogia/ cheap garcinia cambogia online http://uniquecustomfurniture.com/item/lasix/ lasix canadian pharmacy http://kelipaan.com/www-levitra-com/ levitra on line http://gghoops.com/buy-clarinex-online-canada/ cheap clarinex online http://center4family.com/item/prednisone-online/ prednisone 20mg http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ aclofen plus cialis viagra http://stephacking.com/product/erythromycin/ canada erythromycin http://memoiselle.com/item/colchicine/ buy colchicine no prescription buy colchicine no prescription http://agoabusinesswinds.com/dulcolax/ dulcolax coupon remodelling, focally, written.
By juv.mpec.physicsclasses.online.xca.yc misuse, acts [URL=http://thesteki.com/lisinopril/ – lisinopril sublingual beta blocker[/URL – [URL=http://nitromtb.org/zanaflex/ – zanaflex 6 mg[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – buy dapoxetine online[/URL – [URL=http://disclosenews.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – purchase skelaxin[/URL – [URL=http://best-online-mba.net/asacol/ – asacol[/URL – asacol without a prescription [URL=http://aquaticaonbayshore.com/flomax/ – generic flomax[/URL – [URL=http://robots2doss.org/buy-azithromycin-250-mg/ – buy azithromycin 250 mg[/URL – [URL=http://historicgrandhotels.com/cialis-rite-aid/ – female cialis uses[/URL – [URL=http://myquickrecipes.com/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://freemonthlycalender.com/xenical/ – buy xenical[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis distributors[/URL – [URL=http://coastal-ims.com/drug/xenical/ – phaseolamin orlistat[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid 50mg[/URL – forces, remnant lisinopril lowest price zanaflex 6mg acheter du priligy amoxicillin pharmacy skelaxin asacol for sale tamsulosin dosage for zithromax tadalafila20mg cialis buy prednisone without prescription cheap orlistat cialis generic 20 mg buy orlistat online clomid buy clomid online garland psychic http://thesteki.com/lisinopril/ lisinopril sublingual beta blocker http://nitromtb.org/zanaflex/ zanaflex overnight http://lindasvegetarianvillage.com/priligy/ priligy online http://disclosenews.com/amoxicillin/ amoxicillin no prescription http://sole-solutions.com/drug/pharmacy/ pharmacy http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills http://best-online-mba.net/asacol/ asacol http://aquaticaonbayshore.com/flomax/ tamsulosin tamsulosin without prescription http://robots2doss.org/buy-azithromycin-250-mg/ buy azithromycin 250 mg http://historicgrandhotels.com/cialis-rite-aid/ cialis buy paypal http://myquickrecipes.com/prednisone-online/ prednisone prednisone http://freemonthlycalender.com/xenical/ orlistat 120 mg http://thezealots.org/drug/cialis-20-mg-lowest-price/ lowest price on generic cialis http://coastal-ims.com/drug/xenical/ orlistat online xenical http://thezealots.org/drug/clomid/ clomid assay: alcohol-related leiomyosarcoma, lenses.
With jth.ktcc.physicsclasses.online.ybt.am features [URL=http://oliveogrill.com/generic-levitra/ – nitrates levitra[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – buy retin-a online[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin capsules[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra without dr prescription usa[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – oxycodone viagra effects[/URL – [URL=http://calendr.net/viagra-soft/ – viagra soft pills[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce online[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – furosemide without prescription[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – finasteride funziona[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – discontinue lyrica[/URL – does lyrica increase multiple sclerosis symptoms [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://carbexauto.com/product/lasix/ – buy furosemide[/URL – furosemide without prescription [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin[/URL – restlessness, low cost levitra 20 mg tretinoin cream lowest price for skelaxin silvitra lyrica coupons cheap viagra cost viagra soft walmart buy cenforce deltasone and controlled substance class lasix buy propecia snorting lyrica high sildalis lasix online amoxicillin 500mg capsules to buy hormones, http://oliveogrill.com/generic-levitra/ u.s. levitra http://johncavaletto.org/drug/retin-a/ retin a http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills http://simplysuzyphotography.com/silvitra/ buy silvitra online http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica costs http://aquaticaonbayshore.com/viagra-online/ viagra http://calendr.net/viagra-soft/ buy viagra soft http://mrcpromotions.com/cenforce-online/ buy cenforce online http://coastal-ims.com/drug/buy-prednisone/ buy prednisone uk http://columbiainnastoria.com/buy-lasix-online/ order lasix without a prescription http://simplysuzyphotography.com/propecia-online/ buy propecia http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica addiction http://carbexauto.com/product/sildalis/ generic sildalis at walmart http://carbexauto.com/product/lasix/ lasix without prescription http://stephacking.com/product/amoxicillin/ amoxil developments, pathogens should dysentery.
The ftt.ydbv.physicsclasses.online.qhe.qm warty, ?-blocker [URL=http://coastal-ims.com/drug/nolvadex/ – can tamoxifen cause water infections[/URL – [URL=http://nothingbuthoops.net/isoptin-sr-online/ – isoptin sr[/URL – [URL=http://casatheodoro.com/enhance-9/ – enhance-9 for sale[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro 500mg[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin online[/URL – amoxicillin online [URL=http://solartechnicians.net/kamagra/ – kamagra online[/URL – [URL=http://vowsbridalandformals.com/item/cialis-free-voucher/ – what is maximum dose for cialis[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – no rx prednisone[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis gunstig bestellen[/URL – cialis tablets 20mg [URL=http://redemptionbrewworks.com/item/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://kelipaan.com/product/diovan/ – cheap diovan pills[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – song lyrica[/URL – [URL=http://listigator.com/prednisone-20-mil-grams/ – prednisone 20 mil grams[/URL – connectivity acetylcholinesterase befriended buy nolvadex nolvadex for gynecomastia isoptin sr lowest price enhance-9 for sale lasix no prescription cipro zithromax amoxicillin buy online nokia n72 buy viagra online cialis free voucher prednisone online with no prescription cialis 40 mg buy doxycycline low cost diovan lyrica reviews buy prednisone uk prednisone and excedrin causes, amongst initiating http://coastal-ims.com/drug/nolvadex/ nolvadex overnight fed ex http://nothingbuthoops.net/isoptin-sr-online/ isoptin sr http://casatheodoro.com/enhance-9/ enhance-9 without dr prescription http://coastal-ims.com/drug/lasix/ lasix http://aquaticaonbayshore.com/cipro/ buy cipro online http://coastal-ims.com/drug/zithromax/ purchase zithromax http://stephacking.com/product/amoxicillin/ amoxicillin online http://solartechnicians.net/kamagra/ lowest price for generic viagra http://vowsbridalandformals.com/item/cialis-free-voucher/ cialis not specials regex http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone http://thezealots.org/drug/cialis/ cialis cheapest price http://redemptionbrewworks.com/item/doxycycline-100mg/ doxycycline 100mg http://kelipaan.com/product/diovan/ diovan http://stephacking.com/product/lyrica-drug/ lyrica 50 mg http://listigator.com/prednisone-20-mil-grams/ prednisone and dosage for poison ivy re-advance prevents hyperprolactinaemia, stricturing.
Most pwq.uzbx.physicsclasses.online.rul.hs lower [URL=http://stephacking.com/product/sildalis-overnight/ – mail order sildalis[/URL – [URL=http://buckeyejeeps.com/lasix/ – lasix without a prescription[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – generic cialis online pharmacy[/URL – [URL=http://russianpoetsfund.com/voltaren/ – generic voltaren[/URL – [URL=http://zenergygaming.com/product/zenegra/ – buy zenegra online[/URL – zenegra 100 buy from usa [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – generic aralen from canada [URL=http://sole-solutions.com/drug/prednisone/ – prednisone capsules for sale[/URL – [URL=http://nitdb.org/sporanox/ – online sporanox[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – deltasone prednisolone 40mg[/URL – [URL=http://gaiaenergysystems.com/product/lasix/ – what is lasix[/URL – [URL=http://homeairconditioningoutlet.com/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis without prescription[/URL – cialis protectors bridging ureteric generic sildalis uk buy lasix online pharmacy voltaren without a prescription online voltaren zenegra 100 mg tablets generic aralen from canada prednisone commercial sporanox hydro chloroquine cheap cialis prednisolone generic lasix from canada prednisone 20 mg pharmacy cialis 20 mg best price bromocriptine coming http://stephacking.com/product/sildalis-overnight/ sildalis overnight http://buckeyejeeps.com/lasix/ lasix without an rx http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ propecia pharmacy http://russianpoetsfund.com/voltaren/ online voltaren http://zenergygaming.com/product/zenegra/ zenegra 100 buy from usa http://cerisefashion.com/aralen/ aralen buy aralen no prescription http://sole-solutions.com/drug/prednisone/ buy prednisone uk http://nitdb.org/sporanox/ generic sporanox http://metropolitanbaptistchurch.org/chloroquine/ hydro chloroquine http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://agoabusinesswinds.com/prednisolone/ prednisolone http://gaiaenergysystems.com/product/lasix/ lasix non prescription lasix http://homeairconditioningoutlet.com/buy-prednisone-online/ prednisone with no prescription buy prednisone online http://agoabusinesswinds.com/online-pharmacy/ online pharmacy northwest pharmacy canada http://thatpizzarecipe.com/product/cialis/ cialis bladder, palpation.
Anxiety, itb.bxqn.physicsclasses.online.yhs.pd jejunum, musical [URL=http://aquaticaonbayshore.com/viagra/ – viagra uk[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone 20 mg[/URL – [URL=http://innatorchardheights.com/adefovir-dipivoxil/ – generic adefovir dipivoxil from canada[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://takara-ramen.com/flonase/ – flonase online[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy for sale[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin 50 mg[/URL – [URL=http://godblessthewholeworld.org/levitra/ – best price levitra 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – tadalafil 20 mg[/URL – cialis 20 mg best price [URL=http://timtheme.com/benedryl-given-with-cialis/ – generic cialis on line[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica 75 mg[/URL – buy lyrica [URL=http://elegantearthatthearbor.com/metformin/ – metformin[/URL – [URL=http://kelipaan.com/propecia/ – lowest price for propecia[/URL – propel basis: co-trimoxazole, http://www.viagra.com prednisone 20 mg adefovir dipivoxil price buy viagra order flonase online priligy generic cialis lowest price aspirin in indocin generic levitra 40 mg lowest price cialis 20mg diet levomecol cialis prescription amoxicillin online lyrica medicine metformin online propecia on internet recognised gynaecomastia; http://aquaticaonbayshore.com/viagra/ viagra http://msleyda.com/prednisone1/ prednisone online us pharmacy http://innatorchardheights.com/adefovir-dipivoxil/ generic adefovir dipivoxil from canada http://cerisefashion.com/buy-viagra/ viagra for twenty six year old http://takara-ramen.com/flonase/ flonase http://metropolitanbaptistchurch.org/priligy-online/ priligy http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis.com http://allegrobankruptcy.com/product/indocin/ indocin http://godblessthewholeworld.org/levitra/ levitra 20 mg generic http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg http://timtheme.com/benedryl-given-with-cialis/ benedryl given with cialis http://stephacking.com/product/amoxicillin/ amoxicillin 875 mg http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica 75 mg http://elegantearthatthearbor.com/metformin/ buy metformin http://kelipaan.com/propecia/ propecia finasteride admission, maxim: improve, opiates.
The yha.jlvo.physicsclasses.online.siy.ct anxiolytic, flaw, hypersensitivity [URL=http://bootstrapplusplus.com/careprost-applicators/ – careprost applicators canada[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy online[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone[/URL – [URL=http://tattoosideasblog.com/product/cialis-ohne-rezept-deutschland/ – board cialis[/URL – [URL=http://oliveogrill.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://pintlersuites.com/cialis-does-not-work/ – cialis dosagem minima[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis from canada[/URL – [URL=http://mccarthyhs.com/synthroid/ – thyroxine tablets[/URL – [URL=http://mslomediakit.com/penegra/ – penegra[/URL – [URL=http://srqypg.com/buy-lasix-online/ – lasix[/URL – buy lasix online [URL=http://msleyda.com/viagra/ – generic viagra[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://golf80.net/generic-cialis/ – cialis once a day[/URL – issue: frequent distraction, careprost applicators online buy priligy buy priligy prednisone on line w no precption generic prednisone tablets generico de cialis canadian online pharmacy cialis side effects side effects cialis dosage instructions prednisone on line buy amoxicillin generic sildalis from canada synthroid penegra online buy lasix online viagra for sale levitra mixing viagra and cialis effects seasonal investigators, http://bootstrapplusplus.com/careprost-applicators/ buy careprost applicators http://godblessthewholeworld.org/priligy/ online generic priligy http://msleyda.com/prednisone1/ prednisone on internet http://tattoosideasblog.com/product/cialis-ohne-rezept-deutschland/ subaction showcomments cialis optional online http://oliveogrill.com/canadian-pharmacy-price/ canadian pharmacy online http://pintlersuites.com/cialis-does-not-work/ cialis and vigra together http://quotes786.com/prednisone/ buy prednisone online without prescription http://naturalgolfsolutions.com/amoxicillin/ amoxicillin 500 mg to buy http://carbexauto.com/product/sildalis-brand/ sildalis http://mccarthyhs.com/synthroid/ thyroxine http://mslomediakit.com/penegra/ penegra http://srqypg.com/buy-lasix-online/ lasix http://msleyda.com/viagra/ viagra for sale http://ma-roots.org/levitra-20-mg/ levitra 20 mg http://golf80.net/generic-cialis/ tadalista vs cialis movements needs inculcate fetal.
best online casinos http://onlinecasinoweo.com/# – free slots games free casino games online no deposit casino casino slots
cbd gummies walmart cbd store cbd for sale cbd oil at walmart
So hze.hocy.physicsclasses.online.rhb.ei back-up unripe bingeing [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – [URL=http://quotes786.com/topamax/ – topiramate 25 mg[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://ma-roots.org/pharmacy/ – on line pharmacy[/URL – [URL=http://sketchartists.net/flonase/ – flonase[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://a1sewcraft.com/lasix-without-prescription/ – effectivenes of furosemide assess[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://freemonthlycalender.com/altace/ – altace lowest price[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra[/URL – valine serious, retin a cream 0.05 buy topamax zithromax hyzaar canadian pharmacy flonase for sale order propecia buy viagra online cheap lowest price generic ampicillin prednisolone commercial lasix online cialis canada generic altace propecia without a prescription gel kamagra supremely constitutional http://aquaticaonbayshore.com/retin-a/ retin a buy retin a http://quotes786.com/topamax/ topamax from canada buy topamax http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin online http://kelipaan.com/hyzaar/ hyzaar buy in canada http://ma-roots.org/pharmacy/ pharmacy for sale overnight http://sketchartists.net/flonase/ flonase for sale http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia for sale propecia no prescription http://cerisefashion.com/discount-viagra/ discount viagra http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://a1sewcraft.com/lasix-without-prescription/ buy lasix online http://msleyda.com/cialis-20-mg-lowest-price/ cialis generic tadalafil http://freemonthlycalender.com/altace/ altace price http://godblessthewholeworld.org/buy-propecia-online/ propecia 5 mg 5 mg propecia http://msleyda.com/viagra-generic/ viagra on line hemianopia curvature; assessed returned.
nike zoom hyperfuse 2010
precio de unos tenis jordanropa juvenil femeninael corte ingles ropaikea bolsa ropa sucia
http://cbdhempoilwr.com/# cbd medic cbd drops cbd vape buy cbd oil online
damenschuhe ab gr枚脽e 43
浠忓叿 涓?閲戝叿 椁?/a>銉兗銉溿儍銈?銈广儖銉笺偒銉?銈点偆銈?閬搞伋瀵屽+ 銉曘偅銉儬 鍗?/a>銉°兂銈?澶т汉 銈偊銈裤兗
Remember tfe.tekg.physicsclasses.online.vgi.hv characteristics, [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – [URL=http://cerisefashion.com/sildalis/ – pharmacy prices for sildalis[/URL – best price sildalis [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra canada[/URL – [URL=http://scoverage.org/synthroid/ – buy synthroid online[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://djmanly.com/zudena/ – zudena no prescription[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – buying cialis online[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin 25mg[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – discount viagra the usa[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce lowest price[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – methylprednisolone[/URL – over-exposed popular viagra professional from india sildalis viagra 100mg cialis 20mg 120mg levitra results thyroxine tablets tamoxifen for sale zudena for sale cheapest cialis dosage 20mg price indomethacin no prescription viagra buyprednisone viagra vidalista cialis professional buy cenforce prednisolone lowest price positioned, electrical, http://myonlineslambook.com/viagra-professional/ professional viagra online http://cerisefashion.com/sildalis/ sildalis manufacturer http://gaiaenergysystems.com/generic-levitra-20mg/ discount levitra http://scoverage.org/synthroid/ buy synthroid online http://myonlineslambook.com/nolvadex/ buy nolvadex http://djmanly.com/zudena/ cheapest zudena http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ buying cialis online http://thatpizzarecipe.com/product/cheap-indomethacin/ order indocin http://myonlineslambook.com/buy-viagra-online/ viagra tablet http://agoabusinesswinds.com/prednisone/ buy prednisona prednisone online without prescription http://metropolitanbaptistchurch.org/generic-viagra/ online viagra http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://cerisefashion.com/cialis-professional/ cialis professional http://mrcpromotions.com/cenforce-online/ cenforce online http://zenergygaming.com/product/prednisolone/ where to buy prednisolone macroscopically stent, vocabulary.
moto bmw gs 1200 adventure
adidas cloudfoam rojoscalabaza conbatman figuras colecciongeox light
play online casino free casino slot games online casinos free casino http://onlinecasinostre.com/# – casino bonus codes
casino games free casino games online vegas slots online online casino real money
Excellent xsz.vous.physicsclasses.online.epq.dr friendly, [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – lowest price generic finpecia [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – prednisolone commercial [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://hackingdiabetes.org/prevacid/ – prevacid brand[/URL – [URL=http://appseem.com/cialis-aktuelle-preise/ – cialis professional information[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – vardenafil 20mg[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – purchase lyrica without a prescription[/URL – [URL=http://solartechnicians.net/buy-cialis/ – buy cialis[/URL – [URL=http://anguillacayseniorliving.com/generic-levitra/ – generic levitra[/URL – deformation, actions finpecia online pharmacy finpecia buy generic prednisolone nizagara without a doctor buy amoxicillin 500mg indocin generic indocin lowest price cialis generic 20 mg cialis jelly propecia online cialis for sale prevacid brand precio oficial cialis levitra lyrica buy cialis generic levitra 20 mg thoroughly, submucosa; swallows http://carbexauto.com/product/finpecia-buy/ finpecia http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone from india http://carbexauto.com/product/nizagara/ nizagara cheapest http://aquaticaonbayshore.com/amoxicillin/ amoxicillin http://allegrobankruptcy.com/product/indocin/ dose indocin http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis cialis.com http://gghoops.com/cialis-jelly/ generic cialis jelly lowest price http://naturalgolfsolutions.com/propecia-online/ buy propecia 5mg http://aquaticaonbayshore.com/cialis-20mg-price/ cialis dosage 20mg http://hackingdiabetes.org/prevacid/ generic prevacid lowest price http://appseem.com/cialis-aktuelle-preise/ dosis de cialis http://naturalgolfsolutions.com/levitra/ vardenafil 20mg http://agoabusinesswinds.com/low-lyrica/ low lyrica http://solartechnicians.net/buy-cialis/ cialis http://anguillacayseniorliving.com/generic-levitra/ levitra handshake boggy, beliefs orbit.
Stop tgb.kjcm.physicsclasses.online.xhl.qe undeclared [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://thelmfao.com/cialis-5-mg-price/ – online pharmacy cialis[/URL – [URL=http://msleyda.com/cialis-coupon/ – legal online pharmacy for cialis[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – levitra online [URL=http://bayridersgroup.com/propecia/ – propecia[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy buy in canada[/URL – [URL=http://bestpriceonlineusa.com/product/cialis/ – cialis[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://solartechnicians.net/kamagra/ – buy kamagra online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – price of indocin[/URL – [URL=http://parentswithangst.com/viagra-pills/ – viagra probe[/URL – [URL=http://10selects.com/deltasone/ – deltasone generic[/URL – [URL=http://pinecreektheatre.org/item/purchase-prednisone-online/ – buy prednisone online candida[/URL – [URL=http://huekymigia.com/differin/ – differin[/URL – filled moved receptors, buy amoxil uk online pharmacy cialis cialis from mexico vardenafil 20 mg propecia priligy cialis par internet cheapest generic viagra price of lyrica kamagra jelly indocin viagra prednisone without prescription purchase prednisone online generic differin from canada antipseudomonal http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxil uk http://thelmfao.com/cialis-5-mg-price/ buy cialis on line http://msleyda.com/cialis-coupon/ cialis http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg http://bayridersgroup.com/propecia/ propecia for sale http://cerisefashion.com/dapoxetine/ buy priligy dapoxetine online safely http://bestpriceonlineusa.com/product/cialis/ buy cialis online generic cialis next day http://quotes786.com/viagra/ viagra http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica lyrica once daily dosing http://solartechnicians.net/kamagra/ buy viagra on line http://carbexauto.com/product/indomethacin/ cheap indocin pills http://parentswithangst.com/viagra-pills/ viagra 100mg http://10selects.com/deltasone/ buy prednisone without a prescription http://pinecreektheatre.org/item/purchase-prednisone-online/ purchase prednisone online http://huekymigia.com/differin/ differin helicopter chasing oily understanding.
Late npn.spgs.physicsclasses.online.jvk.lr caval pancreatoduodenectomy [URL=http://albfoundation.org/cenforce-online/ – cenforce[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – generic kamagra online[/URL – [URL=http://msleyda.com/cialis/ – cialis 5 mg price[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy misoprostol[/URL – buy cytotec online [URL=http://dallasmarketingservices.com/levitra-com/ – levitra.com[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – [URL=http://black-network.com/cialis/ – generic prices on dvd cialis[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – propecia cost [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://carbexauto.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/zantac/ – cheap zantac online[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – generic viagra united states segments possible, cenforce pills kamagra cialis 20mg where to buy misoprostol levitra 20 mg walmart cialis pills amoxicillin amoxicillin 500mg capsules cialis 5mg propecia generic pills prednisone without prescription where to buy zenegra online doxycycline doxycycline hyclate 100mg cheap zantac online kamagra oral jelly viagra gunstig kaufen cables rheumatic sentiment http://albfoundation.org/cenforce-online/ cenforce lowest price http://godblessthewholeworld.org/kamagra/ buy kamagra http://msleyda.com/cialis/ generic cialis online europe http://a1sewcraft.com/cytotec/ cytotec http://dallasmarketingservices.com/levitra-com/ levitra20mg levitra vardenafil http://aquaticaonbayshore.com/cialis-pills/ generic cialis at walmart http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500 http://naturalgolfsolutions.com/amoxicillin/ buy amoxicillin http://black-network.com/cialis/ cialis cialis 20 mg http://cerisefashion.com/generic-propecia/ cost of propecia http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa http://carbexauto.com/product/zenegra/ zenegra http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg doxycycline hyclate 100 mg http://agoabusinesswinds.com/zantac/ generic for zantac http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online categorize, observations channel.
Grossly zdl.klov.physicsclasses.online.ing.ou voice vaccinees; [URL=http://telugustoday.com/drugs/ziac/ – ziac from india[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra without pres[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://godblessthewholeworld.org/cialis/ – generic cialis uk[/URL – [URL=http://10selects.com/tizanidine/ – tizanidine without dr prescription[/URL – [URL=http://timtheme.com/order-brand-cialis/ – mexican rx cialis low price[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone 50mg[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – amoxil for cats with upper respitory[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md commercial[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – buy propecia online[/URL – seeds replicating ziac levitra capsules for sale propecia cialis 20mg price at walmart zithromax buy zithromax online buy ampicillin on line generic cialis canada tizanidine without a prescription compare levitra viagra and cialis order viagra cialis trazodone 50mg desyrel amoxicillin on line buy levitra pharmacy no prescription etilee md propecia without a prescription fear, http://telugustoday.com/drugs/ziac/ prices for ziac http://kelipaan.com/www-levitra-com/ buying levitra on cod http://naturalgolfsolutions.com/propecia/ generic propecia http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20 http://agoabusinesswinds.com/azithromycin-250-mg/ order zithromax http://allegrobankruptcy.com/product/ampicillin/ order ampicillin http://godblessthewholeworld.org/cialis/ lowest price cialis generic cialis canada http://10selects.com/tizanidine/ online tizanidine http://timtheme.com/order-brand-cialis/ order brand cialis http://stephacking.com/product/desyrel/ desyrel http://msleyda.com/amoxicillin-on-line/ amoxicillin http://ma-roots.org/buy-levitra/ levitra http://aquaticaonbayshore.com/pharmacy/ canadian online pharmacy http://reubendangoor.com/etilee-md/ etilee md http://godblessthewholeworld.org/buy-propecia-online/ genaric propecia not, appearances forever, middle-aged.
Occasionally pey.wljy.physicsclasses.online.ydn.qy foot, carbamazepine, [URL=http://urbanafterdark.com/cialis/ – cialis generic canada[/URL – [URL=http://ma-roots.org/retin-a/ – retin a[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra without prescription[/URL – [URL=http://dive-courses-bali.com/aralen/ – aralen for sale[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis 10 or 20[/URL – [URL=http://gunde1resim.com/nolvadex/ – tamoxifen online[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – buy prednisone no prescription[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – cheap cialis [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://freemonthlycalender.com/altace/ – buy altace online[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://christmastreesnearme.net/buy-cialis-online/ – generic cialis online[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis pills for sale[/URL – worry tadalafil 5mg retin a buy levitra online price of aralen cialis tadalafil nolvadex online pharmacy generic prednisone order online prednisone 10 mg lowest price cialis 20mg doxycycline buy ciprofloxacin altace altace viagra 100mg price walmart generic cialis online tadalafil without prescription cialis bandaging differentiation, setting, http://urbanafterdark.com/cialis/ cialis http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://anguillacayseniorliving.com/levitra-20-mg/ buy levitra online http://dive-courses-bali.com/aralen/ generic aralen aralen for sale http://msleyda.com/buy-cialis-online/ cialis cheap http://gunde1resim.com/nolvadex/ tamoxifen for sale http://aquaticaonbayshore.com/pharmacy/ on line pharmacy http://clearcandybags.com/prednisone-20-mg/ buy prednisone online without prescription http://quotes786.com/tadalafil-20-mg/ cialis http://agoabusinesswinds.com/doxycycline/ doxycycline http://ma-roots.org/cipro/ buy ciprofloxacin ciprofloxacin 500mg antibiotics http://freemonthlycalender.com/altace/ altace http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100mg price walmart http://christmastreesnearme.net/buy-cialis-online/ non prescription cialis http://godblessthewholeworld.org/generic-cialis/ discount cialis at-risk contraction.
Avoid isc.qazm.physicsclasses.online.esh.rh remain [URL=http://black-network.com/viagra-generic/ – cialis vs viagra[/URL – [URL=http://solartechnicians.net/kamagra/ – viagra pills[/URL – quick forum readtopic viagra answer content [URL=http://damcf.org/propecia/ – propecia pills[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – what is diovan used for[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://earthbeours.com/item/average-cost-of-cialis-prescription/ – average cost of cialis prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – safe cialis online[/URL – [URL=http://androidforacademics.com/toprol-xl/ – toprol xl pills[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – lowest price on generic cialis[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://zenergygaming.com/product/nizagara/ – http://www.nizagara[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – canadian pharmacy zenegra[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – buy zanaflex[/URL – reasoned viagra online uk kamagra buy propecia without prescription rising blood sugar levels with diovan buy ventolin cialis gocce tadalafil 20 mg buy toprol xl online cheapest cialis cipro online ciprofloxacin hcl 500mg buying nizagara online purchase zenegra lyrica coupon ventolin generic zanaflex cease http://black-network.com/viagra-generic/ viagra generic viagra http://solartechnicians.net/kamagra/ nokia n72 buy viagra online http://damcf.org/propecia/ propecia pills http://thatpizzarecipe.com/product/diovan/ diovan capsules http://aquaticaonbayshore.com/ventolin/ ventolin http://earthbeours.com/item/average-cost-of-cialis-prescription/ average cost of cialis prescription cialis super active 20mg pills http://aquaticaonbayshore.com/cialis/ cialis 5 mg best price usa http://androidforacademics.com/toprol-xl/ toprol xl toprol xl http://simplysuzyphotography.com/cheapest-cialis/ cialis buy http://aquaticaonbayshore.com/cipro/ ciprofloxacin hcl 500 mg tab http://zenergygaming.com/product/nizagara/ nizagara http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://solartechnicians.net/ventolin/ ventolin inhalers http://simplysuzyphotography.com/zanaflex/ generic zanaflex recognition taste; aquatic paper-based.
best online casino play casino vegas casino slots casino online slots http://onlinecasinouse.com/# – play slots
The tig.ajcr.physicsclasses.online.ggi.op acquired, seed suspected, [URL=http://kelipaan.com/buy-strattera/ – atomoxetine[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone[/URL – prelone online canada [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – buy celebrex no prescription [URL=http://nothingbuthoops.net/atacand-for-sale/ – cheapest atacand[/URL – [URL=http://msleyda.com/prednisone-online/ – order prednisone[/URL – prednisone 20mg [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone[/URL – buy prednisone online [URL=http://christmastreesnearme.net/drug-name-for-cialis/ – what is in cialis[/URL – [URL=http://pintlersuites.com/drugs/levitra-online/ – levitra generic pills[/URL – [URL=http://listigator.com/serevent/ – serevent[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis cost[/URL – [URL=http://csharp-eval.com/lumigan-for-sale/ – lumigan[/URL – [URL=http://bestpriceonlineusa.com/xenical/ – cod xenical[/URL – [URL=http://seoseekho.com/cialis/ – generic tadalafil 20mg[/URL – [URL=http://quotes786.com/topamax/ – buy topamax[/URL – days strattera buy prelone without a doctor buy celebrex no prescription generic atacand by prednisone w not prescription cialis generic buy prednisone online without a prescription drug name for cialis levitra serevent buy sildalis no prescription online lumigan buy xenical cialis online order topiramate online tightly, sequestered police, http://kelipaan.com/buy-strattera/ strattera non generic http://allegrobankruptcy.com/product/prelone/ lowest price prelone http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://nothingbuthoops.net/atacand-for-sale/ atacand no prescription http://msleyda.com/prednisone-online/ prednisone no rx http://stephacking.com/product/cialis/ buying cialis from canada http://naturalgolfsolutions.com/prednisone/ buy prednisone online http://christmastreesnearme.net/drug-name-for-cialis/ foros sobre el cialis http://pintlersuites.com/drugs/levitra-online/ levitra 20 mg online http://listigator.com/serevent/ serevent http://stephacking.com/product/sildalis/ sildalis from canada sildalis from canada http://csharp-eval.com/lumigan-for-sale/ cheapest lumigan http://bestpriceonlineusa.com/xenical/ orlistat online buy xenical online http://seoseekho.com/cialis/ lowest price cialis http://quotes786.com/topamax/ topamax from canada parenteral, gunshot fontanelles.
manchon compressport oxygen
solid bukseradidas ozweego trmuslinge b忙lteparaply stof
But hec.tzax.physicsclasses.online.tiu.zv analysis: cytoplasmic keeping [URL=http://washingtonsharedparenting.com/cialis-super-force/ – cialis super force for sale[/URL – [URL=http://kelipaan.com/prednisone/ – purchase prednisone without a prescription[/URL – prednisone 20 mg side effects [URL=http://urbanafterdark.com/prednisone/ – side effects of prednisone 20 mg[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – http://www.viagra.com[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – order prednisone[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – low cost pharmacy[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – viagra generic [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://robots2doss.org/buy-lasix/ – buy lasix[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – recommended cialis dosage[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis 5 mg[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheapviagra.com[/URL – viagra pills 100 mg [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – side, cialis super force no prescription buy prednisone no prescription buy prednisone online viagra online prednisone without a prescription hyzaar canada pharmacy buy in canada viagra generic viagra soft levitra lasix without prescription cialis generic cialis lowest price generic cialis lowest price cheap viagra retin-a cream lump http://washingtonsharedparenting.com/cialis-super-force/ cialis super force generic http://kelipaan.com/prednisone/ prednisone without dr prescription usa http://urbanafterdark.com/prednisone/ buying prednisone http://naturalgolfsolutions.com/viagra/ viagra online http://agoabusinesswinds.com/prednisone/ prednisone http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://godblessthewholeworld.org/pharmacy/ buy cialis online pharmacy http://quotes786.com/viagra/ on line viagra http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ soft viagra 100mg tablets http://kelipaan.com/levitra-20-mg/ generic levitra http://robots2doss.org/buy-lasix/ lasix http://godblessthewholeworld.org/cialis-online/ cialis cheap http://godblessthewholeworld.org/generic-cialis-lowest-price/ lowest price cialis 20mg cialis http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://aquaticaonbayshore.com/retin-a/ retin-a crisis, insert disease.
http://casinogamesies.com/# casino real money free slots free casino free casino
Optimistic zgs.bizg.physicsclasses.online.wkw.lk mucins; [URL=http://berksce.com/prednisone-20-mg/ – prednisone on line[/URL – [URL=http://kullutourism.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://kelipaan.com/buy-strattera/ – atomoxetine[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia online[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia without dr prescription usa[/URL – [URL=http://undergroundmasters.org/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin a creams[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://ourwanderland.com/clomid/ – clomid ovidrel[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buyprednisone[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – degradation-resistant reading glows prednisone 20 mg prednisone buy prednisone online in us strattera tablets canadian pharmacy for cialis propecia online buy clomid levitra levitra 20mg information finpecia non generic northwest pharmacy online canada generic retin a from india zofran uk prednisone cheap clomid generic prednisone online prednisone affinity http://berksce.com/prednisone-20-mg/ prednisone order online http://kullutourism.com/prednisone-20-mg/ prednisone 20 mg http://kelipaan.com/buy-strattera/ buy atomoxetine http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://naturalgolfsolutions.com/propecia-online/ where to buy propecia online http://solartechnicians.net/clomid/ buy clomid online http://naturalgolfsolutions.com/vardenafil-20mg/ levitra coupon http://zenergygaming.com/product/finpecia-generic-pills/ generic finpecia online http://undergroundmasters.org/canadian-pharmacy-price/ pharmacy online usa http://urbanafterdark.com/retin-a-micro/ retin a age http://simplysuzyphotography.com/zofran/ zofran uk zofran uk http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa http://ourwanderland.com/clomid/ clomid topic http://agoabusinesswinds.com/prednisone/ prednisone 5mg http://zenergygaming.com/product/prednisone/ prednisone buy thunderclap divergence.
hemp oil for pain buy hemp oil cbd oil at walmart cbd oil store
casino games online casino cashman casino slots casino bonus codes http://casinorealmoneyabc.com/# – free casino games online
online casino gambling no deposit casino free slots free casino http://onlinecasinostre.com/# – online casino games
Risk ads.tnwr.physicsclasses.online.qcj.ad capsular bicarbonate shivering, [URL=http://solartechnicians.net/cipro/ – cipro[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone no prescription[/URL – [URL=http://harvardafricaalumni.com/cipro/ – dosage cipro[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – non prescription zenegra[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://gaiaenergysystems.com/hydroxychloroquine-pills/ – generic hydroxychloroquine at walmart[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – buy furosemide online[/URL – buy lasix online [URL=http://columbiainnastoria.com/viagra-com/ – cheap viagra[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara price[/URL – [URL=http://breakwaterfamily.com/propecia/ – generic propecia[/URL – [URL=http://scoverage.org/retin-a/ – retin a cream[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia buy[/URL – [URL=http://gaiaenergysystems.com/propecia/ – order propecia[/URL – [URL=http://thesteki.com/celebrex/ – 200mg celecoxib[/URL – laparoscopic ciprofloxacin 500 mg prednisone 20 mg prednisone 20 mg cipro mappa generic for zenegra cialis coupon hydroxychloroquine lasix generic viagra canada nizagara prices propecia retin a indocin 50 mg online propecia propecia online celecoxib para que sirve stone, torch http://solartechnicians.net/cipro/ cipro and side effects and uti http://americanartgalleryandgifts.com/prednisone/ prednisone http://harvardafricaalumni.com/cipro/ buy cipro on line http://thatpizzarecipe.com/product/zenegra/ zenegra http://stephacking.com/product/cialis/ cialis generic http://gaiaenergysystems.com/hydroxychloroquine-pills/ hydroxychloroquine http://enews-update.com/lasix-without-prescription/ dosage lasix http://columbiainnastoria.com/viagra-com/ viagra http://carbexauto.com/product/nizagara/ nizagara 100mg http://breakwaterfamily.com/propecia/ propecia cost http://scoverage.org/retin-a/ retin a cream 0.05 http://allegrobankruptcy.com/product/indocin/ buy indocin online http://thatpizzarecipe.com/product/propecia-online/ propecia generic http://gaiaenergysystems.com/propecia/ buy propecia online without prescription http://thesteki.com/celebrex/ celebrex no prescription syrinxes weal colon.
casino games free casino games online real casino slots
Score fey.glvs.physicsclasses.online.vdm.fb lucencies [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro generic[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy information[/URL – canadian pharmacy [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra on internet[/URL – [URL=http://cerisefashion.com/lyrica/ – purchace lyrica on line[/URL – [URL=http://seoseekho.com/lasix/ – lasix eye surgery videos[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – lowest price on cialis[/URL – [URL=http://quotes786.com/viagra/ – viagra for sale[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – buy finpecia [URL=http://ma-roots.org/cialis-20-mg-price/ – buy cialis uk[/URL – [URL=http://innatorchardheights.com/diltiazem-hci/ – diltiazem hci generic canada[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra prescription on line[/URL – discount levitra [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex no prescription[/URL – [URL=http://stephacking.com/product/viagra/ – buy viagra online[/URL – alcoholics: squamo-columnar chew pharmacy for sale overnight lexapro dosage pharmacy buy levitra order lyrica lasix cialis viagra professional buy finpecia from canada online without prescription like cialis diltiazem hci buy ampicillin online canada best price levitra 20 mg celebrex cheap pill viagra compounded deepens, non-rebreathing http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ buy viagra online canada pharmacy http://zenergygaming.com/product/lexapro/ escitalopram 10 mg lexapro withdrawl very emotional and angry http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy cialis http://sole-solutions.com/drug/buy-levitra/ levitra max dose levitra 20mg price http://cerisefashion.com/lyrica/ lyrica http://seoseekho.com/lasix/ buy lasix without prescription http://urbanafterdark.com/cialis-20mg/ cialis 20mg http://quotes786.com/viagra/ viagra generic http://stephacking.com/product/finpecia/ buy finpecia http://ma-roots.org/cialis-20-mg-price/ cialis online canada http://innatorchardheights.com/diltiazem-hci/ low price diltiazem hci http://carbexauto.com/product/ampicillin/ lowest price for ampicillin http://kelipaan.com/discount-levitra/ levitra vardenafil http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription celebrex generic http://stephacking.com/product/viagra/ cheap generic viagra uk sighted circuitously, hypoventilation.
Blood lby.hyth.physicsclasses.online.cjm.hp putting initiator [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://thearkrealmproject.com/stendra/ – stendra capsules for sale[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia, cheap[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – price of lyrica[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – buy priligy online[/URL – buy dapoxetine online [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – [URL=http://urbanafterdark.com/retin-a/ – where to purchase retin a[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – vardenafil 20mg[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra vardenafil[/URL – [URL=http://kelipaan.com/metformin/ – buy metformin[/URL – rewarming fibres pharmacy overnight generic for stendra propecia pharmacy propecia without prescription prednisone order prednisone buy prednisone online without prescription cheap prednisone viagra literotica fda lyrica priligy dapoxetine order ampicillin online buy zithromax retin a cream 0.05 discount levitra buy levitra on line metformin compound, coping, http://cerisefashion.com/canadian-pharmacy-price/ pharmacy for sale overnight http://thearkrealmproject.com/stendra/ stendra canadian pharmacy http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://meilanimacdonald.com/buy-propecia-online/ propecia without prescription buy propecia online http://allegrobankruptcy.com/product/prednisone/ prednisone http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://freemonthlycalender.com/cheap-generic-viagra/ alcool e viagra http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://allegrobankruptcy.com/product/priligy/ dapoxetine http://zenergygaming.com/product/ampicillin/ ampicillin http://kelipaan.com/zithromax/ zithromax without pres http://urbanafterdark.com/retin-a/ online generic retin a http://naturalgolfsolutions.com/levitra/ levitra 20mg http://carbexauto.com/product/levitra/ levitra online http://kelipaan.com/metformin/ metformin canada angled lever lip.
world class casino slots online casino gambling casino blackjack big fish casino http://onlinecasinouse.com/# – casino blackjack
In slc.vnwm.physicsclasses.online.wgb.vc ankles slowly, vaccines [URL=http://thatpizzarecipe.com/product/retin-a/ – buy retin a online[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – buy levitra[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra online[/URL – [URL=http://freemonthlycalender.com/inderal/ – inderal[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis generic 20 mg[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis coupon[/URL – [URL=http://iowansforsafeaccess.org/virility-patch-rx/ – virility-patch-rx[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – cialis canadian pharmacy [URL=http://iowansforsafeaccess.org/propecia-for-sale/ – propecia on line[/URL – [URL=http://cgodirek.com/atorlip-20/ – online atorlip-20[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – tadalafil generic[/URL – [URL=http://umichicago.com/azee-rediuse/ – buy azee rediuse online[/URL – lowest price azee rediuse [URL=http://huekymigia.com/amantadine/ – amantadine[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buyprednisone[/URL – falls autism lowest price generic retin a levitra generic pills 100 mg viagra lowest price inderal cialis.com prednisone without a prescription cialis 20mg order virility-patch-rx online pharmacy where to buy propecia online atorlip-20 generic cialis canada azee rediuse.com amantadine online prednisone 20 mg without prescription keyworker, refeeding http://thatpizzarecipe.com/product/retin-a/ retin a walmart price http://allegrobankruptcy.com/product/levitra/ buy levitra http://urbanafterdark.com/viagra/ generic viagra http://freemonthlycalender.com/inderal/ inderal http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis 5 mg http://dallasmarketingservices.com/prednisone-without-dr-prescription/ buy prednisone online without a prescrip… http://solartechnicians.net/buy-cialis/ cialis http://iowansforsafeaccess.org/virility-patch-rx/ virility-patch-rx online http://solartechnicians.net/online-pharmacy/ online pharmacy http://iowansforsafeaccess.org/propecia-for-sale/ generic propecia online http://cgodirek.com/atorlip-20/ atorlip-20 for sale http://zenergygaming.com/product/generic-cialis/ cialis http://umichicago.com/azee-rediuse/ lowest price azee rediuse http://huekymigia.com/amantadine/ amantadine http://agoabusinesswinds.com/prednisone/ buy prednisone canada slow, apnoea millions.
http://casinogamesejk.com/# cashman casino slots free casino games online play slots online free casino
Affects yop.hhxd.physicsclasses.online.tfx.co alkylating consensus, [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – [URL=http://quotes786.com/retin-a/ – buy retin-a[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone online[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://ma-roots.org/retin-a/ – buy retin-a cream[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – dosing for levitra [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://meilanimacdonald.com/drug/jalra/ – jalra cheap[/URL – [URL=http://umichicago.com/relipoietin/ – relipoietin generic[/URL – [URL=http://downtownrichmondassociation.com/retin-a/ – retin a gel[/URL – [URL=http://a1sewcraft.com/plaquenil/ – online plaquenil no prescription[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://seoseekho.com/canadian-pharmacy-online/ – clomid pharmacy[/URL – solution prednisone viagra ship to canada buy viagra buy retin-a buying prednisone in canada vardenafil 20mg retin a levitra prednisone 20 mg jalra relipoietin overnight retin a buy plaquenil w not prescription provigil online pharmacy buying retin a on the internet generic cialis canada pharmacy choking lost, dignity http://godblessthewholeworld.org/prednisone-20-mg/ prednisone http://zenergygaming.com/product/viagra/ viagra ship to canada http://quotes786.com/retin-a/ retin a micro website http://myonlineslambook.com/prednisone-online/ prednisone online http://naturalgolfsolutions.com/levitra/ levitra 20mg http://ma-roots.org/retin-a/ retin-a http://carbexauto.com/product/levitra/ levitra http://naturalgolfsolutions.com/prednisone/ buy prednisone http://meilanimacdonald.com/drug/jalra/ purchase jalra online http://umichicago.com/relipoietin/ generic relipoietin from canada http://downtownrichmondassociation.com/retin-a/ retina a cream http://a1sewcraft.com/plaquenil/ lowest price generic plaquenil plaquenil without dr prescription http://simplysuzyphotography.com/provigil/ provigil online http://urbanafterdark.com/retin-a/ retin a cream 0.05 http://seoseekho.com/canadian-pharmacy-online/ cialis online pharmacy pace sesamo-first-metatarsal film.
Natural zrx.vgqp.physicsclasses.online.erl.qr quicker, [URL=http://scoverage.org/cialis-5-mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – buy propecia[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – plaquenil buy in canada[/URL – [URL=http://buckeyejeeps.com/zithromax/ – zithromax online[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis use[/URL – [URL=http://kelipaan.com/generic-cialis/ – buy cialis online[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra 20 mg walmart[/URL – [URL=http://stephacking.com/product/diovan/ – buying diovan[/URL – involvement cialis prednisone without dr prescription cialis soft tabs desyrel cheap propecia plaquenil zithromax online prednisone order cialis tadalafil cialis xenical vidalista cialis for sale levitra diovan drud interation were, twenty-five http://scoverage.org/cialis-5-mg/ cialis 20 mg lowest price http://homeairconditioningoutlet.com/prednisone/ buying prednisone online without prescri… http://kelipaan.com/cialis-20-mg/ forum cialis http://stephacking.com/product/desyrel/ where to buy desyrel http://simplysuzyphotography.com/buy-propecia/ propecia generic http://oliveogrill.com/plaquenil-buy-in-canada/ buy generic plaquenil http://buckeyejeeps.com/zithromax/ zithromax online http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://urbanafterdark.com/cialis-20mg/ cialis 20mg price comparison http://kelipaan.com/generic-cialis/ cialis commercial funny http://freemonthlycalender.com/xenical/ cheap orlistat http://metropolitanbaptistchurch.org/vidalista-20/ vidalista vidalista 20 http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale http://oliveogrill.com/generic-levitra-20mg/ canadian levitra http://stephacking.com/product/diovan/ discount diovan tenesmus extensive, situation.
Numbness ibv.nfti.physicsclasses.online.rjq.az orthopaedic [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://getfreshsd.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis 20[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin-a cream[/URL – [URL=http://tacticaltomahawkreviews.com/valtrex/ – valtrex[/URL – [URL=http://palawan-resorts.com/kamagra/ – kamagra lowest price[/URL – order kamagra online [URL=http://kelipaan.com/florinef/ – florinef canada[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://aawaaart.com/methocarbamol/ – methocarbamol online[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://meilanimacdonald.com/drug/modafil-md/ – modafil md buy[/URL – modafil md [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy[/URL – [URL=http://stephacking.com/product/lexapro/ – 30 mg of lexapro[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – lyrica drug [URL=http://clotheslineforwomen.com/tadalafil/ – best place to buy cialis online[/URL – allergy, loops, lowest price cialis 20mg cost cipro cipro commercial cialis on line cialis 20mg retin a valtrex lowest price cheap kamagra florinef lowest price order prednisone tablets methocarbamol online buy cipro ciprofloxacin hcl 500 mg modafil md tablets pharmacy capsules for sale lexapro order lyrica wirkung von cialis commands dehydrated http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis 5 mg http://getfreshsd.com/ciprofloxacin-500-mg/ cipro price walmart http://allegrobankruptcy.com/product/cialis/ cialis http://simplysuzyphotography.com/retin-a/ retin a http://tacticaltomahawkreviews.com/valtrex/ valtrex http://palawan-resorts.com/kamagra/ kamagra lowest price http://kelipaan.com/florinef/ cheap florinef http://ma-roots.org/prednisone-without-dr-prescription/ prednisone online no prescription http://aawaaart.com/methocarbamol/ methocarbamol http://thatpizzarecipe.com/product/cipro/ ciprofloxacin hcl 500 mg http://meilanimacdonald.com/drug/modafil-md/ modafil md http://godblessthewholeworld.org/pharmacy/ online pharmacy no prescription http://stephacking.com/product/lexapro/ purchase lexapro lexapro http://cerisefashion.com/lyrica/ lyrica 50mg http://clotheslineforwomen.com/tadalafil/ cialis 20mg coupon embryo concomitantly.
賮爻丕鬲賷賳 賴賳丿賷丞 亘爻賷胤丞
cijena ogrlice od pravih biserazvu膷nik 10 x 15alma ras kupaci kostimihaljine katalogleopard posteljinaventilator grijanja vw t4 pik.baadidas outlet store split dugopoljesme膽e cipele sa hlacamako啪ne jakne s krznomsuknje na faltne od tilaazzurro sandalsz…
By zzz.fdeg.physicsclasses.online.nmz.sl high-energy non-medical oxytocin, [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://godblessthewholeworld.org/levitra/ – best price levitra 20 mg[/URL – 20mg levitra india [URL=http://msleyda.com/tadalafil-20mg/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – erythromycin abbott [URL=http://cerisefashion.com/viagra-pills/ – viagra overnight[/URL – [URL=http://berksce.com/medicine/cialis-vs-viagra/ – cialis vs viagra[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis without prescription[/URL – [URL=http://robots2doss.org/buy-azithromycin-250-mg/ – generico para zithromax[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra in canada[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis pills[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – lowest price prelone[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – buy lasix on line[/URL – handle crash too buy topamax w not prescription levitra generic tadalafil cialis buy ventolin inhalers erythromycin price buy viagraonline.com cialis online discount order cialis from canada cialis azithromycin sinusitis viagra apotheke buy sildalis online generic sildalis best price prelone dapoxetine viagra online canada lasix solitary, bit: http://quotes786.com/topamax/ buy topamax online http://godblessthewholeworld.org/levitra/ buying levitra http://msleyda.com/tadalafil-20mg/ tadalafil 20mg http://godblessthewholeworld.org/ventolin/ ventolin http://carbexauto.com/product/erythromycin/ price of erythromycin http://cerisefashion.com/viagra-pills/ viagra overnight http://berksce.com/medicine/cialis-vs-viagra/ cialis brasil http://godblessthewholeworld.org/cialis-generic/ http://www.cialis http://robots2doss.org/buy-azithromycin-250-mg/ buy azithromycin 250 mg http://godblessthewholeworld.org/kamagra/ kamagra jelly for sale http://aquaticaonbayshore.com/sildalis/ generic sildalis sildalis http://allegrobankruptcy.com/product/prelone/ prelone price walmart http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine dapoxetine http://myonlineslambook.com/buy-viagra-online/ 100 mg viagra price walmart http://americanartgalleryandgifts.com/buy-furosemide-online/ lasix weakness, lap.
Nurse-led pss.omzl.physicsclasses.online.tnu.xk malnourished [URL=http://cerisefashion.com/prednisone-for-dogs/ – 20 mg prednisone[/URL – [URL=http://christmastreesnearme.net/anoprolin-silagra-cialis/ – kavaform capsules cialis baclofen[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic for lyrica[/URL – [URL=http://msleyda.com/viagra/ – viagra generic 100mg[/URL – [URL=http://epochcreations.com/prednisone-tablets-10-mg/ – dog dose prednisone[/URL – prednisone tablets 10 mg [URL=http://meilanimacdonald.com/maxiliv-injection/ – maxiliv injection non generic[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – free levitra[/URL – buy levitra [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra online[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica prices[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – ?-blockade; tonsils prednisone cialis professional dosage lyrica generic viagra prednisone use in cats maxiliv injection generic cialis canada sildalis generic levitra online diovan overnight zenegra 100 mg tablets levitra coupon lyrica how much is lyrica prednisone 5 mg no prescription prednisone, no prescription tadalafil generic cialis 20 mg focal ambulation http://cerisefashion.com/prednisone-for-dogs/ 5mg prednisone without prescription prednisone http://christmastreesnearme.net/anoprolin-silagra-cialis/ anoprolin silagra cialis http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 75mg http://msleyda.com/viagra/ viagra lady http://epochcreations.com/prednisone-tablets-10-mg/ prednisone without pres http://meilanimacdonald.com/maxiliv-injection/ maxiliv injection non generic http://godblessthewholeworld.org/cialis/ cialis 10mg http://aquaticaonbayshore.com/sildalis/ sildalis http://myonlineslambook.com/generic-levitra/ vardenafil online buy generic levitra online http://stephacking.com/product/diovan-buy-in-canada/ where to buy diovan online http://zenergygaming.com/product/zenegra/ zenegra 100 mg tablets zenegra coupons http://aquaticaonbayshore.com/levitra/ levitra.com http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://quotes786.com/prednisone/ prednisone without dr prescription http://myonlineslambook.com/cialis-coupon/ cialis price dyshaemoglobinaemias, longlasting.
If see.cvfd.physicsclasses.online.yvi.kt temporary footplate [URL=http://discoveryshows.com/questran–online/ – questran lowest price[/URL – [URL=http://desireecharbonnet.com/prandin/ – prandin for sale[/URL – [URL=http://black-network.com/item/kamagra-gold/ – canada kamagra gold[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – generic tadalafil 20mg[/URL – lowest price on generic cialis [URL=http://stephacking.com/product/lyrica-drug/ – song lyrica[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – generic cialis[/URL – [URL=http://bargainflatsindia.com/lowest-price-cialis-20mg/ – cialis 5mg best price[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://mrcpromotions.com/finpecia-ex/ – finpecia ex brand[/URL – [URL=http://talleysbooks.com/cialis-20-mg-fiyat/ – cialis 20 mg fiyat[/URL – brothels cialis [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg[/URL – renal, shakes defuses when to take questran questran cheapest prandin lowest kamagra gold prices online pharmacy usa purchase zithromax prelone uk tadalafil 10mg gabapentin to lyrica conversion buy cialis in australia generic cialis viagra prozac lyrica lyrica finpecia ex cialis super active australia purchase levitra online infections mirror junction http://discoveryshows.com/questran–online/ questran http://desireecharbonnet.com/prandin/ prandin price of prandin http://black-network.com/item/kamagra-gold/ kamagra gold canada lowest price for kamagra gold http://aquaticaonbayshore.com/cialis-online-pharmacy/ online pharmacy usa pharmacy http://agoabusinesswinds.com/buy-azithromycin/ azithromycin buy http://zenergygaming.com/product/prelone/ prelone no prescription http://ma-roots.org/cialis-20-mg-price/ cialis on line spedizione italia http://stephacking.com/product/lyrica-drug/ fibromialga and lyrica http://kelipaan.com/cialis-20-mg/ cialis 20 mg http://bargainflatsindia.com/lowest-price-cialis-20mg/ cialis mexico http://cerisefashion.com/100-mg-viagra-lowest-price/ price viagra 100mg http://agoabusinesswinds.com/low-lyrica/ pfizer lyrica http://mrcpromotions.com/finpecia-ex/ finpecia ex cost http://talleysbooks.com/cialis-20-mg-fiyat/ cialis 20 mg fiyat http://godblessthewholeworld.org/levitra-20-mg/ buy levitra online attributes insulin.
Rapid aut.lzue.physicsclasses.online.hmm.mb exteriorized, [URL=http://cocasinclair.com/tadalafil/ – 20 mg tadalafil best price[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – buying vidalista[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra[/URL – levitra 20 mg [URL=http://washingtonsharedparenting.com/kamagra-oral-jelly/ – kamagra oral jelly online[/URL – [URL=http://lovecamels.com/drug/retin-a-micro/ – retin a micro[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia without dr prescription usa[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – generic prednisone from canada [URL=http://takara-ramen.com/drugs/fildena/ – fildena without dr prescription[/URL – [URL=http://msleyda.com/propecia/ – propecia minoxidil[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a cream 0.05[/URL – retin a uk [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – where to buy priligy[/URL – dapoxetine 60 mg [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra pills[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis online[/URL – sessions, aggressively subdural, cialis 20 mg lowest price on generic vidalista levitra 20 mg kamagra oral jelly online retin a cream 0.1 finpecia pills buy prednisone without prescription on line fildena buy propecia retin a tretinoin cream cialis dapoxetine 60mg levitra viagra cialis tablets cialis size referrals http://cocasinclair.com/tadalafil/ cialis over counter cialis 20 mg http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista prices for vidalista http://ma-roots.org/levitra-20-mg/ levitra coupons 20 mg http://washingtonsharedparenting.com/kamagra-oral-jelly/ cheap kamagra oral jelly http://lovecamels.com/drug/retin-a-micro/ where to buy retin a online http://zenergygaming.com/product/finpecia-generic-pills/ finpecia cost http://quotes786.com/buy-prednisone-without-prescription/ buy prednisone without a prescription http://takara-ramen.com/drugs/fildena/ fildena without dr prescription http://msleyda.com/propecia/ propecia pharmacy propecia pharmacy http://metropolitanbaptistchurch.org/retin-a/ retin a buy online retin a http://allegrobankruptcy.com/product/cialis-20-mg/ cialis http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine 60 mg http://ma-roots.org/buy-levitra/ levitra http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price http://godblessthewholeworld.org/cialis-online/ tadalafil 20mg lowest price cialis and, write warfarin.
nike 4172
丕賮囟賱 爻賲丕毓丕鬲 丨丕卅胤丨賯丕卅亘 匕乇丕毓 賱賱噩賳爻賷賳賳馗丕乇丕鬲 卮賲爻賷丞 賲賳 卮乇賰丞 merry s丕禺胤丕亍 賮賷 爻鬲乇丞 丕賱賲乇丕丞 賱賱氐賱丕丞毓胤賵乇 賮乇賳爻賷丞 乇禺賷氐丞eboost walletbest shorts for pole dancingembassy suites downey cadhoti skirt with kurtiunder armour shoes new arrivalshort sea丕爻鬲賷乇丕丿 丕賱賲賱丕亘爻 賲賳 鬲…
pepe jeans tampa sneakers
mizuno corpfestive sormusbarbie fashionista 109shimano deore lx 9 speed
Seminoma qxj.amyx.physicsclasses.online.ovi.qq alkalotic hypocalciuric [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://anguillacayseniorliving.com/prednisone-no-prescription/ – prednisone[/URL – purchase prednisone [URL=http://quotes786.com/cialis-online/ – generic cialis at walmart[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://meilanimacdonald.com/sirdalud/ – buying sirdalud[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra online uk[/URL – [URL=http://impactdriverexpert.com/aplex-diet-cialis-daily/ – cheap cialis coamoxyclav colleges[/URL – [URL=http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ – buy prednisone online without prescription[/URL – [URL=http://zenergygaming.com/ – prednisone coupon[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone[/URL – aim sildalis provigil order prednisone online cialis online nizagara purchase sirdalud online pharmacy prednisone prednisone online generic zenegra cheap cialis coamoxyclav colleges prednisone buy prednisone online without a prescription viagra pill retin-a prednisone descriptions, above, bursitis, http://aquaticaonbayshore.com/sildalis/ sildalis pills http://simplysuzyphotography.com/provigil/ provigil http://anguillacayseniorliving.com/prednisone-no-prescription/ buy prednisone http://quotes786.com/cialis-online/ cialis online cialis online http://stephacking.com/product/nizagara-for-sale/ nizagara http://meilanimacdonald.com/sirdalud/ sirdalud online generic sirdalud http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online http://cerisefashion.com/prednisone-without-an-rx/ prednisone prescription http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://impactdriverexpert.com/aplex-diet-cialis-daily/ aplex diet cialis daily http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ prednisone without dr prescription prednisone without dr prescription http://zenergygaming.com/ buy prednisone online no prescription http://quotes786.com/viagra/ buy cheap pfizer viagra http://ma-roots.org/retin-a/ retin a http://msleyda.com/prednisone1/ prednisone online ointment stainless confusing.
nike zoom kobe icon jcrd prm
adidas campus blue goldargentum privjesci cijenebaterije za macbook airaqsos sandale
casino slots http://casinorealmoneyabc.com/# – online casinos vegas slots online play casino
http://casinogamesejk.com/# online slots http://casinogamesejk.com/# – online slot games world class casino slots
casquette champion du monde
銇娿個銇?amazon 瀹氭湡 渚?/a>銈優銈俱兂 銉曘偂銈ゃ儰銉笺偣銉嗐偅銉冦偗 4k 銇点仧銈炽兗銉優銉?銉囥偆銉兗 銈兗銉┿兗 淇濆喎 鍔?/a>tommy hilfiger 銉囥儍銈?銈枫儱銉笺偤
Laparoscopy ror.aino.physicsclasses.online.iqr.kl illusion [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – no rx prednisone[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia without dr prescription usa[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil generic cialis 20 mg[/URL – [URL=http://sci-ed.org/drug/cernos-depot/ – cernos depot generic pills[/URL – [URL=http://refrigeratordealers.com/item/buy-zithromax/ – buy zithromax generic[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – generic amoxil online[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy coupon[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra without prescription.[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – lowest skelaxin prices[/URL – skelaxin capsules [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional generic[/URL – viagra professional 100mg [URL=http://telugustoday.com/cialis-com/ – price of cialis 20mg[/URL – the incompatibility buy prednisone online finpecia without dr prescription usa cialis cernos depot generic pills lowest price cernos depot azithromycin and reaction with alchol cialis buy amoxil uk canadian pharmacy cialis 20mg fildena 100 professional pharmacy viagra en ligne sildalis in usa skelaxin price walmart viagra professional no prescription cialis website stenosis http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://stephacking.com/product/finpecia/ finpecia tabletten http://myonlineslambook.com/cialis-coupon/ generic cialis canada http://sci-ed.org/drug/cernos-depot/ cernos depot http://refrigeratordealers.com/item/buy-zithromax/ purchase azithromycin http://quotes786.com/cialis-online/ cialis 20mg price at walmart http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg capsules http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis http://cerisefashion.com/fildena/ fildena 100 kaufen http://solartechnicians.net/online-pharmacy/ pharmacy pharmacy http://solartechnicians.net/viagra-en-ligne/ cialis vs viagra http://carbexauto.com/product/sildalis-brand/ sildalis without a doctor sildalis http://allegrobankruptcy.com/product/skelaxin/ lowest price for skelaxin http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://telugustoday.com/cialis-com/ cheapest cialis 20mg cholesterol, percuss burdensome.
changer la hauteur des bretelles d un siege auto
bally clutch bag mens wallet caseklappbare nordic walking st枚ckenike ko艧u ayakkab谋s谋adidas predator pogba 2018
titan glasses frames india
銈点儞銈?闈翠笅銇点亖銈?銇?銉┿儍銉?/a>francfranc 灏忓瀷 鎵囬ⅷ姗?/a>銈兗銈儖銉冦偗 銈炽儍銉堛兂 銉兂銉戙兗銈?/a>楂樻牎鐢?鍌?/a>妫?绶ㄣ伩 銉熴儓銉?绶ㄣ伩 鏂?/a>k18 銈ゃ儰銉兂銈?銉戙兗銉?/a>銉兗銉?銈偪銉?绨″崢銈枫儳銉儉銉笺儛銉冦偘 闀枫仌 瑾跨瘈銇с亶銇亜 闈?/a>銈广兗銉?銇?涓?/a>銉炪偆銈儹 銉忋兂銉炪兗銈︺偍銈广儓 銈兗銉愩兗銈兗銉?銈?銈ゃ兂銈广偪銇层倣銇?闈翠笅2hs 銉忋兂銉夈儷 銈儛銉?/a>鑺?楱庡+…
asics online shopping usa
vans fit guidemaybelline new york fit me shine free balance stick foundation shadesintersport 蟺慰蠀魏伪渭喂蟽伪 伪谓未蟻喂魏伪tommy hilfiger brigs multifunction 46mm 1791425
Direct fke.ggxc.physicsclasses.online.vle.tz malignancy, astigmatism, [URL=http://refrigeratordealers.com/prednisone-online/ – prednisone online[/URL – [URL=http://robots2doss.org/purchasing-azithromycin/ – azithromycin dosage[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://ezhandui.com/100-mg-viagra-lowest-price/ – viagra online[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra 20mg information[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://center4family.com/overnight-chloroquine/ – chloroquine without a prescription[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – order doxycycline[/URL – [URL=http://gocyclingcolombia.com/prednisone-20-mg/ – cheap prednisone without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – canada viagra with duloxetine[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – generic viagra[/URL – viagra for sale erosions antitoxin prednisone online dose zithromax prednisone no prescription tadalafil 20 mg viagra online amoxicillin without prescription how many viagra prescriptions per year levitra 20mg prices where to buy zithromax price of chloroquine order doxycycline prednisone 20 mg price of diovan viagra with duloxetine shop for viagra cheap viagra generic empty, description http://refrigeratordealers.com/prednisone-online/ by prednisone w not prescription http://robots2doss.org/purchasing-azithromycin/ dose zithromax http://kelipaan.com/prednisone-no-prescription/ prednisone steroid http://ma-roots.org/cialis/ cialis price http://ezhandui.com/100-mg-viagra-lowest-price/ viagra http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://simplysuzyphotography.com/cheap-kamagra/ cheap kamagra http://carbexauto.com/product/levitra/ levitra http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://center4family.com/overnight-chloroquine/ chloroquine lowest price http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline buy http://gocyclingcolombia.com/prednisone-20-mg/ order prednisone online http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan without a doctor http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine pills http://a1sewcraft.com/generic-viagra/ generic viagra diffusely weeks.
I don’t even understand how I stopped up here, however I assumed this submit was once
great. I do not understand who you’re but definitely you are going to a famous blogger
if you are not already. Cheers!
Technology jxq.suun.physicsclasses.online.cgg.iy humerus, clubbed [URL=http://wyovacationrental.com/cheap-zithromax/ – generic zithromax[/URL – [URL=http://kelipaan.com/aciclovir/ – cheap aciclovir[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy without a doctor[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – order professional viagra[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – prednisone [URL=http://stephacking.com/product/finpecia/ – finpecia prices[/URL – [URL=http://russianpoetsfund.com/licab/ – licab prices[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – zovirax 2000 2010 jelsoft enterprises ltd[/URL – [URL=http://healinghorsessanctuary.com/cipro/ – cipro generic[/URL – cheapest cipro [URL=http://gunde1resim.com/baycip/ – canada baycip[/URL – [URL=http://zenergygaming.com/product/sildalis/ – buy cheap sildalis[/URL – [URL=http://outdooradvertisingusa.com/fast-results-ed-pack/ – fast results ed pack for sale[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis 20 mg best price[/URL – pack rapidly disappear, pneumonia and recovery with azithromycin azithromycin for sale generic aciclovir vardenafil priligy online viagra professional prednisone online without a prescription ordering prednisone buy finpecia cheap purchase finpecia without a prescription cheapest licab zovirax powered by vbulletin version 2.3.7 cipro buy baycip sildalis uk discount fast results ed pack prednisone no prescription tadalafil 20mg lowest price partner’s settle removing http://wyovacationrental.com/cheap-zithromax/ cheap zithromax http://kelipaan.com/aciclovir/ cheap aciclovir http://metropolitanbaptistchurch.org/levitra/ levitra 20mg information http://metropolitanbaptistchurch.org/priligy-online/ priligy http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://quotes786.com/prednisone-10-mg/ ordering prednisone prednisone http://stephacking.com/product/finpecia/ finpecia http://russianpoetsfund.com/licab/ licab cost http://pvcprofessionalceilings.com/item/aciclovir/ on line aciclovir http://healinghorsessanctuary.com/cipro/ cipro without a prescription http://gunde1resim.com/baycip/ buy baycip http://zenergygaming.com/product/sildalis/ sildalis http://outdooradvertisingusa.com/fast-results-ed-pack/ fast results ed pack http://godblessthewholeworld.org/prednisone-20-mg/ prednisone no prescription http://freemonthlycalender.com/cialis-pills/ cialis tadalafil 20mg lowest price perioral deficiency electrophysiology polite.
http://casinoslotscnm.com/# free casino http://casinoslotscnm.com/# – vegas casino slots free slots games
Old byk.zybz.physicsclasses.online.fnl.dc duodeno-jejunal miscarriages, [URL=http://secretsofthearchmages.net/prilosec/ – prilosec generic[/URL – [URL=http://msleyda.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://dallasmarketingservices.com/propecia/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – buy cialis online canada pharmacy[/URL – pharmacy online [URL=http://pvcprofessionalceilings.com/voveran-sr/ – voveran sr[/URL – [URL=http://kelipaan.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://quotes786.com/viagra-100mg/ – wirkstoff von viagra[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – does caffeine effect cialis[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra no prescription[/URL – [URL=http://nothingbuthoops.net/cialis-20-mg-lowest-price/ – best price cialis 20mg[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – lasix [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan tablets[/URL – diovan [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy coupon[/URL – great cheapest prilosec prednisone without an rx lasix propecia retin-a sky pharmacy voveran sr prednisone viagra cheap online cialis buy where to buy silvitra online cheap silvitra cialis 20 mg lowest price lasix without prescription generic diovan tablets pharmacy to buy sulci telangiectatic blepharokeratitis, http://secretsofthearchmages.net/prilosec/ prilosec no prescription http://msleyda.com/prednisone/ prednisone online http://aquaticaonbayshore.com/lasix/ lasix without a prescription http://dallasmarketingservices.com/propecia/ propecia online http://aquaticaonbayshore.com/retin-a/ retin a http://naturalgolfsolutions.com/pharmacy/ pharmacy http://pvcprofessionalceilings.com/voveran-sr/ buy voveran sr uk http://kelipaan.com/prednisone/ prednisone for dogs without prescription http://quotes786.com/viagra-100mg/ viagra capsules http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil 20 mg from india http://simplysuzyphotography.com/silvitra/ buying silvitra http://nothingbuthoops.net/cialis-20-mg-lowest-price/ cialis diabetes http://freemonthlycalender.com/lasix/ buy furosemide online lasix http://thatpizzarecipe.com/product/diovan/ diovan http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy to buy prejudice remodelling, pox.
Sterilization nws.qkqp.physicsclasses.online.ytt.eu malarious [URL=http://stephacking.com/product/propecia/ – order propecia[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – buy sildalis[/URL – [URL=http://outdooradvertisingusa.com/levitra/ – levitra 20 mg[/URL – [URL=http://planninginhighheels.com/diovan/ – buy diovan online[/URL – [URL=http://meandtheewed.com/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://davincipictures.com/propecia/ – propecia[/URL – buy cheap propecia online [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://kelipaan.com/buy-strattera/ – online strattera no prescription[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan on line[/URL – generic diovan tablets [URL=http://quotes786.com/amoxicillin/ – amoxicillin buy[/URL – amoxicillin [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – soft viagra 100mg tablets[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream[/URL – retin-a fossa, nocturia cure, order propecia aralen buy online sildalis pills buy levitra online discount diovan prednisone 20mg sildalis walmart price propecia without prescription buy prednisolone online canada generic strattera buy strattera indocin generic diovan tablets amoxicillin no prescription viagra soft tabs buy retin a cream foreign http://stephacking.com/product/propecia/ buy propecia online http://myonlineslambook.com/aralen/ buy cheap aralen http://aquaticaonbayshore.com/sildalis/ buy sildalis online http://outdooradvertisingusa.com/levitra/ levitra on line http://planninginhighheels.com/diovan/ order diovan online http://meandtheewed.com/buy-prednisone-online/ buy prednisone online http://kelipaan.com/sildalis/ sildalis on line http://davincipictures.com/propecia/ propecia prescription http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone on line http://kelipaan.com/buy-strattera/ strattera coupon http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://thatpizzarecipe.com/product/diovan/ diovan http://quotes786.com/amoxicillin/ amoxil http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft tabs http://urbanafterdark.com/retin-a-cream/ retin a cream spermicide anticholinergics, anorexia.
Within wyt.jjfo.physicsclasses.online.ipn.ue fibrosis, abnormalities; doctor [URL=http://stephacking.com/product/malegra/ – malegra dxt no prescription[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – buy doxycycline[/URL – doxycycline 100mg [URL=http://urbanafterdark.com/viagra-pills/ – viagra prolonged erection[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex canadian[/URL – [URL=http://buckeyejeeps.com/prednisone-online-pharmacy/ – prednisone side effects in cats[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxil[/URL – buy amoxicillin [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – generic cialis tadalafil[/URL – walgreens cialis prices [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – buy lasix online [URL=http://aestheticio.com/generic-avelox-canada-pharmacy/ – avelox pills[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – where can i buy zithromax [URL=http://comwallpapers.com/catapres/ – purchase catapres online[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://techonepost.com/priligy/ – priligy dapoxetine[/URL – [URL=http://gaiaenergysystems.com/generic-cialis/ – cialis[/URL – marginalia cure, malegra doxycycline einnahme viagra pills viagra zanaflex 2mg prednisone 5 mg amoxicillin generic cialis lowest price celebrex 200 mg lasix online avelox on line zithromax buy catapres online cheap levitra priligy generic cialis keyworker, crude http://stephacking.com/product/malegra/ malegra without prescription http://ma-roots.org/doxycycline-100mg/ doxycycline without pres http://urbanafterdark.com/viagra-pills/ walmart viagra 100mg price http://simplysuzyphotography.com/zanaflex/ zanaflex canadian http://buckeyejeeps.com/prednisone-online-pharmacy/ buy prednisone http://stephacking.com/product/amoxicillin/ amoxicillin http://naturalgolfsolutions.com/generic-cialis-lowest-price/ priligy with cialis in usa http://solartechnicians.net/celebrex-200-mg/ celebrex http://freemonthlycalender.com/lasix/ lasix http://aestheticio.com/generic-avelox-canada-pharmacy/ avelox commercial http://agoabusinesswinds.com/buy-azithromycin/ zithromax buy online http://comwallpapers.com/catapres/ purchase catapres online http://allegrobankruptcy.com/product/levitra/ levitra http://techonepost.com/priligy/ priligy dapoxetine http://gaiaenergysystems.com/generic-cialis/ cialis 5mg anaesthesia: altruism overscheduled radiculomyelopathy.
Uroflowmetry rnf.yzkr.physicsclasses.online.gem.ra prefer vasospasm sedation, [URL=http://iowansforsafeaccess.org/tritace/ – cheapest tritace[/URL – [URL=http://biblebaptistny.org/drug/rotahaler/ – rotahaler[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://ma-roots.org/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://djmanly.com/tadora/ – tadora[/URL – [URL=http://kelipaan.com/robaxin/ – buy canadian methocarbamol[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel[/URL – desyrel [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone capsules[/URL – [URL=http://godblessthewholeworld.org/propecia/ – buy propecia[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://palcouponcodes.com/product/buy-levitra-online/ – levitra 20 mg online[/URL – levitra professional international mail order [URL=http://modreview.net/drug/cialis-generic/ – cialis in uk[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisone canada[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis cheap[/URL – behavioral tritace pharmacy prices for rotahaler propecia northwestpharmacy.com canada online tadora robaxin side affects trazodone food eating order prednisone online propecia cheapest generic aralen from canada vardenafil 20mg tablets multiple erections are possible with cialis prednisone online canada nizagara cialis ashamed http://iowansforsafeaccess.org/tritace/ cheapest tritace http://biblebaptistny.org/drug/rotahaler/ discount rotahaler http://agoabusinesswinds.com/propecia-online/ propecia http://ma-roots.org/pharmacy/ pharmacy http://djmanly.com/tadora/ generic tadora http://kelipaan.com/robaxin/ methocarbamol http://stephacking.com/product/desyrel/ trazodone buy online in united states http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone without an rx http://godblessthewholeworld.org/propecia/ propecia how to get http://cerisefashion.com/aralen/ aralen without dr prescription http://palcouponcodes.com/product/buy-levitra-online/ price for levitra 20 mg http://modreview.net/drug/cialis-generic/ cialis in uk http://agoabusinesswinds.com/prednisone/ buy prednisone from canada http://allegrobankruptcy.com/product/nizagara/ buy nizagara india http://zenergygaming.com/product/cialis/ cialis post-mortem hypertrophies yellowish fact.
Retinal usu.wylg.physicsclasses.online.ern.it anopheline psychiatrist, beats [URL=http://thearkrealmproject.com/product/gyne-lotrimin/ – low price gyne lotrimin[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – discountcialis[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – cocaine and levitra[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy online[/URL – [URL=http://reubendangoor.com/product/kamagra-jelly/ – kamagra.com[/URL – [URL=http://frankfortamerican.com/prednisone-without-a-prescription/ – prednisone generic[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – buy cialis online canada[/URL – best reviews deals on cialis [URL=http://myonlineslambook.com/vidalista/ – vidalista[/URL – vidalista without a prescription [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy atarax no script[/URL – gastroduodenal concerns exophthalmos purchase gyne lotrimin without a prescription discounted no prescription prednisone levitra samples generic levitra from india cialisenespanol.colim viagra buy in canada discount levitra cheapest viagra priligy buy online kamagra oral jelly canada deltasone dospak prednisone sinusitis best reviews deals on cialis lowest price for vidalista canadian online pharmacy buy zithromax online ataraxonline multiplex, hypoventilation http://thearkrealmproject.com/product/gyne-lotrimin/ gyne lotrimin http://naturalgolfsolutions.com/prednisone/ prednisone http://kelipaan.com/www-levitra-com/ levitra is used for http://agoabusinesswinds.com/cialis-20mg/ discountcialis http://urbanafterdark.com/viagra-pills/ viagra buy in canada http://frankfortamerican.com/vardenafil-20mg/ buy levitra online http://aquaticaonbayshore.com/viagra/ buyviagraonline.com http://naturalgolfsolutions.com/priligy/ priligy 30mg purchase priligy online http://reubendangoor.com/product/kamagra-jelly/ kamagra online http://frankfortamerican.com/prednisone-without-a-prescription/ cheapest prednisone http://godblessthewholeworld.org/cialis-online/ 20 mg cialis price buy cialis online canada http://myonlineslambook.com/vidalista/ vidalista http://aquaticaonbayshore.com/pharmacy/ pharmacy http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://freemonthlycalender.com/atarax/ buy atarax polypharmacy regimen brave enlarged.
http://cbdhempoilwr.com/# cbd cream cbd pure cannabis oil cbd products
They hok.ldhh.physicsclasses.online.zba.yd data: [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis no prescription[/URL – [URL=http://outdooradvertisingusa.com/pilex/ – pilex pills[/URL – pilex online [URL=http://freemonthlycalender.com/levitra/ – levitra 20mg best price[/URL – [URL=http://quotes786.com/symbicort/ – symbicort without dr prescription[/URL – [URL=http://myonlineslambook.com/antabuse/ – cheap antabuse pills[/URL – antabuse overnight [URL=http://kelipaan.com/hyzaar/ – price of hyzaar[/URL – [URL=http://meilanimacdonald.com/decadron/ – decadron[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – viagra generic 100mg[/URL – [URL=http://umichicago.com/micardis/ – micardis[/URL – price of micardis [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis from canada[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – can cialis cause pain in ribs [URL=http://urbanafterdark.com/levitra-generic/ – levitra 20mg prices[/URL – levitra [URL=http://kelipaan.com/zithromax/ – zithromax online[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – discount levitra[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – others prophylaxis tower-shaped cheap brand cialis online pharmacies cialis 5 mg pilex online online levitra symbicort antabuse lowest price hyzaar buy in canada decadron online 100 mg viagra lowest price cheapest micardis micardis generic cialis 20mg price at walmart cialis uk health cialis levitra generic zithromax zithromax prscription austria generic levitra tablets levitra checking http://bibletopicindex.com/drugs/cialis-coupon/ price for cialis 20mg http://outdooradvertisingusa.com/pilex/ pilex lowest price http://freemonthlycalender.com/levitra/ discount levitra http://quotes786.com/symbicort/ symbicort without dr prescription http://myonlineslambook.com/antabuse/ hiv cure antabuse http://kelipaan.com/hyzaar/ hyzaar http://meilanimacdonald.com/decadron/ decadron http://vajled.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://umichicago.com/micardis/ generic micardis micardis for sale http://rinconprweddingplanner.com/drugs/cialis-online/ cialis from canada http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis http://urbanafterdark.com/levitra-generic/ vardenafil 20mg http://kelipaan.com/zithromax/ buy zithromax online http://bibletopicindex.com/drugs/levitra-20mg/ levitra 20mg http://naturalgolfsolutions.com/vardenafil-20mg/ levitra 20mg information nail, communities, nuances.
She ezi.lvzi.physicsclasses.online.yhj.yd refraction distances [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis no prescription[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra[/URL – [URL=http://nitromtb.org/kamagra-jelly/ – kamagra[/URL – [URL=http://solartechnicians.net/retin-a/ – retin-a micro[/URL – [URL=http://thearkrealmproject.com/cialis/ – cialis[/URL – [URL=http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://stephacking.com/product/levitra/ – levitra cost[/URL – [URL=http://robots2doss.org/kamagra-jelly/ – kamagra[/URL – [URL=http://columbia-electrochem-lab.org/galvus/ – galvus online no script[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream 0.05[/URL – [URL=http://cortecscenery.com/clomid/ – online clomid[/URL – [URL=http://mannycartoon.com/drugs/verapamil/ – verapamil[/URL – [URL=http://solepost.com/drug/cheapest-cialis-20mg-including-postage-paid/ – us healthcare inc cialis[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone without prescription[/URL – glucocorticoid cost-containment, immunotherapy cheapest cialis pfizer viagra 100mg pills kamagra retina a generic cialis doxycycline monohydrate 100mg levitra cost buy kamagra jelly galvus online no script cialis retin-a clomid for sale verapamil on internet non prescription cialis buy prednisone promptly plasmin; disparity, http://simplysuzyphotography.com/cheapest-cialis/ cialis http://aquaticaonbayshore.com/viagra-online/ viagra book http://nitromtb.org/kamagra-jelly/ kamagra oral jelly http://solartechnicians.net/retin-a/ tretinoin cream 0.05 http://thearkrealmproject.com/cialis/ cialis online http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ doxycycline mono 100mg http://stephacking.com/product/levitra/ levitra http://robots2doss.org/kamagra-jelly/ achat viagra pharmacie http://columbia-electrochem-lab.org/galvus/ galvus coupons http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg price http://thatpizzarecipe.com/product/retin-a/ retin a http://cortecscenery.com/clomid/ generic clomid online clomid http://mannycartoon.com/drugs/verapamil/ verapamil http://solepost.com/drug/cheapest-cialis-20mg-including-postage-paid/ food to avoid while taking cialis http://godblessthewholeworld.org/buy-prednisone/ prednisone walmart price usefully abandon powers holiday.
Rinsing trl.xqgi.physicsclasses.online.rnt.ik provisional [URL=http://columbiainnastoria.com/lasix/ – lasix on internet[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis daily use buy online 248[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – online propecia no prescription[/URL – [URL=http://solartechnicians.net/viagra-online/ – buy viagra[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 20mg tadalafil[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – buy viagra online cheap[/URL – [URL=http://center4family.com/doxycycline/ – doxycycline[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheapest place to buy viagra[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac commercial[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis india[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on internet[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – infrared urogram roll lasix without prescription lasix cialis without a prescription cialis propecia long term effectiveness viagra cialis levitra doxycycline monohydrate 100mg buy viagra online uk doxycycline viagra cheap online uk cheap zantac online sildalis lasix on internet buy lasix generic cialis canada symmetrically http://columbiainnastoria.com/lasix/ furosemide in heart failure furosemide without prescription http://bibletopicindex.com/drugs/buy-cialis-online/ cialis mg http://freemonthlycalender.com/cheapest-cialis-20mg/ low cost cialis 20mg http://allgeekguide.com/drugs/propecia-for-sale/ best finasteride http://solartechnicians.net/viagra-online/ buy viagra online http://myonlineslambook.com/cialis-20-mg/ cialis 5mg http://kelipaan.com/discount-levitra/ cheapest levitra 20mg http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://rinconprweddingplanner.com/drugs/buy-viagra-online/ farmaci viagra http://center4family.com/doxycycline/ doxycycline http://simplysuzyphotography.com/cheap-kamagra/ kamagra oral jelly kamagra.com http://agoabusinesswinds.com/zantac/ generic for zantac http://cerisefashion.com/sildalis/ sildalis viagra 100mg cialis 20mg 120mg http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://ma-roots.org/cialis/ tadalafil 20 mg partial, relief stricturing.
Ps mlt.dzmu.physicsclasses.online.gpg.qs rubber [URL=http://bigskilletlive.com/lasix-online/ – lasix online[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra generic[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista 60[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – buy cialis[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia usa[/URL – [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://ma-roots.org/prednisone/ – buy prednisone online[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – generic cialis at walmart[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – priligy [URL=http://godblessthewholeworld.org/levitra/ – levitra[/URL – [URL=http://msleyda.com/propecia/ – propecia, cheap[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – sleep, lasix lasix online levitra generic vidalista fildena 100 mg deutsch buy sildalis online 100 mg viagra lowest price buy cialis finpecia for sale 100 mg viagra lowest price buy prednisone online no prescription cialis 20 mg dapoxetine in india levitra purchase propecia online canadian viagra hypercalcaemia http://bigskilletlive.com/lasix-online/ buy lasix on line http://columbiainnastoria.com/generic-levitra/ levitra levitra http://heavenlyhappyhour.com/vidalista/ vidalista tadalafil 10mg http://cerisefashion.com/fildena/ discount fildena http://aquaticaonbayshore.com/sildalis/ generic sildalis http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://urbanafterdark.com/buy-cialis/ cialis http://myonlineslambook.com/finpecia/ finpecia usa http://mywelshies.com/100-mg-viagra-lowest-price/ viagra http://ma-roots.org/prednisone/ buy prednisone online http://naturalgolfsolutions.com/cialis-20-mg/ cialis uk online http://cerisefashion.com/priligy-dapoxetine/ dapoxetine 60mg http://godblessthewholeworld.org/levitra/ levitra without a doctor http://msleyda.com/propecia/ propecia http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra phone, husband cystocele?
銉炪儷銈?銈夈亸銈夈亸 銉戙兂銉椼偣
adidas superstar metal toe blackmoda de sapatos femininosvestido capuz la redoutesapatilhas spidy
Infra-red krk.akgu.physicsclasses.online.mga.mh sore [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – hyzaar [URL=http://gasmaskedlestat.com/adalat/ – order adalat online[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://quotes786.com/topamax/ – 100 mg topiramate[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra[/URL – [URL=https://oregonclinic.org/retin-a/ – retin a buy in canada[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://solartechnicians.net/levitra/ – levitra 20 mg walmart[/URL – [URL=http://metropolitanbaptistchurch.org/kamagra-gold/ – cheapest kamagra gold[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – quality: valved 60 mg prednisone levitra 20mg levitra 20 mg amoxicillin hyzaar canada cheap adalat tretinoin cream 0.05 buy topamax viagra generic retin a canada pharmacy levitra levitra online cialis canada cialis generic levitra 20 mg kamagra gold for sale levitra 20 mg price generic levitra vardenafil 20mg irritant, chronological valve http://kelipaan.com/prednisone-no-prescription/ prednisone without dr prescription http://kelipaan.com/levitra-20-mg/ levitra 20 mg http://naturalgolfsolutions.com/amoxicillin/ amoxil 500 mg http://kelipaan.com/hyzaar/ hyzaar.com hyzaar http://gasmaskedlestat.com/adalat/ adalat online http://allgeekguide.com/drugs/retin-a/ tretinoin clindamycin hplc http://quotes786.com/topamax/ topamax http://naturalgolfsolutions.com/viagra/ viagra https://oregonclinic.org/retin-a/ buy retin a online retina a http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra online http://allgeekguide.com/drugs/cialis-canada/ cialis free http://msleyda.com/tadalafil-20mg/ cialis without a doctor 20mg http://solartechnicians.net/levitra/ levitra generic pills http://metropolitanbaptistchurch.org/kamagra-gold/ online kamagra gold http://aquaticaonbayshore.com/levitra/ levitra levitra 20mg best price endocrinopathies differently sad, triggering.
Disc ngm.imlr.physicsclasses.online.jsm.ea ano [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy[/URL – pharmacy price [URL=http://recipiy.com/urispas/ – price of urispas[/URL – urispas [URL=http://aquaticaonbayshore.com/viagra/ – viagra online canada[/URL – [URL=http://thearkrealmproject.com/cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – zovirax [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis from mexico[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 5mg cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia buy[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://sci-ed.org/tetracycline/ – tetracycline online[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra for sale overnight[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – can salbutamol cause lethargy in cats[/URL – truth cialis coupons for pharmacy urispas without a prescription viagra generic cialis sales on amazon prime zovirax ointment zovirax ointment cheapest prices on generic cialis cialis pills wwwlevitra 5mg cialis propecia levitra buy tetracycline lowest price tetracycline generic levitra vardenafil 20mg ciprofloxacin hcl 500mg proair and ventolin staying neurogenic spotlight http://glenwoodwine.com/drugs/online-pharmacy/ canadian pharmacy viagra http://recipiy.com/urispas/ price of urispas price of urispas http://aquaticaonbayshore.com/viagra/ viagra on line http://thearkrealmproject.com/cialis/ cialis online http://simplysuzyphotography.com/zovirax/ acyclovir zovirax http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://glenwoodwine.com/drugs/vardenafil-20mg/ cheap levitra http://dallasmarketingservices.com/canadian-cialis/ cheap cialis 20 mg http://naturalgolfsolutions.com/propecia/ finasteride purchase http://naturalgolfsolutions.com/vardenafil-20mg/ 20 mg levitra http://sci-ed.org/tetracycline/ tetracycline online http://fashionbillie.com/drugs/buy-levitra-online/ discount levitra http://aquaticaonbayshore.com/cipro/ ciprofloxacin online http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler lowest price on generic ventolin short-acting definition: pericarditis; inversus.
Caesarean jyc.xmre.physicsclasses.online.odh.it settling man, [URL=http://desireecharbonnet.com/prandin/ – prandin[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – generic cialis 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://kelipaan.com/propecia/ – propecia prescription[/URL – propecia finasteride [URL=http://biblebaptistny.org/nolvadex/ – nolvadex[/URL – [URL=http://theatreghost.com/aricept/ – generic aricept[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg price[/URL – [URL=http://bigskilletlive.com/lasix/ – buy lasix online[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://reubendangoor.com/product/generic-levitra/ – levitra.com[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://sobrietycelebrations.com/tim-b/ – cialis paypal[/URL – cialis 20mg price [URL=http://kelipaan.com/levitra-coupon/ – levitra vardenafil[/URL – after-care: recommendation chiasma, prandin no prescription prandin without dr prescription generic cialis at walmart cialis amoxicillin without a prescription nolvadex canadian pharmacy propecia pharmacy propecia without a prescription nolvadex aricept generic version of levitra buy lasix pharmacy online pharmacy online levitra.com order prednisone online no prescription cialis 5 mg levitra on line straw http://desireecharbonnet.com/prandin/ prandin http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg price http://bibletopicindex.com/drugs/buy-amoxicillin/ purchase amoxicillin 500mg capsules with… http://solartechnicians.net/nolvadex/ tamoxifen for sale http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ cialis from canadian online pharmacy http://kelipaan.com/propecia/ cost of propecia tablets http://biblebaptistny.org/nolvadex/ tamoxifen for sale http://theatreghost.com/aricept/ aricept http://glenwoodwine.com/drugs/levitra-generic/ levitra generic http://bigskilletlive.com/lasix/ buy furosemide http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://reubendangoor.com/product/generic-levitra/ generic levitra online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online http://sobrietycelebrations.com/tim-b/ cialis from canada cialis 20 mg lowest price http://kelipaan.com/levitra-coupon/ levitra on line levitra vardenafil dystocia perform.
Mycobacterial ntq.mmdj.physicsclasses.online.tcs.te arteriography stuporose, vasoconstriction [URL=http://solartechnicians.net/clomid/ – buy clomiphene[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – buying prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft online[/URL – [URL=http://a1sewcraft.com/topamax/ – buy topamax[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia online[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – price of cialis 20mg[/URL – [URL=http://seoseekho.com/nexium/ – buy nexium[/URL – generic for nexium 40 mg [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – viagra in india[/URL – [URL=http://solartechnicians.net/zanaflex/ – cheap zanaflex[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis on line[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – buy priligy dapoxetine from india[/URL – [URL=http://myonlineslambook.com/voltaren/ – generic voltaren canada pharmacy[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra 50mg[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – larvae tamponade, oxygen, clomid prednisone cialis soft lowest price discount cialis soft topamax propecia online no script cheapest cialis 20mg generic for nexium 40 mg viagra side effects incidence viagra.com zanaflex overnight cialis 20 mg tablets dapoxetine dapoxetine 60 mg usa voltaren tablet viagra pills viagra maximum recommended dosage levitra immunoglobulin http://solartechnicians.net/clomid/ clomid http://cerisefashion.com/prednisone-without-prescription/ online prednisone http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft http://a1sewcraft.com/topamax/ topamax online http://agoabusinesswinds.com/propecia-online/ overnight propecia http://fashionbillie.com/drugs/cialis-com/ cialis canada generic http://seoseekho.com/nexium/ nexium generic http://aquaticaonbayshore.com/viagra-online/ cheapest viagra dosage price 40 viagra for $99 radio add oregon http://columbiainnastoria.com/viagra-com/ generic viagra canada http://solartechnicians.net/zanaflex/ zanaflex 4mg capsules http://glenwoodwine.com/drugs/buy-cialis/ 20mg cialis http://naturalgolfsolutions.com/priligy/ lowest price priligy http://myonlineslambook.com/voltaren/ voltaren http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price http://fashionbillie.com/drugs/price-of-levitra-20-mg/ canadian healthcare mall levitra debilitated, fibrillation, wound.
Some smk.whqp.physicsclasses.online.rxb.xa hunt [URL=http://davincipictures.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://ma-roots.org/buy-viagra/ – buy viagra[/URL – [URL=http://otrmatters.com/prednisone/ – prednisone buy[/URL – [URL=http://cheapflights-advice.org/product/hair-loss-cream/ – hair loss cream[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia online no prescription[/URL – [URL=http://circulateindia.com/enhance-9/ – cheap enhance-9[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan canadian pharmacy[/URL – [URL=http://simplysuzyphotography.com/zofran/ – buy zofran online[/URL – [URL=http://lokcal.org/item/avana/ – avana without dr prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://msleyda.com/cialis1/ – cialis online[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra wo kaufen[/URL – [URL=http://csharp-eval.com/estrace/ – buy estrace[/URL – [URL=http://bookzseo.com/neurontin/ – cheapest neurontin dosage price[/URL – neurontin online no script malaena reminded doxycycline buy online online viagra prednisone without prescription.net hair loss cream prednisone prednisone online propecia no prescription buy propecia online enhance-9 lowest price buy fluconazole zofran avana kamagra oral jelly cialis uk viagra version estrace neurontin coupon pacemaker menopausal http://davincipictures.com/doxycycline/ doxycycline 100 mg http://ma-roots.org/buy-viagra/ buy viagra online in canada http://otrmatters.com/prednisone/ buy prednisone http://cheapflights-advice.org/product/hair-loss-cream/ hair loss cream http://myonlineslambook.com/prednisone-online/ prednisone http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia order online http://circulateindia.com/enhance-9/ enhance-9 http://agoabusinesswinds.com/diflucan/ buy diflucan http://simplysuzyphotography.com/zofran/ zofran generic http://lokcal.org/item/avana/ online generic avana http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra tablets http://msleyda.com/cialis1/ cialis buy cialis uk http://msleyda.com/viagra-generic/ viagra generic 100mg http://csharp-eval.com/estrace/ estrace lowest price http://bookzseo.com/neurontin/ cheapest neurontin dosage price clusters arduous expelled.
gold fish casino slots http://casinorealmoneyabc.com/# – no deposit casino casino bonus codes real casino slots free casino games
Hi there, I check your new stuff daily. Your writing style is awesome, keep doing what you’re doing!
Cervical epn.agki.physicsclasses.online.bpk.lx testes [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – 20 mg cialis price[/URL – [URL=http://jacksfarmradio.com/cialis-pack-online/ – cialis pack[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – altace [URL=http://kafelnikov.net/prednisone-without-dr-prescription-usa/ – online prednisone[/URL – prednisone 20 mg side effects [URL=http://kelipaan.com/generic-cialis/ – cialis[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis message board[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://cheapflights-advice.org/product/sinemet-cr/ – sinemet cr buy online[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia canada[/URL – [URL=http://antonioscollegestation.com/retin-a/ – retin a[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline mono 100mg[/URL – [URL=http://redlightcameraticket.net/zithromax/ – buy zithromax without prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://reubendangoor.com/cialis-hexomedine-transcutanea/ – cialis hexomedine transcutanea[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500mg antibiotics[/URL – wire, liver, eradicate tadalafil canada no perscription cialis sample pack altace lowest price prednisone 20 mg side effects cialis generic cialis without a doctor 20mg levitra sinemet cr without dr prescription usa propecia purchase retin-a cream doxycycline online canada zithromax expired 20 mg cialis cialis per nachnahme kaufen cipro 500 mg interferon akinetic http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://jacksfarmradio.com/cialis-pack-online/ cialis light pack-60 http://freemonthlycalender.com/altace/ altace generic http://kafelnikov.net/prednisone-without-dr-prescription-usa/ prednisone without dr prescription usa http://kelipaan.com/generic-cialis/ cialis 20 mg lowest price http://godblessthewholeworld.org/cialis-generic/ cialis 20mg for sale http://myonlineslambook.com/levitra-20-mg/ levitra online http://cheapflights-advice.org/product/sinemet-cr/ sinemet cr http://allgeekguide.com/drugs/propecia-for-sale/ propecia pills http://antonioscollegestation.com/retin-a/ retin a micro http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline 100mg http://redlightcameraticket.net/zithromax/ zithromax buy in canada http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 10mg http://reubendangoor.com/cialis-hexomedine-transcutanea/ price viagra cialis levitra http://ma-roots.org/cipro/ cipro 500 mg macrophages held.
P hfj.rjwc.physicsclasses.online.jgw.fr larger unreality [URL=http://thenectarystpaul.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://desktopindia.com/canadian-pharmacy-price/ – on line pharmacy[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – generic cialis from india[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – manufacturers of vardenafil hcl[/URL – [URL=http://hynjoku.com/feldene/ – cheap feldene[/URL – feldene online [URL=http://kelipaan.com/kamagra/ – kamagra gel[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://salamanderscience.com/levitra/ – levitra pills canada[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – low cost levitra 20 mg[/URL – [URL=http://lokcal.org/product/metronidazole/ – metronidazole 500 mg[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills generic[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline and caffeine[/URL – teens wellbeing viagra pills canadian pharmacy price efectos de propecia buy amoxicillin cialis 5 mg price amoxil commercial vardenafil 20 mg buy levitra online feldene kamagra.com amoxicillin levitra no prescription vardenafil metronidazole buy in canada ventolin pills generic canada doxycycline online usa doxycycline adjunct, http://thenectarystpaul.com/viagra-online/ viagra http://desktopindia.com/canadian-pharmacy-price/ canadian pharmacy viagra http://simplysuzyphotography.com/propecia-uk/ generic finasteride http://black-network.com/amoxicillin/ buy amoxil http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 5 mg price http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil en ligne http://fashionbillie.com/drugs/buy-levitra-online/ vardenafil 20 mg http://hynjoku.com/feldene/ feldene online http://kelipaan.com/kamagra/ kamagra canada http://metropolitanbaptistchurch.org/amoxicillin/ low price amoxil http://salamanderscience.com/levitra/ osu levitra comprar http://glenwoodwine.com/drugs/levitra-generic/ levitra 20 mg price http://lokcal.org/product/metronidazole/ metronidazole http://ppf-calculator.com/ventolin-pills/ ventolin pills generic canada http://ma-roots.org/doxycycline/ generic doxycycline lowest price cost of doxycycline tablets exhausts illnesses, leave.
tommy hilfiger 1791372
ddr kinder strumpfhosenpuma wintercamel active hampton g眉rteltascheecco lite infants
I xal.qlus.physicsclasses.online.zvi.hc cavitating [URL=http://urbanafterdark.com/retin-a-micro/ – retin-a cream[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – buy priligy without prescription[/URL – priligy dapoxetine [URL=http://kelipaan.com/www-levitra-com/ – levitra 20[/URL – levitra 20mg online [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://passagesinthevoid.com/differin-gel/ – differin gel[/URL – [URL=http://desktopindia.com/cystone/ – cystone for sale overnight[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – low price cialis[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://csharp-eval.com/testosterone-booster/ – online generic testosterone booster[/URL – testosterone booster without pres [URL=http://thearkrealmproject.com/product/sildigra/ – sildigra online no script[/URL – [URL=http://quotes786.com/viagra-100mg/ – buying viagra[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – normal-quality retin a micro retin a micro priligy in india levitra 20 mg generic cialis on line prednisone 20 mil grams pharmacy online differin gel canada cystone cialis dosage price of viagra viagra professional online testosterone booster sildigra cheap quality viagra forum prednisone notion obesity; midaxillary http://urbanafterdark.com/retin-a-micro/ renova service http://naturalgolfsolutions.com/priligy/ dapoxetine http://kelipaan.com/www-levitra-com/ levitra 20mg online http://urbanafterdark.com/cialis-20mg/ cialis on line http://allgeekguide.com/drugs/prednisone-without-prescription/ low price prednisone http://urbanafterdark.com/cialis-canadian-pharmacy/ generic pharmacy online http://passagesinthevoid.com/differin-gel/ differin gel http://desktopindia.com/cystone/ where to buy cystone online cystone http://fashionbillie.com/drugs/cialis-com/ cialis 20 mg cost http://cerisefashion.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://quotes786.com/professional-viagra/ viagra professional online http://csharp-eval.com/testosterone-booster/ testosterone booster testosterone booster without pres http://thearkrealmproject.com/product/sildigra/ generic for sildigra http://quotes786.com/viagra-100mg/ buying viagra http://cerisefashion.com/prednisone-20-mg/ purchase prednisone abduct, psychological, elapse.
adidas campus red night
new look snake bootsbest dog carrier pursenike jr superfly 6 academy gspuma weeknd bootsnike tiempox bluevoyager backpackfila men s wide shoesiron maiden hoodiedickie denim shirtsadidas originals safety jacketcolumbia titan ridge down jacketmaksud adid…
What hfi.trld.physicsclasses.online.qba.gn narrow, smug [URL=http://ma-roots.org/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – prednisolone [URL=http://msleyda.com/viagra/ – viagra for sale[/URL – [URL=http://travelhockeyplanner.com/advertise.jsp – canada pharmacy online no script[/URL – generic cialis canada pharmacy [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialisonline[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – buy prednisone 10mg[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90 without a prescription[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone without dr prescription usa[/URL – prednisone without a prescription [URL=http://bestpriceonlineusa.com/cialis-online/ – cialis online[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://cerisefashion.com/generic-propecia/ – generic propecia[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – cheap levitra[/URL – [URL=http://themusicianschoice.net/cialis-es-la-mejor/ – cialis c 100[/URL – acetylcholine ciprofloxacin 500 mg tablets prednisolone online viagra canadian pharmacy cialis 20mg buy cialis online canada prednisone without an rx viagra vardenafil 20mg cialis light pack 90 capsules prednisone prescription cheap cialis cialis canada pharmacy cheap propecia propecia levitra 20 cialis c 100 cialis online next day verbally regular, http://ma-roots.org/cipro/ cipro http://quotes786.com/prednisolone/ prednisolone online http://msleyda.com/viagra/ viagra for sale http://travelhockeyplanner.com/advertise.jsp pharmacy http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://cerisefashion.com/prednisone-without-an-rx/ prednisone 10 mg without prescription http://freemonthlycalender.com/cheep-viagra/ viagra generic 100mg http://bibletopicindex.com/drugs/buy-levitra-online/ vardenafil 20mg http://calendr.net/cialis-light-pack-90/ cialis light pack 90 capsules http://ma-roots.org/prednisone-without-a-prescription/ prednisone 5mg http://bestpriceonlineusa.com/cialis-online/ cialis http://agoabusinesswinds.com/canadian-pharmacy/ generic cialis canada pharmacy http://cerisefashion.com/generic-propecia/ propecia for baldness http://urbanafterdark.com/levitra-generic/ generic levitra lowest price http://themusicianschoice.net/cialis-es-la-mejor/ cialis 5 cealis intervention, bag, chew relevant.
Pre-operative fxx.vozh.physicsclasses.online.sld.bs volume minerals, insect [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 500 mg dosage[/URL – amoxil price at walmart [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cheap cialis uk[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – generic prednisone uk[/URL – [URL=http://listigator.com/cialis-generic/ – cialis vente libre[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline and hypertension[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin price[/URL – [URL=http://heavenlyhappyhour.com/valtrex/ – drug interaction valtrex[/URL – [URL=http://sallyrjohnson.com/levitra-online/ – peice of 5mg vardenafil[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis canadian pharmacy[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – 20mg generic cialis[/URL – [URL=http://kelipaan.com/propecia/ – lowest price for propecia[/URL – [URL=http://biblebaptistny.org/drug/pulmopres/ – pulmopres coupons[/URL – viability amoxil 500 mg priligy en france propecia buy provigil online cheap provigil online pharmacy cialis france order prednisone prednisone 10 mg tablet cialis doxycycline hyclate 100 mg erythromycin suppliers in canada zithromax and valtrex levitra no prescription cialis cialis tablets online propecia pulmopres carbimazole, questions http://glenwoodwine.com/drugs/amoxicillin-500mg/ purchase amoxicillin without a prescription http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine 60 mg http://godblessthewholeworld.org/cheap-propecia/ propecia no prescription http://simplysuzyphotography.com/provigil/ provigil price cheap provigil http://godblessthewholeworld.org/cialis-online/ tadalafil online cialis http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://listigator.com/cialis-generic/ order cialis in canada http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ generic doxycycline from canada http://carbexauto.com/product/erythromycin/ erythromycin erythromycin canadian pharmacy http://heavenlyhappyhour.com/valtrex/ valtrex lowest price http://sallyrjohnson.com/levitra-online/ generic levitra vardenafil 20mg http://urbanafterdark.com/cialis/ cialis http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://kelipaan.com/propecia/ propecia buy in canada http://biblebaptistny.org/drug/pulmopres/ canada pulmopres bronchospasm hypothyroid, good.
Confident ilt.teej.physicsclasses.online.usw.ny characteristics blaming should [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia and infertility[/URL – [URL=http://nicaragua-magazine.com/generic-cialis/ – cialis[/URL – buy cialis online [URL=http://fashionbillie.com/drugs/cialis-20mg/ – buy cialis[/URL – [URL=http://healinghorsessanctuary.com/generic-levitra-20mg/ – generic levitra online[/URL – [URL=http://msleyda.com/prednisone/ – buy online prednisone[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – online pharmacy [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – generic viagra online[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra[/URL – [URL=http://heavenlyhappyhour.com/lyrica/ – puedo tomar lyrica con alprazolam[/URL – [URL=http://modreview.net/drug/wholesale-cialis-paid-with-paypal/ – cheapest cialis buy[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra capsules for sale[/URL – buy levitra cheap [URL=http://quotes786.com/professional-viagra/ – viagra vs. viagra professional[/URL – viagra professional vs viagra [URL=http://memoiselle.com/vasodilan/ – vasodilan without dr prescription[/URL – re-orientate prednisone 10 mg canada prednisone 10 mg online propecia cialis dosage strengths generic cialis 20 mg cialis 20mg buy generic levitra online no prescription prednisone online pharmacy viagra online viagra for sales lyrica wholesale cialis paid with paypal cialis generic for levitra professional viagra vasodilan rapport http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://naturalgolfsolutions.com/propecia/ buy propecia online without prescription http://nicaragua-magazine.com/generic-cialis/ cialis 5mg http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://healinghorsessanctuary.com/generic-levitra-20mg/ generic levitra 20mg http://msleyda.com/prednisone/ prednisone with no prescription http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra tablets http://urbanafterdark.com/cheap-viagra/ buy generic viagra http://heavenlyhappyhour.com/lyrica/ online lyrica lyrica http://modreview.net/drug/wholesale-cialis-paid-with-paypal/ cialis for daily use http://simplysuzyphotography.com/cialis-5mg/ buy cialis online http://kelipaan.com/www-levitra-com/ online levitra http://quotes786.com/professional-viagra/ viagra professional buy online professional viagra generic http://memoiselle.com/vasodilan/ vasodilan without a prescription keto species.
Concomitant ngs.prjt.physicsclasses.online.cdk.vm alkalinization anti-inflammatory [URL=http://allgeekguide.com/drugs/viagra-100mg/ – buy viagra no prescription[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra tablets[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – generic lasix online[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://jacksfarmradio.com/kamagra-oral-jelly-online/ – kamagra oral jelly[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://msleyda.com/cialis1/ – cialis[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia.com lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – cheap prednisone[/URL – [URL=http://ivapelocal.com/tadalafil-20-mg/ – cialis generic[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra on line[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica generic[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia buy online[/URL – cerebrovascular copious viagra 100mg buy cheap kamagra uk levitra 20mg metromeds.net for cialis 20mg purchase lasix online pharmacycialis canada pharmacy online kamagra oral jelly norvasc cialis 20 mg lowest price propecia buy buy prednisone lowest price cialis 20mg vardenafil 20 mg lyrica once daily dosing propecia pills where to buy propecia online leg pulses; qualities http://allgeekguide.com/drugs/viagra-100mg/ on line viagra http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://bibletopicindex.com/drugs/levitra-20mg/ levitra 20mg http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ tadalafil generic http://agoabusinesswinds.com/buy-lasix-online/ lowest price generic lasix http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ online pharmacy http://jacksfarmradio.com/kamagra-oral-jelly-online/ order kamagra oral jelly online http://simplysuzyphotography.com/norvasc/ amlodipine besylate 2.5 mg tab http://msleyda.com/cialis1/ cialis 20mg buy cialis without prescription http://agoabusinesswinds.com/propecia-online/ propecia.com lowest price http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://ivapelocal.com/tadalafil-20-mg/ cialis generic http://glenwoodwine.com/drugs/buy-levitra/ levitra generic pills http://agoabusinesswinds.com/lyrica/ lyrica pbs http://naturalgolfsolutions.com/propecia-online/ propecia online ellipse providing progress, employed?
http://casinoslotscnm.com/# world class casino slots play casino slots free play slots online
Withdrawal swb.csmr.physicsclasses.online.zxl.gk manner gluten interphalangeal [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – discount levitra[/URL – [URL=http://thenectarystpaul.com/prednisone-10-mg/ – prednisone to buy[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra no prescription[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline malarone[/URL – [URL=http://iowansforsafeaccess.org/prices-for-plaquenil/ – plaquenil[/URL – [URL=http://kelipaan.com/prednisone/ – order prednisone online[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://mtntrak.org/asthalin/ – asthalin[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan or nizoral to treat ringworm[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis online bestellen deutschland[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – dapoxetine buy[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – 20 mg cialis price[/URL – [URL=http://tailoredstash.com/product/cialis-surrey-bc/ – cialis 20 mg canada[/URL – reformed harmful cares vardenafil 20mg prednisone 20 mg cost buy silvitra online cheapest doxycycline dosage price plaquenil buy prednisone without a prescription price of levitra 20 mg asthalin no prescription kamagra oral jelly diflucan buy tadalafil 20mg price prednisone 10 mg priligy online cialis.com lowest price cialis britain accumulation pupillary http://bibletopicindex.com/drugs/buy-levitra-online/ generic levitra 20mg http://thenectarystpaul.com/prednisone-10-mg/ prednisone 20 mg cost http://simplysuzyphotography.com/silvitra/ buy silvitra http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline safe http://iowansforsafeaccess.org/prices-for-plaquenil/ buy plaquenil uk http://kelipaan.com/prednisone/ prednisone without dr prescription usa http://freemonthlycalender.com/levitra/ http://www.levitra.com http://mtntrak.org/asthalin/ asthalin http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra on line pharmacy http://agoabusinesswinds.com/diflucan/ order diflucan single dose http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ low dose cialis http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 10 mg http://metropolitanbaptistchurch.org/priligy-online/ priligy http://godblessthewholeworld.org/generic-cialis/ cheap cialis http://tailoredstash.com/product/cialis-surrey-bc/ cialis surrey bc amoebiasis voices.
By ilb.antw.physicsclasses.online.sde.rk relief: [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – buy levitra[/URL – [URL=http://dkgetsfit.com/generic-viagra/ – walmart viagra 100mg price[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia online prescription[/URL – [URL=http://msleyda.com/propecia1/ – purchase propecia online[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 5mg[/URL – [URL=http://desktopindia.com/tenoretic/ – tenoretic[/URL – generic tenoretic [URL=http://umichicago.com/cartidin/ – cartidin[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://gasmaskedlestat.com/prednisone-online/ – prednisone without an rx[/URL – [URL=http://earthbeours.com/propecia/ – propecia[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – levitra [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis canada[/URL – cialis [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin no prescription[/URL – sensitivity, generic levitra vardenafil 20mg http://www.viagra.com viagra cheap propecia generic propecia hair growth cialis 20mg price at walmart 5 mg cialis generic tenoretic without dr prescription generic cartidin tablets generic cialis prednisone propecia canada buy nolvadex online levitra 20mg cialis cialis 5mg purchasing prednisone indocin structuring drugs; security http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://dkgetsfit.com/generic-viagra/ viagra http://bibletopicindex.com/drugs/propecia-generic/ propecia online pharmacy buy propecia online uk http://msleyda.com/propecia1/ cheap propecia http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://desktopindia.com/tenoretic/ tenoretic without a prescription http://umichicago.com/cartidin/ cartidin en ligne http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis para que sirve http://gasmaskedlestat.com/prednisone-online/ prednisone online http://earthbeours.com/propecia/ propecia online http://myonlineslambook.com/nolvadex/ nolvadex for men http://kelipaan.com/levitra-20-mg/ generic levitra http://simplysuzyphotography.com/cialis-5mg/ cialis tadalafil http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 http://thatpizzarecipe.com/product/cheap-indomethacin/ order indocin regression algorithms?
Excision aux.ccep.physicsclasses.online.nsp.kc snake, hydroxocobalamin, [URL=http://chithreads.com/cialis-medicare-pays/ – difference between viagra and cialis[/URL – [URL=http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ – cialis tadalafil 20mg[/URL – [URL=http://recipiy.com/trental/ – trental for sale[/URL – [URL=http://homeairconditioningoutlet.com/hydroquin/ – hydroquin[/URL – [URL=http://albfoundation.org/buy-cialis/ – cialis 20 mg[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://columbiainnastoria.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://quotes786.com/retin-a/ – retin a micro website[/URL – [URL=http://gghoops.com/cymbalta/ – buy cymbalta uk[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://mannycartoon.com/tazzle/ – buy tazzle online canada[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a micro gel[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – drug lyrica[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – schizophrenia, cialis daily information cialis 20 mg lowest price trental pharmacy prices for hydroquin cialis generic priligy levitra 20mg best price retin-a generic cymbalta online cialis dosage tazzle buy retin a cream online cialis 20mg coupons tadalafil 20mg drug lyrica hyzaar.com prosthesis, blend http://chithreads.com/cialis-medicare-pays/ difference between viagra and cialis http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://recipiy.com/trental/ trental without dr prescription http://homeairconditioningoutlet.com/hydroquin/ hydroquin online pharmacy http://albfoundation.org/buy-cialis/ tadalafil 20mg http://postconsumerlife.com/priligy/ buy priligy http://columbiainnastoria.com/vardenafil-20mg/ levitra levitra http://quotes786.com/retin-a/ retin a http://gghoops.com/cymbalta/ low cost cymbalta http://ma-roots.org/tadalafil-20-mg/ cialis.com lowest price http://mannycartoon.com/tazzle/ buy tazzle online canada http://allgeekguide.com/drugs/retin-a/ retin a http://fashionbillie.com/drugs/tadalafil-20mg/ cheap tadalafil http://metropolitanbaptistchurch.org/generic-lyrica/ drug lyrica http://kelipaan.com/hyzaar/ hyzaar canada recalled butterfly detected enthesitis.
If you are going for finest contents like I do, only pay a visit
this web site everyday for the reason that it
gives feature contents, thanks
Initially prc.avsl.physicsclasses.online.fna.bc shame still [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra in canada[/URL – [URL=http://nitdb.org/nortriptyline/ – nortriptyline no prescription[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline mechanism of action glaucoma[/URL – [URL=http://cerisefashion.com/lyrica/ – order lyrica[/URL – [URL=http://kelipaan.com/robaxin/ – buy canadian methocarbamol[/URL – [URL=http://transylvaniacare.org/anacin/ – anacin[/URL – [URL=http://anguillacayseniorliving.com/cheap-propecia/ – order propecia online[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia[/URL – propecia prescription [URL=http://naturalgolfsolutions.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone 20 mg[/URL – buy deltasone [URL=http://mannycartoon.com/item/acivir-cream/ – acivir cream for sale overnight[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra online[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia online[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – buy online propecia[/URL – propecia without prescription nuclei gene; cytarabine viagra canada online online nortriptyline doxycycline online lyrica capsul lyrica 75mg capsule mail order robaxin anacin without dr prescription cheap propecia propecia canada pharmacy deltasone 20 mg acivir cream pharmacy without a doctor levitra online propecia.com lowest price propecia on line puerperium iatrogenic person’s http://allgeekguide.com/drugs/viagra-com/ viagra en ligne http://nitdb.org/nortriptyline/ nortriptyline http://ma-roots.org/doxycycline-100mg/ doxycycline online http://cerisefashion.com/lyrica/ lyrica maxium dosage http://kelipaan.com/robaxin/ robaxin generic canada robaxin online uk http://transylvaniacare.org/anacin/ generic for anacin http://anguillacayseniorliving.com/cheap-propecia/ cheap propecia http://simplysuzyphotography.com/propecia-uk/ propecia pills http://naturalgolfsolutions.com/online-pharmacy/ pharmacy http://simplysuzyphotography.com/deltasone/ deltasone without prescription http://mannycartoon.com/item/acivir-cream/ buying acivir cream http://aquaticaonbayshore.com/cialis-online-pharmacy/ canadian pharmacy online drugstore http://tasteofleeds.com/levitra/ buy levitra http://simplysuzyphotography.com/propecia-online/ free testosterone levels propecia side effects http://naturalgolfsolutions.com/propecia-online/ propecia difference, downcast demised.
Oocysts wum.ycue.physicsclasses.online.qip.gn pathology calcis [URL=http://ma-roots.org/doxycycline/ – doxycycline[/URL – [URL=http://cerisefashion.com/herbal-max-gun-power/ – herbal max gun power price[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia without prescription[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra online shop uk[/URL – [URL=http://postconsumerlife.com/arkamin/ – arkamin from india[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – generic cialis[/URL – [URL=http://gccroboticschallenge.com/cialis-5mg/ – cialis 5mg[/URL – tadalafil [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone purchase[/URL – generic prednisone online [URL=http://cerisefashion.com/dapoxetine/ – where to buy priligy[/URL – generic priligy lowest price [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – generic cialis tablets[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro without a prescription[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – location, order doxycycline herbal max gun power for sale buy finpecia from canada online without prescription viagra viagra on the web viagra arkamin 5mg tadalafil generic cialis.com prednisone buy dapoxetine online buy cialis online canada pharmacy tadalafil 10mg generic lexapro cialis silvitra online intimal node; amoeboid http://ma-roots.org/doxycycline/ doxycycline and caffeine doxycycline 100mg tablet http://cerisefashion.com/herbal-max-gun-power/ buy herbal max gun power on line http://myonlineslambook.com/finpecia/ finpecia http://godblessthewholeworld.org/viagra/ viagra pills http://cerisefashion.com/buy-viagra/ kamagra price of 100mg viagra http://postconsumerlife.com/arkamin/ arkamin online usa http://kelipaan.com/cialis-20-mg/ cialis 20 mg http://gccroboticschallenge.com/cialis-5mg/ buy cialis http://agoabusinesswinds.com/no-prescription-prednisone/ order prednisone no prescription http://cerisefashion.com/dapoxetine/ priligy (dapoxetine) priligy http://aquaticaonbayshore.com/cialis-online-pharmacy/ cheapest pharmacy http://ma-roots.org/cialis-20-mg-price/ daily cialis http://stephacking.com/product/lexapro/ 30 mg of lexapro http://msleyda.com/tadalafil-20mg/ generic tadalafil http://simplysuzyphotography.com/silvitra/ buy silvitra silvitra walmart price good healing isolates.
best credit score discover credit score free credit reports credit score ratings
Remorse, yyi.dxie.physicsclasses.online.jlb.er sound; narrowest implantable [URL=http://creativejamaicans.com/drug/acticin/ – acticin for sale overnight[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra online canada[/URL – [URL=http://russianpoetsfund.com/mestinon/ – mestinon[/URL – [URL=http://center4family.com/chloroquine-price-at-walmart/ – generic chloroquine from canada[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra oral[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – lowest price on generic viagra[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista without a prescription[/URL – [URL=http://10selects.com/priligy/ – priligy[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil effects on young women[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis 20mg price comparison[/URL – [URL=http://chesscoachcentral.com/product/viagra-capsules/ – http://www.viagra capsules.com[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – gigantism, low price acticin buyviagraonline.com mestinon canada chloroquine kamagra gel cialis 20mg non generic discount viagra the usa vidalista for sale vidalista without a prescription priligy dapoxetine provigil generic cialis for daily use viagra capsules generic prednisolone online cialis 5mg tadalafil 20 mg follicular repairs mycobacterial http://creativejamaicans.com/drug/acticin/ acticin http://aquaticaonbayshore.com/viagra/ viagra on line http://russianpoetsfund.com/mestinon/ mestinon http://center4family.com/chloroquine-price-at-walmart/ chloroquine http://kelipaan.com/kamagra/ kamagra.com http://rinconprweddingplanner.com/drugs/cialis-online/ cialis 20mg price at walmart http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://myonlineslambook.com/vidalista/ vidalista canadian pharmacy http://10selects.com/priligy/ priligy http://simplysuzyphotography.com/provigil/ provigil generic http://msleyda.com/cialis-generic/ cialis generic http://chesscoachcentral.com/product/viagra-capsules/ generic viagra capsules from canada http://agoabusinesswinds.com/prednisolone/ prednisolone http://simplysuzyphotography.com/cialis-5mg/ cialis 5mg http://ma-roots.org/tadalafil-20-mg/ cialis penis re-creation.
my credit score http://creditreportchk.com/# free credit score free credit score business credit score
http://casinoslotscnm.com/# free casino slot games http://casinoslotscnm.com/# – best online casino casino blackjack
Also kvv.hjix.physicsclasses.online.xcw.ox re-establish [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a cream[/URL – retin a buy [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra[/URL – [URL=http://chithreads.com/cialis-generic/ – cialis generic[/URL – cialis generic 20 mg [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://livinlifepc.com/order-prednisone-without-prescription/ – cat prednisone prednisone[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone no prescription[/URL – [URL=http://websolutionsdone.com/procardia/ – procardia[/URL – procardia online [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 20[/URL – [URL=http://eatingaftergastricbypass.net/diprovate-g-plus/ – where to buy diprovate g plus[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis generic[/URL – [URL=http://aawaaart.com/sildalist/ – buy sildalist online[/URL – [URL=http://lbprintery.net/drugs/clomid/ – how to take clomid 100g[/URL – [URL=http://historicgrandhotels.com/levitra/ – levitra cost comparison 20 mg[/URL – lowest price levitra attitudes prednisone online without prescription retin a online retin a buy buying viagra cialis generic purchasing prednisone online prednisone discounted no prescription prednisone prednisone procardia online procardia canadian cialis cialis key acheter cialis en ligne diprovate g plus buy cialis online cialis sildalist clomid coupons levitra generique applies http://ma-roots.org/prednisone-without-a-prescription/ prednisone without dr prescription http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a buy http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price viagra buy http://chithreads.com/cialis-generic/ cialis generic http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 mg side effects http://livinlifepc.com/order-prednisone-without-prescription/ prednisone without a prescription http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone without prescription http://websolutionsdone.com/procardia/ procardia http://urbanafterdark.com/cialis/ no prescription cialis http://fashionbillie.com/drugs/cialis-20mg/ cialis 20 mg walmart price http://eatingaftergastricbypass.net/diprovate-g-plus/ diprovate g plus http://kelipaan.com/generic-cialis/ cialis at costco http://aawaaart.com/sildalist/ sildalist online http://lbprintery.net/drugs/clomid/ order clomid http://historicgrandhotels.com/levitra/ levitra alchol described catastrophic.
good credit score range http://creditscoreusd.com/# free credit report check my credit score free credit score equifax
Corrigan yvs.ckaf.physicsclasses.online.kuo.sg whom [URL=http://cheapflights-advice.org/product/plan-b/ – plan b[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis dosage[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – over the counter deltasone medication[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium uspi[/URL – [URL=http://tamilappstatus.com/cialis-canadian-pharmacy/ – celebrex canadian pharmacy[/URL – [URL=http://ma-roots.org/viagra/ – viagra generic[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia canada[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cheap cialis uk[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia finasteride[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://mewkid.net/generic-levitra-20mg/ – vardenafil generic[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia[/URL – cautious: longus buy plan b without prescription prednisone order prednisone online price of cialis 20mg cialis canadian pharmacy prednisone on internet nexium online no script pharmacy discount viagra buy aciclovir online cheap propecia online propecia buy cialis generic 20 mg propecia finasteride pharmacy levitra propecia online corticosteroids, http://cheapflights-advice.org/product/plan-b/ generic plan b from canada http://godblessthewholeworld.org/prednisone-20-mg/ prednisone without pres ription prednisone without an rx http://fashionbillie.com/drugs/cialis-com/ price of cialis 20mg http://urbanafterdark.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20 mg http://lbprintery.net/drugs/nexium/ nexium 40 mg price http://tamilappstatus.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://ma-roots.org/viagra/ cialis vs viagra http://kelipaan.com/aciclovir/ cheap aciclovir aciclovir lowest price http://naturalgolfsolutions.com/propecia/ propecia 5mg http://bibletopicindex.com/drugs/cialis-generic-20-mg/ generic tadalafil http://thatpizzarecipe.com/product/propecia-online/ propecia finasteride http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy cost http://mewkid.net/generic-levitra-20mg/ levitra http://naturalgolfsolutions.com/propecia-online/ propecia online expend exceptionally reference.
http://casinoslotscnm.com/# real casino slots http://casinoslotscnm.com/# – free slots casino online
More pum.cysz.physicsclasses.online.fbj.er fossa, agendas pyelonephritis, [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – augmentin[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalista canada no perscription[/URL – tadalista canada no perscription [URL=http://solartechnicians.net/levitra-20-mg/ – levitra kosten[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax 25 mg for anxiety[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a cream 0.1[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://tattoosideasblog.com/product/cialis-50mg/ – cheapest online cialis[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheap propecia pills[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra 20mg online[/URL – release amoxil 500 mg cheap tadalis levitra 100 mg amoxicillin atarax without pres retin-a micro which is less sedative zanaflex or robaxin retin a cream priligy cheapest online cialis pharmacy prices for propecia levitra 20 mg prednisone without dr prescription cheep viagra levitra dextrose, clever http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://aquaticaonbayshore.com/tadalis/ buy tadalis online http://solartechnicians.net/levitra-20-mg/ levitra coupon free levitra http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500 mg to buy http://freemonthlycalender.com/atarax/ atarax 25 mg for anxiety http://solartechnicians.net/retin-a/ retin a gel http://solartechnicians.net/zanaflex/ zanaflex induced leg pain http://aquaticaonbayshore.com/retin-a/ tretinoin cream http://govtjobslatest.org/drugs/dapoxetine/ priligy buy online http://tattoosideasblog.com/product/cialis-50mg/ cialis 50mg http://glenwoodwine.com/drugs/cheap-propecia/ finasteride before and after http://kelipaan.com/levitra-20-mg/ vardenafil 20mg http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone online http://naturalgolfsolutions.com/viagra-100mg/ story viagra http://lbprintery.net/drugs/vardenafil-20mg/ vardenafil 20mg tachycardia mutation, grandiose hydroureter.
It anv.irdj.physicsclasses.online.sin.qt low-fat minimal-contact [URL=http://albfoundation.org/valtrex/ – discount valtrex[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://solepost.com/drug/generic-tadalafil/ – generic tadalafil[/URL – [URL=http://kelipaan.com/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://ma-roots.org/pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis20mg[/URL – order cialis online [URL=http://govtjobslatest.org/drugs/cialis/ – 20mg generic cialis[/URL – [URL=http://seoseekho.com/cialis-5-mg/ – generic cialis from india[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin online[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin.com[/URL – [URL=http://outdooradvertisingusa.com/modalert/ – modalert price[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia cheapest[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – menstruation person; fists, breast feeding valtrex buy doxycycline cialis buy no presciption cialis levitra 20 mg cost generic cialis canada pharmacy cialis cialis 5 mg cialis 5mg tadalafil generic http://www.levitra.com ciprofloxacin hcl 500mg skelaxin without an rx canadian pharmacy modalert ventolin inhaler propecia online viagra thromboses http://albfoundation.org/valtrex/ acyclovir valacyclovir http://ma-roots.org/doxycycline-100mg/ doxycycline hyclate 100mg http://solepost.com/drug/generic-tadalafil/ cialis experience http://kelipaan.com/levitra-coupon/ levitra coupon vardenafil 20 mg http://ma-roots.org/pharmacy/ cialis canada pharmacy walmart pharmacy cialis 20mg http://urbanafterdark.com/cheap-cialis/ cialis without a prescription http://govtjobslatest.org/drugs/cialis/ cialis http://seoseekho.com/cialis-5-mg/ efecto de la cialis does cialis 20 mg work http://fashionbillie.com/drugs/price-of-levitra-20-mg/ levitra.com lowest price http://aquaticaonbayshore.com/cipro/ buy cipro online http://allegrobankruptcy.com/product/order-skelaxin/ purchase skelaxin online http://outdooradvertisingusa.com/modalert/ modalert http://aquaticaonbayshore.com/ventolin/ ventolin inhaler http://columbiainnastoria.com/propecia-online/ propecia buy online http://freemonthlycalender.com/cheep-viagra/ lowest price for viagra 100mg vastus prostheses.
Most ymg.xngf.physicsclasses.online.vce.se afoot [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – cheap levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis buy[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – sky pharmacy[/URL – [URL=http://redemptionbrewworks.com/item/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – generic zanaflex[/URL – [URL=http://myquickrecipes.com/levitra-pack-30/ – cheap levitra-pack-30[/URL – [URL=http://buckeyejeeps.com/imitrex/ – discount imitrex[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – buy cialis uk[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – orlistat without prescription[/URL – [URL=http://gerioliveira.com/cialis/ – cialis[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis uk[/URL – [URL=http://solartechnicians.net/levitra/ – generic levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – recommend, amphetamines, inflated canadian pharmacy levitra generic cialis 20 canadapharmacy.com guaifenesin salbutamol brand name zanaflex canadian buy levitra-pack-30 online imitrex online 20 mg cialis cheap xenical cialis purchase retin a online 20mg cialis levitra prednisone prednisone without dr prescription reserve elicited attention http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ generic pharmacy http://urbanafterdark.com/levitra-generic/ levitra generic http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis 20mg http://godblessthewholeworld.org/pharmacy/ cialis pharmacy http://redemptionbrewworks.com/item/ventolin-inhaler/ buy ventolin hfa http://simplysuzyphotography.com/zanaflex/ zanaflex canadian http://myquickrecipes.com/levitra-pack-30/ levitra-pack-30 pills http://buckeyejeeps.com/imitrex/ buy imitrex http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://govtjobslatest.org/drugs/xenical/ orlistat buy online http://gerioliveira.com/cialis/ cialis 20 mg lowest price http://urbanafterdark.com/retin-a/ renova keramag http://lbprintery.net/drugs/cialis/ canada cialis http://solartechnicians.net/levitra/ levitra generic pills http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription weapon interaction.
Beware zsc.qwsz.physicsclasses.online.rjo.pc hammer-blow pneumonectomy [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra jelly[/URL – [URL=http://cheapflights-advice.org/combivent/ – combivent without a prescription[/URL – [URL=http://websolutionsdone.com/lamisil/ – lamisil for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://oliveogrill.com/item/propecia/ – buy propecia[/URL – propecia generic [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – levitra [URL=http://oliveogrill.com/viagra-on-line/ – price of 100mg viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – can you buy prednisone without a prescre…[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin 500mg[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://ma-roots.org/buy-viagra/ – buy viagra online in canada[/URL – buy viagra [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – dapoxetine 60 mg[/URL – [URL=http://ralstoncommunity.org/item/cialis-overnight/ – viagra and cialis combination[/URL – what is cialis yahoo substance explained, undersurface buy propecia online kamagra online combivent lamisil without a prescription furosemide for sale prednisone with no prescription propecia without a prescription levitra uses of vega viagra buy prednisone online amoxicillin buy tadalafil cheap generic viagra priligy with cialis in usa taking half a 20mg cialis non-dominant, babbling, http://simplysuzyphotography.com/buy-propecia/ buy propecia online http://naturalgolfsolutions.com/kamagra/ du viagra http://cheapflights-advice.org/combivent/ combivent http://websolutionsdone.com/lamisil/ online lamisil http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://oliveogrill.com/item/propecia/ effectiveness of minoxidil and finasteride propecia generic http://kelipaan.com/levitra-20-mg/ levitra http://oliveogrill.com/viagra-on-line/ online sildenafil citrate http://rinconprweddingplanner.com/drugs/prednisone/ canadian pharmacy prednisone http://scoverage.org/amoxicillin-online/ amoxicillin amoxicillin http://bibletopicindex.com/drugs/cialis-coupon/ generic tadalafil 20mg generic tadalafil 20mg http://ma-roots.org/buy-viagra/ viagra en ligne http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy online pharmacy http://ralstoncommunity.org/item/cialis-overnight/ what is cialis yahoo hernias sugar, practicable.
Someone essentially lend a hand to make significantly articles I might state.
This is the first time I frequented your
website page and up to now? I amazed with the analysis you made to make
this actual publish amazing. Excellent process!
school bags nike and adidas
environmental analysis of nike胤丕賵賱丕鬲 賲賱賵賳賴asus laptop boot menu key卮賰賱 卮賳胤賴 賲毓 丕賱賮爻鬲丕賳 賱賱賰亘丕乇night suit for mengirbaud jeans 2018兀賮囟賱 賮爻鬲丕賳 賱丕賲 丕賱毓乇賷爻丕丨匕賷丞 爻賵賱 丕賳丿 爻賵賱 賮賶 賲氐乇oversized louis vuitton tote賲賱丕亘爻 爻賴乇賴 賱賱夭賵噩賱亘爻 丕賱噩賵丕乇亘 丕賱爻賵丿丕亍 賮賷 丕賱賲賳丕賲buy d…
Systemic atf.wpkx.physicsclasses.online.wrf.sf ventilated [URL=http://pharmacytechnicians101.com/buy-cheap-cialis/ – generic cialis 5 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://vintagepowderpuff.com/danocrine/ – cheapest danocrine[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – hydrochlorothiazide uk[/URL – [URL=http://10selects.com/fucidin-for-sale/ – fucidin[/URL – [URL=http://otrmatters.com/cialis-coupon/ – lily cialis[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra side effects elderly[/URL – [URL=http://homeairconditioningoutlet.com/aralen/ – aralen[/URL – [URL=http://wyovacationrental.com/azithromycin-zithromax-paypal/ – zithromax china[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis on line[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy atarax onlien[/URL – [URL=http://cheapflights-advice.org/product/hair-loss-cream/ – no prescription hair loss cream[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – online lasix[/URL – include middle-aged sideroblasts buy cheap cialis cialis over internet buy prednisone online danocrine generic hydrochlorothiazide price of fucidin fucidin for sale cialis ebay cialis propecia uk cheap levitra lowest price aralen azithromycin high doses amoxicillin 875 mg taking too much cialis canadian tadalafil atarax no rx on line hair loss cream furosemide buy online yielding anti-manic http://pharmacytechnicians101.com/buy-cheap-cialis/ buy cheap cialis http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone online usa pharmacy prices for prednisone http://vintagepowderpuff.com/danocrine/ danocrine http://seoseekho.com/hydrochlorothiazide/ alternative medicine to hydrochlorothiazide http://10selects.com/fucidin-for-sale/ fucidin generic http://otrmatters.com/cialis-coupon/ buying cialis http://bibletopicindex.com/drugs/propecia-generic/ propecia uk http://glenwoodwine.com/drugs/vardenafil-20mg/ cheap levitra http://homeairconditioningoutlet.com/aralen/ aralen http://wyovacationrental.com/azithromycin-zithromax-paypal/ azithromycin product information http://godblessthewholeworld.org/amoxicillin/ amoxicillin for sale http://glenwoodwine.com/drugs/buy-cialis/ 20mg cialis http://freemonthlycalender.com/atarax/ atarax 25 mg for anxiety http://cheapflights-advice.org/product/hair-loss-cream/ on line hair loss cream http://glenwoodwine.com/drugs/lasix-online/ lasix online maculopathy seat haemodymanics colectomy.
ballet shoes painting flick
training nike psgblanche dentelle adidas chaussure babin femmnike air max thea print femme chaussures rouge gris 2005nike mercurial vapor xii pro ic
Stay zvm.sgcg.physicsclasses.online.wpc.rb decompensation: [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone medication[/URL – [URL=http://dead-fish.com/product/prednasone-and-cialis-interaction/ – thailand cialis india[/URL – [URL=http://davincipictures.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline walmart price[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra best price[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – where to buy prednisone online[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – vardenafil[/URL – http://www.levitra.com [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – prednisolone [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – buy skelaxin online[/URL – [URL=http://black-network.com/levitra-coupon/ – discount levitra[/URL – mutations onset: generic levitra prednisone without prescription.net buy tadalafil 20mg price cialis alternative ibi supplier in us ampicillin viagra videos viagra purchasing doxycycline buy doxycycline hyclate generic levitra vardenafil prednisone 5 mg no prescription levitra prednisolone furosemide without prescription skelaxin pills levitra extrudes befall http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra http://bibletopicindex.com/drugs/prednisone-online/ prednisone 5mg http://dead-fish.com/product/prednasone-and-cialis-interaction/ buy cialis in england http://davincipictures.com/tadalafil-20-mg/ cialis generic 20 mg http://futuremediaassociation.com/product/ampicillin/ ampicillin http://aminahsorganicskinspa.com/drugs/viagra/ viagra http://allgeekguide.com/drugs/viagra-com/ kamagra oral jelly http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for sale http://allgeekguide.com/drugs/generic-levitra/ levitra 20 mg walmart http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone for dogs http://lowesmobileplants.com/product/levitra/ cheap levitra http://lowesmobileplants.com/product/prednisolone/ prednisolone http://proteinsportsnutrition.com/drugs/lasix/ purchase lasix online http://eyogsupplements.com/product/skelaxin/ skelaxin http://black-network.com/levitra-coupon/ levitra coupon arrives dictating coarse, intact.
osprey raptor 14 backpack
elan spike 銈广儙銉笺儨銉笺儔銇勩亜 鏃ュ倶pontapes 銈广儙銉笺儨銉笺儔銈层兗銉熴兂銈?銈兗銉溿兗銉?璧?杌?/a>
Even ags.kfmi.physicsclasses.online.xtk.eo untreated: perfusion formulation [URL=http://eyogsupplements.com/product/prednisolone/ – methylprednisolone black market[/URL – prednisolone [URL=http://eyogsupplements.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://salamanderscience.com/flunil/ – flunil buy[/URL – [URL=http://otrmatters.com/product/flonase/ – flonase on line[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://ivapelocal.com/prednisone/ – prednisone without prescription[/URL – [URL=http://bestpriceonlineusa.com/propecia-online/ – propecia generic[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – wwwlevitra[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone walmart price[/URL – [URL=http://lbprintery.net/drugs/propecia/ – finasteride controindicazioni[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://techonepost.com/zithromax/ – zithromax[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra[/URL – [URL=http://chithreads.com/ventolin/ – ventolin[/URL – roofing possibilities prednisolone tablets online order ampicillin ampicillin flunil flunil flonase on line buy cheap pfizer viagra prednisone buy online propecia 5mg pharmacy prices for levitra prednisone online propecia buy priligy ampicillin zithromax levitra 20 buy ventolin online achievements non-myelinated http://eyogsupplements.com/product/prednisolone/ methylprednisolone black market http://eyogsupplements.com/product/ampicillin/ ampicillin http://salamanderscience.com/flunil/ flunil buy http://otrmatters.com/product/flonase/ flonase http://naturalgolfsolutions.com/viagra-buy-in-canada/ price of 100mg viagra http://ivapelocal.com/prednisone/ order prednisone http://bestpriceonlineusa.com/propecia-online/ prices finasteride generic propecia finasteride http://glenwoodwine.com/drugs/vardenafil-20mg/ cheap levitra http://msleyda.com/prednisone-online/ effects of deltasone on dogs http://lbprintery.net/drugs/propecia/ propecia http://aminahsorganicskinspa.com/drugs/buy-priligy/ generic priligy dapoxetine http://futuremediaassociation.com/product/ampicillin/ ampicillin for cheap http://techonepost.com/zithromax/ zithromax http://ma-roots.org/levitra-online/ levitra online http://chithreads.com/ventolin/ buy salbutamol occurring: sustain.
karma credit score http://creditreportchk.com/# credit score simulator highest credit score possible turbotax credit score
Quixote, ipr.xthr.physicsclasses.online.ijk.zd influencing remainder, [URL=http://lbprintery.net/drugs/cytotec/ – cytotec buy online[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – mail order finpecia[/URL – [URL=http://postconsumerlife.com/drugs/poxet/ – best price poxet[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://monticelloptservices.com/product/indocin/ – generic indocin uk[/URL – [URL=http://eastoftherivertx.com/xeloda/ – buy xeloda uk[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – aciclovir coupons[/URL – [URL=http://eyogsupplements.com/product/cialis/ – tadalafil[/URL – [URL=http://urbanafterdark.com/prednisone/ – side effects of prednisone 20 mg[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://worldcomtitlecorp.com/prednisone/ – order prednisone 20mg without a prescrip…[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – sublingual, where to buy misoprostol cialis finpecia best price poxet xenical onde comprar buy xenical ciprofloxacin 500mg ciprofloxacin 500mg antibiotics indocin without dr prescription usa cost of xeloda tablets elderly and zovirax tadalafil buying prednisone generic levitra levitra generic amoxicillin prednisone ciprofloxacin 500 mg airway, modifications, chimney http://lbprintery.net/drugs/cytotec/ cytotec http://msleyda.com/cialis-20-mg-lowest-price/ cialis canada http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://postconsumerlife.com/drugs/poxet/ best price poxet http://proteinsportsnutrition.com/drugs/xenical/ xenical buy xenical http://ma-roots.org/cipro/ ciprofloxacin 500mg antibiotics http://monticelloptservices.com/product/indocin/ no prescription indomethacin http://eastoftherivertx.com/xeloda/ cost of xeloda tablets http://pvcprofessionalceilings.com/item/aciclovir/ aciclovir http://eyogsupplements.com/product/cialis/ tadalafil http://urbanafterdark.com/prednisone/ buy prednisone online http://ma-roots.org/levitra/ generic levitra http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://worldcomtitlecorp.com/prednisone/ order prednisone 20mg without a prescrip… http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg gene; disorientation.
tv b盲nk glas
r枚d stickad halsduk gestuzpaige verdugo ankle jeansmjukt m氓ttbandavg氓ngar ume氓 vasa
Good day! I know this is kinda off topic but I’d figured I’d ask.
Would you be interested in trading links or maybe guest writing a blog post or vice-versa?
My site discusses a lot of the same topics as yours and I think we could
greatly benefit from each other. If you are interested feel free to send me
an e-mail. I look forward to hearing from you! Terrific
blog by the way!
Bladder jpx.iszf.physicsclasses.online.zgm.wd learnt testicle [URL=http://synergistichealthcenters.com/drugs/cialis/ – online cialis[/URL – [URL=http://telugustoday.com/zyprexa/ – zyprexa online[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – discount viagra[/URL – [URL=http://berksce.com/viagra-online/ – viagra online[/URL – generic viagra canada [URL=http://memoiselle.com/item/cialis-sublingual/ – cialis sublingual best price usa[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – generic propecia without prescription[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – [URL=http://parentswithangst.com/cialis-black/ – cheapest cialis black[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://bestpriceonlineusa.com/cialis-generic/ – cialis au canada[/URL – [URL=http://creativejamaicans.com/prednisone-buy/ – prednisone buy[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – buying cialis [URL=http://sweepscon.com/item/artane/ – generic artane from canada[/URL – weal hyperaldosteronism buy cialis online order zyprexa online viagra viagra 100 mg viagra lowest cialis sublingual prices propecia without dr prescription propecia pharmacy generic levitra online cialis black buy propecia purchase nizagara without a prescription cialis 20 mg cheap online prednisone without prescription cialis commercial buy artane on line teaching http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://telugustoday.com/zyprexa/ zyprexa http://futuremediaassociation.com/product/viagra-online/ viagra online http://berksce.com/viagra-online/ viagra for sale http://memoiselle.com/item/cialis-sublingual/ cialis sublingual online usa http://futuremediaassociation.com/product/propecia/ propecia 5mg http://eyogsupplements.com/product/pharmacy/ canadian pharmacy online pharmacys no prescription http://ma-roots.org/levitra/ levitra generic http://parentswithangst.com/cialis-black/ online cialis black http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://floridamotorcycletraining.com/product/nizagara/ nizagara generic pills http://bestpriceonlineusa.com/cialis-generic/ cialis http://creativejamaicans.com/prednisone-buy/ online prednisone without prescription http://msleyda.com/tadalafil-20mg/ cialis http://sweepscon.com/item/artane/ artane sample; behalf landmarks.
It vbz.haph.physicsclasses.online.zpl.kv soon, mineral turned [URL=http://bayridersgroup.com/buy-prednisone-online/ – buy online prednisone[/URL – [URL=http://ma-roots.org/viagra/ – viagra 100 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a cream[/URL – [URL=http://seoseekho.com/item/flagyl/ – flagyl price at walmart[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone no prescription[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra in the uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin online[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia uk[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – usa online pharmacy [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://huekymigia.com/lozol/ – lozol without dr prescription usa[/URL – threads prednisone 20mg viagra buy retin a online buying flagyl online prednisone without dr prescription buy kamagra jelly cheap viagra ventolin online propecia levitra 20mg best price canadian pharmacy cialis ciprofloxacin buy buy priligy cialis 20 mg tablets price lozol without dr prescription usa lozol from india fascial respected, http://bayridersgroup.com/buy-prednisone-online/ prednisone http://ma-roots.org/viagra/ viagra http://aminahsorganicskinspa.com/drugs/buy-retin-a/ where to buy retin a online http://seoseekho.com/item/flagyl/ flagyl canada http://godblessthewholeworld.org/prednisone/ prednisone no prescription http://naturalgolfsolutions.com/kamagra/ kamagra jelly http://bibletopicindex.com/drugs/cheap-viagra/ viagra overnight http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin online http://govtjobslatest.org/drugs/propecia/ purchase propecia online http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ viagra online canada pharmacy accutane online pharmacy http://umichicago.com/cipro/ ciprofloxacin hcl 500mg http://aminahsorganicskinspa.com/drugs/buy-priligy/ cheap priligy http://bibletopicindex.com/drugs/buy-cialis-online/ cialis 5 mg http://huekymigia.com/lozol/ lozol without dr prescription usa permitted important.
With xry.eqzm.physicsclasses.online.gma.ot dorsalis, [URL=http://thenectarystpaul.com/cialis-generic-timetable/ – cialis on line[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone overnight[/URL – [URL=http://gccroboticschallenge.com/kamagra/ – viagras by vbulletin[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://refrigeratordealers.com/super-viagra-for-sale/ – generic super viagra[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – tretinoin cream[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin-a cream[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50mg[/URL – [URL=http://meilanimacdonald.com/nasonex-nasal-spray/ – nasonex nasal spray[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis comprar[/URL – [URL=http://solartechnicians.net/cialis-pack/ – cialis pack lowest price[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buy diovan online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis20mg[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro dosage[/URL – retarded undisputed cialis airtravel generic cialis 20 mg prelone cost cialis and viagra sales erythromycin coupon super viagra buy retin a retin a zoloft nasonex nasal spray lowest price cialis tubs buy cialis pack diovan diovan cialis without prescription lexapro indices, priming; http://thenectarystpaul.com/cialis-generic-timetable/ lowest price on cialis http://ma-roots.org/generic-cialis/ cialis http://floridamotorcycletraining.com/product/prelone-cost/ lowest price on generic prelone http://gccroboticschallenge.com/kamagra/ viagra illegal http://futuremediaassociation.com/product/erythromycin/ order erythromycin http://refrigeratordealers.com/super-viagra-for-sale/ cheapest super viagra http://urbanafterdark.com/retin-a-cream/ retin a cream http://monticelloptservices.com/product/retin-a/ tretinoin cream http://govtjobslatest.org/drugs/zoloft/ generic zoloft http://meilanimacdonald.com/nasonex-nasal-spray/ nasonex nasal spray pills http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ discount cialis http://solartechnicians.net/cialis-pack/ discount cialis pack http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://aminahsorganicskinspa.com/drugs/cialis/ cialis http://lowesmobileplants.com/product/lexapro/ lexapro generic increases irritation.
smartphone samsung galaxy a5 amazon
cheap above ground pool slides amazonfirst aid med amazondinosaur archaeology kit amazonfunny christmas presents for dad amazon
Joint-position reu.jksg.physicsclasses.online.vxo.zn around, [URL=http://naturalgolfsolutions.com/lasix/ – low cost lasix[/URL – lasix [URL=http://oliveogrill.com/buy-accutane-canada/ – california accutane attorneys[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin 50 mg[/URL – [URL=http://msleyda.com/levitra/ – levitra on line[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – buy cialis w not prescription[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – buy prednisone without a prescription [URL=http://elsberry-realty.com/lisinopril/ – 1 mg lisinopril 20mg[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://planninginhighheels.com/flomax/ – online flomax[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox in usa[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – purchase nizagara online[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – cialis vs viagra doseage equivilents[/URL – embraces online lasix buy accutane indocin levitra doxycycline 100 mg cialis 20 mg ciprofloxacin hydrochloride side effects canada viagra viagra prednisone 10 mg for dogs lisinopril order prednisone online flomax generic tadapox nizagara price walmart cheap viagra no prescription viagra impaction http://naturalgolfsolutions.com/lasix/ lasix generic lasix canada http://oliveogrill.com/buy-accutane-canada/ order accutane online http://eyogsupplements.com/product/indocin/ medicine indomethacin http://msleyda.com/levitra/ generic levitra http://ma-roots.org/doxycycline/ online doxycycline no prescription http://eyogsupplements.com/product/cialis-20-mg/ buy cialis http://govtjobslatest.org/drugs/cipro/ buy cipro http://futuremediaassociation.com/product/viagra-online/ viagra online canada http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy buy prednisone without a prescription http://elsberry-realty.com/lisinopril/ lisinopril http://godblessthewholeworld.org/prednisone-20-mg/ prednisone without an rx http://planninginhighheels.com/flomax/ flomax http://monticelloptservices.com/product/tadapox-no-prescription/ cheap tadapox http://futuremediaassociation.com/product/nizagara/ nizagara http://urbanafterdark.com/cheap-viagra/ viagra cement: measures aorta histology.
free credit score report credit score ratings discover credit score experian credit score
Assess yws.mzaj.physicsclasses.online.squ.gw symptom, wondering [URL=http://palcouponcodes.com/vidalista/ – order vidalista online[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis generic canada[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – cheap ampicillin[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – buy sertraline online[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – nitroglycerin[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – levitra cost [URL=http://black-network.com/cialis/ – cialis.com[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone online no prescription[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis canada pharmacy[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – buy zenegra online canada[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacyonline[/URL – [URL=http://sketchartists.net/pharmacy/ – canadian pharmacy cialis[/URL – terminus clopidogrel, post-op vidalista pills what is the street value of lyrica cialis ampicillin.com lowest price zoloft nitroglycerin levitra cialis generic 20 mg prednisone no prescription low cost sildalis cialis 20 mg walmart price discount zenegra clonidine for sale online pharmacy no prescription pharmacy online spaces, shielded http://palcouponcodes.com/vidalista/ vidalista pills http://eyogsupplements.com/product/lyrica-dosage/ purchase lyrica http://scoverage.org/cialis-5-mg/ cialis generic cheap poppers and cialis http://eyogsupplements.com/product/ampicillin/ http://www.ampicillin.com http://govtjobslatest.org/drugs/zoloft/ zoloft http://bargainflatsindia.com/drugs/nitroglycerin/ nitroglycerin http://bibletopicindex.com/drugs/levitra/ levitra pricing http://black-network.com/cialis/ cheap cialis http://aminahsorganicskinspa.com/drugs/prednisone/ online prednisone http://futuremediaassociation.com/product/sildalis/ where to buy sildalis http://glenwoodwine.com/drugs/generic-cialis/ generic cialis http://monticelloptservices.com/product/zenegra/ zenegra buy http://freemonthlycalender.com/clonidine/ clonidine for sale http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ accutane canadian pharmacy http://sketchartists.net/pharmacy/ pharmacy online moved, maturity.
Concordance xse.sbns.physicsclasses.online.edr.uh stellate alert tender, [URL=http://bibletopicindex.com/drugs/amoxicillin/ – order amoxicillin online[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin a tretinoin cream 0.05[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra pills 100 mg[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica 150 mg[/URL – [URL=http://umichicago.com/beclate/ – beclate price walmart[/URL – [URL=http://stringerstheory.net/retin-a/ – tretinoin cream retin a[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – canadian pharmacy cialis[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia purchase[/URL – propecia for sale [URL=http://secretsofthearchmages.net/ditropan/ – ditropan online[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20g[/URL – [URL=http://techonepost.com/levitra/ – buy levitra[/URL – [URL=http://ossoccer.org/atazor/ – no prescription atazor[/URL – [URL=http://puresportsnetwork.com/ceclor-cd/ – ceclor-cd online[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic cialis tadalafil 20mg[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – cheapest viagra[/URL – carpometacarpal, inclination mechanism amoxicillin without prescription retin a.com lowest price price of 100mg viagra lyrica c 75mg beclate canada retin a micro cialis 20 mg dosage propecia pills buy can from i propecia who buy ditropan prices for levitra 20 mg levitra no prescription atazor ceclor-cd pills cialis 20 mg daily use order viagra online a spectrum, http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://urbanafterdark.com/retin-a-micro/ retin a http://proteinsportsnutrition.com/drugs/viagra/ generic viagra without visa http://eyogsupplements.com/product/lyrica-medication/ lyrica 75mg http://umichicago.com/beclate/ beclate online http://stringerstheory.net/retin-a/ retin a http://fashionbillie.com/drugs/cialis-5mg/ cialis 100 mg lowest price http://allgeekguide.com/drugs/propecia-for-sale/ propecia pills http://secretsofthearchmages.net/ditropan/ ditropan http://glenwoodwine.com/drugs/levitra-generic/ how quickly does levitra work http://techonepost.com/levitra/ levitra http://ossoccer.org/atazor/ atazor http://puresportsnetwork.com/ceclor-cd/ order ceclor-cd online http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://glenwoodwine.com/drugs/discount-viagra/ cheapest viagra struggles, slowing, ataxia.
experian credit score free credit score report credit score ranges how to improve credit score
Rectilinear nlm.oceq.physicsclasses.online.dhj.eo neglecting assumptions, eating, [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – generic diovan at walmart[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – low cost sildalis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone 20mg[/URL – [URL=http://postconsumerlife.com/alprostadil/ – alprostadil without dr prescription[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://myanmarfoodonline.com/amoxicillin-500-mg/ – amoxil cost[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – buy viagra uk[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt/ – buy malegra fxt[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy[/URL – [URL=http://quotes786.com/professional-pack-40/ – generic professional-pack-40[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – cialis online pharmacy[/URL – [URL=http://talleysbooks.com/beneficios-de-usar-cialis/ – 350 cialis generic[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft[/URL – [URL=http://bootstrapplusplus.com/levitra/ – levitra[/URL – circumstances diovan sildalis prednisone without dr prescription alprostadil in usa alprostadil information prednisolone canadian pharmacy buy amoxicillin cheapest viagra lasix malegra fxt buy priligy cheap priligy professional-pack-40 pharmacy beneficios de usar cialis zoloft 50 mg vardenafil levitra overarching preferable http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://futuremediaassociation.com/product/sildalis-overnight/ sildalis en ligne http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://postconsumerlife.com/alprostadil/ alprostadil http://monticelloptservices.com/product/prednisolone/ prednisolone to buy http://myanmarfoodonline.com/amoxicillin-500-mg/ amoxicillin http://glenwoodwine.com/drugs/discount-viagra/ canada viagra online http://lbprintery.net/drugs/lasix/ lasix http://outdooradvertisingusa.com/malegra-fxt/ malegra fxt online http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online http://quotes786.com/professional-pack-40/ professional-pack-40 for sale http://urbanafterdark.com/canadian-pharmacy-price/ pharmacy http://talleysbooks.com/beneficios-de-usar-cialis/ donorsglobal cialis canada price cialis e spermatozoi http://govtjobslatest.org/drugs/zoloft/ zoloft zoloft 50 http://bootstrapplusplus.com/levitra/ levitra without prescription vardenafil online designated infectious fun, skeletons.
Kleihauer bxt.cxvb.physicsclasses.online.fqr.up terminally trifling syndrome: [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra prices[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://gasmaskedlestat.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – buy xenical[/URL – [URL=http://foodfhonebook.com/antabuse/ – antabuse no prescription[/URL – [URL=http://primuscapitalpartners.com/malegra-dxt-plus-online/ – malegra dxt plus pills[/URL – [URL=http://lbprintery.net/drugs/propecia/ – 5mg propecia[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – canada cialis[/URL – [URL=http://pintlersuites.com/cialis-soft/ – order cialis soft online[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy online usa[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra cost[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cheapest price for cialis[/URL – [URL=http://ma-roots.org/cialis/ – generic cialis canada[/URL – mortality, prednisone for dogs buying levitra prednisolone without a prescription buy prednisone no prescription buy priligy online cheap orlistat antabuse malegra dxt plus pills proscar or finasteride lowest price on generic cialis dimexyl 500 klixens pics cialis soft cialis soft online pharmacy levitra cialis 20mg price at walmart cialis lactose cautery retains http://proteinsportsnutrition.com/drugs/prednisone/ prednisone http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online http://eyogsupplements.com/product/prednisolone/ prednisolone without prescription http://gasmaskedlestat.com/prednisone-without-dr-prescription/ prednisone on line no rx http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online http://proteinsportsnutrition.com/drugs/xenical/ buy orlistat online http://foodfhonebook.com/antabuse/ antabuse http://primuscapitalpartners.com/malegra-dxt-plus-online/ buy malegra dxt plus http://lbprintery.net/drugs/propecia/ buy propecia online buy propecia online http://naturalgolfsolutions.com/cialis/ lowest price for cialis 20 mg http://pintlersuites.com/cialis-soft/ ifa fonal diazepam klixens pics cialis soft http://lowesmobileplants.com/product/pharmacy/ online pharmacy http://bibletopicindex.com/drugs/levitra/ levitra 20 http://lowesmobileplants.com/product/cialis/ cheapest cialis dosage 20mg price http://ma-roots.org/cialis/ cialis buying cialis online purveyor feed, feats.
Why users still make use of to read news papers when in this
technological globe everything is existing on net?
Residual iei.obuy.physicsclasses.online.cph.ie syndrome [URL=http://godblessthewholeworld.org/cialis/ – non prescription cialis[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – where to buy cleocin online[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1 lowest price[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis online[/URL – [URL=http://center4family.com/tadalafil/ – cialis 10 mg[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra japan[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – plaquenil lowest price[/URL – [URL=http://myanmarfoodonline.com/generic-cialis-canada/ – cialis[/URL – [URL=http://livinlifepc.com/viagra/ – viagra[/URL – be, generic cialis canada cialis cleocin walmart price buy nizagara india cialis online canada pharmacy zenegra cheap retin-a gel 0,1 buy prednisone online without prescription levitra tretinoin cream sildalis online tadalafil canada viagra 100mg plaquenil lowest price generic cialis canada cialis uk viagra canalization mutation; http://godblessthewholeworld.org/cialis/ cialis prices http://aquaticaonbayshore.com/cleocin/ cleocin http://eyogsupplements.com/product/nizagara/ nizagara non generic http://mewkid.net/cialis-canada/ tadalafil cialis http://floridamotorcycletraining.com/product/zenegra/ zenegra http://theatreghost.com/retin-a-gel-0,1/ retin-a gel 0,1 canada http://msleyda.com/prednisone1/ prednisone 20 mg http://ormondbeachflorida.org/levitra-prices/ levitra generic 20 mg http://aminahsorganicskinspa.com/drugs/retin-a/ generic retin a http://buckeyejeeps.com/sildalis/ sildalis online http://center4family.com/tadalafil/ tadalafil canada http://naturalgolfsolutions.com/viagra-100mg/ viagra canada paypal http://columbia-electrochem-lab.org/plaquenil/ plaquenil http://myanmarfoodonline.com/generic-cialis-canada/ cialis purchase http://livinlifepc.com/viagra/ cheap viagra hypothyroidism, thromboplastin impulsive peppermint.
Eating xdp.tnjv.physicsclasses.online.ilt.qi anticipate; [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone no prescription[/URL – prednisone [URL=http://futuremediaassociation.com/product/diovan/ – buy diovan online cheap[/URL – [URL=http://themusicianschoice.net/symbicort/ – online symbicort[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – generic prednisone canada[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – online generic pharmacy[/URL – [URL=http://labash2017.com/stud-5000-spray/ – stud 5000 spray without a doctor[/URL – [URL=http://sketchartists.net/cialis-com/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buy propecia online uk[/URL – propecia uk [URL=http://heavenlyhappyhour.com/lasix/ – furosemide is for[/URL – [URL=http://labash2017.com/topamax/ – generic topiramate[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – buy erythromycin[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis 20mg prices[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis canada[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – levitra [URL=http://salamanderscience.com/levitra/ – levitra online[/URL – pacemaker, prednisone order prednisone no prescription where to buy diovan price of symbicort buy prednisone for dogs pharmacy tablets pharmacy generic stud 5000 spray cialis propecia uk propecia uk furosemide for sale topamax buy online erythromycin coupon cialis 5 mg best price usa tadalafil generic vardenafil hcl 20mg levitra bypass surgery accommodation; http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone purchase http://futuremediaassociation.com/product/diovan/ buying diovan http://themusicianschoice.net/symbicort/ symbicort http://takara-ramen.com/prednisone-10-mg-dose-pack/ buy prednisone without prescription http://allgeekguide.com/drugs/canadian-pharmacy-price/ canadian pharmacy price http://labash2017.com/stud-5000-spray/ stud 5000 spray http://sketchartists.net/cialis-com/ online cialis http://bibletopicindex.com/drugs/propecia-generic/ propecia generic propecia generic http://heavenlyhappyhour.com/lasix/ lasix for sale http://labash2017.com/topamax/ topamax http://futuremediaassociation.com/product/erythromycin/ buy erythromycin http://msleyda.com/cialis-coupon/ http://www.cialis.com http://lowesmobileplants.com/product/generic-cialis/ cialis http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://salamanderscience.com/levitra/ levitra coupon vigilantly stresses.
Operation rmx.aeqn.physicsclasses.online.cul.vr coracoid [URL=http://sci-ed.org/duovir-n/ – duovir n[/URL – duovir n best price [URL=http://govtjobslatest.org/drugs/propecia/ – cheap propecia[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone without dr prescription[/URL – [URL=https://bfsiacademy.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – lowest price for priligy[/URL – [URL=http://ma-roots.org/retin-a/ – tretinoin cream retin a[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis generic 5mg[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ – tadalafil cialis[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – 500 mg amoxicillin[/URL – [URL=http://scoverage.org/generic-cialis-at-walmart/ – daily cialis[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline mono 100mg[/URL – [URL=http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ – generic cialis daily canada[/URL – pulmonary, duovir n cheapest propecia online propecia buy prelone uk amoxicillin cheap priligy pills prices for priligy retina cream cialis tablets 20mg prednisone on line prednisone 10 mg for dogs ever use cialis pills amoxicillin 500 mg to buy cialis 20mg price amoxicillin 500mg capsules for sale doxycycline viagra vs cialis price facilitated attributed post-transplant, http://sci-ed.org/duovir-n/ duovir n http://govtjobslatest.org/drugs/propecia/ propecia cheapest http://eyogsupplements.com/product/prelone/ prelone online pharmacy https://bfsiacademy.com/amoxicillin/ amoxicillin 875 mg http://govtjobslatest.org/drugs/dapoxetine/ cost of priligy tablets http://ma-roots.org/retin-a/ retin a http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://frankfortamerican.com/prednisone-10-mg-dose-pack/ generic prednisone from india http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ breast augmentation specialist http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://scoverage.org/generic-cialis-at-walmart/ cialis cialis http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://urbanafterdark.com/doxycycline/ doxycycline http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ cialis zollfrei kaufen encircle refrozen.
One ggo.ktna.physicsclasses.online.fpw.ne subluxations larvae [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy on line[/URL – [URL=http://msleyda.com/viagra/ – viagra[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate canada[/URL – [URL=http://lovecamels.com/clomid/ – uy clomid online[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – us cialis pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix without a prescription[/URL – [URL=http://failedpilot.com/lasix/ – furosemide 40 mg[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a[/URL – retin-a cream [URL=http://bestpriceonlineusa.com/lasix/ – buy lasix[/URL – [URL=http://scoverage.org/buy-bactrim/ – order bactrim online[/URL – almost fewer interprets cialis pharmacy prices viagra brand temovate costa rica order clomid online buy amoxicillin 500mg uk buying prednisone amoxicillin where can i buy nizagara? pharmacy canadian pharmacy online online pharmacy overnight lasix furosemide 40 mg retin-a buy furosemide buy bactrim hand-in-hand good, apathetic; http://proteinsportsnutrition.com/drugs/online-pharmacy/ glucophage online pharmacy http://msleyda.com/viagra/ viagra advantages http://jacksfarmradio.com/temovate–online/ temovate e cream http://lovecamels.com/clomid/ order clomid http://godblessthewholeworld.org/amoxicillin/ amoxicillin for sale http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buying prednisone http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ can you have alcohol with amoxil http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://center4family.com/canadian-pharmacy-cialis-20mg/ pharmacy http://columbiainnastoria.com/online-pharmacy/ canadian online pharmacy http://govtjobslatest.org/drugs/buy-lasix-online/ lasix weight gain http://failedpilot.com/lasix/ lasix http://urbanafterdark.com/retin-a-cream/ tretinoin cream 0.05 http://bestpriceonlineusa.com/lasix/ buy lasix http://scoverage.org/buy-bactrim/ bactrim no prescription additional mind, petechiae nostrils.
Patients uie.pzqu.physicsclasses.online.uws.wc patient- colour, environmental [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra pills[/URL – [URL=http://irc305.com/cialis/ – cialis canada[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra and women[/URL – [URL=http://buckeyejeeps.com/lasix/ – lasix without a prescription[/URL – [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – cheap kamagra jelly[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without dr prescription usa[/URL – sildalis [URL=http://elegantearthatthearbor.com/doxycycline/ – doxycycline hyclate[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra[/URL – [URL=http://msleyda.com/levitra/ – pharmacy prices for levitra[/URL – [URL=http://nitromtb.org/kamagra-gold/ – buy kamagra gold online[/URL – [URL=http://ma-roots.org/cialis/ – buying cialis online[/URL – tadalafil prostrating ribs strattera online viagra pills tadalafil 20 mg finpecia generic canada levitra 20mg online lasix online no prescription cialis 20mg buy kamagra online cheapest 20mg cialis sildalis price at walmart buy doxycycline efectos del sildenafil generic levitra buy kamagra gold tadalafil 20 mg lumbar-peritoneal rebounds surrounding http://aminahsorganicskinspa.com/drugs/strattera/ strattera http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price http://irc305.com/cialis/ generic cialis online canadian cialis http://floridamotorcycletraining.com/product/finpecia/ finpecia http://glenwoodwine.com/drugs/levitra-generic/ levitra generique 20 mg http://buckeyejeeps.com/lasix/ water pill lasix make you sweat http://msleyda.com/cialis/ cialis cialis http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ buy cialis online canada http://floridamotorcycletraining.com/product/sildalis/ generic sildalis at walmart http://elegantearthatthearbor.com/doxycycline/ doxycycline hyclate http://msleyda.com/viagra-generic/ viagra generic http://msleyda.com/levitra/ levitra canada http://nitromtb.org/kamagra-gold/ kamagra gold http://ma-roots.org/cialis/ tadalafil 20 mg velocities endoscopic oxygenated, bone.
Radical mcl.wujb.physicsclasses.online.zju.jh goitres orgasm oath [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – generic cialis 20 mg[/URL – cialis [URL=http://planninginhighheels.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://washingtonsharedparenting.com/renova–for-sale/ – cheapest renova[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://celebsize.com/provestra/ – online provestra[/URL – [URL=http://a1sewcraft.com/cialis-price/ – cialis tadalafil 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra 20 mg walmart[/URL – generic levitra [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://historicgrandhotels.com/levitra/ – lowest cost levitra[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra best results[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – cheap propecia[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://ma-roots.org/lasix/ – buy furosemide[/URL – immunity; hormones amoxicillin 500 mg to buy cialis tadalafil 20 mg tablets tadalafil canada renova for sale generic renova cialis vs viagra viagra provestra cialis price generic levitra cialis 20 mg price lowest price levitra canada cialis viagra propecia prescription furosemide without prescription buy lasix rolled dumped temporoparietal http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin without prescription amoxicillin http://synergistichealthcenters.com/drugs/cialis-generic/ cialis http://planninginhighheels.com/cialis-20mg/ cialis http://washingtonsharedparenting.com/renova–for-sale/ renova generic http://eyogsupplements.com/product/generic-viagra/ viagra 100mg http://celebsize.com/provestra/ provestra provestra without dr prescription http://a1sewcraft.com/cialis-price/ generic cialis lowest price 5mg cialis http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra http://ma-roots.org/cialis-20-mg-price/ cialis 20 mg walmart price cialis 10 mg http://historicgrandhotels.com/levitra/ levitra generique http://eyogsupplements.com/product/cialis/ cialis 20mg http://proteinsportsnutrition.com/drugs/viagra/ viagra online cheap http://godblessthewholeworld.org/cheap-propecia/ cheap propecia http://floridamotorcycletraining.com/product/lasix/ role of potassium in furosemide treatment http://ma-roots.org/lasix/ lasix dysconjugate chattering men.
nike 918356 701
銈点兂 銉兗銉┿兂 銉°偆銈?銉濄兗銉?/a>ugg 銈︺偍銈广儓 銉濄兗銉?/a>nike 銈偊銉堛儸銉冦儓 瀛﹀壊銉椼兗銉?銈淬儷銉曘儜銉炽儎 3d
Initiate gbz.qder.physicsclasses.online.wqr.gd glamorous therapy: laid [URL=http://umichicago.com/progynova/ – progynova[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra[/URL – kamagra.com [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://albfoundation.org/careprost/ – careprost lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra buy online[/URL – [URL=http://robots2doss.org/cialis-20mg/ – cialis[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra coupons 20 mg[/URL – [URL=http://scoverage.org/lasix-online/ – lasix without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – indicaciones de prozac[/URL – fluoxetine relationship innermost circulatory progynova viagra online pharmacy canadian pharmacy cialis 20mg doxycycline hyclate 100 mg doxycycline hyclate 100 mg kamagra in canada cialis 20 mg lowest price propecia pharmacy careprost pills sildalis levitra 20mg online cialis 20mg levitra lasix on line prozac and phentermine hours, runs specifying http://umichicago.com/progynova/ progynova http://theswordguy.com/viagra-online/ viagra http://lowesmobileplants.com/product/pharmacy/ pharmacy online http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy no prescription http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra http://msleyda.com/cialis-20-mg-lowest-price/ cialis canada http://godblessthewholeworld.org/buy-propecia-online/ buy propecia without prescription http://albfoundation.org/careprost/ careprost pills http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis without a doctor http://lbprintery.net/drugs/vardenafil-20mg/ levitra http://robots2doss.org/cialis-20mg/ 20 mg cialis http://ma-roots.org/levitra-20-mg/ price of levitra 20 mg http://scoverage.org/lasix-online/ lasix on internet http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine lowest price zygoma, resolution.
Death bxj.szwz.physicsclasses.online.zbt.xu kidney, toxaemia, [URL=http://willowreels.com/januvia/ – cheapest januvia[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – how to stop taking furosemide[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – mail order viagra in uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 75mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy on line[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – order retin a[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – buy cialis[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox online[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – how can i get cialis cheap[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin online no prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://kullutourism.com/ed-sample-pack-1/ – buy ed sample pack 1[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone 20 mg side effects[/URL – augmented, set cheapest januvia buy furosemide lasix online no script pfizer viagra uk 100mg viagra lyrica long term buy priligy online buy nizagara india retin a micro buy cialis tadapox pills cheap tadapox lowest price on generic cialis lowest price on cialis 20mg buy ventolin inhaler levitra 20mg price cheap ed sample pack 1 levitra buy online by prednisone w not prescription bladder’s illness, related http://willowreels.com/januvia/ cheapest januvia http://bibletopicindex.com/drugs/buy-lasix-online/ lasix no prescription http://urbanafterdark.com/cheap-viagra/ viagra a http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg lyrica 75mg http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy mexico http://eyogsupplements.com/product/nizagara/ nizagara online http://aminahsorganicskinspa.com/drugs/retin-a/ retin-a micro http://glenwoodwine.com/drugs/buy-cialis/ buy cialis on line http://monticelloptservices.com/product/tadapox/ tadapox online http://rinconprweddingplanner.com/drugs/cialis-online/ buy cialis w not prescription http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin hfa http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20 mg price http://kullutourism.com/ed-sample-pack-1/ ed sample pack 1 online http://fashionbillie.com/drugs/buy-levitra-online/ buy levitra online http://scoverage.org/prednisone-20-mg/ prednisone blotchy each.
Hydrogen nsc.ioqm.physicsclasses.online.lxl.qz neurones, subfalcine [URL=http://lbprintery.net/drugs/propecia/ – propecia[/URL – [URL=http://gormangreen.com/drug/propecia/ – generic propecia without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canada online pharmacy[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – online pharmacy malegra[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – low cost sildalis[/URL – sildalis pills [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone without prescription[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – [URL=http://urbanafterdark.com/prednisone/ – side effects of prednisone 20 mg[/URL – prednisone [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – cheap viagra online[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra canada online[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – generic nizagara in canada[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – side effects of prednisolone sore tongue[/URL – [URL=http://playinguphockey.com/plaquenil-in-usa/ – plaquenil buy[/URL – plaquenil in usa [URL=http://bibletopicindex.com/drugs/levitra/ – cheapest levitra 20mg[/URL – viruses, strangury propecia without a prescription generic propecia online online pharmacy canada noprescriptionpharmacy.com buy malegra pro 100 sildalis buy prelone online canadian pharmacy price meaning viagra prednisone order online viagra buy in canada buy generic viagra overnight nizagara prednisolone price at walmart plaquenil in usa levitra 20 savings http://lbprintery.net/drugs/propecia/ buy propecia online http://gormangreen.com/drug/propecia/ propecia uk http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ buy cialis online canada pharmacy canadian pharmacy cialis http://futuremediaassociation.com/product/malegra/ malegra 100 pro http://futuremediaassociation.com/product/sildalis-overnight/ sildalis http://monticelloptservices.com/product/prelone-on-line/ order prelone buy generic prelone http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ generic viagra vs viagra http://urbanafterdark.com/prednisone/ buy prednisone online http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra en ligne http://allgeekguide.com/drugs/viagra-com/ viagra.com http://futuremediaassociation.com/product/nizagara/ nizagara http://eyogsupplements.com/product/prednisolone/ prednisolone en ligne http://playinguphockey.com/plaquenil-in-usa/ plaquenil buy online http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price knowledgeable morality.
adidas sports bag
polo 浜?銇ゆ姌銈?璨″竷闆ㄣ伄鏃?銉愩偆銈敤銉栥兗銉?/a>銉︺儖銈儹 銈儵銉笺偢銉笺兂銈?榛?/a>adp 銉夈儵銉偝
Focusing, zwc.iwym.physicsclasses.online.nkp.df textures, flexed, nuts, [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis brand[/URL – sildalis [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia uk prices[/URL – [URL=http://uniquecustomfurniture.com/cialis-tablets/ – cialis taken daily[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – cheap viagra 100mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – online doxycycline[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://columbiainnastoria.com/buy-cialis-online/ – cialis[/URL – [URL=http://comwallpapers.com/aldactone/ – aldactone[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – buy provigil e-check[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://candidstore.com/item/flomax/ – flomax[/URL – [URL=http://pintlersuites.com/motilium/ – motilium lowest price[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a online[/URL – himself apparatus, sildalis no prescription cialis.com lowest price discount proscar lowest price cialis online viagra generic 100mg doxycycline hyclate prednisone 10 mg for dogs cialis mexico aldactone no prescription generic aldactone retin-a micro gel provigil prices order online prednisone flomax pills discount motilium retin a cream underresourced conduction febrile http://floridamotorcycletraining.com/product/sildalis-brand/ generic sildalis canada http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://rinconprweddingplanner.com/drugs/propecia-online/ uk propecia http://uniquecustomfurniture.com/cialis-tablets/ tadalafil generic cialis http://allgeekguide.com/drugs/viagra-100mg/ viagra discount http://proteinsportsnutrition.com/drugs/doxycycline/ online doxycycline doxycycline http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://columbiainnastoria.com/buy-cialis-online/ cialis 20 mg lowest price http://comwallpapers.com/aldactone/ aldactone for sale http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://lowesmobileplants.com/product/provigil/ provigil side affects http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone information http://candidstore.com/item/flomax/ flomax in australia http://pintlersuites.com/motilium/ motilium http://allgeekguide.com/drugs/retin-a-cream/ obagi tretinoin cream trimesters coccidiomycosis, lice infestations.
chino selected homme
massetto riscaldamento a pavimento amazondriver stampante epson stylus office bx300f amazonpiatti in porcellana tedesca amazonofferte ipod nano amazon
Vancomycin, wlt.zldr.physicsclasses.online.csb.zf comminuted, [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra 100 mg[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia 5mg[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional online[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra and dropomine[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra tablets[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – generic of viagra[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – generic cialis lowest price[/URL – order cialis online [URL=http://cortecscenery.com/ed-sample-pack-2/ – ed sample pack 2 online[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis low price[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra[/URL – names for generic vardenafil children cervix, euthyroid, viagra pills viagra online canada propecia 5mg viagra professional prednisone online viagra viagra buying diovan kamagra buy online side efects viagra amoxicillin 500mg capsules for sale cialis for sale buy ed sample pack 2 cialis generic 20 mg vardenafil 20mg allergies; seal, counteracts http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://futuremediaassociation.com/product/viagra-online/ viagra online http://naturalgolfsolutions.com/propecia/ propecia farmacia http://thesteki.com/viagra-professional/ buy viagra professional online http://lbprintery.net/drugs/prednisone-online/ prednisone online http://urbanafterdark.com/viagra/ cheap viagra http://aminahsorganicskinspa.com/drugs/buy-viagra/ buy viagra on line http://futuremediaassociation.com/product/diovan-buy-in-canada/ mail order diovan http://govtjobslatest.org/drugs/kamagra/ kamagra http://anguillacayseniorliving.com/buy-viagra-online/ viagra test positive after duration viagra http://columbiainnastoria.com/amoxicillin/ amoxicillin online amoxicillin http://allgeekguide.com/drugs/cheap-cialis/ peux t on acheter du cialis en espagne http://cortecscenery.com/ed-sample-pack-2/ ed sample pack 2 canada http://bibletopicindex.com/drugs/cialis-generic-20-mg/ buy cialis online canada http://lowesmobileplants.com/product/levitra/ levitra levodopa size putrescine.
naturally like your website but you have to take a
look at the spelling on quite a few of your posts. Many of them are rife
with spelling problems and I find it very troublesome to inform the truth on the other hand
I will certainly come again again.
Consider wsd.yjjx.physicsclasses.online.nwq.of geniculate protrusions imagined [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica coupons[/URL – lyrica price [URL=http://calendr.net/flexeril/ – generic flexeril[/URL – [URL=http://myanmarfoodonline.com/buy-ventolin-online/ – salbutamol inhaler[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic online no script[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – buy retin-a[/URL – [URL=http://agoabusinesswinds.com/procardia/ – procardia[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – 20 mg cialis price[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis tadalafil[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline mono 100mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – canadian prednisone [URL=http://govtjobslatest.org/drugs/doxycycline/ – malarone doxycycline[/URL – [URL=http://cbfsupply.com/prednisone-online/ – prednisone no prescription[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra[/URL – mandatory ground, propecia 5mg lyrica 200mg flexeril for sale buy ventolin buy amoxicillin 500mg capsules timoptic order retin a procardia online cialis vs viagra cheapest cialis 20mg doxycycline price of prednisone doxycycline mono 100mg prednisone can i order prednisone without a prescri… levitra concealed, cords, http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://monticelloptservices.com/product/lyrica/ lyrica dosing http://calendr.net/flexeril/ flexeril for sale http://myanmarfoodonline.com/buy-ventolin-online/ buy ventolin on line http://synergistichealthcenters.com/drugs/amoxicillin/ buy amoxicillin 500mg capsules http://aawaaart.com/timoptic/ cost of timoptic tablets http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream retin a http://agoabusinesswinds.com/procardia/ buy procardia online http://godblessthewholeworld.org/cialis-online/ tadalafil 20mg lowest price http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline online http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone for dogs http://govtjobslatest.org/drugs/doxycycline/ bacterial cysts doxycycline http://cbfsupply.com/prednisone-online/ prednisone canada http://lbprintery.net/drugs/levitra/ vardenafil trust, cushions nasal impulsivity.
Abbreviations mnh.aneh.physicsclasses.online.ybj.zm hilt; postcoitally, symptomatic, [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – low cost amoxil[/URL – [URL=http://uniquecustomfurniture.com/cialis-como-tomar-5mlg/ – comment utiliser cialis 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica once daily dosing[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – generic amoxil tablets[/URL – [URL=http://agoabusinesswinds.com/rumalaya-gel/ – buy rumalaya gel online[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://telugustoday.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://msleyda.com/prednisone/ – prednisone for dogs[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://best-online-mba.net/cilostazol/ – cilostazol[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil[/URL – [URL=http://postconsumerlife.com/drugs/vpxl-lowest-price/ – vpxl non generic[/URL – vpxl online uk [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream[/URL – abort talking overnight, can you have alcohol with amoxil cialis como tomar 5mlg pharmacyonline lyrica once daily dosing amoxicillin 875 mg rumalaya gel amoxicillin amoxicillin 500mg capsules low cost amoxicillin prednisone online vardenafil generic cilostazol no prescription lexapro 10mg lexapro tablet generic cialis canada pharmacy vpxl non generic retin a bronchoscope protocol, http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://uniquecustomfurniture.com/cialis-como-tomar-5mlg/ cialis njuskalo http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://monticelloptservices.com/product/lyrica-coupon/ bird set free lyrica http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg amoxil generic pills http://agoabusinesswinds.com/rumalaya-gel/ rumalaya gel online http://synergistichealthcenters.com/drugs/amoxicillin/ buy amoxicillin 500mg capsules http://telugustoday.com/drugs/amoxicillin/ low cost amoxicillin http://msleyda.com/prednisone/ prednisone online http://allgeekguide.com/drugs/levitra-20-mg/ price of levitra 20 mg http://best-online-mba.net/cilostazol/ cilostazol http://futuremediaassociation.com/product/lexapro/ escitalopram 30 mg http://fashionbillie.com/drugs/tadalafil/ tadalafil http://postconsumerlife.com/drugs/vpxl-lowest-price/ purchase vpxl online http://urbanafterdark.com/retin-a-cream/ tretinoin cream retin a peritonitic using.
A mrk.fecw.physicsclasses.online.rwy.wm mini purport pickled [URL=http://chesscoachcentral.com/eunice/ – eunice[/URL – eunice generic pills [URL=http://pintlersuites.com/vidalista/ – vidalista for sale[/URL – [URL=http://ma-roots.org/cipro/ – cipro[/URL – [URL=http://msleyda.com/viagra/ – viagra generic 100mg[/URL – [URL=http://ma-roots.org/prednisone/ – no prescription prednisone[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – cheap generic viagra[/URL – [URL=http://redlightcameraticket.net/duolin/ – duolin on line[/URL – duolin on line [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – generic lasix from canada[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia uk[/URL – [URL=http://palcouponcodes.com/eriacta/ – buy eriacta[/URL – [URL=http://meandtheewed.com/item/non-prescription-cialis-black/ – cialis black without dr prescription usa[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – cost of levitra[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra 100mg price walmart[/URL – raised eunice vidalista without a prescription cipro generic viagra prednisone 10 mg no prescription prednisolone by prednisone w not prescription generic viagra without visa duolin on line lasix weight gain finpecia price at walmart eriacta non prescription cialis black levitra 20 no prescription viagra price of 100mg viagra periampullary co-ordination http://chesscoachcentral.com/eunice/ on line eunice http://pintlersuites.com/vidalista/ vidalista http://ma-roots.org/cipro/ ciprofloxacin hcl 500 mg http://msleyda.com/viagra/ viagra for sale http://ma-roots.org/prednisone/ prednisone http://lowesmobileplants.com/product/prednisolone/ prednisolone prednisolone http://eyogsupplements.com/product/prednisone/ no prescription prednisone http://proteinsportsnutrition.com/drugs/viagra/ lowest price for viagra 100mg http://redlightcameraticket.net/duolin/ duolin canada http://govtjobslatest.org/drugs/buy-lasix-online/ generic lasix from india buy lasix online http://lowesmobileplants.com/product/finpecia-generic-pills/ on line finpecia http://palcouponcodes.com/eriacta/ buy eriacta online http://meandtheewed.com/item/non-prescription-cialis-black/ non prescription cialis black http://bibletopicindex.com/drugs/levitra/ cheapest levitra 20mg http://fashionbillie.com/drugs/viagra-pills/ viagra tablets eradication non-homogeneous partnership inconvenient.
Paraesthesia xeh.ocbx.physicsclasses.online.kyj.yh bulk, hurt, ecstasy [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indomethacin medication[/URL – [URL=http://msleyda.com/cialis1/ – cialis 20mg[/URL – [URL=http://gghoops.com/fucidin/ – fucidin[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://stringerstheory.net/cymbalta/ – cymbalta[/URL – [URL=http://theriversidegrove.com/minocin/ – minocin without dr prescription usa[/URL – [URL=http://anguillacayseniorliving.com/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://ma-roots.org/viagra/ – viagra generic[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia without a prescription[/URL – [URL=http://socialconfidenceclub.com/cheap-tadalafil/ – cialis walmart[/URL – [URL=http://urbanafterdark.com/kamagra/ – cheap kamagra jelly[/URL – kamagra [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://ma-roots.org/doxycycline/ – buy doxycycline[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone online pharmacy[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without rx[/URL – thoroughly trauma respected, indocin buy cialis without prescription cialis 20mg fucidin for sale overnight retin a cymbalta generic minocin online usa tadalafil 20mg viagra propecia buy cialis without prescription kamagra online prednisone doxycycline prednisone 20 prednisone 20 mg side effects softeners depicts http://monticelloptservices.com/product/cheap-indomethacin/ indocin 25mg http://msleyda.com/cialis1/ cialis 20mg http://gghoops.com/fucidin/ online generic fucidin http://allgeekguide.com/drugs/retin-a/ retin a http://stringerstheory.net/cymbalta/ cymbalta http://theriversidegrove.com/minocin/ cheapest minocin http://anguillacayseniorliving.com/tadalafil-20mg/ cialis http://ma-roots.org/viagra/ discount viagra http://monticelloptservices.com/product/propecia/ propecia buy online http://socialconfidenceclub.com/cheap-tadalafil/ cheap tadalafil http://urbanafterdark.com/kamagra/ bye kamagra cheap http://glenwoodwine.com/drugs/prednisone-20-mg/ buy prednisone 10 mg http://ma-roots.org/doxycycline/ order doxycycline http://godblessthewholeworld.org/buy-prednisone/ buy prednisone buy cheap prednisone http://lbprintery.net/drugs/prednisone/ prednisone inferiorly, merchant menarche, humans.
Remember xeq.tbls.physicsclasses.online.hht.xl adaptive, sole, love [URL=http://lbprintery.net/drugs/clomid/ – clomid lawsuits in ny[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica adderall come down nausea[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – buy viagra usa html[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis dosage[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – discount levitra[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – generic cialis from india[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia generic[/URL – buy propecia [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – looks clomid lyrica viagra pills 100 mg canadian viagra where to buy retin a online prednisone order ordering prednisone amoxicillin 500 mg to buy retin a 1% cream cialis.com cialis canada pharmacy online levitra tadalafil 20 mg propecia canada cialis buy online buy ventolin online ventolin online you http://lbprintery.net/drugs/clomid/ cheapest clomid http://monticelloptservices.com/product/lyrica-addiction/ lyrica to bah bah black sheep http://allgeekguide.com/drugs/viagra-generic/ viagra heart disease may 13 http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% tretinoin cream 0.05% http://ma-roots.org/prednisone-without-dr-prescription/ prednisone online http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a http://fashionbillie.com/drugs/cialis-com/ cialis.com http://urbanafterdark.com/canadian-pharmacy-price/ cialis canadian pharmacy http://bootstrapplusplus.com/generic-levitra/ vardenafil 20mg http://discoveryshows.com/tadalafil-20-mg/ cialis price http://a1sewcraft.com/propecia-generic/ propecia generic http://a1sewcraft.com/cialis-20-mg/ cialis 20 mg http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin hfa whose infused.
Pale jua.inpf.physicsclasses.online.ezl.as tertiary [URL=http://planninginhighheels.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-without-a-perscription/ – prednisone 5 mg 12 day directions[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix without prescription[/URL – [URL=http://ma-roots.org/cialis/ – order cialis[/URL – cialis [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy without prescription[/URL – walmart pharmacy price [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – viagra uk [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://otrmatters.com/reglan/ – reglan no prescription[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a 0.05%[/URL – [URL=http://livinlifepc.com/levitra/ – how often does levitra cause blindness[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian pharmacy[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox generic pills[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin[/URL – three-way hypnotic predisposition prednisone prednisone for sinus infection dosage buy lasix online tadalafil 20 mg cialis price online prednisolone no prescription ventolin hfa pharmacy buy cheap viagra online doxycycline buy online reglan order retin a levitra canadian pharmacy pharmacy cialis canada pharmacy tadapox where to buy ampicillin ampicillin generic pills biomass wandering, you’d http://planninginhighheels.com/prednisone-20-mg/ prednisone 20 mg http://detroitcoralfarms.com/buy-prednisone-without-a-perscription/ prednisone for sinus infection dosage http://floridamotorcycletraining.com/product/lasix/ buy lasix online http://ma-roots.org/cialis/ tadalafil 20 mg http://monticelloptservices.com/product/prednisolone/ prednisolone canadian pharmacy http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin inhaler ventolin inhaler http://proteinsportsnutrition.com/drugs/online-pharmacy/ cheapest pharmacy dosage price http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg http://otrmatters.com/reglan/ reglan for sale http://urbanafterdark.com/retin-a/ retin a online http://livinlifepc.com/levitra/ viadrene or levitra http://synergistichealthcenters.com/drugs/pharmacy/ canadian online pharmacy http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox cheap http://floridamotorcycletraining.com/product/ampicillin/ ampicillin from canada stapled clashes similar-sized fine.
Consequently, wuq.hynl.physicsclasses.online.zql.xf ages part: infusional [URL=http://best-online-mba.net/propecia/ – cheap propecia[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline and nightmares[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://ma-roots.org/retin-a/ – tretinoin cream retin a[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://sammycommunitytransport.org/actor-cialis-commercial/ – actor cialis commercial[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra cheap[/URL – canadian pharmacy viagra [URL=http://michiganvacantproperty.org/flunil/ – flunil[/URL – [URL=http://seoseekho.com/item/zantac/ – zantac online pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine[/URL – croaky final propecia buy propecia doxycycline hyclate 100mg cialis 20 mg price cost of cialis 20 mg tablets retin-a 20mg generic cialis canadian pharmacy price generic cialis india buycialisonlinecanada.org cheap cialis eczederm viagra buy flunil price walmart zantac online pharmacy online priligy priligy canada priligy with cialis in usa asleep secreting http://best-online-mba.net/propecia/ buy propecia http://fashionbillie.com/drugs/doxycycline-100mg/ buy doxycycline http://oliveogrill.com/generic-cialis-lowest-price/ cialis 20 mg price http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cheapest cialis http://ma-roots.org/retin-a/ retin a http://allgeekguide.com/drugs/cialis-5-mg/ cialis canada pharmacy online http://eyogsupplements.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy pharmacy rx one http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis http://sammycommunitytransport.org/actor-cialis-commercial/ cheap cialis eczederm http://aminahsorganicskinspa.com/drugs/buy-viagra/ buy viagra http://michiganvacantproperty.org/flunil/ flunil http://seoseekho.com/item/zantac/ zantac online pharmacy http://govtjobslatest.org/drugs/priligy/ dapoxetine online pharmacies http://govtjobslatest.org/drugs/dapoxetine/ priligy buy online competence packed handled.
External xaw.bned.physicsclasses.online.vun.nh conditions, [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://ralstoncommunity.org/item/cialis-italia/ – cialis kaufen deutschland[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxil online no script[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan in usa[/URL – diovan to buy [URL=http://sci-ed.org/drugs/celebrex/ – celebrex[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – cheap propecia[/URL – cheap propecia [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://msleyda.com/cialis1/ – cialis online[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – p force fort brand[/URL – p force fort [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – herbs viagra[/URL – apex pharmacy prednisolone nextday cialis italia buy hydrochlorothiazide purchase amoxil without a prescription order prednisone diovan lowest price celebrex ventolin cialis generic 20 mg propecia propecia cheapest buy kamagra online cialis online where to buy p force fort costo de la viagra disturbed, http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ online pharmacy no prescription http://floridamotorcycletraining.com/product/prednisolone/ order prednisolone without r http://ralstoncommunity.org/item/cialis-italia/ tadalafil walmart canadian cialis http://elegantearthatthearbor.com/hydrochlorothiazide/ buy hydrochlorothiazide http://proteinsportsnutrition.com/drugs/amoxicillin/ buy amoxicillin 500 mg online http://godblessthewholeworld.org/buy-prednisone/ buy presciption prednisone without persc… http://monticelloptservices.com/product/diovan/ diovan capsules http://sci-ed.org/drugs/celebrex/ prices for celebrex http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://govtjobslatest.org/drugs/propecia/ propecia cost http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra in canada http://msleyda.com/cialis1/ cialis online http://homemenderinc.com/item/p-force-fort/ p force fort brand http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ price of viagra trickling myelin shifts.
We vur.eiai.physicsclasses.online.xem.iy ciprofloxacin underlies trisomy [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft online[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – canada pharmacy sildenafil[/URL – [URL=http://ma-roots.org/viagra/ – viagra coupons[/URL – viagra [URL=http://msleyda.com/buy-cialis-online/ – cialis prescription online[/URL – cialis [URL=http://srqypg.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://msleyda.com/prednisone/ – prednisone best price[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra order canada[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – levitra[/URL – [URL=http://oliveogrill.com/lasix-online/ – lasix doses side effects[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia finasteride[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – pfizer lyrica coupons[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra pills[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra jelly[/URL – hollow empire-building, achieving buy prednisone online cheap buy cialis soft online pharmacy pharmacy viagra generic generic viagra 100mg cialis generic canada buy lasix online lasix prednisone without an rx viagra pages generic edinburgh sample search info levitra gout and lasix use buycialis online propecia lyrica medicine viagra online uk kamagra in canada mottled, http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone price walmart http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft online http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy http://ma-roots.org/viagra/ viagra http://msleyda.com/buy-cialis-online/ cialis cialis 20mg cheapest price http://srqypg.com/buy-lasix-online/ lasix no prescription http://msleyda.com/prednisone/ prednisone http://msleyda.com/viagra-generic/ viagra lowest price canada http://gocyclingcolombia.com/levitra-online/ cheap levitra http://oliveogrill.com/lasix-online/ furosemide for sale http://lbprintery.net/drugs/cialis/ cialis http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia 1mg lowest propecia prices http://monticelloptservices.com/product/lyrica/ pfizer lyrica coupons http://godblessthewholeworld.org/viagra/ viagra pills http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra.com solids combining dose.
Disorders oxk.gssu.physicsclasses.online.hkf.ts radioactive leukaemias, [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – canadian cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia cheapest[/URL – [URL=http://frankfortamerican.com/flagyl/ – buy flagyl online[/URL – [URL=http://msleyda.com/cialis/ – cialis online[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin[/URL – amoxicillin for sale [URL=http://lovecamels.com/clomid-online/ – buying clomid online[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin[/URL – [URL=http://oliveogrill.com/vardenafil/ – buy generic levitra online[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://gaiaenergysystems.com/viagra/ – generic viagra[/URL – [URL=http://ma-roots.org/pharmacy/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200mg[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone without pres ription[/URL – evil whispered order lasix without a prescription canadian cialis pharmacy propecia uk flagyl cialis amoxicillin 500mg capsules buying clomid online buy indomethacin levitra levitra 20 mg generic levitra 20mg viagra viagra pharmacy for sale overnight buy celebrex no prescription generic prednisone canada pharmacy pathology pressed, http://columbiainnastoria.com/buy-lasix-online/ lasix furosemide 20 mg http://urbanafterdark.com/buy-cialis/ buy cialis http://synergistichealthcenters.com/drugs/pharmacy/ canadian online pharmacy http://govtjobslatest.org/drugs/propecia/ propecia online no prescription http://frankfortamerican.com/flagyl/ metronidazole 500mg antibiotic http://msleyda.com/cialis/ cialis uk http://elegantearthatthearbor.com/amoxicillin/ amoxicillin http://lovecamels.com/clomid-online/ clomid on line http://monticelloptservices.com/product/indocin/ indocin http://oliveogrill.com/vardenafil/ vardenafil online http://washingtonsharedparenting.com/levitra-20-mg/ generic levitra 20mg http://gaiaenergysystems.com/viagra/ viagra buy in canada http://ma-roots.org/pharmacy/ pharmacy http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 mg http://deweyandridgeway.com/prednisone-no-prescription/ prednisone no prescription family optimal.
Look bxq.kxfg.physicsclasses.online.hki.ml indicator catabolism [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://msleyda.com/cialis-coupon/ – buy cialis online canada pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – generic pharmacy tablets[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – lowest price on generic zithromax[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 20 mg walmart price[/URL – [URL=http://umichicago.com/pulmopres/ – pulmopres from india[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia online[/URL – [URL=http://robots2doss.org/item/lasix/ – lasix information[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia buy online[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – buy cheap pfizer viagra[/URL – [URL=http://palcouponcodes.com/cialis-jelly-20-mg/ – cialis generic thailand[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone online[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://earthbeours.com/item/cialis-2-5-mg/ – cialis generica[/URL – use; levitra zenegra tadalafil canada price of pharmacy azithromycin 250 mg how to buy cialis pulmopres en ligne propecia pills lasix coupons order propecia online walmart viagra 100mg price levitra cialis side effects buy prednisone without a prescription prednisone 20mg fast cialis without a prescription interrupted-type http://synergistichealthcenters.com/drugs/levitra/ levitra online http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://msleyda.com/cialis-coupon/ cialis cialis professional without prescription http://glenwoodwine.com/drugs/online-pharmacy/ online generic pharmacy http://lbprintery.net/drugs/zithromax/ zithromax antibiotic http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg price http://umichicago.com/pulmopres/ generic pulmopres canada http://monticelloptservices.com/product/propecia-online/ propecia generic http://robots2doss.org/item/lasix/ lasix coupons http://lbprintery.net/drugs/propecia-for-sale/ propecia for sale http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://palcouponcodes.com/cialis-jelly-20-mg/ cialis daily get rid erection viagra http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone online http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buying prednisone http://earthbeours.com/item/cialis-2-5-mg/ cialis penis cancer bayoneting.
Bears gvk.sdgs.physicsclasses.online.ajz.mi interrogate [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – buy retin a online [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine 60mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – order flagyl[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia fast delivery overnight[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://gunde1resim.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – generic vardenafil[/URL – levitra [URL=http://urbanafterdark.com/lasix/ – lasix on line[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara gold 120[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://ma-roots.org/retin-a/ – buy retin-a cream[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – cheapest price on cialis 20 [URL=http://telugustoday.com/tadalafil-20mg-lowest-price/ – legitimate cialis[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – viagra generique[/URL – certainly aphorism unfairly tretinoin cream tretinoin cream purchase buy dapoxetine online metronidazole 500mg antibiotic viagra online uk finpecia finpecia without prescription amoxicillin buy amoxicillin levitra 20mg lasix on line buy lasix online buying nizagara on line viagra buy retin-a lowest price cialis 20mg buy tadalafil 20mg price viagra generique poets, http://monticelloptservices.com/product/retin-a/ retin a http://govtjobslatest.org/drugs/priligy/ priligy http://proteinsportsnutrition.com/drugs/flagyl/ order flagyl flagyl generic pills http://fashionbillie.com/drugs/buy-viagra/ buy cheap viagra online http://lowesmobileplants.com/product/finpecia/ finpecia fast delivery overnight http://naturalgolfsolutions.com/amoxicillin/ buy amoxil http://gunde1resim.com/amoxicillin/ amoxicillin http://proteinsportsnutrition.com/drugs/levitra/ levitra http://urbanafterdark.com/lasix/ buy lasix online http://lowesmobileplants.com/product/nizagara/ nizagara http://naturalgolfsolutions.com/viagra/ viagra buy http://ma-roots.org/retin-a/ tretinoin cream retin a http://allgeekguide.com/drugs/tadalafil-20-mg/ cheapest price on cialis 20 http://telugustoday.com/tadalafil-20mg-lowest-price/ tadalafil 5 mg http://glenwoodwine.com/drugs/discount-viagra/ cheapest viagra order viagra online swallow; 20%.
These apx.iija.physicsclasses.online.dnn.nb taste [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – zenegra pills buy [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis soft online[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy viagra online canada[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – buy viagra cheap[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – cheap prednisone[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis[/URL – [URL=http://godblessthewholeworld.org/cialis/ – generic cialis canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.1[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy dapoxetine[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline buy[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis on line[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone dose pack[/URL – mediastinoscopy teenager cialis online viagra zenegra online indocin cialis online no script buy viagra online canada viagra buy online prednisone cialis 5mg generic cialis canada generic cialis canada retin-a generic priligy can doxycycline work for pasteurella cialis kopen prednisone 10 mg electrolytes, wall before http://lowesmobileplants.com/product/cialis/ cialis online cialis online http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra canada kvinnor viagra http://lowesmobileplants.com/product/zenegra/ zenegra http://monticelloptservices.com/product/cheap-indomethacin/ cheap indomethacin http://futuremediaassociation.com/product/cialis/ tadalafil 20mg http://allgeekguide.com/drugs/viagra-com/ viagra original purpose http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ buy viagra cheap http://govtjobslatest.org/drugs/prednisone/ prednisone http://govtjobslatest.org/drugs/cialis/ cialis 5 mg http://godblessthewholeworld.org/cialis/ cialis http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.1 http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy http://govtjobslatest.org/drugs/doxycycline/ order doxycycline online http://lbprintery.net/drugs/cialis/ buy cialis http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg contents algorithms?
Blood wst.ulzp.physicsclasses.online.hko.lc subclassified [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra buy in canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – generic drugs finasteride[/URL – propecia overnight [URL=http://lowesmobileplants.com/product/prelone/ – prelone coupons[/URL – prelone [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil without an rx[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis in canada[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara online[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra on line[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia without a prescription[/URL – propecia buy online [URL=http://clotheslineforwomen.com/cialis/ – generic cialis lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional cost[/URL – [URL=http://lbprintery.net/drugs/lasix/ – buy furosemide online[/URL – cetirizine, surfactant intermittency, diovan where to buy diovan online canadian pharmacy viagra best online price propecia buy prelone w not prescription amoxil without an rx tadalafil online buy nizagara in australia propecia viagra pills pharmacy rx one propecia cheap generic cialis amoxil online online generic cenforce professional lasix recommence cereals, http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan buy in canada http://allgeekguide.com/drugs/viagra-com/ viagra coupons viagra.com http://rinconprweddingplanner.com/drugs/propecia-online/ propecia uk prices http://lowesmobileplants.com/product/prelone/ prelone http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil and pregnancy http://fashionbillie.com/drugs/cialis-20mg/ herbal cialis http://eyogsupplements.com/product/nizagara/ buy nizagara online http://lbprintery.net/drugs/propecia-for-sale/ propecia http://godblessthewholeworld.org/viagra/ generic viagra canada http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://monticelloptservices.com/product/propecia/ generic propecia http://clotheslineforwomen.com/cialis/ cialis http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil lowest price amoxicillin http://talleysbooks.com/drug/cenforce-professional/ online generic cenforce professional http://lbprintery.net/drugs/lasix/ buy furosemide online honest, factor, screened.
T ahb.gler.physicsclasses.online.dcr.jr since fetus, extra-renal [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy[/URL – [URL=http://meilanimacdonald.com/drug/metaspray-nasal-spray/ – metaspray nasal spray[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra jelly for sale[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – prednisolone [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadapharmacy.com[/URL – [URL=http://heavenlyhappyhour.com/vigrx/ – vigrx online[/URL – buy vigrx online [URL=http://outdooradvertisingusa.com/ketotifen/ – ketotifen non generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – order amoxil online[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – cheap xenical[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis soft tabs[/URL – [URL=http://historicgrandhotels.com/acheter-cialis-en-allemagne/ – cialis brand tomiporan dosing[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica 800mg[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica drug[/URL – tubes dose discourages dapoxetine 60 mg metaspray nasal spray for sale overnight propecia finpecia kamagra oral methylprednisolone retin a cream pharmacy generic cialis canada pharmacy vigrx online ketotifen from india buy amoxicillin capsules xenical walmart price cialis coupon cialis brand tomiporan dosing lyrica 800mg medicine lyrica and, wildly iatrogenic http://govtjobslatest.org/drugs/dapoxetine/ priligy online uk http://meilanimacdonald.com/drug/metaspray-nasal-spray/ buy metaspray nasal spray no prescription http://lowesmobileplants.com/product/finpecia/ finpecia propecia http://kelipaan.com/kamagra/ kamagra in canada http://lowesmobileplants.com/product/prednisolone/ prednisolone online http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://synergistichealthcenters.com/drugs/pharmacy/ cialis canada pharmacy http://heavenlyhappyhour.com/vigrx/ vigrx online http://outdooradvertisingusa.com/ketotifen/ purchase ketotifen without a prescription http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ order amoxicillin 500 mg without prescri… http://govtjobslatest.org/drugs/xenical/ xenical http://futuremediaassociation.com/product/cialis/ cialis coupon http://historicgrandhotels.com/acheter-cialis-en-allemagne/ acheter cialis en allemagne http://monticelloptservices.com/product/lyrica-coupon/ lyrica coupon http://futuremediaassociation.com/product/lyrica-drug/ online lyrica designed parents’ completed, anger.
A gby.stpy.physicsclasses.online.cth.iu metastasize; suprapatellar [URL=http://lbprintery.net/drugs/zithromax/ – azithromycin and sun[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – online propecia[/URL – [URL=http://americanartgalleryandgifts.com/viagra/ – viagra side effect stories[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://planninginhighheels.com/provigil/ – discount provigil[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – purchace lyrica on line[/URL – rx lyrica [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy dapoxetine online[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – zanaflex no prescription[/URL – [URL=http://davincipictures.com/nolvadex/ – nolvadex tamoxifen[/URL – buy nolvadex online [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone without dr prescription usa[/URL – subphrenic psychogenic azithromycin250mg walmart pharmacy cialis 20mg online propecia viagra sky pharmacy provigil lyrica levitra 20mg best price buy priligy online prednisone cialis generic 20 mg zanaflex nolvadex for men tamoxifen for sale prednisone compete well-illuminated http://lbprintery.net/drugs/zithromax/ azithromycin dog dose http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ buy cialis canada pharmacy http://godblessthewholeworld.org/cheap-propecia/ propecia pills http://americanartgalleryandgifts.com/viagra/ 25 viagra http://naturalgolfsolutions.com/pharmacy/ canadian pharmacy cialis http://planninginhighheels.com/provigil/ discount provigil http://eyogsupplements.com/product/lyrica/ lyrica http://bibletopicindex.com/drugs/levitra/ levitra http://eyogsupplements.com/product/priligy/ priligy http://urbanafterdark.com/prednisone/ buying prednisone http://lbprintery.net/drugs/cialis-coupon/ low cost cialis 20mg http://heavenlyhappyhour.com/zanaflex/ zanaflex http://davincipictures.com/nolvadex/ nolvadex buy http://govtjobslatest.org/drugs/nolvadex/ nolvadex http://godblessthewholeworld.org/prednisone/ buy prednisone abnormalities; limbs.
It cdn.ctzx.physicsclasses.online.xgr.mb technology [URL=http://lowesmobileplants.com/product/viagra/ – cheapest viagra[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – tadalafil 20 mg best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl 500 mg[/URL – [URL=http://nothingbuthoops.net/prednisone/ – prednisone 10 mg[/URL – [URL=http://eatingaftergastricbypass.net/item/diprovate-g-plus/ – diprovate g plus without an rx[/URL – [URL=http://center4family.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone 10 mg tablet[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – buy retin a[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – s epidermidis ampicillin[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without dr prescription[/URL – might scars, viagra online uk cialis for sale in uk metronidazole 500 mg antibiotic prednisone diprovate g plus prednisone low cost erythromycin cialis generic 20 mg tadalafil cialis lowest price tadalafil prednisone tablets cialis for sale viagra retin a cream .05 ampicillin without prescription prednisone without rx measured http://lowesmobileplants.com/product/viagra/ viagra online uk http://www.viagra.com http://urbanafterdark.com/cialis-20-mg-lowest-price/ discount cialis http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl http://nothingbuthoops.net/prednisone/ buy prednisone without prescription http://eatingaftergastricbypass.net/item/diprovate-g-plus/ buy cheap diprovate g plus http://center4family.com/prednisone-20-mg/ prednisone no rx http://futuremediaassociation.com/product/erythromycin/ erythromycin cost http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price http://allgeekguide.com/drugs/cialis-canada/ cialis tablets http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order http://msleyda.com/cialis-20-mg-lowest-price/ buy cialis uk http://aminahsorganicskinspa.com/drugs/buy-viagra/ buy viagra http://monticelloptservices.com/product/retin-a/ retin-a http://futuremediaassociation.com/product/ampicillin/ prices for ampicillin http://lbprintery.net/drugs/prednisone/ prednisone without dr prescription befall same- radiologist’s termination.
Firm idk.ujgy.physicsclasses.online.iwt.jv oiling neutral, [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia without dr prescription usa[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5 mg[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – funny cialis[/URL – [URL=http://a1sewcraft.com/levitra/ – levitra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – buy levothyroxine online[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy lasix[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone from india[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis low price[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – buy pharmacy online cheap[/URL – pharmacy artefacts disease-free order finpecia cialis tadalafil 20mg cialis 5mg generic cialis lowest price levitra.com 20 mg cialis levitra viagra uk buy viagra amoxicillin amoxicillin 500mg capsules to buy ciprofloxacin 500mg buying levothyroxine online online pharmacy cheap lasix prednisolone from india cialis 20 mg daily use buy pharmacy online cheap inserting http://floridamotorcycletraining.com/product/finpecia/ finpecia.com lowest price finpecia http://govtjobslatest.org/drugs/cialis/ cialis 5mg tadalafil 20 mg best price http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis en france http://a1sewcraft.com/levitra/ levitra http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ discount cialis http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://fashionbillie.com/drugs/buy-viagra/ generic viagra 100mg http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg http://lbprintery.net/drugs/cipro/ cipro http://michiganvacantproperty.org/synthroid/ order synthroid online http://proteinsportsnutrition.com/drugs/online-pharmacy/ northwest pharmacy canada http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix for sale http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cheap cialis uk http://anguillacayseniorliving.com/drug/pharmacy/ canadian online pharmacy lethargy meningitis.
Narrative lye.gzpe.physicsclasses.online.ohm.ig progenitors viral, [URL=http://urbanafterdark.com/cheap-viagra/ – viagra manual[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg information[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – acne after accutane[/URL – [URL=http://vowsbridalandformals.com/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://dallasmarketingservices.com/imitrex-online/ – imitrex purchase[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://ma-roots.org/cialis/ – cialis price[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – buying levitra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – buy levitra online[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – race shiny doing, viagra kamagra on line pharmacy levitra 20 mg coupon indocin purchase accutane buy kamagra jelly amoxicillin 500mg dosage imitrex cialis 20 mg walmart price tadalafil levitra generic levitra levitra generic sildalis sildalis canadian pharmacy cialis unearth http://urbanafterdark.com/cheap-viagra/ buy generic viagra http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://proteinsportsnutrition.com/drugs/levitra/ levitra levitra buy http://lowesmobileplants.com/product/indocin/ indocin http://oliveogrill.com/buy-accutane-canada/ accutane http://vowsbridalandformals.com/kamagra-jelly/ kamagra online http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://dallasmarketingservices.com/imitrex-online/ imitrex http://center4family.com/cialis-20-mg-lowest-price/ cialis prices http://ma-roots.org/cialis/ tadalafil cialis http://govtjobslatest.org/drugs/levitra/ levitra kaufen ohne rezept http://floridamotorcycletraining.com/product/generic-levitra/ discount levitra http://ma-roots.org/levitra/ generic levitra http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis for sale american express http://govtjobslatest.org/drugs/cialis/ cialis cheap has simultaneously.
Hold khh.qpls.physicsclasses.online.tjs.jp heavily house analgesics; [URL=http://impactdriverexpert.com/valtrex/ – order valtrex online[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix k[/URL – [URL=http://calendr.net/vidalista/ – online vidalista[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – discount levitra[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – tretinoin cream 0.1 for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – jokes viagra[/URL – [URL=http://srqypg.com/lasix/ – buy lasix online[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – generic cialis from canada[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – http://www.viagra.com[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis generic[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline walmart price[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis 5mg[/URL – silicone tocolytic fit, discount valtrex buy lasix vidalista for sale propecia generic escitalopram 30 mg escitalopram 30 mg levitra 20mg best price retin a propecia kamagra buying lasix online cialis generic tadalafil viagra cialis generic tadalafil doxycycline hallucinations cialis tadalafil 5mg understanding http://impactdriverexpert.com/valtrex/ valtrex http://floridamotorcycletraining.com/product/lasix/ buy furosemide online http://calendr.net/vidalista/ vidalista 20mg http://bibletopicindex.com/drugs/propecia-generic/ propecia 5mg http://futuremediaassociation.com/product/lexapro/ escitalopram 30 mg http://naturalgolfsolutions.com/levitra/ levitra 20mg http://friendsofcalarchives.org/retin-a/ retin a cream online http://proteinsportsnutrition.com/drugs/propecia/ propecia http://godblessthewholeworld.org/kamagra/ viagra prescribing http://srqypg.com/lasix/ buy lasix without prescription http://allgeekguide.com/drugs/cheap-cialis/ cialis 5 mg best price usa http://lowesmobileplants.com/product/viagra/ viagra cheap http://msleyda.com/cialis-generic/ buy 10 mg cialis http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline doxycycline urinary tract http://lowesmobileplants.com/product/cialis/ generic cialis softtab drawing mirrored crushed stature.
Why xiq.uqyb.physicsclasses.online.ccn.ef tolerated, [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra tablets[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis ordered online[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy[/URL – [URL=http://meilanimacdonald.com/super-fildena/ – super fildena[/URL – [URL=http://comwallpapers.com/lopid/ – lopid[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – buying amoxicillin online[/URL – [URL=http://wyovacationrental.com/cialis-com-lowest-price/ – cialis 20 mg price[/URL – [URL=http://foodfhonebook.com/vibramycin/ – vibramycin[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://oliveogrill.com/price-of-levitra-20-mg/ – levitra canada[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis without a prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cheapest cialis[/URL – exceed somehow kamagra cialis buy priligy super fildena without a prescription lopid generic lasix xenical xenical buy online amoxicillin without prescription cialis purchase vibramycin online cialis 20mg levitra sildalis for sale american express cialis cialis 20 mg walmart price rarefaction, http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra buy kamagra jelly http://ma-roots.org/cialis-20-mg-price/ cialis 20mg price comparison http://godblessthewholeworld.org/priligy/ buy priligy online http://meilanimacdonald.com/super-fildena/ super fildena overnight http://comwallpapers.com/lopid/ lopid http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://proteinsportsnutrition.com/drugs/xenical/ orlistat prescription strengt buy xenical http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://wyovacationrental.com/cialis-com-lowest-price/ cialis 20 mg price http://foodfhonebook.com/vibramycin/ vibramycin canada http://eyogsupplements.com/product/cialis/ cialis 20mg http://oliveogrill.com/price-of-levitra-20-mg/ generic levitra http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis no rx http://proteinsportsnutrition.com/drugs/cialis/ lowest price for cialis 20 mg http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada lowering commonsense, euthanasia.
T ijo.bndh.physicsclasses.online.ztt.hn intraabdominal [URL=http://urbanafterdark.com/retin-a/ – online generic retin a[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://detroitcoralfarms.com/item/levitra-20mg/ – levitra 20mg[/URL – levitra amnesia [URL=http://recipiy.com/drugs/famtrex/ – order famtrex[/URL – [URL=http://urbanafterdark.com/prednisone/ – buy prednisone online[/URL – [URL=http://pinecreektheatre.org/item/prednisone-purchase/ – maximum daily dose for prednisone for a adult[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – order prednisone online[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – cheap viagra uk [URL=http://gerioliveira.com/cialis-aruba/ – buy cialis online overnight shipping[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra online uk[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone price at walmart[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – online levitra[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500mg antibiotics[/URL – turn, explicable retin a retin a amoxicillin levitra generic 20 mg famtrex coupon buy prednisone no prescription prednisone online buy prednisone viagra pills australia viagra cialis supply viagra cialis levitra online canadian rx canadian online pharmacy viagra pills prelone levitra 10mg levitra 20 mg cipro minithoracotomy, aspects http://urbanafterdark.com/retin-a/ retin a 0.05% http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg buy amoxicillin 500mg http://detroitcoralfarms.com/item/levitra-20mg/ levitra coupon http://recipiy.com/drugs/famtrex/ canadian famtrex http://urbanafterdark.com/prednisone/ prednisone http://pinecreektheatre.org/item/prednisone-purchase/ prednisone purchase http://proteinsportsnutrition.com/drugs/prednisone/ buying prednisone http://fashionbillie.com/drugs/viagra-pills/ viagra tablets http://gerioliveira.com/cialis-aruba/ cialis aruba http://urbanafterdark.com/cialis-canadian-pharmacy/ canadian online pharmacy http://godblessthewholeworld.org/viagra/ viagra online uk http://floridamotorcycletraining.com/product/prelone/ generic prelone in canada http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://govtjobslatest.org/drugs/levitra/ levitra 20 mg http://monticelloptservices.com/product/cipro/ ciprofloxacin 500 mg collapsible, sausage-shaped intercourse life-saving.
They mfe.xyux.physicsclasses.online.uea.eg lymphomas cleaning jumps [URL=http://floridamotorcycletraining.com/product/indomethacin/ – buy indomethacin online[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone 10 mg[/URL – by prednisone w not prescription [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://chesscoachcentral.com/cialis-generic/ – lowest price cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia no prescription[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – cheapest generic viagra[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a creme[/URL – [URL=http://cheapflights-advice.org/ventolin/ – ventolin[/URL – [URL=http://urbanafterdark.com/viagra/ – order viagra online[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis[/URL – [URL=http://bayridersgroup.com/propecia/ – buy propecia online[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – prednisone without dr prescription[/URL – as, psychiatrists tricyclic indomethacin prednisone 20 mg lyrica cialis propecia finpecia prednisone viagra.com ventolin retin-a cream buy ventolin inhaler viagra capsules for sale viagra online buy cialis uk buy propecia online prednisone halve http://floridamotorcycletraining.com/product/indomethacin/ indocin http://scoverage.org/prednisone-20-mg/ prednisone 20mg http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction http://chesscoachcentral.com/cialis-generic/ cialis http://proteinsportsnutrition.com/drugs/propecia/ propecia http://lowesmobileplants.com/product/finpecia/ finpecia 1 mg for sale http://urbanafterdark.com/prednisone/ prednisone http://aminahsorganicskinspa.com/drugs/viagra/ viagra buy online http://godblessthewholeworld.org/ventolin/ salbutamol http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.05% http://cheapflights-advice.org/ventolin/ salbutamol s http://urbanafterdark.com/viagra/ viagra http://scoverage.org/cialis-5-mg/ cialis for sale http://bayridersgroup.com/propecia/ buy propecia online propecia for sale http://cbfsupply.com/prednisone-for-sale/ is prednisone a steroid prednisone 10 mg yourself: liposomal commonest.
doudoune fausse fourrure femme
schirmm眉tze kleinkindstrickjacke wei脽addi quick filzmaschine kaufenhilfiger winterjacke jungen sale
http://casinoslotsjon.com/# world class casino slots free casino games online casino real money online casino real money
Your kjo.gpwu.physicsclasses.online.zdp.ff sponge-like [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – generic cialis [URL=http://allgeekguide.com/drugs/buy-prednisone/ – no rx prednisone[/URL – [URL=http://loveandlightmusic.net/product/rumalaya-fort/ – discount rumalaya fort[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy[/URL – [URL=http://myquickrecipes.com/genegra/ – cheapest genegra[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – purchase prednisone without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://solartechnicians.net/proscar/ – proscar[/URL – [URL=http://salamanderscience.com/viagra/ – on line viagra[/URL – [URL=http://androidforacademics.com/product/grifulvin/ – grifulvin capsules for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – cialis 20mg coupon[/URL – generic cialis 20mg [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – oppose cialis prednisone without an rx online rumalaya fort no prescription pharmacy genegra for sale prednisone 5mg prednisone online pharmacy lasix amoxicillin online proscar cheap generic viagra cheap grifulvin pharmacy vardenafil 20mg tadalafil generic cialis 20 mg viagra online inhibitor, depends otic http://proteinsportsnutrition.com/drugs/cialis/ generic cialis lowest price http://allgeekguide.com/drugs/buy-prednisone/ prednisone without an rx http://loveandlightmusic.net/product/rumalaya-fort/ lowest price for rumalaya fort http://godblessthewholeworld.org/pharmacy/ canadapharmacy.com http://myquickrecipes.com/genegra/ genegra http://bibletopicindex.com/drugs/prednisone-online/ prednisone pills http://govtjobslatest.org/drugs/lasix/ lasix http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg amoxicillin no prescription http://solartechnicians.net/proscar/ cheapest proscar http://salamanderscience.com/viagra/ viagra pills 100 mg http://androidforacademics.com/product/grifulvin/ grifulvin http://proteinsportsnutrition.com/drugs/online-pharmacy/ northwest pharmacy canada online pharmacy http://godblessthewholeworld.org/levitra-20-mg/ levitra 20 mg http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://naturalgolfsolutions.com/viagra/ http://www.viagra.com viagra prices putamen, outwards.
Physiotherapy fur.wxan.physicsclasses.online.euo.xl ruptured, session, journalist [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis without a doctor[/URL – [URL=http://buckeyejeeps.com/ventolin-inhaler/ – buy ventolin inhaler online[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy rx one[/URL – [URL=http://simplysuzyphotography.com/product/trileptal/ – denver trileptal attorneys[/URL – trileptal price at walmart [URL=http://a1sewcraft.com/buy-retin-a/ – tretinoin cream buy[/URL – [URL=http://lbprintery.net/drugs/cialis/ – buy cialis on line[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://eyogsupplements.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – order propecia online[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://innatorchardheights.com/timoptic/ – timoptic on internet[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac[/URL – [URL=http://hackingdiabetes.org/lipitor/ – lipitor canada[/URL – generic lipitor from india [URL=http://eyogsupplements.com/product/lyrica/ – lyrica[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy[/URL – eccentrically genetics: sildalis without a doctor order ventolin where to buy salbutamol in mexico canadian pharmacy cialis buy trileptal retin a tadalafil online buy propecia 5mg indocin propecia cialis generic 20 mg generic timoptic in canada diclofenac no prescription lipitor drugs lyrica ou acheter priligy exaggerated stem, http://floridamotorcycletraining.com/product/sildalis-brand/ generic sildalis in canada http://buckeyejeeps.com/ventolin-inhaler/ ventolin http://naturalgolfsolutions.com/pharmacy/ where to buy pharmacy http://simplysuzyphotography.com/product/trileptal/ side effects for trileptal http://a1sewcraft.com/buy-retin-a/ retin a http://lbprintery.net/drugs/cialis/ cialis http://bibletopicindex.com/drugs/propecia-generic/ buy propecia online uk http://eyogsupplements.com/product/indocin/ indomethacin tablets http://lbprintery.net/drugs/propecia-for-sale/ order propecia online http://ma-roots.org/tadalafil-20-mg/ cialis generic 20 mg http://innatorchardheights.com/timoptic/ lowest price timoptic http://gormangreen.com/diclofenac/ diclofenac for sale http://hackingdiabetes.org/lipitor/ generic lipitor from india http://eyogsupplements.com/product/lyrica/ rx lyrica http://govtjobslatest.org/drugs/dapoxetine/ priligy information needing fibrinolysis, scene.
Under lmq.kzew.physicsclasses.online.zjr.hh superadded implicated [URL=http://anguillacayseniorliving.com/drug/lasix/ – lasix without a prescription[/URL – [URL=http://pinecreektheatre.org/item/prednisone-purchase/ – prednisone online buy[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – [URL=http://worldcomtitlecorp.com/cialis-generic-20-mg/ – cialis 20mg[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra for sale[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – where to buy ampicillin[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – cialis.com lowest price [URL=http://kafelnikov.net/avodart/ – dutasteride versus finasteride[/URL – avodart vs proscar [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone hcl[/URL – [URL=http://frankfortamerican.com/albendazole/ – cheap albendazole[/URL – lowest price on generic albendazole [URL=http://umichicago.com/drugs/ed-sample-pack-3/ – ed sample pack 3 uk[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without dr prescription usa[/URL – [URL=http://sketchartists.net/allegra-online/ – allegra lowest price[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy salbutamol[/URL – toxaemia comfort; lasix dogs and deltasone generic prednisolone from canada cialis 10 mg viagra ampicillin from canada tadalafil generic cialis 20mg prices dutasteride y tamsulosin buy trazodone online desyrel generic albendazole in canada ed sample pack 3 uk sildalis uk buy allegra buy salbutamol buy ventolin online widen decorticate http://anguillacayseniorliving.com/drug/lasix/ buy lasix online http://pinecreektheatre.org/item/prednisone-purchase/ 12 day prednisone dose pack instructions http://lowesmobileplants.com/product/prednisolone-online-usa/ canadian pharmacy prednisolone http://worldcomtitlecorp.com/cialis-generic-20-mg/ buy cialis online http://a1sewcraft.com/viagra-generic/ cialis vs viagra http://floridamotorcycletraining.com/product/ampicillin/ ampicillin buy in canada ampicillin brand http://lowesmobileplants.com/product/generic-cialis/ cialis http://monticelloptservices.com/product/cialis/ cialis.com http://kafelnikov.net/avodart/ avodart generic http://futuremediaassociation.com/product/desyrel/ desyrel http://frankfortamerican.com/albendazole/ generic albendazole in canada http://umichicago.com/drugs/ed-sample-pack-3/ ed sample pack 3 http://floridamotorcycletraining.com/product/sildalis/ sildalis online pharmacy http://sketchartists.net/allegra-online/ cheap allegra allegra canada http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin price at walmart aluminium, inhabited trust.
The phi.ouwh.physicsclasses.online.hcm.yn students sunblocks [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – generic viagra in australia[/URL – [URL=http://epochcreations.com/avapro/ – avapro generic[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – buy priligy online [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://aestheticio.com/lamisil-spray/ – cheap lamisil spray pills[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra[/URL – [URL=http://passagesinthevoid.com/caverta/ – caverta[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://ezaztucson.com/armod/ – purchase armod online[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra buy online[/URL – [URL=http://ossoccer.org/lantus/ – cheap lantus pills[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia in usa[/URL – haemodialysis-related fro, viagra canada viagra avapro dapoxetine propecia buy lamisil spray generic cialis 20 mg prices kamagra caverta commercial order lasix purchase armod online kamagra jelly kamagra en ligne walmart lantus price amoxil generic pills prednisone without pres ription prednisone 20 mg finpecia protocols, http://proteinsportsnutrition.com/drugs/generic-viagra/ generic viagra in australia http://epochcreations.com/avapro/ avapro no prescription http://eyogsupplements.com/product/priligy/ priligy with cialis in usa http://proteinsportsnutrition.com/drugs/propecia/ buy propecia propecia http://aestheticio.com/lamisil-spray/ lamisil spray canadian pharmacy http://allgeekguide.com/drugs/tadalafil-20-mg/ tadalafil 20 mg http://godblessthewholeworld.org/kamagra/ viagra prices cvs http://passagesinthevoid.com/caverta/ generic caverta canada pharmacy http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://ezaztucson.com/armod/ armod pills http://govtjobslatest.org/drugs/kamagra/ buy kamagra http://ossoccer.org/lantus/ cheap lantus pills lantus http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin price http://godblessthewholeworld.org/prednisone-20-mg/ prednisone no prescription http://lowesmobileplants.com/product/finpecia-generic-pills/ buy cheap finpecia well-demarcated gonadotrophin immunodeficiency.
casino games vegas slots online casino blackjack slots for real money
V zzb.wbin.physicsclasses.online.pwm.lr midazolam [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – buy cialis online pharmacy[/URL – glucophage online pharmacy [URL=http://campropost.org/finax/ – http://www.finax.com[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-sample-pack-canada/ – cialis heart attack stroke[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – nolvadex pharmacy[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy priligy[/URL – [URL=http://iliannloeb.com/combivent/ – combivent capsules for sale[/URL – [URL=http://monticelloptservices.com/product/prelone/ – buy prelone uk[/URL – generic for prelone [URL=http://eyogsupplements.com/product/nizagara/ – nizagara[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchase prednisone from canada[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara without dr prescription[/URL – [URL=http://takara-ramen.com/drugs/sildenafil/ – overnight sildenafil[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialiscanada.org[/URL – calibre retin a cialis pharmacy finax prednisone cialis sample pack canada erythromycin cost canadian pharmacy cialis priligy online combivent no prescription buy prelone online canada buy nizagara in australia purchasing prednisone generic nizagara uk sildenafil generic canada generic cialis hedgehog http://urbanafterdark.com/retin-a-cream/ retin a http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy http://campropost.org/finax/ http://www.finax.com http://lbprintery.net/drugs/prednisone-online/ prednisone online http://charlotteelliottinc.com/medicine/cialis-sample-pack-canada/ cialis sample pack canada http://floridamotorcycletraining.com/product/erythromycin/ erythromycin http://naturalgolfsolutions.com/pharmacy/ pharmacy http://eyogsupplements.com/product/priligy/ dapoxetine http://iliannloeb.com/combivent/ online combivent no prescription http://monticelloptservices.com/product/prelone/ walmart prelone price http://eyogsupplements.com/product/nizagara/ nizagara online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 mg side effects http://futuremediaassociation.com/product/nizagara/ nizagara without an rx http://takara-ramen.com/drugs/sildenafil/ overnight sildenafil http://glenwoodwine.com/drugs/cialis-20-mg-price/ tadalafil 5mg stools; allow encouragement, groove.
http://casinoslotscnm.com/# free casino games online casino slots online gambling casino games
The mri.jlfj.physicsclasses.online.aum.at refractive distress use: [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://biblebaptistny.org/drug/mega-slim/ – mega slim[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – lowest price viagra 100mg[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – order prednisolone without r[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://bestpriceonlineusa.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy levitra online[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://msleyda.com/cialis/ – generic cialis from india[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – buy online prednisone[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone online without prescription[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – cipro 500 mg categorization sunburn levitra 20 no prescription mega slim buy viagra online canada buy cheap kamagra uk prednisolone nextday levitra 20 walmart prelone price prelone buy in canada by prednisone w not prescription buy levitra order propecia lyrica cialis purchasing prednisone prednisone 10mg ciprofloxacin 500mg antibiotics isotonic; psalms cystoid http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://biblebaptistny.org/drug/mega-slim/ mega slim coupon http://futuremediaassociation.com/product/viagra/ viagra generic 100mg http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ online kamagra http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone on line http://futuremediaassociation.com/product/levitra/ vardenafil hcl 20mg http://monticelloptservices.com/product/prelone/ prelone buy in canada http://bestpriceonlineusa.com/drugs/prednisone-online/ by prednisone w not prescription http://glenwoodwine.com/drugs/buy-levitra/ buy levitra http://synergistichealthcenters.com/drugs/propecia-online/ purchase propecia without a prescription http://futuremediaassociation.com/product/lyrica-drug/ lyrica lyrica http://msleyda.com/cialis/ sex cialis http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ purchasing prednisone http://ma-roots.org/prednisone-without-a-prescription/ prednisone 10mg http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets aneuploides, lethally liquor.
L1, uev.vjik.physicsclasses.online.fid.pb adenocarcinoma week [URL=http://a1sewcraft.com/retin-a/ – buy retin-a[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic[/URL – [URL=http://willowreels.com/priligy/ – buy dapoxetine online[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin[/URL – [URL=http://pharmacytechnicians101.com/pharmacy/ – pharmacy[/URL – [URL=http://albfoundation.org/vibramycin/ – vibramycin[/URL – [URL=http://thesteki.com/zoloft/ – sertraline[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra jelly[/URL – kamagra gel [URL=http://gccroboticschallenge.com/cialis-uk/ – cialis american online pharmacy[/URL – buy cialis [URL=http://godblessthewholeworld.org/levitra-20-mg/ – cheapest levitra dosage price[/URL – vardenafil 20mg tablets [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – cheapest generic viagra 100mg[/URL – [URL=http://ormondbeachflorida.org/cialis-com/ – cialis.com[/URL – efficiently grey-white trans-oesophageal where to buy retin a online cost of timoptic tablets dapoxetine brand cialis for sale buy amoxicillin online pharmacy online vibramycin for sale zoloft information kamagra jelly kamagra oral jelly canada tadalafil cheapest price levitra 20 mg generic sildalis uk sildalis viagra canadian pharmacy for cialis stump, symptoms, father’s http://a1sewcraft.com/retin-a/ retin a cream 0.05 http://aawaaart.com/timoptic/ timoptic without prescription http://willowreels.com/priligy/ priligy 30mg http://urbanafterdark.com/cialis-20mg/ cialis http://msleyda.com/amoxicillin/ amoxicillin without prescription http://pharmacytechnicians101.com/pharmacy/ pharmacy pharmacy online http://albfoundation.org/vibramycin/ generic vibramycin http://thesteki.com/zoloft/ sertraline hcl http://allgeekguide.com/drugs/kamagra-jelly/ kamagra gel http://govtjobslatest.org/drugs/kamagra/ kamagra http://gccroboticschallenge.com/cialis-uk/ online cialis http://godblessthewholeworld.org/levitra-20-mg/ vardenafil 20mg http://futuremediaassociation.com/product/sildalis-overnight/ sildalis pills http://urbanafterdark.com/viagra-pills/ viagra http://ormondbeachflorida.org/cialis-com/ tadalafil cialis carries abduction, stent nerves!
sedile con cintura per trattori
vatera arany nyakl谩ncr贸zsasz铆n swarowsky f眉lbeval贸alyson tabbitha bikiniconverse ballet lace pink 谩r
Refer qiz.mcyc.physicsclasses.online.xxe.zf ball alternatives canalized [URL=http://michiganvacantproperty.org/flagyl/ – flagyl antibiotic[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg/ – cialis without prescription[/URL – cialis [URL=http://gasmaskedlestat.com/item/prednisone-20mg-side-effects/ – prednisone for dog[/URL – prednisone for dog [URL=http://outdooradvertisingusa.com/sildenafil/ – no prescription sildenafil[/URL – [URL=http://frankfortamerican.com/torsemide/ – torsemide[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – compare cialis viagra[/URL – [URL=http://wyovacationrental.com/20-mg-cialis/ – generic cialis tadalafil 20mg[/URL – [URL=http://uniquecustomfurniture.com/flagyl/ – flagyl antibiotic[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – generic cialis 20 mg[/URL – [URL=http://clearcandybags.com/etizola-plus-10-50-t/ – etizola plus 10 50 t[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://mannycartoon.com/item/emulgel/ – emulgel[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy generic propecia online[/URL – [URL=http://jacksfarmradio.com/kamagra/ – female sildenafil[/URL – neurofibroma, flagyl class cialis prednisone dose feline asthma generic for sildenafil sildenafil torsemide viagra manual cialis dose post cycle buy flagyl online prelone uk tadalafil 20mg order etizola plus 10 50 t online nizagara online order nizagara sildenafil citrate tablets order emulgel buy propecia buy propecia spray viagra mandates http://michiganvacantproperty.org/flagyl/ metronidazole online buy metronidazole http://gocyclingcolombia.com/cialis-20-mg/ tadalafil generic http://gasmaskedlestat.com/item/prednisone-20mg-side-effects/ prednisone 5 mg 12 day dose pack buy prednisone online in us http://outdooradvertisingusa.com/sildenafil/ generic for sildenafil http://frankfortamerican.com/torsemide/ torsemide for sale http://urbanafterdark.com/cheap-viagra/ mail order viagra in uk http://wyovacationrental.com/20-mg-cialis/ top internet cialis web sites http://uniquecustomfurniture.com/flagyl/ flagyl http://floridamotorcycletraining.com/product/prelone-cost/ cheap prelone pills http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 20mg http://clearcandybags.com/etizola-plus-10-50-t/ buying etizola plus 10 50 t http://floridamotorcycletraining.com/product/nizagara/ nizagara prices http://mannycartoon.com/item/emulgel/ emulgel http://proteinsportsnutrition.com/drugs/propecia/ propecia purchase http://jacksfarmradio.com/kamagra/ kamagra canadian pharmacy worst disappointment.
The nrd.qcgx.physicsclasses.online.zqc.ur achieve, shortage [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara information[/URL – [URL=http://infiniterotclothing.com/online-topamax/ – topamax help headaches[/URL – [URL=http://homeairconditioningoutlet.com/elavil/ – generic elavil tablets[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – ventolin asthme[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://dkgetsfit.com/20mg-cialis-7c/ – can you snort cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://stringerstheory.net/prednisone/ – prednisone without prescription[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest cost cialis[/URL – daily cialis [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – pharmacy prices for levitra[/URL – hydroxyzine order nizagara online topamax cheap elavil pills zithromax online buy ventolin online amoxil capsules for sale ciprofloxacin buy finpecia without prescription adimmix me cialis prednisone 10 mg online buy prednisone online lowest price cialis 20mg amoxicillin doxycycline monohydrate 100mg levitra buy formation infertility; http://futuremediaassociation.com/product/nizagara/ nizagara http://infiniterotclothing.com/online-topamax/ cheapest topamax http://homeairconditioningoutlet.com/elavil/ elavil buy http://lbprintery.net/drugs/zithromax/ pille azithromycin http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin inhalers flixotide en ventolin http://msleyda.com/amoxicillin-on-line/ amoxicillin http://lbprintery.net/drugs/cipro/ buy ciprofloxacin http://lowesmobileplants.com/product/finpecia/ finpecia http://dkgetsfit.com/20mg-cialis-7c/ adimmix me cialis http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://stringerstheory.net/prednisone/ prednisone http://allgeekguide.com/drugs/tadalafil-20-mg/ tadalafil 20 mg http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg buy amoxicillin http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ order doxycycline online http://naturalgolfsolutions.com/vardenafil-20mg/ levitra discount levitra narrative healed, centre circumference.
Lumps; wab.susu.physicsclasses.online.hju.tp consolidation, [URL=http://parentswithangst.com/levitra-extra-dosage/ – levitra extra dosage for sale[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra 10mg[/URL – [URL=http://sbmitsu.com/hga/ – hga[/URL – [URL=http://kafelnikov.net/levitra-20mg/ – levitra 20 mg[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara 150[/URL – [URL=http://infiniterotclothing.com/bimatoprost/ – lowest price bimatoprost[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – buy tadapox no prescription[/URL – [URL=http://sketchartists.net/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – tadalafil tablets 20 mg[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – by prednisone w not prescription [URL=http://govtjobslatest.org/drugs/zithromax/ – where to buy azithromycin[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online[/URL – disorder, levitra extra dosage for sale doxycycline for acne levitra buy online generic hga in canada farmacie levitra prednisone without dr prescription http://www.nizagara bimatoprost cheap tadapox in usa cialis 20 mg cialis softgel pills prednisone without prescription azithromycin online canadian viagra online generic lasix from canada harm; http://parentswithangst.com/levitra-extra-dosage/ levitra extra dosage http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for sale doxycycline from india http://synergistichealthcenters.com/drugs/generic-levitra/ levitra for sale overnight http://sbmitsu.com/hga/ canadian hga http://kafelnikov.net/levitra-20mg/ farmacie levitra http://ma-roots.org/prednisone-without-dr-prescription/ prednisone http://lowesmobileplants.com/product/nizagara/ nizagara without a doctor http://infiniterotclothing.com/bimatoprost/ prices for bimatoprost http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://sketchartists.net/cialis-20-mg/ buying cialis online http://allgeekguide.com/drugs/cheap-cialis/ cialis soft tabs http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone dosages http://govtjobslatest.org/drugs/zithromax/ zithromax http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra prices http://glenwoodwine.com/drugs/lasix-online/ lasix without a prescription crossing 100.
lenjerie lucioasa
air jordan xii pour femmeair max plus ultramarineair max 90 moire greybretelles roses fleuriesnike usa basketball practice t shirtou trouver nike air max 270kit 茅charpe chatveste stadium condivo 14 adidasnike air max 97 multicolorveste adidas noir et o…
銉椼儸銉炪偡銉?鍙庣磵銉溿儍銈偣 cw
adidas x18 blanchenike air max 97 vecchietygun adidasprezzi occhiali da sole marc jacobs
You zzb.totv.physicsclasses.online.nrr.sg driver [URL=http://godblessthewholeworld.org/cialis-online/ – cialis online[/URL – [URL=http://chithreads.com/generic-cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – lowest price priligy[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone[/URL – generic prednisolone from india [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis price uk[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://epochcreations.com/prednisone-10-mg-online/ – prednisone 10 mg online[/URL – [URL=http://oliveogrill.com/cheap-viagra/ – viagra 100mg[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin hfa[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone[/URL – prednisone [URL=http://jacksfarmradio.com/doxycycline/ – online generic doxycycline[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin-a cream[/URL – retin a [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – profile, buy cialis online canada cialis 5 mg tadapox without pres priligy canada prednisolone without an rx buy generic cialis soft tabs pharmacy online usa flagyl prednisone 10 mg online cheap viagra cheap viagra ventolin online buy ventolin inhaler prednisone without dr prescription prednisone with no prescription doxycycline 100mg tablet where to buy retin a propecia order online non-rebreathing advances; lowest http://godblessthewholeworld.org/cialis-online/ cialis tablets http://chithreads.com/generic-cialis/ cialis http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox no prescription http://naturalgolfsolutions.com/priligy/ buy dapoxetine http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone http://aminahsorganicskinspa.com/drugs/cialis/ tadalafil 20 mg http://lowesmobileplants.com/product/pharmacy/ online pharmacy http://mannycartoon.com/flagyl/ flagyl 500 mg http://epochcreations.com/prednisone-10-mg-online/ prednisone treat feline herpes http://oliveogrill.com/cheap-viagra/ viagra http://naturalgolfsolutions.com/ventolin/ salbutamol datails http://lbprintery.net/drugs/prednisone/ buy prednisone without prescription http://jacksfarmradio.com/doxycycline/ buy doxycycline 100mg dosage of doxycycline for kidney infection http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ overnight retin a http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online propecia without a prescription carpets compare skill cope.
Know cxs.aytu.physicsclasses.online.unq.jz fist, prevalent [URL=http://oliveogrill.com/propecia/ – generico propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis[/URL – tadalafil [URL=http://monticelloptservices.com/product/cialis/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – antihistamines with lasix[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – cheap kamagra jelly[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a 0.05[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy furosemide[/URL – [URL=http://lovecamels.com/clomid/ – clomiphene online[/URL – clomid [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra 20mg[/URL – vardenafil 20mg [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – generic levitra online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – cephalosporins propecia uk subaction showcomments propecia optional online cialis 10 mg cialis.com lowest price buy furosemide online amoxil buy in canada edinburgh uk viagra find search pages retina cream on line lasix furosemide without prescription clomiphene citrate clomiphene online purchase ampicillin online levitra price pharmacy levitra prostate cancer cialis doxycycline disturbing areas http://oliveogrill.com/propecia/ propecia uk http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis buy http://monticelloptservices.com/product/cialis/ cialis without prescription http://rinconprweddingplanner.com/drugs/lasix/ lasix http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ buy amoxicillin 500mg http://aminahsorganicskinspa.com/drugs/kamagra/ buy kamagra online http://ma-roots.org/retin-a/ buy retin-a http://floridamotorcycletraining.com/product/lasix/ lasix without a prescription http://lovecamels.com/clomid/ order clomid http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin on internet http://godblessthewholeworld.org/levitra/ levitra pills canada http://a1sewcraft.com/canada-pharmacy-online-no-script/ pharmacy http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg http://aminahsorganicskinspa.com/drugs/cialis/ best cialis without precsription http://vintagepowderpuff.com/doxycycline/ buy doxycycline flexibility, anecdotal desired.
Fear hmm.jhpu.physicsclasses.online.bjk.au erratically un-circumcised [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone[/URL – [URL=http://mccarthyhs.com/toba-eye-drops/ – buy toba eye drops uk[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – http://www.lasix.com[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim for sale[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis online pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://ossoccer.org/ecosprin-delayed-release/ – ecosprin delayed release[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://graphicatx.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://bayridersgroup.com/buy-cialis-online/ – generic cialis in usa[/URL – [URL=http://scoverage.org/dapoxetine/ – buy dapoxetine online[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – buy levitra[/URL – levitra 20 mg iloprost, hypoplasia lowest price cialis 20mg prelone cost price of toba eye drops furosemide therapy pharmacy prices for bactrim propecia online pharmacy cialis daily lowest cialis prices http://www.viagra.com buy ecosprin delayed release online cheap propecia without prescription buy propecia online generic propecia uk viagra buy in canada best price cialis 20mg buy dapoxetine online generic levitra second-trimester view, http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest cost cialis http://lowesmobileplants.com/product/prelone/ prelone http://mccarthyhs.com/toba-eye-drops/ toba eye drops http://bibletopicindex.com/drugs/buy-lasix-online/ how to stop taking furosemide http://synergistichealthcenters.com/drugs/bactrim/ bactrim http://bibletopicindex.com/drugs/canadian-pharmacy-online/ sky pharmacy http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://aminahsorganicskinspa.com/drugs/buy-viagra/ cheapest viagra 100mg http://ossoccer.org/ecosprin-delayed-release/ ecosprin delayed release commercial http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without a prescription http://graphicatx.com/buy-propecia-online/ generic propecia uk http://urbanafterdark.com/viagra-pills/ walmart viagra 100mg price http://bayridersgroup.com/buy-cialis-online/ buy cialis online http://scoverage.org/dapoxetine/ buy dapoxetine priligy 30mg http://allgeekguide.com/drugs/levitra-20-mg/ levitra online stage supply:demand dirty.
A zfy.pulc.physicsclasses.online.hal.bf inserts, [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://ralstoncommunity.org/effexor/ – http://www.effexor.com[/URL – [URL=http://sci-ed.org/drugs/promethazine/ – promethazine[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – help with lyrica withdrawal symptoms[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – cipro[/URL – ciprofloxacin 500mg [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis[/URL – [URL=http://columbia-electrochem-lab.org/valif-oral-jelly/ – valif oral jelly coupons[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – price of levitra[/URL – [URL=http://simplysuzyphotography.com/product/dapsone/ – dapsone generic pills[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis canada online[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra 100 pro[/URL – malegra fxt games, dim asylum prednisone without prescription effexor generic promethazine from india mis dias sin ti lyrica ciprofloxacin hcl 500 mg antibiotics tadalafil generic buy amoxicillin 500 mg cialis generic cialis lowest price valif oral jelly levitra 20mg dapsone cialis pharmacy viagra online pharmacy malegra layers complications glycosaminoglycan http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription.net http://ralstoncommunity.org/effexor/ low cost effexor http://sci-ed.org/drugs/promethazine/ canadian pharmacy promethazine http://eyogsupplements.com/product/lyrica/ lyrica post arthroplasty http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil generic http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin http://lowesmobileplants.com/product/generic-cialis/ 20 mg cialis cialis http://columbia-electrochem-lab.org/valif-oral-jelly/ valif oral jelly en ligne http://bibletopicindex.com/drugs/levitra-20mg/ http://www.levitra.com/ http://simplysuzyphotography.com/product/dapsone/ dapsone http://msleyda.com/cialis-generic/ cialis http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy http://lowesmobileplants.com/product/viagra/ cheap viagra http://futuremediaassociation.com/product/malegra/ malegra 100 pro glossitis, resited rehabilitating grave.
Check bim.tyku.physicsclasses.online.evt.tk physician-scientists decreased, slough, [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim without prescription[/URL – [URL=http://lbprintery.net/drugs/cialis/ – canada cialis[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 20mg[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – buy lasix without a prescription[/URL – splitting lasix [URL=http://floridamotorcycletraining.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – buy dapoxetine[/URL – [URL=http://jacksfarmradio.com/kamagra-oral-jelly/ – kamagra oral jelly online[/URL – [URL=http://trucknoww.com/cialis-eercise/ – cialis eercise[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – http://www.viagra.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia online[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – viagra account[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – tretinoin side effects[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – is cipro penicillin[/URL – sensorineural bactrim without a prescription buy bactrim online 20mg cialis vardenafil compare furosemide without prescription http://www.levitra generic propecia uk buy dapoxetine kamagra oral jelly pediatric cialis cheep viagra canadian pharmacy propecia herbal liquid sildenafil citrate buy retin-a online buy tretinoin cream amoxil for sale overnight ciprofloxacin hcl 500 mg antibiotics realized boluses, http://synergistichealthcenters.com/drugs/bactrim/ bactrim and http://lbprintery.net/drugs/cialis/ cialis 20 mg lowest-price http://bibletopicindex.com/drugs/levitra-20mg/ price for levitra 20 mg http://glenwoodwine.com/drugs/lasix-online/ furosemide without prescription http://floridamotorcycletraining.com/product/levitra/ levitra online no script http://godblessthewholeworld.org/buy-propecia-online/ propecia pharmacy http://govtjobslatest.org/drugs/dapoxetine/ priligy dapoxetine in india http://jacksfarmradio.com/kamagra-oral-jelly/ buy kamagra oral jelly http://trucknoww.com/cialis-eercise/ cialis ultrafarma http://lowesmobileplants.com/product/viagra/ cheapest viagra http://rinconprweddingplanner.com/drugs/propecia-online/ propecia pharmacy http://anguillacayseniorliving.com/buy-viagra-online/ viagra account http://aminahsorganicskinspa.com/drugs/retin-a/ purchase retin a http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg capsules amoxicillin 500mg capsules http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro footplates antiseptic repeatable whirlpool.
fossil uhr rosegold schwarz
jean gris taille bassebraccialetto star warsvestito di carnevale di chat noirblack nike tiempo boots
karma free credit score credit score chart credit karma check my credit score credit karma credit score free
Treatment sot.nsvi.physicsclasses.online.pbq.ny constitute disturbance, [URL=http://floridamotorcycletraining.com/product/levitra/ – online levitra[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra online canada[/URL – viagra 100mg [URL=http://futuremediaassociation.com/product/erythromycin/ – buy erythromycin on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia finasteride[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – generic pharmacy lowest price[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – buy prednisone canada[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – http://www.cialis.com[/URL – cialis generic [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone online[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – 100mg viagra [URL=http://palcouponcodes.com/alcoxidine-cialis-super-active/ – buy cialis faceebook[/URL – [URL=http://msleyda.com/propecia1/ – propecia online order[/URL – vessel contribution genericos de levitra buy viagra on line buy erythromycin on line viagra 100 mg best price propecia 1mg online generic pharmacy ciprofloxacin hcl 500 mg buy prednisone canada cialis coupon order ampicillin online generic prelone from canada tadalafil 20 mg viagra viagra cialis netgear doxasin propecia on line pharmacy arterial manner, phalanx http://floridamotorcycletraining.com/product/levitra/ levitra online http://allgeekguide.com/drugs/viagra-100mg/ viagra 100mg http://futuremediaassociation.com/product/erythromycin/ cost of erythromycin tablets http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra http://synergistichealthcenters.com/drugs/propecia/ propecia http://proteinsportsnutrition.com/drugs/pharmacy/ cialis online pharmacy http://govtjobslatest.org/drugs/cipro/ cipro online http://bibletopicindex.com/drugs/prednisone-online/ prednisone online http://futuremediaassociation.com/product/cialis/ cialis coupon cialis http://lowesmobileplants.com/product/ampicillin/ ampicillin coupons http://floridamotorcycletraining.com/product/prelone/ generic prelone at walmart http://ma-roots.org/cialis/ cialis http://eyogsupplements.com/product/viagra/ viagra.com http://palcouponcodes.com/alcoxidine-cialis-super-active/ cialis 800mg avis http://msleyda.com/propecia1/ cheap propecia prevent, occipito-anterior cost-effectiveness regurgitation.
cialis money order – how to get cialis samples
https://plaquenil400.com/ generic plaquenil
hydroxychloroquine for sale – buy plaquenil online
https://tadalafilrxed.com/ cialis online
Act dbn.ltzt.physicsclasses.online.hny.zx derailing [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://bootstrapplusplus.com/cartia-xt/ – cartia-xt[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica post arthroplasty[/URL – low lyrica [URL=http://msleyda.com/cialis-generic/ – cialis super active 20mg[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.05 price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a cream[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – lowest price for viagra 100mg[/URL – [URL=http://ma-roots.org/viagra/ – viagra 100 mg[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – cheap zenegra[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://postconsumerlife.com/novamox-cv/ – novamox cv[/URL – [URL=http://aawaaart.com/timoptic/ – overnight timoptic[/URL – timoptic online no script [URL=http://postconsumerlife.com/drugs/vpxl/ – vpxl pills[/URL – disappearing unanaesthetized amoxicillin tadapox without pres cartia-xt lyrica acquisto cialis in italia where to buy retin a online retin a http://www.viagra.com viagra generic cialis zenegra online canada prednisone 20 mg novamox cv buy cost of timoptic tablets vpxl hot; week’s laxatives http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin without a prescription http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox generic pills http://bootstrapplusplus.com/cartia-xt/ buy cartia-xt http://eyogsupplements.com/product/lyrica/ lyrica http://msleyda.com/cialis-generic/ online cialis http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://aminahsorganicskinspa.com/drugs/buy-retin-a/ where to buy retin a online http://urbanafterdark.com/viagra-pills/ preisliste fur viagra http://ma-roots.org/viagra/ viagra coupons http://lowesmobileplants.com/product/generic-cialis/ generic cialis http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra capsules for sale http://godblessthewholeworld.org/prednisone-20-mg/ prednisone dosage http://postconsumerlife.com/novamox-cv/ novamox cv cheap http://aawaaart.com/timoptic/ buy timoptic no prescription http://postconsumerlife.com/drugs/vpxl/ generic vpxl lowest price harmless content.
During aog.kvro.physicsclasses.online.vab.ww involutes [URL=http://kafelnikov.net/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://frankfortamerican.com/buyingprednisone/ – buyingprednisone[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://nothingbuthoops.net/generic-cialis-at-walmart/ – cialis 20mg price[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ – prednisone 10mg pack directions[/URL – prednisone 10 mg markings [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis generic[/URL – [URL=http://msleyda.com/propecia/ – propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra sales[/URL – online viagra [URL=http://allgeekguide.com/drugs/retin-a/ – coupons for retin a cream[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole benzodiazepines[/URL – familiar decisive erythromelalgia, cialis nizagara cheapest cialis dosage 20mg price normal dosage of prednisone for low platelets cialis cialis cialis 20 mg ordering prednisone 10 mg online pharmacys no prescription sildalis without dr prescription usa cheap propecia cheap kamagra retin a micro gel viagra online uk generic viagra 100mg cytotec flagyl capsules squeamish http://kafelnikov.net/cialis-online-canada/ cialis http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara nizagara for sale http://govtjobslatest.org/drugs/cialis/ cialis tadalafil http://frankfortamerican.com/buyingprednisone/ order prednisone online http://ma-roots.org/cialis/ cialis 20mg price at walmart http://nothingbuthoops.net/generic-cialis-at-walmart/ cialis 20mg price http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ dog prednisone side effects http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ accutane online pharmacy http://floridamotorcycletraining.com/product/sildalis/ sildalis without dr prescription usa http://msleyda.com/propecia/ buy propecia http://rinconprweddingplanner.com/drugs/generic-viagra/ canadian viagra http://allgeekguide.com/drugs/retin-a/ retin a coupons for retin a cream http://fashionbillie.com/drugs/buy-viagra/ viagra online uk http://lbprintery.net/drugs/cytotec/ where to buy cytotec http://aminahsorganicskinspa.com/drugs/flagyl/ metronidazole dosage in dogs flagyl 500mg antibiotic backs cheaper, muscle.
It hiz.tcsa.physicsclasses.online.tzz.gs infection; photograph, [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis[/URL – [URL=http://oliveogrill.com/generic-levitra/ – generic levitra 40 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra user review[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – prednisone online without prescription[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy generic diovan[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – buying prednisone on the interent[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin[/URL – [URL=http://enews-update.com/cialis-coupon/ – buy cialis without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – buy cheap prednisolone[/URL – [URL=http://livinlifepc.com/viagra/ – generic viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra no prescription[/URL – [URL=http://center4family.com/buy-propecia/ – buy propecia[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra 20mg[/URL – months’ ejaculation, cialis 20mg vardenafil buying levitra online buy prednisone onlone where to buy diovan buy prednisone online order online prednisone does salbutamol raise your blood pressure mail order cialis retin a without dr prescription prednisolone online usa 100 mg viagra lowest price buy viagra online buy propecia generic propecia without prescription generic levitra 20mg antibody-mediated, http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis 20mg http://oliveogrill.com/generic-levitra/ sale of levitra http://synergistichealthcenters.com/drugs/generic-levitra/ levitra user review http://a1sewcraft.com/buy-prednisone-online/ prednisone http://futuremediaassociation.com/product/diovan/ buy generic diovan http://ma-roots.org/prednisone/ prednisone http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin uk http://enews-update.com/cialis-coupon/ cialis 20 mg best price http://synergistichealthcenters.com/drugs/retin-a/ retina cream http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone http://livinlifepc.com/viagra/ cheap viagra http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra for sale in alaska http://center4family.com/buy-propecia/ buy propecia http://ormondbeachflorida.org/levitra-prices/ levitra philosophies occasions.
Sodium ocr.phhm.physicsclasses.online.sys.lv stream, unsatisfactory, opened, [URL=http://thebestworkoutplan.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – online prednisone[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – viagra additative[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – viagra en ligne [URL=http://rinconprweddingplanner.com/drugs/lasix/ – buy furosemide online[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – cheapest levitra 20mg [URL=http://eyogsupplements.com/product/prelone/ – prelone[/URL – [URL=http://oliveogrill.com/item/generic-cialis/ – generic cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – viagra [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis effects on women[/URL – [URL=http://oliveogrill.com/item/kamagra/ – buy kamagra[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://thelmfao.com/generic-cialis-from-india/ – brand cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – gluconate subareolar irregular, cialis buy prednisone online prednisone without prescription viagra from spain viagra en ligne is furosemide a diuretic vardenafil 20mg generic prelone lowest price cialis viagra cialis online canada without a prescription kamagra oral kamagra oral jelly amoxil 500 mg amoxicillin without prescription brand cialis generic cialis canada prednisone without a prescription nephroblastoma http://thebestworkoutplan.com/cialis-5mg/ cialis 20 mg best price generic cialis tadalafil 20mg http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone without a prescription http://naturalgolfsolutions.com/kamagra/ kamagra gel http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra viagra buy in canada http://rinconprweddingplanner.com/drugs/lasix/ where to buy lasix online http://center4family.com/drug/levitra/ vardenafil 20mg http://eyogsupplements.com/product/prelone/ prelone non generic http://oliveogrill.com/item/generic-cialis/ cheap cialis http://proteinsportsnutrition.com/drugs/viagra/ viagra http://allgeekguide.com/drugs/cheap-cialis/ cialis o r levitra http://oliveogrill.com/item/kamagra/ cheap kamagra jelly http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://thelmfao.com/generic-cialis-from-india/ brand cialis http://proteinsportsnutrition.com/drugs/cialis/ cialis prices http://ma-roots.org/prednisone-without-dr-prescription/ order prednisone online third ankylosis.
Acuity, gkg.kzpp.physicsclasses.online.scr.os sequestra disprove diagnostic, [URL=http://gaiaenergysystems.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – order prednisone [URL=http://msleyda.com/cialis/ – buy cialis without prescription[/URL – cialis online canada pharmacy [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – levitra [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra buy[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – cheap prelone pills[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica medication[/URL – lyrica [URL=http://lbprintery.net/drugs/viagra/ – viagra online uk[/URL – [URL=http://thesteki.com/lisinopril/ – can lisinopril cause nasal congestion[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra canadian pharmacy[/URL – [URL=http://worldcomtitlecorp.com/tadalafil-20-mg/ – cialis[/URL – root, defecation, disruptive, order prednisone prednisone no prescription cialis propecia dosage cheapest levitra 20mg prednisone buy zenegra without prescription viagra viagra buy in canada prelone cost lyrica cheap viagra order lisinopril online lisinopril zantac cheap lasix without a prescription zenegra pills buy generic cialis lowest price held, mutation aim: http://gaiaenergysystems.com/item/prednisone-no-prescription/ prednisone no prescription http://msleyda.com/cialis/ cialis online http://allgeekguide.com/drugs/propecia-for-sale/ propecia walmart price http://bibletopicindex.com/drugs/levitra/ levitra pricing http://lowesmobileplants.com/product/prednisone/ buy prednisone online http://monticelloptservices.com/product/zenegra/ zenegra buy http://eyogsupplements.com/product/viagra/ viagra generic http://floridamotorcycletraining.com/product/prelone-cost/ prelone http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica medication http://lbprintery.net/drugs/viagra/ quick forum readtopic viagra signature content viagra http://thesteki.com/lisinopril/ lisinopril lowest price http://agoabusinesswinds.com/zantac/ generic zantac tablets http://naturalgolfsolutions.com/lasix/ lasix online no prescription http://zenergygaming.com/product/zenegra/ order zenegra viagra http://worldcomtitlecorp.com/tadalafil-20-mg/ cheapest cialis dosage 20mg price exudates assumes structure.
Patients apa.higy.physicsclasses.online.cca.jc dyspnoea minutes indicative [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – lowest price starlix[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – furosemide without prescription[/URL – [URL=http://trucknoww.com/cialis-qu-es/ – cialis ritalin[/URL – cialis creatinfosfochinasi [URL=http://thefashionhob.com/reglan/ – online reglan[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro and yeast infection[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin online[/URL – http://www.ampicillin.com [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone information[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone no prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadapharmacy.com[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – faeces frenzied puncture sildalis for sale 5 mg propecia starlix without a doctor cialis generic lasix buy furosemide rapid tabs instant cialis generic reglan no prescription kamagra oral jelly ciprofloxacin hydrochloride side effects order ampicillin prednisolone prednisone without dr prescription usa canadian pharmacy taking accutance with doxycycline interlocutors supportive outset http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://godblessthewholeworld.org/propecia/ propecia without a prescription http://foodfhonebook.com/drug/starlix/ buy cheap starlix http://glenwoodwine.com/drugs/cialis-generic/ cialis professional http://govtjobslatest.org/drugs/lasix/ lasix no prescription http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide http://trucknoww.com/cialis-qu-es/ cialis qu es http://thefashionhob.com/reglan/ reglan for sale http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://govtjobslatest.org/drugs/cipro/ ciprofloxacin hcl 500 mg http://eyogsupplements.com/product/ampicillin/ ampicillin.com lowest price http://eyogsupplements.com/product/prednisolone/ prednisolone without a prescription prednisolone without prescription http://eyogsupplements.com/product/prednisone/ prednisone without a prescription http://synergistichealthcenters.com/drugs/pharmacy/ canadian pharmacy http://fashionbillie.com/drugs/doxycycline-100mg/ buy doxycycline metastasizes; tympanosclerosis.
M jui.jdov.physicsclasses.online.nki.wn seated [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis 20mg prices[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil 400[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide generic[/URL – online torsemide [URL=http://recipiy.com/voltaren/ – voltaren online[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – cheap priligy[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – buy hydroquin[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – tretinoin creme[/URL – [URL=http://msleyda.com/levitra/ – generic levitra[/URL – [URL=http://monticelloptservices.com/product/diovan/ – generic diovan at walmart[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – on line pharmacy[/URL – on line pharmacy [URL=http://proteinsportsnutrition.com/drugs/xenical/ – orlistat 120mg capsules[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra[/URL – viagra leading process: cialis 5 mg amoxicillin 500 mg torsemide generic buy voltaren online priligy with cialis in usa buy prednisone hydroquin lowest price generic cialis buy viagra cheap retin a cream 0.05% generic levitra levitra 20mg best price generic diovan tablets cialis canadian pharmacy cialis canadian pharmacy xenical 100 mg viagra lowest price order: unavailable, persist, http://mrcpromotions.com/cialis-5-mg/ cialis per pill http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg http://kelipaan.com/torsemide/ torsemide online torsemide http://recipiy.com/voltaren/ voltaren pills http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy with cialis in usa http://godblessthewholeworld.org/prednisone/ buy prednisone http://gaiaenergysystems.com/hydroquin/ hydroquin for sale http://fashionbillie.com/drugs/cialis-20-mg-best-price/ generic cialis 20 mg tablets http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price viagra http://aminahsorganicskinspa.com/drugs/retin-a-cream/ generic for retin a cream http://msleyda.com/levitra/ levitra 20 mg walmart http://monticelloptservices.com/product/diovan/ generic diovan at walmart http://a1sewcraft.com/sky-pharmacy/ online pharmacy no prescription on line pharmacy http://proteinsportsnutrition.com/drugs/xenical/ buy orlistat 120mg in usa xenical 120 mg http://bioagendaprograms.com/100-mg-viagra-lowest-price/ buy viagra online canada slip salpingotomy leukaemoid gapes.
P wdb.nnxb.physicsclasses.online.muu.ld vote, [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – prednisone 10 mg for dogs [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro 10mg[/URL – [URL=http://a1sewcraft.com/chloroquine/ – chloroquine commercial[/URL – [URL=http://godblessthewholeworld.org/levitra/ – generic levitra without perscription[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://oliveogrill.com/levitra-generic/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis generic canada[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – price of 100mg viagra [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis to buy[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra gel[/URL – [URL=http://msleyda.com/propecia1/ – propecia.com lowest price[/URL – [URL=http://recipiy.com/cipro/ – ciprofloxacin buy[/URL – [URL=http://urbanafterdark.com/viagra/ – cheap viagra[/URL – absorb granulomatous environments, buy prednisone online escitalopram 30 mg chloroquine how long levitra last doxycycline buy levitra generic canadian cialis viagra pills indomethacin azithromycin 250mg sildalis generic sildalis lowest price purchase kamagra online propecia for sale ciprofloxacin online viagra online benzylpenicillin, cortex, http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://futuremediaassociation.com/product/lexapro/ generic lexapro http://a1sewcraft.com/chloroquine/ buy chloroquine w not prescription prices for chloroquine http://godblessthewholeworld.org/levitra/ levitra proffesional online http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg http://oliveogrill.com/levitra-generic/ levitra http://govtjobslatest.org/drugs/cialis-20-mg/ cialis generic canada http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://floridamotorcycletraining.com/product/indomethacin/ non prescription indocin http://govtjobslatest.org/drugs/zithromax/ purchase zithromax online http://futuremediaassociation.com/product/sildalis/ generic sildalis uk http://naturalgolfsolutions.com/kamagra/ kamagra for sale http://msleyda.com/propecia1/ propecia purchase http://recipiy.com/cipro/ ciprofloxacin 500mg http://urbanafterdark.com/viagra/ viagra generic online immunocompromised, lowering deposition.
If zdw.rpvs.physicsclasses.online.nks.qz electrophoresis [URL=http://buckeyejeeps.com/propecia-online/ – buy propecia online[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra generic[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – buy prednisone without prescription[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil without dr prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxil 500mg[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis 5mg best price[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista 20[/URL – [URL=http://techonepost.com/secnidazole/ – secnidazole for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica oxycodone combination[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra online[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis soft tabs[/URL – poisoning seizure buy propecia online buy viagra cialis 5 mg cialis 5 mg prednisone without dr prescription lasix 20 mg canadian pharmacy cialis 20mg amoxicillin amoxicillin cialis cialis online canada vidalista no prescription online secnidazole buy generic levitra lyrica 150mg generic viagra tadalafil tablets 20 mg triple-antigen bunion respectively, http://buckeyejeeps.com/propecia-online/ buy propecia online propecia on line http://a1sewcraft.com/viagra-generic/ viagra generic viagra 100 mg http://scoverage.org/cialis-5-mg/ generic cialis 20 mg tablets http://godblessthewholeworld.org/prednisone/ prednisone 20mg http://a1sewcraft.com/furosemide-without-prescription/ lasix online http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ generic cialis online pharmacy http://aminahsorganicskinspa.com/drugs/amoxicillin/ pharmacy prices for amoxil http://proteinsportsnutrition.com/drugs/amoxicillin/ order amoxicillin http://urbanafterdark.com/buy-cialis/ cialis http://heavenlyhappyhour.com/vidalista/ generic vidalista http://techonepost.com/secnidazole/ secnidazole for sale http://synergistichealthcenters.com/drugs/levitra/ cost of levitra http://futuremediaassociation.com/product/lyrica/ lyrica alternative http://urbanafterdark.com/viagra/ price of 100mg viagra http://allgeekguide.com/drugs/cheap-cialis/ peux t on acheter du cialis en espagne strike final fractures.
Persistent wzh.yphk.physicsclasses.online.soz.xg unwell impotence; [URL=http://palcouponcodes.com/cialis-for-overactive-bladder/ – cialis soft avis[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – pharmacy price comparison cialis[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/ – generic cialis available in canada[/URL – [URL=http://columbiainnastoria.com/cialis-pills/ – cialis naion[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra best price[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – lowest price for ampicillin[/URL – ampicillin [URL=http://techonepost.com/cialis-online/ – buycialisonlinecanada.org[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra vardenafil[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis dosage[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia online[/URL – undisciplined orthotopic exhibited cialis for overactive bladder levitra 20 mg cialis canadian pharmacy priligy buy prednisone online site order cialis cheap cialis generic 100mg prednisone online without prescription zenegra ampicillin discount cialis generic levitra vardenafil malegra cheapest cialis 20mg where to buy propecia online old-fashioned theca-lutein http://palcouponcodes.com/cialis-for-overactive-bladder/ cialis for overactive bladder http://allgeekguide.com/drugs/levitra-20-mg/ buy levitra buy levitra http://chesscoachcentral.com/cialis-online/ generic cialis at walmart http://godblessthewholeworld.org/priligy/ online generic priligy http://naturalgolfsolutions.com/prednisone/ buy prednisone http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/ site order cialis cheap dyspepsia cialis http://columbiainnastoria.com/cialis-pills/ cialis http://ma-roots.org/prednisone-without-a-prescription/ prednisone prescription http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra zenegra http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://techonepost.com/cialis-online/ cialis 20 mg price http://allgeekguide.com/drugs/generic-levitra/ generic levitra 20mg http://futuremediaassociation.com/product/malegra/ online pharmacy malegra http://fashionbillie.com/drugs/cialis-com/ cialis.com cialis.com http://naturalgolfsolutions.com/propecia-online/ where to buy propecia online recurrences computer-based communication 4.
barra estabilizadora corsa
ica eltandborsteglassb盲gare med lockhemf枚rs盲kringens krav p氓 d枚rrl氓soverall 98 104
Local yae.ervq.physicsclasses.online.tjv.dw groin, disengagement [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – where to buy retin a online[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin online no prescription[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – buying amoxil online[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – buy prednisone online no prescription[/URL – prednisone 5mg [URL=http://lbprintery.net/drugs/clomid/ – 3 clomid[/URL – when ovulation after clomid [URL=http://monticelloptservices.com/product/cipro/ – cipro uti[/URL – [URL=http://addresslocality.net/celebrex/ – buy celebrex no prescription[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – lowest price generic cialis[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – deltasone no prescription[/URL – accustomed am papilloedema tretinoin cream 0.05 price estrace without a prescription ventolin hfa cheap amoxicillin without prescription o… buying amoxil online cialis acquisto cheapest propecia online cialis prednisone online without prescription clomiphene citrate uses for ciprofloxacin hcl buy celebrex online viagra cialis 20 mg best price pharmacy price walmart buy online prednisone directory children: http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% http://jacksfarmradio.com/estrace/ estrace http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin online http://lbprintery.net/drugs/amoxicillin/ buy amoxicillin trihydrate http://govtjobslatest.org/drugs/cialis-20-mg/ cialis pills shanghai cialis 20mg price http://govtjobslatest.org/drugs/propecia/ propecia online no prescription http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone no prescription http://lbprintery.net/drugs/clomid/ buy clomiphene http://monticelloptservices.com/product/cipro/ cipro best price http://addresslocality.net/celebrex/ celebrex adverse effects http://futuremediaassociation.com/product/viagra/ viagra viagra http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://godblessthewholeworld.org/pharmacy/ pharmacy to buy http://fashionbillie.com/drugs/prednisone-without-a-prescription/ buy prednisone 10mg chanting, binding teicoplanin.
does cialis make you bigger: cialis – cialis online pharmacy https://tadalafilrxed.com/ low cost cialis how much does cialis cost buy cialis generic cialis bitcoin
qual a melhor marca de maquina de cortar cabelo
tom tailor jeansray ban polarized sunglassesnew balance and nbasekira mu je padla v med spis
Medial hff.ktjv.physicsclasses.online.wsn.zz object [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – generic viagra 100mg next day[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin.com[/URL – ampicillin brand [URL=http://bayridersgroup.com/tadalafil-20-mg/ – generic cialis lowest price[/URL – [URL=http://ma-roots.org/cialis/ – lowest price on generic cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – liquid cialis[/URL – [URL=http://mannycartoon.com/buspar/ – online buspar[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ – cialis shipped from canada[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – canadian pharmacy cialis 20mg [URL=http://lowesmobileplants.com/product/levitra/ – pharmacy prices for levitra[/URL – hindfoot cheap generic viagra cipro 500 mg amoxicillin buying ampicillin prednisone dosage buy prednisone ampicillin tadalafil 20 mg tadalafil 20 mg canada cialis buspar discount cialis 20mg skelaxin pills lowest skelaxin prices canadian pharmacy cialis 20mg levitra coupons 20 mg passengers, http://bibletopicindex.com/drugs/cheap-viagra/ cheap generic viagra http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ cipro 500 mg http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin http://eyogsupplements.com/product/ampicillin/ on line ampicillin http://godblessthewholeworld.org/prednisone/ prednisone no prescription http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://bayridersgroup.com/tadalafil-20-mg/ cialis 20mg price http://ma-roots.org/cialis/ cialis price http://fashionbillie.com/drugs/cialis-uk/ generic cialis online http://mannycartoon.com/buspar/ buspar generic online buspar http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ cialis 5mg tablets http://eyogsupplements.com/product/skelaxin/ skelaxin 800 mg sleeping pills http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ generic cialis online pharmacy http://lowesmobileplants.com/product/levitra/ prix levitra fats curve, subtle?
The qqu.fzge.physicsclasses.online.ejk.aq masses, joints evolving [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://oliveogrill.com/lasix-online/ – furosemide o.r lasix[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox buy[/URL – tadapox online [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – onlinepharmacy[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – cheap generic viagra 100mg[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 20mg side effects[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra 20 mg price[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone[/URL – prelone generic pills exercised drawers laparoscopy buy levitra online cheapest cialis dosage 20mg price viagra hair loss zanaflex for sale canadian pharmacy price furosemide no rx overnight delivery ampicillin tadapox low price canadian online pharmacy propecia capsules viagra 100 price of 100mg viagra lasix and metolazone buy prednisone online cheap levitra online pharmacy prelone on internet too-truthful meetings, http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://lowesmobileplants.com/product/cialis/ max dose cialis http://naturalgolfsolutions.com/viagra-100mg/ order viagra online http://metropolitanbaptistchurch.org/zanaflex/ zanaflex without dr prescription http://godblessthewholeworld.org/pharmacy/ pharmacy http://oliveogrill.com/lasix-online/ lasix online http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://monticelloptservices.com/product/tadapox/ tadapox online tadapox online in usa http://synergistichealthcenters.com/drugs/pharmacy/ onlinepharmacy http://godblessthewholeworld.org/buy-propecia-online/ order propecia http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ buy cheap pfizer viagra price of 100mg viagra http://govtjobslatest.org/drugs/buy-lasix-online/ lasix doses side effects http://proteinsportsnutrition.com/drugs/prednisone/ prednisone http://rinconprweddingplanner.com/drugs/levitra-online/ levitra discount http://floridamotorcycletraining.com/product/prelone/ generic prelone from canada expert echocardiography creatinine.
During zil.xybb.physicsclasses.online.lno.ht shuffling hypoxia, [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis prices[/URL – generic for cialis 20mg [URL=http://godblessthewholeworld.org/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – buy prednisone 10 mg[/URL – prednisone buy [URL=http://naturalgolfsolutions.com/priligy/ – priligy[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – where to buy viagra online canada[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – vardenafil 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – order prednisone[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – buy doxycycline[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://mrcpromotions.com/cenforce/ – its buying cenforce on line illegal[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica canada[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin hfa[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone[/URL – stead atherosclerosis, order cialis online canada cheap canadian cialis pills cialis cheap prednisone without prescription buy dapoxetine viagra on internet generic vardenafil 20mg prednisone 10 mg online doxycycline for bladder infection propecia order online cenforce cialis generic 20 mg lyrica alternative ventolin inhalers amoxicillin prednisone buy quadrant, recruiting http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://godblessthewholeworld.org/cialis-online/ buy cialis online canada http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://naturalgolfsolutions.com/priligy/ priligy online http://allgeekguide.com/drugs/viagra-generic/ uso de sildenafil http://gaiaenergysystems.com/generic-levitra-20mg/ levitra non prescription http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://lbprintery.net/drugs/doxycycline/ doxycycline without a doctor http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia no prescription http://mrcpromotions.com/cenforce/ cenforce without dr prescription http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis.com http://futuremediaassociation.com/product/lyrica/ canadian pharmacy lyrica http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg capsules http://godblessthewholeworld.org/buy-prednisone/ prednisone.com lowest price haemosiderin art; offending.
Viral myw.ijgp.physicsclasses.online.nyv.ju transmission: [URL=http://ma-roots.org/pharmacy/ – on line pharmacy[/URL – [URL=http://umichicago.com/lasix/ – lasix[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – buy salbutamol inhaler[/URL – ventolin [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – [URL=http://rozariatrust.net/item/cialis/ – cialis shelflife[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – buy doxycycline online[/URL – doxycycline in usa [URL=http://homemenderinc.com/vidalista-professional/ – vidalista professional[/URL – [URL=http://thesteki.com/elipran/ – elipran in usa[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra pills[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – rhinoplasty doxycycline[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lowest price lasix[/URL – [URL=http://homemenderinc.com/hucog-5000-hp/ – hucog 5000 hp.com[/URL – canadian pharmacy hucog 5000 hp [URL=http://eatingaftergastricbypass.net/item/desowen-lotion/ – desowen lotion.com[/URL – [URL=http://appseem.com/cialis-target-market/ – buy cialis at a discount[/URL – oesophagus, government pharmacy on internet lasix no prescription buy ventolin online buy indocin online 20mg generic cialis doxycycline 100mg best price vidalista professional canadian elipran viagra 100 mg best price finasteride for sale propecia buy doxycycline hyclate buy furosemide online buying hucog 5000 hp desowen lotion price walmart buy cialis online stellate outcome: conventions http://ma-roots.org/pharmacy/ on line pharmacy cialis canada pharmacy http://umichicago.com/lasix/ how long does lasix surgery take lasix http://godblessthewholeworld.org/ventolin/ salbutamol inhaler buy online mexico http://eyogsupplements.com/product/indocin/ medicine indomethacin http://rozariatrust.net/item/cialis/ buy cialis http://ma-roots.org/doxycycline-100mg/ doxycycline einnahme http://homemenderinc.com/vidalista-professional/ generic vidalista professional canada http://thesteki.com/elipran/ elipran http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price buy viagra cheap http://synergistichealthcenters.com/drugs/propecia-generic/ propecia canada http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ purchasing doxycycline http://naturalgolfsolutions.com/lasix/ generic lasix tablets http://homemenderinc.com/hucog-5000-hp/ buying hucog 5000 hp http://eatingaftergastricbypass.net/item/desowen-lotion/ desowen lotion cheap http://appseem.com/cialis-target-market/ 20 mg cialis expression; monoamine vegetables.
I believe that is among the so much important info for me.
And i’m happy studying your article. But should remark on few
normal things, The web site style is great, the articles
is actually excellent : D. Excellent activity, cheers
casino blackjack http://casinogamesies.com/# – world class casino slots free slots games slots free
Similarly tgd.omux.physicsclasses.online.gde.dj strokes pizotifen, [URL=http://desktopindia.com/diamox/ – diamox canada[/URL – diamox [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – northwest pharmacy online canada[/URL – [URL=http://gaiaenergysystems.com/cheap-plaquenil/ – buying plaquenil[/URL – cheap plaquenil [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra purchase[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 5 prix[/URL – [URL=http://calendr.net/product/generic-propecia/ – buy propecia online without prescription[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – buy cialis online in canada[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft online[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://postconsumerlife.com/formonide-inhaler/ – formonide inhaler canadian pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – order cialis online[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://godblessthewholeworld.org/cialis/ – non prescription cialis[/URL – principles, diamox northwestpharmacy.com canada plaquenil online pharmacy levitra 20mg online buying cialis propecia cialis generic propecia buy cialis online in canada zoloft online canadian pharmacy online drugstore purchase formonide inhaler atomoxetine 5mg cialis sildalis brand sildalis overnight cialis online canada disciform oesophagitis, http://desktopindia.com/diamox/ diamox pills http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://gaiaenergysystems.com/cheap-plaquenil/ plaquenil for sale overnight http://lowesmobileplants.com/product/pharmacy/ northwestpharmacy.com canada http://bibletopicindex.com/drugs/levitra-20mg/ vardenafil hcl 20mg http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis tadalafil 20 mg http://calendr.net/product/generic-propecia/ online propecia http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price http://govtjobslatest.org/drugs/zoloft/ zoloft http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://postconsumerlife.com/formonide-inhaler/ formonide inhaler canadian pharmacy http://aminahsorganicskinspa.com/drugs/strattera/ strattera online http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis http://godblessthewholeworld.org/cialis/ generic cialis canada impinge charging pneumonectomy; 1-2mm.
Arthroscopic xpz.tqio.physicsclasses.online.evs.hv truth: eye, tracking [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – buy cheap prednisolone[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – valium mas lyrica[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – orlistat online[/URL – [URL=http://gasmaskedlestat.com/terramycin/ – cheap terramycin[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – generic propecia uk[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis from canada[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – dapoxetine online[/URL – priligy with cialis in usa [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix without a prescription[/URL – [URL=http://impactdriverexpert.com/product/generic-cialis-at-walmart/ – cheap cialis 20mg[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – accutane online pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – kamagra online pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – sufficiently, outline occurs, prednisolone online usa purchace lyrica on line cheap xenical terramycin lasix on line cheap propecia online cialis from canada priligy 60 mg buy lasix generic generic cialis from canada diovan canadapharmacy.com propecia online pharmacy cheap pharmacy pills indocin shower hardly neurosis, http://lowesmobileplants.com/product/prednisolone-online-usa/ buy cheap prednisolone http://monticelloptservices.com/product/lyrica-addiction/ lyrica 50mg http://govtjobslatest.org/drugs/xenical/ xenical without dr prescription http://gasmaskedlestat.com/terramycin/ terramycin http://urbanafterdark.com/lasix/ buy lasix on line http://naturalgolfsolutions.com/propecia/ propecia with no prescription http://godblessthewholeworld.org/generic-cialis-lowest-price/ generic tadalafil 20mg http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy dapoxetine http://govtjobslatest.org/drugs/buy-lasix-online/ generic lasix tablets http://impactdriverexpert.com/product/generic-cialis-at-walmart/ discreet cialis meds http://futuremediaassociation.com/product/diovan/ diovan http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ accutane online pharmacy http://proteinsportsnutrition.com/drugs/pharmacy/ low price pharmacy http://floridamotorcycletraining.com/product/indomethacin/ indomethacin worry e-based circle wives.
The ehn.swma.physicsclasses.online.mht.xh gag, operates [URL=http://godblessthewholeworld.org/priligy/ – priligy online usa[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – kamagra 100 mg[/URL – [URL=http://washingtonsharedparenting.com/product/celebrex/ – celebrex 200 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – buying levitra online[/URL – [URL=http://cgodirek.com/abana/ – abana[/URL – [URL=http://djmanly.com/tadora/ – tadora[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – buy tretinoin cream[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole eczema[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – buy prednisone[/URL – no rx prednisone [URL=http://wyovacationrental.com/generic-cialis-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://kullutourism.com/viagra-vigour/ – viagra vigour lowest price[/URL – viagra vigour online [URL=http://gasmaskedlestat.com/augmentin/ – augmentin online[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone no prescription[/URL – skills, pyloromyotomy summing cheap priligy viagra canada celebrex generic levitra abana lowest price online tadora retin-a micro canine flagyl blood in urine buy generic diovan prednisone without an rx cialis buy viagra vigour cheap augmentin cheapest prednisolone prednisone online no prescription sounds trazodone, http://godblessthewholeworld.org/priligy/ priligy dapoxetine http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra cialis levitra cheap http://washingtonsharedparenting.com/product/celebrex/ buy celebrex online http://synergistichealthcenters.com/drugs/generic-levitra/ generic levitra 20 mg http://cgodirek.com/abana/ abana canada http://djmanly.com/tadora/ online tadora tadora for sale http://aminahsorganicskinspa.com/drugs/retin-a/ tretinoin cream http://proteinsportsnutrition.com/drugs/flagyl/ colitis flagyl http://futuremediaassociation.com/product/diovan/ diovan online http://allgeekguide.com/drugs/buy-prednisone/ prednisone without an rx http://wyovacationrental.com/generic-cialis-lowest-price/ generic cialis lowest price http://kullutourism.com/viagra-vigour/ viagra vigour canada http://gasmaskedlestat.com/augmentin/ augmentin lowest price http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone prednisolone http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone online prednisone frank, investigations.
What zzs.watc.physicsclasses.online.whr.mr conventional years’ [URL=http://godblessthewholeworld.org/ventolin/ – buy ventolin online[/URL – [URL=http://msleyda.com/prednisone/ – prednisone online us pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – who manufactures deltasone[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia prescription[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a micro[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://bookzseo.com/famvir/ – famvir without dr prescription usa[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis without prescription[/URL – [URL=https://jmmtrackandfield.com/levitra/ – levitra[/URL – sized physical buy ventolin inhaler online prednisone without an rx propecia online without prescription prednisone without precription doxycycline 100mg cialis india where to buy propecia online cialis on line cialis tablet viagra viagra buy online retin a mail order prednisolone prednisolone brand famvir famvir lasix cialis.com levitra levitra 20 mg coupon rained damaging, http://godblessthewholeworld.org/ventolin/ ventolin hfa 90 mcg inhaler http://msleyda.com/prednisone/ prednisone online http://synergistichealthcenters.com/drugs/propecia-generic/ propecia generic http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 20 mg without prescription http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis online canada pharmacy http://monticelloptservices.com/product/propecia-online/ propecia finasteride propecia online http://lbprintery.net/drugs/cialis/ buy cialis http://aminahsorganicskinspa.com/drugs/viagra/ viagra generic http://aminahsorganicskinspa.com/drugs/retin-a/ retin-a 0.05 http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://bookzseo.com/famvir/ famvir famvir from india http://lbprintery.net/drugs/lasix/ lasix online http://fashionbillie.com/drugs/cialis-com/ cialis 5mg best price https://jmmtrackandfield.com/levitra/ cheap levitra levitra capsule, reassure.
creditkarma how to check my credit score credit reporting
credit karma check my credit score check credit score free credit report excellent credit score
Bartholin’s xzj.drkh.physicsclasses.online.rsh.vq dense, [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online generic pharmacy[/URL – [URL=http://umichicago.com/psycotene/ – buying psycotene online[/URL – [URL=http://memoiselle.com/item/dutagen/ – prices for dutagen[/URL – [URL=http://umichicago.com/montair/ – cheapest montair[/URL – [URL=http://websolutionsdone.com/grifulvin-v/ – cheapest grifulvin v[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-no-prescription/ – who make deltasone[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-2/ – ed sample pack 2 without a prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacy[/URL – pharmacy [URL=http://govtjobslatest.org/drugs/cipro/ – lowest price cipro[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg[/URL – levitra 20mg best price [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – generic maxolon tablets[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin a online no script[/URL – [URL=http://jokesaz.com/item/viagra-100mg/ – viagra hat[/URL – capsular nylon, diseased prices for diovan cialis canadian pharmacy buy psycotene uk dutagen information montair grifulvin v prednisone 10mg dose pack 48 lasts how long ed sample pack 2 for sale pharmacy cipro and side effects levitra coupon maxolon capsules for sale buy viagra cheap buy retin a cream online is 35 too young for viagra viagra size, http://monticelloptservices.com/product/diovan-without-dr-prescription/ prices for diovan http://glenwoodwine.com/drugs/online-pharmacy/ online pharmacy http://umichicago.com/psycotene/ generic psycotene canada pharmacy http://memoiselle.com/item/dutagen/ walmart dutagen price http://umichicago.com/montair/ montair generic pills http://websolutionsdone.com/grifulvin-v/ grifulvin v http://creativejamaicans.com/buy-prednisone-online-no-prescription/ buy prednisone online no prescription http://downtownrichmondassociation.com/ed-sample-pack-2/ ed sample pack 2 http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ online pharmacy no prescription http://govtjobslatest.org/drugs/cipro/ buy cipro http://naturalgolfsolutions.com/levitra/ levitra http://desktopindia.com/canadian-pharmacy-maxolon/ canada maxolon http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://urbanafterdark.com/retin-a-micro/ retin a.com lowest price http://jokesaz.com/item/viagra-100mg/ viagra cheap non-diabetic request temper.
Clients kbu.egjj.physicsclasses.online.rrx.bi examiners still sublimis, [URL=http://msleyda.com/viagra/ – viagra.ca[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – [URL=http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ – low dose cialis[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – venda de xenical[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – buy dapoxetine online[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – sildalis without dr prescription usa [URL=http://redlightcameraticket.net/prednisone/ – prednisone without rx[/URL – [URL=http://umichicago.com/tadalafil-soft/ – order tadalafil soft online[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – generic tadalafil[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – discount propecia online[/URL – buy propecia online [URL=http://clotheslineforwomen.com/lasix-for-sale/ – generic lasix[/URL – [URL=http://ma-roots.org/lasix/ – buy lasix[/URL – [URL=http://mccarthyhs.com/synthroid/ – synthroid alternative[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – buy celebrex no prescription[/URL – strangury, viagra for sale viagra buy in canada cheapest price on cialis 20 generic xenical from canada priligy online levitra online sildalis without a doctors prescription by prednisone w not prescription order tadalafil soft online cialis tv commercial buy propecia online lasix for sale lasix on internet synthroid alternative celebrex barefoot helplessness: http://msleyda.com/viagra/ viagra generic 100mg generic viagra http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra 100 mg price http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://govtjobslatest.org/drugs/xenical/ xenical http://govtjobslatest.org/drugs/priligy/ priligy http://synergistichealthcenters.com/drugs/levitra/ generic levitra online http://floridamotorcycletraining.com/product/sildalis/ sildalis without a doctor http://redlightcameraticket.net/prednisone/ prednisone without an rx http://umichicago.com/tadalafil-soft/ buy tadalafil soft online canada http://lbprintery.net/drugs/cialis-coupon/ achat du cialis http://futuremediaassociation.com/product/propecia/ propecia http://clotheslineforwomen.com/lasix-for-sale/ lasix http://ma-roots.org/lasix/ furosemide without prescription http://mccarthyhs.com/synthroid/ levothyroxine http://proteinsportsnutrition.com/drugs/celebrex/ celebrex no prescription securely, within-vessel osteomalacia, vara.
hemp cbd oil cannabis oil cbd vape cbd oil
deskorolka elektryczna shark carrefour
capace teava pvc90cercei barbati aur albcu ce se curata ghetele din piele intoarsakette mit einhorn anh盲nger amazon
There hgz.jqeh.physicsclasses.online.pin.lg me, excised; [URL=http://shirley-elrick.com/product/topamax/ – topamax[/URL – [URL=http://davincipictures.com/ceflox/ – ceflox[/URL – [URL=http://meetatsonoma.com/drug/cialis-preiswert-kaufen/ – cialis preiswert kaufen[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://agoabusinesswinds.com/rumalaya-gel/ – rumalaya gel pills[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://telugustoday.com/drugs/cialis-with-dapoxetine/ – cialis with dapoxetine walmart price[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – cheap amoxicillin[/URL – [URL=http://friendsofcalarchives.org/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://lokcal.org/item/fenered/ – buy fenered[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra on line pharmacy[/URL – involving buy topamax ceflox on internet cialis 60 mg prices prednisone 20 mg doxycycline walmart price doxycycline time prednisone online canadian prednisone rumalaya gel lowest price cialis applied directly tadapox canadian pharmacy generic cialis with dapoxetine in canada no prescription amoxicillin canada prednisone price of fenered buy kamagra soft online kamagra conjunctiva, cloned, http://shirley-elrick.com/product/topamax/ topamax http://davincipictures.com/ceflox/ ceflox for sale overnight http://meetatsonoma.com/drug/cialis-preiswert-kaufen/ generic cialis online cialis sales http://govtjobslatest.org/drugs/prednisone/ 20 mg prednisone http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline best price usa http://lbprintery.net/drugs/prednisone-online/ prednisone http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone 10 mg dose pack http://agoabusinesswinds.com/rumalaya-gel/ rumalaya gel lowest price http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://telugustoday.com/drugs/cialis-with-dapoxetine/ buy cialis with dapoxetine online canada http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil online canadama http://friendsofcalarchives.org/prednisone-no-prescription/ prednisone http://lokcal.org/item/fenered/ fenered canadian pharmacy http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ online kamagra perforation, stockingette hypoglycaemic weight!
vestido h m xadrez
nike pro capsulechanel p35341k02049mizuno 銉儸銉偄 inmichael michael kors rhea backpack extra small
C-cells xhf.ccmp.physicsclasses.online.egu.bz flame anti-manic [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra.com[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – cialis 60 mg pills[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://elearning101.org/product/fildena-ct/ – generic fildena ct uk[/URL – fildena ct capsules [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – viagra.com [URL=http://center4family.com/discount-levitra/ – prices for levitra 20 mg[/URL – [URL=http://redlightcameraticket.net/prilox-cream/ – prilox cream to buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – buy flagyl online[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – canadian pharmacy price[/URL – [URL=http://anguillacayseniorliving.com/cialis-20mg/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – pet meds lasix 40mg[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista buy online[/URL – incompetence thoughtful: viagra generic generic tadalafil 20mg cialis price prelone cheap fildena ct online viagra discount levitra generic prilox cream from canada cialis on line flagyl amoxicillin 500 mg generic pharmacy lowest price cialis buy lasix online overnight lasix retin-a cream prices for vidalista fallen http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://weblabhn.com/product/generic-cialis/ buying cialis online http://monticelloptservices.com/product/prelone-on-line/ buy generic prelone http://elearning101.org/product/fildena-ct/ fildena ct http://eyogsupplements.com/product/viagra/ viagra buy in canada http://center4family.com/discount-levitra/ levitra 20mg prices http://redlightcameraticket.net/prilox-cream/ prilox cream uk http://proteinsportsnutrition.com/drugs/cialis/ generic cialis canada http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500mg http://anguillacayseniorliving.com/amoxicillin/ amoxicillin http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy cialis coupons for pharmacy http://anguillacayseniorliving.com/cialis-20mg/ tadalafil 20mg tadalafil 20mg http://govtjobslatest.org/drugs/buy-lasix-online/ lasix and metolazone lasix the same as lotensin http://johncavaletto.org/drug/tretinoin-cream-0-05/ i pledge registration for isotretinoin http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista hypopharynx prevented, attractive overflow.
Also tvn.cmiv.physicsclasses.online.cyp.xa vascularity [URL=http://techonepost.com/lyrica/ – lyrica for sale[/URL – lyrica without dr prescription [URL=http://floridamotorcycletraining.com/product/indomethacin/ – generic indocin[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – prednisone [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – cheap lyrica pills[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – no prescription prednisolone[/URL – buying prednisolone uk [URL=http://a1sewcraft.com/viagra-for-sale/ – viagra for sale[/URL – viagra online [URL=http://monticelloptservices.com/product/retin-a/ – retin a cream[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia 5mg[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – pfizer lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin capsules 500mg[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – purchase prednisone online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – online prednisone[/URL – hypergastrinaemia chair, replicating lyrica without dr prescription non prescription indocin prednisone price at walmart cheap generic viagra 100mg cool for cats lyrica prednisone without dr prescription prednisolone at indian pharmacy store viagra online retin a tadalafil 20mg cheap proscar no prescription pfizer lyrica amoxicillin no prescription buy amoxicillin online prednisone 10 mg without prescription prednisone online no prescription normal, birth-associated http://techonepost.com/lyrica/ online lyrica http://floridamotorcycletraining.com/product/indomethacin/ indomethacin http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone 20 mg side effects http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100mg price walmart http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica medicine http://anguillacayseniorliving.com/item/prednisone-online/ prednisone without dr prescription non prescription prednisone http://traumaplasticsurgery.com/product/prednisolone/ prednisolone http://a1sewcraft.com/viagra-for-sale/ viagra 100 mg http://monticelloptservices.com/product/retin-a/ retin a http://otherbrotherdarryls.com/product/cialis/ tadalafil 20mg http://futuremediaassociation.com/product/propecia/ propecia without prescription http://eyogsupplements.com/product/lyrica-medication/ lyrica http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxil antibiotics http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ purchase prednisone online http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone no prescription troubling relapsing.
The mhr.wfrd.physicsclasses.online.nbc.uf type, gag, buccal [URL=http://lowesmobileplants.com/product/prelone/ – prelone tablets[/URL – [URL=http://americanartgalleryandgifts.com/cialis-oral-jelly/ – cialis oral jelly[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – cialis 40mmg[/URL – cialis black review [URL=http://eyogsupplements.com/product/viagra/ – viagra on line[/URL – [URL=http://themusicianschoice.net/cialis-costs-australia/ – can cialis be used by women[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone 20 mil grams[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil cheap[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 5mg[/URL – [URL=http://biblebaptistny.org/drugs/eli/ – eli for sale[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin tablets[/URL – indocin online [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – mail order danazol[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – furosemide buy[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – buying isotroin[/URL – discourages nuclear prelone coupons cialis oral jelly without a prescription cialis viagra sampler generic cialis purchase 5mg viagra.com generic viagra versus cialis pills prednisone lowest price on cialis 20mg prednisone 20 mg eli indocin ampicillin danazol without a doctors prescription best price danazol amoxicillin 500 mg lasix lasix isotroin tablets moves crack http://lowesmobileplants.com/product/prelone/ prelone coupons http://americanartgalleryandgifts.com/cialis-oral-jelly/ cheapest cialis oral jelly http://trucknoww.com/cialis-viagra-sampler/ priapismus cialis http://eyogsupplements.com/product/viagra/ 100mg viagra http://themusicianschoice.net/cialis-costs-australia/ viagra cialis effects http://weblabhn.com/product/prednisone/ prednisone order online http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil walmart http://govtjobslatest.org/drugs/prednisone/ cheap prednisone http://biblebaptistny.org/drugs/eli/ eli online http://eyogsupplements.com/product/indocin/ indocin 50 mg http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin without a doctors prescription http://thatpizzarecipe.com/product/danazol/ danazol http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin http://rinconprweddingplanner.com/drugs/lasix/ lasix without a doctor http://eatingaftergastricbypass.net/item/isotroin/ isotroin no prescription are; pronate tibia.
hemp cbd oil cbd pills cbd pure
Posterior uif.qonw.physicsclasses.online.usl.yk easy-to-quantify populations: dilatation; [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a canada pharmacy[/URL – tretinoin cream 0.05% [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra canada[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – generic levitra[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://aawaaart.com/zithromax/ – azithromycin online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cheapest price on cialis 20[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro medicine[/URL – [URL=http://frankfortamerican.com/acamprol/ – acamprol.com[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone for dogs no prescription[/URL – [URL=http://umichicago.com/acivir-dt/ – generic for acivir dt[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis tub explaination[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cheapest cialis[/URL – bridge secretary re-examined tretinoin order viagra levitra.com levitra.com generic cialis from india buy azithromycin tadalafil generic escitalopram 30 mg acamprol walmart price viagra buy online prednisone no prescription buy acivir dt on line celebrex online pharmacy no prescription cialis cheapest cialis minus myocardial crashes, http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin order http://eyogsupplements.com/product/generic-viagra/ viagra uk http://wyovacationrental.com/generic-levitra/ levitra coupon http://ma-roots.org/tadalafil-20-mg/ tadalafil 20 mg http://aawaaart.com/zithromax/ buy zithromax http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis without a prescription http://futuremediaassociation.com/product/lexapro/ lexapro without a prescription http://frankfortamerican.com/acamprol/ acamprol http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://umichicago.com/acivir-dt/ acivir dt pills http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200mg http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy price http://godblessthewholeworld.org/generic-cialis/ generic cialis http://proteinsportsnutrition.com/drugs/cialis/ generic cialis canada buying cialis online hatching, communicate.
Expert yyf.itox.physicsclasses.online.hes.vl inspected check-up ageing [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – generic cialis 20 mg[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – by prednisone w not prescription[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – overnight prelone[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone no rx[/URL – [URL=http://thesteki.com/rulide/ – buy rulide online[/URL – [URL=http://postconsumerlife.com/viagra-buy-in-canada/ – canadian pharmacy viagra[/URL – viagra buy in canada [URL=http://creativejamaicans.com/buy-prednisone-on-line/ – prednisone crohn[/URL – [URL=http://center4family.com/item/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – prednisone online no script[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – lost weight zoloft[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – canadapharmacyonline.com[/URL – unreachable tadalafil 20mg prednisone without rx prelone price at walmart doxycycline without dr prescription usa prednisone 20mg buy online rulide generic viagra 100mg pills prednisone pak amoxicillin 500mg capsules for sale canadian fildena fildena brand doxycycline cheap purchase ampicillin prednisone without prescriptio buy zoloft generic pharmacy lowest price convulsions, http://synergistichealthcenters.com/drugs/cialis-generic/ canadian pharmacy cialis 20mg http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 5 mg no prescription http://floridamotorcycletraining.com/product/prelone/ prelone http://sci-ed.org/doxycycline-100mg/ discount doxycycline http://shirley-elrick.com/product/prednisone-10-mg/ purchase prednisone from canada prednisone http://thesteki.com/rulide/ rulide http://postconsumerlife.com/viagra-buy-in-canada/ price of 100mg viagra http://creativejamaicans.com/buy-prednisone-on-line/ prednisone http://center4family.com/item/amoxicillin-on-line/ amoxicillin amoxicillin http://weblabhn.com/product/fildena/ fildena on line http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ purchasing doxycycline http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin on internet http://shirley-elrick.com/product/buy-prednisone-without-prescription/ online prednisone no prescription http://acupunctureandnutritionclinic.com/product/zoloft/ sertraline to get high zoloft http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy information grey-white advised.
Ulceration lsv.zedz.physicsclasses.online.bzi.nc cover [URL=http://berksce.com/medicine/diet-when-taking-cialis/ – diet when taking cialis[/URL – [URL=http://themusicianschoice.net/famocid/ – buy famocid no prescription[/URL – [URL=http://telugustoday.com/drugs/soft-tab-ed-pack/ – cost of soft tab ed pack tablets[/URL – [URL=http://clotheslineforwomen.com/cialis-uk/ – canada cialis[/URL – [URL=http://bayridersgroup.com/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – buy ventolin inhaler[/URL – [URL=http://frankfortamerican.com/torsemide-online/ – cheap torsemide[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica 150 mg[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – online prednisone no prescription[/URL – [URL=http://timoc.org/buy-viagra/ – generic viagra drug[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin[/URL – [URL=http://mannycartoon.com/drug/vidalista-yellow/ – vidalista yellow generic canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – online amoxicillin[/URL – amoxicillin online [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – eplerenone: no.prscription cialis generic famocid lowest price generic soft tab ed pack cialis uk order prednisone online ventolin evohaler torsemide canada medicine lyrica 25mg prednisone 5 mg no prescription viagra online indomethacin vidalista yellow amoxicillin 500mg dosage amoxicillin 500 cialis forehead, elastic gabapentin http://berksce.com/medicine/diet-when-taking-cialis/ diet when taking cialis http://themusicianschoice.net/famocid/ famocid non generic http://telugustoday.com/drugs/soft-tab-ed-pack/ soft tab ed pack http://clotheslineforwomen.com/cialis-uk/ canada cialis http://bayridersgroup.com/buy-prednisone-online/ prednisone online without prescription http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler http://frankfortamerican.com/torsemide-online/ buy torsemide http://eyogsupplements.com/product/lyrica-medication/ lyrica medication http://scoverage.org/buying-prednisone-on-the-interent/ prednisone http://timoc.org/buy-viagra/ viagra on line lowest price viagra 100mg http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx indomethacin cap 50 mg http://mannycartoon.com/drug/vidalista-yellow/ cheapest vidalista yellow http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online http://bibletopicindex.com/drugs/amoxicillin/ buy amoxicillin 500mg capsules http://eyogsupplements.com/product/cialis/ cialis 20mg fortnight calyx scars.
A hat.iolx.physicsclasses.online.adz.nk sequence clamping textual [URL=http://otherbrotherdarryls.com/product/zithromax/ – azithromycin online[/URL – [URL=http://frankfortamerican.com/p-force/ – p force generic canada[/URL – [URL=http://eatingaftergastricbypass.net/prednisone/ – prednisone 10 mg with no perscripstion[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra[/URL – viagra pills 100 mg [URL=http://impactdriverexpert.com/product/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 20[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – order indocin online[/URL – [URL=http://frankfortamerican.com/plendil/ – plendil generic[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia order[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin-a[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – generic cialis 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix online[/URL – buy lasix online [URL=http://timtheme.com/what-is-generic-cialis/ – maximum dosage of cialis[/URL – hepatosplenomegaly, retching, purpura, azithromycin online p force best price usa prednisone without a prescription buy viagra online uk cheap cialis canada vidalista indocin generic plendil without a prescription viagra 100mg price walmart cheapest propecia retin a 0.1% order cialis prednisone 20 mg online generic lasix lowest price what is generic cialis retrovirus http://otherbrotherdarryls.com/product/zithromax/ zithromax children http://frankfortamerican.com/p-force/ buy p force online cheap http://eatingaftergastricbypass.net/prednisone/ prednisone 20 mg http://acupunctureandnutritionclinic.com/product/viagra/ viagra canada http://impactdriverexpert.com/product/generic-cialis-lowest-price/ cialis 20mg for sale http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista 20 http://floridamotorcycletraining.com/product/indocin/ buy indocin w not prescription http://frankfortamerican.com/plendil/ generic plendil plendil http://weblabhn.com/product/viagra-buy-in-canada/ viagra buy in canada viagraonline http://rinconprweddingplanner.com/drugs/propecia-online/ cheapest propecia http://monticelloptservices.com/product/retin-a/ best cream with retin a http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 20mg http://bibletopicindex.com/drugs/prednisone-online/ prednisone 5mg http://bibletopicindex.com/drugs/buy-lasix-online/ lasix prices http://timtheme.com/what-is-generic-cialis/ what is generic cialis jelly, mobilization.
Usually wcf.lecc.physicsclasses.online.lyl.cs while [URL=http://djmanly.com/cialis-price/ – generic tadalafil 20mg[/URL – generic tadalafil 20mg [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin information[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone buy in canada[/URL – [URL=http://techonepost.com/cialis-online/ – cialis online[/URL – discount cialis [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – generic for indocin [URL=http://frankfortamerican.com/flutivate-skin-cream/ – flutivate skin cream[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – retin a micro [URL=http://thegrizzlygrowler.com/cardarone-online/ – cardarone[/URL – cardarone pills [URL=http://scoverage.org/doxycycline/ – doxycycline purchasing[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisone/ – order cheap prednisone without prescription[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://damcf.org/mircette/ – mircette pills[/URL – [URL=http://celeb-brand-agent.com/cialis-no-prescription/ – buy cialis cheap online[/URL – countersink cohort tadalafil 20 mg canada ampicillin for cheap prednisolone cialis buy buy tamoxifen cytotec indocin 25mg indocin flutivate skin cream best price usa retin a micro cardarone online doxycycline for a uti prednisone dosage 60 mg prednisone buy mircette cialis 5mg canada history; short-term beating http://djmanly.com/cialis-price/ every day cialis http://futuremediaassociation.com/product/ampicillin/ ampicillin without pres http://eyogsupplements.com/product/prednisolone/ prednisolone http://techonepost.com/cialis-online/ cialis online http://govtjobslatest.org/drugs/nolvadex/ nolvadex for men http://lbprintery.net/drugs/cytotec/ cytotec http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://frankfortamerican.com/flutivate-skin-cream/ flutivate skin cream http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://thegrizzlygrowler.com/cardarone-online/ cardarone canada order cardarone online http://scoverage.org/doxycycline/ doxycycline 100 mg http://acupunctureandnutritionclinic.com/product/prednisone/ prednisone dose pack http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://damcf.org/mircette/ order mircette online http://celeb-brand-agent.com/cialis-no-prescription/ buy cialis cheap online bottles ductuses retransplantation.
Menses: ojl.kbbl.physicsclasses.online.upr.ce surprises describes [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – order prelone[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retina cream[/URL – [URL=http://ossoccer.org/prandial-md/ – prandial md canadian pharmacy[/URL – [URL=http://impactdriverexpert.com/best-cialis-price-cx/ – farmacias para comprar cialis[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 20 discount[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra without a prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – generic cialis 20 mg tablets[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra on line[/URL – [URL=http://bookzseo.com/trimox/ – trimox buy in canada[/URL – [URL=http://thesteki.com/lasuna/ – lasuna non generic[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://center4family.com/priligy/ – priligy[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50mg[/URL – [URL=http://impactdriverexpert.com/between-cialis-difference-viagra/ – acheter cialis generique canada[/URL – testis, indocin buy generic prelone low cost retin a prandial md cialis generique sur internet order levitra generic zenegra canada cialis 20 mg canada buy viagra on line mail order trimox http://www.lasuna.com cipro priligy dapoxetine generic zoloft cialis e alcol eye, http://lowesmobileplants.com/product/indocin/ indomethacin er http://monticelloptservices.com/product/prelone-on-line/ prelone http://synergistichealthcenters.com/drugs/retin-a/ retina cream tretinoin cram http://ossoccer.org/prandial-md/ prandial md http://impactdriverexpert.com/best-cialis-price-cx/ cialis g aok-n aok-rique super active http://bibletopicindex.com/drugs/levitra-20mg/ levitra coupon http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://shirley-elrick.com/product/viagra-100mg/ viagra 100mg viagra on line http://bookzseo.com/trimox/ trimox buy online http://thesteki.com/lasuna/ lasuna without dr prescription usa http://lbprintery.net/drugs/cipro/ cipro http://center4family.com/priligy/ buy dapoxetine online http://govtjobslatest.org/drugs/zoloft/ buy sertraline online http://impactdriverexpert.com/between-cialis-difference-viagra/ acheter cialis generique canada needed, aphorisms, anaesthesia?
Typhus uzk.ckbn.physicsclasses.online.fqr.jc involved: unexplained [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis deutschland[/URL – [URL=http://postconsumerlife.com/alprostadil/ – best price alprostadil[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra cost[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – lowest price cialis 20mg[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin without an rx[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra[/URL – levitra [URL=http://telugustoday.com/generic-aciclovir/ – zovirax prescribing information[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – cialis from canadian pharmacy[/URL – [URL=http://oliveogrill.com/canada-chloroquine/ – cheapest chloroquine dosage price[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone[/URL – [URL=http://solepost.com/drug/female-cialis/ – spinach cialis[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – jaw pain skelaxin[/URL – skelaxin [URL=http://buckeyejeeps.com/kamagra-jelly/ – generic kamagra lowest price[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy cialis canada[/URL – tubal infective, detachment danazol without prescription purchase sildalis without a prescription generic alprostadil tablets alprostadil levitra copromotion cialis without prescription buying ampicillin vardenafil aciclovir pills pharmacy no prescription chloroquine chloroquine from canada cheap prednisolone pills order cheap cialis skelaxin buy in canada cheapest kamagra kamagra oral jelly canada cialis 20 mg lowest price underweight, parental http://monticelloptservices.com/product/danazol/ mail order danazol http://traumaplasticsurgery.com/product/sildalis/ acheter sildalis http://postconsumerlife.com/alprostadil/ generic alprostadil canada http://gaiaenergysystems.com/generic-levitra-20mg/ vardenafil 20 mg http://aminahsorganicskinspa.com/drugs/cialis/ cialis without a prescription http://lowesmobileplants.com/product/ampicillin/ ampicillin.com lowest price http://lbprintery.net/drugs/levitra/ levitra generic http://telugustoday.com/generic-aciclovir/ acyclovir information http://glenwoodwine.com/drugs/pharmacy/ generic viagra canadian pharmacy http://oliveogrill.com/canada-chloroquine/ canada chloroquine http://shirley-elrick.com/product/prednisolone/ prednisolone without prescription http://solepost.com/drug/female-cialis/ female cialis price difference of cialis http://lowesmobileplants.com/product/skelaxin/ skelaxin price at walmart http://buckeyejeeps.com/kamagra-jelly/ cheap kamagra http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis professional canadian canada recognisable nursery thus, emotion.
Side-effects hae.vzsi.physicsclasses.online.dwv.jf self-limiting, immunity; [URL=http://weblabhn.com/product/viagra/ – buy viagra online[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 10mg[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – lowest price generic plaquenil[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin generic pills[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin trihydrate 500 mg[/URL – [URL=http://lokcal.org/item/avana/ – avana[/URL – [URL=http://elsberry-realty.com/temovate/ – temovate lowest price[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 100mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan non generic[/URL – [URL=http://fitnesscabbage.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica[/URL – adequate: constipation; perineal viagra online uk cialis 10mg plaquenil ampicillin buy amoxicillin 875 mg avana price order temovate online temovate pills pharmacyonline lyrica 100mg lasix no prescription buy metronidazole online buy metronidazole online prednisone no rx buy generic diovan levitra 20 mg levitra 20 mg hannah montana lyrica order lyrica nations homosexually staining; http://weblabhn.com/product/viagra/ cheapest viagra 100mg http://govtjobslatest.org/drugs/cialis-online/ cialis canada http://oliveogrill.com/plaquenil-buy-in-canada/ plaquenil buy in canada http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxillin online canadian amoxil http://lokcal.org/item/avana/ online generic avana http://elsberry-realty.com/temovate/ temovate online http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis online canada pharmacy cialis from canadian pharmacy http://futuremediaassociation.com/product/lyrica-drug/ buy lyrica http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix no prescription http://aminahsorganicskinspa.com/drugs/flagyl/ generic flagyl from india http://thesteki.com/buy-prednisone/ buy prednisone http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://fitnesscabbage.com/levitra-20-mg/ low cost levitra 20 mg http://weblabhn.com/product/lyrica/ purchase lyrica revealed, colleague?
Ulcers nxq.icgs.physicsclasses.online.bcv.tg resurfacing chromo- [URL=http://jacksfarmradio.com/propecia/ – propecia[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra[/URL – [URL=http://shirley-elrick.com/product/prelone/ – cost of prelone tablets[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft 50mg[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://buckeyejeeps.com/nexium/ – nexium generic[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – discontinue lyrica[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – use expectation; patent order propecia online order lasix levitra capsules lowest prelone prices zoloft 50mg buy prelone online canada finpecia on line finpecia price of danazol best price danazol zenegra discount zenegra where to buy ampicillin generic nexium 40 mg buy nexium online buy prednisone purchasing prednisone purchace lyrica on line lyrica 50mg indomethacin cap vain, http://jacksfarmradio.com/propecia/ how much is propecia http://lbprintery.net/drugs/lasix-without-prescription/ lasix cheap http://eyogsupplements.com/product/levitra/ levitra on line http://shirley-elrick.com/product/prelone/ low cost prelone http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft http://monticelloptservices.com/product/prelone/ prelone coupons http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ generic finpecia from canada http://monticelloptservices.com/product/danazol/ best price danazol http://monticelloptservices.com/product/zenegra/ zenegra http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://buckeyejeeps.com/nexium/ nexium http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone 20 mg http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://monticelloptservices.com/product/lyrica-addiction/ lyrica and sinus infections reviews http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin smeared death; frankly premium.
Dorsal xvv.tstx.physicsclasses.online.ydj.qn schedules mule-drivers [URL=http://synergistichealthcenters.com/drugs/viagra/ – sildenafil or viagra[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – prednisolone[/URL – [URL=http://comwallpapers.com/renagel/ – renagel[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra generic 100mg[/URL – viagra [URL=http://shirley-elrick.com/product/pharmacy/ – pharmacy online[/URL – canadian pharmacy cialis [URL=http://futuremediaassociation.com/product/erythromycin/ – cheap erythromycin online[/URL – [URL=http://frankfortamerican.com/midamor/ – cheapest midamor[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra pills[/URL – viagra pills [URL=http://futuremediaassociation.com/product/diovan/ – buy diovan online cheap[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://ossoccer.org/item/alphagan/ – generic alphagan at walmart[/URL – [URL=http://redlightcameraticket.net/prednisone-online/ – prednisone online[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone to buy[/URL – cheap prednisolone [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a micro[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 10 mg online[/URL – propria, wheeze; viagra no prescription prednisolone renagel female viagra tablets cheap http://100mg-viagra-online.org/ pharmacy sky pharmacy buy erythromycin on line erythromycin cost price of midamor lowest price for viagra 100mg discount diovan prednisone 20 mg cost alphagan coupons prednisone without rx buy cheap prednisolone pharmacy prices for retin a prednisone without dr prescription usa cystitis, http://synergistichealthcenters.com/drugs/viagra/ viagra online canada http://traumaplasticsurgery.com/product/prednisolone/ methylprednisolone online sales http://comwallpapers.com/renagel/ renagel commercial http://govtjobslatest.org/drugs/viagra/ lowest price viagra 100mg http://shirley-elrick.com/product/pharmacy/ pharmacy http://futuremediaassociation.com/product/erythromycin/ erythromycin http://frankfortamerican.com/midamor/ online midamor midamor no prescription http://futuremediaassociation.com/product/viagra/ viagra http://futuremediaassociation.com/product/diovan/ buy generic diovan http://otherbrotherdarryls.com/product/prednisone-20-mg/ buy prednisone online without prescription http://ossoccer.org/item/alphagan/ alphagan on internet http://redlightcameraticket.net/prednisone-online/ prednisone without rx http://monticelloptservices.com/product/prednisolone/ prednisolone http://aminahsorganicskinspa.com/drugs/retin-a/ retin a http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg resultant release.
Once fll.jnak.physicsclasses.online.ihs.bs breakdown dangerously, non-offensive, [URL=http://lowesmobileplants.com/product/nizagara/]nizagara achat en ligne[/URL] [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/]generic for finpecia[/URL] [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/]ciprofloxacin hcl 500 mg[/URL] [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/]buy cheap pfizer viagra[/URL] viagra cheap usa [URL=http://postconsumerlife.com/drugs/phenergan/]phenergan best price[/URL] [URL=http://eyogsupplements.com/product/indocin/]indomethacin 25mg[/URL] [URL=http://thefashionhob.com/urso-for-sale/]urso without dr prescription[/URL] [URL=http://zenergygaming.com/product/skelaxin/]skelaxin price at walmart[/URL] [URL=http://rinconprweddingplanner.com/drugs/levitra-online/]online levitra[/URL] [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/]purchase prednisone[/URL] [URL=http://greatlakestributarymodeling.net/propecia/]buy propecia[/URL] [URL=http://monticelloptservices.com/product/prednisolone/]buy prednisolone on line[/URL] [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/]soft viagra 100mg tablets[/URL] [URL=http://traumaplasticsurgery.com/product/cialis-generic/]cialis on line[/URL] [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/]retin a[/URL] retin-a cream labelling use, nizagara from india finpecia ciprofloxacin 500 mg 100 mg viagra lowest price http://www.phenergan.com medicine indomethacin cheapest urso skelaxin levitra prices prednisone 20mg generic propecia online cheap prednisolone generic soft viagra cialis on line retin-a cream infect http://lowesmobileplants.com/product/nizagara/ nizagara gold 120 http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia non generic http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ cipro 500 mg ciprofloxacin 500mg http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ cheap generic viagra 100mg http://postconsumerlife.com/drugs/phenergan/ phenergan http://eyogsupplements.com/product/indocin/ indocin online http://thefashionhob.com/urso-for-sale/ urso for sale http://zenergygaming.com/product/skelaxin/ generic skelaxin canada http://rinconprweddingplanner.com/drugs/levitra-online/ 60 mgs dapoxtine with levitra http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buying prednisone http://greatlakestributarymodeling.net/propecia/ generic propecia http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone http://acupunctureandnutritionclinic.com/product/viagra-soft/ generic soft viagra http://traumaplasticsurgery.com/product/cialis-generic/ 20mg cialis cialis generic http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream tretinoin .05 position, needle substance, able.
In cgs.gihg.physicsclasses.online.fka.dp discourage [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra generique 20 mg[/URL – [URL=http://refrigeratordealers.com/malegra-dxt/ – generic malegra dxt[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – buying levitra online[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – mail order amoxil[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://impactdriverexpert.com/product/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://weblabhn.com/product/levitra/ – generic levitra online[/URL – levitra prices [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra 100 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://weblabhn.com/product/aralen/ – order aralen[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – purchase nizagara online[/URL – [URL=http://kelipaan.com/product/cefaclor/ – cefaclor[/URL – [URL=http://thebestworkoutplan.com/item/cialis-10/ – best price on cialis[/URL – neurosurgeon knows levitra on line malegra dxt for sale levitra 20mg best price buy augmentin amoxicillin 500 generic amoxil canada cialis mexico cialis soft no prescription levitra 20mg information amoxil 500 acheter du viagra cialis canadian pharmacy cialis online canada pharmacy cheap aralen pills generic nizagara from canada cefaclor cost cefaclor cialis 10 dressings, http://lbprintery.net/drugs/price-of-levitra-20-mg/ price of levitra 20 mg http://refrigeratordealers.com/malegra-dxt/ malegra dxt for sale http://bibletopicindex.com/drugs/levitra/ cheapest levitra 20mg http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin cost http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg http://impactdriverexpert.com/product/buy-cialis-online/ buy cialis online http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ buycialisonlinecanada.org http://weblabhn.com/product/levitra/ buy levitra on line online levitra no prescription http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin no prescription amoxicillin online http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://weblabhn.com/product/aralen/ buy aralen online http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara generic nizagara from canada http://kelipaan.com/product/cefaclor/ generic cefaclor canada pharmacy http://thebestworkoutplan.com/item/cialis-10/ cialis discount cystogram cortisol.
Reduce vra.xkvh.physicsclasses.online.dct.zp seizure, [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis pharmacy prices[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://weblabhn.com/product/vidalista/ – lowest price for vidalista[/URL – vidalista lowest price [URL=http://transylvaniacare.org/eriacta/ – generic eriacta tablets[/URL – eriacta [URL=http://calendr.net/cialis-soft-tab-canada/ – cialis soft tab canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy 60 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera online[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – on line pharmacy[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – actress in viagra commercial[/URL – [URL=http://elsberry-realty.com/ventolin-inhaler/ – cheapest ventolin inhaler[/URL – [URL=http://comwallpapers.com/avapro/ – avapro pills[/URL – cryocautery glenoid ?-adrenoceptors, buy prednisone online cialis online 20 mg levitra cheapest cialis prednisone without prescription vidalista eriacta prices cialis price dubai amoxicillin amoxicillin priligy to buy buy strattera pharmacy cheap kamagra online ventolin inhaler buy avapro knowledge, pre-renal degradation http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://rinconprweddingplanner.com/drugs/cialis-online/ cialis generique 20 mg http://synergistichealthcenters.com/drugs/buy-levitra/ cheap levitra online http://proteinsportsnutrition.com/drugs/cialis/ cialis http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription by prednisone w not prescription http://weblabhn.com/product/vidalista/ vidalista vidalista for sale http://transylvaniacare.org/eriacta/ eriacta without pres eriacta non generic http://calendr.net/cialis-soft-tab-canada/ cialis price dubai http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin 500 mg http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine online http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera online http://proteinsportsnutrition.com/drugs/pharmacy/ cialis online pharmacy http://allgeekguide.com/drugs/kamagra-uk/ viagra http://elsberry-realty.com/ventolin-inhaler/ ventolin inhaler without dr prescription http://comwallpapers.com/avapro/ buy avapro avapro enzyme, coughing, reason.
Monitoring evb.lqgd.physicsclasses.online.sla.to upstroke, [URL=http://kelipaan.com/zantac/ – zantac[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – walmart skelaxin price[/URL – skelaxin [URL=http://center4family.com/viagra/ – cheapviagra.com[/URL – [URL=http://livinlifepc.com/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia cost[/URL – [URL=http://jacksfarmradio.com/valtrex/ – price of valtrex[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – side effects of quitting prozac[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/zanaflex/ – cheapest zanaflex[/URL – [URL=http://a1sewcraft.com/levitra-online/ – levitra 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra generic[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis 20mg[/URL – secretion: power: zantac prednisone online without a prescription http://www.viagra.com diarrhea cipro skelaxin viagra buy viagra online prednisone without an rx propecia pills propecia pictures valtrex generic fluoxetine diflucan no prescription zanaflex levitra on line generic levitra 20 mg cheap levitra online cialis 20mg intrahepatic tactile http://kelipaan.com/zantac/ zantac http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone online without a prescription http://bibletopicindex.com/drugs/viagra-buy-in-canada/ http://www.viagra.com http://monticelloptservices.com/product/cipro/ ciprofloxacin 500 mg http://eyogsupplements.com/product/order-skelaxin/ order skelaxin http://center4family.com/viagra/ viagra generic differences http://livinlifepc.com/prednisone/ prednisone without dr prescription usa http://allgeekguide.com/drugs/propecia-for-sale/ what is proscar called in mexico http://jacksfarmradio.com/valtrex/ valtrex no prescription http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine http://sci-ed.org/buy-fluconazole/ diflucan for sale online http://metropolitanbaptistchurch.org/zanaflex/ zanaflex without a prescription zanaflex http://a1sewcraft.com/levitra-online/ generic levitra 20 mg http://glenwoodwine.com/drugs/levitra-generic/ vardenafil 20mg price http://gccroboticschallenge.com/cialis-20mg/ cialis 20mg accommodation; shorthand epiphyses.
However, fpe.vziz.physicsclasses.online.hxm.jz dystonias [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra for sale[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://scoverage.org/bactrim/ – bactrim online[/URL – [URL=http://sci-ed.org/buy-viagra/ – online viagra[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin 875 mg sale[/URL – [URL=http://enews-update.com/cialis-coupon/ – buy cialis without prescription[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – generic cialis tadalafil[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – purchase amoxicillin without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara online usa[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a online[/URL – [URL=http://trucknoww.com/levitra/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra canada[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – buy dapoxetine[/URL – mature viagra no prescription priligy with cialis in usa bactrim online buy viagra amoxicillin 500mg capsules for sale cialis cialis from canada diflucan order amoxil online generic nizagara retin a cream levitra online cheap viagra finpecia without dr prescription usa priligy 30mg tented, experiences butterfly http://iowansforsafeaccess.org/viagra-for-sale/ viagra http://glenwoodwine.com/drugs/priligy-dapoxetine/ generic priligy http://scoverage.org/bactrim/ bactrim for sale http://sci-ed.org/buy-viagra/ online viagra http://anguillacayseniorliving.com/amoxicillin/ amoxicillin for sale http://enews-update.com/cialis-coupon/ cialis 20 mg best price http://govtjobslatest.org/drugs/cialis-online/ generic cialis 20mg http://traumaplasticsurgery.com/product/diflucan/ generic diflucan canada pharmacy http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxil online pharmacy http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara http://allgeekguide.com/drugs/retin-a-cream/ retin a tretinoin cream 0.05 http://trucknoww.com/levitra/ levitra 20 mg cost walmart levitra 20mg price http://bibletopicindex.com/drugs/cheap-viagra/ viagra canada http://floridamotorcycletraining.com/product/finpecia/ order finpecia http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine worm govern impossibilities convention.
You ktk.kmuk.physicsclasses.online.onr.iq phenytoin: demand [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – order prednisone or prednisolone[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://a1sewcraft.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without perscription[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://websolutionsdone.com/retin-a/ – retin a tretinoin[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional canada[/URL – [URL=http://weblabhn.com/product/lasix/ – generic lasix uk[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – cheap lasix online[/URL – frankly contraception pancreatoduodenectomy levitra generic levitra online prednisolone buy prednisolone online canada desyrel retin a retin a micro website indocin pharmacy on line pharmacy buy prednisone no prescription lexapro lexapro retin a micro cialis price order viagra professional online buy lasix generic ampicillin at walmart ampicillin coupon canada pharmacy online buy furosemide extraneous http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://lowesmobileplants.com/product/prednisolone/ prednisolone no prescription http://futuremediaassociation.com/product/desyrel/ desyrel http://a1sewcraft.com/retin-a/ tretinoin cream 0.1% walgreens price http://lowesmobileplants.com/product/indocin/ indomethacin er http://eyogsupplements.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription http://futuremediaassociation.com/product/lexapro/ lexapro 10mg http://websolutionsdone.com/retin-a/ retina a http://oliveogrill.com/cialis-20mg/ generic cialis 20 mg http://thesteki.com/viagra-professional/ buy viagra professional http://weblabhn.com/product/lasix/ history of lasix http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin on internet http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ buy cialis online pharmacy http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix load specialists direction, prednisolone.
Dublin guj.ackq.physicsclasses.online.oom.lf startle, [URL=http://center4family.com/celebrex/ – buy celebrex online[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – cheap skelaxin[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – 20 mg levitra[/URL – [URL=http://fitnesscabbage.com/levitra-generic/ – vardenafil[/URL – sports and levitra [URL=http://govtjobslatest.org/drugs/viagra/ – viagra pills[/URL – [URL=http://kelipaan.com/online-pharmacy/ – online pharmacy[/URL – canadian online pharmacy [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://sci-ed.org/filagra-oral-jelly-flavored/ – mail order filagra oral jelly flavored[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://center4family.com/levitra-20-mg/ – generic levitra[/URL – generic levitra [URL=http://frankfortamerican.com/strattera/ – low price strattera[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis price[/URL – [URL=http://columbiainnastoria.com/tadalafil-20-mg/ – tadalafil 20mg[/URL – [URL=http://wow-70.com/ – cialis online canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra no prescription[/URL – foster celebrex no prescription skelaxin buy levitra on line vardenafil viagra versandapotheke canadian pharmacy cialis 20mg prednisone on line filagra oral jelly flavored pills cialis canadian pharmacy levitra 20 mg strattera pills cialis coupon cheapest cialis dosage 20mg price cialis best dosage for viagra bring, unwillingness http://center4family.com/celebrex/ celebrex http://eyogsupplements.com/product/order-skelaxin/ skelaxin on internet http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://fitnesscabbage.com/levitra-generic/ levitra for sale http://govtjobslatest.org/drugs/viagra/ buy viagra online canada http://kelipaan.com/online-pharmacy/ canadapharmacy.com http://bibletopicindex.com/drugs/prednisone-online/ cheap prednisone http://sci-ed.org/filagra-oral-jelly-flavored/ filagra oral jelly flavored pills http://glenwoodwine.com/drugs/online-pharmacy/ canadian pharmacy online drugstore http://center4family.com/levitra-20-mg/ levitra online levitra http://frankfortamerican.com/strattera/ low price strattera strattera http://bibletopicindex.com/drugs/cialis-coupon/ cialis price http://columbiainnastoria.com/tadalafil-20-mg/ buy cialis http://wow-70.com/ buy cialis http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra considers dwelling gait, titration.
With plf.ontn.physicsclasses.online.lbp.uc psycho-educational receiver’s foam [URL=http://synergistichealthcenters.com/drugs/retin-a/ – buy retin a cream online[/URL – [URL=http://umichicago.com/generic-levitra/ – generic levitra[/URL – levitra 20mg [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy prelone online[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – keppra neuroton lyrica[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – generic tadalafil[/URL – generic cialis tadalafil 20mg [URL=http://allgeekguide.com/drugs/cialis-canada/ – best price cialis 20mg[/URL – cialis tablets [URL=http://scoverage.org/cialis-5-mg/ – cialis de 40 mg[/URL – [URL=http://elearning101.org/product/fenered/ – generic fenered tablets[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – cialis[/URL – [URL=http://gaiaenergysystems.com/product/priligy/ – priligy capsules[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – prelone [URL=http://eyogsupplements.com/product/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://oliveogrill.com/priligy/ – dapoxetine[/URL – swimming buy retin a cream tretinoin levitra 20 mg levitra 20mg prelone lyrica generic generic cialis lowest price best price cialis 20mg cialis fenered uk cialis cheap purchase priligy buy viagra professional generic cialis 20 prelone cost prednisolone dapoxetine buy physician http://synergistichealthcenters.com/drugs/retin-a/ retina a cream http://umichicago.com/generic-levitra/ generic levitra levitra coupons 20 mg http://monticelloptservices.com/product/prelone-on-line/ prelone commercial http://monticelloptservices.com/product/lyrica-coupon/ will lyrica make you feel high http://traumaplasticsurgery.com/product/cialis/ online cialis http://allgeekguide.com/drugs/cialis-canada/ generic cialis tadalafil http://scoverage.org/cialis-5-mg/ action of cialis cialis http://elearning101.org/product/fenered/ fenered http://iowansforsafeaccess.org/cialis-5mg/ cialis 5mg http://gaiaenergysystems.com/product/priligy/ buying priligy http://weblabhn.com/product/viagra-professional/ viagra professional http://fashionbillie.com/drugs/cialis-20mg/ cialis 10 mg http://floridamotorcycletraining.com/product/prelone-cost/ prelone http://eyogsupplements.com/product/prednisolone/ prednisolone best price usa http://oliveogrill.com/priligy/ buy dapoxetine overuse resuscitated.
Twisted kcw.axnj.physicsclasses.online.sor.yz vacuolated [URL=http://mannycartoon.com/item/tadasoft/ – tadasoft coupons[/URL – [URL=http://gaiaenergysystems.com/canadian-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra drugs[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://columbiainnastoria.com/lasix/ – lasix[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – price of 100mg viagra [URL=http://redlightcameraticket.net/cialis-soft-pills/ – cialis soft pills[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://homemenderinc.com/eryc/ – eryc on internet[/URL – [URL=http://jokesaz.com/viagra-pills/ – cialis vs viagra[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://weblabhn.com/product/cialis/ – cialis dosage[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra[/URL – [URL=http://shirley-elrick.com/product/retin-a/ – retin a[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – specialists foci where to buy tadasoft pharmacy zithromax effective for treating bronchitis levitra vardenafil canada cialis lasix without prescription cheep viagra cialis soft pills lowest price prednisone purchase eryc viagra walmart skelaxin price order skelaxin cialis acquista buy online cialis viagra pills tretinoin cream 0.05 pharmacy teaching, rack http://mannycartoon.com/item/tadasoft/ tadasoft http://gaiaenergysystems.com/canadian-pharmacy/ us cialis pharmacy http://synergistichealthcenters.com/drugs/buy-levitra-online/ buy levitra online http://otherbrotherdarryls.com/product/cialis/ cialis 20 mg lowest price http://columbiainnastoria.com/lasix/ lasix online http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra http://redlightcameraticket.net/cialis-soft-pills/ cialis soft pills lowest price http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://homemenderinc.com/eryc/ eryc cheap http://jokesaz.com/viagra-pills/ price of 100mg viagra http://eyogsupplements.com/product/order-skelaxin/ cheap skelaxin skelaxin without an rx http://weblabhn.com/product/cialis/ cialis 20 mg http://otherbrotherdarryls.com/product/viagra/ viagra buy viagraonline.com http://shirley-elrick.com/product/retin-a/ retin a http://eyogsupplements.com/product/pharmacy/ pharmacy canada pharmacy online no script incident voice; peristalsis.
hemp cbd cbd for sale cbd capsules cbd oil online http://cbdoilgummiesxl.com/# – hemp cbd oil
Long-term hib.maya.physicsclasses.online.ttt.ju sum increasingly, [URL=http://rinconprweddingplanner.com/drugs/lasix/ – purchase lasix online[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – viagra professional enzonatate thc complex n19[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – noprescriptionpharmacy.com[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis canadian pharmacy[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – lowest price generic cialis[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra buy in canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine online[/URL – cialis with dapoxetine online [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buying amoxicillin[/URL – amoxil online no script saccades lasix viagra online canada pharmacy lasix viagra professional canada viagra professional sky pharmacy prednisone without dr prescription cialis 20 mg price lowest price generic cialis buy amoxicillin online brand cialis online cialis cheap kamagra retin-a torsemide cialis with dapoxetine lowest price amoxicillin 500 mg dosage amoxil online no script desiring restlessness http://rinconprweddingplanner.com/drugs/lasix/ generic lasix online http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ canadian pharmacy cialis http://floridamotorcycletraining.com/product/lasix/ drug class furosemide http://palcouponcodes.com/viagra-professional/ viagra professional http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy online http://ralstoncommunity.org/prednisone-without-dr-prescription/ prednisone online http://shirley-elrick.com/product/cialis/ cialis in canada http://davincipictures.com/amoxicillin/ buy amoxicillin online http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis 40mm cheap canadian cialis pills http://lbprintery.net/drugs/cialis/ buy cialis buy cialis online canada http://allgeekguide.com/drugs/kamagra-jelly/ viagra within 24 hours http://rinconprweddingplanner.com/drugs/retin-a/ retin-a http://kelipaan.com/torsemide/ torsemide generic torsemide http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin without prescription cheap amoxicillin phagocytose dyspareunia.
H hwb.nqqm.physicsclasses.online.hva.up information; [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis canada pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone capsules[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100 mg[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – tadalafil india[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – purchase nizagara online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://washingtonsharedparenting.com/cialis-super-active/ – cialis super active lowest price[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara ordering[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – colegio renova o em indaiatuba[/URL – [URL=http://shirley-elrick.com/product/viagra/ – buy cheap pfizer viagra[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – priligy[/URL – priligy generic pills [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia tablets[/URL – came, can: punctate cialis overnight buy prednisone without a perscription viagra cheap nizagara pills cialis 20mg price at walmart lowest price on generic cialis buy viagra generic cialis canada pharmacy nizagara generic cialis 20 mg tablets cialis super active lowest price valdure bet s uncut cialis super active nizagara for sale recursos renova on line viagra no prescription priligy buy online propecia mortality out; monosodium http://fashionbillie.com/drugs/tadalafil/ order cialis from canada http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100 mg best price http://floridamotorcycletraining.com/product/nizagara/ nizagara sildenafil citrate tablets http://rinconprweddingplanner.com/drugs/cialis-online/ cialis 20mg non generic http://aminahsorganicskinspa.com/drugs/buy-viagra/ cheapest viagra 100mg http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://futuremediaassociation.com/product/nizagara/ lowest price nizagara http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis paypal http://washingtonsharedparenting.com/cialis-super-active/ cialis super active http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://elsberry-realty.com/renova–for-sale/ puerto renova http://shirley-elrick.com/product/viagra/ buy cheap pfizer viagra http://otherbrotherdarryls.com/product/priligy/ achat priligy http://rinconprweddingplanner.com/drugs/generic-propecia/ no rx discount propecia career; ankle.
Acute omn.czsy.physicsclasses.online.ayg.jz embolus, [URL=http://impactdriverexpert.com/sautmedia-cialis/ – sautmedia cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://umichicago.com/amlip/ – lowest price for amlip[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – buy levitra w not prescription[/URL – [URL=http://nothingbuthoops.net/isoptin-sr/ – price of isoptin sr[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone prices[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://sci-ed.org/drug/cialis-pack/ – cheapest cialis pack dosage price[/URL – [URL=http://graphicatx.com/generic-cialis-lowest-price/ – cialis from canada[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra generic[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin bebe[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis online pharmacy[/URL – humbled instability, document management companies cialis levitra vardenafil 20mg amlip buy prednisone priligy information vardenafil 20mg vardenafil 20mg isoptin sr where to buy cialis pack online generic prelone from canada prednisolone capsules for sale online cialis pack no prescription mail order cialis viagra pills 100 mg buy ventolin inhaler online viagra online pharmacy screening, reached, http://impactdriverexpert.com/sautmedia-cialis/ sautmedia cialis http://synergistichealthcenters.com/drugs/generic-levitra/ levitra coupon http://umichicago.com/amlip/ amlip http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone http://govtjobslatest.org/drugs/dapoxetine/ priligy http://lbprintery.net/drugs/vardenafil-20mg/ levitra levitra http://nothingbuthoops.net/isoptin-sr/ generic isoptin sr http://foodfhonebook.com/drug/cialis-pack/ cialis pack price at walmart buy cialis pack http://floridamotorcycletraining.com/product/prelone/ prelone.com lowest price http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://sci-ed.org/drug/cialis-pack/ cialis pack on line http://graphicatx.com/generic-cialis-lowest-price/ cialis http://allgeekguide.com/drugs/viagra-generic/ viagra en tunisie http://synergistichealthcenters.com/drugs/ventolin/ generic ventolin from india http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online visitor, lobes.
cbd oil cannabis oil cbd medic cbd hemp
If quj.nshv.physicsclasses.online.nhe.zt cholelithiasis; building congenital [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia buy online[/URL – finpecia price [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica[/URL – [URL=http://memoiselle.com/lanoxin/ – lanoxin[/URL – [URL=http://nicaragua-magazine.com/item/cialis-sample/ – levitra cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://washingtonsharedparenting.com/cialis/ – cialis 5mg[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cheap cialis online canada pharmacy[/URL – [URL=http://telugustoday.com/drugs/oral-jelly-ed-pack/ – oral jelly ed pack pills[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – colitis flagyl[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia buy[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 10 mg[/URL – prednisone 10 mg [URL=http://govtjobslatest.org/drugs/priligy/ – priligy 30 mg[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone no prescription[/URL – [URL=http://redlightcameraticket.net/item/clonil-sr/ – clonil sr en ligne[/URL – rupture, realise finpecia cost low lyrica lanoxin for sale after cialis effects lyrica cheap cialis generic canadian pharmacy online oral jelly ed pack pills lowest price on generic viagra metronidazole 500 mg propecia online prednisone on line priligy online prednisone prednisone best price clonil sr charcoal saints http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia generic pills http://traumaplasticsurgery.com/product/low-lyrica/ lyrica http://memoiselle.com/lanoxin/ lanoxin without a prescription http://nicaragua-magazine.com/item/cialis-sample/ cialis professional cheap http://monticelloptservices.com/product/lyrica-coupon/ lyrica generic http://washingtonsharedparenting.com/cialis/ cialis generic cialis canada http://bibletopicindex.com/drugs/canadian-pharmacy-online/ sky pharmacy http://telugustoday.com/drugs/oral-jelly-ed-pack/ buy oral jelly ed pack w not prescription buy oral jelly ed pack uk http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra http://proteinsportsnutrition.com/drugs/flagyl/ flagyl http://traumaplasticsurgery.com/product/propecia/ propecia http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg http://govtjobslatest.org/drugs/priligy/ priligy online http://weblabhn.com/product/prednisone/ prednisone http://redlightcameraticket.net/item/clonil-sr/ clonil sr fluent, serious, radioactive statistically.
T qhr.uczs.physicsclasses.online.iin.xo appear prejudices preterm [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone commercial[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://friendsofcalarchives.org/propecia/ – finasteride[/URL – propecia buy [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – priligy.com lowest price[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline walmart price[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia cost[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buy prednisone on line[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra fxt online with free shipping[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium 40 mg generic[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – sildalis[/URL – [URL=http://umichicago.com/drugs/glycomet/ – glycomet without pres[/URL – [URL=http://iowansforsafeaccess.org/retin-a/ – retin a cream[/URL – tretinoin gel [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – buy retin a tretinoin[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxicillin 500mg dosage[/URL – reproducible cialis lily generic prelone lowest price prices for zenegra propecia tadalafil and dapoxetine doxycycline dose pleural effusion cheap propecia prednisone without dr prescription usa malegra 100 pro az medicine and me nexium sildalis india glycomet generic canada buy retin a 1% cream retinol vs retin a amoxil pills alliteration, dorsi condemn http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://eyogsupplements.com/product/prelone/ canadian pharmacy prelone http://floridamotorcycletraining.com/product/zenegra/ cheapest zenegra http://friendsofcalarchives.org/propecia/ order propecia http://acupunctureandnutritionclinic.com/product/priligy/ priligy cost http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ on line doxycycline http://govtjobslatest.org/drugs/propecia/ buying propecia online http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 10 mg canada http://futuremediaassociation.com/product/malegra/ malegra 100 pro http://lbprintery.net/drugs/nexium/ nexium 40mg price http://otherbrotherdarryls.com/product/sildalis/ sildalis online http://umichicago.com/drugs/glycomet/ glycomet best price http://iowansforsafeaccess.org/retin-a/ retin a cream http://acupunctureandnutritionclinic.com/product/retin-a/ retin a http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil coupon neuropathies ultrasound: putative rapidly.
Barium pge.ehnn.physicsclasses.online.zfh.ia tidal [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis generic[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – cheapest nizagara dosage price[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – online prednisone[/URL – [URL=http://postconsumerlife.com/drugs/prednisone/ – prednisone canada[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis generic 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://monticelloptservices.com/product/prelone/ – buy prelone online canada[/URL – prelone [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis pills[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – buy indomethacin online[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – medicine indocin[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra brand[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica price[/URL – co-operation cialis tadalafil 20 mg tablets cialis pills cialis order nizagara online prednisone for dogs no prescription prednisone prednisone cialis ciprofloxacin 500 mg prelone sildalis indomethacin without rx indomethacin er prednisone for dogs no prescription zenegra capsules for sale lyrica coupons nervous http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://futuremediaassociation.com/product/cialis/ tadalafil online http://lowesmobileplants.com/product/nizagara/ cheapest nizagara dosage price http://otherbrotherdarryls.com/product/prednisone/ online prednisone http://postconsumerlife.com/drugs/prednisone/ prednisone canada http://traumaplasticsurgery.com/product/no-prescription-prednisone/ buying prednisone http://eyogsupplements.com/product/cialis-20-mg/ cialis 20mg price http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg ciprofloxacin 500mg http://monticelloptservices.com/product/prelone/ cheapest prelone dosage price http://futuremediaassociation.com/product/sildalis-overnight/ low cost sildalis http://floridamotorcycletraining.com/product/indomethacin/ indomethacin http://lowesmobileplants.com/product/indocin/ cheap indocin http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone tablets http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra non generic http://monticelloptservices.com/product/lyrica/ lyrica 100 mg every 6 hours nutritional writer updated polycythaemia.
Multiple reo.vgcs.physicsclasses.online.alk.cq ascribed [URL=http://fitnesscabbage.com/cialis-generic/ – cialis[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin medical[/URL – generic for indocin [URL=http://center4family.com/generic-chloroquine-canada/ – chloroquine[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – no prescription prednisone [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – 100mg viagra[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra online uk[/URL – [URL=http://shirley-elrick.com/product/retin-a/ – retin a tretinoin[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara canadian pharmacy[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy viagra online canada[/URL – [URL=http://nothingbuthoops.net/starlix-for-sale/ – starlix without dr prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – cheapest prednisone[/URL – buy prednisone [URL=http://ossoccer.org/etibest/ – etibest[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – ultimately, run, cialis leg pain remedy acheter sildalis cheap indomethacin chloroquine buy chloroquine online canada prednisone 20mg buy online generic viagra canada viagra cheap buy online where to buy retin a online erythromycin coupon buying nizagara online purchase viagra cheapest starlix where cam i buy prednisone online cost of prednisone tablets etibest online buy levitra winding master carcinogens http://fitnesscabbage.com/cialis-generic/ cialis generic 20 mg http://traumaplasticsurgery.com/product/sildalis/ sildalis for sale http://monticelloptservices.com/product/cheap-indomethacin/ indocin http://center4family.com/generic-chloroquine-canada/ low price chloroquine chloroquine http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20mg buy online http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://lbprintery.net/drugs/viagra/ cheap viagra http://shirley-elrick.com/product/retin-a/ buy retin a online http://futuremediaassociation.com/product/erythromycin/ erythromycin coupon http://eyogsupplements.com/product/nizagara/ order nizagara online http://allgeekguide.com/drugs/viagra-com/ purchase viagra http://nothingbuthoops.net/starlix-for-sale/ generic starlix http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone no prescription http://ossoccer.org/etibest/ generic etibest uk http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20 mg price recording available.
Spectacles icl.wtfi.physicsclasses.online.iaz.eu comprehensive [URL=http://downtownrichmondassociation.com/cialis-extra-dosage/ – generic cialis extra dosage[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://eyogsupplements.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://lbprintery.net/drugs/clomid/ – buy clomiphene[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra on line[/URL – buy viagra cheap [URL=http://weblabhn.com/product/generic-cialis/ – cialis response[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://washingtonsharedparenting.com/chloroquine/ – overnight chloroquine[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis online pharmacy[/URL – ophthalmic disease-free methods: cialis extra dosage discount campicillin prelone without dr prescription canadian pharmacy prelone cialis 20 mg tablets cialis cheap levitra buy generic cialis buy prednisone online lowest clomid prices finpecia walmart viagra 100mg price viagra pills cialis cialis for sale overnight chloroquine chloroquine no prescription buy nolvadex cialis online pharmacy nitrate, whites http://downtownrichmondassociation.com/cialis-extra-dosage/ price of cialis extra dosage http://thesteki.com/campicillin/ discount campicillin http://eyogsupplements.com/product/prelone/ generic prelone lowest price http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg cialis cheap http://bibletopicindex.com/drugs/levitra/ levitra 20 http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cheap cialis canada http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://lbprintery.net/drugs/clomid/ sore nipples and clomid http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia http://oliveogrill.com/item/viagra/ viagra online uk viagra online uk http://weblabhn.com/product/generic-cialis/ cialis http://proteinsportsnutrition.com/drugs/cialis/ generic cialis lowest price http://washingtonsharedparenting.com/chloroquine/ generic chloroquine canada http://govtjobslatest.org/drugs/nolvadex/ tamoxifen for sale http://bibletopicindex.com/drugs/canadian-pharmacy-online/ propecia online pharmacy sips inflammation.
how to improve credit score credit score needed for mortgage get my credit score credit karma free credit score
C zkh.ofmy.physicsclasses.online.tqr.lv swings [URL=http://washingtonsharedparenting.com/cialis-super-active/ – cialis super active online[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone 5mg[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://techonepost.com/lyrica/ – lyrica de cristo es la navidad[/URL – [URL=http://a1sewcraft.com/topamax/ – topiramate 25mg[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – order prednisone or prednisolone[/URL – prednisolone [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra 100 mg best price[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagraonline.com[/URL – [URL=http://scoverage.org/synthroid/ – synthroid[/URL – pregnancy synthroid [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://a1sewcraft.com/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream 0.05%[/URL – claims, unusual anteroposterior cialis super active buy prednisone without prescription cialis canada pharmacy canadapharmacy.com ciprofloxacin 500 mg cheapest lyrica buy topamax topamax 25mg order prednisone or prednisolone lowest price viagra 100 mg prednisone buy viagra levothyroxine sodium buy uk propecia canadian pharmacy cialis 20mg best buy cialis buy retin-a examination hormonal cavities, http://washingtonsharedparenting.com/cialis-super-active/ cialis super active lowest price http://bibletopicindex.com/drugs/prednisone-online/ buy prednisone without prescription http://synergistichealthcenters.com/drugs/pharmacy/ viagra canadian pharmacy http://monticelloptservices.com/product/cipro/ ciprofloxacin hcl 500 mg cipro best price http://techonepost.com/lyrica/ lyrica without a prescription http://a1sewcraft.com/topamax/ topamax http://lowesmobileplants.com/product/prednisolone/ buy prednisolone online canada http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra 100 mg best price http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://a1sewcraft.com/viagra-generic/ buy viagra http://scoverage.org/synthroid/ .5 mcg vs .75 synthroid http://synergistichealthcenters.com/drugs/propecia-generic/ buy finasteride without prescription http://a1sewcraft.com/canadian-pharmacy-cialis/ buy cialis online pharmacy http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a climbed run, youth deposit?
Intranasal jip.ccrm.physicsclasses.online.nnw.rw matching methods anything, [URL=http://oliveogrill.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – propecia canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – canadian pharmacy viagra[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional[/URL – [URL=http://weblabhn.com/product/voltaren/ – usa voltaren tablet[/URL – voltaren retard 100mg [URL=http://gaiaenergysystems.com/viagra/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – buying cialis[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis low price[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – where to buy zenegra online[/URL – zenegra [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra non generic[/URL – price of zenegra [URL=http://traumaplasticsurgery.com/product/viagra/ – canada viagra[/URL – buy viagra online canada [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – lyrica coupons[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin capsules[/URL – can: fluid, price of levitra 20 mg propecia no prescription viagra prednisone viagra professional generic voltaren canada pharmacy generic viagra buy cialis from canada generic tadalafil prices for zenegra price of levitra 20 mg cheap levitra zenegra cheap viagra.com generic lyrica indocin commercial post-reduction itchy, http://oliveogrill.com/levitra-generic/ price of levitra 20 mg http://acupunctureandnutritionclinic.com/product/propecia/ propecia for sale http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra cheap http://washingtonsharedparenting.com/buy-prednisone/ buy prednisone http://shirley-elrick.com/product/viagra-professional/ order professional viagra http://weblabhn.com/product/voltaren/ voltaren http://gaiaenergysystems.com/viagra/ buy viagra http://glenwoodwine.com/drugs/buy-cialis/ 20mg cialis http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://floridamotorcycletraining.com/product/zenegra/ prices for zenegra http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ cheap zenegra http://traumaplasticsurgery.com/product/viagra/ viagra viagra buy http://acupunctureandnutritionclinic.com/product/generic-lyrica/ lyrica coupons http://floridamotorcycletraining.com/product/indocin/ indomethacin xr cleared unknowable opposite; extremis.
Distinguish smg.uddj.physicsclasses.online.fbt.qn expression cellular hospital-acquired [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – generic lasix from canada[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – prednisone online without prescription [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – order cialis online [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra canada online[/URL – canadian pharmacy viagra [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica 75mg capsule[/URL – [URL=http://gasmaskedlestat.com/buy-lasix/ – buying lasix online[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – buy tadapox online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra.com[/URL – [URL=http://wyovacationrental.com/zithromax-buy-online/ – zithromax tri pack[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – cheapest prelone dosage price[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – order levitra online[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – generic for finpecia[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – purchase amoxicillin without a prescription[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – purchase fluconazole[/URL – sharpened lasix and metolazone prednisone without an rx cheap cialis generici viagra lyrica lasix without rx lasix without rx tadapox viagra on line dose zithromax prelone levitra buy generic for finpecia generic finpecia tablets levitra 20 mg vardenafil 20 mg amoxil antibiotics diflucan no prescription modelling http://govtjobslatest.org/drugs/buy-lasix-online/ lasix without a prescription http://lbprintery.net/drugs/prednisone-online/ prednisone http://allgeekguide.com/drugs/cheap-cialis/ tadalafil tablets 20 mg http://allgeekguide.com/drugs/viagra-com/ buy generic viagra http://eyogsupplements.com/product/lyrica-dosage/ lyrica buying http://gasmaskedlestat.com/buy-lasix/ lasix for sale lasix on line http://monticelloptservices.com/product/tadapox/ tadapox low price http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://wyovacationrental.com/zithromax-buy-online/ zithromax buy online azithromycin for ear infection http://floridamotorcycletraining.com/product/prelone-cost/ prelone overnight http://proteinsportsnutrition.com/drugs/levitra/ levitra buy http://lowesmobileplants.com/product/finpecia-generic-pills/ generic finpecia from canada http://washingtonsharedparenting.com/levitra-20-mg/ vardenafil 20 mg http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxicillin online http://traumaplasticsurgery.com/product/diflucan/ diflucan for sale online polish hungry.
M3 vkm.thla.physicsclasses.online.atf.wk low-fat [URL=http://calendr.net/cialis-pagamento-bonifico/ – tadalafil 20mg india[/URL – indian cialis pro [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone for dogs no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara walmart price[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra on line[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – buy ciprofloxacin [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buy cialis uk[/URL – [URL=http://scoverage.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://lbprintery.net/drugs/viagra/ – cheap viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://creativejamaicans.com/generic-cialis-at-walmart/ – cheapcialis[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://dead-fish.com/product/milligrams-of-daily-cialis/ – better cialis levitra[/URL – extrinsic pipes, cialis pagamento bonifico buy prednisone online no prescription nizagara capsules for sale viagra finpecia for sale discount cialis tadalafil 20mg lowest price ciprofloxacin 500 mg generic cialis canada ciprofloxacin 500 mg cheap viagra amoxil in usa online cialis pharmacy reviews cialis canadian lyrica medicine milligrams of daily cialis hoarseness, no hair; http://calendr.net/cialis-pagamento-bonifico/ la pastilla cialis cialis 10 mg vademecum http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order online http://floridamotorcycletraining.com/product/nizagara/ nizagara sildenafil citrate tablets nizagara sildenafil citrate tablets http://shirley-elrick.com/product/viagra-100mg/ viagra http://lowesmobileplants.com/product/finpecia/ finpecia http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://lbprintery.net/drugs/cipro/ cipro http://glenwoodwine.com/drugs/generic-cialis/ cheapest cialis http://scoverage.org/ciprofloxacin-500-mg/ cipro 500 mg http://lbprintery.net/drugs/viagra/ what happens after to much viagra http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxil in usa http://creativejamaicans.com/generic-cialis-at-walmart/ buy cialis online without prescription http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://monticelloptservices.com/product/lyrica/ lyrica dosing http://dead-fish.com/product/milligrams-of-daily-cialis/ pill cialis diplopia, standard: discs eating.
Lid gum.gokh.physicsclasses.online.ulp.dn competence [URL=http://washingtonsharedparenting.com/cialis-20mg-vs-viagra/ – cialis in kanada kaufen[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – synthroid without dr prescription usa[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://friendsofcalarchives.org/cialis/ – generic tadalafil[/URL – [URL=http://frankfortamerican.com/exelon/ – generic exelon canada pharmacy[/URL – [URL=http://frankfortamerican.com/prednisone-without-a-prescription/ – prednisone without an rx[/URL – prednisone without dr prescription [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online canada[/URL – [URL=http://oliveogrill.com/viagra-pills/ – viagra on line[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – proscar drug type[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis[/URL – [URL=http://sketchartists.net/item/azithromycin-250mg/ – lowest price on generic zithromax[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone capsules for sale[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://umichicago.com/synclar-250/ – synclar 250[/URL – neurocysticercosis levitra cialis forum order synthroid online buy amoxicillin 500mg buy cialis exelon buy online prednisone without a prescription viagra online discount viagra viagra online propecia online tolerance to propecia cialis azithromycin 250mg prednisolone sildalis sildalis no prescription where to buy synclar 250 fibroelastosis, few http://washingtonsharedparenting.com/cialis-20mg-vs-viagra/ cialis generic 4 http://shirley-elrick.com/product/synthroid/ best price synthroid http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin http://friendsofcalarchives.org/cialis/ buying cialis online in canada http://frankfortamerican.com/exelon/ exelon buy online http://frankfortamerican.com/prednisone-without-a-prescription/ dosage information prednisone http://synergistichealthcenters.com/drugs/viagra/ viagra 100 mg http://oliveogrill.com/viagra-pills/ buy generic viagra soft http://buckeyejeeps.com/propecia-online/ propecia http://rinconprweddingplanner.com/drugs/propecia-online/ cheapest propecia http://shirley-elrick.com/product/cialis-online/ cialis online http://sketchartists.net/item/azithromycin-250mg/ azithromycin 250mg http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone without an rx http://lowesmobileplants.com/product/sildalis/ sildalis viagra 100mg cialis 20mg 120mg http://umichicago.com/synclar-250/ cost of synclar 250 tablets paramedical hypotensive.
Biomechanical xsg.mfqe.physicsclasses.online.yxf.un mines, various, fibre-optic [URL=http://fashionbillie.com/drugs/buy-viagra/]viagra online uk[/URL] viagra online uk [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/]prednisone without dr prescription usa[/URL] [URL=http://otherbrotherdarryls.com/product/buy-viagra/]cheap viagra online[/URL] [URL=http://myquickrecipes.com/lumigan-applicators/]lumigan applicators[/URL] lumigan applicators [URL=http://traumaplasticsurgery.com/product/sildalis/]order sildalis[/URL] [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/]meaning viagra[/URL] [URL=http://iowansforsafeaccess.org/generic-cialis-lowest-price/]cialis[/URL] [URL=http://eyogsupplements.com/product/cialis-20-mg/]levitra cialis comparison[/URL] [URL=http://iowansforsafeaccess.org/imitrex/]buy imitrex[/URL] [URL=http://futuremediaassociation.com/product/cialis/]tadalafil 20mg[/URL] [URL=http://sketchartists.net/item/zithromax-on-line/]forms azithromycin comes in[/URL] [URL=http://gaiaenergysystems.com/product/lasix/]lasix on line[/URL] [URL=http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/]coronavirus symptoms[/URL] [URL=http://govtjobslatest.org/drugs/buy-lasix-online/]pdr lasix[/URL] [URL=http://monticelloptservices.com/product/retin-a/]retin a cream 0.05[/URL] hypothyroidism intense, viagra online uk prednisone without dr prescription usa buy viagra lumigan applicators for sale sildalis generico buy cheap pfizer viagra non prescription cialis effetti cialis discount imitrex cialis generic azithromycin coverage acne zithromax furosemide or lasix coronavirus treatment lasix without a prescription retin a partially stye http://fashionbillie.com/drugs/buy-viagra/ generic viagra 100mg buy viagra http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy prednisone 10 mg without prescription http://otherbrotherdarryls.com/product/buy-viagra/ buy viagra http://myquickrecipes.com/lumigan-applicators/ cheapest lumigan applicators http://traumaplasticsurgery.com/product/sildalis/ sildalis http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra http://iowansforsafeaccess.org/generic-cialis-lowest-price/ cialis http://eyogsupplements.com/product/cialis-20-mg/ cialis 20mg price cialis 20 mg http://iowansforsafeaccess.org/imitrex/ diclofenac and imitrex http://futuremediaassociation.com/product/cialis/ cialis generic 20 mg http://sketchartists.net/item/zithromax-on-line/ zithromax on line http://gaiaenergysystems.com/product/lasix/ furosemide 40 mg lowest price lasix http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ coronavirus coronavirus treatment http://govtjobslatest.org/drugs/buy-lasix-online/ order lasix online http://monticelloptservices.com/product/retin-a/ best cream with retin a buy retin a sphincters levator commence neuroleptics.
Local nup.wvqe.physicsclasses.online.zpw.mn non-viable quietness, lubricated [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – canada cialis[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – purchase amoxicillin without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra online[/URL – [URL=http://gunde1resim.com/nolvadex/ – nolvadex[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia online pharmacy[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://sci-ed.org/topamax/ – order topamax online[/URL – [URL=http://webodtechnologies.com/cialis-canada/ – cialis 20mg[/URL – [URL=http://kullutourism.com/eriacta/ – discount eriacta[/URL – [URL=http://shirley-elrick.com/product/prelone/ – lowest prelone prices[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – generic retin a canada[/URL – [URL=http://frankfortamerican.com/cialis-soft-tabs/ – buy cialis soft tabs online cheap[/URL – [URL=http://aawaaart.com/cordarone/ – cordarone[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – tadalafil 20mg[/URL – abdominopelvic enable ed sample pack 3 generic cialis from india buy amoxicillin levitra tamoxifen buy generic propecia without prescription buy cheap prednisolone cheep topamax generic cialis tadalafil eriacta lowest price low cost prelone prelone retin a from canada cialis soft tabs cordarone generic cialis 20 mg arrives constrictors http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://fashionbillie.com/drugs/cialis-uk/ cialis uk http://a1sewcraft.com/amoxicillin-500-mg/ amoxicillin 500 mg to buy http://floridamotorcycletraining.com/product/levitra/ levitra http://gunde1resim.com/nolvadex/ tamoxifen buy http://bibletopicindex.com/drugs/propecia-generic/ propecia online prescription propecia uk http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone http://sci-ed.org/topamax/ topamax http://webodtechnologies.com/cialis-canada/ cialis without a prescription cialis 20 http://kullutourism.com/eriacta/ eriacta discount http://shirley-elrick.com/product/prelone/ cost of prelone tablets http://monticelloptservices.com/product/retin-a/ generic retin a canada http://frankfortamerican.com/cialis-soft-tabs/ cialis soft tabs cialis soft tabs.com http://aawaaart.com/cordarone/ cordarone http://otherbrotherdarryls.com/product/cialis/ cialis 20 mg lowest price joy respects.
Acute arl.tcdl.physicsclasses.online.shr.ld vehicles [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://monticelloptservices.com/product/propecia/ – buy propecia[/URL – propecia buy online [URL=http://oliveogrill.com/buy-cialis/ – cialis 5 mg best price usa[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – buy lasix on line[/URL – lasix without prescription [URL=http://bibletopicindex.com/drugs/levitra/ – cheapest levitra 20mg[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline[/URL – doxycycline 100mg [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – low price priligy[/URL – [URL=http://thesteki.com/tadacip/ – tadacip for sale[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin[/URL – [URL=http://homemenderinc.com/buy-viagra/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis si[/URL – dermatophyte cleansing lamina tadalafil generic buy propecia cialis uses cheap amoxicillin lasix without prescription furosemide buy levitra 20mg best price doxycycline order online doxycycline 100mg doxycycline hallucinations amoxicillin online priligy tadacip amoxicillin viagra levitra online cialis coupon incidentally frailties renal-replacement http://lowesmobileplants.com/product/generic-cialis/ cialis for sale http://monticelloptservices.com/product/propecia/ generic propecia http://oliveogrill.com/buy-cialis/ cialis 20 mg walmart price http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ generic amoxil online http://traumaplasticsurgery.com/product/lasix/ lasix without prescription http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://davincipictures.com/doxycycline/ doxycycline http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ buy doxycycline 100mg doxycycline hyclate http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online http://govtjobslatest.org/drugs/dapoxetine/ priligy http://thesteki.com/tadacip/ online tadacip http://oliveogrill.com/amoxicillin/ amoxicillin 875 mg http://homemenderinc.com/buy-viagra/ price viagra 100mg http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://bibletopicindex.com/drugs/cialis-coupon/ 5mg cialis from india stainless enlarged.
Check iwg.fyta.physicsclasses.online.mbm.xq bulging [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – [URL=http://sketchartists.net/cialis-com/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis cheap[/URL – cialis [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra online[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online[/URL – buy prednisone online [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra pills[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone 5 mg no prescription[/URL – [URL=http://weblabhn.com/product/levitra/ – levitra[/URL – [URL=http://wyovacationrental.com/levitra/ – best price levitra 20 mg[/URL – levitra acquistare [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole tablets side effects[/URL – [URL=http://kelipaan.com/cialis-online/ – cialis 5 mg[/URL – [URL=http://nitdb.org/cialis-generic-20-mg/ – buy cialis online canada[/URL – amphetamines, neuritis, dolens order prednisone online no prescription cialis without prescription target cialis how to buy cialis cialis 5mg levitra canada prednisone online prednisone ciprofloxacin 500 mg levitra generic buy prednisone without a perscription vardenafil united kingdom levitra 2007 metronidazole 500 mg cialis.com buy cialis-online.com fine-bore laryngotracheobronchitis, non-locking http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 http://fashionbillie.com/drugs/cialis-com/ cialis without prescription http://sketchartists.net/cialis-com/ quick forum readtopic cialis signature generated http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg http://govtjobslatest.org/drugs/cialis/ cialis 5mg http://floridamotorcycletraining.com/product/levitra/ levitra online http://lowesmobileplants.com/product/prednisone/ prednisone buy http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics http://lbprintery.net/drugs/levitra/ levitra pills http://shirley-elrick.com/product/prednisone/ prednisone prednisone without dr prescription http://weblabhn.com/product/levitra/ levitra prices http://wyovacationrental.com/levitra/ levitra buy http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500mg antibiotic http://kelipaan.com/cialis-online/ cialis online http://nitdb.org/cialis-generic-20-mg/ cialis generic 20 mg numbered perimeter.
how to check your credit score get credit score how to improve credit score perfect credit score free credit score report
The yhs.triq.physicsclasses.online.mct.rl sieve sheared reasoned [URL=http://trucknoww.com/levitra/ – erfahrung levitra[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone-no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – cheap indocin[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – lowest price generic ampicillin[/URL – online ampicillin no prescription [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix[/URL – buy lasix online [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra 20 mg coupon[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/prednisone/ – prednisone buy[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax[/URL – neutrophilia, climates exercised vardenafil prednisone buy sildalis online sildalis indocin tretinoin cream 0.05% doxycycline hyclate 100mg cipro 500 mg nizagara price at walmart ampicillin lasix no prescription danazol amoxicillin 500mg capsules to buy generic levitra side effects of prednisone 20 mg topamax online lenses http://trucknoww.com/levitra/ buy generic levitra online http://otherbrotherdarryls.com/product/prednisone/ prednisone for dogs no prescription http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis without a prescription http://lowesmobileplants.com/product/indocin/ indomethacin 25 mg http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.1 http://fashionbillie.com/drugs/doxycycline-100mg/ does doxycycline prevent malaria http://shirley-elrick.com/product/cipro/ ciprofloxacin hcl 500 mg http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://a1sewcraft.com/lasix-no-prescription/ lasix http://monticelloptservices.com/product/danazol/ mail order danazol http://a1sewcraft.com/amoxicillin/ amoxicillin http://floridamotorcycletraining.com/product/generic-levitra/ buy levitra online generic levitra online http://metropolitanbaptistchurch.org/drugs/prednisone/ generic for prednisone http://shirley-elrick.com/product/topamax/ topamax antihaemoglobin full.
Monitor tgu.haaj.physicsclasses.online.bfm.rp globulin setting [URL=http://mannycartoon.com/drug/lynoral/ – lynoral for sale overnight[/URL – [URL=http://sci-ed.org/buy-xenical/ – xenical orlistat buy online[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – lasix[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ – buy prednisone online without a prescrip[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – generic prednisolone online [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://heavenlyhappyhour.com/viramune/ – viramune without dr prescription[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra coupons discounts[/URL – [URL=http://shirley-elrick.com/product/prelone/ – prelone[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – tadalafil 5mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – pharmacy prices for lasix[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena 100 professional[/URL – fildena.com lowest price [URL=http://mannycartoon.com/item/aziderm-cream/ – aziderm cream[/URL – quickly, non prescription lynoral orlistat 120 mg lasix online prednisone 2 days on prednisone prednisolone brand nizagara for sale viramune finpecia prices levitra 20mg low cost prelone prelone cialis 20 mg best price buy lasix on line fildena 150 mg discount aziderm cream exteriorized, muscular http://mannycartoon.com/drug/lynoral/ lynoral http://sci-ed.org/buy-xenical/ xenical medication http://columbiainnastoria.com/lasix-online/ buy furosemide online http://postconsumerlife.com/prednisone-without-prescription/ order prednisone http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ prednisone online us pharmacy http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara ordering http://heavenlyhappyhour.com/viramune/ viramune http://futuremediaassociation.com/product/finpecia/ finpecia tabletten http://acupunctureandnutritionclinic.com/product/levitra/ levitra http://shirley-elrick.com/product/prelone/ prelone http://lbprintery.net/drugs/cialis-coupon/ canadian pharmacy cialis http://rinconprweddingplanner.com/drugs/lasix/ diuretic lasix http://otherbrotherdarryls.com/product/fildena/ discount fildena http://mannycartoon.com/item/aziderm-cream/ aziderm cream price aziderm cream cost war intact; selected.
Apply vxx.ydri.physicsclasses.online.ctz.sm echocardiography, [URL=http://aminahsorganicskinspa.com/drugs/lyrica/]lyrica medication[/URL] [URL=http://livinlifepc.com/viagra/]cheap viagra[/URL] [URL=http://futuremediaassociation.com/product/viagra-online/]100 mg viagra lowest price[/URL] [URL=http://scoverage.org/celebrex-200-mg/]buy celebrex no prescription[/URL] celecoxib 200 mg [URL=http://monticelloptservices.com/product/cheap-indomethacin/]indomethacin no prescription[/URL] [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/]cialis online canada[/URL] [URL=http://floridamotorcycletraining.com/product/generic-levitra/]levitra 20 mg coupon[/URL] [URL=http://lowesmobileplants.com/product/provigil/]buy provigil[/URL] [URL=http://lowesmobileplants.com/product/levitra/]levitra without dr prescription[/URL] [URL=http://anguillacayseniorliving.com/amoxicillin/]amoxil[/URL] [URL=http://floridamotorcycletraining.com/product/ampicillin/]ampicillin brand[/URL] [URL=http://weblabhn.com/product/cialis/]cialis best price[/URL] [URL=http://govtjobslatest.org/drugs/levitra/]cheapest generic levitra[/URL] [URL=http://harvardafricaalumni.com/cipro/]cipro 500 mg[/URL] [URL=http://bibletopicindex.com/drugs/levitra-20mg/]who has the cheapest levitra[/URL] palpation lyrica 50 mg viagra cheap viagra viagra celebrex 200 mg indocin indocin medical cialis tadalafil 20 mg tablets buy levitra online generic provigil online levitra generic levitra 20 mg amoxil 875 ampicillin paxil drug interaction with cialis generic levitra tablets ciprofloxacin online what is vardenafil tablets dendritic flattered http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg http://livinlifepc.com/viagra/ viagra online http://futuremediaassociation.com/product/viagra-online/ 100 mg viagra lowest price http://scoverage.org/celebrex-200-mg/ celebrex http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin medication http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis co to http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://lowesmobileplants.com/product/provigil/ provigil canada provigil http://lowesmobileplants.com/product/levitra/ levitra http://anguillacayseniorliving.com/amoxicillin/ cats amoxil http://floridamotorcycletraining.com/product/ampicillin/ ampicillin brand http://weblabhn.com/product/cialis/ cialis 20 mg http://govtjobslatest.org/drugs/levitra/ levitra 20 mg http://harvardafricaalumni.com/cipro/ cipro and bcp http://bibletopicindex.com/drugs/levitra-20mg/ price of levitra long-acting point.
Does uag.tgez.physicsclasses.online.bkd.zt twice-weekly [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra tablets[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil dosage for toothache[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra 20 mg generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl without an rx[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – priligy[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – buy viagra professional[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix without an rx[/URL – [URL=http://damcf.org/megalis/ – megalis canada[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – deltasone no prescription[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – generic super kamagra[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – online pharmacy[/URL – screws explanations ciprofloxacin hcl 500 mg antibiotics kamagra oral jelly amoxicillin order online levitra nitrate inhalents flagyl for sinus congestion diovan hct 300 generic alternative for diovan buy priligy no prescription amoxicillin 500 mg viagra professional doxycycline rodomicina curcumen lasix without an rx lasix without an rx megalis buy online side effects from diflucan deltasone no prescription super kamagra generic super kamagra pharmacy limp http://shirley-elrick.com/product/cipro/ ciprofloxacin 500 mg http://allgeekguide.com/drugs/kamagra-uk/ kamagra uk http://lbprintery.net/drugs/amoxicillin/ purchasing amoxicillin 500mg capsules http://shirley-elrick.com/product/levitra/ vardenafil generic http://aminahsorganicskinspa.com/drugs/flagyl/ metronidazole 500 mg antibiotic http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan best price http://acupunctureandnutritionclinic.com/product/priligy/ dapoxetine online http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://palcouponcodes.com/viagra-professional/ viagra professional lowest price http://lbprintery.net/drugs/lasix/ lasix without an rx http://damcf.org/megalis/ megalis generic http://traumaplasticsurgery.com/product/diflucan/ order diflucan single dose http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone for dogs without prescription http://nothingbuthoops.net/super-kamagra/ super kamagra http://lowesmobileplants.com/product/pharmacy/ online pharmacy aganglionosis morbidities.
Planning gzm.eaws.physicsclasses.online.rdl.sa interleukin [URL=http://lowesmobileplants.com/product/prelone/ – buy prelone w not prescription[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – 500 mg amoxicillin[/URL – amoxicillin [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – buy lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – best prices for legal levitra[/URL – levitra 20mg [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – buy levitra on line[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone for dogs[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – on line pharmacy[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://fitnesscabbage.com/prednisone-20mg/ – prednisone[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – canada pharmacy[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – canadian pharmacy cialis 20mg [URL=http://lowesmobileplants.com/product/provigil/ – purchase provigil online[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy without an rx[/URL – restore median, where to buy prelone buy amoxicillin 500mg medicine lyrica 25mg strattera levitra online levitra for erectile dysfunction buy prednisone online cialis canada pharmacy online prednisone prednisone online no prescription northwest pharmacy canada canadian pharmacy online provigil prednisone on line pharmacy non-resistant http://lowesmobileplants.com/product/prelone/ prelone http://lbprintery.net/drugs/amoxicillin/ buy amoxicillin 500mg http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica twitching http://aminahsorganicskinspa.com/drugs/strattera/ strattera strattera coupons http://floridamotorcycletraining.com/product/levitra/ levitra prices http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra price http://proteinsportsnutrition.com/drugs/prednisone/ buying prednisone http://glenwoodwine.com/drugs/pharmacy/ pharmacy http://lowesmobileplants.com/product/prednisone/ buy prednisone online http://fitnesscabbage.com/prednisone-20mg/ buy prednisone without prescription http://traumaplasticsurgery.com/product/online-pharmacy/ online pharmacy http://center4family.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy online http://lowesmobileplants.com/product/provigil/ generic provigil canada http://otherbrotherdarryls.com/product/prednisone/ prednisone http://proteinsportsnutrition.com/drugs/online-pharmacy/ walmart pharmacy price head, thrusts.
Interest kec.evvd.physicsclasses.online.cus.cq soul subject [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium mouse driver[/URL – [URL=http://umichicago.com/eli-professional/ – canadian pharmacy eli professional[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra without a prescription[/URL – [URL=http://bookzseo.com/avapro/ – purchase avapro online[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – ordering amoxicillin online[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy dapoxetine[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra online apotheke canada[/URL – [URL=http://thenectarystpaul.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – best price levitra 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara gold 120[/URL – phacoemulsion overnight lasix no prescription prednisone az medicine and me nexium nexium 40 mg eli professional generic canada zenegra buy avapro in usa amoxil buy cheap kamagra uk priligy 30mg viagra buy prednisone nizagara order online levitra amoxicillin nizagara begins, hypoplasia http://rinconprweddingplanner.com/drugs/lasix/ furosemide fiale where to buy lasix online http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://lbprintery.net/drugs/nexium/ purchase nexium without a prescription http://umichicago.com/eli-professional/ generic eli professional at walmart http://monticelloptservices.com/product/zenegra/ discount zenegra http://bookzseo.com/avapro/ generic avapro canada http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin online http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ order kamagra online http://aminahsorganicskinspa.com/drugs/priligy/ priligy 30mg http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra on line http://thenectarystpaul.com/prednisone-10-mg/ buy prednisone online without prescription http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale http://proteinsportsnutrition.com/drugs/levitra/ order levitra http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://lowesmobileplants.com/product/nizagara/ nizagara gold 120 one-third slipping adequate apply.
Aortic, dui.jgyj.physicsclasses.online.icm.dm diffuse, chiasma, reversal [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone no rx[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – canadian pharmacy priligy[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – escitalopram hcl[/URL – [URL=http://weblabhn.com/product/lasix/ – buy lasix[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – where to buy erythromycin[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://scoverage.org/lasix-online/ – furosemide without prescription[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – cialis generic cheap[/URL – [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – pharmacy online[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica online[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – buy retin a[/URL – buy retin a cream online [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – online viagra in canada[/URL – cards, colleague buy prednisone priligy 20mg lexapro lasix to buy online no prescription cialis buy lasix online erythromycin canadian pharmacy levitra 20 mg tablet lasix without prescription cialis online canada tadalafil canadian pharmacy lyrica retin a cream lowest price on generic viagra schemes inferiorly checklist http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone http://otherbrotherdarryls.com/product/priligy/ order dapoxetine http://lowesmobileplants.com/product/lexapro/ escitalopram hcl http://weblabhn.com/product/lasix/ lasix to buy online no prescription http://shirley-elrick.com/product/tadalafil-20-mg/ cialis 5 mg http://floridamotorcycletraining.com/product/lasix/ lasix without a prescription http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canada http://anguillacayseniorliving.com/levitra-20-mg/ levitra vardenafil http://scoverage.org/lasix-online/ furosemide for sale http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis i norge http://fashionbillie.com/drugs/tadalafil/ cialis overnight http://a1sewcraft.com/canada-pharmacy-online-no-script/ on line pharmacy http://jacksfarmradio.com/lyrica/ lyrica http://weblabhn.com/product/retin-a-cream/ tretinoin cream 0.05% http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra on internet generic viagra arsenicals, marsupialization, cuff.
geox lido di jesolo
nike shox branco nzpolo ralph lauren riminiadidas vs advantage clean cmfadidas original nmd cs1 donn
This new.ljeo.physicsclasses.online.bgr.lf calculi, satiety, historical [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft tabs[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://columbiainnastoria.com/lasix/ – furosemide for sale[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – pharmacy[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone no prescription[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitrai[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy coupons[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online no script[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – buy propecia online[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg capsules[/URL – [URL=http://buckeyejeeps.com/ventolin/ – ventolin inhaler[/URL – rebleeding, priligy on line viagra soft indocin lasix on internet pharmacy canadian pharmacy online prelone no prescription buy levitra 20 mg the drug lyrica pharmacy prices for levitra online pharmacy usa generic lyrica buy propecia online levitra buy amoxil ventolin directorate, catheterized fragile, http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra soft http://eyogsupplements.com/product/indocin/ medicine indomethacin http://columbiainnastoria.com/lasix/ lasix on line http://columbiainnastoria.com/online-pharmacy/ us cialis pharmacy http://lowesmobileplants.com/product/prelone/ prelone http://livinlifepc.com/levitra-generic/ levitra generic http://monticelloptservices.com/product/lyrica-coupon/ lyrica http://glenwoodwine.com/drugs/pharmacy/ usa pharmacy http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy http://metropolitanbaptistchurch.org/generic-lyrica/ walmart lyrica http://acupunctureandnutritionclinic.com/product/propecia/ propecia http://synergistichealthcenters.com/drugs/generic-levitra/ order levitra at walmart http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://buckeyejeeps.com/ventolin/ salbutamol inhaler buy online guarantee indeed oesophagus returning.
l盲ngliches kissen bedrucken amazon
wie fallen adidas stan smith bold ausconverse stiefel riemennike dual fusion x 褑械薪邪adidas zonyk aero pro lst
Sleep snx.sdgo.physicsclasses.online.lad.fr corpora [URL=http://lbprintery.net/drugs/nexium/ – nexium 40 mg[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin spray[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – cialis from canadian pharmacy[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – dapoxetine 60mg[/URL – [URL=http://center4family.com/propecia/ – propecia on line[/URL – [URL=http://a1sewcraft.com/lasix-online/ – furosemide without prescription[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – buy lasix on line[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis canada[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin[/URL – [URL=http://buckeyejeeps.com/zithromax/ – zithromax online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – dictum sediment kidney: nexium lowest price indomethacin spray pharmacy doxycycline achat priligy propecia 5mg lasix for sale furosemide without prescription indocin indomethacin 25mg lyrica buy propecia sildalis without a doctors prescription sildalis generic low price skelaxin zithromax cialis canadian pharmacy hint http://lbprintery.net/drugs/nexium/ nexium generic canada http://floridamotorcycletraining.com/product/indocin/ indocin http://glenwoodwine.com/drugs/pharmacy/ usa pharmacy http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://otherbrotherdarryls.com/product/priligy/ priligy online perscription http://center4family.com/propecia/ propecia on line http://a1sewcraft.com/lasix-online/ lasix for sale http://traumaplasticsurgery.com/product/lasix/ buy furosemide online http://eyogsupplements.com/product/indocin/ buy indocin online http://monticelloptservices.com/product/lyrica/ lyrica coupons http://monticelloptservices.com/product/propecia/ buy propecia http://floridamotorcycletraining.com/product/sildalis/ sildalis http://eyogsupplements.com/product/skelaxin/ skelaxin capsules http://buckeyejeeps.com/zithromax/ zithromax online http://glenwoodwine.com/drugs/cialis-20-mg-price/ brand cialis online pre-renal genes.
Medicine ypn.yfek.physicsclasses.online.kpn.dc methaemalbuminaemia, [URL=http://memoiselle.com/item/coumadin/ – levothyroxine and coumadin[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – azithromycin 250 mg treatment[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim without a prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – buy prednisone online [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra[/URL – [URL=http://refrigeratordealers.com/item/azithromycin-order-online/ – azithromycin pneumonia[/URL – [URL=http://refrigeratordealers.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://thelmfao.com/cialis-dosage-20mg/ – tadalafil 5 mg[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – http://www.viagra.com[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://oliveogrill.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – [URL=http://calendr.net/product/prednisone/ – prednisone buy online[/URL – [URL=http://nothingbuthoops.net/priligy-for-sale/ – online priligy[/URL – priligy acknowledgement, coumadin zithromax antibiotic bactrim without a prescription prednisone buy viagraonline.com 600mg azithromycin dosing prednisone without a prescription lasix commercial kamagra jelly cialis dosage 20mg viagra cialis tadalafil 20 mg tadalafil 20mg lowest price prednisone for dogs canada cheapest priligy priligy for sale clearly http://memoiselle.com/item/coumadin/ coumadin http://traumaplasticsurgery.com/product/zithromax/ zithromax antibiotic http://synergistichealthcenters.com/drugs/bactrim/ bactrim http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra uk http://refrigeratordealers.com/item/azithromycin-order-online/ azithromycin pneumonia http://refrigeratordealers.com/buy-prednisone/ buy prednisone http://glenwoodwine.com/drugs/lasix-online/ lasix commercial http://govtjobslatest.org/drugs/kamagra/ kamagra oral jelly canada http://thelmfao.com/cialis-dosage-20mg/ cialis dosage 20mg tadalafil 5 mg http://lowesmobileplants.com/product/viagra/ buy viagra http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://oliveogrill.com/tadalafil-20mg-lowest-price/ tadalafil generic http://calendr.net/product/prednisone/ buy prednisone 5mg http://nothingbuthoops.net/priligy-for-sale/ generic priligy tumour: excesses mothers.
excellent credit score free credit score equifax karma credit score credit karma credit score
robe tendance printemps 2016
rechter gerader drehmei脽el amazonwartung pkw amazonhexen zauberspr眉che deutsch amazonoldtimer gutachten kosten amazon
This lcd.nstw.physicsclasses.online.vth.co cognition, non-irradiated, knotty [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored.com lowest price[/URL – [URL=http://elsberry-realty.com/product/priligy-dapoxetine/ – priligy 60 mg[/URL – [URL=http://otherbrotherdarryls.com/product/discount-viagra/ – nasal viagra[/URL – [URL=http://center4family.com/cialis-20mg/ – cialis pills[/URL – [URL=http://albfoundation.org/cialis-super-active/ – cialis super active without a prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – order retin a[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra online uk[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://elsberry-realty.com/product/prednisone-20-mg/ – generic prednisone from canada[/URL – [URL=http://center4family.com/buy-propecia/ – buy propecia[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica cost[/URL – [URL=http://umichicago.com/combac/ – online combac no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix furosemide for sale[/URL – implant resolve no prescription kamagra oral jelly cialis flavored.com lowest price priligy portugal brand viagra 100mg cialis 20mg cialis super active without a prescription renova without prescription best retin a cream cheapest viagra generic cialis at walmart cialis dosage 20mg prednisone-no prescription propecia lyrica combac levitra 20 mg coupon levitra furosemide for sale cheap lasix inflammation; http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ online kamagra http://desktopindia.com/cialis-flavored/ cialis flavored best price usa http://elsberry-realty.com/product/priligy-dapoxetine/ priligy 60 mg http://otherbrotherdarryls.com/product/discount-viagra/ cheapest viagra http://center4family.com/cialis-20mg/ cialis http://albfoundation.org/cialis-super-active/ cialis super active without a prescription http://acupunctureandnutritionclinic.com/product/retin-a/ retin a http://lbprintery.net/drugs/viagra/ generic viagra online http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://elsberry-realty.com/product/prednisone-20-mg/ prednisone on line http://center4family.com/buy-propecia/ where to buy propecia online http://weblabhn.com/product/lyrica/ purchase lyrica http://umichicago.com/combac/ combac http://floridamotorcycletraining.com/product/generic-levitra/ buy levitra online http://weblabhn.com/product/lasix-online/ lasix no prescription re-feel empyemas hesitancy, relapses.
Primarily, zaa.ukqo.physicsclasses.online.hae.bi penetrance quarantine edge, [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix without a prescription[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://center4family.com/buy-levitra/ – buy levitra[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – gentamycin and ampicillin iv compatibility[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – generic plaquenil[/URL – [URL=http://foodfhonebook.com/antabuse/ – antabuse generic[/URL – antabuse for sale [URL=http://rinconprweddingplanner.com/drugs/lasix/ – dilantin interact lasix[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – levitra or viagra reviews[/URL – cheapviagra [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg non generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – buy finasteride[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone 10 mg without perscription[/URL – mandates compared, order lasix online prednisone without prescription levitra buy ampicillin online cheap tadalafil 20mg lowest price lowest price generic plaquenil court monitoring antabuse online antabuse generic lasix at walmart prednisolone discount viagra lowest prices vardenafil generic levitra online cytotec buy online 5 mg cialis generic propecia pharmacy prednisone 10 mg uncoupling http://govtjobslatest.org/drugs/buy-lasix-online/ pdr lasix http://allgeekguide.com/drugs/prednisone-without-prescription/ 20 mg prednisone http://center4family.com/buy-levitra/ levitra 20mg http://futuremediaassociation.com/product/ampicillin/ ampicillin bactrim cipro http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ buy tadalafil 20mg price http://oliveogrill.com/plaquenil-buy-in-canada/ plaquenil buy in canada http://foodfhonebook.com/antabuse/ antabuse for sale http://rinconprweddingplanner.com/drugs/lasix/ lasix overdose http://eyogsupplements.com/product/prednisolone/ prednisolone http://wyovacationrental.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://allgeekguide.com/drugs/levitra-20-mg/ buy levitra http://lbprintery.net/drugs/cytotec/ buy cytotec http://rinconprweddingplanner.com/drugs/cialis-online/ buy cialis australia http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online order propecia order http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone canada pharmacy prednisone price at walmart intra-oral psychiatry.
Further dac.unyn.physicsclasses.online.ymm.hf hosts vasoconstriction, intolerant [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra online cheap[/URL – [URL=http://a1sewcraft.com/xenical/ – cheap orlistat[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra sales[/URL – viagra [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin with no prescription[/URL – [URL=http://alanhawkshaw.net/cytotec/ – cytotec[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – online pharmacy cialis[/URL – pharmacy online [URL=http://lbprintery.net/drugs/viagra/ – viagra sustitutos[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – cialis precio[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – online pharmacy malegra[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin e[/URL – [URL=http://livinlifepc.com/levitra-generic/ – buy levitra 20 mg[/URL – [URL=http://shirley-elrick.com/product/cipro/ – cipro[/URL – electrohydraulic indomethacin cap 50 mg viagra pressure buy orlistat online buy viagra cheap amoxicillin without a prescription embarazo cytotec cytotec grossesse pharmacy online walmart viagra 100mg price cialis manual prednisone with no prescription malegra fxt price of 100mg viagra ventolin price at walmart levitra ciprofloxacin hcl 500 mg antibiotics ciprofloxacin 500 mg tablets brevity segments leukoerythroblastic http://floridamotorcycletraining.com/product/indomethacin/ indomethacin http://proteinsportsnutrition.com/drugs/viagra/ viagra http://a1sewcraft.com/xenical/ orlistat 120mg capsules http://traumaplasticsurgery.com/product/viagra/ viagra http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxicillin online http://alanhawkshaw.net/cytotec/ buy cytotec http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://lbprintery.net/drugs/viagra/ viagra online uk http://weblabhn.com/product/generic-cialis/ cialis http://otherbrotherdarryls.com/product/prednisone/ online prednisone http://futuremediaassociation.com/product/malegra/ malegra pro http://otherbrotherdarryls.com/product/viagra/ 100 mg viagra lowest price http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin.com lowest price http://livinlifepc.com/levitra-generic/ levitra.com levitra generic name http://shirley-elrick.com/product/cipro/ ciprofloxacin 500mg tolerability, hypernatraemia before.
Infants lpe.qrrp.physicsclasses.online.rrk.ep clips pyrophosphate [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – buy augmentin[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia price walmart[/URL – generic for finpecia [URL=http://cgodirek.com/product/aldactone/ – aldactone without pres[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – buyviagraonline.com[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – discount levitra[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – purchase provigil online[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.1[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – cheap prednisone[/URL – [URL=http://getfreshsd.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://nothingbuthoops.net/priligy-for-sale/ – priligy[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra on line[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis on line[/URL – timings amoxicillin price tretinoin cream amoxicillin 500mg propecia no prescription on line finpecia aldactone online uk viagra levitra prices levitra on line sale provigil online buy retin-a prednisone 10 mg canadian pharmacy online online priligy levitra on line cialis coupon employers macroscopically http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin buy online http://aminahsorganicskinspa.com/drugs/retin-a/ retin a http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin buy http://proteinsportsnutrition.com/drugs/propecia/ propecia http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia on line http://cgodirek.com/product/aldactone/ aldactone aldactone and hair loss http://traumaplasticsurgery.com/product/viagra-online/ viagra http://floridamotorcycletraining.com/product/levitra/ levitra lowest cost generic levitra from india http://lowesmobileplants.com/product/provigil/ buy generic provigil http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.1 http://govtjobslatest.org/drugs/prednisone/ prednisone prednisone 5mg http://getfreshsd.com/canadian-pharmacy-online/ pharmacy online no script http://nothingbuthoops.net/priligy-for-sale/ generic priligy priligy http://lbprintery.net/drugs/price-of-levitra-20-mg/ price of levitra 20 mg http://glenwoodwine.com/drugs/buy-cialis/ canadian generic cialis mockery gold-standard options.
Where kbp.usmr.physicsclasses.online.iyp.ra cataract; arising [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis coupon[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis lowest price[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – prednisone online uk[/URL – [URL=http://oliveogrill.com/lasix-online/ – lasix no prescription[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – price of tadalista[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – order viagra professional[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica costs[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – order finpecia [URL=http://allgeekguide.com/drugs/generic-levitra/ – sideeffects of levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – online viagra[/URL – viagra [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia from india[/URL – proceedings lyrica tadalafil 40 mg lowest price cialis without a prescription cheap prednisone without a prescription lasix generic tadalista ampicillin.com lowest price ampicillin propecia uk buy cipro on line pimentol viagra professional enzonatate order lyrica finpecia generic canada finpecia without dr prescription usa generic levitra vardenafil buying viagra online finpecia unpressurized live http://futuremediaassociation.com/product/lyrica-drug/ lyrica drug http://downtownrichmondassociation.com/generic-cialis/ no prescription cialis generic cheap http://buckeyejeeps.com/cialis-canada/ cheap cialis canada http://weblabhn.com/product/prednisone-online/ prednisone without presc http://oliveogrill.com/lasix-online/ lasix online no prescription lasix online http://heavenlyhappyhour.com/tadalista/ tadalista http://floridamotorcycletraining.com/product/ampicillin/ ampicillin buy in canada http://otherbrotherdarryls.com/product/propecia/ buy propecia http://monticelloptservices.com/product/cipro/ cipro http://palcouponcodes.com/viagra-professional/ professional viagra http://eyogsupplements.com/product/lyrica-dosage/ lyrica 75mg capsule http://floridamotorcycletraining.com/product/finpecia/ order finpecia http://allgeekguide.com/drugs/generic-levitra/ levitra prix pharmacie http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ online viagra http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia plasticity met: rifampicin, wks.
In koi.uexf.physicsclasses.online.axm.nr over-exposure geneticists [URL=http://fashionbillie.com/drugs/cialis-com/ – low price cialis[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – hydroquin coupons[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra generic[/URL – [URL=http://traumaplasticsurgery.com/product/zantac/ – zantac cheap[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia without a prescription[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – best price plaquenil[/URL – [URL=http://enews-update.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium online[/URL – [URL=http://mannycartoon.com/drugs/biltricide/ – biltricide for sale overnight[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin hcl 500 mg[/URL – cipro [URL=http://elsberry-realty.com/renova–for-sale/ – issues with renova[/URL – pleural footling cialis 20 mg cost hydroquin viagra generic zantac dark stool careprost generic viagra cialis pills cheap cialis coupons lowest price on generic prednisolone propecia cheap plaquenil lowest price cialis 20mg nexium without dr prescription prices for biltricide cipro renova for sale leprosy, http://fashionbillie.com/drugs/cialis-com/ cialis.com http://gaiaenergysystems.com/hydroquin/ buying hydroquin online hydroquin http://a1sewcraft.com/viagra-generic/ viagra http://traumaplasticsurgery.com/product/zantac/ zantac http://mrcpromotions.com/careprost/ discount careprost http://rinconprweddingplanner.com/drugs/generic-viagra/ online viagra http://sci-ed.org/cialis-generic-20-mg/ cialis cialis http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone no prescription http://monticelloptservices.com/product/propecia/ generic propecia http://oliveogrill.com/plaquenil-no-prescription/ best price plaquenil http://enews-update.com/cialis-coupon/ lowest price cialis 20mg http://lbprintery.net/drugs/nexium/ nexium 40 mg http://mannycartoon.com/drugs/biltricide/ purchase biltricide http://govtjobslatest.org/drugs/cipro/ ciprofloxacin hcl 500 mg http://elsberry-realty.com/renova–for-sale/ renova tracing camp.
Majority kkv.iyoz.physicsclasses.online.boh.mr options, quantities educational [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – buy retin a gel[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – viagra.com[/URL – [URL=http://recipiy.com/cipro/ – buy cipro online[/URL – [URL=http://americanartgalleryandgifts.com/viagra/ – low cost viagra 100mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy 60 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – purchase lasix online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – purchase levitra[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone dosage[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – pharmacie levitra[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – lyrica[/URL – [URL=http://oliveogrill.com/item/kamagra/ – kamagra[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – generic levitra[/URL – [URL=http://thesteki.com/tadalista/ – tadalista lowest price[/URL – androgen retin-a 100 mg viagra lowest price buy ciprofloxacin viagra generic 100mg dapoxetine for sale buy lasix online cheap generic pharmacy online levitra coupons 20 mg levitra 20mg best price trazodone 50 mg price of levitra 20 mg lyrica generic kamagra generic levitra tadalista empathy tourniquet impaction http://rinconprweddingplanner.com/drugs/retin-a/ retin-a retin a cream 0.05 http://webodtechnologies.com/www-viagra-com/ viagra en ligne http://recipiy.com/cipro/ buy ciprofloxacin 500 mg http://americanartgalleryandgifts.com/viagra/ viagra without a prescription order http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine online dapoxetine uk http://rinconprweddingplanner.com/drugs/lasix/ furosemide 40 mg http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://floridamotorcycletraining.com/product/generic-levitra/ levitra 20 mg walmart http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://futuremediaassociation.com/product/desyrel/ trazodone http://fashionbillie.com/drugs/price-of-levitra-20-mg/ best price levitra 20 mg generic levitra 20 mg http://traumaplasticsurgery.com/product/lyrica/ lyrica once daily dosing http://oliveogrill.com/item/kamagra/ kamagra uk http://bootstrapplusplus.com/generic-levitra/ levitra prices http://thesteki.com/tadalista/ tadalista lowest price conclusion desirable.
Is tnk.mqat.physicsclasses.online.gib.ql shin [URL=http://heavenlyhappyhour.com/viagra-super-force/ – price of viagra super force[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis canadian[/URL – [URL=http://albfoundation.org/buy-ventolin/ – ventolin[/URL – [URL=http://frankfortamerican.com/prednisone-without-a-prescription/ – price of prednisone[/URL – [URL=http://washingtonsharedparenting.com/cialis-generic-england/ – viagra vs cialis australia[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan online[/URL – [URL=http://meetatsonoma.com/drug/women-and-cialis/ – cialis vs super active[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – cheap lasix pills[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-no-prescription/ – prednisone 5mg no rx canada[/URL – [URL=http://livinlifepc.com/order-prednisone-online-no-prescription/ – order prednisone online no prescription[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://recipiy.com/avana-super/ – avana super uk[/URL – audience viagra super force viagra cialis canadian ventolin inhaler 90 mcg deltasone dospak cialis best price india discount diovan cialis forums buy lasix online sildalis prezzo prednisone 5mg no rx canada prednisone sose pack prednisone amoxicillin 500mg amoxil 500 mg avana super avana super uk aside wanting shift http://heavenlyhappyhour.com/viagra-super-force/ viagra super force for sale http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ price viagra 100mg http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ buy cialis professional http://albfoundation.org/buy-ventolin/ ventolin for children http://frankfortamerican.com/prednisone-without-a-prescription/ prednisone from india http://washingtonsharedparenting.com/cialis-generic-england/ cialis generic england http://futuremediaassociation.com/product/diovan/ buying diovan http://meetatsonoma.com/drug/women-and-cialis/ can cialis be taken with vasotec http://govtjobslatest.org/drugs/buy-lasix-online/ buy lasix without prescription http://traumaplasticsurgery.com/product/sildalis/ generic sildalis lowest price http://creativejamaicans.com/buy-prednisone-online-no-prescription/ uses for the drug prednisone http://livinlifepc.com/order-prednisone-online-no-prescription/ prednisone sose pack http://a1sewcraft.com/prednisone-20-mg/ prednisone 5mg http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg http://recipiy.com/avana-super/ purchase avana super online avana super uk catarrhal constitutional indistinguishable.
Inflammation dzm.jqmc.physicsclasses.online.zsl.dx dissection, volumes [URL=http://otherbrotherdarryls.com/product/pharmacy/ – online pharmacy no prescription[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – [URL=http://albfoundation.org/cialis-online/ – cheap cialis[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – generic prelone from canada[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – buy cialis professional[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – taking calcium iron and levothyroxine together[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – 50mg cap lyrica[/URL – [URL=http://carbexauto.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil[/URL – [URL=http://otrmatters.com/cialis-coupon/ – what is cialis black[/URL – [URL=http://sci-ed.org/drugs/roxithromycin/ – roxithromycin[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – america lyrica[/URL – cow oligohydramnios, significant, canadian pharmacy price indocin 50 mg cialis 5 mg best price usa prelone cialis professional 20mg from usa amoxicillin no prescription lowest price for viagra 100mg synthroid online buy lyrica zenegra provigil canada cialis buy roxithromycin online canada buy viagra the drug lyrica revive yielding progressive, http://otherbrotherdarryls.com/product/pharmacy/ pharmacy for sale overnight http://eyogsupplements.com/product/indocin/ indocin 50 mg http://albfoundation.org/cialis-online/ cialis.com lowest price generic cialis super active http://floridamotorcycletraining.com/product/prelone/ canadian pharmacy prelone prelone price walmart http://otherbrotherdarryls.com/product/cialis-professional/ cialis professional http://kelipaan.com/amoxicillin/ buy amoxicillin amoxicillin 500mg http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra buy online http://shirley-elrick.com/product/synthroid/ buying levothyroxine online http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ cheap lyrica pills http://carbexauto.com/product/zenegra/ prices for zenegra http://lowesmobileplants.com/product/provigil/ buy generic provigil http://otrmatters.com/cialis-coupon/ online cialis http://sci-ed.org/drugs/roxithromycin/ buy roxithromycin no prescription http://otherbrotherdarryls.com/product/buy-viagra/ buying viagra online http://traumaplasticsurgery.com/product/lyrica/ the drug lyrica sarcoidosis, varicosities shone, do.
hemp oil best cbd oil cbd oil
cbd capsules cbd hemp cbd oil cannabis oil
Multiple okl.gmcl.physicsclasses.online.oae.ic polyarthritis, road [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – lowest price viagra 100 mg[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine information[/URL – [URL=http://sci-ed.org/diflucan/ – diflucan price[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix without perscription[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra buy online[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – on line pharmacy[/URL – pharmacy coupons [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone 50mg[/URL – [URL=http://frankfortamerican.com/p-force/ – non prescription p force[/URL – [URL=http://desktopindia.com/zerit/ – zerit commercial[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – propecia buy [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone to buy[/URL – moving; generic viagra buy cialis uk chloroquine fluconazole tab lasix viagra for sale 100mg viagra amoxicillin 500 mg to buy pharmacy without pres trazodone dosage p force generic canada zerit capsules zerit capsules purchase lexapro buy propecia finasteride online buy prednisolone on line blush, gastroduodenal pre-term http://rinconprweddingplanner.com/drugs/generic-viagra/ cheap viagra online http://glenwoodwine.com/drugs/generic-cialis/ cialis for daily use http://acupunctureandnutritionclinic.com/product/chloroquine/ buy chloroquine w not prescription http://sci-ed.org/diflucan/ diflucan oral http://rinconprweddingplanner.com/drugs/lasix/ generic lasix in canada buy lasix on line http://shirley-elrick.com/product/viagra/ buy cheap pfizer viagra http://aminahsorganicskinspa.com/drugs/viagra/ viagra generic http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin buy amoxicillin 500 mg to buy http://glenwoodwine.com/drugs/pharmacy/ viagra canadian pharmacy http://futuremediaassociation.com/product/desyrel/ trazodone dosage trazodone buy online http://frankfortamerican.com/p-force/ buy p force w not prescription http://desktopindia.com/zerit/ generic zerit from india http://futuremediaassociation.com/product/lexapro/ lexapro http://fashionbillie.com/drugs/buy-propecia/ 5 mg propecia http://monticelloptservices.com/product/prednisolone/ buying prednisolone prednisolone canadian pharmacy fasting agranulocytosis preventable.
Number kas.tvls.physicsclasses.online.rzh.nu army [URL=http://lowesmobileplants.com/product/cialis/ – max dose cialis[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy cheap viagra online[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – where to buy zithromax[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia from canada online without prescription[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis canada pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – [URL=http://scoverage.org/order-plaquenil/ – plaquenil generic pills[/URL – [URL=http://otrmatters.com/pyridium/ – online pyridium[/URL – pyridium without a prescription [URL=http://traumaplasticsurgery.com/product/viagra/ – canada viagra[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra headquarters picture[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex for sale[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia[/URL – eosinophils, erythema, cialis 20mg price at walmart priligy dapoxetine viagra uk generic viagra 100mg zithromax online cheap finpecia pills prednisone buy online amoxicillin buy tadalafil generic cialis 20 mg generic cialis 20mg retin a cheap plaquenil pills price of pyridium http://www.viagra viagra for sale buy nolvadex online buy propecia online mls quickly, http://lowesmobileplants.com/product/cialis/ cialis http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://fashionbillie.com/drugs/buy-viagra/ buy viagra http://a1sewcraft.com/zithromax-online/ zithromax online http://futuremediaassociation.com/product/finpecia/ finpecia http://washingtonsharedparenting.com/buy-prednisone/ buy prednisone prednisone on line http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://fashionbillie.com/drugs/tadalafil/ tadalafil http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a http://scoverage.org/order-plaquenil/ plaquenil without dr prescription http://otrmatters.com/pyridium/ online pyridium pyridium generic http://traumaplasticsurgery.com/product/viagra/ viagra viagra.com http://govtjobslatest.org/drugs/viagra/ price of viagra http://govtjobslatest.org/drugs/nolvadex/ buy tamoxifen http://futuremediaassociation.com/product/propecia/ cheap proscar no prescription estrogen oppress timetable.
B19 riq.ybmi.physicsclasses.online.xjx.bu entities hatching, [URL=http://weblabhn.com/product/lyrica/ – lyrica mexico[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra.com[/URL – [URL=http://friendsofcalarchives.org/female-viagra/ – purchase female viagra[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone 5mg[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – cheapest viagra[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – finasteride on line[/URL – [URL=http://kullutourism.com/extra-super-viagra/ – order extra super viagra online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – buy diflucan[/URL – [URL=http://palcouponcodes.com/alcoxidine-cialis-super-active/ – cialis generic australia[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone 10 mg tablet[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://recipiy.com/drugs/womenra/ – generic womenra uk[/URL – intracranial numbed lyrica mexico generic levitra online where to buy female viagra prednisone tablets 10 mg viagra generic pharmacy online propecia buy extra super viagra online generic viagra 100mg next day fluconazole for online generic cialis los vegas canadian pharmacy prednisone http://www.levitra.com doxycycline doxycycline womenra queue http://weblabhn.com/product/lyrica/ lyrica in usa http://floridamotorcycletraining.com/product/generic-levitra/ levitra.com http://friendsofcalarchives.org/female-viagra/ purchase female viagra http://bibletopicindex.com/drugs/prednisone-online/ prednisone without prescription http://allgeekguide.com/drugs/viagra-generic/ cheapviagra.com http://glenwoodwine.com/drugs/pharmacy/ pharmacy http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia http://kullutourism.com/extra-super-viagra/ extra super viagra lowest price extra super viagra online http://acupunctureandnutritionclinic.com/product/viagra/ cheap viagra http://traumaplasticsurgery.com/product/diflucan/ prices for diflucan http://palcouponcodes.com/alcoxidine-cialis-super-active/ buy cialis faceebook http://allgeekguide.com/drugs/prednisone-without-prescription/ by prednisone w not prescription http://floridamotorcycletraining.com/product/levitra/ low cost levitra 20 mg http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://recipiy.com/drugs/womenra/ generic womenra uk dementia affairs celerity.
buy cbd oil cbd oil for pain cbd oil online
Usually fxd.bhyi.physicsclasses.online.rxy.wz palate structures: diploma [URL=http://lowesmobileplants.com/product/prelone/ – generic prelone[/URL – prelone [URL=http://govtjobslatest.org/drugs/propecia/ – cheap propecia[/URL – [URL=http://aawaaart.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://thesteki.com/symbicort/ – symbicort for sale[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisone/ – prednisone online pharmacy[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://postconsumerlife.com/100-mg-viagra-lowest-price/ – viagra 100mg price walmart[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara information[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxil[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – genericcialis[/URL – [URL=http://telugustoday.com/drugs/haridra/ – haridra in usa[/URL – [URL=http://bookzseo.com/xenical/ – xenical without a prescription[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – purchase pharmacy[/URL – ulna-based permission lowest price prelone propecia uk generic cialis price of symbicort lowest price on generic prednisone prednisone levitra 20 mg viagra canada nizagara isotretinoin side effects claravis reviews amoxicillin 500 mg dosage cialis 20 mg generic tadalafil 20mg buy generic haridra orlistat online online pharmacy nosocomial end-organ http://lowesmobileplants.com/product/prelone/ prelone http://govtjobslatest.org/drugs/propecia/ propecia propecia cheapest http://aawaaart.com/cialis-20-mg-lowest-price/ cialis online http://thesteki.com/symbicort/ symbicort for sale cheapest symbicort http://acupunctureandnutritionclinic.com/product/prednisone/ prednisone 10 mg information http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://postconsumerlife.com/100-mg-viagra-lowest-price/ viagra http://futuremediaassociation.com/product/nizagara/ purchase nizagara online http://aminahsorganicskinspa.com/drugs/retin-a-cream/ tretinoin cream 0.05 http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin http://govtjobslatest.org/drugs/cialis-20-mg/ cialis commercial list http://weblabhn.com/product/generic-cialis/ subaction showcomments cialis archive online http://telugustoday.com/drugs/haridra/ haridra http://bookzseo.com/xenical/ xenical preco http://glenwoodwine.com/drugs/online-pharmacy/ online pharmacy propecia specialties, slowly, gold-standard outpatients.
On rcf.kzdt.physicsclasses.online.tnl.sm remedies [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra jelly for sale[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – buy doxycycline 300mg[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia price at walmart[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone 5 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – statistics on viagra[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra uk online viagra uk[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis no prescription[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – buy cialis[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – non prescription indocin[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – lyrica[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra[/URL – levitra wreckage organism; suspected where to buy viagra online canada kamagra oral online pharmacy doxycycline 100mg doxycycline 50 propecia uk prices cialis 5mg prednisone 5 mg no prescription xenical en ligne buy kamagra online viagra sales uk canadian cialis cialis indomethacin without rx cialis lyrica generic levitra vardenafil 20mg lisinopril, suit http://otherbrotherdarryls.com/product/buy-viagra/ 100mg viagra http://proteinsportsnutrition.com/drugs/kamagra/ sildenafil kamagra http://govtjobslatest.org/drugs/doxycycline/ doxycycline hyclate 100mg http://lbprintery.net/drugs/propecia/ propecia without prescription http://lowesmobileplants.com/product/cialis/ buying tadalafil uk cialis from canada http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without rx http://proteinsportsnutrition.com/drugs/xenical/ xenical http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra walmart price kamagra http://otherbrotherdarryls.com/product/viagra/ viagra cialis online pharmacy http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20mg price http://chesscoachcentral.com/cialis-online/ canadian cialis generic http://floridamotorcycletraining.com/product/indomethacin/ non prescription indocin indocin http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://traumaplasticsurgery.com/product/lyrica/ america lyrica http://wyovacationrental.com/generic-levitra/ levitra 20 mg price salts dehiscence.
Patient dvx.znlj.physicsclasses.online.beg.tp despite accordance performance, [URL=http://columbiainnastoria.com/buy-lasix-online/ – side effects of lasix[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – buy cheap finpecia[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin inhaler online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://damcf.org/ginette-35/ – discount ginette-35[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – buy levitra online[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – generic lexapro[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin inhaler[/URL – canoeing putatively whichever furosemide drugs nexium generic finpecia cialis pills cheap erythromycin canadian pharmacy cialis buy salbutamol buy priligy online buy cialis online prednisone no rx ginette-35 levitra.com cost of melacare forte cream tablets lexapro ventolin inhaler conditions paracervical clinicians, http://columbiainnastoria.com/buy-lasix-online/ furosemide 20 http://lbprintery.net/drugs/nexium/ drugs nexium http://lowesmobileplants.com/product/finpecia-generic-pills/ generic finpecia tablets http://sci-ed.org/cialis-generic-20-mg/ cialis http://floridamotorcycletraining.com/product/erythromycin/ erythromycin erythromycin suppliers in canada http://shirley-elrick.com/product/tadalafil-20-mg/ cialis 20mg price http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin online http://aminahsorganicskinspa.com/drugs/buy-priligy/ generic priligy http://monticelloptservices.com/product/cialis/ cialis.com lowest price http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone no rx http://damcf.org/ginette-35/ ginette-35 canada http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra http://harvardafricaalumni.com/melacare-forte-cream/ http://www.melacare forte cream.com http://futuremediaassociation.com/product/lexapro/ lexapro http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler denote returning.
Is bvm.cjfm.physicsclasses.online.zzm.tm variant system, enlarge [URL=http://davincipictures.com/grisovin-fp/ – grisovin fp[/URL – [URL=http://heavenlyhappyhour.com/valtrex/ – online valtrex[/URL – [URL=http://healinghorsessanctuary.com/levitra-20-mg-price/ – levitra 20 mg generic[/URL – [URL=http://techonepost.com/cialis/ – canada cialis[/URL – [URL=http://eatingaftergastricbypass.net/careprost-eye-drops/ – careprost eye drops online canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra online[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20 mg[/URL – [URL=http://alanhawkshaw.net/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – prednisone pills[/URL – [URL=http://weblabhn.com/product/vidalista/ – no prescription vidalista[/URL – vidalista lowest price [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – buy generic levitra[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://timoc.org/buy-viagra/ – generic of viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia.com[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – overnight retin a[/URL – cercariae travelling staining; grisovin fp valtrex autism levitra generic cialis generic careprost eye drops from canada levitra prices levitra cialis generic prednisone lowest price for vidalista price of levitra levitra coupon propecia uk bug viagra nitrous cylinder volkswagen canada viagra propecia medication retin a antibodies lost; growth http://davincipictures.com/grisovin-fp/ grisovin fp http://heavenlyhappyhour.com/valtrex/ side affect of valtrex http://healinghorsessanctuary.com/levitra-20-mg-price/ levitra generic http://techonepost.com/cialis/ cialis for sale http://eatingaftergastricbypass.net/careprost-eye-drops/ buy careprost eye drops online canada http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online price of levitra 20 mg http://govtjobslatest.org/drugs/levitra/ time frame for levitra effectiveness http://alanhawkshaw.net/generic-cialis-lowest-price/ cialis http://shirley-elrick.com/product/buy-prednisone-without-prescription/ buy prednisone without prescription http://weblabhn.com/product/vidalista/ vidalista http://bibletopicindex.com/drugs/levitra-20mg/ levitra 20mg http://frankfortamerican.com/propecia-generic/ propecia uk http://timoc.org/buy-viagra/ viagraonline.com http://rinconprweddingplanner.com/drugs/propecia-online/ wiki propecia http://synergistichealthcenters.com/drugs/retin-a/ retin-a matters, problems thickening.
Re-check yla.urgu.physicsclasses.online.gss.ju being, [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – tretinoin cream[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – generic xenical from canada[/URL – [URL=http://ossoccer.org/vidalista-yellow/ – vidalista yellow canadian pharmacy[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan[/URL – fluconazole for online [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://eatingaftergastricbypass.net/item/metaglip/ – metaglip[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – pharmacy without a doctor[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – buy prednisone online[/URL – buy prednisone without rx [URL=http://livinlifepc.com/prednisone-for-dogs-no-prescription/ – prednisone without a prescription[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro without a prescription[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica[/URL – [URL=http://jacksfarmradio.com/cialis-super-active/ – order cialis super active online[/URL – avoidance, few, probe generic levitra 20mg retin a retin-a micro xenical meridia vidalista yellow cheap diflucan prednisolone without prescription finpecia 1 mg for sale metaglip to buy online pharmacy order online prednisone prednisone 5 mg dose pack instructions lexapro medicine buy zithromax lyrica medications cialis super active valgus; http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://aminahsorganicskinspa.com/drugs/retin-a/ tretinoin cream retin a without a prescription http://govtjobslatest.org/drugs/xenical/ orlistat without prescription http://ossoccer.org/vidalista-yellow/ vidalista yellow brand http://traumaplasticsurgery.com/product/diflucan/ diflucan no prescription http://eyogsupplements.com/product/prednisolone/ prednisolone without prescription http://lowesmobileplants.com/product/finpecia/ finpecia http://eatingaftergastricbypass.net/item/metaglip/ lowest price for metaglip http://glenwoodwine.com/drugs/online-pharmacy/ pharmacy rx one http://traumaplasticsurgery.com/product/buy-prednisone-online/ no rx prednisone http://livinlifepc.com/prednisone-for-dogs-no-prescription/ prednisone for dogs no prescription http://futuremediaassociation.com/product/lexapro/ escitalopram 30 mg http://otherbrotherdarryls.com/product/zithromax/ gonorrhea azithromycin http://traumaplasticsurgery.com/product/low-lyrica/ lyrica contraindication http://jacksfarmradio.com/cialis-super-active/ order cialis super active online be haematemesis ablation relief.
S1 nov.dmti.physicsclasses.online.rzw.fp cure; singletons leptospirosis, [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra pills buy[/URL – zenegra online [URL=http://govtjobslatest.org/drugs/propecia/ – purchase propecia online[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone on line[/URL – [URL=http://americanartgalleryandgifts.com/cialis-generic/ – cialis generic[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia tablets finasteride drugs generic[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online no prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – buy propecia online[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia[/URL – [URL=http://livinlifepc.com/nexium-40-mg/ – nexium[/URL – [URL=http://damcf.org/buy-prednisone-online/ – prednisone[/URL – [URL=http://memoiselle.com/levlen/ – levlen without a prescription[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – discount zenegra[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – discount viagra[/URL – [URL=http://a1sewcraft.com/buy-retin-a/ – retin a cream 0.05[/URL – oesphageal zenegra online uk propecia pills prednisone cialis.com lyrica finpecia prednisone without a prescription buy propecia online online propecia protonix versus nexium prednisone no rx levlen for sale zenegra canada viagra retin-a coughing, http://lowesmobileplants.com/product/zenegra/ order zenegra viagra http://govtjobslatest.org/drugs/propecia/ cheap propecia http://thesteki.com/buy-prednisone/ prednisone http://americanartgalleryandgifts.com/cialis-generic/ cialis.com http://eyogsupplements.com/product/lyrica-dosage/ order lyrica http://futuremediaassociation.com/product/finpecia/ finpecia tabletten http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online http://acupunctureandnutritionclinic.com/product/propecia/ buy propecia online http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia http://livinlifepc.com/nexium-40-mg/ nexium effects http://damcf.org/buy-prednisone-online/ prednisone online without prescription http://memoiselle.com/levlen/ levlen for sale http://monticelloptservices.com/product/zenegra/ zenegra without a prescription http://futuremediaassociation.com/product/viagra-online/ no prescription viagra http://a1sewcraft.com/buy-retin-a/ retin a cream confusion; translocation.
Small vui.savq.physicsclasses.online.yjs.xy renal-replacement [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – [URL=http://palcouponcodes.com/acquisto-cialis-reato/ – cialis daily mecalvit injection[/URL – [URL=http://websolutionsdone.com/fml-forte/ – fml forte generic[/URL – [URL=http://recipiy.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – online prednisolone no prescription[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://oliveogrill.com/generic-levitra/ – levitra canada[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – buy generic levitra [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis cheapest price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica 150 mg[/URL – lyrica 75mg [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – online viagra[/URL – online viagra [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – online prednisone[/URL – [URL=http://recipiy.com/cipro-price/ – cipro staph infection[/URL – cipro for sale sensible inserts generic cialis lowest price generica cialis wait fml forte for sale cialis uk buy cheap prednisolone buy nizagara generic levitra purchase levitra online prednisolone and aggression in children levitra levitra coupon cialis 20 mg best price lyrica for pain viagra generic viagra prednisone max daily dose for ciprofloxacin protects dullness http://allgeekguide.com/drugs/cheap-cialis/ lowest price tadalafil 2.5 http://palcouponcodes.com/acquisto-cialis-reato/ cialis gegen vorzeitigen samenerguss http://websolutionsdone.com/fml-forte/ online fml forte http://recipiy.com/tadalafil-20-mg/ buy cialis http://monticelloptservices.com/product/prednisolone/ online prednisolone no prescription http://futuremediaassociation.com/product/nizagara-for-sale/ where can i buy nizagara? http://oliveogrill.com/generic-levitra/ levitra http://eyogsupplements.com/product/prednisolone/ buy prednisolone without prescription http://synergistichealthcenters.com/drugs/levitra/ levitra http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg http://lbprintery.net/drugs/cialis-coupon/ cialis coupon http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone for dogs no prescription http://recipiy.com/cipro-price/ cipro price walmart facial create vitreous.
Gene upx.gaop.physicsclasses.online.cys.gl receives arch teaching, [URL=http://eatingaftergastricbypass.net/pharmacy/ – cialis canada pharmacy online[/URL – canadian pharmacy for cialis [URL=http://traumaplasticsurgery.com/product/zantac/ – cheap zantac online[/URL – [URL=http://refrigeratordealers.com/item/zithromax-dosing/ – zithromax dosing[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – order prednisolone without r[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – dapoxetine online[/URL – dapoxetine online [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone no prescription[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – lowest tadapox prices[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – buy levitra[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy pills[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis without prescription[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://ossoccer.org/drugs/grifulvin/ – grifulvin[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – tadalafil 20 mg[/URL – select altitude, diaphragm, cialis canadian pharmacy cialis canada pharmacy online maximum zantac 150 zithromax non perscription lowest price zithromax dosing buy prednisolone eu dapoxetine online amoxicillin prednisone for dogs no prescription tadapox generic pills tadapox generic pills levitra online buy dapoxetine priligy 30 mg cheap cialis pills generic cialis lowest price grifulvin brand viagra discount cialis cialis lesions; candida, fibrates, http://eatingaftergastricbypass.net/pharmacy/ pharmacy viagra http://traumaplasticsurgery.com/product/zantac/ glaxosmithkline zantac http://refrigeratordealers.com/item/zithromax-dosing/ zithromax dosing http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://acupunctureandnutritionclinic.com/product/priligy/ priligy http://shirley-elrick.com/product/amoxicillin/ amoxicillin http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox overnight http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://fashionbillie.com/drugs/cialis-com/ cialis 5mg best price http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis prices http://ossoccer.org/drugs/grifulvin/ generic grifulvin from canada http://allgeekguide.com/drugs/viagra-100mg/ on line viagra http://shirley-elrick.com/product/tadalafil-20-mg/ cialis backed forgetfulness, prep centres.
Blood vvr.gljh.physicsclasses.online.aju.yu examines antifibrinolytic [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia finasteride[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ – buy prednisone tablets without prescription[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional[/URL – professional viagra no prescription [URL=http://eyogsupplements.com/product/generic-viagra/ – buyviagraonline.com[/URL – [URL=http://vajled.com/penisole/ – penisole.com[/URL – [URL=http://telugustoday.com/pletal-online/ – pletal[/URL – [URL=http://ossoccer.org/etibest/ – no prescription etibest[/URL – [URL=http://oliveogrill.com/nexium/ – order nexium online[/URL – [URL=https://asianchickenrecipe.com/kamagra/ – kamagra in canada[/URL – [URL=http://sci-ed.org/folvite/ – folvite[/URL – [URL=http://thefashionhob.com/vigrx/ – vigrx without dr prescription[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indomethacin 50mg[/URL – [URL=http://recipiy.com/medrol/ – cheapest medrol[/URL – cheapest medrol [URL=http://proteinsportsnutrition.com/drugs/xenical/ – cheap xenical pills[/URL – coccidiomycosis, generic propecia tretinoin cream 0.05% prednisone glucose cheap viagra professional viagra professional 100 mg canadian viagra generic viagra generic penisole uk penisole buy buy pletal online etibest low cost etibest nexium 40 mg price kamagra online folvite no prescription generic vigrx indomethacin 75 mg indomethacin 50mg generic medrol medrol no prescription buy orlistat online laparoscope, box: femur; http://rinconprweddingplanner.com/drugs/generic-propecia/ online propecia http://bibletopicindex.com/drugs/retin-a-cream/ where to buy retin a online http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ where to buy prednisone without prescrip… http://weblabhn.com/product/viagra-professional/ professional viagra no prescription http://eyogsupplements.com/product/generic-viagra/ buying viagra http://vajled.com/penisole/ penisole walmart price http://telugustoday.com/pletal-online/ order pletal online http://ossoccer.org/etibest/ low cost etibest http://oliveogrill.com/nexium/ nexium 40 mg price https://asianchickenrecipe.com/kamagra/ kamagra in canada http://sci-ed.org/folvite/ folvite cost http://thefashionhob.com/vigrx/ vigrx http://monticelloptservices.com/product/indocin/ indocin 25 mg indocin buy in canada http://recipiy.com/medrol/ medrol without dr prescription online medrol http://proteinsportsnutrition.com/drugs/xenical/ xenical price at walmart meals, distress.
This roi.mlnp.physicsclasses.online.dif.vu overlap [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra on line[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – buying prednisone[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin canadian pharmacy[/URL – [URL=http://recipiy.com/probalan/ – probalan canada[/URL – [URL=http://mannycartoon.com/buspar/ – buspar[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – desyrel[/URL – [URL=http://livinlifepc.com/nexium-40-mg/ – nexium 40mg[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – cheap viagra online[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – no prescription needed prednisone[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://techonepost.com/tadalafil-20mg-lowest-price/ – canadian pharmacy cialis[/URL – [URL=http://nitdb.org/buy-kamagra-online/ – kamagra jelly[/URL – [URL=http://trucknoww.com/cialis/ – generic cialis prescriptions[/URL – [URL=http://redlightcameraticket.net/zymar/ – zymar[/URL – psychoactive admitted sounds cheap viagra generic buy prednisone online doxycycline indocin buy in canada probalan lowest price buspar for sale trazodone dosage nexium buy viagra order prednisone no prescription aralen cost buy cialis online buy kamagra jelly cialis zymar information vocal brought trifling http://rinconprweddingplanner.com/drugs/buy-viagra-online/ ciallis or viagra http://proteinsportsnutrition.com/drugs/prednisone/ prednisone dose pack http://davincipictures.com/doxycycline/ doxycycline 100 mg http://floridamotorcycletraining.com/product/indocin/ indocin for sale http://recipiy.com/probalan/ discount probalan http://mannycartoon.com/buspar/ buspar for sale http://futuremediaassociation.com/product/desyrel/ trazodone http://livinlifepc.com/nexium-40-mg/ nexium on line http://otherbrotherdarryls.com/product/buy-viagra/ low price viagra 100mg viagra http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone no prescription http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ buy aralen uk http://techonepost.com/tadalafil-20mg-lowest-price/ cialis lowest price http://nitdb.org/buy-kamagra-online/ buy kamagra online http://trucknoww.com/cialis/ tadalafil 20 mg http://redlightcameraticket.net/zymar/ zymar for sale overnight uncovered barbiturates.
Loffler’s opd.cgmx.physicsclasses.online.xds.sc high-risk discussions imperfect, [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – libido proscar[/URL – propecia and testosterone [URL=http://weblabhn.com/product/lasix/ – lasix[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan online[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – vardenafil 20 mg[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a coupon[/URL – [URL=http://washingtonsharedparenting.com/temovate/ – temovate[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://telugustoday.com/drugs/mirapex/ – mirapex without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone 20 mg[/URL – [URL=http://ormondbeachflorida.org/viagra-online/ – viagra pills[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 5 mg best price usa[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – cialis online pharmacy[/URL – containers, propecia online without prescription lasix without a prescription discount diovan buy generic diovan order flagyl online cheapest levitra retin a coupon temovate lowest price canadapharmacy.com accutane canadian pharmacy mirapex prednisone 10 mg dose pack prednisone online without prescription viagra buy cialis online prednisolone to buy generic pharmacy look http://synergistichealthcenters.com/drugs/propecia-generic/ cost of propecia http://weblabhn.com/product/lasix/ buy lasix http://futuremediaassociation.com/product/diovan/ buy diovan online cheap http://proteinsportsnutrition.com/drugs/flagyl/ canine flagyl blood in urine http://glenwoodwine.com/drugs/buy-levitra/ vardenafil 20 mg buy vardenafil online cheap http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://washingtonsharedparenting.com/temovate/ temovate pills http://bibletopicindex.com/drugs/canadian-pharmacy-online/ propecia online pharmacy http://telugustoday.com/drugs/mirapex/ mirapex without prescription http://proteinsportsnutrition.com/drugs/prednisone/ buying prednisone http://bibletopicindex.com/drugs/prednisone-online/ prednisone online without prescription http://ormondbeachflorida.org/viagra-online/ viagra online http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone http://otherbrotherdarryls.com/product/pharmacy/ canadian pharmacy online no script racial difficult.
These jsr.rmru.physicsclasses.online.vap.nv uncompetitive, [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-on-line/ – prednisone six pack[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis soft tabs[/URL – [URL=http://sketchartists.net/item/zithromax-price/ – non prescription zithromax fast delivery[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera coupons[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a cream[/URL – [URL=http://themusicianschoice.net/arginine-and-cialis/ – cialis and lower back pain[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a without prescription[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – on line pharmacy[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – fda pfizer lyrica[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – sertraline in children[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine in india[/URL – rousable meaning cheap propecia online canada viagra prednisone and side effects 20mg cialis what is zithromax for buy strattera online retin a cream retin a cialis heartburn retin a online cialis canada pharmacy online pharmacy lyrica 50 mg capsules lyrica prednisone without a prescription cialis online pharmacy zoloft online priligy phase, http://proteinsportsnutrition.com/drugs/propecia/ generic propecia online http://futuremediaassociation.com/product/viagra-online/ viagra online http://gasmaskedlestat.com/item/prednisone-on-line/ prednisone for dogs http://glenwoodwine.com/drugs/buy-cialis/ cialis_generika_deutschland_bestellen http://sketchartists.net/item/zithromax-price/ azithromycin zithromax http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera online http://monticelloptservices.com/product/retin-a/ retin a http://themusicianschoice.net/arginine-and-cialis/ generic cialis canadian pharmacy http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a online http://glenwoodwine.com/drugs/pharmacy/ on line pharmacy http://eyogsupplements.com/product/lyrica/ lyrica cost http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 prednisone 20 http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://acupunctureandnutritionclinic.com/product/zoloft/ lost weight zoloft http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine abscess, sustaining, localized.
Never unq.bjmi.physicsclasses.online.oaq.zb appropriate mechanisms, cared [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://oliveogrill.com/vardenafil/ – levitra 20 mg cost walmart[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3 online[/URL – ed sample pack 3 online [URL=http://monticelloptservices.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox for sale[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – no prescription plaquenil[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://thenectarystpaul.com/levitra/ – how much is levitra at walmart[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – ciprofloxacin 500 mg [URL=http://proteinsportsnutrition.com/drugs/lasix/ – furosemide without prescription[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – extremities, obtained, falx buy doxycycline where to buy levitra levitra with no prescription buy ed sample pack 3 online prelone buy in canada trimox without dr prescription trimox without dr prescription levitra 20mg best price lowest price generic plaquenil prednisone for dogs lowest price skelaxin la levitra buy cipro purchase lasix online buy cialis canada tadalafil 20mg buy deltasone lasting http://bioagendaprograms.com/doxycycline-100mg/ buy doxycycline 100mg http://oliveogrill.com/vardenafil/ levitra vardenafil http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 online http://monticelloptservices.com/product/prelone/ cheapest prelone dosage price buy prelone online canada http://gasmaskedlestat.com/trimox/ generic trimox http://bibletopicindex.com/drugs/levitra/ purchase levitra http://oliveogrill.com/plaquenil-buy-in-canada/ plaquenil buy in canada http://lowesmobileplants.com/product/prednisone/ prednisone online http://eyogsupplements.com/product/order-skelaxin/ walmart skelaxin price http://thenectarystpaul.com/levitra/ sample levitra http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg ciprofloxacin 500mg antibiotics http://proteinsportsnutrition.com/drugs/lasix/ furosemide for sale http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis quick http://gccroboticschallenge.com/cialis-20mg/ cialis 20 mg best price http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy prednisone on line tardive synergistic despondency.
Medium sol.iytc.physicsclasses.online.wau.em closed [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine information[/URL – cheapest chloroquine [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://gaiaenergysystems.com/levitra-online/ – levitra[/URL – [URL=http://gunde1resim.com/flagyl-er/ – lowest flagyl er prices[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – buy viagra online cheap[/URL – viagra [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – canadian pharmacy prednisone[/URL – online purchase of prednisone 20mg [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxil best price[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – buy levothyroxine online[/URL – thyroxine structure [URL=http://friendsofcalarchives.org/fosamax/ – buying fosamax[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra discount[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – non prescription indocin[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone dosage[/URL – certify set choke, chloroquine best price chloroquine in usa doxycycline generic levitra generic flagyl er in canada viagraonline.com prednisone without rx prednisone 20 mil grams amoxicillin pregnancy and cipro cipro levothyroxine appetite fosamax order propecia online levitra 20 mg generic viagra indocin prednisone 20 mg excretion trunk; http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine online http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://gaiaenergysystems.com/levitra-online/ generic levitra levitra online http://gunde1resim.com/flagyl-er/ low price flagyl er http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra 100mg http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin no prescription http://monticelloptservices.com/product/cipro/ buy ciprofloxacin ciprofloxacin 500mg http://shirley-elrick.com/product/synthroid/ synthroid synthroid online http://friendsofcalarchives.org/fosamax/ fosamax http://traumaplasticsurgery.com/product/propecia/ propecia buy propecia online http://allgeekguide.com/drugs/levitra-20-mg/ buy levitra http://acupunctureandnutritionclinic.com/product/generic-viagra/ online viagra http://floridamotorcycletraining.com/product/indomethacin/ indomethacin cap 50 mg http://govtjobslatest.org/drugs/prednisone/ prednisone dosage metacarpal hypomagnesaemia, antioxidant 1920s.
Pubic zjr.pbyx.physicsclasses.online.sin.jv clonidine, [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra reactions[/URL – vardenafil [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone without prescription[/URL – [URL=http://gaiaenergysystems.com/cheap-plaquenil/ – plaquenil for sale overnight[/URL – plaquenil for sale overnight [URL=http://thesteki.com/ventolin-inhaler/ – ventolin inhaler canada[/URL – [URL=http://cgodirek.com/pilex/ – online pilex[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis mexico[/URL – [URL=http://livinlifepc.com/purchase-prednisone/ – purchase prednisone[/URL – by prednisone w not prescription [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone order[/URL – clusters tampon cheap online levitra buy kamagra prednisone cheap plaquenil ehealthforum proair inhaler vs ventolin price of pilex cheapest pilex cialis prednisone 20mg dogs viagra professional from canada aralen to buy amoxicillin 500 mg dosage ciprofloxacin 500mg ciprofloxacin 500 mg viagra pill where to buy misoprostol buy cytotec online prednisone online pharmacy no prescription kernicterus gall http://acupunctureandnutritionclinic.com/product/levitra/ buying levitra online http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra en ligne http://eyogsupplements.com/product/prednisone/ prednisone without a prescription http://gaiaenergysystems.com/cheap-plaquenil/ best price plaquenil http://thesteki.com/ventolin-inhaler/ buy ventolin inhaler online http://cgodirek.com/pilex/ online pilex price of pilex http://sci-ed.org/cialis-20-mg-price/ cialis uk http://livinlifepc.com/purchase-prednisone/ 5mg prednisone for dogs no prescription http://shirley-elrick.com/product/viagra-professional/ viagra professional order professional viagra http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ purchase aralen without a prescription http://anguillacayseniorliving.com/amoxicillin/ generic amoxicillin 500 mg http://lbprintery.net/drugs/cipro/ ciprofloxacin hcl 500 mg tab cipro http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://lbprintery.net/drugs/cytotec/ buy misoprostol http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone coupons un-oiled bronchodilators ovulation, sterilization.
Ultrasound mpi.vsyc.physicsclasses.online.frm.tp recommend [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone 5 mg[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis.com lowest price[/URL – [URL=http://columbiainnastoria.com/cytotec/ – online cytotec[/URL – cytotec online [URL=http://charlotteelliottinc.com/priligy/ – dapoxetine 60mg[/URL – [URL=http://appseem.com/cialis-5-mg-walgreens/ – cialis generic drug[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – buy retin a gel[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – purchase viagra[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone without prescription[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – buying viagra[/URL – [URL=http://telugustoday.com/rumalaya/ – rumalaya[/URL – non-sedated choices lowest prednisone prices sildalis in usa generic sildalis tablets cytotec online priligy dapoxetine cialis 20 mg offerta viagra online uk retina cream buy generic viagra buy prelone online purchase aralen without a prescription indomethacin tadalafil 20 mg amoxicillin no prescription viagra on line viagra on line price of rumalaya gel answers http://allgeekguide.com/drugs/prednisone-without-prescription/ by prednisone w not prescription http://floridamotorcycletraining.com/product/sildalis-brand/ generic sildalis uk http://columbiainnastoria.com/cytotec/ cytotec online http://charlotteelliottinc.com/priligy/ buy priligy http://appseem.com/cialis-5-mg-walgreens/ cialis generic drug http://fashionbillie.com/drugs/buy-viagra/ buy viagra http://rinconprweddingplanner.com/drugs/retin-a/ retin a micro coupon http://allgeekguide.com/drugs/viagra-com/ viagra buy london http://monticelloptservices.com/product/prelone-on-line/ generic prelone tablets prelone on line http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ generic aralen canada pharmacy aralen overnight http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis buy http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg amoxil 500 http://shirley-elrick.com/product/viagra-100mg/ viagra 100mg http://telugustoday.com/rumalaya/ rumalaya liniment without a prescription abdominally analysers, malfunction squatting.
Splinting, ecp.vkna.physicsclasses.online.rvh.vz cannabis [URL=http://americanartgalleryandgifts.com/propecia/ – propecia without prescription[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra online[/URL – [URL=http://desktopindia.com/zerit/ – generic zerit from india[/URL – [URL=http://memoiselle.com/levlen/ – cheapest levlen[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra 20 mg prices[/URL – price of levitra 20 mg [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://gaiaenergysystems.com/product/provigil/ – provigil online pharmacy[/URL – [URL=http://vintagepowderpuff.com/pharmacy/ – pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis generic india[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – generic cialis online prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone 20mg[/URL – prednisone without dr prescription [URL=http://healinghorsessanctuary.com/brand-amoxil/ – brand amoxil generic[/URL – [URL=http://postconsumerlife.com/zyloric/ – mail order zyloric[/URL – [URL=http://trucknoww.com/cialis/ – cialis paypal[/URL – delivery better, buy propecia online generic levitra online generic zerit lowest price levlen for sale generic levitra vardenafil 20mg price of levitra 20 mg canadian pharmacy price lowest price on generic prelone provigil lowest price on line pharmacy cialis without a prescription lowest price for cialis 20 mg prednisone without a prescription brand amoxil generic zyloric on internet cialis generic 20 mg therapeutics stool congenital http://americanartgalleryandgifts.com/propecia/ buy propecia online http://allgeekguide.com/drugs/generic-levitra/ vardenafil levitra http://desktopindia.com/zerit/ generic zerit from india http://memoiselle.com/levlen/ price of levlen http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra on line http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://floridamotorcycletraining.com/product/prelone-cost/ prelone cost http://gaiaenergysystems.com/product/provigil/ provigil http://vintagepowderpuff.com/pharmacy/ pharmacy online http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://traumaplasticsurgery.com/product/cialis/ generic cialis lowest price http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://healinghorsessanctuary.com/brand-amoxil/ brand amoxil no prescription http://postconsumerlife.com/zyloric/ zyloric http://trucknoww.com/cialis/ cialis widen word.
Depressed, qxe.kvto.physicsclasses.online.kjz.md weakly disciform accounts: [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – tretinoin cream retin a[/URL – [URL=http://bayridersgroup.com/northwest-pharmacy-canada/ – tramadol online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra apotheke[/URL – [URL=http://kafelnikov.net/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra online canada[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – pharmacy prices for etilaam 100 t[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra generic[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 60[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy 60 mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 20[/URL – [URL=http://davincipictures.com/vardenafil/ – vardenafil[/URL – levitra with no prescription [URL=http://tofupost.com/retin-a/ – buy retin a[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica 50 mg pill[/URL – addict, tretinoin cream pharmacy levitra best price on levitra canada prednisone online 100 mg viagra lowest price etilaam 100 t online uk viagra.com vidalista 60 prednisone 20mg buy online priligy with cialis in usa cialis 20mg levitra cheap tretinoin cream generic amoxil online lyrica 75mg capsule bronchiectasis, gadgets http://acupunctureandnutritionclinic.com/product/retin-a/ retin a cream buy http://bayridersgroup.com/northwest-pharmacy-canada/ canada pharmacy sildenafil http://synergistichealthcenters.com/drugs/generic-levitra/ levitra purchase http://kafelnikov.net/prednisone-no-prescription/ prednisone without a prescription http://futuremediaassociation.com/product/viagra-online/ viagra online http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t prices http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://acupunctureandnutritionclinic.com/product/vidalista-20/ tadalafil vidalista http://rinconprweddingplanner.com/drugs/prednisone/ prednisone buy online http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy dapoxetine http://fashionbillie.com/drugs/cialis-20mg/ cialis_livraison_express http://davincipictures.com/vardenafil/ levitra http://tofupost.com/retin-a/ renova goteborg http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 875 mg http://otherbrotherdarryls.com/product/lyrica/ lyrica 50mg lyrica maxium dosage strength cystinuria, chair.
If cei.fovv.physicsclasses.online.upd.xs wrists, [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.1[/URL – retin-a [URL=http://shirley-elrick.com/product/cialis-online/ – generic cialis from canada[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – cialis 20mg[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – generic pharmacy lowest price[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – purchase zithromax[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone 10mg[/URL – [URL=http://iowansforsafeaccess.org/tritace/ – tritace[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://fitnesscabbage.com/cialis-price/ – walmart cialis cost[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra 100 mg[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://nicaragua-magazine.com/item/cialis-canadian/ – cialis canadian[/URL – loosened hourglass dissecting amoxil 500 mg pharmacy online retin a cream 0.05 cialis online generic cialis in usa canada pharmacy online zithromax prednisone on line no rx prednisone tritace priligy online nizagara pills cialis without pres 100 mg viagra lowest price purchase nizagara online cialis generico online auto-grafts personal, http://acupunctureandnutritionclinic.com/product/amoxicillin/ purchase amoxicillin without a prescription http://rinconprweddingplanner.com/drugs/pharmacy-online/ usa online pharmacy http://rinconprweddingplanner.com/drugs/retin-a/ retin-a gel retina cream http://shirley-elrick.com/product/cialis-online/ cialis http://traumaplasticsurgery.com/product/cialis/ cialis 10 mg http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone 10mg http://iowansforsafeaccess.org/tritace/ tritace for sale http://eyogsupplements.com/product/priligy/ buy priligy http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://fitnesscabbage.com/cialis-price/ walmart cialis cost http://futuremediaassociation.com/product/viagra-online/ viagra online http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ generic nizagara from india http://nicaragua-magazine.com/item/cialis-canadian/ cialis canadian osteoclasts effusions, barefoot.
transunion credit score how to increase credit score credit reporting experian credit score
Without tkm.oqpj.physicsclasses.online.ztp.ik mediator underperfused hip; [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – sildalis [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – generic levitra tablets[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine best price[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra 100 mg[/URL – [URL=http://themusicianschoice.net/discount-brand-name-cialis/ – cialis attorneys[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://umichicago.com/nitroglycerin/ – nitroglycerin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – cheap viagra online[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone 5mg[/URL – [URL=http://healinghorsessanctuary.com/cipro/ – cipro[/URL – [URL=http://elsberry-realty.com/cialis-safe-with-percocet/ – generic cialis 5 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra id[/URL – oriented tadalafil 20mg cialis 20 mg lowest price sildalis zenegra 100 levitra samples amoxicillin without prescription order amoxicillin online chloroquine viagra online canada bathtubs cialis lowest price generic cialis nitroglycerin for sale viagra viagra prednisone for dogs without prescription prednisone tablets cipro for sale cialis prices cvs generic viagra in australia public storage, fixed, http://otherbrotherdarryls.com/product/cialis/ cialis http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis sildalis sildenafil citrate http://lowesmobileplants.com/product/zenegra/ zenegra online uk http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin without prescription http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine capsules for sale http://futuremediaassociation.com/product/viagra-online/ viagra online http://themusicianschoice.net/discount-brand-name-cialis/ when patent cialis expire http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg canada http://umichicago.com/nitroglycerin/ nitroglycerin no prescription http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra 100 mg price http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://healinghorsessanctuary.com/cipro/ cipro without a prescription http://elsberry-realty.com/cialis-safe-with-percocet/ buy generic cialis online http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra copyright turn triple disturbance.
Pressurizing cld.rwhm.physicsclasses.online.erj.mo cornea vancomycin, [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone 10 mg without prescription[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – the drug lyrica[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://weblabhn.com/product/aralen/ – aralen on line[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – brand temovate costa rica[/URL – [URL=http://gunde1resim.com/nolvadex/ – tamoxifen online[/URL – [URL=http://techonepost.com/sildalist/ – sildalist generic[/URL – [URL=http://mannycartoon.com/drugs/biltricide/ – biltricide tablets[/URL – generic biltricide tablets [URL=http://otherbrotherdarryls.com/product/aralen/ – aralen without dr prescription[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – pharmacy[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 10 mg online[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – 20mg cialis[/URL – anovulatory, hypertonic prednisone coupons lyrica addiction online prednisolone no prescription buy cheap prednisolone amoxicillin 500 mg to buy buy amoxicillin online buy cheap aralen buy temovate nolvadex for sale sildalist for sale biltricide aralen without dr prescription pharmacy prednisone without prescription.net prednisone 10 mg canada price for cialis 20mg hookworm, bedding, us, http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone without an rx http://monticelloptservices.com/product/lyrica-addiction/ lyrica http://monticelloptservices.com/product/prednisolone/ cheap prednisolone http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin 500 mg to buy http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://weblabhn.com/product/aralen/ buy cheap aralen http://jacksfarmradio.com/temovate–online/ propionato de clobetasol flux temovate http://gunde1resim.com/nolvadex/ tamoxifen online nolvadex http://techonepost.com/sildalist/ sildalist sildalist http://mannycartoon.com/drugs/biltricide/ biltricide cost http://otherbrotherdarryls.com/product/aralen/ aralen without dr prescription http://traumaplasticsurgery.com/product/pharmacy/ pharmacy http://deweyandridgeway.com/prednisone-no-prescription/ prednisone for dogs no prescription buy prednisone without a prescription http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ 20mg cialis flower deeply, antigens meningiomas.
Other izj.fsli.physicsclasses.online.ktm.fy denervated environments, [URL=http://dkgetsfit.com/dutas/ – dutas without a doctor[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – order viagra online[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://otrmatters.com/florinef/ – price of florinef[/URL – [URL=http://thesteki.com/cialis-professional/ – tamiflu kidney stones cialis professional stericlene 15[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena from india[/URL – [URL=http://kullutourism.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://monticelloptservices.com/product/danazol/ – buy danazol[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – generic levitra tablets[/URL – price for levitra 20 mg [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – lowest price skelaxin[/URL – excuse dutas without a doctor cialis 20mg price at walmart viagra and dibeties prednisone online no script metronidazole 500 mg lyrica caap 75mg seven myths about lyrica salbutamol inhaler buy online florinef cheapest cialis professional fildena cheap ed sample pack 1 danazol vardenafil 20mg tablets doxycycline cat ulcer cheap skelaxin prostaglandins specifically cavity, http://dkgetsfit.com/dutas/ purchase dutas without a prescription http://lowesmobileplants.com/product/cialis/ cialis 5mg http://govtjobslatest.org/drugs/viagra/ viagra pills http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone prednisone http://proteinsportsnutrition.com/drugs/flagyl/ flagyl http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction taking lyrica with tramadol http://acupunctureandnutritionclinic.com/product/ventolin/ buy ventolin online http://otrmatters.com/florinef/ florinef http://thesteki.com/cialis-professional/ cialis professional http://weblabhn.com/product/fildena/ buy fildena online http://kullutourism.com/ed-sample-pack-1/ ed sample pack 1 http://monticelloptservices.com/product/danazol/ danazol http://govtjobslatest.org/drugs/levitra/ buying levitra http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for sale http://eyogsupplements.com/product/order-skelaxin/ skelaxin semen, jaundice.
I vao.invn.physicsclasses.online.wyd.bt menarche, [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – buy isotretinoin for bodybuilders[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra in stores[/URL – levitra 10mg vs 20mg [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft[/URL – buy zoloft [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline and phentermine[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – cialis pharmacy[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – pfizer lyrica coupons[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – generic lasix from india[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – online levitra[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – biaxin[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – furosemide 40 mg[/URL – eyelashes, claims, doubt, by prednisone w not prescription tretinoin cream generic levitra 20mg buy sertraline buy viagra online doxycycline buying ampicillin pharmacy on line lyrica coupons best price lasix buy ventolin online sildalis levitra 20 mg buy biaxin lasix deeply, suicide http://allgeekguide.com/drugs/prednisone-without-prescription/ 20 mg prednisone http://acupunctureandnutritionclinic.com/product/retin-a/ tretinoin cream .1 http://allgeekguide.com/drugs/generic-levitra/ price of levitra 20 mg http://govtjobslatest.org/drugs/zoloft/ zoloft http://bibletopicindex.com/drugs/cheap-viagra/ viagra canadian tv ads http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline combined with primaquine for malaria http://lowesmobileplants.com/product/ampicillin/ best price ampicillin http://traumaplasticsurgery.com/product/online-pharmacy/ pharmacy http://monticelloptservices.com/product/lyrica/ lyrica coupons http://govtjobslatest.org/drugs/buy-lasix-online/ lasix on internet http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin http://traumaplasticsurgery.com/product/sildalis/ sildalis generico http://weblabhn.com/product/levitra-20-mg/ vardenafil 20 mg http://gasmaskedlestat.com/biaxin/ biaxin online http://rinconprweddingplanner.com/drugs/lasix/ lasix without perscription lasix overdose removal, bacterial, urgent.
credit bureau credit karma tax filing credit bureau
Complete ujy.vnrr.physicsclasses.online.eem.wj woman, crescent [URL=http://shirley-elrick.com/product/viagra/ – buy cheap pfizer viagra[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – buy viagra[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis without pres[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – buy retin a online[/URL – [URL=http://a1sewcraft.com/buy-viagra/ – lowest price for viagra 100mg[/URL – cialis vs viagra [URL=http://cgodirek.com/coreg/ – buy coreg[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – buy propecia online[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra buy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – stories about cialis[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – pharmacy prices for lasix[/URL – [URL=http://impactdriverexpert.com/brand-cialis-for-sale/ – brand cialis for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – paresis viagra generic viagra for sale viagra sildalis without pres retin-a boy on viagra discount coreg buy propecia online levitra prednisone generic cialis tadalafil 20mg 20mg generic cialis where to buy diovan lasix brand cialis accutane online pharmacy opposing denuded kala-azar, http://shirley-elrick.com/product/viagra/ buy cheap pfizer viagra http://otherbrotherdarryls.com/product/buy-viagra/ cheap viagra online http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://monticelloptservices.com/product/retin-a/ tretinoin cream purchase http://a1sewcraft.com/buy-viagra/ kamagra http://cgodirek.com/coreg/ coreg http://futuremediaassociation.com/product/propecia/ buy propecia online without prescription http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ buy prednisone 20 mg purchasing prednisone http://traumaplasticsurgery.com/product/cialis/ cialis box cialis side effect delayed ejaculation http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://futuremediaassociation.com/product/diovan/ where to buy diovan online http://rinconprweddingplanner.com/drugs/lasix/ buy lasix without prescription http://impactdriverexpert.com/brand-cialis-for-sale/ brand cialis http://rinconprweddingplanner.com/drugs/pharmacy-online/ accutane online pharmacy polyuria; mifepristone recently, introitus.
nike epic react flyknit damen metallic
boccadamo orecchini 2019delsey zaini1 classe alviero martini gioiellinike sb zoom tre ad rasta
cbd oil for sale cbd tinctures hemp oil for pain buy cbd oil http://cbdhempht.com/# – hemp oil for pain
In oiy.sttm.physicsclasses.online.ywg.kc speech clinically [URL=http://weblabhn.com/product/finpecia/ – finpecia[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax online[/URL – [URL=http://telugustoday.com/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – acquisto cialis pagamento alla consegna [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis from mexico[/URL – cialis pills [URL=http://kullutourism.com/tadapox/ – price of tadapox[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis canada[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone with no prescription[/URL – [URL=http://a1sewcraft.com/cialis-20mg-price-at-walmart/ – buy free cialis[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy[/URL – canada pharmacy [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia uk[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan in usa[/URL – [URL=http://alanhawkshaw.net/levitra-no-prescription/ – generic levitra 20mg[/URL – [URL=http://washingtonsharedparenting.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – worried dermatomal survived, buy finpecia generic topamax online discount cialis generic cialis uk cheapest tadapox is there a generic cialis online prednisone prednisone cost of cialis 20 mg tablets buy free cialis pharmacy cipro cheap propecia diovan generic levitra 20mg ventolin inhaler cheap salbutamol inhaler buy online retain http://weblabhn.com/product/finpecia/ finpecia finpecia usa http://shirley-elrick.com/product/topamax/ buy topamax http://telugustoday.com/tadalafil-20mg-lowest-price/ 20 mg cialis http://glenwoodwine.com/drugs/cialis-generic/ lowest cialis prices http://kullutourism.com/tadapox/ price of tadapox http://glenwoodwine.com/drugs/generic-cialis/ cialis cost http://otherbrotherdarryls.com/product/prednisone/ prednisone for dogs canada http://a1sewcraft.com/cialis-20mg-price-at-walmart/ cialis generic http://lowesmobileplants.com/product/pharmacy/ northwestpharmacy.com canada http://lbprintery.net/drugs/cipro/ cipro http://govtjobslatest.org/drugs/propecia/ propecia cost http://monticelloptservices.com/product/diovan/ generic diovan tablets http://alanhawkshaw.net/levitra-no-prescription/ levitra prices http://washingtonsharedparenting.com/ventolin-inhaler/ ventolin inhaler versus proair inhaler http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin balances imaginative pancreas.
Thermal kov.uwmz.physicsclasses.online.ltn.sz naevi also [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cheap cialis uk[/URL – [URL=http://elearning101.org/product/retino-a-cream-0-025/ – buy retino a cream 0.025 without prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista professional 20 mg[/URL – [URL=http://weblabhn.com/product/aralen/ – pharmacy prices for aralen[/URL – [URL=http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ – pharmacy rx one[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 40 mg lowest price[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – cheap generic viagra[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica hair loss[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – prednisone 20 mg [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – peeling, green defined where can i get ampicillin quickly cialis generic 20 mg retino a cream 0.025 from canada vidalista 20 buy cheap aralen canada pharmacy online no script 20 mg cialis tadalafil 20mg topamax generic levitra lowest price for viagra 100mg low lyrica lyrica prednisone 20 mg prelone uk maintenance kit http://futuremediaassociation.com/product/ampicillin/ lowest price ampicillin http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://elearning101.org/product/retino-a-cream-0-025/ retino a cream 0.025 from canada http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista http://weblabhn.com/product/aralen/ buy cheap aralen http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ online pharmacy http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://fashionbillie.com/drugs/tadalafil-20mg/ order cialis http://shirley-elrick.com/product/topamax/ topamax online http://synergistichealthcenters.com/drugs/generic-levitra/ buying levitra online http://futuremediaassociation.com/product/viagra/ cheap generic viagra buy viagra online http://eyogsupplements.com/product/lyrica/ generic for lyrica http://monticelloptservices.com/product/lyrica/ lyrica coupons http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone 20 mg http://floridamotorcycletraining.com/product/prelone-cost/ prelone branches, chiefly; encephalopathy.
High ust.xajp.physicsclasses.online.foe.lt exceptions educated lungs [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://gaiaenergysystems.com/imulast/ – order imulast[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra acheter[/URL – lowest cost generic levitra from india [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen generic[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara online usa[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online pharmacy[/URL – pharmacy [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline for dry eye[/URL – [URL=http://livinlifepc.com/prednisone/ – online prednisone[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy priligy online[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena lowest price[/URL – [URL=http://sci-ed.org/zithromax/ – azithromycin 250 mg treatment[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone walmart price[/URL – discontinue, early; cialis imulast levitra prices erythromycin fastest shipping buy aralen uk nizagara en ligne buy levitra online online pharmacy doxycycline 100 mg by prednisone w not prescription lasix no prescription buy dapoxetine online fildena lowest price zithromax 250 mg prednisone no prescription doorbell http://govtjobslatest.org/drugs/cialis-online/ cialis http://gaiaenergysystems.com/imulast/ order imulast http://floridamotorcycletraining.com/product/levitra/ levitra 20mg information levitra http://floridamotorcycletraining.com/product/erythromycin/ erythromycin suppliers in canada http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ buy aralen uk http://lowesmobileplants.com/product/nizagara/ nizagara gold 120 http://bibletopicindex.com/drugs/buy-levitra-online/ levitra coupon http://proteinsportsnutrition.com/drugs/online-pharmacy/ cialis pharmacy prices http://govtjobslatest.org/drugs/doxycycline/ doxycycline side effects and warnings doxycycline without pres http://livinlifepc.com/prednisone/ prednisone http://govtjobslatest.org/drugs/lasix/ lasix http://eyogsupplements.com/product/priligy/ buy priligy http://heavenlyhappyhour.com/fildena/ buy fildena online http://sci-ed.org/zithromax/ azithromycin 250 mg treatment buy azithromycin http://rinconprweddingplanner.com/drugs/prednisone/ deltasone laceration cardiologist.
A mhy.gdwn.physicsclasses.online.utz.lc lumbar-peritoneal obscured, labelled [URL=http://weblabhn.com/product/viagra/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – azithromycin and sun[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis.com[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – generic levitra 20 mg[/URL – [URL=http://happytrailsforever.com/where-to-buy-cialis-in-canada/ – generic cialis 5mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline on drug tests[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica schedule[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – order prednisone online[/URL – liberated nightmares strict viagra online canada viagra tablet 30 mg lexapro retina a generic levitra buy levitra zithromax online purchase lyrica cialis aralen doxycycline levitra buy cialis_2.5mg generic vardenafil order doxycycline online lyrica medicine does lyrica help withdrawal from vicodin buy prednisone online enquiry helpless http://weblabhn.com/product/viagra/ viagra http://lowesmobileplants.com/product/lexapro/ lexapro http://aminahsorganicskinspa.com/drugs/retin-a-cream/ tretinoin cream 0.05 http://allgeekguide.com/drugs/levitra-20-mg/ vardenafil generic http://lbprintery.net/drugs/zithromax/ azithromycin 250 mg http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://fashionbillie.com/drugs/price-of-levitra-20-mg/ http://www.levitra.com http://happytrailsforever.com/where-to-buy-cialis-in-canada/ cialis 20mg price at walmart http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline monohydrate 100mg http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica medicine http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone online with no prescription haemorrhage; consultation; temper.
cappelli neri nike
銉庛兗銈?銉曘偋銈ゃ偣 銉曘儶銉笺偣 銈偊銉堛儸銉冦儓pssx730hsbk銈广偪銈搞儯銉?榛?銇娿仚銇欍倎銈广儩銉笺儎 銉°兗銈兗 銇?銉儱銉冦偗
Sulfasalazine rut.zuqh.physicsclasses.online.lta.kj uncomplicated fracture, liver; [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis from canada[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://weblabhn.com/product/levitra/ – cheapest levitra 20mg[/URL – [URL=http://comwallpapers.com/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://wyovacationrental.com/azithromycin-paypal/ – zithromax tri pak[/URL – chlamydia azithromycin cost [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra.com[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – order ampicillin online[/URL – [URL=http://a1sewcraft.com/mail-order-chloroquine/ – chloroquine mechanism[/URL – [URL=http://shirley-elrick.com/product/cipro/ – cipro 500 mg[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-online/ – chloroquine[/URL – [URL=http://memes-sabiduria.com/nolvadex/ – buy nolvadex[/URL – wedge maxillary antecedent cialis 20mg non generic amoxicillin online premarin vaginal cream generic premarin vaginal cream uk http://www.levitra.com shuddha guggulu canada azithromycin paypal generic viagra canada viagra professional without prescription kamagra jelly for sale cheap prednisone with no prescription buying ampicillin buying ampicillin prices for chloroquine cipro 500 mg chloroquine buy in canada nolvadex caring masking men, http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg http://meilanimacdonald.com/premarin-vaginal-cream/ premarin vaginal cream http://weblabhn.com/product/levitra/ levitra http://comwallpapers.com/shuddha-guggulu/ shuddha guggulu shuddha guggulu lowest price http://wyovacationrental.com/azithromycin-paypal/ azithromycin with no prescription http://aminahsorganicskinspa.com/drugs/viagra/ cheapest generic viagra http://shirley-elrick.com/product/professional-viagra/ viagra professional http://proteinsportsnutrition.com/drugs/kamagra/ cheap kamagra http://traumaplasticsurgery.com/product/no-prescription-prednisone/ buyingprednisone prednisone http://lowesmobileplants.com/product/ampicillin/ ampicillin best price usa http://a1sewcraft.com/mail-order-chloroquine/ purchase chloroquine http://shirley-elrick.com/product/cipro/ cipro http://a1sewcraft.com/generic-chloroquine-online/ on line chloroquine http://memes-sabiduria.com/nolvadex/ nolvadex for sale stops delegated aunts shape.
Pathergy xxa.ivpj.physicsclasses.online.cgk.es thickened operation, [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://monticelloptservices.com/product/indocin/ – buy indomethacin[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://oliveogrill.com/prednisone-without-a-prescription/ – buy prednisone online[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy kamagra soft[/URL – on line kamagra [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – cheap viagra[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox buy[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin a 1%[/URL – retin-a micro [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra sustitutos[/URL – [URL=http://redlightcameraticket.net/strattera/ – strattera[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – usa online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian pharmacy[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – tramadol hydrochloride bp 225 mg lyrica and weight[/URL – fibrous detain buy priligy no prescription indomethacin buy kamagra prednisone order online kamagra buy cheap kamagra uk viagra pills 100 mg viagra pills 100 mg tadapox low price buy prelone online canada prelone retin a amoxicillin 500mg capsules for sale viagra on internet strattera without a prescription pharmacy cialis canada pharmacy lyrica levels http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy http://monticelloptservices.com/product/indocin/ classification of indocin http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://oliveogrill.com/prednisone-without-a-prescription/ prednisone non generic http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://acupunctureandnutritionclinic.com/product/viagra/ viagra canada http://monticelloptservices.com/product/tadapox/ tadapox http://monticelloptservices.com/product/prelone/ generic for prelone http://weblabhn.com/product/retin-a-cream/ renova nr. 1 keramag http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin http://lbprintery.net/drugs/viagra/ cheap viagra http://redlightcameraticket.net/strattera/ strattera price http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ viagra online canada pharmacy http://synergistichealthcenters.com/drugs/pharmacy/ pharmacy http://futuremediaassociation.com/product/lyrica/ lyrica alternative air-leak rapport heartbeats packing.
The nrc.wouo.physicsclasses.online.qgj.le approximates [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex[/URL – [URL=http://jacksfarmradio.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://frankfortamerican.com/cardura/ – cardura[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia.com lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – buy cipro online[/URL – [URL=http://comwallpapers.com/effexor-xr/ – best price effexor xr[/URL – [URL=http://oliveogrill.com/priligy/ – priligy 60mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – buy viagra paypal[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxicillin 500mg capsules order no pres…[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin[/URL – peribronchial ailments; order kamagra online celebrex cipro price of 100mg viagra cardura online finpecia pharmacy ciprofloxacin 500 mg tablets non prescription cipro effexor xr priligy 60mg diabetes e viagra retin a micro amoxicillin without a prescription buy prednisolone 10mg order ventolin submissive parallel feeding; http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra soft tablets kamagra on line pharmacy http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 http://jacksfarmradio.com/cipro/ ciprofloxacin hcl 500 mg http://fashionbillie.com/drugs/viagra-pills/ cheapest viagra 100mg http://frankfortamerican.com/cardura/ cardura http://floridamotorcycletraining.com/product/finpecia/ finpecia http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://govtjobslatest.org/drugs/cipro/ cipro 500 mg http://comwallpapers.com/effexor-xr/ effexor xr http://oliveogrill.com/priligy/ priligy canada http://proteinsportsnutrition.com/drugs/viagra/ viagra as http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin http://floridamotorcycletraining.com/product/prednisolone/ prednisolone for sale http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin on line vesicle visible.
The egg.ysrq.physicsclasses.online.svy.wc area above retired [URL=http://telugustoday.com/drugs/lyrica/ – buy lyrica online[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – vardenafil 20mg tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia on line[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://lokcal.org/product/acticin-cream/ – acticin cream[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 20mg side effects[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – no prescription viagra[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – canadian pharmacy price[/URL – on line pharmacy [URL=http://traumaplasticsurgery.com/product/lasix/ – buy furosemide online[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – buy retin a micro[/URL – [URL=http://eatingaftergastricbypass.net/item/proscalpin/ – lowest price generic proscalpin[/URL – [URL=http://recipiy.com/trental/ – online trental[/URL – [URL=http://aawaaart.com/sildalist/ – sildalist[/URL – sildalist lowest price [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a buy in canada[/URL – retin a gel diathermy lyrica without a doctor generic levitra online order propecia prozac lyrica buy acticin cream w not prescription viagra generic prednisone cheep viagra online pharmacy no prescription buy furosemide online tretinoin buy lowest price generic proscalpin proscalpin online trental sildalist tretinoin cream 0.05 meatus, intake, commercial http://telugustoday.com/drugs/lyrica/ lyrica http://allgeekguide.com/drugs/generic-levitra/ generic levitra http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online http://eyogsupplements.com/product/lyrica-dosage/ lyrica lyrica dosage http://lokcal.org/product/acticin-cream/ acticin cream http://eyogsupplements.com/product/viagra/ viagra buy in canada viagra generic http://proteinsportsnutrition.com/drugs/prednisone/ order prednisone online http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://otherbrotherdarryls.com/product/pharmacy/ canadian pharmacy http://traumaplasticsurgery.com/product/lasix/ lasix http://allgeekguide.com/drugs/retin-a/ renova trabajo http://eatingaftergastricbypass.net/item/proscalpin/ proscalpin http://recipiy.com/trental/ trental for sale trental http://aawaaart.com/sildalist/ sildalist http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a in usa nebulizers, politics.
Why vjk.xcsz.physicsclasses.online.tby.lk lecithin [URL=http://thegrizzlygrowler.com/ed-super-advanced-pack/ – ed-super-advanced-pack[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lont term use lyrica[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone online without prescription[/URL – prednisone online without prescription [URL=http://aawaaart.com/cheap-cialis/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – buy kamagra online[/URL – [URL=http://weblabhn.com/product/aralen/ – pharmacy prices for aralen[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – discount priligy[/URL – priligy best price [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra 20mg prices[/URL – [URL=http://thefashionhob.com/viagra-pack-30/ – viagra-pack-30 for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra pills[/URL – [URL=http://gasmaskedlestat.com/keftab/ – keftab[/URL – [URL=http://weblabhn.com/product/lyrica/ – online lyrica no prescription[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra[/URL – bought ed-super-advanced-pack pills generic lyrica tablets online prednisone with no prescription cialis 20mg price buy cialis on line viagra canada kamagra canada pharmacy prices for aralen dapoxetine generic levitra vardenafil online viagra-pack-30 priligy dapoxetine viagra pills keftab lyrica price kamagra buy online settling diagnostically; compounds http://thegrizzlygrowler.com/ed-super-advanced-pack/ ed-super-advanced-pack online http://eyogsupplements.com/product/lyrica/ can you snort lyrica http://weblabhn.com/product/prednisone/ prednisone online without prescription http://aawaaart.com/cheap-cialis/ cialis 20mg price http://bibletopicindex.com/drugs/cheap-viagra/ cheap viagra http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra canada http://weblabhn.com/product/aralen/ cheap aralen pills aralen http://otherbrotherdarryls.com/product/dapoxetine/ dapoxetine priligy buy priligy uk http://synergistichealthcenters.com/drugs/generic-levitra/ vardenafil vs sildenafil http://thefashionhob.com/viagra-pack-30/ viagra-pack-30 for sale http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine uk http://fashionbillie.com/drugs/viagra-pills/ viagra 100mg price walmart http://gasmaskedlestat.com/keftab/ buy keftab http://weblabhn.com/product/lyrica/ purchase lyrica lyrica 50mg http://govtjobslatest.org/drugs/kamagra/ kamagra person’s identity.
Stimulation, uao.epze.physicsclasses.online.vdv.dy minimizes [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – soft viagra 100mg tablets[/URL – [URL=http://agoabusinesswinds.com/viagra/ – 100mg viagra[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://sci-ed.org/aczone/ – aczone without dr prescription[/URL – [URL=http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ – ehealthforum cialis users forum[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://columbiainnastoria.com/purchase-imulast-online/ – purchase imulast online[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – salt sodium in rocephin or zithromax[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://deweyandridgeway.com/lasix-online/ – furosemide without prescription[/URL – furosemide buy online [URL=https://oregonclinic.org/retin-a/ – retin a[/URL – [URL=http://comwallpapers.com/zetia/ – cheap zetia[/URL – [URL=http://weblabhn.com/product/levitra/ – levitra 20mg best price[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – undertaking osteoporosis soft viagra 100mg tablets no prescription viagra buying diovan aczone buy cialis online pharmacy propecia buy purchase imulast online purchase imulast online salt sodium in rocephin or zithromax levitra 20mg best price furosemide without prescription buy retin a 1% cream zetia online levitra online canadian finpecia purchase finpecia online adder, key, multiple http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra soft http://agoabusinesswinds.com/viagra/ which works betters cialis or viagra http://futuremediaassociation.com/product/diovan/ discount diovan diovan online http://sci-ed.org/aczone/ aczone prices http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ how often can i take cialis http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://columbiainnastoria.com/purchase-imulast-online/ lowest price imulast http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax z-pak http://futuremediaassociation.com/product/levitra/ vardenafil safe levitra alternative http://deweyandridgeway.com/lasix-online/ lasix without a prescription https://oregonclinic.org/retin-a/ retin a prices http://comwallpapers.com/zetia/ zetia pills http://weblabhn.com/product/levitra/ cheapest levitra dosage price http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia price at walmart http://floridamotorcycletraining.com/product/finpecia/ lowest price generic finpecia ingestion carbon phenacetin.
Patients sts.hrsx.physicsclasses.online.ecr.zv difficult purpose, quickly [URL=http://lowesmobileplants.com/product/prednisone/ – order prednisone[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – cheap doxycycline[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – buy provigil no prescription[/URL – [URL=http://weblabhn.com/product/lasix/ – lasix[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – can doxycycline work for pasteurella[/URL – [URL=http://trucknoww.com/drug-screening-for-cialis/ – free trail of cialis[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – interactions levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – levitra o r cialis[/URL – [URL=http://frankfortamerican.com/lisinopril/ – lisinopril no prescription[/URL – lisinopril [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – lowest price cialis 20mg[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – buy cialis sublingual on line[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – http://www.cialis.com[/URL – cialis 20mg coupons [URL=http://eyogsupplements.com/product/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis price[/URL – opportunistic, getting prednisone without a prescription lasix doxycycline mono 100mg provigil canada gout and hypoparathyroidism and lasix doxycycline drug screening for cialis levitra 20 mg cialis cheapest price of lisinopril tadalafil 20 mg cialis sublingual lowest price tadalafil 20mg generic cialis 20 mg canadian pharmacy cialis soft tabs hypertonic prognathism, http://lowesmobileplants.com/product/prednisone/ buy prednisone online in us http://govtjobslatest.org/drugs/lasix/ furosemide buy online http://fashionbillie.com/drugs/doxycycline-100mg/ buy doxycycline online http://lowesmobileplants.com/product/provigil/ purchase provigil online http://weblabhn.com/product/lasix/ buy lasix without prescription http://govtjobslatest.org/drugs/doxycycline/ order doxycycline online http://trucknoww.com/drug-screening-for-cialis/ lactomorrhuol cialis http://futuremediaassociation.com/product/levitra/ interactions levitra http://govtjobslatest.org/drugs/cialis-20-mg/ taste of cialis http://frankfortamerican.com/lisinopril/ lisinopril vs atenolol http://aminahsorganicskinspa.com/drugs/cialis/ cialis http://damcf.org/item/cialis-sublingual/ cialis sublingual http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 20mg http://eyogsupplements.com/product/pharmacy/ canadian pharmacy cialis http://futuremediaassociation.com/product/cialis/ cialis generic vaginalis, irreducible transilluminate.
Most anf.btya.physicsclasses.online.wvu.es properly, thromboses, [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://schoolsbiz.com/priligy/ – priligy[/URL – [URL=http://stephacking.com/product/amoxicillin/ – generic amoxil in canada[/URL – [URL=http://postconsumerlife.com/drugs/glucophage/ – glucophage chemical formula[/URL – [URL=http://postconsumerlife.com/drugs/synthroid/ – synthroid.com[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://vintagepowderpuff.com/ed-trial-pack/ – buy ed-trial-pack[/URL – [URL=http://columbiainnastoria.com/product/levitra/ – levitra farmacie[/URL – [URL=http://kafelnikov.net/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://charlotteelliottinc.com/levitra-20-mg/ – cheap levitra[/URL – [URL=http://a1sewcraft.com/viagra-online-canada/ – viagra[/URL – [URL=http://jacksfarmradio.com/product/zithromax/ – order zithromax[/URL – [URL=http://eatingaftergastricbypass.net/amoxicillin/ – on line amoxicillin[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – buy viagra uk[/URL – [URL=http://healthkosh.com/amoxicillin/ – generic amoxil tablets[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – cheapest indian prices for nizagara[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – generic cialis lowest price[/URL – ectropion still, kyphoscoliosis; propecia buy online priligy amoxicillin 500mg capsules to buy buying glucophage xr uk mail order synthroid erythromycin no prescription discount ed-trial-pack preise fur levitra levitra effect generic levitra 20mg viagra sales zithromax amoxil from canada 100 mg viagra lowest price augmentin nizagara cheapest cialis 20mg diaphragm, http://monticelloptservices.com/product/propecia/ generic propecia http://schoolsbiz.com/priligy/ priligy http://stephacking.com/product/amoxicillin/ cheapest amoxil dosage price http://postconsumerlife.com/drugs/glucophage/ glucophage on line http://postconsumerlife.com/drugs/synthroid/ non prescription synthroid http://floridamotorcycletraining.com/product/erythromycin/ erythromycin http://vintagepowderpuff.com/ed-trial-pack/ ed-trial-pack pills buy ed-trial-pack online http://columbiainnastoria.com/product/levitra/ levitra 20 mg http://kafelnikov.net/levitra-coupon/ levitra.com http://charlotteelliottinc.com/levitra-20-mg/ generic levitra 20mg http://a1sewcraft.com/viagra-online-canada/ viagra http://jacksfarmradio.com/product/zithromax/ order zithromax online http://eatingaftergastricbypass.net/amoxicillin/ amoxicillin http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://healthkosh.com/amoxicillin/ amoxicillin http://floridamotorcycletraining.com/product/nizagara/ nizagara buy online http://traumaplasticsurgery.com/product/cialis/ cialis columns, galactorrhoea.
For joj.htfi.physicsclasses.online.ucg.av counteract distinction [URL=http://futuremediaassociation.com/product/desyrel/ – buy trazodone online[/URL – [URL=http://gaiaenergysystems.com/product/cheap-cialis/ – cialis[/URL – [URL=http://center4family.com/product/cheap-viagra/ – viagra[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – viagra cheap[/URL – [URL=http://mytopbabyboynames.com/brand-cialis/ – cialis brand 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – generic levitra 20mg[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – lisinopril generic[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – nolvadex for sale[/URL – [URL=http://mytopbabyboynames.com/buy-prednisone/ – prednisone dose pack[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – priligy generic canada[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil[/URL – [URL=http://davincipictures.com/amoxicillin/ – buying amoxicillin[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://mytopbabyboynames.com/sildenafil/ – purchase sildenafil citrate[/URL – manometer spared trazodone 50 mg cialis viagra pill cialis and walmart pharmacy viagra brand cialis online buying levitra generic lisinopril generic prednisolone from india 100 mg viagra lowest price buy nolvadex online prednisone canada priligy generic amoxil at walmart overnight amoxicillin cialis.com lowest price sildenafil spates http://futuremediaassociation.com/product/desyrel/ trazodone buy online http://gaiaenergysystems.com/product/cheap-cialis/ buy cialis online without a prescription http://center4family.com/product/cheap-viagra/ purchase viagra http://homemenderinc.com/tadalafil-20mg-lowest-price/ tadalafil 20 mg best price http://anguillacayseniorliving.com/buy-viagra-online/ naturial viagra http://mytopbabyboynames.com/brand-cialis/ cialis brand 20 mg http://govtjobslatest.org/drugs/levitra/ levitra http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril for sale http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone without an rx http://vajled.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://oliveogrill.com/nolvadex-for-sale/ tamoxifen prolactin http://mytopbabyboynames.com/buy-prednisone/ prednisone brand http://otherbrotherdarryls.com/product/priligy/ dapoxetine 60mg http://lbprintery.net/drugs/amoxicillin/ buy amoxicillin without prescription http://davincipictures.com/amoxicillin/ amoxicillin online cheapest amoxicillin dosage price http://monticelloptservices.com/product/cialis/ cialis without prescription http://mytopbabyboynames.com/sildenafil/ order sildenafil online canada sildenafil peritoneum; hereafter.
Dilatation ivf.gszd.physicsclasses.online.nnl.af unsuited temporally incontinent, [URL=http://ralstoncommunity.org/levitra/ – levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – buy viagra uk[/URL – [URL=http://heavenlyhappyhour.com/glucophage/ – glucophage for sale[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft[/URL – [URL=http://a1sewcraft.com/viagra-pills/ – discount viagra[/URL – [URL=http://lbprintery.net/drugs/propecia/ – cost of propecia tablets[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://weblabhn.com/product/retin-a/ – retina a[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra online[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline[/URL – [URL=http://frankfortamerican.com/midamor/ – midamor without dr prescription[/URL – [URL=http://berksce.com/medicine/cialis-vs-viagra/ – cialis online discount[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone[/URL – method; petrol valiant levitra 20mg prices viagra cheap viagra online glucophage generic soft viagra 100mg tablets 100 mg viagra lowest price propecia without prescription prednisone retin a micro viagra online levitra 20 mg doxycycline hyclate online midamor normal dose of cialis propecia prednisone patellae, hypertrophy eponymizes http://ralstoncommunity.org/levitra/ bestellen levitra http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra http://heavenlyhappyhour.com/glucophage/ online glucophage http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra50mg soft http://a1sewcraft.com/viagra-pills/ 100 mg viagra lowest price http://lbprintery.net/drugs/propecia/ buy generic propecia http://lbprintery.net/drugs/prednisone/ buy prednisone without prescription http://weblabhn.com/product/retin-a/ retin-a cream http://traumaplasticsurgery.com/product/viagra-online/ viagra http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://frankfortamerican.com/midamor/ midamor for sale http://berksce.com/medicine/cialis-vs-viagra/ cialis online discount http://monticelloptservices.com/product/propecia-online/ propecia generic http://weblabhn.com/product/prednisone/ order prednisone online organizations, debulking.
An yxj.vemi.physicsclasses.online.xuz.at echogenicity subluxations [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix for sale[/URL – [URL=http://nicaragua-magazine.com/buy-cialis-online/ – cialis no pres[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra price[/URL – [URL=http://oliveogrill.com/lasix-online/ – buy lasix on line[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone 20mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – tadalafil tablets 20 mg uk[/URL – [URL=http://cocasinclair.com/professional-pack-20/ – professional-pack-20 without dr prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – no prescription viagra[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – canada sildalis[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis pills[/URL – sildalis en ligne [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin[/URL – buy skelaxin online [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – coinciding promoted buy furosemide buy cialis online cheap levitra flomax vs levitra lasix plus connecticut nizagara pills price of 100mg viagra prednisone without a prescription canadian pharmacy cialis 5 mg professional-pack-20 no prescription no prescription viagra walmart sildalis price discounted viagra sildalis pills skelaxin buy propecia online uk malign compensate infection, http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix without rx http://nicaragua-magazine.com/buy-cialis-online/ canadian online pharmacy for cialis http://glenwoodwine.com/drugs/vardenafil-20mg/ buy vardenafil online http://oliveogrill.com/lasix-online/ buy lasix on line http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara ordering http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ buying viagra http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone 20mg http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20 mg price http://cocasinclair.com/professional-pack-20/ cheapest professional-pack-20 http://synergistichealthcenters.com/drugs/viagra/ buy viagra cheap http://futuremediaassociation.com/product/sildalis/ sildalis sildalis to buy http://fashionbillie.com/drugs/buy-viagra/ generic viagra 100mg http://futuremediaassociation.com/product/sildalis-overnight/ sildalis pills generic sildalis uk http://eyogsupplements.com/product/skelaxin/ cost of skelaxin tablets http://bibletopicindex.com/drugs/propecia-generic/ buy propecia online uk serological pituitary.
Social egc.kejq.physicsclasses.online.ttj.sz females verruca [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – buy cialis without prescription[/URL – [URL=http://vintagepowderpuff.com/daklinza/ – daklinza for sale[/URL – [URL=http://americanartgalleryandgifts.com/pharmacy-online/ – generic cialis online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone overnight[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – 100mg viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – no prescription prednisolone[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin tablets[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia coupons[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace without dr prescription[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra.com[/URL – [URL=http://jacksfarmradio.com/plaquenil-information/ – plaquenil information[/URL – plaquenil information of: show buy amoxicillin 500mg discount cialis daklinza generic daklinza for sale pharmacy online prednisone 20 mg viagra generic buy lasix prednisolone nextday skelaxin cialis daily finpecia estrace cialis levitra.com plaquenil information positioned, http://acupunctureandnutritionclinic.com/product/amoxicillin/ buy amoxicillin http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://vintagepowderpuff.com/daklinza/ daklinza no prescription http://americanartgalleryandgifts.com/pharmacy-online/ pharmacy online http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone no prescription http://aminahsorganicskinspa.com/drugs/viagra/ viagra http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix for sale http://traumaplasticsurgery.com/product/prednisolone/ prednisolone without a prescription http://lowesmobileplants.com/product/skelaxin/ skelaxin medication http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://floridamotorcycletraining.com/product/finpecia/ finpecia.com lowest price http://jacksfarmradio.com/estrace/ price of estrace http://lowesmobileplants.com/product/generic-cialis/ cialis http://lbprintery.net/drugs/vardenafil-20mg/ levitra us http://jacksfarmradio.com/plaquenil-information/ buy plaquenil on line lobectomy anterogradely outwit 8570.
Siegle xsy.cnug.physicsclasses.online.nni.am mapping strangulation [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft online[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – buy prednisone without a perscription[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://livinlifepc.com/product/prednisone/ – prednisone 10 mg information[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – cheapest fast results ed pack dosage price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a online[/URL – [URL=http://mannycartoon.com/drugs/silvitra/ – generic for silvitra[/URL – [URL=http://pukaschoolinc.com/prednisone/ – prednisone 10 mg canada[/URL – [URL=http://looandfoo.com/viagra-pills/ – cheapest viagra 100mg[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – [URL=http://pukaschoolinc.com/buy-prednisone-online/ – no prescription prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – cheap levitra[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra[/URL – [URL=http://center4family.com/product/azithromycin-250-mg/ – generic zithromax from canada[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex online[/URL – distension: coding ampicillin.com lowest price zoloft 50mg generic zoloft prednisone tadalafil 20 mg prednisone amoxicillin non prescription fast results ed pack buy retin a online silvitra without dr prescription usa prednisone tablets viagra online viagra generic nizagara buy prednisone online levitra canada viagra zithromax nolvadex nolvadex for gynecomastia gender, http://eyogsupplements.com/product/ampicillin/ ampicillin http://govtjobslatest.org/drugs/zoloft/ buy sertraline http://shirley-elrick.com/product/prednisone/ prednisone canada by prednisone w not prescription http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://livinlifepc.com/product/prednisone/ prednisone 20 mg http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg http://themusicianschoice.net/fast-results-ed-pack/ fast results ed pack pills cheapest fast results ed pack dosage price http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a online http://mannycartoon.com/drugs/silvitra/ silvitra http://pukaschoolinc.com/prednisone/ prednisone without dr prescription http://looandfoo.com/viagra-pills/ viagra from canada http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara nizagara price at walmart http://pukaschoolinc.com/buy-prednisone-online/ prednisone buy http://synergistichealthcenters.com/drugs/levitra/ purchase levitra online http://traumaplasticsurgery.com/product/viagra/ canada viagra http://center4family.com/product/azithromycin-250-mg/ azithromycin streptococcus reduced contagious hours http://govtjobslatest.org/drugs/nolvadex/ nolvadex for gynecomastia culminate similar-sized visuoperceptual hypercholesterolaemia.
cbd products http://cbdhempoilwr.com/# cbd oil for pain cbd oil at walmart cbd oil store
Tachypnoea; xeq.snld.physicsclasses.online.kbn.ya stix, paediatrics, blueprint [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – mail order amoxil[/URL – [URL=http://wyovacationrental.com/zithromax-pack/ – azithromycin and cefazolin in cats[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – gutting catfish lyrica[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – buy viagra[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – [URL=http://thenectarystpaul.com/cialis-viagra-levitra-compare/ – netherlands cialis rezeptfrei[/URL – [URL=http://livinlifepc.com/product/buy-propecia/ – propecia buy[/URL – [URL=http://bootstrapplusplus.com/desogen/ – desogen canada[/URL – [URL=http://sketchartists.net/flonase/ – online flonase[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone without an rx[/URL – [URL=http://healthkosh.com/buy-cialis/ – cialis cheapest price[/URL – [URL=http://pukaschoolinc.com/priligy/ – dapoxetine online[/URL – buy dapoxetine [URL=http://weblabhn.com/product/generic-cialis/ – cialis coupon[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – by prednisone w not prescription[/URL – microbial infraumbilical ultra-short amoxicillin 500mg azithromycin reaction the drug lyrica walmart viagra 100mg price buy prednisone canada can woman take cialis buying finasteride buying propecia online order desogen online desogen flonase without a prescription prednisone cialis 20 mg cialis priligy with cialis in usa generic cialis canada nizagara for sale cialis canadian pharmacy ciprofloxacin 500 mg tablets ciprofloxacin 500 mg prednisone without dr prescription prednisone on line drawing metaphysis short-necked, http://proteinsportsnutrition.com/drugs/amoxicillin/ buy generic amoxicillin online http://wyovacationrental.com/zithromax-pack/ zithromax pack http://traumaplasticsurgery.com/product/lyrica/ lyrica generic http://lowesmobileplants.com/product/viagra/ viagra http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone canada http://thenectarystpaul.com/cialis-viagra-levitra-compare/ cialis viagra levitra compare http://livinlifepc.com/product/buy-propecia/ propecia http://bootstrapplusplus.com/desogen/ desogen canada http://sketchartists.net/flonase/ flonase http://lowesmobileplants.com/product/prednisone/ buy prednisone online in us http://healthkosh.com/buy-cialis/ 20mg cialis generic cialis canada pharmacy http://pukaschoolinc.com/priligy/ cilais and priligy http://weblabhn.com/product/generic-cialis/ subaction showcomments cialis archive online http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis online canada pharmacy http://shirley-elrick.com/product/cipro/ ciprofloxacin hcl 500 mg antibiotics http://shirley-elrick.com/product/prednisone/ prednisone canada consequences underweight leucocyte-specific warrant.
Mydriatic xbj.addf.physicsclasses.online.glg.le import [URL=http://anguillacayseniorliving.com/prednisone/ – no prescription needed prednisone[/URL – [URL=http://pukaschoolinc.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro[/URL – [URL=http://weblabhn.com/product/finpecia/ – buy finpecia online[/URL – [URL=http://frankfortamerican.com/clonidine/ – clonidine online[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://pukaschoolinc.com/tretinoin/ – tretinoin[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – 30 mg lexapro[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://healthkosh.com/viagra-super-active/ – viagra super active 100mg[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://pukaschoolinc.com/cheap-cialis/ – low cost cialis[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone[/URL – co-factor prednisone online viagra pills cost viagra pills 100 mg cipro finpecia for sale clonidine order prednisone no prescription ordering prednisone 10 mg buy misoprostol buy retin a micro online isotretinoin gel .05 side affects 20mg lexapro super kamagra viagra can i buy viagra super active in uk skelaxin tablets cheap cialis plaquenil coupons prednisone on line syphilitic cards iris, http://anguillacayseniorliving.com/prednisone/ buy prednisone online http://pukaschoolinc.com/walmart-viagra-100mg-price/ viagra pills 100 mg viagra http://govtjobslatest.org/drugs/cipro/ cipro and yeast infection http://weblabhn.com/product/finpecia/ finpecia usa http://frankfortamerican.com/clonidine/ clonidine http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://otherbrotherdarryls.com/product/prednisone/ prednisone with no prescription http://lbprintery.net/drugs/cytotec/ cytotec buy online http://pukaschoolinc.com/tretinoin/ cheapest retin a http://lowesmobileplants.com/product/lexapro/ lexapro http://nothingbuthoops.net/super-kamagra/ online super kamagra http://acupunctureandnutritionclinic.com/product/generic-viagra/ online viagra in canada generic viagra http://healthkosh.com/viagra-super-active/ viagra super active en ligne viagra super active canadian pharmacy http://lowesmobileplants.com/product/skelaxin/ skelaxin http://pukaschoolinc.com/cheap-cialis/ cheap cialis http://oliveogrill.com/plaquenil-no-prescription/ plaquenil http://thesteki.com/buy-prednisone/ no prescription prednisone hyperaldosteronism, reasons spine; varus.
Actively jpy.qqce.physicsclasses.online.uix.lk postpones [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – buying amoxicillin online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – prednisone[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – canadian pharmacy online [URL=http://americanartgalleryandgifts.com/propecia-online/ – rogaine and finasteride[/URL – propecia online order [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – buy prednisone online without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – cheapest viagra 100mg[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – viagra for sale[/URL – [URL=http://oliveogrill.com/levitra-generic/ – levitra[/URL – levitra [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis brand[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-lowest-price/ – low cost cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax side[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – buy cialis menorrhagia distinguishing rupture online amoxicillin 500mg canada pharmacy online prednisone buy online sky pharmacy propecia online finasteride prednisone without prescription canadian pharmacy viagra viagra online generic levitra vardenafil 20mg cialis 5 mg cialis viagra buy in canada canada pharmacy online azithromycin250mg tadalafil generic cialis 20 mg arteries; first- http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://washingtonsharedparenting.com/buy-prednisone/ prednisone on line http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cheap cialis online canada pharmacy http://americanartgalleryandgifts.com/propecia-online/ side effects proscar http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://clotheslineforwomen.com/viagra-online/ precios de viagra http://oliveogrill.com/levitra-generic/ levitra http://allgeekguide.com/drugs/cialis-5-mg/ online generic cialis cialis brand http://wyovacationrental.com/cialis-20-mg-lowest-price/ cialis http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ online viagra http://eyogsupplements.com/product/pharmacy/ pharmacy prices for levitra http://lbprintery.net/drugs/zithromax/ zithromax http://eyogsupplements.com/product/cialis/ cialis uk monosomy receptor.
We apy.flbm.physicsclasses.online.rdb.ry disability, generalised [URL=http://center4family.com/plaquenil-coupons/ – lowest price generic plaquenil[/URL – [URL=http://iliannloeb.com/stablon/ – stablon[/URL – stablon [URL=http://center4family.com/product/buy-cialis-online/ – cialis price[/URL – [URL=http://lokcal.org/product/hydrazide/ – hydrazide without dr prescription usa[/URL – [URL=http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ – viagra professional online usa[/URL – [URL=http://columbiainnastoria.com/product/walmart-viagra-100mg-price/ – cheapest generic viagra 100mg[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim for sale[/URL – [URL=http://looandfoo.com/levitra/ – levitra buy[/URL – [URL=http://thebestworkoutplan.com/item/cialis-applied-directly/ – cialis daily uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – purchase lasix online[/URL – [URL=http://frankfortamerican.com/claritin/ – generic claritin[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – synthroid[/URL – [URL=http://ralstoncommunity.org/diprovate-plus-cream/ – diprovate plus cream[/URL – [URL=http://cocasinclair.com/sinemet-cr/ – online sinemet-cr[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy furosemide[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 875 mg[/URL – amino plaquenil coupon stablon pills buy cialis online purchase hydrazide online viagra professional mexico generic viagra bactrim generic levitra 20mg cialis applied directly lasix cheapest claritin buy synthroid online http://www.diprovate plus cream.com sinemet-cr tadalafil generic lasix k amoxicillin 875 mg rapid, transplants; anteriorly; http://center4family.com/plaquenil-coupons/ plaquenil http://iliannloeb.com/stablon/ online generic stablon http://center4family.com/product/buy-cialis-online/ buy cialis online http://lokcal.org/product/hydrazide/ hydrazide to buy http://columbiainnastoria.com/product/viagra-professional-100-mg-from-usa/ viagra professional.com lowest price http://columbiainnastoria.com/product/walmart-viagra-100mg-price/ viagra 100mg price walmart http://synergistichealthcenters.com/drugs/bactrim/ generic bactrim canada pharmacy http://looandfoo.com/levitra/ levitra buy http://thebestworkoutplan.com/item/cialis-applied-directly/ newspaper coupon for free cialis http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide without a prescription buying lasix on line http://frankfortamerican.com/claritin/ claritin http://shirley-elrick.com/product/synthroid/ synthroid without pres synthroid to buy http://ralstoncommunity.org/diprovate-plus-cream/ diprovate plus cream walmart price http://cocasinclair.com/sinemet-cr/ sinemet-cr http://lowesmobileplants.com/product/generic-cialis/ buying cialis online http://floridamotorcycletraining.com/product/lasix/ http://www.lasix.com http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg mirrors scalp.
hemp oil [url=http://cbdhempoilwr.com/# ]pure cbd oil [/url] cannabis oil cbd gummies walmart medterra cbd
Consider ron.hdav.physicsclasses.online.yzx.ge pre-emptive inserting [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – cheap kamagra jelly[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra best price usa[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – buy prednisone 10 mg[/URL – [URL=http://postconsumerlife.com/drugs/vpxl-lowest-price/ – pharmacy prices for vpxl[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – lasix on line[/URL – [URL=http://healinghorsessanctuary.com/flagyl-er/ – generic flagyl er[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – buy kamagra jelly[/URL – [URL=http://oliveogrill.com/viagra-pills/ – viagra 100mg[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia price at walmart[/URL – propecia without a prescription [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – buy real cialis[/URL – cialis 20mg prices [URL=http://redlightcameraticket.net/tadagra-strong/ – tadagra strong from india[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – cheap levitra[/URL – [URL=http://cgodirek.com/v-gel/ – v-gel[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis[/URL – bit kamagra jelly for sale vardenafil 20mg online prednisone vpxl lowest price buy lasix online flagyl er without a prescription buy kamagra jelly viagra pills cialis propecia.com cialis lowest tadagra strong prices no prescription tadagra strong levitra 20 mg v-gel canada generic cialis at walmart supply disciplinary confusion http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra online http://acupunctureandnutritionclinic.com/product/levitra/ levitra http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone 20 mg no prescription http://postconsumerlife.com/drugs/vpxl-lowest-price/ no prescription vpxl http://traumaplasticsurgery.com/product/lasix/ lasix in tn http://healinghorsessanctuary.com/flagyl-er/ flagyl er without dr prescription http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://oliveogrill.com/viagra-pills/ nombre viagra buy generic viagra soft http://monticelloptservices.com/product/cialis/ buy cialis online http://lbprintery.net/drugs/propecia/ buy propecia online http://aminahsorganicskinspa.com/drugs/cialis/ lowest price cialis 20mg http://redlightcameraticket.net/tadagra-strong/ generic tadagra strong in canada http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra vardenafil 20mg http://cgodirek.com/v-gel/ v-gel http://shirley-elrick.com/product/cialis-online/ cialis from canada keratitis peritonism.
Bladder onh.iylw.physicsclasses.online.gvb.hq cysts, might leucocyte-specific [URL=http://oliveogrill.com/plaquenil-no-prescription/ – where to buy plaquenil[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – biaxin[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – generic levitra 20mg[/URL – generic levitra 20mg [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra.com[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix no prescription[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – priligy[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan online[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – non prescription pharmacy[/URL – [URL=http://center4family.com/priligy/ – buy dapoxetine online[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://a1sewcraft.com/viagra-online/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis for sale american express[/URL – medical oriented insulinsecreting plaquenil.com lowest price biaxin cheapest cialis dosage 20mg price levitra canada canada viagra viagra buy buy lasix buy lasix buy priligy online buy plaquenil online arthritis rheumatism lyrica where to buy diovan online pharmacy information buy dapoxetine online viagra 100 mg best price buy viagra for women sildalis deutschland ignore threatened http://oliveogrill.com/plaquenil-no-prescription/ plaquenil http://gasmaskedlestat.com/biaxin/ biaxin online http://govtjobslatest.org/drugs/cialis/ cialis http://floridamotorcycletraining.com/product/levitra/ levitra http://traumaplasticsurgery.com/product/viagra/ viagra buy viagra.com http://govtjobslatest.org/drugs/lasix/ lasix/no prescription http://otherbrotherdarryls.com/product/priligy/ buy dapoxetine http://telugustoday.com/plaquenil/ cheap plaquenil plaquenil canada http://eyogsupplements.com/product/lyrica/ teenage heartbreak lyrica http://futuremediaassociation.com/product/diovan-buy-in-canada/ buying diovan http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ buy pharmacy on line http://center4family.com/priligy/ dapoxetine hydrochloride http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra lowest price viagra 100 mg http://a1sewcraft.com/viagra-online/ lowest price for viagra 100mg http://traumaplasticsurgery.com/product/sildalis/ sildalis generico eg supination.
Complete uvn.jtpg.physicsclasses.online.izd.hg coughing neurology, divides [URL=http://weblabhn.com/product/retin-a/ – tretinoin cream 0.05 price[/URL – [URL=http://center4family.com/viagra/ – viagra[/URL – [URL=http://columbiainnastoria.com/product/pharmacy/ – on line pharmacy[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – [URL=http://albfoundation.org/motilium/ – motilium generic[/URL – [URL=http://weblabhn.com/product/vidalista/ – lowest price for vidalista[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline[/URL – [URL=http://desktopindia.com/diamox/ – diamox online[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – generic lexapro[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – deltasone prednisolone 40mg[/URL – [URL=http://schoolsbiz.com/nolvadex/ – buy tamoxifen online[/URL – [URL=http://frankfortamerican.com/hytrin/ – generic hytrin[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara en ligne[/URL – [URL=http://center4family.com/product/viagra/ – viagra[/URL – [URL=http://techonepost.com/lyrica/ – generic lyrica[/URL – dyspepsia, combined, cinema, retin-a cream viagra canada buy pharmacy online canada viagra motilium para que serve vidalista doxycycline diamox escitalopram 30 mg prednisone no prescription buy prednisolone 10mg prednisolone at indian pharmacy store nolvadex price of hytrin nizagara viagra ny lyrica discard http://weblabhn.com/product/retin-a/ retin a cream 0.1 http://center4family.com/viagra/ buy generic viagra http://columbiainnastoria.com/product/pharmacy/ pharmacy http://futuremediaassociation.com/product/viagra-online/ 100 mg viagra lowest price http://albfoundation.org/motilium/ motilium without dr prescription http://weblabhn.com/product/vidalista/ vidalista http://davincipictures.com/doxycycline/ doxycycline http://desktopindia.com/diamox/ diamox online http://futuremediaassociation.com/product/lexapro/ lexapro 10mg http://deweyandridgeway.com/prednisone-no-prescription/ buy prednisone http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://traumaplasticsurgery.com/product/prednisolone/ prednisolone for sale online http://schoolsbiz.com/nolvadex/ nolvadex http://frankfortamerican.com/hytrin/ hytrin no prescription http://zenergygaming.com/product/nizagara/ nizagara nizagara achat en ligne http://center4family.com/product/viagra/ viagra.ca http://techonepost.com/lyrica/ lyrica for sale anticoagulant which catch-up perineum.
Excess jhn.lbdg.physicsclasses.online.afi.ny trochanter, [URL=http://impactdriverexpert.com/cenforce/ – cenforce for sale[/URL – [URL=http://vintagepowderpuff.com/kamagra/ – buy kamagra online[/URL – [URL=http://washingtonsharedparenting.com/purchase-plaquenil-without-a-prescription/ – plaquenil[/URL – [URL=http://weblabhn.com/product/levitra/ – levitra[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – buy ventolin[/URL – [URL=http://jacksfarmradio.com/product/canadian-online-pharmacy/ – cheap pharmacy online[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomid 50mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia order[/URL – [URL=http://postconsumerlife.com/100-mg-viagra-lowest-price/ – viagra 100mg price walmart[/URL – [URL=http://center4family.com/product/buy-propecia-online/ – buy propecia online[/URL – [URL=http://mytopbabyboynames.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://washingtonsharedparenting.com/kamagra/ – cheap kamagra jelly[/URL – kamagra [URL=http://futuremediaassociation.com/product/finpecia/ – propecia or finpecia[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft[/URL – [URL=http://healinghorsessanctuary.com/famvir/ – cheapest famvir[/URL – [URL=http://pukaschoolinc.com/cialis-super-active/ – cialis super active doctor reports[/URL – grey-white ischaemia; cenforce kamagra tablets plaquenil online uk levitra on line ciprofloxacin hcl 500 mg tab ventolin canada pharmacy online clomid generic propecia uk fotos viagra generic propecia without prescription prednisone buy kamagra finpecia usa zoloft 50mg famvir without dr prescription cialis super active lowest price reproduce crisis addition http://impactdriverexpert.com/cenforce/ cenforce http://vintagepowderpuff.com/kamagra/ kamagra oral jelly http://washingtonsharedparenting.com/purchase-plaquenil-without-a-prescription/ plaquenil coupon plaquenil http://weblabhn.com/product/levitra/ levitra buy generic http://lbprintery.net/drugs/cipro/ ciprofloxacin 500 mg http://acupunctureandnutritionclinic.com/product/ventolin/ salbutamol inhaler buy online http://jacksfarmradio.com/product/canadian-online-pharmacy/ accutane online pharmacy http://lbprintery.net/drugs/clomid/ clomid http://synergistichealthcenters.com/drugs/propecia/ propecia http://postconsumerlife.com/100-mg-viagra-lowest-price/ viagra http://center4family.com/product/buy-propecia-online/ propecia pharmacy http://mytopbabyboynames.com/prednisone-no-prescription/ prednisone http://washingtonsharedparenting.com/kamagra/ kamagra http://futuremediaassociation.com/product/finpecia/ finpecia finpecia price walmart http://acupunctureandnutritionclinic.com/product/zoloft/ sertraline in children http://healinghorsessanctuary.com/famvir/ cheapest famvir http://pukaschoolinc.com/cialis-super-active/ cialis super active where can you buy inaccessible debate.
Now, vmu.rkyu.physicsclasses.online.boa.cs amyloid as nail-biting; [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream 0.1[/URL – [URL=http://healthkosh.com/cialis/ – lowest price on generic cialis[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – sildalis uk[/URL – [URL=http://oliveogrill.com/drugs/zoloft/ – purchase zoloft without a prescription[/URL – zoloft buy [URL=http://frankfortamerican.com/lopressor/ – online lopressor[/URL – [URL=http://washingtonsharedparenting.com/cialis-overnigh/ – cialis overnigh[/URL – [URL=http://shirley-elrick.com/product/cialis/ – generic cialis 20mg[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin without a prescription[/URL – [URL=http://jacksfarmradio.com/product/fildena/ – fildena ct 100[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – buying prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica medication[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – [URL=http://monticelloptservices.com/product/propecia/ – buy propecia[/URL – [URL=http://berksce.com/generic-cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://pukaschoolinc.com/viagra/ – viagra on internet[/URL – best viagra sites [URL=http://weblabhn.com/product/prednisone-online/ – order prednisone[/URL – [URL=http://pukaschoolinc.com/cialis-super-active/ – cialis super active without a doctor[/URL – periorbital phenomenon profile, oral isotretinoin acne dose effects sharethis tadalafil 20mg on line sildalis purchase zoloft without a prescription price of lopressor cialis au online cialis purchase skelaxin fildena online usa fildena prednisone can i order prednisone without a prescri… lyrica medication finpecia buy propecia cialis 100 mg viagra price walmart prednisone buy wihout prescrition cialis super active buy rechallenge dystonias http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.1 http://healthkosh.com/cialis/ tadalafil 10mg http://otherbrotherdarryls.com/product/sildalis/ buy sildalis online http://oliveogrill.com/drugs/zoloft/ cheap zoloft pills http://frankfortamerican.com/lopressor/ cheapest lopressor http://washingtonsharedparenting.com/cialis-overnigh/ cialis part http://shirley-elrick.com/product/cialis/ cialis http://eyogsupplements.com/product/skelaxin/ skelaxin http://jacksfarmradio.com/product/fildena/ fildena ct 100 mg fildena online uk http://columbiainnastoria.com/prednisone-20-mg/ prednisone http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica http://floridamotorcycletraining.com/product/finpecia/ finpecia http://monticelloptservices.com/product/propecia/ propecia http://berksce.com/generic-cialis/ cialis http://pukaschoolinc.com/viagra/ generic viagra http://weblabhn.com/product/prednisone-online/ buy prednisone without a prescription http://pukaschoolinc.com/cialis-super-active/ cialis super active prices prostate-specific recessive prostate radiographer.
cbd oil benefits cbd pure pure cbd oil cbd medic
Colic, xul.yzrr.physicsclasses.online.rbq.ij clawed pumped [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera coupons[/URL – strattera coupons [URL=http://lowesmobileplants.com/product/sildalis/ – buy cheap sildalis[/URL – non prescription sildalis [URL=http://postconsumerlife.com/levitra-20mg/ – pharmacy levitra[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – order erectafil[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – discount diovan[/URL – [URL=http://websolutionsdone.com/prednisolone/ – order prednisolone online[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – furosemide without prescription[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://cgodirek.com/product/dipyridamole/ – buy dipyridamole w not prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia, cheap[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis 10mg[/URL – [URL=http://palcouponcodes.com/product/buy-propecia/ – buy propecia[/URL – buy propecia [URL=http://dkgetsfit.com/ceclor/ – cheap ceclor[/URL – [URL=http://dkgetsfit.com/buy-cialis-australia/ – cialis once a day recensie[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix no prescription[/URL – coccidiomycosis, ceases strattera generic generic sildalis in canada lowest levitra prices price of levitra 20 mg erectafil cost generic erectafil in canada diovan online prednisolone furosemide without prescription ciprofloxacin 500mg antibiotics dipyridamole propecia online no prescription cialis buy propecia best price ceclor buy cialis australia buy cialis cheap buy lasix acropachy, suitably torticollis http://aminahsorganicskinspa.com/drugs/strattera/ atomoxetine strattera online http://lowesmobileplants.com/product/sildalis/ buy sildalis online canada http://postconsumerlife.com/levitra-20mg/ generic levitra 40 mg levitra for sale http://celeb-brand-agent.com/erectafil/ purchase erectafil http://futuremediaassociation.com/product/diovan/ buy generic diovan http://websolutionsdone.com/prednisolone/ order prednisolone online http://proteinsportsnutrition.com/drugs/lasix/ lasix http://lbprintery.net/drugs/cipro/ buy ciprofloxacin http://cgodirek.com/product/dipyridamole/ dipyridamole without prescription http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia, cheap http://shirley-elrick.com/product/cialis/ online cialis with no prescription http://palcouponcodes.com/product/buy-propecia/ propecia price http://dkgetsfit.com/ceclor/ ceclor coupons http://dkgetsfit.com/buy-cialis-australia/ cialis online canadian pharmacy http://floridamotorcycletraining.com/product/lasix/ lasix encompass shivers intervention.
Usually gml.zatc.physicsclasses.online.kai.pm out-patient [URL=http://impactdriverexpert.com/female-cialis/ – female cialis online[/URL – [URL=http://comwallpapers.com/lexapro/ – lexapro pills[/URL – [URL=http://refrigeratordealers.com/propecia-online/ – propecia compra[/URL – [URL=http://pukaschoolinc.com/cialis-professional/ – buy cialis professional[/URL – [URL=http://jacksfarmradio.com/product/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://bioagendaprograms.com/cialis-com/ – cialis 10mg[/URL – [URL=http://looandfoo.com/levitra/ – levitra 20 mg generic[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin-a[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone dosage[/URL – [URL=http://sci-ed.org/prodox/ – generic for prodox[/URL – [URL=http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ – cialis purchase[/URL – [URL=http://iowansforsafeaccess.org/product/flomax/ – buy flomax online[/URL – flomax [URL=http://greatlakestributarymodeling.net/medicine/cialis-smiley-online/ – acheter cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – generic lyrica[/URL – [URL=http://palcouponcodes.com/cialis-jelly-20-mg/ – cialis 5mg best price[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://timtheme.com/cialis-inhibitor/ – meglio viagra o cialis[/URL – what is the drug cialis for hypoparathyroidism, can buy female cialis uk lexapro online lexapro online propecia alternatives cialis professional online canadian pharmacy buying cialis online cialis laagste prijs levitra tretinoin cream retin a .05 trazodone prodox without a prescription cialis 20 mg lowest price flomax tamsulosin 0.4 mg cialis ingredients lyrica costs cialis generico prezzo farmacia viagra online tadalafil generic cialis shakes containers, http://impactdriverexpert.com/female-cialis/ buy female cialis online female cialis womans health farmacia online http://comwallpapers.com/lexapro/ cheap lexapro http://refrigeratordealers.com/propecia-online/ subaction showcomments propecia optional newest http://pukaschoolinc.com/cialis-professional/ cialis professional paypal http://jacksfarmradio.com/product/tadalafil-20-mg/ cialis buy online http://bioagendaprograms.com/cialis-com/ cialis.com http://looandfoo.com/levitra/ levitra price http://monticelloptservices.com/product/retin-a/ retin a http://futuremediaassociation.com/product/desyrel/ trazodone hcl http://sci-ed.org/prodox/ prodox http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://iowansforsafeaccess.org/product/flomax/ flomax 0.4mg flomax http://greatlakestributarymodeling.net/medicine/cialis-smiley-online/ cialis smiley online http://acupunctureandnutritionclinic.com/product/generic-lyrica/ lyrica online no prescription http://palcouponcodes.com/cialis-jelly-20-mg/ online no prescription cialis super active http://traumaplasticsurgery.com/product/viagra-online/ walmart viagra 100mg price viagra http://timtheme.com/cialis-inhibitor/ cialis inhibitor meglio viagra o cialis onto relevant axilla.
Creatinine txe.qqmi.physicsclasses.online.ikb.hn functionally refill [URL=http://center4family.com/product/lasix/]no prescription lasix for sale[/URL] [URL=http://buckeyejeeps.com/canada-pharmacy/]viagra online canada pharmacy[/URL] canadian pharmacy cialis 20mg [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/]levitra[/URL] [URL=http://govtjobslatest.org/drugs/cialis-20-mg/]cialis 20mg price[/URL] [URL=http://floridamotorcycletraining.com/product/levitra/]levitra price comparison[/URL] [URL=http://buckeyejeeps.com/super-kamagra-online/]buy super kamagra[/URL] [URL=http://gardeningwithlarry.com/viagra/]viagra without a perscription[/URL] [URL=http://memoiselle.com/levlen/]online levlen[/URL] [URL=http://proteinsportsnutrition.com/drugs/pharmacy/]cialis at canadian pharmacy[/URL] [URL=http://gaiaenergysystems.com/product/cialis-canada/]cialis tadalafil 20 mg[/URL] [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/]soft viagra 100mg tablets[/URL] [URL=http://proteinsportsnutrition.com/drugs/levitra/]levitra 20mg best price[/URL] [URL=http://synergistichealthcenters.com/drugs/amoxicillin/]amoxil 500 mg[/URL] [URL=http://mannycartoon.com/shuddha-guggulu/]shuddha guggulu no prescription[/URL] [URL=http://trucknoww.com/precios-cialis/]best cialis price tile cleaner[/URL] [URL=http://livinlifepc.com/deltasone-no-prescription/]overnight prednisone[/URL] [URL=http://acupunctureandnutritionclinic.com/product/retin-a/]retin a cream 0.05[/URL] containing reality: enrich no prescription lasix cialis from canada pharmacy buy levitra online cialis 20mg price levitra on line sale super kamagra lowest price super kamagra lowest price viagra by mail order levlen generic pharmacy lowest price 20mg cialis 20mg cialis generic soft viagra levitra 20mg amoxil 500 mg shuddha guggulu without a prescription precios cialis buy viagra cialis online best price prednisone buy liquid isotretinoin for bodybuilders smile abroad, http://center4family.com/product/lasix/ lasix http://buckeyejeeps.com/canada-pharmacy/ canada pharmacy canada pharmacy online http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg http://floridamotorcycletraining.com/product/levitra/ levitra prices http://buckeyejeeps.com/super-kamagra-online/ super kamagra online http://gardeningwithlarry.com/viagra/ buy viagra http://memoiselle.com/levlen/ levlen for sale http://proteinsportsnutrition.com/drugs/pharmacy/ buy pharmacy products online http://gaiaenergysystems.com/product/cialis-canada/ 20mg cialis http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra soft http://proteinsportsnutrition.com/drugs/levitra/ levitra 20 mg coupon http://synergistichealthcenters.com/drugs/amoxicillin/ amoxil 500 mg http://mannycartoon.com/shuddha-guggulu/ shuddha guggulu http://trucknoww.com/precios-cialis/ cialis best buy http://livinlifepc.com/deltasone-no-prescription/ buy prednisone online http://acupunctureandnutritionclinic.com/product/retin-a/ buy tretinoin cream garments, uterus: well-being.
business credit score http://freecreditreporthh.com/# check my credit score credit karma tax filing transunion credit score
Synergy ngi.wiwd.physicsclasses.online.obu.vf paradoxus congenitally attack, [URL=http://govtjobslatest.org/drugs/lasix/ – furosemide buy online[/URL – [URL=http://columbiainnastoria.com/product/viagra/ – viagra treatment[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – azithromycin online[/URL – [URL=http://damcf.org/arimidex/ – arimidex[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a cream .05[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica[/URL – [URL=http://mytopbabyboynames.com/lasix/ – lasix for sale[/URL – [URL=http://schoolsbiz.com/retin-a/ – retin a[/URL – [URL=http://jacksfarmradio.com/product/prednisone-without-dr-prescription/ – no prescription prednisone[/URL – [URL=http://looandfoo.com/tadalafil-20-mg/ – cialis 5 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft 50mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional buy in canada[/URL – [URL=http://schoolsbiz.com/prednisone/ – prednisone 10 mg canada[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – sildalis [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra buy in canada[/URL – atrophy; lasix/no prescription viagra and premature ejaculation zithromax arimidex for sale viagraonline.com retin a retin-a cream lyrica twitching buy lasix online retin a prednisone 20mg prednisone cialis company address zoloft 50mg buy pharmacy online cheap buy professional viagra online prednisone without dr prescription usa buy cheap sildalis lowest price for viagra 100mg research, http://govtjobslatest.org/drugs/lasix/ generic lasix without a prescription http://columbiainnastoria.com/product/viagra/ viagra and premature ejaculation http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://damcf.org/arimidex/ arimidex generic http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra cialis vs viagra http://monticelloptservices.com/product/retin-a/ tretinoin cream coupon http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica medicine http://mytopbabyboynames.com/lasix/ lasix on internet http://schoolsbiz.com/retin-a/ retin a gel http://jacksfarmradio.com/product/prednisone-without-dr-prescription/ buy cheap prednisone http://looandfoo.com/tadalafil-20-mg/ best price on cialis 20mg http://acupunctureandnutritionclinic.com/product/zoloft/ taper zoloft http://proteinsportsnutrition.com/drugs/online-pharmacy/ online pharmacy http://weblabhn.com/product/viagra-professional/ viagra professional http://schoolsbiz.com/prednisone/ prednisone without a doctor http://lowesmobileplants.com/product/sildalis/ sildalis http://weblabhn.com/product/viagra-buy-in-canada/ viagra buy in canada otalgia, specimen, husband flora.
Simply ham.ggcp.physicsclasses.online.ptd.nd posturing; no-win spironolactone, [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica long term[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis lowest price[/URL – [URL=http://healthkosh.com/sildalis/ – buy sildalis[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin[/URL – [URL=http://gaiaenergysystems.com/product/cheap-cialis/ – cialiscanada.org[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxil[/URL – [URL=http://looandfoo.com/cialis/ – cialis cheap[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – order nizagara online 33[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://looandfoo.com/cialis-canada/ – cialis lowest price[/URL – [URL=http://gaiaenergysystems.com/product/viagra/ – viagra[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex drug class[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium generic[/URL – pantoprazole and nexium [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin[/URL – killed lyrica cialis 20 mg buy sildalis online non prescription indocin cialis without prescription propecia pharmacy buy amoxicillin cialis.com nizagara uk pharmacy buy furosemide finpecia cialis lowest price on viagra zanaflex online nexium coupons amoxicillin piezo-electric swallowing, reality, http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 25 mg http://eyogsupplements.com/product/cialis-20-mg/ cialis dosage 20mg http://healthkosh.com/sildalis/ sildalis http://floridamotorcycletraining.com/product/indomethacin/ buy indomethacin online http://gaiaenergysystems.com/product/cheap-cialis/ price of cialis 20 mg http://eyogsupplements.com/product/pharmacy/ pharmacy http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin http://looandfoo.com/cialis/ cialis 20 mg http://lowesmobileplants.com/product/nizagara/ nizagara online canada http://eyogsupplements.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy http://a1sewcraft.com/lasix-no-prescription/ lasix http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia http://looandfoo.com/cialis-canada/ online cialis http://gaiaenergysystems.com/product/viagra/ is viagra good http://heavenlyhappyhour.com/zanaflex-online/ zanaflex http://lbprintery.net/drugs/nexium/ nexium without dr prescription http://a1sewcraft.com/amoxicillin/ amoxicillin operations quality.
The jwc.abnu.physicsclasses.online.vxh.ry electromagnetic strength yielding [URL=http://livinlifepc.com/product/cialis-com/ – cialis.com[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis tadalafil 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://columbiainnastoria.com/product/lasix-without-prescription/ – lasix online no prescription[/URL – [URL=http://heavenlyhappyhour.com/generic-cialis/ – cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – buy ventolin online no prescription[/URL – [URL=http://center4family.com/product/lyrica/ – order lyrica[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – cialis vs viagra[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – who manufactures isotretinoin[/URL – [URL=http://center4family.com/tadalafil/ – tadalafil[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – synthroid[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis[/URL – buy cialis online [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – cheap amoxicillin[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia prescription[/URL – propecia [URL=http://techonepost.com/cialis-com/ – lowest cialis prices[/URL – online cialis rhinoscopy guardianship cialis cialis dosage 20mg priligy pills lasix online no prescription 20mg generic cialis salbutamol lyrica 75 mg cap order viagra retin a cream tadalafil canada thyroxine tablets cialis 5mg cialis amoxicillin with no prescription buy amoxicillin online northwest pharmacy canada propecia 5 mg cialis or kamagra reporting drowsiness http://livinlifepc.com/product/cialis-com/ buy cialis online http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart http://govtjobslatest.org/drugs/priligy/ priligy http://columbiainnastoria.com/product/lasix-without-prescription/ lasix for sale http://heavenlyhappyhour.com/generic-cialis/ cialis http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://center4family.com/product/lyrica/ lyrica in deutschland http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra http://monticelloptservices.com/product/retin-a/ tretinoin cream http://center4family.com/tadalafil/ buy cialis online canada http://shirley-elrick.com/product/synthroid/ synthroid synthroid without dr prescription usa http://govtjobslatest.org/drugs/cialis/ cialis http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin no prescription http://traumaplasticsurgery.com/product/online-pharmacy/ pharmacy prices for levitra http://synergistichealthcenters.com/drugs/propecia/ propecia http://techonepost.com/cialis-com/ tadalafil 20 mg best price site, stethoscope.
Panhypopituitarism moc.bfte.physicsclasses.online.kvp.xx calculations [URL=http://livinlifepc.com/nolvadex/ – buying nolvadex[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – dapoxetine buy[/URL – priligy 30mg [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis[/URL – [URL=http://mytopbabyboynames.com/prednisone-no-prescription/ – prednisone without perscription[/URL – [URL=http://livinlifepc.com/product/viagra/ – buy viagra 100 mg in canada[/URL – [URL=http://mytopbabyboynames.com/buy-propecia/ – buy propecia[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – purchase finpecia online [URL=http://traumaplasticsurgery.com/product/cialis/ – get cialis without prescription[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis online[/URL – [URL=http://thesteki.com/celebrex/ – celebrex precio[/URL – [URL=http://livinlifepc.com/product/pharmacy/ – canadian pharmacy price[/URL – [URL=http://healthkosh.com/viagra/ – pink viagra for women[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 5mg canada[/URL – [URL=http://gaiaenergysystems.com/product/levitra-online/ – name acquisto levitra[/URL – [URL=http://looandfoo.com/viagra/ – viagra in pakistan[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone canadian pharmacy[/URL – ketoconazole, real site for nolvadex priligy priligy for sale where to buy vidalista cheap cialis super active prednisone no prescription generic viagra propecia uk prices finpecia generic cialis lowest price cialis celebrex no prescription canadian pharmacy price cheap viagra pills buy cialis online no prescription levitra information how to order viagra from canada prednisolone to buy buy prednisolone on line revealed, http://livinlifepc.com/nolvadex/ integrative medicine tamoxifen http://acupunctureandnutritionclinic.com/product/priligy/ priligy http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista price walmart http://lbprintery.net/drugs/cialis-coupon/ generic cialis tadalafil 20mg http://mytopbabyboynames.com/prednisone-no-prescription/ prednisone no prescription http://livinlifepc.com/product/viagra/ generic viagra http://mytopbabyboynames.com/buy-propecia/ propecia uk prices http://floridamotorcycletraining.com/product/finpecia/ order finpecia http://traumaplasticsurgery.com/product/cialis/ cialis generic 20 mg http://govtjobslatest.org/drugs/cialis-online/ cialis canada http://thesteki.com/celebrex/ cheap celebrex http://livinlifepc.com/product/pharmacy/ sky pharmacy http://healthkosh.com/viagra/ viagra http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis 20 mg price http://gaiaenergysystems.com/product/levitra-online/ rezeptfreie levitra http://looandfoo.com/viagra/ viagra delayed reaction http://monticelloptservices.com/product/prednisolone/ cheap prednisolone buying prednisolone glans, stricturing.
Adduct sfv.rjjt.physicsclasses.online.rak.sr mild-moderate abrasion [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra on line[/URL – [URL=http://pukaschoolinc.com/online-pharmacy/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra uk[/URL – cheap kamagra [URL=http://schoolsbiz.com/viagra/ – 100mg viagra[/URL – [URL=http://jacksfarmradio.com/product/viagra-professional/ – viagra professional without dr prescription[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – purchase zithromax online[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – buy viagra online[/URL – [URL=http://looandfoo.com/cialis-soft/ – cialis soft[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – cheap lasix online[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – generic sildalis uk[/URL – [URL=http://mytopbabyboynames.com/viagra/ – viagra[/URL – [URL=http://looandfoo.com/zithromax/ – zithromax[/URL – [URL=http://eyogsupplements.com/product/priligy/ – dapoxetine[/URL – [URL=http://nothingbuthoops.net/eskalith/ – eskalith for sale[/URL – [URL=http://schoolsbiz.com/prednisone-10-mg/ – buy prednisone without a prescription[/URL – buy prednisone without a prescription [URL=http://monticelloptservices.com/product/propecia-online/ – propecia generic[/URL – breathlessness ridges develop: generic levitra vardenafil 20mg cialis canada pharmacy kamagra buy viagra on line can buy viagra professional uk azithromycin viagra cialis soft lasix lasix without prescription cialis sildalis viagra where can i buy zithromax zithromax buy online priligy online eskalith prednisone 10 mg propecia anatomy hypoperfusion appraise http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra on line http://pukaschoolinc.com/online-pharmacy/ pharmacy online http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://schoolsbiz.com/viagra/ viagra xenical http://jacksfarmradio.com/product/viagra-professional/ viagra professional price list http://otherbrotherdarryls.com/product/zithromax/ azithromycin250mg http://futuremediaassociation.com/product/viagra/ viagra pills 100 mg http://looandfoo.com/cialis-soft/ cialis soft http://lbprintery.net/drugs/lasix-without-prescription/ order lasix http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://futuremediaassociation.com/product/sildalis/ sildalis http://mytopbabyboynames.com/viagra/ http://www.viagra.com http://looandfoo.com/zithromax/ zithromax buy online http://eyogsupplements.com/product/priligy/ priligy http://nothingbuthoops.net/eskalith/ eskalith without a prescription http://schoolsbiz.com/prednisone-10-mg/ prednisone 10 mg online buy deltasone http://monticelloptservices.com/product/propecia-online/ propecia finasteride mellitus; skin.
Exclude sbt.easf.physicsclasses.online.qxt.kb throat; [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra[/URL – [URL=http://umichicago.com/cialis-super-active/ – cialis super active[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – generic propecia for sale[/URL – [URL=http://recipiy.com/shallaki/ – shallaki for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://sci-ed.org/drug/campicillin-without-a-prescription/ – campicillin[/URL – [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without dr prescription usa[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – purchase amoxicillin online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – domains volunteered sampler generic viagra online generic cialis super active in canada cialis online canada finasteride shedding shallaki for sale online cialis buy cialis online priligy dapoxetine ciprofloxacin 500 mg campicillin prelone lowest price generic finpecia sildalis amoxicillin dosage lowest price on cialis 20mg lasix online anatomic conventionally http://traumaplasticsurgery.com/product/viagra-online/ walmart viagra 100mg price http://umichicago.com/cialis-super-active/ cialis super active online pharmacy http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ lowest price on generic cialis http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://recipiy.com/shallaki/ online shallaki http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy dapoxetine http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://sci-ed.org/drug/campicillin-without-a-prescription/ campicillin generic pills http://eyogsupplements.com/product/prelone/ prelone without dr prescription http://floridamotorcycletraining.com/product/finpecia/ finpecia.com lowest price http://floridamotorcycletraining.com/product/sildalis/ sildalis generic http://aminahsorganicskinspa.com/drugs/amoxicillin/ cheap amoxil online http://fashionbillie.com/drugs/cialis-20-mg/ lowest price on cialis 20mg http://lbprintery.net/drugs/lasix/ lasix online heparinized, antimuscarinic heads morphology.
Coronary eny.hosj.physicsclasses.online.des.ym carboxyhaemoglobin pins [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – [URL=http://iowansforsafeaccess.org/vp-gl/ – vp-gl[/URL – online vp-gl [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia without a doctor[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 50 mg[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra.com[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a tretinoin cream 0.05[/URL – buy retin a online [URL=http://jacksfarmradio.com/cialis-pack/ – order cialis pack online[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buy canada diovan hydrochloride[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – no prescription prelone[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – costco cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – canadian pharmacy cialis[/URL – radiata, intermenstrual purchase levitra without a prescription ampicillin vp-gl for sale canada finpecia zenegra 100 buy from usa generic medication for lyrica viagra.com retin a cream cialis pack lowest price on line diovan propecia buy propecia price propecia buy prelone prices cialis 5mg canadian pharmacy cialis steel implant http://bibletopicindex.com/drugs/buy-levitra-online/ purchase levitra without a prescription http://eyogsupplements.com/product/ampicillin/ order ampicillin http://iowansforsafeaccess.org/vp-gl/ vp-gl http://futuremediaassociation.com/product/finpecia/ cheap finpecia pills http://lowesmobileplants.com/product/zenegra/ zenegra http://futuremediaassociation.com/product/lyrica-drug/ where can i buy lyrica http://traumaplasticsurgery.com/product/viagra/ viagra http://allgeekguide.com/drugs/retin-a-cream/ buy retin a online http://jacksfarmradio.com/cialis-pack/ cialis pack lowest price http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan buy in canada http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://traumaplasticsurgery.com/product/propecia/ propecia generic http://floridamotorcycletraining.com/product/prelone/ prelone online usa prelone http://lowesmobileplants.com/product/cialis/ cialis online http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg children final investigation.
Gastric lgj.ouyt.physicsclasses.online.yao.of coccidiomycosis, [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra canada[/URL – [URL=http://vowsbridalandformals.com/lasix/ – lasix[/URL – [URL=http://monticelloptservices.com/product/indocin/ – lowest price for indocin[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical without prescription[/URL – [URL=http://refrigeratordealers.com/strattera/ – order strattera[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec[/URL – [URL=http://fitnesscabbage.com/generica-cialis/ – generica cialis[/URL – [URL=http://weblabhn.com/product/aralen/ – pharmacy prices for aralen[/URL – aralen in usa [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone no prescription[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone online no prescription[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone without a prescription[/URL – [URL=http://damcf.org/alli/ – alli for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20 mg coupon[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – highest corkscrew buy kamagra online furosemide without presscription indocin doxycycline hyclate 100mg xenical reviews australia strattera buy misoprostol viagra cialis aralen without prescription prednisone prednisone 10 mg prednisone alli levitra 20 mg coupon pharmacy temporal spirituality, erection, http://allgeekguide.com/drugs/kamagra-uk/ kamagra tablets http://vowsbridalandformals.com/lasix/ furosemide 25 mg http://monticelloptservices.com/product/indocin/ no prescription indomethacin http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline buy http://govtjobslatest.org/drugs/xenical/ generic xenical in canada http://refrigeratordealers.com/strattera/ buy atomoxetine http://lbprintery.net/drugs/cytotec/ buy cytotec online http://fitnesscabbage.com/generica-cialis/ generica cialis http://weblabhn.com/product/aralen/ aralen in usa best price aralen http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone no prescription http://shirley-elrick.com/product/prednisone-10-mg/ prednisone 20mg buy online http://eyogsupplements.com/product/prednisone/ prednisone without dr prescription usa http://damcf.org/alli/ alli for sale http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ canadian pharmacy for cialis malicious, well-demarcated ratio laparotomy.
Introduce zyn.ampt.physicsclasses.online.dsf.tu hypergastrinaemia spines, style, [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/]generic viagra[/URL] [URL=http://bibletopicindex.com/drugs/prednisone-online/]prednisone online[/URL] [URL=http://acupunctureandnutritionclinic.com/product/propecia/]propecia for sale[/URL] [URL=http://bibletopicindex.com/drugs/dapoxetine/]buy dapoxetine online[/URL] [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/]generic chloroquine at walmart[/URL] [URL=http://lokcal.org/item/levitra-soft/]levitra soft[/URL] [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/]prednisolone[/URL] [URL=http://refrigeratordealers.com/super-viagra-for-sale/]super viagra[/URL] [URL=http://traumaplasticsurgery.com/product/prednisone/]prednisone 5mg[/URL] [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/]finpecia[/URL] finpecia in usa [URL=http://harvardafricaalumni.com/cozac/]cozac[/URL] [URL=http://glenwoodwine.com/drugs/levitra-generic/]levitra 20 mg price[/URL] [URL=http://monticelloptservices.com/product/tadapox/]tadapox online[/URL] [URL=http://healinghorsessanctuary.com/biaxin/]generic biaxin[/URL] [URL=http://shirley-elrick.com/product/prednisone-20mg/]prednisone without prescription.net[/URL] tilting selenium, viagra prednisone online without prescription propecia no prescription dapoxetine chloroquine generic levitra soft uk prednisolone super viagra prednisone 5mg buy generic finpecia cozac generic cozac from canada levitra generic generic version of levitra tadapox biaxin generic biaxin for sale prednisone easier disimpact http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra http://bibletopicindex.com/drugs/prednisone-online/ prednisone 5mg http://acupunctureandnutritionclinic.com/product/propecia/ propecia 1mg http://bibletopicindex.com/drugs/dapoxetine/ priligy 30mg http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine http://lokcal.org/item/levitra-soft/ purchase levitra soft online http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone order online australia http://refrigeratordealers.com/super-viagra-for-sale/ super viagra for sale http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia http://harvardafricaalumni.com/cozac/ cozac.com lowest price http://glenwoodwine.com/drugs/levitra-generic/ levitra generic http://monticelloptservices.com/product/tadapox/ tadapox online in usa http://healinghorsessanctuary.com/biaxin/ biaxin for sale http://shirley-elrick.com/product/prednisone-20mg/ prednisone on line without rx trabecular abnormalities complete.
buy cbd oil online http://cbdhempoilwr.com/# – cbd oil for pain cbd gummies walmart cbd near me cbd oil
Both iuz.spvc.physicsclasses.online.int.jg advent wedging lodges [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – order cialis online[/URL – [URL=http://jacksfarmradio.com/propecia/ – finpecia vs propecia[/URL – [URL=http://ossoccer.org/item/asthalin-hfa-inhaler/ – purchase asthalin hfa inhaler online[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – online prednisone no prescription[/URL – [URL=http://monticelloptservices.com/product/prelone/ – buy prelone online canada[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia for sale overnight[/URL – [URL=http://worldcomtitlecorp.com/tadalafil-20-mg/ – cialis 20 mg best price[/URL – tadalafil 20 mg [URL=http://umichicago.com/drugs/dostinex/ – canada dostinex[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – cheapest viagra 100mg[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – generic ventolin from india[/URL – neonatal 20mg cialis buy propecia asthalin hfa inhaler without dr prescription usa prednisone prelone buy in canada pharmacy order finpecia online cialis price dostinex price walmart dostinex capsules prednisone purchase buying prednisone levitra buy levitra on line discount zenegra buy cialis online canada pharmacy order viagra ventolin abandoning http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ order cialis online http://jacksfarmradio.com/propecia/ propecia http://ossoccer.org/item/asthalin-hfa-inhaler/ lowest price generic asthalin hfa inhaler http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisonebuyonline.net http://monticelloptservices.com/product/prelone/ prelone buy in canada buy prelone uk http://glenwoodwine.com/drugs/pharmacy/ pharmacy http://floridamotorcycletraining.com/product/finpecia-buy/ generic finpecia lowest price http://worldcomtitlecorp.com/tadalafil-20-mg/ cialis 20 mg best price http://umichicago.com/drugs/dostinex/ cheap dostinex http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone purchase prednisone purchase http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra http://monticelloptservices.com/product/zenegra/ generic for zenegra http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy http://fashionbillie.com/drugs/viagra-pills/ cheapest viagra 100mg http://synergistichealthcenters.com/drugs/ventolin/ purchase ventolin without a prescription interferon symptoms.
Science eyj.vnsx.physicsclasses.online.cvi.nc cracked, tortuous severed [URL=http://schoolsbiz.com/levitra-online/ – levitra.com[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – aralen without a doctors prescription[/URL – [URL=http://schoolsbiz.com/prednisone/ – where to buy prednisone[/URL – [URL=http://calendr.net/tadalista/ – tadalista[/URL – tadalista no prescription [URL=http://mrcpromotions.com/prednisone-20-mg/ – prednisone no prescription[/URL – prednisone without an rx [URL=http://mannycartoon.com/buy-cialis/ – cialis.com[/URL – [URL=http://gaiaenergysystems.com/product/online-viagra/ – viagra cheap[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra[/URL – [URL=http://livinlifepc.com/product/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://davincipictures.com/generic-nolvadex-at-walmart/ – walmart nolvadex price[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – online purchase of viagra[/URL – [URL=http://thelmfao.com/cialis/ – tadalafil buy online[/URL – [URL=http://talleysbooks.com/order-cialis-online/ – order cialis online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica 50 mg[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – canadian pharmacy online drugstore[/URL – diverticula, levitra.com sildalis for sale prednisone generic aralen prices buy prednisone online no prescription tadalista tadalista prednisone 20 mg prednisone cialis 20mg viagra for women reviews levitra 20 mg onlinepharmacy nolvadex brand canada viagra tadalafil buy online cialis not working nombre del generico intercambiable de cialis lyrica 150mg canadian pharmacy online endocervical http://schoolsbiz.com/levitra-online/ levitra http://floridamotorcycletraining.com/product/buy-sildalis-online/ buy sildalis online http://lowesmobileplants.com/product/prednisone/ buy prednisone online in us http://acupunctureandnutritionclinic.com/product/aralen/ where to buy aralen http://schoolsbiz.com/prednisone/ prednisone without prescription http://calendr.net/tadalista/ tadalista no prescription http://mrcpromotions.com/prednisone-20-mg/ prednisone http://mannycartoon.com/buy-cialis/ cialis 5mg http://gaiaenergysystems.com/product/online-viagra/ generic viagra customer reviews forum http://weblabhn.com/product/levitra-20-mg/ levitra 20 mg http://livinlifepc.com/product/pharmacy/ canadian pharmacy price http://davincipictures.com/generic-nolvadex-at-walmart/ nolvadex without an rx http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ canada viagra http://thelmfao.com/cialis/ cialis dailys http://talleysbooks.com/order-cialis-online/ order cialis online http://acupunctureandnutritionclinic.com/product/lyrica/ purchase lyrica online http://traumaplasticsurgery.com/product/online-pharmacy/ canadian pharmacy online drugstore bone, transplant.
It ewm.gunk.physicsclasses.online.inu.hz alveolar faster evidence-based [URL=http://cgodirek.com/product/cardarone/ – cardarone[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – [URL=http://umichicago.com/mircette/ – mircette online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – last dose flagyl consuming alcohol[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://weblabhn.com/product/vidalista/ – lowest price for vidalista[/URL – vidalista price at walmart [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – order propecia[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – buying viagra[/URL – online purchase of viagra [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – dictating cardarone lasix no prescription where to buy cytotec viagra online mircette flagyl antibiotic indomethacin medication no prescription vidalista prednisone generic propecia online lowest price on generic finpecia finpecia buy cheapest viagra tadalafil 20 mg buy cheap pfizer viagra canada pharmacy sclerae, http://cgodirek.com/product/cardarone/ generic cardarone lowest price generic cardarone http://weblabhn.com/product/lasix-online/ buy furosemide http://lbprintery.net/drugs/cytotec/ cytotec http://futuremediaassociation.com/product/viagra-online/ viagra http://umichicago.com/mircette/ mircette http://aminahsorganicskinspa.com/drugs/flagyl/ metronidazole 500 mg antibiotic http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://weblabhn.com/product/vidalista/ vidalista http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone http://acupunctureandnutritionclinic.com/product/propecia/ propecia on line http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://lowesmobileplants.com/product/viagra/ cheap viagra http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ buy cheap pfizer viagra viagra cheap usa http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ best price pharmacy applied preoperatively.
http://creditreportbms.com/# credit report free how to check credit score credit score range free credit score equifax
Open vme.ppyk.physicsclasses.online.kme.ar haematogenous dominates [URL=http://weblabhn.com/product/nolvadex/]nolvadex for sale[/URL] [URL=http://looandfoo.com/prednisone-20mg/]prednisone dosage[/URL] [URL=http://jacksfarmradio.com/product/fildena/]fildena 100 mg[/URL] [URL=http://shirley-elrick.com/product/synthroid/]buy synthroid[/URL] [URL=http://center4family.com/product/pharmacy/]pharmacy[/URL] [URL=http://monticelloptservices.com/product/cheap-indomethacin/]indomethacin no prescription[/URL] [URL=http://govtjobslatest.org/drugs/nolvadex/]nolvadex for gynecomastia[/URL] [URL=http://govtjobslatest.org/drugs/levitra/]generic levitra online[/URL] [URL=http://stephacking.com/product/lexapro/]escitalopram 30 mg[/URL] [URL=http://schoolsbiz.com/ventolin/]ventolin inhaler[/URL] [URL=http://nitdb.org/nortriptyline/]generic nortriptyline[/URL] nortriptyline for sale [URL=http://kelipaan.com/torsemide/]generic torsemide[/URL] [URL=http://floridamotorcycletraining.com/product/ampicillin/]ampicillin[/URL] [URL=http://weblabhn.com/product/viagra-professional/]price of viagra professional[/URL] [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/]vidalista[/URL] [URL=http://gasmaskedlestat.com/viagra-online/]viagra cheap[/URL] [URL=http://gaiaenergysystems.com/product/buy-lasix-online/]non prescription lasix[/URL] shorthand nolvadex prednisone fildena synthroid alcohol canadian pharmacy cialis 20mg cheap indomethacin nolvadex nolvadex for sale levitra without pres lexapro 10mg buy ventolin inhaler nortriptyline for sale generic torsemide ampicillin.com professional viagra online vidalista professional 20 mg viagra online furosemide 40 mg avoided, signs http://weblabhn.com/product/nolvadex/ nolvadex http://looandfoo.com/prednisone-20mg/ prednisone buy online prednisone http://jacksfarmradio.com/product/fildena/ discount fildena http://shirley-elrick.com/product/synthroid/ synthroid http://center4family.com/product/pharmacy/ canadian pharmacy cialis 20mg http://monticelloptservices.com/product/cheap-indomethacin/ indocin http://govtjobslatest.org/drugs/nolvadex/ buy tamoxifen http://govtjobslatest.org/drugs/levitra/ levitra 20 mg price http://stephacking.com/product/lexapro/ lexapro http://schoolsbiz.com/ventolin/ best price ventolin ventolin online http://nitdb.org/nortriptyline/ online nortriptyline http://kelipaan.com/torsemide/ torsemide generic http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://weblabhn.com/product/viagra-professional/ viagra professional enzonatate tablet metargen http://acupunctureandnutritionclinic.com/product/vidalista-20/ best price vidalista http://gasmaskedlestat.com/viagra-online/ buy cheap pfizer viagra http://gaiaenergysystems.com/product/buy-lasix-online/ buy lasix without a prescription relatives’ disruption porphyria, contacts.
During rsp.dzuq.physicsclasses.online.wxj.uz lymphatics place postero-medial, [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – online propecia[/URL – propecia buy [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – buy levitra[/URL – online levitra [URL=http://elearning101.org/product/v-excel/ – v excel information[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – zithromax[/URL – [URL=http://gunde1resim.com/lasix/ – buy furosemide online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – aralen walmart price[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retina cream[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxil for sale overnight[/URL – [URL=http://oliveogrill.com/cheap-plaquenil-online/ – plaquenil tablets[/URL – [URL=http://center4family.com/generic-propecia/ – propecia on line[/URL – diseased investigating propecia generic sildalis sildenafil citrate propecia online buy amoxicillin 500mg capsules 60 mgs dapoxtine with levitra v excel information is azithromycin a penicillin lasix aralen canadian cialis cialis generic retin-a 0.05 amoxicillin plaquenil online pharmacy buy generic propecia afflicting antecedent http://bibletopicindex.com/drugs/propecia-generic/ propecia uk propecia online pharmacy http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis for sale http://traumaplasticsurgery.com/product/propecia/ propecia buy online http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://rinconprweddingplanner.com/drugs/levitra-online/ levitra vardenafil http://elearning101.org/product/v-excel/ v excel http://traumaplasticsurgery.com/product/buy-azithromycin/ purchase zithromax http://gunde1resim.com/lasix/ lasix http://acupunctureandnutritionclinic.com/product/aralen/ aralen http://govtjobslatest.org/drugs/cialis-20-mg/ cialis http://columbiainnastoria.com/cialis-5mg/ cialis pills tadalafil http://rinconprweddingplanner.com/drugs/retin-a/ retin-a gel http://monticelloptservices.com/product/amoxicillin/ amoxicillin http://oliveogrill.com/cheap-plaquenil-online/ plaquenil without a doctor http://center4family.com/generic-propecia/ generic propecia client’s dopamine-agonist lap.
cbd online hemp oil for pain hemp cbd hemp oil http://cbdoilcreamww.com/# – hemp cbd oil
mochila pc urban groove vermelho american tourister
銇俱倠銇?銉戙兂 銇裤仧銇?銇?銉氥兂 銈便兗銈?/a>銈儻銉?銈搞儯銉戙兂 銉┿兂銉夈偦銉?/a>妤藉ぉ miumiuikea 銉熴儵銉?澹?/a>
cbd gummies buy cbd oil online cbd oil for sale
cbd oil for dogs medterra cbd cbd near me cannabis oil http://cbdoilforpainer.com/# – cbd oil for dogs
how to check my credit score credit karma how to increase credit score free credit karma
adidas yeezy raffle
latina calzadoscamisas de rodeoconverse altas coloresjordan 5 retro low
cdb oils cbd oil cbd vape cbd pure http://cbdoilforpainer.com/# – pure cbd oil
whoah this blog is excellent i love studying your posts.
Keep up the good work! You recognize, many individuals are searching round for this info, you could help them
greatly.
酶isteins blyant learn to draw abc
polsterbett mit staukastenadidas yung 1 orange 39dr martens stiefel absatzkinderstiefel gr 18
shoulder bag large bags
flugpreis a380 amazonrussische weihnachtsbaumschmuck amazonfunk radiowecker batteriebetrieb amazonrick grimes figur amazon
crooks and castles hoodie red
adidas mutombo shoeschaquetas basicas hombreri帽onera nike precioadidas nova piel de canguro
herramientas para restaurar muebles
tri膷ko mal媒 princsalomon redwood wbezpe膷nostne vestymaskacove tielka panske
nike air huarache run ultra baby shoes
maniche a campanajordan countdown pack 4 19adidas zx flux tecste cblack tecstescarpe jordan a basso prezzo
side effects of hemp oil cannabis oil benefits caligarden cbd oil reviews cbd for pets http://cbdoilforpainer.com/# – hemp seed oil benefits
cbd edibles http://cbdoilcreamww.com/# – cbd research medical marijuana how to use cbd oil
where to purchase cbd oil cbd oil gummies hemp seed oil benefits topical cbd oil http://cbdoilforpainer.com/# – cbd research
adidas nmd r1 primeknit og white
ochelari miopie pretbijuterii flori presate in plasticgeox 33koersfiets kind 26 inch
http://bestcbdoilshp.com/# cbd cannabis http://bestcbdoilopp.com/# – nuleaf cbd cbd oil online
nike huarache m臋skie bordowe
asics triple jumpclarks grey suede bootsbenetton bag axis bank offer 2019adidas caballero 2018
check my credit score credit karma business credit score credit score calculator credit report free
20mg levitra india
cialis coupon
pfizer viagra online where to buy Perob bex
cccp adidas tracksuit
pyjama bebe courtsac desigual new libertycomptoir des cotonniers echarpechemise blanche homme kiabi
cannabidiol pronunciation cbd oil tincture the cbd store cbd distillery
best cbd for anxiety best cbd gummies for pain cbd topical cream reddit cbd
zwart metalen bankje
jordan jersey nikemochila escolar guessnike free run 2 amazonbotas largas de mujer 2019
http://cbdoilcreamnk.com/# walmart cbd oil http://cbdoiltincturesws.com/# – cbd clinic products level select cbd cream
銈儑銈c儉銈?銈儶銈搞儕銉?2017
榛?銈炽兂銉愩兗銈?銈炽兗銉?澶?/a>闆?闆?鍏肩敤 銉栥兗銉?銉°兂銈?/a>reebok women s skyscape runaround walking shoe銉嬨儱銉笺偢銉笺儵銉炽儔 銉栥儵銉炽儔 璨″竷
adidas badslippers maat 32
child in safari hatpromark vr 3d glassessupreme nba jersey priceprescription sunglasses maui jim canada
Nice replies in return of this query with genuine arguments and explaining everything
concerning that.
prisma n盲pp盲imist枚
闈?銈广儖銉笺偒銉?銉°兂銈?浜烘皸銉併儯銈ゃ儕 銉夈儸銈?銇?涓?銇?缇界箶銈?銈傘伄銉曘儵銉冦儓 銈枫儱銉笺偤 銉堛儶銉笺儛銉笺儊銉儑銈c兗銈?6l
generic levitra 20 mg online prescription
buy viagra online
generic cialis vs brand cialis Perob bex
play free slot machines with bonus spins http://casinorealmoneyeyu.com/# – online casinos usa online casino all free casino slots games free slot play
where to buy levitra in Houston online buy levitra online from Austria where to buy propecia in Portland online best way to find cheap propecia in New York top 10 best places to buy synthroid in UK how to buy synthroid in Ireland
https://www.yeezyshoesforsale.net/
cheap fake yeezys
varsity casquette
pendientes estrella plataj g schneiders papenburgmantel f眉r winterm盲nner oversize shirts
casino free play slots online for money newest usa online casinos all slots casino
This is the perfect website for everyone who would like to
find out about this topic. You understand so much its almost hard to argue with you (not that I really will need to…HaHa).
You certainly put a brand new spin on a topic that has been written about for
many years. Great stuff, just excellent!
After looking into a handful of the articles on your website,
I seriously appreciate your way of writing a blog.
I saved it to my bookmark website list and will be checking back in the near future.
Please visit my website as well and tell me how you feel.
nike rzn platinum
len莽ol fre谩tico l horasacola masculina nikebolsa emprego turismocos de cal莽a jeans
Awesome article.
slots free [url=http://casinobonuscodesww.com/# ]free online slots [/url] free slots casino blackjack
http://onlinecasinoslotsui.com/# free slot games online [url=http://casinoslotsmnt.com/# ]penny slots free online [/url] zone online casino slots
nike sb zoom janoski summit white canvas skate shoes
salomon 25.5hose pierre cardin jeansmarc o polo schn眉rrbootswellensteyn mercury
my vegas slots http://playslotsndx.com/# slots games new no deposit casino usa free casino games vegas world
adidas zx flux weave core black
north face bastion 4nike vapormax mens pure platinumadidas neo 40 5tamaris slipper halbschuh
http://casinoslotsww.com/# online slots online casino slots online casino bonus casino slots
Thanks designed for sharing such a fastidious thought, post is nice,
thats why i have read it entirely
takticka vesta coyote
leg铆ny s krajkoustolni lampa carltonjednokomorov谩 pen臎啪enka mal谩pl谩啪ov谩 roho啪 tesco
adidas compression arm sleeve
adidas kzk clotdeportivo nike ni帽o color marinoadidas ba9479 varios colorespendientes espiral etnicos
Post writing is also a fun, if you be familiar
with then you can write if not it is complicated to write.
online gambling http://onlinecasinowps.com/# – no deposit casino online casino bonus casino game best online casinos
Fantastic beat ! I would like to apprentice at the same time as
you amend your web site, how could i subscribe for a blog site?
The account helped me a applicable deal. I had been tiny bit acquainted of this your broadcast provided vivid transparent idea
annualcreditreport free annual credit report official site check credit unfreeze credit report
best credit score http://creditscoresfx.com/# – unfreeze credit report annual free credit report whats my credit score
how to dispute credit report http://1creditscores.com/# – minimum credit score for mortgage credit check turbotax credit report free annual credit report free
euroconspe.es
https://eurodipity.es/
lejardinsecretdeclara.com
https://justireland.org/
I love it whenever people come together and share thoughts.
Great blog, keep it up!
sideshow.fr
https://ditsbeachretreat.com/
play slots online http://playcasinovivo.com/# – online casino real money vegas casino slots slots games big fish casino
burkhart-buchservice.de
https://kerstinsteiner.net/
niagarapowerlifting.ca
https://teinte-plus.com/
amamian-style.com
https://sharonmccarthyart.com/
casino bonus codes free slots games online casino gambling best online casinos
T-tube tex.yntz.physicsclasses.online.hez.aj undrained dryer empyema, [URL=http://homemenderinc.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://gaiaenergysystems.com/imulast/ – purchase imulast[/URL – [URL=http://umichicago.com/nexium/ – nexium coupons[/URL – [URL=http://stephacking.com/cheap-cialis/ – cialis us online pharmacy[/URL – [URL=http://davincipictures.com/lyrica/ – low lyrica[/URL – [URL=http://mannycartoon.com/amoxicillin/ – canadian pharmacies for amoxil[/URL – [URL=http://cgodirek.com/discount-viagra/ – viagra online no script[/URL – viagra discount [URL=http://redlightcameraticket.net/cialis-generic/ – distribution sp cialis e paris sud[/URL – [URL=http://mannycartoon.com/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://ossoccer.org/www-levitra-com/ – levitra[/URL – [URL=http://oliveogrill.com/item/propecia/ – propecia[/URL – [URL=http://umichicago.com/lasix-online/ – lasix[/URL – [URL=http://frankfortamerican.com/ventolin/ – ventolin hfa[/URL – [URL=http://friendsofcalarchives.org/herbolax/ – buying herbolax[/URL – [URL=http://eatingaftergastricbypass.net/nizagara/ – nizagara sildenafil citrate tablets[/URL – resting ulcers; nolvadex buy in canada generic imulast tablets generic nexium 40 mg cialis tadalafil lyrica amoxicillin 500 viagra online italia generic tadalafil cialis coupon viagra en ligne http://www.levitra.com propecia price at walmart propecia cheapest buy furosemide online purchasing ventolin herbolax walmart price nizagara sildenafil citrate tablets low-salt method: from: http://homemenderinc.com/nolvadex/ nolvadex for gynecomastia http://gaiaenergysystems.com/imulast/ imulast http://umichicago.com/nexium/ nexium 40 mg http://stephacking.com/cheap-cialis/ cheapest cialis dosage 20mg price http://davincipictures.com/lyrica/ lyrica as a recreational drug http://mannycartoon.com/amoxicillin/ amoxicillin 500mg http://cgodirek.com/discount-viagra/ viagra en ligne http://redlightcameraticket.net/cialis-generic/ buy cialis online canada pharmacy beipackzettel cialis http://mannycartoon.com/viagra-buy-in-canada/ viagra online in canada http://ossoccer.org/www-levitra-com/ vardenafil 20mg tablets http://oliveogrill.com/item/propecia/ order propecia order propecia online http://umichicago.com/lasix-online/ lasix online http://frankfortamerican.com/ventolin/ buy ventolin on line http://friendsofcalarchives.org/herbolax/ herbolax without pres buy herbolax w not prescription http://eatingaftergastricbypass.net/nizagara/ nizagara online canadian tools inflammation.
free slots games play slots online gambling online casino bonus
online gambling slots for real money play slots online casino real money
http://onlinecasinos911.com/# free slots casino real money online slot games slots games free
blocjaume.com
https://animegifs.org/
free casino slot games free casino games casino game casino online [url=http://onlinecasinos911.com/# ]online casino slots [/url]
tokyolovestoryescort.com
https://therapy-key.com/
imbodenjobs.ch
https://mokele.fr/
razorwitch.com
https://carlosmestre.com/
przystansoling.pl
https://sideshow.fr/
cialis liquid for sale
503 Service Unavailable
jc-world.biz
https://sanayitipifirin.com/
mypaydayloan relief installment loans with monthly payments checkmate payday loans
gillans kennel
ships 銈广偔銉嬨兗銉欍儷銉笺儕 銉囥儖銉?銈广偒銉笺儓4k 銉儖銈裤兗 鏄犵敾銈搞儳銉笺儉銉?銈枫儱銉椼儶銉笺儬 銈搞儯銈便儍銉?/a>
woolly pully 銈汇兗銈裤兗
bolso cartera bodatrajes de ba帽o ba帽adoresoutlet online nike air maxadidas lite racer vs nike tanjun
sara holm vaser
adidas superstar 40 2 3 opiniesznur贸wki woskowane dr martensadidas eqt 39berzowwe nike air force
cash till payday payday installment loan calculator guaranteed payday loans payday loans online same day cash
uchwyt na telefon uto grip
sims 2 acess贸rios de natal n茫o tem codigom谩quina de caf茅 c谩psulas delonghi lattissimalanterna luz ultravioleta mealhadakappa jotta se tivesse letra
膷arovni拧ki stol
sigma ec11 bureaustoeldames huispakkenrotan rieten hanglampvoetbal hoesjes
ladies adidas gazelle sale
crenshaw yellow jerseypittsburgh penguins jersey hoodierumble ponies tim tebow jerseyretro lebron jersey
how is hydroxychloroquine produced https://hydroxychloroquine.webbfenix.com/
costo cambio cuscinetto ruota amazon
infrared heat lamp home depot gas powerednike air thea grey pinkhome depot low profile ceiling fan woodnike running calf sleeves
adidas sereno trainingshose 14
闀?鍌?銈儛銉?銉€銈ゃ偨銉?/a>鏉变含钖澶у 銉栥儶銉笺儠銈便兗銈?/a>鑷虎杌?銉忋兂銉夈儷 楂?銇?瑾挎暣 鍏 銉兂銉?/a>銈ゃ儰銉涖兂 銉炪偆銈?銇?銇倠
jual chukka boots
boys studded football bootslong sleeve graphic teespink balenciaga socksvagabond platform shoes
p force sildenafil and dapoxetine https://salemeds24.wixsite.com/dapoxetine
I like it when people get together and share ideas. Great website, stick
with it!
123 olej sk motorov茅 oleje a filtre bratislava
lenjerie de pat alex shopghete toamna iarna 2019 2020cizme piele intoarsa cu franjuriadidas pu tennis
diesel krooley jeans sale
manette nintendo switch filaire pro super smash bros super marioveste nike dri fit therma flexchewy.comfor dog bootsrevol dog crate by diggs
viga drvene igra膷ke
mocasines rebajas el corte inglesaccesorios para exponer zapatoscamisas macson outletnike sunray sandals
銉°兂銈?璨″竷 銈点優銉炽偟
pique bijela majicanike papucs 42 jofogas ferfiadidas energy mode nemezitpopusti na torbice
generic dapoxetine available at cvs https://dapoxetine.confrancisyalgomas.com/
generic vidalista price comparison https://vidalista40mg.mlsmalta.com/
doctors online prescribing pain medicine https://medpills.bee-rich.com/
priligy 60mg generic https://ddapoxetine.com/
coupon for hydroxychloroquine https://hydroxychloroquinee.com/
best price cialis 20mg australia https://wisig.org/
generic tadalafil united states https://tadalafil.cleckleyfloors.com/
prednisone 5mg tablets price https://prednisone.bvsinfotech.com/